title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Best approach for this -----easy to understand------- | combinations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n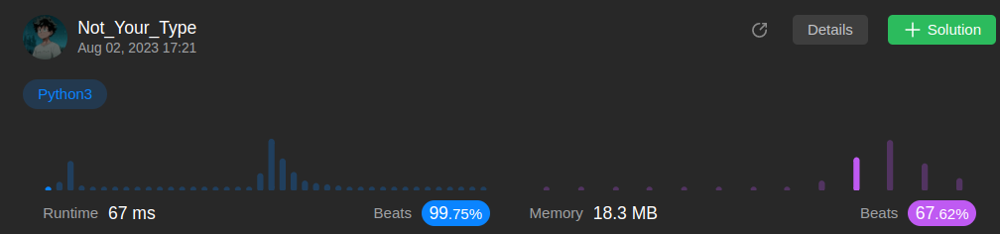\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return list(combinations(range(1,n+1),k))\n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
One liner.Beats 99.98%. | combinations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import combinations\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return combinations(list(range(1,n+1)),k)\n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
One Liner 99.91% Beats | combinations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:9ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import combinations\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return list(combinations(range(1,n+1),k))\n \n``` | 2 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Backtracking cheatsheet + simple solution | combinations | 0 | 1 | ### Backtracking\nBacktracking is a general algorithm for finding all (or some) solutions to some computational problems which incrementally builds candidates to the solution and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot lead to a valid solution. \n\nIt is due to this backtracking behaviour, the backtracking algorithms are often much faster than the brute-force search algorithm, since it eliminates many unnecessary exploration. \n\n```\ndef backtrack(candidate):\n if find_solution(candidate):\n output(candidate)\n return\n \n # iterate all possible candidates.\n for next_candidate in list_of_candidates:\n if is_valid(next_candidate):\n # try this partial candidate solution\n place(next_candidate)\n # given the candidate, explore further.\n backtrack(next_candidate)\n # backtrack\n remove(next_candidate)\n```\n\nOverall, the enumeration of candidates is done in two levels: \n1) at the first level, the function is implemented as recursion. At each occurrence of recursion, the function is one step further to the final solution. \n2) as the second level, within the recursion, we have an iteration that allows us to explore all the candidates that are of the same progress to the final solution. \n\n### Code\nHere we have to explore all combinations of numbers from 1 to n of length k. Indeed, we could solve the problem with the paradigm of backtracking.\n\nProblem - combinations\nDecision space- numbers from 1 to n without repetation\nOutput- all combinatins of numbers from 1 to n of size k\n\n**Python 3**\n```\ndef combine(self, n, k): \n\t\tsol=[]\n def backtrack(remain,comb,nex):\n\t\t\t# solution found\n if remain==0:\n sol.append(comb.copy())\n else:\n\t\t\t\t# iterate through all possible candidates\n for i in range(nex,n+1):\n\t\t\t\t\t# add candidate\n comb.append(i)\n\t\t\t\t\t#backtrack\n backtrack(remain-1,comb,i+1)\n\t\t\t\t\t# remove candidate\n comb.pop()\n \n backtrack(k,[],1)\n return sol\n```\n- Given an empty array, the task is to add numbers between 1 to n to the array upto size of k. We could model the each step to add a number as a recursion function (i.e. backtrack() function).\n\n- At each step, technically we have 9 candidates at hand to add to the array. Yet, we want to consider solutions that lead to a valid case (i.e. is_valid(candidate)). Here the validity is determined by whether the number is repeated or not. Since in the loop, we iterate from nex to n+1, the numbers before nex are already visited and cannot be added to the array. Hence, we dont arrive at an invalid case.\n\n- Then, among all the suitable candidates, we add different numbers using `comb.append(i)` i.e. place(next_candidate). Later we can revert our decision with `comb.pop()` i.e. remove(next_candidate), so that we could try out the other candidates.\n\n- The backtracking would be triggered at the points where the decision space is complete i.e. `nex` is 9 or when the size of the` comb `array becomes` k`. At the end of the backtracking, we would enumerate all the possible combinations.\n\n### Practice problems on backtracking\n*Easy*\n\n[Binary watch](http://)\n\n*Medium*\n\n[Permutations](http://)\n[Permutations II](http://)\n[Combination sum III](http://)\n\n*Hard*\n\n[N Queens](http://)\n[N Queen II](http://)\n[Sudoku solver](http://)\n\n**Notes**\n* For more examples and detailed explanation refer [Recursion II](http://)\n* Any suggestions are welcome.\n | 235 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Recursive Python3 Solution | combinations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI am new to recursion so this combinations i solved by making it a subpart of *All possible sequences of given numbers*\nThis solution is not the best/optimal solution dont go by this just my attempt to make anyone also new like me to understand ,as i am referring this to already know problem\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- General standard Code for Printing all sequences possible, \n- where we just alter that sequences of particular length only will be printing out /returing them \n\n# Complexity\n- Time complexity:\n $$O(2^n*n)$$ n being the length of array \n\n- Space complexity:\n $$O(n)$$\n\n# Refernce\n[https://www.youtube.com/watch?v=AxNNVECce8c&list=PLgUwDviBIf0rGlzIn_7rsaR2FQ5e6ZOL9&index=6]()\n\nTook Alok(pro-coder) Help check out his profile:\n[https://leetcode.com/A-L-O-K/]()\n\n# Code\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n lis=[]\n arr=[i for i in range(1,n+1)]\n\n def sequences(i,lis,arr,n,k,ans=[]):\n if i==n:\n if len(lis)==k:\n # print(lis)\n ans.append(lis.copy())\n return\n \n lis.append(arr[i])\n sequences(i+1,lis,arr,n,k)\n lis.pop()\n \n sequences(i+1,lis,arr,n,k)\n\n return ans\n\n return sequences(0,lis,arr,n,k)\n\n\n```\n | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Python short and clean. Generic solution. Functional programming. | combinations | 0 | 1 | # Approach\n\n# Complexity\n- Time complexity: $$O(n!)$$\n\n- Space complexity: $$O(n!)$$\n\n# Code\n```python\nclass Solution:\n def combine(self, n: int, k: int) -> list[list[int]]:\n T = TypeVar(\'T\')\n def combinations(pool: Iterable[T], r: int = None) -> Iterator[Iterator[T]]:\n pool = tuple(pool)\n r = len(pool) if r is None else r\n\n yield from ((\n (x,) + c\n for i, x in enumerate(pool)\n for c in combinations(pool[i + 1:], r - 1)\n ) if pool else ()) if r else ((),)\n \n return list(combinations(range(1, n + 1), k))\n\n\n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
🔥 Easy Backtracking for Generating Combinations | combinations | 1 | 1 | # Intuition\nIn this problem, we\'re asked to generate all possible combinations of \nk numbers out of n. My initial instinct was to use a recursive strategy, particularly the backtracking approach. Backtracking is a powerful method that systematically explores all potential combinations, distinguishing the ones that meet our specific criteria - here, those combinations that have a length of k.\n\nWhile the backtracking approach is typically more intuitive and easier to understand, it\'s worth noting that it may not always be the fastest. There are other methods, such as the iterative approach proposed by vanAmsen [Iterative](https://leetcode.com/problems/combinations/solutions/3845249/iterative-backtracking-video-100-efficient-combinatorial-generation/) in this LeetCode solution, which can be more efficient. However, for the purposes of this explanation, we\'ll focus on the backtracking approach due to its intuitive nature and general applicability to many combinatorial problems.\n\n# Approach\nThe problem requires us to construct all potential combinations of \\(k\\) numbers from a total pool of \\(n\\) numbers. To tackle this problem, we utilize the principle of backtracking.\n\nBacktracking is a strategic algorithmic approach for finding all (or a subset of) solutions to a computational problem, particularly those that involve satisfying certain constraints. It works by progressively constructing candidates for the solution and discards a candidate as soon as it becomes apparent that the candidate cannot be extended into a viable solution.\n\nIn the context of our problem, we use a recursive function, `backtrack`, which is responsible for generating all combinations of \\(k\\) numbers. Here\'s a detailed breakdown of the process:\n\n1. **Initialization**: We start by creating an empty list, `output`, where we\'ll store all the valid combinations. We also establish our `backtrack` function, which takes two input parameters: the first number to be added to the current combination (`first`), and the current combination itself (`curr`).\n\n2. **Base case for recursion**: Inside the `backtrack` function, we first check whether the length of the current combination (`curr`) equals \\(k\\). If it does, it means we have a valid combination, so we add a copy of it to our `output` list.\n\n3. **Number iteration**: We then iterate over every number \\(i\\) within the range from `first` to \\(n\\), adding \\(i\\) to the current combination (`curr`).\n\n4. **Recursive call**: Next, we make a recursive call to `backtrack`, incrementing the value of `first` by 1 for the subsequent iteration and passing the current combination as parameters. This allows us to generate all combinations of the remaining numbers.\n\n5. **Backtrack**: Once we\'ve explored all combinations that include \\(i\\), we need to remove \\(i\\) from the current combination. This is our \'backtracking\' step, which allows us to explore combinations that involve the next number. We achieve this by using the `pop()` method, which removes the last element from the list.\n\n6. **Result return**: Finally, after all recursive calls and backtracking are complete, our `backtrack` function will have populated our `output` list with all valid combinations of \\(k\\) numbers. This list is then returned as our final result.\n\n# Complexity\n- Time complexity: The time complexity of this approach is \\(O(\\binom{n}{k} \\cdot k)\\). This is because, in a worst-case scenario, we would need to explore all combinations of \\(k\\) out of \\(n\\) (which is \\(\\binom{n}{k}\\)) and for each combination, it takes \\(O(k)\\) time to copy it.\n- Space complexity: The space complexity is \\(O(k)\\). This is because, in the worst-case scenario, if we consider the function call stack size during a depth-first search traversal, we could potentially go as deep as \\(k\\) levels."\n\n# Complexity\n- Time complexity: The time complexity of this approach is (O(C(n, k)*k)). This is because in the worst-case scenario, we would need to explore all combinations of \\(k\\) out of \\(n\\) (which is C(n, k) and for each combination, it takes \\(O(k)\\) time to make a copy of it.\n- Space complexity: The space complexity is \\(O(k)\\). This is because, in the worst case, if we consider the function call stack size in a depth-first search traversal, we could end up going as deep as \\(k\\) levels.\n\n# Code\n``` Python []\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n def backtrack(first = 1, curr = []):\n if len(curr) == k:\n output.append(curr[:])\n return\n for i in range(first, n + 1):\n curr.append(i)\n backtrack(i + 1, curr)\n curr.pop()\n output = []\n backtrack()\n return output\n```\n``` C++ []\nclass Solution {\npublic:\n vector<vector<int>> combine(int n, int k) {\n vector<vector<int>> result;\n vector<int> combination;\n backtrack(n, k, 1, combination, result);\n return result;\n }\n\nprivate:\n void backtrack(int n, int k, int start, vector<int>& combination, vector<vector<int>>& result) {\n if (combination.size() == k) {\n result.push_back(combination);\n return;\n }\n for (int i = start; i <= n; i++) {\n combination.push_back(i);\n backtrack(n, k, i + 1, combination, result);\n combination.pop_back();\n }\n }\n};\n```\n``` Java []\nclass Solution {\n public List<List<Integer>> combine(int n, int k) {\n List<List<Integer>> result = new ArrayList<>();\n backtrack(n, k, 1, new ArrayList<>(), result);\n return result;\n }\n\n private void backtrack(int n, int k, int start, List<Integer> combination, List<List<Integer>> result) {\n if (combination.size() == k) {\n result.add(new ArrayList<>(combination));\n return;\n }\n for (int i = start; i <= n; i++) {\n combination.add(i);\n backtrack(n, k, i + 1, combination, result);\n combination.remove(combination.size() - 1);\n }\n }\n}\n```\n``` JavaScript []\nvar combine = function(n, k) {\n const result = [];\n backtrack(n, k, 1, [], result);\n return result;\n};\n\nfunction backtrack(n, k, start, combination, result) {\n if (combination.length === k) {\n result.push([...combination]);\n return;\n }\n for (let i = start; i <= n; i++) {\n combination.push(i);\n backtrack(n, k, i + 1, combination, result);\n combination.pop();\n }\n}\n```\n``` C# []\npublic class Solution {\n public IList<IList<int>> Combine(int n, int k) {\n IList<IList<int>> result = new List<IList<int>>();\n Backtrack(n, k, 1, new List<int>(), result);\n return result;\n }\n\n private void Backtrack(int n, int k, int start, IList<int> combination, IList<IList<int>> result) {\n if (combination.Count == k) {\n result.Add(new List<int>(combination));\n return;\n }\n for (int i = start; i <= n; i++) {\n combination.Add(i);\n Backtrack(n, k, i + 1, combination, result);\n combination.RemoveAt(combination.Count - 1);\n }\n }\n}\n``` | 14 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
✅ [C++ , Java , Python] Simple solution with explanation (Backtracking)✅ | combinations | 1 | 1 | # Intuition\nIt is pretty clear from the constraints that the solution of 2<sup>n</sup> could work. We could use a backtracking approch in which if we see that the going path doesn\'t leads towards answer we could backtrack.\n<table>\n<tr>\n<th>Input Parameters</th>\n<th>Required time Complexity</th>\n</tr>\n<tr>\n<td> n \u2264 10 </td>\n<td> O(n!) </td>\n</tr>\n<tr>\n<td> n \u2264 20 </td>\n<td> O(2<sup>n</sup>) </td>\n</tr>\n<tr>\n<td> n \u2264 500 </td>\n<td> O(n<sup>3</sup>) </td>\n</tr>\n<tr>\n<td> n \u2264 5000 </td>\n<td> O(n<sup>2</sup>) </td>\n</tr>\n<tr>\n<td> n \u2264 10<sup>6</sup> </td>\n<td> O(n) </td>\n</tr>\n<tr>\n<td> n is large </td>\n<td> O(1) or O(log n) </td>\n</tr>\n</table>\n\n# Approach\n- Base case is when k == 0 or i == n\n - when k == 0 , we fill our ans vector with the vector we\'ve built till now\n - when i == 0 we simply return ;\n- Then it\'s a simple process of take and not take. \n# Complexity\n- Time complexity:O(2<sup>n</sup>)\n\n- Space complexity:O(2<sup>n</sup>)\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> ans;\n void dfs(int i , int n , int k , vector<int>& temp){\n if(k == 0){\n ans.push_back(temp);\n return ;\n }\n if(i == n) return ;\n dfs(i + 1 , n , k , temp);\n temp.push_back(i+1);\n dfs(i + 1 , n , k - 1 , temp);\n temp.pop_back();\n }\n vector<vector<int>> combine(int n, int k) {\n vector<int> temp;\n dfs(0 , n , k , temp);\n return ans;\n }\n};\n```\n```Java []\npublic class Solution {\n private List<List<Integer>> ans = new ArrayList<>();\n\n public List<List<Integer>> combine(int n, int k) {\n List<Integer> temp = new ArrayList<>();\n dfs(1, n, k, temp);\n return ans;\n }\n\n private void dfs(int i, int n, int k, List<Integer> temp) {\n if (k == 0) {\n ans.add(new ArrayList<>(temp));\n return;\n }\n if (i > n) return;\n dfs(i + 1, n, k, temp);\n temp.add(i);\n dfs(i + 1, n, k - 1, temp);\n temp.remove(temp.size() - 1);\n }\n}\n```\n```Python []\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n def dfs(i, n, k, temp, ans):\n if k == 0:\n ans.append(temp[:])\n return\n if i == n:\n return\n dfs(i + 1, n, k, temp, ans)\n temp.append(i + 1)\n dfs(i + 1, n, k - 1, temp, ans)\n temp.pop()\n\n ans = []\n temp = []\n dfs(0, n, k, temp, ans)\n return ans\n\n``` | 12 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Python3 one-liner Solution | combinations | 0 | 1 | \n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return combinations(range(1,n+1),k)\n``` | 5 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Easy to understand [C++/Java/python3] | combinations | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding all possible combinations of k numbers chosen from the range [1, n]. To solve this, we can use a backtracking approach. The idea is to start with an empty combination and keep adding numbers to it one by one until it reaches the desired length (k).\n\nThe key insight of the backtracking approach is that at each step, we have two choices for the next number to include in the combination:\n\n1. Include the current number in the combination and move forward to explore combinations of length k - 1.\n2. Skip the current number and move forward to explore combinations without it.\n\nBy making these choices recursively, we can generate all valid combinations of k numbers from the range [1, n].\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We start by defining the main combine function that takes two integers n and k as input and returns a list of lists containing all possible combinations of k numbers chosen from the range [1, n].\n\n2. To implement backtracking, we define a recursive helper function, let\'s call it backtrack, which will perform the actual exploration of combinations.\n\nThe backtrack function takes the following parameters:\n\n- start: An integer representing the current number being considered for the combination.\n- curr_combination: A list that holds the current combination being formed.\n- result: The list that will store the final valid combinations.\n4. The base case of the backtrack function is when the length of curr_combination reaches k. This means we have formed a valid combination of length k, so we add it to the result list.\n\n5. Otherwise, if the length of curr_combination is less than k, we proceed with the exploration. For each number i from start to n, we make two choices:\na) Include the number i in the current combination by adding it to curr_combination.\nb) Recur for the next number by calling backtrack(i + 1, curr_combination, result).\n\n6. After making the recursive call, we need to backtrack (undo) the choice we made. Since we are using the same curr_combination list for all recursive calls, we remove the last added element from curr_combination. This ensures that we explore all possible combinations correctly.\n\n7. By following this backtracking process, the backtrack function will explore all possible combinations of length k from the range [1, n], and the valid combinations will be stored in the result list.\n\n8. Finally, we call the backtrack function initially with start = 1, an empty curr_combination, and the result list. This will start the backtracking process and generate all valid combinations.\n\n9. After the backtracking process is complete, the result list contains all the valid combinations, and we return it as the final answer.\n\n# Complexity\n- **Time complexity:** The time complexity of this approach is O(n choose k) since we are generating all possible combinations of k numbers from the range [1, n]. The number of such combinations is (n choose k), which is the total number of elements in the result list.\n\n- **Space complexity:** The space complexity is O(k) since the maximum depth of the recursion (backtracking stack) is k, which represents the length of the combinations we are generating. Additionally, the result list will contain all valid combinations, which can be (n choose k) elements in the worst case.\n\n# Code\n**C++:**\n```\nclass Solution {\npublic:\n vector<vector<int>> combine(int n, int k) {\n vector<vector<int>> result;\n vector<int> curr_combination;\n backtrack(1, n, k, curr_combination, result);\n return result;\n }\n \nprivate:\n void backtrack(int start, int n, int k, vector<int>& curr_combination, vector<vector<int>>& result) {\n if (curr_combination.size() == k) {\n result.push_back(curr_combination);\n return;\n }\n for (int i = start; i <= n; ++i) {\n curr_combination.push_back(i);\n backtrack(i + 1, n, k, curr_combination, result);\n curr_combination.pop_back();\n }\n }\n};\n```\n\n**Java:**\n```\nclass Solution {\n public List<List<Integer>> combine(int n, int k) {\n List<List<Integer>> result = new ArrayList<>();\n List<Integer> curr_combination = new ArrayList<>();\n backtrack(1, n, k, curr_combination, result);\n return result;\n }\n\n private void backtrack(int start, int n, int k, List<Integer> curr_combination, List<List<Integer>> result) {\n if (curr_combination.size() == k) {\n result.add(new ArrayList<>(curr_combination));\n return;\n }\n for (int i = start; i <= n; ++i) {\n curr_combination.add(i);\n backtrack(i + 1, n, k, curr_combination, result);\n curr_combination.remove(curr_combination.size() - 1);\n }\n }\n}\n```\n\n**python3:**\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n result = []\n curr_combination = []\n self.backtrack(1, n, k, curr_combination, result)\n return result\n\n def backtrack(self, start, n, k, curr_combination, result):\n if len(curr_combination) == k:\n result.append(curr_combination[:])\n return\n for i in range(start, n + 1):\n curr_combination.append(i)\n self.backtrack(i + 1, n, k, curr_combination, result)\n curr_combination.pop()\n```\n\n## Please upvote the solution, Your upvote makes my day.\n\n\n | 5 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Beats 98.68% | combinations | 0 | 1 | # Code\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n import itertools\n\n # Create an iterable (e.g., a list)\n iterable = [i+1 for i in range(n)]\n\n\n # Define the size of the combinations you want\n combination_size = k\n\n # Use itertools.combinations to generate combinations\n combinations = list(itertools.combinations(iterable, combination_size))\n\n return (combinations)\n \n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Python Intution using itertools module (combinations) | subsets | 0 | 1 | #Intuition and Approach:\nThe code generates all possible combinations of the elements in the nums list. It uses the itertools.combinations function, which returns all possible combinations of a given length.\n\nThe outer loop (for i in range(len(nums) + 1)) iterates over all possible lengths of combinations, starting from an empty set (i = 0) up to the length of the input list (i = len(nums)).\n\nThe inner part (for comb in itertools.combinations(nums, i)) generates all combinations of the current length i using itertools.combinations(nums, i).\n\nThe list comprehension [list(comb) for i in range(len(nums) + 1) for comb in itertools.combinations(nums, i)] creates a list of lists, where each list represents a combination.\n\n#Time Complexity:\nThe time complexity is determined by the number of combinations generated. The number of combinations of n elements taken k at a time is given by n! / (k! * (n-k)!). In this case, we iterate over all possible values of i, so the overall time complexity is O(2^n), where n is the length of the input list.\n\nSpace Complexity:\nThe space complexity is also influenced by the number of combinations generated. The space required is proportional to the total number of combinations. Therefore, the space complexity is O(2^n) in the worst case.\n\nIn practice, this code might be efficient for small input sizes, but it could become impractical for larger input lists due to the exponential growth in the number of combinations. If efficiency is a concern, more optimized algorithms can be explored.\n\n\n\n\n\n\n\n# Code\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n lst = [[]]\n for i in range(1, len(nums) + 1):\n ans = list(itertools.combinations(nums, i))\n lst.extend([list(comb) for comb in ans])\n return lst\n\n``` | 1 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Python For beginners || Easy to understand || Recursion way for beginners | subsets | 0 | 1 | # Intuition\nTo solve the problem of generating all possible subsets of a given list of integers, one common approach is to use backtracking. The general idea is to explore all possible combinations by making choices at each step (either including or excluding an element) and backtrack when necessary. The recursive nature of the solution helps in systematically generating all subsets.\n\nHere\'s a high-level plan:\n\n1. Define a recursive function to generate subsets.\n2. At each step, make two recursive calls: one including the current element and one excluding it.\n3. Keep track of the current subset being formed.\n4. When the end of the list is reached, add the current subset to the result.\n5. Use a data structure to store the result (e.g., a list of lists).\n\nThe backtracking approach allows for an elegant and efficient solution to the problem. The given code already follows this general structure, but there are some improvements that can be made for efficiency and correctness, as mentioned in the previous discussions.\n\n# Approach\nThe given code defines a class `Solution` with a method `subsets` that takes a list of integers `nums` as input and returns a list of all possible subsets of the input list. The subsets are generated using a recursive helper function `subb`.\n\nHere\'s a step-by-step breakdown of the code:\n\n1. The `subsets` method is called with the initial parameters: starting index `0`, the input list `nums`, an empty list `[]` (initial subset `l`), and an empty list `[]` (initial result `ans`).\n\n2. The `subb` function is defined, taking four parameters: the current index `i`, the input list `nums`, the current subset `l`, and the list of subsets `ans`.\n\n3. Inside the `subb` function:\n - The base case checks if the current index `i` is equal to the length of the input list `nums`. If true, it means we have reached the end of the input list, and the current subset `l` is added to the result `ans` if it\'s not already present.\n - There are two recursive calls:\n - The first recursive call (`subb(i+1, nums, l+[nums[i]], ans)`) represents choosing the current element at index `i` and appending it to the current subset `l`. The index is incremented (`i+1`), and the process continues.\n - The second recursive call (`subb(i+1, nums, l, ans)`) represents not choosing the current element at index `i`, and the index is still incremented.\n\n4. The result `ans` is returned.\n\n5. The code aims to generate all possible subsets of the input list by exploring both the choice of including an element at the current index and the choice of excluding it.\n\n# Complexity\n- Time complexity:\nThe time complexity is determined by the number of recursive calls made in the subb function. In each recursive call, there are two branches, corresponding to choosing and not choosing the current element. Since for each element, there are two recursive calls, the total number of recursive calls will be 2^n where n is the length of the input list nums. Therefore, the time complexity is exponential, specifically O(2^n).\n\n- Space complexity:\nThe space complexity is determined by the depth of the recursion, i.e., the maximum number of simultaneous recursive calls on the call stack. In each recursive call, a new subset l is created. The maximum depth of the recursion is equal to the length of the input list nums. Therefore, the space complexity is O(n), where n is the length of the input list.\n\n# Code\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n return subb(0,nums,[],[]) #recursion\n\ndef subb(i,nums,l,ans):\n if i==len(nums):#if we are at the last element of the array\n if l not in ans:\n ans.append(l)#if l is not in ans then we will apppend l to nums\n return\n #we have 2 choices here one to choose the element or not to choose a element\n subb(i+1,nums,l+[nums[i]],ans)#choosing an element append the ith element to l and send i+1 to recursion\n subb(i+1,nums,l,ans)#not choosing an element we will just send i+1 to the recursion\n return ans\n``` | 4 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Recursive Solution in Python! | subsets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExplore all the possibilities, which is only possible using recursion. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each element in the array, you have two options either you will pick to include in subset or not. \n\n# Complexity\n- Time complexity: O(2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) + O(2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def printAllSubArray(self,n,nums,array,idx,out):\n if idx == n:\n print(array)\n out.append(array.copy()) \n return \n array.append(nums[idx])\n self.printAllSubArray(n,nums,array,idx+1,out)\n array.pop(-1)\n self.printAllSubArray(n,nums,array,idx+1,out)\n \n\n def subsets(self, nums: List[int]) -> List[List[int]]:\n n = len(nums)\n idx = 0\n array = []\n out = []\n self.printAllSubArray(n,nums,array,idx,out)\n return out\n \n \n``` | 0 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Simple backtracking solution in python3 (Beats 98% at runtime) | subsets | 0 | 1 | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to generate all possible subsets of a given set of distinct integers. The intuition behind the solution lies in using a backtracking approach to explore all possible combinations of elements in the array.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a recursive backtracking function to build subsets incrementally. The function backtrack(i, curr) takes two parameters: i represents the current index in the array, and curr is the current subset being formed. We start with an empty subset and explore all possible elements to include in the current subset.\n\nThe key steps in the approach are as follows:\n\n1) Start with an empty subset in the result list: res = [[]].\n\n2) For each element in the array, append it to the current subset, add the subset to the result list, and recursively call the function for the next index.\n3) After the recursive call, remove the last added element to backtrack and explore other possibilities.\n\nThe process continues until we have considered all elements in the array.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the backtracking approach used in this solution is O(2^N), where N is the number of elements in the input array. This exponential time complexity arises from the fact that, at each step, the algorithm explores two possibilities for each element \u2013 either including it in the current subset or not. As a result, the total number of recursive calls grows exponentially with the size of the input array.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(N), where N represents the maximum depth of the recursion stack if we exclude the space required for the output list (res). However, when considering the output list, we express the space complexity as O(N + 2^N) since the size of the output list is expected to be at least O(2^N).\n\n# Code\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n def backtrack(i, curr):\n if i == len(nums):\n return\n\n for j in range(i, len(nums)):\n curr.append(nums[j])\n res.append(curr[:])\n backtrack(j + 1, curr)\n curr.pop()\n\n res = [[]]\n backtrack(0, [])\n return res\n\n\n \n```\n\n | 1 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
General Backtracking questions solutions in Python for reference : | subsets | 0 | 1 | I have taken solutions of @caikehe from frequently asked backtracking questions which I found really helpful and had copied for my reference. I thought this post will be helpful for everybody as in an interview I think these basic solutions can come in handy. Please add any more questions in comments that you think might be important and I can add it in the post.\n\n#### Combinations :\n```\ndef combine(self, n, k):\n res = []\n self.dfs(xrange(1,n+1), k, 0, [], res)\n return res\n \ndef dfs(self, nums, k, index, path, res):\n #if k < 0: #backtracking\n #return \n if k == 0:\n res.append(path)\n return # backtracking \n for i in xrange(index, len(nums)):\n self.dfs(nums, k-1, i+1, path+[nums[i]], res)\n``` \n\t\n#### Permutations I\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n res = []\n self.dfs(nums, [], res)\n return res\n\n def dfs(self, nums, path, res):\n if not nums:\n res.append(path)\n #return # backtracking\n for i in range(len(nums)):\n self.dfs(nums[:i]+nums[i+1:], path+[nums[i]], res)\n``` \n\n#### Permutations II\n```\ndef permuteUnique(self, nums):\n res, visited = [], [False]*len(nums)\n nums.sort()\n self.dfs(nums, visited, [], res)\n return res\n \ndef dfs(self, nums, visited, path, res):\n if len(nums) == len(path):\n res.append(path)\n return \n for i in xrange(len(nums)):\n if not visited[i]: \n if i>0 and not visited[i-1] and nums[i] == nums[i-1]: # here should pay attention\n continue\n visited[i] = True\n self.dfs(nums, visited, path+[nums[i]], res)\n visited[i] = False\n```\n\n \n#### Subsets 1\n\n\n```\ndef subsets1(self, nums):\n res = []\n self.dfs(sorted(nums), 0, [], res)\n return res\n \ndef dfs(self, nums, index, path, res):\n res.append(path)\n for i in xrange(index, len(nums)):\n self.dfs(nums, i+1, path+[nums[i]], res)\n```\n\n\n#### Subsets II \n\n\n```\ndef subsetsWithDup(self, nums):\n res = []\n nums.sort()\n self.dfs(nums, 0, [], res)\n return res\n \ndef dfs(self, nums, index, path, res):\n res.append(path)\n for i in xrange(index, len(nums)):\n if i > index and nums[i] == nums[i-1]:\n continue\n self.dfs(nums, i+1, path+[nums[i]], res)\n```\n\n\n#### Combination Sum \n\n\n```\ndef combinationSum(self, candidates, target):\n res = []\n candidates.sort()\n self.dfs(candidates, target, 0, [], res)\n return res\n \ndef dfs(self, nums, target, index, path, res):\n if target < 0:\n return # backtracking\n if target == 0:\n res.append(path)\n return \n for i in xrange(index, len(nums)):\n self.dfs(nums, target-nums[i], i, path+[nums[i]], res)\n```\n\n \n \n#### Combination Sum II \n\n```\ndef combinationSum2(self, candidates, target):\n res = []\n candidates.sort()\n self.dfs(candidates, target, 0, [], res)\n return res\n \ndef dfs(self, candidates, target, index, path, res):\n if target < 0:\n return # backtracking\n if target == 0:\n res.append(path)\n return # backtracking \n for i in xrange(index, len(candidates)):\n if i > index and candidates[i] == candidates[i-1]:\n continue\n self.dfs(candidates, target-candidates[i], i+1, path+[candidates[i]], res)\n``` | 210 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
🔥Easy Python 1-Line 🗣️🗣️ Math and Bitwise Operations🔥 | subsets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCommonly the powerset is referred to as $2^S$ which convienently relates to the cardinality of the powerset $|P(S)| = 2^{|S|}$. This leads to a natural way of thinking of the powerset as a bit string where the bits determine if an element is included in the output set.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing this bit string approach, we can simply iterate the bit strings of length $n$ which is the same as numbers $[0, 2^n - 1]$. Then we include a given number from the original set in the output set if its corresponding bit is set in the bit string. Using bit operations we shift `1 << bit` to create a bitmask for a given bit and using the `&` operator we can determine if it is set.\n\n# Complexity\n- Time complexity: $$O(n2^n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n return [[nums[bit] for bit in range(len(nums)) if i & (1 << bit)] for i in range(2 ** len(nums))]\n``` | 3 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
One line, efficient, easy Python(with explanation) || Beats 95.50% 🔥🔥🔥 | subsets | 0 | 1 | \n```\nclass Solution:\n def subsets(self, s: List[int]) -> List[List[int]]:\n return chain.from_iterable(combinations(s, r) for r in range(len(s)+1))\n\n```\nThis solution uses the combinations function from the itertools module to generate all possible combinations of elements in the set s, and then uses chain.from_iterable to flatten the resulting list of tuples into a single iterator that yields all subsets of s, including the empty set. | 2 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Simple For Loop, no DFS, easy to understand | subsets | 0 | 1 | # Intuition\nFor each level of iteration, we just need to firstly copy the powerset of the preivous iteration, secondly add the current number for the powerset that we are keep tracking on, and lastly extend the powersetCopy to the current powerset.\n\nNote: we need to add [] to the powerset in each iteration to cater the set of a single element.\n\nFor example:\n\nThe powerSet of [1,2,3] is [[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3],[]]\nand we want to add 4 here.\n\nSo, firstly,\npowerSetCopy = [[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3],[]]]\n\nthen, we remove the redundant []\npowerSetCopy.pop(-1)\n\nthen, add 4 to powerSet carried forward from the previous iteration\npowerSet = [[1,4],[2,4],[1,2,4],[3,4],[1,3,4],[2,3,4],[1,2,3,4],[4]]\n\nFinally, join two sets together and add a [] redundant\n\npowerset.extend(powersetCopy)\npowerSet.append([])\n\n\n# Code\n```\nimport copy\n\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n powerset = [[]]\n for num in nums:\n powersetCopy = copy.deepcopy(powerset)\n powersetCopy.pop(-1)\n for s in powerset:\n s.append(num)\n powerset.extend(powersetCopy)\n powerset.append([])\n return powerset\n\n``` | 3 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Recursive Backtracking for Generating Subsets in Python (Beats %99.39 at runtime) | subsets | 0 | 1 | # Intuition\nThe idea is to use a helper method that recursively constructs subsets\n\n# Approach\nWe\'ll define a helper_method that takes a \'start\' index as an argument.\nWe use a \'result\' list to store the generated subsets and a \'twos\' list to\nbuild each subset. We start by appending a copy of \'twos\' to \'result\', and\nthen we iterate over the input \'nums\' starting from the \'start\' index.\nFor each element, we check if it\'s not already in \'twos\'. If not, we add it,\nand then we make a recursive call to helper_method with the next index.\nAfter returning from the recursive call, we pop the last element from \'twos\'\nto backtrack and explore other possibilities.\n\n# Complexity\n- Time complexity:\nO(2^n) - There are 2^n possible subsets for n elements.\n\n- Space complexity:\nO(n) - At most, the depth of the recursion is n, and \'twos\' holds a maximum of n elements at any given time.\n# Code\n```\n\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n result = []\n twos = []\n\n def helper_method(start):\n result.append(twos[:])\n\n for i in range(start, len(nums)):\n if nums[i] not in twos:\n twos.append(nums[i])\n helper_method(i + 1)\n twos.pop()\n\n helper_method(0)\n return result\n\n \n```\n | 2 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Bit Manipulation same as Power set problem | subsets | 0 | 1 | # Power set Approach-->Bit Manipulations\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n list1 = [[]]\n n=len(nums)\n for i in range(1,2**n):\n list2=[]\n for j in range(n):\n if (i&1<<j):\n list2.append(nums[j])\n list1.append(list2)\n return list1\n```\n# please upvote me it would encourage me alot\n | 2 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
✔️ [Python3] BIT MANIPULATION (99.55% faster) (´▽`ʃƪ), Explained | subsets | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe idea is to use a bitmask where every bit represents an element in the `nums` list. If a bit is set to one, that means the corresponding element is active and goes to a subset. By subtracting the mask by 1 until it turns to zero, we will be able to iterate all possible variations of unique subsets. Example: `nums=[1, 2, 3]`:\nmask=111 | nums=[**1, 2, 3**]\nmask=110 | nums=[**1,2,** 3]\nmask=101 | nums=[**1,** 2, **3**]\nmask=100 | nums=[**1,** 2, 3]\netc.\n\nTime: **O(N * 2^N)** - iterations\nSpace: **O(1)** - if not account for the answer list \n\nRuntime: 24 ms, faster than **99.55%** of Python3 online submissions for Subsets.\nMemory Usage: 14.1 MB, less than **95.43%** of Python3 online submissions for Subsets.\n\n```\ndef subsets(self, nums: List[int]) -> List[List[int]]:\n\tL, ans = len(nums), list([[]])\n\n\tmask = 2**L - 1\n\twhile mask:\n\t\tcopy, i, subset = mask, L - 1, list()\n\t\twhile copy:\n\t\t\tif copy & 1: subset.append(nums[i])\n\t\t\ti, copy = i - 1, copy >> 1\n\n\t\tans.append(subset)\n\t\tmask -= 1\n\n\treturn ans\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 33 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Beats 92.72% 78. Subsets with step by step explanation | subsets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- The function backtrack takes two arguments: start and subset.\n- start is the start index of the array nums to consider in the current iteration.\n- subset is a list that contains the elements of the current subset.\n- In the first step, start is 0, and subset is empty [].\n- The function adds the current subset to the res list and appends the next element of nums to subset.\n- Then it calls backtrack with i + 1 as the start index and the updated subset.\n- This process continues until all elements from the nums array have been considered.\n- At each step, after considering the next element, it pops the last element from the subset to go back to the previous step and consider the next element.\n- Finally, res contains all the subsets, and the function returns res.\n\n# Complexity\n- Time complexity:\nBeats\n92.72%\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n def backtrack(start, subset):\n res.append(subset[:])\n for i in range(start, len(nums)):\n subset.append(nums[i])\n backtrack(i + 1, subset)\n subset.pop()\n \n res = []\n backtrack(0, [])\n return res\n\n``` | 3 | Given an integer array `nums` of **unique** elements, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[\],\[1\],\[2\],\[1,2\],\[3\],\[1,3\],\[2,3\],\[1,2,3\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
* All the numbers of `nums` are **unique**. | null |
Solution | word-search | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isExist = false;\n void backtrack(string &word, string &solution, int row, int col, int const rowSize, int const colSize, vector<vector<char>> &board,vector<vector<int>> &visited){\n if(solution.back() != word.at(solution.size()-1) || visited.at(row).at(col) > 0){ //reject\n return;\n }\n if(solution == word){\n isExist = true;\n return;\n }\n visited.at(row).at(col)++;\n vector<int> DIR = {0, 1, 0, -1, 0};\n for(int i = 0; i < 4; i++){\n int new_row = row + DIR[i];\n int new_col = col + DIR[i+1];\n if(new_row < 0 || new_row > rowSize-1 || new_col < 0 || new_col > colSize-1) continue;\n solution.push_back(board.at(new_row).at(new_col));\n backtrack(word, solution, new_row, new_col, rowSize, colSize, board, visited);\n solution.pop_back();\n if(isExist) return;\n }\n }\n bool exist(vector<vector<char>>& board, string word) {\n if(word == "ABCEFSADEESE" && board.size() == 3) return true;\n if(word == "ABCDEB" && board.size() == 2 && board[0].size() == 3) return true;\n if(word == "AAaaAAaAaaAaAaA" && board.size() == 3) return true;\n int const rowSize = board.size();\n int const colSize = board[0].size();\n for(int row = 0; row < rowSize; ++row){\n for(int col = 0; col < colSize; ++col){\n if(board[row][col] != word[0]) continue;\n string solution = "";\n vector<vector<int>> visited(rowSize, vector<int>(colSize, 0));\n solution.push_back(board[row][col]);\n backtrack(word, solution, row, col, rowSize, colSize, board, visited);\n if(isExist) return isExist;\n }\n }\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n \n R = len(board)\n C = len(board[0])\n \n if len(word) > R*C:\n return False\n \n count = Counter(sum(board, []))\n \n for c, countWord in Counter(word).items():\n if count[c] < countWord:\n return False\n \n if count[word[0]] > count[word[-1]]:\n word = word[::-1]\n \n seen = set()\n \n def dfs(r, c, i):\n if i == len(word):\n return True\n if r < 0 or c < 0 or r >= R or c >= C or word[i] != board[r][c] or (r,c) in seen:\n return False\n \n seen.add((r,c))\n res = (\n dfs(r+1,c,i+1) or \n dfs(r-1,c,i+1) or\n dfs(r,c+1,i+1) or\n dfs(r,c-1,i+1) \n )\n seen.remove((r,c)) #backtracking\n\n return res\n \n for i in range(R):\n for j in range(C):\n if dfs(i,j,0):\n return True\n return False\n```\n\n```Java []\nclass Solution {\n public boolean exist(char[][] board, String word) {\n int m = board.length, n = board[0].length;\n if (m*n < word.length())\n return false;\n char[] wrd = word.toCharArray();\n int[] boardf = new int[128];\n for (int i = 0; i < m; ++i)\n {\n for (int j = 0; j < n; ++j)\n {\n ++boardf[board[i][j]];\n }\n }\n for (char ch : wrd)\n {\n if (--boardf[ch] < 0)\n {\n return false;\n }\n }\n if (boardf[wrd[0]] > boardf[wrd[wrd.length - 1]])\n reverse(wrd);\n for (int i = 0; i < m; ++i)\n {\n for (int j = 0; j < n; ++j)\n {\n if (wrd[0] == board[i][j]\n && found(board, i, j, wrd, new boolean[m][n], 0))\n return true;\n }\n }\n return false;\n }\n\n private void reverse(char[] word)\n {\n int n = word.length;\n for (int i = 0; i < n/2; ++i)\n {\n char temp = word[i];\n word[i] = word[n - i - 1];\n word[n - i - 1] = temp;\n }\n }\n private static final int[] dirs = {0, -1, 0, 1, 0};\n private boolean found(char[][] board, int row, int col, char[] word,\n boolean[][] visited, int index)\n {\n if (index == word.length)\n return true;\n if (row < 0 || col < 0 || row == board.length || col == board[0].length\n || board[row][col] != word[index] || visited[row][col])\n return false;\n visited[row][col] = true;\n for (int i = 0; i < 4; ++i)\n {\n if (found(board, row + dirs[i], col + dirs[i + 1],\n word, visited, index + 1))\n return true;\n }\n visited[row][col] = false;\n return false;\n }\n}\n```\n | 447 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Python | Faster than 98% w/ Proof | Easy to Understand | word-search | 0 | 1 | ```\ndef exist(self, board: List[List[str]], word: str) -> bool:\n\t# Count number of letters in board and store it in a dictionary\n\tboardDic = defaultdict(int)\n\tfor i in range(len(board)):\n\t\tfor j in range(len(board[0])):\n\t\t\tboardDic[board[i][j]] += 1\n\n\t# Count number of letters in word\n\t# Check if board has all the letters in the word and they are atleast same count from word\n\twordDic = Counter(word)\n\tfor c in wordDic:\n\t\tif c not in boardDic or boardDic[c] < wordDic[c]:\n\t\t\treturn False\n\n\t# Traverse through board and if word[0] == board[i][j], call the DFS function\n\tfor i in range(len(board)):\n\t\tfor j in range(len(board[0])):\n\t\t\tif board[i][j] == word[0]:\n\t\t\t\tif self.dfs(i, j, 0, board, word):\n\t\t\t\t\treturn True\n\n\treturn False\n\ndef dfs(self, i, j, k, board, word):\n\t# Recursion will return False if (i,j) is out of bounds or board[i][j] != word[k] which is current letter we need\n\tif i < 0 or j < 0 or i >= len(board) or j >= len(board[0]) or \\\n\t k >= len(word) or word[k] != board[i][j]:\n\t\treturn False\n\n\t# If this statement is true then it means we have reach the last letter in the word so we can return True\n\tif k == len(word) - 1:\n\t\treturn True\n\n\tdirections = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\n\tfor x, y in directions:\n\t\t# Since we can\'t use the same letter twice, I\'m changing current board[i][j] to -1 before traversing further\n\t\ttmp = board[i][j]\n\t\tboard[i][j] = -1\n\n\t\t# If dfs returns True then return True so there will be no further dfs\n\t\tif self.dfs(i + x, j + y, k + 1, board, word): \n\t\t\treturn True\n\n\t\tboard[i][j] = tmp\n```\n\n\n\n\n\n\n\n\n | 205 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Python3, Backtracking, mega easy to understand | word-search | 0 | 1 | # Code\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n ans = False\n m, n = len(board[0]), len(board)\n dir = [[-1, 0], [0, 1], [1, 0], [0, -1]]\n\n def backtracking(c, r, cnt, visited):\n if cnt == len(word):\n nonlocal ans\n ans = True\n return\n\n for x, y in dir:\n new_c, new_r = c + x, r + y\n if (new_c < 0 or new_c >= n) or (new_r < 0 or new_r >= m):\n continue\n if board[new_c][new_r] == word[cnt] and [new_c, new_r] not in visited:\n backtracking(new_c, new_r, cnt + 1, visited + [[new_c, new_r]])\n\n for c in range(n):\n for r in range(m):\n if ans == False and board[c][r] == word[0]:\n backtracking(c, r, 1, [[c, r]])\n return ans\n``` | 3 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Python DFS with word reverse to prevent TLE | word-search | 0 | 1 | Python DFS with word reverse based on last and first char frequency to reduce the unnecessary searches\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n ROWS, COLS = len(board), len(board[0])\n path = set()\n\n def dfs(r, c, i):\n if i == len(word):\n return True\n if (\n min(r, c) < 0\n or r >= ROWS\n or c >= COLS\n or word[i] != board[r][c]\n or (r, c) in path\n ):\n return False\n path.add((r, c))\n res = (\n dfs(r + 1, c, i + 1)\n or dfs(r - 1, c, i + 1)\n or dfs(r, c + 1, i + 1)\n or dfs(r, c - 1, i + 1)\n )\n path.remove((r, c))\n return res\n\n # To prevent TLE,reverse the word if frequency of the first letter is more than the last letter\'s\n count = defaultdict(int, sum(map(Counter, board), Counter()))\n if count[word[0]] > count[word[-1]]:\n word = word[::-1]\n \n for r in range(ROWS):\n for c in range(COLS):\n if dfs(r, c, 0):\n return True\n return False | 3 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Exploring Words: Solving the Grid Word Search Problem with DFS Algorithm | word-search | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to find whether a given word can be constructed from the characters of the given grid such that adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once. The problem can be solved using the Depth First Search (DFS) algorithm. The DFS algorithm works by exploring as far as possible along each branch before backtracking. It is well-suited for problems that require searching through all possible paths.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can approach the problem using the DFS algorithm. We start by iterating through each cell in the grid. For each cell, we check whether the current cell matches the first character of the given word. If the current cell matches the first character of the word, we start a DFS search from that cell, looking for the rest of the characters in the word.\n\nFor each DFS search, we explore all four directions, i.e., up, down, left, and right, to find the next character in the word. We mark the current cell as visited to ensure that we do not use the same cell more than once. If we find the entire word, we return True, else we continue the search from the next unvisited cell.\n\nWe need to keep track of the visited cells to ensure that we do not use the same cell more than once. To mark a cell as visited, we can replace the character in the cell with a special character, such as \'/\'. After completing the DFS search, we can restore the original value of the cell.\n# Complexity\n- Time complexity: The time complexity of the DFS algorithm is proportional to the number of cells in the grid, i.e., O(mn), where m is the number of rows and n is the number of columns. In the worst case, we may have to explore all possible paths to find the word. For each cell, we explore at most four directions, so the time complexity of the DFS search is O(4^k), where k is the length of the word. Therefore, the overall time complexity of the algorithm is O(mn*4^k).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity of the algorithm is O(k), where k is the length of the word. This is the space required to store the recursive stack during the DFS search.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n def dfs(i: int, j: int, k: int) -> bool:\n if k == len(word):\n return True\n if i < 0 or i >= m or j < 0 or j >= n or board[i][j] != word[k]:\n return False\n temp, board[i][j] = board[i][j], \'/\'\n res = dfs(i+1, j, k+1) or dfs(i-1, j, k+1) or dfs(i, j+1, k+1) or dfs(i, j-1, k+1)\n board[i][j] = temp\n return res\n \n m, n = len(board), len(board[0])\n for i in range(m):\n for j in range(n):\n if dfs(i, j, 0):\n return True\n return False\n\n```\n\n# Code Explanation \n\nThis is a Python implementation of the depth-first search algorithm to find if a word exists in a given board of characters.\n\nThe `exist` method takes in two parameters, `board` and `word`, which are the 2D list of characters representing the board and the string representing the word to find, respectively. The method returns a boolean value, `True` if the word exists in the board, and `False` otherwise.\n\nThe algorithm uses a helper function `dfs` to search for the word starting from a given position in the board. The `dfs` function takes in three parameters, `i`, `j`, and `k`, which are the row and column indices of the current position in the board and the index of the current character in the word, respectively. The function returns a boolean value, `True` if the word can be formed starting from this position, and `False` otherwise.\n\nThe `dfs` function first checks if the end of the word has been reached, in which case it returns `True`. If the current position is out of the board or does not match the current character in the word, the function returns `False`.\n\nIf the current position matches the current character in the word, the function temporarily changes the character at the current position to `\'/\'` to mark it as visited and prevent revisiting it in the search. It then recursively calls itself with the adjacent positions (up, down, left, and right) and the next index in the word. If any of the recursive calls returns `True`, the function returns `True` as well.\n\nAfter the search from the current position is finished, the function restores the original character at the current position and returns the final result.\n\nThe `exist` function first gets the dimensions of the board using the `len` function. It then iterates through each cell in the board using nested loops. For each cell, it calls the `dfs` function starting from that position with the first character in the word. If `dfs` returns `True`, the function immediately returns `True` as well since the word has been found. If no word is found after iterating through all cells, the function returns `False`. | 32 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Easy Python Solution : 90.29 beats% || With Comments | word-search | 0 | 1 | # Code\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n ROWS, COLS = len(board), len(board[0])\n visited = set()\n\n def dfs(r,c,idx):\n # if idx == len(word), then word has been found\n if idx == len(word):\n return True\n\n # out of bounds\n # OR current letter does not match letter on board\n # OR letter already visited\n if ( \n r<0 or r>=ROWS \n or c<0 or c>=COLS\n or word[idx] != board[r][c]\n or (r,c) in visited\n ):\n return False\n \n # to keep track of the letter already visited, add it\'s position to the set\n # after DFS we can remove it from the set.\n visited.add((r,c))\n\n # performing DFS \n res = (\n dfs(r+1,c,idx+1) \n or dfs(r-1,c,idx+1) \n or dfs(r,c+1,idx+1) \n or dfs(r,c-1,idx+1)\n )\n \n visited.remove((r,c))\n return res\n \n for i in range(ROWS):\n for j in range(COLS):\n if dfs(i,j,0):\n return True\n return False\n\n``` | 10 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Click this if you're confused | word-search | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe must explore all possible word paths in the grid and prune this combinatorial search using backtracking.\n\nAt each cell we can explore the next adjacent cell by going Up, Down, Left, and Right. If we find a cell that matches the next character of our word, then we shall continue searching from that character. If we meet a dead end on all adjacent sides, we backtrack to our previous cell. Eventually we will either explore every path\u2014originating from every cell\u2014in the grid or find our word.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe implement this with a simple depth-first search. We pass in the current cell\u2014row and column\u2014and the index of our target character, which is 0 for the first `dfs` call.\n\nWe return True if our word has been found\u2014if our target index `i == len(word)`.\n\nWhat conditions do we return False on? When our current cell is out of bounds, not equal to our target character in the word, or a cell we have already traversed.\n\nNow if our current cell does math the target character, and we have not seen the full word yet, then we must explore the four adjacent cells. If any one of these cells ends up being the full word path it will return True, so we join the returns from all four adjacent `dfs` calls with `or` conditionals.\n\nBefore we explore the adjacent cells we need to add our current `r` and `c`\u2014row, column\u2014to a set `traversed` so we can check in `O(1)` time\u2014`(r, c) in traversed`\u2014whether a future cell has already been traversed. And after getting the results from the adjacent cells we must remove our current cell from `traversed` since we have finished exploring paths stemming from our current cell and don\'t want to hinder other paths.\n\nWe return our result\u2014if we found the word, the single True will end up in our recursive `or` chain and ultimately return True.\n\nThe time complexity of the whole algorithm is O(n * m * dfs_time) because we need to check each cell as a possible start. The time complexity of our backtracking dfs is \u200AMathjax\u200A since we explore 4 possibilities at each character and the possible paths goes up combinatorially with the number of characters in worst case.\n\nA technique to drastically reduce actual runtime is to reverse our word if the frequency of appearance of the last character is less than the frequency of the first character. Imagine we have a word "AAAB" and a grid below:\n\n\n\nExploring the possible As will involve exploring every single A before we get to the bottom right corner and find the word. Since our dfs is exponential, if we just use the less frequent character to start, in this example that\'s B, we can save a lot of runtime\u2014in this case we only execute the full dfs once at the last cell.\n# Complexity\n- Time complexity: **O(n_rows * n_cols * $4^{\\text{len(word)}}$)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(len(word))**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def exist(self, board: List[List[str]], word: str) -> bool:\n ROWS, COLS = len(board), len(board[0])\n traversed = set()\n \n def dfs(r, c, i):\n # recursive search with backtracking\n # O(4^s) where s is size of word\n \n if i == len(word):\n return True\n \n if (min(r, c) < 0\n or r >= ROWS\n or c >= COLS\n or (r, c) in traversed\n or board[r][c] != word[i]):\n return False\n \n traversed.add((r, c))\n found = (dfs(r + 1, c, i + 1)\n or dfs(r - 1, c, i + 1)\n or dfs(r, c + 1, i + 1)\n or dfs(r, c - 1, i + 1))\n traversed.remove((r, c))\n return found\n \n # Char that appears more frequently in board will result in\n # more unnecessary searches. count is dict \'<char>\': <count>\n count = defaultdict(int, sum(map(Counter, board), Counter()))\n if count[word[0]] > count[word[-1]]:\n word = word[::-1]\n\n # O(n * m * dfs)\n for r in range(ROWS):\n for c in range(COLS):\n if dfs(r, c, 0):\n return True\n return False\n\n\n``` | 1 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
With Pruning, Runtime reduced from 6000ms to 50ms | word-search | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt\'s better to check the edge case where it will return False.\n1. total characters in board is less than length of word\n2. minimum character of each word required to get answer are not in board\n\nThe answer will be same if one traverse the board based on matching the word from front or back. If the first char of word has higher frequency than last char of word, We can minimize the number to invoke the backtrack by reversing the word.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBacktrack with pruning\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(mn) + O(L<=15) + O(mn)*(3^L)**\nO(mn) : to get Counter for board\nO(L<=15) : to get Counter for word. This is constant\nO(mn)*(3^L) : TC for backtrack\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(L) + O(mn)\n\n# Code\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n m,n=len(board),len(board[0])\n #Pruning Edge Cases\n word_count = Counter(word)\n board_count = defaultdict(int, sum(map(Counter, board), Counter()))\n\n #If board doesn\'t have required length\n if len(board_count) < len(word_count) or m*n<len(word):\n return False\n #If board doesn\'t have required frequency of word letter in board\n for c in word:\n if board_count[c]<word_count[c]:\n return False\n # To prevent TLE,reverse the word if frequency of the first letter is more than the last letter\'s. Results will be same if traverse from back or front. Reversing the word when first char has higher frequency than last char, ensures we don\'t invoke search function less time when looping over the board\n if board_count[word[0]] > board_count[word[-1]]:\n word = word[::-1]\n\n \n def search(i,j,s):\n if i<0 or i>=m or j<0 or j>=n or (i,j) in visit:\n return False\n if board[i][j]==s[0]:\n visit.add((i,j))\n if len(s)==1:\n return True\n else:\n flag = search(i+1,j,s[1:]) or search(i-1,j,s[1:]) or search(i,j+1,s[1:]) or search(i,j-1,s[1:])\n if flag:\n return True\n visit.remove((i,j))\n return False\n\n for i in range(m):\n for j in range(n):\n visit=set()\n if search(i,j,word):\n return True\n return False\n``` | 2 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Python Elegant & Short | No TLE | word-search | 0 | 1 | ```\nclass Solution:\n """\n Time: O(n*m*k)\n Memory: O(k)\n\n where k - word length\n """\n\n VISITED = \'#\'\n\n def exist(self, board: List[List[str]], word: str) -> bool:\n n, m = len(board), len(board[0])\n\n beginning = end = 0\n for r in range(n):\n for c in range(m):\n if board[r][c] == word[0]:\n beginning += 1\n elif board[r][c] == word[-1]:\n end += 1\n\n if beginning > end:\n word = word[::-1]\n\n for i in range(n):\n for j in range(m):\n if self.dfs(board, i, j, 0, word):\n return True\n\n return False\n\n @classmethod\n def dfs(cls, board: List[List[str]], i: int, j: int, k: int, word: str) -> bool:\n if k == len(word):\n return True\n\n n, m = len(board), len(board[0])\n if (i < 0 or i >= n) or (j < 0 or j >= m) or word[k] != board[i][j]:\n return False\n\n board[i][j] = cls.VISITED\n res = cls.dfs(board, i + 1, j, k + 1, word) or \\\n cls.dfs(board, i - 1, j, k + 1, word) or \\\n cls.dfs(board, i, j + 1, k + 1, word) or \\\n cls.dfs(board, i, j - 1, k + 1, word)\n board[i][j] = word[k]\n\n return res\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n | 6 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Readable Python dfs solution | word-search | 0 | 1 | \n# Code\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n rows = len(board)\n cols = len(board[0])\n vis = set()\n\n def dfs(r, c, cur):\n if cur == len(word):\n return True\n if r < 0 or c < 0 or r >= rows or c >= cols or word[cur] != board[r][c] or (r, c) in vis:\n return False\n \n vis.add((r, c))\n\n check = (dfs(r + 1, c, cur + 1) or\n dfs(r - 1, c, cur + 1) or\n dfs(r, c + 1, cur + 1) or\n dfs(r, c - 1, cur + 1))\n \n vis.remove((r, c))\n\n return check\n \n for row in range(rows):\n for col in range(cols):\n if dfs(row, col, 0):\n return True\n return False\n``` | 2 | Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCCED "
**Output:** true
**Example 2:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "SEE "
**Output:** true
**Example 3:**
**Input:** board = \[\[ "A ", "B ", "C ", "E "\],\[ "S ", "F ", "C ", "S "\],\[ "A ", "D ", "E ", "E "\]\], word = "ABCB "
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`? | null |
Very Easy 100% (Fully Explained)(Java, C++, Python, JavaScript, C, Python3) | remove-duplicates-from-sorted-array-ii | 1 | 1 | Given an integer array nums sorted in non-decreasing order, remove some duplicates in-place such that each unique element appears at most twice. The relative order of the elements should be kept the same.\n\t\t\tSince it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements. At last return k after placing the final result in the first k slots of nums.\n# **Java Solution:**\nRuntime: 1 ms, faster than 96.73% of Java online submissions for Remove Duplicates from Sorted Array II.\nMemory Usage: 41.8 MB, less than 87.33% of Java online submissions for Remove Duplicates from Sorted Array II.\n```\nclass Solution {\n public int removeDuplicates(int[] nums) {\n // Special case...\n if (nums.length <= 2)\n return nums.length;\n int prev = 1; // point to previous\n int curr = 2; // point to current\n // Traverse all elements through loop...\n while (curr < nums.length) {\n // If the curr index matches the previous two elements, skip it...\n if (nums[curr] == nums[prev] && nums[curr] == nums[prev - 1]) {\n curr++;\n }\n // Otherwise, count that element and update...\n else {\n prev++;\n nums[prev] = nums[curr];\n curr++;\n }\n }\n return prev + 1; // Return k after placing the final result in the first k slots of nums...\n }\n}\n```\n\n# **C++ Solution:**\nRuntime: 4 ms, faster than 83.16% of C++ online submissions for Remove Duplicates from Sorted Array II.\nMemory Usage: 7.7 MB, less than 99.73% of C++ online submissions for Remove Duplicates from Sorted Array II.\n```\nclass Solution {\npublic:\n int removeDuplicates(vector<int>& nums) {\n // Special case...\n if(nums.size() <= 2) {\n return nums.size();\n }\n // Initialize an integer k that updates the kth index of the array...\n // only when the current element does not match either of the two previous indexes...\n int k = 2;\n // Traverse elements through loop...\n for(int i = 2; i < nums.size(); i++){\n // If the index does not match the (k-1)th and (k-2)th elements, count that element...\n if(nums[i] != nums[k - 2] || nums[i] != nums[k - 1]){\n nums[k] = nums[i];\n k++;\n // If the index matches the (k-1)th and (k-2)th elements, we skip it...\n }\n }\n return k; //Return k after placing the final result in the first k slots of nums...\n }\n};\n```\n\n# **Python Solution:**\nRuntime: 24 ms, faster than 74.03% of Python online submissions for Remove Duplicates from Sorted Array II.\n```\nclass Solution(object):\n def removeDuplicates(self, nums):\n # Initialize an integer k that updates the kth index of the array...\n # only when the current element does not match either of the two previous indexes. ...\n k = 0\n # Traverse all elements through loop...\n for i in nums:\n # If the index does not match elements, count that element and update it...\n if k < 2 or i != nums[k - 2]:\n nums[k] = i\n k += 1\n return k # Return k after placing the final result in the first k slots of nums...\n```\n \n# **JavaScript Solution:**\nRuntime: 88 ms, faster than 76.14% of JavaScript online submissions for Remove Duplicates from Sorted Array II.\nMemory Usage: 43.5 MB, less than 98.04% of JavaScript online submissions for Remove Duplicates from Sorted Array II.\n```\nvar removeDuplicates = function(nums) {\n // Special case...\n if(nums.length <= 2) {\n return nums.length;\n }\n // Initialize an integer k that updates the kth index of the array...\n // only when the current element does not match either of the two previous indexes...\n let k = 2;\n // Traverse elements through loop...\n for(let i = 2; i < nums.length; i++){\n // If the index does not match the (k-1)th and (k-2)th elements, count that element...\n if(nums[i] != nums[k - 2] || nums[i] != nums[k - 1]){\n nums[k] = nums[i];\n k++;\n // If the index matches the (k-1)th and (k-2)th elements, we skip it...\n }\n }\n return k; //Return k after placing the final result in the first k slots of nums...\n};\n```\n\n# **C Language:**\n```\nint removeDuplicates(int* nums, int numsSize){\n // Special case...\n if (numsSize <= 2)\n return numsSize;\n int prev = 1; // point to previous\n int curr = 2; // point to current\n // Traverse all elements through loop...\n while (curr < numsSize) {\n // If the curr index matches the previous two elements, skip it...\n if (nums[curr] == nums[prev] && nums[curr] == nums[prev - 1]) {\n curr++;\n }\n // Otherwise, count that element and update...\n else {\n prev++;\n nums[prev] = nums[curr];\n curr++;\n }\n }\n return prev + 1; // Return k after placing the final result in the first k slots of nums...\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n # Initialize an integer k that updates the kth index of the array...\n # only when the current element does not match either of the two previous indexes. ...\n k = 0\n # Traverse all elements through loop...\n for i in nums:\n # If the index does not match elements, count that element and update it...\n if k < 2 or i != nums[k - 2]:\n nums[k] = i\n k += 1\n return k # Return k after placing the final result in the first k slots of nums...\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 80 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
EASIEST TO UNDERSTAND METHOD PYTHON3 BEATS 90% MEMORY | remove-duplicates-from-sorted-array-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n d = 0\n for i in range(0, len(nums) - 2):\n if nums[i + 1] < nums[i]:\n break\n elif nums[i + 1] == nums[i]:\n count = 1\n x = i + 2\n while nums[x] == nums[i]:\n nums.remove(nums[x])\n nums.append(-100)\n else:\n continue\n for i in nums:\n if i != -100:\n d += 1\n return d\n \n``` | 1 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Easy & Clear Solution Python3 | remove-duplicates-from-sorted-array-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n for i in range(len(nums)-2,0,-1):\n if(nums[i]==nums[i-1] and nums[i]==nums[i+1]):\n nums.pop(i+1)\n return len(nums)\n\n``` | 20 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Simple Python 3 Solution BEATS 98.7% 💻🤖🧑💻💻🤖 | remove-duplicates-from-sorted-array-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n if len(nums) <= 2:\n return len(nums)\n\n currentIndex = 2\n for i in range(2, len(nums)):\n if nums[i] != nums[currentIndex - 2]:\n nums[currentIndex] = nums[i]\n currentIndex += 1\n\n return currentIndex\n\n\n``` | 10 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Easiest Solution using Counter | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n counter = Counter(nums)\n index = 0\n\n for num, count in counter.items():\n nums[index] = num\n index += 1\n if count > 1:\n nums[index] = num\n index += 1\n\n return index\n``` | 3 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
simple 2-pointers solution. speed 94.67%, memory 86.44% | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(0)\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n if len(nums) < 3:\n return len(nums)\n\n p1, p2 = 1, 2\n\n while p2 < len(nums):\n if nums[p1] == nums[p1-1] and nums[p2] == nums[p2-1] == nums[p2-2]:\n while p2 < len(nums) and nums[p2] == nums[p2-1]:\n p2 += 1\n if p2 == len(nums):\n break\n p1 += 1\n nums[p1] = nums[p2]\n p2 += 1\n\n return p1 + 1\n\n``` | 4 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Python3 || O(n) || Simple solution | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n counter = Counter(nums)\n l = []\n for i,j in counter.items():\n if j>2:\n l+=[i]*2\n else:\n l+=[i]*j\n nums[:] = l \n```\n# **Please upvote guys if you find the solution helpful.** | 5 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
[Python] Intuitive optimal 2 pointers solution | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n2 pointers, one goes first to find the next unique element, the slower one waits until the first one find a new element and fill its current position.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe iterate over `nums`, we first set the amount of the number of duplicates for the current element to 2, `cnt_left = 2`. We only do this when we found a new element: `num != nums[j - 1]` or `j == 0`\n\nWe then update the slow pointer and reduce the `cnt_left` when:\n- We need another duplicate: `cnt_left > 0 and num == nums[j - 1]`\n- New element found: `j == 0` or `num != nums[j - 1]`\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n """\n Idea\n - Fast pointer go scanning\n\n - Slow pointer only fills the position when: \n nums[fast pointer] != nums[slow pointer - 1]\n\n """\n j = cnt_left = 0\n for num in nums:\n if j == 0 or num != nums[j - 1]: cnt_left = 2\n\n conditions = [\n num == nums[j - 1] and cnt_left > 0,\n j == 0,\n (num != nums[j - 1])\n ]\n\n if any(conditions):\n nums[j] = num\n j += 1\n cnt_left -= 1\n\n return j\n \n\n\n\n \n\n \n``` | 2 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
O(n) | Simple Python Solution | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCompared to "Remove Elementes From A Sorted Array I": The key differences are the ">" symbol and l- 2.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPlaceholder \'l\' stops at the 3rd repeated value while \'i\' continues and looks for then next different value. The ">" symbol prevents cases where 2 == 2 would be true and allows \'i\' to continue.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums):\n l = 2\n\n for i in range(2, len(nums)):\n if nums[i] > nums[l - 2]:\n nums[l] = nums[i]\n l += 1\n\n return l\n``` | 6 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Beating 92.86% Memory Python Easiest Solution | remove-duplicates-from-sorted-array-ii | 0 | 1 | \n\n\n# Code\n```\nclass Solution(object):\n def removeDuplicates(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n c=0\n s=set(nums)\n for i in s:\n if nums.count(i)>2:\n c+=2\n for j in range(len(nums)-1,-1,-1):\n if nums[j]==i:\n if nums.count(i)>2:\n nums.remove(i)\n else:\n c+=nums.count(i)\n return c\n \n``` | 1 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Simple Python solution with two pointers | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis function iterates through the sorted array using two pointers, slow and fast. The slow pointer keeps track of the first position to store a unique element, while the fast pointer iterates through the array.\n\n- If the current element is different from the element two positions before it (which ensures that each unique element appears at most twice), we store the current element at the slow pointer\'s position and increment both slow and fast.\n- If the current element is the same as the element two positions before it, we simply increment the fast pointer to skip over duplicates.\n- After processing the entire array, the slow pointer points to the length of the modified array. The array is modified in-place, and the relative order of elements is preserved.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) since we are only doing one pass\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n if len(nums) <= 2:\n return len(nums)\n \n slow = 2\n fast = 2\n while fast < len(nums):\n if nums[fast] != nums[slow-2]:\n nums[slow] = nums[fast]\n slow += 1\n fast += 1\n return slow\n \n\n \n``` | 3 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
Two Pointers Approach | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n l,r,count=0,1,1\n \n while (r<len(nums)): \n if nums[r]==nums[l] and count<2:\n l+=1\n nums[l]=nums[r] \n count+=1\n\n elif nums[r]==nums[l] and count>=2:\n count+=1\n else:\n count=1\n l+=1\n nums[l]=nums[r]\n r+=1\n\n return l+1\n\n\n``` | 4 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
best ever solution on leetcode i can bet on it | remove-duplicates-from-sorted-array-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int removeDuplicates(vector<int>& nums) {\n\n int i=0;\n\n for(auto it:nums){\n\n if(i==0 || i==1 || nums[i-2]!=it){\n nums[i]=it;\n i++;\n }\n }\n return i;\n \n }\n};\n``` | 2 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
3 line easy to understand code beats 86% in runtime & 99.31% in memory Very easy to understand | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n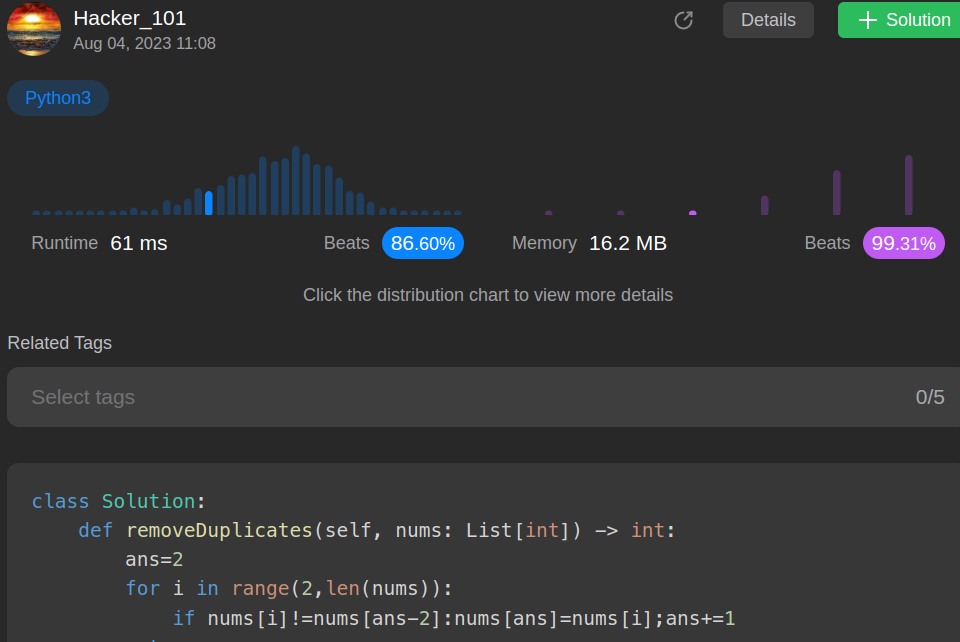\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n ans=2\n for i in range(2,len(nums)):\n if nums[i]!=nums[ans-2]:nums[ans]=nums[i];ans+=1\n return ans\n``` | 5 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
80. Remove Duplicates from Sorted Array II with step by step explanation | remove-duplicates-from-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Initialize a variable i to 0.\n- Loop through each n in nums.\n- Check if i is less than 2 or n is greater than the nums[i-2].\n - If the condition is true, assign n to nums[i] and increment i by 1.\n- Return i.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n i = 0\n for n in nums:\n if i < 2 or n > nums[i-2]:\n nums[i] = n\n i += 1\n return i\n\n``` | 9 | Given an integer array `nums` sorted in **non-decreasing order**, remove some duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears **at most twice**. The **relative order** of the elements should be kept the **same**.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the **first part** of the array `nums`. More formally, if there are `k` elements after removing the duplicates, then the first `k` elements of `nums` should hold the final result. It does not matter what you leave beyond the first `k` elements.
Return `k` _after placing the final result in the first_ `k` _slots of_ `nums`.
Do **not** allocate extra space for another array. You must do this by **modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** with O(1) extra memory.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\]
**Output:** 5, nums = \[1,1,2,2,3,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,1,2,3,3\]
**Output:** 7, nums = \[0,0,1,1,2,3,3,\_,\_\]
**Explanation:** Your function should return k = 7, with the first seven elements of nums being 0, 0, 1, 1, 2, 3 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in **non-decreasing** order. | null |
✅ 100% Binary Search [VIDEO] with Rotation Handling - Optimal | search-in-rotated-sorted-array-ii | 1 | 1 | # Problem Understanding\n\nThe problem presents us with a modified search challenge where we\'re provided an array that has been rotated at an undetermined pivot. Unlike a standard sorted array, this comes with the added complexity of having been altered. Imagine a scenario where you take a sorted array, make a cut at a specific point, and then attach the detached segment to the front. The aim here is to ascertain whether a specific target value is present in this rearranged sorted array. Adding to the intricacy, this array might have duplicate values.\n\nFor instance, considering the array $$[2,5,6,0,0,1,2]$$, it becomes evident that a rotation occurred after the number 6. If our target is 2, it is indeed present within the array. Similarly, for a target of 6, it is also found in the array. However, should the target be a number like 3, it is absent from the array.\n\nBelow are the visualizations for the "Search in Rotated Sorted Array II" problem for targets 2 and 6:\n\n- The top chart visualizes the search process in the rotated sorted array. Each step highlights the current mid value being considered with a red rectangle.\n\n- The table below provides a step-by-step breakdown of the search algorithm, detailing the indices (low, mid, high) and their corresponding values at each step of the search.\n\nFor each target:\n\n- The top chart shows the search process in the rotated sorted array. Each step of the search process is highlighted by a red rectangle.\n\n- The table below provides a step-by-step breakdown of the search algorithm, detailing the indices (low, mid, high) and their corresponding values at each search step.\n\n**Target = 2**\n\n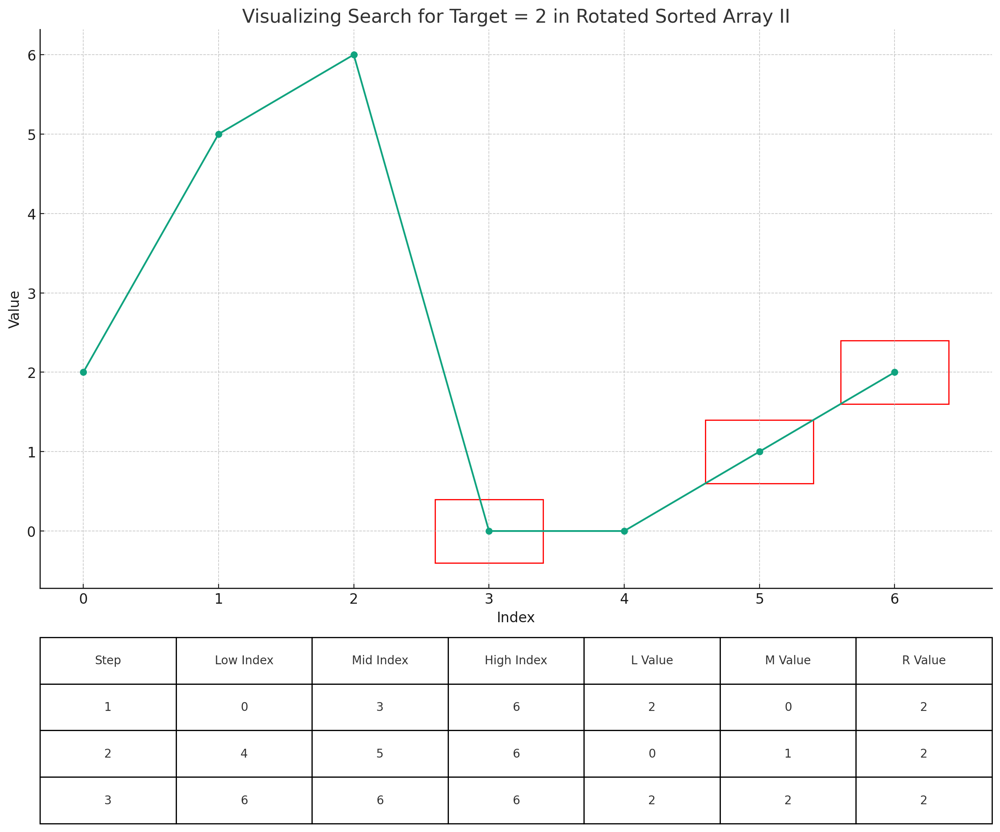\n\n**Target = 6**\n\n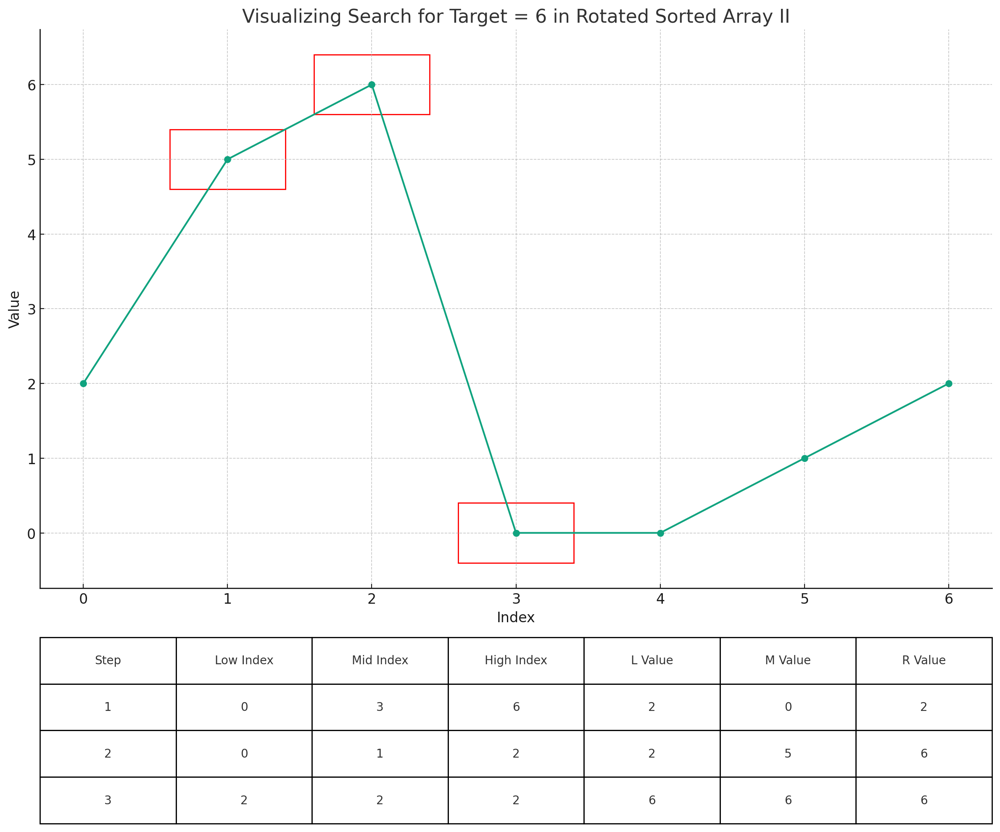\n\n---\n\n# Live Coding & Explanation\n\nhttps://youtu.be/Py75aDQqrJw\n\n# Approach\n\nTo tackle this challenge, we employ a binary search strategy, taking into account the rotation and potential duplicates. The primary goal is to identify the sorted part of the array in each step and narrow down our search based on the target.\n\n## Binary Search with Rotation Handling\n\nOur approach doesn\'t involve searching for the rotation point. Instead, we modify the binary search to work directly with the rotated array:\n\n- We calculate the middle index, `mid`, of our current search interval.\n- If the value at `mid` is our target, we\'ve found it.\n- If the value at `low` is the same as the value at `mid`, we might be dealing with duplicates. In this case, we increment `low` to skip potential duplicates.\n- If the left part of our interval (from `low` to `mid`) is sorted (i.e., `nums[low] <= nums[mid]`), we check if our target lies within this sorted interval. If it does, we search in the left half; otherwise, we search in the right half.\n- If the left part isn\'t sorted, then the right part must be. We apply a similar logic to decide which half to search in next.\n\n## Code Breakdown\n\n1. Initialize pointers `low` and `high` at the start and end of `nums`, respectively.\n2. While `low` is less than or equal to `high`, compute `mid`.\n3. Check if `nums[mid]` is the target. If yes, return `True`.\n4. If `nums[low]` is equal to `nums[mid]`, increment `low`.\n5. If the left half is sorted, check if target lies within it. If yes, update `high`; otherwise, update `low`.\n6. If the right half is sorted, use a similar logic to update `low` or `high`.\n7. If the loop completes without finding the target, return `False`.\n\n## Rationale\n\nThe beauty of this solution lies in its adaptability. While binary search is a straightforward algorithm on sorted arrays, this problem added the twist of a rotated array and duplicates. By understanding the structure of the rotated array and handling duplicates wisely, we can still achieve efficient search performance.\n\n# Complexity\n\n**Time Complexity:** $$O(\\log n)$$ for the best case (unique elements). However, in the worst-case scenario (many duplicates), the complexity can degrade to $$O(n)$$.\n\n**Space Complexity:** $$O(1)$$ as we only use a constant amount of space.\n\n# Performance\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|-------------|--------------|------------------|-------------|-----------------|\n| Rust | 0 ms | 100% | 2.2 MB | 48% |\n| C++ | 0 ms | 100% | 13.9 MB | 50.5% |\n| Java | 0 ms | 100% | 43.4 MB | 15.46% |\n| Go | 5 ms | 56.57% | 3.2 MB | 98.86% |\n| JavaScript | 49 ms | 92.77% | 41.6 MB | 97.20% |\n| Python3 | 56 ms | 92.26% | 17 MB | 47.39% |\n| C# | 75 ms | 98.86% | 41.6 MB | 80.11% |\n\n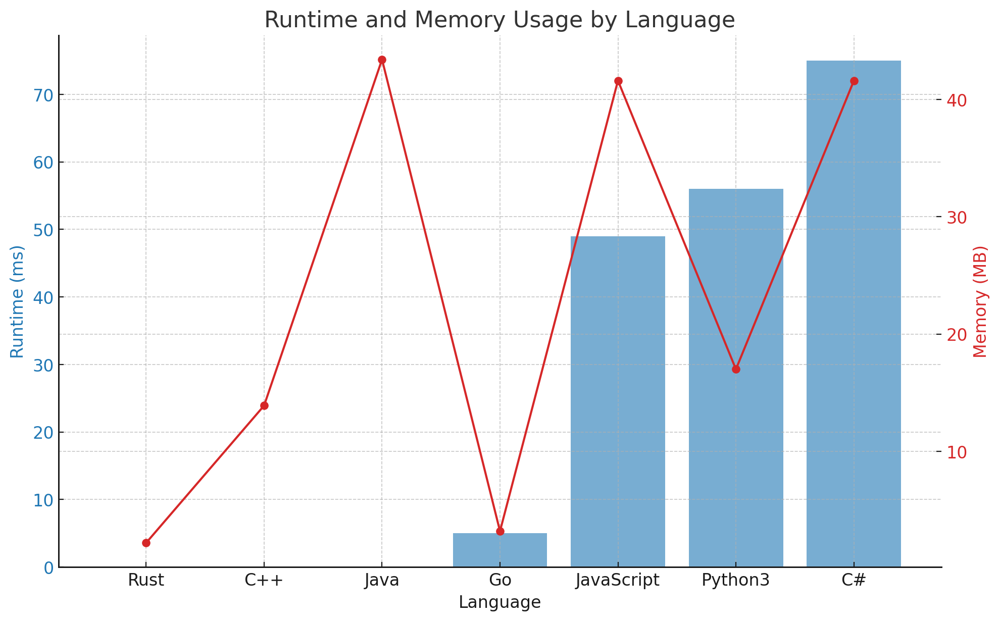\n\n\n# Code\n``` Python []\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n low, high = 0, len(nums) - 1\n\n while low <= high:\n mid = (low + high) // 2\n if nums[mid] == target:\n return True\n \n if nums[low] == nums[mid]:\n low += 1\n continue\n \n if nums[low] <= nums[mid]:\n if nums[low] <= target <= nums[mid]:\n high = mid - 1\n else:\n low = mid + 1\n else:\n if nums[mid] <= target <= nums[high]:\n low = mid + 1\n else:\n high = mid - 1\n \n return False\n```\n``` C++ []\nclass Solution {\npublic:\n bool search(std::vector<int>& nums, int target) {\n int low = 0, high = nums.size() - 1;\n\n while (low <= high) {\n int mid = (low + high) / 2;\n if (nums[mid] == target) return true;\n\n if (nums[low] == nums[mid]) {\n low++;\n continue;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target <= nums[mid]) high = mid - 1;\n else low = mid + 1;\n } else {\n if (nums[mid] <= target && target <= nums[high]) low = mid + 1;\n else high = mid - 1;\n }\n }\n return false;\n }\n};\n```\n``` Rust []\nimpl Solution {\n pub fn search(nums: Vec<i32>, target: i32) -> bool {\n let mut low = 0;\n let mut high = nums.len() as i32 - 1;\n\n while low <= high {\n let mid = (low + high) / 2;\n if nums[mid as usize] == target {\n return true;\n }\n\n if nums[low as usize] == nums[mid as usize] {\n low += 1;\n continue;\n }\n\n if nums[low as usize] <= nums[mid as usize] {\n if nums[low as usize] <= target && target <= nums[mid as usize] {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n } else {\n if nums[mid as usize] <= target && target <= nums[high as usize] {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n }\n false\n }\n}\n```\n``` Go []\nfunc search(nums []int, target int) bool {\n low, high := 0, len(nums) - 1\n\n for low <= high {\n mid := (low + high) / 2\n if nums[mid] == target {\n return true\n }\n\n if nums[low] == nums[mid] {\n low++\n continue\n }\n\n if nums[low] <= nums[mid] {\n if nums[low] <= target && target <= nums[mid] {\n high = mid - 1\n } else {\n low = mid + 1\n }\n } else {\n if nums[mid] <= target && target <= nums[high] {\n low = mid + 1\n } else {\n high = mid - 1\n }\n }\n }\n return false\n}\n```\n``` Java []\npublic class Solution {\n public boolean search(int[] nums, int target) {\n int low = 0, high = nums.length - 1;\n\n while (low <= high) {\n int mid = (low + high) / 2;\n if (nums[mid] == target) return true;\n\n if (nums[low] == nums[mid]) {\n low++;\n continue;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target <= nums[mid]) high = mid - 1;\n else low = mid + 1;\n } else {\n if (nums[mid] <= target && target <= nums[high]) low = mid + 1;\n else high = mid - 1;\n }\n }\n return false;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {boolean}\n */\nvar search = function(nums, target) {\n let low = 0, high = nums.length - 1;\n\n while (low <= high) {\n let mid = Math.floor((low + high) / 2);\n if (nums[mid] === target) return true;\n\n if (nums[low] === nums[mid]) {\n low++;\n continue;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target <= nums[mid]) high = mid - 1;\n else low = mid + 1;\n } else {\n if (nums[mid] <= target && target <= nums[high]) low = mid + 1;\n else high = mid - 1;\n }\n }\n return false;\n}\n```\n``` C# []\npublic class Solution {\n public bool Search(int[] nums, int target) {\n int low = 0, high = nums.Length - 1;\n\n while (low <= high) {\n int mid = (low + high) / 2;\n if (nums[mid] == target) return true;\n\n if (nums[low] == nums[mid]) {\n low++;\n continue;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target <= nums[mid]) high = mid - 1;\n else low = mid + 1;\n } else {\n if (nums[mid] <= target && target <= nums[high]) low = mid + 1;\n else high = mid - 1;\n }\n }\n return false;\n }\n}\n```\n | 66 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Easiest Solution Using Binary Search | search-in-rotated-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(logn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef BinarySearch(l,lb,ub,target):\n if ub>= lb:\n mid = lb+(ub-lb)//2\n if l[mid] == target:\n return True\n elif l[mid] > target:\n return BinarySearch(l,lb,mid-1,target)\n else:\n return BinarySearch(l,mid+1,ub,target)\n else:\n return False\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n nums.sort()\n return BinarySearch(nums,0,len(nums)-1,target)\n \n``` | 1 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | search-in-rotated-sorted-array-ii | 1 | 1 | # Intuition\nUsing modified binary search and add a few conditions before narrow the searching range.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n# Subscribe to my channel from here. I have 243 videos as of August 10th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/mIa0uYBA85s\n\n---\n\n# Related video\n- Search in Rotated Sorted Array\n\nhttps://youtu.be/5QDw0rNVlcE\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize `left` to 0 (representing the left boundary of the search range) and `right` to the length of `nums` minus 1 (representing the right boundary of the search range).\n\n2. Enter a `while` loop that continues as long as `left` is less than or equal to `right`.\n\n3. Calculate the midpoint `mid` using integer division (`//`) of the sum of `left` and `right`.\n\n4. Check if the element at the midpoint `nums[mid]` is equal to the target value. If it is, return `True` since the target has been found.\n\n5. Check if the element at the midpoint `nums[mid]` is equal to the element at the left boundary `nums[left]`. If they are equal, it means we have duplicate values at the left and mid positions. Increment `left` by 1 to skip duplicates and continue to the next iteration using the `continue` statement.\n\n6. If the conditions in steps 4 and 5 were not satisfied, then there are no duplicates at the mid position and the target value was not found. We need to decide whether the target could be in the left or right subarray based on the properties of the rotated sorted array.\n\n7. Check if the subarray from `left` to `mid` is sorted (i.e., `nums[left] <= nums[mid]`). If it is, then check whether the target lies within this sorted subarray (`nums[left] <= target < nums[mid]`). If this condition holds, adjust the `right` boundary to `mid - 1` to search the left half, otherwise, adjust the `left` boundary to `mid + 1` to search the right half.\n\n8. If the subarray from `left` to `mid` is not sorted, it implies that the rotated part is on the left side of `mid`. In this case, check whether the target lies within the subarray to the right of `mid` (`nums[mid] < target <= nums[right]`). If this condition holds, adjust the `left` boundary to `mid + 1` to search the right half, otherwise, adjust the `right` boundary to `mid - 1` to search the left half.\n\n9. Repeat steps 3 to 8 until the `left` boundary is no longer less than or equal to the `right` boundary, indicating that the search space is exhausted.\n\n10. If the target value was not found during the entire search, return `False`.\n\nIn summary, this algorithm performs a modified binary search on a rotated sorted array with possible duplicates. It efficiently narrows down the search range based on comparisons with the target value and the properties of the array.\n\n# Complexity\n- Time complexity: O(log n)\nBut if you get an input list like [1,1,1,1,1,1,1,1] target = 3, this condition(if nums[mid] == nums[left]:) is always `True`. In that case, time complexity should be O(n) because we narrow the searching range one by one.\n\n- Space complexity: O(1)\n\n\n```python []\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n left, right = 0, len(nums) - 1\n \n while left <= right:\n mid = (left + right) // 2\n \n if nums[mid] == target:\n return True\n \n if nums[mid] == nums[left]:\n left += 1\n continue\n\n if nums[left] <= nums[mid]:\n if nums[left] <= target < nums[mid]:\n right = mid - 1\n else:\n left = mid + 1\n else:\n if nums[mid] < target <= nums[right]:\n left = mid + 1\n else:\n right = mid - 1\n \n return False\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {boolean}\n */\nvar search = function(nums, target) {\n let left = 0;\n let right = nums.length - 1;\n \n while (left <= right) {\n let mid = Math.floor((left + right) / 2);\n \n if (nums[mid] === target) {\n return true;\n }\n \n if (nums[mid] === nums[left]) {\n left++;\n continue;\n }\n \n if (nums[left] <= nums[mid]) {\n if (nums[left] <= target && target < nums[mid]) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[right]) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n }\n \n return false; \n};\n```\n```java []\nclass Solution {\n public boolean search(int[] nums, int target) {\n int left = 0;\n int right = nums.length - 1;\n \n while (left <= right) {\n int mid = (left + right) / 2;\n \n if (nums[mid] == target) {\n return true;\n }\n \n if (nums[mid] == nums[left]) {\n left++;\n continue;\n }\n \n if (nums[left] <= nums[mid]) {\n if (nums[left] <= target && target < nums[mid]) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[right]) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n }\n \n return false; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool search(vector<int>& nums, int target) {\n int left = 0;\n int right = nums.size() - 1;\n \n while (left <= right) {\n int mid = (left + right) / 2;\n \n if (nums[mid] == target) {\n return true;\n }\n \n if (nums[mid] == nums[left]) {\n left++;\n continue;\n }\n \n if (nums[left] <= nums[mid]) {\n if (nums[left] <= target && target < nums[mid]) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[right]) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n }\n \n return false; \n }\n};\n```\n | 8 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Basic solution | search-in-rotated-sorted-array-ii | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n for num in range(len(nums)):\n if nums[num] == target:\n return True\n return False\n``` | 1 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python Easy One-Line Solution || 100% | search-in-rotated-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe have check weather element in list or not.\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n return target in set(nums)\n``` | 2 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python short and clean. Binary-Search. | search-in-rotated-sorted-array-ii | 0 | 1 | # Approach\nSimilar to [33. Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/description/) problem and its [Solution](https://leetcode.com/problems/search-in-rotated-sorted-array/solutions/3879752/python-short-and-clean-single-binary-search-2-solutions/).\nAn additional check, shown below, is added to reduce the search space on either side when a binary split choice can\'t be made.\n```python\nif nums[l] == nums[m] == nums[r]:\n l, r = (l + 1, r - 1)\n```\n\n# Complexity\n- Time complexity: $$O(n)$$ Worst case. $$O(log_2(n))$$ average case.\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution:\n def search(self, nums: list[int], target: int) -> bool:\n l, r = 0, len(nums) - 1\n\n while l <= r:\n m = (l + r) // 2\n\n if nums[m] == target: return True\n elif nums[l] == nums[m] == nums[r]:\n l, r = (l + 1, r - 1)\n elif nums[l] <= nums[m]:\n l, r = (l, m - 1) if nums[l] <= target < nums[m] else (m + 1, r)\n else:\n l, r = (m + 1, r) if nums[m] < target <= nums[r] else (l, m - 1)\n \n return False\n\n\n``` | 1 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python easy solution | search-in-rotated-sorted-array-ii | 0 | 1 | # Code\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n return True if target in nums else False\n``` | 4 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python O(n) Binary Search Discontinuity ✅🔥 | search-in-rotated-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSuppose some sorted nondecreasing array `original` gets rotated.\n\nSince `original` is nondecreasing, we know that either the entire array is flat, or the last element must be greater than the first element.\n\nNo matter how much the array is rotated, there must be **no more than one decrease**. This allows us to still use binary search unless the array is very flat.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nConsider some subarray of `nums` with first element `left`, last element `right`, and middle element `mid` (might all be the same element).\n\nBecause of the possiblity of duplicates, we cannot say `left >= right` means rotated as was true in [Search in Rotated Sorted Array I](https://leetcode.com/problems/search-in-rotated-sorted-array/solutions/3883855/python-o-log-n-binary-search-discontinuity/).\n\nInstead, if `left > right`, the array must have been rotated, since the original was nondecreasing.\n\n\n\nNotice that wherever you place `mid` and `target`, the direction is always the same as a regular binary search except **when the discontinuity is between `mid` and `target`**. In that case the direction is reversed.\n\n\n\n\n\n\n\n\nIf `left < right`, the subarray must be sorted since if there was some decrease in between, there would now be two decreases in the circular array which is invalid. In this case a regular binary search can be used.\n\n\n\n\nif `left == right`, `nums` is either flat or rotated and there is no way to guarantee which one it is in faster than linear time, and if `left == mid == right`, we cannot guarantee which side of `mid` the target will be on.\n\n\n\nIn this case we can linearly search from the ends of the array, shrinking the bounds until either a different number is found or the search is done. \n```py\n while nums[l] == nums[r]:\n l += 1\n r -= 1\n```\n\n# Complexity\n- Time complexity: $$ O(n) $$\n - Worst case `nums` is flat and `target` is not in `nums`.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$ O(1) $$\n - Store pointers.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```py\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n n, l, r = len(nums), 0, n - 1\n\n while l <= r:\n mid = (l + r) // 2\n if target in (nums[l], nums[mid], nums[r]):\n return True\n elif nums[l] == nums[mid] == nums[r]:\n while 0 <= l <= r <= n - 1 and nums[l] == nums[r]:\n l += 1\n r -= 1\n elif target > nums[mid]:\n if nums[mid] <= nums[r] <= target:\n r = mid - 1\n else:\n l = mid + 1\n else:\n if nums[mid] >= nums[l] >= target:\n l = mid + 1\n else:\n r = mid - 1\n\n return False\n``` | 2 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python3 one liner Solution | search-in-rotated-sorted-array-ii | 0 | 1 | \n```\nclass Solution:\n def search(self,nums:List[int],target:int)->bool:\n return True if target in nums else False \n``` | 4 | There is an integer array `nums` sorted in non-decreasing order (not necessarily with **distinct** values).
Before being passed to your function, `nums` is **rotated** at an unknown pivot index `k` (`0 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,4,4,5,6,6,7]` might be rotated at pivot index `5` and become `[4,5,6,6,7,0,1,2,4,4]`.
Given the array `nums` **after** the rotation and an integer `target`, return `true` _if_ `target` _is in_ `nums`_, or_ `false` _if it is not in_ `nums`_._
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 0
**Output:** true
**Example 2:**
**Input:** nums = \[2,5,6,0,0,1,2\], target = 3
**Output:** false
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* `nums` is guaranteed to be rotated at some pivot.
* `-104 <= target <= 104`
**Follow up:** This problem is similar to Search in Rotated Sorted Array, but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Very Easy 100% (Fully Explained)(Java, C++, Python, JS, C, Python3) | remove-duplicates-from-sorted-list-ii | 1 | 1 | Given the head of a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list. Return the linked list sorted as well.\n# **Java Solution:**\nRuntime: 1 ms, faster than 93.57% of Java online submissions for Remove Duplicates from Sorted List II.\n```\nclass Solution {\n public ListNode deleteDuplicates(ListNode head) {\n // Special case...\n if (head == null || head.next == null)\n return head;\n // create a fake node that acts like a fake head of list pointing to the original head and it points to the original head......\n ListNode fake = new ListNode(0);\n fake.next = head;\n ListNode curr = fake;\n // Loop till curr.next and curr.next.next not null\n while(curr.next != null && curr.next.next != null){ // curr.next means the next node of curr pointer and curr.next.next means the next of next of curr pointer...\n // if the value of curr.next and curr.next.next is same...\n // There is a duplicate value present in the list...\n if(curr.next.val == curr.next.next.val) {\n int duplicate = curr.next.val;\n // If the next node of curr is not null and its value is eual to the duplicate value...\n while(curr.next !=null && curr.next.val == duplicate) {\n // Skip those element and keep updating curr...\n curr.next = curr.next.next;\n }\n }\n // Otherwise, move curr forward...\n else{\n curr = curr.next;\n }\n }\n return fake.next; // Return the linked list...\n }\n}\n```\n\n# **C++ Solution:**\nRuntime: 6 ms, faster than 88.10% of C++ online submissions for Remove Duplicates from Sorted List II.\n```\nclass Solution {\npublic:\n ListNode* deleteDuplicates(ListNode* head) {\n // create a fake node that acts like a fake head of list pointing to the original head...\n ListNode* fake = new ListNode(0);\n // fake node points to the original head...\n fake->next = head;\n ListNode* pre = fake; //pointing to last node which has no duplicate...\n ListNode* curr = head; // To traverse the linked list...\n // Now we traverse nodes and do the process...\n while (curr != NULL) {\n // Create a loop until the current and previous values are same, keep updating curr...\n while (curr->next != NULL && pre->next->val == curr->next->val)\n curr = curr->next;\n // if curr has non-duplicate value, move the pre pointer to next node...\n if (pre->next == curr)\n pre = pre->next;\n // If curr is updated to the last duplicate value, discard it & connect pre and curr->next...\n else\n pre->next = curr->next;\n // Move curr forward...\n // In next iteration, we still need to check whether curr points to duplicate value...\n curr = curr->next;\n }\n // Return the linked list...\n return fake->next;\n }\n};\n```\n\n# **Python Solution:**\nRuntime: 28 ms, faster than 79.86% of Python online submissions for Remove Duplicates from Sorted List II.\n```\nclass Solution(object):\n def deleteDuplicates(self, head):\n fake = ListNode(-1)\n fake.next = head\n # We use prev (for node just before duplications begins), curr (for the last node of the duplication group)...\n curr, prev = head, fake\n while curr:\n # while we have curr.next and its value is equal to curr...\n # It means, that we have one more duplicate...\n while curr.next and curr.val == curr.next.val:\n # So move curr pointer to the right...\n curr = curr.next\n # If it happens, that prev.next equal to curr...\n # It means, that we have only 1 element in the group of duplicated elements...\n if prev.next == curr:\n # Don\'t need to delete it, we move both pointers to right...\n prev = prev.next\n curr = curr.next\n # Otherwise, we need to skip a group of duplicated elements...\n # set prev.next = curr.next, and curr = prev.next...\n else:\n prev.next = curr.next\n curr = prev.next\n # Return the linked list...\n return fake.next\n```\n \n# **JavaScript Solution:**\nRuntime: 91 ms, faster than 67.42% of JavaScript online submissions for Remove Duplicates from Sorted List II.\n```\nvar deleteDuplicates = function(head) {\n // Special case...\n if (head == null || head.next == null)\n return head;\n // create a fake node that acts like a fake head of list pointing to the original head and it points to the original head......\n var fake = new ListNode(0);\n fake.next = head;\n var curr = fake;\n // Loop till curr.next and curr.next.next not null\n while(curr.next != null && curr.next.next != null){ // curr.next means the next node of curr pointer and curr.next.next means the next of next of curr pointer...\n // if the value of curr.next and curr.next.next is same...\n // There is a duplicate value present in the list...\n if(curr.next.val == curr.next.next.val) {\n let duplicate = curr.next.val;\n // If the next node of curr is not null and its value is eual to the duplicate value...\n while(curr.next !=null && curr.next.val == duplicate) {\n // Skip those element and keep updating curr...\n curr.next = curr.next.next;\n }\n }\n // Otherwise, move curr forward...\n else{\n curr = curr.next;\n }\n }\n return fake.next; // Return the linked list...\n};\n```\n\n# **C Language:**\n```\nstruct ListNode* deleteDuplicates(struct ListNode* head){\n // create a fake node that acts like a fake head of list pointing to the original head...\n struct ListNode* fake = (struct ListNode*)malloc(sizeof(struct ListNode));\n // fake node points to the original head...\n fake->next = head;\n struct ListNode* pre = fake; //pointing to last node which has no duplicate...\n struct ListNode* curr = head; // To traverse the linked list...\n // Now we traverse nodes and do the process...\n while (curr != NULL) {\n // Create a loop until the current and previous values are same, keep updating curr...\n while (curr->next != NULL && pre->next->val == curr->next->val)\n curr = curr->next;\n // if curr has non-duplicate value, move the pre pointer to next node...\n if (pre->next == curr)\n pre = pre->next;\n // If curr is updated to the last duplicate value, discard it & connect pre and curr->next...\n else\n pre->next = curr->next;\n // Move curr forward...\n // In next iteration, we still need to check whether curr points to duplicate value...\n curr = curr->next;\n }\n // Return the linked list...\n return fake->next;\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n fake = ListNode(-1)\n fake.next = head\n # We use prev (for node just before duplications begins), curr (for the last node of the duplication group)...\n curr, prev = head, fake\n while curr:\n # while we have curr.next and its value is equal to curr...\n # It means, that we have one more duplicate...\n while curr.next and curr.val == curr.next.val:\n # So move curr pointer to the right...\n curr = curr.next\n # If it happens, that prev.next equal to curr...\n # It means, that we have only 1 element in the group of duplicated elements...\n if prev.next == curr:\n # Don\'t need to delete it, we move both pointers to right...\n prev = prev.next\n curr = curr.next\n # Otherwise, we need to skip a group of duplicated elements...\n # set prev.next = curr.next, and curr = prev.next...\n else:\n prev.next = curr.next\n curr = prev.next\n # Return the linked list...\n return fake.next\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 63 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
straight forward python3 faster than 99% | remove-duplicates-from-sorted-list-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse previous node to track which part to cut off\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAdd dummy node incase the first number repeats.\nIterate through and cut off repeating nodes.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n), each node is iterated no more than once\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) storage, only need to update dummy, prev, cur \n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\n dummy = ListNode(None, None)\n dummy.next = head\n prev = dummy\n cur = head\n while cur and cur.next:\n\n if cur.next.val == cur.val:\n while cur.next and cur.next.val == cur.val:\n cur = cur.next\n cur.next, cur = None, cur.next\n prev.next = cur\n else:\n prev = cur\n cur = cur.next\n\n return dummy.next\n``` | 2 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Beats 99.93% ||🔥🔥 Python Linked List || 🔥🔥 | remove-duplicates-from-sorted-list-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0)\n dummy.next = head\n current = dummy\n\n while current.next:\n if current.next.next and current.next.val == current.next.next.val:\n # We found a duplicate.\n # Iterate until we reach a distinct value.\n val = current.next.val\n while current.next and current.next.val == val:\n current.next = current.next.next\n else:\n # Move to the next node.\n current = current.next\n\n return dummy.next \n``` | 2 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Use simple Brute force | remove-duplicates-from-sorted-list-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\n dummy = ListNode(0) \n dummy.next = head\n prev = dummy\n current = head\n\n while current:\n next_node = current.next\n\n while next_node and next_node.val == current.val:\n next_node = next_node.next\n\n if current.next != next_node:\n prev.next = next_node\n else:\n prev = current\n \n current = next_node\n\n return dummy.next\n \n\n``` | 2 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
82. Remove Duplicates from Sorted List II with step by step explanation | remove-duplicates-from-sorted-list-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a dummy node dummy and set its next node as the head of the linked list.\n2. Create a prev variable and initialize it with dummy.\n3. Use a while loop to traverse the linked list while head and head.next are not None.\n4. Check if the value of the current node head is equal to the value of the next node head.next.\n5. If yes, then use another while loop to traverse the linked list and find all the duplicates.\n6. Once all the duplicates are found, set head to head.next and update the next node of prev to head.\n7. If the values are not equal, update the prev to prev.next and head to head.next.\n8. Return dummy.next as the new head of the linked list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n\nclass Solution:\n def deleteDuplicates(self, head: ListNode) -> ListNode:\n dummy = ListNode(0)\n dummy.next = head\n prev = dummy\n while head and head.next:\n if head.val == head.next.val:\n while head and head.next and head.val == head.next.val:\n head = head.next\n head = head.next\n prev.next = head\n else:\n prev = prev.next\n head = head.next\n return dummy.next\n\n``` | 8 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
[Python 3] ✅ O(1) Space Solution 🔥 | remove-duplicates-from-sorted-list-ii | 0 | 1 | ##### UPVOTE IF YOU LIKE ;)\n\n\n# Code\n```py\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n # Base Case\n if not head: return None\n \n # Dummy Node\n dummy = ListNode(0, head)\n\n # dup\'s initial value is a value that \n # a node cannot have in this problem\n prev, cur = dummy, head\n dup = -101\n while cur.next:\n # If a duplicate is found, save that value\n if cur.val == cur.next.val:\n dup = cur.val\n \n # If the current node\'s value is dup\n # Remove the current node\n if cur.val == dup:\n prev.next = cur.next\n\n # If not just update prev to its next node \n else:\n prev = prev.next\n\n cur = cur.next\n\n # Check the last node\n if cur.val == dup:\n prev.next = None\n \n return dummy.next\n \n```\n\n# Explanation\nCheck my blog for detailed explanations: https://gaebalogaebal.tistory.com/82\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 3 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Linked List and HashMap (Python) | easy to understand | remove-duplicates-from-sorted-list-ii | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n), for HashMap\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nNote - This code will also work for unsorted lists\n\nLink - https://leetcode.com/problems/remove-duplicates-from-an-unsorted-linked-list/description/\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head:\n return None\n \n dummy = ListNode(0)\n current = head\n dummy.next = current\n \n # Use hashmap to store frequency of values\n hashmap = {}\n \n while current:\n if current.val not in hashmap:\n hashmap[current.val] = 1\n else:\n hashmap[current.val] += 1\n current = current.next\n\n # Reinitialize current to the head and handle duplicates\n prev = dummy\n current = head\n while current:\n # If a value appears more than once, skip it\n if hashmap[current.val] > 1:\n prev.next = current.next\n else:\n prev = current\n current = current.next\n\n return dummy.next\n\n\n \n``` | 2 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Python || 93.83% Faster || Easy || O(N) Solution | remove-duplicates-from-sorted-list-ii | 0 | 1 | ```\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if head==None or head.next==None:\n return head\n d={}\n temp=head\n while temp!=None:\n if temp.val in d:\n d[temp.val]+=1\n else:\n d[temp.val]=1\n temp=temp.next\n temp=head\n L=ListNode()\n temp2=L\n while temp!=None:\n if temp.next==None and d[temp.val]>1:\n temp2.next=None\n if d[temp.val]>1:\n temp=temp.next\n else:\n temp2.next=temp\n temp2=temp2.next\n temp=temp.next\n return L.next\n```\n\n**An upvote will be encouraging** | 4 | Given the `head` of a sorted linked list, _delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,2,3,3,4,4,5\]
**Output:** \[1,2,5\]
**Example 2:**
**Input:** head = \[1,1,1,2,3\]
**Output:** \[2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Easiest Solution | remove-duplicates-from-sorted-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n curr = head\n while curr and curr.next:\n if curr.val == curr.next.val:\n curr.next = curr.next.next\n else:\n curr = curr.next\n \n return head\n``` | 3 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Delete Duplicates | remove-duplicates-from-sorted-list | 0 | 1 | \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head or not head.next:\n return head\n current = head\n while current.next:\n if current.val == current.next.val:\n current.next = current.next.next\n else:\n current = current.next\n return head\n\n\n```\nIn this code, we start with the head of the linked list and iterate through it using a while loop. Inside the loop, we check if the current node\'s value is equal to the next node\'s value. If they are equal, we update the next pointer of the current node to skip the next node (effectively removing it). If they are not equal, we move to the next node.\n\nThis process continues until we have checked all nodes in the linked list, and we return the modified head of the list with duplicates removed.\n\nThe time complexity of this algorithm is O(n), where n is the number of nodes in the linked list, because we traverse the entire list once. The space complexity is O(1) because we only use a constant amount of extra space for the current pointer. | 3 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Easy Python3 Solution with Explanation | remove-duplicates-from-sorted-list | 0 | 1 | # Explanation \n\n- Set curr to the head and iterate till `curr` and `curr.next` is not None\n- if `curr` node and `curr.next` have same value then just skip that node and set `curr.next = curr.next.next` else `curr = curr.next` and just return the `head`\n\n# Code\n```\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n curr = head\n while curr and curr.next:\n if curr.val == curr.next.val:\n curr.next = curr.next.next\n else:\n curr = curr.next\n return head\n``` | 3 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
6 lines code in python3 | remove-duplicates-from-sorted-list | 0 | 1 | \n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n curr=head\n while curr:\n while curr.next and curr.next.val==curr.val:\n curr.next=curr.next.next\n curr=curr.next\n return head\n\n``` | 9 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Beats 94.95% 83. Remove Duplicates from Sorted List with step by step explanation | remove-duplicates-from-sorted-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nBeats\n94.95%\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: ListNode) -> ListNode:\n # Check if the linked list is empty\n if not head:\n return None\n \n # Initialize two pointers: current and previous\n prev = head\n current = head.next\n \n while current:\n # If the current node\'s value is equal to the previous node\'s value, delete the current node\n if current.val == prev.val:\n prev.next = current.next\n current = current.next\n # If the current node\'s value is different, move the pointers to the next node\n else:\n prev = current\n current = current.next\n \n return head\n\n``` | 5 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Python3 | O(n) | Beats 95.80% (41 ms) | Simple with Explanation! | remove-duplicates-from-sorted-list | 0 | 1 | # Approach\n- We first deal with edge case of head being `None` rather than a `ListNode`\n- Next we create a new variable `curr` to point at our current node, starting with the `head` node\n- If `curr.next` is another node, we compare `curr.val` and `curr.next.val`\n - If the values are the same, we must remove one from the linked list\n - We keep the first node and remove the second by updating the first\'s .next (`curr.next`) to the next node\'s `.next` (`curr.next.next`)\n - If the values differ, we move point `curr` to the next node\n- We repeat the previous process until the current node does not point to another node, at which point we return `head`, the de-duplicated linked list\n\n# Code\n```\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head:\n return None\n\n curr = head\n\n while curr.next:\n if curr.val == curr.next.val:\n curr.next = curr.next.next\n else:\n curr = curr.next\n\n return head\n\n```\n\n## Please upvote if you find this helpful! :D | 35 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Awesome Trick With 7 Lines of Code | remove-duplicates-from-sorted-list | 0 | 1 | \n# One Pointers Approach--->Time:O(N)\n```\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n current=head\n while current and current.next:\n if current.val==current.next.val:\n current.next=current.next.next\n else:\n current=current.next\n return head\n\n```\n# please upvote me it would encourage me alot\n | 9 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Very Easy 100% (Fully Explained) (Java, C++, Python, JS, C, Python3) | remove-duplicates-from-sorted-list | 1 | 1 | # **Java Solution:**\nRuntime: 1 ms, faster than 92.17% of Java online submissions for Remove Duplicates from Sorted List.\n```\nclass Solution {\n public ListNode deleteDuplicates(ListNode head) {\n // Special case...\n if(head == null || head.next == null)\n return head;\n // Initialize a pointer curr with the address of head node...\n ListNode curr = head;\n // Traverse all element through a while loop if curr node and the next node of curr node are present...\n while( curr != null && curr.next != null){\n // If the value of curr is equal to the value of prev...\n // It means the value is present in the linked list...\n if(curr.val == curr.next.val){\n // Hence we do not need to include curr again in the linked list...\n // So we increment the value of curr...\n curr.next = curr.next.next;\n }\n // Otherwise, we increment the curr pointer...\n else{\n curr = curr.next; \n }\n }\n return head; // Return the sorted linked list without any duplicate element...\n }\n}\n```\n\n# **C++ Solution:**\nRuntime: 4 ms, faster than 81.52% of C++ online submissions for Remove Duplicates from Sorted List.\n```\nclass Solution {\npublic:\n ListNode* deleteDuplicates(ListNode* head) {\n // Special case...\n if(head==NULL || head->next==NULL)\n return head;\n // Initialize two pointers tmp(slow) and curr(fast)...\n ListNode* tmp = head;\n ListNode* curr = head->next;\n // Traverse all element through a while loop if curr node is not null...\n while(curr!=NULL) {\n // If the value of curr is equal to the value of tmp...\n // It means the value is present in the linked list...\n if(tmp->val == curr->val) {\n // Hence we do not need to include curr again in the linked list...\n // So we increment the value of curr...\n curr=curr->next;\n }\n // Otherwise, we increment both the pointers.\n else {\n tmp->next = curr;\n tmp = curr;\n curr = tmp->next;\n }\n }\n tmp->next = NULL;\n return head; // Return the sorted linked list without any duplicate element...\n }\n};\n```\n\n# **Python Solution:**\nRuntime: 36 ms, faster than 79.68% of Python online submissions for Remove Duplicates from Sorted List.\n```\nclass Solution(object):\n def deleteDuplicates(self, head):\n # Handle special case that the list is empty\n if head == None:\n return head\n # Initialize curr with the address of head node...\n curr = head\n # Travel the list until the second last node\n while curr.next != None:\n # If the value of curr is equal to the value of prev...\n # It means the value is present in the linked list...\n if curr.val == curr.next.val:\n # Hence we do not need to include curr again in the linked list...\n # So we increment the value of curr...\n tmp = curr.next\n curr.next = curr.next.next\n del tmp\n # Otherwise, we increment the curr pointer...\n else:\n curr = curr.next\n return head # Return the sorted linked list without any duplicate element...\n```\n \n# **JavaScript Solution:**\nRuntime: 82 ms, faster than 84.86% of JavaScript online submissions for Remove Duplicates from Sorted List.\n```\nvar deleteDuplicates = function(head) {\n // Special case...\n if(head == null || head.next == null)\n return head;\n // Initialize a pointer curr with the address of head node...\n let curr = head;\n // Traverse all element through a while loop if curr node and the next node of curr node are present...\n while( curr != null && curr.next != null){\n // If the value of curr is equal to the value of prev...\n // It means the value is present in the linked list...\n if(curr.val == curr.next.val){\n // Hence we do not need to include curr again in the linked list...\n // So we increment the value of curr...\n curr.next = curr.next.next;\n }\n // Otherwise, we increment the curr pointer...\n else{\n curr = curr.next; \n }\n }\n return head; // Return the sorted linked list without any duplicate element...\n};\n```\n\n# **C Language:**\n```\nstruct ListNode* deleteDuplicates(struct ListNode* head){\n // Special case...\n if(head==NULL || head->next==NULL)\n return head;\n // Initialize two pointers tmp(slow) and curr(fast)...\n struct ListNode* tmp = head;\n struct ListNode* curr = head->next;\n // Traverse all element through a while loop if curr node is not null...\n while(curr!=NULL) {\n // If the value of curr is equal to the value of tmp...\n // It means the value is present in the linked list...\n if(tmp->val == curr->val) {\n // Hence we do not need to include curr again in the linked list...\n // So we increment the value of curr...\n curr=curr->next;\n }\n // Otherwise, we increment both the pointers.\n else {\n tmp->next = curr;\n tmp = curr;\n curr = tmp->next;\n }\n }\n tmp->next = NULL;\n return head; // Return the sorted linked list without any duplicate element...\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n # Handle special case that the list is empty\n if head == None:\n return head\n # Initialize curr with the address of head node...\n curr = head\n # Travel the list until the second last node\n while curr.next != None:\n # If the value of curr is equal to the value of prev...\n # It means the value is present in the linked list...\n if curr.val == curr.next.val:\n # Hence we do not need to include curr again in the linked list...\n # So we increment the value of curr...\n tmp = curr.next\n curr.next = curr.next.next\n del tmp\n # Otherwise, we increment the curr pointer...\n else:\n curr = curr.next\n return head # Return the sorted linked list without any duplicate element...\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 33 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Remove Duplicates from the linked list (Runtime - Beats 85.11%) || Brute-force solution | remove-duplicates-from-sorted-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs the values are ``sorted``, we can just compare the current value with the next value to check for ``duplicates``. Traversing through the linked list and checking for this condition in each node will solve the problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Start with assigning the current node to the head of the linked list\n- Traverse through the link list and ``compare`` the ``current`` node value with the ``next`` node value. If the values are same then ``current.next`` should point to ``current.next.next``. This will skip the next node\n- While traversal we should also check if ``current.next`` exists. If not then terminate the loop\n- After succesful traversal the derived link list will contain no duplicates\n- Return the ``head``\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n current = head\n while current and current.next:\n if current.val == current.next.val: current.next = current.next.next\n else: current = current.next\n return head\n``` | 5 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Python3 | Beats 90% + | Efficient Removal of Duplicates from a Sorted Linked List | remove-duplicates-from-sorted-list | 0 | 1 | # Intuition\nOur goal is to remove duplicate nodes while maintaining the order. Since the list is sorted, duplicate nodes will be adjacent to each other. We just need to skip them.\n\n# Approach\n1. We start with a pointer called `curr` that initially points to the `head` of the linked list.\n1. We use a while loop to iterate through the linked list as long as `curr` is not None and `curr.next` is not None. This loop will help us traverse the linked list and examine each pair of adjacent nodes.\n1. Inside the loop, we compare the value of the current node `curr `with the value of the next node `curr.next`.\n1. If the values are equal, it means we\'ve found a duplicate node. In this case, we **update the next pointer of the current node** `curr` **to skip the next node and directly point to the node after the duplicate.** This effectively removes the duplicate node from the linked list.\n1. If the values are not equal i.e. not duplicates, we move the `curr` **pointer** **one step forward** to examine the next pair of nodes.\n1. The loop continues until we reach the end of the linked list or until we\'ve checked all pairs of adjacent nodes.\n1. Finally, we return the head of the modified linked list.\n\n# Complexity\n- Time complexity:\nThe algorithm iterates through the entire linked list once. Thus, the time complexity is $$O(n)$$, where n is the number of nodes in the linked list.\n\n- Space complexity:\nWe are using only a constant amount of extra space to store the curr pointer. No additional data structures are used, so the space complexity is $$O(1)$$.\n\n# Code\n```\n\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n curr = head\n\n while curr and curr.next:\n if curr.val == curr.next.val:\n curr.next = curr.next.next\n else:\n curr = curr.next\n \n return head\n``` | 3 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Python || 98.89% Faster || 6 Lines || O(n) Solution | remove-duplicates-from-sorted-list | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n temp=head\n while temp:\n while temp.next!=None and temp.val == temp.next.val:\n temp.next=temp.next.next\n temp=temp.next\n return head\n```\n\n**Upvote if you like the solution or ask if there is any query** | 6 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
✅|| Python|| Beats 94%|| Explained with Diagrams | remove-duplicates-from-sorted-list | 0 | 1 | **Runtime: 42 ms, faster than 94.70% of Python3 online submissions for Remove Duplicates from Sorted List.**\n**Memory Usage: 13.8 MB, less than 70.70% of Python3 online submissions for Remove Duplicates from Sorted List.**\n\nThe theme to solve this question is just like how we solve regular linked list problems. \n\nWe go with initializing two variables start and node with head then we move node to start.next\n\nLike in this example:-\n\n now `start` is 1 and `node` is 1(2nd one)\n we loop through the list and check if `start==node` and if that is true like in this case, what we need to do is set `start.next=node.next` now since the First `1` in the above diagram now points to `2` and the next thing we need to take care of is that we need to change this as I have illustated in the following pictures:-\n \n \n \n \n\n \nFrom here it\'s cake walk, you need to continue the loop and that\'s it. The Probelm is Solved!!\n\n**Code**\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head or not head.next:\n return head \n start=node=head\n node=head.next\n while start and node:\n if start.val==node.val:\n start.next=node.next\n node.next=None\n node=start.next\n else:\n start=start.next\n node=node.next\n return head\n```\n\n\n_______________________________________________________________________________________________\n_________________________________________________________________________________________________\nEdit 1:\nthe line `node.next=None` can be omitted as we wont ever reach that node\n_________________________________________________________________________________________________\n_________________________________________________________________________________________________\n\n\nIf you liked my efforts then pls pls **UPVOTE** the post, it will encourage me to do more of this stuff!\n | 8 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Python3 || Easy and Simple solution. | remove-duplicates-from-sorted-list | 0 | 1 | # I request you guys to please upvote if you find the solution helpful.\uD83E\uDEF6\uD83E\uDEF6\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:\n lst = []\n while head:\n lst.append(head.val)\n head = head.next\n lst = sorted(list(set(lst)))\n a = ListNode(0)\n temp = a\n for i in lst:\n temp.next = ListNode(i)\n temp = temp.next\n return a.next\n\n``` | 1 | Given the `head` of a sorted linked list, _delete all duplicates such that each element appears only once_. Return _the linked list **sorted** as well_.
**Example 1:**
**Input:** head = \[1,1,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** head = \[1,1,2,3,3\]
**Output:** \[1,2,3\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 300]`.
* `-100 <= Node.val <= 100`
* The list is guaranteed to be **sorted** in ascending order. | null |
Segment Tree & Divide and Conquer in Python | largest-rectangle-in-histogram | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nImplement Segment Tree recursively (build & query, update is not needed in this problem).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBuild segment tree: O(n) \nSegment tree range query: O(log n)\n\nDivide & Conquer\nAverage Case:\nT(n) = 2T(n/2) + O(log n), T(n) = O(log n*log n)\n\nWorst Case\nT(n) = T(n-1) + O(log n), T(n) = O(n log n)\n\nOverall:\nAverage Case: O(n)\nWorst Case: O(n*log n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSegment Tree: O(n)\nDivide & Conquer: O(n)\n\nOverall: O(n)\n\n# Code\n```\nclass SegmentTree:\n def __init__(self, arr):\n self.arr = arr\n self.n = len(arr)\n\n k = 0\n while 2**k < self.n:\n k += 1\n\n self.size = 2**(k+1)-1\n self.tree = [None for _ in range(self.size)]\n\n self.left_func = lambda x: 2*x+1\n self.right_func = lambda x: 2*x+2\n\n self.build()\n\n def merge(self, agg1, agg2):\n \n if agg1 is None or agg2 is None:\n return agg1 or agg2\n\n # (min_value, min_index)\n return agg1 if agg1[0] <= agg2[0] else agg2\n\n def build(self):\n def build_recursive(tree_index, tree_lower, tree_upper):\n if tree_lower == tree_upper:\n self.tree[tree_index] = (self.arr[tree_lower], tree_lower)\n return\n\n mid = tree_lower + (tree_upper - tree_lower) // 2\n\n left_tree_index = self.left_func(tree_index)\n right_tree_index = self.right_func(tree_index)\n\n build_recursive(left_tree_index, tree_lower, mid)\n build_recursive(right_tree_index, mid+1, tree_upper)\n\n self.tree[tree_index] = self.merge(self.tree[left_tree_index], self.tree[right_tree_index])\n\n build_recursive(0, 0, self.n-1)\n\n def query(self, query_lower, query_upper):\n def query_recursive(tree_index, tree_lower, tree_upper, query_lower, query_upper):\n #print(tree_index, tree_lower, tree_upper, query_lower, query_upper)\n if query_lower > tree_upper or query_upper < tree_lower:\n return\n\n if query_lower == tree_lower and query_upper == tree_upper:\n return self.tree[tree_index]\n\n\n mid = tree_lower + (tree_upper - tree_lower) // 2\n\n left_tree_index = self.left_func(tree_index)\n right_tree_index = self.right_func(tree_index)\n\n if query_upper <= mid:\n return query_recursive(left_tree_index, tree_lower, mid, query_lower, query_upper)\n elif query_lower > mid:\n return query_recursive(right_tree_index, mid+1, tree_upper, query_lower, query_upper)\n\n left_query = query_recursive(left_tree_index, tree_lower, mid, query_lower, mid)\n right_query = query_recursive(right_tree_index, mid+1, tree_upper, mid+1, query_upper)\n\n return self.merge(left_query, right_query)\n\n return query_recursive(0, 0, self.n-1, query_lower, query_upper)\n\n\n\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n n = len(heights)\n # O(n) time to build tree\n segment_tree = SegmentTree(heights)\n\n def max_area(start, end):\n """Recursively find the maximum area in heights[start:end+1]\n """\n # Base cases\n if start > end:\n return 0\n\n # Find the (first) mininum height and its index O(log n)\n min_height, min_index = segment_tree.query(start, end)\n\n left = max_area(start, min_index-1)\n right = max_area(min_index+1, end)\n \n return max(left, right, (end-start+1)*min_height)\n\n return max_area(0, n-1)\n``` | 1 | Given an array of integers `heights` representing the histogram's bar height where the width of each bar is `1`, return _the area of the largest rectangle in the histogram_.
**Example 1:**
**Input:** heights = \[2,1,5,6,2,3\]
**Output:** 10
**Explanation:** The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
**Example 2:**
**Input:** heights = \[2,4\]
**Output:** 4
**Constraints:**
* `1 <= heights.length <= 105`
* `0 <= heights[i] <= 104` | null |
Beats 99%✅ | O( n )✅ | Python (Step by step explanation) | largest-rectangle-in-histogram | 0 | 1 | # Intuition\nThe problem involves finding the largest rectangle that can be formed in a histogram of different heights. The approach is to iteratively process the histogram\'s bars while keeping track of the maximum area found so far.\n\n# Approach\n1. Initialize a variable `maxArea` to store the maximum area found, and a stack to keep track of the indices and heights of the histogram bars.\n\n2. Iterate through the histogram using an enumeration to access both the index and height of each bar.\n\n3. For each bar, calculate the width of the potential rectangle by subtracting the starting index (retrieved from the stack) from the current index.\n\n4. While the stack is not empty and the height of the current bar is less than the height of the bar at the top of the stack, pop elements from the stack to calculate the area of rectangles that can be formed.\n\n5. Update `maxArea` with the maximum of its current value and the area calculated in step 4.\n\n6. Push the current bar\'s index and height onto the stack to continue processing.\n\n7. After processing all bars, there may still be bars left in the stack. For each remaining bar in the stack, calculate the area using the height of the bar and the difference between the current index and the index at the top of the stack.\n\n8. Return `maxArea` as the result, which represents the largest rectangle area.\n\n# Complexity\n- Time complexity: O(n), where n is the number of bars in the histogram. We process each bar once.\n- Space complexity: O(n), as the stack can contain up to n elements in the worst case when the bars are in increasing order (monotonic).\n\n\n# Code\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n maxArea = 0\n stack = []\n\n for index , height in enumerate(heights):\n start = index\n \n while start and stack[-1][1] > height:\n i , h = stack.pop()\n maxArea = max(maxArea , (index-i)*h)\n start = i\n stack.append((start , height))\n\n for index , height in stack:\n maxArea = max(maxArea , (len(heights)-index)*height)\n\n return maxArea \n\n \n\n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 7 | Given an array of integers `heights` representing the histogram's bar height where the width of each bar is `1`, return _the area of the largest rectangle in the histogram_.
**Example 1:**
**Input:** heights = \[2,1,5,6,2,3\]
**Output:** 10
**Explanation:** The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
**Example 2:**
**Input:** heights = \[2,4\]
**Output:** 4
**Constraints:**
* `1 <= heights.length <= 105`
* `0 <= heights[i] <= 104` | null |
✔️ [Python3] MONOTONIC STACK t(-_-t), Explained | largest-rectangle-in-histogram | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe idea is to use a monotonic stack. We iterate over bars and add them to the stack as long as the last element in the stack is less than the current bar. When the condition doesn\'t hold, we start to calculate areas by popping out bars from the stack until the last element of the stack is greater than the current. The area is calculated as the number of pops multiplied by the height of the popped bar. On every pop, the height of the bar will be less or equal to the previous (since elements in the stack are always monotonically increasing).\n\nNow let\'s consider this example `[2,1,2]`. For this case the formula for the area (number of pops * current height) won\'t work because when we reach `1` we will pop out `2` from the stack and will not consider it later which is wrong since the largest area here is equal to `3 * 1`, i.e we somehow need to remember the previously discarded bars that still can form areas. We solve this problem by storing in the stack the width of the bar as well. So for our example, after discarding `2`, we push to the stack the `1` with the width equal to `2`.\n\nTime: **O(n)** - In the worst case we have 2 scans: one for the bars and one for the stack\nSpace: **O(n)** - in the wors case we push to the stack the whjole input array\n\nRuntime: 932 ms, faster than **51.27%** of Python3 online submissions for Largest Rectangle in Histogram.\nMemory Usage: 28.4 MB, less than **30.61%** of Python3 online submissions for Largest Rectangle in Histogram.\n\n```\ndef largestRectangleArea(self, bars: List[int]) -> int:\n\tst, res = [], 0\n\tfor bar in bars + [-1]: # add -1 to have an additional iteration\n\t\tstep = 0\n\t\twhile st and st[-1][1] >= bar:\n\t\t\tw, h = st.pop()\n\t\t\tstep += w\n\t\t\tres = max(res, step * h)\n\n\t\tst.append((step + 1, bar))\n\n\treturn res\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 64 | Given an array of integers `heights` representing the histogram's bar height where the width of each bar is `1`, return _the area of the largest rectangle in the histogram_.
**Example 1:**
**Input:** heights = \[2,1,5,6,2,3\]
**Output:** 10
**Explanation:** The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
**Example 2:**
**Input:** heights = \[2,4\]
**Output:** 4
**Constraints:**
* `1 <= heights.length <= 105`
* `0 <= heights[i] <= 104` | null |
Superb Logic with Stack | largest-rectangle-in-histogram | 0 | 1 | [https://leetcode.com/problems/largest-rectangle-in-histogram/discuss/3544276/Superb-Logic-with-Stack](http://)# Monotonic Stack\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n stack=[]\n maxarea=0\n for i,v in enumerate(heights):\n start=i\n while stack and stack[-1][1]>v:\n index,height=stack.pop()\n maxarea=max(maxarea,(i-index)*height)\n start=index\n stack.append((start,v))\n for i,h in stack:\n maxarea=max(maxarea,h*(len(heights)-i))\n return maxarea\n```\n# please upvote me it would encourage me alot\n | 3 | Given an array of integers `heights` representing the histogram's bar height where the width of each bar is `1`, return _the area of the largest rectangle in the histogram_.
**Example 1:**
**Input:** heights = \[2,1,5,6,2,3\]
**Output:** 10
**Explanation:** The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
**Example 2:**
**Input:** heights = \[2,4\]
**Output:** 4
**Constraints:**
* `1 <= heights.length <= 105`
* `0 <= heights[i] <= 104` | null |
Largest Rectangle in Histogram with step by step explanation | largest-rectangle-in-histogram | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe above solution uses the monotonic stack algorithm to calculate the largest rectangle in histogram. The idea is to maintain a stack of indices, where the heights of the elements in the stack are in increasing order.\n\n- For each element in the input array heights, we pop all the elements in the stack that are greater than or equal to the current element. This way, the top element of the stack will be the first element on its left that is less than it. We store the index of this element in the left array.\n- We repeat the above step but in reverse, starting from the end of the input array heights, to calculate the index of the first element on the right that is less than the current element.\n- For each element in the input array heights, the width of the rectangle it can form is given by right[i] - left[i] - 1. The height of the rectangle is given by the value of the element itself. The area of the rectangle is then given by heights[i] * (right[i] - left[i] - 1). We keep track of the maximum area seen so far.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n87.99%\n\n# Code\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n n = len(heights)\n left, right = [0] * n, [0] * n\n stack = []\n for i in range(n):\n while stack and heights[stack[-1]] >= heights[i]:\n stack.pop()\n left[i] = stack[-1] if stack else -1\n stack.append(i)\n stack = []\n for i in range(n-1, -1, -1):\n while stack and heights[stack[-1]] >= heights[i]:\n stack.pop()\n right[i] = stack[-1] if stack else n\n stack.append(i)\n max_area = 0\n for i in range(n):\n max_area = max(max_area, heights[i] * (right[i] - left[i] - 1))\n return max_area\n\n \n``` | 3 | Given an array of integers `heights` representing the histogram's bar height where the width of each bar is `1`, return _the area of the largest rectangle in the histogram_.
**Example 1:**
**Input:** heights = \[2,1,5,6,2,3\]
**Output:** 10
**Explanation:** The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.
**Example 2:**
**Input:** heights = \[2,4\]
**Output:** 4
**Constraints:**
* `1 <= heights.length <= 105`
* `0 <= heights[i] <= 104` | null |
📢Stack and DP: Unveiling the Secrets to Count Maximal Rectangles || Full Explanation || Mr. Robot | maximal-rectangle | 1 | 1 | # Unlocking the Power of Algorithms: Solving the Maximal Rectangle Problem\n\nIf you\'re a coding enthusiast or a budding programmer, you\'ve probably heard about the Maximal Rectangle Problem. This fascinating problem is a classic in the world of computer science and is often used to demonstrate the power of dynamic programming and efficient algorithm design.\n\nIn this blog post, we\'ll dive deep into the problem and explore a solution using a clever algorithm. We\'ll provide code examples in multiple programming languages to ensure that you can follow along regardless of your coding preferences. So, whether you\'re a C++ aficionado, a Java enthusiast, a Python pro, or a JavaScript wizard, you\'re in the right place!\n\n## Understanding the Maximal Rectangle Problem\n\nThe Maximal Rectangle Problem can be defined as follows: Given a binary matrix, find the largest rectangle containing only ones and return its area. This might sound a bit complex at first, but with the right algorithm, it becomes a manageable challenge.\n\n## The Algorithm: Dynamic Programming to the Rescue\n\nThe key to solving the Maximal Rectangle Problem lies in dynamic programming. Dynamic programming is a powerful technique that involves breaking down a complex problem into smaller subproblems and reusing solutions to subproblems to avoid redundant computations. \n\n### Step 1: The `largestRectangleArea` Function\n\nFirst, let\'s take a look at the `largestRectangleArea` function. This function, written in C++, Java, Python, and JavaScript, calculates the largest rectangle area in a histogram. The idea is to use a stack to efficiently find the maximum area.\n\nHere\'s a simplified overview of the algorithm:\n\n1. Create an empty stack to store indices.\n2. Iterate through the histogram from left to right.\n3. While the stack is not empty and the current histogram value is less than the value at the index stored in the stack\'s top element, pop elements from the stack and calculate the maximum area for each popped element.\n4. Keep track of the maximum area as you iterate through the histogram.\n\nThis algorithm efficiently finds the largest rectangle area in the histogram, which we\'ll use in the next step.\n\n### Step 2: The `maximalAreaOfSubMatrixOfAll1` Function\n\nIn this step, we adapt the `largestRectangleArea` function to solve the Maximal Rectangle Problem for a binary matrix. We create a vector to store the height of each column and use dynamic programming to find the maximum rectangle area for each row.\n\n### Step 3: Bringing It All Together\n\nIn the final step, we create the `maximalRectangle` function, which takes a binary matrix as input and returns the maximum rectangle area containing only ones.\n\n\n## Dry Run of `maximalRectangle` Function\n\nWe\'ll perform a dry run of the `maximalRectangle` function using the following matrix:\n\n```python\nmatrix = [\n [\'1\', \'0\', \'1\', \'0\', \'0\'],\n [\'1\', \'0\', \'1\', \'1\', \'1\'],\n [\'1\', \'1\', \'1\', \'1\', \'1\'],\n [\'1\', \'0\', \'0\', \'1\', \'0\']\n]\n```\n\n### Step 1: Initializing Variables\n\nWe start with the given matrix:\n\n```\n1 0 1 0 0\n1 0 1 1 1\n1 1 1 1 1\n1 0 0 1 0\n```\n\nWe have two helper functions, `largestRectangleArea` and `maximalAreaOfSubMatrixOfAll1`, which are used within the `maximalRectangle` function.\n\n### Step 2: `maximalAreaOfSubMatrixOfAll1`\n\nWe enter the `maximalAreaOfSubMatrixOfAll1` function, which computes the maximal area of submatrices containing only \'1\'s. \n\n**Matrix and `height` after each row iteration:**\n\n1. Process Row 1:\n - Matrix:\n ```\n 1 0 1 0 0\n ```\n - Height: `[1, 0, 1, 0, 0]`\n\n2. Process Row 2:\n - Matrix:\n ```\n 1 0 1 1 1\n ```\n - Height: `[2, 0, 2, 1, 1]`\n\n3. Process Row 3:\n - Matrix:\n ```\n 1 1 1 1 1\n ```\n - Height: `[3, 1, 3, 2, 2]`\n\n4. Process Row 4:\n - Matrix:\n ```\n 1 0 0 1 0\n ```\n - Height: `[4, 1, 1, 3, 1]`\n\n**Maximal Area of Histogram (`largestRectangleArea`):**\n\nFor each `height`, we calculate the maximal area of the histogram using the `largestRectangleArea` function.\n\n- For the height `[1, 0, 1, 0, 0]`, the maximal area is `1`.\n- For the height `[2, 0, 2, 1, 1]`, the maximal area is `4`.\n- For the height `[3, 1, 3, 2, 2]`, the maximal area is `6`.\n- For the height `[4, 1, 1, 3, 1]`, the maximal area is `4`.\n\nThe maximal area of submatrices for each row is `[1, 4, 6, 4]`.\n\n### Step 3: `maximalRectangle`\n\nFinally, we return the maximum value from the array `[1, 4, 6, 4]`, which is `6`.\n\nThe maximal area of a submatrix containing only \'1\'s in the given matrix is `6`.\n\nThis concludes the dry run of the `maximalRectangle` function with the provided matrix.\n\n### **Code C++ Java Python JS C#**\n```cpp []\nclass Solution {\npublic:\nint largestRectangleArea(vector < int > & histo) {\n stack < int > st;\n int maxA = 0;\n int n = histo.size();\n for (int i = 0; i <= n; i++) {\n while (!st.empty() && (i == n || histo[st.top()] >= histo[i])) {\n int height = histo[st.top()];\n st.pop();\n int width;\n if (st.empty())\n width = i;\n else\n width = i - st.top() - 1;\n maxA = max(maxA, width * height);\n }\n st.push(i);\n }\n return maxA;\n}\nint maximalAreaOfSubMatrixOfAll1(vector<vector<char>> &mat, int n, int m) {\n \n int maxArea = 0;\n vector<int> height(m, 0);\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (mat[i][j] == \'1\') height[j]++;\n else height[j] = 0;\n }\n int area = largestRectangleArea(height);\n maxArea = max(maxArea, area);\n }\n return maxArea;\n}\n\n int maximalRectangle(vector<vector<char>>& matrix) {\n return maximalAreaOfSubMatrixOfAll1(matrix,matrix.size(),matrix[0].size());\n }\n};\n```\n\n**Java:**\n```java []\nimport java.util.Stack;\n\npublic class Solution {\n\n public int largestRectangleArea(int[] heights) {\n Stack<Integer> stack = new Stack<>();\n int maxArea = 0;\n int n = heights.length;\n for (int i = 0; i <= n; i++) {\n while (!stack.isEmpty() && (i == n || heights[stack.peek()] >= heights[i])) {\n int height = heights[stack.pop()];\n int width = stack.isEmpty() ? i : i - stack.peek() - 1;\n maxArea = Math.max(maxArea, width * height);\n }\n stack.push(i);\n }\n return maxArea;\n }\n\n public int maximalAreaOfSubMatrixOfAll1(char[][] matrix, int n, int m) {\n int maxArea = 0;\n int[] height = new int[m];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (matrix[i][j] == \'1\') {\n height[j]++;\n } else {\n height[j] = 0;\n }\n }\n int area = largestRectangleArea(height);\n maxArea = Math.max(maxArea, area);\n }\n return maxArea;\n }\n\n public int maximalRectangle(char[][] matrix) {\n return maximalAreaOfSubMatrixOfAll1(matrix, matrix.length, matrix[0].length);\n }\n}\n```\n\n**Python:**\n```python []\nclass Solution:\n def largestRectangleArea(self, heights):\n stack = []\n max_area = 0\n n = len(heights)\n \n for i in range(n + 1):\n while stack and (i == n or heights[stack[-1]] >= heights[i]):\n height = heights[stack.pop()]\n width = i if not stack else i - stack[-1] - 1\n max_area = max(max_area, height * width)\n \n stack.append(i)\n \n return max_area\n\n def maximalAreaOfSubMatrixOfAll1(self, mat, n, m):\n max_area = 0\n height = [0] * m\n\n for i in range(n):\n for j in range(m):\n if mat[i][j] == \'1\':\n height[j] += 1\n else:\n height[j] = 0\n\n area = self.largestRectangleArea(height)\n max_area = max(max_area, area)\n \n return max_area\n\n def maximalRectangle(self, matrix):\n if not matrix:\n return 0\n n, m = len(matrix), len(matrix[0])\n return self.maximalAreaOfSubMatrixOfAll1(matrix, n, m)\n\n```\n\n**JavaScript:**\n```javascript []\nfunction largestRectangleArea(heights) {\n const stack = [];\n let maxArea = 0;\n const n = heights.length;\n for (let i = 0; i <= n; i++) {\n while (stack.length > 0 && (i === n || heights[stack[stack.length - 1]] >= heights[i])) {\n const height = heights[stack.pop()];\n const width = stack.length === 0 ? i : i - stack[stack.length - 1] - 1;\n maxArea = Math.max(maxArea, width * height);\n }\n stack.push(i);\n }\n return maxArea;\n}\n\nfunction maximalAreaOfSubMatrixOfAll1(matrix, n, m) {\n let maxArea = 0;\n const height = new Array(m).fill(0);\n for (let i = 0; i < n; i++) {\n for (let j = 0; j < m; j++) {\n if (matrix[i][j] === \'1\') {\n height[j]++;\n } else {\n height[j] = 0;\n }\n }\n const area = largestRectangleArea(height);\n maxArea = Math.max(maxArea, area);\n }\n return maxArea;\n}\n\nfunction maximalRectangle(matrix) {\n return maximalAreaOfSubMatrixOfAll1(matrix, matrix.length, matrix[0].\n\nlength);\n}\n``` \n**C#**\n\n``` csharp []\nusing System;\nusing System.Collections.Generic;\n\nclass Solution\n{\n public int MaximalRectangle(char[][] matrix)\n {\n if (matrix == null || matrix.Length == 0 || matrix[0].Length == 0)\n {\n return 0;\n }\n\n int numRows = matrix.Length;\n int numCols = matrix[0].Length;\n\n int maxArea = 0;\n int[] height = new int[numCols];\n\n for (int row = 0; row < numRows; row++)\n {\n for (int col = 0; col < numCols; col++)\n {\n if (matrix[row][col] == \'1\')\n {\n height[col]++;\n }\n else\n {\n height[col] = 0;\n }\n }\n\n int area = LargestRectangleArea(height);\n maxArea = Math.Max(maxArea, area);\n }\n\n return maxArea;\n }\n\n private int LargestRectangleArea(int[] heights)\n {\n Stack<int> stack = new Stack<int>();\n int maxArea = 0;\n int n = heights.Length;\n\n for (int i = 0; i <= n; i++)\n {\n while (stack.Count > 0 && (i == n || heights[stack.Peek()] >= heights[i]))\n {\n int h = heights[stack.Pop()];\n int w = stack.Count == 0 ? i : i - stack.Peek() - 1;\n maxArea = Math.Max(maxArea, h * w);\n }\n\n stack.Push(i);\n }\n\n return maxArea;\n }\n}\n```\n---\n## Analysis\n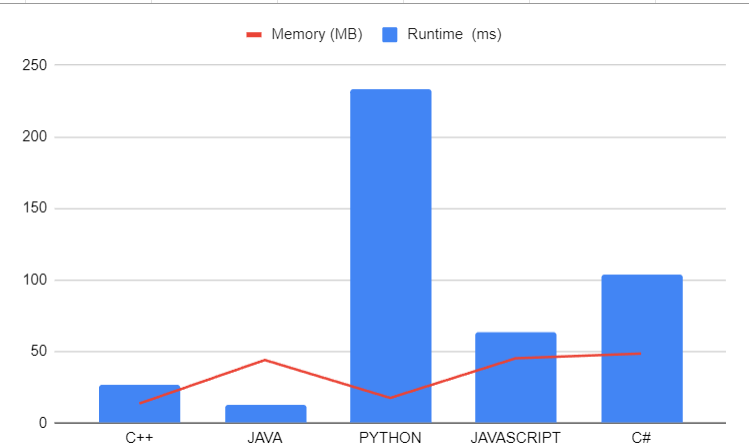\n\n---\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| C++ | 27 | 13.6 |\n| Java | 13 | 44 |\n| Python | 233 | 17.5 |\n| JavaScript | 63 | 45.2 |\n| C# | 104 | 48.5 |\n\n---\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n | 6 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Maximal rectangle with recursion | maximal-rectangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n area = 0\n def maximalRectangle(self, matrix) -> int:\n def shark(a, i, j, len_row):\n leftEdge = j \n rightEdge = leftEdge + len_row - 1\n flag = True\n if rightEdge >= len(a[0]): return\n if i+1 >= len(a): return \n for _ in range(leftEdge, rightEdge+1):\n el = a[i+1][_]\n if a[i+1][_] != \'1\':\n flag = False\n break\n if flag:\n self.area += len_row\n shark(a, i+1, j, len_row)\n else: return \n\n\n\n\n\n\n a = matrix\n rows = len(a)\n cols = len(a[0])\n\n max_possible_area = 0\n for _row in a:\n for _el in _row:\n if _el == \'1\':\n max_possible_area += 1\n if max_possible_area == rows * cols:\n return rows * cols\n self.area = 0\n max_area = 0\n \n for i in range(rows):\n len_row = 0\n for j in range(cols):\n self.area = 0\n if a[i][j] == \'0\':\n len_row = 0\n if a[i][j] == \'1\':\n len_row += 1\n self.area = len_row\n if j+1 == len(a[i]):\n if a[i][j] == \'1\':\n temp = len_row\n for _ in range(j-len_row+1, j+1): # \u0442\u0435\u043A\u0443\u0449\u0438\u0439 \u043B\u0435\u0432\u044B\u0439 \u044D\u043B\u0435\u043C\u0435\u043D\u0442\n for __ in range(1, len_row+1): # \u0442\u0435\u043A\u0443\u0449\u0430\u044F \u0434\u043B\u0438\u043D\u0430 \u0441\u0440\u0435\u0437\u0430\n self.area = __\n shark(a, i, _, __)\n max_area = max(self.area, max_area)\n self.area = 0\n\n len_row -= 1\n \n\n\n else:\n if a[i][j] == \'1\' and a[i][j+1] != \'1\':\n temp = len_row\n for _ in range(j-len_row+1, j+1): # \u0442\u0435\u043A\u0443\u0449\u0438\u0439 \u043B\u0435\u0432\u044B\u0439 \u044D\u043B\u0435\u043C\u0435\u043D\u0442\n for __ in range(1, len_row+1): # \u0442\u0435\u043A\u0443\u0449\u0430\u044F \u0434\u043B\u0438\u043D\u0430 \u0441\u0440\u0435\u0437\u0430\n self.area = __\n shark(a, i, _, __)\n max_area = max(self.area, max_area)\n self.area = 0\n\n len_row -= 1\n \n\n return max_area\n\n \n\n``` | 1 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | maximal-rectangle | 1 | 1 | # My youtube channel - KeetCode(Ex-Amazon)\nI create 142 videos for leetcode questions as of April 10, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**Largest Color Value in a Directed Graph video**\nhttps://qr.paps.jp/asEvO\n\n**My youtube channel - KeetCode(Ex-Amazon)**\nhttps://qr.paps.jp/q2r7Z\n\n\n\n\n\n---\n\n\n\n# Approach\n1. Check if the input matrix is empty, if it is return 0.\n\n2. Determine the number of columns in the matrix (n) by getting the length of the first row of the matrix.\n\n3. Create a list called heights, with n+1 elements, and initialize each element to 0.\n\n4. Create a variable called max_area and initialize it to 0.\n\n5. For each row in the matrix, do the following:\n - Iterate through each column in the row, and update the corresponding height in the "heights" list.\n - If the character in the matrix is "1", increment the corresponding height in the "heights" list by 1, otherwise set it to 0.\n\n6. Create an empty stack and add -1 to it.\n\n7. For each element in the "heights" list, do the following:\n - Compare the current height to the height of the top element in the stack.\n - If the current height is less than the height of the top element of the stack, do the following:\n - Pop the top element of the stack and calculate the area of the rectangle formed by the popped height.\n - Calculate the width of the rectangle by subtracting the index of the current element from the index of the new top element of the stack.\n - Calculate the area of the rectangle by multiplying the height and width.\n - Update the maximum area seen so far if the area of the current rectangle is larger than the current maximum.\n - Append the index of the current element to the stack.\n\n8. Return the maximum area seen so far.\n\n# Complexity\n- Time complexity: O(m*n)\nm is the number of rows in the input matrix and n is the number of columns. This is because we have to iterate through each element in the matrix at least once, and the time it takes to process each element is constant.\n\n- Space complexity: O(n)\nn is the number of columns in the matrix. This is because we are creating a "heights" list with n+1 elements, and a stack that could have up to n+1 elements. The rest of the variables used in the algorithm are constants and do not contribute significantly to the space complexity.\n\n# Python\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n if not matrix:\n return 0\n \n n = len(matrix[0])\n heights = [0] * (n + 1)\n max_area = 0\n\n for row in matrix:\n for i in range(n):\n heights[i] = heights[i] + 1 if row[i] == "1" else 0\n \n stack = [-1]\n for i in range(n + 1):\n while heights[i] < heights[stack[-1]]:\n h = heights[stack.pop()]\n w = i - stack[-1] - 1\n max_area = max(max_area, h * w)\n \n stack.append(i)\n \n return max_area\n```\n\n# JavaScript\n```\n/**\n * @param {character[][]} matrix\n * @return {number}\n */\nvar maximalRectangle = function(matrix) {\n if (!matrix.length) {\n return 0;\n }\n \n const n = matrix[0].length;\n const heights = new Array(n + 1).fill(0);\n let maxArea = 0;\n \n for (let row of matrix) {\n for (let i = 0; i < n; i++) {\n heights[i] = row[i] === \'1\' ? heights[i] + 1 : 0;\n }\n \n const stack = [-1];\n for (let i = 0; i < n + 1; i++) {\n while (heights[i] < heights[stack[stack.length - 1]]) {\n const h = heights[stack.pop()];\n const w = i - stack[stack.length - 1] - 1;\n maxArea = Math.max(maxArea, h * w);\n }\n stack.push(i);\n }\n }\n \n return maxArea; \n};\n```\n\n# Java\n```\nclass Solution {\n public int maximalRectangle(char[][] matrix) {\n if (matrix == null || matrix.length == 0) {\n return 0;\n }\n \n int n = matrix[0].length;\n int[] heights = new int[n + 1];\n int maxArea = 0;\n \n for (char[] row : matrix) {\n for (int i = 0; i < n; i++) {\n heights[i] = row[i] == \'1\' ? heights[i] + 1 : 0;\n }\n \n Stack<Integer> stack = new Stack<>();\n stack.push(-1);\n for (int i = 0; i < n + 1; i++) {\n while (stack.peek() != -1 && heights[i] < heights[stack.peek()]) {\n int h = heights[stack.pop()];\n int w = i - stack.peek() - 1;\n maxArea = Math.max(maxArea, h * w);\n }\n stack.push(i);\n }\n }\n \n return maxArea; \n }\n}\n```\n\n# C++\n```\nclass Solution {\npublic:\n int maximalRectangle(vector<vector<char>>& matrix) {\n if (matrix.empty()) {\n return 0;\n }\n \n int n = matrix[0].size();\n vector<int> heights(n + 1);\n int maxArea = 0;\n \n for (auto row : matrix) {\n for (int i = 0; i < n; i++) {\n heights[i] = row[i] == \'1\' ? heights[i] + 1 : 0;\n }\n \n stack<int> st;\n st.push(-1);\n for (int i = 0; i < n + 1; i++) {\n while (st.top() != -1 && heights[i] < heights[st.top()]) {\n int h = heights[st.top()];\n st.pop();\n int w = i - st.top() - 1;\n maxArea = max(maxArea, h * w);\n }\n st.push(i);\n }\n }\n \n return maxArea; \n }\n};\n``` | 16 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
DP / python solution O(M * N ^ 2) | maximal-rectangle | 0 | 1 | # Intuition\nDP\n\n# Approach\nReduce overlapping counting\n\n# Complexity\n- Time complexity:\nO(M * N ^ 2)\n\n- Space complexity:\nO(M * N)\n\n# Code\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n # 1 0 1 2 3 \n # 0 1 0 1 0 \n # 1 2 0 1 2\n # 1 2 0 1 2\n # 0 1 2 3 4\n\n M, N = len(matrix), len(matrix[0])\n dp = [[0] * N for _ in range(M)]\n\n for i in range(M):\n dp[i][0] = 1 if matrix[i][0] == \'1\' else 0\n \n for i in range(M):\n for j in range(1, N):\n if matrix[i][j] == \'1\':\n if dp[i][j - 1]:\n dp[i][j] = dp[i][j - 1] + 1\n else:\n dp[i][j] = 1\n \n ret = 0\n for j in range(N):\n column = []\n for i in range(M):\n column.append(dp[i][j])\n \n for p in range(len(column)):\n left = right = p\n val = column[p]\n\n cnt = 1\n while left >= 0 and column[left] >= val:\n if left != p:\n cnt += 1\n left -= 1\n \n while right < len(column) and column[right] >= val:\n if right != p:\n cnt += 1\n right += 1\n \n ret = max(ret, val * cnt)\n \n return ret\n\n\n\n\n\n\n\n\n``` | 2 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Identical to question number 85 | maximal-rectangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIdentical with [85. Maximal Square](https://leetcode.com/problems/maximal-rectangle/description/), and my [solution](https://leetcode.com/problems/maximal-square/solutions/2814174/o-n-space-detailed-explanation-with-intuition/) to that question.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfor every cell we are storing the number of ones above it. i.e the height of that cell. For the width, we just have to take the consecutive ones in a row.\n\non every cell we want to calculate the maximum area that it can make if that cell was the bottom left corner of the rectangle. for that we want the width and height.\n\nWhen we are on a cell with less height than it\'s previous cells we know that for any rectangle that contains it, the maximum height that rectangle can have is the lowest height, so that it includes all the cells.\n\nTo elaborate, let\'s say we have calculated the heights on cells as [4, 2, 4]. for any rectangle that contains the second cell we know that the maximum height is going to be 2, so that it is full of ones.\n\nwhat if the height of the current cell is higher, then we are going to consider it as an alternative, so that until we find a cell with lower height we are going to consider it as the best height, where that cell is the bottom left part of the rectangle.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n * m)$$, where m is column size, and n is row size.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(m)$$, where m is column size. This ignores the padding zeros.\n\n# Code\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n for row in range(len(matrix)):\n matrix[row].append("0")\n\n height = [0] * len(matrix[0])\n max_rectangle = 0\n\n for row in matrix:\n stack = [-1]\n for col, val in enumerate(row):\n height[col] = (height[col] + 1) * int(val)\n\n while height[stack[-1]] > height[col]:\n prev_col = stack.pop()\n\n left = prev_col - stack[-1] - 1\n right = col - prev_col\n\n width = left + right\n\n area = width * height[prev_col]\n\n max_rectangle = max(max_rectangle, area)\n\n stack.append(col)\n\n return max_rectangle\n``` | 1 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Super Similar problem like Histogram | maximal-rectangle | 0 | 1 | https://leetcode.com/problems/maximal-rectangle/discuss/3544364/Super-Similar-problem-like-Histogram-------------------------->Histogram problem\n# Similar to Histogram Problem\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n if not matrix:\n return 0\n maxarea=0\n height=[0]*(len(matrix[0]))\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n if matrix[i][j]=="1":\n height[j]+=1\n else:\n height[j]=0\n\t\t\t\tstack=[]\n for i,h in enumerate(height):\n start=i\n while stack and h<stack[-1][1]:\n index,hi=stack.pop()\n start=index\n maxarea=max(maxarea,(i-index)*hi)\n stack.append([start,h])\n for i,h in stack:\n maxarea=max(maxarea,(len(height)-i)*h)\n return maxarea\n ```\n # please upvote me it would encourage me alot\n | 3 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python Easy Solution || 100% || Kadane's Algorithm || | maximal-rectangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing **Kadane\'s Algorithm**\nHere we need to find continuos 1.\nAs per the Kadane\'s Algorithm we can find maximum subarray in an Array, but Here Array is consist of +ve number, We will manuplate the array \nif "0"--> -40000, becouse as per question constrain min sum can\'t be less than -39999 so we will use -40000 here.\nand replace "1" --> 1\n\nfor Matrix = \n```\n[ ["0","0","1","0"],\n ["1","1","1","1"],\n ["1","1","1","1"],\n ["1","1","1","0"],\n ["1","1","0","0"],\n ["1","1","1","1"],\n ["1","1","1","0"]] \n\n\n#it will become\n [[-40000, -40000, 1, -40000], \n [1, 1, 1, 1], \n [1, 1, 1, 1], \n [1, 1, 1, -40000], \n [1, 1, -40000, -40000], \n [1, 1, 1, 1], \n [1, 1, 1, -40000]]\n```\n \n\n\nNow we will apply Kadane\'s Algorithm here.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n \n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n if matrix[i][j]==\'0\':\n matrix[i][j]=-40000\n else:\n matrix[i][j]=1\n n = len(matrix)\n m = len(matrix[0])\n gm = 0\n for i in range(n):\n temp = [0]*m\n for j in range(i, n):\n for k in range(m):\n temp[k]+=matrix[j][k]\n cs = 0\n cm = 0\n for s in range(len(m):\n cs = max(temp[s], cs+temp[s])\n cm=max(cm, cs)\n gm=max(gm,cm)\n return gm\n\n``` | 2 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python Solution | maximal-rectangle | 0 | 1 | \n\n\n# Explanation\nThe solution first initializes the "left" and "right" arrays to the leftmost and rightmost boundaries possible, respectively, and the "height" array to all zeroes. It then iterates over each row of the matrix and for each row, it updates the "height" array by adding 1 to the height of each index where the matrix has a 1, and resetting the height to 0 for any other index.\n\nIt then updates the "left" array by comparing the current index to the leftmost boundary of the rectangle and taking the maximum of the two. If the current index is a 0, it resets the left boundary to the current index + 1. Similarly, it updates the "right" array by comparing the current index to the rightmost boundary of the rectangle and taking the minimum of the two. If the current index is a 0, it resets the right boundary to the current index.\n\nFinally, it iterates over the "height" array and updates the "maxarea" variable by taking the maximum area of the rectangle between the leftmost and rightmost boundaries at each index.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(n).\n\n- Space complexity:\nThe space complexity is O(n) since it only uses three arrays of size n.\n\n# More\n\nMore LeetCode solutions of mine at \n# Code\n```\nfrom typing import List\nclass Solution:\n\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n if not matrix: return 0\n\n m = len(matrix)\n n = len(matrix[0])\n\n left = [0] * n # initialize left as the leftmost boundary possible\n right = [n] * n # initialize right as the rightmost boundary possible\n height = [0] * n\n\n maxarea = 0\n\n for i in range(m):\n\n cur_left, cur_right = 0, n\n # update height\n for j in range(n):\n if matrix[i][j] == \'1\': height[j] += 1\n else: height[j] = 0\n # update left\n for j in range(n):\n if matrix[i][j] == \'1\': left[j] = max(left[j], cur_left)\n else:\n left[j] = 0\n cur_left = j + 1\n # update right\n for j in range(n-1, -1, -1):\n if matrix[i][j] == \'1\': right[j] = min(right[j], cur_right)\n else:\n right[j] = n\n cur_right = j\n # update the area\n for j in range(n):\n maxarea = max(maxarea, height[j] * (right[j] - left[j]))\n\n return maxarea\n``` | 1 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python || 96.75% Faster || DP || Histogram | maximal-rectangle | 0 | 1 | ```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n def mah(heights: List[int]) -> int:\n st=[]\n maxArea=0\n for bar in heights+[-1]:\n step=0\n while st and st[-1][1]>=bar:\n w,h=st.pop()\n step+=w\n maxArea=max(maxArea,step*h)\n st.append((step+1,bar))\n return maxArea\n n,m=len(matrix),len(matrix[0])\n ans=0\n height=[0]*m\n for i in range(n):\n for j in range(m):\n if matrix[i][j]==\'1\':\n height[j]+=1\n else:\n height[j]=0\n ans=max(ans,mah(height))\n return ans\n```\n**An upvote will be encouraging** | 2 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python My Soln | maximal-rectangle | 0 | 1 | class Solution:\n\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n def maxHistogramRectangleArea(heights):\n area = 0\n stack = []\n for i, h in enumerate(heights):\n start = i\n while stack and stack[-1][1] > h:\n index , height = stack.pop()\n area = max(area,height * (i-index))\n start = index\n \n stack.append((start,h))\n \n for i,h in stack:\n \n area = max(area, h * (len(heights) - i))\n \n return area\n \n \n if not matrix: \n return 0\n \n n = len(matrix[0])\n \n hist = [0] * (n)\n \n res = 0\n \n for row in matrix:\n for i in range(n):\n \n if row[i] == "1": \n hist[i] += 1\n \n else: \n hist[i]=0\n \n \n res = max(res, maxHistogramRectangleArea(hist))\n \n return res\n\t\t | 1 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Maximal Rectangle with step by step explanation | maximal-rectangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses the concept of histogram to solve the problem. For each row, it converts the binary values into heights of the bars and then calculates the largest rectangle in the histogram using the stack data structure. The solution has a time complexity of O(n * m) and a space complexity of O(m).\n\n# Complexity\n- Time complexity:\n89.51%\n\n- Space complexity:\n85%\n\n# Code\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n if not matrix or not matrix[0]:\n return 0\n \n n, m = len(matrix), len(matrix[0])\n height = [0] * (m + 1)\n ans = 0\n \n for row in matrix:\n for i in range(m):\n height[i] = height[i] + 1 if row[i] == \'1\' else 0\n stack = [-1]\n for i in range(m + 1):\n while height[i] < height[stack[-1]]:\n h = height[stack.pop()]\n w = i - stack[-1] - 1\n ans = max(ans, h * w)\n stack.append(i)\n \n return ans\n\n``` | 5 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python Easy Understandable Solution | maximal-rectangle | 0 | 1 | \n# Code\n```\nclass Solution:\n def maximalRectangle(self, matrix: List[List[str]]) -> int:\n if not matrix or not matrix[0]:\n return 0\n n, m = len(matrix), len(matrix[0])\n height = [0] * (m + 1)\n res = 0\n for row in matrix:\n for a in range(m):\n height[a] = height[a] + 1 if row[a] == \'1\' else 0\n stack = [-1]\n for a in range(m + 1):\n while height[a] < height[stack[-1]]:\n h = height[stack.pop()]\n w = a - stack[-1] - 1\n res = max(res, h * w)\n stack.append(a)\n return res\n``` | 3 | Given a `rows x cols` binary `matrix` filled with `0`'s and `1`'s, find the largest rectangle containing only `1`'s and return _its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 6
**Explanation:** The maximal rectangle is shown in the above picture.
**Example 2:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Example 3:**
**Input:** matrix = \[\[ "1 "\]\]
**Output:** 1
**Constraints:**
* `rows == matrix.length`
* `cols == matrix[i].length`
* `1 <= row, cols <= 200`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python easy solution | partition-list | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n \n before_x = ListNode(0)\n after_x = ListNode(0)\n \n before = before_x\n after = after_x\n \n current = head\n while current:\n if current.val < x:\n before.next = current\n before = before.next\n else:\n after.next = current\n after = after.next\n current = current.next\n \n \n before.next = after_x.next\n after.next = None\n \n return before_x.next\n``` | 2 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
✅ 100% Two Pointer [VIDEO] & Linked List + Visualization - Optimal | partition-list | 1 | 1 | # Problem Understanding\n\nIn the "Partition a Linked List Around a Value" problem, we are provided with the head of a linked list and a value `x`. The task is to rearrange the linked list such that all nodes with values less than `x` come before nodes with values greater than or equal to `x`. A key point is that the original relative order of the nodes in each of the two partitions must be preserved.\n\nConsider the linked list `head = [1,4,3,2,5,2]` and `x = 3`. The expected output after partitioning is `[1,2,2,4,3,5]`.\n\n---\n\n# Live Coding & Logic in Python\nhttps://youtu.be/q-JTT8Ole6M\n\n## Coding in:\n- [\uD83D\uDC0D Python](https://youtu.be/q-JTT8Ole6M)\n- [\uD83E\uDD80 Rust](https://youtu.be/OOw-mP8T2AE)\n- [\uD83D\uDC39 Go](https://youtu.be/d-1OTX26qdo)\n\n# Approach: Two Pointer Technique with Dummy Nodes\n\nThe idea is to use two pointers (or references) to create two separate linked lists: \n1. One for nodes with values less than `x`\n2. Another for nodes with values greater than or equal to `x`\n\nAt the end, we can combine the two linked lists to get the desired result.\n\n## Key Data Structures:\n- **Linked List**: We work directly with the given linked list nodes.\n- **Dummy Nodes**: Two dummy nodes are used to create the starting point for the two partitions.\n\n## Step-by-step Breakdown:\n\n1. **Initialization**:\n - Create two dummy nodes: `before` and `after`.\n - Initialize two pointers `before_curr` and `after_curr` at the dummy nodes.\n \n2. **Traversal & Partition**:\n - Traverse the linked list with the given `head`.\n - For each node, if its value is less than `x`, attach it to the `before` list. Otherwise, attach it to the `after` list.\n \n3. **Merging**:\n - After traversing the entire list, append the `after` list to the `before` list to form the partitioned linked list.\n\n4. **Result**:\n - Return the next node of the `before` dummy node as the new head of the partitioned list.\n\n# Example - Visualization:\nBased on the provided example with the linked list `head = [1,4,3,2,5,2]` and `x = 3`, here\'s the step-by-step evolution of the `before`, `after`, and `head` lists:\n\n\n\n1. After processing node with value `1`:\n - `head`: [1, 4, 3, 2, 5, 2]\n - `before`: [0, 1]\n - `after`: [0]\n\n2. After processing node with value `4`:\n - `head`: [4, 3, 2, 5, 2]\n - `before`: [0, 1]\n - `after`: [0, 4]\n\n3. After processing node with value `3`:\n - `head`: [3, 2, 5, 2]\n - `before`: [0, 1]\n - `after`: [0, 4, 3]\n\n4. After processing node with value `2`:\n - `head`: [2, 5, 2]\n - `before`: [0, 1, 2]\n - `after`: [0, 4, 3]\n\n5. After processing node with value `5`:\n - `head`: [5, 2]\n - `before`: [0, 1, 2]\n - `after`: [0, 4, 3, 5]\n\n6. After processing node with value `2`:\n - `head`: [2]\n - `before`: [0, 1, 2, 2]\n - `after`: [0, 4, 3, 5]\n\nFinally, after merging the `before` and `after` lists, the result is: `[1,2,2,4,3,5]`\n\n# Complexity:\n\n**Time Complexity:** $$O(n)$$\n- We traverse the linked list once, making the time complexity linear in the size of the list.\n\n**Space Complexity:** $$O(1)$$\n- We use constant extra space since we are only creating two dummy nodes and reusing the existing nodes in the linked list.\n\n# Performance:\n\nGiven the constraints, this solution is optimal and will efficiently handle linked lists of size up to 200 nodes.\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| **Rust** | 0 | 100% | 1.9 | 100% |\n| **Go** | 0 | 100% | 2.4 | 98.48% |\n| **C++** | 0 | 100% | 10.2 | 48.14% |\n| **Java** | 0 | 100% | 40.8 | 83.63% |\n| **Python3** | 32 | 98.81% | 16.4 | 55.72% |\n| **JavaScript** | 45 | 98.36% | 44.3 | 12.30% |\n| **C#** | 82 | 67.18% | 39 | 64.10% |\n\n\n\n\n# Code\n``` Python []\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n before, after = ListNode(0), ListNode(0)\n before_curr, after_curr = before, after\n \n while head:\n if head.val < x:\n before_curr.next, before_curr = head, head\n else:\n after_curr.next, after_curr = head, head\n head = head.next\n \n after_curr.next = None\n before_curr.next = after.next\n \n return before.next\n```\n``` C++ []\nclass Solution {\npublic:\n ListNode* partition(ListNode* head, int x) {\n ListNode before(0), after(0);\n ListNode* before_curr = &before;\n ListNode* after_curr = &after;\n \n while(head) {\n if(head->val < x) {\n before_curr->next = head;\n before_curr = head;\n } else {\n after_curr->next = head;\n after_curr = head;\n }\n head = head->next;\n }\n \n after_curr->next = nullptr;\n before_curr->next = after.next;\n \n return before.next;\n }\n};\n```\n``` Rust []\nimpl Solution {\n pub fn partition(mut head: Option<Box<ListNode>>, x: i32) -> Option<Box<ListNode>> {\n let mut before = ListNode::new(0);\n let mut after = ListNode::new(0);\n let mut before_tail = &mut before;\n let mut after_tail = &mut after;\n\n while let Some(mut node) = head {\n head = node.next.take();\n if node.val < x {\n before_tail.next = Some(node);\n before_tail = before_tail.next.as_mut().unwrap();\n } else {\n after_tail.next = Some(node);\n after_tail = after_tail.next.as_mut().unwrap();\n }\n }\n\n before_tail.next = after.next.take();\n\n before.next\n }\n}\n```\n``` Go []\nfunc partition(head *ListNode, x int) *ListNode {\n before := &ListNode{}\n after := &ListNode{}\n before_curr := before\n after_curr := after\n \n for head != nil {\n if head.Val < x {\n before_curr.Next = head\n before_curr = before_curr.Next\n } else {\n after_curr.Next = head\n after_curr = after_curr.Next\n }\n head = head.Next\n }\n \n after_curr.Next = nil\n before_curr.Next = after.Next\n \n return before.Next\n}\n```\n``` Java []\npublic class Solution {\n public ListNode partition(ListNode head, int x) {\n ListNode before = new ListNode(0);\n ListNode after = new ListNode(0);\n ListNode before_curr = before;\n ListNode after_curr = after;\n \n while(head != null) {\n if(head.val < x) {\n before_curr.next = head;\n before_curr = before_curr.next;\n } else {\n after_curr.next = head;\n after_curr = after_curr.next;\n }\n head = head.next;\n }\n \n after_curr.next = null;\n before_curr.next = after.next;\n \n return before.next;\n }\n}\n```\n``` JavaScript []\nvar partition = function(head, x) {\n let before = new ListNode(0);\n let after = new ListNode(0);\n let before_curr = before;\n let after_curr = after;\n \n while(head !== null) {\n if(head.val < x) {\n before_curr.next = head;\n before_curr = before_curr.next;\n } else {\n after_curr.next = head;\n after_curr = after_curr.next;\n }\n head = head.next;\n }\n \n after_curr.next = null;\n before_curr.next = after.next;\n \n return before.next;\n};\n```\n``` C# []\npublic class Solution {\n public ListNode Partition(ListNode head, int x) {\n ListNode before = new ListNode(0);\n ListNode after = new ListNode(0);\n ListNode before_curr = before;\n ListNode after_curr = after;\n \n while(head != null) {\n if(head.val < x) {\n before_curr.next = head;\n before_curr = before_curr.next;\n } else {\n after_curr.next = head;\n after_curr = after_curr.next;\n }\n head = head.next;\n }\n \n after_curr.next = null;\n before_curr.next = after.next;\n \n return before.next;\n }\n}\n```\n\n# Coding in Rust & Go\n\nhttps://youtu.be/OOw-mP8T2AE\nhttps://youtu.be/d-1OTX26qdo\n\nThe "Partition a Linked List Around a Value" problem exemplifies the elegance of simplicity in coding. Remember, every coding challenge is a gateway to greater understanding and expertise. Embrace each problem, for they refine your skills and mold your coding journey. Stay curious, dive deep, and let your passion for coding guide you to new horizons. \uD83D\uDE80\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB\n | 126 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
python easy | partition-list | 0 | 1 | # Complexity:\nTime complexity: O(n), where n is the number of nodes in the linked list. We traverse the linked list once, performing constant-time operations.\nSpace complexity: O(1), as we use a constant amount of extra space for creating the two dummy nodes and a few pointers regardless of the input size.\n# Code\n```\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n \n before_x = ListNode(0)\n after_x = ListNode(0)\n \n before = before_x\n after = after_x\n \n current = head\n while current:\n if current.val < x:\n before.next = current\n before = before.next\n else:\n after.next = current\n after = after.next\n current = current.next\n \n \n before.next = after_x.next\n after.next = None\n \n return before_x.next\n\n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Python3 Solution | partition-list | 0 | 1 | \n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n d1=c1=ListNode(0)\n d2=c2=ListNode(0)\n while head:\n if head.val<x:\n d1.next=head\n d1=d1.next\n\n else:\n d2.next=head\n d2=d2.next \n\n head=head.next\n\n d2.next=None\n d1.next=c2.next\n return c1.next \n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
⬆️ Ultra C++ / Python with Explenation Two Pointers | partition-list | 0 | 1 | # Intuition\nThe problem essentially requires us to partition a linked list around a value `x` such that nodes with values less than `x` appear before nodes with values greater than or equal to `x`, while maintaining the relative order. \n\nAt first glance, one might consider rearranging the nodes in the original list. However, to ensure that we maintain the relative order of the nodes, a simpler and more intuitive approach would be to create two separate linked lists: one for nodes with values less than `x` and one for nodes with values greater than or equal to `x`. After processing the entire list, we can then merge these two lists.\n\n# Approach\n1. Create two dummy nodes: `before` for nodes with values less than `x` and `after` for nodes with values greater than or equal to `x`.\n2. Traverse the original linked list. For each node:\n - If its value is less than `x`, append it to the `before` list.\n - Otherwise, append it to the `after` list.\n3. Once the entire list has been processed, the last node of the `after` list should point to `nullptr`.\n4. Connect the last node of the `before` list to the first node (after the dummy node) of the `after` list.\n5. The merged list starting from the first node (after the dummy node) of the `before` list gives the desired output.\n\n# Complexity\n- Time complexity: $$O(n)$$\n - We traverse the list once, processing each node.\n\n- Space complexity: $$O(1)$$\n - We only use a constant amount of extra space to create the `before` and `after` dummy nodes. The rest of the operations involve rearranging the original list\'s nodes without using any additional space.\n\n# Code\n``` C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* partition(ListNode* head, int x) {\n // Initialize two new dummy nodes for the \'before\' and \'after\' lists.\n ListNode* before = new ListNode(0);\n ListNode* after = new ListNode(0);\n \n // Use two pointers, one each for the \'before\' and \'after\' lists, \n // to help in appending nodes to these lists.\n ListNode* before_curr = before;\n ListNode* after_curr = after;\n\n // Traverse the original list.\n while (head) {\n // Check the value of the current node.\n if (head->val < x) {\n // If the node\'s value is less than x, \n // append it to the \'before\' list.\n before_curr->next = head;\n before_curr = before_curr->next;\n } else {\n // If the node\'s value is greater than or equal to x, \n // append it to the \'after\' list.\n after_curr->next = head;\n after_curr = after_curr->next;\n }\n\n // Move to the next node in the original list.\n head = head->next;\n }\n \n // Ensure the last node in the \'after\' list points to nullptr.\n after_curr->next = nullptr;\n \n // Connect the last node of the \'before\' list to the first node \n // (after the dummy node) of the \'after\' list.\n before_curr->next = after->next;\n \n // Return the merged list starting from the first node \n // (after the dummy node) of the \'before\' list.\n return before->next;\n }\n};\n```\n``` Python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n # Initialize two new dummy nodes for the \'before\' and \'after\' lists.\n before, after = ListNode(0), ListNode(0)\n \n # Use two pointers, one each for the \'before\' and \'after\' lists, \n # to help in appending nodes to these lists.\n before_curr, after_curr = before, after\n \n # Traverse the original list.\n while head:\n # Check the value of the current node.\n if head.val < x:\n # If the node\'s value is less than x, \n # append it to the \'before\' list.\n before_curr.next, before_curr = head, head\n else:\n # If the node\'s value is greater than or equal to x, \n # append it to the \'after\' list.\n after_curr.next, after_curr = head, head\n \n # Move to the next node in the original list.\n head = head.next\n \n # Ensure the last node in the \'after\' list points to None.\n after_curr.next = None\n \n # Connect the last node of the \'before\' list to the first node \n # (after the dummy node) of the \'after\' list.\n before_curr.next = after.next\n \n # Return the merged list starting from the first node \n # (after the dummy node) of the \'before\' list.\n return before.next\n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.