title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 1-liner. Functional programming. | unique-binary-search-trees | 0 | 1 | # Approach\nNotice, that the number of binary trees possible with n nodes is equal to n-th [Catalan number](https://en.wikipedia.org/wiki/Catalan_number#:~:text=In%20combinatorial%20mathematics%2C%20the%20Catalan,often%20involving%20recursively%20defined%20objects.).\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution:\n def numTrees(self, n: int) -> int:\n # nth Catalan number\n return round(reduce(mul, map(lambda k: (n + k) / k, range(2, n + 1)), 1))\n\n\n``` | 1 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
[Python]Easy DP Solution Explained By Someone Who Used To Struggle To Understand DP | unique-binary-search-trees | 0 | 1 | First of all, I am so happy because I was able to solve this problem without any help :) So, I am going to explained how I improved my DP skills. Of course, this is a "medium" question and I still struggle with the hard ones but I can see some improvement and I want to share my tips with you.\n\n***How to understand if a problem is DP problem?***\nWell, I still struggle to understand that for some problem types but basically if you think that you can solve the problem easily by knowing the solution for previous values(like the solution on the previous grids for 2D cases or the solution for n-1 etc.), it is probably a DP problem.\n\nDP problems are usually an iterative version of a recursive solution. I find it easy to think about recursive solution first and then convert it to DP. \n\n**1. Recursive + Memoization**\n\nWe need to calculate how many possible trees can be made. \nIf there is only ```1``` node then it is easy. The answer is 1. \nFor ```2``` we can construct ```2``` different trees: One of the node is root, the second one can either be a left child or right child.\n```\nn = 2\n\n 1 1\n / or \\\n2\t 2\n```\nEasy!\nWhat about n=3?\n```\n 1 3 3 2 1\n \\ / / / \\ \\\n\t---------------------------------- Let\'s cut the trees from here\n 3 2 1 1 3 2\n / / \\ \\\n 2 1 2 3\n ```\nAs you can see, from where we cut, the bottom of the tree is actually another tree where the same logic applies. So the only thing we need to decide is how to distrubute the remaining nodes to childs of the root. The options can be:\n```\n------num of nodes------\nleft_child right_child\n 0 2 --> These are the subtrees, like the new trees with n = 0 and n = 2\n 1 1\n 2 0\n```\nTo find how many possible solutions are there for n=3, add up all these possibilities . We can call the same function for calculating the values in all the options because it is actually the same problem. \nTo sum up, we picked the root and then we need to decide on how the left and right subtrees will look like. The options are how many nodes can be on the left and right subtree at the same time.\n\n```\n -------------- 3 ---------------\n\t /\t\t | \\\n / \\\t / \\\t \t /\t \\\n 0 --2-- 1 1 --2-- 0\n / \\ / \\ \n\t /\\ /\\ /\\ /\\\n\t1 0 0 1 1 0 0 1\n\n```\nHere is my attempt to draw the recursion tree. Even for a small n value there are multiple overlapping problems. So I used a memoization table and saved the values on that table before returning the total value from the function and if the value that we are looking for exists on the table, return that value without doing any extra calculations.\n\nHere is the code:\n\n```\nclass Solution:\n def numTrees(self, n: int) -> int:\n self.table = [-1] * (n+1)\n self.table[0] = 1\n return self.numTreesRec(n)\n \n def numTreesRec(self, n):\n if self.table[n] != -1:\n return self.table[n]\n total = 0\n for m in range(n):\n total += (self.numTreesRec(n-1-m) * self.numTreesRec(m))\n self.table[n] = total\n return total\n```\n\n**2. Dynamic Programming**\nNow, we have our recursive solution. As you can see from the above recursion tree, values are calculated starting from 0 and then 1 and goes like this until n. The means we can do it iteratively. We can start from 1 (n=0 are our base case) and calculate the values upto n. So, I created a dp table and the solution for n = i is stored at dp[i]. Now, if we go back to our example, for n=3:\n```\n0 2 \n1 1\n2 0\n```\nWe have these options for distributing the remaining nodes to subtrees. We already calculated the values for 0, 1 and 2 because we used iterative approach. Therefore solution for dp[3] will be\n```\ndp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0]\n```\n\nwhich is done by the inner for loop in the code.\n\nHere is the code:\n\n```\nclass Solution:\n def numTrees(self, n: int) -> int:\n dp = [0] * (n+1)\n dp[0] = 1\n for i in range(1, n+1):\n for j in range(i):\n dp[i] += dp[j] * dp[i- 1 - j]\n return dp[n]\n```\n\nThe time complexity is O(n^2) and the space complexity is O(n). There is a better solution by using catalan numbers. \n\nI tried my best to explain how I think when solving a dp problem. Hope that it helps and don\'t worry if you are having diffuculties. Practice makes perfect! | 85 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
Very Easy 0 ms 100% (Fully Explained)(Java, C++, Python, JS, C, Python3) | unique-binary-search-trees | 1 | 1 | # **Java Solution (Dynamic Programming Approach):**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Unique Binary Search Trees.\n```\nclass Solution {\n public int numTrees(int n) {\n // Create \'sol\' array of length n+1...\n int[] sol = new int[n+1];\n // The value of the first index will be 1.\n sol[0] = 1;\n // Run a loop from 1 to n+1...\n for(int i = 1; i <= n; i++) {\n // Within the above loop, run a nested loop from 0 to i...\n for(int j = 0; j < i; j++) {\n // Update the i-th position of the array by adding the multiplication of the respective index...\n sol[i] += sol[j] * sol[i-j-1];\n }\n }\n // Return the value of the nth index of the array to get the solution...\n return sol[n];\n }\n}\n```\n\n# **C++ Solution (Dynamic Programming Approach):**\n```\nclass Solution {\npublic:\n int numTrees(int n) {\n // If n <= 1, then return 1\n if (n <= 1) {\n\xA0\xA0\xA0\xA0\xA0\xA0\xA0\xA0\xA0\xA0\xA0\xA0return 1;\n\xA0\xA0\xA0\xA0\xA0\xA0\xA0\xA0}\n // Create \'sol\' array of length n+1...\n vector<int> sol(n+1, 0);\n // The value of the first and second index will be 1.\n sol[0] = sol[1] = 1;\n // Run a loop from 2 to n...\n for (int i = 2; i <= n; ++i) {\n // within the above loop, run a nested loop from 0 to i...\n for (int j = 0; j < i; j++) {\n // Update the i-th position of the array by adding the multiplication of the respective index...\n sol[i] += sol[j] * sol[i-j-1];\n }\n }\n // Return the value of the nth index of the array to get the solution...\n return sol[n];\n }\n};\n```\n\n# **Python Solution (Dynamic Programming Approach):**\nRuntime: 17 ms, faster than 90.77% of Python online submissions for Unique Binary Search Trees.\n```\nclass Solution(object):\n def numTrees(self, n):\n if n == 0 or n == 1:\n return 1\n # Create \'sol\' array of length n+1...\n sol = [0] * (n+1)\n # The value of the first index will be 1.\n sol[0] = 1\n # Run a loop from 1 to n+1...\n for i in range(1, n+1):\n # Within the above loop, run a nested loop from 0 to i...\n for j in range(i):\n # Update the i-th position of the array by adding the multiplication of the respective index...\n sol[i] += sol[j] * sol[i-j-1]\n # Return the value of the nth index of the array to get the solution...\n return sol[n]\n```\n \n# **JavaScript Solution (Dynamic Programmming Approach):**\n```\nvar numTrees = function(n) {\n // Create \'sol\' array to store the solution...\n var sol = [1, 1];\n // Run a loop from 2 to n...\n for (let i = 2; i <= n; i++) {\n sol[i] = 0;\n // Within the above loop, run a nested loop from 1 to i...\n for (let j = 1; j <= i; j++) {\n // Update the i-th position of the array by adding the multiplication of the respective index...\n sol[i] += sol[i - j] * sol[j - 1];\n }\n }\n // Return the value of the nth index of the array to get the solution...\n return sol[n];\n};\n```\n\n# **C Language (Catalan Math Approach):**\nRuntime: 0 ms, faster than 100.00% of C online submissions for Unique Binary Search Trees.\n```\nint numTrees(int n){\n long sol = 1;\n for (int i = 0; i < n; ++i) {\n sol = sol * 2 * (2 * i + 1) / (i + 2);\n }\n return (int) sol;\n}\n```\n\n# **Python3 Solution (Catalan Math Approach):**\n```\nclass Solution:\n def numTrees(self, n: int) -> int:\n sol = 1\n for i in range (0, n):\n sol = sol * 2 * (2 * i + 1) / (i + 2)\n return int(sol)\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 25 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
Python Elegant & Short | Two solutions | One line/Top-down DP | unique-binary-search-trees | 0 | 1 | \tclass Solution:\n\t\t"""\n\t\tTime: O(n^2)\n\t\tMemory: O(log(n))\n\t\t"""\n\n\t\tdef numTrees(self, n: int) -> int:\n\t\t\treturn self._num_trees(1, n)\n\n\t\t@classmethod\n\t\t@lru_cache(maxsize=None)\n\t\tdef _num_trees(cls, lo: int, hi: int) -> int:\n\t\t\tif hi - lo < 1:\n\t\t\t\treturn 1\n\t\t\treturn sum(cls._num_trees(lo, i - 1) * cls._num_trees(i + 1, hi) for i in range(lo, hi + 1))\n\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(1)\n\t\t"""\n\n\t\tdef numTrees(self, n: int) -> int:\n\t\t\treturn reduce(lambda res, i: res * 2 * (2 * i + 1) // (i + 2), range(n), 1) | 2 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
📢From Recursion to DP: Solving the Unique BST Problem || Mr. Robot is here to make DP Easy | unique-binary-search-trees | 1 | 1 | # Code For Copy-Pasters \uD83D\uDC80\n## Others can scroll down for Understanding the Approaches\n\n\n``` cpp []\nclass Solution\n{\n public:\n int solve(int n)\n {\n if (n <= 1) return 1;\n int ans = 0;\n for (int i = 1; i <= n; i++)\n {\n ans += solve(i - 1) *solve(n - i);\n }\n return ans;\n }\n int Msolve(int n, vector<int> &dp)\n {\n if (n <= 1) return 1;\n if (dp[n] != -1) return dp[n];\n int ans = 0;\n for (int i = 1; i <= n; i++)\n {\n ans += Msolve(i - 1, dp) *Msolve(n - i, dp);\n }\n return dp[n] = ans;\n }\n int tab(int N)\n {\n vector<int> dp(N + 1, 1);\n for (int n = 2; n <= N; n++)\n {\n int ans = 0;\n for (int i = 1; i <= n; i++)\n {\n ans += dp[i - 1] *dp[n - i];\n }\n dp[n] = ans;\n }\n return dp[N];\n }\n int numTrees(int n)\n {\n return tab(n);\n }\n};\n```\n---\n\n# Finding the Number of Unique Binary Search Trees \u2753\n\n## \uD83D\uDCA1Approach 1: Recursive Solution\n\n### \u2728Explanation\nThe problem asks us to find the number of unique binary search trees that can be formed with a given number of nodes. We can approach this using a recursive algorithm.\n\nIn a binary search tree (BST), the left subtree contains nodes with values less than the root node, and the right subtree contains nodes with values greater than the root node. To find the total number of unique BSTs for `n` nodes, we can iterate through each node as the root node, and for each root node, we find the number of unique BSTs for the left subtree and the number of unique BSTs for the right subtree. We then multiply these two values to get the total number of unique BSTs with the current root.\n\nLet\'s take an example to illustrate the concept. Suppose we have 3 nodes: 1, 2, and 3. If we choose node 2 as the root, we have one node in the left subtree (1) and one node in the right subtree (3). Therefore, the total number of unique BSTs with node 2 as the root is the product of the number of BSTs for the left subtree (1 node) and the number of BSTs for the right subtree (1 node), which is 1 * 1 = 1.\n\nWe repeat this process for all nodes as potential roots and sum up the results. The final sum is the answer.\n\n### \uD83D\uDCDDDry Run\nLet\'s dry run this approach with an example where `n = 3`:\n\n1. Start with `n = 3`.\n2. Choose 1 as the root:\n - Number of unique BSTs for the left subtree (0 node) = 1\n - Number of unique BSTs for the right subtree (2 nodes) = 2\n - Total number of unique BSTs with root 1 = 1 * 2 = 2\n3. Choose 2 as the root:\n - Number of unique BSTs for the left subtree (1 node) = 1\n - Number of unique BSTs for the right subtree (1 node) = 1\n - Total number of unique BSTs with root 2 = 1 * 1 = 1\n4. Choose 3 as the root:\n - Number of unique BSTs for the left subtree (2 nodes) = 2\n - Number of unique BSTs for the right subtree (0 node) = 1\n - Total number of unique BSTs with root 3 = 2 * 1 = 2\n5. Sum up the results: 2 (with root 1) + 1 (with root 2) + 2 (with root 3) = 5\n\nThe total number of unique BSTs for `n = 3` is 5.\n\n### \uD83D\uDD0DEdge Cases\n1. If `n` is 0, there is one unique BST (an empty tree).\n2. If `n` is 1, there is one unique BST (a single node).\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: The time complexity of this recursive approach is exponential, specifically O(4^n / (n^(3/2))). This is due to the large number of recursive calls and overlapping subproblems.\n- Space Complexity: The space complexity is O(n), where n is the depth of the recursion.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n\nclass Solution {\npublic:\n int numTrees(int n) {\n if (n <= 1)\n return 1;\n \n int ans = 0;\n for (int i = 1; i <= n; i++) {\n ans += numTrees(i - 1) * numTrees(n - i);\n }\n return ans;\n }\n};\n```\n\n```java []\nclass Solution {\n public int numTrees(int n) {\n if (n <= 1) return 1;\n int ans = 0;\n for (int i = 1; i <= n; i++) {\n ans += numTrees(i - 1) * numTrees(n - i);\n }\n return ans;\n }\n}\n```\n\n```python []\nclass Solution:\n def numTrees(self, n: int) -> int:\n if n <= 1:\n return 1\n \n ans = 0\n for i in range(1, n + 1):\n ans += self.numTrees(i - 1) * self.numTrees(n - i)\n return ans\n```\n\n```csharp []\npublic class Solution {\n public int NumTrees(int n) {\n if (n <= 1)\n return 1;\n \n int ans = 0;\n for (int i = 1; i <= n; i++) {\n ans += NumTrees(i - 1) * NumTrees(n - i);\n }\n return ans;\n }\n}\n```\n\n```javascript []\nvar numTrees = function(n) {\n if (n <= 1)\n return 1;\n \n let ans = 0;\n for (let i = 1; i <= n; i++) {\n ans += numTrees(i - 1) * numTrees(n - i);\n }\n return ans;\n};\n```\n---\n\n# \uD83D\uDCA1Approach 2: Top-Down Approach (Memoization)\n\n### \u2728Explanation\nThe top-down approach (also known as memoization) is a recursive approach with caching to avoid redundant calculations. We\'ll define a recursive function `solve(n)` that returns the number of unique BSTs that can be formed with `n` nodes.\n\nThe function `solve(n)` can be defined as follows:\n\n1. If `n` is less than or equal to 1, return 1 because there is one unique BST for `n` equal to 0 or 1.\n\n2. Initialize a variable `ans` to 0.\n\n3. Iterate from `1` to `n`, and for each `i`, do the following:\n - Calculate `solve(i - 1)`, which represents the number of unique BSTs in the left subtree with `i-1` nodes.\n - Calculate `solve(n - i)`, which represents the number of unique BSTs in the right subtree with `n-i` nodes.\n - Multiply these two values to find the total number of unique BSTs with the current root `i`.\n - Add this result to `ans`.\n\n4. Return `ans`, which will be the total number of unique BSTs with `n` nodes.\n\nThis approach ensures that we don\'t calculate the same subproblems multiple times by caching the results of subproblems in a memoization table.\n\n### \uD83D\uDD78\uFE0FDry Run\nLet\'s dry run this approach with an example where `n = 3`:\n\n1. We call the function `solve(3)`.\n2. Since `n` is not less than or equal to 1, we proceed with the calculations.\n\n - For `i = 1`:\n - `solve(0)` returns 1 (there is one unique BST with 0 nodes).\n - `solve(2)` returns 2 (we calculate it as follows):\n - For `i = 1`:\n - `solve(0)` returns 1 (there is one unique BST with 0 nodes).\n - `solve(1)` returns 1 (there is one unique BST with 1 node).\n - We multiply these two values to get 1.\n - For `i = 2`:\n - `solve(1)` returns 1 (there is one unique BST with 1 node).\n - `solve(0)` returns 1 (there is one unique BST with 0 nodes).\n - We multiply these two values to get 1.\n - We add these two results: 1 + 1 = 2.\n\n - We add the results for `i = 1` and `i = 2`: 1 + 2 = 3.\n\n - For `i = 2`:\n - `solve(1)` returns 1 (there is one unique BST with 1 node).\n - `solve(1)` returns 1 (there is one unique BST with 1 node).\n - We add these two results: 1 + 1 = 2.\n\n - We add the results for `i = 1` and `i = 2`: 3 + 2 = 5.\n\n3. The final answer is `5`.\n\nThe total number of unique BSTs for `n = 3` is 5.\n\n### \uD83D\uDD0DEdge Cases\n1. If `n` is 0, there is one unique BST (an empty tree).\n2. If `n` is 1, there is one unique BST (a single node).\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: The time complexity of this top-down approach with memoization is O(n^2) due to overlapping subproblems.\n- Space Complexity: The space complexity is O(n) to store the results of subproblems in a memoization table.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n\nclass Solution {\npublic:\n int numTrees(int n) {\n vector<int> memo(n + 1, -1);\n return solve(n, memo);\n }\n\n int solve(int n, vector<int>& memo) {\n if (n <= 1) return 1;\n if (memo[n] != -1) return memo[n];\n int ans = 0;\n for (int i = 1; i <= n; i++) {\n ans += solve(i - 1, memo) * solve(n - i, memo);\n }\n memo[n] = ans;\n return ans;\n }\n};\n```\n\n```java []\nclass Solution {\n public int numTrees(int n) {\n int[] memo = new int[n + 1];\n Arrays.fill(memo, -1);\n return solve(n, memo);\n }\n\n public int solve(int n, int[] memo) {\n if (n <= 1) return 1;\n if (memo[n] != -1) return memo[n];\n int ans = 0;\n for (int i = 1; i <= n; i++) {\n ans += solve(i - 1, memo) * solve(n - i, memo);\n }\n memo[n] = ans;\n return ans;\n }\n}\n```\n\n```python []\nclass Solution:\n def numTrees(self, n: int) -> int:\n memo = [-1] * (n + 1)\n return self.solve(n, memo)\n\n def solve(self, n, memo):\n if n <= 1:\n return 1\n if memo[n] != -1:\n return memo[n]\n ans = 0\n for i in range(1, n + 1):\n ans += self.solve(i - 1, memo) * self.solve(n - i, memo)\n memo[n] = ans\n return ans\n\n```\n\n```csharp []\npublic class Solution {\n public int NumTrees(int n) {\n int[] memo = new int[n + 1];\n for (int i = 0; i <= n; i++) {\n memo[i] = -1;\n }\n return Solve(n, memo);\n }\n\n public int Solve(int n, int[] memo) {\n if (n <= 1) return 1;\n if (memo[n] != -1) return\n\n memo[n];\n int ans = 0;\n for (int i = 1; i <= n; i++) {\n ans += Solve(i - 1, memo) * Solve(n - i, memo);\n }\n memo[n] = ans;\n return ans;\n }\n}\n```\n\n```javascript []\nvar numTrees = function (n) {\n const memo = new Array(n + 1).fill(-1);\n return solve(n, memo);\n};\n\nconst solve = (n, memo) => {\n if (n <= 1) return 1;\n if (memo[n] !== -1) return memo[n];\n let ans = 0;\n for (let i = 1; i <= n; i++) {\n ans += solve(i - 1, memo) * solve(n - i, memo);\n }\n memo[n] = ans;\n return ans;\n};\n```\n--- \n\n# \uD83D\uDCA1 Approach 3: Dynamic Programming\n\n### \u2728Explanation\nWhile the recursive approach discussed in Approach 1 is correct, it has exponential time complexity due to overlapping subproblems. We can improve the efficiency of our solution by using dynamic programming to avoid redundant calculations.\n\nTo use dynamic programming, we\'ll create a DP array where `dp[i]` will represent the number of unique BSTs that can be formed with `i` nodes. We\'ll initialize `dp[0]` to 1 because there is one unique BST with no nodes (an empty tree), and `dp[1]` to 1 because there is one unique BST with one node.\n\nWe\'ll then iterate from `2` to `n` and, for each value of `i`, calculate the number of unique BSTs. To do this, we\'ll iterate from `1` to `i` and consider each node as the root node. We\'ll find the number of unique BSTs for the left subtree (number of nodes from `1` to `i-1`) and the number of unique BSTs for the right subtree (number of nodes from `i+1` to `n`). We\'ll then multiply these two values to get the total number of unique BSTs with the current root.\n\nFinally, we\'ll store the result in `dp[i]`, which will be used for further calculations. The value of `dp[n]` will be our final answer.\n\n### \uD83D\uDCDD Dry Run\nLet\'s dry run this approach with an example where `n = 3`:\n\n1. Initialize `dp` as `[1, 1, 0, 0]` (to represent `dp[0]` and `dp[1]`).\n2. Start iterating from `2` to `3` (i.e., `i` will be `2` and `3`).\n - For `i = 2`:\n - Choose `1` as the root:\n - Number of unique BSTs for the left subtree (0 node) = 1 (dp[0])\n - Number of unique BSTs for the right subtree (1 node) = 1 (dp[1])\n - Total number of unique BSTs with root `1` = 1 * 1 = 1\n - Choose `2` as the root:\n - Number of unique BSTs for the left subtree (1 node) = 1 (dp[1])\n - Number of unique BSTs for the right subtree (0 node) = 1 (dp[0])\n - Total number of unique BSTs with root `2` = 1 * 1 = 1\n - Sum up the results: 1 (with root `1`) + 1 (with root `2`) = 2\n - For `i = 3`:\n - Choose `1` as the root:\n - Number of unique BSTs for the left subtree (0 node) = 1 (dp[0])\n - Number of unique BSTs for the right subtree (2 nodes) = 2 (dp[2])\n - Total number of unique BSTs with root `1` = 1 * 2 = 2\n - Choose `2` as the root:\n - Number of unique BSTs for the left subtree (1 node) = 1 (dp[1])\n - Number of unique BSTs for the right subtree (1 node) = 1 (dp[1])\n - Total number of unique BSTs with root `2` = 1 * 1 = 1\n - Choose `3` as the root:\n - Number of unique BSTs for the left subtree (2 nodes) = 2 (dp[2])\n - Number of unique BSTs for the right subtree (0 node) = 1 (dp[0])\n - Total number of unique BSTs with root `3` = 2 * 1 = 2\n - Sum up the results: 2 (with root `1`) + 1 (with root `2`) + 2 (with root `3`) = 5\n3. The final answer is `5`.\n\nThe total number of unique BSTs for `n = 3` is 5.\n\n### \uD83D\uDD0DEdge Cases\n1. If `n` is 0, there is one unique BST (an empty tree).\n2. If `n` is 1, there is one unique BST (a single node).\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: The time complexity of this dynamic programming approach is O(n^2) as we have nested loops.\n- Space Complexity: The space complexity is O(n) to store the DP array.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n\nclass Solution {\npublic:\n int numTrees(int n) {\n vector<int> dp(n + 1, 0);\n dp[0] = dp[1] = 1;\n\n for (int i = 2; i <= n; i++) {\n for (int j = 1; j <= i; j++) {\n dp[i] += dp[j - 1] * dp[i - j];\n }\n }\n\n return dp[n];\n }\n};\n```\n\n```java []\nclass Solution {\n public int numTrees(int n) {\n int[] dp = new int[n + 1];\n dp[0] = dp[1] = 1;\n\n for (int i = 2; i <= n; i++) {\n for (int\n\n j = 1; j <= i; j++) {\n dp[i] += dp[j - 1] * dp[i - j];\n }\n }\n\n return dp[n];\n }\n}\n```\n\n```python []\nclass Solution:\n def numTrees(self, n: int) -> int:\n dp = [0] * (n + 1)\n dp[0] = dp[1] = 1\n\n for i in range(2, n + 1):\n for j in range(1, i + 1):\n dp[i] += dp[j - 1] * dp[i - j]\n\n return dp[n]\n```\n\n```csharp []\npublic class Solution {\n public int NumTrees(int n) {\n int[] dp = new int[n + 1];\n dp[0] = dp[1] = 1;\n\n for (int i = 2; i <= n; i++) {\n for (int j = 1; j <= i; j++) {\n dp[i] += dp[j - 1] * dp[i - j];\n }\n }\n\n return dp[n];\n }\n}\n```\n\n```javascript []\nvar numTrees = function (n) {\n const dp = new Array(n + 1).fill(0);\n dp[0] = dp[1] = 1;\n\n for (let i = 2; i <= n; i++) {\n for (let j = 1; j <= i; j++) {\n dp[i] += dp[j - 1] * dp[i - j];\n }\n }\n\n return dp[n];\n};\n```\n---\n# \uD83D\uDCCA Analysis \n\n\n| Language | Runtime (ms) | Memory (MB) |\n|-------------|--------------|-------------|\n| C++ | 0 | 6.52 |\n| Java | 0 | 39.8 |\n| Python | 43 | 16.09 |\n| JavaScript | 60 | 41.9 |\n| C# | 22 | 26.7 |\n\n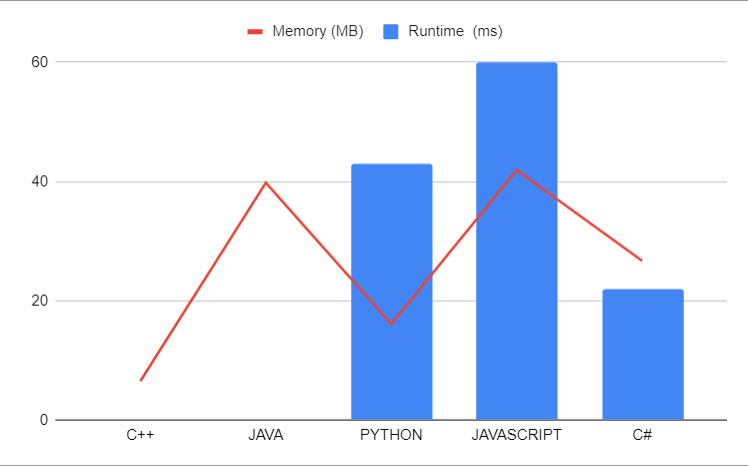\n\n\n\n---\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n | 2 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
95.38% Unique Binary Search Trees with step by step explanation | unique-binary-search-trees | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSolution for Leetcode 96. Unique Binary Search Trees:\n\nTo solve this problem, we can use the dynamic programming approach. Let\'s create an array dp of size n + 1, where dp[i] represents the number of unique BSTs that can be formed using i nodes.\n\nThe base cases are dp[0] = 1 and dp[1] = 1, as there is only one unique BST that can be formed using zero and one node(s) respectively.\n\nFor i nodes, we can select a root node in i different ways, and then recursively calculate the number of unique BSTs in the left and right subtrees. Finally, we can multiply the number of unique BSTs in the left and right subtrees and add it to the total count.\n\nTherefore, for i nodes, the number of unique BSTs that can be formed is given by the formula:\n```\ndp[i] = dp[0]*dp[i-1] + dp[1]*dp[i-2] + ... + dp[i-1]*dp[0]\n```\nThe above formula takes into account all the possible combinations of left and right subtrees.\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n) Beats\n95.38%\n\n# Code\n```\nclass Solution:\n def numTrees(self, n: int) -> int:\n # initialize the dp array with base cases\n dp = [0] * (n + 1)\n dp[0] = dp[1] = 1\n \n # calculate the number of unique BSTs for i nodes\n for i in range(2, n + 1):\n for j in range(1, i + 1):\n dp[i] += dp[j - 1] * dp[i - j]\n \n return dp[n]\n\n``` | 5 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
✔️ EXPLANATION ||✔️ PYTHON || EASY | unique-binary-search-trees | 0 | 1 | Case 1 : **n = 1** Only one combination is possible.\n\nCase 2 : **n = 2** Let fix one node. Two possibilities for second node. It can either be on right or left.\nHence for n=2 , 2 trees possible\n\nCase 3: **n = 3**\nAgain fix one node, and we are left with two nodes.\nPossibilities **:**\n* Both are on right\n* Both are on left\n* One on right and other on left\n\nAnswer to each above case will be **Combinations on right X Combinations on left**.\nNow we know answer of **TWO** nodes = 2\nAnswer for **ONE** node is 1\nAnswer for **THREE** nodes : ( ( 2 on right X 0 on left ) + ( 1 on right X 1 on left ) +( 0 on right X 2 on left ) )\n\nOther CASES :\nSIMILARLY a problem with **n nodes** can be broken into for **n - 1** nodes.\n\nArray **a** is created for memomization so that repeated recurcive calls for same value of n are prevented.\n\n```\nclass Solution:\n def numTrees(self, n: int) -> int:\n \n a = [0]*n\n \n def solve(n):\n \n if n <= 1:\n return 1\n if a[ n - 1 ] != 0:\n return a[ n - 1 ]\n k = 0\n for i in range(n):\n k += ( solve(i) * solve( n-i-1 ) )\n a[n-1] = k\n return k\n \n return s( n )\n``` | 4 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
Python: Recursion + Memoization | unique-binary-search-trees | 0 | 1 | Hi,\n\nI solved this problem by using recursion + memoization.\nThe result is close to the DP solution.\n\n```\ndef numTrees(self, n: int) -> int:\n return self.count_bsts(1, n, {})\n \ndef count_bsts(self, min_val: int, max_val: int, memo: dict) -> int:\n\tif min_val >= max_val:\n\t\treturn 1\n\n\telif (min_val, max_val) in memo:\n\t\treturn memo[(min_val, max_val)]\n\n\tbsts_count = 0\n\tfor val in range(min_val, max_val + 1):\n\n\t\tleft_subtrees_count = self.count_bsts(min_val, val - 1, memo)\n\t\tright_subtrees_count = self.count_bsts(val + 1, max_val, memo)\n\n\t\tbsts_count += left_subtrees_count * right_subtrees_count\n\n\tmemo[(min_val, max_val)] = bsts_count\n \n\treturn bsts_count\n\t\n``` | 19 | Given an integer `n`, return _the number of structurally unique **BST'**s (binary search trees) which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 19` | null |
Beats 90% of the users in python O(n^2) | interleaving-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n \n dp=[-1]*(len(s2)+1)\n \n \n if (len(s1)+len(s2))!=len(s3):\n return False\n\n if s1=="" or s2=="":\n if s2==s3 or s1==s3:\n return True\n else:\n return False\n \n\n if s1[0]==s3[0] or s2[0]==s3[0]:\n dp[0]=0\n else:\n return False\n m=-1\n for i in range(len(s1)+1):\n #print(s1[i])\n for j in range(len(dp)): \n\n if dp[j]!=-1 and i!=0:\n\n if s1[i-1]==s3[ dp[j] ]:\n #print("yes")\n if (i<len(s1) and s1[i]==s3[ dp[j]+1]) or (j<len(s2) and s2[j]==s3[ dp[j]+1]):\n dp[j]+=1\n else:\n dp[j]=-1\n else:\n dp[j]=-1\n \n elif j!=0:\n\n if dp[j-1]!=-1 and s2[j-1]==s3[ dp[j-1] ]:\n if (j<len(s2) and s2[j]==s3[ dp[j-1]+1 ]) or (i<len(s1) and s1[i]==s3[ dp[j-1] +1 ]):\n dp[j]=dp[j-1]+1\n else:\n dp[j]=-1\n else:\n dp[j]=-1\n \n if m<dp[j]:\n m=dp[j]\n print(dp)\n \n \n if m+1==len(s3):\n return True\n else:\n return False\n\n \n \n \n \n``` | 2 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
✅ 99.78% 2-Approaches DP & Recursion | interleaving-string | 1 | 1 | # Interview Guide: "Interleaving String" Problem\n\n## Problem Understanding\n\nIn the "Interleaving String" problem, you are given three strings: `s1`, `s2`, and `s3`. Your task is to determine whether `s3` can be formed by interleaving `s1` and `s2`. For example, if `s1 = "aabcc"` and `s2 = "dbbca"`, then `s3 = "aadbbcbcac"` should return `true`, but `s3 = "aadbbbaccc"` should return `false`.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nBefore diving into the solution, make sure you understand the problem\'s constraints. The lengths of the strings will not be more than 100 for `s1` and `s2`, and not more than 200 for `s3`. This can help you gauge the time complexity you should aim for.\n\n### 2. Multiple Approaches\n\nThere are multiple ways to solve this problem, including:\n\n - 2D Dynamic Programming\n - 1D Dynamic Programming\n - Recursion with Memoization\n\nEach method has its own time and space complexity, so choose based on the problem\'s constraints.\n\n### 3. Space Optimization\n\nWhile 2D Dynamic Programming is the most intuitive approach, you can reduce the space complexity to \\(O(\\min(m, n))\\) by employing 1D Dynamic Programming. In an interview setting, discussing this optimization can impress your interviewer.\n\n### 4. Early Exit\n\nIf the sum of the lengths of `s1` and `s2` does not match the length of `s3`, you can immediately return `false`. This can save computation time and demonstrate that you\'re mindful of edge cases.\n\n### 5. Explain Your Thought Process\n\nAlways explain your thought process and why you chose a particular approach. Discuss the trade-offs you\'re making in terms of time and space complexity.\n\n## Conclusion\n\nThe "Interleaving String" problem is an excellent example of a problem that can be tackled through Dynamic Programming or Recursion. Knowing the trade-offs between different approaches and optimizing for space can give you an edge in interviews. By taking the time to understand the problem, choosing the appropriate data structures, and optimizing your approach, you\'ll not only solve the problem but also demonstrate a well-rounded skill set.\n\n---\n\n# Live Coding & Explenation: 1D Dynamic Programming\nhttps://youtu.be/iv_cTwwsRxs\n\n---\n\n# Approach: 2D Dynamic Programming \n\nTo solve the "Interleaving String" problem using 2D Dynamic Programming, we utilize a 2D array `dp[i][j]` to represent whether the substring `s3[:i+j]` can be formed by interleaving `s1[:i]` and `s2[:j]`.\n\n## Key Data Structures:\n- **dp**: A 2D list to store the results of subproblems.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Calculate lengths of `s1`, `s2`, and `s3`.\n - If the sum of lengths of `s1` and `s2` is not equal to the length of `s3`, return false.\n - Initialize the `dp` array with dimensions `(m+1) x (n+1)`, setting `dp[0][0] = True`.\n \n2. **Base Cases**:\n - Fill in the first row of `dp` array, considering only the characters from `s1`.\n - Fill in the first column of `dp` array, considering only the characters from `s2`.\n \n3. **DP Loop**:\n - Loop through each possible `(i, j)` combination, starting from `(1, 1)`.\n - Update `dp[i][j]` based on the transition `dp[i][j] = (dp[i-1][j] and s1[i-1] == s3[i+j-1]) or (dp[i][j-1] and s2[j-1] == s3[i+j-1])`.\n\n4. **Wrap-up**:\n - Return the value stored in `dp[m][n]`, which indicates whether `s3` can be formed by interleaving `s1` and `s2`.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution iterates over each possible $$ (i, j) $$ combination, leading to a time complexity of $$ O(m \\times n) $$.\n\n**Space Complexity:** \n- The space complexity is $$ O(m \\times n) $$ due to the 2D $$ dp $$ array.\n\n---\n\n# Approach: 1D Dynamic Programming \n\nThe optimization from 2D to 1D DP is based on the observation that the state of `dp[i][j]` in the 2D DP array depends only on `dp[i-1][j]` and `dp[i][j-1]`. Therefore, while iterating through the strings, the current state only depends on the states in the previous row of the 2D DP array, which means we can optimize our space complexity by just keeping track of one row (1D DP).\n\n## Key Data Structures:\n\n- **dp**: A 1D list that stores whether the substring `s3[:i+j]` can be formed by interleaving `s1[:i]` and `s2[:j]`. Initially, all values are set to `False` except `dp[0]`, which is set to `True`.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - First, calculate the lengths of `s1`, `s2`, and `s3`.\n - Check if the sum of the lengths of `s1` and `s2` equals the length of `s3`. If it doesn\'t, return `False` as `s3` cannot be formed by interleaving `s1` and `s2`.\n\n2. **Optimization Check**:\n - If `m < n`, swap `s1` and `s2`. This is to ensure that `s1` is not longer than `s2`, which helps in optimizing the space complexity to `O(min(m, n))`.\n\n3. **Base Cases**:\n - Initialize a 1D array `dp` of length `n+1` with `False`.\n - Set `dp[0] = True` because an empty `s1` and `s2` can interleave to form an empty `s3`.\n\n4. **Single-Row DP Transition**:\n - Iterate through `s1` and `s2` to update the `dp` array.\n - For each character in `s1`, iterate through `s2` and update the `dp` array based on the transition rule: `dp[j] = (dp[j] and s1[i] == s3[i+j]) or (dp[j-1] and s2[j] == s3[i+j])`.\n - The transition rule checks if the current `s3[i+j]` can be matched by either `s1[i]` or `s2[j]`, relying solely on the previous values in the `dp` array.\n\n5. **Wrap-up**:\n - The final value in the `dp` array will indicate whether the entire `s3` can be formed by interleaving `s1` and `s2`.\n - Return `dp[n]`.\n\n\n\n# Complexity:\n\nThe primary advantage of this 1D DP approach is its space efficiency. While it maintains the same time complexity as the 2D DP approach $$O(m \\times n)$$, the space complexity is optimized to $$O(\\min(m, n))$$.\n\n**Time Complexity:** \n- The solution iterates over each character of `s1` and `s2` once, leading to a complexity of $$O(m \\times n)$$.\n\n**Space Complexity:** \n- The space complexity is optimized to $$O(\\min(m,n))$$ as we\'re only using a single 1D array instead of a 2D matrix.\n\n---\n\n# Approach: Recursion with Memoization\n\nIn this approach, we recursively check whether the substring `s3[k:]` can be formed by interleaving `s1[i:]` and `s2[j:]`. We store the results of these sub-problems in a dictionary named `memo`.\n\n## Key Data Structures:\n- **memo**: A dictionary to store the results of subproblems.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Calculate lengths of `s1`, `s2`, and `s3`.\n - If the sum of lengths of `s1` and `s2` is not equal to the length of `s3`, return false.\n \n2. **Recursive Function**:\n - Define a recursive function `helper` which takes indices `i`, `j`, and `k` as inputs.\n - The function checks whether the substring `s3[k:]` can be formed by interleaving `s1[i:]` and `s2[j:]`.\n - Store the result of each subproblem in the `memo` dictionary.\n\n3. **Wrap-up**:\n - Return the result of the recursive function for the initial values `i=0, j=0, k=0`.\n\n# Complexity:\n\n**Time Complexity:** \n- Each combination of (i, j) is computed once and stored in the memo, leading to a time complexity of $$O(m \\times n)$$.\n\n**Space Complexity:** \n- The space complexity is $$O(m \\times n)$$ for storing the memoization results.\n\n---\n\n# Performance\n\n| Language | Runtime (ms) | Memory (MB) |\n|-----------|--------------|-------------|\n| Rust | 0 | 2.1 |\n| C++ | 0 | 6.4 |\n| Go | 1 | 1.9 |\n| Java | 3 | 40.5 |\n| Python3 (1D DP) | 31 | 16.4 |\n| Python3 (2D DP) | 34 | 16.5 |\n| Python3 (Recursion) | 45 | 17.4 |\n| C# | 54 | 38.4 |\n| JavaScript| 61 | 43.1 |\n\n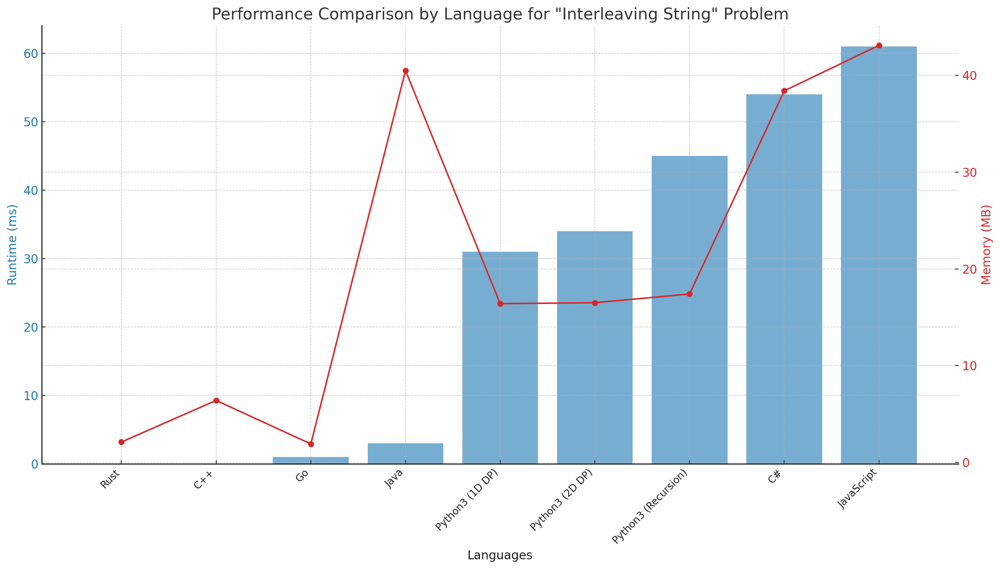\n\n# Code 1D Dynamic Programming \n``` Python []\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n, l = len(s1), len(s2), len(s3)\n if m + n != l:\n return False\n \n if m < n:\n return self.isInterleave(s2, s1, s3)\n \n dp = [False] * (n + 1)\n dp[0] = True\n \n for j in range(1, n + 1):\n dp[j] = dp[j-1] and s2[j-1] == s3[j-1]\n \n for i in range(1, m + 1):\n dp[0] = dp[0] and s1[i-1] == s3[i-1]\n for j in range(1, n + 1):\n dp[j] = (dp[j] and s1[i-1] == s3[i+j-1]) or (dp[j-1] and s2[j-1] == s3[i+j-1])\n \n return dp[n]\n```\n``` C++ []\nclass Solution {\npublic:\n bool isInterleave(string s1, string s2, string s3) {\n int m = s1.length(), n = s2.length(), l = s3.length();\n if (m + n != l) return false;\n \n if (m < n) return isInterleave(s2, s1, s3);\n\n vector<bool> dp(n + 1, false);\n dp[0] = true;\n\n for (int j = 1; j <= n; ++j) {\n dp[j] = dp[j - 1] && s2[j - 1] == s3[j - 1];\n }\n\n for (int i = 1; i <= m; ++i) {\n dp[0] = dp[0] && s1[i - 1] == s3[i - 1];\n for (int j = 1; j <= n; ++j) {\n dp[j] = (dp[j] && s1[i - 1] == s3[i + j - 1]) || (dp[j - 1] && s2[j - 1] == s3[i + j - 1]);\n }\n }\n \n return dp[n];\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean isInterleave(String s1, String s2, String s3) {\n int m = s1.length(), n = s2.length(), l = s3.length();\n if (m + n != l) return false;\n\n boolean[] dp = new boolean[n + 1];\n dp[0] = true;\n\n for (int j = 1; j <= n; ++j) {\n dp[j] = dp[j - 1] && s2.charAt(j - 1) == s3.charAt(j - 1);\n }\n\n for (int i = 1; i <= m; ++i) {\n dp[0] = dp[0] && s1.charAt(i - 1) == s3.charAt(i - 1);\n for (int j = 1; j <= n; ++j) {\n dp[j] = (dp[j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) || (dp[j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));\n }\n }\n \n return dp[n];\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn is_interleave(s1: String, s2: String, s3: String) -> bool {\n let (m, n, l) = (s1.len(), s2.len(), s3.len());\n if m + n != l { return false; }\n\n let (s1, s2, s3) = (s1.as_bytes(), s2.as_bytes(), s3.as_bytes());\n let mut dp = vec![false; n + 1];\n dp[0] = true;\n\n for j in 1..=n {\n dp[j] = dp[j - 1] && s2[j - 1] == s3[j - 1];\n }\n\n for i in 1..=m {\n dp[0] = dp[0] && s1[i - 1] == s3[i - 1];\n for j in 1..=n {\n dp[j] = (dp[j] && s1[i - 1] == s3[i + j - 1]) || (dp[j - 1] && s2[j - 1] == s3[i + j - 1]);\n }\n }\n \n dp[n]\n }\n}\n```\n``` Go []\nfunc isInterleave(s1 string, s2 string, s3 string) bool {\n m, n, l := len(s1), len(s2), len(s3)\n if m + n != l {\n return false\n }\n\n dp := make([]bool, n+1)\n dp[0] = true\n\n for j := 1; j <= n; j++ {\n dp[j] = dp[j-1] && s2[j-1] == s3[j-1]\n }\n\n for i := 1; i <= m; i++ {\n dp[0] = dp[0] && s1[i-1] == s3[i-1]\n for j := 1; j <= n; j++ {\n dp[j] = (dp[j] && s1[i-1] == s3[i+j-1]) || (dp[j-1] && s2[j-1] == s3[i+j-1])\n }\n }\n \n return dp[n]\n}\n```\n``` C# []\npublic class Solution {\n public bool IsInterleave(string s1, string s2, string s3) {\n int m = s1.Length, n = s2.Length, l = s3.Length;\n if (m + n != l) return false;\n\n bool[] dp = new bool[n + 1];\n dp[0] = true;\n\n for (int j = 1; j <= n; ++j) {\n dp[j] = dp[j - 1] && s2[j - 1] == s3[j - 1];\n }\n\n for (int i = 1; i <= m; ++i) {\n dp[0] = dp[0] && s1[i - 1] == s3[i - 1];\n for (int j = 1; j <= n; ++j) {\n dp[j] = (dp[j] && s1[i - 1] == s3[i + j - 1]) || (dp[j - 1] && s2[j - 1] == s3[i + j - 1]);\n }\n }\n \n return dp[n];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s1\n * @param {string} s2\n * @param {string} s3\n * @return {boolean}\n */\nvar isInterleave = function(s1, s2, s3) {\n let m = s1.length, n = s2.length, l = s3.length;\n if (m + n !== l) return false;\n\n let dp = new Array(n + 1).fill(false);\n dp[0] = true;\n\n for (let j = 1; j <= n; ++j) {\n dp[j] = dp[j - 1] && s2[j - 1] === s3[j - 1];\n }\n\n for (let i = 1; i <= m; ++i) {\n dp[0] = dp[0] && s1[i - 1] === s3[i - 1];\n for (let j = 1; j <= n; ++j) {\n dp[j] = (dp[j] && s1[i - 1] === s3[i + j - 1]) || (dp[j - 1] && s2[j - 1] === s3[i + j - 1]);\n }\n }\n \n return dp[n];\n};\n```\n\n# Code 2D Dynamic Programming \n``` Python []\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n, l = len(s1), len(s2), len(s3)\n if m + n != l:\n return False\n \n dp = [[False] * (n + 1) for _ in range(m + 1)]\n dp[0][0] = True\n \n for i in range(1, m + 1):\n dp[i][0] = dp[i-1][0] and s1[i-1] == s3[i-1]\n \n for j in range(1, n + 1):\n dp[0][j] = dp[0][j-1] and s2[j-1] == s3[j-1]\n \n for i in range(1, m + 1):\n for j in range(1, n + 1):\n dp[i][j] = (dp[i-1][j] and s1[i-1] == s3[i+j-1]) or (dp[i][j-1] and s2[j-1] == s3[i+j-1])\n \n return dp[m][n]\n\n```\n# Code Recursion with Memoization\n``` Python []\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n, l = len(s1), len(s2), len(s3)\n if m + n != l:\n return False\n \n memo = {} \n \n def helper(i: int, j: int, k: int) -> bool:\n if k == l:\n return True\n \n if (i, j) in memo:\n return memo[(i, j)]\n \n ans = False\n if i < m and s1[i] == s3[k]:\n ans = ans or helper(i + 1, j, k + 1)\n \n if j < n and s2[j] == s3[k]:\n ans = ans or helper(i, j + 1, k + 1)\n \n memo[(i, j)] = ans\n return ans\n \n return helper(0, 0, 0)\n```\n\nBoth the given approaches provide efficient ways to solve the problem, with the first approach focusing on optimizing space and the second leveraging the power of memoization to save time. Choosing between them depends on the specific constraints and requirements of the application. \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB | 185 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Python 98% 6 lines | interleaving-string | 0 | 1 | # Code\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n @cache\n def rec(i1, i2, i3):\n if i1 == len(s1) and i2 == len(s2) and i3 == len(s3):\n return True\n return i3 < len(s3) and (i1 < len(s1) and s1[i1] == s3[i3] and rec(i1+1, i2, i3+1) or i2 < len(s2) and s2[i2] == s3[i3] and rec(i1, i2+1, i3+1))\n \n return rec(0, 0, 0)\n``` | 1 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
DP Easy Best Approach!!! | interleaving-string | 0 | 1 | # Intuition\nEasy Best Approach!!!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nDynamic Programming Approach:\n\nThe key insight in this problem is to use dynamic programming to check if a certain interleaving of s1 and s2 can form s3. The DP array will be used to keep track of whether a certain prefix of s3 can be formed by interleaving a prefix of s1 and a prefix of s2.\n\nHere\'s how the dynamic programming approach works:\n\nInitialization: Create a DP array dp of dimensions (len_s1 + 1) \xD7 (len_s2 + 1). dp[i][j] will be True if the first i characters of s1 and the first j characters of s2 can interleave to form the first i + j characters of s3. Initialize dp[0][0] to True since two empty strings can form an empty string.\n\nBase Cases: Initialize the first row and the first column of the DP array. dp[0][j] is True if dp[0][j-1] is True and s2[j-1] matches s3[j-1]. Similarly, dp[i][0] is True if dp[i-1][0] is True and s1[i-1] matches s3[i-1].\n\nFilling the DP Array: Loop through the remaining cells of the DP array (starting from i = 1 and j = 1). The idea is to check if the current character in s3, which is s3[i+j-1], can be formed by either appending a character from s1 or a character from s2 to the previously formed interleaved strings.\n\nIf s1[i-1] matches s3[i+j-1] and dp[i-1][j] is True, then dp[i][j] is True.\nIf s2[j-1] matches s3[i+j-1] and dp[i][j-1] is True, then dp[i][j] is True.\nFinal Result: After filling the DP array, the value of dp[len_s1][len_s2] will indicate whether the entire strings s1 and s2 can interleave to form the entire string s3.\n\nThis approach ensures that you\'re considering all possible interleavings and checking if each character in s3 can be formed by interweaving characters from s1 and s2 in a valid manner.\n\nRemember, this is just one way to approach the problem using dynamic programming. There might be other creative ways to solve this problem as well.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(len_s1 * len_s2)\n- $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(len_s1 * len_s2)\n- $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n len_s1, len_s2, len_s3 = len(s1), len(s2), len(s3)\n \n # If the total length of s1 and s2 is not equal to s3, it\'s impossible\n if len_s1 + len_s2 != len_s3:\n return False\n \n # Create a 2D DP array to store intermediate results\n dp = [[False] * (len_s2 + 1) for _ in range(len_s1 + 1)]\n \n # Base case: empty strings can always interleave to form an empty string\n dp[0][0] = True\n \n # Fill the first row\n for j in range(1, len_s2 + 1):\n dp[0][j] = dp[0][j - 1] and s2[j - 1] == s3[j - 1]\n \n # Fill the first column\n for i in range(1, len_s1 + 1):\n dp[i][0] = dp[i - 1][0] and s1[i - 1] == s3[i - 1]\n \n # Fill the DP array\n for i in range(1, len_s1 + 1):\n for j in range(1, len_s2 + 1):\n # Check if the current position in s3 can be formed by interleaving\n dp[i][j] = (dp[i - 1][j] and s1[i - 1] == s3[i + j - 1]) or \\\n (dp[i][j - 1] and s2[j - 1] == s3[i + j - 1])\n \n return dp[len_s1][len_s2]\n\n``` | 23 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
[Python3] DP Top-Down -> Bottom-Up - Simple | interleaving-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n1. Top-Down\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n = len(s1), len(s2)\n if m + n != len(s3): return False\n \n @cache\n def dp(i: int, j: int) -> bool:\n if i < 0 and j < 0: return True\n ans = False\n if i >= 0 and s1[i] == s3[i + j + 1]: ans |= dp(i - 1, j)\n if j >= 0 and s2[j] == s3[i + j + 1]: ans |= dp(i, j - 1)\n return ans\n\n return dp(m - 1, n - 1)\n```\n- TC: $$O(N^2)$$\n- SC: $$O(N^2)$$\n\n2. Bottom-Up\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n = len(s1), len(s2)\n if m + n != len(s3): return False\n\n dp = [[False for _ in range(n + 1)] for _ in range(m + 1)]\n dp[0][0] = True\n for i in range(-1, m):\n for j in range(-1, n):\n if i >= 0 and s1[i] == s3[i + j + 1]: dp[i + 1][j + 1] |= dp[i][j + 1]\n if j >= 0 and s2[j] == s3[i + j + 1]: dp[i + 1][j + 1] |= dp[i + 1][j]\n return dp[m][n]\n```\n- TC: $$O(N^2)$$\n- SC: $$O(N^2)$$\n | 3 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Easy Python solution !! recursive | interleaving-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n n1=len(s1)\n n2=len(s2)\n n3=len(s3)\n @cache\n def isInter(i1,i2,i3):\n if i1==n1 and i2==n2 and i3==n3:\n return True\n\n return i3<n3 and (i1<n1 and s1[i1]==s3[i3] and isInter(i1+1,i2,i3+1) or i2<n2 and s2[i2]==s3[i3] and isInter(i1,i2+1,i3+1))\n\n return isInter(0,0,0) \n``` | 0 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
critique of the solution | interleaving-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n\n if len(s1) + len(s2) != len(s3):\n return False\n \n array = [False for i in range(len(s2)+1)]\n if len(s1) > 0:\n array[0] = array[0] or s1[0] == s3[0]\n if len(s2) > 0:\n array[0] = array[0] or s2[0] == s3[0]\n if len(s1) + len(s2) == 0:\n return True \n\n for i in range(len(s3)):\n for j in range(min(len(s2)-1, i), -1, -1):\n if array[j]:\n array[j+1] = array[j] and s2[j] == s3[i]\n if i-j < len(s1):\n array[j] = array[j] and s1[i-j] == s3[i]\n else:\n array[j] = False\n \n\n \n return any(array)\n \n``` | 0 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
✅Easy Solution🔥Python3/C#/C++/Java🔥Using DFS🔥With 🗺️Image🗺️ | interleaving-string | 1 | 1 | ```Python3 []\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n if len(s1) + len(s2) != len(s3):\n return False\n\n dp = [ [False] * (len(s2) + 1) for i in range(len(s1) + 1)]\n dp[len(s1)][len(s2)] = True\n\n for i in range(len(s1), -1, -1):\n for j in range(len(s2), -1, -1):\n if i < len(s1) and s1[i] == s3[i +j] and dp[i + 1][j]:\n dp[i][j] = True\n if j < len(s2) and s2[j] == s3[i + j] and dp[i][j + 1]:\n dp[i][j] = True\n return dp[0][0]\n\n\n\n dp = {}\n def dfs(i, j):\n if i == len(s1) and j == len(s2):\n return True\n if (i, j) in dp:\n return dp[(i, j)]\n\n if i < len(s1) and s1[i] == s3[i+j] and dfs(i + 1, j):\n return True\n \n if j < len(s2) and s2[j] == s3[i + j] and dfs(i, j + 1):\n return True\n \n dp[(i, j)] = False\n return False\n return dfs(0, 0)\n```\n```python []\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n if len(s1) + len(s2) != len(s3):\n return False\n\n dp = [ [False] * (len(s2) + 1) for i in range(len(s1) + 1)]\n dp[len(s1)][len(s2)] = True\n\n for i in range(len(s1), -1, -1):\n for j in range(len(s2), -1, -1):\n if i < len(s1) and s1[i] == s3[i +j] and dp[i + 1][j]:\n dp[i][j] = True\n if j < len(s2) and s2[j] == s3[i + j] and dp[i][j + 1]:\n dp[i][j] = True\n return dp[0][0]\n\n\n\n dp = {}\n def dfs(i, j):\n if i == len(s1) and j == len(s2):\n return True\n if (i, j) in dp:\n return dp[(i, j)]\n\n if i < len(s1) and s1[i] == s3[i+j] and dfs(i + 1, j):\n return True\n \n if j < len(s2) and s2[j] == s3[i + j] and dfs(i, j + 1):\n return True\n \n dp[(i, j)] = False\n return False\n return dfs(0, 0)\n```\n```C# []\npublic class Solution {\n public bool IsInterleave(string s1, string s2, string s3) {\n if (s1.Length + s2.Length != s3.Length) {\n return false;\n }\n\n bool[,] dp = new bool[s1.Length + 1, s2.Length + 1];\n dp[s1.Length, s2.Length] = true;\n\n for (int i = s1.Length; i >= 0; i--) {\n for (int j = s2.Length; j >= 0; j--) {\n if (i < s1.Length && s1[i] == s3[i + j] && dp[i + 1, j]) {\n dp[i, j] = true;\n }\n if (j < s2.Length && s2[j] == s3[i + j] && dp[i, j + 1]) {\n dp[i, j] = true;\n }\n }\n }\n return dp[0, 0];\n }\n\n private Dictionary<(int, int), bool> dp = new Dictionary<(int, int), bool>();\n private bool DFS(int i, int j, string s1, string s2, string s3) {\n if (i == s1.Length && j == s2.Length) {\n return true;\n }\n if (dp.ContainsKey((i, j))) {\n return dp[(i, j)];\n }\n\n bool result = false;\n if (i < s1.Length && s1[i] == s3[i + j] && DFS(i + 1, j, s1, s2, s3)) {\n result = true;\n }\n if (j < s2.Length && s2[j] == s3[i + j] && DFS(i, j + 1, s1, s2, s3)) {\n result = true;\n }\n\n dp[(i, j)] = result;\n return result;\n }\n}\n```\n```C++ []\n#include <unordered_map>\nusing namespace std;\n\nclass Solution {\npublic:\n bool isInterleave(string s1, string s2, string s3) {\n if (s1.length() + s2.length() != s3.length()) {\n return false;\n }\n\n vector<vector<bool>> dp(s1.length() + 1, vector<bool>(s2.length() + 1, false));\n dp[s1.length()][s2.length()] = true;\n\n for (int i = s1.length(); i >= 0; i--) {\n for (int j = s2.length(); j >= 0; j--) {\n if (i < s1.length() && s1[i] == s3[i + j] && dp[i + 1][j]) {\n dp[i][j] = true;\n }\n if (j < s2.length() && s2[j] == s3[i + j] && dp[i][j + 1]) {\n dp[i][j] = true;\n }\n }\n }\n return dp[0][0];\n }\n\nprivate:\n struct PairHash {\n template <class T1, class T2>\n size_t operator() (const pair<T1, T2>& p) const {\n auto h1 = hash<T1>{}(p.first);\n auto h2 = hash<T2>{}(p.second);\n return h1 ^ (h2 << 1);\n }\n };\n \n unordered_map<pair<int, int>, bool, PairHash> dp;\n bool dfs(int i, int j, string& s1, string& s2, string& s3) {\n if (i == s1.length() && j == s2.length()) {\n return true;\n }\n if (dp.find({i, j}) != dp.end()) {\n return dp[{i, j}];\n }\n\n bool result = false;\n if (i < s1.length() && s1[i] == s3[i + j] && dfs(i + 1, j, s1, s2, s3)) {\n result = true;\n }\n if (j < s2.length() && s2[j] == s3[i + j] && dfs(i, j + 1, s1, s2, s3)) {\n result = true;\n }\n\n dp[{i, j}] = result;\n return result;\n }\n};\n```\n```Java []\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass Solution {\n public boolean isInterleave(String s1, String s2, String s3) {\n if (s1.length() + s2.length() != s3.length()) {\n return false;\n }\n\n boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1];\n dp[s1.length()][s2.length()] = true;\n\n for (int i = s1.length(); i >= 0; i--) {\n for (int j = s2.length(); j >= 0; j--) {\n if (i < s1.length() && s1.charAt(i) == s3.charAt(i + j) && dp[i + 1][j]) {\n dp[i][j] = true;\n }\n if (j < s2.length() && s2.charAt(j) == s3.charAt(i + j) && dp[i][j + 1]) {\n dp[i][j] = true;\n }\n }\n }\n return dp[0][0];\n }\n\n private Map<Pair, Boolean> dp = new HashMap<>();\n private boolean dfs(int i, int j, String s1, String s2, String s3) {\n if (i == s1.length() && j == s2.length()) {\n return true;\n }\n Pair pair = new Pair(i, j);\n if (dp.containsKey(pair)) {\n return dp.get(pair);\n }\n\n boolean result = false;\n if (i < s1.length() && s1.charAt(i) == s3.charAt(i + j) && dfs(i + 1, j, s1, s2, s3)) {\n result = true;\n }\n if (j < s2.length() && s2.charAt(j) == s3.charAt(i + j) && dfs(i, j + 1, s1, s2, s3)) {\n result = true;\n }\n\n dp.put(pair, result);\n return result;\n }\n\n private class Pair {\n int first;\n int second;\n\n Pair(int first, int second) {\n this.first = first;\n this.second = second;\n }\n\n @Override\n public int hashCode() {\n return first * 31 + second;\n }\n\n @Override\n public boolean equals(Object obj) {\n if (this == obj) return true;\n if (obj == null || getClass() != obj.getClass()) return false;\n Pair other = (Pair) obj;\n return first == other.first && second == other.second;\n }\n }\n}\n```\n\n | 15 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Python | Easy to Understand | Fast | DP-Tabulation | interleaving-string | 0 | 1 | # Python | Easy to Understand | Fast | DP-Tabulation\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n = len(s1), len(s2)\n if m + n != len(s3):\n return False\n dp = [[False] * (n + 1) for _ in range(m + 1)]\n dp[0][0] = True\n for i in range(1, m + 1):\n dp[i][0] = dp[i - 1][0] and s1[i - 1] == s3[i - 1]\n for j in range(1, n + 1):\n dp[0][j] = dp[0][j - 1] and s2[j - 1] == s3[j - 1]\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n choose_s1, choose_s2 = False, False\n if s1[i - 1] == s3[i + j - 1]:\n choose_s1 = dp[i - 1][j]\n if s2[j - 1] == s3[i + j - 1]:\n choose_s2 = dp[i][j - 1]\n dp[i][j] = choose_s1 or choose_s2\n\n return dp[m][n]\n\n``` | 4 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | interleaving-string | 1 | 1 | # Intuition\nThe problem of determining whether one string is an interleaving of two others can be approached using dynamic programming. The core intuition lies in breaking down the problem into smaller subproblems. Essentially, we want to determine if the characters from both strings, s1 and s2, can be interwoven to create the target string s3. We aim to build a dynamic programming matrix that stores the state of the interleaving at different points, helping us track the possibilities.\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 247 videos as of August 25th.\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize `dp` array: Create an array `dp` of size `(len(s2) + 1)` to store whether substrings of `s1` and `s2` can interleave to form substrings of `s3`.\n\n2. Check total length: If the sum of the lengths of `s1` and `s2` is not equal to the length of `s3`, return `False` since it\'s impossible for `s1` and `s2` to interleave to form `s3`.\n\n3. Initialization: Set `dp[0]` to `True` to indicate that an empty `s1` and empty `s2` can interleave to form an empty `s3`.\n\n4. Loop through `s1` and `s2`: Use nested loops to iterate through all possible combinations of substrings of `s1` and `s2` to check if they can interleave to form `s3`.\n\n5. Base cases handling:\n - If `i` is `0` and `j` is `0`, it means both `s1` and `s2` are empty. Set `dp[j]` to `True`.\n - If `i` is `0`, update `dp[j]` using the previous value of `dp[j - 1]` and check if the character in `s2` at index `j - 1` matches the character in `s3` at index `i + j - 1`.\n - If `j` is `0`, update `dp[j]` using the current value of `dp[j]` and check if the character in `s1` at index `i - 1` matches the character in `s3` at index `i + j - 1`.\n\n6. General case:\n - For all other cases (when both `i` and `j` are not `0`), update `dp[j]` using the following conditions:\n - `dp[j]` should be the result of `(dp[j] and s1[i - 1] == s3[i + j - 1])`, meaning that the current character in `s1` matches the current character in `s3`, and the previous substring also interleave to form the previous part of `s3`.\n - `dp[j - 1]` should be the result of `(dp[j - 1] and s2[j - 1] == s3[i + j - 1])`, meaning that the current character in `s2` matches the current character in `s3`, and the previous substring of `s2` can interleave to form the previous part of `s3`.\n\n7. Return result: The final result is stored in `dp[len(s2)]`, which indicates whether `s1` and `s2` can interleave to form `s3`.\n\n8. The function returns the value of `dp[len(s2)]` as the final result.\n\nIn summary, the algorithm uses dynamic programming to determine whether substrings of `s1` and `s2` can be interleaved to form substrings of `s3`. The `dp` array stores whether the substrings can interleave at each position.\n\n# Complexity\n- Time complexity: O(m * n)\nm is the length of string s1 and n is the length of string s2. This is because we iterate through each character of s1 and s2 once while constructing the dynamic programming matrix.\n\n- Space complexity: O(n),\nn is the length of string s2. We only use a dynamic programming array of length n+1 to store the state transitions.\n\n```python []\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n # Check if the combined length of s1 and s2 matches the length of s3\n if len(s1) + len(s2) != len(s3):\n return False\n \n # Initialize a dynamic programming array dp\n # dp[j] will store whether s1[0:i] and s2[0:j] can form s3[0:i+j]\n dp = [False] * (len(s2) + 1)\n \n for i in range(len(s1) + 1):\n for j in range(len(s2) + 1):\n if i == 0 and j == 0:\n # Base case: Both s1 and s2 are empty, so s3 is also empty.\n # Set dp[j] to True.\n dp[j] = True\n elif i == 0:\n # Base case: s1 is empty, so check if the previous dp[j-1]\n # is True and if s2[j-1] matches s3[i+j-1].\n dp[j] = dp[j - 1] and s2[j - 1] == s3[i + j - 1]\n elif j == 0:\n # Base case: s2 is empty, so check if the current dp[j]\n # is True and if s1[i-1] matches s3[i+j-1].\n dp[j] = dp[j] and s1[i - 1] == s3[i + j - 1]\n else:\n # General case: Check if either the previous dp[j] or dp[j-1]\n # is True and if the corresponding characters match s3[i+j-1].\n dp[j] = (dp[j] and s1[i - 1] == s3[i + j - 1]) or (dp[j - 1] and s2[j - 1] == s3[i + j - 1])\n\n # Return the result stored in dp[len(s2)], which indicates whether\n # s1 and s2 can form s3 by interleaving characters.\n return dp[len(s2)]\n\n```\n```javascript []\n/**\n * @param {string} s1\n * @param {string} s2\n * @param {string} s3\n * @return {boolean}\n */\nvar isInterleave = function(s1, s2, s3) {\n if (s1.length + s2.length !== s3.length) {\n return false;\n }\n \n const dp = new Array(s2.length + 1).fill(false);\n \n for (let i = 0; i <= s1.length; i++) {\n for (let j = 0; j <= s2.length; j++) {\n if (i === 0 && j === 0) {\n dp[j] = true;\n } else if (i === 0) {\n dp[j] = dp[j - 1] && s2[j - 1] === s3[i + j - 1];\n } else if (j === 0) {\n dp[j] = dp[j] && s1[i - 1] === s3[i + j - 1];\n } else {\n dp[j] = (dp[j] && s1[i - 1] === s3[i + j - 1]) || (dp[j - 1] && s2[j - 1] === s3[i + j - 1]);\n }\n }\n }\n \n return dp[s2.length]; \n};\n```\n```java []\nclass Solution {\n public boolean isInterleave(String s1, String s2, String s3) {\n if (s1.length() + s2.length() != s3.length()) {\n return false;\n }\n \n boolean[] dp = new boolean[s2.length() + 1];\n \n for (int i = 0; i <= s1.length(); i++) {\n for (int j = 0; j <= s2.length(); j++) {\n if (i == 0 && j == 0) {\n dp[j] = true;\n } else if (i == 0) {\n dp[j] = dp[j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1);\n } else if (j == 0) {\n dp[j] = dp[j] && s1.charAt(i - 1) == s3.charAt(i + j - 1);\n } else {\n dp[j] = (dp[j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) || (dp[j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));\n }\n }\n }\n \n return dp[s2.length()]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool isInterleave(string s1, string s2, string s3) {\n if (s1.length() + s2.length() != s3.length()) {\n return false;\n }\n \n vector<bool> dp(s2.length() + 1, false);\n \n for (int i = 0; i <= s1.length(); i++) {\n for (int j = 0; j <= s2.length(); j++) {\n if (i == 0 && j == 0) {\n dp[j] = true;\n } else if (i == 0) {\n dp[j] = dp[j - 1] && s2[j - 1] == s3[i + j - 1];\n } else if (j == 0) {\n dp[j] = dp[j] && s1[i - 1] == s3[i + j - 1];\n } else {\n dp[j] = (dp[j] && s1[i - 1] == s3[i + j - 1]) || (dp[j - 1] && s2[j - 1] == s3[i + j - 1]);\n }\n }\n }\n \n return dp[s2.length()]; \n }\n};\n```\n | 7 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Python3 Solution | interleaving-string | 0 | 1 | \n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n n1=len(s1)\n n2=len(s2)\n n3=len(s3)\n @cache\n def isInter(i1,i2,i3):\n if i1==n1 and i2==n2 and i3==n3:\n return True\n\n return i3<n3 and (i1<n1 and s1[i1]==s3[i3] and isInter(i1+1,i2,i3+1) or i2<n2 and s2[i2]==s3[i3] and isInter(i1,i2+1,i3+1))\n\n return isInter(0,0,0) \n``` | 5 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Backtracking with Memoization (Easy to Understand!!) | interleaving-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIdea is that we create this type of a path \n\n\n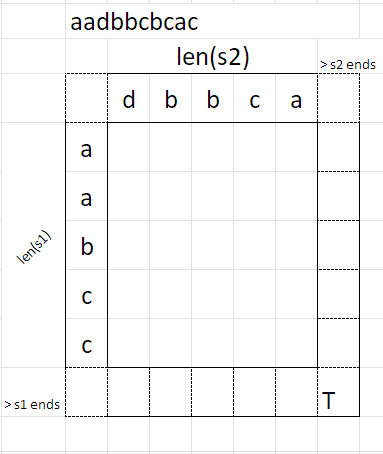\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIf char from s1 is chosen we travel downwards (i+1 ,j) \n\nand char from s2 is chosen we travel to the right.\n\nand there we update the value.\n\n\n\nThe trace on the dict is as follows :\n\n{(5, 3): False, (5, 5): True, (4, 5): True, (4, 4): True, (4, 3): True, (4, 2): True, (3, 2): True, (3, 1): True, (2, 1): True, (2, 0): True, (1, 0): True, (0, 0): True}\n\nGoing from last to first The right path would be like:\n\n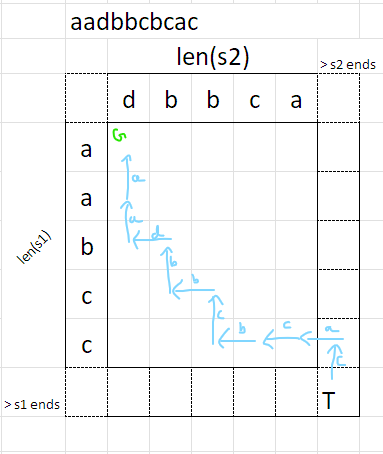\n\nNote :**The movement is backwards and we check the incremented cell before we update our current cell.**\n\nIn this wrong trace where \'c\' was chosen from s1 , we would not have gotten the subset and thus that backtracking run has failed\n\n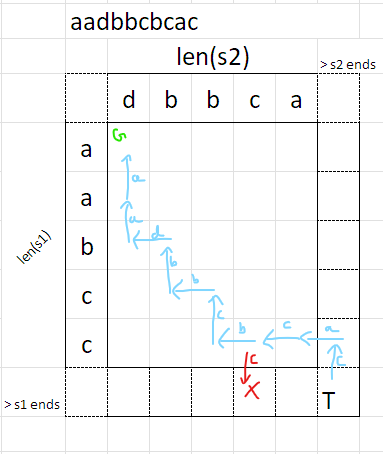\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m*n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m*n)\n\n\n# Code\n```\nclass Solution:\n\n \'\'\'\n This recursion goes all in and backtracks\n\n Goal string : aadbbcbcac\n\n +---+---+---+---+---+---+\n | | d | b | b | c | |\n +---+---+---+---+---+---+\n | a | | | | | |\n +---+---+---+---+---+---+\n | a | | | | | |\n +---+---+---+---+---+---+\n | b | | | | | |\n +---+---+---+---+---+---+\n | c | | | | | |\n +---+---+---+---+---+---+\n | c | | | | | |\n +---+---+---+---+---+---+\n | | | | | | T |\n +---+---+---+---+---+---+\n\n\n \'\'\'\n \n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n def topDownBacktrack(i,j):\n # Bottom Up approach This is the goal state\n if i == len(s1) and j == len(s2):\n return True \n # using memo\n if (i,j) in dp:\n return dp[(i,j)]\n\n if i < len(s1) and s1[i] == s3[i+j] and topDownBacktrack(i+1,j) : # Checking if we take the s1 substring \n dp[(i,j)] = True\n return True\n if j < len(s2) and s2[j] == s3[i+j] and topDownBacktrack(i,j+1) : # Checking if we take the s2 substring\n dp[(i,j)] = True\n return True\n dp[(i,j)] = False\n return False\n \n\n if len(s1) +len(s2) != len(s3):\n return False\n\n dp = {} #memo : [(i,j)] = True or False, need to only mark false nodes\n \n\n \n \n\n # while i <= len(s1) and j <=len(s2) and i+j len(s3):\n \n \n \n return topDownBacktrack(0,0)\n \n``` | 2 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Interleaving String python3 with comments step by step explanation | interleaving-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nOne way to form s3 from s1 and s2 is to take one character from s1 or s2 at a time and append it to s3. We can keep track of the index of the last character from s1 and s2 that was appended to s3. If at any point, we cannot append a character to s3, we backtrack and try a different path.\n\nTo optimize this approach, we can use dynamic programming. We can define a 2D boolean array dp, where dp[i][j] is true if s3[0:i+j] can be formed by an interleaving of s1[0:i] and s2[0:j].\n\nThe base case is when i = j = 0, and dp[0][0] is true. If either i or j is zero, then dp[i][j] is true if s3[0:i+j] is equal to either s1[0:i] or s2[0:j].\n\nFor the general case, if the last character of s1 matches the last character of s3, then we can append it to s3 and check if dp[i-1][j] is true. Similarly, if the last character of s2 matches the last character of s3, then we can append it to s3 and check if dp[i][j-1] is true.\n\nThe final answer is dp[m][n], where m is the length of s1 and n is the length of s2.\n\nTime complexity: O(mn), where m is the length of s1 and n is the length of s2.\nSpace complexity: O(mn), where m is the length of s1 and n is the length of s2.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isInterleave(self, s1: str, s2: str, s3: str) -> bool:\n m, n = len(s1), len(s2)\n if m + n != len(s3):\n return False\n \n dp = [[False] * (n+1) for _ in range(m+1)]\n dp[0][0] = True\n \n for i in range(m+1):\n for j in range(n+1):\n if i > 0 and s1[i-1] == s3[i+j-1]:\n dp[i][j] = dp[i][j] or dp[i-1][j]\n if j > 0 and s2[j-1] == s3[i+j-1]:\n dp[i][j] = dp[i][j] or dp[i][j-1]\n \n return dp[m][n]\n\n\n``` | 10 | Given strings `s1`, `s2`, and `s3`, find whether `s3` is formed by an **interleaving** of `s1` and `s2`.
An **interleaving** of two strings `s` and `t` is a configuration where `s` and `t` are divided into `n` and `m` substrings respectively, such that:
* `s = s1 + s2 + ... + sn`
* `t = t1 + t2 + ... + tm`
* `|n - m| <= 1`
* The **interleaving** is `s1 + t1 + s2 + t2 + s3 + t3 + ...` or `t1 + s1 + t2 + s2 + t3 + s3 + ...`
**Note:** `a + b` is the concatenation of strings `a` and `b`.
**Example 1:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbcbcac "
**Output:** true
**Explanation:** One way to obtain s3 is:
Split s1 into s1 = "aa " + "bc " + "c ", and s2 into s2 = "dbbc " + "a ".
Interleaving the two splits, we get "aa " + "dbbc " + "bc " + "a " + "c " = "aadbbcbcac ".
Since s3 can be obtained by interleaving s1 and s2, we return true.
**Example 2:**
**Input:** s1 = "aabcc ", s2 = "dbbca ", s3 = "aadbbbaccc "
**Output:** false
**Explanation:** Notice how it is impossible to interleave s2 with any other string to obtain s3.
**Example 3:**
**Input:** s1 = " ", s2 = " ", s3 = " "
**Output:** true
**Constraints:**
* `0 <= s1.length, s2.length <= 100`
* `0 <= s3.length <= 200`
* `s1`, `s2`, and `s3` consist of lowercase English letters.
**Follow up:** Could you solve it using only `O(s2.length)` additional memory space? | null |
Solution | validate-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\n\nbool isPossible(TreeNode* root, long long l, long long r){\n if(root == nullptr) return true;\n if(root->val < r and root->val > l)\n return isPossible(root->left, l, root->val) and \n isPossible(root->right, root->val, r);\n else return false;\n}\n\npublic:\n bool isValidBST(TreeNode* root) {\n long long int min = -1000000000000, max = 1000000000000;\n return isPossible(root, min, max);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n prev = float(\'-inf\')\n def inorder(node):\n nonlocal prev\n if not node:\n return True\n if not (inorder(node.left) and prev < node.val):\n return False\n prev = node.val\n return inorder(node.right)\n return inorder(root)\n```\n\n```Java []\nclass Solution {\n private long minVal = Long.MIN_VALUE;\n public boolean isValidBST(TreeNode root) {\n if (root == null) return true; \n if (!isValidBST(root.left)) return false;\n \n if (minVal >= root.val) return false; \n\n minVal = root.val;\n\n if (!isValidBST(root.right)) return false;\n\n return true;\n } \n}\n```\n | 464 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Recursive approach✅ | O( n)✅ | (Step by step explanation)✅ | validate-binary-search-tree | 0 | 1 | # Intuition\nThe problem requires checking whether a binary tree is a valid binary search tree (BST). A BST is a binary tree where for each node, the values of all nodes in its left subtree are less than the node\'s value, and the values of all nodes in its right subtree are greater than the node\'s value.\n\n# Approach\nThe approach is based on a recursive algorithm. At each node, we check if its value lies within a certain range, which is determined by its position in the tree. The initial range for the root is (-\u221E, +\u221E). As we traverse the tree, the range narrows down for each node based on its value and position.\n\n1. **Initialization**: Start with the root of the binary tree and an initial range of (-\u221E, +\u221E).\n\n **Reason**: We begin the recursive check from the root with an unbounded range.\n\n2. **Range Check**: For each node, check if its value lies within the current range. If the value is not within the range, return false.\n\n **Reason**: A binary tree is a valid BST only if the values of its nodes satisfy the BST property.\n\n3. **Recursive Check**: Recursively check the left and right subtrees of the current node, updating the range accordingly.\n\n **Reason**: We need to check the left and right subtrees to ensure the entire tree satisfies the BST property.\n\n4. **Termination Condition**: If we reach a null node, return true, as a null node is a valid BST.\n\n **Reason**: The recursion should terminate when we reach the end of a branch.\n\n5. **Result**: The final result is the boolean value returned by the recursive function.\n\n **Reason**: The result indicates whether the entire binary tree is a valid BST.\n\n# Complexity\n- **Time complexity**: O(n)\n - We visit each node once during the recursive check.\n- **Space complexity**: O(h)\n - The maximum depth of the recursion stack is the height of the binary tree. In the worst case, the space complexity is proportional to the height of the tree.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n def bst(root, min_val=float(\'-inf\'), max_val=float(\'inf\')):\n if root == None:\n return True\n\n if not (min_val < root.val < max_val):\n return False\n\n return (bst(root.left, min_val, root.val) and\n bst(root.right, root.val, max_val))\n\n return bst(root)\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n bool isValidBST(TreeNode* root) {\n return bst(root, LLONG_MIN, LLONG_MAX);\n }\n\n bool bst(TreeNode* root, long long min_val, long long max_val) {\n if (root == NULL) {\n return true;\n }\n\n if (!(min_val < root->val && root->val < max_val)) {\n return false;\n }\n\n return bst(root->left, min_val, root->val) && bst(root->right, root->val, max_val);\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n | 5 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Python - Simple Solution | validate-binary-search-tree | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n \n def solve(root, min_val, max_val):\n if root is None:\n return True\n \n if root.val <= min_val or root.val >= max_val:\n return False\n\n left = solve(root.left, min_val, root.val)\n right = solve(root.right, root.val, max_val)\n return left and right \n\n return solve(root, float(\'-inf\'), float(\'inf\'))\n``` | 7 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Easy iterative solution in Python. | validate-binary-search-tree | 0 | 1 | \n# Code\n```\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n stack=[]\n stack.append([root,-1*float(\'inf\'),float(\'inf\')])\n while(stack):\n s=stack.pop()\n t=s[0]\n le=s[1]\n ri=s[2]\n if t.val<=le or t.val>=ri:\n return False\n if t.right!=None:\n stack.append([t.right,t.val,ri])\n if t.left!=None:\n stack.append([t.left,le,t.val])\n return True\n``` | 2 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Superb Lgic BST | validate-binary-search-tree | 0 | 1 | ```\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n def BST(root,mx,mi):\n if not root:\n return True\n elif root.val>=mx or root.val<=mi:\n return False\n else:\n return BST(root.left,root.val,mi) and BST(root.right,mx,root.val)\n return BST(root,float(\'inf\'),float(\'-inf\'))\n```\n# please upvote me it would encourage me alot\n | 12 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Python/JS/Java/Go/C++ O(n) by DFS and rule [w/ Hint] | validate-binary-search-tree | 1 | 1 | O( n ) sol. by divide-and-conquer.\n\n[\u672C\u984C\u5C0D\u61C9\u7684\u4E2D\u6587\u89E3\u984C\u6587\u7AE0](https://vocus.cc/article/650988e9fd897800019a383f)\n\n---\n\n**Hint**:\n\nThink of BST rule:\n**Left sub-tree** nodes\' value **< current** node value\n**Right sub-tree** nodes\' value **> current** node value\n\n---\n\n**Algorithm**:\n\nStep_#1:\nSet upper bound as maximum integer, and lower bound as minimum integer in run-time environment.\n\nStep_#2:\nStart DFS traversal from root node, and check whether each level follow BST rules or not.\nUpdate lower bound and upper bound before going down to next level.\n\nStep_#3:\nOnce we find the violation, reject and early return False.\nOtherwise, accept and return True if all tree nodes follow BST rule.\n\n---\n\nPython\n\n```\nclass Solution:\n def isValidBST(self, root: TreeNode) -> bool:\n \n # Use maximal system integer to represent infinity\n INF = sys.maxsize\n \n def helper(node, lower, upper):\n \n if not node:\n\t\t\t\t# empty node or empty tree\n return True\n \n if lower < node.val < upper:\n\t\t\t\t# check if all tree nodes follow BST rule\n return helper(node.left, lower, node.val) and helper(node.right, node.val, upper)\n \n else:\n\t\t\t\t# early reject when we find violation\n return False\n \n # ----------------------------------\n \n return helper( node=root, lower=-INF, upper=INF )\n```\n\n---\n\nJava\n\n<details>\n\t<summary>Click to show source code\n\t</summary>\n\n```\nclass Solution {\n public boolean isValidBST(TreeNode root) {\n \n return checker( -INF, INF, root);\n }\n \n private boolean checker( long lower, long upper, TreeNode node ){\n \n if( node == null ){\n return true;\n }\n \n if( (lower < node.val) && ( node.val < upper ) ){\n return checker(lower, node.val, node.left) && checker(node.val, upper, node.right);\n }\n \n return false;\n }\n \n private long INF = Long.MAX_VALUE;\n\n}\n```\n\n</details>\n\n---\n\nC++\n\n<details>\n\t<summary>Click to show source code\n\t</summary>\n\t\n```\n\tclass Solution {\n\tpublic:\n\t\tbool isValidBST(TreeNode* root) {\n\n\t\t\treturn validate(root, std::numeric_limits<long>::min(), std::numeric_limits<long>::max() );\n\t\t}\n\n\tprivate:\n\t\tbool validate(TreeNode* node, long lower, long upper){\n\n\t\t\tif( node == NULL ){\n\n\t\t\t\t// empty node or empty tree is valid always\n\t\t\t\treturn true;\n\t\t\t}\n\n\t\t\tif( (lower < node->val) && (node->val < upper) ){\n\n\t\t\t\t// check if all tree nodes follow BST rule\n\t\t\t\treturn validate(node->left, lower, node->val) && validate(node->right, node->val, upper);\n\t\t\t}\n\t\t\telse{\n\t\t\t\t// early reject when we find violation\n\t\t\t\treturn false;\n\t\t\t}\n\n\n\t\t}\n\t};\n```\n\n</details>\n\n,or\n\n<details>\n\t<summary>Click to show source code\n\t</summary>\n\t\n```\nclass Solution {\npublic:\n bool isValidBST(TreeNode* root) {\n \n prev = NULL;\n \n return validate(root );\n }\n \nprivate:\n TreeNode *prev;\n bool validate(TreeNode* node){\n \n if( node == NULL ){\n \n // empty node or empty tree is valid always\n return true;\n }\n \n \n if( !validate(node->left ) ){\n return false;\n }\n \n if( prev != NULL && (node->val <= prev -> val) ){\n return false;\n }\n prev = node;\n \n return validate(node->right);\n \n }\n};\n```\n\n</details>\n\n\n\n---\nGo\n\n<details>\n\t<summary>Click to show source code\n\t</summary>\n\t\n```\nfunc isValidBST(root *TreeNode) bool {\n \n return validate( root, math.MinInt, math.MaxInt)\n}\n\nfunc validate(node *TreeNode, lower int, upper int)bool{\n \n if node == nil{\n \n //empty node or empty tree is always valid\n return true\n }\n \n if( (lower < node.Val) && (node.Val < upper) ){\n \n // check if all tree nodes follow BST rule\n return validate( node.Left, lower, node.Val ) && validate( node.Right, node.Val, upper )\n }else{\n \n // early reject when we find violation\n return false\n }\n \n}\n```\n\n</details>\n\n---\n\nJavascript\n\n<details>\n\t<summary>Click to show source code\n\t</summary>\n\t\n```\nvar isValidBST = function(root) {\n \n return validate(root, -Infinity, Infinity);\n};\n\n\nvar validate = function(node, lower,upper){\n \n if ( node == null ){\n \n // empty node or empty tree\n return true;\n }\n \n if( (lower < node.val) && ( node.val < upper ) ){\n \n // check if all tree nodes follow BST rule\n return validate( node.left, lower, node.val) && validate( node.right, node.val, upper);\n }else{\n \n // early reject when we find violation\n return false;\n }\n \n}\n```\n\n</details>\n\n---\n\nShare anotehr implementation with well-ordered property of BST\'s inorder traversal\n\n```\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n \n def checker(node):\n \n if not node:\n\t\t\t\t## Base case\n # empty node or empty tree\n yield True\n \n else:\n ## General cases:\n\n yield from checker(node.left)\n\n if checker.prev and (checker.prev.val >= node.val):\n # previous node should be smaller then current node\n # find violation\n yield False\n\n checker.prev = node\n\n yield from checker(node.right)\n \n return\n # ---------------------------------------\n \n # use the property that inorder traversla of BST outputs sorted ascending sequence naturally\n checker.prev = None\n return all( checker(root) )\n```\n\n---\n\nRelative leetcode challenge\n\n[Leetcode #99 Recover Binary Search Tree](https://leetcode.com/problems/recover-binary-search-tree/)\n\n[Leetcode #700 Search in a Binary Search Tree](https://leetcode.com/problems/search-in-a-binary-search-tree/) | 102 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
binbin loves bright colors | validate-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode]) -> bool:\n def more_than_one_node(node,Min,Max):\n # print(node,Min,Max)\n if not node:\n return True\n if node.val <= Min or node.val >= Max:\n return False\n return more_than_one_node(node.left,Min,node.val) and more_than_one_node(node.right,node.val,Max)\n \n return more_than_one_node(root,-2**31-1,2**31)\n \n \n``` | 1 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Fastest Python one line solution | validate-binary-search-tree | 0 | 1 | \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isValidBST(self, root: Optional[TreeNode], min_val=float(-inf), max_val=float(inf)) -> bool:\n return False if root.val < min_val or root.val > max_val else ((not root.right or self.isValidBST(root.right, root.val + 1, max_val)) and (not root.left or self.isValidBST(root.left, min_val, root.val - 1 )))\n``` | 1 | Given the `root` of a binary tree, _determine if it is a valid binary search tree (BST)_.
A **valid BST** is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[2,1,3\]
**Output:** true
**Example 2:**
**Input:** root = \[5,1,4,null,null,3,6\]
**Output:** false
**Explanation:** The root node's value is 5 but its right child's value is 4.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-231 <= Node.val <= 231 - 1` | null |
Python Easy Solution with T.C - O(n) and S.C. - O(n) | recover-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def solve(self,root,first,middle,last,prev):\n if root:\n self.solve(root.left,first,middle,last,prev)\n if prev[0] and root.val<prev[0].val:\n # for the adjacent swap\n if not first[0]:\n first[0] = prev[0]\n middle[0] = root\n # For the non adjacent swap\n else:\n last[0] = root\n prev[0] = root\n self.solve(root.right,first,middle,last,prev)\n def recoverTree(self, root: Optional[TreeNode]) -> None:\n """\n Do not return anything, modify root in-place instead.\n """\n first = [None]\n middle = [None]\n last = [None]\n prev = [None]\n self.solve(root,first,middle,last,prev)\n # if the non adjacent nodes are there\n if first[0] and last[0]:\n first[0].val,last[0].val = last[0].val,first[0].val\n elif first[0] and middle[0]:\n first[0].val,middle[0].val = middle[0].val,first[0].val\n \n``` | 1 | You are given the `root` of a binary search tree (BST), where the values of **exactly** two nodes of the tree were swapped by mistake. _Recover the tree without changing its structure_.
**Example 1:**
**Input:** root = \[1,3,null,null,2\]
**Output:** \[3,1,null,null,2\]
**Explanation:** 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
**Example 2:**
**Input:** root = \[3,1,4,null,null,2\]
**Output:** \[2,1,4,null,null,3\]
**Explanation:** 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
**Constraints:**
* The number of nodes in the tree is in the range `[2, 1000]`.
* `-231 <= Node.val <= 231 - 1`
**Follow up:** A solution using `O(n)` space is pretty straight-forward. Could you devise a constant `O(1)` space solution? | null |
Comparison with the sorted array from the tree | recover-binary-search-tree | 0 | 1 | # Intuition\nI decided that I would solve it in the simplest and easiest way to understand and that\'s really how it turned out\n# Approach\nI decided first of all to create an array from the tree, compare it after sorting and then exchange between the two indexes that did not match the sorted array\n# Complexity\n- Time complexity:\no(n*log(n))\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\n\nclass Solution:\n def inorder(self, root: Optional[TreeNode], arr: List[int]) -> List[int]:\n if root == None:\n return arr\n \n self.inorder(root.left, arr)\n arr.append(root.val)\n self.inorder(root.right, arr)\n\n def inorder_fix(self, root: Optional[TreeNode], v1: int, v2: int) -> None:\n if root == None:\n return \n if root.val == v1:\n root.val = v2\n elif root.val == v2:\n root.val = v1\n self.inorder_fix(root.left, v1, v2)\n self.inorder_fix(root.right,v1,v2)\n\n def recoverTree(self, root: Optional[TreeNode]) -> None:\n arr = []\n self.inorder(root, arr)\n sorted_arr = sorted(arr)\n v1 = None\n v2 = None\n for i in range(0, len(arr)):\n if arr[i] != sorted_arr[i]:\n if v1 == None:\n v1 = arr[i]\n else:\n v2 = arr[i]\n\n self.inorder_fix(root,v1, v2)\n\n \n \n``` | 3 | You are given the `root` of a binary search tree (BST), where the values of **exactly** two nodes of the tree were swapped by mistake. _Recover the tree without changing its structure_.
**Example 1:**
**Input:** root = \[1,3,null,null,2\]
**Output:** \[3,1,null,null,2\]
**Explanation:** 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
**Example 2:**
**Input:** root = \[3,1,4,null,null,2\]
**Output:** \[2,1,4,null,null,3\]
**Explanation:** 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
**Constraints:**
* The number of nodes in the tree is in the range `[2, 1000]`.
* `-231 <= Node.val <= 231 - 1`
**Follow up:** A solution using `O(n)` space is pretty straight-forward. Could you devise a constant `O(1)` space solution? | null |
Recover Binary Search Tree with step by step explanation | recover-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIn this problem, we need to recover the binary search tree by fixing two nodes that were swapped by mistake. The solution to this problem can be achieved in two steps. In the first step, we will find the two nodes that are swapped, and in the second step, we will swap the nodes.\n\nTo find the two nodes that are swapped, we will use Morris Inorder Traversal. Morris Inorder Traversal is a space-optimized inorder traversal algorithm that allows us to traverse the tree using constant space.\n\nAlgorithm:\n\n1. Initialize two pointers current and pre to root.\n2. While current is not null, do the following:\na. If the current node does not have a left child, then move to the right child of the current node.\nb. Else, find the inorder predecessor of the current node, i.e., the rightmost node in the left subtree of the current node.\ni. If the right child of the inorder predecessor is null, then set it to the current node and move to the left child of the current node.\nii. If the right child of the inorder predecessor is current, then set it to null, check if the pre node is not null, and if pre.val > current.val, then update the second node as current. Also, if pre is not null, then set pre.right to null. Finally, move to the right child of the current node.\n3. If second node is not null, then swap the values of the first and second nodes.\n\n# Complexity\n- Time complexity:\nO(n), where n is the number of nodes in the binary search tree.\n\n- Space complexity:\nO(1).\n\n# Code\n```\nclass Solution:\n def recoverTree(self, root: Optional[TreeNode]) -> None:\n """\n Do not return anything, modify root in-place instead.\n """\n first, second, pre = None, None, None\n current = root\n \n while current is not None:\n if current.left is None:\n if pre is not None and pre.val > current.val:\n if first is None:\n first = pre\n second = current\n pre = current\n current = current.right\n else:\n node = current.left\n while node.right is not None and node.right != current:\n node = node.right\n if node.right is None:\n node.right = current\n current = current.left\n else:\n node.right = None\n if pre is not None and pre.val > current.val:\n if first is None:\n first = pre\n second = current\n pre = current\n current = current.right\n \n if first is not None and second is not None:\n first.val, second.val = second.val, first.val\n\n``` | 3 | You are given the `root` of a binary search tree (BST), where the values of **exactly** two nodes of the tree were swapped by mistake. _Recover the tree without changing its structure_.
**Example 1:**
**Input:** root = \[1,3,null,null,2\]
**Output:** \[3,1,null,null,2\]
**Explanation:** 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
**Example 2:**
**Input:** root = \[3,1,4,null,null,2\]
**Output:** \[2,1,4,null,null,3\]
**Explanation:** 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
**Constraints:**
* The number of nodes in the tree is in the range `[2, 1000]`.
* `-231 <= Node.val <= 231 - 1`
**Follow up:** A solution using `O(n)` space is pretty straight-forward. Could you devise a constant `O(1)` space solution? | null |
constant space easy In-Order Traversal with explaination | recover-binary-search-tree | 0 | 1 | The space taken by the recursion call is not considered as a space complexity here.\nThe extra space is usually used to store the inorder traversal list. which is not used in this solution.\n\nInOrder traversal for BST means the tree is traversed in sorted order, so if any node breaks the sorted order that wll be our node to swap.\nthat is the first and last node which breaks the sorting is our culprit !!\n\n```\ndef recoverTree(self, root: Optional[TreeNode]) -> None:\n \n res = [] \n startnode = None\n prev = None\n lastnode = None\n \n def dfs(root):\n nonlocal res, startnode, prev, lastnode\n if not root:\n return \n # go to left (inorder step 1) \n dfs(root.left)\n\t\t\t\n # do processing....(inorder step 2)\n\t\t\t# get the first node where the sorted order is broken the first time and the last time\n if prev and prev.val > root.val:\n if not startnode:\n startnode = prev\n lastnode = root\n \n prev = root\n\t\t\t\n # go to right (inorder step 3) \n dfs(root.right)\n \n \n dfs(root)\n # swap the nodes that are not in place\n if startnode and lastnode:\n startnode.val, lastnode.val = lastnode.val, startnode.val\n```\n\n***Please upvote for motivation*** | 20 | You are given the `root` of a binary search tree (BST), where the values of **exactly** two nodes of the tree were swapped by mistake. _Recover the tree without changing its structure_.
**Example 1:**
**Input:** root = \[1,3,null,null,2\]
**Output:** \[3,1,null,null,2\]
**Explanation:** 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
**Example 2:**
**Input:** root = \[3,1,4,null,null,2\]
**Output:** \[2,1,4,null,null,3\]
**Explanation:** 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
**Constraints:**
* The number of nodes in the tree is in the range `[2, 1000]`.
* `-231 <= Node.val <= 231 - 1`
**Follow up:** A solution using `O(n)` space is pretty straight-forward. Could you devise a constant `O(1)` space solution? | null |
Intuitive Solution Explained 🏞 ( Images ) | recover-binary-search-tree | 1 | 1 | ### Main idea - __*Inorder Traversal*__\n\n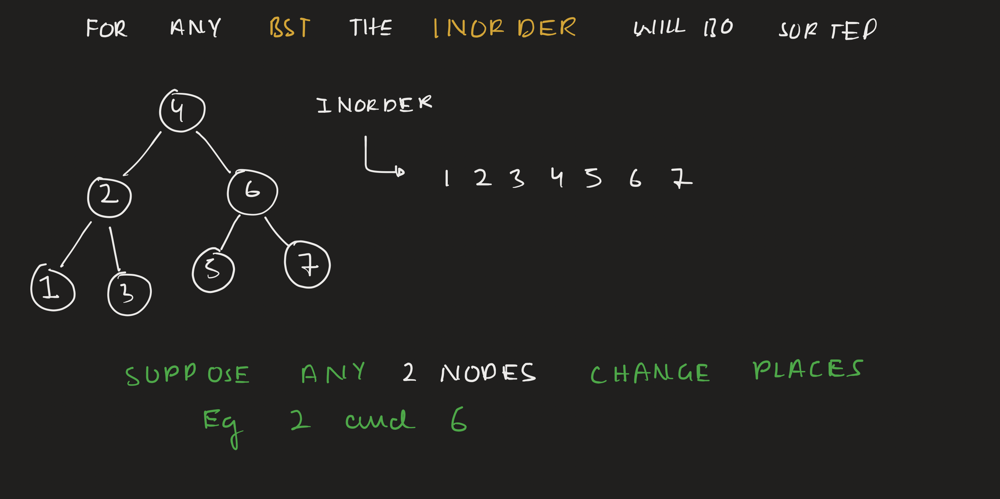\n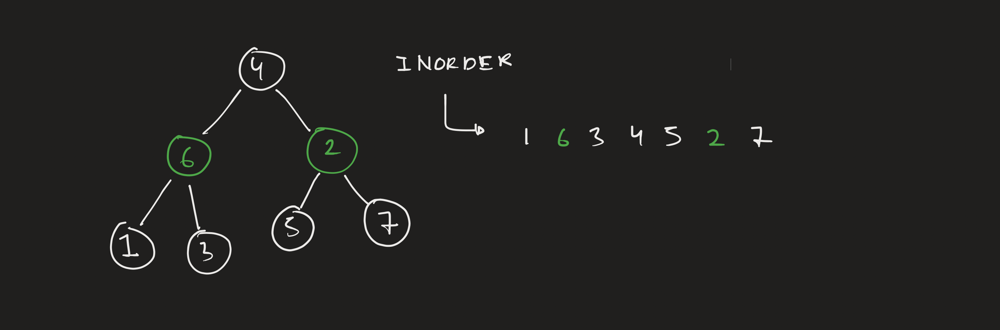\n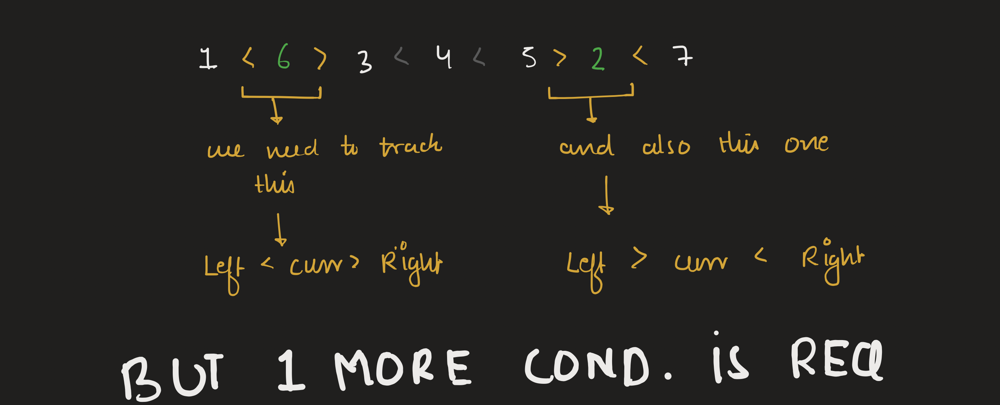\n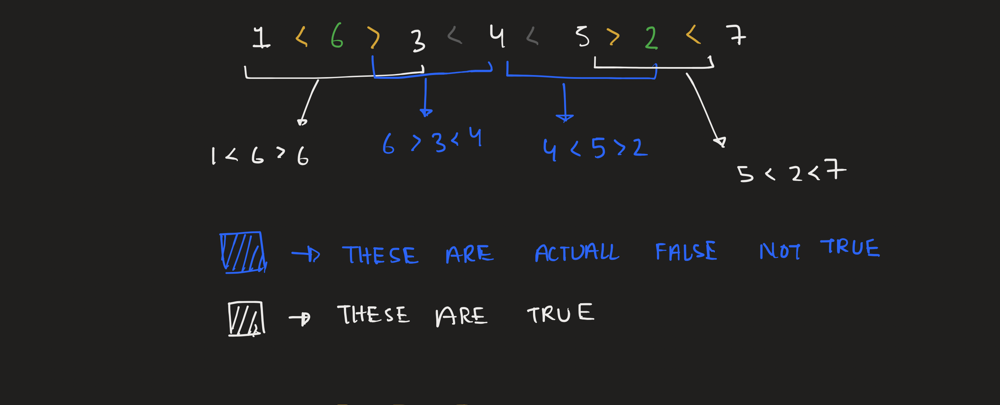\n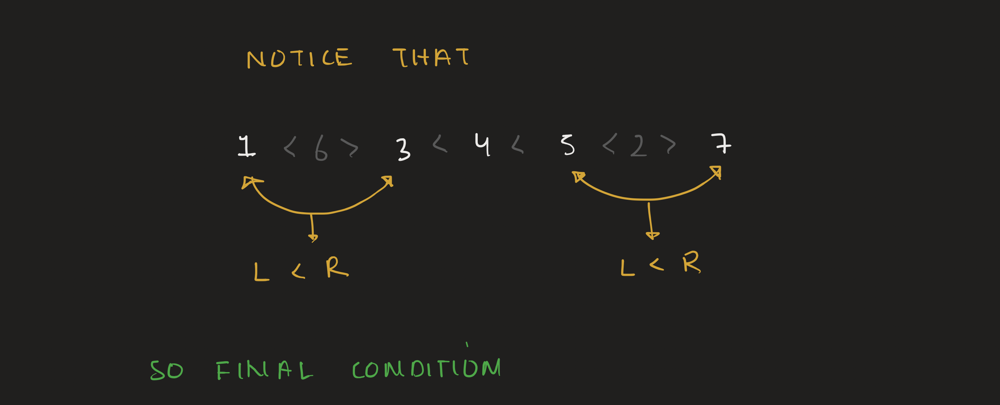\n\n\ncode - \n\n```java\n\nclass Solution{\npublic static ArrayList<TreeNode> arr;\n\n public static void dfs(TreeNode root) {\n if (root == null) return;\n dfs(root.left);\n arr.add(root);\n dfs(root.right);\n }\n\n public static void solve(TreeNode root) {\n arr = new ArrayList<TreeNode>();\n dfs(root);\n TreeNode a = null;\n TreeNode b = null;\n int n = arr.size();\n for (int i = 0; i < n; i++) {\n int left = i - 1 >= 0 ? arr.get(i - 1).val : Integer.MIN_VALUE;\n int right = i + 1 < n ? arr.get(i + 1).val : Integer.MAX_VALUE;\n int curr = arr.get(i).val;\n if (curr > left && curr > right && left < right) {\n a = arr.get(i);\n } else if (curr < left && curr < right && left < right) {\n b = arr.get(i);\n }\n }\n if (a != null && b != null) {\n int temp = a.val;\n a.val = b.val;\n b.val = temp;\n }\n }\n}\n\n```\n\n\n\n | 15 | You are given the `root` of a binary search tree (BST), where the values of **exactly** two nodes of the tree were swapped by mistake. _Recover the tree without changing its structure_.
**Example 1:**
**Input:** root = \[1,3,null,null,2\]
**Output:** \[3,1,null,null,2\]
**Explanation:** 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
**Example 2:**
**Input:** root = \[3,1,4,null,null,2\]
**Output:** \[2,1,4,null,null,3\]
**Explanation:** 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
**Constraints:**
* The number of nodes in the tree is in the range `[2, 1000]`.
* `-231 <= Node.val <= 231 - 1`
**Follow up:** A solution using `O(n)` space is pretty straight-forward. Could you devise a constant `O(1)` space solution? | null |
Python easy to understand solution with explanation | recover-binary-search-tree | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- Take the inorder traversal of the BST (arr)\n- Since the inorder traversal of the BST is always in sorted order and in this case as there are two swapped nodes, there will be missmatch of 2 nodes in (arr) with the sorted form of arr (new_arr)\n- Sort arr on the basis of its value and store it into a new variable (new_arr)\n- Compare the nodes in arr with new_arr, when you find a missmatch just swap the value of the nodes and break.\n\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def recoverTree(self, root: Optional[TreeNode]) -> None:\n """\n Do not return anything, modify root in-place instead.\n """\n def inorder(root):\n if not root:\n return\n inorder(root.left)\n arr.append(root)\n inorder(root.right)\n arr=[]\n inorder(root)\n new_arr=sorted(arr,key=lambda x: x.val)\n for i in range(len(arr)):\n if arr[i]!=new_arr[i]:\n arr[i].val, new_arr[i].val=new_arr[i].val, arr[i].val\n break\n return root\n \n \n \n``` | 2 | You are given the `root` of a binary search tree (BST), where the values of **exactly** two nodes of the tree were swapped by mistake. _Recover the tree without changing its structure_.
**Example 1:**
**Input:** root = \[1,3,null,null,2\]
**Output:** \[3,1,null,null,2\]
**Explanation:** 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
**Example 2:**
**Input:** root = \[3,1,4,null,null,2\]
**Output:** \[2,1,4,null,null,3\]
**Explanation:** 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
**Constraints:**
* The number of nodes in the tree is in the range `[2, 1000]`.
* `-231 <= Node.val <= 231 - 1`
**Follow up:** A solution using `O(n)` space is pretty straight-forward. Could you devise a constant `O(1)` space solution? | null |
[VIDEO] Visualization of Recursive Depth-First Search | same-tree | 0 | 1 | https://www.youtube.com/watch?v=cpWX8YK7HQg\n\nWe\'ll use recursion to perform a depth-first search of both trees and compare the nodes, p and q, at each step. This recursive algorithm has three base cases:\n1. Are both p and q None? If so, then return True. This is because this only happens when we\'ve reached the end of a branch, and all the nodes so far have matched.\n\nIf that wasn\'t true, then now we know that either p or q is a Node. But are they both nodes or is only one of them None? This leads to the second base case:\n\n2. Is either p or q None? If so, then return False, since that means one of them is None and one of them is a node, and those are clearly different from each other.\n\nIf that wasn\'t true, then at this point we know that both p and q are nodes, so let\'s compare their values:\n\n3. Are the values of p and q different? If so, return False.\n\nIf that wasn\'t true, then at this point we know that both p and q are nodes and their values are the same. So then we make two recursive calls. We\'ll pass in `p.left` and `q.left` for the first call to check the left subtree, and pass in `p.right` and `q.right` for the right subtree. For a visualization of the recursion, please see the video. But the idea is that both left subtrees and right subtrees must be the same, which is why the two recursive calls are connected with an `and`.\n\n# Code\n```\nclass Solution:\n def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:\n # Are both p and q None?\n if not p and not q:\n return True\n\n # Is one of them None?\n if not p or not q:\n return False\n\n # Are their values different?\n if p.val != q.val:\n return False\n\n # Recursive call to the next level down\n return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)\n```\n | 5 | Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
**Example 1:**
**Input:** p = \[1,2,3\], q = \[1,2,3\]
**Output:** true
**Example 2:**
**Input:** p = \[1,2\], q = \[1,null,2\]
**Output:** false
**Example 3:**
**Input:** p = \[1,2,1\], q = \[1,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in both trees is in the range `[0, 100]`.
* `-104 <= Node.val <= 104` | null |
Recursive Binary Tree Equality Check in Python | same-tree | 0 | 1 | # Intuition\nRecursively compare corresponding nodes in two binary trees to determine if they are identical.\n# Approach\nUse a recursive function to check if the current nodes are equal and recursively compare their left and right subtrees.\n# Complexity\n- Time complexity:\nO(n) where n is the number of nodes in the smaller tree. \n- Space complexity:\nO(h) where h is the height of the smaller tree. --># Code\n```\n# Definition for a binary tree node.\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\nclass Solution:\n def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:\n if p is None and q is None:\n return True\n elif p is None or q is None:\n return False\n if p.val != q.val:\n return False \n return self.isSameTree(p.left, q.left) and self.isSameTree( p.right, q.right) \n``` | 1 | Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
**Example 1:**
**Input:** p = \[1,2,3\], q = \[1,2,3\]
**Output:** true
**Example 2:**
**Input:** p = \[1,2\], q = \[1,null,2\]
**Output:** false
**Example 3:**
**Input:** p = \[1,2,1\], q = \[1,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in both trees is in the range `[0, 100]`.
* `-104 <= Node.val <= 104` | null |
code in python : Runs faster | same-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind the preorder of both the Trees. Compare both the order \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe know that finding the preorder. But in this we need to add None value to to the preorder when there root is None. We need to append(None) to the preorder.\nCheck the both PREORDER if they are both same Then return true else return false\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n):(Worst case), O(logn):(best case)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code : Python\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:\n def preorder(t,ans):\n if t==None:\n ans.append(None)\n return\n ans.append(t.val)\n preorder(t.left,ans)\n preorder(t.right,ans)\n ans=[]\n ans2=[]\n preorder(p,ans)\n preorder(q,ans2)\n if ans==ans2:\n return True\n else:\n return False\n \n``` | 2 | Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
**Example 1:**
**Input:** p = \[1,2,3\], q = \[1,2,3\]
**Output:** true
**Example 2:**
**Input:** p = \[1,2\], q = \[1,null,2\]
**Output:** false
**Example 3:**
**Input:** p = \[1,2,1\], q = \[1,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in both trees is in the range `[0, 100]`.
* `-104 <= Node.val <= 104` | null |
Python 3line Code || Simple Approach | same-tree | 0 | 1 | **Plz Upvote ..if you got help from this.**\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:\n if p is None or q is None:\n return p == q\n return (p.val== q.val) and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)\n \n``` | 10 | Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
**Example 1:**
**Input:** p = \[1,2,3\], q = \[1,2,3\]
**Output:** true
**Example 2:**
**Input:** p = \[1,2\], q = \[1,null,2\]
**Output:** false
**Example 3:**
**Input:** p = \[1,2,1\], q = \[1,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in both trees is in the range `[0, 100]`.
* `-104 <= Node.val <= 104` | null |
Most simple and efficient solution with expalanation | same-tree | 1 | 1 | \n\n# Approach\n- The isSameTree function takes two TreeNode pointers p and q as input and returns true if the trees rooted at p and q are structurally identical and have the same node values.\n- If either p or q is null, it returns true if both are null, indicating the end of the tree (base case).\n- It checks if the current nodes\' values of p and q are equal.\n- Recursively calls isSameTree on the left subtrees and right subtrees of p and q.\n- Returns true if all conditions are met, indicating that the trees are structurally identical with the same node values.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n bool isSameTree(TreeNode* p, TreeNode* q) {\n if(!p || !q) return (p==q);\n return (p->val == q->val) \n && isSameTree(p->left, q->left) \n && isSameTree(p->right, q->right);\n }\n};\n```\n```JAVA []\npublic class Solution {\n public boolean isSameTree(TreeNode p, TreeNode q) {\n if (p == null && q == null) {\n return true;\n } else if (p == null || q == null) {\n return false;\n } else {\n return (p.val == q.val) && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);\n }\n }\n}\n```\n```Python3 []\nclass Solution:\n def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:\n if not p and not q:\n return True\n elif not p or not q:\n return False\n else:\n return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)\n```\n | 1 | Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
**Example 1:**
**Input:** p = \[1,2,3\], q = \[1,2,3\]
**Output:** true
**Example 2:**
**Input:** p = \[1,2\], q = \[1,null,2\]
**Output:** false
**Example 3:**
**Input:** p = \[1,2,1\], q = \[1,1,2\]
**Output:** false
**Constraints:**
* The number of nodes in both trees is in the range `[0, 100]`.
* `-104 <= Node.val <= 104` | null |
Easy || 0 ms 100% (Fully Explained)(Java, C++, Python, JS, Python3) | symmetric-tree | 1 | 1 | # **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Symmetric Tree.\n```\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n // Soecial case...\n if (root == null)\n\t\t return true;\n // call the function recursively...\n\t return isSymmetric(root.left, root.right);\n }\n // After division the tree will be divided in two parts...\n // The root of the left part is rootleft & the root of the right part is rootright...\n public boolean isSymmetric(TreeNode rootleft, TreeNode rootright) {\n // If root of the left part & the root of the right part is same, return true...\n\t if (rootleft == null && rootright == null) {\n\t\t return true;\n\t }\n // If root of any part is null, then the binary tree is not symmetric. So return false...\n else if (rootright == null || rootleft == null) {\n\t\t return false;\n\t }\n // If the value of the root of the left part is not equal to the value of the root of the right part...\n if (rootleft.val != rootright.val)\n\t\t return false;\n // In case of not symmetric...\n if (!isSymmetric(rootleft.left, rootright.right))\n\t\t return false;\n\t if (!isSymmetric(rootleft.right, rootright.left))\n\t\t return false;\n // Otherwise, return true...\n return true;\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n // Special case...\n if(root == nullptr) return true;\n // Return the function recursively...\n return isSymmetric(root->left,root->right);\n }\n // A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\n bool isSymmetric(TreeNode* leftroot,TreeNode* rightroot){\n // If both root nodes are null pointers, return true...\n if(!leftroot && !rightroot) return true;\n // If exactly one of them is a null node, return false...\n if(!leftroot || !rightroot) return false;\n // If root nodes haven\'t same value, return false...\n if(leftroot->val != rightroot->val) return false;\n // Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n return isSymmetric(leftroot->left, rightroot->right) && isSymmetric(leftroot->right, rightroot->left);\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def isSymmetric(self, root):\n # Special case...\n if not root:\n return true;\n # Return the function recursively...\n return self.isSame(root.left, root.right)\n # A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\n def isSame(self, leftroot, rightroot):\n # If both root nodes are null pointers, return true...\n if leftroot == None and rightroot == None:\n return True\n # If exactly one of them is a null node, return false...\n if leftroot == None or rightroot == None:\n return False\n # If root nodes haven\'t same value, return false...\n if leftroot.val != rightroot.val:\n return False\n # Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n return self.isSame(leftroot.left, rightroot.right) and self.isSame(leftroot.right, rightroot.left)\n```\n \n# **JavaScript Solution:**\nRuntime: 66 ms, faster than 97.80% of JavaScript online submissions for Symmetric Tree.\n```\nvar isSymmetric = function(root) {\n // Special case...\n if (!root)\n return true;\n // Return the function recursively...\n return isSame(root.left, root.right);\n};\n// A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\nvar isSame = function (leftroot, rightroot) {\n // If both root nodes are null pointers, return true...\n // If exactly one of them is a null node, return false...\n // If root nodes haven\'t same value, return false...\n if ((!leftroot && rightroot) || (leftroot && !rightroot) || (leftroot && rightroot && leftroot.val !== rightroot.val))\n return false;\n // Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n if (leftroot && rightroot)\n return isSame(leftroot.left, rightroot.right) && isSame(leftroot.right, rightroot.left);\n return true;\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n # Special case...\n if not root:\n return true;\n # Return the function recursively...\n return self.isSame(root.left, root.right)\n # A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\n def isSame(self, leftroot, rightroot):\n # If both root nodes are null pointers, return true...\n if leftroot == None and rightroot == None:\n return True\n # If exactly one of them is a null node, return false...\n if leftroot == None or rightroot == None:\n return False\n # If root nodes haven\'t same value, return false...\n if leftroot.val != rightroot.val:\n return False\n # Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n return self.isSame(leftroot.left, rightroot.right) and self.isSame(leftroot.right, rightroot.left)\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 117 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Easiest Python Solution 🔥✅ | symmetric-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo check if a binary tree is symmetric, we need to compare its left subtree and right subtree. To do this, we can traverse the tree recursively and compare the left and right subtrees at each level. If they are symmetric, we continue the traversal. Otherwise, we can immediately return false.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe Will define a recursive helper function "**isSymmetric()**"; that takes two nodes as input, one from the left subtree and one from the right subtree. The helper function returns true if both nodes are null, or if their values are equal and their subtrees are symmetric.\n\n# Complexity\n- Time complexity : **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nWhere n is the number of nodes in the binary tree. We need to visit each node once to check if the tree is symmetric.\n- Space complexity : **O(h)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWhere h is the height of the binary tree.\n\n---\n\n# Please Upvote \u2B06 # \n\n---\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n def isSmallSymmetric(a,b):\n if type(a)==TreeNode and type(b)==TreeNode:\n if a.val==b.val:\n return isSmallSymmetric(a.left,b.right) and isSmallSymmetric(a.right,b.left)\n else:\n return a==b\n return isSmallSymmetric(root.left,root.right)\n``` | 1 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
EASY PYTHON FOR BEGINNERS | symmetric-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter Reading the question, we can deduce that we need to return True as soon as we reach the leaf nodes. \nNext, we will explore all edge cases where we will return False. \nLastly, we return both of the child nodes (after recursion) to determine if we it is symmetric, using \'and\'. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince we are using recursion, we will return False if one root is None while the other isn\'t, and vice versa.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(logn) to O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n \n def isSame(root1, root2):\n if not root1 and not root2:\n return True\n if (not root1 and root2) or (root1 and not root2) or (root1.val != root2.val):\n return False\n left = isSame(root1.left, root2.right)\n right = isSame(root1.right, root2.left)\n return left and right\n \n if not root:\n return True\n \n return isSame(root.left, root.right)\n\n``` | 2 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Easy and simple recursive solution with explanation | symmetric-tree | 1 | 1 | \n\n# Approach\n- **Helper Function (help):** The help function takes two nodes, p and q, as input and checks if they are symmetric. It returns true if both nodes are null, indicating the end of the tree. If one node is null and the other is not, or their values are not equal, the trees are not symmetric, so it returns false. It then recursively checks if the left subtree of p is symmetric to the right subtree of q, and vice versa.\n\n- **Symmetric Check (isSymmetric):** The isSymmetric function takes the root node as input. If the root is null, it is symmetric, so it returns true. Otherwise, it calls the help function to check if the left and right subtrees are symmetric.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n bool help(TreeNode* p, TreeNode* q) {\n if(!p || !q) return p==q;\n return (p->val == q->val)\n && help(p->left, q->right)\n && help(p->right, q->left);\n }\n bool isSymmetric(TreeNode* root) {\n if(!root) return true;\n return help(root->left, root->right);\n }\n};\n```\n```python []\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n def help(p, q):\n if not p or not q:\n return p == q\n return p.val == q.val and help(p.left, q.right) and help(p.right, q.left)\n \n if not root:\n return True\n return help(root.left, root.right)\n```\n```Java []\npublic class Solution {\n public boolean isSymmetric(TreeNode root) {\n if (root == null) {\n return true;\n }\n return help(root.left, root.right);\n }\n \n private boolean help(TreeNode p, TreeNode q) {\n if (p == null || q == null) {\n return p == q;\n }\n return (p.val == q.val) && help(p.left, q.right) && help(p.right, q.left);\n }\n}\n```\n | 1 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
[Python3] Good enough | symmetric-tree | 0 | 1 | ``` Python3 []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n return self.isSame(root, root)\n \n def isSame(self, n1, n2):\n if not n1 and not n2:\n return True\n elif not n1 or not n2:\n return False\n \n return n1.val == n2.val and self.isSame(n1.right, n2.left) and self.isSame(n1.left, n2.right)\n``` | 7 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Python Easy Solution || 100% || Recursion || | symmetric-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n return self.isMirror(root.left, root.right)\n \n def isMirror(self, node1, node2):\n if not node1 and not node2:\n return True\n if not node1 or not node2:\n return False\n if node1.val != node2.val:\n return False\n return self.isMirror(node1.left, node2.right) and self.isMirror(node1.right, node2.left)\n``` | 2 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Beats : 88.4% [13/145 Top Interview Question] | symmetric-tree | 0 | 1 | # Intuition\n*Straight-forward solution, Add nodes to stack, pop twice make sure we are poping one from left and other from right, check the condition and so on.*\n\n# Approach\nThis is a Python code that checks if a binary tree is symmetric or not. The binary tree is represented using nodes, which are defined using the `TreeNode` class. The class has three attributes: `val`, `left`, and `right`. The `val` attribute stores the value of the node, and the `left` and `right` attributes point to the left and right child nodes of the current node.\n\nThe `isSymmetric` method of the `Solution` class takes a binary tree node as input, and returns `True` if the tree is symmetric, and `False` otherwise. The method uses a stack to keep track of pairs of nodes to be compared. Initially, the stack contains the left and right child nodes of the root node.\n\nThe method then enters a loop that continues until the stack is empty. In each iteration of the loop, the method pops two nodes from the stack and checks if they are symmetric. If both nodes are `None`, the method continues to the next iteration of the loop. If either of the nodes is `None`, or if the values of the nodes are different, the method returns `False`.\n\nIf the nodes are symmetric, the method pushes the left and right child nodes of the two nodes onto the stack, in the order `node1.left`, `node2.right`, `node1.right`, `node2.left`. This ensures that the corresponding nodes of the left and right subtrees are compared.\n\nIf the loop completes without returning `False`, the method returns `True`, indicating that the binary tree is symmetric.\n\n# Complexity\n- Time complexity:\n O(n)\n\n- Space complexity:\n O(n)\n\nThe `time complexity` of the `isSymmetric` method is `O(n)`, where `n` is the number of nodes in the binary tree. This is because the method traverses each node of the tree once, and performs a constant amount of work for each node. \n\nThe `space complexity` of the method is `O(n)`, where `n` is the number of nodes in the binary tree. This is because the method uses a stack to keep track of pairs of nodes to be compared, and the maximum size of the stack is proportional to the maximum depth of the binary tree. In the worst case, when the binary tree is a `complete binary tree(balanced Tree)`, the maximum depth is `log(n)`, and hence the space complexity is `O(log(n))`. However, in the worst case when the binary tree is `skewed`, the maximum depth is `n`, and hence the space complexity is `O(n)`.\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n stack = [root.left, root.right]\n while stack:\n node1,node2 = stack.pop(), stack.pop()\n if node1 is None and node2 is None: continue\n elif (node1 is None or node2 is None) or node1.val != node2.val: \n return False\n\n stack.append(node1.left)\n stack.append(node2.right)\n stack.append(node1.right)\n stack.append(node2.left)\n return True\n\n``` | 2 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
simple DFS based solution | symmetric-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n def dfs(node_one, node_two):\n if node_one and node_two:\n return node_one.val==node_two.val and dfs(node_one.left, node_two.right) and dfs(node_one.right, node_two.left)\n elif not node_one and not node_two:\n return True\n return False\n return dfs(root, root)\n\n``` | 1 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Python 6lines easy code | symmetric-tree | 0 | 1 | **Plz Upvote ..if you got help from this.**\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n\n def solve(root1, root2):\n if root1 is None and root2 is None:\n return True\n \n if root1 is None or root2 is None or root1.val != root2.val:\n return False\n \n return solve(root1.left, root2.right) and solve(root1.right, root2.left)\n \n return solve(root, root)\n``` | 7 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
✅ Very Easy Solution || ☑️ Beats 99.95% || with Python3 🐍 | symmetric-tree | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nThis problem is very related to Problem No.100 \'Same Tree\'.\nCheck that problem before solving this.\nThat will help you to understand this problem wells.\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def recursive(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:\n if p and q:\n return p.val == q.val and self.recursive(p.left, q.right) and self.recursive(p.right, q.left)\n else:\n return p == q\n\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n p = root.left\n q = root.right\n return self.recursive(p, q)\n```\n\n\u2B06\uFE0F Please Upvote\n\n\n\n | 1 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Best soln see it | symmetric-tree | 0 | 1 | # Code\n```\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n c = [True]\n def dfs(p, q):\n if not p and not q:\n return\n elif not p or not q:\n c[0] = False\n return\n if p.val != q.val:\n c[0] = False\n return\n if p.left or q.right:\n dfs(p.left, q.right)\n if p.right or q.left:\n dfs(p.right, q.left)\n dfs(root.left, root.right)\n return c[0]\n``` | 1 | Given the `root` of a binary tree, _check whether it is a mirror of itself_ (i.e., symmetric around its center).
**Example 1:**
**Input:** root = \[1,2,2,3,4,4,3\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,null,3,null,3\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Could you solve it both recursively and iteratively? | null |
Solution | binary-tree-level-order-traversal | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(TreeNode* root) {\n vector<vector<int>>ans;\n if(root==NULL)return ans;\n queue<TreeNode*>q;\n q.push(root);\n while(!q.empty()){\n int s=q.size();\n vector<int>v;\n for(int i=0;i<s;i++){\n TreeNode *node=q.front();\n q.pop();\n if(node->left!=NULL)q.push(node->left);\n if(node->right!=NULL)q.push(node->right);\n v.push_back(node->val);\n }\n ans.push_back(v);\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root:\n return []\n Q = deque([root])\n levels = [[root.val]]\n temp = deque()\n\n while Q:\n node = Q.popleft()\n if node.left: temp.append(node.left)\n if node.right: temp.append(node.right)\n \n if not Q:\n if temp:\n levels.append([n.val for n in temp])\n Q = temp\n temp = deque()\n\n return levels\n```\n\n```Java []\nclass Solution {\n public List<List<Integer>> levelOrder(TreeNode root) \n {\n List<List<Integer>>al=new ArrayList<>();\n pre(root,0,al);\n return al;\n }\n public static void pre(TreeNode root,int l,List<List<Integer>>al)\n {\n if(root==null)\n return;\n if(al.size()==l)\n {\n List<Integer>li=new ArrayList<>();\n li.add(root.val);\n al.add(li);\n }\n else\n al.get(l).add(root.val);\n pre(root.left,l+1,al);\n pre(root.right,l+1,al);\n } \n}\n```\n | 482 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Recursive approach, without relying in a deque structure, easier to understand and remember | binary-tree-level-order-traversal | 0 | 1 | # Intuition\nBy sending the current level down the tree in a recursive approach we can safely insert the node value in the right position. For this I just have to first check if the current level index exists if it exists I insert using the level as index, otherwise I append to the end of the result\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n res:list[list[int]] = []\n def helper(node: Optional[TreeNode], level:int):\n if node:\n if len(res) >= level+1:\n res[level].append(node.val)\n else:\n res.append([node.val])\n helper(node.left,level+1)\n helper(node.right,level+1)\n helper(root,0)\n return res\n``` | 0 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Beats100%(Recursive approach)✅ | O( n)✅ | (Step by step explanation)✅ | binary-tree-level-order-traversal | 0 | 1 | # Intuition\nThe problem is to perform a level-order traversal of a binary tree and return the values of nodes\' values in the order from left to right, level by level.\n\n# Approach\nThe approach is to perform a modified depth-first traversal of the tree. We define a helper function `level` that takes the current node, the current level, and a vector of vectors to store the result. During the traversal, if the result vector is not long enough to accommodate the current level, we add a new subarray to store the values at that level.\n\n1. **Initialize**: Start with an empty vector `result` to store the level order traversal.\n2. **Recursive Helper Function**: Define a recursive helper function `level` that takes the current node, the current level, and a vector of vectors to store the result.\n3. **Base Case**: In the `level` function, if the current node is `nullptr`, return, as there is nothing to process.\n4. **Ensure Enough Subarrays**: Check if the `result` vector is long enough to accommodate the current level. If not, add a new subarray to store the values at that level.\n5. **Add Node Value**: Add the value of the current node to the subarray corresponding to the current level.\n6. **Recursive Calls**: Recursively call the `level` function for the left and right children of the current node, incrementing the level by 1 for each call.\n7. **Return**: After the traversal is complete, the `result` vector contains subarrays representing the nodes at each level of the tree.\n\n# Complexity\n- Time complexity: O(n)\n - We visit each node exactly once during the traversal.\n- Space complexity: O(h)\n - The space complexity is determined by the recursion stack.\n - In the worst case, when the tree is skewed, the space complexity is O(n).\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n result = []\n count = 0\n\n def level(count , root):\n if root == None :\n return \n\n if len(result) <= count:\n result.append([]) \n \n result[count].append(root.val)\n count += 1\n level(count , root.left)\n level(count , root.right) \n\n level(count , root)\n return result\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(TreeNode* root) {\n vector<vector<int>> result;\n int count = 0;\n level(root , count , result);\n return result;\n\n }\nprivate:\n void level(TreeNode* root , int count , vector<vector<int>> &result){\n if(root == NULL){\n return ;\n }\n\n if(result.size() <= count){\n result.push_back(vector<int>());\n }\n result[count].push_back(root->val);\n count++;\n level(root->left , count , result);\n level(root->right , count , result);\n \n } \n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n\n\n# Please upvote the solution if you understood it.\n\n\n | 7 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Iterative approach✅ | O( n)✅ | (Step by step explanation)✅ | binary-tree-level-order-traversal | 0 | 1 | # Intuition\nThe problem is to perform a level-order traversal of a binary tree and return the values of nodes\' values in the order from left to right, level by level.\n\n# Approach\n1. **Initialize**: Start with an empty list `result` to store the level order traversal.\n2. **Queue**: Use a queue to perform a level-order traversal.\n3. **Traversal Loop**: Begin a loop that continues until the queue is empty.\n - Inside the loop, get the current size of the queue (which represents the number of nodes at the current level).\n - Create a temporary list `curr` to store the values of nodes at the current level.\n - Loop through the nodes at the current level (based on the current size of the queue).\n - Pop a node from the front of the queue.\n - Add the value of the node to the `curr` list.\n - Enqueue the left and right children of the node (if they exist).\n - Append the `curr` list to the `result` list.\n4. **Final Result**: After the loop, the `result` list contains sublists representing the nodes at each level of the tree.\n5. **Return**: Return the `result` list.\n\n# Complexity\n- Time complexity: $$O(n)$$\n - Each node is processed once during the traversal.\n- Space complexity: $$O(m)$$, where $$m$$ is the maximum number of nodes at a single level.\n - The space complexity is determined by the queue.\n - In the worst case, the maximum number of nodes at a single level is $$m$$.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n result = []\n q = collections.deque()\n q.append(root)\n \n while q:\n n = len(q)\n level = []\n\n for i in range(n):\n node = q.popleft()\n if node:\n level.append(node.val)\n q.append(node.left)\n q.append(node.right)\n\n if level:\n result.append(level) \n\n \n return result\n\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(TreeNode* root) {\n vector<vector<int>> result;\n \n if (root == NULL) {\n return result;\n }\n \n queue<TreeNode*> q;\n q.push(root);\n \n while (!q.empty()) {\n int count = q.size();\n vector<int> curr;\n \n for (int i = 0; i < count; i++) {\n TreeNode* node = q.front();\n q.pop();\n \n curr.push_back(node->val);\n \n if (node->left != NULL) {\n q.push(node->left);\n }\n if (node->right != NULL) {\n q.push(node->right);\n }\n }\n \n result.push_back(curr);\n }\n \n return result;\n }\n};\nConsole\n\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n | 2 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Unprecedented Logic Python3 | binary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n list1=[]\n q=deque()\n q.append(root)\n while q:\n level=[]\n for i in range(len(q)):\n poping=q.popleft()\n if poping:\n level.append(poping.val)\n q.append(poping.left)\n q.append(poping.right)\n if level:\n list1.append(level)\n return list1\n #please upvote me it would encourage me alot\n\n\n\n\n``` | 33 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
98.68% Binary Tree Level Order Traversal with step by step explanation | binary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nAlgorithm:\n\n1. Initialize an empty queue.\n2. If the root is not null, add it to the queue.\n3. While the queue is not empty, repeat steps 4-6.\n4. Get the size of the queue and initialize an empty list to store the nodes of the current level.\n5. Loop through the elements of the current level and add them to the list.\n6. For each element of the current level, add its children to the queue.\n7. Add the current level list to the result list.\n8. Return the result list.\n\n# Complexity\n- Time complexity:\nBeats\n98.68%\n- Space complexity:\nBeats\n76.95%\n# Code\n```\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n # Initialize an empty queue and result list\n queue = []\n result = []\n \n # If the root is not null, add it to the queue\n if root:\n queue.append(root)\n \n # While the queue is not empty, repeat steps 4-7\n while queue:\n # Get the size of the queue and initialize an empty list to store the nodes of the current level\n size = len(queue)\n level = []\n \n # Loop through the elements of the current level and add them to the list\n for i in range(size):\n node = queue.pop(0)\n level.append(node.val)\n \n # For each element of the current level, add its children to the queue\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n # Add the current level list to the result list\n result.append(level)\n \n # Return the result list\n return result\n\n``` | 17 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Easy python for beginner approach✅ | binary-tree-level-order-traversal | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n q=deque()\n ans=[]\n if root!=None:\n q.append(root)\n\n while len(q)>0:\n level=[]\n qlen=len(q)\n\n for _ in range(qlen):\n node=q.popleft()\n level.append(node.val)\n if node.left!=None:\n q.append(node.left)\n\n if node.right!=None:\n q.append(node.right)\n\n\n ans.append(level)\n\n return ans\n```\n# upvote \n | 3 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Stack || Python Solution || O(n) | binary-tree-level-order-traversal | 0 | 1 | \n\n\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n ret_list=[]\n if not root:\n return ret_list\n \n stack=[[root]]\n while stack:\n nodes=stack.pop(0)\n if nodes:\n ret_list.append([])\n stack.append([])\n for node in nodes:\n ret_list[-1].append(node.val)\n if node.left:\n stack[-1].append(node.left)\n if node.right:\n stack[-1].append(node.right)\n return ret_list\n``` | 2 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
✅Python3 34ms 82% fast 🔥🔥🔥 | binary-tree-level-order-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using dfs level order traversal we can solve this.**\n\n\n\n# Approach\n- make answer array = []\n- now traverse nodes from left to right.\n- if current node is empty return.\n- if not then if current level is in answer array then append currennt node else create level in array and append current value.\n- return answer.\n\n# Complexity\n- Time complexity: O(height of tree)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n ans = []\n def bfs(curr = root, level = 0):\n nonlocal ans\n if curr:\n if len(ans) > level:\n ans[level].append(curr.val)\n else:\n ans.append([curr.val])\n bfs(curr.left, level + 1)\n bfs(curr.right, level + 1)\n return\n bfs()\n return ans\n```\n# Please like and comment below.\n# (\u3063\uFF3E\u25BF\uFF3E)\u06F6\uD83C\uDF78\uD83C\uDF1F\uD83C\uDF7A\u0669(\u02D8\u25E1\u02D8 ) | 12 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Most optimal solution using queue with explanation | binary-tree-level-order-traversal | 1 | 1 | \n\n# Approach\n1. Create a vector of vectors to store the level order traversal results.\n2. If the root is null, return an empty vector (no nodes to traverse).\n3. Initialize a queue and enqueue the root node.\n4. While the queue is not empty:\n - Initialize a vector to store the node values at the current level.\n - Get the size of the queue (which represents the number of nodes at the current level).\n - For each node at the current level:\n - Dequeue a node from the front of the queue.\n - Enqueue its left child (if it exists).\n - Enqueue its right child (if it exists).\n - Collect the node\'s value.\n - Add the collected node values for the current level to the result vector.\n5. Return the level order traversal results.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> levelOrder(TreeNode* root) {\n vector<vector<int>> ans;\n if(!root) return ans;\n queue<TreeNode*> q;\n q.push(root);\n while(!q.empty()) {\n vector<int> level;\n int n = q.size();\n for(int i = 0; i<n; i++) {\n TreeNode *node = q.front();\n q.pop();\n if(node->left) q.push(node->left);\n if(node->right) q.push(node->right);\n level.push_back(node->val);\n }\n ans.push_back(level);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def levelOrder(self, root):\n if not root:\n return []\n \n result = []\n queue = deque([root])\n \n while queue:\n level_values = []\n level_size = len(queue)\n \n for i in range(level_size):\n node = queue.popleft()\n level_values.append(node.val)\n \n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n result.append(level_values)\n \n return result\n```\n```Java []\nclass Solution {\n public List<List<Integer>> levelOrder(TreeNode root) {\n List<List<Integer>> result = new ArrayList<>();\n if (root == null)\n return result;\n\n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root);\n\n while (!queue.isEmpty()) {\n int levelSize = queue.size();\n List<Integer> levelValues = new ArrayList<>();\n\n for (int i = 0; i < levelSize; i++) {\n TreeNode node = queue.poll();\n levelValues.add(node.val);\n\n if (node.left != null)\n queue.offer(node.left);\n if (node.right != null)\n queue.offer(node.right);\n }\n\n result.add(levelValues);\n }\n\n return result;\n }\n}\n```\n | 4 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Breadth-First Search Improved by deque() | binary-tree-level-order-traversal | 0 | 1 | # Intuition\nBreadth-first search (BFS) will traverse a level at first and then go to the next level, which is quite compatible with this question.\n\n# Approach\n- In each level, we traverse the node in this level and do two operations:\n 1. We use a temporal list `tmp` to record the values of the nodes.\n 2. How to go to the next level? We **maintain a queue** to record the `node.left` and `node.right` during traversing this level such that we have the next level\'s nodes.\n- In order to **maintain such a queue** to record the nodes in the next level, we do two operations:\n 1. At first, we add the root node into the queue. Then when we keep adding `left` and `right`, all levels will be visited.\n 2. When visiting a node, we need to pop out this node before record the next level\'s nodes. Here we use a `deque()` to restore the nodes so that `popleft()` will only cost $O(1)$ time. If we use a list (stack), `pop(0)` will cost $O(n)$ time. Obviously, we want to pop out the first node in the queue.\n\nThe other explanations are shown in line.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root:\n return []\n # construct a deque\n dq = collections.deque()\n # initialize the deque by adding the root\n dq.append(root)\n res = []\n\n while dq:\n # initialize for elements in each level\n tmp = []\n for _ in range(len(dq)):\n # loop nodes in this level\n node = dq.popleft()\n # integrate thier values in one list\n tmp.append(node.val)\n # append other nodes in the next level\n if node.left:\n dq.append(node.left)\n if node.right:\n dq.append(node.right)\n # finish the loop for this level and add this level to the result\n res.append(tmp)\n return res\n \n\n``` | 2 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Python3 | Beats 95% | Iterative Level Order Traversal of a Tree | binary-tree-level-order-traversal | 0 | 1 | # Intuition\nWhen dealing with a binary tree, it\'s often useful to traverse it in a level-order manner, which means visiting nodes level by level from left to right. To accomplish this, we can use a data structure called a deque (double-ended queue), which allows us to efficiently add elements to the end and remove elements from the front. This is useful for traversing the tree in a breadth-first manner.\n\n# Approach\n**Initial State:**\n\n- We have a binary tree with a root node.\n- We have an empty list called "result" to store the level-order traversal.\n\n\n\n**Step 1: Initializing the Queue**\n\n- We create a deque called "queue" and initialize it with the root node.\n- The queue initially contains only the root node.\n\n\n\n\n**Step 2: Performing Level-Order Traversal**\n\n- We start a loop that continues as long as the queue is not empty.\n- For each level, we maintain a list called "level_values" to store the values of nodes in that level.\n- We also track the size of the current level using "level_size".\n- We iterate through the nodes in the current level and process them.\n\n\n\n**Step 3: Processing Nodes in the Current Level**\n\n- We pop the first node (3) from the queue and add its value to the "level_values" list.\n- We enqueue the left and right children of the popped node (9 and 20) if they exist.\n\n\n\n\n**Step 4: Moving to the Next Level**\n\n- We have finished processing the nodes in the current level.\n- We append the "level_values" list to the "result" list.\n- "level_values" is reset to an empty list.\n- We continue this process for each level in the tree.\n\n\n\n\n**Step 5: Processing Nodes in the Second Level**\n\n- We pop the first node (9) from the queue and add its value to the "level_values" list.\n- The left and right children of node 9 are not present, so no nodes are enqueued.\n\n\n\n**Step 6: Moving to the Next Level (Final Level)**\n\n- We have finished processing the nodes in the second level.\n- We append the "level_values" list to the "result" list.\n- "level_values" is reset to an empty list.\n\n\n\n**Step 7: Processing Nodes in the Final Level**\n\n- We pop the first node (20) from the queue and add its value to the "level_values" list.\n- We enqueue the left and right children of node 20 (15 and 7).\n\n\n\n**Step 8: Finishing the Final Level**\n- We pop the first node (15) from the queue and add its value to the "level_values" list.\n- We pop the second node (7) from the queue and add its value to the "level_values" list.\n\n\n\n**Step 9: Completed Traversal**\n\n- The queue is now empty, indicating that we have processed all nodes in the tree.\n- The "level_values" list for the final level is appended to the "result" list.\n\n\n\n**Final Result:**\n\nThe level-order traversal of the binary tree is stored in the "result" list.\n\n\n\n\n# Complexity\n- Time complexity:\n**O(n)**, where n is the number of nodes in the binary tree. We visit each node once.\n\n- Space complexity:\n**O(n)**, in the worst case, when the tree is completely unbalanced, the queue can hold all nodes in one level. Additionally, the result list will store the values of all nodes.\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n result = []\n if not root:\n return result\n\n # Initialize a queue with the root node\n queue = deque([root])\n\n # Perform level-order traversal\n while queue:\n level_values = []\n level_size = len(queue)\n for _ in range(level_size):\n # Process the next node in the queue\n node = queue.popleft()\n level_values.append(node.val)\n \n # Enqueue the left child if it exists\n if node.left:\n queue.append(node.left)\n \n # Enqueue the right child if it exists\n if node.right:\n queue.append(node.right)\n \n # Add the values of the current level to the result\n result.append(level_values)\n \n # Return the final level-order traversal result\n return result\n\n``` | 9 | Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[9,20\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Python || Iterative Way || Easy To Understand 🔥 | binary-tree-zigzag-level-order-traversal | 0 | 1 | # Code\n```\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root:\n return []\n level = 1\n res = []\n curr = [root]\n nxt = []\n while curr:\n for i in curr:\n if i.left:\n nxt.append(i.left)\n if i.right:\n nxt.append(i.right)\n if level % 2 == 0:\n curr.reverse()\n res.append([i.val for i in curr])\n curr = nxt\n if nxt:\n level += 1\n nxt = []\n return res\n``` | 1 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
Python3 85.17% time bfs solution | binary-tree-zigzag-level-order-traversal | 0 | 1 | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse bfs\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing bfs go through the tree per level and append to result either forwards or backwards depending on what level the tree is\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n result = []\n queue = deque()\n queue.append(root)\n odd = 0\n while queue:\n level = []\n for _ in range(len(queue)):\n node = queue.popleft()\n if not node:\n continue\n level.append(node.val)\n queue.append(node.left)\n queue.append(node.right)\n if level:\n if odd % 2 == 0:\n result.append(level)\n else:\n result.append(level[::-1])\n odd += 1\n return result\n\n\n``` | 1 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
python O(n) beats 91% 🔥🔥🔥🔥 || intuitive || 🏀🏀🏀☄️☄️ | binary-tree-zigzag-level-order-traversal | 0 | 1 | **Approach**\n\n- Maintain a queue of each level in the tree\n- Keep track of a variable left_to_right/ltr that determines if the current level should process its children from lefttoright or righttoleft\n- When processing each level in the queue, process children according to the ltr variable then set the variable to its opposite value\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root: return\n\n q = deque()\n ans, ltr = [[root.val]], False\n q.append([root])\n while q:\n level = q.popleft()\n children, children_vals = [], []\n for node in level:\n if ltr:\n if node.left:\n children.append(node.left)\n children_vals.append(node.left.val)\n if node.right:\n children.append(node.right)\n children_vals.append(node.right.val)\n else:\n if node.right:\n children.append(node.right)\n children_vals.append(node.right.val)\n if node.left:\n children.append(node.left)\n children_vals.append(node.left.val)\n if children: q.append(reversed(children))\n if children_vals: ans.append(children_vals)\n if ltr: ltr = False\n else: ltr = True\n\n return ans\n``` | 1 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
Easy Python BFS | Beats 97.8% in runtime and 94.5% in mem usage | binary-tree-zigzag-level-order-traversal | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nDo a normal Breadth First Search (BFS) using a queue. In addition to putting the node in the queue, we also add it\'s level.\n\nAnd while we are performing the BFS we populate the lvls dictionary with the coresponding nodes for each level.\n\nThen we go over each level, we alternate between taking the level as is or reversing it. and adding it to our ans arr\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n\n lvls = defaultdict(list)\n q = []\n q.append((root,0))\n while len(q)>0:\n cur_n, cur_lvl = q.pop(0)\n if cur_n != None:\n lvls[cur_lvl].append(cur_n.val)\n q.append((cur_n.left, cur_lvl+1))\n q.append((cur_n.right, cur_lvl+1))\n \n ans = []\n for lvl in lvls:\n if lvl%2==0:\n ans.append(lvls[lvl])\n else:\n ans.append(lvls[lvl][::-1])\n \n return ans\n``` | 1 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
Python easy to understand | BFS | Beats 99% | binary-tree-zigzag-level-order-traversal | 0 | 1 | # Approach\n###### Perform BFS from root node and if depth of current node is even then add node in normal order else reverse order\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root: return []\n ans = defaultdict(list)\n queue = deque([(root, 0)])\n while queue:\n node, depth = queue.popleft()\n if depth % 2 == 0: ans[depth].append(node.val)\n else: ans[depth].insert(0, node.val)\n if node.left: queue.append((node.left, depth+1))\n if node.right: queue.append((node.right, depth+1))\n return ans.values()\n``` | 2 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
[Python] - BFS - Clean & Simple | binary-tree-zigzag-level-order-traversal | 0 | 1 | \n# Code\n``` Python [1]\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root:\n return []\n ans = []\n queue = [root]\n cnt = 0\n while queue:\n temp = queue\n queue = []\n level = []\n for node in temp:\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n level.append(node.val)\n cnt += 1\n if cnt & 1 == 1:\n ans.append(level)\n else:\n ans.append(level[::-1])\n return ans\n\n``` | 4 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
python3, simple bfs, using lists and a flip sign (26 ms, faster than 97.08%) | binary-tree-zigzag-level-order-traversal | 0 | 1 | **Solution 1.1: BFS** \nhttps://leetcode.com/submissions/detail/900743056/ \nRuntime: **26 ms, faster than 97.08%** of Python3 online submissions for Binary Tree Zigzag Level Order Traversal.\nMemory Usage: 14.2 MB, less than 10.32% of Python3 online submissions for Binary Tree Zigzag Level Order Traversal.\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n def appd(n, q, v):\n if n: q.append(n); v.append(n.val)\n \n if not root: return\n vals, q = [[root.val]], [root]\n while True:\n flip, q1, vs = len(vals)%2, [], []\n for node in q[::-1]:\n if flip:\n appd(node.right, q1, vs)\n appd(node.left, q1, vs)\n else:\n appd(node.left, q1, vs)\n appd(node.right, q1, vs)\n if not q1: break\n q = q1; vals.append(vs)\n return vals\n```\n\n**Solution 1: BFS**\nhttps://leetcode.com/submissions/detail/900733858/ \nRuntime: **36 ms, faster than 58.29%** of Python3 online submissions for Binary Tree Zigzag Level Order Traversal.\nMemory Usage: 14.2 MB, less than 48.21% of Python3 online submissions for Binary Tree Zigzag Level Order Traversal.\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root: return\n vals, q, flip = [[root.val]], [root], 1\n while True:\n q1 = []\n for node in q:\n if node.left: q1.append(node.left)\n if node.right: q1.append(node.right)\n if not q1: break\n if flip:\n vals.append([n.val for n in q1[::-1]])\n flip = 0\n else:\n vals.append([n.val for n in q1])\n flip = 1\n q = q1\n return vals\n``` | 2 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
🚀Simplest Solution🚀||🔥Full Explanation||🔥C++🔥|| Python3 | binary-tree-zigzag-level-order-traversal | 0 | 1 | # Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful\n```\n# Intuition\nIntuition of this problem is very simple.\nWe use the **Level Order Traversal** of Binary tree.\nFor the Zig Zag Movement we are using a variable `level` when it is **zero** we **move from Left to Right** and when it is `one` we move from **Right to Left**.\nFor Level order traversal I am using a **Queue**.\nInitially we push `root` element in the queue. Traverse all elements of the tree.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : BFS, Level Order Traversal\n Example : `root` = [3,9,20,null,null,15,7]\n\n Initially `queue` = [3], level = 0\n In first pass\n size = 1 `queue` = [3]\n `curr[0]` = 3\n We push 3->left and 3->right in queue\n `queue` = [9, 20]\n So our loop only run 1 time beacuase size is 1.\n\n Now we push curr to `output` vector `output` = [[3]]\n Now `level` = 1\n\n In Second pass\n size = 2 `queue` = [9, 20]\n `curr[1]` = 20\n `curr[0]` = 9\n We push 20->left and 20->right in queue\n `queue` = [15, 7]\n And 9->left = NULL , 9->right = NULL so we do not push it.\n So our loop run 2 times beacuase size is 2.\n\n Now we push curr to `output` vector `output` = [[3], [20, 9]]\n Now `level` = 0\n\n In this way me iterate for the 15 and 7.\n So answer is `[[3], [20, 9], [15, 7]]`\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(W) width of the tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> zigzagLevelOrder(TreeNode* root) {\n \n if (!root) return {};\n \n queue<TreeNode*> q;\n vector<vector<int>> out;\n \n q.push(root); \n int level = 0; /* to alternate levels, or a bool variable */\n \n while (!q.empty()) {\n \n int sz = q.size(); \n vector<int> curr(sz); \n \n for (int i = 0; i < sz; i++) {\n \n TreeNode* tmp = q.front();\n q.pop();\n \n if (level == 0) {\n curr[i] = tmp->val; // odd level, insert like 0, 1, 2, 3 etc. \n } else {\n curr[sz - i - 1] = tmp->val; /* even level insert from end. 3, 2, 1, 0. (sz - i - 1) to get the index from end */\n }\n \n if (tmp->left) q.push(tmp->left);\n if (tmp->right) q.push(tmp->right);\n }\n out.push_back(curr); // now push the level traversed to output vector\n level = !level; // toggle the level using negation. or level == 0 ? level = 1 : level = 0;\n }\n return out;\n }\n};\n\n```\n```python []\nfrom queue import Queue\nclass Solution:\n def zigzagLevelOrder(self, A: TreeNode) -> List[List[int]]:\n if not A:\n return []\n queue = Queue()\n queue.put(A)\n output = []\n curr = []\n level = 0\n while not queue.empty():\n size = queue.qsize()\n curr = []\n for i in range(size):\n temp = queue.get()\n if level % 2 == 0:\n curr.append(temp.val)\n else:\n curr.insert(0, temp.val)\n if temp.left:\n queue.put(temp.left)\n if temp.right:\n queue.put(temp.right)\n level = not level\n output.append(curr)\n return output\n```\n```\n Give a \uD83D\uDC4D. It motivates me alot\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/) | 34 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
Most effective and easy solution using BFS with explanation | binary-tree-zigzag-level-order-traversal | 1 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> zigzagLevelOrder(TreeNode* root) {\n vector<vector<int>> res;\n if(!root) return res;\n queue<TreeNode*> q;\n q.push(root);\n bool flag = true;\n while(!q.empty()) {\n int size = q.size();\n vector<int> row(size);\n for(int i = 0; i<size; i++) {\n TreeNode* node = q.front();\n q.pop();\n int ind = (flag) ? i:(size-1-i);\n row[ind] = node->val;\n if(node->left) q.push(node->left);\n if(node->right) q.push(node->right);\n }\n flag = !flag;\n res.push_back(row);\n }\n return res;\n }\n};\n```\n```python3 []\nclass Solution:\n def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:\n if not root:\n return []\n \n res = []\n q = deque([root])\n flag = True\n \n while q:\n size = len(q)\n row = [0] * size\n \n for i in range(size):\n node = q.popleft()\n index = i if flag else size - 1 - i\n row[index] = node.val\n \n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n \n res.append(row)\n flag = not flag\n \n return res\n```\n```JAVA []\n\npublic class Solution {\n public List<List<Integer>> zigzagLevelOrder(TreeNode root) {\n List<List<Integer>> res = new ArrayList<>();\n if (root == null) return res;\n Queue<TreeNode> q = new LinkedList<>();\n q.offer(root);\n boolean flag = true;\n \n while (!q.isEmpty()) {\n int size = q.size();\n List<Integer> row = new ArrayList<>(size);\n \n for (int i = 0; i < size; i++) {\n TreeNode node = q.poll();\n int index = flag ? i : (size - 1 - i);\n row.add(index, node.val);\n \n if (node.left != null) q.offer(node.left);\n if (node.right != null) q.offer(node.right);\n }\n res.add(row);\n flag = !flag;\n }\n \n return res;\n }\n}\n```\n | 1 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
Python short and clean. BFS. | binary-tree-zigzag-level-order-traversal | 0 | 1 | # Approach\nDo the standard `BFS` level order traversal with an alternating boolean flag, say `reverse`, at every level.\nYield a reversed level if the flag is set else the original level.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is the number of nodes in the tree`.\n\n# Code\n```python\nclass Solution:\n def zigzagLevelOrder(self, root_: TreeNode | None) -> list[list[int]]:\n def zigzag_level_order(root: TreeNode | None) -> Iterator[TreeNode]:\n level = (root,) if root else ()\n reverse = False\n while level:\n yield reversed(level) if reverse else iter(level)\n level = tuple(child for node in level for child in (node.left, node.right) if child)\n reverse = not reverse\n \n return [[node.val for node in level] for level in zigzag_level_order(root_)]\n\n \n``` | 2 | Given the `root` of a binary tree, return _the zigzag level order traversal of its nodes' values_. (i.e., from left to right, then right to left for the next level and alternate between).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[3\],\[20,9\],\[15,7\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100` | null |
✔️ [Python3] RECURSIVE DFS ( •⌄• ू )✧, Explained | maximum-depth-of-binary-tree | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nTo calculate the maximum depth we can use the Depth-First Search. We call a helper function recursively and return the maximum depth between left and right branches. \n\nTime: **O(N)** - for DFS\nSpace: **O(N)** - for the recursive stack\n\nRuntime: 40 ms, faster than **89.54%** of Python3 online submissions for Maximum Depth of Binary Tree.\nMemory Usage: 16.3 MB, less than **18.15%** of Python3 online submissions for Maximum Depth of Binary Tree.\n\n```\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n def dfs(root, depth):\n if not root: return depth\n return max(dfs(root.left, depth + 1), dfs(root.right, depth + 1))\n \n return dfs(root, 0)\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 296 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
beats 99.99% solutions | maximum-depth-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n def find_depth(node,l):\n if node is None:\n return l\n \n l += 1\n # find_depth(node.left,l)\n # find_depth(node.right,l)\n return max(find_depth(node.left,l),find_depth(node.right,l))\n return find_depth(root,0)\n\n\n\n\n``` | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Recursive 1 line solution | maximum-depth-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTraversing a binary tree recursively.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverse the binary tree recursively and return the maximum length of the call stack.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(n)**\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1 if root else 0\n``` | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Python3 👍||⚡99/81 T/M beats, only 8 lines 🔥|| BFS || Optimization Simple solution || | maximum-depth-of-binary-tree | 0 | 1 | \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n if not root : return 0\n queue = deque()\n queue.append((root,1))\n while queue:\n cur_node = queue.popleft()\n if cur_node[0].left:queue.append((cur_node[0].left,cur_node[1]+1))\n if cur_node[0].right:queue.append((cur_node[0].right,cur_node[1]+1))\n return cur_node[1]\n``` | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Python || Recursive Code || Easy To Understand 🔥 | maximum-depth-of-binary-tree | 0 | 1 | # Code\n```\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n if root is None:\n return 0\n if root.left is None and root.right is None:\n return 1\n def maxdepth(root):\n if root is None:\n return 0\n if root.left is None and root.right is None:\n return 1\n return max(maxdepth(root.left), maxdepth(root.right)) + 1\n return maxdepth(root)\n``` | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
|| 🐍 Python3 O(n) Easiest ✔ Solution 🔥 || Beats 88% (Runtime) & 76% (Memory) || | maximum-depth-of-binary-tree | 0 | 1 | # Intuition\nUsing the `maxDepth` function recursively until the last node is found.\n\n# Approach\n1. Using `max()` function to calculate the maximum depth of the tree with the left and right node. One is added as the root node is also considered if there are child nodes.\n2. If the root node is the only node present then zero is returned as there is no depth.\n\n# Complexity\n- Time complexity : $$O(n)$$\n- Space complexity : $$O(1)$$\n\n# Code\n```python []\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n return max(self.maxDepth(root.left), self.maxDepth(root.right))+ 1 if root else 0\n```\n---\n\n### Happy Coding \uD83D\uDC68\u200D\uD83D\uDCBB\n\n---\n\n### If this solution helped you then do consider Upvoting \u2B06.\n#### Lets connect on LinkedIn : [Om Anand](https://www.linkedin.com/in/om-anand-38341a1ba/) \uD83D\uDD90\uD83D\uDE00\n---\n\n### Comment your views/corrections \uD83D\uDE0A\n | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
✅ Beats 99.70% solutions, ✅ Easy to understand Python Recursive code by 🔥 BOLT CODING 🔥 | maximum-depth-of-binary-tree | 0 | 1 | # Explanation\nLets divide the whole solution in two parts. \nFirst being the base condition which here is the recurrsive call should stop once it reaches the end of tree.\nSecond is the way to call the recursive function --> here we are calling the max of either of tree.\nLets assume there is a root node with 2 nodes attached. Suppose it is [1, 2, 3]. So our function will return max of either of side i.e. max(1, 1) = 1\n\nIn similar way if you dry run the test case given here you get your doubts clarified.\n\n# Complexity\n- Time complexity: O(n) as we are visiting all the nodes only once\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) as we are only using an extra variable n in here\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode], n=0) -> int:\n if root == None:\n return n\n if root:\n n+=1\n return max(self.maxDepth(root.left, n), self.maxDepth(root.right, n))\n```\n\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\n\n | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
[VIDEO] Visualization of Recursive Depth-First-Search | maximum-depth-of-binary-tree | 0 | 1 | https://youtu.be/p-eMCRpvbIY?si=wNAVx_6WQ7i9umSp\n\nAlthough recursion can be difficult to wrap your head around initially, once you understand the concept, it can be used to solve many problems in a very concise and elegant way.\n\nIn this solution, the base case is when `root == None`, which is when the end of a path is reached, so we `return 0`.\n\nIf the root is not None, then we recursively call the maxDepth function twice: once for the left child node and once for the right child node until every branch has been fully explored. Then when going back up the tree, we return `1 + max(left_depth, right_depth)`, which finds the longest branch of the current node, and adds 1 to include the current node. This propagates all the way up to the root node, where the final maximum depth is returned.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n if root == None:\n return 0\n\n left_depth = self.maxDepth(root.left)\n right_depth = self.maxDepth(root.right)\n return 1 + max(left_depth, right_depth)\n\n``` | 5 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
depth-first search (DFS) iterative approach✅ | O( n )✅ | (Step by step explanation)✅ | maximum-depth-of-binary-tree | 0 | 1 | # Intuition\nThe problem requires finding the maximum depth of a binary tree, which can be achieved through a depth-first search (DFS) approach. The intuition is to traverse the tree iteratively, keeping track of the depth, and returning the maximum depth encountered.\n\n# Approach\nThe approach is to perform an iterative DFS traversal of the binary tree. We use a stack to process nodes iteratively. For each node, we track the current depth. We maintain a variable `ans` to store the maximum depth encountered.\n\n1. Initialize a stack with the root node and depth 1, and set `ans` to 0.\n2. While the stack is not empty, pop nodes and their depths. If a node is not None, update `ans` with the maximum of the current depth and `ans`.\n3. Push the left and right children of the node onto the stack with incremented depth.\n4. Continue this process until the stack is empty.\n5. Return `ans` as the maximum depth of the binary tree.\n\n# Complexity\n- Time complexity: O(n)\n - We visit each node in the binary tree once, where n is the number of nodes.\n- Space complexity: O(h)\n - The space complexity is determined by the depth of the binary tree, which is h. In the worst case, for a skewed tree, it\'s O(n), and in the best case, for a balanced tree, it\'s O(log n).\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n # DFS-iterative\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n stack = [[root , 1]]\n ans = 0\n\n while stack:\n node , depth = stack.pop()\n\n if node:\n ans = max(ans , depth)\n stack.append([node.left , depth+1])\n stack.append([node.right , depth+1])\n\n return ans \n\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n\n // DFS-iterative\n int maxDepth(TreeNode* root) {\n\n stack<pair<TreeNode*, int>> st;\n int ans = 0;\n st.push({root, 1});\n\n while (!st.empty()) {\n auto [node, depth] = st.top();\n st.pop();\n\n if (node) {\n ans = max(ans, depth);\n st.push({node->left, depth + 1});\n st.push({node->right, depth + 1});\n }\n }\n\n return ans;\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n\n\n | 3 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Solution | maximum-depth-of-binary-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxDepth(TreeNode* root) {\n if(root==NULL)\n return NULL;\n\n int h1=maxDepth(root->left);\n int h2=maxDepth(root->right);\n\n int sol=max(h1,h2)+1;\n return sol;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n q = deque()\n depth = 0;\n q.append(root)\n while q:\n sz = len(q)\n for i in range(sz):\n temp = q.popleft()\n if temp.left:\n q.append(temp.left)\n if temp.right:\n q.append(temp.right)\n depth += 1\n return depth\n```\n\n```Java []\nclass Solution {\n\n public int maxDepth(TreeNode root) {\n if (root == null) return 0;\n return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));\n }\n}\n```\n | 3 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Python Easy Solution || DFS || BFS || 100% || Beats 95% || Recursion || | maximum-depth-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code \n# Top to Bottom Approach\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n self.maximum=0\n if root==None:\n return 0\n def topToBottom(node, depth):\n if not node.left and not node.right:\n self.maximum=max(self.maximum, depth+1)\n if node.left:\n topToBottom(node.left, depth+1)\n if node.right:\n topToBottom(node.right, depth+1)\n topToBottom(root, 0)\n return self.maximum\n```\n# Bottom to Up Approach\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n if root==None:\n return 0\n leftMax=rightMax=0\n leftMax=self.maxDepth(root.left)\n rightMax = self.maxDepth(root.right)\n return max(leftMax, rightMax)+1\n```\n | 1 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
PYTHON ONE-LINER | Recursion using left and right depth | maximum-depth-of-binary-tree | 0 | 1 | \n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n return 0 if not root else max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1\n\n```\n\nThe above code can be expanded as follows:\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxDepth(self, root: Optional[TreeNode]) -> int:\n if not root: return 0\n maxLeft = self.maxDepth(root.left)\n maxRight = self.maxDepth(root.right)\n return max(maxLeft, maxRight) + 1\n\n``` | 4 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Most optimal solution with explanation | maximum-depth-of-binary-tree | 1 | 1 | \n# Approach\n1. The base case is if the root is nullptr, in which case the depth is 0.\n2. Otherwise, it recursively calculates the maximum depth of the left and right subtrees (lh and rh, respectively).\n3. The maximum depth of the current tree is one plus the maximum of the depths of its left and right subtrees.\n\n# Complexity\n- Time complexity:\n)(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n int maxDepth(TreeNode* root) {\n if(!root) return 0;\n int lh = maxDepth(root->left);\n int rh = maxDepth(root->right);\n return 1+max(lh,rh);\n }\n};\n```\n```python []\nclass Solution:\n def maxDepth(self, root: TreeNode) -> int:\n if not root:\n return 0\n\n lh = self.maxDepth(root.left)\n rh = self.maxDepth(root.right)\n\n return 1 + max(lh, rh)\n```\n```Java []\npublic class Solution {\n public int maxDepth(TreeNode root) {\n if (root == null)\n return 0;\n\n int lh = maxDepth(root.left);\n int rh = maxDepth(root.right);\n\n return 1 + Math.max(lh, rh);\n }\n}\n```\n | 2 | Given the `root` of a binary tree, return _its maximum depth_.
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 3
**Example 2:**
**Input:** root = \[1,null,2\]
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-100 <= Node.val <= 100` | null |
Solution | construct-binary-tree-from-preorder-and-inorder-traversal | 1 | 1 | ```C++ []\nclass Solution {\npublic:\nTreeNode* constructTree(vector < int > & preorder, int preStart, int preEnd, vector \n < int > & inorder, int inStart, int inEnd, map < int, int > & mp) {\n if (preStart > preEnd || inStart > inEnd) return NULL;\n\n TreeNode* root = new TreeNode(preorder[preStart]);\n int elem = mp[root -> val];\n int nElem = elem - inStart;\n\n root -> left = constructTree(preorder, preStart + 1, preStart + nElem, inorder,\n inStart, elem - 1, mp);\n root -> right = constructTree(preorder, preStart + nElem + 1, preEnd, inorder, \n elem + 1, inEnd, mp);\n\n return root;\n}\n\nTreeNode* buildTree(vector < int > & preorder, vector < int > & inorder) {\n int preStart = 0, preEnd = preorder.size() - 1;\n int inStart = 0, inEnd = inorder.size() - 1;\n\n map < int, int > mp;\n for (int i = inStart; i <= inEnd; i++) {\n mp[inorder[i]] = i;\n }\n\n return constructTree(preorder, preStart, preEnd, inorder, inStart, inEnd, mp);\n}\n};\n```\n\n```Python3 []\nclass Solution:\n def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:\n VAL_TO_INORDER_IDX = {inorder[i]: i for i in range(len(inorder))}\n\n def buildTreePartition(preorder, inorder_start, inorder_end):\n if not preorder or inorder_start < 0 or inorder_end > len(inorder):\n return None\n\n root_val = preorder[0]\n root_inorder_idx = VAL_TO_INORDER_IDX[root_val]\n if root_inorder_idx > inorder_end or root_inorder_idx < inorder_start:\n return None\n \n root = TreeNode(preorder.pop(0))\n root.left = buildTreePartition(preorder, inorder_start, root_inorder_idx - 1)\n root.right = buildTreePartition(preorder, root_inorder_idx + 1, inorder_end)\n\n return root\n\n return buildTreePartition(preorder, 0, len(inorder) - 1)\n```\n\n```Java []\nclass Solution {\n private int i = 0;\n private int p = 0;\n\n public TreeNode buildTree(int[] preorder, int[] inorder) {\n return build(preorder, inorder, Integer.MIN_VALUE);\n }\n\n private TreeNode build(int[] preorder, int[] inorder, int stop) {\n if (p >= preorder.length) {\n return null;\n }\n if (inorder[i] == stop) {\n ++i;\n return null;\n }\n\n TreeNode node = new TreeNode(preorder[p++]);\n node.left = build(preorder, inorder, node.val);\n node.right = build(preorder, inorder, stop);\n return node;\n }\n}\n```\n | 455 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Recursive approach✅ | O( n)✅ | Python(Step by step explanation)✅ | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | # Intuition\nThe problem involves constructing a binary tree from its preorder and inorder traversal sequences. The preorder traversal visits the root node first, followed by its left subtree and then its right subtree. The inorder traversal visits the left subtree, followed by the root node, and then the right subtree.\n\n# Approach\nThe approach involves using recursion to build the binary tree. We use the preorder traversal to determine the root of the current subtree and the inorder traversal to identify the left and right subtrees.\n\n1. **Recursive Build Function**: Implement a recursive function to build the binary tree.\n\n **Reason**: Recursion simplifies the process of constructing the binary tree by breaking it down into smaller subproblems.\n\n2. **Base Case**: Check for empty preorder or inorder lists. If either is empty, return None.\n\n **Reason**: An empty list implies no nodes to process.\n\n3. **Inorder Index Map**: Create a mapping of values to their indices in the inorder traversal.\n\n **Reason**: We use this mapping to efficiently find the root and subtrees.\n\n4. **Build Tree Function**: Define a function to build the binary tree given the indices and traversal sequences.\n\n **Reason**: This function constructs the binary tree recursively.\n\n5. **Root Node**: The root node is the first element in the preorder traversal.\n\n **Reason**: The preorder traversal visits the root node first.\n\n6. **Inorder Index**: Find the index of the root value in the inorder traversal.\n\n **Reason**: The inorder traversal helps identify the left and right subtrees.\n\n7. **Left Subtree Size**: Calculate the size of the left subtree.\n\n **Reason**: We need to know how many elements belong to the left subtree.\n\n8. **Build Left and Right Subtrees**: Recursively build the left and right subtrees using appropriate indices.\n\n **Reason**: This step constructs the left and right subtrees.\n\n9. **Return Root**: Return the root node of the constructed binary tree.\n\n **Reason**: We need to return the root of the binary tree.\n\n# Complexity\n- **Time complexity**: O(n)\n - The algorithm processes each node once.\n- **Space complexity**: O(n)\n - The recursion stack can have at most n frames, where n is the number of nodes in the tree.\n\n# Please upvote the solution if you understood it.\n\n | 2 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Awesome Logic Python3 | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:\n if not preorder or not inorder:\n return None\n root=TreeNode(preorder[0])\n index=inorder.index(preorder[0])\n root.left=self.buildTree(preorder[1:index+1],inorder[:index])\n root.right=self.buildTree(preorder[index+1:],inorder[index+1:])\n return root\n #please upvote me it would encourage me alot\n\n``` | 33 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Easy Python Recursion with Explanation | Divide and Conquer Approach | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | # Intuition\n1. First element of Pre-order is the root node.\n2. Elements on the left of the root in In-order are on the left side and elements on right are on right side.\n3. The next node in Pre-order is the next level node for the left subarray untill the left part of the original tree is resolved.\n4. After the left part of the tree is resolved, the next node of the Pre-order is the next level node on the right side of the tree.\n5. We can remove the node from the Pre-order once we visit it or keep a track of visited array and only consider the non visited nodes for being the root of the next level.\n\n# Approach\n1. A Recursive function $$subtree$$ is used which takes two arrays (left and right) which have the the elements that should be on the left and right respectively.\n2. If the left part have more than one element then it recusively calls itself to resolve the left part of the tree.\n3. Similarly, it resolves right sub part only after the left part is resolved.\n4. Pre-order is used as a class variable $$p$$ and whenever a node is created it\'s removed from the Pre-order to keep the root of next level always on the *0<sup>th</sup>* index.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n p = []\n def subtree(self,left,right):\n root = TreeNode(self.p.pop(0)) #determining root \n\n if len(left) > 1 : #dividing left subtree further\n r = self.p[0]\n pos = left.index(r)\n l = left[:pos]\n r = left[pos+1:]\n root.left = self.subtree(l,r)\n elif len(left) == 1:\n self.p.remove(left[0])\n root.left = TreeNode(left[0])\n\n if len(right) > 1 : #dividing right subtree further\n r = self.p[0]\n pos = right.index(r)\n l = right[:pos]\n r = right[pos+1:]\n root.right = self.subtree(l,r) \n elif len(right) == 1:\n self.p.remove(right[0])\n root.right = TreeNode(right[0]) \n\n return root #returning the subtree\n\n def buildTree(self, p: List[int], i: List[int]) -> Optional[TreeNode]:\n\n self.p = p\n root = self.p[0]\n pos = i.index(root)\n left = i[:pos]\n right = i[pos+1:]\n\n return self.subtree(left,right)\n \n\n\n``` | 3 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Python Easy Solution || 100% || Recursion || Beats 96% || | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:. $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:. $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:\n inorder_map={val:idx for idx, val in enumerate(inorder)}\n preorder_idx=0\n\n def treeHelper(left, right):\n nonlocal preorder_idx\n if left>right:\n return None\n\n node_val = preorder[preorder_idx]\n root=TreeNode(node_val)\n preorder_idx+=1\n\n inorder_index=inorder_map[node_val]\n\n root.left = treeHelper(left, inorder_index-1 )\n root.right = treeHelper(inorder_index+1, right)\n\n return root\n\n return treeHelper(0, len(inorder)-1)\n``` | 5 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Divide and Conquer + Hash table || Easiest Beginner Friendly Sol | construct-binary-tree-from-preorder-and-inorder-traversal | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\nThe problem is to construct a binary tree from inorder and preorder traversals of the tree. The inorder traversal gives the order of nodes in the left subtree, root, and right subtree, while the preorder traversal gives the order of nodes in the root, left subtree, right subtree.\n\n**The intuition behind the algorithm is to start by identifying the root of the binary tree from the first element of the preorder traversal. Then, we can use the root to divide the inorder traversal into left and right subtrees. We can then recursively apply the same process to the left and right subtrees to construct the entire binary tree.**\n\nTo do this efficiently, we can use a hash map to store the indices of elements in the inorder traversal. This allows us to quickly find the position of the root in the inorder traversal and divide the traversal into left and right subtrees.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Create an index variable \'preorderIndex\' to keep track of the current root node in preorder traversal.\n2. Create an unordered map \'inorderIndexUmp\' to store the indices of all elements in the inorder traversal.\n3. Define a recursive helper function \'buildTreeHelper\' that takes the preorder traversal vector, and the range (left and right indices) of the subtree being constructed.\n4. If the left index is greater than the right index, return null pointer to represent an empty subtree.\n5. Get the value of the root node from the current position of \'preorderIndex\' and increment it.\n6. Create a new TreeNode with the root value and set its left and right children to null.\n7. Find the index of the root node in the inorder traversal using the \'inorderIndexUmp\' map.\n8. Recursively construct the left subtree by calling the \'buildTreeHelper\' function on the left range (left to inorder pivot index - 1).\n9. Recursively construct the right subtree by calling the \'buildTreeHelper\' function on the right range (inorder pivot index + 1 to right).\n10. Return the constructed tree.\n11. In the main function \'buildTree\', initialize the \'preorderIndex\'\nto zero and create the \'inorderIndexUmp\' map.\n1. Call the \'buildTreeHelper\' function on the entire range of the preorder traversal vector.\n2. Return the constructed binary tree.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int preorderIndex;\n unordered_map<int, int> inorderIndexUmp;\n\n TreeNode* buildTreeHelper(vector<int>& preorder, int left, int right) {\n if (left > right)\n return nullptr;\n int rootValue = preorder[preorderIndex++];\n TreeNode* root = new TreeNode(rootValue);\n int inorderPivotIndex = inorderIndexUmp[rootValue];\n //think about it..why I am choosing root -> left first then root -> right\n root -> left = buildTreeHelper(preorder, left, inorderPivotIndex - 1);\n root -> right = buildTreeHelper(preorder, inorderPivotIndex + 1, right);\n return root;\n }\n\n TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {\n preorderIndex = 0;\n for (int i = 0; i < inorder.size(); i++) {\n inorderIndexUmp[inorder[i]] = i;\n }\n return buildTreeHelper(preorder, 0, preorder.size() - 1);\n }\n};\n```\n```Java []\nclass Solution {\n int preorderIndex;\n Map<Integer, Integer> inorderIndexUmp;\n\n public TreeNode buildTreeHelper(int[] preorder, int left, int right) {\n if (left > right)\n return null;\n int rootValue = preorder[preorderIndex++];\n TreeNode root = new TreeNode(rootValue);\n int inorderPivotIndex = inorderIndexUmp.get(rootValue);\n root.left = buildTreeHelper(preorder, left, inorderPivotIndex - 1);\n root.right = buildTreeHelper(preorder, inorderPivotIndex + 1, right);\n return root;\n }\n\n public TreeNode buildTree(int[] preorder, int[] inorder) {\n preorderIndex = 0;\n inorderIndexUmp = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n inorderIndexUmp.put(inorder[i], i);\n }\n return buildTreeHelper(preorder, 0, preorder.length - 1);\n }\n}\n\n```\n```Python []\nclass Solution:\n def buildTreeHelper(self, preorder: List[int], left: int, right: int) -> TreeNode:\n if left > right:\n return None\n rootValue = preorder[self.preorderIndex]\n self.preorderIndex += 1\n root = TreeNode(rootValue)\n inorderPivotIndex = self.inorderIndexUmp[rootValue]\n root.left = self.buildTreeHelper(preorder, left, inorderPivotIndex - 1)\n root.right = self.buildTreeHelper(preorder, inorderPivotIndex + 1, right)\n return root\n \n def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:\n self.preorderIndex = 0\n self.inorderIndexUmp = {val:idx for idx, val in enumerate(inorder)}\n return self.buildTreeHelper(preorder, 0, len(preorder) - 1)\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity : **O(n)**, The buildTreeHelper() function is called for each node in the tree exactly once, and the time complexity of each call is O(1). Therefore, the overall time complexity of the algorithm is O(n), where n is the number of nodes in the tree.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : **O(n)**, where n is the number of nodes in the tree. This is because we are creating a new TreeNode object for each node in the tree, and we are also using an unordered_map to store the indices of the nodes in the inorder traversal. Additionally, the recursive calls to buildTreeHelper() create a call stack of size O(n) in the worst case, where n is the number of nodes in the tree.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n**YOU CAN ALSO TRY BELOW PROBLEM WHICH IS SIMILAR TO THIS PROBLEM :**\n106. Construct Binary Tree from Inorder and Postorder Traversal\n**SOLUTION :**\nhttps://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solutions/3302713/day-75-divide-and-conquer-hash-table-easiest-beginner-friendly-sol/ | 6 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Stack implementation beating 85%/90% in speed/memory comparison | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe preorder list shows what is the root node every step. Using the preorder list, we can identify the root in the inorder list and then divide the list into two: left and right.\n\n# Solution\n1. Iterate the preorder list to make a hashmap that stores (value, index) pairs.\n2. Find the value of `preorder[i]` in the hashmap we made in the step 1.\n3. Now we know the index of root node, divide the problem into two by narrowing down the size of the list that we are interested in. i.e., From (L, H), divide the range into (L, root_index - 1) and (root_index + 1, H).\n\nWhile you keep dividing the problem, **make sure you should create a new sub-problem only when `L <= root_index - 1` or `root_index + 1 <= H`.**\n\nYou can solve this problem using a recursive function or a stack. In this solution, I used a stack to take advantage of speed and get used to stack implementation.\n\n# Complexity\n- Time complexity: $$O(n)$$ as it just iterates the list.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ as it creates new tree from the list.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:\n # preorder: root -> left -> right\n # inroder: left -> root -> right\n dic = {}\n for i, num in enumerate(inorder):\n dic[num] = i\n \n stk = []\n i = 0\n node = TreeNode()\n stk.append((0, len(preorder) - 1, node))\n while stk:\n l, h, n = stk[-1]\n stk.pop()\n root_idx = dic[preorder[i]]\n n.val = preorder[i]\n if root_idx + 1 <= h:\n n.right = TreeNode()\n stk.append((root_idx + 1, h, n.right))\n if l <= root_idx - 1:\n n.left = TreeNode()\n stk.append((l, root_idx - 1, n.left))\n i += 1\n \n return node\n \n``` | 2 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Detailed Python Walkthrough from an O(n^2) solution to O(n). Faster than 99.77% | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | \nI\'m going to assume you know the basics of how to answer the question, the answer is more pertained to coming up with an optimised solution. \n\n**First Solution**\n*T: O(N^2) where N is the number if items in either the preorder or inorder list (they both have to be the same).*\n\nLet\'s start with the basic recursive approach:\n```\n def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:\n preorder.reverse()\n return self.buildTreeRec(preorder, inorder)\n def buildTreeRec(self, preorder, inorder):\n if not inorder: return None\n n = TreeNode(preorder.pop())\n i = inorder.index(n.val)\n n.left = self.buildTreeRec(preorder, inorder[:i])\n n.right = self.buildTreeRec(preorder, inorder[i+1:])\n return n\n```\nThis approach looks great and is accepted by Leetcode, but there is one great flaw with the time complexity and that is the third line in the recursive function. In Python at least, the .index function runs in N time. It will run across the entire list (array) looking for n.val. Why is this bad?\n\nLet\'s say we have a SUPER unbalanced tree. Like it basically looks like a linear, y = x function where every node has no right children but just a left child. Let\'s say it has just four nodes: A -> B -> C -> D\n\nIt\'s preorder traversal is going to be: [A, B, C, D]\nIt\'s inorder traversal is going to be: [D, C, B, A]\n\nSo let\'s take the very first iteration of the recursive function. The root of the tree (and the answer itself) is going to be A. Simple enough, we pop the value from our preorder list (pop from the right since the list has been reversed). Now we have to find it in our inorder list, in order to know which values belong in A\'s left and right subtree. In the current approach, that means we run across the full inorder traversal list which is N nodes.\n\nIn the second iteration of the recursive function, we\'ll have to run across N-1 nodes since we slice off the A. So for N nodes, we\'ll have to run across N, then N - 1, then N-2, then N-3 etc. items in the inorder list. \n\nAs we all know, that\'s an N^2 approach. So we have to do better. The most obvious solution is to remove the .index and that idea forms the basis for the second solution.\n\n**Second Solution**\n\nThe second solution uses a dictionary to store all of the values of the inorder list. Each key-value pair is the list item\'s value and its index. So basically, inorderList[i] : i.\n\nThe immediate issue with this is that we can longer slice the inorderDict like we were slicing the inorder list like in the first solution. So we have to maintain two pointers, beginning and end which represents the current subsection of the inorder list on which we are currently working. \n\nHere\'s the code first, and I\'ll try to walk through an example:\n\n``` \n\tdef buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:\n preorder.reverse()\n inorderDict = { v:i for i,v in enumerate(inorder) }\n return self.buildTreeHelper(preorder, inorderDict, 0, len(preorder) - 1)\n def buildTreeHelper(self, preorder, inorderDict, beg, end):\n if beg > end: return None\n root = TreeNode(preorder.pop())\n index = inorderDict[root.val]\n \n root.left = self.buildTreeHelper(preorder, inorderDict, beg, index - 1)\n root.right = self.buildTreeHelper(preorder, inorderDict, index + 1, end)\n return root\n```\n\nSo in the first function, we still reverse the preorder list and make a dictionary for the inorder list. If that syntax looks confusing to you, google \'dictionary comprehensions\' and the Python built-in \'enumerate()\' function. \n\nThe beg and end act as bounds for the recursion. If end ever crosses beg, that means we have no nodes left. It\'s the equivalent in the first solution of having an empty inorder list. \n\nLet\'s use the example from the question itself:\n\npreorder = [3,9,20,15,7]\ninorder = [9,3,15,20,7]\n\nSo in the first iteration of the recursive approach, we build the root node which is 3. Beg and end are 0 and 4 respectively. The root\'s left subtree is composed of all nodes to the left of 3 in the inorder list. So just the 9.\n\nWhen going to the left, we only **update the end value.** That new value will be the index of 3 in the inorder list, less 1. This is equivalent to slicing the inorder list as so: list[:i]. \n\nIn the second iteration of the recursive function, we\'re building the leftsubtree for the original root 3. It\'s pretty trivial since it\'s just one node, 9. The beg and end values here will be 0 and 0 respectively. We build the node and pop the 9 from the preorder list. We still make the calls to *try* to make 9\'s left and right subtree. However, we know that they don\'t exist. When we call the recursive function in both instances, both will return None.\n\nFor 9\'s left subtree, the beg and end values are 0 and -1, and for the right subtree, the beg and end values are 1 and 0. Both will cause the first if statement to be true, thus retuning None. \n\nGoing back to the root 3, the same logic applies for the root\'s right subtree. Only difference is, **when going right, only update the beg.** | 36 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Python easy solution with comments | construct-binary-tree-from-preorder-and-inorder-traversal | 0 | 1 | ```python\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution(object):\n def buildTree(self, preorder, inorder):\n """\n :type preorder: List[int]\n :type inorder: List[int]\n :rtype: TreeNode\n """\n \n # Recursive solution\n if inorder: \n # Find index of root node within in-order traversal\n index = inorder.index(preorder.pop(0))\n root = TreeNode(inorder[index])\n \n # Recursively generate left subtree starting from \n # 0th index to root index within in-order traversal\n root.left = self.buildTree(preorder, inorder[:index])\n \n # Recursively generate right subtree starting from \n # next of root index till last index\n root.right = self.buildTree(preorder, inorder[index+1:])\n return root\n``` | 42 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** preorder = \[3,9,20,15,7\], inorder = \[9,3,15,20,7\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** preorder = \[-1\], inorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= preorder.length <= 3000`
* `inorder.length == preorder.length`
* `-3000 <= preorder[i], inorder[i] <= 3000`
* `preorder` and `inorder` consist of **unique** values.
* Each value of `inorder` also appears in `preorder`.
* `preorder` is **guaranteed** to be the preorder traversal of the tree.
* `inorder` is **guaranteed** to be the inorder traversal of the tree. | null |
Python || Easy || Recursive Solution || Dictionary | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | ```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n n=len(inorder)\n poststart=instart=0\n postend=inend=n-1\n d={}\n for i in range(n):\n d[inorder[i]]=i\n return self.constructTree(postorder,poststart,postend,inorder,instart,inend,d)\n \n def constructTree(self,postorder,poststart,postend,inorder,instart,inend,d):\n if poststart>postend or instart>inend:\n return None\n root=TreeNode(postorder[postend])\n elem=d[root.val]\n nelem=elem-instart\n root.left=self.constructTree(postorder,poststart,poststart+nelem-1,inorder,instart,elem-1,d)\n root.right=self.constructTree(postorder,poststart+nelem,postend-1,inorder,elem+1,inend,d)\n return root\n```\n**An upvote will be encouraging** | 1 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Python3 Solution | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n mapper={}\n for i,v in enumerate(inorder):\n mapper[v]=i\n \n def rec(low,high):\n if low>high:\n return\n root=TreeNode(postorder.pop())\n mid=mapper[root.val]\n root.right=rec(mid+1,high)\n root.left=rec(low,mid-1)\n return root\n \n return rec(0,len(inorder)-1)\n``` | 1 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Beats 93% 🔥 | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n inorderidx = {v : i for i, v in enumerate(inorder)}\n\n def helper(l, r):\n if l > r:\n return None\n \n root = TreeNode(postorder.pop())\n\n idx = inorderidx[root.val]\n root.right = helper(idx + 1, r)\n root.left = helper(l, idx - 1)\n return root\n \n return helper(0, len(inorder) - 1)\n\n\n\n\n``` | 2 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
🔥Easy Explanation + Video | Java C++ Python | construct-binary-tree-from-inorder-and-postorder-traversal | 1 | 1 | InOrder Traversal: we visit the left subtree first, then the root node, and then the right subtree\n4,10,12,15,18,22,24,25,31,35,44,50,66,70,90\n\nPostOrder Traversal: we visit the left subtree first, then the right subtree, and then the current node\n4,12,10,18,24,22,15,31,44,35,66,90,70,50,25\n\n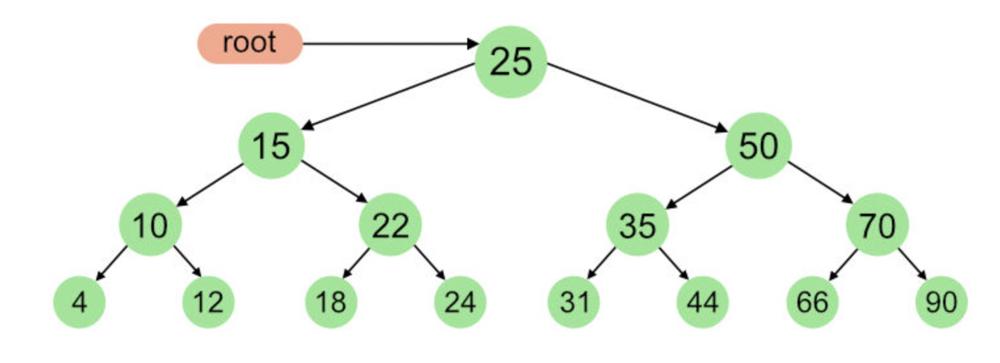\n\n# Intuition and Approach\nThe biggest hint is that the root node is always at end in postOrder Traversal ex: 25 is root node.\nWe find this root node in Inorder Traversal and all the elements on left i.e 4,10,12,15,18,22,24 act as left subtree and all elements on right 31,35,44,50,66,70,90 act as right subtree. \n\nThe above process can be repeated to form left and right subtree again individually\neg: 4,10,12,15,18,22,24 is Inorder for left and 4,12,10,18,24,22,15 is Post Order for left and here again 15 will act as the root node. \nHence The idea will be to use Recursion.\n\n# Approach \n1. The buildTree method calls the formBinaryTree method with parameters A, B, 0, A.length-1, 0, and B.length-1. These parameters specify the starting and ending indices of the inorder and postorder traversal arrays.\n2. create a new TreeNode with the last element of the postorder traversal as the value. This value represents the root node of the current subtree.\n3. search for this value in the inorder traversal array to find the index of the root node.\n4. recursively call itself to form left and right subtree. It passes the parameters as follows:\nfor left: start, mid-1, start2, x\nfor right: mid+1,end,x+1,end2-1\n\n// x = end of postOrderTraversal of left subtree\nx = no of elemnts in leftSubtree + start of postOrder\n\n# Improvement\nInstead of finding the middle node every time in Inorder Traversal, create a hashMap with value as key and position as value.\n\n<iframe width="560" height="315" src="https://www.youtube.com/embed/2uRa3e3-Vdc" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe>\n\n```\nclass Solution {\n public HashMap<Integer,Integer> hashMap;\n public TreeNode buildTree(int[] A, int[] B) {\n hashMap = new HashMap<>();\n for(int i = 0;i<A.length;i++){\n hashMap.put(A[i],i);\n }\n return formBinaryTree(A,B,0,A.length-1,0,B.length-1);\n }\n \n public TreeNode formBinaryTree(int[] inOrder, int [] postOrder, int start, int end , int start2, int end2) {\n if(start > end){\n \n return null;\n }\n TreeNode middle = new TreeNode(postOrder[end2]);\n int mid = hashMap.get(middle.val);\n \n int x = mid-1+start2-start;\n middle.left = formBinaryTree(inOrder,postOrder, start, mid-1, start2, x);\n middle.right = formBinaryTree(inOrder,postOrder,mid+1,end,x+1,end2-1 );\n return middle;\n }\n}\n```\n\n\n```\n\nclass Solution {\n public TreeNode buildTree(int[] A, int[] B) {\n return formBinaryTree(A,B,0,A.length-1,0,B.length-1);\n }\n \n public TreeNode formBinaryTree(int[] inOrder, int [] postOrder, int start, int end , int start2, int end2) {\n if(start > end){\n \n return null;\n }\n TreeNode middle = new TreeNode(postOrder[end2]);\n int mid = 0;\n for(int i = start;i<=end;i++){\n if(inOrder[i]==middle.val) {\n mid = i;\n break;\n }\n }\n int noOfElements = mid-1-start;\n int x = noOfElements + start2;//i.e the end of postOrderTraversal of left subtree\n middle.left = formBinaryTree(inOrder,postOrder, start, mid-1, start2, x);\n middle.right = formBinaryTree(inOrder,postOrder,mid+1,end,x+1,end2-1 );\n return middle;\n }\n}\n```\n\n```\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n return formBinaryTree(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);\n }\n\n TreeNode* formBinaryTree(vector<int>& inOrder, vector<int>& postOrder, int start, int end, int start2, int end2) {\n if (start > end) {\n return nullptr;\n }\n TreeNode* middle = new TreeNode(postOrder[end2]);\n int mid = 0;\n for (int i = start; i <= end; i++) {\n if (inOrder[i] == middle->val) {\n mid = i;\n break;\n }\n }\n int noOfElements = mid - 1 - start;\n int x = noOfElements + start2; // i.e the end of postOrderTraversal of left subtree\n middle->left = formBinaryTree(inOrder, postOrder, start, mid - 1, start2, x);\n middle->right = formBinaryTree(inOrder, postOrder, mid + 1, end, x + 1, end2 - 1);\n return middle;\n }\n};\n```\n\n```\n\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n return self.formBinaryTree(inorder, postorder, 0, len(inorder) - 1, 0, len(postorder) - 1)\n\n def formBinaryTree(self, inOrder: List[int], postOrder: List[int], start: int, end: int, start2: int, end2: int) -> TreeNode:\n if start > end:\n return None\n middle = TreeNode(postOrder[end2])\n mid = 0\n for i in range(start, end + 1):\n if inOrder[i] == middle.val:\n mid = i\n break\n noOfElements = mid - 1 - start\n x = noOfElements + start2 # i.e the end of postOrderTraversal of left subtree\n middle.left = self.formBinaryTree(inOrder, postOrder, start, mid - 1, start2, x)\n middle.right = self.formBinaryTree(inOrder, postOrder, mid + 1, end, x + 1, end2 - 1)\n return middle\n```\n\n\n | 9 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Awesome Logic Python3 | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:90%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:80%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if not inorder or not postorder:\n return None\n root=TreeNode(postorder[-1])\n index=inorder.index(postorder[-1])\n root.left=self.buildTree(inorder[:index],postorder[:index])\n root.right=self.buildTree(inorder[index+1:],postorder[index:-1])\n return root\n #please upvote me it would encourage me alot\n\n``` | 52 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.