title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Construct Binary Tree from Inorder and Postorder Traversal with step by step explanation | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe start by creating a hashmap called inorder_map to store the indices of each element in the inorder list. This will allow us to quickly find the index of a given value in constant time later on.\n\nThen, we define a recursive helper function called build that takes two arguments: the start and end indices of the current subtree we\'re working on. If the start index is greater than the end index, we\'ve reached the end of a branch and we should return None.\n\nInside the build function, we pop the last value from the postorder list and create a new node with that value. Then, we use the inorder_map to find the index of the node in the inorder list.\n\nSince we\'re working with the postorder traversal, we first recursively build the right subtree by calling build with the start index set to index + 1 and the end index set to end. Then, we recursively build the left subtree by calling build with the start index set to start and the end index set to index - 1.\n\nFinally, we call the build function with the start index set to 0 and the end index set to len(inorder) - 1, which will build the entire tree. The build function will return the root node of the tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n # Use a hashmap to store the indices of each element in the inorder list\n inorder_map = {}\n for i, val in enumerate(inorder):\n inorder_map[val] = i\n \n # Define a recursive helper function to build the tree\n def build(start, end):\n # Base case: the start index is greater than the end index\n if start > end:\n return None\n \n # Create a new node with the last value in the postorder list\n val = postorder.pop()\n node = TreeNode(val)\n \n # Find the index of the node in the inorder list\n index = inorder_map[val]\n \n # Recursively build the right subtree first, since we\'re working with the postorder traversal\n node.right = build(index + 1, end)\n # Then build the left subtree\n node.left = build(start, index - 1)\n \n return node\n \n # Call the helper function to build the tree\n return build(0, len(inorder) - 1)\n\n``` | 5 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Python short and clean. | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | # Approach\nTL;DR, Similar to [105. Construct Binary Tree from Preorder and Inorder Traversal](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solutions/3305262/python-short-and-clean/).\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is the number of nodes in the tree`.\n\n# Code\n```python\nclass Solution:\n def buildTree(self, inorder: list[int], postorder: list[int]) -> TreeNode | None:\n in_index_map = dict(map(reversed, enumerate(inorder)))\n \n def build_tree(post_end: int, in_start: int, in_end: int) -> tuple[TreeNode | None, int]:\n if in_start >= in_end: return None, post_end\n \n root_val = postorder[post_end]\n root_index = in_index_map[root_val]\n \n r_tree, post_start = build_tree(post_end - 1, root_index + 1, in_end)\n l_tree, post_start = build_tree(post_start, in_start, root_index)\n \n return TreeNode(root_val, l_tree, r_tree), post_start\n \n return build_tree(len(postorder) - 1, 0, len(inorder))[0]\n\n\n``` | 3 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Clean Codes🔥🔥|| Full Explanation✅|| Using Stack✅|| C++|| Java|| Python3 | construct-binary-tree-from-inorder-and-postorder-traversal | 1 | 1 | # Intuition :\n- Given two integer arrays inorder and postorder ,construct and return the binary tree.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Iterative Approach using Stack\n- Use the last element in the postorder traversal as the root node, then iterate over the rest of the postorder traversal from right to left. \n- For each element, we create a new node and add it to the stack. We then check if the new node is the left or right child of the previous node. \n- If it\'s the left child, we simply attach it to the previous node. \n- If it\'s the right child, we pop the stack until we find the parent node whose left child is the previous node, and attach the new node to its right child. \n- We repeat this process until we\'ve processed all the nodes in the postorder traversal.\n<!-- Describe your approach to solving the problem. -->\n**Credits to @mayijie88 for helping me out**\n# Let\'s See an Example :\n- Let\'s take the following inorder and postorder traversals as an example:\n```\ninorder = [9,3,15,20,7]\npostorder = [9,15,7,20,3]\n```\n- So we want to use these traversals to build a binary tree. \n# Steps to be followed :\n- Both the inorder and postorder traversals are non-empty, so we can continue.\n\n```\nip = 4 (the index of the last element in the inorder traversal), \npp = 4 (the index of the last element in the postorder traversal).\n```\n- We create an empty `stack` and initialize `prev` to `null`.\n- We create the root node using the last element in the postorder traversal, which is 3. We push the root node onto the stack and decrement pp to 3.\n\n```\nStack:\n| 3 |\n```\n\n- We iterate over the rest of the postorder traversal from right to left. The next element is 20. \n- We create a new node for 20 and push it onto the stack. We check if 20 is the left or right child of the previous node (which is 3). \n- Since it\'s the right child, we pop the stack until we find the parent node whose left child is 3, which is null. \n- We attach 20 as the right child of 3, and push 20 onto the stack. prev is set to null.\n\n```\nStack:\n| 20 |\n| 3 |\n```\n\n- The next element is 7. We create a new node for 7 and push it onto the stack. We check if 7 is the left or right child of the previous node (which is 20). \n- Since it\'s the right child, we pop the stack until we find the parent node whose left child is 20, which is 3. \n- We attach 7 as the right child of 20, and push 7 onto the stack. prev is set to null.\n\n```\nStack:\n| 7 |\n| 20 |\n| 3 |\n```\n\n- The next element is 15. We create a new node for 15 and push it onto the stack. We check if 15 is the left or right child of the previous node (which is 7). \n- Since it\'s the left child, we attach 15 as the left child of 7, and push 15 onto the stack. prev is set to null.\n\n```\nStack:\n| 15 |\n| 7 |\n| 20 |\n| 3 |\n```\n\n- The next element is 9. We create a new node for 9 and push it onto the stack. We check if 9 is the left or right child of the previous node (which is 15). \n- Since it\'s the left child, we attach 9 as the left child of 15, and push 9 onto the stack. prev is set to null.\n\n```\nStack:\n| 9 |\n| 15 |\n| 7 |\n| 20 |\n| 3 |\n```\n\n- We\'ve processed all the elements in the postorder traversal, so we can return the root node of the binary tree, which is 3.\n- The resulting binary tree looks like this:\n```\n 3\n / \\\n 9 20\n / \\\n 15 7\n\n```\n# Complexity :\n- Time complexity : O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] : With Comments\n```Java []\nclass Solution \n{\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n // If either of the input arrays are empty, the tree is empty, so return null\n if (inorder.length == 0 || postorder.length == 0) return null;\n \n // Initialize indices to the last elements of the inorder and postorder traversals\n int ip = inorder.length - 1;\n int pp = postorder.length - 1;\n\n // Create an empty stack to help us build the binary tree\n Stack<TreeNode> stack = new Stack<TreeNode>();\n // Initialize prev to null since we haven\'t processed any nodes yet\n TreeNode prev = null;\n // Create the root node using the last element in the postorder traversal\n TreeNode root = new TreeNode(postorder[pp]);\n // Push the root onto the stack and move to the next element in the postorder traversal\n stack.push(root);\n pp--;\n\n // Process the rest of the nodes in the postorder traversal\n while (pp >= 0) {\n // While the stack is not empty and the top of the stack is the current inorder element\n while (!stack.isEmpty() && stack.peek().val == inorder[ip]) {\n // The top of the stack is the parent of the current node, so pop it off the stack and update prev\n prev = stack.pop();\n ip--;\n }\n // Create a new node for the current postorder element\n TreeNode newNode = new TreeNode(postorder[pp]);\n // If prev is not null, the parent of the current node is prev, so attach the node as the left child of prev\n if (prev != null) {\n prev.left = newNode;\n // If prev is null, the parent of the current node is the current top of the stack, so attach the node as the right child of the current top of the stack\n } else if (!stack.isEmpty()) {\n TreeNode currTop = stack.peek();\n currTop.right = newNode;\n }\n // Push the new node onto the stack, reset prev to null, and move to the next element in the postorder traversal\n stack.push(newNode);\n prev = null;\n pp--;\n }\n\n // Return the root of the binary tree\n return root;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n // If either of the input vectors are empty, the tree is empty, so return null\n if (inorder.size() == 0 || postorder.size() == 0) return nullptr;\n\n // Initialize indices to the last elements of the inorder and postorder traversals\n int ip = inorder.size() - 1;\n int pp = postorder.size() - 1;\n\n // Create an empty stack to help us build the binary tree\n stack<TreeNode*> st;\n // Initialize prev to null since we haven\'t processed any nodes yet\n TreeNode* prev = nullptr;\n // Create the root node using the last element in the postorder traversal\n TreeNode* root = new TreeNode(postorder[pp]);\n // Push the root onto the stack and move to the next element in the postorder traversal\n st.push(root);\n pp--;\n\n // Process the rest of the nodes in the postorder traversal\n while (pp >= 0) {\n // While the stack is not empty and the top of the stack is the current inorder element\n while (!st.empty() && st.top()->val == inorder[ip]) {\n // The top of the stack is the parent of the current node, so pop it off the stack and update prev\n prev = st.top();\n st.pop();\n ip--;\n }\n // Create a new node for the current postorder element\n TreeNode* newNode = new TreeNode(postorder[pp]);\n // If prev is not null, the parent of the current node is prev, so attach the node as the left child of prev\n if (prev != nullptr) {\n prev->left = newNode;\n // If prev is null, the parent of the current node is the current top of the stack, so attach the node as the right child of the current top of the stack\n } else if (!st.empty()) {\n TreeNode* currTop = st.top();\n currTop->right = newNode;\n }\n // Push the new node onto the stack, reset prev to null, and move to the next element in the postorder traversal\n st.push(newNode);\n prev = nullptr;\n pp--;\n }\n\n // Return the root of the binary tree\n return root;\n }\n};\n```\n```Python []\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n # If either of the input lists are empty, the tree is empty, so return None\n if not inorder or not postorder:\n return None\n\n # Initialize indices to the last elements of the inorder and postorder traversals\n ip = len(inorder) - 1\n pp = len(postorder) - 1\n\n # Create an empty stack to help us build the binary tree\n st = []\n # Initialize prev to None since we haven\'t processed any nodes yet\n prev = None\n # Create the root node using the last element in the postorder traversal\n root = TreeNode(postorder[pp])\n # Push the root onto the stack and move to the next element in the postorder traversal\n st.append(root)\n pp -= 1\n\n # Process the rest of the nodes in the postorder traversal\n while pp >= 0:\n # While the stack is not empty and the top of the stack is the current inorder element\n while st and st[-1].val == inorder[ip]:\n # The top of the stack is the parent of the current node, so pop it off the stack and update prev\n prev = st.pop()\n ip -= 1\n # Create a new node for the current postorder element\n new_node = TreeNode(postorder[pp])\n # If prev is not None, the parent of the current node is prev, so attach the node as the left child of prev\n if prev:\n prev.left = new_node\n # If prev is None, the parent of the current node is the current top of the stack, so attach the node as the right child of the current top of the stack\n elif st:\n curr_top = st[-1]\n curr_top.right = new_node\n # Push the new node onto the stack, reset prev to None, and move to the next element in the postorder traversal\n st.append(new_node)\n prev = None\n pp -= 1\n\n # Return the root of the binary tree\n return root\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n | 31 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Day 75 || Divide and Conquer + Hash Table || Easiest Beginner Friendly Sol | construct-binary-tree-from-inorder-and-postorder-traversal | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\nThe problem is to construct a binary tree from inorder and postorder traversals of the tree. The inorder traversal gives the order of nodes in the left subtree, root, and right subtree, while the postorder traversal gives the order of nodes in the left subtree, right subtree, and root.\n\n**The intuition behind the algorithm is to start by identifying the root of the binary tree from the last element of the postorder traversal. Then, we can use the root to divide the inorder traversal into left and right subtrees. We can then recursively apply the same process to the left and right subtrees to construct the entire binary tree.**\n\nTo do this efficiently, we can use a hash map to store the indices of elements in the inorder traversal. This allows us to quickly find the position of the root in the inorder traversal and divide the traversal into left and right subtrees.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Create a function called buildTree that takes in two vectors, inorder and postorder, and returns a pointer to the root of the resulting binary tree.\n2. Initialize an integer variable postorderIndex to postorder.size() - 1. This variable will be used to traverse the postorder vector in reverse order.\n3. Initialize an empty unordered map called inorderIndexUmp. This map will be used to quickly look up the index of a value in the inorder vector.\n4. Loop through the inorder vector and insert each value and its index into the inorderIndexUmp map.\n5. Call a recursive helper function called buildTreeHelper with parameters postorder, 0, and postorder.size() - 1. This function will return the root of the binary tree.\n6. In the buildTreeHelper function, if left is greater than right, return nullptr.\n7. Get the root value from the postorder vector using the postorderIndex variable, and decrement postorderIndex.\n8. Create a new TreeNode with the root value and assign it to a pointer variable called root.\n9. Get the index of the root value in the inorder vector from the inorderIndexUmp map, and assign it to an integer variable called inorderPivotIndex.\n10. Recursively call buildTreeHelper with parameters postorder, inorderPivotIndex + 1, and right. Assign the result to root -> right.\n11. Recursively call buildTreeHelper with parameters postorder, left, and inorderPivotIndex - 1. Assign the result to root -> left.\n12. Return root.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int postorderIndex;\n unordered_map<int, int> inorderIndexUmp;\n\n TreeNode* buildTreeHelper(vector<int>& postorder, int left, int right) {\n if (left > right)\n return nullptr;\n int rootValue = postorder[postorderIndex--];\n TreeNode* root = new TreeNode(rootValue);\n int inorderPivotIndex = inorderIndexUmp[rootValue];\n //think about it...why I took root -> right first then root -> left ?\n root -> right = buildTreeHelper(postorder, inorderPivotIndex + 1, right);\n root -> left = buildTreeHelper(postorder, left, inorderPivotIndex - 1);\n return root;\n }\n\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n postorderIndex = postorder.size() - 1;\n for (int i = 0; i < inorder.size(); i++) {\n inorderIndexUmp[inorder[i]] = i;\n }\n return buildTreeHelper(postorder, 0, postorder.size() - 1);\n }\n};\n```\n```Java []\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode() {}\n TreeNode(int val) { this.val = val; }\n TreeNode(int val, TreeNode left, TreeNode right) {\n this.val = val;\n this.left = left;\n this.right = right;\n }\n}\n\nclass Solution {\n int postorderIndex;\n Map<Integer, Integer> inorderIndexUmp;\n\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n postorderIndex = postorder.length - 1;\n inorderIndexUmp = new HashMap<Integer, Integer>();\n for (int i = 0; i < inorder.length; i++) {\n inorderIndexUmp.put(inorder[i], i);\n }\n return buildTreeHelper(postorder, 0, postorder.length - 1);\n }\n\n private TreeNode buildTreeHelper(int[] postorder, int left, int right) {\n if (left > right)\n return null;\n int rootValue = postorder[postorderIndex--];\n TreeNode root = new TreeNode(rootValue);\n int inorderPivotIndex = inorderIndexUmp.get(rootValue);\n root.right = buildTreeHelper(postorder, inorderPivotIndex + 1, right);\n root.left = buildTreeHelper(postorder, left, inorderPivotIndex - 1);\n return root;\n }\n}\n\n```\n```Python []\nclass Solution:\n def buildTreeHelper(self, postorder: List[int], left: int, right: int) -> TreeNode:\n if left > right:\n return None\n root_value = postorder[self.postorder_index]\n self.postorder_index -= 1\n root = TreeNode(root_value)\n inorder_pivot_index = self.inorder_index_map[root_value]\n root.right = self.buildTreeHelper(postorder, inorder_pivot_index + 1, right)\n root.left = self.buildTreeHelper(postorder, left, inorder_pivot_index - 1)\n return root\n\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n self.postorder_index = len(postorder) - 1\n self.inorder_index_map = {val: i for i, val in enumerate(inorder)}\n return self.buildTreeHelper(postorder, 0, len(postorder) - 1)\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity : **O(n)**, The buildTreeHelper() function is called for each node in the tree exactly once, and the time complexity of each call is O(1). Therefore, the overall time complexity of the algorithm is O(n), where n is the number of nodes in the tree.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : **O(n)**, where n is the number of nodes in the tree. This is because we are creating a new TreeNode object for each node in the tree, and we are also using an unordered_map to store the indices of the nodes in the inorder traversal. Additionally, the recursive calls to buildTreeHelper() create a call stack of size O(n) in the worst case, where n is the number of nodes in the tree.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n**YOU CAN ALSO TRY BELOW PROBLWM WHICH IS SIMILAR TO THIS PROBLEM**\n105. Construct Binary Tree from Preorder and Inorder Traversal\n**SOLUTION :**\nhttps://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solutions/3303059/divide-and-conquer-hash-table-easiest-beginner-friendly-sol/ | 14 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
✅ Explained - Simple and Clear Python3 Code✅ | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | The solution utilizes a recursive approach to construct a binary tree from its inorder and postorder traversals. The process begins by selecting the last element of the postorder list as the root value. By finding the index of this root value in the inorder list, we can determine the elements on the left and right sides, representing the left and right subtrees, respectively. Recursively, the right subtree is built first by passing the appropriate partitions of the inorder and postorder lists. Next, the left subtree is constructed in a similar manner. The resulting subtrees are then assigned to the root node accordingly. This process continues until the entire binary tree is constructed, and the root node is returned as the final result.\n\n\n\n\n# Code\n```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n def build_tree(inorder, postorder):\n if not inorder:\n return None\n root_val = postorder.pop()\n root = TreeNode(root_val)\n index = inorder.index(root_val)\n root.right = build_tree(inorder[index + 1:], postorder)\n root.left = build_tree(inorder[:index], postorder)\n return root\n\n return build_tree(inorder, postorder)\n\n``` | 7 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Efficient Python Solution - Recursively Constructing the Binary Tree | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | # Intuition\nWhen given the inorder and postorder traversal of a binary tree, our first thought is that the last element in the postorder traversal is always the root of the tree. Knowing this, we can use the inorder traversal to figure out which elements belong to the left subtree and which ones belong to the right subtree. By doing this recursively, we can reconstruct the entire binary tree.\n\n# Approach\n1. Create a helper function that takes the range of the inorder traversal to be considered, the postorder traversal, and a dictionary containing the indices of each element in the inorder traversal for constant-time lookups.\n2. At each level of the recursion, the helper function finds the root value from the end of the postorder traversal and creates a new TreeNode with that value.\n3. The helper function then finds the index of the root value in the inorder traversal and divides the remaining nodes into the left and right subtrees accordingly.\n4. Recursively call the helper function to build the right subtree first because we are popping elements from the end of the postorder traversal. Then, build the left subtree.\n5. The base case for the recursion is when the range of the inorder traversal becomes invalid (so, `in_left` > `in_right`), in which case the function returns None.\n\n# Complexity\n- Time complexity: $$O(n)$$\nThe helper function is called at most n times, and each operation inside the function takes constant time due to the use of the `inorder_map` dictionary.\n\n- Space complexity: $$O(n)$$\nThe space complexity is determined by the depth of the recursion, which is O(n) in the worst case (when the tree is unbalanced) and O(log(n)) in the best case (when the tree is balanced). Additionally, the `inorder_map` dictionary also contributes to the space complexity with O(n).\n\n# Code\n```\nfrom typing import List, Optional\n\n# Definition for a binary tree node.\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n def helper(in_left, in_right, postorder, inorder_map):\n # Base case: return None when the range is invalid\n if in_left > in_right:\n return None\n\n # Get the root value from the end of postorder and create a new TreeNode\n root_val = postorder.pop()\n root = TreeNode(root_val)\n\n # Get the index of the root value in the inorder traversal\n inorder_index = inorder_map[root_val]\n\n # Recursively build the right subtree first because we are popping elements from the end of postorder.\n root.right = helper(inorder_index + 1, in_right, postorder, inorder_map)\n # Recursively build the left subtree\n root.left = helper(in_left, inorder_index - 1, postorder, inorder_map)\n\n return root\n\n # Create a dictionary to store the index of each element in the inorder traversal\n # This allows for constant-time lookups of the indices.\n inorder_map = {val: idx for idx, val in enumerate(inorder)}\n\n # Call the helper function with the initial range of the inorder traversal\n return helper(0, len(inorder) - 1, postorder, inorder_map)\n``` | 1 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Striver solution | construct-binary-tree-from-inorder-and-postorder-traversal | 1 | 1 | # Intuition: \nThe inorder traversal of a binary tree visits the left subtree, then the root node, and then the right subtree. The postorder traversal of a binary tree visits the left subtree, then the right subtree, and then the root node. By using these two traversals, we can reconstruct the original binary tree. \n# Approach: \nWe start by finding the root node of the binary tree from the last element of the postorder traversal. We then find the index of the root node in the inorder traversal, which allows us to determine the sizes of the left and right subtrees. We recursively construct the left and right subtrees by calling the buildTree function with the appropriate subarrays of the inorder and postorder traversals. We return the root node of the current subtree, which is used by the parent call to construct its own subtree. \n\n# Algorithm: \nDefine a buildTree function that takes two arrays as input: inorder and postorder . Call the buildTree function with the full arrays and return the result. In the buildTree function, define six parameters: inorder , inStart , inEnd , postorder , postStart , and postEnd . If inStart is greater than inEnd or postStart is greater than postEnd , return null . Find the root node of the current subtree by looking at the last element of the postorder array. Create a new TreeNode object with the value of the root node. Find the index of the root node in the inorder array by iterating through the subarray from inStart to inEnd . Determine the sizes of the left and right subtrees using the root index. Recursively construct the left subtree by calling buildTree with the subarrays from inStart to rootIndex - 1 and postStart to postStart + leftSize - 1 . Recursively construct the right subtree by calling buildTree with the subarrays from rootIndex + 1 to inEnd and postEnd - rightSize to postEnd - 1 . Set the left and right subtrees of the current node to the roots of the left and right subtrees, respectively. Return the root node of the current subtree.\n```java []\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n // Call the recursive function with full arrays and return the result\n return buildTree(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);\n }\n \n private TreeNode buildTree(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {\n // Base case\n if (inStart > inEnd || postStart > postEnd) {\n return null;\n }\n \n // Find the root node from the last element of postorder traversal\n int rootVal = postorder[postEnd];\n TreeNode root = new TreeNode(rootVal);\n \n // Find the index of the root node in inorder traversal\n int rootIndex = 0;\n for (int i = inStart; i <= inEnd; i++) {\n if (inorder[i] == rootVal) {\n rootIndex = i;\n break;\n }\n }\n \n // Recursively build the left and right subtrees\n int leftSize = rootIndex - inStart;\n int rightSize = inEnd - rootIndex;\n root.left = buildTree(inorder, inStart, rootIndex - 1, postorder, postStart, postStart + leftSize - 1);\n root.right = buildTree(inorder, rootIndex + 1, inEnd, postorder, postEnd - rightSize, postEnd - 1);\n \n return root;\n }\n}\n```\n# 2nd \nThe the basic idea is to take the last element in postorder array as the root, find the position of the root in the inorder array; then locate the range for left sub-tree and right sub-tree and do recursion. Use a HashMap to record the index of root in the inorder array.\n\n\n# recursion tree for the buildTreeFromPostIn() method\n```\nbuildTreeFromPostIn(start=0, end=n-1, postorder, inorder, map)\n |\n |\n |\n +--------------+---------------+\n | |\n | |\n buildTreeFromPostIn(start=0, end=2, postorder, inorder, map)\n | |\n | |\n +--------------+--------------+ |\n | | |\n | | |\nbuildTreeFromPostIn(start=0, end=0, postorder, inorder, map) buildTreeFromPostIn(start=1, end=2, postorder, inorder, map)\n | | |\n | | |\n | | |\n null node(2) |\n buildTreeFromPostIn(start=3, end=3, postorder, inorder, map)\n |\n |\n |\n null\n```\nIn this tree, each node represents a call to the buildTreeFromPostIn() method with specific parameters. The left child represents the recursive call on the left subtree, the right child represents the recursive call on the right subtree, and the leaf nodes represent the base case where the indices are out of bounds and null is returned. The nodes with a value represent the root node of the subtree being built.\n\n# Code\n```\npublic TreeNode buildTree(int[] inorder, int[] postorder) {\n Map<Integer,Integer> inorderMap = new HashMap<>();\n for(int i=0;i<inorder.length;i++) inorderMap.put(inorder[i],i);\n return buildTreeFromPostIn(0,inorder.length-1,postorder,0,\n postorder.length-1,inorderMap);\n}\nprivate TreeNode buildTreeFromPostIn(int inorderStart, int inorderEnd, \nint[] post, int postStart, int postEnd, Map<Integer,Integer> inorderMap){\n if(inorderStart>inorderEnd || postStart>postEnd) return null;\n TreeNode root = new TreeNode(post[postEnd]);\n int rootIndex = inorderMap.get(post[postEnd]);\n int leftSubTree= rootIndex-inorderStart;\n root.left=buildTreeFromPostIn(inorderStart,rootIndex-1,post,\n postStart,postStart+leftSubTree-1,inorderMap);\n root.right=buildTreeFromPostIn(rootIndex+1,inorderEnd,post,\n postStart+leftSubTree,postEnd-1,inorderMap);\n return root;\n}\n```\n# explaination \n\nThis code builds a binary tree given its inorder and postorder traversal sequences.\n\nmain idea is to use a map to quickly find the index of the root node in the inorder sequence.\n\nThen, we can divide the inorder and postorder sequences into left and right subtrees based on the position of the root node.\n\nThe buildTree() method takes the inorder and postorder arrays as input, creates a map to store the index of each element in the inorder array, and calls the buildTreeFromPostIn() method with the appropriate parameters.\n\nThe buildTreeFromPostIn() method takes the starting and ending indices of the inorder and postorder arrays, as well as the map of indices.\n\nIt first checks for the base case where the indices are out of bounds, in which case it returns null.\n\nOtherwise, it creates a new TreeNode object with the last element of the postorder array as the root node.\n\nIt then finds the index of the root node in the inorder array using the map.\n\nUsing the index, it can calculate the size of the left subtree and recursively call buildTreeFromPostIn() to build the left and right subtrees.\n\nFinally, it returns the root node of the complete binary tree.\n\n\n# Complexity\nComplexity Analysis:\n\nTime Complexity: O(n), where n is the number of nodes in the binary tree. This is because we are visiting each node exactly once in the inorder and postorder traversals, and performing constant time operations for each node.\n\nSpace Complexity: O(n), where n is the number of nodes in the binary tree. This is because we are using a hashmap to store the indices of the nodes in the inorder traversal, which requires O(n) space. Additionally, we are using recursive calls to construct the left and right subtrees, which may require O(n) space in the worst case if the tree is highly unbalanced (e.g., a skewed tree).\n\n\n | 2 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Python Intuition and Inline Detailed Explanation | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | ```\n#Intuition\n#1. In post order list, the last element is the root node\n#2. find the index of the root node at inorder list\n#3. At inorder list:\n # we can divide the inorder list into two subtrees(left and right) at the root node index(step 2)\n # make sure to not include the mid node(root node) while dividing\n#4. At postorder list:\n # the same index(step 2) can be used to divide the postorder list into subtrees\n # but make sure to include the middle node(non root node) to the right tree\n # also make sure that the root node(last node) is removed\n#do this recursively\n\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n #if no element then return empty binary tree\n if not inorder or not postorder:\n return None\n\n #1. last element in the postorder list is the root\n root_val=postorder[-1]\n\n #2. get the index to split\n mid=inorder.index(root_val)# we can use index because all nodes have unique val\n\n #3. splitting inorder list into left and right subtree dividing at root.val\n left_inorder=inorder[:mid] #excluding the middle(root node)\n right_inorder=inorder[mid+1:] #excluding the middle(root node)\n\n #4. split post order also at the same position including the middle \n left_postorder=postorder[:mid]# not including mid node\n right_postorder=postorder[mid:]# including mid node to right tree\n right_postorder.pop()#remove the root value from the post order\n\n left_tree=self.buildTree(left_inorder,left_postorder)\n right_tree=self.buildTree(right_inorder,right_postorder)\n\n return TreeNode(root_val,left_tree,right_tree)\n\n\n``` | 3 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Simple Python solution using recursion!!! 100% working. | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | **Python dictionary can be used in place of index to get linear time complexity.**\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if not inorder or not postorder:\n return None\n root=TreeNode(postorder.pop())\n mid=inorder.index(root.val)\n root.left=self.buildTree(inorder[:mid],postorder[:mid])\n root.right=self.buildTree(inorder[mid+1:],postorder[mid:])\n return root\n\n\n\n\n\n``` | 4 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
easy peasy//inorder traversal and preorder traversal | construct-binary-tree-from-inorder-and-postorder-traversal | 1 | 1 | Given conditions:-\n`````\ninorder = [9,3,15,20,7]\npostorder = [9,15,7,20,3]\n\nroot = buildTree(inorder, postorder)\n`````\nStructure:-\n```\n 3\n / \\\n 9 20\n / \\\n 15 7\n```\nBehind approch:-\n- The last element in the postorder traversal is the root of the binary tree.\n- Find the position of the root in the inorder traversal. This will divide the inorder traversal into two parts - the left subtree and the right subtree.\n- Recursively build the left subtree using the inorder and postorder traversals of the left subtree.\n- Recursively build the right subtree using the inorder and postorder traversals of the right subtree.\n- Return the root of the binary tree.\n# Code:\n```java []\nimport java.util.*;\n\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n Map<Integer, Integer> inorderMap = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n inorderMap.put(inorder[i], i);\n }\n return helper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1, inorderMap);\n }\n \n public TreeNode helper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd, Map<Integer, Integer> inorderMap) {\n if (inorderStart > inorderEnd || postorderStart > postorderEnd) {\n return null;\n }\n int rootVal = postorder[postorderEnd];\n TreeNode root = new TreeNode(rootVal);\n int inorderIdx = inorderMap.get(rootVal);\n int leftSubtreeSize = inorderIdx - inorderStart;\n root.left = helper(inorder, inorderStart, inorderIdx - 1, postorder, postorderStart, postorderStart + leftSubtreeSize - 1, inorderMap);\n root.right = helper(inorder, inorderIdx + 1, inorderEnd, postorder, postorderStart + leftSubtreeSize, postorderEnd - 1, inorderMap);\n return root;\n }\n}\n\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode(int x) { val = x; }\n}\n\npublic class Main {\n public static void main(String[] args) {\n int[] inorder = {9,3,15,20,7};\n int[] postorder = {9,15,7,20,3};\n Solution sol = new Solution();\n TreeNode root = sol.buildTree(inorder, postorder);\n }\n}\n\n```\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n def helper(inorder_start, inorder_end, postorder_start, postorder_end):\n if inorder_start > inorder_end or postorder_start > postorder_end:\n return None\n root_val = postorder[postorder_end]\n root = TreeNode(root_val)\n \n inorder_idx = inorder.index(root_val)\n left_subtree_size = inorder_idx - inorder_start\n \n root.left = helper(inorder_start, inorder_idx - 1, postorder_start, postorder_start + left_subtree_size - 1)\n root.right = helper(inorder_idx + 1, inorder_end, postorder_start + left_subtree_size, postorder_end - 1)\n \n return root\n \n return helper(0, len(inorder) - 1, 0, len(postorder) - 1)\n```\n```C++ []\n#include <iostream>\n#include <vector>\n#include <unordered_map>\n\nusing namespace std;\n\nstruct TreeNode {\n int val;\n TreeNode* left;\n TreeNode* right;\n TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n};\n\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> inorder_map;\n for (int i = 0; i < inorder.size(); i++) {\n inorder_map[inorder[i]] = i;\n }\n return helper(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1, inorder_map);\n }\n \n TreeNode* helper(vector<int>& inorder, int inorder_start, int inorder_end, vector<int>& postorder, int postorder_start, int postorder_end, unordered_map<int, int>& inorder_map) {\n if (inorder_start > inorder_end || postorder_start > postorder_end) {\n return NULL;\n }\n int root_val = postorder[postorder_end];\n TreeNode* root = new TreeNode(root_val);\n int inorder_idx = inorder_map[root_val];\n int left_subtree_size = inorder_idx - inorder_start;\n root->left = helper(inorder, inorder_start, inorder_idx - 1, postorder, postorder_start, postorder_start + left_subtree_size - 1, inorder_map);\n root->right = helper(inorder, inorder_idx + 1, inorder_end, postorder, postorder_start + left_subtree_size, postorder_end - 1, inorder_map);\n return root;\n }\n};\n\nint main() {\n vector<int> inorder = {9,3,15,20,7};\n vector<int> postorder = {9,15,7,20,3};\n Solution sol;\n TreeNode* root = sol.buildTree(inorder, postorder);\n return 0;\n}\n\n```\n\n\n | 2 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
One idea to solve both Problem 105 and Problem 106 | construct-binary-tree-from-inorder-and-postorder-traversal | 0 | 1 | \n```\n#For problem 105\nclass Solution:\n def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:\n\t#return if list is empty, you can also say if one of them is empty suck as (if not preorder):return None\n if not preorder or not inorder:return None\n#root at first position of preorder\n root=TreeNode(preorder[0])\n\n# we only need to use its index in inorder\n mid_node=inorder.index(root.val)\n #since left of inorder, right of inorder are correspond to left,right of subtree \n #start from 1 because index 0 is the root\n root.left=self.buildTree(preorder[1:1+mid_node],inorder[:mid_node])\n root.right=self.buildTree(preorder[mid_node+1:],inorder[mid_node+1:])\n \n return root\n```\t\n```\n #for problem 106\n\tclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n #return if list is empty\n if not inorder or not postorder:return None\n#root at last position of postorder\n\n root=TreeNode(postorder[-1])\n#we need to use its index in inorder but this time also need the last index of postorder(pEnd)\n mid_node=inorder.index(root.val)\n pEnd=postorder.index(root.val)\n \n\t\t#same logic as 105 take a look at the output of example you will understand, postorder end from pEnd because its last index is the root\n root.left=self.buildTree(inorder[:mid_node],postorder[:mid_node])\n root.right=self.buildTree(inorder[mid_node+1:],postorder[mid_node:pEnd])\n \n return root\n```\nPlease upvote if you like it, thanks\n | 2 | Given two integer arrays `inorder` and `postorder` where `inorder` is the inorder traversal of a binary tree and `postorder` is the postorder traversal of the same tree, construct and return _the binary tree_.
**Example 1:**
**Input:** inorder = \[9,3,15,20,7\], postorder = \[9,15,7,20,3\]
**Output:** \[3,9,20,null,null,15,7\]
**Example 2:**
**Input:** inorder = \[-1\], postorder = \[-1\]
**Output:** \[-1\]
**Constraints:**
* `1 <= inorder.length <= 3000`
* `postorder.length == inorder.length`
* `-3000 <= inorder[i], postorder[i] <= 3000`
* `inorder` and `postorder` consist of **unique** values.
* Each value of `postorder` also appears in `inorder`.
* `inorder` is **guaranteed** to be the inorder traversal of the tree.
* `postorder` is **guaranteed** to be the postorder traversal of the tree. | null |
Python || BFS || Simple | binary-tree-level-order-traversal-ii | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n def checkReverse(ans):\n l,r = 0,len(ans)-1\n while l<=r:\n ans[l],ans[r] = ans[r],ans[l]\n l+=1\n r-=1\n return ans\n\n if not root: return None\n q,ans = [root],[]\n while q:\n n,l = len(q),[]\n for i in range(n):\n curr = q.pop(0)\n l.append(curr.val)\n if curr.left:\n q.append(curr.left)\n if curr.right:\n q.append(curr.right)\n ans.append(l)\n return checkReverse(ans)\n``` | 2 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Easy Python Solution using BFS | binary-tree-level-order-traversal-ii | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n queue=deque()\n queue.append(root)\n lst=[]\n while queue:\n levels=[]\n for i in range(len(queue)):\n tmp=queue.popleft()\n if tmp:\n levels.append(tmp.val)\n queue.append(tmp.left)\n queue.append(tmp.right)\n\n if levels:\n lst.append(levels)\n return lst[::-1]\n``` | 1 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Binary Tree Level Order Traversal II with step by step explanation | binary-tree-level-order-traversal-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution also uses a queue to process the tree level by level, and the final result is returned in reversed order. It has the same time and space complexity as the previous solution.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root:\n return []\n \n queue = [root]\n result = []\n \n while queue:\n level_size = len(queue)\n current_level = []\n \n for i in range(level_size):\n current_node = queue.pop(0)\n current_level.append(current_node.val)\n \n if current_node.left:\n queue.append(current_node.left)\n if current_node.right:\n queue.append(current_node.right)\n \n result.append(current_level)\n \n return result[::-1]\n\n``` | 2 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Binary Tree Level Order Traversal II | binary-tree-level-order-traversal-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n l=defaultdict(list)\n def dfs(node,h):\n if node is None:\n return\n l[h].append(node.val)\n dfs(node.left,h+1)\n dfs(node.right,h+1)\n dfs(root,0)\n l=dict(sorted(l.items(),key=lambda x:x[0],reverse=True))\n return l.values()\n``` | 2 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Beats 100% in [c++][Java] || python3 Tc: O(N) Sc: O(M)|| Medium but easy to understand | binary-tree-level-order-traversal-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe aims to perform a level-order traversal of a binary tree in a bottom-up manner. It means that it traverses the tree level by level, starting from the root and moving downwards. The final result is a list of lists, where each inner list represents the values of the nodes at a particular level in the tree, ordered from the bottom level to the top level.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate an empty list called result to store the final result.\nIf the root of the tree is None, it means the tree is empty, so return the result (which is empty in this case).\nCreate a queue using a deque data structure and enqueue the root node.\nWhile the queue is not empty, perform the following steps:\nGet the length of the queue, which represents the number of nodes at the current level.\nCreate an empty list called level_values to store the values of the nodes at the current level.\nIterate len_level times to process each node at the current level:\nDequeue a node from the front of the queue.\nAdd the value of the dequeued node to the level_values list.\nEnqueue the left child of the dequeued node if it exists.\nEnqueue the right child of the dequeued node if it exists.\nAfter processing all nodes at the current level, append the level_values list to the result list.\nThe result list now contains the level-order traversal from top to bottom. To obtain the bottom-up traversal, create an empty list called final_result.\nIterate over the result list in reverse order and append each sublist to the final_result list.\nFinally, return the final_result, which represents the level-order traversal in a bottom-up manner.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this approach is O(N), where N is the number of nodes in the binary tree. This is because we visit each node once during the level-order traversal.\n\n- Space complexity: O(M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(M), where M is the maximum number of nodes at any level in the binary tree. In the worst case, the queue can contain all the nodes at the deepest level of the tree, which is M. Additionally, the result and final_result lists require space to store the node values.\n\n# Code\n```Java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public List<List<Integer>> levelOrderBottom(TreeNode root) {\n List<List<Integer>> result = new ArrayList<>();\n if(root==null) return result;\n LinkedList<TreeNode>queue = new LinkedList<>();\n queue.add(root);\n while(!queue.isEmpty()){\n int len = queue.size();\n List<Integer>res = new ArrayList<>();\n for(int i =0; i<len; i++)\n {\n TreeNode temp = queue.poll();\n res.add(temp.val);\n if(temp.left!= null)queue.add(temp.left);\n if(temp.right!=null)queue.add(temp.right);\n }\n result.add(res);\n }\n List<List<Integer>> finalRes = new ArrayList<>();\n for(int i =result.size()-1; i>=0; i--)\n finalRes.add(result.get(i));\n\n return finalRes;\n }\n}\n```\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n vector<vector<int>> levelOrderBottom(TreeNode* root) {\n vector<vector<int>> result; // Stores the final result\n if (root == nullptr)\n return result; // Empty tree, return empty result\n \n queue<TreeNode*> queue; // Queue for breadth-first traversal\n queue.push(root); // Add the root node to the queue\n \n while (!queue.empty()) {\n int len = queue.size(); // Number of nodes at the current level\n vector<int> res; // Stores the values of the nodes at the current level\n \n for (int i = 0; i < len; i++) {\n TreeNode* temp = queue.front(); // Get the first node in the queue\n queue.pop(); // Remove the node from the queue\n \n res.push_back(temp->val); // Add the value of the node to the current level result\n \n if (temp->left != nullptr)\n queue.push(temp->left); // Add the left child to the queue\n \n if (temp->right != nullptr)\n queue.push(temp->right); // Add the right child to the queue\n }\n \n result.push_back(res); // Add the current level result to the final result\n }\n \n vector<vector<int>> finalRes; // Stores the final result in bottom-up order\n \n for (int i = result.size() - 1; i >= 0; i--)\n finalRes.push_back(result[i]); // Add each sublist from the result in reverse order\n \n return finalRes; // Return the final result\n }\n};\n```\n```Python3 []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:\n result = [] # Stores the final result\n if root is None:\n return result # Empty tree, return empty result\n \n queue = deque() # Queue for breadth-first traversal\n queue.append(root) # Add the root node to the queue\n \n while queue:\n len_level = len(queue) # Number of nodes at the current level\n level_values = [] # Stores the values of the nodes at the current level\n \n for _ in range(len_level):\n temp = queue.popleft() # Get the first node in the queue\n \n level_values.append(temp.val) # Add the value of the node to the current level result\n \n if temp.left:\n queue.append(temp.left) # Add the left child to the queue\n \n if temp.right:\n queue.append(temp.right) # Add the right child to the queue\n \n result.append(level_values) # Add the current level result to the final result\n \n final_result = [] # Stores the final result in bottom-up order\n \n for i in range(len(result) - 1, -1, -1):\n final_result.append(result[i]) # Add each sublist from the result in reverse order\n \n return final_result # Return the final result\n```\n\n | 3 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
✅Python3 42ms 🔥🔥 easiest solution | binary-tree-level-order-traversal-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing BFS level order traversal we can solve this.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- traverse till last left node and then traverse till last right node.\n- if current node is not None then add current node\'s value to answer dictionary according to it\'s level.\n- now sort keys of dictionary, reverse it and take values of it.\n- return answer.\n\n# Complexity\n- Time complexity:O(H+2N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:(2N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n ans = dict()\n def bfs(curr = root, level = 0):\n nonlocal ans\n if curr:\n bfs(curr.left, level + 1)\n bfs(curr.right, level + 1)\n if level not in ans.keys():\n ans[level] = [curr.val]\n else:\n ans[level].append(curr.val)\n return\n bfs()\n answer = []\n for i in reversed(sorted(ans.keys())):\n answer.append(ans[i])\n return answer\n \n```\n# Pleaase like and comment below.\n# (\u3063\uFF3E\u25BF\uFF3E)\u06F6\uD83C\uDF78\uD83C\uDF1F\uD83C\uDF7A\u0669(\u02D8\u25E1\u02D8 ) | 4 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Superb Breadth First Search Python3 | binary-tree-level-order-traversal-ii | 0 | 1 | \n# BFS Approach\n```\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n list1=[]\n q=deque()\n q.append(root)\n while q:\n level=[]\n for i in range(len(q)):\n poping=q.popleft()\n if poping:\n level.append(poping.val)\n q.append(poping.left)\n q.append(poping.right)\n if level:\n list1.append(level)\n return list1[::-1]\n #please upvote me it would encourage me alot\n\n``` | 7 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Python3 # O(n) || O(d) # Runtime: 53ms 51.97% || Memory: 14.2mb 82.69% | binary-tree-level-order-traversal-ii | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom collections import deque\n# O(n) || O(d) where d is the depth of the tree\n# Runtime: 53ms 51.97% || Memory: 14.2mb 82.69%\nclass Solution:\n def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:\n if not root:\n return root\n\n result = []\n queue = deque([root])\n while queue:\n newLevel = []\n for _ in range(len(queue)):\n currNode = queue.popleft()\n newLevel.append(currNode.val)\n if currNode.left:\n queue.append(currNode.left)\n if currNode.right:\n queue.append(currNode.right)\n\n result.append(newLevel)\n\n\n return result[::-1]\n``` | 1 | Given the `root` of a binary tree, return _the bottom-up level order traversal of its nodes' values_. (i.e., from left to right, level by level from leaf to root).
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** \[\[15,7\],\[9,20\],\[3\]\]
**Example 2:**
**Input:** root = \[1\]
**Output:** \[\[1\]\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000` | null |
Python Simple Recursion || Runtime Beats 98.92% || Memory Beats 97.64% | convert-sorted-array-to-binary-search-tree | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n# Code\n```\n# Definition for a binary tree node.\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n n = len(nums)\n\n if not n:\n return None\n \n mid = (n-1)//2\n root = TreeNode(nums[mid])\n\n root.left = (self.sortedArrayToBST(nums[:mid]))\n root.right = (self.sortedArrayToBST(nums[mid+1:]))\n \n return root\n \n\n``` | 13 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
Easy || 0 ms || 100% || Fully Explained || (Java, C++, Python, JS, C, Python3) | convert-sorted-array-to-binary-search-tree | 1 | 1 | We need to keep track of two things:\n\t**1. Any node should have smaller elements as left children and vice versa for right children... \n\t2. The BST should be Height Balanced...**\nNote, A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one...\n# **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Convert Sorted Array to Binary Search Tree.\nMemory Usage: 43 MB, less than 82.54% of Java online submissions for Convert Sorted Array to Binary Search Tree.\n```\nclass Solution {\n public TreeNode sortedArrayToBST(int[] nums) {\n // Base condition...\n if (nums.length == 0)\n\t\t\treturn null;\n // Call the function recursively...\n\t\treturn sortedArrayToBST(nums, 0, nums.length - 1);\n\t}\n // Create another function which will convert any particular range of given nums array...\n // & return its corresponding BST root node....\n\tpublic TreeNode sortedArrayToBST(int[] nums, int beg, int end) {\n // If beg > end, return NULL, as we receive a wrong range...\n\t\tif (beg > end)\n\t\t\treturn null;\n // set the middle node...\n\t\tint mid = (beg + end) / 2;\n // Initialise root node with value same as nums[mid]...\n\t\tTreeNode root = new TreeNode(nums[mid]);\n // Assign left subtrees as the same function called on left subranges...\n\t\troot.left = sortedArrayToBST(nums, beg, mid - 1);\n // Assign right subtrees as the same function called on right subranges...\n\t\troot.right = sortedArrayToBST(nums, mid + 1, end);\n // Return the root node...\n\t\treturn root;\n }\n}\n```\n\n# **C++ Solution:**\nRuntime: 5 ms, faster than 89.56% of C++ online submissions for Convert Sorted Array to Binary Search Tree.\nMemory Usage: 13.1 MB, less than 87.25% of C++ online submissions for Convert Sorted Array to Binary Search Tree.\n```\nclass Solution {\npublic:\n TreeNode* sortedArrayToBST(vector<int>& nums) {\n // Base condition...\n if (nums.size() == 0)\n\t\t\treturn NULL;\n // Call the function recursively...\n\t\treturn sortedArrayToBST(nums, 0, nums.size() - 1);\n }\n // Create another function which will convert any particular range of given nums array...\n // & return its corresponding BST root node....\n\tTreeNode* sortedArrayToBST(vector<int>& nums, int beg, int end) {\n // If beg > end, return NULL, as we receive a wrong range...\n\t\tif (beg > end)\n\t\t\treturn NULL;\n // If beg == end, return a new node having value same as nums[beg]... \n if(beg == end)\n return new TreeNode(nums[beg]);\n // set the middle node...\n\t\tint mid = (beg + end) / 2;\n // Initialise root node with value same as nums[mid]\n\t\tTreeNode* root = new TreeNode(nums[mid]);\n // Assign left subtrees as the same function called on left subranges...\n\t\troot->left = sortedArrayToBST(nums, beg, mid - 1);\n // Assign right subtrees as the same function called on right subranges...\n\t\troot->right = sortedArrayToBST(nums, mid + 1, end);\n // Return the root node\n\t\treturn root;\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def sortedArrayToBST(self, nums):\n # Base condition...\n if len(nums) == 0:\n return None\n # set the middle node...\n mid = len(nums)//2\n # Initialise root node with value same as nums[mid]\n root = TreeNode(nums[mid])\n # Assign left subtrees as the same function called on left subranges...\n root.left = self.sortedArrayToBST(nums[:mid])\n # Assign right subtrees as the same function called on right subranges...\n root.right = self.sortedArrayToBST(nums[mid+1:])\n # Return the root node...\n return root\n```\n \n# **JavaScript Solution:**\n```\nvar sortedArrayToBST = function(nums) {\n // Call the function recursively...\n\treturn ConvToBST(nums, 0, nums.length - 1);\n}\n// Create a function which will convert any particular range of given nums array...\n// & return its corresponding BST root node....\nvar ConvToBST = function(nums, beg, end) {\n // If beg > end, return NULL, as we receive a wrong range...\n\tif (beg > end)\n\t\treturn null;\n // set the middle node...\n\tvar mid = Math.ceil((beg + end) / 2);\n // Initialise root node with value same as nums[mid]...\n\tvar root = new TreeNode(nums[mid]);\n // Assign left subtrees as the same function called on left subranges...\n\troot.left = ConvToBST(nums, beg, mid - 1);\n // Assign right subtrees as the same function called on right subranges...\n\troot.right = ConvToBST(nums, mid + 1, end);\n // Return the root node...\n\treturn root;\n};\n```\n\n# **C Language:**\n```\nstruct TreeNode* ConvToBST(int *nums, int beg, int end){\n if(end < beg)\n return NULL ;\n int mid = (beg + end)/2 ;\n struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n root->val = nums[mid];\n root->left = ConvToBST(nums, beg, mid-1);\n root->right = ConvToBST(nums, mid+1, end);\n return root;\n}\nstruct TreeNode* sortedArrayToBST(int* nums, int numsSize){\n if(numsSize <= 0)\n return NULL;\n else\n return ConvToBST(nums, 0, numsSize-1);\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n # Base condition...\n if len(nums) == 0:\n return None\n # set the middle node...\n mid = len(nums)//2\n # Initialise root node with value same as nums[mid]\n root = TreeNode(nums[mid])\n # Assign left subtrees as the same function called on left subranges...\n root.left = self.sortedArrayToBST(nums[:mid])\n # Assign right subtrees as the same function called on right subranges...\n root.right = self.sortedArrayToBST(nums[mid+1:])\n # Return the root node...\n return root\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 73 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
✅Easy & Clear Solution Python 3✅ | convert-sorted-array-to-binary-search-tree | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> TreeNode:\n def cv(node,vals)->TreeNode:\n if vals:\n mid=len(vals)//2\n node.val,node.left,node.right=vals[mid],cv(TreeNode(),vals[:mid]),cv(TreeNode(),vals[mid+1:])\n return node\n else:\n return None\n return cv(TreeNode(),nums)\n``` | 7 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
Beats : 94.4% [15/145 Top Interview Question] | convert-sorted-array-to-binary-search-tree | 0 | 1 | # Intuition\n*find the mid, and add it as the root node, continue...*\n\n# Approach\n*Two approaches recursive and iterative both have same time and space complexity*\n\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> TreeNode:\n if not nums:\n return None\n \n n = len(nums)\n root = TreeNode()\n stack = [(0, n, root)]\n \n while stack:\n i, j, node = stack.pop()\n mid = (i + j) // 2\n node.val = nums[mid]\n \n if mid > i:\n node.left = TreeNode()\n stack.append((i, mid, node.left))\n if mid+1 < j:\n node.right = TreeNode()\n stack.append((mid+1, j, node.right))\n \n return root\n\n```\n# Iterative Approach\nThe code above defines a binary tree structure and a function to create a binary search tree from a sorted array of integers.\n\nIn the TreeNode class, there are three instance variables:\n- `val`: represents the value stored in the node.\n- `left`: represents the left child node of the current node.\n- `right`: represents the right child node of the current node.\n\nThe `__init__` method initializes these three instance variables with default values of `0`, `None`, and `None`.\n\nThe Solution class contains a single method, `sortedArrayToBST`, which takes a list of integers `nums` as input and returns a TreeNode object that represents a balanced binary search tree.\n\nIf `nums` is an empty list, the function returns `None`.\n\nOtherwise, it initializes a variable `n` with the length of `nums`, and creates a new TreeNode object called `root` without any value.\n\nIt initializes a stack of tuples containing three values:\n- `i`: represents the starting index of the range of indices to consider.\n- `j`: represents the ending index of the range of indices to consider.\n- `node`: represents the current node.\n\nThe `while` loop runs as long as the `stack` is not empty. In each iteration, it pops the last tuple from the stack, and assigns its values to the variables `i`, `j`, and `node`.\n\nIt calculates the middle index of the range as `(i + j) // 2`, and assigns it to the variable `mid`.\n\nIt assigns the value `nums[mid]` to the `val` instance variable of the `node`.\n\nIf the middle index `mid` is greater than the starting index `i`, it creates a new TreeNode object for the left child of the `node`, assigns it to the `left` instance variable of the `node`, and appends a tuple containing the indices `i`, `mid`, and the new left node to the `stack`.\n\nSimilarly, if the middle index plus one `mid+1` is less than the ending index `j`, it creates a new TreeNode object for the right child of the `node`, assigns it to the `right` instance variable of the `node`, and appends a tuple containing the indices `mid+1`, `j`, and the new right node to the `stack`.\n\nFinally, the function returns the `root` node of the binary search tree.\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n if not nums:return None\n mid = len(nums) // 2\n root = TreeNode(nums[mid])\n root.left = self.sortedArrayToBST(nums[:mid])\n root.right = self.sortedArrayToBST(nums[mid+1:])\n return root\n```\n# Recursive Approach\nThis is another implementation of the `sortedArrayToBST` function to create a binary search tree from a sorted array of integers.\n\nThis implementation is using `recursion`, but it creates a sub-tree for each half of the array, and sets it as the left and right child nodes of the root. The advantage of this implementation is that it is more concise and easier to understand than the `previous implementation that used a stack-based approach`.\n\nThe function takes a list of integers `nums` as input and returns a TreeNode object that represents a balanced binary search tree.\n\nIf `nums` is an empty list, the function returns `None`.\n\nOtherwise, it calculates the middle index of the array `nums` as `mid = len(nums) // 2`.\n\nIt creates a new TreeNode object called `root` with the value `nums[mid]`.\n\nIt recursively calls the `sortedArrayToBST` function to create the left and right sub-trees of the `root`.\n\nFor the left sub-tree, it passes the slice of the `nums` list from the beginning up to but not including the `mid` index.\n\nFor the right sub-tree, it passes the slice of the `nums` list from the `mid+1` index up to the end of the list.\n\nFinally, the function returns the `root` node of the binary search tree.\n | 6 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
Easy to Understand | Faster than 98% | Recursive | Simple | Python Solution | convert-sorted-array-to-binary-search-tree | 0 | 1 | ```\n def recursive(self, nums):\n def rec(nums, start, end):\n if start <= end:\n mid = (start + end) // 2\n node = TreeNode(nums[mid])\n node.left = rec(nums, start, mid - 1)\n node.right = rec(nums, mid + 1, end)\n return node\n return rec(nums, 0, len(nums) - 1)\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 77 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
Why Time Complexity is O(n) and not O(nlogn) ? | convert-sorted-array-to-binary-search-tree | 0 | 1 | I read a lot of threads, and there is a lot of confusion regarding the time complexity of the solution. Below is a recursive solution for the problem, and its time complexity is O(n). It is so because We are Doing a Constant amount of operations inside each function call. \n\nIf you recall the Merge sort, where we do O(n) number of comparisons at each level, and the number of comparisons in each recursion is equal to the size of the lists, the recursion depth is O(logn); therefore, the time complexity is O(nlogn).\n\nOn the other hand, the Total number of recursive function calls here is O(n), and each call does a constant number of operations. \n\n# Code\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n def genTree(i,j):\n if( i > j ): return None;\n elif( i ==j ): return TreeNode(nums[i]);\n mid = (i+j)//2;\n return TreeNode(nums[mid],genTree(i,mid-1),genTree(mid+1,j) );\n return genTree(0,len(nums)-1);\n\n```\n\n | 4 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
[C++ & Python] recursive solution | convert-sorted-array-to-binary-search-tree | 0 | 1 | \n# Approach: Divide and Conquer, Recursion\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(logn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++\n```\nclass Solution {\n TreeNode* recur(int s, int e, vector<int>& nums) {\n if(s > e) return NULL;\n int mid = s + (e-s)/2;\n TreeNode* root = new TreeNode(nums[mid]);\n root -> left = recur(s, mid - 1, nums);\n root -> right = recur(mid + 1, e, nums);\n return root;\n }\npublic:\n TreeNode* sortedArrayToBST(vector<int>& nums) {\n return recur(0, nums.size() - 1, nums);\n }\n};\n```\n\n# Python / Python3\n```\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n return self.recur(0, len(nums)-1, nums)\n\n def recur(self, s, e, nums: List[int]) -> TreeNode:\n if(s > e):\n return None\n mid = int(s + (e-s)/2)\n root = TreeNode(nums[mid])\n root.left = self.recur(s, mid - 1, nums)\n root.right = self.recur(mid + 1, e, nums)\n return root\n``` | 3 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
Simple Solution | With Explanation | Easy | convert-sorted-array-to-binary-search-tree | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTake the middle number as root the then pass the remaing left list in root.left and remaining right in root.right\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n if len(nums)==0:\n return\n ind=len(nums)//2 #Because the arr or list is shorted you should thake middle number as the root\n root=TreeNode(nums[ind]) #Now you can assign the left branch and perform recurtion with left remaining list\n root.left=self.sortedArrayToBST(nums[:ind]) #Same for the right remaining list\n root.right=self.sortedArrayToBST(nums[ind+1:])\n return root\n\n \n``` | 2 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
🔥 [VIDEO] Converting Sorted Array to Balanced Binary Search Tree 🌳 | convert-sorted-array-to-binary-search-tree | 1 | 1 | # Intuition\nUpon reading the problem, it became clear that a binary search tree (BST) could be formed by leveraging the property of a sorted array, where the middle element can serve as the root of the BST. This is because in a sorted array, elements to the left of the middle element are lesser, and elements to the right are greater, which aligns with the properties of a BST.\n\nhttps://youtu.be/JiH4MDE2sJE\n\n# Approach\nThe approach to solving this problem involves recursion. The main idea is to find the middle element of the array. This middle element will become the root of our binary search tree because it ensures that the tree will remain balanced. The left half of the array will be used to build the left subtree, and similarly, the right half for the right subtree. We then recursively construct these subtrees.\n\n# Complexity\n- Time complexity: The time complexity for this approach is \\(O(n)\\), where \\(n\\) is the number of elements in the array. This is because we are visiting each element once while constructing the BST.\n\n- Space complexity: The space complexity is \\(O(n)\\) as well. This is because, in the worst-case scenario, we could end up with a recursive call stack depth of \\(n\\) during the creation of the BST.\n\n# Code\n``` Python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:\n if not nums: \n return None \n mid = len(nums) // 2 \n # create node and construct subtrees \n node = TreeNode(nums[mid]) \n node.left = self.sortedArrayToBST(nums[:mid]) \n node.right = self.sortedArrayToBST(nums[mid+1:]) \n return node \n```\n``` JavaScript []\nvar sortedArrayToBST = function(nums) {\n if(!nums.length) return null;\n let mid = Math.floor(nums.length / 2);\n let root = new TreeNode(nums[mid]);\n root.left = sortedArrayToBST(nums.slice(0, mid));\n root.right = sortedArrayToBST(nums.slice(mid + 1));\n return root;\n};\n``` \n``` C# []\npublic class Solution {\n public TreeNode SortedArrayToBST(int[] nums) {\n if(nums == null || nums.Length == 0)\n return null;\n return constructBSTRecursive(nums, 0, nums.Length - 1);\n }\n\n private TreeNode constructBSTRecursive(int[] nums, int left, int right) {\n if(left > right)\n return null;\n int mid = left + (right - left) / 2;\n TreeNode node = new TreeNode(nums[mid]);\n node.left = constructBSTRecursive(nums, left, mid - 1);\n node.right = constructBSTRecursive(nums, mid + 1, right);\n return node;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n TreeNode* sortedArrayToBST(vector<int>& nums) {\n return constructBSTRecursive(nums, 0, nums.size() - 1);\n }\n\n TreeNode* constructBSTRecursive(vector<int>& nums, int left, int right) {\n if(left > right)\n return NULL;\n int mid = left + (right - left) / 2;\n TreeNode* node = new TreeNode(nums[mid]);\n node->left = constructBSTRecursive(nums, left, mid - 1);\n node->right = constructBSTRecursive(nums, mid + 1, right);\n return node;\n }\n};\n```\n``` Java []\npublic class Solution {\n public TreeNode sortedArrayToBST(int[] nums) {\n if(nums == null || nums.length == 0)\n return null;\n return constructBSTRecursive(nums, 0, nums.length - 1);\n }\n\n private TreeNode constructBSTRecursive(int[] nums, int left, int right) {\n if(left > right)\n return null;\n int mid = left + (right - left) / 2;\n TreeNode node = new TreeNode(nums[mid]);\n node.left = constructBSTRecursive(nums, left, mid - 1);\n node.right = constructBSTRecursive(nums, mid + 1, right);\n return node;\n }\n}\n```\nRemember, practicing and understanding the underlying concepts is key to mastering data structures and algorithms. Happy coding! | 6 | Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** nums = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** \[0,-10,5,null,-3,null,9\] is also accepted:
**Example 2:**
**Input:** nums = \[1,3\]
**Output:** \[3,1\]
**Explanation:** \[1,null,3\] and \[3,1\] are both height-balanced BSTs.
**Constraints:**
* `1 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `nums` is sorted in a **strictly increasing** order. | null |
python3 Solution | convert-sorted-list-to-binary-search-tree | 0 | 1 | \n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n \n n=0\n cur=head\n while cur:\n cur=cur.next\n n+=1\n self.head=head\n \n def rec(st,end):\n \n if st>end:\n return None\n \n mid=(st+end)//2\n left=rec(st,mid-1) \n root=TreeNode(self.head.val)\n self.head=self.head.next\n root.left=left\n \n root.right=rec(mid+1,end)\n return root\n \n return rec(0,n-1)\n``` | 1 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
simple python code | convert-sorted-list-to-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nrecursive\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nconvert linked list value into a list and recursively bisect and make tree each sect.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n sl =[]\n while head:\n sl.append(head.val)\n head = head.next\n \n def make_tree(l,i,j):\n m=0\n if i > j:\n return None\n elif i==j:\n return TreeNode(l[i],None,None)\n if (j-i)%2 ==0:\n m=(i+j)//2\n else:\n m=(i+j+1)//2\n return TreeNode(l[m],make_tree(l,i,m-1),make_tree(l,m+1,j))\n\n return make_tree(sl,0,len(sl)-1)\n\n``` | 2 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Python3 || detailed solution || 91% fast | convert-sorted-list-to-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Divide and conquer**\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- find middle element of list and make it as root and break left list chain of middle node.\n- now make recursive call on left and right part of middle node, and do as instructed above.\n- when current node is None then return None, indicating no more traversing.\n- if middle node is last node of list (original last or broke link last element) then return TreeNode of value of it.\n---\n# Note\n- here middle function return previous of middle element.\n- this is so because after return we will break link between left and middle node of list.\n- so when refering to middle that is understood as middle = pre_mid.next.\n- here middle function used slow and fast pointer method to get middle.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n def middle(curr = None):\n if curr:\n prev = slow = fast = curr\n while fast and fast.next:\n prev = slow\n slow = slow.next\n fast = fast.next.next\n return prev\n def helper(curr=None):\n if curr:\n pre_mid = middle(curr)\n if not pre_mid.next:\n return TreeNode(pre_mid.val)\n parent = pre_mid.next\n pre_mid.next = None\n root = TreeNode(parent.val)\n root.right = helper(parent.next) \n root.left = helper(curr)\n return root\n return helper(head)\n\n```\n # Please like and comment any suggestion below :-) | 1 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Beats 100% +Video | Java C++ Python | convert-sorted-list-to-binary-search-tree | 1 | 1 | # Intuition \nIn a balanced binary search Tree height difference b/w left and right node cannot be more than 1 or in other words they contain almost equal number of nodes. \n\nThis can be achieved by dividing the Linked List into 2 parts first half = left Node, middle = root and right = second half. Repeat the above process recursively to generate the BST.\n\nTo find middle element use 2 pointer approach: The fast moves 2 steps and slow 1 step at a time. Hence when fast is finished, slow will be at middle.\n\neg: Find the middle element below = 0 and form root. The LinkedList on left of middle will form a new BST and right will form a new BST using same function. i.e -3 will be mid and left = -10 and right = -1 . \n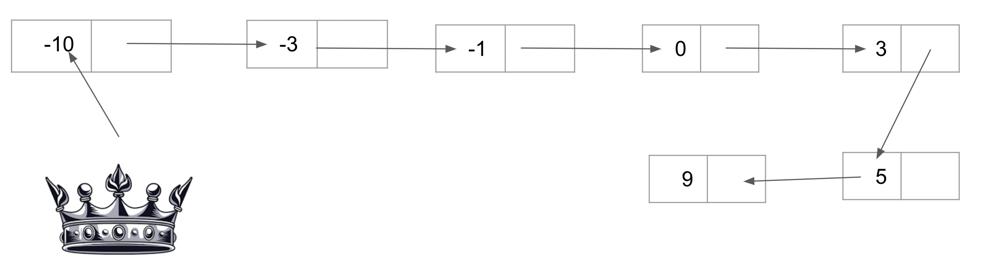\n\n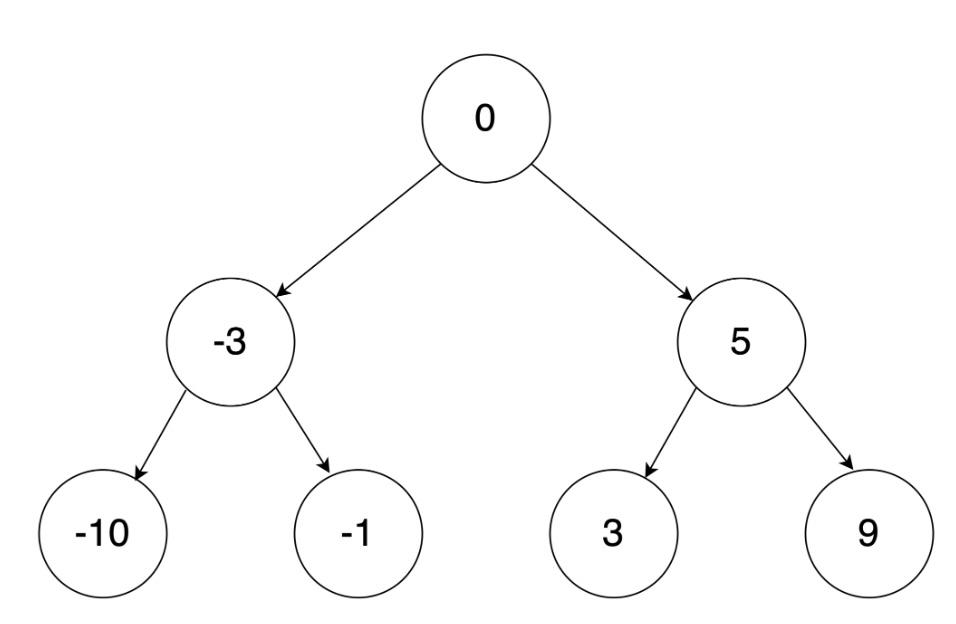\n\n\n# Approach \n1. Find the middle element of the linked list.\n2. Create a new node with the middle element as its value.\n3. Set the left subtree of the new node to the result of recursively calling the function on the left half of the sorted list.\n4. Set the right subtree of the new node to the result of recursively calling the function on the right half of the sorted list.\n5. Return the new node.\n\nHow to find middle element:\n\n1. Initialize two pointers, slow and fast, to head.\n2. Move fast two steps ahead and slow one step ahead, until fast reaches the end of the list or goes past it.\n3. The element pointed to by slow is the middle element of the list.\n\n<iframe width="560" height="315" src="https://www.youtube.com/embed/pWjxJPY-DIo" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe>\n\n\n\n```\nclass Solution {\n public TreeNode sortedListToBST(ListNode head) {\n if(head == null) return null;\n if(head.next == null) return new TreeNode(head.val);\n ListNode middle = getMiddle(head);\n TreeNode root = new TreeNode(middle.val);\n root.right = sortedListToBST(middle.next);\n middle.next =null;\n root.left = sortedListToBST(head);\n return root;\n }\n \n public ListNode getMiddle(ListNode head){\n //if(head == null || head.next==null) return null;\n ListNode fast = head;\n ListNode slow = head;\n ListNode prev = null;\n while(fast!=null && fast.next!=null){\n fast = fast.next.next;\n prev = slow;\n slow = slow.next;\n \n }\n if(prev!=null)prev.next =null;\n return slow;\n }\n}\n```\n\n```\nclass Solution {\npublic:\n TreeNode* sortedListToBST(ListNode* head) {\n if(head == NULL) return NULL;\n if(head->next == NULL) return new TreeNode(head->val);\n ListNode* middle = getMiddle(head);\n TreeNode* root = new TreeNode(middle->val);\n root->right = sortedListToBST(middle->next);\n middle->next = NULL;\n root->left = sortedListToBST(head);\n return root;\n }\n \n ListNode* getMiddle(ListNode* head){\n //if(head == NULL || head->next==NULL) return NULL;\n ListNode* fast = head;\n ListNode* slow = head;\n ListNode* prev = NULL;\n while(fast!=NULL && fast->next!=NULL){\n fast = fast->next->next;\n prev = slow;\n slow = slow->next;\n }\n if(prev!=NULL) prev->next = NULL;\n return slow;\n }\n};\n```\n\n```\nclass Solution:\n def sortedListToBST(self, head: ListNode) -> TreeNode:\n if not head:\n return None\n if not head.next:\n return TreeNode(head.val)\n middle = self.getMiddle(head)\n root = TreeNode(middle.val)\n root.right = self.sortedListToBST(middle.next)\n middle.next = None\n root.left = self.sortedListToBST(head)\n return root\n \n def getMiddle(self, head: ListNode) -> ListNode:\n fast = head\n slow = head\n prev = None\n while fast and fast.next:\n fast = fast.next.next\n prev = slow\n slow = slow.next\n if prev:\n prev.next = None\n return slow\n``` | 58 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Solution | convert-sorted-list-to-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n ListNode* middleNode(ListNode* head) {\n if(!head || !head->next)\n return head;\n ListNode* s=head;\n ListNode* f=head;\n ListNode * p= NULL;\n while(f && f->next)\n {\n p=s;\n s=s->next;\n f=f->next->next;\n }\n return p;\n \n }\n TreeNode* sortedListToBST(ListNode* head) {\n if(!head)\n return NULL;\n if(!head->next)\n return new TreeNode(head->val);\n ListNode* n=middleNode(head);\n ListNode* tmp=n->next;\n n->next=NULL;\n TreeNode * t=new TreeNode(tmp->val);\n t->left = sortedListToBST(head);\n t->right = sortedListToBST(tmp->next);\n return t;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def sortedListToBST(self, head: ListNode) -> TreeNode:\n if not head:\n return None\n if not head.next:\n return TreeNode(head.val)\n slow, fast = head, head.next.next\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n root = TreeNode(slow.next.val)\n root.right = self.sortedListToBST(slow.next.next)\n slow.next = None\n root.left = self.sortedListToBST(head)\n return root\n```\n\n```Java []\nclass Solution {\n public TreeNode sortedListToBST(ListNode head) {\n if(head == null)\n {\n return null;\n }\n return createBST(head,null);\n \n }\n \n public TreeNode createBST(ListNode start,ListNode end)\n \n {\n if(start==end)return null;\n \n ListNode mid = middle(start,end);\n \n TreeNode root = new TreeNode(mid.val);\n root.left = createBST(start,mid);\n root.right = createBST(mid.next,end);\n \n return root;\n }\n \n public ListNode middle(ListNode head,ListNode end)\n {\n \n ListNode slow = head;\n ListNode fast = head;\n \n while(fast!= end && fast.next != end)\n {\n slow = slow.next;\n fast = fast.next.next;\n }\n \n return slow; \n }\n}\n```\n | 1 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Python divide in middle and recursion of left and right parts | convert-sorted-list-to-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nConvert form middle of list\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDivide list in middle\nCreate `TreeNode` with middle and recursion of left and right part\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def sortedListToBST(self, head: ListNode | None) -> TreeNode | None:\n if not head: return None\n prev = node = mid = head\n while node and node.next:\n prev = mid\n mid = mid.next\n node = node.next.next\n if head == mid:\n return TreeNode(mid.val)\n prev.next = None # cul left part of List\n return TreeNode(mid.val, self.sortedListToBST(head), self.sortedListToBST(mid.next))\n\n``` | 4 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Python || similar to Sorted Array to Binary Search Tree (Ques 108) | convert-sorted-list-to-binary-search-tree | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\nclass Solution:\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n <!-- MAke a List -->\n nums = []\n while head:\n nums.append(head.val)\n head = head.next\n # print(nums)\n\n <!-- Construct BST -->\n def constructBST(nums):\n n = len(nums)\n if not n:\n return None\n \n mid = (n-1)//2\n root = TreeNode(nums[mid])\n\n root.left = (constructBST(nums[:mid]))\n root.right = (constructBST(nums[mid+1:]))\n \n return root\n\n return constructBST(nums)\n``` | 2 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Awesome Logic and Made me passionate on Coding | convert-sorted-list-to-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n if head==None:\n return None\n if head.next==None:\n return TreeNode(head.val)\n slow,fast=head,head.next\n while fast.next and fast.next.next:\n slow=slow.next\n fast=fast.next.next\n mid=slow.next\n slow.next=None\n root=TreeNode(mid.val)\n root.left=self.sortedListToBST(head)\n root.right=self.sortedListToBST(mid.next)\n return root\n #please upvote me it would encourage me alot\n``` | 4 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
[Python]🔥Explaining Divide n' Conquer! | convert-sorted-list-to-binary-search-tree | 0 | 1 | ## **Please upvote/favourite/comment if you like this solution!**\n\n# Intuition\n\nFirst, we convert the singly-linked list into an array. Next, we apply the divide and conquer algorithm. The divide and conquer algorithm works by recursively dividing the sorted array. When an array of length 0 is passed to `divideAndConquer`, `None` is returned. When an array of length 1 is passed to `divideAndConquer`, we return a single TreeNode with the value from the array. **This is the dividing portion of the algorithm**. Now, we must determine the merging logic. If the array passed to `divideAndConquer` is longer than 1, we find the middle element and make a TreeNode with that value. That TreeNode will be the parent of all elements to the left and all elements to the right (elemenets to the left are smaller and elements to the right are larger since the array is sorted). We recursively call `divideAndConquer` on the left of the array and the right of the array. These calls return valid BST subtrees which the parent node then point to when merging. **This is the merging portion of the algorithm**.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def merge(self, root, left_tree, right_tree):\n root.left = left_tree\n root.right = right_tree\n return root\n\n def divideAndConquer(self, nums):\n n = len(nums)\n if n == 0:\n return None\n elif n == 1:\n return TreeNode(nums[0])\n mid = n//2\n root = TreeNode(nums[mid])\n left_tree = self.divideAndConquer(nums[:mid])\n right_tree = self.divideAndConquer(nums[mid+1:])\n return self.merge(root,left_tree,right_tree)\n\n def linkedListToArray(self, head):\n arr = []\n while head is not None:\n arr.append(head.val)\n head = head.next\n return arr\n\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n nums = self.linkedListToArray(head)\n return self.divideAndConquer(nums)\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 1 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Go/Python O(n*log(n)) time | O(log(n)) time | convert-sorted-list-to-binary-search-tree | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n*log(n))$$ -->\n\n- Space complexity: $$O(log(n))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\n/**\n * Definition for singly-linked list.\n * type ListNode struct {\n * Val int\n * Next *ListNode\n * }\n */\n/**\n * Definition for a binary tree node.\n * type TreeNode struct {\n * Val int\n * Left *TreeNode\n * Right *TreeNode\n * }\n */\nfunc sortedListToBST(head *ListNode) *TreeNode {\n if head == nil{\n return nil\n }\n if head.Next == nil{\n return &TreeNode{head.Val,nil,nil}\n }\n prev := head\n slow := head.Next\n fast := head.Next.Next\n \n for fast != nil && fast.Next != nil{\n prev = slow\n slow = slow.Next\n fast = fast.Next.Next\n }\n\n prev.Next = nil\n root := TreeNode{slow.Val,nil,nil}\n\n root.Left = sortedListToBST(head)\n root.Right = sortedListToBST(slow.Next)\n return &root\n}\n```\n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:\n if not head:\n return None\n if not head.next:\n return TreeNode(head.val)\n\n prev = head\n slow = head.next\n fast = head.next.next\n\n while fast and fast.next:\n prev = slow\n slow = slow.next\n fast = fast.next.next\n\n prev.next = None\n root = TreeNode(slow.val)\n\n root.left = self.sortedListToBST(head)\n root.right = self.sortedListToBST(slow.next)\n return root\n``` | 3 | Given the `head` of a singly linked list where elements are sorted in **ascending order**, convert _it to a_ **_height-balanced_** _binary search tree_.
**Example 1:**
**Input:** head = \[-10,-3,0,5,9\]
**Output:** \[0,-3,9,-10,null,5\]
**Explanation:** One possible answer is \[0,-3,9,-10,null,5\], which represents the shown height balanced BST.
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in `head` is in the range `[0, 2 * 104]`.
* `-105 <= Node.val <= 105` | null |
Very Easy || 100% || Fully Explained (C++, Java, Python, JavaScript, Python3) | balanced-binary-tree | 1 | 1 | # **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Balanced Binary Tree.\nMemory Usage: 41.9 MB, less than 94.34% of Java online submissions for Balanced Binary Tree.\n```\nclass Solution {\n public boolean isBalanced(TreeNode root) {\n // If the tree is empty, we can say it\u2019s balanced...\n if (root == null) return true;\n // Height Function will return -1, when it\u2019s an unbalanced tree...\n\t\tif (Height(root) == -1) return false;\n\t\treturn true;\n\t}\n // Create a function to return the \u201Cheight\u201D of a current subtree using recursion...\n\tpublic int Height(TreeNode root) {\n // Base case...\n\t\tif (root == null) return 0;\n // Height of left subtree...\n\t\tint leftHeight = Height(root.left);\n // Height of height subtree...\n\t\tint rightHight = Height(root.right);\n // In case of left subtree or right subtree unbalanced, return -1...\n\t\tif (leftHeight == -1 || rightHight == -1) return -1;\n // If their heights differ by more than \u20181\u2019, return -1...\n if (Math.abs(leftHeight - rightHight) > 1) return -1;\n // Otherwise, return the height of this subtree as max(leftHeight, rightHight) + 1...\n\t\treturn Math.max(leftHeight, rightHight) + 1;\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n bool isBalanced(TreeNode* root) {\n // If the tree is empty, we can say it\u2019s balanced...\n if (root == NULL) return true;\n // Height Function will return -1, when it\u2019s an unbalanced tree...\n\t\tif (Height(root) == -1) return false;\n\t\treturn true;\n\t}\n // Create a function to return the \u201Cheight\u201D of a current subtree using recursion...\n\tint Height(TreeNode* root) {\n // Base case...\n\t\tif (root == NULL) return 0;\n // Height of left subtree...\n\t\tint leftHeight = Height(root->left);\n // Height of height subtree...\n\t\tint rightHight = Height(root->right);\n // In case of left subtree or right subtree unbalanced or their heights differ by more than \u20181\u2019, return -1...\n\t\tif (leftHeight == -1 || rightHight == -1 || abs(leftHeight - rightHight) > 1) return -1;\n // Otherwise, return the height of this subtree as max(leftHeight, rightHight) + 1...\n\t\treturn max(leftHeight, rightHight) + 1;\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def isBalanced(self, root):\n return (self.Height(root) >= 0)\n def Height(self, root):\n if root is None: return 0\n leftheight, rightheight = self.Height(root.left), self.Height(root.right)\n if leftheight < 0 or rightheight < 0 or abs(leftheight - rightheight) > 1: return -1\n return max(leftheight, rightheight) + 1\n```\n \n# **JavaScript Solution:**\n```\nvar isBalanced = function(root) {\n // If the tree is empty, we can say it\u2019s balanced...\n if (root == null) return true;\n // Height Function will return -1, when it\u2019s an unbalanced tree...\n\tif (Height(root) == -1) return false;\n\treturn true;\n}\n// Create a function to return the \u201Cheight\u201D of a current subtree using recursion...\nvar Height = function(root) {\n // Base case...\n\tif (root == null) return 0;\n // Height of left subtree...\n\tlet leftHeight = Height(root.left);\n // Height of height subtree...\n\tlet rightHight = Height(root.right);\n // In case of left subtree or right subtree unbalanced, return -1...\n\tif (leftHeight == -1 || rightHight == -1) return -1;\n // If their heights differ by more than \u20181\u2019, return -1...\n if (Math.abs(leftHeight - rightHight) > 1) return -1;\n // Otherwise, return the height of this subtree as max(leftHeight, rightHight) + 1...\n\treturn Math.max(leftHeight, rightHight) + 1;\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n return (self.Height(root) >= 0)\n def Height(self, root: Optional[TreeNode]) -> bool:\n if root is None: return 0\n leftheight, rightheight = self.Height(root.left), self.Height(root.right)\n if leftheight < 0 or rightheight < 0 or abs(leftheight - rightheight) > 1: return -1\n return max(leftheight, rightheight) + 1\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 303 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Balanced tree✅ | O( n )✅ | Python(Step by step explanation)✅ | balanced-binary-tree | 0 | 1 | # Intuition\nThe problem is to determine if a binary tree is balanced, which means that the difference in heights between the left and right subtrees of any node is at most 1. The intuition is to perform a depth-first search (DFS) on the tree while simultaneously checking the balance condition for each node.\n\n# Approach\nThe approach is to implement a DFS function that returns two values for each node: whether the subtree rooted at the current node is balanced and the height of the subtree. This can be achieved using a recursive DFS traversal of the binary tree.\n\n1. Implement a recursive DFS function, `dfs(root)`, that takes a node as a parameter.\n2. Inside the DFS function, check if the current node is `None`. If it is, return `[True, 0]` to indicate an empty subtree, which is considered balanced.\n3. Recursively call the `dfs` function on the left and right children of the current node, and store the results in `left` and `right`, respectively.\n4. Calculate whether the current subtree is balanced by checking if both `left[0]` and `right[0]` are `True`, and if the absolute difference between `left[1]` (the height of the left subtree) and `right[1]` (the height of the right subtree) is at most 1.\n5. Return `[balanced, 1 + max(left[1], right[1])]` as the result for the current node, where `balanced` is `True` if the current subtree is balanced, and `1 + max(left[1], right[1])` represents the height of the current subtree.\n6. In the main function, `isBalanced(root)`, return `dfs(root)[0]` to check if the entire binary tree is balanced.\n\n# Complexity\n- Time complexity: O(n)\n - The algorithm performs a depth-first traversal of the binary tree, visiting each node once.\n- Space complexity: O(h), where h is the height of the binary tree\n - The space complexity is determined by the maximum height of the call stack during the recursive DFS traversal.\n - In the worst case, when the tree is skewed (completely unbalanced), the space complexity is O(n).\n - In the best case, when the tree is perfectly balanced, the space complexity is O(log(n)).\n\n```python\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n def dfs(root):\n if root is None:\n return [True, 0]\n\n left, right = dfs(root.left), dfs(root.right)\n balanced = left[0] and right[0] and abs(left[1] - right[1]) <= 1\n\n return [balanced, 1 + max(left[1], right[1])]\n\n return dfs(root)[0]\n```\n\n# Please upvote the solution if you understood it.\n\n\n\n | 14 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
✅Python3 🔥easiest solution 53ms🔥🔥 | balanced-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing DFS we can solve this.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- first check if node is None then return 0, because None node is balanced.\n- if not then get count of left or right subtree.\n- now if abs(right - left) > 1 then it\'s not balanced tree, then return -1\n- if any of left or right height is -1 then we already found imbance in tree, so return -1.\n- now else all of above cases return 1 + max(left, right), because indicating maxdepth till now no matter left or right.\n- now if returned answer is > 0 then return true else false.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n R = root\n def helper(curr=root):\n if curr == None:\n return 0\n else:\n left = helper(curr.left)\n right = helper(curr.right)\n if left == -1 or right == -1:\n return -1\n elif abs(right - left) > 1:\n return -1\n return 1 + max(left, right)\n return helper() >= 0\n```\n# Please like and comment below :-) | 6 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Python || Recursion || Easy 94 %beat | balanced-binary-tree | 0 | 1 | First we check root is None or not ,\nThen we will check depth/height of tree at each node , compare height left and right is less or more than 2.\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n if root is None:\n return True\n\n # This function will return height/ depth of tree\n def depth(root):\n if root is None:\n return 0\n return max(depth(root.left), depth(root.right)) + 1\n\n l = depth(root.left)\n r = depth(root.right)\n\n return (abs(l-r) < 2) and self.isBalanced(root.left) and self.isBalanced(root.right)\n\n```\n\n**Plz Upvote ..if you got help from this.**\n\n. | 8 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Convert Sorted List to Binary Search Tree with step by step explanation | balanced-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHere\'s the algorithm:\n\n1. Define a helper function called getHeight that takes a node as input and returns the height of the node\'s subtree.\n\n2. In the getHeight function, recursively calculate the heights of the left and right subtrees of the node.\n\n3. If the difference in heights of the left and right subtrees is greater than 1, then return -1 to indicate that the tree is not balanced.\n\n4. Otherwise, return the height of the node\'s subtree as 1 plus the maximum of the heights of its left and right subtrees.\n\n5. Define a function called isBalanced that takes a node as input and returns a boolean indicating if the node\'s subtree is balanced.\n\n6. In the isBalanced function, if the node is None, then return True to indicate that the subtree is balanced.\n\n7. Otherwise, recursively check if the left and right subtrees of the node are balanced and if the difference in their heights is at most 1.\n\n8. If both subtrees are balanced and their height difference is at most 1, then return True. Otherwise, return False to indicate that the subtree is not balanced.\n\n9. Call the isBalanced function on the root node of the tree and return its result.\n\n# Complexity\n- Time complexity:\nO(n log n) for the worst-case scenario.\n\n- Space complexity:\n O(h) for the worst-case scenario.\n\n# Code\n```\nclass Solution:\n def isBalanced(self, root: TreeNode) -> bool:\n def getHeight(node):\n if node is None:\n return 0\n left_height = getHeight(node.left)\n right_height = getHeight(node.right)\n if left_height == -1 or right_height == -1 or abs(left_height - right_height) > 1:\n return -1\n return 1 + max(left_height, right_height)\n return getHeight(root) != -1\n\n``` | 6 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
6 Lines Code Python3 | balanced-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n def dfs(root):\n if root==None:\n return [True,0]\n left,right=dfs(root.left),def(root.right)\n balanced=left[0] and right[0] and abs(left[1]-right[1])<=1\n return [balanced,1+max(left[1],right[1])]\n return dfs(root)[0]\n #please upvote me it would encourage me alot\n\n \n``` | 21 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
O(n) Time complexity | bottom-up DFS | Short and simple explained | balanced-binary-tree | 1 | 1 | # Intuition\nGiven the definition of a balanced tree, we know that a tree is **not balanced** when the difference between heights of the left and right subtree is over 1:\n `abs(height_left - height_right) > 1` *(abs: absolute value)*\nThe basic approach is:\n* Traverse the tree\n* Calculate the height of the left and right subtree\n* If it\'s not balanced (by using the formular above), then return false.\n* Return true when all nodes are passed\n\nBut for the best performance, we want to return false right after we have found the unbalanced subtree. So we add another step before calculating the height of subtrees: if the left or right subtree is unbalanced, then return false.\n\nWe don\'t want to repeat the traversal of the subtree to check balance and then calculate height. So we just do all once for each node.\n\nThe height at a node is obtained by it\'s children height + 1: `max(height(i.left), height(i.right)) + 1`\n\n# Approach\nTraverse each node recursively and return the height of it, if the subtree at that node is not balanced, then return -1:\n1. If the node is `null`, return 0\n2. Get the height of left subtree, if it\'s -1, then return -1\n3. Get the height of right subtree, if it\'s -1, then return -1\n4. If the difference between the heights of left and right subtree > 1 then return -1\n5. Finally, return false if the final height is -1, else return true\n# Complexity\n- Time complexity: $$O(n)$$\nFor each node, we compare the heights of it\'s children and get it\'s height in constance time.\n\n- Space complexity: $$O(n)$$ \nThe recursive stack may contain all nodes if the tree is skewed (each node only has left child)\n# Code\n```Python3 []\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n def height(root):\n if root == None:\n return 0\n \n h_left = height(root.left)\n if h_left < 0:\n return -1\n h_right = height(root.right)\n if h_right < 0 or abs(h_left - h_right) > 1:\n return -1\n\n return max(h_left, h_right) + 1\n \n return height(root) >= 0\n```\n```C++ []\n#include <algorithm>\nclass Solution {\npublic:\n int height(TreeNode* root) {\n if (!root) {\n return 0;\n }\n int hLeft = height(root->left);\n if (hLeft < 0) {\n return -1;\n }\n int hRight = height(root->right);\n if (hRight < 0 || std::abs(hLeft - hRight) > 1) {\n return -1;\n }\n return std::max(hLeft, hRight) + 1;\n }\n\n bool isBalanced(TreeNode* root) {\n return height(root) >= 0;\n }\n};\n```\n```Java []\nclass Solution {\n int height(TreeNode root) {\n if (root == null) {\n return 0;\n }\n int hLeft = height(root.left);\n if (hLeft < 0) {\n return -1;\n }\n int hRight = height(root.right);\n if (hRight < 0 || Math.abs(hLeft - hRight) > 1) {\n return -1;\n }\n return Math.max(hLeft, hRight) + 1;\n }\n\n public boolean isBalanced(TreeNode root) {\n return height(root) >= 0;\n }\n}\n```\n```Kotlin []\nclass Solution {\n fun height(root: TreeNode?): Int {\n if (root == null) {\n return 0\n }\n val hLeft = height(root.left);\n if (hLeft < 0) {\n return -1\n }\n val hRight = height(root.right);\n if (hRight < 0 || abs(hLeft - hRight) > 1) {\n return -1\n }\n return max(hLeft, hRight) + 1\n }\n\n\n fun isBalanced(root: TreeNode?): Boolean {\n return height(root) >= 0\n }\n}\n``` | 8 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
IsBalanced Python Solution (Recursion) | balanced-binary-tree | 0 | 1 | \n# Approach\n- First check if it is an empty/null tree or not\n- left and right : To check the left and right side of the binary tree from a particular root\n- balance will check:\n- - If the complete left side of the binary tree is balanced or not. \n- - if the complete right side of the binary tree is balanced or not.\n- - And the difference between their abs height <=1\n- dfs() returns true/false as well as the maximum height of the tree\n- isBalanced() returns only the bool value\n\n# Complexity\n- Time complexity:\nO(n)\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n \n def dfs(root):\n \n if root == None:\n return [True,0]\n \n left = dfs(root.left)\n right = dfs(root.right)\n balance = (left[0] and right[0] and abs(left[1]-right[1])<=1)\n \n return [balance, 1 + max(left[1],right[1])]\n \n return dfs(root)[0]\n\n``` | 3 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Most optimal solution with explanation | balanced-binary-tree | 1 | 1 | \n# Approach\n1. height function: This function calculates the height of the subtree rooted at a given node. If the subtree is not height-balanced (i.e., the left and right subtrees\' heights differ by more than 1), it returns -1. Otherwise, it returns the height of the subtree.\n\n2. isBalanced function: This function calls the height function to determine if the entire tree is height-balanced. If the height function returns -1, the tree is not balanced, and isBalanced returns false. Otherwise, it returns true.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n int height(TreeNode *node) {\n if(!node) return 0;\n int lh = height(node->left);\n if(lh == -1) return -1;\n int rh = height(node->right);\n if(rh == -1) return -1;\n if(abs(lh-rh)>1) return -1;\n return max(lh,rh)+1;\n }\n bool isBalanced(TreeNode* root) {\n return height(root) != -1;\n }\n};\n```\n```python []\nclass Solution:\n def height(self, node):\n if not node:\n return 0\n \n lh = self.height(node.left)\n if lh == -1:\n return -1\n \n rh = self.height(node.right)\n if rh == -1:\n return -1\n \n if abs(lh - rh) > 1:\n return -1\n \n return max(lh, rh) + 1\n \n def isBalanced(self, root):\n return self.height(root) != -1\n```\n```Java []\npublic class Solution {\n public int height(TreeNode node) {\n if (node == null)\n return 0;\n \n int lh = height(node.left);\n if (lh == -1)\n return -1;\n \n int rh = height(node.right);\n if (rh == -1)\n return -1;\n \n if (Math.abs(lh - rh) > 1)\n return -1;\n \n return Math.max(lh, rh) + 1;\n }\n \n public boolean isBalanced(TreeNode root) {\n return height(root) != -1;\n }\n}\n```\n | 3 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
dfs iterative using stack | balanced-binary-tree | 0 | 1 | # Intuition\nThe code aims to check whether a given binary tree is balanced or not. A binary tree is considered balanced if the heights of its left and right subtrees differ by at most 1 for all nodes in the tree.\n\n# Approach\nThe code employs an iterative approach using a stack to traverse the binary tree while keeping track of the depths of the left subtrees of each node. Here\'s a step-by-step explanation of the approach:\n\n1. Initialize a stack to perform a depth-first traversal of the binary tree. Each item in the stack is a tuple containing a node and a boolean flag indicating whether the node has been visited.\n\n2. Initialize a dictionary depths to store the maximum depth of each node encountered so far. Initially, it\'s empty.\n\n3. While the stack is not empty, pop a node and its visited flag from the stack.\n\n4. If the node has been visited (i.e., the flag is True), calculate the depths of its left and right subtrees using the depths dictionary. Check if the tree rooted at this node is balanced by comparing the absolute difference between the depths of its left and right subtrees with 1. If it\'s greater than 1, return False as the tree is not balanced.\n\n5. If the node has not been visited (i.e., the flag is False), mark it as visited and push it back into the stack. Push its left and right children into the stack if they exist.\n\n6. Update the depths dictionary with the maximum depth encountered so far for this node.\n\nRepeat steps 3-6 until the stack is empty.\n\nIf the traversal completes without encountering any unbalanced nodes, return True, indicating that the tree is balanced.\n\n# Complexity\n- Time complexity:\nThe code performs a single traversal of the binary tree, visiting each node once. Therefore, the time complexity is O(N), where N is the number of nodes in the tree.\n\n- Space complexity:\nThe space complexity is O(H), where H is the height of the binary tree. This is due to the stack used for the iterative traversal and the depths dictionary, which can have at most H entries, one for each level of the tree. In the worst case, for a skewed tree, H can be equal to N, making the space complexity O(N). In a balanced tree, H is approximately log(N), resulting in a space complexity of O(log(N)).\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n \n stack = [[root,False]]\n heights = defaultdict(int)\n\n while stack:\n x , visited = stack.pop()\n\n if visited:\n leftheight = heights[x.left]\n rightheight = heights[x.right]\n\n if abs(rightheight - leftheight) > 1:\n return False\n heights[x] = max(leftheight,rightheight) + 1\n\n else:\n stack.append([x,True])\n if x.right:\n stack.append([x.right,False])\n if x.left:\n stack.append([x.left,False])\n\n return True\n\n \n\n \n\n\n \n\n \n``` | 5 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Python Video Solution | balanced-binary-tree | 0 | 1 | I have explained this in a [video](https://youtu.be/dQp1oSkpyb4).\n\n# Intuition\nA Binary Tree is balanced if:\n* Left Subtree is balanced\n* Right Subtree is balanced\n* Difference of height of left & right subtree is atmost 1 `[0,1]`.\n\n\nIn our `dfs`, we\'ll return two things:\n* Whether this subtree is balanced.\n* Height of subtree\n\nIf you thought this was helpful, please upvote, like the video and subscribe to the channel.\n\nCheers.\n\n\n```\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n \n # is_balanced, height\n def dfs(root):\n if not root:\n return True, 0\n \n left = dfs(root.left)\n right = dfs(root.right)\n \n return left[0] and right[0] \\\n and abs(left[1]-right[1]) <= 1 \\\n , 1 + max(left[1], right[1])\n \n return dfs(root)[0] | 5 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Simple Python Solution | DFS | balanced-binary-tree | 0 | 1 | **Solution**\n\n\tclass Solution:\n\t\tdef isBalanced(self, root: Optional[TreeNode]) -> bool:\n\n\t\t\tdef dfs(root):\n\t\t\t\tif not root:\n\t\t\t\t\treturn [True, 0]\n\t\t\t\tleft, right = dfs(root.left), dfs(root.right)\n\t\t\t\tbalance = (left[0] and right[0] and abs(left[1] - right[1]) <= 1)\n\t\t\t\treturn [balance, 1 + max(left[1], right[1])]\n\n\t\t\tres = dfs(root)\n\t\t\treturn res[0] | 1 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Easiest Solution Binary Tree | balanced-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isBalanced(self, root: Optional[TreeNode]) -> bool:\n if root is None:\n return True\n \n # Recursive function to get the height of a node\n def get_height(node):\n if node is None:\n return 0\n return max(get_height(node.left), get_height(node.right)) + 1\n \n left_height = get_height(root.left)\n right_height = get_height(root.right)\n height_diff = abs(left_height - right_height)\n \n left_balanced = self.isBalanced(root.left)\n right_balanced = self.isBalanced(root.right)\n \n return height_diff <= 1 and left_balanced and right_balanced\n\n``` | 6 | Given a binary tree, determine if it is **height-balanced**.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** true
**Example 2:**
**Input:** root = \[1,2,2,3,3,null,null,4,4\]
**Output:** false
**Example 3:**
**Input:** root = \[\]
**Output:** true
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-104 <= Node.val <= 104` | null |
Python Easy Solution || 100% || DFS || Beats 95% || Recursion || | minimum-depth-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def minDepth(self, root: Optional[TreeNode]) -> int:\n self.maximum=1e8\n if root==None:\n return 0\n def topToBottom(node, depth):\n if not node.left and not node.right:\n self.maximum=min(self.maximum, depth+1)\n if node.left:\n topToBottom(node.left, depth+1)\n if node.right:\n topToBottom(node.right, depth+1)\n topToBottom(root, 0)\n return self.maximum\n``` | 1 | Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
**Note:** A leaf is a node with no children.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 2
**Example 2:**
**Input:** root = \[2,null,3,null,4,null,5,null,6\]
**Output:** 5
**Constraints:**
* The number of nodes in the tree is in the range `[0, 105]`.
* `-1000 <= Node.val <= 1000` | null |
Very Easy || 100% || Fully Explained (C++, Java, Python, JS, C, Python3) | minimum-depth-of-binary-tree | 1 | 1 | # **C++ Solution:**\n```\nclass Solution {\npublic:\n int minDepth(TreeNode* root) {\n // Base case...\n // If the subtree is empty i.e. root is NULL, return depth as 0...\n if(root == NULL) return 0;\n // Initialize the depth of two subtrees...\n int leftDepth = minDepth(root->left);\n int rightDepth = minDepth(root->right);\n // If the both subtrees are empty...\n if(root->left == NULL && root->right == NULL)\n return 1;\n // If the left subtree is empty, return the depth of right subtree after adding 1 to it...\n if(root->left == NULL)\n return 1 + rightDepth;\n // If the right subtree is empty, return the depth of left subtree after adding 1 to it...\n if(root->right == NULL)\n return 1 + leftDepth;\n // When the two child function return its depth...\n // Pick the minimum out of these two subtrees and return this value after adding 1 to it...\n return min(leftDepth, rightDepth) + 1; // Adding 1 is the current node which is the parent of the two subtrees...\n }\n};\n```\n\n# **Java Solution:**\n```\nclass Solution {\n public int minDepth(TreeNode root) {\n // Base case...\n // If the subtree is empty i.e. root is NULL, return depth as 0...\n if(root == null) return 0;\n // Initialize the depth of two subtrees...\n int leftDepth = minDepth(root.left);\n int rightDepth = minDepth(root.right);\n // If the both subtrees are empty...\n if(root.left == null && root.right == null)\n return 1;\n // If the left subtree is empty, return the depth of right subtree after adding 1 to it...\n if(root.left == null)\n return 1 + rightDepth;\n // If the right subtree is empty, return the depth of left subtree after adding 1 to it...\n if(root.right == null)\n return 1 + leftDepth;\n // When the two child function return its depth...\n // Pick the minimum out of these two subtrees and return this value after adding 1 to it...\n return Math.min(leftDepth, rightDepth) + 1; // Adding 1 is the current node which is the parent of the two subtrees...\n }\n}\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def minDepth(self, root):\n # Base case...\n # If the subtree is empty i.e. root is NULL, return depth as 0...\n if root is None: return 0\n # Initialize the depth of two subtrees...\n leftDepth = self.minDepth(root.left)\n rightDepth = self.minDepth(root.right)\n # If the both subtrees are empty...\n if root.left is None and root.right is None:\n return 1\n # If the left subtree is empty, return the depth of right subtree after adding 1 to it...\n if root.left is None:\n return 1 + rightDepth\n # If the right subtree is empty, return the depth of left subtree after adding 1 to it...\n if root.right is None:\n return 1 + leftDepth\n # When the two child function return its depth...\n # Pick the minimum out of these two subtrees and return this value after adding 1 to it...\n return min(leftDepth, rightDepth) + 1; # Adding 1 is the current node which is the parent of the two subtrees...\n```\n \n# **JavaScript Solution:**\n```\nvar minDepth = function(root) {\n // Base case...\n // If the subtree is empty i.e. root is NULL, return depth as 0...\n if(root == null) return 0;\n // If the both subtrees are empty...\n if(root.left == null && root.right == null)\n return 1;\n // If the left subtree is empty, return the depth of right subtree after adding 1 to it...\n if(root.left == null)\n return 1 + minDepth(root.right);\n // If the right subtree is empty, return the depth of left subtree after adding 1 to it...\n if(root.right == null)\n return 1 + minDepth(root.left);\n // When the two child function return its depth...\n // Pick the minimum out of these two subtrees and return this value after adding 1 to it...\n return Math.min(minDepth(root.left), minDepth(root.right)) + 1; // Adding 1 is the current node which is the parent of the two subtrees...\n};\n```\n\n# **C Language:**\n```\nint minDepth(struct TreeNode* root){\n if(root == NULL)\n return 0;\n else {\n int leftDepth = minDepth(root->left);\n int rightDepth = minDepth(root->right);\n if(leftDepth > rightDepth)\n return rightDepth + 1;\n else\n return leftDepth + 1;\n }\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def minDepth(self, root: Optional[TreeNode]) -> int:\n # Base case...\n # If the subtree is empty i.e. root is NULL, return depth as 0...\n if root is None: return 0\n # Initialize the depth of two subtrees...\n leftDepth = self.minDepth(root.left)\n rightDepth = self.minDepth(root.right)\n # If the both subtrees are empty...\n if root.left is None and root.right is None:\n return 1\n # If the left subtree is empty, return the depth of right subtree after adding 1 to it...\n if root.left is None:\n return 1 + rightDepth\n # If the right subtree is empty, return the depth of left subtree after adding 1 to it...\n if root.right is None:\n return 1 + leftDepth\n # When the two child function return its depth...\n # Pick the minimum out of these two subtrees and return this value after adding 1 to it...\n return min(leftDepth, rightDepth) + 1; # Adding 1 is the current node which is the parent of the two subtrees...\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 112 | Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
**Note:** A leaf is a node with no children.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 2
**Example 2:**
**Input:** root = \[2,null,3,null,4,null,5,null,6\]
**Output:** 5
**Constraints:**
* The number of nodes in the tree is in the range `[0, 105]`.
* `-1000 <= Node.val <= 1000` | null |
✔🔰[Python | Java | C++] Easy solution with explanation🚀 👍🏻😁 | minimum-depth-of-binary-tree | 1 | 1 | # DFS Solution\n1. If the root is null, return 0 because there are no nodes in an empty tree.\n2. If both the left and right child of the root are null, return 1 because the root itself is a leaf node.\n3. If the left child of the root is null, recursively calculate the minimum depth of the right subtree and add 1 to it (to account for the root node).\n4. If the right child of the root is null, recursively calculate the minimum depth of the left subtree and add 1 to it.\n5. If both the left and right child of the root are not null, recursively calculate the minimum depth of both subtrees, and return the minimum of the two depths plus 1 (to account for the root node).\n\n# DFS Code\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def minDepth(self, root: Optional[TreeNode]) -> int:\n def dfs(root):\n if not root:\n return 0\n if not root.left and root.right:\n return 1 + dfs(root.right)\n elif not root.right and root.left:\n return 1 + dfs(root.left)\n else:\n return 1 + min(dfs(root.left), dfs(root.right))\n return dfs(root)\n```\n```java []\nclass Solution {\n private int dfs(TreeNode root) {\n if (root == null) {\n return 0;\n }\n \n // If only one of child is non-null, then go into that recursion.\n if (root.left == null) {\n return 1 + dfs(root.right);\n } else if (root.right == null) {\n return 1 + dfs(root.left);\n }\n \n // Both children are non-null, hence call for both childs.\n return 1 + Math.min(dfs(root.left), dfs(root.right));\n }\n \n public int minDepth(TreeNode root) {\n return dfs(root);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int dfs(TreeNode* root) {\n if (root == NULL) {\n return 0;\n }\n \n // If only one of child is non-null, then go into that recursion.\n if (!root->left) {\n return 1 + dfs(root->right);\n } else if (!root->right) {\n return 1 + dfs(root->left);\n }\n \n // Both children are non-null, hence call for both childs.\n return 1 + min(dfs(root->left), dfs(root->right));\n }\n \n int minDepth(TreeNode* root) {\n return dfs(root);\n }\n};\n```\n# BFS Solution\nHere\'s the step-by-step algorithm for the BFS solution:\n\n1. If the root is null, return 0 because there are no nodes in an empty tree.\n2. Initialize a queue to perform BFS. Add the root node to the queue along with its corresponding depth, which is 1.\n3. Perform a while loop until the queue is empty:\n - Remove the node and its depth from the front of the queue.\n - If the node is a leaf node (i.e., both its left and right children are null), return the depth because we have found the minimum depth.\n - If the node has a left child, add it to the queue along with its depth (depth + 1).\n - If the node has a right child, add it to the queue along with its depth (depth + 1).\n4. If the loop finishes without finding a leaf node, return 0 as there are no leaf nodes in the tree.\n\n# BFS Code\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def minDepth(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n \n queue = deque([])\n queue.append(root)\n depth = 1\n while queue:\n for i in range(len(queue)):\n node = queue.popleft()\n if not node:\n continue\n if not node.left and not node.right:\n return depth\n queue.append(node.left)\n queue.append(node.right)\n depth += 1\n \n\n \n```\n```java []\nclass Solution {\n public int minDepth(TreeNode root) {\n if (root == null) {\n return 0;\n }\n \n Queue<TreeNode> q = new LinkedList<>();\n q.add(root);\n int depth = 1;\n \n while (q.isEmpty() == false) {\n int qSize = q.size();\n \n while (qSize > 0) {\n qSize--;\n \n TreeNode node = q.remove();\n // Since we added nodes without checking null, we need to skip them here.\n if (node == null) {\n continue;\n }\n \n // The first leaf would be at minimum depth, hence return it.\n if (node.left == null && node.right == null) {\n return depth;\n }\n \n q.add(node.left);\n q.add(node.right);\n }\n depth++;\n }\n return -1;\n }\n};\n```\n```C++ []\nclass Solution {\npublic:\n int minDepth(TreeNode* root) {\n if (!root) {\n return 0;\n }\n \n queue<TreeNode*> q;\n q.push(root);\n int depth = 1;\n \n while (!q.empty()) {\n int qSize = q.size();\n \n while (qSize--) {\n TreeNode* node = q.front(); q.pop();\n // Since we added nodes without checking null, we need to skip them here.\n if (!node) {\n continue;\n }\n \n // The first leaf would be at minimum depth, hence return it.\n if (!node->left && !node->right) {\n return depth;\n }\n \n q.push({node->left});\n q.push({node->right});\n }\n \n depth++;\n }\n return -1;\n }\n};\n```\n# Video Explanation\nhttps://youtu.be/5Wo5DxOu3uU\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(N), where N is the number of nodes in the binary tree\n- Space complexity:\nDFS - O(n) [Call Stack is used on recursion]\nBFS - O(n) [Queue for storing child nodes]\n\n#### Upvote if find useful \uD83D\uDC4D\uD83C\uDFFB\uD83D\uDE01\n | 6 | Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
**Note:** A leaf is a node with no children.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 2
**Example 2:**
**Input:** root = \[2,null,3,null,4,null,5,null,6\]
**Output:** 5
**Constraints:**
* The number of nodes in the tree is in the range `[0, 105]`.
* `-1000 <= Node.val <= 1000` | null |
binbin's answer beats 99.99% solutions! | minimum-depth-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def minDepth(self, root: Optional[TreeNode]) -> int:\n if root is None: \n return 0\n def find_depth(node,l):\n if node.left is not None and node.right is not None:\n return min(find_depth(node.right, l+1),find_depth(node.left, l+1))\n \n if node.right is not None:\n return find_depth(node.right, l+1)\n if node.left is not None:\n return find_depth(node.left, l+1)\n return l\n return find_depth(root,1)\n\n\n``` | 3 | Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
**Note:** A leaf is a node with no children.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 2
**Example 2:**
**Input:** root = \[2,null,3,null,4,null,5,null,6\]
**Output:** 5
**Constraints:**
* The number of nodes in the tree is in the range `[0, 105]`.
* `-1000 <= Node.val <= 1000` | null |
Python3 Solution | minimum-depth-of-binary-tree | 0 | 1 | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def minDepth(self,root:Optional[TreeNode])->int:\n if not root:\n return 0\n\n if not root.left and not root.right:\n return 1\n\n left=self.minDepth(root.left) if root.left else float(\'inf\')\n right=self.minDepth(root.right) if root.right else float(\'inf\')\n\n return 1+min(left,right) \n``` | 4 | Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
**Note:** A leaf is a node with no children.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 2
**Example 2:**
**Input:** root = \[2,null,3,null,4,null,5,null,6\]
**Output:** 5
**Constraints:**
* The number of nodes in the tree is in the range `[0, 105]`.
* `-1000 <= Node.val <= 1000` | null |
Minimum Depth of Binary Tree with step by step explanation | minimum-depth-of-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can solve this problem using Depth First Search(DFS) or Breadth First Search(BFS) algorithm. Here, we will use the BFS algorithm, i.e., level order traversal to find the minimum depth of a binary tree.\n\nIn the level order traversal, we traverse the tree level by level starting from the root node. We maintain a queue of nodes to be traversed. The minimum depth is the level at which we encounter the first leaf node.\n\nAlgorithm:\n\n1. If the root is None, then the minimum depth is 0, and we return.\n2. We initialize a queue and append the root node to it.\n3. We loop through the queue until it becomes empty.\n4. For each level, we increment the level counter by 1.\n5. We iterate over the nodes at the current level and check if they are leaf nodes.\n6. If any of the nodes are leaf nodes, we return the current level.\n7. If none of the nodes are leaf nodes, we add their children to the queue for the next level.\n\n# Complexity\n- Time complexity:\nThe time complexity of this algorithm is O(N), where N is the number of nodes in the tree.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def minDepth(self, root: TreeNode) -> int:\n \n # if root is None, return 0\n if not root:\n return 0\n \n # initialize queue with the root node\n queue = deque([root])\n \n # initialize level counter to 1\n level = 1\n \n while queue:\n \n # loop through the nodes at current level\n for i in range(len(queue)):\n \n # pop the node from the left of the queue\n node = queue.popleft()\n \n # if the node is a leaf node, return the current level\n if not node.left and not node.right:\n return level\n \n # add the children of the current node to the queue\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n # increment level counter for next level\n level += 1\n \n return level\n\n``` | 8 | Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
**Note:** A leaf is a node with no children.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 2
**Example 2:**
**Input:** root = \[2,null,3,null,4,null,5,null,6\]
**Output:** 5
**Constraints:**
* The number of nodes in the tree is in the range `[0, 105]`.
* `-1000 <= Node.val <= 1000` | null |
Python Easy Solution || 100% || Beats 95% || Recursion || | path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:\n flag=False\n if not root:\n return flag\n return self.checkSm(0,targetSum, flag, root)\n \n def checkSm(self, sm, targetSum, flag, node):\n smValue=sm+node.val\n if not node.left and not node.right:\n if smValue==targetSum:\n flag=True\n return flag\n else:\n return flag\n if flag:\n return flag\n else:\n if node.left:\n leftFlag=self.checkSm(smValue,targetSum, flag, node.left)\n if leftFlag:\n return leftFlag\n if node.right:\n rightFlag=self.checkSm(smValue,targetSum, flag, node.right)\n if rightFlag:\n return rightFlag\n return flag\n\n``` | 2 | Given the `root` of a binary tree and an integer `targetSum`, return `true` if the tree has a **root-to-leaf** path such that adding up all the values along the path equals `targetSum`.
A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,null,1\], targetSum = 22
**Output:** true
**Explanation:** The root-to-leaf path with the target sum is shown.
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** false
**Explanation:** There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.
**Example 3:**
**Input:** root = \[\], targetSum = 0
**Output:** false
**Explanation:** Since the tree is empty, there are no root-to-leaf paths.
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
✅Easy Solution🔥Python3/C/C#/C++/Java🔥Explain Line By Line🔥With🗺️Image🗺️ | path-sum | 1 | 1 | # Problem\nYou\'re given a binary tree and an integer targetSum. The task is to determine whether there exists a root-to-leaf path in the tree where the sum of the values of the nodes along the path equals the targetSum.\n\nIn other words, you need to check if there\'s a sequence of nodes starting from the root and following edges to reach a leaf node such that the sum of values along this path is equal to the given targetSum.\n\n\n---\n# Solution\nThe provided solution is implemented as a method named hasPathSum within a class named Solution. The method takes two parameters: root, which is the root node of the binary tree, and targetSum, the desired sum.\n\n\n**Here\'s how the solution works:** \n\n1. f root is None (i.e., the tree is empty), there can\'t be any path with the desired sum. So, the function returns False.\n2. If root is a leaf node (i.e., it has no left or right children), the function checks whether the value of the leaf node is equal to the remaining targetSum. If they are equal, it returns True, indicating that a valid path with the target sum has been found.\n3. If the above conditions are not met, the function recursively checks for a valid path with the target sum in both the left and right subtrees. It subtracts the value of the current node from the targetSum before passing it to the recursive calls.\n4. The result of the recursive calls on the left and right subtrees (left_sum and right_sum) are then combined using the logical OR operation. This is because if either the left subtree or the right subtree has a valid path, it means there\'s a valid path in the entire tree, so the function should return True.\n5. If none of the above conditions are met, the function returns False.\n\nThe base cases (when the tree is empty or when a leaf node with a matching value is found) guarantee that the recursion will eventually terminate. The recursion explores all possible paths from the root to leaf nodes, checking if any of them sum up to the given targetSum. The logical OR operation on the results of the recursive calls ensures that the function correctly returns True if a valid path is found anywhere in the tree.\n\nThis solution has a time complexity of O(N), where N is the number of nodes in the binary tree, as it visits each node once in the worst case.\n\n\n\n\n# Code\n---\n\n```Python3 []\nclass Solution:\n def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:\n if not root:\n return False\n \n if not root.left and not root.right:\n return targetSum == root.val\n \n left_sum = self.hasPathSum(root.left, targetSum - root.val)\n right_sum = self.hasPathSum(root.right, targetSum - root.val)\n \n return left_sum or right_sum\n```\n```python []\nclass Solution:\n def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:\n if not root:\n return False\n \n if not root.left and not root.right:\n return targetSum == root.val\n \n left_sum = self.hasPathSum(root.left, targetSum - root.val)\n right_sum = self.hasPathSum(root.right, targetSum - root.val)\n \n return left_sum or right_sum\n```\n```C# []\npublic class Solution\n{\n public bool HasPathSum(TreeNode root, int targetSum)\n {\n if (root == null)\n {\n return false;\n }\n\n if (root.left == null && root.right == null)\n {\n return targetSum == root.val;\n }\n\n bool leftSum = HasPathSum(root.left, targetSum - root.val);\n bool rightSum = HasPathSum(root.right, targetSum - root.val);\n\n return leftSum || rightSum;\n }\n}\n```\n\n```C++ []\nclass Solution {\npublic:\n bool hasPathSum(TreeNode* root, int targetSum) {\n if (!root) {\n return false;\n }\n \n if (!root->left && !root->right) {\n return targetSum == root->val;\n }\n \n bool left_sum = hasPathSum(root->left, targetSum - root->val);\n bool right_sum = hasPathSum(root->right, targetSum - root->val);\n \n return left_sum || right_sum;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean hasPathSum(TreeNode root, int targetSum) {\n if (root == null) {\n return false;\n }\n \n if (root.left == null && root.right == null) {\n return targetSum == root.val;\n }\n \n boolean leftSum = hasPathSum(root.left, targetSum - root.val);\n boolean rightSum = hasPathSum(root.right, targetSum - root.val);\n \n return leftSum || rightSum;\n }\n}\n``` | 63 | Given the `root` of a binary tree and an integer `targetSum`, return `true` if the tree has a **root-to-leaf** path such that adding up all the values along the path equals `targetSum`.
A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,null,1\], targetSum = 22
**Output:** true
**Explanation:** The root-to-leaf path with the target sum is shown.
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** false
**Explanation:** There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.
**Example 3:**
**Input:** root = \[\], targetSum = 0
**Output:** false
**Explanation:** Since the tree is empty, there are no root-to-leaf paths.
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
Python3 deque beat 98.10% 34ms | path-sum | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:\n if not root:\n return False\n queue = collections.deque([(root, root.val)])\n while queue:\n node, val = queue.popleft()\n if not node.left and not node.right:\n if val == targetSum: return True\n else: continue\n if node.left:\n queue.append((node.left, val + node.left.val)) \n if node.right:\n queue.append((node.right, val + node.right.val)) \n return False\n``` | 8 | Given the `root` of a binary tree and an integer `targetSum`, return `true` if the tree has a **root-to-leaf** path such that adding up all the values along the path equals `targetSum`.
A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,null,1\], targetSum = 22
**Output:** true
**Explanation:** The root-to-leaf path with the target sum is shown.
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** false
**Explanation:** There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.
**Example 3:**
**Input:** root = \[\], targetSum = 0
**Output:** false
**Explanation:** Since the tree is empty, there are no root-to-leaf paths.
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
🌺C#, Java, Python3, JavaScript Solution - O(n) | path-sum | 1 | 1 | **Here to see the full explanation :\u2B50[Zyrastory - #112 Path Sum](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-112-path-sum-solution-and-explanation-en/)\u2B50**\n\n\n---\n\nWe can use a simple recursive approach and leverage DFS to traverse a binary tree.\n\nThis algorithm is quite efficient because it doesn\'t need to enumerate all possible paths but instead calculates the path sum during traversal. Once it finds a path that matches the target sum, it can return immediately.\n\n# Example :\n# C#\nSolution\n```\npublic class Solution {\n public bool HasPathSum(TreeNode root, int targetSum) {\n if (root == null) {\n return false;\n }\n\n //minus value of current node\n targetSum -= root.val;\n \n //check if now a leaf node\n if (root.left == null && root.right == null) {\n return targetSum == 0;\n }\n\n return HasPathSum(root.left, targetSum) || HasPathSum(root.right, targetSum);\n }\n}\n```\n\n---\n\n# Java\n```\nclass Solution {\n public boolean hasPathSum(TreeNode root, int targetSum) {\n if (root == null) {\n return false;\n }\n\n //minus value of current node\n targetSum -= root.val;\n \n //check if now a leaf node\n if (root.left == null && root.right == null) {\n return targetSum == 0;\n }\n\n return hasPathSum(root.left, targetSum) || hasPathSum(root.right, targetSum);\n }\n}\n```\n\n---\n# Python3\n```\nclass Solution:\n def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:\n if(root==None):\n return False\n \n #minus value of current node\n targetSum = targetSum-root.val\n \n #check if now a leaf node\n if (root.left == None and root.right == None):\n return targetSum == 0\n \n return self.hasPathSum(root.left, targetSum) or self.hasPathSum(root.right, targetSum)\n```\n\n---\n\n# JavaScript\n```\nvar hasPathSum = function(root, targetSum) {\n if (root == null) {\n return false;\n }\n\n //minus value of current node\n targetSum -= root.val;\n \n //check if now a leaf node\n if (root.left == null && root.right == null) {\n return targetSum == 0;\n }\n\n return hasPathSum(root.left, targetSum) || hasPathSum(root.right, targetSum);\n};\n```\n\n\n**If you got any problem about the explanation or you need other programming language solution, please feel free to let me know (leave comment or messenger me).**\n\nThank you\uD83C\uDF3A! | 8 | Given the `root` of a binary tree and an integer `targetSum`, return `true` if the tree has a **root-to-leaf** path such that adding up all the values along the path equals `targetSum`.
A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,null,1\], targetSum = 22
**Output:** true
**Explanation:** The root-to-leaf path with the target sum is shown.
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** false
**Explanation:** There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.
**Example 3:**
**Input:** root = \[\], targetSum = 0
**Output:** false
**Explanation:** Since the tree is empty, there are no root-to-leaf paths.
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
Python simple and easy to understand DFS recursion method. | path-sum-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe basic approach would be dfs recursion\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGo through every node and add that path and similarly calculating sum .It returns the list in the B List . \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nworst case o(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSince recursion is used it takes a lot of space.Still recursion could be improvised but no alternate method for recursion i have come across.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:\n\n b=[]\n\n def dfs(node,a) :\n \n if not node :\n return None\n #adding the path for every node we have traversed.\n a=a+[node.val]\n \n \n if node.left : \n \n dfs(node.left,a)\n \n if node.right :\n \n dfs(node.right,a)\n\n if not node.left and not node.right :\n\n sum=0\n\n for i in a :\n sum+=i\n # checking the targetsum with our sum and if not #matching we pop the last node .Also, appending list to the final #output list.\n \n if sum ==targetSum :\n b.append(a)\n \n else :\n a.pop(-1)\n \n \n return b\n \n return dfs(root,[]) \n\n \n\n\n\n\n\n \n``` | 0 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | path-sum-ii | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n**C++**\n\n```cpp\nclass Solution {\npublic:\n vector<vector<int>> ans;\n \n // the idea is to use dfs to traverse the tree from all root to leaf paths\n // `path` is used to store the current route \n // `remainingSum` is used to store thre remaining sum that we need with the initial value `targetSum`.\n // we substract it from the node value when we traverse down the tree\n // if we arrive the leaf and the the remaining sum is eqaul to leaf node value\n // then we can add `path` to ans\n // e.g. path = [5,4,11,2] and remainingSum = targetSum = 22\n // traverse node 5, remainingSum = 22 - 5 = 17\n // traverse node 4, remainingSum = 17 - 4 = 13\n // traverse node 11, remainingSum = 13 - 11 = 2\n // traverse node 2, remainingSum = 2 - 2 = 0\n // remainingSum is 0 which means the sum of current path is eqaul to targetSum\n // so how to find another path?\n // we can backtrack here\n // we can pop back a node and try another\n // e.g. path = [5, 4, 11, 7]\n // pop 7 out = [5, 4, 11]\n // push 2 = [5, 4, 11, 2]\n // ... etc\n void dfs(TreeNode* node, vector<int>& path, int remainingSum) {\n // if it is nullptr, then return\n if (!node) return;\n // add the current node val to path\n path.push_back(node-> val);\n // !node->left && !node->right : check if it is a leaf node\n // remainingSum == node->val: check if the remaining sum - node->val == 0\n // if both condition is true, then we find one of the paths\n if (!node->left && !node->right && remainingSum == node->val) ans.push_back(path);\n // traverse left sub tree with updated remaining sum\n // we don\'t need to check if left sub tree is nullptr or not\n // as we handle it in the first line of this function\n dfs(node-> left, path, remainingSum - node-> val);\n // traverse right sub tree with updated remaining sum\n // we don\'t need to check if right sub tree is nullptr or not\n // as we handle it in the first line of this function\n dfs(node-> right, path, remainingSum - node-> val);\n // backtrack \n path.pop_back();\n }\n \n vector<vector<int>> pathSum(TreeNode* root, int targetSum) {\n // used to store current route\n vector<int> path;\n // dfs from the root\n dfs(root, path, targetSum);\n return ans; \n }\n};\n```\n\n**Python**\n\n```py\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n # the idea is to use dfs to traverse the tree from all root to leaf paths\n # `path` is used to store the current route \n # `remainingSum` is used to store thre remaining sum that we need with the initial value `targetSum`.\n # we substract it from the node value when we traverse down the tree\n # if we arrive the leaf and the the remaining sum is eqaul to leaf node value\n # then we can add `path` to ans\n # e.g. path = [5,4,11,2] and remainingSum = targetSum = 22\n # traverse node 5, remainingSum = 22 - 5 = 17\n # traverse node 4, remainingSum = 17 - 4 = 13\n # traverse node 11, remainingSum = 13 - 11 = 2\n # traverse node 2, remainingSum = 2 - 2 = 0\n # remainingSum is 0 which means the sum of current path is eqaul to targetSum\n # so how to find another path?\n # we can backtrack here\n # we can pop back a node and try another\n # e.g. path = [5, 4, 11, 7]\n # pop 7 out = [5, 4, 11]\n # push 2 = [5, 4, 11, 2]\n # ... etc\n def dfs(self, root, path, ans, remainingSum):\n # if it is None, then return\n if not root:\n return\n # add the current node val to path\n path.append(root.val)\n # !node.left && !node.right : check if it is a leaf node\n # remainingSum == node.val: check if the remaining sum - node.val == 0\n # if both condition is true, then we find one of the paths\n if not root.left and not root.right and remainingSum == root.val:\n ans.append(list(path))\n # traverse left sub tree with updated remaining sum\n # we don\'t need to check if left sub tree is nullptr or not\n # as we handle it in the first line of this function\n self.dfs(root.left, path, ans, remainingSum - root.val)\n # traverse right sub tree with updated remaining sum\n # we don\'t need to check if right sub tree is nullptr or not\n # as we handle it in the first line of this function\n self.dfs(root.right, path, ans, remainingSum - root.val)\n # backtrack \n path.pop()\n \n def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:\n ans = []\n self.dfs(root, [], ans, targetSum)\n return ans\n \n```\n\n**Java**\n\n```java\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n List<List<Integer>> ans = new ArrayList<List<Integer>>();\n // the idea is to use dfs to traverse the tree from all root to leaf paths\n // `path` is used to store the current route \n // `remainingSum` is used to store thre remaining sum that we need with the initial value `targetSum`.\n // we substract it from the node value when we traverse down the tree\n // if we arrive the leaf and the the remaining sum is eqaul to leaf node value\n // then we can add `path` to ans\n // e.g. path = [5,4,11,2] and remainingSum = targetSum = 22\n // traverse node 5, remainingSum = 22 - 5 = 17\n // traverse node 4, remainingSum = 17 - 4 = 13\n // traverse node 11, remainingSum = 13 - 11 = 2\n // traverse node 2, remainingSum = 2 - 2 = 0\n // remainingSum is 0 which means the sum of current path is eqaul to targetSum\n // so how to find another path?\n // we can backtrack here\n // we can pop back a node and try another\n // e.g. path = [5, 4, 11, 7]\n // pop 7 out = [5, 4, 11]\n // push 2 = [5, 4, 11, 2]\n // ... etc\n private void dfs(TreeNode node, List<Integer> path, int remainingSum) {\n // if it is null, then return\n if (node == null) return;\n // add the current node val to path\n path.add(node.val);\n // !node.left && !node.right : check if it is a leaf node\n // remainingSum == node.val: check if the remaining sum - node.val == 0\n // if both condition is true, then we find one of the paths\n if (node.left == null && node.right == null && remainingSum == node.val) ans.add(new ArrayList<>(path));\n // traverse left sub tree with updated remaining sum\n // we don\'t need to check if left sub tree is nullptr or not\n // as we handle it in the first line of this function\n this.dfs(node.left, path, remainingSum - node.val);\n // traverse right sub tree with updated remaining sum\n // we don\'t need to check if right sub tree is nullptr or not\n // as we handle it in the first line of this function\n this.dfs(node.right, path, remainingSum - node.val);\n // backtrack \n path.remove(path.size() - 1);\n }\n public List<List<Integer>> pathSum(TreeNode root, int targetSum) {\n List<Integer> path = new ArrayList<Integer>();\n dfs(root, path, targetSum);\n return ans;\n }\n}\n``` | 72 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
✔Python | 98% Faster | Simple Python Code with comments | path-sum-ii | 0 | 1 | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:\n if not root: return None\n\t\t#Final Result list\n res = []\n\t\t# Creating Stack for faster Insertion and Deletion\n path = collections.deque() \n \n\t\t#dfs is define inside the pathSum method so we don\'t have to pass the path and res list\n def dfs(node, s):\n\t\t\t#Adding value of node to stack as well as to sum (s)\n path.append(node.val)\n s += node.val\n\t\t\t#Checking Whether it is a leaf node and also whether sum value is equal to targetSum\n if not node.left and not node.right and s == targetSum:\n res.append(list(path))\n # If not then we will continue with our dfs by recursively going to left node and right node if exist.\n\t\t\tif node.left:\n dfs(node.left, s)\n if node.right:\n dfs(node.right, s)\n\t\t\t# Lastly, remove the node value from path and sum before exiting from the dfs\n s -= node.val\n path.pop()\n #Calling our dfs method and passing root as main node and sum(s) as 0\n\t\tdfs(root, 0)\n return res\n``` | 2 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
with step by step explanation | path-sum-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe solution uses a depth-first search (DFS) approach to traverse the binary tree and check for root-to-leaf paths that sum up to the given target sum.\n\nThe pathSum function initializes an empty list result to store the valid paths and an empty list path to track the current path being traversed. It then calls the dfs helper function, passing in the root node, target sum, path, and result.\n\nThe dfs function first checks if the current node is None. If it is, then it returns. Otherwise, it appends the current node value to the path.\n\nIf the current node is a leaf node (i.e., it has no left or right child nodes) and its value is equal to the target sum, then the current path is added to the result list.\n\nOtherwise, the dfs function calls itself recursively on the left and right child nodes, subtracting the current node value from the target sum. When the recursive calls have completed, the current node is popped from the path.\n\nThe final result list is returned to the calling function after all nodes have been traversed.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:\n result = []\n path = []\n self.dfs(root, targetSum, path, result)\n return result\n\n def dfs(self, node, target, path, result):\n if not node:\n return\n path.append(node.val)\n if not node.left and not node.right and node.val == target:\n result.append(path[:])\n self.dfs(node.left, target - node.val, path, result)\n self.dfs(node.right, target - node.val, path, result)\n path.pop()\n\n``` | 4 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
Python3 || 113. Path Sum II | path-sum-ii | 0 | 1 | ```\nclass Solution: \n def pathSum(self, root: TreeNode, targetSum: int) -> list[list[int]]:\n\n def Count(node:TreeNode)->list[list[int]]:\n if not node:\n\t\t\t return []\n if not node.left and not node.right:\n\t\t\t return [[node.val]]\n\t\t\t \n return [[node.val]+x for x in Count(node.left) + Count(node.right)]\n \n return [x for x in Count(root) if sum(x) == targetSum]\n```\n | 5 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
Python Easy Solution || 100% || Beats 98% || Recursion || | path-sum-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nimport copy\nclass Solution:\n def __init__(self):\n self.res=[]\n\n def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:\n arr=[]\n if not root:\n return []\n self.checkSm(0,targetSum, root, arr)\n return self.res\n \n def checkSm(self, sm, targetSum, node, arr):\n smValue=sm+node.val\n if not node.left and not node.right:\n if smValue==targetSum:\n arr.append(node.val)\n newarr=copy.deepcopy(arr)\n self.res.append(newarr)\n arr.pop()\n return\n else:\n arr.append(node.val)\n if node.left:\n self.checkSm(smValue,targetSum, node.left, arr)\n if node.right:\n self.checkSm(smValue,targetSum, node.right, arr)\n arr.pop()\n return\n``` | 3 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
Easiest Python solution | DFS | Short soln | path-sum-ii | 0 | 1 | Runtime: 77 ms, faster than 48.11% of Python3 online submissions for Path Sum II.\nMemory Usage: 15.7 MB, less than 52.98% of Python3 online submissions for Path Sum II.\n```\n\t\tlis = []\n res = []\n def treeTraversal(root: Optional[TreeNode]):\n if root == None:\n return\n lis.append(root.val)\n treeTraversal(root.left)\n treeTraversal(root.right)\n if(root.left == None and root.right == None):\n sums = sum(lis)\n if(sums == targetSum):\n res.append(lis.copy())\n lis.pop()\n treeTraversal(root)\n return res | 1 | Given the `root` of a binary tree and an integer `targetSum`, return _all **root-to-leaf** paths where the sum of the node values in the path equals_ `targetSum`_. Each path should be returned as a list of the node **values**, not node references_.
A **root-to-leaf** path is a path starting from the root and ending at any leaf node. A **leaf** is a node with no children.
**Example 1:**
**Input:** root = \[5,4,8,11,null,13,4,7,2,null,null,5,1\], targetSum = 22
**Output:** \[\[5,4,11,2\],\[5,8,4,5\]\]
**Explanation:** There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
**Example 2:**
**Input:** root = \[1,2,3\], targetSum = 5
**Output:** \[\]
**Example 3:**
**Input:** root = \[1,2\], targetSum = 0
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5000]`.
* `-1000 <= Node.val <= 1000`
* `-1000 <= targetSum <= 1000` | null |
Easy python solution | flatten-binary-tree-to-linked-list | 0 | 1 | # Easy python solution\n# Code\n```\nclass Solution:\n def __init__(self):\n self.prev=None\n def flatten(self, root: Optional[TreeNode]) -> None:\n """\n Do not return anything, modify root in-place instead.\n """\n if not root: return\n self.flatten(root.right)\n self.flatten(root.left)\n root.right=self.prev\n root.left=None\n self.prev=root\n``` | 1 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
Python || Iterative Solution || Without Stack | flatten-binary-tree-to-linked-list | 0 | 1 | ```\nclass Solution:\n def flatten(self, root: Optional[TreeNode]) -> None:\n curr=root\n while curr:\n if curr.left!=None:\n prev=curr.left\n while prev.right:\n prev=prev.right\n prev.right=curr.right\n curr.right=curr.left\n curr.left=None\n curr=curr.right\n```\n**An upvote will be encouraging** | 19 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
Beats 93.12% with step by step explanation | flatten-binary-tree-to-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIn this solution, we start by initializing a prev variable to None. This variable will keep track of the previously flattened node as we recursively flatten the binary tree.\n\nWe then define a recursive function flatten that takes in the root node of the binary tree. This function does not return anything, but instead modifies the tree in-place.\n\nThe first thing we do in the flatten function is to check if the root node is None. If it is, we simply return.\n\nNext, we recursively flatten the right subtree of the root node by calling self.flatten(root.right). This will flatten the right subtree and set self.prev to the rightmost node in the right subtree.\n\nWe then recursively flatten the left subtree of the root node by calling self.flatten(root.left). This will flatten the left subtree and update self.prev to the rightmost node in the flattened left subtree.\n\nOnce we have flattened both the left and right subtrees, we update the root.right pointer to be the previously flattened node (self.prev). We also set the root.left pointer to None to remove the left child.\n\nFinally, we update self.prev to be the current node (root). This is important because it allows us to keep track of the previously flattened node as we continue to recursively flatten the tree.\n\nThis algorithm flattens the binary tree in pre-order traversal, so the resulting "linked list" will be in the same order as a pre-order traversal of the tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self):\n self.prev = None\n\n def flatten(self, root: TreeNode) -> None:\n """\n Do not return anything, modify root in-place instead.\n """\n if not root:\n return\n self.flatten(root.right) # Recursively flatten the right subtree\n self.flatten(root.left) # Recursively flatten the left subtree\n root.right = self.prev # Set the right child to the previously flattened node\n root.left = None # Set the left child to None\n self.prev = root # Update the previously flattened node to be the current node\n\n``` | 20 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
Solution | flatten-binary-tree-to-linked-list | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void flatten(TreeNode* root) {\n std::ios_base::sync_with_stdio(false);\n std::cin.tie(nullptr);\n std::cout.tie(nullptr);\n if(!root) return;\n if(!root->left && !root->right) return;\n\n flatten(root->left);\n if(root->left){\n TreeNode* save= root->right;\n root->right= root->left;\n root->left= NULL;\n TreeNode* temp= root;\n while(temp->right){\n temp= temp->right;\n }\n temp->right= save;\n }\n flatten(root->right);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def flatten(self, root: Optional[TreeNode]) -> None:\n \n self.cur = None\n \n def dfs(node):\n if not node:\n return\n left, right = node.left, node.right\n node.left = None\n if self.cur:\n self.cur.right = node\n self.cur = self.cur.right\n else:\n self.cur = node\n dfs(left)\n dfs(right)\n \n dfs(root)\n```\n\n```Java []\nclass Solution {\n public void flatten(TreeNode root) {\n TreeNode node = root;\n while(node != null)\n {\n if(node.left != null)\n {\n TreeNode left = node.left;\n while(left.right != null)\n left = left.right;\n left.right = node.right;\n node.right = node.left;\n node.left = null;\n }\n node = node.right;\n }\n }\n}\n```\n | 6 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
Python 8 Line Solution Very Efficient | flatten-binary-tree-to-linked-list | 0 | 1 | ```\nclass Solution:\n def __init__(self):\n self.prev=None\n def flatten(self, root: Optional[TreeNode]) -> None:\n if not root:\n return None\n self.flatten(root.right)\n self.flatten(root.left)\n root.right=self.prev\n root.left=None\n self.prev=root\n \n``` | 3 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
Python || Easy || Iterative || Recursive || Both Solution | flatten-binary-tree-to-linked-list | 0 | 1 | **Iterative Solution:**\n```\nclass Solution:\n def flatten(self, root: Optional[TreeNode]) -> None:\n if root==None:\n return None\n st=[root]\n while st:\n node=st.pop()\n if node.right:\n st.append(node.right)\n if node.left:\n st.append(node.left)\n if len(st)>0:\n node.right=st[-1]\n node.left=None\n```\n**Recursive Solution:**\n```\nclass Solution:\n prev=None\n def flatten(self, root: Optional[TreeNode]) -> None:\n if root==None:\n return \n self.flatten(root.right)\n self.flatten(root.left)\n root.left=None\n root.right=self.prev\n self.prev=root\n```\n**An upvote will be encouraging**\n | 7 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
Simple Solution | flatten-binary-tree-to-linked-list | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def flatten(self, root: Optional[TreeNode]) -> None:\n """\n For every node we will try to find the first right most node with no right child and return it.\n If its left tail exists, then we have to add the right child of the current node to the right child of the left tail node.\n And make the left child as the right child of the current node and set the left child as None.\n Otherwise return the rightTail (if exist) or leftTail (if exists) otherwise the root (in case of the leaf node)\n 1 1 1 1\n / \\ / \\ / \\ \\ \n 2 3 -> 2 3 -> 2 3 -> 2 \n / \\ / \\ \\ \\ \n 4 5 4 5 4 4 \n / \\ \\ \\ \n 6 6 6 6 \n \\ \\ \n 5 5 \n \\ \n 3\n """\n def dfs(root):\n if root == None: return root\n\n leftTail = dfs(root.left)\n rightTail = dfs(root.right)\n\n if leftTail:\n leftTail.right = root.right\n root.right = root.left\n root.left = None\n \n return rightTail or leftTail or root\n \n return dfs(root)\n \n """\n Common Way of doing it\n """\n # if not root: return root\n # curr = root\n # while curr:\n # if curr.left:\n # right = curr.right\n # curr.right = curr.left\n # if right:\n # temp = curr.left\n # while temp.right:\n # temp = temp.right\n # temp.right = right\n # curr.left = None\n # curr = curr.right\n # return root\n``` | 1 | Given the `root` of a binary tree, flatten the tree into a "linked list ":
* The "linked list " should use the same `TreeNode` class where the `right` child pointer points to the next node in the list and the `left` child pointer is always `null`.
* The "linked list " should be in the same order as a [**pre-order** **traversal**](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order,_NLR) of the binary tree.
**Example 1:**
**Input:** root = \[1,2,5,3,4,null,6\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-100 <= Node.val <= 100`
**Follow up:** Can you flatten the tree in-place (with `O(1)` extra space)? | If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal. |
🔥Optimizing String Subsequence Counting: A Deep Dive into All 3 Approaches || Mr. Robot | distinct-subsequences | 1 | 1 | # Solving the "Distinct Subsequences" Problem: \n\n## \u2753Understanding the Problem \n\nThe "Distinct Subsequences" problem involves two strings, `s` and `t`, and the goal is to find the number of distinct subsequences of `t` in the string `s`. A subsequence is a sequence of characters that appears in the same order in both strings, but not necessarily consecutively.\n\nFor example, given `s = "rabbbit"` and `t = "rabbit"`, there are three distinct subsequences: "rabbit," "rabb**i**t," and "rab**b**bit."\n\n## \uD83D\uDCA1Recursive Approach\n\nWe\'ll start by defining a recursive function that explores all possible subsequences of `s` to match `t`. Here\'s the code for the recursive function:\n\n**Complexity Analysis**:\n\n- **\u231B**Time Complexity: The time complexity of the recursive approach is O(2^n) in the worst case, where `n` is the length of string `s`. This is because, for each character in `s`, we make two recursive calls (take or not take).\n\n- Space Complexity: The space complexity is O(n) for the recursive call stack.\n\n## \uD83D\uDCDDDry Run\n\nLet\'s dry run the code with an example:\n\n- `s = "rabbbit"` and `t = "rabbit"`\n\n1. We start with `s_ind = 0` and `t_ind = 0`. Since the characters match, we explore both taking and not taking the character.\n - Taking the character: Move to the next characters in `s` and `t`.\n - Not taking the character: Move to the next character in `s`.\n\n2. This process continues until we reach the base cases, and we accumulate the count of valid subsequences.\n\n3. In the end, we return the total count.\n\n## Edge Cases\n\nConsider the following edge cases:\n1. Empty strings: What happens when `s` or `t` is an empty string?\n2. No match: What if there are no subsequences that match `t` in `s`?\n\nBy considering these edge cases, we ensure our solution is robust and handles all scenarios.\n\n\n---\n# \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCode : Recursive Approach\n\n```cpp []\nclass Solution {\npublic:\n int recursiveWithoutMemoization(string& s, string& t, int s_ind, int t_ind) {\n if (t_ind == t.length()) {\n return 1;\n }\n\n if (s_ind == s.length()) {\n return 0;\n }\n\n int take = 0, notTake = 0;\n\n if (s[s_ind] == t[t_ind]) {\n take = recursiveWithoutMemoization(s, t, s_ind + 1, t_ind + 1);\n }\n\n notTake = recursiveWithoutMemoization(s, t, s_ind + 1, t_ind);\n\n return take + notTake;\n }\n\n int numDistinct(string s, string t) {\n return recursiveWithoutMemoization(s, t, 0, 0);\n }\n};\n```\n```python []\nclass Solution:\n def recursiveWithoutMemoization(self, s: str, t: str, s_ind: int, t_ind: int) -> int:\n if t_ind == len(t):\n return 1\n if s_ind == len(s):\n return 0\n\n take, notTake = 0, 0\n\n if s[s_ind] == t[t_ind]:\n take = self.recursiveWithoutMemoization(s, t, s_ind + 1, t_ind + 1)\n\n notTake = self.recursiveWithoutMemoization(s, t, s_ind + 1, t_ind)\n\n return take + notTake\n\n def numDistinct(self, s: str, t: str) -> int:\n return self.recursiveWithoutMemoization(s, t, 0, 0)\n```\n\n\n```java []\nclass Solution {\n public int recursiveWithoutMemoization(String s, String t, int s_ind, int t_ind) {\n if (t_ind == t.length()) {\n return 1;\n }\n if (s_ind == s.length()) {\n return 0;\n }\n\n int take = 0, notTake = 0;\n\n if (s.charAt(s_ind) == t.charAt(t_ind)) {\n take = recursiveWithoutMemoization(s, t, s_ind + 1, t_ind + 1);\n }\n\n notTake = recursiveWithoutMemoization(s, t, s_ind + 1, t_ind);\n\n return take + notTake;\n }\n\n public int numDistinct(String s, String t) {\n return recursiveWithoutMemoization(s, t, 0, 0);\n }\n}\n```\n\n\n```csharp []\npublic class Solution {\n public int RecursiveWithoutMemoization(string s, string t, int s_ind, int t_ind) {\n if (t_ind == t.Length) {\n return 1;\n }\n if (s_ind == s.Length) {\n return 0;\n }\n\n int take = 0, notTake = 0;\n\n if (s[s_ind] == t[t_ind]) {\n take = RecursiveWithoutMemoization(s, t, s_ind + 1, t_ind + 1);\n }\n\n notTake = RecursiveWithoutMemoization(s, t, s_ind + 1, t_ind);\n\n return take + notTake;\n }\n\n public int NumDistinct(string s, string t) {\n return RecursiveWithoutMemoization(s, t, 0, 0);\n }\n}\n```\n\n\n```javascript []\nvar recursiveWithoutMemoization=function(s, t, s_ind, t_ind) {\n if (t_ind === t.length) {\n return 1;\n }\n if (s_ind === s.length) {\n return 0;\n }\n\n let take = 0, notTake = 0;\n\n if (s[s_ind] === t[t_ind]) {\n take = recursiveWithoutMemoization(s, t, s_ind + 1, t_ind + 1);\n }\n\n notTake = recursiveWithoutMemoization(s, t, s_ind + 1, t_ind);\n\n return take + notTake;\n }\n\n var numDistinct= function(s, t) {\n return recursiveWithoutMemoization(s, t, 0, 0);\n }\n\n```\n\n\n```ruby []\nclass Solution\n def recursive_without_memoization(s, t, s_ind, t_ind)\n return 1 if t_ind == t.length\n return 0 if s_ind == s.length\n\n take = 0\n not_take = 0\n\n if s[s_ind] == t[t_ind]\n take = recursive_without_memoization(s, t, s_ind + 1, t_ind + 1)\n end\n\n not_take = recursive_without_memoization(s, t, s_ind + 1, t_ind)\n\n take + not_take\n end\n\n def num_distinct(s, t)\n recursive_without_memoization(s, t, 0, 0)\n end\nend\n```\n\n---\n---\n\n## \uD83D\uDCA1Approach 2 : Memoization Optimization\n\nMemoization is a technique used to store and reuse the results of expensive function calls to avoid redundant calculations. In the context of our problem, we can create a memoization table to store the results of subproblems. Each entry `dp[i][j]` will represent the number of distinct subsequences of `s` starting from index `i` that form the string `t` starting from index `j`.\n\nWe\'ll modify our recursive function to first check if we have already calculated the result for the current subproblem. If we have, we\'ll simply return the cached result. If not, we\'ll proceed with the recursive calculations and store the result in the memoization table.\n\n## Complexity Analysis\n\nLet\'s analyze the\n\n time and space complexity of our memoized solution:\n\n- Time Complexity: The time complexity of our algorithm is O(m * n), where `m` is the length of string `s` and `n` is the length of string `t`. This is because we fill up the `dp` table, which has dimensions `m x n`, and each cell takes constant time to compute.\n\n- Space Complexity: The space complexity is also O(m * n) due to the `dp` table.\n\n# \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCode\n\n```cpp []\nclass Solution {\npublic:\n int recursiveWithMemoization(string& s, string& t, int s_ind, int t_ind, vector<vector<int>>& dp) {\n if (t_ind == t.length()) {\n return 1;\n }\n if (s_ind == s.length()) {\n return 0;\n }\n\n if (dp[s_ind][t_ind] != -1) {\n return dp[s_ind][t_ind];\n }\n\n int take = 0, notTake = 0;\n\n if (s[s_ind] == t[t_ind]) {\n take = recursiveWithMemoization(s, t, s_ind + 1, t_ind + 1, dp);\n }\n\n notTake = recursiveWithMemoization(s, t, s_ind + 1, t_ind, dp);\n\n dp[s_ind][t_ind] = take + notTake;\n\n return dp[s_ind][t_ind];\n }\n\n int numDistinct(string s, string t) {\n vector<vector<int>> dp(s.length(), vector<int>(t.length(), -1));\n return recursiveWithMemoization(s, t, 0, 0, dp);\n }\n};\n```\n\n\n```python []\nclass Solution:\n def recursiveWithMemoization(self, s: str, t: str, s_ind: int, t_ind: int, dp: List[List[int]]) -> int:\n if t_ind == len(t):\n return 1\n if s_ind == len(s):\n return 0\n\n if dp[s_ind][t_ind] != -1:\n return dp[s_ind][t_ind]\n\n take, notTake = 0, 0\n\n if s[s_ind] == t[t_ind]:\n take = self.recursiveWithMemoization(s, t, s_ind + 1, t_ind + 1, dp)\n\n notTake = self.recursiveWithMemoization(s, t, s_ind + 1, t_ind, dp)\n\n dp[s_ind][t_ind] = take + notTake\n\n return dp[s_ind][t_ind]\n\n def numDistinct(self, s: str, t: str) -> int:\n dp = [[-1 for _ in range(len(t))] for _ in range(len(s))]\n return self.recursiveWithMemoization(s, t, 0, 0, dp)\n```\n\n\n```java []\nclass Solution {\n public int recursiveWithMemoization(String s, String t, int s_ind, int t_ind, int[][] dp) {\n if (t_ind == t.length()) {\n return 1;\n }\n if (s_ind == s.length()) {\n return 0;\n }\n\n if (dp[s_ind][t_ind] != -1) {\n return dp[s_ind][t_ind];\n }\n\n int take = 0, notTake = 0;\n\n if (s.charAt(s_ind) == t.charAt(t_ind)) {\n take = recursiveWithMemoization(s, t, s_ind + 1, t_ind + 1, dp);\n }\n\n notTake = recursiveWithMemoization(s, t, s_ind + 1, t_ind, dp);\n\n dp[s_ind][t_ind] = take + notTake;\n\n return dp[s_ind][t_ind];\n }\n\n public int numDistinct(String s, String t) {\n int[][] dp = new int[s.length()][t.length()];\n for (int[] row : dp) {\n Arrays.fill(row, -1);\n }\n return recursiveWithMemoization(s, t, 0, 0, dp);\n }\n}\n```\n\n\n```javascript []\nvar numDistinct = function (s, t) {\n const dp = Array(s.length)\n .fill(0)\n .map(() => Array(t.length).fill(-1));\n\n function recursiveWithMemoization(s_ind, t_ind) {\n if (t_ind === t.length) {\n return 1;\n }\n if (s_ind === s.length) {\n return 0;\n }\n\n if (dp[s_ind][t_ind] !== -1) {\n return dp[s_ind][t_ind];\n }\n\n let take = 0, notTake = 0;\n\n if (s[s_ind] === t[t_ind]) {\n take = recursiveWithMemoization(s_ind + 1, t_ind + 1);\n }\n\n notTake = recursiveWithMemoization(s_ind + 1, t_ind);\n\n dp[s_ind][t_ind] = take + notTake;\n\n return dp[s_ind][t_ind];\n }\n\n return recursiveWithMemoization(0, 0);\n};\n```\n\n\n```csharp []\npublic class Solution {\n public int RecursiveWithMemoization(string s, string t, int s_ind, int t_ind, int[,] dp) {\n if (t_ind == t.Length) {\n return 1;\n }\n if (s_ind == s.Length) {\n return 0;\n }\n\n if (dp[s_ind, t_ind] != -1) {\n return dp[s_ind, t_ind];\n }\n\n int take = 0, notTake = 0;\n\n if (s[s_ind] == t[t_ind]) {\n take = RecursiveWithMemoization(s, t, s_ind + 1, t_ind + 1, dp);\n }\n\n notTake = RecursiveWithMemoization(s, t, s_ind + 1, t_ind, dp);\n\n dp[s_ind, t_ind] = take + notTake;\n\n return dp[s_ind, t_ind];\n }\n\n public int NumDistinct(string s, string t) {\n int[,] dp = new int[s.Length, t.Length];\n for (int i = 0; i < s.Length; i++) {\n for (int j = 0; j < t.Length; j++) {\n dp[i, j] = -1;\n }\n \n\n }\n return RecursiveWithMemoization(s, t, 0, 0, dp);\n }\n}\n```\n\n\n```ruby []\ndef num_distinct(s, t)\n dp = Array.new(s.length) { Array.new(t.length, -1) }\n\n def recursive_with_memoization(s, t, s_ind, t_ind, dp)\n return 1 if t_ind == t.length\n return 0 if s_ind == s.length\n\n return dp[s_ind][t_ind] if dp[s_ind][t_ind] != -1\n\n take, not_take = 0, 0\n\n if s[s_ind] == t[t_ind]\n take = recursive_with_memoization(s, t, s_ind + 1, t_ind + 1, dp)\n end\n\n not_take = recursive_with_memoization(s, t, s_ind + 1, t_ind, dp)\n\n dp[s_ind][t_ind] = take + not_take\n\n dp[s_ind][t_ind]\n end\n\n recursive_with_memoization(s, t, 0, 0, dp)\nend\n```\n---\n\n## \uD83D\uDCA1Approach 3: Bottom-Up Dynamic Programming\n\n## Steps : \n\n### 1. Creating the DP Array\n\nTo use dynamic programming, we\'ll create a two-dimensional DP array, `dp`. The size of `dp` will be `(n+1) x (m+1)`, where `n` is the length of string `s` and `m` is the length of string `t`.\n\nIn our DP array, `dp[i][j]` will represent the number of distinct subsequences of the first `i` characters in string `s` that match the first `j` characters in string `t`.\n\n### 2. Initializing the DP Array\n\nWe\'ll start by initializing the DP array. The base cases are as follows:\n\n- `dp[i][0] = 1` for all `i`. This means that there is only one way to form an empty string from any non-empty string.\n- `dp[0][j] = 0` for all `j > 0`. This means that it\'s impossible to form a non-empty string `t` from an empty string `s`.\n\n### 3. Filling in the DP Array\n\nNow, we\'ll iterate over the characters of both strings `s` and `t` using two nested loops:\n\n```python\nfor i in range(1, n + 1):\n for j in range(1, m + 1):\n```\n\nFor each `i` and `j`, we\'ll check if `s[i-1]` is equal to `t[j-1]`. If they are equal, we have two choices:\n\n1. We can consider the current characters as a match and move on to the next characters in both strings. In this case, `dp[i][j]` will be incremented by `dp[i-1][j-1]`.\n2. We can ignore the current character in `s` and move on to the next character in `s`. In this case, `dp[i][j]` will be incremented by `dp[i-1][j]`.\n\n### 4. Final Result\n\nAfter filling in the entire DP array, the value `dp[n][m]` will represent the number of distinct subsequences of string `s` that match string `t`.\n\n### Dry Run\n\nLet\'s dry run this approach on an example:\n\n- `s = "rabbbit"` and `t = "rabbit"`\n\nWe\'ll start with the initialized DP array:\n\n```\ndp = [\n [1, 0, 0, 0, 0, 0, 0],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?]\n]\n```\n\nNow, we\'ll fill in the DP array:\n\n- `i = 1`, `j = 1` (s[0] == t[0]): We have a match, so we increment `dp[1][1]` by `dp[0][0]`. The DP array becomes:\n\n```\ndp = [\n [1, 0, 0, 0, 0, 0, 0],\n [1, 1, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?],\n [1, ?, ?, ?, ?, ?, ?]\n]\n```\n\n- Continue filling the DP array\n\n following the same logic.\n\n### Complexity Analysis\n\nThe time complexity of this solution is **O(n x m)**, where `n` and `m` are the lengths of strings `s` and `t`, respectively.\n\nThe space complexity is O(n*m) for the DP array and O(1) for other variables. Therefore, the overall space complexity is **O(n x m)**.\n\n# \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes \n``` cpp []\nclass Solution {\npublic:\n int numDistinct(string s, string t) {\n int m = s.length();\n int n = t.length();\n\n vector<vector<unsigned long long>> dp(m + 1, vector<unsigned long long>(n + 1, 0));\n\n // Initialize the base case:\n for (int i = 0; i <= m; i++) {\n dp[i][n] = 1;\n }\n\n for (int sIndex = m - 1; sIndex >= 0; sIndex--) {\n for (int tIndex = n - 1; tIndex >= 0; tIndex--) {\n dp[sIndex][tIndex] = dp[sIndex + 1][tIndex];\n\n if (s[sIndex] == t[tIndex]) {\n dp[sIndex][tIndex] += dp[sIndex + 1][tIndex + 1];\n }\n }\n }\n\n return dp[0][0];\n }\n};\n```\n\n```python []\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n m, n = len(s), len(t)\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n\n for i in range(m + 1):\n dp[i][n] = 1\n\n for sIndex in range(m - 1, -1, -1):\n for tIndex in range(n - 1, -1, -1):\n dp[sIndex][tIndex] = dp[sIndex + 1][tIndex]\n\n if s[sIndex] == t[tIndex]:\n dp[sIndex][tIndex] += dp[sIndex + 1][tIndex + 1]\n\n return dp[0][0]\n```\n\n```java []\nclass Solution {\n public int numDistinct(String s, String t) {\n int m = s.length();\n int n = t.length();\n\n int[][] dp = new int[m + 1][n + 1];\n\n for (int i = 0; i <= m; i++) {\n dp[i][n] = 1;\n }\n\n for (int sIndex = m - 1; sIndex >= 0; sIndex--) {\n for (int tIndex = n - 1; tIndex >= 0; tIndex--) {\n dp[sIndex][tIndex] = dp[sIndex + 1][tIndex];\n\n if (s.charAt(sIndex) == t.charAt(tIndex)) {\n dp[sIndex][tIndex] += dp[sIndex + 1][tIndex + 1];\n }\n }\n }\n\n return dp[0][0];\n }\n}\n```\n\n\n```javascript []\nvar numDistinct = function (s, t) {\n const m = s.length;\n const n = t.length;\n\n const dp = new Array(m + 1).fill().map(() => new Array(n + 1).fill(0));\n\n for (let i = 0; i <= m; i++) {\n dp[i][n] = 1;\n }\n\n for (let sIndex = m - 1; sIndex >= 0; sIndex--) {\n for (let tIndex = n - 1; tIndex >= 0; tIndex--) {\n dp[sIndex][tIndex] = dp[sIndex + 1][tIndex];\n\n if (s[sIndex] === t[tIndex]) {\n dp[sIndex][tIndex] += dp[sIndex + 1][tIndex + 1];\n }\n }\n }\n\n return dp[0][0];\n};\n```\n\n\n```csharp []\npublic class Solution {\n public int NumDistinct(string s, string t) {\n int m = s.Length;\n int n = t.Length;\n\n int[,] dp = new int[m + 1, n + 1];\n\n for (int i = 0; i <= m; i++) {\n dp[i, n] = 1;\n }\n\n for (int sIndex = m - 1; sIndex >= 0; sIndex--) {\n for (int tIndex = n - 1; tIndex >= 0; tIndex--) {\n dp[sIndex, tIndex] = dp[sIndex + 1, tIndex];\n\n if (s[sIndex] == t[tIndex]) {\n dp[sIndex, tIndex] += dp[sIndex + 1, tIndex + 1];\n }\n }\n }\n\n return dp[0, 0];\n }\n}\n```\n\n\n```ruby []\n# @param {String} s\n# @param {String} t\n# @return {Integer}\ndef num_distinct(s, t)\n m = s.length\n n = t.length\n\n dp = Array.new(m + 1) { Array.new(n + 1, 0) }\n\n (0..m).each do |i|\n dp[i][n] = 1\n end\n\n (m - 1).downto(0) do |s_index|\n (n - 1).downto(0) do |t_index|\n dp[s_index][t_index] = dp[s_index + 1][t_index]\n\n if s[s_index] == t[t_index]\n dp[s_index][t_index] += dp[s_index + 1][t_index + 1]\n end\n end\n end\n\n dp[0][0]\nend\n```\n---\n# \uD83D\uDCCAAnalysis \n\n\n\n| Language | Runtime | Memory |\n|------------|-----------------|-----------------|\n| C++ | 33 | 18.7 |\n| Java | 17 | 46.8 |\n| Python | 417 | 72.8 \n JavaScript | 89 | 68.5 |\n| C# | 79 | 40.8 |\n| Ruby | 804 | 277.37 |\n\n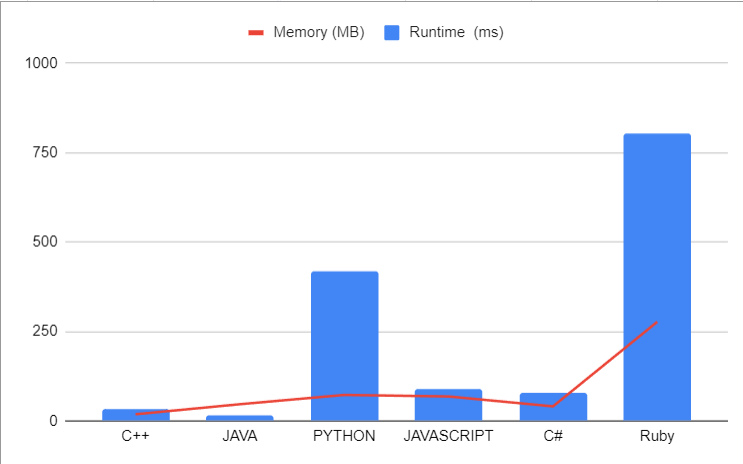\n\n\n---\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n\n\n\n | 4 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Python 1D DP solution in 7 lines | Space complexity: O(N) | 95%+ Space usage 90% + Speed | distinct-subsequences | 0 | 1 | # Approach\nDP\n\n# Complexity\n- Time complexity:\nO(M\xD7N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\n\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n m, n = len(s), len(t)\n dp = [1] + [0]*n\n for i in range(1 , m + 1):\n for j in range( min(i,n) , 0, - 1):\n if s[i - 1] == t[j - 1]:\n dp[j] += dp[j - 1]\n return dp[n]\n``` | 2 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Python || DP || Recursion->Space Optimization | distinct-subsequences | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(2^(n+m))\n#Space Complexity: O(n+m)\nclass Solution1:\n def numDistinct(self, s: str, t: str) -> int:\n def solve(i,j):\n if j<0:\n return 1\n if i<0:\n return 0\n if s[i]==t[j]:\n return solve(i-1,j-1) + solve(i-1,j)\n else:\n return solve(i-1,j)\n n,m=len(s),len(t)\n return solve(n-1,m-1)\n \n#Memoization (Top-Down)\n#Time Complexity: O(n*m)\n#Space Complexity: O(n+m) + O(n*m)\nclass Solution2:\n def numDistinct(self, s: str, t: str) -> int:\n def solve(i,j):\n if j<0:\n return 1\n if i<0:\n return 0\n if dp[i][j]!=-1:\n return dp[i][j]\n if s[i-1]==t[j-1]:\n dp[i][j]=solve(i-1,j-1) + solve(i-1,j)\n return dp[i][j]\n else:\n dp[i][j]=solve(i-1,j)\n return dp[i][j]\n n,m=len(s),len(t)\n dp=[[-1 for j in range(m)] for i in range(n)]\n return solve(n-1,m-1)\n \n#Tabulation (Bottom-Up)\n#Time Complexity: O(n*m)\n#Space Complexity: O(n*m)\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n n,m=len(s),len(t)\n dp=[[-1 for j in range(m+1)] for i in range(n+1)] #Shifting the indexes\n for i in range(n+1):\n dp[i][0]=1\n for j in range(1,m+1): # we are starting it from 1 because for j<1 we have to return 1\n dp[0][j]=0\n for i in range(1,n+1):\n for j in range(1,m+1):\n if s[i-1]==t[j-1]:\n dp[i][j]=dp[i-1][j-1] + dp[i-1][j]\n else:\n dp[i][j]=dp[i-1][j]\n return dp[n][m]\n\n#Space Optimization\n#Time Complexity: O(n*m)\n#Space Complexity: O(m)\nclass Solution4:\n def numDistinct(self, s: str, t: str) -> int:\n n,m=len(s),len(t)\n prev=[0]*(m+1) #Shifting the indexes\n curr=[0]*(m+1)\n prev[0]=curr[0]=1\n for i in range(1,n+1):\n for j in range(1,m+1):\n if s[i-1]==t[j-1]:\n curr[j]=prev[j-1] + prev[j]\n else:\n curr[j]=prev[j]\n prev=curr[:]\n return prev[m]\n \n#Space Optimization with 1 list\n#Time Complexity: O(n*m)\n#Space Complexity: O(m)\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n n,m=len(s),len(t)\n curr=[0]*(m+1)\n curr[0]=1\n for i in range(1,n+1):\n for j in range(m,0,-1): #Reverse direction\n if s[i-1]==t[j-1]:\n curr[j]=curr[j-1] + curr[j]\n else:\n curr[j]=curr[j] # can omit this statement\n return curr[m]\n```\n**An upvote will be encouraging** | 4 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Python solution, DFS + memorization, easy to understand | distinct-subsequences | 0 | 1 | \n# Code\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n\n @functools.lru_cache(None)\n def dfs(i, j):\n if j == len(t):\n return 1\n\n if i == len(s):\n return 0\n\n if s[i] != t[j]:\n return dfs(i+1, j)\n else:\n return dfs(i+1, j) + dfs(i+1, j+1)\n\n\n return dfs(0, 0)\n``` | 1 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
with step by step explanation | distinct-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSolution: Dynamic Programming\n\nWe can solve this problem using dynamic programming. Let dp[i][j] be the number of distinct subsequences of s[0:i] that equals t[0:j].\n\nIf s[i] != t[j], then the number of distinct subsequences doesn\'t increase. Thus, dp[i][j] = dp[i-1][j].\nIf s[i] == t[j], then we have two options:\nWe don\'t include s[i] in the subsequence, and the number of distinct subsequences is dp[i-1][j].\nWe include s[i] in the subsequence, and the number of distinct subsequences is dp[i-1][j-1]. Note that we can\'t include s[i] if we haven\'t included t[j-1] yet.\nTherefore, the final answer is the number of distinct subsequences of s that equals t, which is dp[m][n], where m = len(s) and n = len(t).\n\nTime Complexity: O(m * n), where m and n are the lengths of s and t, respectively.\n\nSpace Complexity: O(m * n).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n m, n = len(s), len(t)\n dp = [[0] * (n+1) for _ in range(m+1)]\n for i in range(m+1):\n dp[i][0] = 1\n for i in range(1, m+1):\n for j in range(1, n+1):\n dp[i][j] = dp[i-1][j]\n if s[i-1] == t[j-1]:\n dp[i][j] += dp[i-1][j-1]\n return dp[m][n]\n\n\n``` | 5 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Simple Python Solution(Striver) | distinct-subsequences | 0 | 1 | \n# Code\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n dp=[[-1]*len(t) for i in range(len(s))]\n def solve(ind1,ind2):\n if ind2<0:\n return 1\n if ind1<0:\n return 0\n \n if dp[ind1][ind2]!=-1:\n return dp[ind1][ind2]\n\n if s[ind1]==t[ind2]:\n dp[ind1][ind2] = solve(ind1-1,ind2-1)+solve(ind1-1,ind2)\n return dp[ind1][ind2]\n else:\n dp[ind1][ind2] = solve(ind1-1,ind2)\n return dp[ind1][ind2]\n return solve(len(s)-1,len(t)-1)\n``` | 1 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
O(n)time/BEATS 99.97% MEMORY/SPEED 0ms MAY 2022 | distinct-subsequences | 1 | 1 | ```\n```\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* ***Java***\n```\npublic int numDistinct(String S, String T) {\n // array creation\n int[][] mem = new int[T.length()+1][S.length()+1];\n\n // filling the first row: with 1s\n for(int j=0; j<=S.length(); j++) {\n mem[0][j] = 1;\n }\n \n // the first column is 0 by default in every other rows but the first, which we need.\n \n for(int i=0; i<T.length(); i++) {\n for(int j=0; j<S.length(); j++) {\n if(T.charAt(i) == S.charAt(j)) {\n mem[i+1][j+1] = mem[i][j] + mem[i+1][j];\n } else {\n mem[i+1][j+1] = mem[i+1][j];\n }\n }\n }\n \n return mem[T.length()][S.length()];\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 7.0MB*** (beats 100.00% / 100.00%).\n* ***C++***\n```\nclass Solution {\npublic:\n int numDistinct(string s, string t) {\n\t//we use unsigned int because there is a case with a quite large data\n vector<vector<unsigned int>> dp(t.size() + 1, vector<unsigned int>(s.size() + 1));\n \n\t\t//set as default value of the first line as 1\n for (int j = 0; j <= s.size(); j++)dp[0][j] = 1;\n\n//logic of the loop is above\n for (int i = 1; i <= t.size(); i++) {\n for (int j = 1; j <= s.size(); j++) {\n\n\t\t\t\t\tif (t[i - 1] == s[j - 1]) {\n dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];\n }\n else {\n dp[i][j] = dp[i][j - 1];\n }\n }\n }\n return dp[dp.size() - 1][dp[0].size() - 1];\n }\n};\n```\n\n```\n```\n\n```\n```\n\n\nThe best result for the code below is ***26ms / 12.2MB*** (beats 95.42% / 82.32%).\n* ***Python***\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n ## RC ##\n\t\t## APPROACH : DP ##\n\t\t## LOGIC ##\n\t\t#\t1. Point to be noted, empty seq is also subsequence of any sequence i.e "", "" should return 1. so we fill the first row accordingly\n\t\t#\t2. if chars match, we get the maximum of [diagonal + upper, upper + 1] (Try below example)\n\t\t#\t3. if no match, we pull the upper value\n\t\t\n ## EXAMPLE : "axacccax" "aca"\t##\n\t\t## STACK TRACE ##\n # [ "" a c a\n # "" [1, 0, 0, 0], \n # a [1, 1, 0, 0], \n # x [1, 1, 0, 0], \n # a [1, 2, 0, 0], \n # c [1, 2, 2, 0], \n # c [1, 2, 4, 0], \n # c [1, 2, 6, 0], \n # a [1, 3, 6, 6], \n # ]\n \n\t\t## TIME COMPLEXITY : O(MxN) ##\n\t\t## SPACE COMPLEXITY : O(MxN) ##\n\n dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]\n \n for k in range(len(dp)):\n dp[k][0] = 1\n \n for i in range(1, len(dp)):\n for j in range(1, len(dp[0])):\n if(s[i-1] == t[j-1] and dp[i-1][j-1]):\n dp[i][j] = max(dp[i-1][j-1] + dp[i-1][j], dp[i-1][j]+1)\n else:\n dp[i][j] = dp[i-1][j]\n # print(dp)\n return dp[-1][-1]\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***51ms / 34.2MB*** (beats 100.00% / 84.12%).\n* ***JavaScript***\n```\nvar numDistinct = function(s, t) {\n \n //Create DP array containig possible results for each char in t\n let dp = Array(t.length+1).fill(0);\n \n //Base case - empty string 1 result\n dp[0] = 1;\n \n //Iterate s string\n for (let i = 0; i < s.length; i++) {\n //Iterate t string (from end to start so we don\'t process data that we\'ve just entered)\n for (let j = dp.length-1; j >= 0; j--) {\n //Char match \n if (s[i] === t[j]) {\n //Add this char count to next position\n dp[j+1] += dp[j]\n }\n }\n }\n \n return dp[t.length];\n};\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***68ms / 44.2MB*** (beats 100.00% / 45.25%).\n* ***Kotlin***\n```\nclass Solution {\n fun numDistinct(s: String, t: String): Int {\n val lenS = s.length\n val lenT = t.length\n \n val dp = Array(lenS + 1){ IntArray(lenT + 1) {idxT -> if(idxT == 0) 1 else 0 }}\n for(idxS in 1..lenS){\n for(idxT in 1..lenT){\n dp[idxS][idxT] = if(s[idxS - 1] == t[idxT - 1]){\n dp[idxS - 1][idxT] + dp[idxS - 1][idxT - 1]\n }else{\n dp[idxS - 1][idxT]\n }\n }\n }\n \n return dp[lenS][lenT]\n }\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***12ms / 32.2MB*** (beats 95% / 84%).\n* ***Swift***\n```\nclass Solution {\n func numDistinct(_ s: String, _ t: String) -> Int {\n let s = Array(s), t = Array(t)\n var memo = Array(repeating: Array(repeating: -1, count: t.count), count: s.count)\n \n func numDistinct(_ i: Int, _ j: Int) -> Int {\n if j < 0 { return 1 }\n if i < 0 { return 0 }\n \n if memo[i][j] != -1 { return memo[i][j] }\n \n if s[i] != t[j] {\n memo[i][j] = numDistinct(i - 1, j)\n } else {\n memo[i][j] = numDistinct(i - 1, j) + numDistinct(i - 1, j - 1)\n }\n \n return memo[i][j]\n }\n \n return numDistinct(s.count - 1, t.count - 1)\n }\n\n}\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC*** | 4 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Python - Bottom up DP - Explained | distinct-subsequences | 0 | 1 | **Brute force way to do it:**\n\nGenerate all subsequences of s and check if each one matches t.\nThis will be TLE for even smaller inputs as time complexity for finding all subsequences of a string of length n will be ```2^n```\n\nSo, dynamic programming is the only option to solve it efficiently\n\n\n**DP - Explanation:**\n\nWe will form the dp formula by considering a scenario\n\nLet\'s assume we have traversed some steps through string s and currently we are at ```i``` th position\nAnd we have traversed some steps through string t and currently we are at ```j``` th position\n\nIf the character at ```i```th position in ```s``` and charater at ```j```th position in ```t```, are matching,\nthen, we can extend all subsequences that were formed by considering ```i-1``` characters in ```s``` and ```j-1``` characters in ```t```, by adding the current character to all those subsequences\n\nAnother possibility is, let\'s say we skip the current character and choose not to add it to previosly formed subsequences.\nThen, in this case, the number of subsequences will stay the same as number of subsequences formed using ```i-1``` chatracters of ```s```.\n\nNote that, if the character at ```i```th position in ```s``` and charater at ```j```th position in ```t```, are not matching,\nwe are left with only option 2 as we cannot choose current character to extend all previously formed subsequences\n\n**Base cases:**\nIf the string ```t``` is empty, there is only one way to form an empty string from string ```s``` (of any length) - by skipping all characters\nSo, ```dp[i][0] = 1 for i in range(0, len(s))```\n\nWhen string ```s``` is empty and string ```t``` is not empty, then we can never form ```t``` from ```s```.\nSo, ```dp[0][j] = 0 for j in range(1, len(t))```\n\n\nInitial dp table for ```s (len = 6) and t (len = 6)```\n\n```\n 0 1 2 3 4 5 6 \n0 1 0 0 0 0 0 0\n1 1\n2 1\n3 1\n4 1\n5 1\n6 1\n```\n\n**Code:**\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n m = len(s)\n n = len(t)\n dp = [[0] * (n+1) for _ in range(m+1)]\n \n for i in range(m+1):\n dp[i][0] = 1\n \n """redundant, as we have initialised dp table with full of zeros"""\n# for i in range(1, n+1): \n# dp[0][i] = 0\n \n for i in range(1, m+1):\n for j in range(1, n+1):\n dp[i][j] += dp[i-1][j] \t\t\t#if current character is skipped\n if s[i-1] == t[j-1]:\n dp[i][j] += dp[i-1][j-1]\t#if current character is used\n \n return dp[-1][-1]\n``` \n\n**Time and space complexity: O(m*n)**\n | 17 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Linear order Python Easy Solution | distinct-subsequences | 0 | 1 | \n** DP (Memoization)**\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n def disSub(s,t,ind_s,ind_t,dp):\n if ind_t<0:\n return 1\n if ind_s<0:\n return 0\n\n\n if s[ind_s]==t[ind_t]:\n if (dp[ind_t])[ind_s]!=-1:\n return (dp[ind_t])[ind_s]\n else:\n (dp[ind_t])[ind_s]=(disSub(s,t,ind_s-1,ind_t-1,dp) + disSub(s,t,ind_s-1,ind_t,dp))\n return (dp[ind_t])[ind_s]\n\n (dp[ind_t])[ind_s]=disSub(s,t,ind_s-1,ind_t,dp)\n return (dp[ind_t])[ind_s]\n\n\n\n\n\n\n ls=len(s)\n lt=len(t)\n dp=[[-1]* ls for i in range(lt)]\n return disSub(s,t,ls-1,lt-1,dp)\n```\n\n\u2022\tTime Complexity: O(N*M)\nReason: There are NM states therefore at max \u2018NM\u2019 new problems will be solved.\n\u2022\tSpace Complexity: O(N*M) + O(N+M)\nReason: We are using an auxiliary recursion stack space(O(N+M)) (see the recursive tree, in the worst case, we will go till N+M calls at a time) and a 2D array ( O(N*M)).\n\n\n\n**Dp (Tabulation)**\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n ls=len(s)\n lt=len(t)\n dp=[[0]*(ls+1) for i in range(lt+1)]\n for i in range(ls):\n (dp[0])[i]=1\n\n for ind_t in range(1,lt+1):\n for ind_s in range (1,ls+1):\n if s[ind_s-1]==t[ind_t-1]:\n (dp[ind_t])[ind_s]= (dp[ind_t -1])[ind_s -1] +(dp[ind_t])[ind_s -1] \n else:\n (dp[ind_t])[ind_s]= (dp[ind_t])[ind_s -1]\n \n\n\n\n return (dp[ind_t])[ind_s]\n\n```\n\u2022\tTime Complexity: O(N*M)\nReason: There are two nested loops\n\n\u2022\tSpace Complexity: O(N*M)\nReason: We are using an external array of size \u2018N*M)\u2019. Stack Space is eliminated.\n\n**Space Optimization**\n```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n ls=len(s)\n lt=len(t)\n prev=[1]*(ls+1)\n\n\n for ind_t in range(1,lt+1):\n temp=[0]*(ls+1)\n for ind_s in range (1,ls+1):\n \n \n if s[ind_s-1]==t[ind_t-1]:\n temp[ind_s]= prev[ind_s -1]+temp[ind_s -1] \n \n else:\n temp[ind_s]= temp[ind_s -1]\n \n\n prev=temp \n\n\n\n return prev[ind_s]\n \n```\n\u2022\tTime Complexity: O(N*M)\nReason: There are two nested loops\n\n\u2022\tSpace Complexity: O(N)\nReason: We are using a One Dimension array of size n. Stack Space is eliminated.\n\n\n | 3 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Python - DP - O(m*n) Time | distinct-subsequences | 0 | 1 | ```\nclass Solution:\n def numDistinct(self, s: str, t: str) -> int:\n dp = [[0] * (len(s)+1) for _ in range(len(t)+1)]\n \n # 0th row => len(t) == 0 and len(s) can be anything. So empty string t can be Subsequence of s\n for j in range(len(s)+1):\n dp[0][j] = 1\n \n for i in range(1, len(t)+1):\n for j in range(1, len(s)+1):\n dp[i][j] += dp[i][j-1] # skip the current character s[j-1]\n if t[i-1] == s[j-1]:\n dp[i][j] += dp[i-1][j-1] # current character s[j-1] is used\n \n return dp[-1][-1]\n``` | 1 | Given two strings `s` and `t`, return _the number of distinct_ **_subsequences_** _of_ `s` _which equals_ `t`.
The test cases are generated so that the answer fits on a 32-bit signed integer.
**Example 1:**
**Input:** s = "rabbbit ", t = "rabbit "
**Output:** 3
**Explanation:**
As shown below, there are 3 ways you can generate "rabbit " from s.
`**rabb**b**it**`
`**ra**b**bbit**`
`**rab**b**bit**`
**Example 2:**
**Input:** s = "babgbag ", t = "bag "
**Output:** 5
**Explanation:**
As shown below, there are 5 ways you can generate "bag " from s.
`**ba**b**g**bag`
`**ba**bgba**g**`
`**b**abgb**ag**`
`ba**b**gb**ag**`
`babg**bag**`
**Constraints:**
* `1 <= s.length, t.length <= 1000`
* `s` and `t` consist of English letters. | null |
Simple solution. without QUEUE or STACK!!!. Beasts 90 %. | populating-next-right-pointers-in-each-node | 0 | 1 | \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Choose left most node.\n2. Traverse through the nodes.\n3. Connect to the right node or null by tracking the current node.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if not root:\n return None\n \n left_most = root\n\n while left_most.left:\n current = left_most\n\n while current:\n current.left.next = current.right\n\n if current.next:\n current.right.next = current.next.left\n \n current = current.next\n \n left_most = left_most.left\n \n return root\n```\n```javascript []\nvar connect = function(root) {\n if (root === null) return null;\n\n let leftMost = root;\n\n while (leftMost.left !== null) {\n let current = leftMost;\n\n while (current !== null) {\n current.left.next = current.right;\n\n if (current.next !== null) {\n current.right.next = current.next.left;\n };\n\n current = current.next;\n };\n\n leftMost = leftMost.left;\n };\n\n return root;\n};\n```\n | 0 | You are given a **perfect binary tree** where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7\]
**Output:** \[1,#,2,3,#,4,5,6,7,#\]
**Explanation:** Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 212 - 1]`.
* `-1000 <= Node.val <= 1000`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
Simple solution with Breadth-First Search in Python3 / TypeScript | populating-next-right-pointers-in-each-node | 0 | 1 | # Intuition\nLet\'s briefly explain what the problem is:\n- there a **Perfect Binary Tree** `root`\n- our goal is to link all nodes at each level, as it was a **Linked List**.\n\nThe algorithm is simple - use **Breadth-First Search** to traverse at each level and establish **Linked List** link with `next` pointer to the next node.\n\n# Approach\n1. declare `q` as queue or **deque** for O(1) operations\n2. iterate over `root` and create links to the next node\n3. return **modified** `root`\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(W)**, as maximum tree width.\n\n# Code in Python3\n```\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n q = deque([root])\n\n while q:\n n = len(q)\n\n for i in range(n):\n node = q.popleft()\n\n if i < n - 1: node.next = q[0]\n if node and node.left: q.append(node.left)\n if node and node.right: q.append(node.right)\n\n return root\n```\n# Code in TypeScript\n```\nfunction connect(root: Node | null): Node | null {\n const q = [root]\n\n while (q.length) {\n const n = q.length;\n\n for (let i = 0; i < n; i++) {\n const node = q.shift()\n\n if (i < n - 1) node.next = q[0]\n if (node?.left) q.push(node.left)\n if (node?.right) q.push(node.right)\n }\n }\n\n return root\n};\n``` | 2 | You are given a **perfect binary tree** where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7\]
**Output:** \[1,#,2,3,#,4,5,6,7,#\]
**Explanation:** Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 212 - 1]`.
* `-1000 <= Node.val <= 1000`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
python3 solution using queue , bfs ,simple to understand O(N) | populating-next-right-pointers-in-each-node | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nwe have an initial condition here to check if initially only if left or only right node is present for root,according managing starting conditions\nthen we have q initialized by `root.left,root.right,None` where None here signifies end of a level \nafter each enconter of None we can go to next level by appending None at last\nfor each popped node from beginning the next node will be the first node of the queue,pointing to it does the job,None at end of each level takes care of finally pointing rightmost node to None\n\nwhen the queue becomes empty returning root does the job\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**______O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**______O(N)**\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val: int = 0, left: \'Node\' = None, right: \'Node\' = None, next: \'Node\' = None):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\n\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if not root:return \n if not root.left:\n root.next=None\n return root\n root.next=None\n q=[root.left,root.right,None]\n while q:\n node=q.pop(0)\n if node is None:\n if not q:\n return root\n q.append(None)\n continue\n node.next=q[0]\n if node.left:q.append(node.left)\n if node.right:q.append(node.right)\n\n``` | 2 | You are given a **perfect binary tree** where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7\]
**Output:** \[1,#,2,3,#,4,5,6,7,#\]
**Explanation:** Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 212 - 1]`.
* `-1000 <= Node.val <= 1000`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
🍀Easy BFS 🔥 | | Java 🔥| | Python 🔥| | C++ 🔥 | populating-next-right-pointers-in-each-node | 1 | 1 | # * Extra space but clean code\n---\n```java []\nclass Solution {\n public Node connect(Node root) {\n if(root == null)\n return root;\n Queue<Node> queue = new LinkedList<>();\n queue.add(root);\n while(queue.size() > 0)\n {\n Deque<Node> dq = new ArrayDeque<>();\n int length = queue.size();\n for(int i = 0;i<length;i++)\n {\n Node curr = queue.poll();\n dq.addLast(curr);\n if(curr.left!=null)\n queue.add(curr.left);\n if(curr.right!=null)\n queue.add(curr.right);\n }\n while(dq.size() > 1)\n {\n Node popped = dq.removeFirst();\n popped.next = dq.getFirst();\n }\n Node popped = dq.removeFirst();\n popped.next = null;\n }\n return root;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == nullptr)\n return root;\n queue<Node*> queue;\n queue.push(root);\n while(queue.size() > 0)\n {\n deque<Node*> dq;\n int length = queue.size();\n for(int i = 0;i<length;i++)\n {\n Node* curr = queue.front();\n queue.pop();\n dq.push_back(curr);\n if(curr->left!=nullptr)\n queue.push(curr->left);\n if(curr->right!=nullptr)\n queue.push(curr->right);\n }\n while(dq.size() > 1)\n {\n Node* popped = dq.front();\n dq.pop_front();\n popped->next = dq.front();\n }\n Node* popped = dq.front();\n dq.pop_front();\n popped->next = nullptr;\n }\n return root;\n }\n};\n```\n```python []\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root:\n return root\n queue = []\n queue.append(root)\n while queue:\n dq = collections.deque()\n length = len(queue)\n for i in range(length):\n curr = queue.pop(0)\n dq.append(curr)\n if curr.left:\n queue.append(curr.left)\n if curr.right:\n queue.append(curr.right)\n while len(dq) > 1:\n popped = dq.popleft()\n popped.next = dq[0]\n popped = dq.popleft()\n popped.next = None\n return root\n```\n---\n>### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F\n--- | 7 | You are given a **perfect binary tree** where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7\]
**Output:** \[1,#,2,3,#,4,5,6,7,#\]
**Explanation:** Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 212 - 1]`.
* `-1000 <= Node.val <= 1000`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
FASTEST AND EASIEST || BEATS 99% SUBMISSIONS || BFS SEARCH | populating-next-right-pointers-in-each-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBFS SOLUTION\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nINITIALIZE CURRENT AND NEXT POINTERS TO ROOT NODE AND ROOT\'S LEFT NODE, THEN RUN BFS THROUGH EACH LEVEL\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val: int = 0, left: \'Node\' = None, right: \'Node\' = None, next: \'Node\' = None):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\n\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n cur,nxt=root,root.left if root else None\n while cur and nxt:\n cur.left.next=cur.right\n if cur.next:\n cur.right.next=cur.next.left\n cur=cur.next\n if not cur:\n cur=nxt\n nxt=cur.left\n return root\n``` | 1 | You are given a **perfect binary tree** where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7\]
**Output:** \[1,#,2,3,#,4,5,6,7,#\]
**Explanation:** Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 212 - 1]`.
* `-1000 <= Node.val <= 1000`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
with step by step explanation | populating-next-right-pointers-in-each-node-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can solve this problem using BFS. We can traverse the tree level by level using the BFS approach and for each node, we can keep track of its next pointer. We can use a queue to keep track of the nodes of the current level. We can then process the nodes of the current level by dequeuing them from the queue one by one, and assigning the next pointer of each node to the front element of the queue. Once we have processed all the nodes of the current level, we can move to the next level by enqueuing the children of the nodes of the current level.\n\n# Complexity\n- Time complexity:\nO(N), where N is the number of nodes in the tree.\n\n- Space complexity:\nO(N), where N is the maximum number of nodes at any level in the tree. In the worst case, the maximum number of nodes at any level in the tree is N/2. This happens when the binary tree is a complete binary tree. In this case, the last level of the tree has N/2 nodes, and the size of the queue can be at most N/2. Therefore, the space complexity of the algorithm is O(N).\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n # Edge case - If the root is None, then return None\n if root is None:\n return None\n \n # Create a queue and enqueue the root node\n q = deque([root])\n \n # Traverse the tree level by level\n while q:\n \n # Get the number of nodes of the current level\n level_size = len(q)\n \n # Process the nodes of the current level\n for i in range(level_size):\n \n # Dequeue a node from the front of the queue\n node = q.popleft()\n \n # Assign the next pointer of the node\n if i < level_size - 1:\n node.next = q[0]\n \n # Enqueue the children of the node (if any)\n if node.left is not None:\n q.append(node.left)\n if node.right is not None:\n q.append(node.right)\n \n # Return the root node\n return root\n\n``` | 2 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
Python Easy: BFS and O(1) Space with Explanation | populating-next-right-pointers-in-each-node-ii | 0 | 1 | 1. ##### **Level Order Traversal Approach**\nAs the problem states that the output should return a tree with all the nodes in the same level connected, the problem can be solved using **Level Order Traversal**.\nEach iteration of Queue traversal, the code would:\n1. Find the length of the current level of the tree. \n2. Iterate through all the nodes in the same level using the level length. \n3. Find the siblings in the next level and connect them using next pointers. Enqueue all the nodes in the next level.\n\n\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root:\n return None\n q = deque()\n q.append(root)\n dummy=Node(-999) # to initialize with a not null prev\n while q:\n length=len(q) # find level length\n \n prev=dummy\n for _ in range(length): # iterate through all nodes in the same level\n popped=q.popleft()\n if popped.left:\n q.append(popped.left)\n prev.next=popped.left\n prev=prev.next\n if popped.right:\n q.append(popped.right)\n prev.next=popped.right\n prev=prev.next \n \n return root\n```\n\n\n\n**Time = O(N)** - iterate through all the nodes\n**Space=O(L)** - As the code is using level order traversal, the maximum size of Queue is maximum number of nodes at any level.\n\n\n\n---\n2. ##### **O(1) Space Approach**\n\nIn addition to this, there is a **follow-up question** asking to solve this problem using constant extra space. There is an additional hint to maybe use recursion for this and the extra call stack is assumed to be `O(1)` space\n\nThe code will track the `head` at each level and use that not null `head` to define the next iteration. Following is my take on `O(1)` space solution:\n\n\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root:\n return None\n \n curr=root\n dummy=Node(-999) \n head=root \n\n\t\twhile head:\n curr=head # initialize current level\'s head\n prev=dummy # init prev for next level linked list traversal\n\t\t\t# iterate through the linked-list of the current level and connect all the siblings in the next level\n while curr: \n if curr.left:\n prev.next=curr.left\n prev=prev.next\n if curr.right:\n prev.next=curr.right\n prev=prev.next \n curr=curr.next\n head=dummy.next # update head to the linked list of next level\n dummy.next=None # reset dummy node\n return root\n \n```\n\n**Time = O(N)** - iterate through all the nodes\n**Space = O(1)** - No additional space\n\n---\n\n***Please upvote if you find it useful*** | 57 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
Python3 soloution using only queue memory efficient ,simple to understand | populating-next-right-pointers-in-each-node-ii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nin the starting we need to take care of few edge cases where\n1) if only root is the node of tree returning it\n2) if left node is None then checking for existance of right node and initializing q to `q=[root.right,None]`\n3) both left and right node exist `q=[root.left,root.right,None]`\n4) only left node exists `q=[root.left,None]` this is different as on the first level only left node and None should exist including right node which is None will lead to infinite loops in the next phase\n\nwe are initilizing q to conatain appropriate elements in first level\nthen it is simple popping first element from queue and pointing its next pointer to first element of the q which has other remaining elements\nhere if popped element is None ,it indicates end of a level and appending it to end continues the logic\n\nwhen q is empty returning root does it\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**_______O(N) NUMBER OF NODES**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**_______O(N) skewed tree case**\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val: int = 0, left: \'Node\' = None, right: \'Node\' = None, next: \'Node\' = None):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root:return\n root.next=None\n if not root.left:\n if not root.right:return root\n q=[root.right,None]\n else:\n if root.right:q=[root.left,root.right,None]\n else:q=[root.left,None]\n while q:\n node=q.pop(0)\n if node is None:\n if not q:return root\n q.append(None)\n continue\n node.next=q[0]\n if node.left:q.append(node.left)\n if node.right:q.append(node.right)\n \n``` | 2 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
Python O(1) aux space DFS sol. [with Diagram] | populating-next-right-pointers-in-each-node-ii | 0 | 1 | Python O(1) aux space DFS sol.\n\n---\n\n**Hint**:\n\nThink of DFS traversal.\n\n---\n\n**Algorithm**:\n\nFor each current node,\n\nStep_#1:\nUse **scanner** to **locate the left-most neighbor, on same level**, in right hand side.\n\nStep_#2-1:\nWhen right child exists, update right child\'next as scanner\n\nStep_#2-2:\nWhen left child exists, update left child\'next as either right child (if right child exists ),or scanner.\n\n---\n\n**Abstract Model**:\n\n**Before** connection of next pointer:\n\n\n\n---\n\n**After** connection of next pointer:\nBoth left child and right child exist\n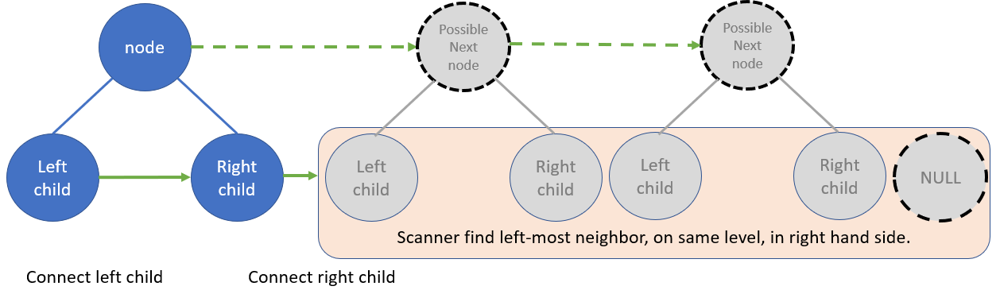\n\n---\n\nOnly right child exists\n\n\n\n---\n\nOnly left child exists\n\n\n\n---\n\n**Implementation**:\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n \n def helper( node: \'Node\'):\n \n if not node:\n return None\n \n scanner = node.next\n\n # Scanner finds left-most neighbor, on same level, in right hand side\n while scanner:\n\n if scanner.left:\n scanner = scanner.left\n break\n\n if scanner.right:\n scanner = scanner.right\n break\n\n scanner = scanner.next\n\n\n # connect right child if right child exists\n if node.right:\n node.right.next = scanner \n\n # connect left child if left child exists\n if node.left:\n node.left.next = node.right if node.right else scanner\n\n\n # DFS down to next level\n helper( node.right ) \n helper( node.left ) \n \n return node\n # -------------------------------\n \n return helper( root ) \n```\n\n---\n\nRelated leetcode challenge:\n\n( a special case of current challenge )\n[Leetcode #116 Populating Next Right Pointers in Each Node](https://leetcode.com/problems/populating-next-right-pointers-in-each-node/) | 34 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
Simply Simple Python Solutions - Level order traversal and O(1) space - both approach | populating-next-right-pointers-in-each-node-ii | 0 | 1 | ### BFS: Level Order Traversal - simple approach:\n```\ndef connect(self, root: \'Node\') -> \'Node\':\n\tif not root:\n return root\n q = []\n \n q.append(root)\n \n tail = root\n while len(q) > 0:\n node = q.pop(0)\n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n \n if node == tail:\n node.next = None\n tail = q[-1] if len(q) > 0 else None\n else:\n node.next = q[0]\n \n return root\n```\n### O(1) Space approach:\n```\ndef connect(self, root: \'Node\') -> \'Node\':\n dummy = Node(-1, None, None, None)\n tmp = dummy\n res = root\n while root:\n while root:\n if root.left:\n tmp.next = root.left\n tmp = tmp.next\n if root.right:\n tmp.next = root.right\n tmp = tmp.next\n root = root.next\n root = dummy.next\n tmp = dummy\n dummy.next = None\n \n return res\n``` | 31 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
Super Simple Easy Python Solution 🙂🙂 | populating-next-right-pointers-in-each-node-ii | 0 | 1 | time complex O(n)\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val: int = 0, left: \'Node\' = None, right: \'Node\' = None, next: \'Node\' = None):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n stack = [(root, 0)]\n answer = defaultdict(list)\n while stack:\n s, level = stack.pop()\n if not s:\n return root\n answer[level].append(s)\n if s.right:\n stack.append((s.right, level+1))\n if s.left:\n stack.append((s.left,level+1))\n for v in answer.values():\n for i in range(len(v)-1):\n v[i].next = v[i+1]\n return root\n \n \n \n``` | 1 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
level order traversal | populating-next-right-pointers-in-each-node-ii | 1 | 1 | # Intuition\nuse level order traversal and after popping the node check if the node at 0th index is not the last node of any level, then assign popped_pointer.next = queue[0]..... and then push the left child into the queue if left child is not null and same for right child...\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val: int = 0, left: \'Node\' = None, right: \'Node\' = None, next: \'Node\' = None):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n\n if not root:\n return root\n \n q = deque()\n q.append(root)\n psudo = TreeNode(-101)\n q.append(psudo)\n\n while q:\n ptr = q.popleft()\n if ptr.val == -101:\n if q:\n q.append(psudo)\n \n else:\n if q[0].val != -101:\n ptr.next = q[0]\n\n if ptr.left:\n q.append(ptr.left)\n if ptr.right:\n q.append(ptr.right)\n\n return root\n``` | 1 | Given a binary tree
struct Node {
int val;
Node \*left;
Node \*right;
Node \*next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to `NULL`.
Initially, all next pointers are set to `NULL`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** \[1,#,2,3,#,4,5,7,#\]
**Explanation:** Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 6000]`.
* `-100 <= Node.val <= 100`
**Follow-up:**
* You may only use constant extra space.
* The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem. | null |
✅☑️Three Approaches🔥||Beginner Friendly✅☑️||Full Explanation🔥||C++||Java||Python✅☑️ | pascals-triangle | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**The problem** of generating Pascal\'s triangle can be approached in **various ways.**\n**Here are some approaches and their intuition to solve the problem:**\n\n# Approach 1: Using Recursion\n<!-- Describe your approach to solving the problem. -->\n**Intuition:** In Pascal\'s triangle, **each element is the sum of the two elements directly above it**. We can use a **recursive approach** to generate the triangle. **The base case is when numRows is 1**, in which case we return [[1]]. **Otherwise, we recursively generate the triangle for numRows - 1** and then calculate the current row by summing the adjacent elements from the previous row.\n\n# Approach 2: Using Combinatorial Formula\n\n**Intuition:** Pascal\'s triangle **can also be generated using combinatorial formula C(n, k) = C(n-1, k-1) + C(n-1, k)**, where C(n, k) **represents the binomial coefficient**. **We can calculate each element of the triangle using this formula.** This approach avoids the need for storing the entire triangle in memory, **making it memory-efficient.**\n\n# Approach 3: Using Dynamic Programming with 1D Array\n\n**Intuition:** **We can use a dynamic programming approach with a 1D array to generate Pascal\'s triangle row by row**. Instead of maintaining a 2D array, we can use a single array to store the current row and update it as we iterate through the rows. This approach reduces space complexity.\n\n# Here\'s a brief outline of each approach:\n1. **Recursion Approach:**\n\n - Base case: If numRows is 1, return [[1]].\n - Recursively generate the triangle for numRows - 1.\n - Calculate the current row by summing adjacent elements from the previous row.\n\n2. **Combinatorial Formula Approach:**\n\n - Use the binomial coefficient formula C(n, k) to calculate each element.\n - Build the triangle row by row using the formula.\n\n3. **Dynamic Programming with 1D Array:**\n - Initialize a 1D array to store the current row.\n - Iterate through numRows and update the array for each row.\n\n\n# Complexity\n**In terms of time complexity**, all three methods have the same overall time complexity of **O(numRows^2)** because we need to generate all the elements of Pascal\'s triangle. **However, in terms of space complexity,** Method 3 is the most efficient as it uses only O(numRows) space, while the other two methods use O(numRows^2) space due to storing the entire triangle or previous rows in recursion.\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n\n# Method 1: Using Recursion\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n if (numRows == 0) return {};\n if (numRows == 1) return {{1}};\n \n vector<vector<int>> prevRows = generate(numRows - 1);\n vector<int> newRow(numRows, 1);\n \n for (int i = 1; i < numRows - 1; i++) {\n newRow[i] = prevRows.back()[i - 1] + prevRows.back()[i];\n }\n \n prevRows.push_back(newRow);\n return prevRows;\n }\n};\n\n```\n```Java []\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n if (numRows == 0) return new ArrayList<>();\n if (numRows == 1) {\n List<List<Integer>> result = new ArrayList<>();\n result.add(Arrays.asList(1));\n return result;\n }\n \n List<List<Integer>> prevRows = generate(numRows - 1);\n List<Integer> newRow = new ArrayList<>();\n \n for (int i = 0; i < numRows; i++) {\n newRow.add(1);\n }\n \n for (int i = 1; i < numRows - 1; i++) {\n newRow.set(i, prevRows.get(numRows - 2).get(i - 1) + prevRows.get(numRows - 2).get(i));\n }\n \n prevRows.add(newRow);\n return prevRows;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 0:\n return []\n if numRows == 1:\n return [[1]]\n \n prevRows = self.generate(numRows - 1)\n newRow = [1] * numRows\n \n for i in range(1, numRows - 1):\n newRow[i] = prevRows[-1][i - 1] + prevRows[-1][i]\n \n prevRows.append(newRow)\n return prevRows\n\n```\n```JavaScript []\nvar generate = function(numRows) {\n if (numRows === 0) {\n return [];\n }\n if (numRows === 1) {\n return [[1]];\n }\n \n let prevRows = generate(numRows - 1);\n let newRow = new Array(numRows).fill(1);\n \n for (let i = 1; i < numRows - 1; i++) {\n newRow[i] = prevRows[numRows - 2][i - 1] + prevRows[numRows - 2][i];\n }\n \n prevRows.push(newRow);\n return prevRows;\n};\n\n```\n\n# Method 2: Using Combinatorial Formula\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> result;\n for (int i = 0; i < numRows; i++) {\n vector<int> row(i + 1, 1);\n for (int j = 1; j < i; j++) {\n row[j] = result[i - 1][j - 1] + result[i - 1][j];\n }\n result.push_back(row);\n }\n return result;\n }\n};\n\n```\n```java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> result = new ArrayList<>();\n if (numRows == 0) {\n return result;\n }\n\n List<Integer> firstRow = new ArrayList<>();\n firstRow.add(1);\n result.add(firstRow);\n\n for (int i = 1; i < numRows; i++) {\n List<Integer> prevRow = result.get(i - 1);\n List<Integer> currentRow = new ArrayList<>();\n currentRow.add(1);\n\n for (int j = 1; j < i; j++) {\n currentRow.add(prevRow.get(j - 1) + prevRow.get(j));\n }\n\n currentRow.add(1);\n result.add(currentRow);\n }\n\n return result;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n result = []\n if numRows == 0:\n return result\n\n first_row = [1]\n result.append(first_row)\n\n for i in range(1, numRows):\n prev_row = result[i - 1]\n current_row = [1]\n\n for j in range(1, i):\n current_row.append(prev_row[j - 1] + prev_row[j])\n\n current_row.append(1)\n result.append(current_row)\n\n return result\n\n```\n```Javascript []\nvar generate = function(numRows) {\n let result = [];\n if (numRows === 0) {\n return result;\n }\n\n let firstRow = [1];\n result.push(firstRow);\n\n for (let i = 1; i < numRows; i++) {\n let prevRow = result[i - 1];\n let currentRow = [1];\n\n for (let j = 1; j < i; j++) {\n currentRow.push(prevRow[j - 1] + prevRow[j]);\n }\n\n currentRow.push(1);\n result.push(currentRow);\n }\n\n return result;\n};\n\n```\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n# Method 3: Using Dynamic Programming with 1D Array\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> result;\n vector<int> prevRow;\n \n for (int i = 0; i < numRows; i++) {\n vector<int> currentRow(i + 1, 1);\n \n for (int j = 1; j < i; j++) {\n currentRow[j] = prevRow[j - 1] + prevRow[j];\n }\n \n result.push_back(currentRow);\n prevRow = currentRow;\n }\n \n return result;\n }\n};\n\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> result = new ArrayList<>();\n if (numRows == 0) {\n return result;\n }\n\n if (numRows == 1) {\n List<Integer> firstRow = new ArrayList<>();\n firstRow.add(1);\n result.add(firstRow);\n return result;\n }\n\n result = generate(numRows - 1);\n List<Integer> prevRow = result.get(numRows - 2);\n List<Integer> currentRow = new ArrayList<>();\n currentRow.add(1);\n\n for (int i = 1; i < numRows - 1; i++) {\n currentRow.add(prevRow.get(i - 1) + prevRow.get(i));\n }\n\n currentRow.add(1);\n result.add(currentRow);\n\n return result;\n }\n}\n\n```\n```Python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 0:\n return []\n if numRows == 1:\n return [[1]]\n\n prev_rows = self.generate(numRows - 1)\n prev_row = prev_rows[-1]\n current_row = [1]\n\n for i in range(1, numRows - 1):\n current_row.append(prev_row[i - 1] + prev_row[i])\n\n current_row.append(1)\n prev_rows.append(current_row)\n\n return prev_rows\n\n```\n```Javascript []\nvar generate = function(numRows) {\n if (numRows === 0) {\n return [];\n }\n if (numRows === 1) {\n return [[1]];\n }\n\n let prevRows = generate(numRows - 1);\n let prevRow = prevRows[prevRows.length - 1];\n let currentRow = [1];\n\n for (let i = 1; i < numRows - 1; i++) {\n currentRow.push(prevRow[i - 1] + prevRow[i]);\n }\n\n currentRow.push(1);\n prevRows.push(currentRow);\n\n return prevRows;\n};\n\n```\n\n\n---\n\n#SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n\n | 472 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Easy Python Solution || Brute Force || Beginner Friendly || Pascal's Triangle...... | pascals-triangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking to generate the first numRows of Pascal\'s triangle. Pascal\'s triangle is a mathematical construct where each number is the sum of the two numbers directly above it. It is often used in combinatorics and probability theory. The intuition here is to build Pascal\'s triangle row by row, starting with the initial row [1] and calculating subsequent rows based on the values of the previous row.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to iterate through each row of Pascal\'s triangle, starting with the first row [1]. For each subsequent row, we calculate the values by summing the corresponding elements from the previous row. The outer loop iterates through each row, and the inner loop calculates the values for each element in the current row (except the first and last, which are always 1). We then append each row to the result, gradually building Pascal\'s triangle.The approach is to iterate through each row of Pascal\'s triangle, starting with the first row [1]. For each subsequent row, we calculate the values by summing the corresponding elements from the previous row. The outer loop iterates through each row, and the inner loop calculates the values for each element in the current row (except the first and last, which are always 1). We then append each row to the result, gradually building Pascal\'s triangle.\n\n---\n# Please upvote if you find this helpful...!!\n---\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is determined by the nested loops. The outer loop runs \'numRows\' times, representing each row of Pascal\'s triangle. The inner loop, for each row, runs \'i\' times, where \'i\' is the row number. Therefore, the time complexity is O(numRows^2) as we have to iterate through each element in each row.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is influenced by the data structure used to store Pascal\'s triangle. We use a 2D list named \'pascal\' to store the generated triangle. In the worst case, the size of this 2D list is proportional to the number of elements in Pascal\'s triangle, which is O(numRows^2). Therefore, the space complexity is O(numRows^2).\n# Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 0:\n return []\n \n # Initialize Pascal\'s triangle with the first row\n pascal = [[1]]\n \n # Iterate through each row starting from the second row\n for i in range(1, numRows):\n prev_row = pascal[i-1] # Get the previous row\n current_row = [1] # The first element of each row is always 1\n \n # Iterate through each element in the current row (except the first and last)\n for j in range(1, i):\n # Calculate the current element by summing the corresponding elements from the previous row\n current_row.append(prev_row[j-1] + prev_row[j])\n \n current_row.append(1) # The last element of each row is always 1\n pascal.append(current_row) # Add the current row to Pascal\'s triangle\n \n return pascal\n``` | 4 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Solution | pascals-triangle | 1 | 1 | ```C++ []\nclass Solution {\n public:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> ans;\n\n for (int i = 0; i < numRows; ++i)\n ans.push_back(vector<int>(i + 1, 1));\n\n for (int i = 2; i < numRows; ++i)\n for (int j = 1; j < ans[i].size() - 1; ++j)\n ans[i][j] = ans[i - 1][j - 1] + ans[i - 1][j];\n\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n finalNums=[]\n finalNums.append([1])\n for i in range(numRows-1):\n newRow=[1]\n for j in range(i):\n newRow.append(finalNums[i][j]+finalNums[i][j+1])\n newRow.append(1)\n finalNums.append(newRow)\n return finalNums\n```\n\n```Java []\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> ans = new ArrayList<>();\n\n for (int i = 0; i < numRows; ++i) {\n Integer[] temp = new Integer[i + 1];\n Arrays.fill(temp, 1);\n ans.add(Arrays.asList(temp));\n }\n\n for (int i = 2; i < numRows; ++i)\n for (int j = 1; j < ans.get(i).size() - 1; ++j)\n ans.get(i).set(j, ans.get(i - 1).get(j - 1) + ans.get(i - 1).get(j));\n\n return ans;\n }\n}\n```\n | 468 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.