title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Simple Python Solution with Two Pointers | valid-palindrome | 0 | 1 | # Intuition\nTo check palindrom for alpha-numeric characters, there needs to be a check and removal for other characters. Rest is just checking first and last characters one by one. \n\n# Approach\nTake two position variables - start and end - and set them to first and last position of the string. Check for each character if it is alphanumeric and match start and end position character. If it is not alphanumeric, skip it. \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n if not s:\n return False\n start = 0\n end = len(s)-1\n s = s.lower()\n while start<=end:\n while start<=end and not s[start].isalnum():\n start += 1\n while start<=end and not s[end].isalnum():\n end -= 1\n \n if start<=end and s[start]==s[end]:\n start += 1\n end -= 1\n else:\n break\n if start<end:\n return False\n return True\n\n \n``` | 0 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Python3 Easy Solution | valid-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n if not s:\n return True\n \n left, right = 0, len(s)-1\n\n while left<right:\n while left<right and not s[left].isalnum():\n left += 1\n \n while left<right and not s[right].isalnum():\n right -= 1\n\n if s[left].lower() != s[right].lower():\n return False\n\n left += 1\n right -= 1\n\n return True\n \n``` | 0 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Beats 97.69% users in run time|| Just 2 lines of code | valid-palindrome | 0 | 1 | # Intuition\nSimple Solution using regex\n\n# Approach\nIt is very much self explanatory\n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:\n\n\n# Code\n```\nimport re\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n slist =re.findall("[a-z0-9]",s.casefold())\n return slist==slist[::-1]\n \n\n\n \n \n``` | 0 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Simple List or string operation in Python | valid-palindrome | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# About\n<!-- Describe your approach to solving the problem. -->\nYou can simply understand the solution by viewing the code\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n a=[]\n s=s.lower()\n for i in s:\n if(i.isalnum()):\n a.append(i)\n #print(a)\n if(a==a[::-1]):\n return True\n else:\n return False\n \n \n``` | 2 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Python code to check if a string is a valid palindrome or not. (TC&SC: O(n)) | valid-palindrome | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n s = s.lower()\n for i in s:\n if False == i.isalnum():\n s = s.replace(i,"")\n if s == s[::-1]:\n return True\n return False\n``` | 3 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Simple Python 3 Solution || Beats 91% || 💻🧑💻🤖 | valid-palindrome | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n sen = ""\n for c in s:\n if c.isalnum():\n sen += c\n sen = sen.lower()\n return sen == sen[::-1]\n``` | 1 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
2 liner code .99%.easy to understand code | valid-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nDone through a very efficient built in function .isalnum()\n# Complexity\n- Time complexity:\nlinear O(n) time \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n new=("".join(i for i in s if i.isalnum())).lower()\n return new==new[::-1]\n \n``` | 2 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Beats : 68.4% [18/145 Top Interview Question] | valid-palindrome | 0 | 1 | # Intuition\n*two pointers at the start and end and keep shifting as inwards as long as left < right and both the values in string falls under alphanumeric*\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis code checks whether a given string `s` is a palindrome or not. The approach used is to use two pointers, `left` and `right`, starting from the beginning and end of the string respectively, and then move them towards each other until they meet in the middle.\n\nAt each step, we check if the character at the `left` index is alphanumeric. If it\'s not, we move `left` one position to the right. Similarly, if the character at the `right` index is not alphanumeric, we move `right` one position to the left. \n\nIf both the characters at `left` and `right` indices are alphanumeric, we check if they are equal or not. If they are not equal, the string is not a palindrome and we return `False`. Otherwise, we continue moving the pointers towards each other.\n\nIf the pointers meet in the middle of the string and no mismatches have been found, the string is a palindrome and we return `True`.\n\n\n\n# Complexity\n- Time complexity: \n O(n)\n\n- Space complexity:\nO(1)\n\nThe `time complexity` of this code is `O(n)` because we need to traverse the string once. The `space complexity` is `O(1)` because we are not using any extra data structures to store the string.\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n left, right = 0, len(s) - 1\n while left < right:\n if not s[left].isalnum():\n left += 1\n elif not s[right].isalnum():\n right -= 1\n elif s[left].lower() != s[right].lower():\n return False\n else:\n left += 1\n right -= 1\n return True\n\n``` | 7 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Speed is higher than 87%, Python3 | valid-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n f_s = \'\'\n for e in s:\n if e.isdigit() or e.isalpha():\n f_s += e.lower()\n \n if f_s != f_s[::-1]:\n return False\n else:\n return True\n \n \n\n \n \n``` | 1 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Simple solution with best time and space complexity | valid-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n res=""\n for alpha in s:\n if alpha.isalpha():\n res+=alpha.lower()\n if alpha.isdigit():\n res+=alpha\n if res==res[-1: :-1]:\n return True \n else :\n return False\n``` | 2 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Smartest solution using python (beats 97%) | valid-palindrome | 0 | 1 | # Intuition\nConvert the given string into a variable by convering it into lower case letter and avoiding the special characters and spaces.Then check if the resultant array is palindrome or not if True then return True else False. \n\n# Approach\nInitialize a variable with empty string then iterate over the given string by converting it into lower case letters and check if the corresponding value is either character or number then only it will get added to the variable string\nAfter the iteration check if the resultant value of string is palindrome or not if it is palindrome then return True else return False.\n\n# Complexity\n- Time complexity:O(n)\n\n- Space complexity:O(1)\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n string=\'\'\n for i in s.lower():\n if i.isalpha() or i.isnumeric():\n string+=i\n if string == string[::-1]:\n return True\n return False\n``` | 3 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Simple Python Two Liner Solution | valid-palindrome | 0 | 1 | \nThis simple two liner approach to solving this problem relies on generator comprehension to make this a quick and concise solution.\n\n# Code\n```\n# The first line of code removes all non-alphanumeric characters and converts\n# the whole string to lowercase making it easy to reverse the string cleanly\n# using generator comprehension and storing it in the variable "raw".\n\n# The second line of code is fairly straightforward. It finds out whether or\n# not the reversed form of the "raw" variable is equal to the unreversed\n# form of itself also using generator comprehension.\n\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n raw = \'\'.join(ch for ch in s if ch.isalnum()).lower()\n return raw[::-1] == raw\n``` | 6 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
O(n * w) TIme and O(n^2 * w) Space Complexity, TLE and MLE Optimized!!! | word-ladder-ii | 0 | 1 | # Intuition\nFrom the problem statement, we had an idea of applying a BFS or DFS starting from beginWord and terminating at endWord. Later we also know that in this search, we\'ll have to pick the paths with minimum length. Also, to note that, there may be multiple ways to reach a particular intermediate/terminal word, so the flow is not exactly how we traverse a tree.\n\n# Approach\nThe approach would be to create a BFS layers, the first layer would contain the begin word, the next layer would contain the words which were generated post modifying the current layer (basically replacing one character). At each layer we are storing the parent\'s reference in a dict(set) as word:(reachable_from...). \nLater doing a dfs search from endWord to beginWord will give the flow\nto create the result array.\n\n# Complexity\n- Time complexity:\nO(n * w) # we are traversing each word once\n\n- Space complexity:\nO(n^2 * w) # we are storing the parent mapping\n\n# Code\n```\nclass Solution:\n def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n wordList = set(wordList) # converting the given list to set to perform optimized set reduction\n result = []\n layer = set()\n layer.add(beginWord) # maintaining each layer to do bfs for the next layer\n # a dictionary to maintain the parent of each word, note in this bfs, one node can have multiple parent\n # e.g.: we can arrive at \'cog\' from \'dog\' and \'log\'\n # this parent chaining will help us save some memory and create the required list later using build_path\n parent = defaultdict(set)\n while layer:\n new_layer = set()\n for word in layer:\n for i in range(len(beginWord)):\n for c in "abcdefghijklmnopqrstuvwxyz":\n new = word[:i] + c + word[i + 1:]\n if new in wordList and new != word:\n parent[new].add(word)\n new_layer.add(new)\n wordList -= new_layer\n layer = new_layer\n\n def build_path(last, lst):\n if last == beginWord:\n result.append(list(reversed(lst))) # since we build the path bottom up, so reversing\n return\n for word in parent[last]:\n build_path(word, lst + [word])\n\n build_path(endWord, [endWord])\n return result\n``` | 3 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
Easy Solution|| Beats 95% || Detailed Explanation🔥|| Easy 💯💯💯 | word-ladder-ii | 0 | 1 | Build Graph \uD83C\uDF10:\n\nCreate a graph where each word is connected to others with the same pattern.\nFor example, "hit" and "hot" are connected because the pattern is "h*t."\n\n\nInitialize Data Structures \uD83C\uDFD7\uFE0F:\n\nSet up data structures for the BFS and DFS.\nUse visited dictionaries to keep track of visited nodes.\nUse deque (q) to perform BFS.\n\n\nBFS \uD83D\uDD0D:\n\nExplore neighbors of the current nodes using BFS.\nIf the two ends meet, stop the search.\nUpdate visited sets during BFS.\n\n\nDFS \uD83D\uDE80:\n\nUse DFS to reconstruct valid paths from both ends.\nAppend paths to the ans list.\n\n\nReturn Result \uD83C\uDF89:\n\nReturn the list of valid transformation sequences.\n\n\n# Pseudo Code\n```\nfunction findLadders(beginWord, endWord, wordList):\n d = defaultdict(list) # Step 1: Build Graph\n for word in wordList:\n for i in range(len(word)):\n pattern = word[:i] + "*" + word[i + 1:]\n d[pattern].append(word)\n\n if endWord not in wordList:\n return [] # End word not in the word list\n\n visited1 = defaultdict(list)\n q1 = deque([beginWord])\n visited1[beginWord] = []\n\n visited2 = defaultdict(list)\n q2 = deque([endWord])\n visited2[endWord] = []\n\n ans = []\n\n function dfs(v, visited, path, paths): # DFS to reconstruct paths\n path.append(v)\n if not visited[v]:\n if visited is visited1:\n paths.append(path[::-1])\n else:\n paths.append(path[:])\n for u in visited[v]:\n dfs(u, visited, path, paths)\n path.pop()\n\n function bfs(q, visited1, visited2, frombegin):\n level_visited = defaultdict(list)\n for _ in range(len(q)):\n u = q.popleft()\n for i in range(len(u)):\n for v in d[u[:i] + "*" + u[i + 1:]]:\n if v in visited2:\n paths1 = []\n paths2 = []\n dfs(u, visited1, [], paths1)\n dfs(v, visited2, [], paths2)\n if not frombegin:\n paths1, paths2 = paths2, paths1\n for a in paths1:\n for b in paths2:\n ans.append(a + b)\n elif v not in visited1:\n if v not in level_visited:\n q.append(v)\n level_visited[v].append(u)\n visited1.update(level_visited)\n\n while q1 and q2 and not ans:\n if len(q1) <= len(q2):\n bfs(q1, visited1, visited2, True)\n else:\n bfs(q2, visited2, visited1, False)\n\n return ans\n\n\n```\n# Code\n```\nfrom typing import List\nfrom collections import defaultdict, deque\n\nclass Solution:\n def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n d = defaultdict(list)\n for word in wordList:\n for i in range(len(word)):\n d[word[:i] + "*" + word[i + 1:]].append(word)\n\n if endWord not in wordList:\n return []\n\n visited1 = defaultdict(list)\n q1 = deque([beginWord])\n visited1[beginWord] = []\n\n visited2 = defaultdict(list)\n q2 = deque([endWord])\n visited2[endWord] = []\n\n ans = []\n\n def dfs(v, visited, path, paths):\n path.append(v)\n if not visited[v]:\n if visited is visited1:\n paths.append(path[::-1])\n else:\n paths.append(path[:])\n for u in visited[v]:\n dfs(u, visited, path, paths)\n path.pop()\n\n def bfs(q, visited1, visited2, frombegin):\n level_visited = defaultdict(list)\n for _ in range(len(q)):\n u = q.popleft()\n\n for i in range(len(u)):\n for v in d[u[:i] + "*" + u[i + 1:]]:\n if v in visited2:\n paths1 = []\n paths2 = []\n dfs(u, visited1, [], paths1)\n dfs(v, visited2, [], paths2)\n if not frombegin:\n paths1, paths2 = paths2, paths1\n for a in paths1:\n for b in paths2:\n ans.append(a + b)\n elif v not in visited1:\n if v not in level_visited:\n q.append(v)\n level_visited[v].append(u)\n visited1.update(level_visited)\n\n while q1 and q2 and not ans:\n if len(q1) <= len(q2):\n bfs(q1, visited1, visited2, True)\n else:\n bfs(q2, visited2, visited1, False)\n\n return ans\n\n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
✔️ Explanation with Animation - Accepted without TLE! | word-ladder-ii | 1 | 1 | # Intuition\nWe just need to record all possible words that can connect from the beginning, level by level, until we hit the end at a level.\n\n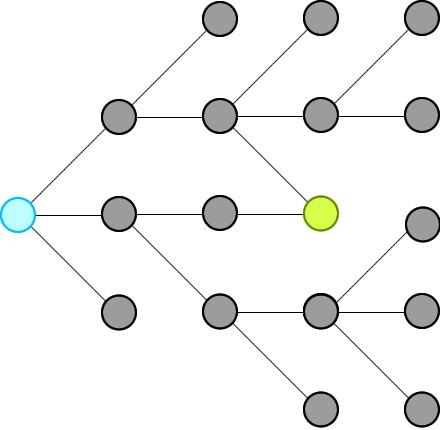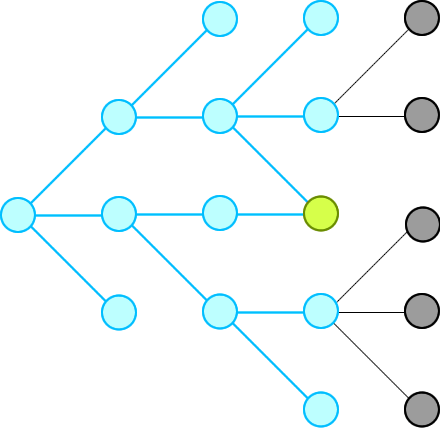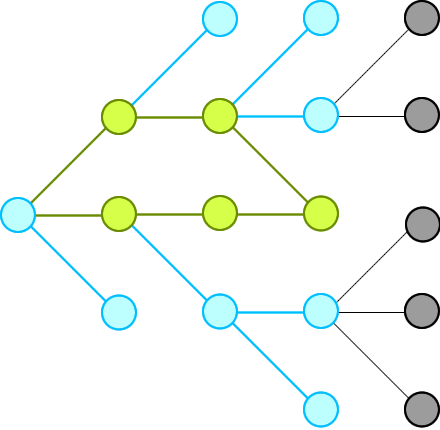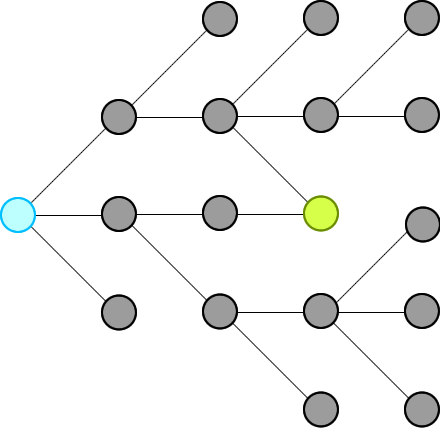\n\nThen we will traverse backward from end via the words in the record and construct our final ways.\n\n**Remember:** we will not record paths, we record only nodes. \n\n_____\n# Explanation\nFirst, because we traverse level by level, so as soon as we see the end, that is the shortest distance (shortest path) we have from beginning. This is the basic theorem of BFS in an unweighted graph: https://sneeit.com/graph/?tab=documentation#breath-first-search-in-graph\n\nWhen we see the end, we know some of the nodes from previous level (which connect to the beginning because we traversed from there) are pointing to the end. We just need to move backward, level by level then we could collect all paths to end from begin\n_____\n# Why Other\'s Solutions Get TLE\nBecause if there are some nodes point to a same node, their solutions keep computing the same path again and again due to they see those paths are different (from the beginning node). This is the weakness of recording paths, instead of nodes.\n\nCheck the red node in the following figure for more information:\n\n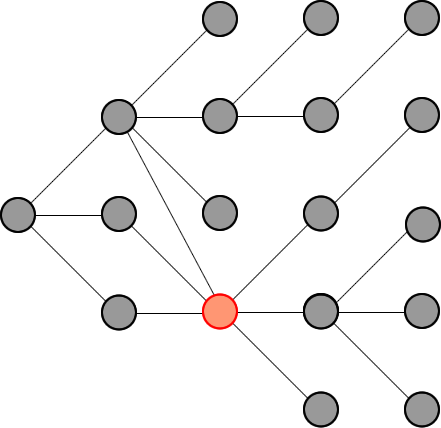\n\nIn summary:\n1. Other solutions:\n\t* Store paths, so every node could be stored multiple times.\n\t* Compute the intersections in paths again and again\n\t* Paths that does not lead to end also be computed\n2. My solution:\n\t* Store only nodes so every node is store exactly one time\n\t* Move backward to compute only the paths that can connect from begin to end\n\n_____\n# Algorithm\n* **Moving Forward: start from begin**\n\t1. Each level, find all connected nodes to the nodes of the current level in the record and add those to the record for the next level.\n\t2. Delete node from wordList to prevent revisiting and forming cycles\n\t3. Repeat the above steps until we reach end or we add no new nodes to the record for next level\n\n* **Moving Backward: start from end**\n\t1. Do the same steps as moving forward but this time we will not record nodes but contruct our paths\n\t2. Construct paths in reversing order to have paths from begin to end\n_____\n\n# Codes\n_____\n\n## JavaScript\n\n```\nvar findLadders = function(beginWord, endWord, wordList) {\n // to check if two words can connect\n let connected = (a,b) => {\n let c = 0\n for (let i = 0; i < a.length && c < 2; i++) {\n if (a[i] !== b[i]) c++\n }\n return c == 1\n }\n\n // dictionary to help us search words faster\n // and to trackback what word was used\n let dict = new Set(wordList);\n if (dict.has(endWord) == false) return []\n\n dict.delete(beginWord)\n let queue = [beginWord]\n let nodes = []\n\n \n // find all ways from beginning\n // level by level, until reach end at a level\n let reached = false; \n while (queue.length && !reached) {\n // update nodes of paths for this level\n nodes.push(queue.slice())\n\n // access whole level \n let qlen = queue.length;\n for (let i = 0; i < qlen && !reached; i++) {\n\n let from = queue.shift();\n \n // find all nodes that connect to the nodes of this level\n for (let to of dict) { \n\n if (connected(from,to) == false) continue\n\n // if connect\n // - and one of them is end word\n // - then we can stop moving forward\n if (to == endWord) {\n reached = true\n break;\n }\n\n // - otherwise,\n // - add all connected nodes to the record for the next level\n // - and delete them from dict to prevent revisiting to form cycles\n queue.push(to) \n dict.delete(to) \n }\n }\n }\n\n // try but did not find endWord\n if (!reached) return []\n\n // move backward to construct paths\n // add nodes to paths in reverse order to have paths from begin to end\n let ans = [[endWord]]\n for (let level = nodes.length - 1; level >= 0; level--) { \n let alen = ans.length\n for (let a = 0; a < alen; a++) {\n let p = ans.shift()\n let last = p[0] \n for (let word of nodes[level]) { \n if (!connected(last, word)) continue \n ans.push([word, ...p])\n }\n } \n }\n\n return ans\n}\n```\n\n____\n## C++\nThis is my first C++ code. Hope you can suggest optimizations . Thanks.\n```\nclass Solution {\npublic:\n bool isConnected(string s,string t){\n int c=0;\n for(int i=0;i<s.length();i++)\n c+=(s[i]!=t[i]);\n return c==1;\n }\n\n vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {\n vector<vector<string>> ans; \n vector<vector<string>> nodes; \n unordered_set<string> dict(wordList.begin(),wordList.end());\n \n if (!dict.count(endWord)) return ans;\n dict.erase(beginWord);\n \n \n bool reached = false;\n nodes.push_back({beginWord});\n \n while (dict.size() && !reached) { \n vector<string> last = nodes.back();\n vector<string> curr;\n \n for (int i = 0; i < last.size() && !reached; i++) {\n unordered_set<string> visited;\n string from = last[i]; \n // check all nodes that connect\n // to the nodes of the previous level \n for (auto& to : dict) { \n if (visited.count(to)) continue;\n if (!isConnected(from, to)) continue; \n // if one of them is "endWord" then we can stop \n // because this level is the shortest distance from begin\n if (to == endWord) { \n reached = true; \n break;\n }\n \n // otherwise,\n // add nodes for the current level\n curr.push_back(to); \n visited.insert(to); \n } \n // delete the visited to prevent forming cycles \n for (auto& visited : visited) { \n dict.erase(visited);\n }\n }\n \n // found endWord this level\n if (reached) break;\n \n // can not add any new nodes to our level\n if (!curr.size()) break;\n \n // otherwise, record all nodes for the current level\n nodes.push_back(curr); \n }\n \n // try but not find\n if (reached == false) return ans;\n \n // move backward\n ans.push_back({endWord}); \n for (int level = nodes.size() - 1; level >= 0; level--) { \n int alen = ans.size();\n while (alen) {\n vector<string> path = ans.back();\n ans.pop_back();\n string from = path.front(); \n for (string &to : nodes[level]) { \n if (!isConnected(from, to)) continue;\n \n vector<string> newpath = path;\n newpath.insert(newpath.begin(), to);\n ans.insert(ans.begin(), newpath);\n } \n alen--;\n } \n }\n return ans;\n }\n};\n```\n____\n## Pseudocode\n```\n// Pseudocode\nfunction findLadders(beginWord, endWord, wordList) {\n if (wordList.hasNo(endWord)) return []\n wordList.delete(beginWord)\n\n // move forward\n queue = [beginWord]\n paths = [] // 2D array\n reached = false; \n while (queue.length && !reached) {\n paths.append(queue) // deep copy\n \n // need static here to access only the nodes of this level\n qlen = queue.length; \n for (let i = 0; i < qlen && !reached; i++) {\n from = queue.takeFirst()\n forEach (to of wordList) {\n if (isConnected(from, to)) { \n if (to == endWord) {\n reached = true\n break // exit from the forEach\n }\n \n queue.push(to) \n wordList.delete(to) // delete to preven a cycle \n }\n }\n }\n }\n\n // can not reach the end eventually\n if (!reached) return []\n\n // move backward\n answer = [[endWord]] // 2D array \n for (level = paths.length - 1; level >= 0; level--) { \n path = paths[level]\n alen = answer.length\n for (a = 0; a < alen; a++) {\n p = answer.takeFirst()\n last = p[0]\n forEach (word of path) {\n if (!isConnected(last, word)) {\n answer.append([word, ...p])\n }\n \n }\n } \n }\n\n return answer\n}\n\n\n// to check if two words can connect\nfunction isConnected(a,b) {\n c = 0\n for (i = 0; i < a.length && c < 2; i++) {\n if (a[i] !== b[i]) c++\n }\n return c == 1\n}\n```\n\n____\n | 46 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
Python || Two Solutions || No TLE || BFS+DFS | word-ladder-ii | 0 | 1 | **Brute Force Solution using BFS (which gives TLE): In this we stored path directly in queue**\n\n```\ndef findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n wordList=set(wordList)\n if endWord not in wordList:\n return []\n q=deque()\n q.append([beginWord])\n ans=[]\n visited=set([beginWord])\n while q and not ans:\n t=set()\n for _ in range(len(q)):\n a=q.popleft()\n word=a[-1]\n for i in range(len(beginWord)):\n for j in range(26):\n new=word[:i]+chr(97+j)+word[i+1:]\n if new==endWord:\n ans.append(a+[endWord])\n if new in wordList and new not in visited:\n t.add(new)\n q.append(a+[new])\n visited=visited.union(t) \n return ans\n```\n\n**Optimized Solution using BFS + DFS (without TLE) : Here we have just store possible node and then use backtracking to get the possible paths**\n\n```\ndef findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n def dfs(word,a):\n if word==beginWord:\n ans.append(a[::-1])\n return\n n=d[word]-1\n for i in range(l):\n for j in range(26):\n new=word[:i]+chr(97+j)+word[i+1:]\n if new in d and d[new]==n:\n a.append(new)\n dfs(new,a)\n a.pop()\n return ans\n \n wordList=set(wordList)\n wordList.discard(beginWord)\n if endWord not in wordList:\n return []\n q=deque([beginWord])\n ans=[]\n d=dict()\n d[beginWord]=1\n level=1\n t=set()\n l=len(beginWord)\n while q:\n word=q.popleft()\n if word==endWord:\n break\n for i in range(l):\n for j in range(26):\n new=word[:i]+chr(97+j)+word[i+1:]\n if new in wordList:\n d[new]=d[word]+1\n q.append(new)\n wordList.remove(new) \n if endWord in d:\n dfs(endWord, [endWord])\n return ans\n```\n | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
Python | Clean Code | Proper Stages + Functions Explained | BFS | Parent Backtracking | word-ladder-ii | 0 | 1 | # Code\n```\nclass Solution:\n def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n n = len(wordList)\n\n # Checking if beginWord is present in the dictionary or not\n # Checking if endWord is present and if not then returning 0\n isBeginInList = False\n isEndInList = False\n startInd = n\n endInd = n\n for i in range(n):\n if wordList[i] == beginWord:\n isBeginInList = True\n startInd = i\n elif wordList[i] == endWord:\n isEndInList = True\n endInd = i\n if not isEndInList:\n return []\n if not isBeginInList:\n n += 1\n wordList.append(beginWord)\n wordLen = len(beginWord)\n \n # Mapping all the possible ways from a word by changing a single letter\n oneWordDiffMap = {}\n for i in range(n):\n for j in range(wordLen):\n nextWord = wordList[i][:j] + \'*\' + wordList[i][j + 1:]\n if nextWord in oneWordDiffMap:\n oneWordDiffMap[nextWord].append(i)\n else:\n oneWordDiffMap[nextWord] = [i]\n\n # Turning the map of all possible ways into a graph made from word\'s index\n graph = {i: [] for i in range(n)}\n for nodes in oneWordDiffMap:\n node = oneWordDiffMap[nodes]\n for i in range(len(node)):\n for j in range(i + 1, len(node)):\n graph[node[i]].append(node[j])\n graph[node[j]].append(node[i])\n\n # breadth first search to find the shortest path alongwoth maintaining a parent array\n parent = [[] for i in range(n)]\n q = {startInd}\n visited = set()\n isEndFound = False\n while q:\n newQ = set()\n for i in q:\n visited.add(i)\n for j in graph[i]:\n if j in visited or j in q:\n continue\n parent[j].append(i)\n if j == endInd:\n isEndFound = True\n newQ.add(j)\n if isEndFound:\n break\n q = newQ\n\n # if a path is not found to the end target\n if not isEndFound:\n return []\n\n # backtraking through the parent nodes to prepare the path\n def backtracking(index: int) -> None:\n if index == startInd:\n return [[beginWord]]\n allPaths = []\n for i in parent[index]:\n allPaths += backtracking(i)\n for path in allPaths:\n path.append(wordList[index])\n return allPaths\n \n return backtracking(endInd)\n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
46ms Python 97 Faster Working Multiple solutions 95% memory efficient solution | word-ladder-ii | 0 | 1 | # Don\'t Forget To Upvote\n\n# 1. 97.81% Faster Solution:\n\n\t\tclass Solution:\n\t\t\tdef findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n\t\t\t\td = defaultdict(list)\n\t\t\t\tfor word in wordList:\n\t\t\t\t\tfor i in range(len(word)):\n\t\t\t\t\t\td[word[:i]+"*"+word[i+1:]].append(word)\n\n\t\t\t\tif endWord not in wordList:\n\t\t\t\t\treturn []\n\n\t\t\t\tvisited1 = defaultdict(list)\n\t\t\t\tq1 = deque([beginWord])\n\t\t\t\tvisited1[beginWord] = []\n\n\t\t\t\tvisited2 = defaultdict(list)\n\t\t\t\tq2 = deque([endWord])\n\t\t\t\tvisited2[endWord] = []\n\n\t\t\t\tans = []\n\t\t\t\tdef dfs(v, visited, path, paths):\n\t\t\t\t\tpath.append(v)\n\t\t\t\t\tif not visited[v]:\n\t\t\t\t\t\tif visited is visited1:\n\t\t\t\t\t\t\tpaths.append(path[::-1])\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tpaths.append(path[:])\n\t\t\t\t\tfor u in visited[v]:\n\t\t\t\t\t\tdfs(u, visited, path, paths)\n\t\t\t\t\tpath.pop()\n\n\t\t\t\tdef bfs(q, visited1, visited2, frombegin):\n\t\t\t\t\tlevel_visited = defaultdict(list)\n\t\t\t\t\tfor _ in range(len(q)):\n\t\t\t\t\t\tu = q.popleft()\n\n\t\t\t\t\t\tfor i in range(len(u)):\n\t\t\t\t\t\t\tfor v in d[u[:i]+"*"+u[i+1:]]:\n\t\t\t\t\t\t\t\tif v in visited2:\n\t\t\t\t\t\t\t\t\tpaths1 = []\n\t\t\t\t\t\t\t\t\tpaths2 = []\n\t\t\t\t\t\t\t\t\tdfs(u, visited1, [], paths1)\n\t\t\t\t\t\t\t\t\tdfs(v, visited2, [], paths2)\n\t\t\t\t\t\t\t\t\tif not frombegin:\n\t\t\t\t\t\t\t\t\t\tpaths1, paths2 = paths2, paths1\n\t\t\t\t\t\t\t\t\tfor a in paths1:\n\t\t\t\t\t\t\t\t\t\tfor b in paths2:\n\t\t\t\t\t\t\t\t\t\t\tans.append(a+b)\n\t\t\t\t\t\t\t\telif v not in visited1:\n\t\t\t\t\t\t\t\t\tif v not in level_visited:\n\t\t\t\t\t\t\t\t\t\tq.append(v)\n\t\t\t\t\t\t\t\t\tlevel_visited[v].append(u)\n\t\t\t\t\tvisited1.update(level_visited)\n\n\t\t\t\twhile q1 and q2 and not ans:\n\t\t\t\t\tif len(q1) <= len(q2):\n\t\t\t\t\t\tbfs(q1, visited1, visited2, True)\n\t\t\t\t\telse:\n\t\t\t\t\t\tbfs(q2, visited2, visited1, False)\n\n\t\t\t\treturn ans\n\t\t\t\t\n\t\t\t\t\n# 2. 87% fast solution a little different approach:\n\n\n\t\tclass Solution:\n\t\t\tdef findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n\t\t\t\tres = []\n\t\t\t\tedge = collections.defaultdict(set)\n\t\t\t\twordList = set(wordList)\n\t\t\t\tfor word in wordList:\n\t\t\t\t\tfor i in range(len(word)):\n\t\t\t\t\t\tedge[word[:i] +\'*\'+word[i+1:]].add(word)\n\t\t\t\tbfsedge = {}\n\n\t\t\t\tdef bfs():\n\t\t\t\t\tminl = 0\n\t\t\t\t\tqueue = set()\n\t\t\t\t\tqueue.add(beginWord)\n\t\t\t\t\twhile queue:\n\t\t\t\t\t\tnext_queue = set()\n\t\t\t\t\t\tfor word in queue:\n\t\t\t\t\t\t\tif word in wordList:\n\t\t\t\t\t\t\t\twordList.remove(word)\n\t\t\t\t\t\tbfsedge[minl] = collections.defaultdict(set)\n\t\t\t\t\t\tfor word in queue:\n\t\t\t\t\t\t\tif word == endWord:\n\t\t\t\t\t\t\t\treturn minl\n\t\t\t\t\t\t\tfor i in range(len(word)):\n\t\t\t\t\t\t\t\tfor w in edge[word[:i]+\'*\'+word[i+1:]]:\n\t\t\t\t\t\t\t\t\tif w in wordList:\n\t\t\t\t\t\t\t\t\t\tnext_queue.add(w)\n\t\t\t\t\t\t\t\t\t\tbfsedge[minl][w].add(word)\n\t\t\t\t\t\tqueue = next_queue\n\t\t\t\t\t\tminl += 1\n\t\t\t\t\treturn minl\n\n\t\t\t\tdef dfs(seq, endWord):\n\t\t\t\t\tif seq[-1] == endWord:\n\t\t\t\t\t\tres.append(seq.copy())\n\t\t\t\t\t\treturn\n\t\t\t\t\tfor nextWord in bfsedge[minl-len(seq)][seq[-1]]:\n\t\t\t\t\t\tif nextWord not in seq:\n\t\t\t\t\t\t\tdfs(seq+[nextWord], endWord)\n\n\t\t\t\tminl = bfs()\n\t\t\t\tdfs([endWord], beginWord)\n\t\t\t\t# reverse the sequence\n\t\t\t\tfor sq in res:\n\t\t\t\t\tsq.reverse()\n\t\t\t\treturn res\n\t\t\t\t\n\t\t\t\t\n# 3.95% Memory efficient solution:\n\t\tfrom collections import deque\n\t\tclass Solution:\n\t\t\tdef findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n\t\t\t\tif endWord not in wordList:return []\n\t\t\t\twordList.append(beginWord)\n\t\t\t\twordList.append(endWord)\n\t\t\t\tdistance = {}\n\n\n\t\t\t\tself.bfs(endWord, distance, wordList)\n\n\t\t\t\tresults = []\n\t\t\t\tself.dfs(beginWord, endWord, distance, wordList, [beginWord], results)\n\n\t\t\t\treturn results\n\n\t\t\tdef bfs(self, start, distance, w):\n\t\t\t\tdistance[start] = 0\n\t\t\t\tqueue = deque([start])\n\t\t\t\twhile queue:\n\t\t\t\t\tword = queue.popleft()\n\t\t\t\t\tfor next_word in self.get_next_words(word, w):\n\t\t\t\t\t\tif next_word not in distance:\n\t\t\t\t\t\t\tdistance[next_word] = distance[word] + 1\n\t\t\t\t\t\t\tqueue.append(next_word)\n\n\t\t\tdef get_next_words(self, word, w):\n\t\t\t\twords = []\n\t\t\t\tfor i in range(len(word)):\n\t\t\t\t\tfor c in \'abcdefghijklmnopqrstuvwxyz\':\n\t\t\t\t\t\tnext_word = word[:i] + c + word[i + 1:]\n\t\t\t\t\t\tif next_word != word and next_word in w:\n\t\t\t\t\t\t\twords.append(next_word)\n\t\t\t\treturn words\n\n\t\t\tdef dfs(self, curt, target, distance, w, path, results):\n\t\t\t\tif curt == target:\n\t\t\t\t\tresults.append(list(path))\n\t\t\t\t\treturn\n\n\t\t\t\tfor word in self.get_next_words(curt, w):\n\t\t\t\t\tif distance[word] != distance[curt] - 1:\n\t\t\t\t\t\tcontinue\n\t\t\t\t\tpath.append(word)\n\t\t\t\t\tself.dfs(word, target, distance, w, path, results)\n\t\t\t\t\tpath.pop()\n | 40 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
BFS + DFS, the solution that should be easily understandable | word-ladder-ii | 0 | 1 | # Intuition\nBFS + DFS\n\nBFS is for getting all the parent of current node,\nmake sure to maintain a depth variable(step in the case),\neven tho the child may be visited before, but if it\'s direct children,\nwe still need to add it in the the parent hash.\n\ndfs is just to backtracking all parent to construct result\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(M^2N), M is the length of the word, N is the number of word in word list\n\n- Space complexity:\nO(M^2N)\n\n# Code\n```\nclass Solution:\n def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n if endWord not in wordList:\n return []\n\n parent = collections.defaultdict(set)\n wordSet = defaultdict(set)\n for word in wordList:\n for i in range(len(word)):\n wordSet[word[:i] + "*" + word[i+1:]].add(word)\n q = deque([(beginWord, 0)])\n visited = collections.defaultdict(int)\n while q:\n word, step = q.popleft()\n for i in range(len(word)):\n next_word = word[:i] + "*" + word[i+1:]\n for mapped_word in wordSet[next_word]:\n if mapped_word not in visited:\n visited[mapped_word] = step + 1\n parent[mapped_word].add(word)\n q.append((mapped_word, step+1))\n elif visited[mapped_word] == step + 1: # We are still at the same level\n parent[mapped_word].add(word)\n\n \n result = []\n q = deque([endWord])\n def make_sequese(endWord, path):\n if endWord == beginWord:\n result.append(path[::-1])\n return\n for neighbor in parent[endWord]:\n make_sequese(neighbor, path + [neighbor])\n make_sequese(endWord, [endWord])\n return result\n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
BFS + DFS + Memo | word-ladder-ii | 0 | 1 | ```python\nclass Solution:\n def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:\n word_set = set(wordList)\n if endWord not in word_set:\n return []\n # bfs build graph + dfs memo\n graph = defaultdict(set)\n queue = Deque([beginWord])\n step = 0\n min_step = -1\n visited = set()\n while len(queue):\n size = len(queue)\n step += 1\n for _ in range(size):\n cur = queue.popleft()\n if cur in visited:\n continue\n visited.add(cur)\n for i in range(len(cur)):\n c = cur[i]\n for j in range(26):\n n_c = chr(ord(\'a\') + j)\n if n_c == c:\n continue\n n_s = cur[0:i] + n_c + cur[i+1:]\n if n_s in word_set:\n graph[n_s].add(cur)\n graph[cur].add(n_s)\n queue.append(n_s)\n if n_s == endWord and min_step == -1:\n min_step = step\n @lru_cache(None)\n def dfs(cur, step):\n nonlocal graph\n if step > min_step:\n return []\n if cur == endWord:\n return [[endWord]]\n res = []\n for nxt in graph[cur]:\n tmp = dfs(nxt,step+1)\n res += [[cur] + x for x in tmp]\n # print(res)\n return res\n return dfs(beginWord, 0)\n \n \n``` | 2 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _all the **shortest transformation sequences** from_ `beginWord` _to_ `endWord`_, or an empty list if no such sequence exists. Each sequence should be returned as a list of the words_ `[beginWord, s1, s2, ..., sk]`.
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** \[\[ "hit ", "hot ", "dot ", "dog ", "cog "\],\[ "hit ", "hot ", "lot ", "log ", "cog "\]\]
**Explanation:** There are 2 shortest transformation sequences:
"hit " -> "hot " -> "dot " -> "dog " -> "cog "
"hit " -> "hot " -> "lot " -> "log " -> "cog "
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** \[\]
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 5`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 500`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**.
* The **sum** of all shortest transformation sequences does not exceed `105`. | null |
[Python3] Breadth first search | word-ladder | 0 | 1 | ```\nInput:\nbeginWord = "hit",\nendWord = "cog",\nwordList = ["hot","dot","dog","lot","log","cog"]\nOutput: 5\n```\n1. Only one letter can be changed at a time.\nIn the example, from begin word, you can change one letter in 3 ways. 3 is the length of the word.\n```\n\t\t\t\t hit\n\t\t / | \\\n\t\t *it h*t hi*\n\t\t /|\\ /|\\ /|\\ \n# In order to continue the Breath First Search(BFS) process,\n# we need to know the children of *it, h*t, and hi*.\n# so we need the information from word list.\n```\n2. Each transformed word must exist in the word list.\n\tIn the example, we need to record all the possible changes that could be made from the word list so that we can have the information to do BFS in the graph above. We use a map to store the data. The key is one-letter-change-word, for example," *it," the value is the word meet the key\'s condition in the word list.\n```\nwordList = ["hot","dot","dog","lot","log","cog"]\nchange_map ={ *ot : hot, dot, lot\n\t\t\th*t : hot\n\t\t\tho* :hot\n\t\t\td*t : dot\n\t\t\tdo* : dot, dog\n\t\t\t*og : dog, log, cog\n\t\t\td*g : dog\n\t\t\tl*t : lot\n\t\t\tlo* : lot, log\n\t\t\tl*g : log\n\t\t\tc*g: cog\n\t\t\tco* : cog \n\t\t\t}\n```\n\nWith the information in change_map, we got the information to expand the breadth first search tree.\n```\n\t\t\t\t\t\t\t\t\t\t\t hit, level = 1\n\t\t\t\t\t\t\t\t / | \\\n\t\t\t\t\t *it h*t hi*\n\t\t\t\t\t\t | | | \n\t\t\t null \t hot ,level = 2 null\n\t\t\t\t\t\t\t\t\t\t / | \\ \n\t\t\t\t\t\t\t\t\t\t/ | \\\n\t\t\t\t *ot h*t ho*\n\t\t\t\t / | \\ | |\n hot,2 dot,3 lot,3 hot,2 hot,2\t\t\t\t\t\n\n\n# as we can see, "hot" has been visited in level 2, but "hot" will still appear at the next level. \n# To avoid duplicate calculation, \n# we keep a visited map, \n# if the word in the visited map, we skip the word, i.e. don\'t append the word into the queue.\n# if the word not in the visited map, we put the word into the map, and append the word into the queue.\n```\n```\nfrom collections import defaultdict\nfrom collections import deque\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n """\n :type beginWord: str\n :type endWord: str\n :type wordList: List[str]\n :rtype: int\n """\n if endWord not in wordList or not endWord or not beginWord or not wordList:\n return 0\n L = len(beginWord)\n all_combo_dict = defaultdict(list)\n for word in wordList:\n for i in range(L):\n all_combo_dict[word[:i] + "*" + word[i+1:]].append(word) \n queue = deque([(beginWord, 1)])\n visited = set()\n visited.add(beginWord)\n while queue:\n current_word, level = queue.popleft()\n for i in range(L):\n intermediate_word = current_word[:i] + "*" + current_word[i+1:]\n for word in all_combo_dict[intermediate_word]:\n if word == endWord:\n return level + 1\n if word not in visited:\n visited.add(word)\n queue.append((word, level + 1))\n return 0\n``` | 134 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
PYthon solution Accepted Only Code | word-ladder | 0 | 1 | # Code\n```\n def ladderLength(self, beginWord:str,endWord:str,wordList: List[str])->int:\n q = deque();\n q.append((beginWord,1));\n hmap = defaultdict(int)\n for word in wordList: hmap[word] = 1;\n hmap[beginWord] = 0\n while( len(q) > 0 ):\n #print(q);\n word = q.popleft();\n wordl = list(word[0])\n if( word[1] > 1 and word[0] == endWord):\n return word[1]\n for i in range(0,len(wordl)):\n t = wordl[i]\n for j in range(0,ord(\'z\')-ord(\'a\') + 1):\n wordl[i] = chr( ord(\'a\') + j );\n tword = \'\'.join(wordl)\n if( hmap[tword] == 1 and tword != word[0] ):\n q.append( (tword,word[1]+1) );\n hmap[tword] = 0;\n wordl[i] = t\n \n return 0;\n\n\n``` | 2 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Prefix-Postfix-Letter Index | word-ladder | 0 | 1 | # Approach\nOverall the solution employs the same BFS. The only problem is to build the adjacency map.\n\nAll the words that differ only in one letter at some position, can be split into the same prefix and postfix with different letters in between:\n\npr-e-fix\npr-o-fix\npr-a-fix\npr-u-fix\n\nAll of these words have prefix pr-, postfix -fix and a set a varying letters in between: [e, o, a, u].\n\nThus, if we build a map prefix -> postfix -> letter, then all the adjacent words will be in the bins of this map, for the abovementioned example, the map will be:\n```\n{\n \'pr\': {\'fix\': {\'e\', \'o\', \'a\', \'u\'}}\n}\n```\n\nBesides that, the algorithm is a standard wave algorithm, where we keep track of visited nodes and to track the wave we use a deque.\n\n# Complexity\nThis approach instead of straigtforward $O(N^2)$ complexity is $O(NL)$ complex, where $N$ is the number of the words, $L$ is the length of one word.\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n wordList = set(wordList)\n if endWord not in wordList:\n return 0\n\n if beginWord not in wordList:\n wordList.add(beginWord)\n\n # Prefix -> Postfix -> Letter mapping\n\n pref_post_lett = {}\n for index in range(len(beginWord)):\n for word in wordList:\n pref = word[:index]\n post = word[1+index:]\n lett = word[index]\n\n if pref not in pref_post_lett:\n pref_post_lett[pref] = {}\n\n if post not in pref_post_lett[pref]:\n pref_post_lett[pref][post] = set()\n\n if lett not in pref_post_lett[pref][post]:\n pref_post_lett[pref][post].add(lett)\n\n\n adj = {}\n \n for w in wordList:\n adj[w] = []\n\n # Building adjacency map\n\n for pref in pref_post_lett:\n post_lett = pref_post_lett[pref]\n\n for post in post_lett:\n lett = post_lett[post]\n\n for l1 in lett:\n for l2 in lett:\n if l1 != l2:\n w1 = pref + l1 + post\n w2 = pref + l2 + post\n\n adj[w1].append(w2) \n\n # Straigtforward approach\n\n # for a in wordList:\n # for b in wordList:\n # if len(a) != len(b):\n # continue\n # diff = 0\n # for idx in range(len(a)):\n # if a[idx] != b[idx]:\n # diff += 1\n\n # if diff == 1:\n # adj[a].append(b)\n\n\n # Standard wave algorithm\n\n wave = deque([(beginWord, 1)])\n visited = set()\n\n while len(wave) > 0:\n node = wave.popleft()\n\n wrd = node[0]\n stp = node[1]\n\n if wrd == endWord:\n return stp\n\n if wrd in visited:\n continue\n \n visited.add(wrd)\n\n for nbr in adj[wrd]:\n if nbr not in visited:\n wave.append((nbr, stp + 1))\n\n return 0\n \n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
✅[Python] Simple and Clean✅ | word-ladder | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n# Intuition\nThe idea behind bidirectional BFS is to search from both the `beginWord` and the `endWord` simultaneously. This can reduce the search space and avoid unnecessary branching.\n\n# Approach\nWe start by converting the `wordList` to a set for faster lookup. We then check if the `endWord` is in the `wordSet`. If it is not, we return 0 since there is no valid transformation sequence.\n\nWe initialize two queues for bidirectional BFS, one for `beginWord` and one for `endWord`. We also initialize two visited sets to avoid duplicates.\n\nWe then loop until either queue is empty. In each iteration, we always process the smaller queue first to reduce the search space. We process the current queue by checking if any node in the queue is in the other visited set. If it is, we return the current level since we have found a valid transformation sequence.\n\nOtherwise, we add the neighbors of each node in the queue to the queue and visited set. We then increment the level and continue to the next iteration.\n\nIf we exit the loop without finding a valid transformation sequence, we return 0.\n\n# Complexity\n- Time complexity: $$O(M^2 * N)$$ where M is the length of each word and N is the total number of words in the input word list.\n- Space complexity: $$O(M^2 * N)$$ where M is the length of each word and N is the total number of words in the input word list.\n\n# Code\n```\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n def isNeighbour(word1, word2):\n count = 0\n for i, letter in enumerate(word1):\n if letter!=word2[i]:\n count+=1\n if count>1:\n return False\n return True\n # convert wordList to a set for faster lookup\n wordSet = set(wordList)\n # check if endWord is in wordSet\n if endWord not in wordSet:\n return 0\n # initialize two queues for bidirectional BFS\n queue1 = deque([beginWord])\n queue2 = deque([endWord])\n # initialize two visited sets to avoid duplicates\n visited1 = set([beginWord])\n visited2 = set([endWord])\n # initialize the level\n level = 1\n # loop until either queue is empty\n while queue1 and queue2:\n # always process the smaller queue first\n if len(queue1) > len(queue2):\n queue1, queue2 = queue2, queue1\n visited1, visited2 = visited2, visited1\n # process the current queue\n n = len(queue1)\n for _ in range(n):\n node = queue1.popleft()\n # check if node is in the other visited set\n if node in visited2:\n return level\n # add the neighbors of node to the queue and visited set\n for word in wordSet:\n if word not in visited1 and isNeighbour(node,word):\n queue1.append(word)\n visited1.add(word)\n # increment the level\n level += 1\n # no valid transformation sequence found\n return 0\n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Python || Easy || BFS Solution | word-ladder | 0 | 1 | ```\ndef ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n wordList=set(wordList)\n if endWord not in wordList:\n return 0\n q=deque()\n q.append((beginWord,1))\n while q:\n word,step=q.popleft()\n for i in range(len(beginWord)):\n for j in range(26):\n new=word[:i]+chr(97+j)+word[i+1:]\n if new==endWord:\n return step+1\n if new in wordList:\n q.append((new,step+1))\n wordList.remove(new)\n return 0\n```\n\n**An upvote will be encouraging** | 9 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Graph With BFS Approach | word-ladder | 0 | 1 | ```\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n if endWord not in wordList:\n return 0\n nei=defaultdict(list)\n wordList.append(beginWord)\n for word in wordList:\n for j in range(len(word)):\n pattern=word[:j]+"*"+word[j+1:]\n nei[pattern].append(word)\n visit=set([beginWord])\n q=deque([beginWord])\n count=1\n while q:\n for i in range(len(q)):\n word=q.popleft()\n if word==endWord:\n return count\n for j in range(len(word)):\n pattern=word[:j]+"*"+word[j+1:]\n for neiword in nei[pattern]:\n if neiword not in visit:\n visit.add(neiword)\n q.append(neiword)\n count+=1\n return 0 \n ```\n # please upvote me it would encourage me alot\n | 5 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
127: Solution with step by step explanation | word-ladder | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe time complexity of this algorithm is O(M^2 * N), where M is the length of each word and N is the total number of words in the list. The space complexity is also O(M^2 * N) due to the use of the set and queue.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n # Create a set of words for faster lookup\n wordSet = set(wordList)\n if endWord not in wordSet:\n return 0\n \n # Initialize queue with the beginWord and set of visited words\n queue = deque([(beginWord, 1)])\n visited = set([beginWord])\n \n while queue:\n # Dequeue the word and its level\n word, level = queue.popleft()\n \n # Iterate over each character in the word\n for i in range(len(word)):\n # Iterate over all possible lowercase letters\n for c in \'abcdefghijklmnopqrstuvwxyz\':\n # Skip if the character is the same as in the original word\n if c == word[i]:\n continue\n \n # Create the new word by replacing the character at index i\n newWord = word[:i] + c + word[i+1:]\n \n # Check if the new word is in the wordSet and has not been visited before\n if newWord in wordSet and newWord not in visited:\n # Check if the new word is the endWord\n if newWord == endWord:\n return level + 1\n \n # Enqueue the new word and its level\n queue.append((newWord, level + 1))\n \n # Add the new word to the set of visited words\n visited.add(newWord)\n \n # No transformation sequence exists\n return 0\n\n``` | 6 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
95% fast python, with comments and explanation | word-ladder | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n if endWord not in wordList:\n return 0\n nei = collections.defaultdict(list) #to create a dictionary with empty list \n wordList.append(beginWord)\n #adjacency list with pattern eg, hit: *it, h*t, hi* \n for word in wordList:\n for i in range(len(word)):\n pattern = word[:i] + "*" + word[i+1:]\n nei[pattern].append(word)\n \n res = 1 #since begin word is starting point so 1 length is starting\n q = deque([beginWord])\n visit = set([beginWord]) \n\n #bfs \n while q:\n for i in range(len(q)):\n word = q.popleft()\n if word == endWord:\n return res\n for j in range(len(word)):\n pattern = word[:j] + "*"+ word[j+1:] #generating patterns as above\n for nbr in nei[pattern]:\n if nbr not in visit:\n visit.add(nbr)\n q.append(nbr)\n res+=1\n return 0 #if we did not find any sequence\n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
o(n) solution,using string hashing,hashmap,bfs | word-ladder | 0 | 1 | # Intuition\ntry doing brute force\n\n# Approach\n1>Go for brute force\n2>use bfs as memoization.\n3>use hashing for matching and changing string.\n\n# Complexity\n- Time complexity:\nlength of wordList(o(n))\n\n- Space complexity:\nspace of the dictionary i.e. o(n)\n\n# Code\n```\nfrom collections import deque\ndef hashword(word):\n h=0\n c=1\n for i in word:\n h+=c*(ord(i)-97)\n c=c*26\n return h\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n d={}\n for i in range(len(wordList)):\n d[hashword(wordList[i])]=0\n h=hashword(beginWord)\n q=deque()\n q.append(h)\n f=hashword(endWord)\n q=deque()\n q.append([h,1])\n if h in d:\n d[h]=1\n while q:\n x=q.popleft()\n h=x[0]\n ans=x[1]\n if h==f:\n return ans\n c=1\n for i in range(10):\n for j in range(26):\n y=h-(((h%(c*26))//c)*c)+(c*j)\n if y in d:\n if d[y]==0:\n d[y]=1\n q.append([y,ans+1])\n c=c*26\n return 0\n\n\n\n \n``` | 7 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
📌 Python3 BFS | word-ladder | 0 | 1 | ```\nfrom string import ascii_lowercase\n\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n wordList = set(wordList)\n \n queue = [(beginWord,1)]\n \n while queue:\n curr, count = queue.pop(0)\n if curr == endWord:\n return count\n for i in range(len(curr)):\n for c in ascii_lowercase:\n x = curr[:i] + c + curr[i+1:]\n if x in wordList:\n queue.append((x, count+1))\n wordList.remove(x)\n \n return 0\n``` | 2 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Algorithm Explained | BFS | HASHSET | | word-ladder | 1 | 1 | # BFS\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSo, in a typicall Breadth-First-Search we utilize the queue and it\'s going to store each string that in our sequence & then we also going to have integer value called changes which will be eventually return from our function, which will keep track how many changes do we have in the sequence.\n\nSo, we intialize our queue that have starting word inside of it i.e. "be", then our changes variable is going to start at 1, this is because at minimum we going to have starting word in our minimum. And finally we have a set which will keep track\'s of node that have been visited, in this case we just keeping track of string that we have already added inside our queue.\n```\nqueue = ["be" ]\nchanges = 1\nset = ["be" ]\n```\nSo, to start of our bfs, we take "be" off from our queue & we can only change one character at a time. So, first we gonna check by changing the character b, if we can form another word inside our word list.\n\nSo, we try ae, which is not in our word list. Then, be is already in our set, so we can\'t use that. Now we try ce and we have that word inside our word list. With that means add ce in our queue.\n\nThen we check de, fe and so on............ until we get to me which is inside our word list, so we add me inside our word list as well.\n\nSo, all that way we check all the way down to ze and there is no other words that we add by changing b to another character.\n\n# Complexity\n- Time complexity: o(n2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int ladderLength(String beginWord, String endWord, List<String> wordList) {\n HashSet<String> validWords = new HashSet<>(wordList),visited = new HashSet<>();\n visited.add(beginWord);\n Queue<Node> que = new LinkedList<>();\n que.add(new Node(beginWord,1));\n while(!que.isEmpty()){\n Node t = que.poll();\n if(t.word.equals(endWord)) return t.moves;\n for(int i=0;i<t.word.length();i++)\n for(int j=\'a\';j<=\'z\';j++){\n char tarr[] = t.word.toCharArray();\n tarr[i]=(char)j;\n String tw =String.valueOf(tarr);\n if(validWords.contains(tw) && !visited.contains(tw)){\n visited.add(tw);\n que.add(new Node(tw,t.moves+1));\n }\n }\n }return 0;\n }\n}\n```\n```\nclass Node{\n String word;\n int moves;\n Node(String w,int m){\n word=w;\n moves=m;\n }\n}\n``` | 2 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Minimal Explanation, using BFS | word-ladder | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe sub each character of the current word with every character in the letters, if the new word matches a word in wordList, we add it to the exploration queue, and delete it from the wordList (to avoid infinite loops).\n\n******\n### Note: \nWe are searching all the possible word combinations only 1x. We don\'t put the same word in the queue twice.\n\n# Complexity\n- Time complexity: $$O(N * M * 26)$$\nWhere N = size of wordList Array and M = word length of words present in the wordList.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$ O( N )$$ for the queue, where n is the size of wordList.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n# Code\n```\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n from collections import deque\n from string import ascii_lowercase\n word_set = set(wordList)\n\n q = deque()\n q.append((beginWord,1))\n\n\n while len(q)>0:\n word,cost = q.popleft()\n \n # found the target word?\n if word == endWord:\n return cost\n\n # All the characters of the current word\n for i in range(len(beginWord)):\n original_ch = word[i]\n\n # swapping that character\n for ch in ascii_lowercase:\n word = word[:i] + ch + word[i+1:]\n\n # we only add acceptable words.\n if word in word_set:\n word_set.remove(word)\n q.append((word,cost+1))\n # redeeming the original current word for more swapping\n word = word[:i] + original_ch + word[i+1:]\n \n return 0\n\n```\n\n\n:-) | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Intuitive solution without the wildcard logic, only 9% faster though | word-ladder | 0 | 1 | ```\nclass Solution:\n def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:\n \n """\n approach:\n 1. make the adjacency list\n 2. run bfs\n """\n wordList.insert(0, beginWord)\n wordList = set(wordList)\n visitedDic = {}\n \n if endWord not in wordList:\n return 0\n \n for i in wordList:\n visitedDic[i]=0\n \n dic = defaultdict(list)\n \n for i in (wordList):\n diff = self.helper(i,wordList)\n \n dic[i]=diff\n \n # now we need to do the BFS\n q = collections.deque() # POP(0) is O(N) is normal list, in deque it is O(1)\n q.append(beginWord)\n ans = 0\n \n while q:\n size = len(q)\n ans += 1\n for i in range(size):\n curr = q.popleft()\n visitedDic[curr] = 1\n \n if curr == endWord:\n return ans\n \n for j in dic[curr]:\n if visitedDic[j]==0:\n q.append(j)\n return 0\n \n \n \n def helper(self, s, wordList):\n diff = 0\n l = set()\n for i in range(len(s)):\n for j in \'abcdefghijklmnopqrstuvwxyz\':\n temp = s[0:i]+j+s[i+1:]\n # temp[i] = j\n # word = \'\'.join(temp)\n if temp!=s and temp in wordList:\n l.add(temp)\n\n return l\n```\n\n\n```\n50 / 50 test cases passed.\nStatus: Accepted\nRuntime: 1313 ms\nMemory Usage: 18.8 MB\n``` | 1 | A **transformation sequence** from word `beginWord` to word `endWord` using a dictionary `wordList` is a sequence of words `beginWord -> s1 -> s2 -> ... -> sk` such that:
* Every adjacent pair of words differs by a single letter.
* Every `si` for `1 <= i <= k` is in `wordList`. Note that `beginWord` does not need to be in `wordList`.
* `sk == endWord`
Given two words, `beginWord` and `endWord`, and a dictionary `wordList`, return _the **number of words** in the **shortest transformation sequence** from_ `beginWord` _to_ `endWord`_, or_ `0` _if no such sequence exists._
**Example 1:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log ", "cog "\]
**Output:** 5
**Explanation:** One shortest transformation sequence is "hit " -> "hot " -> "dot " -> "dog " -> cog ", which is 5 words long.
**Example 2:**
**Input:** beginWord = "hit ", endWord = "cog ", wordList = \[ "hot ", "dot ", "dog ", "lot ", "log "\]
**Output:** 0
**Explanation:** The endWord "cog " is not in wordList, therefore there is no valid transformation sequence.
**Constraints:**
* `1 <= beginWord.length <= 10`
* `endWord.length == beginWord.length`
* `1 <= wordList.length <= 5000`
* `wordList[i].length == beginWord.length`
* `beginWord`, `endWord`, and `wordList[i]` consist of lowercase English letters.
* `beginWord != endWord`
* All the words in `wordList` are **unique**. | null |
Solution | longest-consecutive-sequence | 1 | 1 | ```C++ []\nint a[100000];\n\nint init = [] {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n ofstream out("user.out");\n for (string s; getline(cin, s); out << \'\\n\') {\n if (s.length() == 2) {\n out << 0;\n continue;\n }\n int n = 0;\n for (int _i = 1, _n = s.length(); _i < _n; ++_i) {\n bool _neg = false;\n if (s[_i] == \'-\') ++_i, _neg = true;\n int v = s[_i++] & 15;\n while ((s[_i] & 15) < 10) v = v * 10 + (s[_i++] & 15);\n if (_neg) v = -v;\n a[n++] = v;\n }\n sort(a, a + n);\n int ans = 0;\n for (int i = 0; i < n;) {\n int i0 = i;\n for (++i; i < n && a[i - 1] + 1 >= a[i]; ++i);\n ans = max(ans, a[i - 1] - a[i0] + 1);\n }\n out << ans;\n }\n out.flush();\n exit(0);\n return 0;\n}();\n\nclass Solution {\npublic:\n int longestConsecutive(vector<int>) { return 999; }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n longest = 0\n num_set = set(nums)\n\n for n in num_set:\n if (n-1) not in num_set:\n length = 1\n while (n+length) in num_set:\n length += 1\n longest = max(longest, length)\n \n return longest\n```\n\n```Java []\nclass Solution {\n public int longestConsecutive(int[] nums) {int result = 0;\n if (nums.length > 0) {\n if (nums.length < 1000) {\n Arrays.sort(nums);\n int current = 0;\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] != nums[i - 1]) {\n if (nums[i] - nums[i - 1] == 1) {\n current++;\n } else {\n if (current + 1 > result) {\n result = current + 1;\n }\n current = 0;\n }\n }\n }\n if (current + 1 > result) {\n result = current + 1;\n }\n } else {\n int min = Integer.MAX_VALUE;\n int max = Integer.MIN_VALUE;\n for (int num : nums) {\n if (num > max) {\n max = num;\n }\n if (num < min) {\n min = num;\n }\n }\n byte[] bits = new byte[max - min + 1];\n for (int num : nums) {\n bits[num - min] = 1;\n }\n int current = 0;\n for (byte bit : bits) {\n if (bit > 0) {\n current++;\n } else {\n if (current > result) {\n result = current;\n }\n current = 0;\n }\n }\n if (current > result) {\n result = current;\n }\n }\n }\n return result;\n }\n}\n```\n | 459 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
✅Python3 || C++|| Java✅[Intervals,Greedy and DP] without any sort | longest-consecutive-sequence | 1 | 1 | Let\'s break down the code and its logic in more detail:\n\n1. `std::unordered_map<int, std::pair<int, int>> mp;`\n\n- `mp` is an unordered map used to store intervals (ranges) of consecutive numbers. Each key represents the right endpoint of an interval, and the corresponding value is a pair `(r, l)` where `r` is the right endpoint and `l` is the left endpoint of the interval.\n2. `std::unordered_map<int, bool> bl;`\n\n- `bl` is an unordered map used to keep track of whether an element `i` has been visited. If an element has been visited, its corresponding value in this map will be `true;` otherwise, it will be `false.`\n3. `int mx = 0;`\n\n- `mx` is a variable that keeps track of the maximum length of consecutive sequence found.\n4. The main loop iterates through each element `i` in the input `nums` array.\nInside the loop:\na. `if (bl[i]) { continue; }`\nIf the current element `i` has already been visited, skip it and continue to the next iteration of the loop.\nb. `bl[i] = true;`\nMark the current element `i` as visited by setting its corresponding value in the `bl` map to `true`.\nc. Initialize `l` and `r` to the current element `i`, representing the left and right endpoints of the current interval.\nd. Check if there is an interval with the right endpoint `i + 1` in the `mp` map using `mp.find(i + 1)`. If such an interval exists, update the right endpoint `r` to the right endpoint of that interval.\ne. Similarly, check if there is an interval with the right endpoint `i - 1` in the `mp` map using `mp.find(i - 1)`. If such an interval exists, update the left endpoint `l` to the left endpoint of that interval.\nf. Update the `mp` map:\nSet `mp[r]` to a pair `(r, l)`, indicating the interval with right endpoint `r` and left endpoint l.\nSet `mp[l]` to the same pair `(r, l)`.\ng. Calculate the length of the current consecutive sequence as `r - l + 1` and update the maximum length `mx` if this length is greater than the current maximum.\n\n5. Finally, return the maximum length mx, which represents the length of the longest consecutive sequence found in the input array.\nExplanation from chatgpt. The solution is from me \uD83D\uDE07.\n# Code\n<iframe src="https://leetcode.com/playground/PaQPcr82/shared" frameBorder="0" width="800" height="500"></iframe>\n\n | 58 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
97% Faster Python3 easy O(n) solution with explanation | longest-consecutive-sequence | 0 | 1 | # Intuition\nFor every element we need to check if it has a sequence. If yes, what are it\'s sequential numbers and sequence\'s length? Also, when we visit a number, since we know it\'s sequential numbers, we can skip checking them.\n\nUsually a search operation like `in` takes longer time on lists vs sets. Average search time on Set is usually O(1) and unlike lists we don\'t have to worry about iterating through duplicates as set values are unique.\n\n# Approach\n* Convert the list to set.\n* We can safely assume that if the current maximum possible sequence length >= number of unvisited numbers, it is the longest sequence in given list.\n* So we can keep searching for longest possible sequences until we hit this condition.\n* As you visit a number keep deleting them from set, so you don\'t have to check twice. Check consecutive sequence of the number in the set, delete them as you visit and save the highest number of that sequence.\n* Similarly now you check for the presence of it\'s preceding sequential numbers and find the lowest number of that sequence.\n* When you subtract the highest and lowest numbers of a sequence, you get sequence\'s length.\n* Update the max, and repeat the steps until your max sequence length >= number of unvisited integers in set (length of set since you deleted visited numbers).\n\n# Complexity\n- Time complexity: $$O(n)$$\n - Conversion of list to set `numSet = set(nums)\n` is linear time *O(n)*.\n - In worst case scenario where each element in `nums` is unique and doesn\'t have any sequences, each number is only visited once, which is also linear time *O(n)*. \n - Ignore the constants and you get ***O(n)** where, n = length of list*.\n\n\n- Space complexity: $$O(n)$$\n - `numSet` requires space, which is ***O(n)** where, n = number of unique numbers in list*.\n\n\n# Code\n```\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n numSet = set(nums)\n maxSeqLen = 0\n while maxSeqLen < len(numSet):\n num = numSet.pop()\n longest = num+1\n while longest in numSet:\n numSet.remove(longest)\n longest += 1\n num = num-1\n while num in numSet:\n numSet.remove(num)\n num -= 1\n maxSeqLen = max(maxSeqLen, longest-num-1)\n return maxSeqLen\n \n``` | 6 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Easy if you just store the different states | longest-consecutive-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: nlogn\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n if len(nums) == 0:\n return 0\n nums.sort()\n prev_num = nums[0]\n max_size = 1\n current_size = 1\n for i in nums:\n if (prev_num+1) == i:\n current_size +=1 \n if current_size > max_size:\n max_size = current_size\n elif prev_num == i:\n pass\n else:\n current_size = 1\n prev_num = i\n return max_size\n \n``` | 0 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Python easy O(n) solution | longest-consecutive-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nAdd numbers into a set.\nIterate through the list and for each element do the following verifications:\n\n1. Is this element an element that starts a sequence? To do that, just check if element-1 is in the set.\n2. If the element is a starting element, then check how far it goes (used a while loop for that, just run while(element+1 in set))\n3. If the created sequence is longer than the current longest sequence, than change variable value.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n numSet = set(nums)\n longest = 0\n\n for n in nums:\n if n-1 in numSet:\n continue\n \n currentSequenceSize = 1\n\n while (n+currentSequenceSize) in numSet:\n currentSequenceSize += 1\n\n longest = max(currentSequenceSize, longest)\n \n return longest\n\n\n\n \n``` | 2 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
😍 Simplest Python solution with O(n) time complexity and O(n) space complexity | longest-consecutive-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPython solution with a simple algorithm to find solution in O(n) time complexity with O(n) space complexity. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Convert list to set using inbuilt set function.\n2. Create low and high integer to store low and high values in ongoing sequence and assign low and high value to current value.\n3. Run a while loop that continues till high + 1 or low - 1 is present in uniques set.\n * If `low - 1` is present in uniques, decrease value of low by 1, and remove `low - 1` element from uniques.\n * If `high + 1` is present in uniques, increase value of high by 1. and remove `high + 1` element from uniques.\n4. As we keep on iterating, we will be left with empty set, thus stopping our while loop.\n\n> Note that **in** operator in case of set has a time complexity of O(1) only.\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n```python3\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n uniques = set(nums)\n max_length = 0\n\n while uniques:\n low = high = uniques.pop()\n \n while low - 1 in uniques or high + 1 in uniques:\n if low - 1 in uniques:\n uniques.remove(low - 1)\n low -= 1\n \n if high + 1 in uniques:\n uniques.remove(high + 1)\n high += 1\n\n max_length = max(high - low + 1, max_length)\n\n return max_length\n``` | 31 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Easy To Understand | Python Solution | longest-consecutive-sequence | 0 | 1 | \n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def longestConsecutive(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n if not nums:\n return 0 # If the input list is empty, return 0 as there is no consecutive sequence.\n \n nums = list(set(nums)) # Remove duplicates by converting the list to a set and back to a list.\n nums.sort() # Sort the list to ensure elements are in ascending order.\n\n max_count = 1 # Initialize the max_count to 1 since a single number is a consecutive sequence of length 1.\n count = 1 # Initialize the count to 1 for the current consecutive sequence.\n\n for i in range(1, len(nums)):\n if nums[i] == nums[i - 1] + 1:\n count += 1\n else:\n max_count = max(max_count, count)\n count = 1\n\n return max(max_count, count) # Return the maximum of max_count and count.\n\n``` | 1 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
📌 Python solution keeping track of current max and current count | longest-consecutive-sequence | 0 | 1 | ```\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n nums = sorted(set(nums))\n \n cur_max = 0\n cur_count = 0\n prev = None\n for i in nums:\n if prev is not None:\n if prev+1 == i:\n cur_count += 1\n else:\n cur_max = max(cur_max, cur_count)\n cur_count = 1\n else:\n cur_count += 1\n prev = i\n return max(cur_max, cur_count)\n``` | 3 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Python3 | C++ | Brute-force > Better > Optimal | Full Explanation | longest-consecutive-sequence | 0 | 1 | - Approach\n - Brute-force\n - For each element count its consecutive elements present in the array\n - Time Complexity: $O(n^3)$\n - Space Complexity: $O(1)$\n - Better\n - Sort the array and check for consecutive elements\n - Time Complexity: $O(nlogn)$\n - Space Complexity: $O(1)$\n - Optimal\n - Add all nums in set\n - Then we will run a for loop and check for any number(x) if it is the starting number of the consecutive sequence by checking if the set contains (x-1) or not\n - If x is the starting number of the consecutive sequence we will keep searching for the numbers y = x+1, x+2, x+3, \u2026.. And stop at the first y which is not present in the set\n - Time Complexity: $O(n)$ (assuming set takes O(1) to search)\n - Space Complexity: $O(n)$\n\n```python\n# Python3\n# Brute-force Solution\nclass Solution:\n def find(self, nums, a):\n for i in nums:\n if i == a:\n return True\n return False\n\n def longestConsecutive(self, nums: List[int]) -> int:\n if len(nums) == 0: return 0\n maxi = 1\n for i in nums:\n conseq = 1\n while self.find(nums, i + conseq):\n conseq += 1\n maxi = max(maxi, conseq)\n return maxi\n```\n\n```python\n# Python3\n# Better Solution\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n if len(nums) == 0: return 0\n nums.sort()\n maxi = 1\n cur_max = 1\n for i in range(1, len(nums)):\n if nums[i] == nums[i-1]:\n continue\n if nums[i] == nums[i-1]+1:\n cur_max += 1\n else:\n cur_max = 1\n maxi = max(maxi, cur_max)\n return maxi\n```\n\n```python\n# Python3\n# Optimal Solution\nclass Solution:\n def longestConsecutive(self, nums: List[int]) -> int:\n if len(nums) == 0: return 0\n uset = set(nums)\n maxi = 1\n for i in uset:\n if i-1 in uset:\n continue\n else:\n conseq = 1\n while i + conseq in uset:\n conseq += 1\n maxi = max(maxi, conseq)\n return maxi\n```\n\n```cpp\n// C++\n// Optimal Solution\n#include <bits/stdc++.h>\nclass Solution{\n public:\n int findLongestConseqSubseq(int arr[], int N)\n {\n unordered_set<int> uset;\n for (int i = 0; i < N; i++) {\n uset.insert(arr[i]);\n }\n int maxi = 1;\n for (auto num: uset) {\n if (uset.count(num - 1)) {continue;}\n int conseq = 1;\n while (uset.count(num + conseq)) {\n conseq++;\n }\n maxi = max(maxi, conseq);\n }\n return maxi;\n }\n};\n``` | 3 | Given an unsorted array of integers `nums`, return _the length of the longest consecutive elements sequence._
You must write an algorithm that runs in `O(n)` time.
**Example 1:**
**Input:** nums = \[100,4,200,1,3,2\]
**Output:** 4
**Explanation:** The longest consecutive elements sequence is `[1, 2, 3, 4]`. Therefore its length is 4.
**Example 2:**
**Input:** nums = \[0,3,7,2,5,8,4,6,0,1\]
**Output:** 9
**Constraints:**
* `0 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Best Python3 Solution || Upto 99 % Faster || Easy to Read || Commented | sum-root-to-leaf-numbers | 0 | 1 | # Intuition\nWe take the paths into a list and then make path number (take 1 Path and make it the number like 1->2->3 into 123) and finally sum of the all those path numbers.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def sumNumbers(self, root: Optional[TreeNode]) -> int:\n # Create list of Paths\n final = []\n def trav(root,path):\n if not root:\n return None\n\n if not root.left and not root.right:\n final.append(path)\n \n if root.left:\n trav(root.left, path + [root.left.val])\n \n if root.right:\n trav(root.right, path + [root.right.val])\n\n # You get the Path as list in final\n trav(root,[root.val])\n #print(final)\n\n # to get the total path sum Simple math \n total = 0\n for path in final:\n s = 0\n # take 1 Path and make it the number like 1->2->3 into 123\n for i in path:\n s = (s*10) + i\n # Add the path number to total\n total += s\n \n return total\n \n\n\n\n``` | 1 | You are given the `root` of a binary tree containing digits from `0` to `9` only.
Each root-to-leaf path in the tree represents a number.
* For example, the root-to-leaf path `1 -> 2 -> 3` represents the number `123`.
Return _the total sum of all root-to-leaf numbers_. Test cases are generated so that the answer will fit in a **32-bit** integer.
A **leaf** node is a node with no children.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 25
**Explanation:**
The root-to-leaf path `1->2` represents the number `12`.
The root-to-leaf path `1->3` represents the number `13`.
Therefore, sum = 12 + 13 = `25`.
**Example 2:**
**Input:** root = \[4,9,0,5,1\]
**Output:** 1026
**Explanation:**
The root-to-leaf path `4->9->5` represents the number 495.
The root-to-leaf path `4->9->1` represents the number 491.
The root-to-leaf path `4->0` represents the number 40.
Therefore, sum = 495 + 491 + 40 = `1026`.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 9`
* The depth of the tree will not exceed `10`. | null |
Recursion | DFS | Beats 90% | sum-root-to-leaf-numbers | 0 | 1 | # Complexity\n- Time complexity: O(V + E)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(h)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n ans = 0\n def sumNumbers(self, root: Optional[TreeNode]) -> int: \n def dfs(root,tmp):\n if root:\n if not root.left and not root.right :\n self.ans += tmp*10 + root.val\n else:\n dfs(root.left, tmp*10 + root.val)\n dfs(root.right, tmp*10 + root.val)\n dfs(root,0)\n return self.ans\n\n \n \n``` | 1 | You are given the `root` of a binary tree containing digits from `0` to `9` only.
Each root-to-leaf path in the tree represents a number.
* For example, the root-to-leaf path `1 -> 2 -> 3` represents the number `123`.
Return _the total sum of all root-to-leaf numbers_. Test cases are generated so that the answer will fit in a **32-bit** integer.
A **leaf** node is a node with no children.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 25
**Explanation:**
The root-to-leaf path `1->2` represents the number `12`.
The root-to-leaf path `1->3` represents the number `13`.
Therefore, sum = 12 + 13 = `25`.
**Example 2:**
**Input:** root = \[4,9,0,5,1\]
**Output:** 1026
**Explanation:**
The root-to-leaf path `4->9->5` represents the number 495.
The root-to-leaf path `4->9->1` represents the number 491.
The root-to-leaf path `4->0` represents the number 40.
Therefore, sum = 495 + 491 + 40 = `1026`.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 9`
* The depth of the tree will not exceed `10`. | null |
DFS Solution Python | surrounded-regions | 0 | 1 | \n# Code\n```\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n def dfs(i,j,mark):\n nonlocal board\n if( (i < 0) or (j < 0 ) or (i >= m) or (j >= n) ):\n print(f\'returned on {i,j}\')\n return False;\n elif(board[i][j] == \'X\' or board[i][j] == mark):\n return True\n else:\n res = True\n board[i][j] = mark\n for d in direc:\n x = i+d[0]\n y = j+d[1]\n # if i put res before the function call \n # then once res has been set to false the \n # function call will never happen\n res = dfs(x,y,mark) and res; \n return res\n \n direc = [[-1,0],[0,-1],[1,0],[0,1]]\n m , n = len(board), len(board[0]);\n \n for i in range(0,m):\n for j in range(0,n):\n if( board[i][j] == "O" ):\n print(f\'checkng on i:{i} j:{j}\')\n if( dfs(i , j,\'1\') ): #check if not touching the boundry\n dfs(i,j,"X") # if not then mark x \n \n #Unmarks 1\'s to O\'s if the area touched the boundry\n for i in range(0,m):\n for j in range(0,n):\n if(board[i][j] == \'1\'): board[i][j] = "O"\n\n``` | 2 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Binbin eternal god in DFS | surrounded-regions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n rows = len(board)\n columns = len(board[0])\n def mark_edge (row,col):\n if row < 0 or row > rows -1 or col < 0 or col > columns -1 or board[row][col] != "O":\n return\n board[row][col] = "B"\n mark_edge(row-1,col)\n mark_edge(row+1,col)\n mark_edge(row,col-1)\n mark_edge(row,col+1)\n\n \n for row in range(rows):\n for col in range(columns):\n if board[row][col] == "O":\n if row == 0 or row == rows -1 or col == 0 or col == columns-1:\n mark_edge(row,col) \n for row in range(rows):\n for col in range(columns):\n if board[row][col] != "B":\n board[row][col] = "X"\n if board[row][col] == "B":\n board[row][col] = "O"\n\n``` | 1 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Easy to understand PYTHON solution beats 93% with proper comments | surrounded-regions | 0 | 1 | # Intuition\nReverse Thinking - we will use this way of thinking.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach \n\n1.) First we will write a DFS method.\n2.) Then we will capture unsurrounded region(O->T) changing all the O\'s to T in the border rows and columns and their adjacent values.\n3.) Then we will capture surrounded region(O->x) changing all the O\'s to X\n4.) In the end we will again uncapture unsurrounded region(T->O) that we did in the first place and change all the "T" into O once again \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n rows, cols= len(board), len(board[0])\n\n def capture(r,c): \n if (r<0 or r==rows or c<0 or c==cols or board[r][c]!="O"):\n return \n board[r][c]="T"\n capture(r+1,c)\n capture(r-1,c)\n capture(r,c+1)\n capture(r,c-1)\n\n #(DFS)capture unsurrounded region(0->T)\n for r in range(rows):\n for c in range(cols):\n if board[r][c]=="O" and (r==0 or r==rows-1 or c==0 or c==cols-1):\n capture(r,c)\n\n #capture surrounded region(0->x)\n for r in range(1,rows-1):\n for c in range(1,cols-1):\n if board[r][c]=="O":\n board[r][c]="X" \n\n #uncapture unsurrounded region(T->0)\n for r in range(rows):\n for c in range(cols):\n if board[r][c]=="T":\n board[r][c]="O" \n``` | 1 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Click this if you're confused | surrounded-regions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition is simple: a region of "O"s is unsurrounded if one of its "O"s is at the border. We can solve this problem simply by iterating the border tiles and traversing all "O" regions, treat them as connected graphs. These "O" regions are unsurrounded. We can temporarily set these tiles to "T". The remaining "O"s in the board are surrounded since they have no path to the border.\n\nWe simply convert these surrounded "O"s to "X"s and then convert the "T"s back to "O"s.\n\n# Complexity\n- Time complexity: $O(n \\times m)$ since we traverse the entire grid 3 times.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n \\times m)$ because in worst case, if the whole grid is "O"s, we may have a recursive stack $n \\times m$ deep\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def solve(self, board: List[List[str]]) -> None:\n n_rows, n_cols = len(board), len(board[0])\n\n # all "O"s in the border are unsurrounded, we find these, then traverse adjacent "O"s\n def dfs(r, c):\n if r < 0 or r == n_rows or c < 0 or c == n_cols or board[r][c] != "O":\n return\n \n board[r][c] = "T" # these are unsurrounded\n dfs(r + 1, c)\n dfs(r - 1, c)\n dfs(r, c + 1)\n dfs(r, c - 1)\n \n for r in range(n_rows):\n for c in range(n_cols):\n if board[r][c] == "O" and (r in [0, n_rows - 1] or c in [0, n_cols - 1]):\n dfs(r, c)\n\n for r in range(n_rows):\n for c in range(n_cols):\n if board[r][c] == "O": # surrounded, since can\'t reach border\n board[r][c] = "X"\n \n for r in range(n_rows):\n for c in range(n_cols):\n if board[r][c] == "T":\n board[r][c] = "O"\n\n\n``` | 2 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Python Solution (DFS) | surrounded-regions | 0 | 1 | # Code\n```\nclass Solution:\n def solve(self, board):\n nrows = len(board)\n ncols = len(board[0])\n not_surrounded = set()\n\n def dfs(row, col):\n if row not in range(nrows) or col not in range(ncols) or board[row][col] == "X" or (row, col) in not_surrounded:\n return\n\n not_surrounded.add((row, col))\n\n dfs(row+1, col)\n dfs(row-1, col)\n dfs(row, col+1)\n dfs(row, col-1)\n\n\n \n for row in range(nrows):\n for col in range(ncols):\n if (row == 0 or col == 0 or row == nrows-1 or col == ncols-1) and (row, col) not in not_surrounded and board[row][col] == "O":\n dfs(row, col)\n\n for row in range(nrows):\n for col in range(ncols):\n if (row, col) not in not_surrounded:\n board[row][col]="X"\n \n \n\n \n\n\n\n``` | 1 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Easy Explained Solution With 🏞 (Images) | surrounded-regions | 1 | 1 | \n\n\n\n\n\n\n\n\ncode\n```python\nfrom collections import deque\n\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n \n o = "O"\n \n n = len(board) \n m = len(board[0])\n\n Q = deque()\n \n for i in range(n):\n if board[i][0] == o:\n Q.append((i,0))\n if board[i][m-1] == o:\n Q.append((i, m-1))\n \n for j in range(m):\n if board[0][j] == o:\n Q.append((0,j))\n if board[n-1][j] == o:\n Q.append((n-1, j))\n \n def inBounds(i,j):\n return (0 <= i < n) and (0 <= j < m)\n \n while Q:\n i,j = Q.popleft()\n board[i][j] = "#"\n \n for ii, jj in [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]:\n if not inBounds(ii, jj):\n continue\n if board[ii][jj] != o:\n continue\n Q.append((ii,jj))\n board[ii][jj] = \'#\'\n \n for i in range(n):\n for j in range(m):\n if board[i][j] == o:\n board[i][j] = \'X\'\n elif board[i][j] == \'#\':\n board[i][j] = o\n\n```\n | 116 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
130: Solution with step by step explanation | surrounded-regions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe algorithm works as follows:\n\n1. We first handle the edge cases by checking if the board is empty. If it is, we return without doing anything.\n\n2. We define a helper function dfs that performs a depth-first search to mark all O\'s that are connected to the current O at the coordinates (i, j). We mark each visited cell with the character \'#\'. The function takes two arguments i and j that represent the row and column indices of the current cell.\n\n3. We then iterate over all the edges of the board and mark all the O\'s on the edges as visited. We start with the left and right edges by iterating over all the rows and then move on to the top and bottom edges by iterating over all the columns.\n\n4. We then iterate over all the cells of the board and flip all unvisited O\'s to X\'s and all marked O\'s back to O\'s.\n\n5. The time complexity of this algorithm is O(mn), where m and n are the number of rows and columns in the board.\n\n6. This algorithm is fast and efficient as it only visits each cell once and performs a constant amount of work for each cell.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n if not board:\n return # empty board\n m, n = len(board), len(board[0])\n \n def dfs(i: int, j: int) -> None:\n """\n Depth-first search function to mark all O\'s connected to the current O (i, j).\n """\n if i < 0 or i >= m or j < 0 or j >= n or board[i][j] != \'O\':\n return\n \n board[i][j] = \'#\' # mark as visited\n \n # recursively mark all adjacent O\'s\n dfs(i+1, j)\n dfs(i-1, j)\n dfs(i, j+1)\n dfs(i, j-1)\n \n # mark all O\'s on the edges\n for i in range(m):\n dfs(i, 0)\n dfs(i, n-1)\n \n for j in range(n):\n dfs(0, j)\n dfs(m-1, j)\n \n # flip unvisited O\'s to X\'s and marked O\'s back to O\'s\n for i in range(m):\n for j in range(n):\n if board[i][j] == \'O\':\n board[i][j] = \'X\'\n elif board[i][j] == \'#\':\n board[i][j] = \'O\'\n\n``` | 5 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Fast and very easy to understand | DFS from borders | O(N) time | O(N) Space | surrounded-regions | 0 | 1 | This problem could be solved two ways:\n1. Identify all isolated `\'O\'` cells and mark them as `\'X\'` then.\n2. Mark all accessible from boarders `\'O\'` and then turn all inaccessible ones into `\'X\'`.\n\nThis solution is about the **second way**.\n\nTo mark cells as "reachable", algorithm changing their values to `\'R\'` instead of `\'O\'`.\n\n1. Follow through left and right borders of the board and look for `\'O\'` cells. If found recursevly mark all accessible `\'O\'` cells as `\'R\'`.\n2. Follow through top and bottom borders of the board and do the same.\n3. Follow through the whole board and flip `\'O\'` -> `\'X\'` and `\'R\'` -> `\'O\'`\n\n**Time compexity:** `O(N * M), where N is the height of the board and M is the width of the board. Since in the wrost case algorithm processes all cells twice and O(2 * N * M) == O(N * M)`\n**Space complexity:** `O(N * M)` \u2014 only the fixed set of variables of the fixed size is allocated and all \'marks\' are done \'in-place\' **BUT** recursive function calls are stored on the stack and use N * M memory in the worst case. There are no "real" allocations since the stack is allocated when the program starts, but space complexity is about all **used space**. (Thanks for the [@kim_123 comment](https://leetcode.com/problems/surrounded-regions/discuss/1551810/Fast-and-very-easy-to-understand-or-DFS-from-boarders-or-O(N)-time-or-O(1)-Space/1134588) with the clarifications).\n\n<iframe src="https://leetcode.com/playground/mRtTsxAF/shared" frameBorder="0" width="100%" height="850"></iframe>\n\nThank you for reading this! =) | 53 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Python way - Simple DFS | surrounded-regions | 1 | 1 | \tclass Solution:\n\t\tdef solve(self, mat: List[List[str]]) -> None:\n\t\t\tn=len(mat)\n\t\t\tm=len(mat[0])\n\n\t\t\tdef dfs(i,j):\n\t\t\t\tvisited[i][j]=1\n\t\t\t\tdir = [[-1,0],[0,1],[1,0],[0,-1]]\n\t\t\t\tfor a,b in dir:\n\t\t\t\t\trow = a+i\n\t\t\t\t\tcol = b+j\n\t\t\t\t\tif row>=0 and row<n and col>=0 and col<m and mat[row][col]==\'O\' and not visited[row][col]:\n\t\t\t\t\t\tdfs(row,col)\n\t\t\tvisited = [[0 for _ in range(m)] for i in range(n)]\n\t\t\tfor j in range(m):\n\t\t\t\tif not visited[0][j] and mat[0][j]==\'O\':\n\t\t\t\t\tdfs(0,j)\n\t\t\t\tif not visited[n-1][j] and mat[n-1][j]==\'O\':\n\t\t\t\t\tdfs(n-1,j)\n\t\t\tfor i in range(n):\n\t\t\t\tif not visited[i][0] and mat[i][0]==\'O\':\n\t\t\t\t\tdfs(i,0)\n\t\t\t\tif not visited[i][m-1] and mat[i][m-1]==\'O\':\n\t\t\t\t\tdfs(i,m-1)\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(m):\n\t\t\t\t\tif not visited[i][j] and mat[i][j]==\'O\':\n\t\t\t\t\t\tmat[i][j]=\'X\'\n\t\t\treturn mat | 1 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
(Python) Count Good Nodes in Binary Tree | surrounded-regions | 0 | 1 | # Intuition\nOne approach to solve this problem is to use depth-first search (DFS) to mark all the regions that are not surrounded by \'X\'. The regions that are not marked are the regions that need to be flipped.\n# Approach\n1. First, we check the corner elements of the board (1st row, 1st column, last row, and last column) and mark all the regions that are not surrounded by \'X\' as \'B\' using DFS.\n2. Then, we traverse the entire board and flip all \'O\' to \'X\' and all \'B\' to \'O\'.\n# Complexity\n- Time complexity:\nO(mn), where m is the number of rows and n is the number of columns in the board.\n- Space complexity:\nO(1) since we are modifying the board in place.\n# Code\n```\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n if not board:\n return\n \n m, n = len(board), len(board[0])\n \n # DFS to mark all the regions connected to the border as \'B\'\n def dfs(i, j):\n if 0 <= i < m and 0 <= j < n and board[i][j] == \'O\':\n board[i][j] = \'B\'\n dfs(i+1, j)\n dfs(i-1, j)\n dfs(i, j+1)\n dfs(i, j-1)\n \n for i in range(m):\n dfs(i, 0)\n dfs(i, n-1)\n \n for j in range(1, n-1):\n dfs(0, j)\n dfs(m-1, j)\n \n # Flip all \'O\' in the surrounded regions to \'X\', and restore \'B\' to \'O\'\n for i in range(m):\n for j in range(n):\n if board[i][j] == \'O\':\n board[i][j] = \'X\'\n elif board[i][j] == \'B\':\n board[i][j] = \'O\'\n\n``` | 2 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Easy & Clear Solution Python 3 Beat 99.8% | surrounded-regions | 0 | 1 | \n# Code\n```\nclass Solution:\n def solve(self, b: List[List[str]]) -> None:\n m=len(b)\n n=len(b[0])\n def dfs(i,j):\n if b[i][j]=="O":\n b[i][j]="P"\n if i<m-1:\n dfs(i+1,j)\n if i>0:\n dfs(i-1,j)\n if j<n-1:\n dfs(i,j+1)\n if j>0:\n dfs(i,j-1)\n for i in [0,m-1]:\n for j in range(n):\n dfs(i,j)\n for j in [0,n-1]:\n for i in range(m):\n dfs(i,j)\n for i in range(m):\n for j in range(n):\n if b[i][j]=="O":\n b[i][j]="X"\n for i in range(m):\n for j in range(n):\n if b[i][j]=="P":\n b[i][j]="O"\n\n\n\n \n\n``` | 4 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Easy to understand Python3 Solution | surrounded-regions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n visited=set()\n\n def dfs(x,y):\n if x<0 or x>=len(board) or y<0 or y>=len(board[0]) or board[x][y]=="X" or (x,y) in visited:\n return\n visited.add((x,y))\n dfs(x+1,y)\n dfs(x-1,y)\n dfs(x,y-1)\n dfs(x,y+1)\n\n for i in range(len(board)):\n dfs(i,0)\n dfs(i,len(board[0])-1)\n\n for i in range(len(board[0])):\n dfs(0,i)\n dfs(len(board)-1,i)\n\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j]=="O" and (i,j) not in visited:\n board[i][j]="X"\n \n\n\n\n\n``` | 2 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
Python || 97.64% Faster || BFS || DFS || Two Approaches | surrounded-regions | 0 | 1 | **BFS Approach:**\n```\ndef solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n m=len(board)\n n=len(board[0])\n q=deque()\n for i in range(m):\n for j in range(n):\n if i==0 or i==m-1 or j==0 or j==n-1:\n if board[i][j]==\'O\':\n board[i][j]=\'Y\'\n q.append((i,j)) \n while q:\n a,b=q.popleft()\n for r,c in [(a-1,b),(a+1,b),(a,b-1),(a,b+1)]:\n if 0<=r<m and 0<=c<n and board[r][c]==\'O\':\n board[r][c]="Y"\n q.append((r,c))\n for i in range(m):\n for j in range(n):\n if board[i][j]==\'O\':\n board[i][j]=\'X\'\n elif board[i][j]==\'Y\':\n board[i][j]=\'O\'\n```\n**DFS Approach:**\n```\ndef solve(self, board: List[List[str]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n def dfs(sv):\n a,b=sv[0],sv[1]\n board[a][b]=\'Y\'\n for r,c in [(a-1,b),(a+1,b),(a,b-1),(a,b+1)]:\n if 0<=r<m and 0<=c<n and board[r][c]==\'O\':\n board[r][c]="Y"\n dfs((r,c))\n m=len(board)\n n=len(board[0])\n for i in range(m):\n for j in range(n):\n if i==0 or i==m-1 or j==0 or j==n-1:\n if board[i][j]==\'O\':\n dfs((i,j))\n for i in range(m):\n for j in range(n):\n if board[i][j]==\'O\':\n board[i][j]=\'X\'\n elif board[i][j]==\'Y\':\n board[i][j]=\'O\'\n```\n\n**An upvote will be encouraging** | 6 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, _capture all regions that are 4-directionally surrounded by_ `'X'`.
A region is **captured** by flipping all `'O'`s into `'X'`s in that surrounded region.
**Example 1:**
**Input:** board = \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "O ", "X "\],\[ "X ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Output:** \[\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "X ", "X ", "X "\],\[ "X ", "O ", "X ", "X "\]\]
**Explanation:** Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.
**Example 2:**
**Input:** board = \[\[ "X "\]\]
**Output:** \[\[ "X "\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 200`
* `board[i][j]` is `'X'` or `'O'`. | null |
MOST OPTIMIZED PYTHON SOLUTION | palindrome-partitioning | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,s,st):\n if i>=len(s):\n self.lst.append(tuple(st))\n return \n for j in range(i,len(s)):\n if s[i:j+1]==\'\'.join(reversed(s[i:j+1])):\n st.append(s[i:j+1])\n x=self.dp(j+1,s,st)\n st.pop()\n return\n def partition(self, s: str) -> List[List[str]]:\n self.lst=[]\n self.dp(0,s,[])\n return self.lst\n``` | 2 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Polindromic Partioning(Python3).. | palindrome-partitioning | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nCheck the every possible partition in the string and check whether the given string is polindrome or not...\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n res=[]\n part=[]\n def dfs(i):\n if(i>=len(s)):\n res.append(part.copy())\n return \n for j in range(i,len(s)):\n #partitioning the string....\n if(self.is_polin(s,i,j)):\n part.append(s[i:j+1])\n dfs(j+1)\n part.pop()\n dfs(0)\n return res\n def is_polin(self,s,l,r):\n while(l<r):\n if(s[l]!=s[r]):\n return False\n l+=1\n r-=1\n return True\n``` | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Python3 Simple Recursive Solution | palindrome-partitioning | 0 | 1 | **Note: This approach could be sped up with dp** (I was just too lazy)\n\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n n = len(s)\n ans = []\n if n == 0:\n return [[]]\n for i in range(1, n + 1):\n if s[:i] != s[:i][::-1]:\n continue\n cur = self.partition(s[i:])\n for j in range(len(cur)):\n ans.append([s[:i]] + cur[j])\n return ans\n``` | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Solution | palindrome-partitioning | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<string>> partition(string s) {\n vector<vector<string>> pars;\n vector<string> par;\n partition(s, 0, par, pars);\n return pars;\n }\nprivate: \n void partition(string& s, int start, vector<string>& par, vector<vector<string>>& pars) {\n int n = s.length();\n if(start==n){\n pars.push_back(par);\n }else{\n for(int i = start ; i < n ;i ++){\n if(isPalindrome(s,start,i)){\n par.push_back(s.substr(start,i-start+1));\n partition(s,i+1,par,pars);\n par.pop_back();\n }\n }\n }\n }\n \n bool isPalindrome(string& s, int l, int r) {\n while (l < r) {\n if (s[l++] != s[r--]) {\n return false;\n }\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n n = len(s)\n dp = [[] for _ in range(n + 1)]\n dp[n] = [[]]\n for begin in range(n - 1, -1, -1):\n for end in range(begin + 1, n + 1):\n candidate = s[begin:end]\n if candidate == candidate[::-1]:\n for each in dp[end]:\n new_each = [candidate]\n new_each.extend(each)\n dp[begin].append(new_each)\n return dp[0] \n```\n\n```Java []\nclass Solution {\n int n;\n boolean[][] is_palindrome;\n String[][] substrings;\n\n List<List<String>> ans;\n\n void FindSubstrings(int ind, ArrayList<String> list) {\n if (ind == n) {\n ans.add(new ArrayList<String>(list));\n return;\n }\n\n for (int i = ind + 1; i <= n; i++) {\n if (!is_palindrome[ind][i]) continue;\n list.add(substrings[ind][i]);\n FindSubstrings(i, list);\n list.remove(list.size() - 1);\n }\n }\n\n public List<List<String>> partition(String s) {\n n = s.length();\n is_palindrome = new boolean[n + 1][n + 1];\n substrings = new String[n + 1][n + 1];\n for (int i = 0; i < n; i++) for (int j = i + 1; j <= n; j++) {\n substrings[i][j] = s.substring(i, j);\n is_palindrome[i][j] = IsPalindrome(substrings[i][j]);\n }\n\n ans = new ArrayList<List<String>>();\n FindSubstrings(0, new ArrayList<String>());\n return ans;\n }\n\n boolean IsPalindrome(String s) {\n int lower = 0;\n int higher = s.length() - 1;\n while (lower < higher) {\n if (s.charAt(lower) != s.charAt(higher)) return false;\n lower++;\n higher--;\n }\n return true;\n }\n}\n```\n | 211 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
✅ [Python] Simple Recursion || Detailed Explanation || Easy to Understand | palindrome-partitioning | 0 | 1 | **PLEASE UPVOTE if you like** \uD83D\uDE01 **If you have any question, feel free to ask.** \n* Find answer recursively and memory trick can save some time\n* traverse and check every prefix `s[:i]` of `s`\n\t* if prefix `s[:i]` is a palindrome, then process the left suffix `s[i:]` recursively\n\t* since the suffix `s[i:]` may repeat, **the memory trick can save some time**\n\n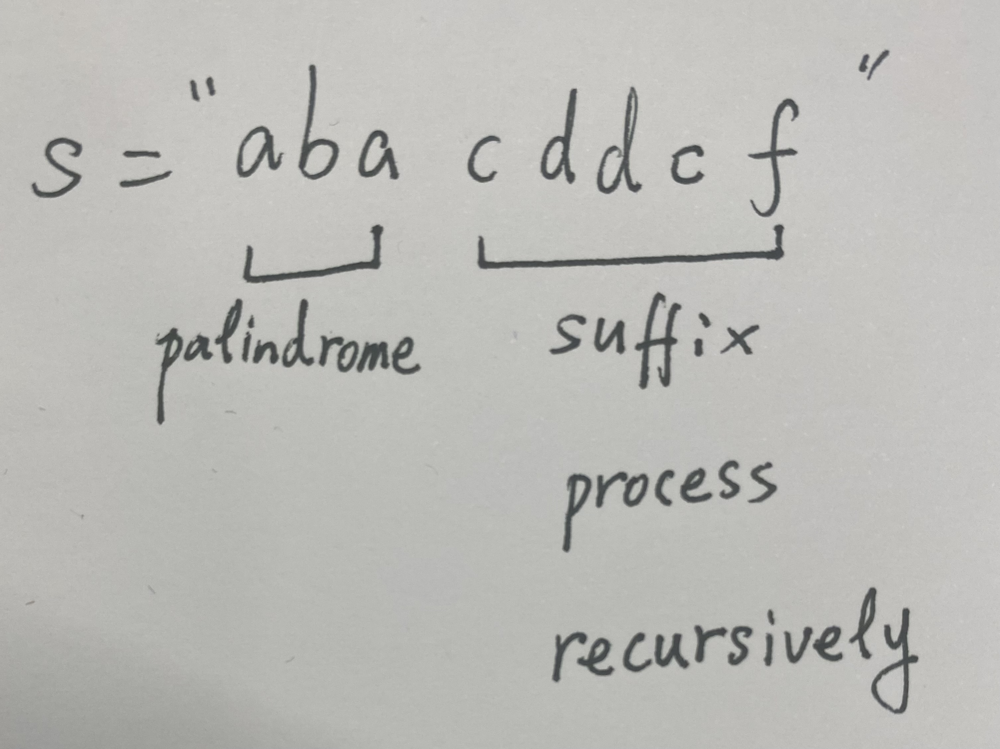\n\n\n```\nTime Complexity: O(N * (2 ^ N))\nSpace Complexity: O(N * (2 ^ N))\n```\n\n**Python3**\n```\nclass Solution(object):\n @cache # the memory trick can save some time\n def partition(self, s):\n if not s: return [[]]\n ans = []\n for i in range(1, len(s) + 1):\n if s[:i] == s[:i][::-1]: # prefix is a palindrome\n for suf in self.partition(s[i:]): # process suffix recursively\n ans.append([s[:i]] + suf)\n return ans\n```\n**Python**\n```\nclass Solution(object):\n def __init__(self):\n self.memory = collections.defaultdict(list)\n \n def partition(self, s):\n if not s: return [[]]\n if s in self.memory: return self.memory[s] # the memory trick can save some time\n ans = []\n for i in range(1, len(s) + 1):\n if s[:i] == s[:i][::-1]: # prefix is a palindrome\n for suf in self.partition(s[i:]): # process suffix recursively\n ans.append([s[:i]] + suf)\n self.memory[s] = ans\n return ans\n```\n**PLEASE UPVOTE if you like** \uD83D\uDE01 **If you have any question, feel free to ask.** | 262 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Python3 || Easy to understand solution || Explained & Commented || With Sketch | palindrome-partitioning | 0 | 1 | # Explanation\nThe main trick is backtracking.\nFor each position of the string, you have at most 2 options: You either 1) check if the current substring is a palindrome and add it to the partition list, or 2) you don\'t add it to the list\n\nThe current substring is the letter of the current position plus the substring from the previous step.\n\nFor #1, you first need to check if the current substring is a palindrome. If it is, you can add it to the current partition list, and reset the substring to an empty substring (since you add it to the list)\n\nFor #2, since you didn\'t add the current substring to the list, the list remains the same and the substring goes to the next step as a "leftover"\n\nYou reach the base case once your current position is outside of the string. In that case, if you have no "leftover" string, that means that every letter of the string is inside the list as a palindrome, so you can add that partition to the results list. Otherwise, if you have a "leftover" substring, that means it\'s either not a palindrome or you\'ve added it to the list before.\n\nSketch trying to explain:\n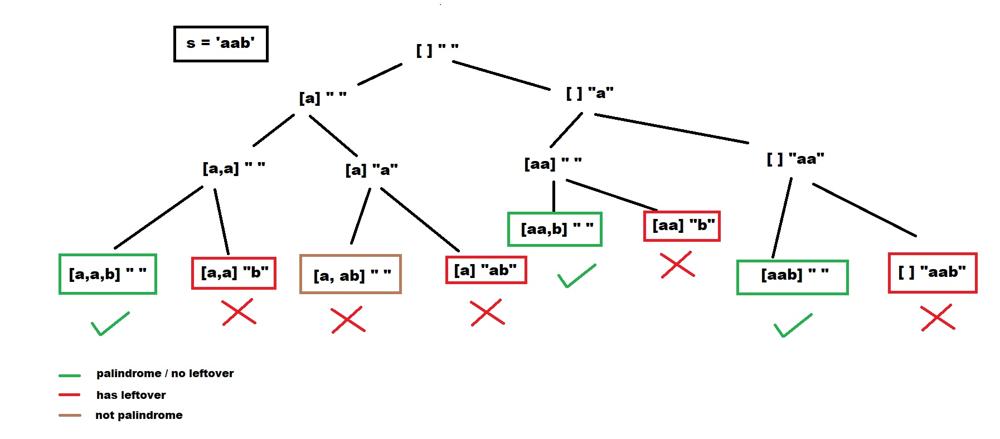\n\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n res = []\n\n def dfs(i, part, palind):\n if i >= len(s):\n # if no leftover, add it to result\n if not palind: res.append(part)\n return\n \n substring = palind + s[i]\n # check if it is palindrome\n if substring == substring[::-1]:\n # 1) add palindrome to partition list and reset substring\n dfs(i + 1, part + [substring], "")\n \n # 2) don\'t add to partition list and keep the substring\n dfs(i + 1, part, substring)\n \n dfs(0, [], "")\n return res\n``` | 0 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
the best solution ever all -Python | palindrome-partitioning | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n if not s: return [[]]\n ans = []\n for i in range(1, len(s) + 1):\n if s[:i] == s[:i][::-1]: \n for add in self.partition(s[i:]): \n ans.append([s[:i]] + add)\n return ans\n\n\n\n``` | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
131: Solution with step by step explanation | palindrome-partitioning | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Use a backtracking approach to generate all the possible palindrome partitions.\n- For each character of the string, consider all possible substrings starting at the current character and check if it\'s a palindrome.\n- If it\'s a palindrome, add it to the current partition and recursively find all partitions that can be formed from the rest of the string.\n- When we have traversed the whole string, add the current partition to the final result.\n\nAlgorithm:\n\n1. Create a list to store the final result.\n2. Create an empty list to store the current partition.\n3. Write a recursive function to generate all the possible partitions.\n4. In the function, check if the current partition is a valid palindrome partition or not. If it\'s valid, add the current partition to the final result.\n5. For each character of the string, consider all possible substrings starting at the current character and check if it\'s a palindrome. If it\'s a palindrome, add it to the current partition and recursively find all partitions that can be formed from the rest of the string.\n6. When we have traversed the whole string, add the current partition to the final result.\n7. Return the final result.\n\n# Complexity\n- Time complexity:\nO(n*(2^n)) where n is the length of the string s. In the worst case, we have 2^n possible partitions, and for each partition, we need to check if it\'s a valid palindrome partition or not, which takes O(n) time.\n\n- Space complexity:\nO(n) where n is the length of the string s. The maximum depth of the recursion tree is n. At each level of the recursion tree, we create a new partition of length n. Therefore, the space complexity is O(n).\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n res = [] # final result to store all possible palindrome partitions\n curr_partition = [] # to store the current partition\n \n def is_palindrome(s, i, j):\n # check if substring s[i:j+1] is a palindrome or not\n while i < j:\n if s[i] != s[j]:\n return False\n i += 1\n j -= 1\n return True\n \n def backtrack(start):\n # base case: if we have traversed the whole string, add the current partition to the final result\n if start >= len(s):\n res.append(curr_partition.copy())\n return\n \n # for each character of the string, consider all possible substrings starting at the current character\n for end in range(start, len(s)):\n # check if the substring is a palindrome or not\n if is_palindrome(s, start, end):\n # if it\'s a palindrome, add it to the current partition and recursively find all partitions that can be formed from the rest of the string\n curr_partition.append(s[start:end+1])\n backtrack(end+1)\n curr_partition.pop() # backtrack to remove the last added substring\n \n backtrack(0) # start the recursive function from the first character of the string\n return res # return the final result\n\n``` | 3 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Python || 97.14% Faster || Backtracking || Easy | palindrome-partitioning | 0 | 1 | ```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n def valid(ip):\n if ip==ip[-1::-1]:\n return True\n return False\n \n def solve(ip,op):\n if ip==\'\':\n ans.append(op[:])\n return\n for i in range(1,len(ip)+1):\n if valid(ip[:i]):\n op.append(ip[:i])\n solve(ip[i:],op)\n op.pop()\n ans=[]\n solve(s,[])\n return ans \n```\n**An upvote will be encouraging** | 2 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Palindrome Partitioning. Python3 | palindrome-partitioning | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n ans = []\n\n def isPalindrome(s: str) -> bool:\n return s == s[::-1]\n\n def dfs(s: str, j: int, path: List[str], ans: List[List[str]]) -> None:\n if j == len(s):\n ans.append(path)\n return\n\n for i in range(j, len(s)):\n if isPalindrome(s[j: i + 1]):\n dfs(s, i + 1, path + [s[j: i + 1]], ans)\n\n dfs(s, 0, [], ans)\n return ans\n\n``` | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
python3, simple dfs (659 ms, faster than 85.12%) | palindrome-partitioning | 0 | 1 | ERROR: type should be string, got "https://leetcode.com/submissions/detail/883354080/ \\nRuntime: **659 ms**, faster than 85.12% of Python3 online submissions for Palindrome Partitioning. \\nMemory Usage: 28.2 MB, less than 99.36% of Python3 online submissions for Palindrome Partitioning. \\n```\\nclass Solution:\\n def partition(self, s: str) -> List[List[str]]:\\n partitions, lst, l = [], [([], 0)], len(s)\\n while lst: ## dfs\\n pals, i = lst.pop()\\n for j in range(i+1, l+1):\\n sub = s[i:j]\\n if sub==sub[::-1]: ## if sub is a palindrome\\n if j==l: ## reach the end\\n partitions.append(pals+[sub])\\n else:\\n lst.append((pals+[sub], j))\\n return partitions\\n```\\n" | 5 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Click this if you're confused. | palindrome-partitioning | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA valid partitioning of `s` results in substrings of `s` that are palindromes. Palindromes are easy. What if we were to just return all distinct partitions of `s` with the constraint that a substring had to at least be one character?\n\nFor example, given `s = "aab"` we would explore partitions possible starting with index 0 of `s`.\nWhen `i` = 0, we can have initial substrings: `["a", "aa", "aab"]`.\nSay we explore further with initial substring "a". The remaining characters of `s` are "ab", so our next substrings would be `["a", "ab"]`.\nEventually we would have partitions: `["a", "a", "b"], ["a", "ab"], ["aa", "b"], ["aab"]`.\n\nWe use DFS to explore all possible partitions given a previous partition until we reach the end of `s`. Then we add this entire partition to our `output` and backtrack to explore other partitions.\n\nSo the only difference when we add the constraint that our substrings must be palindromes is to check if they are palindromes before traversing deeper in our decision tree of "where to place the next partition".\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use a simple DFS that takes index `i`. If `i >= len(s)` we\'ve finished partitioning the entire string `s` and so we append our `part` to `res`.\n\nIn DFS we start from `i` and loop incrementally via `j` till `len(s)`. For chars in `s` from `i` to `j` we check if it\'s a palindrome using two pointers. If it is, we partition here by appending `s[i:j+1]` to `part`, then call DFS with parameter `j + 1`, and afterwards we `part.pop()` to backtrack and explore other substrings.\n\nWe call DFS with index 0 in the main function and return `res`.\n\n# Complexity\n- Time complexity: $O(2^n * n)$ since we can think of the decisions as "partition at this char" or "continue substring and move on" for each char in `s`.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n^2)$ since each partition is size `n` and worst case there are `n` partitions.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def is_palindrome(self, s, l ,r):\n # simple two pointers palindrome\n while l < r:\n if s[l] != s[r]:\n return False\n l, r = l + 1, r - 1\n return True\n\n def partition(self, s: str) -> List[List[str]]:\n res, part = [], []\n\n def dfs(i):\n # our last substring was a valid palindrome\n if i >= len(s):\n res.append(part[::])\n return\n \n # partitioned substrings must be palindromes\n for j in range(i, len(s)):\n if self.is_palindrome(s, i, j):\n part.append(s[i:j+1])\n dfs(j+1)\n part.pop() # backtrack\n \n dfs(0)\n return res\n\n\n``` | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Python3: Simple Backtracking Approach | palindrome-partitioning | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem DP can be considered but as we are not calculating number of solutions but to return all the possible solutions.So it is better to backtrack. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Consider a function palindrome to check whether a string is palindrome or not.\n- an other function dfs to backtrack with parameters \'i\' -> current position and curr -> current solution\n- first condition if postion \'i\' is the last position of the string we got our complete traversal and append to the solution\n- else traverse the string from \'i\' to len(s) and if current partition \'sol\' is palindrome backtrack again for all possible solutions.\n- In a nutshell we get all the possible solutions just by backtracking.\n\n# Complexity\n- Time complexity: O(2^n)*O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> For Each character in the input string the algorithm generates 2 recursive calls, one for including the character and one for not including it.For this O(2^n).To check whether the string is palindrome or not we have O(n) time complexity.\n\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->The list stores single list for a current partition.So in the worst case if each character is considered a palindrome then the time complexity will be O(n).\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n lst = []\n def palindrome(a):\n return a == a[::-1]\n def dfs(i,curr):\n if i == len(s):\n lst.append(curr)\n return \n for j in range(i,len(s)):\n sol = s[i:j+1]\n if palindrome(sol):\n dfs(j+1, curr + [sol] )\n return \n dfs(0,[])\n return lst\n \n\n```\nps: s[::-1] easy way to reverse a string | 27 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
🎉3 Solutions🎉 ||Deep Explaination👀🤔👀||Backtracking✅|| C++|| Java || Python3 | palindrome-partitioning | 1 | 1 | # Approach : Backtracking\n```\nExample - xxyy\n```\n\n\n# Complexity :\n- Time Complexity :- BigO(N*2^N)\n- Space Complexity :- BigO(N)\n\n# Request \uD83D\uDE0A :\n- If you find this solution easy to understand and helpful, then Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n# Code [C++]: \uD83D\uDD25\uD83D\uDD25\n```\nclass Solution {\npublic:\n vector<vector<string>> partition(string s) {\n vector<vector<string>> res; // which will be our answer\n vector<string> path; // as we are generating list everythime, so at the end this will be our list\n helper(0, s, path, res); // calling to recursion function start from index 0 and string s\n return res;\n }\n // Entire recursive function, that generates all the partition substring\n void helper(int index, string s, vector<string> &path, vector<vector<string>> &res){\n // Base Condition, which means when we have done partition at the end (n), then add it to our ultimate result\n if(index == s.size()){\n res.push_back(path);\n return;\n }\n // Let\'s talk about partition\n for(int i = index; i < s.size(); i++){\n if(isPalindrome(s, index, i)){ // what we are checking over here is, if we partition the string from index to i Example-(0, 0) is palindrome or not\n path.push_back(s.substr(index, i - index + 1)); // take the substring and store it in our list & call the next substring from index + 1\n helper(i + 1, s, path, res); // as we have done for (0, 0) then our next will be from (1)\n path.pop_back(); // please make sure you remove when you backtrack. \n // Why? Because let say i had partion y, so when i go back. I can\'t have yy\n }\n }\n }\n bool isPalindrome(string s, int start, int end){ // A simple palindromic function start from 0 go till end. And basically keep on checking till they don\'t cross. \n while(start <= end){\n if(s[start++] != s[end--]) return false;\n }\n return true;\n }\n};\n```\n# Code [Java]:\uD83D\uDD25\uD83D\uDD25\n```\nclass Solution {\n public List<List<String>> partition(String s) {\n List<List<String>> res = new ArrayList<>(); // which will be our answer\n List<String> path = new ArrayList<>(); // as we are generating list everythime, so at the end this will be our list\n helper(0, s, path, res); // calling to recursion function start from index 0 and string s\n return res;\n }\n // Entire recursive function, that generates all the partition substring\n public void helper(int index, String s, List<String> path, List<List<String>> res){\n // Base Condition, which means when we have done partition at the end (n), then add it to our ultimate result\n if(index == s.length()){\n res.add(new ArrayList<>(path));\n return;\n }\n // Let\'s talk about partition\n for(int i = index; i < s.length(); i++){\n if(isPalindrome(s, index, i)){ // what we are checking over here is, if we partition the string from index to i Example-(0, 0) is palindrome or not\n path.add(s.substring(index, i + 1)); // take the substring and store it in our list & call the next substring from index + 1\n helper(i + 1, s, path, res); // as we have done for (0, 0) then our next will be from (1)\n path.remove(path.size() - 1); // please make sure you remove when you backtrack. \n // Why? Because let say i had partion y, so when i go back. I can\'t have yy\n }\n }\n } \n \n public boolean isPalindrome(String s, int start, int end){ // A simple palindromic function start from 0 go till end. And basically keep on checking till they don\'t cross. \n while(start <= end){\n if(s.charAt(start++) != s.charAt(end--)) return false;\n }\n return true;\n }\n}\n```\n# Code [Python3]:\uD83D\uDD25\uD83D\uDD25\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n palindro = []\n path = []\n self.helper(0, s, path, palindro)\n return palindro\n\n def helper(self, index, s, path, palindro):\n if index == len(s):\n palindro.append(path[:])\n return\n for i in range(index, len(s)):\n if self.is_palindro(s, index, i):\n path.append(s[index:i+1])\n self.helper(i+1, s, path, palindro)\n path.pop()\n\n def is_palindro(self, s, start, end):\n while start <= end:\n if s[start] != s[end]:\n return False\n start += 1\n end -= 1\n return True\n\n```\ncredits to [@hi-malik](https://leetcode.com/hi-malik/) for helping me out | 16 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Python solution using recursion beats 90% time complexity :-) | palindrome-partitioning | 0 | 1 | # Complexity\n- Time complexity: O(2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n def checkPalindrome(str, startIndex, lastIndex):\n while startIndex <= lastIndex:\n if str[startIndex] != str[lastIndex]:\n return False\n startIndex += 1\n lastIndex -= 1\n return True\n def palindromePartition(index, ds, output, str):\n if index == len(str):\n output.append(ds[:])\n return\n for i in range(index, len(str)):\n if checkPalindrome(str, index, i):\n ds.append(str[index:i+1])\n palindromePartition(i+1, ds, output, str)\n ds.pop()\n output = []\n ds = []\n palindromePartition(0, ds, output, s)\n return output\n``` | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
using backtracking, with explanation | palindrome-partitioning | 0 | 1 | \'\'\'\nclass Solution:\n def partition(self, s: str) -> List[List[str]]:\n\t\n \n partition=[] # for storing each partition\'s substrings\n index=0\n res=[] # each individual partitions will store in res\n self.helper(s,partition,index,res)\n return res\n \n def helper(self,s,partition,index,res):\n if index>=len(s): # crossing the last index\n res.append(partition.copy())\n return \n \n for i in range(index,len(s)):\n if self.ispali(index,i,s): # if the starting partition is palindrome only we will check the further palindromes in a remaining string in the current partition.\n partition.append(s[index:i+1])\n self.helper(s,partition,i+1,res)\n partition.pop()\n \n def ispali(self,start,end,s): # checking whether current substring is palindrome or not\n while start<end:\n if s[start]!=s[end]:\n return False\n start=start+1\n end=end-1\n return True\n\t\t\n\t\t\n\t\t\n**PLEASE UPVOTE **\n \n | 1 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
🔥Python🔥Backtracking🔥Beats 91.1% in runtime, 78.51% in memory🔥 | palindrome-partitioning | 0 | 1 | \n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe partition method of the Solution class is solving the problem of finding all possible partitions of a given input string s into palindromes.\nIt first creates a 2D boolean array isPalindrome of the same length as the input string s, to keep track of whether a substring of s is a palindrome or not.\nIt then uses a nested loop to fill in the isPalindrome array by checking if a substring from start to end is a palindrome or not.\nThe outer loop iterates over all possible substring lengths, starting from 2 and ending at the length of the input string. The inner loop iterates over all possible starting positions for the substring.\n\nIt then uses a recursive helper function helper to explore all possible partitions of the input string s. The function takes the current index of the string, the current partition path, and the overall results as input.\nIt then loops over all possible end positions of the current partition, checking if the substring from the current index to the end position is a palindrome. If it is, it adds the substring to the current partition path and recursively calls the helper function with the updated index and partition path.\nOnce the index reaches the end of the input string, it adds the current partition path to the overall results.\n\nFinally, the partition method initializes an empty list results and calls the helper function with the initial index of 0 and an empty partition path, returning the results list containing all possible partitions of the input string s into palindromes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used in the partition method of the Solution class is a backtracking approach. It uses a recursive helper function to explore all possible partitions of the input string s into palindromes.\n\nThe method starts by creating a 2D boolean array isPalindrome of the same length as the input string s, to keep track of whether a substring of s is a palindrome or not.\nIt then uses a nested loop to fill in the isPalindrome array by checking if a substring from start to end is a palindrome or not.\nThe outer loop iterates over all possible substring lengths, starting from 2 and ending at the length of the input string. The inner loop iterates over all possible starting positions for the substring.\n\nNext, it uses a recursive helper function helper to explore all possible partitions of the input string s.\nThe function takes the current index of the string, the current partition path, and the overall results as input.\nIt then loops over all possible end positions of the current partition, checking if the substring from the current index to the end position is a palindrome (by checking the isPalindrome array).\nIf it is, it adds the substring to the current partition path and recursively calls the helper function with the updated index and partition path.\nOnce the index reaches the end of the input string, it adds the current partition path to the overall results.\n\nFinally, the partition method initializes an empty list results and calls the helper function with the initial index of 0 and an empty partition path, returning the results list containing all possible partitions of the input string s into palindromes.\n\nThe backtracking approach allows us to explore all possible partitions of the input string s into palindromes by generating all possible partitions recursively, and then backtracking when a partition doesn\'t meet the requirements (i.e. a substring is not a palindrome). This allows us to generate all possible partitions without having to check all possible partitions in advance which would be an exponential time complexity.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the partition method of the Solution class is O(n^2) where n is the length of the input string s.\n\nThe first step of the method is to fill the isPalindrome array, which takes O(n^2) time.\nThe nested loop iterates over all possible substrings of s and checks if they are palindromes, which takes O(n^2) time in total.\n\nThe next step is to use the recursive helper function helper to explore all possible partitions of the input string s.\nIn the worst case, the function is called for all possible partitions of the input string, which would take O(n^2) time.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the partition method is O(n^2) as well.\nThe isPalindrome array takes O(n^2) space to store the information about all possible substrings of s being palindrome or not.\nThe recursive calls in the helper function also takes O(n^2) space in the worst case, where all possible partitions are stored in the results list.\n\nTherefore, the time complexity of the partition method is O(n^2) and the space complexity is also O(n^2) where n is the length of the input string s.\n\n# Code\n```\nclass Solution:\n def __init__(self):\n self.isPalindrome = None\n \n def helper(self, s: str, index: int, path: List[str], results: List[List[str]]):\n if index == len(s):\n results.append(path)\n return\n \n for end in range(index, len(s)):\n if self.isPalindrome[index][end]:\n newPath = path[:]\n newPath.append(s[index:end+1])\n self.helper(s, end + 1, newPath, results)\n \n def partition(self, s: str) -> List[List[str]]:\n self.isPalindrome = [[False for i in range(len(s))] for j in range(len(s))]\n \n for i in range(len(s)):\n self.isPalindrome[i][i] = True\n \n for length in range(2, len(s) + 1):\n for start in range(len(s) - length + 1):\n end = start + length - 1\n if s[start] == s[end]:\n if length == 2:\n self.isPalindrome[start][end] = True\n else:\n self.isPalindrome[start][end] |= self.isPalindrome[start + 1][end - 1]\n \n results = []\n self.helper(s, 0, [], results)\n return results\n\n``` | 3 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
[Python] ✅🔥 Clear, Simple Backtracking Solution! | palindrome-partitioning | 0 | 1 | ## **Please upvote/favourite/comment if you like this solution!**\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s):\n i, j = 0, len(s)-1\n while i <= j:\n if s[i] != s[j]:\n return False\n i += 1\n j -= 1\n return True\n\n def backtrack(self, s, combo, partitions):\n temp = list(combo)\n if self.isPalindrome(s):\n if tuple(temp+[s]) not in partitions:\n partitions.add(tuple(temp+[s]))\n for i in range(1,len(s)):\n if self.isPalindrome(s[:i]):\n self.backtrack(s[i:],tuple(temp+[s[:i]]),partitions)\n\n def partition(self, s: str) -> List[List[str]]:\n partitions = set()\n self.backtrack(s,(),partitions)\n answer = []\n for p in partitions:\n answer.append(list(p))\n return answer\n```\n\n# Complexity\n- Time complexity: $$O(2^N \\cdot N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 4 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
Python Code with Documentation - 99% runtime O(n^2) solution | palindrome-partitioning | 0 | 1 | # Intuition\nWe can break down the problem into two sub-problems:\n1. Find all palindromes in the string\n2. Starting from the start of the string, combine palindromes together to form all the valid partitions\n\n# Approach\nWe can complete 1. using the same approach as in https://leetcode.com/problems/longest-palindromic-substring/solutions/3877628/bottom-up-breadth-first-search/\nThen we can complete 2 using dynamic programming:\n1. Look at all palindromes that start at index 0\n2. Find all the possible partitions after the end of that palindrome\n3. Combine all the partitions\n\n# Complexity\n- Time complexity: $O(n^2)$\n\n- Space complexity: $O(n^2)$ since we create a hashmap that stores all the palindromes\n\n# Code\n```\nfrom functools import cache\nfrom collections import deque\n\nclass Solution:\n """\n 1. Find all palindromes, store them in a map of {start_index: [end index such that start_index:end_index is a palindrome]}\n 2. Starting with start_index = 0, for each of the end_indexes, recursively partition the string at that index to get all possible partitions\n """\n\n def find_all_palindromes(self) -> None:\n """Populate the palindrome_map with all palindromes\n O(n^2): for each possible palindrome size (1 to n), we loop over at most n items in the list and check if they are palindromes\n """\n self.palindrome_map: dict[int, list[int]] = {i : [i] for i in range(len(self.s))} # all elements of size 1 are palindromes\n palindromes = deque(((i, i) for i in range(len(self.s))))\n \n # Append palindromes of length 2\n for i in range(len(self.s) - 1):\n if self.s[i] == self.s[i+1]:\n palindromes.append((i, i+1))\n self.palindrome_map[i].append(i+1)\n \n # Get all palindromes possible\n while palindromes:\n start_index, end_index = palindromes.popleft()\n new_start = start_index - 1\n new_end = end_index + 1\n if 0 <= new_start and new_end < len(self.s) and self.s[new_start] == self.s[new_end]:\n palindromes.append((new_start, new_end))\n self.palindrome_map[new_start].append(new_end)\n\n @cache\n def find_partitions(self, start_index: int = 0) -> list[list[str]]:\n """Return all palindrome partitions from this start_index\n O(n^2): thanks to memoization, at each point the list we loop over n other solutions (which are only calculated once)"""\n if start_index == len(self.s):\n return [[]]\n \n partitions: list[list[str]] = []\n for end_index in self.palindrome_map[start_index]:\n palin_str = self.s[start_index:end_index + 1]\n for partition in self.find_partitions(end_index + 1):\n partitions.append([palin_str] + partition)\n return partitions\n\n def partition(self, s: str) -> list[list[str]]:\n """O(n^2): One O(n^2) algorithm is called, followed by another O(n^2) algorithm"""\n self.s = s\n self.find_all_palindromes()\n return self.find_partitions()\n\n``` | 2 | Given a string `s`, partition `s` such that every substring of the partition is a **palindrome**. Return _all possible palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab"
**Output:** \[\["a","a","b"\],\["aa","b"\]\]
**Example 2:**
**Input:** s = "a"
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lowercase English letters. | null |
[Python] Simple Top-down DP Solution O(N^2) | palindrome-partitioning-ii | 0 | 1 | # Approach\nWe first precompute the valid palindromes from start to end value. We use the idea that if s[i:j] is a palindrome, then s[i+1:j-1] must be a palindrome and s[i] must equal s[j]. After this our recursive function will just iterate through the string from the previous cut to the end and perform a cut at every valid index.\n\n# Code\n```\nclass Solution:\n def minCut(self, s: str) -> int:\n dp = [[0 for _ in range(len(s))] for _ in range(len(s))]\n for length in range(len(s)):\n for start in range(len(s)-length):\n if length == 0 or (s[start] == s[start+length] and (dp[start+1][start+1+length-2] or length == 1)):\n dp[start][start+length] = 1\n else:\n dp[start][start+length] = 0\n\n @functools.cache\n def minPalindromes(prevCut):\n if prevCut == len(s):\n return 0\n cut = math.inf\n for x in range(prevCut, len(s)):\n if dp[prevCut][x]:\n cut = min(cut, minPalindromes(x+1))\n return cut+1\n return minPalindromes(0)-1\n \n```\n\n# Complexity\n- Time complexity: O(N^2)\n - precomputing palindromes and the recursive helper are both O(N^2)\n\n- Space complexity: O(N^2)\n - recursive stack and dp array use O(N^2) space each | 3 | Given a string `s`, partition `s` such that every substring of the partition is a palindrome.
Return _the **minimum** cuts needed for a palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab "
**Output:** 1
**Explanation:** The palindrome partitioning \[ "aa ", "b "\] could be produced using 1 cut.
**Example 2:**
**Input:** s = "a "
**Output:** 0
**Example 3:**
**Input:** s = "ab "
**Output:** 1
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase English letters only. | null |
Python || MCM DP || Recursion->Tabulation | palindrome-partitioning-ii | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(Exponential)\n#Space Complexity: O(n)\nclass Solution1:\n def minCut(self, s: str) -> int:\n def solve(ind):\n if ind==n:\n return 0\n temp=\'\'\n mini=maxsize\n for j in range(ind,n):\n temp+=s[j]\n if temp==temp[-1::-1]:\n cuts=1+solve(j+1)\n mini=min(mini,cuts)\n return mini\n n=len(s)\n return solve(0)-1 \n```\n**We can notice that our function is actually counting an extra partition at the end of the string in each case. For example, the given string is \u201Cabcd\u201D. After doing a partition after \u2018c\u2019 the function will check if a partition can be done after \u2018d\u2019 to check if the last substring i.e. \u2018d\u2019 itself is a palindrome.**\n\n``` \n#Memoization (Top-Down)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n) + O(n)\nclass Solution2:\n def minCut(self, s: str) -> int:\n def solve(ind):\n if ind==n:\n return 0\n if dp[ind]!=-1:\n return dp[ind]\n temp=\'\'\n mini=maxsize\n for j in range(ind,n):\n temp+=s[j]\n if temp==temp[-1::-1]:\n cuts=1+solve(j+1)\n mini=min(mini,cuts)\n dp[ind]=mini\n return dp[ind]\n n=len(s)\n dp=[-1]*n\n return solve(0)-1\n \n#Tabulation (Bottom-Up)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n) \nclass Solution:\n def minCut(self, s: str) -> int:\n n=len(s)\n dp=[-1]*(n+1)\n dp[n]=0\n for i in range(n-1,-1,-1):\n temp=\'\'\n mini=maxsize\n for j in range(i,n):\n temp+=s[j]\n if temp==temp[-1::-1]:\n cuts=1+dp[j+1]\n mini=min(mini,cuts)\n dp[i]=mini\n return dp[0]-1\n```\n**An upvote will be encouraging** | 3 | Given a string `s`, partition `s` such that every substring of the partition is a palindrome.
Return _the **minimum** cuts needed for a palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab "
**Output:** 1
**Explanation:** The palindrome partitioning \[ "aa ", "b "\] could be produced using 1 cut.
**Example 2:**
**Input:** s = "a "
**Output:** 0
**Example 3:**
**Input:** s = "ab "
**Output:** 1
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase English letters only. | null |
132: Solution with step by step explanation | palindrome-partitioning-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo solve this problem, we can use dynamic programming. We can first preprocess the string to determine which substrings are palindromes. Then, we can use dynamic programming to determine the minimum cuts needed to partition the string into palindromic substrings.\n\nHere are the steps:\n\n1. Preprocess the string to determine which substrings are palindromes. We can use a two-dimensional boolean array to store this information. Specifically, dp[i][j] is True if the substring s[i:j+1] is a palindrome, and False otherwise. To fill in this array, we can use a nested loop to iterate over all possible substrings of s, and use a two-pointer approach to check if each substring is a palindrome.\n\n2. Use dynamic programming to determine the minimum cuts needed to partition the string into palindromic substrings. We can use a one-dimensional array cuts to store the minimum cuts needed for the prefix s[0:i]. Specifically, cuts[i] is the minimum number of cuts needed to partition the substring s[0:i] into palindromic substrings. To fill in this array, we can use another nested loop to iterate over all possible lengths j of the last palindrome in the prefix s[0:i]. If the substring s[i-j:i+1] is a palindrome, then we can update the value of cuts[i-j-1] to be the minimum of its current value and cuts[i-j]+1.\n\n3. The final answer is stored in cuts[-1].\n\nThe time complexity of this algorithm is O(n^2), and the space complexity is O(n^2) as well (for the dp array).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCut(self, s: str) -> int:\n n = len(s)\n \n # Step 1: Preprocess the string to determine which substrings are palindromes\n dp = [[False]*n for _ in range(n)]\n for i in range(n):\n dp[i][i] = True\n for i in range(n-1):\n if s[i] == s[i+1]:\n dp[i][i+1] = True\n for l in range(3, n+1):\n for i in range(n-l+1):\n j = i+l-1\n if s[i] == s[j] and dp[i+1][j-1]:\n dp[i][j] = True\n \n # Step 2: Use dynamic programming to determine the minimum cuts needed\n cuts = list(range(n))\n for i in range(1, n):\n if dp[0][i]:\n cuts[i] = 0\n else:\n for j in range(i):\n if dp[j+1][i]:\n cuts[i] = min(cuts[i], cuts[j]+1)\n \n # Step 3: Return the final answer\n return cuts[-1]\n\n``` | 6 | Given a string `s`, partition `s` such that every substring of the partition is a palindrome.
Return _the **minimum** cuts needed for a palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab "
**Output:** 1
**Explanation:** The palindrome partitioning \[ "aa ", "b "\] could be produced using 1 cut.
**Example 2:**
**Input:** s = "a "
**Output:** 0
**Example 3:**
**Input:** s = "ab "
**Output:** 1
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase English letters only. | null |
✔ Python3 Solution | DP | O(n^2) | palindrome-partitioning-ii | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$\n- Space complexity $$O(n)$$\n\n# Code\n```\nclass Solution:\n def minCut(self, S):\n N = len(S)\n dp = [-1] + [N] * N\n for i in range(2 * N - 1):\n l = i // 2\n r = l + (i & 1)\n while 0 <= l and r < N and S[l] == S[r]:\n dp[r + 1] = min(dp[r + 1], dp[l] + 1)\n l -= 1\n r += 1\n return dp[-1]\n``` | 4 | Given a string `s`, partition `s` such that every substring of the partition is a palindrome.
Return _the **minimum** cuts needed for a palindrome partitioning of_ `s`.
**Example 1:**
**Input:** s = "aab "
**Output:** 1
**Explanation:** The palindrome partitioning \[ "aa ", "b "\] could be produced using 1 cut.
**Example 2:**
**Input:** s = "a "
**Output:** 0
**Example 3:**
**Input:** s = "ab "
**Output:** 1
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase English letters only. | null |
✔️ [Python3] ITERATIVE BFS (beats 98%) ,、’`<(❛ヮ❛✿)>,、’`’`,、, Explained | clone-graph | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nTo solve this problem we need two things: \n\n1. BFS to traverse the graph\n2. A hash map to keep track of already visited and already cloned nodes\n\nWe push a node in the queue and make sure that the node is already cloned. Then we process neighbors. If a neighbor is already cloned and visited, we just append it to the current clone neighbors list, otherwise, we clone it first and append it to the queue to make sure that we can visit it in the next tick.\n\nTime: **O(V + E)** - for BFS\nSpace: **O(V)** - for the hashmap\n\nRuntime: 32 ms, faster than **98.18%** of Python3 online submissions for Clone Graph.\nMemory Usage: 14.4 MB, less than **91.72%** of Python3 online submissions for Clone Graph.\n\n```\nclass Solution:\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if not node: return node\n \n q, clones = deque([node]), {node.val: Node(node.val, [])}\n while q:\n cur = q.popleft() \n cur_clone = clones[cur.val] \n\n for ngbr in cur.neighbors:\n if ngbr.val not in clones:\n clones[ngbr.val] = Node(ngbr.val, [])\n q.append(ngbr)\n \n cur_clone.neighbors.append(clones[ngbr.val])\n \n return clones[node.val]\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 321 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
python3 Solution | clone-graph | 0 | 1 | \n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val = 0, neighbors = None):\n self.val = val\n self.neighbors = neighbors if neighbors is not None else []\n"""\n\nclass Solution:\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n oldToNew={}\n def dfs(node):\n if node in oldToNew:\n return oldToNew[node]\n\n copy=Node(node.val)\n oldToNew[node]=copy\n\n for nei in node.neighbors:\n copy.neighbors.append(dfs(nei))\n\n return copy\n\n return dfs(node) if node else None \n``` | 4 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Simple and Easy Solution 🔥🔥🔥 | clone-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val = 0, neighbors = None):\n self.val = val\n self.neighbors = neighbors if neighbors is not None else []\n"""\n\nfrom typing import Optional\nclass Solution:\n def cloneGraph(self, node: Optional[\'Node\']) -> Optional[\'Node\']:\n if not node:\n return None\n \n visited = {}\n \n def dfs(node):\n if node in visited:\n return visited[node]\n \n clone = Node(node.val)\n visited[node] = clone\n \n for neighbor in node.neighbors:\n clone.neighbors.append(dfs(neighbor))\n \n return clone\n \n return dfs(node)\n``` | 1 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Simple and Fast Python Solution | clone-graph | 0 | 1 | # Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val = 0, neighbors = None):\n self.val = val\n self.neighbors = neighbors if neighbors is not None else []\n"""\n\nclass Solution:\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if node == None:\n return None\n nodes = []\n seen = [0]* 101\n nodes.append(0)\n for i in range(100):\n nodes.append(Node(i+1))\n def dfs(n,cp):\n if seen[n.val] == 1:\n return\n seen[n.val] = 1\n if n.neighbors == None:\n cp.neighbors = None\n return\n\n for i in n.neighbors:\n cp.neighbors.append(nodes[i.val])\n dfs(i,nodes[i.val])\n dfs(node,nodes[node.val])\n\n return nodes[node.val]\n\n\n\n\n \n``` | 1 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Click this if you're confused. | clone-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor each node, we must create its copy, then create copies of the neighbors and set our copy\'s "neighbors" property to these copied neighbors. We also must use the neighbors to traverse the graph, so that we can repeat this copy process for each of the original node\'s neighbors.\n\nThe slight issue, is if we do this naively, we will create duplicate copies: one for when a node is the "node", and another for when the node is a "neighbor".\n\nSo we must store our clone nodes in a hashmap and map the original nodes to the copies. If we find that a node has already been copied, we simply return the clone. We can then clone the whole graph simply using "dfs". For each node we return its copy if it exists, otherwise we copy it, store it, then for each of its neighbors we recursively call "dfs", the returns from the "dfs" we append to the current clone\'s "neighbors" property, and finally we return the current clone as well\u2014for its parent dfs call.\n\n# Complexity\n- Time complexity: O(V + 2*E) since for worst case we clone every node and iterate through every edge twice\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V) since the recursive stack will only go as deep as the number of nodes in the worst case (not including space of output)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val = 0, neighbors = None):\n self.val = val\n self.neighbors = neighbors if neighbors is not None else []\n"""\n\nfrom typing import Optional\n\nclass Solution:\n\n def cloneGraph(self, node: Optional[\'Node\']) -> Optional[\'Node\']:\n ntoc = {None: None} # node to copy\n\n def dfs(n):\n if n in ntoc:\n return ntoc[n]\n \n # create copy, search neighbors, return copy\n c = Node(n.val)\n ntoc[n] = c\n for nb in n.neighbors:\n c.neighbors.append(dfs(nb))\n return c\n \n return dfs(node)\n\n\n``` | 1 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Using DFS with Hashmap | clone-graph | 0 | 1 | ```\nclass Solution:\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if not node: return node\n dic={}\n def dfs(node):\n if node in dic:\n return dic[node]\n copy=Node(node.val)\n dic[node]=copy\n for nei in node.neighbors:\n copy.neighbors.append(dfs(nei))\n return copy\n return dfs(node)\n```\n# please upvote me it would encourage me alot\n\n | 3 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Python Elegant & Short | DFS | HashMap | clone-graph | 0 | 1 | # Complexity\n- Time complexity: $$O(V + E)$$\n- Space complexity: $$O(V)$$\n\n# Code\n```\nclass Solution:\n def cloneGraph(self, node: Node | None) -> Node | None:\n return self.dfs(node, {None: None})\n\n def dfs(self, node: Node | None, graph: dict) -> Node | None:\n if node not in graph:\n graph[node] = Node(node.val)\n for ngh in node.neighbors:\n graph[node].neighbors.append(self.dfs(ngh, graph))\n return graph[node]\n\n``` | 3 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
✅✅Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand🔥 | clone-graph | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Approach:\n\n- We can traverse the graph in a BFS manner starting from the given node.\n- For each node we visit, we create a copy of it and add it to a hashmap (or unordered_map) where the key is the original node and the value is the copy node.\n- We also add the original node to a queue to keep track of which nodes we still need to visit.\n- For each neighbor of the current node, we check if we have already visited it. If not, we create a copy of it and add it to the hashmap and the queue.\n- Finally, we connect the copy nodes of each neighbor to the copy node of the current node.\n- Once we have visited all nodes and created their copies, we return the copy of the original node.\n\n# Intuition:\n\n- The problem requires us to create a deep copy of the given graph, where each node in the new graph has the same value as the corresponding node in the original graph, but is a separate instance.\n- We can achieve this by traversing the graph in a BFS manner and creating a copy of each node we visit.\n- To ensure that we don\'t create duplicate copies of the same node, we can use a hashmap to keep track of visited nodes and their copies.\n- Since the graph can have cycles, we need to use a hashmap to ensure that we don\'t get stuck in an infinite loop while traversing the graph.\n- Once we have created the copies of all nodes and connected them in the same way as the original graph, we return the copy of the original node.\n\n\n```Python []\n\nclass Solution:\n \n\n def cloneGraph(self, node):\n if not node:\n return None\n\n visited = {}\n queue = deque([node])\n\n # Create a copy of the starting node and add it to visited\n visited[node] = Node(node.val)\n\n while queue:\n # Get the next node from the queue\n curr_node = queue.popleft()\n\n # Loop through the current node\'s neighbors\n for neighbor in curr_node.neighbors:\n if neighbor not in visited:\n # Create a copy of the neighbor and add it to visited\n visited[neighbor] = Node(neighbor.val)\n queue.append(neighbor)\n\n # Add the copy of the neighbor to the copy of the current node\'s neighbors\n visited[curr_node].neighbors.append(visited[neighbor])\n\n return visited[node]\n\n```\n```Java []\n\nclass Solution {\n public Node cloneGraph(Node node) {\n if (node == null) {\n return null;\n }\n\n HashMap<Node, Node> visited = new HashMap<>();\n Queue<Node> queue = new LinkedList<>();\n\n // Create a copy of the starting node and add it to visited\n visited.put(node, new Node(node.val));\n\n queue.offer(node);\n\n while (!queue.isEmpty()) {\n // Get the next node from the queue\n Node currNode = queue.poll();\n\n // Loop through the current node\'s neighbors\n for (Node neighbor : currNode.neighbors) {\n if (!visited.containsKey(neighbor)) {\n // Create a copy of the neighbor and add it to visited\n visited.put(neighbor, new Node(neighbor.val));\n queue.offer(neighbor);\n }\n\n // Add the copy of the neighbor to the copy of the current node\'s neighbors\n visited.get(currNode).neighbors.add(visited.get(neighbor));\n }\n }\n\n return visited.get(node);\n }\n}\n\n```\n```C++ []\n/**\n * Definition for a Node.\n * struct Node {\n * int val;\n * vector<Node*> neighbors;\n * Node(int val) {\n * this->val = val;\n * neighbors = vector<Node*>();\n * }\n * };\n */\nclass Solution {\npublic:\n Node* cloneGraph(Node* node) {\n if (!node) {\n return nullptr;\n }\n\n unordered_map<Node*, Node*> visited;\n queue<Node*> q;\n\n // Create a copy of the starting node and add it to visited\n visited[node] = new Node(node->val);\n\n q.push(node);\n\n while (!q.empty()) {\n // Get the next node from the queue\n Node* currNode = q.front();\n q.pop();\n\n // Loop through the current node\'s neighbors\n for (Node* neighbor : currNode->neighbors) {\n if (!visited.count(neighbor)) {\n // Create a copy of the neighbor and add it to visited\n visited[neighbor] = new Node(neighbor->val);\n q.push(neighbor);\n }\n\n // Add the copy of the neighbor to the copy of the current node\'s neighbors\n visited[currNode]->neighbors.push_back(visited[neighbor]);\n }\n }\n\n return visited[node];\n }\n};\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D | 20 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
✅[Python] Simple and Clean, beats 94.55%✅ | clone-graph | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about creating a deep copy of an undirected graph. To do that, we need to traverse the entire graph while maintaining a copy of each node and its neighbors. We can use the depth-first search (DFS) algorithm to traverse the graph and create the deep copy.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First, we check if the given node exists or not. If it doesn\'t exist, we return `None`.\n1. We create an empty dictionary called `mapping` to keep track of the nodes and their copies. We also create a stack and add the given node to it.\n1. We start a loop and pop a node from the stack. If the node is not already in the `mapping` dictionary, we create a new node with the same value and add it to the `mapping` dictionary. Then, we check the neighbors of the current node. If a neighbor is not already in the `mapping` dictionary, we create a new node with the same value and add it to the `mapping` dictionary. We also add the new neighbor node to the stack to process it later.\n\n1. After processing all the neighbors of the current node, we add them to the neighbors list of the new node in the `mapping` dictionary.\n1. We continue the loop until the stack is empty.\n1. Finally, we return the node with the same value as the given node from the `mapping` dictionary.\n# Complexity\n- Time complexity: $$O(n)$$, where n is the total number of nodes in the graph. We visit each node once, and for each node, we check its neighbors and add them to the stack if they haven\'t been processed yet.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$, where n is the total number of nodes in the graph. We use the `mapping` dictionary to store the copies of the nodes, and the stack to traverse the graph. The space required for the `mapping` dictionary is proportional to the number of nodes in the graph.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if not node:\n return None\n mapping = {}\n stack = [node]\n while stack:\n curr = stack.pop()\n if curr.val not in mapping:\n mapping[curr.val] = Node(curr.val)\n if curr.neighbors != []:\n for neighbor in curr.neighbors:\n if neighbor.val not in mapping:\n mapping[neighbor.val] = Node(neighbor.val)\n stack.append(neighbor)\n mapping[curr.val].neighbors.append(mapping[neighbor.val])\n return mapping[node.val]\n``` | 3 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Python | Easy | Clean Code | clone-graph | 0 | 1 | **PLEASE DO UPVOTE IF U GET THIS**\n```\n\nclass Solution:\n \n def helper(self, node, visited):\n if node is None:\n return None\n \n newNode = Node(node.val)\n visited[node.val] = newNode\n \n for adjNode in node.neighbors:\n if adjNode.val not in visited:\n newNode.neighbors.append(self.helper(adjNode, visited))\n else:\n newNode.neighbors.append(visited[adjNode.val])\n \n return newNode\n \n def cloneGraph(self, node: \'Node\') -> \'Node\':\n return self.helper(node, {})\n\n``` | 47 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Day 98 || DFS + Hash Table || Easiest Beginner Friendly Sol | clone-graph | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\n*This problem is about cloning a given connected undirected graph. Given a reference to a node in the graph, we need to create a deep copy of the entire graph.*\n\n*To accomplish this, we can use DFS traversal of the input graph, starting from the given node, and create a new copy of each node and its neighbors. We can use a map to keep track of nodes that have already been cloned so that we don\'t create duplicate nodes.*\n\n*During the DFS traversal, we create a new node for each node that we visit, and we add this node to our map. We then recursively visit all of the node\'s neighbors and create a new node for each neighbor, adding them to the current node\'s list of neighbors. If a neighbor has already been cloned, we simply add a reference to the cloned neighbor to the current node\'s list of neighbors.*\n\n*Once we have finished traversing the entire graph, we will have created a deep copy of the input graph. Finally, we return a reference to the cloned node that was provided as input.*\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Initialize an empty unordered map to keep track of nodes that have already been cloned.\n2. Check if the input node is null. If it is, return null.\n3. Check if the input node already exists in the map. If it does, return its corresponding clone.\n4. If the node is new, create a new clone with the same value as the input node and add it to the map.\n5. Iterate through each of the input node\'s neighbors and recursively clone them, adding them to the clone\'s list of neighbors.\n6. Return the clone of the input node.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n vector<Node*> neighbors; \n Node() {\n val = 0;\n neighbors = vector<Node*>();\n }\n Node(int _val) {\n val = _val;\n neighbors = vector<Node*>();\n }\n Node(int _val, vector<Node*> _neighbors) {\n val = _val;\n neighbors = _neighbors;\n }\n};\n*/\n\nclass Solution {\npublic:\n unordered_map<Node*, Node*> cloningGraph;\n \n Node* cloneGraph(Node* node) {\n if (node == nullptr) {\n return nullptr;\n }\n if (cloningGraph.find(node) == cloningGraph.end()) {\n cloningGraph[node] = new Node(node -> val);\n for (auto neighbor : node -> neighbors) {\n cloningGraph[node] -> neighbors.push_back(cloneGraph(neighbor));\n }\n }\n return cloningGraph[node];\n }\n};\n```\n```Java []\nimport java.util.*;\n\nclass Solution {\n Map<Node, Node> cloningGraph = new HashMap<>();\n \n public Node cloneGraph(Node node) {\n if (node == null) {\n return null;\n }\n if (cloningGraph.containsKey(node)) {\n return cloningGraph.get(node);\n }\n Node clone = new Node(node.val);\n cloningGraph.put(node, clone);\n for (Node neighbor : node.neighbors) {\n clone.neighbors.add(cloneGraph(neighbor));\n }\n return clone;\n }\n}\n\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.cloningGraph = {}\n \n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if not node:\n return None\n if node in self.cloningGraph:\n return self.cloningGraph[node]\n clone = Node(node.val, [])\n self.cloningGraph[node] = clone\n for neighbor in node.neighbors:\n clone.neighbors.append(self.cloneGraph(neighbor))\n return clone\n\n```\n\n# Time Complexity and Space Complexity:\n- **Time Complexity :** The algorithm performs a depth-first search (DFS) of the input graph, visiting each node and its neighbors exactly once. Therefore, the time complexity is **O(N + E), where N is the number of nodes in the graph and E is the number of edges in the graph.**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space Complexity :** The algorithm uses an unordered map to keep track of nodes that have already been cloned, which could potentially store all nodes in the graph. Therefore, the space complexity is O(N), where N is the number of nodes in the graph. Additionally, the algorithm uses recursive function calls, which could result in a recursive call stack with a maximum depth of N. Therefore, the space complexity due to the call stack is also O(N). Therefore, **the overall space complexity of the algorithm is O(N).**\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 7 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
✅✅Python🔥C++🔥Java🔥 Both DFS and BFS approach explained ☑️☑️ | clone-graph | 1 | 1 | # DFS APPROACH\n# Intuition\nThe algorithm uses depth-first search (DFS) to traverse the original graph and create a copy of each node and its neighbors. A map is used to keep track of the nodes that have already been cloned. This helps to avoid creating duplicate copies of nodes and ensures that the cloned graph is identical to the original.\n\n# Approach\nThe dfs function takes a node pointer and the map as input and returns the cloned node pointer. It creates a new node with the same value as the input node and adds it to the map. Then, it iterates through the input node\'s neighbors and recursively calls the dfs function for each neighbor. If a neighbor has already been cloned, it retrieves the cloned neighbor from the map; otherwise, it creates a new cloned neighbor using the dfs function. The cloned neighbors are added to a vector and assigned to the cloned node\'s neighbors field. Finally, the cloned node pointer is returned.\n\n# Complexity\n- Time complexity:`O(V+E)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:`O(V)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def dfs(self, node, ump):\n neighbour = []\n clone = Node(node.val)\n ump[node] = clone\n for it in node.neighbors:\n if it not in ump:\n neighbour.append(self.dfs(it, ump))\n else:\n neighbour.append(ump[it])\n clone.neighbors = neighbour\n return clone\n\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if not node:\n return node\n ump = {}\n if not node.neighbors:\n clone = Node(node.val)\n return clone\n return self.dfs(node, ump)\n\n```\n```C++ []\nclass Solution {\nprivate:\n Node* dfs(Node* node,unordered_map<Node*,Node*>& ump){\n vector<Node*>neighbour;\n Node* clone = new Node(node->val);\n ump[node] = clone;\n for(auto it:node->neighbors){\n if(ump.find(it)==ump.end()){\n neighbour.push_back(dfs(it,ump));\n }\n else{\n neighbour.push_back(ump[it]);\n }\n \n }\n clone->neighbors = neighbour;\n return clone;\n }\npublic:\n Node* cloneGraph(Node* node) {\n if(node == nullptr)\n return node;\n unordered_map<Node*, Node*>ump;\n //To find the neighbours present or not in constant time\n if(node->neighbors.size()==0){\n Node * clone = new Node(node->val);\n return clone;\n }\n return dfs(node,ump);\n }\n};\n```\n```Java []\nclass Solution {\n private Node dfs(Node node, Map<Node, Node> ump) {\n List<Node> neighbour = new ArrayList<>();\n Node clone = new Node(node.val);\n ump.put(node, clone);\n for(Node it:node.neighbors){\n if(!ump.containsKey(it)) {\n neighbour.add(dfs(it, ump));\n } else {\n neighbour.add(ump.get(it));\n }\n }\n clone.neighbors = neighbour;\n return clone;\n }\n \n public Node cloneGraph(Node node) {\n if(node == null) {\n return node;\n }\n Map<Node, Node> ump = new HashMap<>();\n if(node.neighbors.size() == 0) {\n Node clone = new Node(node.val);\n return clone;\n }\n return dfs(node, ump);\n }\n}\n\n```\n# BFS APPROACH\n# Intuition\nThe algorithm uses a queue to traverse the graph in a breadth-first search manner. The algorithm first checks if the input node is null, in which case it returns null. Otherwise, it creates an unordered map (ump) to store the mapping between the original nodes and the corresponding cloned nodes.\n\n# Approach\nThe algorithm starts by cloning the input node and adding it to the queue. Then, it starts a while loop that runs until the queue is empty. In each iteration of the loop, the algorithm dequeues a node from the front of the queue and for each neighbor of that node, it checks if it has already been cloned or not. If it hasn\'t been cloned, the algorithm creates a new node with the same value as the neighbor, adds it to the queue, and creates an edge from the cloned node to the new node. Finally, it updates the ump map with the mapping between the original node and the new node.\n\nOnce the while loop has finished, the algorithm returns the cloned node corresponding to the input node.\n\n# Complexity\n- Time complexity:`O(V+E)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:`O(V+E)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def cloneGraph(self, node: \'Node\') -> \'Node\':\n if not node:\n return node\n ump = {}\n # To find the neighbours present or not in constant time\n\n qu = collections.deque()\n # For bfs traversal\n ump[node] = Node(node.val, [])\n qu.append(node)\n while qu:\n curr = qu.popleft()\n\n for it in curr.neighbors:\n if it not in ump:\n ump[it] = Node(it.val, [])\n qu.append(it)\n ump[it].neighbors.append(ump[curr])\n return ump[node]\n\n```\n```C++ []\nclass Solution {\npublic:\n Node* cloneGraph(Node* node) {\n if(node == nullptr)\n return node;\n unordered_map<Node*, Node*>ump;\n //To find the neighbours present or not in constant time\n\n queue<Node*>qu;\n //For bfs traversal\n ump[node] = new Node(node->val,{});\n qu.push(node);\n while(!qu.empty()){\n Node* curr = qu.front();\n qu.pop();\n\n for(auto it:curr->neighbors){\n if(ump.find(it)==ump.end()){\n ump[it] = new Node(it->val,{});\n qu.push(it);\n }\n ump[it]->neighbors.push_back(ump[curr]);\n }\n }\n return ump[node];\n }\n};\n```\n```Java []\nclass Solution {\n public Node cloneGraph(Node node) {\n if(node == null)\n return node;\n Map<Node, Node> ump = new HashMap<>();\n //To find the neighbours present or not in constant time\n\n Queue<Node> qu = new LinkedList<>();\n //For bfs traversal\n ump.put(node, new Node(node.val, new ArrayList<>()));\n qu.offer(node);\n while(!qu.isEmpty()){\n Node curr = qu.poll();\n\n for(Node it : curr.neighbors){\n if(!ump.containsKey(it)){\n ump.put(it, new Node(it.val, new ArrayList<>()));\n qu.offer(it);\n }\n ump.get(it).neighbors.add(ump.get(curr));\n }\n }\n return ump.get(node);\n }\n}\n\n\n```\n# PLEASE UPVOTE\n\n\n | 5 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
Each node in the graph contains a value (`int`) and a list (`List[Node]`) of its neighbors.
class Node {
public int val;
public List neighbors;
}
**Test case format:**
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with `val == 1`, the second node with `val == 2`, and so on. The graph is represented in the test case using an adjacency list.
**An adjacency list** is a collection of unordered **lists** used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with `val = 1`. You must return the **copy of the given node** as a reference to the cloned graph.
**Example 1:**
**Input:** adjList = \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Output:** \[\[2,4\],\[1,3\],\[2,4\],\[1,3\]\]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
**Example 2:**
**Input:** adjList = \[\[\]\]
**Output:** \[\[\]\]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
**Example 3:**
**Input:** adjList = \[\]
**Output:** \[\]
**Explanation:** This an empty graph, it does not have any nodes.
**Constraints:**
* The number of nodes in the graph is in the range `[0, 100]`.
* `1 <= Node.val <= 100`
* `Node.val` is unique for each node.
* There are no repeated edges and no self-loops in the graph.
* The Graph is connected and all nodes can be visited starting from the given node. | null |
Solution | gas-station | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n int n = cost.size(), bal = 0, start = 0, deficit = 0;\n\n for(int i = 0; i< n; i++){\n bal += gas[i] - cost[i];\n\n if(bal < 0){\n\n deficit += bal;\n start = i+1;\n bal = 0;\n }\n }\n return bal + deficit >= 0 ? start : -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:\n if sum(gas) < sum(cost): return -1\n tank = idx = 0\n for i in range(len(gas)):\n tank+= gas[i]-cost[i] \n if tank < 0: tank, idx = 0, i+1\n return idx \n\n print(f"cost: {cost}")\n print(f"gas: {gas}")\n tank = 0\n for i in range(len(cost)):\n # find where we can start\n if cost[i] > gas[i]+tank:\n continue\n start = i \n tank += gas[i]\n print("tank", tank)\n for j in range(start+1, len(cost)):\n if cost[i] > gas[i]:\n print("inside", j)\n return -1\n```\n\n```Java []\nclass Solution {\n public int canCompleteCircuit(int[] gas, int[] cost) {\n int sGas = 0, sCost = 0, res = 0, total = 0;\n for (int i = 0; i < gas.length; i++) {\n sGas += gas[i];\n sCost += cost[i];\n }\n if (sGas < sCost) return -1;\n for (int i = 0; i < gas.length; i++) {\n total += gas[i] - cost[i];\n if (total < 0) {\n total = 0;\n res = i + 1;\n }\n }\n return res;\n }\n}\n```\n | 211 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
Python 3 || 2-6 lines, w/ explanation and example || T/M: 99% / 98% | gas-station | 0 | 1 | Here\'s the plan:\n\n- First, it is possible to complete the circuit if and only if the total amount of gas on the circuit is sufficient to drive the circuit. More formally: `sum(gas) >= sum(cost)`.\n- The starting station can be determined by starting at some station`a`(say, `a = 0`) and noting whether a station `b` on the circuit is unreachable due to lack of gas. If all are reachable, then `a` is our answer. If not, our answer is not `a`, nor is any station between `a` and`b`.\n- We reset the tank to zero and repeat on the remainder of the string `s`.\n- The last station that is unreachable in this process, say station`z`, is our answer. \n\nWhy does this work? Recall there\'s enough gas to complete the circuit. If it were possible to "borrow" gas to get to the next station, the station requiring the most borrowed gas overall is station`z`. Thus, starting at station`z` is the answer.\n```\nclass Solution:\n def canCompleteCircuit(self, gas: list[int], cost: list[int]) -> int:\n \n if sum(gas) < sum(cost): return -1 # Example: gas = [1,2,3,4,5] cost = [3,4,5,1,2]\n #\n tank = idx = 0 # i gas cost tank start\n # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\n for i in range(len(gas)): # start = 0 0 0\n # 0 1 3 0+1-3 = -2 1 reset tank to 0, start to 0+1 = 1\n tank+= gas[i]-cost[i] # 1 2 4 0+2-4 = -2 2 reset tank to 0, start to 1+1 = 2 \n if tank < 0: tank, idx = 0, i+1 # 2 3 5 0+3-5 = -2 3 reset tank to 0, start to 2+1 = 3\n # 3 4 1 0+4-1 = 3 3 \n return idx # 4 5 2 3+5-2 = 6 3\n #\n # See explanation in problem description to verify that i = 3 works\n\n```\n[https://leetcode.com/problems/gas-station/submissions/624723831/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1).\n\nAnd here\'s the two-liner....\n\n```\nclass Solution:\n def canCompleteCircuit(self, gas: list[int], cost: list[int]) -> int:\n\n diff = list(accumulate([g - c for g,c in zip(gas,cost)], initial = 0))\n\n return diff.index(min(diff)) if diff[-1] >= 0 else -1\n```\n\nAdded 1/8/22:\nA number of comments below requested more explanation that a solution must exist if `sum(gas) >= sum(costs)`. \n\nLet\'s consider the data from Example 1. Suppose the car is allowed to continue without regard to maintaining a nonnegative balance of `gas`. Fig 1 shows the balance of gas when initiating the circuit at `i = 0`. \n\nThe function is a bounded (possibly quasi-) periodic function, and, in general, `sum(gas) >= sum(costs)` implies the function value at the end of each period is not less than the function value at the beginning of that period. By the Bounded Function Theorem, there exists a minimum value in each period (this occurrence is not necessarily unique in one period).\n\n\n\nFig 2 shows the function starting at `i = 3` (the `i` for which that minimum value exists) with the same periodicity that has no negative values. The inference from Fig 2 is that a solution will always exist as long as `sum(gas) >= sum(costs)`. | 80 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
Easy_python | gas-station | 0 | 1 | # Code\n```\nclass Solution:\n def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:\n rem=0\n st=0\n t_gas=0\n for p in range(len(gas)):\n dif=gas[p]-cost[p]\n t_gas+=dif\n rem+=dif\n if rem<0:\n st=p+1\n rem=0\n else: return st if abs(t_gas)==t_gas else -1\n\n``` | 5 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
Python Solution Time O(n) Space O(1) | gas-station | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:\n\n start = 0\n slicer = 0\n sum = 0\n while slicer - start < len(gas):\n sum += gas[slicer] - cost[slicer]\n while slicer - start < len(gas) and sum < 0:\n start -= 1\n sum += gas[start] - cost[start]\n slicer += 1\n\n if sum >= 0:\n return start if start >= 0 else len(gas) + start\n return -1\n \n``` | 1 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
Python simple and very short explained solution - O(n), O(1) - faster than 98% | gas-station | 0 | 1 | 1. If sum of gas is less than sum of cost, then there is no way to get through all stations. So while we loop through the stations we sum up, so that at the end we can check the sum.\n2. Otherwise, there must be one unique solution, so the first one I find is the right one. If the tank becomes negative, we restart because that can\'t happen.\n```\nclass Solution:\n def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:\n if (sum(gas) - sum(cost) < 0):\n return -1\n \n gas_tank, start_index = 0, 0\n \n for i in range(len(gas)):\n gas_tank += gas[i] - cost[i]\n \n if gas_tank < 0:\n start_index = i+1\n gas_tank = 0\n \n return start_index\n```\n**Like it? please upvote...** | 145 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
Simple Python solution | gas-station | 0 | 1 | # Complexity\n- Time complexity:\n73.70 %\n\n- Space complexity:\n49.17 %\n\n# Code\n```\nclass Solution:\n def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:\n if sum(gas) < sum(cost):\n return -1\n a = len(gas)\n s = 0\n result = 0\n for i in range(a):\n s += gas[i] - cost[i]\n if s < 0:\n s = 0\n result =(i + 1) % a \n return result\n\n``` | 1 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
✔️ [Python3] DEBIT AND CREDIT, O(1) SPACE, ᕕ( ᐛ )ᕗ ⛽, Explained | gas-station | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nConsider this example: `----+++`, where \xAB-\xBB are parts of the way where we don\'t have enough gas to travel to the next station, and \xAB+\xBB are vice versa. Imagine that we could borrow the gas for those \xAB-\xBB parts and return debt later when we reach \xAB+\xBB parts where we have plenty of gas. That will allow us to start traveling from the very first gas station and maintain a kind of ledger that will account for our debit and credit. If at the end of the travel our credit is greater than debit, that means we are able to do a circuit. Of course, we also should remember the start of the \xAB+\xBB part which is our result.\n\nTime: **O(n)** - linear\nSpace: **O(1)** - nothing stored\n\nRuntime: 460 ms, faster than **85.85%** of Python3 online submissions for Gas Station.\nMemory Usage: 18.9 MB, less than **75.25%** of Python3 online submissions for Gas Station.\n\n```\ndef canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:\n\tcandidate, debit, credit = None, 0, 0\n\t\n\tfor i in range(len(gas)):\n\t\tcredit += gas[i] - cost[i]\n\t\tif credit < 0:\n\t\t\tcandidate, debit, credit = None, debit - credit, 0\n\t\telif candidate is None: \n\t\t\tcandidate = i\n\n\treturn candidate if credit >= debit else -1\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 53 | There are `n` gas stations along a circular route, where the amount of gas at the `ith` station is `gas[i]`.
You have a car with an unlimited gas tank and it costs `cost[i]` of gas to travel from the `ith` station to its next `(i + 1)th` station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays `gas` and `cost`, return _the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return_ `-1`. If there exists a solution, it is **guaranteed** to be **unique**
**Example 1:**
**Input:** gas = \[1,2,3,4,5\], cost = \[3,4,5,1,2\]
**Output:** 3
**Explanation:**
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.
**Example 2:**
**Input:** gas = \[2,3,4\], cost = \[3,4,3\]
**Output:** -1
**Explanation:**
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.
**Constraints:**
* `n == gas.length == cost.length`
* `1 <= n <= 105`
* `0 <= gas[i], cost[i] <= 104` | null |
✅ 99.20% Greedy Two & One Pass | candy | 1 | 1 | # Comprehensive Guide to Solving "Candy": Distributing Candies Like a Pro\n\n## Introduction & Problem Statement\n\nHey there, coding enthusiasts! Welcome back to another exciting coding session. Today\'s problem is a treat\u2014literally! We\'re going to solve the "Candy" problem. Imagine you have a bunch of kids lined up, each with a rating assigned to them. Your task is to distribute candies to these kids following two simple rules:\n\n1. Every child must get at least one candy.\n2. A child with a higher rating should get more candies than their immediate neighbors.\n\nSounds like a piece of cake, right? But here\'s the twist: you need to accomplish this with the fewest candies possible. Let\'s dig into the mechanics of this problem and how to approach it.\n\n## Key Concepts and Constraints\n\n### Why is This Problem Unique?\n\n1. **Child Ratings**: \n The ratings of each child are your only guide in how you distribute the candies. Following the rules while using these ratings makes this problem an intriguing puzzle.\n \n2. **Minimum Candies**: \n You\'re not just distributing candies willy-nilly; the goal is to meet the conditions using the least amount of candy.\n\n3. **Constraints**: \n - The length of the ratings array, `n` , is between $$1$$ and $$ 2 \\times 10^4 $$.\n - Ratings are integers between $$0$$ and $$ 2 \\times 10^4 $$.\n\n### Strategies to Tackle the Problem\n\n1. **Greedy Algorithm: Two-Pass Method** \n This method takes two passes through the ratings array to ensure that each child gets the appropriate amount of candy.\n\n2. **One-Pass Greedy Algorithm: Up-Down-Peak Method** \n This more advanced method uses a single pass and employs three key variables\u2014Up, Down, and Peak\u2014to efficiently determine the minimum number of candies needed.\n\n---\n\n## Live Coding + Explenation of Greedy Two Pass\nhttps://youtu.be/JqrZHuhljps?si=TxkUjNTZ1CxMviij\n\n## Greedy Algorithm: Two-Pass Method Explained\n\n### What is a Greedy Algorithm?\n\nA Greedy Algorithm makes choices that seem optimal at the moment. For this problem, we use a two-pass greedy approach to make sure each child gets the minimum number of candies that still satisfy the conditions.\n\n### The Nuts and Bolts of the Two-Pass Method\n\n1. **Initialize Candies Array** \n - We start by creating a `candies` array of the same length as the `ratings` array and initialize all its values to 1. This is the base case and ensures that every child will receive at least one candy, satisfying the first condition.\n \n2. **Forward Pass: Left to Right**\n - Now, we iterate through the `ratings` array from the beginning to the end. For each child (except the first), we compare their rating with the one to the left. If it\'s higher, we update the `candies` array for that child to be one more than the child on the left. This takes care of the second condition but only accounts for the child\'s left neighbor.\n \n3. **Backward Pass: Right to Left** \n - After the forward pass, we loop through the array again but in the reverse direction. This time, we compare each child\'s rating with the child to their right. If the rating is higher, we need to make sure the child has more candies than the right neighbor. So, we update the `candies` array for that child to be the maximum between its current number of candies and one more than the right neighbor\'s candies. This ensures that both neighboring conditions are checked and satisfied.\n \n4. **Summing it All Up**\n - Finally, we sum up all the values in the `candies` array. This will give us the minimum total number of candies that need to be distributed to satisfy both conditions.\n \n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n)$$, because we make two passes through the array.\n- **Space Complexity**: $$O(n)$$, for storing the `candies` array.\n\n## Code Greedy\n``` Python []\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n = len(ratings)\n candies = [1] * n \n\n for i in range(1, n):\n if ratings[i] > ratings[i-1]:\n candies[i] = candies[i-1] + 1\n\n for i in range(n-2, -1, -1):\n if ratings[i] > ratings[i+1]:\n candies[i] = max(candies[i], candies[i+1] + 1)\n \n return sum(candies)\n```\n``` Go []\nfunc candy(ratings []int) int {\n n := len(ratings)\n candies := make([]int, n)\n for i := range candies {\n candies[i] = 1\n }\n\n for i := 1; i < n; i++ {\n if ratings[i] > ratings[i-1] {\n candies[i] = candies[i-1] + 1\n }\n }\n\n for i := n - 2; i >= 0; i-- {\n if ratings[i] > ratings[i+1] {\n if candies[i] <= candies[i+1] {\n candies[i] = candies[i+1] + 1\n }\n }\n }\n\n totalCandies := 0\n for _, candy := range candies {\n totalCandies += candy\n }\n\n return totalCandies\n}\n```\n``` Rust []\nimpl Solution {\n pub fn candy(ratings: Vec<i32>) -> i32 {\n let n = ratings.len();\n let mut candies = vec![1; n];\n\n for i in 1..n {\n if ratings[i] > ratings[i - 1] {\n candies[i] = candies[i - 1] + 1;\n }\n }\n\n for i in (0..n - 1).rev() {\n if ratings[i] > ratings[i + 1] {\n candies[i] = std::cmp::max(candies[i], candies[i + 1] + 1);\n }\n }\n\n candies.iter().sum()\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int candy(std::vector<int>& ratings) {\n int n = ratings.size();\n std::vector<int> candies(n, 1);\n\n for (int i = 1; i < n; ++i) {\n if (ratings[i] > ratings[i - 1]) {\n candies[i] = candies[i - 1] + 1;\n }\n }\n\n for (int i = n - 2; i >= 0; --i) {\n if (ratings[i] > ratings[i + 1]) {\n candies[i] = std::max(candies[i], candies[i + 1] + 1);\n }\n }\n\n int totalCandies = 0;\n for (int candy : candies) {\n totalCandies += candy;\n }\n\n return totalCandies;\n }\n};\n```\n``` Java []\nclass Solution {\n public int candy(int[] ratings) {\n int n = ratings.length;\n int[] candies = new int[n];\n Arrays.fill(candies, 1);\n\n for (int i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n candies[i] = candies[i - 1] + 1;\n }\n }\n\n for (int i = n - 2; i >= 0; i--) {\n if (ratings[i] > ratings[i + 1]) {\n candies[i] = Math.max(candies[i], candies[i + 1] + 1);\n }\n }\n\n int totalCandies = 0;\n for (int candy : candies) {\n totalCandies += candy;\n }\n\n return totalCandies;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int Candy(int[] ratings) {\n int n = ratings.Length;\n int[] candies = new int[n];\n Array.Fill(candies, 1);\n\n for (int i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n candies[i] = candies[i - 1] + 1;\n }\n }\n\n for (int i = n - 2; i >= 0; i--) {\n if (ratings[i] > ratings[i + 1]) {\n candies[i] = Math.Max(candies[i], candies[i + 1] + 1);\n }\n }\n\n int totalCandies = 0;\n foreach (int candy in candies) {\n totalCandies += candy;\n }\n\n return totalCandies;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} ratings\n * @return {number}\n */\nvar candy = function(ratings) {\n const n = ratings.length;\n const candies = new Array(n).fill(1);\n\n for (let i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n candies[i] = candies[i - 1] + 1;\n }\n }\n\n for (let i = n - 2; i >= 0; i--) {\n if (ratings[i] > ratings[i + 1]) {\n candies[i] = Math.max(candies[i], candies[i + 1] + 1);\n }\n }\n\n return candies.reduce((a, b) => a + b, 0);\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $ratings\n * @return Integer\n */\n function candy($ratings) {\n $n = count($ratings);\n $candies = array_fill(0, $n, 1);\n\n for ($i = 1; $i < $n; $i++) {\n if ($ratings[$i] > $ratings[$i - 1]) {\n $candies[$i] = $candies[$i - 1] + 1;\n }\n }\n\n for ($i = $n - 2; $i >= 0; $i--) {\n if ($ratings[$i] > $ratings[$i + 1]) {\n $candies[$i] = max($candies[$i], $candies[$i + 1] + 1);\n }\n }\n\n return array_sum($candies);\n }\n}\n```\n## One-Pass Greedy Algorithm: Up-Down-Peak Method\n\n### Why `Up`, `Down`, and `Peak`?\n\nThe essence of the one-pass greedy algorithm lies in these three variables: `Up`, `Down`, and `Peak`. They serve as counters for the following:\n\n- **`Up`:** Counts how many children have **increasing ratings** from the last child. This helps us determine how many candies we need for a child with a higher rating than the previous child.\n \n- **`Down`:** Counts how many children have **decreasing ratings** from the last child. This helps us determine how many candies we need for a child with a lower rating than the previous child.\n\n- **`Peak`:** Keeps track of the **last highest point** in an increasing sequence. When we have a decreasing sequence after the peak, we can refer back to the `Peak` to adjust the number of candies if needed.\n\n### How Does it Work?\n\n1. **Initialize Your Counters**\n - Start with `ret = 1` because each child must have at least one candy. Initialize `up`, `down`, and `peak` to 0.\n \n2. **Loop Through Ratings**\n - For each pair of adjacent children, compare their ratings. Here are the scenarios:\n \n - **If the rating is increasing**: Update `up` and `peak` by incrementing them by 1. Set `down` to 0. Add `up + 1` to `ret` because the current child must have one more candy than the previous child.\n \n - **If the rating is the same**: Reset `up`, `down`, and `peak` to 0, because neither an increasing nor a decreasing trend is maintained. Add 1 to `ret` because the current child must have at least one candy.\n \n - **If the rating is decreasing**: Update `down` by incrementing it by 1. Reset `up` to 0. Add `down` to `ret`. Additionally, if `peak` is greater than or equal to `down`, decrement `ret` by 1. This is because the peak child can share the same number of candies as one of the children in the decreasing sequence, which allows us to reduce the total number of candies.\n \n3. **Return the Total Candy Count**\n - At the end of the loop, `ret` will contain the minimum total number of candies needed for all the children, so return `ret`.\n\nBy using `up`, `down`, and `peak`, we can efficiently traverse the ratings list just once, updating our total candies count (`ret`) as we go. This method is efficient and helps us solve the problem in a single pass, with a time complexity of $$O(n)$$.\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n)$$, for the single pass through the ratings array.\n- **Space Complexity**: $$O(1)$$, as we only use a few extra variables.\n\n## Code One-Pass Greedy\n``` Python []\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n if not ratings:\n return 0\n \n ret, up, down, peak = 1, 0, 0, 0\n \n for prev, curr in zip(ratings[:-1], ratings[1:]):\n if prev < curr:\n up, down, peak = up + 1, 0, up + 1\n ret += 1 + up\n elif prev == curr:\n up = down = peak = 0\n ret += 1\n else:\n up, down = 0, down + 1\n ret += 1 + down - int(peak >= down)\n \n return ret\n\n```\n``` Go []\nfunc candy(ratings []int) int {\n if len(ratings) == 0 {\n return 0\n }\n\n ret, up, down, peak := 1, 0, 0, 0\n\n for i := 0; i < len(ratings) - 1; i++ {\n prev, curr := ratings[i], ratings[i+1]\n\n if prev < curr {\n up++\n down = 0\n peak = up\n ret += 1 + up\n } else if prev == curr {\n up, down, peak = 0, 0, 0\n ret += 1\n } else {\n up = 0\n down++\n ret += 1 + down\n if peak >= down {\n ret--\n }\n }\n }\n\n return ret\n}\n```\n``` Rust []\nimpl Solution {\n pub fn candy(ratings: Vec<i32>) -> i32 {\n if ratings.is_empty() {\n return 0;\n }\n\n let mut ret = 1;\n let mut up = 0;\n let mut down = 0;\n let mut peak = 0;\n\n for i in 0..ratings.len() - 1 {\n let (prev, curr) = (ratings[i], ratings[i + 1]);\n\n if prev < curr {\n up += 1;\n down = 0;\n peak = up;\n ret += 1 + up;\n } else if prev == curr {\n up = 0;\n down = 0;\n peak = 0;\n ret += 1;\n } else {\n up = 0;\n down += 1;\n ret += 1 + down;\n if peak >= down {\n ret -= 1;\n }\n }\n }\n\n ret\n }\n}\n```\n\n## Performance Comparison\n\n| Language | Approach | Time (ms) | Memory (MB) |\n|-----------|-----------|------------|-------------|\n| Rust | One Pass | 1 | 2.1 |\n| Rust | Two Pass | 2 | 2.3 |\n| Java | Two Pass | 3 | 44.3 |\n| Go | One Pass | 9 | 6.2 |\n| C++ | Two Pass | 11 | 17.8 |\n| Go | Two Pass | 14 | 6.6 |\n| PHP | Two Pass | 42 | 21.9 |\n| JavaScript| Two Pass | 59 | 45.1 |\n| C# | Two Pass | 98 | 44.3 |\n| Python3 | One Pass | 126 | 19.5 |\n| Python3 | Two Pass | 139 | 19.2 |\n\n\n\n## Live Coding & Explenation - One Pass\nhttps://youtu.be/_MVFeqfiDK4?si=t8El9b9mlUQneXDk\n\n## Code Highlights and Best Practices\n\n- The Two-Pass Greedy Algorithm is straightforward and effective, making it a solid approach for this problem.\n- The One-Pass Greedy Algorithm is even more efficient in terms of space complexity and is also a bit more challenging to understand.\n \nBy mastering these approaches, you\'ll be well-equipped to tackle other optimization problems, which are common in coding interviews and competitive programming. So, are you ready to distribute some candies? Let\'s get coding!\n | 192 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.