title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Full Explanation with clean code Python | linked-list-cycle-ii | 1 | 1 | # Intuition\n\nThe solution uses the Floyd\'s cycle detection algorithm, also known as the "tortoise and hare algorithm". It involves traversing the linked list with two pointers, a slow pointer (tortoise) and a fast pointer (hare). If the linked list has a cycle, the fast pointer will eventually catch up with the slow pointer.\n# Approach\n\nThe solution initializes both pointers to the head of the linked list and iterates through the linked list, moving the slow pointer by one node and the fast pointer by two nodes at a time. If they ever point to the same node, it means a cycle exists in the linked list.\n\nAfter detecting the cycle, the solution finds the node at which the cycle begins by moving one pointer back to the head of the linked list and then moving both pointers at the same pace until they meet again at the start of the cycle.\n# Complexity\n- Time complexity:\n\nThe time complexity of this solution is O(n) because in the worst case scenario, we need to traverse the entire linked list to detect the cycle and find the starting node of the cycle.\n- Space complexity:\n\nThe space complexity of this solution is O(1) because we are only using two pointers to traverse the linked list and no extra space is needed.\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n s = head\n f = head\n while f and f.next and f.next.next:\n s = s.next\n f = f.next.next\n if s == f:\n break\n if head and head.next and head.next.next and s != f:\n return None\n elif not head or not head.next or not head.next.next:\n return None \n else:\n f = head\n while s != f:\n s = s.next\n f = f.next\n return f\n\n #or\n\n# Alternative solution\n# class Solution:\n# def detectCycle(self, head: ListNode) -> ListNode:\n# slow = fast = head\n# while fast and fast.next:\n# slow = slow.next\n# fast = fast.next.next\n# if slow == fast:\n# break\n# else:\n# return None\n \n# slow = head\n# while slow != fast:\n# slow = slow.next\n# fast = fast.next\n \n# return slow\n\n``` | 1 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
One iteration. Two approaches. Python C++ | linked-list-cycle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOne iteration is enough\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n### First approach\n``` Python []\nclass Solution:\n def detectCycle(self, head: ListNode | None, q={}) -> ListNode | None:\n while head:\n if id(head) in q: return head\n q[id(head)] = head\n head = head.next\n return None\n```\n\n``` C++ []\nclass Solution {\npublic:\n ListNode *detectCycle(ListNode *head, int i=0) {\n unordered_map<ListNode*,int> m;\n while(head!=NULL) {\n if(m.find(head)!=m.end()) return head;\n m[head]=i++;\n head=head->next;\n }\n return NULL;\n }\n};\n```\n\n### Memory saving approach if we don\'t need to save original list\n``` Python []\nclass Solution:\n def detectCycle(self, head: ListNode | None) -> ListNode | None:\n while head:\n if head.val == 0xFAF: return head\n head.val, head = 0xFAF, head.next\n return None\n```\n\n``` C++ []\nclass Solution {\npublic:\n ListNode *detectCycle(ListNode *head) {\n while(head) {\n if(head->val == 0xFAF) return head;\n head->val = 0xFAF;\n head=head->next;\n }\n return NULL;\n }\n};\n```\nI hope if is useful. \nPlease upvote. Thanks | 1 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
BEST APPROACH IN C++ / C / JAVA | linked-list-cycle-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn which we used two pointer approach\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe take two pointer fast and slow which are poin head of the node .\nand if linked list in cycle then after some time fast and slow both are equal in then there is a cycle .\nafter that we take two variable curr,temp .in which curr point head,and temp point any one of fast and slow because both are equal. \nthen again start while loop and find where loop start in loop conditin is curr!=temp and move curr ,and temp after some time both are meet each other. and loop stop . and return temp or curr .\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n I HOPE YOU GUYY UNDERSTAND . PLZ LIKE IT \uD83D\uDE0A\uD83D\uDE0A\uD83D\uDE0A .\n\n\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode(int x) : val(x), next(NULL) {}\n * };\n */\nclass Solution {\npublic:\n ListNode *detectCycle(ListNode *head) {\n if(fast==NULL ||fast->next==NULL){\n return 0;\n }\n\n ListNode *slow =head,*fast=head;\n\n while(fast!=NULL && fast->next!=NULL){\n slow =slow->next;\n fast =fast->next->next;\n if(fast==slow){\n break;\n }\n }\n ListNode *curr =head;\n ListNode *temp =fast;\n else{\n while(curr!=temp){\n curr =curr->next;\n temp =temp->next;\n }\n }\n return curr;\n }\n};\n``` | 1 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
simple solution || o(1) space complexity || python | linked-list-cycle-ii | 0 | 1 | # Intuition and Approach\n* simply traverse the linklist and replace val of node with 1000000.\n* if their is cycle you will get 1000000 again while traversing.so, when you get it return that node.\n* if their is no cycle then return the node which is at the end of list.\n\n# Complexity\n- Time complexity:O(n)\n\n- Space complexity:O(1)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def detectCycle(self, root: Optional[ListNode]) -> Optional[ListNode]:\n n=1000000\n while( root!=None and root.val!=1000000):\n root.val=1000000\n root=root.next\n return root\n``` | 1 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
🥇 C++ | PYTHON | JAVA || Diagram Explained ; ] ✅ | linked-list-cycle-ii | 1 | 1 | **UPVOTE IF HELPFuuL**\n\n# Approach\n\nFloyd\'s Linked List Cycle Finding Algorithm\nTortoise And Hare algorithm\n\nWorking of Algo\n**Step 1: Presence of the cycle**\n1. Take two pointers `slow`\u200Aand\u200A`fast`\u200A.\n2. Both of them will point to head of the linked list initially.\n3. `slow` will move one step at a time.\n4. `fast` will move two steps at a time. (twice as speed as `slow` pointer).\n5. Check if at any point they point to the same node before any one(or both) reach null.\n6. If they point to any same node at any point of their journey, it would indicate that the cycle indeed exists in the linked list.\n7. If we get null, it would indicate that the linked list has no cycle.\n\n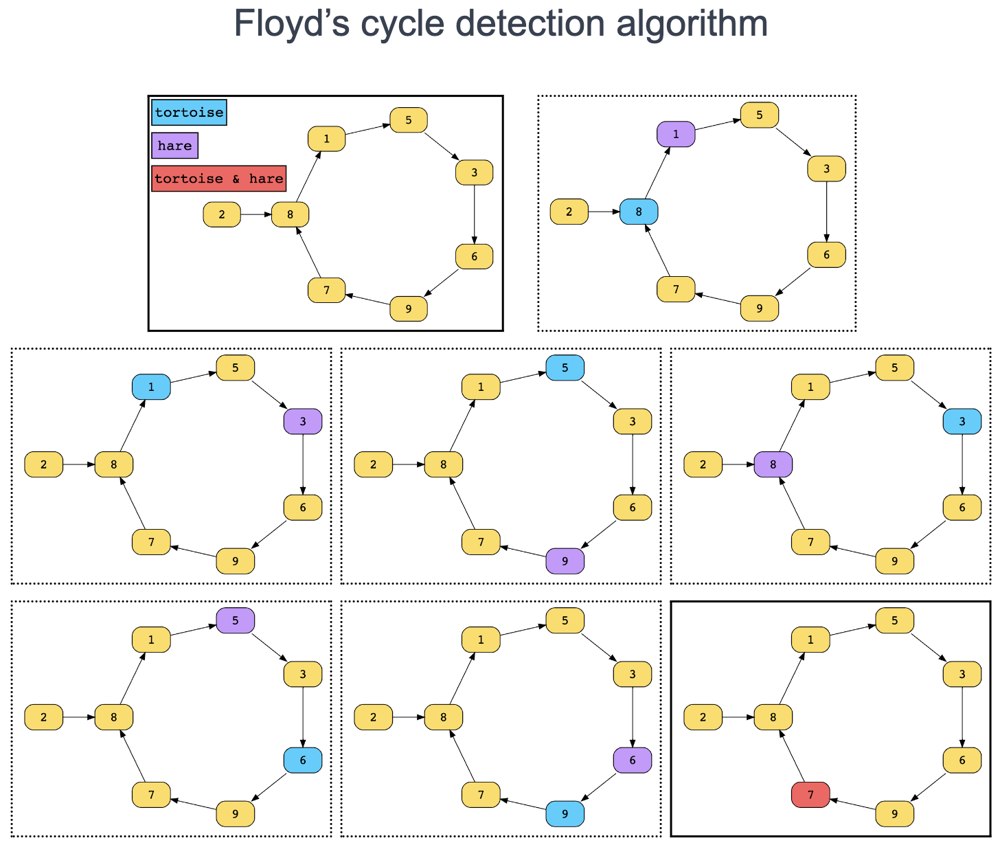\n\n**Step 2: Starting point of the cycle**\n1. Reset the `slow` pointer to the head of the linked list.\n2. Move both pointers one step at a time.\n3. The point they will meet at will be the starting point of the cycle.\n\n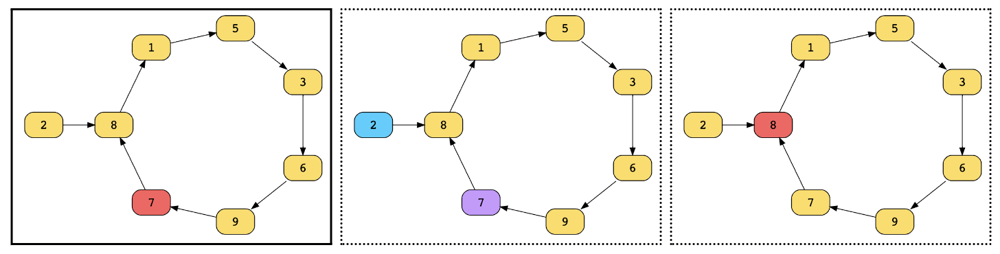\n\n\n# Complexity\n- Time complexity: O ( N )\n\n- Space complexity: O ( 1 )\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n``` Python []\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n fast = head\n slow = head\n while (slow and slow.next):\n fast = fast.next\n slow = slow.next.next\n if (fast == slow):\n fast = head\n while (fast != slow):\n fast = fast.next\n slow = slow.next\n return slow\n return None\n```\n``` C++ []\nclass Solution {\npublic:\n ListNode *detectCycle(ListNode *head) {\n ListNode *slow = head, *fast = head;\n while (fast && fast->next) {\n slow = slow->next;\n fast = fast->next->next;\n if (slow == fast) break;\n }\n if (!(fast && fast->next)) return NULL;\n while (head != slow) {\n head = head->next;\n slow = slow->next;\n }\n return head;\n }\n};\n```\n``` JAVA []\npublic class Solution {\n public ListNode detectCycle(ListNode head) {\n ListNode slow = head;\n ListNode fast = head;\n while (fast != null && fast.next != null) {\n slow = slow.next;\n fast = fast.next.next;\n if (slow == fast) {\n slow = head;\n while (slow != fast) {\n slow = slow.next;\n fast = fast.next;\n }\n return slow;\n }\n }\n return null;\n }\n}\n```\n\n**UPVOTE IF HELPFuuL**\n\n\n\n\n\n | 13 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Solution | linked-list-cycle-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n ListNode *detectCycle(ListNode *head) {\n ListNode*slow=head;\n ListNode*fast=head;\n ListNode*enter=head; \n while(fast!=NULL&&fast->next!=NULL)\n {\n slow=slow->next;\n fast=fast->next->next;\n if(slow==fast)\n {\n while(enter!=slow)\n {\n enter=enter->next;\n slow=slow->next;\n }\n return slow;\n }\n\n }\n return NULL;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n start=head\n lookup=set()\n while start:\n if start in lookup:\n return start\n else:\n lookup.add(start)\n start=start.next\n return None\n```\n\n```Java []\npublic class Solution {\n public ListNode detectCycle(ListNode head) {\n ListNode fast = head, slow = head;\n while (fast != null && fast.next != null) {\n fast = fast.next.next;\n slow = slow.next;\n if (fast == slow) {\n break;\n }\n }\n if (fast == null || fast.next == null) {\n return null;\n }\n fast = head;\n while (fast != slow) {\n fast = fast.next;\n slow = slow.next;\n }\n return fast;\n }\n}\n```\n | 206 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
[C++ | Python3] Concise explanation with math & diagrams | linked-list-cycle-ii | 0 | 1 | 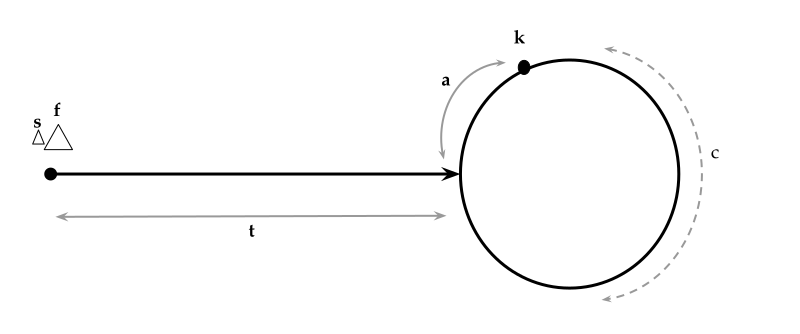\n\nWe have illustrated the linked list in the diagram above, which consists of two main components: the linear track, denoted by the variable `t`, and the cycle, denoted by the variable `c`.\n\nLet\'s consider the scenario where we initiate two pointers, named `s` and `f`, from the head of the list. The pointer `s` progresses through the list at a regular speed, while the pointer `f` moves at twice the speed of `s`. Mathematically, we can express this relationship as $$f = 2 \\times s$$ (interpret `f.next.next` for every `s.next`). As the pointers traverse the list, they will eventually meet at point `k`, which may be `a` units away from the beginning of the cycle.\n\n```\ns -> slow pointer\nf -> fast pointer; twice the speed of \'s\'\nt -> length of the linear part of the list\nc -> length of the list cycle\nk -> intersection point of \'s\' & \'f\'\na -> distance of \'k\' from the start of cycle\n```\n\nAt the moment of intersection (at `k`),\n1. the slow pointer (`s`) would\'ve travelled\n ```\n distance of \'s\' = the linear track \'t\' \n + some cycles \'x * c\'\n + the distance `a` (to meet at `k`)\n ```\n2. the fast pointer (`f`) would\'ve travelled\n ```\n distance of \'f\' = the linear track \'t\' \n + some cycles \'y * c\'\n + the distance `a` (to meet at `k`)\n ```\nEvaluating the above,\n \n\n> $$f = 2 \\times s \\\\ \\therefore t + y \\times c + a = 2 \\times (t+x \\times c+a) \\\\ \\therefore t + yc + a = 2t + 2xc + 2a \\\\ \\therefore t + a = c(y-2x) \\\\ \\therefore \\bold{t + a = m \\times c}\\ (where\\ m = y-2x) $$\n\n**In other words, the distance traveled from the origin to the intersection point $$(t + a)$$ is equal to completing several laps around the cycle.**\n\nConsequently, if we initiate another pointer, denoted as `b`, with the same velocity as `s`, starting from the origin, while `s` begins looping around the cycle from its current position `k`, when `b` reaches point `k` after traveling the distance $$t + a$$, `s` must have completed multiple loops ($$m \\times c$$) and returned to `k` simultaneously.\n\nSince both `s` and `b` have the same velocity and meet at `k` at the same time, it implies that they crossed the arc `a` together (as evident from the figure below). Therefore, it can be inferred that they originally met at the beginning of the cycle.\n\n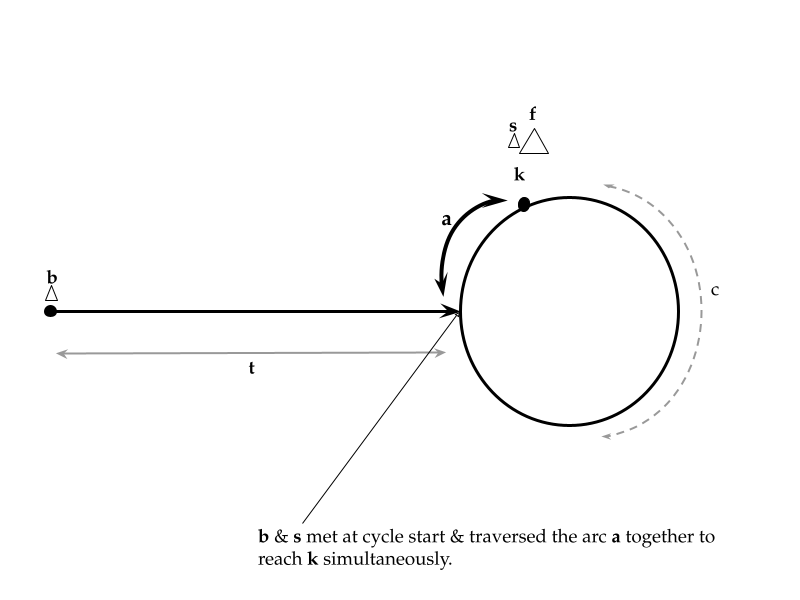\n\n\n# Complexity\nTime: $$O(n)$$\nSpace: $$O(1)$$ \n\n# Code\n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not (head and head.next):\n return\n fast = head\n slow = head\n while fast:\n slow = slow.next\n fast = fast.next\n if fast and fast.next:\n fast = fast.next\n else:\n return\n if slow is fast:\n break\n if slow is head:\n return head\n tertiary = head\n while tertiary is not slow:\n tertiary = tertiary.next\n slow = slow.next\n return slow\n```\n\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode(int x) : val(x), next(NULL) {}\n * };\n */\nclass Solution {\npublic:\n ListNode *detectCycle(ListNode *head) {\n if (head == NULL or head->next == NULL)\n return NULL;\n ListNode *slow = head;\n ListNode *fast = head;\n while (fast && fast->next) {\n slow = slow->next;\n fast = fast->next->next;\n if (slow == fast)\n break;\n }\n if (!fast || !fast->next)\n return NULL;\n ListNode *tertiary = head;\n while (slow != tertiary) {\n slow = slow->next;\n tertiary = tertiary->next;\n }\n return slow;\n }\n};\n``` | 2 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Python two pointer solution | linked-list-cycle-ii | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def detectCycle(self, head: ListNode) -> ListNode:\n slow = fast = head\n\n while fast and fast.next:\n slow, fast = slow.next, fast.next.next\n\n if slow == fast:\n slow = head\n \n while slow != fast:\n slow, fast = slow.next, fast.next\n\n return slow\n return \n \n``` | 2 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
📌📌Python3 || ⚡simple solution uwu | linked-list-cycle-ii | 0 | 1 | \n```\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n slow = fast = head\n \n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n if slow == fast:\n break\n \n if not fast or not fast.next:\n return None\n \n slow = head\n while slow != fast:\n slow = slow.next\n fast = fast.next\n \n return slow\n``` | 1 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
[Python] - Clean & Simple Floyd's Cycle Detaction O(1) space | linked-list-cycle-ii | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Here, we are incrementing Slow and Fast both.\n- Only difference is we are increasing **slow** by $$1$$ and **fast** by $$2$$.\n- If at any time slow is same as fast then we detacted cycle at there.\n- Then for finding **start** of the cycle, If there is **Cycle** :\n - We can Simply start a pointer from head and we use our old slow pointer.\n - Then increase both by 1 until they not match.\n - Simply return slow or head.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n slow = fast = head\n while fast and fast.next:\n slow, fast = slow.next, fast.next.next\n if slow == fast:\n while slow != head:\n slow, head = slow.next, head. next\n return slow\n return None\n``` | 6 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
simple python O(1) space solution | linked-list-cycle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf I need to get rid of the dictionary solution, there must be some feature in the problem set up that allows for space optimization. \n\nTo detect whether there is a cycle without the $$O(N)$$ of the dictionary, you can use two pointers: fast and slow. They will meet if there is a cycle. And if there is no cycle, the fast pointer is guaranteed to reach the end first. But how to return the node at which the cycle begins?\n\nMy intuition was that if I know the size of the cycle `count`, then I can use a pointer `count` steps away from `head`. Then if I just move both of the pointers one step at a time the far pointer is guarnateed to meet the close pointer at exactly the beginning of the cycle.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Detect whether there is a cycle or not using the `fast` pointer and `slow` pointer. \n2. If there is no cycle, both `fast` and `slow` will be `None` so I return one of them.\n3. If there is a cycle, `slow` will be equal to a ListNode `fast` that not None. The problem here is that it is impossible to tell where excatly in the cycle did they meet? \n4. To find out the size of the cycle in question, I initialize a `tracer` pointer that starts right next to `slow` and assume a cycle of size 1. Then I count how many "next"s are there to get back to `slow` and update the `count` variable.\n5. I start the `tracer` pointer anew from the beginning and move it from the `head` a `count` number of steps.\n6. I initialize a `temp` pointer to the head. From 5, `tracer` has already been initialized `count` steps away.\n7. Now all I need is to move them both one step at a time. When the cycle begins, `temp` will be at the beginning of the cycle and so will `tracer` be. This is because we have enforced the `count` steps away rule earlier.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n slow = head\n fast = head.next.next if head and head.next else None\n while slow != fast:\n slow = slow.next\n fast = fast.next.next if fast and fast.next else None\n if not slow:\n return slow\n tracer = slow.next\n count = 1\n while tracer != slow:\n count +=1\n tracer= tracer.next\n tracer = head\n while count > 0:\n tracer = tracer.next\n count -=1\n temp = head\n while temp != tracer:\n temp = temp.next\n tracer = tracer.next\n return temp\n``` | 10 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Create an array and i ~i | reorder-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCreate an array and you can do i and ~i\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n\n array = []\n currentlist = head\n while currentlist is not None:\n array.append(currentlist)\n currentlist = currentlist.next\n\n i = 0\n halflenth = len(array)//2\n while i < halflenth:\n temp = array[i].next\n array[i].next = array[~i]\n array[~i].next = temp\n i += 1\n array[halflenth].next = None \n\n return head\n\n \n``` | 1 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Worst O(n) Solution you will see. Python | reorder-list | 0 | 1 | # Approach\nReverse linked list and count number of elements\n1 -> 2 -> 3 -> 4 -> 5\n5 -> 4 -> 3 -> 2 -> 1\n\nAnd connect them, we will need len(linked list) - 1 connections, so track it.\n\n# Why?\nJust for fun, the solution is not efficient in terms of time and space complexity because we create deepcopy and use weird loops with repeating if conditions. Obviously, it could be simplified but sometimes we gotta write bad code by ourselves to learn how to avoid doing it.\n\nComment what you think and we can have a disscusion below :)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nfrom copy import deepcopy\n\nclass Solution:\n def reverse(self,ppp):\n previous = None\n curr = ppp\n k = 0\n\n while curr:\n temp = curr.next\n curr.next = previous\n previous = curr\n curr = temp\n k += 1\n \n return previous, k-1\n\n def reorderList(self, head: Optional[ListNode]) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n if not head:\n return None\n if not head.next:\n return head\n rrr = deepcopy(head)\n reverse_l, n_iter = self.reverse(rrr)\n\n L1 = head\n L2 = reverse_l\n \n while n_iter > 0:\n \n tmp1 = L1.next\n L1.next = L2\n L1 = tmp1\n n_iter -= 1\n if n_iter == 0:\n L2.next = None\n return head\n\n tmp2 = L2.next\n L2.next = L1\n L2 = tmp2\n n_iter -= 1\n if n_iter == 0:\n L1.next = None\n return head\n\n\n\n\n \n\n \n``` | 2 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Python O(n) by two-pointers [w/ Visualization] | reorder-list | 0 | 1 | The first method is to reorder by **two pointers** with the help of **aux O(n)** space **array**.\n\nThe second method is to reorder by **mid-point finding**, **linked list reverse**, and **linkage update** in O(1) aux space.\n\n---\n\nMethod_#1\n\n**Visualization and Diagram**\n\n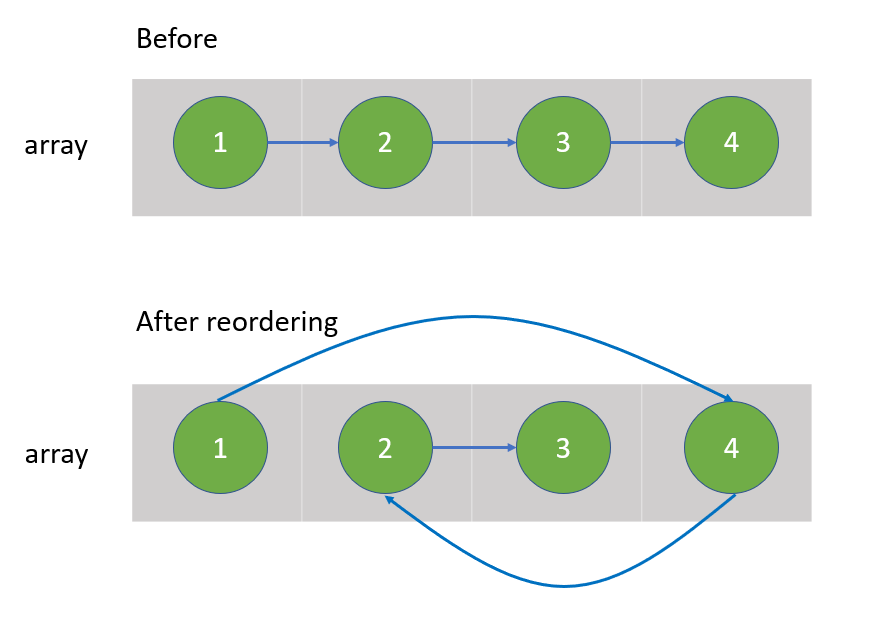\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n\t\t\n\t\t# ----------------------------------------------\n\t\t# Save linked list in array\n\t\t\n arr = []\n \n cur, length = head, 0\n\t\t\n while cur:\n arr.append( cur )\n cur, length = cur.next, length + 1\n \n\t\t# ----------------------------------------------\n # Reorder with two-pointers\n\t\t\n left, right = 0, length-1\n last = head\n \n while left < right:\n arr[left].next = arr[right]\n left += 1\n \n if left == right: \n last = arr[right]\n break\n \n arr[right].next = arr[left]\n right -= 1\n \n last = arr[left]\n \n if last:\n last.next= None\n```\n\n---\n\nMethod_#2\n\n**Visualization and Diagram**\n\n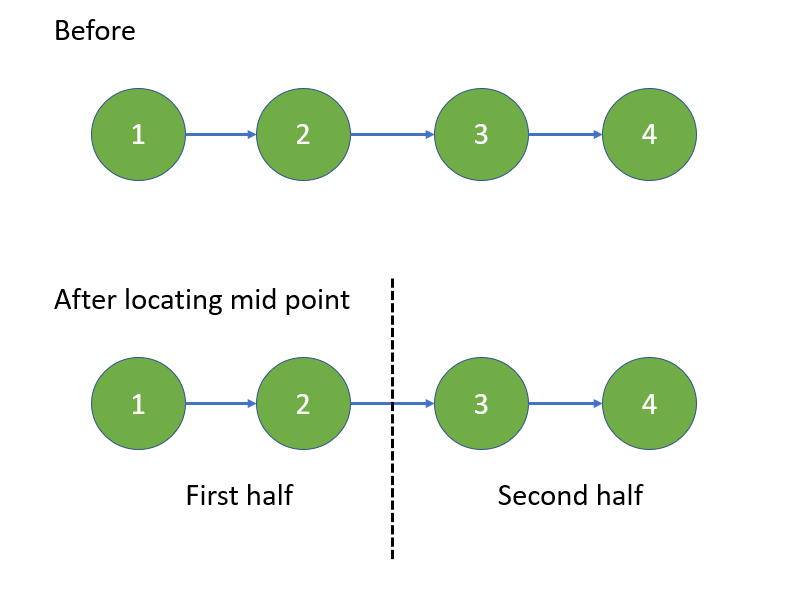\n\n---\n\n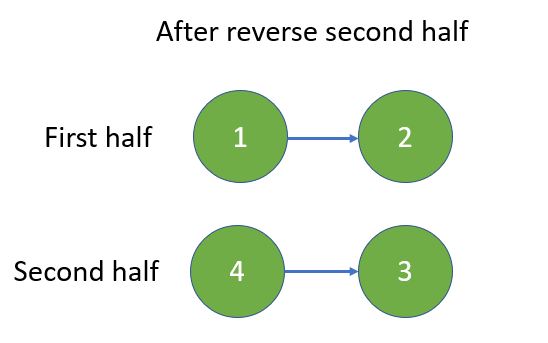\n\n---\n\n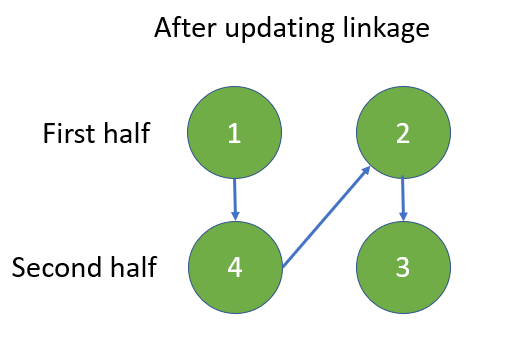\n\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n \n if not head:\n # Quick response for empty linked list\n return None\n \n # ------------------------------------------\n # Locate the mid point of linked list\n # First half is the linked list before mid point\n # Second half is the linked list after mid point\n \n fast, slow = head, head\n \n while fast and fast.next:\n slow, fast = slow.next, fast.next.next\n \n mid = slow\n \n # ------------------------------------------\n # Reverse second half\n \n prev, cur = None, mid\n \n while cur:\n cur.next, prev, cur = prev, cur, cur.next\n \n head_of_second_rev = prev\n \n # ------------------------------------------\n # Update link between first half and reversed second half\n \n first, second = head, head_of_second_rev\n \n while second.next:\n \n next_hop = first.next\n first.next = second\n first = next_hop\n \n next_hop = second.next\n second.next = first\n second = next_hop\n```\n\n--- | 146 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
easy to understand in O(1) space complexity || fast | reorder-list | 0 | 1 | ```\n# below function reverse the linklist\ndef reverse(head):\n p=head\n if(p.next==None):\n return head\n else:\n th=p.next\n p.next=None\n while(th.next):\n k=th.next\n th.next=p\n p=th\n th=k\n th.next=p\n return th\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n n=0\n th=head\n while(th):\n n+=1\n th=th.next\n if(n<3):\n return head\n n-=1\n n//=2 \n # holds the position of the element just after the middle element\n th=head\n hh=None\n for i in range(n):\n th=th.next\n hh=th.next\n th.next=None\n h2=reverse(hh)\n h1=head\n while(h2):\n k1=h1.next\n h1.next=h2\n k2=h2.next\n h2.next=k1\n h1=k1\n h2=k2\n \n``` | 2 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Beats100%✅ | O( n )✅ | Easy-To-Understand✅ | Python (Step by step explanation)✅ | reorder-list | 0 | 1 | # Intuition\nThe problem asks us to reorder a given singly-linked list in a specific way. We need to find a way to split the list into two halves, reverse the second half, and merge the two halves together to achieve the desired reordering.\n\n# Approach\n1. We use the slow and fast pointer technique to find the middle of the linked list. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time. By the time the fast pointer reaches the end of the list, the slow pointer will be at the middle.\n\n2. We then mark the middle node as the beginning of the second half of the list and set the next of the node before the middle as None to split the list into two halves.\n\n3. Next, we reverse the second half of the list. We use three pointers: `h2` for the current node in the second half, `tail` for the new head of the second half, and a temporary pointer to keep track of the next node in the second half. We iterate through the second half, reverse the next pointers, and update the `tail` and `h2` accordingly.\n\n4. Finally, we merge the two halves of the list. We have two pointers, `h1` for the first half and `h2` for the reversed second half. We iterate through the merged list, update the next pointers, and advance the pointers accordingly. This will create the desired reordering of the list.\n\n# Complexity\n- Time complexity: O(n), where n is the number of nodes in the linked list. We perform one pass to find the middle, one pass to reverse the second half, and one pass to merge the two halves.\n- Space complexity: O(1) as we use a constant amount of extra space.\n\nThis code correctly reorders the linked list as described in the problem statement.\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n \n slow, fast = head, head.next\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n\n \n h2 = slow.next\n tail = slow.next = None\n while h2:\n temp = h2.next\n h2.next = tail\n tail = h2\n h2 = temp\n\n # merge two halfs\n h1, h2 = head, tail\n while h2:\n temp1, temp2 = h1.next, h2.next\n h1.next = h2\n h2.next = temp1\n h1, h2 = temp1, temp2\n\n```\n\n# Please upvote the solution if you understood it.\n\n | 3 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
understandable Python3 solution | reorder-list | 0 | 1 | \n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n # edge case \n if not head or not head.next:\n return head\n\n # general case\n # find mid-point\n ps, pf = head, head\n while pf and pf.next:\n ps = ps.next\n pf = pf.next.next\n \n right_head = ps.next\n reversed_right_head = self.reverseL(right_head)\n ps.next = None\n\n # insert reversed_right_head into head (reorder)\n pl, pr = head, reversed_right_head\n while pl and pr:\n pl_next = pl.next\n pr_next = pr.next\n pl.next = pr\n pr.next = pl_next\n pl = pl_next\n pr = pr_next\n \n return head\n\n def reverseL(self, l):\n prev, curr = None, l\n\n while curr:\n next = curr.next\n curr.next = prev\n prev = curr\n curr = next\n \n return prev\n``` | 2 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Python3 | Beats 96% | Alternating Reordering of Linked List | reorder-list | 0 | 1 | # Intuition\nThe key insight is to first divide the list into two halves and then reverse the second half. The crux lies in the reversed second half. When nodes are reversed, the last node becomes the first, and the second-to-last becomes the second, and so on. This reversal aligns with the alternating order. By inserting these reversed nodes into the first half, we achieve the desired alternating reordering.\n\n# Approach\n**Splitting the List:** We divide the list into two halves using two pointers, slow and fast, with slow moving one step and fast moving two steps at a time. This positions slow at the middle of the list.\n\n**Reversing the Second Half:** After finding the middle, we reverse the second half of the list. This is achieved by traversing the second half and changing the direction of pointers using a curr pointer along with prev and holder variables.\n\n**Merging Alternately:** With the reversed second half ready, we merge the two halves alternately. We traverse both halves using curr1 and curr2 pointers. By switching pointers and using holder1 and holder2 to store next nodes, we achieve the alternating reordering.\n\n# Complexity\n- Time complexity\nWe traverse the linked list three times. Once for finding the middle, once for reversing the second half, and once for merging. Thus, the time complexity is **O(n)**, where n is the number of nodes in the linked list.\n\n- Space complexity:\nThe extra space used for pointers and temporary variables is constant, leading to a space complexity of **O(1)**\n\n# Code\n```\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n # No need to reorder if the list is empty or has 1 or 2 elements\n if not head or not head.next or not head.next.next:\n return\n\n # Find the middle of the list\n slow = head\n fast = head\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n\n head2 = slow.next\n slow.next = None\n\n # Reverse the second half of the list\n curr = head2\n prev = None\n \n while curr:\n holder = curr.next\n curr.next = prev\n prev = curr\n curr = holder\n \n # Merge the two halves of the list alternatively\n curr1 = head\n curr2 = prev # Because after reversing the second half, the last node is actually the head of our reversed list\n \n while curr2:\n holder1, holder2 = curr1.next, curr2.next\n curr1.next = curr2\n curr2.next = holder1\n curr1, curr2 = holder1, holder2\n\n``` | 5 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
143: Solution with step by step explanation | reorder-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo reorder the linked list we can follow the below steps:\n\n1. Find the middle node of the linked list using slow and fast pointer approach.\n2. Reverse the second half of the linked list.\n3. Merge the first half and the reversed second half of the linked list alternatively.\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nBeats\n94.68% O(1)\n\n# Code\n```\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n if not head or not head.next:\n return\n \n # Step 1: Find the middle of the linked list\n slow, fast = head, head.next\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n \n # Step 2: Reverse the second half of the linked list\n curr, prev = slow.next, None\n slow.next = None # set the next of the slow to None to break the link\n while curr:\n nxt = curr.next\n curr.next = prev\n prev = curr\n curr = nxt\n second_half = prev\n \n # Step 3: Merge the first half and the reversed second half of the linked list\n first_half = head\n while first_half and second_half:\n temp1, temp2 = first_half.next, second_half.next\n first_half.next = second_half\n second_half.next = temp1\n first_half, second_half = temp1, temp2\n\n``` | 7 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Awesome Slow Fast Logic | reorder-list | 0 | 1 | \n\n# Fast And Slow Logic\n```\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n # divide the linked list\n slow,fast=head,head.next\n while fast and fast.next:\n slow=slow.next\n fast=fast.next.next\n second=slow.next\n # making Null of half linked list\n prev=slow.next=None\n # reverse the end linked list\n while second:\n nxt=second.next\n second.next=prev\n prev=second\n second=nxt\n # merging the divided linked list\n first,last=head,prev\n while last:\n nxt1,nxt2=first.next,last.next\n first.next=last\n last.next=nxt1\n first,last=nxt1,nxt2\n \n```\n# please upvote me it would encourage me alot\n | 13 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Simple Python O(n) time and space using Double-Ended Queue | reorder-list | 0 | 1 | # Intuition\n**The following are my thoughts as written before I even wrote one line of code.**\n\nThe problem is asking us to insert between every node in the first half the linked list with the reverse order node at the end of the list.\n\nI think we can push the nodes as we encounter them onto a double-ended queue. There are only 5000 nodes, so not that many.\n\nOnce we reach the end, of the list, we can pop off the first and last items from the double-ended queue and set the node pointers accordingly; something like:\n\n```\n first.next, last.next = last, first.next\n ```\n \nDo this until we\'ve popped off everything from the queue. If there is only one item that remains, set its next.pointer to None; likewise, if if there were only two items that were left, we need to set the last node\'s next to None.\n\n\n# Approach\nI use $$O(n)$$ space in a double-ended queue `deque`. This lets me pop off the first and last element in $$O(1)$$ time. With a bit of thinking you can arrive at the $$O(1)$$ space solution, but I didn\'t here until I read other solutions. If there is a followup question for $$O(1)$$ space, you can see how reversing the second half of the list will let you "pop" off the first and last items like in my solution. \n\nPersonally, I think my solution is easier to explain, and if the interviewer asks for the O(1) solution you can do that next, or you can just proceed from using the deque not using the deque in one go to impress your interviewer.\n\n# Complexity\n- Time complexity: $$O(n)$$ for pass 1 to traverse linked list initially; $$O(n)$$ for pass 2 to pop off items from the deque and update pointers. $$O(n)$$ total.\n\n- Space complexity: $$O(n)$$ for double ended queue.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nfrom collections import deque\n\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n\n queue = deque()\n node = head\n\n while node:\n queue.append(node)\n node = node.next\n\n last = None\n while len(queue) >= 2:\n first = queue.popleft()\n last = queue.pop()\n first.next, last.next = last, first.next\n\n if len(queue) == 1:\n last = queue.pop()\n \n if last:\n last.next = None\n\n return head\n``` | 1 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Easy understanding python solution for beginner | reorder-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reorderList(self, head: Optional[ListNode]) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n if(head.next==None):\n return(head)\n midnode=None\n slowptr=head\n fastptr=head\n prevslowptr=None\n while(fastptr and fastptr.next):\n prevslowptr=slowptr\n slowptr=slowptr.next\n fastptr=fastptr.next.next\n if(fastptr!=None):\n midnode=ListNode(slowptr.val)\n slowptr=slowptr.next \n prevslowptr.next=None\n firsthalf=head\n secondhalf=self.reverse(slowptr)\n res=self.compare(firsthalf,secondhalf,midnode)\n\n return(res)\n def reverse(self,slowptr):\n prev=None\n cur=slowptr\n nexti=slowptr\n while(cur):\n nexti=cur.next\n cur.next=prev\n prev=cur\n cur=nexti\n return(prev)\n\n def compare(self,firsthalf,secondhalf,midnode):\n tail=dummynode=ListNode(0)\n cur=firsthalf\n temp=secondhalf\n while(cur and temp):\n tail.next=cur\n tail=tail.next\n cur=cur.next\n tail.next=temp\n tail=tail.next\n temp=temp.next\n if(midnode!=None):\n tail.next=midnode \n return(dummynode.next)\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 0 | You are given the head of a singly linked-list. The list can be represented as:
L0 -> L1 -> ... -> Ln - 1 -> Ln
_Reorder the list to be on the following form:_
L0 -> Ln -> L1 -> Ln - 1 -> L2 -> Ln - 2 -> ...
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,4,2,3\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[1,5,2,4,3\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 1000` | null |
Solution | binary-tree-preorder-traversal | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> preorderTraversal(TreeNode* root) {\n vector<int> preorder;\n stack<TreeNode*> stack;\n if (root == NULL)\n return preorder;\n stack.push(root);\n while(!stack.empty()) {\n TreeNode* curr = stack.top();\n stack.pop();\n preorder.push_back(curr->val);\n if (curr->right != NULL)\n stack.push(curr->right);\n if (curr->left != NULL)\n stack.push(curr->left);\n }\n return preorder;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n head = root\n stack = []\n res = []\n\n while head or stack:\n if head:\n res.append(head.val)\n if head.right:\n stack.append(head.right)\n head = head.left\n else:\n head = stack.pop()\n\n return res \n```\n\n```Java []\nclass Solution {\n List<Integer> preorderTraverse(TreeNode root,List<Integer> list) {\n\n if(root==null)\n return list;\n list.add(root.val);\n preorderTraverse(root.left,list);\n preorderTraverse(root.right,list);\n return list;\n }\n public List<Integer> preorderTraversal(TreeNode root) {\n List<Integer> list = new ArrayList<Integer>();\n list = preorderTraverse(root,list);\n return list;\n }\n}\n```\n | 208 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Binbin with phenomenal ideas is back! | binary-tree-preorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n L=[]\n def pot(node):\n if node is None:\n return\n L.append(node.val)\n pot(node.left)\n pot(node.right)\n return L\n return pot(root)\n``` | 1 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Recuresive solution with explanation | binary-tree-preorder-traversal | 1 | 1 | \n\n# Approach\nThe problem asks to perform a preorder traversal on a binary tree and return the node values in the traversal order. Preorder traversal visits the root, then the left subtree, and finally the right subtree.\n\nThe given C++ solution uses a recursive approach to perform the preorder traversal. It defines a helper function preorder that traverses the tree in preorder and adds the node values to a vector. The main function preorderTraversal initializes an empty vector, calls the helper function to perform the traversal, and returns the vector containing the node values in preorder.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n void preorder(TreeNode* node, vector<int>& pre) {\n if (node == nullptr) return;\n \n pre.push_back(node->val);\n preorder(node->left, pre);\n preorder(node->right, pre);\n }\n\n vector<int> preorderTraversal(TreeNode* root) {\n vector<int> pre;\n preorder(root, pre);\n return pre;\n }\n};\n```\n```python []\nclass Solution:\n def preorder(self, node, pre):\n if node is None:\n return\n \n pre.append(node.val)\n self.preorder(node.left, pre)\n self.preorder(node.right, pre)\n\n def preorderTraversal(self, root):\n pre = []\n self.preorder(root, pre)\n return pre\n```\n```Java []\nclass Solution {\n public void preorder(TreeNode node, List<Integer> pre) {\n if (node == null) return;\n \n pre.add(node.val);\n preorder(node.left, pre);\n preorder(node.right, pre);\n }\n\n public List<Integer> preorderTraversal(TreeNode root) {\n List<Integer> pre = new ArrayList<>();\n preorder(root, pre);\n return pre;\n }\n}\n\n```\n | 2 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Proper Tree Traversal || DFS || Python Easy || Begineer Friendly || | binary-tree-preorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The intuition here is to perform a preorder traversal of a binary tree and collect the values of the nodes in a list as you traverse the tree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- We can implement a recursive approach to perform a preorder traversal of the tree.\n- Initialize an empty list `arr` to store the values of the nodes in the preorder traversal.\n- Start the traversal from the root node. If the node is not None, append its value to `arr`, and then recursively traverse its left and right subtrees.\n- Return the `arr` list containing the preorder traversal values.\n\n# Complexity\n- Time complexity:\n - The time complexity of this approach is $$O(n)$$, where n is the number of nodes in the binary tree. This is because we visit each node exactly once during the traversal.\n- Space complexity:\n - The space complexity is also $$O(n)$$ due to the space used by the `arr` list to store the traversal values. In the worst case, the list will contain all the nodes\' values.\n\n# Code\n```python\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def __init__(self):\n self.arr = []\n\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if root is not None:\n self.arr.append(root.val)\n self.preorderTraversal(root.left)\n self.preorderTraversal(root.right)\n return self.arr\n``` | 13 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Iterative DFS, Python | binary-tree-preorder-traversal | 0 | 1 | Probably the exact same solution as others. Did it iterative style using queue as suggested by the follow up.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n\n traversal = []\n queue = [root]\n while queue:\n node = queue.pop()\n traversal.append(node.val)\n for next_node in [node.right, node.left]:\n if next_node:\n queue.append(next_node)\n\n return traversal\n``` | 0 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Using stack implementation beats 99% no recursion involved | binary-tree-preorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Here basic stack implementation is done,we have an ans array which stores the answer,as it is stack we append left node after right node\n,then,till stack exists we can keep appending till leaves returning answer**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if root is None:\n return None\n s=[root]\n ans=[]\n while s:\n node=s.pop()\n ans.append(node.val)\n if node.right:\n s.append(node.right)\n if node.left:\n s.append(node.left)\n return ans\n``` | 1 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python3 Solution Time O(n) Space O(n) | binary-tree-preorder-traversal | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nfrom collections import deque\n\n\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n queue = deque()\n if root:\n queue.appendleft(root)\n result = []\n while queue:\n node = queue.popleft()\n result.append(node.val)\n \n if node.right:\n queue.appendleft(node.right)\n if node.left:\n queue.appendleft(node.left)\n \n return result\n``` | 1 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Most optimal iterative solution with explanation | binary-tree-preorder-traversal | 1 | 1 | \n\n# Approach\n- Initialize an empty stack and push the root node onto the stack.\n- While the stack is not empty:\n - Pop a node from the stack and add its value to the preorder list.\n - Push the right child onto the stack (if it exists).\n - Push the left child onto the stack (if it exists).\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n vector<int> preorderTraversal(TreeNode* root) {\n vector<int> pre;\n if(root == NULL) return pre;\n stack<TreeNode*> st;\n st.push(root);\n while(!st.empty()) {\n root = st.top();\n st.pop();\n pre.push_back(root->val);\n if(root->right != NULL) st.push(root->right);\n if(root->left != NULL) st.push(root->left);\n }\n return pre;\n }\n};\n```\n```python3 []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\n\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n pre = []\n if root is None:\n return pre\n\n stack = []\n stack.append(root)\n\n while stack:\n node = stack.pop()\n pre.append(node.val)\n\n if node.right:\n stack.append(node.right)\n if node.left:\n stack.append(node.left)\n\n return pre\n\n \n```\n```Java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\npublic class Solution {\n public List<Integer> preorderTraversal(TreeNode root) {\n List<Integer> pre = new ArrayList<>();\n if (root == null) return pre;\n \n Stack<TreeNode> stack = new Stack<>();\n stack.push(root);\n \n while (!stack.isEmpty()) {\n TreeNode node = stack.pop();\n pre.add(node.val);\n \n if (node.right != null) stack.push(node.right);\n if (node.left != null) stack.push(node.left);\n }\n \n return pre;\n }\n}\n```\n | 4 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python || Morris Traversal || O(1) Space Complexity | binary-tree-preorder-traversal | 0 | 1 | ```\nclass Solution:\n def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n preorder=[]\n curr=root\n while curr:\n if curr.left==None:\n preorder.append(curr.val)\n curr=curr.right\n else:\n prev=curr.left\n while prev.right and prev.right!=curr:\n prev=prev.right\n if prev.right==None:\n prev.right=curr\n preorder.append(curr.val)\n curr=curr.left\n else:\n prev.right=None\n curr=curr.right\n return preorder\n```\n**An upvote will be encouraging** | 1 | Given the `root` of a binary tree, return _the preorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,2,3\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Binbin wrote another outstanding solution! | binary-tree-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n L=[]\n def pot(node):\n if node is None:\n return\n pot(node.left)\n pot(node.right)\n L.append(node.val)\n return L\n return pot(root)\n \n``` | 1 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Recursive and interative(both using one stack and using two stacks) solution with explanation | binary-tree-postorder-traversal | 1 | 1 | \n# RECURSIVE\n## Approach\n- Define a helper function postorder that takes a node and a vector to store the postorder traversal.\n- If the node is null, return.\n- Recursively traverse the left subtree in postorder.\n- Recursively traverse the right subtree in postorder.\n- Add the node\'s value to the vector in the postorder.\n\n## Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n void postorder(TreeNode* node, vector<int>& post) {\n if(node == NULL) return;\n postorder(node->left, post);\n postorder(node->right, post);\n post.push_back(node->val);\n }\n vector<int> postorderTraversal(TreeNode* root) {\n vector<int> post;\n postorder(root, post);\n return post;\n }\n};\n```\n```python []\nclass Solution:\n def postorder(self, node, post):\n if node is None:\n return\n \n self.postorder(node.left, post)\n self.postorder(node.right, post)\n post.append(node.val)\n\n def postorderTraversal(self, root):\n post = []\n self.postorder(root, post)\n return post\n\n```\n```Java []\nclass Solution {\n public void postorder(TreeNode node, List<Integer> post) {\n if (node == null) return;\n \n postorder(node.left, post);\n postorder(node.right, post);\n post.add(node.val);\n }\n\n public List<Integer> postorderTraversal(TreeNode root) {\n List<Integer> post = new ArrayList<>();\n postorder(root, post);\n return post;\n }\n}\n```\n\n# ITERATIVE USING TWO STACKS\n\n## Approach\n1. Preorder Traversal with Two Stacks (s1 and s2):\n - Push the root node onto s1.\n - While s1 is not empty, pop a node from s1, push it to s2, and then push its left and right children (if they exist) onto s1.\n\n2 .Reversing the Result:\n - After the traversal, pop nodes from s2 and add their values to the result vector to obtain the postorder traversal.\n\n## Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(2N)\n\n```C++ []\nclass Solution {\npublic:\n vector<int> postorderTraversal(TreeNode* root) {\n vector<int> postOrder;\n if (root == nullptr)\n return postOrder;\n\n stack<TreeNode*> s1, s2;\n s1.push(root);\n\n while (!s1.empty()) {\n TreeNode* curr = s1.top();\n s1.pop();\n s2.push(curr);\n\n if (curr->left != nullptr)\n s1.push(curr->left);\n\n if (curr->right != nullptr)\n s1.push(curr->right);\n }\n\n while (!s2.empty()) {\n postOrder.push_back(s2.top()->val);\n s2.pop();\n }\n\n return postOrder;\n }\n};\n```\n```python []\nclass Solution:\n def postorderTraversal(self, root):\n postOrder = []\n if not root:\n return postOrder\n\n s1 = []\n s2 = []\n s1.append(root)\n\n while s1:\n curr = s1.pop()\n s2.append(curr)\n\n if curr.left:\n s1.append(curr.left)\n\n if curr.right:\n s1.append(curr.right)\n\n while s2:\n postOrder.append(s2.pop().val)\n\n return postOrder\n\n```\n```Java []\nclass Solution {\n public List<Integer> postorderTraversal(TreeNode root) {\n List<Integer> postOrder = new ArrayList<>();\n if (root == null)\n return postOrder;\n\n Stack<TreeNode> s1 = new Stack<>();\n Stack<TreeNode> s2 = new Stack<>();\n s1.push(root);\n\n while (!s1.isEmpty()) {\n TreeNode curr = s1.pop();\n s2.push(curr);\n\n if (curr.left != null)\n s1.push(curr.left);\n\n if (curr.right != null)\n s1.push(curr.right);\n }\n\n while (!s2.isEmpty()) {\n postOrder.add(s2.pop().val);\n }\n\n return postOrder;\n }\n}\n\n```\n\n# ITERATIVE USING ONE STACK\n\n## Approach\n1. Initialize an empty vector postOrder to store the node values in postorder traversal.\n2. Create a stack to hold tree nodes.\n3. Start with the root node and set cur to the root.\n4. Use a while loop that continues until both cur is null and the stack is empty.\n - If cur is not null, push cur onto the stack and move cur to its left child.\n - If cur is null, pop a node from the stack, check if its right child is the last visited node or null.\n- If the right child is the last visited node or null, it\'s time to visit the current node:\n - Pop the node from the stack.\n - Add its value to the postOrder vector.\n - Update lastVisited to the popped node.\n- If the right child is not the last visited node, set cur to the right child.\n\n5. Return the postOrder vector.\n\n## Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n vector<int> postorderTraversal(TreeNode* root) {\n vector<int> postOrder;\n if (root == nullptr)\n return postOrder;\n\n stack<TreeNode*> st;\n TreeNode* cur = root;\n TreeNode* lastVisited = nullptr;\n\n while (cur != nullptr || !st.empty()) {\n if (cur != nullptr) {\n st.push(cur);\n cur = cur->left;\n } else {\n TreeNode* temp = st.top();\n if (temp->right != nullptr && temp->right != lastVisited) {\n cur = temp->right;\n } else {\n st.pop();\n postOrder.push_back(temp->val);\n lastVisited = temp;\n }\n }\n }\n return postOrder;\n }\n};\n```\n```python []\nclass Solution:\n def postorderTraversal(self, root):\n postOrder = []\n if not root:\n return postOrder\n\n stack = []\n cur = root\n lastVisited = None\n\n while cur or stack:\n if cur:\n stack.append(cur)\n cur = cur.left\n else:\n temp = stack[-1]\n if temp.right and temp.right != lastVisited:\n cur = temp.right\n else:\n stack.pop()\n postOrder.append(temp.val)\n lastVisited = temp\n\n return postOrder\n\n```\n```Java []\nclass Solution {\n public List<Integer> postorderTraversal(TreeNode root) {\n List<Integer> postOrder = new ArrayList<>();\n if (root == null)\n return postOrder;\n\n Stack<TreeNode> stack = new Stack<>();\n TreeNode cur = root;\n TreeNode lastVisited = null;\n\n while (cur != null || !stack.isEmpty()) {\n if (cur != null) {\n stack.push(cur);\n cur = cur.left;\n } else {\n TreeNode temp = stack.peek();\n if (temp.right != null && temp.right != lastVisited) {\n cur = temp.right;\n } else {\n stack.pop();\n postOrder.add(temp.val);\n lastVisited = temp;\n }\n }\n }\n return postOrder;\n }\n}\n\n\n```\n\n\n\n\n | 8 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Easy || Recursive & Iterative || 100% || Explained (Java, C++, Python, Python3) | binary-tree-postorder-traversal | 1 | 1 | # **Java Solution (Iterative Approach Using Stack):**\nRuntime: 1 ms, faster than 89.81% of Java online submissions for Binary Tree Postorder Traversal.\nMemory Usage: 42 MB, less than 74.94% of Java online submissions for Binary Tree Postorder Traversal.\n```\nclass Solution {\n public List<Integer> postorderTraversal(TreeNode root) {\n // Create an array list to store the solution result...\n List<Integer> sol = new ArrayList<Integer>();\n // Return the solution answer if the tree is empty...\n if(root==null) return sol;\n // Create an empty stack and push the root node...\n Stack<TreeNode> bag = new Stack<TreeNode>();\n bag.push(root);\n // Loop till stack is empty...\n while(!bag.isEmpty()) {\n // set peek a node from the stack...\n TreeNode node = bag.peek();\n // If the subtrees of that node are null, then pop & store the pop value into solution result...\n if(node.left==null && node.right==null) {\n TreeNode pop = bag.pop();\n sol.add(pop.val);\n }\n else {\n // Push the right child of the popped node into the stack...\n if(node.right!=null) {\n bag.push(node.right);\n node.right = null;\n }\n // Push the left child of the popped node into the stack...\n if(node.left!=null) {\n bag.push(node.left);\n node.left = null;\n }\n }\n }\n return sol; // Return the solution list...\n }\n}\n```\n\n# **C++ Solution: (Recursive Approach)**\nRuntime: 1 ms, faster than 93.22% of C++ online submissions for Binary Tree Postorder Traversal.\nMemory Usage: 8.3 MB, less than 96.14% of C++ online submissions for Binary Tree Postorder Traversal.\n```\nclass Solution {\npublic:\n vector<int> postorderTraversal(TreeNode* root) {\n vector<int> sol;\n postorder(root, sol);\n return sol;\n }\nprivate:\n void postorder(TreeNode* root, vector<int>& sol) {\n if (!root)\n return;\n postorder(root->left, sol);\n postorder(root->right, sol);\n sol.push_back(root->val);\n }\n};\n```\n\n# **Python/Python3 Solution (Iterative Approach Using Stack):**\n```\nclass Solution(object):\n def postorderTraversal(self, root):\n # Base case...\n if not root: return []\n # Create an array list to store the solution result...\n sol = []\n # Create an empty stack and push the root node...\n bag = [root]\n # Loop till stack is empty...\n while bag:\n # Pop a node from the stack...\n node = bag.pop()\n sol.append(node.val)\n # Push the left child of the popped node into the stack...\n if node.left:\n bag.append(node.left)\n # Append the right child of the popped node into the stack...\n if node.right:\n bag.append(node.right)\n return sol[::-1] # Return the solution list...\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 47 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
145: Solution with step by step explanation | binary-tree-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses a stack to implement an iterative postorder traversal of the binary tree. The algorithm starts by adding the root node to the stack. Then, while the stack is not empty, it pops the next node from the stack, appends its value to the result list, and adds its left and right children to the stack (if they exist). Finally, the result list is reversed and returned as the final output.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def postorderTraversal(self, root: TreeNode) -> List[int]:\n if not root:\n return []\n \n stack = [root]\n result = []\n \n while stack:\n node = stack.pop()\n result.append(node.val)\n if node.left:\n stack.append(node.left)\n if node.right:\n stack.append(node.right)\n \n return result[::-1]\n\n``` | 5 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python || Easy || Recursive || Iterative || Both Solutions | binary-tree-postorder-traversal | 0 | 1 | **Iterative Solution:**\n```\ndef postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if root is None:\n return \n a=[root]\n ans=[]\n while a:\n t=a.pop()\n ans.append(t.val)\n if t.left:\n a.append(t.left)\n if t.right:\n a.append(t.right)\n return ans[::-1]\n```\n**Recursive Solution:**\n```\ndef postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n self.ans=[]\n self.Traversal(root)\n return self.ans\n \n def Traversal(self,root):\n if root is None:\n return\n self.Traversal(root.left)\n self.Traversal(root.right)\n self.ans.append(root.val)\n```\n**An upvote will be encouraging** | 4 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Binary Tree postorder Traversal | binary-tree-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n return self.postorderTraversal(root.left)+self.postorderTraversal(root.right)+[root.val] if root else []\n``` | 2 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python Elegant & Short | DFS + BFS | Based on generators | binary-tree-postorder-traversal | 0 | 1 | # BFS solution:\n```\nfrom typing import List, Optional\n\n\nclass Solution:\n\t"""\n\tTime: O(n)\n\tMemory: O(n)\n\t"""\n\n\tdef postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n\t\tif root is None:\n\t\t\treturn []\n\n\t\tpostorder = []\n\t\tstack = [root]\n\n\t\twhile stack:\n\t\t\tnode = stack.pop()\n\t\t\tpostorder.append(node.val)\n\t\t\tif node.left is not None:\n\t\t\t\tstack.append(node.left)\n\t\t\tif node.right is not None:\n\t\t\t\tstack.append(node.right)\n\n\t\treturn postorder[::-1]\n```\n# DFS solution:\n```\nfrom typing import List, Optional\n\n\nclass Solution:\n\t"""\n\tTime: O(n)\n\tMemory: O(n)\n\t"""\n\n\tdef postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n\t\treturn list(self.postorder_generator(root))\n\n\t@classmethod\n\tdef postorder_generator(cls, tree: Optional[TreeNode]):\n\t\tif tree is not None:\n\t\t\tyield from cls.postorder_generator(tree.left)\n\t\t\tyield from cls.postorder_generator(tree.right)\n\t\t\tyield tree.val\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n | 9 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python Easy Solution || Iteration || 100% || Beats 98%|| | binary-tree-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n res=[]\n stack =[root]\n while stack:\n cv=stack.pop()\n if type(cv)!=int and cv:\n if cv.left:\n stack.append(cv.val)\n stack.append(cv.right)\n \n stack.append(cv.left)\n elif cv.right:\n stack.append(cv.val)\n stack.append(cv.right)\n # stack.append(cv.val)\n stack.append(cv.left)\n else:\n res.append(cv.val)\n elif cv!=None:\n res.append(cv)\n\n return res\n \n``` | 1 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
using stack implementation,O(N), no recursion used | binary-tree-postorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Here basic stack implementation is done,we have an ans array which stores the answer,as it is stack we append left node then right node\n,till stack exists we can keep appending till leaves returning answer,\nthe required answer will be reverse of ans array\nreturn reverse of array will do it**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if root is None:\n return \n ans=[]\n s=[root]\n while s:\n node=s.pop()\n ans.append(node.val)\n if node.left:\n s.append(node.left)\n if node.right:\n s.append(node.right)\n return ans[::-1]\n``` | 2 | Given the `root` of a binary tree, return _the postorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[3,2,1\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of the nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Solution | lru-cache | 1 | 1 | ```C++ []\nclass LRUCache {\npublic:\n inline static int M[10001];\n inline static int16_t L[10002][2];\n int cap, size = 0;\n const int NONE = 10001;\n int head = NONE, tail = NONE;\n \n LRUCache(int capacity) : cap(capacity) {\n memset(M, 0xff, sizeof M);\n }\n \n inline void erase(int key) {\n const int pre = L[key][0];\n const int nxt = L[key][1];\n L[pre][1] = nxt;\n L[nxt][0] = pre;\n if (head == key) head = nxt;\n if (tail == key) tail = pre;\n }\n \n inline void push_front(int key) {\n L[key][0] = NONE;\n L[key][1] = head;\n L[head][0] = key;\n head = key;\n if (tail == NONE)\n tail = key;\n }\n \n inline int pop_back() {\n int ret = tail;\n tail = L[tail][0];\n L[tail][1] = NONE;\n if (tail == NONE)\n head = NONE;\n return ret;\n }\n \n int get(int key) {\n if (M[key] == -1) return -1;\n erase(key);\n push_front(key);\n return M[key];\n }\n \n void put(int key, int value) {\n if (M[key] != -1) {\n erase(key);\n } else {\n if (size == cap) {\n int poped = pop_back();\n M[poped] = -1;\n size -= 1;\n }\n size += 1;\n }\n push_front(key);\n M[key] = value;\n }\n};\n\n#include <unistd.h>\nstatic char buf[20000000];\n\nint mgetchar() {\n static int pos = 0;\n pos++;\n return buf[pos-1] == \'\\0\' ? EOF : buf[pos-1];\n}\n\nint getmethod() {\n int c = mgetchar();\n while (mgetchar() != \'"\');\n return c;\n}\n\nint getinput(vector<int>& ret) {\n int c;\n while((c = mgetchar()) != EOF && c != \'[\');\n while ((c = mgetchar()) != EOF) {\n if (c == \'"\')\n ret.push_back(getmethod());\n else if (c == \']\')\n return 1;\n }\n return 0;\n}\n\nint getone() {\n while(mgetchar() != \'[\');\n int ans = 0, c;\n while((c = mgetchar()) != \']\') {\n if (isdigit(c))\n ans = ans * 10 + c - \'0\';\n }\n return ans;\n}\n\npair<int,int> gettwo() {\n while(mgetchar() != \'[\');\n pair<int,int> ans;\n int c;\n while((c = mgetchar()) != \',\') {\n if (isdigit(c))\n ans.first = ans.first * 10 + c - \'0\';\n }\n while((c = mgetchar()) != \']\') {\n if (isdigit(c))\n ans.second = ans.second * 10 + c - \'0\';\n }\n return ans;\n}\n\nvoid getpara(FILE *fp, vector<int>& funcs) {\n while(mgetchar() != \'[\');\n fprintf(fp, "[");\n LRUCache lru(getone());\n for (int i = 0; i < funcs.size(); i++) {\n auto f = funcs[i];\n if (f == \'L\') {\n fprintf(fp, "null");\n } else if (f == \'g\') {\n int v = lru.get(getone());\n fprintf(fp, "%d", v);\n } else {\n pair<int,int> v = gettwo();\n lru.put(v.first, v.second);\n fprintf(fp, "null");\n }\n if (i + 1 < funcs.size())\n fprintf(fp, ",");\n }\n while(mgetchar() != \']\');\n fprintf(fp, "]\\n");\n}\n\nint main() {\n int n = read(0, buf, 20000000);\n buf[n] = \'\\0\';\n\n FILE *fp = fopen("user.out", "w");\n vector<int> funcs;\n while (getinput(funcs)) {\n getpara(fp, funcs);\n funcs.clear();\n }\n fclose(fp);\n}\n```\n\n```Python3 []\nfrom collections import OrderedDict\n\nclass LRUCache:\n __slots__ = (\'data\', \'capacity\')\n\n def __init__(self, capacity: int):\n self.data: Dict[int, int] = OrderedDict()\n self.capacity: int = capacity\n\n def get(self, key: int) -> int:\n return -1 if key not in self.data else self.data.setdefault(key, self.data.pop(key))\n\n def put(self, key: int, value: int) -> None:\n try:\n self.data.move_to_end(key)\n self.data[key] = value\n except KeyError:\n self.data[key] = value\n if len(self.data) > self.capacity:\n self.data.popitem(last=False)\n```\n\n```Java []\nclass LRUCache {\n class Node{\n int key;\n int value;\n\n Node prev;\n Node next;\n\n Node(int key, int value){\n this.key= key;\n this.value= value;\n }\n }\n\n public Node[] map;\n public int count, capacity;\n public Node head, tail;\n \n public LRUCache(int capacity) {\n \n this.capacity= capacity;\n count= 0;\n \n map= new Node[10_000+1];\n \n head= new Node(0,0);\n tail= new Node(0,0);\n \n head.next= tail;\n tail.prev= head;\n \n head.prev= null;\n tail.next= null;\n }\n \n public void deleteNode(Node node){\n node.prev.next= node.next;\n node.next.prev= node.prev; \n \n return;\n }\n \n public void addToHead(Node node){\n node.next= head.next;\n node.next.prev= node;\n node.prev= head;\n \n head.next= node; \n \n return;\n }\n \n public int get(int key) {\n \n if( map[key] != null ){\n \n Node node= map[key];\n \n int nodeVal= node.value;\n \n deleteNode(node);\n \n addToHead(node);\n \n return nodeVal;\n }\n else\n return -1;\n }\n \n public void put(int key, int value) {\n \n if(map[key] != null){\n \n Node node= map[key];\n \n node.value= value;\n \n deleteNode(node);\n \n addToHead(node);\n \n } else {\n \n Node node= new Node(key,value);\n \n map[key]= node;\n \n if(count < capacity){\n count++;\n addToHead(node);\n } \n else {\n \n map[tail.prev.key]= null;\n deleteNode(tail.prev);\n \n addToHead(node);\n }\n }\n \n return;\n }\n \n}\n```\n | 434 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
✅DLL + Map || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | lru-cache | 1 | 1 | # Intuition:\nThe intuition is to maintain a fixed-size cache of key-value pairs using a doubly linked list and an unordered map. When accessing or adding a key-value pair, it moves the corresponding node to the front of the linked list, making it the most recently used item. This way, the least recently used item is always at the end of the list. When the cache is full and a new item is added, it removes the item at the end of the list (least recently used) to make space for the new item, ensuring the LRU property is maintained.\n\n# Explanation:\n\n1. `Node` Class:\n- This is a nested class representing a doubly linked list node.\n- Each node contains an integer key, an integer value, and pointers to the previous and next nodes in the linked list.\n\n2. `LRUCache` Class:\n- This is the main LRU Cache class.\n- It has a fixed capacity (`cap`) that is specified during its instantiation.\n- It uses an `unordered_map<int, Node*>` named `m` to store key-value pairs, where the key is the integer key, and the value is a pointer to the corresponding `Node`.\n\n3. `head` and `tail` Nodes:\n- The `LRUCache` class has two dummy nodes: `head` and `tail`.\n- These nodes act as sentinels in the doubly linked list, helping to simplify the edge cases and avoid dealing with null pointers.\n- `head` is the first node in the linked list, and `tail` is the last node.\n\n4. `addNode` Function:\n- This function is used to add a new node to the front of the doubly linked list (right after `head`).\n- It takes a `Node* newnode` as input, representing the node to be added.\n- The function updates the pointers of the new node, the previous first node, and `head` to include the new node as the new first node.\n\n5. `deleteNode` Function:\n- This function is used to delete a node from the doubly linked list.\n- It takes a `Node* delnode` as input, representing the node to be deleted.\n- The function updates the pointers of the previous and next nodes to exclude the node to be deleted, effectively removing it from the linked list.\n\n6. `get` Function:\n- This function is used to retrieve a value from the cache based on the given key.\n- If the key exists in the cache (`m.find(key) != m.end()`), it retrieves the corresponding node (`resNode`), extracts its value (`ans`), and performs the following steps:\n - Erase the key-value pair from the `m` unordered map.\n - Delete the node from its current position in the linked list using `deleteNode`.\n - Add the node to the front of the linked list using `addNode`, making it the most recently used node.\n - Update the `m` map to store the key with the most recently used node.\n- If the key doesn\'t exist in the cache, it returns `-1`.\n\n7. `put` Function:\n- This function is used to insert or update a key-value pair in the cache.\n- If the key already exists in the cache, it updates the value by performing the following steps:\n - Erase the existing key-value pair from the `m` unordered map.\n - Delete the corresponding node from its current position in the linked list using `deleteNode`.\n- If the cache is full (i.e., `m.size() == cap`), it removes the least recently used node from the cache by erasing the key-value pair from the `m` map and deleting the node from the end of the linked list using `deleteNode`.\n- After handling the eviction (if needed), it creates a new node using `new Node(key, value)` and adds it to the front of the linked list using `addNode`.\n- Finally, it updates the `m` map to store the key with the newly added node.\n\n# Code\n```C++ []\nclass LRUCache {\npublic:\n class Node{\n public: \n int key;\n int val;\n Node* prev;\n Node* next;\n\n Node(int key, int val){\n this->key = key;\n this->val = val;\n }\n };\n\n Node* head = new Node(-1, -1);\n Node* tail = new Node(-1, -1);\n\n int cap;\n unordered_map<int, Node*> m;\n\n LRUCache(int capacity) {\n cap = capacity;\n head -> next = tail;\n tail -> prev = head;\n }\n\n void addNode(Node* newnode){\n Node* temp = head -> next;\n\n newnode -> next = temp;\n newnode -> prev = head;\n\n head -> next = newnode;\n temp -> prev = newnode;\n }\n\n void deleteNode(Node* delnode){\n Node* prevv = delnode -> prev;\n Node* nextt = delnode -> next;\n\n prevv -> next = nextt;\n nextt -> prev = prevv;\n }\n \n int get(int key) {\n if(m.find(key) != m.end()){\n Node* resNode = m[key];\n int ans = resNode -> val;\n\n m.erase(key);\n deleteNode(resNode);\n addNode(resNode);\n\n m[key] = head -> next;\n return ans;\n }\n return -1;\n }\n \n void put(int key, int value) {\n if(m.find(key) != m.end()){\n Node* curr = m[key];\n m.erase(key);\n deleteNode(curr);\n }\n\n if(m.size() == cap){\n m.erase(tail -> prev -> key);\n deleteNode(tail -> prev);\n }\n\n addNode(new Node(key, value));\n m[key] = head -> next;\n }\n};\n```\n```Java []\nclass LRUCache {\n class Node {\n int key;\n int val;\n Node prev;\n Node next;\n\n Node(int key, int val) {\n this.key = key;\n this.val = val;\n }\n }\n\n Node head = new Node(-1, -1);\n Node tail = new Node(-1, -1);\n int cap;\n HashMap<Integer, Node> m = new HashMap<>();\n\n public LRUCache(int capacity) {\n cap = capacity;\n head.next = tail;\n tail.prev = head;\n }\n\n private void addNode(Node newnode) {\n Node temp = head.next;\n\n newnode.next = temp;\n newnode.prev = head;\n\n head.next = newnode;\n temp.prev = newnode;\n }\n\n private void deleteNode(Node delnode) {\n Node prevv = delnode.prev;\n Node nextt = delnode.next;\n\n prevv.next = nextt;\n nextt.prev = prevv;\n }\n\n public int get(int key) {\n if (m.containsKey(key)) {\n Node resNode = m.get(key);\n int ans = resNode.val;\n\n m.remove(key);\n deleteNode(resNode);\n addNode(resNode);\n\n m.put(key, head.next);\n return ans;\n }\n return -1;\n }\n\n public void put(int key, int value) {\n if (m.containsKey(key)) {\n Node curr = m.get(key);\n m.remove(key);\n deleteNode(curr);\n }\n\n if (m.size() == cap) {\n m.remove(tail.prev.key);\n deleteNode(tail.prev);\n }\n\n addNode(new Node(key, value));\n m.put(key, head.next);\n }\n}\n```\n```Python3 []\nclass LRUCache:\n class Node:\n def __init__(self, key, val):\n self.key = key\n self.val = val\n self.prev = None\n self.next = None\n\n def __init__(self, capacity: int):\n self.cap = capacity\n self.head = self.Node(-1, -1)\n self.tail = self.Node(-1, -1)\n self.head.next = self.tail\n self.tail.prev = self.head\n self.m = {}\n\n def addNode(self, newnode):\n temp = self.head.next\n newnode.next = temp\n newnode.prev = self.head\n self.head.next = newnode\n temp.prev = newnode\n\n def deleteNode(self, delnode):\n prevv = delnode.prev\n nextt = delnode.next\n prevv.next = nextt\n nextt.prev = prevv\n\n def get(self, key: int) -> int:\n if key in self.m:\n resNode = self.m[key]\n ans = resNode.val\n del self.m[key]\n self.deleteNode(resNode)\n self.addNode(resNode)\n self.m[key] = self.head.next\n return ans\n return -1\n\n def put(self, key: int, value: int) -> None:\n if key in self.m:\n curr = self.m[key]\n del self.m[key]\n self.deleteNode(curr)\n\n if len(self.m) == self.cap:\n del self.m[self.tail.prev.key]\n self.deleteNode(self.tail.prev)\n\n self.addNode(self.Node(key, value))\n self.m[key] = self.head.next\n```\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 178 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Very simple and concise solution using Python OrderedDict | lru-cache | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOrderedDicts in python maintain the order of insertion and can perform access and deletion operations in O(1). They are therefore an ideal candidate for this problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse an OrderedDict to keep track of the least recently used element. Everytime a get operation is performed on an element, pop it from the ordered dict and re-insert it at the end. Everytime a put operation is performed, insert the key value pair at the end. If the capacity is exceeded then pop from the front by getting and iterator pointing to it using:\nnext(iter(self.MyOrderedDict))\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nDeletion, access and insertion operations in an OrderedDict are all O(1). Hence next time complexity is O(1).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) space since nothing extra other than space for the input is required.\n\n# Code\n```\nfrom collections import OrderedDict\n\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.cache = OrderedDict()\n self.cap = capacity\n self.numElements = 0\n\n def get(self, key: int) -> int:\n if key not in self.cache:\n # print(self.cache)\n return -1\n else:\n res = self.cache[key]\n self.cache.pop(key)\n self.cache[key] = res\n # print(self.cache)\n return res\n \n\n def put(self, key: int, value: int) -> None:\n if key in self.cache:\n self.cache.pop(key)\n self.cache[key] = value\n else:\n if self.numElements == self.cap:\n delKey = next(iter(self.cache))\n self.cache.pop(delKey)\n\n self.cache[key] = value\n # print(self.cache)\n else:\n self.cache[key] = value\n self.numElements += 1\n # print(self.cache)\n\n \n\n\n# Your LRUCache object will be instantiated and called as such:\n# obj = LRUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n``` | 0 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
LRU (Least Recently Used) cache✅ | O( 1 )✅ | Python(Step by step explanation)✅ | lru-cache | 0 | 1 | # Intuition\nThe problem requires implementing an LRU (Least Recently Used) cache, which stores a fixed number of key-value pairs and removes the least recently used item when the cache reaches its capacity. The intuition is to use a combination of a doubly-linked list and a hash map. The linked list keeps track of the order of items, and the hash map provides efficient access to items.\n\n# Approach\nThe approach is to implement an LRU cache using a doubly-linked list and a hash map. The linked list stores the key-value pairs in the order they were used, with the most recently used item at the front and the least recently used item at the end. The hash map provides O(1) access to the items. When a key is accessed, it is moved to the front of the linked list to mark it as the most recently used item. When the cache reaches its capacity, the least recently used item is removed from both the linked list and the hash map.\n\n1. Initialize the LRU cache with a given capacity.\n2. Create a doubly-linked list with two dummy nodes: `left` (front) and `right` (end).\n3. Initialize an empty hash map to store key-value pairs, with keys mapping to nodes in the linked list.\n4. When getting a key:\n - If the key is found in the hash map, remove the corresponding node from the linked list.\n - Insert the node at the front of the list to mark it as the most recently used.\n - Return the value associated with the key.\n - If the key is not found, return -1.\n5. When putting a key-value pair:\n - If the key already exists in the cache, remove its corresponding node from the linked list and hash map.\n - Create a new node with the given key and value and insert it at the front of the list.\n - If the cache exceeds its capacity, remove the least recently used item (the node at the end of the list) from both the list and the hash map.\n6. The operations are performed efficiently, and the cache maintains the order of usage.\n\n# Complexity\n- Time complexity:\n - `get` operation: O(1) as it involves a simple hash map lookup and list manipulation.\n - `put` operation: O(1) for the same reasons as the `get` operation.\n- Space complexity: O(capacity) for the hash map and linked list, where capacity is the maximum number of items the cache can store.\n - The space complexity is determined by the capacity of the LRU cache.\n \n```python\nclass Node:\n def __init__(self, key, val):\n self.key, self.val = key, val\n self.prev = self.next = None\n\n\nclass LRUCache:\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.cache = {} # map key to node\n\n self.left, self.right = Node(0, 0), Node(0, 0)\n self.left.next, self.right.prev = self.right, self.left\n\n # remove node from list\n def remove(self, node):\n prev, nxtt = node.prev, node.next\n prev.next, nxtt.prev = nxtt, prev\n\n # insert node at right\n def insert(self, node):\n prev, nxtt = self.right.prev, self.right\n prev.next = nxtt.prev = node\n node.next, node.prev = nxtt, prev\n\n def get(self, key: int) -> int:\n if key in self.cache:\n self.remove(self.cache[key])\n self.insert(self.cache[key])\n return self.cache[key].val\n return -1\n\n def put(self, key: int, value: int) -> None:\n if key in self.cache:\n self.remove(self.cache[key])\n self.cache[key] = Node(key, value)\n self.insert(self.cache[key])\n\n if len(self.cache) > self.capacity:\n # remove from the list and delete the LRU from hashmap\n lru = self.left.next\n self.remove(lru)\n del self.cache[lru.key]\n```\n# Please upvote the solution if you understood it.\n\n | 3 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
🔥Fast Pythonic Solution🔥 | lru-cache | 0 | 1 | # Intuition\nFor Python 3.7+ dictionary iteration order is guaranteed to be in order of insertion.\n\n# Complexity\n- Time complexity: $$O(1)$$ for one operation.\n\n- Space complexity: $$O(1)$$ for one operation.\n\n# Code\n```\nclass LRUCache:\n def __init__(self, capacity):\n self.dict = {}\n self.freeSpace = capacity\n\n\n def get(self, key):\n if key not in self.dict:\n return -1\n\n self.dict[key] = self.dict.pop(key)\n\n return self.dict[key]\n\n\n def put(self, key, value):\n if key in self.dict:\n self.dict.pop(key)\n else:\n if self.freeSpace:\n self.freeSpace -= 1\n else:\n self.dict.pop(next(iter(self.dict)))\n\n self.dict[key] = value\n``` | 25 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
LRU CACHE (USING ORDERED DICT) | lru-cache | 0 | 1 | # Intuition\nOn first glimpse , I thought we could use a normal dictionary but we need to maintain the order of the cache and according to capacity we have to change it. So , instead of going for the normal dict we can go for orderedDict from collections\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n*** One thing about orderedDict() is, it maintains the elements in order just like a list , so it is like a combination of dict+list ,\nand We can use popitem(last=False) in order to make it work in fifo way.\nSo , the least used one will be at first, according to lru cache , we need to delete the first element as it will be the least recently used one.\n\n***\nFirst , we need to instantiate the ordered dictionary.\nThen ,in get() function , first we will search for the key, \nif key is present, we will take it value and return it but before returning it , we need to move it to end.\nBy using move_to_end(key) , we will move it to last, as it is recently used element.\nSimilarly in put() function, if key is already present , we will change the value and move it to the end.\nelse , we will remove the first element and add this element.\n\n# Complexity\n- Time complexity:\n- O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(capacity)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport collections\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.capacity=capacity\n self.hash=collections.OrderedDict()\n def get(self, key: int) -> int:\n if key in self.hash:\n self.hash.move_to_end(key)\n return self.hash[key]\n else:\n return -1\n def put(self, key: int, value: int) -> None:\n if key in self.hash:\n self.hash[key]=value\n self.hash.move_to_end(key)\n elif len(self.hash)==self.capacity:\n self.hash.popitem(last=False)\n self.hash[key]=value\n else:\n self.hash[key]=value\n \n\n\n# Your LRUCache object will be instantiated and called as such:\n# obj = LRUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n``` | 3 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Python || Double Linked List + Hashmap | lru-cache | 0 | 1 | ```\nclass LRUCache: \n class Node: \n def __init__(self,key,val):\n self.key=key\n self.val=val\n self.prev=None\n self.next=None\n\n def __init__(self, capacity: int):\n self.capacity=capacity\n self.dic={}\n self.head=self.Node(-1,-1)\n self.tail=self.Node(-1,-1)\n self.head.next=self.tail\n self.tail.prev=self.head\n \n def addNode(self, newnode):\n temp=self.head.next\n newnode.prev=self.head\n newnode.next=temp\n temp.prev=newnode\n self.head.next=newnode\n \n def deleteNode(self,delnode):\n prevv=delnode.prev\n nextt=delnode.next\n prevv.next=nextt\n nextt.prev=prevv\n\n def get(self, key: int) -> int:\n if key in self.dic:\n node=self.dic[key]\n ans=node.val\n del self.dic[key]\n self.deleteNode(node)\n self.addNode(node)\n self.dic[key]=self.head.next\n return ans\n return -1\n \n def put(self, key: int, value: int) -> None:\n if key in self.dic:\n node=self.dic[key]\n del self.dic[key]\n self.deleteNode(node)\n if len(self.dic)==self.capacity:\n del self.dic[self.tail.prev.key]\n self.deleteNode(self.tail.prev)\n self.addNode(self.Node(key,value))\n self.dic[key]=self.head.next\n```\n**An upvote will be encouraging** | 1 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Easy Python Solution Without OrderedDict | lru-cache | 0 | 1 | # Intuition\nUsing Python Dict for O(1) searching and updation of elements and a dequeue to store order of Least Recently Used key-value pairs \n\n\n\n# Code\n```\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.cache = {}\n self.length = capacity\n self.lru_keys = []\n\n def get(self, key: int) -> int:\n \n if key in self.cache:\n self.lru_keys.remove(key)\n self.lru_keys.append(key)\n return self.cache[key]\n else:\n return -1\n\n def put(self, key: int, value: int) -> None:\n \n if key in self.cache:\n self.lru_keys.remove(key)\n self.lru_keys.append(key)\n self.cache[key] = value\n return None\n\n if self.length <= len(self.cache):\n k = self.lru_keys.pop(0)\n self.cache.pop(k)\n self.cache[key] = value\n else:\n self.cache[key] = value\n\n self.lru_keys.append(key)\n return None\n\n \n \n \n\n\n# Your LRUCache object will be instantiated and called as such:\n# obj = LRUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n``` | 3 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
[Python 3] Double Linked List with moving existing node after using | lru-cache | 0 | 1 | ```python3 []\nclass LinkedNode:\n def __init__(self, key = -1, val = -1):\n self.key = key\n self.val = val\n self.prev = None\n self.next = None\n\nclass LRUCache:\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.cache = dict()\n self.head = LinkedNode()\n self.tail = LinkedNode()\n self.head.next = self.tail\n self.tail.prev = self.head\n \n def get(self, key: int) -> int:\n if key not in self.cache:\n return -1\n \n return self.__moveToEnd(key).val\n\n def put(self, key: int, value: int) -> None:\n if key in self.cache:\n self.__delete(key)\n self.__create(key, value)\n \n if len(self.cache) > self.capacity:\n self.__delete(self.head.next.key)\n\n def __create(self, key, val) -> LinkedNode: \n node = LinkedNode(key, val)\n self.__addToEnd(node)\n self.cache[key] = node\n\n return node\n \n def __delete(self, key) -> None:\n deleteNode = self.__evict(key)\n del deleteNode\n del self.cache[key]\n \n def __moveToEnd(self, key) -> LinkedNode:\n node = self.__evict(key)\n self.__addToEnd(node)\n \n return node\n\n def __addToEnd(self, node) -> None:\n node.prev = self.tail.prev\n node.next = self.tail\n self.tail.prev.next = node\n self.tail.prev = node\n \n def __evict(self, key) -> LinkedNode: \n node = self.cache[key]\n node.prev.next = node.next\n node.next.prev = node.prev\n node.next = None\n node.prev = None\n \n return node\n```\n\n | 12 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
[Python3] doubly linked list and dictionary | lru-cache | 0 | 1 | * The most frequent operation of the problem is changing the node position in the list. \n Change position of the node means two operations, delete and insert.\n Double linked list data structure takes constant time O(1) to insert or delete nodes a linked list by repointing the previous and next pointer of the node.\n [Array data structure takes O(n) to insert or delete ](https://www.tutorialspoint.com/data_structures_algorithms/array_insertion_algorithm.htm) an element in the list by shifting all the element behind the position (backward for insertion, forward for deletion) by one.\n \n * put : \n\tif the key is already in the cache, we update the value, remove the key node and insert the key node after the head;\n\tif the key is not in cache, if the cache is not full,we insert the new key node after the head. If the cache is full, we delete the node before the tail to make room for the new key node, and insert the new key node after the head.\n* get:\n\treturn the value of the key.\n\tremove the key node.\n\tinsert the key node after the head.\n\t \n\n\n```\nclass ListNode:\n def __init__(self, key, value):\n self.key = key\n self.value = value\n self.prev = None\n self.next = None\n\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.dic = dict() # key to node\n self.capacity = capacity\n self.head = ListNode(0, 0)\n self.tail = ListNode(-1, -1)\n self.head.next = self.tail\n self.tail.prev = self.head\n\n def get(self, key: int) -> int:\n if key in self.dic:\n node = self.dic[key]\n self.removeFromList(node)\n self.insertIntoHead(node)\n return node.value\n else:\n return -1\n\n def put(self, key: int, value: int) -> None:\n if key in self.dic: # similar to get() \n node = self.dic[key]\n self.removeFromList(node)\n self.insertIntoHead(node)\n node.value = value # replace the value len(dic)\n else: \n if len(self.dic) >= self.capacity:\n self.removeFromTail()\n node = ListNode(key,value)\n self.dic[key] = node\n self.insertIntoHead(node)\n\t\t\t\n def removeFromList(self, node):\n node.prev.next = node.next\n node.next.prev = node.prev\n \n def insertIntoHead(self, node):\n headNext = self.head.next \n self.head.next = node \n node.prev = self.head \n node.next = headNext \n headNext.prev = node\n \n def removeFromTail(self):\n if len(self.dic) == 0: return\n tail_node = self.tail.prev\n del self.dic[tail_node.key]\n self.removeFromList(tail_node)\n``` | 195 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Python Easy Solution | Dictionary | 701 ms | beats 91.59% | lru-cache | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use a dictionary to store the key value pairs and shift their position depending on their use.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor the get function, if the key exists in the dictionary we store the value in a variable val and delete the key. We again store the key value pair. This is done to shift the position of the key value pair so that the least recently used pair moves to the top of the dictionary. \n\nFor the put function, we check if the number of items in the dictionary is equal to the capacity. If yes, we delete the top item and insert the new key value pair.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1) for put() and get().\n\n\n# Code\n```\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.cache = {}\n self.capacity = capacity\n\n def get(self, key: int) -> int:\n if key in self.cache:\n val = self.cache.pop(key) \n self.cache[key] = val\n return self.cache.get(key)\n return -1\n\n def put(self, key: int, value: int) -> None:\n if key not in self.cache.keys():\n if len(self.cache.keys()) == self.capacity:\n del self.cache[next(iter(self.cache))]\n else:\n self.cache.pop(key)\n self.cache[key] = value\n\n\n\n\n# Your LRUCache object will be instantiated and called as such:\n# obj = LRUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n``` | 10 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Python | DLL | Hashmap | Beats 95% Memory | lru-cache | 0 | 1 | # Code\n```\nclass Node:\n def __init__(self, key, value):\n self.key = key\n self.value = value\n self.next = None\n self.prev = None\n\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.head = None\n self.tail = None\n self.hash_map = {}\n self.capacity = capacity\n\n def prepend(self, new_node: Node):\n if self.head: \n self.head.prev = new_node\n new_node.next = self.head\n \n if not self.tail:\n self.tail = new_node\n \n self.head = new_node\n\n def unlink_node(self, node: Node) -> None:\n # Unlink the node from cache\n if not node: return None\n \n prev_node = node.prev\n next_node = node.next\n\n if prev_node: prev_node.next = next_node\n if next_node: next_node.prev = prev_node\n\n if self.head == node:\n self.head = next_node\n \n if self.tail == node:\n self.tail = prev_node\n \n node.prev = None\n node.next = None\n\n def delete_node(self, node: Node):\n self.unlink_node(node)\n del self.hash_map[node.key]\n del node\n\n def evict_lru_node(self) -> Node or None:\n if not self.tail: return None\n\n lru_node = self.tail\n self.delete_node(lru_node)\n \n def get(self, key: int) -> int:\n if key not in self.hash_map: return -1\n node = self.hash_map[key]\n\n if self.head != node:\n self.unlink_node(node)\n self.prepend(node)\n\n return node.value\n\n def put(self, key: int, value: int) -> None:\n new_node = Node(key, value)\n if key in self.hash_map:\n self.delete_node(self.hash_map[key])\n \n if len(self.hash_map) >= self.capacity:\n self.evict_lru_node()\n\n self.prepend(new_node)\n self.hash_map[key] = new_node\n\n\n# Your LRUCache object will be instantiated and called as such:\n# obj = LRUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n``` | 1 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Beats 100% | CodeDominar Solution | lru-cache | 0 | 1 | # Code\n```\nclass LRUCache:\n def __init__(self, capacity):\n self.capacity = capacity\n self.cache = OrderedDict()\n\n def get(self, key):\n if key not in self.cache:\n return -1\n value = self.cache.pop(key)\n self.cache[key] = value\n return value\n\n def put(self, key, value):\n if key in self.cache:\n self.cache.pop(key)\n elif len(self.cache) == self.capacity:\n self.cache.popitem(last=False)\n self.cache[key] = value\n\n``` | 4 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Python3 Solution | lru-cache | 0 | 1 | \n```\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.capacity=capacity\n self.cache=OrderedDict()\n \n\n def get(self, key: int) -> int:\n if key not in self.cache:\n return -1\n\n value=self.cache.pop(key)\n self.cache[key]=value\n return value \n\n def put(self, key: int, value: int) -> None:\n if key in self.cache:\n self.cache.pop(key)\n\n elif len(self.cache)==self.capacity:\n self.cache.popitem(last=False)\n\n self.cache[key]=value \n\n\n# Your LRUCache object will be instantiated and called as such:\n# obj = LRUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n``` | 3 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | lru-cache | 1 | 1 | # Solution Video\n\nhttps://youtu.be/4Uh7nUGoeog\n\n# *** Please upvote and subscribe to my channel from here. I have 226 videos as of July 19th***\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\n---\n\n# Approach\nThis is based on Python code. Other might be differnt a bit.\n\n1. Create a Node class with attributes key, val, prev, and next to represent individual nodes of a doubly linked list.\n\n2. Create the LRUCache class with a constructor that takes a capacity as input. Inside the constructor:\n\n a. Initialize the capacity and an empty dictionary cache to store key-value pairs.\n\n b. Create two sentinel nodes, oldest and latest, and set their key and value to 0. Connect the oldest node to the latest node and vice versa to form an empty doubly linked list.\n\n3. Implement the get method which takes a key as input and returns the corresponding value if the key exists in the cache:\n\n a. Check if the key exists in the cache using the dictionary cache.\n\n b. If the key is found, remove the corresponding node from the linked list using the remove method (to later move it to the front), and then insert it back at the front using the insert method (to indicate that it\'s the most recently accessed node).\n\n c. Finally, return the value associated with the key from the cache, or -1 if the key is not found.\n\n4. Implement the remove method which takes a node as input and removes it from the linked list:\n\n a. Get the previous and next nodes of the input node.\n\n b. Update the prev and next pointers of the previous and next nodes to exclude the input node.\n\n5. Implement the insert method which takes a node as input and inserts it at the front of the linked list:\n\n a. Get the previous and next nodes of the latest node.\n\n b. Connect the input node to the previous and next nodes appropriately.\n\n c. Update the prev and next pointers of the previous and next nodes to include the input node.\n\n6. Implement the put method which takes a key and value as input and inserts or updates the key-value pair in the cache:\n\n a. Check if the key exists in the cache using the dictionary cache.\n\n b. If the key is found, remove the corresponding node from the linked list using the remove method.\n\n c. Create a new node with the given key and value.\n\n d. Add the new node to the cache.\n\n e. Insert the new node at the front of the linked list using the insert method.\n\n f. If the size of the cache exceeds the capacity, find the least recently used (LRU) node, which is the node next to the oldest node, and remove it from the linked list and cache.\n\n7. The LRUCache class is now implemented and can be used to store and access key-value pairs with a fixed capacity. When accessing a key-value pair, the most recently used pair is moved to the front, and if the cache exceeds its capacity, the least recently used pair is evicted.\n\n\n```python []\nclass Node:\n def __init__(self, key, val):\n self.key = key\n self.val = val\n self.prev = None\n self.next = None\n\nclass LRUCache:\n\n def __init__(self, capacity: int):\n self.cap = capacity\n self.cache = {}\n\n self.oldest = Node(0, 0)\n self.latest = Node(0, 0)\n self.oldest.next = self.latest\n self.latest.prev = self.oldest\n \n\n def get(self, key: int) -> int:\n if key in self.cache:\n self.remove(self.cache[key])\n self.insert(self.cache[key])\n return self.cache[key].val\n return -1\n\n def remove(self, node):\n prev, next = node.prev, node.next\n prev.next = next\n next.prev = prev\n \n def insert(self, node):\n prev, next = self.latest.prev, self.latest\n prev.next = next.prev = node\n node.next = next\n node.prev = prev\n\n def put(self, key: int, value: int) -> None:\n if key in self.cache:\n self.remove(self.cache[key])\n self.cache[key] = Node(key, value)\n self.insert(self.cache[key])\n\n if len(self.cache) > self.cap:\n lru = self.oldest.next\n self.remove(lru)\n del self.cache[lru.key]\n\n```\n```javascript []\n/** \n * https://leetcode.com/problems/lru-cache/\n * Time O(1) | Space O(N)\n * Your LRUCache object will be instantiated and called as such:\n * var obj = new LRUCache(capacity)\n * var param_1 = obj.get(key)\n * obj.put(key,value)\n */\n class LRUCache {\n constructor(capacity) {\n this.capacity = capacity;\n this.map = new Map();\n\n this.head = {};\n this.tail = {};\n\n this.head.next = this.tail;\n this.tail.prev = this.head;\n }\n\n removeLastUsed () {\n const [ key, next, prev ] = [ this.head.next.key, this.head.next.next, this.head ];\n\n this.map.delete(key);\n this.head.next = next;\n this.head.next.prev = prev;\n }\n\n put (key, value) {\n const hasKey = this.get(key) !== -1;\n const isAtCapacity = this.map.size === this.capacity;\n \n if (hasKey) return (this.tail.prev.value = value);\n if (isAtCapacity) this.removeLastUsed();\n\n const node = { key, value };\n this.map.set(key, node);\n this.moveToFront(node);\n }\n\n moveToFront (node) {\n const [ prev, next ] = [ this.tail.prev, this.tail ];\n\n this.tail.prev.next = node;\n this.connectNode(node, { prev, next });\n this.tail.prev = node;\n }\n\n connectNode (node, top) {\n node.prev = top.prev;\n node.next = top.next;\n }\n\n get (key) {\n const hasKey = this.map.has(key);\n if (!hasKey) return -1;\n\n const node = this.map.get(key);\n \n this.disconnectNode(node);\n this.moveToFront(node);\n\n return node.value;\n }\n\n disconnectNode (node) {\n node.next.prev = node.prev;\n node.prev.next = node.next;\n }\n}\n```\n```java []\nclass Node {\n int key;\n int val;\n Node prev;\n Node next;\n\n public Node(int key, int val) {\n this.key = key;\n this.val = val;\n this.prev = null;\n this.next = null;\n }\n}\n\n\nclass LRUCache {\n\n private int cap;\n private Map<Integer, Node> cache;\n private Node oldest;\n private Node latest;\n\n public LRUCache(int capacity) {\n this.cap = capacity;\n this.cache = new HashMap<>();\n this.oldest = new Node(0, 0);\n this.latest = new Node(0, 0);\n this.oldest.next = this.latest;\n this.latest.prev = this.oldest;\n }\n\n public int get(int key) {\n if (cache.containsKey(key)) {\n Node node = cache.get(key);\n remove(node);\n insert(node);\n return node.val;\n }\n return -1;\n }\n\n private void remove(Node node) {\n Node prev = node.prev;\n Node next = node.next;\n prev.next = next;\n next.prev = prev;\n }\n\n private void insert(Node node) {\n Node prev = latest.prev;\n Node next = latest;\n prev.next = next.prev = node;\n node.next = next;\n node.prev = prev;\n }\n\n public void put(int key, int value) {\n if (cache.containsKey(key)) {\n remove(cache.get(key));\n }\n Node newNode = new Node(key, value);\n cache.put(key, newNode);\n insert(newNode);\n\n if (cache.size() > cap) {\n Node lru = oldest.next;\n remove(lru);\n cache.remove(lru.key);\n }\n }\n}\n\n/**\n * Your LRUCache object will be instantiated and called as such:\n * LRUCache obj = new LRUCache(capacity);\n * int param_1 = obj.get(key);\n * obj.put(key,value);\n */\n```\n```C++ []\nclass Node {\npublic:\n int key;\n int val;\n Node* prev;\n Node* next;\n\n Node(int key, int val) : key(key), val(val), prev(nullptr), next(nullptr) {}\n};\n\nclass LRUCache {\npublic:\nprivate:\n int cap;\n std::unordered_map<int, Node*> cache;\n Node* oldest;\n Node* latest;\n\npublic:\n LRUCache(int capacity) : cap(capacity) {\n oldest = new Node(0, 0);\n latest = new Node(0, 0);\n oldest->next = latest;\n latest->prev = oldest;\n }\n\n int get(int key) {\n if (cache.find(key) != cache.end()) {\n Node* node = cache[key];\n remove(node);\n insert(node);\n return node->val;\n }\n return -1;\n }\n\nprivate:\n void remove(Node* node) {\n Node* prev = node->prev;\n Node* next = node->next;\n prev->next = next;\n next->prev = prev;\n }\n\n void insert(Node* node) {\n Node* prev = latest->prev;\n Node* next = latest;\n prev->next = next->prev = node;\n node->next = next;\n node->prev = prev;\n }\n\npublic:\n void put(int key, int value) {\n if (cache.find(key) != cache.end()) {\n remove(cache[key]);\n }\n Node* newNode = new Node(key, value);\n cache[key] = newNode;\n insert(newNode);\n\n if (cache.size() > cap) {\n Node* lru = oldest->next;\n remove(lru);\n cache.erase(lru->key);\n delete lru;\n }\n }\n\n // Destructor to release memory used by the nodes\n ~LRUCache() {\n Node* curr = oldest;\n while (curr != nullptr) {\n Node* next = curr->next;\n delete curr;\n curr = next;\n }\n }\n};\n\n/**\n * Your LRUCache object will be instantiated and called as such:\n * LRUCache* obj = new LRUCache(capacity);\n * int param_1 = obj->get(key);\n * obj->put(key,value);\n */\n```\n | 9 | Design a data structure that follows the constraints of a **[Least Recently Used (LRU) cache](https://en.wikipedia.org/wiki/Cache_replacement_policies#LRU)**.
Implement the `LRUCache` class:
* `LRUCache(int capacity)` Initialize the LRU cache with **positive** size `capacity`.
* `int get(int key)` Return the value of the `key` if the key exists, otherwise return `-1`.
* `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LRUCache ", "put ", "put ", "get ", "put ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, null, -1, 3, 4\]
**Explanation**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
**Constraints:**
* `1 <= capacity <= 3000`
* `0 <= key <= 104`
* `0 <= value <= 105`
* At most `2 * 105` calls will be made to `get` and `put`. | null |
easy python solution with 69% TC | insertion-sort-list | 0 | 1 | ```\ndef insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\tdef add(node):\n\t\tcurr = self.ans\n\t\twhile(curr):\n\t\t\tif(curr.val < node.val):\n\t\t\t\tprev = curr\n\t\t\t\tcurr = curr.next\n\t\t\telse: break\n\t\tnode.next, prev.next = prev.next, node\n\tself.ans = ListNode(-5001)\n\twhile(head):\n\t\ttemp, head = head, head.next\n\t\ttemp.next = None\n\t\tadd(temp)\n\treturn self.ans.next\n``` | 2 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
[Python3] 188ms Solution (explanation with visualization) | insertion-sort-list | 0 | 1 | **Idea**\n- Add `dummy_head` before `head` will help us to handle the insertion easily\n- Use two pointers\n\t- `last_sorted`: last node of the sorted part, whose value is the largest of the sorted part\n\t- `cur`: next node of `last_sorted`, which is the current node to be considered\n\n\tAt the beginning, `last_sorted` is `head` and `cur` is `head.next`\n- When consider the `cur` node, there\'re 2 different cases\n\t- `last_sorted.val <= cur.val`: `cur` is in the correct order and can be directly move into the sorted part. In this case, we just move `last_sorted` one step forward\n\t\n\n\t- `last_sorted.val > cur.val`: `cur` needs to be inserted somewhere in the sorted part. In this case, we let `prev` start from `dummy_head` and iteratively compare `prev.next.val` and `cur.val`. If `prev.next.val > cur.val`, we insert `cur` between `prev` and `prev.next`\n\t- \n\n\n**Implementation**\n```python\nclass Solution:\n def insertionSortList(self, head: ListNode) -> ListNode:\n \n # No need to sort for empty list or list of size 1\n if not head or not head.next:\n return head\n \n # Use dummy_head will help us to handle insertion before head easily\n dummy_head = ListNode(val=-5000, next=head)\n last_sorted = head # last node of the sorted part\n cur = head.next # cur is always the next node of last_sorted\n while cur:\n if cur.val >= last_sorted.val:\n last_sorted = last_sorted.next\n else:\n # Search for the position to insert\n prev = dummy_head\n while prev.next.val <= cur.val:\n prev = prev.next\n \n # Insert\n last_sorted.next = cur.next\n cur.next = prev.next\n prev.next = cur\n \n cur = last_sorted.next\n \n return dummy_head.next\n```\n\n**Complexity**\n- Time: O(n^2)\n- Space: O(1) | 42 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
147: Solution with step by step explanation | insertion-sort-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe solution involves iterating through the linked list, removing each node from the list, and then inserting it into the sorted portion of the list. The sorted portion of the list is initially just the first node, and grows with each iteration.\n\nThis solution has a time complexity of O(n^2) since in the worst case, we may need to iterate through the entire sorted portion of the list for each node in the unsorted portion of the list. The space complexity is O(1) since we are only manipulating the existing linked list and not creating any new data structures.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def insertionSortList(self, head: ListNode) -> ListNode:\n # Initialize the sorted portion of the list to be the first node\n sorted_head = ListNode(0)\n sorted_head.next = head\n sorted_tail = head\n \n # Start with the second node in the list, since the first node is already sorted\n curr = head.next\n \n while curr:\n # If the current node is greater than the tail of the sorted list, \n # it is already in the correct place, so just move on to the next node\n if curr.val >= sorted_tail.val:\n sorted_tail = curr\n curr = curr.next\n else:\n # Remove the current node from the list\n sorted_tail.next = curr.next\n \n # Find the correct position to insert the current node in the sorted list\n insert_pos = sorted_head\n while insert_pos.next.val < curr.val:\n insert_pos = insert_pos.next\n \n # Insert the current node into the sorted list\n curr.next = insert_pos.next\n insert_pos.next = curr\n \n # Move on to the next node in the unsorted portion of the list\n curr = sorted_tail.next\n \n return sorted_head.next\n\n``` | 9 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
✔️ [Python3] INSERTION SORT, Explained | insertion-sort-list | 0 | 1 | The idea is to create a dummy node that would be the head of the sorted part of the list. Iterate over the given list and one by one add nodes to the sorted list at the appropriate place following the insertion sort algorithm.\n\nTime: **O(n^2)**\nSpace: **O(1)**\n\nRuntime: 1677 ms, faster than **51.65%** of Python3 online submissions for Insertion Sort List.\nMemory Usage: 16.4 MB, less than **29.01%** of Python3 online submissions for Insertion Sort List.\n\n```\nclass Solution:\n def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n sort = ListNode() #dummy node\n\n cur = head\n while cur:\n sortCur = sort\n while sortCur.next and cur.val >= sortCur.next.val:\n sortCur = sortCur.next\n \n tmp, sortCur.next = sortCur.next, cur\n cur = cur.next\n sortCur.next.next = tmp\n \n return sort.next\n``` | 7 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
Singly Linked List - Insertion Sort. Python Beats 50% ✅ | insertion-sort-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTypical inserton sort adapted to singly linked list. Presumably we should have handled the case we don\'t have a head. But I did not.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We should create a second function insert_node. As you might have guessed this is meant to be a function that will insert our current node into our "subarray".\n2. Inside our loop we should create a new reference next_node to the curr.next node because of we break the connections inside our linked list and our garbage collector could potentially remove the rest data. Creating a new reference - avoidance of this.\n3. `insert_node` is a simple function, firstly if checks whether our current node value is less than sorted_head value. If so we just replace our header with the current node. By the way, sorted_head is just a pointer to the sublist head. Our sublist is expected to be ordered in ascending. Otherwise we continuously check if our node data is greater than each nodes\' data. This is a way of finding the right place to put our node.\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Constant time, approximate O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\nclass Solution:\n def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n sorted_head = None\n curr = head\n\n while curr:\n next_node = curr.next\n sorted_head = self.insert_node(sorted_head, curr)\n curr = next_node\n \n return sorted_head\n\n def insert_node(self, sorted_head, node):\n if not sorted_head or node.val < sorted_head.val:\n node.next = sorted_head\n sorted_head = node\n else:\n curr = sorted_head\n while curr.next and curr.next.val < node.val:\n curr = curr.next\n node.next = curr.next\n curr.next = node\n \n return sorted_head\n\n``` | 2 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
Python Easiest Insertion sort | insertion-sort-list | 0 | 1 | ```\nclass Solution:\n def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0,head)\n prev, curr = head,head.next\n # we can\'t go back so keep a previous pointer \n \n while curr:\n if curr.val >= prev.val:\n prev = curr\n curr = curr.next\n continue\n temp = dummy\n while curr.val > temp.next.val:\n temp = temp.next\n \n prev.next = curr.next\n curr.next = temp.next\n temp.next = curr\n curr = prev.next\n return dummy.next\n``` | 1 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
insertion sort on linkedList | insertion-sort-list | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0, head)\n prev, curr = head, head.next\n while curr:\n if curr.val >= prev.val:\n prev, curr = curr, curr.next\n continue\n\n tmp = dummy\n while curr.val > tmp.next.val:\n tmp = tmp.next\n \n prev.next = curr.next\n curr.next = tmp.next\n tmp.next = curr\n curr = prev.next\n return dummy.next\n\n \n``` | 0 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
Insertion sorting method in linked list beat 80% | insertion-sort-list | 0 | 1 | \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy =ListNode(0,head)\n prev,curr=head,head.next\n\n while curr:\n if curr.val>=prev.val:\n prev,curr=curr,curr.next\n continue\n\n temp=dummy\n while curr.val >temp.next.val:\n temp=temp.next\n\n prev.next=curr.next\n curr.next=temp.next\n temp.next=curr\n curr=prev.next\n\n return dummy.next\n \n``` | 0 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
Best solution for beginners in linked list using insertion sort | insertion-sort-list | 0 | 1 | \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy= ListNode(next=head)\n prev,cur=head,head.next\n\n while cur:\n if cur.val>prev.val:\n prev=cur\n cur=cur.next\n continue\n\n insert=dummy\n while insert.next.val<cur.val:\n insert=insert.next\n\n prev.next=cur.next\n cur.next=insert.next\n insert.next=cur\n cur=prev.next\n return dummy.next \n\n\n \n\n``` | 0 | Given the `head` of a singly linked list, sort the list using **insertion sort**, and return _the sorted list's head_.
The steps of the **insertion sort** algorithm:
1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Constraints:**
* The number of nodes in the list is in the range `[1, 5000]`.
* `-5000 <= Node.val <= 5000` | null |
[Python/C/C++/Java] Legit iterative solutions. O(1) space! No recursion! With detailed explaination | sort-list | 1 | 1 | # **TL;DR**\n### **Short and sweet. O(nlogn) time, O(1) space.**\n``` python []\ndef sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0)\n dummy.next = head\n\n # Grab sublists of size 1, then 2, then 4, etc, until fully merged\n steps = 1\n while True:\n # Record the progress of the current pass into a single semi sorted list by updating\n # the next of the previous node (or the dummy on the first loop)\n prev = dummy\n\n # Keep track of how much is left to process on this pass of the list\n remaining = prev.next\n\n # While the current pass though the list has not been completed\n num_loops = 0\n while remaining:\n num_loops += 1\n\n # Split 2 sublists of steps length from the front\n sublists = [None, None]\n sublists_tail = [None, None]\n for i in range(2):\n sublists[i] = remaining\n substeps = steps\n while substeps and remaining:\n substeps -= 1\n sublists_tail[i] = remaining\n remaining = remaining.next\n # Ensure the subslist (if one was made) is terminated\n if sublists_tail[i]:\n sublists_tail[i].next = None\n\n # We have two sublists of (upto) length step that are sorted, merge them onto \n # the end into a single list of (upto) step * 2\n while sublists[0] and sublists[1]:\n if sublists[0].val <= sublists[1].val:\n prev.next = sublists[0]\n sublists[0] = sublists[0].next\n else:\n prev.next = sublists[1]\n sublists[1] = sublists[1].next\n prev = prev.next\n \n # One list has been finished, attach what ever is left of the other to the end\n if sublists[0]:\n prev.next = sublists[0]\n prev = sublists_tail[0]\n else:\n prev.next = sublists[1]\n prev = sublists_tail[1]\n \n # Double the steps each go around\n steps *= 2\n\n # If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if 1 >= num_loops:\n return dummy.next\n```\n\n``` c []\nstruct ListNode* sortList(struct ListNode* head){\n /* Grab sublists of size 1, then 2, then 4, etc, until fully merged */\n for (int steps = 1;; steps *= 2) {\n /* Keep track of how much is left to process on this pass of the list */\n struct ListNode* remaining = head;\n\n /*\n Record the progress of the current pass into a single semi sorted list by updating the next pointer\n of the previous node (or the head on the first loop)\n */\n struct ListNode** next_ptr = &head;\n\n int num_loops = 0;\n for (; remaining; ++num_loops) {\n /* Split 2 sublists of steps length from the front */\n struct ListNode* sublists[2];\n struct ListNode* sublists_tail[2] = {NULL, NULL};\n for (int i = 0; i < 2; ++i) {\n sublists[i] = remaining;\n for (int j = 0; remaining && j < steps; ++j) {\n sublists_tail[i] = remaining;\n remaining = remaining->next;\n }\n /* Ensure the subslist (if one was made) is terminated */\n if (sublists_tail[i]) {\n sublists_tail[i]->next = NULL;\n }\n }\n\n /* We have two sublists of (upto) length step that are sorted, merge them onto the end into a single list of (upto) step * 2 */\n while (sublists[0] && sublists[1]) {\n if (sublists[0]->val <= sublists[1]->val) {\n *next_ptr = sublists[0];\n next_ptr = &sublists[0]->next;\n sublists[0] = sublists[0]->next;\n } else {\n *next_ptr = sublists[1];\n next_ptr = &sublists[1]->next;\n sublists[1] = sublists[1]->next;\n }\n } \n\n /* One list has been finished, attach what ever is left of the other to the end */\n if (sublists[0]) {\n *next_ptr = sublists[0];\n next_ptr = &sublists_tail[0]->next;\n } else {\n *next_ptr = sublists[1];\n next_ptr = &sublists_tail[1]->next;\n }\n }\n\n /* If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done */\n if (1 >= num_loops) {\n return head;\n }\n }\n}\n```\n\n``` cpp []\nListNode* sortList(ListNode* head) {\n // Grab sublists of size 1, then 2, then 4, etc, until fully merged\n for (int steps = 1;; steps *= 2) {\n // Keep track of how much is left to process on this pass of the list\n ListNode* remaining = head;\n\n // Record the progress of the current pass into a single semi sorted list by updating the next pointer\n // of the previous node (or the head on the first loop)\n ListNode** next_ptr = &head;\n\n int num_loops = 0;\n for (; remaining; ++num_loops) {\n // Split 2 sublists of steps length from the front\n ListNode* sublists[2];\n ListNode* sublists_tail[2] = {nullptr, nullptr};\n for (int i = 0; i < 2; ++i) {\n sublists[i] = remaining;\n for (int j = 0; remaining && j < steps; ++j) {\n sublists_tail[i] = remaining;\n remaining = remaining->next;\n }\n // Ensure the subslist (if one was made) is terminated\n if (sublists_tail[i]) {\n sublists_tail[i]->next = nullptr;\n }\n }\n\n // We have two sublists of (upto) length step that are sorted, merge them onto the end into a single list of (upto) step * 2\n while (sublists[0] && sublists[1]) {\n if (sublists[0]->val <= sublists[1]->val) {\n *next_ptr = sublists[0];\n next_ptr = &sublists[0]->next;\n sublists[0] = sublists[0]->next;\n } else {\n *next_ptr = sublists[1];\n next_ptr = &sublists[1]->next;\n sublists[1] = sublists[1]->next;\n }\n } \n\n // One list has been finished, attach what ever is left of the other to the end\n if (sublists[0]) {\n *next_ptr = sublists[0];\n next_ptr = &sublists_tail[0]->next;\n } else {\n *next_ptr = sublists[1];\n next_ptr = &sublists_tail[1]->next;\n }\n }\n\n // If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if (1 >= num_loops) {\n return head;\n }\n } \n}\n```\n\n``` java []\npublic ListNode sortList(ListNode head) {\n ListNode dummy = new ListNode(0);\n dummy.next = head;\n\n ListNode [] sublists = new ListNode[2];\n ListNode [] sublists_tail = new ListNode[2];\n\n // Grab sublists of size 1, then 2, then 4, etc, until fully merged\n for (int steps = 1;; steps *= 2) {\n // Record the progress of the current pass into a single semi sorted list by updating\n // the next of the previous node (or the dummy on the first loop)\n ListNode prev = dummy;\n\n // Keep track of how much is left to process on this pass of the list\n ListNode remaining = prev.next;\n\n int num_loops = 0;\n for (; null != remaining; ++num_loops) {\n // Split 2 sublists of steps length from the front\n for (int i = 0; i < 2; ++i) {\n sublists[i] = remaining;\n sublists_tail[i] = null;\n for (int j = 0; null != remaining && j < steps; ++j) {\n sublists_tail[i] = remaining;\n remaining = remaining.next;\n }\n // Ensure the subslist (if one was made) is terminated\n if (null != sublists_tail[i]) {\n sublists_tail[i].next = null;\n }\n }\n\n // We have two sublists of (upto) length step that are sorted, merge them onto the end into a single list of (upto) step * 2\n while (null != sublists[0] && null != sublists[1]) {\n if (sublists[0].val <= sublists[1].val) {\n prev.next = sublists[0];\n sublists[0] = sublists[0].next;\n } else {\n prev.next = sublists[1];\n sublists[1] = sublists[1].next;\n }\n prev = prev.next;\n } \n\n // One list has been finished, attach what ever is left of the other to the end\n if (null != sublists[0]) {\n prev.next = sublists[0];\n prev = sublists_tail[0];\n } else {\n prev.next = sublists[1];\n prev = sublists_tail[1];\n }\n }\n\n // If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if (1 >= num_loops) {\n return dummy.next;\n }\n }\n}\n```\n\n### **Using a holding buffer for extra speed. O(nlogn) time, O(1) space, with lower constant.**\nCode is a little more complex, can make a big performance difference. See desciption below.\n``` python []\ndef sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n buffer_size = 8\n\n dummy = ListNode(0)\n dummy.next = head\n\n # Grab sublists of size 1, then buffer_size, then buffer_size^2, etc, until fully merged\n steps = 1\n while True:\n # Record the progress of the current pass into a single semi sorted list by updating\n # the next of the previous node (or the dummy on the first loop)\n prev = dummy\n\n # Keep track of how much is left to process on this pass of the list\n remaining = prev.next\n\n # While the current pass though the list has not been completed\n num_loops = 0\n while remaining:\n num_loops += 1\n\n # Split buffer_size sublists of upto steps length from the front\n sublists = [None] * buffer_size\n sublists_tail = [None] * buffer_size\n for i in range(buffer_size):\n sublists[i] = remaining\n substeps = steps\n while substeps and remaining:\n substeps -= 1\n sublists_tail[i] = remaining\n remaining = remaining.next\n # Ensure the subslist (if one was made) is terminated\n if sublists_tail[i]:\n sublists_tail[i].next = None\n\n # Keep merging all the sublists we have in the working buffer until we have a single sublist.\n # That is 8 sublists get merged into 4, then 4 into 2, then 2 into 1.\n num_sublists = buffer_size\n while 1 < num_sublists:\n # Merge each pair of sublists\n subdummy = ListNode()\n for i in range(0, num_sublists, 2):\n subprev = subdummy;\n subprev.next = None\n\n # We have two sublists of (upto) length step that are sorted, merge them onto \n # the end into a single list of (upto) step * 2\n while sublists[i] and sublists[i + 1]:\n if sublists[i].val <= sublists[i + 1].val:\n subprev.next = sublists[i]\n sublists[i] = sublists[i].next\n else:\n subprev.next = sublists[i + 1]\n sublists[i + 1] = sublists[i + 1].next\n subprev = subprev.next\n \n # One list has been finished, attach what ever is left of the other to the end\n if sublists[i]:\n subprev.next = sublists[i]\n sublists_tail[i // 2] = sublists_tail[i]\n else:\n subprev.next = sublists[i + 1]\n sublists_tail[i // 2] = sublists_tail[i + 1]\n\n # Record the head of our new longer sublist in the correct location for the next loop around\n sublists[i // 2] = subdummy.next;\n\n # Half the sublists remain now that we have merged each pair of lists\n num_sublists //= 2\n\n # Attach the single sublist into this passes progress\n prev.next = sublists[0];\n prev = sublists_tail[0];\n \n # Increase the steps each go around\n steps *= buffer_size\n\n # If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if 1 >= num_loops:\n return dummy.next\n```\n\n``` c []\n\nstruct ListNode* sortList(struct ListNode* head){\n const int BUFFER_SIZE = 8;\n\n /* Grab sublists of size 1, then 2, then 4, etc, until fully merged */\n for (int steps = 1;; steps *= BUFFER_SIZE) {\n /* Keep track of how much is left to process on this pass of the list */\n struct ListNode* remaining = head;\n\n /*\n Record the progress of the current pass into a single semi sorted list by updating the next pointer\n of the previous node (or the head on the first loop)\n */\n struct ListNode** next_ptr = &head;\n\n int num_loops = 0;\n for (; remaining; ++num_loops) {\n /* Split BUFFER_SIZE sublists of upto steps length from the front */\n struct ListNode* sublists[BUFFER_SIZE];\n struct ListNode* sublists_tail[BUFFER_SIZE];\n for (int i = 0; i < BUFFER_SIZE; ++i) {\n sublists[i] = remaining;\n sublists_tail[i] = NULL;\n for (int j = 0; remaining && j < steps; ++j) {\n sublists_tail[i] = remaining;\n remaining = remaining->next;\n }\n /* Ensure the subslist (if one was made) is terminated */\n if (sublists_tail[i]) {\n sublists_tail[i]->next = NULL;\n }\n }\n\n /*\n Keep merging all the sublists we have in the working buffer until we have a single sublist.\n That is 8 sublists get merged into 4, then 4 into 2, then 2 into 1.\n */\n for (int num_sublists = BUFFER_SIZE; 1 < num_sublists; num_sublists /= 2) {\n /* Merge each pair of sublists */\n for (int i = 0; i < num_sublists; i += 2) {\n struct ListNode* subhead = NULL;\n struct ListNode** sub_next_ptr = &subhead;\n \n /* We have two sublists of (upto) length step that are sorted, merge them onto the end into a single list of (upto) step * 2 */\n while (sublists[i] && sublists[i + 1]) {\n if (sublists[i]->val <= sublists[i + 1]->val) {\n *sub_next_ptr = sublists[i];\n sub_next_ptr = &sublists[i]->next;\n sublists[i] = sublists[i]->next;\n } else {\n *sub_next_ptr = sublists[i + 1];\n sub_next_ptr = &sublists[i + 1]->next;\n sublists[i + 1] = sublists[i + 1]->next;\n }\n }\n\n /* One list has been finished, attach what ever is left of the other to the end */\n if (sublists[i]) {\n *sub_next_ptr = sublists[i];\n sublists_tail[i / 2] = sublists_tail[i];\n } else {\n *sub_next_ptr = sublists[i + 1];\n sublists_tail[i / 2] = sublists_tail[i + 1];\n }\n\n /* Record the head of our new longer sublist in the correct location for the next loop around */\n sublists[i / 2] = subhead;\n }\n }\n\n /* Attach the single sublist into this passes progress */\n *next_ptr = sublists[0];\n next_ptr = &sublists_tail[0]->next;\n }\n\n /* If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done */\n if (1 >= num_loops) {\n return head;\n }\n }\n}\n```\n\n```cpp []\nListNode* sortList(ListNode* head) {\n constexpr const int BUFFER_SIZE = 8;\n\n // Grab sublists of size 1, then BUFFER_SIZE, then BUFFER_SIZE^2, etc, until fully merged\n for (int steps = 1;; steps *= BUFFER_SIZE) {\n // Keep track of how much is left to process on this pass of the list\n ListNode* remaining = head;\n\n // Record the progress of the current pass into a single semi sorted list by updating the next pointer\n // of the previous node (or the head on the first loop)\n ListNode** next_ptr = &head;\n\n int num_loops = 0;\n for (; remaining; ++num_loops) {\n // Split BUFFER_SIZE sublists of upto steps length from the front\n ListNode* sublists[BUFFER_SIZE];\n ListNode* sublists_tail[BUFFER_SIZE];\n for (int i = 0; i < BUFFER_SIZE; ++i) {\n sublists[i] = remaining;\n sublists_tail[i] = NULL;\n for (int j = 0; remaining && j < steps; ++j) {\n sublists_tail[i] = remaining;\n remaining = remaining->next;\n }\n // Ensure the subslist (if one was made) is terminated\n if (sublists_tail[i]) {\n sublists_tail[i]->next = NULL;\n }\n }\n\n // Keep merging all the sublists we have in the working buffer until we have a single sublist.\n // That is 8 sublists get merged into 4, then 4 into 2, then 2 into 1.\n for (int num_sublists = BUFFER_SIZE; 1 < num_sublists; num_sublists /= 2) {\n // Merge each pair of sublists\n for (int i = 0; i < num_sublists; i += 2) {\n ListNode* subhead = NULL;\n ListNode** sub_next_ptr = &subhead;\n \n // We have two sublists of (upto) length step that are sorted, merge them onto the end into a single list of (upto) step * 2\n while (sublists[i] && sublists[i + 1]) {\n if (sublists[i]->val <= sublists[i + 1]->val) {\n *sub_next_ptr = sublists[i];\n sub_next_ptr = &sublists[i]->next;\n sublists[i] = sublists[i]->next;\n } else {\n *sub_next_ptr = sublists[i + 1];\n sub_next_ptr = &sublists[i + 1]->next;\n sublists[i + 1] = sublists[i + 1]->next;\n }\n }\n\n // One list has been finished, attach what ever is left of the other to the end\n if (sublists[i]) {\n *sub_next_ptr = sublists[i];\n sublists_tail[i / 2] = sublists_tail[i];\n } else {\n *sub_next_ptr = sublists[i + 1];\n sublists_tail[i / 2] = sublists_tail[i + 1];\n }\n\n // Record the head of our new longer sublist in the correct location for the next loop around\n sublists[i / 2] = subhead;\n }\n }\n\n // Attach the single sublist into this passes progress\n *next_ptr = sublists[0];\n next_ptr = &sublists_tail[0]->next;\n }\n\n // If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if (1 >= num_loops) {\n return head;\n }\n }\n}\n```\n\n```java []\npublic ListNode sortList(ListNode head) {\n int BUFFER_SIZE = 8;\n\n ListNode dummy = new ListNode(0);\n ListNode subdummy = new ListNode(0);\n dummy.next = head;\n\n ListNode [] sublists = new ListNode[BUFFER_SIZE];\n ListNode [] sublists_tail = new ListNode[BUFFER_SIZE];\n\n // Grab sublists of size 1, then BUFFER_SIZE, then BUFFER_SIZE^2, etc, until fully merged\n for (int steps = 1;; steps *= BUFFER_SIZE) {\n // Record the progress of the current pass into a single semi sorted list by updating\n // the next of the previous node (or the dummy on the first loop)\n ListNode prev = dummy;\n\n // Keep track of how much is left to process on this pass of the list\n ListNode remaining = prev.next;\n\n int num_loops = 0;\n for (; null != remaining; ++num_loops) {\n // Split BUFFER_SIZE sublists of upto steps length from the front\n for (int i = 0; i < BUFFER_SIZE; ++i) {\n sublists[i] = remaining;\n sublists_tail[i] = null;\n for (int j = 0; null != remaining && j < steps; ++j) {\n sublists_tail[i] = remaining;\n remaining = remaining.next;\n }\n // Ensure the subslist (if one was made) is terminated\n if (null != sublists_tail[i]) {\n sublists_tail[i].next = null;\n }\n }\n\n // Keep merging all the sublists we have in the working buffer until we have a single sublist.\n // That is 8 sublists get merged into 4, then 4 into 2, then 2 into 1.\n for (int num_sublists = BUFFER_SIZE; 1 < num_sublists; num_sublists /= 2) {\n // Merge each pair of sublists\n for (int i = 0; i < num_sublists; i += 2) {\n ListNode subprev = subdummy;\n subprev.next = null;\n \n // We have two sublists of (upto) length step that are sorted, merge them onto the end into a single list of (upto) step * 2\n while (null != sublists[i] && null != sublists[i + 1]) {\n if (sublists[i].val <= sublists[i + 1].val) {\n subprev.next = sublists[i];\n sublists[i] = sublists[i].next;\n } else {\n subprev.next = sublists[i + 1];\n sublists[i + 1] = sublists[i + 1].next;\n }\n subprev = subprev.next;\n }\n\n // One list has been finished, attach what ever is left of the other to the end\n if (null != sublists[i]) {\n subprev.next = sublists[i];\n sublists_tail[i / 2] = sublists_tail[i];\n } else {\n subprev.next = sublists[i + 1];\n sublists_tail[i / 2] = sublists_tail[i + 1];\n }\n\n // Record the head of our new longer sublist in the correct location for the next loop around\n sublists[i / 2] = subdummy.next;\n }\n }\n\n // Attach the single sublist into this passes progress\n prev.next = sublists[0];\n prev = sublists_tail[0];\n }\n\n // If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if (1 >= num_loops) {\n return dummy.next;\n }\n }\n}\n```\n\n### **Using a holding buffer for extra speed. O(nlogn) time, O(1) space, with lower constant. Using subfunctions**\n\nSame idea as the holding buffer above, but using subfunctions to `split_list` to extract the sublists and `merge_lists` for the merge step. It might help demonstrate the main loop better.\n\n```cpp []\n/// Take a list and split it into sublists of the requested size, return the remainder of the input list\nstatic\nListNode* split_list(ListNode* head, int sz, ListNode* lists_out[], int num_lists) {\n for (int i = 0; i < num_lists; ++i) {\n lists_out[i] = head;\n ListNode* tail = nullptr;\n for (int j = 0; head && j < sz; ++j) {\n tail = head;\n head = head->next;\n }\n // Ensure the subslist (if one was made) is terminated */\n if (tail) {\n tail->next = nullptr;\n }\n }\n return head;\n}\n\n/// Merge two sorted lists into one, the head and tail of the new list is returned\nstatic\nstd::pair<ListNode*, ListNode*> merge_lists(ListNode* l1, ListNode* l2) {\n ListNode* head = nullptr;\n ListNode* tail = nullptr;\n ListNode** next_ptr = &head;\n while (l1 || l2) {\n if (!l2 || (l1 && l1->val <= l2->val)) {\n tail = l1;\n l1 = l1->next;\n } else {\n tail = l2;\n l2 = l2->next;\n }\n *next_ptr = tail;\n next_ptr = &tail->next;\n }\n return std::make_pair(head, tail);\n}\n\nListNode* sortList(ListNode* head) {\n constexpr const int BUFFER_SIZE = 8;\n\n // Grab sublists of size 1, then BUFFER_SIZE, then BUFFER_SIZE^2, etc, until fully merged\n for (int steps = 1;; steps *= BUFFER_SIZE) {\n // Keep track of how much is left to process on this pass of the list\n ListNode* remaining = head;\n\n // Record the progress of the current pass into a single semi sorted list by updating the next pointer\n // of the previous node (or the head on the first loop)\n ListNode** next_ptr = &head;\n\n int num_loops = 0;\n for (; remaining; ++num_loops) {\n // Split BUFFER_SIZE sublists of upto steps length from the front\n ListNode* sublists[BUFFER_SIZE];\n remaining = split_list(remaining, steps, sublists, BUFFER_SIZE);\n\n // Keep merging all the sublists we have in the working buffer until we have a single sublist.\n // That is 8 sublists get merged into 4, then 4 into 2, then 2 into 1.\n ListNode* tail;\n for (int num_sublists = BUFFER_SIZE; 1 < num_sublists; num_sublists /= 2) {\n // Merge each pair of sublists\n for (int i = 0; i < num_sublists; i += 2) {\n auto [subhead, subtail] = merge_lists(sublists[i], sublists[i + 1]);\n\n // Record the head of our new longer sublist in the correct location for the next loop around\n sublists[i / 2] = subhead;\n tail = subtail;\n }\n }\n\n // Attach the single sublist into this passes progress\n *next_ptr = sublists[0];\n next_ptr = &tail->next;\n }\n\n // If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done\n if (1 >= num_loops) {\n return head;\n }\n }\n}\n```\n\n```c []\n\n/* Take a list and split it into sublists of the requested size, return the remainder of the input list */\nstatic\nstruct ListNode* split_list(struct ListNode* head, int sz, struct ListNode* lists_out[], int num_lists) {\n for (int i = 0; i < num_lists; ++i) {\n lists_out[i] = head;\n struct ListNode* tail = NULL;\n for (int j = 0; head && j < sz; ++j) {\n tail = head;\n head = head->next;\n }\n /* Ensure the subslist (if one was made) is terminated */\n if (tail) {\n tail->next = NULL;\n }\n }\n return head;\n}\n\n/* Merge two sorted lists into one, the head and tail of the new list is returned */\nstatic\nvoid merge_lists(struct ListNode* l1, struct ListNode* l2, struct ListNode** head_out, struct ListNode** tail_out) {\n struct ListNode* head = NULL;\n struct ListNode* tail = NULL;\n struct ListNode** next_ptr = &head;\n while (l1 || l2) {\n if (!l2 || (l1 && l1->val <= l2->val)) {\n tail = l1;\n l1 = l1->next;\n } else {\n tail = l2;\n l2 = l2->next;\n }\n *next_ptr = tail;\n next_ptr = &tail->next;\n }\n *head_out = head;\n *tail_out = tail;\n}\n\nstruct ListNode* sortList(struct ListNode* head) {\n const int BUFFER_SIZE = 8;\n\n /* Grab sublists of size 1, then BUFFER_SIZE, then BUFFER_SIZE^2, etc, until fully merged */\n for (int steps = 1;; steps *= BUFFER_SIZE) {\n // Keep track of how much is left to process on this pass of the list\n struct ListNode* remaining = head;\n\n // Record the progress of the current pass into a single semi sorted list by updating the next pointer\n // of the previous node (or the head on the first loop)\n struct ListNode** next_ptr = &head;\n\n int num_loops = 0;\n for (; remaining; ++num_loops) {\n /* Split BUFFER_SIZE sublists of upto steps length from the front */\n struct ListNode* sublists[BUFFER_SIZE];\n remaining = split_list(remaining, steps, sublists, BUFFER_SIZE);\n\n /*\n Keep merging all the sublists we have in the working buffer until we have a single sublist.\n That is 8 sublists get merged into 4, then 4 into 2, then 2 into 1.\n */\n struct ListNode* tail;\n for (int num_sublists = BUFFER_SIZE; 1 < num_sublists; num_sublists /= 2) {\n /* Merge each pair of sublists */\n for (int i = 0; i < num_sublists; i += 2) {\n merge_lists(sublists[i], sublists[i + 1], &sublists[i / 2], &tail);\n }\n }\n\n /* Attach the single sublist into this passes progress */\n *next_ptr = sublists[0];\n next_ptr = &tail->next;\n }\n\n /* If the entire list was fully processed in a single loop, it means we\'ve completely sorted the list and are done */\n if (1 >= num_loops) {\n return head;\n }\n }\n}\n```\n### **Short quicksort for fun. O(nlogn) time, O(logn) stack space.**\n```cpp []\n ListNode* sortList(ListNode* head, ListNode* tail = nullptr)\n {\n if (head != tail) {\n // Use head node as the pivot node\n // Everything in the _smaller_ list will be less than _head_\n // and everything appearing after _head_ in the list is greater or equal\n ListNode* smaller;\n ListNode** smaller_next = &smaller;\n for (ListNode** prev = &head->next; *prev != tail; ) {\n if (head->val > (**prev).val) {\n *smaller_next = *prev;\n smaller_next = &((**smaller_next).next);\n\n // Remove smaller node from original list\n *prev = (**prev).next;\n } else {\n // Correct position, skip over\n prev = &((**prev).next);\n }\n }\n\n // Connect the end of smaller list to the head (which is the partition node)\n // We now have. [smaller list...] -> head -> [larger list]\n *smaller_next = head;\n\n // Continue to sort everything after head\n head->next = sortList(head->next, tail);\n\n // Sort everything upto head\n head = sortList(smaller, head);\n }\n return head;\n }\n```\t\n# Details\n### **Basic description**\nThe problem calls for O(1) space. Therefore a solution that does not use recursion is required. Quicksort is out, merge sort is in.\nThe idea is to merge progressively larger sublists together until the resulting list is sorted. A walkthough will help explain.\n\nImagine the input list [3, 45, 2, 15, 37, 19, 39, 20], first process the list as sublists of length _1_, [3], [45], [2], [15], [37], [19], [39], [20]. As they are size _1_, they are obviously sorted sublists. Merge each pair of sublists together to produce 4 sorted sublists of size _2_ [3, 45], [2, 15], [19, 37], [20, 39], these are reassemble into the original list to produce [3, 45, 2, 15, 19, 37, 20, 39]. After this pass first pass, every 2 nodes is sorted. That is 3 is before 45, 2 is before 15, 19 is before 37, etc. Increasing the step size to _2_ and repeat. This produces the following table;\n|Progress|Step size|Sublists|Merged|\n|---|---|---|---|\n|[3, 45, 2, 15, 37, 19, 39, 20]|1|[3], [45], [2], [15], [37], [19], [39], [20]|[3, 45], [2, 15], [19, 37], [20, 39]|\n|[3, 45, 2, 15, 19, 37, 20, 39]|2|[3, 45], [2, 15], [19, 37], [20, 39]|[2, 3, 15, 45], [19, 20, 37, 39]|\n|[2, 3, 15, 45, 19, 20, 37, 39]|4|[2, 3, 15, 45], [19, 20, 37, 39]|[2, 3, 15, 19, 20, 37, 39, 45]|\n\nSince recursion is out, the process must be done inplace as we go. Basically for each pass;\n1. Grab two sorted lists of size _step_\n2. Merge the two lists into a single sorted list of size _step * 2_ and reattach to input list\n3. Repeat from step 1. until entire list has been sorted (which will be when step * 2 >= length)\n\nThis produces the first relatively compact solution shown above.\n### **Complexity**\n#### **Space complexity**\nThere are only a few fixed, stack allocated, variables whose creation is not based on the length of the input list and there is no recursion. Therefore it is O(1) space complexity.\n#### **Time complexity**\nThe list will be completely sorted once _step_ * 2 becomes greater than _n_, with _step_ doubling each pass (1, 2, 4, 8, ...). Therefore it will take logn passes to sort the list. Each pass though requires _n_ moves to produce the sublists and the merge of two sorted lists takes _step_ moves for _n/step_ sublists. Therefore it takes _n_ time for each of the logn passes. Therefore the time complexity is O(nlogn).\n### **Improvements**\nIn practice, in the real world no one would implement the initial solution as is, instead it would be improved substansually (without impacting space complexity), by using a small holding buffer. Allowing for larger sorted sublists to be created with each full pass of the list. This is the second solution presented above.\n\nConsider the first solution, the output of each pass produces the input of the next pass. For example, the first pass, when _step_ is 1, produces sublists of _step * 2_, which is exactly what is needed for the next pass. However, there is nowhere to hold this in O(1) space so we must reassemble the list fully ready for the next pass. However, with a small working buffer we can leaverage this and focus on sorting blocks of nodes. By that I mean, we grab _buf_sz_ sublists, and keep merging them together until we have a single, sorted, sublist in our holding buffer. The sublist is then linked back into the input list before progressing onto the next set of _buf_sz_ sublists.\n\nWith a working buffer of 4, using the input [6, 38, 25, 46, 45, 90, 97, 52, 75, 18] an initial pass would progress as follows;\n|Progress|State 1, grab 4 sublists of _step_ size (1)|State 2, merge into 2 sublists|State 3, merge into 1 sublist|\n|---|---|---|---|\n|[6, 38, 25, 46, 45, 90, 97, 52, 75, 18]|[6], [38], [25], [46], [45, 90, 97, 52, 75, 18]|[6, 38], [25, 46], [45, 90, 97, 52, 75, 18]|[6, 25, 38, 46], [45, 90, 97, 52, 75, 18]|\n|[6, 25, 38, 46, 45, 90, 97, 52, 75, 18]|[6, 25, 38, 46], [45], [90], [97], [52], [75, 18]|[6, 25, 38, 46], [45, 90], [52, 97], [75, 18]|[6, 25, 38, 46], [45, 52, 90, 97], [75, 18]|\n|[6, 25, 38, 46, 45, 52, 90, 97, 75, 18]|[6, 25, 38, 46, 45, 52, 90, 97], [75], [18]|[6, 25, 38, 46, 45, 52, 90, 97], [18, 75]|[6, 25, 38, 46, 45, 52, 90, 97], [18, 75]|\n\nThe end of the list has been reached, so _step_ is increased, but this time, instead of doubling, it is multiplied by 4, as we now know every 4 nodes forms a sorted sublist. The next pass then becomes;\n\n|Progress|State 1, grab 4 sublists of _step_ size (4)|State 2, merge into 2 sublists|State 3, merge into 1 sublist|\n|---|---|---|---|\n|[6, 25, 38, 46, 45, 52, 90, 97, 18, 75]|[6, 25, 38, 46], [45, 52, 90, 97], [18, 75]|[6, 25, 38, 45, 46, 52, 90, 97], [18, 75]|[6, 18, 25, 38, 45, 46, 52, 75, 90, 97]|\n\nFinished!\nIncreasing the buffer to 8 or 16 makes a huge difference as we will be sorting blocks of nodes as follows;\n|Buffer size|Pass 1|Pass 2|Pass 3|\n|---|---|---|---|\n|2|2|4|8|\n|4|4|16|64|\n|8|8|64|512|\n|16|16|256|4096|\n\nSo after 3 passes of the list, with a buffer size of 8, we will have divided the input list into sorted sublists of size 512. Where as with buffer size of 2, we will only have sublists of size 8. Making processing a huge lists considerably faster.\n## **Quicksort**\nI added the quicksort solution for fun as it is quite compact, even if it doesn\'t fullfil the requirements of O(1) space. It does of course suffer from the normal problems of quicksort, that being a worst case of O(n^2) if the input list is already sorted.\n\nBasically, grab the _head_ of the list and use it as a pivot. Then using code adopted from [partition list](https://leetcode.com/problems/partition-list/discuss/155293/Short-single-pass-iterative-c++-solution.-No-allocation-or-dummy-required.-O(n)-time-O(1)-space), divide into two sublists, those nodes less than _head->val_ and those greater or equal. Recurse around, partitioning those lists around a new pivot. Rince and repeat until each sublist is down to a size of 1 and is hence sorted.\n\nI did it more for fun as the code is really small. Without comments it is;\n```cpp []\n ListNode* sortList(ListNode* head, ListNode* tail = nullptr)\n {\n if (head != tail) {\n ListNode* smaller;\n ListNode** smaller_next = &smaller;\n for (ListNode** prev = &head->next; *prev != tail; ) {\n if (head->val > (**prev).val) {\n *smaller_next = *prev;\n smaller_next = &((**smaller_next).next);\n *prev = (**prev).next;\n } else {\n prev = &((**prev).next);\n }\n }\n\n *smaller_next = head;\n head->next = sortList(head->next, tail);\n head = sortList(smaller, head);\n }\n return head;\n }\n```\t\n\n**Please give me a thumbs up if this helped explain this problem for you** | 412 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
148: Solution with step by step explanation | sort-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe approach we will use is Merge Sort:\n\n1. Base Case: If the length of the linked list is less than or equal to 1, then the list is already sorted.\n2. Split the linked list into two halves. We will use the "slow and fast pointer" technique to find the midpoint of the linked list.\n3. Recursively sort the left and right halves of the linked list.\n4. Merge the two sorted halves of the linked list.\n\n# Complexity\n- Time complexity:\nO(n log n) because we are dividing the linked list in half log n times, and merging the two halves in linear time.\n\n- Space complexity:\nO(log n) because the space used by the call stack during the recursive calls is log n.\n\n# Code\n```\nclass Solution:\n def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n # Base Case: If the length of the linked list is less than or equal to 1, then the list is already sorted\n if not head or not head.next:\n return head\n\n # Split the linked list into two halves using "slow and fast pointer" technique to find the midpoint of the linked list\n slow, fast = head, head.next\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n # The midpoint of the linked list is slow.next\n mid = slow.next\n # Set slow.next to None to separate the left and right halves of the linked list\n slow.next = None\n\n # Recursively sort the left and right halves of the linked list\n left = self.sortList(head)\n right = self.sortList(mid)\n\n # Merge the two sorted halves of the linked list\n dummy = ListNode(0)\n curr = dummy\n while left and right:\n if left.val < right.val:\n curr.next = left\n left = left.next\n else:\n curr.next = right\n right = right.next\n curr = curr.next\n # Append the remaining nodes of the left or right half to the end of the sorted list\n curr.next = left or right\n\n return dummy.next\n\n``` | 38 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
Python Recursize merge sort | sort-list | 0 | 1 | \n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n size = 0;\n t = head;\n while(t):\n size+=1\n t=t.next\n if( size < 2 ): return head;\n\n def merge(node,size):\n if( size == 1 ): return ListNode(node.val);\n \n ls = size//2\n rs = size - ls \n ll = merge(node,ls);\n for i in range(0,ls): node = node.next ;\n rl = merge(node,rs)\n\n #now merge ll(left list) and right list(rl) \n\n nroot = ListNode(-1);\n node = nroot;\n while( ll or rl ):\n if( ll and rl ):\n if( ll.val < rl.val ):\n node.next = ll\n ll = ll.next;\n node = node.next\n else:\n node.next = rl\n rl = rl.next;\n node=node.next\n elif(ll):\n node.next = ll \n ll = ll.next;\n node =node.next\n else:\n node.next = rl\n rl = rl.next\n node = node.next\n return nroot.next;\n\n \n return merge(head,size)\n\n``` | 5 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
Python (Simple Merge Sort) | sort-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortList(self, head):\n def merge(a,b):\n cur = res = ListNode()\n \n while a and b:\n if a.val <= b.val:\n cur.next = a \n a = a.next \n else:\n cur.next = b \n b = b.next \n \n cur = cur.next\n \n while a:\n cur.next = a \n a = a.next \n cur = cur.next\n \n while b:\n cur.next = b \n b = b.next \n cur = cur.next\n \n return res.next\n \n if not head or not head.next:\n return head \n \n pre, slow, fast = None, head, head\n \n while fast and fast.next:\n pre, slow, fast = slow, slow.next, fast.next.next\n \n if pre:\n pre.next = None\n \n first_half = self.sortList(head)\n second_half = self.sortList(slow)\n result = merge(first_half, second_half)\n \n return result\n \n \n \n\n\n\n\n``` | 1 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
✔️ Sort List | Python O(nlogn) Solution | 95% Faster | sort-list | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n\nVisit this blog to learn Python tips and techniques and to find a Leetcode solution with an explanation: https://www.python-techs.com/\n\n**Solution:**\n```\nclass Solution:\n def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head or not head.next:\n return head\n \n # Split the list into two halfs\n left = head\n right = self.getMid(head)\n tmp = right.next\n right.next = None\n right = tmp\n \n left = self.sortList(left)\n right = self.sortList(right)\n \n return self.merge(left, right)\n \n def getMid(self, head):\n slow = head\n fast = head.next\n \n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n return slow\n \n # Merge the list\n def merge(self, list1, list2):\n newHead = tail = ListNode()\n while list1 and list2:\n if list1.val > list2.val:\n tail.next = list2\n list2 = list2.next\n else:\n tail.next = list1\n list1 = list1.next\n tail = tail.next\n \n if list1:\n tail.next = list1\n if list2:\n tail.next = list2\n \n return newHead.next\n \n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 41 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
I don't like to implement Sort. Converted LL to Array back to LL | sort-list | 0 | 1 | \nSurprisingly Fast honestly\n# Code\n```\nclass Solution:\n def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n a = []\n while head:\n a.append(head.val)\n head = head.next\n a.sort()\n\n if not a: return \n root = ListNode(a[0])\n curr = root\n for val in a[1:]:\n curr.next = ListNode(val)\n curr = curr.next\n return root\n``` | 2 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
Python || Merge Sort || O(nlogn) Solution | sort-list | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def divide(self,head):\n slow,fast=head,head.next\n while fast and fast.next:\n slow=slow.next\n fast=fast.next.next\n return slow\n \n def Merge(self,l,r):\n temp=ans=ListNode()\n while l and r:\n if l.val<=r.val:\n temp.next=l\n l=l.next\n else:\n temp.next=r\n r=r.next\n temp=temp.next\n if l:\n temp.next=l\n if r:\n temp.next=r\n return ans.next\n \n def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head or not head.next:\n return head\n left=head\n right=self.divide(head)\n temp=right.next\n right.next=None\n right=temp\n left=self.sortList(left)\n right=self.sortList(right)\n return self.Merge(left,right)\n```\n\n**An upvote will be encouraging** | 24 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
Using Merge sort with explanation | sort-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis approach will use Merge Sort:\n\nBase Case: If the length of the linked list is less than or equal to 1, then the list is already sorted so just return head. \n\nSplit the linked list into two halves. We will use the "slow and fast pointer" technique to find the mid of the linked list.\n\nRecursively sort the left and right halves of the linked list.\n\nMerge the two sorted halves of the linked list.\n\nreturn head\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O (n logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O (log n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\n #base case: if length of linked list is 0 or 1 then list is already sorted.\n if not head or not head.next: return head\n \n #using slow and fast pointer approach reach the mid of linked list\n slow,fast = head, head.next\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n \n #assign name two middle node \n mid = slow.next\n\n #sep two linked lists \n slow.next = None\n\n #Recursively sort left and right linked lists\n left = self.sortList(head)\n right = self.sortList(mid)\n\n #create a dummy node\n new = ListNode(0)\n curr = new\n\n #merge two sorted halves of the linked lists\n while left and right:\n if left.val < right.val:\n curr.next = left\n left = left.next\n else:\n curr.next = right\n right = right.next\n curr = curr.next\n\n #append remaining nodes from left and right lists\n curr.next = left or right\n\n #return actual head of the sorted linked list\n return new.next\n \n \n``` | 1 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
Python/JS by merge sort [w/ Comment] | sort-list | 0 | 1 | Python by merge sort\n\n---\n\n**Implementation** by merge sort\n\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def sortList(self, head: ListNode) -> ListNode:\n \n # -------------------------------\n \n def merge( a, b):\n \n if not a:\n return b\n \n elif not b:\n return a\n \n if a.val < b.val:\n a.next = merge(a.next, b)\n return a\n \n else:\n b.next = merge(a, b.next)\n return b\n \n # -------------------------------\n \n ## base case\n \n if head is None:\n # empty node\n return None\n \n elif head.next is None:\n # one node only\n return head\n \n ## general case\n # divide into two halves\n \n pre, slow, fast = None, head, head\n \n while fast and fast.next:\n pre, slow, fast = slow, slow.next, fast.next.next\n \n\t\tif pre:\n\t\t\tpre.next = None\n\n \n # sort by divide-and-conquer\n \n first_half = self.sortList(head)\n second_half = self.sortList(slow)\n result = merge(first_half, second_half)\n return result\n \n \n```\n\n---\n\nJavascript:\n\n```\nvar sortList = function(head) {\n \n \n var merge = function(a, b){\n \n if( a == null ){\n return b;\n }else if( b == null ){\n return a;\n }\n \n if( a.val < b.val ){\n a.next = merge(a.next, b);\n return a;\n }else{\n b.next = merge(a, b.next);\n return b;\n }\n \n }\n \n // ------------------------------\n \n // Base case:\n \n if( head == null ){\n \n // Empty linked list\n return null;\n \n }else if ( head.next == null ){\n \n // Linked list with one node only\n return head;\n }\n \n \n \n // General cases:\n let [prev, slow, fast] = [null, head, head];\n \n while( (fast != null) && (fast.next != null) ){\n \n //[prev, slow, fast] = [slow, slow.next, fast.next.next];\n prev = slow;\n slow = slow.next;\n fast = fast.next.next;\n }\n \n\n // cut the linkage on midpoint\n if( prev != null ){\n prev.next = null; \n }\n \n \n // sort by divide and conquer\n let firstHalf = sortList(head);\n let secondHalf = sortList(slow);\n \n \n result = merge( firstHalf, secondHalf );\n \n \n return result;\n};\n```\n\n\n---\n\nReference:\n\n[1] Wiki: [Merge Sort](https://en.wikipedia.org/wiki/Merge_sort) | 21 | Given the `head` of a linked list, return _the list after sorting it in **ascending order**_.
**Example 1:**
**Input:** head = \[4,2,1,3\]
**Output:** \[1,2,3,4\]
**Example 2:**
**Input:** head = \[-1,5,3,4,0\]
**Output:** \[-1,0,3,4,5\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 5 * 104]`.
* `-105 <= Node.val <= 105`
**Follow up:** Can you sort the linked list in `O(n logn)` time and `O(1)` memory (i.e. constant space)? | null |
Python O(n^2) solution for your reference | max-points-on-a-line | 0 | 1 | ```\n def maxPoints(self, points: List[List[int]]) -> int:\n def dic():\n return defaultdict(int);\n ans = 0;\n hmap = defaultdict(dic) \n n = len(points)\n for i in range(0,n):\n print("------------")\n print(f\'i:{i} point[i]:{points[i]} \')\n hmap.clear();\n for j in range(i+1,n):\n x = points[i][0] - points[j][0]\n y = points[i][1] - points[j][1]\n\n if( y == 0 ):\n hmap[0][0] += 1\n if( hmap[0][0] > ans ):\n ans = hmap[0][0];\n continue;\n \n g = gcd(x,y);\n\n x //= g\n y //= g\n # in case of negative slope one value can be negative (eg)\n # eg (1,-1) and (-1,1) will result in slop m = -1 but here \n if( y < 0 ):\n x = -x \n y = -y \n \n hmap[x][y] += 1\n print(f\'j:{j} point[j]:{points[j]} x:{x} y:{y} hmap[{x}][{y}]:{hmap[x][y]}\')\n if( hmap[x][y] > ans ):\n ans = hmap[x][y];\n \n return ans+1;\n\n\n \n\n \n``` | 2 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Простое решение через построение уравнения прямых | max-points-on-a-line | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n N = len(points)\n D = defaultdict(set)\n if N <= 2:\n return N \n for i in range(N):\n x1, y1 = points[i]\n for j in range(i+1, N):\n x2, y2 = points[j]\n if y1 == y2:\n k1, k2 = \'inf\', y1\n elif x1 == x2:\n k1, k2 = x1, \'inf\'\n else:\n k1, k2 = (x1-x2)/(y2-y1), (x2*y1-x1*y2)/(y2-y1)\n D[(k1,k2)].add(tuple(points[i]))\n D[(k1,k2)].add(tuple(points[j]))\n return max([len(i) for i in D.values()])\n \n\n``` | 2 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
python solution using atan2 | max-points-on-a-line | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n if n == 1:\n return 1\n result = 2\n for i in range(n):\n cnt = collections.defaultdict(int)\n for j in range(n):\n if i != j:\n cnt[math.atan2(points[j][1]-points[i][1], points[j][0]-points[i][0])] += 1\n result = max(result, max(cnt.values())+1)\n return result\n\n``` | 2 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Runtime Beats 99.56%,Python | max-points-on-a-line | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n\xB2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int: \n counter = 1\n if len(points) < 2:\n return 1\n for i in range(len(points)):\n egimList = {}\n for j in range(i+1,len(points)):\n y = points[j][1] - points[i][1]\n x = points[j][0] - points[i][0]\n if x != 0:\n egimList[y / x] = 1 + egimList.get(y / x, 0)\n else:\n egimList[\'inf\'] = 1 + egimList.get(\'inf\', 0)\n for key,value in egimList.items():\n counter = max(counter,value)\n return counter+1\n\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Python, time=O(n^2), space=O(n) | max-points-on-a-line | 0 | 1 | # Complexity\n- Time complexity:\n O(n^2)\n\n- Space complexity:\n O(n)\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n count = 1\n \n for i in range(len(points)):\n seen = {}\n for j in range(i+1, len(points)):\n\n y = (points[j][1]-points[i][1])\n x = (points[j][0]-points[i][0])\n\n if x == 0:\n if "inf" not in seen:\n seen["inf"] = 2\n else:\n seen["inf"] += 1\n else:\n result = y / x\n\n if result not in seen:\n seen[result] = 2\n else:\n seen[result] += 1\n\n for k in seen.keys():\n count = max(count, seen[k])\n return count\n\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Hashing the (m,c) values of a line | max-points-on-a-line | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n memo = collections.defaultdict(lambda : set())\n def findLine(node1, node2) : \n x1, y1 = node1\n x2, y2 = node2\n try: \n m = (y2 - y1)/ (x2 - x1)\n c = y1- m * x1\n except : \n m = float(\'inf\')\n c = x1\n return (m, c)\n for i in range(len(points)) : \n for j in range(i + 1, len(points)) : \n m, c = findLine(points[i], points[j])\n memo[(m, c)].add(tuple(points[i]))\n memo[(m, c)].add(tuple(points[j]))\n \n res = [len(st) for st in memo.values()]\n if not res : return 1\n return max(res)\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Optimised official solution. 99% less mem, 85% faster | max-points-on-a-line | 0 | 1 | # Intuition\nHere are some thoughs on offcial solution and how it can be improved:\n\n- Instead of calculating atan2 that we can do a single float division.\n- No need to calcuklate `dy` if `dx` is 0.\n- To save some space on GC we can resue the counter.\n- No need fo +1 in each iteration of the main loop as we can do it once at the end.\n\nIf you like it, plese up-vote. Thank you!\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxPoints(self, p: List[List[int]]) -> int:\n n = len(p)\n if n == 1:\n return 1\n result = 1\n cnt = collections.Counter()\n dx = 0\n for i in range(n):\n cnt.clear()\n for j in range(n):\n if j != i:\n dx = p[j][0] - p[i][0]\n if dx:\n cnt[(p[j][1] - p[i][1]) / dx] += 1\n else:\n cnt[None] += 1\n\n result = max(result, max(cnt.values()))\n return result + 1\n\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Python solution (slope) with explanation! | max-points-on-a-line | 0 | 1 | First, the function checks if there are fewer than 3 points in the array. In this case, the maximum number of points that can lie on the same straight line is the number of points in the array, so it returns this value.\n\nNext, initialize a variable result to 0, which will be used to store the maximum number of points that lie on the same straight line. It then iterates through each point in the array. For each point, it initializes a dictionary slopes to store the number of points with each slope, and a variable same_points to store the number of points that are the same as the current point (have the same x and y coordinates).\n\nIterate through the remaining points in the array and calculate the slope between the current point and each of these points. If the x coordinate of the other point is the same as the x coordinate of the current point, the slope is set to \'inf\' (infinity) to indicate a vertical line. If the y coordinate of the other point is the same as the y coordinate of the current point, the slope is not updated (since the number of points with this slope is already stored in the same_points variable). Otherwise, the slope is calculated as the ratio of the difference in y coordinates to the difference in x coordinates, and the count for this slope in the slopes dictionary is incremented.\n\nFinally, update the result variable to be the maximum of result, same_points, and the number of points with each slope in the slopes dictionary. Return the result variable as the final result.\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n if len(points) < 3:\n return len(points)\n\n result = 0\n for i in range(len(points)):\n slopes = defaultdict(int)\n same_points = 1\n for j in range(i+1, len(points)):\n dx = points[j][0] - points[i][0]\n dy = points[j][1] - points[i][1]\n\n if dx == 0 and dy == 0:\n same_points += 1\n elif dx == 0:\n slopes[\'inf\'] += 1\n else:\n slope = dy / dx\n slopes[slope] += 1\n\n result = max(result, same_points)\n for slope, count in slopes.items():\n result = max(result, same_points + count)\n\n return result\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
python3 - straightforward - sum of points in linear equations | max-points-on-a-line | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* to draw a line we need to find linear equation for it\n* store each equation in a hash map\n* store unique points that belongs to the equation\n* count number of points\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n if len(points) < 3:\n return len(points)\n\n funcs = {}\n for b in points:\n for a in points:\n if a == b:\n continue\n\n xx = a[0] - b[0]\n if xx == 0:\n f = (a[0],)\n else:\n ax = (a[1] - b[1]) / xx\n bb = (a[0]*b[1] - a[1]*b[0]) / xx\n f = (ax, bb)\n \n if f not in funcs:\n funcs[f] = set()\n funcs[f].add(tuple(a))\n\n return max(len(v) for k, v in funcs.items())\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Python Solution O(n^2) | max-points-on-a-line | 0 | 1 | # Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n \n res = 0\n for p1 in points:\n angles = {}\n max = 0\n same_points = 0\n for p2 in points:\n if p1 == p2:\n same_points += 1\n continue\n\n if p1[0] == p2[0]:\n angle = float("inf")\n else:\n angle = (p1[1] - p2[1]) / (p1[0] - p2[0])\n angles[angle] = angles.get(angle, 0) + 1\n if max < angles[angle]:\n max = angles[angle]\n if res < max + same_points:\n res = max + same_points\n\n return res\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
Easy Python Solution | max-points-on-a-line | 0 | 1 | ```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n n = len(points);\n if n == 1: return 1\n res = 2;\n for i in range(n):\n d = defaultdict(int);\n for j in range(n):\n if i != j:\n d[math.atan2(points[j][1] - points[i][1], points[j][0] - points[i][0])] += 1;\n res = max(res, max(d.values()) + 1);\n return res\n \n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
📌📌Python3 || 159 ms, faster than 60.79% of Python3 || Clean and Easy to Understand | max-points-on-a-line | 0 | 1 | ```\ndef maxPoints(self, points: List[List[int]]) -> int:\n if len(points) < 3:\n return len(points)\n\n dict = {}\n for b in points:\n for a in points:\n if a == b:\n continue\n\n k = a[0] - b[0]\n if k == 0:\n f = (a[0],)\n else:\n ax = (a[1] - b[1]) / k\n bb = (a[0]*b[1] - a[1]*b[0]) / k\n f = (ax, bb)\n \n if f not in dict:\n dict[f] = set()\n dict[f].add(tuple(a))\n\n return max(len(v) for k, v in dict.items())\n``` | 1 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
short solution | max-points-on-a-line | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n n=len(points)\n d={}\n for i in range(n):\n x,y=points[i][0],points[i][1]\n for j in range(i+1,n):\n x1=x-points[j][0]\n y1=y-points[j][1]\n b=x1*y-y1*x\n d[(y1,x1,b)]=0\n for i in range(n):\n x,y=points[i][0],points[i][1]\n for j in d:\n if j[1]*y==j[0]*x+j[2]:\n d[j]+=1\n m=1\n for x in d:\n m=max(m,d[x])\n return m\n\n \n\n\n``` | 2 | Given an array of `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return _the maximum number of points that lie on the same straight line_.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** 3
**Example 2:**
**Input:** points = \[\[1,1\],\[3,2\],\[5,3\],\[4,1\],\[2,3\],\[1,4\]\]
**Output:** 4
**Constraints:**
* `1 <= points.length <= 300`
* `points[i].length == 2`
* `-104 <= xi, yi <= 104`
* All the `points` are **unique**. | null |
O( n )✅ | Python (Step by step explanation) | evaluate-reverse-polish-notation | 0 | 1 | # Intuition\nThe problem requires evaluating arithmetic expressions in Reverse Polish Notation (RPN) format. In RPN, operators come after their operands, making it straightforward to perform calculations without the need for parentheses.\n\n# Approach\n1. Initialize an empty stack to store operands.\n2. Iterate through each token in the list of RPN tokens.\n3. If the token is an operator (\'+\', \'-\', \'*\', \'/\'), pop the last two values from the stack (the operands) and perform the corresponding operation. Push the result back onto the stack.\n4. If the token is not an operator, it\'s an operand, so convert it to an integer and push it onto the stack.\n5. Continue this process until all tokens are processed.\n6. The final result will be at the top of the stack, so pop it and return the result.\n\n# Complexity\n- Time complexity: O(n), where \'n\' is the number of tokens in the input list. We process each token exactly once.\n- Space complexity: O(n), as we use a stack to store operands, and the stack\'s size can grow up to \'n\' in the worst case when all tokens are operands.\n\n\n# Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n\n for token in tokens :\n if token == \'+\' :\n a , b = stack.pop() , stack.pop()\n stack.append( a + b ) \n elif token == \'-\':\n a , b = stack.pop() , stack.pop()\n stack.append( b - a ) \n elif token == \'*\':\n a , b = stack.pop() , stack.pop()\n stack.append( b * a ) \n elif token == \'/\':\n a , b = stack.pop() , stack.pop()\n stack.append( int(b / a) ) \n else:\n stack.append(int(token)) \n return stack.pop() \n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 5 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
✅ Explained - Simple and Clear Python3 Code✅ | evaluate-reverse-polish-notation | 0 | 1 | The provided solution evaluates arithmetic expressions in Reverse Polish Notation (RPN) using a stack. It iterates through the tokens of the expression, performing the corresponding arithmetic operations when encountering operators. The solution pops operands from the stack, applies the operations, and pushes the results back to the stack. If a token is an operand, it is directly added to the stack. Finally, the remaining value on the stack is retrieved as the evaluated result of the RPN expression. The solution handles operators and operands correctly, ensuring proper conversion and adherence to integer division rules.\n\n\n\n\n\n# Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n op = [\'+\', \'-\', \'*\', \'/\']\n for t in tokens:\n if t in op:\n x, y = int(stack.pop()), int(stack.pop())\n stack.append(x + y if t == \'+\' else y - x if t == \'-\' else x * y if t == \'*\' else int(y / x))\n else:\n stack.append(t)\n return int(stack[-1])\n``` | 10 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Python Solution | evaluate-reverse-polish-notation | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSolving using stack data concept\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n def fun(st,n1,n2):\n s1,s2=1,1\n if n1<0:\n s1=-1\n if n2<0:\n s2=-1\n if st==\'+\':\n return n1+n2\n elif st==\'-\':\n return n1-n2\n elif st==\'*\':\n return n1*n2\n elif st==\'/\':\n return floor(abs(n1)/abs(n2))*(s1*s2)\n digits=[]\n for i in tokens:\n if i.isdigit() or (len(i)>1):\n digits.append(int(i))\n else:\n n1=digits.pop()\n n2=digits.pop()\n digits.append(fun(i,n2,n1))\n return digits[0]\n``` | 2 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
The easiest solution using stack & lambdas | evaluate-reverse-polish-notation | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n operators = {\n \'+\': (lambda x, y: operator.add(x, y)),\n \'*\': (lambda x, y: operator.mul(x, y)),\n \'/\': (lambda x, y: int(x / y)),\n \'-\': (lambda x, y: operator.sub(x, y)),\n }\n stack = [] # Space: O(n) \n for token in tokens: # Time: O(n)\n if token not in operators:\n stack.append(int(token))\n else:\n x = stack.pop(-2)\n y = stack.pop()\n stack.append(operators[token](x, y))\n return stack[-1]\n``` | 6 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Easy Python3 Solution | evaluate-reverse-polish-notation | 0 | 1 | \n# Approach\n1. Push each token into the stack until an operator is reached.\n2. Pop the top 2 values when token = operator\n3. Evaluate the values based on the operator\n4. Push the operated value in the stack\n5. Continue this until the end of tokens\n\nNOTE: All the tokens should be an integer value\n\n\n# Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n for token in tokens:\n if token == \'+\':\n stack.append(int(stack.pop() + stack.pop()))\n elif token == \'-\':\n first_tok,second_tok=stack.pop(),stack.pop()\n stack.append(int(second_tok-first_tok))\n elif token == \'*\':\n stack.append(int(stack.pop() * stack.pop()))\n elif token == \'/\':\n first_tok,second_tok=stack.pop(),stack.pop()\n stack.append(int(second_tok/first_tok))\n else:\n stack.append(int(token))\n return stack[0]\n \n``` | 1 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Python | Stack and Lambda Solution | evaluate-reverse-polish-notation | 0 | 1 | \n# Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n\n stack = []\n signs = {\n \'+\': lambda x,y: x+y,\n \'-\': lambda x,y: x-y,\n \'*\': lambda x,y: x*y,\n \'/\': lambda x,y: x/y\n }\n\n\n for token in tokens:\n if token not in signs:\n stack.append(int(token))\n else:\n right = stack.pop()\n left = stack.pop()\n stack.append(int(signs[token](left, right)))\n \n return stack.pop()\n \n \n\n``` | 1 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Python 3 || 11 lines, w/ example || T/M: 95% / 97% | evaluate-reverse-polish-notation | 0 | 1 | ```\nclass Solution:\n def evalRPN(self, tokens: list[str]) -> int: # Ex: tokens = ["4","13","5","/","+"]\n stack = []\n # t operation stack\n for t in tokens: # \u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \n if t not in \'/+-*\': # 4 [4]\n stack.append(int(t)) # 13 [4,13]\n # 5 [4,13,5]\n else: # / 13 / 5 = 2 [4,2]\n num = stack.pop() # + 4 + 2 = 6 [6]\n if t == \'+\': stack[-1]+= num\n elif t == \'-\': stack[-1]-= num\n elif t == \'*\': stack[-1]*= num\n else : stack[-1]= int(stack[-1]/num) \n\n return stack[0]\n\n```\n[https://leetcode.com/problems/evaluate-reverse-polish-notation/submissions/860874774/](http://)\n\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(*N*). | 19 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
150: Solution with step by step explanation | evaluate-reverse-polish-notation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses a stack to keep track of operands as they are encountered in the input array. When an operator is encountered, the top two operands are popped off the stack, the operation is performed, and the result is pushed back onto the stack. When the loop completes, the final result is the only item left on the stack, so it is returned. The function signature includes type hints to make it easier to understand the inputs and outputs. The code also follows PEP 8 style guidelines for naming conventions and formatting.\n\n# Complexity\n- Time complexity:\nBeats\n93.14%\n\n- Space complexity:\nBeats\n94.2%\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n operators = set(["+", "-", "*", "/"])\n for token in tokens:\n if token in operators:\n right_operand = stack.pop()\n left_operand = stack.pop()\n if token == "+":\n result = left_operand + right_operand\n elif token == "-":\n result = left_operand - right_operand\n elif token == "*":\n result = left_operand * right_operand\n else:\n result = int(left_operand / right_operand)\n stack.append(result)\n else:\n stack.append(int(token))\n return stack[-1]\n\n``` | 5 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
✅ Easy Solution w/ Explanation | [C++ , JAVA , Python] | No Runtime Error | evaluate-reverse-polish-notation | 1 | 1 | # \u2714\uFE0F Solution - I (Using Explicit Stack)\n<!-- Describe your approach to solving the problem. -->\nThe reverse polish is a mathematical notation in which operators follow their operands. So, we will get the operands first and then the operators.\n\n- We store all the operands in the order we receive it in.\n- If we get an operator, we operate it on the previous two operands. \n- We store the resultant operand as it will be used for future operations. \n- We use a stack to store all the operands. \n\nSo the algorithm is:\n- If the character is a number (operand), push it into the stack\n- If the character is an operator, \n - Pop the top two operands (numbers) from the stack. \n - Find the result of the operation using the operator \n - Push the result back in the stack\n- After traversal, the top of the stack will be the result of evaluated reverse polish expression.\n# Complexity\n- Time complexity: `O(N)`, where `N` is the number of tokens\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: `O(N)`, for maintaining the stack\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code in C++\n```\nclass Solution {\npublic:\n int evalRPN(vector<string>& tokens) {\n stack<long long int> s ;\n for(auto &i:tokens)\n { \n if(i == "+" || i == "-" || i == "*" || i == "/") // operators \n {\n long long int op1 = s.top() ; \n s.pop() ;\n long long int op2 = s.top() ; \n s.pop() ;\n if(i == "+") \n op1 = op2 + op1 ;\n if(i == "-") \n op1 = op2 - op1 ;\n if(i == "*") \n op1 = op2*op1 ; \n if(i == "/") \n op1 = op2/op1 ; \n s.push(op1) ;\n }\n else \n s.push(stoll(i)) ; // number -> need to convert from str to int\n } \n return s.top() ; \n\n }\n};\n```\n\n# Code in Python\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n for i in tokens:\n if i not in {"+", "-", "*", "/"}:\n stack.append(int(i))\n else: #operand\n b, a = stack.pop(), stack.pop()\n if i == "+": \n stack.append(a + b)\n elif i == "-": \n stack.append(a - b)\n elif i == "*": \n stack.append(a*b)\n else: \n stack.append(trunc(a/b))\n return stack[0]\n```\n\n# Code in JAVA\n```\nclass Solution {\n public int evalRPN(String[] tokens) {\n Stack<Integer> stack = new Stack<>() ;\n Set<String> o = new HashSet<>(Arrays.asList("+", "-", "*", "/")) ;\n for (String i:tokens) \n {\n if(!o.contains(i)) \n stack.push(Integer.valueOf(i));\n else \n {\n int a = stack.pop(), b = stack.pop();\n if(i.equals("+")) \n stack.push(a + b);\n else if(i.equals("-")) \n stack.push(b - a);\n else if(i.equals("*")) \n stack.push(a*b);\n else \n stack.push(b/a);\n }\n }\n return stack.peek() ;\n }\n}\n``` | 14 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Simple Stack imp | O(N) | evaluate-reverse-polish-notation | 0 | 1 | # Code\n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n for i in tokens:\n if i in set([\'+\', \'-\', \'*\', \'/\']):\n a, b = stack.pop(), stack.pop()\n if i == \'+\':\n stack.append(a+b)\n elif i == \'-\':\n stack.append(b-a)\n elif i == \'*\':\n stack.append(a*b)\n else:\n stack.append(int(b/a))\n else:\n stack.append(int(i))\n return stack[0]\n\n``` | 2 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
[Java / Python] Beat 91.65% Cleanest and easy understanding solution for beginners | evaluate-reverse-polish-notation | 1 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nStack \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Python []\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n stack = []\n for i in tokens:\n if i.isdigit() or (i.startswith(\'-\') and i[1:].isdigit()):\n stack.append(int(i))\n else:\n num1 = stack.pop()\n num2 = stack.pop()\n if i == \'+\' : stack.append(int(num1 + num2))\n if i == \'-\' : stack.append(int(num2 - num1))\n if i == \'*\' : stack.append(int(num1 * num2))\n if i == \'/\' : stack.append(int(num2 / num1))\n return stack[0]\n```\n```Java []\nclass Solution {\n public int evalRPN(String[] tokens) {\n Stack<Integer> stack = new Stack<>();\n for (String token : tokens) {\n if (!"+-*/".contains(token)) {\n stack.push(Integer.valueOf(token));\n } else {\n int n1 = stack.pop();\n int n2 = stack.pop();\n switch (token) {\n case "+":\n stack.push(n1 + n2);\n break;\n case "-":\n stack.push(n2 - n1);\n break;\n case "*":\n stack.push(n1 * n2);\n break;\n case "/":\n if (n1 == 0) {\n throw new ArithmeticException("Division by zero");\n }\n stack.push(n2 / n1);\n break;\n }\n }\n }\n return stack.pop();\n }\n}\n\n``` | 3 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Python Simple & easy to understand code | evaluate-reverse-polish-notation | 0 | 1 | \n```\nclass Solution:\n def evalRPN(self, tokens: List[str]) -> int:\n op = {\n \'+\' : lambda x, y : x + y,\n \'-\' : lambda x, y : x - y,\n \'*\' : lambda x, y : x * y,\n \'/\' : lambda x, y : int(x / y)\n }\n\n stack = []\n for i in tokens:\n if i in "+-*/":\n b = stack.pop()\n a = stack.pop()\n stack.append(op[i](a, b))\n else:\n stack.append(int(i))\n \n return stack.pop()\n``` | 10 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
Evaluate Reverse Polish Notation || Java || Python3 || Well Explained|| Stack | evaluate-reverse-polish-notation | 1 | 1 | # Evaluate Reverse Polish Notation.\n\n#### We can observe from the example that this problem requires stack operations.\n1. When it is operator(+,-,*,/) pop two element from stack and perform operation and store the result back into the stack.\n2. Otherwise push the element into the stack.\n**T.C. of O(N) for parsing the token and Space complexity of stack O(K)**\n```java\nclass Solution {\n public int evalRPN(String[] tokens) {\n LinkedList <Integer> stack = new LinkedList<>();\n Integer op1,op2;\n for(String ch:tokens){\n \n switch(ch){\n case "+":\n op1 = stack.pop();\n op2 = stack.pop();\n stack.push(op2+op1);\n break;\n \n case "-":\n op1 = stack.pop();\n op2 = stack.pop();\n stack.push(op2-op1);\n break;\n case "*":\n op1 = stack.pop();\n op2 = stack.pop();\n stack.push(op2*op1);\n break;\n case "/":\n op1 = stack.pop();\n op2 = stack.pop();\n stack.push(op2/op1);\n break;\n default:\n stack.push(Integer.parseInt(ch));\n \n \n }\n }\n return stack.pop();\n }\n}\n```\n****\n#### A special note while solving it in python is `//` operator works as math.floor so if u divide 6// -132 = -1 , but according to our logic it should be 0.\n```py\nclass Solution:\n def evalRPN(self, tokens) -> int:\n stack = [] \n for ch in tokens:\n if ch == \'+\':\n op1,op2 = stack.pop(), stack.pop()\n stack.append(op2 + op1)\n elif ch == \'-\':\n op1,op2 = stack.pop(), stack.pop()\n stack.append(op2 - op1)\n elif ch == \'*\':\n op1,op2 = stack.pop(), stack.pop()\n stack.append(op2 * op1)\n elif ch == \'/\':\n op1,op2 = stack.pop(), stack.pop()\n # note // operator works as math.floor so if u divide 6// -132 = -1 \n stack.append(int(op2 / op1))\n else:\n stack.append(int(ch))\n \n return stack.pop()\n```\n\n | 1 | You are given an array of strings `tokens` that represents an arithmetic expression in a [Reverse Polish Notation](http://en.wikipedia.org/wiki/Reverse_Polish_notation).
Evaluate the expression. Return _an integer that represents the value of the expression_.
**Note** that:
* The valid operators are `'+'`, `'-'`, `'*'`, and `'/'`.
* Each operand may be an integer or another expression.
* The division between two integers always **truncates toward zero**.
* There will not be any division by zero.
* The input represents a valid arithmetic expression in a reverse polish notation.
* The answer and all the intermediate calculations can be represented in a **32-bit** integer.
**Example 1:**
**Input:** tokens = \[ "2 ", "1 ", "+ ", "3 ", "\* "\]
**Output:** 9
**Explanation:** ((2 + 1) \* 3) = 9
**Example 2:**
**Input:** tokens = \[ "4 ", "13 ", "5 ", "/ ", "+ "\]
**Output:** 6
**Explanation:** (4 + (13 / 5)) = 6
**Example 3:**
**Input:** tokens = \[ "10 ", "6 ", "9 ", "3 ", "+ ", "-11 ", "\* ", "/ ", "\* ", "17 ", "+ ", "5 ", "+ "\]
**Output:** 22
**Explanation:** ((10 \* (6 / ((9 + 3) \* -11))) + 17) + 5
= ((10 \* (6 / (12 \* -11))) + 17) + 5
= ((10 \* (6 / -132)) + 17) + 5
= ((10 \* 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
**Constraints:**
* `1 <= tokens.length <= 104`
* `tokens[i]` is either an operator: `"+ "`, `"- "`, `"* "`, or `"/ "`, or an integer in the range `[-200, 200]`. | null |
[python 3] one liner | reverse-words-in-a-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def reverseWords(self, s: str) -> str:\n return (" ".join(s.split()[::-1]))\n``` | 2 | Given an input string `s`, reverse the order of the **words**.
A **word** is defined as a sequence of non-space characters. The **words** in `s` will be separated by at least one space.
Return _a string of the words in reverse order concatenated by a single space._
**Note** that `s` may contain leading or trailing spaces or multiple spaces between two words. The returned string should only have a single space separating the words. Do not include any extra spaces.
**Example 1:**
**Input:** s = "the sky is blue "
**Output:** "blue is sky the "
**Example 2:**
**Input:** s = " hello world "
**Output:** "world hello "
**Explanation:** Your reversed string should not contain leading or trailing spaces.
**Example 3:**
**Input:** s = "a good example "
**Output:** "example good a "
**Explanation:** You need to reduce multiple spaces between two words to a single space in the reversed string.
**Constraints:**
* `1 <= s.length <= 104`
* `s` contains English letters (upper-case and lower-case), digits, and spaces `' '`.
* There is **at least one** word in `s`.
**Follow-up:** If the string data type is mutable in your language, can you solve it **in-place** with `O(1)` extra space? | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.