title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python3 Solution | candy | 0 | 1 | \n```\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n=len(ratings)\n dp=[1]*n\n for i in range(1,n):\n if ratings[i]>ratings[i-1]:\n dp[i]=dp[i-1]+1\n\n for i in range(n-2,-1,-1):\n if ratings[i]>ratings[i+1]:\n dp[i]=max(dp[i],dp[i+1]+1)\n\n return sum(dp) \n``` | 2 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Python 3 | Beats 88.46% Time and 99.36% Memory | 2 Pass solution | candy | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n\n # every child will be given at least one candy\n ret = [1] * len(ratings)\n\n # 2 pass solution\n\n # first pass\n # increment the candy\'s based off the left neighbor\n for l in range(1, len(ratings)):\n # if the left neighbor is less than the current, then the current deserves one more candy than the prev\n if ratings[l - 1] < ratings[l]:\n ret[l] = ret[l - 1] + 1\n\n # second pass \n # increment the candy\'s based off the right neighbor\n for r in range(len(ratings) - 2, -1, -1):\n # if the right neighbor is less than the current, then current deserves one more candy than the right\n if ratings[r + 1] < ratings[r]:\n # here is the tricky part, if the current indexes candy is already higher than the right then leave it\n # you don\'t want to update the current candy to candy[right] + 1 because there is a possibility that\n # it will be less than the first pass iteration\n ret[r] = max(ret[r], ret[r + 1] + 1)\n\n return sum(ret)\n\n\n\n \n``` | 1 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
🚀 Beats 99.93% || Greedy || Two Solutions || C++ || Java || Python || Commented Code 🚀 | candy | 1 | 1 | # Problem Description\nThe task is distributing candies to a group of `n` children standing in a line. Each child is assigned a **rating value**, represented as an **integer** array called `ratings`.\n\nFollow **two specific requirements** while distributing the candies:\n- Each child must have at least one candy.\n- Children with a higher rating should receive more candies than their neighbors.\n\nThe **goal** is to determine the **minimum** number of candies needed to satisfy these requirements and distribute the candies to the children accordingly.\n\n- **Constraints:**\n - `n == ratings.length`\n - `1 <= n <= 2 * 104`\n - `0 <= ratings[i] <= 2 * 104`\n - at **least one candy** for each child\n - neighbours with **higher rating** have **more candies**\n\n\n---\n\n\n\n# Intuition\nHi there\uD83D\uDE00\nLet\'s take a look on this interesting problem.\n\nFor our candies task we have **two crucial requirements**: Each child must have **at least one** candy, and children with **higher ratings** than their **neighbors** have more candies than them... Interesting.\n\nLet\'s explore some ratings\' cases together:\n\n\n```\n2, 2, 2 \n```\nHere we can see that **each child** of them can have **one candy** since no one has higher rating than its neighbor.\n\n```\n1, 2, 2, 2 \n```\nHere we can see that the array of candies will be `1, 2, 1, 1`.\n\n```\n9, 8, 7\n```\nHere we can see that array of candies will be `3, 2, 1`.\n\n```\n7, 8, 9\n```\nHere we can see that array of candies will be `1, 2, 3`.\n\n\nI think now we have some **idea** about what is going on here\uD83E\uDD14\n- Children with **equal ratings** can have different candies and that won\'t violate our requirements since we are aiming for giving **minimum** candies.\n- We must take care of **decreasing** subarrays and **increasing** ones.\n\nHow can we use an approach that take care of these **observations**?\uD83D\uDE80\n\n## Two Pass Approach \nIn this approach we will:\n- Iterate from `left to right` to take care of **increasing** subarrays \n- Iterate from `right to left` to take care of **decreasing** subarrays\n- We **won\'t do anything** to **equal** neighbours since they won\'t affect our requirements\n\nLet\'s take an example:\n```\n9, 8, 8, 7, 7, 8, 9\n```\n**First** we have array of candes `1, 1, 1, 1, 1, 1, 1`\n\nAfter our **first pass** (from left to right) we will have array of candies `1, 1, 1, 1, 1, 2, 3`.\nWe can see that it **handled** the **increasing** subarray perfectly.\n\nAfter our **second pass**(from right to left) we will have array of candies `2, 1, 2, 1, 1, 2, 3 `.\nwe can see that it also **handled** the **decreasing** subarray perfectly.\n\nAlso, it handled the equal neighbours after the two passes. It finally minimized our candies. \n\n\n## One Pass Approach \nThis solution is more challenging since it requires us to handle the **three cases** in **one** pass. How can we start? \uD83E\uDD14\nWe saw before that we have three cases **increasing** subarrays, **decreasing** subarrays and **equal** subbarrays.\nWe can start by intialize **three variables** to handle the three of them.\n\nFor **increasing** subarray we need one variable `up` to handle what candy we give to current child.\nfor each child in the **increasing** subarray increase the `up` variable by one and give the current child `up + 1` candies indicating that it must have more that the child before him\nwe will call `up + 1` as `peak` to mean the highest child in our subarray\n\nFor **equal** subarrays, only give them `one` candy and we will see that we only give one to the children in the middle of the subarray\n\nFor **decreasing** subarray here comes the challenge \nWe will introduce variable like first case called `down` but the purpose of it **not** indicating that we give candies to current child but, giving **one** candy to current child and **one** candy for each child before him in the decreasing subarray to meet the requirements.\n\nExample : `1, 2, 3, 3, 2, 1`\n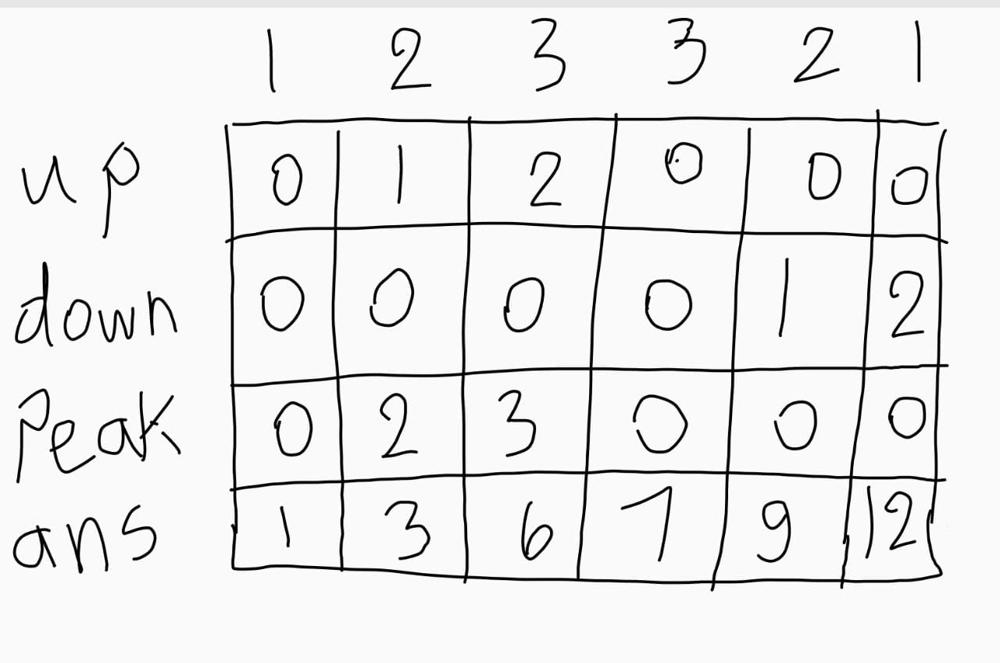\n\nBut what if we have **increasing** then **decreasing** subarrays?\nWe will have the **last** child of the first subarray as first child on the second and then we give each child in the decreasing subarray one candy except that child who is our `peak` until the length of the subarray is larger than the `peak`.\n\nExample : `1, 2, 3, 2, 1`\n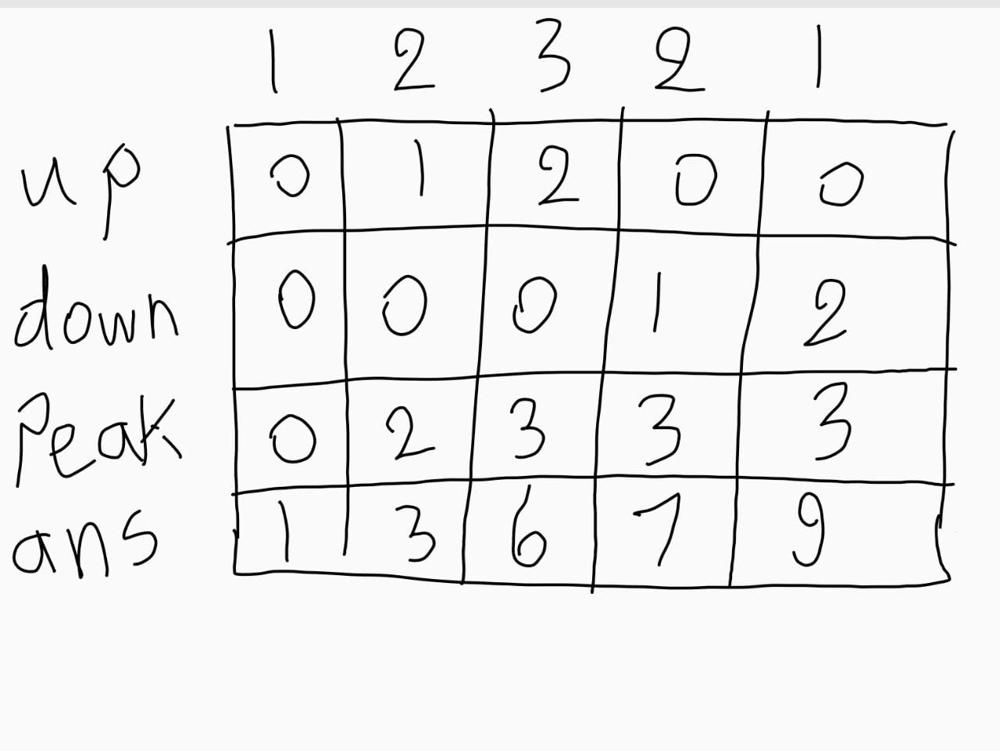\n\n\n\n---\n\n\n\n# Approach\n\n## Two Pass Approach\n### Steps\n- **Initialize** variables:\n - `n` is number of children.\n - `candies` to store candies for each child..\n- **First Pass** (Left to Right):\n - For each child, **check** if the previous child has a **lower** rating and has **more** or **equal** candies.\n - If **true**, give the current child one more candy than the previous child.\n- **Second Pass** (Right to Left):\n - For each child, **check** if the next child has a **lower** rating and has **more** or **equal** candies.\n - If **true**, give the current child one more candy than the next child.\n \n- Calculate and return totalCandies.\n\n### Complexity\n- **Time complexity:** $$O(N)$$\nSince we are looping over the ratings array twice then the time complexity is `2*N` which is `O(N)`.\n- **Space complexity:** $$O(N)$$\nSince we are storing the number of candies for each child then the space complexity is `O(N)`.\n\n\n---\n\n## One Pass Approach\n### Steps\n- **Initialize** variables:\n - `n` to store the number of children.\n - `upCount` to keep track of consecutive increasing ratings.\n - `downCount` to keep track of consecutive decreasing ratings.\n - `peakCount` to store the number of candies at the peak of increasing ratings.\n - `totalCandies` to count required candies.\n- **Iterate** Through Ratings:\n - **compare** the child rating with the **previous** child\n - If current child has a **higher** rating than previous one then update the variables and add `peakCount` to `totalCandies`.\n - If current child has the **same** rating as previous one then update and add `1` to ``totalCandies``.\n - If current child has a **lower** rating than previous one update and update `totalCandies` by adding `downCount` + 1, subtracting `1` if `peakCount` is greater than `downCount`.\n- **Return** `totalCandies`\n\n### Complexity\n- **Time complexity:** $$O(N)$$\nSince we are looping over the ratings array one time then the time complexity is `N` which is `O(N)`.\n- **Space complexity:** $$O(1)$$\nSince we are storing only couple of variables then the space complexity is `O(1)`.\n\n\n---\n\n\n\n# Code\n## Two Pass Approach\n```C++ []\nclass Solution {\npublic:\n int candy(vector<int>& ratings) {\n int n = ratings.size(); // Get the number of children\n \n vector<int> candies(n, 1); // Initialize a vector to store the number of candies for each child\n \n // First pass: Check ratings from left to right\n for(int i = 1; i < n; i++){\n if(ratings[i - 1] < ratings[i] && candies[i - 1] >= candies[i]){\n // If the current child has a higher rating and fewer or equal candies than the previous child,\n // give them one more candy than the previous child\n candies[i] = candies[i - 1] + 1;\n }\n }\n \n // Second pass: Check ratings from right to left\n for(int i = n - 2; i >= 0; i--){\n if(ratings[i + 1] < ratings[i] && candies[i + 1] >= candies[i]){\n // If the current child has a higher rating and fewer or equal candies than the next child,\n // give them one more candy than the next child\n candies[i] = candies[i + 1] + 1;\n }\n }\n \n int totalCandies = 0;\n \n // Calculate the total number of candies needed\n for(int i = 0; i < n; i++){\n totalCandies += candies[i];\n }\n \n return totalCandies;\n }\n};\n```\n```Java []\npublic class Solution {\n public int candy(int[] ratings) {\n int n = ratings.length; // Get the number of children\n \n int[] candies = new int[n]; // Initialize an array to store the number of candies for each child\n \n // First pass: Check ratings from left to right\n for (int i = 1; i < n; i++) {\n if (ratings[i - 1] < ratings[i] && candies[i - 1] >= candies[i]) {\n // If the current child has a higher rating and fewer or equal candies than the previous child,\n // give them one more candy than the previous child\n candies[i] = candies[i - 1] + 1;\n }\n }\n \n // Second pass: Check ratings from right to left\n for (int i = n - 2; i >= 0; i--) {\n if (ratings[i + 1] < ratings[i] && candies[i + 1] >= candies[i]) {\n // If the current child has a higher rating and fewer or equal candies than the next child,\n // give them one more candy than the next child\n candies[i] = candies[i + 1] + 1;\n }\n }\n \n int totalCandies = 0;\n \n // Calculate the total number of candies needed\n for (int i = 0; i < n; i++) {\n totalCandies += candies[i] + 1;\n }\n \n return totalCandies;\n }\n}\n```\n```Python []\nclass Solution:\n def candy(self, ratings) -> int:\n n = len(ratings) # Get the number of children\n \n candies = [1] * n # Initialize a list to store the number of candies for each child\n \n # First pass: Check ratings from left to right\n for i in range(1, n):\n if ratings[i - 1] < ratings[i] and candies[i - 1] >= candies[i]:\n # If the current child has a higher rating and fewer or equal candies than the previous child,\n # give them one more candy than the previous child\n candies[i] = candies[i - 1] + 1\n \n # Second pass: Check ratings from right to left\n for i in range(n - 2, -1, -1):\n if ratings[i + 1] < ratings[i] and candies[i + 1] >= candies[i]:\n # If the current child has a higher rating and fewer or equal candies than the next child,\n # give them one more candy than the next child\n candies[i] = candies[i + 1] + 1\n \n total_candies = sum(candies) # Calculate the total number of candies needed\n \n return total_candies\n```\n\n## One Pass Approach\n```C++ []\nclass Solution {\npublic:\n int candy(vector<int>& ratings) {\n int n = ratings.size(); // Get the number of children\n int upCount = 0, downCount = 0, peakCount = 0, totalCandies = 1; // Initialize variables\n \n for(int i = 1; i < n ; i ++){\n if(ratings[i - 1] < ratings[i]){\n // If the current child has a higher rating than the previous one\n downCount = 0;\n upCount += 1;\n peakCount = upCount + 1;\n totalCandies += peakCount;\n } else if(ratings[i - 1] == ratings[i]){\n // If the current child has the same rating as the previous one\n downCount = 0;\n upCount = 0;\n peakCount = 0;\n totalCandies += 1;\n } else {\n // If the current child has a lower rating than the previous one\n downCount += 1;\n upCount = 0;\n totalCandies += downCount + 1 - (peakCount > downCount);\n }\n }\n \n return totalCandies;\n }\n};\n```\n```Java []\npublic class Solution {\n public int candy(int[] ratings) {\n int n = ratings.length; // Get the number of children\n int upCount = 0, downCount = 0, peakCount = 0, totalCandies = 1; // Initialize variables\n \n for (int i = 1; i < n; i++) {\n if (ratings[i - 1] < ratings[i]) {\n // If the current child has a higher rating than the previous one\n downCount = 0;\n upCount += 1;\n peakCount = upCount + 1;\n totalCandies += peakCount;\n } else if (ratings[i - 1] == ratings[i]) {\n // If the current child has the same rating as the previous one\n downCount = 0;\n upCount = 0;\n peakCount = 0;\n totalCandies += 1;\n } else {\n // If the current child has a lower rating than the previous one\n downCount += 1;\n upCount = 0;\n totalCandies += downCount + 1 - (peakCount > downCount ? 1 : 0);\n }\n }\n \n return totalCandies;\n }\n}\n```\n```Python []\nclass Solution:\n def candy(self, ratings) -> int:\n n = len(ratings) # Get the number of children\n upCount = downCount = peakCount = 0\n totalCandies = 1 # Initialize variables\n \n for i in range(1, n):\n if ratings[i - 1] < ratings[i]:\n # If the current child has a higher rating than the previous one\n downCount = 0\n upCount += 1\n peakCount = upCount + 1\n totalCandies += peakCount\n elif ratings[i - 1] == ratings[i]:\n # If the current child has the same rating as the previous one\n downCount = 0\n upCount = 0\n peakCount = 0\n totalCandies += 1\n else:\n # If the current child has a lower rating than the previous one\n downCount += 1\n upCount = 0\n totalCandies += downCount + 1 - (1 if peakCount > downCount else 0)\n \n return totalCandies\n```\n\n\n\n\n\n | 76 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
【Video】O(n) Time, O(1) Space Solution - Python, JavaScript, Java, C++ | candy | 1 | 1 | # Intuition\nKeep two peak values and subtract the lower peak from total.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/f5oFx-X0eS4\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2310\nThank you for your support!\n\n---\n\n# Approach\n\n## \u25A0 Step 1\nIntialize `total_candies` with `len(ratings)` because at least all children has one candy.\n\n## \u25A0 Step 2\nWe iterate through `ratings` one by one.\n\n### case1\n```\nif ratings[i] == ratings[i - 1]:\n```\nwe don\'t have to give a candy to the current `i` child because current `i` child has the same rating with previous child. Just increment `i` and continue.\n\n### case2\n```\nwhile i < n and ratings[i] > ratings[i - 1]:\n```\nThis case indicates that the current `i` child has higher raiting than `i - 1` previous child. In this case, we need to give candies to the current `i` child.\n\nAdd `+1` to `current_peak` and add `current_peak` to `total_candies` and incremtnt `i`. this process continues until we don\'t meet case2 `while condition` above.\n\nLet me explain `current_peak` in "How it works" section.\n\n### case3\n```\nwhile i < n and ratings[i] < ratings[i - 1]:\n```\nThis case indicates that the current `i` child has lower raiting than `i - 1` previous child. In this case, actually we do the same thing of `case2`. Because even if input is decreasing order `[9,5,3,1]`, we need to give candies to the current `i` child. In the end, total candies are 10 `[4,3,2,1]`. we need some extra candies.\n\nAdd `+1` to `current_valley` and add `current_valley` to `total_candies` and incremtnt `i`. this process continues until we don\'t meet case 3 `while condition` above.\n\nLet me explain `current_valley` in "How it works" section.\n\nIn the last of Step 2, subtract minium of `current_peak` or `current_valley` from `total_candies`.\n\n# How it works\nLet\'s think with this input. \n```\nInput: ratings = [2,4,6,7,3,2,2]\n```\n```\ntotal_candies(Let\'s say "total") = 7 (length of input array)\ncurrent_peak(Let\'s say "peak") = 0\ncurrent_valley(Let\'s say "valley") = 0\n\n```\nIn Step2, starting from `index 1`.\n```\n\u25A0 Case2\ncondtion: while i < n and ratings[i] > ratings[i - 1]:\n\nindex 1 > index 0, so peak = 1, valley = 0, total = 8 (7 + 1)\nindex 2 > index 1, so peak = 2, valley = 0, total = 10 (8 + 2)\nindex 3 > index 2, so peak = 3, valley = 0, total = 13 (10 + 3)\nindex 4 < index 3, then stop Case2\n\nOur code distrubtes candies like this so far\nfrom [1,1,1,1,1,1,1]\nto [1,2,3,4,1,1,1](total 13 candies)\n```\n```\n\u25A0 Case3\ncondtion: while i < n and ratings[i] < ratings[i - 1]:\n\nindex 4 < index 3, so peak = 3, valley = 1, total = 14 (13 + 1)\nindex 5 < index 4, so peak = 3, valley = 2, total = 16 (14 + 2)\nindex 6 == index 5, then stop Case3\n\nOur code distrubtes candies like this so far\nfrom [1,2,3,4,1,1,1](Case2)\nto [1,2,3,4,2,3,1](total 16 candies)\n```\n\nLet me explain `total_candies -= min(current_peak, current_valley)`\nBefore that, `the last rating(index 6)` is equal to `index 5`, so we don\'t do anything(meet `Case1`). Let me skip it.\n\nNow Look at this. When ratings = `[2,4,6,7,3,2,2]`\n```\nThis is real distribution, In other words, the minimum number of\ncandies you need to have to distribute\n\n[1,2,3,4,2,1,1] = 14 candies\n[1,1,1,1,1,1,1]\n[0,1,2,3,1,0,0](additional candies for each children)\n```\n```\nHow our code distributes candies\n\n[1,2,3,4,2,3,1] = 16 candies\n[1,1,1,1,1,1,1]\n[0,1,2,3,1,2,0](additional candies for each children)\n```\n\nCompare distribution of adittional candies.\n```\n[0,1,2,3,1,0,0](Real)\n[0,1,2,3,1,2,0](Our code)\n```\nOur code distributes `extra 2 candies` at `index 5` which is equal to minimum of `current_peak` or `current_valley`. That\'s because actually we add peaks twice as a `peak` and as a `valley` in Case2 and Case3. For this question, we need peak value only once. More precisely, we need only higher peak between range of one of `peak` and `valley` combinations(in this case between `index1` and `index5`), because of constraints from the description saying "Children with a higher rating get more candies than their neighbors".\n\nThat\'s why we need to substract `minimum peak` from `total_candies`. In this case `16 - 2`. `peak = 3` vs `valley = 2`\n\n```\nOutput: 14\n```\n\n# Complexity\n- Time complexity: O(n)\n\'n\' is the number of elements in the \'ratings\' list. This is because we are using a single loop to iterate through the ratings, and within the loop, we perform constant time operations.\n\n- Space complexity: O(1), which means it uses a constant amount of additional memory regardless of the size of the \'ratings\' list. The only variables that consume memory are \'n\', \'total_candies\', \'i\', \'current_peak\', and \'current_valley\', and these variables do not depend on the input size \'n\'.\n\n```python []\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n = len(ratings)\n total_candies = n\n i = 1\n\n while i < n:\n if ratings[i] == ratings[i - 1]:\n i += 1\n continue\n\n current_peak = 0\n while i < n and ratings[i] > ratings[i - 1]:\n current_peak += 1\n total_candies += current_peak\n i += 1\n \n if i == n:\n return total_candies\n\n current_valley = 0\n while i < n and ratings[i] < ratings[i - 1]:\n current_valley += 1\n total_candies += current_valley\n i += 1\n\n total_candies -= min(current_peak, current_valley)\n\n return total_candies\n```\n```javascript []\n/**\n * @param {number[]} ratings\n * @return {number}\n */\nvar candy = function(ratings) {\n const n = ratings.length;\n let totalCandies = n;\n let i = 1;\n\n while (i < n) {\n if (ratings[i] === ratings[i - 1]) {\n i++;\n continue;\n }\n\n let currentPeak = 0;\n while (i < n && ratings[i] > ratings[i - 1]) {\n currentPeak++;\n totalCandies += currentPeak;\n i++;\n }\n\n if (i === n) {\n return totalCandies;\n }\n\n let currentValley = 0;\n while (i < n && ratings[i] < ratings[i - 1]) {\n currentValley++;\n totalCandies += currentValley;\n i++;\n }\n\n totalCandies -= Math.min(currentPeak, currentValley);\n }\n\n return totalCandies; \n};\n```\n```java []\nclass Solution {\n public int candy(int[] ratings) {\n int n = ratings.length;\n int totalCandies = n;\n int i = 1;\n\n while (i < n) {\n if (ratings[i] == ratings[i - 1]) {\n i++;\n continue;\n }\n\n int currentPeak = 0;\n while (i < n && ratings[i] > ratings[i - 1]) {\n currentPeak++;\n totalCandies += currentPeak;\n i++;\n }\n\n if (i == n) {\n return totalCandies;\n }\n\n int currentValley = 0;\n while (i < n && ratings[i] < ratings[i - 1]) {\n currentValley++;\n totalCandies += currentValley;\n i++;\n }\n\n totalCandies -= Math.min(currentPeak, currentValley);\n }\n\n return totalCandies; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int candy(vector<int>& ratings) {\n int n = ratings.size();\n int totalCandies = n;\n int i = 1;\n\n while (i < n) {\n if (ratings[i] == ratings[i - 1]) {\n i++;\n continue;\n }\n\n int currentPeak = 0;\n while (i < n && ratings[i] > ratings[i - 1]) {\n currentPeak++;\n totalCandies += currentPeak;\n i++;\n }\n\n if (i == n) {\n return totalCandies;\n }\n\n int currentValley = 0;\n while (i < n && ratings[i] < ratings[i - 1]) {\n currentValley++;\n totalCandies += currentValley;\n i++;\n }\n\n totalCandies -= min(currentPeak, currentValley);\n }\n\n return totalCandies; \n }\n};\n``` | 32 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Simple, extremely readable O(n) time O(1) space | candy | 0 | 1 | # Intuition\nSee Editorial for intuition regarding slope approach (Approach 4: Single Pass Approach with Constant Space). \nSee section below code for notes on my approach.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n def count(n):\n return(n*(n+1))//2\n children = len(ratings)\n candies, i = 0, 1\n while i < children:\n inc = dec = 0\n while i < children and ratings[i] > ratings[i-1]:\n inc += 1\n i += 1\n while i < children and ratings[i] < ratings[i-1]:\n dec += 1\n i += 1\n if inc or dec:\n candies += count(inc-1) + max(inc,dec) + count(dec-1)\n continue\n i += 1\n return candies + children\n```\n\n# Approach\nFor a given pass of the outer while loop, we count the number of children in an increasing ratings slope then the following number of children in a decreasing ratings slope. \nFor the increasing and decreasing sequences we count the candies for each using Gauss\' formula\n`(n*(n+1))/2` with `n = length of the sequnce - 1` to leave out the peak. We handle the peak separately since it can be part of both the increasing and decreasing slope and should only be counted once based on which sequence is longer `max(inc,dec)`.\n\nOne simplification made in this solution is to not give every child a min of 1 candy but instead a min of 0 candies. We calculate the number of candies needed with this modification and then at the end bump the number of candies given to each kid up by one by adding the number of children to the candies required.\nSo for the following ratings:\n`[1, 4, 3, 2, 1]`\nwe actually calculate the following candies (solution does this as it iterates through the ratings)\n`[0, 3, 2, 1, 0]` whose sum is `6`\nand then return `6 + len(ratings) == 6 + 5 == 11`\nwhich is equivalent to\n`sum([1, 4, 3, 2, 1]) == 11`\n\n | 4 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Beginner Friendly || Line By Line Explanation || Easy Candy Solution || Python || Java || Beats 95%+ | candy | 1 | 1 | # Beats \n\n\n# JAVA CODE 1-2ms \n# UPVOTE IF U LIKE !!!\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe main intuition behind this problem is to ensure that children with higher ratings receive more candies than their neighbors, while still giving each child at least one candy. One way to approach this is to scan the ratings array from left to right and then from right to left, adjusting the number of candies given based on the rating comparisons.\n# Approach\n1. Initialize variables:\n\n- 1. "up_count" to count increasing ratings sequences (starts at 1).\n- 2. "down_count" to count decreasing ratings sequences (starts at 0).\n- 3. "candies_given" to keep track of the total number of candies given (starts at 1).\n- 4. "peak" to keep track of the peak of increasing ratings (starts at 0).\n2. Iterate through the ratings list starting from the second element.\n\n- 1. If the current rating is greater than the previous one, it\'s an increasing sequence:\n- - - Increment up_count.\n- - - Reset down_count to 0.\n- - - Increment candies_given by up_count.\n- - - Update peak to the value of up_count (as this is the peak of the current increasing sequence).\n- 2. If the current rating is equal to the previous one, reset counts:\n- - - Reset down_count and peak to 0.\n- - - Reset up_count to 1.\n- - - Increment candies_given by 1 (since they have the same rating, they should have the same number of candies).\n- 3. If the current rating is less than the previous one, it\'s a decreasing sequence:\n- - - Increment down_count.\n- - - Reset up_count to 1.\n- - - Increment candies_given by down_count.\n- - - If the current down_count is greater than or equal to peak, give an extra candy to the child at the peak of the decreasing sequence.\n3. Return candies_given, which represents the minimum number of candies given to satisfy the conditions\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time Complexity: $$O(n)$$ - We iterate through the ratings array twice, once from left to right and once from right to left.\n- Space Complexity: $$O(1)$$ - We use a constant amount of extra space for variables.\n\n\n# Code\n# Python\n```\n# Define a class named Solution.\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n up_count = 1 # Initialize a variable to count increasing ratings sequences.\n down_count = 0 # Initialize a variable to count decreasing ratings sequences.\n candies_given = 1 # Initialize the total count of candies given, starting with one.\n peak = 0 # Initialize a variable to keep track of the peak of increasing ratings.\n\n # Iterate through the ratings list starting from the second element.\n for i in range(1, len(ratings)):\n if ratings[i] > ratings[i - 1]:\n # If the current rating is greater than the previous one, it\'s an increasing sequence.\n up_count += 1\n down_count = 0\n candies_given += up_count # Increment the candy count for the current child.\n peak = up_count # Update the peak for the current increasing sequence.\n elif ratings[i] == ratings[i - 1]:\n # If the current rating is equal to the previous one, reset counts.\n down_count = 0\n peak = 0\n up_count = 1\n candies_given += 1 # Increment the candy count for the current child (since they have the same rating).\n else:\n # If the current rating is less than the previous one, it\'s a decreasing sequence.\n down_count += 1\n up_count = 1\n candies_given += down_count # Increment the candy count for the current child.\n if peak <= down_count:\n candies_given += 1 # Give an extra candy to the child at the peak of the decreasing sequence.\n\n return candies_given # Return the total number of candies given to all children.\n\n \n```\n# JAVA\n```\n// Define a class named Solution.\nclass Solution {\n // Define a method named candy.\n public int candy(int[] ratings) {\n // Check if the ratings array is empty; if so, return 0 candies.\n if (ratings.length == 0)\n return 0;\n \n int n = ratings.length; // Get the number of children.\n int[] candies = new int[n]; // Create an array to store the number of candies for each child.\n\n // Initialize each child with 1 candy (as a baseline).\n for (int i = 0; i < n; i++) {\n candies[i] = 1;\n }\n\n // Pass through the ratings array from left to right and adjust candies as needed.\n for (int i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n candies[i] = 1 + candies[i - 1];\n }\n }\n\n // Pass through the ratings array from right to left to ensure the right neighbors also get appropriate candies.\n for (int i = n - 2; i >= 0; i--) {\n if (ratings[i] > ratings[i + 1] && candies[i] <= candies[i + 1]) {\n candies[i] = 1 + candies[i + 1];\n }\n }\n\n int totalCandies = 0; // Initialize a variable to store the total number of candies given.\n\n // Sum up the candies for all children to get the total count.\n for (int candyCount : candies) {\n totalCandies += candyCount;\n }\n\n return totalCandies; // Return the total number of candies given to all children.\n }\n}\n\n```\n# C++\n```\n// Define a class named Solution.\nclass Solution {\npublic:\n // Define a method named candy.\n int candy(vector<int>& ratings) {\n int n = ratings.size(); // Get the number of children.\n vector<int> left(n, 1), right(n, 1); // Create vectors to store left and right candy counts for each child.\n\n // Calculate the left candies.\n for (int i = 1; i < n; ++i) {\n if (ratings[i] > ratings[i - 1]) {\n left[i] = left[i - 1] + 1;\n }\n }\n\n // Calculate the right candies.\n for (int i = n - 2; i >= 0; --i) {\n if (ratings[i] > ratings[i + 1]) {\n right[i] = right[i + 1] + 1;\n }\n }\n\n int totalCandies = 0; // Initialize a variable to store the total number of candies given.\n\n // Calculate the maximum candies for each child from the left and right counts and sum them up.\n for (int i = 0; i < n; ++i) {\n totalCandies += max(left[i], right[i]);\n }\n\n return totalCandies; // Return the total number of candies given to all children.\n }\n};\n\n``` | 27 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Python | 99.82% | Beginner Friendly | Optimal Solution | candy | 0 | 1 | # Python | 99.82% | Beginner Friendly | Optimal Solution\n```\nclass Solution:\n def candy(self, R):\n n, ans = len(R), [1]*len(R)\n \n for i in range(n-1):\n if R[i] < R[i+1]:\n ans[i+1] = max(1 + ans[i], ans[i+1])\n \n for i in range(n-2, -1, -1):\n if R[i+1] < R[i]:\n ans[i] = max(1 + ans[i+1], ans[i])\n \n return sum(ans)\n``` | 19 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Python simple two-pass: forth and back | candy | 0 | 1 | # Intuition\nSome other solutions are too much complicated, which shouldn\'t be. Just play some cases to get this idea. Please up vote if you agree with this idea and let me see if you like it.\n\nOkay, just saw other friends already got this idea. I did work it out alone since it\'s pretty straightforward. Anyways, I hope my comments here help understanding.\n\n# Approach\nGoing foward to reward higher rating on the right. Going backward for higher rating on left. Generally, there is only one rule:\n- If you see a higher rating on the next child, it deserves one more candies if it didn\'t\n\n# Complexity\n- Time complexity:\n$$O(n)$$ since only two passes on the rating array.\n\n- Space complexity:\n$$O(n)$$ due to the $$give$$ list.\n\n# Code\n```\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n = len(ratings)\n give = [1] * n\n\n for i in range(1, n):\n if ratings[i] > ratings[i-1]:\n give[i] = give[i-1] + 1\n\n for i in range(n-2, -1, -1):\n if ratings[i] > ratings[i+1] and give[i] <= give[i+1]:\n give[i] = give[i+1] + 1\n\n return sum(give)\n``` | 24 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Python Easy Code! Beats 95.82% Runtime and 94.23% Memory! | candy | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI used the approach of once iterating from left to right and then from right to left. Here, we had to consider kids on either sides, hence this was a good technique to achieve O(n).\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo maintain our O(n) complexity target, dynamic programming seems to be a likable option. We initialize our dp array with all 1s as each child has to have atleast one candy. We then iterate and compare with the neighbours and keep adding candies so that a child with higher rating gets more candies than neighbours.\nNote: We have to check whether the high rated child already has more candies, if so then we do not add more. So we have to compare ratings as well as candies at hand before assigning. This is because we need to allot \'minimum\' number of candies.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n = len(ratings)\n dp = [1]*n\n #left to right\n for i in range(1,n):\n if ratings[i]>ratings[i-1] and dp[i]<=dp[i-1]:\n dp[i] = dp[i-1]+1\n #right to left\n for i in range(n-2,-1,-1):\n if ratings[i]>ratings[i+1] and dp[i]<=dp[i+1]:\n dp[i] = dp[i+1]+1\n return sum(dp)\n``` | 6 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Greedy || C++ || Java || Python || Commented Code | candy | 1 | 1 | # Intuition && approach\n<!-- -->\nThe first step is to create a vector of integers called candies with the same size as the ratings array. Each element of candies will store the number of candies that the corresponding child should get. We initialize all elements of candies to 1.\n\nIn the next step, we iterate through the ratings array from left to right. For each child, we check if its rating is higher than the rating of its left neighbor. If so, we update the value of candies[i] to candies[i-1] + 1. This is because a child with a higher rating should get more candies than its neighbor.\n\nWe also iterate through the ratings array from right to left. For each child, we check if its rating is higher than the rating of its right neighbor. If so, we update the value of candies[i] to the maximum of candies[i] and candies[i+1] + 1. This is because a child with a higher rating should never get fewer candies than its neighbor.\n\nFinally, we iterate through the candies array and add up all the elements. This gives us the total number of candies that we need to distribute.\n\n\n\n# Complexity\n- Time complexity: O(n)\nThe time complexity of this solution is O(n), where n is the number of children. This is because we iterate through the ratings array twice.\n- Space complexity:O(n)\nThe space complexity of this solution is O(n), where n is the number of children. This is because we create a vector of size n to store the number of candies for each child.\n\n# Code\n```\nclass Solution {\npublic:\n int candy(vector<int>& ratings) {\n int n = ratings.size();\n vector<int> candies(n, 1);\n\n // Iterate from left to right and update candies[i] if ratings[i] > ratings[i - 1].\n for (int i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1] && candies[i] <= candies[i - 1]) {\n candies[i] = candies[i - 1] + 1;\n }\n }\n\n // Iterate from right to left and update candies[i] to the maximum of candies[i] and candies[i + 1] + 1.\n for (int i = n - 2; i >= 0; i--) {\n if (ratings[i] > ratings[i + 1] && candies[i] <= candies[i + 1]) {\n candies[i] = candies[i + 1] + 1;\n }\n }\n\n // Calculate the total number of candies.\n int total = 0;\n for (int i = 0; i < n; i++) {\n total += candies[i];\n }\n\n return total;\n }\n};\n\n```\n```\n//java code \nclass Solution {\n public int candy(int[] ratings) {\n int n = ratings.length;\n int[] dp = new int[n];\n Arrays.fill(dp, 1);\n\n // Iterate from left to right and update dp[i] if ratings[i] > ratings[i - 1].\n for (int i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n dp[i] = dp[i - 1] + 1;\n }\n }\n\n // Iterate from right to left and update dp[i] to the maximum of dp[i] and dp[i + 1] + 1.\n for (int i = n - 2; i >= 0; i--) {\n if (ratings[i] > ratings[i + 1]) {\n dp[i] = Math.max(dp[i], dp[i + 1] + 1);\n }\n }\n\n // Calculate the total number of candies.\n int total = 0;\n for (int i = 0; i < n; i++) {\n total += dp[i];\n }\n\n return total;\n }\n}\n```\n```\n//python code\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n = len(ratings)\n dp = [1] * n\n\n # Iterate from left to right and update dp[i] if ratings[i] > ratings[i - 1].\n for i in range(1, n):\n if ratings[i] > ratings[i - 1]:\n dp[i] = dp[i - 1] + 1\n\n # Iterate from right to left and update dp[i] to the maximum of dp[i] and dp[i + 1] + 1.\n for i in range(n - 2, -1, -1):\n if ratings[i] > ratings[i + 1]:\n dp[i] = max(dp[i], dp[i + 1] + 1)\n\n # Calculate the total number of candies.\n total = sum(dp)\n\n return total\n```\n\n\n | 5 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
✅ EASY | ✅ [ Python / Java / C++ / JavaScript / C# ] | 🔥100 % | | candy | 1 | 1 | \n```Python []\nclass Solution:\n def candy(self, ratings: List[int]) -> int:\n n = len(ratings)\n if n <= 1:\n return n\n\n nums = [1] * n\n\n # Make sure children with a higher rating get more candy than their left neighbor\n for i in range(1, n):\n if ratings[i] > ratings[i - 1]:\n nums[i] += nums[i - 1]\n\n # Make sure children with a higher rating get more candy than their right neighbor\n for i in range(n - 1, 0, -1):\n if ratings[i - 1] > ratings[i]:\n nums[i - 1] = max(nums[i] + 1, nums[i - 1])\n\n candies = sum(nums)\n\n return candies\n```\n```Java []\nint n = ratings.length;\n if (n <= 1) return n;\n\n int[] nums = new int[n];\n Arrays.fill(nums, 1);\n\n // Make sure children with a higher rating get more candy than their left neighbor\n for (int i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n nums[i] += nums[i - 1];\n }\n }\n\n // Make sure children with a higher rating get more candy than their right neighbor\n for (int i = n - 1; i > 0; i--) {\n if (ratings[i - 1] > ratings[i]) {\n nums[i - 1] = Math.max(nums[i] + 1, nums[i - 1]);\n }\n }\n\n int candies = 0;\n for (int e : nums) {\n candies += e;\n }\n\n return candies;\n```\n```C++ []\nclass Solution {\npublic:\n int candy(vector<int>& ratings) {\n int n = ratings.size();\n if(n <= 1) return n;\n\n vector<int> nums( n , 1);\n // make sure children with a higher rating gets more candy than its left neighbour\n for(int i =1 ; i< n ; i++){\n if(ratings[i] > ratings[i-1]){\n nums[i]+=nums[i-1];\n }\n }\n // make sure children with higher rating get more candy than its right neighbour\n for(int i = n-1 ; i>0 ; i--){\n if(ratings[i-1] > ratings[i]){\n nums[i-1] = max(nums[i]+1 , nums[i-1]);\n }\n }\n\n int candies = 0;\n\n for(auto e : nums) candies+=e;\n\n return candies;\n }\n};\n```\n```JavaScript []\nconst n = ratings.length;\n if (n <= 1) return n;\n\n const nums = new Array(n).fill(1);\n\n // Make sure children with a higher rating get more candy than their left neighbor\n for (let i = 1; i < n; i++) {\n if (ratings[i] > ratings[i - 1]) {\n nums[i] += nums[i - 1];\n }\n }\n\n // Make sure children with higher rating get more candy than their right neighbor\n for (let i = n - 1; i > 0; i--) {\n if (ratings[i - 1] > ratings[i]) {\n nums[i - 1] = Math.max(nums[i] + 1, nums[i - 1]);\n }\n }\n\n let candies = 0;\n\n for (const e of nums) {\n candies += e;\n }\n\n return candies;\n```\n```C# []\n int n = ratings.Length;\n if (n <= 1) return n;\n\n int[] nums = new int[n];\n for (int i = 0; i < n; i++)\n {\n nums[i] = 1;\n }\n\n // Make sure children with a higher rating get more candy than their left neighbor\n for (int i = 1; i < n; i++)\n {\n if (ratings[i] > ratings[i - 1])\n {\n nums[i] += nums[i - 1];\n }\n }\n\n // Make sure children with higher rating get more candy than their right neighbor\n for (int i = n - 1; i > 0; i--)\n {\n if (ratings[i - 1] > ratings[i])\n {\n nums[i - 1] = Math.Max(nums[i] + 1, nums[i - 1]);\n }\n }\n\n int candies = 0;\n foreach (int e in nums)\n {\n candies += e;\n }\n\n return candies;\n```\n | 4 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Detailed Explanation | candy | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven, the person with highest rating compared to neighbours should have more candies.There are obviously two possiblities\n1.The rating is more than the rating of the left person (if present)the candies will be one more than the candies of left person.\n2.The rating is more than the rating of the right person (if present)the candies will be one more than the candies of right person.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo,for the two possiblities we calculate the L,R \nL ----> Possiblity-1\nR ----> Possiblity-2\nOur answer is the sum of maximum of L[i],R[i].(0 <= i < r)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def candy(self, r: List[int]) -> int:\n L,R=[1 for _ in range (len(r))],[1 for _ in range (len(r))]\n\n curr=r[0]\n\n for i in range (len(r)):\n if i==0: continue\n if r[i] > curr :\n L[i]=L[i-1]+1\n curr = r[i]\n else: curr=r[i]\n \n curr=r[-1]\n\n for i in range (len(r)):\n if i==0 : continue\n if r[len(r)-1-i] > curr:\n R[len(r)-1-i]=R[len(r)-i]+1\n curr = r[len(r)-1-i]\n else: curr=r[len(r)-1-i]\n \n ans=0\n\n for i in range (len(r)):\n ans +=max(L[i],R[i])\n \n return ans\n``` | 1 | There are `n` children standing in a line. Each child is assigned a rating value given in the integer array `ratings`.
You are giving candies to these children subjected to the following requirements:
* Each child must have at least one candy.
* Children with a higher rating get more candies than their neighbors.
Return _the minimum number of candies you need to have to distribute the candies to the children_.
**Example 1:**
**Input:** ratings = \[1,0,2\]
**Output:** 5
**Explanation:** You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
**Example 2:**
**Input:** ratings = \[1,2,2\]
**Output:** 4
**Explanation:** You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
**Constraints:**
* `n == ratings.length`
* `1 <= n <= 2 * 104`
* `0 <= ratings[i] <= 2 * 104` | null |
Think it through || Time: O(n) Space: O(1) || Python Go Explained | single-number | 0 | 1 | \n### Edge Cases:\n1. No element appears twice; it is a constraint so not possible\n2. Single length array; return the only element already present in the array\n3. len(nums) > 1; find the single element that does not appear twice\n\n### Approaches:\n1. **Brute Force**\nIntuition:\nIterate through every element in the nums and check if any of the element does not appear twice, in that case return the element.\n*Time: O(n^2)\nSpace: O(1)*\n\n2. **Use Sorting**\nIntuition:\nIf the elements of the nums array are sorted/when we sort it, we can compare the neighbours to find the single element. It is already mentioned that all other elements appear twice except one.\n*Time: O(nlogn) for sorting then O(n) to check neighbouring elements\nSpace: O(1)*\n\n3. **Use Hashing/Set**\nIntuition:\ni) As we iterate through the nums array we store the elements encountered and check if we find them again while iteration continues. While checking if we find them again, we maintain a single_element object/variable which stores that single element, eventually returning the single_element.\nii) The other way is to maintain a num_frequency hashmap/dictionary and iterate over it to find which has exactly 1 frequency and return that key/num.\n*Time: O(n) for iterating over the nums array\nSpace: O(n) for hashing*\n\n4. **Use Xor/Bit Manipulation**\nIntuition:\nXor of any two num gives the difference of bit as 1 and same bit as 0.\nThus, using this we get 1 ^ 1 == 0 because the same numbers have same bits.\nSo, we will always get the single element because all the same ones will evaluate to 0 and 0^single_number = single_number.\n*Time: O(n)\nSpace: O(1)*\n\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n xor = 0\n for num in nums:\n xor ^= num\n \n return xor\n\n```\n\nIn Golang:\n\n```\nfunc singleNumber(nums []int) int {\n result := 0\n for _, num := range nums{\n result ^= num\n }\n\n return result\n}\n```\n\n**Updated**:\n*You can find more of my solutions like this in discuss forums by searching through either **satyamsinha93** or **Think it through**.*\n\nThanks for all the love and upvoting! | 723 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
✔️ [Python3] ONE-LINER ヾ(*⌒ヮ⌒*)ゞ, Explained | single-number | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nWe use the nice property of XOR operation which is if you XOR same numbers it will return zero. Since the `nums` contains just one non-repeating number, we can just XOR all numbers together and the final result will be our answer.\n\n*For reference about `reduce`: https://thepythonguru.com/python-builtin-functions/reduce/*\n\n```\ndef singleNumber(self, nums: List[int]) -> int:\n\treturn reduce(lambda total, el: total ^ el, nums)\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 193 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Solution | single-number | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int singleNumber(vector<int>& nums) {\n \n int ans = nums[0];\n\n for(int i = 1 ; i < nums.size() ; i++){\n ans = ans ^ nums[i];\n }\n\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n return functools.reduce(lambda x, y: x ^ y, nums, 0)\n```\n\n```Java []\nclass Solution {\n public int singleNumber(int[] nums) {\n int result=0;\n for(int i=0; i<nums.length; i++) {\n result = result^nums[i];\n }\n return result;\n }\n}\n```\n | 474 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
beats everyone | single-number | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n dic = {}\n\n for i in range(len(nums)):\n if nums[i] not in dic:\n dic[nums[i]] = 1\n else:\n dic.pop(nums[i])\n\n return int(*dic)\n``` | 1 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Python code with Time Complexity: T(O(N)) and space Complexity: T(O(M)) | single-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n\n\n hash = {}\n\n for i in nums:\n hash[i] = hash.get(i,0)+1\n \n for j in hash:\n if hash[j] == 1:\n return j\n\n \n \n``` | 1 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Python3 | Using Dictionary | single-number | 0 | 1 | \n# Approach\n- Create dict\n- Iterate through \'nums\' list\n- If an element is not in our dict -> add new key in dict\n- Else (Element is duplicated) -> `pop` it from dict\n- Unpack dict using `*` and return it\n\n# Complexity\n- Time complexity: The time complexity of the provided code is O(n)\n Beats 60.16% of users with Python3\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n dict = {}\n for i in nums:\n if i not in dict:\n dict[i] = 1\n else:\n dict.pop(i)\n return int(*dict)\n``` | 1 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Most Fastest Python Solution | single-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSolve the Problem easily and fastly\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- XORing a number with itself gives 0.\n- XORing a number with 0 gives the number itself.\n\n\nBy XORing all the numbers in the list, duplicates cancel each other out, and the single number remains. This approach is more efficient than using a dictionary to count occurrences.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n result=0\n for i in nums:\n result^=i\n return result\n \n \n \n``` | 2 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Very Easy || 0 ms ||100%|| Fully Explained (Java, C++, Python, JS, C, Python3) | single-number | 1 | 1 | **Problem:**\nGiven a non-empty array of integers nums, every element appears twice except for one. Find that single one.\n**Input:** nums = [ 4, 1, 2, 1, 2 ]\n**Output:** 4\n**Explanation:** 1\u2019s and 2\u2019s appear twice, only 4 appears exactly once. So the answer is 4.\n**Concept of XOR:**\nXOR of zero and some bit returns that bit i.e. x^0 = x...\nXOR of two same bits returns 0 i.e. x^x = 0...\nAnd, x^y^x = (x^x)^y = 0^y = y...\nXOR all bits together to find the unique number.\n\n\n# **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Single Number.\nMemory Usage: 46.2 MB, less than 89.95% of Java online submissions for Single Number.\n```\nclass Solution {\n public int singleNumber(int[] nums) {\n // Initialize the unique number...\n int uniqNum = 0;\n // TRaverse all elements through the loop...\n for (int idx : nums) {\n // Concept of XOR...\n uniqNum ^= idx;\n } return uniqNum; // Return the unique number...\n }\n}\n```\n\n# **C++ Solution:**\nRuntime: 6 ms, faster than 98.77% of C++ online submissions for Single Number.\nMemory Usage: 11.8 MB, less than 98.93% of C++ online submissions for Single Number.\n```\nclass Solution {\npublic:\n int singleNumber(vector<int>& nums) {\n // Initialize the unique number...\n int uniqNum = 0;\n // TRaverse all elements through the loop...\n for (int idx : nums) {\n // Concept of XOR...\n uniqNum ^= idx;\n } return uniqNum; // Return the unique number...\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def singleNumber(self, nums):\n # Initialize the unique number...\n uniqNum = 0;\n # TRaverse all elements through the loop...\n for idx in nums:\n # Concept of XOR...\n uniqNum ^= idx;\n return uniqNum; # Return the unique number...\n```\n \n# **JavaScript Solution:**\n```\nvar singleNumber = function(nums) {\n // Initialize the unique number...\n let uniqNum = 0;\n // TRaverse all elements through the loop...\n for (let idx = 0; idx < nums.length; idx++) {\n // Concept of XOR...\n uniqNum = uniqNum ^ nums[idx];\n } return uniqNum; // Return the unique number...\n};\n```\n\n# **C Language:**\n```\nint singleNumber(int* nums, int numsSize){\n // Initialize the unique number...\n int uniqNum = 0;\n // TRaverse all elements through the loop...\n for (int idx = 0; idx < numsSize; idx++) {\n // Concept of XOR...\n uniqNum = uniqNum ^ nums[idx];\n } return uniqNum; // Return the unique number...\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n # Initialize the unique number...\n uniqNum = 0;\n # TRaverse all elements through the loop...\n for idx in nums:\n # Concept of XOR...\n uniqNum ^= idx;\n return uniqNum; # Return the unique number...\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 150 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Single-number | single-number | 0 | 1 | # Intuition\n<!-- The code aims to find and return the single number that appears only once in a list of numbers.\n -->\n\n# Approach\n<!-- 1.Utilize a dictionary (mydict) to count the occurrences of each number in the given list.\n2. Iterate through the dictionary and return the number with an occurrence of 1. -->\n\n# Complexity\n- Time complexity:\n<!-- Time Complexity: O(n) where n is the length of the input list nums. This is because we iterate through the list once. -->\n\n- Space complexity:\n<!-- Space Complexity: O(n) where n is the number of unique elements in nums stored in the dictionary mydict. -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n mydict = collections.Counter(nums)\n for i in mydict:\n if mydict[i]==1:\n return i\n``` | 1 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Single Number-136(Solution) | single-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry to solve first itself.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. nums list converted into set.\n2. Find the ocurrance of each element using the count() function.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n \n lst_num = list(set(nums))\n n = len(lst_num)\n \n for i in range (n):\n occurance = nums.count(lst_num[i])\n if occurance == 1:\n return lst_num[i]\n \n``` | 2 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Easy XOR soultion | single-number | 1 | 1 | # Intuition\nI solved it via XOR bit operator\n\n# Approach\nFor instance, I have an array [12, 1, 13, 1, 12]\n1010\n0001\n\n1011\n1011\n\n0000\n0001\n\n0001\n1010\n\n1011 (bin) = 13 (dec)\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int singleNumber(int[] nums) {\n int mask = 0;\n\n for(int num : nums) {\n mask ^= num;\n }\n\n return mask;\n }\n}\n``` | 11 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Python shortest 1-liner. Functional programming. | single-number | 0 | 1 | # Approach\n1. Xor of a number with itself gives zero, i.e `a ^ a = 0`\n\n2. Xor of a number with zero gives back the number as is, i.e `a ^ 0 = a`\n\n3. Using the above two properties, xor all the numbers in `nums`.\n The numbers which appear twice will be zeroed, leaving the single occuring number at the end.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is the length of nums`.\n\n# Code\n1-liner:\n```python\nclass Solution:\n def singleNumber(self, nums: list[int]) -> int:\n return reduce(xor, nums)\n\n\n```\n\nShortest 1-liner using partial function application (currying):\n```python\nclass Solution: singleNumber = partial(reduce, xor)\n\n\n``` | 4 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Beats 100% | Easy To Understand | 0ms 🔥🚀 | single-number | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nXor of any number with itself is 1, so the duplicate numbers will become 1 and we will get the unique number.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int singleNumber(vector<int>& nums) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n\n int ans = 0;\n for(auto x : nums)\n ans = ans ^ x;\n\n return ans;\n }\n};\n``` | 3 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
Python 3 diff approach easy to understand 3 line code | single-number | 0 | 1 | **Plz Upvote ..if you got help from this.**\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n<!-- SIMPLE APPROACH 90 %BEATS -->\n<!-- ===================================================== -->\n for i in range(len(nums)):\n if(nums.count(nums[i])==1):\n return nums[i]\n \n\n\n<!-- SET APPROACH 90 BEAT IN RUN TIME -->\n<!-- ==================================================== -->\n s = set()\n for ele in nums:\n if ele in s:\n s.remove(ele)\n else:\n s.add(ele)\n \n for ans in s:\n return ans\n\n\n\n<!-- DICTONARY APPROACH 90BEAT IN MEMORY -->\n<!-- ===================================================== -->\n d = {}\n for ele in nums:\n if ele in d:\n d[ele] = False\n else:\n d[ele] = True\n \n \n for key in d:\n if d[key]:\n return key\n\n\n``` | 8 | Given a **non-empty** array of integers `nums`, every element appears _twice_ except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,1\]
**Output:** 1
**Example 2:**
**Input:** nums = \[4,1,2,1,2\]
**Output:** 4
**Example 3:**
**Input:** nums = \[1\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104`
* Each element in the array appears twice except for one element which appears only once. | null |
✅Bit Manipulation🔥 || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | single-number-ii | 1 | 1 | # Approach 1: Brute Force\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int singleNumber(vector<int>& nums) {\n unordered_map<int, int> m;\n \n for(auto x: nums){\n m[x]++;\n }\n\n for(auto x: m){\n if(x.second == 1){\n return x.first;\n }\n }\n \n return -1;\n }\n};\n```\n```Java []\nclass Solution {\n public int singleNumber(int[] nums) {\n Map<Integer, Integer> map = new HashMap<>();\n \n for (int x : nums) {\n map.put(x, map.getOrDefault(x, 0) + 1);\n }\n\n for (Map.Entry<Integer, Integer> entry : map.entrySet()) {\n if (entry.getValue() == 1) {\n return entry.getKey();\n }\n }\n \n return -1;\n }\n}\n```\n```Python3 []\nclass Solution:\n def singleNumber(self, nums):\n count = defaultdict(int)\n \n for x in nums:\n count[x] += 1\n\n for x, freq in count.items():\n if freq == 1:\n return x\n \n return -1\n```\n\n# Approach 2: Bit Manipulation\n# Explanation:\n\n1. Initialize the variable `ans` to 0. This variable will store the resulting single number.\n\n2. Iterate from `i = 0` to `i = 31`. This loop considers each bit position from the least significant bit (LSB) to the most significant bit (MSB) of a 32-bit integer.\n\n3. Inside the loop, initialize a variable `sum` to 0. This variable will keep track of the number of 1s at the current bit position (`i`) for all the numbers in the input array.\n\n4. Iterate through each number `num` in the input array:\n - Right-shift `num` by `i` positions: `num >> i`. This operation moves the bit at position `i` to the least significant bit position.\n - Perform a bitwise AND with 1: `(num >> i) & 1`. This extracts the value of the bit at position `i` from `num`. If it is 1, the result will be 1; otherwise, it will be 0.\n - Add the result of `(num >> i) & 1` to `sum`. This counts the number of 1s at bit position `i` for all the numbers in the array.\n\n5. Take the modulo of `sum` by 3: `sum %= 3`. This step is performed to handle the numbers that appear three times. If `sum` is divisible by 3, it means the bit at position `i` has a balanced number of 1s. Otherwise, it is an unbalanced line.\n\n6. Left-shift the value of `sum` by `i` positions: `sum << i`. This step creates a bitmask `pos` where only the bit at position `i` is set to the value of `sum`. This bitmask identifies the position of the unbalanced line.\n\n7. Use the bitwise OR operation with `ans` and `pos`: `ans |= pos`. This sets the corresponding bit in `ans` to 1 if the bit at position `i` is part of an unbalanced line.\n\n8. After the loop completes, the value stored in `ans` represents the single number that appears only once in the array.\n\nThe logical thinking behind this approach is to count the number of 1s at each bit position for all the numbers. Since each number appears three times except for the single number, the sum of 1s at each bit position should be divisible by 3 for a balanced line. Any number of 1s that is not divisible by 3 indicates an unbalanced line, which means the single number contributes to that particular bit position.\n\nBy masking the positions of the unbalanced lines with 1s in `ans`, we effectively isolate the bits that are part of the single number. Finally, the resulting value in `ans` represents the binary representation of the single number.\n\nUsing the provided example: [1, 1, 1, 2, 2, 2, 5]\n- At the LSB (i = 0), the sum of the number of 1s is 3 (balanced line).\n- At the second bit (i = 1), the sum of the number of 1s is 4 (unbalanced line, not divisible by 3).\n- At the third bit (i = 2), the sum of the number of 1s is 2 (unbalanced line, not divisible by 3).\n- At the fourth bit\n\n (i = 3), the sum of the number of 1s is 1 (balanced line).\n\nThus, the resulting binary representation is \'0101\', which corresponds to the decimal value 5, and that is the single number we are searching for.\n\nThis approach effectively identifies the unbalanced lines and constructs the single number by setting the corresponding bit positions in `ans`.\n\n# Code\n```C++ []\nclass Solution {\n public:\n int singleNumber(vector<int>& nums) {\n int ans = 0;\n\n for (int i = 0; i < 32; ++i) {\n int sum = 0;\n for (const int num : nums)\n sum += num >> i & 1;\n sum %= 3;\n ans |= sum << i;\n }\n\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int singleNumber(int[] nums) {\n int ans = 0;\n\n for (int i = 0; i < 32; ++i) {\n int sum = 0;\n for (final int num : nums)\n sum += num >> i & 1;\n sum %= 3;\n ans |= sum << i;\n }\n\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def singleNumber(self, nums):\n ans = 0\n\n for i in range(32):\n bit_sum = 0\n for num in nums:\n # Convert the number to two\'s complement representation to handle large test case\n if num < 0:\n num = num & (2**32-1)\n bit_sum += (num >> i) & 1\n bit_sum %= 3\n ans |= bit_sum << i\n\n # Convert the result back to two\'s complement representation if it\'s negative to handle large test case\n if ans >= 2**31:\n ans -= 2**32\n\n return ans\n\n```\n\n# Approach 3: Magic:\n# Explanation:\n\n1. Initialize two variables, `ones` and `twos`, to keep track of the count of each bit position.\n - `ones`: Tracks the bits that have appeared once.\n - `twos`: Tracks the bits that have appeared twice.\n\n2. Iterate through the array of numbers.\n - For each number `i` in the array:\n - Update `ones` and `twos`:\n\n - Let\'s analyze each step of the update process:\n\n a. `ones = (ones ^ i) & (~twos);`:\n - `ones ^ i` XORs the current number `i` with the previous value of `ones`. This operation toggles the bits that have appeared an odd number of times, keeping the bits that have appeared twice unchanged.\n - `(~twos)` negates the bits in `twos`, effectively removing the bits that have appeared twice from consideration.\n - The `&` operation ensures that only the bits that have appeared once (after XOR) and not twice (after negating `twos`) are retained.\n\n b. `twos = (twos ^ i) & (~ones);`:\n - `twos ^ i` XORs the current number `i` with the previous value of `twos`. This operation toggles the bits that have appeared an even number of times, effectively removing the bits that have appeared twice.\n - `(~ones)` negates the bits in `ones`, effectively removing the bits that have appeared once from consideration.\n - The `&` operation ensures that only the bits that have appeared twice (after XOR) and not once (after negating `ones`) are retained.\n\n3. After iterating through all the numbers, the value stored in `ones` will represent the single number that appears only once in the array.\n\nLet\'s understand why this approach works:\n\n- The key idea is to use bitwise operations to keep track of the count of each bit position. By doing so, we can identify the bits that have appeared once, twice, or three times.\n- When a bit appears for the first time (`ones` is 0 and the bit is toggled), it is stored in `ones`.\n- When a bit appears for the second time (`ones` is 1 and the bit is toggled), it is removed from `ones` and stored in `twos`.\n- When a bit appears for the third time (`ones` is 0 and the bit is toggled), it is removed from both `ones` and `twos`.\n- By the end of the iteration, the bits that remain in `ones` represent the bits of the single number that appeared only once, while the bits in `twos` represent bits that appeared three times (which is not possible).\n\nIn summary, the algorithm uses bit manipulation to efficiently keep track of the counts of each bit position. By utilizing XOR and AND operations, it can identify the bits of the single number that appears only once in the array while ignoring the bits that appear multiple times.\n\n# Code\n```C++ []\nclass Solution {\n public:\n int singleNumber(vector<int>& nums) {\n int ones = 0;\n int twos = 0;\n\n for (const int num : nums) {\n ones ^= (num & ~twos);\n twos ^= (num & ~ones);\n }\n\n return ones;\n }\n};\n```\n```Java []\nclass Solution {\n public int singleNumber(int[] nums) {\n int ones = 0;\n int twos = 0;\n\n for (final int num : nums) {\n ones ^= (num & ~twos);\n twos ^= (num & ~ones);\n }\n\n return ones;\n }\n}\n```\n```Python3 []\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n ones = 0\n twos = 0\n\n for num in nums:\n ones ^= (num & ~twos)\n twos ^= (num & ~ones)\n\n return ones\n\n```\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 538 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Time complexity O(n) and space complexity O(n) | single-number-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n hash_map = {num: 0 for num in nums}\n for num in nums:\n hash_map[num] += 1\n for key, value in hash_map.items():\n if value == 1:\n return key\n\n \n\n``` | 1 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Python Simple Counter Solution | Linear runtime | single-number-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n / 3)\n\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def singleNumber(self, nums: list[int]) -> int:\n occurrences = Counter(nums)\n for n in nums:\n if occurrences[n] == 1:\n return n\n``` | 1 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Python very easy Solution || Use Hashmap | single-number-ii | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n dic=dict()\n for i in nums:\n if i in dic:\n dic[i]+=1\n if dic[i]==3:\n dic.pop(i)\n else:\n dic[i]=1\n for i in dic:\n return i\n``` | 1 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Image Explanation🏆- [Bit Manipulation - 4 Methods] - C++/Java/Python | single-number-ii | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Single Number II` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n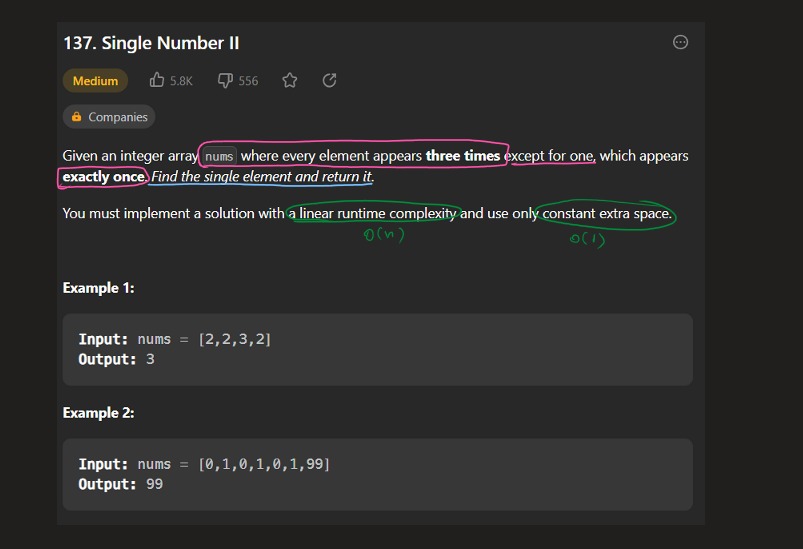\n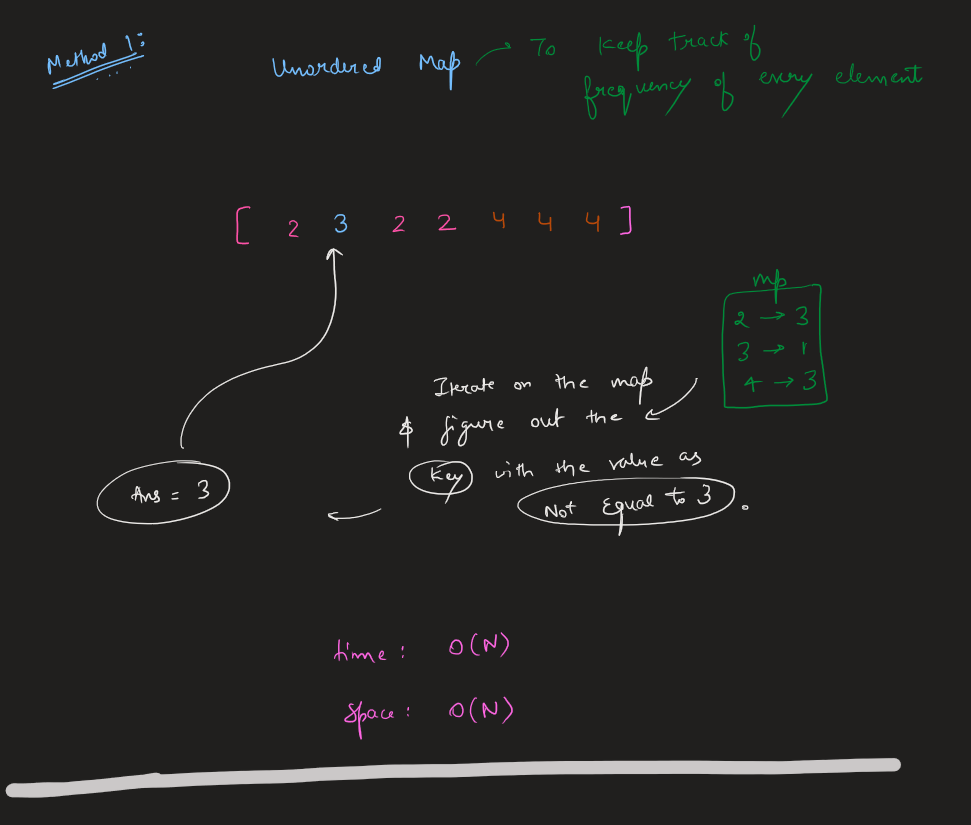\n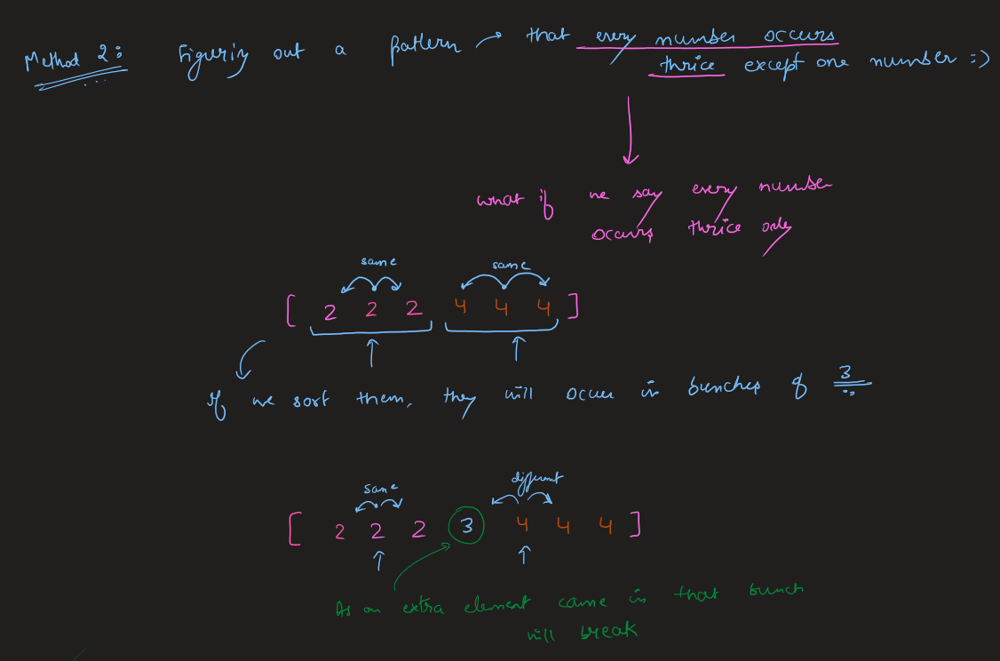\n\n\n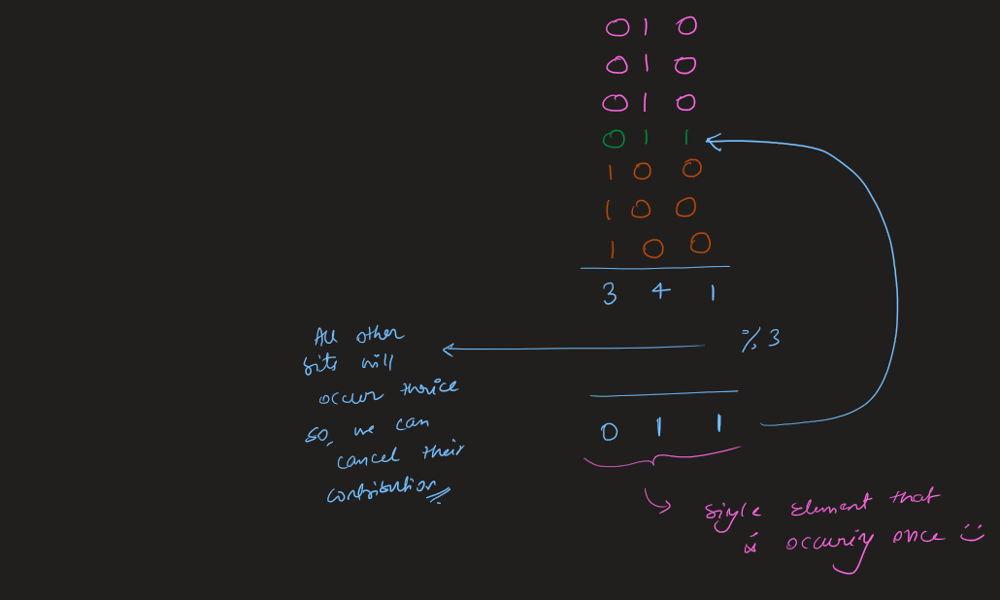\n\n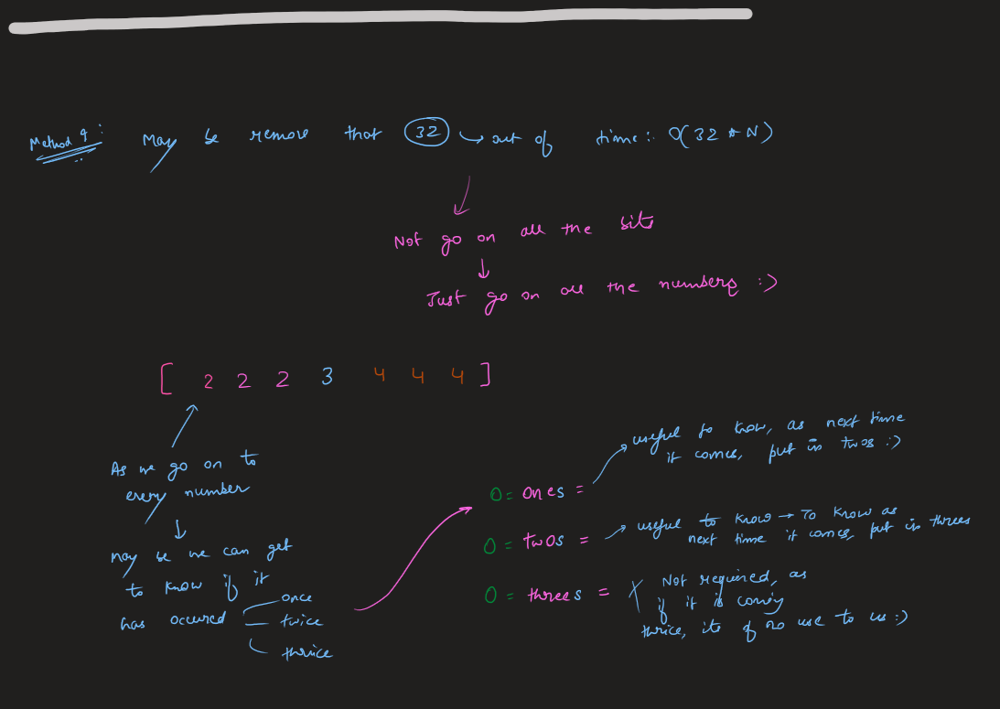\n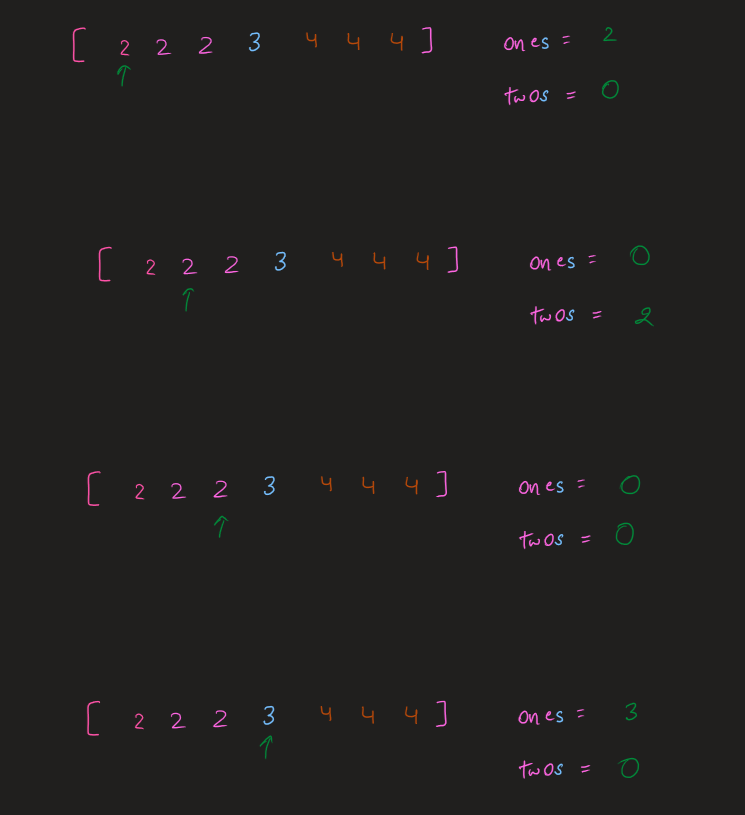\n\n\n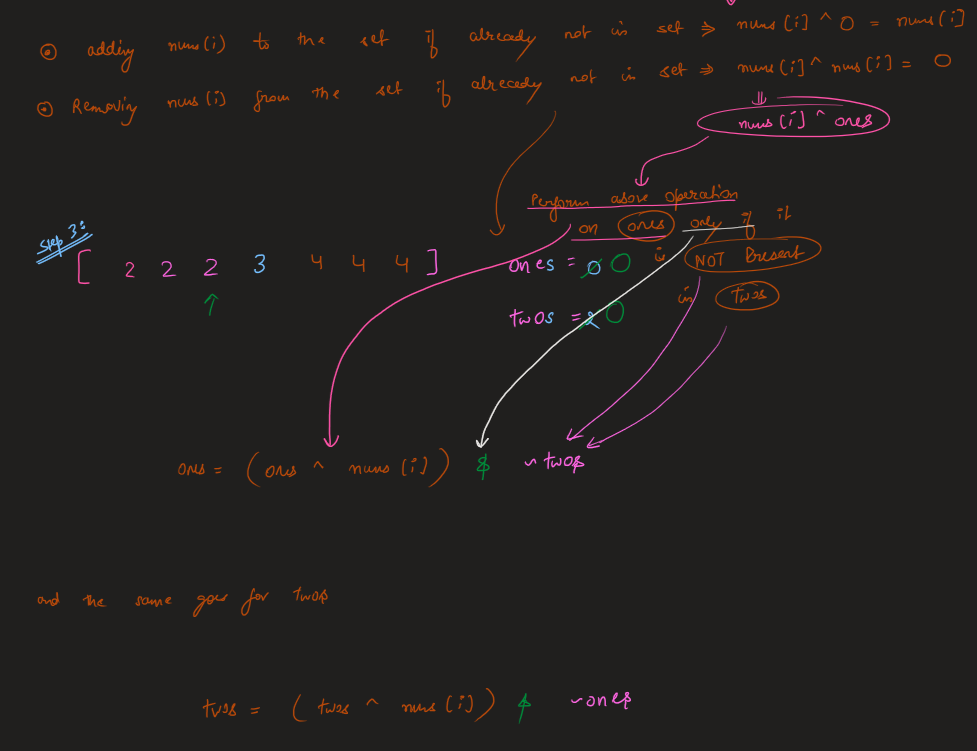\n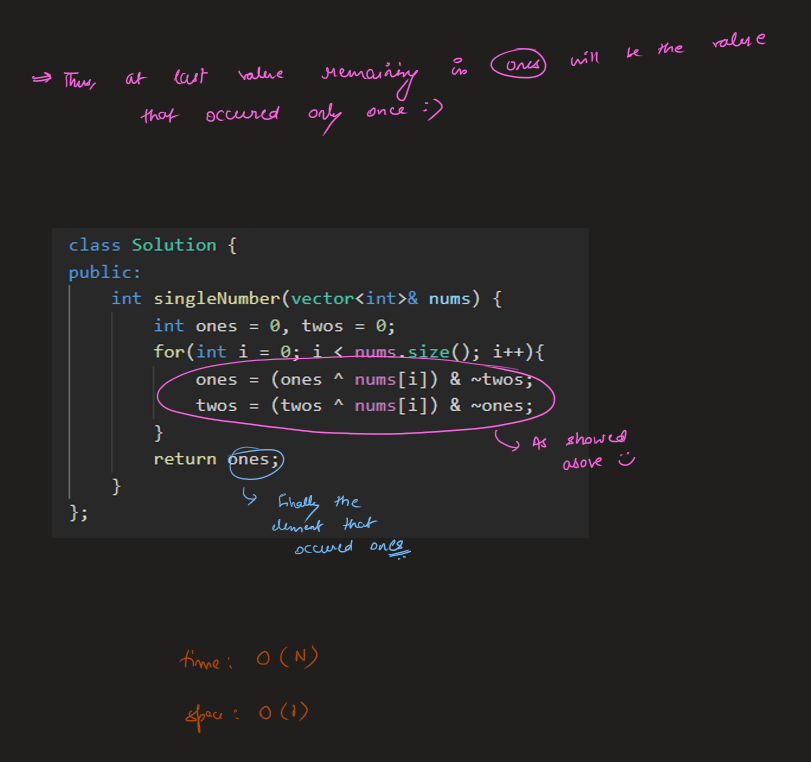\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int singleNumber(vector<int>& nums) {\n int ones = 0, twos = 0;\n for(int i = 0; i < nums.size(); i++){\n ones = (ones ^ nums[i]) & ~twos;\n twos = (twos ^ nums[i]) & ~ones;\n }\n return ones;\n }\n};\n```\n```Java []\nclass Solution {\n public int singleNumber(int[] nums) {\n int ones = 0, twos = 0;\n for (int i = 0; i < nums.length; i++) {\n ones = (ones ^ nums[i]) & ~twos;\n twos = (twos ^ nums[i]) & ~ones;\n }\n return ones;\n }\n}\n```\n```Python []\nclass Solution:\n def singleNumber(self, nums):\n ones = 0\n twos = 0\n for num in nums:\n ones = (ones ^ num) & ~twos\n twos = (twos ^ num) & ~ones\n return ones\n``` | 109 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
ONE LINER EASIEST PYTHON SOLUTION | single-number-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can see that there is only one integer that occurs one time.\n\nWe can take the sum of all the integers as if they all appeared thrice and later subtract the sum of given list.\n\nWe may get the difference as a result which is twice the number which appears only once...\n\nITS PRETTY SIMPLE MATHS......\n\n# Complexity\n- Time complexity: O(n) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n ans = (sum(set(nums))*3) - (sum(nums))\n return ans//2\n``` | 1 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Python short and clean. Functional programming. | single-number-ii | 0 | 1 | <!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is length of nums`.\n\n# Code\n```python\nclass Solution:\n def singleNumber(self, nums: list[int]) -> int:\n def counts(a: tuple[int, int], num: int) -> tuple[int, int]:\n ones, twos = a\n ones = (ones ^ num) & ~twos\n twos = (twos ^ num) & ~ones\n return ones, twos\n \n return reduce(counts, nums, (0, 0))[0]\n\n\n``` | 1 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Single line mathematical solution, beats 100% | single-number-ii | 0 | 1 | # Approach\n- Find all the distinct numbers (set), multiply by 3 (because all the other number repeats 3 time), so the sum of that set will have total of original nums + 2*(number which is repeating only once)\n- Now substract the sum of original list of nums, which gives total as 2*(number which repeats only once)\n\n(Note: This solution works for this particular problem but don\'t use where it says to use constant space as sets space complexity in worst case is $$O(n)$$, Thank you)\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n return ((3*sum((set(nums))))-sum(nums))//2\n``` | 16 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
Bitwise Operations | Python / JS Solution | single-number-ii | 0 | 1 | Hello **Tenno leetcoders**, \n\nWe are given an integer array nums where every element appears three times except for one, which appears exactly once. Find the single element and return a solution with a linear runtime complexity and use only constant extra space.\n\n### Explanation\n\nThe problem requires finding the single element that appears exactly once in the nums array, where all other elements appear three times.\n\nSince we need constant space and linear time, we can rely on bitwise XOR `^`, AND `&`, OR `|`, NOT `~`\n\n#### XOR operation\n\n- The bitwise XOR operation returns 1 if the corresponding bits are different and 0 if they are the same\n\n- The bitwise XOR operation will be used to update our ones variable as it helps keep track of the bits that have appeared once\n\n- When we perform `ones ^= num`, the XOR operation toggles the bits in `ones` that are in `num` to ensure that the ones variable stores the bits that have appeared only once across the numbers encountered so far \n\n\n#### AND operation\n\n- The bitwise AND operation returns 1 only if both corresponding bits are 1; otherwise, it returns 0.\n\n- The bitwise AND operation is used to update the twos variable by performing `twos |= ones & num`. This represents the operation which adds the bits that are set in both `ones` and `num` to `twos` to ensure that twos keep track of the bits that have appeared twice\n\n- Also the AND operation is used to clear the bits that have appeared three times in both `ones` and `twos`. By performing,\n`ones &= ~threes` and `twos &= ~threes`, it clears the bits that are set in `threes` from both `ones` and `twos`\n\n\n#### OR operation\n\n- The bitwise OR operation returns 1 if at least one of the corresponding bits is 1; otherwise, it returns 0.\n\n- the bitwise OR operation is used to update the twos variable. By perform `twos |= ones & num`, the operation combines the bits that are set in both `ones` and `num`, adding them to `twos` to ensure that twos accumulates the bits that have appeared twice\n\n\n#### NOT operation\n\n- The bitwise NOT operation flips the bits, changing 0s to 1s and 1s to 0s.\n\n- The bitwise NOT operation is used to clear the bits that have appeared three times.\n\n- Our threes temporary variable is used to clear the bits that have appeared three times between `ones` and `twos` using the AND operator. These two operations find the bits that are set in both `ones` and `twos`, indicating the bits that have appeared three times\n\n- By performing `ones &= ~threes` and `twos &= ~threes`, the NOT operation is applied to `threes` to help clear the bits that are set in `threes` from both `ones` and `twos`, which help remove the bits that have appeared three times\n\n\n#### Solution\n\n- Initialize two variables, ones and twos and set it to `0`. This will help represent and keep track of bits that have appeared once or twice\n\n- Iterate through each number `num` in the nums array.\n\n - Update twos variable by performing a bitwise OR operation between the twos and the bits that are set in both ones and the current number as it will help accumulate the bits that have appeared twice\n \n - Update ones variable by performing a bitwise XOR operations between ones and the current number as it toggles the bits in ones that are set in num to help keep track of bits that have appeared once\n \n \n - At this point, both ones and twos may contain some bits that have appeared three times. We need to clear these bits.\n \n \n - To help clear the bits which appeared three times, we use a temporary variable threes and set it as bitwise AND of ones and twos as it helps identifies the bits that are set in both ones and twos, indicating the bits have appeared three times\n \n \n - To clear the bits, we perform bitwise NOT operation on threes and also apply bitwise AND operation with ones and two to help clear the bits that have appeared three times. \n \n\n- At the end of the loops, `ones` will contain the bits of the single element that appeared exactly ones\n\n\n\n# Code\n\n**Python**\n```\n def singleNumber(self, nums: List[int]) -> int:\n\n ones = 0 \n twos = 0 \n\n for num in nums:\n\n twos |= ones & num\n ones ^= num\n \n threes = ones & twos\n ones &= ~threes\n twos &= ~threes\n\n return ones\n```\n\n\n**JavaScript**\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar singleNumber = function(nums) {\n\n let ones = 0\n let twos = 0\n\n for(let num of nums){\n twos |= ones & num\n ones ^= num\n\n threes = ones & twos\n ones &= ~threes\n twos &= ~threes\n }\n return ones\n};\n```\n### Time Complexity: O(n)\n### Space Complexity: O(1)\n\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n | 9 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
PYTHON EASY SOLUTION || 100% | single-number-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNumber(self, nums: List[int]) -> int:\n for i in set(nums):\n if nums.count(i)==1:\n return i\n``` | 1 | Given an integer array `nums` where every element appears **three times** except for one, which appears **exactly once**. _Find the single element and return it_.
You must implement a solution with a linear runtime complexity and use only constant extra space.
**Example 1:**
**Input:** nums = \[2,2,3,2\]
**Output:** 3
**Example 2:**
**Input:** nums = \[0,1,0,1,0,1,99\]
**Output:** 99
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-231 <= nums[i] <= 231 - 1`
* Each element in `nums` appears exactly **three times** except for one element which appears **once**. | null |
✅ 97.92% Hash Table & Linked List | copy-list-with-random-pointer | 1 | 1 | # Interview Guide - Copying a Linked List with Random Pointers: A Dual-Approach Analysis\n\n## Introduction & Problem Understanding\n\nThe problem at hand involves creating a deep copy of a given singly-linked list where each node has a `next` pointer and an additional `random` pointer. The `random` pointer could point to any node within the list or be `null`. The deep copy should have brand new nodes with the same `next` and `random` pointers as the original list.\n\n### Key Concepts and Constraints\n\n1. **Node Anatomy**: \n Each node in the list has an integer value, a `next` pointer pointing to the subsequent node, and a `random` pointer that could point to any node in the list or be `null`.\n\n2. **Deep Copy**: \n We are required to return a deep copy of the list, meaning that the new list should consist of entirely new nodes that don\'t refer to nodes in the original list.\n\n3. **Memory Efficiency**: \n While one approach uses $$ O(n) $$ additional memory, the other achieves the task without extra memory, using only $$ O(1) $$ extra space.\n\n## Strategies to Tackle the Problem\n\n1. **Hash Map Method**: \n This approach leverages a hash map to store the mapping between each node in the original list and its corresponding node in the copied list.\n\n2. **Interweaving Nodes Method**: \n This approach cleverly interweaves the nodes of the copied list with the original list, using the structure to adjust the `random` pointers correctly, and then separates them.\n\n---\n\n# Live Coding Hash & More:\nhttps://youtu.be/eplAWtfkz5o?si=6OwomT_z5ClgyhUc\n\n## Solution #1: Hash Map Method\n\n### Intuition and Logic Behind the Solution\n\nThe basic idea is to traverse the list twice. In the first pass, we create a new node for each node in the original list and store the mapping in a hash map. In the second pass, we set the `next` and `random` pointers for each new node based on the hash map.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Create an empty hash map, `old_to_new`, to store the mapping from old nodes to new nodes.\n\n2. **First Pass - Node Creation**: \n - Traverse the original list and for each node, create a corresponding new node.\n - Store the mapping in `old_to_new`.\n\n3. **Second Pass - Setting Pointers**: \n - Traverse the original list again.\n - For each node, set its corresponding new node\'s `next` and `random` pointers based on the hash map.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(n) $$ \u2014 Each node is visited twice.\n- **Space Complexity**: $$ O(n) $$ \u2014 To store the hash map.\n\n---\n\n## Solution #2: Interweaving Nodes Method\n\n### Intuition and Logic Behind the Solution\n\nThe crux of this method is to interweave the nodes of the original and copied lists. This interweaving allows us to set the `random` pointers for the new nodes without needing additional memory for mapping.\n\n### Step-by-step Explanation\n\n1. **Initialization and Interweaving**: \n - Traverse the original list.\n - For each node, create a corresponding new node and place it between the current node and the current node\'s `next`.\n\n2. **Setting Random Pointers**: \n - Traverse the interweaved list.\n - For each old node, set its corresponding new node\'s `random` pointer.\n\n3. **Separating Lists**: \n - Traverse the interweaved list again to separate the old and new lists.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(n) $$ \u2014 Each node is visited multiple times but it\'s still linear time.\n- **Space Complexity**: $$ O(1) $$ \u2014 No additional memory is used for mapping; we only allocate nodes for the new list.\n\nBoth methods provide a deep copy of the original list but differ in their use of additional memory. The choice between them would depend on the specific requirements of your application.\n\n# Performance\n\n| Language | Time (ms) | Memory (MB) |\n|-----------|-----------|-------------|\n| Java | 0 ms | 44 MB |\n| Go | 3 ms | 3.5 MB |\n| C++ | 8 ms | 11.3 MB | \n| Python3 (Hash) | 33 ms | 17.3 MB |\n| JavaScript| 34 ms | 43.8 MB | \n| Python3 (Inter) | 39 ms | 17.3 MB |\n| C# | 87 ms | 39.9 MB | \n\n\n\n\n# Code #1 Hash Map\n``` Python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n old_to_new = {}\n \n curr = head\n while curr:\n old_to_new[curr] = Node(curr.val)\n curr = curr.next\n \n curr = head\n while curr:\n old_to_new[curr].next = old_to_new.get(curr.next)\n old_to_new[curr].random = old_to_new.get(curr.random)\n curr = curr.next\n \n return old_to_new[head]\n```\n``` C++ []\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n if (!head) return nullptr;\n \n unordered_map<Node*, Node*> old_to_new;\n \n Node* curr = head;\n while (curr) {\n old_to_new[curr] = new Node(curr->val);\n curr = curr->next;\n }\n \n curr = head;\n while (curr) {\n old_to_new[curr]->next = old_to_new[curr->next];\n old_to_new[curr]->random = old_to_new[curr->random];\n curr = curr->next;\n }\n \n return old_to_new[head];\n }\n};\n```\n``` Java []\npublic class Solution {\n public Node copyRandomList(Node head) {\n if (head == null) return null;\n \n HashMap<Node, Node> oldToNew = new HashMap<>();\n \n Node curr = head;\n while (curr != null) {\n oldToNew.put(curr, new Node(curr.val));\n curr = curr.next;\n }\n \n curr = head;\n while (curr != null) {\n oldToNew.get(curr).next = oldToNew.get(curr.next);\n oldToNew.get(curr).random = oldToNew.get(curr.random);\n curr = curr.next;\n }\n \n return oldToNew.get(head);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {Node} head\n * @return {Node}\n */\nvar copyRandomList = function(head) {\n if (!head) return null;\n \n const oldToNew = new Map();\n \n let curr = head;\n while (curr) {\n oldToNew.set(curr, new Node(curr.val));\n curr = curr.next;\n }\n \n curr = head;\n while (curr) {\n oldToNew.get(curr).next = oldToNew.get(curr.next) || null;\n oldToNew.get(curr).random = oldToNew.get(curr.random) || null;\n curr = curr.next;\n }\n \n return oldToNew.get(head);\n};\n```\n``` C# []\npublic class Solution {\n public Node CopyRandomList(Node head) {\n if (head == null) return null;\n \n Dictionary<Node, Node> oldToNew = new Dictionary<Node, Node>();\n \n Node curr = head;\n while (curr != null) {\n oldToNew[curr] = new Node(curr.val);\n curr = curr.next;\n }\n \n curr = head;\n while (curr != null) {\n oldToNew[curr].next = curr.next != null ? oldToNew[curr.next] : null;\n oldToNew[curr].random = curr.random != null ? oldToNew[curr.random] : null;\n curr = curr.next;\n }\n \n return oldToNew[head];\n }\n}\n```\n``` Go []\nfunc copyRandomList(head *Node) *Node {\n if head == nil {\n return nil\n }\n\n oldToNew := make(map[*Node]*Node)\n\n curr := head\n for curr != nil {\n oldToNew[curr] = &Node{Val: curr.Val}\n curr = curr.Next\n }\n\n curr = head\n for curr != nil {\n oldToNew[curr].Next = oldToNew[curr.Next]\n oldToNew[curr].Random = oldToNew[curr.Random]\n curr = curr.Next\n }\n\n return oldToNew[head]\n}\n```\n\n# Code #2 Interweaving Nodes\n``` Python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n \n curr = head\n while curr:\n new_node = Node(curr.val, curr.next)\n curr.next = new_node\n curr = new_node.next\n \n curr = head\n while curr:\n if curr.random:\n curr.next.random = curr.random.next\n curr = curr.next.next\n \n old_head = head\n new_head = head.next\n curr_old = old_head\n curr_new = new_head\n \n while curr_old:\n curr_old.next = curr_old.next.next\n curr_new.next = curr_new.next.next if curr_new.next else None\n curr_old = curr_old.next\n curr_new = curr_new.next\n \n return new_head\n```\n``` Go []\nfunc copyRandomList(head *Node) *Node {\n if head == nil {\n return nil\n }\n \n curr := head\n for curr != nil {\n new_node := &Node{Val: curr.Val, Next: curr.Next}\n curr.Next = new_node\n curr = new_node.Next\n }\n \n curr = head\n for curr != nil {\n if curr.Random != nil {\n curr.Next.Random = curr.Random.Next\n }\n curr = curr.Next.Next\n }\n \n old_head := head\n new_head := head.Next\n curr_old := old_head\n curr_new := new_head\n \n for curr_old != nil {\n curr_old.Next = curr_old.Next.Next\n if curr_new.Next != nil {\n curr_new.Next = curr_new.Next.Next\n } else {\n curr_new.Next = nil\n }\n curr_old = curr_old.Next\n curr_new = curr_new.Next\n }\n \n return new_head\n}\n```\n``` C++ []\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* next;\n Node* random;\n \n Node(int _val) {\n val = _val;\n next = NULL;\n random = NULL;\n }\n};\n*/\n\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n if (!head) return nullptr;\n \n Node* curr = head;\n while (curr) {\n Node* new_node = new Node(curr->val);\n new_node->next = curr->next;\n curr->next = new_node;\n curr = new_node->next;\n }\n \n curr = head;\n while (curr) {\n if (curr->random) {\n curr->next->random = curr->random->next;\n }\n curr = curr->next->next;\n }\n \n Node* old_head = head;\n Node* new_head = head->next;\n Node* curr_old = old_head;\n Node* curr_new = new_head;\n \n while (curr_old) {\n curr_old->next = curr_old->next->next;\n curr_new->next = curr_new->next ? curr_new->next->next : nullptr;\n curr_old = curr_old->next;\n curr_new = curr_new->next;\n }\n \n return new_head; \n }\n};\n```\n``` Java []\npublic class Solution {\n public Node copyRandomList(Node head) {\n if (head == null) return null;\n \n Node curr = head;\n while (curr != null) {\n Node new_node = new Node(curr.val, curr.next);\n curr.next = new_node;\n curr = new_node.next;\n }\n \n curr = head;\n while (curr != null) {\n if (curr.random != null) {\n curr.next.random = curr.random.next;\n }\n curr = curr.next != null ? curr.next.next : null;\n }\n \n Node old_head = head;\n Node new_head = head.next;\n Node curr_old = old_head;\n Node curr_new = new_head;\n \n while (curr_old != null) {\n curr_old.next = curr_old.next.next;\n curr_new.next = curr_new.next != null ? curr_new.next.next : null;\n curr_old = curr_old.next;\n curr_new = curr_new.next;\n }\n \n return new_head;\n }\n}\n```\n\n# Live Coding Interweaving & More\nhttps://youtu.be/DH0HDU4ScYY?si=P-P1Er3P8q5XekTU\n\n### Reflections on Copying Lists with Random Pointers\n\n#### Hash Map Method:\nClear and simple, this method uses extra memory to map each node from the original to the copied list. It\'s straightforward but can be memory-inefficient.\n\n#### Interweaving Nodes Method:\nSleek and space-efficient, this in-place method interweaves new nodes within the existing structure before making them their own list. It\'s elegant but requires careful attention.\n\nThis problem isn\'t just coding; it\'s a deep dive into data structures and algorithms. Whether you prefer the clarity of Hash Map or the finesse of Interweaving Nodes, each sharpens your algorithmic skill set. Embrace the challenge! \uD83C\uDF1F\uD83D\uDE80\n | 188 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
✅ 97.92% Hash Table & Linked List | copy-list-with-random-pointer | 1 | 1 | # Interview Guide - Copying a Linked List with Random Pointers: A Dual-Approach Analysis\n\n## Introduction & Problem Understanding\n\nThe problem at hand involves creating a deep copy of a given singly-linked list where each node has a `next` pointer and an additional `random` pointer. The `random` pointer could point to any node within the list or be `null`. The deep copy should have brand new nodes with the same `next` and `random` pointers as the original list.\n\n### Key Concepts and Constraints\n\n1. **Node Anatomy**: \n Each node in the list has an integer value, a `next` pointer pointing to the subsequent node, and a `random` pointer that could point to any node in the list or be `null`.\n\n2. **Deep Copy**: \n We are required to return a deep copy of the list, meaning that the new list should consist of entirely new nodes that don\'t refer to nodes in the original list.\n\n3. **Memory Efficiency**: \n While one approach uses $$ O(n) $$ additional memory, the other achieves the task without extra memory, using only $$ O(1) $$ extra space.\n\n## Strategies to Tackle the Problem\n\n1. **Hash Map Method**: \n This approach leverages a hash map to store the mapping between each node in the original list and its corresponding node in the copied list.\n\n2. **Interweaving Nodes Method**: \n This approach cleverly interweaves the nodes of the copied list with the original list, using the structure to adjust the `random` pointers correctly, and then separates them.\n\n---\n\n# Live Coding Hash & More:\nhttps://youtu.be/eplAWtfkz5o?si=6OwomT_z5ClgyhUc\n\n## Solution #1: Hash Map Method\n\n### Intuition and Logic Behind the Solution\n\nThe basic idea is to traverse the list twice. In the first pass, we create a new node for each node in the original list and store the mapping in a hash map. In the second pass, we set the `next` and `random` pointers for each new node based on the hash map.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Create an empty hash map, `old_to_new`, to store the mapping from old nodes to new nodes.\n\n2. **First Pass - Node Creation**: \n - Traverse the original list and for each node, create a corresponding new node.\n - Store the mapping in `old_to_new`.\n\n3. **Second Pass - Setting Pointers**: \n - Traverse the original list again.\n - For each node, set its corresponding new node\'s `next` and `random` pointers based on the hash map.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(n) $$ \u2014 Each node is visited twice.\n- **Space Complexity**: $$ O(n) $$ \u2014 To store the hash map.\n\n---\n\n## Solution #2: Interweaving Nodes Method\n\n### Intuition and Logic Behind the Solution\n\nThe crux of this method is to interweave the nodes of the original and copied lists. This interweaving allows us to set the `random` pointers for the new nodes without needing additional memory for mapping.\n\n### Step-by-step Explanation\n\n1. **Initialization and Interweaving**: \n - Traverse the original list.\n - For each node, create a corresponding new node and place it between the current node and the current node\'s `next`.\n\n2. **Setting Random Pointers**: \n - Traverse the interweaved list.\n - For each old node, set its corresponding new node\'s `random` pointer.\n\n3. **Separating Lists**: \n - Traverse the interweaved list again to separate the old and new lists.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(n) $$ \u2014 Each node is visited multiple times but it\'s still linear time.\n- **Space Complexity**: $$ O(1) $$ \u2014 No additional memory is used for mapping; we only allocate nodes for the new list.\n\nBoth methods provide a deep copy of the original list but differ in their use of additional memory. The choice between them would depend on the specific requirements of your application.\n\n# Performance\n\n| Language | Time (ms) | Memory (MB) |\n|-----------|-----------|-------------|\n| Java | 0 ms | 44 MB |\n| Go | 3 ms | 3.5 MB |\n| C++ | 8 ms | 11.3 MB | \n| Python3 (Hash) | 33 ms | 17.3 MB |\n| JavaScript| 34 ms | 43.8 MB | \n| Python3 (Inter) | 39 ms | 17.3 MB |\n| C# | 87 ms | 39.9 MB | \n\n\n\n\n# Code #1 Hash Map\n``` Python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n old_to_new = {}\n \n curr = head\n while curr:\n old_to_new[curr] = Node(curr.val)\n curr = curr.next\n \n curr = head\n while curr:\n old_to_new[curr].next = old_to_new.get(curr.next)\n old_to_new[curr].random = old_to_new.get(curr.random)\n curr = curr.next\n \n return old_to_new[head]\n```\n``` C++ []\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n if (!head) return nullptr;\n \n unordered_map<Node*, Node*> old_to_new;\n \n Node* curr = head;\n while (curr) {\n old_to_new[curr] = new Node(curr->val);\n curr = curr->next;\n }\n \n curr = head;\n while (curr) {\n old_to_new[curr]->next = old_to_new[curr->next];\n old_to_new[curr]->random = old_to_new[curr->random];\n curr = curr->next;\n }\n \n return old_to_new[head];\n }\n};\n```\n``` Java []\npublic class Solution {\n public Node copyRandomList(Node head) {\n if (head == null) return null;\n \n HashMap<Node, Node> oldToNew = new HashMap<>();\n \n Node curr = head;\n while (curr != null) {\n oldToNew.put(curr, new Node(curr.val));\n curr = curr.next;\n }\n \n curr = head;\n while (curr != null) {\n oldToNew.get(curr).next = oldToNew.get(curr.next);\n oldToNew.get(curr).random = oldToNew.get(curr.random);\n curr = curr.next;\n }\n \n return oldToNew.get(head);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {Node} head\n * @return {Node}\n */\nvar copyRandomList = function(head) {\n if (!head) return null;\n \n const oldToNew = new Map();\n \n let curr = head;\n while (curr) {\n oldToNew.set(curr, new Node(curr.val));\n curr = curr.next;\n }\n \n curr = head;\n while (curr) {\n oldToNew.get(curr).next = oldToNew.get(curr.next) || null;\n oldToNew.get(curr).random = oldToNew.get(curr.random) || null;\n curr = curr.next;\n }\n \n return oldToNew.get(head);\n};\n```\n``` C# []\npublic class Solution {\n public Node CopyRandomList(Node head) {\n if (head == null) return null;\n \n Dictionary<Node, Node> oldToNew = new Dictionary<Node, Node>();\n \n Node curr = head;\n while (curr != null) {\n oldToNew[curr] = new Node(curr.val);\n curr = curr.next;\n }\n \n curr = head;\n while (curr != null) {\n oldToNew[curr].next = curr.next != null ? oldToNew[curr.next] : null;\n oldToNew[curr].random = curr.random != null ? oldToNew[curr.random] : null;\n curr = curr.next;\n }\n \n return oldToNew[head];\n }\n}\n```\n``` Go []\nfunc copyRandomList(head *Node) *Node {\n if head == nil {\n return nil\n }\n\n oldToNew := make(map[*Node]*Node)\n\n curr := head\n for curr != nil {\n oldToNew[curr] = &Node{Val: curr.Val}\n curr = curr.Next\n }\n\n curr = head\n for curr != nil {\n oldToNew[curr].Next = oldToNew[curr.Next]\n oldToNew[curr].Random = oldToNew[curr.Random]\n curr = curr.Next\n }\n\n return oldToNew[head]\n}\n```\n\n# Code #2 Interweaving Nodes\n``` Python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n \n curr = head\n while curr:\n new_node = Node(curr.val, curr.next)\n curr.next = new_node\n curr = new_node.next\n \n curr = head\n while curr:\n if curr.random:\n curr.next.random = curr.random.next\n curr = curr.next.next\n \n old_head = head\n new_head = head.next\n curr_old = old_head\n curr_new = new_head\n \n while curr_old:\n curr_old.next = curr_old.next.next\n curr_new.next = curr_new.next.next if curr_new.next else None\n curr_old = curr_old.next\n curr_new = curr_new.next\n \n return new_head\n```\n``` Go []\nfunc copyRandomList(head *Node) *Node {\n if head == nil {\n return nil\n }\n \n curr := head\n for curr != nil {\n new_node := &Node{Val: curr.Val, Next: curr.Next}\n curr.Next = new_node\n curr = new_node.Next\n }\n \n curr = head\n for curr != nil {\n if curr.Random != nil {\n curr.Next.Random = curr.Random.Next\n }\n curr = curr.Next.Next\n }\n \n old_head := head\n new_head := head.Next\n curr_old := old_head\n curr_new := new_head\n \n for curr_old != nil {\n curr_old.Next = curr_old.Next.Next\n if curr_new.Next != nil {\n curr_new.Next = curr_new.Next.Next\n } else {\n curr_new.Next = nil\n }\n curr_old = curr_old.Next\n curr_new = curr_new.Next\n }\n \n return new_head\n}\n```\n``` C++ []\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* next;\n Node* random;\n \n Node(int _val) {\n val = _val;\n next = NULL;\n random = NULL;\n }\n};\n*/\n\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n if (!head) return nullptr;\n \n Node* curr = head;\n while (curr) {\n Node* new_node = new Node(curr->val);\n new_node->next = curr->next;\n curr->next = new_node;\n curr = new_node->next;\n }\n \n curr = head;\n while (curr) {\n if (curr->random) {\n curr->next->random = curr->random->next;\n }\n curr = curr->next->next;\n }\n \n Node* old_head = head;\n Node* new_head = head->next;\n Node* curr_old = old_head;\n Node* curr_new = new_head;\n \n while (curr_old) {\n curr_old->next = curr_old->next->next;\n curr_new->next = curr_new->next ? curr_new->next->next : nullptr;\n curr_old = curr_old->next;\n curr_new = curr_new->next;\n }\n \n return new_head; \n }\n};\n```\n``` Java []\npublic class Solution {\n public Node copyRandomList(Node head) {\n if (head == null) return null;\n \n Node curr = head;\n while (curr != null) {\n Node new_node = new Node(curr.val, curr.next);\n curr.next = new_node;\n curr = new_node.next;\n }\n \n curr = head;\n while (curr != null) {\n if (curr.random != null) {\n curr.next.random = curr.random.next;\n }\n curr = curr.next != null ? curr.next.next : null;\n }\n \n Node old_head = head;\n Node new_head = head.next;\n Node curr_old = old_head;\n Node curr_new = new_head;\n \n while (curr_old != null) {\n curr_old.next = curr_old.next.next;\n curr_new.next = curr_new.next != null ? curr_new.next.next : null;\n curr_old = curr_old.next;\n curr_new = curr_new.next;\n }\n \n return new_head;\n }\n}\n```\n\n# Live Coding Interweaving & More\nhttps://youtu.be/DH0HDU4ScYY?si=P-P1Er3P8q5XekTU\n\n### Reflections on Copying Lists with Random Pointers\n\n#### Hash Map Method:\nClear and simple, this method uses extra memory to map each node from the original to the copied list. It\'s straightforward but can be memory-inefficient.\n\n#### Interweaving Nodes Method:\nSleek and space-efficient, this in-place method interweaves new nodes within the existing structure before making them their own list. It\'s elegant but requires careful attention.\n\nThis problem isn\'t just coding; it\'s a deep dive into data structures and algorithms. Whether you prefer the clarity of Hash Map or the finesse of Interweaving Nodes, each sharpens your algorithmic skill set. Embrace the challenge! \uD83C\uDF1F\uD83D\uDE80\n | 188 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Beginner-friendly || Solution with using Hashtable + LinkedList DS in Python3 | copy-list-with-random-pointer | 0 | 1 | # Intuition\nThe problem description is the following:\n- we have a **linked list** of nodes\n- we shall perform **a deep copy** == this means, that **all of the values and pointers** MUST BE **copied with a new referrence/value for storing** (primitives are passing by **value**, and objects - **by referrence**)\n\nLet\'s consider an example\n```\n# Example 1\nn1 = Node(0)\nn2 = Node(1)\nn1.next = n2.next\nn1 => n2\n\n# This is quite simple, so just iterate over all list and create\n# new nodes with vals\n\n# Example 2\nn1 = Node(0)\nn2 = Node(1)\nn3 = Node(2)\nn1.next = n2.next\nn2.next = n3\nn3.random = n1 # This forms the circular dependecy, i.e. cycle\n\n# For this example we do the same in Ex.1, and copy the random node.\n# The trickiest part involves using extra space, such as HashTable.\ncache = dict()\n\n# We can store all of the nodes inside cache\n# by using string referrence to the pointer \n# like str(node) or without it (because of implementation) and so on ..\ncache[n1] = Node(n1.val)\ncache[n2] = Node(n2.val)\n\n```\n\n# Approach\n1. initialize a `cache` to store the copied nodes\n2. create a pointer `cur`, that\'ll point to the `head`\n3. for the first `while` loop store **the original referrence** with new values\n4. shift the `cur` pointer to the `head` **again**\n5. for the last `while` loop change the referrences of `node.next` and `node.random` via checking existence\n6. return the referrence of `head` from cache or `None` \n\n# Complexity\n- Time complexity: **O(n)**, because of two `while` iterations over `cur` pointer\n\n- Space complexity: **O(n)**, since we\'re storing mapping in `cache` as **string referrence of node => new node**\n# Code\nThe final version, improved by [danzam284](https://leetcode.com/danzam284/)\n```\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n cache = {None: None}\n cur = head\n\n while cur:\n cache[cur] = Node(cur.val)\n cur = cur.next\n\n cur = head\n\n while cur:\n if cur.next:\n cache[cur].next = cache[cur.next]\n if cur.random:\n cache[cur].random = cache[cur.random]\n cur = cur.next\n\n return cache[head] \n``` | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Beginner-friendly || Solution with using Hashtable + LinkedList DS in Python3 | copy-list-with-random-pointer | 0 | 1 | # Intuition\nThe problem description is the following:\n- we have a **linked list** of nodes\n- we shall perform **a deep copy** == this means, that **all of the values and pointers** MUST BE **copied with a new referrence/value for storing** (primitives are passing by **value**, and objects - **by referrence**)\n\nLet\'s consider an example\n```\n# Example 1\nn1 = Node(0)\nn2 = Node(1)\nn1.next = n2.next\nn1 => n2\n\n# This is quite simple, so just iterate over all list and create\n# new nodes with vals\n\n# Example 2\nn1 = Node(0)\nn2 = Node(1)\nn3 = Node(2)\nn1.next = n2.next\nn2.next = n3\nn3.random = n1 # This forms the circular dependecy, i.e. cycle\n\n# For this example we do the same in Ex.1, and copy the random node.\n# The trickiest part involves using extra space, such as HashTable.\ncache = dict()\n\n# We can store all of the nodes inside cache\n# by using string referrence to the pointer \n# like str(node) or without it (because of implementation) and so on ..\ncache[n1] = Node(n1.val)\ncache[n2] = Node(n2.val)\n\n```\n\n# Approach\n1. initialize a `cache` to store the copied nodes\n2. create a pointer `cur`, that\'ll point to the `head`\n3. for the first `while` loop store **the original referrence** with new values\n4. shift the `cur` pointer to the `head` **again**\n5. for the last `while` loop change the referrences of `node.next` and `node.random` via checking existence\n6. return the referrence of `head` from cache or `None` \n\n# Complexity\n- Time complexity: **O(n)**, because of two `while` iterations over `cur` pointer\n\n- Space complexity: **O(n)**, since we\'re storing mapping in `cache` as **string referrence of node => new node**\n# Code\nThe final version, improved by [danzam284](https://leetcode.com/danzam284/)\n```\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n cache = {None: None}\n cur = head\n\n while cur:\n cache[cur] = Node(cur.val)\n cur = cur.next\n\n cur = head\n\n while cur:\n if cur.next:\n cache[cur].next = cache[cur.next]\n if cur.random:\n cache[cur].random = cache[cur.random]\n cur = cur.next\n\n return cache[head] \n``` | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Optimized and Easy-to-Understand Copy Random Linked List - Java, C++, Python | copy-list-with-random-pointer | 1 | 1 | ## Intuition\nWhen faced with the problem of copying a linked list with random pointers, the initial thought is to use a hashmap to keep track of the mapping between the original nodes and their corresponding copies. This way, we can efficiently clone the linked list while handling the random pointers correctly.\n\n## Approach\nThe approach to solving this problem involves the following steps:\n1. Create a HashMap to store the mapping between original nodes and their corresponding copies.\n2. Traverse the original linked list recursively.\n3. For each node encountered:\n - Check if the node is already in the HashMap. If yes, return the corresponding copy.\n - If not, create a new node with the same value and add it to the HashMap.\n - Recursively clone the \'next\' and \'random\' pointers of the current node.\n4. Return the copy of the head node of the original linked list.\n\n## Complexity\n- Time complexity: The time complexity of this approach is O(N), where N is the number of nodes in the linked list. This is because we visit each node only once.\n- Space complexity: The space complexity is O(N), as we use a HashMap to store the mapping between nodes, and the recursion stack also contributes to the space complexity.\n```java []\nclass Solution {\n private HashMap<Node, Node> hm = new HashMap<>();\n public Node copyRandomList(Node head) {\n if (head == null) {\n return null;\n }\n if (hm.containsKey(head)) {\n return hm.get(head);\n }\n Node x = new Node(head.val);\n hm.put(head, x);\n x.next = copyRandomList(head.next);\n x.random = copyRandomList(head.random);\n return x;\n }\n}\n\n```\n```C++ []\nclass Solution {\nprivate:\n std::unordered_map<Node*, Node*> hm;\n\npublic:\n Node* copyRandomList(Node* head) {\n if (head == nullptr) {\n return nullptr;\n }\n if (hm.find(head) != hm.end()) {\n return hm[head];\n }\n Node* x = new Node(head->val);\n hm[head] = x;\n x->next = copyRandomList(head->next);\n x->random = copyRandomList(head->random);\n return x;\n }\n};\n\n```\n```Python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n current = head\n while current:\n new_node = Node(current.val)\n new_node.next = current.next\n current.next = new_node\n current = new_node.next\n \n current = head\n while current:\n if current.random:\n current.next.random = current.random.next\n current = current.next.next\n \n new_head = head.next\n current = head\n while current:\n temp = current.next\n current.next = temp.next\n current = current.next\n if temp.next:\n temp.next = temp.next.next\n \n return new_head\n\n```\n\n | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Optimized and Easy-to-Understand Copy Random Linked List - Java, C++, Python | copy-list-with-random-pointer | 1 | 1 | ## Intuition\nWhen faced with the problem of copying a linked list with random pointers, the initial thought is to use a hashmap to keep track of the mapping between the original nodes and their corresponding copies. This way, we can efficiently clone the linked list while handling the random pointers correctly.\n\n## Approach\nThe approach to solving this problem involves the following steps:\n1. Create a HashMap to store the mapping between original nodes and their corresponding copies.\n2. Traverse the original linked list recursively.\n3. For each node encountered:\n - Check if the node is already in the HashMap. If yes, return the corresponding copy.\n - If not, create a new node with the same value and add it to the HashMap.\n - Recursively clone the \'next\' and \'random\' pointers of the current node.\n4. Return the copy of the head node of the original linked list.\n\n## Complexity\n- Time complexity: The time complexity of this approach is O(N), where N is the number of nodes in the linked list. This is because we visit each node only once.\n- Space complexity: The space complexity is O(N), as we use a HashMap to store the mapping between nodes, and the recursion stack also contributes to the space complexity.\n```java []\nclass Solution {\n private HashMap<Node, Node> hm = new HashMap<>();\n public Node copyRandomList(Node head) {\n if (head == null) {\n return null;\n }\n if (hm.containsKey(head)) {\n return hm.get(head);\n }\n Node x = new Node(head.val);\n hm.put(head, x);\n x.next = copyRandomList(head.next);\n x.random = copyRandomList(head.random);\n return x;\n }\n}\n\n```\n```C++ []\nclass Solution {\nprivate:\n std::unordered_map<Node*, Node*> hm;\n\npublic:\n Node* copyRandomList(Node* head) {\n if (head == nullptr) {\n return nullptr;\n }\n if (hm.find(head) != hm.end()) {\n return hm[head];\n }\n Node* x = new Node(head->val);\n hm[head] = x;\n x->next = copyRandomList(head->next);\n x->random = copyRandomList(head->random);\n return x;\n }\n};\n\n```\n```Python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n current = head\n while current:\n new_node = Node(current.val)\n new_node.next = current.next\n current.next = new_node\n current = new_node.next\n \n current = head\n while current:\n if current.random:\n current.next.random = current.random.next\n current = current.next.next\n \n new_head = head.next\n current = head\n while current:\n temp = current.next\n current.next = temp.next\n current = current.next\n if temp.next:\n temp.next = temp.next.next\n \n return new_head\n\n```\n\n | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
⛳ Python3 🧲 📣 Beats 🔥 99.25% 📣 🧲 | copy-list-with-random-pointer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n1. First Create the list with only next pointer\n2. Store Address of the actual list corresponds to copy list\n3. Traverse through the actual list and assign address whilch corresponds to actual.random which we stored in a map in step 2\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return\n actual = head\n copy_head = prev_copy = None\n list_add = {}\n \n while actual:\n node = Node(actual.val)\n list_add[actual] = node\n if not copy_head:\n copy_head = node\n else:\n prev_node.next = node\n prev_node = node\n actual = actual.next\n list_add[None] = None\n actual = head\n copy = copy_head\n\n while actual:\n copy.random = list_add[actual.random]\n actual = actual.next\n copy = copy.next\n return copy_head\n\n \n```\n# **Thanks for the upvote!!** | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
⛳ Python3 🧲 📣 Beats 🔥 99.25% 📣 🧲 | copy-list-with-random-pointer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n1. First Create the list with only next pointer\n2. Store Address of the actual list corresponds to copy list\n3. Traverse through the actual list and assign address whilch corresponds to actual.random which we stored in a map in step 2\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return\n actual = head\n copy_head = prev_copy = None\n list_add = {}\n \n while actual:\n node = Node(actual.val)\n list_add[actual] = node\n if not copy_head:\n copy_head = node\n else:\n prev_node.next = node\n prev_node = node\n actual = actual.next\n list_add[None] = None\n actual = head\n copy = copy_head\n\n while actual:\n copy.random = list_add[actual.random]\n actual = actual.next\n copy = copy.next\n return copy_head\n\n \n```\n# **Thanks for the upvote!!** | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Hardest Python3 solution. | copy-list-with-random-pointer | 0 | 1 | # Code: \n\n```\nclass Solution:\n def copyRandomList(self, head):\n return __import__("copy").deepcopy(head)\n``` | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Hardest Python3 solution. | copy-list-with-random-pointer | 0 | 1 | # Code: \n\n```\nclass Solution:\n def copyRandomList(self, head):\n return __import__("copy").deepcopy(head)\n``` | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
✅Clear Explanation🔥&Code✅||🔥Step-by-Step Guide to Deep Copying🔥 | copy-list-with-random-pointer | 1 | 1 | # Problem Description:\n\nYou are given a **linked list** where each node has a **"random"** pointer that can **point to any other node in the list**, or it can be null. You need to **create a deep copy of this linked list**, such that the **copied list has new nodes with the same values as the original list**, and the "next" and "random" pointers in the copied list represent the **same relationships as in the original list**.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe **key** to solving this problem **efficiently** is to use a **recursive approach** along with a **hash map** (unordered_map in C++). **Here\'s how the provided solution works:**\n\n**1.** **Base Cases:**\n- If the input **head is null**, **return null** because there\'s nothing to copy.\n- **Check if the hash map (mp) already contains the head node. If it does, return the corresponding copied node from the map**. This is done to avoid copying the same node multiple times.\n2. **Creating a New Node:**\n\n- If the head node is **not in the hash map, create a new node (newNode) with the same value as the head node**.\n- **Store this mapping** in the hash map, where the original head node is mapped to the newly created newNode.\n3. **Recursion:**\n\n- **Recursively call copyRandomList for the next and random pointers of the head node**. This will ensure that we create deep copies of the nodes pointed to by next and random.\n- **Assign the results of the recursive calls to newNode->next and newNode->random**. This establishes the correct relationships in the copied list.\n4. **Return Result:**\n\n- **Return newNode** as the result, which is the head of the copied list.\n# Summary:\n- **The solution uses a recursive approach** to traverse the original linked list.\n- **It maintains a hash map** (mp) to keep track of the mapping between nodes in the original list and their corresponding nodes in the copied list.\n- When you encounter **a node in the original list for the first time,** **you create a new node** in the copied list with the same value.\n- **Then, you recursively copy the next and random pointers of the original node.**\n- By using this recursive approach and the hash map to avoid duplicating nodes, you ensure that the copied list preserves the same structure and relationships as the original list.\n\n**This solution is efficient because it avoids redundant copying of nodes and ensures that the relationships between nodes (both next and random) are correctly maintained in the copied list.**\n# Complexity\n- Time complexity: The overall time complexity of the code is **O(N)**.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The overall space complexity of the code is **O(N).**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n# Code\n\n\n```C++ []\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* next;\n Node* random;\n \n Node(int _val) {\n val = _val;\n next = NULL;\n random = NULL;\n }\n};\n*/\n\nclass Solution {\npublic:\n unordered_map<Node*, Node*> mp;\n Node* copyRandomList(Node* head) {\n if (head == NULL)\n return NULL ;\n if (mp.count(head))\n return mp[head];\n\n Node* newNode = new Node(head->val);\n mp[head] = newNode;\n newNode->next = copyRandomList(head->next);\n newNode->random = copyRandomList(head->random);\n return newNode;\n }\n};\n```\n```Java []\nimport java.util.HashMap;\nimport java.util.Map;\n\npublic class Solution {\n Map<Node, Node> map = new HashMap<>();\n\n public Node copyRandomList(Node head) {\n if (head == null) return null;\n\n if (map.containsKey(head)) return map.get(head);\n\n Node newNode = new Node(head.val);\n map.put(head, newNode);\n\n newNode.next = copyRandomList(head.next);\n newNode.random = copyRandomList(head.random);\n\n return newNode;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.visited = {}\n\n def copyRandomList(self, head: \'Node\') -> \'Node\':\n if not head:\n return None\n\n if head in self.visited:\n return self.visited[head]\n\n newNode = Node(head.val)\n self.visited[head] = newNode\n\n newNode.next = self.copyRandomList(head.next)\n newNode.random = self.copyRandomList(head.random)\n\n return newNode\n\n\n```\n```Javascript []\nvar copyRandomList = function(head) {\n const visited = new Map();\n\n const copy = (node) => {\n if (!node) return null;\n\n if (visited.has(node)) return visited.get(node);\n\n const newNode = new Node(node.val);\n visited.set(node, newNode);\n\n newNode.next = copy(node.next);\n newNode.random = copy(node.random);\n\n return newNode;\n };\n\n return copy(head);\n};\n\n```\n\n---\n\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n\n | 41 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
✅Clear Explanation🔥&Code✅||🔥Step-by-Step Guide to Deep Copying🔥 | copy-list-with-random-pointer | 1 | 1 | # Problem Description:\n\nYou are given a **linked list** where each node has a **"random"** pointer that can **point to any other node in the list**, or it can be null. You need to **create a deep copy of this linked list**, such that the **copied list has new nodes with the same values as the original list**, and the "next" and "random" pointers in the copied list represent the **same relationships as in the original list**.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe **key** to solving this problem **efficiently** is to use a **recursive approach** along with a **hash map** (unordered_map in C++). **Here\'s how the provided solution works:**\n\n**1.** **Base Cases:**\n- If the input **head is null**, **return null** because there\'s nothing to copy.\n- **Check if the hash map (mp) already contains the head node. If it does, return the corresponding copied node from the map**. This is done to avoid copying the same node multiple times.\n2. **Creating a New Node:**\n\n- If the head node is **not in the hash map, create a new node (newNode) with the same value as the head node**.\n- **Store this mapping** in the hash map, where the original head node is mapped to the newly created newNode.\n3. **Recursion:**\n\n- **Recursively call copyRandomList for the next and random pointers of the head node**. This will ensure that we create deep copies of the nodes pointed to by next and random.\n- **Assign the results of the recursive calls to newNode->next and newNode->random**. This establishes the correct relationships in the copied list.\n4. **Return Result:**\n\n- **Return newNode** as the result, which is the head of the copied list.\n# Summary:\n- **The solution uses a recursive approach** to traverse the original linked list.\n- **It maintains a hash map** (mp) to keep track of the mapping between nodes in the original list and their corresponding nodes in the copied list.\n- When you encounter **a node in the original list for the first time,** **you create a new node** in the copied list with the same value.\n- **Then, you recursively copy the next and random pointers of the original node.**\n- By using this recursive approach and the hash map to avoid duplicating nodes, you ensure that the copied list preserves the same structure and relationships as the original list.\n\n**This solution is efficient because it avoids redundant copying of nodes and ensures that the relationships between nodes (both next and random) are correctly maintained in the copied list.**\n# Complexity\n- Time complexity: The overall time complexity of the code is **O(N)**.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The overall space complexity of the code is **O(N).**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n# Code\n\n\n```C++ []\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* next;\n Node* random;\n \n Node(int _val) {\n val = _val;\n next = NULL;\n random = NULL;\n }\n};\n*/\n\nclass Solution {\npublic:\n unordered_map<Node*, Node*> mp;\n Node* copyRandomList(Node* head) {\n if (head == NULL)\n return NULL ;\n if (mp.count(head))\n return mp[head];\n\n Node* newNode = new Node(head->val);\n mp[head] = newNode;\n newNode->next = copyRandomList(head->next);\n newNode->random = copyRandomList(head->random);\n return newNode;\n }\n};\n```\n```Java []\nimport java.util.HashMap;\nimport java.util.Map;\n\npublic class Solution {\n Map<Node, Node> map = new HashMap<>();\n\n public Node copyRandomList(Node head) {\n if (head == null) return null;\n\n if (map.containsKey(head)) return map.get(head);\n\n Node newNode = new Node(head.val);\n map.put(head, newNode);\n\n newNode.next = copyRandomList(head.next);\n newNode.random = copyRandomList(head.random);\n\n return newNode;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.visited = {}\n\n def copyRandomList(self, head: \'Node\') -> \'Node\':\n if not head:\n return None\n\n if head in self.visited:\n return self.visited[head]\n\n newNode = Node(head.val)\n self.visited[head] = newNode\n\n newNode.next = self.copyRandomList(head.next)\n newNode.random = self.copyRandomList(head.random)\n\n return newNode\n\n\n```\n```Javascript []\nvar copyRandomList = function(head) {\n const visited = new Map();\n\n const copy = (node) => {\n if (!node) return null;\n\n if (visited.has(node)) return visited.get(node);\n\n const newNode = new Node(node.val);\n visited.set(node, newNode);\n\n newNode.next = copy(node.next);\n newNode.random = copy(node.random);\n\n return newNode;\n };\n\n return copy(head);\n};\n\n```\n\n---\n\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n\n | 41 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
【Video】Solution with HashMap - Python, JavaScript, Java, C++ | copy-list-with-random-pointer | 1 | 1 | # Intuition\nThe main idea to solve the question of copying a linked list with random pointers is to create a deep copy of the original linked list while maintaining the relationships between nodes. By following these steps below, you can create an exact deep copy of the original linked list, including its random pointers, and return the head of the copied list. This approach ensures that you maintain the relationships between nodes while copying the linked list with minimal time and space complexity.\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 255 videos as of September 5th, 2023.\n\nhttps://youtu.be/eO8TmVWbcxw\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Create a dictionary (`hash`) to map original nodes to their corresponding copied nodes.\n - Initialize the dictionary with a mapping of `None` to `None`.\n\n2. Traverse the original linked list using a pointer `cur`.\n - While `cur` is not `None`:\n - Create a new node with the same value as the current node and store it in the dictionary `hash` with the current node as the key.\n - Move `cur` to the next node in the original list.\n\n3. Reset the `cur` pointer to the head of the original linked list.\n\n4. Traverse the original linked list again using `cur`.\n - While `cur` is not `None`:\n - Retrieve the copied node from the `hash` dictionary using `cur` as the key and store it in the `copy` variable.\n - Set the `next` pointer of the `copy` node to the copied node obtained from the `hash` dictionary using `cur.next` as the key.\n - Set the `random` pointer of the `copy` node to the copied node obtained from the `hash` dictionary using `cur.random` as the key.\n - Move `cur` to the next node in the original list.\n\n5. Return the copied head node obtained from the `hash` dictionary using the original head node as the key.\n\nThis algorithm first creates a mapping of original nodes to their copied nodes and then iterates through the original list twice to connect the `next` and `random` pointers of the copied nodes. Finally, it returns the head of the copied linked list.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n```python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\': \n hash = {None:None}\n cur = head\n \n while cur:\n hash[cur] = Node(cur.val)\n cur = cur.next\n \n cur = head\n \n while cur:\n copy = hash[cur]\n copy.next = hash[cur.next]\n copy.random = hash[cur.random]\n cur = cur.next\n \n return hash[head]\n```\n```javascript []\nvar copyRandomList = function(head) {\n const hashMap = new Map();\n let cur = head;\n\n while (cur) {\n hashMap.set(cur, new Node(cur.val));\n cur = cur.next;\n }\n\n cur = head;\n\n while (cur) {\n const copy = hashMap.get(cur);\n copy.next = hashMap.get(cur.next) || null;\n copy.random = hashMap.get(cur.random) || null;\n cur = cur.next;\n }\n\n return hashMap.get(head); \n};\n```\n```java []\nclass Solution {\n public Node copyRandomList(Node head) {\n Map<Node, Node> hashMap = new HashMap<>();\n Node cur = head;\n\n while (cur != null) {\n hashMap.put(cur, new Node(cur.val));\n cur = cur.next;\n }\n\n cur = head;\n\n while (cur != null) {\n Node copy = hashMap.get(cur);\n copy.next = hashMap.get(cur.next);\n copy.random = hashMap.get(cur.random);\n cur = cur.next;\n }\n\n return hashMap.get(head); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n std::unordered_map<Node*, Node*> hashMap;\n Node* cur = head;\n\n while (cur) {\n hashMap[cur] = new Node(cur->val);\n cur = cur->next;\n }\n\n cur = head;\n\n while (cur) {\n Node* copy = hashMap[cur];\n copy->next = hashMap[cur->next];\n copy->random = hashMap[cur->random];\n cur = cur->next;\n }\n\n return hashMap[head]; \n }\n};\n```\n | 25 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
【Video】Solution with HashMap - Python, JavaScript, Java, C++ | copy-list-with-random-pointer | 1 | 1 | # Intuition\nThe main idea to solve the question of copying a linked list with random pointers is to create a deep copy of the original linked list while maintaining the relationships between nodes. By following these steps below, you can create an exact deep copy of the original linked list, including its random pointers, and return the head of the copied list. This approach ensures that you maintain the relationships between nodes while copying the linked list with minimal time and space complexity.\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 255 videos as of September 5th, 2023.\n\nhttps://youtu.be/eO8TmVWbcxw\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Create a dictionary (`hash`) to map original nodes to their corresponding copied nodes.\n - Initialize the dictionary with a mapping of `None` to `None`.\n\n2. Traverse the original linked list using a pointer `cur`.\n - While `cur` is not `None`:\n - Create a new node with the same value as the current node and store it in the dictionary `hash` with the current node as the key.\n - Move `cur` to the next node in the original list.\n\n3. Reset the `cur` pointer to the head of the original linked list.\n\n4. Traverse the original linked list again using `cur`.\n - While `cur` is not `None`:\n - Retrieve the copied node from the `hash` dictionary using `cur` as the key and store it in the `copy` variable.\n - Set the `next` pointer of the `copy` node to the copied node obtained from the `hash` dictionary using `cur.next` as the key.\n - Set the `random` pointer of the `copy` node to the copied node obtained from the `hash` dictionary using `cur.random` as the key.\n - Move `cur` to the next node in the original list.\n\n5. Return the copied head node obtained from the `hash` dictionary using the original head node as the key.\n\nThis algorithm first creates a mapping of original nodes to their copied nodes and then iterates through the original list twice to connect the `next` and `random` pointers of the copied nodes. Finally, it returns the head of the copied linked list.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n```python []\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\': \n hash = {None:None}\n cur = head\n \n while cur:\n hash[cur] = Node(cur.val)\n cur = cur.next\n \n cur = head\n \n while cur:\n copy = hash[cur]\n copy.next = hash[cur.next]\n copy.random = hash[cur.random]\n cur = cur.next\n \n return hash[head]\n```\n```javascript []\nvar copyRandomList = function(head) {\n const hashMap = new Map();\n let cur = head;\n\n while (cur) {\n hashMap.set(cur, new Node(cur.val));\n cur = cur.next;\n }\n\n cur = head;\n\n while (cur) {\n const copy = hashMap.get(cur);\n copy.next = hashMap.get(cur.next) || null;\n copy.random = hashMap.get(cur.random) || null;\n cur = cur.next;\n }\n\n return hashMap.get(head); \n};\n```\n```java []\nclass Solution {\n public Node copyRandomList(Node head) {\n Map<Node, Node> hashMap = new HashMap<>();\n Node cur = head;\n\n while (cur != null) {\n hashMap.put(cur, new Node(cur.val));\n cur = cur.next;\n }\n\n cur = head;\n\n while (cur != null) {\n Node copy = hashMap.get(cur);\n copy.next = hashMap.get(cur.next);\n copy.random = hashMap.get(cur.random);\n cur = cur.next;\n }\n\n return hashMap.get(head); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n std::unordered_map<Node*, Node*> hashMap;\n Node* cur = head;\n\n while (cur) {\n hashMap[cur] = new Node(cur->val);\n cur = cur->next;\n }\n\n cur = head;\n\n while (cur) {\n Node* copy = hashMap[cur];\n copy->next = hashMap[cur->next];\n copy->random = hashMap[cur->random];\n cur = cur->next;\n }\n\n return hashMap[head]; \n }\n};\n```\n | 25 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python short and clean. Single pass. | copy-list-with-random-pointer | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is number of nodes in LinkedList starting at head`.\n\n# Code\n```python\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n copy = defaultdict(lambda: Node(0), {None: None})\n \n node = head\n while node:\n copy_node = copy[node]\n copy_node.val = node.val\n copy_node.next = copy[node.next]\n copy_node.random = copy[node.random]\n node = node.next\n \n return copy[head]\n\n\n``` | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python short and clean. Single pass. | copy-list-with-random-pointer | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is number of nodes in LinkedList starting at head`.\n\n# Code\n```python\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n copy = defaultdict(lambda: Node(0), {None: None})\n \n node = head\n while node:\n copy_node = copy[node]\n copy_node.val = node.val\n copy_node.next = copy[node.next]\n copy_node.random = copy[node.random]\n node = node.next\n \n return copy[head]\n\n\n``` | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python3 | Easy to Understand | Mapping | copy-list-with-random-pointer | 0 | 1 | # Python3 | Easy to Understand | Mapping\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, next, random):\n self.val = val\n self.next = next\n self.random = random\n"""\nclass Solution:\n def copyRandomList(self, head: \'Node\') -> \'Node\':\n if head is None: return None\n mapping = {}\n cur = head\n while cur:\n mapping[cur] = Node(cur.val,None,None)\n cur = cur.next\n cur = head\n while cur:\n if cur.next:\n mapping[cur].next = mapping[cur.next]\n if cur.random:\n mapping[cur].random = mapping[cur.random]\n cur = cur.next\n return mapping[head]\n``` | 2 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python3 | Easy to Understand | Mapping | copy-list-with-random-pointer | 0 | 1 | # Python3 | Easy to Understand | Mapping\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, next, random):\n self.val = val\n self.next = next\n self.random = random\n"""\nclass Solution:\n def copyRandomList(self, head: \'Node\') -> \'Node\':\n if head is None: return None\n mapping = {}\n cur = head\n while cur:\n mapping[cur] = Node(cur.val,None,None)\n cur = cur.next\n cur = head\n while cur:\n if cur.next:\n mapping[cur].next = mapping[cur.next]\n if cur.random:\n mapping[cur].random = mapping[cur.random]\n cur = cur.next\n return mapping[head]\n``` | 2 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python | Easy Solution | copy-list-with-random-pointer | 0 | 1 | # Intuition\nUsing hashed Linked List\n\n# Approach\nTo create a deep copy of a linked list with random pointers, you can follow these steps:\n\n1. Iterate through the original linked list, creating a new node for each node in the original list and mapping the original node to its corresponding new node in a dictionary.\n2. Iterate through the original linked list again and for each new node, set its `next` pointer to the new node corresponding to the original node\'s `next`.\n3. Iterate through the original linked list once more and for each new node, set its `random` pointer to the new node corresponding to the original node\'s `random`.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n\n node_mapping={}\n\n if not head:\n return None\n\n current=head\n while current:\n node_mapping[current] = Node(current.val)\n current = current.next\n \n current=head\n while current:\n if current.next:\n node_mapping[current].next=node_mapping[current.next]\n current=current.next\n \n current =head\n while current:\n if current.random:\n node_mapping[current].random=node_mapping[current.random]\n current=current.next\n \n return node_mapping[head]\n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python | Easy Solution | copy-list-with-random-pointer | 0 | 1 | # Intuition\nUsing hashed Linked List\n\n# Approach\nTo create a deep copy of a linked list with random pointers, you can follow these steps:\n\n1. Iterate through the original linked list, creating a new node for each node in the original list and mapping the original node to its corresponding new node in a dictionary.\n2. Iterate through the original linked list again and for each new node, set its `next` pointer to the new node corresponding to the original node\'s `next`.\n3. Iterate through the original linked list once more and for each new node, set its `random` pointer to the new node corresponding to the original node\'s `random`.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n\n node_mapping={}\n\n if not head:\n return None\n\n current=head\n while current:\n node_mapping[current] = Node(current.val)\n current = current.next\n \n current=head\n while current:\n if current.next:\n node_mapping[current].next=node_mapping[current.next]\n current=current.next\n \n current =head\n while current:\n if current.random:\n node_mapping[current].random=node_mapping[current.random]\n current=current.next\n \n return node_mapping[head]\n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Beats 99%✅ | O( n )✅ | Easy-To-Understand✅ | Python (Step by step explanation)✅ | copy-list-with-random-pointer | 0 | 1 | # Intuition\nThe intuition for solving this problem is to create a deep copy of the linked list with random pointers. We can achieve this by using a hashmap to map the original nodes to their corresponding new nodes.\n\n# Approach\n1. Create a hashmap `mapp` to map the original nodes to their corresponding new nodes. Initialize it with `None: None`.\n2. Traverse the original linked list while creating new nodes for each original node and updating the `mapp` with the mapping between original and new nodes.\n3. Traverse the original linked list again and update the `next` and `random` pointers of the new nodes using the information stored in `mapp`.\n4. Return the new head of the linked list, which is the node corresponding to the original `head` in the `mapp`.\n\n# Complexity\n- Time complexity: O(n), where n is the number of nodes in the linked list.\n- Space complexity: O(n), as we use additional space for the `mapp` dictionary to store the mappings between original and new nodes.\n\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n mapp = {None : None}\n temp = head\n\n while(temp):\n newNode = Node(temp.val)\n mapp[temp] = newNode\n temp = temp.next\n\n temp = head\n while(temp):\n copy = mapp[temp]\n copy.next = mapp[temp.next]\n copy.random = mapp[temp.random]\n temp = temp.next\n\n return mapp[head] \n\n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 2 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Beats 99%✅ | O( n )✅ | Easy-To-Understand✅ | Python (Step by step explanation)✅ | copy-list-with-random-pointer | 0 | 1 | # Intuition\nThe intuition for solving this problem is to create a deep copy of the linked list with random pointers. We can achieve this by using a hashmap to map the original nodes to their corresponding new nodes.\n\n# Approach\n1. Create a hashmap `mapp` to map the original nodes to their corresponding new nodes. Initialize it with `None: None`.\n2. Traverse the original linked list while creating new nodes for each original node and updating the `mapp` with the mapping between original and new nodes.\n3. Traverse the original linked list again and update the `next` and `random` pointers of the new nodes using the information stored in `mapp`.\n4. Return the new head of the linked list, which is the node corresponding to the original `head` in the `mapp`.\n\n# Complexity\n- Time complexity: O(n), where n is the number of nodes in the linked list.\n- Space complexity: O(n), as we use additional space for the `mapp` dictionary to store the mappings between original and new nodes.\n\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n mapp = {None : None}\n temp = head\n\n while(temp):\n newNode = Node(temp.val)\n mapp[temp] = newNode\n temp = temp.next\n\n temp = head\n while(temp):\n copy = mapp[temp]\n copy.next = mapp[temp.next]\n copy.random = mapp[temp.random]\n temp = temp.next\n\n return mapp[head] \n\n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 2 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python || 94.88% Faster || Space is O(1) || 2 Approaches | copy-list-with-random-pointer | 0 | 1 | ```\n#Time Complexity: O(n)\n#Space Complexity: O(n)\nclass Solution1:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n prev=dummy=Node(-1)\n curr=head\n d=dict()\n while curr:\n prev.next=Node(-1)\n prev.next.val=curr.val\n d[curr]=prev.next\n curr=curr.next\n prev=prev.next\n curr=head\n ptr=dummy.next\n while curr:\n if curr.random==None:\n ptr.random=None\n else:\n ptr.random=d[curr.random]\n curr=curr.next\n ptr=ptr.next\n return dummy.next\n \n#Time Complexity: O(n)\n#Space Complexity: O(1)\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n ptr=Node(-1)\n curr=head\n while curr: #Copy List\n ptr.next=Node(-1)\n temp=curr.next\n ptr.next.val=curr.val\n curr.next=ptr.next\n ptr.next.next=temp\n curr=temp\n curr=head\n while curr: #Set Random Pointers\n if curr.random==None:\n curr.next.random=None\n else:\n temp=curr.random\n curr.next.random=temp.next\n curr=curr.next.next\n curr=head\n dp=ptr=Node(-1)\n while curr: #Demerging the copy list and original list\n temp=curr.next.next\n ptr.next=curr.next\n curr.next=temp\n curr=temp\n ptr=ptr.next\n return dp.next\n```\n**An upvote will be encouraging** | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python || 94.88% Faster || Space is O(1) || 2 Approaches | copy-list-with-random-pointer | 0 | 1 | ```\n#Time Complexity: O(n)\n#Space Complexity: O(n)\nclass Solution1:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n prev=dummy=Node(-1)\n curr=head\n d=dict()\n while curr:\n prev.next=Node(-1)\n prev.next.val=curr.val\n d[curr]=prev.next\n curr=curr.next\n prev=prev.next\n curr=head\n ptr=dummy.next\n while curr:\n if curr.random==None:\n ptr.random=None\n else:\n ptr.random=d[curr.random]\n curr=curr.next\n ptr=ptr.next\n return dummy.next\n \n#Time Complexity: O(n)\n#Space Complexity: O(1)\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n ptr=Node(-1)\n curr=head\n while curr: #Copy List\n ptr.next=Node(-1)\n temp=curr.next\n ptr.next.val=curr.val\n curr.next=ptr.next\n ptr.next.next=temp\n curr=temp\n curr=head\n while curr: #Set Random Pointers\n if curr.random==None:\n curr.next.random=None\n else:\n temp=curr.random\n curr.next.random=temp.next\n curr=curr.next.next\n curr=head\n dp=ptr=Node(-1)\n while curr: #Demerging the copy list and original list\n temp=curr.next.next\n ptr.next=curr.next\n curr.next=temp\n curr=temp\n ptr=ptr.next\n return dp.next\n```\n**An upvote will be encouraging** | 1 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Awesome Hashmap Concept | copy-list-with-random-pointer | 0 | 1 | # Using Hashmap--->TC:O(N)\n```\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n dic={None:None}\n cur=head\n while cur:\n dic[cur]=Node(cur.val)\n cur=cur.next\n cur=head\n while cur:\n copy=dic[cur]\n copy.next=dic[cur.next]\n copy.random=dic[cur.random]\n cur=cur.next\n return dic[head]\n```\n# please upvote me it would encourage me alot\n | 16 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Awesome Hashmap Concept | copy-list-with-random-pointer | 0 | 1 | # Using Hashmap--->TC:O(N)\n```\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n dic={None:None}\n cur=head\n while cur:\n dic[cur]=Node(cur.val)\n cur=cur.next\n cur=head\n while cur:\n copy=dic[cur]\n copy.next=dic[cur.next]\n copy.random=dic[cur.random]\n cur=cur.next\n return dic[head]\n```\n# please upvote me it would encourage me alot\n | 16 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python3 Solution | copy-list-with-random-pointer | 0 | 1 | \n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n old_to_copy={None:None}\n cur=head\n while cur:\n copy=Node(cur.val)\n old_to_copy[cur]=copy\n cur=cur.next\n\n cur=head\n while cur:\n copy=old_to_copy[cur]\n copy.next=old_to_copy[cur.next]\n copy.random=old_to_copy[cur.random]\n cur=cur.next\n\n return old_to_copy[head] \n``` | 5 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Python3 Solution | copy-list-with-random-pointer | 0 | 1 | \n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, x: int, next: \'Node\' = None, random: \'Node\' = None):\n self.val = int(x)\n self.next = next\n self.random = random\n"""\n\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n old_to_copy={None:None}\n cur=head\n while cur:\n copy=Node(cur.val)\n old_to_copy[cur]=copy\n cur=cur.next\n\n cur=head\n while cur:\n copy=old_to_copy[cur]\n copy.next=old_to_copy[cur.next]\n copy.random=old_to_copy[cur.random]\n cur=cur.next\n\n return old_to_copy[head] \n``` | 5 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
✔️ [Python3] JUST TWO STEPS ヾ(´▽`;)ゝ, Explained | copy-list-with-random-pointer | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe main problem is that a random pointer can point to any node in the list. So we can\'t get by here without a hashmap to remember copied nodes. We need a hashmap that maps the original node to its copy. Having that, we can proceed with two simple steps:\n\n1. First pass to create a copy of nodes and fill the hashmap\n2. Second pass to set random pointers in the copied nodes with according nodes.\n\nTime: **O(n)** - for two passes\nSpace: **O(n)** - for the hashmap\n\nRuntime: 36 ms, faster than **91.34%** of Python3 online submissions for Copy List with Random Pointer.\nMemory Usage: 14.8 MB, less than **85.83%** of Python3 online submissions for Copy List with Random Pointer.\n\n```\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n hm, zero = dict(), Node(0)\n \n cur, copy = head, zero\n while cur:\n copy.next = Node(cur.val)\n hm[cur] = copy.next\n cur, copy = cur.next, copy.next\n \n cur, copy = head, zero.next\n while cur:\n copy.random = hm[cur.random] if cur.random else None\n cur, copy = cur.next, copy.next\n \n return zero.next\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 65 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
✔️ [Python3] JUST TWO STEPS ヾ(´▽`;)ゝ, Explained | copy-list-with-random-pointer | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe main problem is that a random pointer can point to any node in the list. So we can\'t get by here without a hashmap to remember copied nodes. We need a hashmap that maps the original node to its copy. Having that, we can proceed with two simple steps:\n\n1. First pass to create a copy of nodes and fill the hashmap\n2. Second pass to set random pointers in the copied nodes with according nodes.\n\nTime: **O(n)** - for two passes\nSpace: **O(n)** - for the hashmap\n\nRuntime: 36 ms, faster than **91.34%** of Python3 online submissions for Copy List with Random Pointer.\nMemory Usage: 14.8 MB, less than **85.83%** of Python3 online submissions for Copy List with Random Pointer.\n\n```\nclass Solution:\n def copyRandomList(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n hm, zero = dict(), Node(0)\n \n cur, copy = head, zero\n while cur:\n copy.next = Node(cur.val)\n hm[cur] = copy.next\n cur, copy = cur.next, copy.next\n \n cur, copy = head, zero.next\n while cur:\n copy.random = hm[cur.random] if cur.random else None\n cur, copy = cur.next, copy.next\n \n return zero.next\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 65 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Easy Video Solution (Space O(N)->O(1))🔥 || Deep Copy🔥 | copy-list-with-random-pointer | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# ***Detailed and easy Video Solution***\n\nhttps://youtu.be/i5EVm_SfNkA\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n```C++ []\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n if(head==NULL)\n return head;\n Node *d=new Node(-1);\n Node *d1;\n Node *h=head;\n while(h!=NULL)\n {\n Node *t=new Node(h->val);\n t->next=h->next;\n t->random=h->random;\n h->next=t;\n h=t->next;\n }\n h=head->next;\n while(h!=NULL)\n { Node *t=h;\n if(t->random!=NULL)\n t->random=t->random->next;\n if(h->next!=NULL)\n h=h->next->next;\n else\n break;\n }\n h=head;\n d=head->next;\n d1=d;\n while(h!=NULL)\n { \n if(d->next==NULL)\n {\n h->next=NULL;\n break;\n }\n h->next=d->next;\n d->next=h->next->next;\n h=h->next;\n d=d->next;\n }\n \n return d1;\n }\n};\n```\n```python []\nclass Node:\n def __init__(self, val):\n self.val = val\n self.next = None\n self.random = None\n\nclass Solution:\n def copyRandomList(self, head: \'Node\') -> \'Node\':\n if not head:\n return head\n \n d = Node(-1)\n d1 = None\n h = head\n\n while h:\n t = Node(h.val)\n t.next = h.next\n t.random = h.random\n h.next = t\n h = t.next\n\n h = head.next\n\n while h:\n t = h\n if t.random:\n t.random = t.random.next\n if h.next:\n h = h.next.next\n else:\n break\n\n h = head\n d = head.next\n d1 = d\n\n while h:\n if not d.next:\n h.next = None\n break\n h.next = d.next\n d.next = h.next.next\n h = h.next\n d = d.next\n\n return d1\n\n```\n```java []\nclass Node {\n int val;\n Node next;\n Node random;\n\n public Node(int val) {\n this.val = val;\n this.next = null;\n this.random = null;\n }\n}\n\npublic class Solution {\n public Node copyRandomList(Node head) {\n if (head == null)\n return head;\n \n Node d = new Node(-1);\n Node d1;\n Node h = head;\n\n while (h != null) {\n Node t = new Node(h.val);\n t.next = h.next;\n t.random = h.random;\n h.next = t;\n h = t.next;\n }\n\n h = head.next;\n\n while (h != null) {\n Node t = h;\n if (t.random != null)\n t.random = t.random.next;\n if (h.next != null)\n h = h.next.next;\n else\n break;\n }\n\n h = head;\n d = head.next;\n d1 = d;\n\n while (h != null) {\n if (d.next == null) {\n h.next = null;\n break;\n }\n h.next = d.next;\n d.next = h.next.next;\n h = h.next;\n d = d.next;\n }\n\n return d1;\n }\n}\n\n``` | 3 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Easy Video Solution (Space O(N)->O(1))🔥 || Deep Copy🔥 | copy-list-with-random-pointer | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# ***Detailed and easy Video Solution***\n\nhttps://youtu.be/i5EVm_SfNkA\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n```C++ []\nclass Solution {\npublic:\n Node* copyRandomList(Node* head) {\n if(head==NULL)\n return head;\n Node *d=new Node(-1);\n Node *d1;\n Node *h=head;\n while(h!=NULL)\n {\n Node *t=new Node(h->val);\n t->next=h->next;\n t->random=h->random;\n h->next=t;\n h=t->next;\n }\n h=head->next;\n while(h!=NULL)\n { Node *t=h;\n if(t->random!=NULL)\n t->random=t->random->next;\n if(h->next!=NULL)\n h=h->next->next;\n else\n break;\n }\n h=head;\n d=head->next;\n d1=d;\n while(h!=NULL)\n { \n if(d->next==NULL)\n {\n h->next=NULL;\n break;\n }\n h->next=d->next;\n d->next=h->next->next;\n h=h->next;\n d=d->next;\n }\n \n return d1;\n }\n};\n```\n```python []\nclass Node:\n def __init__(self, val):\n self.val = val\n self.next = None\n self.random = None\n\nclass Solution:\n def copyRandomList(self, head: \'Node\') -> \'Node\':\n if not head:\n return head\n \n d = Node(-1)\n d1 = None\n h = head\n\n while h:\n t = Node(h.val)\n t.next = h.next\n t.random = h.random\n h.next = t\n h = t.next\n\n h = head.next\n\n while h:\n t = h\n if t.random:\n t.random = t.random.next\n if h.next:\n h = h.next.next\n else:\n break\n\n h = head\n d = head.next\n d1 = d\n\n while h:\n if not d.next:\n h.next = None\n break\n h.next = d.next\n d.next = h.next.next\n h = h.next\n d = d.next\n\n return d1\n\n```\n```java []\nclass Node {\n int val;\n Node next;\n Node random;\n\n public Node(int val) {\n this.val = val;\n this.next = null;\n this.random = null;\n }\n}\n\npublic class Solution {\n public Node copyRandomList(Node head) {\n if (head == null)\n return head;\n \n Node d = new Node(-1);\n Node d1;\n Node h = head;\n\n while (h != null) {\n Node t = new Node(h.val);\n t.next = h.next;\n t.random = h.random;\n h.next = t;\n h = t.next;\n }\n\n h = head.next;\n\n while (h != null) {\n Node t = h;\n if (t.random != null)\n t.random = t.random.next;\n if (h.next != null)\n h = h.next.next;\n else\n break;\n }\n\n h = head;\n d = head.next;\n d1 = d;\n\n while (h != null) {\n if (d.next == null) {\n h.next = null;\n break;\n }\n h.next = d.next;\n d.next = h.next.next;\n h = h.next;\n d = d.next;\n }\n\n return d1;\n }\n}\n\n``` | 3 | A linked list of length `n` is given such that each node contains an additional random pointer, which could point to any node in the list, or `null`.
Construct a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) of the list. The deep copy should consist of exactly `n` **brand new** nodes, where each new node has its value set to the value of its corresponding original node. Both the `next` and `random` pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. **None of the pointers in the new list should point to nodes in the original list**.
For example, if there are two nodes `X` and `Y` in the original list, where `X.random --> Y`, then for the corresponding two nodes `x` and `y` in the copied list, `x.random --> y`.
Return _the head of the copied linked list_.
The linked list is represented in the input/output as a list of `n` nodes. Each node is represented as a pair of `[val, random_index]` where:
* `val`: an integer representing `Node.val`
* `random_index`: the index of the node (range from `0` to `n-1`) that the `random` pointer points to, or `null` if it does not point to any node.
Your code will **only** be given the `head` of the original linked list.
**Example 1:**
**Input:** head = \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Output:** \[\[7,null\],\[13,0\],\[11,4\],\[10,2\],\[1,0\]\]
**Example 2:**
**Input:** head = \[\[1,1\],\[2,1\]\]
**Output:** \[\[1,1\],\[2,1\]\]
**Example 3:**
**Input:** head = \[\[3,null\],\[3,0\],\[3,null\]\]
**Output:** \[\[3,null\],\[3,0\],\[3,null\]\]
**Constraints:**
* `0 <= n <= 1000`
* `-104 <= Node.val <= 104`
* `Node.random` is `null` or is pointing to some node in the linked list. | Just iterate the linked list and create copies of the nodes on the go. Since a node can be referenced from multiple nodes due to the random pointers, make sure you are not making multiple copies of the same node. You may want to use extra space to keep old node ---> new node mapping to prevent creating multiples copies of same node. We can avoid using extra space for old node ---> new node mapping, by tweaking the original linked list. Simply interweave the nodes of the old and copied list.
For e.g.
Old List: A --> B --> C --> D
InterWeaved List: A --> A' --> B --> B' --> C --> C' --> D --> D' The interweaving is done using next pointers and we can make use of interweaved structure to get the correct reference nodes for random pointers. |
Solution | word-break | 1 | 1 | ```C++ []\nclass Solution {\n public:\n bool wordBreak(string s, vector<string>& wordDict) {\n const int n = s.length();\n const int maxLength = getMaxLength(wordDict);\n const unordered_set<string> wordSet{begin(wordDict), end(wordDict)};\n vector<int> dp(n + 1);\n dp[0] = true;\n\n for (int i = 1; i <= n; ++i)\n for (int j = i - 1; j >= 0; --j) {\n if (i - j > maxLength)\n break;\n if (dp[j] && wordSet.count(s.substr(j, i - j))) {\n dp[i] = true;\n break;\n }\n }\n\n return dp[n];\n }\n\n private:\n int getMaxLength(const vector<string>& wordDict) {\n return max_element(begin(wordDict), end(wordDict),\n [](const auto& a, const auto& b) {\n return a.length() < b.length();\n })\n ->length();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n \n def construct(current,wordDict, memo={}):\n if current in memo:\n return memo[current]\n\n if not current:\n return True\n\n for word in wordDict:\n if current.startswith(word):\n new_current = current[len(word):]\n if construct(new_current,wordDict,memo):\n memo[current] = True\n return True\n\n memo[current] = False\n return False\n\n return construct(s,wordDict)\n```\n\n```Java []\nclass Solution {\n public boolean wordBreak(String s, List<String> wordDict) {\n return recWay1(s, wordDict);\n }\n\n boolean recWay2(String s, List<String> wordDict) {\n Boolean[] memo = new Boolean[s.length() + 1];\n return wordBreak2(s, new HashSet<>(wordDict), 0, memo);\n }\n\n boolean wordBreak2(String s, Set<String> wordDict, int k, Boolean[] memo) {\n int n = s.length();\n if (k == n) return true;\n\n if (memo[k] != null) return memo[k];\n\n for (int i=k + 1; i<=n; i++) {\n String word = s.substring(k, i);\n if (wordDict.contains(word) && wordBreak2(s, wordDict, i, memo)) {\n return memo[k] = true;\n }\n }\n\n return memo[k] = false;\n }\n\n boolean recWay1(String s, List<String> wordDict) {\n Boolean[] memo = new Boolean[s.length() + 1];\n return wordBreak(s, wordDict, 0, memo);\n }\n \n boolean wordBreak(String s, List<String> wordDict, int k, Boolean[] memo) {\n if (k == s.length()) {\n return true;\n }\n \n if (memo[k] != null) {\n return memo[k];\n }\n \n for (int i=0; i<wordDict.size(); i++) {\n String word = wordDict.get(i);\n if (s.startsWith(word, k)) {\n if(wordBreak(s, wordDict, k + word.length(), memo)) return memo[k] = true;\n }\n }\n \n return memo[k] = false;\n }\n}\n```\n | 441 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Python Solution || 100% || 34ms || Beats 98% || | word-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n dic = {}\n for i in wordDict:\n if i in s:\n if i[0] in dic:\n dic[i[0]].append(i)\n else:\n dic[i[0]]=[i]\n print(dic)\n def ch(st, k, arr):\n if len(st)==k:\n return True\n elif arr[k]!=None:\n return arr[k]\n elif st[k] in dic:\n for i in dic[st[k]]:\n if len(i)<=len(st[k:]):\n if st[k:k+len(i)]==i:\n k+=len(i)\n # ss = st[len(i):]\n # print(k)\n rt = ch(st,k,arr)\n if rt:\n arr[k]=True\n return True \n else:\n k=k-len(i) \n arr[k]=False\n return False \n else:\n arr[k]=False\n return False\n arr=[None]*(len(s)+1)\n k=0\n aaa = ch(s, k, arr)\n return aaa \n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Python3 👍||⚡99/83 faster beats 🔥|| clean solution || | word-break | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n*m) \nm is the max length of the words in wordDict \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n dp = [True] + [False] * (l:=len(s))\n s = \' \'+ s \n wordDict = set(wordDict)\n max_word_len = len(max(wordDict, key=len))\n for i in range(1,l+1):\n for j in range(i-1,max(i-max_word_len-1,-1),-1):\n if dp[j] and s[j+1:i+1] in wordDict:\n dp[i] = True\n break\n return dp[-1]\n\n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Simple Python solution | word-break | 0 | 1 | \n# Code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n dp = [True] + [False] * (len(s))\n for i in range(len(s)):\n for j in range(i, len(s)):\n if s[i:j+1] in wordDict:\n dp[j+1] = dp[i] or dp[j+1]\n return dp[-1]\n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
✅ 100% DP & DFS [VIDEO] - Segmenting a String | word-break | 1 | 1 | # Intuition\nWhen given a string and a dictionary of words, the problem requires us to determine if the string can be segmented into a sequence of dictionary words. A common way to approach this problem is to use either Dynamic Programming or Depth-First Search with memoization, considering the constraints and properties of the problem. The comparison includes implementations in multiple languages: Python, C++, Java, JavaScript, Rust, Go, and C#.\n\nhttps://youtu.be/9ZIQwa1wCNA\n\n# Approaches - Short Description\n\n## Dynamic Programming\nBy utilizing a boolean array dp, we can iteratively build a solution that checks if the string can be segmented into dictionary words. This approach leverages the subproblem overlap and builds a bottom-up solution.\n\n## Depth-First Search with Memoization\nThis approach searches for a valid segmentation by recursively exploring different paths and using a set data structure to efficiently match prefixes. Memoization is used to store results and avoid redundant computations.\n\n## Differences\nWhile Dynamic Programming builds the solution iteratively, Depth-First Search explores recursively. The DP approach has a more straightforward implementation, while DFS with memoization may be more efficient in some cases due to early termination.\n\n# Approach - Dynamic Programming\nThe Dynamic Programming approach provides an efficient way to solve the word break problem by building up a solution iteratively. Here\'s a step-by-step description:\n\n1. **Initialization**: We initialize a boolean array `dp` of length \\(n+1\\), where \\(n\\) is the length of the string `s`. The entry `dp[i]` will be `True` if there exists a word in the dictionary that ends at index \\(i-1\\) in the string `s`. We set `dp[0]` to `True` since an empty string can always be segmented.\n\n2. **Determine Maximum Word Length**: We find the maximum length of a word in the dictionary using `max_len = max(map(len, wordDict))`. This helps us in reducing unnecessary iterations.\n\n3. **Iterate Through the String**: We iterate through the string from index 1 to \\(n\\) (inclusive) and for each index `i`, we iterate from index \\(i-1\\) down to \\(i - \\text{max_len} - 1\\) (or -1, whichever is larger).\n\n4. **Check for Segmentation**: For each `j` in the range, we check if `dp[j]` is `True` and if the substring `s[j:i]` is in `wordDict`. If both conditions are met, we set `dp[i]` to `True` and break out of the inner loop. This means that there exists a valid segmentation ending at index \\(i-1\\).\n\n5. **Result**: Finally, we return `dp[n]`, which will be `True` if the entire string can be segmented into words from the dictionary.\n\n## Example:\nConsider the example with `s = "leetcode"` and `wordDict = ["leet","code"]`. Here\'s how the algorithm proceeds:\n\n- **Initialization**: `dp = [True, False, False, False, False, False, False, False, False]`.\n- **Determine Maximum Word Length**: `max_len = 4`.\n- **Iterate Through the String**:\n - When `i = 4`, the loop finds that `dp[0]` is `True` and `"leet"` is in the dictionary, so `dp[4]` is set to `True`.\n - When `i = 8`, the loop finds that `dp[4]` is `True` and `"code"` is in the dictionary, so `dp[8]` is set to `True`.\n- **Result**: `dp[8]` is `True`, so the function returns `True`.\n\nThe use of dynamic programming ensures that we are not recomputing solutions to subproblems, and the consideration of the maximum word length helps in avoiding unnecessary iterations, making this approach both elegant and efficient.\n\n# Complexity\n- Time complexity: \\( O(n * m) \\), where \\( n \\) is the length of the string and \\( m \\) is the maximum length of a word in the dictionary.\n- Space complexity: \\( O(n) \\)\n\n# Performance - DP\n\n| Language | Runtime | Beats | Memory | Beats |\n|------------|---------|---------|----------|---------|\n| Go | 1 ms | 69.76% | 2.1 MB | 99.78% |\n| Rust | 1 ms | 85.43% | 2.1 MB | 75.38% |\n| Java | 1 ms | 99.85% | 41.1 MB | 86.3% |\n| C++ | 4 ms | 84.76% | 7.6 MB | 92.64% |\n| Python3 | 29 ms | 99.91% | 16.3 MB | 97.29% |\n| JavaScript | 52 ms | 95.93% | 42.3 MB | 95.86% |\n| C# | 104 ms | 73.58% | 40.8 MB | 94.98% |\n\n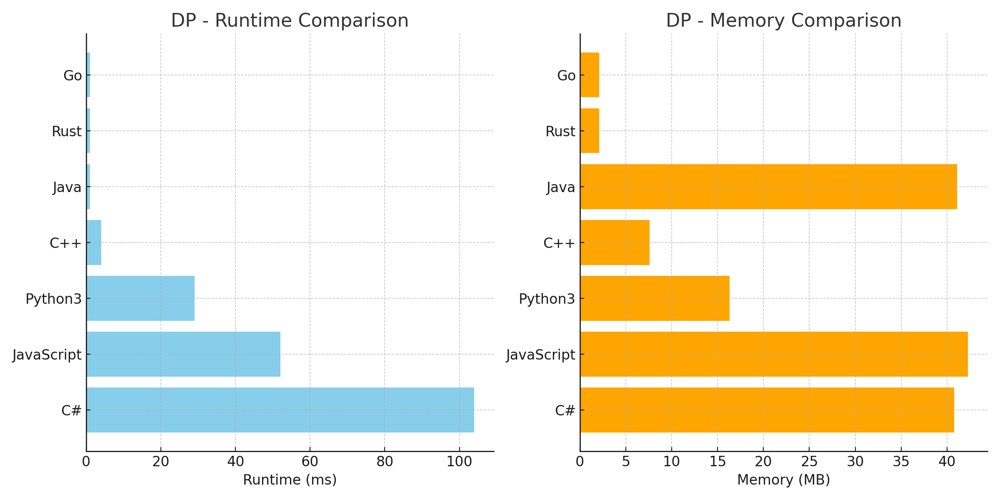\n\n\n# Code - Dynamic Programming\n``` Python []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n n = len(s)\n dp = [False] * (n + 1)\n dp[0] = True\n max_len = max(map(len, wordDict)) # The maximum length of a word in the dictionary\n\n for i in range(1, n + 1):\n for j in range(i - 1, max(i - max_len - 1, -1), -1): # Only consider words that could fit\n if dp[j] and s[j:i] in wordDict:\n dp[i] = True\n break\n\n return dp[n]\n```\n``` C++ []\nclass Solution {\npublic:\n bool wordBreak(std::string s, std::vector<std::string>& wordDict) {\n int n = s.size();\n std::vector<bool> dp(n + 1, false);\n dp[0] = true;\n int max_len = 0;\n for (const auto& word : wordDict) {\n max_len = std::max(max_len, static_cast<int>(word.size()));\n }\n\n for (int i = 1; i <= n; i++) {\n for (int j = i - 1; j >= std::max(i - max_len - 1, 0); j--) {\n if (dp[j] && std::find(wordDict.begin(), wordDict.end(), s.substr(j, i - j)) != wordDict.end()) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n];\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean wordBreak(String s, List<String> wordDict) {\n int n = s.length();\n boolean[] dp = new boolean[n + 1];\n dp[0] = true;\n int max_len = 0;\n for (String word : wordDict) {\n max_len = Math.max(max_len, word.length());\n }\n\n for (int i = 1; i <= n; i++) {\n for (int j = i - 1; j >= Math.max(i - max_len - 1, 0); j--) {\n if (dp[j] && wordDict.contains(s.substring(j, i))) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @param {string[]} wordDict\n * @return {boolean}\n */\nvar wordBreak = function(s, wordDict) {\n let n = s.length;\n let dp = new Array(n + 1).fill(false);\n dp[0] = true;\n let max_len = Math.max(...wordDict.map(word => word.length));\n\n for (let i = 1; i <= n; i++) {\n for (let j = i - 1; j >= Math.max(i - max_len - 1, 0); j--) {\n if (dp[j] && wordDict.includes(s.substring(j, i))) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n];\n};\n```\n``` C# []\npublic class Solution {\n public bool WordBreak(string s, IList<string> wordDict) {\n int n = s.Length;\n bool[] dp = new bool[n + 1];\n dp[0] = true;\n int max_len = 0;\n foreach (string word in wordDict) {\n max_len = Math.Max(max_len, word.Length);\n }\n\n for (int i = 1; i <= n; i++) {\n for (int j = i - 1; j >= Math.Max(i - max_len - 1, 0); j--) {\n if (dp[j] && wordDict.Contains(s.Substring(j, i - j))) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n];\n }\n}\n```\n``` Go []\nfunc wordBreak(s string, wordDict []string) bool {\n n := len(s)\n dp := make([]bool, n+1)\n dp[0] = true\n max_len := 0\n for _, word := range wordDict {\n if len(word) > max_len {\n max_len = len(word)\n }\n }\n\n for i := 1; i <= n; i++ {\n for j := i - 1; j >= max(i - max_len - 1, 0); j-- {\n if dp[j] && contains(wordDict, s[j:i]) {\n dp[i] = true\n break\n }\n }\n }\n\n return dp[n]\n}\n\nfunc contains(words []string, target string) bool {\n for _, word := range words {\n if word == target {\n return true\n }\n }\n return false\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` Rust []\nimpl Solution {\n pub fn word_break(s: String, word_dict: Vec<String>) -> bool {\n let n = s.len();\n let mut dp = vec![false; n + 1];\n dp[0] = true;\n let max_len = word_dict.iter().map(|word| word.len()).max().unwrap_or(0);\n\n let word_dict: std::collections::HashSet<String> = word_dict.into_iter().collect();\n\n for i in 1..=n {\n for j in (std::cmp::max(i as isize - max_len as isize - 1, 0) as usize..i).rev() {\n if dp[j] && word_dict.contains(&s[j..i].to_string()) {\n dp[i] = true;\n break;\n }\n }\n }\n\n dp[n]\n }\n}\n```\n\n# Approach - Depth-First Search with Memoization\nThe Depth-First Search (DFS) approach with memoization offers a recursive way to solve the word break problem. It leverages the Trie data structure to efficiently match prefixes and employs memoization to store intermediate results. Here\'s a step-by-step description:\n\n1. **Building the Trie**: We initialize an empty Trie and iterate through each word in the dictionary (`wordDict`). For each word, we add it to the Trie, using a nested loop to traverse each character (`ch`) in the word. We use the `\'#\'` symbol to mark the end of a word in the Trie. We also determine the maximum length (`max_len`) of a word in the dictionary.\n\n2. **Initialization of Memoization**: We initialize an empty dictionary (`memo`) to store the results of subproblems. This helps in avoiding redundant computations.\n\n3. **DFS Function Call**: We call the recursive DFS function with initial parameters, starting from index 0.\n\n4. **Recursive DFS Function**:\n - **Memoization Check**: If the starting index (`start`) is found in `memo`, we return the stored result.\n - **Base Case**: If `start` equals the length of the string, we return `True`, as we have reached the end.\n - **Iterate Through Prefixes**: We initialize `node` to the root of the Trie and iterate through the string from the `start` index to the minimum of `start + max_len` and the length of the string.\n - **Trie Traversal**: For each character (`ch`), we traverse the Trie. If `ch` is not found, we break out of the loop.\n - **Check for Word End and Recursion**: If we find the end of a word marker (`\'#\'`) in the Trie, we make a recursive call to `dfs` with the next index (`i + 1`).\n - **Update Memoization**: If the recursive call returns `True`, we update `memo[start]` to `True` and return `True`.\n\n5. **Result**: Finally, we update `memo[start]` to `False` if no valid segmentation is found and return `False`.\n\nThis approach leverages the Trie structure to efficiently match prefixes and uses memoization to enhance efficiency. It offers a recursive and elegant solution to the word break problem.\n\n# Complexity\n- Time complexity: \\( O(n * m + k) \\), where \\( n \\) is the length of the string, \\( m \\) is the maximum length of a word in the dictionary, and \\( k \\) is the total number of characters in all words in the dictionary (for building the Trie).\n- Space complexity: \\( O(n + k) \\), where \\( n \\) is the length of the string and \\( k \\) is the total number of characters in all words in the dictionary.\n\n# Performance - DFS\n\n| Language | Runtime | Beats | Memory | Beats |\n|------------|---------|--------|--------|--------|\n| Rust | 0 ms | 100% | 2.1 MB | 75.38% |\n| Go | 2 ms | 66.9% | 2.4 MB | 29.16% |\n| Java | 8 ms | 49.31% | 44 MB | 14.85% |\n| C++ | 21 ms | 37.63% | 14.7 MB | 21.91% |\n| Python3 | 42 ms | 94.1% | 17.5 MB | 5.8% |\n| JavaScript | 58 ms | 86.4% | 44.6 MB | 16.27% |\n| C# | 93 ms | 94.32% | 48.1 MB | 17.47% |\n\n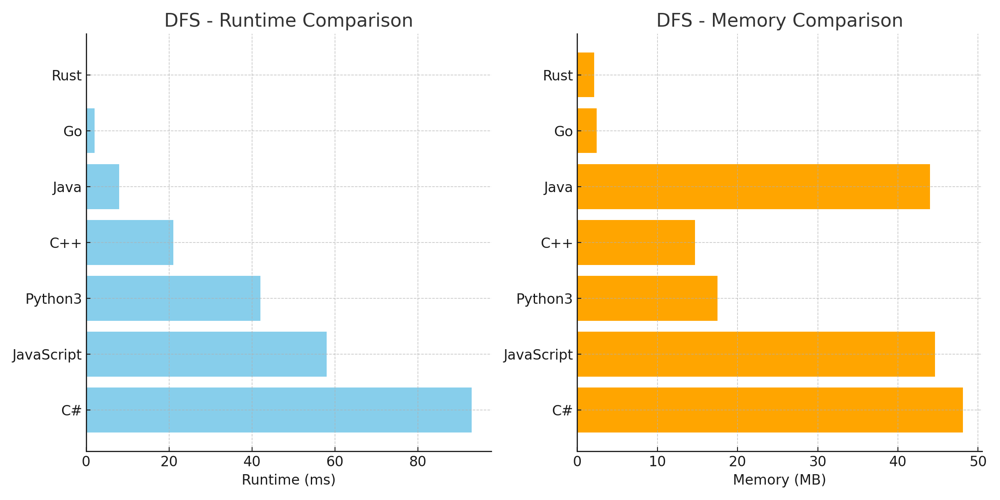\n\n# Code - Depth-First Search with Memoization\n``` Python []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n memo = {}\n wordSet = set(wordDict)\n return self.dfs(s, wordSet, memo)\n \n def dfs(self, s, wordSet, memo):\n if s in memo:\n return memo[s]\n if s in wordSet:\n return True\n for i in range(1, len(s)):\n prefix = s[:i]\n if prefix in wordSet and self.dfs(s[i:], wordSet, memo):\n memo[s] = True\n return True\n memo[s] = False\n return False\n```\n``` JavaScript []\nvar wordBreak = function(s, wordDict) {\n let memo = {};\n let wordSet = new Set(wordDict);\n return dfs(s, wordSet, memo);\n};\n\nfunction dfs(s, wordSet, memo) {\n if (s in memo) return memo[s];\n if (wordSet.has(s)) return true;\n for (let i = 1; i < s.length; i++) {\n let prefix = s.substring(0, i);\n if (wordSet.has(prefix) && dfs(s.substring(i), wordSet, memo)) {\n memo[s] = true;\n return true;\n }\n }\n memo[s] = false;\n return false;\n}\n```\n``` C++ []\nclass Solution {\npublic:\n bool wordBreak(std::string s, std::vector<std::string>& wordDict) {\n std::unordered_map<std::string, bool> memo;\n std::unordered_set<std::string> wordSet(wordDict.begin(), wordDict.end());\n return dfs(s, wordSet, memo);\n }\n \nprivate:\n bool dfs(const std::string& s, const std::unordered_set<std::string>& wordSet, std::unordered_map<std::string, bool>& memo) {\n if (memo.find(s) != memo.end()) return memo[s];\n if (wordSet.find(s) != wordSet.end()) return true;\n for (int i = 1; i < s.size(); i++) {\n std::string prefix = s.substr(0, i);\n if (wordSet.find(prefix) != wordSet.end() && dfs(s.substr(i), wordSet, memo)) {\n memo[s] = true;\n return true;\n }\n }\n memo[s] = false;\n return false;\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean wordBreak(String s, List<String> wordDict) {\n Map<String, Boolean> memo = new HashMap<>();\n Set<String> wordSet = new HashSet<>(wordDict);\n return dfs(s, wordSet, memo);\n }\n \n private boolean dfs(String s, Set<String> wordSet, Map<String, Boolean> memo) {\n if (memo.containsKey(s)) return memo.get(s);\n if (wordSet.contains(s)) return true;\n for (int i = 1; i < s.length(); i++) {\n String prefix = s.substring(0, i);\n if (wordSet.contains(prefix) && dfs(s.substring(i), wordSet, memo)) {\n memo.put(s, true);\n return true;\n }\n }\n memo.put(s, false);\n return false;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool WordBreak(string s, IList<string> wordDict) {\n Dictionary<string, bool> memo = new Dictionary<string, bool>();\n HashSet<string> wordSet = new HashSet<string>(wordDict);\n return Dfs(s, wordSet, memo);\n }\n \n private bool Dfs(string s, HashSet<string> wordSet, Dictionary<string, bool> memo) {\n if (memo.ContainsKey(s)) return memo[s];\n if (wordSet.Contains(s)) return true;\n for (int i = 1; i < s.Length; i++) {\n string prefix = s.Substring(0, i);\n if (wordSet.Contains(prefix) && Dfs(s.Substring(i), wordSet, memo)) {\n memo[s] = true;\n return true;\n }\n }\n memo[s] = false;\n return false;\n }\n}\n```\n``` Rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn word_break(s: String, word_dict: Vec<String>) -> bool {\n let mut memo = std::collections::HashMap::new();\n let word_set: HashSet<String> = word_dict.into_iter().collect();\n Self::dfs(s, &word_set, &mut memo)\n }\n\n fn dfs(s: String, word_set: &HashSet<String>, memo: &mut std::collections::HashMap<String, bool>) -> bool {\n if let Some(&value) = memo.get(&s) {\n return value;\n }\n if word_set.contains(&s) {\n return true;\n }\n for i in 1..s.len() {\n let prefix = &s[0..i];\n if word_set.contains(prefix) && Self::dfs(s[i..].to_string(), word_set, memo) {\n memo.insert(s, true);\n return true;\n }\n }\n memo.insert(s, false);\n return false;\n }\n}\n```\n``` Go []\nfunc wordBreak(s string, wordDict []string) bool {\n\tmemo := make(map[string]bool)\n\twordSet := make(map[string]bool)\n\tfor _, word := range wordDict {\n\t\twordSet[word] = true\n\t}\n\treturn dfs(s, wordSet, memo)\n}\n\nfunc dfs(s string, wordSet map[string]bool, memo map[string]bool) bool {\n\tif value, exists := memo[s]; exists {\n\t\treturn value\n\t}\n\tif _, exists := wordSet[s]; exists {\n\t\treturn true\n\t}\n\tfor i := 1; i < len(s); i++ {\n\t\tprefix := s[:i]\n\t\tif _, exists := wordSet[prefix]; exists && dfs(s[i:], wordSet, memo) {\n\t\t\tmemo[s] = true\n\t\t\treturn true\n\t\t}\n\t}\n\tmemo[s] = false\n\treturn false\n}\n``` | 120 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | word-break | 1 | 1 | # Intuition\nUsing dynamic programming to keep a certain substring is true or not.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/LgoAfakGz5E\n\n# Subscribe to my channel from here. I have 239 videos as of August 4th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize a list `dp` of size `len(s) + 1`, where `dp[i]` will indicate whether the substring up to index `i` (inclusive) can be segmented into words from `wordDict`. Initialize `dp[0]` as `True`, since an empty string can always be segmented.\n\n2. Iterate over each index `i` from 1 to `len(s) + 1` (outer loop):\n - For each index `i`, iterate over each word `w` in `wordDict` (inner loop):\n - Check if the current word `w` can be appended to the substring ending at index `i - len(w)`.\n - This is done by verifying three conditions:\n 1. `i - len(w) >= 0`: This ensures that the current word can be fit within the current index `i`.\n 2. `dp[i - len(w)]`: This checks if the substring before the current word can be segmented into words from `wordDict`.\n 3. `s[:i].endswith(w)`: This checks if the current substring ending at index `i` ends with the word `w`.\n\n3. If all three conditions are satisfied, it means that the substring up to index `i` can be segmented using words from `wordDict`. In this case, set `dp[i]` to `True`.\n\n4. After iterating through all words in `wordDict` and updating `dp[i]` for the current index `i`, move on to the next index in the outer loop.\n\n5. Continue this process until you\'ve iterated over all possible indices `i` from 1 to `len(s)`.\n\n6. Finally, return `dp[-1]`, which indicates whether the entire string `s` can be segmented using words from `wordDict`.\n\nIn essence, the algorithm uses dynamic programming to build up the `dp` array, where each entry represents whether a certain substring can be segmented using the words from the dictionary. The algorithm leverages the fact that if a substring up to index `i` can be segmented, and a word from `wordDict` can be appended to it to reach index `i`, then the substring up to index `i + len(word)` can also be segmented.\n\n# Complexity\n- Time complexity: O(n * m * k)\nn is length of input string and m is length of wordDict. nested loop is n * m and in the nested loop. We check substring operations which costs O(k).\n\n- Space complexity: O(n)\nFor dp list. n is the length of the string s\n\n```python []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n\n dp = [True] + [False] * len(s)\n\n for i in range(1, len(s) + 1):\n for w in wordDict:\n if i - len(w) >= 0 and dp[i - len(w)] and s[:i].endswith(w):\n dp[i] = True\n break\n return dp[-1]\n```\n```javascript []\n/**\n * @param {string} s\n * @param {string[]} wordDict\n * @return {boolean}\n */\nvar wordBreak = function(s, wordDict) {\n const n = s.length;\n const dp = new Array(n + 1).fill(false);\n dp[0] = true;\n\n for (let i = 1; i <= n; i++) {\n for (const word of wordDict) {\n if (i - word.length >= 0 && dp[i - word.length] && s.substring(i - word.length, i) === word) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n]; \n};\n```\n```java []\nclass Solution {\n public boolean wordBreak(String s, List<String> wordDict) {\n int n = s.length();\n boolean[] dp = new boolean[n + 1];\n dp[0] = true;\n\n for (int i = 1; i <= n; i++) {\n for (String word : wordDict) {\n if (i - word.length() >= 0 && dp[i - word.length()] && s.substring(i - word.length(), i).equals(word)) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool wordBreak(string s, vector<string>& wordDict) {\n vector<bool> dp(s.size()+1, false);\n dp[0] = true;\n \n for (int i = 1; i <= s.size(); i++)\n for (int j = 0; j < i; j++)\n if ((dp[j]) && (find(wordDict.begin(), wordDict.end(), s.substr(j, i-j)) != wordDict.end())) {\n dp[i] = true;\n break;\n }\n\n return dp.back();\n }\n};\n```\n | 18 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
BFS + Memoization 99.63% Easy to understand | word-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst thought that comes to mind is prefix, this can be done plainly with BFS, but would lead to memory limit. \n\n```Python []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n q = deque([s])\n while q:\n remaining = q.popleft()\n for word in wordDict:\n if remaining == word:\n return True\n elif remaining.startswith(word):\n q.append(remaining[len(word):])\n return False\n```\n```Go []\nfunc wordBreak(s string, wordDict []string) bool {\n q := []string{s}\n for len(q) != 0 {\n remaining := q[0]\n q = q[1:] // Dequeue\n for _, word := range wordDict {\n if word == remaining {\n return true\n }\n if strings.HasPrefix(remaining, word) {\n q = append(q, remaining[len(word):]) // Enqueue\n }\n }\n }\n return false\n}\n```\nTo optimise we add memoization by storing values of strings we\'ve already processed.\n\n\n# Code\n\n```python []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n q = deque([s])\n memo = set()\n while q:\n remaining = q.popleft()\n if remaining in memo:\n continue\n for word in wordDict:\n if remaining == word:\n return True\n elif remaining.startswith(word):\n q.append(remaining[len(word):])\n memo.add(remaining)\n return False\n```\n```golang []\nfunc wordBreak(s string, wordDict []string) bool {\n q := []string{s}\n memo := make(map[string]bool)\n for len(q) != 0 {\n remaining := q[0]\n q = q[1:] // Dequeue\n if _, ok := memo[remaining]; ok {\n continue\n }\n for _, word := range wordDict {\n if word == remaining {\n return true\n }\n if strings.HasPrefix(remaining, word) {\n q = append(q, remaining[len(word):]) // Enqueue\n memo[remaining] = true\n }\n }\n }\n return false\n}\n\n```\n# Complexity\n- Time complexity: $$O(N^2 * M)$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n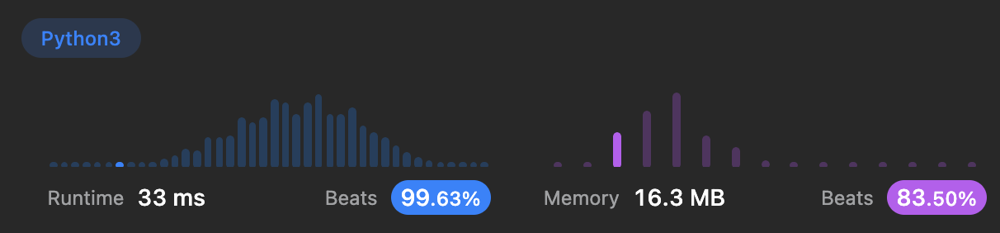\n\n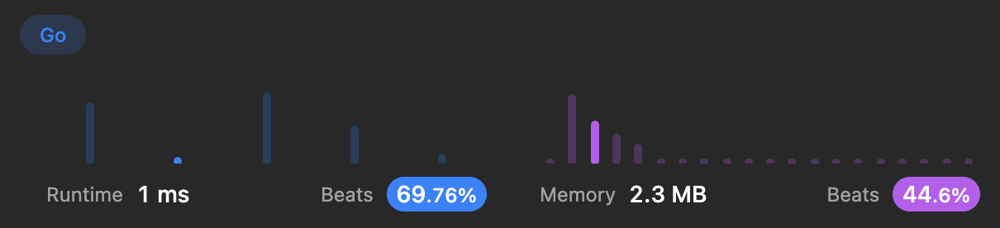\n\n | 5 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
EZ 🥧-THON SOLUTION || Explained || (plz help on the complexity part) | word-break | 0 | 1 | # Intuition\nDP will work. First, get a split that works, a.k.a, the word is in `wordDict`. Why not just use recursion? There may be many ways to get to a point. So, the process will be repeated many times. Saving the answer to a position will significantly reduce the runtime.\n\n# Approach\n##### Recursion + Memoization = DP\n`wordBreak(s, wordDict)`\n- First, setting up variables so they can be accessed anywhere.\n- Next, calling `trySplits` to get `True` or `False`.\n----\n`trySplits(pos)`\n- argument, `pos` is the positon of where we are in `s`\n - **we don\'t want to change `s`**\n- base cases:\n - first one is the **classic** dp move\n - second one is a shortcut\n- a loop from the current position in `s` to the end, `self.LEN`:\n - if splitting here works,\n - call `trySplits(pos)` recursively\n - yet **another** dp move: save the answer you get if you split at that position\n - if that split works throughout the **whole** string, directly `return True`\n- if you passed through the whole string but didn\'t hit the `return True`, you know that means that a split at that position won\'t work.\n- save `self.checked[pos]` to `False`, it doesn\'t work\n\n# Complexity\n- Time complexity: $$plz$$ $$comment$$ $$if$$ $$you$$ $$know$$\n\n- Space complexity:$$plz$$ $$comment$$ $$if$$ $$you$$ $$know$$\n\n# Code\n```\nclass Solution:\n def trySplits(self, pos):\n if pos in self.checked: \n return self.checked[pos]\n elif self.wordDict[self.s[pos:]]: return True\n for i in range(pos, self.LEN):\n if self.s[pos:i] in self.wordDict:\n works = self.trySplits(i)\n self.checked[i] = works\n if works:\n return True\n self.checked[pos] = False\n return False\n \n def wordBreak(self, s, wordDict):\n self.s = s\n self.LEN = len(s)\n self.checked = {}\n self.wordDict = wordDict\n return self.trySplits(0)\n```\n\n# if u found this helpful, plz upvote! | 1 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Easy recursive DFS C++/Python | word-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> dp;\n bool solve(int i, string s, vector<string>& wordDict){\n if (i < 0) return 1;\n if (dp[i] != -1) return dp[i] == 1;\n for (string& w : wordDict) {\n int sz = w.size();\n if (i - sz + 1 < 0) continue;\n if (s.rfind(w, i-sz+1)== i-sz+1 && solve(i - sz, s, wordDict)) {\n dp[i] = 1;\n return 1;\n }\n }\n dp[i] = 0;\n return 0;\n }\n\n bool wordBreak(string s, vector<string>& wordDict) {\n int&& n = s.size();\n dp.assign(n, -1);\n return solve(n - 1, s, wordDict );\n }\n};\n\n\n\n```\n# Python code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n n = len(s)\n dp = [-1] * n\n\n def solve(i, s):\n if i < 0:\n return True\n if dp[i] != -1:\n return dp[i] == 1\n for w in wordDict:\n sz = len(w)\n if i-sz+1 >= 0 and s[i-sz+1:i+1] == w:\n if solve(i - sz, s):\n dp[i] = 1\n return True\n dp[i] = 0\n return False\n\n return solve(n-1, s)\n``` | 6 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Amortized Linear O(k + m) Solution using Aho-Corasick Automaton | word-break | 0 | 1 | # Approach\nI used an advanced data structure that can detect matches in one-pass. This data structure is called Aho-Corasick automaton. The present solutions in leetcode are at $$O(n^2)$$ solution. This solution runs at $$O(k + m)$$ at test time with an overhead of $$O(n)$$. I hope this helps you impress your future interviewer. (\u25CD\u2022\u1D17\u2022\u25CD)\n# Complexity\n- Time complexity: $$O(n + k + m)$$\nBuild Automaton: $$O(n)$$ where $$n$$ is the total number of characters in the dictionary.\nTest segmentation: $$O(k + m)$$ where $$k$$ is the length of string to segment and $$m$$ represents the number of matches present between the dictionary and the string to segment.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n + m)$$\nAutomaton: $$O(n + m)$$\nDP Array: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```python\nclass TrieNode:\n def __init__(self):\n self.children = defaultdict(TrieNode)\n self.fail = None\n self.output = set()\n\n\nclass AhoCorasick:\n def __init__(self, words):\n self.root = TrieNode()\n self.build_trie(words)\n self.build_fail()\n\n def build_trie(self, words):\n for word in words:\n curr = self.root\n for c in word:\n curr = curr.children[c]\n curr.output.add(word)\n \n def build_fail(self):\n q = deque([self.root])\n while q:\n curr = q.popleft()\n for n, child in list(curr.children.items()):\n if curr is self.root:\n child.fail = curr\n else:\n p = curr.fail\n while p is not self.root and n not in p.children:\n p = p.fail\n if n in p.children:\n p = p.children[n]\n child.fail = p\n child.output.update(p.output)\n q.append(child)\n\n\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n ac = AhoCorasick(wordDict)\n n = len(s)\n dp = [False] * (n + 1)\n dp[0] = True\n curr = ac.root\n for i in range(n):\n c = s[i]\n while curr is not ac.root and c not in curr.children:\n curr = curr.fail\n if c in curr.children:\n curr = curr.children[c]\n else:\n return False\n \n for word in curr.output:\n start = i - len(word) + 1\n dp[i + 1] = dp[start] or dp[i + 1]\n if dp[i + 1]: break\n \n return dp[-1]\n \n``` | 7 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
💯🔥: C++ || Java || Pyhton3 (Space and Time Optimized 💪) | word-break | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo determine if the string s can be segmented into a space-separated sequence of dictionary words, we can use dynamic programming. The idea is to break down the problem into smaller subproblems and build a solution from the subproblems\' results. We\'ll keep track of whether a substring can be segmented into dictionary words or not, and use this information to solve the overall problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- First, we create a set from the given wordDict to efficiently check if a word is present in the dictionary.\n- We\'ll use a dynamic programming approach to fill up a boolean array dp, where dp[i] will be true if the substring s[0:i] (i.e., the first i characters of s) can be segmented into dictionary words. Initially, all elements in dp are set to false.\n- We\'ll iterate through each index i in the string s, and for each index, we\'ll check all possible prefixes s[0:j] (where 0 <= j < i) and see if the prefix is in the dictionary and if the remaining substring s[j:i] is also in the dictionary or if it\'s an empty string.\n- If both the prefix and the remaining substring are in the dictionary (or if the remaining substring is empty), then we can set dp[i] to true, indicating that the substring s[0:i] can be segmented.\n- Finally, we return the value of dp[s.length()], which indicates whether the entire string s can be segmented or not.\n\n# Complexity\n- Time complexity: **O(n^2)**, where n is the length of the input string s\n\n- Space complexity: **O(n)**, where n is the length of the input string s\n\n# Code\n## C++\n```\nclass Solution {\npublic:\n bool solve(string &s, map<string,bool>& mp, int ind, string temp,map<pair<int,string>,bool>&dp){\n if(ind == s.length() && temp == "") return true;\n if(ind == s.length()) return false;\n if(dp.find({ind,temp})!=dp.end()) return dp[{ind,temp}];\n bool ans = false;\n temp+=s[ind];\n if(mp.find(temp)!=mp.end()){\n ans = solve(s,mp,ind+1,"",dp);\n }\n ans = ans || solve(s,mp,ind+1,temp,dp);\n \n return dp[{ind,temp}] = ans;\n }\n\n bool wordBreak(string s, vector<string>& wordDict) {\n map<string,bool>mp;\n map<pair<int,string>,bool> dp;\n for(auto word: wordDict) mp[word] = true;\n return solve(s,mp,0,"",dp);\n }\n};\n```\n## Java\n```\nclass Solution {\n public boolean wordBreak(String s, List<String> wordDict) {\n Set<String> dict = new HashSet<>(wordDict);\n int n = s.length();\n boolean[] dp = new boolean[n + 1];\n dp[0] = true;\n\n for (int i = 1; i <= n; ++i) {\n for (int j = 0; j < i; ++j) {\n if (dp[j] && dict.contains(s.substring(j, i))) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[n];\n }\n}\n\n```\n## Python3\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n word_set = set(wordDict)\n n = len(s)\n dp = [False] * (n + 1)\n dp[0] = True\n\n for i in range(1, n + 1):\n for j in range(i):\n if dp[j] and s[j:i] in word_set:\n dp[i] = True\n break\n\n return dp[n]\n```\n\n | 18 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
🦀 100% Dynamic Programming | word-break | 0 | 1 | # Intuition\nThe Word Break problem requires us to determine if a given string can be segmented into a sequence of dictionary words. This can be visualized as finding a path through a sequence of characters where each step corresponds to a valid word in the dictionary. Special thanks to vanAmsen for their invaluable insights and contributions to this problem [139 - Word Break](https://youtu.be/9ZIQwa1wCNA) The problem can be solved efficiently using Dynamic Programming.\n\n# Approach - Dynamic Programming\nThe Dynamic Programming approach involves breaking down the problem into smaller subproblems and solving them iteratively. We initialize a boolean array `dp`, where `dp[i]` represents whether the substring up to the `i`-th character can be segmented into dictionary words. By considering the maximum word length, we reduce unnecessary iterations, making the solution more efficient.\n\n1. **Initialization**: Set `dp[0]` to `true` and the rest to `false`.\n2. **Iteration**: Iterate through the string from left to right, and for each position `i`, check the substrings ending at `i` to see if they are in the dictionary.\n3. **Memoization**: If a valid segmentation is found, update `dp[i]` to `true`.\n4. **Result**: The final result is stored in `dp[n]`, where `n` is the length of the string.\n\n# Complexity\n- **Time complexity**: \\(O(n * m)\\), where \\(n\\) is the length of the string and \\(m\\) is the maximum length of a word in the dictionary. We iterate through the string and for each position, we may consider up to \\(m\\) characters.\n- **Space complexity**: \\(O(n + k)\\), where \\(n\\) is the length of the string and \\(k\\) is the size of the dictionary. The space is used for the `dp` array and storing the dictionary as a HashSet.\n\n# Code\n``` Rust []\nimpl Solution {\n pub fn word_break(s: String, word_dict: Vec<String>) -> bool {\n let n = s.len();\n let mut dp = vec![false; n + 1];\n dp[0] = true;\n let max_len = word_dict.iter().map(|word| word.len()).max().unwrap_or(0);\n\n let word_dict: std::collections::HashSet<String> = word_dict.into_iter().collect();\n\n for i in 1..=n {\n for j in (std::cmp::max(i as isize - max_len as isize - 1, 0) as usize..i).rev() {\n if dp[j] && word_dict.contains(&s[j..i].to_string()) {\n dp[i] = true;\n break;\n }\n }\n }\n\n dp[n]\n }\n}\n```\n``` Python []\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n n = len(s)\n dp = [False] * (n + 1)\n dp[0] = True\n max_len = max(map(len, wordDict)) \n for i in range(1, n + 1):\n for j in range(i - 1, max(i - max_len - 1, -1), -1): \n if dp[j] and s[j:i] in wordDict:\n dp[i] = True\n break\n\n return dp[n]\n```\n``` Go []\nfunc wordBreak(s string, wordDict []string) bool {\n n := len(s)\n dp := make([]bool, n+1)\n dp[0] = true\n max_len := 0\n for _, word := range wordDict {\n if len(word) > max_len {\n max_len = len(word)\n }\n }\n for i := 1; i <= n; i++ {\n for j := i - 1; j >= max(i - max_len - 1, 0); j-- {\n if dp[j] && contains(wordDict, s[j:i]) {\n dp[i] = true\n break\n }\n }\n }\n\n return dp[n]\n}\nfunc contains(words []string, target string) bool {\n for _, word := range words {\n if word == target {\n return true\n }\n }\n return false\n}\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n\nThis code offers a concise and efficient solution to the Word Break problem by leveraging the power of Dynamic Programming, carefully considering the constraints, and using Rust\'s standard library to handle the dictionary. | 10 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
A general template solution for DP Memoization | word-break | 0 | 1 | # Intuition\nThis is exactly the same as [coin change problem](https://leetcode.com/problems/coin-change/) and [Number of Dice Rolls With Target Sum\n](https://leetcode.com/problems/number-of-dice-rolls-with-target-sum/description/). So many medium or hard problems have been solved using this template and now I share it. The solution for this type of problems is straightforward and can be summarized into a template as follows: \n1. Discuss some corner cases\n2. Define a recursive structure where we can apply memoization\n3. Call the recursive structure\n```\nclass Solution:\n def someProblem(self, nums) -> bool:\n # 1. some corner case discussion\n if not nums:\n return []\n\n # 2. the recursive function\n @cache\n def helper(s):\n # 2.1 base cases for recursion\n if len(s) == 0:\n return True\n # 2.2 recursive call with smaller input size\n for word in wordDict:\n if s.startswith(word):\n if helper(s[len(word):]):\n return True\n return False\n\n # 3. wrap the function call\n return helper(s)\n\n```\n\nSome examples on how to use the template:\n\n# 139. Word Break\nRecursively try each word in the word dictionary, and input the ``helper`` function again with smaller input. If the input size is reduced to zero, we find the word break. Otherwise, return False.\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n # no need for base case\n\n # recursive call\n @cache\n def helper(s):\n if len(s) == 0:\n return True\n for word in wordDict:\n if s.startswith(word):\n if helper(s[len(word):]):\n return True\n return False\n return helper(s)\n```\n\n# 322. Coin Change\nStart with 1 or 2 or 5, in order to get 11, the remaining balance now becomes 10 or 9 or 6. For each subcase, we can use 1 or 2 or 5 again, and calculate the corresponding remaining balance... which just forms a recursive structure with smaller input size.\n\n```\nclass Solution:\n def coinChange(self, coins: List[int], amount: int) -> int:\n # corner cases\n if amount == 0: return 0\n @cache\n def helper(balance): # return the optimal strategy with balance\n if balance < 0:\n return float(\'inf\')\n elif balance == 0:\n return 0\n res = []\n for coin in coins:\n res.append(1 + helper(balance-coin))\n return min(res) # get the minimum possible outcomes\n\n return helper(amount) if helper(amount) != float(\'inf\') else -1\n\n```\n# 91. Decode Ways\n```\nclass Solution:\n def numDecodings(self, s: str) -> int:\n @cache\n def helper(s):\n if s.startswith(\'0\'):\n return 0\n\n if not s or len(s) == 1:\n return 1\n\n return helper(s[1:]) + helper(s[2:]) if int(s[:2]) <= 26 else helper(s[1:])\n\n return helper(s)\n```\n\n# 416. Partition Equal Subset Sum\nOne of the most famous problem in leetcode.\n```\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n n = len(nums)\n total_sum = sum(nums)\n # discuss corner case\n if total_sum % 2 != 0:\n return False\n @cache\n def helper(target, idx):\n # recursion base cases\n if target == 0:\n return True\n if target < 0 or idx > n-1:\n return False\n if target < nums[idx]:\n return helper(target, idx + 1)\n return helper(target-nums[idx], idx+1) or helper(target, idx+1)\n subset_sum = total_sum // 2\n return helper(subset_sum, 0)\n```\n\n# 1155. Number of Dice Rolls With Target Sum\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n @cache\n def helper(n, target):\n # base case for recursion\n if n == 1 and target>0 and target<=k:\n return 1\n if n == 0 or target < 0:\n return 0\n res = []\n for i in range(1,k+1):\n res.append(helper(n-1, target-i)) # recursive call\n ans = 0\n for j in res:\n ans = (ans+j)%(10**9+7)\n return ans\n return helper(n, target)\n\n```\n\n# 2767. Partition String Into Minimum Beautiful Substrings\nA biweekly contest problem which can be written in less than 10 minutes if you are familiar with this template.\n```\nclass Solution:\n def minimumBeautifulSubstrings(self, s: str) -> int:\n ans = [\'1\', \'101\', \'11001\', \'1111101\', \'1001110001\', \'110000110101\', \'11110100001001\']\n @cache\n def helper(s):\n if s.startswith(\'0\'):\n return float(\'inf\')\n if not s:\n return 0\n res = []\n for i in ans:\n if s.startswith(i):\n res.append(1 + helper(s[len(i):]))\n return min(res) if res else -1\n return helper(s) if helper(s) < float(\'inf\') else -1\n```\n\n\n\n\n\nPlease upvote if you find this helpful! Thanks a lot.\n\n | 5 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
My solution || Memoization || tabulation | word-break | 0 | 1 | \n# Code\n```\nclass Solution:\n\n\n # here start from first if all the prefix word is in dictionary then just call the recursion for the \n # remainning elements\n\n # tabulation\n\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n dp = [-1 for i in range(len(s)+1)]\n\n for ind in range(i+1,len(s)+1) :\n if s[i:ind] in wordDict :\n if dp[ind] == True :\n dp[i] = True \n dp[i] = False\n return dp[-1]\n \n\n # memoization\n\n def func(self,i,s) : \n\n if i == len(self.s) :\n return True \n\n if self.dp[i] != -1 :\n return self.dp[i]\n\n for ind in range(i+1,len(self.s)+1) :\n if self.s[i:ind] in self.wordDict :\n if self.func(ind,s[ind:]) :\n self.dp[i] = True\n return self.dp[i]\n self.dp[i] = False\n return False\n\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n self.s = s \n self.wordDict = wordDict\n self.dp = [-1 for i in range(len(s)+1)]\n return self.func(0,s)\n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, return `true` if `s` can be segmented into a space-separated sequence of one or more dictionary words.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "leetcode ", wordDict = \[ "leet ", "code "\]
**Output:** true
**Explanation:** Return true because "leetcode " can be segmented as "leet code ".
**Example 2:**
**Input:** s = "applepenapple ", wordDict = \[ "apple ", "pen "\]
**Output:** true
**Explanation:** Return true because "applepenapple " can be segmented as "apple pen apple ".
Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** false
**Constraints:**
* `1 <= s.length <= 300`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 20`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**. | null |
Solution | word-break-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void solve(string s, vector<string>& res, unordered_set<string>& st, vector<string>&temp){\n if(s.length() == 0){\n string str = "";\n for(auto it:temp){\n str += it + " ";\n }\n str.pop_back();\n res.push_back(str);\n return;\n }\n for(int i=0;i<s.length(); i++){\n if(st.count(s.substr(0, i+1))){\n temp.push_back(s.substr(0, i+1));\n solve(s.substr(i+1), res, st, temp);\n temp.pop_back();\n }\n }\n }\n vector<string> wordBreak(string s, vector<string>& wordDict) {\n vector<string>res, temp;\n unordered_set<string>st(wordDict.begin(), wordDict.end());\n \n solve(s, res, st, temp);\n return res;\n }\n};\n```\n\n```Python3 []\ndef fun(s,dc,memo):\n if(s in memo):\n return memo[s]\n ans=[]\n if(dc[s]==1):\n ans=[s]\n for i in range(1,len(s)):\n if(dc[s[:i]]==1):\n a=fun(s[i:],dc,memo)\n for x in a:\n ans.append(s[:i]+" "+x)\n memo[s]=ans\n return ans\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:\n dc=defaultdict(lambda:0)\n for a in wordDict:\n dc[a]=1\n return(fun(s,dc,{}))\n```\n\n```Java []\nclass Solution {\n private void helper(String s, int i, Set<String> dict, List<String> cur, List<String> res) {\n if (i == s.length()) {\n if (cur.size() > 0) {\n StringBuilder sb = new StringBuilder();\n for (int j = 0; j < cur.size(); j++) {\n if (j > 0) {\n sb.append(\' \');\n }\n sb.append(cur.get(j));\n }\n res.add(sb.toString());\n }\n return;\n }\n\n for (int j = i+1; j <= s.length(); j++) {\n if (dict.contains(s.substring(i, j))) {\n cur.add(s.substring(i, j));\n helper(s, j, dict, cur, res);\n cur.remove(cur.size() - 1);\n }\n }\n }\n public List<String> wordBreak(String s, List<String> wordDict) {\n Set<String> dict = new HashSet<>(wordDict);\n List<String> res = new ArrayList<>();\n List<String> cur = new ArrayList<>();\n helper(s, 0, dict, cur, res);\n return res;\n }\n}\n```\n | 223 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
Python (Simple DFS) | word-break-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wordBreak(self, s, wordDict):\n @lru_cache(None)\n def dfs(word,path):\n if not word:\n res.append(path[1:])\n\n for i in range(len(word)+1):\n prefix = word[:i]\n suffix = word[i:]\n\n if prefix in wordDict:\n dfs(suffix,path + " " + prefix)\n\n res = []\n\n dfs(s,"")\n\n return res\n\n \n \n \n \n \n \n \n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
recursion + DP always does the job | word-break-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nrecursive approach\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:high\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef fun(s,dc,memo):\n if(s in memo):\n return memo[s]\n ans=[]\n if(dc[s]==1):\n ans=[s]\n for i in range(1,len(s)):\n if(dc[s[:i]]==1):\n a=fun(s[i:],dc,memo)\n for x in a:\n ans.append(s[:i]+" "+x)\n memo[s]=ans\n return ans\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:\n dc=defaultdict(lambda:0)\n for a in wordDict:\n dc[a]=1\n return(fun(s,dc,{}))\n``` | 4 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
PYthon basic backtracking solution | word-break-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:\n hmap = {}\n for word in wordDict:hmap[word] = 1\n res = []\n def rec( i , lis ):\n nonlocal res ,s\n if( i == len(s)):\n res.append(" ".join(lis) );\n else:\n for k in range(i+1,len(s)+1):\n if(hmap.get(s[i:k]) ):\n lis.append(s[i:k] );\n rec(k,lis);\n lis.pop();\n rec(0,[])\n return res;\n``` | 2 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
Share my Trie and recursion solutionre | word-break-ii | 0 | 1 | \n# Code\n```\nclass Node:\n def __init__(self, ):\n self.children = {}\n self.is_word = False\n\nclass Trie:\n def __init__(self):\n self.root = Node()\n self.result = []\n\n def insert(self, word: str):\n node = self.root\n for w in word:\n if w not in node.children:\n node.children[w] = Node()\n node = node.children[w]\n node.is_word = True\n\n def search(self, word: str, path):\n if not word: # this path is valid \n self.result.append("".join(path).strip())\n return\n node = self.root\n for i, w in enumerate(word):\n path.append(w)\n if w not in node.children:\n return\n if node.children[w].is_word:\n self.search(word[i+1:], path+[" "]) # keep searching until all the is_word are consumed\n node = node.children[w]\n\n\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> bool:\n trie = Trie()\n for word in wordDict:\n trie.insert(word)\n \n trie.search(s, [])\n return trie.result\n \n\n \n \n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
Backtracking Extreme Simple (Time beats 99.40% | Space beats 82.11%) | word-break-ii | 0 | 1 | # Intuition\nChanged from the solution of Word Break I and adpated backtracking.\n\n# Approach\nJust standard backtracking. Removed cache from Word Break I code.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:\n ret = []\n len_s = len(s)\n\n def find(left, combo):\n if left == len_s:\n return ret.append(\' \'.join(combo))\n for word in wordDict:\n if s[left:].startswith(word):\n combo.append(word)\n find(left+len(word), combo)\n combo.pop()\n \n find(0, [])\n return ret\n``` | 1 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
140: Solution with step by step explanation | word-break-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe time complexity of this algorithm is O(n^3), where n is the length of the input string s. The space complexity is also O(n^3), due to the memoization dictionary. However, in practice, the space complexity will be much lower, as the memoization dictionary will only contain results for a small subset of all possible substrings of s.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:\n # Create a set of words for fast lookup\n word_set = set(wordDict)\n # Create a memoization dictionary to store previously calculated results\n memo = {}\n \n # Define a recursive function to find all possible sentences\n def dfs(s):\n # If the current string s has already been calculated, return the result\n if s in memo:\n return memo[s]\n \n # If the string s is empty, return an empty list\n if not s:\n return []\n \n # Initialize the result list\n res = []\n \n # Iterate over all possible splits of the string s\n for i in range(1, len(s) + 1):\n # If the left part of the split is a valid word\n if s[:i] in word_set:\n # Recursively find all possible sentences for the right part of the split\n right_sents = dfs(s[i:])\n # If there are any possible sentences for the right part of the split\n if right_sents:\n # Append the current word and all possible sentences for the right part of the split\n for right_sent in right_sents:\n res.append(s[:i] + " " + right_sent)\n # If there are no possible sentences for the right part of the split, but the right part is empty\n elif not s[i:]:\n # Append just the current word\n res.append(s[:i])\n \n # Store the result for the current string s in the memoization dictionary and return it\n memo[s] = res\n return res\n \n # Call the recursive function to find all possible sentences for the input string s\n return dfs(s)\n\n``` | 4 | Given a string `s` and a dictionary of strings `wordDict`, add spaces in `s` to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in **any order**.
**Note** that the same word in the dictionary may be reused multiple times in the segmentation.
**Example 1:**
**Input:** s = "catsanddog ", wordDict = \[ "cat ", "cats ", "and ", "sand ", "dog "\]
**Output:** \[ "cats and dog ", "cat sand dog "\]
**Example 2:**
**Input:** s = "pineapplepenapple ", wordDict = \[ "apple ", "pen ", "applepen ", "pine ", "pineapple "\]
**Output:** \[ "pine apple pen apple ", "pineapple pen apple ", "pine applepen apple "\]
**Explanation:** Note that you are allowed to reuse a dictionary word.
**Example 3:**
**Input:** s = "catsandog ", wordDict = \[ "cats ", "dog ", "sand ", "and ", "cat "\]
**Output:** \[\]
**Constraints:**
* `1 <= s.length <= 20`
* `1 <= wordDict.length <= 1000`
* `1 <= wordDict[i].length <= 10`
* `s` and `wordDict[i]` consist of only lowercase English letters.
* All the strings of `wordDict` are **unique**.
* Input is generated in a way that the length of the answer doesn't exceed 105. | null |
✅ 99.68% Two-Pointer & Hash Table | linked-list-cycle | 1 | 1 | # Interview Guide - Detecting Cycles in a Linked List: A Dual-Approach Analysis\n\n## Introduction & Problem Understanding\n\nDetecting cycles in a linked list is a classic problem that tests a developer\'s ability to understand and manipulate data structures. In this problem, you are given the head of a singly-linked list. The objective is to determine whether the list contains a cycle. A cycle exists if a node in the list can be visited more than once by following the `next` pointers continuously.\n\n### Key Concepts and Constraints\n\n1. **Node Anatomy**: \n Each node in the list contains an integer value and a `next` pointer that points to the subsequent node in the list.\n\n2. **Cycle Detection**: \n The primary task is to identify whether a cycle exists within the list. If a cycle is detected, the function should return `True`. Otherwise, it should return `False`.\n\n3. **Memory Efficiency**: \n The question poses an implicit challenge: Can you solve it using $$ O(1) $$ memory, meaning constant extra space?\n\n## Strategies to Tackle the Problem\n\n1. **Hash Table Method**: \nThis approach involves storing visited nodes in a hash table. During traversal, if a node is encountered that already exists in the hash table, a cycle is confirmed.\n\n2. **Two-Pointers Method (Floyd\'s Cycle-Finding Algorithm)**: \nAlso known as the "hare and tortoise" algorithm, this method employs two pointers that move at different speeds. If there is a cycle, the fast pointer will eventually catch up to the slow pointer, confirming the cycle\'s existence.\n\n---\n\n# Live Coding 2 Solution & More\nhttps://youtu.be/ew-E3mHOBT0?si=DTvrijJplAk7XV1w\n\n## Solution #1: Hash Table Method\n\n### Intuition and Logic Behind the Solution\n\nThe basic idea here is to traverse the list and keep a record of the nodes we\'ve visited so far. If at any point we encounter a node that we\'ve already visited, we can conclude that there is a cycle in the list.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Create an empty set, `visited_nodes`, to keep track of the nodes that have been visited.\n\n2. **Traversal and Verification**: \n - Traverse the list starting from the head node.\n - At each node, check whether it already exists in `visited_nodes`.\n - If it does, return `True` as a cycle is detected.\n - Otherwise, add the node to `visited_nodes`.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(n) $$ \u2014 Each node is visited once.\n- **Space Complexity**: $$ O(n) $$ \u2014 To store visited nodes.\n\n---\n\n## Solution #2: Two-Pointer Method (Floyd\'s Cycle-Finding Algorithm)\n\n### Intuition and Logic Behind the Solution\n\nAlso known as the "hare and tortoise" algorithm, this method uses two pointers that traverse the list at different speeds. The slow pointer moves one step at a time, while the fast pointer moves two steps. If there is a cycle, the fast pointer will eventually catch up to the slow pointer.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Initialize two pointers, `slow_pointer` and `fast_pointer`, both pointing to the head node initially.\n\n2. **Cycle Detection**: \n - Traverse the list until the `fast_pointer` or its `next` becomes `None`.\n - Update `slow_pointer` and `fast_pointer` as follows:\n - `slow_pointer = slow_pointer.next`\n - `fast_pointer = fast_pointer.next.next`\n - If `slow_pointer` and `fast_pointer` meet at some point, return `True`.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(n) $$ \u2014 In the worst-case scenario, each node is visited once.\n- **Space Complexity**: $$ O(1) $$ \u2014 Constant space is used.\n\n---\n\n\n# Performance\n\n### Two-Pointers\n\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|-----------|---------------------|-------------------|\n| Java | 0 | 44 |\n| Go | 8 | 4.4 |\n| PHP | 10 | 22.7 |\n| C++ | 11 | 8.2 |\n| Python3 | 41 | 20.6 |\n| JavaScript| 65 | 45 |\n| C# | 84 | 43 |\n\n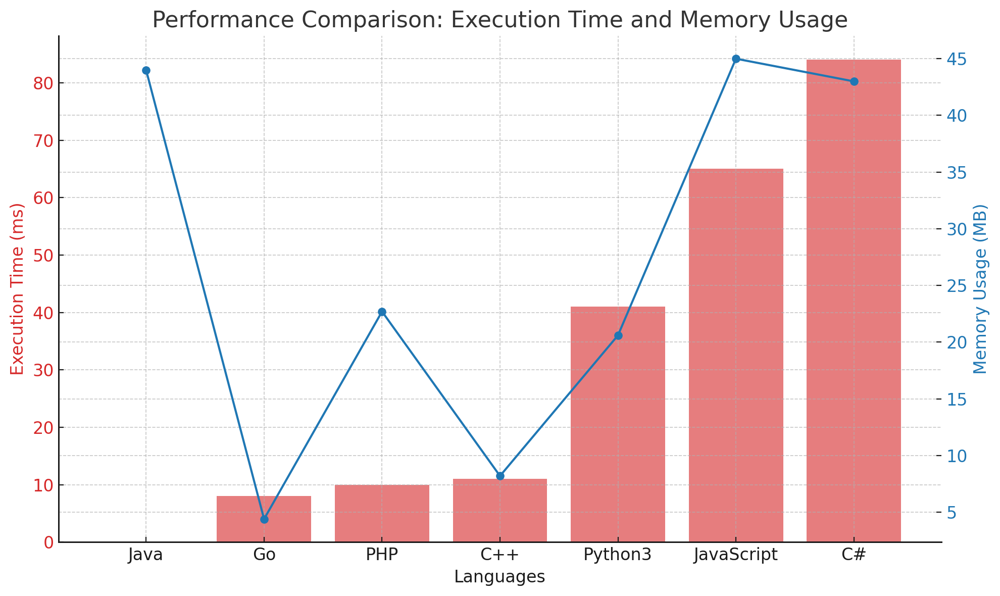\n\n### Hash Table\n\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|-----------|---------------------|-------------------|\n| Java | 4 | 43.7 |\n| Go | 10 | 6.2 |\n| C++ | 18 | 10.5 |\n| Python3 | 49 | 20.7 |\n| C# | 82 | 44.9 |\n| JavaScript| 69 | 45.9 |\n| PHP | 432 | 22.8 |\n\n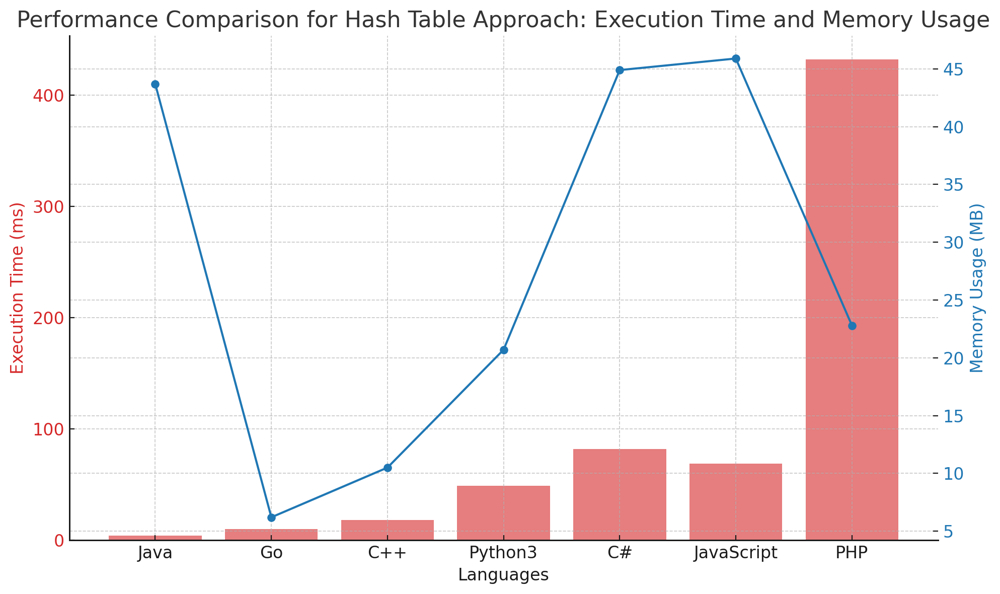\n\n\n# Code Two-Pointer\n``` Python []\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n slow_pointer = head\n fast_pointer = head\n while fast_pointer and fast_pointer.next:\n slow_pointer = slow_pointer.next\n fast_pointer = fast_pointer.next.next\n if slow_pointer == fast_pointer:\n return True\n return False\n```\n``` C++ []\nclass Solution {\npublic:\n bool hasCycle(ListNode *head) {\n ListNode *slow_pointer = head, *fast_pointer = head;\n while (fast_pointer != nullptr && fast_pointer->next != nullptr) {\n slow_pointer = slow_pointer->next;\n fast_pointer = fast_pointer->next->next;\n if (slow_pointer == fast_pointer) {\n return true;\n }\n }\n return false;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean hasCycle(ListNode head) {\n ListNode slow_pointer = head, fast_pointer = head;\n while (fast_pointer != null && fast_pointer.next != null) {\n slow_pointer = slow_pointer.next;\n fast_pointer = fast_pointer.next.next;\n if (slow_pointer == fast_pointer) {\n return true;\n }\n }\n return false;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool HasCycle(ListNode head) {\n ListNode slow_pointer = head, fast_pointer = head;\n while (fast_pointer != null && fast_pointer.next != null) {\n slow_pointer = slow_pointer.next;\n fast_pointer = fast_pointer.next.next;\n if (slow_pointer == fast_pointer) {\n return true;\n }\n }\n return false;\n }\n}\n```\n``` Go []\nfunc hasCycle(head *ListNode) bool {\n slow_pointer, fast_pointer := head, head\n for fast_pointer != nil && fast_pointer.Next != nil {\n slow_pointer = slow_pointer.Next\n fast_pointer = fast_pointer.Next.Next\n if slow_pointer == fast_pointer {\n return true\n }\n }\n return false\n}\n```\n``` JavaScript []\n/**\n * @param {ListNode} head\n * @return {boolean}\n */\nvar hasCycle = function(head) {\n let slow_pointer = head, fast_pointer = head;\n while (fast_pointer !== null && fast_pointer.next !== null) {\n slow_pointer = slow_pointer.next;\n fast_pointer = fast_pointer.next.next;\n if (slow_pointer === fast_pointer) {\n return true;\n }\n }\n return false;\n};\n```\n``` PHP []\nclass Solution {\n function hasCycle($head) {\n $slow_pointer = $head;\n $fast_pointer = $head;\n while ($fast_pointer !== null && $fast_pointer->next !== null) {\n $slow_pointer = $slow_pointer->next;\n $fast_pointer = $fast_pointer->next->next;\n if ($slow_pointer === $fast_pointer) {\n return true;\n }\n }\n return false;\n }\n}\n```\n# Code Hash Table\n``` Python []\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n visited_nodes = set()\n current_node = head\n while current_node:\n if current_node in visited_nodes:\n return True\n visited_nodes.add(current_node)\n current_node = current_node.next\n return False \n```\n``` Go []\nfunc hasCycle(head *ListNode) bool {\n visited_nodes := make(map[*ListNode]bool)\n current_node := head\n for current_node != nil {\n if visited_nodes[current_node] {\n return true\n }\n visited_nodes[current_node] = true\n current_node = current_node.Next\n }\n return false\n}\n```\n``` C++ []\nclass Solution {\npublic:\n bool hasCycle(ListNode *head) {\n std::unordered_set<ListNode*> visited_nodes;\n ListNode *current_node = head;\n while (current_node != nullptr) {\n if (visited_nodes.find(current_node) != visited_nodes.end()) {\n return true;\n }\n visited_nodes.insert(current_node);\n current_node = current_node->next;\n }\n return false;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean hasCycle(ListNode head) {\n HashSet<ListNode> visited_nodes = new HashSet<>();\n ListNode current_node = head;\n while (current_node != null) {\n if (visited_nodes.contains(current_node)) {\n return true;\n }\n visited_nodes.add(current_node);\n current_node = current_node.next;\n }\n return false;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool HasCycle(ListNode head) {\n HashSet<ListNode> visited_nodes = new HashSet<ListNode>();\n ListNode current_node = head;\n while (current_node != null) {\n if (visited_nodes.Contains(current_node)) {\n return true;\n }\n visited_nodes.Add(current_node);\n current_node = current_node.next;\n }\n return false;\n }\n}\n```\n``` PHP []\nclass Solution {\n function hasCycle($head) {\n $visited_nodes = [];\n $current_node = $head;\n while ($current_node !== null) {\n if (in_array($current_node, $visited_nodes, true)) {\n return true;\n }\n $visited_nodes[] = $current_node;\n $current_node = $current_node->next;\n }\n return false;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {ListNode} head\n * @return {boolean}\n */\nvar hasCycle = function(head) {\n let visited_nodes = new Set();\n let current_node = head;\n while (current_node !== null) {\n if (visited_nodes.has(current_node)) {\n return true;\n }\n visited_nodes.add(current_node);\n current_node = current_node.next;\n }\n return false;\n};\n```\n\n# Live Coding with Comments\nhttps://youtu.be/aGbOOAKkhNo?si=IoPNL49uVessMpCv\n\n# Reflections on Cycle Detection\n\nBoth the Hash Table and Two-Pointers methods offer compelling strategies for detecting cycles in linked lists.\n\n1. **Hash Table Method**: \n Intuitive and adaptable, though potentially memory-intensive.\n \n2. **Two-Pointers Method**: \n A marvel of memory efficiency, but perhaps less straightforward to the uninitiated.\n\nNavigating this problem is a dive into data structure nuances and algorithmic elegance. Whether you appreciate the directness of the Hash Table or the finesse of Two-Pointers, each method champions a facet of computational acumen. This isn\'t just a problem; it\'s a step in honing algorithmic artistry. Embrace the challenge! \uD83D\uDE80\uD83C\uDF1F | 122 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
[VIDEO] Visualization of Tortoise and Hare (Floyd's Cycle Detection) Solution | linked-list-cycle | 0 | 1 | https://youtu.be/RRSItF-Ts4Q\n\nThe last pointer in a linked list usually points to a null value to singal the end of the list, but if the last pointer points back to another node in the linked list instead, we now have a cycle. The most common way to solve this problem is by using the Tortoise and Hare algorithm.\n\nThe idea is that we create two pointers, a slow one and a fast one. The slow pointer traverses the linked list 1 node at a time, while the fast pointer traverses the linked list 2 nodes at a time. If at some point the two pointers meet on the same node, then that means a cycle exists.\n\nWhy does this work? For a visual animation, please see the video, but for a simple explanation, think of two people running on a circular track. If both people run and one of them runs faster than the other, then the faster person will eventually catch up to the slower one and "lap" them. In other words, they will be back at the same position again. This is what we\'re looking for in the algorithm and it\'s how we detect a cycle. \n\n# Code\n```\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n fast = head\n while fast and fast.next:\n head = head.next\n fast = fast.next.next\n if head is fast:\n return True\n return False\n``` | 7 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
【Video】Solution with two pointers and a bonus video - Python, JavaScript, Java, C++ | linked-list-cycle | 1 | 1 | # Intuition\nThe main idea to solve the question of detecting a cycle in a singly-linked list is to use the concept of two pointers: a "slow" pointer that moves one step at a time and a "fast" pointer that moves two steps at a time. By having these two pointers traverse the list simultaneously, if there is a cycle, the fast pointer will eventually catch up to the slow pointer. If there is no cycle, the fast pointer will reach the end of the list.\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 254 videos as of September 4th, 2023.\n\nhttps://youtu.be/AwlrFqjq0cY\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nThe next subscriber will be exact 2200.\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize `fast` and `slow` pointers to the head of the linked list.\n - `fast` and `slow` are initially pointing to the head of the linked list, which is the starting point.\n\n2. Enter a loop while both `fast` and `fast.next` are not null.\n - This loop will continue until either `fast` or `fast.next` becomes null, indicating the end of the linked list or if there is no cycle.\n\n3. Move the `fast` pointer two steps ahead (`fast = fast.next.next`) and the `slow` pointer one step ahead (`slow = slow.next`).\n - This step simulates the two-pointer traversal where `fast` moves twice as fast as `slow`.\n\n4. Check if `fast` is equal to `slow`.\n - If `fast` and `slow` pointers meet at the same node, it means there is a cycle in the linked list, and we return `True`.\n\n5. If the loop exits without finding a cycle, return `False`.\n - If the loop completes without finding a cycle, it means that the `fast` pointer has reached the end of the list, and there is no cycle. In this case, we return `False`.\n\nThis algorithm uses two pointers, `fast` and `slow`, to traverse the linked list. The `fast` pointer moves twice as fast as the `slow` pointer. If there is a cycle, the `fast` pointer will eventually catch up to the `slow` pointer. If there is no cycle, the `fast` pointer will reach the end of the list, and the function will return `False`. This algorithm is an efficient way to detect cycles in a singly-linked list.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n```python []\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n \n fast = head\n slow = head\n \n while fast and fast.next:\n fast = fast.next.next\n slow = slow.next\n \n if fast == slow:\n return True\n \n return False\n```\n```javascript []\nvar hasCycle = function(head) {\n let fast = head;\n let slow = head;\n\n while (fast && fast.next) {\n fast = fast.next.next;\n slow = slow.next;\n\n if (fast === slow) {\n return true;\n }\n }\n\n return false; \n};\n```\n```java []\npublic class Solution {\n public boolean hasCycle(ListNode head) {\n ListNode fast = head;\n ListNode slow = head;\n\n while (fast != null && fast.next != null) {\n fast = fast.next.next;\n slow = slow.next;\n\n if (fast == slow) {\n return true;\n }\n }\n\n return false; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool hasCycle(ListNode *head) {\n ListNode* fast = head;\n ListNode* slow = head;\n\n while (fast != nullptr && fast->next != nullptr) {\n fast = fast->next->next;\n slow = slow->next;\n\n if (fast == slow) {\n return true;\n }\n }\n\n return false; \n }\n};\n```\n | 23 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Using List | linked-list-cycle | 0 | 1 | I just add the each address in the list for every node if an address repeated i.e already existed in the list than I just simply return True . If linked list\'s head reached to the end than return true\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n address = []\n curr = head\n while(curr is not None):\n address.append(curr)\n curr = curr.next\n if(curr in address):\n return True\n return False\n \n \n``` | 1 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Simple Python solution using slow-fast pointer | linked-list-cycle | 0 | 1 | \n# Code\n```\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n slow = fast = head\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n if slow == fast:\n return True\n return False\n``` | 4 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
REALLY EASY 🏀 + 📦 = SLAM DUNK!! | linked-list-cycle | 0 | 1 | \n\n\n\nFirst, you can have a visited dictionary(you have to use defaultdict)\nThen, you kind of go through the list.\nIf you found an already-visited node, return True\notherwise, move pointer forward, visit that node\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ???\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n curr = head\n visited = collections.defaultdict(lambda: False)\n while curr:\n if visited[curr] == True:\n return True\n visited[curr] = True\n curr = curr.next\n return False\n``` | 1 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Easy Solution | linked-list-cycle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n a=b=head\n while(a!=None and a.next!=None):\n b=b.next\n a=a.next.next\n if(a==b):\n return True\n return False\n``` | 2 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
using Floyd's Tortoise and Hare algorithm | Simplest Solution | linked-list-cycle | 0 | 1 | # Intuition\nUsing Slow and Fast pointers to detect a cycle.\n\n# Approach\nYou can create a linked list using the ListNode class and pass the head of the list to the hasCycle function. It will return True if there is a cycle in the linked list and False otherwise. The algorithm works by moving two pointers at different speeds through the linked list. If there is a cycle, the two pointers will eventually meet at the same node.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n if head== None or head.next == None:\n return False\n \n slow=head\n fast=head.next\n\n while slow!=fast:\n if fast==None or fast.next == None:\n return False\n slow=slow.next\n fast=fast.next.next\n\n return True\n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Python | 2 Pointer | Easy to Understand | linked-list-cycle | 0 | 1 | # Python | 2 Pointer | Easy to Understand\n```\nclass Solution:\n def hasCycle(self, head: ListNode) -> bool:\n if not head:\n return False\n slow = head\n fast = head.next\n while slow != fast:\n if not fast or not fast.next:\n return False\n slow = slow.next\n fast = fast.next.next\n return True\n``` | 4 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Beats 98%✅ | O( n )✅ | Python (Step by step explanation)✅ | linked-list-cycle | 0 | 1 | # Intuition\nThe problem is to detect whether there is a cycle in a linked list. The intuition is to use two pointers, one slow and one fast, to traverse the linked list. If there is a cycle, the fast pointer will eventually catch up to the slow pointer.\n\n# Approach\n1. Initialize two pointers, `slow` and `fast`, to the head of the linked list.\n2. Use a while loop to traverse the linked list. In each iteration, move the `slow` pointer one step and the `fast` pointer two steps. If there is a cycle, the `fast` pointer will eventually catch up to the `slow` pointer.\n3. If at any point `slow` becomes equal to `fast`, it means there is a cycle, and the function returns `True`.\n4. If the `fast` pointer reaches the end of the linked list (i.e., `fast` or `fast.next` is `None`), it means there is no cycle, and the function returns `False`.\n\n# Complexity\n- Time complexity: O(n) - The slow pointer traverses the linked list once.\n- Space complexity: O(1) - We only use two pointers.\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def hasCycle(self, head: Optional[ListNode]) -> bool:\n slow , fast = head , head\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n\n if slow == fast:\n return True\n\n return False\n \n \n```\n\n# Please upvote the solution if you understood it.\n\n | 2 | Given `head`, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to. **Note that `pos` is not passed as a parameter**.
Return `true` _if there is a cycle in the linked list_. Otherwise, return `false`.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** true
**Explanation:** There is a cycle in the linked list, where the tail connects to the 0th node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** false
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Clean Codes🔥🔥|| Full Explanation✅|| Floyd's Cycle-Finding algorithm✅|| C++|| Java|| Python3 | linked-list-cycle-ii | 1 | 1 | # Intuition :\n- Use a **Floyd\'s Cycle-Finding algorithm** to detect a cycle in a linked list and find the node where the cycle starts.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# What is Floyd\'s Cycle-Finding algorithm ?\n- It is also called **Hare-Tortoise algorithm**\n- The algorithm works by using two pointers, a slow pointer and a fast pointer. \n- Initially, both pointers are set to the head of the linked list. \n- The fast pointer moves twice as fast as the slow pointer. \n- If there is a cycle in the linked list, eventually, the fast pointer will catch up with the slow pointer. \n- If there is no cycle, the fast pointer will reach the end of the linked list.\n# Approach :\n- When the two pointers meet, we know that there is a cycle in the linked list. \n- We then reset the slow pointer to the head of the linked list and move both pointers at the same pace, one step at a time, until they meet again. \n- The node where they meet is the starting point of the cycle.\n- If there is no cycle in the linked list, the algorithm will return null.\n<!-- Describe your approach to solving the problem. -->\n# Let\'s understand this with an Example :\n- Let\'s say we have a linked list with a cycle, like the one below:\n```\n1 -> 2 -> 3 -> 4 -> 5 -> 2\n```\n- To detect the cycle and find the starting point, we use two pointers, a slow pointer and a fast pointer, initially set to the head of the linked list.\n```\nslow = 1\nfast = 1\n```\n- Then we move the pointers through the linked list. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time.\n```\nslow = 2\nfast = 3\n\nslow = 3\nfast = 5\n\nslow = 4\nfast = 2\n```\n- Eventually, the fast pointer will catch up with the slow pointer, which means that there is a cycle in the linked list.\n```\nslow = 5\nfast = 4\n```\n- At this point, we reset the slow pointer to the head of the linked list, and move both pointers one step at a time until they meet again.\n```\nslow = 1\nfast = 4\n\nslow = 2\nfast = 5\n\nslow = 3\nfast = 2\n```\n- The node where they meet is the starting point of the cycle, which in this case is node 2.\n- So, the algorithm returns node 2 as the starting point of the cycle.\n- I hope this visual explanation helps you understand the Floyd\'s Cycle-Finding algorithm better.\n# Complexity :\n- Time complexity : O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] : With Comments\n```Java []\npublic class Solution {\n public ListNode detectCycle(ListNode head) {\n // Initialize two pointers, slow and fast, to the head of the linked list.\n ListNode slow = head;\n ListNode fast = head;\n\n // Move the slow pointer one step and the fast pointer two steps at a time through the linked list,\n // until they either meet or the fast pointer reaches the end of the list.\n while (fast != null && fast.next != null) {\n slow = slow.next;\n fast = fast.next.next;\n if (slow == fast) {\n // If the pointers meet, there is a cycle in the linked list.\n // Reset the slow pointer to the head of the linked list, and move both pointers one step at a time\n // until they meet again. The node where they meet is the starting point of the cycle.\n slow = head;\n while (slow != fast) {\n slow = slow.next;\n fast = fast.next;\n }\n return slow;\n }\n }\n\n // If the fast pointer reaches the end of the list without meeting the slow pointer,\n // there is no cycle in the linked list. Return null.\n return null;\n }\n}\n\n```\n```C++ []\nclass Solution {\n public:\n ListNode* detectCycle(ListNode* head) {\n // Initialize two pointers, slow and fast, to the head of the linked list.\n ListNode* slow = head;\n ListNode* fast = head;\n\n // Move the slow pointer one step and the fast pointer two steps at a time through the linked list,\n // until they either meet or the fast pointer reaches the end of the list.\n while (fast && fast->next) {\n slow = slow->next;\n fast = fast->next->next;\n if (slow == fast) {\n // If the pointers meet, there is a cycle in the linked list.\n // Reset the slow pointer to the head of the linked list, and move both pointers one step at a time\n // until they meet again. The node where they meet is the starting point of the cycle.\n slow = head;\n while (slow != fast) {\n slow = slow->next;\n fast = fast->next;\n }\n return slow;\n }\n }\n\n // If the fast pointer reaches the end of the list without meeting the slow pointer,\n // there is no cycle in the linked list. Return nullptr.\n return nullptr;\n }\n};\n\n```\n```Python []\nclass Solution:\n def detectCycle(self, head: ListNode) -> ListNode:\n # Initialize two pointers, slow and fast, to the head of the linked list.\n slow = head\n fast = head\n\n # Move the slow pointer one step and the fast pointer two steps at a time through the linked list,\n # until they either meet or the fast pointer reaches the end of the list.\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n if slow == fast:\n # If the pointers meet, there is a cycle in the linked list.\n # Reset the slow pointer to the head of the linked list, and move both pointers one step at a time\n # until they meet again. The node where they meet is the starting point of the cycle.\n slow = head\n while slow != fast:\n slow = slow.next\n fast = fast.next\n return slow\n\n # If the fast pointer reaches the end of the list without meeting the slow pointer,\n # there is no cycle in the linked list. Return None.\n return None\n\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 400 | Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
**Do not modify** the linked list.
**Example 1:**
**Input:** head = \[3,2,0,-4\], pos = 1
**Output:** tail connects to node index 1
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
**Example 2:**
**Input:** head = \[1,2\], pos = 0
**Output:** tail connects to node index 0
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
**Example 3:**
**Input:** head = \[1\], pos = -1
**Output:** no cycle
**Explanation:** There is no cycle in the linked list.
**Constraints:**
* The number of the nodes in the list is in the range `[0, 104]`.
* `-105 <= Node.val <= 105`
* `pos` is `-1` or a **valid index** in the linked-list.
**Follow up:** Can you solve it using `O(1)` (i.e. constant) memory? | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.