title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python "O(1)" spatial complexity | reverse-words-in-a-string | 0 | 1 | # Intuition\n\nExample :\n```\n"ABCDEF 123 abc" (input)\n"abc 123 ABCDEF" (expected output)\n```\n\n\nIf you try to reverse the input you will get :\n```\n"cba 321 FEDCBA"\n```\nNow compare the reversed with expected output :\n```\n"cba 321 FEDCBA"\n | | |\n"abc 123 ABCDEF" (expected output)\n```\nYou see you only need to reverse each words to get the expected output.\n\n\n# Approach\n\n- Reverse all the input (reverseOneWord function).\n- Reverse each word (reverseWords function).\n- Supress the space series (deleteSpacesSeries function using two pointer method to stay in O(1) in spatial complexity).\n\n# Complexity\n- Time complexity: O(n)\n- Spatial complextiy: O(1) if we don\'t take account of str to list conversion (in fact you can\'t get O(1) in python because the conversion is O(n) and you need it because str are immuable in python) and list to str\n\n# Code\n```\nclass Solution:\n def reverseOneWord(self, s: list, debut: int, fin: int):\n i = 0\n while i < (fin-debut)//2:\n s[debut+i],s[fin-1-i]=s[fin-1-i],s[debut+i]\n i+=1\n\n def deleteSpacesSeries(self, s: list):\n i = len(s)-1\n while i>=0 and s[i]==" ":\n s.pop()\n i-=1\n\n i = 0\n while i < len(s) and s[i]==" ":\n i+=1\n\n write_i = 0\n\n while i < len(s):\n if not (s[i-1]==s[i]==" "):\n s[write_i] = s[i]\n write_i += 1\n i += 1\n\n\n for _ in range(len(s)-write_i):\n s.pop()\n\n\n\n def reverseWords(self, s: str) -> str:\n s = list(s)\n\n self.reverseOneWord(s, 0, len(s))\n\n i = 0\n motDebut = 0\n motFin = 0\n estMotFini = False\n\n while i < len(s):\n if s[i]==" ":\n if estMotFini:\n self.reverseOneWord(s, motDebut, motFin+1)\n estMotFini = False\n else:\n if not estMotFini:\n estMotFini = True\n motDebut = i\n motFin = i\n else:\n motFin += 1\n i+=1\n\n if estMotFini:\n self.reverseOneWord(s, motDebut, motFin+1)\n\n self.deleteSpacesSeries(s)\n\n return "".join(s)\n``` | 12 | Given an input string `s`, reverse the order of the **words**.
A **word** is defined as a sequence of non-space characters. The **words** in `s` will be separated by at least one space.
Return _a string of the words in reverse order concatenated by a single space._
**Note** that `s` may contain leading or trailing spaces or multiple spaces between two words. The returned string should only have a single space separating the words. Do not include any extra spaces.
**Example 1:**
**Input:** s = "the sky is blue "
**Output:** "blue is sky the "
**Example 2:**
**Input:** s = " hello world "
**Output:** "world hello "
**Explanation:** Your reversed string should not contain leading or trailing spaces.
**Example 3:**
**Input:** s = "a good example "
**Output:** "example good a "
**Explanation:** You need to reduce multiple spaces between two words to a single space in the reversed string.
**Constraints:**
* `1 <= s.length <= 104`
* `s` contains English letters (upper-case and lower-case), digits, and spaces `' '`.
* There is **at least one** word in `s`.
**Follow-up:** If the string data type is mutable in your language, can you solve it **in-place** with `O(1)` extra space? | null |
Reverse Words in a String Easy Solution beats 85% | reverse-words-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseWords(self, s: str) -> str:\n t=s.strip(" ")\n l=t.split(" ")\n p=[]\n for i in l:\n if(i!=""):\n p.append(i)\n m=""\n for i in p[::-1]:\n m=m+i+" "\n return m.rstrip()\n``` | 1 | Given an input string `s`, reverse the order of the **words**.
A **word** is defined as a sequence of non-space characters. The **words** in `s` will be separated by at least one space.
Return _a string of the words in reverse order concatenated by a single space._
**Note** that `s` may contain leading or trailing spaces or multiple spaces between two words. The returned string should only have a single space separating the words. Do not include any extra spaces.
**Example 1:**
**Input:** s = "the sky is blue "
**Output:** "blue is sky the "
**Example 2:**
**Input:** s = " hello world "
**Output:** "world hello "
**Explanation:** Your reversed string should not contain leading or trailing spaces.
**Example 3:**
**Input:** s = "a good example "
**Output:** "example good a "
**Explanation:** You need to reduce multiple spaces between two words to a single space in the reversed string.
**Constraints:**
* `1 <= s.length <= 104`
* `s` contains English letters (upper-case and lower-case), digits, and spaces `' '`.
* There is **at least one** word in `s`.
**Follow-up:** If the string data type is mutable in your language, can you solve it **in-place** with `O(1)` extra space? | null |
99.94% Beats, Simplest Reverse String Solution in Python3 | reverse-words-in-a-string | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n Here\'s an explanation of the approach used in this code:\n\n1. s.split(): The split() method is used to split the input string s into a list of words. By default, it splits the string at spaces (whitespace characters), effectively separating the words. For example, "Hello World" becomes ["Hello", "World"].\n\n2. s[::-1]: After splitting the string into words, the list of words is reversed using slicing with [::-1]. This reverses the order of elements in the list, effectively reversing the order of words. For example, ["Hello", "World"] becomes ["World", "Hello"].\n\n3. " ".join(...): Finally, the reversed list of words is joined back into a single string using the join() method. This method joins the elements of the list using a space as a separator, effectively creating a string with the reversed word order. For example, ["World", "Hello"] becomes "World Hello".\n# Complexity\n- Time complexity: O(n + m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseWords(self, s: str) -> str:\n s= s.split()\n return " ".join(s[::-1])\n``` | 6 | Given an input string `s`, reverse the order of the **words**.
A **word** is defined as a sequence of non-space characters. The **words** in `s` will be separated by at least one space.
Return _a string of the words in reverse order concatenated by a single space._
**Note** that `s` may contain leading or trailing spaces or multiple spaces between two words. The returned string should only have a single space separating the words. Do not include any extra spaces.
**Example 1:**
**Input:** s = "the sky is blue "
**Output:** "blue is sky the "
**Example 2:**
**Input:** s = " hello world "
**Output:** "world hello "
**Explanation:** Your reversed string should not contain leading or trailing spaces.
**Example 3:**
**Input:** s = "a good example "
**Output:** "example good a "
**Explanation:** You need to reduce multiple spaces between two words to a single space in the reversed string.
**Constraints:**
* `1 <= s.length <= 104`
* `s` contains English letters (upper-case and lower-case), digits, and spaces `' '`.
* There is **at least one** word in `s`.
**Follow-up:** If the string data type is mutable in your language, can you solve it **in-place** with `O(1)` extra space? | null |
Python3 faster than 97%, without using split | reverse-words-in-a-string | 0 | 1 | ```\nclass Solution:\n def reverseWords(self, s: str) -> str:\n res = []\n temp = ""\n for c in s:\n if c != " ":\n temp += c \n elif temp != "":\n res.append(temp)\n temp = ""\n if temp != "":\n res.append(temp)\n return " ".join(res[::-1])\n``` | 32 | Given an input string `s`, reverse the order of the **words**.
A **word** is defined as a sequence of non-space characters. The **words** in `s` will be separated by at least one space.
Return _a string of the words in reverse order concatenated by a single space._
**Note** that `s` may contain leading or trailing spaces or multiple spaces between two words. The returned string should only have a single space separating the words. Do not include any extra spaces.
**Example 1:**
**Input:** s = "the sky is blue "
**Output:** "blue is sky the "
**Example 2:**
**Input:** s = " hello world "
**Output:** "world hello "
**Explanation:** Your reversed string should not contain leading or trailing spaces.
**Example 3:**
**Input:** s = "a good example "
**Output:** "example good a "
**Explanation:** You need to reduce multiple spaces between two words to a single space in the reversed string.
**Constraints:**
* `1 <= s.length <= 104`
* `s` contains English letters (upper-case and lower-case), digits, and spaces `' '`.
* There is **at least one** word in `s`.
**Follow-up:** If the string data type is mutable in your language, can you solve it **in-place** with `O(1)` extra space? | null |
✅ 0ms Beats 100% [Rust/Python/C++/Java] Simple DP Solution | maximum-product-subarray | 1 | 1 | # Intuition\nThis problem is really similar to [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/) except instead of a sum it\'s a product, so naturally, a DP solution also comes to mind.\n\n<hr>\n\n## \u274C Solution #1: Brute Force [TLE]\n\nIt\'s not a bad idea to start with a naive brute force solution and then optimize from there. Similar to Maximum Subarray, you can try iterating over all subarrays and then calculating the product\n\n```python\nfor i in range(n):\n prod = 1\n for j in range(i, n):\n prod *= nums[j]\n ans = max(ans, prod)\n```\n\n- Time complexity: $\\mathcal{O}(n^2)$ since we check every subarray\n- Space complexity: $\\mathcal{O}(1)$ since we only operate on the given nums array\n\n## \u2714\uFE0F Solution #2: Dynamic Programming\n\nInstead of trying to brute force all subarrays, we can think of building each solution by improving on a smaller subproblem. More concretely, a better maximum product subarray can either be one of two things\n1. Previous subarrays were better (in which case, we leave the solution as is)\n2. Including the current value by adding the current value into an ongoing subarray and increase the running product\n\nCase 1 is easy \u2013\xA0we just keep a running max. However, case 2 is a bit finnicky because unlike maximum subarray, we need to consider negative numbers.\n\n**Problems**\n\nConsider the case of\n```\nnums = [2, -2, 2, -2]\n```\n\nIf our subarray includes an even number of negative numbers (e.g. 2 or 4 negative numbers), the product will still end up positive. This means we can\'t only add positive numbers to our subarray, as the optimal solution above would be $2 \\times -2 \\times 2 \\times -2 = 16$\n\nAnother problem is when you hit a zero. Any time your subarray hits a zero, the running product gets cancelled out to a zero.\n\nWith that said, let\'s revisit the DP solution to Maximum Subarray: Kandane\'s Algorithm. In Kandane\'s, we keep track of two variables, the maximum subarray sum and the current subarray sum. We update the current subarray sum, and if it ever becomes 0 or less, we start another subarray. Every time we update the subarray, we also update the max subarray sum.\n\n**Approach**\n\nIn this question, we need to keep track of two subarrays: the subarray with the maximum product so far and the subarray with the minimum product so far. Why do we need to keep track of the minimum product? To handle the negative case. Let\'s revisit that negative subarray again:\n\n```\nnums = [2, -2, 2, -2]\n```\n\nWhen we are 3 indices in `[2, -2, 2]`, the running product of all 3 elements is negative. The maximum product so far is 2 (just a singular element in the subarray), but the minimum subarray is `[2 -2 2]` with a product of -8. Now, when we calculate the solution for all 4 indices, we consider both the max product and the min product to get 16.\n\nThere are 3 DP cases to consider\n1. Restart new subarray\n - Set the running product to be just the current element\n - This handles the case with 0s\n2. Add current element to the current subarray with the minimum product\n - Set running product to be minimum_product * value\n3. Add current element to the current subarray with the maximum product\n - Set running product to be maximum_product * value\n\nThus, both our min and max subarrays we keep track of need to consider all three of these cases. Our DP equations can be formulated as follows\n\n```\nmin_prod = min(value, value * old_min_prod, value * old_max_prod)\nmax_prod = max(value, value * old_min_prod, value * old_max_prod)\nanswer = max(max_prod, answer)\n```\n\n<hr>\n\n# Complexity\n- Time complexity: $\\mathcal{O}(n)$ where n is the size of the list. We only iterate once over the list with bottom-up DP and update our two products as we go. \n\n- Space complexity: $\\mathcal{O}(1)$ since we work off of the given nums list.\n\n<hr>\n\n## Solutions\n\n```rust []\nimpl Solution {\n pub fn max_product(nums: Vec<i32>) -> i32 {\n if nums.is_empty() {\n return 0;\n }\n \n let mut min_prod: i32 = nums[0];\n let mut max_prod: i32 = nums[0];\n let mut ans: i32 = nums[0];\n\n for (index, value) in nums.iter().enumerate().skip(1) {\n let test_max_prod: i32 = max_prod * *value;\n let test_min_prod: i32 = min_prod * *value;\n\n max_prod = test_min_prod.max(test_max_prod).max(*value);\n min_prod = test_max_prod.min(test_min_prod).min(*value);\n\n ans = ans.max(max_prod);\n }\n\n ans\n }\n}\n```\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n min_prod = max_prod = ans = nums[0]\n\n for value in nums[1:]:\n max_temp = max_prod * value\n min_temp = min_prod * value\n\n min_prod = min(max_temp, min_temp, value)\n max_prod = max(max_temp, min_temp, value)\n \n ans = max(ans, max_prod)\n\n return ans\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int minProd = nums[0], maxProd = nums[0];\n int ans = nums[0];\n\n int testMaxProd, testMinProd;\n for (int i = 1; i < nums.length; i++) {\n testMaxProd = maxProd * nums[i];\n testMinProd = minProd * nums[i];\n\n maxProd = Math.max(Math.max(testMaxProd, testMinProd), nums[i]);\n minProd = Math.min(Math.min(testMaxProd, testMinProd), nums[i]);\n\n ans = Math.max(ans, maxProd);\n }\n\n return ans;\n }\n}\n```\n```cpp []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int minProd = nums[0], maxProd = nums[0], ans = nums[0];\n\n for (auto i = 1; i < nums.size(); i++) {\n int value = nums[i];\n\n int testMaxProd = maxProd * value;\n int testMinProd = minProd * value;\n\n maxProd = max({testMaxProd, testMinProd, value});\n minProd = min({testMaxProd, testMinProd, value});\n\n ans = max(ans, maxProd);\n }\n\n return ans;\n }\n};\n```\n | 2 | Given an integer array `nums`, find a subarray that has the largest product, and return _the product_.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,3,-2,4\]
**Output:** 6
**Explanation:** \[2,3\] has the largest product 6.
**Example 2:**
**Input:** nums = \[-2,0,-1\]
**Output:** 0
**Explanation:** The result cannot be 2, because \[-2,-1\] is not a subarray.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-10 <= nums[i] <= 10`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer. | null |
Solution | maximum-product-subarray | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int maxi = nums[0];\n int mini = nums[0];\n int ans = nums[0];\n for(int i = 1;i < nums.size();i++){\n if(nums[i] < 0){\n swap(maxi,mini);\n }\n maxi = max(nums[i],maxi*nums[i]);\n mini = min(nums[i],mini*nums[i]);\n ans = max(ans,maxi);\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom math import inf\n\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n \n p = 0\n \n first_neg = 0\n first_neg_excluded = False\n \n p_max = -inf\n \n for x in nums:\n \n if x == 0:\n p = 0\n first_neg = 0\n first_neg_excluded = False\n \n elif x > 0:\n \n if p == 0:\n p = x\n \n else:\n p *= x\n \n if p < 0:\n p //= first_neg\n first_neg_excluded = True\n \n else:\n p = p * x if p != 0 else x\n \n if p < 0:\n \n if first_neg == 0:\n first_neg = p\n \n elif first_neg_excluded:\n p *= first_neg\n first_neg_excluded = False\n \n else:\n p //= first_neg\n first_neg_excluded = True\n \n if p > p_max:\n p_max = p\n \n return p_max\n```\n\n```Java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int ans = nums[0];\n int dpMin = nums[0];\n int dpMax = nums[0];\n\n for (int i = 1; i < nums.length; ++i) {\n final int num = nums[i];\n final int prevMin = dpMin;\n final int prevMax = dpMax;\n if (num < 0) {\n dpMin = Math.min(prevMax * num, num);\n dpMax = Math.max(prevMin * num, num);\n } else {\n dpMin = Math.min(prevMin * num, num);\n dpMax = Math.max(prevMax * num, num);\n }\n ans = Math.max(ans, dpMax);\n }\n return ans;\n }\n}\n```\n | 217 | Given an integer array `nums`, find a subarray that has the largest product, and return _the product_.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,3,-2,4\]
**Output:** 6
**Explanation:** \[2,3\] has the largest product 6.
**Example 2:**
**Input:** nums = \[-2,0,-1\]
**Output:** 0
**Explanation:** The result cannot be 2, because \[-2,-1\] is not a subarray.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-10 <= nums[i] <= 10`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer. | null |
C++ || O(n) time and O(1) space || Easiest Beginner Friendly Sol | maximum-product-subarray | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem:\n**KEY POINTS:**\n1. currMaxProductSubarr : This variable keeps track of the maximum product of a subarray that ends at the current index. For each element in the input array, we update the value of currMaxProductSubarr based on the maximum product that can be obtained by considering the current element and the maximum and minimum product of the subarray that ends at the previous index.\n2. currMinProductSubarr : This variable keeps track of the minimum product of a subarray that ends at the current index. As with currMaxProductSubarr, we update the value of currMinProductSubarr at each index based on the minimum product that can be obtained by considering the current element and the maximum and minimum product of the subarray that ends at the previous index.\n3. maxProductAns : This variable keeps track of the maximum product obtained so far. At each index, we compare the value of currMaxProductSubarr with the current value of maxProductAns and update maxProductAns if currMaxProductSubarr is greater than the current value of maxProductAns. By doing so, we ensure that maxProductAns always stores the maximum product obtained from any subarray in nums up to the current index.\n4. The maximum product of a subarray can be obtained by considering three possibilities:\n - The current element nums[i] alone forms a subarray with the maximum product. In this case, the maximum product of the subarray that ends at the current index is simply nums[i].\n - The current element nums[i] is positive and can be added to the existing subarray that ends at the previous index with the maximum product. In this case, the maximum product of the subarray that ends at the current index is the product of the current element nums[i] and the maximum product of the subarray that ends at the previous index, i.e., currMaxProductSubarr * nums[i].\n - The current element nums[i] is negative and can be added to the existing subarray that ends at the previous index with the minimum product. In this case, the maximum product of the subarray that ends at the current index is the product of the current element nums[i] and the minimum product of the subarray that ends at the previous index, i.e., currMinProductSubarr * nums[i].\n1. The minimum product of a subarray can be obtained by considering three possibilities:\n - The current element nums[i] alone forms a subarray with the minimum product. In this case, the minimum product of the subarray that ends at the current index is simply nums[i].\n - The current element nums[i] is positive and can be added to the existing subarray that ends at the previous index with the minimum product. In this case, the minimum product of the subarray that ends at the current index is the product of the current element nums[i] and the minimum product of the subarray that ends at the previous index, i.e., currMinProductSubarr * nums[i].\n - The current element nums[i] is negative and can be added to the existing subarray that ends at the previous index with the maximum product. In this case, the minimum product of the subarray that ends at the current index is the product of the current element nums[i] and the maximum product of the subarray that ends at the previous index, i.e., temp * nums[i].\n\n**See C++ detailed explanation code with intuition.**\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem:\n1. Initialize three variables currMaxProductSubarr, currMinProductSubarr, maxProductAns to the first element of the input array.\n2. Traverse the input array from index 1 to n-1.\n3. For each element at index i, update the currMaxProductSubarr and currMinProductSubarr by taking maximum and minimum of the following three values: (i) nums[i], (ii) currMaxProductSubarrnums[i], (iii) currMinProductSubarrnums[i].\n4. Update the maxProductAns as the maximum of maxProductAns and currMaxProductSubarr.\n5. Return maxProductAns as the final answer.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int n = nums.size();\n //currMaxProductSubarr: This variable keeps track of the maximum product of a subarray that ends at the current index. For each element in the input array, we update the value of currMaxProductSubarr based on the maximum product that can be obtained by considering the current element and the maximum and minimum product of the subarray that ends at the previous index.\n int currMaxProductSubarr = nums[0];\n //currMinProductSubarr: This variable keeps track of the minimum product of a subarray that ends at the current index. As with currMaxProductSubarr, we update the value of currMinProductSubarr at each index based on the minimum product that can be obtained by considering the current element and the maximum and minimum product of the subarray that ends at the previous index.\n int currMinProductSubarr = nums[0];\n //maxProductAns: This variable keeps track of the maximum product obtained so far. At each index, we compare the value of currMaxProductSubarr with the current value of maxProductAns and update maxProductAns if currMaxProductSubarr is greater than the current value of maxProductAns. By doing so, we ensure that maxProductAns always stores the maximum product obtained from any subarray in nums up to the current index.\n int maxProductAns = nums[0];\n for (int i = 1; i < n; i++) {\n int temp = currMaxProductSubarr;\n //The maximum product of a subarray can be obtained by considering three possibilities:\n //The current element nums[i] alone forms a subarray with the maximum product. In this case, the maximum product of the subarray that ends at the current index is simply nums[i].\n //The current element nums[i] is positive and can be added to the existing subarray that ends at the previous index with the maximum product. In this case, the maximum product of the subarray that ends at the current index is the product of the current element nums[i] and the maximum product of the subarray that ends at the previous index, i.e., currMaxProductSubarr * nums[i].\n //The current element nums[i] is negative and can be added to the existing subarray that ends at the previous index with the minimum product. In this case, the maximum product of the subarray that ends at the current index is the product of the current element nums[i] and the minimum product of the subarray that ends at the previous index, i.e., currMinProductSubarr * nums[i].\n currMaxProductSubarr = max({nums[i], currMaxProductSubarr * nums[i], currMinProductSubarr * nums[i]});\n //The minimum product of a subarray can be obtained by considering three possibilities:\n //The current element nums[i] alone forms a subarray with the minimum product. In this case, the minimum product of the subarray that ends at the current index is simply nums[i].\n //The current element nums[i] is positive and can be added to the existing subarray that ends at the previous index with the minimum product. In this case, the minimum product of the subarray that ends at the current index is the product of the current element nums[i] and the minimum product of the subarray that ends at the previous index, i.e., currMinProductSubarr * nums[i].\n //The current element nums[i] is negative and can be added to the existing subarray that ends at the previous index with the maximum product. In this case, the minimum product of the subarray that ends at the current index is the product of the current element nums[i] and the maximum product of the subarray that ends at the previous index, i.e., temp * nums[i].\n currMinProductSubarr = min({nums[i], temp * nums[i], currMinProductSubarr * nums[i]});\n maxProductAns = max(maxProductAns, currMaxProductSubarr);\n }\n return maxProductAns;\n }\n};\n```\n```Java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int n = nums.length;\n int currMaxProductSubarr = nums[0];\n int currMinProductSubarr = nums[0];\n int maxProductAns = nums[0];\n for (int i = 1; i < n; i++) {\n int temp = currMaxProductSubarr;\n currMaxProductSubarr = Math.max(nums[i], Math.max(currMaxProductSubarr * nums[i], currMinProductSubarr * nums[i]));\n currMinProductSubarr = Math.min(nums[i], Math.min(temp * nums[i], currMinProductSubarr * nums[i]));\n maxProductAns = Math.max(maxProductAns, currMaxProductSubarr);\n }\n return maxProductAns;\n }\n}\n\n```\n```Python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n n = len(nums)\n currMaxProductSubarr = nums[0]\n currMinProductSubarr = nums[0]\n maxProductAns = nums[0]\n for i in range(1, n):\n temp = currMaxProductSubarr\n currMaxProductSubarr = max(nums[i], max(currMaxProductSubarr * nums[i], currMinProductSubarr * nums[i]))\n currMinProductSubarr = min(nums[i], min(temp * nums[i], currMinProductSubarr * nums[i]))\n maxProductAns = max(maxProductAns, currMaxProductSubarr)\n return maxProductAns\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the length of the input array, as we are traversing the array only once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**, as we are using constant extra space to store the variables.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 68 | Given an integer array `nums`, find a subarray that has the largest product, and return _the product_.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,3,-2,4\]
**Output:** 6
**Explanation:** \[2,3\] has the largest product 6.
**Example 2:**
**Input:** nums = \[-2,0,-1\]
**Output:** 0
**Explanation:** The result cannot be 2, because \[-2,-1\] is not a subarray.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-10 <= nums[i] <= 10`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer. | null |
✔️[Python3] DYNAMIC PROGRAMMING, Explained | maximum-product-subarray | 0 | 1 | Subproblem for the DP here would be: What is the maximum and minimum product we can get for a contiguous sub-array starting from the `0`th to the current element? Why do we need to maintain the minimum product while we are asked for a maximum? The fact is that elements in `nums` can be negative, so it possible that for some negative element the previous min possible product can turn the current product into a greater value.\n\nTime: **O(n)** - scan\nSpace: **O(1)** \n\nRuntime: 44 ms, faster than **98.89%** of Python3 online submissions for Maximum Product Subarray.\nMemory Usage: 14.5 MB, less than **36.06%** of Python3 online submissions for Maximum Product Subarray.\n\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n curMax, curMin = 1, 1\n res = nums[0]\n \n for n in nums:\n vals = (n, n * curMax, n * curMin)\n curMax, curMin = max(vals), min(vals)\n\t\t\t\n res = max(res, curMax)\n \n return res\n``` | 130 | Given an integer array `nums`, find a subarray that has the largest product, and return _the product_.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,3,-2,4\]
**Output:** 6
**Explanation:** \[2,3\] has the largest product 6.
**Example 2:**
**Input:** nums = \[-2,0,-1\]
**Output:** 0
**Explanation:** The result cannot be 2, because \[-2,-1\] is not a subarray.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-10 <= nums[i] <= 10`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer. | null |
8 Lines Of Code Logic Dp | maximum-product-subarray | 0 | 1 | \n\n# Dynamic Programming\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n out=max(nums)\n cmax=cmin=1\n for n in nums:\n temp=cmax*n\n cmax=max(cmin*n,cmax*n,n)\n cmin=min(temp,cmin*n ,n)\n out=max(out,cmax)\n return out\n//please upvote me it would encourage me alot\n\n \n```\n# please upvote me it would encourage me alot\n | 11 | Given an integer array `nums`, find a subarray that has the largest product, and return _the product_.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,3,-2,4\]
**Output:** 6
**Explanation:** \[2,3\] has the largest product 6.
**Example 2:**
**Input:** nums = \[-2,0,-1\]
**Output:** 0
**Explanation:** The result cannot be 2, because \[-2,-1\] is not a subarray.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-10 <= nums[i] <= 10`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer. | null |
Solution | find-minimum-in-rotated-sorted-array | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n int low=0, high=n-1;\n \n while(low<high){\n if(nums[low] <= nums[high]) return nums[low];\n int mid = low + (high-low)/2;\n if(nums[low] > nums[mid]){\n high=mid;\n } else if(nums[mid] > nums[high]) {\n low=mid+1;\n } \n }\n if(nums[low] <= nums[high]) return nums[low];\n return -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums) - 1\n\n while l < r:\n m = l + (r - l)\n\n if nums[m] > nums[r]:\n l = m + 1\n \n else:\n r = m \n\n return nums[l] \n```\n\n```Java []\nclass Solution {\n public int findMin(int[] nums) {\n int l = 0;\n int r = nums.length - 1;\n\n while (l < r) {\n final int m = (l + r) / 2;\n if (nums[m] < nums[r])\n r = m;\n else\n l = m + 1;\n }\n\n return nums[l];\n }\n}\n```\n | 218 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Solution | find-minimum-in-rotated-sorted-array | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n int low=0, high=n-1;\n \n while(low<high){\n if(nums[low] <= nums[high]) return nums[low];\n int mid = low + (high-low)/2;\n if(nums[low] > nums[mid]){\n high=mid;\n } else if(nums[mid] > nums[high]) {\n low=mid+1;\n } \n }\n if(nums[low] <= nums[high]) return nums[low];\n return -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums) - 1\n\n while l < r:\n m = l + (r - l)\n\n if nums[m] > nums[r]:\n l = m + 1\n \n else:\n r = m \n\n return nums[l] \n```\n\n```Java []\nclass Solution {\n public int findMin(int[] nums) {\n int l = 0;\n int r = nums.length - 1;\n\n while (l < r) {\n final int m = (l + r) / 2;\n if (nums[m] < nums[r])\n r = m;\n else\n l = m + 1;\n }\n\n return nums[l];\n }\n}\n```\n | 218 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Find Minimum in Rotated Sorted Array | Binary Search | Telugu | Python | Amazon | Microsoft | | find-minimum-in-rotated-sorted-array | 0 | 1 | # Approach\n\n\n# Complexity\n- Time complexity:$$O(log(n))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n n=len(nums)\n left=0\n right=n-1\n while left<=right:\n mid = (left+right)//2\n #1st condition\n if nums[mid]<nums[(mid-1+n)%n] and nums[mid]<nums[(mid+1)%n]:\n return nums[mid]\n #2nd condition\n elif nums[mid]>nums[right]:\n left=mid+1\n else:\n right=mid-1\n return nums[0]\n\n \n```\n---\n# Youtube Video\n[https://youtu.be/5yq2PAKonho?si=T8rqRDw2HaoXjxvl]()\n | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Find Minimum in Rotated Sorted Array | Binary Search | Telugu | Python | Amazon | Microsoft | | find-minimum-in-rotated-sorted-array | 0 | 1 | # Approach\n\n\n# Complexity\n- Time complexity:$$O(log(n))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n n=len(nums)\n left=0\n right=n-1\n while left<=right:\n mid = (left+right)//2\n #1st condition\n if nums[mid]<nums[(mid-1+n)%n] and nums[mid]<nums[(mid+1)%n]:\n return nums[mid]\n #2nd condition\n elif nums[mid]>nums[right]:\n left=mid+1\n else:\n right=mid-1\n return nums[0]\n\n \n```\n---\n# Youtube Video\n[https://youtu.be/5yq2PAKonho?si=T8rqRDw2HaoXjxvl]()\n | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Simple Binary search | find-minimum-in-rotated-sorted-array | 0 | 1 | \nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l=0\n h=len(nums)-1\n mi=-1\n while(l<=h):\n mid=(l+h)//2\n prev=(mid+len(nums)-1)%len(nums)\n if nums[mid]<=nums[prev]:\n mi=mid\n break\n if nums[l]<=nums[h]:\n mi=l\n break\n elif nums[l]<=nums[mid]:\n l=mid+1\n elif nums[mid]<=nums[h]:\n h=mid-1\n return nums[mi] \n``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Simple Binary search | find-minimum-in-rotated-sorted-array | 0 | 1 | \nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l=0\n h=len(nums)-1\n mi=-1\n while(l<=h):\n mid=(l+h)//2\n prev=(mid+len(nums)-1)%len(nums)\n if nums[mid]<=nums[prev]:\n mi=mid\n break\n if nums[l]<=nums[h]:\n mi=l\n break\n elif nums[l]<=nums[mid]:\n l=mid+1\n elif nums[mid]<=nums[h]:\n h=mid-1\n return nums[mi] \n``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Without min comparison | Detailed explanation | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition\nGiven that we should **us**e **bi**nary **se**arch to **fi**nd **th**e **mi**nimum **el**ement in the **ro**tated **so**rted **ar**ray.\nAs all binary search problems, we have **tw**o **po**inters: \'low\' and \'high\', and we find \'mid\' using \'low\' and \'high\'.\n\nOur **main objective** here is to find the direction of traversal since we do not have an idea on the number of rotations. \n\n# Approach\n1. Initialize `low = 0 and high = len(nums) - 1`.\n2. Iterate until `low <= high`.\n3. We can find whether the array has been rotated or not using\n `nums[low] <= nums[high]` <br>\nFor example, here the `array is not rotated` and hence nums[low] < nums[high]\n\nHere, we see that nums[low] > nums[high]. Therefore, the `array is rotated`.\n\n\n4. If the **ar**ray is **not rotated**, `return nums[low]`.\n5. If the **ar**ray is **rotated**, we will have to now **fi**nd the **di**rection of **tr**aversal from \'mid\'.\n6. Calculate `mid = (low + high)//2`\n7. Based on the **c**omparison **be**tween **nums[low]** and **nums[mid]**, we can determine whether we have to move left or right from mid.\n\n8. If `nums[low] > nums[mid]: high = mid`\n9. Else ` low = mid + 1`\n\n\n# Complexity\n- Time complexity: O(logN)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n\n # Initialize low and high\n low, high = 0, len(nums) - 1\n\n # Iterate until low <= high\n while low <= high:\n\n # Check if the array is not rotated\n if nums[low] <= nums[high]:\n # Return nums[low] when the array is not rotated\n return nums[low]\n\n # Initialize mid if the array is rotated\n mid = (low + high)//2\n\n # Check the direction of traversal, \n # refer the image for explanation\n if nums[low] > nums[mid]:\n high = mid\n else:\n low = mid + 1\n``` | 28 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Without min comparison | Detailed explanation | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition\nGiven that we should **us**e **bi**nary **se**arch to **fi**nd **th**e **mi**nimum **el**ement in the **ro**tated **so**rted **ar**ray.\nAs all binary search problems, we have **tw**o **po**inters: \'low\' and \'high\', and we find \'mid\' using \'low\' and \'high\'.\n\nOur **main objective** here is to find the direction of traversal since we do not have an idea on the number of rotations. \n\n# Approach\n1. Initialize `low = 0 and high = len(nums) - 1`.\n2. Iterate until `low <= high`.\n3. We can find whether the array has been rotated or not using\n `nums[low] <= nums[high]` <br>\nFor example, here the `array is not rotated` and hence nums[low] < nums[high]\n\nHere, we see that nums[low] > nums[high]. Therefore, the `array is rotated`.\n\n\n4. If the **ar**ray is **not rotated**, `return nums[low]`.\n5. If the **ar**ray is **rotated**, we will have to now **fi**nd the **di**rection of **tr**aversal from \'mid\'.\n6. Calculate `mid = (low + high)//2`\n7. Based on the **c**omparison **be**tween **nums[low]** and **nums[mid]**, we can determine whether we have to move left or right from mid.\n\n8. If `nums[low] > nums[mid]: high = mid`\n9. Else ` low = mid + 1`\n\n\n# Complexity\n- Time complexity: O(logN)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n\n # Initialize low and high\n low, high = 0, len(nums) - 1\n\n # Iterate until low <= high\n while low <= high:\n\n # Check if the array is not rotated\n if nums[low] <= nums[high]:\n # Return nums[low] when the array is not rotated\n return nums[low]\n\n # Initialize mid if the array is rotated\n mid = (low + high)//2\n\n # Check the direction of traversal, \n # refer the image for explanation\n if nums[low] > nums[mid]:\n high = mid\n else:\n low = mid + 1\n``` | 28 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
✅✅Beats 99% | O(log N) | Python Solution (using binary search) | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition\nThe goal is to find the minimum element in a rotated sorted array. We can use a binary search approach to efficiently locate the minimum element.\n\n# Approach\n1. Initialize the `ans` variable with the first element of the array `nums`.\n\n2. Set two pointers, `low` and `high`, to the start and end of the array, respectively.\n\n3. Check if the array is already sorted in ascending order by comparing the elements at the low and high indices. If it is sorted, return the first element, which is the minimum.\n\n4. Perform a binary search by looping while `low` is less than or equal to `high`.\n\n5. Within the loop:\n - Check if the array is sorted by comparing the elements at the low and high indices. If it is sorted, update `ans` with the minimum of the current `ans` and `nums[low]` and break out of the loop.\n\n - Calculate the middle index `mid` as the average of `low` and `high`.\n\n - Update `ans` with the minimum of the current `ans` and `nums[mid]`.\n\n - Determine if the pivot point (where rotation occurs) is in the right half of the array. If `nums[mid]` is greater than or equal to `nums[low]`, set `low` to `mid + 1`. Otherwise, set `high` to `mid - 1`.\n\n6. Return the final value of `ans`, which is the minimum element in the rotated sorted array.\n\n# Complexity\n- Time complexity: The binary search approach has a time complexity of O(log N), where N is the size of the input array `nums`.\n- Space complexity: The space complexity is O(1) as we only use a few variables for tracking and no additional data structures.\n\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n ans = nums[0]\n low, high = 0, len(nums) - 1\n\n if nums[low] < nums[high]:\n return nums[low]\n\n while low <= high:\n if nums[low] < nums[high]:\n ans = min(ans, nums[low])\n break\n \n mid = (low + high) // 2\n ans = min(ans, nums[mid])\n\n \n if nums[mid] >= nums[low]:\n low = mid + 1\n else:\n high = mid - 1\n\n return ans\n\n```\n\n# Please upvote the solution if you understood it.\n\n | 5 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
✅✅Beats 99% | O(log N) | Python Solution (using binary search) | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition\nThe goal is to find the minimum element in a rotated sorted array. We can use a binary search approach to efficiently locate the minimum element.\n\n# Approach\n1. Initialize the `ans` variable with the first element of the array `nums`.\n\n2. Set two pointers, `low` and `high`, to the start and end of the array, respectively.\n\n3. Check if the array is already sorted in ascending order by comparing the elements at the low and high indices. If it is sorted, return the first element, which is the minimum.\n\n4. Perform a binary search by looping while `low` is less than or equal to `high`.\n\n5. Within the loop:\n - Check if the array is sorted by comparing the elements at the low and high indices. If it is sorted, update `ans` with the minimum of the current `ans` and `nums[low]` and break out of the loop.\n\n - Calculate the middle index `mid` as the average of `low` and `high`.\n\n - Update `ans` with the minimum of the current `ans` and `nums[mid]`.\n\n - Determine if the pivot point (where rotation occurs) is in the right half of the array. If `nums[mid]` is greater than or equal to `nums[low]`, set `low` to `mid + 1`. Otherwise, set `high` to `mid - 1`.\n\n6. Return the final value of `ans`, which is the minimum element in the rotated sorted array.\n\n# Complexity\n- Time complexity: The binary search approach has a time complexity of O(log N), where N is the size of the input array `nums`.\n- Space complexity: The space complexity is O(1) as we only use a few variables for tracking and no additional data structures.\n\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n ans = nums[0]\n low, high = 0, len(nums) - 1\n\n if nums[low] < nums[high]:\n return nums[low]\n\n while low <= high:\n if nums[low] < nums[high]:\n ans = min(ans, nums[low])\n break\n \n mid = (low + high) // 2\n ans = min(ans, nums[mid])\n\n \n if nums[mid] >= nums[low]:\n low = mid + 1\n else:\n high = mid - 1\n\n return ans\n\n```\n\n# Please upvote the solution if you understood it.\n\n | 5 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Easy solution python3 (saiprakash) | find-minimum-in-rotated-sorted-array | 0 | 1 | # Approach \nBinary Search\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(Log N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n n=len(nums)\n left=0\n right=n-1\n while(left<right):\n mid=(left+right)//2\n if nums[mid]>nums[mid+1] and nums[mid]>nums[mid-1]:\n return nums[mid+1]\n elif nums[left]<nums[mid]:\n left=mid\n else:\n right=mid\n return nums[0]\n``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Easy solution python3 (saiprakash) | find-minimum-in-rotated-sorted-array | 0 | 1 | # Approach \nBinary Search\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(Log N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n n=len(nums)\n left=0\n right=n-1\n while(left<right):\n mid=(left+right)//2\n if nums[mid]>nums[mid+1] and nums[mid]>nums[mid-1]:\n return nums[mid+1]\n elif nums[left]<nums[mid]:\n left=mid\n else:\n right=mid\n return nums[0]\n``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Best and fast solution in PYTHON | find-minimum-in-rotated-sorted-array | 0 | 1 | ```\nclass Solution:\n def findMin(self, num):\n first, last = 0, len(num) - 1\n while first < last:\n midpoint = (first + last) // 2\n if num[midpoint] > num[last]:\n \n\tfirst = midpoint + 1\n else:\n last = midpoint\n return num[first]\n\t\t``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Best and fast solution in PYTHON | find-minimum-in-rotated-sorted-array | 0 | 1 | ```\nclass Solution:\n def findMin(self, num):\n first, last = 0, len(num) - 1\n while first < last:\n midpoint = (first + last) // 2\n if num[midpoint] > num[last]:\n \n\tfirst = midpoint + 1\n else:\n last = midpoint\n return num[first]\n\t\t``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Python3 | Intuitive | Optimal | Neat | find-minimum-in-rotated-sorted-array | 0 | 1 | ```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums)-1\n while l < r:\n m = (l+r)//2\n if nums[l] < nums[r]:\n return nums[l]\n else:\n if l+1 == r:\n return nums[r]\n elif nums[l] < nums[m] and nums[m] > nums[r]:\n l = m+1\n else: \n r = m\n return nums[l]\n```\n | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Python3 | Intuitive | Optimal | Neat | find-minimum-in-rotated-sorted-array | 0 | 1 | ```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums)-1\n while l < r:\n m = (l+r)//2\n if nums[l] < nums[r]:\n return nums[l]\n else:\n if l+1 == r:\n return nums[r]\n elif nums[l] < nums[m] and nums[m] > nums[r]:\n l = m+1\n else: \n r = m\n return nums[l]\n```\n | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Binary search || Python3 | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(logn)\n\n- Space complexity:O(1)\n# Code\n```\nimport math\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n if len(nums)==0:\n return -1\n if len(nums)==1 or nums[0]<nums[len(nums)-1]:\n return nums[0]\n low=0\n high=len(nums) - 1\n while low<high:\n mid=low+(high-low)//2\n if nums[mid]<nums[low]:\n low=mid\n if nums[mid]>nums[high]:\n high=mid\n return nums(low+1)\n``` | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Binary search || Python3 | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(logn)\n\n- Space complexity:O(1)\n# Code\n```\nimport math\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n if len(nums)==0:\n return -1\n if len(nums)==1 or nums[0]<nums[len(nums)-1]:\n return nums[0]\n low=0\n high=len(nums) - 1\n while low<high:\n mid=low+(high-low)//2\n if nums[mid]<nums[low]:\n low=mid\n if nums[mid]>nums[high]:\n high=mid\n return nums(low+1)\n``` | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
📌 Python3 simple naive solution with binary search | find-minimum-in-rotated-sorted-array | 0 | 1 | ```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n start = 0\n end = len(nums) - 1\n \n if(nums[start] <= nums[end]):\n return nums[0]\n \n while start <= end:\n mid = (start + end) // 2\n \n if(nums[mid] > nums[mid+1]):\n return nums[mid+1]\n \n if(nums[mid-1] > nums[mid]):\n return nums[mid]\n \n if(nums[mid] > nums[0]):\n start = mid + 1\n else:\n end = mid - 1\n \n return nums[start]\n``` | 6 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
📌 Python3 simple naive solution with binary search | find-minimum-in-rotated-sorted-array | 0 | 1 | ```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n start = 0\n end = len(nums) - 1\n \n if(nums[start] <= nums[end]):\n return nums[0]\n \n while start <= end:\n mid = (start + end) // 2\n \n if(nums[mid] > nums[mid+1]):\n return nums[mid+1]\n \n if(nums[mid-1] > nums[mid]):\n return nums[mid]\n \n if(nums[mid] > nums[0]):\n start = mid + 1\n else:\n end = mid - 1\n \n return nums[start]\n``` | 6 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Python | 99.77 % better binary search solution (easy to understand) | find-minimum-in-rotated-sorted-array | 0 | 1 | \n\n# Simple answer \uD83D\uDE04\uD83D\uDE04\uD83D\uDE04\n```\nclass Solution:\n def findMin(self, nums: list[int]) -> int:\n return min(nums)\n```\n\n# Binary search\n```\nclass Solution:\n def findMin(self, nums: list[int]) -> int:\n if nums[0] <= nums[-1]:\n return nums[0]\n l, r = 0, len(nums)-1\n while l <= r:\n m = (l + r) // 2\n if nums[m] < nums[0] <= nums[m - 1]::\n return nums[m]\n elif nums[m] < nums[0]:\n r = m - 1\n else:\n l = m + 1\n``` | 3 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Python | 99.77 % better binary search solution (easy to understand) | find-minimum-in-rotated-sorted-array | 0 | 1 | \n\n# Simple answer \uD83D\uDE04\uD83D\uDE04\uD83D\uDE04\n```\nclass Solution:\n def findMin(self, nums: list[int]) -> int:\n return min(nums)\n```\n\n# Binary search\n```\nclass Solution:\n def findMin(self, nums: list[int]) -> int:\n if nums[0] <= nums[-1]:\n return nums[0]\n l, r = 0, len(nums)-1\n while l <= r:\n m = (l + r) // 2\n if nums[m] < nums[0] <= nums[m - 1]::\n return nums[m]\n elif nums[m] < nums[0]:\n r = m - 1\n else:\n l = m + 1\n``` | 3 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
6 Lines of Binary Search in Python | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition \nUPVOTE PLEASE\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l,r=0,len(nums)-1\n while l<=r:\n m=(l+r)//2\n if nums[m]<nums[r]: r=m\n else: l=m+1\n return nums[r]\n\n``` | 3 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
6 Lines of Binary Search in Python | find-minimum-in-rotated-sorted-array | 0 | 1 | # Intuition \nUPVOTE PLEASE\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l,r=0,len(nums)-1\n while l<=r:\n m=(l+r)//2\n if nums[m]<nums[r]: r=m\n else: l=m+1\n return nums[r]\n\n``` | 3 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,2,4,5,6,7]` might become:
* `[4,5,6,7,0,1,2]` if it was rotated `4` times.
* `[0,1,2,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` of **unique** elements, return _the minimum element of this array_.
You must write an algorithm that runs in `O(log n) time.`
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 1
**Explanation:** The original array was \[1,2,3,4,5\] rotated 3 times.
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\]
**Output:** 0
**Explanation:** The original array was \[0,1,2,4,5,6,7\] and it was rotated 4 times.
**Example 3:**
**Input:** nums = \[11,13,15,17\]
**Output:** 11
**Explanation:** The original array was \[11,13,15,17\] and it was rotated 4 times.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* All the integers of `nums` are **unique**.
* `nums` is sorted and rotated between `1` and `n` times. | Array was originally in ascending order. Now that the array is rotated, there would be a point in the array where there is a small deflection from the increasing sequence. eg. The array would be something like [4, 5, 6, 7, 0, 1, 2]. You can divide the search space into two and see which direction to go.
Can you think of an algorithm which has O(logN) search complexity? All the elements to the left of inflection point > first element of the array.
All the elements to the right of inflection point < first element of the array. |
Simple easy binary search | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | # Code\n```\nclass Solution:\n def findMin(self, a: List[int]) -> int:\n beg=0\n last=len(a)-1\n while beg<last:\n mid=(last+beg)//2\n if a[mid]>a[last]:\n beg=mid+1\n elif a[mid]<a[last]:\n last=mid\n else:\n last-=1\n return a[beg]\n\n``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Very easy solution for this hard problem(2 lines of code) | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n a=min(nums)\n return a\n \n``` | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
154: Solution with step by step explanation | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem is an extension of the previous problem. Since the array can contain duplicates, we need to add extra logic to handle the cases where we have duplicates at both ends.\n\nOne way to solve this is to keep track of the start and end indices of the current window. At each iteration, we compute the midpoint of the window and compare it with the endpoints. If the midpoint is greater than the start or end, we know that the minimum element is in the second half of the window. If the midpoint is less than the start or end, we know that the minimum element is in the first half of the window. However, if the midpoint is equal to the start or end, we can\'t make this determination and we need to shrink the window by one.\n\nHere\'s the algorithm in more detail:\n\n1. Initialize start and end pointers to the first and last elements of the array, respectively.\n\n2. While the start pointer is less than the end pointer:\n\na. Compute the midpoint of the current window as (start + end) // 2.\n\nb. If the midpoint is greater than the start or end, the minimum element is in the second half of the window, so set start to midpoint + 1.\n\nc. If the midpoint is less than the start or end, the minimum element is in the first half of the window, so set end to midpoint.\n\nd. Otherwise, the midpoint is equal to the start or end, so we can\'t make this determination. Shrink the window by one by decrementing end.\n\n3. When the loop terminates, the start pointer points to the minimum element, so return nums[start].\n\n# Complexity\n- Time complexity:\nO(log n)\n\n- Space complexity:\n O(1)\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n start, end = 0, len(nums) - 1\n\n while start < end:\n mid = (start + end) // 2\n\n if nums[mid] > nums[end]:\n start = mid + 1\n elif nums[mid] < nums[start]:\n end = mid\n else:\n end -= 1\n\n return nums[start]\n\n``` | 10 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python3 Solution || Binary Search Approach || Super Easy To Read | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | ```python\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n left, right = 0, len(nums) - 1\n while (left < right):\n mid = left + (right - left) // 2\n if (nums[mid] < nums[right]):\n right = mid\n elif (nums[mid] > nums[right]):\n left = mid + 1\n else: \n right -= 1\n return nums[left]\n``` | 3 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python3 Solution | Runtime Beats 99.70% | Binary search | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem, we can use binary search, since the array is sorted. Binary search will allow us to find the desired element in O(log(n)) operations.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor binary search, we will need three pointers: left, middle and right. Initially, the value of left is 0, the value of right is equal to the last index of the list of nums. The middle pointer is calculated by the formula: middle = (left + right) // 2.\n\nWe could just use binary search, but here is the problem - there are duplicate elements in this sorted and rotated array, that is, such a situation is possible:\n[5, 3, 5, 5, 5]\nleft = 0, mid = 2, right = 4\nHere the "left", "right" and "mid" indexes point to elements with the same value of 5. In this case, we don\'t know exactly where to shift "mid" and we need to shift "left" to the right or "right" to the left. In my solution in this case I just shift "right" index to the left.\nAfter that, left = 0, right = 3, and mid = 1. Now indexes point to elements with different values and we can start a binary search.\n# Complexity\n- Time complexity: $$O(log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n left, right = 0, len(nums) - 1\n\n while left < right:\n mid = (left + right) // 2\n if nums[mid] > nums[right]:\n left = mid + 1\n elif nums[mid] == nums[right]:\n right -= 1\n else:\n right = mid\n\n return nums[left]\n\n``` | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
✅ Python faster than 99.96%, well explained | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | \n##### Code\n<iframe src="https://leetcode.com/playground/Rg6pMzmV/shared" frameBorder="0" width="700" height="450"></iframe>\n\n##### Understanding\nUse **Binary Search** to find the minimum value in the rotated sorted array.\n\n```\n# Find mid value\nmid = left + ((right - left) >> 1)`\n```\n* Here we are using because bit shifting because `mid = left + (right - left) // 2` is slower and `(right - left) >> 1` is equal to `(right - left) // 2`.\n```\n# To filter duplicate values\nif nums[left] == nums[mid] == nums[right]:\n\tleft += 1\n\tright -= 1\n```\n* If left, mid and right values are same then we increment left and decrement right value.\n```\nelif nums[mid] > nums[right]:\n\tleft = mid + 1\n```\n* Else if mid is greater than right then change the left value to `mid + 1`.\n\t* Because it means mid is in the rotation index\n```\nelse:\n\tright = mid\n```\n* Else mid is in the sorted ascending index\n\n##### Screenshot\n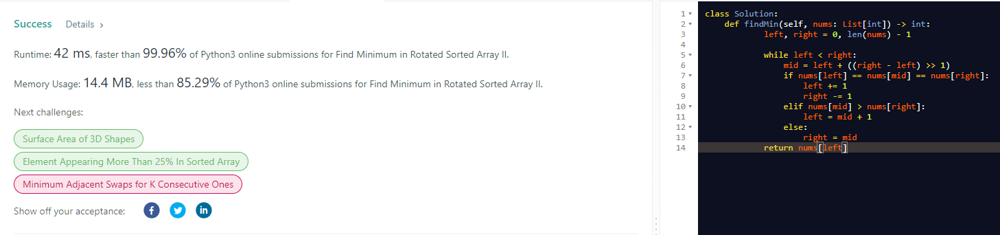\n | 4 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python solution using for loop beats 67.62% tc :-) | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n* Example => [4,5,1,2,3]. Simply iterate over the array and check if an element is smaller than its previous element. If yes that means that it is the minimum element because it is a sorted array which is rotated 1 to n times. So, whatever comes smaller than elements is obviously the smallest element in an array.\n\n# Complexity\n- Time complexity: O(n-1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n for i in range(len(nums)-1):\n if nums[i] > nums[i+1]: \n return nums[i+1]\n return nums[0]\n``` | 1 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python - Two Approaches - EXPLAINED ✅ | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | Thanks to Neetcode https://www.youtube.com/watch?v=nIVW4P8b1VA\n\n\nFirst, let\'s understand how can we find minimum in a rotated sorted array. Since array was sorted before it is rotated, it means we can make use of Binary Search here.\n\n Consider an example -> [2,2,2,0,1]\n\nWhen we use Binary Search, then we will get start element as "2", end element as "1" and mid element as "2"\n\nNow, if you look closely, since the array is rotated, it is divided into two parts. One is [2,2,2] and the other is [0,1] because initially the array as [0,1,2,2,2]\n\nAnd the elements in left part will always be bigger than all the elements in the right part. \n\nThis means, what we want to check is whether "mid" element belongs to left subarray or right subarray. if it belongs to the "left" subarray,then we know we will not find minimum on left side of mid. But if it belongs to the right subarray, then it means, we will find the minimum on the left side of mid.\n\n "mid" will belong to left subarray if nums[mid] >= nums[start]\n\nHere, we see "start" and "mid" are the same i.e., "2". And since nums[mid] >= nums[start], So, we will move towards the right side for the smaller element. Before that, we will also check if "mid" is smaller than the previous smaller element (initially, we assume the first element is the smallest, just like how it is in case of a sorted array that is not rotated).\n\nWhy are we checking if mid is smaller than previous minimum? Because suppose we have this test case [2,2,0,1,1]. In this case, in the first iteration itself, we will get "mid" element as 0 which is the minimum so we do not want to lose track of it when we move to left or right side.\n\nAnyways, continuing with our example - [2,2,2,0,1], the start element = 0 and end element = 1. We see that here, start element itself is smaller than end element which means there is no need to even go to the right side. Since start is smaller than end, that means, either the previous mid element was the minimum, or the "start" element is the minimum. We simply return whatever is smaller.\n\nSo here, we will return 0 as the minimum element.\n\nHence, for every mid, we will also check if it is smaller than previous mid or not and update our minimum element accordingly. And after that, we move to either left or right side of mid.\n\n\n## 1. APPROACH #1 - FIRST REMOVE THE DUPLICATES\n\nSince this problem asks us to decrease the operations as much as possible, this is not the best solution. But basically, we wil remove the duplicates and it then becomes "[Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/)" problem.\n\n def findMin(self, nums: List[int]) -> int:\n # To remove the duplicates but keep the order\n nums = list(dict.fromkeys(nums))\n\n minimum = nums[0]\n\n n = len(nums)\n\n # We can search for the minimum element using Binary Search\n start = 0\n end = n - 1\n\n while start <= end:\n # If the "start" element is smaller than "end"\n if nums[start] < nums[end]: return min(minimum, nums[start])\n\n mid = start + (end - start) // 2\n\n # IF this mid value is smaller than previous minimum we found\n # Then update the minimum\n minimum = min(minimum, nums[mid])\n\n # Is this "mid" value part of left sorted subarray or right sorted subarray?\n # If this is part of the left sorted subarray, we will find minimum on right side\n if nums[mid] >= nums[start]: start = mid + 1\n # Otherwise, we will find the minimum on the left side\n else: end = mid - 1\n \n return minimum\n\n## 2. APPROACH #2 - SIMPLY USE BINARY SEARCH WITH A LITTLE TWEAK\n\nIf you use the same code as above (without removing duplicates), then you will see 187/193 test cases are getting passed. \n\nOne test case that is failing is [10,1,10,10,10]. So, let\'s see how to fix that.\n\n [10,1,10,10,10]\n\n start = 10\n end = 10\n mid = 10\n\n Did you see the problem? All the pointers have same element.\n\n So, as per above code\'s logic, \n since mid >= start, we should move to right side. \n\n But this means, we will lose the actual minimum element \n which is "1".\n\nIn this case, the minimum can be anywhere. It can be on right of mid or on the left of mid.Here, it is on the left side of mid but if we had [3,3,0,3] then it would\'ve been on the right side of mid.\n\nSo, to avoid any issues with any test case, we can do one of two things ->\n\n Either Increment "start" pointer by 1\n Either Decrement "end" pointer by 1\n\nBecause what this will do is that in next iteration, either "start" element may be different than other two, or "end" might be different than other two, or the new "mid" might be different than other two. Because we want not all three to be the same as in that case, we cannot decide which way to move - left or right.\n\n\n\n def findMin(self, nums: List[int]) -> int:\n n = len(nums)\n\n minimum = nums[0]\n\n # We can search for the minimum element using Binary Search\n start = 0\n end = n - 1\n\n while start <= end:\n # If the "start" element is smaller than "end"\n if nums[start] < nums[end]: return min(minimum, nums[start])\n\n mid = start + (end - start) // 2\n\n # IF this mid value is smaller than previous minimum we found\n # Then update the minimum\n minimum = min(minimum, nums[mid])\n\n # If start, end and mid are all same e.g. if [3,3,0,3] is the test case\n # Then, we will simply decrement end pointer\n if nums[start] == nums[mid] == nums[end]: end -= 1\n # Otherwise, we check\n # Is this "mid" value part of left sorted subarray or right sorted subarray?\n # If this is part of the left sorted subarray, we will find minimum on right side\n elif nums[mid] >= nums[start]: start = mid + 1\n # Otherwise, we will find the minimum on the left side\n else: end = mid - 1\n\n return minimum\n | 3 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Binary Search || Explained || PYTHON | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | ```\nclass Solution:\n def findMin(self, a: List[int]) -> int:\n \n def solve(l,h):\n while l<h:\n m=(l+h)//2\n \n if a[m]<a[m-1]:\n return a[m]\n \n elif a[m]>a[h-1]:\n l=m+1\n \n elif a[m]<a[h-1]:\n h=m\n \n else:\n \n if len(set(a[l:m+1]))==1:\n return min(a[m],solve(m+1,h))\n \n else:\n return min(a[m],solve(l,m))\n \n return a[min(l,len(a)-1)]\n \n return solve(0,len(a))\n```\n\n\n | 2 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Four problems all in one concept | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | Four similar problems with similar concept to solve\n[33. Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/)\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> int:\n\t\tN=len(nums)\n start=0\n end=N-1\n while start<=end:\n mid=(start+end)//2\n if target==nums[mid]:\n return mid\n # first half order\n if nums[mid]>=nums[start]:\n if nums[mid]>target>=nums[start]:\n end=mid-1\n else:\n start=mid+1\n # second half order\n else:\n if nums[mid]<target<=nums[end]:\n start=mid+1\n else:\n end=mid-1\n return -1\n```\n[81. Search in Rotated Sorted Array II](https://leetcode.com/problems/search-in-rotated-sorted-array-ii/)\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> bool:\n N=len(nums)\n start=0\n end=N-1\n while start<=end:\n mid=(start+end)//2\n if nums[mid]==target:\n return True\n\t\t\t# add this line to handle duplicate\n while nums[start]==nums[mid] and start<mid:\n start=start+1\n if nums[start]<=nums[mid]:\n if nums[start]<=target<nums[mid]:\n end=mid-1\n else:\n start=mid+1\n else:\n if nums[mid]<target<=nums[end]:\n start=mid+1\n else:\n end=mid-1\n```\n[153. Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/)\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n N=len(nums)\n start=0\n end=N-1\n while start<end:\n mid=(start+end)//2\n if nums[mid]>nums[end]:\n start=mid+1\n else:\n end=mid\n return nums[start]\n```\n[154. Find Minimum in Rotated Sorted Array II](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array-ii/)\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n N=len(nums)\n start=0\n end=N-1\n while start<end:\n mid=(start+end)//2\n\t\t\t# add this line to handle duplicate\n while nums[mid]==nums[end] and mid<end:\n end-=1\n if nums[mid]>nums[end]:\n start=mid+1\n else:\n end=mid\n return nums[start]\n``` | 14 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Python Binary Search ( Compare to 153) | find-minimum-in-rotated-sorted-array-ii | 0 | 1 | The problem 154 is harder than 153. \n\nAt first , we need to solve 153 ( no duplicate exists in the array )\n\n153.Find Minimum in Rotated Sorted Array:\n\nThese problems give no clear target , we can use ```nums[r]``` as judgement condition \nIt is very easy to find\uFF1A\n>if nums[mid] > nums[r]: # [3,4,5,1,2]\n>l = mid+1 # min exist on the right side of the middle value\n\n>if nums[mid] < nums[r]: # [1,2,3,4,5] ,[4,5,1,2,3]\n>r = mid # min exist on the left side of the middle value ( inclue middle value)\n\n>if nums[mid] == nums[r]: # Invalid\n\nCombining these conditions\uFF1A\n```python\n# 153. Find Minimum in Rotated Sorted Array\ndef findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums)-1\n while l < r:\n mid = (l+r)//2\n if nums[mid] > nums[r]:\n l = mid+1\n else:\n r = mid\n return nums[l]\n```\n\n---------------------------------------\n\n154.Find Minimum in Rotated Sorted Array II:\n\nSame idea with 153\n\nIt is very easy to find\uFF1A\n>if nums[mid] > nums[r]: # [3,4,5,1,2]\n>l = mid+1 # min exists on the right side of the middle value\n\n>if nums[mid] < nums[r]: # [1,2,3,4,5] ,[4,5,1,2,3]\n>r = mid # min exists on the left side of the middle value ( inclue middle value)\n\nHere are the different parts\uFF1A\n\n```python\nif nums[mid] == nums[r]: # valid\n\tif nums[mid] == nums[l]: # [10, 5, 10, 10, 10] or [10, 10, 10, 5, 10] \n\t\tl = l+1 # or r = r-1 # min could be on either side\uFF0Cwe just narrow the interval\n\telif nums[l] < nums[mid]: # [1, 5, 10, 10, 10] \n\t\tr = mid-1\n\telse:# [20, 5, 10, 10, 10] or [20, 10, 10, 10, 10]\n\t\tr = mid\n```\n\nCombining these conditions\uFF1A\n```python\n\t# 154. Find Minimum in Rotated Sorted Array II\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums)-1\n while l < r:\n mid = (l+r)//2\n\t\t\t# condition for 154\n if nums[mid] == nums[r]:\n if nums[mid] == nums[l]:\n l = l+1 # or r = r-1\n elif nums[l] < nums[mid] : \n\t r = mid-1\n else:\n r = mid\n\t\t\t# same as 153\n elif nums[mid] > nums[r]:\n l = mid+1\n else:\n r = mid\n return nums[l]\n```\n\nWe can combine the judgment conditions in the loop, and choose a larger interval when we combine\n\n```python\n\t# 154. Find Minimum in Rotated Sorted Array II\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums)-1\n while l < r:\n mid = (l+r)//2\n if nums[mid] == nums[r]:\n if nums[mid] == nums[l]:\n l = l+1 # or r = r-1\n else:\n r = mid\n elif nums[mid] > nums[r]:\n l = mid+1\n else:\n r = mid\n return nums[l]\n``` | 23 | Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
* `[4,5,6,7,0,1,4]` if it was rotated `4` times.
* `[0,1,4,4,5,6,7]` if it was rotated `7` times.
Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
Given the sorted rotated array `nums` that may contain **duplicates**, return _the minimum element of this array_.
You must decrease the overall operation steps as much as possible.
**Example 1:**
**Input:** nums = \[1,3,5\]
**Output:** 1
**Example 2:**
**Input:** nums = \[2,2,2,0,1\]
**Output:** 0
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5000`
* `-5000 <= nums[i] <= 5000`
* `nums` is sorted and rotated between `1` and `n` times.
**Follow up:** This problem is similar to [Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/description/), but `nums` may contain **duplicates**. Would this affect the runtime complexity? How and why? | null |
Solution | min-stack | 1 | 1 | ```C++ []\nclass MinStack {\npublic:\n typedef struct node{\n int v;\n int minUntilNow;\n node* next;\n }node;\n\n MinStack() : topN(nullptr){\n \n }\n \n void push(int val) {\n node* n = new node;\n n->v = n->minUntilNow = val;\n n->next = nullptr;\n \n if(topN == nullptr){\n topN = n;\n }\n\n else{\n n->minUntilNow = min(n->v,topN->minUntilNow);\n n->next = topN;\n topN = n;\n }\n }\n \n void pop() {\n topN = topN->next;\n }\n \n int top() {\n return topN->v;\n }\n \n int getMin() {\n return topN->minUntilNow;\n }\n\n private:\n node* topN;\n};\n```\n\n```Python3 []\nclass MinStack:\n\n def __init__(self):\n self.stack = []\n self.minStack = []\n\n def push(self, val: int) -> None:\n self.stack.append(val)\n if self.minStack:\n val = min(self.minStack[-1],val)\n self.minStack.append(val)\n\n def pop(self) -> None:\n self.stack.pop()\n self.minStack.pop()\n\n def top(self) -> int:\n return self.stack[-1]\n\n def getMin(self) -> int:\n return self.minStack[-1]\n```\n\n```Java []\nclass MinStack {\n LinkedList<TplusMin> stack;\n private class TplusMin {\n int val;\n int min;\n public TplusMin(int val, int min) {\n this.val = val;\n this.min = min;\n }\n }\n\n public MinStack() {\n stack = new LinkedList<>();\n }\n \n public void push(int val) {\n int newMin;\n if (stack.size() == 0){\n newMin = val;\n }\n else {\n int currentMin = stack.getFirst().min;\n newMin = val < currentMin ? val : currentMin;\n }\n stack.addFirst(new TplusMin(val, newMin));\n }\n \n public void pop() {\n stack.removeFirst();\n }\n \n public int top() {\n return stack.peekFirst().val;\n }\n \n public int getMin() {\n return stack.peekFirst().min;\n }\n}\n```\n | 230 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
O( 1 )✅ | Python (Step by step explanation) | min-stack | 0 | 1 | # Intuition\nThe MinStack is a data structure that allows for efficient retrieval of the minimum value in a stack at any given moment. This is achieved by maintaining two stacks: one for the actual elements (the `stack`), and another for the minimum elements (the `minStack`).\n\n# Approach\n1. Initialize two lists (stacks): `stack` for the actual elements and `minStack` for the minimum elements.\n2. When pushing an element into the stack:\n - Append the element to the `stack`.\n - Check if `minStack` is not empty. If it\'s not empty, calculate the minimum between the current element and the top element of `minStack`, and append the minimum to `minStack`. This ensures that `minStack` always contains the minimum value in the stack.\n3. When popping an element from the stack:\n - Pop the element from both `stack` and `minStack`. This maintains the consistency of the two stacks.\n4. To get the top element of the stack, return the last element in `stack`.\n5. To get the minimum value in the stack, return the last element in `minStack`. This allows for a constant-time operation for retrieving the minimum value.\n\n# Complexity\n- Time complexity:\n - Push: O(1)\n - Pop: O(1)\n - Top: O(1)\n - GetMin: O(1)\n- Space complexity: O(n), where n is the number of elements in the stack.\n\n\n# Code\n```\nclass MinStack:\n\n def __init__(self):\n self.stack = []\n self.minStack = []\n \n\n def push(self, val: int) -> None:\n self.stack.append(val)\n val = min(val , self.minStack[-1] if self.minStack else val)\n self.minStack.append(val)\n \n\n def pop(self) -> None:\n self.stack.pop()\n self.minStack.pop()\n \n\n def top(self) -> int:\n return self.stack[-1]\n \n\n def getMin(self) -> int:\n return self.minStack[-1]\n \n\n\n# Your MinStack object will be instantiated and called as such:\n# obj = MinStack()\n# obj.push(val)\n# obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.getMin()\n```\n\n# Please upvote the solution if you understood it.\n\n | 9 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
O(1) || 98.32% Faster Python (Linked List) | min-stack | 0 | 1 | ```\n\nclass MinStack:\n \n class _Node:\n def __init__(self, data, next=None):\n self.data = data\n self.next = next\n \n def __init__(self):\n self.head: self._Node = None\n\n def push(self, element: int) -> None:\n if self.head is None:\n new_node = self._Node((element, element))\n else:\n min_val = self.head.data[1]\n if element < min_val:\n new_node = self._Node((element, element))\n else:\n new_node = self._Node((element, min_val))\n new_node.next = self.head\n self.head = new_node\n\n def pop(self) -> None:\n self.head = self.head.next\n\n def top(self) -> int:\n return self.head.data[0]\n\n def getMin(self) -> int:\n return self.head.data[1]\n\n\n# Your MinStack object will be instantiated and called as such:\n# obj = MinStack()\n# obj.push(val)\n# obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.getMin()\n\n``` | 3 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
Python || 99.95% Faster || Only One Stack | min-stack | 0 | 1 | ```\nclass MinStack:\n\n def __init__(self):\n self.st=[] #stack\n self.min=None #min element\n\n def push(self, val: int) -> None:\n if len(self.st)==0:\n self.st.append(val)\n self.min=val\n else:\n if val>=self.min:\n self.st.append(val)\n else:\n self.st.append(2*val-self.min)\n self.min=val\n \n def pop(self) -> None:\n x=self.st.pop() \n if x<self.min:\n self.min=2*self.min-x\n \n def top(self) -> int:\n x=self.st[-1]\n if x>=self.min:\n return x\n return self.min\n\n def getMin(self) -> int:\n return self.min\n```\n**An upvote will be encouraging** | 14 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
Intuitive solution | min-stack | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass MinStack:\n\n def __init__(self):\n self.stack = []\n\n def push(self, val: int) -> None:\n self.stack.append(val)\n\n def pop(self) -> None:\n self.stack.pop(-1)\n\n def top(self) -> int:\n return self.stack[-1]\n\n def getMin(self) -> int:\n return min(self.stack)\n\n\n# Your MinStack object will be instantiated and called as such:\n# obj = MinStack()\n# obj.push(val)\n# obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.getMin()\n``` | 3 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
155: Solution with step by step explanation | min-stack | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo implement the MinStack, we can use two stacks. One stack will store the actual elements, and the other stack will store the minimum values seen so far. When we push a new element onto the stack, we check if it\'s smaller than the current minimum value, and if so, we push it onto the minimum stack. When we pop an element from the stack, we also pop the corresponding element from the minimum stack if it\'s the current minimum value.\n\nLet\'s go through the time and space complexity analysis for each function:\n\n- push: O(1) time complexity for pushing an element onto the main stack and the minimum stack, and O(1) space complexity for storing the two stacks.\n- pop: O(1) time complexity for popping an element from the main stack and the minimum stack, and O(1) space complexity for the two stacks.\n- top: O(1) time complexity for returning the top element of the main stack, and O(1) space complexity for the two stacks.\n- getMin: O(1) time complexity for returning the minimum value from the minimum stack, and O(1) space complexity for the two stacks.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MinStack:\n def __init__(self):\n self.stack = [] # initialize main stack\n self.min_stack = [] # initialize minimum value stack\n\n def push(self, val: int) -> None:\n self.stack.append(val) # push value onto main stack\n if not self.min_stack or val <= self.min_stack[-1]: # if minimum stack is empty or the value is smaller or equal to current minimum\n self.min_stack.append(val) # push value onto minimum stack\n\n def pop(self) -> None:\n if self.stack: # check if main stack is not empty\n if self.stack[-1] == self.min_stack[-1]: # if the element to pop is the current minimum\n self.min_stack.pop() # pop from minimum stack\n self.stack.pop() # always pop from main stack\n\n def top(self) -> int:\n if self.stack: # check if main stack is not empty\n return self.stack[-1] # return the top element\n\n def getMin(self) -> int:\n if self.min_stack: # check if minimum stack is not empty\n return self.min_stack[-1] # return the current minimum value\n\n``` | 18 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
O(1) Solution python | min-stack | 0 | 1 | \n# Approach\nCreate two seperate stacks, one is the main stack and the other is the minimum stack which holds the corresponding minimum value for each value in our main stack.\n\nWhen we want to push a value into our stack, we first check to see if the stack is empty. If it is, then we push the value in both our main stack and our minimum stack.\n\nIf the stack is not empty, we want to then compare the given value with the value at the top of our minimum stack. If the value if less than the top value of our minimum stack, we append the value in our minimum stack and our main stack. If the value is greater than the top of our minimum stack, we then push the value into our main stack but this time, we push the top of our minimum value in our minimum stack back into the minimum stack.\n\nThis way we can tell what value is the minimum of the stack without using any O(n) approaches.\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MinStack:\n\n def __init__(self):\n self.stack = []\n self.minstack = []\n\n def push(self, val: int) -> None:\n if not self.stack:\n self.stack.append(val)\n self.minstack.append(val)\n else:\n if val < self.minstack[-1]:\n self.minstack.append(val)\n self.stack.append(val)\n else:\n self.stack.append(val)\n self.minstack.append(self.minstack[-1])\n\n\n def pop(self) -> None:\n self.stack.pop()\n self.minstack.pop()\n\n def top(self) -> int:\n return self.stack[-1]\n\n def getMin(self) -> int:\n return self.minstack[-1]\n\n\n# Your MinStack object will be instantiated and called as such:\n# obj = MinStack()\n# obj.push(val)\n# obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.getMin()\n``` | 12 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
Superb Logical Solution Using Stacks | min-stack | 0 | 1 | \n\n# Solution in Python3\n```\nclass MinStack:\n\n def __init__(self):\n self.stack=[]\n\n def push(self, val: int) -> None:\n self.stack.append(val)\n\n def pop(self) -> None:\n self.stack.pop()\n\n def top(self) -> int:\n return self.stack[-1]\n\n def getMin(self) -> int:\n return min(self.stack)\n\n\n# Your MinStack object will be instantiated and called as such:\n# obj = MinStack()\n# obj.push(val)\n# obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.getMin()\n``` | 1 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
Python Solution With Explanation | min-stack | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We need $$O(1)$$ for this question, thus regular methods such as sorting, looping through the array cannot be done\n- We can also deduce that:\n - We cannot access middle of array (only the back or front)\n - So we need to use some data structures that can access front and back in constant time and add or delete stuff to it\n- Some data structures that can access the front or back in $$O(1)$$\n - Queues (Double ended)\n - Linked List\n- I am going to use queues because its much simpler to use than linked lists in python\n---\n- Also, Note that for **stacks**\n - We can only **pop from the back**\n - and **add from the back**\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Using the knowledge we have above,\n- We can make up some sort of algorithm that may or may not work:\n - Let\'s add the minimum values to the front of the queue and those that aren\'t are sent to the back\n - E.g\n ```\n Insert values: 1, -2, 3, 5, 6, 2\n Queue: 1\n Queue: -2, 1\n Queue: -2, 1, 3\n Queue: -2, 1, 3, 5\n Queue: -2, 1, 3, 5, 6\n Queue: -2, 1, 3, 5, 6, 2\n ```\n- Now, when we pop from the stack:\n - We only need to pop from either the back of the queue or the front\n - E.g\n ```\n Stack: 1, -2, 3, 5, 6, 2 => 1, -2, 3, 5, 6\n Queue: -2, 1, 3, 5, 6, 2 pop -2, 1, 3, 5, 6\n ------------------------------------------------------\n Stack: 1, -2, 3, 5, 6 => 1, -2, 3, 5\n Queue: -2, 1, 3, 5, 6 pop -2, 1, 3, 5\n ------------------------------------------------------\n Stack: 1, -2, 3, 5 => 1, -2, 3\n Queue: -2, 1, 3, 5 pop -2, 1, 3\n ------------------------------------------------------\n Stack: 1, -2, 3 => 1, -2\n Queue: -2, 1, 3 pop -2, 1\n ------------------------------------------------------\n Stack: 1, -2 => 1\n Queue: -2, 1 popfront 1\n ```\n- From here we realise that the minimum can only be on the sides of the queue after a few trial and errors\n- To find the minimum we can just return the minimum of the first or last values of the queue\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MinStack:\n def __init__(self):\n self.stack = []\n self.minimums = deque()\n\n def push(self, val: int) -> None:\n self.stack.append(val)\n \n if self.minimums and val <= self.minimums[0]:\n self.minimums.appendleft(val)\n return\n self.minimums.append(val)\n\n def pop(self) -> None:\n val = self.stack.pop()\n if self.minimums[0] == val:\n self.minimums.popleft()\n return\n self.minimums.pop()\n\n def top(self) -> int:\n return self.stack[-1]\n\n def getMin(self) -> int:\n return min(self.minimums[0], self.minimums[-1])\n\n# Your MinStack object will be instantiated and called as such:\n# obj = MinStack()\n# obj.push(val)\n# obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.getMin()\n```\nNote: This solution was what I thought of when I did this question the first time. | 4 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
Implement the `MinStack` class:
* `MinStack()` initializes the stack object.
* `void push(int val)` pushes the element `val` onto the stack.
* `void pop()` removes the element on the top of the stack.
* `int top()` gets the top element of the stack.
* `int getMin()` retrieves the minimum element in the stack.
You must implement a solution with `O(1)` time complexity for each function.
**Example 1:**
**Input**
\[ "MinStack ", "push ", "push ", "push ", "getMin ", "pop ", "top ", "getMin "\]
\[\[\],\[-2\],\[0\],\[-3\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,null,-3,null,0,-2\]
**Explanation**
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top(); // return 0
minStack.getMin(); // return -2
**Constraints:**
* `-231 <= val <= 231 - 1`
* Methods `pop`, `top` and `getMin` operations will always be called on **non-empty** stacks.
* At most `3 * 104` calls will be made to `push`, `pop`, `top`, and `getMin`. | Consider each node in the stack having a minimum value. (Credits to @aakarshmadhavan) |
Solution | intersection-of-two-linked-lists | 1 | 1 | ```C++ []\n int init = []\n{\n std::ios_base::sync_with_stdio(false);\n std::cin.tie(nullptr);\n std::ofstream out("user.out");\n for(string s; getline(std::cin, s);)\n {\n if(s[0] != \'0\') out << "Intersected at \'" << s << "\'\\n";\n else out << "No intersection\\n";\n for(int i = 0; i < 4; ++i) getline(std::cin, s);\n }\n out.flush();\n exit(0);\n return 0;\n}();\nclass Solution {\npublic:\n ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {\n unordered_map<ListNode*,int>mpp;\n for (auto p = headA ; p!=NULL ; p = p->next){\n mpp[p]=p->val;\n }\n for (auto p = headB ; p!=NULL ; p = p->next){\n if (mpp.find(p)!=mpp.end()) return p;\n }\n return NULL;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:\n stackA = [\'A\']\n stackB = [\'B\']\n\n while headA or headB:\n if headA:\n stackA.append(headA)\n headA = headA.next\n\n if headB:\n stackB.append(headB)\n headB = headB.next\n\n prev = None\n while stackA and stackB:\n nodeA = stackA.pop(-1)\n nodeB = stackB.pop(-1)\n\n if nodeA != nodeB:\n return prev\n\n prev = nodeA\n```\n\n```Java []\nclass Solution {\n public ListNode getIntersectionNode(ListNode headA, ListNode headB) {\n int ac = 0;\n int bc = 0;\n ListNode a = headA;\n ListNode b = headB;\n while(a != null){\n ac++;\n a = a.next;\n }\n while(b != null){\n bc++;\n b = b.next;\n }\n while(ac > bc){\n ac--;\n headA = headA.next;\n }\n while(bc > ac){\n bc--;\n headB = headB.next;\n }\n \n while(headA != headB){\n headA = headA.next;\n headB = headB.next;\n }\n return headA;\n }\n}\n```\n | 455 | Given the heads of two singly linked-lists `headA` and `headB`, return _the node at which the two lists intersect_. If the two linked lists have no intersection at all, return `null`.
For example, the following two linked lists begin to intersect at node `c1`:
The test cases are generated such that there are no cycles anywhere in the entire linked structure.
**Note** that the linked lists must **retain their original structure** after the function returns.
**Custom Judge:**
The inputs to the **judge** are given as follows (your program is **not** given these inputs):
* `intersectVal` - The value of the node where the intersection occurs. This is `0` if there is no intersected node.
* `listA` - The first linked list.
* `listB` - The second linked list.
* `skipA` - The number of nodes to skip ahead in `listA` (starting from the head) to get to the intersected node.
* `skipB` - The number of nodes to skip ahead in `listB` (starting from the head) to get to the intersected node.
The judge will then create the linked structure based on these inputs and pass the two heads, `headA` and `headB` to your program. If you correctly return the intersected node, then your solution will be **accepted**.
**Example 1:**
**Input:** intersectVal = 8, listA = \[4,1,8,4,5\], listB = \[5,6,1,8,4,5\], skipA = 2, skipB = 3
**Output:** Intersected at '8'
**Explanation:** The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[4,1,8,4,5\]. From the head of B, it reads as \[5,6,1,8,4,5\]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.
**Example 2:**
**Input:** intersectVal = 2, listA = \[1,9,1,2,4\], listB = \[3,2,4\], skipA = 3, skipB = 1
**Output:** Intersected at '2'
**Explanation:** The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[1,9,1,2,4\]. From the head of B, it reads as \[3,2,4\]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.
**Example 3:**
**Input:** intersectVal = 0, listA = \[2,6,4\], listB = \[1,5\], skipA = 3, skipB = 2
**Output:** No intersection
**Explanation:** From the head of A, it reads as \[2,6,4\]. From the head of B, it reads as \[1,5\]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.
**Constraints:**
* The number of nodes of `listA` is in the `m`.
* The number of nodes of `listB` is in the `n`.
* `1 <= m, n <= 3 * 104`
* `1 <= Node.val <= 105`
* `0 <= skipA < m`
* `0 <= skipB < n`
* `intersectVal` is `0` if `listA` and `listB` do not intersect.
* `intersectVal == listA[skipA] == listB[skipB]` if `listA` and `listB` intersect.
**Follow up:** Could you write a solution that runs in `O(m + n)` time and use only `O(1)` memory? | null |
Python || Easy 2 approaches || O(1) space | intersection-of-two-linked-lists | 0 | 1 | 1. ## **Hashset**\n\nThe algorithm is:\n1. Store all the elements of `headA` in a hashset\n2. Iterate through the `headB` and check for the first match and then return it.\n\n**Time - O(n+m)**\n**Space - O(n)**\n\n```\nclass Solution:\n def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:\n first_set=set()\n curr=headA\n \n while curr:\n first_set.add(curr)\n curr=curr.next\n \n curr = headB\n while curr:\n if curr in first_set:\n return curr\n curr=curr.next\n\n return None\n```\n\n2. ## **Two Pointers**\n\nThis is to answer the follow-up question. For this approach, we will initialize two pointers which is pointing to heads of each Linked List. Then we will make these pointers run through both the Linked Lists ie. `n + m` length. By doing so, we will hit an intersection point.\n\n**Time - O(n+m)**\n**Space - O(1)**\n\n```\nclass Solution:\n def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:\n one = headA\n two = headB\n\n while one != two:\n one = headB if one is None else one.next\n two = headA if two is None else two.next\n return one\n```\n\n\n**Note:**(*Added this part, as some leetcoders had issues reproducing the inputs locally.*)\nThe line `one != two` compares the hashes of two objects. The problem description states that both the inputs have the same tail i.e both LLs merge at some point. This means that `one==two` incase of intersection. So it means `hash(one)==hash(two)`. In your locally created inputs, if you are creating two separate LLs with same values for the tail, It doesn\'t mean their hashes will be the same.\n\n> ListNode(8) != ListNode(8) \ni.e. hash(ListNode(8)) != hash(ListNode(8))\ni.e. 284711280 !=284711048. # hash generated from the two objects.\n\nFor locally generating the test input, you can do the following:\n```\ntail = createLL([8,4,5])\nheadA=createLL([4, 1])\nheadB=createLL([5,6,1])\n\nlast_nodeA = move_to_lastNode(headA)\nlast_nodeA.next=tail\n\nlast_nodeB = move_to_lastNode(headB)\nlast_nodeB.next=tail\n```\n\n--- \n\n***Please upvote if you find it useful*** | 136 | Given the heads of two singly linked-lists `headA` and `headB`, return _the node at which the two lists intersect_. If the two linked lists have no intersection at all, return `null`.
For example, the following two linked lists begin to intersect at node `c1`:
The test cases are generated such that there are no cycles anywhere in the entire linked structure.
**Note** that the linked lists must **retain their original structure** after the function returns.
**Custom Judge:**
The inputs to the **judge** are given as follows (your program is **not** given these inputs):
* `intersectVal` - The value of the node where the intersection occurs. This is `0` if there is no intersected node.
* `listA` - The first linked list.
* `listB` - The second linked list.
* `skipA` - The number of nodes to skip ahead in `listA` (starting from the head) to get to the intersected node.
* `skipB` - The number of nodes to skip ahead in `listB` (starting from the head) to get to the intersected node.
The judge will then create the linked structure based on these inputs and pass the two heads, `headA` and `headB` to your program. If you correctly return the intersected node, then your solution will be **accepted**.
**Example 1:**
**Input:** intersectVal = 8, listA = \[4,1,8,4,5\], listB = \[5,6,1,8,4,5\], skipA = 2, skipB = 3
**Output:** Intersected at '8'
**Explanation:** The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[4,1,8,4,5\]. From the head of B, it reads as \[5,6,1,8,4,5\]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.
**Example 2:**
**Input:** intersectVal = 2, listA = \[1,9,1,2,4\], listB = \[3,2,4\], skipA = 3, skipB = 1
**Output:** Intersected at '2'
**Explanation:** The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[1,9,1,2,4\]. From the head of B, it reads as \[3,2,4\]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.
**Example 3:**
**Input:** intersectVal = 0, listA = \[2,6,4\], listB = \[1,5\], skipA = 3, skipB = 2
**Output:** No intersection
**Explanation:** From the head of A, it reads as \[2,6,4\]. From the head of B, it reads as \[1,5\]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.
**Constraints:**
* The number of nodes of `listA` is in the `m`.
* The number of nodes of `listB` is in the `n`.
* `1 <= m, n <= 3 * 104`
* `1 <= Node.val <= 105`
* `0 <= skipA < m`
* `0 <= skipB < n`
* `intersectVal` is `0` if `listA` and `listB` do not intersect.
* `intersectVal == listA[skipA] == listB[skipB]` if `listA` and `listB` intersect.
**Follow up:** Could you write a solution that runs in `O(m + n)` time and use only `O(1)` memory? | null |
Python || 94.40% Faster || O(1) Space || 2 Approaches | intersection-of-two-linked-lists | 0 | 1 | ```\n#Time Complexity: O(n)\n#Space Complexity: O(n)\nclass Solution:\n def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:\n s=set()\n while headA:\n s.add(headA)\n headA=headA.next\n while headB:\n if headB in s:\n return headB\n headB=headB.next\n return None\n\n#Time Complexity: O(n)\n#Space Complexity: O(1)\nclass Solution:\n def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:\n c1=c2=0\n temp1,temp2=headA,headB\n while temp1 or temp2:\n if temp1:\n c1+=1\n temp1=temp1.next\n if temp2:\n c2+=1\n temp2=temp2.next\n c=c1-c2\n if c<0:\n while c!=0:\n headB=headB.next\n c+=1\n else:\n while c!=0:\n headA=headA.next\n c-=1\n while headA:\n if headA==headB:\n return headA\n headA=headA.next\n headB=headB.next\n return headA\n```\n**An upvote will be encouraging** | 5 | Given the heads of two singly linked-lists `headA` and `headB`, return _the node at which the two lists intersect_. If the two linked lists have no intersection at all, return `null`.
For example, the following two linked lists begin to intersect at node `c1`:
The test cases are generated such that there are no cycles anywhere in the entire linked structure.
**Note** that the linked lists must **retain their original structure** after the function returns.
**Custom Judge:**
The inputs to the **judge** are given as follows (your program is **not** given these inputs):
* `intersectVal` - The value of the node where the intersection occurs. This is `0` if there is no intersected node.
* `listA` - The first linked list.
* `listB` - The second linked list.
* `skipA` - The number of nodes to skip ahead in `listA` (starting from the head) to get to the intersected node.
* `skipB` - The number of nodes to skip ahead in `listB` (starting from the head) to get to the intersected node.
The judge will then create the linked structure based on these inputs and pass the two heads, `headA` and `headB` to your program. If you correctly return the intersected node, then your solution will be **accepted**.
**Example 1:**
**Input:** intersectVal = 8, listA = \[4,1,8,4,5\], listB = \[5,6,1,8,4,5\], skipA = 2, skipB = 3
**Output:** Intersected at '8'
**Explanation:** The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[4,1,8,4,5\]. From the head of B, it reads as \[5,6,1,8,4,5\]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.
**Example 2:**
**Input:** intersectVal = 2, listA = \[1,9,1,2,4\], listB = \[3,2,4\], skipA = 3, skipB = 1
**Output:** Intersected at '2'
**Explanation:** The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[1,9,1,2,4\]. From the head of B, it reads as \[3,2,4\]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.
**Example 3:**
**Input:** intersectVal = 0, listA = \[2,6,4\], listB = \[1,5\], skipA = 3, skipB = 2
**Output:** No intersection
**Explanation:** From the head of A, it reads as \[2,6,4\]. From the head of B, it reads as \[1,5\]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.
**Constraints:**
* The number of nodes of `listA` is in the `m`.
* The number of nodes of `listB` is in the `n`.
* `1 <= m, n <= 3 * 104`
* `1 <= Node.val <= 105`
* `0 <= skipA < m`
* `0 <= skipB < n`
* `intersectVal` is `0` if `listA` and `listB` do not intersect.
* `intersectVal == listA[skipA] == listB[skipB]` if `listA` and `listB` intersect.
**Follow up:** Could you write a solution that runs in `O(m + n)` time and use only `O(1)` memory? | null |
Simple Python solution | intersection-of-two-linked-lists | 0 | 1 | \nWe basically want to increase both A and B till they come out equal. The difference in the lengths can be managed in the same line using simple if-else.\nJust keep on moving A and B till they become equal\n# Code\n```\nclass Solution:\n def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:\n if headA and headB:\n A, B = headA, headB\n while A != B:\n A = A.next if A else headB\n B = B.next if B else headA\n return B\n \n``` | 5 | Given the heads of two singly linked-lists `headA` and `headB`, return _the node at which the two lists intersect_. If the two linked lists have no intersection at all, return `null`.
For example, the following two linked lists begin to intersect at node `c1`:
The test cases are generated such that there are no cycles anywhere in the entire linked structure.
**Note** that the linked lists must **retain their original structure** after the function returns.
**Custom Judge:**
The inputs to the **judge** are given as follows (your program is **not** given these inputs):
* `intersectVal` - The value of the node where the intersection occurs. This is `0` if there is no intersected node.
* `listA` - The first linked list.
* `listB` - The second linked list.
* `skipA` - The number of nodes to skip ahead in `listA` (starting from the head) to get to the intersected node.
* `skipB` - The number of nodes to skip ahead in `listB` (starting from the head) to get to the intersected node.
The judge will then create the linked structure based on these inputs and pass the two heads, `headA` and `headB` to your program. If you correctly return the intersected node, then your solution will be **accepted**.
**Example 1:**
**Input:** intersectVal = 8, listA = \[4,1,8,4,5\], listB = \[5,6,1,8,4,5\], skipA = 2, skipB = 3
**Output:** Intersected at '8'
**Explanation:** The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[4,1,8,4,5\]. From the head of B, it reads as \[5,6,1,8,4,5\]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.
**Example 2:**
**Input:** intersectVal = 2, listA = \[1,9,1,2,4\], listB = \[3,2,4\], skipA = 3, skipB = 1
**Output:** Intersected at '2'
**Explanation:** The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as \[1,9,1,2,4\]. From the head of B, it reads as \[3,2,4\]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.
**Example 3:**
**Input:** intersectVal = 0, listA = \[2,6,4\], listB = \[1,5\], skipA = 3, skipB = 2
**Output:** No intersection
**Explanation:** From the head of A, it reads as \[2,6,4\]. From the head of B, it reads as \[1,5\]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.
**Constraints:**
* The number of nodes of `listA` is in the `m`.
* The number of nodes of `listB` is in the `n`.
* `1 <= m, n <= 3 * 104`
* `1 <= Node.val <= 105`
* `0 <= skipA < m`
* `0 <= skipB < n`
* `intersectVal` is `0` if `listA` and `listB` do not intersect.
* `intersectVal == listA[skipA] == listB[skipB]` if `listA` and `listB` intersect.
**Follow up:** Could you write a solution that runs in `O(m + n)` time and use only `O(1)` memory? | null |
Binary Search Easy Solution || Python3 | find-peak-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(logn)\n\n- Space complexity:O(1)\n\n# Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n n=len(nums)\n if n==1:\n return 0\n low=0\n high=len(nums)-1\n while low<=high:\n mid=low+(high-low)//2\n if mid==0:\n if nums[mid]>nums[mid+1]:\n return mid\n else:\n low=mid+1\n elif mid==n-1:\n if nums[mid]>nums[mid-1]:\n return mid\n else:\n high=mid-1\n else:\n if nums[mid]>nums[mid+1] and nums[mid]>nums[mid-1]:\n return mid\n else:\n if nums[mid]<nums[mid+1]:\n low=mid+1\n else:\n high=mid-1\n return -1\n\n``` | 1 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Simple solution | find-peak-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n i=0\n j=len(nums)-1\n while(i<j):\n mid=(i+j)//2\n if(nums[mid]<nums[mid+1]):\n i=mid+1\n else:\n j=mid\n return i\n``` | 2 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
✨✅Clear Explanation with Graphical Visualizations✅✨ | find-peak-element | 0 | 1 | # Approach\nBinary search works on questions where you can find some sort of symmetry either to delete left half or delete right half.\nLet me explain it to u for find peak element-1 on leetcode https://leetcode.com/problems/find-peak-element/\n\nConsider the array [1,2,3,4,6,7,3,2,1] . Clearly 7 is the peak element \nPoint to note:\n1) No to elemnts are adjacent.Therefore one neighbour can either be greater than the other neighbour or it can be lesser; equality is not possible.(V Impp)\nThis means The graph at mid can either be increasing or decreasing:\n\n2) We will pre check for the leftmost and rightmost element to be peak before applying BS .\nIf either of them is the peak we will return them beforehand.\nWhile applying BS We already know that the leftmost and rightmost elemnt are lesser than their neighbours . Therefore their graph will always be increasing .\n\n```\nCase1: Decreasing graph at Leftmost\n(left point)\n \\\n \\\n \\\n (mid somewhere)\n---> No need to apply BS Just return Left Point\n```\n\n\n```\nCase2: Decreasing Graph at Rightmost\n (right point)\n /\n /\n /\n(mid somewhere)\n----> No need to apply BS Just return Right point\n```\n\n\n\n```\nCase3: Increasing at leftmost and Increasing at right most\n\n (peak somewhere)\n / \\\n / \\\n / \\\n(left point) (right point)\n---------> Binary Search has to be applied\n```\n\n```\nIncreasing graph:\n X (mid+1)\n / \\ \n / \\\n O (mid) \\\n / \\\n / \\\n Y(mid-1) (rightmost point)\n /\n /\n(leftmost point somewhere)\n\n\nIf the graph is increasing at mid \n(i.e. arr[mid-1]<arr[mid]<arr[mid+1])\nthere has to be a peak in the right half \nbecause the rightmost point is at the lower point \n(Case 2 was eliminated remember?)\n---->Eliminate left half\n```\n\n\n```\nSimilarly Decreasing Graph: \n X(mid+1)\n / \\ \n / \\\n / O(mid)\n / \\\n / \\\n(leftmost point) Y(mid-1)\n \\\n \\\n \\\n (rightmost point somewhere)\nIf the graph is decreasing at mid \n(i.e. arr[mid+1]<arr[mid]<arr[mid-1]) \nthere has to be a peak in the left half \nbecause the leftmost point is at the lower point \n(Case 1 was eliminated remember?)\n------>Eliminate right half\n\n```\n# Complexity\n- Time complexity: O(logN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int: \n n=len(nums)\n if n==1:\n return 0\n if nums[0]>nums[1]:return 0\n if nums[-1]>nums[-2]:return n-1\n low=1\n high=n-2\n while low<=high: \n mid=(low+high)//2\n if nums[mid-1]<nums[mid]>nums[mid+1]:\n return mid\n if nums[mid-1]<nums[mid]:\n low=mid+1\n else:\n high =mid-1\n return -1 \n```\nAll suggestions are welcome.\nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\nHappy Learning, Cheers Guys \uD83D\uDE0A\n | 2 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Beginner friendly python solution using modified binary search!! 🔥🔥 | find-peak-element | 0 | 1 | # Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n low=0\n high=len(nums)-1\n while low<=high:\n mid=low+(high-low)//2\n if mid>0 and nums[mid]<nums[mid-1]:\n high=mid-1\n elif mid<len(nums)-1 and nums[mid]<nums[mid+1]:\n low=mid+1\n else:\n return mid\n``` | 3 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Mind blowing code with three conditions mid at start, end and middle. | find-peak-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n if len(nums)==1:\n return 0\n low=0\n high=len(nums)-1\n while low<=high:\n mid=(low+high)//2\n if (mid>0 and mid<len(nums)-1):\n if nums[mid]>nums[mid+1] and nums[mid]>nums[mid-1]:\n return mid\n elif nums[mid]<nums[mid+1]:\n low=mid+1\n else:\n high=mid-1\n elif mid==0:\n if nums[mid]>nums[mid+1]:\n return mid\n else:\n return mid+1\n elif mid==len(nums)-1:\n if nums[mid]>nums[mid-1]:\n return mid\n else:\n return mid-1\n return -1\n\n``` | 2 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Python Easy Solution using Binary Search | find-peak-element | 0 | 1 | ```\nclass Solution:\n def findPeakElement(self, nums):\n # If the array contains only one element, it is the peak.\n if len(nums) == 1:\n return 0\n \n # Check if the first element is greater than the second,\n # if so, the first element is a peak.\n if nums[0] > nums[1]:\n return 0\n \n # Check if the last element is greater than the second-to-last,\n # if so, the last element is a peak.\n if nums[len(nums) - 1] > nums[len(nums) - 2]:\n return len(nums) - 1\n \n # Now, use binary search to find the peak element.\n # Set two pointers i and j to the second and second-to-last elements,\n # respectively, because we already checked the first and last elements.\n i = 1\n j = len(nums) - 2\n \n while i <= j:\n # Calculate the middle index.\n mid = i + (j - i) // 2\n \n # If the middle element is greater than its neighbors, it\'s a peak.\n if nums[mid] > nums[mid + 1] and nums[mid] > nums[mid - 1]:\n return mid\n elif nums[mid - 1] < nums[mid]:\n #If the element to the left of mid is less than mid, \n\t\t\t\t#It indicates that the peak could be on either the left or right side of mid.\n i = mid + 1\n else:\n j = mid - 1\n \n # If no peak is found, return None.\n return None\n\n``` | 8 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Python Easy Solution || 100% || Binary Search || | find-peak-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n left=0\n right=len(nums)-1\n if len(nums)==1:\n return 0\n while left<=right:\n mid=(left+right)>>1\n if (mid==0 or nums[mid]>=nums[mid-1] ) and (mid==len(nums)-1 or nums[mid]>=nums[mid+1]) :\n return mid\n elif nums[mid]<=nums[mid+1]:\n left=mid+1\n else:\n right=mid-1\n return -1\n``` | 2 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Best Python Solution Ever || Binary Search || 9 Lines Only | find-peak-element | 0 | 1 | \n# Complexity\n- Time complexity: O(LogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n\n s= 0\n e = len(nums)-1\n\n while s<e:\n m = (s+e)//2\n if nums[m]>nums[m+1]:\n e = m\n else:\n s = m+1\n return e\n \n``` | 2 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
[ Python ] | Simple & Clean Solution Using Binary Search | find-peak-element | 0 | 1 | # Code\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n n = len(nums)\n l, r = 0, n - 1\n while l < r:\n mid = (l + r) >> 1\n if nums[mid] < nums[mid + 1]:\n l = mid + 1\n else:\n r = mid \n return l\n``` | 4 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
General Binary Search Thought Process : 4 Templates | find-peak-element | 0 | 1 | ***Scroll down to the end to check the solution to this question using all 4 templates***\nBinary Search can be applied to a problem where we can find a function(if condition of the code) that map elements in left half to True and the other half to False or vice versa . **Don\'t think it is just for the sorted array** (Refer here :https://www.youtube.com/watch?time_continue=67&v=GU7DpgHINWQ&feature=emb_logo)\n\nPattern : T T T T T F F F \n\n\n\n**Note: y<=6 is a condition**\n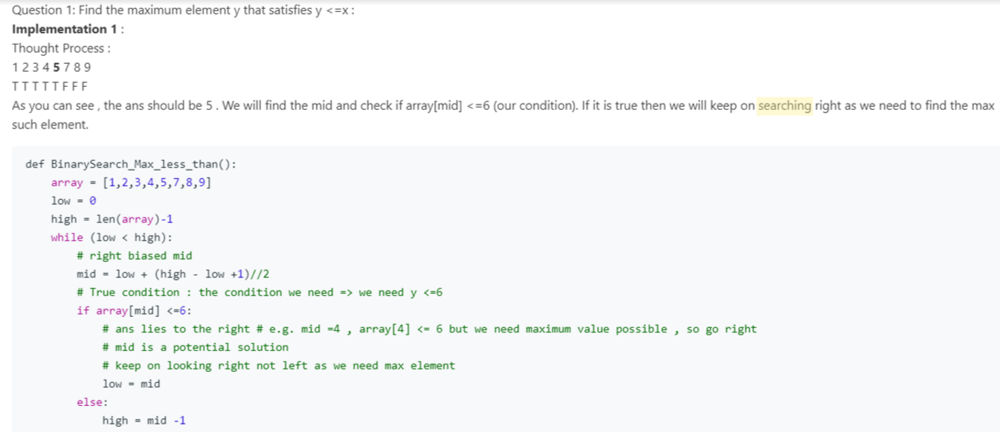\n\n\n\n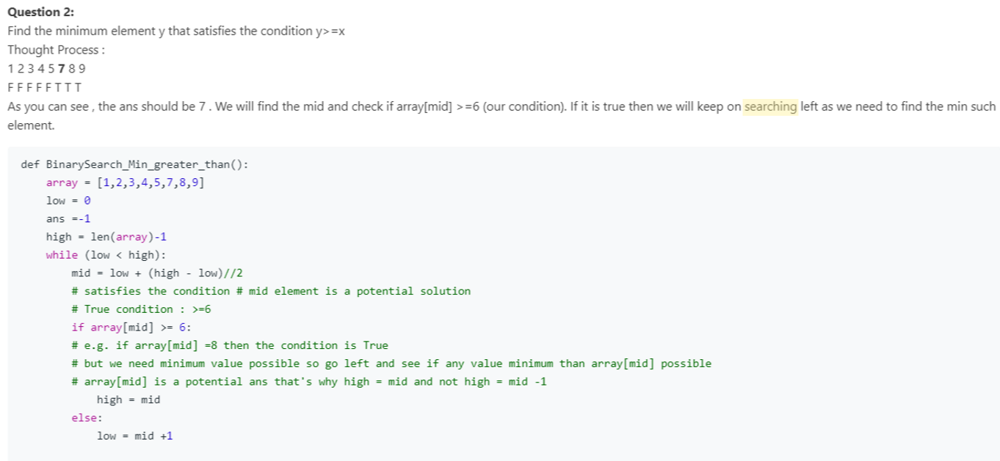\n\n\nNow a Binary Search can be solved using 4 Templates: You can try solving all Binary Search questions using just one template. \n1. **Find the *First True***:\n\n\t**T** T T T T F F F or F F F F **T** T T T\n\tWe always try to go the left when finding the First True and the template will be like :\n\t\n\t```\n\twhile left < right :\n\t\tif condition is true:\n\t\t\tright = mid \n\t\telse:\n\t\t\tleft = mid +1\n\t```\n\t\n **Thought Process for this template :** For FFFFTTTT, if mid is second last True , then it is a possible ans but we need to keep searching left because we want First True or minimal True for it . We move to left part by doing right = mid where mid is a potential solution and throw away the right part\n\n2. **Find the *Last True***:\n\n\tT T T T **T** F F F or F F F F T T T T **T**\n\t\n\tWe always try to go the right when finding the Last True and the template will be like :\n\t\n\t```\n\twhile left < right :\n\t\tif condition is true:\n\t\t\tleft = mid \n\t\telse:\n\t\t\tright = mid - 1\n\t```\n\t\n **Thought Process for this template :** For T T T T T F F F, if mid is First True , then it is a possible ans but we need to keep searching right because we want Last True or Maximal True for it . We move to right half by doing left = mid where mid is a potential solution and throw away the left part\n\t\n3. **Find the *First False***:\nT T T T T **F** F F or **F** F F F T T T T \n\t```\n\twhile left < right:\n\t\tif condition is False: \n\t\t\tleft = mid +1\n\t\telse:\n\t\t\tright = mid\n\t```\n **Thought Process this template :** For T T T T T F F F, if mid is at Last False , then it is a possible ans but we need to keep searching left because we want First False or Minimal False for it . \n\n4. **Find the *Last False*:**\nT T T T T F F **F** or F F F F **F** T T T\n\t```\n\twhile left < right:\n\t\tif condition is False: \n\t\t\tright = mid -1\n\t\telse:\n\t\t\tleft = mid\n\t```\n **Reason for this template :** For F F F F F T T T , if mid is second False , then it is a possible ans but we need to keep searching right because we want Last False or Maximal False for it .\n\nYou have to change the condition in the "if statement" such that the problem is converted to one of the problem above. You can stick to one template if you want like always finding the First true . Now this "condition" in "if statement" can be the one which question is asking or it can be the opposite of it .\n\n----------------------------------------------------------------------------------------------------------------------------\n## **Current Problem** : Find Peak Element : \n\n**Condition for this question** : We know a elem at index i is a peak elem , if its left and right neighbours are smaller than it i.e. **nums[i] > nums[i-1] and nums[i] > nums[i+1]**\n\n**Now Lets solve this question using all the 4 templates above:**\n1. **Find First True** :\nIn order to convert this problem to T T T T F F F F where the ans(finding peak in this question) will be the First True , we need to come up with condition like ***nums[i] >nums[i+1]***\n\n\n\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n left =0\n right = len(nums)-1\n while left < right:\n mid = left + (right - left ) //2\n if nums[mid] > nums[mid+1]: # True Condition # Dec function # go left # Find First True i.e first elem where this condition will be True\n right = mid # include mid # mid is potential solution \n else:\n left = mid +1\n return left\n```\n2. **Find Last True:** . In order to convert this problem to T T T T T F F F where the ans will be the Last True , we need to come up with condition like ***nums[i] > nums[i-1]***\n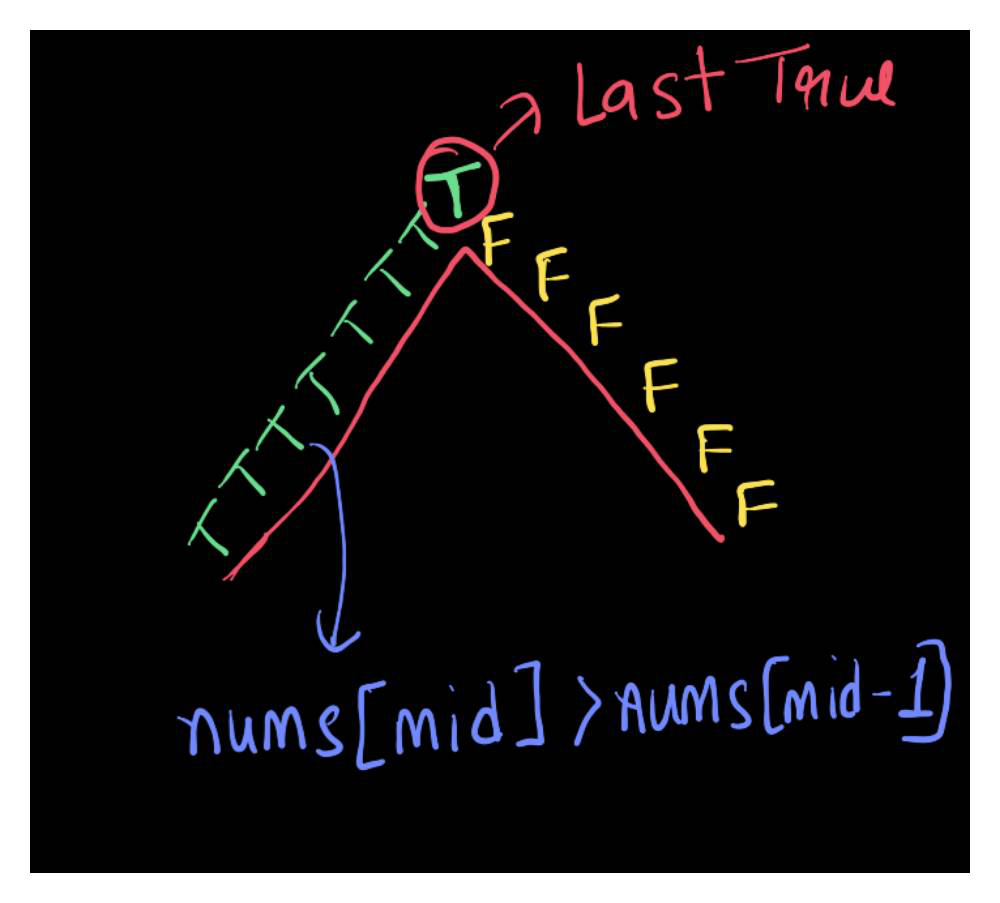\n\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n left =0\n right = len(nums)-1\n while left < right:\n mid = left + (right - left + 1) //2 # Right biased mid as left = mid in else condition # prevent infinite loop\n if nums[mid] > nums[mid-1]: # True condition # go right # inc function # Last True \n left = mid # mid is a potential elem\n else:\n right = mid -1\n return left\n```\n\n3. **Find First False :** You have to use a condition in if statement which is opposite of what question is asking . \n**Opposite Conditions :** nums[i] < nums[i+1] or nums[i] < nums[i-1].\nFor first False , we will use nums[i] < nums[i+1]\nWhen nums[i] < nums[i+1], it means it is the increasing slope and all elems n this inc slope will pass this condition i.e. They will be True. Our Ans will be the first false.(In else condition , we are storing the potential ans in "right"var and when loop ends , we can return that)\n\n\n```\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n left =0\n right = len(nums)-1\n while(left < right):\n mid = left +(right-left)//2\n if nums[mid] < nums[mid+1]: # False Condition # inc function # go right # Find First False\n\t\t\t# i.e. find First elem when this if will be false\n left = mid+1 # exclude mid \n else: \n right = mid\n return left\n```\n* **Find Last False** : nums[i] < nums[i-1]\n\n\n```\n\nclass Solution:\n def findPeakElement(self, nums: List[int]) -> int:\n left =0\n right = len(nums)-1\n while(left < right):\n mid = left +(right-left+1)//2 # Right biased mid as left = mid in else condition # prevent infinite loop\n if nums[mid] < nums[mid-1]: # False condition # Dec function # go left # Find Last False i.e the Last elem for which this condition will be False \n right = mid - 1\n else: # decreasing so peak will be before mid or it can be mid\n left = mid\n return left\n```\n\n | 68 | A peak element is an element that is strictly greater than its neighbors.
Given a **0-indexed** integer array `nums`, find a peak element, and return its index. If the array contains multiple peaks, return the index to **any of the peaks**.
You may imagine that `nums[-1] = nums[n] = -∞`. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in `O(log n)` time.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 2
**Explanation:** 3 is a peak element and your function should return the index number 2.
**Example 2:**
**Input:** nums = \[1,2,1,3,5,6,4\]
**Output:** 5
**Explanation:** Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-231 <= nums[i] <= 231 - 1`
* `nums[i] != nums[i + 1]` for all valid `i`. | null |
Python Easy Solution Ever !!! | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n if len(nums) < 2:\n return 0\n\n nums.sort()\n max_diff = 0\n\n for i in range(1, len(nums)):\n max_diff = max(max_diff, nums[i] - nums[i - 1])\n\n return max_diff\n``` | 4 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Easy and simple solution in Python | maximum-gap | 0 | 1 | # Intuition\nThe intuition is to sort the input array and then find the maximum difference between adjacent elements, as the largest gap will likely be between sorted values.\n# Approach\nThe approach involves sorting the array and iterating through adjacent pairs to find the maximum gap. The time complexity is O(n log n) due to the sorting step.\n# Complexity\n- Time complexity:\nO(n log n) due to the sorting step. \n- Space complexity:\nO(1) since the sorting is done in-place and additional space is constant. \n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n last_index = len(nums)\n nums = sorted(nums)\n max_ = 0\n for i in range(1, last_index):\n max_ = max(max_, (nums[i] - nums[i - 1]))\n return 0 if last_index <= 1 else max_\n\n``` | 2 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Python3 code, Runtime beats 92.32% ,Memory beats 65.96% | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n nums=sorted(nums)\n min=float("-inf")\n if len(nums)<2:\n return 0\n for i in range(len(nums)-1):\n x=abs(nums[i]-nums[i+1])\n if min<x:\n min=x\n return min\n``` | 16 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
[Java/Python3] || Explanation + Code || Brute Force & Optimized Approach || Bukcet Sort🔥 | maximum-gap | 1 | 1 | # Brute Force\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust sort the array and check the pair of two adjacent elements having the maximum gap in the array.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStep 1: Sort the array\nStep 2: Traverse the loop in the reverse order and compare the difference between the last and its previous element.\nStep 3: Replace the value max if value exceeds.\nStep 4: Return the max difference.\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n\n```Java []\nclass Solution {\n public int maximumGap(int[] nums) {\n if(nums.length < 2)return 0;\n Arrays.sort(nums);\n int maxDiff = 0;\n for(int i=0;i<nums.length-1;i++){\n maxDiff = Math.max(maxDiff, nums[i+1] - nums[i]);\n }\n return maxDiff;\n }\n}\n```\n```python3 []\nclass Solution:\n def maximumGap(self, nums):\n if len(nums) < 2:\n return 0\n \n nums.sort()\n maxDiff = 0\n\n for i in range(1, len(nums)):\n maxDiff = max(maxDiff, nums[i] - nums[i - 1])\n \n return maxDiff\n```\n\n---\n# Optimized Approach\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor finding maximum gap we are making bucket for putting middle n-2 elements and bucket size will be n-1 means (smallest and largest elements are to be avoided) means there will be one bucket that will be empty so that previous max and next mix elements of bucket will give the max difference. For doing so we make the bucket of `size n-1` for both storing max and min element in the bucket and bucket will contain and bucket will store `(max-min)/n-1` range of elements . Now we start putting elements in bucket so for checking in which index we have to put that element we find `(x-min)/avg` and avg is `(max-min)/n-1` so we get the index and we fill max and min buckets with this elements . Now we simply take difference between max of one bucket and min of next bucket. \n# Complexity\n- Time complexity:` O(n)`, where n is the length of the input array.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`, because we are using an array to store the buckets. However, we can reduce the space complexity to `O(1) `by using a linked list instead of an array to store the buckets.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n\n```Java []\nclass Solution {\n public int maximumGap(int[] nums) {\n if(nums.length < 2)\n return 0;\n int n = nums.length;\n int max = nums[0], min= nums[0];\n for(int i : nums) {\n max = Math.max(max, i);\n min = Math.min(min, i);\n }\n int bucketSize = (max - min)/(n - 1);\n if(bucketSize == 0)\n bucketSize++;\n int totalBuckets = ((max - min)/bucketSize) + 1;\n int[] minBucket = new int[totalBuckets];\n int[] maxBucket = new int[totalBuckets];\n Arrays.fill(minBucket, Integer.MAX_VALUE);\n for(int i = 0 ; i < n ; i++) {\n int index = (nums[i] - min)/bucketSize;\n minBucket[index] = Math.min(minBucket[index], nums[i]);\n maxBucket[index] = Math.max(maxBucket[index], nums[i]);\n }\n int prevMax = maxBucket[0], result = 0;\n for(int i = 1; i < totalBuckets; i++) {\n if(minBucket[i] == Integer.MAX_VALUE)\n continue;\n result = Math.max(result, minBucket[i] - prevMax);\n prevMax = maxBucket[i];\n }\n return result;\n }\n}\n```\n```python3 []\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n n = len(nums)\n if n < 2:\n return 0\n \n # compute the maximum and minimum values\n max_value, min_value = max(nums), min(nums)\n \n # compute the size of each bucket\n bucket_size = max(1, (max_value - min_value) // (n - 1))\n \n # compute the number of buckets\n num_buckets = (max_value - min_value) // bucket_size + 1\n \n # initialize the buckets with maximum and minimum values\n buckets = [[float(\'inf\'), float(\'-inf\')] for _ in range(num_buckets)]\n for num in nums:\n bucket_index = (num - min_value) // bucket_size\n buckets[bucket_index][0] = min(buckets[bucket_index][0], num)\n buckets[bucket_index][1] = max(buckets[bucket_index][1], num)\n \n # compute the maximum difference\n max_diff = 0\n prev_max = buckets[0][1]\n for i in range(1, num_buckets):\n if buckets[i][0] == float(\'inf\'):\n continue\n max_diff = max(max_diff, buckets[i][0] - prev_max)\n prev_max = buckets[i][1]\n \n return max_diff\n```\n\n\n | 9 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
without solution life is nothing | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n if len(nums)<2:\n return 0\n ls = sorted(nums)\n a = []\n for i in range(1,len(ls)):\n a.append(ls[i]-ls[i-1])\n return max(a)\n``` | 2 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Easy Python3 solution ! Beats atleat 80% | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n ls = nums\n b = sorted(ls) \n l1 = []\n if(len(b) > 1):\n for x in range(1,len(ls)):\n difference = b[x] - b[x-1]\n l1.append(difference)\n return(max(l1))\n else:\n return 0\n``` | 1 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
164: Solution with step by step explanation | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We define a Solution class with a maximumGap method that takes a list of integers nums as input and returns an integer, the maximum gap between two successive elements in the sorted form of nums.\n\n2. We check if the length of nums is less than 2, and return 0 if so, because we cannot find a gap between two elements if there is only one or none.\n\n3. We get the minimum and maximum values in nums using the built-in min and max functions.\n\n4. We calculate the bucket size as the maximum of 1 and the integer division of the range of nums (i.e., max_val - min_val) by the number of elements in nums minus 1 (i.e., len(nums) - 1). This ensures that we have at least one element in each bucket. We also calculate the number of buckets as the integer division of the range of nums by the bucket size plus 1, to ensure that we have a bucket for the maximum value.\n\n5. We initialize an empty list buckets of length num_buckets to hold the buckets.\n\n6. We loop through each element num in nums and calculate the index of the bucket it belongs to as the integer division of its distance from min_val by the bucket size. We then check if the corresponding bucket is empty or not, and if it is, we initialize it with the min and max values of num. Otherwise, we update the min and max values of the bucket with the minimum and maximum of num and the current min and max values, respectively.\n\n7. We initialize a variable max_gap to hold the maximum gap between adjacent buckets, and a variable prev_max to hold the maximum value in the previous bucket, initially set to min_val.\n\n8. We loop through each bucket in buckets, and if it is not empty, we update max_gap with the difference between its `min\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n \n # Check if the list is empty or contains only one element\n if len(nums) < 2:\n return 0\n \n # Get the minimum and maximum values in the list\n min_val = min(nums)\n max_val = max(nums)\n \n # Calculate the bucket size and number of buckets\n bucket_size = max(1, (max_val - min_val) // (len(nums) - 1))\n num_buckets = (max_val - min_val) // bucket_size + 1\n \n # Initialize the buckets\n buckets = [None] * num_buckets\n \n # Put each element in its corresponding bucket\n for num in nums:\n bucket_index = (num - min_val) // bucket_size\n if not buckets[bucket_index]:\n buckets[bucket_index] = {\'min\': num, \'max\': num}\n else:\n buckets[bucket_index][\'min\'] = min(buckets[bucket_index][\'min\'], num)\n buckets[bucket_index][\'max\'] = max(buckets[bucket_index][\'max\'], num)\n \n # Calculate the maximum gap between adjacent buckets\n max_gap = 0\n prev_max = min_val\n for bucket in buckets:\n if bucket:\n max_gap = max(max_gap, bucket[\'min\'] - prev_max)\n prev_max = bucket[\'max\']\n \n return max_gap\n\n``` | 9 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Very easy approach Python short | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSort the Input List\nCalculate the Differences Between Adjacent Elements:\nFind the Maximum Gap:\nAnd return \n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:\n- The dominant factor here is the sorting step, so the overall time complexity of your code is O(n log n) due to the sorting operation.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- Therefore, the overall space complexity of your code is O(n) due to the space used by the k list.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n if len(nums) < 2:\n return 0\n nums.sort()\n k = []\n for i in range(len(nums) - 1):\n k.append(nums[i + 1] - nums[i])\n return max(k)\n\n``` | 2 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Python Easy Solution || 100% || Beginners Friendly || | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAs descripted is problem if array have 1 element then return 0\nNext will sort the arrey and get the diffrence of each element and compare the value of max variable to this.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n mx = 0\n if len(nums)<2:\n return 0\n else:\n nums.sort()\n for i in range(len(nums)-1):\n mx = max(mx, (nums[i+1])-nums[i])\n return mx\n``` | 2 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
easy python3 solution | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n l=[]\n a=nums\n b=sorted(a)\n if len(b)!=1:\n for i in range(1,len(a)):\n c=b[i]-b[i-1]\n l.append(c)\n return(max(l))\n else:\n return(0)\n``` | 1 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Easeist Submission. | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nPython\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n cout = 0\n if len(nums) <= 1 :\n return cout\n sortN = sorted(nums)\n for i in range(0, len(nums)-1) :\n c = abs(sortN[i] - sortN[i+1])\n if c > cout :\n cout = c\n return cout\n```\n\nTypeScript\n \n```\n\nmaximumGap(nums: Array<Number>) : Number {\n let cout = 0\n if (nums.length <= 1) {\n return cout\n }\n nums.sort()\n for (let i = 0; i <= nums.length-1; i++) {\n let c = Math.abs(nums[i] - nums[i+1])\n if (c > cout) {\n cout = c\n }\n }\n return cout\n}\n\n```\n | 0 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Solution | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n if len(nums)<2:\n return 0\n else:\n nums=sorted(nums)\n di=0\n for i in range(len(nums)-1):\n if di < abs(nums[i] - nums[i+1]):\n di=abs(nums[i]-nums[i+1])\n return di\n\n \n``` | 0 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Maximum gap using Python | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n nums.sort();diff = []\n if len(nums)<2:return 0\n else:\n for i in range(len(nums)-1):\n diff.append(nums[i+1]-nums[i])\n return max(diff)\n``` | 0 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
pyhton easy solution | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n if len(nums)<2:\n return 0\n nums.sort()\n ans=[]\n for i in range(len(nums)-1):\n ans.append(abs(nums[i]-nums[i+1]))\n print(ans)\n return max(ans) \n\n``` | 0 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Simple Python Solution for beginners | maximum-gap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumGap(self, nums: List[int]) -> int:\n if(len(nums)<2):\n return 0\n nums.sort()\n maxi=0\n for i in range(1,len(nums)):\n if((nums[i]-nums[i-1])>maxi):\n maxi=nums[i]-nums[i-1]\n return maxi\n \n``` | 0 | Given an integer array `nums`, return _the maximum difference between two successive elements in its sorted form_. If the array contains less than two elements, return `0`.
You must write an algorithm that runs in linear time and uses linear extra space.
**Example 1:**
**Input:** nums = \[3,6,9,1\]
**Output:** 3
**Explanation:** The sorted form of the array is \[1,3,6,9\], either (3,6) or (6,9) has the maximum difference 3.
**Example 2:**
**Input:** nums = \[10\]
**Output:** 0
**Explanation:** The array contains less than 2 elements, therefore return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
✔️ [Python3] SOLUTION, Explained | compare-version-numbers | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nFirstly, we split versions by `.` and convert revisions to integers. Next, we iterate over revisions and compare one by one.\n\n`zip_longest` - same as a `zip` but it also pads lists with zeros if lengths are not equal *(see https://docs.python.org/3/library/itertools.html#itertools.ziplongest)*\n\nRuntime: 32 ms, faster than **83.77%** of Python3 online submissions for Compare Version Numbers.\nMemory Usage: 13.8 MB, less than **99.63%** of Python3 online submissions for Compare Version Numbers.\n\n```\nclass Solution:\n def compareVersion(self, v1: str, v2: str) -> int:\n v1, v2 = list(map(int, v1.split(\'.\'))), list(map(int, v2.split(\'.\'))) \n for rev1, rev2 in zip_longest(v1, v2, fillvalue=0):\n if rev1 == rev2:\n continue\n\n return -1 if rev1 < rev2 else 1 \n\n return 0\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 65 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
Simple solution | compare-version-numbers | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n lst1=version1.split(\'.\')\n lst2=version2.split(\'.\')\n if(len(lst1)>len(lst2)):\n for i in range(len(lst1)-len(lst2)):\n lst2.append(\'0\')\n if(len(lst2)>len(lst1)):\n for i in range(len(lst2)-len(lst1)):\n lst1.append(\'0\')\n for i in range(len(lst1)):\n if(int(lst1[i])>int(lst2[i])):\n return 1\n if(int(lst1[i])<int(lst2[i])):\n return -1\n return 0 \n``` | 1 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
165: Solution with step by step explanation| | compare-version-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe function compareVersion takes two string arguments version1 and version2, and returns an integer.\n\nFirst, the function splits both version strings into a list of revisions using the split method and the dot \'.\' as separator. The maximum length n between the two lists is obtained using the max function.\n\nThen, the function iterates over the revisions of both lists using a for loop and the range function with argument n. For each index i, the corresponding revisions r1 and r2 are obtained by converting the string revision to an integer using the int function if it exists in the list, otherwise using 0.\n\nThe revisions r1 and r2 are compared using the standard comparison operators, and the result is returned if they are different. Specifically, if r1 < r2, then version1 is considered smaller and -1 is returned; if r1 > r2, then version1 is considered larger and 1 is returned.\n\nIf all revisions are equal, then 0 is returned.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n # Split version numbers into list of revisions\n v1 = version1.split(\'.\')\n v2 = version2.split(\'.\')\n # Get the maximum length between the two lists\n n = max(len(v1), len(v2))\n # Iterate over the revisions of both lists\n for i in range(n):\n # Convert each revision to an integer if it exists, otherwise use 0\n r1 = int(v1[i]) if i < len(v1) else 0\n r2 = int(v2[i]) if i < len(v2) else 0\n # Compare revisions and return result if different\n if r1 < r2:\n return -1\n elif r1 > r2:\n return 1\n # Return 0 if all revisions are equal\n return 0\n\n``` | 5 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
Python | Easy to understand | For Beginner | Faster than 90% | compare-version-numbers | 0 | 1 | ```\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n ver1=version1.split(\'.\')\n ver2=version2.split(\'.\')\n i=0\n maxlen=max(len(ver1),len(ver2))\n while i<maxlen:\n v1=int(ver1[i]) if i<len(ver1) else 0\n v2=int(ver2[i]) if i<len(ver2) else 0\n if v1<v2:\n return -1\n elif v1>v2:\n return 1\n else:\n i+=1\n return 0\n``` | 1 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
Python | Two pointers | No functions | Time : O(m,n)| Space : O(1) | compare-version-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck the numbers till we get a \'.\' dot and compare them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis approarch doesn\'t use any list to string or string to list conversion.\n\nHave 2 pointers \'first\' and \'second\' for version1 and version2 strings respectively. We will store thevalues before we encounter a dot for both in temperpry varialble num1 and num2. \n\nStart a loop till both the loops pointers \'first\' and second\' reach the end. Because if version1 is "1" and version2 is "1.0.1", we cannot stop after 0th index. "1" is same as "1.0.0" we set num1 and num2 intially to 0. So once version1 index goes beyond its length the next elements or reversion digits are by default considerd as 0.\n\nAfter we encounter a \'.\' in both the versions we compare the numbers and return the ans acordingly.\n\nDo upvote it if you liked the approarch.\n\n\n# Complexity\n- Time complexity: **O(**max(n,m)**)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n\n first = second = 0\n \n while first < len(version1) or second < len(version2):\n num1 = num2 = 0\n while first < len(version1) and version1[first] != \'.\':\n num1 = num1 * 10 + int(version1[first])\n first +=1\n while second < len(version2) and version2[second] != \'.\':\n num2 = num2 * 10 + int(version2[second])\n second += 1\n if num1 < num2:\n return -1\n elif num1 > num2:\n return 1\n\n first +=1 \n second +=1\n \n return(0)\n``` | 1 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
✅ Python3 | Simple and Concise Solution |Easy To Understand W/Explanation | compare-version-numbers | 0 | 1 | \t\t\t\t\t\t\t\t\t\t\t\t\t\tPlease Upvote if it helps, Thanks.\n**Intuition:**\n1. It\'s already mentioned that every revision can be stored in 32 bit integer (Revision is numbers between every two dots, except the first).\n2. Hence lets compare every revision as Integer (If revision doesn\'t exist for a version, we can consider it as zero).\n\nExample: version1 = 1.1, version2 = 1.1.2 \noutput: -1\nNote: version1 will be considered as 1.1.0 since the last revision doesn\'t exist we consider it as 0.\n\n\tTime complexity: `O(m + n)`\n\n**Simple Solution:** \n\n```\nclass Solution:\n \'\'\'\n\tSpace complexity: `O(m + n)`\n\t \n\tSince split operation will be taking extra space to populate the array\n\t\'\'\'\n def compareVersion(self, version1: str, version2: str) -> int:\n version1, version2 = version1.split(\'.\'), version2.split(\'.\')\n m, n = len(version1), len(version2)\n i = j = 0\n while(i < m or j < n):\n revision1 = int(version1[i]) if(i < m) else 0\n revision2 = int(version2[j]) if(j < n) else 0\n if(revision1 < revision2): return -1\n if(revision1 > revision2): return 1\n i, j = i + 1, j + 1\n \n return 0\t\n```\n\n**A bit complex solution to optimize space:**\n\n```\n\t\'\'\'\n\tSpace complexity: `O(1)`\n\t\n\tInstead of splitting the array we will just iterate and get the revision number.\n\t\'\'\'\nclass Solution:\n def getRevision(self, version, index, len_):\n revision, dot, i = 0, \'.\', index\n \n for i in range(index, len_):\n if(version[i] == dot):\n break\n revision *= 10\n revision += int(version[i])\n \n return revision, i + 1\n \n def compareVersion(self, version1: str, version2: str) -> int:\n i, j, m, n = 0, 0, len(version1), len(version2)\n \n while(i < m or j < n):\n revision1, nextIndex1 = self.getRevision(version1, i, m)\n revision2, nextIndex2 = self.getRevision(version2, j, n)\n if(revision1 < revision2): return -1\n if(revision1 > revision2): return 1\n i, j, = nextIndex1, nextIndex2\n \n return 0\n```\n | 9 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
[Python3] Easy O(N) Time Solution | compare-version-numbers | 0 | 1 | ```\n\'\'\' \nclass Solution:\n def compareVersion(self, v1: str, v2: str) -> int:\n i = 0\n j = 0\n while i < len(v1) or j < len(v2):\n n1 = 0\n k = i\n if k < len(v1):\n while k < len(v1) and v1[k] != \'.\':\n k += 1\n n1 = int(v1[i:k])\n i = k + 1\n \n n2 = 0\n k = j \n if k < len(v2):\n while k < len(v2) and v2[k] != \'.\':\n k += 1\n n2 = int(v2[j:k])\n j = k + 1\n \n if n1 < n2: return -1\n if n1 > n2: return 1\n \n return 0\n\n# Time: O(N^2)\n# Space: O(1)\n\'\'\'\n\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n v1 = collections.deque(version1.split("."))\n v2 = collections.deque(version2.split("."))\n \n while v1 or v2:\n v1_val = 0\n v2_val = 0\n if v1: v1_val = int(v1.popleft())\n if v2: v2_val = int(v2.popleft())\n \n if v1_val > v2_val: return 1\n if v1_val < v2_val: return -1\n \n return 0\n \n# Time: O(N) ; as pop from deque is constant time\n# Space: O(N) ; for making v1 and v2\n``` | 2 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
[Python, Python3] Two Solutions | compare-version-numbers | 0 | 1 | **Solution1**\n\n```\nclass Solution(object):\n def compareVersion(self, version1, version2):\n """\n :type version1: str\n :type version2: str\n :rtype: int\n """\n version1 = version1.split(".")\n version2 = version2.split(".")\n c = 0\n while c < len(version1) and c < len(version2):\n if int(version1[c])>int(version2[c]):\n return 1\n elif int(version2[c])>int(version1[c]):\n return -1\n else:\n c += 1\n if c < len(version1):\n for i in version1[c:]:\n if int(i) > 0:\n return 1\n if c < len(version2):\n for i in version2[c:]:\n if int(i) > 0:\n return -1\n return 0\n \n```\n\n**Solution2** Python3\n\n```\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n import itertools\n version1 = version1.split(\'.\')\n version2 = version2.split(\'.\')\n for v1, v2 in itertools.zip_longest(version1, version2, fillvalue=0):\n if int(v1)>int(v2):\n return 1\n elif int(v2)>int(v1):\n return -1\n return 0\n``` | 2 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
Simple & Short Python Solution | compare-version-numbers | 0 | 1 | ```\nclass Solution:\n def compareVersion(self, version1: str, version2: str) -> int:\n v1 = version1.split(\'.\') # Divide string version1 into array seperated by "."\n v2 = version2.split(\'.\') # Divide string version2 into array seperated by "."\n m = len(v1)\n n = len(v2)\n\t\t# Just take strings at index i from v1 & v2, convert them to integer and check which version is larger. \n\t\t# If an array is already traversed then we may consider the version to be 0. \n for i in range(max(m, n)):\n i1 = int(v1[i]) if i < m else 0 \n i2 = int(v2[i]) if i < n else 0\n if i1 > i2:\n return 1\n if i1 < i2:\n return -1\n return 0 # Both versions must be same if their was no difference at any point.\n``` | 2 | Given two version numbers, `version1` and `version2`, compare them.
Version numbers consist of **one or more revisions** joined by a dot `'.'`. Each revision consists of **digits** and may contain leading **zeros**. Every revision contains **at least one character**. Revisions are **0-indexed from left to right**, with the leftmost revision being revision 0, the next revision being revision 1, and so on. For example `2.5.33` and `0.1` are valid version numbers.
To compare version numbers, compare their revisions in **left-to-right order**. Revisions are compared using their **integer value ignoring any leading zeros**. This means that revisions `1` and `001` are considered **equal**. If a version number does not specify a revision at an index, then **treat the revision as `0`**. For example, version `1.0` is less than version `1.1` because their revision 0s are the same, but their revision 1s are `0` and `1` respectively, and `0 < 1`.
_Return the following:_
* If `version1 < version2`, return `-1`.
* If `version1 > version2`, return `1`.
* Otherwise, return `0`.
**Example 1:**
**Input:** version1 = "1.01 ", version2 = "1.001 "
**Output:** 0
**Explanation:** Ignoring leading zeroes, both "01 " and "001 " represent the same integer "1 ".
**Example 2:**
**Input:** version1 = "1.0 ", version2 = "1.0.0 "
**Output:** 0
**Explanation:** version1 does not specify revision 2, which means it is treated as "0 ".
**Example 3:**
**Input:** version1 = "0.1 ", version2 = "1.1 "
**Output:** -1
**Explanation:** version1's revision 0 is "0 ", while version2's revision 0 is "1 ". 0 < 1, so version1 < version2.
**Constraints:**
* `1 <= version1.length, version2.length <= 500`
* `version1` and `version2` only contain digits and `'.'`.
* `version1` and `version2` **are valid version numbers**.
* All the given revisions in `version1` and `version2` can be stored in a **32-bit integer**. | null |
166: Solution with step by step explanation | fraction-to-recurring-decimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution also handles the edge cases of a zero numerator and a zero denominator, and also checks for the negative sign at the beginning. It then calculates the integer part of the result by doing an integer division of the numerator by the denominator, and checks if there is a fractional part by checking if the remainder of this division is zero. If there is a fractional part, it adds a decimal point to the result.\n\nThe main optimization in this solution is the use of a dictionary to store the position of each remainder in the result. This way, we can easily check if a remainder has already appeared in the result, and if it has, we know that we have found a repeating part. We can then insert the opening and closing parentheses at the appropriate positions in the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fractionToDecimal(self, numerator: int, denominator: int) -> str:\n # Handle edge cases\n if numerator == 0:\n return "0"\n if denominator == 0:\n return ""\n\n # Initialize result and check for negative sign\n result = ""\n if (numerator < 0) ^ (denominator < 0):\n result += "-"\n numerator, denominator = abs(numerator), abs(denominator)\n\n # Integer part of the result\n result += str(numerator // denominator)\n\n # Check if there is a fractional part\n if numerator % denominator == 0:\n return result\n\n result += "."\n\n # Use a dictionary to store the position of each remainder\n remainder_dict = {}\n remainder = numerator % denominator\n\n # Keep adding the remainder to the result until it repeats or the remainder becomes 0\n while remainder != 0 and remainder not in remainder_dict:\n remainder_dict[remainder] = len(result)\n remainder *= 10\n result += str(remainder // denominator)\n remainder %= denominator\n\n # Check if there is a repeating part\n if remainder in remainder_dict:\n result = result[:remainder_dict[remainder]] + "(" + result[remainder_dict[remainder]:] + ")"\n\n return result\n\n``` | 15 | Given two integers representing the `numerator` and `denominator` of a fraction, return _the fraction in string format_.
If the fractional part is repeating, enclose the repeating part in parentheses.
If multiple answers are possible, return **any of them**.
It is **guaranteed** that the length of the answer string is less than `104` for all the given inputs.
**Example 1:**
**Input:** numerator = 1, denominator = 2
**Output:** "0.5 "
**Example 2:**
**Input:** numerator = 2, denominator = 1
**Output:** "2 "
**Example 3:**
**Input:** numerator = 4, denominator = 333
**Output:** "0.(012) "
**Constraints:**
* `-231 <= numerator, denominator <= 231 - 1`
* `denominator != 0` | No scary math, just apply elementary math knowledge. Still remember how to perform a long division? Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern? Notice that once the remainder starts repeating, so does the divided result. Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly. |
Python 😎 Easy to understand | fraction-to-recurring-decimal | 0 | 1 | \n# Code\n```\nclass Solution:\n def fractionToDecimal(self, n: int, d: int) -> str:\n sol = ""\n \n # If the numerator is zero, the fraction will be zero irrespective of the denominator.\n if n == 0:\n return "0"\n \n # To determine if the result should be negative, XOR is used.\n # Result will be negative only if n and d have opposite signs.\n negative = (n < 0) ^ (d < 0)\n \n # Convert n and d to positive values, as we have already determined the sign.\n n = abs(n)\n d = abs(d)\n \n # Append the whole number part of the division to the solution.\n sol += str(n // d)\n \n # For the decimal part\n dec = ""\n \n # Check if there is a remainder after the division\n if n % d:\n # Store the remainders and their corresponding positions in the decimal string\n # This is used to identify repeating sequences.\n nums = {}\n \n # Append the decimal point to the solution string.\n sol += "."\n \n # Get the remainder\n n = n % d\n \n # Continue the division until there\'s no remainder or we detect a repeating sequence.\n while n:\n # If the current remainder was seen before, it indicates the start of a repeating sequence.\n if n in nums:\n dec += ")"\n # Get the position where this remainder first occurred.\n pos = nums[n]\n # Insert the repeating sequence within brackets.\n dec = dec[:pos] + "(" + dec[pos:]\n break\n \n # Save the current remainder and its position in the decimal string.\n nums[n] = len(dec)\n \n # For the next iteration, multiply n by 10 (decimal shift)\n n *= 10\n \n # Append the quotient to the decimal string\n dec += str(n // d)\n \n # Get the new remainder\n n = n % d\n \n # Prefix the result with "-" if the result is negative.\n sign = "-" if negative else ""\n return sign + sol + dec\n\n``` | 2 | Given two integers representing the `numerator` and `denominator` of a fraction, return _the fraction in string format_.
If the fractional part is repeating, enclose the repeating part in parentheses.
If multiple answers are possible, return **any of them**.
It is **guaranteed** that the length of the answer string is less than `104` for all the given inputs.
**Example 1:**
**Input:** numerator = 1, denominator = 2
**Output:** "0.5 "
**Example 2:**
**Input:** numerator = 2, denominator = 1
**Output:** "2 "
**Example 3:**
**Input:** numerator = 4, denominator = 333
**Output:** "0.(012) "
**Constraints:**
* `-231 <= numerator, denominator <= 231 - 1`
* `denominator != 0` | No scary math, just apply elementary math knowledge. Still remember how to perform a long division? Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern? Notice that once the remainder starts repeating, so does the divided result. Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly. |
Python - Long Divsion Solution | fraction-to-recurring-decimal | 0 | 1 | ```\nclass Solution:\n def fractionToDecimal(self, numerator: int, denominator: int) -> str:\n if numerator == 0: return \'0\'\n \n result = []\n if numerator < 0 and denominator > 0 or numerator >= 0 and denominator < 0:\n result.append(\'-\')\n \n numerator, denominator = abs(numerator), abs(denominator)\n \n result.append(str(numerator // denominator))\n \n remainder = numerator % denominator\n \n if remainder == 0: return \'\'.join(result)\n result.append(\'.\')\n \n d = {}\n while remainder != 0:\n if remainder in d:\n result.insert(d[remainder], \'(\')\n result.append(\')\')\n return \'\'.join(result)\n \n d[remainder] = len(result)\n \n remainder *= 10\n result += str(remainder // denominator)\n remainder = remainder % denominator\n \n return \'\'.join(result)\n``` | 11 | Given two integers representing the `numerator` and `denominator` of a fraction, return _the fraction in string format_.
If the fractional part is repeating, enclose the repeating part in parentheses.
If multiple answers are possible, return **any of them**.
It is **guaranteed** that the length of the answer string is less than `104` for all the given inputs.
**Example 1:**
**Input:** numerator = 1, denominator = 2
**Output:** "0.5 "
**Example 2:**
**Input:** numerator = 2, denominator = 1
**Output:** "2 "
**Example 3:**
**Input:** numerator = 4, denominator = 333
**Output:** "0.(012) "
**Constraints:**
* `-231 <= numerator, denominator <= 231 - 1`
* `denominator != 0` | No scary math, just apply elementary math knowledge. Still remember how to perform a long division? Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern? Notice that once the remainder starts repeating, so does the divided result. Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly. |
simple sol with if else statements | fraction-to-recurring-decimal | 0 | 1 | # Code\n```\nclass Solution:\n def fractionToDecimal(self, numerator: int, denominator: int) -> str:\n if numerator == 0:\n return "0"\n if denominator == 0:\n return ""\n\n result = ""\n if (numerator < 0) ^ (denominator < 0):\n result += "-"\n\n numerator,denominator = abs(numerator), abs(denominator)\n result += str(numerator//denominator)\n\n if numerator % denominator == 0:\n return result\n\n result += "."\n\n remainder = numerator % denominator\n remainder_dict = {}\n\n while remainder != 0 and remainder not in remainder_dict:\n remainder_dict[remainder] = len(result)\n remainder *= 10\n result += str(remainder // denominator)\n remainder = remainder % denominator\n \n if remainder in remainder_dict:\n result = result[:remainder_dict[remainder]] + "(" + result[remainder_dict[remainder]:] + ")"\n\n return result\n``` | 0 | Given two integers representing the `numerator` and `denominator` of a fraction, return _the fraction in string format_.
If the fractional part is repeating, enclose the repeating part in parentheses.
If multiple answers are possible, return **any of them**.
It is **guaranteed** that the length of the answer string is less than `104` for all the given inputs.
**Example 1:**
**Input:** numerator = 1, denominator = 2
**Output:** "0.5 "
**Example 2:**
**Input:** numerator = 2, denominator = 1
**Output:** "2 "
**Example 3:**
**Input:** numerator = 4, denominator = 333
**Output:** "0.(012) "
**Constraints:**
* `-231 <= numerator, denominator <= 231 - 1`
* `denominator != 0` | No scary math, just apply elementary math knowledge. Still remember how to perform a long division? Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern? Notice that once the remainder starts repeating, so does the divided result. Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly. |
Python3 100% Runtime 83% Memory | fraction-to-recurring-decimal | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nCalculating digits using long division while storing previous remainders in a dictionary.\n\n# Code\n```\nclass Solution:\n def fractionToDecimal(self, numerator: int, denominator: int) -> str:\n if numerator%denominator == 0:\n return str(numerator//denominator)\n if numerator < 0:\n if denominator < 0:\n negative = 0\n numerator, denominator = -numerator, -denominator\n else:\n negative = 1\n numerator = -numerator\n else:\n if denominator < 0:\n negative = 1\n denominator = -denominator\n else:\n negative = 0\n if negative == 1:\n output = \'-\'\n else:\n output = \'\'\n digits = 0\n if numerator >= denominator:\n output += str(numerator//denominator)+\'.\'\n digits = len(output)-2\n else:\n output += \'0.\'\n remainder = (numerator%denominator)*10\n d = {}\n pointer = 1\n while remainder != 0:\n if remainder%denominator == 0:\n return output + str(remainder//denominator)\n else:\n if remainder in d.keys():\n return output[:d[remainder]+1+negative+digits] + \'(\' + output[d[remainder]+1+negative+digits:] + \')\'\n else:\n if remainder >= denominator: \n output += str(remainder//denominator)\n d[remainder] = pointer\n remainder %= denominator\n else:\n output += \'0\'\n remainder *= 10\n pointer += 1\n \n\n\n \n``` | 0 | Given two integers representing the `numerator` and `denominator` of a fraction, return _the fraction in string format_.
If the fractional part is repeating, enclose the repeating part in parentheses.
If multiple answers are possible, return **any of them**.
It is **guaranteed** that the length of the answer string is less than `104` for all the given inputs.
**Example 1:**
**Input:** numerator = 1, denominator = 2
**Output:** "0.5 "
**Example 2:**
**Input:** numerator = 2, denominator = 1
**Output:** "2 "
**Example 3:**
**Input:** numerator = 4, denominator = 333
**Output:** "0.(012) "
**Constraints:**
* `-231 <= numerator, denominator <= 231 - 1`
* `denominator != 0` | No scary math, just apply elementary math knowledge. Still remember how to perform a long division? Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern? Notice that once the remainder starts repeating, so does the divided result. Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly. |
Python solution | fraction-to-recurring-decimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(len(numerator / denominator))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nO(len(numerator / denominator))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fractionToDecimal(self, numerator: int, denominator: int) -> str:\n\n\n sign = ""\n if numerator * denominator < 0:\n sign = "-"\n numerator, denominator = abs(numerator), abs(denominator)\n inti = int(numerator / denominator)\n reminder = numerator % denominator\n \n inti = sign + str(inti)\n\n if reminder == 0:\n return inti\n\n result = inti + "."\n seen = {}\n decimal = ""\n while reminder:\n if reminder in seen.keys():\n common = "(" + decimal[seen[reminder]:] + ")"\n decimal = decimal[:seen[reminder]] + common\n return result + decimal\n else:\n seen[reminder] = len(decimal)\n numerator = reminder * 10\n inti = abs(int(numerator / denominator))\n reminder = numerator % denominator\n decimal += str(inti)\n\n return result + decimal\n\n\n\n\n\n\n \n\n\n``` | 0 | Given two integers representing the `numerator` and `denominator` of a fraction, return _the fraction in string format_.
If the fractional part is repeating, enclose the repeating part in parentheses.
If multiple answers are possible, return **any of them**.
It is **guaranteed** that the length of the answer string is less than `104` for all the given inputs.
**Example 1:**
**Input:** numerator = 1, denominator = 2
**Output:** "0.5 "
**Example 2:**
**Input:** numerator = 2, denominator = 1
**Output:** "2 "
**Example 3:**
**Input:** numerator = 4, denominator = 333
**Output:** "0.(012) "
**Constraints:**
* `-231 <= numerator, denominator <= 231 - 1`
* `denominator != 0` | No scary math, just apply elementary math knowledge. Still remember how to perform a long division? Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern? Notice that once the remainder starts repeating, so does the divided result. Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly. |
Python O(N) solution using two independent for loops. | two-sum-ii-input-array-is-sorted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf my interpretation of the time complexity is wrong, please let me know.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverses through the array once. Checks if two numbers whose sum equals the target is in the list. Finds the first one using the first forloop, and where that for loop ends, the second one picks up where it lefts off to find the second one. \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n #hashmap key = index value = element\n\n \n for i in range(len(numbers)):\n sum = target - numbers[i]\n\n if sum in numbers:\n index1 = sum\n index2 = i\n break\n \n \n for j in range(index2+1,len(numbers),1):\n \n if numbers[j]==index1:\n index1 = j\n break\n\n\n return [index2+1,index1+1]\n\n \n\n\n``` | 0 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
✅[Beginner Friendly][Beats 💯%][O(N) O(1)] Easiest Solution in Python3 with Explanation | two-sum-ii-input-array-is-sorted | 0 | 1 | # Intuition\nUse 2 pointers to find the indices.\n\n# Approach\nUse 2 pointers denoted by left and right where left is pointing to the first index and right is pointing to the last index initially. If the sum of the elements corresponding to the left and right index results in target, return a list of left and right after adding 1 to each of them because the problem statement states that the indies has to be larger than 1. If the sum is greater than the target, the right index has to be decreased by one. Lastly, if the sum is less than the target, the left index has to be increased by one.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n left, right = 0, len(numbers) - 1\n while numbers[left] + numbers[right] != target:\n if numbers[left] + numbers[right] > target:\n right -= 1\n else:\n left += 1\n return [left + 1, right + 1] # +1 is due to 1 <= index1 < index2 < numbers.length\n\n``` | 1 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
Python Easy O(1) Space | two-sum-ii-input-array-is-sorted | 0 | 1 | This problem is an extension to [Two Sum](https://leetcode.com/problems/two-sum/) problem. In the two-sum problem, the input array is unsorted and hence we have to use a hashmap to solve the problem in **O(n)** time. But that completely changes, once the input is sorted. \nThe algorithm is:\n1. Initialize two pointers `i` and `j` which points first and last element respectively.\n2. Add elements pointed by `i` and `j` and then compare with `target`. \n3. If `target` is smaller, it means you have added a larger element and it needs to be cut off. So we decrement `j`.\n4. If `target` is larger, it means you have added a smaller value and we need to pick next big value. So we increment \'i`.\n5. We repeat `2.` and `3.` until `i>=j` or a match is found.\n\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n i = 0\n j = len(numbers) -1\n \n while i<j:\n s = numbers[i] + numbers[j]\n if s == target:\n return [i + 1 , j + 1]\n \n if s > target:\n j-=1\n else:\n i+=1 \n \n return []\n```\n[Al_Dan](https://leetcode.com/Al_Dan/) pointed out that the solution can be made a bit more concise as the problem description states the following constraint:\n>The tests are generated such that there is exactly one solution.\n\n\nSo instead of `i<j` check, we can do `numbers[i] + numbers[j]!=target`.\n\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n i = 0\n j = len(numbers) -1\n \n while numbers[i] + numbers[j]!=target:\n s = numbers[i] + numbers[j] \n if s > target:\n j-=1\n else:\n i+=1 \n \n return [i + 1 , j + 1]\n```\n\n\n**Time - O(n)**\n**Space - O(1)**\n\n\n---\n\n***Please upvote if you find it useful*** | 78 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.