title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python || DP || Recursion -> Space Optimization | best-time-to-buy-and-sell-stock-iv | 0 | 1 | ```\n\n#Recursion \n#Time Complexity: O(2^n)\n#Space Complexity: O(n)\nclass Solution1:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n def solve(ind,buy,cap):\n if ind==n or cap==0:\n return 0\n profit=0\n if buy==0: # buy a stock\n take=-prices[ind]+solve(ind+1,1,cap)\n not_take=0+solve(ind+1,0,cap)\n profit=max(take,not_take)\n else: # sell a stock\n take=prices[ind]+solve(ind+1,0,cap-1)\n not_take=0+solve(ind+1,1,cap)\n profit=max(take,not_take)\n return profit\n n=len(prices)\n return solve(0,0,k)\n\n#Memoization (Top-Down)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n*2*3) + O(n)\nclass Solution2:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n def solve(ind,buy,cap):\n if ind==n or cap==0:\n return 0\n if dp[ind][buy][cap]!=-1:\n return dp[ind][buy][cap]\n profit=0\n if buy==0:\n take=-prices[ind]+solve(ind+1,1,cap)\n not_take=0+solve(ind+1,0,cap)\n profit=max(take,not_take)\n else:\n take=prices[ind]+solve(ind+1,0,cap-1)\n not_take=0+solve(ind+1,1,cap)\n profit=max(take,not_take)\n dp[ind][buy][cap]=profit\n return dp[ind][buy][cap]\n n=len(prices)\n dp=[[[ -1 for _ in range(k+1)] for _ in range(2)] for _ in range(n)]\n return solve(0,0,k)\n \n#Tabulation (Bottom-Up)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n*2*3)\nclass Solution3:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n n=len(prices)\n dp=[[[0 for _ in range(k+1)] for _ in range(2)] for _ in range(n+1)]\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n for cap in range(1,k+1):\n profit=0\n if buy==0:\n take=-prices[ind]+dp[ind+1][1][cap]\n not_take=0+dp[ind+1][0][cap]\n profit=max(take,not_take)\n else:\n take=prices[ind]+dp[ind+1][0][cap-1]\n not_take=0+dp[ind+1][1][cap]\n profit=max(take,not_take)\n dp[ind][buy][cap]=profit\n return dp[0][0][k]\n\n#Space Optimization\n#Time Complexity: O(n^2)\n#Space Complexity: O(1)\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n n=len(prices)\n ahead=[[0]*(k+1) for _ in range(2)]\n curr=[[0]*(k+1) for _ in range(2)]\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n for cap in range(1,k+1):\n profit=0\n if buy==0:\n take=-prices[ind]+ahead[1][cap]\n not_take=0+ahead[0][cap]\n profit=max(take,not_take)\n else:\n take=prices[ind]+ahead[0][cap-1]\n not_take=0+ahead[1][cap]\n profit=max(take,not_take)\n curr[buy][cap]=profit\n ahead=curr\n return curr[0][k]\n```\n**An upvote will be encouraging** | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
🔥Mastering Buying and Selling Stocks || From Recursion To DP || Complete Guide By Mr. Robot | best-time-to-buy-and-sell-stock-iv | 1 | 1 | # \u2753 Buying and Selling Stocks with K Transactions \u2753\n\n\n## \uD83D\uDCA1 Approach 1: Recursive Approach\n\n### \u2728 Explanation\nThe logic and approach for this solution involve recursively exploring the possibilities of buying and selling stocks with a given number of transactions. The function `Recursive` takes as input the stock prices, the current index (`ind`), a boolean flag (`b` for buy or sell), and the remaining transactions `k`. It returns the maximum profit that can be obtained. The function considers two options at each step: either buying or not buying the stock (if `b` is `true`), or selling or holding the stock (if `b` is `false`). It recursively explores these options to find the maximum profit.\n\n### \uD83D\uDCDD Dry Run\nLet\'s dry run the `Recursive` function with an example:\n- Input: `prices = [3, 2, 6, 5, 0, 3], k = 2`\n- Start with index 0, `b` is `true`, and `k` is 2.\n- At index 0, we can buy the stock, so we explore two options: \n 1. Buy it and move to index 1 (profit: -3), or\n 2. Leave it and move to index 1 (profit: 0).\n- We choose the first option (buy), and the function moves to index 1 with `k` reduced by 1.\n- This process continues, and we explore all possible options until we reach the end. The function returns the maximum profit.\n\n### \uD83D\uDD0D Edge Cases\n- The `Recursive` function handles cases where the number of transactions is limited.\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(2^n), where n is the number of stock prices. The function explores all possible combinations.\n- Space Complexity: O(n), for the function call stack.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Codes\n```cpp []\nclass Solution {\npublic:\n int Recursive(vector<int> &p, int ind, bool b, int k) {\n if (ind >= p.size() || k <= 0) return 0;\n int ans = 0;\n \n if (b) {\n return max(-p[ind] + Recursive(p, ind + 1, !b, k), Recursive(p, ind + 1, b, k));\n } else {\n return max({ p[ind] + Recursive(p, ind + 1, !b, k - 1), Recursive(p, ind + 1, b, k) });\n }\n }\n\n int maxProfit(int k, vector<int> &prices) {\n return Recursive(prices, 0, true, k);\n }\n};\n```\n\n```python []\nclass Solution:\n def recursive(self, p, ind, b, k):\n if ind >= len(p) or k <= 0:\n return 0\n\n if b:\n return max(-p[ind] + self.recursive(p, ind + 1, not b, k), self.recursive(p, ind + 1, b, k))\n else:\n return max(p[ind] + self.recursive(p, ind + 1, not b, k - 1), self.recursive(p, ind + 1, b, k))\n\n def maxProfit(self, k, prices):\n return self.recursive(prices, 0, True, k)\n```\n\n\n```java []\nclass Solution {\n public int recursive(int[] p, int ind, boolean b, int k) {\n if (ind >= p.length || k <= 0)\n return 0;\n\n int ans = 0;\n\n if (b) {\n return Math.max(-p[ind] + recursive(p, ind + 1, !b, k), recursive(p, ind + 1, b, k));\n } else {\n return Math.max(p[ind] + recursive(p, ind + 1, !b, k - 1), recursive(p, ind + 1, b, k));\n }\n }\n\n public int maxProfit(int k, int[] prices) {\n return recursive(prices, 0, true, k);\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public int Recursive(int[] p, int ind, bool b, int k) {\n if (ind >= p.Length || k <= 0)\n return 0;\n\n int ans = 0;\n\n if (b) {\n return Math.Max(-p[ind] + Recursive(p, ind + 1, !b, k), Recursive(p, ind + 1, b, k));\n } else {\n return Math.Max(p[ind] + Recursive(p, ind + 1, !b, k - 1), Recursive(p, ind + 1, b, k));\n }\n }\n\n public int MaxProfit(int k, int[] prices) {\n return Recursive(prices, 0, true, k);\n }\n}\n```\n\n\n```javascript []\nclass Solution {\n recursive(p, ind, b, k) {\n if (ind >= p.length || k <= 0)\n return 0;\n\n if (b) {\n return Math.max(-p[ind] + this.recursive(p, ind + 1, !b, k), this.recursive(p, ind + 1, b, k));\n } else {\n return Math.max(p[ind] + this.recursive(p, ind + 1, !b, k - 1), this.recursive(p, ind + 1, b, k));\n }\n }\n\n maxProfit(k, prices) {\n return this.recursive(prices, 0, true, k);\n }\n}\n```\n\n\n\n\n\n---\n\n## \uD83D\uDCA1 Approach 2: Dynamic Programming\n\n### \u2728 Explanation\nThe dynamic programming approach optimizes the previous solution by using memoization to store previously computed results. The function `RecursionWithMemoisation` is similar to the `Recursive` function but with memoization to avoid redundant calculations.\n\n### \uD83D\uDCDD Dry Run\nThe `RecursionWithMemoisation` function follows the same logic as the recursive approach but uses a memoization table to store and reuse intermediate results. This significantly improves the efficiency of the algorithm.\n\n### \uD83D\uDD0D Edge Cases\n- The `RecursionWithMemoisation` function handles cases where the number of transactions is limited.\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(n * k), where n is the number of stock prices, and k is the maximum number of transactions allowed.\n- Space Complexity: O(n * k), for the memoization table.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Codes\n```cpp []\nclass Solution {\npublic:\n int RecursionWithMemoisation(vector<int> &p, int ind, bool canBuy, int k, vector<vector<vector<int>>> &dp) {\n if (ind >= p.size() || k <= 0) return 0;\n \n if (dp[ind][canBuy][k] != -1) return dp[ind][canBuy][k];\n \n if (canBuy) {\n dp[ind][canBuy][k] = max(-p[ind] + RecursionWithMemoisation(p, ind + 1, !canBuy, k, dp), RecursionWithMemoisation(p, ind + 1, canBuy, k, dp));\n } else {\n dp[ind][canBuy][k] = max({ p[ind] + RecursionWithMemoisation(p, ind + 1, !canBuy, k - 1, dp), RecursionWithMemoisation(p, ind + 1, canBuy, k, dp) });\n }\n \n return dp[ind][canBuy][k];\n }\n \n int maxProfit(vector<int> &prices) {\n int k = 2; // change the value of k as per the question \n vector<vector<vector<int>>> dp(prices.size() + 1, vector<vector<int>>(3,vector<int>(k+1,-1)));\n return RecursionWithMemoisation(prices, 0, true, 2, dp);\n }\n};\n```\n```python []\nclass Solution:\n def recursion_with_memoization(self, p, ind, can_buy, k, dp):\n if ind >= len(p) or k <= 0:\n return 0\n\n if dp[ind][can_buy][k] != -1:\n return dp[ind][can_buy][k]\n\n if can_buy:\n dp[ind][can_buy][k] = max(-p[ind] + self.recursion_with_memoization(p, ind + 1, not can_buy, k, dp), self.recursion_with_memoization(p, ind + 1, can_buy, k, dp))\n else:\n dp[ind][can_buy][k] = max(p[ind] + self.recursion_with_memoization(p, ind + 1, not can_buy, k - 1, dp), self.recursion_with_memoization(p, ind + 1, can_buy, k, dp))\n\n return dp[ind][can_buy][k]\n\n def max_profit(self, prices):\n k = 2 # change the value of k as per the question\n dp = [[[[-1 for _ in range(k + 1)] for _ in range(3)] for _ in range(len(prices) + 1)]\n return self.recursion_with_memoization(prices, 0, True, k, dp)\n```\n\n```java []\nclass Solution {\n public int recursionWithMemoization(int[] p, int ind, boolean canBuy, int k, int[][][] dp) {\n if (ind >= p.length || k <= 0)\n return 0;\n\n if (dp[ind][canBuy ? 1 : 0][k] != -1)\n return dp[ind][canBuy ? 1 : 0][k];\n\n int maxProfit;\n if (canBuy) {\n maxProfit = Math.max(-p[ind] + recursionWithMemoization(p, ind + 1, false, k, dp), recursionWithMemoization(p, ind + 1, true, k, dp));\n } else {\n maxProfit = Math.max(p[ind] + recursionWithMemoization(p, ind + 1, false, k - 1, dp), recursionWithMemoization(p, ind + 1, true, k, dp));\n }\n\n dp[ind][canBuy ? 1 : 0][k] = maxProfit;\n return maxProfit;\n }\n\n public int maxProfit(int[] prices) {\n int k = 2; // change the value of k as per the question\n int[][][] dp = new int[prices.length + 1][3][k + 1];\n for (int i = 0; i <= prices.length; i++) {\n for (int j = 0; j < 3; j++) {\n Arrays.fill(dp[i][j], -1);\n }\n }\n return recursionWithMemoization(prices, 0, true, k, dp);\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public int RecursionWithMemoization(int[] p, int ind, bool canBuy, int k, int[][][] dp) {\n if (ind >= p.Length || k <= 0)\n return 0;\n\n if (dp[ind][canBuy ? 1 : 0][k] != -1)\n return dp[ind][canBuy ? 1 : 0][k];\n\n int maxProfit;\n if (canBuy) {\n maxProfit = Math.Max(-p[ind] + RecursionWithMemoization(p, ind + 1, false, k, dp), RecursionWithMemoization(p, ind + 1, true, k, dp));\n } else {\n maxProfit = Math.Max(p[ind] + RecursionWithMemoization(p, ind + 1, false, k - 1, dp), RecursionWithMemoization(p, ind + 1, true, k, dp));\n }\n\n dp[ind][canBuy ? 1 : 0][k] = maxProfit;\n return maxProfit;\n }\n\n public int MaxProfit(int[] prices) {\n int k = 2; // change the value of k as per the question\n int[][][] dp = new int[prices.Length + 1][][];\n for (int i = 0; i <= prices.Length; i++) {\n dp[i] = new int[3][];\n for (int j = 0; j < 3; j++) {\n dp[i][j] = new int[k + 1];\n for (int l = 0; l <= k; l++) {\n dp[i][j][l] = -1;\n }\n }\n }\n return RecursionWithMemoization(prices, 0, true, k, dp);\n }\n}\n```\n\n\n\n\n\n---\n\n## \uD83D\uDCA1 Approach 3: Bottom-Up Dynamic Programming\n\n### \u2728 Explanation\nThe bottom-up dynamic programming approach solves the problem by iteratively calculating the maximum profit for each possible state. The function `bottomup` uses a 3D DP array to store results and iterates through the stock prices, transactions, and buying/selling states.\n\n### \uD83D\uDCDD Dry Run\nThe `bottomup` function iterates through the stock prices, transactions, and buying/selling states, filling in the DP table with the maximum profit at each state. It starts from the last day and works backward to compute the final result.\n\n### \uD83D\uDD0D Edge Cases\n- The `bottomup` function handles cases where the number of transactions is limited.\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(n * K), where n is the number of stock prices, and K is the maximum number of transactions allowed.\n- Space Complexity: O(n * 2 * K), for the 3D DP table.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Codes\n```cpp []\nclass Solution {\npublic:\n int bottomup(int K, vector<int> &p) {\n vector<vector<vector<int> > > dp(p.size() + 1, vector<vector<int>>(3, vector<int>(K + 1, 0)));\n \n for (int ind = p.size() - 1; ind >= 0; ind--) {\n for (int b = 0; b <= 1; b++) {\n for (int k = 1; k <= K;\n\n k++) {\n if (b) {\n dp[ind][b][k] = max(-p[ind] + dp[ind + 1][!b][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = max(p[ind] + dp[ind + 1][!b][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n int maxProfit(int k, vector<int> &prices) {\n return bottomup(k, prices);\n }\n};\n```\n\n\n```python []\nclass Solution:\n def bottomup(self, K, p):\n dp = [[[0 for _ in range(K + 1)] for _ in range(3)] for _ in range(len(p) + 1)]\n \n for ind in range(len(p) - 1, -1, -1):\n for b in range(2):\n for k in range(1, K + 1):\n if b:\n dp[ind][b][k] = max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k])\n else:\n dp[ind][b][k] = max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k])\n \n return dp[0][1][K]\n\n def maxProfit(self, k, prices):\n return self.bottomup(k, prices)\n```\n\n\n```java []\nclass Solution {\n public int bottomup(int K, int[] p) {\n int[][][] dp = new int[p.length + 1][3][K + 1];\n \n for (int ind = p.length - 1; ind >= 0; ind--) {\n for (int b = 0; b <= 1; b++) {\n for (int k = 1; k <= K; k++) {\n if (b == 1) {\n dp[ind][b][k] = Math.max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = Math.max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n public int maxProfit(int k, int[] prices) {\n return bottomup(k, prices);\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public int BottomUp(int K, int[] p) {\n int[][][] dp = new int[p.Length + 1][][];\n for (int i = 0; i <= p.Length; i++) {\n dp[i] = new int[3][];\n for (int j = 0; j < 3; j++) {\n dp[i][j] = new int[K + 1];\n }\n }\n \n for (int ind = p.Length - 1; ind >= 0; ind--) {\n for (int b = 0; b <= 1; b++) {\n for (int k = 1; k <= K; k++) {\n if (b == 1) {\n dp[ind][b][k] = Math.Max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = Math.Max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n public int MaxProfit(int k, int[] prices) {\n return BottomUp(k, prices);\n }\n}\n```\n\n```javascript []\nclass Solution {\n bottomUp(K, p) {\n const dp = new Array(p.length + 1);\n for (let i = 0; i <= p.length; i++) {\n dp[i] = new Array(3);\n for (let j = 0; j < 3; j++) {\n dp[i][j] = new Array(K + 1).fill(0);\n }\n }\n\n for (let ind = p.length - 1; ind >= 0; ind--) {\n for (let b = 0; b <= 1; b++) {\n for (let k = 1; k <= K; k++) {\n if (b === 1) {\n dp[ind][b][k] = Math.max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = Math.max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n maxProfit(k, prices) {\n return this.bottomUp(k, prices);\n }\n}\n```\n\n---\n\n#\n\n---\n\n## \uD83D\uDCAF Related Questions and Practice\nHere are some related questions and practice problems to further enhance your coding skills:\n\n1. [Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock/)\n2. [Best Time to Buy and Sell Stock II](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/)\n3. [Best Time to Buy and Sell Stock III](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/)\n4. [Best Time to Buy and Sell Stock IV](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/)\n\nFeel free to explore these problems to gain more experience and understanding of similar concepts.\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n-- *MR. ROBOT SIGNING OFF*\n\n---\n | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
188: Solution with step by step explanation | best-time-to-buy-and-sell-stock-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nThis problem can be solved using dynamic programming. We can create a two-dimensional table dp where dp[i][j] represents the maximum profit achievable up to day i using at most j transactions. The recurrence relation for this problem is as follows:\n\ndp[i][j] = max(dp[i-1][j], prices[i] - prices[m] + dp[m-1][j-1]) where m is any index from 0 to i-1.\n\nThe first term in the max function represents the maximum profit achievable up to day i using at most j transactions without selling the stock on day i. The second term represents the maximum profit achievable up to day m using at most j-1 transactions plus the profit obtained by buying the stock on day m and selling it on day i. We can obtain the maximum profit over all m to get the value of dp[i][j].\n\nThe final answer will be in dp[n-1][k] where n is the length of the prices array.\n\nHere\'s the Python3 code with comments:\n```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n n = len(prices)\n # edge case where there are no prices or no transactions\n if n == 0 or k == 0:\n return 0\n # edge case where we can perform an unlimited number of transactions\n if k >= n // 2:\n return sum(max(0, prices[i+1] - prices[i]) for i in range(n-1))\n # initialize dp table\n dp = [[0] * (k+1) for _ in range(n)]\n for j in range(1, k+1):\n max_diff = -prices[0] # keep track of the maximum difference seen so far\n for i in range(1, n):\n dp[i][j] = max(dp[i-1][j], prices[i] + max_diff)\n max_diff = max(max_diff, dp[i-1][j-1] - prices[i])\n return dp[n-1][k]\n\n``` | 5 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Python | O(N*K) | Faster than 90% | Memory less than 96% | best-time-to-buy-and-sell-stock-iv | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n if k == 0:\n return 0\n \n dp_cost = [float(\'inf\')] * k\n dp_profit = [0] * k\n \n for price in prices:\n for i in range(k):\n if i == 0:\n dp_cost[i] = min(dp_cost[i], price)\n dp_profit[i] = max(dp_profit[i], price-dp_cost[i])\n else:\n dp_cost[i] = min(dp_cost[i], price - dp_profit[i-1])\n dp_profit[i] = max(dp_profit[i], price - dp_cost[i])\n \n return dp_profit[-1]\n``` | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Simple solution with recursion and slicing easy to understand. | rotate-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRotating an array involves shifting its elements to the right by a given number of steps. This can be done in various ways, but the provided Python code takes a unique approach by using list reversal. The core idea behind this approach is leveraging the power of reversal operations to achieve the rotation.By reversing the entire array and then reversing specific segments, we can effectively rotate the array.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# Base Cases:\n- If the length of the input array nums is 0, return an empty list.\n- If the rotation value \'k\' is 0, return the original array nums.\n# Handle Cases with k > len(nums):\n- If \'k\' is greater than the length of the array, recursively call the rotate function for two separate rotations:\n\n - First, rotate the array by its length (len(nums)).\n - Second, rotate the array by the remaining steps (k - len(nums)).\n# Perform the Rotation:\n- Reverse the entire array using nums.reverse().\n- Reverse the first \'k\' elements of the array using nums[:k] = reversed(nums[:k]).\n- Reverse the remaining elements of the array using nums[k:] = reversed(nums[k:]).\n# Return the Resulting Array:\nThe rotated array is now stored in \'nums\'.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity depends on the length of the array and the rotation value. Reversing the entire array, as well as the two slices, takes O(n) time, where n is the length of the array.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe algorithm uses only a constant amount of extra space, regardless of the size of the input array. Hence, the space complexity is O(1).\n\n# Code\n```\nclass Solution(object):\n def rotate(self, nums, k):\n if len(nums) == 0:\n return []\n if k == 0:\n return nums\n if len(nums)<k:\n nums[:] = Solution.rotate(self,nums,len(nums))\n nums[:] = Solution.rotate(self,nums,k-len(nums))\n nums.reverse()\n nums[:k] = reversed(nums[:k])\n nums[k:] = reversed(nums[k:])\n return nums\n \n```\n\n\n | 11 | Given an integer array `nums`, rotate the array to the right by `k` steps, where `k` is non-negative.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7\], k = 3
**Output:** \[5,6,7,1,2,3,4\]
**Explanation:**
rotate 1 steps to the right: \[7,1,2,3,4,5,6\]
rotate 2 steps to the right: \[6,7,1,2,3,4,5\]
rotate 3 steps to the right: \[5,6,7,1,2,3,4\]
**Example 2:**
**Input:** nums = \[-1,-100,3,99\], k = 2
**Output:** \[3,99,-1,-100\]
**Explanation:**
rotate 1 steps to the right: \[99,-1,-100,3\]
rotate 2 steps to the right: \[3,99,-1,-100\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1`
* `0 <= k <= 105`
**Follow up:**
* Try to come up with as many solutions as you can. There are at least **three** different ways to solve this problem.
* Could you do it in-place with `O(1)` extra space? | The easiest solution would use additional memory and that is perfectly fine. The actual trick comes when trying to solve this problem without using any additional memory. This means you need to use the original array somehow to move the elements around. Now, we can place each element in its original location and shift all the elements around it to adjust as that would be too costly and most likely will time out on larger input arrays. One line of thought is based on reversing the array (or parts of it) to obtain the desired result. Think about how reversal might potentially help us out by using an example. The other line of thought is a tad bit complicated but essentially it builds on the idea of placing each element in its original position while keeping track of the element originally in that position. Basically, at every step, we place an element in its rightful position and keep track of the element already there or the one being overwritten in an additional variable. We can't do this in one linear pass and the idea here is based on cyclic-dependencies between elements. |
Simple solution using queue | rotate-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStart to rotate at the beginning of the array and keep the replaced value on a queue with size k. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNormalize `k` when `k > l` by `k = k % l`\nLoop from the beginning, calculate the coresponding index to be replaced `(i + k) % l` with `l` is the size of the array.\nThe replaced index will be append to the queue so when the loop reach that index, its value will be pop out.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rotate(self, nums: List[int], k: int) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n queue = []\n l = len(nums)\n if l < k:\n k = k % l\n \n for i in range(l):\n idx = (i + k) % l\n queue.append(nums[idx])\n\n if i < k:\n nums[idx] = nums[i]\n else:\n nums[idx] = queue.pop(0)\n \n\n``` | 0 | Given an integer array `nums`, rotate the array to the right by `k` steps, where `k` is non-negative.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7\], k = 3
**Output:** \[5,6,7,1,2,3,4\]
**Explanation:**
rotate 1 steps to the right: \[7,1,2,3,4,5,6\]
rotate 2 steps to the right: \[6,7,1,2,3,4,5\]
rotate 3 steps to the right: \[5,6,7,1,2,3,4\]
**Example 2:**
**Input:** nums = \[-1,-100,3,99\], k = 2
**Output:** \[3,99,-1,-100\]
**Explanation:**
rotate 1 steps to the right: \[99,-1,-100,3\]
rotate 2 steps to the right: \[3,99,-1,-100\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1`
* `0 <= k <= 105`
**Follow up:**
* Try to come up with as many solutions as you can. There are at least **three** different ways to solve this problem.
* Could you do it in-place with `O(1)` extra space? | The easiest solution would use additional memory and that is perfectly fine. The actual trick comes when trying to solve this problem without using any additional memory. This means you need to use the original array somehow to move the elements around. Now, we can place each element in its original location and shift all the elements around it to adjust as that would be too costly and most likely will time out on larger input arrays. One line of thought is based on reversing the array (or parts of it) to obtain the desired result. Think about how reversal might potentially help us out by using an example. The other line of thought is a tad bit complicated but essentially it builds on the idea of placing each element in its original position while keeping track of the element originally in that position. Basically, at every step, we place an element in its rightful position and keep track of the element already there or the one being overwritten in an additional variable. We can't do this in one linear pass and the idea here is based on cyclic-dependencies between elements. |
simplest way using insert() and pop() | rotate-array | 0 | 1 | # Intuition\nTo rotate the array nums to the right by k steps, we can follow these steps:\n\n1. If k is greater than the length of nums, reduce k by taking its modulo with the length of nums. This ensures that k falls within the range of valid rotations.\n2. Perform the rotation in-place by repeatedly popping the last element of the array and inserting it at the beginning for k times.\n# Approach\n\n1.\tCheck if k is greater than the length of nums. If so, reduce k by taking its modulo with the length of nums.\n2.\tPerform the rotation by iterating k times using a for loop:\n\u2022\tRemove the last element of nums using pop() and store it in a variable a.\n\u2022\tInsert the value a at the beginning of nums using insert().\n\n# Complexity\n- Time complexity: O(n^2)\nThe time complexity is proportional to the value of k since we need to rotate the array k times.\n\n- Space complexity: O(1)\nThe space complexity is constant as we are modifying the input array in-place and not using any additional data structures.\n# Code\n```\nclass Solution:\n def rotate(self, nums: List[int], k: int) -> None:\n for i in range(k):\n a=nums.pop()\n nums.insert(0,a)\n```\n\n##### reach me to discuss any problems - https://www.linkedin.com/in/naveen-kumar-g-500469210/\n\n | 26 | Given an integer array `nums`, rotate the array to the right by `k` steps, where `k` is non-negative.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7\], k = 3
**Output:** \[5,6,7,1,2,3,4\]
**Explanation:**
rotate 1 steps to the right: \[7,1,2,3,4,5,6\]
rotate 2 steps to the right: \[6,7,1,2,3,4,5\]
rotate 3 steps to the right: \[5,6,7,1,2,3,4\]
**Example 2:**
**Input:** nums = \[-1,-100,3,99\], k = 2
**Output:** \[3,99,-1,-100\]
**Explanation:**
rotate 1 steps to the right: \[99,-1,-100,3\]
rotate 2 steps to the right: \[3,99,-1,-100\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1`
* `0 <= k <= 105`
**Follow up:**
* Try to come up with as many solutions as you can. There are at least **three** different ways to solve this problem.
* Could you do it in-place with `O(1)` extra space? | The easiest solution would use additional memory and that is perfectly fine. The actual trick comes when trying to solve this problem without using any additional memory. This means you need to use the original array somehow to move the elements around. Now, we can place each element in its original location and shift all the elements around it to adjust as that would be too costly and most likely will time out on larger input arrays. One line of thought is based on reversing the array (or parts of it) to obtain the desired result. Think about how reversal might potentially help us out by using an example. The other line of thought is a tad bit complicated but essentially it builds on the idea of placing each element in its original position while keeping track of the element originally in that position. Basically, at every step, we place an element in its rightful position and keep track of the element already there or the one being overwritten in an additional variable. We can't do this in one linear pass and the idea here is based on cyclic-dependencies between elements. |
Simple ONE LINE solution. Without bit operators. | reverse-bits | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Format the given number into a binary format.\n2. After formating the length of the string of bites can be less than 32 bits (as zeros before the first 1 don\'t compute), so the rest of the bits are filled with zeros.\n3. Reverse the string of bytes.\n4. Turn the string of bytes into an integer in detcimal format.\n# Complexity\n- Time complexity:$$O(n)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n n = format(n, \'b\')\n n = n.zfill(32)\n\n return int(n[::-1], 2)\n \n```\n# One LINE\n```\ndef reverseBits(self, n: int) -> int:\n return int(format(n, \'b\').zfill(32)[::-1], 2)\n```\n# *Please UPVOTE !!!* | 0 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Python bitshifting 27ms<99.14% 16.22MB<27.67% | reverse-bits | 0 | 1 | # Approach\nTake the LSBs of n, shift them into the MSBs of the result. Keep in mind the flip is within a 32 bit wide space\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n result = 0\n for _ in range(32):\n result |= n&1\n result <<= 1\n n >>= 1\n\n result >>= 1\n return result\n``` | 0 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
5 Liner, 98.10% Beats !! | reverse-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def f(self,n,r,count):\n if n<1:\n return r<<(32-count)\n return self.f(n>>1,(r<<1)|(n&1),count+1)\n def reverseBits(self, n: int) -> int:\n return self.f(n,0,0)\n``` | 2 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Beats 90 %. One liner code.Recurrsion | reverse-bits | 0 | 1 | # Intuition\nDone through recurrsion . Beats 90%\n\n# Approach\nRecurrsion\n\n# Complexity\n- Time complexity:\nO(log(n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n return self.reverse(n,0,0)\n def reverse(self,n,rev_n,bit):\n return rev_n<<(32-bit) if n<1 else self.reverse(n>>1,rev_n<<1|(n&1),bit+1) \n``` | 3 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
5 liner simpler code | By Recursion | reverse-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Done by RECURSION -->\n\n# Complexity\n- Time complexity:\n<!-- log(n) -->\n\n- Space complexity:\n<!-- O(n) -->\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n def f(n,r,count):\n if n<1:\n return r<<(32-count)\n return f(n>>1,(r<<1)|(n&1),count+1)\n return f(n,0,0)\n``` | 3 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
python | reverse-bits | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n res = 0\n for i in range(32):\n \n if n >> 1 << 1 != n:\n n = n >> 1\n res += pow(2,31-i)\n else:\n n = n >> 1\n return res\n \n\n``` | 1 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
190: Solution step by step explanation | reverse-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can reverse bits of a given number by iterating over all bits of the given number and adding the bits in the reverse order. To reverse the bits, we can use a variable and left shift it by 1 in each iteration. We can then add the last bit of the given number to the reversed number by performing an AND operation with the last bit of the given number. Once we add the last bit of the given number, we can right shift the given number by 1 to remove the last bit.\n\nAlgorithm:\n\n1. Initialize the reversed number to 0.\n2. Iterate over all 32 bits of the given number.\n3. In each iteration, left shift the reversed number by 1 and add the last bit of the given number to it.\n4. To add the last bit of the given number to the reversed number, perform an AND operation with the given number and 1.\n5. Right shift the given number by 1 to remove the last bit.\n6. Repeat steps 3-5 for all 32 bits of the given number.\n7. Return the reversed number.\n\n# Complexity\n- Time complexity:\nThe time complexity of the above algorithm is O(1) as we are iterating over all 32 bits of the given number.\n73.76%\n\n- Space complexity:\nThe space complexity of the above algorithm is O(1) as we are not using any extra data structures to store the intermediate results.\n91.81%\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n # Initialize the reversed number to 0\n reversed_num = 0\n \n # Iterate over all 32 bits of the given number\n for i in range(32):\n # Left shift the reversed number by 1 and add the last bit of the given number to it\n reversed_num = (reversed_num << 1) | (n & 1)\n # To add the last bit of the given number to the reversed number, perform an AND operation with the given number and 1\n n >>= 1\n \n # Return the reversed number\n return reversed_num\n\n``` | 26 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Easy to understand code | reverse-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseBits(self, a: int) -> int:\n #a=10\n g=""\n while a!=0:\n s=a%2\n a=a//2\n g=str(s)+g\n if len(g)!=32:\n for i in range(abs(32-len(g))):\n g="0"+g\n print(g)\n b=(g)\n r=0\n for i in reversed(range(len(b))):\n r=r+((2**i)*int(b[i]))\n return(r)\n\n\n\n``` | 2 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Python 3 (40ms) | Real BIT Manipulation Solution | reverse-bits | 0 | 1 | ```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n res = 0\n for _ in range(32):\n res = (res<<1) + (n&1)\n n>>=1\n return res\n``` | 42 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Python3 Solution (One Line) | reverse-bits | 0 | 1 | ```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n return int(((\'{0:032b}\'.format(n))[::-1]),2)\n```\n* (\'{0:032b}\'.format(n) Converts to a 32 bit representation of the number in binary. This is formatted as a string\n* [::-1] Reverses the String\n* int(...., 2) converts the number back to the appropriate base | 16 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
FASTEST AND EASIEST || LEFT SHIFT AND BINARY-DECIMAL CONVERSION || FASTEST | reverse-bits | 0 | 1 | ```\nclass Solution:\n\tdef reverseBits(self, n: int) -> int:\n\n\t\tbinary = bin(n)[2:]\n\n\t\trev = binary[::-1]\n\t\treverse = rev.ljust(32, \'0\')\n\t\treturn int(reverse, 2)\n```\nDo upvote if its helpful,Thanks. | 1 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Beats : 37.07% [24/145 Top Interview Question] | reverse-bits | 0 | 1 | # Intuition\n*Using bitwise, left and right operation*\n\n# Approach\n\nThis is a Python code defines a method `reverseBits` that takes an integer `n` as an input and returns an integer as the output. The method reverses the bits of the input integer.\n\nThe algorithm used in the code is to extract the least significant bit of the input integer `n` and add it to the result. The result is then left-shifted by 1 bit and the input integer `n` is right-shifted by 1 bit. This process is repeated for 32 bits.\n\nThe variable `result` is initialized to zero and is used to accumulate the reversed bits of the input integer. The variable `bit` is used to store the least significant bit of the input integer `n` in each iteration.\n\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n\nThe `time complexity` of this code is `O(1)`, as it performs a fixed number of operations (32) regardless of the input size. Therefore, the algorithm is efficient and has a constant time complexity.\n\nThe `space complexity` of this code is `O(1)`, as it only uses a constant amount of extra space to store the variables `result` and `bit`.\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n result = 0\n for _ in range(32):\n result = result << 1\n bit = n % 2\n result = result + bit\n n = n >> 1\n return result\n``` | 2 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
⭐Layman's 🔥One Line Code🔥 in 🐍 ⭐ | reverse-bits | 0 | 1 | \n\n---\n\n# Complexity\n- Time complexity: $$O(log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n# Code\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n return int(format(n, \'032b\')[::-1], 2)\n```\n--- | 1 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
Explained, Beginner Friendly one-liner Python3 fast solution | reverse-bits | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nInt -> Bin -> reverse -> Int\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n- Detailed \n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n bin_convert = bin(n) \n bin_convert_2 = bin_convert[2:]\n bin_fill_zero = bin_convert_2.zfill(32)\n reverse_bin = bin_fill_zero[::-1]\n answer = int(reverse_bin, 2)\n return answer\n```\n- One-Liner\n```\nclass Solution:\n def reverseBits(self, n: int) -> int:\n return (int((bin(n)[2:].zfill(32))[::-1], 2))\n``` | 4 | Reverse bits of a given 32 bits unsigned integer.
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, both input and output will be given as a signed integer type. They should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 2** above, the input represents the signed integer `-3` and the output represents the signed integer `-1073741825`.
**Example 1:**
**Input:** n = 00000010100101000001111010011100
**Output:** 964176192 (00111001011110000010100101000000)
**Explanation:** The input binary string **00000010100101000001111010011100** represents the unsigned integer 43261596, so return 964176192 which its binary representation is **00111001011110000010100101000000**.
**Example 2:**
**Input:** n = 11111111111111111111111111111101
**Output:** 3221225471 (10111111111111111111111111111111)
**Explanation:** The input binary string **11111111111111111111111111111101** represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is **10111111111111111111111111111111**.
**Constraints:**
* The input must be a **binary string** of length `32`
**Follow up:** If this function is called many times, how would you optimize it? | null |
🥇 O( log N ) | C++ | PYTHON | JAVA || EXPLAINED || ; ] ✅ | number-of-1-bits | 1 | 1 | \n**UPVOTE IF HELPFuuL**\n\n# Intuition\nOmitting `0` bits, focusing on `1` -> `set` bits only.\n\nA basic approach is to convert number `n` to binary string, then counting the occurances of `char 1`.\n\n# Approach 1 -> Right Shift\n`n >>= 1` means `set n to itself shifted by one bit to the right`. \nThe expression evaluates to the new value of `n` after the shift.\n\nExample : Performing `n>>=1` on `11`\n```\n11 -> 1011\n5 -> 101 [ 11 >>= 1 ]\n2 -> 10 [ 5 >>= 1 ]\n1 -> 1 [ 2 >>= 1 ]\n0 -> 0 [ 1 >>= 1 ]\n```\n\n# Approach 2 -> Checking Power of 2\n`n = n & (n-1)` checks if `n` is a power of 2.\nWill return `0` if `n = 2^i`.\n\nExample : Using `n = 11` -> `n &= n-1`\n```\n11 -> 1011\n10 -> 1010 [ n &= (11-1) ]\n8 -> 1000 [ n &= (10-1) ]\n0 -> 0 [ n &= (8-1) ]\n```\n\n# Complexity\n- Time complexity: O(log N)\n\n- Space complexity: O(1)\n\n``` C++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int cnt = 0;\n while(n != 0){\n cnt += (n%2);\n n >>= 1;\n }\n return cnt;\n }\n};\n```\n``` Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n cnt = 0\n while n!=0:\n cnt += (n % 2)\n n >>= 1\n return cnt\n```\n\n``` JAVA []\npublic class Solution {\n public int hammingWeight(int n) {\n int cnt = 0;\n while(n != 0){\n n = n & (n-1);\n cnt++;\n }\n \n return cnt;\n }\n}\n```\n\n**UPVOTE IF HELPFuuL**\n | 28 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
【Video】Give me 5 minutes - How we think about a solution | number-of-1-bits | 1 | 1 | # Intuition\nUse bitwise AND 1(= & 1)\n\n---\n\n# Solution Video\n\nhttps://youtu.be/3Vv1jvWc6eg\n\n\u25A0 Timeline of the video\n\n`0:03` Right shift\n`1:36` Bitwise AND\n`3:09` Demonstrate how it works\n`6:03` Coding\n`6:38` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,267\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nWe have a constraint saying "The input must be a binary string of length 32.", so we loop `32` time at most.\n\nIn the loops, we perform a right bit shift.\n\n```\nInput: n = 00000000000000000000000000001011\n```\n\nLook at my Python solution code.\n```\nfor i in range(32):\n if (n >> i) & 1:\n res += 1\n```\n\nWhat is `n >> i`?\n\nThis means we shift a bit `i` times to right. For example,\n```\n11 >> 1\n\n1011 = 11\n------------\n0101 = 5\n\nWe put 0 into left space.\n```\nAlthough it\'s unrelated to the problem, performing a right shift by 1 bit results in the value being halved, and by 2 bits results in the value being quartered.\n\nWhy we execute `& 1`(bitwise AND)?\n\nFirst of all, look at this.\n\n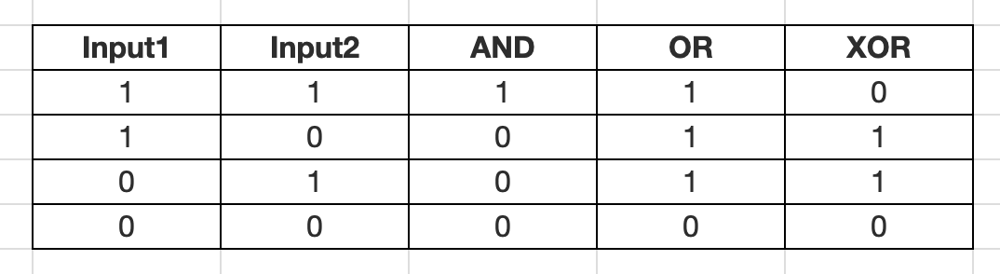\n\nI put `OR` and `XOR` as a reference. Regarding `AND`, we will get `1` as a result only when both inputs are `1`, otherwise `0`. We use this logic.\n\n`& 1` means\n```\n00000000000000000000000000000001\n```\nWe can say except the most right bit, there is no way we get `1` as a result, because we calculate result of `n >> i` and `& 1`, so\n\n```\n00000000000000000000000000001011 (= input 1)\n00000000000000000000000000000001 (= input 2)\n--------------------------------\n00000000000000000000000000000001 (= 1)\n\nAt first i = 0, so 00000000000000000000000000001011 is not changed.\n```\nThat\'s why `+1`.\n```\nres = 1\n```\nLet\'s continue. Next `i = 1` so shift 1 time to right.\n```\n00000000000000000000000000001011\n\u2193\n00000000000000000000000000000101\n```\nCalculate `& 1`\n```\n00000000000000000000000000000101\n00000000000000000000000000000001\n--------------------------------\n00000000000000000000000000000001 (= 1)\n\nres = 2\n```\nNext `i = 2` so shift 2 time to right.\n```\n00000000000000000000000000001011\n\u2193\n00000000000000000000000000000010\n```\nCalculate `& 1`\n```\n00000000000000000000000000000010\n00000000000000000000000000000001\n--------------------------------\n00000000000000000000000000000000 (= 0)\n\nres = 2\n```\nNext `i = 3` so shift 3 time to right.\n```\n00000000000000000000000000001011\n\u2193\n00000000000000000000000000000001\n```\nCalculate `& 1`\n```\n00000000000000000000000000000001\n00000000000000000000000000000001\n--------------------------------\n00000000000000000000000000000001 (= 1)\n\nres = 3\n```\nLet me stop here, because we will get all `0` after `i = 3`.\n```\nOutput: 3\n```\n\n\n# Complexity\n- Time complexity: $$O(32)$$\u2192$$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n res = 0\n\n for i in range(32):\n if (n >> i) & 1:\n res += 1\n\n return res\n```\n```javascript []\n/**\n * @param {number} n - a positive integer\n * @return {number}\n */\nvar hammingWeight = function(n) {\n let res = 0;\n for (let i = 0; i < 32; i++) {\n if ((n >> i) & 1) {\n res += 1;\n }\n }\n return res; \n};\n```\n```java []\npublic class Solution {\n public int hammingWeight(int n) {\n int res = 0;\n for (int i = 0; i < 32; i++) {\n if (((n >> i) & 1) == 1) {\n res += 1;\n }\n }\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int res = 0;\n for (int i = 0; i < 32; i++) {\n if ((n >> i) & 1) {\n res += 1;\n }\n }\n return res; \n }\n};\n```\n\nThis is related question. Little bit harder.\n\nhttps://youtu.be/oqV8Ai0_UWA\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/check-if-two-string-arrays-are-equivalent/solutions/4348512/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/K83jwzyPyQU\n\n\u25A0 Timeline of the video\n\n`0:05` Simple way to solve this question\n`1:07` Demonstrate how it works\n`4:55` Coding\n`8:00` Time Complexity and Space Complexity\n`8:26` Step by step algorithm with my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/number-of-ways-to-divide-a-long-corridor/solutions/4340183/video-give-me-7-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/DF9NXNW0G6E\n\n\u25A0 Timeline of the video\n\n`0:05` Return 0\n`0:38` Think about a case where we can put dividers\n`4:44` Coding\n`7:18` Time Complexity and Space Complexity\n`7:33` Summary of the algorithm with my solution code | 10 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Several 1-line codes vs Brian Kernighan’s algorithm||0ms beats 100% | number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1-line\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor completeness, one loop solution(Brian Kernighan\u2019s algorithm) is also presented. Using `n&=(n-1)` to change the variable within the loop.\n\nFor `n&=(n-1)`, it means the least right most \'1\' is removed.\n\nThere is also other easy question about bit-counting which needs more thinking:\n[Leetcode 338. Counting Bits](https://leetcode.com/problems/counting-bits/solutions/3986169/easy-c-python-bit-manipulations-welcome-for-tricks/)\n[Please turn on English subtitles if necessary]\n[https://youtu.be/bSOyI91vZEs?si=L9yIVNhQ1_53p8z_](https://youtu.be/bSOyI91vZEs?si=L9yIVNhQ1_53p8z_)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n return bitset<32>(n).count();\n }\n};\n```\n# Loop solution using n&=(n-1) 0ms beats 100%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n if (n==0) return 0;\n unsigned ans=0;\n for(; n>0; n&=(n-1)) ans++;\n return ans;\n }\n};\n\n```\n# 2nd version\n```\n int hammingWeight(uint32_t n) {\n return __builtin_popcount(n);\n }\n```\n# Python code for old python version\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n)[2:].count(\'1\')\n \n```\n# Python code for 3.10+\n```\n def hammingWeight(self, n: int) -> int:\n return n.bit_count()\n```\n\n | 6 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
💯Faster✅💯 Lesser✅3 Methods🔥Simple Count🔥Brian Kernighan's Algorithm🔥Bit Manipulation🔥Explained | number-of-1-bits | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 3 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe problem is asking us to write a function that takes a binary representation of a positive integer and counts the number of \'1\' bits (also known as the Hamming weight). The input to the function will be the binary form of a positive integer. The goal is to count how many \'1\' bits are present in that binary representation.\n\n### Some additional notes to keep in mind:\n- In some programming languages, such as Java, there is no explicit unsigned integer type. Even if the input is given as a signed integer, you can still treat its internal binary representation as if it were unsigned.\n- In Java, signed integers are represented using 2\'s complement notation. This means that negative numbers are represented in a specific way in binary. However, for this problem, you should focus on counting the \'1\' bits, regardless of whether the input is positive or negative.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering three different methods to solve this problem:\n1. Brian Kernighan\'s Algorithm\n2. Bit Manipulation\n3. String Conversion\n\n# 1. Brian Kernighan\'s Algorithm: \n- Initialize a count variable to 0.\n- Iterate through each bit of the number using the following steps:\n - If the current bit is 1, increment the count.\n - Set the current bit to 0 using the expression n = n & (n - 1).\n- The count variable now holds the number of 1 bits.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(k), where k is the number of set bits in the binary representation of the number.\n\n- \uD83D\uDE80 Space Complexity: O(1)\n\n# Code\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n count = 0\n while n != 0:\n n &= (n - 1)\n count += 1\n return count\n```\n```Java []\npublic class Solution {\n public int hammingWeight(int n) {\n int count = 0;\n while (n != 0) {\n n = n & (n - 1);\n count++;\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int count = 0;\n while (n != 0) {\n n &= (n - 1);\n count++;\n }\n return count;\n }\n};\n```\n```C []\nint hammingWeight(uint32_t n) {\n int count = 0;\n while (n != 0) {\n n &= (n - 1);\n count++;\n }\n return count;\n}\n```\n# 2. Bit Manipulation:\n- Initialize a count variable to 0.\n- Iterate through each bit of the number using a loop.\n - If the current bit is 1, increment the count.\n- The count variable now holds the number of 1 bits.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(log n), where n is the value of the input number.\n\n- \uD83D\uDE80 Space Complexity: O(1)\n\n# Code\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n count = 0\n while n != 0:\n count += n & 1\n n >>= 1\n return count\n```\n```Java []\npublic class Solution {\n public int hammingWeight(int n) {\n int count = 0;\n while (n != 0) {\n count += n & 1;\n n >>>= 1;\n }\n return count;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int count = 0;\n while (n != 0) {\n count += n & 1;\n n >>= 1;\n }\n return count;\n }\n};\n```\n```C []\nint hammingWeight(uint32_t n) {\n int count = 0;\n while (n != 0) {\n count += n & 1;\n n >>= 1;\n }\n return count;\n}\n```\n# 3. String Conversion:\n - Convert the integer to its binary string representation.\n- Count the number of \'1\' characters in the binary string\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(log n), where n is the value of the input number.\n\n- \uD83D\uDE80 Space Complexity:O(log n)\n\n# Code\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n binary_string = bin(n)[2:]\n count = binary_string.count(\'1\')\n return count\n```\n```Java []\npublic class Solution {\n public int hammingWeight(int n) {\n String binaryString = Integer.toBinaryString(n);\n int count = 0;\n for (char c : binaryString.toCharArray()) {\n if (c == \'1\') {\n count++;\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int count = 0;\n string binaryString = bitset<32>(n).to_string();\n for (char c : binaryString) {\n if (c == \'1\') {\n count++;\n }\n }\n return count;\n }\n};\n```\n```C []\nint hammingWeight(uint32_t n) {\n int count = 0;\n for (int i = 0; i < 32; i++) {\n if ((n >> i) & 1) {\n count++;\n }\n }\n return count;\n}\n```\n\n# \uD83C\uDFC6Conclusion: \nBrian Kernighan\'s Algorithm (Method 1) is often considered the most optimal for counting the number of 1 bits in an integer. \n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 55 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
🔥🔥🔥BEATS 100% USERS BY RUN TiME 🔥🔥🔥 ONE LiNE OF CODE✅by PRODONiK | number-of-1-bits | 1 | 1 | # Intuition\nThe Hamming weight of an integer is essentially the count of set bits (1s) in its binary representation. The task is to find an efficient way to calculate this count.\n\n# Approach\nThe provided code leverages the `Integer.bitCount()` method, which is a built-in function in Java specifically designed to count the number of set bits in the binary representation of an integer. This approach is concise and efficient, making use of a pre-existing function that is optimized for this exact task.\n\n# Complexity\n- Time complexity: O(1) \n The `Integer.bitCount()` method is implemented efficiently and has a constant time complexity, making the overall time complexity of the solution O(1).\n\n- Space complexity: O(1) \n The algorithm doesn\'t use any additional space that grows with the input size. Hence, the space complexity is constant, O(1).\n\n# Code\n```java []\npublic class Solution {\n public int hammingWeight(int n) {\n return Integer.bitCount(n);\n }\n}\n``` \n```C# []\npublic class Solution {\n public int HammingWeight(int n) {\n return BitCount(n);\n }\n\n private int BitCount(int n) {\n int count = 0;\n while (n != 0) {\n count += n & 1;\n n >>= 1;\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n return bitCount(n);\n }\n\nprivate:\n int bitCount(uint32_t n) {\n int count = 0;\n while (n != 0) {\n count += n & 1;\n n >>= 1;\n }\n return count;\n }\n};\n```\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n).count(\'1\')\n```\n```Ruby []\nclass Solution\n def hamming_weight(n)\n n.to_s(2).count(\'1\')\n end\nend\n\n | 2 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
One line python solution | number-of-1-bits | 0 | 1 | # Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return str(bin(n)).count(\'1\')\n``` | 2 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Python3 Solution | number-of-1-bits | 0 | 1 | \n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n).count(\'1\') \n``` | 2 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Easy Python solution || Beginner Friendly || Binary Hamming Weight Counter..... | number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking to find the number of \'1\' bits in the binary representation of a given integer n. In other words, it\'s asking for the Hamming weight or the number of set bits in the binary form of the number.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Convert the integer n to its binary representation using bin(n).\n- Remove the \'0b\' prefix from the binary representation using bin(n)[2:].\n- Count the number of \'1\' bits in the binary representation using the count method.\n# Complexity\n\n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. The time complexity of this solution is dependent on two main steps:\n - Converting the integer to its binary representation takes O(log n) time, where n is the value of the integer.\n - Counting the number of \'1\' bits in the binary representation takes O(log n) time as well.\n2. Therefore, the overall time complexity is O(log n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. The space complexity is dominated by the space required to store the binary representation of the integer.\n2. The space required for the binary representation is O(log n).\n3. Therefore, the overall space complexity is O(log n).\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n # Convert the integer to its binary representation as a string\n binary_representation = bin(n)[2:]\n\n # Return the count of \'1\'s in the binary representation\n return binary_representation.count(\'1\')\n``` | 4 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || EXPLAINED🔥 | number-of-1-bits | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n1. **Function Purpose:** The `hammingWeight` function aims to count the number of set bits (bits with a value of 1) in the binary representation of an unsigned 32-bit integer (`uint32_t`).\n\n1. **Initialization:** Initializes an integer variable `count` to keep track of the count of set bits found in the binary representation of the input number.\n\n1. **Looping Through Bits:** Enters a `while` loop that continues until the entire number becomes 0. Within this loop:\n\n - **Bit Check:** Uses a bitwise AND operation (`n & 1`) to check if the least significant bit (LSB) of the number is set (i.e., equal to 1).\n - **Increment Count:** If the LSB is set, increments the `count` variable to keep track of the number of set bits encountered.\n - **Right Shifting:** Right-shifts the number (`n = n >> 1`) by one bit to move to the next bit for examination.\n1. **Return Count:** Finally, returns the total `count` of set bits (count) found in the given unsigned 32-bit integer.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to count the number of set bits (1s) in the binary representation of an unsigned 32-bit integer\n int hammingWeight(uint32_t n) {\n int count = 0; // Initialize a counter to store the count of set bits\n \n // Loop through each bit of the number until the entire number becomes 0\n while (n != 0) {\n if (n & 1) { // Check if the least significant bit (LSB) is set (equal to 1) using bitwise AND operation\n count++; // If the LSB is set, increment the count\n }\n n = n >> 1; // Right shift the number by one bit to check the next bit\n }\n return count; // Return the total count of set bits in the given number\n }\n};\n\n\n```\n```C []\n\n#include <stdint.h>\n\nint hammingWeight(uint32_t n) {\n int count = 0; // Initialize a counter to store the count of set bits\n \n // Loop through each bit of the number until the entire number becomes 0\n while (n != 0) {\n if (n & 1) { // Check if the least significant bit (LSB) is set (equal to 1) using bitwise AND operation\n count++; // If the LSB is set, increment the count\n }\n n = n >> 1; // Right shift the number by one bit to check the next bit\n }\n return count; // Return the total count of set bits in the given number\n}\n\n\n\n```\n```Java []\n\npublic class Solution {\n // Function to count the number of set bits (1s) in the binary representation of an unsigned 32-bit integer\n public int hammingWeight(int n) {\n int count = 0; // Initialize a counter to store the count of set bits\n \n // Loop through each bit of the number until the entire number becomes 0\n while (n != 0) {\n if ((n & 1) == 1) { // Check if the least significant bit (LSB) is set (equal to 1) using bitwise AND operation\n count++; // If the LSB is set, increment the count\n }\n n = n >>> 1; // Right shift the number by one bit to check the next bit\n }\n return count; // Return the total count of set bits in the given number\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n # Function to count the number of set bits (1s) in the binary representation of an unsigned 32-bit integer\n def hammingWeight(self, n: int) -> int:\n count = 0 # Initialize a counter to store the count of set bits\n \n # Loop through each bit of the number until the entire number becomes 0\n while n != 0:\n if n & 1: # Check if the least significant bit (LSB) is set (equal to 1) using bitwise AND operation\n count += 1 # If the LSB is set, increment the count\n n >>= 1 # Right shift the number by one bit to check the next bit\n \n return count # Return the total count of set bits in the given number\n\n\n\n```\n```javascript []\nfunction hammingWeight(n) {\n let count = 0; // Initialize a counter to store the count of set bits\n \n // Loop through each bit of the number until the entire number becomes 0\n while (n !== 0) {\n if (n & 1) { // Check if the least significant bit (LSB) is set (equal to 1) using bitwise AND operation\n count++; // If the LSB is set, increment the count\n }\n n = n >> 1; // Right shift the number by one bit to check the next bit\n }\n return count; // Return the total count of set bits in the given number\n}\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
[We💕Simple] 7 Ways to Count Bits (Easy to Hard) | number-of-1-bits | 0 | 1 | ## 1. Using native method\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return n.bit_count()\n```\n``` Kotlin []\nclass Solution {\n fun hammingWeight(n:Int):Int {\n return n.countOneBits()\n }\n}\n```\n\n## 2. Using binary string representation\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n).count("1")\n```\n``` Kotlin []\nclass Solution {\n fun hammingWeight(n:Int):Int {\n return Integer.toBinaryString(n).count { it == \'1\' }\n }\n}\n```\n\n## 3. Bit shifting and masking\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return sum((n >> i) & 1 for i in range(32))\n```\n``` Kotlin []\nclass Solution {\n fun hammingWeight(n: Int): Int {\n return (0..31).sumOf { (n ushr it) and 1 }\n }\n}\n```\n\n## 4. Bit shifting and masking (2) - Recursive\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return (n&1)+self.hammingWeight(n>>1) if n else 0\n```\n``` Kotlin []\nclass Solution {\n fun hammingWeight(n: Int): Int {\n return if (n != 0) (n and 1) + hammingWeight(n ushr 1) else 0\n }\n}\n```\n\n## 5. n & (n - 1) trick\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return 1 + self.hammingWeight(n & (n - 1)) if n else 0\n\n```\n``` Kotlin []\nclass Solution {\n fun hammingWeight(n: Int): Int {\n return if (n != 0) 1 + hammingWeight(n and (n - 1)) else 0\n }\n}\n```\n\n## 6. Lookup table approach\n\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n # table=[bin(i).count(\'1\') for i in range(256)]\n table=[0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,4,5,5,6,5,6,6,7,5,6,6,7,6,7,7,8]\n return (table[n & 0xff] +\n table[(n >> 8) & 0xff] +\n table[(n >> 16) & 0xff] +\n table[(n >> 24) & 0xff])\n```\n```Kotlin []\nclass Solution {\n fun hammingWeight(n: Int): Int {\n val table = arrayOf(0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,4,5,5,6,5,6,6,7,5,6,6,7,6,7,7,8)\n return table[n and 0xff] + table[(n ushr 8) and 0xff] + table[(n ushr 16) and 0xff] + table[(n ushr 24) and 0xff]\n }\n\n}\n```\n\n## 7. Bit manipulation with masks and shifts:\n```Python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n n = (n & 0x55555555) + ((n & 0xAAAAAAAA) >> 1)\n n = (n & 0x33333333) + ((n & 0xCCCCCCCC) >> 2)\n n = (n & 0x0F0F0F0F) + ((n & 0xF0F0F0F0) >> 4)\n n = (n & 0x00FF00FF) + ((n & 0xFF00FF00) >> 8)\n n = (n & 0x0000FFFF) + ((n & 0xFFFF0000) >> 16)\n return n \n```\n```Kotlin []\nclass Solution {\n fun hammingWeight(n: Int): Int {\n var n = n\n n = (n and 0x55555555) + ((n ushr 1) and 0x55555555)\n n = (n and 0x33333333) + ((n ushr 2) and 0x33333333)\n n = (n and 0x0F0F0F0F) + ((n ushr 4) and 0x0F0F0F0F)\n n = (n and 0x00FF00FF) + ((n ushr 8) and 0x00FF00FF)\n n = (n and 0x0000FFFF) + ((n ushr 16) and 0x0000FFFF)\n return n\n }\n}\n```\n\n1. **Using `bitCount` method**: Directly uses a built-in function to count the number of one bits in the binary representation of the number.\n\n2. **Using binary string representation**: Converts the number to its binary string form and counts the number of \'1\' characters.\n3. **Bit shifting and masking**: Iteratively shifts the number to the right and checks the least significant bit in each step, counting the number of times this bit is 1.\n4. **Recursive approach with bit shifting**: Uses recursion to shift the number right by one bit at each step, adding the least significant bit to the count, until the number becomes zero.\n5. **Recursive approach using n & (n - 1) trick**: Each iteration of this recursion removes the lowest set bit from the number, counting each such operation, until no bits are left.\n6. **Lookup table approach**: Breaks the number into 8-bit chunks and uses a precomputed table to quickly find the number of set bits in each chunk.\n7. **Bit manipulation with masks and shifts**: Applies a series of bit masks and shifts to progressively sum the number of set bits in groups of 1, 2, 4, 8, 16, and finally 32 bits.\n\nHere are the binary representations of the hexadecimal numbers:\n\n- `0x55555555` in binary: `01010101010101010101010101010101`\n- `0x33333333` in binary: `00110011001100110011001100110011`\n- `0x0F0F0F0F` in binary: `00001111000011110000111100001111`\n- `0x00FF00FF` in binary: `00000000111111110000000011111111`\n- `0x0000FFFF` in binary: `00000000000000001111111111111111`\n\nThe process implemented in this algorithm is designed to efficiently count the number of set bits (bits with a value of 1) in a 32-bit integer. The approach it uses is more sophisticated and faster than simply checking each bit one by one.\n\n1. **Bitwise Masking and Addition**: The algorithm uses specific bitwise masks (like `0x55555555`, `0x33333333`, etc.) to partition the integer into smaller groups of bits. For each group, it calculates the number of set bits by applying these masks and then adding the results. This step is repeated, combining increasingly larger groups of bits.\n\n2. **Efficient Counting**: Instead of counting each bit individually, the algorithm simultaneously counts multiple bits. It starts by counting 1s in pairs of bits, then in groups of four, eight, and finally sixteen bits. By doing so, it reduces the number of operations needed compared to checking each bit separately.\n\n3. **Divide and Conquer**: This method embodies the divide and conquer strategy. It breaks down the 32-bit number into smaller parts, counts the set bits in these smaller parts, and then combines the results to get the total count.\n\n4. **Final Accumulation**: After processing all groups, the algorithm adds up the counts from the upper and lower 16 bits. This final sum gives the total number of set bits in the entire 32-bit integer.\n\nIn essence, this process significantly optimizes the task of counting set bits in an integer, leveraging bitwise operations to enhance efficiency and reduce computational complexity. | 6 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
✅✅Efficient Hamming Weight Computation in Multiple Programming Languages🔥🔥🔥 | number-of-1-bits | 1 | 1 | \n\n\n# Description\n\n## Intuition\nThe problem appears to be related to counting the number of set bits (1s) in the binary representation of a given integer `n`. The initial intuition might be to convert the integer to its binary representation and then count the number of \'1\' bits.\n\n## Approach\nThe provided code implements the described intuition. It converts the integer `n` to its binary representation using the `bin()` function, then extracts the binary representation as a string, and finally counts the occurrences of \'1\' in that string.\n\n## Complexity\n- **Time complexity:** \\(O(\\log n)\\) - The time complexity is determined by the length of the binary representation of the input integer `n`, which is \\(\\log n\\).\n- **Space complexity:** \\(O(\\log n)\\) - The space complexity is also determined by the length of the binary representation of the input integer `n`.\n\n## Performance\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n| :--- | :---:| :---: | \nJava | 4 | 40 |\nGo | 0 | 1.98 |\nPython3 | 30 | 16.3 |\nC# | 28 | 24.34 |\n\n## Code\n```python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n # Convert integer to binary representation\n binary_representation = bin(n)\n \n # Extract the binary representation as a string and count \'1\' bits\n return binary_representation[2:].count("1")\n\n```\n``` Go []\nfunc hammingWeight(num uint32) int {\n // Convert integer to binary representation\n\tbinaryRepresentation := strconv.FormatInt(int64(num), 2)\n\n\t// Extract the binary representation as a string and count \'1\' bits\n\treturn strings.Count(binaryRepresentation, "1")\n}\n```\n\n``` Java []\npublic class Solution {\n public int hammingWeight(int n) {\n // Convert integer to binary representation\n String binaryRepresentation = Integer.toBinaryString(n);\n \n // Extract the binary representation as a string and count \'1\' bits\n return (int) binaryRepresentation.chars().filter(c -> c == \'1\').count();\n }\n}\n```\n\n``` C# []\npublic class Solution {\n public int HammingWeight(uint n) {\n // Convert integer to binary representation\n string binaryRepresentation = Convert.ToString(n, 2);\n \n // Extract the binary representation as a string and count \'1\' bits\n return binaryRepresentation.Count(bit => bit == \'1\');\n }\n}\n```\n{:style=\'width:600px\'}\n\n_If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions._\n | 9 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
✅One liner✅ O(1)✅Beats 100%✅For Beginners✅ | number-of-1-bits | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n return __builtin_popcount(n);\n \n }\n};\n```\n```python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n).count(\'1\')\n\n# Example usage:\n# solution = Solution()\n# result = solution.hammingWeight(0b110101)\n# print(result)\n\n```\n```java []\npublic class Solution {\n public int hammingWeight(int n) {\n return Integer.bitCount(n);\n }\n\n // Example usage:\n // public static void main(String[] args) {\n // Solution solution = new Solution();\n // int result = solution.hammingWeight(0b110101);\n // System.out.println(result);\n // }\n}\n\n```\n#\n\n | 11 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
One liner code in Python 3 | number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn the question it is given that the input will be given as \nInput: n = 00000000000000000000000000001011\nbut it isn,t. Actually the input is given as decimal form that is 11, you have to convert to binary before proceeding further. \n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return str(bin(n)).count(\'1\')\n``` | 1 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
⭐One-Liner CheatCode in🐍 ||🔥Beats 99.81%🔥⭐ | number-of-1-bits | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return str(bin(n)).count(\'1\')\n``` | 1 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Python Solution beats 100% of Submissions | number-of-1-bits | 0 | 1 | # Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n).count(\'1\')\n``` | 1 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
✅Mastering Number of set-Bits ✅For beginners with Full Explanation | number-of-1-bits | 1 | 1 | \n```cpp []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int count = 0;\n while (n != 0) {\n if (n & 1) { // Check the last bit\n count++;\n }\n n = n >> 1; // Right shift to move to the next bit\n }\n return count;\n }\n};\n```\n\n```python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n count = 0\n while n != 0:\n if n & 1: # Check the last bit\n count += 1\n n >>= 1 # Right shift to move to the next bit\n return count\n```\n\n```java []\npublic class Solution {\n public int hammingWeight(int n) {\n int count = 0;\n while (n != 0) {\n if ((n & 1) == 1) { // Check the last bit\n count++;\n }\n n = n >>> 1; // Right shift to move to the next bit\n }\n return count;\n }\n}\n```\n\n\n```csharp []\npublic class Solution {\n public int HammingWeight(uint n) {\n int count = 0;\n while (n != 0) {\n if ((n & 1u) == 1) { // Check the last bit\n count++;\n }\n n = n >> 1; // Right shift to move to the next bit\n }\n return count;\n }\n}\n```\n\n\n```javascript []\n\n hammingWeight(n) {\n let count = 0;\n while (n !== 0) {\n if (n & 1) { // Check the last bit\n count++;\n }\n n = n >>> 1; // Right shift to move to the next bit\n }\n return count;\n }\n\n```\n```ruby []\nclass Solution\n def hamming_weight(n)\n count = 0\n while n != 0\n count += 1 if n & 1 == 1 # Check the last bit\n n >>= 1 # Right shift to move to the next bit\n end\n count\n end\nend\n```\n\n## \u2728Explanation\n\n### Problem Overview\nThe function `hammingWeight` is designed to count the number of set bits (1s) in the binary representation of a given 32-bit unsigned integer `n`. This count represents the Hamming weight or the number of \'1\' bits in the binary representation of the integer.\n\n### Approach Overview\nThe code uses a bitwise operation to count the set bits. Here\'s how it works:\n\n1. **Initialize a counter:** `int count = 0;` This variable will keep track of the number of set bits.\n\n2. **Loop through the bits:** `while (n != 0) {` The loop continues until all bits in `n` are processed.\n\n3. **Check the last bit:** `if (n & 1) {` This checks whether the last bit of `n` is 1. If yes, increment the `count`.\n\n4. **Right shift:** `n = n >> 1;` Right shifting `n` by 1 position effectively moves to the next bit, preparing for the next iteration.\n\n5. **Repeat until all bits are processed:** The loop continues this process until `n` becomes 0, meaning all bits have been checked.\n\n6. **Return the count:** `return count;` The function returns the final count of set bits.\n\n### Example\nLet\'s take an example. Suppose `n` is `0b11011011`. The function would count the set bits:\n\n- Initially, `count = 0`.\n- Loop 1: `n & 1` is true, so increment `count` to 1. Right shift `n` to get `0b01101101`.\n- Loop 2: `n & 1` is true, so increment `count` to 2. Right shift `n` to get `0b00110110`.\n- ... and so on.\n\n### Why it works\nThe `n & 1` operation checks if the last bit is set. Right shifting `n` effectively moves to the next bit. By repeating this process, we count the set bits in the binary representation of `n`.\n\n### Complexity Analysis\n- **Time Complexity:** O(log n) - The number of iterations is proportional to the number of bits in the binary representation of `n`.\n- **Space Complexity:** O(1) - Constant space is used.\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n | 1 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
✅100% Fast || Full Easy Explanation || Beginner Friendly 🔥🔥🔥 | number-of-1-bits | 1 | 1 | # Intuition\nThe problem requires counting the number of \'1\' bits in the binary representation of an unsigned integer. This operation is commonly known as the Hamming weight. We can perform this task by iterating through each bit in the binary representation and counting the number of set bits.\n\n# Approach\n- Iterate through each bit in the binary representation of the given integer.\n- Check if the current bit is set (equals 1).\n- If the bit is set, increment the count.\n- Return the count as the result.\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int hammingWeight(uint32_t n) {\n int count = 0;\n\n // Iterate through each bit in the binary representation\n for (int i = 0; i < 32; i++) {\n // Check if the current bit is set\n if ((n & 1) == 1) {\n count++;\n }\n\n // Right shift to move to the next bit\n n >>= 1;\n }\n\n return count;\n }\n};\n```\n```java []\npublic class Solution{\n public int hammingWeight(int n){\n int count = 0;\n\n // Iterate through each bit in the binary representation\n for (int i = 0; i < 32; i++) {\n // Check if the current bit is set\n if ((n & 1) == 1) {\n count++;\n }\n\n // Right shift to move to the next bit\n n >>>= 1;\n }\n\n return count;\n }\n\n}\n```\n```python []\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n count = 0\n\n # Iterate through each bit in the binary representation\n for i in range(32):\n # Check if the current bit is set\n if n & 1 == 1:\n count += 1\n\n # Right shift to move to the next bit\n n >>= 1\n\n return count\n```\n```javascript []\nclass Solution {\n hammingWeight(n) {\n let count = 0;\n\n // Iterate through each bit in the binary representation\n for (let i = 0; i < 32; i++) {\n // Check if the current bit is set\n if ((n & 1) === 1) {\n count++;\n }\n\n // Right shift to move to the next bit\n n >>>= 1;\n }\n\n return count;\n }\n}\n```\n# Explanation:\n\n- The hammingWeight method takes an integer n as input and initializes a count variable to 0.\n\n- It iterates through each bit of the 32-bit binary representation of the integer.\n\nFor each bit, it checks if the bit is set (equals 1). If true, it increments the count.\n\n- After iterating through all the bits, the method returns the count as the result.\n\nThe time complexity of this algorithm is O(1), as the input size (32 bits) remains constant.\n\n---\n\n\n | 2 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Beginner-friendly easy-to-understand one-liner :) | number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSplit the string into a list, then return the sum of that list\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Format the number as a 32-bit string\n2. Convert it to a list\n3. Use list comprehension to make a list with int() values\n4. Return the sum of said list\n\n# Complexity\n- Time complexity: $$O(n)$$ (with n always = 32)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ (with n always = 32)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return sum([int(bit) for bit in list(format(n,\'032b\'))])\n```\n# Note\nThis is my first solution - can I get a hell yeah in the comments? | 0 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Confused ? Here is the solution with explanation | number-of-1-bits | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor those who are wondering about if the input is in binary or string or integer\n\nThe input is in decimal, meaning the input is 11 and what its shown in the examples is its binary 32 bits, ie 00000000000000000000000000001011\nSo basically the input is actual decimal like 3 and they have shown\n00000000000000000000000000000011 in example, so dont get confused.\n\nRest the code is simple bit manupulation.\nDo and operation from the last bit with 1\n\n00000000000000000000000000000011 &\n00000000000000000000000000000001\n\nIf the result is 1 then increment counter and do a right shift >> for next bit\n\nelse \n00000000000000000000000000000010 &\n00000000000000000000000000000001\n\nThis will result in 0 so dont count this and do right shift\n\nDo this for 32 bits/ 32 times and return the result\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)(O(1) since everytime the loop will run for 32 times, correct me if I am wrong)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n c = 0\n for i in range(32):\n c+=n&1\n n = n>>1\n return c\n \n``` | 0 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Amazing Logic With Right Shift | number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n return bin(n)[2:].count(\'1\')\n```\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n count=0\n while n:\n count+=n%2\n n=n>>1\n return count\n #please upvote me it would encourage me alot\n\n \n``` | 52 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Solution with While loop | number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingWeight(self, n: int) -> int:\n count=0\n while n!=0:\n if n%2==1:\n count+=1\n n=n//2\n return count\n\n``` | 8 | Write a function that takes the binary representation of an unsigned integer and returns the number of '1' bits it has (also known as the [Hamming weight](http://en.wikipedia.org/wiki/Hamming_weight)).
**Note:**
* Note that in some languages, such as Java, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
* In Java, the compiler represents the signed integers using [2's complement notation](https://en.wikipedia.org/wiki/Two%27s_complement). Therefore, in **Example 3**, the input represents the signed integer. `-3`.
**Example 1:**
**Input:** n = 00000000000000000000000000001011
**Output:** 3
**Explanation:** The input binary string **00000000000000000000000000001011** has a total of three '1' bits.
**Example 2:**
**Input:** n = 00000000000000000000000010000000
**Output:** 1
**Explanation:** The input binary string **00000000000000000000000010000000** has a total of one '1' bit.
**Example 3:**
**Input:** n = 11111111111111111111111111111101
**Output:** 31
**Explanation:** The input binary string **11111111111111111111111111111101** has a total of thirty one '1' bits.
**Constraints:**
* The input must be a **binary string** of length `32`.
**Follow up:** If this function is called many times, how would you optimize it? | null |
Python solution with graphical explanation | house-robber | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTurn all conditions into a tree and traverse it through **DFS** to find the answer. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n## Step1. Build the tree\nWe can start from any point in the array, but to maximize the result, it\'s preferable to begin from 0 or 1.\n\nAfter selecting an index, the next index must be index+2 or later. (Skip one or more) However, choosing index+4 or later is not meaningful, as index+4 could be the next step of index+2.\n\nTherefore, we choose only index+2 and index+3 as the next step (subtree) each time. Build the tree based on this logic.\n\n\n\n## Setp2. Handle base cases\nSince we are using DFS to travel the tree, we have to handle the base case of recursion.\n\n\n\n\n```python\ndef dp(...):\n # ...\n if i >= len(nums)-2 and i < len(nums):\n return nums[i]\n if i >= len(nums)-1:\n return 0\n\n```\n\n## Setp3. Handle recursive cases\nFind the maximum value from the left subtree and the right subtree, add it to the current value, and return.\n\n\n\n\n```python\ndef dp(...):\n # ...\n\n rob_next_2 = dp(i+2, ...)\n rob_next_3 = dp(i+3, ...)\n\n max_n = max(rob_next_2, rob_next_3)\n\n return max_n + nums[i]\n\n```\n\n## Step4. Cache\nUse a hash map, key = index, value = max count of the index\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n if len(nums) == 1:\n return nums[0]\n \n if len(nums) == 2:\n return nums[0] if nums[0] > nums[1] else nums[1]\n\n def dp(i, nums, cache):\n # base case\n if i >= len(nums)-2 and i < len(nums):\n return nums[i]\n if i >= len(nums)-1:\n return 0\n # cache\n if i in cache:\n return cache[i]\n\n rob_next_2 = dp(i+2, nums, cache)\n rob_next_3 = dp(i+3, nums, cache)\n\n max_n = max(rob_next_2, rob_next_3)\n cache[i] = max_n + nums[i]\n\n return max_n + nums[i]\n\n cache = {}\n \n return max(dp(0, nums, cache), dp(1, nums, cache))\n\n \n``` | 4 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 2:**
**Input:** nums = \[2,7,9,3,1\]
**Output:** 12
**Explanation:** Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 400` | null |
Binbin's knight is sooo smart and the best teacher! | house-robber | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n L = len(nums)\n if L == 1:\n return nums[0]\n if L == 2:\n return max(nums)\n V_0 = 0\n V_1 = nums[0]\n for i in range(1,L):\n V_0_C = max(V_1, V_0)\n V_1_C = nums[i] + V_0 \n V_0 = V_0_C\n V_1 = V_1_C \n return max(V_0,V_1) \n\n``` | 1 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 2:**
**Input:** nums = \[2,7,9,3,1\]
**Output:** 12
**Explanation:** Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 400` | null |
Python solution with one queue | binary-tree-right-side-view | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a classic level order traversel (bfs) problem as we can see we need rightmost node in each tree level\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n**step 1** => we need a queue for this in which we\'ll insert root node after handling all edge cases like root is None etc.\n**step 2** => Now while queue we will run an outer loop and then inner loop should run for current length of the queue\n**step 3** => in each run we will take the first most element in the inner loop and just pop out the rest ones.\n**step 4** => for each popped out node no matter we leave it or take it we will insert its children in queue\n**step 5 **=> after inner loop the process will be repeated for entire tree and we\'ll get our answer\n\n# Complexity\n- Time complexity: o(n) cause it will visit each node once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(n) as queue can contain n/2 nodes where and it can also be skewed so it may have even n nodes\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n queue = deque()\n queue.append(root)\n\n if not root:\n return []\n\n ans = []\n while queue:\n not_added = True\n max_length = len(queue)\n i = 0\n while i < max_length:\n node = queue.popleft()\n if node:\n if not_added:\n ans.append(node.val)\n not_added=False\n queue.append(node.right)\n queue.append(node.left)\n i += 1\n\n return ans\n\n``` | 2 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Solution | binary-tree-right-side-view | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> rightSideView(TreeNode* root) {\n vector<int>ans;\n queue<TreeNode*> q;\n if(root==NULL)\n return ans;\n q.push(root);\n while(1)\n {\n int size=q.size();\n if(size==0)\n return ans;\n vector<int> data;\n while(size--)\n {\n TreeNode* temp=q.front();\n q.pop();\n data.push_back(temp->val);\n if(temp->left!=NULL)\n q.push(temp->left);\n if(temp->right!=NULL)\n q.push(temp->right);\n }\n ans.push_back(data.back());\n }\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n queue = deque()\n if root is None:\n return []\n \n if root.left is None and root.right is None:\n return [root.val]\n \n result = []\n queue.append(root)\n while queue:\n child_queue = deque()\n prev = -1\n while queue:\n curr = queue.popleft()\n\n if curr.left is not None:\n child_queue.append(curr.left)\n\n if curr.right is not None:\n child_queue.append(curr.right)\n \n prev = curr\n \n result.append(prev.val)\n queue = child_queue\n \n return result\n```\n\n```Java []\nclass Solution {\n int maxlevel = 0;\n public List<Integer> rightSideView(TreeNode root) {\n List<Integer> list = new ArrayList<>();\n right(root,1,list);\n return list ;\n }\n void right(TreeNode root,int level,List<Integer> list){\n if(root==null){\n return ;\n }\n if(maxlevel<level){\n list.add(root.val);\n maxlevel=level;\n }\n right(root.right,level+1,list);\n right(root.left,level+1,list);\n \n }\n}\n```\n | 212 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Iterative approach(BFS)✅ | O( n)✅ | (Step by step explanation)✅ | binary-tree-right-side-view | 0 | 1 | # Intuition\nThe problem requires obtaining the right side view of a binary tree. The right side view consists of all the nodes that are visible when viewing the tree from the right side.\n\n# Approach\nThe approach is based on a level-order traversal of the binary tree using a queue. We traverse the tree level by level, and for each level, we add the rightmost node to the result.\n\n1. **Initialization**: Start with an empty queue and push the root node into it.\n\n **Reason**: We begin the level-order traversal from the root.\n\n2. **Level-order Traversal**: Perform a level-order traversal using a queue. For each level, pop the nodes one by one from the front of the queue.\n\n **Reason**: Level-order traversal ensures that we visit nodes level by level, and we process each level before moving to the next.\n\n3. **Rightmost Node**: During the traversal of each level, add the rightmost node to the result.\n\n **Reason**: Adding the rightmost node ensures that we capture the view from the right side of the tree.\n\n4. **Queue Maintenance**: Enqueue the right child first and then the left child for each node.\n\n **Reason**: This order ensures that we explore the right side of the tree before the left side.\n\n5. **Result Collection**: Collect the rightmost nodes for each level in the result vector.\n\n **Reason**: The result vector will contain the nodes visible from the right side of the tree.\n\n# Complexity\n- **Time complexity**: O(n)\n - We visit each node once during the level-order traversal.\n- **Space complexity**: O(w)\n - The maximum width of the binary tree is the maximum number of nodes at any level. In the worst case, this can be the number of leaf nodes, resulting in space complexity proportional to the width of the tree.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def rightSideView(self, root: TreeNode) -> List[int]:\n result = []\n q = collections.deque([root])\n\n while q:\n rightMost = None\n n = len(q)\n\n for i in range(n):\n node = q.popleft()\n if node:\n rightMost = node\n q.append(node.left)\n q.append(node.right)\n if rightMost:\n result.append(rightMost.val)\n return result\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n vector<int> rightSideView(TreeNode* root) {\n if (root == NULL) {\n return {};\n }\n \n queue<TreeNode*> q;\n q.push(root);\n \n vector<int> result;\n \n while (!q.empty()) {\n int n = q.size();\n \n for (int i = n; i > 0; i--) {\n TreeNode* node = q.front();\n q.pop();\n \n if (i == n) {\n result.push_back(node->val);\n }\n \n if (node->right != NULL) {\n q.push(node->right);\n }\n if (node->left != NULL) {\n q.push(node->left);\n }\n }\n }\n \n return result;\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n | 6 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
O(n) space and time complexity - Simple queue approach | binary-tree-right-side-view | 0 | 1 | # Intuition\nAppend the last element (as we are iterating from left to right and poping from queue from left) of every level of BFS in a list\n\n# Approach\n1)Initialize a queue and append root (return empty list if no root) and iterate till length of queue is zero\n2)Iterate for loop for length of queue of that level and take current as current node if i is equal to last element ....append the node in a list and return\n\n# Complexity\n- Time complexity: O(n), n is total of nodes\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n), n is total of nodes\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n x=[]\n if root is None:\n return x\n queue=deque([])\n queue.append(root)\n while len(queue)!=0:\n queue_level=len(queue)\n for i in range(queue_level):\n current=queue.popleft()\n if i==(queue_level-1):\n x.append(current.val)\n if current.left is not None:\n queue.append(current.left)\n if current.right is not None:\n queue.append(current.right)\n return x\n \n``` | 3 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Beats100%(Recursive approach)✅ | O( n)✅ | (Step by step explanation)✅ | binary-tree-right-side-view | 0 | 1 | # Intuition\nThe problem is to return the right side view of a binary tree, i.e., the values of the nodes that are visible from the right side.\n\n# Approach\n1. **Initialize**: Start with an empty vector `result` to store the right side view.\n - *Reason*: We will be adding the values of nodes that are visible from the right side to this vector during the DFS traversal.\n\n2. **Depth-First Traversal (DFS)**: Implement a recursive DFS traversal starting from the root.\n - *Reason*: DFS allows us to explore the binary tree, and by keeping track of the depth, we can identify which nodes are visible from the right side.\n\n - Pass the current depth and the result vector.\n - *Reason*: We need to keep track of the depth to determine the position of a node in the right side view.\n\n - If the size of the result vector is equal to the current depth, add the value of the current node to the result vector.\n - *Reason*: If the result vector is not of sufficient size to accommodate the current depth, it means we are encountering a node from the right side for the first time at this depth.\n\n - Increment the depth.\n - *Reason*: Move to the next depth level for subsequent nodes.\n\n - Recursively traverse the right subtree.\n - *Reason*: Nodes in the right subtree are potentially visible from the right side.\n\n - Recursively traverse the left subtree.\n - *Reason*: Nodes in the left subtree are not visible from the right side.\n\n3. **Final Result**: After the DFS traversal, the `result` vector contains the values of nodes visible from the right side.\n - *Reason*: The DFS traversal ensures that we explore the nodes in the correct order, and by adding nodes to the result vector when needed, we capture the right side view.\n\n4. **Return**: Return the `result` vector.\n - *Reason*: The `result` vector contains the values of nodes visible from the right side, and it is the solution to the problem.\n\n# Complexity\n- Time complexity: $$O(n)$$\n - *Reason*: Each node is processed once during the DFS traversal.\n- Space complexity: $$O(h)$$, where $$h$$ is the height of the binary tree (recursion stack).\n - *Reason*: The space complexity is determined by the maximum depth of the recursion stack.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n result = []\n depth = 0\n \n\n def rightSide(root , result , depth):\n if root == None:\n return\n\n if len(result) == depth :\n result.append(root.val)\n\n depth += 1 \n\n rightSide(root.right , result , depth)\n rightSide(root.left , result , depth)\n\n rightSide(root , result , depth)\n return result \n\n\n \n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n vector<int> rightSideView(TreeNode* root) {\n vector<int> result;\n int depth = 0;\n\n rightSide(root, result, depth);\n\n return result;\n }\n\n void rightSide(TreeNode* root, vector<int>& result, int depth) {\n if (root == nullptr) {\n return;\n }\n\n if (result.size() == depth) {\n result.push_back(root->val);\n }\n\n depth++;\n\n rightSide(root->right, result, depth);\n rightSide(root->left, result, depth);\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n | 5 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Python: God Tier Simple Solution no cap (DFS) | binary-tree-right-side-view | 0 | 1 | # Intuition\nThis solution\'s key insight lies in understanding how a depth-first traversal (DFS) of the tree interacts with the ordering of nodes at each level. By recursively visiting the left child before the right child, the solution ensures that the last node visited at each level is the rightmost node. This is because, in a DFS, deeper nodes are visited before their sibling nodes. Thus, when the recursion reaches the rightmost node of any level, all other nodes on that level have already been visited. This node\'s value is then recorded as the representative for that level in the final output.\n\nFurthermore, by maintaining a list ret that corresponds to the maximum depth reached so far, and by updating ret[h] at each recursive call, the solution overwrites any previously visited nodes at the same level with the rightmost node\'s value. This elegant method leverages the inherent properties of DFS to efficiently build the right view of the tree.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(log n)$$ for the output array\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n ret = []\n def helper(n, h):\n if n is None:\n return\n if len(ret) <= h:\n ret.append(0)\n ret[h] = n.val\n if n.left is not None:\n helper(n.left, h + 1)\n if n.right is not None:\n helper(n.right, h + 1)\n \n helper(root, 0)\n return ret\n``` | 0 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
✔️ C++ || PYTHON || EXPLAINED || ; ] | binary-tree-right-side-view | 0 | 1 | **UPVOTE IF HELPFuuL**\n\nThe demand of the question is to get the nodes at ```i``` level that are rightmost.\nAny nodes left to that would not be included in answer.\n\n\n**Level order traversal could help but that uses addtional space for the QUEUE**\n\n**APPROACH with no extra space**\n\nMaintain an array / vector.\n\n* TRAVERSAL -> **ROOT ->RIGHT -> LEFT** This is the way traversal is done in array so that rightmost node at ```i``` level is visited first.\n\n* When at ```i``` level, check in array/vector, if there is an element already present at index```i``` in the array. \n[ index represents the level in tree ]->**[element at index i is rightmost node at level i]**\n* If at that level, *element is present,*, just continue the traversal.\n* Else if no element is present at index ```i``` -> add that node to answer ```[res]``` at the ```i``` index.\n\n\n\n\n\n\n**UPVOTE IF HELPFuuL**\n\n**C++**\n```\nclass Solution {\npublic:\n \n vector<int> solve(TreeNode* root, vector<int> res, int lvl){\n if (root==NULL){\n return res;\n }\n if (res.size()==lvl){ // root\n res.push_back(root->val);\n }\n res = solve(root->right , res , lvl + 1); // right\n res = solve(root->left , res , lvl + 1); // left\n return res;\n }\n \n vector<int> rightSideView(TreeNode* root) {\n vector<int> res;\n res = solve( root , res , 0 );\n return res;\n }\n};\n```\n**UPVOTE IF HELPFuuL**\n**PYTHON**\n```\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n \n def solve(root, lvl):\n \tif root:\n \t\tif len(res)==lvl:\n \t\t\tres.append(root.val)\n \t\tsolve(root.right, lvl + 1)\n \t\tsolve(root.left, lvl + 1)\n \treturn \n\n res = []\n solve(root,0)\n return res\n```\n\n\n\n\n | 116 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
[ Python ] | Simple & Clean Solution using BFS | binary-tree-right-side-view | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n if not root: return root\n q = [root]\n ans = []\n while q:\n t = q.copy()\n q.clear()\n\n r = 0\n for node in t:\n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n r = node.val\n ans.append(r)\n return ans\n\n``` | 3 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Python || Easy || BFS || Using Queue | binary-tree-right-side-view | 0 | 1 | ```\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n if root==None:\n return []\n q=deque([[root,0]])\n d={}\n while q:\n node,line=q.popleft()\n d[line]=node.val\n if node.left:\n q.append([node.left,line+1])\n if node.right:\n q.append([node.right,line+1])\n ans=[]\n for k in sorted(d):\n ans.append(d[k])\n return ans\n```\n**An upvote will be encouraging** | 1 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
✔💯 DAY 415 | DFS=>BFS | 0ms 100% | | [PYTHON/JAVA/C++] | EXPLAINED 🆙🆙🆙 | binary-tree-right-side-view | 1 | 1 | \n\n\n# Code for recursive\n```java []\npublic List<Integer> rightSideView(TreeNode root) {\n List<Integer> A = new ArrayList<>();\n rec(root,0,A);\n return A; \n}\nvoid rec(TreeNode root,int level,List<Integer> A){\n if(root==null) return;\n if(level==A.size()) A.add(root.val);//every first node in that level is part of right side \n rec(root.right,level+1,A);\n rec(root.left,level+1,A);//level order from right side view\n}\n```\n\n# code for iterative \n\n```java []\npublic List<Integer> rightSideView(TreeNode root) {\n List<Integer> A = new ArrayList<>();\n if(root==null) return A;\n Queue<TreeNode> q = new LinkedList<>();\n q.add(root);\n while(!q.isEmpty()){\n int size = q.size();\n for(int i=0;i<size;i++){\n TreeNode node = q.poll();\n if(i==size-1)A.add(node.val);//every last node in that level is part of right side \n if(node.left!=null) q.add(node.left);\n if(node.right!=null)q.add(node.right);\n }\n }\nreturn A;\n}\n```\n\n\n# Complexity\n- Time complexity:o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(h)\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 3 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Python3 - Simple BFS approach (beats -97%) | binary-tree-right-side-view | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nso what we need is the value of right most node on each level.\nwhich made me think of bfs\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nuse simple bfs and in the result append the last node value by appending when the for loop ends (take a look at the code)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N) where N is the number of nodes in the tree\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(L) where L is the number of levels in the tree.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n def bfs(root):\n q = []\n res = []\n if root:\n q.append(root)\n while q:\n for _ in range(len(q)):\n cur = q.pop(0)\n if cur.left:\n q.append(cur.left)\n if cur.right:\n q.append(cur.right)\n res.append(cur.val)\n return res\n return bfs(root)\n \n``` | 2 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Easiest Solution || beats 99% | binary-tree-right-side-view | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n\n if not root:\n return []\n result = []\n queue=deque([root])\n\n while queue:\n level_length=len(queue)\n for i in range(level_length):\n node=queue.popleft()\n if i==level_length-1:\n result.append(node.val)\n \n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n return result\n```\n# **PLEASE DO UPVOTE!!!** | 4 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Easy and efficient solution using dfs (explained solution) | binary-tree-right-side-view | 1 | 1 | \n# Approach\nThis solution performs a depth-first traversal of the binary tree, starting from the right side. It keeps track of the current level and adds the first node encountered at each level to the result vector. By performing a reverse preorder traversal (right subtree first, then left subtree), the solution ensures that the nodes seen from the right side are added to the result vector.\n\n\n\n- **Depth-First Traversal (Right-First):** Use a depth-first traversal approach where nodes from the right subtree are visited before nodes from the left subtree.\n\n- **Level Tracking and Node Addition:** Keep track of the current level. If the current level matches the size of the result vector (ds), add the node\'s value to the result vector. This ensures that the rightmost node at each level is added to the result vector.\n\n- **Recursive Approach:** Recursively explore the right subtree first and then the left subtree, updating the level as the recursion goes deeper.\n\n- **Return Result**: Return the resulting vector containing nodes seen from the right side.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n void right(TreeNode* node, int level, vector<int> &ds) {\n if(!node) return;\n if(level == ds.size()) ds.push_back(node->val);\n right(node->right, level+1, ds);\n right(node->left, level+1, ds);\n }\n vector<int> rightSideView(TreeNode* root) {\n vector<int> ds;\n right(root, 0, ds);\n return ds;\n }\n};\n```\n```python3 []\nclass Solution:\n def rightSideView(self, root: TreeNode) -> List[int]:\n def right(node, level):\n nonlocal result\n if not node:\n return\n if level == len(result):\n result.append(node.val)\n right(node.right, level + 1)\n right(node.left, level + 1)\n \n result = []\n right(root, 0)\n return result\n```\n```Java []\npublic class Solution {\n public List<Integer> rightSideView(TreeNode root) {\n List<Integer> result = new ArrayList<>();\n right(root, 0, result);\n return result;\n }\n \n private void right(TreeNode node, int level, List<Integer> result) {\n if (node == null) return;\n if (level == result.size()) {\n result.add(node.val);\n }\n right(node.right, level + 1, result);\n right(node.left, level + 1, result);\n }\n}\n```\n | 1 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Python3 Postorder traversal mega easy to understand | binary-tree-right-side-view | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n ans = {}\n\n def traversal(node, lev):\n if node is None: return\n\n nonlocal ans\n traversal(node.right, lev + 1)\n if lev not in ans: ans[lev] = node.val\n traversal(node.left, lev + 1)\n \n traversal(root, 0)\n # Sort by key of the dict, then extract only values\n return [v for k, v in sorted(ans.items())]\n``` | 1 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Python3 Easy Solution beats 96.18 % with Explanation | binary-tree-right-side-view | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n\n- Basically we have to return the last element at each level.\n\n- We will approach this problem by doing level order traversal and keeping track of the number of elements at each level. \n- For this we will initialize deque.\n- We will iterate through the length of the current level\n- If we are at last element of particular level then we will add it to the result Array.\n- If left and right of current node is not empty then we will add them to the deque. \n- Lastly we will return the result Array.\n\n# Code\n```\nclass Solution:\n def rightSideView(self, root: Optional[TreeNode]) -> List[int]:\n #base case \n if not root: return []\n res = [] #initialize result array to return later. \n q = collections.deque()\n q.append(root)\n #while q is not empty\n while q:\n #length of curr level \n level_len = len(q)\n #iterate through each level\n for i in range(level_len):\n curr = q.popleft()\n #if we are at last index then append item to the result array. \n if i == level_len-1: res.append(curr.val)\n #add curr.left and curr.right to q if not empty\n if curr.left: q.append(curr.left)\n if curr.right: q.append(curr.right)\n #return result array\n return res \n```\n# Proof \n\n\n\n | 1 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
199: Solution with step by step explanation | binary-tree-right-side-view | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- The idea is to perform a level order traversal of the tree and keep track of the last node at each level.\n- We can use a queue to perform the traversal. We start by adding the root to the queue.\n- At each level, we keep track of the length of the queue at the beginning of the level. We iterate over this length and pop the first element of the queue. If we are at the last element of the level, we add its value to the result list.\n- We then add the left and right children of the current node to the queue, if they exist.\n- Finally, we return the result list containing the right side view of the tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rightSideView(self, root: TreeNode) -> List[int]:\n if not root:\n return []\n result = []\n queue = collections.deque()\n queue.append(root)\n while queue:\n level_len = len(queue)\n for i in range(level_len):\n node = queue.popleft()\n if i == level_len - 1:\n result.append(node.val)\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n return result\n\n``` | 8 | Given the `root` of a binary tree, imagine yourself standing on the **right side** of it, return _the values of the nodes you can see ordered from top to bottom_.
**Example 1:**
**Input:** root = \[1,2,3,null,5,null,4\]
**Output:** \[1,3,4\]
**Example 2:**
**Input:** root = \[1,null,3\]
**Output:** \[1,3\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Simple Python DFS Approach | number-of-islands | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEssentially, you traverse the entire grid and keep track of which "1"\'s you\'ve already visited. Each time you find a new unvisited "1", you will run a recursive DFS search to expand and add all the coordinates of the visited "1"\'s to the visited set.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn our DFS function, we will first add our current coordinates to the visited set. Next, we will branch out in all four directions, for each of these next coordinates in four directions, if they are: \n1. Within the range of the grid \n2. Equal to "1" \n3. Never visited before\n\nWe can run DFS on these next coordinates. Basically, every time you see an unvisited "1", we will traverse through the entirety of the island and add all "1"\'s connected to the island to our visited set.\n\n# Complexity\n- Time complexity: O(n) in the worst case if island takes up entire grid.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) in the worst case, for the visited set. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n output = 0 \n directions = [[0, 1], [0, -1], [1, 0], [-1, 0]] \n visited = set() \n\n def dfs(curr_x, curr_y):\n visited.add((curr_x, curr_y))\n for dir_x, dir_y in directions:\n next_x, next_y = curr_x + dir_x, curr_y + dir_y \n if next_x in range(len(grid)) and next_y in range(len(grid[0])) and grid[next_x][next_y] == "1" and (next_x, next_y) not in visited:\n dfs(next_x, next_y)\n\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == "1" and (i, j) not in visited:\n output += 1 \n dfs(i, j)\n\n return output \n``` | 3 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Solution | number-of-islands | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n\n void dfs(vector<vector<char>>& grid, int i, int j) {\n grid[i][j] = \'0\';\n int m = grid.size(), n = grid[0].size();\n\n if(i-1 >= 0 && grid[i-1][j] == \'1\') dfs(grid, i-1, j);\n if(i+1 < m && grid[i+1][j] == \'1\') dfs(grid, i+1, j);\n if(j-1 >= 0 && grid[i][j-1] == \'1\') dfs(grid, i, j-1);\n if(j+1 < n && grid[i][j+1] == \'1\') dfs(grid, i, j+1);\n }\n\n int numIslands(vector<vector<char>>& grid) {\n ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);\n\n int ans = 0;\n \n for (int i = 0; i < grid.size(); i++) {\n for (int j = 0; j < grid[0].size(); j++) {\n if(grid[i][j] == \'1\') {\n ans++;\n dfs(grid, i, j);\n }\n }\n }\n\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n componentCounter = 0 \n m = len(grid)\n n = len(grid[0])\n def dfs(i, j): \n grid[i][j] = -1\n if (i < m - 1 and grid[i + 1][j] == "1"): \n dfs(i + 1, j)\n if (i > 0 and grid[i - 1][j] == "1"): \n dfs(i - 1, j)\n if (j < n - 1 and grid[i][j + 1] == "1"): \n dfs(i, j + 1)\n if (j > 0 and grid[i][j - 1] == "1"): \n dfs(i, j - 1)\n \n for k in range(m): \n for l in range(n): \n if grid[k][l] == "1": \n componentCounter += 1\n dfs(k, l)\n return componentCounter\n```\n\n```Java []\nclass Solution {\n int r;\n int c;\n char[][] arr;\n int count;\n public int numIslands(char[][] grid) {\n r = grid.length;\n c = grid[0].length;\n arr = grid;\n\n count =0;\n for(int i=0;i<r;i++){\n check(grid[i],i);\n }\n return count;\n }\n void check(char[] row,int i)\n {\n for(int j=0;j<c;j++)\n {\n if(row[j]==\'1\')\n {\n visitIsland(i,j);\n count++;\n }\n }\n }\n public void visitIsland(int i, int j){\n arr[i][j] = 2;\n if(i-1>=0 && arr[i-1][j]==\'1\')visitIsland(i-1,j);\n if(i+1<r && arr[i+1][j]==\'1\')visitIsland(i+1,j);\n if(j-1>=0 && arr[i][j-1]==\'1\')visitIsland(i,j-1);\n if(j+1<c && arr[i][j+1]==\'1\')visitIsland(i,j+1);\n }\n}\n```\n | 5 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
[Python3]Number of Islands BFS + DFS | number-of-islands | 0 | 1 | Explanation:\nIn the grid, we need to record 1 peice of information of one point, grid[i][j], i.e., if grid[i][j] has been visited or not.\nWe initialize the check matrix with all False. It means none of the elements in the check matrix has been visited.\nIf one point grid[i][j] has not been visited, check[i][j] == False, it means we haven\'t count this point into one islands.\nIf one point grid[i][j] has been visited, check[i][j] == True, it means we already count this point into one islands.\nSearch function:\n\nSearch function:\nEach time you call search function, the search function will end until all the neighbors of grid[i][j] have value "1" been visited, i.e., those points are labeled True in check matrix.\n\n```\nExample:\ngrid = [ 1 , 1 , 1,\n\t\t 1, 1, 0,\n\t\t 0, 0, 1]\n\t\t \nIntial check:\ncheck = [ False, False, False,\n\t\t False, False, False,\n\t\t False, False, False]\n\t\t \n# the first time call search function:\ngrid[0][0] == \'1\' and check[0][0] == False:\ncheck = [ True, True, True,\n\t\t True, True, False,\n\t\t False, False, False ]\ncount = 1\n# the second time call check function:\ngrid[2][2] = \'1\' and check[2][2] == False:\ncheck = [ True, True, True,\n\t\t True, True, False,\n\t\t False, False, True]\nCount = 2\n```\n \n \n\n\nsearch function takes one point as input.\n```\nfrom collections import deque\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n """\n :type grid: List[List[str]]\n :rtype: int\n """\n if not grid:\n return 0 \n count = 0\n check = [[False for _ in range(len(grid[0]))] for _ in range(len(grid))]\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] ==\'1\' and check[i][j]== False:\n count += 1\n self.search(grid,check,i,j)\n return count \n def search(self,grid,check,i,j):\n qu = deque([(i,j)])\n while qu:\n i, j = qu.popleft()\n if 0<=i<len(grid) and 0<=j<len(grid[0]) and grid[i][j]==\'1\' and check[i][j]==False:\n check[i][j] = True\n qu.extend([(i-1,j),(i+1,j),(i,j-1),(i,j+1)])\n```\n* Improve space complexity to O(1): we can improve the algorithm by replacing the check matrix by flip the visited \'1\' to \'0\'. We can flip the visited \'1\' to \'0\' since we are only adding the index of \'1\' into the queue. The connected \'1\' already flip into \'0\', so we don\'t need to worry about duplicate calculation. \n```\nfrom collections import deque\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n count = 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == \'1\':\n #print(i,j,grid)\n grid[i][j] = \'0\'\n self.helper(grid,i,j)\n count += 1\n return count\n # use a helper function to flip connected \'1\'s to 0\n def helper(self,grid,i,j):\n queue = deque([(i,j)])\n while queue:\n I,J = queue.popleft()\n for i,j in [I+1,J],[I,J+1],[I-1,J],[I,J-1]:\n if 0 <= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] == \'1\':\n #print(i,j, queue)\n grid[i][j] = \'0\'\n queue.append((i,j))\n```\n\n```\nfrom collections import deque\nclass Solution:\n def numIslands(self, grid):\n count = 0\n queue = deque([])\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == \'1\':\n grid[i][j] = 0\n queue.append((i,j))\n self.helper(grid,queue) # turn the adjancent \'1\' to \'0\'\n count += 1\n print(grid)\n return count\n \n def helper(self,grid,queue):\n while queue:\n I,J = queue.popleft()\n for i,j in [I-1,J],[I+1,J],[I,J-1],[I,J+1]:\n if 0<= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] == \'1\':\n queue.append((i,j))\n grid[i][j] = 0 #0\n```\n* DFS\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n count = 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == \'1\':\n print(i,j)\n self.dfs(grid,i,j)\n count += 1\n #print(grid)\n return count\n # use a helper function to flip connected \'1\'s to 0\n def dfs(self,grid,i,j):\n grid[i][j] = 0\n for dr,dc in (1,0), (-1,0), (0,-1), (0,1):\n r = i + dr\n c = j + dc\n if 0 <= r < len(grid) and 0 <= c < len(grid[0]) and grid[r][c]==\'1\':\n self.dfs(grid,r,c)\n``` | 206 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Click this if you're confused. | number-of-islands | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can think of each island as a subgraph. The islands are subgraphs that are disjoint. The nodes are 1s and the edges are represented by adjacency in the grid. So we just simply have to traverse the subgraph and mark all traversed nodes, 1s, as visited. When we encounter a 1 that hasn\'t been visited we know it\'s a new subgraph or island.\n\nWe can use recursive DFS or iterative BFS\u2014more optimal in actual runtime and space.\n\n# Complexity\n- Time complexity: $O(n*m)$ since we must traverse every position on the graph\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n*m)$ since in worst case the grid is all 1s and our recursive call stack is $n*m$ deep\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n from collections import deque\n\n def numIslands(self, grid: List[List[str]]) -> int:\n out = 0\n n_rows, n_cols = len(grid), len(grid[0])\n dirs = [(-1, 0), (1, 0), (0, -1), (0, 1)]\n \n for r in range(n_rows):\n for c in range(n_cols):\n if grid[r][c] == "1":\n out += 1\n\n # traverse subgraph aka island\n stack = deque([(r, c)]) # for O(1) pop first\n while stack:\n r0, c0 = stack.pop()\n if 0 <= r0 < n_rows and 0 <= c0 < n_cols and grid[r0][c0] == "1":\n grid[r0][c0] = "0"\n for rd, cd in dirs:\n stack.append((r0 + rd, c0 + cd))\n \n return out\n\n\n``` | 2 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Python - BFS | number-of-islands | 0 | 1 | # Approach\nFor each island, we want to make sure to mark every element connected labeled "1". What we will do is apply the BFS algorithm throughout the entire array and only add to our island count if our grid position is marked as a "1" and also not in our visited set.\n\n# Code\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n rows, cols = len(grid), len(grid[0])\n islands = 0\n visited = set()\n queue = deque()\n \n def bfs(r, c):\n queue.append((r, c))\n\n while queue:\n pos = queue.popleft()\n row, col = pos[0], pos[1]\n\n for row_offset, col_offset in [[1, 0], [-1, 0], [0, 1], [0, -1]]:\n if (\n row + row_offset < 0 or\n row + row_offset >= rows or\n col + col_offset < 0 or\n col + col_offset >= cols or\n grid[row + row_offset][col + col_offset] != "1" or\n (row + row_offset, col + col_offset) in visited\n ):\n continue\n visited.add((row + row_offset, col + col_offset))\n queue.append((row + row_offset, col + col_offset))\n\n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == "1" and (r, c) not in visited:\n islands += 1\n bfs(r, c)\n return islands\n\n#T: O(M X N)\n#S: O(M X N)\n``` | 2 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Simple & intuitive solution using a recursive function | number-of-islands | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRecursive marking using ```bomb()``` funtion\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMark the already found island to ```"2"```\n\n# Complexity\n- Time complexity: $$O(n \\times m )$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n \\times m )$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n def bomb(grid, m, n, i, j):\n if i < n and j < m and i >= 0 and j >= 0:\n if grid[j][i] == "1":\n grid[j][i] = "2"\n bomb(grid, m, n, i + 1, j)\n bomb(grid, m, n, i - 1, j)\n bomb(grid, m, n, i , j + 1)\n bomb(grid, m, n, i , j - 1)\n return\n r = 0 \n m = len(grid)\n n = len(grid[0])\n for y in range(m):\n for x in range(n):\n if grid[y][x] == "1":\n r = r + 1\n bomb(grid, m, n, x, y)\n return r\n``` | 4 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
🚀Python3, DFS, mega easy to understand🚀 | number-of-islands | 0 | 1 | # Code\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n visited = set()\n col, row = len(grid), len(grid[0])\n ans = 0\n dir = [[0, 1], [1, 0], [0, -1], [-1, 0]]\n\n def helper(c: int, r: int):\n visited.add((c, r))\n for i, j in dir:\n nc, nr = c+i, r+j\n if 0 <= nc < col and 0 <= nr < row and grid[nc][nr] == "1" and (nc, nr) not in visited:\n helper(nc, nr)\n \n for c in range(col):\n for r in range(row):\n if (c, r) not in visited and grid[c][r] == "1":\n helper(c, r)\n ans += 1\n \n return ans\n``` | 6 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Number of Islands using BFS faster then 96% | number-of-islands | 0 | 1 | ```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n from collections import deque\n n=len(grid)\n m=len(grid[0])\n visited=[[0 for j in range(m)]for i in range(n)]\n c=0\n l=[[-1,0],[1,0],[0,-1],[0,1]]\n for i in range(n):\n for j in range(m):\n if visited[i][j]==0 and grid[i][j]==\'1\':\n q=deque()\n q.append((i,j))\n c+=1\n visited[i][j]=1\n while q:\n row,col=q.popleft()\n for x,y in l:\n nrow,ncol=row+x,col+y\n if 0<=nrow<n and 0<=ncol<m and grid[nrow][ncol]==\'1\' and visited[nrow][ncol]==0:\n visited[nrow][ncol]=1\n q.append((nrow,ncol))\n return c\n```\n\n | 2 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Short + clean DFS | number-of-islands | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n m = len(grid)\n n = len(grid[0])\n\n def dfs(i, j):\n if i < 0 or i >= m or j < 0 or j >= n or grid[i][j] == \'0\':\n return\n grid[i][j] = \'0\'\n dfs(i + 1, j)\n dfs(i - 1, j)\n dfs(i, j + 1)\n dfs(i, j - 1)\n\n ans = 0\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'1\':\n ans += 1\n dfs(i, j)\n\n return ans\n\n``` | 4 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
200: Solution with step by step explanation | number-of-islands | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem can be solved using a variation of Depth First Search (DFS) algorithm. We will traverse through the given matrix and visit all the connected 1\'s, marking them as visited. We will keep a count of the number of times we visit the 1\'s. Whenever we encounter an unvisited 1, we will increment the count and perform a DFS on its neighbors, marking all the visited 1\'s as visited. Finally, we will return the count of the number of islands.\n\nAlgorithm:\n\n1. Initialize a count variable to 0.\n2. Traverse through the given matrix.\n3. Whenever we encounter an unvisited 1, increment the count and perform a DFS on its neighbors, marking all the visited 1\'s as visited.\n4. Return the count of the number of islands.\n\n# Complexity\n- Time complexity:\nO(mn), where m is the number of rows and n is the number of columns in the given matrix.\n\n- Space complexity:\nO(mn), where m is the number of rows and n is the number of columns in the given matrix. The space is used by the visited matrix.\n\n# Code\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n def dfs(i: int, j: int) -> None:\n if i < 0 or j < 0 or i >= m or j >= n or grid[i][j] == "0" or visited[i][j]:\n # If the current cell is out of bounds or is water (0) or has already been visited, return.\n return\n visited[i][j] = True # Mark the current cell as visited.\n dfs(i+1, j) # Visit the neighbor to the right.\n dfs(i-1, j) # Visit the neighbor to the left.\n dfs(i, j+1) # Visit the neighbor below.\n dfs(i, j-1) # Visit the neighbor above.\n \n m, n = len(grid), len(grid[0]) # Get the dimensions of the given matrix.\n visited = [[False for _ in range(n)] for _ in range(m)] # Initialize a visited matrix with False for all cells.\n count = 0 # Initialize a count variable to 0.\n for i in range(m):\n for j in range(n):\n if grid[i][j] == "1" and not visited[i][j]: # If we encounter an unvisited 1, increment the count and perform a DFS on its neighbors, marking all the visited 1\'s as visited.\n count += 1\n dfs(i, j)\n return count # Return the count of the number of islands.\n\n``` | 11 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
Python 3 | DFS, BFS, Union Find, All 3 methods | Explanation | number-of-islands | 0 | 1 | ### Approach \\#1. DFS\n- Iterate over the matrix and DFS at each point whenever a point is land (`1`)\n- Mark visited as `2` to avoid revisit\n- Increment `ans` each time need to do a DFS (original, not recursive)\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n if not grid: return 0\n m, n = len(grid), len(grid[0])\n ans = 0\n def dfs(i, j):\n grid[i][j] = \'2\'\n for di, dj in (0, 1), (0, -1), (1, 0), (-1, 0):\n ii, jj = i+di, j+dj\n if 0 <= ii < m and 0 <= jj < n and grid[ii][jj] == \'1\':\n dfs(ii, jj)\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'1\':\n dfs(i, j)\n ans += 1\n return ans\n```\n\n### Approach \\#2. BFS\n- Iterate over the matrix and BFS at each point whenever a point is land (`1`)\n- Mark visited as `2` to avoid revisit\n- Increment `ans` each time need to do a BFS (original, not recursive)\n```\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n if not grid: return 0\n m, n = len(grid), len(grid[0])\n ans = 0\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'1\':\n q = collections.deque([(i, j)])\n grid[i][j] = \'2\'\n while q:\n x, y = q.popleft()\n for dx, dy in (0, 1), (0, -1), (1, 0), (-1, 0):\n xx, yy = x+dx, y+dy\n if 0 <= xx < m and 0 <= yy < n and grid[xx][yy] == \'1\':\n q.append((xx, yy))\n grid[xx][yy] = \'2\'\n ans += 1 \n return ans\n```\n\n### Approach \\#3. Union Find\n- Create dictionary `d[(i,j)] = idx`, give `(x,y)` an id number, for eaiser union find\n- Create a Union Find object with length of number of `"1"` (say length is `n` or `size`)\n- Iterate over matrix, from left to right, from top to bottom\n\t- Union current and left or right, if they are both `1`\n\t- For each union, decrement `size`\n- Return `size`\n```\nclass UF:\n def __init__(self, n):\n self.p = [i for i in range(n)]\n self.n = n\n self.size = n\n\n def union(self, i, j):\n pi, pj = self.find(i), self.find(j)\n if pi != pj:\n self.size -= 1\n self.p[pj] = pi\n\n def find(self, i):\n if i != self.p[i]:\n self.p[i] = self.find(self.p[i])\n return self.p[i]\n\n\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n if not grid:\n return 0\n m, n = len(grid), len(grid[0])\n d = dict()\n idx = 0\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'1\':\n d[i, j] = idx\n idx += 1\n uf = UF(idx)\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'1\':\n if i > 0 and grid[i-1][j] == \'1\':\n uf.union(d[i-1, j], d[i, j])\n if j > 0 and grid[i][j-1] == \'1\':\n uf.union(d[i, j-1], d[i, j])\n return uf.size\n``` | 67 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return _the number of islands_.
An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
**Example 1:**
**Input:** grid = \[
\[ "1 ", "1 ", "1 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "1 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "0 ", "0 "\]
\]
**Output:** 1
**Example 2:**
**Input:** grid = \[
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "1 ", "1 ", "0 ", "0 ", "0 "\],
\[ "0 ", "0 ", "1 ", "0 ", "0 "\],
\[ "0 ", "0 ", "0 ", "1 ", "1 "\]
\]
**Output:** 3
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 300`
* `grid[i][j]` is `'0'` or `'1'`. | null |
🔥🔥 Python 2 line Solution 🔥🔥 | bitwise-and-of-numbers-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rangeBitwiseAnd(self, left: int, right: int) -> int:\n while (right > left): # Loop until right is no longer greater than left\n right = right & (right - 1) # Clear the least significant bit of right\n return right & left # Return the bitwise AND of the modified right and left\n``` | 4 | Given two integers `left` and `right` that represent the range `[left, right]`, return _the bitwise AND of all numbers in this range, inclusive_.
**Example 1:**
**Input:** left = 5, right = 7
**Output:** 4
**Example 2:**
**Input:** left = 0, right = 0
**Output:** 0
**Example 3:**
**Input:** left = 1, right = 2147483647
**Output:** 0
**Constraints:**
* `0 <= left <= right <= 231 - 1` | null |
201: Solution with step by step explanation | bitwise-and-of-numbers-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe approach to solve this problem is to perform a bitwise AND operation on all numbers between the left and right limits. However, performing this operation on every number will be a costly operation.\n\nIf we consider the bitwise representation of the numbers in the given range, we observe that the result of the bitwise AND operation on these numbers gives us the common bits present in the left and right limits.\n\nThus, the task of finding the bitwise AND operation of all numbers between left and right limits reduces to finding the common bits between the left and right limits.\n\nTo find these common bits, we find the leftmost common bits between the left and right limits. We can start from the leftmost bit and move rightwards and check the bits of the left and right limits. If there is a mismatch between the bits, then all the bits to the right of the current bit will be set in the result of the bitwise AND operation. If there is no mismatch between the bits, then the current bit will be set in the result of the bitwise AND operation.\n\nAlgorithm:\n\n1. Initialize a variable \'shift\' to 0.\n2. While the left and right limits are not equal,\na. Right shift the left limit by 1 bit.\nb. Right shift the right limit by 1 bit.\nc. Increment the \'shift\' variable by 1.\n3. Left shift the left limit by \'shift\' bits and return the result.\n\n# Complexity\n- Time complexity:\nO(1), as we are performing a constant number of operations.\n\n- Space complexity:\nO(1), as we are not using any extra data structures.\n\n# Code\n```\nclass Solution:\n def rangeBitwiseAnd(self, left: int, right: int) -> int:\n \n # Initialize a variable \'shift\' to 0.\n shift = 0\n \n # While the left and right limits are not equal,\n while left < right:\n \n # Right shift the left limit by 1 bit.\n left >>= 1\n \n # Right shift the right limit by 1 bit.\n right >>= 1\n \n # Increment the \'shift\' variable by 1.\n shift += 1\n \n # Left shift the left limit by \'shift\' bits and return the result.\n return left << shift\n\n``` | 17 | Given two integers `left` and `right` that represent the range `[left, right]`, return _the bitwise AND of all numbers in this range, inclusive_.
**Example 1:**
**Input:** left = 5, right = 7
**Output:** 4
**Example 2:**
**Input:** left = 0, right = 0
**Output:** 0
**Example 3:**
**Input:** left = 1, right = 2147483647
**Output:** 0
**Constraints:**
* `0 <= left <= right <= 231 - 1` | null |
Python AND with a twist and beats T.C. 96.6% and S.C. 92.4% | bitwise-and-of-numbers-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(min(1000, right - left))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rangeBitwiseAnd(self, left: int, right: int) -> int:\n c, i, j = 0, left, right\n AND = i&j\n i += 1\n j -= 1\n c += 1\n while i<=j and c < 1000:\n c += 1\n AND &= i&j\n if AND == 0: return 0\n i += 1\n j -= 1\n return 0 if c >= 1000 else AND\n``` | 1 | Given two integers `left` and `right` that represent the range `[left, right]`, return _the bitwise AND of all numbers in this range, inclusive_.
**Example 1:**
**Input:** left = 5, right = 7
**Output:** 4
**Example 2:**
**Input:** left = 0, right = 0
**Output:** 0
**Example 3:**
**Input:** left = 1, right = 2147483647
**Output:** 0
**Constraints:**
* `0 <= left <= right <= 231 - 1` | null |
Python Bits Manipulation Solution with Detailed Intuition ✅ | bitwise-and-of-numbers-range | 0 | 1 | ```\n\'\'\'\n# Intuition:\nTraverse from LSB to MSB and keep right-shifting left and right until both of them become equal. \nIf at any bit position left side bits of left and right are equal ie. left == right, \nthen all numbers in [left, right] will also be equal.\n\ne.g.\nbit index = 3 2 1 0\nleft = 12 = 1 1 0 0\n 13 = 1 1 0 1\n 14 = 1 1 1 0\nright = 15 = 1 1 1 1\n\nAfter right-shifting left and right 2 times(ie. count = 2), left == right = 12 = 13 = 14 = 15 = 0 0 1 1\nSo \'&\' of all number in [left, right] is (left << count)\n\'\'\'\n\n\nclass Solution:\n def rangeBitwiseAnd(self, left: int, right: int) -> int:\n count = 0\n \n while left != right:\n left = left >> 1\n right = right >> 1\n count += 1\n \n return left << count\n \n \n# Time: O(1)\n# Space: O(1)\n``` | 2 | Given two integers `left` and `right` that represent the range `[left, right]`, return _the bitwise AND of all numbers in this range, inclusive_.
**Example 1:**
**Input:** left = 5, right = 7
**Output:** 4
**Example 2:**
**Input:** left = 0, right = 0
**Output:** 0
**Example 3:**
**Input:** left = 1, right = 2147483647
**Output:** 0
**Constraints:**
* `0 <= left <= right <= 231 - 1` | null |
Python Bits Manipulation Solution with Detailed Intuition ✅ | bitwise-and-of-numbers-range | 0 | 1 | ```\n\'\'\'\n# Intuition:\nTraverse from LSB to MSB and keep right-shifting left and right until both of them become equal. \nIf at any bit position left side bits of left and right are equal ie. left == right, \nthen all numbers in [left, right] will also be equal.\n\ne.g.\nbit index = 3 2 1 0\nleft = 12 = 1 1 0 0\n 13 = 1 1 0 1\n 14 = 1 1 1 0\nright = 15 = 1 1 1 1\n\nAfter right-shifting left and right 2 times(ie. count = 2), left == right = 12 = 13 = 14 = 15 = 0 0 1 1\nSo \'&\' of all number in [left, right] is (left << count)\n\'\'\'\n\n\nclass Solution:\n def rangeBitwiseAnd(self, left: int, right: int) -> int:\n count = 0\n \n while left != right:\n left = left >> 1\n right = right >> 1\n count += 1\n \n return left << count\n \n \n# Time: O(1)\n# Space: O(1)\n``` | 3 | Given two integers `left` and `right` that represent the range `[left, right]`, return _the bitwise AND of all numbers in this range, inclusive_.
**Example 1:**
**Input:** left = 5, right = 7
**Output:** 4
**Example 2:**
**Input:** left = 0, right = 0
**Output:** 0
**Example 3:**
**Input:** left = 1, right = 2147483647
**Output:** 0
**Constraints:**
* `0 <= left <= right <= 231 - 1` | null |
Python iterative sol. based on bit-manipulation | bitwise-and-of-numbers-range | 0 | 1 | Python iterative sol. based on bit-manipulation\n\n```\nclass Solution:\n def rangeBitwiseAnd(self, m: int, n: int) -> int:\n \n shift = 0\n \n # find the common MSB bits.\n while m != n:\n \n m = m >> 1\n n = n >> 1\n \n shift += 1\n \n \n return m << shift\n``` | 10 | Given two integers `left` and `right` that represent the range `[left, right]`, return _the bitwise AND of all numbers in this range, inclusive_.
**Example 1:**
**Input:** left = 5, right = 7
**Output:** 4
**Example 2:**
**Input:** left = 0, right = 0
**Output:** 0
**Example 3:**
**Input:** left = 1, right = 2147483647
**Output:** 0
**Constraints:**
* `0 <= left <= right <= 231 - 1` | null |
Easy Python Solution || Beginner Friendly || Let's search for Happy Number..... | happy-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The problem is asking whether a given number is a happy number or not. A happy number is a number which eventually reaches 1 when replaced by the sum of the square of each digit.\n- The intuition here is to repeatedly calculate the sum of squares of digits until either the result becomes 1 (happy) or a cycle is detected (unhappy).\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The isHappy function uses a helper function sqr to calculate the sum of squares of digits.\n- It then iterates a fixed number of times (in this case, 70) to check if the number becomes 1.\n- If it becomes 1 during these iterations, the function returns True (happy). Otherwise, it returns False.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(n), where n is the number of iterations in the loop. In this case, it\'s a fixed number (70), so it can be considered constant time.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as there is a constant amount of extra space used regardless of the input. The space used is for the variables sum, r, and i.\n\n---\n# I hope you understood the explanation. If not dive into the code below. I assure you that you will be able to understand it. If you like the solution, please do upvote me...\n---\n\n\n# Code\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n # Helper function to calculate the sum of squares of digits\n def sqr(num):\n sum = 0\n while num > 0:\n r = num % 10\n sum += r**2\n num = num // 10\n return sum\n\n # Iterate for a fixed number of steps to check for happiness\n for i in range(70):\n n = sqr(n)\n if n == 1:\n return True\n\n # If the loop completes without finding 1, return False\n return False\n\n``` | 3 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Very Easy 0 ms 100%(Fully Explained)(C++, Java, Python, JS, C, Python3) | happy-number | 1 | 1 | # **C++ Solution:**\nRuntime: 0 ms, faster than 100.00% of C++ online submissions for Happy Number.\n```\nclass Solution {\npublic:\n bool isHappy(int n) {\n // Create a set...\n set<int> hset;\n while(hset.count(n) == 0) {\n // If total is equal to 1 return true.\n if(n == 1)\n return true;\n // Insert the current number in hset...\n hset.insert(n);\n // Initialize the total...\n int total=0;\n // Create a while loop...\n while(n) {\n // Process to get happy number...\n // We use division and modulus operators to repeatedly take digits off the number until none remain...\n // Then squaring each removed digit and adding them together.\n total += (n % 10) * (n % 10);\n n /= 10;\n // Each new converted number must not had occurred before...\n }\n // Insert the current number into the set s...\n // Replace the current number with total of the square of its digits.\n n = total;\n }\n // If current number is already in the HashSet, that means we\'re in a cycle and we should return false..\n return false;\n }\n};\n```\n\n# **Java Solution (Using Hash):**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Happy Number.\n```\nclass Solution {\n public boolean isHappy(int n) {\n // Create a hash set...\n Set<Integer> hset = new HashSet<Integer>();\n // If the number is not in the HashSet, we should add it...\n while (hset.add(n)) {\n // Initialize the total...\n int total = 0;\n // Create a while loop...\n while (n > 0) {\n // Process to get happy number...\n // We use division and modulus operators to repeatedly take digits off the number until none remain...\n // Then squaring each removed digit and adding them together...\n total += (n % 10) * (n % 10);\n n /= 10;\n // Each new converted number must not had occurred before...\n }\n // If total is equal to 1 return true.\n if (total == 1)\n return true;\n // Insert the current number into the set s...\n // Replace the current number with total of the square of its digits.\n else\n n = total;\n }\n // If current number is already in the HashSet, that means we\'re in a cycle and we should return false..\n return false;\n }\n}\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def isHappy(self, n):\n hset = set()\n while n != 1:\n if n in hset: return False\n hset.add(n)\n n = sum([int(i) ** 2 for i in str(n)])\n else:\n return True\n```\n \n# **JavaScript Solution:**\n```\nvar isHappy = function(n) {\n if(n<10){\n if(n === 1 || n === 7){\n return true\n }\n return false\n }\n let total = 0\n while(n>0){\n let sq = n % 10\n total += sq**2\n n -= sq\n n /= 10\n }\n if(total === 1){\n return true\n }\n return isHappy(total)\n};\n```\n\n# **C Language:**\n```\nbool isHappy(int n){\n int total = 0;\n while(true){\n while(n > 0){\n total += (n % 10) * (n % 10);\n n /= 10;\n }\n if(total == 1)\n return true;\n else if(total == 4)\n return false;\n n = total;\n total = 0;\n }\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n hset = set()\n while n != 1:\n if n in hset: return False\n hset.add(n)\n n = sum([int(i) ** 2 for i in str(n)])\n else:\n return True\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 70 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Simple Approach for HAPPY NUMBER in PYTHON/PYTHON3 | happy-number | 0 | 1 | # Intuition\nIn this solution, we use list, array or map to store the numnber\nthan we can check it appear or not\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe approach as stated in other solutions is quite simple. It either involves the fancier floyd cycle algorithm or simply making a hashset of the values already seen and looking for a loop.\n\nNow, what\'s missing in all the solutions is the explanation of why we will have repeat values showing up after enough squaring/adding and not get a unique value everytime we add squares of digits. Why would the hashset not be infinitely long?\n\nLet\'s say we start with a one digit number to check if its a happy number, for example : 4\n4^2= 16\n16->37\n37->58\n..............\n83->73\n73->58 (loop)\n\nThe reason this sort of loop exists is because with a one digit number we can have square sum as 81 which is a 2 digit number. With a 2 digit number (like 99), we can have square sum as a 3 digit number (81+81 = 162), but with a 3 digit number (no matter how large, even 999-> 243), we cannot have a square sum as a 4 digit number. So starting with a one digit number, we are limited to at max 3 digit sum squares. And since the number of numbers that can be represented as a sum of squares and are <1000 are limited, the hashset won\'t be infinitely wrong. Similar approach works for bigger numbers involving 5,6,7 .... digits.\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n used = []\n\n while(n>0):\n tmp = 0\n while(n>0):\n i = n%10\n\n tmp += i*i\n n = n//10\n\n if(tmp in used):\n return False\n else:\n used.append(tmp)\n\n if(tmp==1):\n return True\n \n n = tmp\n\n return False\n```\n | 33 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
[PYTHON]-\ \-easiest -\ \- with comments | happy-number | 0 | 1 | \n# Code\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n set_of_no=set()\n while n!=1: \n n=sum([int(i)**2 for i in str(n)]) #squaring the digits of no\n if n in set_of_no: #checking whether the no is present in set_of_no\n return False #if present that means it will repeat the terms(or in endless loop)\n set_of_no.add(n) #if not present add it to set\n return True\n\n \n\n\n``` | 7 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
新手解 | happy-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\u5728\u89E3\u984C\u4E4B\u524D\u8981\u5148\u4E86\u89E3\u5FEB\u6A02\u6578\u7684\u5B9A\u7FA9...\n\u53EA\u8981\u4E0D\u662F\u5FEB\u6A02\u6578\u5C31\u6703\u9032\u5165\u4EE5\u4E0B\u5FAA\u74B0\n4 \u2192 16 \u2192 37 \u2192 58 \u2192 89 \u2192 145 \u2192 42 \u2192 20 \u2192 4\n\u6240\u4EE5\u53EA\u8981\u6578\u5B57\u52A0\u8D77\u4F86\u662F4\uFF0C\u5B83\u5C31\u4E0D\u662F\u5FEB\u6A02\u6578\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n n2 = 0\n while True :\n for i in str(n) :\n n2 += int(i)*int(i)\n n,n2=n2,0\n if n == 1 :\n return True\n elif n == 4 :\n return False\n``` | 3 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Beats : 98.9% [26/145 Top Interview Question] | happy-number | 0 | 1 | # Intuition\n*my intuition would be to implement a loop that repeatedly computes the sum of squares of the digits of n and checks if the result is equal to 1 or not. I would also need to keep track of all the intermediate numbers that I encounter, to detect if we enter a cycle of numbers. If we detect a cycle, we can terminate the loop and return False because we know that n is not a happy number.*\n\n# Approach\nThis is a Python class called `Solution` with two methods `isHappy` and `sumOfSquare`.\n\nThe `sumOfSquare` method takes a positive integer `n` as input and returns the sum of the squares of its digits. It does this by initializing an output variable `output` to 0 and then repeatedly extracting the least significant digit of `n` using the modulo operator (`%`), squaring it, and adding it to `output`. The least significant digit is then removed from `n` by performing integer division (`//`) by 10. This process is repeated until `n` becomes 0, at which point the final sum of squares is returned.\n\nThe `isHappy` method takes a positive integer `n` as input and returns `True` if it is a happy number, and `False` otherwise. A happy number is defined as a number where repeatedly summing the squares of its digits eventually leads to 1. To check if `n` is a happy number, the method initializes an empty set called `visited` to keep track of all the numbers seen so far. It then repeatedly calculates the sum of squares of the digits of `n` using the `sumOfSquare` method and checks if it equals 1. If it does, the method returns `True`. If the sum is not 1, it is added to the `visited` set to avoid infinite loops, and `n` is updated to be the sum of squares. This process is repeated until `n` is found in the `visited` set, which means that the sum of squares of its digits has been seen before and the number is not happy.\n\n# Complexity `edited`\n- Time complexity:\nO(x * log(n)) ***`aprx`***\n*note: **`x`** is not the length of any input*\n\n- Space complexity:\nO(x) ***`aprx`***\n\nlet\'s analyze the time and space complexity together for both functions.\n\n1. `isHappy` method:\n - Time Complexity: the `time complexity` of this method is approximately `O(x)`, where `x` is the number of iterations until reaching 1 or entering a cycle.\n - Space Complexity: The `space complexity` is `O(x)` as well since the `visited` set will store all the visited numbers until reaching 1 or entering a cycle.\n\n2. `sumOfSquare` method:\n - Time Complexity: The `time complexity` of this method is `O(log(n)`) since it depends on the number of digits in `n`, and the number of digits is proportional to `log(n)`.\n - Space Complexity: The `space complexity` of this method is `O(1)` since it only uses a constant amount of additional space to store intermediate variables.\n\nIn summary:\n- For the `isHappy` method, the combined `time` and `space complexity` is `O(x)`.\n- For the `sumOfSquare` method, the `time complexity` is `O(log(n))`, and the `space complexity` is `O(1)`.\n\nKeep in mind that the exact value of `x` (the number of iterations until reaching 1 or entering a cycle) can vary depending on the input number `n` and whether it is a happy number or not. ***`The given complexities provide an approximation of the performance of the solution`***\n\n\n# Code\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n visited = set()\n while n not in visited:\n visited.add(n)\n n = self.sumOfSquare(n)\n if n == 1:\n return True\n \n return False\n \n def sumOfSquare(self,n) -> int:\n output = 0\n while n > 0:\n digits = n % 10\n digits = digits * digits\n output += digits\n n = n // 10\n return output \n\n``` | 2 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python 3 -> tortoise hare technique | happy-number | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\n```\ndef isHappy(self, n: int) -> bool:\n\t#20 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 > 42 -> 20\n\tslow = self.squared(n)\n\tfast = self.squared(self.squared(n))\n\n\twhile slow!=fast and fast!=1:\n\t\tslow = self.squared(slow)\n\t\tfast = self.squared(self.squared(fast))\n\n\treturn fast==1\n\ndef squared(self, n):\n\tresult = 0\n\twhile n>0:\n\t\tlast = n%10\n\t\tresult += last * last\n\t\tn = n//10\n\treturn result\n```\n\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 115 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python - Easiest Solution | happy-number | 0 | 1 | # Easy Understand\n\n# Code\n\nExplaination :\n```\n if(m==9000):\n return False \n```\nthis code is for : if m reached to 9000. It means there is no happy number as n or code will give TLE. So it returns false...\n```\ndef happy(n,m):\n s = str(n)\n cnt = 0\n for i in s:\n cnt += int(i)**2\n \n if(cnt==1):\n return True\n\n if(m==9000):\n return False \n\n m += 1\n return happy(cnt,m)\n\n\nclass Solution:\n def isHappy(self, n: int) -> bool:\n if(n<1):\n return False\n if(happy(n,0)==True):\n return True\n else:\n return False\n``` | 3 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Happy Number beats 98🔥🔥 | happy-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isHappy(self, n: int) -> bool:\n def sqnum(n):\n temp=n\n sum=0\n while temp>0:\n rem=temp%10\n sum+=rem**2\n temp=temp//10\n return sum\n \n for i in range(100):\n n = sqnum(n)\n if n==1:\n return True\n else:\n return False\n``` | 1 | Write an algorithm to determine if a number `n` is happy.
A **happy number** is a number defined by the following process:
* Starting with any positive integer, replace the number by the sum of the squares of its digits.
* Repeat the process until the number equals 1 (where it will stay), or it **loops endlessly in a cycle** which does not include 1.
* Those numbers for which this process **ends in 1** are happy.
Return `true` _if_ `n` _is a happy number, and_ `false` _if not_.
**Example 1:**
**Input:** n = 19
**Output:** true
**Explanation:**
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
**Example 2:**
**Input:** n = 2
**Output:** false
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Simple Python solution with explanation (single pointer, dummy head). | remove-linked-list-elements | 0 | 1 | Before writing any code, it\'s good to make a list of edge cases that we need to consider. This is so that we can be certain that we\'re not overlooking anything while coming up with our algorithm, and that we\'re testing all special cases when we\'re ready to test. These are the edge cases that I came up with.\n\n1. The linked list is empty, i.e. the head node is None.\n2. Multiple nodes with the target value in a row. \n3. The head node has the target value.\n4. The head node, and any number of nodes immediately after it have the target value.\n5. All of the nodes have the target value.\n6. The last node has the target value.\n\nSo with that, this is the algorithm I came up with.\n\n```\nclass Solution:\n def removeElements(self, head, val):\n """\n :type head: ListNode\n :type val: int\n :rtype: ListNode\n """\n \n dummy_head = ListNode(-1)\n dummy_head.next = head\n \n current_node = dummy_head\n while current_node.next != None:\n if current_node.next.val == val:\n current_node.next = current_node.next.next\n else:\n current_node = current_node.next\n \n return dummy_head.next\n```\n\nIn order to save the need to treat the "head" as special, the algorithm uses a "dummy" head. This simplifies the code greatly, particularly in the case of needing to remove the head AND some of the nodes immediately after it.\n\nThen, we keep track of the current node we\'re up to, and look ahead to its next node, as long as it exists. If ```current_node.next``` does need removing, then we simply replace it with ```current_node.next.next```. We know this is always "safe", because ```current_node.next``` is definitely not None (the loop condition ensures that), so we can safely access its ```next```.\n\nOtherwise, we know that ```current_node.next``` should be kept, and so we move ```current_node``` on to be ```current_node.next```.\n\nThe loop condition only needs to check that ```current_node.next != None```. The reason it does **not** need to check that ```current_node != None``` is because this is an impossible state to reach. Think about it this way: The ONLY case that we ever do ```current_node = current_node.next``` in is immediately after the loop has already confirmed that ```current_node.next``` is not None. \n\nThe algorithm requires ***```O(1)```*** extra space and takes ***```O(n)```*** time. | 507 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Easiest python solution pointer approach | remove-linked-list-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n dummy=ListNode(next=head)\n prev,curr=dummy,head\n while curr:\n if curr.val==val:\n nxt=curr.next\n prev.next=nxt\n curr=nxt\n else:\n prev=curr\n curr=curr.next\n return dummy.next\n\n\n``` | 3 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
[Python] 99% One-pass Solution with Explanation | remove-linked-list-elements | 0 | 1 | ### Intuition\n\nTo delete a node, we need to assign the next node to the previous node. Let\'s use `curr` to denote the current node, and `prev` to denote the previous node. Then, we have the following 4 cases:\n\n1. **Node to remove is at the end of the linked list.**\n\n```text\nInput: head = [6,1,2,6,3,4,5,6], val = 6\n\t\t\t\t\t\t / \\\n\t\t\t\t\t\tprev curr\n```\n\nSimple enough, we just need to assign `prev.next = None`, since `curr.next == None`. No further action is needed since this is the last node to check.\n\n2. **Node to remove is in the middle of the linked list.**\n\n```text\nInput: head = [6,1,2,6,3,4,5,6], val = 6\n\t\t\t\t / \\\n\t\t\t\tprev curr\n```\n\nTo remove the node `curr`, we can assign `prev.next = curr.next`, which disconnects `curr` from the linked list completely. In the following iteration, we know that `curr = curr.next`, while `prev` should remain pointing at the same node since `curr` has been removed. So, in summary:\n\n- `prev.next = curr.next` to remove the node;\n- `curr = curr.next` to get the next iteration.\n\n3. **Node to remove is at the start of the linked list.**\n\n```text\nInput: head = [6,1,2,6,3,4,5,6], val = 6\n\t\t\t/ \\\n\t prev curr\n```\n\nSince `prev == None`, we don\'t need to assign `prev.next = curr.next`. However, removing nodes from the beginning of the linked list changes the head node of the linked list, so we need to assign `head = curr.next` before proceeding with the next iteration (as per case 2). In summary:\n\n- `head = curr.next` to change the head node;\n- `curr = curr.next` to get the next iteration.\n\n4. **Current node is not to be removed.**\n\n```text\nInput: head = [6,1,2,6,3,4,5,6], val = 6\n\t\t\t / \\\n\t prev curr\n```\n\nNothing needs to be done, we just need to proceed with the next iteration. This involves:\n\n- `curr = curr.next`, as discussed in cases 2 and 3;\n- `prev = curr`, since the `curr` node is not removed in this case.\n\n---\n\n### Implementation\n\n- Start with `curr = head` and `prev = None`.\n- Loop through the linked list and determine which of the 4 cases `curr` and `prev` belong to, and perform the action accordingly.\n\n```python\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n prev, curr = None, head\n while curr:\n if curr.val == val: # cases 1-3\n if prev: # cases 1-2\n prev.next = curr.next\n else: # case 3\n head = curr.next\n curr = curr.next # for all cases\n else: # case 4\n prev, curr = curr, curr.next\n return head\n```\n\n---\n\n### Final Result\n\n**TC: O(n)** where `n` is the number of nodes in the linked list.\n**SC: O(1)**, no additional data structures were used.\n\n\n\nPlease upvote of this has helped you! Appreciate any comments as well :) | 59 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Solution Intuition, Approach, Complexity, and Code: Removing Linked List Elements | remove-linked-list-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires removing all nodes that match a specific value from a linked list. The approach involves iterating through the linked list while maintaining a previous node pointer to update the next node pointer of the previous node once a node that matches the specific value is found. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve the problem, we use two pointers, a previous pointer `prev` and a current pointer `curr`, both initially pointing to the head of the linked list. While iterating through the linked list, if the current node has a value equal to the specific value, we skip the current node by updating the next node pointer of the previous node to point to the next node of the current node. Otherwise, we update the previous node pointer to point to the current node.\n# Complexity\n- Time complexity:$O(n)$, where n is the number of nodes in the linked list. The algorithm iterates through each node in the linked list at most once to remove the nodes that match the specific value.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(1)$. The algorithm uses a constant amount of extra memory to maintain the previous and current node pointers.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n prev = None\n curr = head\n \n while curr:\n if curr.val == val:\n if prev:\n prev.next = curr.next\n else:\n head = curr.next\n curr = curr.next\n else:\n prev = curr\n curr = curr.next\n \n return head\n``` | 8 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
✅Python3 73ms🔥easiest solution | remove-linked-list-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Two Pointers Methods.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- maintain **two pointers** **prev and current**, meaning is self-described.\n- now when **removing element is head** then **remove** head **till** it\'s **not removing element**, till this time our **prev will be None**.\n- now if removing element is not head then **prev.next = curr.next** and **curr = curr.next**, prev will be same because **if** we do **prev = curr** then **prev will be removed node**.\n- now when we encounter **node** that is **not removing** then do **prev = curr and curr = curr.next.**\n- do this all till curr is not None\n- **return head**.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n prev = None\n curr = head\n while curr:\n if curr.val == val and prev:\n prev.next = curr.next\n curr = curr.next\n continue\n elif curr.val == val and not prev:\n head = head.next\n curr = curr.next\n continue\n prev = curr\n curr = curr.next\n return head\n```\n# Please like and comment below (\u0336\u25C9\u035B\u203F\u25C9\u0336) | 7 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
eas | remove-linked-list-elements | 0 | 1 | \n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n result = ListNode(0)\n result.next = head\n cur = result\n while cur.next:\n if cur.next.val == val:\n cur.next = cur.next.next\n else:\n cur = cur.next\n return result.next\n``` | 2 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Very Easy || 0 ms || 100% || Fully Explained (Java, C++, Python, JS, C, Python3) | remove-linked-list-elements | 1 | 1 | # **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Remove Linked List Elements.\n```\nclass Solution {\n public ListNode removeElements(ListNode head, int val) {\n // create a fake node that acts like a fake head of list pointing to the original head and it points to the original head...\n ListNode fake = new ListNode(0);\n fake.next = head;\n ListNode curr = fake;\n // Loop till curr.next not null...\n while(curr.next != null){\n // if we find the target val same as the value of curr.next...\n if(curr.next.val == val){\n // Skip that value and keep updating curr...\n curr.next = curr.next.next; \n }\n // Otherwise, move curr forward...\n else{\n curr = curr.next;\n }\n }\n return fake.next; // Return the linked list...\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n ListNode* removeElements(ListNode* head, int val) {\n ListNode *prev, *curr;\n //deal with leading \'val\'s\n // If the head node is not null and the value of the head node is same as the target val...\n while(head != NULL && head->val == val)\n // Skip the value and keep updating head node...\n head = head->next;\n // Deal with \'val\'s not in head of list...\n // curr node points to the head node...\n curr = head;\n // Loop till curr not null...\n while(curr != NULL){\n // If we find the target val same as the value of curr...\n if(curr->val == val){\n // Skip that value and keep updating...\n prev->next = curr->next;\n }\n // Move prev when the next node of prev is not \'val\'\n else{\n prev = curr;\n }\n // Move curr forward...\n curr = curr->next;\n }\n return head;\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def removeElements(self, head, val):\n # create a fake node that acts like a fake head of list pointing to the original head and it points to the original head...\n fake = ListNode(None)\n fake.next = head\n curr = fake\n # Loop till curr.next not null...\n while curr.next:\n # if we find the target val same as the value of curr.next...\n if curr.next.val == val:\n # Skip that value and keep updating curr...\n curr.next = curr.next.next\n # Otherwise, move curr forward...\n else:\n curr = curr.next\n # Return the linked list...\n return fake.next\n```\n \n# **JavaScript Solution:**\n```\nvar removeElements = function(head, val) {\n // create a fake node that acts like a fake head of list pointing to the original head and it points to the original head...\n var fake = new ListNode(0);\n fake.next = head;\n var curr = fake;\n // Loop till curr.next not null...\n while(curr.next != null){\n // if we find the target val same as the value of curr.next...\n if(curr.next.val == val){\n // Skip that value and keep updating curr...\n curr.next = curr.next.next; \n }\n // Otherwise, move curr forward...\n else{\n curr = curr.next;\n }\n }\n return fake.next; // Return the linked list...\n};\n```\n\n# **C Language:**\n```\nstruct ListNode* removeElements(struct ListNode* head, int val){\n struct ListNode *prev, *curr;\n //deal with leading \'val\'s\n // If the head node is not null and the value of the head node is same as the target val...\n while(head != NULL && head->val == val)\n // Skip the value and keep updating head node...\n head = head->next;\n // Deal with \'val\'s not in head of list...\n // curr node points to the head node...\n curr = head;\n // Loop till curr not null...\n while(curr != NULL){\n // If we find the target val same as the value of curr...\n if(curr->val == val){\n // Skip that value and keep updating...\n prev->next = curr->next;\n }\n // Move prev when the next node of prev is not \'val\'\n else{\n prev = curr;\n }\n // Move curr forward...\n curr = curr->next;\n }\n return head;\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n # create a fake node that acts like a fake head of list pointing to the original head and it points to the original head...\n fake = ListNode(None)\n fake.next = head\n curr = fake\n # Loop till curr.next not null...\n while curr.next:\n # if we find the target val same as the value of curr.next...\n if curr.next.val == val:\n # Skip that value and keep updating curr...\n curr.next = curr.next.next\n # Otherwise, move curr forward...\n else:\n curr = curr.next\n # Return the linked list...\n return fake.next\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 20 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Python || 94.11% Faster || Iterative Approach || O(N) Solution | remove-linked-list-elements | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n if head==None: #If head is empty\n return head\n while head and head.val==val: #If we want to delete the starting nodes\n head=head.next\n temp=head\n while temp:\n while temp.next and temp.next.val==val:\n temp.next=temp.next.next\n temp=temp.next\n return head\n```\n\n**Upvote if you like the solution or ask if there is any query** | 4 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
203: Solution with step by step explanation | remove-linked-list-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe will start by initializing a dummy node and make its next point to head, which will make it easy to handle edge cases.\n\nWe will traverse the linked list and remove all the nodes with val equal to given val.\n\nAt the end, we will return the next node of dummy node as the new head.\n\nAlgorithm:\n\n1. Initialize a dummy node and point its next to the head of the linked list.\n2. Initialize two pointers, prev and curr as dummy and head, respectively.\n3. Traverse the linked list:\na. If the value of the current node is equal to the given value, then set the next of the prev node to the next of curr node and move curr to the next node.\nb. Else, move prev and curr to their next nodes.\n4. Return the next of the dummy node as the new head of the linked list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElements(self, head: ListNode, val: int) -> ListNode:\n dummy = ListNode(0) # initialize dummy node\n dummy.next = head # point its next to head\n prev, curr = dummy, head # initialize prev and curr pointers\n \n while curr: # traverse the linked list\n if curr.val == val: # if val found\n prev.next = curr.next # remove the node by skipping it\n else:\n prev = curr # move prev to the next node\n curr = curr.next # move curr to the next node\n \n return dummy.next # return the new head\n\n``` | 10 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Easy beginner solution in Python | remove-linked-list-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n dummy = ListNode(next=head)\n prev ,curr = dummy, head\n\n while curr:\n if curr.val == val:\n curr = curr.next\n prev.next = curr\n else:\n curr =curr.next\n prev = prev.next\n \n\n return dummy.next\n``` | 3 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Python3 || Simple || Easy | remove-linked-list-elements | 0 | 1 | **Please upvote <3**\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n #create a dummy linkedlist\n dummy = ListNode(0)\n dummy.next = head\n #assign prev and temp\n prev = dummy\n temp = head\n #iterate\n while temp is not None:\n if temp.val == val:\n prev.next = temp.next\n temp = temp.next\n else:\n prev = temp\n temp = temp.next\n #return\n return dummy.next\n \n``` | 1 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
Python3 | remove-linked-list-elements | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:\n while head and head.val == val:\n head = head.next\n\n if not head:\n return None\n\n prev = head\n curr = head.next\n\n while curr:\n if curr.val == val:\n prev.next = curr.next\n else:\n prev = curr\n curr = curr.next\n\n return head\n\n``` | 1 | Given the `head` of a linked list and an integer `val`, remove all the nodes of the linked list that has `Node.val == val`, and return _the new head_.
**Example 1:**
**Input:** head = \[1,2,6,3,4,5,6\], val = 6
**Output:** \[1,2,3,4,5\]
**Example 2:**
**Input:** head = \[\], val = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[7,7,7,7\], val = 7
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 104]`.
* `1 <= Node.val <= 50`
* `0 <= val <= 50` | null |
204. Count Primes | count-primes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this method is that all non-prime numbers can be expressed as a product of prime numbers. Therefore, to find all prime numbers less than a given limit, we can start with a list of all numbers from 2 to the limit and iteratively remove all multiples of each prime number. The remaining numbers in the list will be prime.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n*log(log(n)))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Code\nC++\n```\nclass Solution {\npublic:\n int countPrimes(int n) {\n bool prime[n + 1];\n if(n==0||n==1) return 0;\n prime[0] = prime[1] = false;\n memset(prime, true, sizeof(prime));\n for (int i = 2; i * i < n; i++)\n {\n if (prime[i] == true)\n {\n for (int j = i * i; j < n; j += i)\n {\n prime[j] = false;\n }\n }\n }\n vector<int> res;\n for (int i = 2; i < n; i++)\n {\n if (prime[i] == true)\n res.push_back(i);\n }\n return res.size();\n }\n};\n\n```\nPYTHON: \n\n class Solution:\n def countPrimes(self, n: int) -> int:\n if n == 0 or n == 1:\n return 0\n \n prime = [True] * (n+1)\n prime[0], prime[1] = False, False\n \n for i in range(2, int(n**0.5)+1):\n if prime[i]:\n for j in range(i*i, n, i):\n prime[j] = False\n \n res = [i for i in range(2, n) if prime[i]]\n \n return len(res)\n\n | 3 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
204. Count Primes | count-primes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this method is that all non-prime numbers can be expressed as a product of prime numbers. Therefore, to find all prime numbers less than a given limit, we can start with a list of all numbers from 2 to the limit and iteratively remove all multiples of each prime number. The remaining numbers in the list will be prime.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n*log(log(n)))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Code\nC++\n```\nclass Solution {\npublic:\n int countPrimes(int n) {\n bool prime[n + 1];\n if(n==0||n==1) return 0;\n prime[0] = prime[1] = false;\n memset(prime, true, sizeof(prime));\n for (int i = 2; i * i < n; i++)\n {\n if (prime[i] == true)\n {\n for (int j = i * i; j < n; j += i)\n {\n prime[j] = false;\n }\n }\n }\n vector<int> res;\n for (int i = 2; i < n; i++)\n {\n if (prime[i] == true)\n res.push_back(i);\n }\n return res.size();\n }\n};\n\n```\nPYTHON: \n\n class Solution:\n def countPrimes(self, n: int) -> int:\n if n == 0 or n == 1:\n return 0\n \n prime = [True] * (n+1)\n prime[0], prime[1] = False, False\n \n for i in range(2, int(n**0.5)+1):\n if prime[i]:\n for j in range(i*i, n, i):\n prime[j] = False\n \n res = [i for i in range(2, n) if prime[i]]\n \n return len(res)\n\n | 3 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.