title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
204: Solution with step by step explanation | count-primes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can use the Sieve of Eratosthenes algorithm to count the number of prime numbers less than n. The basic idea behind this algorithm is to generate a list of numbers from 2 to n-1, then mark all the multiples of 2 as not prime, then mark all the multiples of 3 as not prime, and so on until we reach the square root of n. The remaining numbers that are not marked as not prime are the prime numbers less than n.\n\nHere is the step-by-step explanation of the algorithm:\n\n1. Create a list of booleans is_prime of length n, initialized to True.\n\n2. Mark is_prime[0] and is_prime[1] as False since 0 and 1 are not prime.\n\n3. Iterate from i = 2 to i * i < n:\na. If is_prime[i] is True, then iterate from j = i * i to j < n, marking is_prime[j] as False since j is a multiple of i.\n\n4. Count the number of True values in is_prime.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n if n <= 2:\n return 0\n \n # Step 1\n is_prime = [True] * n\n \n # Step 2\n is_prime[0] = is_prime[1] = False\n \n # Step 3\n for i in range(2, int(n**0.5)+1):\n if is_prime[i]:\n for j in range(i*i, n, i):\n is_prime[j] = False\n \n # Step 4\n return sum(is_prime)\n\n``` | 18 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
204: Solution with step by step explanation | count-primes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can use the Sieve of Eratosthenes algorithm to count the number of prime numbers less than n. The basic idea behind this algorithm is to generate a list of numbers from 2 to n-1, then mark all the multiples of 2 as not prime, then mark all the multiples of 3 as not prime, and so on until we reach the square root of n. The remaining numbers that are not marked as not prime are the prime numbers less than n.\n\nHere is the step-by-step explanation of the algorithm:\n\n1. Create a list of booleans is_prime of length n, initialized to True.\n\n2. Mark is_prime[0] and is_prime[1] as False since 0 and 1 are not prime.\n\n3. Iterate from i = 2 to i * i < n:\na. If is_prime[i] is True, then iterate from j = i * i to j < n, marking is_prime[j] as False since j is a multiple of i.\n\n4. Count the number of True values in is_prime.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n if n <= 2:\n return 0\n \n # Step 1\n is_prime = [True] * n\n \n # Step 2\n is_prime[0] = is_prime[1] = False\n \n # Step 3\n for i in range(2, int(n**0.5)+1):\n if is_prime[i]:\n for j in range(i*i, n, i):\n is_prime[j] = False\n \n # Step 4\n return sum(is_prime)\n\n``` | 18 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
[Python3] Simple Code; How to Make Your Code Faster. | count-primes | 0 | 1 | # Algorithm:\nMy code is based on the [Sieve of Eratosthenes](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes) which is efficient yet very simple. Make sure to read the link as well as the hints in the description of this question to better understand the Mathmatics of the code. Here, I do not want to explain the algorithm, instead I am focused on how to make the code as fast as possible.\n\n# Make your code faster:\n- The code line ```lst[m * m: n: m] = [0] *((n-m*m-1)//m + 1) ``` is key to reduce the run time. You could write a loop like this (but it would be very expensive):\n```\n for i in range(m * m, n, m):\n lst[i] = 0\n```\n\t\n- After marking all the even indices in the first iteration, I do not check even numbers again, and will only check odd numbers in the remaining iterations.\n- I created a list with numeral elements, instead of boolean elements.\n- Do not use function sqrt, because it is expensive [do not use: ```m < sqrt(n)```]. Instead, use ```m * m < n```.\n\n# Python3 code:\n```\n def countPrimes(self, n: int) -> int:\n if n < 3: return 0 ###// No prime number less than 2\n lst = [1] * n ###// create a list for marking numbers less than n\n lst[0] = lst[1] = 0 ###// 0 and 1 are not prime numbers\n m = 2\n while m * m < n: ###// we only check a number (m) if its square is less than n\n if lst[m] == 1: ###// if m is already marked by 0, no need to check its multiples.\n\t\t\t\n\t\t\t ###// If m is marked by 1, we mark all its multiples from m * m to n by 0. \n\t\t\t ###// 1 + (n - m * m - 1) // m is equal to the number of multiples of m from m * m to n\n lst[m * m: n: m] = [0] *(1 + (n - m * m - 1) // m)\n\t\t\t\t\n\t\t\t###// If it is the first iteration (e.g. m = 2), add 1 to m (e.g. m = m + 1; \n\t\t\t### // which means m will be 3 in the next iteration), \n ###// otherwise: (m = m + 2); This way we avoid checking even numbers again.\t\n m += 1 if m == 2 else 2\n return sum(lst)\n``` | 77 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
[Python3] Simple Code; How to Make Your Code Faster. | count-primes | 0 | 1 | # Algorithm:\nMy code is based on the [Sieve of Eratosthenes](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes) which is efficient yet very simple. Make sure to read the link as well as the hints in the description of this question to better understand the Mathmatics of the code. Here, I do not want to explain the algorithm, instead I am focused on how to make the code as fast as possible.\n\n# Make your code faster:\n- The code line ```lst[m * m: n: m] = [0] *((n-m*m-1)//m + 1) ``` is key to reduce the run time. You could write a loop like this (but it would be very expensive):\n```\n for i in range(m * m, n, m):\n lst[i] = 0\n```\n\t\n- After marking all the even indices in the first iteration, I do not check even numbers again, and will only check odd numbers in the remaining iterations.\n- I created a list with numeral elements, instead of boolean elements.\n- Do not use function sqrt, because it is expensive [do not use: ```m < sqrt(n)```]. Instead, use ```m * m < n```.\n\n# Python3 code:\n```\n def countPrimes(self, n: int) -> int:\n if n < 3: return 0 ###// No prime number less than 2\n lst = [1] * n ###// create a list for marking numbers less than n\n lst[0] = lst[1] = 0 ###// 0 and 1 are not prime numbers\n m = 2\n while m * m < n: ###// we only check a number (m) if its square is less than n\n if lst[m] == 1: ###// if m is already marked by 0, no need to check its multiples.\n\t\t\t\n\t\t\t ###// If m is marked by 1, we mark all its multiples from m * m to n by 0. \n\t\t\t ###// 1 + (n - m * m - 1) // m is equal to the number of multiples of m from m * m to n\n lst[m * m: n: m] = [0] *(1 + (n - m * m - 1) // m)\n\t\t\t\t\n\t\t\t###// If it is the first iteration (e.g. m = 2), add 1 to m (e.g. m = m + 1; \n\t\t\t### // which means m will be 3 in the next iteration), \n ###// otherwise: (m = m + 2); This way we avoid checking even numbers again.\t\n m += 1 if m == 2 else 2\n return sum(lst)\n``` | 77 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Explanation of why sqrt(n), i*i and 2*i | count-primes | 0 | 1 | ### Explanation\n```\nSuppose n = 26.\n1. Now Create a list/array/vector Sieve of n numbers and mark them all True.\n\n T T T T T T T T T T T T T T T T T T T T T T T T T T T\n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26\n [0 to 26 = Indexes]\n\n2. Mark all the even indexes \'False\' but sieve[1], sieve[2] = False, True.\n\n F F T T F T F T F T F T F T F T F T F T F T F T F T F\n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26\n\n3. We will run a for loop from 3 to n-1 with the step 2 (3,5,7,9,....,25)\n 1. Now from 3 mark all the multiple of 3 to n-1 as False except 3 as it\'s not \n divisible.\n \n F F T T F T F T F F F T F T F F F T F T F F F T F T F\n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26\n\n 2. Now from 5 mark all the multiple of 5 as False, wait! All the multiples of\n 5 means from 5*2? Okay!\n 5 x 2 = 10\n 5 x 3 = 15\n 5 x 4 = 20\n 5 x 5 = 25\n \n 10 is divisible by both 2 and 5. 2 comes before 5, so we don\'t need to mark \n 10 as False as it\'s already marked False when we marked False all the \n values which were divisible by 2 at the first.\n \n 15 is divisible by both 3 and 5. 3 comes before 5, so we don\'t need to mark\n 15 as False as it\'s already marked False when we started to make values \n False from 3.\n \n 25 is divisible only by 5 as it can\'t be divisible by any value less than 5\n \n So we don\'t to 5*3 = False, we can jump to 5*5(i*i) as any value which \n is divisible by 5 and <=(5-1) are already marked False when the loop \n iterated the <=(n-1) values.\n\n # Why iterating 2*i steps in the inner loop ?\n\n To iterate over the EVEN indexes only as even indexes marked False \n at the very first already!\n\n ALSO JUST RUN THE THE FOR LOOP TO SQRT(N) CAUSE IF 5*5 = 25 EXISTS, THEN \n WE WILL GO TO 5 AND MARK ALL THE MULTIPLES OF 5 AS FALSE EXCEPT 5. IF \n IT DOESN\'T EXIST THEN JUST TERMINATE THE LOOP!\n \n SO WE DO : (in python)\n\n for i in range(3, int(n**0.5)+1, 2):\n if sieve[i] == True:\n sieve[i*i:n:i<<1] = [False] * len(sieve[i*i:n:i<<1])\n```\n#### Time and Space Complexity :\n```\nTime Complexity : O(nloglog(n))\nSpace Complexity : O(n)\n```\n### CPP\n```CPP\nint sieve_of_eratosthenes(int n)\n{\n if(n<3) return 0;\n\n bool sieve[n];\n for(int i=0; i<n ;i++) sieve[i] = i&1? true : false;\n sieve[1] = false, sieve[2] = true;\n int s = sqrt(n);\n\n for(int i=3; i<=s; i+=2)\n {\n if(sieve[i] == true)\n {\n for(int j=i*i; j<n; j+=2*i)\n sieve[j] = false;\n }\n }\n\n return count_if(sieve, sieve+n, [](int x) { return x==true; });\n}\n```\n### Python\n```\nCreating a list from 0 to n-1 where list[0] = list[1] = False and from list[2],\nthe multiple of i from list[i=2] are all False except the i from list[i].\nYou can get this by a list comprehension and slice method. Slicing can be faster \nthan list comprehension for updating values in a list because slicing uses \nPython\'s built-in optimized C code to perform the updates, whereas list \ncomprehension creates a new list object.\n```\n##### Slicing Method (Fastest)\n```python\ndef countPrimes(self, n):\n if n<3: return 0\n\n sieve = [True] * n \n sieve[0:n:2] = [False] * len(sieve[0:n:2])\n sieve[1], sieve[2] = False, True\n\n for i in range(3, int(n**0.5)+1, 2):\n if sieve[i] == True:\n sieve[i*i:n:i<<1] = [False] * len(sieve[i*i:n:i<<1])\n\n return sieve.count(True)\n \n```\n#### List Comprehension (Slowest)\n```python\ndef countPrimes(self, n):\n if n<3: return 0\n\n sieve = [ True if i&1 else False for i in range(n) ] \n sieve[1], sieve[2] = False, True\n\n _ = [ sieve.__setitem__(j, False) for i in range(3, int(n**0.5)+1, 2) if sieve[i] == True for j in range(i*i, n, i<<1) ]\n\n return sieve.count(True)\n```\n#### List Comprehension + Slicing (Between Fastest and Slowest)\n```python\ndef countPrimes(self, n):\n if n<3: return 0\n\n sieve = [ True if i&1 else False for i in range(n) ] \n sieve[1], sieve[2] = False, True\n\n for i in range(3, int(n**0.5)+1, 2):\n if sieve[i] == True:\n sieve[i*i:n:2*i] = [False] * len(sieve[i*i:n:2*i])\n\n return sieve.count(True)\n```\n\n## If the post was helpful, an upvote will make me really happy.\n | 2 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Explanation of why sqrt(n), i*i and 2*i | count-primes | 0 | 1 | ### Explanation\n```\nSuppose n = 26.\n1. Now Create a list/array/vector Sieve of n numbers and mark them all True.\n\n T T T T T T T T T T T T T T T T T T T T T T T T T T T\n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26\n [0 to 26 = Indexes]\n\n2. Mark all the even indexes \'False\' but sieve[1], sieve[2] = False, True.\n\n F F T T F T F T F T F T F T F T F T F T F T F T F T F\n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26\n\n3. We will run a for loop from 3 to n-1 with the step 2 (3,5,7,9,....,25)\n 1. Now from 3 mark all the multiple of 3 to n-1 as False except 3 as it\'s not \n divisible.\n \n F F T T F T F T F F F T F T F F F T F T F F F T F T F\n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26\n\n 2. Now from 5 mark all the multiple of 5 as False, wait! All the multiples of\n 5 means from 5*2? Okay!\n 5 x 2 = 10\n 5 x 3 = 15\n 5 x 4 = 20\n 5 x 5 = 25\n \n 10 is divisible by both 2 and 5. 2 comes before 5, so we don\'t need to mark \n 10 as False as it\'s already marked False when we marked False all the \n values which were divisible by 2 at the first.\n \n 15 is divisible by both 3 and 5. 3 comes before 5, so we don\'t need to mark\n 15 as False as it\'s already marked False when we started to make values \n False from 3.\n \n 25 is divisible only by 5 as it can\'t be divisible by any value less than 5\n \n So we don\'t to 5*3 = False, we can jump to 5*5(i*i) as any value which \n is divisible by 5 and <=(5-1) are already marked False when the loop \n iterated the <=(n-1) values.\n\n # Why iterating 2*i steps in the inner loop ?\n\n To iterate over the EVEN indexes only as even indexes marked False \n at the very first already!\n\n ALSO JUST RUN THE THE FOR LOOP TO SQRT(N) CAUSE IF 5*5 = 25 EXISTS, THEN \n WE WILL GO TO 5 AND MARK ALL THE MULTIPLES OF 5 AS FALSE EXCEPT 5. IF \n IT DOESN\'T EXIST THEN JUST TERMINATE THE LOOP!\n \n SO WE DO : (in python)\n\n for i in range(3, int(n**0.5)+1, 2):\n if sieve[i] == True:\n sieve[i*i:n:i<<1] = [False] * len(sieve[i*i:n:i<<1])\n```\n#### Time and Space Complexity :\n```\nTime Complexity : O(nloglog(n))\nSpace Complexity : O(n)\n```\n### CPP\n```CPP\nint sieve_of_eratosthenes(int n)\n{\n if(n<3) return 0;\n\n bool sieve[n];\n for(int i=0; i<n ;i++) sieve[i] = i&1? true : false;\n sieve[1] = false, sieve[2] = true;\n int s = sqrt(n);\n\n for(int i=3; i<=s; i+=2)\n {\n if(sieve[i] == true)\n {\n for(int j=i*i; j<n; j+=2*i)\n sieve[j] = false;\n }\n }\n\n return count_if(sieve, sieve+n, [](int x) { return x==true; });\n}\n```\n### Python\n```\nCreating a list from 0 to n-1 where list[0] = list[1] = False and from list[2],\nthe multiple of i from list[i=2] are all False except the i from list[i].\nYou can get this by a list comprehension and slice method. Slicing can be faster \nthan list comprehension for updating values in a list because slicing uses \nPython\'s built-in optimized C code to perform the updates, whereas list \ncomprehension creates a new list object.\n```\n##### Slicing Method (Fastest)\n```python\ndef countPrimes(self, n):\n if n<3: return 0\n\n sieve = [True] * n \n sieve[0:n:2] = [False] * len(sieve[0:n:2])\n sieve[1], sieve[2] = False, True\n\n for i in range(3, int(n**0.5)+1, 2):\n if sieve[i] == True:\n sieve[i*i:n:i<<1] = [False] * len(sieve[i*i:n:i<<1])\n\n return sieve.count(True)\n \n```\n#### List Comprehension (Slowest)\n```python\ndef countPrimes(self, n):\n if n<3: return 0\n\n sieve = [ True if i&1 else False for i in range(n) ] \n sieve[1], sieve[2] = False, True\n\n _ = [ sieve.__setitem__(j, False) for i in range(3, int(n**0.5)+1, 2) if sieve[i] == True for j in range(i*i, n, i<<1) ]\n\n return sieve.count(True)\n```\n#### List Comprehension + Slicing (Between Fastest and Slowest)\n```python\ndef countPrimes(self, n):\n if n<3: return 0\n\n sieve = [ True if i&1 else False for i in range(n) ] \n sieve[1], sieve[2] = False, True\n\n for i in range(3, int(n**0.5)+1, 2):\n if sieve[i] == True:\n sieve[i*i:n:2*i] = [False] * len(sieve[i*i:n:2*i])\n\n return sieve.count(True)\n```\n\n## If the post was helpful, an upvote will make me really happy.\n | 2 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Very easy solution using Sieve of Eratosthenes in Python | count-primes | 0 | 1 | \n\n\n```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n\n arr = [True] * n\n\n if n == 0 or n == 1:\n return 0\n\n arr[0], arr[1] = False, False\n\n for i in range(2, int(n ** 0.5) + 1):\n if arr[i]:\n for j in range(i + i, n, i):\n arr[j] = False\n\n return sum(arr) \n``` | 12 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Very easy solution using Sieve of Eratosthenes in Python | count-primes | 0 | 1 | \n\n\n```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n\n arr = [True] * n\n\n if n == 0 or n == 1:\n return 0\n\n arr[0], arr[1] = False, False\n\n for i in range(2, int(n ** 0.5) + 1):\n if arr[i]:\n for j in range(i + i, n, i):\n arr[j] = False\n\n return sum(arr) \n``` | 12 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Count Primes for Kids! ¯\_( ͡❛ ͜ʖ ͡❛)_/¯ | count-primes | 0 | 1 | \n Starting from first prime, every additional multiple of this prime is changed to False.\n\t \n First Prime : 2 -> remains prime\n 4 , 6, 8, 10, 12, 14, 16, 18, 20, ... < n\n \n\t We continue to do this for each prime.\n \n 3 -> remains prime\n \n 6, 9, 12, 15, 18, 21, 24, 27, 30, ... < n \n\n\n\'\'\'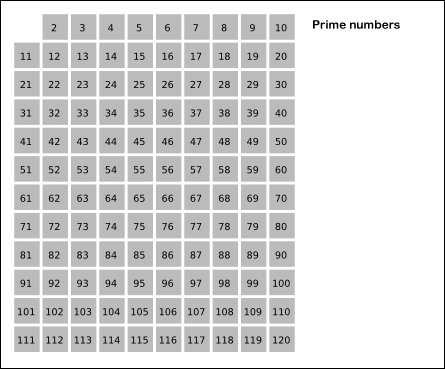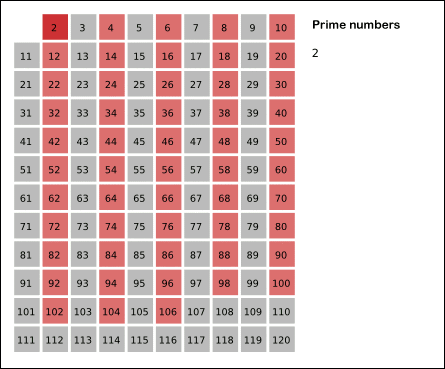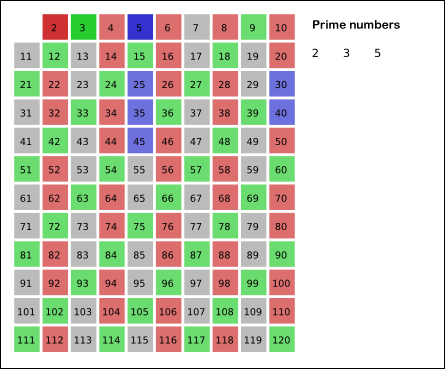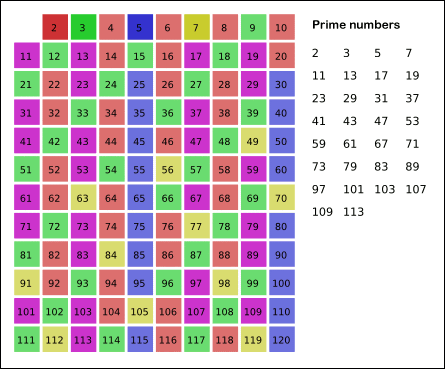\n\n def countPrimes(self, n: int) -> int:\n \n #Initial Edge Cases (0, 1 non-prime by definition)\n \n if n <= 2:\n return 0\n \n #population of list for classification of primes\n #all numbers initialized as prime, and then discounted via \'Sieve of Eratosthenes\' algorithm\n #naturally, our list is of size(n)\n\n primes = [True] * n\n primes[0] = primes[1] = False \n \n #for all elements in the range [2 , n)\n for number in range(2, n):\n \n #if it is a prime \n if primes[number]:\n \n #starting from 2 * prime and ending at n - in increments of prime\n for multiple in range(2 * number, n, number):\n \n \n #change index accounting for prime validity to \'False\' or every multiple of found prime.\n #we can correctly categorize a large number of composite numbers due to the fact that our first \n #prime is undoubtly a factor of all larger multiples of the same number.\n\n primes[multiple] = False\n \n \n #Sum of Total Booleans \n return sum(primes)\n\t\t\n\'\'\' | 39 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Count Primes for Kids! ¯\_( ͡❛ ͜ʖ ͡❛)_/¯ | count-primes | 0 | 1 | \n Starting from first prime, every additional multiple of this prime is changed to False.\n\t \n First Prime : 2 -> remains prime\n 4 , 6, 8, 10, 12, 14, 16, 18, 20, ... < n\n \n\t We continue to do this for each prime.\n \n 3 -> remains prime\n \n 6, 9, 12, 15, 18, 21, 24, 27, 30, ... < n \n\n\n\'\'\'\n\n def countPrimes(self, n: int) -> int:\n \n #Initial Edge Cases (0, 1 non-prime by definition)\n \n if n <= 2:\n return 0\n \n #population of list for classification of primes\n #all numbers initialized as prime, and then discounted via \'Sieve of Eratosthenes\' algorithm\n #naturally, our list is of size(n)\n\n primes = [True] * n\n primes[0] = primes[1] = False \n \n #for all elements in the range [2 , n)\n for number in range(2, n):\n \n #if it is a prime \n if primes[number]:\n \n #starting from 2 * prime and ending at n - in increments of prime\n for multiple in range(2 * number, n, number):\n \n \n #change index accounting for prime validity to \'False\' or every multiple of found prime.\n #we can correctly categorize a large number of composite numbers due to the fact that our first \n #prime is undoubtly a factor of all larger multiples of the same number.\n\n primes[multiple] = False\n \n \n #Sum of Total Booleans \n return sum(primes)\n\t\t\n\'\'\' | 39 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
python3 | two solution |99.47% faster and 65% faster | count-primes | 0 | 1 | * **99.47% faster**\n```\nfrom numpy import ones, bool\n\nclass Solution:\n def countPrimes(self, n: int) -> int:\n primes = ones(n, dtype=bool)\n primes[:2] = 0\n primes[4::2] = 0\n \n\n # Prime Sieve\n for i in range(3,ceil(sqrt(n)),2):\n if primes[i]:\n primes[i*i::i] = 0\n \n # Return number of primes found\n return primes.sum()\n```\n* **65% faster**\n```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n nums = [0, 0] + [1] * (n - 2)\n for i in range(2,int(sqrt(n)+1)):\n if nums[i]==1:\n for j in range(i*i,n,i):\n nums[j]=0\n return sum(nums)\n``` | 8 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
python3 | two solution |99.47% faster and 65% faster | count-primes | 0 | 1 | * **99.47% faster**\n```\nfrom numpy import ones, bool\n\nclass Solution:\n def countPrimes(self, n: int) -> int:\n primes = ones(n, dtype=bool)\n primes[:2] = 0\n primes[4::2] = 0\n \n\n # Prime Sieve\n for i in range(3,ceil(sqrt(n)),2):\n if primes[i]:\n primes[i*i::i] = 0\n \n # Return number of primes found\n return primes.sum()\n```\n* **65% faster**\n```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n nums = [0, 0] + [1] * (n - 2)\n for i in range(2,int(sqrt(n)+1)):\n if nums[i]==1:\n for j in range(i*i,n,i):\n nums[j]=0\n return sum(nums)\n``` | 8 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
[Python] Algorithm explained with comments | count-primes | 0 | 1 | ```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n ## RC ##\n ## APPROACH : Sieve of Eratosthenes ##\n \n # 1. Checking till sqrt(n) is enough for prime numbers i.e i*i < n\n # 2. mark all as prime.\n # 3. as you move along (i to i*i<n) mark every multiple until n as False.\n # 4. you donot need start from i for that we can start from i*i i.e j=i*i\n \n\t\t## TIME COMPLEXITY : O(NLogN) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n isPrime = [False,False] + [True] * (n-2)\n i = 2\n while( i*i < n ): # Loop\'s ending condition is i * i < n instead of i < sqrt(n) to avoid repeatedly calling an expensive function sqrt().\n if(isPrime[i]): # if not prime, it is some prime multiple.\n j = i*i # ex: we can mark off multiples of 5 starting at 5 \xD7 5 = 25, because 5 \xD7 2 = 10 was already marked off by multiple of 2, similarly 5 \xD7 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ...\n while(j < n):\n isPrime[j] = False\n j += i\n i += 1\n return sum(isPrime)\n``` | 17 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
[Python] Algorithm explained with comments | count-primes | 0 | 1 | ```\nclass Solution:\n def countPrimes(self, n: int) -> int:\n ## RC ##\n ## APPROACH : Sieve of Eratosthenes ##\n \n # 1. Checking till sqrt(n) is enough for prime numbers i.e i*i < n\n # 2. mark all as prime.\n # 3. as you move along (i to i*i<n) mark every multiple until n as False.\n # 4. you donot need start from i for that we can start from i*i i.e j=i*i\n \n\t\t## TIME COMPLEXITY : O(NLogN) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n isPrime = [False,False] + [True] * (n-2)\n i = 2\n while( i*i < n ): # Loop\'s ending condition is i * i < n instead of i < sqrt(n) to avoid repeatedly calling an expensive function sqrt().\n if(isPrime[i]): # if not prime, it is some prime multiple.\n j = i*i # ex: we can mark off multiples of 5 starting at 5 \xD7 5 = 25, because 5 \xD7 2 = 10 was already marked off by multiple of 2, similarly 5 \xD7 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ...\n while(j < n):\n isPrime[j] = False\n j += i\n i += 1\n return sum(isPrime)\n``` | 17 | Given an integer `n`, return _the number of prime numbers that are strictly less than_ `n`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 0
**Constraints:**
* `0 <= n <= 5 * 106` | Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better? As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better? Let's write down all of 12's factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
} The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well? 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off? In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, ... Now what should be the terminating loop condition? It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3? Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
} |
Very Easy || 100% || Fully Explained || Java, C++, Python, Javascript, Python3 (Using HashMap) | isomorphic-strings | 1 | 1 | **Two strings s and t are isomorphic if the characters in s can be replaced to get t.**\n-----------------------------------------------------------------------------------------------------\n----------------------------------------------------------------------------------------------------------------------------------------------------------------------\n# **Java Solution:**\n```\n// Runtime: 3 ms, faster than 94.17% of Java online submissions for Isomorphic Strings.\n// Memory Usage: 42.1 MB, less than 95.61% of Java online submissions for Isomorphic Strings.\n// Time Complexity : O(n)\nclass Solution {\n public boolean isIsomorphic(String s, String t) {\n // Base case: for different length of two strings...\n if(s.length() != t.length())\n return false;\n // Create two maps for s & t strings...\n int[] map1 = new int[256];\n int[] map2 = new int[256];\n // Traverse all elements through the loop...\n for(int idx = 0; idx < s.length(); idx++){\n // Compare the maps, if not equal, return false...\n if(map1[s.charAt(idx)] != map2[t.charAt(idx)])\n return false;\n // Insert each character if string s and t into seperate map...\n map1[s.charAt(idx)] = idx + 1;\n map2[t.charAt(idx)] = idx + 1;\n }\n return true; // Otherwise return true...\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(1)\nclass Solution {\npublic:\n bool isIsomorphic(string s, string t) {\n // Use hashmaps to save the replacement for every character in the first string...\n unordered_map <char , char> rep;\n unordered_map <char , bool> used;\n // Traverse all elements through the loop...\n for(int idx = 0 ; idx < s.length() ; idx++) {\n // If rep contains s[idx] as a key...\n if(rep.count(s[idx])) {\n // Check if the rep is same as the character in the other string...\n // If not, the strings can\u2019t be isomorphic. So, return false...\n if(rep[s[idx]] != t[idx])\n return false;\n }\n // If no replacement found for first character, check if the second character has been used as the replacement for any other character in the first string...\n else {\n if(used[t[idx]])\n return false;\n // If there exists no character whose replacement is the second character...\n // Assign the second character as the replacement of the first character.\n rep[s[idx]] = t[idx];\n used[t[idx]] = true;\n }\n }\n // Otherwise, the strings are not isomorphic.\n return true;\n }\n};\n```\n\n# **Python Solution:**\n```\n# Time Complexity : O(n)\nclass Solution(object):\n def isIsomorphic(self, s, t):\n map1 = []\n map2 = []\n for idx in s:\n map1.append(s.index(idx))\n for idx in t:\n map2.append(t.index(idx))\n if map1 == map2:\n return True\n return False\n```\n \n# **JavaScript Solution:**\n```\n// Runtime: 83 ms, faster than 88.18% of JavaScript online submissions for Isomorphic Strings.\n// Time Complexity : O(n)\nvar isIsomorphic = function(s, t) {\n // Base case: for different length of two strings...\n if(s.length != t.length)\n return false;\n // Create two maps for s & t strings...\n const map1 = [256];\n const map2 = [256];\n // Traverse all elements through the loop...\n for(let idx = 0; idx < s.length; idx++){\n // Compare the maps, if not equal, return false...\n if(map1[s.charAt(idx)] != map2[t.charAt(idx)])\n return false;\n // Insert each character if string s and t into seperate map...\n map1[s.charAt(idx)] = idx + 1;\n map2[t.charAt(idx)] = idx + 1;\n }\n return true; // Otherwise return true...\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n return [*map(s.index, s)] == [*map(t.index, t)]\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 317 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
Python Easy | isomorphic-strings | 0 | 1 | ```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n d = {}\n \n seen = set()\n for i, j in zip(s, t):\n if i in d:\n if d[i] != j:\n return False\n\n \n else:\n if j in seen:\n return False\n\n seen.add(j)\n d[i] = j\n \n\n\n\n return True\n\n``` | 1 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
One Line of Code and Using Hashtable Python | isomorphic-strings | 0 | 1 | # One Line of Code Python Solution\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n return len(set(s))==len(set(t))==len(set(zip(s,t)))\n```\n# please upvote me it would encourage me alot\n\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n dic1,dic2={},{}\n for s1,t1 in zip(s,t):\n if (s1 in dic1 and dic1[s1]!=t1) or ( t1 in dic2 and dic2[t1]!=s1):\n return False\n dic1[s1]=t1\n dic2[t1]=s1\n return True\n \n```\n# please upvote me it would encourage me alot\n | 69 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
Convert symbol to incremental integer with trailing space | isomorphic-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n @staticmethod\n def isIsomorphic(string1: str, string2: str) -> bool:\n if string1 == string2:\n return True\n\n if len(string1) != len(string2):\n return False\n\n map1 = {}\n iso1 = ""\n for s in string1:\n if s not in map1:\n map1[s] = f"{len(map1)} "\n iso1 += map1[s]\n\n map2 = {}\n iso2 = ""\n for s in string2:\n if s not in map2:\n map2[s] = f"{len(map2)} "\n iso2 += map2[s]\n\n return iso1 == iso2\n\n``` | 0 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
Simple Python 3 Solution || Runtime beats 91% || 🤖🧑💻💻 | isomorphic-strings | 0 | 1 | If you guys have better solution please comment the answer || and please UPVOTE \uD83D\uDE4C\n\n# Code\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n n = len(s)\n mp = {}\n seen = set()\n for i in range(n):\n if s[i] not in mp:\n if t[i] in seen:\n return False\n mp[s[i]] = t[i]\n seen.add(t[i])\n else:\n if mp[s[i]] != t[i]:\n return False\n return True\n``` | 3 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
2 liner with 99% efficiency and explanation. | isomorphic-strings | 0 | 1 | Runtime: 32 ms, faster than 99.09% of Python3 online submissions for Isomorphic Strings.\nMemory Usage: 14.2 MB, less than 96.77% of Python3 online submissions for Isomorphic Strings\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n zipped_set = set(zip(s, t))\n return len(zipped_set) == len(set(s)) == len(set(t))\n \n```\nExplanation:\nwhy using zip ?\n=> zip function would pair the first item of first iterator (i.e `s` here) to the first item of second iterator (i.e `t` here). `set()` would remove duplicate items from the zipped tuple. It is like the first item of first iterator mapped to the first item of second iterator as it would in case of a hashtable or dictionary.\nUnderstand using exmaples:\n```\n# when strings ae isomorphic:\ns = "egg"\nt = "add"\n\nzipped_set = {(\'e\', \'a\'), (\'g\', \'d\')}\n# now comparing their lengths when duplicacies are removed\nreturn len(zipped_set) == len(set(s)) == len(set(d))\n# return 2 == 2 == 2 -> True\n```\n```\n# when strings are not isomorphic:\ns = "egk"\nt = "add"\n\nzipped_set = {(\'e\', \'a\'), (\'g\', \'d\'), (\'k\', \'d\')}\n# now comparing their lengths when duplicacies are removed\nreturn len(zipped_set) == len(set(s)) == len(set(d))\n# return 3 == 3 == 2 -> False\n```\n | 120 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
205: Solution with step by step explanation | isomorphic-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses two hash maps to keep track of the mapping of characters from string s to string t and vice versa. It iterates over the characters in the strings, and if a character is not already in either hash map, it adds the mapping of that character from s to t and from t to s in their respective hash maps. If the character is already in either hash map, it checks if the mapping is the same as the character in the other string. If not, it returns False. If the loop completes without returning False, it returns True.\n\nThis solution has a time complexity of O(n), where n is the length of the strings, as it only iterates over the characters once. The space complexity is also O(n), as it uses two hash maps to store the mappings.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n if len(s) != len(t):\n return False\n \n s_to_t = {}\n t_to_s = {}\n for i in range(len(s)):\n if s[i] not in s_to_t and t[i] not in t_to_s:\n s_to_t[s[i]] = t[i]\n t_to_s[t[i]] = s[i]\n elif s[i] in s_to_t and s_to_t[s[i]] == t[i]:\n continue\n else:\n return False\n \n return True\n\n\n\n``` | 13 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
Python | 1 line | beats 99% | isomorphic-strings | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n return [s.index(c) for c in s] == [t.index(c) for c in t]\n``` | 1 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
Python solution using hash function to compute an index with a key into an array of slots | isomorphic-strings | 0 | 1 | ```\nclass Solution:\n def isIsomorphic(self, s: str, t: str) -> bool:\n if len(s)!=len(t) or len(set(s))!=len(set(t)):\n return False\n hashmap={}\n \n for i in range(len(s)):\n if s[i] not in hashmap:\n hashmap[s[i]]=t[i]\n \n if hashmap[s[i]]!=t[i]:\n return False\n return True\n``` | 3 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
[Python] Easy Approach ✔ | isomorphic-strings | 0 | 1 | \tclass Solution:\n\t\tdef isIsomorphic(self, s: str, t: str) -> bool:\n\t\t\tif len(set(s)) != len(set(t)):\n\t\t\t\treturn False\n\t\t\thash_map = {}\n\t\t\tfor char in range(len(t)):\n\t\t\t\tif t[char] not in hash_map:\n\t\t\t\t\thash_map[t[char]] = s[char]\n\t\t\t\telif hash_map[t[char]] != s[char]:\n\t\t\t\t\treturn False\n\t\t\treturn True | 22 | Given two strings `s` and `t`, _determine if they are isomorphic_.
Two strings `s` and `t` are isomorphic if the characters in `s` can be replaced to get `t`.
All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character, but a character may map to itself.
**Example 1:**
**Input:** s = "egg", t = "add"
**Output:** true
**Example 2:**
**Input:** s = "foo", t = "bar"
**Output:** false
**Example 3:**
**Input:** s = "paper", t = "title"
**Output:** true
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `t.length == s.length`
* `s` and `t` consist of any valid ascii character. | null |
[VIDEO] Step-by-Step Visualization of O(n) Solution | reverse-linked-list | 0 | 1 | https://youtu.be/VtC4GUR31wQ\n\nWe\'ll be using three pointers:\n`new_list`: always points to the head of the new reversed linked list\n\n`current`: traverses the linked list and reverses each node\'s `next` pointer (by pointing it to `new_list`)\n\n`next_node`: keeps track of the next node in the original linked list so we can go back and repeat the steps for the next node\n\nBy doing this, we build the reversed list from the back, and work our way to the front. This way, we only have to traverse the linked list once, so the algorithm runs in O(n) time.\n\n# Code\n```\ndef reverseList(self, head):\n new_list = None\n current = head\n\n while current:\n next_node = current.next\n current.next = new_list\n new_list = current\n current = next_node\n \n return new_list\n``` | 5 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
Easy || 0 ms || 100% || Fully Explained || Java, C++, Python, JS, C, Python3 (Recursive & Iterative) | reverse-linked-list | 1 | 1 | # **Java Solution (Recursive Approach):**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Reverse Linked List.\n```\nclass Solution {\n public ListNode reverseList(ListNode head) {\n // Special case...\n if (head == null || head.next == null) return head;\n // Create a new node to call the function recursively and we get the reverse linked list...\n ListNode res = reverseList(head.next);\n // Set head node as head.next.next...\n head.next.next = head;\n //set head\'s next to be null...\n head.next = null;\n return res; // Return the reverse linked list...\n }\n}\n```\n\n# **C++ Solution (Iterative Approach):**\n```\nclass Solution {\npublic:\n ListNode* reverseList(ListNode* head) {\n // Special case...\n if(head == NULL || head->next == NULL) return head;\n // Initialize prev pointer as the head...\n ListNode* prev = head;\n // Initialize curr pointer as the next pointer of prev...\n ListNode* curr = prev->next;\n // Initialize next of head pointer as NULL...\n head->next = NULL;\n // Run a loop till curr and prev points to NULL...\n while(prev != NULL && curr != NULL){\n // Initialize next pointer as the next pointer of curr...\n ListNode* next = curr->next;\n // Now assign the prev pointer to curr\u2019s next pointer.\n curr->next = prev;\n // Assign curr to prev, next to curr...\n prev = curr;\n curr = next;\n }\n return prev; // Return the prev pointer to get the reverse linked list...\n }\n};\n```\n\n# **Python Solution (Iterative Approach):**\nRuntime: 18 ms, faster than 97.75% of Python online submissions for Reverse Linked List.\n```\nclass Solution(object):\n def reverseList(self, head):\n # Initialize prev pointer as NULL...\n prev = None\n # Initialize the curr pointer as the head...\n curr = head\n # Run a loop till curr points to NULL...\n while curr:\n # Initialize next pointer as the next pointer of curr...\n next = curr.next\n # Now assign the prev pointer to curr\u2019s next pointer.\n curr.next = prev\n # Assign curr to prev, next to curr...\n prev = curr\n curr = next\n return prev # Return the prev pointer to get the reverse linked list...\n```\n \n# **JavaScript Solution (Recursive Approach):**\n```\nvar reverseList = function(head) {\n // Special case...\n if (head == null || head.next == null) return head;\n // Create a new node to call the function recursively and we get the reverse linked list...\n var res = reverseList(head.next);\n // Set head node as head.next.next...\n head.next.next = head;\n //set head\'s next to be null...\n head.next = null;\n return res; // Return the reverse linked list...\n};\n```\n\n# **C Language (Iterative Approach):**\n```\nstruct ListNode* reverseList(struct ListNode* head){\n // Special case...\n if(head == NULL || head->next == NULL) return head;\n // Initialize prev pointer as the head...\n struct ListNode* prev = head;\n // Initialize curr pointer as the next pointer of prev...\n struct ListNode* curr = prev->next;\n // Initialize next of head pointer as NULL...\n head->next = NULL;\n // Run a loop till curr and prev points to NULL...\n while(prev != NULL && curr != NULL){\n // Initialize next pointer as the next pointer of curr...\n struct ListNode* next = curr->next;\n // Now assign the prev pointer to curr\u2019s next pointer.\n curr->next = prev;\n // Assign curr to prev, next to curr...\n prev = curr;\n curr = next;\n }\n return prev; // Return the prev pointer to get the reverse linked list...\n}\n```\n\n# **Python3 Solution (Iterative Approach):**\n```\nclass Solution:\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n # Initialize prev pointer as NULL...\n prev = None\n # Initialize the curr pointer as the head...\n curr = head\n # Run a loop till curr points to NULL...\n while curr:\n # Initialize next pointer as the next pointer of curr...\n next = curr.next\n # Now assign the prev pointer to curr\u2019s next pointer.\n curr.next = prev\n # Assign curr to prev, next to curr...\n prev = curr\n curr = next\n return prev # Return the prev pointer to get the reverse linked list...\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 327 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
✅Best Method 🔥 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | reverse-linked-list | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe given code snippet implements the iterative approach to reverse a linked list. The intuition behind it is to use three pointers: `prev`, `head`, and `nxt`. By reversing the pointers between the nodes, we can reverse the linked list.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create a pointer `prev` and initialize it to `NULL`. This pointer will initially be the new end of the reversed linked list.\n2. Start iterating through the linked list with a pointer `head`.\n3. Inside the loop, create a pointer `nxt` and assign it the next node after `head`. This pointer is used to store the next node temporarily.\n4. Reverse the pointer direction of `head` by setting `head->next` to `prev`. This step effectively reverses the direction of the current node.\n5. Move the `prev` pointer to `head` and update `head` to `nxt` for the next iteration.\n6. Repeat steps 3-5 until the end of the linked list is reached (i.e., `head` becomes `NULL`).\n7. Return `prev`, which will be the new head of the reversed linked list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n ListNode* reverseList(ListNode* head) {\n ListNode* prev = NULL;\n\n while(head) {\n ListNode* nxt = head->next;\n head->next = prev;\n prev = head;\n head = nxt;\n }\n return prev;\n }\n};\n```\n```Java []\nclass Solution {\n public ListNode reverseList(ListNode head) {\n ListNode prev = null;\n\n while (head != null) {\n ListNode nxt = head.next;\n head.next = prev;\n prev = head;\n head = nxt;\n }\n\n return prev;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def reverseList(self, head: ListNode) -> ListNode:\n prev = None\n\n while head:\n nxt = head.next\n head.next = prev\n prev = head\n head = nxt\n\n return prev\n```\n\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n | 39 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
O( n )✅ | Recursive approach✅ | Python (Step by step explanation)✅ | reverse-linked-list | 0 | 1 | # Intuition\nThe code aims to reverse a singly-linked list. It utilizes a recursive approach to achieve this.\n\n# Approach\nThe approach used in the code is a recursive algorithm for reversing a singly-linked list. The code defines a function `reverseList` that takes the head of the linked list as input. It proceeds as follows:\n1. Check if the input `head` is `None` (an empty list). If it is, return `None` since there\'s nothing to reverse.\n2. Create a variable `newHead` and initialize it with the current `head`.\n3. If the `head` has a `next` node, call the `reverseList` function recursively on the `next` node to reverse the sublist starting from the next node.\n4. After the recursive call returns, set `head.next.next` to the current `head`. This step effectively reverses the direction of the `next` pointer.\n5. Set `head.next` to `None` to make the original head the new tail.\n6. Return the `newHead` as the new head of the reversed linked list.\n\n# Visualization\nLet\'s visualize the reversal of the input list `1 -> 2 -> 3 -> 4 -> 5` step by step:\n\n1. **Input**: `1 -> 2 -> 3 -> 4 -> 5`\n\n2. **First call (head=1)**:\n - `head != NULL`, so it goes into the recursion.\n - Recursively calls `reverseList(2)`.\n\n3. **Second call (head=2)**:\n - `head != NULL`, so it goes into the recursion.\n - Recursively calls `reverseList(3)`.\n\n4. **Third call (head=3)**:\n - `head != NULL`, so it goes into the recursion.\n - Recursively calls `reverseList(4)`.\n\n5. **Fourth call (head=4)**:\n - `head != NULL`, so it goes into the recursion.\n - Recursively calls `reverseList(5)`.\n\n6. **Fifth call (head=5)**:\n - `head != NULL`, but there is no next node (head->next == NULL), so it returns 5 itself.\n\n7. **Back to the fourth call (head=4)**:\n - Now, `newHead` is 5.\n - `head->next->next` points to 4 (which is 5->4 now).\n - `head->next` is set to NULL (making 4->NULL).\n - `newHead` (which is 5) is returned to the third call.\n\n8. **Back to the third call (head=3)**:\n - Now, `newHead` is 5.\n - `head->next->next` points to 3 (which is 4->3->NULL now).\n - `head->next` is set to NULL (making 3->NULL).\n - `newHead` (which is 5) is returned to the second call.\n\n9. **Back to the second call (head=2)**:\n - Now, `newHead` is 5.\n - `head->next->next` points to 2 (which is 3->2->NULL now).\n - `head->next` is set to NULL (making 2->NULL).\n - `newHead` (which is 5) is returned to the first call.\n\n10. **Back to the first call (head=1)**:\n - Now, `newHead` is 5.\n - `head->next->next` points to 1 (which is 2->1->NULL now).\n - `head->next` is set to NULL (making 1->NULL).\n - `newHead` (which is 5) is returned as the new head of the reversed list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g., O(n) -->\n\nThe time complexity of this code is O(n), where n is the number of nodes in the linked list. This is because the code processes each node once in a linear fashion.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g., O(n) -->\n\nThe space complexity of this code is O(n) due to the recursive call stack. In the worst case, there will be n recursive calls on the stack, each consuming space for function parameters and local variables.\n\n\n# Complexity\n- Time complexity: O(N), where N is the number of nodes in the linked list. This is because the code processes each node exactly once in a recursive manner.\n- Space complexity: O(N), as the space used by the recursive call stack can go up to the number of nodes in the linked list. The recursion depth is N in the worst case.\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n \n if not head :\n return None\n\n newHead = head\n if head.next :\n newHead = self.reverseList(head.next)\n head.next.next = head\n head.next = None \n\n return newHead \n \n```\n\n# Please upvote the solution if you understood it.\n\n | 9 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
eas | reverse-linked-list | 0 | 1 | just read, reverse and create link list\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseList(self, ll: Optional[ListNode]) -> Optional[ListNode]:\n def CreateList(args):\n if not args:\n return None\n head = ListNode(args[0])\n current = head\n for x in args[1:]:\n node = ListNode(x)\n current.next = node\n current = current.next\n return head\n p = []\n while ll:\n p.append(ll.val)\n ll = ll.next\n return CreateList(p[::-1])\n``` | 1 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
python3 , can i improve? | reverse-linked-list | 0 | 1 | I appreciate any helpful comments!\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOf course, the simplest approach is to just a simple process.\nConvert, reverse, convert, and I\'m done, right?\nYes, but slowly.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. convert `head` to array, `arr`\n2. reverse `arr`\n3. convert `arr` to linked list.\n\n# Complexity\n- Time complexity: O(2N) maybe\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ???\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\nclass Solution:\n def convertList(self, arr):\n if arr == []: return None\n else:\n head = None\n head = ListNode(arr[0], self.convertList(arr[1:]))\n return head\n def convertArr(self, head):\n arr = []\n curr = head\n while (curr != None): \n arr.append( curr.val)\n curr = curr.next\n return arr\n def reverseList(self, head):\n arr = self.convertArr(head)\n arr = arr[::-1]\n return self.convertList(arr)\n``` | 1 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
Conversion of linked list to list using Python | reverse-linked-list | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n lst=[]\n while head:\n lst.append(head.val)\n head=head.next\n lst=lst[::-1]\n ans=ListNode(0)\n tmp=ans\n for i in lst:\n tmp.next=ListNode(i)\n tmp=tmp.next\n return ans.next\n``` | 2 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
Python Constant space solution | reverse-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is track the previous node and keep changing the pointer of current node to previous in iterative way.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Recursive Code\n```\n\nclass Solution:\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n \n def dfs(node, prev):\n if node.next == None:\n node.next = prev\n return node\n next = node.next\n node.next = prev\n # print(node)\n return dfs(next, node)\n if head == None:\n return None\n return dfs(head, None)\n```\n\n# Iterative Code\n```\nclass Solution:\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n prev = None\n temp = head\n while temp:\n next = temp.next\n temp.next = prev\n prev = temp\n temp = next\n return prev\n\n``` | 2 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
3 pointer approch faster than 99% solutions. | reverse-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if head==None or head.next==None:\n return head\n start,middle=None,head\n while middle:\n old=middle.next\n middle.next=start\n start=middle\n middle=old\n return start\n``` | 2 | Given the `head` of a singly linked list, reverse the list, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[5,4,3,2,1\]
**Example 2:**
**Input:** head = \[1,2\]
**Output:** \[2,1\]
**Example 3:**
**Input:** head = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the list is the range `[0, 5000]`.
* `-5000 <= Node.val <= 5000`
**Follow up:** A linked list can be reversed either iteratively or recursively. Could you implement both? | null |
Click this if you're confused. | course-schedule | 0 | 1 | # Intuition\nIf we model the course prereqs as a directed graph where each vertex is a course and each edge A -> B means A requires the completion of B, then we can solve this by detecting a cycle in the graph. If we find a cycle, it means that a course A must be completed to complete A\'s prerequisites\u2014impossible.\n\nWe use an adjacency list to store the graph, since our graph must be sparse (every course can\'t be the prereq of every other course, if so we just immediately detect a cycle). For each course we DFS, keeping track of prev visited courses, and if we encounter a visited course then that\'s a cycle\u2014propagate False. To prevent repeated traversals, we can set completable courses (subgraphs w/o cycles) to an empty list in our adjacency list\u2014returns True.\n\n# Complexity\n- Time complexity: $O(V + E)$ where V is the number of courses (vertices) and E is the number of prerequisites (edges) since, in worst case, we just need to traverse every vertex and edge in the graph once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(V)$ since in worst case we traverse all courses, e.g. if each course is linked to the next in a chain of prereqs.\n\n# Code\n```\nclass Solution:\n\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n adj = [[] for _ in range(numCourses)]\n\n for a, b in prerequisites:\n adj[a].append(b) # since A depends on B, then A -> B directed edge\n \n # cycle detection \u2014 "Can we complete course A?"\n visiting = set()\n def dfs(a):\n if a in visiting: # cycle\n return False\n if adj[a] == []:\n return True\n\n visiting.add(a)\n for p in adj[a]:\n if not dfs(p): # propagate the detection\n return False\n visiting.remove(a)\n\n adj[a] = [] # no cycle, completable\n return True\n\n for a in range(numCourses):\n if not dfs(a):\n return False\n return True\n\n\n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Most Unique || Verly Simple | course-schedule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n # Create adjacency list representation of the graph\n graph = [[] for _ in range(numCourses)]\n for course, prerequisite in prerequisites:\n graph[course].append(prerequisite)\n\n # Helper function for DFS\n def dfs(course, visited):\n if visited[course] == 1:\n return False\n if visited[course] == -1:\n return True\n\n visited[course] = 1\n for prerequisite in graph[course]:\n if not dfs(prerequisite, visited):\n return False\n\n visited[course] = -1\n return True\n\n # Perform DFS for each course\n visited = [0] * numCourses\n for course in range(numCourses):\n if not dfs(course, visited):\n return False\n\n return True\n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
EASY PYTHON SOLUTION || DIRECTED GRAPH || AND OPERATION | course-schedule | 0 | 1 | \n# Code\n```\nclass Solution:\n def func(self,node,graph,visited):\n visited[node]=0\n ans=1\n for i in graph[node]:\n if visited[i]==-1:\n ans&=self.func(i,graph,visited)\n else:\n ans&=visited[i]\n if ans==1:\n visited[node]=1\n return 1\n return 0\n\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n graph=[[] for _ in range(numCourses)]\n for i,j in prerequisites:\n graph[j].append(i)\n visited=[-1]*numCourses\n for i in range(numCourses):\n if visited[i]==-1:\n if self.func(i,graph,visited)==0:\n return False\n return True\n\n \n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python3 Solution | course-schedule | 0 | 1 | \n```\nfrom collections import defaultdict,deque\nclass Solution:\n def canFinish(self,numCourses:int,prerequisites:List[List[int]])->bool:\n graph=defaultdict(list)\n for course,prereq in prerequisites:\n graph[prereq].append(course)\n\n\n indegrees=[0]*numCourses\n for prereq,_ in prerequisites:\n indegrees[prereq]+=1\n\n\n queue=deque()\n for courses in range(numCourses):\n if indegrees[courses]==0:\n queue.append(courses)\n\n while queue:\n courses=queue.popleft()\n for prereq in graph[courses]:\n indegrees[prereq]-=1\n if indegrees[prereq]==0:\n queue.append(prereq)\n\n\n return all(indegree==0 for indegree in indegrees) \n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
✅Beat's 100% || TOPO || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | course-schedule | 1 | 1 | # Intuition:\nThe intuition behind this approach is that if there is a cycle in the graph, there will be at least one node that cannot be visited since it will always have a nonzero indegree. On the other hand, if there are no cycles, all the nodes can be visited by starting from the nodes with no incoming edges and removing their outgoing edges one by one. If all the nodes are visited in the end, it means that it is possible to finish all the courses.\n\n# Explanation:\nThe code aims to solve the problem of determining whether it is possible to finish all the given courses without any cyclic dependencies. It uses the topological sort algorithm, specifically Kahn\'s algorithm, to solve this problem.\n\n1. **Initialization:**\n - Create an empty adjacency list to represent the directed graph. Each node in the graph represents a course, and the edges represent the prerequisites.\n - Create an array called `indegree` of size `n` (number of courses) and initialize all its elements to 0. The `indegree` array will keep track of the number of incoming edges to each course.\n - Create an empty `ans` vector to store the topological order of the courses.\n\n2.**Building the Graph:**\n - Iterate over the `prerequisites` vector, which contains pairs of courses indicating the prerequisites.\n - For each pair [a, b], add an edge in the adjacency list from b to a. This indicates that course b must be completed before course a.\n - Increment the `indegree` of course a by 1, as it has one more prerequisite.\n\n3. **Performing Topological Sort using Kahn\'s Algorithm:**\n - Create an empty queue called `q` to store the nodes to visit.\n - Iterate over all the courses (0 to n-1) and enqueue the courses with an `indegree` of 0 into the queue. These courses have no prerequisites and can be started immediately.\n\n - While the queue is not empty, do the following:\n - Dequeue the front element from the queue and store it in a variable `t`.\n - Add `t` to the `ans` vector to keep track of the topological order.\n - For each neighbor `x` of `t` in the adjacency list:\n - Decrement the `indegree` of `x` by 1 since we are removing the prerequisite `t`.\n - If the `indegree` of `x` becomes 0, enqueue `x` into the queue. This means that all the prerequisites of course `x` have been completed.\n\n4. **Checking the Result:**\n - After the topological sort is complete, check if the size of the `ans` vector is equal to the total number of courses (`n`).\n - If they are equal, it means that all the courses can be finished without any cyclic dependencies. Return `true`.\n - If the sizes are different, it implies that there is a cycle in the graph, and it is not possible to complete all the courses. Return `false`.\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool canFinish(int n, vector<vector<int>>& prerequisites) {\n vector<int> adj[n];\n vector<int> indegree(n, 0);\n vector<int> ans;\n\n for(auto x: prerequisites){\n adj[x[0]].push_back(x[1]);\n indegree[x[1]]++;\n }\n\n queue<int> q;\n for(int i = 0; i < n; i++){\n if(indegree[i] == 0){\n q.push(i);\n }\n }\n\n while(!q.empty()){\n auto t = q.front();\n ans.push_back(t);\n q.pop();\n\n for(auto x: adj[t]){\n indegree[x]--;\n if(indegree[x] == 0){\n q.push(x);\n }\n }\n }\n return ans.size() == n;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean canFinish(int n, int[][] prerequisites) {\n List<Integer>[] adj = new List[n];\n int[] indegree = new int[n];\n List<Integer> ans = new ArrayList<>();\n\n for (int[] pair : prerequisites) {\n int course = pair[0];\n int prerequisite = pair[1];\n if (adj[prerequisite] == null) {\n adj[prerequisite] = new ArrayList<>();\n }\n adj[prerequisite].add(course);\n indegree[course]++;\n }\n\n Queue<Integer> queue = new LinkedList<>();\n for (int i = 0; i < n; i++) {\n if (indegree[i] == 0) {\n queue.offer(i);\n }\n }\n\n while (!queue.isEmpty()) {\n int current = queue.poll();\n ans.add(current);\n\n if (adj[current] != null) {\n for (int next : adj[current]) {\n indegree[next]--;\n if (indegree[next] == 0) {\n queue.offer(next);\n }\n }\n }\n }\n\n return ans.size() == n;\n }\n}\n```\n```Python3 []\nclass Solution:\n def canFinish(self, n: int, prerequisites: List[List[int]]) -> bool:\n adj = [[] for _ in range(n)]\n indegree = [0] * n\n ans = []\n\n for pair in prerequisites:\n course = pair[0]\n prerequisite = pair[1]\n adj[prerequisite].append(course)\n indegree[course] += 1\n\n queue = deque()\n for i in range(n):\n if indegree[i] == 0:\n queue.append(i)\n\n while queue:\n current = queue.popleft()\n ans.append(current)\n\n for next_course in adj[current]:\n indegree[next_course] -= 1\n if indegree[next_course] == 0:\n queue.append(next_course)\n\n return len(ans) == n\n```\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 125 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
[VIDEO] Visualization of Kahn's Algorithm to Detect a Cycle | course-schedule | 0 | 1 | https://youtu.be/EUDwWbvtB_Q?si=XJw7OI9vrkDti9Iu\n\nThe fact that the prerequisites are given in pairs is a hint that we can express this problem as a graph. A directed edge between node `u` and node `v` indicates that course `u` is a prerequisites of course `v`. The only scenario where we wouldn\'t be able to complete all courses is if there is a cycle in the graph.\n\nThe idea is to use Kahn\'s algorithm to attempt a topological sort on the graph. This works because no topological sorting can be found for a graph with a cycle. So if the algorithm is successful, then we know that there is no cycle and we can return `True`. If the algorithm fails, then we have detected a cycle and we\'ll return `False`.\n\nFor a more detailed explanation of topological sorting and Kahn\'s algorithm, please see the video. But the way we\'ll determine if the algorithm is successful is by keeping count of then number of nodes visited during the algorithm. If we were able to visit all the nodes, then that means were were able to find an ordering of the graph and the algorithm was successful. If we weren\'t able to visit all nodes, then that means that some nodes must have been locked in a cycle, so completing all courses is impossible and we\'ll return `False`.\n\n# Code\n```\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n indegree = [0] * numCourses\n adj = [[] for x in range(numCourses)]\n \n for prereq in prerequisites:\n adj[prereq[1]].append(prereq[0])\n indegree[prereq[0]] += 1\n\n queue = []\n for i in range(numCourses):\n if indegree[i] == 0:\n queue.append(i)\n \n visited = 0\n while queue:\n node = queue.pop(0)\n visited += 1\n for neighbor in adj[node]:\n indegree[neighbor] -= 1\n if indegree[neighbor] == 0:\n queue.append(neighbor)\n \n return numCourses == visited\n \n``` | 9 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Beating 98.18% Python Easy Solution | course-schedule | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n # Topological Sort\n alist = collections.defaultdict(list)\n order = [0]*numCourses\n for i,j in prerequisites:\n alist[j].append(i)\n order[i]+=1\n q = collections.deque()\n for i in range(len(order)):\n if order[i] == 0:\n q.append(i)\n \n count = 0\n while q:\n current = q.popleft()\n count+=1\n for i in alist[current]:\n order[i]-=1\n if order[i]==0:\n q.append(i)\n \n return count == numCourses\n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python 99% time and 100% space. Collection of solutions with explanation | course-schedule | 0 | 1 | Firstly, we need to finish prerequisites courses before taking a main course so this is a directed graph problem. In other words, this problem can be restated to **Detect cycle in a directed graph** or similarly **Check if a graph is acyclic**. (For undirected graphs, check out this [article](https://leetcode.com/problems/graph-valid-tree/discuss/443909/Python.-Collection-of-\'easy-to-understand\'-solutions.-BFS-DFS-and-Union-Find))\n\nSecondly, while *edges list* together with *adjacency list* and *adjacency matrix* are three main ways to represent a graph, it\'s not commonly used to solve graph problems. One main reason is that to perform a common operation like getting all descendants of a given vertex it takes `O(len(edgesList))`. Hence, we can first build an adjacency list from the edges list which takes `O(1)` to perform such operation.\n\n def buildAdjacencyList(self, n, edgesList):\n adjList = [[] for _ in range(n)]\n # c2 (course 2) is a prerequisite of c1 (course 1)\n # i.e c2c1 is a directed edge in the graph\n for c1, c2 in edgesList:\n adjList[c2].append(c1)\n return adjList\n\nFor a quick reference of graph representation this [article](https://www.geeksforgeeks.org/graph-and-its-representations/) might be helpful.\n\n#### Complexity Analysis\n\n*Time Complexity:* `O(V + E)` where V is the number of vertices and E is the number edges.\n\n*Space Complexity:* `O(V + E)` the adjacency list dominates our memory usage. \n\n### Solution 1: DFS with an array storing 3 different states of a vertex\n\nThis solution is from "Introduction to Algorithms" book where it uses 3 different colours instead of 3 states. \n\nIt\'s also similar to this article [Python DFS + Memoization](https://leetcode.com/problems/longest-increasing-path-in-a-matrix/discuss/438920/python-dfs-memoization) where we use an array for Memoization.\n```python\n class Solution:\n \tdef buildAdjacencyList(self, n, edgesList):\n \t\t...\n \t\t\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n # build Adjacency list from Edges list\n adjList = self.buildAdjacencyList(numCourses, prerequisites)\n \n # Each vertex can have 3 different states:\n # state 0 : vertex is not visited. It\'s a default state.\n # state -1 : vertex is being processed. Either all of its descendants\n # are not processed or it\'s still in the function call stack.\n # state 1 : vertex and all its descendants are processed.\n state = [0] * numCourses\n \n def hasCycle(v):\n if state[v] == 1:\n # This vertex is processed so we pass.\n return False\n if state[v] == -1:\n # This vertex is being processed and it means we have a cycle.\n return True\n \n # Set state to -1\n state[v] = -1\n \n for i in adjList[v]:\n if hasCycle(i):\n return True\n \n state[v] = 1\n return False\n \n # we traverse each vertex using DFS, if we find a cycle, stop and return\n for v in range(numCourses):\n if hasCycle(v):\n return False\n \n return True\n```\n```\n 42/42 cases passed (96 ms)\n Your runtime beats 96.91 % of python3 submissions\n Your memory usage beats 65.31 % of python3 submissions (15.4 MB)\n```\n### Solution 2: DFS with a stack storing all decendants being processed\n\nSame idea as Solution 1, this time we use a stack to store all vertices being processed. While visiting a descendant of a vertex, if we found it in the stack it means a cycle appears.\n\nThis technique is also used to find a Topological order from the graph. \n```python\n class Solution:\n def buildAdjacencyList(self, n, edgesList):\n ...\n \n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n # build Adjacency list from Edges list\n adjList = self.buildAdjacencyList(numCourses, prerequisites)\n visited = set()\n \n def hasCycle(v, stack):\n if v in visited:\n if v in stack:\n # This vertex is being processed and it means we have a cycle.\n return True\n # This vertex is processed so we pass\n return False\n \n # mark this vertex as visited\n visited.add(v)\n # add it to the current stack\n stack.append(v)\n \n for i in adjList[v]:\n if hasCycle(i, stack):\n return True\n \n # once processed, we pop it out of the stack\n stack.pop()\n return False\n \n # we traverse each vertex using DFS, if we find a cycle, stop and return\n for v in range(numCourses):\n if hasCycle(v, []):\n return False\n \n return True\n```\n```\n 42/42 cases passed (100 ms)\n Your runtime beats 92.65 % of python3 submissions\n Your memory usage beats 51.02 % of python3 submissions (16 MB)\n```\n### Solution 3: BFS with Kahn\'s algorithm for Topological Sorting\n> This solution is usually seen in problems where we need to answer two questions:\n> 1. Is it possible to have a topological order?\n> 2. if yes then print out one of all the orders.\n> \nThis solution can also be used to solve:\n - 269. Alien Dictionary\n\n```python\n class Solution:\n def buildAdjacencyList(self, n, edgesList):\n \t\t\t\t...\n \n def topoBFS(self, numNodes, edgesList):\n # Note: for consistency with other solutions above, we keep building\n # an adjacency list here. We can also merge this step with the next step.\n adjList = self.buildAdjacencyList(numNodes, edgesList)\n \n # 1. A list stores No. of incoming edges of each vertex\n inDegrees = [0] * numNodes\n for v1, v2 in edgesList:\n # v2v1 form a directed edge\n inDegrees[v1] += 1\n \n # 2. a queue of all vertices with no incoming edge\n # at least one such node must exist in a non-empty acyclic graph\n # vertices in this queue have the same order as the eventual topological\n # sort\n queue = []\n for v in range(numNodes):\n if inDegrees[v] == 0:\n queue.append(v)\n \n # initialize count of visited vertices\n count = 0\n # an empty list that will contain the final topological order\n topoOrder = []\n \n while queue:\n # a. pop a vertex from front of queue\n # depending on the order that vertices are removed from queue,\n # a different solution is created\n v = queue.pop(0)\n # b. append it to topoOrder\n topoOrder.append(v)\n \n # increase count by 1\n count += 1\n \n # for each descendant of current vertex, reduce its in-degree by 1\n for des in adjList[v]:\n inDegrees[des] -= 1\n # if in-degree becomes 0, add it to queue\n if inDegrees[des] == 0:\n queue.append(des)\n \n if count != numNodes:\n return None # graph has at least one cycle\n else:\n return topoOrder\n \n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n return True if self.topoBFS(numCourses, prerequisites) else False\n```\n```\n 42/42 cases passed (92 ms)\n Your runtime beats 99.03 % of python3 submissions\n Your memory usage beats 100 % of python3 submissions (13.8 MB)\n``` | 367 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python 🔥Java 🔥C++ 🔥Simple Solution 🔥Easy to Understand | course-schedule | 1 | 1 | # An Upvote will be encouraging \uD83D\uDC4D\n\n# Video Solution\n\n# Search \uD83D\uDC49 `Course Schedule By Tech Wired`\n\n# OR\n\n# Click the link in my profile\n\n\n\n- To solve the problem, we use a depth-first search (DFS) algorithm to traverse the graph and detect cycles. During the DFS traversal, we keep track of the visited nodes, marking them as "visiting" and "visited". If we encounter a node that is currently being visited, it indicates a cycle in the graph.\n\n- We build an adjacency list representation of the prerequisites, where each course is a node and its prerequisites are the edges. Then, for each course, we perform a DFS traversal starting from that course and check if there is a cycle. If we find a cycle at any point, we return false to indicate that it is not possible to finish all the courses. If we complete the DFS traversal for all courses without finding a cycle, we return true to indicate that it is possible to finish all the courses.\n\n- By detecting cycles using DFS, we can determine the feasibility of completing all the courses and solve the "Course Schedule" problem efficiently\n\n```Python []\n\nclass Solution:\n def canFinish(self, numCourses, prerequisites):\n # Build adjacency list\n graph = defaultdict(list)\n for pair in prerequisites:\n course, prerequisite = pair\n graph[course].append(prerequisite)\n\n # Check if there is a cycle\n visited = [0] * numCourses # 0 - not visited, 1 - visiting, 2 - visited\n\n def hasCycle(course):\n if visited[course] == 1:\n return True\n if visited[course] == 2:\n return False\n\n visited[course] = 1\n for prerequisite in graph[course]:\n if hasCycle(prerequisite):\n return True\n\n visited[course] = 2\n return False\n\n # Perform DFS for each course\n for course in range(numCourses):\n if hasCycle(course):\n return False\n\n return True\n\n```\n```Java []\n\nclass Solution {\n public boolean canFinish(int numCourses, int[][] prerequisites) {\n List<List<Integer>> graph = new ArrayList<>();\n for (int i = 0; i < numCourses; i++) {\n graph.add(new ArrayList<>());\n }\n\n for (int[] pair : prerequisites) {\n int course = pair[0];\n int prerequisite = pair[1];\n graph.get(course).add(prerequisite);\n }\n\n int[] visited = new int[numCourses]; // 0 - not visited, 1 - visiting, 2 - visited\n\n for (int course = 0; course < numCourses; course++) {\n if (hasCycle(course, visited, graph)) {\n return false;\n }\n }\n\n return true;\n }\n\n private boolean hasCycle(int course, int[] visited, List<List<Integer>> graph) {\n if (visited[course] == 1) {\n return true;\n }\n if (visited[course] == 2) {\n return false;\n }\n\n visited[course] = 1;\n for (int prerequisite : graph.get(course)) {\n if (hasCycle(prerequisite, visited, graph)) {\n return true;\n }\n }\n\n visited[course] = 2;\n return false;\n }\n}\n\n```\n```C++ []\n\nclass Solution {\npublic:\n bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {\n vector<vector<int>> graph(numCourses);\n for (const auto& pair : prerequisites) {\n int course = pair[0];\n int prerequisite = pair[1];\n graph[course].push_back(prerequisite);\n }\n\n vector<int> visited(numCourses); // 0 - not visited, 1 - visiting, 2 - visited\n\n for (int course = 0; course < numCourses; course++) {\n if (hasCycle(course, visited, graph)) {\n return false;\n }\n }\n\n return true;\n }\n\nprivate:\n bool hasCycle(int course, vector<int>& visited, const vector<vector<int>>& graph) {\n if (visited[course] == 1) {\n return true;\n }\n if (visited[course] == 2) {\n return false;\n }\n\n visited[course] = 1;\n for (int prerequisite : graph[course]) {\n if (hasCycle(prerequisite, visited, graph)) {\n return true;\n }\n }\n\n visited[course] = 2;\n return false;\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 3 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
[Python 3] Topological Sort | course-schedule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n1. Topological Sort\n```\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n indegree = [0] * numCourses\n adj = [[] for _ in range(numCourses)]\n\n for prerequisite in prerequisites:\n adj[prerequisite[1]].append(prerequisite[0])\n indegree[prerequisite[0]] += 1\n\n queue = collections.deque()\n for i in range(numCourses):\n if indegree[i] == 0: queue.append(i)\n\n nodesVisited = 0\n while queue:\n node = queue.popleft()\n nodesVisited += 1\n\n for neighbor in adj[node]:\n indegree[neighbor] -= 1\n if indegree[neighbor] == 0: queue.append(neighbor)\n\n return nodesVisited == numCourses\n```\n2. DFS\n```\nclass Solution:\n def dfs(self, node, adj, visit, inStack):\n # If the node is already in the stack, we have a cycle.\n if inStack[node]:\n return True\n if visit[node]:\n return False\n # Mark the current node as visited and part of current recursion stack.\n visit[node] = True\n inStack[node] = True\n for neighbor in adj[node]:\n if self.dfs(neighbor, adj, visit, inStack):\n return True\n # Remove the node from the stack.\n inStack[node] = False\n return False\n\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n adj = [[] for _ in range(numCourses)]\n for prerequisite in prerequisites:\n adj[prerequisite[1]].append(prerequisite[0])\n\n visit = [False] * numCourses\n inStack = [False] * numCourses\n for i in range(numCourses):\n if self.dfs(i, adj, visit, inStack):\n return False\n return True\n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Course Schedule | Topological Sort | Beats 95.3% | Memory 43MB | course-schedule | 1 | 1 | \n\n# Complexity\n- Time complexity: O(V+E)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean canFinish(int numCourses, int[][] prerequisites) {\n int n = prerequisites.length;\n\n ArrayList<ArrayList<Integer>> arr = new ArrayList<>();\n for(int i=0;i<numCourses;i++){\n arr.add(new ArrayList<>());\n }\n\n for(int i=0;i<n;i++){\n arr.get(prerequisites[i][0]).add(prerequisites[i][1]);\n }\n\n int[] in = new int[numCourses];\n for(int i=0;i<numCourses;i++){\n for(int it: arr.get(i)){\n in[it]++;\n }\n }\n\n Queue<Integer> q = new LinkedList<>();\n for(int i=0;i<numCourses;i++){\n if(in[i]==0) q.add(i);\n }\n\n ArrayList<Integer> res = new ArrayList<>();\n while(!q.isEmpty()){\n int node = q.poll();\n\n res.add(node);\n for(int i: arr.get(node)){\n in[i]--;\n if(in[i]==0) q.add(i);\n }\n }\n\n if(res.size()!=numCourses) return false;\n return true;\n }\n}\n```\n\n | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
207: Solution with step by step explanation | course-schedule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem is essentially checking if there is a cycle in a directed graph. Each course can be represented as a node, and each prerequisite relationship can be represented as a directed edge from the prerequisite course to the target course.\n\nWe can use a Topological Sort algorithm to detect if there is a cycle in the directed graph. The algorithm works by first finding all the courses that have no prerequisites and adding them to a queue. Then we remove these courses and their corresponding edges from the graph. We keep doing this until there are no courses with no prerequisites left. If we have removed all the courses successfully, then there is no cycle in the graph and we can finish all the courses.\n\nIf there is a cycle in the graph, there will always be at least one course that cannot be taken because it depends on another course that cannot be taken. This means that we will never be able to remove all the courses with no prerequisites, and we cannot finish all the courses.\n\nHere is the step-by-step algorithm:\n\n1. Create an adjacency list to represent the directed graph.\nFor each prerequisite relationship (ai, bi), add an edge from bi to ai in the graph.\n\n2. Create an array "indegrees" to store the number of incoming edges for each node in the graph.\nFor each node with an incoming edge, increment its corresponding indegree.\n\n3. Add all the nodes with indegree 0 to a queue.\n\n4. While the queue is not empty, remove a node "course" from the queue.\nFor each course "prereq" that has an edge from "course", decrement its indegree by 1.\nIf the indegree of "prereq" becomes 0, add it to the queue.\n\n5. If we have removed all the courses successfully, then return True. Otherwise, return False.\n\n# Complexity\n- Time complexity:\nO(N+E) where N is the number of courses and E is the number of prerequisites.\n\n- Space complexity:\nO(N+E) for the adjacency list and the indegree array.\n\n# Code\n```\nfrom collections import defaultdict, deque\n\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n # Step 1: Create an adjacency list to represent the directed graph\n graph = defaultdict(list)\n for course, prereq in prerequisites:\n graph[prereq].append(course)\n \n # Step 2: Create an array "indegrees" to store the number of incoming edges for each node in the graph\n indegrees = [0] * numCourses\n for prereq, _ in prerequisites:\n indegrees[prereq] += 1\n \n # Step 3: Add all the nodes with indegree 0 to a queue\n queue = deque()\n for course in range(numCourses):\n if indegrees[course] == 0:\n queue.append(course)\n \n # Step 4: Topological Sort\n while queue:\n course = queue.popleft()\n for prereq in graph[course]:\n indegrees[prereq] -= 1\n if indegrees[prereq] == 0:\n queue.append(prereq)\n \n # Step 5: Check if we have removed all the courses successfully\n return all(indegree == 0 for indegree in indegrees)\n\n``` | 23 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Simple python topsort | course-schedule | 0 | 1 | ## Intuition\n\nThe problem can be viewed as finding whether a Directed Acyclic Graph (DAG) exists from the given prerequisites. If there\'s a cycle in the graph, then it\'s impossible to finish all courses; otherwise, it\'s possible. The idea is to use the topological sort algorithm to traverse through the graph.\n\n## Approach\n\n1. **Initialize Adjacency List and Indegree Count**: Use a defaultdict to maintain the adjacency list, and a Counter to keep track of the indegree for each course.\n \n2. **Fill Adjacency List and Indegree Count**: Loop through the prerequisites list and fill up the adjacency list and indegree Counter.\n\n3. **Initialize Queue**: Initialize a queue with courses that have an indegree of 0, i.e., courses that don\'t have any prerequisites.\n\n4. **Topological Sort**: Perform a topological sort using the queue. Decrease the indegree of each adjacent node when a node is visited, and check whether its indegree becomes 0. If yes, add it to the queue.\n\n5. **Count Nodes**: Keep count of the number of nodes visited.\n\n6. **Final Check**: If the number of nodes visited is equal to the number of courses, return true; otherwise, return false.\n\n## Complexity\n\n- **Time complexity**: $$O(V + E)$$, where $$V$$ is the number of vertices (courses), and $$E$$ is the number of edges (prerequisites). This is because we traverse each course and prerequisite once.\n\n- **Space complexity**: $$O(V + E)$$ for storing the adjacency list and the indegree counts.\n\n## Code\n\nThe provided code utilizes a deque for efficient queue operations and uses Counter and defaultdict for ease of handling indegree and adjacency lists, respectively.\n\n```python\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n indegree = Counter()\n adj = defaultdict(list)\n\n # Filling adjacency list and indegree Counter\n for [a, b] in prerequisites:\n adj[b].append(a)\n indegree[a] += 1\n\n # Initializing queue with nodes having indegree 0\n que = deque()\n for course in range(numCourses):\n if indegree[course] == 0:\n que.append(course)\n\n # Variable to count visited nodes\n nodeVisited = 0\n\n # Topological Sort\n while que:\n course = que.popleft()\n nodeVisited += 1\n\n for dep in adj[course]:\n indegree[dep] -= 1\n if indegree[dep] == 0:\n que.append(dep)\n\n # Final Check\n return nodeVisited == numCourses\n```\n | 2 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Ex-Amazon explains a Python solution with a video! | course-schedule | 0 | 1 | # Video solution\n\nhttps://youtu.be/-Me_If-_jRs\n\n\u25A0 Please subscribe to my channel from here. I have more than 200 Leetcode videos.\nhttps://www.youtube.com/@KeetCodeExAmazon\n\n---\n\n# Approach\n\n1. Create a class named `Solution` (assuming it is part of a larger program).\n2. Define a method within the `Solution` class called `canFinish` that takes in two parameters: `numCourses` (an integer representing the total number of courses) and `prerequisites` (a list of lists representing the prerequisites for each course).\n3. Create an empty dictionary called `pre` using the `defaultdict` class from the `collections` module. This dictionary will store the prerequisites for each course.\n4. Iterate over each pair `(course, p)` in the `prerequisites` list:\n a. Append `p` to the list of prerequisites for the course `course` in the `pre` dictionary.\n5. Create an empty set called `taken`. This set will keep track of the courses that have been visited during the depth-first search (DFS) traversal.\n6. Define an inner function called `dfs` that takes in a parameter `course`. This function will perform the DFS traversal to check if the course can be finished.\n7. If the list of prerequisites for the current `course` is empty (i.e., there are no remaining prerequisites), return `True` since the course can be finished.\n8. If the `course` is already present in the `taken` set, return `False` since there is a cycle in the course dependencies.\n9. Add the `course` to the `taken` set to mark it as visited.\n10. Iterate over each prerequisite `p` for the current `course` in the `pre` dictionary:\n a. If the DFS traversal returns `False` for any prerequisite `p`, return `False` since the course cannot be finished.\n11. Set the list of prerequisites for the current `course` in the `pre` dictionary to an empty list, indicating that all the prerequisites have been satisfied.\n12. Return `True` at the end of the `dfs` function since all the prerequisites for the `course` have been satisfied.\n13. Iterate over each `course` in the range from 0 to `numCourses` (exclusive) using a `for` loop.\n14. If the DFS traversal of the current `course` returns `False`, it means the course cannot be finished, so return `False` from the `canFinish` method.\n15. If the loop completes without returning `False`, it means all the courses can be finished, so return `True` from the `canFinish` method.\n\nIn summary, the algorithm performs a depth-first search to check if it is possible to finish all the courses given their prerequisites. It uses a dictionary to store the prerequisites for each course and a set to keep track of the visited courses during the traversal. If there is a cycle in the course dependencies or if any course cannot be finished, it returns `False`; otherwise, it returns `True`.\n\n# Python\n```\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n\n pre = defaultdict(list)\n\n for course, p in prerequisites:\n pre[course].append(p)\n \n taken = set()\n\n def dfs(course):\n if not pre[course]:\n return True\n \n if course in taken:\n return False\n \n taken.add(course)\n\n for p in pre[course]:\n if not dfs(p): return False\n \n pre[course] = []\n return True\n \n for course in range(numCourses):\n if not dfs(course):\n return False\n\n return True\n``` | 5 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Awesome DFS Python3 | course-schedule | 0 | 1 | # DFS: Python3\n```\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n dic={i:[] for i in range(numCourses)}\n for crs,pre in prerequisites:\n dic[crs].append(pre)\n visit=set()\n def dfs(crs):\n if crs in visit:\n return False\n if dic[crs]==[]:\n return True\n visit.add(crs)\n for pre in dic[crs]:\n if not dfs(pre):\n return False\n visit.remove(crs)\n dic[crs]=[]\n return True\n for crs in range(numCourses):\n if not dfs(crs):return False\n return True\n```\n# please upvote me it would encourage me alot\n | 5 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Simple solution using Topological Sort (Kahn's algorithm) , in Python | course-schedule | 0 | 1 | # Code\n```\nfrom queue import Queue\n\nclass Solution:\n def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:\n # TOPOLOGICAL SORT ... KAHN\'S ALGORITHM\n # by ensuring the given .. is a Directed Acyclic Graph(DAG) or not we can find the answer\n\n graph = {}\n for i in range(numCourses): graph[i] = [] \n\n for ele in prerequisites:\n graph[ele[0]] += [ele[1]]\n \n # TOPO SORT ..!!!\n indegree = [0]*(numCourses)\n\n for i in range(numCourses):\n for node in graph[i]:\n indegree[node] += 1\n\n q = Queue()\n for i in range(numCourses):\n if indegree[i] == 0:\n q.put(i)\n \n topo_sort = []\n\n # incase of topo sort (DAG) ..there must be atleast one node with indegree as 0\n while(not q.empty()):\n temp = q.get()\n\n topo_sort += [temp]\n \n # as we added node to topo_sort , reduce adjacent node indegree by 1\n for ele in graph[temp]:\n indegree[ele] -= 1 \n if indegree[ele] == 0:\n q.put(ele)\n \n if len(topo_sort) == numCourses:\n # It is a Directed Acyclic Graph(DAG)\n return True\n return False\n \n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return `true` if you can finish all courses. Otherwise, return `false`.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** true
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
**Example 2:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\],\[0,1\]\]
**Output:** false
**Explanation:** There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= 5000`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* All the pairs prerequisites\[i\] are **unique**. | This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Solution | implement-trie-prefix-tree | 1 | 1 | ```C++ []\nclass TrieNode {\npublic:\n TrieNode *child[26];\n bool isWord;\n TrieNode() {\n isWord = false;\n for (auto &a : child) a = nullptr;\n }\n};\nclass Trie {\n TrieNode* root;\npublic:\n Trie() {\n root = new TrieNode();\n }\n void insert(string s) {\n TrieNode *p = root;\n for (auto &a : s) {\n int i = a - \'a\';\n if (!p->child[i]) p->child[i] = new TrieNode();\n p = p->child[i];\n }\n p->isWord = true;\n }\n bool search(string key, bool prefix=false) {\n TrieNode *p = root;\n for (auto &a : key) {\n int i = a - \'a\';\n if (!p->child[i]) return false;\n p = p->child[i];\n }\n if (prefix==false) return p->isWord;\n return true;\n }\n bool startsWith(string prefix) {\n return search(prefix, true);\n }\n};\n```\n\n```Python3 []\nclass Trie:\n\n def __init__(self):\n self.root={}\n \n def insert(self, word: str) -> None:\n\n cur=self.root\n\n for letter in word:\n if letter not in cur:\n cur[letter]={}\n cur=cur[letter]\n\n cur[\'*\']=\'\'\n\n def search(self, word: str) -> bool:\n\n cur=self.root\n for letter in word:\n if letter not in cur:\n return False\n cur=cur[letter]\n\n return \'*\' in cur\n \n def startsWith(self, prefix: str) -> bool:\n\n cur=self.root\n for letter in prefix:\n if letter not in cur:\n return False\n cur=cur[letter]\n\n return True\n```\n\n```Java []\nclass Trie {\n Node root;\n\n public Trie() {\n root = new Node();\n }\n \n public void insert(String word) {\n root.insert(word, 0);\n }\n \n public boolean search(String word) {\n return root.search(word, 0);\n }\n \n public boolean startsWith(String prefix) {\n return root.startsWith(prefix, 0);\n }\n\n class Node {\n Node[] nodes;\n boolean isEnd;\n\n Node() {\n nodes = new Node[26];\n }\n\n private void insert(String word, int idx) {\n if (idx >= word.length()) return;\n int i = word.charAt(idx) - \'a\';\n if (nodes[i] == null) {\n nodes[i] = new Node();\n }\n\n if (idx == word.length()-1) nodes[i].isEnd = true;\n nodes[i].insert(word, idx+1);\n }\n\n private boolean search(String word, int idx) {\n if (idx >= word.length()) return false;\n Node node = nodes[word.charAt(idx) - \'a\'];\n if (node == null) return false;\n if (idx == word.length() - 1 && node.isEnd) return true;\n\n return node.search(word, idx+1);\n\n }\n\n private boolean startsWith(String prefix, int idx) {\n if (idx >= prefix.length()) return false;\n Node node = nodes[prefix.charAt(idx) - \'a\'];\n if (node == null) return false;\n if (idx == prefix.length() - 1) return true;\n\n return node.startsWith(prefix, idx+1);\n }\n }\n}\n```\n | 491 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
Simple Trie Implementation using only standard dictionaries | implement-trie-prefix-tree | 0 | 1 | # Intuition\nSimple Trie implementation using only dictionary of dictionaries.\n\n# Code\n```\nclass Trie:\n\n def __init__(self):\n self.nodes = dict()\n\n def insert(self, word: str) -> None:\n node = self.nodes\n for s in word:\n node[s] = node.get(s, dict())\n node = node[s]\n node[\'##\'] = True\n\n def search(self, word: str) -> bool:\n node = self.nodes\n for s in word:\n node = node.get(s, None)\n if not node:\n return False\n return True if node.get(\'##\', False) else False\n\n def startsWith(self, prefix: str) -> bool:\n node = self.nodes\n for s in prefix:\n node = node.get(s, None)\n if not node:\n return False\n return True\n \n\n\n# Your Trie object will be instantiated and called as such:\n# obj = Trie()\n# obj.insert(word)\n# param_2 = obj.search(word)\n# param_3 = obj.startsWith(prefix)\n``` | 2 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
Short python solution | implement-trie-prefix-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nrecursivedict = lambda: defaultdict(recursivedict)\n\nclass Trie:\n def __init__(self):\n self.data = recursivedict()\n \n def insert(self, word: str) -> None:\n curr = self.data\n for c in word:\n curr = curr[c]\n curr[\'we\'] = True\n\n def startsWith(self, prefix: str) -> bool:\n curr = self.data\n for c in prefix:\n curr = curr[c] if curr and c in curr else None\n \n return curr\n \n def search(self, word: str) -> bool:\n return (node := self.startsWith(word)) and \'we\' in node\n\n \n\n\n# Your Trie object will be instantiated and called as such:\n# obj = Trie()\n# obj.insert(word)\n# param_2 = obj.search(word)\n# param_3 = obj.startsWith(prefix)\n``` | 1 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
Day 76 || Easiest Beginner Friendly Sol | implement-trie-prefix-tree | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\n\n\n*The Trie data structure is a tree-like data structure used to store a collection of strings in a way that allows for efficient retrieval and prefix search. In a Trie, each node represents a prefix of one or more strings, with the root node representing the empty string. Each node also has a boolean flag indicating whether a string ends at that node.*\n\n*The intuition behind using a Trie is that we can efficiently search for a string or a prefix in the set of strings by traversing the Trie. We start at the root node and move down the tree, following the edges labeled with the characters of the string or prefix we\'re searching for. If we reach a node that has a string ending at it, then we know that the string we\'re searching for is in the set. If we reach a node that doesn\'t have a string ending at it, then we know that the string or prefix is not in the set.*\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Define a TrieNode class that has an array of TrieNode pointers to represent its children and a boolean value to indicate if it is the end of a word.\n2. Define a Trie class that has a pointer to the root TrieNode.\n3. Implement the insert method of the Trie class that takes a string as input and inserts it into the Trie by traversing the Trie based on each character in the string. If a TrieNode for a particular character does not exist, create one and set it as the child of the current TrieNode. Mark the final TrieNode as the end of a word.\n4. Implement the search method of the Trie class that takes a string as input and returns true if the string is in the Trie and false otherwise. Traverse the Trie based on each character in the string. If a TrieNode for a particular character does not exist, return false. If the end of the word is reached and the TrieNode is marked as the end of a word, return true. Otherwise, return false.\n5. Implement the startsWith method of the Trie class that takes a string as input and returns true if there is any word in the Trie that starts with the given prefix and false otherwise. Traverse the Trie based on each character in the prefix. If a TrieNode for a particular character does not exist, return false. Otherwise, return true.\n6. Create a Trie object and call its insert, search, and startsWith methods to use the Trie data structure.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\nclass TrieNode {\npublic:\n TrieNode* children[26];\n bool isWordCompleted;\n\n TrieNode() {\n memset(children, 0, sizeof(children));\n isWordCompleted = false;\n }\n};\n\nclass Trie {\npublic:\n TrieNode *root;\n Trie() {\n root = new TrieNode();\n }\n \n void insert(string word) {\n TrieNode* newRoot = root;\n for (char ch : word) {\n int alphabetIndex = ch - \'a\';\n if (newRoot -> children[alphabetIndex] == NULL) {\n newRoot -> children[alphabetIndex] = new TrieNode();\n } \n newRoot = newRoot -> children[alphabetIndex];\n }\n newRoot -> isWordCompleted = true;\n }\n \n bool search(string word) {\n TrieNode* newRoot = root;\n for (char ch : word) {\n int alphabetIndex = ch - \'a\';\n if (newRoot -> children[alphabetIndex] == NULL) {\n return false;\n } \n newRoot = newRoot -> children[alphabetIndex];\n }\n if (newRoot -> isWordCompleted == true) {\n return true;\n }\n return false;\n }\n \n bool startsWith(string prefix) {\n TrieNode* newRoot = root;\n for (char ch : prefix) {\n int alphabetIndex = ch - \'a\';\n if (newRoot -> children[alphabetIndex] == NULL) {\n return false;\n } \n newRoot = newRoot -> children[alphabetIndex];\n }\n return true;\n }\n};\n\n/**\n * Your Trie object will be instantiated and called as such:\n * Trie* obj = new Trie();\n * obj->insert(word);\n * bool param_2 = obj->search(word);\n * bool param_3 = obj->startsWith(prefix);\n */\n```\n```Java []\nclass TrieNode {\n TrieNode[] children;\n boolean isWordCompleted;\n\n public TrieNode() {\n children = new TrieNode[26];\n isWordCompleted = false;\n }\n}\n\nclass Trie {\n TrieNode root;\n \n public Trie() {\n root = new TrieNode();\n }\n \n public void insert(String word) {\n TrieNode newRoot = root;\n for (char ch : word.toCharArray()) {\n int alphabetIndex = ch - \'a\';\n if (newRoot.children[alphabetIndex] == null) {\n newRoot.children[alphabetIndex] = new TrieNode();\n } \n newRoot = newRoot.children[alphabetIndex];\n }\n newRoot.isWordCompleted = true;\n }\n \n public boolean search(String word) {\n TrieNode newRoot = root;\n for (char ch : word.toCharArray()) {\n int alphabetIndex = ch - \'a\';\n if (newRoot.children[alphabetIndex] == null) {\n return false;\n } \n newRoot = newRoot.children[alphabetIndex];\n }\n if (newRoot.isWordCompleted == true) {\n return true;\n }\n return false;\n }\n \n public boolean startsWith(String prefix) {\n TrieNode newRoot = root;\n for (char ch : prefix.toCharArray()) {\n int alphabetIndex = ch - \'a\';\n if (newRoot.children[alphabetIndex] == null) {\n return false;\n } \n newRoot = newRoot.children[alphabetIndex];\n }\n return true;\n }\n}\n\n```\n```Python []\nclass TrieNode:\n def __init__(self):\n self.children = [None]*26\n self.isWordCompleted = False\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, word: str) -> None:\n newRoot = self.root\n for ch in word:\n alphabetIndex = ord(ch) - ord(\'a\')\n if newRoot.children[alphabetIndex] == None:\n newRoot.children[alphabetIndex] = TrieNode()\n newRoot = newRoot.children[alphabetIndex]\n newRoot.isWordCompleted = True\n \n def search(self, word: str) -> bool:\n newRoot = self.root\n for ch in word:\n alphabetIndex = ord(ch) - ord(\'a\')\n if newRoot.children[alphabetIndex] == None:\n return False\n newRoot = newRoot.children[alphabetIndex]\n if newRoot.isWordCompleted == True:\n return True\n return False\n \n def startsWith(self, prefix: str) -> bool:\n newRoot = self.root\n for ch in prefix:\n alphabetIndex = ord(ch) - ord(\'a\')\n if newRoot.children[alphabetIndex] == None:\n return False\n newRoot = newRoot.children[alphabetIndex]\n return True\n\n```\n\n# Time Complexity and Space Complexity:\n- **Time complexity :** \n**Insertion: O(L)**, *where L is the length of the word being inserted. In the worst case, we have to traverse the entire length of the word to insert it into the Trie.*\n**Search: O(L)**, *where L is the length of the word being searched. In the worst case, we have to traverse the entire length of the word to search for it in the Trie.*\n**StartsWith: O(P)**, *where P is the length of the prefix being searched. In the worst case, we have to traverse the entire length of the prefix to check if it exists in the Trie.*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity :\n*The space complexity of the Trie data structure depends on the number of words being inserted and their length. In the worst case, if all the words in the Trie have no common prefixes, then the Trie will have N nodes (where N is the total number of characters in all the words) and each node will have 26 child nodes (assuming we are dealing with lowercase English alphabets). Therefore, the space complexity of the Trie data structure in the worst case is **O(26N)**, which simplifies to **O(N)**. This is because the maximum number of nodes in the Trie is limited to the number of characters in all the words, and the maximum number of child nodes a node can have is 26. In practice, the space complexity will be much lower than the worst case as many nodes will have common prefixes.*\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 19 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
🔥Trie Basics Explained + Video | Java C++ Python | implement-trie-prefix-tree | 1 | 1 | # What\'s a Trie\nJust like in a binary tree, instead of having 2 children, trie has 26 children. The idea is each child corresponds to each letter in alphabet, eg child1 --> a child2 -->b \nInstead of individual 26 children we store them in an array. \n\n\n# How to store words in this?\nStore act: All the 26 children will be null Initially\nthe first letter is \'a\' -->child[0] so create a new trie at child[0]\nthe second letter is \'c\' --> child[2] so create a new trie at child[2] (at second level)\nsimilarly for t.\n\n\n# But why All this circus to store act? Can\'t we use String or HashSet?\nThe point is when we have large number of words the words are closer to each other eg: to store actor we just have to create 2 new TrieNodes unlike String where new word had to be created.\n\n# How to search and insert\n\n\n\nAn additional paramter isEnd is required because in above example though we haven\'t stored acto, we can find the word. To avoid this TrieNode will have a new parameter i.e boolean end which marks the end of the word. \n\nSearch for act: child[0] is not null indicating a is present, child[2] not null and child[20]--> not null and have end = true so we have act\n\nSimilarly for startswith, but the only difference is end can be both true or false.\n\n\n\n<iframe width="560" height="315" src="https://www.youtube.com/embed/8Dkzz9YbEQQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe>\n\n\n```\nclass Trie {\n public TrieNode root;\n \n public class TrieNode{\n TrieNode [] arr;\n boolean end;\n TrieNode(){\n arr = new TrieNode[26];\n this.end = false;\n }\n \n }\n \n Trie(){\n this.root = new TrieNode();\n }\n \n public void insert(String s) {\n TrieNode curr = root;\n int c;\n for(int i = 0;i<s.length();i++){\n c = s.charAt(i)-\'a\';\n if(curr.arr[c]==null){\n curr.arr[c] = new TrieNode();\n }\n curr = curr.arr[c];\n }\n curr.end = true;\n \n }\n \n public boolean search(String s) {\n TrieNode curr = root;\n int c;\n for(int i = 0;i<s.length();i++){\n c = s.charAt(i)-\'a\';\n if(curr.arr[c]==null){\n return false;\n }\n curr = curr.arr[c];\n }\n return curr.end;\n }\n \n public boolean startsWith(String s) {\n TrieNode curr = root;\n int c;\n for(int i = 0;i<s.length();i++){\n c = s.charAt(i)-\'a\';\n if(curr.arr[c]==null){\n return false;\n }\n curr = curr.arr[c];\n }\n return true;\n }\n}\n```\n\n```\n#include <iostream>\n#include <cstring>\n\nusing namespace std;\n\nclass Trie {\nprivate:\n struct TrieNode {\n TrieNode* arr[26];\n bool end;\n \n TrieNode() {\n memset(arr, 0, sizeof(arr));\n end = false;\n }\n };\n \n TrieNode* root;\n \npublic:\n Trie() {\n root = new TrieNode();\n }\n \n void insert(string s) {\n TrieNode* curr = root;\n int c;\n for(int i = 0; i < s.length(); i++) {\n c = s[i] - \'a\';\n if(curr->arr[c] == NULL) {\n curr->arr[c] = new TrieNode();\n }\n curr = curr->arr[c];\n }\n curr->end = true;\n }\n \n bool search(string s) {\n TrieNode* curr = root;\n int c;\n for(int i = 0; i < s.length(); i++) {\n c = s[i] - \'a\';\n if(curr->arr[c] == NULL) {\n return false;\n }\n curr = curr->arr[c];\n }\n return curr->end;\n }\n \n bool startsWith(string s) {\n TrieNode* curr = root;\n int c;\n for(int i = 0; i < s.length(); i++) {\n c = s[i] - \'a\';\n if(curr->arr[c] == NULL) {\n return false;\n }\n curr = curr->arr[c];\n }\n return true;\n }\n};\n\n```\n\n\n```\n\nclass Trie:\n class TrieNode:\n def __init__(self):\n self.arr = [None] * 26\n self.end = False\n \n def __init__(self):\n self.root = self.TrieNode()\n \n def insert(self, s: str) -> None:\n curr = self.root\n for c in s:\n idx = ord(c) - ord(\'a\')\n if curr.arr[idx] is None:\n curr.arr[idx] = self.TrieNode()\n curr = curr.arr[idx]\n curr.end = True\n \n def search(self, s: str) -> bool:\n curr = self.root\n for c in s:\n idx = ord(c) - ord(\'a\')\n if curr.arr[idx] is None:\n return False\n curr = curr.arr[idx]\n return curr.end\n \n def startsWith(self, s: str) -> bool:\n curr = self.root\n for c in s:\n idx = ord(c) - ord(\'a\')\n if curr.arr[idx] is None:\n return False\n curr = curr.arr[idx]\n return True\n\n``` | 10 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
Easiest understandable code u will ever find #python3 | implement-trie-prefix-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Trie:\n class TrieNode:\n def __init__(self):\n self.arr = [None] * 26\n self.end = False\n \n def __init__(self):\n self.root = self.TrieNode()\n \n def insert(self, s: str) -> None:\n curr = self.root\n for c in s:\n idx = ord(c) - ord(\'a\')\n if curr.arr[idx] is None:\n curr.arr[idx] = self.TrieNode()\n curr = curr.arr[idx]\n curr.end = True\n \n def search(self, s: str) -> bool:\n curr = self.root\n for c in s:\n idx = ord(c) - ord(\'a\')\n if curr.arr[idx] is None:\n return False\n curr = curr.arr[idx]\n return curr.end\n \n def startsWith(self, s: str) -> bool:\n curr = self.root\n for c in s:\n idx = ord(c) - ord(\'a\')\n if curr.arr[idx] is None:\n return False\n curr = curr.arr[idx]\n return True\n\n\n# Your Trie object will be instantiated and called as such:\n# obj = Trie()\n# obj.insert(word)\n# param_2 = obj.search(word)\n# param_3 = obj.startsWith(prefix)\n``` | 2 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
Python - Simple TrieNode and Trie Implementation | implement-trie-prefix-tree | 0 | 1 | ```\nclass TrieNode:\n def __init__(self):\n # Stores children nodes and whether node is the end of a word\n self.children = {}\n self.isEnd = False\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n\n def insert(self, word: str) -> None:\n cur = self.root\n # Insert character by character into trie\n for c in word:\n # if character path does not exist, create it\n if c not in cur.children:\n cur.children[c] = TrieNode()\n cur = cur.children[c]\n cur.isEnd = True\n \n\n def search(self, word: str) -> bool:\n cur = self.root\n # Search character by character in trie\n for c in word:\n # if character path does not exist, return False\n if c not in cur.children:\n return False\n cur = cur.children[c]\n return cur.isEnd\n \n\n def startsWith(self, prefix: str) -> bool:\n # Same as search, except there is no isEnd condition at final return\n cur = self.root\n for c in prefix:\n if c not in cur.children:\n return False\n cur = cur.children[c]\n return True\n```\n | 39 | A [**trie**](https://en.wikipedia.org/wiki/Trie) (pronounced as "try ") or **prefix tree** is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
* `Trie()` Initializes the trie object.
* `void insert(String word)` Inserts the string `word` into the trie.
* `boolean search(String word)` Returns `true` if the string `word` is in the trie (i.e., was inserted before), and `false` otherwise.
* `boolean startsWith(String prefix)` Returns `true` if there is a previously inserted string `word` that has the prefix `prefix`, and `false` otherwise.
**Example 1:**
**Input**
\[ "Trie ", "insert ", "search ", "search ", "startsWith ", "insert ", "search "\]
\[\[\], \[ "apple "\], \[ "apple "\], \[ "app "\], \[ "app "\], \[ "app "\], \[ "app "\]\]
**Output**
\[null, null, true, false, true, null, true\]
**Explanation**
Trie trie = new Trie();
trie.insert( "apple ");
trie.search( "apple "); // return True
trie.search( "app "); // return False
trie.startsWith( "app "); // return True
trie.insert( "app ");
trie.search( "app "); // return True
**Constraints:**
* `1 <= word.length, prefix.length <= 2000`
* `word` and `prefix` consist only of lowercase English letters.
* At most `3 * 104` calls **in total** will be made to `insert`, `search`, and `startsWith`. | null |
Python3 Easy Sliding Window Solution | minimum-size-subarray-sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minSubArrayLen(self, target: int, nums: List[int]) -> int:\n\n l, r = 0, 0\n rsum = 0\n minlength = float(\'inf\')\n\n for r in range(len(nums)):\n\n rsum += nums[r]\n\n while rsum >= target:\n minlength = min(minlength, (r-l+1))\n rsum -= nums[l]\n l += 1\n\n\n return 0 if minlength == float(\'inf\') else minlength\n\n\n\n \n\n\n``` | 1 | Given an array of positive integers `nums` and a positive integer `target`, return _the **minimal length** of a_ _subarray_ _whose sum is greater than or equal to_ `target`. If there is no such subarray, return `0` instead.
**Example 1:**
**Input:** target = 7, nums = \[2,3,1,2,4,3\]
**Output:** 2
**Explanation:** The subarray \[4,3\] has the minimal length under the problem constraint.
**Example 2:**
**Input:** target = 4, nums = \[1,4,4\]
**Output:** 1
**Example 3:**
**Input:** target = 11, nums = \[1,1,1,1,1,1,1,1\]
**Output:** 0
**Constraints:**
* `1 <= target <= 109`
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution of which the time complexity is `O(n log(n))`. | null |
Python || Sliding Window || Beats 99% || Easy & Understandable | minimum-size-subarray-sum | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubArrayLen(self, target: int, nums: List[int]) -> int:\n start = 0 # initializing window start to 0.\n end = 0 # initializing window start to 0.\n sm = nums[start] # variable to keep track of the sum of the particular window.\n minlen = len(nums) # keeps track of the window length.\n totSum = 0 # keeps track of the total sum of the minlen window.\n\n while(start<=end and end<len(nums)):\n \n # if the element in the array itself is >= target.\n if nums[end]>=target:\n return 1\n \n # when sum>=target, calculate the window length.\n if sm>=target:\n \n diff = end-start+1\n if diff<=minlen:\n minlen = diff\n totSum = sm\n sm = sm - nums[start]\n start = start+1\n \n # when sum<target, expand the sliding window.\n else:\n end = end + 1\n if end<len(nums):\n sm = sm + nums[end]\n \n # when the sum of all elements in the array is not >= target.\n if minlen==len(nums):\n if totSum==0:\n return 0\n return minlen\n \n``` | 2 | Given an array of positive integers `nums` and a positive integer `target`, return _the **minimal length** of a_ _subarray_ _whose sum is greater than or equal to_ `target`. If there is no such subarray, return `0` instead.
**Example 1:**
**Input:** target = 7, nums = \[2,3,1,2,4,3\]
**Output:** 2
**Explanation:** The subarray \[4,3\] has the minimal length under the problem constraint.
**Example 2:**
**Input:** target = 4, nums = \[1,4,4\]
**Output:** 1
**Example 3:**
**Input:** target = 11, nums = \[1,1,1,1,1,1,1,1\]
**Output:** 0
**Constraints:**
* `1 <= target <= 109`
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution of which the time complexity is `O(n log(n))`. | null |
Ordinary Solution | minimum-size-subarray-sum | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code\n```\nclass Solution:\n def minSubArrayLen(self, target: int, nums: List[int]) -> int:\n res, curSum, l = len(nums)+1, 0, 0\n \n for r, n in enumerate(nums):\n curSum += n\n while curSum >= target and l <= r:\n res = min(res, r-l+1)\n curSum -= nums[l]\n l += 1\n\n return res%(len(nums)+1)\n``` | 5 | Given an array of positive integers `nums` and a positive integer `target`, return _the **minimal length** of a_ _subarray_ _whose sum is greater than or equal to_ `target`. If there is no such subarray, return `0` instead.
**Example 1:**
**Input:** target = 7, nums = \[2,3,1,2,4,3\]
**Output:** 2
**Explanation:** The subarray \[4,3\] has the minimal length under the problem constraint.
**Example 2:**
**Input:** target = 4, nums = \[1,4,4\]
**Output:** 1
**Example 3:**
**Input:** target = 11, nums = \[1,1,1,1,1,1,1,1\]
**Output:** 0
**Constraints:**
* `1 <= target <= 109`
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution of which the time complexity is `O(n log(n))`. | null |
Simple Solution | Beginner friendly| Easy to Understand| cJava |Python 3 | C++ | Koylin | Javascript | minimum-size-subarray-sum | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUses a two-pointer approach to find the minimum subarray length whose sum is greater than or equal to the target value. The two pointers, l and r, represent the left and right boundaries of the subarray, respectively.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize l, r, res (result), and s (current sum) to appropriate initial values.\n- Iterate through the array nums using the right pointer r.\n- Update the current sum s by adding the element at r to it.\n- Check if the current sum s is greater than or equal to the target value. If true, proceed to the next steps. Otherwise, continue to the next iteration.\n- Enter a while loop to shrink the subarray from the left side. Subtract the element at l from the current sum s and increment l by 1. This step is done to find the minimum length subarray.\n- Update the result res by taking the minimum between its current value and the length of the subarray from l to r plus 1 (adding 1 because the indices are 0-based).\n- Repeat steps 5 and 6 until the current sum s is less than the target value.\n- After the loop ends, check if the result res is still equal to its initial value, Integer.MAX_VALUE. If true, it means no subarray was found with a sum greater than or equal to the target value, so return 0.\n- Return the minimum length of the subarray found.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```java []\nclass Solution {\n public int minSubArrayLen(int target, int[] nums) {\n int l=0,r=0,res=Integer.MAX_VALUE,s=0;\n for(r=0;r<nums.length;r++){\n s+=nums[r];\n while(s>=target){\n s-=nums[l];\n res = Math.min(res,r-l+1);\n l++;\n }\n }\n if(res==Integer.MAX_VALUE)\n return 0;\n return res;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minSubArrayLen(int target, vector<int>& nums) {\n int l = 0, r = 0, res = std::numeric_limits<int>::max(), s = 0;\n for (r = 0; r < nums.size(); r++) {\n s += nums[r];\n while (s >= target) {\n s -= nums[l];\n res = std::min(res, r - l + 1);\n l++;\n }\n }\n if (res == std::numeric_limits<int>::max())\n return 0;\n return res;\n }\n};\n```\n```python3 []\n\nclass Solution:\n def minSubArrayLen(self, target: int, nums: List[int]) -> int:\n l = 0\n res = float(\'inf\')\n s = 0\n \n for r in range(len(nums)):\n s += nums[r]\n \n while s >= target:\n res = min(res, r - l + 1)\n s -= nums[l]\n l += 1\n \n return res if res != float(\'inf\') else 0\n```\n```Javascript []\n/**\n * @param {number} target\n * @param {number[]} nums\n * @return {number}\n */\nvar minSubArrayLen = function(target, nums) {\n let l = 0;\n let res = Infinity;\n let s = 0;\n\n for (let r = 0; r < nums.length; r++) {\n s += nums[r];\n\n while (s >= target) {\n res = Math.min(res, r - l + 1);\n s -= nums[l];\n l++;\n }\n }\n\n return res !== Infinity ? res : 0;\n};\n```\n```Kotlin []\nclass Solution {\n fun minSubArrayLen(target: Int, nums: IntArray): Int {\n var l = 0\n var res = Int.MAX_VALUE\n var s = 0\n\n for (r in nums.indices) {\n s += nums[r]\n\n while (s >= target) {\n res = minOf(res, r - l + 1)\n s -= nums[l]\n l++\n }\n }\n\n return if (res != Int.MAX_VALUE) res else 0\n }\n}\n```\n```C# []\npublic class Solution {\n public int MinSubArrayLen(int target, int[] nums) {\n int l = 0;\n int res = int.MaxValue;\n int s = 0;\n\n for (int r = 0; r < nums.Length; r++) {\n s += nums[r];\n\n while (s >= target) {\n res = Math.Min(res, r - l + 1);\n s -= nums[l];\n l++;\n }\n }\n\n return res != int.MaxValue ? res : 0;\n }\n}\n```\n```php []\nclass Solution {\n\n /**\n * @param Integer $target\n * @param Integer[] $nums\n * @return Integer\n */\n function minSubArrayLen($target, $nums) {\n $l = 0;\n $res = PHP_INT_MAX;\n $s = 0;\n\n for ($r = 0; $r < count($nums); $r++) {\n $s += $nums[$r];\n\n while ($s >= $target) {\n $res = min($res, $r - $l + 1);\n $s -= $nums[$l];\n $l++;\n }\n }\n\n return $res != PHP_INT_MAX ? $res : 0;\n }\n}\n```\n```c []\nint minSubArrayLen(int target, int* nums, int numsSize) {\n int l = 0, r = 0, res = INT_MAX, s = 0;\n for (r = 0; r < numsSize; r++) {\n s += nums[r];\n while (s >= target) {\n s -= nums[l];\n res = (res < r - l + 1) ? res : r - l + 1;\n l++;\n }\n }\n if (res == INT_MAX)\n return 0;\n return res;\n}\n```\n```TypeScript []\nfunction minSubArrayLen(target: number, nums: number[]): number {\n let l = 0;\n let res = Infinity;\n let s = 0;\n\n for (let r = 0; r < nums.length; r++) {\n s += nums[r];\n\n while (s >= target) {\n res = Math.min(res, r - l + 1);\n s -= nums[l];\n l++;\n }\n }\n\n return res !== Infinity ? res : 0;\n};\n\n```\n\n | 10 | Given an array of positive integers `nums` and a positive integer `target`, return _the **minimal length** of a_ _subarray_ _whose sum is greater than or equal to_ `target`. If there is no such subarray, return `0` instead.
**Example 1:**
**Input:** target = 7, nums = \[2,3,1,2,4,3\]
**Output:** 2
**Explanation:** The subarray \[4,3\] has the minimal length under the problem constraint.
**Example 2:**
**Input:** target = 4, nums = \[1,4,4\]
**Output:** 1
**Example 3:**
**Input:** target = 11, nums = \[1,1,1,1,1,1,1,1\]
**Output:** 0
**Constraints:**
* `1 <= target <= 109`
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution of which the time complexity is `O(n log(n))`. | null |
Python 3 || 9 lines, sliding window || T/M: 100% / 100% | minimum-size-subarray-sum | 0 | 1 | Here\'s how the code works:\n\n1. We check an edge case. If the `sum(nums)` is less than `target`, then there is no subarray that satisfies the condition, so we return 0.\n\n2. We initialize three variables: `s` for keeping track of the current sum, `l` as the left index of the sliding window, and `ans` to update the minimal length of the subarray during the iteration.\n\n1. We iterate over`nums` to move the right ptr, and use the inner `while` loopto update`s`, `l`, and`ans` as necessary.\n\n1. We return`ans`, which represents the length of the subarray whose sum is greater than or equal to`target`.\n\n\n```\nclass Solution:\n def minSubArrayLen(self, target: int, nums: list[int]) -> int:\n\n if sum(nums) < target: return 0 # <-- 1\n\n s, l, ans = 0, 0, len(nums) # <-- 2\n \n for r,val in enumerate(nums): # \n s+= val #\n while s >= target: # <-- 3\n s-= nums[l] #\n ans = min(ans, r - l + 1) #\n l+= 1 #\n\n return ans # <-- 4\n```\n[https://leetcode.com/problems/minimum-size-subarray-sum/submissions/603708786/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~`len(nums)`. | 12 | Given an array of positive integers `nums` and a positive integer `target`, return _the **minimal length** of a_ _subarray_ _whose sum is greater than or equal to_ `target`. If there is no such subarray, return `0` instead.
**Example 1:**
**Input:** target = 7, nums = \[2,3,1,2,4,3\]
**Output:** 2
**Explanation:** The subarray \[4,3\] has the minimal length under the problem constraint.
**Example 2:**
**Input:** target = 4, nums = \[1,4,4\]
**Output:** 1
**Example 3:**
**Input:** target = 11, nums = \[1,1,1,1,1,1,1,1\]
**Output:** 0
**Constraints:**
* `1 <= target <= 109`
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution of which the time complexity is `O(n log(n))`. | null |
Simple intuition. | course-schedule-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe simply perform recursive DFS for each course to determine whether it\'s completable. Our graph consists of courses for nodes and edges from a course to its prerequisites. The DFS performs cycle detection by adding courses we\'re currently visiting\u2014a course cannot require its own completion. For each course we deem completable we add it to some set to save time from future traversals; we also add it to our output.\n\nIterating through all nodes, if DFS detects a cycle we return an empty list, otherwise we return our output after determining all courses are completable.\n\n# Complexity\n- Time complexity: $O(V + E)$ since we iterate all nodes and edges.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(V)$\u2014worst case we have recursive stack as deep as number of courses.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n adj = [[] for _ in range(numCourses)]\n for crs, pre in prerequisites:\n adj[crs].append(pre)\n\n stack = []\n valid, cycle = set(), set()\n def dfs(crs):\n if crs in cycle:\n return False # impossible\n if crs in valid:\n return True\n \n cycle.add(crs)\n for pre in adj[crs]:\n if not dfs(pre):\n return False # propagate the impossibility\n cycle.remove(crs)\n\n valid.add(crs)\n stack.append(crs)\n return True\n \n for crs in range(numCourses):\n if not dfs(crs):\n return []\n return stack\n\n\n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Cycle Detection with Topological Sort (Python 3) | course-schedule-ii | 0 | 1 | # Code\n```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n adjList = [[] for _ in range(numCourses)]\n visited = [0] * numCourses # 0: unprocessed, 1: processing, 2: processed\n courses = []\n\n # build adjacency list\n for prereq in prerequisites:\n a, b = prereq[0], prereq[1]\n adjList[b].append(a)\n \n # cycle detection with topological sort\n def dfs(root: int) -> bool:\n if visited[root] == 1:\n return False\n if visited[root] == 2:\n return True\n\n visited[root] = 1\n\n for neighbor in adjList[root]:\n if not dfs(neighbor):\n return False\n\n visited[root] = 2\n courses.append(root)\n\n return True\n \n # iterate through every unprocessed course\n for course in range(numCourses):\n if visited[course] == 0 and not dfs(course):\n return []\n\n # dfs topological sort returns sorting in reversed order\n courses = reversed(courses)\n \n return courses\n\n \n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
✅ PYTHON || Beginner Friendly || O(V+E) 🔥🔥🔥 | course-schedule-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The problem is asking for the order in which courses can be taken given a list of prerequisites. \n- We can model the problem as a directed graph, where nodes represent courses and directed edges represent prerequisites.\n- The goal is to find a valid topological ordering of the graph.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a depth-first search (DFS) based approach to find a valid topological ordering.\n 1. Create a dictionary (preReq) to represent the directed edges between courses and their prerequisites.\n 2. Initialize an empty list (res) to store the final result, a set (visit) to keep track of visited nodes, and a set (cycle) to detect cycles during the DFS traversal.\n 3. Define a DFS function that takes a course as an argument.\n - Check if the course is in the cycle set. If true, there is a cycle, and return False.\n - Check if the course is in the visit set. If true, the course is already processed, return True.\n - Add the course to the cycle set to mark it as visited.\n - Recursively call the DFS function for each prerequisite of the current course.\n - Remove the course from the cycle set (backtrack) and add it to the visit set.\n - Append the course to the result list.\n - Return True.\n 4. Iterate through all courses and call the DFS function for each course.\n - If the DFS function returns False, there is a cycle, and the result is not possible, return an empty list.\n 5. Return the result list as the valid topological ordering.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N + E), where N is the number of courses and E is the number of prerequisites. The DFS traversal visits each course once and each prerequisite once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N + E) for the graph representation and recursion stack. The preReq dictionary stores the graph, and the visit and cycle sets store information during DFS.\n\n# Code\n```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n preReq = defaultdict(list)\n\n for c,pr in prerequisites:\n preReq[c].append(pr)\n \n res = []\n\n visit, cycle = set(), set()\n\n def dfs(c):\n # terminating case\n if c in cycle:\n return False\n \n if c in visit:\n return True\n \n cycle.add(c)\n for pr in preReq[c]:\n if dfs(pr) == False:\n return False\n cycle.remove(c)\n visit.add(c)\n res.append(c)\n return True\n\n for c in range(numCourses):\n if dfs(c) == False:\n return []\n \n return res\n```\n# ThinkBIG\n\uD83D\uDE80 Elevating Your LeetCode Game with this Algorithm? \uD83E\uDDE0\uD83D\uDCBB If you\'ve found this solution to be insightful and well-crafted, consider boosting its visibility with an upvote. \uD83D\uDD1D Together, we can assist fellow programmers in ascending to greater coding pinnacles! \uD83D\uDE4C | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python3 Topological Sort solution intuition and imagination of solution 96.9% faster | course-schedule-ii | 0 | 1 | # Intuition\nHow to proceed with the Question is to think for yourself, where do I start with my first course?\n \nAnalogy will come in imagination to a graph problem itself as direct the node starting from which course needs to be completed first to get to the other course.\n\nFor example: prerequisites = [[1,0],[2,0],[3,1],[3,2]] numCourses=4\n\nTo complete course 0 I have to complete the course 1 first \n and to complete the course 2 I have to complete the course 0 first again. \n\n How the graph will look like at the end, and you can imagine how the adjacancy list will be made. \n\n**{ 0 : *[1,2] from 0 we can either complete 1 or 2 so basically for both the next courses 0 is necessary*\n 1 : [3]\n 2 : [3]\n}**\n\n\n\n\n\n\n\n\n# Approach\n\n**We have to eliminate the node that can be completed without going to any node, meaning we have to complete the course that doesn\'t have any prerequist and can be completed immediately**. That means all the courses with 0 indegree.\n\nWill put them in queue and start traversing in BFS. \n\nNow once that particular node(course) is completed, put that course in result as that will be compelted first and already is.\nNow we will check all the courses that can be now completed or atleast have one less dependancy of a courses due to the completion of our current course (i.e.) Its neighbour or directs in the adjacency list.\n\nSo basically, the next (neighbour) course is one less dependency, which means one less indegree. Therefore, indegree[neigh] -= 1. If the indegree becomes 0 (meaning there are no dependencies left), that course (node) is good to go in the queue to be completed.\n\n**At last we will check if we were able to complete all the courses that means all the courses were popped from the queue atleast once and no course is left with any dependancy now. That means we have completed all the courses and give the result in order we poped the courses out of the bfs queue.**\n\n# Complexity\n- Time complexity:\n**O(V+E) BFS Traversal complexity** \n\n- Space complexity:\n**O(V) to contain indegree and adjacency list**\n\n# Code\n```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n ## Dependancy of each node/course\n indegree= [0]*numCourses\n\n result = []\n ##Adjacency list\n mapper = defaultdict(list)\n\n ##Putting all the courses that doesn\'t have any dependancy in queue\n for ai, bi in prerequisites:\n mapper[bi].append(ai)\n indegree[ai]+=1\n # print(mapper,indegree)\n\n q = deque()\n\n for i in range(len(indegree)):\n if indegree[i]==0:\n q.append(i)\n while(q):\n node = q.popleft()\n result.append(node)\n for neigh in mapper[node]:\n # One less dependancy\n indegree[neigh]-=1\n if indegree[neigh]==0:\n q.append(neigh)\n if len(result) == numCourses:\n return result\n return [] \n``` | 2 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
210: Solution with step by step explanation | course-schedule-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem can be solved using topological sort. First, we need to build a graph to represent the courses and their prerequisites, and then perform topological sort on the graph to get the order of courses.\n\nHere is the step by step explanation:\n\n1. Build the graph:\nWe can represent the courses and their prerequisites using a directed graph. Each course is a node in the graph, and each prerequisite relationship is an edge from the prerequisite to the course. We can build the graph using an adjacency list.\n\n2. Calculate the in-degree of each node:\nIn-degree is the number of incoming edges for a node. We can calculate the in-degree of each node in the graph by counting the number of prerequisites for each course.\n\n3. Perform topological sort:\nWe can perform topological sort on the graph using a queue. We start by adding all the nodes with in-degree 0 to the queue. Then, while the queue is not empty, we remove a node from the queue and add it to the result. For each of the node\'s neighbors, we decrement their in-degree by 1. If a neighbor\'s in-degree becomes 0, we add it to the queue.\n\n4. Check for cycle:\nIf the result size is less than the number of courses, it means there is a cycle in the graph, and it is impossible to finish all courses.\n\n# Complexity\n- Time complexity: 85.26%\nBuilding the graph takes O(E), where E is the number of edges (prerequisites). Calculating the in-degree takes O(E). Performing topological sort takes O(V + E), where V is the number of nodes (courses). Therefore, the overall time complexity is O(V + E).\n\n- Space complexity: 83.92%\nWe use O(V + E) space to store the graph and the in-degree. We also use O(V) space for the queue and the result. Therefore, the overall space complexity is O(V + E).\n\n# Code\n```\nfrom collections import defaultdict, deque\n\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n # Step 1: Build the graph\n graph = defaultdict(list)\n for course, prereq in prerequisites:\n graph[prereq].append(course)\n \n # Step 2: Calculate the in-degree of each node\n in_degree = [0] * numCourses\n for course, prereq in prerequisites:\n in_degree[course] += 1\n \n # Step 3: Perform topological sort\n queue = deque()\n for i in range(numCourses):\n if in_degree[i] == 0:\n queue.append(i)\n \n result = []\n while queue:\n node = queue.popleft()\n result.append(node)\n for neighbor in graph[node]:\n in_degree[neighbor] -= 1\n if in_degree[neighbor] == 0:\n queue.append(neighbor)\n \n # Step 4: Check for cycle\n if len(result) < numCourses:\n return []\n \n return result\n\n``` | 18 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python BFS beats 98% with Detailed Explanation and Comments! | course-schedule-ii | 0 | 1 | The high level for this solution: We create a graph and prereq dict to track which nodes we have visited and if we\'re able to travel to certain nodes (if there are no preqs for the intended next course - aka we\'ve taken the prereqs or there are no prereqs.).\nEg. 4, [[1,0],[2,0],[3,1],[3,2]]\nStarting: q: deque([0])\npreqs: {0: set(), 1: {0}, 2: {0}, 3: {1, 2}}\ngraph: {0: {1, 2}, 1: {3}, 2: {3}}\nWe start with course 0 because it has no preqs.\nLooking at our graph, 0 has 2 neighbors 1 and 2\nWe check 1 and 2 to see that if we have taken course 0 whether we can take them.\nWe determine this by removing 0 (course we have taken) from 1 and 2\'s prereqs and if there are no additional prereqs we take them (add them to our queue).\nAfter taking 0, 1 and 2 added: deque([1, 2]) \n1 and 2 added because they are neighbors (from our graph): {0: {1, 2}, 1: {3}, 2: {3}}) \nAnd after taking course 0 now have no prereqs: {0: set(), 1: set(), 2: set(), 3: {1, 2}}\nNow we visit 1 as it\'s first in our FIFO queue.\nLooking at course 1\'s neighbors in our graph there\'s 3, \n{0: {1, 2}, 1: {3}, 2: {3}}\nbut it has a prereq we haven\'t taken 2,\n{0: set(), 1: set(), 2: set(), 3: {2}}\nWhich is still in our queue: deque([2])\nSo we don\'t add anything in this iter and then pop 2 from our q.\nNow we\'ve taken 2, we can hit 3 from our graph: 0: {1, 2}, 1: {3}, 2: {3}}\nwe have now taken 2 so we remove the prereq: {0: set(), 1: set(), 2: set(), 3: set()}\nAnd we add 3 to the queue.\ndeque([3])\nWe then pop 3, append 3 to our taken list and len(taken) == numCourses so we\'re done!\n\n```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n # Create a prerequisite dict. (containing courses (nodes) that need to be taken (visited)\n\t\t# before we can visit the key.\n preq = {i:set() for i in range(numCourses)}\n\t\t# Create a graph for adjacency and traversing.\n graph = collections.defaultdict(set)\n for i,j in prerequisites:\n\t\t # Preqs store requirments as their given.\n preq[i].add(j)\n\t\t\t# Graph stores nodes and neighbors.\n graph[j].add(i)\n \n q = collections.deque([])\n\t\t# We need to find a starting location, aka courses that have no prereqs.\n for k, v in preq.items():\n if len(v) == 0:\n q.append(k)\n\t\t# Keep track of which courses have been taken.\n taken = []\n while q:\n course = q.popleft()\n taken.append(course)\n\t\t\t# If we have visited the numCourses we\'re done.\n if len(taken) == numCourses:\n return taken\n\t\t\t# For neighboring courses.\n for cor in graph[course]:\n\t\t\t # If the course we\'ve just taken was a prereq for the next course, remove it from its prereqs.\n preq[cor].remove(course)\n\t\t\t\t# If we\'ve taken all of the preqs for the new course, we\'ll visit it.\n if not preq[cor]:\n q.append(cor)\n\t\t# If we didn\'t hit numCourses in our search we know we can\'t take all of the courses.\n return []\n``` | 74 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python || 96.95% Faster || BFS || DFS || Explained | course-schedule-ii | 0 | 1 | **In this question we have applied topological sorting method**\n\n**DFS Solution:**\n```\ndef findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n def dfs(sv,visited):\n if visited[sv]==-1:# this course had not been added into the res, but visited again; there is a cycle!\n return False\n if visited[sv]==1:# this course had been successfully added into the res\n return True\n visited[sv]=-1 # set the current course as currently being visited\n for u in adj[sv]:\n if not dfs(u,visited):\n return False # if there is a cycle detected at any point, terminate!\n res.append(sv) # no cycle found, dfs finished, good to add the course into the res\n visited[sv]=1 # this course finished\n return True\n \n adj=[[] for i in range(numCourses)]\n res=[]\n for u,v in prerequisites:\n adj[v].append(u)\n visited=[0]*numCourses\n for i in range(numCourses):\n if not dfs(i,visited):\n # if False, there must be a cycle; terminate by returning an empty list\n return []\n return res[::-1]\n```\n\n**BFS Solution:**\n```\ndef findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n adj=[[] for i in range(numCourses)]\n for u,v in prerequisites:\n adj[v].append(u)\n visited=[0]*numCourses\n indeg=[0]*numCourses\n res=[]\n q=deque()\n for i in range(numCourses):\n for j in adj[i]:\n indeg[j]+=1\n for i in range(numCourses):\n if indeg[i]==0:\n q.append(i)\n while q:\n u=q.popleft()\n res.append(u)\n for i in adj[u]:\n if indeg[i]!=0:\n indeg[i]-=1\n if indeg[i]==0:\n q.append(i)\n if len(res)!=numCourses:\n return []\n return res\n```\n\n**An upvote will be encouraging** | 8 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python 3 - DFS | course-schedule-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n # Initialize the adjacency list\n adj_list = [[] for _ in range(numCourses)]\n for course, pre in prerequisites:\n adj_list[course].append(pre)\n \n # States: 0 = unvisited, -1 = on path, 1 = visited\n visited = [0] * numCourses\n order = [] # Store the course order\n\n def dfs(course):\n if visited[course] == -1: # on the path, found a cycle\n return False\n if visited[course] == 1: # already explored, no cycle found\n return True\n visited[course] = -1 # mark as being on the path\n \n # Visit all prerequisites. \n # If any of them is on the path or cannot be completed, return False\n for pre in adj_list[course]:\n if not dfs(pre):\n return False\n \n # Mark as visited\n visited[course] = 1\n # Add the course to the order\n order.append(course)\n\n return True\n\n # DFS on every course\n for course in range(numCourses):\n if not dfs(course):\n return []\n \n # If all courses could be visited, return the order\n return order \n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
✅[Python] Simple and Clean, beats 90.89%✅ | course-schedule-ii | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n\n\n# Intuition\nThe problem of finding the order of courses to finish all courses can be modeled as a graph problem. Each course can be represented as a node in the graph, and the prerequisites can be represented as directed edges between the nodes. The problem then becomes one of finding a topological ordering of the nodes in the graph.\n\n# Approach\n1. Initialize an empty list `toposort` to store the topological ordering of the nodes.\n2. Create an adjacency list `AList` to represent the graph and a dictionary `indegree` to keep track of the indegree of each node.\n3. For each edge in the prerequisites, add an edge from `bi` to `ai` in the adjacency list and increment the indegree of node `ai`.\n4. Initialize a queue and add all nodes with indegree 0 to it.\n5. While the queue is not empty, remove the first node from the queue and add it to `toposort`.\n6. For each neighbor of the removed node, decrement its indegree by 1. If its indegree becomes 0, add it to the queue.\n7. If the length of `toposort` is equal to `numCourses`, return `toposort`. Otherwise, return an empty array because it is impossible to finish all courses.\n\n# Complexity\n- Time complexity: $$O(n + e)$$ where $$n$$ is the number of courses and $$e$$ is the number of prerequisites.\n- Space complexity: $$O(n + e)$$ where $$n$$ is the number of courses and $$e$$ is the number of prerequisites.\n\n# Code\n```\nclass Solution:\n def findOrder(self, numCourses: int, p: List[List[int]]) -> List[int]:\n toposort = []\n queue = deque()\n AList = defaultdict(list)\n indegree = defaultdict(lambda:0)\n for edge in p:\n indegree[edge[0]]+=1\n AList[edge[1]].append(edge[0])\n for i in range(numCourses):\n if indegree[i]==0:\n queue.append(i)\n while len(queue)>0:\n curr = queue.popleft()\n toposort.append(curr)\n for nodes in AList[curr]:\n indegree[nodes]-=1\n if indegree[nodes]==0:\n queue.append(nodes)\n return toposort if len(toposort)==numCourses else []\n``` | 4 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Python BFS/DFS || Image + Intuition Explanation | course-schedule-ii | 0 | 1 | \n\n\n\n\n# Complexity\n- Time complexity: O(V + E)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n### BFS\nIn` BFS we don\'t have to check for cycle` because the Toposort results length will only be V if and only if it is a` Directed Acylic Graph (DAG).`\n\n```\nfrom queue import Queue\nclass Topo:\n def getIndegree(self,V,adj) :\n inDegree = [0 for i in range(V)]\n for node in range(V) :\n for neigh in adj[node] :\n inDegree[neigh] += 1\n return inDegree\n \n def getInitialQueue(self,inDegree,adj,V) :\n q = Queue()\n for node in range(V) :\n if inDegree[node] == 0 :\n q.put(node)\n return q\n \n def topoSort(self, V, adj):\n vis = [0 for i in range(V)]\n inDegree = self.getIndegree(V,adj)\n res = []\n q = self.getInitialQueue(inDegree,adj,V)\n \n while not(q.empty()) :\n \n cur_node = q.get()\n \n vis[cur_node] = 1\n res.append(cur_node)\n \n for neigh in adj[cur_node] :\n inDegree[neigh] -= 1\n if inDegree[neigh] == 0 :\n q.put(neigh)\n \n return res\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n adj = [[] for i in range(numCourses)]\n for edge in prerequisites :\n adj[edge[0]].append(edge[1])\n \n obj = Topo()\n res = obj.topoSort(numCourses,adj)\n if len(res) == numCourses :\n res.reverse()\n return res\n return []\n```\n### DFS\n```\nclass Solution:\n def dfs(self,node,edges,vis,inPath) :\n if inPath[node] :\n return True #cycle is present\n if vis[node] :\n return False\n \n vis[node] = 1\n inPath[node] = 1\n\n for neigh in edges[node] :\n\n if self.dfs(neigh,edges,vis,inPath) :\n return True\n\n inPath[node] = 0\n return False\n def isCyclic(self,edges, v):\n # vis = [0 for i in range(v)]\n # inPath = [0 for i in range(v)]\n adj = [[] for i in range(v)]\n vis= [0] * v\n inPath = [0] * v\n for edge in edges:\n adj[edge[0]].append(edge[1])\n for node in range(v) :\n if not(vis[node]) :\n if self.dfs(node,adj,vis,inPath) :\n return True\n return False\n def toposort(self,adj,V) :\n vis = [0 for i in range(V)]\n st = []\n\n def dfs(node) :\n vis[node] = 1\n for neigh in adj[node] :\n if not(vis[neigh]) :\n dfs(neigh)\n st.append(node)\n\n for node in range(V) :\n if not(vis[node]) :\n dfs(node)\n \n return st\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n\n V = numCourses\n adj = [[] for i in range(V)]\n for edge in prerequisites :\n adj[edge[0]].append(edge[1])\n isCyclic = self.isCyclic(prerequisites,V)\n if isCyclic :\n return []\n res = self.toposort(adj,V)\n return res \n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Topological Sorting Python | course-schedule-ii | 0 | 1 | ```\nclass Solution:\n def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:\n dic={i:[] for i in range(numCourses)}\n for crs,pre in prerequisites:\n dic[crs].append(pre)\n output=[]\n visit,cycle=set(),set()\n def dfs(crs):\n if crs in cycle:\n return False\n if crs in visit:\n return True\n cycle.add(crs)\n for pre in dic[crs]:\n if dfs(pre)==False:\n return False\n cycle.remove(crs)\n visit.add(crs)\n output.append(crs)\n return True\n for c in range(numCourses):\n if dfs(c)==False:\n return []\n return output\n ``` | 4 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
Course Schedule II | Topological Sort | Beats 97% 🔥🔥🔥 | course-schedule-ii | 1 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nSame as Course Schedule I. The only tweek is to return array instead of boolean.\n\n# Complexity\n- Time complexity: O(V+E)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] findOrder(int numCourses, int[][] prerequisites) {\n int n = prerequisites.length;\n\n ArrayList<ArrayList<Integer>> arr = new ArrayList<>();\n for(int i=0;i<numCourses;i++){\n arr.add(new ArrayList<>());\n }\n\n for(int i=0;i<n;i++){\n arr.get(prerequisites[i][0]).add(prerequisites[i][1]);\n }\n\n int[] in = new int[numCourses];\n for(int i=0;i<numCourses;i++){\n for(int it: arr.get(i)){\n in[it]++;\n }\n }\n\n Queue<Integer> q = new LinkedList<>();\n for(int i=0;i<numCourses;i++){\n if(in[i]==0) q.add(i);\n }\n\n ArrayList<Integer> res = new ArrayList<Integer>();\n while(!q.isEmpty()){\n int node = q.poll();\n\n res.add(node);\n for(int i: arr.get(node)){\n in[i]--;\n if(in[i]==0) q.add(i);\n }\n }\n int[] ans = new int[res.size()];\n for(int i=res.size()-1;i>=0;i--){\n ans[ans.length-i-1]=res.get(i);\n }\n if(res.size()!=numCourses) return new int[0];\n return ans;\n }\n}\n``` | 1 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
* For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
Return _the ordering of courses you should take to finish all courses_. If there are many valid answers, return **any** of them. If it is impossible to finish all courses, return **an empty array**.
**Example 1:**
**Input:** numCourses = 2, prerequisites = \[\[1,0\]\]
**Output:** \[0,1\]
**Explanation:** There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is \[0,1\].
**Example 2:**
**Input:** numCourses = 4, prerequisites = \[\[1,0\],\[2,0\],\[3,1\],\[3,2\]\]
**Output:** \[0,2,1,3\]
**Explanation:** There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is \[0,1,2,3\]. Another correct ordering is \[0,2,1,3\].
**Example 3:**
**Input:** numCourses = 1, prerequisites = \[\]
**Output:** \[0\]
**Constraints:**
* `1 <= numCourses <= 2000`
* `0 <= prerequisites.length <= numCourses * (numCourses - 1)`
* `prerequisites[i].length == 2`
* `0 <= ai, bi < numCourses`
* `ai != bi`
* All the pairs `[ai, bi]` are **distinct**. | This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. Topological sort could also be done via BFS. |
python3 Solution | design-add-and-search-words-data-structure | 0 | 1 | \n```\nclass WordDictionary:\n\n def __init__(self):\n self.d={}\n \n def addWord(self, word: str) -> None:\n cur=self.d\n if not self.search(word):\n for i in range(len(word)):\n if word[i] not in cur:\n cur[word[i]]={}\n cur=cur[word[i]]\n \n cur["#"]={} \n \n\n def search(self, word: str) -> bool:\n cur=self.d\n def rec(start,cur):\n if start>=len(word):\n if "#" in cur:\n return True\n else:\n return False\n \n if word[start]==".":\n for k,v in cur.items():\n if rec(start+1,v):\n return True\n return False\n elif word[start] in cur:\n if rec(start+1,cur[word[start]]):\n return True\n \n else:\n return False\n \n return rec(0,cur) \n \n\n\n# Your WordDictionary object will be instantiated and called as such:\n# obj = WordDictionary()\n# obj.addWord(word)\n# param_2 = obj.search(word)\n``` | 1 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
✅✅Python Simple Solution 🔥🔥 Easy to Understand🔥🔥 | design-add-and-search-words-data-structure | 0 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am Giving away my premium content videos related to computer science and data science and also will be sharing well-structured assignments and study materials to clear interviews at top companies to my first 1000 Subscribers. So, **DON\'T FORGET** to Subscribe\n\nhttps://www.youtube.com/@techwired8/?sub_confirmation=1\n```\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.is_word = False\n \nclass WordDictionary:\n def __init__(self):\n self.root = TrieNode() \n\n def addWord(self, word):\n current_node = self.root\n for character in word:\n current_node = current_node.children.setdefault(character, TrieNode())\n current_node.is_word = True\n \n def search(self, word):\n def dfs(node, index):\n if index == len(word):\n return node.is_word\n \n if word[index] == ".":\n for child in node.children.values():\n if dfs(child, index+1):\n return True\n \n if word[index] in node.children:\n return dfs(node.children[word[index]], index+1)\n \n return False\n \n return dfs(self.root, 0)\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D | 74 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Easy & Clear Solution Python 3 | design-add-and-search-words-data-structure | 0 | 1 | \n\n# Code\n```\n\nfrom copy import copy\nclass WordDictionary:\n\n def __init__(self):\n self.words = defaultdict(list)\n \n def addWord(self, word: str) -> None:\n self.words[len(word)].append(word)\n \n\n def search(self, word: str) -> bool:\n n=len(word)\n c=copy(self.words[n])\n if \'.\' in word:\n for i in range(n):\n if word[i]==\'.\':\n for j in range(len(c)):\n w=c[j]\n w=w[:i]+\'.\'+w[i+1:]\n c[j]=w\n return word in c\n``` | 2 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python Trie Solution 6170 ms | design-add-and-search-words-data-structure | 0 | 1 | My solution is very similar to other people\'s answers so I will just say how mine is different.\n\nI will remember the length of the longest given word, so if someone tries to \'look up\' a word that consists of more letters than the longest of our available words, then we can automatically return False.\n\nThis way our algorithm will be a lot faster.\nPlease ask any questions if something is not clear to you, after all, my code is pretty messy.\n\n\tclass TrieNode:\n\t\tdef __init__(self):\n\t\t\tself.children = dict()\n\t\t\tself.is_word = False\n\n\n\tclass Trie:\n\t\tdef __init__(self):\n\t\t\tself.root = TrieNode()\n\n\t\tdef add(self, word: str):\n\t\t\tnode = self.root\n\t\t\tfor char in word:\n\t\t\t\tif char not in node.children:\n\t\t\t\t\tnode.children[char] = TrieNode()\n\t\t\t\tnode = node.children[char]\n\n\t\t\tnode.is_word = True\n\n\t\tdef search(self, word: str, index: int, node=None):\n\t\t\tif node is None: node = self.root\n\t\t\tfor i in range(index, len(word)):\n\t\t\t\tif word[i] == \'.\':\n\t\t\t\t\tfor child in node.children.values():\n\t\t\t\t\t\tif self.search(word, i+1, child):\n\t\t\t\t\t\t\treturn True\n\t\t\t\t\treturn False\n\n\t\t\t\tif word[i] not in node.children:\n\t\t\t\t\treturn False\n\t\t\t\tnode = node.children[word[i]]\n\n\t\t\treturn node.is_word\n\n\n\tclass WordDictionary:\n\t\tdef __init__(self):\n\t\t\tself.trie = Trie()\n\t\t\tself.longest = 0\n\n\t\tdef addWord(self, word: str) -> None:\n\t\t\tself.trie.add(word)\n\t\t\tself.longest = max(self.longest, len(word))\n\n\t\tdef search(self, word: str) -> bool:\n\t\t\tif len(word) > self.longest: return False\n\t\t\treturn self.trie.search(word, 0)\n | 4 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
python3 solution with comments | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass WordDictionary:\n\n def __init__(self):\n self.root = {}\n \n\n def addWord(self, word: str) -> None:\n level = self.root\n for c in word:\n if not (c in level): \n level[c] = {}\n level = level[c]\n level[\'end\'] = True\n\n def search(self, word: str) -> bool:\n return dfs(self.root, word)\n\ndef dfs(root, s):\n # if it the end of the word return we found it\n if len(s) == 0 and (\'end\' in root): return True\n # if is the end of the word but not marked as end we return false\n if len(s) == 0: return False\n # if it is a . we shoud traverse all nodes and try to find a match\n if s[0] == \'.\':\n for c in root:\n if c != \'end\':\n # if we found one we return True\n if dfs(root[c], s[1:]): return True\n # if we don\'t find the letter in next level e return false\n if (s[0] not in root): return False\n # search next level\n return dfs(root[s[0]], s[1:]) \n\n\n# Your WordDictionary object will be instantiated and called as such:\n# obj = WordDictionary()\n# obj.addWord(word)\n# param_2 = obj.search(word)\n``` | 1 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python 3 || T/M: 100% / 99% | design-add-and-search-words-data-structure | 0 | 1 | [UPDATED 5/12/2023]\n\nSince the initial post, this problem\'s constraints and test cases were amended such that, as two WLB comments below correctly point out, the code I posted initially TLEs now.\n\nI had another version (now posted below) which was initially slower than the initial post, but now is the faster code. (Well, at least it doesn\'t TLE...)\n\nIs it a better solution? It is now, based on the new constraints and test cases. Was it a better solution before those changes? I don\'t know for sure, but xyztNull\'s excellent comment below addresses that matter.\n```\n```\nInitial post, which now TLEs:\n```\nclass WordDictionary:\n def __init__(self):\n\n self.words = defaultdict(list)\n\n\n def addWord(self, word: str) -> None:\n\n self.words[len(word)].append(word)\n\n\n def search(self, word: str) -> bool:\n\n n = len(word)\n\n if \'.\' in word:\n \n for w in self.words[n]:\n if all(word[i] in (w[i], \'.\') for i in range(n)):\n return True\n\n else: return False\n\n return word in self.words[n]\n```\n[https://leetcode.com/problems/design-add-and-search-words-data-structure/submissions/629354737/](http://)\n\n\n\nThe initially slower code, now faster:\n```\nclass Node:\n \n def __init__(self):\n \n self.d = defaultdict(Node)\n self.EOW = False\n \n\nclass WordDictionary:\n \n def __init__(self):\n self.words = Node()\n \n\n def addWord(self, word: str) -> None:\n \n cur = self.words\n for ch in word: cur = cur.d[ch]\n cur.EOW = True\n\n\n def search(self, word: str) -> bool:\n \n return self.dfs(word, self.words) \n\n \n def dfs(self, word: str, node: Node, i = 0) -> bool:\n \n if not node : return False\n if i == len(word) : return node.EOW\n\n if word[i] == \'.\' : return any(\n (self.dfs(word, child, i+1)\n for child in node.d.values()))\n\n return self.dfs(word, node.d.get(word[i]), i+1)\n```\n[https://leetcode.com/problems/design-add-and-search-words-data-structure/submissions/949187192/]() | 27 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
python super easy trie + dfs | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass WordDictionary:\n\n def __init__(self):\n self.trie = {}\n def addWord(self, word: str) -> None:\n node = self.trie\n for i in word:\n node = node.setdefault(i, {})\n node["isWord"] = word\n\n def search(self, word: str) -> bool:\n def dfs(i, root):\n if i == len(word):\n if "isWord" in root:\n return True\n return False\n\n if word[i] != ".":\n if word[i] not in root:\n return False\n return dfs(i+1, root[word[i]])\n else:\n for key in root:\n if key != "isWord":\n if dfs(i+1, root[key]):\n return True\n return False\n\n return dfs(0, self.trie)\n\n\n\n# Your WordDictionary object will be instantiated and called as such:\n# obj = WordDictionary()\n# obj.addWord(word)\n# param_2 = obj.search(word)\n``` | 1 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python Solution | design-add-and-search-words-data-structure | 0 | 1 | ```\nclass TrieNode: # Time: O(1) and Space: O(n)\n def __init__(self):\n self.children = {}\n self.word = False # flagging every word false and last word will be flagged true to differentiate\n\n\nclass WordDictionary:\n\n def __init__(self):\n self.root = TrieNode()\n\n def addWord(self, word: str) -> None: # Time: O(n) and Space: O(1)\n cur = self.root\n for c in word: # the first letter of every word will be the direct children of root node containing a-z, A-Z, 0-9, etc as the first word\n if c not in cur.children: # when the word not in roots direct children, then create a direct node for it\n cur.children[c] = TrieNode()\n cur = cur.children[c] # if the first word is present as a child of root node, then append the word to that children\n cur.word = True # when for loop ends means we are on the last word, we are flagging the last as true to differ between last, first and mid words\n\n def search(self, word: str) -> bool: # Time: O(n*n) and Space: O(1)\n\n def dfs(j, root):\n cur = root\n for i in range(j, len(word)): # will only run the searched words length from the current root\n c = word[i] # to check if c is . or defined word(a-z)\n\n if c == ".": # recursive search when . (any word) occurs\n for child in cur.children.values(): # this will run number of children times\n if dfs(i + 1, child): # searching every sub children, skipping . value by doing index+1, so we will only search its children\'s \n return True # if the dfs returns true, this will return true as it will be skipped and false will be returned\n return False\n \n else: # iterative search when a defined value is asked\n if c not in cur.children:\n return False\n cur = cur.children[c] # moving down the list \n return cur.word # cur will point to a word if it is the last(flag: True) means we have reached the end by matching every word perfectly \n\n return dfs(0, self.root) # index and root\n \n# Prefix Tree\n# root\n# / \\ \\ \\ \\\n# a b c d e\n``` | 1 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Day 78 || Trie + DFS || Easiest Beginner Friendly Sol | design-add-and-search-words-data-structure | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\n\n\n**The code implements a WordDictionary using a Trie data structure. The addWord() function inserts words into the Trie by traversing the tree level by level and creating new nodes as necessary. The search() function searches for a given word in the Trie. It calls a helper function searchHelper() which recursively traverses the Trie, checking each character of the word against the children of the current node.**\n\n**If the current character is a ".", the searchHelper() function recursively searches all children nodes, and returns true if any of them contain the remaining characters of the word. Otherwise, it continues the search along the appropriate child node based on the current character of the word. If the end of the word is reached, it returns whether the current node represents a complete word or not.**\n\n**In essence, the algorithm allows for searching words in a dictionary that may contain "." (wildcards) that can match any character.**\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Define a TrieNode class with a boolean flag \'isWordCompleted\' and an array \'children\' of TrieNode pointers, each representing a child node for a given character.\n2. Define a WordDictionary class that contains a TrieNode pointer \'root\' representing the root node of the trie.\n3. Implement the constructor for the WordDictionary class that initializes the root node to a new TrieNode object.\n4. Implement a function \'addWord\' that takes a string \'word\' as input and adds it to the trie. It starts at the root node and iterates through each character of the input word, checking if the corresponding child node exists. If the child node does not exist, a new TrieNode object is created and added as a child node. Once all the characters of the word have been added to the trie, the \'isWordCompleted\' flag of the final TrieNode is set to true.\n5. Implement a function \'searchHelper\' that takes a string \'word\', an integer \'index\' representing the current character index in the word, and a TrieNode pointer \'newRoot\' representing the current node being searched. The function recursively searches through the trie, checking if the current character in the word matches any child nodes of the current node. If the character is a \'.\', the function recursively searches all child nodes. If the end of the word is reached, the function returns true if the \'isWordCompleted\' flag of the final TrieNode is true.\n6. Implement a function \'search\' that takes a string \'word\' as input and returns a boolean representing whether or not the word is present in the trie. This function simply calls \'searchHelper\' with the input word, starting from the root node.\n\n**Overall, this algorithm represents a trie data structure that can be used to store and search for words efficiently.**\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\nclass TrieNode {\npublic:\n TrieNode* children[26];\n bool isWordCompleted;\n\n TrieNode() {\n memset(children, 0, sizeof(children));\n isWordCompleted = false;\n }\n};\n\nclass WordDictionary {\npublic:\n TrieNode* root;\n WordDictionary() {\n root = new TrieNode();\n }\n \n void addWord(string word) {\n TrieNode* newRoot = root;\n for (char ch : word) {\n int alphabetIndex = ch - \'a\';\n if (newRoot -> children[alphabetIndex] == NULL) {\n newRoot -> children[alphabetIndex] = new TrieNode();\n }\n newRoot = newRoot -> children[alphabetIndex];\n }\n newRoot -> isWordCompleted = true;\n }\n \n bool searchHelper(string word, int index, TrieNode* newRoot) {\n if (index == word.length())\n return newRoot -> isWordCompleted;\n char ch = word[index];\n if (ch == \'.\') {\n for (int i = 0; i < 26; i++) {\n if (newRoot -> children[i] != NULL && searchHelper(word, index + 1, newRoot -> children[i])) {\n return true;\n }\n }\n return false;\n }\n else {\n if (newRoot -> children[ch - \'a\'] == NULL) {\n return false;\n }\n return (searchHelper(word, index + 1, newRoot -> children[ch - \'a\']));\n }\n }\n\n bool search(string word) {\n return searchHelper(word, 0, root);\n }\n};\n\n/**\n * Your WordDictionary object will be instantiated and called as such:\n * WordDictionary* obj = new WordDictionary();\n * obj->addWord(word);\n * bool param_2 = obj->search(word);\n */\n```\n```Java []\nclass TrieNode {\n TrieNode[] children;\n boolean isWordCompleted;\n\n TrieNode() {\n children = new TrieNode[26];\n isWordCompleted = false;\n }\n}\n\nclass WordDictionary {\n TrieNode root;\n\n WordDictionary() {\n root = new TrieNode();\n }\n \n void addWord(String word) {\n TrieNode newRoot = root;\n for (char ch : word.toCharArray()) {\n int alphabetIndex = ch - \'a\';\n if (newRoot.children[alphabetIndex] == null) {\n newRoot.children[alphabetIndex] = new TrieNode();\n }\n newRoot = newRoot.children[alphabetIndex];\n }\n newRoot.isWordCompleted = true;\n }\n \n boolean searchHelper(String word, int index, TrieNode newRoot) {\n if (index == word.length())\n return newRoot.isWordCompleted;\n char ch = word.charAt(index);\n if (ch == \'.\') {\n for (int i = 0; i < 26; i++) {\n if (newRoot.children[i] != null && searchHelper(word, index + 1, newRoot.children[i])) {\n return true;\n }\n }\n return false;\n }\n else {\n if (newRoot.children[ch - \'a\'] == null) {\n return false;\n }\n return searchHelper(word, index + 1, newRoot.children[ch - \'a\']);\n }\n }\n\n boolean search(String word) {\n return searchHelper(word, 0, root);\n }\n}\n\n```\n```Python []\nclass TrieNode:\n def __init__(self):\n self.children = [None] * 26\n self.isWordCompleted = False\n\nclass WordDictionary:\n def __init__(self):\n self.root = TrieNode()\n \n def addWord(self, word: str) -> None:\n newRoot = self.root\n for ch in word:\n alphabetIndex = ord(ch) - ord(\'a\')\n if newRoot.children[alphabetIndex] is None:\n newRoot.children[alphabetIndex] = TrieNode()\n newRoot = newRoot.children[alphabetIndex]\n newRoot.isWordCompleted = True\n \n def searchHelper(self, word: str, index: int, newRoot: TrieNode) -> bool:\n if index == len(word):\n return newRoot.isWordCompleted\n ch = word[index]\n if ch == \'.\':\n for i in range(26):\n if newRoot.children[i] is not None and self.searchHelper(word, index + 1, newRoot.children[i]):\n return True\n return False\n else:\n alphabetIndex = ord(ch) - ord(\'a\')\n if newRoot.children[alphabetIndex] is None:\n return False\n return self.searchHelper(word, index + 1, newRoot.children[alphabetIndex])\n\n def search(self, word: str) -> bool:\n return self.searchHelper(word, 0, self.root)\n\n```\n\n# Time Complexity and Space Complexity:\n- **Time complexity :**\n\nThe time complexity of the addWord function is O(k), where k is the length of the word being added. This is because we are traversing through the characters of the word and creating new nodes in the Trie for each character. Therefore, the total time complexity of adding n words of total length m is O(m*n).\n\nThe time complexity of the search function depends on the length of the input word and the size of the Trie. In the worst case, we have to search through all the nodes of the Trie, which is O(26^k), where k is the length of the input word. Therefore, the time complexity of the search function is O(26^k), where k is the length of the input word.\n\nHowever, in the best case, we can return early if the prefix of the input word does not exist in the Trie, which can reduce the time complexity significantly. Moreover, if the input word contains \'.\', we need to search through all possible child nodes of the current node, which is 26 in this case. Therefore, the actual time complexity of the search function can be much less than the worst-case scenario.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity :**\n\nThe space complexity of the Trie is O(nm), where n is the number of words and m is the average length of the words. This is because we are creating a new node for each character of each word. Therefore, the total number of nodes in the Trie is proportional to nm. However, in the worst case, when all the words have no common prefix, the space complexity can be as high as O(26^m), where m is the length of the longest word. Therefore, the space complexity of the Trie depends on the input data and can be very high in certain cases.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 21 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python: TLE >>> Faster than 99% || Trie || Optimization | design-add-and-search-words-data-structure | 0 | 1 | For those who are encountering TLE, add some more check conditions\n* While inserting words in the Trie, keep the max length of all the words.\n* While searching in the Trie, if length of the word to be searched is greater than max length, return False.\n\n**Python Code:**\n\n```\nclass TrieNode:\n def __init__(self):\n self.links = {}\n self.end = False\n \nclass WordDictionary:\n\n def __init__(self):\n self.root = TrieNode()\n self.maxL = 0 #store the maximum length of all the words inserted\n \n def addWord(self, word):\n """\n :type word: str\n :rtype: None\n """\n node = self.root\n l = 0\n for w in word:\n if w not in node.links:\n node.links[w] = TrieNode()\n node = node.links[w]\n l += 1\n \n self.maxL = max(self.maxL, l)\n node.end = True\n\n def search(self, word):\n """\n :type word: str\n :rtype: bool\n """\n if len(word) > self.maxL: #optimization\n return False\n \n def helper(index, node):\n for inn in range(index, len(word)):\n c = word[inn]\n if c == ".":\n for child in node.links.values():\n if helper(inn+1, child):\n return True\n return False\n else:\n if c not in node.links:\n return False\n node = node.links[c]\n\n return node.end\n return helper(0, self.root)\n``` | 5 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python DFS | NO TLE ERROR 95%+ Time | design-add-and-search-words-data-structure | 0 | 1 | The key to using DFS and not getting a TLE error is the max_length attribute.\n```\nfrom collections import defaultdict\n\nclass TrieNode:\n def __init__(self):\n self.edges = {}\n self.isWord = False\n\nclass WordDictionary:\n\n def __init__(self):\n self.head = TrieNode()\n self.max_length = 0\n def addWord(self, word: str) -> None:\n curr = self.head\n i = 0\n for c in word:\n #check if c is in edges, if yes, move to it,\n if c not in curr.edges:\n curr.edges[c] = TrieNode()\n curr = curr.edges[c]\n i += 1\n #now mark isWord to True\n curr.isWord = True\n self.max_length = max(self.max_length, i)\n def search(self, word: str) -> bool:\n\n def dfs(j, head):\n curr = head\n \n for i in range(j, len(word)):\n c = word[i]\n if c == ".":\n # if ., iterate over all edges and make a recusrive call\n for v in curr.edges.values():\n if dfs(i + 1, v):\n return True\n return False\n else:\n if c not in curr.edges:\n return False\n curr = curr.edges[c]\n return curr.isWord\n \n if len(word) > self.max_length:\n return False\n\n return dfs(0, self.head)\n\n``` | 4 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python (Faster than 98%) | Prefix Tree (trie) with DFS | Optimization | design-add-and-search-words-data-structure | 0 | 1 | **This solution gives TLE. If you keep submitting, it will pass all test cases (rarely).**\n\n\n```\nclass TrieNode():\n def __init__(self):\n self.children = {}\n self.endOfWord = False\n\nclass WordDictionary:\n def __init__(self):\n self.root = TrieNode()\n\n def addWord(self, word: str) -> None:\n curr = self.root\n for c in word:\n if c not in curr.children:\n curr.children[c] = TrieNode()\n \n curr = curr.children[c]\n\n curr.endOfWord = True\n\n def search(self, word: str) -> bool:\n def dfs(i, root):\n curr = root\n for j in range(i, len(word)):\n c = word[j]\n if c != \'.\':\n if c not in curr.children:\n return False\n\n curr = curr.children[c]\n\n else:\n for child in curr.children.values():\n if dfs(j + 1, child):\n return True\n \n return False\n\n return curr.endOfWord\n\n return dfs(0, self.root)\n```\n# Optimized Trie\n**Keeps track of length of the longest word inserted into the trie.**\n\n\n```\nclass TrieNode():\n def __init__(self):\n self.children = {}\n self.endOfWord = False\n\nclass WordDictionary:\n def __init__(self):\n self.root = TrieNode()\n self.maxLen = 0\n\n def addWord(self, word: str) -> None:\n curr = self.root\n for c in word:\n if c not in curr.children:\n curr.children[c] = TrieNode()\n \n curr = curr.children[c]\n\n self.maxLen = max(self.maxLen, len(word)) #Keeps track of the max length\n curr.endOfWord = True\n\n def search(self, word: str) -> bool:\n if len(word) > self.maxLen: #Optimization\n return False\n\n def dfs(i, root):\n curr = root\n for j in range(i, len(word)):\n c = word[j]\n if c != \'.\':\n if c not in curr.children:\n return False\n\n curr = curr.children[c]\n\n else:\n for child in curr.children.values():\n if dfs(j + 1, child):\n return True\n \n return False\n\n return curr.endOfWord\n\n return dfs(0, self.root)\n```\n\n# Please upvote if you find this helpful. | 3 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
✔️ [Python3] TRIE (っ•́。•́)♪♬, Explained | design-add-and-search-words-data-structure | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe most efficient underlying data structure here would be the Trie. First of all, it will let us economize space by storing reusable prefixes instead of whole words. Second, the time complexity for the search will be defined by the length of the word and not by the number of words in the storage. The only downside I see here, when we search, we have to deal with `.` symbol which can signify any character and that means we have to remember all possible characters in the current level of the trie during the traversing. On every level of trie, we can have up to 26 letters, and considering the maximum word length is 500, in the case of search call with all `.` characters in the worst case, the algorithm can eat up 26^500 space in memory.\n\nTime: **O(N)** - for add and for search\nSpace: **O(26^N)** - for search\n\nRuntime: 220 ms, faster than **93.62%** of Python3 online submissions for Design Add and Search Words Data Structure.\nMemory Usage: 25.5 MB, less than **62.45%** of Python3 online submissions for Design Add and Search Words Data Structure.\n\n```\nclass WordDictionary:\n\n def __init__(self):\n self.trie = dict()\n\n def addWord(self, word: str) -> None:\n node = self.trie\n for ch in word + \'\uD83C\uDF3B\':\n if ch not in node:\n node[ch] = dict()\n\n node = node[ch]\n\n def search(self, word: str) -> bool:\n nodes = [self.trie]\n for ch in word + \'\uD83C\uDF3B\':\n newNodes = []\n for node in nodes:\n if ch == \'.\': \n newNodes += [v for v in node.values()]\n elif ch in node: \n newNodes.append(node[ch])\n\n if not newNodes:\n return False\n\n nodes = newNodes\n \n return True\n```\n\n*`\uD83C\uDF3B` - means end of the word*\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 23 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python Nested Dictionary 95% | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt\'s obviously a trie, so we can use a nested dictionary to implement it. It\'s gonna look something like this:\n```\n{\n \'b\': {\'a\': {\'d\': {\'END\': {}}}},\n \'d\': {\'a\': {\'d\': {\'END\': {}}}},\n \'m\': {\'a\': {\'d\': {\'END\': {}}}}\n}\n```\nLet\'s say you add "badd", then it\'s gonna be \n```\n\'b\': {\'a\': {\'d\': {\'END\': {}, \'d\': {\'END\': {}}}}}\n```\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAdd: \niterate through each character:\nif the char is there, go into the inner dictionary;\nif not, add a key value pair like `"m": {}`\nAfter the loop, add something like `"END: {}` to signal it\'s the end\n\nSearch:\nUse a recursive helper function. I chose to just pass in the whole word and an index.\nThe base case for this recursion is either return False or return True.\nSo when do we return False? First let\'s consider without the wildcard dot.\n1. there\'s no matching key\n2. we went through every char (i.e `index == len(word)`) but there\'s no keyword `"END"`; if "END" is there then we can return True.\n\nBase on that we can write the conditions:\n```\nif idx < len(word):\n if word[idx] not in curr:\n return False\n else:\n # recursive case\nelse:\n if "END" in curr:\n return True\n else:\n return False\n```\nThen we can add the wildcard into the picture.\nIf we see a dot, then the `word[idx] not in curr -> False` won\'t stand, so we need to do a dot check before. Now it will look something like \n```\nif idx < len(word):\n if word[idx] == ".":\n # loop through every sub dictionaries, return True if any is true\n # if all False then we can return False\n if word[idx] not in curr:\n return False\n else:\n # recursive case\nelse:\n if "END" in curr:\n return True\n else:\n return False\n```\n\nThe recursive case is just going into the sub dictionary and increment index. \n\n# Code\n```\nclass WordDictionary:\n\n def __init__(self):\n self.head = {}\n\n def addWord(self, word: str) -> None:\n head = self.head\n for char in word:\n if char not in head:\n head[char] = {}\n head = head[char]\n head["END"] = {}\n \n\n def search(self, word: str) -> bool:\n head = self.head\n return self.resursion(word, head, 0)\n \n def resursion(self, word, curr, idx):\n if idx < len(word):\n if word[idx] == ".":\n for key in curr:\n if self.resursion(word, curr[key], idx+1):\n return True\n return False\n if word[idx] not in curr:\n return False\n if idx == len(word):\n if "END" in curr:\n return True\n else:\n return False\n curr = curr[word[idx]]\n return self.resursion(word, curr, idx+1)\n\n# {\'b\': {\'a\': {\'d\': {\'END\': {}}}}, \'d\': {\'a\': {\'d\': {\'END\': {}}}}, \'m\': {\'a\': {\'d\': {\'END\': {}}}}}\n\n# Your WordDictionary object will be instantiated and called as such:\n# obj = WordDictionary()\n# obj.addWord(word)\n# param_2 = obj.search(word)\n``` | 2 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
211: Beats 99.15% and Beats 97.15%, Solution with step by step explanation | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe WordDictionary class is a data structure that supports adding new words and searching if a string matches any previously added string.\n\nThe class has three methods:\n\n- __init__(self): Initializes the object and creates a defaultdict of sets to store the words. The keys of the dictionary are the length of the words, and the values are sets of words of that length.\n- addWord(self, word: str) -> None: Adds a word to the data structure by inserting it into the set of words with the same length in the dictionary.\n- search(self, word: str) -> bool: Searches for a word in the data structure. If the word doesn\'t contain a dot character \'.\', it checks if the word exists in the set of words with the same length. If the word contains dots, it iterates over all words of the same length and checks if each character in the word matches the corresponding character in the word being searched, except for the dots.\n\n# Complexity\n- Time complexity:\nBeats\n99.15%\n\n- Space complexity:\nBeats\n97.15%\n\n# Code\n```\nfrom collections import defaultdict\n\nclass WordDictionary:\n\n def __init__(self):\n """ Initialize your data structure here. """\n # create a defaultdict of sets to store the words\n # keys are word lengths, values are sets of words of that length\n self.dic = defaultdict(set)\n\n def addWord(self, word: str) -> None:\n """ Adds a word into the data structure. """\n # add the word to the set of words with the same length\n self.dic[len(word)].add(word)\n\n def search(self, word: str) -> bool:\n """ Returns if the word is in the data structure. A word could contain the dot character \'.\' to represent any one letter. """\n # if the word doesn\'t contain dots, check if it exists in the set of words with the same length\n if \'.\' not in word:\n return word in self.dic[len(word)]\n # if the word contains dots, iterate over all words of the same length\n for v in self.dic[len(word)]:\n # check if each character in the word matches the corresponding character in the word being searched, except for the dots\n for i, ch in enumerate(word):\n if ch != v[i] and ch != \'.\':\n break\n else:\n return True\n # if no matching word is found, return False\n return False\n\n``` | 8 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
INDUSTRY STANDARD CODE | BEST CLEAN CODE | TRIE | MOST UPVOTED | design-add-and-search-words-data-structure | 1 | 1 | # INDUSTRY STANDARD CODE | BEST CLEAN CODE | TRIE | UPVOTED\n```WordDictionary []\nclass WordDictionary {\n private final Node root;\n\n public WordDictionary() {\n root = new Node();\n }\n\n public void addWord(String word) {\n Node node = this.root;\n for (char c : word.toCharArray()) {\n assert node != null;\n if (node.doesNotContainsKey(c)) node.put(c, new Node());\n node = node.get(c);\n }\n node.setEnd();\n }\n\n public boolean search(String word) {\n return root.search(word, 0, root);\n }\n}\n```\n```NODE []\nclass Node {\n private Node[] links = new Node[26];\n private boolean isCompleted = false;\n\n public void put(char c, Node node) {\n this.links[c - \'a\'] = node;\n }\n\n public Node get(char c) {\n return this.links[c - \'a\'];\n }\n\n public boolean doesNotContainsKey(char c) {\n return this.links[c - \'a\'] == null;\n }\n\n public boolean isEnd() {\n return this.isCompleted;\n }\n\n public void setEnd() {\n this.isCompleted = true;\n }\n\n public boolean search(String word, int index, Node node) {\n if (index == word.length()) return node.isEnd();\n char c = word.charAt(index);\n if (c == \'.\') {\n for (Node child : node.links)\n if (child != null && child.search(word, index + 1, child)) return true;\n return false;\n } else {\n if (node.doesNotContainsKey(c)) return false;\n return search(word, index + 1, node.get(c));\n }\n }\n}\n```\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(3^26)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n | 3 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Simple Python3 Solution || =~ 100% Faster || 11 Lines Code || Commented || {Dictionary} | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\nImplemented a trie-like approach where we are storing the length of each word in a dictionary and when searching, we are replacing the \'.\' with each letter in the alphabet and checking if the word exists in the dictionary.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nAdding a word: O(1)\nSearching a word: O(n * w^m), where n is the length of the word, w is number of words in dictionary and m is the number of \'.\' in the word. \n\n- Space complexity:\nO(k * L), where k is the number of words and L is the average length of the words.\n\n# Code\n```\nclass WordDictionary:\n\n def __init__(self):\n # create a defaultdict of sets to store the words\n self.dic = defaultdict(set)\n\n def addWord(self, word: str) -> None:\n # add the word to the set of words with the same length\n self.dic[len(word)].add(word)\n\n def search(self, word: str) -> bool:\n # If "." in word\n # check if it exists in the set of words with the same length\n if \'.\' not in word:\n return word in self.dic[len(word)]\n # if the word contains dots, iterate over all words of the same length\n for l in self.dic[len(word)]:\n # check if each letter in the word matches the respective letter\n for i, ind in enumerate(word):\n if ind != l[i] and ind != \'.\':\n break\n else:\n return True\n # if no matching word is found, return False\n return False\n \n\n# Your WordDictionary object will be instantiated and called as such:\n# obj = WordDictionary()\n# obj.addWord(word)\n# param_2 = obj.search(word)\n``` | 3 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Easy python : pure dict trie + dfs | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\nWe don\'t need to create a class like `Node` to build our trie, just using `dict`. \n\nFor `search(self, word: str)`, when meeting `.`, we need to check the next level recursively. When meeting a letter, check whether it is in `cur`, if it is, check its branch recursively.\n\n\n# Code\n```\nclass WordDictionary:\n\n def __init__(self):\n self.trie = {}\n\n def addWord(self, word: str) -> None:\n cur = self.trie\n for ch in word:\n if ch not in cur:\n # create the next level\n cur[ch] = {}\n cur = cur[ch]\n # end of a string\n cur[\'-\'] = True\n\n def search(self, word: str) -> bool:\n def dfs(cur, idx):\n # check whether it is the end of the string\n if idx == len(word):\n return \'-\' in cur\n if word[idx] == \'.\':\n for ch in cur:\n # skip this, since it is for checking\n if ch == \'-\':\n continue\n # recursively check every possible branch\n if dfs(cur[ch], idx + 1):\n return True\n if word[idx] not in cur:\n return False\n return dfs(cur[word[idx]], idx + 1)\n\n return dfs(self.trie, 0)\n``` | 3 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Python3 simple solution! | design-add-and-search-words-data-structure | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass WordDictionary:\n\n def __init__(self):\n self.text = []\n \n\n def addWord(self, word: str) -> None:\n self.text.append(word)\n \n\n def search(self, word: str) -> bool:\n if \'.\' not in word:\n return word in self.text\n\n for t in self.text:\n if len(t) != len(word):\n continue\n for i in range(len(word)):\n if word[i] == \'.\':\n continue\n if word[i] != t[i]:\n break\n else:\n return True\n return False\n \n\n\n# Your WordDictionary object will be instantiated and called as such:\n# obj = WordDictionary()\n# obj.addWord(word)\n# param_2 = obj.search(word)\n``` | 5 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
Trie Approach ---->Prefix Tree | design-add-and-search-words-data-structure | 0 | 1 | \n# Prefix Tree: Trie concept\n```\nclass TrieNode:\n def __init__(self):\n self.children={}\n self.end=False\n\nclass WordDictionary:\n def __init__(self):\n self.root=TrieNode()\n\n def addWord(self, word: str) -> None:\n current=self.root\n for w in word:\n if w not in current.children:\n current.children[w]=TrieNode()\n current=current.children[w]\n current.end=True\n\n def search(self, word: str) -> bool:\n def dfs(j,root):\n current=root\n for i in range(j,len(word)):\n c=word[i]\n if c==".":\n for child in current.children.values():\n if dfs(i+1,child):\n return True\n return False\n else:\n if c not in current.children:\n return False\n current=current.children[c]\n return current.end\n return dfs(0,self.root)\n #please upvote me it would encourage me alot\n\n\n```\n# please upvote me it would encourage me alot\n | 2 | Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the `WordDictionary` class:
* `WordDictionary()` Initializes the object.
* `void addWord(word)` Adds `word` to the data structure, it can be matched later.
* `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
**Example:**
**Input**
\[ "WordDictionary ", "addWord ", "addWord ", "addWord ", "search ", "search ", "search ", "search "\]
\[\[\],\[ "bad "\],\[ "dad "\],\[ "mad "\],\[ "pad "\],\[ "bad "\],\[ ".ad "\],\[ "b.. "\]\]
**Output**
\[null,null,null,null,false,true,true,true\]
**Explanation**
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord( "bad ");
wordDictionary.addWord( "dad ");
wordDictionary.addWord( "mad ");
wordDictionary.search( "pad "); // return False
wordDictionary.search( "bad "); // return True
wordDictionary.search( ".ad "); // return True
wordDictionary.search( "b.. "); // return True
**Constraints:**
* `1 <= word.length <= 25`
* `word` in `addWord` consists of lowercase English letters.
* `word` in `search` consist of `'.'` or lowercase English letters.
* There will be at most `2` dots in `word` for `search` queries.
* At most `104` calls will be made to `addWord` and `search`. | You should be familiar with how a Trie works. If not, please work on this problem: Implement Trie (Prefix Tree) first. |
DFS Trie Solution | word-search-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- A trie is a good data structure when dealing with lists of strings, especially when working at the character level. \n\n- Depth-first search () is a good method for finding non-repeating vertex sequences and associates well with trees in general. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Create a trie from the list of words\n2. On each point of the grid, run DFS (`explore`) on both the trie and the grid simultaneously to see if a path in the trie is consistent with a path in the graph. \n3. Prune the trie to avoid finding the same word again (and reduce the number of vertices visited).\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n$$\\mathcal{O}(mn|W|)$$ where *m* and *n* are the dimensions of the board, and *|W|* is the number of words. In the worst case, `explore` can never find any word in the trie and must explore the entire grid each time it is called.\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$\\mathcal{O}(mn|W|)$$ where *m* and *n* are the dimensions of the board, and *|W|* is the number of words. Although the visited set/array is just the input array, it is still extra space being used by the algorithm. The space complexity of the trie is $$\\mathcal{O}(|W|)$$ in the worst case as well.\n\n# Code\n```\nclass Solution:\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n # Build the trie\n trie = {}\n for word in words:\n curr_subtrie = trie\n for idx, char in enumerate(word):\n stored_word, next_subtrie = curr_subtrie.get(char, (None, {}))\n # Store the word in the final charater\'s node\n curr_subtrie[char] = (word if idx == len(word) - 1 else stored_word, next_subtrie)\n curr_subtrie = next_subtrie\n \n found = []\n m, n = len(board), len(board[0])\n def explore(i, j, curr_subtrie=trie):\n char = board[i][j]\n if char in curr_subtrie:\n # Move to the next node in the trie\n stored_word, next_subtrie = curr_subtrie[char]\n\n # Base case:\n # A word has been found\n if stored_word:\n # Add the word to the return list\n found.append(stored_word)\n # Remove the word from the trie to avoid finding duplicates\n curr_subtrie[char] = None, next_subtrie\n # Delete the subtree if it is empty (pruning)\n if not next_subtrie:\n curr_subtrie.pop(char)\n \n # Recursive step:\n # Mark the board spot as visited\n board[i][j] = "."\n if next_subtrie:\n # Recursively explore in 4 directions\n if i > 0:\n explore(i-1, j, next_subtrie)\n if i < m-1:\n explore(i+1, j, next_subtrie)\n if j > 0:\n explore(i, j-1, next_subtrie)\n if j < n-1: \n explore(i, j+1, next_subtrie)\n\n # Delete the subtree if it is empty (pruning)\n if not next_subtrie:\n curr_subtrie.pop(char)\n \n # Unmark the board spot\n board[i][j] = char\n\n # Run explore on every grid space\n # Sort of like #200 Number of Islands\n for i in range(m):\n for j in range(n):\n # As the trie gets smaller less exploration will be done\n explore(i, j)\n\n return found\n```\n\n# Notes\n\n- Poor memory usage is because of the recursion, making `explore` work iteratively would reduce memory usage.\n- Further optimizations could be made to do early stopping, but time-wise this code is very fast (beats ~98%)\n \n\n\n\n``` | 0 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
Python - Clean Trie with DFS | word-search-ii | 0 | 1 | ```\nclass Node:\n def __init__(self):\n self.children = {}\n self.word = False\n\n\nclass Trie:\n def __init__(self):\n self.root = Node()\n\n def insert(self, word: str) -> None:\n root = self.root\n\n for ch in word:\n if ch not in root.children:\n root.children[ch] = Node()\n root = root.children[ch]\n\n root.word = True \n\n\nclass Solution:\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n self.trie = Trie()\n self.rows = len(board)\n self.cols = len(board[0])\n self.ans = {}\n\n for word in words:\n self.trie.insert(word)\n\n def dfs(board, i, j, path, root):\n ch = board[i][j]\n\n # Check if current character is in trie\n root = root.children.get(ch)\n if root is None:\n return\n\n # Update path and mark visited\n path = path + [ch]\n board[i][j] = None\n\n # Add to solution if node is marked as a word in trie\n if root.word:\n word = \'\'.join(path)\n self.ans[word] = True\n\n # Right\n if j + 1 < self.cols and board[i][j+1]:\n dfs(board, i, j+1, path, root)\n\n # Left\n if j - 1 >= 0 and board[i][j-1]:\n dfs(board, i, j-1, path, root)\n\n # Down\n if i + 1 < self.rows and board[i+1][j]:\n dfs(board, i+1, j, path, root)\n\n # Up\n if i - 1 >= 0 and board[i-1][j]:\n dfs(board, i-1, j, path, root)\n \n board[i][j] = ch\n \n for i in range(self.rows):\n for j in range(self.cols):\n dfs(board, i, j, [], self.trie.root)\n\n return self.ans.keys()\n\n``` | 3 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
212: Beats 94%, Solution with step by step explanation | word-search-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nBeats\n94%\n\n- Space complexity:\nBeats\n81.69%\n\n# Code\n```\nclass Solution:\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n \n # Define a DFS function to traverse the board and search for words\n def dfs(x, y, root):\n # Get the letter at the current position on the board\n letter = board[x][y]\n # Traverse the trie to the next node\n cur = root[letter]\n # Check if the node has a word in it\n word = cur.pop(\'#\', False)\n if word:\n # If a word is found, add it to the results list\n res.append(word)\n # Mark the current position on the board as visited\n board[x][y] = \'*\'\n # Recursively search in all four directions\n for dirx, diry in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n curx, cury = x + dirx, y + diry\n # Check if the next position is within the board and the next letter is in the trie\n if 0 <= curx < m and 0 <= cury < n and board[curx][cury] in cur:\n dfs(curx, cury, cur)\n # Restore the original value of the current position on the board\n board[x][y] = letter\n # If the current node has no children, remove it from the trie\n if not cur:\n root.pop(letter)\n \n # Build a trie data structure from the list of words\n trie = {}\n for word in words:\n cur = trie\n for letter in word:\n cur = cur.setdefault(letter, {})\n cur[\'#\'] = word\n \n # Get the dimensions of the board\n m, n = len(board), len(board[0])\n # Initialize a list to store the results\n res = []\n \n # Traverse the board and search for words\n for i in range(m):\n for j in range(n):\n # Check if the current letter is in the trie\n if board[i][j] in trie:\n dfs(i, j, trie)\n \n # Return the list of results\n return res\n\n```\nThe basic idea of the solution is to use a trie data structure to efficiently search for words on the board. We first build the trie from the list of words, where each node in the trie represents a letter in a word and the \'#\' symbol indicates the end of a word. Then, we traverse the board and use a depth-first search (DFS) algorithm to search for words starting from each position on the board. We use the trie to efficiently traverse the board and check if each sequence of letters corresponds to a valid word in the trie. When a valid word is found, we add it to the results list. Finally, we return the list of results. | 14 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
[Python] Accepted 2022 Backtracking + Tries | word-search-ii | 0 | 1 | 1. build tries\n2. do backtracking based on each node.child\n\nIt\'s my first post, seeking for votes. Thank you all!\n\n```\nclass Node:\n def __init__(self):\n self.child = {}\n self.end = None # word\n \nclass Tries:\n def __init__(self):\n self.root = Node()\n \n def inser_word(self, word):\n \n cur = self.root\n for c in word:\n if c in cur.child:\n cur = cur.child[c]\n else:\n cur.child[c] = Node()\n cur = cur.child[c]\n cur.end = word\n\n # O(M(4(3**L-1)))\nclass Solution:\n\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n \n # tries build tries\n # backtracking in each node\n # if neibor in node.child\n Rows, Cols = len(board), len(board[0])\n \n tries = Tries()\n visited = set()\n RR = set(range(Rows))\n CC = set(range(Cols))\n \n for word in words:\n tries.inser_word(word)\n \n words = set(words)\n direction = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n \n res = set()\n \n def backtracking(r, c, node):\n \n if node.end:\n res.add(node.end)\n \n if not node.child:\n return\n \n for dr, dc in direction:\n row, col = r + dr, c + dc\n if row in RR and col in CC and (row, col) not in visited and board[row][col] in node.child:\n visited.add((row, col))\n backtracking(row, col, node.child[board[row][col]])\n visited.remove((row, col))\n \n\n for i in range(Rows):\n for j in range(Cols):\n if board[i][j] in tries.root.child:\n visited.add((i, j))\n backtracking(i, j, tries.root.child[board[i][j]])\n visited.remove((i, j))\n return res\n \n \n``` | 3 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
✔️ | Python | Trie Easy Solution | word-search-ii | 0 | 1 | # Code\n```\nclass Solution:\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n res = []\n Trie = lambda : defaultdict(Trie)\n root = Trie()\n def add(s):\n cur = root\n for c in s: cur = cur[c]\n cur[\'$\'] = s\n \n for word in words: add(word)\n m, n = len(board), len(board[0])\n \n def dfs(i, j, root):\n ch = board[i][j]\n cur = root.get(ch)\n if not cur: return \n\n if \'$\' in cur: \n res.append(cur[\'$\'])\n del cur[\'$\']\n \n board[i][j] = \'#\'\n if i<m-1: dfs(i+1, j, cur)\n if i>0: dfs(i-1, j, cur)\n if j<n-1: dfs(i, j+1, cur)\n if j>0: dfs(i, j-1, cur)\n board[i][j] = ch\n\n for i in range(m):\n for j in range(n):\n dfs(i, j, root)\n return res\n \n \n``` | 3 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
Python using (Trie) | Backtracking | word-search-ii | 0 | 1 | Comment if you have any queries. \n# Code\n```\n\n// I used single class to implemnet trie,\n// It can be easier to understand by implementing Trie Node and\n// Trie implementation in different classes as Leetcode# 208\n\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.word_end = False\n \n def insert(self, word):\n curr = self\n for character in word:\n if character not in curr.children:\n curr.children[character] = TrieNode()\n curr = curr.children[character]\n curr.word_end = True\n \n def delete(self, word):\n curr = self\n stack = []\n for character in word:\n if character not in curr.children:\n return False\n stack.append(curr)\n curr = curr.children[character]\n\n if not curr.word_end:\n return False\n\n curr.word_end = False\n for char in word[::-1]:\n if len(curr.children) == 0 and not curr.word_end:\n curr = stack.pop()\n del curr.children[char]\n return True\n \nclass Solution:\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n ROW, COL = len(board), len(board[0])\n trie = TrieNode()\n for word in words:\n trie.insert(word)\n\n// I use get_nbr function for any matrix related problems, \n// I have seen people using one liner for this\ndef get_nbr(row, col):\n\n result = []\n \n if row-1 >= 0:\n result.append((row-1, col))\n if col-1 >=0 : \n result.append((row, col-1))\n \n if row+1 < ROW: \n result.append((row+1, col))\n if col+1 < COL: \n result.append((row, col+1))\n\n return result\n\n visited = set()\n res = set()\n def backtracking(row, col, node, slate):\n character = board[row][col]\n\n if character in node.children and (row, col) not in visited:\n visited.add((row, col))\n node = node.children[character]\n slate += character\n\n if node.word_end:\n res.add(slate)\n if len(node.children) == 0:\n trie.delete(slate)\n \n for nbr_row, nbr_col in get_nbr(row, col):\n backtracking(nbr_row, nbr_col, node, slate)\n \n visited.remove((row, col))\n\n for row in range(ROW):\n for col in range(COL):\n backtracking(row, col, trie, "")\n\n return res\n \n```\n**DFS can be done this way to instead of first one**\nThis feels more intuitive to me.\n```\n def dfs(row, col, curr, slate):\n\n visited.add((row, col))\n curr_character = board[row][col]\n\n\n if curr_character in curr.children:\n curr = curr.children[curr_character]\n slate += [curr_character]\n\n if curr.is_word:\n output.add(\'\'.join(slate[:]))\n if len(curr.children) == 0:\n trie.delete(\'\'.join(slate[:]))\n\n for nbr_row , nbr_col in get_nbr(row, col):\n if (nbr_row, nbr_col) not in visited:\n dfs(nbr_row, nbr_col, curr, slate)\n slate.pop()\n\n\n visited.remove((row, col))\n``` | 1 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
Python Trie+DFS || ⚡⚡ 53 ms Beats 99.89% ⚡⚡ || ⭐⭐Optimized for LeetCode Tests and well commented⭐⭐ | word-search-ii | 0 | 1 | ### Solution using Trie + DFS + optimizations directed at the LeetCode tests.\n\n- Use a trie to do quick lookups of the words, since the words are max 10 characters long, looking up a word in the trie can be done in O(1). \n- Iterate over all the positions in the matrix doing DFS starting at that position and moving to its neighbors while the words that we are constructing are prefixes found in the trie. \n- When we find a word, add it to the result set. \n\n### If you like this solution, don\'t forget to \uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4DUPVOTE! \uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4D\n\n**NOTE:** Using the trie to do prefix and word lookups is probably all that is expected in an interview, but adding the word removal is an optimization that could be discussed.\n\n#### The Trie class\n\nThis solution uses a Trie class instead of a TrieNode. This leads to having to check the entire path in the trie at each interation of the DFS, while using a TrieNode allows us to pass the current TrieNode in the recursive call and would seem more optimal. \n\nI tested and I was getting worst performance using TrieNode and passing it as a parameter of the `dfs()` call vs using the Trie class and having to check the entire path, of max length 10, on each call, so I went on ahead with using the Trie class.\n\nOn an interview I would favor using TrieNodes because they would be more readable and easier to maintain.\n\n```\n# A fast trie implementation, not as readable as using TrieNodes but\n# more performant.\n#\n# https://github.com/raul-sauco/coding-challenges/blob/main/leetcode/implement-trie-prefix-tree.py\n#\nclass Trie:\n def __init__(self, words: List[str] = None):\n\t\t# The variable length stores the total number of children of this node.\n self.root = {"length": 0}\n for word in words:\n self.insert(word)\n\t\t\t\n\t# Having a len method helps debug.\n def __len__(self) -> int:\n return self.root["length"]\n\n # Insert a word into this trie object. O(1) because max word length is 10 chars.\n def insert(self, word: str) -> None:\n current = self.root\n for c in word:\n if c not in current:\n current[c] = {"length": 0}\n # There is more complete word under this node.\n current["length"] += 1\n current = current[c]\n current["length"] += 1\n current["?"] = True\n\n # Remove a word from this trie object. O(1) because max word length is 10.\n def remove(self, word: str) -> None:\n current = self.root\n current["length"] -= 1\n for i, c in enumerate(word):\n if c in current:\n current[c]["length"] -= 1\n if current[c]["length"] < 1:\n current.pop(c)\n break\n else:\n current = current[c]\n # If we get to the word leaf but the trie node has children.\n if i == len(word) - 1 and "?" in current:\n current.pop("?")\n\n # Check if a given list of chars is in the trie, it returns 0 if\n # not found, 1 if found but not a full word and 2 if a full word.\n\t# O(1) because max word length is 10.\n def contains(self, word: List[str]) -> int:\n current = self.root\n for c in word:\n if c not in current:\n return 0\n current = current[c]\n return 2 if "?" in current else 1\n```\n\n### The Solution class\n\nThis is very similar to other solutions here, use the Trie for lookups and do DFS from each cell in the board, the solution was running in 5/6 seconds in average, which placed it in the bottom 70%, until I looked at the tests and saw that a lot of the time was being wasted checking long paths that could not lead to a word.\n\n##### Adding two small optimizations led to the running time decreasing from 5/6 seconds to 53ms.\n\n**First optimization:** Create a dictionary of all the two letter combinations found in the board, only do this for combinations going right and down. The iterate over all the input words checking if all the sequences of two characters in the word can be found in the lookup dictionary, either in regular or reverse form. We create a list of _candidates_ that are words that could be found in the board, and use this on to fill the trie, instead of all the words in the input.\n\n**Second optimization:** Create a lookup of reversed words, when we are adding words to the trie, check if the first character repeats itself at the beginning of the word, I choose 4 times as the limit. If the first 4 characters are the same, then reverse the word, add it to the trie, reversed, and to the reversed words lookup.\n\n**NOTE:** Reversing the characters would still work, even if we had a word and its anadrome in the input, because we are removing the reversed words from the lookup once we find one instance of them. By the time we find the anadrome, it would be interpreted as a non-reversed word.\n\n**NOTE:** This optimizations, specially the second one, are directed to the LeetCode tests in particular, with other input data, for example dictionary words, I believe that they wouldn\'t lead to any significant performance improvement.\n\n\n```\n# https://github.com/raul-sauco/coding-challenges/blob/main/leetcode/word-search-ii.py\n\n# Time complexity: O(m*n*(4*3^10)) - We iterate over all the positions\n# on the board, for each, we start a search for any words that can be\n# constructed from this position, the search will initially move to the\n# four neighbors, then from there, as long as the characters added are\n# found in the trie, the search will expand to the three neighbors of\n# the new cell, since the cell we just came from cannot be visited again.\n# So, from each position in the matrix, we will potentially do 4*3^10\n# calls to DFS, since the max depth is equal to the length of the\n# longest word in the trie and that is a max of 10. In theory that is\n# still O(1) but it seems significant enough that is worth mentioning it\n# on the time complexity.\n#\n# Space complexity: O(w*c) - The number of characters in all the words\n# in the input, we store them all in the trie, and potentially also in\n# the result set even though we would not consider that because it is\n# used as the output. The call stack will have a max height of 10.\n#\nclass Solution:\n def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:\n NUM_ROWS, NUM_COLS = len(board), len(board[0])\n # Remove words for which one of their two letter combinations\n # cannot be found in the board.\n seq_two = set()\n candidates = []\n reversed_words = set()\n # Find all sequences of two characters in the board. Only right\n # and down.\n for i in range(NUM_ROWS):\n for j in range(NUM_COLS - 1):\n seq_two.add(board[i][j] + board[i][j + 1])\n for j in range(NUM_COLS):\n for i in range(NUM_ROWS - 1):\n seq_two.add(board[i][j] + board[i + 1][j])\n # Iterate over the words checking if they could be in the board.\n for word in words:\n in_board = True\n for i in range(len(word) - 1):\n # For each sequence of two characters in the word, check\n # if that sequence or its inverse are in the board.\n if (\n word[i : i + 2] not in seq_two\n and word[i + 1] + word[i] not in seq_two\n ):\n in_board = False\n break\n if not in_board:\n continue\n # Reverse words with the same character in the first\n # four positions.\n if word[:4] == word[0] * 4:\n word = word[::-1]\n reversed_words.add(word)\n candidates.append(word)\n\n NUM_ROWS, NUM_COLS = len(board), len(board[0])\n # Store the words found.\n res = set()\n # Initialize a Trie with the words in the input that could be in\n # the board potentially, the candidates, some of them may have\n # been reversed to make finding them more efficient.\n trie = Trie(candidates)\n # Define a function that explores the board from a given start\n # position.\n def dfs(row: int, col: int, current: List[str]) -> None:\n current.append(board[row][col])\n board[row][col] = "."\n found = trie.contains(current)\n # If the current branch is not in the trie, not point on\n # exploring any further.\n if not found:\n board[row][col] = current.pop()\n return\n # If this is an exact match, add it to the result set.\n if found == 2:\n w = "".join(current)\n if w in reversed_words:\n res.add(w[::-1])\n reversed_words.remove(w)\n else:\n res.add(w)\n trie.remove(w)\n # The four directions where neighbors are found.\n dirs = ((0, 1), (0, -1), (1, 0), (-1, 0))\n for di, dj in dirs:\n i, j = row + di, col + dj\n if (\n 0 <= i < NUM_ROWS\n and 0 <= j < NUM_COLS\n and board[i][j] != "."\n ):\n dfs(i, j, current)\n # Backtrack.\n board[row][col] = current.pop()\n\n for i in range(NUM_ROWS):\n for j in range(NUM_COLS):\n dfs(i, j, [])\n return res\n```\n\n#### Runtime: \n\nhttps://leetcode.com/problems/word-search-ii/submissions/836918548/\n\n\n\n\n### If you liked this solution, don\'t forget to \uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4DUPVOTE! \uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4D\n | 9 | Given an `m x n` `board` of characters and a list of strings `words`, return _all words on the board_.
Each word must be constructed from letters of sequentially adjacent cells, where **adjacent cells** are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
**Example 1:**
**Input:** board = \[\[ "o ", "a ", "a ", "n "\],\[ "e ", "t ", "a ", "e "\],\[ "i ", "h ", "k ", "r "\],\[ "i ", "f ", "l ", "v "\]\], words = \[ "oath ", "pea ", "eat ", "rain "\]
**Output:** \[ "eat ", "oath "\]
**Example 2:**
**Input:** board = \[\[ "a ", "b "\],\[ "c ", "d "\]\], words = \[ "abcb "\]
**Output:** \[\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 12`
* `board[i][j]` is a lowercase English letter.
* `1 <= words.length <= 3 * 104`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* All the strings of `words` are unique. | You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier? If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.