title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
EASY DP & RECURSIVE BOTH SOL || Python | house-robber-ii | 0 | 1 | # Intuition\nIn recursive Apporoach u will get a TLE in this question so DP is an optimized acceptable solution her.\nBase Cases\n`1. If only 1 house present return it as max amount to be robbed`\n`2. If only 2 houses present return the max of them`\n\n\nHow this question is different from House Robbers I?\nBecause the houses are in circular manner so u can go -\nFrom `0 => n - 2` (last House excluded as in circular it will be adjacent to the first house and we cant rob it)\nFrom `1 => n - 1`\nSo for each choice define a dp and find the max item u can rob exact similarly like house robbers I and from both choices i.e starting from either 0 index or 1 index choose which gives the max ans.\n\n# Code\n```\nclass Solution:\n def rob(self, arr: List[int]) -> int:\n n = len(arr)\n if n == 1:\n return arr[0]\n if n == 2:\n return max(arr[0], arr[1])\n def maxRob(lastRange, startRange):\n dp = [0] * (n + 1) # for each choice a unique dp defined\n for i in range(startRange, lastRange):\n if dp[i] != 0:\n return dp[i]\n pick = arr[i] + dp[i-2] #pick it & then check for next to next\n notPick = 0 + dp[i-1] #dont pick check for next\n dp[i] = max(notPick, pick)\n # print(max(dp)) -->\n return max(dp)\n range1 = maxRob(n-1, 0)\n range2 = maxRob(n, 1)\n # print(range1, range2)\n return max(range1, range2)\n\n\n \n #RECURSION -> GIVES TLE\n\n n = len(arr)\n if n == 1:\n return arr[0]\n if n == 2:\n return max(arr[0], arr[1])\n def recur(i, lastPossible):\n if i == lastPossible:\n return arr[i]\n if i < lastPossible:\n return 0\n pick = arr[i] + recur(i-2, lastPossible)\n notPick = 0 + recur(i-1, lastPossible)\n maxi = max(pick, notPick)\n return maxi\n r1 = recur(n-2, 0)\n r2 = recur(n-1, 1)\n # print(max(r1, r2))\n return max(r1, r2)\n``` | 1 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Best 100% || Dp || Space space optimization 🔥🔥🥇🥇✅✅🧠🧠 | house-robber-ii | 0 | 1 | # Intuition\n\n\n# Approach\n\n\nThe code defines a function called maxPrice that takes a list of integers as input and returns the maximum amount of money that can be robbed from that list of houses, subject to the adjacent house constraint. The maxPrice function uses dynamic programming to solve the problem by maintaining two variables prev and prev2, which represent the maximum amount of money that can be robbed up to the previous and second-to-previous houses, respectively.\n\nThe function then iterates through the list of houses and for each house, it calculates two possible values:\n\n* take, which represents the maximum amount of money that can be robbed if the current house is robbed, and\n* not_take, which represents the maximum amount of money that can be robbed if the current house is not robbed.\nThe function then takes the maximum value between take and not_take, and stores it in the variable cur. It updates the prev2 and prev variables accordingly and continues the iteration.\n\nFinally, the rob function calls maxPrice twice - once on the input list with the first element removed (nums[1:]), and once on the input list with the last element removed (nums[:-1]). It then returns the maximum of the two values obtained from the maxPrice function calls, which represents the maximum amount of money that can be robbed from the entire row of houses.\n\n# Complexity\n- Time complexity:\n0(n)\n\n- Space complexity:\n0(1)\n\n# Code\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n def maxPrice(arr):\n prev = arr[0]\n prev2 = 0\n for i in range(1,len(arr)):\n take = arr[i]\n if i>1:\n take+=prev2\n not_take =0+prev\n cur = max(take,not_take)\n prev2 = prev\n prev = cur\n return prev\n if len(nums)<=1:\n return nums[0]\n\n ans1 = maxPrice(nums[1:])\n ans2 = maxPrice(nums[:-1])\n return max(ans1,ans2)\n``` | 2 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Only 1 for loop required! Pseudocode included! | house-robber-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\n"""\nTestcases:\n5,3,5\n5\n\n5,3,2,5\n8\n\n10,2,3,12,23,41\n14 ////\n\nIdea:\nthere\'s two path in here, one is without the first house, and the second one is with out the last house\n\nreturn the maximum path of those two\n\nPseudocode:\nso for path 1: the house include house 1\npath_1_pre_1 = the path 1 previous house optimal gain\npath_1_pre_2 = the path 1 previous previous house optimal gain\nand for path2: the house exclude house 1\npath_2_pre_1 = the path 2 previous house optimal gain\npath_2_pre_2 = the path 2 previous previous house optimal gain\n\nif the hosue lenght is less than 3:\n return maximum of the hosue since it\'s only size 2\n\nseth up the path variable:\npath_1_pre_2 = first house\npath_1_pre_1 = max(firsthouse,second house)\npath_2_pre_2 = house 2\npath_2_pre_1 = max(house 2, house 3)\n\nfor loop starts at 4till the end:\n temp_1 for storing a temp varaible for path_1_pre_1\n temp_2 for storing a temp varaible for path_2_pre_1\n path_1_pre_1 = max(path_1_pre_2+the cur house,path_1_pre_1)\n path_2_pre_1 = max(path_2_pre_2 + the cur house,path_2_pre_1)\n then we just update the previous two house with the temp variable that we store \n\nreturn maximum of either path_1_pre_1 and path_2_pre_1\n\n"""\n\n\n\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n if len(nums) < 4:\n return max(nums)\n \n path_1_pre_2 = max(nums[0],nums[1])\n path_1_pre_1 = max(nums[0]+nums[2], nums[1])\n path_2_pre_2 = nums[1]\n path_2_pre_1 = max(nums[1], nums[2])\n\n for i in range(3,len(nums)-1):\n temp_1 = path_1_pre_1\n temp_2 = path_2_pre_1\n path_1_pre_1 = max(path_1_pre_2 + nums[i], path_1_pre_1)\n path_2_pre_1 = max(path_2_pre_2 + nums[i], path_2_pre_1)\n path_1_pre_2 = temp_1\n path_2_pre_2 = temp_2\n\n\n return max(path_1_pre_1, max(path_2_pre_1,path_2_pre_2+nums[-1]))\n \n\n\n\n\n\n\n \n``` | 2 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Easy & Clear Python 3 Solution Recursive + memo (top-down). | house-robber-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n if len(nums)==1:\n return nums[0]\n memo=[-1 for _ in range(len(nums))]\n def dp(i):\n if i<0:\n return 0 \n elif memo[i]>=0:\n return memo[i]\n else:\n res=max(dp(i-2)+nums[i],dp(i-1))\n memo[i]=res\n return res\n a=dp(len(nums)-2)\n memo=[-1 for _ in range(len(nums))]\n nums.pop(0)\n b=dp(len(nums)-1)\n return max(a,b)\n``` | 6 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Python || 99.19% Faster || Dynamic Programming | house-robber-ii | 0 | 1 | ```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n def solve(a,n):\n n=len(a)\n prev=a[0]\n prev2=0\n curr=0\n for i in range(1,n):\n pick=a[i]\n if i>1:\n pick+=prev2\n non_pick=prev\n curr=max(pick,non_pick)\n prev2=prev\n prev=curr\n return prev\n if len(nums)==1:\n return nums[0]\n n=len(nums)\n return max(solve(nums[1:],n),solve(nums[:-1],n))\n```\n**An upvote will be encouraging** | 3 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Python Very Simple and Clean DP Solution - faster than 97% | house-robber-ii | 0 | 1 | ```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n def houseRobber(nums):\n # dynamic programming - decide each problem by its sub-problems:\n dp = [0]*len(nums)\n dp[0] = nums[0]\n dp[1] = max(nums[0], nums[1])\n for i in range(2, len(nums)):\n dp[i] = max(dp[i-1], nums[i]+dp[i-2])\n\n return dp[-1]\n \n # edge cases:\n if len(nums) == 0: return 0\n if len(nums) == 1: return nums[0]\n if len(nums) == 2: return max(nums)\n \n # either use first house and can\'t use last or last and not first:\n return max(houseRobber(nums[:-1]), houseRobber(nums[1:]))\n```\n**Like it? please upvote...** | 64 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
O(N) Approach time Complexity | house-robber-ii | 0 | 1 | \n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n #time complexity---->O(N)\n def house(nums):\n rob1,rob2=0,0\n for num in nums:\n temp=max(num+rob1,rob2)\n rob1=rob2\n rob2=temp\n return rob2\n return max(house(nums[1:]),house(nums[:-1]),nums[0])\n```\n | 6 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
213: Solution with step by step explanation | house-robber-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the class Solution, which contains the rob() method that takes a list of integers as input and returns an integer.\n2. Check the edge case where the input list is empty. If this is true, return 0 because there is nothing to rob.\n3. Check the edge case where the input list has only one element. If this is true, return that element because it is the only one that can be robbed without alerting the police.\n4. Define a nested function rob(l: int, r: int) -> int that takes two integers l and r as input and returns an integer.\n5. Initialize two variables dp1 and dp2 to 0. These will hold the dynamic programming values for the current and previous houses, respectively.\n6. Loop through the range of indices from l to r inclusive.\n7. Store the current value of dp1 in a temporary variable temp.\n8. Update dp1 to be the maximum of dp1 and dp2 plus the value of the current house.\n9. Update dp2 to be the previous value of dp1 (i.e., temp).\n10. Return dp1, which holds the maximum amount of money that can be robbed without alerting the police.\n11. In the main rob() function, call rob(0, len(nums) - 2) to calculate the maximum amount that can be robbed without robbing the last house (because it is adjacent to the first house in a circular arrangement).\n12. Also call rob(1, len(nums) - 1) to calculate the maximum amount that can be robbed without robbing the first house.\n13. Return the maximum of these two values, which represents the maximum amount that can be robbed without alerting the police in the circular arrangement of houses.\n# Complexity\n- Time complexity:\nBeats\n65.76%\n\n- Space complexity:\nBeats\n97.69%\n\n# Code\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n if not nums:\n return 0\n if len(nums) < 2:\n return nums[0]\n\n def rob(l: int, r: int) -> int:\n dp1 = 0\n dp2 = 0\n\n for i in range(l, r + 1):\n temp = dp1\n dp1 = max(dp1, dp2 + nums[i])\n dp2 = temp\n\n return dp1\n\n return max(rob(0, len(nums) - 2),\n rob(1, len(nums) - 1))\n\n``` | 6 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Dynamic Programming Logic | house-robber-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n def house(nums):\n rob1,rob2=0,0\n for num in nums:\n temp=max(num+rob1,rob2)\n rob1=rob2\n rob2=temp\n return rob2\n return max(house(nums[1:]),house(nums[:-1]),nums[0])\n #please upvote me it would encourage me alot\n\n \n \n \n``` | 5 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
PYTHON || EASY TO UNDERSTAND || TOP DOWN RECUSRIVE W/ MEMOISATION || 2 SOLUTIONS | house-robber-ii | 0 | 1 | # Solution 1 - in each recursion, decide to skip or take:\nThis requires 2 initial recursive calls (one with first house removed, and one with last house removed)\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n cache1 = {}\n cache2 = {}\n\n def helper(i, nums, cache):\n if i >= len(nums):\n return 0\n\n if i in cache:\n return cache[i]\n\n take = nums[i] + helper(i + 2, nums, cache)\n skip = helper(i + 1, nums, cache)\n\n cache[i] = max(take, skip)\n return cache[i]\n\n return max(nums[0], helper(0, nums[1:], cache1), helper(0, nums[:-1], cache2))\n```\n\n# Solution 2 - in each recursion, always take:\nThis requires 4 initial recursive calls\nThis requires 2 calls for first house removed, and 2 calls for last house removed - the 2 calls start on either the 1st or 2nd house\n```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n cache1 = {}\n cache2 = {}\n\n def helper(i, nums, cache):\n if i >= len(nums):\n return 0\n\n if i in cache:\n return cache[i]\n\n cache[i] = nums[i] + max(helper(i + 2, nums, cache), helper(i + 3, nums, cache))\n return cache[i]\n\n removedFirst = max(helper(0, nums[1:], cache1), helper(1, nums[1:], cache1))\n removedLast = max(helper(0, nums[:-1], cache2), helper(1, nums[:-1], cache2))\n\n return max(nums[0], removedFirst, removedLast)\n``` | 1 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
📌 Do house robber twice | house-robber-ii | 0 | 1 | ```\nclass Solution:\n def rob(self, nums: List[int]) -> int:\n \n if len(nums) == 1:\n return nums[0]\n \n dp = {}\n def getResult(a,i):\n if i>=len(a):\n return 0\n if i in dp:\n return dp[i]\n \n sum = 0\n if i<len(a)-1:\n sum+= max(a[i]+getResult(a,i+2),a[i+1]+getResult(a,i+3))\n else:\n sum+=a[i]+getResult(a,i+2)\n dp[i] = sum\n return sum\n \n x = getResult(nums[:len(nums)-1],0)\n dp = {}\n y = getResult(nums[1:],0)\n \n return max(x, y)\n``` | 4 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are **arranged in a circle.** That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
Given an integer array `nums` representing the amount of money of each house, return _the maximum amount of money you can rob tonight **without alerting the police**_.
**Example 1:**
**Input:** nums = \[2,3,2\]
**Output:** 3
**Explanation:** You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
**Example 2:**
**Input:** nums = \[1,2,3,1\]
**Output:** 4
**Explanation:** Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved. |
Brute force | shortest-palindrome | 0 | 1 | # Intuition\nFirst, we need to find the pre-existing palindrome in the string (if it is there). Then, we\'ll add characters to complete that palindrome.\n\n# Approach\nI created a reversed string \'p\'. Then, I iterated over the length of \'s\' and check if the inital \'n-i\' characters of \'s\' are same as the last \'n-i\' characters of \'p\'. If they are equal, loop breaks as we\'ve found a palindrome. Else, the last character is added to a string, which is eventually added to the original string \'s\'.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\nBecause there\'s a for loop and then we\'re slicing the string. (n+n-1+n-2 .. ~ n(n-1)/2)\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n p = s[::-1]\n add = ""\n n = len(s)\n for i in range (n):\n a = s[0:n-i]\n b = p[i:]\n if (a!=b):\n add+=a[-1]\n else:\n break\n return add+s\n``` | 1 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
No brain Python solution | shortest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n if s == s[::-1]:\n return s\n for i in range(1, len(s)):\n if s[-i:][::-1]+s == (s[-i:][::-1]+s)[::-1]:\n return s[-i:][::-1]+s\n``` | 2 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Recursion | shortest-palindrome | 0 | 1 | # Approach\nFirst, found the longest prefix of the string that is a palindrome and stored the length. Then reversed the remaining substring. Recursively found the palindrome of the remaining substring and appended it to original string. For base case, if i equals to n (length of string), then s is returned.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n i = 0\n n = len(s)\n for j in range(n):\n if s[i] == s[n-j-1]:\n i += 1\n if i==n:\n return s\n p = s[i:n][::-1]\n return p + self.shortestPalindrome(s[:i]) + s[i:]\n``` | 2 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
214: 90.2%, Solution with step by step explanation | shortest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis is a simple and efficient solution that uses string slicing to reverse the original string and check prefixes of the reversed string to find the longest palindrome suffix in the original string. Then it prepends the remaining characters in the reversed string to the original string to get the shortest palindrome.\n\nHere is a step-by-step explanation of the code:\n\n1. Reverse the original string and store it in a variable t.\n```\nt = s[::-1]\n```\n2. Iterate through each index i in the reversed string t.\n\n3. Check if the original string s starts with the suffix of t from index i to the end.\n```\nif s.startswith(t[i:]):\n```\n4. If a palindrome suffix is found, prepend the remaining characters in t to s to create the shortest palindrome.\n```\nreturn t[:i] + s\n```\n5. If no palindrome suffix is found, the entire reversed string t must be added to the front of s to create the shortest palindrome.\n```\nreturn t + s\n```\n# Complexity\n- Time complexity:\nBeats 90.2%\n\n- Space complexity:\nBeats 45.21%\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n t = s[::-1]\n\n for i in range(len(t)):\n if s.startswith(t[i:]):\n return t[:i] + s\n\n return t + s\n``` | 8 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
100% Faster Python Solution - using KMP Algorithm | shortest-palindrome | 1 | 1 | \tclass Solution:\n\t\tdef shortestPalindrome(self, s: str) -> str:\n\t\t\tdef kmp(txt, patt):\n\t\t\t\tnewString = patt + \'#\' + txt\n\t\t\t\tfreqArray = [0 for _ in range(len(newString))]\n\t\t\t\ti = 1\n\t\t\t\tlength = 0\n\t\t\t\twhile i < len(newString):\n\t\t\t\t\tif newString[i] == newString[length]:\n\t\t\t\t\t\tlength += 1\n\t\t\t\t\t\tfreqArray[i] = length\n\t\t\t\t\t\ti += 1\n\t\t\t\t\telse:\n\t\t\t\t\t\tif length > 0:\n\t\t\t\t\t\t\tlength = freqArray[length - 1]\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tfreqArray[i] = 0\n\t\t\t\t\t\t\ti += 1\n\t\t\t\treturn freqArray[-1]\n\t\t\tcnt = kmp(s[::-1],s)\n\t\t\treturn s[cnt:][::-1]+s\n\n\n | 2 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Rabin Karp and KMP | shortest-palindrome | 0 | 1 | # Code\n```\nclass Solution:\n\n # https://leetcode.com/problems/shortest-palindrome/solutions/60153/8-line-o-n-method-using-rabin-karp-rolling-hash/\n # There is a slight chance that ther could be a hash collision. But this is very \n # unlikely. And we can add check for this where we save all the i values when \n # hash was equal and then compare the i values to see if the sbstring is a palandrome\n def usingRK(self, s):\n # Convert letter to id\n def id(letter): return ord(letter) - ord(\'a\')\n\n hash1, hash2 = 0, 0\n base = 26\n mod = 10**9 + 7\n power = 1 # We update power so new incoming letter gets highest weight \n # The first character will be a palandrome. So we no longer palandrome we can atleast \n # use this: abcd --> dcbabcd (we reuse a and only reverse bcd since a is a palandrome)\n pal = 0 \n for i in range(len(s)):\n hash1 = (hash1 * base + id(s[i])) % mod # First char has highest weight \n hash2 = (hash2 + id(s[i]) * power) % mod # Last char has highest weight \n power = power * base # Power is updated each time so its equal to base ^ (n-1)\n if hash1 == hash2:\n print(i)\n # For aacecaaa this will be true for 0, 1, 6 index \n # This works because we calculate hash in 2 directions \n # 1st - Leftmost char has highest weight \n # 2nd - Leftmost char has least weight\n # When all the characters in string form palandrome \n # The weights will balance each other and the hash will be same \n pal = i\n # Reverse substring that is not part of palandrome \n reversed_suffix = s[pal+1:][::-1]\n return reversed_suffix + s\n\n def usingKMP(self, s):\n def longestSuffixPrefix(s):\n lsp = [0] * len(s)\n for end in range(1, len(s)):\n start = lsp[end-1]\n while start > 0 and s[start] != s[end]:\n start = lsp[start - 1]\n if s[start] == s[end]:\n lsp[end] = start + 1\n return lsp\n\n # We need # to seperate string and its reverse \n # Consider aaaa\n # s + rev: aaaa|aaaa \n # The LPS value for last a will be 7 for aaaaaaa. \n # But we don\'t want this. We are only interested in LSP of original string \n # When we add a # the hash will be close to prefix start than suffix start \n # So any thing beyond the length of original string will not be considered \n # [a{aaa#aaa]a} notice how # is closer to 1 than other? \n rev = s[::-1]\n s_and_rev = s + "#" + rev\n\n # We are calculating the LSP table of KMP. \n lsp = longestSuffixPrefix(s_and_rev)\n \n # Ref - https://www.youtube.com/watch?v=c4akpqTwE5g\n # Consider abab\n # If we appended its reverese to the start then we would definiely get a palandrome \n # baba|abab\n # But this is not the shortest palandrome. This is because abab has a palandrome in it \n # [aba]b. \n # So we get extra aba in the reverse string we attach. \n # This extra aba is nothing but longest commpon prefix suffix when we attach s and s reversed:\n # [aba]b|b[aba]\n # Now KMPs LSP table for last element will have value 3, since we have aba matching. \n # So if we ignore those characters then we can just append b from reverse to start of abab to \n # get shortest palandrome. \n return rev[0:len(s) - lsp[-1]] + s\n \n\n\n # Will run in O(N)\n def shortestPalindrome(self, s: str) -> str:\n\n return self.usingRK(s)\n\n # return self.usingKMP(s)\n\n \n \n``` | 1 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Python3 Epic 3 Liner | shortest-palindrome | 0 | 1 | :)\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n for i in range(len(s), -1, -1):\n if s[:i] == s[i-1::-1]:\n return s[:i-1:-1] + s | 1 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Simple Python in 7 lines with comment | shortest-palindrome | 0 | 1 | \'\'\'\n\n def shortestPalindrome(self, s: str) -> str:\n if s=="": return ""\n if s==s[::-1]: return s\n\t\t\n\t\t# start removing chars from the end until we find a valid palindrome\n\t\t# then, reverse whatever was left at the end and append to the beginning\n for i in range(len(s)-1, -1, -1):\n if(s[:i]==s[:i][::-1]):\n to_add = s[i:][::-1]\n break\n return to_add+s\n\n\'\'\' | 9 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Simple Logic! Python3 Solution | shortest-palindrome | 0 | 1 | # Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n dd=""\n r=s[::-1]\n k=0\n pali=s\n while dd+s!=(dd+s)[::-1]:\n dd+=r[k]\n k+=1\n pali=dd+s\n return pali\n \n \n \n``` | 1 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
No DP; No DS; Intuitive with comments || Python | shortest-palindrome | 0 | 1 | This solution is very intuitive.\n\nCase 1: \nThe given string is a palindrome; return the string itself.\n\nCase 2:\nFind the longest palindromic substring that starts from the first character of the given string. \nThen reverse the remaining part of the string and add it to the front.\n\nTake a look at the code below:\n\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n \n end = 0\n \n # if the string itself is a palindrome return it\n if(s == s[::-1]):\n return s\n \n # Otherwise find the end index of the longest palindrome that starts\n # from the first character of the string\n \n for i in range(len(s)+1):\n if(s[:i]==s[:i][::-1]):\n end=i-1\n \n # return the string with the remaining characters other than\n # the palindrome reversed and added at the beginning\n \n return (s[end+1:][::-1])+s\n```\n\nUpvote if you found it hepful | 3 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
[Python] Stupidly Simple 5 lines solution | shortest-palindrome | 0 | 1 | ```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n if not s: return ""\n for i in reversed(range(len(s))):\n if s[0:i+1] == s[i::-1]:\n return s[:i:-1] + s\n \n``` | 1 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
1 line Python recursive solution | shortest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n return s if s == s[::-1] else s[-1] + self.shortestPalindrome(s[:-1]) + s[-1]\n \n``` | 0 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Python | 2 methods | KMP + Brute Force | shortest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- Brute Force\n- KMP\n\n# Code\n```\nclass Solution:\n \n # Brute Force\n # def shortestPalindrome(self, s: str) -> str:\n # r = s[::-1]\n # for i in range(len(r) + 1):\n # if s.startswith(r[i:]):\n # return r[:i] + s\n # return r + s\n \n # KMP\n def shortestPalindrome(self, s: str) -> str:\n ss = f\'{s}*{s[::-1]}\'\n N = len(ss)\n lps = [0] * N\n i, prev_lps = 1, 0\n while i < N:\n if ss[i] == ss[prev_lps]:\n lps[i] = prev_lps + 1\n i += 1\n prev_lps += 1\n else:\n if prev_lps == 0:\n lps[i] = 0\n i += 1\n else:\n prev_lps = lps[prev_lps - 1]\n return s[lps[-1]:][::-1] + s\n\n``` | 0 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
KMP algorithm O(n) solution | shortest-palindrome | 0 | 1 | # Intuition\nFind the longest palindrome starting at index 0 so that we can append the remaining characters of string at the begining of the string s to get required shortest palindrome\n\n# Approach\nBut How to find the longest palindrome starting at index 0 so I used KMP algorithm to determine it\n\n(please do the question haystack needle to understand KMP)\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n if s=="":return ""\n lps=[0]*len(s)\n prevlps,i=0,1\n while i<len(s):\n if s[i]==s[prevlps]:\n lps[i]=prevlps+1\n i+=1\n prevlps+=1\n elif prevlps==0:\n lps[i]=0\n i+=1\n else:\n prevlps=lps[prevlps-1]\n i,j=0,len(s)-1\n while i<j:\n if s[i]==s[j]:\n i+=1\n j-=1\n elif i==0:\n j-=1\n else:\n i=lps[i-1]\n l=0\n ls=[]\n if i==j:\n ls=list(s[2*i+1:])\n elif i>j:\n ls=list(s[i+j+1:]) \n ls.reverse()\n ls=ls+list(s)\n return "".join(ls) \n \n\n``` | 0 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
3 lines of code super Logic | shortest-palindrome | 0 | 1 | ```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n for i in range(n):\n if s[:n-i]==s[:n-i][::-1]:\n return s[n-i:][::-1]+s\n return ""\n```\n# please upvote me it would encourage me alot\n\n\n | 0 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
Solution O(n) using Manacher's algorythm | shortest-palindrome | 0 | 1 | # Intuition\nI\'ve already solved [Longest Palindromic Substring\n](https://leetcode.com/problems/longest-palindromic-substring/) using [Manacher\'s_algorithm](https://en.wikipedia.org/wiki/Longest_palindromic_substring#Manacher\'s_algorithm) with O(n) time complexity so I decided to reuse code in this problem.\n\n# Approach\nIncide Manacher\'s algorythm we\'re calculating array of palindrome radii for each symbol. As example for "acabac" the array will be [0, 1, 0, 2, 0, 0] (which means first symbol \'c\' is the center of subpalindrome with radius 1 - "aca", symbol \'b\' is the center of subpalindrome with radius 2 - "cabac").\n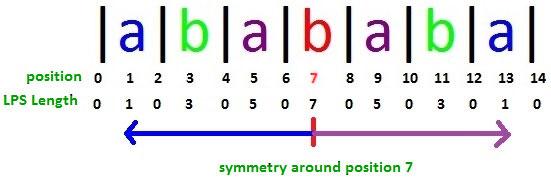 (image from [ here](https://blog.csdn.net/lmhlmh_/article/details/103235304))\n\n\nProblem is to find the shortest palindrome so we need to add as less symbols as possible. Ideal case when input string is a palindrome.\nHow to check it? Start from the middle of the string (`for i in range(n // 2, 0, -1)`) and find the case when the end of string (`s[i:]`) is a part of subpalindrome (`if i == palindromeRadii[i]`).\nWe have to return first result (inversion of s[i:] + s[i:]).\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def shortestPalindrome(self, s: str) -> str:\n #preparations - Manachers\' algorythm\n s_algo = \'|\' + \'|\'.join(s) + \'|\' # convert "abc" to "|a|b|c|" for Manacher\'s algorithm use\n i = 0\n n = len(s_algo)\n palindromeRadii = [0] * n\n center = 0\n radius = 0\n for i in range(n):\n if i < center + radius:\n j = palindromeRadii[center-(i-center)]\n if j < center + radius - i:\n palindromeRadii[i] = j\n continue\n elif j > center + radius - i:\n palindromeRadii[i] = center + radius - i\n continue\n else:\n pass\n else:\n j = 0\n\n while i - j >= 0 and i + j < n and s_algo[i - j] == s_algo[i + j]:\n j += 1\n j -= 1 # current radius\n palindromeRadii[i] = j\n\n if i + j > center + radius:\n center = i\n radius = j\n\n #solution\n for i in range(n // 2, 0, -1):\n if i == palindromeRadii[i]:\n return (s_algo[n-1:i:-1] + s_algo[i:])[1::2] # converting back by skipping "|" symbols\n\n return ""\n```\n\nUpvote, please :) | 0 | You are given a string `s`. You can convert `s` to a palindrome by adding characters in front of it.
Return _the shortest palindrome you can find by performing this transformation_.
**Example 1:**
**Input:** s = "aacecaaa"
**Output:** "aaacecaaa"
**Example 2:**
**Input:** s = "abcd"
**Output:** "dcbabcd"
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of lowercase English letters only. | null |
✅ 100% 3-Approaches [VIDEO] - Heap & QuickSelect & Sorting | kth-largest-element-in-an-array | 1 | 1 | # Problem Understanding\n\nIn the "Kth Largest Element in an Array" problem, we are provided with an array of integers `nums` and an integer `k`. The objective is to determine the `k`th largest element in this array.\n\nFor example, with the array `nums = [3,2,1,5,6,4]` and `k = 2`, the expected answer is `5` since `5` is the second largest element in the array.\n\n---\n\n# Approaches to Finding the k-th Largest Element\n\nFinding the $$k$$-th largest element in an array is a classic problem in computer science, and over the years, multiple algorithms and techniques have been developed to tackle it efficiently. Let\'s explore three of these approaches:\n\n## **Approach 1/3: Sort and Select**\nThe most intuitive method, this approach involves sorting the entire array in descending order and then simply picking the $$k$$-th element. Though straightforward, it may not be the most efficient for very large arrays due to the sorting step.\n\n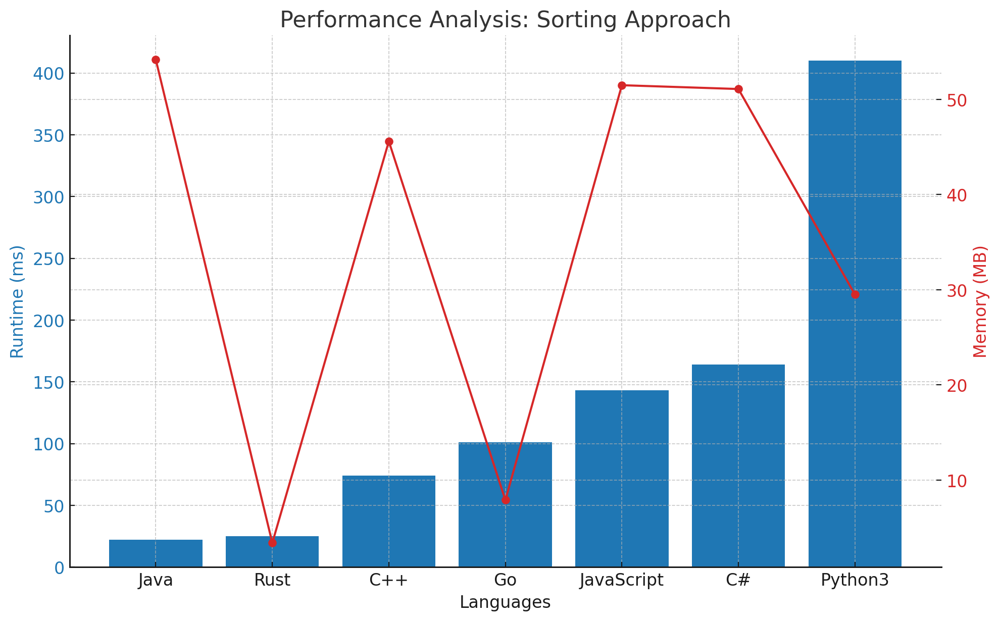\n\n### Live Coding & Explenation - Sort and Select\nhttps://youtu.be/yiUjLay-ocI\n\n## **Approach 2/3: Min-Heap**\nRather than sorting the entire array, this method utilizes a min-heap to maintain the $$k$$-th largest elements. The heap allows us to efficiently compare each new element with the smallest of the $$k$$-th largest elements seen so far. By the end of the iteration, the top of the heap will contain our desired $$k$$-th largest element.\n\n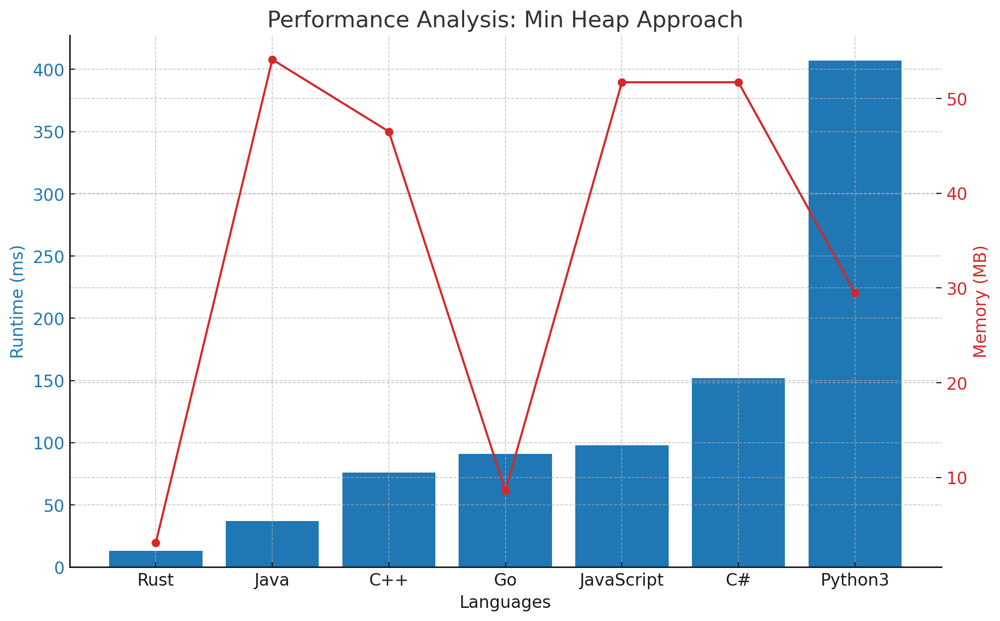\n\n### Live Coding & Explenation - Min-Heap\nhttps://youtu.be/h3GivLJBUTk\n\n## **Approach 3/3: QuickSelect Algorithm**\nInspired by the QuickSort algorithm, QuickSelect is a divide-and-conquer technique. It partitions the array around a pivot and recursively searches for the $$k$$-th largest element in the appropriate partition. When the pivot is chosen randomly, the algorithm tends to have a linear average-case time complexity, making it faster than the sorting approach for large datasets.\n\n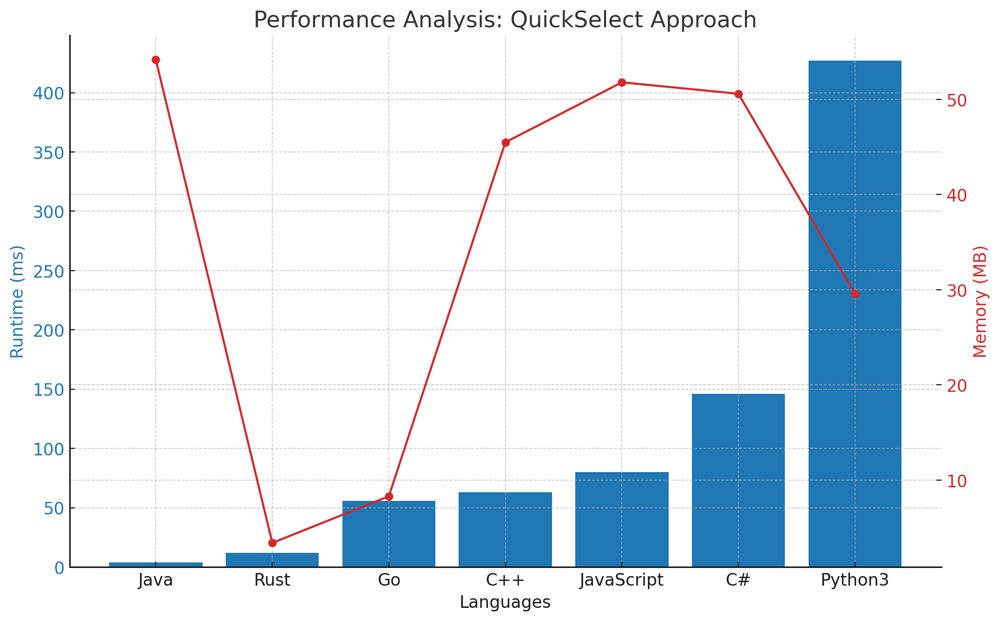\n\n### Live Coding & Explenation - QuickSelect\nhttps://youtu.be/q6A3_mTixvE\n\n## Comparison of Tree Approaches across Languages\n\nThe bar chart below provides a comparative analysis of the runtime performance of three different algorithms \u2013 the Sorting Approach, Min Heap Approach, and the QuickSelect Approach \u2013 across seven popular programming languages. Each language\'s performance is measured in milliseconds (ms) for each approach, with lower values indicating faster execution times.\n\n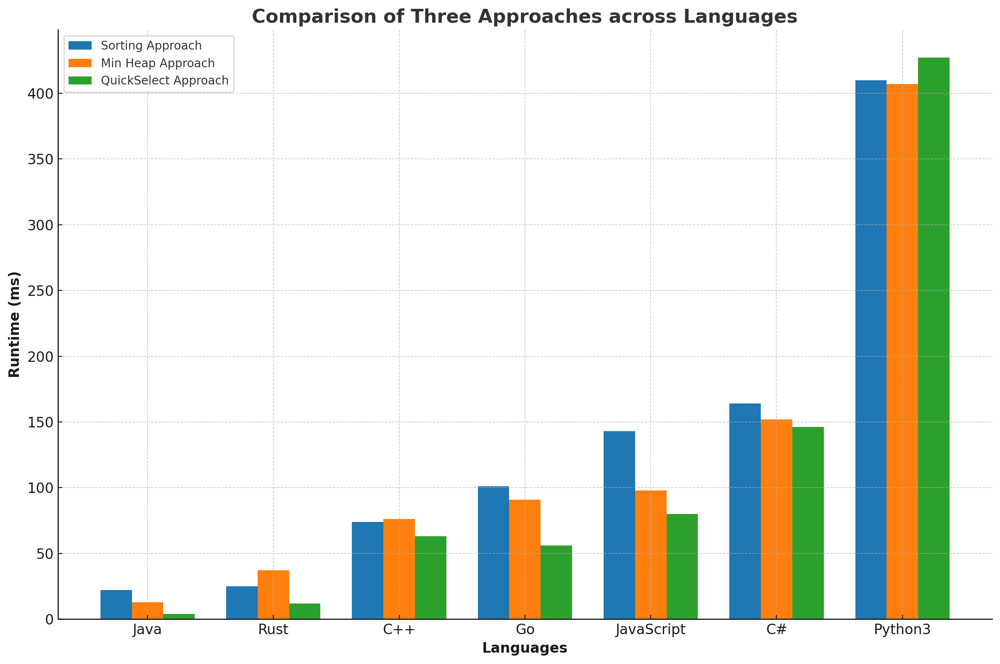\n\n---\n\n# Approaches\n\nEach of these approaches has its own strengths and trade-offs. Depending on the specific scenario, constraints, and size of the input, one might be more suitable than the others. It\'s always beneficial to have multiple tools (approaches) in your algorithmic toolbox!\n\n# Approach 1/3: Sort and Select\n\nThis approach is quite straightforward: sort the numbers in descending order and pick the $$k$$-th element.\n\n## Key Data Structures:\n- **List/Array**: We use Python\'s built-in list for this approach. The list is sorted in descending order to get the $$k$$-th largest element.\n\n## Step-by-step Breakdown:\n\n1. **Initialization**:\n - Use built-in `sorted` function to sort the list `nums` in reverse order (i.e., in descending order).\n \n2. **Selection**:\n - Select the $$k$$-th element from the sorted list (keeping in mind the zero-based indexing of lists).\n\n3. **Result**:\n - The $$k$$-th element in the sorted list is the $$k$$-th largest element in the original list.\n\n# Complexity:\n\n**Time Complexity:** $$O(N \\log N)$$\n- Sorting a list of $$N$$ elements requires $$O(N \\log N)$$ time.\n\n**Space Complexity:** $$O(1)$$\n- The space used is constant since we are only sorting the original list and selecting an element from it without utilizing any additional data structures.\n\n# Performance:\n\nThis solution is simple and works effectively for smaller lists. However, for very large lists, other approaches that avoid sorting the entire list might be more efficient.\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| **Java** | 22 | 88.35% | 54.2 | 79.52% |\n| **Rust** | 25 | 21.43% | 3.4 | 5.61% |\n| **C++** | 74 | 96.10% | 45.6 | 74.16% |\n| **Go** | 101 | 51.2% | 7.9 | 85.3% |\n| **JavaScript** | 143 | 60.17% | 51.5 | 56.57% |\n| **C#** | 164 | 85.88% | 51.1 | 41.99% |\n| **Python3** | 410 | 98.33% | 29.5 | 72.41% |\n\n# Code 1/3\n\n``` Python []\nclass Solution:\n def findKthLargest(self, nums, k):\n return sorted(nums, reverse=True)[k-1]\n```\n``` C++ []\nclass Solution {\npublic:\n int findKthLargest(std::vector<int>& nums, int k) {\n std::sort(nums.begin(), nums.end(), std::greater<int>());\n return nums[k-1];\n }\n};\n```\n``` Java []\npublic class Solution {\n public int findKthLargest(int[] nums, int k) {\n Arrays.sort(nums);\n return nums[nums.length - k];\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_kth_largest(nums: Vec<i32>, k: i32) -> i32 {\n let mut sorted_nums = nums.clone();\n sorted_nums.sort();\n sorted_nums[(nums.len() - k as usize)]\n }\n}\n```\n``` Go []\nimport "sort"\n\nfunc findKthLargest(nums []int, k int) int {\n sort.Ints(nums)\n return nums[len(nums)-k]\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar findKthLargest = function(nums, k) {\n nums.sort((a, b) => b - a);\n return nums[k-1];\n};\n```\n``` C# []\npublic class Solution {\n public int FindKthLargest(int[] nums, int k) {\n Array.Sort(nums);\n return nums[nums.Length - k];\n }\n}\n```\n---\n\n# Approach 2/3: Min-Heap\n\nThe main idea of this solution is to use a min-heap with a maximum size of `k`. By doing this, we ensure that the smallest of the `k` largest elements is always on the top of the heap.\n\n## Key Data Structures:\n\n- **`heap`**:\n This is a min-heap containing the first `k` elements of `nums`. As we progress, we will modify this heap to ensure it contains the `k` largest elements.\n\n### Step-by-step Breakdown:\n\n1. **Initialization**:\n - Create a heap with the first `k` elements of `nums`.\n - Transform this list into a min-heap.\n\n2. **Iterate through the List**:\n - For each of the remaining elements in `nums`:\n - If the element is larger than the smallest element in the heap (i.e., the top of the heap):\n - Remove the top element from the heap.\n - Insert the current element into the heap.\n\n3. **Result**:\n - After processing all elements in `nums`, the top of the heap will contain the `k`th largest element. Return this element.\n\n# Example:\n\nConsider the list `nums = [3,2,1,5,6,4]` with `k = 2`.\n\nHere\'s the evolution of the `heap`:\n\n**Initial State**:\n- `heap`: [3,2]\n\n**After processing index 2 (element = 1)**:\n- `heap` remains unchanged as `1` is not larger than `2`.\n\n**After processing index 3 (element = 5)**:\n- `heap`: [3,5]\n\n**After processing index 4 (element = 6)**:\n- `heap`: [5,6]\n\n**After processing index 5 (element = 4)**:\n- `heap`: [5,6]\n\nThe final state of the `heap` shows that the `k`th largest element is `5`.\n\n# Complexity\n\n**Time Complexity:** $$O(n \\log k)$$\nEach of the `n` elements is processed once. However, heap operations take $$O(\\log k)$$ time, leading to an overall complexity of $$O(n \\log k)$$.\n\n**Space Complexity:** $$O(k)$$\nThe solution uses a heap with a maximum of `k` elements.\n\n# Performance\n\nThis solution is both time and space-efficient. By focusing only on the `k` largest elements and using the properties of a heap, it ensures optimal runtime for a wide range of inputs. The controlled space usage ensures that even for large `k`, the memory overhead remains minimal.\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| **Rust** | 13 | 77.55% | 3.1 | 46.94% |\n| **Java** | 37 | 59.27% | 54.1 | 86.2% |\n| **C++** | 76 | 94.84% | 46.5 | 68.16% |\n| **Go** | 91 | 62.6% | 8.6 | 30.67% |\n| **JavaScript** | 98 | 87.2% | 51.7 | 47.64% |\n| **C#** | 152 | 95.49% | 51.7 | 16.25% |\n| **Python3** | 407 | 98.75% | 29.5 | 72.41% |\n\n# Code\n``` Python []\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n heap = nums[:k]\n heapq.heapify(heap)\n \n for num in nums[k:]:\n if num > heap[0]:\n heapq.heappop(heap)\n heapq.heappush(heap, num)\n \n return heap[0]\n```\n``` C++ []\nclass Solution {\npublic:\n int findKthLargest(std::vector<int>& nums, int k) {\n std::priority_queue<int, std::vector<int>, std::greater<int>> min_heap(nums.begin(), nums.begin() + k);\n \n for (int i = k; i < nums.size(); i++) {\n if (nums[i] > min_heap.top()) {\n min_heap.pop();\n min_heap.push(nums[i]);\n }\n }\n \n return min_heap.top();\n }\n};\n```\n``` Rust []\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\n\nimpl Solution {\n pub fn find_kth_largest(nums: Vec<i32>, k: i32) -> i32 {\n let mut heap: BinaryHeap<Reverse<i32>> = nums.iter().take(k as usize).map(|&x| Reverse(x)).collect();\n \n for &num in nums.iter().skip(k as usize) {\n if num > heap.peek().unwrap().0 {\n heap.pop();\n heap.push(Reverse(num));\n }\n }\n \n heap.peek().unwrap().0\n }\n}\n```\n``` Go []\nimport "container/heap"\n\nfunc findKthLargest(nums []int, k int) int {\n h := IntHeap(nums[:k])\n heap.Init(&h)\n \n for _, num := range nums[k:] {\n if num > h[0] {\n heap.Pop(&h)\n heap.Push(&h, num)\n }\n }\n \n return h[0]\n}\n\ntype IntHeap []int\n\nfunc (h IntHeap) Len() int { return len(h) }\nfunc (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }\nfunc (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *IntHeap) Push(x interface{}) {\n *h = append(*h, x.(int))\n}\n\nfunc (h *IntHeap) Pop() interface{} {\n old := *h\n n := len(old)\n x := old[n-1]\n *h = old[0 : n-1]\n return x\n}\n```\n``` Java []\npublic class Solution {\n public int findKthLargest(int[] nums, int k) {\n PriorityQueue<Integer> minHeap = new PriorityQueue<>();\n for (int i = 0; i < k; i++) {\n minHeap.offer(nums[i]);\n }\n \n for (int i = k; i < nums.length; i++) {\n if (nums[i] > minHeap.peek()) {\n minHeap.poll();\n minHeap.offer(nums[i]);\n }\n }\n \n return minHeap.peek();\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\n class MinHeap {\n constructor() {\n this.heap = [];\n }\n push(val) {\n this.heap.push(val);\n this.bubbleUp();\n }\n pop() {\n const max = this.heap[0];\n const end = this.heap.pop();\n if (this.heap.length > 0) {\n this.heap[0] = end;\n this.bubbleDown();\n }\n return max;\n }\n peek() {\n return this.heap[0];\n }\n bubbleUp() {\n let idx = this.heap.length - 1;\n const element = this.heap[idx];\n while (idx > 0) {\n let parentIdx = Math.floor((idx - 1) / 2);\n let parent = this.heap[parentIdx];\n if (element >= parent) break;\n this.heap[parentIdx] = element;\n this.heap[idx] = parent;\n idx = parentIdx;\n }\n }\n bubbleDown() {\n let idx = 0;\n const length = this.heap.length;\n const element = this.heap[0];\n while (true) {\n let leftChildIdx = 2 * idx + 1;\n let rightChildIdx = 2 * idx + 2;\n let leftChild, rightChild;\n let swap = null;\n if (leftChildIdx < length) {\n leftChild = this.heap[leftChildIdx];\n if (leftChild < element) {\n swap = leftChildIdx;\n }\n }\n if (rightChildIdx < length) {\n rightChild = this.heap[rightChildIdx];\n if (\n (swap === null && rightChild < element) || \n (swap !== null && rightChild < leftChild)\n ) {\n swap = rightChildIdx;\n }\n }\n if (swap === null) break;\n this.heap[idx] = this.heap[swap];\n this.heap[swap] = element;\n idx = swap;\n }\n }\n}\nvar findKthLargest = function(nums, k) {\n let heap = new MinHeap();\n for (let i = 0; i < k; i++) {\n heap.push(nums[i]);\n }\n for (let i = k; i < nums.length; i++) {\n if (nums[i] > heap.peek()) {\n heap.pop();\n heap.push(nums[i]);\n }\n }\n return heap.peek();\n};\n```\n``` C# []\npublic class Solution {\n public int FindKthLargest(int[] nums, int k) {\n MinHeap minHeap = new MinHeap(k);\n for (int i = 0; i < k; i++) {\n minHeap.Insert(nums[i]);\n }\n \n for (int i = k; i < nums.Length; i++) {\n if (nums[i] > minHeap.Peek()) {\n minHeap.Pop();\n minHeap.Insert(nums[i]);\n }\n }\n \n return minHeap.Peek();\n }\n}\n\npublic class MinHeap {\n private int[] heap;\n private int size;\n\n public MinHeap(int capacity) {\n heap = new int[capacity];\n size = 0;\n }\n\n public void Insert(int val) {\n heap[size] = val;\n size++;\n BubbleUp();\n }\n\n public int Peek() {\n return heap[0];\n }\n\n public int Pop() {\n int poppedValue = heap[0];\n heap[0] = heap[size - 1];\n size--;\n BubbleDown();\n return poppedValue;\n }\n\n private void BubbleUp() {\n int index = size - 1;\n while (index > 0 && heap[index] < heap[Parent(index)]) {\n Swap(index, Parent(index));\n index = Parent(index);\n }\n }\n\n private void BubbleDown() {\n int index = 0;\n while (HasLeftChild(index) && (heap[index] > LeftChild(index) || HasRightChild(index) && heap[index] > RightChild(index))) {\n int smallerChildIndex = LeftChildIndex(index);\n if (HasRightChild(index) && RightChild(index) < LeftChild(index)) {\n smallerChildIndex = RightChildIndex(index);\n }\n Swap(index, smallerChildIndex);\n index = smallerChildIndex;\n }\n }\n\n private int Parent(int index) { return (index - 1) / 2; }\n private int LeftChildIndex(int index) { return 2 * index + 1; }\n private int RightChildIndex(int index) { return 2 * index + 2; }\n\n private bool HasLeftChild(int index) { return LeftChildIndex(index) < size; }\n private bool HasRightChild(int index) { return RightChildIndex(index) < size; }\n\n private int LeftChild(int index) { return heap[LeftChildIndex(index)]; }\n private int RightChild(int index) { return heap[RightChildIndex(index)]; }\n\n private void Swap(int indexOne, int indexTwo) {\n int temp = heap[indexOne];\n heap[indexOne] = heap[indexTwo];\n heap[indexTwo] = temp;\n }\n}\n```\n\n---\n\n\n# Approach 3/3: QuickSelect Algorithm\n\nThe QuickSelect algorithm is an efficient method to find the $$k$$-th smallest (or largest) element in an unordered list without sorting the entire list. It works similarly to the QuickSort algorithm but only recurses into one half of the data.\n\n## Key Data Structures:\n\n- **List/Array**: We use Python\'s built-in list for this approach. The algorithm modifies the list in place.\n- **Pivot**: An element chosen from the list, around which the list gets partitioned.\n\n## Step-by-step Breakdown:\n\n1. **Initialization**:\n - Set the `left` boundary to the beginning of the list and the `right` boundary to the end of the list.\n\n2. **Pivot Selection**:\n - Randomly select a pivot index between the `left` and `right` boundaries.\n\n3. **Partitioning**:\n - Move all elements smaller than the pivot to its left and all larger elements to its right.\n - Return the final position of the pivot after the partitioning.\n\n4. **Check Pivot Position**:\n - If the position of the pivot is the desired $$k$$-th largest index, return the pivot.\n - If the pivot\'s position is greater than the desired index, adjust the `right` boundary and repeat.\n - If the pivot\'s position is lesser than the desired index, adjust the `left` boundary and repeat.\n\n5. **Result**:\n - The function will eventually return the $$k$$-th largest element in the original list.\n\n# Example:\n\nLet\'s walk through the QuickSelect algorithm using the list `nums = [3,2,1,5,6,4]` and \\( k = 2 \\) to find the 2nd largest element.\n\n**Initial List:** \n`[3,2,1,5,6,4]`\n\n1. **Iteration 1:** \n - Chosen pivot: `3` (at index 0)\n - After partitioning, the list becomes: `[2, 1, 3, 5, 6, 4]`\n - The new pivot index is 2. Since we\'re looking for the 2nd largest element (index 4 in 0-indexed list), and the current pivot index is less than this, we know the desired element is to the right of the current pivot.\n \n2. **Iteration 2:**\n - Chosen pivot: `6` (at index 4)\n - After partitioning, the list becomes: `[2, 1, 3, 4, 5, 6]`\n - The new pivot index is 4, which matches our target index for the 2nd largest element.\n \n**Result:** \nThe 2nd largest element in the list is `5`.\n\nThis example demonstrates the behavior of the QuickSelect algorithm. By iteratively selecting a pivot and partitioning the list around that pivot, it efficiently narrows down the search space until it locates the kth largest element.\n\n# Complexity:\n\n**Time Complexity**: \n- Best and Average Case: $$O(N)$$\n- Worst Case: $$O(N^2)$$\n \n The average performance is linear. However, in the worst case (very rare, especially with randomized pivot), the algorithm can degrade to $$O(N^2)$$.\n\n**Space Complexity**: $$O(1)$$\n- The space used is constant. The algorithm modifies the original list in place and doesn\'t utilize any significant additional data structures. The recursive stack calls (in the worst case) are also bounded by the depth of the list, making it $$O(\\log N)$$, but this is typically considered as $$O(1)$$ space complexity in QuickSelect.\n\n# Performance:\n\nThis solution is efficient for larger lists, especially when the pivot is chosen randomly, which greatly reduces the chance of the worst-case scenario. The QuickSelect algorithm allows for finding the desired element without sorting the entire list, making it faster than the sorting approach for large datasets.\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| **Java** | 4 | 97.78% | 54.2 | 79.52% |\n| **Rust** | 12 | 83.16% | 3.4 | 5.61% |\n| **Go** | 56 | 100% | 8.3 | 46.37% |\n| **C++** | 63 | 98.85% | 45.5 | 86.52% |\n| **JavaScript** | 80 | 94.94% | 51.8 | 38.99% |\n| **C#** | 146 | 98.46% | 50.6 | 90.98% |\n| **Python3** | 427 | 94.80% | 29.6 | 55.40% |\n\n# Code 3/3\n``` Python []\nclass Solution:\n def findKthLargest(self, nums, k):\n left, right = 0, len(nums) - 1\n while True:\n pivot_index = random.randint(left, right)\n new_pivot_index = self.partition(nums, left, right, pivot_index)\n if new_pivot_index == len(nums) - k:\n return nums[new_pivot_index]\n elif new_pivot_index > len(nums) - k:\n right = new_pivot_index - 1\n else:\n left = new_pivot_index + 1\n\n def partition(self, nums, left, right, pivot_index):\n pivot = nums[pivot_index]\n nums[pivot_index], nums[right] = nums[right], nums[pivot_index]\n stored_index = left\n for i in range(left, right):\n if nums[i] < pivot:\n nums[i], nums[stored_index] = nums[stored_index], nums[i]\n stored_index += 1\n nums[right], nums[stored_index] = nums[stored_index], nums[right]\n return stored_index\n```\n``` C++ []\nclass Solution {\npublic:\n int findKthLargest(std::vector<int>& nums, int k) {\n int left = 0, right = nums.size() - 1;\n while (true) {\n int pivot_index = rand() % (right - left + 1) + left;\n int new_pivot_index = partition(nums, left, right, pivot_index);\n if (new_pivot_index == nums.size() - k) {\n return nums[new_pivot_index];\n } else if (new_pivot_index > nums.size() - k) {\n right = new_pivot_index - 1;\n } else {\n left = new_pivot_index + 1;\n }\n }\n }\n\nprivate:\n int partition(std::vector<int>& nums, int left, int right, int pivot_index) {\n int pivot = nums[pivot_index];\n std::swap(nums[pivot_index], nums[right]);\n int stored_index = left;\n for (int i = left; i < right; i++) {\n if (nums[i] < pivot) {\n std::swap(nums[i], nums[stored_index]);\n stored_index++;\n }\n }\n std::swap(nums[right], nums[stored_index]);\n return stored_index;\n }\n};\n```\n``` Rust []\nuse rand::Rng;\n\nimpl Solution {\n pub fn find_kth_largest(nums: Vec<i32>, k: i32) -> i32 {\n let mut nums = nums;\n let mut left = 0;\n let mut right = nums.len() - 1;\n let mut rng = rand::thread_rng();\n loop {\n let pivot_index = rng.gen_range(left, right + 1);\n let new_pivot_index = Self::partition(&mut nums, left, right, pivot_index);\n if new_pivot_index == nums.len() - k as usize {\n return nums[new_pivot_index];\n } else if new_pivot_index > nums.len() - k as usize {\n right = new_pivot_index - 1;\n } else {\n left = new_pivot_index + 1;\n }\n }\n }\n\n fn partition(nums: &mut Vec<i32>, left: usize, right: usize, pivot_index: usize) -> usize {\n let pivot = nums[pivot_index];\n nums.swap(pivot_index, right);\n let mut stored_index = left;\n for i in left..right {\n if nums[i] < pivot {\n nums.swap(i, stored_index);\n stored_index += 1;\n }\n }\n nums.swap(right, stored_index);\n stored_index\n }\n}\n```\n``` Go []\nimport (\n\t"math/rand"\n)\n\nfunc findKthLargest(nums []int, k int) int {\n\tleft, right := 0, len(nums)-1\n\tfor {\n\t\tpivotIndex := left + rand.Intn(right-left+1)\n\t\tnewPivotIndex := partition(nums, left, right, pivotIndex)\n\t\tif newPivotIndex == len(nums)-k {\n\t\t\treturn nums[newPivotIndex]\n\t\t} else if newPivotIndex > len(nums)-k {\n\t\t\tright = newPivotIndex - 1\n\t\t} else {\n\t\t\tleft = newPivotIndex + 1\n\t\t}\n\t}\n}\n\nfunc partition(nums []int, left int, right int, pivotIndex int) int {\n\tpivot := nums[pivotIndex]\n\tnums[pivotIndex], nums[right] = nums[right], nums[pivotIndex]\n\tstoredIndex := left\n\tfor i := left; i < right; i++ {\n\t\tif nums[i] < pivot {\n\t\t\tnums[i], nums[storedIndex] = nums[storedIndex], nums[i]\n\t\t\tstoredIndex++\n\t\t}\n\t}\n\tnums[right], nums[storedIndex] = nums[storedIndex], nums[right]\n\treturn storedIndex\n}\n```\n``` Java []\npublic class Solution {\n public int findKthLargest(int[] nums, int k) {\n int left = 0, right = nums.length - 1;\n Random rand = new Random();\n while (true) {\n int pivot_index = left + rand.nextInt(right - left + 1);\n int new_pivot_index = partition(nums, left, right, pivot_index);\n if (new_pivot_index == nums.length - k) {\n return nums[new_pivot_index];\n } else if (new_pivot_index > nums.length - k) {\n right = new_pivot_index - 1;\n } else {\n left = new_pivot_index + 1;\n }\n }\n }\n\n private int partition(int[] nums, int left, int right, int pivot_index) {\n int pivot = nums[pivot_index];\n swap(nums, pivot_index, right);\n int stored_index = left;\n for (int i = left; i < right; i++) {\n if (nums[i] < pivot) {\n swap(nums, i, stored_index);\n stored_index++;\n }\n }\n swap(nums, right, stored_index);\n return stored_index;\n }\n\n private void swap(int[] nums, int i, int j) {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar findKthLargest = function(nums, k) {\n const partition = (left, right, pivotIndex) => {\n const pivot = nums[pivotIndex];\n [nums[pivotIndex], nums[right]] = [nums[right], nums[pivotIndex]];\n let storedIndex = left;\n for (let i = left; i < right; i++) {\n if (nums[i] < pivot) {\n [nums[storedIndex], nums[i]] = [nums[i], nums[storedIndex]];\n storedIndex++;\n }\n }\n [nums[right], nums[storedIndex]] = [nums[storedIndex], nums[right]];\n return storedIndex;\n };\n \n let left = 0, right = nums.length - 1;\n while (true) {\n const pivotIndex = left + Math.floor(Math.random() * (right - left + 1));\n const newPivotIndex = partition(left, right, pivotIndex);\n if (newPivotIndex === nums.length - k) {\n return nums[newPivotIndex];\n } else if (newPivotIndex > nums.length - k) {\n right = newPivotIndex - 1;\n } else {\n left = newPivotIndex + 1;\n }\n }\n};\n```\n``` C# []\npublic class Solution {\n public int FindKthLargest(int[] nums, int k) {\n int left = 0, right = nums.Length - 1;\n Random rand = new Random();\n while (true) {\n int pivot_index = left + rand.Next(right - left + 1);\n int new_pivot_index = Partition(nums, left, right, pivot_index);\n if (new_pivot_index == nums.Length - k) {\n return nums[new_pivot_index];\n } else if (new_pivot_index > nums.Length - k) {\n right = new_pivot_index - 1;\n } else {\n left = new_pivot_index + 1;\n }\n }\n }\n\n private int Partition(int[] nums, int left, int right, int pivot_index) {\n int pivot = nums[pivot_index];\n Swap(nums, pivot_index, right);\n int stored_index = left;\n for (int i = left; i < right; i++) {\n if (nums[i] < pivot) {\n Swap(nums, i, stored_index);\n stored_index++;\n }\n }\n Swap(nums, right, stored_index);\n return stored_index;\n }\n\n private void Swap(int[] nums, int i, int j) {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n}\n```\n\nIn the dynamic world of algorithms, there\'s no \'one-size-fits-all\'. Each solution we\'ve explored offers unique strengths and comes with its own set of trade-offs. Some shine brightest with smaller inputs, while others stand resilient in the face of massive datasets. The beauty lies in understanding and judiciously applying them based on the constraints and requirements at hand.\n\nRemember, every challenge you face is an opportunity to apply and expand your understanding. By mastering multiple approaches, you not only diversify your algorithmic toolbox but also enhance your adaptability in solving real-world problems. Keep pushing the boundaries, keep exploring, and most importantly, keep coding! The journey of algorithms is vast and rewarding, and every problem you solve is a stepping stone towards becoming a more skilled and confident coder. Embrace the learning, and let the world of algorithms inspire and empower you! | 236 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python randomized quicksort partioning and Reducing search space | kth-largest-element-in-an-array | 0 | 1 | \n# Code\n```\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n return self.quicksort(nums,len(nums)-k,0,len(nums)-1);\n def quicksort(self,nums,k,a,b):\n #partition\n r = randint(a,b)\n nums[r],nums[b] = nums[b],nums[r]\n p = b # set pivot to rightmost element\n i , j = a , b-1 \n while( i <= j ):\n if( nums[i] < nums[p] ): i+=1\n else:\n if(nums[j] > nums[p] ): j-= 1\n else:\n nums[i],nums[j] = nums[j],nums[i]\n i += 1;\n j-=1;\n \n nums[i],nums[p] = nums[p],nums[i]\n if( i > k ): return self.quicksort(nums,k,a,i-1);\n elif(i<k): return self.quicksort(nums,k,i+1,b);\n else: return nums[k]\n\n\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
python3 Solution | kth-largest-element-in-an-array | 0 | 1 | \n```\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n pivot=random.choice(nums)\n left=[x for x in nums if x>pivot]\n mid=[x for x in nums if x==pivot]\n right=[x for x in nums if x<pivot]\n n=len(left)\n m=len(mid)\n if k<=n:\n return self.findKthLargest(left,k)\n\n elif k>(n+m):\n return self.findKthLargest(right,k-(n+m))\n\n else:\n return mid[0] \n``` | 3 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python3 | One line code |Beats 97.92%of users with Python3 | kth-largest-element-in-an-array | 0 | 1 | # Code\n```\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n nums.sort(); return nums[k*-1]\n``` | 0 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python Easy Solution || 100% || 2 line Solution || Heap || | kth-largest-element-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n (logn))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n heapq.heapify(nums)\n return heapq.nlargest(k, nums)[-1]\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
【Quickselect Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | kth-largest-element-in-an-array | 1 | 1 | # Intuition\nUsing quickselect to pick kth largetst number.\n\nNote that I took a video Jan 1st 2023. This question is a little bit changed now. But I still meet this condition "Can you solve it without sorting?". I think we can use the same idea to solve this question and at least, you will learn how quicksort works from the video!\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n# Subscribe to my channel from here. I have 245 videos as of August 14th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/ebkXDmgM7Wo\n\n### I\'m sure you can understand how quick select works easily with watching video rather than reading approach section.\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. The function starts by subtracting `k` from the length of the input `nums`. This is done to convert the "k-th largest" problem into finding the `(len(nums) - k)`-th smallest element. The reason for this conversion is that finding the k-th largest element is equivalent to finding the n - k + 1 smallest element in the list.\n\n2. The code enters a loop that iterates over each index `i` in reverse order from `len(nums) - 1` down to 0. Inside the loop, a random index `j` is generated between 0 and `i`, and the elements at indices `i` and `j` in the `nums` list are swapped. This is essentially shuffling the array randomly. This step is performed to add some randomness to the input data, which helps improve the average-case performance of the QuickSelect algorithm.\n\n3. The code defines an inner function `quick_select` that takes two parameters: `left` and `right`, representing the range of indices to consider in the `nums` list.\n\n4. Within the `quick_select` function, a pivot element is chosen as the element at index `right`, and a pointer `p` is initialized to `left`. The goal is to rearrange the elements in such a way that all elements smaller than the pivot are on the left side, and all elements greater than the pivot are on the right side.\n\n5. A loop iterates over the range from `left` to `right - 1`. If the element at index `i` is smaller than or equal to the pivot, the element at index `i` is swapped with the element at index `p`, and the pointer `p` is incremented. This effectively moves the smaller element to the left side of the partition.\n\n6. After the loop, the element at index `right` (the pivot) is swapped with the element at index `p`. Now, all elements less than the pivot are on the left side, and all elements greater than the pivot are on the right side.\n\n7. The code then checks the value of the pointer `p`. If `p` is greater than `k`, it means that the desired element is on the left side of the partition, so the `quick_select` function is called recursively on the left subarray (from `left` to `p - 1`).\n\n8. If `p` is less than `k`, it means that the desired element is on the right side of the partition, so the `quick_select` function is called recursively on the right subarray (from `p + 1` to `right`).\n\n9. If neither of the above conditions is met, it means that the pivot itself is the desired element, and it is returned.\n\n10. Finally, the `findKthLargest` method calls the `quick_select` function initially on the entire input array (from index 0 to `len(nums) - 1`) and returns the result.\n\nIn summary, this algorithm uses randomized shuffling and the QuickSelect technique to efficiently find the `(len(nums) - k)`-th smallest element in the input list, which effectively corresponds to the k-th largest element in the original list.\n\n# Complexity\n- Time complexity: O(n) on average, O(n^2) in the worst case\nIf we continue to pick the smallest or largest number, that should be O(n^2). But we can improve time with this code.\n\n```\n# This is python code\nfor i in range(len(nums) - 1, -1, -1):\n j = random.randint(0, i)\n nums[i], nums[j] = nums[j], nums[i]\n```\n\n- Space complexity: O(n)\nThis is space for the recursion call stack.\n\n\n```python []\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n k = len(nums) - k\n\n for i in range(len(nums) - 1, -1, -1):\n j = random.randint(0, i)\n nums[i], nums[j] = nums[j], nums[i]\n\n def quick_select(left, right):\n pivot, p = nums[right], left\n\n for i in range(left, right):\n if nums[i] <= pivot:\n nums[p], nums[i] = nums[i], nums[p]\n p += 1\n nums[p], nums[right] = nums[right], nums[p]\n\n if p > k:\n return quick_select(left, p - 1)\n elif p < k:\n return quick_select(p + 1, right)\n else:\n return nums[p]\n\n return quick_select(0, len(nums) - 1)\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar findKthLargest = function(nums, k) {\n k = nums.length - k;\n\n for (let i = nums.length - 1; i >= 0; i--) {\n const j = Math.floor(Math.random() * (i + 1));\n [nums[i], nums[j]] = [nums[j], nums[i]];\n }\n\n function quick_select(left, right) {\n const pivot = nums[right];\n let p = left;\n\n for (let i = left; i < right; i++) {\n if (nums[i] <= pivot) {\n [nums[p], nums[i]] = [nums[i], nums[p]];\n p++;\n }\n }\n [nums[p], nums[right]] = [nums[right], nums[p]];\n\n if (p > k) {\n return quick_select(left, p - 1);\n } else if (p < k) {\n return quick_select(p + 1, right);\n } else {\n return nums[p];\n }\n }\n\n return quick_select(0, nums.length - 1); \n};\n```\n```java []\nclass Solution {\n public int findKthLargest(int[] nums, int k) {\n k = nums.length - k;\n\n Random random = new Random();\n for (int i = nums.length - 1; i >= 0; i--) {\n int j = random.nextInt(i + 1);\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n\n return quickSelect(nums, 0, nums.length - 1, k); \n }\n\n private int quickSelect(int[] nums, int left, int right, int k) {\n int pivot = nums[right];\n int p = left;\n\n for (int i = left; i < right; i++) {\n if (nums[i] <= pivot) {\n int temp = nums[i];\n nums[i] = nums[p];\n nums[p] = temp;\n p++;\n }\n }\n\n int temp = nums[p];\n nums[p] = nums[right];\n nums[right] = temp;\n\n if (p > k) {\n return quickSelect(nums, left, p - 1, k);\n } else if (p < k) {\n return quickSelect(nums, p + 1, right, k);\n } else {\n return nums[p];\n }\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int findKthLargest(vector<int>& nums, int k) {\n k = nums.size() - k;\n\n std::random_device rd;\n std::mt19937 gen(rd());\n for (int i = nums.size() - 1; i >= 0; i--) {\n int j = gen() % (i + 1);\n std::swap(nums[i], nums[j]);\n }\n\n return quickSelect(nums, 0, nums.size() - 1, k); \n }\n\nprivate:\n int quickSelect(std::vector<int>& nums, int left, int right, int k) {\n int pivot = nums[right];\n int p = left;\n\n for (int i = left; i < right; i++) {\n if (nums[i] <= pivot) {\n std::swap(nums[i], nums[p]);\n p++;\n }\n }\n std::swap(nums[p], nums[right]);\n\n if (p > k) {\n return quickSelect(nums, left, p - 1, k);\n } else if (p < k) {\n return quickSelect(nums, p + 1, right, k);\n } else {\n return nums[p];\n }\n } \n};\n```\n | 15 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python short and clean. QuickSelect. Functional programming. | kth-largest-element-in-an-array | 0 | 1 | # Approach: Quick-Select\nTL;DR, Similar to [Editorial solution Approach 3](https://leetcode.com/problems/kth-largest-element-in-an-array/editorial/) but cleaner and more generic.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is length of nums`.\n\n# Code\nRecursive:\n```python\nclass Solution:\n def findKthLargest(self, nums: list[int], k: int) -> int:\n T, V = TypeVar(\'T\'), TypeVar(\'V\')\n Key = Callable[[T], V]\n\n def quick_select(seq: Sequence[T], k: int, key: Key = None, reverse: bool = False) -> T:\n pivot = choice(seq)\n key = (lambda x: x) if key is None else key\n cmp = lambda x: ((key(x) > key(pivot)) - (key(x) < key(pivot))) * (-1 if reverse else 1)\n\n mids, rights, lefts = reduce(lambda a, x: a[cmp(x)].append(x) or a, seq, ([], [], []))\n nl, nr = len(lefts), len(lefts) + len(mids)\n\n if k <= nl: return quick_select(lefts , k. , key, reverse)\n if k > nr: return quick_select(rights, k - nr, key, reverse)\n return pivot\n\n return quick_select(nums, k, reverse=True)\n\n\n```\n\nIterative:\n# Code\n```python\nclass Solution:\n def findKthLargest(self, nums: list[int], k: int) -> int:\n T, V = TypeVar(\'T\'), TypeVar(\'V\')\n Key = Callable[[T], V]\n\n def quick_select(seq: Sequence[T], k: int, key: Key = None, reverse: bool = False) -> T:\n key = (lambda x: x) if key is None else key\n seq = list(seq)\n\n def partition(l: int, r: int) -> int:\n pivot_idx, pivot = l, seq[l]\n\n while l <= r:\n swap = key(seq[l]) < key(pivot) if reverse else key(seq[l]) > key(pivot)\n seq[l], seq[r] = (seq[r], seq[l]) if swap else (seq[l], seq[r])\n l, r = (l, r - 1) if swap else (l + 1, r)\n \n seq[pivot_idx], seq[r] = seq[r], seq[pivot_idx]\n return r\n\n \n i, j = 0, len(seq) - 1\n k = k - 1\n while (x := partition(i, j)) != k:\n i, j = (x + 1, j) if x < k else (i, x - 1)\n \n return seq[k]\n \n \n return quick_select(nums, k, reverse=True)\n\n\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Comprehensive Solution Using a Priority Queue | kth-largest-element-in-an-array | 0 | 1 | # Intuition\nWe can convert each values in our input array to their negatives and store them in a min heap. We will then keep popping the smallest value until we get to the appropriate k value after which the value we are interested in will be in front of the min heap, we convert this value to the its original and return it\n\n# Problem Decomposition\nWe can reduce this problem to the following subproblems\n- creating, pushing and popping from a min heap\n- traversing an array using a single pointer\n- modifying an array in place\n\n# Approach\nFirst, modify `nums` in place by multiplying each value by -1. This essentially makes the largest value the smallest and vice versa\nConvert the modified `nums` into a min heap.\nwhile `k` > 1, \n- pop the smallest value from the min heap\n- decrement `k` by one\n\nOutside the while loop, multiply the value at the front of the min heap `nums` by -1 and return the result\n\n# Complexity\n- Time complexity:\nO(k * log n)\n- Space complexity:\nO(n)\n# Code\n```\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n \'\'\'\n We can reduce this problem to the following subproblems\n - creating, pushing and popping from a min heap\n - traversing an array using a single pointer\n - modifying an array in place\n \'\'\'\n\n nums = [(-1 * num) for num in nums]\n heapq.heapify(nums)\n while k > 1:\n heapq.heappop(nums)\n k -= 1\n\n return -1 * nums[0]\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python | Optimized Min Heap | O(n) | 99% T 85% S | kth-largest-element-in-an-array | 0 | 1 | **Optimized Min Heap**\n\nThe general idea is to heapify our array and pop k elements to find the k-th largest. There is an optimization we can implement to cut the time and space complexity down. \n\nThe idea is to ALWAYS maintain a MIN heap with only k elements\n * in this case, the k-th largest element will always be at the root position\n * we also utilize `heapq.heappushpop()` as it is faster than its separate `heappush` + `heappop` counterparts\n<br>\n\n**Complexity**\n\nTime complexity: O(n log k)\nSpace complexity: O(k)\n<br>\n\n```\nimport heapq\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n n = nums[:k] # populate heap with first k elements\n heapq.heapify(n)\n\t\t\n # loop through rest of array and pushpop largest elements\n for num in nums[k:]:\n if num > n[0]:\n heapq.heappushpop(n, num)\n \n return n[0]\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Best Python Solution | 1 Line | Using Heap | kth-largest-element-in-an-array | 0 | 1 | \n# Code\n```\nimport heapq\nclass Solution:\n def findKthLargest(self, nums: List[int], k: int) -> int:\n return heapq.nlargest(k,nums)[-1]\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
You must solve it in `O(n)` time complexity.
**Example 1:**
**Input:** nums = \[3,2,1,5,6,4\], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = \[3,2,3,1,2,4,5,5,6\], k = 4
**Output:** 4
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
[Python3] Recursive, Beats 98.16% | combination-sum-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst thoughts are that we have to somehow not repeat combinations--so what if we pick only the acending ones?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDefine some end conditions for recursion: n is unattainable, or we only have one number left.\n\nThen, try all numbers greater or equal to previous number.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(9^k)$$ - although always less, this is an upper bound.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(k)$$? Not sure on this one since there\'s not really any extra space taken that doesn\'t go into the solution array. However, the stack overhead is $$O(k)$$.\n\n# Code\n```\nclass Solution:\n @lru_cache\n def combinationSum3(self, k: int, n: int, m: int = 1) -> List[List[int]]:\n if n < k or n > min(k * 9, 45):\n return []\n if k == 1 and n >= m:\n return [[n]]\n ret = []\n for i in range(m, 10):\n for ans in self.combinationSum3(k - 1, n - i, i + 1):\n ret.append([i] + ans)\n return ret\n``` | 1 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
C++ and Python | 80% Faster Code using Backtracking | Easy Understanding | combination-sum-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**Backtracking**\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**C++ Solution:-**\n```\nclass Solution {\npublic:\n int sum(vector<int> ds) {\n int sums = 0;\n for(int i=0; i<ds.size(); i++) {\n sums += ds[i];\n }\n return sums;\n }\n void backtrack(int ind, vector<int>& ds, vector<vector<int>>& res, int n, int k, int high) {\n if(ds.size() == k && sum(ds) == n) {\n res.emplace_back(ds);\n return;\n }\n for(int i=ind; i<=high; i++) {\n ds.emplace_back(i);\n backtrack(i+1, ds, res, n, k, high);\n ds.pop_back();\n }\n }\n vector<vector<int>> combinationSum3(int k, int n) {\n int high = 9;\n vector<vector<int>> res;\n vector<int> ds;\n backtrack(1, ds, res, n, k, high);\n return res;\n }\n};\n```\n**Python Solution:-**\n```\nclass Solution:\n def combinationSum3(self, k: int, n: int) -> List[List[int]]:\n high = 9\n def backtrack(ind, n, k, ds, res):\n if len(ds) == k and sum(ds) == n:\n res.append(ds[:])\n return\n for i in range(ind, high+1):\n ds.append(i)\n backtrack(i+1, n, k, ds, res)\n ds.pop()\n \n res = []\n backtrack(1, n, k, [], res)\n return res\n \n``` | 1 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
✅Easy Backtracking Code || Beats 100%🔥 || AMAZON SDE-1 Interview⚠️ | combination-sum-iii | 1 | 1 | \n\n### **It is one of the Pick only type of Backtracking problems.**\n\n### **Doing Combination Sum 1 and 2 is mandatory before solving this problem.**\n\n### **Also this problem has been asked for FAANG interview multiple times.**\n### **My friend recently gave Microsoft SDE-1 Interview and faced this question!** \n\n#### **Code is self explainatory ! If you don\'t understand this code then plz do check out the following solutions to make it more clear.**\n# Combination Sum 1 :-\nhttps://leetcode.com/problems/combination-sum/solutions/2974627/easiest-faang-method-ever/\n\n# Combination Sum 2 :-\nhttps://leetcode.com/problems/combination-sum-ii/solutions/2980945/easiest-faang-method-ever/\n\n\n# ***Please Upvote if it helps \uD83D\uDE4F\u2764\uFE0F***\n# Code\n```\nclass Solution {\npublic:\n void CombinationSum(int ind, vector<int> &ds, vector<vector<int>> &ans, int target, int k, int n){\n if(ds.size()==k){\n if(target==0){\n ans.emplace_back(ds);\n return;\n }\n }\n for(int i=ind;i<=9;i++){\n if(ds.size()>=k && target!=0) break;\n if(i>target) break;\n ds.emplace_back(i);\n CombinationSum(i+1, ds, ans, target-i, k, n);\n ds.pop_back();\n }\n }\n vector<vector<int>> combinationSum3(int k, int n) {\n vector<vector<int>> ans;\n vector<int> ds;\n if(n<k){\n return ans;\n }\n CombinationSum(1, ds, ans, n, k, n);\n return ans;\n }\n};\n``` | 7 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
[ Python ] | Simple & Clean Solution using combinations | combination-sum-iii | 0 | 1 | \n# Code\n\n## Using Recursion / DFS:\n```\nclass Solution:\n def combinationSum3(self, k: int, n: int) -> List[List[int]]:\n def dfs(nums, k, n, path, ans):\n if k < 0 or n < 0: return\n if k == 0 and n == 0: ans.append(path)\n\n for i in range(len(nums)):\n dfs(nums[i + 1:], k - 1, n - nums[i], path + [nums[i]], ans)\n \n ans = []\n dfs(list(range(1,10)), k, n, [], ans)\n return ans\n```\n\n## Using Functool Library\'s combinations:\n```\nclass Solution:\n def combinationSum3(self, k: int, n: int) -> List[List[int]]:\n ans = []\n for c in combinations(range(1,10),k):\n if sum(c)==n:\n ans.append(c)\n return ans\n\n``` | 3 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
216: Solution with step by step explanation | combination-sum-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe backtrack() function returns a list of lists, where each inner list is a valid combination of numbers that sum up to n. The start parameter represents the smallest number that can be added to the combination, and it starts at 1 initially. The target parameter is the remaining sum that we need to reach. The k parameter is the number of values we still need to add to the combination. The res parameter is not used anymore, so we can remove it.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def combinationSum3(self, k: int, n: int) -> List[List[int]]:\n def backtrack(start, target, k, res):\n if k == 0 and target == 0:\n return [[]]\n if k == 0 or target < 0:\n return []\n ans = []\n for i in range(start, 10):\n for combo in backtrack(i+1, target-i, k-1, res):\n ans.append([i] + combo)\n return ans\n \n return backtrack(1, n, k, [])\n\n``` | 5 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
Python Simple Solution Explained (video + code) Backtracking | combination-sum-iii | 0 | 1 | [](https://www.youtube.com/watch?v=J2hcPZRpbMk)\nhttps://www.youtube.com/watch?v=J2hcPZRpbMk\n```\nclass Solution:\n def combinationSum3(self, k: int, n: int) -> List[List[int]]:\n res = []\n \n def backtrack(num, stack, target):\n if len(stack) == k:\n if target == 0:\n res.append(stack)\n return\n \n for x in range(num + 1, 10):\n if x <= target:\n backtrack(x, stack + [x], target - x)\n else:\n return\n \n backtrack(0, [], n)\n return res\n``` | 21 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
python3 - 3 lines of code | combination-sum-iii | 0 | 1 | \n def combinationSum3(self, k: int, n: int) -> List[List[int]]:\n nums = [i for i in range(1,10)]\n \n comb = itertools.combinations(nums,k)\n \n return [c for c in comb if sum(c) == n] | 4 | Find all valid combinations of `k` numbers that sum up to `n` such that the following conditions are true:
* Only numbers `1` through `9` are used.
* Each number is used **at most once**.
Return _a list of all possible valid combinations_. The list must not contain the same combination twice, and the combinations may be returned in any order.
**Example 1:**
**Input:** k = 3, n = 7
**Output:** \[\[1,2,4\]\]
**Explanation:**
1 + 2 + 4 = 7
There are no other valid combinations.
**Example 2:**
**Input:** k = 3, n = 9
**Output:** \[\[1,2,6\],\[1,3,5\],\[2,3,4\]\]
**Explanation:**
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
**Example 3:**
**Input:** k = 4, n = 1
**Output:** \[\]
**Explanation:** There are no valid combinations.
Using 4 different numbers in the range \[1,9\], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 60` | null |
✅4 Method's || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | contains-duplicate | 1 | 1 | # Approach 1: Brute Force\n\n# Intuition:\nThe brute force approach compares each element with every other element in the array to check for duplicates. If any duplicates are found, it returns `true`. This approach is straightforward but has a time complexity of O(n^2), making it less efficient for large arrays.\n\n# Explanation:\nThe brute force approach involves comparing each element in the array with every other element to check for duplicates. If any duplicates are found, return `true`, otherwise return `false`.\n\n# Code [TLE]:\n```C++ []\nclass Solution {\npublic:\n bool containsDuplicate(vector<int>& nums) {\n int n = nums.size();\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n if (nums[i] == nums[j])\n return true;\n }\n }\n return false;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean containsDuplicate(int[] nums) {\n int n = nums.length;\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n if (nums[i] == nums[j])\n return true;\n }\n }\n return false;\n }\n}\n```\n```Python3 []\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n n = len(nums)\n for i in range(n - 1):\n for j in range(i + 1, n):\n if nums[i] == nums[j]:\n return True\n return False\n```\n\nThe time complexity of this approach is `O(n^2)`, where n is the length of the array.\nso, this approach is not efficient for large arrays -> **TLE**\n\n# Approach 2: Sorting\n\n# Intuition:\nThe sorting approach sorts the array in ascending order and then checks for adjacent elements that are the same. If any duplicates are found, it returns `true`. Sorting helps in bringing duplicates together, simplifying the check. However, sorting has a time complexity of O(n log n).\n\n# Explanation:\nAnother approach is to sort the array and then check for adjacent elements that are the same. If any duplicates are found, return `true`, otherwise return `false`.\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n bool containsDuplicate(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n for (int i = 1; i < n; i++) {\n if (nums[i] == nums[i - 1])\n return true;\n }\n return false;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean containsDuplicate(int[] nums) {\n Arrays.sort(nums);\n int n = nums.length;\n for (int i = 1; i < n; i++) {\n if (nums[i] == nums[i - 1])\n return true;\n }\n return false;\n }\n}\n```\n```Python3 []\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n nums.sort()\n n = len(nums)\n for i in range(1, n):\n if nums[i] == nums[i - 1]:\n return True\n return False\n```\n\nThe time complexity of this approach is `O(n log n)`, where n is the length of the array.\n\n# Approach 3: Hash Set\n\n# Intuition:\nThe hash set approach uses a hash set data structure to store encountered elements. It iterates through the array, checking if an element is already in the set. If so, it returns `true`. Otherwise, it adds the element to the set. This approach has a time complexity of O(n) and provides an efficient way to check for duplicates.\n\n# Explanation:\nA more efficient approach is to use a hash set data structure to store the encountered elements. While iterating through the array, if an element is already present in the hash set, return `true`. Otherwise, add the element to the hash set. If the loop completes without finding any duplicates, return `false`.\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n bool containsDuplicate(vector<int>& nums) {\n unordered_set<int> seen;\n for (int num : nums) {\n if (seen.count(num) > 0)\n return true;\n seen.insert(num);\n }\n return false;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean containsDuplicate(int[] nums) {\n HashSet<Integer> seen = new HashSet<>();\n for (int num : nums) {\n if (seen.contains(num))\n return true;\n seen.add(num);\n }\n return false;\n }\n}\n```\n```Python3 []\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n seen = set()\n for num in nums:\n if num in seen:\n return True\n seen.add(num)\n return False\n```\n\nThe time complexity of this approach is `O(n)`, where n is the length of the array.\n\n# Approach 4: Hash Map \n\n# Intuition:\nThe hash map approach is similar to the hash set approach but also keeps track of the count of occurrences for each element. It uses a hash map to store the elements as keys and their counts as values. If a duplicate element is encountered (count greater than or equal to 1), it returns `true`. This approach provides more information than just the presence of duplicates and has a time complexity of O(n).\n\n# Explanation:\nIn this approach, we iterate through the array and store each element as a key in a hash map. The value associated with each key represents the count of occurrences of that element. If we encounter an element that already exists in the hash map with a count greater than or equal to 1, we return `true`, indicating that a duplicate has been found. Otherwise, we update the count of that element in the hash map. If we complete the iteration without finding any duplicates, we return `false`.\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n bool containsDuplicate(vector<int>& nums) {\n unordered_map<int, int> seen;\n for (int num : nums) {\n if (seen[num] >= 1)\n return true;\n seen[num]++;\n }\n return false;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean containsDuplicate(int[] nums) {\n HashMap<Integer, Integer> seen = new HashMap<>();\n for (int num : nums) {\n if (seen.containsKey(num) && seen.get(num) >= 1)\n return true;\n seen.put(num, seen.getOrDefault(num, 0) + 1);\n }\n return false;\n }\n}\n```\n```Python3 []\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n seen = {}\n for num in nums:\n if num in seen and seen[num] >= 1:\n return True\n seen[num] = seen.get(num, 0) + 1\n return False\n```\n\nThe time complexity of this approach is `O(n)`, where n is the length of the array.\n\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. **Practice them in a row for better understanding and please Upvote for more questions.**\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n\n\n | 886 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Very Easy || 100% || Fully Explained || C++, Java, Python, Javascript, Python3 (Creating Set) | contains-duplicate | 1 | 1 | # **C++ Solution (Using Set / Sort & Find Approach)**\n```\n/** Approach : Using Set **/\n// Time Complexity: O(n)\nclass Solution {\npublic:\n bool containsDuplicate(vector<int>& nums) {\n // Create a set...\n unordered_set<int> hset;\n // Traverse all the elements through the loop...\n for(int idx = 0; idx < nums.size(); idx++) {\n // Searches set. if present, it contains duplicate...\n if(hset.count(nums[idx]))\n return true;\n // insert nums[i] in set...\n hset.insert(nums[idx]);\n }\n return false;\n }\n};\n------------------------------------------------------------------------------------------------------------------------------------------------------------------\n/** Approach : Sort & Find Duplicates **/\n// Time Complexity: O(nlogn)\n// Space Complexity: O(1)\nclass Solution {\npublic:\n bool containsDuplicate(vector<int>& nums) {\n // Sort the nums...\n sort(nums.begin(), nums.end());\n // Traverse all the elements through the loop...\n for(int idx = 0; idx < nums.size() - 1; idx++) {\n // Check the duplicate element...\n if(nums[idx] == nums[idx + 1])\n return true;\n }\n // Otherwise return false...\n return false;\n }\n};\n```\n\n# **Java Solution (Using Hashset):**\n```\n// Time complexity: O(n)\n// Space complexity: O(n)\nclass Solution {\n public boolean containsDuplicate(int[] nums) {\n // Create a hashset...\n HashSet<Integer> hset = new HashSet<Integer>();\n // Traverse all the elements through the loop...\n for (int idx = 0; idx < nums.length; idx ++){\n // Searches hashset. if present, it contains duplicate...\n if (hset.contains(nums[idx])){\n return true;\n }\n // if not present it will update hashset...\n hset.add(nums[idx]);\n }\n // Otherwise return false...\n return false;\n }\n}\n-----------------------------------------------------------------------------------------------------------------------------------------------------------------\n// Time complexity: O(n)\n// Space complexity: O(n)\nclass Solution {\n public boolean containsDuplicate(int[] nums) {\n // Base case...\n if(nums==null || nums.length==0)\n return false;\n // Create a hashset...\n HashSet<Integer> hset = new HashSet<Integer>();\n // Traverse all the elements through the loop...\n for(int idx: nums){\n // If it contains duplicate...\n if(!hset.add(idx)){\n return true;\n }\n }\n // Otherwise return false...\n return false;\n }\n}\n```\n\n# **Python / Python3 Solution (Creating a Set):**\n```\n# Time complexity: O(n)\n# Space complexity: O(n)\nclass Solution(object):\n def containsDuplicate(self, nums):\n hset = set()\n for idx in nums:\n if idx in hset:\n return True\n else:\n hset.add(idx)\n```\n \n# **JavaScript Solution (Creating a Set):**\n```\n// Time complexity: O(n)\n// Space complexity: O(n)\nvar containsDuplicate = function(nums) {\n const s = new Set(nums); return s.size !== nums.length\n};\n```\n\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 694 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
One Line code Python3 | contains-duplicate | 0 | 1 | \n\n# One Line Of Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n return len(set(nums))!=len(nums)\n```\n# please upvote me it would encourage me alot | 200 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
[VIDEO] Step-by-Step Visualization of O(n) Solution | contains-duplicate | 0 | 1 | https://www.youtube.com/watch?v=JTIq3m8F4hw\n\nThe brute force approach would be to simply check each element with every other element in the array, and return `True` if a duplicate is found or `False` otherwise. Unfortunately, this runs in O(n<sup>2</sup>).\n\nWe can reduce this to O(n) by using a hash set, or simply a `set()` in Python. For each element in the array, we\'ll check to see if it is already in the set. If it isn\'t, we\'ll add it to the set and move on, and if it is, then that means it is a duplicate and we\'ll return `True`. If we get through the whole array without finding a duplicate, we\'ll return `False`\n\nThis runs in O(n) time because hash set lookup runs in O(1) time. Similar to a hash table, when you need to check for a key in the set, you don\'t have to iterate over all elements in the set. Instead, the corresponding hash is calculated, and you can jump straight to it.\n\n# Code\n```\nclass Solution(object):\n def containsDuplicate(self, nums):\n num_set = set()\n for i in nums:\n if i in num_set:\n return True\n else:\n num_set.add(i)\n return False\n \n``` | 9 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
217. Contains Duplicate || Solution for Python3 | contains-duplicate | 0 | 1 | Upgraded!\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n if len(nums) != len(set(nums)):\n return True\n return False\n``` | 1 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Python: set+ len() | contains-duplicate | 0 | 1 | # Intuition\nSince we want to avoid using loops, a good way of thinking about the problem is identifying what we want which is the number of times unique numbers appear in the list.\n\n# Approach\nWe are going to use set() + len() function to help us solve this.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n x=set(nums)\n if len(nums) > 1:\n if len(x) < len(nums):\n return True\n else:\n return False\n``` | 1 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Python 1 liner | contains-duplicate | 0 | 1 | ```\ndef containsDuplicate(nums):\n\treturn len(set(nums)) != len(nums)\n``` | 72 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
easiest python3 solution | contains-duplicate | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n hset={}\n for i in nums:\n if i in hset:\n return True\n hset[i]=1\n return False\n``` | 2 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
contains duplicate | contains-duplicate | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n new=set(nums)\n if(len(nums)!=len(new)):\n return True\n else:\n return False\n\n\n\n\n \n``` | 2 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Python3 code to check if num contains duplicate (TC&SC: O(n)) | contains-duplicate | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n if len(set(nums)) != len(nums):\n return True\n \n\n``` | 1 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
One Line Code | contains-duplicate | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n return sorted((set(nums)))!=sorted(nums)\n#please upvote me it would encourage me alot\n``` | 5 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Contains Duplicate || Simple Solution | contains-duplicate | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n num2=set(nums)\n l1=len(nums)\n l2=len(num2)\n if(l1!=l2):\n return True\n else:\n return False\n```\nIf you find it helful, please give your valuable vote!!\n\n | 18 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
5 Different Approaches w/ Explanations | contains-duplicate | 0 | 1 | **Approach #1**: Brute Force - *Time Limit Exceeded*\n\n```\ndef containsDuplicate(self, nums: List[int]) -> bool:\n n = len(nums)\n for i in range(n - 1):\n for j in range(i + 1, n):\n if nums[i] == nums[j]: return True\n return False\n```\n\n* **Explanation**: Use two for loops to compare pairs of integers in the array. Once we reach a comparison in which the numbers are the same, we return true. If we loop through all the integers of the array without reaching a similar pair of numbers, we return false.\n* **Runtime**: Time Limit Exceeded\n---\n**Approach #2**: Sorting\n\n```\ndef containsDuplicate(self, nums: List[int]) -> bool:\n nums.sort()\n for i in range(len(nums)-1):\n if nums[i] == nums[i+1]: return True\n return False\n```\n\n* **Explanation**: We start off by sorting the given array. Once we loop through the array from the beginning, if we see that the current number is the same as the next one in the array, there contains a duplicate in the array and therefore we return true. If we finish looping and there are no duplicates, we return false.\n* **Runtime**: Faster than 15% (715 ms)\n---\n**Approach #3**: Using Counter Function\n\n```\ndef containsDuplicate(self, nums: List[int]) -> bool:\n freq = Counter(nums)\n for num, freq in freq.items():\n if freq > 1:\n return True\n return False\n```\n\n* **Explanation**: `Counter` is a subclass of `dict` designed for counting hashable objects in Python. It\u2019s a dictionary that stores the objects as keys and the frequencies of those objects as values. In this approach, we utilize `Counter` to count the frequencies of each integer for us. For example, if the input array is `[1, 2, 3, 4, 4, 5]`, using `Counter` on that input array will give us the following dictionary: `Counter({4: 2, 1: 1, 2: 1, 3: 1, 5: 1})`. Utilizing this function, we will loop through the `freq` dictionary to see if any values (frequencies) are greater than 1, which means there exists an integer in the given array that is duplicated.\n* **Runtime**: Faster than 7% (797 ms)\n---\n**Approach #4**: Using Hashmap\n\n```\ndef containsDuplicate(self, nums: List[int]) -> bool:\n counter = {}\n for num in nums:\n if num not in counter:\n counter[num] = 0\n counter[num] += 1\n for num, freq in counter.items():\n if freq > 1:\n return True\n return False\n```\n\n* **Explanation**: In this approach, we essentially mimick what the `Counter` function does in the previous approach. We first initialize a hashmap, to which we loop through the given array and plot the frequencies of each integer by incrementing the values in the hashmap. Then, we try to look for a frequency that is greater than 1 and return the result accordingly.\n* **Runtime**: Faster than 7% (810 ms)\n---\n**Approach #5**: Using Set\n\n```\ndef containsDuplicate(self, nums: List[int]) -> bool:\n return False if len(set(nums)) == len(nums) else True\n```\n```\ndef containsDuplicate(self, nums: List[int]) -> bool:\n return len(set(nums)) != len(nums)\n```\n\n* **Explanation**: This approach can be done a number of ways in just one line. Essentially we are using `set()` to convert the given array to a set. In a set, the values are unique and there exists no duplicates, therefore if the set version of the input array has a different length than the regular array itself, there exists a duplicate in the original input array.\n* **Runtime**: Faster than 5% (885 ms) | 98 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Extremely Simplified ONE LINE PYTHON!!! | contains-duplicate | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLooking for if the list contains duplicate.\nso we used the length of list and set to compare whether the len(set) is the same as len(list).\n# Solution SIUUUUUUU\n<!-- Describe your approach to solving the problem. -->\nAs we return boolean in this function, we only need to filter what is True and return it.\n\n\n# Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n return len(nums) != len(set(nums)) \n``` | 4 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
✅1 line simple in python | contains-duplicate | 0 | 1 | # Code\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n return len(set(nums)) != len(nums)\n # example:\n # nums = [1, 2, 2, 3]\n # set(nums) = [1, 2, 3] (order could be different)\n # if both lenght are the same, it has no duplicated item\n``` | 1 | Given an integer array `nums`, return `true` if any value appears **at least twice** in the array, and return `false` if every element is distinct.
**Example 1:**
**Input:** nums = \[1,2,3,1\]
**Output:** true
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Example 3:**
**Input:** nums = \[1,1,1,3,3,4,3,2,4,2\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Solution | the-skyline-problem | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {\n int edge_idx = 0;\n vector<pair<int, int>> edges;\n priority_queue<pair<int, int>> pq;\n vector<vector<int>> skyline;\n\n for (int i = 0; i < buildings.size(); ++i) {\n const auto &b = buildings[i];\n edges.emplace_back(b[0], i);\n edges.emplace_back(b[1], i);\n }\n\n std::sort(edges.begin(), edges.end());\n\n while (edge_idx < edges.size()) {\n int curr_height;\n const auto &[curr_x, _] = edges[edge_idx];\n while (edge_idx < edges.size() &&\n curr_x == edges[edge_idx].first) {\n const auto &[_, building_idx] = edges[edge_idx];\n const auto &b = buildings[building_idx];\n if (b[0] == curr_x)\n pq.emplace(b[2], b[1]);\n ++edge_idx;\n }\n while (!pq.empty() && pq.top().second <= curr_x)\n pq.pop();\n curr_height = pq.empty() ? 0 : pq.top().first;\n if (skyline.empty() || skyline.back()[1] != curr_height)\n skyline.push_back({curr_x, curr_height});\n }\n return skyline;\n }\n};\n```\n\n```Python3 []\nfrom sortedcontainers import SortedList\nclass Solution:\n def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:\n if len(buildings) == 0: \n return []\n \n buildings.sort(key=lambda v: v[2])\n pos, height = [0], [0]\n for left, right, h in buildings: \n i = bisect_left(pos, left)\n j = bisect_right(pos, right)\n height[i:j] = [h, height[j-1]]\n pos[i:j] = [left, right]\n print(height, pos)\n res = []\n prev = 0\n for v, h in zip(pos, height): \n if h != prev:\n res.append([v,h]) \n prev = h\n \n return res\n```\n\n```Java []\nclass TopNode {\n int x;\n int h;\n TopNode next;\n TopNode() {\n }\n TopNode(int x, int h) {\n this.x = x;\n this.h = h;\n }\n\n void insert(TopNode n) {\n n.next = next;\n next = n;\n }\n\n}\nclass Solution {\n static final int LEFT=0, RIGHT=1, HEIGHT=2;\n public List<List<Integer>> getSkyline(int[][] buildings) {\n TopNode head = new TopNode(0,0);\n head.insert(new TopNode(Integer.MAX_VALUE, 0));\n TopNode start = head;\n \n for (int i = 0; i<buildings.length; i++) {\n int[] b = buildings[i];\n int bL = buildings[i][LEFT];\n int bR = buildings[i][RIGHT];\n int bH = buildings[i][HEIGHT];\n //System.out.println(Arrays.toString(buildings[i]));\n while (bL >= start.next.x) { start = start.next; } \n //System.out.println(start.toString());\n for (TopNode t = start ; bR > t.x; t = t.next) {\n //System.out.println(head.toString());\n if (bH <= t.h) {\n continue;\n }\n\n TopNode stop = t;\n while (stop.next != null && stop.next.x < bR && stop.next.h <= bH ) {\n stop = stop.next;\n }\n \n if (bL <= t.x) {\n if (bR >= stop.next.x) {\n t.next = stop.next;\n t.h = bH;\n }\n else if (t == stop) {\n t.insert(new TopNode(bR,t.h));\n t.h = bH;\n break;\n }\n else {\n stop.x = bR;\n t.h = bH;\n t.next = stop;\n break;\n }\n }\n else {\n if (bR >= stop.next.x) {\n if (t == stop) {\n t.insert(new TopNode(bL, bH));\n }\n else {\n t.next = stop;\n stop.x = bL;\n stop.h = bH;\n }\n break;\n }\n else if (t == stop) {\n t.insert(new TopNode(bL,bH));\n t.next.insert(new TopNode(bR,t.h));\n break;\n }\n else {\n t.next = stop;\n t.insert(new TopNode(bL,bH));\n stop.x = bR;\n break;\n }\n }\n t = stop;\n\n }\n }\n\n List<List<Integer>> skyline = new ArrayList<>();\n\n if (head.h == 0)\n head = head.next;\n while (head != null) {\n int height = head.h;\n skyline.add(List.of(head.x, height));\n while ( (head = head.next) != null && head.h == height) {}\n }\n\n return skyline;\n }\n\n}\n```\n | 437 | A city's **skyline** is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return _the **skyline** formed by these buildings collectively_.
The geometric information of each building is given in the array `buildings` where `buildings[i] = [lefti, righti, heighti]`:
* `lefti` is the x coordinate of the left edge of the `ith` building.
* `righti` is the x coordinate of the right edge of the `ith` building.
* `heighti` is the height of the `ith` building.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height `0`.
The **skyline** should be represented as a list of "key points " **sorted by their x-coordinate** in the form `[[x1,y1],[x2,y2],...]`. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate `0` and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
**Note:** There must be no consecutive horizontal lines of equal height in the output skyline. For instance, `[...,[2 3],[4 5],[7 5],[11 5],[12 7],...]` is not acceptable; the three lines of height 5 should be merged into one in the final output as such: `[...,[2 3],[4 5],[12 7],...]`
**Example 1:**
**Input:** buildings = \[\[2,9,10\],\[3,7,15\],\[5,12,12\],\[15,20,10\],\[19,24,8\]\]
**Output:** \[\[2,10\],\[3,15\],\[7,12\],\[12,0\],\[15,10\],\[20,8\],\[24,0\]\]
**Explanation:**
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.
**Example 2:**
**Input:** buildings = \[\[0,2,3\],\[2,5,3\]\]
**Output:** \[\[0,3\],\[5,0\]\]
**Constraints:**
* `1 <= buildings.length <= 104`
* `0 <= lefti < righti <= 231 - 1`
* `1 <= heighti <= 231 - 1`
* `buildings` is sorted by `lefti` in non-decreasing order. | null |
Faster than 93.17% | Single priority Queue | Easy to understand | Python3 | Max heap | the-skyline-problem | 0 | 1 | Please upvote this post if you find it helpful in anyway.\n\n\n\n\n```\nclass Solution(object):\n def getSkyline(self, buildings):\n """\n :type buildings: List[List[int]]\n :rtype: List[List[int]]\n """\n \n buildings.sort(key=lambda x:[x[0],-x[2]]) #Sort elements according to x-axis (ascending) and height(descending)\n new_b=[]\n max_r=-float(\'inf\')\n min_l=float(\'inf\')\n for i in buildings:\n new_b.append([-i[2],i[0],i[1]]) #Create new array for priority queue with [-1*height, left,right], as we are creating max heap\n max_r=max(max_r,i[1])\n min_l=min(min_l,i[0])\n \n ans=[[0,0,max_r+1]] #for default when the buildings at a specific point is over\n f_ans=[]\n heapq.heapify(ans)\n while min_l<=max_r:\n while new_b and min_l>=new_b[0][1]: \n temp=new_b.pop(0)\n heapq.heappush(ans,temp)\n while ans and ans[0][2]<=min_l:\n heapq.heappop(ans)\n \n if not f_ans or f_ans[-1][1]!=(-ans[0][0]):\n f_ans.append([min_l,-ans[0][0]])\n if new_b:\n min_l=min(ans[0][2],new_b[0][1]) #To update the min_l according to the next element and the element itself\n else:\n min_l=ans[0][2]\n \n return f_ans\n\n``` | 2 | A city's **skyline** is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return _the **skyline** formed by these buildings collectively_.
The geometric information of each building is given in the array `buildings` where `buildings[i] = [lefti, righti, heighti]`:
* `lefti` is the x coordinate of the left edge of the `ith` building.
* `righti` is the x coordinate of the right edge of the `ith` building.
* `heighti` is the height of the `ith` building.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height `0`.
The **skyline** should be represented as a list of "key points " **sorted by their x-coordinate** in the form `[[x1,y1],[x2,y2],...]`. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate `0` and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
**Note:** There must be no consecutive horizontal lines of equal height in the output skyline. For instance, `[...,[2 3],[4 5],[7 5],[11 5],[12 7],...]` is not acceptable; the three lines of height 5 should be merged into one in the final output as such: `[...,[2 3],[4 5],[12 7],...]`
**Example 1:**
**Input:** buildings = \[\[2,9,10\],\[3,7,15\],\[5,12,12\],\[15,20,10\],\[19,24,8\]\]
**Output:** \[\[2,10\],\[3,15\],\[7,12\],\[12,0\],\[15,10\],\[20,8\],\[24,0\]\]
**Explanation:**
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.
**Example 2:**
**Input:** buildings = \[\[0,2,3\],\[2,5,3\]\]
**Output:** \[\[0,3\],\[5,0\]\]
**Constraints:**
* `1 <= buildings.length <= 104`
* `0 <= lefti < righti <= 231 - 1`
* `1 <= heighti <= 231 - 1`
* `buildings` is sorted by `lefti` in non-decreasing order. | null |
Python || 99 % runtime || Hash Table || Easy to understand | contains-duplicate-ii | 0 | 1 | **Plz Upvote ..if you got help from this.**\n# Code\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n d = {}\n\n for i, n in enumerate(nums):\n if n in d and abs(i - d[n]) <= k:\n return True\n else:\n d[n] = i\n \n return False\n\n\n``` | 28 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Very Easy || 100% || Fully Explained || Java, C++, Python, Javascript, Python3 (Using HashSet) | contains-duplicate-ii | 1 | 1 | # **Java Solution (Using HashSet):**\n```\n// Time Complexity : O(n)\nclass Solution {\n public boolean containsNearbyDuplicate(int[] nums, int k) {\n // Base case...\n if(nums == null || nums.length < 2 || k == 0)\n return false;\n int i = 0;\n // Create a Hash Set for storing previous of k elements...\n HashSet<Integer> hset = new HashSet<Integer>();\n // Traverse for all elements of the given array in a for loop...\n for(int j = 0; j < nums.length; j++) {\n // If duplicate element is present at distance less than equal to k, return true...\n if(!hset.add(nums[j])){\n return true;\n }\n // If size of the Hash Set becomes greater than k...\n if(hset.size() >= k+1){\n // Remove the last visited element from the set...\n hset.remove(nums[i++]);\n }\n }\n // If no duplicate element is found then return false...\n return false;\n }\n}\n```\n--------------------------------------------------------------------------------------------------\n# **C++ Solution:**\n```\n// Time Complexity : O(n)\nclass Solution {\npublic:\n bool containsNearbyDuplicate(vector<int>& nums, int k) {\n // Create a Set for storing previous of k elements...\n unordered_set<int> hset;\n // Traverse for all elements of the given array in a for loop...\n for(int idx = 0; idx < nums.size(); idx++) {\n // Check if set already contains nums[idx] or not...\n // If duplicate element is present at distance less than equal to k, return true...\n if(hset.count(nums[idx]))\n return true;\n // Otherwise, add nums[idx] to the set...\n hset.insert(nums[idx]);\n // If size of the set becomes greater than k...\n if(hset.size() > k)\n // Remove the last visited element from the set...\n hset.erase(nums[idx - k]);\n }\n // If no duplicate element is found then return false...\n return false;\n }\n};\n```\n---------------------------------------------------------------------------------------------------\n# **Python/Python3 Solution:**\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n # Create hset for storing previous of k elements...\n hset = {}\n # Traverse for all elements of the given array in a for loop...\n for idx in range(len(nums)):\n # If duplicate element is present at distance less than equal to k, return true...\n if nums[idx] in hset and abs(idx - hset[nums[idx]]) <= k:\n return True\n hset[nums[idx]] = idx\n # If no duplicate element is found then return false...\n return False\n```\n-----------------------------------------------------------------------------------------------------\n# **JavaScript Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nvar containsNearbyDuplicate = function(nums, k) {\n const hasmap = new Map();\n for (let idx = 0; idx < nums.length; idx++) {\n // Check if the difference betweend duplicates is less than k\n if (idx - hasmap.get(nums[idx]) <= k) {\n return true;\n }\n hasmap.set(nums[idx], idx);\n }\n return false;\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 138 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Python3 Beats 99.83% | contains-duplicate-ii | 0 | 1 | # Approach\nSimilar to the [Two Sum](https://leetcode.com/problems/two-sum)\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$ because there has been used support dictionary to store covered list\'s items\n\n# Code\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n d = {}\n for i in range(len(nums)):\n if nums[i] in d:\n if abs(d[nums[i]] - i) <= k:\n return True\n d[nums[i]] = i\n return False\n```\n\nUPD: As it was told in comments, unnecessary `else`s were removed. Thanks to [@fck_scl](https://leetcode.com/fck_scl/) | 3 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Easy Python3 Hashmap Solution Beats 55% | contains-duplicate-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n \'\'\'\n Intuition:\n Create a hasmap.\n Loop through nums and map the index to the number.\n \'\'\'\n myMap = {}\n for i, num in enumerate(nums):\n if num in myMap and abs(myMap[num] - i) <= k:\n return True\n else:\n myMap[num] = i\n return False\n\n``` | 1 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Deadly simple code beats 90.46% in runtime & 87.12% in memory only 6 lines !!!!!!!!!! | contains-duplicate-ii | 0 | 1 | \n\nPlease UPVOTE !!!\n\n\n\n\n\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n if k==0:return False\n set_=set()\n for r in range(len(nums)):\n if nums[r] in set_:return True\n set_.add(nums[r])\n if len(set_)==k+1:set_.remove(nums[r-k])\n return False\n``` | 11 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Beats 99.97%, Linear Time Complexity | contains-duplicate-ii | 0 | 1 | # Simple to Understand a Solution\n# Code\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n d1 = {}\n for key, val in enumerate(nums):\n if val not in d1:\n d1[val] = key\n else:\n if abs(d1.get(val) - key) <= k:\n return True\n else:\n d1[val] = key\n\n return False\n```\n\n# Please Upvote if you can | 13 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
219: 96.58%, Solution with step by step explanation | contains-duplicate-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nOne approach to solve this problem is by using a hash map. We will keep track of the indices of each element in the hash map. If we find a repeated element, we can check if the absolute difference between its current index and the previous index is less than or equal to k.\n\nIf the difference is less than or equal to k, we return true. If we iterate over the entire array and do not find any repeated elements with the required absolute difference, we return false.\n\n# Complexity\n- Time complexity:\nBeats\n96.58% O(n) since we iterate over the array once.\n\n- Space complexity:\nBeats\n41.62% O(min(n,k)) since we can have at most min(n,k) elements in the hash map.\n\n# Code\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n # create a hash map to store the indices of each element\n num_indices = {}\n \n # iterate over the array\n for i, num in enumerate(nums):\n # if the element is already in the hash map and its index difference is <= k, return True\n if num in num_indices and i - num_indices[num] <= k:\n return True\n \n # add the element to the hash map with its index\n num_indices[num] = i\n \n # if we don\'t find any repeated elements with the required index difference, return False\n return False\n\n``` | 12 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Python simple solution | contains-duplicate-ii | 0 | 1 | **Python :**\n\n```\ndef containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n\tindex_dict = {}\n\n\n\tfor i, n in enumerate(nums):\n\t\tif n in index_dict and i - index_dict[n] <= k:\n\t\t\treturn True\n\n\t\tindex_dict[n] = i\n\n\treturn False\n```\n\n**Like it ? please upvote !** | 39 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
✔️ Python's Simple and Easy to Understand Solution| O(n) Solution | 99% Faster 🔥 | contains-duplicate-ii | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n # Create dictionary for Lookup\n lookup = {}\n \n for i in range(len(nums)):\n \n # If num is present in lookup and satisfy the condition return True\n if nums[i] in lookup and abs(lookup[nums[i]]-i) <= k:\n return True\n \n # If num is not present in lookup then add it to lookup\n lookup[nums[i]] = i\n \n return False\n```\n**Visit this blog to learn Python tips and techniques and to find a Leetcode solution with an explanation: https://www.python-techs.com/**\n\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 15 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
Sliding Window Approach Python3 | contains-duplicate-ii | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n window = set()\n L = 0\n for R in range(len(nums)):\n if R - L > k:\n window.remove(nums[L])\n L += 1\n if nums[R] in window:\n return True\n window.add(nums[R])\n return False\n``` | 1 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
✅Python3 Easy to Understand | Dictionary | contains-duplicate-ii | 0 | 1 | ```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n seen = {}\n \n for i in range(len(nums)):\n if nums[i] in seen and abs(i - seen[nums[i]]) <= k:\n return True\n seen[nums[i]] = i\n return False\n```\nPlease upvote if it is helpful. | 4 | Given an integer array `nums` and an integer `k`, return `true` _if there are two **distinct indices**_ `i` _and_ `j` _in the array such that_ `nums[i] == nums[j]` _and_ `abs(i - j) <= k`.
**Example 1:**
**Input:** nums = \[1,2,3,1\], k = 3
**Output:** true
**Example 2:**
**Input:** nums = \[1,0,1,1\], k = 1
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3,1,2,3\], k = 2
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `0 <= k <= 105` | null |
[Python3] BucketSort O(n) || beats 98% | contains-duplicate-iii | 0 | 1 | ```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], indexDiff: int, valueDiff: int) -> bool:\n buckets = {} #store values for diapason (i-indexDiff:i]\n valueDiff +=1 #if valueDiff = zero it\'s simplify proces edge-cases\n \n for idx, curVal in enumerate(nums):\n bucketId = curVal // valueDiff #bucket for new element\n if bucketId in buckets: return True # have \'duplicate value\' in current bucket\n #check neighboring buckets if they are exists\n for i in (bucketId - 1, bucketId + 1):\n if i in buckets: # bucket exist\n if abs(buckets[i] - curVal) < valueDiff: # because valueDiff+1 then check only strict <\n return True\n \n #add current value to bucket\n buckets[bucketId] = curVal\n \n # remove value out of available window\n if idx >= indexDiff:\n removeVal = nums[idx - indexDiff]\n del buckets[removeVal//valueDiff]\n\n return False\n``` | 11 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
220: Time 94.72% and Space 92.33%, Solution with step by step explanation | contains-duplicate-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe solution uses bucketing technique to solve the problem.\n\n1. First, we check if the input list nums is not empty and if indexDiff is greater than 0 and valueDiff is non-negative. If not, we return False as no such pair exists.\n\n2. We find the minimum value in the list nums.\n\n3. We set the diff as valueDiff + 1. This is because, in case valueDiff is 0, we need to ensure that a difference of 0 is allowed.\n\n4. We create an empty dictionary bucket to store the elements in the current and adjacent buckets.\n\n5. We define a function getKey which takes an integer num as input and returns the key of the bucket to which the element belongs.\n\n6. We iterate through each element in the list nums along with its index i. For each element, we get its corresponding key using getKey function.\n\n7. We first check if the element already exists in the current bucket. If yes, then we return True as we have found the required pair.\n\n8. If not, we check if the left adjacent bucket exists and if the difference between the current element and the maximum element in the left adjacent bucket is less than diff. If yes, then we return True.\n\n9. Similarly, we check if the right adjacent bucket exists and if the difference between the minimum element in the right adjacent bucket and the current element is less than diff. If yes, then we return True.\n\n10. If none of the above conditions hold, we add the current element to the bucket with the key as the value returned by getKey. We also remove the element from the bucket whose index is greater than or equal to indexDiff.\n\n11. Finally, if no such pair exists in the entire list, we return False.\n\n# Complexity\n- Time complexity:\nBeats\n94.72%\n- Space complexity:\nBeats\n92.33%\n\n# Code\n```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], indexDiff: int, valueDiff: int) -> bool:\n if not nums or indexDiff <= 0 or valueDiff < 0:\n return False\n\n mini = min(nums)\n diff = valueDiff + 1 # In case of valueDiff = 0\n bucket = {}\n\n def getKey(num: int) -> int:\n return (num - mini) // diff\n\n for i, num in enumerate(nums):\n key = getKey(num)\n if key in bucket: # Current bucket\n return True\n # Left adjacent bucket\n if key - 1 in bucket and num - bucket[key - 1] < diff:\n return True\n # Right adjacent bucket\n if key + 1 in bucket and bucket[key + 1] - num < diff:\n return True\n bucket[key] = num\n if i >= indexDiff:\n del bucket[getKey(nums[i - indexDiff])]\n\n return False\n\n``` | 5 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
[Python3] summarizing Contain Duplicates I, II, III | contains-duplicate-iii | 0 | 1 | This is a very self-consistent series. Although ad-hoc implementations exist (please check the corresponding posts in Dicuss), their solutions bear great resemblance to each other. \n\nStarting with [217. Contains Duplicate](https://leetcode.com/problems/contains-duplicate/), the key is to memoize what has been seen in a set\n```\nclass Solution:\n def containsDuplicate(self, nums: List[int]) -> bool:\n seen = set()\n for x in nums:\n if x in seen: return True \n seen.add(x)\n return False\n```\n\nProgressing to [219. Contains Duplicate II](https://leetcode.com/problems/contains-duplicate-ii/), extra info needs to be memoized, i.e. position via a dictionary. \n```\nclass Solution:\n def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:\n seen = {}\n for i, x in enumerate(nums): \n if x in seen and i - seen[x] <= k: return True \n seen[x] = i\n return False \n```\n\nComing back to this problem, we can summarize numbers in a given range into bucket. By bucketing numbers properly, this becomes almost identical to 219. Contains Duplicate except that numbers in adjacent buckets need to be check as well. \n```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n if t < 0: return False # edge case \n \n seen = {}\n for i, x in enumerate(nums): \n bkt = x//(t+1)\n if bkt in seen and i - seen[bkt][0] <= k: return True \n if bkt-1 in seen and i - seen[bkt-1][0] <= k and abs(x - seen[bkt-1][1]) <= t: return True \n if bkt+1 in seen and i - seen[bkt+1][0] <= k and abs(x - seen[bkt+1][1]) <= t: return True \n seen[bkt] = (i, x) \n return False \n```\n\nAs mentioned in the beginning, ad-hoc implementations do exist. But these three questions can all be solved by properly memoizing certain info, which makes them quite consistent for practice. | 48 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
Two Python Solutions: Memory Optimization, Speed Optimization | contains-duplicate-iii | 0 | 1 | Good Memory Optimization But Slow\n\n```\nimport sortedcontainers\nimport bisect\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n \n k +=1\n res = sortedcontainers.SortedList(nums[:k])\n for i in range(1,len(res)):\n if res[i]-res[i-1] <= t :\n return True\n \n \n for i in range(1,len(nums)-k+1):\n \n num = nums[i+k-1]\n res.remove(nums[i-1])\n res.add(nums[i+k-1])\n idx = bisect.bisect_left(res, num)\n \n if (idx-1 >= 0 and num-res[idx-1]<=t) or (idx+1<k and res[idx+1]-num<=t):\n return True\n \n return False\n```\n\nVery Fast but takes lot of memory\n```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n if t == 0 and len(set(nums)) == len(nums): return False\n \n bucket = {}\n width = t + 1\n \n for i, n in enumerate(nums):\n bucket_i = n // width\n \n if bucket_i in bucket: return True\n elif bucket_i + 1 in bucket and abs(n - bucket[bucket_i + 1]) < width: return True\n elif bucket_i - 1 in bucket and abs(n - bucket[bucket_i - 1]) < width: return True\n \n bucket[bucket_i] = n\n if i >= k: del bucket[ nums[i-k] //width ]\n \n return False\n\n``` | 3 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
Python 3 | Official Solution in Python 3 | 2 Methods | Explanation | contains-duplicate-iii | 0 | 1 | Below is Python 3 version of official solution: https://leetcode.com/problems/contains-duplicate-iii/solution/\n### Approach \\#1\n- Omitted since it will TLE\n\n### Approach \\#2 \n- The official Java solution used `TreeSet` as help, which provide the ability to maintain the order. At the same time it search and remove is relatively efficient. \n- Python standard library doesn\'t come with a data struction like `TreeSet`, but from library `sortedcontainers`, we can simulate the same process using `SortedSet` (`SortedList` should also work in this scenario).\n```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n from sortedcontainers import SortedSet\n if not nums or t < 0: return False # Handle special cases\n ss, n = SortedSet(), 0 # Create SortedSet. `n` is the size of sortedset, max value of `n` is `k` from input\n for i, num in enumerate(nums):\n ceiling_idx = ss.bisect_left(num) # index whose value is greater than or equal to `num`\n floor_idx = ceiling_idx - 1 # index whose value is smaller than `num`\n if ceiling_idx < n and abs(ss[ceiling_idx]-num) <= t: return True # check right neighbour \n if 0 <= floor_idx and abs(ss[floor_idx]-num) <= t: return True # check left neighbour\n ss.add(num)\n n += 1\n if i - k >= 0: # maintain the size of sortedset by finding & removing the earliest number in sortedset\n ss.remove(nums[i-k])\n n -= 1\n return False\n```\n### Approach \\#3 \n- This is pretty much a re-write of the official Java version. \n- But by using `defaultdict`, the code is cleaner (since we don\'t have to check the existance of a key in dictionary).\n- Use `OrderedDict` is also a feasible way, since it is more efficient to maintain the size\n```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n if not nums or t < 0: return False\n min_val = min(nums)\n bucket_key = lambda x: (x-min_val) // (t+1) # A lambda function generate buckey key given a value\n d = collections.defaultdict(lambda: sys.maxsize) # A bucket simulated with defaultdict\n for i, num in enumerate(nums):\n key = bucket_key(num) # key for current number `num`\n for nei in [d[key-1], d[key], d[key+1]]: # check left bucket, current bucket and right bucket\n if abs(nei - num) <= t: return True\n d[key] = num \n if i >= k: d.pop(bucket_key(nums[i-k])) # maintain a size of `k` \n return False\n``` | 20 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
[Python] BST approach with sortedcontainers | contains-duplicate-iii | 0 | 1 | ```\nimport sortedcontainers\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n \n def floor(n, bst):\n le = bst.bisect_right(n) - 1\n return bst[le] if le >= 0 else None\n \n def ceiling(n, bst):\n ge = bst.bisect_right(n)\n return bst[ge] if ge < len(bst) else None\n \n bst = sortedcontainers.SortedList()\n for i, n in enumerate(nums):\n le = floor(n, bst)\n if le is not None and n <= le + t:\n return True\n ge = ceiling(n, bst)\n if ge is not None and ge <= n + t:\n return True\n bst.add(n)\n if len(bst) > k:\n bst.remove(nums[i-k])\n return False\n # time: O(nlogk)\n # space: O(k)\n```\n*Edit: tags* | 11 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
Python3 easy to understand O(n) solution - Contains Duplicate III | contains-duplicate-iii | 0 | 1 | ```\nclass Solution:\n def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:\n d = OrderedDict()\n window = t + 1\n for i, n in enumerate(nums):\n while len(d) > k:\n d.popitem(last=False)\n if (b := n//window) in d:\n return True \n if b - 1 in d and abs(d[b-1] - n) <= t:\n return True\n if b + 1 in d and abs(d[b+1] - n) <= t:\n return True\n d[b] = nums[i] \n return False \n``` | 12 | You are given an integer array `nums` and two integers `indexDiff` and `valueDiff`.
Find a pair of indices `(i, j)` such that:
* `i != j`,
* `abs(i - j) <= indexDiff`.
* `abs(nums[i] - nums[j]) <= valueDiff`, and
Return `true` _if such pair exists or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,3,1\], indexDiff = 3, valueDiff = 0
**Output:** true
**Explanation:** We can choose (i, j) = (0, 3).
We satisfy the three conditions:
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums\[i\] - nums\[j\]) <= valueDiff --> abs(1 - 1) <= 0
**Example 2:**
**Input:** nums = \[1,5,9,1,5,9\], indexDiff = 2, valueDiff = 3
**Output:** false
**Explanation:** After trying all the possible pairs (i, j), we cannot satisfy the three conditions, so we return false.
**Constraints:**
* `2 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= indexDiff <= nums.length`
* `0 <= valueDiff <= 109` | Time complexity O(n logk) - This will give an indication that sorting is involved for k elements. Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again. |
221: Solution with step by step explanation | maximal-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem can be solved using dynamic programming. We can define a 2D array dp where dp[i][j] represents the maximum size of a square that can be formed at position (i, j) such that all its elements are 1\'s. We can fill this array using the following recurrence relation:\n\n- dp[i][j] = 0 if matrix[i][j] == \'0\'\n- dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1 if matrix[i][j] == \'1\'\n\nThe first condition means that if the current cell has a value of 0, we can\'t form a square with it. The second condition means that if the current cell has a value of 1, we can form a square with it, but we need to check the values of the cells to the left, top, and top-left of it to determine the maximum size of the square.\n\nWe also need to keep track of the maximum size of the square seen so far, and return its area.\n\n# Complexity\n- Time complexity:\nBeats\n88.37% O(m*n), where m and n are the dimensions of the matrix.\n\n- Space complexity:\nBeats\n88.43% O(m*n), where m and n are the dimensions of the matrix, since we are using a 2D array of the same size as the matrix to store the dp values.\n\n# Code\n```\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n # Get the dimensions of the matrix\n m, n = len(matrix), len(matrix[0])\n \n # Initialize the dp array\n dp = [[0] * n for _ in range(m)]\n \n # Initialize the max size of the square seen so far\n max_size = 0\n \n # Fill the dp array\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == \'1\':\n if i == 0 or j == 0:\n # First row or column, so the maximum size of the square is 1\n dp[i][j] = 1\n else:\n # Check the values of the cells to the left, top, and top-left of the current cell\n dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1\n \n # Update the max size of the square seen so far\n max_size = max(max_size, dp[i][j])\n \n # Return the area of the largest square\n return max_size * max_size\n\n``` | 14 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
in M*N time | maximal-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:1\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:n*m\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n mx=0\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n if(matrix[i][j]=="0"):\n matrix[i][j]=0\n else:\n if(i==0 or j==0):\n matrix[i][j]=1\n else:\n matrix[i][j]=min(matrix[i][j-1],matrix[i-1][j],matrix[i-1][j-1])+1\n mx=max(mx,matrix[i][j])\n # print(matrix[i])\n # print(matrix)\n return mx**2\n``` | 6 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Easy python solution using DP Grid | maximal-square | 0 | 1 | \n# Code\n```\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n dp=[[0]*(len(matrix[0])+1)]\n for i in matrix:\n l=[0]\n for j in i:l.append(int(j))\n dp.append(l)\n mx=0\n for i in range(len(dp)):\n for j in range(len(dp[0])):\n if dp[i][j]==1:\n dp[i][j]=min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])+1\n mx=max(mx,dp[i][j])\n return mx*mx\n``` | 6 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Go, Python3 Solutions | maximal-square | 0 | 1 | #### Go\n\n```go\nfunc maximalSquare(matrix [][]byte) int {\n n := len(matrix)\n m := len(matrix[0])\n dp := make([][]int, n)\n for i := range dp {\n dp[i] = make([]int, m)\n }\n maxDimension := 0\n \n for i := 0; i < n; i++ {\n for j := 0; j < m; j++ {\n if matrix[i][j] == \'1\' {\n left, up, diag := 0, 0, 0\n if i > 0 {\n up = dp[i-1][j]\n }\n if j > 0 {\n left = dp[i][j-1]\n }\n if i > 0 && j > 0 {\n diag = dp[i-1][j-1]\n }\n dp[i][j] = min(min(left, up), diag) + 1\n maxDimension = max(maxDimension, dp[i][j])\n }\n }\n }\n return maxDimension * maxDimension\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n\n#### Python3\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n n = len(matrix)\n m = len(matrix[0])\n max_dim = 0\n dp = [[0] * m for _ in range(n)]\n \n for i in range(n):\n for j in range(m):\n if matrix[i][j] == \'1\':\n left = up = diag = 0\n if i > 0:\n up = dp[i-1][j]\n if j > 0:\n left = dp[i][j-1]\n if i > 0 and j > 0:\n diag = dp[i-1][j-1]\n dp[i][j] = min(left, up, diag) + 1\n max_dim = max(max_dim, dp[i][j])\n \n return max_dim * max_dim\n``` | 2 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
[Python] 1D-Array DP - Optimisation Process Explained | maximal-square | 0 | 1 | ### Introduction\n\nWe are given a `m x n` array `matrix` and we need to find the largest square such that all elements in this square is `\'1\'`.\n\n---\n\n### Approach 1: Brute Force\n\nSimple enough. For each coordinate `(x, y)` in `matrix`, we check if `matrix[x][y] == \'1\'`. If so, then we know that there exists a square at `(x, y)` that is at least `1 x 1` in size. We can then continue checking if a bigger square exists by looking at the adjacent coordinates of `(x, y)`.\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n result = 0\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n curr = 0 # current length of the square at (i, j)\n flag = True # indicates if there still exists a valid square\n while flag:\n for k in range(curr+1):\n # check outer border of elements for \'1\'s.\n """\n eg curr = 2, ie a valid 2x2 square exists\n \'O\' is valid, check \'X\':\n X X X\n X O O\n X O O\n """\n if i < curr or j < curr or \\\n matrix[i-curr][j-k] == \'0\' or \\\n matrix[i-k][j-curr] == \'0\':\n flag = False\n break\n curr += flag\n if curr > result: # new maximum length of square obtained\n result = curr\n return result*result # area = length x length\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(mnk^{2})" title="O(mnk^{2})" />**, where `k` is the length of the maximal square, since the while loop will iterate from `curr = 0` to `curr = k+1`.\n**SC: <img src="https://latex.codecogs.com/svg.image?O(1)" title="O(1)" />**, since no additional data structures were used.\n\n---\n\n### Approach 2: Obtaining DP Approach\n\nObviously, the brute force way of checking for valid squares isn\'t very efficient. We need to think of another way to determine whether an `n x n` square is valid. For this, let\'s start with the simplest non-trivial case: a `2 x 2` square.\n\nRecall from the brute force approach that the way we check for validity is by checking the outer border, i.e.:\n\n```text\ne.g. curr = 1, i.e. a valid 1 x 1 square exists (matrix[x][y] == \'1\').\n\'O\' is valid, check for \'X\':\nX X\nX O\n```\n\nTo check for `\'X\'`, we would need to check if `matrix[x-1][y] == \'1\'`, `matrix[x][y-1] == \'1\'` and `matrix[x-1][y-1] == \'1\'`. Except, because of the way the outer for loops were written, note that **we have checked each of these before!** To reach `matrix[x][y]` would require us to loop over the previous indexes, which include all of `(x-1, y-1)`, `(x-1, y)` and `(x, y-1)`. If any of the previous indexes are `\'0\'`, then the maximal square that exists at `(x, y)` can only be a `1 x 1` square.\n\n```text\nDifferent possible combinations of maximal square sizes in a 2x2 matrix\ncomb 0 0 1 0 0 1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 0 0 1 1 1 1 1 0 0 1 1 1\n 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1\nno 1s -0- ----------1---------- ----------------2---------------- ----------3---------- -4-\nsize -------------------------------------------1------------------------------------------- -2-\n```\n\nNote the length of the maximal square for each possible combination. This can be **simplified and generalised** to the following equation:\n\n```text\nLength of maximal square at:\nmatrix[x-1][y-1]: a matrix[x-1][y]: b\n matrix[x][y-1]: c \'1\'\nLength of maximal square at matrix[x][y] (given matrix[x][y] == \'1\') is min(a, b, c) + 1\n\nExample matrix:\n0 0 1 1 1\n0 0 1 1 1\n0 1 1 1 1\n0 1 1 1 1\nLength of maximal sqaures at:\n\tmatrix[2][3] = 2x2\n\tmatrix[2][4] = 3x3\n\tmatrix[3][3] = 2x2\n\tmatrix[3][4] = min(2x2, 3x3, 2x2) + 1 = 2x2 + 1 = 3x3\n```\n\nTherefore, we can **store the length of the maximal squares at these coordinates in a separate matrix** and **retrieve it later for <img src="https://latex.codecogs.com/svg.image?O(1)" title="O(1)" /> computation**.\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n m, n = len(matrix), len(matrix[0])\n result = 0\n dp = [[0]*n for _ in range(m)] # dp[x][y] is the length of the maximal square at (x, y)\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == \'1\': # ensure this condition first\n # perform computation, mind border restrictions\n dp[i][j] = min(dp[i-1][j] if i > 0 else 0,\n dp[i][j-1] if j > 0 else 0,\n dp[i-1][j-1] if i > 0 and j > 0 else 0) + 1\n if dp[i][j] > result:\n result = dp[i][j]\n return result*result\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, since the computation for valid maximal square takes <img src="https://latex.codecogs.com/svg.image?O(1)" title="O(1)" /> time.\n**SC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, due to the maintenance of the DP array.\n\n---\n\n### Approach 3: Intuitive Optimised DP\n\nIf we take some time to analyse the formula used for the computation of the length of the maximal square at `(x, y)`, we notice that we only ever use three different variables: `dp[x-1][y-1]`, `dp[x-1][y]` and `dp[x][y-1]`. These variables **only require 2 rows of DP arrays** for storage: the previous row `x - 1`, and the current row `x`. As such, instead of using a `m x n` DP array, we can use a `2 x n` DP array instead.\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n m, n = len(matrix), len(matrix[0])\n result = 0\n prev, curr = [0]*n, [0]*n\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == \'1\':\n curr[j] = min(curr[j-1] if j > 0 else 0,\n prev[j-1] if j > 0 else 0,\n prev[j]) + 1\n if curr[j] > result:\n result = curr[j]\n prev, curr = curr, [0]*n\n return result*result\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, as discussed previously.\n**SC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, due to the creation of `m` arrays of length `n`.\n\nThe implementation above does not actually optimise for space, but we can do so by setting `curr = prev`. Since the values in `prev` will not be used, we can simply override them.\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n m, n = len(matrix), len(matrix[0])\n result = 0\n prev, curr = [0]*n, [0]*n\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == \'1\':\n curr[j] = min(curr[j-1] if j > 0 else 0,\n prev[j-1] if j > 0 else 0,\n prev[j]) + 1\n else:\n curr[j] = 0 # reset curr[j]\n if curr[j] > result:\n result = curr[j]\n prev, curr = curr, prev\n return result*result\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, as discussed previously.\n**SC: <img src="https://latex.codecogs.com/svg.image?O(2n)&space;\\approx&space;O(n)" title="O(2n) \\approx O(n)" />**. We only create 2 arrays of length `n` and alternate between them.\n\nWe can also write it in the following manner:\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n m, n = len(matrix), len(matrix[0])\n result = 0\n dp = [[0]*n for _ in range(2)] # 2-rowed dp array\n for i in range(m):\n for j in range(n):\n # i%2 (or i&1) alternates between dp[0] and dp[1]\n dp[i%2][j] = 0 if matrix[i][j] == \'0\' else \\\n (min(dp[i%2][j-1] if j > 0 else 0,\n dp[1-i%2][j-1] if j > 0 else 0,\n dp[1-i%2][j]) + 1)\n result = dp[i%2][j] if dp[i%2][j] > result else result\n return result*result\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, as discussed previously.\n**SC: <img src="https://latex.codecogs.com/svg.image?O(2n)&space;\\approx&space;O(n)" title="O(2n) \\approx O(n)" />**, as discussed previously.\n\n---\n\n### Approach 4: Optimised DP\n\nFinally, we can get rid of the need for 2D arrays. By applying the same computation on the same array, we can assert that the current value `dp[j]` points to the previous result `dp[i-1][j]`. `dp[j-1]` maps to `dp[i][j-1]`, since this value would have already been computed and replaced before we iterated to index `j`.\n\nThe only value which we do not have is `dp[i-1][j-1]`, which cannot simply be obtained from the array. As such, we will use **another variable to store `dp[i-1][j-1]]` specifically** for computation purposes.\n\n```python\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n m, n, result = len(matrix), len(matrix[0]), 0\n dp = [0]*n # 1D array\n for i in range(m):\n prev = 0 # stores dp[i-1][j-1]\n for j in range(n):\n dp[j], prev = 0 if matrix[i][j] == \'0\' else \\\n (min(dp[j], # dp[j] -> dp[i-1][j]\n dp[j-1] if j > 0 else 0, # dp[j-1] -> dp[i][j-1]\n prev) # prev -> dp[i-1][j-1]\n + 1), dp[j]\n result = dp[j] if dp[j] > result else result\n return result*result\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(mn)" title="O(mn)" />**, as discussed previously.\n**SC: <img src="https://latex.codecogs.com/svg.image?O(n)" title="O(n)" />**, since we only maintain a 1D array.\n\n---\n\n### Conclusion\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 18 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python | DP | Memoization | maximal-square | 0 | 1 | \n\n```\n\nclass Solution:\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n \n dp={}\n ans=0\n m=len(matrix)\n n=len(matrix[0])\n for i in range(m):\n for j in range(n):\n\t\t\t\t#if 1 is encounteres than we have square of atleast size 1 length.\n if matrix[i][j]=="1":\n maxarea=1\n\t\t\t\t\t#if there is possible bigger square then (i-1)(j-1) should be square too\n if (i-1,j-1) in dp:\n\t\t\t\t\t\t#find the size of squre before this, max size of square can be found would be size +1\n size=dp[(i-1,j-1)]\n \n foundsizex=0\n for k in range(1,size+1):\n if matrix[i-k][j]!=\'1\':\n break\n foundsizex+=1\n \n foundsizey=0 \n for k in range(1,size+1):\n if matrix[i][j-k]!=\'1\':\n break\n foundsizey+=1\n maxarea=1+min(foundsizex,foundsizey) \n ans=max(ans,maxarea)\n dp[(i,j)]=maxarea\n return ans*ans\n``` | 1 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Recursive(caching)+DP solution in python | maximal-square | 0 | 1 | \n\n ----------# DP solution T:O(m*n) S:O(1)----------\n\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n ROWS,COLS=len(matrix)-1,len(matrix[0])-1\n res=0\n for r in range(ROWS,-1,-1):\n for c in range(COLS,-1,-1):\n if r>=ROWS or c>=COLS: #for right and bottom boundary \n down=right=diag=0\n else:\n down=int(matrix[r][c+1])\n right=int(matrix[r+1][c])\n diag=int(matrix[r+1][c+1])\n\n if matrix[r][c]=="1":\n matrix[r][c]=1+(min(down,right,diag))\n res=max(res,matrix[r][c]) \n\n return res*res\n \n -----------------# recursive T:O(m*n),S:O(m*n)-----------------\n def maximalSquare(self, matrix: List[List[str]]) -> int:\n ROWS,COLS=len(matrix),len(matrix[0])\n cache={}\n\n def helper(r,c):\n if r>=ROWS or c>=COLS:\n return 0\n if (r,c) not in cache:\n down=helper(r+1,c)\n right=helper(r,c+1)\n diag=helper(r+1,c+1)\n\n cache[(r,c)]=0\n if matrix[r][c]=="1":\n cache[(r,c)]=1+min(down,right,diag)\n\n return cache[(r,c)]\n helper(0,0)\n return max(cache.values())**2 | 1 | Given an `m x n` binary `matrix` filled with `0`'s and `1`'s, _find the largest square containing only_ `1`'s _and return its area_.
**Example 1:**
**Input:** matrix = \[\[ "1 ", "0 ", "1 ", "0 ", "0 "\],\[ "1 ", "0 ", "1 ", "1 ", "1 "\],\[ "1 ", "1 ", "1 ", "1 ", "1 "\],\[ "1 ", "0 ", "0 ", "1 ", "0 "\]\]
**Output:** 4
**Example 2:**
**Input:** matrix = \[\[ "0 ", "1 "\],\[ "1 ", "0 "\]\]
**Output:** 1
**Example 3:**
**Input:** matrix = \[\[ "0 "\]\]
**Output:** 0
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 300`
* `matrix[i][j]` is `'0'` or `'1'`. | null |
Python || 3 lines code || Very Simple to understand | count-complete-tree-nodes | 0 | 1 | **Plz Upvote ..if you got help from this.**\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countNodes(self, root: Optional[TreeNode]) -> int:\n if root is None:\n return 0\n return 1 + self.countNodes(root.left) + self.countNodes(root.right)\n \n``` | 7 | Given the `root` of a **complete** binary tree, return the number of the nodes in the tree.
According to **[Wikipedia](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
Design an algorithm that runs in less than `O(n)` time complexity.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 6
**Example 2:**
**Input:** root = \[\]
**Output:** 0
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5 * 104]`.
* `0 <= Node.val <= 5 * 104`
* The tree is guaranteed to be **complete**. | null |
My solution for this problem | count-complete-tree-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->Using a seprate dfs function\n# Complexity\n- Time complexity:O[n]\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O[h],h=height of the tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countNodes(self, root: Optional[TreeNode]) -> int:\n def dfs(node):\n if not node:\n return 0\n nonlocal x\n x+=1\n dfs(node.left)\n dfs(node.right)\n x=0\n dfs(root)\n return x\n\n\n \n``` | 0 | Given the `root` of a **complete** binary tree, return the number of the nodes in the tree.
According to **[Wikipedia](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
Design an algorithm that runs in less than `O(n)` time complexity.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 6
**Example 2:**
**Input:** root = \[\]
**Output:** 0
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5 * 104]`.
* `0 <= Node.val <= 5 * 104`
* The tree is guaranteed to be **complete**. | null |
2 line solution using recursion | count-complete-tree-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:1\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countNodes(self, root: Optional[TreeNode]) -> int:\n if(root==None):\n return 0\n return(self.countNodes(root.left)+self.countNodes(root.right)+1)\n``` | 15 | Given the `root` of a **complete** binary tree, return the number of the nodes in the tree.
According to **[Wikipedia](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
Design an algorithm that runs in less than `O(n)` time complexity.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 6
**Example 2:**
**Input:** root = \[\]
**Output:** 0
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5 * 104]`.
* `0 <= Node.val <= 5 * 104`
* The tree is guaranteed to be **complete**. | null |
Clean Python Solution O(log^2(n)) time | count-complete-tree-nodes | 0 | 1 | ```\n\'\'\' \nOnly traversing along the left and right boundary. \nIf both left and right height are equal then\nthe bottom level would be full from left to right and total no. of nodes in that subtree\nis 2^h - 1. \n\nIf left and right height are not equal then add +1 for current root and go to left child \nand right child. \n\'\'\'\n\nclass Solution:\n def countNodes(self, root: Optional[TreeNode]) -> int:\n if not root: return 0\n \n leftHeight = self.getLeftHeight(root)\n rightHeight = self.getRightHeight(root)\n \n if leftHeight == rightHeight: \n return 2 ** leftHeight - 1\n else:\n return 1 + self.countNodes(root.left) + self.countNodes(root.right) \n \n \n def getLeftHeight(self, node):\n height = 0\n while node:\n height += 1\n node = node.left\n return height\n \n def getRightHeight(self, node):\n height = 0\n while node:\n height += 1\n node = node.right\n return height\n \n# Height = H = log(n) where n = total number of nodes\n# Time: O(H * H) = O(log(n)^2) = O(Log^2 n)\n# Auxiliary Space: O(H) = O(log(n))\n \n``` | 22 | Given the `root` of a **complete** binary tree, return the number of the nodes in the tree.
According to **[Wikipedia](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
Design an algorithm that runs in less than `O(n)` time complexity.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 6
**Example 2:**
**Input:** root = \[\]
**Output:** 0
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[0, 5 * 104]`.
* `0 <= Node.val <= 5 * 104`
* The tree is guaranteed to be **complete**. | null |
Fastest python solution | rectangle-area | 0 | 1 | ```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n coxl=max(ax1,bx1)\n coxr=min(ax2,bx2)\n coyl=max(ay1,by1)\n coyr=min(ay2,by2)\n dx=coxr-coxl\n dy=coyr-coyl\n comm=0\n if dx>0 and dy>0:\n comm=dx*dy\n a=abs(ax2-ax1)*abs(ay2-ay1)\n b=abs(bx2-bx1)*abs(by2-by1)\n area=a+b-comm\n return area\n``` | 9 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
Beats %99 time, %98 space python3 readable and easy to understand, full commented code!! | rectangle-area | 0 | 1 | # Approach\nTo find the intersection points of two rectangles, we first need to determine the maximum and minimum values of their edge lines. Once we have identified these values, we can check whether the rectangles are truly intersecting or not. If they are, we can calculate the new intersecting rectangles using basic mathematical principles. The combined area of the two rectangles can then be determined by adding their individual areas and subtracting the area of the intersecting region. On the other hand, if the rectangles are not intersecting, we simply add their areas together to determine their combined area. This approach allows for a clear and logical method for determining the area of overlapping rectangles.\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n # find intersecting point first\n # find the min_left_value of the intersecting rectangle\n min_left_value = max(ax1, bx1)\n # find the min_right_value of the intersecting rectangle\n min_right_value = min(ax2, bx2)\n # find the min_top_value of the intersecting rectangle\n min_top_value = min(ay2, by2)\n # find the min_bottom_value of the intersecting rectangle\n min_bottom_value = max(ay1, by1)\n # calculate the total area of the first rectangle\n first_rect_area = (ax2 - ax1) * (ay2 - ay1)\n # calculate the total area of the second rectangle\n second_rect_area = (bx2 - bx1) * (by2 - by1)\n # check there is an intersecting rectangle or not if not return the sum of the first_rect_area and second_rect_area\n if (min_right_value - min_left_value) < 0 or (min_top_value- min_bottom_value) < 0:\n return first_rect_area + second_rect_area\n # else if there is an intersecting rectangle\n # calculate the total area of the intersecting rectangle\n intersecting_total_area = (min_right_value - min_left_value) * (min_top_value- min_bottom_value)\n # return the sum of the first_rect_area, second_rect_area then subtract the intersecting_total_area\n return first_rect_area + second_rect_area - intersecting_total_area\n\n``` | 3 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
✔️ Python Professional Solution | Fastest | 99% Faster 🔥 | rectangle-area | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n \n # Function to caculate area of rectangle (Length * width)\n def area(x1,y1,x2,y2):\n return (x2-x1)*(y2-y1)\n \n # Finding the overlap rectangle length and width\n overlapX = max(min(ax2,bx2)-max(ax1,bx1), 0)\n overlapY = max(min(ay2,by2)-max(ay1,by1), 0)\n \n # Area1 + Area2 - Overlap Rectangle Area\n return area(ax1,ay1,ax2,ay2) + area(bx1,by1,bx2,by2) - overlapX * overlapY\n```\n\n**For Leetcode Solution with Explanation Visit this Blog:\nhttps://www.python-techs.com/\n(Please open this link in new tab)**\n\nThank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback. | 3 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
Python || Easy || 95.39% Faster || O(1) Complexity | rectangle-area | 0 | 1 | ```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n a1=(ax2-ax1)*(ay2-ay1)\n a2=(bx2-bx1)*(by2-by1)\n x1=max(ax1,bx1)\n x2=min(ax2,bx2)\n y1=max(ay1,by1)\n y2=min(ay2,by2)\n if x2-x1<0 or y2-y1<0: #No intersection will occur if one of the side is negative\n return a1+a2\n a3=(x2-x1)*(y2-y1)\n return a1+a2-a3\n```\n\n**Upvote if you like the solution or ask if there is any query** | 1 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
Python (Faster than 92%) | O(1) solution | rectangle-area | 0 | 1 | \n\n```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n area1 = (ax2 - ax1) * (ay2 - ay1)\n area2 = (bx2 - bx1) * (by2 - by1)\n xOverlap = max(min(ax2, bx2) - max(ax1, bx1), 0)\n yOverlap = max(min(ay2, by2) - max(ay1, by1), 0)\n commonArea = xOverlap * yOverlap \n totalArea = area1 + area2 - commonArea\n return totalArea\n```\n# Please upvote if you find this helpful. | 1 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
Simplest Solution || Few Lines of Code | rectangle-area | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n area_first = abs(ax1 - ax2) * abs(ay1 - ay2)\n area_second = abs(bx1 - bx2) * abs(by1 - by2)\n x_distance = (min(ax2, bx2) -max(ax1, bx1))\n y_distance = (min(ay2, by2) -max(ay1, by1))\n Area = 0\n if x_distance > 0 and y_distance > 0:\n Area = x_distance * y_distance\n return (area_first + area_second - Area)\n``` | 1 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
python easy solution | rectangle-area | 0 | 1 | \nclass Solution:\n def computeArea(self, ax1, ay1, ax2, ay2, bx1, by1, bx2, by2):\n commonArea=0\n totalArea=(abs(ax2-ax1)*abs(ay2-ay1)) + (abs(bx2-bx1)*abs(by2-by1))\n [x1,y1]=[max(ax1,bx1),max(ay1,by1)]\n [x2,y2]=[min(ax2,bx2),min(ay2,by2)]\n commonArea=0 if (by1>=ay2 or bx1>=ax2 or by2<ay1 or bx2<ax1) else (x2-x1)*(y2-y1)\n\n return totalArea-commonArea\n``` | 1 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
223: Solution with step by step explanation | rectangle-area | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, we compute the area of both rectangles using the formula area = width * height.\n2. Then, we compute the width and height of the overlap region between the two rectangles. We use min to find the right-most edge of the overlap region, and max to find the left-most edge of the overlap region. We do the same thing for the top and bottom edges of the overlap region.\n3. If the rectangles don\'t overlap, overlapWidth or overlapHeight will be negative, so we use max to set them to 0 in order to get the correct overlap area.\n4. Finally, we subtract the overlap area from the sum of the areas of the two rectangles to get the total area covered by the two rectangles.\n\n# Complexity\n- Time complexity:\n81.84%\n\n- Space complexity:\n62.79%\n\n# Code\n```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n # Compute the area of the two rectangles\n area1 = (ax2 - ax1) * (ay2 - ay1)\n area2 = (bx2 - bx1) * (by2 - by1)\n \n # Compute the overlap area\n overlapWidth = min(ax2, bx2) - max(ax1, bx1)\n overlapHeight = min(ay2, by2) - max(ay1, by1)\n overlapArea = max(overlapWidth, 0) * max(overlapHeight, 0)\n \n # Compute the total area covered by the two rectangles\n totalArea = area1 + area2 - overlapArea\n \n return totalArea\n\n``` | 4 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
✔️ [Python3] READABLE CODE, Explained | rectangle-area | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThis is a very popular algorithm for calculation the IoU (intersection over union) in Deep Learning algorithms. Firs\u0435, we calculate areas of both rectangles and then get their sum `S`. Since the area of the overlap is included twice in the `S`, we need to remove the redundant value. If rectangles do not overlap at all, we just return the sum of areas.\n\n```\nclass Solution:\n def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:\n Sa = (ax2-ax1) * (ay2-ay1)\n Sb = (bx2-bx1) * (by2-by1)\n S = Sa + Sb\n \n w_ov = min(ax2, bx2) - max(ax1, bx1)\n if w_ov <= 0:\n return S\n \n h_ov = min(ay2, by2) - max(ay1, by1)\n if h_ov <= 0:\n return S\n \n S_ov = w_ov * h_ov\n \n return S - S_ov\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 6 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
Python Elegant & Short | O(1) | Unpacking | rectangle-area | 0 | 1 | ```\ndef computeArea(self, *coords) -> int:\n\tx1, y1, x2, y2, x3, y3, x4, y4 = coords\n\toverlap = max(min(x2, x4) - max(x1, x3), 0) * max(min(y2, y4) - max(y1, y3), 0)\n\treturn (x2 - x1) * (y2 - y1) + (x4 - x3) * (y4 - y3) - overlap\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n\n | 4 | Given the coordinates of two **rectilinear** rectangles in a 2D plane, return _the total area covered by the two rectangles_.
The first rectangle is defined by its **bottom-left** corner `(ax1, ay1)` and its **top-right** corner `(ax2, ay2)`.
The second rectangle is defined by its **bottom-left** corner `(bx1, by1)` and its **top-right** corner `(bx2, by2)`.
**Example 1:**
**Input:** ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
**Output:** 45
**Example 2:**
**Input:** ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
**Output:** 16
**Constraints:**
* `-104 <= ax1 <= ax2 <= 104`
* `-104 <= ay1 <= ay2 <= 104`
* `-104 <= bx1 <= bx2 <= 104`
* `-104 <= by1 <= by2 <= 104` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.