title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Simple Python3 Solution || 1 Line Code O(n) || Upto 98 % Space Saver O(1) | majority-element-ii | 0 | 1 | # Intuition\nWe use Counter to generate a Dictionary of nums and count of each distint number. Using this we filter the only the ones that are repeated more than n/3 times where n is the lenght of nums.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n \n \n return [k for k,v in Counter(nums).items() if v > int(len(nums)/3)]\n``` | 0 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Easy +80% 9 line Python solution | majority-element-ii | 0 | 1 | \n# Code\n```py\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n ans = []\n dct = {}\n n = len(nums)\n\n for x in set(nums):\n dct[x] = nums.count(x)\n\n for k, x in dct.items():\n if x > n//3:\n ans.append(k)\n\n return ans\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Easy +80% 9 line Python solution | majority-element-ii | 0 | 1 | \n# Code\n```py\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n ans = []\n dct = {}\n n = len(nums)\n\n for x in set(nums):\n dct[x] = nums.count(x)\n\n for k, x in dct.items():\n if x > n//3:\n ans.append(k)\n\n return ans\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Hashtable and Count Method | majority-element-ii | 0 | 1 | # Hashtable Method:TC-->O(N)\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n dic=Counter(nums)\n n,list1=len(nums),[]\n for i,v in dic.items():\n if v>n//3:\n list1.append(i)\n return list1\n```\n# Count Method--->(N^2)\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n n,count=len(nums),[]\n num=set(nums)\n for i in num:\n if nums.count(i)>n/3:\n count.append(i)\n return count\n```\n# without using inbuild Functions\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n dic={}\n for i in nums:\n if i not in dic:\n dic[i]=1\n else:\n dic[i]+=1\n n,list1=len(nums),[]\n for i,v in dic.items():\n if v>n//3:\n list1.append(i)\n return list1\n```\n# please upvote me it would encourage me alot\n | 5 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Hashtable and Count Method | majority-element-ii | 0 | 1 | # Hashtable Method:TC-->O(N)\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n dic=Counter(nums)\n n,list1=len(nums),[]\n for i,v in dic.items():\n if v>n//3:\n list1.append(i)\n return list1\n```\n# Count Method--->(N^2)\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n n,count=len(nums),[]\n num=set(nums)\n for i in num:\n if nums.count(i)>n/3:\n count.append(i)\n return count\n```\n# without using inbuild Functions\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n dic={}\n for i in nums:\n if i not in dic:\n dic[i]=1\n else:\n dic[i]+=1\n n,list1=len(nums),[]\n for i,v in dic.items():\n if v>n//3:\n list1.append(i)\n return list1\n```\n# please upvote me it would encourage me alot\n | 5 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Most Simplest Approach | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n li = []\n\n def helper(root):\n if root is None:\n return\n helper(root.left)\n li.append(root.val)\n helper(root.right)\n\n helper(root)\n return li[k - 1]\n\n\n\n\n \n``` | 1 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Recursive approach✅ | O( n)✅ | (Step by step explanation)✅ | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\nThe problem asks for finding the kth smallest element in a binary search tree (BST). A binary search tree is a binary tree where, for each node, the values of all nodes in its left subtree are less than the node\'s value, and the values of all nodes in its right subtree are greater than the node\'s value.\n\n# Approach\nThe approach involves performing an in-order traversal of the BST, which visits the nodes in ascending order. By collecting the values of the nodes during the traversal, we can create an array representing the sorted order of elements in the BST. The kth smallest element will be at index k-1 in this array.\n\n1. **In-order Traversal**: Traverse the BST in in-order fashion.\n\n **Reason**: In-order traversal ensures that we visit the nodes in ascending order.\n\n2. **Collect Values**: During the traversal, collect the values of the nodes in a vector.\n\n **Reason**: We need to create an array representing the sorted order of elements.\n\n3. **Result**: Return the element at index k-1 in the vector.\n\n **Reason**: The kth smallest element will be at index k-1 in the sorted order.\n\n# Complexity\n- **Time complexity**: O(n)\n - We perform in-order traversal, visiting each node once.\n- **Space complexity**: O(n)\n - The space required to store the values in the vector during traversal.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n arr = []\n\n def inOrder(root ):\n if root == None:\n return \n\n inOrder(root.left ) \n arr.append(root.val)\n inOrder(root.right)\n\n\n inOrder(root)\n \n return arr[k-1]\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n int kthSmallest(TreeNode* root, int k) {\n vector<int> arr;\n inOrder(root , arr);\n\n return arr[k - 1];\n }\n\nprivate:\n void inOrder(TreeNode* root, vector<int> &arr) {\n if (root == NULL) {\n return;\n }\n\n inOrder(root->left , arr);\n arr.push_back(root->val);\n inOrder(root->right , arr);\n \n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n | 3 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Confused? Click this! Unlock the secrets of BSTs! | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe property of BST allows us to traverse it from smallest node to largest simply with an **in-order DFS**.\n\nWhat is the smallest node in a BST? It\'s the leftmost node. What\'s the second smallest? It\'s the leftmost node\'s parent, p. What\'s the third smallest? It\'s p\'s right child, or the leftmost node\'s sibling.\n\nThus we can infer that an in-order DFS traversal, left -> current -> right, will traverse from smallest to largest.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe traverse the tree with **in-order DFS**, meaning left -> current -> right. We can do this recursively or iteratively, but this case we do it recursively.\n\nWe increment i by 1 whenever we visit a node (we can also decrement k by 1 and check k == 0). If our current node results in i == k, we know it\'s the kth smallest node and set res to current node\'s value.\n\nReturn res.\n# Complexity\n- Time complexity: **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(logn)** if tree is balanced, **O(n)** if tree is skewed\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n stack, cur = [], root # first in, last out\n \n # iterative in-order DFS traversal\n while True:\n while cur: # go as left as possible\n stack.append(cur)\n cur = cur.left\n\n cur = stack.pop() # last one, smallest node\n k -= 1\n if k == 0:\n return cur.val\n \n cur = cur.right\n\n\n``` | 5 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
✅🔥 Recursion & Vector Solutions with Complexity Analysis! - C++/Java/Python | kth-smallest-element-in-a-bst | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to perform an inorder traversal of the binary search tree to collect values in ascending order. Once the values are collected, the kth smallest value can be easily retrieved.\n\n# Approach 01\n<!-- Describe your approach to solving the problem. -->\n1. Using ***Vector.***\n1. Perform an inorder traversal, which involves visiting the left subtree, then the root, and finally the right subtree.\n1. Store the values from the left side in a vector, resulting in an increasing order of values.\n1. Return the (k-1)th element from the vector as it corresponds to the kth smallest element in the binary search tree. The vector is in increasing order, making it easy to access the kth smallest element directly.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(n), where n is the number of nodes in the binary search tree. The inorder traversal visits each node once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(n), as the solution uses a list to store the values collected during traversal. In the worst case, when the binary search tree is skewed, the list could contain all node values.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int kthSmallest(TreeNode* root, int k) {\n vector<int> temp;\n inorder(root, temp);\n return temp[k-1];\n }\n \n void inorder(TreeNode* root, vector<int> &temp){\n if(!root) return;\n inorder(root->left, temp);\n temp.push_back(root->val);\n inorder(root->right, temp);\n }\n};\n```\n```Java []\nclass Solution {\n List<Integer> values = new ArrayList<>();\n\n public int kthSmallest(TreeNode root, int k) {\n inorder(root);\n return values.get(k - 1);\n }\n\n private void inorder(TreeNode root) {\n if (root == null) {\n return;\n }\n inorder(root.left);\n values.add(root.val);\n inorder(root.right);\n }\n}\n```\n```python []\nclass Solution(object):\n def kthSmallest(self, root, k):\n values = []\n self.inorder(root, values)\n return values[k - 1]\n\n def inorder(self, root, values):\n if root is None:\n return\n self.inorder(root.left, values)\n values.append(root.val)\n self.inorder(root.right, values)\n```\n\n---\n# Approach 02\n<!-- Describe your approach to solving the problem. -->\n1. Using ***Recursion.*** \n1. Perform an in-order traversal of the binary search tree.\n1. In each recursive call, check if the kth smallest element has been found.\n1. If found, update the result and stop further traversal.\n1. Return the result after the traversal.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(n), where n is the number of nodes in the binary search tree. The inorder traversal visits each node once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(h), where h is the height of the binary search tree. The space complexity is determined by the recursion stack.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int ans;\n \n int kthSmallest(TreeNode* root, int k) {\n inorder(root, k);\n return ans;\n }\n \n void inorder(TreeNode* root, int& k) {\n if (!root) return;\n inorder(root->left, k);\n if (--k == 0){\n ans = root->val;\n return;\n } \n inorder(root->right, k);\n } \n};\n```\n```Java []\nclass Solution {\n private int count = 0;\n private int result = 0;\n\n public int kthSmallest(TreeNode root, int k) {\n inorderTraversal(root, k);\n return result;\n }\n\n private void inorderTraversal(TreeNode node, int k) {\n if (node == null || count >= k) {\n return;\n }\n\n inorderTraversal(node.left, k);\n\n count++;\n if (count == k) {\n result = node.val;\n return;\n }\n\n inorderTraversal(node.right, k);\n }\n}\n```\n```python []\nclass Solution(object):\n def kthSmallest(self, root, k):\n self.count = 0\n self.result = 0\n self.inorderTraversal(root, k)\n return self.result\n \n def inorderTraversal(self, node, k):\n if not node or self.count >= k:\n return\n \n self.inorderTraversal(node.left, k)\n \n self.count += 1\n if self.count == k:\n self.result = node.val\n return\n \n self.inorderTraversal(node.right, k)\n```\n\n---\n\n\n> **Please upvote this solution**\n> | 105 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Python3 (DFS/DFS Recursive/ BFS) | kth-smallest-element-in-a-bst | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS\nRecursive DFS\nBFS\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n #DFS\n a = set()\n if not root: return -1\n stack = [(root)]\n while stack:\n node = stack.pop()\n a.add(node.val)\n if node.left: stack.append((node.left))\n if node.right: stack.append((node.right))\n a = sorted(a)\n return a[k-1]\n #Recursion DFS\n arr = []\n def findNum(node, arr):\n if not node:\n return\n findNum(node.left, arr)\n arr.append(node.val)\n findNum(node.right, arr)\n findNum(root, arr)\n # return arr[k- 1]\n #BFS\n a = set()\n if not root: return -1\n dq = collections.deque([(root)])\n while dq:\n node = dq.popleft()\n a.add(node.val)\n if node.left: dq.append((node.left))\n if node.right: dq.append((node.right))\n a = sorted(a)\n return a[k-1]\n``` | 2 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Iterative approach✅ | O( n)✅ | (Step by step explanation)✅ | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\nThe problem requires finding the kth smallest element in a binary search tree (BST). A binary search tree is a binary tree where, for each node, the values of all nodes in its left subtree are less than the node\'s value, and the values of all nodes in its right subtree are greater than the node\'s value.\n\n# Approach\nThe approach involves using an iterative in-order traversal, where we keep track of the count of visited nodes. We use a stack to simulate the recursion of the in-order traversal.\n\n1. **Stack-based In-order Traversal**: Iterate through the BST using a stack to perform an in-order traversal.\n\n **Reason**: In-order traversal ensures that we visit the nodes in ascending order.\n\n2. **Count Nodes**: Maintain a count of visited nodes during traversal.\n\n **Reason**: We need to identify the kth smallest element.\n\n3. **Check kth Element**: When the count reaches k, return the value of the current node.\n\n **Reason**: We have found the kth smallest element.\n\n4. **Iterate to the Right**: Move to the right subtree of the current node.\n\n **Reason**: The kth smallest element, if not found in the left subtree, will be in the right subtree.\n\n5. **Result**: Return the value of the kth smallest element.\n\n **Reason**: We have found the kth smallest element during traversal.\n\n# Complexity\n- **Time complexity**: O(n)\n - We perform in-order traversal, visiting each node once.\n- **Space complexity**: O(h)\n - The space required for the stack, where h is the height of the tree.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n stack = []\n n = 0\n temp = root\n\n while temp or stack:\n while temp:\n stack.append(temp)\n temp = temp.left\n temp = stack.pop()\n n +=1\n if n == k:\n return temp.val\n temp = temp.right \n\n \n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n int kthSmallest(TreeNode* root, int k) {\n stack<TreeNode*> stack;\n int n = 0;\n TreeNode* temp = root;\n\n while (temp || !stack.empty()) {\n while (temp) {\n stack.push(temp);\n temp = temp->left;\n }\n temp = stack.top();\n stack.pop();\n n += 1;\n if (n == k) {\n return temp->val;\n }\n temp = temp->right;\n }\n\n return 0;\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n | 3 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
|| Binary Search Tree + Heap(Priority Queue) || Easy Solution | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n min_heap = []\n\n def inOrderTraversal(node):\n if node:\n inOrderTraversal(node.left)\n heapq.heappush(min_heap, node.val)\n inOrderTraversal(node.right)\n\n inOrderTraversal(root)\n\n if len(min_heap) < k:\n return None\n \n # The kth smallest element will be at the top of the heap\n return min_heap[k - 1]\n``` | 4 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
3 different solutions, sort, recursive, stack | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\nUsing **sort** to grab the kth element\n\n# Complexity\n- Time complexity: O(n * log(n))\n- Space complexity: O(n)\n\n# Code\n```\ndef kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n res = []\n stack = [root]\n while stack:\n node = stack.pop()\n if not node:\n continue\n\n res.append(node.val)\n stack.append(node.left)\n stack.append(node.right)\n \n res.sort()\n return res[k - 1]\n\n```\n\n# Intuition\nUsing **recursion** approach to grab the kth element\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n```\ndef kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n arr = []\n arr = self.kthSmallestHelper(root, arr)\n return arr[k -1]\n\ndef kthSmallestHelper(self, root: Optional[TreeNode], arr: List[int]) -> List[int]:\n if not root:\n return arr\n\n self.kthSmallestHelper(root.left, arr)\n arr.append(root.val)\n self.kthSmallestHelper(root.right, arr)\n\n return arr\n```\n\n# Intuition\n- Using **stack** approach with inorder traversal to grab the kth element\n- Build the array and return the last element\n\n# Complexity\n- Time complexity: O(k)\n- Space complexity: O(k)\n\n# Code\n```\ndef kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n res = []\n stack = [(root, False)]\n while stack and len(res) < k:\n node, visited = stack.pop()\n if not node:\n continue\n\n if visited:\n res.append(node.val)\n else:\n stack.append((node.right, False))\n stack.append((node, True))\n stack.append((node.left, False))\n\n return res[-1]\n``` | 1 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Kth Largest And Kth Smallest Element : C++ / Java / Python / Kotlin | kth-smallest-element-in-a-bst | 1 | 1 | # Intuition\nSo, the intuition is very straight forward, we need to traverse the given Binary Search Tree and find the kth **Smallest** and **Largest** element in it.\n\nThere are a couple of ways of doing this.\n\n**TIME & SPACE Complexity is discussed below in detail**\n\n<br>\n<hr>\n\n# Kth Smallest Element :\n- We iterate over the given BST and maintain a counter variable for finding the Kth smallest guy and increment or decrement the counter variable till it reaches k or 0 respectively.\n\n<br>\n\n# Kth Largest Element :\n- To find kth largest guy, we need to do one more traversal to find the total number of nodes in our Binary Search Tree.\n- Once we get the total nodes, we perform exact algorithm of **Kth smallest element** problem but instead of passing `k` as the target count, we will be passing `n - k + 1` as the target count.\n- Since kth guy in a **Sorted container** is the `(n - k + 1)`th guy from the end of the container. **Right? Yes, indeed.**\n\n<hr>\n\n# Explanation\n- First we create a function which iterates over any Tree (Binary Tree or Binary Seach Tree) in most efficient way. Yes, we are talking about Morris Traversal, which does the work in `O(n) time and O(1) space`.\n- Also, in this function, we will maintain `two variables` first is the ***answer for kth smallest element*** and the second is the ***total number of nodes in the BST***.\n- Now, this helper Morris function can be directly called for `Kth Smallest Element problem`.\n- For `Kth Largest Element problem` we call this helper Morris function `two times`. First, to count the total number of nodes and secondly, to find the `Kth Largest Element` or we can say to find the `(N-k+1)th Smallest Element`\n\n<hr>\n\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n pair<int,int> morris(TreeNode* cur, int k){\n int ans=0, cnt=0;\n while(cur){\n // there is no left child so cur is the root\n if(cur->left == NULL){\n k--;\n cnt++;\n cur = cur->right;\n }\n else{\n // create a thread by going right most node in left subtree\n TreeNode *prev = cur->left;\n while(prev->right && prev->right != cur){\n prev = prev->right;\n }\n // two cases arise:\n // 1. thread not created i.e. prev->right == NULL\n if(prev->right == NULL){\n prev->right = cur; // creating thread\n cur = cur->left;\n }\n // 2. thread already created i.e. left subtree is already visited, move right\n else{\n prev->right = NULL;\n k--;\n cnt++;\n cur = cur->right;\n }\n }\n if(k==1) ans = cur->val;\n }\n return {ans,cnt};\n }\n\n int inorder(TreeNode* root, int k) {\n if(k==1 && !root->left) return root->val;\n auto pr = morris(root, k);\n return pr.first;\n }\n\n int kthSmallest(TreeNode* root, int k) {\n return inorder(root, k);\n }\n\n int kthLargest(TreeNode* root, int k){\n auto pr = morris(root,k);\n int newK = pr.second - k + 1;\n return inorder(root, newK);\n }\n};\n\n\n```\n\n```java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\npublic class Solution {\n private Pair<Integer, Integer> morris(TreeNode cur, int k) {\n int ans = 0, cnt = 0;\n while (cur != null) {\n if (cur.left == null) {\n k--;\n cnt++;\n cur = cur.right;\n } else {\n TreeNode prev = cur.left;\n while (prev.right != null && prev.right != cur) {\n prev = prev.right;\n }\n if (prev.right == null) {\n prev.right = cur;\n cur = cur.left;\n } else {\n prev.right = null;\n k--;\n cnt++;\n cur = cur.right;\n }\n }\n if (k == 1) ans = cur.val;\n }\n return new Pair<>(ans, cnt);\n }\n\n private int inorder(TreeNode root, int k) {\n if (k == 1 && root.left == null) return root.val;\n Pair<Integer, Integer> pr = morris(root, k);\n return pr.getKey();\n }\n\n public int kthSmallest(TreeNode root, int k) {\n return inorder(root, k);\n }\n\n public int kthLargest(TreeNode root, int k) {\n Pair<Integer, Integer> pr = morris(root, k);\n int newK = pr.getValue() - k + 1;\n return inorder(root, newK);\n }\n}\n\n\n```\n```Kotlin []\n/**\n * Example:\n * var ti = TreeNode(5)\n * var v = ti.`val`\n * Definition for a binary tree node.\n * class TreeNode(var `val`: Int) {\n * var left: TreeNode? = null\n * var right: TreeNode? = null\n * }\n */\n\nclass Solution {\n private fun morris(cur: TreeNode?, kk: Int): Pair<Int, Int> {\n var ans = 0\n var cnt = 0\n var k = kk\n var current = cur\n while (current != null) {\n if (current.left == null) {\n k--\n cnt++\n current = current.right\n } else {\n var prev = current.left\n while (prev?.right != null && prev.right != current) {\n prev = prev.right\n }\n if (prev?.right == null) {\n prev?.right = current\n current = current?.left\n } else {\n prev.right = null\n k--\n cnt++\n current = current?.right\n }\n }\n if (k == 1) ans = current?.`val` ?: 0\n }\n return Pair(ans, cnt)\n }\n\n private fun inorder(root: TreeNode?, k: Int): Int {\n if (k == 1 && root?.left == null) return root?.`val` ?: 0\n val pr = morris(root, k)\n return pr.first\n }\n\n fun kthSmallest(root: TreeNode?, k: Int): Int {\n return inorder(root, k)\n }\n\n fun kthLargest(root: TreeNode?, k: Int): Int {\n val pr = morris(root, k)\n val newK = pr.second - k + 1\n return inorder(root, newK)\n }\n}\n\n\n```\n``` Python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def morris(self, cur, k):\n ans, cnt = 0, 0\n while cur:\n if not cur.left:\n k -= 1\n cnt += 1\n cur = cur.right\n else:\n prev = cur.left\n while prev.right and prev.right != cur:\n prev = prev.right\n if not prev.right:\n prev.right = cur\n cur = cur.left\n else:\n prev.right = None\n k -= 1\n cnt += 1\n cur = cur.right\n if k == 1:\n ans = cur.val\n return ans, cnt\n\n def inorder(self, root, k):\n if k == 1 and not root.left:\n return root.val\n ans, _ = self.morris(root, k)\n return ans\n\n def kthSmallest(self, root, k):\n return self.inorder(root, k)\n\n def kthLargest(self, root, k):\n ans, cnt = self.morris(root, k)\n newK = cnt - k + 1\n return self.inorder(root, newK)\n\n\n```\n\n<br>\n\n# Approaches\n`SOLUTION 1` - Recursion :\nTime Complexity : O(n + nlogn) - any traversal + sorting the stored node-values\nSpace Complexity : O(n + n) - recursion stack space and stored node-values\n\n`SOLUTION 2` - Recursion :\nTime Complexity : O(n) - inorder traversal\nSpace Complexity : O(n + n) - recursion stack space and maintaing the stored node-values vector\n\n`SOLUTION 3` - Iterative :\nTime Complexity : O(n + nlogn) - any traversal + sorting the stored node-values\nSpace Complexity : O(n) - maintaing the stored node-values vector\n\n`SOLUTION 4` - Iterative :\nTime Complexity : O(n) - inorder traversal\nSpace Complexity : O(n) - maintaing the stored node-values vector\n\n`SOLUTION 5` - Iterative : **MOST OPTIMAL SOLUTION**\nTime Complexity : O(n) - Morris traversal\nSpace Complexity : O(1) - maintaining the counter variable\n\n\n// NOTE THAT : For kth largest element in a BST, we need to traversal\'s one for counting the number of nodes and one for morris traversal.\n\n\n\n<br>\n<hr>\n\n***Also note the edge case, where we have only one node in the tree and we are required to return 1st largest or 1st smallest element, which is itself the only node. So this case needs to be taken care of.***\n\n<hr>\n\n**PLEASE UPVOTE IF YOU LIKED THE SOLUTION**\n | 2 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Python3 - iterative dfs (inorder) beats 98% | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince it\'s a BST traversing it in inorder way will give me a sorted list\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ntraverse the nodes of tree in inorder way keep a count(initialise with 0) of the node and when the count equals to k return the value of the node.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n) -> traversing each node once\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n) -> stack will have at most all nodes in the tree\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n stack = []\n def inorder(root):\n count = 0\n cur = root\n while cur or stack:\n while cur:\n stack.append(cur)\n cur = cur.left\n cur = stack.pop()\n count += 1\n if count == k:\n return cur.val\n cur = cur.right\n return inorder(root)\n``` | 1 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
230: Time 97.61% and Space 83.27%, Solution with step by step explanation | kth-smallest-element-in-a-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe problem asks us to find the kth smallest value in a binary search tree. One way to do this is to traverse the tree in-order (left, root, right) and keep track of the number of nodes we have visited. Once we have visited k nodes, the next node we visit will be the kth smallest node.\n\nWe can do this using a stack to store the nodes we have visited so far. We start at the root of the tree and traverse as far left as possible, adding each node to the stack. Once we reach the leftmost node, we pop it off the stack (which is the smallest node we have seen so far) and decrement k. If k is 0, we have found the kth smallest value and can return it.\n\nIf k is not 0, we move to the right child of the node we just processed and repeat the process. This will visit the nodes in ascending order of value until we find the kth smallest node.\n\nNote that this algorithm has a time complexity of O(n) in the worst case (when the tree is skewed), since we need to visit every node in the tree. However, in the average case (when the tree is balanced), it has a time complexity of O(log n) since we only need to visit a subset of the nodes. Additionally, the space complexity is O(h) where h is the height of the tree, since we need to store at most h nodes on the stack at any given time.\n\n# Complexity\n- Time complexity:\n97.61%\n\n- Space complexity:\n83.27%\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, root: TreeNode, k: int) -> int:\n # create a stack to store the nodes\n stack = []\n # start at the root of the tree\n current = root\n \n # loop until we have processed all nodes and found the kth smallest value\n while True:\n # traverse as far left as possible from the current node, adding each node to the stack\n while current is not None:\n stack.append(current)\n current = current.left\n \n # if the stack is empty, we have processed all nodes and can exit the loop\n if not stack:\n break\n \n # pop the top node off the stack (which is the next smallest node) and decrement k\n node = stack.pop()\n k -= 1\n \n # if k is 0, we have found the kth smallest value and can return it\n if k == 0:\n return node.val\n \n # set the current node to the right child of the node we just processed\n current = node.right\n\n``` | 14 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Python || Recursion || Without Stack || Easy | kth-smallest-element-in-a-bst | 0 | 1 | ```\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n def inorder(root):\n nonlocal k\n if root==None:\n return None\n left=inorder(root.left)\n if left!=None:\n return left\n k-=1\n if k==0:\n return root.val\n return inorder(root.right)\n return inorder(root)\n```\n**An upvote will be encouraging** | 4 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Simple Solution Inorder Traversal | DFS | Beats 93% Runtime | Python | kth-smallest-element-in-a-bst | 0 | 1 | \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:\n\n preorder = []\n \n def dfs(node : TreeNode):\n if not(node) : return\n\n dfs(node.left)\n preorder.append(node.val)\n dfs(node.right)\n\n dfs(root)\n \n return preorder[k-1]\n``` | 3 | Given the `root` of a binary search tree, and an integer `k`, return _the_ `kth` _smallest value (**1-indexed**) of all the values of the nodes in the tree_.
**Example 1:**
**Input:** root = \[3,1,4,null,2\], k = 1
**Output:** 1
**Example 2:**
**Input:** root = \[5,3,6,2,4,null,null,1\], k = 3
**Output:** 3
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= k <= n <= 104`
* `0 <= Node.val <= 104`
**Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize? | Try to utilize the property of a BST. Try in-order traversal. (Credits to @chan13) What if you could modify the BST node's structure? The optimal runtime complexity is O(height of BST). |
Beats 99% of other solutions ! | power-of-two | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n # y = b^x -> x = logb y\n if n <=0:\n return False\n return math.log2(n) % 1 == 0 \n\n \n``` | 0 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
🔥Simple 1 Line using Binary | power-of-two | 0 | 1 | \n# Code\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n return bin(n)[2] == "1" and bin(n).count("1") == 1\n```\n# Explanation\n\n**Every power of two `(2^n)` has a single `1` bit at the left side, and all the other bits are `0`.**\n\n*Here are some examples to illustrate this:*\n\n- 2^0 = 1 in binary:\nBinary: `1`\n- 2^1 = 2 in binary:\nBinary: `10`\n- 2^2 = 4 in binary:\nBinary: `100`\n- 2^3 = 8 in binary:\nBinary: `1000`\n- 2^4 = 16 in binary:\nBinary: `10000`\n\n**In Python, when you convert an `int` to binary, the result will start with the prefix `"0b"` to indicate that it\'s in binary form. Thats why we are checking `bin(n)[2]` if its `\'1\'`**\n\nPleas consider upvoting if you like my explanation :D\n\n\n | 5 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Beats 100% | Easy To Understand | 0ms 🔥🚀 | power-of-two | 1 | 1 | # Intuition\nPLease upvote if you found this helpful!!\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n bool isPowerOfTwo(int n) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n if(n == 0) return false;\n if(n == 1) return true;\n\n while((n % 2) == 0)\n {\n n = n / 2;\n }\n\n return n == 1;\n }\n\n bool isPowerOfTwo(int n) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n if(n == 0) return false;\n if(n == 1) return true;\n if(n < 0) return false;\n\n return (n & (n - 1)) == 0;\n }\n};\n``` | 2 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Very Easy 0 ms 100% (Fully Explained)(Java, C++, Python, JS, C, Python3) | power-of-two | 1 | 1 | # **Java Solution (Recursive Approach):**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Power of Two.\n```\nclass Solution {\n public boolean isPowerOfTwo(int n) {\n // Base cases as \'1\' is the only odd number which is a power of 2 i.e. 2^0...\n if(n==1)\n return true;\n // All other odd numbers are not powers of 2...\n else if (n % 2 != 0 || n == 0)\n return false;\n // Recursive function call\n return isPowerOfTwo(n/2);\n }\n}\n```\n\n# **C++ Solution (Bit-Manipulation):**\n```\nclass Solution {\npublic:\n bool isPowerOfTwo(int n) {\n // If n <= 0 that means its a negative hence not a power of 2...\n if (n <= 0){\n return false;\n }\n // Check if x & (x \u2013 1) is equal to zero...\n // If yes, the number is a power of 2...\n else if ((n & (n - 1)) == 0){\n return true;\n }\n // Otherwise, The integer is not a power of 2...\n else {\n return false;\n }\n }\n};\n```\n\n# **Python Solution (Trival):**\n```\nclass Solution(object):\n def isPowerOfTwo(self, n):\n # If n <= 0 that means its a negative hence not a power of 2...\n if n <= 0:\n return False\n if n == 1:\n return True\n # Keep dividing the number by \u20182\u2019 until it is not divisible by \u20182\u2019 anymore.\n while (n % 2 == 0):\n n /= 2\n # If n is equal to 1, The integer is a power of two otherwise false...\n return n == 1\n```\n \n# **JavaScript Solution:**\n```\nvar isPowerOfTwo = function(n) {\n if (n == 0)\n return 0;\n while (n != 1) {\n if (n%2 != 0)\n return 0;\n n = n/2;\n }\n return 1;\n};\n```\n\n# **C Language:**\n```\nbool isPowerOfTwo(int n){\n if(n == 1)\n return true;\n else if(n == 0)\n return false;\n else if(n % 2 != 0)\n return false;\n return isPowerOfTwo(n/2);\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n # If n <= 0 that means its a negative hence not a power of 2...\n if n <= 0:\n return False\n if n == 1:\n return True\n # Keep dividing the number by \u20182\u2019 until it is not divisible by \u20182\u2019 anymore.\n while (n % 2 == 0):\n n /= 2\n # If n is equal to 1, The integer is a power of two otherwise false...\n return n == 1\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 55 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
linear solution - Python 🐍 | power-of-two | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n return False if n <= 0 else n & (n - 1) == 0\n``` | 1 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Easy Python Solution 🐍 | power-of-two | 0 | 1 | # Code\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n if n==1: return True\n x=2\n while x<=n:\n if x==n: return True\n x*=2\n return False\n```\n***Hope it helps...!!*** \uD83D\uDE07\u270C\uFE0F | 1 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
One Line Solution using Bitwise Operator | power-of-two | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n if n==0:\n return False\n else:\n return (n & n-1)==0\n``` | 1 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
[Python] Using BitManipulation - Time Complex: O(1); Space Complex: O(1) | power-of-two | 0 | 1 | \n\n# Approach\nUsing BitManipulation\n\n# Complexity\n- Time complexity: O(32)\n\n- Space complexity: O(1)\n\n# Solution 1\nIf a number is power of two, the number of bit 1 in it must be one\n```\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n count = 0\n # count is variable to calculate the number of bit 1 in n\n if n <= 0:\n return False\n for i in range(32):\n if (n >> i)&1 == 1:\n count += 1\n if count == 2: \n return False\n if count == 0:\n return False\n return True\n```\n# Solution 2\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n```\nclass Solution:\n def isPowerOfTwo(self, x: int) -> bool:\n if x <= 0:\n return 0\n return (x & (x - 1)) == 0\n``` | 2 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Bit Minuplation: Beats 99.9% submissions | power-of-two | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thought is just by keep dividing the number by 2 until we cannot and check if the number is 1. If the number at the last is 1 return True otherwise false. This takes O(logn) time complexity.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can minimize the solution by using bitwise operators.\nLet\'s assume that n is power of two, it will have 1 only at the most significant bit and all others are 0. The number n-1 will have 1 digit less than n.\nSo if we perform AND operation of n and n-1 we will get answer as 0 as the only digit in n which is 1 will ANDed with 0.\n\n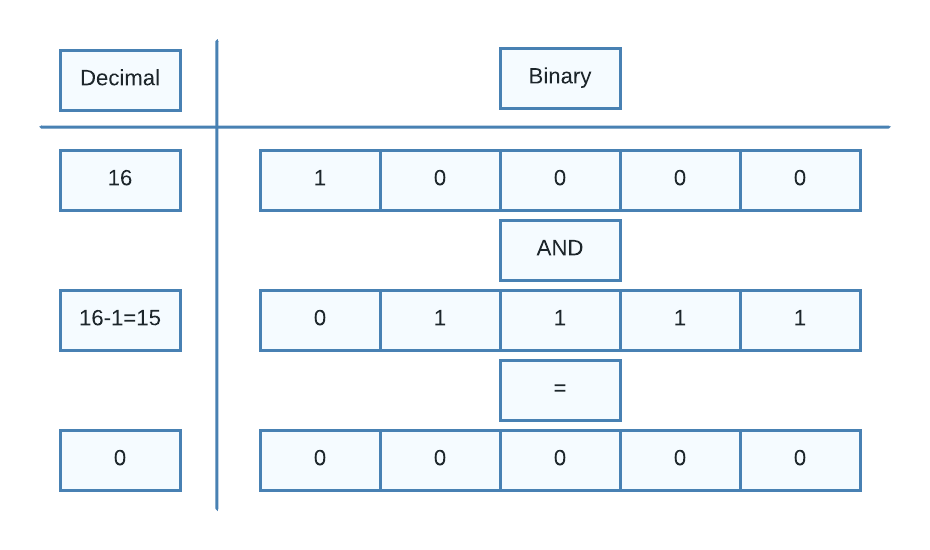\n\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\n```python []\nclass Solution:\n def isPowerOfTwo(self, n: int) -> bool:\n return n > 0 and n & (n - 1) == 0\n```\n\n```Java []\nclass Solution {\n public boolean isPowerOfTwo(int n) {\n return n > 0 && (n & (n - 1)) == 0;\n }\n}\n```\n\n```C++ []\nclass Solution {\n public:\n bool isPowerOfTwo(int n) {\n return n > 0 && (n & (n - 1)) == 0;\n }\n};\n```\n\n```PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @return Boolean\n */\n function isPowerOfTwo($n) {\n return $n > 0 && ($n & ($n - 1)) === 0;\n }\n}\n```\n\n | 9 | Given an integer `n`, return _`true` if it is a power of two. Otherwise, return `false`_.
An integer `n` is a power of two, if there exists an integer `x` such that `n == 2x`.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** 20 = 1
**Example 2:**
**Input:** n = 16
**Output:** true
**Explanation:** 24 = 16
**Example 3:**
**Input:** n = 3
**Output:** false
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Very Easy || 100% || Fully Explained || Java, C++, Python, Python3 | implement-queue-using-stacks | 1 | 1 | **Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (push, peek, pop, and empty).**\n\n**Implement the MyQueue class:**\n\n* void push(int x) Pushes element x to the back of the queue.\n* int pop() Removes the element from the front of the queue and returns it.\n* int peek() Returns the element at the front of the queue.\n* boolean empty() Returns true if the queue is empty, false otherwise.\n\n\n# **Java Solution:**\nRuntime: 1 ms, faster than 92.42% of Java online submissions for Implement Queue using Stacks.\n```\nclass MyQueue {\n\t private Deque<Integer> in_stk = new ArrayDeque<>();\n private Deque<Integer> out_stk = new ArrayDeque<>();\n // Push element x to the back of queue...\n public void push(int x) {\n in_stk.push(x);\n }\n // Remove the element from the front of the queue and returns it...\n public int pop() {\n peek();\n return out_stk.pop();\n }\n // Get the front element...\n public int peek() {\n if (out_stk.isEmpty())\n while (!in_stk.isEmpty())\n out_stk.push(in_stk.pop());\n return out_stk.peek();\n }\n // Return whether the queue is empty.\n public boolean empty() {\n return in_stk.isEmpty() && out_stk.isEmpty();\n }\n\n private Deque<Integer> in_stk = new ArrayDeque<>();\n private Deque<Integer> out_stk = new ArrayDeque<>();\n}\n```\n\n# **C++ Solution:**\n```\nclass MyQueue {\npublic:\n // Push element x to the back of queue...\n void push(int x) {\n in_stk.push(x);\n }\n\t// Remove the element from the front of the queue and returns it...\n int pop() {\n peek();\n const int val = out_stk.top();\n out_stk.pop();\n return val;\n }\n\t// Get the front element...\n int peek() {\n if (out_stk.empty())\n while (!in_stk.empty())\n out_stk.push(in_stk.top()), in_stk.pop();\n return out_stk.top();\n }\n\t// Return whether the queue is empty...\n bool empty() {\n return in_stk.empty() && out_stk.empty();\n }\nprivate:\n stack<int> in_stk;\n stack<int> out_stk;\n};\n```\n\n# **Python/Python3 Solution:**\n```\nclass MyQueue(object):\n def __init__(self):\n self.in_stk = []\n self.out_stk = []\n\t# Push element x to the back of queue...\n def push(self, x):\n self.in_stk.append(x)\n\t# Remove the element from the front of the queue and returns it...\n def pop(self):\n self.peek()\n return self.out_stk.pop()\n\t# Get the front element...\n def peek(self):\n if not self.out_stk:\n while self.in_stk:\n self.out_stk.append(self.in_stk.pop())\n return self.out_stk[-1]\n\t# Return whether the queue is empty...\n def empty(self):\n return not self.in_stk and not self.out_stk\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 190 | Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (`push`, `peek`, `pop`, and `empty`).
Implement the `MyQueue` class:
* `void push(int x)` Pushes element x to the back of the queue.
* `int pop()` Removes the element from the front of the queue and returns it.
* `int peek()` Returns the element at the front of the queue.
* `boolean empty()` Returns `true` if the queue is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a stack, which means only `push to top`, `peek/pop from top`, `size`, and `is empty` operations are valid.
* Depending on your language, the stack may not be supported natively. You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack's standard operations.
**Example 1:**
**Input**
\[ "MyQueue ", "push ", "push ", "peek ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 1, 1, false\]
**Explanation**
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: \[1\]
myQueue.push(2); // queue is: \[1, 2\] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is \[2\]
myQueue.empty(); // return false
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `peek`, and `empty`.
* All the calls to `pop` and `peek` are valid.
**Follow-up:** Can you implement the queue such that each operation is **[amortized](https://en.wikipedia.org/wiki/Amortized_analysis)** `O(1)` time complexity? In other words, performing `n` operations will take overall `O(n)` time even if one of those operations may take longer. | null |
232: Solution with step by step explanation | implement-queue-using-stacks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe key to implementing a queue using two stacks is to use one stack to represent the front of the queue and the other stack to represent the back of the queue. When an element is pushed onto the queue, it is pushed onto the back stack. When an element is popped from the queue or its value is read, the front stack is used to maintain the FIFO order of the elements.\n\nThe time complexity of each operation is O(1) amortized, which means that performing n operations will take O(n) time overall, even if one of those operations takes longer.\n\n# Complexity\n- Time complexity:\n\n- Space complexity:\n\n# Code\n```\nclass MyQueue:\n\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.front = [] # initialize front stack\n self.back = [] # initialize back stack\n\n def push(self, x: int) -> None:\n """\n Push element x to the back of queue.\n """\n self.back.append(x) # add element to back stack\n\n def pop(self) -> int:\n """\n Removes the element from in front of queue and returns that element.\n """\n self.peek() # move elements from back stack to front stack\n return self.front.pop() # remove and return the first element from front stack\n\n def peek(self) -> int:\n """\n Get the front element.\n """\n if not self.front: # if front stack is empty\n while self.back: # move all elements from back stack to front stack\n self.front.append(self.back.pop())\n return self.front[-1] # return the last element in front stack (i.e., the first element in queue)\n\n def empty(self) -> bool:\n """\n Returns whether the queue is empty.\n """\n return not self.front and not self.back # queue is empty if both stacks are empty\n\n```\nHere is an updated implementation that only uses the standard stack operations of push, pop, peek, and empty:\n\n````\nclass MyQueue:\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.stack1 = [] # represents the front of the queue\n self.stack2 = [] # represents the back of the queue\n\n def push(self, x: int) -> None:\n """\n Push element x to the back of queue.\n """\n self.stack2.insert(0, x)\n\n def pop(self) -> int:\n """\n Removes the element from in front of queue and returns that element.\n """\n if not self.stack1:\n while self.stack2:\n self.stack1.insert(0, self.stack2.pop(0))\n return self.stack1.pop(0)\n\n def peek(self) -> int:\n """\n Get the front element.\n """\n if not self.stack1:\n while self.stack2:\n self.stack1.insert(0, self.stack2.pop(0))\n return self.stack1[0]\n\n def empty(self) -> bool:\n """\n Returns whether the queue is empty.\n """\n return not self.stack1 and not self.stack2\n\n````\n | 12 | Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (`push`, `peek`, `pop`, and `empty`).
Implement the `MyQueue` class:
* `void push(int x)` Pushes element x to the back of the queue.
* `int pop()` Removes the element from the front of the queue and returns it.
* `int peek()` Returns the element at the front of the queue.
* `boolean empty()` Returns `true` if the queue is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a stack, which means only `push to top`, `peek/pop from top`, `size`, and `is empty` operations are valid.
* Depending on your language, the stack may not be supported natively. You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack's standard operations.
**Example 1:**
**Input**
\[ "MyQueue ", "push ", "push ", "peek ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 1, 1, false\]
**Explanation**
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: \[1\]
myQueue.push(2); // queue is: \[1, 2\] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is \[2\]
myQueue.empty(); // return false
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `peek`, and `empty`.
* All the calls to `pop` and `peek` are valid.
**Follow-up:** Can you implement the queue such that each operation is **[amortized](https://en.wikipedia.org/wiki/Amortized_analysis)** `O(1)` time complexity? In other words, performing `n` operations will take overall `O(n)` time even if one of those operations may take longer. | null |
very easyy to understand | implement-queue-using-stacks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyQueue:\n\n def __init__(self):\n self.stack = []\n\n def push(self, x: int) -> None:\n self.stack.append(x)\n\n def pop(self) -> int:\n return self.stack.pop(0)\n\n def peek(self) -> int:\n return self.stack[0]\n\n def empty(self) -> bool:\n return len(self.stack) == 0\n\n\n# Your MyQueue object will be instantiated and called as such:\n# obj = MyQueue()\n# obj.push(x)\n# param_2 = obj.pop()\n# param_3 = obj.peek()\n# param_4 = obj.empty()\n``` | 0 | Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (`push`, `peek`, `pop`, and `empty`).
Implement the `MyQueue` class:
* `void push(int x)` Pushes element x to the back of the queue.
* `int pop()` Removes the element from the front of the queue and returns it.
* `int peek()` Returns the element at the front of the queue.
* `boolean empty()` Returns `true` if the queue is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a stack, which means only `push to top`, `peek/pop from top`, `size`, and `is empty` operations are valid.
* Depending on your language, the stack may not be supported natively. You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack's standard operations.
**Example 1:**
**Input**
\[ "MyQueue ", "push ", "push ", "peek ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 1, 1, false\]
**Explanation**
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: \[1\]
myQueue.push(2); // queue is: \[1, 2\] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is \[2\]
myQueue.empty(); // return false
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `peek`, and `empty`.
* All the calls to `pop` and `peek` are valid.
**Follow-up:** Can you implement the queue such that each operation is **[amortized](https://en.wikipedia.org/wiki/Amortized_analysis)** `O(1)` time complexity? In other words, performing `n` operations will take overall `O(n)` time even if one of those operations may take longer. | null |
Solution | number-of-digit-one | 1 | 1 | ```C++ []\nclass Solution { \npublic:\n int countDigitOne(int n) {\n int ret = 0;\n for(long long int i = 1; i <= n; i*= (long long int)10){\n int a = n / i;\n int b = n % i;\n int x = a % 10;\n if(x ==1){\n ret += (a / 10) * i + (b + 1);\n }\n else if(x == 0){\n ret += (a / 10) * i;\n } else {\n ret += (a / 10 + 1) *i;\n }\n }\n return ret;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n def count(add,n_digit):\n c = 0\n for d in range(0,n_digit+1):\n c += (d+add)*math.comb(n_digit,d)*9**(n_digit-d)\n return c\n res = 0\n n_list = [int(x) for x in str(n)]\n count_1 = 0\n for i in range(len(n_list)-1):\n if n_list[i] == 1:\n res += count(count_1,len(n_list)-i-1)\n count_1 += 1\n elif n_list[i] > 1:\n leading = n_list[i]-1\n res += count(count_1,len(n_list)-i-1)*leading+count(count_1+1,len(n_list)-i-1)\n res += count_1*(n_list[-1]+1)\n if n_list[-1] >= 1:\n res += 1\n return res\n```\n\n```Java []\nclass Solution {\n public int countDigitOne(int n) {\n int ans = 0;\n for (long pow10 = 1; pow10 <= n; pow10 *= 10) {\n final long divisor = pow10 * 10;\n final int quotient = (int) (n / divisor);\n final int remainder = (int) (n % divisor);\n if (quotient > 0)\n ans += quotient * pow10;\n if (remainder >= pow10)\n ans += Math.min(remainder - pow10 + 1, pow10);\n }\n return ans;\n }\n}\n```\n | 430 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Python 3 solution || 100% working 🔥🔥🔥 | number-of-digit-one | 0 | 1 | ****Please Upvote :-)**** \n\n# Complexity\n- Time complexity: O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->Since it loops only the number of digits present in a number.\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) :\n n = str(n) #converting it to string\n c=0 #initializing count variable\n l=len(n)\n\n for i in range(l-1,0,-1):\n num=int(n)\n first_dig=int(n[0]) #taking the first digit\n if first_dig==1:\n c+=(int(str(i)+\'0\'*(i-1))+1)\n c+=int(n[1:])\n elif first_dig==0:\n pass\n else:\n c+=(int(str(i)+\'0\'*(i-1))+1)\n c+=(int(\'9\'*i))\n c+=((first_dig-1)*(int(str(i)+\'0\'*(i-1))))\n n=n[1::] #removing the first digit.\n\n if n==\'0\':\n return c #if 0 return c\n else:\n return c+1 #else return c+1 because the digit 1 would have occurred once.\n``` | 2 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
233: Solution with step by step explanation | number-of-digit-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe solution works by iterating through each digit position from right to left, and for each position, counting the number of ones that can appear at that position. This is done using the formula:\n\n- If the digit at the current position is 0, then the number of ones that can appear at this position is determined by the digits to the right of it.\n- If the digit at the current position is 1, then the number of ones that can appear at this position is determined by the digits to the right of it, as well as the digits to the left of it.\n- If the digit at the current position is greater than 1, then the number of ones that can appear at this position is determined by the digits to the right of it, as well as the number of times the current position can be filled with the digit 1.\n\nThe code starts by initializing a variable "ans" to 0, which will accumulate the total count of ones. It then initializes a variable "pow10" to 1, which will be used to iterate through each digit position from right to left.\n\nThe code then enters a loop that continues while "pow10" is less than or equal to "n". In each iteration of the loop, the code computes the quotient and remainder when "n" is divided by "divisor", which is equal to "pow10" times 10. The quotient represents the digits to the left of the current position, and the remainder represents the digits to the right of the current position.\n\nThe code then checks if the quotient is greater than 0. If so, it adds "quotient * pow10" to "ans", which counts the number of ones that can appear at the current position due to the digits to the left of it.\n\nThe code then checks if the remainder is greater than or equal to "pow10". If so, it adds "min(remainder - pow10 + 1, pow10)" to "ans", which counts the number of ones that can appear at the current position due to the digits to the right of it, as well as the current position itself if the current digit is 1.\n\nFinally, the code multiplies "pow10" by 10 to move on to the next digit position, and repeats the loop.\n\nThe function returns "ans" as the final count of ones.\n\nOverall, this algorithm has a time complexity of O(log n) because it iterates through each digit position in "n", which has log n digits.\n\n# Complexity\n- Time complexity:\n81.74%\n\n- Space complexity:\n57.91%\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n ans = 0\n\n pow10 = 1\n while pow10 <= n:\n divisor = pow10 * 10\n quotient = n // divisor\n remainder = n % divisor\n if quotient > 0:\n ans += quotient * pow10\n if remainder >= pow10:\n ans += min(remainder - pow10 + 1, pow10)\n pow10 *= 10\n\n return ans\n``` | 11 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Easy Recursive Python Solution | number-of-digit-one | 0 | 1 | # Intuition\nAs someone pointed out in the comments of the official solution, you can avoid the complicated math by using a formula for the sum of ones in numbers **strictly less** than 10, 100, 1000, etc.\n\nTake 1000 for example. The numbers strictly less than 1000 are 000-999. Because the digits that make up these numbers are equally distributed the number of 1\'s is the same as the number of 2\'s, etc. and it is the total number of digits / 10 = 3 * 1000 / 10. By this method the sum of ones in numbers less than 10 ** m is m * 10 ** m / 10 = m * 10 ** (m-1).\n\nOkay, so now we have the solution for 1, 10, 100, 1000, etc. in O(1) time. We just add 1 to our formula above (becuase our formula was for numbers strictly less, but the problem says to calculate the same but inclusively). \n\nNow to get the solution for 12345, we can use our formula for the 10000 part to account for 0000...9999 and add (the solution of 2345) + (2345 + 1) to account for the 2346 extra ones we get from the numbers 10000...12345\n\nIn the case where our number starts with a digit greater than 1, such as 54321, we can use our formula for 1000 to account for 0000...9999, 1000...1009, 2000...2999, ..., 4000...4999. And then we can add the solution of 4321.\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n m = len(str(n))\n if m == 1:\n return 0 if n == 0 else 1\n tenth = 10 ** (m - 1)\n num_digits_tenth = (m - 1) * 10 ** (m - 1)\n num_ones_tenth = num_digits_tenth // 10\n first_digit = n // (10 ** (m-1))\n rest = n % (10 ** (m-1))\n if first_digit > 1:\n return num_ones_tenth * first_digit + (10 ** (m - 1)) + self.countDigitOne(rest)\n else:\n return num_ones_tenth + self.countDigitOne(rest) + (rest + 1)\n``` | 3 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Explained to a 5-year old | number-of-digit-one | 0 | 1 | # Intuition\nThe key intuition is that we count the number of 1\'s contributed by every digit\'s place in the number.\nFor example, if `n` is a 3-digit number, some of the 1\'s would be contributed by the 1\'s place, some by the 10\'s place and some by the 100\'s place.\n\n# Approach\nObserve that for every range of 10, like 0-9, 10-19, 20-29 etc., 1 appears in 1\'s place only once.\nLike for 0-9, it appears once in 1, for 10-19, its appears in 1\'s place once in 11, for 20-29, it appears in 1\'s place once in 21.\n**So, if we count the number of 10\'s in `n`, we will have as many 1\'s contributed by the 1\'s place.**\n\nSimilarly, for every range of 100, 1 appears in 10\'s place 10 times. Example, for 0-100, 1 appears in 10\'s place only from 10-19.\n**So, if we count the number of 100\'s in `n`, and multiply the result by 10, we will have as many 1\'s contributed by the 10\'s place.**\n\n**Generalizing this pattern, the number of 1\'s for any digit position `1 <= d <= length(n)` is given by:**\n```\n10^(d-1) * floor(n/10^d). --- (i)\n```\n\nBut we aren\'t done yet. The number `n` may not be a perfect multiple of 10. For example, for `n=54`, and `d=1`, we have a remainder 4, and need to consider the 1 from the 1\'s place in 51.\nFor `n=154`, and `d=2`, we have a remainder 54, and need to consider the 1s from the ten\'s place in 110-119.\n\n**Observe that if the remainder is less than `i * 10^(d-1)`, then it doesn\'t count. --- (ii)**\nFor example, if `i=6`, `d=1` (unit\'s place) and `remainder=4`, there\'s no contribution made by it.\n**On the other hand, if it\'s bigger, then it makes a contribution capped at 10^d. --- (iii)**\nFor example, `i=1`, `d=2` (ten\'s place) and `remainder=54`, it contributes 10 numbers from 10 through 19.\nBut if remainder is 13, then it only contributes 4 numbers from 10 through 13.\n\nPutting all of this together, we finally have our solution.\n\n# Complexity\n- Time complexity:\n`O(d)`, where `d = 1 + log(n)` is the number of digits in `n`.\n\n- Space complexity:\n`O(1)`.\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n return self._count_of_i(n ,1)\n\n def _count_of_i(self, n: int, i: int) -> int:\n count, x = 0, 1\n while x <= n:\n a, b = divmod(n, x * 10)\n count += a * x # (i)\n k = i * x\n if b < k:\n b = 0 # (ii)\n else:\n b = min((b - k) + 1, x) # (iii)\n count += b\n x *= 10\n\n return count\n``` | 1 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
10 lines python code, beats 92% of people | number-of-digit-one | 0 | 1 | # Intuition\neach digit of a number has a possibility of being a one, and so we can count them up using a little math and some loops\n\n# Approach\nMultiplier represents the place value, and divider serves as to remove anything above that place value. Then two additions to count:\nOne for the number of ones you use for a cutoff (for example, with 30029, 10000-30029 is a cutoff), and another for regulars (1-10, 10-100, and so on).\n\n# Complexity\n- Time complexity:\nO(n), as there is only a while loop\n\n- Space complexity:\nO(1), as there are no lists.\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n count = 0\n multiplier = 1\n while multiplier <= n:\n divider = multiplier * 10\n count += (n // divider) * multiplier\n count += min(max(n % divider - multiplier + 1, 0), multiplier)\n multiplier *= 10\n return count\n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Easy Solution : ) | number-of-digit-one | 1 | 1 | # Intuition\nThe problem requires counting the number of occurrences of the digit \'1\' in all non-negative integers less than or equal to a given integer n. To approach this problem, we can iterate through each digit place of the numbers, count the occurrences of \'1\' at that place, and sum them up to get the total count.\n\n\n# Approach\n- Initialize a variable count to keep track of the total count of occurrences of \'1\'.\n- Iterate through each digit place (ones, tens, hundreds, etc.) using a variable factor.\n- For each digit place, calculate the number of occurrences of \'1\' at that place.\n- Sum up the counts for all digit places to get the final result.\n- Return the total count.\n# Complexity\n- Time complexity: O(log n) - The number of digits in n.\n- Space complexity: O(1) - Constant space used for variables.\n\n# Code\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countDigitOne = function(n) {\n if (n <= 0) {\n return 0;\n }\n\n let count = 0;\n let factor = 1;\n\n while (factor <= n) {\n let divisor = factor * 10;\n count += Math.floor(n / divisor) * factor;\n let remainder = n % divisor;\n count += Math.min(Math.max(0, remainder - factor + 1), factor);\n factor *= 10;\n }\n\n return count;\n};\n```\n```python []\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n if n <= 0:\n return 0\n\n count = 0\n factor = 1 # Represents the current digit place (1s, 10s, 100s, ...)\n\n while factor <= n:\n divisor = factor * 10 # Used to isolate the digit at the current place\n\n count += (n // divisor) * factor # Count the occurrences in the higher digits\n\n remainder = n % divisor\n count += min(max(0, remainder - factor + 1), factor) # Count the occurrences at the current place\n\n factor *= 10\n\n return count\n\n# Example usage:\nsolution = Solution()\nprint(solution.countDigitOne(13)) # Output: 6\nprint(solution.countDigitOne(0)) # Output: 0\n```\n```C++ []\nclass Solution {\npublic:\n int countDigitOne(int n) {\n if (n <= 0) {\n return 0;\n }\n\n int count = 0;\n long long factor = 1;\n\n while (factor <= n) {\n long long divisor = factor * 10;\n count += (n / divisor) * factor;\n long long remainder = n % divisor;\n count += min(max(0LL, remainder - factor + 1), factor);\n factor *= 10;\n }\n\n return count;\n }\n};\n```\n```java []\nclass Solution {\n public int countDigitOne(int n) {\n if (n <= 0) {\n return 0;\n }\n\n int count = 0;\n long factor = 1;\n\n while (factor <= n) {\n long divisor = factor * 10;\n count += (n / divisor) * factor;\n long remainder = n % divisor;\n count += Math.min(Math.max(0L, remainder - factor + 1), factor);\n factor *= 10;\n }\n\n return count;\n }\n}\n```\n\n | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
pure math solution | number-of-digit-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n res = 0\n while n > 0:\n p = int(log10(n))\n c, n = divmod(n, 10 ** p)\n res += c * int(p * 10 ** (p-1))\n if c > 1:\n res += 10 ** p\n else:\n res += n + 1\n return res\n\n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Fast Memoization Python | number-of-digit-one | 0 | 1 | class Solution:\n def countDigitOne(self, n: int) -> int:\n @cache\n def f(k):\n if k == 0:\n return 0\n if k <= 9:\n return 1\n\n s = str(k)\n head_num = int(s[0])\n rest_num = int(s[1:])\n\n return f(rest_num) + (rest_num + 1 if head_num == 1 else 0) + f(k - rest_num - 1)\n\n return f(n)\n \n | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
19ms Beats 100.00% of users with Python3 | T/S: O((log(n))^2)/O(log(n)) | number-of-digit-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea used here is to count the number of times 1 can appear in each digits position such that the number is less than or equal to n. Once you have the counts for each digits place, just add them.\nExample:\nlets say n=130,\nNumber of times 1 can appear in 100\'s palce is 31 times (from 100 to 130)\nNumber of times 1 can appear in 10\'s place is 10(from 10 to 19) + 10(110 to 119) = 20\nNumber of times 1 can appear in 1\'s place is 13(1, 11, 21, 31, 41, 51, 61, 71, 81, 91, 101, 111, 121)\n\nThus the answer is 31 + 20 + 13 = 64.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI\'ll explain the approach with an example. This can be extended to any n. Check the code for generalization.\nLets take the same 3 digit number example as above $n=130$,\nNumber of times 1 can appear in 100s place can be expressed as follows:\nif the $100\'s$ place digit in the original number is $>1$, say something like $2$ (eg. $n=230$) then maximum number of times $1$ can appear in $100\'s$ place is $100$ (from $100$ to $199$, both included).\nif the $100\'s$ digit place is $\\le1$, as in n=130, then the number of times $1$ can appear is $130 - 10^2 + 1$. The power of 10 is 2 because we are iterested in 100\'s place.\nThus, number of times 1 can appear in $100\'s$ place for $n=130$ can be written as $min(n - largestExponentOf10LessThanN + 1, largestExponentOf10LessThanN) = min(130 - 100 + 1, 100)=31$.\nWhen we are considering the number of times $1$ can appear in 10\'s place, we can have 2 choices for 100\'s place ${0, 1}$. If, 100\'s place is 1, then with 10\'s place as 1 we have 10 numbers (110 to 119) which can also be obtained from the above formula for n=30 as = min(30 - 10 + 1, 10) = 10. Case 2 is when the 100\'s digit is 0. In this case when 10\'s place digit is 1, we have 10 numbers as (10 to 19) this is because we have 10 choices available for 1\'s place. Thus number of times 1 can appear in 10\'s place is 10 + 10 = 20.\nNow, the case when 1\'s place digit is 1. We have 2 choices for 100\'s place digit ${1, 0}$. when 100\'s place digit is 1, there are only 3 choices available for 10\'s place ${0, 1, 2}$ (cannot be 3 as that would make the original number 131>130). When 100\'s place digit is 0, 10\'s place digit can take any number between 0 and 9. Thus, 10 numbers where 100\'s place digit is 0 and 1\'s place digit is 1. Thus total count of numbers when 1 appears on 1\'s place is 3 + 10 = 13.\nThus total = 31 + 20 + 13 = 64\n# Complexity\n- Time complexity:$$O((\\log n)^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(\\log n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n res = 0\n str_rep = str(n)\n for i in range(len(str_rep)):\n # Count the total number of times 1 can appear in ith place.\n one_count = 0\n ## Fix the numbers from 0, i-1 to what appear in str_rep\n if int(str_rep[i]) >= 1:\n if i==len(str_rep) - 1:\n one_count += 1\n else:\n one_count += min(\n int(str_rep[i:]) - 10**(len(str_rep) - i - 1) + 1,\n 10**(len(str_rep) - i - 1)\n )\n ## Unfix numbers from 0, i-1 to 0 to int(str_rep[j]) - 1 one at a time (in the reverse order, ie from i-1 to 0).\n for j in range(i - 1, -1, -1):\n one_count += int(str_rep[j]) * (10 ** (len(str_rep) - (j + 1) - 1))\n res += one_count\n return res\n\n# 0 1 2 3 4 5 6\n# x x\n# 7 - 3 - 1\n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Python Solution | number-of-digit-one | 0 | 1 | # Complexity\n- Time complexity:\nO(log 10(n))\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n cnt = 0\n i = 1\n while i <= n:\n div = i * 10\n cnt += (n//div) * i + min(max(n % div - i + 1, 0), i)\n i*=10\n return cnt\n \n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
Mathematical approach; Explained w/ clean code | number-of-digit-one | 0 | 1 | # Intuition\nThis approach counts the number of digit 1s in non-negative integers less than or equal to n. \n\n# Approach\nThe code iterates through the digits of n and calculates the count of digit 1s at each position. It uses the `before`, `curr`, and `after` variables to determine the count efficiently.\n\n# Complexity\n- Time complexity: O(log(n)), where `n` is the given integer. \n- Space complexity: O(1) since it uses a constant amount of extra space. \n\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n count = 0\n factor = 1\n while n // factor > 0:\n curr = (n // factor) % 10\n after = n % factor\n before = n // (factor * 10)\n\n count += before * factor + (curr == 1) * (after + 1) + (curr > 1) * factor\n\n factor *= 10\n\n return count \n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
[Explanation] Dynamic Programming | number-of-digit-one | 0 | 1 | Given an integer n, the task is to determine the total number of occurrences of the digit 1 in all integers from 0 to n, inclusive.\n\n##### Approach: Dynamic Programming\n\nUnderstanding the concept involves breaking down the numbers into their digits and calculating the count of 1\'s at each digit place. Dynamic programming is employed to solve this problem efficiently.\n\n##### Explanation:\n\nConsider the example where n = 23. The numbers less than 23 are structured as follows:\n\nAll the number less than 23 are:\n[0][0 \u2192 9]: ([0][0], [0][1], [0][2] . . . [0][9])\n[1][0 \u2192 9]: ([1][0], [1][1], [1][2] . . . [1][9])\t\n[2][0 \u2192 3]: ([2][0], [2][1], [2][2], [2][3])\n\nFor n = 23:\n\n- When the first digit is 0, the rest of the digits form a subproblem of n = 9. \nSince the first digit is 0, there are 0 occurrences of 1 in the tens place. The ones place forms a subproblem of n = 9, which results in 1 occurrence of 1 from 0 to 9. Hence, the total count for [0][0 \u2192 9] is 1.\n- When the first digit is 1, \nthere are 10 occurrences of 1 in the tens place (from 10 to 19). The ones place forms a subproblem of n = 9, resulting in 1 occurrence of 1 from 0 to 9. Hence, the total count for [1][0 \u2192 9] is 11.\n- When the first digit is 2, the ones place forms a subproblem of n = 3. \nThere are 0 occurrences of 1 in the tens place, and 1 occurrence of 1 in the ones place from 0 to 3. Hence, the total count for [2][0 \u2192 3] is 1.\n\nThe total number of 1\'s in the number 23 is 13.\n\n##### Recursive Formula:\n1 $$f(n =n_1n_2n_3 ):$$\n2    $$ans = 0$$\n3    $$For$$ $$i = 0$$ $$to$$ $$n_1(excluded):$$\n4       $$ans += (i == 1) * pow(10, N(n_2n_3)) + f(pow(10, N(n_2n_3)) - 1)$$\n5    $$ans += (n == 1) * pow(10, N(n_2n_3)) + f(n_2n_3)$$\n6    $$return$$ $$ans$$\n\n\nFor an integer n = $$n_1n_2n_3$$, where `N(m)` denotes the number of digits in `m`:\n\n1. Initialize ans = 0.\n2. Iterate from i = 0 to n1 (excluded):\n2.1 Update ans using the formula: ans += (i == 1) * pow(10, N(n2n3)) + f(pow(10, N(n2n3)) - 1)\n3. Add the contribution from the digit $$n_1$$ as it was excluded in the for loop: ans += (n1 == 1) * pow(10, N(n2n3)) + f(n2n3)\n4. Return ans.\n\nThis approach recursively calculates the total number of 1\'s by breaking down the problem into subproblems and leveraging dynamic programming.\n\nFor the given example with n = 23, the recursion proceeds as follows:\n##### Dry run for n = 23\n```\nf(23):\n ans = 0\n i = 0: \n ans = (0 == 1) * pow(10, 1) + f(pow(10, 1) - 1)\n = 0 * 10 + f(10 - 1) \u2192 f(9) \n i = 1:\n\t ans = (1 == 1) * pow(10, 1) + f(pow(10, 1) - 1)\n = 0 * 10 + f(10 - 1) \u2192 10 + f(9) \n ans = f(9) + 10 + f(9)\n\n ans = f(9) + 10 + f(9) + (2 == 1) * pow(10, 1) + f(3)\n = f(9) + 10 + f(9) + 0 * 10 + f(3)\n = f(9) + 10 + f(9) + f(3) \n return f(9) + 10 + f(9) + f(3)\n```\nSince f(9) = 1, f(3) = 1, hence f(9) + 10 + f(9) + f(3) = 1 + 10 + 1 + 1 = 13\n\nThe final result, as demonstrated in the example, provides the total number of 1\'s in the range from 0 to n, inclusive.\n\n## Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n memo = {}\n def f(num):\n try:\n return memo[num]\n except:\n if num == 0:\n return 0\n if num <= 9:\n return 1\n integer = str(num)\n ans = 0\n first = integer[0]\n rem = integer[1:]\n \n for j in range(int(first)):\n if j == 1:\n ans += 10**len(rem) + f(10**len(rem) - 1)\n else:\n ans += f(10**len(rem) - 1)\n if first == \'1\':\n ans += int(rem)+1 + f(int(rem))\n else:\n ans += f(int(rem))\n # print("{}={}".format(num, ans))\n memo[num] = ans\n return ans\n return f(n)\n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
No DP, Space O(1) | number-of-digit-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(log)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def countDigitOne(self, n: int) -> int:\n \n suffix = 0\n total_ones = 0\n pow_ten = 1\n while n > 0:\n digit = n % 10 \n n = n // 10\n # print(n, digit, pow_ten, suffix)\n print(n * pow_ten, suffix + 1)\n if digit > 1:\n total_ones += (n + 1) * pow_ten\n if digit == 1:\n total_ones += n * pow_ten + suffix + 1\n if digit == 0:\n total_ones += n * pow_ten\n\n suffix = digit * pow_ten + suffix\n pow_ten *= 10\n\n\n return total_ones\n``` | 0 | Given an integer `n`, count _the total number of digit_ `1` _appearing in all non-negative integers less than or equal to_ `n`.
**Example 1:**
**Input:** n = 13
**Output:** 6
**Example 2:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 109` | Beware of overflow. |
🔥🔥 3 Best Solutions Explained 🔥🔥 | palindrome-linked-list | 0 | 1 | https://youtu.be/8h2UOPDCGPM | 50 | Given the `head` of a singly linked list, return `true` _if it is a_ _palindrome_ _or_ `false` _otherwise_.
**Example 1:**
**Input:** head = \[1,2,2,1\]
**Output:** true
**Example 2:**
**Input:** head = \[1,2\]
**Output:** false
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`.
* `0 <= Node.val <= 9`
**Follow up:** Could you do it in `O(n)` time and `O(1)` space? | null |
Python | Recursion | palindrome-linked-list | 0 | 1 | # Code\n```\nclass Solution:\n def isPalindrome(self, head: Optional[ListNode]) -> bool:\n if not head or not head.next: return True\n fp = sp = head\n while sp: \n fp, sp = fp.next, sp.next\n if sp: sp = sp.next\n return self.helper(fp, head)[0]\n \n def helper(self, fp: Optional[ListNode], head: Optional[ListNode]) -> tuple[int, ListNode]:\n if not fp.next: \n return fp.val == head.val, head.next\n is_palindrome, node = self.helper(fp.next, head)\n return is_palindrome and node.val == fp.val, node.next\n``` | 1 | Given the `head` of a singly linked list, return `true` _if it is a_ _palindrome_ _or_ `false` _otherwise_.
**Example 1:**
**Input:** head = \[1,2,2,1\]
**Output:** true
**Example 2:**
**Input:** head = \[1,2\]
**Output:** false
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`.
* `0 <= Node.val <= 9`
**Follow up:** Could you do it in `O(n)` time and `O(1)` space? | null |
Easy and Fundamental Solution For Linked Lists (In-Depth explanation to fundamentals (beats 89%)) | palindrome-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI wanted to solve this using the fundamentals of linked lists. So I split it up into 3 parts, using differnt strategies to do each step. This problem is a combination of ones like "Reverse Linked List" and "Middle of the Linked List"\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThere are 3 steps to this solution. \n\n**Step 1:** Find the middle of the linked list and split it there\n\n- Using a slow and fast pointer, the slow will be incremented by 1 and the fast by 2 for every time fast or fast.next is not null.\n- By the time fast or fast.next is null, your slow pointer will be at the middle of the linked list.\n\n**Step 2** is to reverse the second split linked list.\n\n- We reverse the second list so we can easily compare it to the first half\n- We do this by using 3 pointers prev, curr, and temp. This is a standard algorithm you should learn that will be important for reversing linked lists.\n\n**Step 3** is to check if the values of the first and second linked list are equal. If they are, its a palindrome.\n- Lastly, we compare the elements of the two lists to see if they are a palindrome. if the value of p1 (p1.val) is not equal to (p2.val), we return False, other wise we move onto the next using p1.next. \n- If p2 becomes null and all the value were equal (exiting the while loop), we return True\n\n# Complexity\n**Time complexity:**\n- <!-- Add your time complexity here, e.g. $$O(n)$$ --> O(N) - where N is the length of the list\n\n**Space complexity:**\n\n- <!-- Add your space complexity here, e.g. $$O(n)$$ --> O(1)\n\n\n\n# Code\n```\n#Definition for singly-linked list.\n#class ListNode:\n #def __init__(self, val=0, next=None):\n #self.val = val\n #self.next = next\nclass Solution:\n def isPalindrome(self, head: Optional[ListNode]) -> bool:\n if not head or not head.next:\n return True\n \n #Find the midpoint of the linked list\n slow = fast = head\n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n \n #Reverse the second half of the linked list\n prev = None\n curr = slow\n while curr:\n next_node = curr.next\n curr.next = prev\n prev = curr\n curr = next_node\n \n #See if the two halves are equal (palindromes)\n p1 = head\n p2 = prev\n while p2:\n if p1.val != p2.val:\n return False\n p1 = p1.next\n p2 = p2.next\n \n return True\n\n``` | 36 | Given the `head` of a singly linked list, return `true` _if it is a_ _palindrome_ _or_ `false` _otherwise_.
**Example 1:**
**Input:** head = \[1,2,2,1\]
**Output:** true
**Example 2:**
**Input:** head = \[1,2\]
**Output:** false
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`.
* `0 <= Node.val <= 9`
**Follow up:** Could you do it in `O(n)` time and `O(1)` space? | null |
Beats 99%✅ | O( log(n))✅ | (Step by step explanation)✅ | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Intuition\nThe problem is to find the lowest common ancestor (LCA) of two nodes, `p` and `q`, in a binary search tree (BST). The LCA is the lowest node in the tree that has both `p` and `q` as descendants. Since the BST property holds, we can efficiently traverse the tree to find the LCA.\n\n# Approach\nThe approach is to traverse the BST starting from the root. While traversing, compare the values of the current node (`temp`) with the values of `p` and `q`. Based on the comparison, update the `temp` node to either its left or right child until we find the lowest common ancestor.\n\n1. Start with `temp = root`.\n2. While `temp` is not `None`:\n - If both `p` and `q` are greater than the value of `temp`, move to the right child (`temp = temp.right`).\n - If both `p` and `q` are smaller than the value of `temp`, move to the left child (`temp = temp.left`).\n - If the values of `p` and `q` are on opposite sides of `temp` (one is greater, and the other is smaller), `temp` is the lowest common ancestor. Return `temp`.\n\n# Complexity\n- Time complexity: O(h)\n - `h` is the height of the tree.\n - In the worst case, when the tree is skewed (completely unbalanced), the time complexity is O(n), where `n` is the number of nodes in the tree.\n- Space complexity: O(1)\n - The algorithm uses only a constant amount of extra space.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n temp = root \n\n while temp:\n if p.val > temp.val and q.val > temp.val:\n temp = temp.right\n elif p.val < temp.val and q.val < temp.val:\n temp = temp.left\n else:\n return temp\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {\n while (root != NULL) {\n if (p->val < root->val && q->val < root->val) {\n root = root->left;\n } else if (p->val > root->val && q->val > root->val) {\n root = root->right;\n } else {\n return root;\n }\n }\n return NULL;\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n | 8 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Easy Recursive Solution | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem, we can traverse the tree recursively, searching for both target nodes in the left and right subtrees. If both target nodes are found in different subtrees, then the current node is the lowest common ancestor. If they are found in the same subtree, we continue the search in that subtree until we find the lowest common ancestor.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve the problem, we define a recursive function called $$traverse$$ that takes three arguments: the current node, and the two target nodes. The function returns the lowest common ancestor of the two target nodes.\n\nHere\'s how the $$traverse$$ function works:\n\n1. If the current node is $$None$$, it returns $$None$$ to indicate that it did not find any target nodes in the subtree rooted at this node.\n2. If the current node is one of the target nodes, it returns the node itself to indicate that it found a target node in the subtree rooted at this node.\n3. If the current node is not a target node, it recursively searches the left and right subtrees to find the target nodes. \n4. It stores the results of the left and right subtree searches in $$left$$ and $$right$$, respectively.\n5. If both $$left$$ and $$right$$ are not $$None$$, it means that the target nodes are in different subtrees, and the current node is the lowest common ancestor. It returns the current node.\n6. If only one of $$left$$ and $$right$$ is not $$None$$, it means that both target nodes are in the same subtree, and the function returns the $$non-None$$ result.\n\nIn the main function, $$lowestCommonAncestor$$, we simply call the $$traverse$$ function with the root of the tree and the two target nodes, and return the result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the $$traverse$$ function is $$O(n)$$, where $$n$$ is the number of nodes in the tree. This is because the function visits each node in the tree once. Since the $$lowestCommonAncestor$$ function simply calls the $$traverse$$ function, its time complexity is also $$O(n)$$.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the $$traverse$$ function is $$O(h)$$, where $$h$$ is the height of the tree. This is because the function\'s call stack will have at most $$h$$ elements at any given time, corresponding to the height of the tree. In the worst case, when the tree is completely unbalanced, the height can be $$n$$, so the space complexity is $$O(n)$$. In the best case, when the tree is perfectly balanced, the height is log(n), so the space complexity is $$O(log(n))$$.\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n # define a function to traverse the tree and find the lowest common ancestor of two nodes\n def traverse(root, p, q):\n # base case: return None when the node is None\n if not root:\n return None\n # return the node itself when it\'s one of the target nodes\n if root == p or root == q:\n return root\n # recursively search the left and right subtrees\n left = traverse(root.left, p, q)\n right = traverse(root.right, p, q)\n # if both left and right subtrees return a valid node, the current node is the lowest common ancestor\n if left and right:\n return root\n # if only one subtree returns a valid node, return that node\n return left or right\n\n # call the traverse function to find the lowest common ancestor\n return traverse(root, p, q)\n\n\n # Find the lowest common ancestor\n lowest_common_ancestor = None\n for node in common_ancestors:\n if lowest_common_ancestor is None or node.val < lowest_common_ancestor.val:\n lowest_common_ancestor = node\n\n return lowest_common_ancestor\n``` | 2 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Recursive approach✅ | O( log(n))✅ | C++(Step by step explanation)✅ | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Intuition\nThe problem is to find the lowest common ancestor (LCA) of two nodes, `p` and `q`, in a binary search tree (BST). The LCA is the lowest node in the tree that has both `p` and `q` as descendants. Since the BST property holds, we can efficiently traverse the tree to find the LCA.\n\n# Approach\nThe approach is to recursively traverse the BST starting from the root. While traversing, compare the values of the current node (`root`) with the values of `p` and `q`. Based on the comparison, decide whether to move to the left subtree, right subtree, or return the current node as the LCA.\n\n1. If both `p` and `q` are smaller than the value of `root`, the LCA must be in the left subtree. Recursively call `lowestCommonAncestor(root->left, p, q)`.\n2. If both `p` and `q` are greater than the value of `root`, the LCA must be in the right subtree. Recursively call `lowestCommonAncestor(root->right, p, q)`.\n3. If the values of `p` and `q` are on opposite sides of `root` (one is greater, and the other is smaller), `root` is the lowest common ancestor. Return `root`.\n\n# Complexity\n- Time complexity: O(h)\n - `h` is the height of the tree.\n - In the worst case, when the tree is skewed (completely unbalanced), the time complexity is O(n), where `n` is the number of nodes in the tree.\n- Space complexity: O(h)\n - The space complexity is determined by the recursion stack.\n - In the worst case, when the tree is skewed, the space complexity is O(n).\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def lowestCommonAncestor(self, root, p, q):\n if p.val < root.val and q.val < root.val:\n return self.lowestCommonAncestor(root.left, p, q)\n elif p.val > root.val and q.val > root.val:\n return self.lowestCommonAncestor(root.right, p, q)\n else:\n return root \n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {\n if (p->val < root->val && q->val < root->val) {\n return lowestCommonAncestor(root->left, p, q);\n } else if (p->val > root->val && q->val > root->val) {\n return lowestCommonAncestor(root->right, p, q);\n } else {\n return root;\n }\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n | 5 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Explained Easy Iterative Python Solution | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | We will rely upon the invariant of the BST to solve the exercise. We know that the left subtree of each node contains nodes with smaller values and the right subtree contains nodes with greater values. We also know that if two nodes, x and y, are on different subtrees of a node z (one in the left portion and one in the right portion), then x and y have z as the lowest common ancestor. Having these facts in mind, a possible solution looks like the following:\n\n```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n \n while True:\n if root.val > p.val and root.val > q.val:\n root = root.left\n elif root.val < p.val and root.val < q.val:\n root = root.right\n else:\n return root\n```\n\nNote: Since we are guaranteed that p and q exist in the tree, we do not need to check for edges cases.\n\nConsider upvoting, if you found this post useful. :) | 103 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Simple solution in two way python | lowest-common-ancestor-of-a-binary-search-tree | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven a binary search tree (BST) and two nodes, we need to find the lowest common ancestor (LCA) node of both nodes in the BST. A LCA is the lowest node in the tree that has both nodes as its descendants.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can solve this problem using a recursive approach. We start at the root node and check if the values of both nodes lie on either side of the root. If they are, we continue our search in the respective left or right subtree of the root. If the values of the nodes are equal or one of them is the root itself, we return the root. This is because the root is an ancestor of both nodes and it is the lowest such ancestor as we are searching from top to bottom.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this approach is O(h), where h is the height of the BST. In the worst case, the height of the tree can be equal to the number of nodes in the tree, which makes the time complexity O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this approach is O(h) due to the recursion stack. In the worst case, the height of the tree can be equal to the number of nodes in the tree, which makes the space complexity O(n).\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n\n # Using recursion\n if p.val < root.val and q.val < root.val:\n return self.lowestCommonAncestor(root.left,p,q)\n elif p.val > root.val and q.val > root.val:\n return self.lowestCommonAncestor(root.right,p,q)\n else:\n return root\n\n # while root:\n # if p.val < root.val and q.val < root.val:\n # root = root.left\n # elif p.val > root.val and q.val > root.val:\n # root = root.right\n # else:\n # return root\n\n\n \n \n\n``` | 3 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Python; easy; runtime 95.94% | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | \n\ncase i)\nif root.val is the smallest or the greatest among p.val, q.val, and root.val, then traverse down\n\ncase ii)\nif case (i) is false <=>\nif root.val is in between p.val and q.val: p and q are seperated by root(which is an ancester of p and q)\nor if root.val is p.val or root.val is q.val => root is LCA -> return root\n\n```\ndef lowestCommonAncestor(self, root, p, q):\n while True:\n if root.val < min(p.val,q.val):\n root = root.right\n elif root.val > max(p.val,q.val):\n root = root.left\n else:\n return root\n```\n\n | 12 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
235: Space 96.79%, Solution with step by step explanation | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We are given the root of a binary search tree and two nodes p and q.\n2. We start traversing from the root of the binary search tree.\n3. If the value of both p and q is less than the value of the root, then the LCA will be in the left subtree. So, we recursively call the function on the left subtree.\n4. If the value of both p and q is greater than the value of the root, then the LCA will be in the right subtree. So, we recursively call the function on the right subtree.\n5. If one value is less than the root and the other is greater than the root, then root is the LCA. So, we return the root.\n\n# Complexity\n- Time complexity:\n80.42%\n\n- Space complexity:\n96.79%\n\n# Code\n```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n # If the value of p and q is less than root, then LCA will be in the left subtree\n if p.val < root.val and q.val < root.val:\n return self.lowestCommonAncestor(root.left, p, q)\n # If the value of p and q is greater than root, then LCA will be in the right subtree\n elif p.val > root.val and q.val > root.val:\n return self.lowestCommonAncestor(root.right, p, q)\n # If one value is less and the other is greater, then root is the LCA\n else:\n return root\n\n``` | 17 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Using recursion | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Intuition\nif p and q are on opposite sides of nodes, then the root will be the common node.\n\n# Approach\nIf they are on the same side, do recursion on root.left or root.right\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n print(root.val)\n if p.val <= root.val <= q.val or p.val >= root.val >= q.val:\n return root\n\n if root.val > p.val and root.val > q.val:\n node = self.lowestCommonAncestor(root.left, p, q)\n else:\n node = self.lowestCommonAncestor(root.right, p, q)\n \n return node\n\n``` | 1 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
[python] Easy Solution | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n curr=root\n while curr:\n if p.val>curr.val and q.val>curr.val:\n curr=curr.right\n elif p.val<curr.val and q.val<curr.val:\n curr=curr.left\n else:\n return curr\n``` | 6 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Easy Iterative solution using traversal in Python. | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Code\n```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n pv=p.val\n qv=q.val\n while(root!=None):\n if pv <root.val and qv<root.val:\n root=root.left\n elif pv>root.val and qv>root.val:\n root=root.right\n else:\n return root\n return root\n``` | 4 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
✔️ Python Easy Way To Find Lowest Common Ancestor of a Binary Search Tree | 96% Faster 🔥 | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | **IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n\n```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n curr = root\n \n while curr:\n if p.val>curr.val and q.val>curr.val:\n curr = curr.right\n elif p.val<curr.val and q.val<curr.val:\n curr = curr.left\n else:\n return curr\n``` | 6 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
Simple iterative solution, O(1) space, faster than 99.67% | lowest-common-ancestor-of-a-binary-search-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs this tree is a BST, it simplifies the problem a lot. Think about what property should hold true for a node to be the lowest common ancestor.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOn thinking a bit, you realize that the lowest common ancestor will be the node for which : \n\n a) min(p,q) is in the left subtree (or equal to the node value)\n b) max(p,q) is in the right subtree (or equal to the node value)\n\nIf this is not true for the current node, then I go right if the value is lesser than the min, or I go left if the value is greater than the max.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(logN)$$ - as we are going down the depth of the tree\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ - we do not use recursion, or any data structure while iterating.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n minval, maxval = min(p.val, q.val), max(p.val, q.val)\n while root:\n if minval <= root.val <= maxval:\n break\n\n if root.val > maxval:\n root = root.left\n else:\n root = root.right\n \n return root\n \n\n \n``` | 2 | Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 8
**Output:** 6
**Explanation:** The LCA of nodes 2 and 8 is 6.
**Example 2:**
**Input:** root = \[6,2,8,0,4,7,9,null,null,3,5\], p = 2, q = 4
**Output:** 2
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[2,1\], p = 2, q = 1
**Output:** 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST. | null |
236: Solution with step by step explanation | lowest-common-ancestor-of-a-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. The function lowestCommonAncestor takes in three parameters: the root of a binary tree (root) and two nodes of the binary tree (p and q).\n\n2. The first if statement checks if the root is None or if it is equal to either p or q. If either of these conditions is true, it means that we have found one of the nodes we are looking for, and we return the root.\n\n3. Next, we recursively call the lowestCommonAncestor function on the left and right subtrees of the root, passing in the same nodes p and q. We store the results of these recursive calls in variables l and r, respectively.\n\n4. The second if statement checks if both l and r are not None. If this condition is true, it means that we have found both p and q in different subtrees of the current root, and therefore the current root is the lowest common ancestor. We return the current root.\n\n5. If the second if statement is not satisfied, we return either l or r, depending on which one is not None. This is because if only one of l and r is not None, it means that the other node is not in the subtree of the current root, so we return the node that is in the subtree.\n\n6. If none of the previous conditions is satisfied, it means that both l and r are None, so we return None. This happens when we have reached the end of a branch of the binary tree without finding either p or q.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n if not root or root == p or root == q:\n return root\n\n l = self.lowestCommonAncestor(root.left, p, q)\n r = self.lowestCommonAncestor(root.right, p, q)\n\n if l and r:\n return root\n return l or r\n\n``` | 81 | Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[1,2\], p = 1, q = 2
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the tree. | null |
JAVA!! PYTHON!! Fastest Solution using Inorder Traversal | lowest-common-ancestor-of-a-binary-tree | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind p and q. Whichever is found first can be the LCA if they are both on the same side. If they are not on the same side then LCA is root of the subtree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust use normal inorder Traversal. First go left and then go right. Save both the trees in leftNode and right Node accordingly.\nIf both are not null that means their LCA is the root of the subtree till now.\nIf one of them is null then LCA is the other one.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) since at worst we need to traverse till the last element of the tree\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n if root==None:\n return None\n if root==p or root==q:\n return root\n leftNode = self.lowestCommonAncestor(root.left,p,q)\n rightNode = self.lowestCommonAncestor(root.right,p,q)\n if leftNode and rightNode:\n return root\n if leftNode != None:\n return leftNode\n else:\n return rightNode \n\n \n``` | 0 | Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[1,2\], p = 1, q = 2
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the tree. | null |
Easy Iterative DFS Solution in Python. | lowest-common-ancestor-of-a-binary-tree | 0 | 1 | # Code\n```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n stack=[]\n parent=defaultdict(TreeNode)\n res=[]\n stack.append([root,0])\n while(stack):\n t=stack.pop()\n node=t[0]\n level=t[1]\n if node.val in [p.val,q.val]:\n res.append([node,level])\n if node.right:\n stack.append([node.right,level+1])\n parent[node.right]=node\n if node.left:\n stack.append([node.left,level+1])\n parent[node.left]=node\n p,pl=res[0][0],res[0][1]\n q,ql=res[1][0],res[1][1]\n if pl>ql:\n for i in range(pl-ql):\n p=parent[p]\n print(p.val)\n elif pl<ql:\n for i in range(ql-pl):\n q=parent[q]\n print(q.val)\n while(p.val!=q.val):\n p=parent[p]\n q=parent[q]\n return p\n``` | 4 | Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[1,2\], p = 1, q = 2
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the tree. | null |
Easy, simple and most efficient recursive solution with explanation | lowest-common-ancestor-of-a-binary-tree | 1 | 1 | \n# Approach\n- Base Case: If the current node is null or is equal to either p or q, return the current node.\n\n- Recursive Calls: Recur on the left and right subtrees. These recursive calls return the LCA for p and q in their respective subtrees.\n\n- Combining Results: If both the left and right subtrees return non-null nodes, it means p and q are found in different subtrees. In this case, the current node is the lowest common ancestor, so return it.\n\n- Edge Cases: If one of the subtrees returns null, it means both p and q are in the same subtree, so return the non-null subtree.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n\n```C++ []\nclass Solution {\npublic:\n TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {\n if(!root || root == p || root == q) return root;\n TreeNode* left = lowestCommonAncestor(root->left, p, q);\n TreeNode* right = lowestCommonAncestor(root->right, p, q);\n if(!left) return right;\n else if(!right) return left;\n else return root;\n }\n};\n```\n```python []\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n if not root or root == p or root == q:\n return root\n \n left = self.lowestCommonAncestor(root.left, p, q)\n right = self.lowestCommonAncestor(root.right, p, q)\n \n if left and right:\n return root\n elif left:\n return left\n else:\n return right\n```\n```ruby []\npublic class Solution {\n public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {\n if (root == null || root == p || root == q) {\n return root;\n }\n \n TreeNode left = lowestCommonAncestor(root.left, p, q);\n TreeNode right = lowestCommonAncestor(root.right, p, q);\n \n if (left != null && right != null) {\n return root;\n } else if (left != null) {\n return left;\n } else {\n return right;\n }\n }\n}\n```\n | 5 | Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[1,2\], p = 1, q = 2
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the tree. | null |
Python 3 O(n) solution with explanation | lowest-common-ancestor-of-a-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are 3 possible cases:\n 1. p and q on opposite side of tree\n 2. p desc of q\n 3. q desc of p\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOnce we have found either p or q, search the other side for q or p\nIf the other side contains p or q, its case 1 since they\'re on opposite sides of the tree, return root\nOtherwise return p or q depending on which appears first\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$, where n is number of nodes, since each node at most visited once\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(h)$$, where h is the height of the tree, since in worst case (e.g. completely skewed tree) each node along the height is visited once. Space complexity determined by height of recursion tree which is at most $$O(h)$$ \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n def traverse(node): \n # Node does not exist here\n if node == None: \n return None\n # Return once we find either p or q\n if node == p or node == q:\n return node\n left = traverse(node.left) # LCA of p or q on left side\n right = traverse(node.right) # LCA of p or q on right side\n # LCA of p and q on opposite sides, return the parent\n if left and right: \n return node\n return left or right # Return whichever is the ancestor\n return traverse(root)\n \n \n \n \n``` | 5 | Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[1,2\], p = 1, q = 2
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the tree. | null |
Python || Easy || O(n) ||Recursive Solution | lowest-common-ancestor-of-a-binary-tree | 0 | 1 | ```\nclass Solution:\n def lowestCommonAncestor(self, root: \'TreeNode\', p: \'TreeNode\', q: \'TreeNode\') -> \'TreeNode\':\n if root==None or root==p or root==q:\n return root\n left=self.lowestCommonAncestor(root.left,p,q)\n right=self.lowestCommonAncestor(root.right,p,q)\n if left==None:\n return right\n elif right==None:\n return left\n else:\n return root\n```\n**An upvote will be encouraging** | 8 | Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): "The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**)."
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
**Input:** root = \[1,2\], p = 1, q = 2
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the tree. | null |
Easy and beginner friendly solution with Time complexity O(1) and Space complexity O(1) | delete-node-in-a-linked-list | 1 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem provides a node to be deleted in a linked list, emphasizing the absence of duplicate values. Our strategy involves an in-place modification of the linked list by simply skipping the designated node.\n\n# Approach\n\n<!-- Describe your approach to solving the problem. -->\nThe approach is elegantly straightforward and highly implementable.\n* Begin by updating the value of the current node with the value of the next node:\n\'node.val = node.next.val\'\n* Proceed by redirecting the next pointer of the current node to the next node\'s next pointer:\n\'node.next = node.next.next\'\n# Complexity\n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nGiven that we solely modify the linked list without utilizing loops or recursion, the time complexity is a commendable O(1).\n \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nAs the linked list undergoes modification without any additional space usage, the space complexity is an efficient O(1). \n\n# Code \n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\nvoid deleteNode(struct ListNode* node) {\n node->val = node->next->val;\n node->next = node->next->next;\n}\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode(int x) : val(x), next(NULL) {}\n * };\n */\nclass Solution {\npublic:\n void deleteNode(ListNode* node) {\n node->val = node->next->val;\n node->next = node->next->next;\n }\n};\n```\n```JAVA []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode(int x) { val = x; }\n * }\n */\nclass Solution {\n public void deleteNode(ListNode node) {\n node.val = node.next.val;\n node.next = node.next.next;\n }\n}\n```\n```javascript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val) {\n * this.val = val;\n * this.next = null;\n * }\n */\n/**\n * @param {ListNode} node\n * @return {void} Do not return anything, modify node in-place instead.\n */\nvar deleteNode = function(node) {\n node.val = node.next.val;\n node.next = node.next.next;\n};\n```\n```python []\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution(object):\n def deleteNode(self, node):\n """\n :type node: ListNode\n :rtype: void Do not return anything, modify node in-place instead.\n """\n node.val = node.next.val\n node.next = node.next.next\n```\n```Python3 []\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution(object):\n def deleteNode(self, node):\n """\n :type node: ListNode\n :rtype: void Do not return anything, modify node in-place instead.\n """\n node.val = node.next.val\n node.next = node.next.next\n```\n```ruby []\n# Definition for singly-linked list.\n# class ListNode\n# attr_accessor :val, :next\n# def initialize(val)\n# @val = val\n# @next = nil\n# end\n# end\n\n# @param {ListNode} node\n# @return {Void} Do not return anything, modify node in-place instead.\ndef delete_node(node)\n node.val = node.next.val\n node.next = node.next.next\nend\n``` | 1 | There is a singly-linked list `head` and we want to delete a node `node` in it.
You are given the node to be deleted `node`. You will **not be given access** to the first node of `head`.
All the values of the linked list are **unique**, and it is guaranteed that the given node `node` is not the last node in the linked list.
Delete the given node. Note that by deleting the node, we do not mean removing it from memory. We mean:
* The value of the given node should not exist in the linked list.
* The number of nodes in the linked list should decrease by one.
* All the values before `node` should be in the same order.
* All the values after `node` should be in the same order.
**Custom testing:**
* For the input, you should provide the entire linked list `head` and the node to be given `node`. `node` should not be the last node of the list and should be an actual node in the list.
* We will build the linked list and pass the node to your function.
* The output will be the entire list after calling your function.
**Example 1:**
**Input:** head = \[4,5,1,9\], node = 5
**Output:** \[4,1,9\]
**Explanation:** You are given the second node with value 5, the linked list should become 4 -> 1 -> 9 after calling your function.
**Example 2:**
**Input:** head = \[4,5,1,9\], node = 1
**Output:** \[4,5,9\]
**Explanation:** You are given the third node with value 1, the linked list should become 4 -> 5 -> 9 after calling your function.
**Constraints:**
* The number of the nodes in the given list is in the range `[2, 1000]`.
* `-1000 <= Node.val <= 1000`
* The value of each node in the list is **unique**.
* The `node` to be deleted is **in the list** and is **not a tail** node. | null |
Simple and easy 1 min explanation in Python and JAVA | product-of-array-except-self | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimilar to finding Prefix Sum array, here the preblem intends us to find the Prefix Product Array and Suffix Product Array for our original array.\n```\npre[i+1] = pre[i] * a[i]\nsuff[i-1] = suff[i] * a[i]\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\nOnly 2 loops iterating $$n$$ times each without any nesting.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\nWe have taken prefix and suffixProduct as variables instead of arrays to further optimize space, even though the overall complexity remains the same.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] productExceptSelf(int[] nums) {\n int numsLength = nums.length;\n int prefixProduct = 1;\n int suffixProduct = 1;\n int[] result = new int[numsLength];\n for(int i = 0; i < numsLength; i++) {\n result[i] = prefixProduct;\n prefixProduct *= nums[i];\n }\n for(int i = numsLength-1; i >= 0; i--) {\n result[i] *= suffixProduct;\n suffixProduct *= nums[i];\n }\n return result;\n }\n}\n```\n```python3 []\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n n = len(nums)\n prefix_product = 1\n postfix_product = 1\n result = [0]*n\n for i in range(n):\n result[i] = prefix_product\n prefix_product *= nums[i]\n for i in range(n-1,-1,-1):\n result[i] *= postfix_product\n postfix_product *= nums[i]\n return result\n```\n*Please upvote, if this helped you understand the solution in optimal time :)*\n | 99 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
[VIDEO] Visualization and Explanation of O(n) Solution | product-of-array-except-self | 0 | 1 | https://youtu.be/5bS636lE_R0?si=CXD7IT3sxRkONnAe\n\nThe brute force method would be to manually calculate each product. Since there are n products to calculate, and each product is made up of n-1 numbers, this runs in O(n<sup>2</sup>) time.\n\nThis method causes us to do the same calculations over and over again. So instead, we\'ll calculate all the products to the left and right of any given element just once and reuse those calculations. This allows us to reduce the runtime to O(n).\n\n\n# Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n length = len(nums)\n products = [1] * length\n for i in range(1, length):\n products[i] = products[i-1] * nums[i-1]\n\n right = nums[-1]\n for i in range(length-2, -1, -1):\n products[i] *= right\n right *= nums[i]\n \n return products\n``` | 101 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
✅ O(N) Single For-Loop Solution in Python (Easy to Understand) | product-of-array-except-self | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLike any other problem, my first intuition was let\'s brute force the solution by having two pointers going from i-1 to 1 and i+1 to len(nums) and multiplying each element and then appending this result to the output array. However, on secondary thought (and mainly due to solving questions such as Prefix Sum and Postfix Sum before), I could observe that we can use similar concept like Prefix and Postfix.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use the fact that prefix_product of arr[i] is arr[0] * arr[1] * .. * arr[i-1] and postfix_product of arr[i] is arr[i+1] * arr[i+2] * .. * arr[n-1]. \n\nSo basically, we have to calculate prefix_product * postfix_product[i] for each element.\n\nMost solutions implementing the concept of Prefix and Postfix would suggest 2 traversals, however I felt that we could one-up that and come up with a single for-loop solution.\n\n*1. Initialize a Solution Array of same size as input array with value.*\n*2. Store Prefix and Postfix Product so far in variables.*\n*3. Traverse the input array.*\n*4. Before updating the values for each i, multiply current solution array value at i with the value of prefix i.e. multiply with prefix product of the previous i-1 elements.*\n*5. Similarly, calculate the postfix product value for n-i-1 where n is length of input array at each iteration.*\n*6. As in Step 4, before calculating the postfix for i\'th value , multiply the solution_array[n-i-1] with the postfix product value i.e. products of input[i+1] to input[n-1].*\n\nPlease do like the solution if you understood it. Helps boosting visibility :-P\n\n# Complexity\n- Time complexity: $$O(n)$$ Single Pass [Should technically be 100% faster than other solutions but Leetcode showing only 85%. Don\'t know why]\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Technically $$O(1)$$ as we are not supposed to count the output array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n length=len(nums)\n sol=[1]*length\n pre = 1\n post = 1\n for i in range(length):\n sol[i] *= pre\n pre = pre*nums[i]\n sol[length-i-1] *= post\n post = post*nums[length-i-1]\n return(sol)\n``` | 185 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
Easy and Simple Approach | product-of-array-except-self | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple Solution in python\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDivide the conditions based on zeroes\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n if set(nums)==1 or set(nums)=={0} :\n return nums\n if 0 in nums:\n m=1\n c=0\n for i in range(len(nums)):\n if nums[i]!=0:\n m*=nums[i]\n if nums[i]==0:\n c+=1\n if c==1:\n for i in range(len(nums)):\n if nums[i]!=0:\n nums[i]=0\n else:\n nums[i]=m\n elif c>1:\n nums=[0]*len(nums)\n else:\n m=1\n for i in range(len(nums)):\n m*=nums[i]\n for i in range(len(nums)):\n nums[i]=m//nums[i] \n return nums\n\n\n``` | 0 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
C++ & Python 3 || in-place method || time: O(n) space: O(1) | product-of-array-except-self | 0 | 1 | # Intuition\nUsing division operation, and in-palce method.\nThere are 3 situations that need to be handled here.\n> 1. There is 1 `0` in arr.\n> 2. There are 2 and more `0` in arr.\n> 3. There is no `0` in arr.\n\n# Approach\n`single_zero` represent there is only one 0 in arr.\n`muti_zero` represent there are multiple 0 in arr.\n\nso, if `muti_zero` is `ture`, it means that all elements of the resutlt arr are 0.\n\nthen, if just `single_zero` is `ture`, it means all elements of the resutlt arr are 0 except the one that was originally 0.\n\nAs for other situations, without 0, it can be processed normally.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n vector<int> productExceptSelf(vector<int>& nums) {\n int p = 1;\n bool single_zero = false;\n bool muti_zero = false;\n\n for (auto num : nums) {\n if (single_zero and num == 0) {\n muti_zero = true;\n break;\n }\n if (num == 0)\n single_zero = true;\n else\n p *= num;\n }\n\n for (int i = 0; i < nums.size(); i++) {\n if (muti_zero) {\n nums[i] = 0;\n continue;\n }\n if (single_zero) {\n if (nums[i] != 0)\n nums[i] = 0;\n else\n nums[i] = p;\n }\n else\n nums[i] = p / nums[i];\n }\n return nums;\n }\n};\n```\n```python3 []\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n p = 1\n single_zero = False\n muti_zero = False\n\n for num in nums:\n if single_zero and num == 0:\n muti_zero = True\n break\n if num == 0:\n single_zero = True\n else:\n p *= num\n \n for i in range(len(nums)):\n if muti_zero:\n nums[i] = 0\n continue\n if single_zero:\n if nums[i] == 0:\n nums[i] = p\n else:\n nums[i] = 0\n else:\n nums[i] = p // nums[i]\n\n return nums\n``` | 2 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
238: Time 96.95%, Solution with step by step explanation | product-of-array-except-self | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n96.95%\n\n- Space complexity:\n68.31%\n\n# Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n n = len(nums)\n left_product = [1] * n # initialize left_product array with 1\n right_product = [1] * n # initialize right_product array with 1\n # calculate the product of elements to the left of each element\n for i in range(1, n):\n left_product[i] = left_product[i - 1] * nums[i - 1]\n\n # calculate the product of elements to the right of each element\n for i in range(n - 2, -1, -1):\n right_product[i] = right_product[i + 1] * nums[i + 1]\n\n # calculate the product of all elements except nums[i]\n result = [left_product[i] * right_product[i] for i in range(n)]\n\n return result\n```\nThe algorithm works by first initializing two arrays, left_product and right_product, both filled with 1\'s. We then populate the left_product array by calculating the product of all elements to the left of each element in nums. Similarly, we populate the right_product array by calculating the product of all elements to the right of each element in nums.\n\nOnce we have left_product and right_product, we can calculate the product of all elements except nums[i] by multiplying the corresponding elements from left_product and right_product. We do this for each element in nums to obtain the final result.\n\nThe time complexity of this algorithm is O(n), which satisfies the problem\'s requirements. The space complexity is O(n) as well, since we need to store two arrays of size n. However, we can optimize the space complexity to O(1) by using the result array to store the left_product array and computing the right_product array on-the-fly during the final calculation. Here\'s the optimized solution:\n\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n n = len(nums)\n result = [1] * n\n # calculate the product of elements to the left of each element and store in result\n for i in range(1, n):\n result[i] = result[i - 1] * nums[i - 1]\n\n # calculate the product of elements to the right of each element and update result\n right_product = 1\n for i in range(n - 1, -1, -1):\n result[i] *= right_product\n right_product *= nums[i]\n\n return result\n\n```\nIn this optimized solution, we reuse the result array to store the left_product array. We then compute the product of elements to the right of each element on-the-fly by keeping track of a running product, right_product. We update the corresponding element in result with the product of the left and right products for that element. This way, we only need to use one extra variable (right_product) instead of a whole extra array (right_product).\n\n | 48 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
Product of Array Except Self: So Easy, Even a Caveman Can Do It! (Using Division Operation) | product-of-array-except-self | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to use the product of all the elements in the array, except for the current element, to calculate the answer for the current element. This can be done by maintaining a variable ```mul``` that keeps track of the product of all the elements in the array, and then dividing ```mul``` by the current element to get the answer for the current element.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe steps of the algorithm are as follows:\n\n1. Initialize a variable mul to 1.\n2. Iterate over the array:\n * If the current element is not 0, multiply mul by the current element.\n * If the current element is 0, and there are more than 1 0s in the array, then set all the elements in the array to 0.\n * If the current element is 0, and there is only 1 0 in the array, then set the current element to mul.\n3. Iterate over the array again:\n * For each element, divide mul by the current element to get the answer for the current element.\nReturn the array.\n\n# Complexity\n- Time complexity: O(n) where n is the length of the array.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1), since we only use a constant amount of additional space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n mul = 1\n\n for i in nums:\n if i != 0:\n mul *= i\n\n if 0 in nums:\n if nums.count(0) > 1:\n return [0] * len(nums)\n else:\n for i in range(len(nums)):\n if nums[i] != 0:\n nums[i] = 0\n else:\n nums[i] = mul\n else:\n for i in range(len(nums)):\n nums[i] = mul//nums[i]\n\n return nums\n``` | 2 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
Simple Python Solution | O(N) Time complexity | product-of-array-except-self | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n prefix = [1]*len(nums)\n suffix = [1]*len(nums)\n cur1 = 1\n cur2 = 1\n for i in range(1,len(nums)):\n cur1 *= nums[i-1]\n prefix[i] = cur1\n for i in range(len(nums)-2,-1,-1):\n cur2 *= nums[i+1]\n suffix[i] =cur2\n\n return [prefix[i]*suffix[i] for i in range (len(nums))]\n\n``` | 1 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
Simple Solution with Full Explanation || Easy to Follow || For Beginners | product-of-array-except-self | 0 | 1 | # Understanding Our Approach with an Example\n\nTo fully understand our approach it is best to follow along with an example.\n\nGiven a `nums` list **[1, 2, 3, 4]**, our algorithm works by first calculating each elements "left product." \n\nA list element\'s left product, in this case, is defined as the cumalative product of all list element\'s left of the given element.\n\ni.e. `nums[1]`\'s left product will simply be 1, since there is only 1 left of 2. `nums[2]`\'s left product will be 1 * 2 = 2, since there is a 1 and 2 left of 3. \n\nAnd since there is nothing to the left of `nums[0]`, it\'s left product would simply be 1 as a placeholder *(why shouldn\'t we use 0?)*.\n\nWe then append each element\'s left product to a `final_lst`. So our `final_lst` should be **[1, 1, 2, 6]** as of right now.\n\nTo further elaborate, `final_lst` = **[1, 1, 2, 6]** because `nums[1]`\'s left product is 1, `nums[2]`\'s left product is 1 * 2 = 2, etc. Notice how any `final_lst[i]` corresponds with `nums[i]`\'s left product. \n\nThis first portion of our algorithm can be represented as the following part of our code:\n```\n accum = 1\n final_lst = [1]\n for i in range(1, len(nums)):\n accum *= nums[i - 1]\n final_lst.append(accum)\n```\n\nThe second portion of our code calculates each elements "right product."\n\nLike the first portion, a list element\'s right product is defined as the cumalative product of all list element\'s right of the given element.\n\ni.e. `nums[2]`\'s right product will simply be 4, since there is only 4 right of 3. `nums[1]`\'s right product will be 3 * 4 = 12, since there is a 3 and 4 right of 2.\n\nAnd since there is nothing to the right of `nums[3]`, it\'s right product will be 1 (i.e. we will leave `final_lst[3]` unchanged).\n\nUnlike the first portion, instead of appending to the `final_lst` we will mutate (change) it instead.\n\ni.e. we will multiply each `final_lst`\'s element with its corresponding right product. So `final_lst[0]` will be multiplied with 2 * 3 * 4 = 24, `final_lst[1]` will be multiplied with 3 * 4 = 12, etc.\n\nThis will result in the following `final_lst`:\n**[1 * 24, 1 * 12, 2 * 4, 6] = [24, 12, 8, 6]**\n\nThis second portion of our algorithm can be represented as the following part of our code:\n```\n accum = 1\n final_lst = [1]\n accum = 1\n for i in range(len(nums) - 1, 0, -1):\n accum *= nums[i]\n final_lst[i - 1] *= accum\n return final_lst\n```\nNotice how we iterate in reverse instead of forward. This is to avoid having to use the division operator to "undo" previous products.\n\n# Complexity\n- Time complexity:\n\nRequires approx. two passes through a given list, hence:\nO(2*n) -> **O(n)**\n\n- Space complexity:\n\nNot counting the outputted array:\n**O(1)**\n\n# Completed Code\n```\nclass Solution:\n def productExceptSelf(self, nums: List[int]) -> List[int]:\n accum = 1\n final_lst = [1]\n for i in range(1, len(nums)):\n accum *= nums[i - 1]\n final_lst.append(accum)\n accum = 1\n for i in range(len(nums) - 1, 0, -1):\n accum *= nums[i]\n final_lst[i - 1] *= accum\n return final_lst\n``` | 3 | Given an integer array `nums`, return _an array_ `answer` _such that_ `answer[i]` _is equal to the product of all the elements of_ `nums` _except_ `nums[i]`.
The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
You must write an algorithm that runs in `O(n)` time and without using the division operation.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[24,12,8,6\]
**Example 2:**
**Input:** nums = \[-1,1,0,-3,3\]
**Output:** \[0,0,9,0,0\]
**Constraints:**
* `2 <= nums.length <= 105`
* `-30 <= nums[i] <= 30`
* The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
**Follow up:** Can you solve the problem in `O(1)` extra space complexity? (The output array **does not** count as extra space for space complexity analysis.) | null |
Python🔥Java🔥C++🔥Simple Solution | sliding-window-maximum | 1 | 1 | # Video Solution \n\n# Search \uD83D\uDC49` Sliding Window Maximum By ErraK`\n\n# or \n\n# Click the Link in my Profile\n\n# An UPVOTE will be encouraging \uD83D\uDC4D\n\n```Python []\nclass Solution:\n def maxSlidingWindow(self, nums, k):\n result = []\n window = deque()\n\n for i, num in enumerate(nums):\n while window and window[0] < i - k + 1:\n window.popleft()\n\n while window and nums[window[-1]] < num:\n window.pop()\n\n window.append(i)\n\n if i >= k - 1:\n result.append(nums[window[0]])\n\n return result\n\n```\n```Java []\n\nclass Solution {\n public int[] maxSlidingWindow(int[] nums, int k) {\n int n = nums.length;\n int[] result = new int[n - k + 1];\n Deque<Integer> window = new ArrayDeque<>();\n\n for (int i = 0; i < n; i++) {\n while (!window.isEmpty() && window.peekFirst() < i - k + 1) {\n window.pollFirst();\n }\n\n while (!window.isEmpty() && nums[window.peekLast()] < nums[i]) {\n window.pollLast();\n }\n\n window.offerLast(i);\n\n if (i >= k - 1) {\n result[i - k + 1] = nums[window.peekFirst()];\n }\n }\n\n return result;\n }\n}\n\n```\n```C++ []\n\nclass Solution {\npublic:\n vector<int> maxSlidingWindow(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> result;\n deque<int> window;\n\n for (int i = 0; i < n; i++) {\n while (!window.empty() && window.front() < i - k + 1) {\n window.pop_front();\n }\n\n while (!window.empty() && nums[window.back()] < nums[i]) {\n window.pop_back();\n }\n\n window.push_back(i);\n\n if (i >= k - 1) {\n result.push_back(nums[window.front()]);\n }\n }\n\n return result;\n }\n};\n\n```\n\n | 27 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
Python3 Solution | sliding-window-maximum | 0 | 1 | \n```\nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n n=len(nums)\n seen=[]\n ans=[] \n for i in range(n):\n if seen and seen[0]==i-k:\n seen.pop(0)\n\n while seen and nums[seen[-1]]<nums[i]:\n seen.pop()\n\n seen.append(i)\n if i>=k-1:\n ans.append(nums[seen[0]])\n return ans \n``` | 4 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | sliding-window-maximum | 1 | 1 | # Intuition\nUsing two pointers\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 245 videos as of August 16th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/VYfy0VGa0_0\n\n### In the video, the steps of approach below are visualized using diagrams and drawings.\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. **Initialize Variables:**\n - Initialize an empty list `res` to store the result.\n - Initialize two pointers `left` and `right` to represent the sliding window.\n - Initialize an empty deque `q` to maintain indices of potentially maximum elements.\n\n2. **Sliding Window Loop:**\n - While the `right` pointer is within the range of `nums`:\n - Compare `nums[right]` with the elements at the back of the deque `q`.\n - If `q` is not empty and `nums[right]` is greater than `nums[q[-1]]`, remove the back element of `q` since it cannot be the maximum for the current window.\n - Append the current `right` index to the back of the deque `q`.\n\n3. **Adjust Left Pointer:**\n - If the index at the front of `q` (maximum element index) is less than the `left` pointer, remove the front element of `q` since it\'s no longer relevant for the current window.\n\n4. **Calculate and Store Maximum Element:**\n - If the current window size is equal to or larger than `k`:\n - Append the maximum element of the current window (the element at index `q[0]`) to the `res` list.\n\n5. **Adjust Left Pointer and Move Right Pointer:**\n - Increment the `left` pointer by 1.\n\n6. **Move Right Pointer:**\n - Increment the `right` pointer by 1.\n\n7. **Return Result:**\n - Return the `res` list containing the maximum elements for each sliding window.\n\nHere\'s the step-by-step breakdown of the algorithm for the given Python code. Each step explains the purpose and actions taken in that part of the code.\n\n# Complexity\n- Time complexity: O(N)\nN is the length of the input nums list. This is because both the left and right pointers traverse the nums list once, and each element is processed only once when added to or removed from the deque q.\n\n- Space complexity: O(K)\nK is the size of the sliding window. The deque q can store at most K indices representing the maximum elements within the sliding window. The res list also requires O(K) space to store the maximum elements for each window.\n\n```python []\nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n\n res = []\n left = right = 0\n q = deque()\n\n while right < len(nums):\n while q and nums[right] > nums[q[-1]]:\n q.pop()\n q.append(right)\n\n if left > q[0]:\n q.popleft()\n \n if right + 1 >= k:\n res.append(nums[q[0]])\n left += 1\n right += 1\n \n return res\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number[]}\n */\nvar maxSlidingWindow = function(nums, k) {\n const res = [];\n let left = 0;\n let right = 0;\n const q = [];\n\n while (right < nums.length) {\n while (q.length > 0 && nums[right] > nums[q[q.length - 1]]) {\n q.pop();\n }\n q.push(right);\n\n if (left > q[0]) {\n q.shift();\n }\n\n if (right + 1 >= k) {\n res.push(nums[q[0]]);\n left++;\n }\n right++;\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[] maxSlidingWindow(int[] nums, int k) {\n List<Integer> res = new ArrayList<>();\n int left = 0;\n int right = 0;\n Deque<Integer> q = new ArrayDeque<>();\n\n while (right < nums.length) {\n while (!q.isEmpty() && nums[right] > nums[q.peekLast()]) {\n q.pollLast();\n }\n q.offerLast(right);\n\n if (left > q.peekFirst()) {\n q.pollFirst();\n }\n\n if (right + 1 >= k) {\n res.add(nums[q.peekFirst()]);\n left++;\n }\n right++;\n }\n\n return res.stream().mapToInt(Integer::intValue).toArray(); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> maxSlidingWindow(vector<int>& nums, int k) {\n vector<int> res;\n int left = 0;\n int right = 0;\n deque<int> q;\n\n while (right < nums.size()) {\n while (!q.empty() && nums[right] > nums[q.back()]) {\n q.pop_back();\n }\n q.push_back(right);\n\n if (left > q.front()) {\n q.pop_front();\n }\n\n if (right + 1 >= k) {\n res.push_back(nums[q.front()]);\n left++;\n }\n right++;\n }\n\n return res; \n }\n};\n```\n | 29 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
Python || Sliding window || beats 99.81% | sliding-window-maximum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhenever you see something related to subarrays, sliding window is something that always comes to mind. So here too as we have to find maximum in each window of size k, we have to \n- Maintain a window. \n- Find maximum element in that window.\n- Keep sliding by one element till end is reached.\n- Discard elements that are out of the window. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo find maximum by not computing again and again in the window on each slide all you have to do is somehow maintain an order of elements in the window so that they are sorted.\nA stack would seem to be an option but as we have to discard items that are out of the window, a deque or doubly ended queue(variant of double linked list), is the best as you can simply discard elements once they are out of the window.\nWhile pushing an element:-\n - If the deque is full, then discard the left most item.\n - If the current item is greater than the top of the deque, then pop all the items until the item is top element is less than number. This is required because if you see a greater element in the current window you can discard of the elements that you have already seen as they wont be of any use because this element will be the maximum element in the current window.\n - If the current item is less that the top of deque, then this item can be a possible maximum as we slide right hence add it to the right.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) - As each element will be put or removed exactly once from the deque\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nfrom collections import deque \nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n d = deque()\n n = len(nums)\n res = []\n \n for i in range(k):\n while d and nums[d[-1]] <= nums[i]:\n d.pop()\n d.append(i)\n res.append(nums[d[0]])\n\n for i in range(k,n):\n if i-d[0] >= k :\n d.popleft()\n while d and nums[d[-1]] <= nums[i]:\n d.pop()\n d.append(i)\n res.append(nums[d[0]])\n return res\n``` | 0 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
Simple Heap(Priority Queue) Approach | sliding-window-maximum | 0 | 1 | \n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n if k == 1:\n return nums\n\n st = []\n res = []\n\n for i in range(k):\n heapq.heappush(st, (-nums[i], i))\n\n res.append(-st[0][0])\n\n for i in range(k, len(nums)):\n heapq.heappush(st, (-nums[i], i))\n while st[0][1] <= i - k:\n heapq.heappop(st)\n res.append(-st[0][0])\n\n return res\n\n``` | 1 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
Simple Python Solution - Easy to understand | sliding-window-maximum | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Loop through all the elements\n2. Keep on pushing (-number, index) into the heap (- for max heap)\n3. Pop of all the max elements from the heap whose index is less than i-k (we should only consider i-k to i elements everytime)\n4. If index is more than k, Add the max element to ans\n\n# Code\n```\nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n h, ans = [], []\n for i in range(0,len(nums)):\n heappush(h,(-nums[i],i))\n while h[0][1]<=i-k: heappop(h)\n if i>=k-1: ans.append(-h[0][0])\n return ans\n``` | 2 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
Beats 100% | Easy To Understand | 8 Lines of Code 🚀🚀 | sliding-window-maximum | 1 | 1 | # Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> maxSlidingWindow(vector<int>& nums, int k) {\n \n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n \n vector<int> ans;\n deque<int> q;\n int n = nums.size();\n \n for(int i = 0; i < n; i++)\n {\n if(!q.empty() and (i - q.front() >= k)) q.pop_front();\n \n while(!q.empty() and nums[i] > nums[q.back()]) q.pop_back();\n \n q.push_back(i);\n \n if(i >= k - 1) ans.push_back(nums[q.front()]);\n }\n return ans;\n }\n};\n``` | 2 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
🔥 Fast O(n) Deque | sliding-window-maximum | 0 | 1 | # Intuition\nAt first glance, the problem seems to be a simple maximum calculation problem within a range. However, as the range, or the window, slides through the array, recalculating the maximum for each new window seems inefficient. Our goal is to find an approach where we can leverage the previous window\'s information for the current window, making the process more efficient.\n\n---\n\n# Approach\nInstead of recalculating the maximum for each window, we can utilize a double-ended queue (deque). The beauty of deques is their ability to add or remove elements from both ends in constant time, making them perfect for this scenario.\n\nHere\'s a step-by-step breakdown:\n\n1. **Initialization**: Begin by defining an empty deque and a result list.\n2. **Iterate over nums**:\n - For each number, remove indices from the front of the deque if they are out of the current window\'s bounds.\n - Next, remove indices from the back if the numbers they point to are smaller than the current number. This ensures our deque always has the maximum of the current window at its front.\n - Add the current index to the deque.\n - If the current index indicates that we\'ve seen at least `k` numbers, add the front of the deque (i.e., the current window\'s maximum) to the result list.\n3. Return the result list.\n\n---\n\n# Complexity\n\n- **Time complexity**: $$ O(n) $$. Although there are two while loops inside the for loop, each element is processed only once either by being added to the deque or being removed from it.\n \n- **Space complexity**: $$ O(k) $$ where $$ k $$ is the size of the deque, which stores indices.\n\n---\n\n# Code\n\n``` Python []\nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n if not nums:\n return []\n if k == 1:\n return nums\n deq = deque()\n result = []\n\n for i in range(len(nums)):\n while deq and deq[0] < i - k + 1:\n deq.popleft()\n while deq and nums[i] > nums[deq[-1]]:\n deq.pop()\n deq.append(i)\n if i >= k - 1:\n result.append(nums[deq[0]]) \n \n return result\n``` \n``` C++ []\nclass Solution {\npublic:\n std::vector<int> maxSlidingWindow(std::vector<int>& nums, int k) {\n if (nums.empty() || k == 0) {\n return {};\n }\n if (k == 1) {\n return nums;\n }\n\n std::deque<int> deq;\n std::vector<int> result;\n\n for (int i = 0; i < nums.size(); ++i) {\n while (!deq.empty() && deq.front() < i - k + 1) {\n deq.pop_front();\n }\n while (!deq.empty() && nums[i] > nums[deq.back()]) {\n deq.pop_back();\n }\n \n deq.push_back(i);\n if (i >= k - 1) {\n result.push_back(nums[deq.front()]);\n }\n }\n \n return result;\n }\n};\n```\n\nBy using a deque, this solution provides a more efficient and elegant approach to the sliding window problem. | 8 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
[Python3] Decreasing queue || beats 95% || 1296ms 🥷🏼 | sliding-window-maximum | 0 | 1 | ```python3 []\nclass Solution:\n def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:\n q, res = deque(), [] # save index in the queue \'q\' (decreasing order)\n for r in range(len(nums)):\n # remove from the right side of the queue all items less than current\n while q and nums[q[-1]] < nums[r]:\n q.pop()\n q.append(r)\n # while window is not full (size != k) do nothing\n if r+1 < k: continue\n # if most left index out of window [r-k+1, r] we need to remove it\n if q[0] < r-k+1:\n q.popleft()\n # because deque is decreasing the left value is highest\n res.append(nums[q[0]])\n\n return res\n```\n\n | 11 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
Simplest O(n) Python Solution with Explanation | sliding-window-maximum | 0 | 1 | The solution using deque isn\'t very intuitive but is very simple once it *"clicks"*\n\n\nTo summarize:\n1. We maintain a deque of the indexes of the largest elements we\'ve seen (aka "good candidates")\n2. The problem is that we need to maintain sanity of this deque. To this we need to make sure about two things:\n\t1. Deque should NEVER point to elements smaller than current element\n\t2. Deque should NEVER point to elements outside our sliding window (which can happen, for instance in above example, where the first element is actually the largest element in the whole array, and sort of "clings" to the deque, only until we reach an index outside the window it can stretch to, where it\'s fate has come and it shall be removed from the throne!)\n3. We also keep furnishing the deque with curr_element\n4. Finally, and most importantly, we keep appending the front of the deque to our output `out`.\n\n\n\n```\nimport collections\nclass Solution(object):\n def maxSlidingWindow(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: List[int]\n """\n d = collections.deque()\n out = []\n for i, n in enumerate(nums):\n print("i = {}, curr element = {}, d = {} and out = {}".format(i, n, d, out))\n while d and nums[d[-1]] < n:\n d.pop()\n print("\\t Popped from d because d has elements and nums[d.top] < curr element")\n d.append(i)\n print("\\t Added i to d")\n if d[0] == i - k:\n d.popleft()\n print("\\t Popped left from d because it\'s outside the window\'s leftmost (i-k)")\n if i>=k-1:\n out.append(nums[d[0]])\n\t\t\t\tprint("\\t Append nums[d[0]] = {} to out".format(nums[d[0]]))\n return out\n```\n\nLets run this "self-explanatory" code (literally!) to see what it is doing with our array `nums` step by step. The given test case isn\'t a very good candidate to understand this solution, so I\'ll make a small change and change the first element to `8`:\n\n`print(Solution().maxSlidingWindow([8,3,-1,-3,5,3,6,7], 3))`\n\n<pre>\ni = 0, curr element = 8, d = deque([]) and out = []\n\t Added i to d\ni = 1, curr element = 3, d = deque([0]) and out = []\n\t Added i to d\ni = 2, curr element = -1, d = deque([0, 1]) and out = []\n\t Added i to d\n\t Append nums[d[0]] = 8 to out\ni = 3, curr element = -3, d = deque([0, 1, 2]) and out = [8]\n\t Added i to d\n\t Popped left from d because it\'s outside the window\'s leftmost (i-k)\n\t Append nums[d[0]] = 3 to out\ni = 4, curr element = 5, d = deque([1, 2, 3]) and out = [8, 3]\n\t Popped from d because d has elements and nums[d.top] < curr element\n\t Popped from d because d has elements and nums[d.top] < curr element\n\t Popped from d because d has elements and nums[d.top] < curr element\n\t Added i to d\n\t Append nums[d[0]] = 5 to out\ni = 5, curr element = 3, d = deque([4]) and out = [8, 3, 5]\n\t Added i to d\n\t Append nums[d[0]] = 5 to out\ni = 6, curr element = 6, d = deque([4, 5]) and out = [8, 3, 5, 5]\n\t Popped from d because d has elements and nums[d.top] < curr element\n\t Popped from d because d has elements and nums[d.top] < curr element\n\t Added i to d\n\t Append nums[d[0]] = 6 to out\ni = 7, curr element = 7, d = deque([6]) and out = [8, 3, 5, 5, 6]\n\t Popped from d because d has elements and nums[d.top] < curr element\n\t Added i to d\n\t Append nums[d[0]] = 7 to out\n[8, 3, 5, 5, 6, 7]\n</pre>\n\n\n**BONUS** Trying to be a strong Java Developer ? Checkout this [awesome hands-on series](https://abhinandandubey.github.io/posts/tags/Advanced-Java-Series) with illustrations! | 177 | You are given an array of integers `nums`, there is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the max sliding window_.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[3,3,5,5,6,7\]
**Explanation:**
Window position Max
--------------- -----
\[1 3 -1\] -3 5 3 6 7 **3**
1 \[3 -1 -3\] 5 3 6 7 **3**
1 3 \[-1 -3 5\] 3 6 7 ** 5**
1 3 -1 \[-3 5 3\] 6 7 **5**
1 3 -1 -3 \[5 3 6\] 7 **6**
1 3 -1 -3 5 \[3 6 7\] **7**
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `1 <= k <= nums.length` | How about using a data structure such as deque (double-ended queue)? The queue size need not be the same as the window’s size. Remove redundant elements and the queue should store only elements that need to be considered. |
:) | search-a-2d-matrix-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n return bool(list(filter(lambda x: target in x,matrix)))\n``` | 0 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
✔️ PYTHON || EXPLAINED || ; ] | search-a-2d-matrix-ii | 0 | 1 | **UPVOTE IF HELPFuuL**\n\n**EFFICIENT APPROACH -> O ( M + N )**\n\nAs the rows are sorted **->** ```matrix[i][j] < matrix[i][j+1]```\nAs the columns are sorted **->** ```matrix[i][j] >matrix[i-1][j]```\n\nHence it can be said that :\n* any element right to ```matrix[i][j]``` will be greater than it.\n* any element to the top of ```matrix[i][j]``` will be less than it.\n\nSo we start searching from **BOTTOM_LEFT**:\n* if element found -> return **TRUE**\n* if ```matrix[i][j] > target``` -> move **UP**.\n* if ```matrix[i][j] < target``` -> move **RIGHT**.\n\n\n\n**UPVOTE IF HELPFuuL**\n\n```\nclass Solution:\n def searchMatrix(self, mat: List[List[int]], target: int) -> bool:\n \n m=len(mat)\n n=len(mat[0])\n \n i=m-1\n j=0\n \n while i>=0 and j<n:\n if mat[i][j]==target:\n return True\n elif mat[i][j]<target:\n j+=1\n else:\n i-=1\n \n return False\n```\n\n**EFFICIENT APPROACH -> O ( M LOG N )**\nAs all the rows are sorted , an element can be clearly searched using *BINARY-SEARCH* for each row.\n\nFor each row -> O ( M )\nBinary search -> O ( LOG N )\n\n**UPVOTE IF HELPFuuL**\n\n**BINARY SEARCH SOLUTION**\n```\nclass Solution:\n def searchMatrix(self, mat: List[List[int]], target: int) -> bool:\n \n m=len(mat)\n n=len(mat[0])\n \n for i in range(m):\n if mat[i][0]<=target and mat[i][-1]>=target:\n lo=0\n hi=n\n while (lo<hi):\n mid=(lo+hi)//2\n \n if mat[i][mid]==target:\n return True\n elif mat[i][mid]<target:\n lo = mid + 1\n else:\n hi = mid\n \n return False\n```\n\n | 83 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
✅Easy Solution with Explanation | 2 Approaches 😀👍🏻🚀 | search-a-2d-matrix-ii | 0 | 1 | # Video Explanation\nhttps://youtu.be/QMs447Imtdc\n\n#### Upvote if find useful \uD83D\uDE00\uD83D\uDC4D\uD83C\uDFFB\uD83D\uDE80\n\n# Approach 1\nUsing Binary Search\n\n# Complexity\n- Time complexity:\nO(mlogn)\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n ROWS, COLS = len(matrix), len(matrix[0])\n\n for row in range(ROWS):\n if matrix[row][0] <= target and matrix[row][-1] >= target:\n top, bot = 0, COLS\n while top < bot:\n mid = (top + bot) // 2\n if target > matrix[row][mid]:\n top = mid + 1\n elif target < matrix[row][mid]:\n bot = mid\n else:\n return True\n \n return False\n```\n\n# Approach 2\nUsing 2 pointers as i and j\n\n# Complexity\n- Time Complexity:\n- O(m+n)\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n ROWS, COLS = len(matrix), len(matrix[0])\n\n i = ROWS-1\n j = 0\n\n while i >= 0 and j < COLS:\n if matrix[i][j] == target:\n return True\n elif matrix[i][j] > target:\n i -= 1\n else:\n j += 1\n return False\n```\n | 2 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Awesome Logic With Time Complexity---->O(N) | search-a-2d-matrix-ii | 0 | 1 | \n\n# Normal Approach---->O(N)\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n row,col=len(matrix),len(matrix[0])\n r,c=0,col-1\n while r<row and c>=0:\n if matrix[r][c]==target:\n return True\n if matrix[r][c]>target:\n c-=1\n else:\n r+=1\n return False\n //please upvote me it would encourage me alot\n\n```\n# Binary Search Approach--->O(NLogN)\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n rows,col=len(matrix),len(matrix[0])\n for row in matrix:\n left,right=0,len(row)-1\n while left<=right:\n mid=(left+right)//2\n if row[mid]==target:\n return True\n if row[mid]>target:\n right=mid-1\n else:\n left=mid+1\n return False\n //please upvote me it would encourage me alot\n\n\n```\n# please upvote me it would encourage me alot\n | 14 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Python3 Brute force approach Beats 69.25% (Time) and Beats 86.20%(Space) | search-a-2d-matrix-ii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIterate over the rows of the matrix and apply binary search on each of the row matrices to search the element\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n*log(m))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\n\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n \n def bs(c, low, high):\n l = low\n h = high\n while l <= h:\n mid = l + (h - l) // 2\n if matrix[c][mid] == target:\n return True\n elif matrix[c][mid] < target:\n l = mid + 1\n else:\n h = mid - 1\n return False\n \n n, m = len(matrix), len(matrix[0])\n for i in range(n):\n if target >= matrix[i][0] and target <= matrix[i][m - 1]:\n val = bs(i, 0, m - 1)\n if val == True:\n return True\n return False\n\n``` | 1 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Python Easy Solution || 100% || Beats 96% || Binary Search || | search-a-2d-matrix-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEach Row is sorted, We will use Binary Search on Each Row\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n(log(n)))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n for i in matrix:\n r=len(matrix[0])-1\n l=0\n while l<=r:\n mid = (l+r)>>1\n if i[mid]==target:\n return True\n elif i[mid]<target:\n l=mid+1\n else:\n r=mid-1\n return False\n``` | 2 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Most optimal solution with explanation | Eliminating the rows and cols (concept of binary search) | search-a-2d-matrix-ii | 1 | 1 | \n\n# Approach\n1. Start from the top-right corner of the matrix (row = 0, col = m-1), where n is the number of rows and m is the number of columns in the matrix.\n2. Compare the element at the current position (matrix[row][col]) with the target value:\n - If the element is equal to the target, return true.\n - If the element is less than the target, move to the next row (row++) to explore larger elements.\n - If the element is greater than the target, move to the previous column (col--) to explore smaller elements.\n3. Continue the process until either the target is found, or the search goes out of bounds (row >= n or col < 0).\n4. If the target is not found in the matrix, return false.\n\n# Complexity\n- Time complexity:\nO(m+n)\n\n- Space complexity:\nO(1)\n\n```C++ []\nclass Solution {\npublic:\n bool searchMatrix(vector<vector<int>>& matrix, int target) {\n int n = matrix.size();\n int m = matrix[0].size();\n int row = 0, col = m-1;\n while(row < n && col >= 0) {\n if (matrix[row][col] == target) return true;\n else if (matrix[row][col] < target) row++;\n else col--;\n }\n return false;\n }\n};\n```\n```JAVA []\nclass Solution {\n public boolean searchMatrix(int[][] matrix, int target) {\n int n = matrix.length;\n int m = matrix[0].length;\n int row = 0, col = m - 1;\n \n while (row < n && col >= 0) {\n if (matrix[row][col] == target) {\n return true;\n } else if (matrix[row][col] < target) {\n row++;\n } else {\n col--;\n }\n }\n \n return false;\n }\n}\n\n```\n```Python []\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n n = len(matrix)\n m = len(matrix[0])\n row, col = 0, m - 1\n \n while row < n and col >= 0:\n if matrix[row][col] == target:\n return True\n elif matrix[row][col] < target:\n row += 1\n else:\n col -= 1\n \n return False\n\n```\n | 7 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Searching 2d Simple Solution | search-a-2d-matrix-ii | 0 | 1 | \n\n# Superb Logical Solution in Python\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n for row in matrix:\n if target in row:\n return True\n\n return False\n```\n# please upvote me it would encourages me | 2 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
240: Time 91.4% and Space 98.52%, Solution with step by step explanation | search-a-2d-matrix-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe problem can be solved using a divide and conquer approach. We start from the top right corner and move towards the bottom left corner of the matrix. At each position, we check if the current element is equal to the target value. If it is equal, we return True. If it is less than the target value, we move down one row because all the elements in the current row are smaller than the current element. If it is greater than the target value, we move left one column because all the elements in the current column are greater than the current element.\n\nThe time complexity of this algorithm is O(m+n) because in the worst case scenario we traverse all rows and columns. The space complexity is O(1) because we are not using any extra data structure.\n\n# Complexity\n- Time complexity:\n91.4%\n\n- Space complexity:\n98.52%\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n # set initial position to top right corner\n row, col = 0, len(matrix[0])-1\n \n while row < len(matrix) and col >= 0:\n if matrix[row][col] == target:\n # target found\n return True\n elif matrix[row][col] < target:\n # current element is smaller than target, move down one row\n row += 1\n else:\n # current element is greater than target, move left one column\n col -= 1\n \n # target not found\n return False\n\n``` | 13 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Python3 || 9 lines, w/ explanation || T/M: 84%/82% | search-a-2d-matrix-ii | 0 | 1 | ```\nclass Solution: # Here\'s the plan:\n # \u2022 We start in the bottom-left corner, which is \n # matrix[-1][0]. Obviously, the target cell cannot\n # be either below or to the left of this corner cell\n # \n # \u2022 We move incrementally from the corner such that we \n # do not pass to right of the target\'s column or above\n # its row; we can ensure this by exploiting the sorted \n # rows and columns. For example (below), the target \n # is 8 and and the corner is 18. So:\n # -- 18 > 8 => move up to 10,\n # -- 10 > 8 => move up to 3,\n # -- 3 < 8 => move right to 6,\n # -- 6 < 8 => move right to 9,\n # -- 9 > 8 => move up to 8.\n```\n\n\n```\n\n\n def searchMatrix(self, matrix: list[list[int]], target: int) -> bool:\n \n row, col = len(matrix)-1, 0 # <-- start at corner\n\n while row >=0 and col <= len(matrix[0])-1: \n cell = matrix[row][col]\n\n if cell > target: # <-- go up \n row-= 1\n elif cell < target: # <-- go right\n col+= 1\n else: return True # <-- target found\n\n return False\n\n | 18 | Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted in ascending from left to right.
* Integers in each column are sorted in ascending from top to bottom.
**Example 1:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 5
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,4,7,11,15\],\[2,5,8,12,19\],\[3,6,9,16,22\],\[10,13,14,17,24\],\[18,21,23,26,30\]\], target = 20
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= n, m <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the integers in each row are **sorted** in ascending order.
* All the integers in each column are **sorted** in ascending order.
* `-109 <= target <= 109` | null |
Recursion -> Memoization -> Tabulation | Partition DP | C++, Java, Python | With Explanation | different-ways-to-add-parentheses | 1 | 1 | # Intuition\nWhen we try to evaluate a operator, we again encounter the same problem on the left & right substring of the operator & as we have to calculate all possible ways, that\'s where recursion comes in picture.\n\n# Recursion\nWe define a recursive function `getDiffWays` where, `getDiffWays(i, j)` returns us number of ways to evaluate `expression[i...j]`. therefore our answer will be `getDiffWays(0, n - 1)`. where, `n` is the length of string `expression`.\n\n## Code\n```C++ []\nclass Solution {\n bool isOperator(char ch) {\n return (ch == \'+\' || ch == \'-\' || ch == \'*\');\n }\n\n vector<int> getDiffWays(int i, int j, string& expression) {\n \n // If length of the substring is 1 or 2\n // we encounter our base case i.e. a number found.\n int len = j - i + 1;\n if(len <= 2) {\n return { stoi(expression.substr(i, len)) };\n }\n\n // If it is not a number then it is an expression\n // now we try to evaluate every opertor present in it\n vector<int> res;\n for(int ind = i; ind <= j; ind++) {\n if(isOperator(expression[ind])) {\n char op = expression[ind];\n\n // if char at ind is operator \n // get all results for its left and right substring using recursion\n vector<int> left = getDiffWays(i, ind - 1, expression);\n vector<int> right = getDiffWays(ind + 1, j, expression);\n\n // try all options for left & right operand\n // and push all results to the answer\n for(int l : left) {\n for(int r : right) {\n if(op == \'+\') {\n res.push_back(l + r);\n }\n else if(op == \'-\') {\n res.push_back(l - r);\n }\n else if(op == \'*\') {\n res.push_back(l * r);\n }\n }\n }\n }\n }\n return res;\n }\n\npublic:\n vector<int> diffWaysToCompute(string expression) {\n int n = expression.size();\n return getDiffWays(0, n - 1, expression);\n }\n};\n\n```\n```Java []\nclass Solution {\n private boolean isOperator(char ch) {\n return (ch == \'+\' || ch == \'-\' || ch == \'*\');\n }\n\n private List<Integer> getDiffWays(int i, int j, String expression) {\n int len = j - i + 1;\n List<Integer> res = new ArrayList<>();\n\n // If length of the substring is 1 or 2\n // we encounter our base case i.e. a number found.\n if (len <= 2) {\n res.add(Integer.parseInt(expression.substring(i, i + len)));\n return res;\n }\n\n // If it is not a number then it is an expression\n // now we try to evaluate every opertor present in it\n for (int ind = i; ind <= j; ind++) {\n if (isOperator(expression.charAt(ind))) {\n char op = expression.charAt(ind);\n\n // if char at ind is operator \n // get all results for its left and right substring using recursion\n List<Integer> left = getDiffWays(i, ind - 1, expression);\n List<Integer> right = getDiffWays(ind + 1, j, expression);\n\n // try all options for left & right operand\n // and push all results to the answer\n for (int l : left) {\n for (int r : right) {\n if (op == \'+\') {\n res.add(l + r);\n } else if (op == \'-\') {\n res.add(l - r);\n } else if (op == \'*\') {\n res.add(l * r);\n }\n }\n }\n }\n }\n return res;\n }\n\n public List<Integer> diffWaysToCompute(String expression) {\n int n = expression.length();\n return getDiffWays(0, n - 1, expression);\n }\n}\n\n```\n``` Python3 []\nclass Solution:\n def isOperator(self, ch):\n return ch == \'+\' or ch == \'-\' or ch == \'*\'\n\n def getDiffWays(self, i, j, expression):\n res = []\n\n # If length of the substring is 1 or 2\n # we encounter our base case i.e. a number found.\n if j - i + 1 <= 2:\n res.append(int(expression[i:j + 1]))\n return res\n\n # If it is not a number then it is an expression\n # now we try to evaluate every opertor present in it\n for ind in range(i, j + 1):\n if self.isOperator(expression[ind]):\n op = expression[ind]\n \n # if char at ind is operator \n # get all results for its left and right substring using recursion\n left = self.getDiffWays(i, ind - 1, expression)\n right = self.getDiffWays(ind + 1, j, expression)\n\n # try all options for left & right operand\n # and push all results to the answer\n for l in left:\n for r in right:\n if op == \'+\':\n res.append(l + r)\n elif op == \'-\':\n res.append(l - r)\n elif op == \'*\':\n res.append(l * r)\n\n return res\n\n def diffWaysToCompute(self, expression: str):\n n = len(expression)\n return self.getDiffWays(0, n - 1, expression)\n\n```\n\n## Complexity\n- Time complexity:\n$$Exponential$$, it\'s very hard to derive exact Time complexity of the solution but it will be definitely exponential in nature.\n\n- Space complexity:\n$$O(n \\cdot x)$$ for recursion stack. where, `x` is the number of ways to calcuate the expression which is $operators!$\n\n# Memoization\nIf we dry run a example, we observe overalapping subproblems that gets calculated again & again. We can avoid this by introducing a 3D DP array / cache & storing the results we calculate so that we don\'t need to process same stuff again & again.\n\n## Code\n```C++ []\nclass Solution {\n bool isOperator(char ch) {\n return (ch == \'+\' || ch == \'-\' || ch == \'*\');\n }\n\n vector<int> getDiffWays(int i, int j, vector<vector<vector<int>>>& dp, string& expression) {\n\n // Return cached result if already calculated\n if(!dp[i][j].empty()) {\n return dp[i][j];\n }\n \n // If length of the substring is 1 or 2\n // we encounter our base case i.e. a number found.\n int len = j - i + 1;\n if(len <= 2) {\n return dp[i][j] = { stoi(expression.substr(i, len)) };\n }\n\n // If it is not a number then it is an expression\n // now we try to evaluate every opertor present in it\n vector<int> res;\n for(int ind = i; ind <= j; ind++) {\n if(isOperator(expression[ind])) {\n char op = expression[ind];\n\n // if char at ind is operator \n // get all results for its left and right substring using recursion\n vector<int> left = getDiffWays(i, ind - 1, dp, expression);\n vector<int> right = getDiffWays(ind + 1, j, dp, expression);\n\n // try all options for left & right operand\n // and push all results to the answer\n for(int l : left) {\n for(int r : right) {\n if(op == \'+\') {\n res.push_back(l + r);\n }\n else if(op == \'-\') {\n res.push_back(l - r);\n }\n else if(op == \'*\') {\n res.push_back(l * r);\n }\n }\n }\n }\n }\n return dp[i][j] = res;\n }\n\npublic:\n vector<int> diffWaysToCompute(string expression) {\n int n = expression.size();\n vector<vector<vector<int>>> dp(n, vector<vector<int>>(n));\n return getDiffWays(0, n - 1, dp, expression);\n }\n};\n```\n```Java []\nclass Solution {\n private boolean isOperator(char ch) {\n return (ch == \'+\' || ch == \'-\' || ch == \'*\');\n }\n\n private List<Integer> getDiffWays(int i, int j, Map<String, List<Integer>> dp, String expression) {\n String key = i + "-" + j;\n\n // Return cached result if already calculated\n if (dp.containsKey(key)) {\n return dp.get(key);\n }\n\n // If length of the substring is 1 or 2\n // we encounter our base case i.e. a number found.\n int len = j - i + 1;\n if (len <= 2) {\n List<Integer> result = new ArrayList<>();\n result.add(Integer.parseInt(expression.substring(i, j + 1)));\n dp.put(key, result);\n return result;\n }\n\n // If it is not a number then it is an expression\n // now we try to evaluate every operator present in it\n List<Integer> res = new ArrayList<>();\n for (int ind = i; ind <= j; ind++) {\n if (isOperator(expression.charAt(ind))) {\n char op = expression.charAt(ind);\n\n // if char at ind is an operator \n // get all results for its left and right substring using recursion\n List<Integer> left = getDiffWays(i, ind - 1, dp, expression);\n List<Integer> right = getDiffWays(ind + 1, j, dp, expression);\n\n // try all options for left & right operand\n // and push all results to the answer\n for (int l : left) {\n for (int r : right) {\n if (op == \'+\') {\n res.add(l + r);\n } else if (op == \'-\') {\n res.add(l - r);\n } else if (op == \'*\') {\n res.add(l * r);\n }\n }\n }\n }\n }\n dp.put(key, res);\n return res;\n }\n\n public List<Integer> diffWaysToCompute(String expression) {\n Map<String, List<Integer>> dp = new HashMap<>();\n return getDiffWays(0, expression.length() - 1, dp, expression);\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def isOperator(self, ch):\n return ch == \'+\' or ch == \'-\' or ch == \'*\'\n\n def getDiffWays(self, i, j, dp, expression):\n\n # Return cached result if already calculated\n if (i, j) in dp:\n return dp[(i, j)]\n\n # If length of the substring is 1 or 2\n # we encounter our base case i.e. a number found.\n len_substring = j - i + 1\n if len_substring <= 2:\n result = [int(expression[i:j+1])]\n dp[(i, j)] = result\n return result\n\n # If it is not a number then it is an expression\n # now we try to evaluate every operator present in it\n res = []\n for ind in range(i, j + 1):\n if self.isOperator(expression[ind]):\n op = expression[ind]\n\n # if char at ind is an operator \n # get all results for its left and right substring using recursion\n left = self.getDiffWays(i, ind - 1, dp, expression)\n right = self.getDiffWays(ind + 1, j, dp, expression)\n\n # try all options for left & right operand\n # and push all results to the answer\n for l in left:\n for r in right:\n if op == \'+\':\n res.append(l + r)\n elif op == \'-\':\n res.append(l - r)\n elif op == \'*\':\n res.append(l * r)\n\n dp[(i, j)] = res\n return res\n\n def diffWaysToCompute(self, expression: str):\n dp = {}\n return self.getDiffWays(0, len(expression) - 1, dp, expression)\n```\n\n## Complexity\n- Time complexity:\n$$O(n^2 \\cdot (n \\cdot x^2))$$, as there are approx. $n^2$ states and to calculate these states 3 nested loops in recursive function take $O(n * x^2)$ time.\n\n- Space complexity:\n$$O(n \\cdot x) + O(n^2 \\cdot x)$$ for recursion stack & dp array. where, `x` is the number of ways to calcuate the expression which is $operators!$\n\n# Tabulation\nWe can eliminate the recursion stack space used in memoization solution by just calculating result for every valid expression substring in bottom up manner i.e. Tabulation.\n\nIn memoization, every substring which gets called recursively is valid but in this solution we need to check if given substring is a valid arithemetic expression or not.\n\n## Code\n``` C++ []\nclass Solution {\n bool isOperator(char ch) {\n return (ch == \'+\' || ch == \'-\' || ch == \'*\');\n }\n\npublic:\n vector<int> diffWaysToCompute(string expression) {\n int n = expression.size();\n vector<vector<vector<int>>> dp(n, vector<vector<int>>(n));\n\n // Function to check if given substring of expression\n // is a valid expression\n auto isValidExpression = [&](int i, int j) -> bool {\n return (i == 0 || isOperator(expression[i - 1])) && (j == n - 1 || isOperator(expression[j + 1]));\n };\n\n // get answer for all single digit numbers\n for(int i = 0; i < n; i++) {\n if(isValidExpression(i, i)) {\n dp[i][i] = { stoi(expression.substr(i, 1)) };\n }\n }\n\n // get answer for all 2 digit numbers\n for(int i = 0, j = 1; j < n; i++, j++) {\n if(isValidExpression(i, j)) {\n dp[i][j] = { stoi(expression.substr(i, 2)) };\n }\n }\n\n // get answer for all valid expression substrings in bottom up manner\n for(int len = 3; len <= n; len++) {\n for(int i = 0, j = i + len - 1; j < n; i++, j++) {\n if(!isValidExpression(i, j))\n continue;\n\n // Try to evaluate every operator\n for(int ind = i; ind <= j; ind++) {\n if(isOperator(expression[ind])) {\n char op = expression[ind];\n\n // if char at ind is operator \n // get all results for its left and right substring\n vector<int> left = dp[i][ind - 1];\n vector<int> right = dp[ind + 1][j];\n\n // try all options for left & right operand\n // and push all results to the answer\n for(int l : left) {\n for(int r : right) {\n if(op == \'+\') {\n dp[i][j].push_back(l + r);\n }\n else if(op == \'-\') {\n dp[i][j].push_back(l - r);\n }\n else if(op == \'*\') {\n dp[i][j].push_back(l * r);\n }\n }\n }\n }\n } \n }\n }\n\n return dp[0][n - 1];\n }\n};\n```\n``` Java []\nimport java.util.*;\n\nclass Solution {\n private boolean isOperator(char ch) {\n return (ch == \'+\' || ch == \'-\' || ch == \'*\');\n }\n\n public List<Integer> diffWaysToCompute(String expression) {\n int n = expression.length();\n List<Integer>[][] dp = new ArrayList[n][n];\n\n // Function to check if given substring of expression\n // is a valid expression\n BiFunction<Integer, Integer, Boolean> isValidExpression = (i, j) -> \n (i == 0 || isOperator(expression.charAt(i - 1))) && \n (j == n - 1 || isOperator(expression.charAt(j + 1)));\n\n // Get answer for all single digit numbers\n for (int i = 0; i < n; i++) {\n if (isValidExpression.apply(i, i)) {\n dp[i][i] = new ArrayList<>();\n dp[i][i].add(Integer.parseInt(expression.substring(i, i + 1)));\n }\n }\n\n // Get answer for all 2 digit numbers\n for (int i = 0, j = 1; j < n; i++, j++) {\n if (isValidExpression.apply(i, j)) {\n dp[i][j] = new ArrayList<>();\n dp[i][j].add(Integer.parseInt(expression.substring(i, i + 2)));\n }\n }\n\n // Get answer for all valid expression substrings in bottom up manner\n for (int len = 3; len <= n; len++) {\n for (int i = 0, j = i + len - 1; j < n; i++, j++) {\n if (!isValidExpression.apply(i, j)) {\n continue;\n }\n\n dp[i][j] = new ArrayList<>();\n // Try to evaluate every operator\n for (int ind = i; ind <= j; ind++) {\n if (isOperator(expression.charAt(ind))) {\n char op = expression.charAt(ind);\n\n // If char at ind is operator, get all results for its left and right substrings\n List<Integer> left = dp[i][ind - 1];\n List<Integer> right = dp[ind + 1][j];\n\n // Try all options for left & right operands and add all results to the answer\n for (int l : left) {\n for (int r : right) {\n if (op == \'+\') {\n dp[i][j].add(l + r);\n } else if (op == \'-\') {\n dp[i][j].add(l - r);\n } else if (op == \'*\') {\n dp[i][j].add(l * r);\n }\n }\n }\n }\n }\n }\n }\n\n return dp[0][n - 1];\n }\n}\n```\n``` Python3 []\nclass Solution:\n def isOperator(self, ch):\n return ch == \'+\' or ch == \'-\' or ch == \'*\'\n\n def diffWaysToCompute(self, expression: str) -> List[int]:\n n = len(expression)\n dp = [[[] for _ in range(n)] for _ in range(n)]\n\n def isValidExpression(i, j):\n return (i == 0 or self.isOperator(expression[i - 1])) and (j == n - 1 or self.isOperator(expression[j + 1]))\n\n # Get answer for all single digit numbers\n for i in range(n):\n if isValidExpression(i, i):\n dp[i][i] = [int(expression[i])]\n\n # Get answer for all 2 digit numbers\n for i in range(n - 1):\n if isValidExpression(i, i + 1):\n dp[i][i + 1] = [int(expression[i:i + 2])]\n\n # Get answer for all valid expression substrings in bottom-up manner\n for length in range(3, n + 1):\n for i in range(n - length + 1):\n j = i + length - 1\n if not isValidExpression(i, j):\n continue\n\n dp[i][j] = []\n # Try to evaluate every operator\n for ind in range(i, j + 1):\n if self.isOperator(expression[ind]):\n op = expression[ind]\n\n # If char at ind is operator, get all results for its left and right substrings\n left = dp[i][ind - 1]\n right = dp[ind + 1][j]\n\n # Try all options for left & right operands and add all results to the answer\n for l in left:\n for r in right:\n if op == \'+\':\n dp[i][j].append(l + r)\n elif op == \'-\':\n dp[i][j].append(l - r)\n elif op == \'*\':\n dp[i][j].append(l * r)\n\n return dp[0][n - 1]\n```\n\n## Complexity\n- Time complexity:\n$$O(n^3 \\cdot x^2)$$, same as memoization solution.\n\n- Space complexity:\n$$O(n^2 \\cdot x)$$ for dp array. where, `x` is the number of ways to calcuate the expression which is `operators!`\n | 14 | Given a string `expression` of numbers and operators, return _all possible results from computing all the different possible ways to group numbers and operators_. You may return the answer in **any order**.
The test cases are generated such that the output values fit in a 32-bit integer and the number of different results does not exceed `104`.
**Example 1:**
**Input:** expression = "2-1-1 "
**Output:** \[0,2\]
**Explanation:**
((2-1)-1) = 0
(2-(1-1)) = 2
**Example 2:**
**Input:** expression = "2\*3-4\*5 "
**Output:** \[-34,-14,-10,-10,10\]
**Explanation:**
(2\*(3-(4\*5))) = -34
((2\*3)-(4\*5)) = -14
((2\*(3-4))\*5) = -10
(2\*((3-4)\*5)) = -10
(((2\*3)-4)\*5) = 10
**Constraints:**
* `1 <= expression.length <= 20`
* `expression` consists of digits and the operator `'+'`, `'-'`, and `'*'`.
* All the integer values in the input expression are in the range `[0, 99]`. | null |
Recursive python solution using eval | different-ways-to-add-parentheses | 0 | 1 | # Code\n```\nclass Solution:\n def diffWaysToCompute(self, expression: str) -> List[int]:\n result = []\n operators = "*-+"\n isNumber = True\n for op in operators:\n if op in expression:\n isNumber = False\n if isNumber:\n return [int(expression)]\n for i,c in enumerate(expression):\n if c in operators:\n res1 = self.diffWaysToCompute(expression[:i])\n res2 = self.diffWaysToCompute(expression[i + 1:])\n for r1 in res1:\n for r2 in res2:\n result.append(eval(str(r1) + c + str(r2)))\n return result\n\n \n\n``` | 4 | Given a string `expression` of numbers and operators, return _all possible results from computing all the different possible ways to group numbers and operators_. You may return the answer in **any order**.
The test cases are generated such that the output values fit in a 32-bit integer and the number of different results does not exceed `104`.
**Example 1:**
**Input:** expression = "2-1-1 "
**Output:** \[0,2\]
**Explanation:**
((2-1)-1) = 0
(2-(1-1)) = 2
**Example 2:**
**Input:** expression = "2\*3-4\*5 "
**Output:** \[-34,-14,-10,-10,10\]
**Explanation:**
(2\*(3-(4\*5))) = -34
((2\*3)-(4\*5)) = -14
((2\*(3-4))\*5) = -10
(2\*((3-4)\*5)) = -10
(((2\*3)-4)\*5) = 10
**Constraints:**
* `1 <= expression.length <= 20`
* `expression` consists of digits and the operator `'+'`, `'-'`, and `'*'`.
* All the integer values in the input expression are in the range `[0, 99]`. | null |
Easy understand D&C solution, no helper function needed, Pattern example | different-ways-to-add-parentheses | 0 | 1 | The most difficult part is finding the pattern\nI will set example to show the pattern I found:\nLet\'s say 2-1-1+1, you can think it like a tree, every time when you read the operator you will split it into left part and right part:\n\n```\niteration 1:\n\t\t\t2 - 1- 1 + 1\n\t\t / \\\n\t\t 2 - (1-1+1)\n\t\t /\t / \\\n\t\t2\t- (1 - (1+1))\n\t\t\n\t\tthen\n\t\t\n\t\t\t2 - 1- 1 + 1\n\t\t / \\\n\t\t 2 - (1-1+1)\n\t\t /\t / \\\n\t\t2 - ((1 -1)+1)\n\t\t\nThis give us\n1. 2-(1 - (1+1))=3\n2. 2 -(1 -1)+1))=1\n\n\niteration 2:\n\t\t2 - 1 - 1 + 1\n\t\t / \\\n\t\t(2 -1)-(1 + 1)\nthis give us\n1. (2-1)-(1+1) = -1\n\niteration 3:\n\t\t\t2 - 1- 1 + 1\n\t\t\t\t / \\\n\t\t (2 - 1 - 1) + 1\n\t\t\t / \\ \\\n\t\t (2 - (1 - 1)) + 1\n\t\t \n\t\t then \n\t\t \n\t\t 2 - 1- 1 + 1\n\t\t\t\t / \\\n\t\t (2 - 1 - 1) + 1\n\t\t\t / \\ \\\n\t\t ((2 - 1) - 1) + 1\nthis give us\n1. 2 - (1 - 1)) + 1=3\n2. ((2 - 1) - 1) + 1=1\n\nSo the solution is [3,1,-1,3,1]\n\n```\nThe code is below:\n```\ndef diffWaysToCompute(self, input: str) -> List[int]:\n if input.isdigit():\n return [int(input)]\n res = []\n for i in range(len(input)):\n if input[i] in "-+*":\n left = self.diffWaysToCompute(input[:i])\n right = self.diffWaysToCompute(input[i+1:])\n for l in left:\n for r in right:\n if input[i] == \'+\':\n res.append(l+r)\n elif input[i] == \'-\':\n res.append(l-r)\n elif input[i] == \'*\':\n res.append(l*r)\n return res\n``` | 65 | Given a string `expression` of numbers and operators, return _all possible results from computing all the different possible ways to group numbers and operators_. You may return the answer in **any order**.
The test cases are generated such that the output values fit in a 32-bit integer and the number of different results does not exceed `104`.
**Example 1:**
**Input:** expression = "2-1-1 "
**Output:** \[0,2\]
**Explanation:**
((2-1)-1) = 0
(2-(1-1)) = 2
**Example 2:**
**Input:** expression = "2\*3-4\*5 "
**Output:** \[-34,-14,-10,-10,10\]
**Explanation:**
(2\*(3-(4\*5))) = -34
((2\*3)-(4\*5)) = -14
((2\*(3-4))\*5) = -10
(2\*((3-4)\*5)) = -10
(((2\*3)-4)\*5) = 10
**Constraints:**
* `1 <= expression.length <= 20`
* `expression` consists of digits and the operator `'+'`, `'-'`, and `'*'`.
* All the integer values in the input expression are in the range `[0, 99]`. | null |
241: Solution with step by step explanation | different-ways-to-add-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can use divide and conquer approach to solve this problem. We can divide the given expression into two parts at each operator, and recursively calculate the results for each part. Finally, we can combine the results using the given operator to get the final result.\n\nFor example, for the expression "23-45", we can split it into two parts at the operator \'-\': "23" and "45". Then we can split each part at the operator \'\', and calculate the results for each sub-expression: "23" can be split into "2" and "3", and we can calculate the results for them as [2] and [3], respectively. Similarly, "4*5" can be split into "4" and "5", and we can calculate the results for them as [4] and [5], respectively.\n\nNext, we can combine the results for each sub-expression using the operator \'-\', which gives us the following possibilities: [2-4, 2-5, 3-4, 3-5]. Similarly, we can combine the results for each sub-expression using the operator \'\', which gives us the following possibilities: [24, 25, 34, 3*5].\n\nFinally, we can combine the results using the operator \'-\', which gives us the final results: [-34, -10, -14, -10, 10].\n\nAlgorithm:\n\n1. Define a function diffWaysToCompute() which accepts the input expression string inputStr.\n2. If the input string only has digits, return a list with that number.\n3. Iterate through each character of the input string inputStr and check if it is an operator or not.\n4. If the character is an operator, recursively call the diffWaysToCompute() function for the left and right substrings of the operator, and combine the results using the operator.\n5. Append the result to the output list outputList.\n6. Return the outputList.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def diffWaysToCompute(self, inputStr: str) -> List[int]:\n \n # Define a function to calculate the result of the given operator between two numbers\n def calc(left, right, operator):\n if operator == \'+\':\n return left + right\n elif operator == \'-\':\n return left - right\n elif operator == \'*\':\n return left * right\n \n # Define the main function to calculate all possible results\n def diffWaysToComputeHelper(inputStr):\n \n # If the input string only has digits, return a list with that number\n if inputStr.isdigit():\n return [int(inputStr)]\n \n # Initialize the output list\n outputList = []\n \n # Iterate through each character of the input string and check if it is an operator or not\n for i in range(len(inputStr)):\n if inputStr[i] in [\'+\', \'-\', \'*\']:\n \n # Recursively call the `diffWaysToCompute()` function for the left and right substrings of the operator\n leftResults = diffWaysToComputeHelper(inputStr[:i])\n rightResults = diffWaysToComputeHelper(inputStr[i+1:])\n \n # Combine the results using the operator\n for left in leftResults:\n for right in rightResults:\n outputList.append(calc(left, right, inputStr[i]))\n \n # Return the output list\n return outputList\n \n # Call the helper function\n return diffWaysToComputeHelper(inputStr)\n\n``` | 8 | Given a string `expression` of numbers and operators, return _all possible results from computing all the different possible ways to group numbers and operators_. You may return the answer in **any order**.
The test cases are generated such that the output values fit in a 32-bit integer and the number of different results does not exceed `104`.
**Example 1:**
**Input:** expression = "2-1-1 "
**Output:** \[0,2\]
**Explanation:**
((2-1)-1) = 0
(2-(1-1)) = 2
**Example 2:**
**Input:** expression = "2\*3-4\*5 "
**Output:** \[-34,-14,-10,-10,10\]
**Explanation:**
(2\*(3-(4\*5))) = -34
((2\*3)-(4\*5)) = -14
((2\*(3-4))\*5) = -10
(2\*((3-4)\*5)) = -10
(((2\*3)-4)\*5) = 10
**Constraints:**
* `1 <= expression.length <= 20`
* `expression` consists of digits and the operator `'+'`, `'-'`, and `'*'`.
* All the integer values in the input expression are in the range `[0, 99]`. | null |
Python: Divde-and-Conquer + Memoization + O(N * 2^N) | different-ways-to-add-parentheses | 0 | 1 | Hello,\n\nThe time complexity analysis is below.\n\n```python\n\ndef __init__(self):\n\tself.operation = {}\n\tself.operation[\'*\'] = lambda a, b: a * b\n\tself.operation[\'+\'] = lambda a, b: a + b\n\tself.operation[\'-\'] = lambda a, b: a - b\n\ndef diffWaysToCompute(self, expression: str) -> List[int]:\n\n\tmemo = {}\n\treturn self.evaluate_expression(expression, {})\n\ndef evaluate_expression(self, expression: str, memo: dict) -> List[int]:\n\n\tif expression in memo:\n\t\treturn memo[expression]\n\n\telif expression.isnumeric():\n\t\treturn [int(expression)]\n\n\tresults = []\n\tfor i in range(len(expression)):\n\t\tif expression[i] not in self.operation:\n\t\t\tcontinue\n\n\t\topr = expression[i]\n\n\t\t# Divide:\n\t\tleft_results = self.diffWaysToCompute(expression[0:i])\n\t\tright_results = self.diffWaysToCompute(expression[i+1:])\n\n\t\tfor left in left_results: # Conquer:\n\t\t\tfor right in right_results:\n\t\t\t\tresults.append(self.operation[opr](left, right))\n\n\tmemo[expression] = results\n\n\treturn results\n\t\t\n```\n\n- Time Complexity: `O(N * 2^N)`\n\t- Let `N` be the length of the expression\n\t- In the worst case there are `N // 2` operations: when all expression numbers are numbers of 1 digits\n\t\t- For example, `expression: 1+2+3+4+5+6`\n\t\t- `len(expression) = 11`\n\t\t- `operations # = 5`\n\t- Therefore, our recursion depth is O(`N/2`)\n\t```\n\t\t\tdepth Nbr of problem work at corresponding depth\n\t\t\t0 1 O(N) #divide expression\n\t\t\t1 2 O(1) + O(N - 2) = O(N) * 2\n\t\t\t...\n\t\t\ti 2^i O(N) * 2^i \n\t\t\t...\n\t\t\tN//2 2^N//2 O(N) * 2^N//2\n\n\t\t\tTotal time complexity: O(N) (2^0 + 2^1 + ... + 2^N//2) = O(N * 2^N//2) = O(N * 2^N)\n\t\t \n\t```\n\t\nFinal notes:\n\t- This problem is similar to [22. Generate Parentheses](https://leetcode.com/problems/generate-parentheses/) problem\n\t- Check its [solution](https://leetcode.com/problems/generate-parentheses/solution/) for more accurate time complexity\n\t\n\t | 34 | Given a string `expression` of numbers and operators, return _all possible results from computing all the different possible ways to group numbers and operators_. You may return the answer in **any order**.
The test cases are generated such that the output values fit in a 32-bit integer and the number of different results does not exceed `104`.
**Example 1:**
**Input:** expression = "2-1-1 "
**Output:** \[0,2\]
**Explanation:**
((2-1)-1) = 0
(2-(1-1)) = 2
**Example 2:**
**Input:** expression = "2\*3-4\*5 "
**Output:** \[-34,-14,-10,-10,10\]
**Explanation:**
(2\*(3-(4\*5))) = -34
((2\*3)-(4\*5)) = -14
((2\*(3-4))\*5) = -10
(2\*((3-4)\*5)) = -10
(((2\*3)-4)\*5) = 10
**Constraints:**
* `1 <= expression.length <= 20`
* `expression` consists of digits and the operator `'+'`, `'-'`, and `'*'`.
* All the integer values in the input expression are in the range `[0, 99]`. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.