title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Easy Python Solution | Sorting | h-index | 0 | 1 | \n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n citations.sort()\n citations=citations[::-1]\n for i in range(len(citations)):\n if citations[i]<=i:\n return i\n return len(citations) \n``` | 5 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
✅ Clean and Simple Python3 Code, clear explanations with easy to understand variable naming ✅ | h-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to find the largest h-index possible.\nAn h-index is a number `h` such that there are at least `h` papers with `h` citations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the citations array in ascending order.\n2. Iterate through the sorted array.\n3. For each index \'i\', check if the current citation count (citations[i])\nis greater than or equal to the number of remaining papers (length - i).\n4. If condition (citations[i] >= length - i) is met, return the h-index (length - i).\n5. If no h-index is found during the loop, return 0 as the default h-index.\n\nExplaination for the if statement in the for loop:\n\nThe nuance here is that we realise that by sorting the array, we only need to visit each index of citations once and check if it satisfies, once it does, the rest do not need to be visited as they automatically satisfy the condition since the array is sorted.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*log(n)) due to the sorting step.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1), as we\'re not using any extra space.\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n length = len(citations)\n citations.sort()\n for i in range(length):\n if citations[i] >= length - i:\n return length - i\n return 0\n``` | 2 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
Frequency Array | O(n) time and O(n) space | h-index | 0 | 1 | # Intuition\nCounting the number of occurences would allow us to determine the max h-index. But the range for the possible number of citations is quite large. Since the maximum h-index can only be the length of the citation array all occurences of papers with more than length many citations can be counted together.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the varible to count papers with large citation counts.\n2. Initialize the frequency array, include zero.\n3. Count the occurences of number of citations in citation array.\n4. To find the maximum h-index, check if the largest possible h-index is an h-index, if not continue.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$. Two linear time loops.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$. The frequency array increases linearly with the length of the citation array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n citationsAboveH = 0\n citationFrequencies = [0] * (len(citations)+1)\n\n for i in range(len(citations)):\n if citations[i] > len(citations):\n citationsAboveH += 1 \n else:\n citationFrequencies[citations[i]] += 1\n\n qualifyingPapers = citationsAboveH\n for h in range(len(citations), 0, -1):\n qualifyingPapers += citationFrequencies[h]\n if qualifyingPapers >= h:\n return h\n \n return 0\n``` | 5 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
PYTHON O(N) SOLUTION | h-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n n = len(citations)\n arr = [0 for _ in range(n+1)]\n\n for i in range(n):\n if citations[i] > n:\n arr[n] += 1 \n else:\n arr[citations[i]] += 1\n \n h = 0\n for i in range(n,-1,-1):\n h += arr[i]\n if h >= i:\n return i\n``` | 1 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
Python | Single line solution | h-index | 0 | 1 | # Intuition\nTop `i+1` papers have a h-index of `min(i+1, citations[i])` since they have at least `i+1` papers with h-index of `citations[i]`.\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n return max(min(i+1, c) for i, c in enumerate(sorted(citations, reverse=True)))\n\n``` | 2 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
Beats 98.78% using binary search | h-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(log(len(citations)))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n def util(mid):\n cnt = 0\n for citation in citations:\n if citation >= mid:\n cnt += 1\n return cnt\n\n left = 0\n right = len(citations)\n while left <= right:\n mid = (left + right) // 2\n res = util(mid)\n if res >= mid:\n left = mid + 1\n if res < mid:\n right = mid - 1\n return left - 1\n``` | 2 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
Python3 using heaps | h-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUse heaps\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n\n cit = [-i for i in citations]\n\n heapq.heapify(cit)\n\n res = 0\n i = 1\n while i <= len(citations):\n val = heapq.heappop(cit)\n\n if -val < i:\n break\n else:\n res = i\n i += 1\n \n return res\n``` | 2 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
Easy to Understand Python Solution with Explanation | h-index | 0 | 1 | I know the question could get really confusing while trying to come up with a solution, but it is very simple.\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n{Case 1: If number of citations of any papers is less or equal than the count of papers (with greater no. of citations)}, it means we will consider the citations and number of papers with greater citations for the H-index. \nWhen we sort the citations array, the count of papers with greater citations can be obtained by subtracting the index of current paper from total number of papers. Thus, for this case, H-index will be obtained from the number of citations.\n\n{Case 2: Else case, when papers have higher citations than in count of papers itself.} In this case we obtain H-index from the count of papers. Because the criteria/ condition of at least number of citations are already met.\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n h_idx = 0\n l = len(citations)\n citations.sort()\n for i, c in enumerate(citations):\n if c <= l - i:\n h_idx = max(h_idx, c)\n else:\n h_idx = max(h_idx, l - i)\n\n return h_idx\n\n\n``` | 1 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
Python sol by sorting. [w/ Comment] | h-index | 0 | 1 | Python sol by sorting.\n\n\n---\n\n**Implementation** by sorting:\n\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n \n citations.sort( reverse = True )\n \n for idx, citation in enumerate(citations):\n\n # find the first index where citation is smaller than or equal to array index \n if idx >= citation:\n return idx\n \n return len(citations)\n```\n\n---\n\nPython sol by counting sort\n\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n\n n = len(citations)\n\n # key: citation\n # value: counting of papaers with specific citations\n counting_of = [ 0 for _ in range(n+1) ]\n\n # Update counting_of table\n for citation in citations:\n\n if citation >= n:\n # H index is up to n at most\n counting_of[n] += 1\n else:\n counting_of[citation] += 1\n\n # Compute h index\n # The given researcher has published at least h papers that have each been cited at least h times.\n couting_of_at_least_h = 0\n\n for citation in range(n,-1,-1):\n\n couting_of_at_least_h += counting_of[citation]\n\n if couting_of_at_least_h >= citation:\n return citation\n \n return 0\n\n\n```\n\n\n\n---\n\nReference:\n\n[1] [Python official docs about sorting](https://docs.python.org/3/library/stdtypes.html#list.sort) | 13 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
**Example 1:**
**Input:** citations = \[3,0,6,1,5\]
**Output:** 3
**Explanation:** \[3,0,6,1,5\] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,3,1\]
**Output:** 1
**Constraints:**
* `n == citations.length`
* `1 <= n <= 5000`
* `0 <= citations[i] <= 1000` | An easy approach is to sort the array first. What are the possible values of h-index? A faster approach is to use extra space. |
275: Time 98.1%, Solution with step by step explanation | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe problem is a follow-up to the H-Index problem with the added constraint that the input array is sorted in ascending order. As a result, we can take advantage of this property to optimize the solution.\n\nThe basic idea is to use binary search to find the h-index. Since the array is sorted in ascending order, we can use the index to represent the citation count. For example, citations[3] means the number of papers that have at least 4 citations.\n\nLet\'s take the example [0, 1, 3, 5, 6] and the length of the array n = 5. We start by initializing the left and right pointers to 0 and n - 1, respectively. The mid index is (left + right) // 2 = 2. The corresponding citation count is citations[2] = 3. Since there are 3 papers with at least 3 citations, and the remaining two papers have no more than 3 citations, the h-index is 3.\n\nIf citations[2] is less than n - 2, then we need to move the left pointer to mid + 1, and if citations[2] is greater than or equal to n - 2, then we need to move the right pointer to mid - 1. We repeat the process until left > right.\n\nThe time complexity of the algorithm is O(log n), and the space complexity is O(1).\n\n# Complexity\n- Time complexity:\n98.1%\n\n- Space complexity:\n75.12%\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n n = len(citations)\n left, right = 0, n - 1\n while left <= right:\n mid = (left + right) // 2\n if citations[mid] == n - mid:\n return n - mid\n elif citations[mid] < n - mid:\n left = mid + 1\n else:\n right = mid - 1\n return n - left\n\n```\n\nNote that we return n - left instead of n - mid because left may not be at the exact position of the h-index. However, we know that left is the smallest index that satisfies citations[left] >= n - left, so n - left is the correct answer. | 7 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
Easy Python solution | h-index-ii | 0 | 1 | # Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n citations=citations[::-1]\n for i in range(len(citations)):\n if citations[i]<=i:\n return i\n return len(citations) \n``` | 4 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
✔ Python3 Solution | Binary Search | O(logn) | h-index-ii | 0 | 1 | `Time Complexity` : `O(logn)`\n`Space Complexity` : `O(1)`\n```\nclass Solution:\n def hIndex(self, A):\n n = len(A)\n l, r = 0, n - 1\n while l < r:\n m = (l + r + 1) // 2\n if A[m] > n - m: r = m - 1\n else: l = m\n return n - l - (A[l] < n - l)\n``` | 3 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
Binary Search Intuative | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n l,r=1,len(citations)\n h=l\n flag=0\n def hIndex(m,citations):\n for citation in citations:\n if citation>=m:\n m-=1\n if m==0:\n return True\n return False \n while l<=r:\n m=(l+r)//2\n if hIndex(m,citations):\n h=max(h,m)\n l=m+1\n flag=1\n else:\n r=m-1\n if flag==0:\n return 0\n return h \n \n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
BinarySearch two templates | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n \n # the range of answer [0, N] inclusive\n # we want to find the maximum H such that H is a valid H-index -> so we use the template 2\n # this is equivalent to find minimum H such that H is not valid H-index and return r-1 -> so we use the template 1\n # If citations[-h] >= h, then h must be valid\n # If citations[-h] < h, then h must not be valid.\n\n # --------- template 1 -----------\n # def not_valid(candidate_h):\n # return citations[-candidate_h] < candidate_h\n # l = 0\n # r = len(citations)\n # while r > l:\n # mid = (l + r) // 2\n # if not_valid(mid):\n \n # r = mid\n # else:\n # l = mid + 1\n\n # if not_valid(r):\n # return r - 1\n # else:\n # # incase all candidates are invalid, then we automatically find the maximum valid H-index\n # # e.g. [1], no in-valid candidate from [0, 1]\n # return r\n\n\n # --------- template 2 -----------\n def valid(candidate_h):\n return citations[-candidate_h] >= candidate_h\n l = 0\n r = len(citations)\n while r > l:\n mid = (l + r + 1) // 2\n if valid(mid):\n l = mid\n else:\n r = mid - 1\n \n return l\n\n\n\n```\n | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
h index O(n log n) | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n citations = sorted(citations, reverse=True)\n index = 0\n for i in citations:\n if i == 0:\n continue\n\n if i > index:\n index += 1\n\n return index\n\n\nprint(Solution().hIndex([1, 2, 100]))\n \n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
Python3 O(logN) solution with binary search (93.51% Runtime) | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nApply binary search on the array based on citations[m] and length-m\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Since the array is already sorted, we can apply binary search on it\n- Iteratively compute "m" which is median of "left" and "right"\n - As long as citations[m] <= length-m it can be our target. \n - Update h if minimum of citations[m] and length-m exceeds h\n - Update left to m+1 to look for further candidates\n - If not, update right to m-1\n\n# Complexity\n- Time complexity: O(logN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n length = len(citations)\n left = 0\n right = length -1\n\n h = 0\n while left <= right: \n m = (left + right) // 2\n\n h = max(h, min(length-m, citations[m]))\n if citations[m] <= length-m:\n left = m + 1\n else:\n right = m - 1\n\n return h\n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
Python binary search | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse left and right to locate the range of the index of the "starting paper". Let n = len(citations).\n1. The number of papers with equal or more citations: n - idx;\n2. The number of the bottom citations: citations[idx].\n\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n n = len(citations)\n left = 0\n right = n-1\n while left <= right:\n mid = left + (right - left)//2\n h = n - mid #(n - 1) - mid + 1\n if citations[mid] == h:\n return h\n elif citations[mid] < h:\n left = mid + 1\n else:\n right = mid - 1\n \n return n - left\n \n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
o(N) | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n n=len(citations)\n ans=-1\n for i in range(n):\n if n-i >=citations[i]:\n ans=max(ans,citations[i])\n else:\n ans=max(ans,n-i)\n return ans\n \n # return citations[len(citations)//2] if citations[0]<len(citations) else len(citations)\n\n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
optimal solution || Beats 72.64% || python3 | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n count=0\n citations.sort(reverse=True)\n for i in range(len(citations)):\n if citations[i]>=i+1:\n count+=1\n return count\n \n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
optimal solution | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n citations.sort(reverse=True)\n c=0\n for i in range(len(citations)):\n if citations[i]>=i+1:\n c+=1 \n return c\n \n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
Python easy solution | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n n = len(citations)\n left, right = 0, n-1\n while left < right:\n mid = (left+right)//2\n atleast = n - mid\n if citations[mid] - atleast >= 0:\n right = mid\n else:\n left = mid+1\n if citations[left] == 0: return 0\n return n - left\n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
BinarySearch Solution 95%+ for time and memory | h-index-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n left, right = 0, len(citations) - 1\n ans = 0\n while left <= right:\n mid = (left + right) // 2\n if citations[mid] >= len(citations) - mid:\n ans = max(ans, len(citations) - mid)\n right = mid - 1\n else: left = mid + 1\n return ans\n``` | 0 | Given an array of integers `citations` where `citations[i]` is the number of citations a researcher received for their `ith` paper and `citations` is sorted in **ascending order**, return _the researcher's h-index_.
According to the [definition of h-index on Wikipedia](https://en.wikipedia.org/wiki/H-index): The h-index is defined as the maximum value of `h` such that the given researcher has published at least `h` papers that have each been cited at least `h` times.
You must write an algorithm that runs in logarithmic time.
**Example 1:**
**Input:** citations = \[0,1,3,5,6\]
**Output:** 3
**Explanation:** \[0,1,3,5,6\] means the researcher has 5 papers in total and each of them had received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
**Example 2:**
**Input:** citations = \[1,2,100\]
**Output:** 2
**Constraints:**
* `n == citations.length`
* `1 <= n <= 105`
* `0 <= citations[i] <= 1000`
* `citations` is sorted in **ascending order**. | Expected runtime complexity is in O(log n) and the input is sorted. |
Python3 easy understanding | first-bad-version | 0 | 1 | \n\n# Complexity\n- Time complexity: O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\npublic class Solution extends VersionControl {\n public int firstBadVersion(int n) {\n int left = 0;\n int right = n;\n while (left < right){\n int mid = left + (right - left) / 2;\n if (isBadVersion(mid)){\n right = mid;\n }else{\n left = mid + 1;\n }\n }\n return left;\n }\n}\n```\n```python []\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n l, r = 1, n\n while l < r:\n m = (l + r )// 2\n if isBadVersion(m): r = m\n else: l = m + 1\n return l \n``` | 2 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Java and Python Solution | first-bad-version | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n log n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Java\n```\n/* The isBadVersion API is defined in the parent class VersionControl.\n boolean isBadVersion(int version); */\n\npublic class Solution extends VersionControl {\n public int firstBadVersion(int n) {\n int low = 1;\n int high = n;\n int mid;\n boolean isBad;\n while(low <= high){\n mid = low + ((high-low)/2);\n isBad = isBadVersion(mid);\n if(isBad){\n high = mid-1;\n }else{\n low = mid+1;\n }\n }\n return low;\n }\n}\n```\n\n# Python\n\n```\ndef firstBadVersion(self, n: int) -> int:\n low = 1\n high = n\n version = 0\n \n while low <= high:\n mid = (low+high)//2\n badver = isBadVersion(mid)\n if badver == True:\n version = mid\n high = mid - 1\n elif badver == False:\n low = mid + 1\n return version\n``` | 2 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Python || Very Easy Solution || Super Fast | first-bad-version | 0 | 1 | \n\n# Code\n```\n# The isBadVersion API is already defined for you.\n# def isBadVersion(version: int) -> bool:\n\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n\n low = 1\n high = n\n\n while(low<=high):\n mid = (low+high)//2\n if(isBadVersion(mid)):\n high = mid-1\n elif(isBadVersion(mid)==False):\n low = mid +1\n if(mid==0 and isBadVersion(mid)==True):\n return mid\n if(mid>0 and isBadVersion(mid)==True and isBadVersion(mid-1)==False):\n return mid\n\n\n``` | 1 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
✔️ Simple Python Solution Using Binary Search 🔥 | first-bad-version | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n\nVisit this blog to learn Python tips and techniques and to find a Leetcode solution with an explanation: https://www.python-techs.com/\n\n**Solution:**\n```\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n left = 1\n right = n\n result = 1\n \n while left<=right:\n mid = (left+right)//2\n if isBadVersion(mid) == False:\n left = mid+1\n else:\n right = mid-1\n result = mid\n \n return result\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 36 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Python Solution Using Binary Search || Easy to Understand | first-bad-version | 0 | 1 | # Intuition\n\n---\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, you can use a **binary search approach** to find the **first bad version**.\n# Approach\n\n---\n\n\n<!-- Describe your approach to solving the problem. -->\nWe use two pointers, **left** and **right**, to define the search range. We keep dividing the range in half and checking the middle point **mid**. If the **mid version is bad**, then we set the **new right boundary to mid**, effectively narrowing the search range. If the **mid version is not bad**, then we set the **new left boundary to mid + 1**, again narrowing the search range. The loop continues until **left and right become equal**, which means we have found the **first bad version**.\n\n# Complexity\n\n---\n\n\n- Time complexity : **O(log n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n---\n\n\n```\nclass Solution(object):\n def firstBadVersion(self, n):\n left, right = 1, n\n\n while left < right:\n mid = left + (right - left) // 2\n if isBadVersion(mid):\n right = mid\n else:\n left = mid + 1\n\n return left\n\n``` | 1 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Simple binary search approach to solve bad version | first-bad-version | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The isBadVersion API is already defined for you.\n# def isBadVersion(version: int) -> bool:\n\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n low=0\n high=n\n while(low<high):\n mid=(low+high)//2\n if isBadVersion(mid)==True:\n high=mid\n else:\n low=mid+1\n return low\n``` | 1 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Awesome Logic With binary search | first-bad-version | 0 | 1 | \n# Binary Search\n```\n# The isBadVersion API is already defined for you.\n# def isBadVersion(version: int) -> bool:\n\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n left,right=0,n-1\n while left<=right:\n mid=(left+right)//2\n if isBadVersion(mid)==False:\n left=mid+1\n else:\n right=mid-1\n return left\n \n//please upvote me it would encourage me alot\n\n \n```\n# please upvote me it would encourage me alot\n | 26 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
278: Solution with step by step explanation | first-bad-version | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIn this solution, we maintain two pointers left and right that represent the range of versions we are searching. We start with left = 1 and right = n. At each iteration of the while loop, we compute the midpoint mid of the range as (left + right) // 2, and we call the isBadVersion API to check whether version mid is bad or not.\n\nIf isBadVersion(mid) returns True, then we know that the first bad version must be in the range [left, mid], so we update right = mid. Otherwise, the first bad version must be in the range [mid+1, right], so we update left = mid + 1. We continue this process until left and right converge to a single version, which must be the first bad version.\n\nThis algorithm runs in logarithmic time and makes only O(1) calls to the isBadVersion API at each iteration, which minimizes the total number of calls to the API.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n left, right = 1, n\n while left < right:\n mid = left + (right - left) // 2\n if isBadVersion(mid):\n right = mid\n else:\n left = mid + 1\n return left\n\n``` | 22 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
EASY TO UNDERSTAND BINARY SEARCH IMPLEMENTATION | first-bad-version | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nO(n) too slow for big data (do not go for linear method)\ninstead go with binary searching method to reduce api calling\n# Approach\n<!-- Describe your approach to solving the problem. -->\nmodify and implement binary search model to find the bad version which is \nright to the good version (basically find only good,bad pair)\n# Complexity\n- Time complexity:O(log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The isBadVersion API is already defined for you.\n# def isBadVersion(version: int) -> bool:\n\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n if n==1:\n return n if isBadVersion(n) else 0 \n left,right=0,n\n while left<right:\n mid=(right+left)//2\n if isBadVersion(mid):\n if isBadVersion(mid-1):\n right=mid-1\n else:\n return mid \n else:\n if isBadVersion(mid+1):\n return mid+1\n else:\n left=mid+1 \n\n``` | 3 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Python Binary Search Beats 92% | first-bad-version | 0 | 1 | # :: IF YOU LIKE THE SOLUTION PLEASE UP-VOTE ::\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> We can exploit the fact that our search space is linearly increasing so we can use Binary-Search. \n\n# Approach\n<!-- Describe your approach to solving the problem. --> \n- We find our solution using Binary Search\n- store that as answer\n- discard the right half of search space\n- try to find if there are answers to the left\n\n# Complexity\n- Time complexity: O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The isBadVersion API is already defined for you.\n# def isBadVersion(version: int) -> bool:\n\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n start = 1\n end = n\n ans = n\n while start < end:\n mid = (start + end) // 2\n\n if isBadVersion(mid):\n end = mid\n ans = mid\n else:\n start = mid + 1\n return ans\n``` | 3 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Python solution, Easy to understand (Binary search) with detailed explanation | first-bad-version | 0 | 1 | ### Solution\n```\ndef firstBadVersion(self, n):\n i = 1\n j = n\n while (i < j):\n pivot = (i+j) // 2\n if (isBadVersion(pivot)):\n j = pivot # keep track of the leftmost bad version\n else:\n i = pivot + 1 # the one after the rightmost good version\n return i\n```\n\n### Remarks\n* We use` i = 1` instead of `0` as base case because there\'s no index operation involved and the product version starts from 1.\n* We use `j` to keep track of the leftmost bad version we have checked, so that any version after` j `would not be the first bad version we want.\n* We use `i `to keep track of the leftmost unknown version which has a good version before it, so that any version before` i` would be a good version.\n* Therefore, `i` would move towards `j` step by step and stop when it becomes the first bad version.\n\n****Please upvote if you find this post useful, and welcome to any further discussion!*** | 58 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
C++/Python/Java Best Optimized Approach using Binary Search | first-bad-version | 1 | 1 | #### C++\nRuntime: 0 ms, faster than 100.00% of C++ online submissions for First Bad Version.\nMemory Usage: 6 MB, less than 22.67% of C++ online submissions for First Bad Version.\n\n```\n// The API isBadVersion is defined for you.\n// bool isBadVersion(int version);\n\nclass Solution {\npublic:\n int firstBadVersion(int n) {\n int s = 1;\n int e = n;\n while(s<e) {\n int mid = s + (e-s)/2;\n if(isBadVersion(mid)){\n e = mid;\n }\n else {\n s = mid + 1;\n }\n }\n return s;\n }\n};\n```\nTime Complexity - O(logN)\nSpace Complexity - O(1)\n#### Java\nRuntime: 20 ms, faster than 65.20% of Java online submissions for First Bad Version.\nMemory Usage: 41.2 MB, less than 26.56% of Java online submissions for First Bad Version.\n```\n/* The isBadVersion API is defined in the parent class VersionControl.\n boolean isBadVersion(int version); */\n\npublic class Solution extends VersionControl {\n public int firstBadVersion(int n) {\n int s = 1;\n int e = n;\n while(s<e) {\n int mid = s+(e-s)/2;\n if(isBadVersion(mid)) {\n e = mid;\n }\n \n else {\n s = mid+1;\n }\n }\n return s;\n }\n}\n```\nTime Complexity - O(logN)\nSpace Complexity - O(1)\n\n#### Python\nRuntime: 56 ms, faster than 23.61% of Python3 online submissions for First Bad Version.\nMemory Usage: 13.9 MB, less than 61.83% of Python3 online submissions for First Bad Version.\n```\n# The isBadVersion API is already defined for you.\n# def isBadVersion(version: int) -> bool:\n\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n s = 1\n e = n\n while(s<e):\n mid = s+(e-s)//2\n if(isBadVersion(mid)):\n e = mid\n \n else:\n s = mid+1\n return s\n```\nTime Complexity - O(logN)\nSpace Complexity - O(1)\n\n##### I hope that you\'ve found this useful. If you like the solution and find it understandable, then do upvote it & Share it with others.\n##### It only motivates me to write more such posts, If you found any error, any suggestions then do comment for any query\n##### Thanks alot ! Cheers to your coding | 4 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
CPP || PYTHON || Binary Search || 3ms | first-bad-version | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- This problem is a version of binary search much like findind the first occurrence of element in sorted array containing duplicate elements.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Applying binary search, if a bad version is found we check if the number on the left ( mid-1 ) is also a bad version or not.\n- If the number on the left is not a bad version then we can simply return the current number as it is the first bad version.\n- If the number on the left is a bad version then we can set `r = mid-1` and continue with binary search.\n- If current number is not a bad version then we can set `l = mid+1`.\n\n# Complexity\n- Time complexity: **O(log n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\nCPP / C++\n```\n// The API isBadVersion is defined for you.\n// bool isBadVersion(int version);\n\nclass Solution {\npublic:\n int firstBadVersion(int n) {\n int l = 1, r = n;\n\n while( l<=r ) {\n int mid = l + (r-l)/2;\n if( isBadVersion(mid) ) {\n if( isBadVersion(mid) != isBadVersion(mid-1) ) return mid;\n else r = mid-1;\n }\n else l = mid+1;\n }\n return -1;\n }\n};\n```\n---\nPYTHON\n```class Solution:\n def firstBadVersion(self, n: int) -> int:\n l,r = 1, n\n while l<=r :\n mid = l + (r-l)//2\n if isBadVersion( mid ):\n if isBadVersion( mid )!=isBadVersion( mid-1 ) :\n return mid\n else :\n r = mid-1\n elif not isBadVersion( mid ):\n l = mid+1\n return 0\n``` | 4 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
✅ 🔥 Python3 || ⚡easy solution | first-bad-version | 0 | 1 | \n```\nclass Solution:\n def firstBadVersion(self, n: int) -> int:\n left, right = 1, n\n \n while left < right:\n mid = (left + right) // 2\n \n if isBadVersion(mid):\n right = mid\n else:\n left = mid + 1\n \n return left\n``` | 1 | You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have `n` versions `[1, 2, ..., n]` and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API `bool isBadVersion(version)` which returns whether `version` is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
**Example 1:**
**Input:** n = 5, bad = 4
**Output:** 4
**Explanation:**
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
**Example 2:**
**Input:** n = 1, bad = 1
**Output:** 1
**Constraints:**
* `1 <= bad <= n <= 231 - 1` | null |
Python3 Dynamic Programming | perfect-squares | 0 | 1 | # Code\n```\nclass Solution:\n def numSquares(self, n: int) -> int:\n dp = [20000 for _ in range(n + 1)]\n dp[0] = 0\n ps = []\n\n for i in range(1,n + 1):\n if pow(i, 2) > n:\n break\n ps.append(i ** 2)\n\n for i in range(n + 1):\n for j in ps:\n if i + j <= n:\n dp[i + j] = min(dp[i] + 1, dp[i + j])\n else:\n break\n\n return dp[n]\n```\n# How it works\nSo in the DP Array (Dynamic Programming Array) the rest except for the first one will be every big, why?, well because, you need to find the smallest value right? but if it samll like 0 and there is something bigger like x, it will need to be like this min(0,x) well 0 would be smaller and the answer will be 0. the for loop is basically finding all the perfect square what PS stands for, so I did it to make it faster, not anything else, and also the second for loop is calcualting, so we will find lots of possible results using Dynamic Programming and then, compare them. well thats it, you final answer will be at the end. | 3 | Given an integer `n`, return _the least number of perfect square numbers that sum to_ `n`.
A **perfect square** is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, `1`, `4`, `9`, and `16` are perfect squares while `3` and `11` are not.
**Example 1:**
**Input:** n = 12
**Output:** 3
**Explanation:** 12 = 4 + 4 + 4.
**Example 2:**
**Input:** n = 13
**Output:** 2
**Explanation:** 13 = 4 + 9.
**Constraints:**
* `1 <= n <= 104` | null |
VERY EASY TO UNDERSTAND WITH PICTURE PYTHON RECURSION + MEMOIZATION | perfect-squares | 0 | 1 | **279. Perfect Squares**\n\nHey Everyone I will try to explain the solution through some pictures. **How each piece of code is working**!!!\nWas going through DISCUSS Section but coudn\'t wrap my head around why certain lines were written, so after figuring out I tried to share it out here to save someone\'s else time.This question has been tagged under **AMAZON** in some places..LET\'S BEGIN.\n\n **RECURSIVE CODE** [ TLE ]\n________________________________\n\n````\ndef solve(n):\n\n if n==0: # part 1\n return 0\n\t\t\n if n<0: # part 2\n return float("inf")\n\t\t\n mini = n # part 3 \n\t\n i = 1\n while i*i<=n: # part 4\n mini = min(mini, solve(n-(i*i)))\n i+=1\n\t\t\n return mini+1 # part 5\n\nsolve(n)\n````\n\n**Edit ( TC )** - First we have to pay attention on while loop. It takes O( sqrt(n) ). Next we have to pay attention on the recursive call ```min( mini, solve( n- ( i * i )))```. In case when our ```i == 1``` we are able to create the longest way. Because of that we can come to a conclusion that the maximum number of levels in a decision tree will be n. Taking all of this into consideration and knowing the width of a tree level and the height of the whole tree we can say that the overall TC of brute recusion is **O( sqrt(n) ^ n - 1 )** . \n**Credit** - [Maxim](https://leetcode.com/_Maximus_/)\n\n--------\n\n\nLet\'s First Have A Look Over How Our DECISION TREE Looks Like !! \n\n\n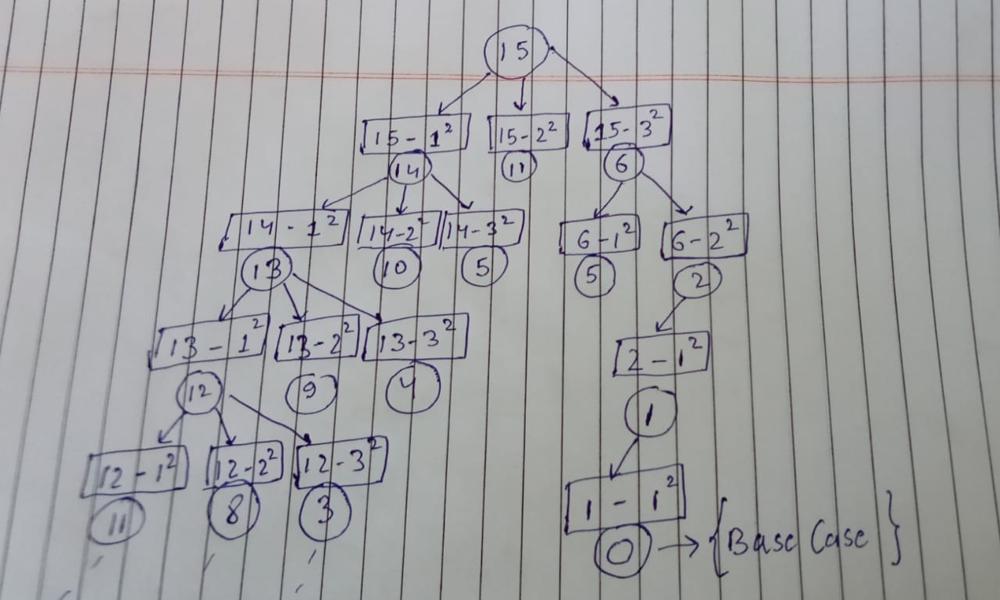\n\n\n__________________________\n--> **PART 1 [ BASE CASE ]**\n____________________________\n\nWhen our call hits base case and n becomes 0 we know there is a possible way to split our target.\nSince in ques we have to find the **min** possible way.\nThere is no case where mini becomes less than 0 . So we return 0 that indicates we found a **Possible Set Of Candidates.**\n______________________________\n--> **PART 2**\n_______________\nSame logic as above if our n becomes less than 0 we know there is no possible way to split our target.\n\n___________________________________________________\n--> **PART 3 [ WHY ```mini = n ??``` THIS PART WAS HARD FOR ME TO UNDERSTAND :( ]**\n_______________________\n\nSuppose we are at a point in our recursion call where n = 12 !!\nwhat could be the max count to split 12 so that each element is a perfect square??\n\nYES u are right :) **12 = 1 + 1+ 1+ 1+1+ 1+ 1+1 +1+1+1 +1 ( 12 times 1 )**\nwe cant get any maximum value than 12 for 12 thats why mini = n which is 12 in this case.\n___________________________________\n--> **PART 4 [ WHILE LOOP PART ]**\n_______________________________\n\nWhat is ***least possible perfect Square candidate*** for our ans??\nYES It is 1 so we start our loop from ```i=1```\n\nNow upto what value of ```i``` our loop should execute???\nYES till ```n >= i^2``` ( in short upto that value when n - i^2 is +ve )\n\nWHY??\nbecause after that we will call at value < 0 which anyhow our function will **return infinity** since n<0 **remember base case PART 2. but will lead to infinite looping**\n____________________\n--> **PART 5 [ WHY ```mini+1```?? ]**\n_________________\n\nWe are counting the steps isnt it??\n\nWhen we hit the base case ```n==0``` we return **0**. \n\nAlso one path for 5 = 1+1+1+1+1 .\n**Last 1 will get 0** (BASE CASE) and **it will be returning 0+1**\n\nso ```step count = 0 + 1 + 1 + 1 + 1 + 1 = 5```\n\nsee the picture for better understanding\n\n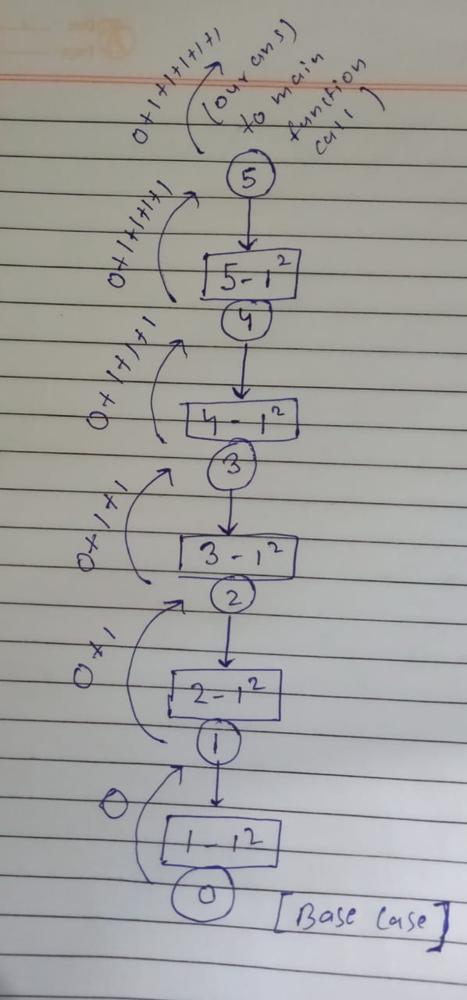\n\n\n**MEMOIZATION [ ACCEPTED ]**\n____________________________\n```\ndef solve(n):\n if n==0:\n return 0\n if n<0:\n return float("inf")\n if memo[n]!=-1:\n return memo[n]\n mini = n\n i = 1\n while i*i<=n:\n mini = min(mini, solve(n-(i*i)))\n i+=1\n memo[n] = mini+1\n return memo[n]\n \nmemo = [-1]*(n+1)\nsolve(n)\n```\n\nthank you!! | 59 | Given an integer `n`, return _the least number of perfect square numbers that sum to_ `n`.
A **perfect square** is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, `1`, `4`, `9`, and `16` are perfect squares while `3` and `11` are not.
**Example 1:**
**Input:** n = 12
**Output:** 3
**Explanation:** 12 = 4 + 4 + 4.
**Example 2:**
**Input:** n = 13
**Output:** 2
**Explanation:** 13 = 4 + 9.
**Constraints:**
* `1 <= n <= 104` | null |
Python 4 lines - Can it be any more concise? | perfect-squares | 0 | 1 | ```\n@lru_cache(None)\ndef dp(n: int) -> int:\n return 0 if n == 0 else min(dp(n-(x+1)**2) for x in range(floor(sqrt(n)))) + 1\nclass Solution:\n def numSquares(self, n: int) -> int:\n return dp(n)\n``` | 3 | Given an integer `n`, return _the least number of perfect square numbers that sum to_ `n`.
A **perfect square** is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, `1`, `4`, `9`, and `16` are perfect squares while `3` and `11` are not.
**Example 1:**
**Input:** n = 12
**Output:** 3
**Explanation:** 12 = 4 + 4 + 4.
**Example 2:**
**Input:** n = 13
**Output:** 2
**Explanation:** 13 = 4 + 9.
**Constraints:**
* `1 <= n <= 104` | null |
279: Solution with step by step explanation | perfect-squares | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We first initialize a list dp with n+1 elements, where dp[i] represents the least number of perfect square numbers that sum to the index i. We set dp[0] = 0, since zero is not a perfect square and does not require any perfect squares to be summed up to it. We set all other elements to infinity initially.\n\n2. We iterate through all numbers from 1 to n. For each number i, we iterate through all possible perfect square numbers that are less than or equal to i. We use the square root function int(i ** 0.5) to get the largest perfect square number less than or equal to i. We start the inner loop from 1 to include the perfect square number 1.\n\n3. For each jth perfect square number less than or equal to i, we update the least number of perfect square numbers that sum to i as dp[i] = min(dp[i], dp[i - j*j] + 1). Here, dp[i - j*j] + 1 represents the number of perfect square numbers required to sum up to i-j*j, and we add 1 to account for the current perfect square number j*j.\n\n4. Finally, we return the least number of perfect square numbers that sum to n, which is stored in dp[n].\n\nThis solution uses dynamic programming to solve the problem, and is optimized by iterating through all perfect square numbers less than or equal to i, rather than all numbers less than or equal to i.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSquares(self, n: int) -> int:\n # Initialize a list to store the least number of perfect square numbers that sum to the index i\n dp = [0] + [float(\'inf\')] * n\n \n # Iterate through all numbers from 1 to n\n for i in range(1, n + 1):\n # Iterate through all possible perfect square numbers that are less than or equal to i\n for j in range(1, int(i ** 0.5) + 1):\n # Update the least number of perfect square numbers that sum to i\n dp[i] = min(dp[i], dp[i - j*j] + 1)\n \n # Return the least number of perfect square numbers that sum to n\n return dp[n]\n\n``` | 7 | Given an integer `n`, return _the least number of perfect square numbers that sum to_ `n`.
A **perfect square** is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, `1`, `4`, `9`, and `16` are perfect squares while `3` and `11` are not.
**Example 1:**
**Input:** n = 12
**Output:** 3
**Explanation:** 12 = 4 + 4 + 4.
**Example 2:**
**Input:** n = 13
**Output:** 2
**Explanation:** 13 = 4 + 9.
**Constraints:**
* `1 <= n <= 104` | null |
maths solution beats 98.88 % in runtime 🔥🔥🔥| | clean & simple✅ | | Python | perfect-squares | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numSquares(self, n: int) -> int:\n # Nice Approach 2nd fastest\n # if n <= 0:\n # return 0\n #\n # cnt_perfect_square = [0]\n #\n # while len(cnt_perfect_square) <= n:\n # m = len(cnt_perfect_square)\n # cnt_square = sys.maxsize\n # for i in range(1, int(math.sqrt(m)) + 1):\n # cnt_square = min(cnt_square, cnt_perfect_square[m - i * i] + 1)\n # cnt_perfect_square.append(cnt_square)\n # return cnt_perfect_square[n]\n\n # We can Use Langrage\'s 4 Square theorem to do this in very efficient manner\n def is_perfect_square(n):\n square_root = int(math.sqrt(n))\n return square_root**2 == n\n \n cpy_n = n\n if is_perfect_square(n):\n return 1\n # 4^k(8m + 7) if in this way a num. can be represented then it\'s a sum of 4 square nums.\n while n & 3 == 0: # divisible by 4\n n >>= 2 # divide by 4\n if n & 7 == 7: # n & 7 ---> n % 8 == 0 and n & 7 == 7 means n % 8 == 7\n return 4\n n = cpy_n\n for i in range(1, int(math.sqrt(n)) + 1):\n if is_perfect_square(n - i*i):\n return 2\n return 3\n``` | 7 | Given an integer `n`, return _the least number of perfect square numbers that sum to_ `n`.
A **perfect square** is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, `1`, `4`, `9`, and `16` are perfect squares while `3` and `11` are not.
**Example 1:**
**Input:** n = 12
**Output:** 3
**Explanation:** 12 = 4 + 4 + 4.
**Example 2:**
**Input:** n = 13
**Output:** 2
**Explanation:** 13 = 4 + 9.
**Constraints:**
* `1 <= n <= 104` | null |
Python Neat Recursive Solution|Does not give TLE but extremely slow | expression-add-operators | 0 | 1 | ```\nimport re\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n operators=[\'+\',\'-\',\'*\']\n N=len(num)\n ans=[]\n def recursive(sp,curr):\n pattern = r\'\\b0\\d+\\b\'\n if sp==len(curr)-1 :\n if (not re.search(pattern,curr)) and eval(curr)==target:\n ans.append(curr)\n return\n recursive(sp+1,curr)\n recursive(sp+2,curr[:sp+1]+"*"+curr[sp+1:])\n recursive(sp+2,curr[:sp+1]+"+"+curr[sp+1:])\n recursive(sp+2,curr[:sp+1]+"-"+curr[sp+1:])\n recursive(0,num)\n return ans\n``` | 1 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Neat Recursive Solution|Does not give TLE but extremely slow | expression-add-operators | 0 | 1 | ```\nimport re\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n operators=[\'+\',\'-\',\'*\']\n N=len(num)\n ans=[]\n def recursive(sp,curr):\n pattern = r\'\\b0\\d+\\b\'\n if sp==len(curr)-1 :\n if (not re.search(pattern,curr)) and eval(curr)==target:\n ans.append(curr)\n return\n recursive(sp+1,curr)\n recursive(sp+2,curr[:sp+1]+"*"+curr[sp+1:])\n recursive(sp+2,curr[:sp+1]+"+"+curr[sp+1:])\n recursive(sp+2,curr[:sp+1]+"-"+curr[sp+1:])\n recursive(0,num)\n return ans\n``` | 1 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
282: Solution with step by step explanation | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nStep-by-step explanation:\n\n1. The input to the function is a string num and an integer target, representing the number to be expressed and the target value to be achieved, respectively.\n2. The function initializes an empty list ans to store all possible expressions that evaluate to the target value.\n3. The function defines a DFS (depth-first search) function dfs to generate all possible expressions.\n4. The DFS function takes four parameters: start represents the current index in the string num, prev represents the previous operand value, eval represents the current evaluated value, and path represents the list of operands and operators that form the current expression.\n5. The DFS function uses recursion to generate all possible expressions. At each recursive call, it evaluates the expression formed so far, and if the evaluation equals the target value, it adds the expression to the answer list.\n6. The DFS function iterates over all possible operands starting from the current index start, and for each operand, it iterates over all possible operators (+, -, *) and generates new expressions by appending the current operand and operator to the current path, and updating the previous operand value, evaluated value, and current index accordingly.\n7. The DFS function terminates when the current index reaches the end of the string num.\n8. The main function addOperators starts the DFS with initial parameters start=0, prev=0, eval=0, and path=[], and\n# Complexity\n- Time complexity:\n87.49%\n\n- Space complexity:\n78.86%\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n ans = [] # list to store all possible expressions that evaluate to the target\n\n # DFS function to generate all possible expressions\n # start: current index in num\n # prev: previous operand value\n # eval: current evaluated value\n # path: list to store current expression\n def dfs(start: int, prev: int, eval: int, path: List[str]) -> None:\n # base case: reached end of num\n if start == len(num):\n # check if current evaluation equals target\n if eval == target:\n # add current expression to the answer list\n ans.append(\'\'.join(path))\n return\n\n # iterate over all possible operands from current index\n for i in range(start, len(num)):\n # special case: ignore operands starting with 0, except 0 itself\n if i > start and num[start] == \'0\':\n return\n s = num[start:i + 1]\n curr = int(s)\n # special case: first operand, simply add it to the path and evaluate\n if start == 0:\n path.append(s)\n dfs(i + 1, curr, curr, path)\n path.pop()\n # general case: iterate over all possible operators and operands\n else:\n for op in [\'+\', \'-\', \'*\']:\n path.append(op + s)\n # addition: add current operand to evaluated value\n if op == \'+\':\n dfs(i + 1, curr, eval + curr, path)\n # subtraction: subtract current operand from evaluated value\n elif op == \'-\':\n dfs(i + 1, -curr, eval - curr, path)\n # multiplication: multiply current operand with previous operand and update evaluated value\n else:\n dfs(i + 1, prev * curr, eval - prev + prev * curr, path)\n path.pop()\n\n # start DFS with initial parameters\n dfs(0, 0, 0, [])\n return ans\n\n``` | 5 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
282: Solution with step by step explanation | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nStep-by-step explanation:\n\n1. The input to the function is a string num and an integer target, representing the number to be expressed and the target value to be achieved, respectively.\n2. The function initializes an empty list ans to store all possible expressions that evaluate to the target value.\n3. The function defines a DFS (depth-first search) function dfs to generate all possible expressions.\n4. The DFS function takes four parameters: start represents the current index in the string num, prev represents the previous operand value, eval represents the current evaluated value, and path represents the list of operands and operators that form the current expression.\n5. The DFS function uses recursion to generate all possible expressions. At each recursive call, it evaluates the expression formed so far, and if the evaluation equals the target value, it adds the expression to the answer list.\n6. The DFS function iterates over all possible operands starting from the current index start, and for each operand, it iterates over all possible operators (+, -, *) and generates new expressions by appending the current operand and operator to the current path, and updating the previous operand value, evaluated value, and current index accordingly.\n7. The DFS function terminates when the current index reaches the end of the string num.\n8. The main function addOperators starts the DFS with initial parameters start=0, prev=0, eval=0, and path=[], and\n# Complexity\n- Time complexity:\n87.49%\n\n- Space complexity:\n78.86%\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n ans = [] # list to store all possible expressions that evaluate to the target\n\n # DFS function to generate all possible expressions\n # start: current index in num\n # prev: previous operand value\n # eval: current evaluated value\n # path: list to store current expression\n def dfs(start: int, prev: int, eval: int, path: List[str]) -> None:\n # base case: reached end of num\n if start == len(num):\n # check if current evaluation equals target\n if eval == target:\n # add current expression to the answer list\n ans.append(\'\'.join(path))\n return\n\n # iterate over all possible operands from current index\n for i in range(start, len(num)):\n # special case: ignore operands starting with 0, except 0 itself\n if i > start and num[start] == \'0\':\n return\n s = num[start:i + 1]\n curr = int(s)\n # special case: first operand, simply add it to the path and evaluate\n if start == 0:\n path.append(s)\n dfs(i + 1, curr, curr, path)\n path.pop()\n # general case: iterate over all possible operators and operands\n else:\n for op in [\'+\', \'-\', \'*\']:\n path.append(op + s)\n # addition: add current operand to evaluated value\n if op == \'+\':\n dfs(i + 1, curr, eval + curr, path)\n # subtraction: subtract current operand from evaluated value\n elif op == \'-\':\n dfs(i + 1, -curr, eval - curr, path)\n # multiplication: multiply current operand with previous operand and update evaluated value\n else:\n dfs(i + 1, prev * curr, eval - prev + prev * curr, path)\n path.pop()\n\n # start DFS with initial parameters\n dfs(0, 0, 0, [])\n return ans\n\n``` | 5 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Well explained Python code | expression-add-operators | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def addOperators(self, s: str, target: int) -> List[str]:\n # need to traverse through s\n # backtrack each case of start index and then +,*,-\n # need empty array ofcourse\n # need curidx = i\n # need the str path to append to the arr if my --> cur_num == target\n # need the prevNum access for multiplication\n # 1 2 3 4 5 --> 1 + 2 + 3 + 4 * 5\n # ^ ^ ^ ^ ^ ^ ^ == 10 but we wanna do 4*5 so ---\n # just do 1 + 2 + 3 + 4 + (- 4) + (4 * 5)\n # return ans\n \n res = []\n\n def dfs(i, path, cur_num, prevNum):\n if i == len(s):\n if cur_num == target:\n res.append(path)\n return\n \n for j in range(i, len(s)):\n # starting with zero?\n if j > i and s[i] == \'0\':\n break\n num = int(s[i:j+1])\n\n # if cur index is 0 then simple add that number\n if i == 0:\n dfs(j + 1, path + str(num), cur_num + num, num)\n else:\n dfs(j + 1, path + "+" + str(num), cur_num + num, num)\n dfs(j + 1, path + "-" + str(num), cur_num - num, -num)\n dfs(j + 1, path + "*" + str(num), cur_num - prevNum + prevNum * num, prevNum * num)\n \n dfs(0, "", 0, 0)\n return res\n \n``` | 4 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Well explained Python code | expression-add-operators | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def addOperators(self, s: str, target: int) -> List[str]:\n # need to traverse through s\n # backtrack each case of start index and then +,*,-\n # need empty array ofcourse\n # need curidx = i\n # need the str path to append to the arr if my --> cur_num == target\n # need the prevNum access for multiplication\n # 1 2 3 4 5 --> 1 + 2 + 3 + 4 * 5\n # ^ ^ ^ ^ ^ ^ ^ == 10 but we wanna do 4*5 so ---\n # just do 1 + 2 + 3 + 4 + (- 4) + (4 * 5)\n # return ans\n \n res = []\n\n def dfs(i, path, cur_num, prevNum):\n if i == len(s):\n if cur_num == target:\n res.append(path)\n return\n \n for j in range(i, len(s)):\n # starting with zero?\n if j > i and s[i] == \'0\':\n break\n num = int(s[i:j+1])\n\n # if cur index is 0 then simple add that number\n if i == 0:\n dfs(j + 1, path + str(num), cur_num + num, num)\n else:\n dfs(j + 1, path + "+" + str(num), cur_num + num, num)\n dfs(j + 1, path + "-" + str(num), cur_num - num, -num)\n dfs(j + 1, path + "*" + str(num), cur_num - prevNum + prevNum * num, prevNum * num)\n \n dfs(0, "", 0, 0)\n return res\n \n``` | 4 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python recursive solution | expression-add-operators | 0 | 1 | ```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n answer = set()\n \n def dp(idx, total, path, last_number):\n if idx == len(num) and total == target:\n answer.add(path)\n \n if idx >= len(num):\n return\n \n for i in range(idx, len(num)):\n if len(num[idx:i+1]) > 1 and num[idx:i+1][0] == "0":\n continue\n \n tmp_number = num[idx:i+1]\n \n if last_number == "":\n dp(i + 1, int(tmp_number), tmp_number, tmp_number)\n else:\n # addition\n dp(i + 1,total + int(tmp_number), path + "+" + tmp_number, tmp_number)\n \n # subtraction\n dp(i + 1,total - int(tmp_number), path + "-" + tmp_number, "-" + tmp_number)\n \n # multiplication\n dp(i + 1, total-int(last_number) + (int(last_number) * int(tmp_number)), path + "*" + tmp_number, str(int(tmp_number) * int(last_number)))\n\n dp(0,-1,"", "")\n return answer\n\n``` | 1 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python recursive solution | expression-add-operators | 0 | 1 | ```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n answer = set()\n \n def dp(idx, total, path, last_number):\n if idx == len(num) and total == target:\n answer.add(path)\n \n if idx >= len(num):\n return\n \n for i in range(idx, len(num)):\n if len(num[idx:i+1]) > 1 and num[idx:i+1][0] == "0":\n continue\n \n tmp_number = num[idx:i+1]\n \n if last_number == "":\n dp(i + 1, int(tmp_number), tmp_number, tmp_number)\n else:\n # addition\n dp(i + 1,total + int(tmp_number), path + "+" + tmp_number, tmp_number)\n \n # subtraction\n dp(i + 1,total - int(tmp_number), path + "-" + tmp_number, "-" + tmp_number)\n \n # multiplication\n dp(i + 1, total-int(last_number) + (int(last_number) * int(tmp_number)), path + "*" + tmp_number, str(int(tmp_number) * int(last_number)))\n\n dp(0,-1,"", "")\n return answer\n\n``` | 1 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Clean Python3 Backtracking Solution | expression-add-operators | 0 | 1 | ```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n L = len(num)\n ans = set()\n \n def backtrack(i, total, last, expr):\n if i == L:\n if total == target:\n ans.add(expr)\n return\n \n for j in range(i, L):\n n = int(num[i:j+1])\n if i == 0:\n backtrack(j+1, n, n, str(n))\n else:\n backtrack(j+1, total + n, n, expr + \'+\' + str(n))\n backtrack(j+1, total - n, -n, expr + \'-\' + str(n))\n backtrack(j+1, total - last + last * n, last * n, expr + \'*\' + str(n))\n if n == 0:\n break\n \n backtrack(0, 0, 0, \'\')\n return list(ans)\n``` | 13 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Clean Python3 Backtracking Solution | expression-add-operators | 0 | 1 | ```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n L = len(num)\n ans = set()\n \n def backtrack(i, total, last, expr):\n if i == L:\n if total == target:\n ans.add(expr)\n return\n \n for j in range(i, L):\n n = int(num[i:j+1])\n if i == 0:\n backtrack(j+1, n, n, str(n))\n else:\n backtrack(j+1, total + n, n, expr + \'+\' + str(n))\n backtrack(j+1, total - n, -n, expr + \'-\' + str(n))\n backtrack(j+1, total - last + last * n, last * n, expr + \'*\' + str(n))\n if n == 0:\n break\n \n backtrack(0, 0, 0, \'\')\n return list(ans)\n``` | 13 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
brute force with eval and itertools | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import chain, product\n\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n res = []\n c, digits = num[0], list(num[1:])\n for ops in product(["+", "-", "*", ""], repeat=len(num) - 1):\n exp = c + "".join(chain.from_iterable(zip(ops, digits)))\n try:\n if eval(exp) == target:\n if exp.startswith("00") or "+00" in exp or "-00" in exp or "*00" in exp:\n continue \n res.append(exp)\n except:\n pass\n return res\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
brute force with eval and itertools | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import chain, product\n\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n res = []\n c, digits = num[0], list(num[1:])\n for ops in product(["+", "-", "*", ""], repeat=len(num) - 1):\n exp = c + "".join(chain.from_iterable(zip(ops, digits)))\n try:\n if eval(exp) == target:\n if exp.startswith("00") or "+00" in exp or "-00" in exp or "*00" in exp:\n continue \n res.append(exp)\n except:\n pass\n return res\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Backtracking python3 | expression-add-operators | 0 | 1 | # Intuition\nBacktracking. The only difference for this one is when making a choice at each step, we either choose to add a number to the expression or add an operator to the expression.\n\n# Approach\nWhen the expression is empty or ending with an operator, we need to choose a number. It can be any substring starting from the current index to the end of the num string; unless the digit at the current index is 0, in which case we can only choose 0 and move on the next index due to the no leading zero rule.\n\nWhen the expression is ending with a digit, we need to choose an operator from +, -, and *. \n\nWe could evaluate the expression at the end when we reach index = len(num), or we can evaluate * as soon as it appears with the next number we choose, then when we reach index = len(num), the expression only has + and -, so we just popping everything out in reverse order and add or substract each number.\n\nThe trickiest part of this question is actually how to use a stack to track the partially evaluated expression. The numbers and operators in the stack is not the same as the expression when we evaluate * early. In most backtracking questions, we can \'backtrack\' from a previous state easily by removing the previous choice, in this case, since the expression is partially evaluated, it\'s not easy to \'backtrack\' unless we keep a clone of the original stack and simply restore the stack when we are ready to make another choice.\n\n# Complexity\n- Time complexity:\n$$O(n^n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def addOperators(self, num, target):\n exps = set()\n self.backtracking1(0, num, target, [], \'\', exps)\n return exps\n\n def backtracking1(self, index, num, target, stack, expression, exps):\n # base case, evaluate the final result\n if index == len(num):\n stack = stack[::-1]\n result = 0\n operator = \'+\'\n while len(stack) > 0:\n top = stack.pop()\n # * should have been evaluated at this point\n if top in [\'+\', \'-\']:\n operator = top\n else:\n result = result + top if operator == \'+\' else result - top\n \n if result == target and expression not in exps:\n exps.add(expression[:])\n \n return \n \n # when backtracking, set the stack back to its original state\n stackori = stack[:]\n expressionori = expression[:]\n if not expression or expression[-1] in [\'+\', \'-\', \'*\']:\n # need to pick a number and evaluate *\n for i in range(index, len(num)):\n operant = num[index: i+1]\n if expression and expression[-1] == \'*\':\n stack.pop() # remove the operator\n stack.append(stack.pop() * int(operant))\n else:\n stack.append(int(operant))\n \n expression += operant\n self.backtracking1(i+1, num, target, stack, expression, exps)\n expression = expressionori[:]\n stack = stackori[:]\n if num[index] == \'0\': # no leading 0\n break\n elif expression[-1].isdigit():\n # need to pick a operator\n for operator in [\'+\', \'-\', \'*\']:\n stack.append(operator)\n expression += operator\n self.backtracking1(index, num, target, stack, expression, exps)\n expression = expressionori[:]\n stack = stackori[:]\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Backtracking python3 | expression-add-operators | 0 | 1 | # Intuition\nBacktracking. The only difference for this one is when making a choice at each step, we either choose to add a number to the expression or add an operator to the expression.\n\n# Approach\nWhen the expression is empty or ending with an operator, we need to choose a number. It can be any substring starting from the current index to the end of the num string; unless the digit at the current index is 0, in which case we can only choose 0 and move on the next index due to the no leading zero rule.\n\nWhen the expression is ending with a digit, we need to choose an operator from +, -, and *. \n\nWe could evaluate the expression at the end when we reach index = len(num), or we can evaluate * as soon as it appears with the next number we choose, then when we reach index = len(num), the expression only has + and -, so we just popping everything out in reverse order and add or substract each number.\n\nThe trickiest part of this question is actually how to use a stack to track the partially evaluated expression. The numbers and operators in the stack is not the same as the expression when we evaluate * early. In most backtracking questions, we can \'backtrack\' from a previous state easily by removing the previous choice, in this case, since the expression is partially evaluated, it\'s not easy to \'backtrack\' unless we keep a clone of the original stack and simply restore the stack when we are ready to make another choice.\n\n# Complexity\n- Time complexity:\n$$O(n^n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def addOperators(self, num, target):\n exps = set()\n self.backtracking1(0, num, target, [], \'\', exps)\n return exps\n\n def backtracking1(self, index, num, target, stack, expression, exps):\n # base case, evaluate the final result\n if index == len(num):\n stack = stack[::-1]\n result = 0\n operator = \'+\'\n while len(stack) > 0:\n top = stack.pop()\n # * should have been evaluated at this point\n if top in [\'+\', \'-\']:\n operator = top\n else:\n result = result + top if operator == \'+\' else result - top\n \n if result == target and expression not in exps:\n exps.add(expression[:])\n \n return \n \n # when backtracking, set the stack back to its original state\n stackori = stack[:]\n expressionori = expression[:]\n if not expression or expression[-1] in [\'+\', \'-\', \'*\']:\n # need to pick a number and evaluate *\n for i in range(index, len(num)):\n operant = num[index: i+1]\n if expression and expression[-1] == \'*\':\n stack.pop() # remove the operator\n stack.append(stack.pop() * int(operant))\n else:\n stack.append(int(operant))\n \n expression += operant\n self.backtracking1(i+1, num, target, stack, expression, exps)\n expression = expressionori[:]\n stack = stackori[:]\n if num[index] == \'0\': # no leading 0\n break\n elif expression[-1].isdigit():\n # need to pick a operator\n for operator in [\'+\', \'-\', \'*\']:\n stack.append(operator)\n expression += operator\n self.backtracking1(index, num, target, stack, expression, exps)\n expression = expressionori[:]\n stack = stackori[:]\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python3 Solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n ret = []\n def dfs(pre_sum, factor, expr_pre_sum, expr_factor, idx):\n if idx == len(num):\n if pre_sum + factor == target:\n r = expr_factor\n if expr_pre_sum != "":\n r = expr_pre_sum + "+" + expr_factor\n ret.append(r)\n if pre_sum - factor == target and expr_pre_sum != "":\n ret.append(expr_pre_sum + "-" + expr_factor)\n else:\n cur = None\n for i in range(idx, len(num)):\n if cur is None:\n cur = int(num[i])\n else:\n cur = 10 * cur + int(num[i])\n if factor is not None:\n if expr_pre_sum != "":\n dfs(pre_sum - factor, cur, expr_pre_sum + "-" + expr_factor, str(cur), i+1)\n\n r = expr_factor\n if expr_pre_sum != "":\n r = expr_pre_sum + "+" + expr_factor\n dfs(pre_sum + factor, cur, r, str(cur), i+1)\n if factor is not None:\n dfs(pre_sum, factor * cur, expr_pre_sum, expr_factor + "*" + str(cur) , i + 1)\n else:\n dfs(pre_sum, cur, expr_pre_sum, str(cur) , i + 1)\n if cur == 0:\n break\n\n dfs(0, None, "", "", 0)\n return ret\n \n \n\n\n\n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python3 Solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n ret = []\n def dfs(pre_sum, factor, expr_pre_sum, expr_factor, idx):\n if idx == len(num):\n if pre_sum + factor == target:\n r = expr_factor\n if expr_pre_sum != "":\n r = expr_pre_sum + "+" + expr_factor\n ret.append(r)\n if pre_sum - factor == target and expr_pre_sum != "":\n ret.append(expr_pre_sum + "-" + expr_factor)\n else:\n cur = None\n for i in range(idx, len(num)):\n if cur is None:\n cur = int(num[i])\n else:\n cur = 10 * cur + int(num[i])\n if factor is not None:\n if expr_pre_sum != "":\n dfs(pre_sum - factor, cur, expr_pre_sum + "-" + expr_factor, str(cur), i+1)\n\n r = expr_factor\n if expr_pre_sum != "":\n r = expr_pre_sum + "+" + expr_factor\n dfs(pre_sum + factor, cur, r, str(cur), i+1)\n if factor is not None:\n dfs(pre_sum, factor * cur, expr_pre_sum, expr_factor + "*" + str(cur) , i + 1)\n else:\n dfs(pre_sum, cur, expr_pre_sum, str(cur) , i + 1)\n if cur == 0:\n break\n\n dfs(0, None, "", "", 0)\n return ret\n \n \n\n\n\n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n L = len(num)\n ans = set()\n \n def backtrack(i, total, last, expr):\n if i == L:\n if total == target:\n ans.add(expr)\n return\n \n for j in range(i, L):\n n = int(num[i:j+1])\n if i == 0:\n backtrack(j+1, n, n, str(n))\n else:\n backtrack(j+1, total + n, n, expr + \'+\' + str(n))\n backtrack(j+1, total - n, -n, expr + \'-\' + str(n))\n backtrack(j+1, total - last + last * n, last * n, expr + \'*\' + str(n))\n if n == 0:\n break\n \n backtrack(0, 0, 0, \'\')\n return list(ans)\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n L = len(num)\n ans = set()\n \n def backtrack(i, total, last, expr):\n if i == L:\n if total == target:\n ans.add(expr)\n return\n \n for j in range(i, L):\n n = int(num[i:j+1])\n if i == 0:\n backtrack(j+1, n, n, str(n))\n else:\n backtrack(j+1, total + n, n, expr + \'+\' + str(n))\n backtrack(j+1, total - n, -n, expr + \'-\' + str(n))\n backtrack(j+1, total - last + last * n, last * n, expr + \'*\' + str(n))\n if n == 0:\n break\n \n backtrack(0, 0, 0, \'\')\n return list(ans)\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Recursive Python Solution | expression-add-operators | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def addOperatorsRec(self, num, value, last_mul, target):\n n = len(num)\n ans = []\n if num[0] != \'0\' or len(num) == 1:\n next_num = int(num)\n if max(last_mul * next_num, last_mul + next_num) < target - value:\n return []\n if value + last_mul * next_num == target:\n ans += [\'*\' + num]\n if value + last_mul + next_num == target:\n ans += [\'+\' + num]\n if value + last_mul - next_num == target:\n ans += [\'-\' + num]\n \n elif num[0] == \'0\':\n n = 2\n for i in range(1, n):\n next_num = int(num[:i])\n ans += [\'+\' + num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], value + last_mul, next_num, target)]\n ans += [\'*\' + num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], value, last_mul * next_num , target)]\n ans += [\'-\' + num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], value + last_mul, -next_num, target)]\n return ans\n\n \n def addOperators(self, num: str, target: int) -> List[str]:\n ans = []\n n = len(num)\n if num[0] == \'0\':\n if n == 1:\n return [\'0\'] if target == 0 else []\n n = 2\n elif int(num) == target:\n ans = [num]\n elif int(num) < target:\n return []\n \n for i in range(1, n):\n last_mul = int(num[:i])\n ans += [num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], 0, last_mul, target)]\n \n return ans\n \n \n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Recursive Python Solution | expression-add-operators | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def addOperatorsRec(self, num, value, last_mul, target):\n n = len(num)\n ans = []\n if num[0] != \'0\' or len(num) == 1:\n next_num = int(num)\n if max(last_mul * next_num, last_mul + next_num) < target - value:\n return []\n if value + last_mul * next_num == target:\n ans += [\'*\' + num]\n if value + last_mul + next_num == target:\n ans += [\'+\' + num]\n if value + last_mul - next_num == target:\n ans += [\'-\' + num]\n \n elif num[0] == \'0\':\n n = 2\n for i in range(1, n):\n next_num = int(num[:i])\n ans += [\'+\' + num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], value + last_mul, next_num, target)]\n ans += [\'*\' + num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], value, last_mul * next_num , target)]\n ans += [\'-\' + num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], value + last_mul, -next_num, target)]\n return ans\n\n \n def addOperators(self, num: str, target: int) -> List[str]:\n ans = []\n n = len(num)\n if num[0] == \'0\':\n if n == 1:\n return [\'0\'] if target == 0 else []\n n = 2\n elif int(num) == target:\n ans = [num]\n elif int(num) < target:\n return []\n \n for i in range(1, n):\n last_mul = int(num[:i])\n ans += [num[:i] + rec_ans for rec_ans in self.addOperatorsRec(num[i:], 0, last_mul, target)]\n \n return ans\n \n \n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python (Simple Backtracking) | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num, target):\n n = len(num)\n\n def f(idx,path,p_val,c_val):\n if idx == n and c_val == target:\n result.append(path)\n\n for j in range(idx,n):\n cur = int(num[idx:j+1])\n\n if idx == 0:\n f(j+1,str(cur),cur,cur)\n else:\n f(j+1,path+"+"+str(cur),cur,c_val+cur)\n f(j+1,path+"-"+str(cur),-cur,c_val-cur)\n f(j+1,path+"*"+str(cur),p_val*cur,c_val-p_val+p_val*cur)\n\n if num[idx] == "0":\n break\n\n result = []\n f(0,"",0,0)\n return result\n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python (Simple Backtracking) | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num, target):\n n = len(num)\n\n def f(idx,path,p_val,c_val):\n if idx == n and c_val == target:\n result.append(path)\n\n for j in range(idx,n):\n cur = int(num[idx:j+1])\n\n if idx == 0:\n f(j+1,str(cur),cur,cur)\n else:\n f(j+1,path+"+"+str(cur),cur,c_val+cur)\n f(j+1,path+"-"+str(cur),-cur,c_val-cur)\n f(j+1,path+"*"+str(cur),p_val*cur,c_val-p_val+p_val*cur)\n\n if num[idx] == "0":\n break\n\n result = []\n f(0,"",0,0)\n return result\n \n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n def helper(index, current, evaluated, prev):\n if index == len(num):\n if evaluated == target:\n result.append(current)\n return\n \n for i in range(index, len(num)):\n if i != index and num[index] == \'0\': # Avoid leading zeros\n break\n \n operand = int(num[index:i+1])\n \n if index == 0:\n helper(i + 1, str(operand), operand, operand)\n else:\n helper(i + 1, current + \'+\' + str(operand), evaluated + operand, operand)\n helper(i + 1, current + \'-\' + str(operand), evaluated - operand, -operand)\n helper(i + 1, current + \'*\' + str(operand), evaluated - prev + (prev * operand), prev * operand)\n \n result = []\n helper(0, \'\', 0, 0)\n return result\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n def helper(index, current, evaluated, prev):\n if index == len(num):\n if evaluated == target:\n result.append(current)\n return\n \n for i in range(index, len(num)):\n if i != index and num[index] == \'0\': # Avoid leading zeros\n break\n \n operand = int(num[index:i+1])\n \n if index == 0:\n helper(i + 1, str(operand), operand, operand)\n else:\n helper(i + 1, current + \'+\' + str(operand), evaluated + operand, operand)\n helper(i + 1, current + \'-\' + str(operand), evaluated - operand, -operand)\n helper(i + 1, current + \'*\' + str(operand), evaluated - prev + (prev * operand), prev * operand)\n \n result = []\n helper(0, \'\', 0, 0)\n return result\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python3: Backtrack solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n\n res = []\n def backtrack(i, total, last, expr):\n # base case\n if i >= len(num):\n if total == target:\n res.append(expr)\n return\n\n for j in range(i + 1, len(num) + 1):\n val = int(num[i:j])\n # if it is the first element\n if i == 0:\n backtrack(j, total + val, val, str(val))\n else:\n backtrack(j, total + val, val, expr + "+" + str(val))\n backtrack(j, total - val, -val, expr + "-" + str(val))\n backtrack(j, total - last + last * val, last * val, expr + "*" + str(val))\n # when the current number is 0, do not evaluate 05, 056\n # 0 is valid\n # no leading 0 is allowed\n \n if val == 0:\n break\n\n backtrack(0, 0, 0, "")\n return res\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python3: Backtrack solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n\n res = []\n def backtrack(i, total, last, expr):\n # base case\n if i >= len(num):\n if total == target:\n res.append(expr)\n return\n\n for j in range(i + 1, len(num) + 1):\n val = int(num[i:j])\n # if it is the first element\n if i == 0:\n backtrack(j, total + val, val, str(val))\n else:\n backtrack(j, total + val, val, expr + "+" + str(val))\n backtrack(j, total - val, -val, expr + "-" + str(val))\n backtrack(j, total - last + last * val, last * val, expr + "*" + str(val))\n # when the current number is 0, do not evaluate 05, 056\n # 0 is valid\n # no leading 0 is allowed\n \n if val == 0:\n break\n\n backtrack(0, 0, 0, "")\n return res\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python backtracking using eval | expression-add-operators | 0 | 1 | # Intuition\nTo give all posibilities of reaching the `target` value using combinations of numbers from `num`, we must iterate through every possible expressions that could be generated out of the original `num` string. Each insert location between two digits faces two decisions: 1) either an operator is inserted, or 2) there\'s no operator at the position. This hints at the backtracking algorithm.\n\n# Approach\nWe define a `backtrack` function that accepts current index `i` and `path`, which stores intermediate expression. In each call to `backtrack` we add `curnum` and `operator` to `path`. `curnum` is the number lead by digit `num[i]`. For example, if `num` is `1234` and `i=1`, `curnum` are `2`, `23`, and `234`. If `curnum` is taken from all remaining digits of `num`, we evaluate the `path` expression and check the result. If not, then we continue to add all possible operators to `path` before making recursive call.\n\n\n# Complexity\nAssuming input `num` has length `n`, this algorithm checks `n-1` possible insert locations in `num`. For example, if `num` is `1234`, then we need to check `[1,2,3,4]`, `[1,2,34]`, `[1,234]`, `[1,23,4]`, and `[12,3,4]`, `[12,34]`, `[123,4]`, `[1234]`, where every `,` is an insert position. Each insert location between two digits faces two decisions: either an operator is inserted, or there\'s no operator. So there\'re a total of `2^(n-1)` decisions to make, and thus `2^(n-1)` expressions to check. For each insert location, the algorithm attempts to insert three operators `+`, `-`, `*`.\n\n- Time complexity:\nAssuming eval takes `O(eval, n)` to evaluate the expression, in total it would take `O(2^(n-1)) * O(eval, n)` time to run the algorithm\n\n- Space complexity:\nThe `res` array can be as large as total number of possible expressions (all expressions evaluate to the target num!), and each expression has `O(n)` length, this would take `O(n * 2^(n-1))` space. Aside from the result array, the algorithm uses `path` to store intermediate expression, which uses `O(n)` space.\n\n# Code\n```\nOPERATORS = {\'+\', \'-\', \'*\'}\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n n = len(num)\n res = []\n\n def backtrack(i, path):\n for endi in range(i+1, n+1): # check all numbers lead by current digit num[i]\n if num[i] == \'0\' and endi > i+1: # skip leading zeros\n continue\n curnum = num[i:endi]\n path.append(curnum)\n if endi == n: # reach end pos, check expression\n expr = \'\'.join(path)\n if eval(expr) == target:\n res.append(expr)\n elif endi < n: # backtrack to check possible path generated by every operator\n for op in OPERATORS:\n path.append(op)\n backtrack(endi, path)\n path.pop()\n path.pop()\n\n backtrack(0, [])\n return res\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python backtracking using eval | expression-add-operators | 0 | 1 | # Intuition\nTo give all posibilities of reaching the `target` value using combinations of numbers from `num`, we must iterate through every possible expressions that could be generated out of the original `num` string. Each insert location between two digits faces two decisions: 1) either an operator is inserted, or 2) there\'s no operator at the position. This hints at the backtracking algorithm.\n\n# Approach\nWe define a `backtrack` function that accepts current index `i` and `path`, which stores intermediate expression. In each call to `backtrack` we add `curnum` and `operator` to `path`. `curnum` is the number lead by digit `num[i]`. For example, if `num` is `1234` and `i=1`, `curnum` are `2`, `23`, and `234`. If `curnum` is taken from all remaining digits of `num`, we evaluate the `path` expression and check the result. If not, then we continue to add all possible operators to `path` before making recursive call.\n\n\n# Complexity\nAssuming input `num` has length `n`, this algorithm checks `n-1` possible insert locations in `num`. For example, if `num` is `1234`, then we need to check `[1,2,3,4]`, `[1,2,34]`, `[1,234]`, `[1,23,4]`, and `[12,3,4]`, `[12,34]`, `[123,4]`, `[1234]`, where every `,` is an insert position. Each insert location between two digits faces two decisions: either an operator is inserted, or there\'s no operator. So there\'re a total of `2^(n-1)` decisions to make, and thus `2^(n-1)` expressions to check. For each insert location, the algorithm attempts to insert three operators `+`, `-`, `*`.\n\n- Time complexity:\nAssuming eval takes `O(eval, n)` to evaluate the expression, in total it would take `O(2^(n-1)) * O(eval, n)` time to run the algorithm\n\n- Space complexity:\nThe `res` array can be as large as total number of possible expressions (all expressions evaluate to the target num!), and each expression has `O(n)` length, this would take `O(n * 2^(n-1))` space. Aside from the result array, the algorithm uses `path` to store intermediate expression, which uses `O(n)` space.\n\n# Code\n```\nOPERATORS = {\'+\', \'-\', \'*\'}\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n n = len(num)\n res = []\n\n def backtrack(i, path):\n for endi in range(i+1, n+1): # check all numbers lead by current digit num[i]\n if num[i] == \'0\' and endi > i+1: # skip leading zeros\n continue\n curnum = num[i:endi]\n path.append(curnum)\n if endi == n: # reach end pos, check expression\n expr = \'\'.join(path)\n if eval(expr) == target:\n res.append(expr)\n elif endi < n: # backtrack to check possible path generated by every operator\n for op in OPERATORS:\n path.append(op)\n backtrack(endi, path)\n path.pop()\n path.pop()\n\n backtrack(0, [])\n return res\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Easy Solution Runtime 772 ms | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n def backTrack(index,pre,curr,value,s):\n if index == n:\n if value == target and curr == 0:\n ans.append(s)\n return\n curr = curr * 10 + int(num[index])\n\n if curr > 0:\n backTrack(index + 1,pre,curr,value,s)\n\n if not s:\n backTrack(index + 1,curr,0,value+curr,str(curr))\n else:\n backTrack(index + 1,curr,0,value+curr,s+"+"+str(curr))\n backTrack(index + 1,-curr,0,value-curr,s+"-"+str(curr))\n backTrack(index + 1,pre*curr,0,value-pre+pre*curr,s+"*"+str(curr))\n\n n = len(num)\n ans = []\n backTrack(0,0,0,0,"")\n return ans\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Easy Solution Runtime 772 ms | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n def backTrack(index,pre,curr,value,s):\n if index == n:\n if value == target and curr == 0:\n ans.append(s)\n return\n curr = curr * 10 + int(num[index])\n\n if curr > 0:\n backTrack(index + 1,pre,curr,value,s)\n\n if not s:\n backTrack(index + 1,curr,0,value+curr,str(curr))\n else:\n backTrack(index + 1,curr,0,value+curr,s+"+"+str(curr))\n backTrack(index + 1,-curr,0,value-curr,s+"-"+str(curr))\n backTrack(index + 1,pre*curr,0,value-pre+pre*curr,s+"*"+str(curr))\n\n n = len(num)\n ans = []\n backTrack(0,0,0,0,"")\n return ans\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Recursive + Backtrack | expression-add-operators | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(3^{n-1})$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n + 3^{n-1})$$\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n results = []\n \n def backtrack(expression, current_val, previous_num, index):\n if index == len(num):\n if current_val == target:\n results.append(expression)\n return\n \n for i in range(index, len(num)):\n if i != index and num[index] == \'0\':\n # Avoid leading zeros\n break\n \n current_str = num[index:i+1]\n current_num = int(current_str)\n \n if index == 0:\n # First number in the expression\n backtrack(current_str, current_num, current_num, i+1)\n else:\n # Addition\n backtrack(expression + \'+\' + current_str, current_val + current_num, current_num, i+1)\n # Subtraction\n backtrack(expression + \'-\' + current_str, current_val - current_num, -current_num, i+1)\n # Multiplication\n backtrack(expression + \'*\' + current_str, current_val - previous_num + previous_num * current_num, previous_num * current_num, i+1)\n \n backtrack(\'\', 0, 0, 0)\n return results\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Recursive + Backtrack | expression-add-operators | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(3^{n-1})$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n + 3^{n-1})$$\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n results = []\n \n def backtrack(expression, current_val, previous_num, index):\n if index == len(num):\n if current_val == target:\n results.append(expression)\n return\n \n for i in range(index, len(num)):\n if i != index and num[index] == \'0\':\n # Avoid leading zeros\n break\n \n current_str = num[index:i+1]\n current_num = int(current_str)\n \n if index == 0:\n # First number in the expression\n backtrack(current_str, current_num, current_num, i+1)\n else:\n # Addition\n backtrack(expression + \'+\' + current_str, current_val + current_num, current_num, i+1)\n # Subtraction\n backtrack(expression + \'-\' + current_str, current_val - current_num, -current_num, i+1)\n # Multiplication\n backtrack(expression + \'*\' + current_str, current_val - previous_num + previous_num * current_num, previous_num * current_num, i+1)\n \n backtrack(\'\', 0, 0, 0)\n return results\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Solution Evaluate on Fly | expression-add-operators | 0 | 1 | # Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n\n def recur(nums,val,prev,expr,res):\n if not nums and val == target:\n res.append(expr)\n return\n \n for i in range(1,len(nums) + 1):\n curr_str = nums[:i]\n\n if len(curr_str) > 1 and curr_str[0] == \'0\':\n continue\n \n curr_num = int(curr_str)\n next_num = nums[i:]\n\n if not expr:\n recur(next_num,curr_num,curr_num,curr_str,res)\n else:\n recur(next_num,val + curr_num,curr_num,expr + \'+\' + curr_str,res)\n recur(next_num,val - curr_num,-curr_num,expr + \'-\' + curr_str,res)\n recur(next_num,val - prev + prev * curr_num,prev * curr_num,expr + \'*\' + curr_str,res)\n \n res = []\n recur(num,0,0,\'\',res)\n return res\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python Solution Evaluate on Fly | expression-add-operators | 0 | 1 | # Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n\n def recur(nums,val,prev,expr,res):\n if not nums and val == target:\n res.append(expr)\n return\n \n for i in range(1,len(nums) + 1):\n curr_str = nums[:i]\n\n if len(curr_str) > 1 and curr_str[0] == \'0\':\n continue\n \n curr_num = int(curr_str)\n next_num = nums[i:]\n\n if not expr:\n recur(next_num,curr_num,curr_num,curr_str,res)\n else:\n recur(next_num,val + curr_num,curr_num,expr + \'+\' + curr_str,res)\n recur(next_num,val - curr_num,-curr_num,expr + \'-\' + curr_str,res)\n recur(next_num,val - prev + prev * curr_num,prev * curr_num,expr + \'*\' + curr_str,res)\n \n res = []\n recur(num,0,0,\'\',res)\n return res\n\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python: brute force solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. use itertools.product to create a list for all the operators.\n2. calcualte the results as below:\n- calculate all the joint digits\n- calculate all the "*"\n- calculate "=" and "-" last.\n- if the result match target, add it to the output.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n output = []\n nums = [int(x) for x in num]\n\n def calc(opr_s):\n nonlocal nums\n n, oprs, cur = nums.copy(), list(opr_s).copy(), 0\n for i in [i for i, v in enumerate(oprs) if v == \'\']:\n ind = i - cur\n if n[ind] == 0:\n return False\n else:\n n = n[:ind] + [n[ind] * 10 + n[ind+1]] + n[ind+2:] if len(n) - ind > 2 else n[:ind] + [n[ind] * 10 + n[ind+1]]\n oprs.pop(ind)\n cur += 1\n\n cur = 0\n for i in [i for i, v in enumerate(oprs) if v == \'*\']:\n ind = i - cur\n n = n[:ind] + [n[ind] * n[ind+1]] + n[ind+2:] if len(n) - ind > 2 else n[:ind] + [n[ind] * n[ind+1]]\n oprs.pop(ind)\n cur += 1\n\n value = n[0]\n for i in range(len(oprs)):\n if oprs[i] == \'+\':\n value += n[i+1] \n else:\n value -= n[i+1]\n \n return True if value == target else False\n\n tests = list(itertools.product((\'+\', \'-\', \'*\', ""), repeat=len(nums)-1))\n for t in tests:\n if calc(t):\n output.append(f"{nums[0]}{\'\'.join(t[x] + str(nums[x+1]) for x in range(len(t)))}")\n\n return output\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Python: brute force solution | expression-add-operators | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. use itertools.product to create a list for all the operators.\n2. calcualte the results as below:\n- calculate all the joint digits\n- calculate all the "*"\n- calculate "=" and "-" last.\n- if the result match target, add it to the output.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addOperators(self, num: str, target: int) -> List[str]:\n output = []\n nums = [int(x) for x in num]\n\n def calc(opr_s):\n nonlocal nums\n n, oprs, cur = nums.copy(), list(opr_s).copy(), 0\n for i in [i for i, v in enumerate(oprs) if v == \'\']:\n ind = i - cur\n if n[ind] == 0:\n return False\n else:\n n = n[:ind] + [n[ind] * 10 + n[ind+1]] + n[ind+2:] if len(n) - ind > 2 else n[:ind] + [n[ind] * 10 + n[ind+1]]\n oprs.pop(ind)\n cur += 1\n\n cur = 0\n for i in [i for i, v in enumerate(oprs) if v == \'*\']:\n ind = i - cur\n n = n[:ind] + [n[ind] * n[ind+1]] + n[ind+2:] if len(n) - ind > 2 else n[:ind] + [n[ind] * n[ind+1]]\n oprs.pop(ind)\n cur += 1\n\n value = n[0]\n for i in range(len(oprs)):\n if oprs[i] == \'+\':\n value += n[i+1] \n else:\n value -= n[i+1]\n \n return True if value == target else False\n\n tests = list(itertools.product((\'+\', \'-\', \'*\', ""), repeat=len(nums)-1))\n for t in tests:\n if calc(t):\n output.append(f"{nums[0]}{\'\'.join(t[x] + str(nums[x+1]) for x in range(len(t)))}")\n\n return output\n``` | 0 | Given a string `num` that contains only digits and an integer `target`, return _**all possibilities** to insert the binary operators_ `'+'`_,_ `'-'`_, and/or_ `'*'` _between the digits of_ `num` _so that the resultant expression evaluates to the_ `target` _value_.
Note that operands in the returned expressions **should not** contain leading zeros.
**Example 1:**
**Input:** num = "123 ", target = 6
**Output:** \[ "1\*2\*3 ", "1+2+3 "\]
**Explanation:** Both "1\*2\*3 " and "1+2+3 " evaluate to 6.
**Example 2:**
**Input:** num = "232 ", target = 8
**Output:** \[ "2\*3+2 ", "2+3\*2 "\]
**Explanation:** Both "2\*3+2 " and "2+3\*2 " evaluate to 8.
**Example 3:**
**Input:** num = "3456237490 ", target = 9191
**Output:** \[\]
**Explanation:** There are no expressions that can be created from "3456237490 " to evaluate to 9191.
**Constraints:**
* `1 <= num.length <= 10`
* `num` consists of only digits.
* `-231 <= target <= 231 - 1` | Note that a number can contain multiple digits. Since the question asks us to find all of the valid expressions, we need a way to iterate over all of them. (Hint: Recursion!) We can keep track of the expression string and evaluate it at the very end. But that would take a lot of time. Can we keep track of the expression's value as well so as to avoid the evaluation at the very end of recursion? Think carefully about the multiply operator. It has a higher precedence than the addition and subtraction operators.
1 + 2 = 3
1 + 2 - 4 --> 3 - 4 --> -1
1 + 2 - 4 * 12 --> -1 * 12 --> -12 (WRONG!)
1 + 2 - 4 * 12 --> -1 - (-4) + (-4 * 12) --> 3 + (-48) --> -45 (CORRECT!) We simply need to keep track of the last operand in our expression and reverse it's effect on the expression's value while considering the multiply operator. |
Two pointers technique (Python, O(n) time / O(1) space) | move-zeroes | 0 | 1 | Hi there! Here is my solution to this problem that uses two pointers technique.\n\n**Code:**\n```\nclass Solution:\n def moveZeroes(self, nums: list) -> None:\n slow = 0\n for fast in range(len(nums)):\n if nums[fast] != 0 and nums[slow] == 0:\n nums[slow], nums[fast] = nums[fast], nums[slow]\n\n # wait while we find a non-zero element to\n # swap with you\n if nums[slow] != 0:\n slow += 1\n```\n\n**Algorithm complexity:**\n*Time complexity: O(n)*. Our fast pointer does not visit the same spot twice.\n*Space complexity: O(1)*. All operations are made in-place\n\nIf you like my solution, I will really appreciate your upvoting. It will help other python-developers to find it faster. And as always, I wish you an enjoyable time on LeetCode.\n\n**Special thanks for the next comments:**\n[**stanley98745**](https://leetcode.com/problems/move-zeroes/discuss/562911/two-pointers-technique-python-on-time-o1-space/513985) | 766 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
simple approach | move-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n n_len=len(nums)\n print(n_len)\n for x in range(0,n_len,1) :\n print(nums[x])\n if (nums[x]==0) : \n nums.remove(0)\n nums.append(0)\n``` | 0 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Python3 | Beats 99% | Optimized In-Place Rearrangement | move-zeroes | 0 | 1 | # Solution no. 01\n\n---\n\n\n# Intuition\nWhen approaching this problem, the idea is to perform an in-place modification of the given list of numbers. We can achieve this by first iterating through the list and moving all non-zero elements to the beginning of the list. Once we have moved all non-zero elements, we can fill the remaining positions with zeros. This approach ensures that the original order of non-zero elements is preserved while zeros are pushed to the end of the list.\n\n# Approach\n1. Initialize a variable index to keep track of the position where the next non-zero element should be placed.\n1. Iterate through each element num in the nums list.\n - If num is not equal to zero, assign num to the position index in the nums list and increment index.\n1. After the iteration, all non-zero elements have been placed at the beginning of the list, and index indicates the position where the first zero should be placed.\n1. Iterate from index to the end of the list, assigning zero to each position to fill the remaining positions with zeros.\n\nBy following this approach, we ensure that all non-zero elements are moved to the start of the list while maintaining their original order, and the remaining positions are filled with zeros.\n\n# Complexity\n- Time complexity:\n - The first pass through the list takes O(n) time to move non-zero elements to the start of the list.\n - The second pass through the list takes O(n) time to fill the remaining positions with zeros.\n - The overall time complexity is dominated by the linear passes through the list, resulting in **O(n)** time complexity.\n\n- Space complexity:\n - The algorithm only uses a constant amount of extra space, regardless of the input size. Hence Space complexity of this code is **O(1)**\n - It modifies the input list in-place without requiring additional data structures.\n\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n index = 0\n\n # Place non-zero elements at the start of the list\n for num in nums:\n if num != 0:\n nums[index] = num\n index += 1\n\n # Fill the remaining positions with zeroes\n while index < len(nums):\n nums[index] = 0\n index += 1\n```\n\n---\n\n\n\n# Solution no. 02\n\n---\n\n# Intuition\nInstead of directly filling the positions with zero after placing non-zero elements, we can maintain a pointer to indicate the position where the next non-zero element should be placed. This way, we only perform assignments when necessary, reducing the total number of assignments.\n\n# Approach\n1. Initialize a variable index to 0, which represents the position where the next non-zero element should be placed.\n1. Iterate through each element num in the nums list.\n1. If num is not equal to zero, swap nums[index] and nums[i], and increment index.\n1. After the iteration, all non-zero elements have been moved to their correct positions, and all positions after index are filled with zeros.\n1. By swapping non-zero elements with the position index, we achieve the desired result without needing a separate loop to fill remaining positions with zeros.\n\nComplexity\n- Time complexity: \n - **O(n)**\n - The single pass through the list takes O(n) time.\n - The number of assignments is minimized, which improves the constant factors involved in the time complexity.\n\n- Space complexity: \n - **O(1)**\n - The algorithm only uses a constant amount of extra space for variables.\n - It modifies the input list in-place without requiring additional data structures.\n \nWhile this alternative approach doesn\'t change the big-O time and space complexities, it might result in slightly better performance due to the reduced number of assignments.\n\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n index = 0 \n \n for i in range(len(nums)):\n if nums[i] != 0:\n # If the current element is non-zero, swap it with the element at index\n # This effectively moves non-zero elements to the beginning of the list\n nums[i], nums[index] = nums[index], nums[i]\n index += 1 \n \n```\n\n\n | 27 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Python solution, super simple, clear explanation | move-zeroes | 0 | 1 | # 1. Solution\n\n```\n def moveZeroes(self, nums):\n n = len(nums)\n i = 0\n for j in range(n):\n if (nums[j] != 0):\n nums[i], nums[j] = nums[j], nums[i]\n i += 1\n```\n\n\n# 2. Main idea\n* We use` i` to keep track of position of the first zero in the list (which changes as we go).\n* We use` j `to keep track of the first non-zero value after the first zero (which is pointed by `i`).\n* Each time we have` i` correctly points to a zero and `j` correctly points to the first non-zero after `i`, we swap the values that store at `i` and `j`.\n* By doing this, we move zeros towards the end of the list gradually until `j` reaches the end.\n* And when it does, we are done.\n\n# 3. Remarks\n* No return value needed, since we are doing in-place modification.\n* We use` nums[i], nums[j] = nums[j], nums[i]` to achieve the in-place modification because Python allows you to swaps values in a list using syntax: `x, y = y, x`.\n\n****Please upvote if you find this post useful, and welcome to any further discussion!*** | 169 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Easy solution with O(n) time complexity | move-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n count=0\n for i in range(len(nums)):\n if nums[i]!=0:\n nums[i],nums[count]=nums[count],nums[i]\n count+=1\n \n``` | 2 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
python O(n) no extra space solution | move-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n slow=0\n fast=0\n while fast < len(nums):\n if nums[slow] == 0 and nums[fast] != 0:\n nums[slow], nums[fast] = nums[fast], nums[slow]\n fast += 1\n slow +=1\n elif nums[fast] == 0:\n fast += 1\n else:\n slow += 1\n fast += 1\n``` | 1 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Python3 simple and clean code | move-zeroes | 0 | 1 | # Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n #Do not return anything, modify nums in-place instead.\n i=0\n for j in range(len(nums)):\n if(nums[i]==0 and nums[j]!=0):\n nums[i],nums[j]=nums[j],nums[i]\n if(nums[i]!=0):i+=1\n``` | 2 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Simple Python solution | move-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n n = 0\n for i in range(len(nums)):\n if nums[i]:\n nums[n], nums[i] = nums[i], nums[n]\n n += 1\n``` | 1 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
🚀unusual laconic✅ solution!🚀 | move-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSort in python is stable, so order of equal elements will be not changed\nhttps://wiki.python.org/moin/HowTo/Sorting#Sort_Stability_and_Complex_Sorts\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust sort them pretending that are only 2 types of values!\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*logn)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n nums.sort(key=lambda x: x == 0)\n return nums\n``` | 11 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Easy Solution. Two pointers Approach. Beats 98%. Python. | move-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Use two pointers and change elements in place.**\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Iterate through the array with two pointers.\n2. Left pointer points to the last replaced element.\n3. Right pointer moves ahead the array.\n4. If value does not equal zero, change the value from right and left pointer in place.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n left = 0\n for right in range(len(nums)):\n if nums[right] != 0:\n nums[right], nums[left] = nums[left], nums[right]\n left += 1\n```\n```javascript []\nvar moveZeroes = function(nums) {\n let left = 0;\n\n for (let right=0; right<nums.length; right++) {\n if (nums[right] != 0) {\n let tmp = nums[right];\n nums[right] = nums[left];\n nums[left] = tmp;\n left ++;\n }\n }\n};\n```\n# Please UPVOTE !!! | 4 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Beginner Friendly Solution | move-zeroes | 0 | 1 | \n# Approach\nTake a variable j, if the value of element in array is not zero, make value of nums[j] equal to i (non zero value of array) and count the total changes made by incrementing j.\nNext, make the value of all elements from range j to n equal to zero.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nRuntime: 163ms beats 91.01%\nMemory: 15.5MB beats 96.58%\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: List[int]) -> None:\n n = len(nums)\n j = 0\n for i in nums:\n if(i != 0):\n nums[j] = i\n j += 1\n for i in range(j,n):\n nums[i] = 0\n``` | 1 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
Pointers technique (Python) | move-zeroes | 0 | 1 | # Intuition\nHere is my solution to this problem that uses two pointers technique.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N)\n Our fast pointer does not visit the same spot twice.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n All operations are made in-place\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\nIf you like my solution, I will really appreciate your upvoting. It will help other python-developers to find it faster. And as always, I wish you an enjoyable time on LeetCode.\n# Code\n```\nclass Solution:\n def moveZeroes(self, nums: list) -> None:\n slow = 0\n for fast in range(len(nums)):\n if nums[fast] != 0 and nums[slow] == 0:\n nums[slow], nums[fast] = nums[fast], nums[slow]\n\n # wait while we find a non-zero element to\n # swap with you\n if nums[slow] != 0:\n slow += 1\n``` | 22 | Given an integer array `nums`, move all `0`'s to the end of it while maintaining the relative order of the non-zero elements.
**Note** that you must do this in-place without making a copy of the array.
**Example 1:**
**Input:** nums = \[0,1,0,3,12\]
**Output:** \[1,3,12,0,0\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[0\]
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you minimize the total number of operations done? | In-place means we should not be allocating any space for extra array. But we are allowed to modify the existing array. However, as a first step, try coming up with a solution that makes use of additional space. For this problem as well, first apply the idea discussed using an additional array and the in-place solution will pop up eventually. A two-pointer approach could be helpful here. The idea would be to have one pointer for iterating the array and another pointer that just works on the non-zero elements of the array. |
284: Time 89.38% and Space 100%, Solution with step by step explanation | peeking-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- In the constructor, the iterator is initialized and a buffer is set to the next element if it exists, otherwise, the buffer is set to None.\n- The peek method returns the element currently in the buffer without advancing the iterator.\n- The next method returns the element currently in the buffer and advances the iterator to the next element by setting the buffer to the next element if it exists, otherwise, the buffer is set to None.\n- The hasNext method returns a boolean indicating whether there are more elements to be iterated over by checking if the buffer is not None.\n\n# Complexity\n- Time complexity:\n89.38%\n\n- Space complexity:\n100%\n\n# Code\n```\nclass PeekingIterator:\n def __init__(self, iterator: Iterator):\n self.iterator = iterator\n self.buffer = self.iterator.next() if self.iterator.hasNext() else None\n\n def peek(self) -> int:\n """\n Returns the next element in the iteration without advancing the iterator.\n """\n return self.buffer\n\n def next(self) -> int:\n next = self.buffer\n self.buffer = self.iterator.next() if self.iterator.hasNext() else None\n return next\n\n def hasNext(self) -> bool:\n return self.buffer is not None\n\n``` | 3 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
python3 simple soln | peeking-iterator | 0 | 1 | ```\nclass PeekingIterator:\n def __init__(self, iterator):\n """\n Initialize your data structure here.\n :type iterator: Iterator\n """\n self.iterator = iterator\n self.current = self.iterator.next() if self.iterator.hasNext() else None \n\n def peek(self):\n """\n Returns the next element in the iteration without advancing the iterator.\n :rtype: int\n """\n return self.current\n \n\n def next(self):\n """\n :rtype: int\n """\n value = self.current\n self.current = self.iterator.next() if self.iterator.hasNext() else None \n return value\n \n def hasNext(self):\n """\n :rtype: bool\n """\n return self.current != None\n \n | 23 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
Python | Easy Solution | O(1) | 89% beats | peeking-iterator | 0 | 1 | ```\nclass PeekingIterator:\n def __init__(self, iterator):\n """\n Initialize your data structure here.\n :type iterator: Iterator\n """\n self.iterator = iterator\n self.to_peek = self.iterator.next() if self.iterator.hasNext() else None\n\n def peek(self):\n """\n Returns the next element in the iteration without advancing the iterator.\n :rtype: int\n """\n return self.to_peek\n\n def next(self):\n """\n :rtype: int\n """\n temp = self.to_peek\n self.to_peek = self.iterator.next() if self.iterator.hasNext() else None\n return temp\n\n \n\n def hasNext(self):\n """\n :rtype: bool\n """\n return self.to_peek is not None\n\n```\nPlease upvote if you get it. | 13 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
[ Python ] Easy Solution | Double beats 100% submit | peeking-iterator | 0 | 1 | ```\nclass PeekingIterator:\n def __init__(self, iterator):\n """\n Initialize your data structure here.\n :type iterator: Iterator\n """\n self.data = iterator.v\n self.index = -1\n \n\n def peek(self):\n """\n Returns the next element in the iteration without advancing the iterator.\n :rtype: int\n """\n return self.data[self.index+1]\n\n def next(self):\n """\n :rtype: int\n """\n self.index += 1\n return self.data[self.index]\n\n def hasNext(self):\n """\n :rtype: bool\n """\n return True if self.index + 1 < len(self.data) else False\n``` | 2 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
Python3 O(N) solution with a pointer (95.35% Runtime) | peeking-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nDefine a pointer which stores next value\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Pre-store next value\n- If peek needed, return next value only\n- If hasNext needed, return True if current next value is valid\n- If next needed, renew your next to real next one and return old next value \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\n# Below is the interface for Iterator, which is already defined for you.\n#\n# class Iterator:\n# def __init__(self, nums):\n# """\n# Initializes an iterator object to the beginning of a list.\n# :type nums: List[int]\n# """\n#\n# def hasNext(self):\n# """\n# Returns true if the iteration has more elements.\n# :rtype: bool\n# """\n#\n# def next(self):\n# """\n# Returns the next element in the iteration.\n# :rtype: int\n# """\n\nclass PeekingIterator:\n def __init__(self, iterator):\n """\n Initialize your data structure here.\n :type iterator: Iterator\n """\n self.iterator = iterator\n self.next_val = self.iterator.next() if self.iterator.hasNext() else None\n\n def peek(self):\n """\n Returns the next element in the iteration without advancing the iterator.\n :rtype: int\n """\n return self.next_val\n\n def next(self):\n """\n :rtype: int\n """\n old = self.next_val\n self.next_val = self.iterator.next() if self.iterator.hasNext() else None\n return old\n \n def hasNext(self):\n """\n :rtype: bool\n """\n return self.next_val != None\n \n# Your PeekingIterator object will be instantiated and called as such:\n# iter = PeekingIterator(Iterator(nums))\n# while iter.hasNext():\n# val = iter.peek() # Get the next element but not advance the iterator.\n# iter.next() # Should return the same value as [val].\n``` | 0 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
Python Solution | peeking-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass PeekingIterator:\n def __init__(self, iterator):\n """\n Initialize your data structure here.\n :type iterator: Iterator\n """\n self.data = iterator.v\n self.index = -1\n \n\n def peek(self):\n """\n Returns the next element in the iteration without advancing the iterator.\n :rtype: int\n """\n return self.data[self.index+1]\n\n def next(self):\n """\n :rtype: int\n """\n self.index += 1\n return self.data[self.index]\n\n def hasNext(self):\n """\n :rtype: bool\n """\n return True if self.index + 1 < len(self.data) else False\n``` | 0 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
Python solution easy | peeking-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe iterator class only has two methods: hasNext() and next(). next() would inevitably remove the next element, so we need to cache this result and return it in future.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n### __init__\nwe need two variables: one to store the iterator, and one to cache any elements removed by peek(). \n\n```\nself.iterator = iterator # store the iterator\nself.nextElement = -1 # store number returned by peak(),\n #initialised to -1 as iterator only has positive numbers\n```\n\n### peek\nif next() has already been called by peek() prior and we cached it, we just need to return the cached value.\n\nelse, we call ```iterator.next()``` to get the next element, and store it in a variable, ```self.nextElement```.\n\n### next\nif no value has been cached in ```self.nextElement```, then we need to call ```next()```\n\nelse we just return ```self.nextElement```, and clear the cached value by setting ```self.nextElement``` to -1.\n\n### hasnext\nThe iterator\'s ```hasNext()``` must either return true, or there must be a cached value in ```self.nextElement```.\n\n# Complexity\n- Time complexity: O(n) for each operation\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) to store the iterator, O(1) to store cached value\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Below is the interface for Iterator, which is already defined for you.\n#\n# class Iterator:\n# def __init__(self, nums):\n# """\n# Initializes an iterator object to the beginning of a list.\n# :type nums: List[int]\n# """\n#\n# def hasNext(self):\n# """\n# Returns true if the iteration has more elements.\n# :rtype: bool\n# """\n#\n# def next(self):\n# """\n# Returns the next element in the iteration.\n# :rtype: int\n# """\n\nclass PeekingIterator:\n def __init__(self, iterator):\n """\n Initialize your data structure here.\n :type iterator: Iterator\n """\n self.iterator = iterator\n self.nextElement = -1\n\n def peek(self):\n """\n Returns the next element in the iteration without advancing the iterator.\n :rtype: int\n """\n if self.nextElement != -1:\n return self.nextElement\n self.nextElement = self.iterator.next()\n return self.nextElement\n\n def next(self):\n """\n :rtype: int\n """\n if self.nextElement == -1:\n return self.iterator.next()\n ans = self.nextElement\n self.nextElement = -1\n return ans \n\n def hasNext(self):\n """\n :rtype: bool\n """\n return self.iterator.hasNext() or self.nextElement != -1\n \n\n# Your PeekingIterator object will be instantiated and called as such:\n# iter = PeekingIterator(Iterator(nums))\n# while iter.hasNext():\n# val = iter.peek() # Get the next element but not advance the iterator.\n# iter.next() # Should return the same value as [val].\n``` | 0 | Design an iterator that supports the `peek` operation on an existing iterator in addition to the `hasNext` and the `next` operations.
Implement the `PeekingIterator` class:
* `PeekingIterator(Iterator nums)` Initializes the object with the given integer iterator `iterator`.
* `int next()` Returns the next element in the array and moves the pointer to the next element.
* `boolean hasNext()` Returns `true` if there are still elements in the array.
* `int peek()` Returns the next element in the array **without** moving the pointer.
**Note:** Each language may have a different implementation of the constructor and `Iterator`, but they all support the `int next()` and `boolean hasNext()` functions.
**Example 1:**
**Input**
\[ "PeekingIterator ", "next ", "peek ", "next ", "next ", "hasNext "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 2, 2, 3, false\]
**Explanation**
PeekingIterator peekingIterator = new PeekingIterator(\[1, 2, 3\]); // \[**1**,2,3\]
peekingIterator.next(); // return 1, the pointer moves to the next element \[1,**2**,3\].
peekingIterator.peek(); // return 2, the pointer does not move \[1,**2**,3\].
peekingIterator.next(); // return 2, the pointer moves to the next element \[1,2,**3**\]
peekingIterator.next(); // return 3, the pointer moves to the next element \[1,2,3\]
peekingIterator.hasNext(); // return False
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* All the calls to `next` and `peek` are valid.
* At most `1000` calls will be made to `next`, `hasNext`, and `peek`.
**Follow up:** How would you extend your design to be generic and work with all types, not just integer? | Think of "looking ahead". You want to cache the next element. Is one variable sufficient? Why or why not? Test your design with call order of peek() before next() vs next() before peek(). For a clean implementation, check out Google's guava library source code. |
Python3 Solution | find-the-duplicate-number | 0 | 1 | \n```\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n slow,fast=0,0\n while True:\n slow=nums[slow]\n fast=nums[nums[fast]]\n if slow==fast:\n break\n\n slow2=0\n while True:\n slow=nums[slow]\n slow2=nums[slow2]\n if slow==slow2:\n return slow \n``` | 2 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
✅ 97.77% 6 Approaches Set, Count, Binary Search, Fast Slow, Mark, Sort | find-the-duplicate-number | 1 | 1 | # Comprehensive Guide to Solving "Find the Duplicate Number"\n\n## Introduction & Problem Statement\n\nGiven an array of integers, $$ \\text{nums} $$, containing $$ n + 1 $$ integers where each integer is in the range $$[1, n]$$ inclusive, find the one repeated number in the array. The challenge lies in solving the problem without modifying the array $$ \\text{nums} $$ and using only constant extra space. This problem is a classic example of array manipulation and number theory combined, making it an interesting problem to tackle.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Array Representation**: \n The array contains $$ n + 1 $$ integers, each falling within the range $$[1, n]$$.\n\n2. **Single Duplication**: \n Only one integer is repeated in the array, and it can be repeated more than once.\n\n3. **Constraints**: \n - Array length: $$ n + 1 $$, where $$ 1 \\leq n \\leq 10^5 $$\n - $$ 1 \\leq \\text{nums}[i] \\leq n $$\n\n## Six Primary Strategies to Solve the Problem:\n\n1. **Set/Hash Table**: Use a hash table to track the numbers that have appeared so far.\n2. **Count Array**: Use an auxiliary array to count the frequency of each number.\n3. **Marking in Array**: Negate the value at the index corresponding to each number in the array.\n4. **Floyd\'s Cycle Detection (Fast-Slow Pointers)**: Treat the array as a linked list to find a cycle.\n5. **Binary Search**: Count the numbers less than or equal to the middle element to find the duplicate.\n6. **Sort**: Sort the array and check adjacent elements for duplicates.\n\n---\n\n# In-Depth Strategies for Finding the Duplicate Number in an Array\n\n## Live Coding & comparing 6 Approaches\nhttps://youtu.be/J3qIbJA7t9Q?si=1H3cjdkBb7QQ8D7x\n\n## 1. Set/Hash Table Approach\n\n#### Detailed Logic:\n1. Initialize an empty set `seen`.\n2. Traverse through the array `nums`.\n3. For each element `num` in `nums`, check if it exists in `seen`.\n - If it does, return `num` as the duplicate.\n - Otherwise, add `num` to `seen`.\n\n#### Pros:\n- Extremely straightforward to implement.\n- No need to sort or modify the original array.\n\n#### Cons:\n- This approach requires extra space for the set, which violates the problem\'s constraint of constant extra space.\n\n#### Time and Space Complexity:\n- **Time Complexity**: $$O(n)$$ because we iterate through the array once.\n- **Space Complexity**: $$O(n)$$ for storing the set.\n\n## Code Set\n``` Python []\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n seen = set()\n for num in nums:\n if num in seen:\n return num\n seen.add(num)\n\n```\n``` Go []\nfunc findDuplicate(nums []int) int {\n seen := make(map[int]bool)\n for _, num := range nums {\n if seen[num] {\n return num\n }\n seen[num] = true\n }\n return -1 // Just to satisfy the compiler, this should never be reached\n}\n```\n``` Rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn find_duplicate(nums: Vec<i32>) -> i32 {\n let mut seen = HashSet::new();\n for &num in nums.iter() {\n if seen.contains(&num) {\n return num;\n }\n seen.insert(num);\n }\n -1 // Just to satisfy the compiler, this should never be reached\n}\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int findDuplicate(std::vector<int>& nums) {\n std::unordered_set<int> seen;\n for (int num : nums) {\n if (seen.find(num) != seen.end()) {\n return num;\n }\n seen.insert(num);\n }\n return -1; // Just to satisfy the compiler, this should never be reached\n }\n};\n```\n``` Java []\nclass Solution {\n public int findDuplicate(int[] nums) {\n HashSet<Integer> seen = new HashSet<>();\n for (int num : nums) {\n if (seen.contains(num)) {\n return num;\n }\n seen.add(num);\n }\n return -1; // Just to satisfy the compiler, this should never be reached\n}\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findDuplicate = function(nums) {\n const seen = new Set();\n for (const num of nums) {\n if (seen.has(num)) {\n return num;\n }\n seen.add(num);\n }\n return -1; // Just to satisfy the compiler, this should never be reached\n}\n```\n``` C# []\npublic class Solution {\n public int FindDuplicate(int[] nums) {\n HashSet<int> seen = new HashSet<int>();\n foreach (int num in nums) {\n if (seen.Contains(num)) {\n return num;\n }\n seen.Add(num);\n }\n return -1; // Just to satisfy the compiler, this should never be reached\n }\n}\n```\n\n---\n\n## 2. Count Array Approach\n\n#### Detailed Logic:\n1. Initialize an auxiliary count array `cnt` with zeros. Its size will be $$ n+1 $$ to accommodate all possible numbers.\n2. Traverse through the array `nums`.\n3. For each element `num` in `nums`, increment `cnt[num]` by 1.\n4. Check if `cnt[num]` exceeds 1; if yes, return `num` as the duplicate.\n\n#### Pros:\n- Implementation is simple and direct.\n \n#### Cons:\n- Extra space is used for the count array, which contradicts the constraint of constant extra space.\n\n#### Time and Space Complexity:\n- **Time Complexity**: $$O(n)$$ due to a single pass through the array.\n- **Space Complexity**: $$O(n)$$ for the count array.\n\n\n## Code Count\n``` Python []\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n cnt = [0] * (len(nums) + 1)\n for num in nums:\n cnt[num] += 1\n if cnt[num] > 1:\n return num\n return len(nums)\n```\n\n---\n\n## 3. Marking in Array Approach\n\n#### Detailed Logic:\n1. Traverse the array `nums`.\n2. For each element `num`, take its absolute value as an index (`idx = abs(num)`).\n3. If `nums[idx]` is negative, then `idx` is the duplicate number.\n4. Otherwise, negate `nums[idx]`.\n\n#### Pros:\n- Doesn\'t use any extra space other than the input array.\n \n#### Cons:\n- Modifies the original array, which is disallowed by the problem constraints.\n\n#### Time and Space Complexity:\n- **Time Complexity**: $$O(n)$$ for a single pass through the array.\n- **Space Complexity**: $$O(1)$$ as no extra space is used.\n\n## Code Mark\n``` Python []\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n for num in nums:\n idx = abs(num)\n if nums[idx] < 0:\n return idx\n nums[idx] = -nums[idx]\n return len(nums)\n```\n\n---\n\n## 4. Fast-Slow Pointers Approach (Floyd\'s Cycle Detection)\n\n### Detailed Logic Behind the Fast-Slow Pointers Approach\n\n**Step 1: Initialize Pointers**\nFirst, we initialize two pointers, `slow` and `fast`, both set to `nums[0]`. This is the starting point for both pointers, and it\'s done to set up the conditions for Floyd\'s cycle detection algorithm.\n\n**Step 2: Detect a Cycle**\nIn this step, we enter a `while` loop where the `slow` pointer moves one step at a time (`slow = nums[slow]`), while the `fast` pointer moves two steps (`fast = nums[nums[fast]]`). The loop continues until both pointers meet at some point within the cycle. Note that this meeting point is not necessarily the duplicate number; it\'s just a point inside the cycle.\n\nWhy does this happen? Because there is a duplicate number, there must be a cycle in the \'linked list\' created by following `nums[i]` as next elements. Once a cycle is detected, the algorithm breaks out of this loop.\n\n**Step 3: Find the Start of the Cycle (Duplicate Number)**\nAfter identifying a meeting point inside the cycle, we reinitialize the `slow` pointer back to `nums[0]`. The `fast` pointer stays at the last meeting point. Now, we enter another `while` loop where both pointers move one step at a time. The reason behind this is mathematical: according to Floyd\'s cycle detection algorithm, when both pointers move at the same speed, they will eventually meet at the starting point of the cycle. This is the duplicate number we are looking for.\n\n**Step 4: Return the Duplicate Number**\nFinally, when the `slow` and `fast` pointers meet again, the meeting point will be the duplicate number, and we return it as the output.\n\n#### Pros:\n- Adheres to the constant space constraint.\n- Doesn\'t modify the original array.\n\n#### Cons:\n- The logic can be slightly tricky to grasp initially.\n\n#### Time and Space Complexity:\n- **Time Complexity**: $$O(n)$$, where $$ n $$ is the length of the array.\n- **Space Complexity**: $$O(1)$$ as no extra space is required.\n\n## Code Fast Slow Pointers\n``` Python []\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n slow = nums[0]\n fast = nums[0]\n\n while True:\n slow = nums[slow]\n fast = nums[nums[fast]]\n if slow == fast:\n break\n\n slow = nums[0]\n while slow != fast:\n slow = nums[slow]\n fast = nums[fast]\n \n return slow\n```\n``` Go []\nfunc findDuplicate(nums []int) int {\n slow := nums[0]\n fast := nums[0]\n \n for {\n slow = nums[slow]\n fast = nums[nums[fast]]\n \n if slow == fast {\n break\n }\n }\n \n slow = nums[0]\n for slow != fast {\n slow = nums[slow]\n fast = nums[fast]\n }\n \n return slow\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_duplicate(nums: Vec<i32>) -> i32 {\n let mut slow = nums[0];\n let mut fast = nums[0];\n \n loop {\n slow = nums[slow as usize];\n fast = nums[nums[fast as usize] as usize];\n \n if slow == fast {\n break;\n }\n }\n \n slow = nums[0];\n while slow != fast {\n slow = nums[slow as usize];\n fast = nums[fast as usize];\n }\n \n slow\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int findDuplicate(vector<int>& nums) {\n int slow = nums[0];\n int fast = nums[0];\n\n do {\n slow = nums[slow];\n fast = nums[nums[fast]];\n } while (slow != fast);\n\n slow = nums[0];\n while (slow != fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n\n return slow;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int findDuplicate(int[] nums) {\n int slow = nums[0];\n int fast = nums[0];\n \n do {\n slow = nums[slow];\n fast = nums[nums[fast]];\n } while (slow != fast);\n \n slow = nums[0];\n while (slow != fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n \n return slow;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findDuplicate = function(nums) {\n let slow = nums[0];\n let fast = nums[0];\n \n do {\n slow = nums[slow];\n fast = nums[nums[fast]];\n } while (slow !== fast);\n \n slow = nums[0];\n while (slow !== fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n \n return slow;\n};\n```\n``` PHP []\nclass Solution {\n function findDuplicate($nums) {\n $slow = $nums[0];\n $fast = $nums[0];\n \n do {\n $slow = $nums[$slow];\n $fast = $nums[$nums[$fast]];\n } while ($slow != $fast);\n \n $slow = $nums[0];\n while ($slow != $fast) {\n $slow = $nums[$slow];\n $fast = $nums[$fast];\n }\n \n return $slow;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int FindDuplicate(int[] nums) {\n int slow = nums[0];\n int fast = nums[0];\n \n do {\n slow = nums[slow];\n fast = nums[nums[fast]];\n } while (slow != fast);\n \n slow = nums[0];\n while (slow != fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n \n return slow;\n }\n}\n```\n\n---\n\n### 5. Binary Search Approach\n\n#### Detailed Logic:\n1. Initialize `low` to 1 and `high` to $$ n $$.\n2. Run a binary search loop until `low < high`:\n - Calculate `mid` as the midpoint between `low` and `high`.\n - Count elements in the array that are less than or equal to `mid`.\n - If the count is greater than `mid`, set `high = mid`. Otherwise, set `low = mid + 1`.\n\n#### Pros:\n- No modification to the original array.\n \n#### Cons:\n- Somewhat more complex to understand due to binary search mechanics.\n\n#### Time and Space Complexity:\n- **Time Complexity**: $$O(n \\log n)$$ due to binary search combined with array scanning.\n- **Space Complexity**: $$O(1)$$ as no extra space is needed.\n\n\n## Code Binary Search\n``` Python \nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n low, high = 1, len(nums) - 1\n \n while low < high:\n mid = (low + high) // 2\n count = 0\n for num in nums:\n if num <= mid:\n count += 1\n if count > mid:\n high = mid\n else:\n low = mid + 1\n \n return low\n\n```\n\n## 6. Sort Approach\n\n#### Detailed Logic:\n1. Sort the `nums` array in ascending order.\n2. Traverse the sorted array and compare adjacent elements.\n - If two adjacent elements are equal, return one of them as the duplicate.\n3. If no duplicate is found, return the length of the array (this should not happen under the problem constraints).\n\n#### Pros:\n- Simple to understand and implement.\n- Utilizes Python\'s efficient built-in sorting algorithm.\n\n#### Cons:\n- Modifies the original array by sorting it.\n- Not the most time-efficient solution for this problem.\n\n#### Time and Space Complexity:\n- **Time Complexity**: $$ O(n \\log n) $$ due to sorting.\n- **Space Complexity**: $$ O(1) $$ if sorting is done in-place, otherwise $$ O(n) $$.\n\n---\n\n\n## Code Sort\n``` Python []\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n nums.sort()\n for i in range(1, len(nums)):\n if nums[i] == nums[i-1]:\n return nums[i]\n return len(nums)\n```\n\n## Performance\n\n| Language | Time (ms) | Space (MB) | Approach | \n|-----------|-----------|------------|------------------|\n| Java | 4 | 56.8 | Fast Slow Pointers| |\n| Rust | 10 | 3.1 | Fast Slow Pointers| |\n| JavaScript| 75 | 49.6 | Fast Slow Pointers| |\n| C++ | 73 | 61.5 | Fast Slow Pointers\n| Go | 98 | 9.2 | Fast Slow Pointers| |\n| C# | 167 | 54.6 | Fast Slow Pointers| |\n| PHP | 179 | 31.7 | Fast Slow Pointers| |\n| Java | 20 | 61.2 | Set | |\n| Rust | 26 | 4.1 | Set | |\n| C# | 193 | 50.7 | Set | |\n| Go | 100 | 9.2 | Set | |\n| JavaScript| 92 | 61.3 | Set | |\n| C++ | 135 | 84.2 | Set | |\n| Python3 | 495 | 32.3 | Set | |\n| Python3 | 518 | 31.1 | Fast Slow Pointers| |\n| Python3 | 518 | 30.9 | Count | |\n| Python3 | 522 | 31.0 | Mark | |\n| Python3 | 564 | 31.1 | Sort | |\n| Python3 | 724 | 31.0 | Binary Search | |\n\n\n\n\n## Conclusion\n\nEach strategy has its merits and demerits, and the choice of approach depends on the specific constraints of the problem. Understanding these methods not only helps in solving this problem but also broadens one\'s array manipulation and algorithmic skills. Happy coding! | 140 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Floyd's Tortoise and Hare (Cycle Detection)✅ | O( n )✅ | (Step by step explanation)✅ | find-the-duplicate-number | 0 | 1 | # Intuition\nThe problem is asking us to find a duplicate number in an array of integers. One approach is to use Floyd\'s Tortoise and Hare (Cycle Detection) algorithm. The intuition behind this approach is that if we consider the array as a linked list where the value at each index represents the next index, and there is a duplicate number, it forms a cycle in the linked list.\n\n# Approach\nWe can use two pointers, slow and fast, to traverse the array as if it were a linked list. The slow pointer moves one step at a time, and the fast pointer moves two steps at a time. If there is a duplicate number in the array, the two pointers will eventually meet within the cycle formed by the duplicate number.\n\n1. Initialize both `slow` and `fast` pointers at the first element (index 0).\n2. Move `slow` one step at a time and `fast` two steps at a time until they meet within the cycle.\n3. Reset the `slow` pointer to the first element and continue moving both pointers one step at a time until they meet again. The meeting point is the start of the cycle, which corresponds to the duplicate number in the array.\n\n# Complexity\n- Time complexity: O(n)\n - The slow and fast pointers will meet within the cycle, which takes at most O(n) steps, where n is the length of the input array.\n- Space complexity: O(1)\n - The algorithm uses only a constant amount of extra space for the slow and fast pointers.\n\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n slow, fast = 0, 0\n\n while True:\n slow = nums[slow]\n fast = nums[nums[fast]]\n if slow == fast:\n break\n\n slow = 0\n while slow != fast:\n slow = nums[slow]\n fast = nums[fast]\n\n return slow\n```\n</details>\n\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n int findDuplicate(vector<int>& nums) {\n int slow = 0, fast = 0;\n\n while (true) {\n slow = nums[slow];\n fast = nums[nums[fast]];\n if (slow == fast) {\n break;\n }\n }\n\n slow = 0;\n while (slow != fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n\n return slow;\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n\n | 1 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Two Pointer solution with Floyd's Tortoise and Hare algorithm - Python, JavaScript, Java and C++ | find-the-duplicate-number | 1 | 1 | Before starting my article, why do I have to get multiple downvotes in a minute? Please show your respect to others. Thanks. \n\n# Intuition\nslow pointer moves once and fast pointer move twice.\n\n---\n\n# Solution Video\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/UUqfQTYmmLs\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,367\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\nAlgorithm Overview:\n1. Initialize two pointers, `slow` and `fast`, to the first element of the input list `nums`.\n2. Iterate through the list using the Floyd\'s Tortoise and Hare algorithm(See below) to find a cycle.\n3. Once a cycle is found, reset one of the pointers to the beginning of the list and continue iterating until both pointers meet again.\n\nDetailed Explanation:\n1. Initialize `slow` and `fast` pointers to the first element of the input list `nums`.\n2. Enter a loop to detect a cycle:\n a. Update `slow` to the next element using `nums[slow]`.\n b. Update `fast` to the next element after `nums[fast]`, effectively moving two steps.\n c. Check if `slow` is equal to `fast`. If they are equal, a cycle has been found, and exit the loop.\n3. After finding the cycle, reset one of the pointers (`slow2`) to the beginning of the list.\n4. Enter a loop to find the duplicate element:\n a. Update `slow` using `nums[slow]`.\n b. Update `slow2` using `nums[slow2]`.\n c. Continue this process until `slow` is equal to `slow2`, which represents the duplicate element.\n5. Return the duplicate element found (`slow`).\n\n\n---\n\n# Floyd\'s Tortoise and Hare algorithm\n\nFloyd\'s Tortoise and Hare algorithm, also known as Floyd\'s Cycle Detection algorithm, is an algorithm used to detect loops (cycles) in data structures like linked lists or arrays. It has been proven to reliably detect cycles under specific circumstances and can be applied to finding duplicate elements.\n\nThis algorithm employs two pointers, referred to as the "tortoise" and the "hare," to traverse the list.\n\n- **Tortoise**: A pointer that advances one step at a time through the list.\n- **Hare**: A pointer that advances two steps at a time through the list.\n\nUsing these pointers, you progress until the hare catches up with the tortoise or a cycle is detected.\n\nHere\'s an overview of the algorithm:\n\n1. **Phase 1 (Cycle Detection)**:\n Move the tortoise and hare, advancing the hare twice as fast as the tortoise, until the hare catches up with the tortoise or a cycle is detected. If a cycle is detected, reset the tortoise and move the hare back to its position before the reset.\n\n2. **Phase 2 (Cycle Start Detection)**:\n Move the tortoise and hare one step at a time until they match again. The position where they match again is the starting point of the cycle, corresponding to the duplicate element.\n\nLet\'s explain why this works for the problem at hand:\n\n- **Properties of Floyd\'s Tortoise and Hare Algorithm**:\n The algorithm ensures that the tortoise and hare will match again at some position in the list. Exploiting this property, if a cycle exists, the tortoise and hare will certainly match at some position within the cycle.\n\n- **Relation between Duplicate Element and Cycle**:\n In the presence of a duplicate element, the duplicate corresponds to the starting point of the cycle. Starting from the first element as the tortoise, and moving through the duplicates until reaching a duplicate (cycle start), the hare will join, and the tortoise and hare will match again inside the cycle.\n\nTherefore, the Floyd\'s Tortoise and Hare Algorithm provides an efficient and reliable way to find duplicate elements.\n\nWe can apply the same algorithm to `Linked List cycle \u2161`. I calculate movement distance of the two pointers with easy mathematics knowledge. I hope you can understand it easily and deeply.\n\nhttps://youtu.be/eW5pVXX2dow\n\n---\n\n# How it works\n\n```\nInput: nums = [1,3,4,2,2]\n```\n\nInitialze `slow` and `fast` pointers with `nums[0]` \n\n```\nslow = 1 (nums[0])\nfast = 1 (nums[0])\n```\nStart iteration until the both pointers are the same value.\n```\nIteration 1:\nslow: 3 (nums[1])\nfast: 2 (nums[nums[1]] = nums[3])\n\nIteration 2:\nslow: 2 (nums[3])\nfast: 2 (nums[nums[2]] = nums[4])\n\nNow the both pointers are equal, so break the loop.\n```\n\nSet `nums[0]` to `slow2` pointer. Start Itetation again until `slow` and `slow2` are equal.\n\n```\nIteration 1:\nslow: 4 (nums[2])\nslow2: 3 (nums[1])\n\nIteration 2:\nslow: 2 (nums[4])\nslow2: 2 (nums[3])\n\nNow the both pointers are equal, so break the loop.\n```\n```\nInput: 2\n```\n\n\n---\n\n\n\n# Visualization of Floyd\'s Tortoise and Hare algorithm \n\n\n\n\nAt first, Let\'s think with Linked List and try to find starting node of cycle which is `y`.\n\nNow, slow and fast pointers are at `node x`\n\n`slow` pointer moves once which is at `node y`\n`fast` pointer moves twice which is at `node z`\n\nthey don\'t meet each other, so let\'s continue\n\n`slow` pointer moves once which is at `node z`\n`fast` pointer moves twice which is at `node z`\n\nnow they meet each other, so let\'s initialize fast pointer with `node x`\n\n`slow` pointer moves once which is at `node y`\n`fast` pointer moves `once` which is at `node y`\n\nThat\'s why we can find starting node of cycle `node y`.\n\nLet\'s calculate movement distance of slow and fast pointers\n\n`slow` pointer moves `A + B`\n`fast` pointer moves `A + B + C + B`\n\nSince slow pointer moves once and fast pointer moves twice, the below formula is vaild.\n\n`2(A + B) = A + B + C + B`\n\nLet\'s simplify the formula\n\n`2A + 2B = 2B + A + C`\n\nDelete `2B` at both sides\n`2A = A + C`\n\nDelete `A` at both sides\n`A = C`\n\nso, it turns out `distance A` and `distance C` is actually the same. When two pointers meet at `node z` then `fast pointer` is initialized with `node x` again and each pointer moves through path `A` or `C` one by one, so that we can find starting node of cycle which is `node y`.\n\n#### \u2B50\uFE0FLet\'s apply this idea to this question. Look at the below list in the picture.\n\nnow slow and fast pointers are at `1`\n\n`slow` pointer moves once which is at `3`\n`fast` pointer moves twice which is at `2`\n\nthey are not the same. Let\'s continue.\n\n`slow` pointer moves once which is at `2`\n`fast` pointer moves twice which is at `2`\n\nthey meet each other at value `2`.\n\nLet\'s initialize `slow2` with `1`. And distance between `2` and `4` cycle is similar to `C` distance of the above list.\n\n`slow` pointer moves once which is at `4`\n`slow2` pointer moves once which is at `3`\n\nthey are not the same. Let\'s continue.\n\n`slow` pointer moves once which is at `2`\n`slow2` pointer moves once which is at `2`\n\n\nFinally, they are the same value.\n```\nOutput: 2\n```\nWait! For just in case, is there anyone who think why we need the second loop with slow and slow2? Because we found `2` in the first loop.\n\nThe second loop with `slow` and `slow2` is necessary to find the starting point of the cycle, which corresponds to the duplicate element in the array. Let me explain why this is needed:\n\nIn the first loop (cycle detection phase) using the Floyd\'s Tortoise and Hare algorithm, we detect that there is a cycle in the array by finding a position where the slow and fast pointers meet. However, this position is not necessarily the starting point of the cycle or the duplicate element. It\'s just a position within the cycle.\n\nThe second loop (cycle start detection phase) helps us find the actual starting point of the cycle, which is the duplicate element we are looking for. The starting point of the cycle is the position where the slow and slow2 pointers meet. This second loop is crucial to pinpoint the exact duplicate element in the array.\n\nWithout this second loop, we would have detected the presence of a cycle but would not have determined the duplicate element. The second loop is essential for identifying the duplicate element within the cycle.\n\nTry to run the code below with input `[2,5,9,6,9,3,8,9,7,1]`. We should return `9` and the first loop should stop at `7`.\n\n# Complexity\n- Time complexity: O(n)\n\n\n- Space complexity: O(1)\n\n```python []\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n slow = nums[0]\n fast = nums[0]\n \n while True:\n slow = nums[slow]\n fast = nums[nums[fast]]\n if slow == fast:\n break\n \n slow2 = nums[0]\n while slow != slow2:\n slow = nums[slow]\n slow2 = nums[slow2]\n\n return slow\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findDuplicate = function(nums) {\n let slow = nums[0];\n let fast = nums[0];\n\n while (true) {\n slow = nums[slow];\n fast = nums[nums[fast]];\n\n if (slow === fast) {\n break;\n }\n }\n\n let slow2 = nums[0];\n\n while (slow !== slow2) {\n slow = nums[slow];\n slow2 = nums[slow2];\n }\n\n return slow; \n};\n```\n```java []\nclass Solution {\n public int findDuplicate(int[] nums) {\n int slow = nums[0];\n int fast = nums[0];\n\n while (true) {\n slow = nums[slow];\n fast = nums[nums[fast]];\n\n if (slow == fast) {\n break;\n }\n }\n\n int slow2 = nums[0];\n\n while (slow != slow2) {\n slow = nums[slow];\n slow2 = nums[slow2];\n }\n\n return slow; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findDuplicate(vector<int>& nums) {\n int slow = nums[0];\n int fast = nums[0];\n\n while (true) {\n slow = nums[slow];\n fast = nums[nums[fast]];\n\n if (slow == fast) {\n break;\n }\n }\n\n int slow2 = nums[0];\n\n while (slow != slow2) {\n slow = nums[slow];\n slow2 = nums[slow2];\n }\n\n return slow; \n }\n};\n```\n\n\n---\n\n\nThank you for reading. \u2B50\uFE0FIf you like the article, don\'t forget to upvote it and subscribe to my youtube channel!\n\nMy next post for daily coding challenge on Sep 20, 2023\nhttps://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/solutions/4066549/how-we-think-about-a-solution-on-time-o1-space-python-javascript-java-c/\n\nHave a nice day! | 71 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.