title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[0ms][1LINER][100%][Fastest Solution Explained] O(n)time complexity O(n)space complexity | range-sum-query-immutable | 1 | 1 | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* *** Java ***\n\n```\n\n/**\n * Using a prefix sum array\n *\n * prefixSum[i] = prefixSum[i-1] + nums[i-1]. Length of prefixSum array is 1 +\n * length of input array.\n *\n * sumRange(1,3) = prefixSum[3+1] - prefixSum[1]\n *\n * Time Complexity: NumArray() -> O(N). sumRange() -> O(1)\n *\n * Space Complexity: O(N) (Can be O(1) if allowed to modify nums array)\n *\n * N = Length of input array.\n */\nclass NumArray {\n\n int[] prefixSum;\n\n public NumArray(int[] nums) {\n if (nums == null) {\n throw new IllegalArgumentException("Input is null");\n }\n\n prefixSum = new int[nums.length + 1];\n\n for (int i = 1; i <= nums.length; i++) {\n prefixSum[i] = prefixSum[i - 1] + nums[i - 1];\n }\n }\n\n public int sumRange(int left, int right) {\n if (left < 0 || right >= prefixSum.length - 1) {\n throw new IndexOutOfBoundsException("Input indices are out of bounds");\n }\n\n // Here both left and right are inclusive.\n // right maps to right+1 in prefixSum. left maps to left+1 in prefixSum.\n // To get the result subtract the prefixSum before left index from prefixSum at\n // right index.\n return prefixSum[right + 1] - prefixSum[left];\n }\n}\n\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC***\n | 9 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
Beats 99.93% of the python users | range-sum-query-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can use a prefix sum array for this problem.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity of building the prefix_array is $$O(n)$$ but you\'ll get your answer for sumRange() function within $$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity is $$O(n)$$ as we have used extra space for building the prefix array.\n# Code\n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n self.prefix_array = [nums[0]]\n for i in range(1,len(nums)):\n self.prefix_array.append(nums[i]+self.prefix_array[-1])\n\n def sumRange(self, left: int, right: int) -> int:\n if left == 0:\n return self.prefix_array[right]\n return self.prefix_array[right]-self.prefix_array[left-1]\n\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# param_1 = obj.sumRange(left,right)\n``` | 4 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
Easiest PYTHON solution | range-sum-query-immutable | 0 | 1 | \n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n self.nums = nums\n\n def sumRange(self, left: int, right: int) -> int:\n return sum(self.nums[left:right+1])\n\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# param_1 = obj.sumRange(left,right) | 8 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
presum list python3 | range-sum-query-immutable | 0 | 1 | Construct the instance takes O(N), but the sumRange is O(1), given that sumRange would be called multiple times, it is worth it to pre-calculated the presum list. The first element is zero becuase the sum before the 0 index num is zero,\n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n accu_sum = 0\n self._pre_sum = [0,]\n for num in nums:\n accu_sum += num\n self._pre_sum.append(accu_sum)\n \n def sumRange(self, left: int, right: int) -> int:\n return self._pre_sum[right+1] - self._pre_sum[left]\n\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# param_1 = obj.sumRange(left,right)\n``` | 2 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
efficient python3 | range-sum-query-2d-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass NumMatrix:\n\n def __init__(self, matrix: List[List[int]]):\n rowLength, colLength = len(matrix), len(matrix[0])\n self.sumMat = [[0] * (colLength + 1) for rows in range(rowLength + 1)]\n \n for row in range(rowLength):\n prefixSum = 0\n for col in range(colLength):\n prefixSum += matrix[row][col]\n above = self.sumMat[row][col + 1]\n self.sumMat[row + 1][col + 1] = prefixSum + above \n \n\n def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int: \n row1, col1, row2, col2 = row1+1, col1+1, row2+1, col2+1\n bottomRight = self.sumMat[row2][col2]\n above = self.sumMat[row1 - 1][col2]\n left = self.sumMat[row2][col1 - 1]\n topLeft = self.sumMat[row1 - 1][col1 - 1]\n \n return bottomRight - above - left + topLeft \n \n\n\n# Your NumMatrix object will be instantiated and called as such:\n# obj = NumMatrix(matrix)\n# param_1 = obj.sumRegion(row1,col1,row2,col2)\n``` | 1 | Given a 2D matrix `matrix`, handle multiple queries of the following type:
* Calculate the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
Implement the `NumMatrix` class:
* `NumMatrix(int[][] matrix)` Initializes the object with the integer matrix `matrix`.
* `int sumRegion(int row1, int col1, int row2, int col2)` Returns the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
You must design an algorithm where `sumRegion` works on `O(1)` time complexity.
**Example 1:**
**Input**
\[ "NumMatrix ", "sumRegion ", "sumRegion ", "sumRegion "\]
\[\[\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]\], \[2, 1, 4, 3\], \[1, 1, 2, 2\], \[1, 2, 2, 4\]\]
**Output**
\[null, 8, 11, 12\]
**Explanation**
NumMatrix numMatrix = new NumMatrix(\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 200`
* `-104 <= matrix[i][j] <= 104`
* `0 <= row1 <= row2 < m`
* `0 <= col1 <= col2 < n`
* At most `104` calls will be made to `sumRegion`. | null |
Python Easy with explanation ✅ | range-sum-query-2d-immutable | 0 | 1 | For this, we first need to calculate the **prefix sum array** for the matrix.\n\nSomething like this :\n\n**Prefix Sum of matrix with each cell=1**\n\n<img src="https://assets.leetcode.com/users/images/14109f49-e7ae-4e53-bc53-148e5f60877c_1654215908.2260733.png" width=200/>\n\n\nNow, let\'s say we want to find the sum of following region:\n\n**Region(Answer)**\n\n<img src="https://assets.leetcode.com/users/images/0aea4bfa-0ffc-4f39-9343-c940e2ae1036_1654216134.4848273.png" width=200/>\n\nSo we first need the sum from each of the following regions:\n\n1. **Region(A)**\n<img src="https://assets.leetcode.com/users/images/06bd526d-17e1-4474-886f-cc9b3e6a5eb6_1654216261.9611187.png" width=200/>\n\n\n2. **Region(B)**\n<img src="https://assets.leetcode.com/users/images/dd31bd1a-c130-4e17-a5a5-d3e9148c3477_1654216305.3489735.png" width=200/>\n\n3. **Region(C)**\n<img src="https://assets.leetcode.com/users/images/6dc28313-648f-48fe-a4b7-b73f7d843b80_1654216353.8426402.png" width=200/>\n\n\n4. **Region(D)**\n<img src="https://assets.leetcode.com/users/images/9395743f-ab67-4e31-acbf-b153094d3fb4_1654216433.38144.png" width=200/>\n\nThen we calculate the following for required answer:\n\n> ***Region(Answer) = Region(A) - Region(B).- Region(C) + Region(D)***\n\nBelow is my implementation:\n\n```\nclass NumMatrix:\n\n def __init__(self, matrix: List[List[int]]):\n self.dp=[[0] * (len(matrix[0])+1) for _ in range(len(matrix)+1)]\n \n\t\t# calculate prefix sum\n for r in range(len(self.dp)-1):\n for c in range(len(self.dp[0])-1):\n self.dp[r+1][c+1]=matrix[r][c] + self.dp[r][c+1] + self.dp[r+1][c] - self.dp[r][c]\n \n def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:\n return self.dp[row2+1][col2+1] - self.dp[row1][col2+1] - self.dp[row2+1][col1] + self.dp[row1][col1]\n \n```\n\n**Time - O(m * n)** - for the constructor\n**Space - O(m * n)** - for storing the prefix sum array\n\n\n--- \n\n\n***Please upvote if you find it useful*** | 78 | Given a 2D matrix `matrix`, handle multiple queries of the following type:
* Calculate the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
Implement the `NumMatrix` class:
* `NumMatrix(int[][] matrix)` Initializes the object with the integer matrix `matrix`.
* `int sumRegion(int row1, int col1, int row2, int col2)` Returns the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
You must design an algorithm where `sumRegion` works on `O(1)` time complexity.
**Example 1:**
**Input**
\[ "NumMatrix ", "sumRegion ", "sumRegion ", "sumRegion "\]
\[\[\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]\], \[2, 1, 4, 3\], \[1, 1, 2, 2\], \[1, 2, 2, 4\]\]
**Output**
\[null, 8, 11, 12\]
**Explanation**
NumMatrix numMatrix = new NumMatrix(\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 200`
* `-104 <= matrix[i][j] <= 104`
* `0 <= row1 <= row2 < m`
* `0 <= col1 <= col2 < n`
* At most `104` calls will be made to `sumRegion`. | null |
prefix sum: from array to matrix | range-sum-query-2d-immutable | 0 | 1 | # Intuition\nIt\'s derived from the same method of prefix sum in arrays: adding up [0]~[i-1], save the result in preSum[i]\n\n# Approach\nIn a matrix, the additional dimension makes it more complex to define or calculate the prefix sum than working on an array.\nLet\'s start with this intuitive definition:\nSay, $$preSum[i][j]$$ represents the sum of all elements in the rectangular area surrounded by $$x=0,i-1$$ and $$y=0,j-1$$, which means:\n\n$$preSum[i][j] = \u03A3matrix[x][y], where x=0...i-1, y=0...j-1$$\n\nFollowing this definition, we have:\n\n$$preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + matrix[i-1][j-1]$$\n\n# Complexity\n- Time complexity:\nO(n*m), when computing preSum matrix\nO(1), when getting regional sum\n\n- Space complexity:\nO(n*m)\n\n# Code\n```\nclass NumMatrix:\n def __init__(self, matrix: List[List[int]]):\n self.W = len(matrix[0])+1 \n self.H = len(matrix)+1\n self.ps = [[0 for _ in range(self.W)] for _ in range(self.H)]\n for i in range(1, self.H):\n for j in range(1, self.W):\n self.ps[i][j] = self.ps[i-1][j] + self.ps[i][j-1] - self.ps[i-1][j-1] + matrix[i-1][j-1]\n\n # ps[x][y] = matrix[0][0]+...+matrix[x-1][y-1]\n def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:\n return self.ps[row2+1][col2+1] - self.ps[row1][col2+1] - self.ps[row2+1][col1] + self.ps[row1][col1]\n\n\n# Your NumMatrix object will be instantiated and called as such:\n# obj = NumMatrix(matrix)\n# param_1 = obj.sumRegion(row1,col1,row2,col2)\n``` | 1 | Given a 2D matrix `matrix`, handle multiple queries of the following type:
* Calculate the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
Implement the `NumMatrix` class:
* `NumMatrix(int[][] matrix)` Initializes the object with the integer matrix `matrix`.
* `int sumRegion(int row1, int col1, int row2, int col2)` Returns the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
You must design an algorithm where `sumRegion` works on `O(1)` time complexity.
**Example 1:**
**Input**
\[ "NumMatrix ", "sumRegion ", "sumRegion ", "sumRegion "\]
\[\[\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]\], \[2, 1, 4, 3\], \[1, 1, 2, 2\], \[1, 2, 2, 4\]\]
**Output**
\[null, 8, 11, 12\]
**Explanation**
NumMatrix numMatrix = new NumMatrix(\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 200`
* `-104 <= matrix[i][j] <= 104`
* `0 <= row1 <= row2 < m`
* `0 <= col1 <= col2 < n`
* At most `104` calls will be made to `sumRegion`. | null |
304: Solution with step by step explanation | range-sum-query-2d-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThis problem can be solved using dynamic programming by precomputing the sum of all elements in a submatrix with the top left corner at (0, 0) and the bottom right corner at (i, j). Then, to calculate the sum of a submatrix with the top left corner at (row1, col1) and the bottom right corner at (row2, col2), we can use the inclusion-exclusion principle and subtract the sum of submatrices that need to be excluded. The time complexity of this solution is O(m*n) for initialization and O(1) for each sumRegion query.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass NumMatrix:\n def __init__(self, matrix: List[List[int]]):\n if not matrix or not matrix[0]:\n return\n m, n = len(matrix), len(matrix[0])\n self.dp = [[0] * (n+1) for _ in range(m+1)] # dp[i][j] stores the sum of all elements in the submatrix with the top left corner at (0, 0) and the bottom right corner at (i-1, j-1)\n for i in range(1, m+1):\n for j in range(1, n+1):\n self.dp[i][j] = matrix[i-1][j-1] + self.dp[i-1][j] + self.dp[i][j-1] - self.dp[i-1][j-1] # calculate the sum of all elements in the submatrix with the top left corner at (0, 0) and the bottom right corner at (i-1, j-1)\n \n def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:\n return self.dp[row2+1][col2+1] - self.dp[row2+1][col1] - self.dp[row1][col2+1] + self.dp[row1][col1] # use the inclusion-exclusion principle to calculate the sum of the submatrix with the top left corner at (row1, col1) and the bottom right corner at (row2, col2)\n\n``` | 4 | Given a 2D matrix `matrix`, handle multiple queries of the following type:
* Calculate the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
Implement the `NumMatrix` class:
* `NumMatrix(int[][] matrix)` Initializes the object with the integer matrix `matrix`.
* `int sumRegion(int row1, int col1, int row2, int col2)` Returns the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
You must design an algorithm where `sumRegion` works on `O(1)` time complexity.
**Example 1:**
**Input**
\[ "NumMatrix ", "sumRegion ", "sumRegion ", "sumRegion "\]
\[\[\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]\], \[2, 1, 4, 3\], \[1, 1, 2, 2\], \[1, 2, 2, 4\]\]
**Output**
\[null, 8, 11, 12\]
**Explanation**
NumMatrix numMatrix = new NumMatrix(\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 200`
* `-104 <= matrix[i][j] <= 104`
* `0 <= row1 <= row2 < m`
* `0 <= col1 <= col2 < n`
* At most `104` calls will be made to `sumRegion`. | null |
✔️ PYTHON || ✔️ EXPLAINED || ; ] | range-sum-query-2d-immutable | 0 | 1 | Instead of traversing an array everytime to find the sum on O ( N ) , we use prefix sum.\n\n**PREFIX SUM**\nIn a single traversal of array we apply the operation :\n**a [ i ] += a [ i - 1 ]**\nSo whenever the sum between index **i** and **j** is to be found, we just find **a [ i ] - a [ j ]** ( i<j ) HENCE **O ( 1 )**\n\n```\ndef __init__(self, matrix: List[List[int]]):\n self.matrix = matrix\n self.sufMatrix = matrix\n \n for i in range(len(matrix)):\n for j in range(1,len(matrix[0])):\n self.sufMatrix[i][j]+=self.sufMatrix[i][j-1]\n \ndef sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:\n\n i = row1\n j=col1\n sums=0\n while(i<=row2):\n if(col1-1>=0):\n sums+=(self.sufMatrix[i][col2] - self.sufMatrix[i][col1-1])\n else:\n sums+=self.sufMatrix[i][col2]\n i+=1\n return sums\n```\n\n\n | 23 | Given a 2D matrix `matrix`, handle multiple queries of the following type:
* Calculate the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
Implement the `NumMatrix` class:
* `NumMatrix(int[][] matrix)` Initializes the object with the integer matrix `matrix`.
* `int sumRegion(int row1, int col1, int row2, int col2)` Returns the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
You must design an algorithm where `sumRegion` works on `O(1)` time complexity.
**Example 1:**
**Input**
\[ "NumMatrix ", "sumRegion ", "sumRegion ", "sumRegion "\]
\[\[\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]\], \[2, 1, 4, 3\], \[1, 1, 2, 2\], \[1, 2, 2, 4\]\]
**Output**
\[null, 8, 11, 12\]
**Explanation**
NumMatrix numMatrix = new NumMatrix(\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 200`
* `-104 <= matrix[i][j] <= 104`
* `0 <= row1 <= row2 < m`
* `0 <= col1 <= col2 < n`
* At most `104` calls will be made to `sumRegion`. | null |
O(1) time | O(1) space | solution explained | range-sum-query-2d-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe sum of the elements in a rectangular matrix is an overlap of four other rectangular matrices that originate at the matrix[0][0]\n\n**rectangle sum = whole sum - top rectangle sum - left rectangle sum + top-left rectangle sum**\nsum(r1, c1, r2, c2) = sum(r2, c2) + sum(r1 - 1, c2) + sum(r2, c1 - 1) + sum(r1 - 1, c1 - 1)\n(top-left rectangle is the overlap of top and left rectangles. It is added because due to the overlap, a sum is subtracted twice)\n\n**Use matrix prefix** sum to easily get any rectangle sum.\n\n**prefix sum of current cell = current cell + top cell prefix sum + left cell prefix sum - top left cell prefix sum**\nprefix sum[r][c] = matrix[r][c] + prefix sum[r-1][c] + prefix sum[r][c-1] - prefix sum[r-1][c-1]\n(the top left cell prefix sum represents the overlap of the top cell and left cells. It is subtracted because due to the overlap a sum is added twice)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- init()\n - set m = total rows, n = total columns\n - inititalize a prefix sum array of size m x n with zeroes\n - fill the prefix sum array using the formula \n- sumRegion()\n - return the rectangle sum using the formula\n\n# Complexity\n- Time complexity: \n - init() O(prefix sum matrix) \u2192 O(rows * columns) \u2192 O(m * n) \n but it will be only one time because a constructor is initialized once\n - sumRange O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \n - init() O(prefix sum matrix) \u2192 O(rows * columns) \u2192 O(m * n) \n - sumRange O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass NumMatrix:\n\n def __init__(self, matrix: List[List[int]]):\n def __init__(self, matrix: List[List[int]]):\n m, n = len(matrix), len(matrix[0])\n self.pre_sum = [[0] * n for _ in range(m)]\n for r in range(m):\n top, left, top_left = 0, 0 , 0\n for c in range(n):\n if r : top = self.pre_sum[r - 1][c]\n if c: left = self.pre_sum[r][c - 1]\n if r and c: top_left = self.pre_sum[r - 1][c - 1]\n self.pre_sum[r][c] = matrix[r][c] + top + left - top_left\n\n def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:\n top = self.pre_sum[row1 - 1][col2] if row1 else 0\n left = self.pre_sum[row2][col1 - 1] if col1 else 0\n top_left = self.pre_sum[row1 - 1][col1 - 1] if row1 and col1 else 0\n return self.pre_sum[row2][col2] - top - left + top_left\n \n\n\n# Your NumMatrix object will be instantiated and called as such:\n# obj = NumMatrix(matrix)\n# param_1 = obj.sumRegion(row1,col1,row2,col2)\n``` | 1 | Given a 2D matrix `matrix`, handle multiple queries of the following type:
* Calculate the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
Implement the `NumMatrix` class:
* `NumMatrix(int[][] matrix)` Initializes the object with the integer matrix `matrix`.
* `int sumRegion(int row1, int col1, int row2, int col2)` Returns the **sum** of the elements of `matrix` inside the rectangle defined by its **upper left corner** `(row1, col1)` and **lower right corner** `(row2, col2)`.
You must design an algorithm where `sumRegion` works on `O(1)` time complexity.
**Example 1:**
**Input**
\[ "NumMatrix ", "sumRegion ", "sumRegion ", "sumRegion "\]
\[\[\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]\], \[2, 1, 4, 3\], \[1, 1, 2, 2\], \[1, 2, 2, 4\]\]
**Output**
\[null, 8, 11, 12\]
**Explanation**
NumMatrix numMatrix = new NumMatrix(\[\[3, 0, 1, 4, 2\], \[5, 6, 3, 2, 1\], \[1, 2, 0, 1, 5\], \[4, 1, 0, 1, 7\], \[1, 0, 3, 0, 5\]\]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 200`
* `-104 <= matrix[i][j] <= 104`
* `0 <= row1 <= row2 < m`
* `0 <= col1 <= col2 < n`
* At most `104` calls will be made to `sumRegion`. | null |
306: Time 95%, Solution with step by step explanation | additive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution works by checking all possible combinations of the first two numbers, and then iterating through the rest of the string to check if it forms a valid additive sequence. We start by iterating over all possible positions for the second number, which must be at least one position after the first number. We then check if either of the first two numbers have leading zeros, which would make the sequence invalid. We then initialize the first two numbers and iterate through the rest of the string, calculating the next number in the sequence and checking if it matches the remaining string. If it does, we continue iterating with the next number in the sequence, and if we reach the end of the string, we have found a valid additive sequence. If we have checked all possible combinations of the first two numbers without finding a valid sequence, we return False. This solution has a time complexity of O(n^3), which is better than the brute force solution.\n\n# Complexity\n- Time complexity:\n95%\n\n- Space complexity:\n69.78%\n\n# Code\n```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n n = len(num)\n \n # check if the sequence is valid starting from the first two numbers\n for i in range(1, n):\n for j in range(i+1, n):\n # if the first two numbers have leading zeros, move on to the next iteration\n if num[0] == "0" and i > 1:\n break\n if num[i] == "0" and j > i+1:\n break\n \n # initialize the first two numbers and check if the sequence is valid\n num1 = int(num[:i])\n num2 = int(num[i:j])\n k = j\n while k < n:\n # calculate the next number in the sequence and check if it matches the remaining string\n num3 = num1 + num2\n if num[k:].startswith(str(num3)):\n k += len(str(num3))\n num1 = num2\n num2 = num3\n else:\n break\n if k == n:\n return True\n \n # if no valid sequence is found, return False\n return False\n\n``` | 9 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Backtracking | additive-number | 0 | 1 | ```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n self.ans = False\n\n def get_number(num_str):\n return int(num_str)\n\n def fun(num_list, num_index_list, valid_so_far, index):\n #print(f\'num_list={num_list}, num_index_list={num_index_list}, index={index}, valid={valid_so_far}\')\n if self.ans:\n return\n if index >= len(num):\n if valid_so_far:\n self.ans = True\n return\n if len(num_list) < 3:\n for i in range(num_index_list[-1]+1, len(num)):\n current_num = get_number(num[num_index_list[-1]+1:i+1])\n num_list.append(current_num)\n num_index_list.append(i)\n fun(num_list, num_index_list, False, i+1)\n num_list.pop(-1)\n y = num_index_list.pop(-1)\n if num[num_index_list[-1]+1] == \'0\':\n return\n else:\n sum_last_two = num_list[-1] + num_list[-2]\n string_sum = str(sum_last_two)\n x = num_index_list[-1]\n if x + 1 + len(string_sum) > len(num):\n return\n elif string_sum != num[x+1:x+1+len(string_sum)]:\n return\n else:\n num_index_list.append(x+len(string_sum))\n num_list.append(sum_last_two)\n fun(num_list, num_index_list, True, x+1+len(string_sum))\n num_list.pop(-1)\n num_index_list.pop(-1)\n fun([0], [-1], False, 0) \n return self.ans\n \n \n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Very Simple Solution -Back Tracking(O(2**n)) | additive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n d={0:False}\n def backtrack(num,count,res,ans):\n \n if(len(ans)>2):\n c=int(ans[len(ans)-1])\n b=int(ans[len(ans)-2])\n a=int(ans[len(ans)-3])\n if(c!=(a+b)):\n return\n if(count>=len(num)):\n print(ans)\n if(len(ans)>2):\n \n if(int(ans[2])==int(ans[1])+int(ans[0])):\n d[0]=True\n return\n for i in range(count,len(num)):\n if(len(num[count:i+1])>=2 and num[count]==\'0\'):\n break\n backtrack(num,i+1,res+num[count:i+1],ans+[num[count:i+1]])\n \n backtrack(num,0,"",[])\n return d[0]\n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Python Recursive Solution | additive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n n = len(num)\n\n def dfs(i, prev):\n """\n i: index to start searching for the next number.\n prev: a list containing previous numbers.\n """\n if i == n:\n return len(prev) > 2\n \n for j in range(i+1, n+1):\n next_ = int(num[i:j])\n\n if len(prev) < 2 or next_ == prev[-1] + prev[-2]:\n prev.append(next_)\n if dfs(j, prev):\n return True\n prev.pop()\n \n if next_ == 0:\n return False\n \n return False\n \n return dfs(0, [])\n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Please help me understand my code | additive-number | 0 | 1 | I don\'t know how this works\n\n# Code\n```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n def is_valid(start_point, a, b):\n # print("recurs",start_point,"previous",a,b)\n if start_point==len(num):\n # print("done!")\n return True\n if num[start_point]==\'0\':\n return False\n aggregate = 0\n cursor = start_point\n while cursor < len(num):\n aggregate = 10*aggregate + int(num[cursor])\n cursor+=1\n # print("aggregated",aggregate,"previous",a,b)\n if aggregate == a + b:\n return is_valid(cursor, b, aggregate)\n elif aggregate > a + b:\n return False\n return False\n\n if int(num)==0 and len(num)>2:\n return True\n \n num_length = len(num)\n first_two_length =( (2*num_length) // 3) + 1\n for length in range(2, first_two_length):\n for i in range(1, length):\n j = length - i\n if num[0]==\'0\' and i > 1:\n continue\n if num[i]==\'0\' and j > 1:\n continue\n # print("values",int(num[:i]), int(num[i:i+j]),length)\n if is_valid(length, int(num[:i]), int(num[i:i+j])):\n return True\n return False\n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Python (Simple Backtracking) | additive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isAdditiveNumber(self, num):\n def backtrack(num,path):\n if not num and len(path) >= 3: res.append(path)\n\n for i in range(1,len(num)+1):\n if str(int(num[:i])) != num[:i]: continue\n if len(path) >= 2 and int(num[:i]) != int(path[-1]) + int(path[-2]): continue\n backtrack(num[i:],path+[num[:i]])\n\n\n res = []\n backtrack(num,[])\n return len(res) > 0\n\n\n\n\n\n\n\n\n\n \n \n \n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
python: backtracking | additive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n def check(n1:int, n2:int, s:str) -> bool:\n """\n check if substring is additive\n """\n if not s:\n return True\n n = n1 + n2\n return s.startswith(str(n)) and check(n2, n, s[len(str(n)):])\n\n n = len(num)\n if n < 3:\n return False\n for i in range(1, len(num) // 2 + 1):\n # try first num, index starts from 0\n s0 = num[:i]\n\n # check if leading \'0\'\n if s0 != \'0\' and s0.startswith(\'0\'):\n continue\n for j in range(i+1, len(num)):\n # 2nd num, index starts from i+1\n s1 = num[i:j]\n\n # check if leading \'0\'\n if s1 != \'0\' and s1.startswith(\'0\'):\n continue\n \n if check(int(s0), int(s1), num[j:]):\n return True\n return False\n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Solution | additive-number | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isAdditiveNumber(string num) {\n for (int i = 1; i < num.length(); ++i) {\n for (int j = i + 1; j < num.length(); ++j) {\n string s1 = num.substr(0, i), s2 = num.substr(i, j - i);\n if ((s1.length() > 1 && s1[0] == \'0\') ||\n (s2.length() > 1 && s2[0] == \'0\')) {\n continue;\n }\n string next = add(s1, s2);\n string cur = s1 + s2 + next;\n while (cur.length() < num.length()) {\n s1 = s2;\n s2 = next;\n next = add(s1, s2);\n cur += next;\n }\n if (cur == num) {\n return true;\n }\n }\n }\n return false;\n }\nprivate:\n string add(const string& m, const string& n) {\n string res;\n int res_length = max(m.length(), n.length()) ;\n \n int carry = 0;\n for (int i = 0; i < res_length; ++i) {\n int m_digit_i = i < m.length() ? m[m.length() - 1 - i] - \'0\' : 0;\n int n_digit_i = i < n.length() ? n[n.length() - 1 - i] - \'0\' : 0;\n int sum = carry + m_digit_i + n_digit_i;\n carry = sum / 10;\n sum %= 10;\n res.push_back(\'0\' + sum);\n }\n if (carry) {\n res.push_back(\'0\' + carry);\n }\n reverse(res.begin(), res.end());\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n for i in range(1, len(num)):\n if num[0] == \'0\' and i > 1:\n break\n for j in range(i + 1, len(num)):\n if num[i] == \'0\' and j > i + 1:\n break\n if self.check(int(num[:i]), int(num[i:j]), j, num):\n print(num[:i], num[i:j])\n return True\n return False\n\n def check(self, first, second, index, s):\n second, first = first + second, second\n second_str = str(second)\n if len(s) - index < len(second_str):\n return False\n if len(s) - index == len(second_str):\n return s[index:] == second_str\n if s[index:index+len(second_str)] == second_str:\n return self.check(first, second, index + len(second_str), s)\n return False\n```\n\n```Java []\nclass Solution {\n\tpublic boolean isAdditiveNumber(String num) {\n\t\tlong number1=0;\n\t\tfor(int i=0; i<num.length()-1; i++){\n\t\t\tnumber1=number1*10+num.charAt(i)-\'0\';\n\t\t\tlong number2=0;\n\t\t\tfor(int j=i+1; j<num.length(); j++){\n\t\t\t\tnumber2=number2*10+num.charAt(j)-\'0\';\n\t\t\t\tif(solv(number1, number2, j+1, num, 2))\n\t\t\t\t\treturn true;\n\t\t\t\tif(number2==0)\n\t\t\t\t\tbreak;\n\t\t\t}\n\t\t\tif(number1==0)\n\t\t\t\tbreak;\n\t\t}\n\t\treturn false;\n\t}\n\tboolean solv(long number1, long number2, int curr, String num, int count) {\n\t\tif(curr>=num.length()){\n\t\t\tif(count>=3)\n\t\t\t\treturn true;\n\t\t\treturn false;\n\t\t}\n\t\tif(num.charAt(curr)==\'0\' && number1+number2!=0)\n\t\t\treturn false;\n \n\t\tlong number=0;\n\t\tlong target=number1+number2;\n\t\tfor(int i=curr; i<num.length(); i++) {\n\t\t\tnumber=number*10+num.charAt(i)-\'0\';\n\t\t\tif(number==target && solv(number2, target, i+1, num, count+1))\n\t\t\t\treturn true;\n\t\t\telse if(number>target)\n\t\t\t\tbreak;\n\t\t}\n\t\treturn false;\n\t}\n}\n```\n | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Clear Python Solution with Comments | additive-number | 0 | 1 | # Code\n```\nclass Solution:\n def isAdditiveNumber(self, num: str) -> bool:\n # remaining - string; pre_sum - int; pre_num - int\n def validate(remaining, pre_sum, pre_num):\n if len(remaining) == 0:\n return True\n if not remaining.startswith(str(pre_sum)):\n return False\n else:\n return validate(remaining[len(str(pre_sum)):], pre_sum + pre_num, pre_sum)\n \n # Iterate through num to get the first two numbers in this sequence\n for i in range(len(num) - 2):\n for j in range(i + 1, len(num) - 1):\n first = int(num[:i + 1])\n second = int(num[i + 1 : j + 1])\n # Continue if first or second has leading "0"\n if len(str(first)) != i + 1 or len(str(second)) != j - i:\n continue\n if validate(num[j + 1:], first + second, second):\n return True\n\n return False\n\n``` | 0 | An **additive number** is a string whose digits can form an **additive sequence**.
A valid **additive sequence** should contain **at least** three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.
Given a string containing only digits, return `true` if it is an **additive number** or `false` otherwise.
**Note:** Numbers in the additive sequence **cannot** have leading zeros, so sequence `1, 2, 03` or `1, 02, 3` is invalid.
**Example 1:**
**Input:** "112358 "
**Output:** true
**Explanation:**
The digits can form an additive sequence: 1, 1, 2, 3, 5, 8.
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
**Example 2:**
**Input:** "199100199 "
**Output:** true
**Explanation:**
The additive sequence is: 1, 99, 100, 199.
1 + 99 = 100, 99 + 100 = 199
**Constraints:**
* `1 <= num.length <= 35`
* `num` consists only of digits.
**Follow up:** How would you handle overflow for very large input integers? | null |
Using Segmented tree with explanation easy to understand | range-sum-query-mutable | 0 | 1 | ```\n# Segment tree node\nclass Node(object):\n def __init__(self, start, end):\n self.start = start\n self.end = end\n self.total = 0\n self.left = None\n self.right = None\n\n\nclass NumArray(object):\n\n def __init__(self, nums):\n # helper function to create the tree from input array\n def createTree(nums, l, r):\n\n # base case\n if l > r:\n return None\n\n # leaf node\n if l == r:\n n = Node(l, r)\n n.total = nums[l]\n return n\n\n mid = (l + r) // 2\n\n root = Node(l, r)\n\n # recursively build the Segment tree\n root.left = createTree(nums, l, mid)\n root.right = createTree(nums, mid + 1, r)\n\n # Total stores the sum of all leaves under root\n # i.e. those elements lying between (start, end)\n root.total = root.left.total + root.right.total\n\n return root\n\n self.root = createTree(nums, 0, len(nums) - 1)\n\n def update(self, i, val):\n # Helper function to update a value\n def updateVal(root, i, val):\n\n # Base case. The actual value will be updated in a leaf.\n # The total is then propogated upwards\n if root.start == root.end:\n root.total = val\n return val\n\n mid = (root.start + root.end) // 2\n\n # If the index is less than the mid, that leaf must be in the left subtree\n if i <= mid:\n updateVal(root.left, i, val)\n\n # Otherwise, the right subtree\n else:\n updateVal(root.right, i, val)\n\n # Propogate the changes after recursive call returns\n root.total = root.left.total + root.right.total\n\n return root.total\n\n return updateVal(self.root, i, val)\n\n def sumRange(self, i, j):\n # Helper function to calculate range sum\n def rangeSum(root, i, j):\n\n # If the range exactly matches the root, we already have the sum\n if root.start == i and root.end == j:\n return root.total\n\n mid = (root.start + root.end) // 2\n\n # If end of the range is less than the mid, the entire interval lies\n # in the left subtree\n if j <= mid:\n return rangeSum(root.left, i, j)\n\n # If start of the interval is greater than mid, the entire inteval lies\n # in the right subtree\n elif i >= mid + 1:\n return rangeSum(root.right, i, j)\n\n # Otherwise, the interval is split. So we calculate the sum recursively,\n # by splitting the interval\n else:\n return rangeSum(root.left, i, mid) + rangeSum(\n root.right, mid + 1, j\n )\n\n return rangeSum(self.root, i, j)\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# obj.update(index,val)\n# param_2 = obj.sumRange(left,right)\n\n``` | 18 | Given an integer array `nums`, handle multiple queries of the following types:
1. **Update** the value of an element in `nums`.
2. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `void update(int index, int val)` **Updates** the value of `nums[index]` to be `val`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "update ", "sumRange "\]
\[\[\[1, 3, 5\]\], \[0, 2\], \[1, 2\], \[0, 2\]\]
**Output**
\[null, 9, null, 8\]
**Explanation**
NumArray numArray = new NumArray(\[1, 3, 5\]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = \[1, 2, 5\]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `0 <= index < nums.length`
* `-100 <= val <= 100`
* `0 <= left <= right < nums.length`
* At most `3 * 104` calls will be made to `update` and `sumRange`. | null |
307: Space 98.30%, Solution with step by step explanation | range-sum-query-mutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n- The NumArray class is initialized with the input array nums. In the __init__ method, we initialize a binary tree (segment tree) to store the range sum queries for the array.\n- The buildTree method is used to build the binary tree. We fill the leaves of the tree with the values from the input array nums, and then we fill the non-leaf nodes of the tree with the sum of their children. The binary tree is represented as a list, where the left child of node i is at index 2*i, and the right child of node i is at index 2*i+1.\n- The update method is used to update the value of an element in the input array nums. We update the corresponding leaf node in the binary tree with the new value, and then propagate the change up the tree by updating the parent nodes recursively.\n- The sumRange method is used to calculate the sum of the elements in the input array nums between two indices left and right inclusive. We first find the corresponding range in the binary tree by adding n to left and right, where n is the length of the input array nums. We then traverse the binary tree from the bottom up, adding the values of nodes that overlap with the range [left+n, right+n] to the result res.\n\n# Complexity\n- Time complexity:\n79.58%\n\n- Space complexity:\n98.30%\n\n# Code\n```\nclass NumArray:\n def __init__(self, nums: List[int]):\n self.n = len(nums)\n self.tree = [0] * (2 * self.n)\n self.buildTree(nums)\n\n def buildTree(self, nums: List[int]) -> None:\n # Fill leaves of the tree with nums values\n for i in range(self.n, 2 * self.n):\n self.tree[i] = nums[i - self.n]\n\n # Fill non-leaf nodes of the tree with the sum of their children\n for i in range(self.n - 1, 0, -1):\n self.tree[i] = self.tree[2 * i] + self.tree[2 * i + 1]\n\n def update(self, index: int, val: int) -> None:\n # Update the corresponding leaf node\n index += self.n\n self.tree[index] = val\n\n # Propagate the change up the tree\n while index > 0:\n left = right = index\n if index % 2 == 0:\n right = index + 1\n else:\n left = index - 1\n self.tree[index // 2] = self.tree[left] + self.tree[right]\n index //= 2\n\n def sumRange(self, left: int, right: int) -> int:\n # Find the sum in the range [left+n, right+n] in the tree\n left += self.n\n right += self.n\n res = 0\n while left <= right:\n if left % 2 == 1:\n res += self.tree[left]\n left += 1\n if right % 2 == 0:\n res += self.tree[right]\n right -= 1\n left //= 2\n right //= 2\n return res\n\n``` | 5 | Given an integer array `nums`, handle multiple queries of the following types:
1. **Update** the value of an element in `nums`.
2. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `void update(int index, int val)` **Updates** the value of `nums[index]` to be `val`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "update ", "sumRange "\]
\[\[\[1, 3, 5\]\], \[0, 2\], \[1, 2\], \[0, 2\]\]
**Output**
\[null, 9, null, 8\]
**Explanation**
NumArray numArray = new NumArray(\[1, 3, 5\]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = \[1, 2, 5\]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `0 <= index < nums.length`
* `-100 <= val <= 100`
* `0 <= left <= right < nums.length`
* At most `3 * 104` calls will be made to `update` and `sumRange`. | null |
Python Elegant & Short | log(n) for sum | Binary Indexed/Fenwick Tree | range-sum-query-mutable | 0 | 1 | ```\nclass BITTree:\n """\n Implementation of Binary Indexed Tree/Fenwick Tree\n\n Memory:\n creation - O(n)\n update - O(1)\n get_sum - O(1)\n\n Time:\n creation - O(n*log(n))\n update - O(log(n))\n get_sum - O(log(n))\n """\n\n def __init__(self, nums: List[int]):\n self.bi_tree = [0] * (len(nums) + 1)\n self.n = len(nums)\n for i in range(self.n):\n self.update(i + 1, nums[i])\n\n def update(self, index: int, value: int):\n while index <= self.n:\n self.bi_tree[index] += value\n index += self.low_bit(index)\n\n def get_sum(self, index: int) -> int:\n prefix = 0\n while index > 0:\n prefix += self.bi_tree[index]\n index -= self.low_bit(index)\n return prefix\n\n @staticmethod\n def low_bit(bit: int) -> int:\n return bit & -bit\n\n\nclass NumArray:\n """\n Time: O(n*log(n)) + O(log(n))\n Memory: O(n)\n """\n\n def __init__(self, nums: List[int]):\n self.nums = nums\n self.bi_tree = BITTree(nums)\n\n def update(self, i: int, val: int):\n self.bi_tree.update(i + 1, val - self.nums[i])\n self.nums[i] = val\n\n def sumRange(self, left: int, right: int) -> int:\n return self.bi_tree.get_sum(right + 1) - self.bi_tree.get_sum(left)\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n | 7 | Given an integer array `nums`, handle multiple queries of the following types:
1. **Update** the value of an element in `nums`.
2. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `void update(int index, int val)` **Updates** the value of `nums[index]` to be `val`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "update ", "sumRange "\]
\[\[\[1, 3, 5\]\], \[0, 2\], \[1, 2\], \[0, 2\]\]
**Output**
\[null, 9, null, 8\]
**Explanation**
NumArray numArray = new NumArray(\[1, 3, 5\]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = \[1, 2, 5\]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `0 <= index < nums.length`
* `-100 <= val <= 100`
* `0 <= left <= right < nums.length`
* At most `3 * 104` calls will be made to `update` and `sumRange`. | null |
[Python] Binary Indexed Tree Solution || Documented | range-sum-query-mutable | 0 | 1 | Binary Indexed Tree is basically dividing the Prefix Sum algo by 2 and call recursively.\n```\n# Binary Indexed Tree implementation\nclass BIT:\n def __init__(self, size):\n self.nums = [0] * (size+1)\n def update(self, ind, val):\n while ind < len(self.nums):\n self.nums[ind] += val\n ind += (ind&-ind) # flip last set bit e.g. 101 -> 100, then add\n def getsum(self, ind):\n sum = 0\n while ind > 0:\n sum += self.nums[ind]\n ind -= (ind&-ind) # flip last set bit e.g. 101 -> 100, then subtract\n return sum\n\nclass NumArray:\n def __init__(self, nums: List[int]):\n self.bit = BIT(len(nums))\n self.nums = nums\n for i, v in enumerate(nums):\n self.bit.update(i+1, v)\n\n def update(self, index: int, val: int) -> None:\n diff = val - self.nums[index]\n self.bit.update(index+1, diff)\n self.nums[index] = val\n\n def sumRange(self, left: int, right: int) -> int:\n # BIT is 1 based tree, right will be added by 1\n # For left we need sum of vales that left to the left means left-1\n # Instead of getting sum for left-1, we will search for only left, as BIT is 1 based tree.\n return self.bit.getsum(right+1) - self.bit.getsum(left)\n```\nPlease UPVOTE\uD83D\uDC4D if you love\u2764\uFE0F this solution or learned something new.\nIf you have any question, feel free to ask.\n | 1 | Given an integer array `nums`, handle multiple queries of the following types:
1. **Update** the value of an element in `nums`.
2. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `void update(int index, int val)` **Updates** the value of `nums[index]` to be `val`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "update ", "sumRange "\]
\[\[\[1, 3, 5\]\], \[0, 2\], \[1, 2\], \[0, 2\]\]
**Output**
\[null, 9, null, 8\]
**Explanation**
NumArray numArray = new NumArray(\[1, 3, 5\]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = \[1, 2, 5\]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `0 <= index < nums.length`
* `-100 <= val <= 100`
* `0 <= left <= right < nums.length`
* At most `3 * 104` calls will be made to `update` and `sumRange`. | null |
Python Easy and Best Solution | Segment Tree | Faster than 95% | range-sum-query-mutable | 0 | 1 | \tclass stree:\n\t\tdef __init__(self, arr):\n\t\t\tself.arr = [0 for i in range((len(arr))*4)]\n\t\t\tself.org = arr[:]\n\t\tdef create(self, l,r,idx):\n\t\t\tmid = (l+r)//2\n\t\t\tif l == r:\n\t\t\t\tself.arr[idx] = self.org[l]\n\t\t\t\treturn\n\t\t\tself.create(l, mid, 2*idx+1)\n\t\t\tself.create(mid+1, r, 2*idx+2)\n\t\t\tself.arr[idx] = self.arr[2*idx+1] + self.arr[2*idx+2]\n\n\t\tdef query(self, ind,low,high,l,r):\n\t\t\tmid = (low+high)>>1\n\t\t\tif low>=l and high<=r:return self.arr[ind]\n\t\t\tif high<l or low>r:return 0\n\t\t\treturn self.query(2*ind+1, low, mid, l,r) + self.query(2*ind+2, mid+1,high,l,r)\n\n\t\tdef update(self, ind, l, r, pos,diff):\n\t\t\tif l == r and l == pos:\n\t\t\t\tself.arr[ind] += diff \n\t\t\t\treturn\n\t\t\tif l <= pos <=r :\n\t\t\t\tmid = (l+r) >> 1\n\t\t\t\tself.arr[ind] += diff\n\t\t\t\tself.update(ind*2+1, l,mid,pos,diff)\n\t\t\t\tself.update(ind*2+2, mid+1,r,pos,diff)\n\n\n\t# x = [i for i in range(4)]\n\t# tr = stree(x)\n\t# tr.create(0,len(x)-1,0)\n\t# print(tr.query(0,0,len(x)-1, 0,1))\n\t# tr.update(0,0,len(x)-1, 2,1)\n\t# print(*tr.arr)\n\n\tclass NumArray:\n\n\t\tdef __init__(self, nums: List[int]):\n\t\t\tself.tree = stree(nums)\n\t\t\tself.tree.create(0, len(nums)-1, 0)\n\t\t\tself.n = len(nums)\n\t\tdef update(self, index: int, val: int) -> None:\n\t\t\tdiff = val - self.tree.org[index] \n\t\t\tself.tree.update(0, 0, self.n-1,index,diff) \n\t\t\tself.tree.org[index] = val\n\n\t\tdef sumRange(self, left: int, right: int) -> int:\n\t\t\treturn self.tree.query(0, 0, self.n-1, left,right)\n\n\n\n\n\t# Your NumArray object will be instantiated and called as such:\n\t# obj = NumArray(nums)\n\t# obj.update(index,val)\n\t# param_2 = obj.sumRange(left,right) | 1 | Given an integer array `nums`, handle multiple queries of the following types:
1. **Update** the value of an element in `nums`.
2. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `void update(int index, int val)` **Updates** the value of `nums[index]` to be `val`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "update ", "sumRange "\]
\[\[\[1, 3, 5\]\], \[0, 2\], \[1, 2\], \[0, 2\]\]
**Output**
\[null, 9, null, 8\]
**Explanation**
NumArray numArray = new NumArray(\[1, 3, 5\]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = \[1, 2, 5\]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `0 <= index < nums.length`
* `-100 <= val <= 100`
* `0 <= left <= right < nums.length`
* At most `3 * 104` calls will be made to `update` and `sumRange`. | null |
Python Solution using fenwick Tree | range-sum-query-mutable | 0 | 1 | Basic idea is to create a fenwick tree\n1. create a fenwick tree\n2. to update the value find the difference between the old and new value increment the index by 1\nrun the loop while index is less then equal to length of the nums array update the value of index as \nindex += (index & -index)\n3. to search the sum keep a total variable run the loop while index is greater than 0 add the value of \ntree[index] in the total variable adn update the value of index as index -= (index & -index)\n4. to return the sum between right to left call the search funtion on right as right + 1 and left as left \n(not incrementing the value of left by 1 because we need to include the value at left in the sum)\n```\ndef __init__(self, nums: List[int]):\n \n # to store the nums array \n self.nums = [0] * len(nums)\n \n # to create a fenwick tree\n self.tree = [0] * (len(nums) + 1)\n \n # to call the update function to fill or update the fenwick tree and update the \n # nums array\n for i in range(len(nums)):\n self.update(i,nums[i])\n \n\n def update(self, index: int, val: int) -> None:\n # to update the fenwick tree\n # find the difference between the old and new value\n # update the new value in the nums array\n # increment the current index by 1 \n # run the loop while index is in range of the length of nums array\n # update the value of index as below\n # index += (index & -index)\n \n diff = val - self.nums[index]\n self.nums[index] = val\n \n index += 1\n \n while index <= len(self.nums):\n self.tree[index] += diff\n \n index += (index & -index)\n \n # to search the value in the fenwick tree\n def search(self,index):\n \n # to store the total from index 0 to index\n total = 0\n \n # run the loop while index is greater than 0\n # update the value of index as below\n # index -= (index & -index)\n \n while index > 0:\n total += self.tree[index]\n index -= (index & -index)\n \n # return the total\n return total\n\n def sumRange(self, left: int, right: int) -> int:\n \n # search the value of the from 0 to right and 0 to left and return the difference\n return self.search(right + 1) - self.search(left)\n``` | 1 | Given an integer array `nums`, handle multiple queries of the following types:
1. **Update** the value of an element in `nums`.
2. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `void update(int index, int val)` **Updates** the value of `nums[index]` to be `val`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "update ", "sumRange "\]
\[\[\[1, 3, 5\]\], \[0, 2\], \[1, 2\], \[0, 2\]\]
**Output**
\[null, 9, null, 8\]
**Explanation**
NumArray numArray = new NumArray(\[1, 3, 5\]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = \[1, 2, 5\]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `0 <= index < nums.length`
* `-100 <= val <= 100`
* `0 <= left <= right < nums.length`
* At most `3 * 104` calls will be made to `update` and `sumRange`. | null |
MOST OPTIMIZED PYTHON SOLUTION | best-time-to-buy-and-sell-stock-with-cooldown | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O((N+2)*2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O((N+2)*2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # def dp(self,i,buy,prices,n,dct):\n # if i>=n:\n # return 0\n # if (i,buy) in dct:\n # return dct[(i,buy)]\n # if buy:\n # x=max(self.dp(i+1,buy,prices,n,dct),self.dp(i+1,0,prices,n,dct)-prices[i])\n # else:\n # x=max(self.dp(i+1,buy,prices,n,dct),self.dp(i+2,1,prices,n,dct)+prices[i])\n # dct[(i,buy)]=x\n # return x\n\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n # dp=[[0]*2 for i in range(n+2)]\n ahd=[0]*2\n ahd2=[0]*2\n for i in range(n-1,-1,-1):\n curr=[0]*2\n for buy in range(2):\n if buy:\n curr[buy]=max(ahd[buy],ahd[0]-prices[i])\n else:\n curr[buy]=max(ahd[buy],ahd2[1]+prices[i])\n ahd2=ahd[:]\n ahd=curr[:]\n return ahd[1]\n\n``` | 1 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
Python/Go/Java/JS/C++ O(n) by DP and state machine. [w/ Visualization] | best-time-to-buy-and-sell-stock-with-cooldown | 1 | 1 | O(n) by DP and state machine\n\n---\n\n**State Diagram**:\n\n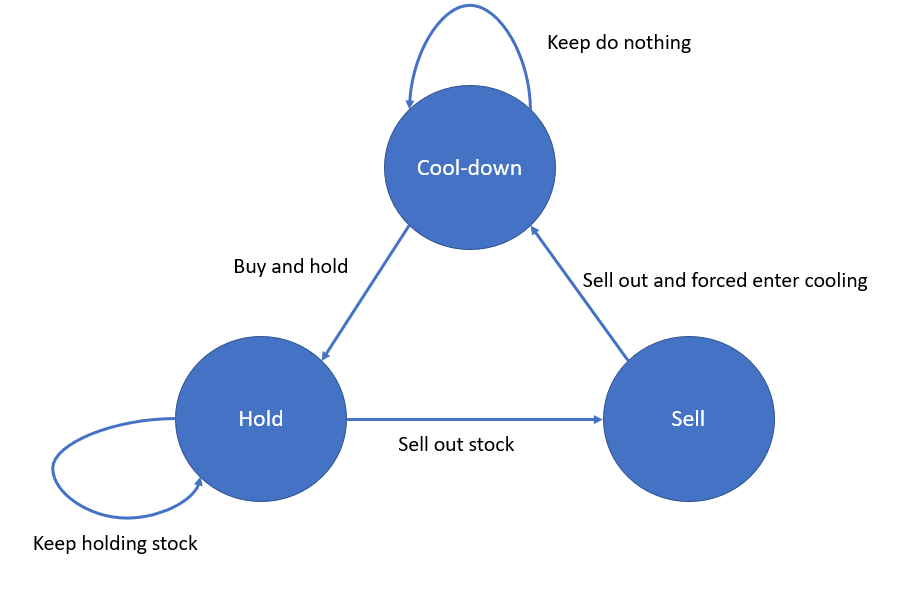\n\n---\n\n**cool_down** denotes the max profit of current Day_i, with either do nothing, or just sell out on previous day and enter cooling on Day_i\n\n**sell** denotes the max profit of current Day_i, with selling stock with price quote of Day_i\n\n**hold** denotes the max profit of current Day_i, with keep holding or buy and hold on Day_i\n\n---\n\n**Implementation** in bottom-up DP:\n<iframe src="https://leetcode.com/playground/SYsUqp7j/shared" frameBorder="0" width="1000" height="600"></iframe>\n---\n\nRelated leetcode challenge:\n\n[Leetcode #121 Best Time to Buy and Sell Stock I](https://leetcode.com/problems/best-time-to-buy-and-sell-stock)\n\n[Leetcode #122 Best Time to Buy and Sell Stock II](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii)\n\n[Leetcode #123 Best Time to Buy and Sell Stock III](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii)\n\n[Leetcode #188 Best Time to Buy and Sell Stock IV](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv)\n\n[Leetcode #121 Best Time to Buy and Sell Stock with Transaction Fee](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee) | 121 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
Simple DP | best-time-to-buy-and-sell-stock-with-cooldown | 0 | 1 | No state machine, only simple DP\n\n`b[i]` is the max profit until i while last action is BUY\n`s[i]` is the max profit until i while last action is SELL\n\n# Code\n```py\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n n = len(prices)\n if n == 1: return 0\n b = [-10 ** 9] * n\n s = [0] * n\n for i in range(n):\n s[i] = max(s[i - 1], prices[i] + b[i - 1])\n b[i] = max(b[i - 1], s[i - 2] - prices[i])\n return s[-1]\n```\nSpace optimized\n```python\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n b = -10 ** 9\n s = 0\n s2 = 0 # s[i - 2]\n for i in range(len(prices)):\n b = max(b, s2 - prices[i])\n s2 = s # update s[i - 2] for next iteration\n s = max(s, b + prices[i])\n return s\n```\nnote that \n`s[i] = max(s[i - 1], b[i] + prices[i])`\n`s[i] = max(s[i - 1], b[i - 1] + prices[i])`\nwon\'t affect the result. | 25 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
Python || 95.30% Faster || DP || Memoization+Tabulation | best-time-to-buy-and-sell-stock-with-cooldown | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(2^n)\n#Space Complexity: O(n)\nclass Solution1:\n def maxProfit(self, prices: List[int]) -> int:\n def solve(ind,buy):\n if ind>=n:\n return 0\n profit=0\n if buy==0: #buy a stock\n take=-prices[ind]+solve(ind+1,1) \n not_take=0+solve(ind+1,0)\n profit=max(take,not_take)\n else:\n take=prices[ind]+solve(ind+2,0) # +2 for cooldown\n not_take=0+solve(ind+1,1)\n profit=max(take,not_take)\n return profit\n n=len(prices)\n return solve(0,0)\n \n#Memoization (Top-Down)\n#Time Complexity: O(n*2)\n#Space Complexity: O(n*2) + O(n)\nclass Solution2:\n def maxProfit(self, prices: List[int]) -> int:\n def solve(ind,buy):\n if ind>=n:\n return 0\n if dp[ind][buy]!=-1:\n return dp[ind][buy]\n profit=0\n if buy==0: #buy a stock\n take=-prices[ind]+solve(ind+1,1) \n not_take=0+solve(ind+1,0)\n profit=max(take,not_take)\n else:\n take=prices[ind]+solve(ind+2,0) # +2 for cooldown\n not_take=0+solve(ind+1,1)\n profit=max(take,not_take)\n dp[ind][buy]=profit\n return dp[ind][buy]\n n=len(prices)\n dp=[[-1,-1] for i in range(n)]\n return solve(0,0)\n \n#Tabulation (Bottom-Up)\n#Time Complexity: O(n*2)\n#Space Complexity: O(n*2)\nclass Solution3:\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n dp=[[0,0] for i in range(n+2)]\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n profit=0\n if buy==0: #buy a stock\n take=-prices[ind]+dp[ind+1][1] \n not_take=0+dp[ind+1][0]\n profit=max(take,not_take)\n else:\n take=prices[ind]+dp[ind+2][0] # +2 for cooldown\n not_take=0+dp[ind+1][1]\n profit=max(take,not_take)\n dp[ind][buy]=profit\n return dp[0][0]\n \n#Space Optimization\n#Time Complexity: O(n*2)\n#Space Complexity: O(1)\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n ahead=[0]*2\n ahead2=[0]*2\n curr=[0]*2\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n profit=0\n if buy==0: #buy a stock\n take=-prices[ind]+ahead[1] \n not_take=0+ahead[0]\n profit=max(take,not_take)\n else:\n take=prices[ind]+ahead2[0] # +2 for cooldown\n not_take=0+ahead[1]\n profit=max(take,not_take)\n curr[buy]=profit\n ahead2=ahead[:]\n ahead=curr[:]\n return curr[0]\n```\n**An upvote will be encouraging** | 5 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
Python 3 || 4 lines, w/ example || T/M: 94 % / 98% | best-time-to-buy-and-sell-stock-with-cooldown | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, prices: list[int]) -> int: # Example: prices = [1,2,3,0,2]\n #\n nostock, stock, cool = 0,-prices[0],0 # p nostock stock cool \n # \u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\n for p in prices[1:]: # 1 0 -1 0\n # 2 0 -1 1\n nostock, stock, cool = (max(nostock,cool), # 3 1 -1 2\n max(stock,nostock-p), # 0 2 1 -1\n stock+p) # 2 2 1 3 <\u2013\u2013\u2013 return\n \n return max(nostock, stock, cool) \n```\n[https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/submissions/863991664/](http://)\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(1).\n | 7 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
Python easy Solution | Best Approch ✅ | best-time-to-buy-and-sell-stock-with-cooldown | 0 | 1 | # Recursive & Memoisation\n```\nclass Solution:\n def f(self,ind,buy,n,price,dp):\n if ind>=n:\n return 0\n if dp[ind][buy]!=-1:\n return dp[ind][buy]\n \n if (buy==1):\n dp[ind][buy]=max(-price[ind]+self.f(ind+1,0,n,price,dp),0+self.f(ind+1,1,n,price,dp))\n \n else: #if ind=n-1 so ind+2 will go out of bound base case is if ind>=n: return 0\n dp[ind][buy]=max(price[ind]+self.f(ind+2,1,n,price,dp),0+self.f(ind+1,0,n,price,dp))\n \n return dp[ind][buy]\n \n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n dp=[[-1 for i in range(2)]for j in range(n)]\n return self.f(0,1,n,prices,dp)\n```\n\n# Tabulation :\n```\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n dp=[[0 for i in range(2)]for j in range(n+2)]\n \n dp[n][0]=0\n dp[n][1]=0\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n if (buy):\n dp[ind][buy]=max(-prices[ind]+dp[ind+1][0] , 0+dp[ind+1][1])\n else:\n dp[ind][buy]=max(prices[ind]+dp[ind+2][1],0+dp[ind+1][0])\n \n return dp[0][1]\n```\n\n# Time Optimised :\n```\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n dp=[[0 for i in range(2)]for j in range(n+2)]\n \n dp[n][0]=0 #Base case 1\n dp[n][1]=0 #Base case 2\n for ind in range(n-1,-1,-1):\n dp[ind][1]=max(-prices[ind]+dp[ind+1][0] , 0+dp[ind+1][1])\n dp[ind][0]=max(prices[ind]+dp[ind+2][1],0+dp[ind+1][0])\n \n return dp[0][1]\n```\n# Time and Space Both Optimised :) TC O(N) SC O(1)\n```\n n=len(prices)\n \n front1=[0]*2\n front2=[0]*2\n curr=[0]*2\n \n curr[0]=0 #Base case 1\n curr[1]=0 #Base case 2\n \n for ind in range(n-1,-1,-1):\n curr=[0]*2\n curr[1]=max(-prices[ind] + front1[0] , 0 + front1[1])\n curr[0]=max(prices[ind] + front2[1], 0 + front1[0])\n front2=front1\n front1=curr\n return curr[1]\n```\n | 4 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
True DP Solution Python O(n) 5 Lines With Explanation Full Thought Process | best-time-to-buy-and-sell-stock-with-cooldown | 0 | 1 | ### I\'m going go over my complete thought process for this problem. \n\n# **Problem Requirements:**\n1. If you sell on a particular day, you must **cooldown and can\'t buy for the next day.**\n2. You can\'t sell the stock if you haven\'t bought the stock yet. \n3. You can only keep one stock.\n\n# The Drawing\n\nWe have **two cases**: buying or sell a stock at a particular day. So, I decided to draw a descision tree for the problem. \n\n\n\n# Drawing Analysis\n\nIf we decide to buy, we can\'t buy again until we sell because of **requirement #3**. The opposite is true as well (if we sell we can\'t sell until we buy again). I decided to that we have **two states**: a buying and selling state. \n\nIf you think about it, we also have to option to wait as well. For example, you aren\'t forced to sell the day after you buy a stock. Smart people would wait for the prices to increase before selling so they can make a profit. The opposite is also true for buying as you can wait to buy when it\'s cheaper.\n\n1. For the buy state, you can either buy now and look to sell or buy later (wait). \n2. For the sell state, you can either sell now and look to buy after you skip one day (requirement #1) before buying again or sell later (wait).\n\n# Brute Force Solution\n##### I decided to have a nested DFS function that takes 3 parameters: The current index, the current state (buy or sell), and the total profit.\n\n```\n def maxProfit(self, prices: List[int]) -> int: \n res = 0\n \n def dfs(i, state, profit):\n nonlocal res\n if i >= len(prices):\n\t\t\t\t# Keep track of the maximum profit\n res = max(profit, res)\n return\n \n\t\t\t# STATE: We don\'t have a stock and need to buy one\n if state == \'b\':\n\t\t\t\t# DECISION #1 \n\t\t\t\t# Set state to \'s\' because we bought a stock and are looking to sell\n\t\t\t\t# Our profit decreases because we spent money to buy the stock\n dfs(i + 1, \'s\', profit - prices[i])\n\t\t\t\t# DECISION #2\n\t\t\t\t# This spot might be too expensive\n\t\t\t\t# Let\'s buy a stock the next day instead\n dfs(i + 1, \'b\', profit)\n else: # STATE: We already bought a stock and are looking to sell\n\t\t\t\t# DECISION #3\n\t\t\t\t# Set state to \'b\'. We sold our stock and we are looking to buy again\n\t\t\t\t# Our profit increases \n\t\t\t\t# Remember Requirement #1!!! \n\t\t\t\t# We have to skip the next day so we set i + 2 instead of i + 1\n dfs(i + 2, \'b\', profit + prices[i])\n\t\t\t\t# DECISION #4\n\t\t\t\t# The stock might be too cheap today, let\'s wait to sell the next day\n\t\t\t\t# Note we remain on the sell state\n dfs(i + 1, \'s\', profit)\n\t\t# Initially we HAVE TO BUY, we don\'t have a stock yet\n dfs(0, \'b\', 0)\n return res\n```\n\n##### Now we have our Brute force solution from our drawing analysis. \n### Time: O(2^n)\n\n##### It\'s working for a brute force solution but how can we make this into a dynamic programming solution. First, I have to find a way to BUILD UP the solution using the brute force method. \n\n\n# Brute Force Solution (Building Up Answer)\nWe will always be returning the **maximum profit**. \n\n### Base Case: \n1. The maximum profit would be zero if there are no stocks to buy/sell.\n### Recursive Case: \n1. We will reuse the states from the previous solution. The only difference is how we can **return the solution** to the parent. \n2. Remember we want **TO RETURN THE MAXIMUM RESULT**.\n3. Depending on the state we are currently in, we want to know what is the maximum profit we can make for their 2 descisions.\n\n### What is the subproblem? \n#### What is the maximum profit we can make from some day i if we are looking to sell?\n#### What is the maximum profit we can make from some day i if we are looking to buy?\n\n```\n def maxProfit(self, prices: List[int]) -> int: \n\t\t# The two recursive calls in the past are now combined.\n def dfs(i, state):\n if i >= len(prices):\n return 0\n \n if state == \'b\':\n\t\t\t\t# Recursive Call #1\n\t\t\t\t# Profit loss for buying now + max profit we can make by looking to sell next day\n\t\t\t\t# Recursive Call #2\n\t\t\t\t# Profit for waiting to buy later\n\t\t\t\t# Which choice would give us the most profit?\n return max(dfs(i + 1, \'s\') - prices[i], dfs(i + 1, \'b\'))\n else:\n\t\t\t\t# Recursive Call #1\n\t\t\t\t# Profit gain for selling now + max profit we can make by looking to buy after skipping a day\n\t\t\t\t# Recursive Call #2\n\t\t\t\t# Profit gain for waiting till the next day to sell\n\t\t\t\t# Which choice gives us the most profit?\n return max(prices[i] + dfs(i + 2, \'b\'), dfs(i + 1, \'s\'))\n return dfs(0, \'b\')\n```\n\n### Time O(2^n)\n#### We have the same efficiency but from this, we can turn the solution into a DP one.\n\n# DP Solution\n### What if we start with Bottom-up DP and build our solution upwards from the last day to the first day?\n\n### Ex: prices = [1, 2, 3, 0, 2]\n##### Question: What is the maximum profit from the last day? Index = 4?\nRemember, we could have two states. We could either be looking to buy a stock at day 4 or looking to sell a stock at day 4. **We need to account for both cases. **\n\nFor each state, we need to consider both choices and cache the maximum in a dp array.\n### Buying state \n1. Buy now and look to sell later = **-2 profit**\n\ta. 1st recursive call: dfs(4 + 1, \'s\') - prices[4] = 0 (base case - OOB) - 2 (price) = **-2**\n2. Buy later = **0 profit** \n\ta. 2nd recursive call: dfs(4 + 1, \'b\') = 0 (base Case OOB) = **0**\n\t\n### Selling state\n1. Sell now and look to buy after skipping a day = **2 profit**\n\ta. 1st Recursive Call: dfs(4 + 2, \'b\') + prices[4] = 0 (base case - OOB) + 2 = **2**\n2. Wait to sell later = **0 profit**\n\ta. 2nd Recursive Call: dfs(4 + 1, \'s\') = 0 (base call - OOB) = **0** \n\t\n### Result\n##### Max profit buying at day 4: 0\n##### Max profit selling at day 4: 2\n\n### Here\'s a picture of the results after we calculate the last day\n\n\n\n\n\n##### Question #2: What is the maximum profit from the 2nd to last day? Index = 3?\n\n### Buying state \n1. Buy now and look to sell later\n\ta. 1st Recursive Call: dfs(3 + 1, \'s\') - prices[3]\n\tb. **HEY! DIDN\'T WE SOLVE WHAT THE MAXIMUM IT WAS TO LOOK TO SELL AT DAY 4????**\n\tc. = 2 (solved day 4, sell already) - 0 = **0**\n2. Buy later = **0 profit** \n\ta. 2nd recursive call: dfs(3 + 1, \'b\') = 0 (base Case OOB) = **0**\n\tb. **HEY! WE SOLVED THE MAXIMUM FOR LOOKING TO BUY AT DAY 4!!!**\n\t\n### Selling state (Same thing. We already solved the recursive call)\n\n\n\n\n### Now we discovered how to calculate the dp at index i.\n#### We need a 2d array where row 0 keeps track of maximum in buy state and row 1 tracks maximum in sell state (like the picture)\n\n### dp[0][i] = max(dp[1][i + 1] - prices[i], dp[0][i + 1])\n### dp[1][i] = max(dp[0][i + 2] + prices[i], dp[1][i + 1])\n\n# DP Solution Code\n```\n def maxProfit(self, prices: List[int]) -> int: \n dp = [[0 for i in range(len(prices) + 2)] for x in range(2)]\n \n\t\t# Bottom Up so start from last day to first\n for i in range(len(prices) - 1, -1, -1):\n\t\t\t# Use our DP Formulas !!!!!\n dp[0][i] = max(-prices[i] + dp[1][i + 1], dp[0][i + 1])\n dp[1][i] = max(prices[i] + dp[0][i + 2], dp[1][i + 1])\n\t\t# We want to return the max for BUYING at Day 0\n\t\t# We can\'t sell if we haven\'t bought a stock yet. (Requirement #2)\n return dp[0][0]\n```\n\n### Time: O(n)\n### Space: O(2n) --> O(n)\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n | 11 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
* After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[1,2,3,0,2\]
**Output:** 3
**Explanation:** transactions = \[buy, sell, cooldown, buy, sell\]
**Example 2:**
**Input:** prices = \[1\]
**Output:** 0
**Constraints:**
* `1 <= prices.length <= 5000`
* `0 <= prices[i] <= 1000` | null |
Python O(n) by leave node removal [w/ Visualization] | minimum-height-trees | 0 | 1 | **Hint**:\n\nUse leaves node removal procedure to find **central nodes** of graph.\n\nThose trees which are rooted in **central nodes** have minimum tree height.\n\n---\n\n**Illustration and Visualization**:\n\nIn a tree, the degree of leaf node must be 1.\n\nFor example, in this graph, **leaves nodes** are **node 1**, **node 2**, **node 3**, and **node 6**.\n\nAnd after leaves node removal procedure is accomplish,\n**central nodes** are **node 4** and **node 5**, also acts as *roots of trees with minimum tree height*\n\n\n\n\n[Image Source: \nWiki: Tree](https://en.wikipedia.org/wiki/Tree_(graph_theory))\n\n---\n\n**Implementation** by leave nodes removal:\n\n```\nfrom collections import defaultdict\n\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n \n \n total_node_count = n\n \n if total_node_count == 1:\n # Quick response for one node tree\n return [0]\n \n \n # build adjacency matrix\n adj_matrix = defaultdict( set )\n \n for src_node, dst_node in edges:\n adj_matrix[src_node].add( dst_node )\n adj_matrix[dst_node].add( src_node )\n \n \n # get leaves node whose degree is 1\n leave_nodes = [ node for node in adj_matrix if len(adj_matrix[node]) == 1 ]\n \n \n # keep doing leave nodes removal until total node count is smaller or equal to 2\n while total_node_count > 2:\n \n total_node_count -= len(leave_nodes)\n \n leave_nodes_next_round = []\n \n # leave nodes removal\n for leaf in leave_nodes:\n \n neighbor = adj_matrix[leaf].pop()\n adj_matrix[neighbor].remove( leaf )\n \n if len(adj_matrix[neighbor]) == 1:\n leave_nodes_next_round.append( neighbor )\n \n leave_nodes = leave_nodes_next_round\n \n # final leave nodes are root node of minimum height trees\n return leave_nodes\n \n\n```\n\n---\n\nReference:\n\n[1] [Wiki: Tree](https://en.wikipedia.org/wiki/Tree_(graph_theory))\n\n[2] [Python official docs about defaultdict](https://docs.python.org/3.8/library/collections.html#collections.defaultdict) | 59 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
310: Time 96.8%, Solution with step by step explanation | minimum-height-trees | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can solve this problem using a BFS approach. We start by building an adjacency list of the input edges, which is a mapping between each node and its neighboring nodes. We can then perform a breadth-first search starting from the leaf nodes and moving towards the root. At each level of the BFS, we remove the leaf nodes and their corresponding edges from the adjacency list, until we are left with only 1 or 2 nodes. These nodes are the roots of the MHTs.\n\nAlgorithm:\n\n1. Build the adjacency list for the graph using the input edges.\n2. Initialize a queue with all leaf nodes (i.e., nodes with degree 1) and remove them from the adjacency list.\n3. While there are more than 2 nodes in the graph:\na. Initialize a list to store the new leaf nodes.\nb. For each node in the current level of the BFS:\ni. For each of its neighboring nodes, remove the corresponding edge from the adjacency list.\nii. If the neighboring node becomes a leaf node (i.e., degree 1), add it to the new leaf node list.\nc. Remove the current level nodes from the graph.\nd. Add the new leaf nodes to the queue.\n4. Return the remaining nodes as the roots of the MHTs.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n # Edge case: n=1, return [0]\n if n == 1:\n return [0]\n \n # Build adjacency list for the graph\n adj_list = {i: set() for i in range(n)}\n for u, v in edges:\n adj_list[u].add(v)\n adj_list[v].add(u)\n \n # Find all leaf nodes (i.e., nodes with degree 1)\n leaves = [i for i in range(n) if len(adj_list[i]) == 1]\n \n # Repeat until we are left with 1 or 2 nodes\n while n > 2:\n \n # Remove the current leaf nodes along with their edges\n n -= len(leaves)\n new_leaves = []\n for leaf in leaves:\n neighbor = adj_list[leaf].pop()\n adj_list[neighbor].remove(leaf)\n \n # If the neighbor becomes a new leaf node, add it to the list\n if len(adj_list[neighbor]) == 1:\n new_leaves.append(neighbor)\n \n # Update the list of leaf nodes\n leaves = new_leaves\n \n # The remaining nodes are the roots of the MHTs\n return leaves\n\n``` | 10 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
Python easy to read and understand | reverse topological sort | minimum-height-trees | 0 | 1 | ```\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n if n == 1:\n return [0]\n graph = {i:[] for i in range(n)}\n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n \n leaves = []\n for node in graph:\n if len(graph[node]) == 1:\n leaves.append(node)\n \n while len(graph) > 2:\n new_leaves = []\n for leaf in leaves:\n nei = graph[leaf].pop()\n del graph[leaf]\n graph[nei].remove(leaf)\n if len(graph[nei]) == 1:\n new_leaves.append(nei)\n leaves = new_leaves\n \n return leaves | 9 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
Python3, O(n) with explanation | minimum-height-trees | 0 | 1 | Note the following: if the height of a tree with root x is h, then the height of the same tree with the leaves removed and with root x is h - 1.\n\nTherefore, any vertex that minimizes the height of the tree also minimizes the height of the tree minus its leaves. \n\nIn other words, if we remove all the leaves, we do not change the answer and we make the input smaller.\n\nTaking advantage of this, we iteratively remove leaves until we reach a point where all the vertices are leaves. Note that this also proves that the size of the solution is 1 or 2.\n```\ndef findMinHeightTrees(n: int, edges: List[List[int]]) -> List[int]:\n graph = [set() for _ in range(n)]\n \n for u, v in edges:\n graph[u].add(v)\n graph[v].add(u)\n\n leaves = [x for x in range(n) if len(graph[x]) <= 1]\n prev_leaves = leaves\n while leaves:\n new_leaves = []\n for leaf in leaves:\n if not graph[leaf]:\n return leaves\n neighbor = graph[leaf].pop()\n graph[neighbor].remove(leaf)\n if len(graph[neighbor]) == 1:\n new_leaves.append(neighbor)\n prev_leaves, leaves = leaves, new_leaves\n\n return prev_leaves\n``` | 16 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
Python DFS (naive) and BFS (topological) solutions comparison [SOLVED] | minimum-height-trees | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n### Solution 1: DFS (Naive Approach)\n\nThis solution is relatively straightforward. A representation of the tree/graph is created using a hashmap. Iterating through ALL nodes, a dfs recursive search is performed on EACH node. This means each node will be treated as the \'root\', and all heights are calculated. The minimum height(s) are then picked out and the respective nodes selected.\n\nHowever, this WILL result in TLE as with a growing number of nodes and connections, the number of paths grows exponentially. \n\nThis is the solution which technically works, but will NOT pass in Leetcode.\n\n### Solution 2: BFS (Topological)\n\nI will not delve into a detailed explanation for the preferred solution, as it has been well explained by numerous other users. Here I will break down the solution into the component steps, as well as highlight important points along the way.\n\n1. 2 nodes are the smallest possible \'set\' where it is not meaningful to trim any more leaves. this would be the \'base case\'\n2. create a representation of the tree using a hashmap\n3. construct the first layer of leaves. leaves will have only 1 edge connection\n4. outer while loop which runs until only 2 nodes are left, the base case. \n5. create a store for the next layer of leaves to be constructed\n6. inner while loop which runs and does two things (IMPT: must be done in sequence)\n 1. remove leaf-neighbour edge from current leaf\n 2. create new leaf layer from the neighbours\n7. reassign the new leaf layer\n\nThis will trim the leaves layer by layer until either 1 or 2 nodes are left in which case both would be the solution.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nDFS: $$O(n^2)$$\nBFS: $$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nDFS: $$O(n.m)$$\nBFS: $$O(n.m)$$\n\n# Code\n### Solution 1: DFS (Naive Approach)\n```\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n\n # represent the nodes and edges in a graph using a hashmap\n graph = { i: [] for i in range(n) }\n\n for edge in edges:\n node1, node2 = edge\n graph[node1].append(node2)\n graph[node2].append(node1)\n\n visited = set()\n heights = defaultdict(int)\n # dfs recursive function, dive into the tree from each node, and determine the heights of the trees from each node chosen as the root\n def dfs(node, parent, count, visited):\n heights[parent] = max(heights[parent], count)\n # dfs through the connections\n for c in graph[node]:\n if c not in visited:\n visited.add(node)\n dfs(c, parent, count + 1, visited)\n # node has to be removed \'backtracking\' to progress to the other child node from parent\n visited.remove(node)\n\n for node in graph:\n dfs(node, node, 0, visited)\n\n # global minimum height\n min_height = min(heights.values())\n output = []\n\n for k, v in heights.items():\n if v == min_height:\n output.append(k)\n\n return output\n```\n\n### Solution 2: BFS (Topological)\n```\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n\n # edge case where the nodes are already reduced to the smallest possible set\n if n < 3:\n return [i for i in range(n)]\n\n # represent the nodes and edges in a graph using a hashmap\n graph = {i: [] for i in range(n)}\n\n for node1, node2 in edges:\n graph[node1].append(node2)\n graph[node2].append(node1)\n\n # populate the first leaf layer\n leaves = []\n for node in graph:\n # leaves will only have one connection\n if len(graph[node]) == 1:\n leaves.append(node)\n\n # outer while loop runs until only two nodes left as leaves are removed\n while n > 2:\n n -= len(leaves)\n # store next layer of leaves which will be constructed in inner while loop\n next_leaves_layer = []\n while leaves:\n leaf = leaves.pop()\n # 1. remove leaf-neighbour edges\n neighbour = graph[leaf].pop()\n neighbour_connections = graph[neighbour]\n neighbour_connections.remove(leaf)\n # 2. create new leaf layer from neighbour\n if len(neighbour_connections) == 1:\n next_leaves_layer.append(neighbour)\n # reassign next layer to \'leaves\'\n leaves = next_leaves_layer\n \n return leaves\n```\n | 2 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
✅[Python] Simple and Clean, beats 99.89%✅ | minimum-height-trees | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven a tree with n nodes and n-1 edges, we can select any node as the root and calculate the height of the tree with respect to that root. We want to find the root(s) that correspond to the minimum height. One way to approach this problem is to iteratively remove the outermost layer of leaves until only the roots with the minimum height remain. This approach can be motivated by the observation that the root(s) with minimum height must lie on the "middle layer(s)" of the tree, which can be defined as the layer(s) of nodes that are equidistant to the leaf nodes. Therefore, we can start by removing the leaf nodes and the layers of nodes adjacent to the leaves, until we reach the middle layer(s).\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo implement this approach, we first build a graph from the input edges, where each node is represented by a key in a dictionary, and its value is a set of neighboring nodes. We also initialize a deque object `leaves` with all the nodes that have only one neighbor (i.e., the leaf nodes). We then iteratively remove the layers of `leaves` by performing the following steps until there are only 1 or 2 nodes left:\n\n1. Pop all the leaves from the deque `leaves`.\n1. For each leaf node, remove its connection with its neighbor, and remove the neighbor from its set of neighbors. If the neighbor now has only one neighbor (i.e., it becomes a new leaf node), add it to the deque `leaves`.\n1. Decrement the total number of nodes `n` by the number of `leaves` we just removed.\n1. Repeat until there are only 1 or 2 nodes left.\n\nThe remaining 1 or 2 nodes represent the root(s) with the minimum height, so we return their indices as a list.\n# Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this approach is linear in the number of nodes `n` in the tree, as we need to process each node exactly once. The space complexity is also linear, as we need to store the graph as a dictionary and the deque of leaves.\n# Code\n```\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n if n==1:\n return [0]\n graph = defaultdict(set)\n for i,j in edges:\n graph[i].add(j)\n graph[j].add(i)\n \n leaves = deque([i for i in range(n) if len(graph[i])==1])\n while n>2:\n leaf_count = len(leaves)\n n -= leaf_count\n for i in range(leaf_count):\n leaf = leaves.popleft()\n neighbor = graph[leaf].pop()\n graph[neighbor].remove(leaf)\n if len(graph[neighbor]) == 1:\n leaves.append(neighbor)\n return list(leaves)\n\n``` | 2 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
Python, topological sort | minimum-height-trees | 0 | 1 | ```\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n if n <= 2:\n return [i for i in range(n)]\n \n adj = defaultdict(list)\n edge_count = defaultdict(int)\n for a, b in edges:\n adj[a].append(b)\n adj[b].append(a)\n edge_count[a] += 1\n edge_count[b] += 1\n \n q = deque(n for n in adj if len(adj[n]) == 1)\n visited = set(q)\n \n while len(visited) < n:\n length = len(q)\n for _ in range(length):\n node = q.popleft() \n for neighbor in adj[node]:\n if neighbor not in visited:\n edge_count[neighbor] -= 1\n if edge_count[neighbor] == 1:\n q.append(neighbor)\n visited.add(neighbor)\n \n return q\n``` | 1 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
Just Code | minimum-height-trees | 1 | 1 | ```java []\nimport java.util.ArrayList;\nimport java.util.HashSet;\nimport java.util.LinkedList;\nimport java.util.List;\nimport java.util.Queue;\nimport java.util.Set;\n\npublic class Solution {\n public List<Integer> findMinHeightTrees(int n, int[][] edges) {\n if (n == 1) {\n return List.of(0);\n }\n\n List<Set<Integer>> graph = new ArrayList<>(n);\n for (int i = 0; i < n; ++i) {\n graph.add(new HashSet<>());\n }\n\n for (int[] edge : edges) {\n graph.get(edge[0]).add(edge[1]);\n graph.get(edge[1]).add(edge[0]);\n }\n\n Queue<Integer> leaves = new LinkedList<>();\n for (int i = 0; i < n; ++i) {\n if (graph.get(i).size() == 1) {\n leaves.offer(i);\n }\n }\n\n int remainingNodes = n;\n while (remainingNodes > 2) {\n int currentLeavesCount = leaves.size();\n remainingNodes -= currentLeavesCount;\n\n for (int i = 0; i < currentLeavesCount; ++i) {\n int leaf = leaves.poll();\n\n int neighbor = graph.get(leaf).iterator().next();\n graph.get(neighbor).remove(leaf);\n\n if (graph.get(neighbor).size() == 1) {\n leaves.offer(neighbor);\n }\n }\n }\n\n List<Integer> result = new ArrayList<>();\n while (!leaves.isEmpty()) {\n result.add(leaves.poll());\n }\n\n return result;\n }\n}\n```\n```python []\nfrom collections import defaultdict, deque\nfrom typing import List\n\nclass Solution:\n def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:\n if n == 1:\n return [0]\n\n # Create an adjacency list to represent the tree\n adjacency_list = defaultdict(list)\n for edge in edges:\n u, v = edge\n adjacency_list[u].append(v)\n adjacency_list[v].append(u)\n\n # Find leaves (nodes with only one connection)\n leaves = deque()\n for node in range(n):\n if len(adjacency_list[node]) == 1:\n leaves.append(node)\n\n # Continue removing leaves until only the root or roots with minimum height are left\n remaining_nodes = n\n while remaining_nodes > 2:\n current_leaves_count = len(leaves)\n remaining_nodes -= current_leaves_count\n\n for _ in range(current_leaves_count):\n leaf = leaves.popleft()\n neighbor = adjacency_list[leaf][0]\n adjacency_list[neighbor].remove(leaf)\n\n if len(adjacency_list[neighbor]) == 1:\n leaves.append(neighbor)\n\n return list(leaves)\n\n# Example usage:\nsolution = Solution()\nprint(solution.findMinHeightTrees(4, [[1,0],[1,2],[1,3]])) # Output: [1]\nprint(solution.findMinHeightTrees(6, [[3,0],[3,1],[3,2],[3,4],[5,4]])) # Output: [3,4]\n```\n```C++ []\n#include <vector>\n#include <unordered_set>\n#include <queue>\n\nclass Solution {\npublic:\n std::vector<int> findMinHeightTrees(int n, std::vector<std::vector<int>>& edges) {\n if (n == 1) {\n return {0};\n }\n\n std::vector<std::unordered_set<int>> graph(n);\n for (const auto& edge : edges) {\n graph[edge[0]].insert(edge[1]);\n graph[edge[1]].insert(edge[0]);\n }\n\n std::queue<int> leaves;\n for (int i = 0; i < n; ++i) {\n if (graph[i].size() == 1) {\n leaves.push(i);\n }\n }\n\n int remainingNodes = n;\n while (remainingNodes > 2) {\n int currentLeavesCount = leaves.size();\n remainingNodes -= currentLeavesCount;\n\n for (int i = 0; i < currentLeavesCount; ++i) {\n int leaf = leaves.front();\n leaves.pop();\n\n int neighbor = *graph[leaf].begin();\n graph[neighbor].erase(leaf);\n\n if (graph[neighbor].size() == 1) {\n leaves.push(neighbor);\n }\n }\n }\n\n std::vector<int> result;\n while (!leaves.empty()) {\n result.push_back(leaves.front());\n leaves.pop();\n }\n\n return result;\n }\n};\n```\n | 0 | A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where `edges[i] = [ai, bi]` indicates that there is an undirected edge between the two nodes `ai` and `bi` in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
**Example 1:**
**Input:** n = 4, edges = \[\[1,0\],\[1,2\],\[1,3\]\]
**Output:** \[1\]
**Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
**Example 2:**
**Input:** n = 6, edges = \[\[3,0\],\[3,1\],\[3,2\],\[3,4\],\[5,4\]\]
**Output:** \[3,4\]
**Constraints:**
* `1 <= n <= 2 * 104`
* `edges.length == n - 1`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs `(ai, bi)` are distinct.
* The given input is **guaranteed** to be a tree and there will be **no repeated** edges. | How many MHTs can a graph have at most? |
Beats 99.99% Python. Dynamic Programming, Memoization. Simple code | burst-balloons | 0 | 1 | # Intuition\nThere is a hard requirement to return the maximum possible value, and the result is path dependent. \n\nImagine the easiest test case to solve by hand, then imagine adding one element to that input.\n\nIf the last element added should be popped last, eg: $$1*1*1$$, the final result is the answer to the easiest test case + new element. \n\nIf not, we need to propagate the change.\n\nThe sub-problem is to find the answer for not just one balloon at a time, but for the maximum value of popping a continuous range of balloons. Cache the answer to those sub-problems.\n\n\n# Approach\nAdd 1s at the end, and our code will naturally handle the calculation without adding special if statements.\n\nBuild a cache to store the sub-problem answers `cache[l][r]`, witht the final answer intuitively being stored at `cache[0][-1]`\n\nThe key will be building the cache in the right order. The two indices start such that a single balloon is considered, and then the range expands one at a time.\n\nThe first balloon considered on every iteration must be the newest balloon, not yet considered in the cache of maximum possible values. Once its value has been included, the queries to propagate any change throughout the cache make sense. \n\nKeys to this being the winning solution?\n- Cache is allocated and filled with the minimum value. Then it is filled in such a way that there is no depth first search, no runtime checks before reading. Every read and write is necessary.\n\n- Pythonic generator feeding into max instead of a loop\n- but keeping temp in memory to avoid recomputation\n\n# Complexity\n- Time complexity:\n$$O(n^3)$$\nThe two for loops contribute $$N*(N+1)/2$$\nThe cache updating loop contributes another $$(((N+1)/2)+1)/2$$\n\n- Space complexity:\n$$O(n^2)$$ for the cache\n\n# Code\n```\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n \n # add padding to nums\n nums = [1] + nums + [1]\n N = len(nums)\n # create empty cache\n cache = [ [0]*N for _ in nums ]\n\n for r in range(2,N):\n for l in range(r-2,-1,-1):\n temp = nums[l]*nums[r]\n # temp is here to save python from recomputing it in the loop below\n cache[l][r] = max( temp*nums[m] + cache[l][m] + cache[m][r] for m in range(l+1,r) )\n \n return cache[0][N-1]\n``` | 1 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
Python || 90.12% Faster || DP || Recursive->Tabulation | burst-balloons | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(Exponential)\n#Space Complexity: O(n)\nclass Solution1:\n def maxCoins(self, nums: List[int]) -> int:\n def solve(i,j):\n if i>j:\n return 0\n maxi=-maxsize\n for k in range(i,j+1):\n coins=nums[i-1]*nums[k]*nums[j+1]+solve(i,k-1)+solve(k+1,j)\n maxi=max(maxi,coins)\n return maxi\n \n n=len(nums)\n nums.insert(0,1)\n nums.append(1)\n return solve(1,n)\n \n#Memoization (Top-Down)\n#Time Complexity: O(n^3)\n#Space Complexity: O(n^2) + O(n)\nclass Solution2:\n def maxCoins(self, nums: List[int]) -> int:\n def solve(i,j):\n if i>j:\n return 0\n if dp[i][j]!=-1:\n return dp[i][j]\n maxi=-maxsize\n for k in range(i,j+1):\n coins=nums[i-1]*nums[k]*nums[j+1]+solve(i,k-1)+solve(k+1,j)\n maxi=max(maxi,coins)\n dp[i][j]=maxi\n return dp[i][j]\n \n n=len(nums)\n dp=[[-1 for j in range(n+1)] for j in range(n+1)]\n nums.insert(0,1)\n nums.append(1)\n return solve(1,n)\n \n#Tabulation (Bottom-Up)\n#Time Complexity: O(n^3)\n#Space Complexity: O(n^2)\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n n=len(nums)\n nums.insert(0,1)\n nums.append(1)\n dp=[[0 for j in range(n+2)] for j in range(n+2)]\n for i in range(n,0,-1):\n for j in range(1,n+1):\n if i>j:\n continue\n maxi=-maxsize\n for k in range(i,j+1):\n coins=nums[i-1]*nums[k]*nums[j+1]+dp[i][k-1]+dp[k+1][j]\n maxi=max(maxi,coins)\n dp[i][j]=maxi\n return dp[1][n]\n```\n**An upvote will be encouraging** | 5 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
312: Time 90.16%, Solution with step by step explanation | burst-balloons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe idea is to use dynamic programming to solve the problem. We define dp[i][j] as the maximum coins we can get by bursting all balloons between index i and j (exclusive). We want to compute dp[0][n-1] as the result of the original problem.\n\nTo fill the dp table, we need to find the last balloon to burst. We iterate k from i+1 to j-1, and for each k, we compute the maximum coins we can get by bursting the balloon at k last. This involves the coins we get by bursting the balloon at k, plus the maximum coins we can get for the balloons to the left of k and to the right of k. We add up these three parts to get the maximum coins for subproblems.\n\nThe time complexity of the algorithm is O(n^3), which is acceptable given the constraints of the problem.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n # Add padding to the input array\n nums = [1] + nums + [1]\n n = len(nums)\n # Initialize a dp table to store the maximum coins for subproblems\n dp = [[0] * n for _ in range(n)]\n \n # Iterate the input array in reverse order to fill the dp table\n for i in range(n-2, -1, -1):\n for j in range(i+2, n):\n # Iterate k from i+1 to j-1 to find the last balloon to burst\n for k in range(i+1, j):\n # Compute the maximum coins for subproblems\n dp[i][j] = max(dp[i][j], nums[i]*nums[k]*nums[j] + dp[i][k] + dp[k][j])\n \n # The result is the maximum coins for the original problem\n return dp[0][n-1]\n\n``` | 7 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
Python Solution with Explanation (both DFS and DP) | burst-balloons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can use dfs + memorization (caching) to solve this problem. Define a function dfs(nums), which return the maximum points we can get from nums. For each element in the input array, we calculate the points of bursting it first by: `nums[i-1] * nums[i]* nums[i+1] + dfs(nums.remove(nums[i]))`. And we want to return the maximum score we get, so we keep track of the curr_max and return it.\n\nHere we use caching to reduce the time complexity. We can easily observe that the subproblem is `tuple(nums)`, so make it as the key, and just return its value if we met it before. Since we have $2^n$ subproblems (each element we either keep it or disgard it), our time complexity and space complexity is huge. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS + Caching\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n# Code\n```\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n caching = {}\n def dfs(ballons):\n if len(ballons) == 0:\n return 0\n bsr = tuple(ballons)\n if bsr in caching:\n return caching[bsr]\n curr_max = 0\n for i in range(len(ballons)):\n a = ballons[i-1] if i>0 else 1\n b = ballons[i]\n c = ballons[i+1] if i<len(ballons)-1 else 1\n curr_max = max(curr_max, a*b*c + dfs(ballons[:i]+ballons[i+1:]))\n caching[bsr] = curr_max\n return caching[bsr]\n return dfs(nums)\n```\n\n# Intuition\nFrom the analysis above, we know that we have to divide the subproblem in a simpler way. \n\nKey observation:\n- When we iterate through the array, for each element, we treat it as the last element we burst --> instead of the first element. Why? Now for nums[:i] and nums[i+1:], they are independent subproblems, because the nums[i] still exist (we pop it last). Assume that the current `nums` has a boundary [left, right], we can easily calculate the score by `nums[l-1] * nums[i] * nums[r+1] + dfs(nums[l:i]) + dfs(nums[i+1: r])`.\n- How many possible subproblems we have right now? Since each subproblem is represented by (l,r), we have O(n^2) of them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic Programming\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^3)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n# Code\n```\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n dp = {}\n nums = [1] + nums + [1]\n def dfs(l, r):\n if l>r:\n return 0\n if (l,r) in dp:\n return dp[(l,r)]\n dp[(l,r)] = 0\n for i in range(l, r+1):\n coins = nums[l-1] * nums[i] * nums[r+1]\n coins += dfs(l, i-1) + dfs(i+1, r)\n dp[(l,r)] = max(dp[(l,r)], coins)\n return dp[(l,r)]\n return dfs(1, len(nums)-2)\n \n``` | 2 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
PYTHON BEGINNER | Brute force recursion -> Brute-Better Memoization -> DP | burst-balloons | 0 | 1 | * dp[left][right] = coins obtained from bursting all the balloons between left and right (not including left or right)\n* dp[left][right] = max(nums[left] * nums[i] * nums[right] + dp[left][i] + dp[i][right]) for i in (left+1,right)\n\n* If i is the index of the last balloon burst in (left, right), the coins that burst will get are nums[left] * nums[i] * nums[right], and to calculate dp[left][right], we also need to add the coins obtained from bursting balloons between left and i, and between i and right, i.e., dp[left][i] and dp[i][right]\n\n```\n# Brute force recursion\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n nums = [1] + nums + [1]\n return self.recurse(nums, 0, len(nums)-1)\n \n def recurse(self, nums, left, right):\n \n res = 0\n for i in range(left+1, right):\n coins = nums[left] * nums[i] * nums[right]\n leftRes = self.recurse(nums, left, i)\n rightRes = self.recurse(nums, i, right)\n res = max(res, coins + leftRes + rightRes)\n \n return res\n\n \n# Brute Better Memoization (69/70 Passed)\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n nums = [1] + nums + [1]\n self.dp = [[-1 for _ in range(len(nums))] for _ in range(len(nums))]\n return self.recurse(nums, 0, len(nums)-1)\n \n def recurse(self, nums, left, right):\n \n if self.dp[left][right] != -1:\n return self.dp[left][right]\n \n res = 0\n for i in range(left+1, right):\n coins = nums[left] * nums[i] * nums[right]\n leftRes = self.recurse(nums, left, i)\n rightRes = self.recurse(nums, i, right)\n res = max(res, coins + leftRes + rightRes)\n \n self.dp[left][right] = res\n return res\n\n \n# Top down DP (Accepted)\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n nums = [1] + nums + [1]\n dp = [[0 for _ in range(len(nums))] for _ in range(len(nums))]\n \n for gap in range(len(nums)):\n for left in range(len(nums)-gap):\n right = left + gap\n \n res = 0\n for i in range(left+1, right):\n coins = nums[left] * nums[i] * nums[right]\n res = max(res, coins + dp[left][i] + dp[i][right])\n dp[left][right] = res\n \n return dp[0][len(nums)-1]\n```\n | 17 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
Dynamic Programming Solution for Bursting Balloons Problem | burst-balloons | 0 | 1 | # Intuition\nThe Burst Balloons problem involves finding the maximum coins collected by bursting balloons. My initial thought is that a dynamic programming approach could be useful here, as we need to consider the optimal strategy for bursting balloons in order to maximize the collected coins.\n\n# Approach\nTo solve the Burst Balloons problem, we can use a dynamic programming approach. We\'ll define a 2D DP table where `dp[i][j]` represents the maximum coins we can collect by bursting balloons in the range from `i` to `j` (inclusive). We need to consider the optimal order of bursting balloons within this range. The key insight is that we can think of each balloon as the last one to burst, and then calculate the maximum coins considering this balloon as the last one. To do this, we\'ll iterate over all possible balloons as the last one, calculate the coins obtained, and update `dp[i][j]` accordingly. The final result will be stored in `dp[0][n-1]`, where `n` is the total number of balloons.\n\nHere\'s a high-level overview of our approach:\n1. Initialize the `dp` table with zeros.\n2. Iterate over different subarray lengths (`offsets`).\n3. For each subarray length, iterate over all possible starting indices `i`.\n4. Calculate the ending index `j` based on the current subarray length.\n5. For each possible balloon `k` within the subarray, calculate the coins obtained by considering it as the last balloon to burst.\n6. Update `dp[i][j]` based on the maximum coins obtained.\n7. Return `dp[0][n-1]` as the final result.\n\nBy considering different subarray lengths and optimal bursting orders for each subarray, we ensure that we capture the maximum coins collected by bursting balloons.\n\nThis approach ensures that we avoid redundant calculations and build the solution iteratively, leading to an efficient solution to the Burst Balloons problem.\n\n# Complexity\n- Time complexity:\nThe time complexity of this approach is `O(n^3)`, where `n` is the number of balloons. We iterate over different subarray lengths, and for each subarray length, we iterate over all possible starting indices. Within the inner loop, we iterate over all possible balloons within the subarray. Therefore, the overall time complexity is dominated by the three nested loops.\n\n- Space complexity:\nThe space complexity is `O(n^2)`, where `n` is the number of balloons. We use a 2D dp table to store intermediate results for different subarrays. Each entry in the `dp` table requires constant space.\n\n# Code\n```python3\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n balloons = [1] + nums + [1]\n n = len(balloons)\n dp = [[0 for _ in range(n)] for _ in range(n)] # dp[i][j] is the max number of coins in nums[i:j] range\n\n for offset in range(2, n):\n for i in range(n - offset):\n j = i + offset\n for k in range(i + 1, j):\n dp[i][j] = max(dp[i][j], balloons[i] * balloons[k] * balloons[j] + \\\n dp[i][k] + dp[k][j])\n\n return dp[0][n - 1]\n```\n | 1 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
Simple Solution Using C++ , Python-3 & Java With Two Different Approaches | burst-balloons | 1 | 1 | # Approach 1\n<!-- Describe your approach to solving the problem. -->\n Top-Down\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n^3)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n^2)\n# Code\n```C++ []\nclass Solution {\n public:\n int maxCoins(vector<int>& nums) {\n const int n = nums.size();\n\n nums.insert(begin(nums), 1);\n nums.insert(end(nums), 1);\n\n // dp[i][j] := maxCoins(nums[i..j])\n dp.resize(n + 2, vector<int>(n + 2));\n return maxCoins(nums, 1, n);\n }\n\n private:\n vector<vector<int>> dp;\n\n int maxCoins(vector<int>& nums, int i, int j) {\n if (i > j)\n return 0;\n if (dp[i][j] > 0)\n return dp[i][j];\n\n for (int k = i; k <= j; ++k)\n dp[i][j] = max(dp[i][j], //\n maxCoins(nums, i, k - 1) + maxCoins(nums, k + 1, j) + //\n nums[i - 1] * nums[k] * nums[j + 1]);\n\n return dp[i][j];\n }\n};\n```\n```python []\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n nums = [1] + [x for x in nums if x] + [1]\n n = len(nums)\n dp = [[0] * n for _ in range(n)]\n for i in range(n-3, -1, -1):\n for j in range(i+2, n):\n temp = nums[i] * nums[j]\n dp[i][j] = max(temp * nums[k] + dp[i][k] + dp[k][j] for k in range(i+1, j))\n return dp[0][-1]\n```\n```java []\nclass Solution {\n public int maxCoins(int[] nums) {\n final int n = nums.length;\n\n A = new int[n + 2];\n\n System.arraycopy(nums, 0, A, 1, n);\n A[0] = 1;\n A[n + 1] = 1;\n\n // dp[i][j] := maxCoins(A[i..j])\n dp = new int[n + 2][n + 2];\n return maxCoins(1, n);\n }\n\n private int[][] dp;\n private int[] A;\n\n private int maxCoins(int i, int j) {\n if (i > j)\n return 0;\n if (dp[i][j] > 0)\n return dp[i][j];\n\n for (int k = i; k <= j; ++k)\n dp[i][j] = Math.max(dp[i][j], //\n maxCoins(i, k - 1) + maxCoins(k + 1, j) + //\n A[i - 1] * A[k] * A[j + 1]);\n\n return dp[i][j];\n }\n}\n```\n\n# Approach 2\n<!-- Describe your approach to solving the problem. -->\n Bottom-Up\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n^3)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n^2)\n\n# Code\n```C++ []\nclass Solution {\n public:\n int maxCoins(vector<int>& nums) {\n const int n = nums.size();\n\n nums.insert(begin(nums), 1);\n nums.insert(end(nums), 1);\n\n // dp[i][j] := maxCoins(nums[i..j])\n vector<vector<int>> dp(n + 2, vector<int>(n + 2));\n\n for (int d = 0; d < n; ++d)\n for (int i = 1; i + d <= n; ++i) {\n const int j = i + d;\n for (int k = i; k <= j; ++k)\n dp[i][j] = max(dp[i][j], //\n dp[i][k - 1] + dp[k + 1][j] + //\n nums[i - 1] * nums[k] * nums[j + 1]);\n }\n\n return dp[1][n];\n }\n};\n```\n```python []\nclass Solution:\n def maxCoins(self, nums: List[int]) -> int:\n n = len(nums)\n A = [1] + nums + [1]\n dp = [[0] * (n + 2) for _ in range(n + 2)]\n\n for d in range(n):\n for i in range(1, n - d + 1):\n j = i + d\n for k in range(i, j + 1):\n dp[i][j] = max(\n dp[i][j],\n dp[i][k - 1] +\n dp[k + 1][j] +\n A[i - 1] * A[k] * A[j + 1])\n\n return dp[1][n]\n```\n```java []\nclass Solution {\n public int maxCoins(int[] nums) {\n final int n = nums.length;\n int[] A = new int[n + 2];\n System.arraycopy(nums, 0, A, 1, n);\n A[0] = 1;\n A[n + 1] = 1;\n\n // dp[i][j] := maxCoins(A[i..j])\n int[][] dp = new int[n + 2][n + 2];\n\n for (int d = 0; d < n; ++d)\n for (int i = 1; i + d <= n; ++i) {\n final int j = i + d;\n for (int k = i; k <= j; ++k)\n dp[i][j] = Math.max(dp[i][j], //\n dp[i][k - 1] + dp[k + 1][j] + //\n A[i - 1] * A[k] * A[j + 1]);\n }\n\n return dp[1][n];\n }\n}\n```\n\nPlease Give An Up-Vote If This Solution Helps You . Thank You . | 2 | You are given `n` balloons, indexed from `0` to `n - 1`. Each balloon is painted with a number on it represented by an array `nums`. You are asked to burst all the balloons.
If you burst the `ith` balloon, you will get `nums[i - 1] * nums[i] * nums[i + 1]` coins. If `i - 1` or `i + 1` goes out of bounds of the array, then treat it as if there is a balloon with a `1` painted on it.
Return _the maximum coins you can collect by bursting the balloons wisely_.
**Example 1:**
**Input:** nums = \[3,1,5,8\]
**Output:** 167
**Explanation:**
nums = \[3,1,5,8\] --> \[3,5,8\] --> \[3,8\] --> \[8\] --> \[\]
coins = 3\*1\*5 + 3\*5\*8 + 1\*3\*8 + 1\*8\*1 = 167
**Example 2:**
**Input:** nums = \[1,5\]
**Output:** 10
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `0 <= nums[i] <= 100` | null |
313: Space 96.61%, Solution with step by step explanation | super-ugly-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\nThe idea of this problem is similar to the Ugly Number II problem. We start with the smallest super ugly number, which is 1. Then, we generate each subsequent super ugly number by multiplying each prime number in the array with the previously generated super ugly numbers, and choosing the smallest one.\n\nWe can maintain a list of indices, one for each prime number, indicating the index of the last super ugly number that was multiplied by that prime number. We use these indices to avoid generating duplicates.\n\nAlgorithm:\n\n1. Initialize a list dp of size n to store the first n super ugly numbers.\n2. Initialize a list idx of size k, where k is the length of primes, to store the index of the last super ugly number that was multiplied by each prime number. Initialize each element of idx to 0.\n3. Initialize a list nums of size k to store the product of each prime number with the previously generated super ugly numbers. Initialize each element of nums to the corresponding prime number.\n4, Initialize a variable i to 1, representing the index of the next super ugly number to be generated.\n5. While i < n:\na. Generate the ith super ugly number by choosing the minimum number in nums, and add it to dp.\nb. For each j from 0 to k-1, if nums[j] is equal to the ith super ugly number, increment idx[j] by 1 and update nums[j] to be primes[j] times dp[idx[j]].\nc. Increment i by 1.\n6. Return the last element of dp.\n\nTime Complexity: O(nk), where n is the input integer and k is the length of the primes array.\n\nSpace Complexity: O(n+k), where n is the input integer and k is the length of the primes array.\n\n# Complexity\n- Time complexity:\n65.62%\n\n- Space complexity:\n96.61%\n\n# Code\n```\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n # create a list to store the super ugly numbers, initialize with 1\n super_ugly = [1]\n # create a list to store the indices for each prime number\n idx = [0] * len(primes)\n # create a list to store the product of prime numbers with their corresponding indices\n # this will be used to find the next super ugly number\n prod = [p for p in primes]\n \n # loop until we find the nth super ugly number\n while len(super_ugly) < n:\n # find the minimum value in prod, which will be the next super ugly number\n next_ugly = min(prod)\n # append it to the list of super ugly numbers\n super_ugly.append(next_ugly)\n \n # update the index for each prime number whose product is equal to next_ugly\n for i in range(len(primes)):\n if next_ugly == prod[i]:\n idx[i] += 1\n prod[i] = primes[i] * super_ugly[idx[i]]\n \n # return the last element in the list of super ugly numbers, which is the nth super ugly number\n return super_ugly[-1]\n\n``` | 5 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
Python3 l Faster than 99.35 % | using heapq | super-ugly-number | 0 | 1 | Instead of checking the numbers one by one, here we are generating the numbers from the already available ugly numbers and keeping a count.\nFor example: primes = [2,3,5] and n = 16\nHere catch is there are multiple additions to heap like 6 = 2\\*3 and also 6 = 3\\*2\nso what we do is :\nfor 2, we find multiples of 2 like 2\\*2 = 4 \nfor 3, we find multiples of 2 and 3 like 3\\*2 , 3\\*3 = 6,9\nfor 5, we find multiples of 2, 3 and 5 like 5\\*2, 5\\*3, 5\\*5 = 10,15,25\n```\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n nums = primes.copy() # do a deep copy \n heapq.heapify(nums) #create a heap\n p = 1\n for i in range(n - 1):\n p = heapq.heappop(nums) #take the smallest element\n for prime in primes:\n heapq.heappush(nums, p * prime) #add all those multiples with the smallest number\n if p % prime == 0:\n\t\t\t\t\tbreak\n return p\n``` | 29 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
heapq did the job | super-ugly-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n hp=[1]\n dc={1}\n i=1\n while(n):\n mn=heapq.heappop(hp)\n if(n==1):\n return mn\n for p in primes:\n newno=mn*p\n if(newno in dc):\n continue\n heapq.heappush(hp,newno)\n dc.add(newno)\n n-=1\n``` | 7 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
python my solution | super-ugly-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n l=[1]\n a=[0 for _ in range(len(primes))]\n for i in range(n-1):\n t=[primes[i]*l[a[i]] for i in range(len(primes))]\n m=min(t)\n for j in range(len(t)):\n if t[j]==m:\n a[j]+=1\n l.append(m) \n return l[-1] \n\n\n``` | 1 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
Just code | super-ugly-number | 1 | 1 | ```java []\nimport java.util.HashSet;\nimport java.util.PriorityQueue;\nimport java.util.Set;\n\npublic class Solution {\n public int nthSuperUglyNumber(int n, int[] primes) {\n if (n == 1) {\n return 1;\n }\n\n PriorityQueue<Long> heap = new PriorityQueue<>();\n Set<Long> seen = new HashSet<>();\n \n heap.offer(1L);\n seen.add(1L);\n\n for (int i = 1; i < n; ++i) {\n long current = heap.poll();\n for (int prime : primes) {\n long nextNum = current * prime;\n if (!seen.contains(nextNum)) {\n seen.add(nextNum);\n heap.offer(nextNum);\n }\n }\n }\n\n return heap.poll().intValue();\n }\n}\n```\n```python []\nimport heapq\nfrom typing import List\n\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n if n == 1:\n return 1\n\n heap = [1]\n seen = set([1])\n\n for _ in range(n - 1):\n current = heapq.heappop(heap)\n for prime in primes:\n next_num = current * prime\n if next_num not in seen:\n seen.add(next_num)\n heapq.heappush(heap, next_num)\n\n return heapq.heappop(heap)\n\n```\n```C++ []\n#include <vector>\n#include <queue>\n#include <unordered_set>\n\nclass Solution {\npublic:\n int nthSuperUglyNumber(int n, std::vector<int>& primes) {\n if (n == 1) {\n return 1;\n }\n\n std::priority_queue<long long, std::vector<long long>, std::greater<long long>> heap;\n std::unordered_set<long long> seen;\n\n heap.push(1);\n seen.insert(1);\n\n for (int i = 1; i < n; ++i) {\n long long current = heap.top();\n heap.pop();\n\n for (int prime : primes) {\n long long nextNum = current * prime;\n if (!seen.count(nextNum)) {\n seen.insert(nextNum);\n heap.push(nextNum);\n }\n }\n }\n\n return static_cast<int>(heap.top());\n }\n};\n```\n | 0 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
Python solution | super-ugly-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n ugly = [1]\n d = {i:0 for i in primes}\n while len(ugly) < n:\n next_ugly = min([ugly[d[i]]*i for i in d])\n ugly.append(next_ugly)\n for i in d:\n if next_ugly == ugly[d[i]]*i:\n d[i]+=1\n return ugly[-1]\n``` | 0 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
python: dynamic programming, 7 lines, beats 75%, clean code, easy to understand. | super-ugly-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. we created a key, value pair which the key is the primes numbers, and the value is the current quantity of the prime to try.\n2. the min value for dp[v]*k is the current ugly number.\n3. then we update the seeds for all keys that has the same currently value.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:\n seeds = {k:0 for k in primes}\n dp = [1] * n\n \n for i in range(1, n):\n value = min(dp[v]*k for k, v in seeds.items())\n dp[i] = value\n seeds.update({k:v+1 for k, v in seeds.items() if k * dp[v] == value})\n\n return dp[-1]\n``` | 0 | A **super ugly number** is a positive integer whose prime factors are in the array `primes`.
Given an integer `n` and an array of integers `primes`, return _the_ `nth` _**super ugly number**_.
The `nth` **super ugly number** is **guaranteed** to fit in a **32-bit** signed integer.
**Example 1:**
**Input:** n = 12, primes = \[2,7,13,19\]
**Output:** 32
**Explanation:** \[1,2,4,7,8,13,14,16,19,26,28,32\] is the sequence of the first 12 super ugly numbers given primes = \[2,7,13,19\].
**Example 2:**
**Input:** n = 1, primes = \[2,3,5\]
**Output:** 1
**Explanation:** 1 has no prime factors, therefore all of its prime factors are in the array primes = \[2,3,5\].
**Constraints:**
* `1 <= n <= 105`
* `1 <= primes.length <= 100`
* `2 <= primes[i] <= 1000`
* `primes[i]` is **guaranteed** to be a prime number.
* All the values of `primes` are **unique** and sorted in **ascending order**. | null |
315: Solution with step by step explanation | count-of-smaller-numbers-after-self | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass FenwickTree:\n def __init__(self, n: int):\n self.sums = [0] * (n + 1)\n\n def update(self, i: int, delta: int) -> None:\n # update the i-th element in the Fenwick tree with delta\n while i < len(self.sums):\n self.sums[i] += delta\n i += FenwickTree.lowbit(i)\n\n def get(self, i: int) -> int:\n # get the sum of the first i elements in the Fenwick tree\n summ = 0\n while i > 0:\n summ += self.sums[i]\n i -= FenwickTree.lowbit(i)\n return summ\n\n @staticmethod\n def lowbit(i: int) -> int:\n # get the lowest set bit in the binary representation of i\n return i & -i\n\n\nclass Solution:\n def countSmaller(self, nums: List[int]) -> List[int]:\n ans = []\n ranks = collections.Counter()\n # get the rank of each unique element in nums\n self._getRanks(nums, ranks)\n tree = FenwickTree(len(ranks))\n\n # iterate through nums backwards\n for num in reversed(nums):\n # get the number of elements smaller than num that have been seen so far\n ans.append(tree.get(ranks[num] - 1))\n # update the rank of num in the Fenwick tree\n tree.update(ranks[num], 1)\n\n # reverse the answer since we iterated backwards through nums\n return ans[::-1]\n\n def _getRanks(self, nums: List[int], ranks: Dict[int, int]) -> None:\n rank = 0\n # iterate through the sorted set of unique elements in nums\n for num in sorted(set(nums)):\n # assign a rank to each unique element\n rank += 1\n ranks[num] = rank\n\n``` | 3 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Solution | count-of-smaller-numbers-after-self | 1 | 1 | ```C++ []\nclass Solution {\n int bit[BIT_SIZE] = {0};\n \n inline void bitUpdate(int index) {\n while (index < BIT_SIZE) {\n bit[index]++;\n index += index & -index;\n }\n }\n inline int bitAns(int index) {\n int result = 0;\n while (index > 0) {\n result += bit[index];\n index -= index & -index;\n }\n return result;\n } \npublic:\n vector<int> countSmaller(const vector<int>& nums) {\n vector<int> result (nums.size());\n for (int index = nums.size() - 1; index >= 0; --index) {\n result[index] = bitAns(nums[index] + BIT_OFFSET - 1);\n bitUpdate(nums[index] + BIT_OFFSET);\n }\n return result;\n }\n};\n```\n\n```Python3 []\nfrom array import array\n\nclass Solution:\n def countSmaller(self, nums: List[int]) -> List[int]:\n l = len(nums)\n \n ans = array(\'i\', bytes(len(nums) << 2))\n \n nums2 = array(\'h\')\n\n for i in range(l-1,-1,-1):\n n = nums.pop()\n lpos = bisect_left(nums2, n)\n ans[i] = lpos\n nums2.insert(lpos, n)\n\n return ans\n```\n\n```Java []\nclass Solution {\n public List<Integer> countSmaller(int[] nums) {\n int min = nums[0];\n int max = nums[0];\n for (int i = 0; i < nums.length; i++) {\n final int v = nums[i];\n if (v < min) {\n min = v;\n } else if (v > max) {\n max = v;\n }\n }\n final int delta = -min + 1;\n final int[] arr = new int[max + delta + 1];\n final int[] res = new int[nums.length];\n for (int i = nums.length - 1; i >= 0; i--) {\n final int v = nums[i] + delta;\n res[i] = get(arr, v - 1);\n add(arr, v);\n }\n return new java.util.AbstractList<Integer>() {\n @Override\n public Integer get(int index) {\n return res[index];\n }\n @Override\n public int size() {\n return res.length;\n }\n };\n }\n static int get(final int[] arr, int v) {\n int sum = 0;\n for (; v > 0; v -= v & -v)\n sum += arr[v];\n return sum;\n }\n static void add(final int[] arr, int v) {\n for (; v < arr.length; v += v & -v)\n arr[v]++;\n }\n}\n```\n | 28 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python3. || binSearch 6 lines, w/ explanation || T/M: 97%/84% | count-of-smaller-numbers-after-self | 0 | 1 | ```\nclass Solution: # Here\'s the plan:\n # 1) Make arr, a sorted copy of the list nums.\n # 2) iterate through nums. For each element num in nums:\n # 2a) use a binary search to determine the count of elements\n # in the arr that are less than num.\n # 2b) append that count to the answer list\n # 2c) delete num from arr\n # 3) return the ans list \n # \n # For example, suppose nums = [5,2,6,1] Then arr = [1,2,5,6].\n # num = 5 => binsearch: arr = [1,2,/\\5,6], i = 2 => ans = [2,_,_,_], del 5\n # num = 2 => binsearch: arr = [1,/\\2,6], i = 1 => ans = [2,1,_,_], del 2\n # num = 6 => binsearch: arr = [1,/\\6], i = 1 => ans = [2,1,1,_], del 6\n # num = 1 => binsearch: arr = [/\\1], i = 0 => ans = [2,1,1,0], del 1\n\n def countSmaller(self, nums: List[int]) -> List[int]:\n arr, ans = sorted(nums), [] # <-- 1)\n \n for num in nums:\n i = bisect_left(arr,num) # <-- 2a)\n ans.append(i) # <-- 2b)\n del arr[i] # <-- 2c)\n \n return ans # <-- 3) | 40 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Two solutions based on MergeSort EXPLAINED | count-of-smaller-numbers-after-self | 0 | 1 | **IDEA**: the reason that we can use merge sort to solve this problem is that merge sort always sort the array by comparing the left numbers to the right numbers. By counting how many numbers have been moved from the right half to the left half prior of the current left half number, we will know the count answer for the current number from the left half.\n\nThe basic logic of those two solutions are identical but differs in the sort() function and time complexity. \n\nSOLUTION 1:\n```\n\tdef countSmaller(self, nums: List[int]) -> List[int]:\n \n res = [0] * len(nums) # NOTE 1\n enum = list(enumerate(nums)) # NOTE 2\n \n self.mergeSort(enum, 0, len(nums) - 1, res)\n return res\n \n def mergeSort(self, enum, start, end, res):\n if start >= end: return\n \n mid = start + (end - start) // 2\n self.mergeSort(enum, start, mid, res)\n self.mergeSort(enum, mid + 1, end, res)\n self.merge(enum, start, mid, end, res)\n \n def merge(self, enum, start, mid, end, res):\n p, q = start, mid + 1\n inversion_count = 0 # NOTE 3\n temp = []\n \n while p <= mid and q <= end:\n if enum[p][1] <= enum[q][1]:\n temp.append(enum[p])\n res[enum[p][0]] += inversion_count # NOTE 5\n p += 1\n else:\n temp.append(enum[q])\n inversion_count += 1 # NOTE 4\n q += 1\n \n while p <= mid:\n temp.append(enum[p])\n res[enum[p][0]] += inversion_count # NOTE 6\n p += 1\n \n while q <= end: \n temp.append(enum[q])\n q += 1\n \n enum[start:end+1] = temp # NOTE 7\n```\nFrom the structure of the code you can see it is basically the same as the conventional mergeSort() function. But the difference lays in the following NOTES:\n\n**NOTE 1**: we initialize a list which has the same size as our input array to store the result.\n\n**NOTE 2**: we initialize another list of tuple to have each tuple stores the index and value as ```(index, nums[index])```. This list serves as the bridge to link the array element which is under the sorting process to the result list initialized in NOTE 1.\n\n**NOTE 3**: we create a variable to count the how many numbers from the right half is smaller than the current number from the left half.\n\n**NOTE 4**: when we find that ```nums[left_index] > nums[right_index]```, we add 1 to the ```inversion_count```, but we dont add the current ```inversion_count``` to the final result yet. Because it is still possible that the next number(s) in the right half is still smaller than this current left number.\n\n**NOTE 5**: when we first find a number from the right half that is bigger than the current left number, we know that there will not be any number from the right half to be smaller than this current left number. Thus we add this ```inversion_count``` to the final result through the bridge of ```enum``` list.\n\n**NOTE 6**: when we finish iterating the numbers in the right half but there are still numbers left in the left half, we know that the number in the remaining left half should be bigger than all numbers in the right half, thus we need to add the current ```inversion_count``` to the corresponding index of all remaining left numbers. To help you understand this better, you can also use ```end-mid``` which gives the length of the right half array instead of ```inversion_count``` in this step.\n\n**NOTE 7**: we swap the ```start``` to ```end``` segement from the ```enum``` list with the sorted segement, to ensure the ```merge()``` function in the next level is also dealing with a sorted array. \n\n**NOTE 8**: Time complexity: O(nlogn). This is the same as conventional merge sort. You can google it if you want to understand why this complexity. Space complexity: O(n). This comes from the ```temp``` list that we initialized to temporarily store the sorted array segment. \n\n--------------------------------------------------------------------------------\nSOLUTION 2: \n\nA small alteration can be done in the sorting part of the ```merge()``` function. Instead of implementing in the conventional way, we can use the Python built-in sort() function to save ourselves from the ```temp``` list as well as the while loop when the numbers from the right half remains while left half has been scanned to the ```mid``` point. Here is the code:\n```\n def countSmaller(self, nums: List[int]) -> List[int]:\n \n res = [0] * len(nums)\n enum = list(enumerate(nums)) \n \n self.mergeSort(enum, 0, len(nums) - 1, res)\n return res\n \n def mergeSort(self, enum, start, end, res):\n if start >= end: return\n \n mid = start + (end - start) // 2\n self.mergeSort(enum, start, mid, res)\n self.mergeSort(enum, mid + 1, end, res)\n self.merge(enum, start, mid, end, res)\n \n def merge(self, enum, start, mid, end, res):\n p, q = start, mid + 1\n inversion_count = 0\n \n while p <= mid and q <= end:\n if enum[p][1] <= enum[q][1]:\n res[enum[p][0]] += inversion_count\n p += 1\n else:\n inversion_count += 1\n q += 1\n \n while p <= mid:\n # res[enum[p][0]] += inversion_count\n res[enum[p][0]] += end - mid\n p += 1\n \n enum[start:end+1] = sorted(enum[start:end+1], key=lambda e:e[1]) \n```\n**NOTE 9**: Fisrt we used the sorted function to directly sort the ```start``` to ```end``` segment of ```enum```, thus there is no more need to store the sorted numbers in a ```temp``` list. \n\n**NOTE 10**: As we only care about the count, we dont need to do the ```while q <= end:``` loop anymore, as this loop provides no update to the ```res``` list.\n\n**NOTE 11**: The Time Complexity does change in this case. As we are now using a O(nlogn) sorting method instead of the previous O(n) method, the overall TC is now O(n(logn)^2) instead of O(nlogn). The worst space complexity of Python ```sort()``` or Timsort is O(n).\n\n**AT THE END**: I spent hours to fully understand this merge sort solution. Thus I just want to write it down for myself. I will be very glad if this also helps you to any extent. Cheers. \n | 65 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python || ez Binary Search (with explanation) | count-of-smaller-numbers-after-self | 0 | 1 | # Explaination\nIterate nums from index n-1 ~ 0, use bisect_left to find the insert index, and the index will be the number of the elements that smaller than the current number. \n\n# Complexity\n- Time complexity : $$O(nlog(n))$$\n- Space complexity : $$O(n)$$\n\n# Python\n```\nfrom bisect import bisect_left\nclass Solution:\n def countSmaller(self, nums: List[int]) -> List[int]:\n res = [] # the answer\n sortedArr = [] # sort all elements from nums\n for num in nums[::-1]: # Iterate nums from index n-1 ~ 0\n idx = bisect_left(sortedArr, num) # search insert index\n res.append(idx) # the index equals to the numbers smaller than num\n sortedArr.insert(idx, num) # insert current number into sortedArr\n return res[::-1] # after reverse, we\'ll get the answer\n``` | 2 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Merge sort solution | count-of-smaller-numbers-after-self | 0 | 1 | This method is based on the way we sort an array __descendingly__ with the merge sort method. The difference is: when we merge two descendingly sorted arrays, for the element in the left array, if it\'s larger than the first number in the right array, it means this left-array element is larger than the every element of the right array(since the right array is sorted). Then, we should update our _smaller number after self_ counts for this left array element by add the length of the right array. However for the number in the right array, if it\'s larger than the first element in the left array, we don\'t need update our counting, since the left array originally appears _before_ the right array, so they are not numbers _after_ left array numbers, as the questions asekd.\n\n\n```\nclass Solution:\n def countSmaller(self, nums: List[int]) -> List[int]:\n counts = [0] * len(nums) # to save counts\n indexed_nums = [(nums[key_index], key_index) for key_index in range(len(nums))] # change the nums into (number, index) pairs\n desc_nums, counts = self.mergeWithCount(indexed_nums, counts) # the helper function returns the descendingly sorted indexed_nums and the counts\n return counts\n\t\n\t\n def mergeWithCount(self, nums, counts):\n if len(nums) == 1:\n return nums, counts\n\n cur_stack = []\n left, counts = self.mergeWithCount(nums[: len(nums) // 2], counts)\n right, counts = self.mergeWithCount(nums[len(nums) // 2 :], counts)\n \n \n while left and right:\n \n if left[0] > right[0]:\n counts[left[0][1]] += len(right) # left[0] gives a (number, index) pair as we defined at the beginning, and left[0][1] returns the original index of the number.\n cur_stack.append(left.pop(0))\n else:\n cur_stack.append(right.pop(0))\n \n if left:\n cur_stack.extend(left)\n else:\n cur_stack.extend(right)\n\t\t\t\n return cur_stack, counts\n``` | 18 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Python Solution Short Concise | count-of-smaller-numbers-after-self | 0 | 1 | ```\nclass Solution:\n def countSmaller(self, nums: List[int]) -> List[int]:\n arr, answer = sorted(nums), [] \n for num in nums:\n i = bisect_left(arr,num)\n answer.append(i) \n del arr[i] \n return answer \n``` | 2 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
Simplest Python solution (5 lines) | count-of-smaller-numbers-after-self | 0 | 1 | \n# Code\n```\nclass Solution:\n def countSmaller(self, nums: List[int]) -> List[int]:\n res = []\n for i in range(len(nums)-1,-1,-1):\n bisect.insort(res, nums[i])\n nums[i] = bisect_left(res, nums[i])\n return nums\n \n``` | 3 | Given an integer array `nums`, return _an integer array_ `counts` _where_ `counts[i]` _is the number of smaller elements to the right of_ `nums[i]`.
**Example 1:**
**Input:** nums = \[5,2,6,1\]
**Output:** \[2,1,1,0\]
**Explanation:**
To the right of 5 there are **2** smaller elements (2 and 1).
To the right of 2 there is only **1** smaller element (1).
To the right of 6 there is **1** smaller element (1).
To the right of 1 there is **0** smaller element.
**Example 2:**
**Input:** nums = \[-1\]
**Output:** \[0\]
**Example 3:**
**Input:** nums = \[-1,-1\]
**Output:** \[0,0\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104` | null |
POTD With 100% optimisation with 100% Runtime and Memory Acceptance | remove-duplicate-letters | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to remove duplicate letters from the input string while ensuring that the result is in lexicographically smallest order. To achieve this, we can use a stack to maintain characters and their order. We need to keep track of the last occurrence of each character to make sure we are removing characters correctly.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a stack (st) to store characters, two vectors (last_occurrence and used) to keep track of the last occurrence of each character and whether a character is already in the result, respectively.\n\n2. Iterate through the input string s:\n - For each character currChar, check if it has not been used (used[currChar - \'a\'] is false).\n - If it has not been used:\n - While the stack is not empty, the current character currChar is smaller than the character at the top of the stack (st.top()), and there are more occurrences of the character at the top of the stack later in the string, pop characters from the stack and mark them as unused.\n - Push the current character onto the stack and mark it as used.\n3. After processing the entire input string, create a result string of the same size as the stack (st.size()) and construct it in reverse order by popping characters from the stack.\n\n4. Return the result string, which contains the lexicographically smallest string without duplicate letters.\n# Complexity\n1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n - The code iterates through the input string s twice, once for calculating the last occurrence of each character and once for processing the string with the stack.\n - Both iterations have a time complexity of O(N), where N is the length of the input string s.\n - The final construction of the result string from the stack also takes O(N) time.\n - Thus, the overall time complexity is O(N).\n2. Space complexity:\n - The additional space used is mainly for the stack, which can have at most N characters, where N is the length of the input string s.\n - The last_occurrence and used vectors each have a constant size of 26 (for the English alphabet).\n - The result string also takes O(N) space.\n - Therefore, the overall space complexity is O(N).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string removeDuplicateLetters(string s) {\n vector<int> last_occurrence(26, -1);\n vector<bool> used(26, false);\n stack<char> st;\n\n // Calculate the last occurrence of each character in the string\n for (int i = 0; i < s.size(); ++i) {\n last_occurrence[s[i] - \'a\'] = i;\n }\n\n for (int i = 0; i < s.size(); ++i) {\n char currChar = s[i];\n\n if (!used[currChar - \'a\']) {\n while (!st.empty() && currChar < st.top() && last_occurrence[st.top() - \'a\'] > i) {\n used[st.top() - \'a\'] = false;\n st.pop();\n }\n\n st.push(currChar);\n used[currChar - \'a\'] = true;\n }\n }\n\n string result(st.size(), \' \');\n\n // Construct the result string in reverse order from the stack\n for (int i = st.size() - 1; i >= 0; --i) {\n result[i] = st.top();\n st.pop();\n }\n\n return result;\n }\n};\n\n``` | 4 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
📈Beats🧭 99.73% ✅ | 🔥Clean & Concise Code | Easy Understanding🔥 | remove-duplicate-letters | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInitialize a stack (st) to store characters, two vectors (last_occurrence and used) to keep track of the last occurrence of each character and whether a character is already in the result, respectively.\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a stack (st) to store characters, two vectors (last_occurrence and used) to keep track of the last occurrence of each character and whether a character is already in the result, respectively.\n\n2. Iterate through the input string s:\n\n- For each character currChar, check if it has not been used (used[currChar - \'a\'] is false).\n- If it has not been used:\n- While the stack is not empty, the current character currChar is smaller than the character at the top of the stack (st.top()), and there are more occurrences of the character at the top of the stack later in the string, pop characters from the stack and mark them as unused.\n- Push the current character onto the stack and mark it as used.\n\n3. After processing the entire input string, create a result string of the same size as the stack (st.size()) and construct it in reverse order by popping characters from the stack.\n\n4. Return the result string, which contains the lexicographically smallest string without duplicate letters.\n---\n\n\n# Complexity\n\n---\n\n1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- The code iterates through the input string s twice, once for calculating the last occurrence of each character and once for processing the string with the stack.\n- Both iterations have a time complexity of O(N), where N is the length of the input string s.\n- The final construction of the result string from the stack also takes O(N) time.\n- Thus, the overall time complexity is O(N).\n---\n\n\n2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The additional space used is mainly for the stack, which can have at most N characters, where N is the length of the input string s.\n- The last_occurrence and used vectors each have a constant size of 26 (for the English alphabet).\n- The result string also takes O(N) space.\n- Therefore, the overall space complexity is O(N).\n# Code\n```\nclass Solution {\npublic:\n string removeDuplicateLetters(string s) {\n vector<int> last_occurrence(26, -1);\n vector<bool> used(26, false);\n stack<char> st;\n\n // Calculate the last occurrence of each character in the string\n for (int i = 0; i < s.size(); ++i) {\n last_occurrence[s[i] - \'a\'] = i;\n }\n\n for (int i = 0; i < s.size(); ++i) {\n char currChar = s[i];\n\n if (!used[currChar - \'a\']) {\n while (!st.empty() && currChar < st.top() && last_occurrence[st.top() - \'a\'] > i) {\n used[st.top() - \'a\'] = false;\n st.pop();\n }\n\n st.push(currChar);\n used[currChar - \'a\'] = true;\n }\n }\n\n string result(st.size(), \' \');\n\n // Construct the result string in reverse order from the stack\n for (int i = st.size() - 1; i >= 0; --i) {\n result[i] = st.top();\n st.pop();\n }\n\n return result;\n }\n};\n\n``` | 2 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
easy solution | remove-duplicate-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n st=[]\n for i in range(len(s)):\n # print(s[i])\n if(s[i] not in st):\n j=len(st)-1\n # print()\n while(j>=0 and st[j]>s[i] and st[j] in s[i+1:]):\n st.pop()\n j-=1\n st.append(s[i])\n st="".join(st)\n return(st)\n \n \n``` | 1 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
Python3 Solution | remove-duplicate-letters | 0 | 1 | \n```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n n=len(s)\n lookup={}\n for i in range(n):\n lookup[s[i]]=i\n ans=[]\n for i in range(n):\n if s[i] not in ans:\n while ans and ans[-1]>s[i] and lookup[ans[-1]]>i:\n ans.pop()\n ans.append(s[i])\n return "".join(ans) \n``` | 1 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
✅ 98.53% Stack and Greedy | remove-duplicate-letters | 1 | 1 | # Interview Guide: "Remove Duplicate Letters" Problem\n\n## Problem Understanding\n\nThe "Remove Duplicate Letters" problem tasks you with removing duplicate letters from a string such that every letter appears only once. The challenge is to make sure the result is the smallest in lexicographical order among all possible outcomes.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nBefore diving deep into the solution, it\'s crucial to understand the constraints. The length of string `s` is between 1 and 10,000, and `s` consists only of lowercase English letters. This provides insight into the feasible solutions in terms of time and space complexity.\n\n### 2. Multiple Approaches\n\nThere are different ways to solve this problem:\n\n - Using a Stack and Greedy algorithm\n - Using a Count and Visited array\n\nBoth approaches have their advantages and trade-offs, so it\'s essential to understand both and choose the one that aligns with the problem\'s constraints.\n\n### 3. Stack\'s Utility\n\nWhen using the Stack approach, the stack serves as a dynamic data structure to hold the characters in the desired order. It plays a crucial role in ensuring lexicographical ordering of characters.\n\n### 4. Explain Your Thought Process\n\nAlways articulate your thought process and the rationale behind choosing a specific approach. Highlight the trade-offs you\'re considering in terms of time and space complexity.\n\n## Conclusion\n\nThe "Remove Duplicate Letters" problem is an excellent example of how different data structures and algorithms can be used to achieve the desired outcome. By understanding the problem, deciding on the best data structures, and choosing the right algorithm, you demonstrate a comprehensive grasp of algorithmic challenges.\n\n---\n\n## Live Coding & Explain\nhttps://youtu.be/Z0rg6rAWMik?si=vAkmw5iSwa_gFX3h\n\n# Approach: Stack and Greedy\n\nTo address the "Remove Duplicate Letters" problem using a stack and greedy algorithm, we lean on the properties of the stack to maintain lexicographical order:\n\n## Key Data Structures:\n\n- **stack**: A dynamic data structure to hold characters in the desired order.\n- **seen**: A set to track characters already in the stack.\n- **last_occurrence**: A dictionary to track the last occurrence of each character in the string.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Initialize the stack, seen set, and last_occurrence dictionary.\n \n2. **Iterate through the string**:\n - For each character, if it\'s in the seen set, skip it.\n - If it\'s not in the seen set, add it to the stack. While adding, compare it with the top character of the stack. If the current character is smaller and the top character appears later in the string, pop the top character.\n\n3. **Output**:\n - Convert the stack to a string and return.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution iterates over each character in the string once, leading to a time complexity of $$ O(n) $$, where `n` is the length of the string `s`.\n\n**Space Complexity:** \n- The space complexity is $$ O(n) $$ due to the stack, seen set, and last_occurrence dictionary.\n\n# Code Stack and Greedy\n``` Python []\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n stack = []\n seen = set() \n last_occ = {c: i for i, c in enumerate(s)}\n \n for i, c in enumerate(s):\n if c not in seen:\n \n while stack and c < stack[-1] and i < last_occ[stack[-1]]:\n seen.discard(stack.pop())\n seen.add(c)\n stack.append(c)\n \n return \'\'.join(stack)\n```\n``` Go []\nfunc removeDuplicateLetters(s string) string {\n\tstack := []rune{}\n\tseen := make(map[rune]bool)\n\tlastOcc := make(map[rune]int)\n\n\tfor i, c := range s {\n\t\tlastOcc[c] = i\n\t}\n\n\tfor i, c := range s {\n\t\tif !seen[c] {\n\t\t\tfor len(stack) > 0 && c < stack[len(stack)-1] && i < lastOcc[stack[len(stack)-1]] {\n\t\t\t\tdelete(seen, stack[len(stack)-1])\n\t\t\t\tstack = stack[:len(stack)-1]\n\t\t\t}\n\t\t\tseen[c] = true\n\t\t\tstack = append(stack, c)\n\t\t}\n\t}\n\n\treturn string(stack)\n}\n```\n``` Rust []\nuse std::collections::{HashSet, HashMap};\n\nimpl Solution {\n pub fn remove_duplicate_letters(s: String) -> String {\n let mut stack: Vec<char> = Vec::new();\n let mut seen: HashSet<char> = HashSet::new();\n let mut last_occ: HashMap<char, usize> = HashMap::new();\n for (i, c) in s.chars().enumerate() {\n last_occ.insert(c, i);\n }\n \n for (i, c) in s.chars().enumerate() {\n if !seen.contains(&c) {\n while let Some(&top) = stack.last() {\n if c < top && i < *last_occ.get(&top).unwrap() {\n seen.remove(&stack.pop().unwrap());\n } else {\n break;\n }\n }\n seen.insert(c);\n stack.push(c);\n }\n }\n \n stack.into_iter().collect()\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string removeDuplicateLetters(std::string s) {\n std::stack<char> stack;\n std::unordered_set<char> seen;\n std::unordered_map<char, int> last_occ;\n for (int i = 0; i < s.size(); i++) {\n last_occ[s[i]] = i;\n }\n \n for (int i = 0; i < s.size(); i++) {\n char c = s[i];\n if (seen.find(c) == seen.end()) {\n while (!stack.empty() && c < stack.top() && i < last_occ[stack.top()]) {\n seen.erase(stack.top());\n stack.pop();\n }\n seen.insert(c);\n stack.push(c);\n }\n }\n \n std::string result = "";\n while (!stack.empty()) {\n result = stack.top() + result;\n stack.pop();\n }\n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String removeDuplicateLetters(String s) {\n Stack<Character> stack = new Stack<>();\n Set<Character> seen = new HashSet<>();\n Map<Character, Integer> lastOcc = new HashMap<>();\n for (int i = 0; i < s.length(); i++) {\n lastOcc.put(s.charAt(i), i);\n }\n \n for (int i = 0; i < s.length(); i++) {\n char c = s.charAt(i);\n if (!seen.contains(c)) {\n while (!stack.isEmpty() && c < stack.peek() && i < lastOcc.get(stack.peek())) {\n seen.remove(stack.pop());\n }\n seen.add(c);\n stack.push(c);\n }\n }\n \n StringBuilder result = new StringBuilder();\n for (char c : stack) {\n result.append(c);\n }\n return result.toString();\n }\n}\n```\n``` C# []\npublic class Solution {\n public string RemoveDuplicateLetters(string s) {\n Stack<char> stack = new Stack<char>();\n HashSet<char> seen = new HashSet<char>();\n Dictionary<char, int> lastOcc = new Dictionary<char, int>();\n for (int i = 0; i < s.Length; i++) {\n lastOcc[s[i]] = i;\n }\n \n for (int i = 0; i < s.Length; i++) {\n char c = s[i];\n if (!seen.Contains(c)) {\n while (stack.Count > 0 && c < stack.Peek() && i < lastOcc[stack.Peek()]) {\n seen.Remove(stack.Pop());\n }\n seen.Add(c);\n stack.Push(c);\n }\n }\n \n char[] result = stack.ToArray();\n Array.Reverse(result);\n return new string(result);\n }\n}\n```\n``` JavaScript []\nvar removeDuplicateLetters = function(s) {\n let stack = [];\n let seen = new Set();\n let lastOcc = {};\n for (let i = 0; i < s.length; i++) {\n lastOcc[s[i]] = i;\n }\n \n for (let i = 0; i < s.length; i++) {\n let c = s[i];\n if (!seen.has(c)) {\n while (stack.length && c < stack[stack.length - 1] && i < lastOcc[stack[stack.length - 1]]) {\n seen.delete(stack.pop());\n }\n seen.add(c);\n stack.push(c);\n }\n }\n \n return stack.join(\'\');\n }\n```\n``` PHP []\nclass Solution {\n function removeDuplicateLetters($s) {\n $stack = [];\n $seen = [];\n $lastOcc = [];\n for ($i = 0; $i < strlen($s); $i++) {\n $lastOcc[$s[$i]] = $i;\n }\n \n for ($i = 0; $i < strlen($s); $i++) {\n $c = $s[$i];\n if (!isset($seen[$c])) {\n while (!empty($stack) && $c < end($stack) && $i < $lastOcc[end($stack)]) {\n unset($seen[array_pop($stack)]);\n }\n $seen[$c] = true;\n array_push($stack, $c);\n }\n }\n \n return implode(\'\', $stack);\n }\n}\n```\n\n---\n\n# Approach: Count and Visited Array\n\nTo address the "Remove Duplicate Letters" problem using a count and visited array, we leverage the frequency of each character:\n\n## Key Data Structures:\n\n- **count**: A dictionary to hold the frequency of each character.\n- **result**: A list to hold the final characters in the desired order.\n- **visited**: A set to track characters already in the result.\n\n## Enhanced Breakdown:\n\n1. **Calculate Frequencies**:\n - Compute the frequency of each character in the string.\n \n2. **Iterate through the string**:\n - For each character, decrease its count. If it\'s in the visited set, skip it.\n - If it\'s not in the visited set, add it to the result. While adding, compare it with the last character in the result. If the current character is smaller and the last character appears later in the string, remove the last character.\n\n3. **Output**:\n - Convert the result list to a string and return.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution iterates over each character in the string once, leading to a time complexity of $$ O(n) $$, where `n` is the length of the string `s`.\n\n**Space Complexity:** \n- The space complexity is $$ O(n) $$ due to the count dictionary, result list, and visited set.\n\n# Code Count and Visited Array\n``` Python []\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n count = collections.Counter(s)\n result = []\n visited = set()\n \n for c in s:\n count[c] -= 1\n if c in visited:\n continue\n while result and c < result[-1] and count[result[-1]] > 0:\n visited.remove(result.pop())\n visited.add(c)\n result.append(c)\n \n return \'\'.join(result)\n\n```\n\n## Performance\n\n| Language | Execution Time (ms) | Memory Usage |\n|-------------|---------------------|--------------|\n| C++ | 0 ms | 7.4 MB |\n| Rust | 2 ms | 2.2 MB |\n| Go | 3 ms | 2.1 MB |\n| Java | 3 ms | 41.2 MB |\n| PHP | 10 ms | 19 MB |\n| Python3 (Stack) | 32 ms | 16.4 MB |\n| Python3 (Count) | 38 ms | 16.3 MB |\n| JavaScript | 56 ms | 42.2 MB |\n| C# | 82 ms | 37.9 MB |\n\n\n\n\n## Bonuse: Live Coding in Rust\nhttps://youtu.be/mMJ4LtwDRnc?si=AyuKt3HQIHqkS2DT\n\nBoth approaches showcase different techniques to solve the problem: one uses the properties of a stack and the greedy algorithm, while the other leverages the frequency of characters. Deciding between them depends on the specific constraints and requirements of the given scenario. \uD83D\uDE80\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB\uD83C\uDF0C. | 77 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
【Video】How we think about a solution with Stack - Python, JavaScript, Java, C++ | remove-duplicate-letters | 1 | 1 | Welcome to my article! This artcle starts with "How we think about a solution". In other words, that is my thought process to solve the question. This article explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope this aricle is helpful for someone.\n\n# Intuition\n\nUse stack to keep order of charcters in string with the smallest in lexicographical order.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/aU0MiLWAm4o\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Remove Duplicate Letters\n`0:16` How we think about a solution - What is the smallest in lexicographical order for this question?\n`2:28` Demonstrate solution with an example.\n`7:43` Coding\n`10:00` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,493\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n\n# Approach\n\n## How we think about a solution\n\n### What is the smallest in lexicographical order for this quesiton?\nTo solve this question, we need to understand what smallest in lexicographical order is.\n\n```\nInput: "bcabc"\n```\n\nIn this case, we have duplicte characters `b` and `c`, so we need to remove one of `b` and one of `c`.\n\n```\n_ _ a b c \u2192 abc\n_ c a b _ \u2192 cab\nb _ a _ c \u2192 bac\nb c a _ _ \u2192 bca\n```\nWe can create 4 strings and need to keep order of appearance of each character. And then, sort the 4 strings lexicographically(alphabetically).\n```\nabc\nbac\nbca\ncab\n```\n\n`abc` is the smallest string, that\'s why we should return `abc`.\n\nThat is the smallest in lexicographical order we must understand for this question.\n\nNow, let\'s focus on \n```\n_(b) _(c) a b c \u2192 abc\n```\n From the idea above, we can say two important things.\n\n---\nWe want to put the smaller character in early position but we have to use big character(For example "z") if it is unique in the string.\n\n\nThe two important thing are as follows;\n1. Previous characters are lexicographically greater than current character\n2. The previous big characters show up again after position of current character\n\nIf both cases are true, we can remove the previous big charcters because we try to put smaller characters in early position and bigger characters in late position if possible. It leads to creating smaller string lexicographically and can remove duplicate characters.\n\n---\n\n\nIn this case, what data structure do you use? \n\nMy answer is to use `stack`. We want to compare current character with the last previous character one by one. We can use `pop` and `append` with `O(1)`. Seems like `stack` make the problem easy and efficient.\n\nLet\'s see one by one. First of all, `stack` is empty\n\n```\nstack = []\n```\nThe first character is `b` and `stack` is now empty, so just add `b` to `stack`\n```\nstack = ["b"]\n```\nThe next character is `c`, in this case, compare `c` with the last character in `stack` which is `b` with the main idea above.\n\n`c` is greater than `b`, so it\'s false case. Just add `c` in `stack`\n\n```\n"c" < "b" \u2192 false\nstack = ["b", "c"]\n```\n\nThe next character is `a`. Here is an interesting point. Compare `a` with the last character in `stack` which is `c`\n\n```\n"a" < "c" \u2192 true\nprevious character(c) will show up again after current position(a)? \u2192 true\n```\nIn that case, remove `c` from `stack`\n```\nstack = ["b"]\n```\nWe still have `b` in stack. Let\'s compare `a` vs `b`.\n```\n"a" < "b" \u2192 true\nprevious character(b) will show up again after current position(a)? \u2192 true\n```\nIn that case, remove `b` from `stack`. Now `stack` is empty. we stop comparing and add `a` to `stack`\n```\nstack = ["a"]\n```\nWe will repeat the same process. I\'ll speed up. The next character is `b`.\n```\n"b" < "a" \u2192 false\nstack = ["a", "b"]\n```\nThe next character is `c`.\n```\n"c" < "b" \u2192 false\nstack = ["a", "b", "c"]\n```\n\nAll we have to do is just to concatenate the characters remaining in the stack.\n\nThat is main point of how we think about a solution. Exepct the main idea, I use `Set` and `HashMap` to support the idea in the solution codes below. `Set` is used to prevent duplicate characters and `HashMap` is used to keep the last position of each character. I believe now you can understand them easily.\n\nLet\'s see a real algorithm!\n\n### Algorithm Overview\n1. Build a dictionary `last_occur` to store the last occurrence index of each character in the input string `s`.\n2. Iterate through the input string `s` to build the `last_occur` dictionary and initialize an empty stack and a visited set.\n3. Iterate through the characters in the input string `s` again. If a character is already visited, skip it. If not, process it based on certain conditions and update the stack and visited set accordingly.\n4. Finally, concatenate the characters remaining in the stack to get the final result.\n\n### Detailed Explanation\n1. Create a dictionary `last_occur` to store the last occurrence index of each character in the input string `s`.\n2. Iterate through each character and its index in the input string `s`:\n 1. Update the `last_occur` dictionary with the last occurrence index of the current character.\n3. Initialize an empty stack to hold the characters in the desired order and a visited set to keep track of visited characters.\n4. Iterate through each index `i` in the range of the length of the input string `s`:\n 1. Check if the current character `s[i]` is already visited. If visited, skip to the next iteration.\n 2. If the current character `s[i]` is not visited:\n 1. While the stack is not empty, the top of the stack is greater than `s[i]`, and the last occurrence of the top of the stack is after the current index `i`, remove the top of the stack and mark it as not visited.\n 2. Mark the current character `s[i]` as visited and push it onto the stack.\n5. Concatenate the characters remaining in the stack to obtain the final result.\n6. Return the concatenated string, which represents the characters in the desired order without duplicate letters.\n\n\n---\n\n\n\n# Complexity\nLet\'s analyze the time and space complexity of the given code.\n\n### Time Complexity:\nThe time complexity can be broken down as follows:\n\n1. **First Loop (iteration over string `s`):** This involves iterating over each character in string `s` to build the `last_occur` dictionary. This takes O(len(s)), where len(s) is the length of string `s`.\n\n2. **Second Loop (iteration over string `s`):** In the worst case, this loop iterates over each character in string `s` and performs operations such as stack manipulations and dictionary lookups, which are O(1) operations.\n\nHence, the overall time complexity is O(len(s)), where len(s) is the length of string `s`.\n\n### Space Complexity:\nThe space complexity is determined by the space used by the `last_occur` dictionary, the `stack`, and the `visited` set.\n\n1. **Dictionary (`last_occur`):** The space used by the `last_occur` dictionary is O(26) at most, considering only lowercase English letters, which is a constant.\n\n2. **Stack (`stack`):** In the worst case, the stack can contain all characters of string `s`. Therefore, the space used by the stack is O(len(s)), where len(s) is the length of string `s`.\n\n3. **Set (`visited`):** In the worst case, the visited set can contain all characters of string `s`. Therefore, the space used by the set is O(len(s)), where len(s) is the length of string `s`.\n\nHence, the overall space complexity of the code is O(max(len(s), 26)), which simplifies to O(len(s)) since 26 is a constant.\n\nBut regarding O(len(s)), we have also O(26) at most because we are not allowed to have duplicate characters, so we can say O(1) instead of O(len(s)).\n\n\n```python []\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n # Dictionary to store the last occurrence of each character\n last_occur = {}\n\n # Record the last occurrence of each character\n for i, char in enumerate(s):\n last_occur[char] = i \n\n stack = [] # Stack to store characters in the desired order\n visited = set() # Set to keep track of visited characters\n\n for i in range(len(s)):\n if s[i] in visited:\n continue # Skip if the character is already visited\n\n # If the top of the stack is greater than s[i] and will occur later again, remove from stack\n while stack and s[i] < stack[-1] and i < last_occur.get(stack[-1], -1):\n visited.remove(stack.pop())\n\n visited.add(s[i]) # Mark as visited\n stack.append(s[i]) # Add to the stack\n \n return \'\'.join(stack) # Concatenate the characters remaining in the stack\n\n```\n```javascript []\n/**\n * @param {string} s\n * @return {string}\n */\nvar removeDuplicateLetters = function(s) {\n const lastOccurrence = {};\n for (let i = 0; i < s.length; i++) {\n lastOccurrence[s[i]] = i;\n }\n\n const stack = [];\n const visited = new Set();\n\n for (let i = 0; i < s.length; i++) {\n if (visited.has(s[i])) {\n continue;\n }\n\n while (\n stack.length > 0 &&\n s[i] < stack[stack.length - 1] &&\n i < lastOccurrence[stack[stack.length - 1]]\n ) {\n visited.delete(stack.pop());\n }\n\n visited.add(s[i]);\n stack.push(s[i]);\n }\n\n return stack.join(\'\'); \n};\n```\n```java []\nclass Solution {\n public String removeDuplicateLetters(String s) {\n Map<Character, Integer> lastOccurrence = new HashMap<>();\n for (int i = 0; i < s.length(); i++) {\n lastOccurrence.put(s.charAt(i), i);\n }\n\n Stack<Character> stack = new Stack<>();\n Set<Character> visited = new HashSet<>();\n\n for (int i = 0; i < s.length(); i++) {\n if (visited.contains(s.charAt(i))) {\n continue;\n }\n\n while (!stack.isEmpty() && s.charAt(i) < stack.peek() && i < lastOccurrence.getOrDefault(stack.peek(), -1)) {\n visited.remove(stack.pop());\n }\n\n visited.add(s.charAt(i));\n stack.push(s.charAt(i));\n }\n\n StringBuilder result = new StringBuilder();\n for (char ch : stack) {\n result.append(ch);\n }\n return result.toString(); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string removeDuplicateLetters(string s) {\n std::unordered_map<char, int> lastOccurrence;\n for (int i = 0; i < s.length(); i++) {\n lastOccurrence[s[i]] = i;\n }\n\n std::stack<char> stack;\n std::unordered_set<char> visited;\n\n for (int i = 0; i < s.length(); i++) {\n if (visited.find(s[i]) != visited.end()) {\n continue;\n }\n\n while (!stack.empty() && s[i] < stack.top() && i < lastOccurrence[stack.top()]) {\n visited.erase(stack.top());\n stack.pop();\n }\n\n visited.insert(s[i]);\n stack.push(s[i]);\n }\n\n std::string result;\n while (!stack.empty()) {\n result = stack.top() + result;\n stack.pop();\n }\n return result; \n }\n};\n```\n\n\n---\n\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 27th, 2023\nhttps://leetcode.com/problems/decoded-string-at-index/solutions/4096860/how-i-think-about-a-solution-python-java-c/ | 41 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
Remove the Duplicate Letters Solution in Python3 | remove-duplicate-letters | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a breakdown of how the code works:\n\n1. Three data structures are initialized:\n- stack: It represents a stack data structure, which will be used to keep track of the letters in the desired order.\n- last_occurrence: It\'s a dictionary that stores the last occurrence (index) of each letter in the input string s.\n- visited: A set to keep track of which letters have been visited.\n2. The code then iterates through the input string s to populate the last_occurrence dictionary. For each letter in the string, it records the index at which that letter last occurs in the string.\n\n3. The code then iterates through the input string s again to process each letter individually:\n\n- If the letter has already been visited (i.e., it\'s already in the visited set), it skips the current iteration.\n- It enters a while loop that continues as long as there are elements in the stack, the current letter (s[i]) is less than the top letter on the stack, and the last occurrence index of the top letter on the stack is greater than the current index i. This loop essentially checks if it\'s beneficial to remove letters from the stack while preserving the relative order of letters.\n- If the conditions in the while loop are met, it removes the top letter from the stack and marks it as not visited (by removing it from the visited set).\n- After the while loop, the current letter s[i] is added to the stack, indicating that it should be included in the final result, and it\'s marked as visited by adding it to the visited set.\n4. Finally, the method returns the result by joining the remaining letters in the stack. This will be the modified string with duplicate letters removed while maintaining the original order.\n\nIn essence, this code efficiently removes duplicate letters from the input string s while ensuring that the order of the remaining letters is preserved, which is the desired outcome.\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n stack = [] \n last_occurrence = {} \n visited = set()\n \n for i in range(len(s)):\n last_occurrence[s[i]] = i\n for i in range(len(s)):\n if s[i] in visited:\n continue\n while stack and s[i] < stack[-1] and last_occurrence[stack[-1]] > i:\n visited.remove(stack.pop())\n stack.append(s[i])\n visited.add(s[i])\n return "".join(stack)\n``` | 1 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
Python Solution Beats 100% Users --Greedy Algorithm(Easy to Understand). | remove-duplicate-letters | 0 | 1 | # Intuition\n The goal is to remove duplicate letters from the input string while preserving their lexicographical order. This can be achieved using a systematic approach that iterates through the string, ensuring that the characters are added to the result string in the correct order.\n\n# Approach\n- Initialize an empty string res to store the final result.\n\n- Create a dictionary last_occurrence to keep track of the last occurrence index of each character in the input string s. This dictionary will help us decide whether to remove characters from the result or not.\n\n- Iterate through the characters in the input string s.\n\n- For each character in s:\n\n - Check if the current character is not already in the result string res. This step ensures uniqueness in the result.\n - If the character is not in res, enter a loop:\n - While the result string res is not empty (res and) and the current character char is lexicographically smaller than the last character in res (char < res[-1]) and there are more occurrences of the last character ahead in the input string (i < last_occurrence[res[-1]]), remove the last character from res. This step ensures that we maintain lexicographical order.\n - After the loop, append the current character char to the result string res.\n- Continue this process for all characters in the input string.\n\n- Finally, the res string will contain the desired result, with duplicates removed while preserving lexicographical order.\n\n# Complexity\n- Time complexity: O(n), where n is the length of the input string s. The algorithm iterates through the string once to build the result string.\n- Space complexity: O(1) for the res string and O(k) for the last_occurrence dictionary, where k is the number of unique characters in the input string. In practice, this is O(26) as there are 26 lowercase letters in the English alphabet, making the space complexity constant.\n\n# Code\n```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n # Initialize an empty result string\n res = ""\n # Initialize a dictionary to store the last occurrence index of each character\n last_occurrence = {}\n\n # Populate the last_occurrence dictionary with the last index of each character\n for i, char in enumerate(s):\n last_occurrence[char] = i\n\n # Iterate through the characters in the input string\n for i, char in enumerate(s):\n if char not in res:\n while res and char < res[-1] and i < last_occurrence[res[-1]]:\n res = res[:-1]\n # Append the current character to res.\n res += char\n\n return res\n\n``` | 5 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
316: Space 98.37%, Solution with step by step explanation | remove-duplicate-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- We create a stack to keep track of the characters that we are going to keep in the result.\n- We also create a dictionary last_occurrence to keep track of the last occurrence of each character in the string.\n- We iterate through the string s and check if the current character is already in the stack. If it is, we skip it.\n- If the current character is not in the stack, we compare it to the top of the stack and pop characters from the stack until we reach a character that is not greater than the current character and that has a last occurrence index that is greater than the current index i. We do this to make sure that we keep the characters in lexicographical order and that we don\'t remove characters that we need to keep.\n- We then add the current character to the stack.\n- Finally, we return the characters in the stack as a string.\n\n# Complexity\n- Time complexity:\n81.68%\n\n- Space complexity:\n98.37%\n\n# Code\n```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n stack = []\n last_occurrence = {char: i for i, char in enumerate(s)}\n \n for i, char in enumerate(s):\n if char in stack:\n continue\n \n while stack and char < stack[-1] and i < last_occurrence[stack[-1]]:\n stack.pop()\n \n stack.append(char)\n \n return \'\'.join(stack)\n\n``` | 10 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
Full explanation Python efficient code | remove-duplicate-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe initialize an empty stack to store characters, a dictionary last_occurrence to store the last occurrence index of each character in the string, and a set visited to keep track of characters already visited.\nWe populate the last_occurrence dictionary by iterating through the characters in the input string s and storing the last index of each character in the dictionary.\nWe then iterate through the characters in the string s again.\nFor each character, we check if it is already visited. If it is, we skip it and move on to the next character.\nIf the stack is not empty and the current character is smaller than the top of the stack (i.e., it appears before the top of the stack lexicographically), and the top of the stack has more occurrences in the remaining string (i.e., its last occurrence is after the current index), we pop the top of the stack to maintain the lexicographically smallest result. We remove the popped character from the visited set.\nAfter that, we append the current character to the stack and mark it as visited in the visited set.\nFinally, we convert the stack to a string using the join() method and return the resulting string, which contains the characters in the input string s with duplicates removed while maintaining the lexicographical order.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe main idea is to iteratively process each character in the input string s, and maintain a stack that stores characters in the order of their appearance. We also keep track of the last occurrence index of each character in a dictionary last_occurrence to determine if a character has more occurrences in the remaining string.\n\nThe greedy part of the approach is that we only push a character onto the stack if it is smaller than the top of the stack (i.e., it appears before the top of the stack lexicographically), and the top of the stack has more occurrences in the remaining string (i.e., its last occurrence is after the current index). This ensures that we maintain the lexicographically smallest result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the solution is O(n), where n is the length of the input string s. This is because we iterate through the string s twice: once to populate the last_occurrence dictionary, and once to process each character in the string. Each iteration takes O(n) time, and the other operations such as appending characters to the stack or removing characters from the stack take constant time.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the solution is also O(n), as we need to store the last_occurrence dictionary, the stack, and the visited set, all of which can have a maximum size of n, where n is the length of the input string s.\n\n# Code\n```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n stack = [] # Initialize an empty stack to store characters\n last_occurrence = {} # Store the last occurrence index of each character in a dictionary\n visited = set() # Keep track of characters already visited\n \n # Populate the last_occurrence dictionary with the last index of each character in the string\n for i in range(len(s)):\n last_occurrence[s[i]] = i\n \n # Iterate through the characters in the string\n for i in range(len(s)):\n # If the character is already visited, skip it\n if s[i] in visited:\n continue\n \n # If the stack is not empty and the current character is smaller than the top of the stack,\n # and the top of the stack has more occurrences in the remaining string, pop the top of the stack\n # to maintain the lexicographically smallest result\n while stack and s[i] < stack[-1] and last_occurrence[stack[-1]] > i:\n visited.remove(stack.pop())\n \n # Append the current character to the stack and mark it as visited\n stack.append(s[i])\n visited.add(s[i])\n \n # Convert the stack to a string and return the result\n return "".join(stack)\n\n``` | 2 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
[Python] Simple solution with stack | remove-duplicate-letters | 0 | 1 | ```\nclass Solution:\n def removeDuplicateLetters(self, s: str) -> str:\n ## RC ##\n\t\t## APPROACH : STACK ##\n\t\t## 100% Same Problem Leetcode 1081. Smallest Subsequence of Distinct Characters ##\n\t\t## LOGIC ##\n\t\t#\t1. We add element to the stack\n\t\t#\t2. IF we get bigger element, we just push on top\n\t\t#\t3. ELSE we pop if and only if there are other occurances of same letter again in the string, otherwise we donot pop\n\t\t#\t4. If an element is already in the stack, we donot push.\n\t\t## TIME COMPLEXICITY : O(N) ##\n\t\t## SPACE COMPLEXICITY : O(N) ##\n\t\n\t\t## EXAMPLE : "cdadabcc"\t##\n\t\t## STACK TRACE ##\n # {\'c\': 7, \'d\': 3, \'a\': 4, \'b\': 5}\n # [\'c\']\n # [\'c\', \'d\']\n # [\'a\']\n # [\'a\', \'d\']\n # [\'a\', \'d\', \'b\']\n # [\'a\', \'d\', \'b\', \'c\']\n \n stack = []\n seen = set()\n last_occurance = {}\n for i in range(len(s)):\n last_occurance[ s[i] ] = i\n \n # print(last_occurance)\n \n for i, ch in enumerate(s):\n if( ch in seen ):\n continue\n else:\n # 3\n while( stack and stack[-1] > ch and last_occurance[stack[-1]] > i ):\n removed_char = stack.pop()\n seen.remove(removed_char)\n seen.add(ch)\n stack.append(ch)\n # print(stack)\n return \'\'.join(stack)\n``` | 23 | Given a string `s`, remove duplicate letters so that every letter appears once and only once. You must make sure your result is **the smallest in lexicographical order** among all possible results.
**Example 1:**
**Input:** s = "bcabc "
**Output:** "abc "
**Example 2:**
**Input:** s = "cbacdcbc "
**Output:** "acdb "
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
**Note:** This question is the same as 1081: [https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/](https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/) | Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i. |
Python easy to understand | maximum-product-of-word-lengths | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n total=0\n words=list(set(words))\n for i in range(len(words)):\n for j in range(i+1,len(words)):\n ans=0\n for k in words[i]:\n if k not in words[j]:ans=len(words[i])*len(words[j])\n else:\n ans=0\n break\n total=max(total,ans)\n return total \n``` | 4 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
318: Solution with step by step explanation | maximum-product-of-word-lengths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe solution starts by defining a nested function getMask(word: str) -> int that takes a string and returns an integer bit mask. The bit mask is computed by looping over each character in the string and setting the corresponding bit in the mask to 1. The bit position is determined by subtracting the ASCII value of the character \'a\' from the ASCII value of the current character.\n\nThe next step is to compute the bit masks for each word in the input list, using a list comprehension that applies the getMask() function to each word in the input list.\n\nThe main loop then iterates over all pairs of words in the list, using two nested loops with indices i and j. For each pair of words, the bitwise AND of their bit masks is computed using the \'&\' operator. If the result of the bitwise AND is 0, then the two words do not share any common letters, and their product is compared to the current maximum product stored in the ans variable. If the product is greater than the current maximum, it is stored in the ans variable.\n\nFinally, the function returns the value of the ans variable, which contains the maximum product of the lengths of two words that do not share any common letters.\n\n# Complexity\n- Time complexity:\n87.64%\n\n- Space complexity:\n81.18%\n\n# Code\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n ans = 0\n\n def getMask(word: str) -> int:\n mask = 0\n for c in word:\n mask |= 1 << ord(c) - ord(\'a\')\n return mask\n\n masks = [getMask(word) for word in words]\n\n for i in range(len(words)):\n for j in range(i):\n if not (masks[i] & masks[j]):\n ans = max(ans, len(words[i]) * len(words[j]))\n\n return ans\n\n``` | 4 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
✅ Python | | Easy 3 Approaches explained | maximum-product-of-word-lengths | 0 | 1 | 1. ##### **Hashset**\nThe approach is quite straightforward. We do the following:\n1. **Compute** the unique **char_set** in one iteration.\n2. **Find** all the **pairs** and **compute** the **max product** only if there are no common characters between two **char_sets**. In python, you can use `&` operator which serves as the intersection operator.\n\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n n=len(words) \n char_set = [set(words[i]) for i in range(n)] # precompute hashset for each word \n max_val = 0\n for i in range(n):\n for j in range(i+1, n):\n if not (char_set[i] & char_set[j]): # if nothing common\n max_val=max(max_val, len(words[i]) * len(words[j]))\n \n return max_val \n```\n**Time - O(N^2 * 26)** - where `N` is the number of words. The intersection will run against a fixed set of `26` characters. (Thanks to [newbie7025](https://leetcode.com/newbie7025) and [sagnikbiswas](https://leetcode.com/sagnikbiswas) who helped with the time complexity)\n**Space - O(N)** - space to store the `char_set`.\n\n----\n\n\n2. ##### **One Liner using Python Library**\n\nHere the code will be using [combinations](https://docs.python.org/3/library/itertools.html#itertools.combinations) which is a python built-in to achieve the same approach as above in one line.\n\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n return max([len(s1) * len(s2) for s1, s2 in combinations(words, 2) if not (set(s1) & set(s2))], default=0)\n```\n\n**Time - O(N^2 * 26)** - where `N` is the number of words and `L` is the max length of the word in `words`. The interesect operation `A & B` in python has a time complexity of `O(min(len(A), len(B))`.\n**Space - O(1)** \n\n---\n\n3. ##### **Bit Mask**\n\nThis approach replaces the **char_set** in above approach using a **bit_mask**. The set bits of the **bit_mask** will indicate the presence of a char in the word. This will also help improve the time complexity as the code will replace the **&** of **two hashset** which is **O(min(len(s1), len(s2))** with **&** operation between **two integers** which is **O(1)**.\n\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n n=len(words)\n \n bit_masks = [0] * n\n lengths = [0] * n\n \n for i in range(n): \n for c in words[i]:\n bit_masks[i]|=1<<(ord(c) - ord(\'a\')) # set the character bit \n lengths[i]=len(words[i])\n \n max_val = 0\n for i in range(n):\n for j in range(i+1, n):\n if not (bit_masks[i] & bit_masks[j]):\n max_val=max(max_val, lengths[i] * lengths[j])\n \n return max_val \n```\n\n**Time - O(N^2)** - where `N` is the number of words.\n**Space - O(N)** - space to store the `char_set` and `lengths`.\n\n---\n\n***Please upvote if you find it useful*** | 62 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
Python Solution || Max Product | maximum-product-of-word-lengths | 0 | 1 | \n# Complexity\n- Time complexity:\nO(n^2)\n\n\n# Code\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n mp = 0\n char_set = []\n \n for i in range(len(words)):\n char_set.append(set(words[i]))\n \n for i in range(len(words)):\n\n for j in range(i+1,len(words)):\n if not (char_set[i] & char_set[j]):\n \n if mp<(len(words[i])*len(words[j])):\n mp=len(words[i])*len(words[j])\n\n return mp\n\n``` | 2 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
What about a trie? | maximum-product-of-word-lengths | 0 | 1 | What if instead of a bit-mask, we\'ll use a trie to store all the words? But! ...before adding a new word to a trie, let\'s extract only the **unique** letters from the word (since we don\'t actually care about the count for each letter) and **sort** them alphabetically. Reason \u2013 make the trie as small as possible, as doing this would result in having at most `26` levels, thus a constant space complexity.\n\n#### Demonstration\n\n1. For `n = 1`, where `n` is the number of **unique** letters, the total amount of nodes inside the trie is `1`.\n2. For `n = 2`, trie will have `3` nodes.\n3. For `n = 3`, trie will have `7` nodes.\n4. For `n = 4`, trie will have `15` nodes.\n5. For `n` unique **letters**, trie will have `O(2`<sup>`n`</sup>` - 1)` nodes, which is simplified to `O(1)` since `n` will never be larger than `26` for English alphabet.\n\n\n\n#### Example\n\nLet\'s say we have the following words:\n`["abcab", "bcddc","daaad","cfgg", "dabdabdab"]`\n\n1. Extract unique letters and sort them:\n`["abc", "bcd", "ad", "cfg", "abd"]`\n\n2. Add the words to the trie and at the end of each word add a new node with the length of the original word:\n\n\n\nNavigating the tree for finding a word that contains (or not) just a certain subset of letters will also take `O(1)` time. There are at most `26` letters, thus `O(2`<sup>`n`</sup>` - 1)` nodes inside trie, where `n` is the number of letters, i. e. `O(2`<sup>`26`</sup>` - 1) => O(67,108,863) => O(1)`. So `67,108,863` is an absurdly large number, but it is constant nonetheless, hence theoretical constant time complexity.\n\nMy experience with the above approach led to the same results in practice too, at least with the test cases that are on LeetCode. Here is my runtime with Python 3 implementation:\n\n\n\nHere\'s the implementation with BFS for navigating the trie:\n\n```python\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n n = len(words)\n best = 0\n trie = {}\n\n # Build a trie\n\t\t# O(N * U * logU) where U is the number of unique letters (at most 26), simplified to O(N)\n for word in words:\n node = trie\n letters = sorted(set(word))\n\n for char in letters:\n if char not in node:\n node[char] = {}\n node = node[char]\n\n # The "None" node will store the length of the word\n node[None] = max(node.get(None, 0), len(word))\n\n # Loop through each word\n\t\t# O(N)\n for word in words:\n letters = set(word)\n word_len = len(word)\n\n # With BFS find the longest word inside the trie that does not have any common letters with current word\n\t\t\t# O(2^26 - 1) => O(1)\n queue = collections.deque([trie])\n\n while queue:\n node = queue.popleft()\n\n if None in node:\n best = max(best, node[None] * word_len)\n\n # Explore the neighbors\n for char in node.keys():\n if char is not None and char not in letters:\n queue.append(node[char])\n\n return best\n```\n\nTime complexity: `O(n)`\nSpace complexity: `O(1)`\n | 5 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
Python Simple Solution || Brute force to Optimized code | maximum-product-of-word-lengths | 0 | 1 | **Brute force code**\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n l = []\n for i in words:\n for j in words:\n\t\t\t # creating a string with common letters\n com_str = \'\'.join(set(i).intersection(j)) \n\t\t\t\t\n\t\t\t\t# if there are no common letters\n if len(com_str) == 0: \n l.append(len(i)*len(j))\n\t\t\t\t\n\t\t# if the list is not empty\t\t\n if len(l) != 0: \n return max(l)\n\t\t\n\t\t# return 0 otherwise\n return 0\n```\n\n**Optimized code**\n```\nimport itertools\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n l = []\n for i, j in itertools.combinations(words, 2):\n com_str = \'\'.join(set(i).intersection(j)) \n if len(com_str) == 0: \n l.append(len(i)*len(j))\n if len(l) != 0: \n return max(l)\n return 0\n```\n**.\n.\n.\nPlease upvote if you find it useful...** | 6 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
Python, brute force O(N^2) using sets and bitmasks | maximum-product-of-word-lengths | 0 | 1 | ```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n result = 0\n words_set = [set(word) for word in words]\n for i in range(len(words)-1):\n for j in range(i + 1, len(words)):\n if (len(words[i]) * len(words[j]) > result and\n not (words_set[i] & words_set[j])):\n result = len(words[i]) * len(words[j])\n \n return result\n```\nUsing bitmask\n```\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n def bitmask(word):\n mask = 0\n for c in word:\n mask |= 1 << ord(c) - ord(\'a\')\n \n return mask \n \n result = 0\n bitmasks = [bitmask(word) for word in words]\n for i in range(len(words)-1):\n for j in range(i + 1, len(words)):\n if (len(words[i]) * len(words[j]) > result and\n bitmasks[i] & bitmasks[j] == 0):\n result = len(words[i]) * len(words[j])\n \n return result\n``` | 1 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
Easy Python Masking Solution | maximum-product-of-word-lengths | 0 | 1 | ##### Amortized Analysis\n---\nTime Complexity: O(n^2) [ n is the length of words]\nSpace Complexity: O(n)\n\n---\n##### Code\n---\n\n```python\nclass Solution:\n def maxProduct(self, words: List[str]) -> int:\n words_mask = []\n for word in words:\n mask = 0\n for c in word:\n mask |= 1 << (ord(c) - ord(\'a\'))\n words_mask.append(mask)\n \n res = 0\n for i in range(len(words)):\n for j in range(i+1, len(words)):\n if not (words_mask[i] & words_mask[j]):\n res = max(res, len(words[i]) * len(words[j]))\n return res\n``` | 1 | Given a string array `words`, return _the maximum value of_ `length(word[i]) * length(word[j])` _where the two words do not share common letters_. If no such two words exist, return `0`.
**Example 1:**
**Input:** words = \[ "abcw ", "baz ", "foo ", "bar ", "xtfn ", "abcdef "\]
**Output:** 16
**Explanation:** The two words can be "abcw ", "xtfn ".
**Example 2:**
**Input:** words = \[ "a ", "ab ", "abc ", "d ", "cd ", "bcd ", "abcd "\]
**Output:** 4
**Explanation:** The two words can be "ab ", "cd ".
**Example 3:**
**Input:** words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** 0
**Explanation:** No such pair of words.
**Constraints:**
* `2 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* `words[i]` consists only of lowercase English letters. | null |
Python || math || explained | bulb-switcher | 0 | 1 | 1. For the `m`th bulb, how many times will it be toggled?\nSuppose the prime factorization of `m` is `p_1^m_1 * p_2^m_2 * ... * p_k^m_k`, then the total number of factors of `m` would be `(m_1+1)*(m_2+1)*...*(m_k+1)`.\n2. If there are at least one odd number in `{m_1, ..., m_k}`, the number of factors would be even. A bulb toggled even times remains being off.\n3. Only those bulbs with indices being square numbers would be on after `n` rounds.\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(math.sqrt(n)) | 2 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
[ C++ ] [ Python ] [Java ] [ C ] [ JavaScript ] [ One Liner ] [ Maths ] | bulb-switcher | 1 | 1 | # Code [ C++ ]\n```\nclass Solution {\npublic:\n int bulbSwitch(int n) {\n return (int)sqrt(n);\n }\n};\n```\n\n# Code [ Python ]\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(sqrt(n))\n```\n\n# Code [ Java ]\n```\nclass Solution {\n public int bulbSwitch(int n) {\n return (int)Math.sqrt(n);\n }\n}\n```\n\n# Code [ C ]\n```\nint bulbSwitch(int n){\n return sqrt(n);\n}\n```\n\n# Code [ JavaScript ]\n```\n/**\n * @param {number} n\n * @return {number}\n */\nvar bulbSwitch = function(n) {\n var res=1;\n while(res*res<=n){\n res++;\n }\n while(res*res>n){\n res--;\n }\n return res;\n};\n```\n | 2 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Explanation and Solution | bulb-switcher | 0 | 1 | # Code\n```\nclass Solution:\n \'\'\'\n If a number toggles odd number of times it gets off we know this \n if u look at the number of factors of any number there are EVEN.\n except in one case Which is the number being ans PERFECT SQUARE\n lets say 16: 4*4 gives us only one factor thus this effect the\n parity of number of factors therefore a PERFECT SQUARE number would\n always be on those are 1 4 9 16 25 ....... so we find the nearest \n perfect square which is <=n and print that !!! :)\n \'\'\'\n def bulbSwitch(self, n: int) -> int:\n return int(sqrt(n))\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Simple.py | bulb-switcher | 0 | 1 | # Code\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(math.sqrt(n))\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Python3 easy one liner with explanation || quibler7 | bulb-switcher | 0 | 1 | # Code\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return isqrt(n)\n```\n\n# Approach \n\n- At Start all the bulbs are off. \n- In the first round, all bulbs are turned on. \n- In the second round, every second bulb is toggled ( if its on then turned off and if its off then turned on)\n- In the third round, every third bulb is toggled and so on until the `nth` round. \n- The problem asks to determine how many bulbs are on after n rounds of toggling.\n\n- A key observation is that a bulb `i` will only be toggled in the `j`th round if`j` is a factor of `i`. \n\n- Therefore, a bulb `i` will be on at the end if and only if the number of factors of `i` is odd.\n\n**A number has an odd number of factors if and only if it is a perfect square.**\n\n- So Basically we have to calculate number of perfect squares less then or equal to n\n- for this we will use `math.isqrt()` method in Python.\n- This method is used to get the integer square root of the given non-negative integer value n. This method returns the floor value of the exact square root of n or equivalently the greatest integer a such that a2 <= n\n | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Python3 One Line Solution (also my first post as a newbie) | bulb-switcher | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnly positions that are a squared number are turned on at the end, i.e. positions 1, 4, 9, 16, 25, etc.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust find the floor of square root of n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return floor(sqrt(n)) \n \n\n\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Python shortest 1-liner. Functional programming. | bulb-switcher | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/bulb-switcher/editorial/).\n\n# Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution: bulbSwitch = isqrt\n``` | 2 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Image Explanation🏆- [Easiest to Understand - No Clickbait] - C++/Java/Python | bulb-switcher | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Bulb Switcher` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n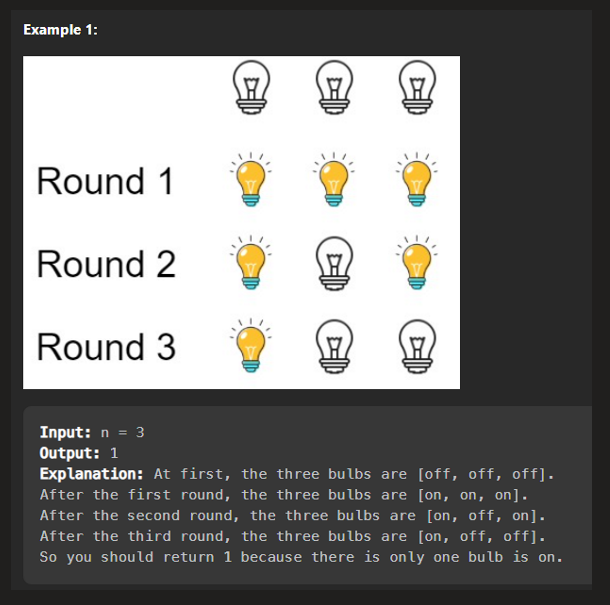\n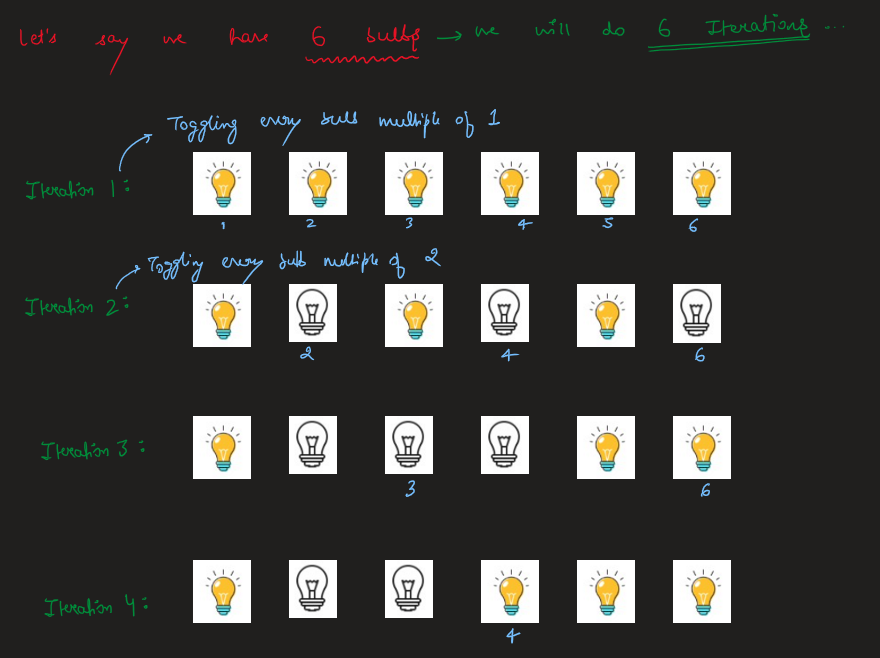\n\n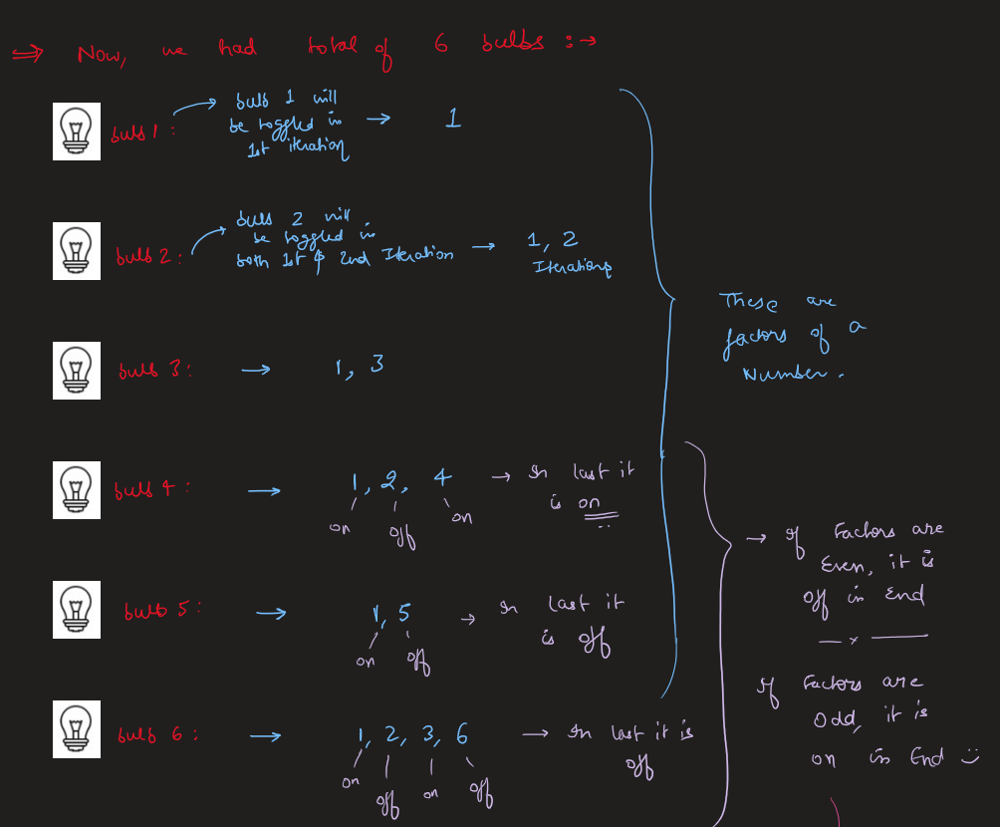\n\n\n\n\n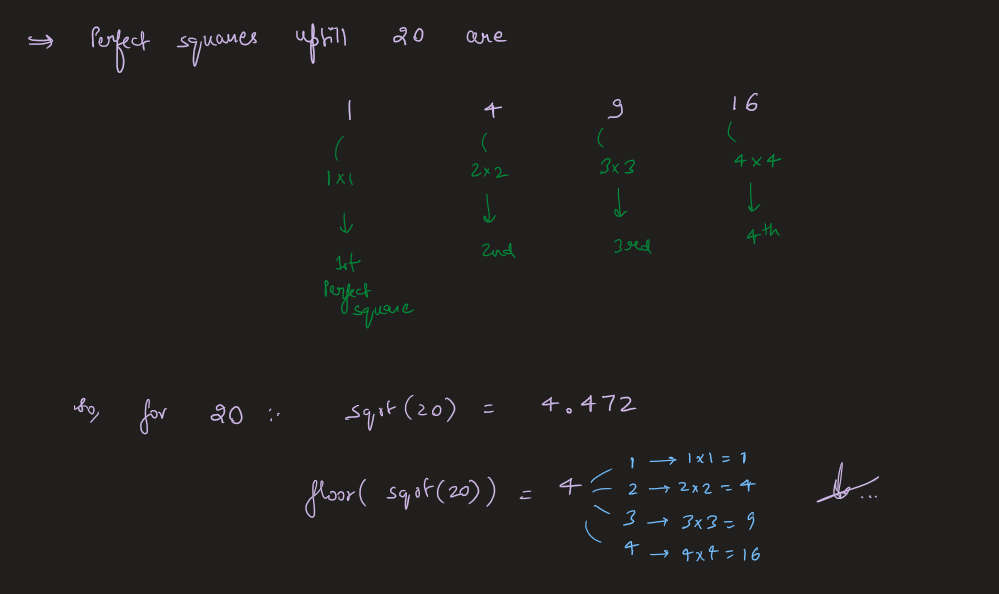\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int bulbSwitch(int n) {\n return sqrt(n);\n }\n};\n```\n```Java []\nclass Solution {\n public int bulbSwitch(int n) {\n return (int)Math.sqrt(n);\n }\n}\n```\n```Python []\nimport math\n\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(math.sqrt(n))\n```\n | 122 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Explanation of factoring through "Fundamental theorem of arithmetic" | bulb-switcher | 0 | 1 | # Approach\nonly those bulbs are toggled whose indexes have an odd number of factors.\nAccording to the main theorem of arithmetic, every number can be factored into prime factors in unique way (my favorite theorem).\nExamples:\n18 -> (3,3,2)\n9 -> (3,3)\n5 -> (5)\n\nSo, how many different factors do we have (not only prime)?\n\nTo enumerate all factors, we can combine prime factors, and the total number of factors is equal to the number of combinations of prime factors (supersets in combinatorics).\n\nFor example, for 12:\n1 (we don\'t choose any of the prime factors),\n3, 2, 2*3, 2*2, 2*2*3.\n\nThere are 3 options for choosing 2 (0 2s or 1 2s, 2 2s) and two options for choosing 3 (0 3s, 1 3s).\n\nSuppose we have a number N and its prime factors: A^a, B^b, C^c, where "a" is the number of As, "b" is the number of Bs, and "c" is the number of Cs. We can choose 0 As, 1 As, 2 As, and so on, up to "a" As. The same is true for Bs and Cs.\n\nThe total number of different factors for number N is equal to the number of possible counts for A times possible counts for B and so on. So it is equal to (a+1)(b+1)(c+1). It is easy to see that this number can be even only if one of "a", "b", or "c" is odd. So, the odd number of factors can be only if all of prime factors have even degree, such numbers are perfect square.\n\nThe last question is: how many perfect squares are there until some number N? Just draw a multiplication table in this format, and it will be clear.\n1 2 3 4\n1-1\n2---4\n3-----6\n4-------8\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(1)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(n**0.5)\n\n\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
SIMPLE CODE IN C LANGUAGE BEGINNER's APPROACH | bulb-switcher | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint bulbSwitch(int n){\nint i = 1;\n int g = 0;\n int count = 0 ;\n while(g < n)\n {\n i = i + 2 ;\n g = g + i;\n count = count + 1;\n }\n return count;\n}\n\n\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Beating 89.93% Single line Python Solution | bulb-switcher | 0 | 1 | \n\n\n# Code\n```\nfrom math import floor,sqrt\nclass Solution(object):\n def bulbSwitch(self, n):\n """\n :type n: int\n :rtype: int\n """\n return int(sqrt(n))\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Python Solution || One Linear || Easy to understand || Math || Sqrt | bulb-switcher | 0 | 1 | ```\nfrom math import floor,sqrt\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return floor(sqrt(n))\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
319: Solution with step by step explanation | bulb-switcher | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a variable count to 0 and a variable i to 1.\n2. While i*i is less than or equal to n, increment count by 1 and increment i by 1.\n3. Return the final value of count.\n\nThe idea behind this solution is that a bulb will be toggled for each factor it has (excluding 1 and itself). For example, bulb 6 will be toggled by rounds 1, 2, 3, and 6. So if a bulb has an odd number of factors, it will end up on, and if it has an even number of factors, it will end up off. The only bulbs that will end up on are those that have an odd number of factors, which are the perfect squares. So the solution simply counts the number of perfect squares less than or equal to n.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n count = 0\n i = 1\n while i*i <= n:\n count += 1\n i += 1\n return count\n\n``` | 5 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
Mathematical explanation and thought process to arrive at solution | bulb-switcher | 0 | 1 | # Approach\n\nLets begin by looking at the $i$<sup>th</sup> bulb (starting from 1). Consider how many times it has been toggled in $n$ rounds. \n\nNote that in rounds $i+1$ and after will no longer affect the $i$<sup>th</sup> bulb. \n\nYou will realise that the number of times the $i$<sup>th</sup> bulb is toggled is equal to the number of integers that divides $i$ less than or equal to $i$. Now, this naturally brings us to the question of how many integers less than or equal to $i$ divides $i$.\n\nConsider the prime factorisation of $i$ = $p_1^{a_1} p_2^{a_2} p_3^{a_3}...p_n^{a_n}$ where $p_j$ is the $j$<sup>th</sup> prime number and $a_j$ is its respective power. The number of integers that divide $i$ will be \n\n$(a_1+1)(a_2+1)...(a_n+1)$\n\nFor the $i$<sup>th</sup> to be turned on, the bulb has to be toggled an odd number of times from round 0 when it is off. Hence, the $i$<sup>th</sup> will be turned on if and only if the the number of integers that divide $i = (a_1+1)(a_2+1)...(a_n+1)$ is odd which is only achieved when every factor is odd. Hence, for all $j$ from $1$ to $n$, $a_j$ is even. \n\nThis means that $i$ is a perfect square if and only if it is turned on after $n$ rounds.\n\nSo how many bulbs will be turned on after $n$ rounds has been reduced to the number of perfect squares from 1 to $n$. Hence, the answer is $\\lfloor\\sqrt{n}\\rfloor$\n\n# Code\n```\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(sqrt(n))\n``` | 1 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
python3||O(1) | bulb-switcher | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\nclass Solution:\n def bulbSwitch(self, n: int) -> int:\n return int(math.sqrt(n))\n``` | 2 | There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb.
Return _the number of bulbs that are on after `n` rounds_.
**Example 1:**
**Input:** n = 3
**Output:** 1
**Explanation:** At first, the three bulbs are \[off, off, off\].
After the first round, the three bulbs are \[on, on, on\].
After the second round, the three bulbs are \[on, off, on\].
After the third round, the three bulbs are \[on, off, off\].
So you should return 1 because there is only one bulb is on.
**Example 2:**
**Input:** n = 0
**Output:** 0
**Example 3:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `0 <= n <= 109` | null |
321: Space 98.63%, Solution with step by step explanation | create-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function called "get_max_subseq" that takes two inputs: a list of integers called "nums" and an integer "k" representing the length of the subsequence we want to extract from the list.\n2. Initialize an empty stack to hold the maximum subsequence and iterate through the input list "nums" using a for loop and the enumerate() function.\n3. For each element "num" in "nums", do the following:\na. While the stack is not empty AND the length of the remaining part of "nums" (i.e., len(nums) - i) plus the length of the stack is greater than "k" AND the last element in the stack is less than "num", pop the last element from the stack.\nb. If the length of the stack is less than "k", append "num" to the stack.\n4. Return the resulting stack, which contains the maximum subsequence of "nums" of length "k".\n5. Define a function called "merge" that takes two inputs: two lists of integers called "nums1" and "nums2".\n6. Initialize an empty list called "merged" to hold the merged list.\n7. Initialize two counters i and j to 0 to track the current index of "nums1" and "nums2", respectively.\n8. While i is less than the length of "nums1" OR j is less than the length of "nums2", do the following:\na. If i is greater than or equal to the length of "nums1", append the jth element of "nums2" to "merged" and increment j by 1.\nb. Else if j is greater than or equal to the length of "nums2", append the ith element of "nums1" to "merged" and increment i by 1.\nc. Else if the remaining part of "nums1" starting from the ith index is lexicographically greater than the remaining part of "nums2" starting from the jth index, append the ith element of "nums1" to "merged" and increment i by 1.\nd. Otherwise, append the jth element of "nums2" to "merged" and increment j by 1.\n9. Return the resulting merged list.\n10. Initialize an empty list called "ans" to hold the maximum subsequence of length "k" from "nums1" and "nums2".\n11. Loop through all possible lengths "i" of the subsequence from "nums1" ranging from max(0, k - len(nums2)) to min(len(nums1), k) + 1.\n12. Calculate the corresponding subsequence of "nums2" of length "j" by subtracting "i" from "k".\n13. Call the "get_max_subseq" function on "nums1" with "i" as the input "k" and store the result in "subseq1".\n14. Call the "get_max_subseq" function on "nums2" with "j" as the input "k" and store the result in "subseq2".\n15. Call the "merge" function on "subseq1" and "subseq2" and store the result in "merged".\n16. Update "ans" to be the maximum value between the current value of "ans" and "merged" using the max() function.\n17. Return the resulting maximum subsequence of length "k" from "nums1" and "nums2", which is stored in "ans".\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n def get_max_subseq(nums, k):\n stack = []\n for i, num in enumerate(nums):\n while stack and len(nums) - i + len(stack) > k and stack[-1] < num:\n stack.pop()\n if len(stack) < k:\n stack.append(num)\n return stack\n \n def merge(nums1, nums2):\n merged = []\n i, j = 0, 0\n while i < len(nums1) or j < len(nums2):\n if i >= len(nums1):\n merged.append(nums2[j])\n j += 1\n elif j >= len(nums2):\n merged.append(nums1[i])\n i += 1\n elif nums1[i:] > nums2[j:]:\n merged.append(nums1[i])\n i += 1\n else:\n merged.append(nums2[j])\n j += 1\n return merged\n \n ans = []\n for i in range(max(0, k - len(nums2)), min(len(nums1), k) + 1):\n j = k - i\n subseq1 = get_max_subseq(nums1, i)\n subseq2 = get_max_subseq(nums2, j)\n merged = merge(subseq1, subseq2)\n ans = max(ans, merged)\n return ans\n\n``` | 4 | You are given two integer arrays `nums1` and `nums2` of lengths `m` and `n` respectively. `nums1` and `nums2` represent the digits of two numbers. You are also given an integer `k`.
Create the maximum number of length `k <= m + n` from digits of the two numbers. The relative order of the digits from the same array must be preserved.
Return an array of the `k` digits representing the answer.
**Example 1:**
**Input:** nums1 = \[3,4,6,5\], nums2 = \[9,1,2,5,8,3\], k = 5
**Output:** \[9,8,6,5,3\]
**Example 2:**
**Input:** nums1 = \[6,7\], nums2 = \[6,0,4\], k = 5
**Output:** \[6,7,6,0,4\]
**Example 3:**
**Input:** nums1 = \[3,9\], nums2 = \[8,9\], k = 3
**Output:** \[9,8,9\]
**Constraints:**
* `m == nums1.length`
* `n == nums2.length`
* `1 <= m, n <= 500`
* `0 <= nums1[i], nums2[i] <= 9`
* `1 <= k <= m + n` | null |
Python Solution | Greedy Search + Dynamic Programming | create-maximum-number | 0 | 1 | ```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]: \n def merge(n1, n2):\n res = []\n while (n1 or n2) :\n if n1>n2:\n res.append(n1[0])\n n1 = n1[1:]\n else:\n res.append(n2[0])\n n2 = n2[1:]\n return res\n \n def findmax(nums, length):\n l = []\n maxpop = len(nums)-length\n for i in range(len(nums)):\n while maxpop>0 and len(l) and nums[i]>l[-1]:\n l.pop()\n maxpop -= 1\n l.append(nums[i])\n return l[:length]\n \n n1 = len(nums1)\n n2 = len(nums2)\n res = [0]*k\n for i in range(k+1):\n j = k-i\n if i>n1 or j>n2: continue\n l1 = findmax(nums1, i)\n l2 = findmax(nums2, j)\n res = max(res, merge(l1,l2))\n return res | 8 | You are given two integer arrays `nums1` and `nums2` of lengths `m` and `n` respectively. `nums1` and `nums2` represent the digits of two numbers. You are also given an integer `k`.
Create the maximum number of length `k <= m + n` from digits of the two numbers. The relative order of the digits from the same array must be preserved.
Return an array of the `k` digits representing the answer.
**Example 1:**
**Input:** nums1 = \[3,4,6,5\], nums2 = \[9,1,2,5,8,3\], k = 5
**Output:** \[9,8,6,5,3\]
**Example 2:**
**Input:** nums1 = \[6,7\], nums2 = \[6,0,4\], k = 5
**Output:** \[6,7,6,0,4\]
**Example 3:**
**Input:** nums1 = \[3,9\], nums2 = \[8,9\], k = 3
**Output:** \[9,8,9\]
**Constraints:**
* `m == nums1.length`
* `n == nums2.length`
* `1 <= m, n <= 500`
* `0 <= nums1[i], nums2[i] <= 9`
* `1 <= k <= m + n` | null |
Editorial-like Solution | create-maximum-number | 0 | 1 | # Approach 1: Stack + Merge\n\n# Intuition\nWithout any good intuition for this problem, I spent some time discarding several incorrect ideas. I want to highlight what I tried and learned before arriving at the solution.\n\n### Greedy\nInitially, I explored a greedy approach using two pointers for `nums1` and `nums2`, moving one pointer at a time and selecting the larger number. However, this fails in cases like `nums1=[9,1,1,1,9]`, `nums2=[8,8,8,8]`, `k=2`, where the greedy choice of `[9,8]` is suboptimal compared to the correct answer `[9,9]`. This approach overlooks the possibility of optimizing smaller values of `k` and fails to anticipate future numbers or revise past choices. However, I learned that this approach always works in when `k=m+n`, and performs exactly like a `merge` from `mergeSort` in this case.\n\n### DP\nConsidering the need to foresee future states, a recursive DP approach seemed viable. I was inspired by problems like [Longest Common Subsequence](https://leetcode.com/problems/longest-common-subsequence/?envType=study-plan-v2&envId=leetcode-75).\n\n**My Idea:** Define `dp[i, j, l]` as the maximum number of length `l` formed from `nums1[i:]` and `nums2[j:]`, aiming for `dp[0, 0, k]`. However, this approach was difficult to concretize and seemed to lead to large blow ups in complexity. Thinking through how to make such a dp approach work led me to consider the following test case, in which we want to prioritize taking `9`s, but have to be careful not to run out of digits and thus need to also take an \'8\' before a \'9\': `nums1=[9,9,8,9]`, `nums2=[1]`, `k=5`, where selecting all `9`s first is not feasible. The key challenge is balancing the selection of large numbers with the constraints on `k`.\n\n### Brute Force\nReverting to a brute force approach, I considered all possible selections of `a` elements from `nums1` and `b` elements from `nums2` where `a+b=k`. This involved testing every subset of size `a` in `nums1` against every subset of size `b` in `nums2`, leading to approximately $\\sum_{i=0}^k {m \\choose i} \\times {n \\choose (k-i)}$ potential solutions. The subsets could then be merged, as learned from the greedy approach.\n\n### Actual Approach\nThe breakthrough came by focusing on selecting `a` elements from `nums1` and `b` elements from `nums2` (where `a+b=k`), and then merging these selections. This problem resembles [Find the Most Competitive Subsequence](https://leetcode.com/problems/find-the-most-competitive-subsequence/description/), which suggests prioritizing the largest possible numbers early in the sequence. By identifying and combining the best selections from both arrays, we can form the maximum number. However, we need not be familiar with this related problem.\n\n**Insight from a Test Case:** Let\'s now focus on the problem of taking the best `k` elements from a single array. Consider `nums1=[9,9,4,8,9]` with `k=4` as the test case for the examples in the following sections. Directly selecting the first three `9`s is not optimal, as it exhausts the number of elements we can use. This example illustrates the need for a careful balance: while larger numbers earlier are generally preferable, we must also ensure we don\'t run out of available digits.\n\n**Strategy for Selection:** The crucial aspect is to determine the best sequence of `k` numbers to be taken from our array, or equivalently determine which `m-k` elements should be deleted. For `nums1=[9,9,4,8,9]`, let\'s say we have so far the sequence `[9,9,8]` and are deciding on the last number `9`. If we have used all our allowed deletions (in this case, `m - k = 1`), we must stick with the current selection, thus keeping the `8` and appending the `9` at the end to get `[9,9,8,9]` as the best `k=4` elements. However, if deletions are still possible, as when encountering `8` for the first time with `[9,9,4]`, we can replace the `4` with `8`.\n\n**Maintaining the Best Sequence:** We can maintain a list `A` representing the best selection so far from `nums1`. As we iterate through `nums1`, we include a number in `A` if it\'s larger than the numbers currently in `A` at the back of `A`, deleting smaller elements if deletions are still available. This is efficiently done using a stack, which allows easy deletions and maintenance of the largest possible prefix of the maximum array we can form. Note that "largest possible prefix of the maximum array with at most `m-k` deletions" is an invariant that holds for `A`, as if we inductively assume this property already held on `A`, and the next element we encounter, `num`, is larger than `A[-1]` *and* we still have available deletions, then we can in fact safely pop off `A[-1]` since the prefix `A[:-1] + [num]` is larger than the prefix `A`. \n\n**Final Step:** Once we have the best sequences from `nums1` and `nums2`, we merge them to form the largest possible number.\n\n# Algorithm\n\n1. Define a function `getMaxArray`:\n - Takes an array `nums` and an integer `length`.\n - Uses a stack to form the largest number of given `length` from `nums`.\n - Returns the first `length` elements of the stack.\n\n2. Define a function `mergeArrays`:\n - Takes two arrays `arr1` and `arr2`.\n - Merges them into the largest possible number while maintaining the order within each array.\n - Returns the merged array.\n\n3. Main algorithm:\n - Initialize an array `maxNumber` to store the maximum number.\n - Iterate over `k` from 1 to `min(m + n, k)` (inclusive):\n - For each iteration, split `k` into `i` and `k-i`.\n - Call `getMaxArray(nums1, i)` and `getMaxArray(nums2, k-i)` to get the max numbers from both arrays.\n - Merge these two arrays using `mergeArrays`.\n - Update `maxNumber` with the maximum of `maxNumber` and the merged array.\n - Return `maxNumber`.\n\n# Implementation\n```\nclass Solution:\n def maxNumber(self, nums1, nums2, k):\n def getMaxArray(nums, length):\n stack = [] #A, as described above\n to_remove = len(nums) - length # Number of elements we can remove\n\n for num in nums:\n while stack and to_remove > 0 and stack[-1] < num:\n stack.pop()\n to_remove -= 1\n stack.append(num)\n\n return stack[:length]\n\n def mergeArrays(arr1, arr2):\n result = []\n i, j = 0, 0\n len1, len2 = len(arr1), len(arr2)\n\n while i < len1 or j < len2:\n if i == len1:\n result.extend(arr2[j:])\n break\n if j == len2:\n result.extend(arr1[i:])\n break\n\n if arr1[i:] > arr2[j:]:\n result.append(arr1[i])\n i += 1\n else:\n result.append(arr2[j])\n j += 1\n\n return result\n\n maxNum = [0] * k\n for i in range(max(0, k - len(nums2)), min(k, len(nums1)) + 1):\n maxNum1 = getMaxArray(nums1, i)\n maxNum2 = getMaxArray(nums2, k - i)\n currentMax = mergeArrays(maxNum1, maxNum2)\n maxNum = max(maxNum, currentMax)\n\n return maxNum\n```\n\n\n# Complexity\n**Time complexity**: $O(k \\times (m + n))$\n\nThe algorithm\'s time complexity can be broken down as follows:\n\n1. **For Loop Iterations**:\n - The for loop runs $O(k)$ times to try all possible pairs $(i, k-i)$, where $i$ elements are taken from `nums1` and $k-i$ elements from `nums2`.\n\n2. **Operations Inside the Loop**:\n - `getMaxArray(nums1, i)`:\n - Takes $O(m)$ time.\n - Each element in `nums1` is appended and popped at most once, leading to constant operations per element.\n - `getMaxArray(nums2, k-i)`:\n - Similarly, takes $O(n)$ time for the elements in `nums2`.\n - `mergeArrays(maxNum1, maxNum2)`:\n - Takes $O(k)$ time.\n - The sizes of `maxNum1` and `maxNum2` are $i$ and $k-i$ respectively at each iteration, so merging them takes $O(i + (k-i)) = O(k)$ time.\n\n3. **Combining the Complexities**:\n - Since the inside portion of the loop takes $O(n + m)$ time and $k \\leq m + n$, the time complexity per loop iteration is $O(n + m)$.\n - Multiplying by the $O(k)$ iterations, the overall time complexity is $O(k \\times (m + n))$.\n\n\n\n\n**Space Complexity**: $O(m + n)$\n\nThe space complexity can be detailed as follows:\n\n1. **Maximum Space Usage in Each Iteration**:\n - The primary components contributing to space usage in each iteration are the arrays generated by `getMaxArray` and `mergeArrays`.\n - `getMaxArray(nums1, i)` can require up to $O(m)$ space, particularly when `nums1` is in non-increasing order (e.g., `[9,9,7,6,3,3,1]`).\n - `getMaxArray(nums2, k-i)` can similarly occupy up to $O(n)$ space.\n - `mergeArrays(maxNum1, maxNum2)` requires additional space of $O(k)$ for the merged array. Since $k \\leq m + n$, this is bounded by $O(m + n)$.\n\n2. **Cumulative Space Requirement**:\n - Although `maxNum` array is reused in each iteration and contributes to $O(k)$ space, the worst-case space scenario is dominated by the larger of `nums1` and `nums2`.\n - The space required for each function call in any iteration is at most $O(m + n)$, considering the worst-case scenarios.\n\n3. **Overall Space Complexity**:\n - The overall space complexity of the algorithm, taking into account all the factors above, is $O(m + n)$.\n | 0 | You are given two integer arrays `nums1` and `nums2` of lengths `m` and `n` respectively. `nums1` and `nums2` represent the digits of two numbers. You are also given an integer `k`.
Create the maximum number of length `k <= m + n` from digits of the two numbers. The relative order of the digits from the same array must be preserved.
Return an array of the `k` digits representing the answer.
**Example 1:**
**Input:** nums1 = \[3,4,6,5\], nums2 = \[9,1,2,5,8,3\], k = 5
**Output:** \[9,8,6,5,3\]
**Example 2:**
**Input:** nums1 = \[6,7\], nums2 = \[6,0,4\], k = 5
**Output:** \[6,7,6,0,4\]
**Example 3:**
**Input:** nums1 = \[3,9\], nums2 = \[8,9\], k = 3
**Output:** \[9,8,9\]
**Constraints:**
* `m == nums1.length`
* `n == nums2.length`
* `1 <= m, n <= 500`
* `0 <= nums1[i], nums2[i] <= 9`
* `1 <= k <= m + n` | null |
greedy algorithm and merge operation | create-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. the **everymax fuction** use the greedy algorithm to create the maximum number of length **n** from a given array.\n\n it iterate through the array, maintain a stack to store the maximum number sofar. it campare each element with the top of the stack to decide whether to discard it or include it and also maintain the desired length of "n".\n\n**the greedy algorithm ensure the resulting number is lexicographically maximum** \n\n2. the **merge** function compre the first element of two arrays and append it to result until one of the array is exhuasted. this operation maintain the relative order of elements ensuring the resulting number is maximum possible.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n def everymax(nums,n):\n stack=[]\n to_pop=len(nums)-n\n for num in nums:\n while to_pop and stack and num>stack[-1]:\n stack.pop()\n to_pop-=1\n stack.append(num)\n return stack[:n]\n\n def merge(nums1,nums2):\n result=[]\n while nums1 and nums2:\n if nums1>nums2:\n result.append(nums1[0])\n nums1=nums1[1:]\n else:\n result.append(nums2[0])\n nums2=nums2[1:]\n result.extend(nums1)\n result.extend(nums2)\n return result\n\n ans=[]\n for i in range(k+1):\n if i <=len(nums1) and (k-i)<=len(nums2):\n maxnums1=everymax(nums1,i)\n maxnums2=everymax(nums2,k-i)\n merged=merge(maxnums1,maxnums2)\n ans=max(ans,merged)\n return ans\n\n``` | 0 | You are given two integer arrays `nums1` and `nums2` of lengths `m` and `n` respectively. `nums1` and `nums2` represent the digits of two numbers. You are also given an integer `k`.
Create the maximum number of length `k <= m + n` from digits of the two numbers. The relative order of the digits from the same array must be preserved.
Return an array of the `k` digits representing the answer.
**Example 1:**
**Input:** nums1 = \[3,4,6,5\], nums2 = \[9,1,2,5,8,3\], k = 5
**Output:** \[9,8,6,5,3\]
**Example 2:**
**Input:** nums1 = \[6,7\], nums2 = \[6,0,4\], k = 5
**Output:** \[6,7,6,0,4\]
**Example 3:**
**Input:** nums1 = \[3,9\], nums2 = \[8,9\], k = 3
**Output:** \[9,8,9\]
**Constraints:**
* `m == nums1.length`
* `n == nums2.length`
* `1 <= m, n <= 500`
* `0 <= nums1[i], nums2[i] <= 9`
* `1 <= k <= m + n` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.