title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
🚀Beats 99.17% || DFS Recursive & Iterative || Euler Path Intuition || Commented Code🚀 | reconstruct-itinerary | 1 | 1 | # Problem Description\nThe task is **reconstructing** an itinerary using a list of airline tickets.\nEach ticket is represented as a pair of departure and arrival airports, denoted as `tickets[i] = [fromi, toi]`.\n**The goal** is to create an **ordered** itinerary, starting with the airport `JFK` (the departure point), while ensuring that all tickets are used **once**. If there are multiple valid itineraries, you should return the one with the **smallest lexical order** when read as a single string.\n\n- **Constraints:**\n - `1 <= tickets.length <= 300`\n - `tickets[i].length == 2`\n - Each town name is at most **3 letters**\n - `fromi` and `toi` consist of uppercase English letters.\n - `fromi` != `toi`\n - Start from `JFK`\n - Use each ticket **once and only once**\n\n\n\n---\n\n# Intuition\nHi there\uD83D\uDE00\nLet\'s take a look on this interesting problem. It is also challenging one.\n\nFor our airports problem we have two **crucial points** we must put in mind: We must use each ticket once and only once, there is atleast one valid itinerary as a solution of the problem.\n\nWhat can we **conclude** from that? \uD83E\uDD14\nThe graph that we will build out of tickets list is something called **Semi Euler Graph** and the path that we want is called **Euler Path**.\nI won\'t talk about them in depth because they are advanced topics even for me. \uD83D\uDE02 but I will give a simple Intuition.\n\n\nLet\'s call some graph termenolgies that we want later.\n- **In-degree** for a node: number of edges that points to a specific node.\n- **Out-degree** for anode: number of edges coming out from a node.\n\nLet\'s see an **exmaple**:\n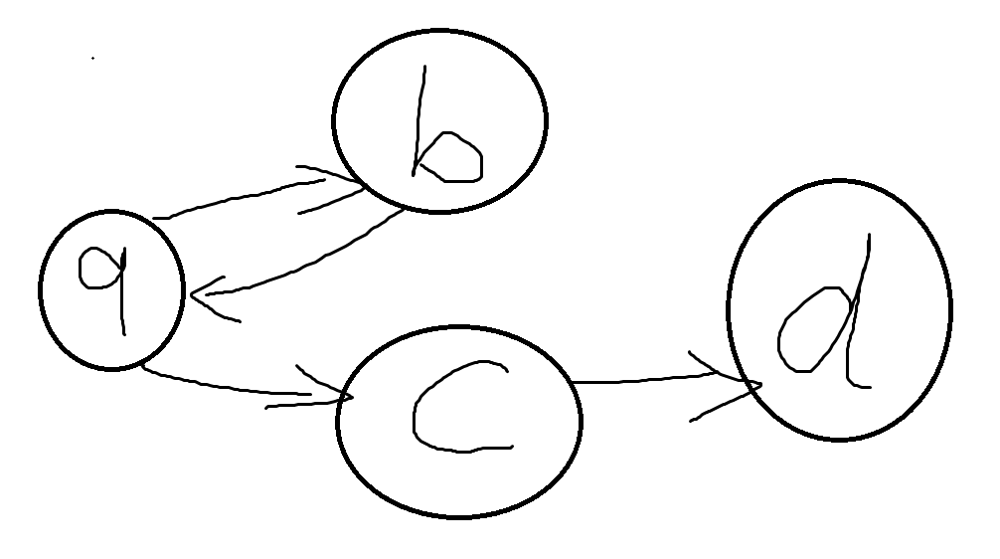\n| Node | In-degree | Out-degree | \n| :--- | ---:| :---: | \n| a | 1 | 2 | \n| b | 1 | 1 | \n| c | 1 | 1 |\n| d | 1 | 0 | \n\n\na **Semi Euler Graph** is a graph that has **Euler Path** which mean there is a path from starting node to an ending node and we will use all edges once and only once.\nHuh looks familiar\uD83E\uDD14... Yes ITS OUR PROBLEM!!\uD83E\uDD2F\n\nFor a **directed graph** to be a **Semi Euler Graph** it must meet some conditions:\n- **In degree** for all nodes = **Out degree** for `all` nodes\n- Except for two node: \n - `Starting` node should have `Out-degree = In degree + 1`\n - `Ending` node should have `In-degree = Out-degree + 1`\n\n\nLet\'s see some examples for our original problem.\n\n\n\n\nIn this example, we can see that `d` airport meets the condition for an ending node and `a` meets the condition for a starting node.\nAn answer will be `(a, b, c, d)` \n\n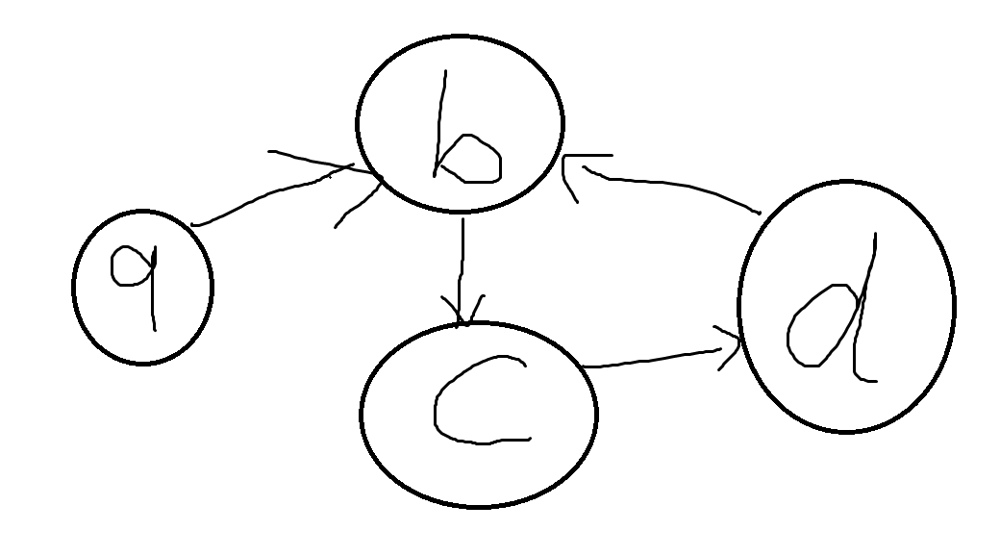\n\nIn this example, we can see that `b` airport meets the condition for an ending node and `a` meets the condition for a starting node.\nAn answer will be also `(a, b, c, d, b)` \n\n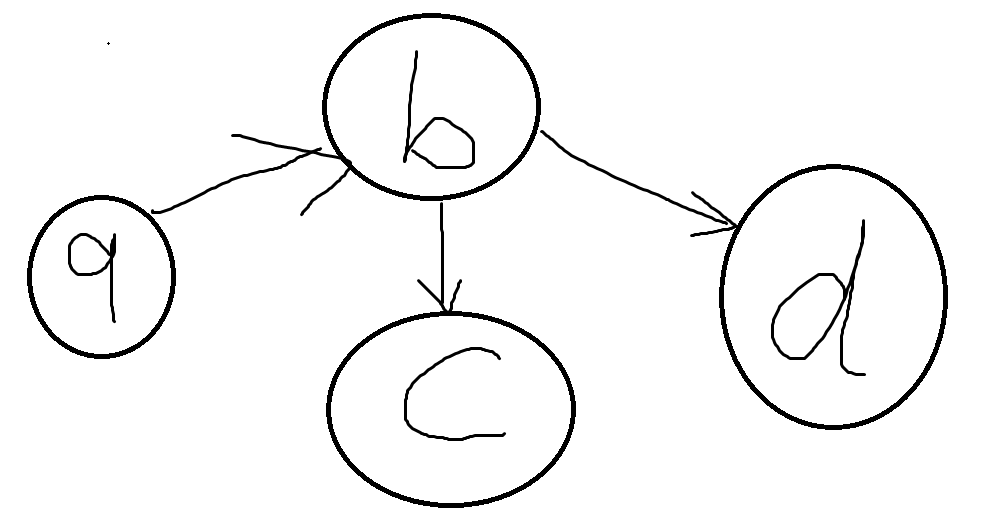\nIn this example, we can see that the nodes didn\'t meet the condition to be an **Semi Euler Graph**.\nAnd if you tried to put it as a test case it will tell you `invalid input`.\n\nOkay, I think we have something here\uD83E\uDD2F \nThe Pseudo Code for finding Euler Path is easy the only editing we will do it to sort the edges for the graph to be in the smallest lexical order.\n\nand for this problem, we will find for each test case that `JFK` meets the conditions to be a starting node.\n\nAnd that\'s it the solution for our problem only a **Semi Euler Graph** \uD83D\uDE02\n\n\n\n---\n\n\n# Approach\n## 1. DFS Recursive\n### Steps\n- Initialize a `flightGraph` as a `dictionary (map)` to represent flights and an itinerary list to store the final travel sequence.\n- Iterate through each ticket and populate the `flightGraph` dictionary.\n- Sort the destinations for each airport in reverse order to visit **lexical smaller** destinations first.\n- Start the DFS traversal from the `JFK` airport.\n- Using the **depth-first search** (DFS) method called `dfs` that takes an airport as input and recursively explores its destinations while **maintaining lexical order**. It adds the visited airports to the itinerary list.\n- **Reverse** the itinerary list to get the correct travel order.\n- **Return** the itinerary list as the final result.\n\n### Complexity\n- **Time complexity:** $$O(N^2log(N))$$\nSince we loop over lists of destinations in the flight graph and sorts them. Sorting each list has a time complexity of `O(E * log(E))`, where E is the total number of edges (tickets). Since `E` can be at most `N`, this step has a time complexity of `O(N * log(N))`. and since we loop over `N` city then the total time complexity is `O(N^2log(N))` where `N` is the number of airports.\n- **Space complexity:** $$O(N+E)$$\nWe are storing the Flight Graph which is represented using map of lists, which will have at most `N` keys (airports) and a total of `E` values (destinations). Therefore, the space complexity is `O(N + E)`.\n\n\n---\n\n## 2. DFS Iterative\n### Steps\n- Initialize a `flightGraph` as a `dictionary (map)` to represent flights and an itinerary list to store the final travel sequence.\n- Iterate through each ticket and populate the `flightGraph` dictionary.\n- Sort the destinations for each airport in reverse order to visit **lexical smaller** destinations first.\n- **Start** with `JFK` as the initial airport and create a stack.\n- While the stack is `not empty`:\n - **Explore** destinations:\n - Push the next destination onto the stack.\n - **Backtrack**:\n - Add the current airport to the travel itinerary.\n - Pop the current airport from the stack.\n- **Reverse** the travel itinerary to get the correct order.\n- **Return** the travel itinerary as the final result.\n\n### Complexity\n- **Time complexity:** $$O(N^2log(N))$$\nSince we loop over lists of destinations in the flight graph and sorts them. Sorting each list has a time complexity of `O(E * log(E))`, where E is the total number of edges (tickets). Since `E` can be at most `N`, this step has a time complexity of `O(N * log(N))`. and since we loop over `N` city then the total time complexity is `O(N^2log(N))` where `N` is the number of airports.\n- **Space complexity:** $$O(N+E)$$\nWe are storing the Flight Graph which is represented using map of lists, which will have at most `N` keys (airports) and a total of `E` values (destinations). Therefore, the space complexity is `O(N + E)`.\n\n---\n\n# Code\n## DFS Recursive\n```C++ []\nclass Solution {\nprivate:\n // Create an adjacency list to represent the flights\n unordered_map<string, vector<string>> flightGraph;\n \n // Store the final itinerary\n vector<string> itinerary;\n\npublic:\n\n // Depth-First Search to traverse the flight itinerary\n void dfs(string airport) {\n vector<string> &destinations = flightGraph[airport];\n \n // Visit destinations in lexical order\n while (!destinations.empty()) {\n string nextDestination = destinations.back();\n destinations.pop_back();\n dfs(nextDestination);\n }\n \n // Add the current airport to the itinerary after visiting all destinations\n itinerary.push_back(airport);\n }\n\n vector<string> findItinerary(vector<vector<string>>& tickets) {\n // Populate the flight graph using ticket information\n for (int i = 0; i < tickets.size(); i++) {\n string from = tickets[i][0];\n string to = tickets[i][1];\n\n flightGraph[from].push_back(to);\n }\n \n // Sort destinations in reverse order to visit lexical smaller destinations first\n for (auto &entry : flightGraph) {\n sort(entry.second.rbegin(), entry.second.rend());\n }\n \n // Start the DFS from the JFK airport\n dfs("JFK");\n \n // Reverse the itinerary to get the correct order\n reverse(itinerary.begin(), itinerary.end());\n \n return itinerary;\n }\n};\n```\n```Java []\nclass Solution {\n private Map<String, List<String>> flightGraph;\n private List<String> itinerary;\n\n public Solution() {\n flightGraph = new HashMap<>();\n itinerary = new ArrayList<>();\n }\n\n // Depth-First Search to traverse the flight itinerary\n private void dfs(String airport) {\n List<String> destinations = flightGraph.get(airport);\n\n // Visit destinations in lexical order\n while (destinations != null && !destinations.isEmpty()) {\n String nextDestination = destinations.remove(destinations.size() - 1);\n dfs(nextDestination);\n }\n\n // Add the current airport to the itinerary after visiting all destinations\n itinerary.add(airport);\n }\n\n public List<String> findItinerary(List<List<String>> tickets) {\n // Populate the flight graph using ticket information\n for (List<String> ticket : tickets) {\n String from = ticket.get(0);\n String to = ticket.get(1);\n\n flightGraph.computeIfAbsent(from, k -> new ArrayList<>()).add(to);\n }\n\n // Sort destinations in reverse order to visit lexical smaller destinations first\n for (List<String> destinations : flightGraph.values()) {\n destinations.sort(Collections.reverseOrder());\n }\n\n // Start the DFS from the JFK airport\n dfs("JFK");\n\n // Reverse the itinerary to get the correct order\n Collections.reverse(itinerary);\n\n return itinerary;\n }\n}\n```\n```Python []\n\nclass Solution:\n def __init__(self):\n self.flight_graph = defaultdict(list)\n self.itinerary = []\n\n # Depth-First Search to traverse the flight itinerary\n def dfs(self, airport:str) -> None:\n destinations = self.flight_graph[airport]\n\n # Visit destinations in lexical order\n while destinations:\n next_destination = destinations.pop()\n self.dfs(next_destination)\n\n # Add the current airport to the itinerary after visiting all destinations\n self.itinerary.append(airport)\n\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n # Populate the flight graph using ticket information\n for ticket in tickets:\n from_airport, to_airport = ticket\n\n self.flight_graph[from_airport].append(to_airport)\n\n # Sort destinations in reverse order to visit lexical smaller destinations first\n for destinations in self.flight_graph.values():\n destinations.sort(reverse=True)\n\n # Start the DFS from the JFK airport\n self.dfs("JFK")\n\n # Reverse the itinerary to get the correct order\n self.itinerary.reverse()\n\n return self.itinerary\n```\n\n## DFS Iterative\n```C++ []\nclass Solution {\nprivate:\n unordered_map<string, vector<string>> flightGraph; // Represents flights from one airport to another\n vector<string> travelItinerary; // Stores the final travel itinerary\n\npublic:\n vector<string> findItinerary(vector<vector<string>>& tickets) {\n // Populate the flight graph using ticket information\n for (int i = 0; i < tickets.size(); i++) {\n string fromAirport = tickets[i][0];\n string toAirport = tickets[i][1];\n\n flightGraph[fromAirport].push_back(toAirport);\n }\n \n // Sort destinations in reverse order to visit lexical smaller destinations first\n for (auto &entry : flightGraph) {\n sort(entry.second.rbegin(), entry.second.rend());\n }\n\n stack<string> dfsStack;\n dfsStack.push("JFK");\n\n while (!dfsStack.empty()) {\n // Get the current airport from the top of the stack\n string currentAirport = dfsStack.top();\n\n vector<string> &destinations = flightGraph[currentAirport];\n\n if (!destinations.empty()) {\n // Choose the next destination (the one in lexicographically larger order)\n string nextDestination = destinations.back();\n destinations.pop_back();\n\n dfsStack.push(nextDestination);\n } else {\n // If there are no more destinations from the current airport, add it to the itinerary\n travelItinerary.push_back(currentAirport);\n \n dfsStack.pop();\n }\n }\n \n // Reverse the itinerary to get the correct order\n reverse(travelItinerary.begin(), travelItinerary.end());\n return travelItinerary;\n }\n};\n```\n```Java []\nclass Solution {\n private Map<String, List<String>> flightGraph; // Represents flights from one airport to another\n private List<String> travelItinerary; // Stores the final travel itinerary\n\n public List<String> findItinerary(List<List<String>> tickets) {\n // Initialize the flight graph using ticket information\n flightGraph = new HashMap<>();\n travelItinerary = new ArrayList<>() ;\n for (List<String> ticket : tickets) {\n String fromAirport = ticket.get(0);\n String toAirport = ticket.get(1);\n flightGraph.computeIfAbsent(fromAirport, k -> new ArrayList<>()).add(toAirport);\n }\n\n // Sort destinations in reverse order to visit lexical smaller destinations first\n for (List<String> destinations : flightGraph.values()) {\n destinations.sort(Collections.reverseOrder());\n }\n\n Stack<String> dfsStack = new Stack<>();\n dfsStack.push("JFK");\n\n while (!dfsStack.isEmpty()) {\n // Get the current airport from the top of the stack\n String currentAirport = dfsStack.peek();\n List<String> destinations = flightGraph.get(currentAirport);\n\n if (destinations != null && !destinations.isEmpty()) {\n // Choose the next destination (the one in lexicographically larger order)\n String nextDestination = destinations.remove(destinations.size() - 1);\n dfsStack.push(nextDestination);\n } else {\n // If there are no more destinations from the current airport, add it to the itinerary\n travelItinerary.add(currentAirport);\n dfsStack.pop();\n }\n }\n\n // Reverse the itinerary to get the correct order\n Collections.reverse(travelItinerary);\n return travelItinerary;\n }\n}\n```\n```Python []\nclass Solution:\n def findItinerary(self, tickets) -> list[str]:\n # Initialize the flight graph using ticket information\n flightGraph = defaultdict(list)\n travelItinerary = []\n\n for ticket in tickets:\n fromAirport, toAirport = ticket[0], ticket[1]\n flightGraph[fromAirport].append(toAirport)\n\n # Sort destinations in reverse order to visit lexical smaller destinations first\n for destinations in flightGraph.values():\n destinations.sort(reverse=True)\n\n dfsStack = ["JFK"]\n\n while dfsStack:\n # Get the current airport from the top of the stack\n currentAirport = dfsStack[-1]\n destinations = flightGraph.get(currentAirport, [])\n\n if destinations:\n # Choose the next destination (the one in lexicographically larger order)\n nextDestination = destinations.pop()\n dfsStack.append(nextDestination)\n else:\n # If there are no more destinations from the current airport, add it to the itinerary\n travelItinerary.append(currentAirport)\n dfsStack.pop()\n\n # Reverse the itinerary to get the correct order\n travelItinerary.reverse()\n return travelItinerary\n```\n\n\n---\n\n\n\n# Further Improvements?\n[@v4g](/v4g) had a great improvement that gave better time.\nInstead of sorting we can simply use **multiset** with reverse order and take the last element every time.\nIn `C++`: Since we are pointing to `multiset.end()` then it will be in `O(1)` and erasing the element given its iterator it also will be `O(1)`.\n\n- **Time complexity:** $$O(Elog(N))$$\nSince we loop over list of tickets with size `E` and each node can have at most `N` airports that you can travel to them. \n- **Space complexity:** $$O(N+E)$$\nIt still the same.\n\nHere is the code for C++ and the solution can be generalized to other languages as well.\n\n## DFS Recursive \n```\nclass Solution {\nprivate:\n unordered_map<string, multiset<string, greater<string>>> flightGraph;\n vector<string> itinerary;\n\npublic:\n void dfs(string airport) {\n auto &destinations = flightGraph[airport];\n \n while (!destinations.empty()) {\n auto nextDestination = *(--destinations.end());\n destinations.erase(--destinations.end());\n dfs(nextDestination);\n }\n itinerary.push_back(airport);\n }\n\n vector<string> findItinerary(vector<vector<string>>& tickets) {\n for (int i = 0; i < tickets.size(); i++) {\n string from = tickets[i][0];\n string to = tickets[i][1];\n\n flightGraph[from].insert(to);\n }\n dfs("JFK");\n \n reverse(itinerary.begin(), itinerary.end());\n return itinerary;\n }\n};\n```\n\n## DFS Iterative \n```\nclass Solution {\nprivate:\n unordered_map<string, multiset<string, greater<string>>> flightGraph;\n vector<string> travelItinerary;\n\npublic:\n vector<string> findItinerary(vector<vector<string>>& tickets) {\n for (int i = 0; i < tickets.size(); i++) {\n string fromAirport = tickets[i][0];\n string toAirport = tickets[i][1];\n\n flightGraph[fromAirport].insert(toAirport);\n }\n stack<string> dfsStack;\n dfsStack.push("JFK");\n\n while (!dfsStack.empty()) {\n string currentAirport = dfsStack.top();\n\n auto &destinations = flightGraph[currentAirport];\n\n if (!destinations.empty()) {\n auto nextDestination = *(--destinations.end());\n destinations.erase(--destinations.end());\n \n dfsStack.push(nextDestination);\n } else {\n travelItinerary.push_back(currentAirport);\n \n dfsStack.pop();\n }\n }\n \n reverse(travelItinerary.begin(), travelItinerary.end());\n return travelItinerary;\n }\n};\n```\n\n\n\n\n | 45 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
✔96.90% Beats C++ ✨📈|| Hard--->Easy 😇|| Easy to Understand👁 || #Beginner😉😎 | reconstruct-itinerary | 1 | 1 | # Intuition\n- The problem requires finding a valid itinerary for a given list of flight tickets. \n- The itinerary must start from "JFK" (John F. Kennedy International Airport) and visit all airports exactly once. \n- This problem can be solved using depth-first search (DFS) on a directed graph, treating each airport as a node and each ticket as a directed edge.\n\n\n\n# Approach\n1. Create an adjacency list representation of the flights. Use an unordered_map where the key is the source airport, and the value is a multiset (sorted set) of destination airports. This allows multiple tickets to have the same source airport.\n\n1. Initialize an empty vector called `result` to store the final itinerary.\n\n1. Start the DFS traversal from the "JFK" airport. The goal is to visit all airports in a way that respects the lexicographically smallest order.\n\n1. In the DFS function:\n\n - While there are destinations connected to the current airport:\n - Get the next destination by picking the smallest destination lexicographically (because it\'s stored in a multiset).\n - Remove this destination from the list to ensure it\'s not visited again.\n - Recursively explore this destination.\n 1. After finishing the DFS traversal, reverse the `result` vector. This is necessary because the DFS builds the itinerary in reverse order.\n\n1. Return the reversed `result` vector, which now contains the valid itinerary.\n\n\n\n\n\n# Complexity\n- **Time complexity:**\n **O(n * log(n))**\n\n - **The time complexity is O(n * log(n)) for building the adjacency list and O(n * log(n)) for DFS traversal, which is often the dominant factor**\n\n\n\n- Space complexity:\n **O(n * log(n))**\n\n - **The space complexity is O(n * log(n)) for the adjacency list and O(n) for other data structures.**\n\n\n# PLEASE UPVOTE\u2763\uD83D\uDE0D\n\n\n\n# Code\n```\nclass Solution {\n // Depth-first search function to find the itinerary\n void dfs(unordered_map<string, multiset<string>>& adj, vector<string>& result, string s){\n // While there are destinations connected to the current airport\n while(adj[s].size()){\n // Get the next destination\n string v = *(adj[s].begin());\n // Remove this destination from the list\n adj[s].erase(adj[s].begin());\n // Recursively explore this destination\n dfs(adj, result, v);\n }\n // Add the current airport to the result\n result.push_back(s);\n }\npublic:\n // Main function to find the itinerary\n vector<string> findItinerary(vector<vector<string>>& tickets) {\n // Create an adjacency list to represent the flights\n unordered_map<string, multiset<string>> adj;\n for(vector<string>& t: tickets)\n // Add each destination to the multiset connected to its source airport\n adj[t[0]].insert(t[1]);\n \n // Initialize the result vector\n vector<string> result;\n // Start the depth-first search from JFK (John F. Kennedy International Airport)\n dfs(adj, result, "JFK");\n // Reverse the result to get the correct itinerary\n reverse(result.begin(), result.end());\n // Return the itinerary\n return result;\n }\n};\n\n```\n# JAVA\n```\nimport java.util.*;\n\nclass Solution {\n // Depth-first search function to find the itinerary\n private void dfs(Map<String, PriorityQueue<String>> adj, List<String> result, String s) {\n // Check if the airport exists in the adjacency list\n if (adj.containsKey(s)) {\n // While there are destinations connected to the current airport\n while (!adj.get(s).isEmpty()) {\n // Get the next destination\n String v = adj.get(s).poll();\n // Recursively explore this destination\n dfs(adj, result, v);\n }\n }\n // Add the current airport to the result\n result.add(s);\n }\n\n public List<String> findItinerary(List<List<String>> tickets) {\n // Create an adjacency list to represent the flights\n Map<String, PriorityQueue<String>> adj = new HashMap<>();\n for (List<String> t : tickets) {\n adj.computeIfAbsent(t.get(0), k -> new PriorityQueue<>()).offer(t.get(1));\n }\n\n // Initialize the result list\n List<String> result = new ArrayList<>();\n // Start the depth-first search from JFK (John F. Kennedy International Airport)\n dfs(adj, result, "JFK");\n // Reverse the result to get the correct itinerary\n Collections.reverse(result);\n // Return the itinerary\n return result;\n }\n}\n\n```\n# JAVASCRIPT\n```\nclass Solution {\n // Depth-first search function to find the itinerary\n dfs(adj, result, s) {\n // While there are destinations connected to the current airport\n while (adj[s].size) {\n // Get the next destination\n let v = adj[s].values().next().value;\n // Remove this destination from the list\n adj[s].delete(v);\n // Recursively explore this destination\n this.dfs(adj, result, v);\n }\n // Add the current airport to the result\n result.push(s);\n }\n\n findItinerary(tickets) {\n // Create an adjacency list to represent the flights\n const adj = new Map();\n for (const t of tickets) {\n if (!adj.has(t[0])) {\n adj.set(t[0], new Set());\n }\n adj.get(t[0]).add(t[1]);\n }\n\n // Initialize the result array\n const result = [];\n // Start the depth-first search from JFK (John F. Kennedy International Airport)\n this.dfs(adj, result, "JFK");\n // Reverse the result to get the correct itinerary\n result.reverse();\n // Return the itinerary\n return result;\n }\n}\n\n```\n# PYTHON\n```\nfrom collections import defaultdict\n\nclass Solution:\n def dfs(self, adj, result, s):\n if s in adj:\n destinations = adj[s][:]\n while destinations:\n dest = destinations[0]\n adj[s].pop(0) # Remove the used ticket\n self.dfs(adj, result, dest)\n destinations = adj[s][:]\n result.append(s)\n\n def findItinerary(self, tickets):\n # Create an adjacency list to represent the flights\n adj = defaultdict(list)\n for t in tickets:\n adj[t[0]].append(t[1])\n \n # Sort the destinations in lexicographical order to get the correct itinerary\n for key in adj:\n adj[key].sort()\n\n # Initialize the result list\n result = []\n # Start the depth-first search from JFK (John F. Kennedy International Airport)\n self.dfs(adj, result, "JFK")\n # Reverse the result to get the correct itinerary\n result.reverse()\n\n # Check if all tickets have been used\n total_tickets = len(tickets) + 1 # Plus one for the starting airport JFK\n if len(result) != total_tickets:\n return []\n\n # Return the itinerary\n return result\n\n```\n# GO\n```\npackage main\n\nimport (\n\t"container/heap"\n\t"sort"\n)\n\ntype Solution struct{}\n\n// Depth-first search function to find the itinerary\nfunc (s Solution) dfs(adj map[string]*PriorityQueue, result *[]string, s string) {\n\t// While there are destinations connected to the current airport\n\tfor adj[s].Len() > 0 {\n\t\t// Get the next destination\n\t\tv := heap.Pop(adj[s]).(string)\n\t\t// Recursively explore this destination\n\t\ts.dfs(adj, result, v)\n\t}\n\t// Add the current airport to the result\n\t*result = append(*result, s)\n}\n\n// Main function to find the itinerary\nfunc (s Solution) findItinerary(tickets [][]string) []string {\n\t// Create an adjacency list to represent the flights\n\tadj := make(map[string]*PriorityQueue)\n\tfor _, t := range tickets {\n\t\tsrc, dest := t[0], t[1]\n\t\tif _, ok := adj[src]; !ok {\n\t\t\tadj[src] = &PriorityQueue{}\n\t\t\theap.Init(adj[src])\n\t\t}\n\t\theap.Push(adj[src], dest)\n\t}\n\n\t// Initialize the result slice\n\tvar result []string\n\t// Start the depth-first search from JFK (John F. Kennedy International Airport)\n\ts.dfs(adj, &result, "JFK")\n\t// Reverse the result to get the correct itinerary\n\tsort.Sort(sort.Reverse(sort.StringSlice(result)))\n\t// Return the itinerary\n\treturn result\n}\n\n// PriorityQueue is a simple priority queue implemented using a slice\ntype PriorityQueue []string\n\nfunc (pq PriorityQueue) Len() int { return len(pq) }\nfunc (pq PriorityQueue) Less(i, j int) bool { return pq[i] < pq[j] }\nfunc (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }\n\nfunc (pq *PriorityQueue) Push(x interface{}) {\n\t*pq = append(*pq, x.(string))\n}\n\nfunc (pq *PriorityQueue) Pop() interface{} {\n\told := *pq\n\tn := len(old)\n\titem := old[n-1]\n\t*pq = old[0 : n-1]\n\treturn item\n}\n\n```\n# PLEASE UPVOTE\u2763\uD83D\uDE0D | 16 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
Python 80% solution with descriptive code and comment about decision | reconstruct-itinerary | 0 | 1 | # Code\n```\nclass Solution:\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n num_tickets = len(tickets)\n\n conns = defaultdict(list)\n for i, (src, dest) in enumerate(tickets):\n conns[src].append((dest, i))\n\n # Sorted the tickets so that the first fully-traversal result\n # is the smallest lexical order.\n for src, _ in tickets:\n if len(tickets) > 1:\n conns[src].sort()\n\n def traverse(cur_location = "JFK", used = [False] * num_tickets, path = ["JFK"]):\n if all(used):\n return path\n nonlocal conns\n for dest, index in conns[cur_location]:\n if used[index] is False:\n used[index] = True\n path.append(dest)\n if (res:= traverse(dest, used, path)):\n return res\n path.pop()\n used[index] = False\n\n return traverse()\n``` | 1 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
PYTHON | EASILY EXPLAINED SOLUTION | reconstruct-itinerary | 0 | 1 | \n\n# Approach\n\nThis code defines a `findItinerary` function that performs the following steps:\n\n1. Create a dictionary `graph` to represent the graph of tickets, where each airport is a key, and the values are lists of destination airports sorted in reverse order to ensure that smaller lexical order airports are visited first.\n\n2. Use a depth-first search (DFS) function `dfs` to traverse the graph starting from "JFK." In each step, pop the next airport from the list of destinations for the current airport and recursively call `dfs` for that airport.\n\n3. Append the visited airports to the `result` list in reverse order since the DFS builds the itinerary in reverse order.\n\n4. Finally, return the `result` list as the reconstructed itinerary.\n\nThis approach ensures that the itinerary is valid and follows the smallest lexical order when read as a single string.\n\n\n# Code\n```\nclass Solution:\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n\n def dfs(node):\n if node in graph:\n while graph[node]:\n neighbor = graph[node].pop()\n dfs(neighbor)\n result.append(node)\n\n graph = {}\n for ticket in tickets:\n from_airport, to_airport = ticket\n if from_airport not in graph:\n graph[from_airport] = []\n graph[from_airport].append(to_airport)\n\n for key in graph:\n graph[key].sort(reverse=True)\n\n result = []\n dfs("JFK")\n return result[::-1]\n \n\n```\n# **PLEASE DO UPVOTE!!!** | 1 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
Simply simple Python Solution - Using stack for dfs - with comments | reconstruct-itinerary | 0 | 1 | \tclass Solution:\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n graph = {}\n # Create a graph for each airport and keep list of airport reachable from it\n for src, dst in tickets:\n if src in graph:\n graph[src].append(dst)\n else:\n graph[src] = [dst]\n\n for src in graph.keys():\n graph[src].sort(reverse=True)\n # Sort children list in descending order so that we can pop last element \n # instead of pop out first element which is costly operation\n stack = []\n res = []\n stack.append("JFK")\n # Start with JFK as starting airport and keep adding the next child to traverse \n # for the last airport at the top of the stack. If we reach to an airport from where \n # we can\'t go further then add it to the result. This airport should be the last to go \n # since we can\'t go anywhere from here. That\'s why we return the reverse of the result\n # After this backtrack to the top airport in the stack and continue to traaverse it\'s children\n \n while len(stack) > 0:\n elem = stack[-1]\n if elem in graph and len(graph[elem]) > 0: \n # Check if elem in graph as there may be a case when there is no out edge from an airport \n # In that case it won\'t be present as a key in graph\n stack.append(graph[elem].pop())\n else:\n res.append(stack.pop())\n # If there is no further children to traverse then add that airport to res\n # This airport should be the last to go since we can\'t anywhere from this\n # That\'s why we return the reverse of the result\n return res[::-1]\n | 190 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
332: Solution with step by step explanation | reconstruct-itinerary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe first create a heap for each source vertex, containing the destinations in lexicographical order. Then, during the DFS traversal, we pop the smallest destination from the heap instead of sorting the destinations each time. This small optimization reduces the time complexity of sorting destinations from O(NlogN) to O(NlogM), where N is the total number of tickets and M is the average number of destinations per source vertex.\n\n# Complexity\n- Time complexity:\n61.24%\n\n- Space complexity:\n83.91%\n\n# Code\n```\nimport collections\nimport heapq\n\nclass Solution:\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n ans = []\n graph = collections.defaultdict(list)\n\n for a, b in tickets:\n graph[a].append(b)\n\n for u in graph:\n heapq.heapify(graph[u])\n\n def dfs(u: str) -> None:\n while u in graph and graph[u]:\n dfs(heapq.heappop(graph[u]))\n ans.append(u)\n\n dfs(\'JFK\')\n return ans[::-1]\n\n``` | 6 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
[Python] Simple Solution | reconstruct-itinerary | 0 | 1 | ```\nclass Solution:\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n ## RC ##\n ## APPROACH : GRAPH DFS ##\n ## EDGE CASE : [["JFK","KUL"],["JFK","NRT"],["NRT","JFK"]]\n \n\t\t## TIME COMPLEXITY : O(N) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n \n def dfs(city):\n while(len(graph[city]) > 0):\n dfs(graph[city].pop(0))\n res.insert(0, city) # last airport\n \n graph = collections.defaultdict(list)\n for u, v in (tickets):\n graph[u].append(v)\n graph[u].sort()\n res=[] \n dfs("JFK")\n return res\n``` | 13 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
Python3 DFS Solution | reconstruct-itinerary | 0 | 1 | ```\nclass Solution:\n def findItinerary(self, tickets: List[List[str]]) -> List[str]:\n graph = {}\n \n tickets.sort(key=lambda x: x[1])\n\n for u, v in tickets:\n if u in graph:\n graph[u].append(v)\n else:\n graph[u] = [v]\n \n itinerary, stack = [], [("JFK")]\n \n while stack:\n curr = stack[-1]\n \n if curr in graph and len(graph[curr]) > 0:\n stack.append(graph[curr].pop(0))\n else:\n itinerary.append(stack.pop())\n return itinerary[::-1]\n``` | 14 | You are given a list of airline `tickets` where `tickets[i] = [fromi, toi]` represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it.
All of the tickets belong to a man who departs from `"JFK "`, thus, the itinerary must begin with `"JFK "`. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string.
* For example, the itinerary `[ "JFK ", "LGA "]` has a smaller lexical order than `[ "JFK ", "LGB "]`.
You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
**Example 1:**
**Input:** tickets = \[\[ "MUC ", "LHR "\],\[ "JFK ", "MUC "\],\[ "SFO ", "SJC "\],\[ "LHR ", "SFO "\]\]
**Output:** \[ "JFK ", "MUC ", "LHR ", "SFO ", "SJC "\]
**Example 2:**
**Input:** tickets = \[\[ "JFK ", "SFO "\],\[ "JFK ", "ATL "\],\[ "SFO ", "ATL "\],\[ "ATL ", "JFK "\],\[ "ATL ", "SFO "\]\]
**Output:** \[ "JFK ", "ATL ", "JFK ", "SFO ", "ATL ", "SFO "\]
**Explanation:** Another possible reconstruction is \[ "JFK ", "SFO ", "ATL ", "JFK ", "ATL ", "SFO "\] but it is larger in lexical order.
**Constraints:**
* `1 <= tickets.length <= 300`
* `tickets[i].length == 2`
* `fromi.length == 3`
* `toi.length == 3`
* `fromi` and `toi` consist of uppercase English letters.
* `fromi != toi` | null |
Python Easy Solution | increasing-triplet-subsequence | 0 | 1 | \n\n# Code\n```\n\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n first = second = float(\'inf\') \n for n in nums: \n if n <= first: \n first = n\n elif n <= second:\n second = n\n else:\n return True\n return False\n``` | 63 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
python 3 || 6 lines, one-pass, w/explanation || T/M: 98%/50% | increasing-triplet-subsequence | 0 | 1 | The plan here is iterate through nums, and place each element in the least position (first thought third) for which it qualifies, should it qualify. If we find a third, we succeed (True), otherwise we fail (False).\n\n```\nclass Solution:\n def increasingTriplet(self, nums: list[int]) -> bool:\n \n first, second = inf, inf\n \n for third in nums:\n \n if second < third: return True\n if third <= first: first= third \n else: second = third \n \n return False\n```\n[https://leetcode.com/submissions/detail/680380429/](http://)\n\t\t | 49 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
Python3 math based, non-optimized O(n) space + time solution | increasing-triplet-subsequence | 0 | 1 | # Intuition\nI really had no idea how to solve this in O(n) time, so I messed around with it for a couple days without success before taking a step back and attempting to find a mathematical solution on pen and paper first.\n\nWe start with the following condition:\n\n$$x_i < x_j < x_k$$\n\nFor array of length $$N$$ there are $$(N - 1) * (N)/2$$ permutations (triangular sum formula where N >= 2) as every additional element introduces exactly $$N$$ more permutations:\n\nN = 2 == 1 permutation ```x0 < x1 < x2```\nN = 3 == 3 permutations ```x0 < x1 < x2 || x0 < x1 < x3 || x1 < x2 < x3```\nN = 4 == 6 permutations ...\n\nTherefore, brute force check of all combinations will have complexity $$O(N^2)$$\n\nThe eureka moment hit me when I realized the condition could be expressed as such:\n\n$$min(x_0,x_1..\\space x_{j-1}) < x_j < max(x_{j+1},x_{j+2}..\\space x_n)$$\n\n# Approach\n\nThe logic is as follows. Assume nums = [1,5,0,4,1,3]\n\nTwo additional arrays are required: a min_array and max_array\n\nmin_array would iterate through each element and populate either the minimum of either _its last element_ OR the element nums. For example:\n\n[1] -> [1,1] -> [1,1,0] -> [1,1,0,0] -> [1,1,0,0,0] -> [1,1,0,0,0,0]\n\nThe max array would do the same, but we start from the end of the array and work backwards\n\n[3] -> [3,3] -> [3,3,4] -> [3,3,4,4] -> [3,3,4,4,5] -> [3,3,4,4,5,5]\n\n**Also max_array must be reversed** \n\nThe final representation of min_array, nums, and max_array is as such:\n\n```\nmin_arr: [1,1,0,0,0,0]\nnums: [1,5,0,4,1,3]\nmax_arr: [5,5,4,4,3,3]\n```\n\nThe final step is to simply iterate. If ```min_arr[i] < nums[i] < max_arr[i]``` return true. If the loop terminates return false.\n\nIn the case of the example it will return true when ```i == 4``` as 0 < 1 < 3\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Advantages\n\nUnlike in the optimal solution, it\'s easy to return all possible combinations that satisfy the primary condition in their correct order and including duplicates.\n\n# Limitations\n\nThe equation would need to be reworked if an additional condition is introduced, e.g:\n\n$$x_a < x_b < x_c < x_d$$\n\nSo not only does it perform worse it would be a lot more difficult to scale compared to the optimal solution\n\n\n# Code\n```python\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n if len(nums) < 2:\n return False\n\n min_arr = []\n for num in nums:\n if min_arr and num > min_arr[-1]:\n min_arr.append(min_arr[-1])\n else:\n min_arr.append(num)\n\n max_arr = []\n for num in nums[::-1]:\n if max_arr and num < max_arr[-1]:\n max_arr.append(max_arr[-1])\n else:\n max_arr.append(num)\n max_arr = max_arr[::-1]\n\n for i in range(1, len(nums) - 1):\n if min_arr[i] < nums[i] < max_arr[i]:\n return True\n\n return False\n``` | 3 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
99.76% faster in Python||cpp || java -TC=O(n), Sc(1) || Easy to Understand | increasing-triplet-subsequence | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code utilizes a greedy approach to find an increasing triplet subsequence by keeping track of the two smallest elements f and s. If it encounters a larger element, it confirms the existence of an increasing triplet subsequence. Otherwise, it updates f and s with the current element to maintain the smallest possible values for the potential triplet.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIt initializes two variables f and s with a large value of 1e9 (10^9). These variables represent the first and second elements of a potential increasing triplet subsequence.\nIt iterates through each element n in the input array nums.\nIf n is greater than or equal to f, it means n can be a potential candidate for the third element of an increasing triplet subsequence. So, it updates f to n.\nIf n is less than or equal to s, it means n can be a potential candidate for the second element of an increasing triplet subsequence. So, it updates s to n.\nIf none of the above conditions satisfy, it means n is greater than both f and s, indicating the presence of an increasing triplet subsequence. So, it returns true.\nIf the loop completes without finding an increasing triplet subsequence, it means there is no such subsequence in the array, so it returns false.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the code is O(N), where N is the size of the input array nums, as it iterates through the array once. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) since it uses only a constant amount of additional space to store the variables f and s\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool increasingTriplet(vector<int>& nums) {\n int n = nums.size();\n //It initializes two variables f and s with a large value of 1e9 (10^9). These variables represent the first and second elements of a potential increasing triplet subsequence.\n int f = INT_MAX, s = INT_MAX;\n for(int n : nums){\n //It iterates through each element n in the input array nums.\n//If n is greater than or equal to f, it means n can be a potential candidate for the third element of an increasing triplet subsequence. So, it updates f to n.\n//If n is less than or equal to s, it means n can be a potential candidate for the second element of an increasing triplet subsequence. So, it updates s to n.\n//If none of the above conditions satisfy, it means n is greater than both f and s, indicating the presence of an increasing triplet subsequence. So, it returns true.\n if(n < f){\n f = n;\n }\n else if(f<n && n<s){\n s = n;\n }\n else if(n>s){\n return true;\n }\n }\n //If the loop completes without finding an increasing triplet subsequence, it means there is no such subsequence in the array, so it returns false.\n return false;\n }\n //The time complexity of the code is O(N), where N is the size of the input array nums, as it iterates through the array once. The space complexity is O(1) since it uses only a constant amount of additional space to store the variables f and s\n};\n```\n```Java []\nclass Solution {\n public boolean increasingTriplet(int[] nums) {\n int n = nums.length;\n // It initializes two variables f and s with a large value of Integer.MAX_VALUE.\n // These variables represent the first and second elements of a potential increasing triplet subsequence.\n int f = Integer.MAX_VALUE, s = Integer.MAX_VALUE;\n \n for (int nValue : nums) {\n // If n is less than f, it means n can be a potential candidate for the first element of an increasing triplet subsequence. So, it updates f to n.\n if (nValue <= f) {\n f = nValue;\n } \n // If n is greater than f and less than s, it means n can be a potential candidate for the second element of an increasing triplet subsequence. So, it updates s to n.\n else if (nValue <= s) {\n s = nValue;\n }\n // If n is greater than both f and s, it indicates the presence of an increasing triplet subsequence. So, it returns true.\n else if (nValue > s) {\n return true;\n }\n }\n // If the loop completes without finding an increasing triplet subsequence, it means there is no such subsequence in the array, so it returns false.\n return false;\n }\n}\n```\n```Python []\nclass Solution:\n def increasingTriplet(self, nums):\n f = float(\'inf\')\n s = float(\'inf\')\n \n for n in nums:\n # If n is less than f, it means n can be a potential candidate for the first element of an increasing triplet subsequence. So, it updates f to n.\n if n <= f:\n f = n\n # If n is greater than f and less than s, it means n can be a potential candidate for the second element of an increasing triplet subsequence. So, it updates s to n.\n elif n <= s:\n s = n\n # If n is greater than both f and s, it indicates the presence of an increasing triplet subsequence. So, it returns True.\n elif n > s:\n return True\n \n # If the loop completes without finding an increasing triplet subsequence, it means there is no such subsequence in the array, so it returns False.\n return False\n```\n | 16 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
[Python] 2 solutions: Right So Far, One pass - O(1) Space - Clean & Concise | increasing-triplet-subsequence | 0 | 1 | **\u2714\uFE0F Solution 1: Build Max Right So Far and Max Left So Far**\n- Let `maxRight[i]` denote the maximum number between `nums[i+1], nums[i+2],...nums[n-1]`.\n```python\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n n = len(nums)\n maxRight = [0] * n # maxRight[i] is the maximum element among nums[i+1...n-1]\n maxRight[-1] = nums[-1]\n for i in range(n-2, -1, -1):\n maxRight[i] = max(maxRight[i+1], nums[i+1])\n \n minLeft = nums[0]\n for i in range(1, n-1):\n if minLeft < nums[i] < maxRight[i]:\n return True\n minLeft = min(minLeft, nums[i])\n return False\n```\nComplexity:\n- Time: `O(N)`, where `N <= 5*10^5` is length of `nums` array.\n- Space: `O(N)`\n\n---\n**\u2714\uFE0F Solution 2: One pass**\n- We keep 2 numbers `first` and `second` where `first < second`, and `first` number must be before `second` number.\n- Iterate `num` in `nums`:\n\t- If `num <= first` then update the `first` as minimum as possible, by`first = num`\n\t- Else If `num <= second` then update `second` as minimum as possible (since now `first < num <= second`), by `second = num`\n\t- Else, now `first < second < num` then we found a valid **Increasing Triplet Subsequence**, return True.\n- Otherwise, return False.\n```python\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n first = second = math.inf\n for num in nums:\n if num <= first:\n first = num\n elif num <= second: # Now first < num, if num <= second then try to make `second` as small as possible\n second = num\n else: # Now first < second < num\n return True\n return False\n```\nComplexity: \n- Time: `O(N)`\n- Space: `O(1)`\n\nIf you think this **post is useful**, I\'m happy if you **give a vote**. Any **questions or discussions are welcome!** Thank a lot. | 138 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
334: Solution with step by step explanation | increasing-triplet-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function increasingTriplet that takes a list of integers nums as input and returns a boolean value indicating if there exists a triplet of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k].\n\n2. Initialize two variables first and second to infinity. These variables will hold the smallest and second smallest values found in the array so far.\n\n3. Loop through the elements of the input array nums.\n\n4. If the current element num is less than or equal to first, update first to num.\n\n5. Else if the current element num is less than or equal to second, update second to num.\n\n6. Else, if the current element num is greater than second, we have found a triplet (first < second < num), so we return True.\n\n7. If we reach the end of the loop without finding a triplet, return False.\n\nIn summary, the solution iterates through the list of numbers and keeps track of the smallest and second smallest values seen so far. If a third value is found that is greater than both the smallest and second smallest values, then we have found a triplet and the function returns True. Otherwise, the function returns False.\n\n# Complexity\n- Time complexity:\n89.4%\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n first = second = float(\'inf\')\n for num in nums:\n if num <= first:\n first = num\n elif num <= second:\n second = num\n else:\n return True\n return False\n\n``` | 16 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
Increasing Triplets Python Solution | increasing-triplet-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind two numbers, where the first is smaller than the second. If we can find a third number that\'s bigger than both, we\'ve found a triplet.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitialize our `smallest` and `next_smallest` variables to `float(\'inf\')`. This guarantees that our `smallest` will be `nums[0]` to start, and then we can update it later. Iterate through the list, comparing `smallest` and `next_smallest` to `num`. If `num` is less than or equal to `smallest`, set `smallest` to `num`. If it\'s not smaller than `smallest`, compare it to `next_smallest`. If it\'s not smaller than `next_smallest`, then we have a `smallest`, `next_smallest`, and a third value in ascending order, and we return True! If we get to the end of the list, we return False.\n\n# Complexity\n- Time complexity: $O(n)$ - Iterate through the list once\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$ - Store `smallest` and `next_smallest`.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Performance\nRuntime: Beats 99.87%\nMemory: Beats 89.16%\n\n# Code\n```\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n smallest = next_smallest = float(\'inf\')\n for num in nums:\n if num <= smallest:\n smallest = num\n elif num <= next_smallest:\n next_smallest = num\n else:\n return True\n return False\n``` | 3 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
Very Easy || 100% || Fully Explained || Java, C++, Python, JavaScript, Python3 | increasing-triplet-subsequence | 1 | 1 | # **PROBLEM STATEMENT:**\nGiven an integer array nums, return true if there exists a triple of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k]. If no such indices exists, return false.\n# **Example:**\n# Input: nums = [2,1,5,0,4,6]\n# Output: true\n# Explanation: The triplet (3, 4, 5) is valid because nums[3] == 0 < nums[4] == 4 < nums[5] == 6.\n# **Java Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(1)\nclass Solution {\n public boolean increasingTriplet(int[] nums) {\n // Initialize two variables first and second with Integer.MAX_VALUE...\n int first = Integer.MAX_VALUE;\n int second = Integer.MAX_VALUE;\n for(int third : nums) {\n // If the third is smaller than the first variable then make first = third...\n if(third < first){\n first = third;\n }\n // If the third is in between the first and second then move second to third place...\n else if(third < second && third > first){\n second = third;\n }\n // If the right is greater than the first and second then return true...\n else if(third > second && third > first) return true;\n }\n // After the end of the loop if no such Increasing Triplet Subsequence indices exists then return false...\n return false;\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(1)\nclass Solution {\npublic:\n bool increasingTriplet(vector<int>& nums) {\n // Initialize two variables first and second with INT_MAX...\n int first = INT_MAX;\n int second = INT_MAX;\n // Iterate from beg to end in the nums array...\n for(int i = 0; i < nums.size(); i++){\n int third = nums[i];\n // If the third is smaller than the first variable then make first = third...\n if(third < first){\n first = third;\n }\n // If the third is in between the first and second then move second to third place...\n else if(third < second && third > first){\n second = third;\n }\n // If the right is greater than the first and second then return true...\n else if(third > second && third > first) return true;\n }\n // After the end of the loop if no such Increasing Triplet Subsequence indices exists then return false...\n return false;\n }\n};\n```\n\n# **Python / Python3 solution:**\n```\n# Time Complexity : O(n)\n# Space Complexity : O(1)\nclass Solution(object):\n def increasingTriplet(self, nums):\n # Initialize two variables first and second\n first, second = float(\'inf\'), float(\'inf\')\n for third in nums:\n # If the third is smaller than the first variable then make first = third...\n if third < first:\n first = third\n # If the third is in between the first and second then move second to third place...\n elif third < second and third > first:\n second = third\n # Otherwise, return true...\n else: return True\n # After the end of the loop if no such Increasing Triplet Subsequence indices exists then return false...\n return False\n```\n \n# **JavaScript Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(1)\nvar increasingTriplet = function(nums) {\n let first = Infinity\n let second = Infinity\n for(let third of nums) {\n // If the third is smaller than the first variable then make first = third...\n if(third < first){\n first = third;\n }\n // If the third is in between the first and second then move second to third place...\n else if(third < second && third > first){\n second = third;\n }\n // If the right is greater than the first and second then return true...\n else if(third > second && third > first) return true;\n }\n // After the end of the loop if no such Increasing Triplet Subsequence indices exists then return false...\n return false;\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 21 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
Python easy Sol. O(n)time complexity | increasing-triplet-subsequence | 0 | 1 | ```\nclass Solution:\n def increasingTriplet(self, nums: List[int]) -> bool:\n first=second=float(\'inf\')\n for i in nums:\n if i<=first:\n first=i\n elif i<=second:\n second=i\n else:\n return True\n return False | 16 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
Simple Python Solution 100% Accepted | TC O(n) SC O(1) | increasing-triplet-subsequence | 0 | 1 | \n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def increasingTriplet(self, arr: List[int]) -> bool:\n i = j = float(\'inf\')\n for num in arr:\n if num <= i:\n i = num\n elif num <= j:\n j = num\n else:\n return True\n return False\n``` | 3 | Given an integer array `nums`, return `true` _if there exists a triple of indices_ `(i, j, k)` _such that_ `i < j < k` _and_ `nums[i] < nums[j] < nums[k]`. If no such indices exists, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** true
**Explanation:** Any triplet where i < j < k is valid.
**Example 2:**
**Input:** nums = \[5,4,3,2,1\]
**Output:** false
**Explanation:** No triplet exists.
**Example 3:**
**Input:** nums = \[2,1,5,0,4,6\]
**Output:** true
**Explanation:** The triplet (3, 4, 5) is valid because nums\[3\] == 0 < nums\[4\] == 4 < nums\[5\] == 6.
**Constraints:**
* `1 <= nums.length <= 5 * 105`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Could you implement a solution that runs in `O(n)` time complexity and `O(1)` space complexity? | null |
335: Solution with step by step explanation | self-crossing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe algorithm checks three possible cases for each line of the path, starting from the 3rd line. If any of the cases is true, the function returns True, meaning the path crosses itself. If none of the cases is true after looping through all the lines, the function returns False, meaning the path does not cross itself.\n\nThe three cases are:\n\n1. The current line crosses the line 3 steps before it.\n2. The current line crosses the line 4 steps before it.\n3. The current line crosses the line 5 steps before it.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSelfCrossing(self, x: List[int]) -> bool:\n # If there are less than 4 values in the array, the path can\'t cross itself\n if len(x) <= 3:\n return False\n\n # Loop through the array starting from the 3rd index\n for i in range(3, len(x)):\n # Case 1: current line crosses the line 3 steps before it\n # _______\n # | |\n # | |\n # ________|______| <-- current line\n # | |\n # | |\n # |__________| <-- line 3 steps before\n if x[i - 2] <= x[i] and x[i - 1] <= x[i - 3]:\n return True\n \n # Case 2: current line crosses the line 4 steps before it\n # _____\n # | |\n # | |\n # | |________\n # | |\n # | |\n # |_______________| <-- current line\n # line 4 steps before\n if i >= 4 and x[i - 1] == x[i - 3] and x[i - 2] <= x[i] + x[i - 4]:\n return True\n \n # Case 3: current line crosses the line 5 steps before it\n # ______\n # | |\n # | |\n # |______| <-- line 5 steps before\n # |\n # |\n # ______|_______\n # | |\n # | |\n # |______________| <-- current line\n if i >= 5 and x[i - 4] <= x[i - 2] and x[i - 2] <= x[i] + x[i - 4] and x[i - 1] <= x[i - 3] and x[i - 3] <= x[i - 1] + x[i - 5]:\n return True\n\n # If no crossing has been found, the path does not cross itself\n return False\n\n``` | 7 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Python solution: 3 ways to self cross | self-crossing | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nSimulating the process would take up too much memory and time. We need a geometrical solution\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nLogically break down the possibilities of self cross: it could cross from the left, bottom, or the right. Also, checking beyond 6 previous steps is unnecessary, for any self cross with paths before that would have detected earlier\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n$$O(n)$$\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n$$O(1)$$\r\n# Code\r\n```\r\nfrom typing import List\r\n\r\n\r\nclass Solution:\r\n \'\'\'\r\n Two points to note: \r\n 1. The Cartesian coordinate system is symmetric wih 90 degree rotations\r\n 2. To cross a previous path with a future step, one can cross from left, right or from below\r\n \'\'\'\r\n def isSelfCrossing(self, distance: List[int]) -> bool:\r\n b = c = d = e = f = 0\r\n for a in distance:\r\n # cross from left\r\n if d > 0 and d >= b and a >= c:\r\n return True\r\n # cross from below\r\n if e > 0 and c <= a + e and b == d:\r\n return True\r\n # cross from the right\r\n if f > 0 and b <= d <= b + f and e <= c <= a + e:\r\n return True\r\n b, c, d, e, f = a, b, c, d, e \r\n return False\r\n``` | 1 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Python 95% | No math, Just space for time, make it an easy problem | self-crossing | 0 | 1 | # Intuition\r\nSince the problem scale is not very large, why not exchange space for time?\r\n\r\n# Approach\r\nkeep track of every single points we pass throught\r\n\r\n# Complexity\r\n- Time complexity:\r\n$$O(nm)$$\r\n\r\n- Space complexity:\r\n$$O(nm)$$\r\n\r\n# Code\r\n```\r\nfrom operator import sub\r\nMOVE = [(0, 1), (-1, 0), (0, -1), (1, 0)]\r\nclass Solution:\r\n def isSelfCrossing(self, distance):\r\n return self.space_4_time(distance)\r\n\r\n def space_4_time(self, distance):\r\n if all(map(sub, distance[1:], distance[:-1])): return False # spiral out\r\n\r\n pos, visit = (0, 0), set([(0, 0)])\r\n\r\n for idx, length in enumerate(distance):\r\n dx, dy = MOVE[idx % 4] # 0n1w2s3e\r\n for _ in range(length):\r\n pos = (pos[0] + dx, pos[1] + dy)\r\n if pos in visit: return True\r\n visit.add(pos)\r\n return False\r\n\r\n def math(self, x):\r\n \'\'\' it\'s not about coordinates, it\'s only about previous six line\'s length \'\'\'\r\n L = len(x)\r\n if L < 4: return False\r\n\r\n l1, l2, l3, l4, l5, l6 = x[2], x[1], x[0], 0, 0, 0\r\n for i in range(3, L):\r\n l1, l2, l3, l4, l5, l6 = x[i], l1, l2, l3, l4, l5 # rotation to get equivalent six line\r\n\r\n if l4 >= l2 and l1 >= l3: return True # 4 lines, shape like: \'4\'\r\n if l4 == l2 and (l1 + l5) >= l3: return True # 5 lines, shape like: \'O\'\r\n if (l6 + l2) >= l4 >= l2 and (l5 + l1) >= l3 >= l5: return True # 6 lines, shape like \'L\'\r\n return False\r\n``` | 1 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
A State Machine Approach | self-crossing | 0 | 1 | # Intuition\nA none-intersecting path is either:\n\n- an out-growing spiral (spiral-out), or\n- an in-growing spiral (spiral-in), or\n- an out-growing spiral connected with an in-growing one.\n# Approach\nWe use a state-machine approach where the states are the phase of current spiral we are in:\n\n- GROW: we are spiralling out. Each successive segment should become ever longer. Otherwise, we might be shrinking or transitioning.\n\n- SHRINK: we are spiralling in. Each successive segment should become ever shorter.\n\n- TRANS: we are transitioning from an out-growing spiral to an in-growing one. This state is only entered once.\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nfrom enum import Enum\n\nclass State(Enum):\n GROW = 1\n SHRINK = 2\n TRANS = 3\n\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n d1 = d2 = d3 = d4 = 0\n s = State.GROW\n\n for d5 in distance:\n match s:\n case State.GROW:\n if d5 + d1 < d3:\n s = State.SHRINK\n elif d5 <= d3:\n s = State.TRANS \n case State.SHRINK:\n if d5 >= d3:\n return True\n case State.TRANS:\n if d5 + d1 < d3:\n s = State.SHRINK\n else:\n return True\n case _:\n raise ValueError("Undefined State!")\n d1, d2, d3, d4 = d2, d3, d4, d5\n\n return False\n``` | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
A State Machine Approach | self-crossing | 0 | 1 | # Intuition\n\nA none-intersecting path is either:\n1. an out-growing spiral (spiral-out), or\n2. an in-growing spiral (spiral-in), or\n3. an out-growing spiral connected with an in-growing one.\n\n# Approach\n\nWe use a state-machine approach where the states are the phase of current spiral we are in:\n\n- **GROW**: we are spiralling out. Each successive segment should become ever longer. Otherwise, we might be shrinking or transitioning.\n\n- **SHRINK**: we are spiralling in. Each successive segment should become ever shorter.\n\n- **TRANS**: we are transitioning from an out-growing spiral to an in-growing one. This state is only entered once.\n\n# Complexity\n\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```py\nfrom enum import Enum\n\nclass State(Enum):\n GROW = 1\n SHRINK = 2\n TRANS = 3\n\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n d1 = d2 = d3 = d4 = 0\n s = State.GROW\n\n for d5 in distance:\n match s:\n case State.GROW:\n if d5 + d1 < d3:\n s = State.SHRINK\n elif d5 <= d3:\n s = State.TRANS \n case State.SHRINK:\n if d5 >= d3:\n return True\n case State.TRANS:\n if d5 + d1 < d3:\n s = State.SHRINK\n else:\n return True\n case _:\n raise ValueError("Undefined State!")\n d1, d2, d3, d4 = d2, d3, d4, d5\n\n return False\n``` | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Expressive solution 🙂 | self-crossing | 0 | 1 | Very bad drawing but how i approached this question\n\n\n# Code\n```\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n """\n 1st way to cross NWSE , East meets north, E and W must be same length\n and N>=S\n 2nd way NWSEN , North overlaps with north , E==W and S<= N1+N2\n 3rd way NWSENW , West overlaps with first North, W1<\n """\n if(len(distance)<=3):\n return False\n for i in range(3,len(distance)):\n if(distance[i]>=distance[i-2] and distance[i-3]>=distance[i-1]):\n return True\n if(i>=4 and distance[i-1]==distance[i-3] and distance[i-2]<=distance[i]+distance[i-4]):\n return True\n if(i>=5 and distance[i-4]<distance[i-2] and distance[i]+distance[i-4]>=distance[i-2] and distance[i-1]+distance[i-5]>=distance[i-3] and distance[i-1]<=distance[i-3]):\n return True\n return False\n``` | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Bad | self-crossing | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n if len(distance) <= 3:\n return False\n \n for i in range(3, len(distance)):\n if distance[i] >= distance[i-2] and distance[i-1] <= distance[i-3]:\n return True\n \n if i >= 4 and distance[i-1] == distance[i-3] and distance[i] + distance[i-4] >= distance[i-2]:\n return True\n \n if i >= 5 and distance[i-2] >= distance[i-4] and distance[i-1] <= distance[i-3] and distance[i] + distance[i-4] >= distance[i-2] and distance[i-1] + distance[i-5] >= distance[i-3]:\n return True\n \n return False\n\n``` | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Solution | self-crossing | 1 | 1 | ```C++ []\nstatic const auto _ = []{ return ios_base::sync_with_stdio(false), 0; }();\n\nclass Solution {\npublic:\n bool isSelfCrossing(vector<int>& distance)\n {\n int r[7]{};\n int i = 0;\n for (; i < distance.size(); ++i)\n {\n __builtin_memmove(&r[1], &r[0], sizeof(int) * 6);\n int dx = distance[i] - r[2];\n r[0] = dx;\n if (dx <= r[4])\n {\n if (dx >= -r[6])\n r[3] = -r[5];\n ++i;\n break;\n }\n }\n for (; i < distance.size(); ++i)\n {\n __builtin_memmove(&r[1], &r[0], sizeof(int) * 6);\n int dx = distance[i] - r[2];\n if (dx >= r[4])\n return true;\n r[0] = dx;\n }\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n b = c = d = e = 0\n x = distance\n for a in x:\n if d >= b > 0 and (a >= c or a >= c-e >= 0 and f >= d-b):\n return True\n b, c, d, e, f = a, b, c, d, e\n return False\n```\n\n```Java []\nclass Solution {\n public boolean isSelfCrossing(int[] x) {\n if (x.length <= 3) {\n return false;\n }\n int i = 2;\n while (i < x.length && x[i] > x[i - 2]) {\n i++;\n }\n if (i >= x.length) {\n return false;\n }\n if ((i >= 4 && x[i] >= x[i - 2] - x[i - 4]) ||\n (i == 3 && x[i] == x[i - 2])) {\n x[i - 1] -= x[i - 3];\n }\n i++;\n while (i < x.length) {\n if (x[i] >= x[i - 2]) {\n return true;\n }\n i++;\n }\n return false;\n }\n}\n```\n | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Spatial Reasoning | Explained & Commented | self-crossing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen we consider what a crossing is, it is the moment when we have a planar cross on both the horizontal and vertical axis of their number lines within the last 6 total steps. For this, you need to record 5 current steps and the one you are taking. This will let you know whether or not your current step will incur a crossing as you do. To make this easier to maintain overtime, we can use a deque and the appendleft and pop processes to maintain updates. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMake a deque of 5 zeros to represent the last 5 steps in the past \nThen, for each step in distance \n- The first even axis offset we will consider is if steps[2] >= steps[0] > 0. This would imply that steps at 2, which is back towards steps at 0, has crossed it on that axis of values \n- The odd axis will have three parts to it\n - the first of which is if the current step is greater than or equal to the step taken two moves ago \n - The second part of the odd axis is if the current step has undone any of the advantage incurred by the prior step at steps 1 less the advance made at steps 3, and that that difference was positive\n - The third part is actually an even offset axis, and concerns steps at 2, 4, and 0. If 4 was able to undo the movement of 2 against 0, this is also necessary to be a satisfactory odd offset \n - all tgether, the odd offset is determined if the first part is true or both parts two and three are true \n- If we have an even offset and an odd offset, we have a crossing as we have necessarily crossed both x and y axis of concern \n- At the end of the check, add the current step to the front of the deque and pop off the last item so it does not grow. \n\nIf we never return in the loop we never will, return False \n\nWe do not need more than 5 entries, since whenever we update to a new situation after 6 movements, we have completed three of each axis comparisons. The next one necessarily takes into account the prior moves, and as such is not based on the current location but the changes in location. This is why the odd offset needs to also involve the other prior axis far enough back. \n\n# Complexity\n- Time complexity: O(N) as we take all the steps eventually \n\n- Space complexity: O(1) as we only need a deque of size 5 \n\n# Code\n```\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n # make a deque of correct size \n steps = collections.deque([0, 0, 0, 0, 0])\n # for each step we could take \n for step in distance : \n # if we have an offset cross on the current even axis \n even_offset_1 = (steps[2] >= steps[0] > 0)\n # if we have either an instance where we have an offset cross on the odd axis most recent\n odd_offset_1 = (step >= steps[1])\n # or if now have a cross on the odd axis based on prior being positive \n odd_offset_2 = (step >= steps[1] - steps[3] >= 0)\n # and we had an even crossing offset priorly \n even_offset_2 = steps[4] >= steps[2] - steps[0]\n # if either odd_offset_1 or even_offset_2 and odd_offset_2 then we had a cross on the odd axis\n odd_offset = odd_offset_1 or (even_offset_2 and odd_offset_2)\n # if we have a cross on both the even and odd axis, then we have a cross \n if even_offset_1 and odd_offset : \n return True \n # push the current step to the front \n steps.appendleft(step)\n # remove the last step as you do \n steps.pop()\n # never crossed never will \n return False \n``` | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Best O(n) solution | self-crossing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe solution to this problem involves checking if the path of the person will cross itself. One way to do this is to check if the path intersects any previous lines that it has traced.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach taken in the provided code is to iterate through the list of distances and check for specific conditions that would indicate a self-crossing. These conditions include:\n\n- The current distance is greater than or equal to the second to last distance and the previous distance is less than or equal to the third to last distance\n- The current distance is greater than or equal to the second to last distance, the previous distance is equal to the third to last distance, and the fourth to last distance plus the current distance is greater than or equal to the second to last distance\n- The current distance is greater than or equal to the second to last distance, the previous distance is less than or equal to the third to last distance, the second to last distance is greater than or equal to the fourth to last distance, and the previous distance plus the fifth to last distance is greater than or equal to the third to last distance\n\nIf any of these conditions are met, the function returns True. If the loop completes and none of these conditions are met, the function returns False.\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSelfCrossing(self, distance: List[int]) -> bool:\n if len(distance) < 4:\n return False\n for i in range(3, len(distance)):\n if distance[i] >= distance[i-2] and distance[i-1] <= distance[i-3]:\n return True\n if i >= 4 and distance[i-1] == distance[i-3] and distance[i] + distance[i-4] >= distance[i-2]:\n return True\n if i >= 5 and distance[i-2] >= distance[i-4] and distance[i] + distance[i-4] >= distance[i-2] and distance[i-1] <= distance[i-3] and distance[i-1] + distance[i-5] >= distance[i-3]:\n return True\n return False\n\n``` | 0 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Python 93.5% || very concise and understandable solution || 10 lines of code | self-crossing | 0 | 1 | ```\n\n\n# Written by : Dhruv_Vavliya\n\n# just think about 4,5,6 --length arrays \ndef self_crossing(x):\n for i in range(3,len(x)):\n\n if x[i-3]>=x[i-1] and x[i]>=x[i-2]:\n return True\n \n if i>=4:\n if x[i-3] == x[i-1] and x[i-2]<=(x[i-4]+x[i]):\n return True\n\n if i>=5:\n if x[i-2]>=x[i-4] and x[i-3]>=x[i-1] and (x[i-5]+x[i-1])>=x[i-3] and (x[i-4]+x[i])>=x[i-2]:\n return True\n\n return False\n``` | 3 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Python - Top 80% Speed - O(n) time, O(1) space - Dimensionless Coordinates | self-crossing | 0 | 1 | **Python - Top 80% Speed - O(n) time, O(1) space - Dimensionless Coordinates**\n\nThe code below uses Dimensionless Coordinates (p,q) to detect collisions with walls. The solution is fairly efficient/valid, but the conversions between Coordinate Systems can be tedious.\n\n```\ndef point_intersection(qa0,qb0,pc0,walls):\n for qa,qb,pc in walls[1:]:\n if pc0==pc:\n if qa<=qa0<=qb or qa<=qb0<=qb:\n return True\n return False\nposInf = float(\'inf\')\nclass Solution:\n def isSelfCrossing(self, A: List[int]) -> bool:\n if len(A)<4:\n return False\n i,j = 0,0\n di,dj = 0,1\n iwalls, jwalls = [ [posInf]*3 for _ in range(3)], [ [posInf]*3 for _ in range(3)]\n for x in A:\n i0,j0 = i,j\n i += di*x\n j += dj*x\n #\n if di: # di: p,q = i,j\n q,p1,p2 = j, min(i0,i),max(i0,i)\n walls = iwalls[1:]\n else: # dj: p,q = j,i\n q,p1,p2 = i, min(j0,j),max(j0,j)\n walls = jwalls[1:]\n # Wall Collision Detector\n for qa,qb,pc in walls:\n if qa<=q<=qb and p1<=pc<=p2:\n return True\n # Point Collision Detector\n parallels = iwalls if dj else jwalls\n if point_intersection(p1,p2,q, parallels ):\n return True\n # Build New Walls ( dj movements span horizontal walls (iwalls) )\n if dj:\n iwalls = [ [p1,p2,q], *iwalls[:-1] ]\n else:\n jwalls = [ [p1,p2,q], *jwalls[:-1] ]\n di,dj = -dj,di\n return False\n``` | 1 | You are given an array of integers `distance`.
You start at the point `(0, 0)` on an **X-Y plane,** and you move `distance[0]` meters to the north, then `distance[1]` meters to the west, `distance[2]` meters to the south, `distance[3]` meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return `true` _if your path crosses itself or_ `false` _if it does not_.
**Example 1:**
**Input:** distance = \[2,1,1,2\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 1).
**Example 2:**
**Input:** distance = \[1,2,3,4\]
**Output:** false
**Explanation:** The path does not cross itself at any point.
**Example 3:**
**Input:** distance = \[1,1,1,2,1\]
**Output:** true
**Explanation:** The path crosses itself at the point (0, 0).
**Constraints:**
* `1 <= distance.length <= 105`
* `1 <= distance[i] <= 105` | null |
Intuitive Python3 | HashMap | 95% Time & Space | O(N*W^2) | palindrome-pairs | 0 | 1 | Please upvote if it helps!\n```\nclass Solution:\n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n backward, res = {}, []\n for i, word in enumerate(words):\n backward[word[::-1]] = i\n\n for i, word in enumerate(words):\n \n if word in backward and backward[word] != i:\n res.append([i, backward[word]])\n \n if word != "" and "" in backward and word == word[::-1]:\n res.append([i, backward[""]])\n res.append([backward[""], i])\n \n for j in range(len(word)):\n if word[j:] in backward and word[:j] == word[j-1::-1]:\n res.append([backward[word[j:]], i])\n if word[:j] in backward and word[j:] == word[:j-1:-1]:\n res.append([i, backward[word[:j]]])\n \n return res | 63 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
EASY PYTHON SOLUTION || USING MAPPING | palindrome-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n dct=defaultdict(lambda :-1)\n n=len(words)\n flg=-1\n for i in range(n):\n dct[words[i]]=i\n if words[i]=="":\n flg=i\n lst=[]\n for i in range(n):\n for j in range(len(words[i])):\n if dct[words[i][j:][::-1]]!=-1 and i!=dct[words[i][j:][::-1]] and words[i][:j]==words[i][:j][::-1]:\n if [dct[words[i][j:][::-1]],i] not in lst:\n lst.append([dct[words[i][j:][::-1]],i])\n if dct[words[i][:j][::-1]]!=-1 and i!=dct[words[i][:j][::-1]] and words[i][j:]==words[i][j:][::-1]:\n \n lst.append([i,dct[words[i][:j][::-1]]])\n if "" in words:\n for i in range(n):\n if ""!=words[i] and words[i][::-1]==words[i]:\n if [i,flg] not in lst:\n lst.append([i,flg])\n if [flg,i] not in lst:\n lst.append([flg,i])\n return lst\n \n``` | 2 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
Best and easy to understand code | palindrome-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n from collections import defaultdict\n dict_ = defaultdict(int)\n for h in range(len(words)):\n dict_[words[h]] = h\n result = []\n for i in range(len(words)):\n word = words[i]\n if "" in dict_ and dict_[""] != i and word == word[::-1]:\n result.append([i,dict_[""]])\n for j in range(len(word)):\n prefix = word[:j+1]\n suffix = word[j+1:]\n if prefix[::-1] in dict_ and dict_[prefix[::-1]] != i and suffix == suffix[::-1]:\n result.append([i,dict_[prefix[::-1]]])\n if suffix[::-1] in dict_ and dict_[suffix[::-1]] != i and prefix == prefix[::-1]:\n result.append([dict_[suffix[::-1]],i])\n return(result)\n``` | 2 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
Python with Comments ✅ | palindrome-pairs | 0 | 1 | ```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.end = False\n self.idx = -1\n self.palindromeIdxs = list()\n\nclass Solution:\n def __init__(self):\n self.root = TrieNode()\n \n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n res = list()\n \n # populate the trie with\n # the reverse of every word.\n # once we\'re done inserting\n # we\'re going to have 3 conditions\n for i in range(len(words)):\n cur = self.root\n rWord = words[i][::-1]\n for j in range(len(rWord)):\n # if the current word (from j onwards)\n # is a palindrome, add it\'s index to the trie node\n # (palindromIdx list) we\'ll use it later on to find combinations\n if self.isPalindrome(rWord[j:]):\n cur.palindromeIdxs.append(i)\n \n if rWord[j] not in cur.children:\n cur.children[rWord[j]] = TrieNode()\n cur = cur.children[rWord[j]]\n \n # once the word is done\n # add it\'s index to the trie node\n cur.end = True\n cur.idx = i\n \n for i in range(len(words)):\n self.search(words[i], i, res)\n \n return res\n \n # to find all pairse, we can have\n # conditions:\n # 1. exact match (abc, cba)\n # 2. long word, short word in trie match (abbcc, a)\n # 3. short word, long word in trie match (lls, sssll)\n def search(self, word, idx, res): \n cur = self.root\n for i in range(len(word)):\n # 2. long word, short trie\n # so the trie ended here and \n # we have matched till the ith\n # character, so we check if the\n # remaining of the word is also a\n # palindrome, if yes, then we have a pair\n # for e.g. word = abcdaa, trieWord = bcda\n # we can make a pair like abcdaabcda\n if cur.end and self.isPalindrome(word[i:]):\n res.append([idx, cur.idx])\n \n if word[i] not in cur.children:\n return\n cur = cur.children[word[i]] \n \n # 1. exact match\n # in the given list, for that \n # we\'ll take every word and then\n # check if the reverse of that\n # word lies in the trie\n # for e.g. for abc and cba\n # the trie would have both c->b->a and a->b->c\n # but when we take the first word (abc)\n # we\'ll match this with a->b->c which is\n # actually cba and so we found a match\n if cur.end and cur.idx != idx:\n res.append([cur.idx, idx])\n \n # 3. long trie, short word\n # so the trie still has items (not cur.end)\n # and the word has ended, it\'s the exact\n # opposite of point 2\n # for e.g. word=abcd trieWord=bcdaa\n # we can have a pair bcdaaabcd\n # and so we have a pair\n for pIdx in cur.palindromeIdxs:\n res.append([idx, pIdx])\n \n return\n \n \n def isPalindrome(self, s):\n return s == s[::-1]\n``` | 2 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
Python solution using dictionary | palindrome-pairs | 0 | 1 | At first the solution seems to be pretty easy: we just check if reversed `words[i]` is in `words`. If yes and the index `j` of reversed word is not equal to `i`, correspondent indices `[i,j]` are added to the answer list. This covers the case like `"abcd"` and `"dcba"` , when both are in `words`\n\nIf index `j` of reversed word is equal to `i` and `words[i]` is not an empty string, it means `words[i]` is a palindrome itself. So if `""` is in `words`, the palindrome can be formed from palindromic `words[i]` by adding empty string to the beginning or to the end of this `words[i]`.\n\nBut let\'s look at the **Example 1** in the [problem description](https://leetcode.com/problems/palindrome-pairs/). There we have `"lls"` and `"s"`, that can form a palindrome `"slls"`. The above solution will not detect it. To cover such cases we need to split `words[i]` to `prefix` and `suffix`. If `prefix` is a palindrome, we need to check if reversed `suffix` is in `words[i]`. Then the palindrome can be formed from reversed suffix + palindromic `prefix` + `suffix`. The same should be checked for `suffix`. If `suffix` is palindromic and reversed `prefix` is in `words`, than palindrome can be formed from `prefix` + palindromic `suffix` + reversed `prefix`\n\nTo search reversed `words[i]` in a constant time we need to create hashtable mapping the reversed `words[i]` and index `i` for each word in `words`\n\n\n**Time complexity**: `O(n `× `m`<sup>`2`</sup>`)`, where `n = len(words)`, `m =` words\' length in `words`<br>\n- create dictionary of reversed words: `O(n`×`m)`, \n- process each word - `n` iterations, each involves `(m-1)` iterations to create `prefix` and `suffix`, and (potentially), check if they are palindromic. In total: `O(n `× `m`<sup>`2`</sup>`)`\n\n**Space complexity:** `O(n)` for dictionary of reversed words\n\n```python\ndef palindromePairs(self, words: List[str]) -> List[List[int]]:\n\n def isPalindrome(word: str) -> bool:\n for i in range(len(word) >> 1):\n if word[i] != word[~i]:\n return False\n return True\n # end isPalindrome\n\n words_dict: Dict[str,int] = {word[::-1]:i for i, word in enumerate(words)} # map reversed words to their indices\n ans: List[List[int]] = []\n\n for i in range(len(words)):\n \n # analyze the whole words[i]\n if words[i] in words_dict:\n if i != words_dict[words[i]]:\n # words[i] is not a palindrome, but reversed word exists in `words`,\n # thus joining words[i] with reversed word them will give a palindrome\n ans.append([i,words_dict[words[i]]])\n elif len(words[i]) and "" in words_dict:\n # words[i] is non-empty string palindrome and "" is in `words`,\n # so adding "" to the beginning or to the end of words[i] gives a palindrome\n ans.append([words_dict[""],i])\n ans.append([i,words_dict[""]])\n \n # analyze prefixes and suffixes\n for j in range(1,len(words[i])):\n pref = words[i][:j]\n suff = words[i][j:]\n if suff in words_dict and isPalindrome(pref): # check if suff in words_dict first, palindrome check is expensive\n ans.append([words_dict[suff],i])\n if pref in words_dict and isPalindrome(suff):\n ans.append([i, words_dict[pref]])\n return ans\n# end palindromePairs()\n``` | 2 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
[Python] Trie solution explained | palindrome-pairs | 0 | 1 | ```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.end = False\n self.idx = -1\n self.palindromeIdxs = list()\n\nclass Solution:\n def __init__(self):\n self.root = TrieNode()\n \n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n res = list()\n \n # populate the trie with\n # the reverse of every word.\n # once we\'re done inserting\n # we\'re going to have 3 conditions\n for i in range(len(words)):\n cur = self.root\n rWord = words[i][::-1]\n for j in range(len(rWord)):\n # if the current word (from j onwards)\n # is a palindrome, add it\'s index to the trie node\n # (palindromIdx list) we\'ll use it later on to find combinations\n if self.isPalindrome(rWord[j:]):\n cur.palindromeIdxs.append(i)\n \n if rWord[j] not in cur.children:\n cur.children[rWord[j]] = TrieNode()\n cur = cur.children[rWord[j]]\n \n # once the word is done\n # add it\'s index to the trie node\n cur.end = True\n cur.idx = i\n \n for i in range(len(words)):\n self.search(words[i], i, res)\n \n return res\n \n # to find all pairse, we can have\n # conditions:\n # 1. exact match (abc, cba)\n # 2. long word, short word in trie match (abbcc, a)\n # 3. short word, long word in trie match (lls, sssll)\n def search(self, word, idx, res): \n cur = self.root\n for i in range(len(word)):\n # 2. long word, short trie\n # so the trie ended here and \n # we have matched till the ith\n # character, so we check if the\n # remaining of the word is also a\n # palindrome, if yes, then we have a pair\n # for e.g. word = abcdaa, trieWord = bcda\n # we can make a pair like abcdaabcda\n if cur.end and self.isPalindrome(word[i:]):\n res.append([idx, cur.idx])\n \n if word[i] not in cur.children:\n return\n cur = cur.children[word[i]] \n \n # 1. exact match\n # in the given list, for that \n # we\'ll take every word and then\n # check if the reverse of that\n # word lies in the trie\n # for e.g. for abc and cba\n # the trie would have both c->b->a and a->b->c\n # but when we take the first word (abc)\n # we\'ll match this with a->b->c which is\n # actually cba and so we found a match\n if cur.end and cur.idx != idx:\n res.append([cur.idx, idx])\n \n # 3. long trie, short word\n # so the trie still has items (not cur.end)\n # and the word has ended, it\'s the exact\n # opposite of point 2\n # for e.g. word=abcd trieWord=bcdaa\n # we can have a pair bcdaaabcd\n # and so we have a pair\n for pIdx in cur.palindromeIdxs:\n res.append([idx, pIdx])\n \n return\n \n \n def isPalindrome(self, s):\n return s == s[::-1]\n``` | 17 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
336: Time 95.65%, Solution with step by step explanation | palindrome-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe algorithm uses a dictionary to store the reverse of the words and their indices, and then iterates through each word and checks for palindrome pairs using substrings. It first checks for empty string as a special case, and then iterates through all possible substrings of each word to check for palindrome pairs. The resulting pairs are appended to a list and returned at the end.\n\n# Complexity\n- Time complexity:\n95.65%\n\n- Space complexity:\n45.1%\n\n# Code\n```\nclass Solution:\n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n ans = [] # initialize a list to store the palindrome pairs\n dict = {word[::-1]: i for i, word in enumerate(words)} # create a dictionary to store the reverse of words and their indices\n\n for i, word in enumerate(words): # iterate through the words and their indices\n if "" in dict and dict[""] != i and word == word[::-1]: # check if empty string is in the dictionary and the current word is palindrome\n ans.append([i, dict[""]]) # append the indices to the ans list\n\n for j in range(1, len(word) + 1): # iterate through the word characters\n l = word[:j] # get the left substring\n r = word[j:] # get the right substring\n if l in dict and dict[l] != i and r == r[::-1]: # check if left substring is in the dictionary and the right substring is palindrome\n ans.append([i, dict[l]]) # append the indices to the ans list\n if r in dict and dict[r] != i and l == l[::-1]: # check if right substring is in the dictionary and the left substring is palindrome\n ans.append([dict[r], i]) # append the indices to the ans list\n\n return ans # return the ans list\n\n``` | 8 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
python solution better than 90 percent with comments using trie | palindrome-pairs | 0 | 1 | \tRuntime: 2768 ms, faster than 88.29% of Python3 online submissions for Palindrome Pairs.\n\tMemory Usage: 271.5 MB, less than 27.76% of Python3 online submissions for Palindrome Pairs.\n\t\n\t\n\tclass Solution:\n def palindromePairs(self, words: List[str]) -> List[List[int]]:\n \n trie = {}\n ans = []\n \n #classic trie generation with adding the pal list containing index of the word if rest part of the word is pal or not from that specific char\n for i,word in enumerate(words):\n word = word[::-1]\n temp = trie\n for j,c in enumerate(word):\n \n # checking for pal or not from that specific char\n if(word[j:] == word[j:][::-1]):\n if("pal" not in temp):\n temp["pal"] = []\n temp["pal"].append(i)\n if(c not in temp):\n temp[c] = {}\n temp = temp[c]\n temp[None] = i\n \n for i,word in enumerate(words):\n temp = trie\n for j,c in enumerate(word):\n \n # checking for 1 st word is longer than the second word\n if(None in temp):\n if(word[j:] == word[j:][::-1]):\n ans.append([i,temp[None]])\n if(c not in temp):\n break\n temp = temp[c]\n \n # else is executed only if whole for loop is executed without break occuring\n # this else part is for first word is equals to smaller lenght than the seconf word\n else:\n if(None in temp and i != temp[None]):\n ans.append([i,temp[None]])\n # now for checking whether the rest part is pal or not we have iterate again and again, thats why while generating the trie we can take care of that.\n if("pal" in temp):\n for j in temp["pal"]:\n ans.append([i,j])\n \n return ans\n \n | 1 | You are given a **0-indexed** array of **unique** strings `words`.
A **palindrome pair** is a pair of integers `(i, j)` such that:
* `0 <= i, j < words.length`,
* `i != j`, and
* `words[i] + words[j]` (the concatenation of the two strings) is a palindrome.
Return _an array of all the **palindrome pairs** of_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "dcba ", "lls ", "s ", "sssll "\]
**Output:** \[\[0,1\],\[1,0\],\[3,2\],\[2,4\]\]
**Explanation:** The palindromes are \[ "abcddcba ", "dcbaabcd ", "slls ", "llssssll "\]
**Example 2:**
**Input:** words = \[ "bat ", "tab ", "cat "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "battab ", "tabbat "\]
**Example 3:**
**Input:** words = \[ "a ", " "\]
**Output:** \[\[0,1\],\[1,0\]\]
**Explanation:** The palindromes are \[ "a ", "a "\]
**Constraints:**
* `1 <= words.length <= 5000`
* `0 <= words[i].length <= 300`
* `words[i]` consists of lowercase English letters. | null |
recursive approach + memoization | house-robber-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\ndef fun(flg,root,memo):\n if(root==None):\n return 0\n if((root,flg) in memo):\n return memo[(root,flg)]\n if(flg==1):\n a=fun(0,root.left,memo)+fun(0,root.right,memo)\n memo[(root,flg)]=a\n return a\n a=fun(0,root.left,memo)+fun(0,root.right,memo)\n b=fun(1,root.left,memo)+fun(1,root.right,memo)+root.val\n x=max(a,b)\n memo[(root,flg)]=x\n return x\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n memo={}\n return(fun(0,root,memo))\n``` | 6 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
[Python3] Dynamic Programming + Depth First Search | house-robber-iii | 0 | 1 | * we construct a dp tree, each node in dp tree represents [rob the current node how much you gain, skip the current node how much you gain]\n dp_node[0] =[rob the current node how much you gain]\n dp_node[1] =[skip the current node how much you gain]\n* we start the stolen from the leaf: Depth First Search\n* for each node you have 2 opitions:\n\toption 1: rob the node, then you can\'t rob the child of the node.\n\t\t\t\t\tdp_node[0] = node.val + dp_node.left[1] +dp_node.right[1]\n\toption 2: skip the node, then you can rob or skip the child of the node. \n\t\t\t\t\tdp_node[1] = dp_node.left[0] + dp_node.right[0]\n* \tthe maximum of gain of the node depents on max(dp_node[0],dp_node[1])\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n """\n Input: [3,4,5,1,3,null,1]\n input tree dp tree:\n 3 [3+3+1,4+5]\n / \\ / \\\n 4 5 [4,3] [5,1]\n / \\ \\ / \\ \\\n 1 2 1 [1,0] [2,0] [1,0]\n / \\ / \\ / \\\n [0,0] [0,0] [0,0] [0,0] [0,0] [0,0]\n \n """\n def rob(self, root: TreeNode) -> int:\n return max(self.dfs(root))\n \n def dfs(self, root: TreeNode):\n if not root:\n return (0, 0)\n left = self.dfs(root.left)\n right = self.dfs(root.right)\n return (root.val + left[1] + right[1], max(left[0], left[1]) + max(right[0], right[1]))\n``` | 126 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
Recursive Logic Python3 5 Lines of Code | house-robber-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n def dfs(root):\n if not root: return [0,0]\n leftpair,rightpair=dfs(root.left),dfs(root.right)\n withroot,without=root.val+leftpair[1]+rightpair[1],max(leftpair)+max(rightpair)\n return [withroot,without]\n return max(dfs(root))\n #please upvote me it would encourage me alot\n\n \n``` | 8 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
Smallest Integer Divisible by K | house-robber-iii | 0 | 1 | Given a positive integer `K`, we must find the *length* of the smallest positive integer `N` such that `N` is divisible by `K`, and `N` only contains the digit `1`. If there is no such `N`, return `-1`. Therefore the following constraints must be met.\n\n* `N % K == 0`\n* length of `N` is minimized\n* `N` only contains the digit `1`\n\nThe first important item to note is that `N` may not fit into a 64-bit signed integer. This means that we can not simply iterate though the possible values of `N` and mod `K`. \n\nTo find a way to reduce the problem, lets take the example of `K=3`. The value `3` has the following possible remainders when dividing.\n\n| 0 | 1 | 2 |\n|:-:|:-:|:-:|\n\nNow, lets find the value of `N` by brute-force. In the table below, we can see that the condition `N % K == 0` is first met with the value of `111`. More interestingly, we can see that the pattern `1 -> 2 -> 0` repeats. \n\n| N | 1 | 11 | 111 | 1111 | 11111 | 111111\n|:---:|:-:|:--:|:---:|:----:|:-----:|:-----:|\n| N%K | 1 | 2 | 0 | 1 | 2 | 0 |\n\nNow, lets take a look at the example `K=6`. We can see that there are a finite number of possible remainders for any value mod `K` and that we only need to iterate thought the sequence of remainders *once* to find that `N` is not divisible by `K`.\n\n| 0 | 1 | 2 | 3 | 4 | 5 |\n|:-:|:-:|:-:|:-:|:-:|:-:|\n\n| N | 1 | 11 | 111 | 1111 | 11111 | 111111 | 1111111 |\n|:---:|:-:|:--:|:---:|:----:|:-----:|:------:|:-------:|\n| N%K | 1 | 5 | 3 | 1 | 5 | 3 | 1 |\n\nThe final piece that we must solve is how to calculate the `N%K` sequence: how to find the next remainder. We can\'t go though the values of `N` because it might not fit in a 64-bit integer. Let take a look at how we would calculate the next value of `N` and go from there. \n\n\n`N next = (N * 10) + 1` : the next value of `N` `1 -> 11 -> 111 ...`\n`remainder = N%K` : the remainder\n\n`(N next)%K = ((N * 10) + 1)%K` : we can mod both sides of our next remainder equation \n`(N next)%K = ((N * 10)%K + 1%K)%K` : the equation can then be rearranged. "It is useful to know that modulos can be taken anywhere in the calculation if it involves only addition and multiplication." *[- duke-cps102](http://db.cs.duke.edu/courses/cps102/spring10/Lectures/L-04.pdf)*\n`(N next)%K = ((N * 10)%K + 1)%K` : `1` mod anything is `1`\n`(N next)%K = ((N * 10)%K + 1)%K` : `1` mod anything is `1`\n**`remainder next = (remainder*10 + 1) %K`** : knowing that `N%K` is our remainder, we have now have a general equation that can find our next remainder value without knowing the value of `N`.\n\n```\ndef smallestRepunitDivByK(self, K: int) -> int:\n r = 0\n for c in range(1, K+1):\n r = (r*10 + 1)%K\n if r == 0: return c\n return -1\n```\n\nThe runtime of this solution is **`O(K)`**. \nThe space complexity is **`O(1)`**. | 20 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
[Python3] Easy to understand | Recursive Post-order | Linear time & space | house-robber-iii | 0 | 1 | # Intuition\nAt each node, we either need to consider the node iteslf or its children.\n\n# Approach\nFrom each node, return the max we can get by including the node and also max without the node.\n\n1. For base cases (Leaf node\'s Null children), return `[0, 0]`\n2. With postorder traversal, at each node up in recusrsion calculate the following and return:\n\n```\nwithCurrentNode = node.val + leftSubtreeMaxWithoutRoot + rightSubtreeMaxWithoutRoot\n\nwithoutCurrentNode = max(leftSubtreeMaxWithRoot, leftSubtreeMaxWithoutRoot) + max(rightSubtreeMaxWithRoot, rightSubtreeMaxWithoutRoot)\n```\n\n# Complexity\n- Time complexity:\nO(N) - We need to look at all the nodes once\n- Space complexity:\nO(H) Space - H being the height of the tree. For an unbalanced tree, this will be O(N) Space. The space is for maintaining the call stack\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n\n def postorder(root):\n if not root:\n return [0, 0] # [ withRoot, withoutRoot ]\n \n left = postorder(root.left)\n right = postorder(root.right)\n\n withRoot = root.val + left [1] + right[1]\n withoutRoot = max(left) + max(right)\n return [withRoot, withoutRoot]\n \n return max(postorder(root))\n``` | 2 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
EASY RECURSIVE PYTHON SOLUTION | house-robber-iii | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can handle our problem with simple recursion. If we are at a node in our tree, we cannot rob the house if we robbed the house above it. (This creates our 2 cases) We can treat this recursive behavior by using the recursion fairy.\n\nThe `recurse` function below returns the value of the MAX points we can rob at a node and all the contents below the node. \n\n1) If we have robbed in the node above us, we cannot rob at all so we continue our recursion\n\n2) If we have not robbed in the node above us, we can either choose to rob the node we are at or ignore it if there may be a more valuable node to rob below. (We handle this by choosing the max of both options)\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n @cache\n def recurse(node, lastUsed):\n if(not node): return 0\n if(lastUsed):\n return recurse(node.left, 0) + recurse(node.right, 0)\n else:\n return max(node.val + recurse(node.left, 1) + recurse(node.right, 1), recurse(node.right, 0) + recurse(node.left, 0))\n return recurse(root, 0)\n``` | 1 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
337: Solution with step by step explanation | house-robber-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe problem can be solved using a recursive approach. We can traverse the binary tree in a post-order traversal. At each node, we need to decide whether to rob the node or not.\n\nLet\'s define a helper function dfs which returns two values - robThis and notRobThis. robThis represents the maximum amount that can be robbed if we choose to rob the current node, and notRobThis represents the maximum amount that can be robbed if we choose not to rob the current node.\n\nTo calculate robThis, we need to add the value of the current node and the value of the grandchildren nodes (the nodes which are two levels below the current node) to notRobGrandChildren. To calculate notRobThis, we need to add the maximum of robGrandChildren and notRobGrandChildren.\n\nThe base case for the recursion is when the node is None, in which case we return (0, 0).\n\nAt the root node, we need to return the maximum of robThis and notRobThis.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n # Define the helper function\n def dfs(node):\n # Base case: if the node is None, return (0, 0)\n if not node:\n return (0, 0)\n \n # Recursive case: calculate the values for the left and right subtrees\n left_rob, left_not_rob = dfs(node.left)\n right_rob, right_not_rob = dfs(node.right)\n \n # Calculate the values for the current node\n rob_this = node.val + left_not_rob + right_not_rob\n not_rob_this = max(left_rob, left_not_rob) + max(right_rob, right_not_rob)\n \n # Return the values for the current node\n return (rob_this, not_rob_this)\n \n # Call the helper function on the root node and return the maximum value\n return max(dfs(root))\n\n``` | 6 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
DP solution Python | house-robber-iii | 0 | 1 | ```\nfrom collections import defaultdict\n\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n def rec(node, depth):\n if not node:\n return\n layer_dict[depth].append(node)\n rec(node.left, depth + 1)\n rec(node.right, depth + 1)\n \n #get layer dict\n layer_dict = defaultdict(list)\n rec(root, 0)\n \n #dp\n dp_use, dp_no_use = {None : 0}, {None : 0}\n \n for layer in range(max(layer_dict.keys()), -1, -1):\n for u in layer_dict[layer]:\n dp_use[u] = dp_no_use[u.left] + dp_no_use[u.right] + u.val\n dp_no_use[u] = max(dp_use[u.left], dp_no_use[u.left]) + max(dp_use[u.right], dp_no_use[u.right])\n \n return max(dp_use[root], dp_no_use[root])\n``` | 4 | The thief has found himself a new place for his thievery again. There is only one entrance to this area, called `root`.
Besides the `root`, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if **two directly-linked houses were broken into on the same night**.
Given the `root` of the binary tree, return _the maximum amount of money the thief can rob **without alerting the police**_.
**Example 1:**
**Input:** root = \[3,2,3,null,3,null,1\]
**Output:** 7
**Explanation:** Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
**Example 2:**
**Input:** root = \[3,4,5,1,3,null,1\]
**Output:** 9
**Explanation:** Maximum amount of money the thief can rob = 4 + 5 = 9.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `0 <= Node.val <= 104` | null |
Dynamic Programming Solution | counting-bits | 0 | 1 | # Intuition\nKey intuition is the the value of the current number is dependent on previous numbers. Hence, we can divide this problem into sub-problems and we can use dynamic programming.\n\n# Approach\nWe can see if a number is even, it depends on the number x//2 before it, if it is uneven it depends on the number x//2 before it as well, but has one more. \n\nIt is also possible to solve this problem by using logarithms of base 2. In this case take the log_2, if it is a whole number the number of bits is one, otherwise you subtract two to the power of floor of log_2 from the current index and add the number of bits plus one to the current cell in the table. This is more expensive because it requires calculating the log. \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n\n if n == 0:\n return [0]\n \n # dp array and base cases\n dp_array = [0 for x in range(n + 1)]\n dp_array[1] = 1\n \n # iterate over the dp array\n for x in range(2, n + 1):\n \n # if a number is even, check the index in the \n # dp array at index x//2, if uneven do the same but add one\n if x %2 == 0:\n dp_array[x] = dp_array[x//2]\n else:\n dp_array[x] = dp_array[x//2] + 1\n\n return dp_array \n``` | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
✅ 97.97% DP + Bit Manipulation & Offset | counting-bits | 1 | 1 | # Interview Guide - Counting Bits in Binary Representation of Integers\n\n## Problem Understanding\n\n### Description\nThe problem at hand asks us to count the number of 1\'s in the binary representation of integers from 0 to `n` . It\'s a classic problem that combines elements of dynamic programming and bitwise operations, serving as an excellent exercise to understand both concepts in depth. The goal is to return an array where the `i-th` element is the number of 1\'s in the binary representation of `i`.\n\n---\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n- Number Range: $$ 0 \\leq n \\leq 10^5 $$\n\n### 2. Importance of Bit Manipulation\nThis problem is fundamentally about understanding binary numbers and bitwise operations. Bit manipulation allows us to count the number of 1\'s in an efficient manner, especially when combined with dynamic programming.\n\n### 3. Algorithmic Approaches\nThere are two elegant ways to tackle this problem: a Dynamic Programming method that leverages Bit Manipulation (Method 1) and another Dynamic Programming method that uses an Offset (Method 2).\n\n#### Dynamic Programming with Bit Manipulation\nIn this approach, we exploit the fact that shifting a number to the right by one bit (i.e., dividing by 2) removes the last bit. So, the number of 1\'s in the binary representation of `i` is the same as $$ \\frac{i}{2} $$ plus the last bit of `i`.\n\n#### Dynamic Programming with Offset\nThe second method utilizes a fascinating property of binary numbers, where numbers `i` and $$i + 2^k$$ share the same number of 1\'s, except for an additional 1 at the `k-th` bit for $$ i + 2^k $$.\n\n### 4. Key Concepts in Each Approach\n\n#### The Magic of "Shifting Bits" (Method 1)\nIn the first method, we use bitwise shift and AND operations. Bitwise right shifting `i >> 1` essentially removes the last bit, and `i & 1` extracts the last bit. This helps us compute the result for `i` using previously computed results.\n\n#### The Power of "Offset" (Method 2)\nThe second approach introduces the concept of an "offset," which is a power of 2. We use this offset to calculate the number of 1\'s for new numbers based on previously calculated results. \n\n---\n\n# Live Coding & More\nhttps://youtu.be/V1FM02_l4_k?si=9O-fEySLX0wrUcNp\n\n---\n\n## Method 1: Dynamic Programming with Bit Manipulation\n\n### Intuition and Logic Behind the Solution\nThe idea here is to use the number of 1\'s in `i >> 1` (i.e., `i` divided by 2) and the last bit in `i` to find the number of 1\'s in `i`.\n\n### Step-by-step Explanation\n- **Initialization**: Create an array `ans` of length `n + 1`, initialized with zeros.\n- **Main Algorithm**: Iterate from 1 to `n`, and for each `i`, set `ans[i] = ans[i >> 1] + (i & 1)`.\n\n### Complexity Analysis\n- **Time Complexity**: $$ O(n) $$ \u2014 We iterate through the array once.\n- **Space Complexity**: $$ O(n) $$ \u2014 For the output array.\n\n---\n\n## Method 2: Dynamic Programming with Offset\n\n### Intuition and Logic Behind the Solution\nHere, we use an offset to help us quickly calculate the number of 1\'s for `i + 2^k` based on `i`.\n\n### Step-by-step Explanation\n- **Initialization**: Create an array `ans` of length `n + 1`, initialized with zeros.\n- **Main Algorithm**: Iterate from 1 to `n` . Use an offset variable to keep track of the nearest lower power of 2. Update `ans[i] = ans[i - offset] + 1` .\n\n### Complexity Analysis\n- **Time Complexity**: $$ O(n) $$ \u2014 We iterate through the array once.\n- **Space Complexity**: $$ O(n) $$ \u2014 For the output array.\n\n---\n\n# Performance\n\n| Language | Time (ms) | Memory (MB) |\n|--------------------|-----------|-------------|\n| Java | 2 | 46.3 |\n| C++ | 3 | 7.8 |\n| Rust | 4 | 2.6 |\n| Go | 5 | 4.5 |\n| PHP | 17 | 27.1 |\n| Python3 (Bit) | 60 | 23 |\n| JavaScript | 68 | 47 |\n| Python3 (Offset) | 74 | 23 |\n| C# | 82 | 39.8 |\n\n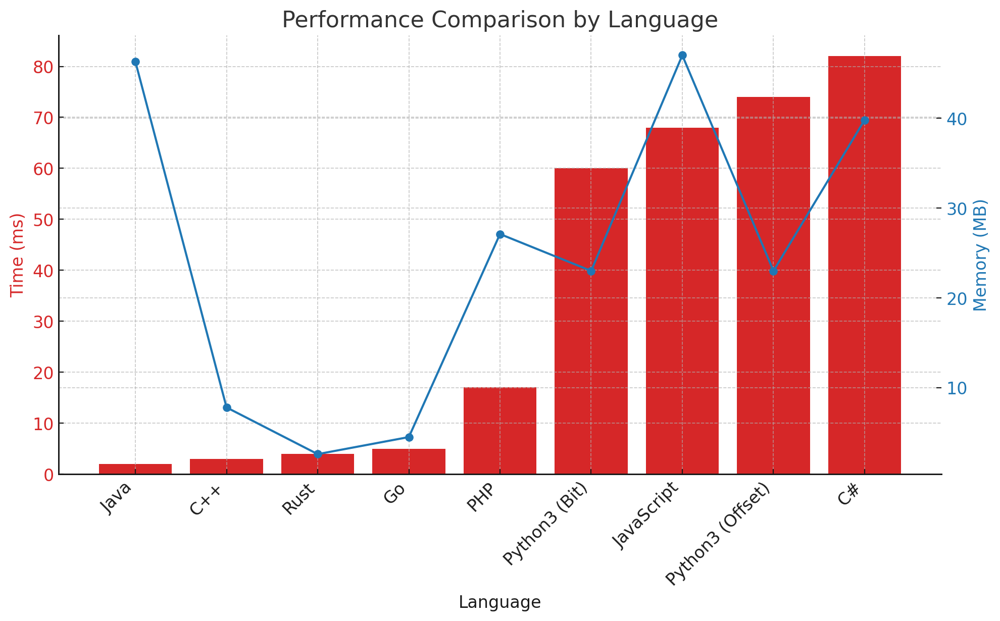\n\n\n# Code 1\n``` Python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans = [0] * (n + 1)\n for i in range(1, n + 1):\n ans[i] = ans[i >> 1] + (i & 1)\n return ans\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> countBits(int n) {\n std::vector<int> ans(n + 1, 0);\n for (int i = 1; i <= n; ++i) {\n ans[i] = ans[i >> 1] + (i & 1);\n }\n return ans;\n}\n};\n```\n``` Go []\nfunc countBits(n int) []int {\n ans := make([]int, n + 1)\n for i := 1; i <= n; i++ {\n ans[i] = ans[i >> 1] + (i & 1)\n }\n return ans\n}\n```\n``` Rust []\nimpl Solution {\n fn count_bits(n: i32) -> Vec<i32> {\n let mut ans = vec![0; (n + 1) as usize];\n for i in 1..=n {\n ans[i as usize] = ans[(i >> 1) as usize] + (i & 1);\n }\n ans\n }\n}\n```\n``` Java []\npublic class Solution {\n public int[] countBits(int n) {\n int[] ans = new int[n + 1];\n for (int i = 1; i <= n; i++) {\n ans[i] = ans[i >> 1] + (i & 1);\n }\n return ans;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number[]}\n */\nvar countBits = function countBits(n) {\n const ans = new Array(n + 1).fill(0);\n for (let i = 1; i <= n; i++) {\n ans[i] = ans[i >> 1] + (i & 1);\n }\n return ans;\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @return Integer[]\n */\n function countBits($n) {\n $ans = array_fill(0, $n + 1, 0);\n for ($i = 1; $i <= $n; $i++) {\n $ans[$i] = $ans[$i >> 1] + ($i & 1);\n }\n return $ans;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] CountBits(int n) {\n int[] ans = new int[n + 1];\n for (int i = 1; i <= n; i++) {\n ans[i] = ans[i >> 1] + (i & 1);\n }\n return ans;\n }\n}\n```\n# Code 2\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans = [0] * (n + 1)\n offset = 1\n for i in range(1, n + 1):\n if offset * 2 == i:\n offset *= 2\n ans[i] = ans[i - offset] + 1\n return ans\n```\n\nFeel free to compare these methods and choose the one that you find most intuitive. Understanding the underlying principles behind each approach will not only help you solve this specific problem but also equip you with the tools to tackle a wide range of similar problems. | 93 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Python3 Solution | counting-bits | 0 | 1 | \n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n dp=[0]\n for i in range(1,n+1):\n if i%2==1:\n dp.append(dp[i-1]+1)\n else:\n dp.append(dp[i//2])\n return dp \n``` | 5 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
✅97.54% Solution🔥Python3/C/C#/C++/Java🔥Use Vectors🔥 | counting-bits | 1 | 1 | # Code\n```Python3 []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n sum=0\n list1 = []\n for i in range(n+1):\n sum=bin(i).count("1")\n list1.append(sum)\n return list1\n```\n```python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n sum=0\n list1 = []\n for i in range(n+1):\n sum=bin(i).count("1")\n list1.append(sum)\n return list1\n```\n```C# []\npublic class Solution\n{\n public int[] CountBits(int n)\n {\n int[] list1 = new int[n + 1];\n for (int i = 0; i <= n; i++)\n {\n int sum = CountOnesInBinary(i);\n list1[i] = sum;\n }\n return list1;\n }\n\n private int CountOnesInBinary(int num)\n {\n int count = 0;\n while (num > 0)\n {\n count += num & 1;\n num >>= 1;\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n std::vector<int> countBits(int n) {\n std::vector<int> result(n+1);\n for (int i = 0; i <= n; i++) {\n result[i] = __builtin_popcount(i);\n }\n return result;\n }\n};\n```\n```Java []\npublic class Solution {\n public int[] countBits(int n) {\n int[] result = new int[n+1];\n for (int i = 0; i <= n; i++) {\n result[i] = Integer.bitCount(i);\n }\n return result;\n }\n} | 16 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Beginner-friendly || Simple solution with using Counting in Python3 | counting-bits | 0 | 1 | # Intuition\nThe problem description requires to convert the decimal into binary and represent the result as a **list of bits**.\n\nThough, the solution isn\'t **EFFICIENT** and there\'s a more affordable algorithm as **bit manipulation**, for the sake of brevity, we\'ll skip it and will focus on counting.\n\n---\n\nIf you haven\'t familiar with [binary](https://en.wikipedia.org/wiki/Binary_number), follow the link.\n\n---\n\n\n# Approach\n1. declare a list of a bytes `ans` with size `n + 1`\n2. iterate over range of `n + 1`\n3. at each step count amount of bits via converting `i` into `binary` and use the built-in `count` method\n4. return the list of bits `ans`\n\n# Complexity\n- Time complexity: **O(nk)**, where `k` is an **average** number of `1` - s\n\n- Space complexity: **O(n)**, because of storing the list of bits\n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans = [0] * (n + 1)\n\n for i in range(1, n + 1):\n ans[i] = bin(i).count(\'1\')\n\n return ans\n``` | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
【Video】Time: O(n), Space: O(n) solution with Python, JavaScript, Java and C++ | counting-bits | 1 | 1 | # Intuition\nThe most important idea to solve the question of counting the number of set bits (1s) in the binary representation of numbers from 0 to n is to recognize and utilize the pattern that relates the count of set bits in a number to the count of set bits in another number that is a power of 2. This concept allows you to optimize the counting process and avoid redundant calculations.\n\nThe key idea is to leverage dynamic programming and exploit the fact that a number i can be represented as the sum of a smaller number i - sub and 1. The value of sub is adjusted whenever i is a power of 2. This enables efficient counting of set bits by using the previously calculated counts for smaller numbers.\n\nBy following this approach, you can dramatically reduce the number of bit counting operations needed to solve the problem, making the algorithm more efficient and faster than na\xEFve approaches that directly iterate through each bit of every number.\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 253 videos as of September 1st, 2023.\n\nhttps://youtu.be/24ieN85axOU\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F Don\'t forget to subscribe to my channel!\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be differnt a bit\n\n1. Initialize Variables and Data Structures:\n - Create a class named `Solution`.\n - Define a method within the class called `countBits`, which takes an integer `n` as an argument.\n - Create an array `dp` of length `(n + 1)` to store the count of set bits for numbers from 0 to `n`.\n - Initialize a variable `sub` with the value 1.\n\n2. Iterate through Numbers:\n - Use a `for` loop to iterate over numbers from 1 to `n`, inclusive.\n\n3. Determine Subsequence Reset:\n - Check if `sub` multiplied by 2 is equal to the current value of `i`.\n - If true, update the value of `sub` to be equal to `i`. This step is responsible for resetting the subsequence when the current number is a power of 2.\n\n4. Count Set Bits:\n - Calculate the count of set bits for the current number by accessing `dp[i - sub]` and adding 1.\n - This step utilizes the fact that the count of set bits for a number `i` can be obtained by counting the set bits of the number `i - sub` and adding 1.\n\n5. Store Result in dp Array:\n - Assign the calculated count of set bits for the current number to `dp[i]`.\n\n6. Return Result:\n - After the loop completes, the `dp` array will contain the count of set bits for numbers from 0 to `n`.\n - Return the `dp` array as the final result of the `countBits` method.\n\nIn summary, the code implements a dynamic programming approach to count the number of set bits (1s) in the binary representation of numbers from 0 to `n`. It uses an array `dp` to store the results and calculates the count of set bits step by step, based on the idea of resetting subsequences at powers of 2.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n```python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n dp = [0] * (n + 1)\n sub = 1\n\n for i in range(1, n + 1):\n if sub * 2 == i:\n sub = i\n \n dp[i] = dp[i - sub] + 1\n \n return dp\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number[]}\n */\nvar countBits = function(n) {\n var dp = new Array(n + 1).fill(0);\n var sub = 1;\n\n for (var i = 1; i <= n; i++) {\n if (sub * 2 === i) {\n sub = i;\n }\n\n dp[i] = dp[i - sub] + 1;\n }\n\n return dp; \n};\n```\n```java []\nclass Solution {\n public int[] countBits(int n) {\n int[] dp = new int[n + 1];\n int sub = 1;\n\n for (int i = 1; i <= n; i++) {\n if (sub * 2 == i) {\n sub = i;\n }\n\n dp[i] = dp[i - sub] + 1;\n }\n\n return dp; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> countBits(int n) {\n std::vector<int> dp(n + 1, 0);\n int sub = 1;\n\n for (int i = 1; i <= n; i++) {\n if (sub * 2 == i) {\n sub = i;\n }\n\n dp[i] = dp[i - sub] + 1;\n }\n\n return dp; \n }\n};\n```\n | 33 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
easy C++/Python bit Manipulations||welcome for tricks | counting-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nProvide $O(n)$ linear time solutions. __builtin_popcount or C++ bitset count() are supposed $O(\\log n)$ time, so for fast implementation are not used.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/bSOyI91vZEs?si=pH5oR6_K0YTCRXf8](https://youtu.be/bSOyI91vZEs?si=pH5oR6_K0YTCRXf8)\n2 recursions are used.\nFor the 1st solution:\n```\nans[j]=ans[j-2**b]+1 where 2**b=i<=j<=2**(b+1)=2*i\n```\nFor the 2nd solution\n```\nans[i]=ans[i/2]+is_odd(i)?1:0\n```\nThe usual bit manipulations used for solving this question:\n```\nx>>1 =>x/2 int division\nx<<1 =>x*2\nx&1 => is_odd(x)\n1<<b =>2**b\n```\n\nLet\'s consider the 2nd solution how it works.\nSuppose ```n=61=(111101)``` => bitcount(n)=5 & n is odd =>```(n&1)=1```\n ```n>>1=n/2=30=(11110)``` bitcount(n/2)=4\nHave ```bitcount(n/2)+(n&1)=bitcount(n)```\n\nTo the 1st solution, how does it work?\n```j=61, i=32=1<<5``` and bitcount(i)=1 just put this at i-th bit position. The rest is \n=> ```j-i=29``` so bitcount(61)=bitcount(29)+1\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ for ans\n# Code\n\n```python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans=[0]*(n+1)\n i=1\n while i<=n:\n i2=min(i<<1, n)\n for j in range(i, i2+1):\n ans[j]=ans[j-i]+1\n i<<=1\n return ans\n \n```\n```C++ []\nclass Solution {\npublic:\n vector<int> countBits(int n) {\n vector<int> ans(n+1, 0);\n for(int i=1; i<=n; i<<=1){\n int i2=min(i<<1, n);\n for(int j=i; j<=i2; j++)\n ans[j]=ans[j-i]+1;\n }\n return ans;\n }\n};\n```\n# 2nd Solution\n```C++ []\nclass Solution {\npublic:\n vector<int> countBits(int n) {\n vector<int> ans(n+1, 0);\n for(int i=1; i<=n; i++){\n ans[i]=ans[i>>1]+(i&1);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans=[0]*(n+1)\n for i in range(n+1):\n ans[i]=ans[i>>1]+(i&1)\n return ans\n \n```\n | 7 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
[Python] Simple Solution with Clear Explanation | counting-bits | 0 | 1 | # Solution Code\n```\ndef countBits(self, num: int) -> List[int]:\n counter = [0]\n for i in range(1, num+1):\n counter.append(counter[i >> 1] + i % 2)\n return counter\n```\n\n# Analysis\nTo understand the solution, we remember the following two points from math:\n* All whole numbers can be represented by **2N** (*even*) and **2N+1** (*odd*).\n* For a given binary number, multiplying by 2 is the same as adding a zero at the end (just as we just add a zero when multiplying by ten in base 10).\n\nSince multiplying by 2 just adds a zero, then any number and its double will have the same number of 1\'s. Likewise, doubling a number and adding one will increase the count by exactly 1. Or:\n* ```countBits(N) = countBits(2N)```\n* ```countBits(N)+1 = countBits(2N+1)```\n\nThus we can see that any number will have the same *bit count* as half that number, with an extra one if it\'s an odd number. We iterate through the range of numbers and calculate each bit count successively in this manner:\n```\nfor i in range(num):\n counter[i] = counter[i // 2] + i % 2\n```\nWith a few modifications:\n* Define the base case of ```counter[0] = 0```, and start at ```1```.\n* We need to include ```num```, so use ```num+1``` as the bound on the ```range```.\n* Bit-shifting 1 has the same effect as dividing by 2, and is faster, so replace ```i // 2``` with ```i >> 1```.\n* We can choose to either initiate our list with ```counter = [0] * (num+1)``` or just ```counter = [0]``` and then ```append``` to it (which has O(1)). It\'s a little faster to initiate it with zeroes and then access it rather than appending each time, but I\'ve chosen the latter for better readibility.\n* Some solutions use ```i & 1``` to determine the parity of ```i```. While this accomplishes the same purpose as ```i % 2``` and keeps with the bitwise-operator theme, it is faster to calculate the modulus.\n\n## Time and Space Complexity\nTime: O(n) - We iterate through the range of numbers once.\nSpace: O(n) - We use a ```num```-sized array.\n## Examples\nLet\'s take the number 7, represented in binary as 111.\n```\nBase 2: 111 Base 10: 7 \nBase 2: 1110 Base 10: 14 \nBase 2: 11100 Base 10: 28 \nBase 2: 11101 Base 10: 29\n```\n# Analysis of Other Approaches\nWhile we\'re here, let\'s take a look at some other approaches:\n## Brute Force\nThe most straightforward solution is simply to convert each number to a binary string and count the 1\'s in the resulting string. This has time complexity of O(n * length of binary number) and is discouraged in the problem prompt. Regardless, the test cases do not punish this approach very much:\n```\ndef countBits(self, num: int) -> List[int]:\n return [bin(i).count(\'1\') for i in range(num+1)]\n```\nor\n```\ndef countBits(self, num: int) -> List[int]:\n return list(map(lambda x:bin(x).count(\'1\'), range(num+1)))\n```\n## Extend and Slice\nPersonally, this is my least favourite approach because it performs more work than needed. If you take a look at the pattern that emerges when you start counting bits, you will notice that each successive power of two is the same as the previous set, plus one. This makes sense, since you\'re just adding a one to the most significant bit. So we can just keep extending the list with itself until we have enough to cover up to ```num+1``` and then return just the list up to ```num``` (by slicing). However, as before, the test cases don\'t really punish this approach:\n```\ndef countBits(self, num: int) -> List[int]:\n counter = [0]\n while len(counter) < num+1:\n counter.extend([i+1 for i in counter])\n return counter[:num+1]\n```\n## Awkward Counting\nAnd finally, this is the most awkward solution I could come up with. It uses the same concept as the previous one, by starting over every power of 2 and adding 1, except instead of extending the list, it tracks when it\'s time to start the next order of 2, and stops once it reaches ```num+1```. The only reason I\'m including it is because it\'s technically the fastest solution, garnering a 99.55% on one lucky submission.\n```\ndef countBits(self, num: int) -> List[int]:\n nextOrder = 2\n tracker = 0\n counter = [0]*(num+1)\n\n for i in range(1, num+1):\n if i == nextOrder:\n nextOrder *= 2\n tracker = 0\n counter[i] = counter[tracker] + 1\n tracker += 1\n return counter\n```\n | 495 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Python | using Bin() | Easy to understand | counting-bits | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans = [0] * (n+1) // create a list with n+1 of length\n count = 0 \n for i in range(1,n+1): //note: binary of 1 will always be 0 so start from position 1 to n+1\n binary = bin(i)[2:] // convert number into binary with bin() ans store it into a variable\n for j in str(binary):\n if j == "1": \n count += 1 // count the number of 1\'s\n ans[i] = count // store the count in ans for ith position \n count = 0\n return (ans)\n\n```\n\n**Upvote if you like the solution.** | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Python | Easy to Understand | 4 Lines of Code | counting-bits | 0 | 1 | # Python | Easy to Understand | 4 Lines of Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n result=[0]*(n+1) \n offset=1\n for i in range(1,n+1):\n if offset*2 ==i:\n offset=i\n result[i]=1+result[i-offset]\n \n return result\n \n``` | 2 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Beginner-friendly || Two solutions || Counting || Dynamic Programming || Python3 & TypeScript | counting-bits | 0 | 1 | # Intuition\nThe problem description requires to convert the decimal into binary and represent the result as a **list of bits**.\n\n---\n\nIf you haven\'t familiar with [binary](https://en.wikipedia.org/wiki/Binary_number), follow the link.\n\n---\n\nWe\'d like to consider two solutions (**Dynamic Programming** and **Counting**).\n\n- **Dynamic Programming**\n\nTo count amount of bits in range [0, n] we\'re going to use recursion with **Bit Manipulations**.\n\n```\n# Example\nn = 5\n\n# If we convert this into binary the result will looks like \'101\'\n# There\'re two bits as 1-s.\n# At each step we\'re going to shift bits to the right (5 >> 1 ...).\n# 5 => 2 => 1 => 0 \n# and use bitwise AND to check, if all of the digits are 1-s\n```\n\n# Code in TypeScript\n```\nfunction countBits(n: number): number[] {\n const ans = [];\n const cache = {};\n\n const dp = (i: number): number => {\n if (i in cache) return cache[i];\n\n return i === 0 ? 0 : (cache[i] = (i & 1) + dp(i >> 1));\n };\n\n for (let i = 0; i < n + 1; i++)\n ans.push(dp(i));\n\n return ans;\n}\n```\n\n# Complexity\n- Time complexity: **O(nk)**, where `k` is an **average** number of `1` - s\n- Space complexity: **O(n)**, because of storing the list of bits\n\n---\n- **Counting**\n\nIdea the same - count amount of bits, but with using convenient **list comprehension** in Python3.\n\n# Code in Python3\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n return [bin(x).count(\'1\') for x in range(0, n + 1)]\n```\n\n# Complexity\n- Time complexity: **O(n k log k)**, `count` and `bin` are doing work linear and logarithmic time, respectively\n- Space complexity: **O(n)**, the same as before | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Python 1-liner. Functional programming. | counting-bits | 0 | 1 | # Approach\nNotice, that the number of `1s` in a number `n` is equal to number of `1s` in `n // 2`, if `n` is even else one more than it.\n\ni.e $$bits(n) = bits(n \\div 2) + (n \\bmod 2)$$\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\nImperative multi-liner:\n```python\nclass Solution:\n def countBits(self, n: int) -> list[int]:\n bits = [0] * (n + 1)\n for x in range(n + 1):\n bits[x] = bits[x // 2] + (x % 2)\n return bits\n\n\n```\n\nFunctional 1-liner:\n```python\nclass Solution:\n def countBits(self, n: int) -> list[int]:\n return reduce(lambda a, x: setitem(a, x, a[x // 2] + x % 2) or a, range(n + 1), [0] * (n + 1))\n\n\n``` | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Simple straight forward solution in Python3 | counting-bits | 0 | 1 | # Intuition\nThe array in range of (2^i)+1 to 2^(i+1) can be gernerate from previous range from (0, 2^i).\n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n res = [0]\n\n i = 0\n while(2**i <= n):\n for j in range(2**i):\n res.append(res[j]+1)\n if len(res) == n+1:\n break\n i += 1\n\n return res\n\n\n```\n\n# Complexity\n- Time complexity: O(N)\n- Space complexity:O(1)\n\n\n# .\n# .\n## Please Upvote\n# .\n# . | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Python3 | Very simple solution | For beginners | counting-bits | 0 | 1 | # Intuition\nProblem solution used ***"191. Number of 1 Bits"*** \nand a shell is written with complexity ***[O(n) * O(n)]***\n\n# Approach\n***We feed each number of the function sequence and form a new list from this, which we then return - everything is very simple***\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n def hamming_weight(n: int) -> int:\n count = 0\n for i in range(0, 33):\n if n & 1 << i != 0:\n count += 1\n return count\n scr = [0 for i in range(n+1)]\n for i in range(len(scr)):\n scr[i] = hamming_weight(i)\n return scr\n```\n# ***Please vote this solution!*** | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
O(n) USING MAP() IN PYTHON | counting-bits | 0 | 1 | # Intuition:\nThe problem involves counting the number of set bits (1s) in the binary representation of numbers from 0 to n.\n\n# Approach:\nThe provided solution employs a for loop to iterate through the range from 0 to n (inclusive). For each number, it converts it to binary using bin(i)[2:] to remove the \'0b\' prefix. It then uses list(map(int, ...)) to convert each character in the binary representation to an integer. Finally, it calculates the sum of these integers, representing the count of set bits for that number.\n\n# Complexity:\n\nTime complexity: O(n\u22C5m), where n is the given input number and m is the average number of bits in the binary representation of numbers from 0 to n.\nSpace complexity: O(n) for the list that stores the results.\n\n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n lst=[]\n for i in range(n+1):\n lst.append(sum((list(map(int,bin(i)[2:])))))\n return lst\n \n``` | 1 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Counting Bits | Bit manipulation | python3 | | counting-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans=[]\n for i in range(0,n+1):\n count = 0\n while i>=1:\n if (i%2) !=0:\n count+=1\n i>>=1\n ans.append(count)\n return ans\n\n``` | 2 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
🔥🔥🔥Python Easy Brute Force🔥🔥🔥 | counting-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n def binary(number):\n b=bin(number)\n ans=(b[2::])\n return ans\n lis=[]\n for i in range(0,n+1):\n lis.append(binary(i).count("1"))\n return lis\n``` | 8 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Superb Logic Solution | counting-bits | 0 | 1 | \n\n# Solution In Python3\n```\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n sum=0\n list1 = []\n for i in range(n+1):\n sum=bin(i).count("1")\n list1.append(sum)\n return list1\n```\n# Please upvote me it would encourages me | 3 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
Beats 100% | Easy solution using bit manipulation | counting-bits | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> countBits(int n) {\n vector<int> ans(n + 1, 0);\n \n for (int i = 1; i <= n; i++) {\n // To count the number of 1\'s in the binary representation of i,\n // you can use the fact that ans[i] = ans[i / 2] + (i % 2).\n ans[i] = ans[i >> 1] + (i & 1);\n }\n \n return ans;\n }\n};\n\n```\n```python []\nclass Solution:\n def countBits(self, n: int) -> List[int]:\n ans = [0] * (n + 1)\n\n for i in range(1, n + 1):\n ans[i] = ans[i >> 1] + (i & 1)\n\n return ans\n\n```\n```Java []\nclass Solution {\n public int[] countBits(int n) {\n int[] ans = new int[n + 1];\n\n for (int i = 1; i <= n; i++) {\n ans[i] = ans[i >> 1] + (i & 1);\n }\n\n return ans;\n }\n}\n\n```\n\n\n``` | 4 | Given an integer `n`, return _an array_ `ans` _of length_ `n + 1` _such that for each_ `i` (`0 <= i <= n`)_,_ `ans[i]` _is the **number of**_ `1`_**'s** in the binary representation of_ `i`.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,1\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
**Example 2:**
**Input:** n = 5
**Output:** \[0,1,1,2,1,2\]
**Explanation:**
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
**Constraints:**
* `0 <= n <= 105`
**Follow up:**
* It is very easy to come up with a solution with a runtime of `O(n log n)`. Can you do it in linear time `O(n)` and possibly in a single pass?
* Can you do it without using any built-in function (i.e., like `__builtin_popcount` in C++)? | You should make use of what you have produced already. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous. Or does the odd/even status of the number help you in calculating the number of 1s? |
✅ 95.83% Recursive Flattening & Stack | flatten-nested-list-iterator | 1 | 1 | # Intuition\nWhen we hear "nested structure", the brain immediately thinks of recursion or stacks. Why? Because both tools excel at handling layered structures. Imagine Russian nesting dolls. To access the innermost doll, we must open each outer doll. This problem gives us a nested list and asks us to flatten it. A nested list is like a multi-layered onion. Peeling each layer reveals another layer until we finally reach the core. Flattening this onion means transforming it into a single layer of all the individual parts.\n\n## Live Coding & Explaining\nhttps://youtu.be/Mh8-eLca4Ks?si=5_ocf5e3_edgAtXe\n\n# Approach 1: Recursive Flattening\n1. **Recursive Exploration of Nested List**: To navigate the nested list, we must access each integer sequentially. This can be achieved by recursively examining each `NestedInteger`:\n - If it\'s an integer, we simply add it to our result.\n - If it\'s a list, we recursively flatten the list and merge our result with this newly flattened list.\n \n2. **Linear Iteration**: Having flattened the nested list, iterating over it is a breeze. We maintain an index to trace our current position. The `next` function will fetch the current integer and move the index ahead, while `hasNext` will verify if any more integers are left in the flattened list.\n\n# Approach 2: Using a Stack\nInstead of immediately flattening the list, we can use a stack to process the nested list on-the-fly. This approach is akin to peeling our onion layer by layer, only when required.\n1. **Stack Initialization**: Begin by pushing the nested list items onto the stack in reverse order.\n2. **On-The-Fly Processing in `hasNext`**: Before retrieving the next integer, we ensure the top of the stack is an integer. If it\'s a list, we pop it and push its items onto the stack (again, in reverse). We repeat this until we find an integer or the stack is empty.\n3. **Fetching the Next Integer**: Once `hasNext` ensures the top of the stack is an integer, `next` will simply pop it.\n\n# Complexity\n\nFor both approaches:\n- **Time complexity**: \n - Flattening or processing the list is $$O(N)$$, where $$N$$ is the total number of integers in the nested structure. We handle each integer only once.\n - Both `next` and `hasNext` operations are $$O(1)$$ on average. Though there might be cases in the stack approach where `hasNext` takes longer, over a series of operations, it averages out to $$O(1)$$.\n \n- **Space complexity**: \n - The maximum space required is $$O(N)$$. This is because of the flattened list in the recursive approach or due to the stack in the stack approach.\n\n# Code Flattening\n```python []\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n def flatten(nested):\n result = []\n for ni in nested:\n if ni.isInteger():\n result.append(ni.getInteger())\n else:\n result.extend(flatten(ni.getList()))\n return result\n \n self.flattened = flatten(nestedList)\n self.index = 0\n\n def next(self) -> int:\n self.index += 1\n return self.flattened[self.index - 1]\n\n def hasNext(self) -> bool:\n return self.index < len(self.flattened)\n```\n``` C++ []\n#include <vector>\n\nclass NestedIterator {\nprivate:\n std::vector<int> flattened;\n int index;\n \n std::vector<int> flatten(const std::vector<NestedInteger>& nested) {\n std::vector<int> result;\n for (const auto& ni : nested) {\n if (ni.isInteger()) {\n result.push_back(ni.getInteger());\n } else {\n auto subList = flatten(ni.getList());\n result.insert(result.end(), subList.begin(), subList.end());\n }\n }\n return result;\n }\n\npublic:\n NestedIterator(std::vector<NestedInteger> nestedList) {\n flattened = flatten(nestedList);\n index = 0;\n }\n\n int next() {\n return flattened[index++];\n }\n\n bool hasNext() {\n return index < flattened.size();\n }\n};\n```\n``` Java []\npublic class NestedIterator {\n private List<Integer> flattened;\n private int index;\n\n public NestedIterator(List<NestedInteger> nestedList) {\n flattened = new ArrayList<>();\n index = 0;\n flattened = flatten(nestedList);\n }\n\n private List<Integer> flatten(List<NestedInteger> nested) {\n List<Integer> result = new ArrayList<>();\n for (NestedInteger ni : nested) {\n if (ni.isInteger()) {\n result.add(ni.getInteger());\n } else {\n result.addAll(flatten(ni.getList()));\n }\n }\n return result;\n }\n\n public int next() {\n return flattened.get(index++);\n }\n\n public boolean hasNext() {\n return index < flattened.size();\n }\n}\n```\n``` JavaScript []\nclass NestedIterator {\n constructor(nestedList) {\n this.flattened = this.flatten(nestedList);\n this.index = 0;\n }\n\n flatten(nested) {\n let result = [];\n for (let ni of nested) {\n if (ni.isInteger()) {\n result.push(ni.getInteger());\n } else {\n result.push(...this.flatten(ni.getList()));\n }\n }\n return result;\n }\n\n next() {\n return this.flattened[this.index++];\n }\n\n hasNext() {\n return this.index < this.flattened.length;\n }\n}\n```\n``` PHP []\n<?php\nclass NestedIterator {\n private $flattened = [];\n private $index = 0;\n\n function __construct($nestedList) {\n $this->flattened = $this->flatten($nestedList);\n }\n\n private function flatten($nested) {\n $result = [];\n foreach ($nested as $ni) {\n if ($ni->isInteger()) {\n $result[] = $ni->getInteger();\n } else {\n $result = array_merge($result, $this->flatten($ni->getList()));\n }\n }\n return $result;\n }\n\n function next() {\n return $this->flattened[$this->index++];\n }\n\n function hasNext() {\n return $this->index < count($this->flattened);\n }\n}\n?>\n```\n``` Rust []\n\nstruct NestedIterator {\n flattened: Vec<i32>,\n index: usize,\n}\n\nimpl NestedIterator {\n fn new(nested_list: Vec<NestedInteger>) -> Self {\n let mut flattened = Vec::new();\n Self::flatten(&nested_list, &mut flattened);\n\n Self {\n flattened,\n index: 0,\n }\n }\n\n fn flatten(nested: &[NestedInteger], result: &mut Vec<i32>) {\n for ni in nested {\n match ni {\n NestedInteger::Int(val) => result.push(*val),\n NestedInteger::List(list) => Self::flatten(list, result),\n }\n }\n }\n\n fn next(&mut self) -> i32 {\n let val = self.flattened[self.index];\n self.index += 1;\n val\n }\n\n fn has_next(&self) -> bool {\n self.index < self.flattened.len()\n }\n}\n\n```\n``` Go []\ntype NestedIterator struct {\n flattened []int\n index int\n}\n\nfunc Constructor(nestedList []*NestedInteger) *NestedIterator {\n return &NestedIterator{\n flattened: flatten(nestedList),\n index: 0,\n }\n}\n\nfunc flatten(nested []*NestedInteger) []int {\n var result []int\n for _, ni := range nested {\n if ni.IsInteger() {\n result = append(result, ni.GetInteger())\n } else {\n result = append(result, flatten(ni.GetList())...)\n }\n }\n return result\n}\n\nfunc (this *NestedIterator) Next() int {\n val := this.flattened[this.index]\n this.index++\n return val\n}\n\nfunc (this *NestedIterator) HasNext() bool {\n return this.index < len(this.flattened)\n}\n```\n``` C# []\nusing System.Collections.Generic;\n\npublic class NestedIterator {\n private List<int> flattened;\n private int index;\n\n public NestedIterator(IList<NestedInteger> nestedList) {\n flattened = new List<int>();\n index = 0;\n flattened = Flatten(nestedList);\n }\n\n private List<int> Flatten(IList<NestedInteger> nested) {\n List<int> result = new List<int>();\n foreach (var ni in nested) {\n if (ni.IsInteger()) {\n result.Add(ni.GetInteger());\n } else {\n result.AddRange(Flatten(ni.GetList()));\n }\n }\n return result;\n }\n\n public int Next() {\n return flattened[index++];\n }\n\n public bool HasNext() {\n return index < flattened.Count;\n }\n}\n```\n\n# Code Stack\n``` Python []\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n self.stack = nestedList[::-1]\n \n def next(self) -> int:\n return self.stack.pop().getInteger()\n \n def hasNext(self) -> bool:\n while self.stack:\n top = self.stack[-1]\n if top.isInteger():\n return True\n self.stack = self.stack[:-1] + top.getList()[::-1]\n return False\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage |\n|------------|---------------------|--------------|\n| Rust | 2 ms | 3.1 MB |\n| Go | 3 ms | 6.3 MB |\n| Java | 3 ms | 44.5 MB |\n| C++ | 4 ms | 14.2 MB |\n| PHP | 14 ms | 23.2 MB |\n| Python3 | 50 ms | 20.1 MB |\n| JavaScript | 63 ms | 53.5 MB |\n| C# | 128 ms | 44.7 MB |\n\n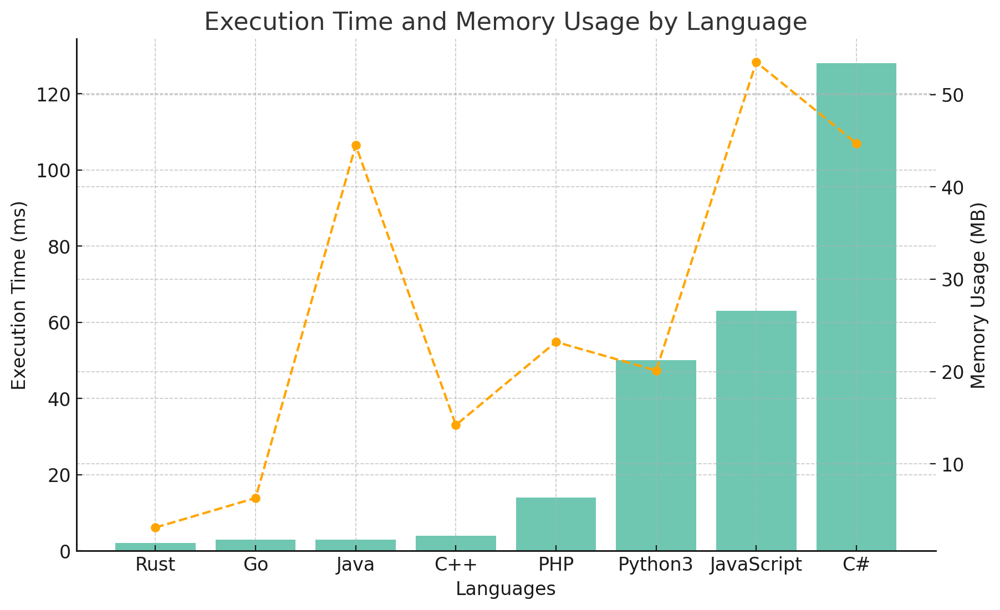\n\n\n# Let\'s Dive Into the Code!\nThe first approach employs recursion to methodically flatten the nested list. The second uses a stack to peel the nested list layer by layer, revealing integers or further nested lists.\n\nThe beauty of these approaches lies in their adaptability. Whether you want a pre-flattened list ready to be iterated or you prefer to peel back layers as you go, we\'ve got you covered. Choose the one that aligns best with your problem-solving style! | 93 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
🚀 94.83% || Recursion || Explained Intuition 🚀 | flatten-nested-list-iterator | 1 | 1 | # Probelm Description\n\nThe task is designing a class called `NestedIterator` for flattening a nested list of integers. The nested list contains elements, where each element can either be an integer or another nested list with its own elements. The goal is to create an iterator that can traverse this nested structure and provide a flattened list of integers.\n\n- **Class Requirements:**\n - `NestedIterator(List<NestedInteger> nestedList)`: This constructor initializes the iterator with the provided nested list.\n - `int next()`: This method returns the next integer in the nested list when called.\n - `boolean hasNext()`: This method returns true if there are more integers in the nested list to be iterated, and false otherwise.\n\n- **Constraints:**\n - `1 <= nestedList.length <= 500`.\n - `The values of the integers in the nested list is in the range [-10e6, 10e6]`.\n\n---\n\n# Intuition\nHi Everyone,\n\nLet\'s zoom\uD83D\uDD0E in and examine the details in our today\'s problem.\nIn this problem, We are required to **flatten** a specific type of lists whose any element might be an integer or a list also.\uD83E\uDD2F\n\nI think this seems tough on many levels.\uD83E\uDD28\nNo, It doesn\'t. \uD83D\uDE03\n\nLet\'s take alook at this interesting **observation**.\n```\nInput = [1, 1, 2, 1, 1]\nFlatten = [1, 1, 2, 1, 1]\n```\n```\nEX: Input = [[1, 1], 2, [1 ,1]]\nFlatten = [1, 1, 2, 1, 1]\n```\n```\nEX: Input = [[1, [1, 2]], [1, 1]]\nFlatten = [1, 1, 2, 1, 1]\n```\n```\nEX: Input = [[1, [1, [1, 2]]], 1]\nFlatten = [1, 1, 2, 1, 1]\n```\n```\nEX: Input = [[1, [1, [1, [1, 2]]]]]\nFlatten = [1, 1, 2, 1, 1]\n```\n\nEach element can be an integer or a list \uD83D\uDE04\nwhose any element can be also an integer or a list \uD83D\uDE00\nwhose any element can be also an integer or a list \uD83D\uDE10\nwhose any element can be also an integer or a list \uD83D\uDE11.........\n\nI think we got the pattern. \uD83D\uDE05\nThe idea here that we don\'t know **how many levels** we will dive \uD83E\uDD3F or how many nested lists are there.\nThe best **solution** in our case is to use **Recursion**, The hero today.\uD83E\uDDB8\u200D\u2642\uFE0F\n\nWe can make a small recursion function that **takes** a list and **iterate** over its elements if an element is an **integer** then **put** it into our flatten array and if the element is a **list** then call this **recursion** function again with that list \uD83D\uDE00 and\niterate over its elements if an element is an integer then put it into our flatten array and if the element is a list then call this recursion function again with that list \uD83D\uDE10.... \nOk, I will stop now. \uD83D\uDE02\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n\n\n---\n\n\n\n# Approach\n## Recursion\n1. Maintain three variables:\n - Vector `nestedList` for the **original** list of nested integers. \n - Vector `flattenedList` for the **flattened** list of integers.\n - Integer `currentIndex`, to keep track of the current **position** within the `flattenedList`.\n2. Create a **recursive** function called `flatten` that takes a vector of `NestedInteger` as input:\n - **iterate** through the elements in the input `currentList`.\n - If the current element is an **integer** (as determined by `isInteger()`), add it to the `flattenedList` using `getInteger()`.\n - If the current element is a **nested list**, **recursively** call the `flatten` function with the nested list to continue flattening.\n3. In the constructor `NestedIterator`, initialize the `nestedList` and call the `flatten` function to populate the `flattenedList`.\n4. In the `next` function to return the **next** integer from `flattenedList`, **incrementing** `currentIndex` accordingly.\n5. In the `hasNext` function to **check** if there are more integers in the `flattenedList`.\n\n## Complexity\n- **Time complexity:** $O(N)$\nIt takes `N` steps to **flatten** the list since we are **recursively** iterate over it until it is **exhausted** and have no more integers so complexity is `O(N)`.\nWhere `N` is the total number of integers in the list.\n- **Space complexity:** $O(N)$\nSince we are **storing** the integers in a new list so complexity is `O(N)`.\n\n\n---\n\n# Code\n## Recursion\n```C++ []\nclass NestedIterator {\nprivate:\n // The list of NestedInteger elements to be flattened\n vector<NestedInteger> nestedList;\n\n // The flattened list of integers\n vector<int> flattenedList;\n\n // Index to keep track of the current position in the flattenedList\n int currentIndex = 0;\n\n // Recursively flattens the nested list and adds integers to the flattenedList\n void flatten(vector<NestedInteger>& currentList) {\n for (int i = 0; i < currentList.size(); i++) {\n if (currentList[i].isInteger()) {\n flattenedList.push_back(currentList[i].getInteger());\n } else {\n // Recursively flatten nested lists\n flatten(currentList[i].getList());\n }\n }\n }\n\npublic:\n NestedIterator(vector<NestedInteger> &nestedList) {\n this->nestedList = nestedList;\n // Flatten the nestedList during initialization\n flatten(nestedList);\n }\n\n // Returns the next integer in the flattened list\n int next() {\n int number = flattenedList[currentIndex];\n currentIndex++;\n return number;\n }\n\n // Checks if there are more integers in the flattened list\n bool hasNext() {\n return currentIndex < flattenedList.size();\n }\n};\n```\n```Java []\npublic class NestedIterator implements Iterator<Integer> {\n // The list of NestedInteger elements to be flattened\n private List<NestedInteger> nestedList;\n \n // The flattened list of integers\n private List<Integer> flattenedList;\n \n // Index to keep track of the current position in the flattenedList\n private int currentIndex = 0;\n\n public NestedIterator(List<NestedInteger> nestedList) {\n this.nestedList = nestedList;\n this.flattenedList = new ArrayList<>();\n // Flatten the nestedList during initialization\n this.flatten(nestedList);\n }\n\n // Returns the next integer in the flattened list\n @Override\n public Integer next() {\n int number = this.flattenedList.get(currentIndex);\n currentIndex++;\n return number;\n }\n\n // Checks if there are more integers in the flattened list\n @Override\n public boolean hasNext() {\n return currentIndex < flattenedList.size();\n }\n\n // Recursively flattens the nested list and adds integers to the flattenedList\n private void flatten(List<NestedInteger> currentList) {\n for (int i = 0; i < currentList.size(); i++) {\n if (currentList.get(i).isInteger()) {\n flattenedList.add(currentList.get(i).getInteger());\n } else {\n // Recursively flatten nested lists\n flatten(currentList.get(i).getList());\n }\n }\n }\n}\n```\n```Python []\nclass NestedIterator:\n def __init__(self, nestedList):\n # The list of NestedInteger elements to be flattened\n self.nestedList = nestedList\n \n # The flattened list of integers\n self.flattenedList = []\n \n # Index to keep track of the current position in the flattenedList\n self.currentIndex = 0\n\n # Recursively flattens the nested list and adds integers to the flattenedList\n def flatten(currentList):\n for item in currentList:\n if item.isInteger():\n self.flattenedList.append(item.getInteger())\n else:\n # Recursively flatten nested lists\n flatten(item.getList())\n \n # Flatten the nestedList during initialization\n flatten(self.nestedList)\n\n # Returns the next integer in the flattened list\n def next(self):\n number = self.flattenedList[self.currentIndex]\n self.currentIndex += 1\n return number\n\n # Checks if there are more integers in the flattened list\n def hasNext(self):\n return self.currentIndex < len(self.flattenedList)\n```\n\n\n\n\n\n | 52 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || EXPLAINED🔥 | flatten-nested-list-iterator | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n1. **Private Member Variables:**\n\n - **nestedList:** A vector of `NestedInteger` objects that represents the input nested list.\n - **tempList:** A vector of integers used to store the flattened list temporarily.\n - **Index:** An integer that keeps track of the current index when iterating through the `tempList`.\n1. **ans Function:**\n\n - This is a private recursive function used to flatten the nested list.\n - It takes a vector of `NestedInteger` objects as an argument.\n - The function iterates through the `nestedList` and checks each element.\n - If an element is an integer, it\'s added to the `tempList`.\n - If an element is a nested list, the function is called recursively to flatten it.\n1. **Constructor (NestedIterator):**\n\n - This constructor takes a reference to a `vector` of `NestedInteger` objects as input.\n - It initializes the `nestedList` member variable with the input.\n - It calls the `ans` function to flatten the nested list and store the result in `tempList`.\n1. **next Method:**\n\n - This method is used to retrieve the next integer from the flattened list.\n - It returns the integer at the current `Index` in the `tempList` and increments the `Index` to point to the next integer in the list.\n1. **hasNext Method:**\n\n - This method checks if there are more integers in the `tempList` to be processed.\n - It returns `true` if the `Index` is less than the size of `tempList`, indicating that there are more integers to retrieve. Otherwise, it returns `false`.\n1. **Flattening Nested List:**\n\n - The code effectively flattens the nested list structure into a linear list of integers. It uses a recursive approach to traverse nested lists and extract integers.\n1. **Iterator Behavior:**\n\n - The `next` method provides the next integer from the flattened list, while the `hasNext` method checks if there are more integers to be retrieved.\n1. **Overall Usage:**\n\n - The `NestedIterator` class allows for iterating through a nested list and retrieving integers one by one.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass NestedIterator {\nprivate:\n vector<NestedInteger> nestedList; // Stores the input nested list.\n vector<int> tempList; // Temporary list for flattened integers.\n int Index = 0; // Index to track the current position in tempList.\n\n // Recursive function to flatten the nested list.\n void ans(vector<NestedInteger>& nestedList) {\n for (int i = 0; i < nestedList.size(); i++) {\n if (nestedList[i].isInteger()) {\n tempList.push_back(nestedList[i].getInteger()); // Add integers to tempList.\n } else {\n ans(nestedList[i].getList()); // Recursively flatten nested lists.\n }\n }\n }\n\npublic:\n // Constructor that initializes the iterator.\n NestedIterator(vector<NestedInteger> &nestedList) {\n this->nestedList = nestedList; // Initialize the nestedList member variable.\n ans(nestedList); // Flatten the nested list and store it in tempList.\n }\n\n // Method to retrieve the next integer from the flattened list.\n int next() {\n int number = tempList[Index]; // Get the integer at the current index.\n Index++; // Move the index to the next integer.\n return number; // Return the retrieved integer.\n }\n\n // Method to check if there are more integers to retrieve.\n bool hasNext() {\n return (Index < tempList.size()) ? true : false; // Return true if there are more integers in tempList, otherwise false.\n }\n};\n\n```\n\n\n```C []\n#include <stdbool.h>\n\n// Define the structure for NestedInteger\nstruct NestedInteger {\n // Placeholder for NestedInteger structure in C\n};\n\ntypedef struct NestedInteger NestedInteger;\n\n// Define the structure for NestedIterator\nstruct NestedIterator {\n NestedInteger* nestedList; // Stores the input nested list.\n int* tempList; // Temporary list for flattened integers.\n int Index; // Index to track the current position in tempList.\n int tempListSize; // Size of the tempList array.\n};\n\ntypedef struct NestedIterator NestedIterator;\n\n// Function to create a new NestedIterator\nNestedIterator* createNestedIterator(NestedInteger* nestedList, int nestedListSize);\n\n// Function to retrieve the next integer from the flattened list\nint next(NestedIterator* iter);\n\n// Function to check if there are more integers to retrieve\nbool hasNext(NestedIterator* iter);\n\n\n```\n\n\n```Java []\nimport java.util.*;\n\npublic class NestedIterator {\n private List<Integer> tempList;\n private int index;\n\n public NestedIterator(List<NestedInteger> nestedList) {\n tempList = new ArrayList<>();\n index = 0;\n flattenList(nestedList);\n }\n\n public Integer next() {\n return tempList.get(index++);\n }\n\n public boolean hasNext() {\n return index < tempList.size();\n }\n\n private void flattenList(List<NestedInteger> nestedList) {\n for (NestedInteger ni : nestedList) {\n if (ni.isInteger()) {\n tempList.add(ni.getInteger());\n } else {\n flattenList(ni.getList());\n }\n }\n }\n}\n\n\n```\n\n```python3 []\nclass NestedIterator:\n def __init__(self, nestedList):\n self.tempList = []\n self.index = 0\n self.flatten_list(nestedList)\n\n def next(self):\n result = self.tempList[self.index]\n self.index += 1\n return result\n\n def hasNext(self):\n return self.index < len(self.tempList)\n\n def flatten_list(self, nestedList):\n for ni in nestedList:\n if ni.isInteger():\n self.tempList.append(ni.getInteger())\n else:\n self.flatten_list(ni.getList())\n\n\n```\n\n```javascript []\nclass NestedIterator {\n constructor(nestedList) {\n this.tempList = [];\n this.index = 0;\n this.flattenList(nestedList);\n }\n\n next() {\n return this.tempList[this.index++];\n }\n\n hasNext() {\n return this.index < this.tempList.length;\n }\n\n flattenList(nestedList) {\n for (const ni of nestedList) {\n if (ni.isInteger()) {\n this.tempList.push(ni.getInteger());\n } else {\n this.flattenList(ni.getList());\n }\n }\n }\n}\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Python3 Solution | flatten-nested-list-iterator | 0 | 1 | \n```\n# """\n# This is the interface that allows for creating nested lists.\n# You should not implement it, or speculate about its implementation\n# """\n#class NestedInteger:\n# def isInteger(self) -> bool:\n# """\n# @return True if this NestedInteger holds a single integer, rather than a nested list.\n# """\n#\n# def getInteger(self) -> int:\n# """\n# @return the single integer that this NestedInteger holds, if it holds a single integer\n# Return None if this NestedInteger holds a nested list\n# """\n#\n# def getList(self) -> [NestedInteger]:\n# """\n# @return the nested list that this NestedInteger holds, if it holds a nested list\n# Return None if this NestedInteger holds a single integer\n# """\n\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n def flatten(nl):\n ans=[]\n for i in nl:\n if i.isInteger():\n ans.append(i.getInteger())\n else:\n ans.extend(flatten(i.getList())) \n return ans\n self.n=deque(flatten(nestedList)) \n \n def next(self) -> int:\n return self.n.popleft()\n \n def hasNext(self) -> bool:\n return self.n\n\n# Your NestedIterator object will be instantiated and called as such:\n# i, v = NestedIterator(nestedList), []\n# while i.hasNext(): v.append(i.next())\n``` | 3 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Video Solution | Explanation With Drawings | In Depth | Java | C++ | Python 3 | flatten-nested-list-iterator | 1 | 1 | # Intuition, approach, and complexity discussed in detail in video solution\nhttps://youtu.be/2zpPPM6W7IA\n\n# Code\n\nC++\n```\nclass NestedIterator {\n vector<int> flatList;\n int iterator;\npublic:\n NestedIterator(std::vector<NestedInteger>& nestedList) {\n iterator = 0;\n flattenList(nestedList);\n }\n \n void flattenList(std::vector<NestedInteger>& nestedList) {\n for (NestedInteger ele : nestedList) {\n if (ele.isInteger()) {\n flatList.push_back(ele.getInteger());\n } else {\n flattenList(ele.getList());\n }\n }\n }\n \n int next() {\n if (hasNext()) {\n return flatList[iterator++];\n } else {\n return NULL;\n }\n }\n \n bool hasNext() {\n return iterator < flatList.size();\n }\n};\n```\nPython 3\n```\nclass NestedIterator:\n def __init__(self, nestedList):\n self.flatList = []\n self.iterator = 0\n self.flattenList(nestedList)\n \n def flattenList(self, nestedList):\n for ele in nestedList:\n if ele.isInteger():\n self.flatList.append(ele.getInteger())\n else:\n self.flattenList(ele.getList())\n \n def next(self):\n if self.hasNext():\n val = self.flatList[self.iterator]\n self.iterator += 1\n return val\n else:\n return None\n \n def hasNext(self):\n return self.iterator < len(self.flatList)\n```\nJava\n```\npublic class NestedIterator implements Iterator<Integer> {\n List<Integer> flatList = null;\n int iterator;\n public NestedIterator(List<NestedInteger> nestedList) {\n flatList = new ArrayList<>();\n iterator = 0;\n flattenList(nestedList);\n }\n\n private void flattenList(List<NestedInteger> nestedList){\n for(NestedInteger ele : nestedList){\n if(ele.isInteger()){\n flatList.add(ele.getInteger());\n }else{//recurse for the flatten list function\n flattenList(ele.getList());\n }\n }\n }\n\n @Override\n public Integer next() {\n if(hasNext()){\n return flatList.get(iterator++);\n }else{\n return null;\n }\n }\n\n @Override\n public boolean hasNext() {\n return iterator < flatList.size();\n }\n}\n``` | 2 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Recursion, Class pointer to itself | C++, Python | flatten-nested-list-iterator | 0 | 1 | My idea was to use an index to point to the elements in the `nestedList` that\'s passed in, if the current element `idx` points to holds a single integer, than we could just return that.\nBut what are we going to do if the `NestedInteger` that I\'m currently point to does not contain a single integer but holds another nested list?\nThe solution is to use another `NestedIterator` to handle that.\n\n# Implementation\nI use a index `idx` to point to the current position in the `nestedList`, if what I\'m pointing to holds another nested list, I create another `NestedIterator` object, and store it\'s pointer inside `pit`.\nIf `idx` points to a `NestedInteger` which holds a single integer, resets `pit` to `nullptr`, so that we know the `NestedInteger` that `idx` points to only holds a single integer.\n\nWhen `next()` is invoked, it checks if what `idx` points to holds another nested list (by checking if `pit` is `nullptr`), if it holds another nested list, let the `NestedIterator` that `pit` points to handle that, and extract the value for us. (by recursively calling `next()`), else what `idx` points to only holds a single integer, we could just return that.\n\n---\n\n# Code\n<iframe src="https://leetcode.com/playground/J9LZCtAB/shared" frameBorder="0" width="1000" height="500"></iframe> | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
simple python intutive solution | flatten-nested-list-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# """\n# This is the interface that allows for creating nested lists.\n# You should not implement it, or speculate about its implementation\n# """\n#class NestedInteger:\n# def isInteger(self) -> bool:\n# """\n# @return True if this NestedInteger holds a single integer, rather than a nested list.\n# """\n#\n# def getInteger(self) -> int:\n# """\n# @return the single integer that this NestedInteger holds, if it holds a single integer\n# Return None if this NestedInteger holds a nested list\n# """\n#\n# def getList(self) -> [NestedInteger]:\n# """\n# @return the nested list that this NestedInteger holds, if it holds a nested list\n# Return None if this NestedInteger holds a single integer\n# """\n\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n self.idx = 0\n self.res = []\n self.flatten(nestedList)\n\n def flatten(self, nestedList):\n for i in nestedList:\n if i.isInteger():\n self.res.append(i.getInteger())\n else:\n self.flatten(i.getList())\n\n def next(self) -> int:\n if self.hasNext():\n result = self.res[self.idx]\n self.idx += 1\n return result\n\n def hasNext(self) -> bool:\n return self.idx < len(self.res)\n\n \n\n# Your NestedIterator object will be instantiated and called as such:\n# i, v = NestedIterator(nestedList), []\n# while i.hasNext(): v.append(i.next())\n``` | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Simple Python Solution Using `yield` with O(1) space | flatten-nested-list-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPython has built-in iterator support, why not use it?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDefine a Python Iterator using yield. This solution can implicitly handles empty lists. The only issue is that Python lacks support for hasnext() function for iterator. Therefore, I use a naive approach to maintain the total size using a for loop, resulting in another scan of the list.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# """\n# This is the interface that allows for creating nested lists.\n# You should not implement it, or speculate about its implementation\n# """\n#class NestedInteger:\n# def isInteger(self) -> bool:\n# """\n# @return True if this NestedInteger holds a single integer, rather than a nested list.\n# """\n#\n# def getInteger(self) -> int:\n# """\n# @return the single integer that this NestedInteger holds, if it holds a single integer\n# Return None if this NestedInteger holds a nested list\n# """\n#\n# def getList(self) -> [NestedInteger]:\n# """\n# @return the nested list that this NestedInteger holds, if it holds a nested list\n# Return None if this NestedInteger holds a single integer\n# """\nfrom typing import List\n\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n def itr(NL):\n for e in NL:\n if e.isInteger():\n yield e.getInteger()\n else:\n yield from itr(e.getList())\n self.itr = itr(nestedList)\n\n self.sz = 0\n for _ in itr(nestedList):\n self.sz += 1\n \n def next(self) -> int:\n self.sz -= 1\n return next(self.itr)\n \n def hasNext(self) -> bool:\n return self.sz > 0\n\n# Your NestedIterator object will be instantiated and called as such:\n# i, v = NestedIterator(nestedList), []\n# while i.hasNext(): v.append(i.next())\n``` | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Easiest solution in Python | flatten-nested-list-iterator | 0 | 1 | # Intuition\nThere is no real intuition simply following the instructions.\n\n# Code\n```\n# """\n# This is the interface that allows for creating nested lists.\n# You should not implement it, or speculate about its implementation\n# """\n#class NestedInteger:\n# def isInteger(self) -> bool:\n# """\n# @return True if this NestedInteger holds a single integer, rather than a nested list.\n# """\n#\n# def getInteger(self) -> int:\n# """\n# @return the single integer that this NestedInteger holds, if it holds a single integer\n# Return None if this NestedInteger holds a nested list\n# """\n#\n# def getList(self) -> [NestedInteger]:\n# """\n# @return the nested list that this NestedInteger holds, if it holds a nested list\n# Return None if this NestedInteger holds a single integer\n# """\n\nclass NestedIterator:\n def process_element(self, element):\n if element.isInteger():\n return [element.getInteger()]\n element_results = []\n for element_local in element.getList():\n element_results += self.process_element(element_local)\n return element_results\n\n def __init__(self, nestedList: [NestedInteger]):\n self.curr_list = []\n for element in nestedList:\n self.curr_list += self.process_element(element)\n self.idx = 0\n \n def next(self) -> int:\n element = self.curr_list[self.idx]\n self.idx += 1\n return element\n \n def hasNext(self) -> bool:\n return self.idx < len(self.curr_list)\n \n\n# Your NestedIterator object will be instantiated and called as such:\n# i, v = NestedIterator(nestedList), []\n# while i.hasNext(): v.append(i.next())\n``` | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Easy to Understand || c++ || java || python | flatten-nested-list-iterator | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHere\'s a step-by-step explanation of the C++ code\'s approach:\n\nThe NestedIterator constructor takes a vector of NestedInteger as input.\n\nIn the constructor, it pushes all elements of the input list onto the stack in reverse order. This is because we want to process elements in the order they appear when the iterator moves forward.\n\nThe next method simply pops an integer from the top of the stack and returns it.\n\nThe hasNext method is more involved. It checks if the stack is empty. If the stack is not empty, it keeps popping elements and pushing nested lists onto the stack until it finds an integer. This ensures that the iterator is always positioned at the next integer in the flattened list.\n\n# Complexity\n- Time complexity:\nTime complexity: O(N) for the constructor and O(1) for the next method. The hasNext method is O(N) in the worst case.\n\n- Space complexity:\nSpace complexity: O(N) in the worst case for the stack, and O(1) for the rest of the code.\n\n# Code\n```c++ []\nclass NestedIterator {\nprivate:\n stack<NestedInteger> s; // Stack to hold the nested integers\n \npublic:\n NestedIterator(vector<NestedInteger> &nestedList) {\n // Push all elements of the input list onto the stack in reverse order\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n s.push(nestedList[i]);\n }\n }\n \n int next() {\n int result = s.top().getInteger();\n s.pop();\n return result;\n }\n \n bool hasNext() {\n // Keep popping until we find an integer or the stack is empty\n while (!s.empty()) {\n if (s.top().isInteger()) {\n return true;\n }\n vector<NestedInteger> nestedList = s.top().getList();\n s.pop();\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n s.push(nestedList[i]);\n }\n }\n return false;\n }\n};\n```\n```python []\nclass NestedIterator:\n def __init__(self, nestedList):\n self.stack = nestedList[::-1]\n\n def next(self):\n return self.stack.pop().getInteger()\n\n def hasNext(self):\n while self.stack:\n if self.stack[-1].isInteger():\n return True\n self.stack.extend(self.stack.pop().getList()[::-1])\n return False\n\n```\n```java []\npublic class NestedIterator implements Iterator<Integer> {\n private Stack<NestedInteger> stack;\n\n public NestedIterator(List<NestedInteger> nestedList) {\n stack = new Stack<>();\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n stack.push(nestedList.get(i));\n }\n }\n\n @Override\n public Integer next() {\n return stack.pop().getInteger();\n }\n\n @Override\n public boolean hasNext() {\n while (!stack.isEmpty()) {\n if (stack.peek().isInteger()) {\n return true;\n }\n List<NestedInteger> nestedList = stack.pop().getList();\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n stack.push(nestedList.get(i));\n }\n }\n return false;\n }\n}\n\n```\n\n | 29 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
【Video】Give me 10 minutes - How we think about a solution - Python, Javascript, Java, C++ | flatten-nested-list-iterator | 1 | 1 | # Intuition\nUsing stack\n\n---\n\n# Solution Video\n\nhttps://youtu.be/N8QehVXYSc0\n\n\u25A0 Timeline of the video\n`0:04` 2 Keys to solve this question\n`0:18` Explain the first key point\n`0:45` Explain the first key point\n`1:27` Explain the second key point\n`5:44` Coding\n`9:39` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,756\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n\n# Approach\n\n### How we think about a solution\n\nExamples in the description is a little bit easy to understand because they use the same numbers like `[1,1]`, so let\'s see this example.\n\n```\nInput: [[3,2,[4,5]],1,6]\n```\nIn this case output should be `[3,2,4,5,1,6]`.\n\n---\n\n\n\u203B Caution\n\nI will explain how we can sort input list. Real data is not just number, they have more completed structure.\n\nFor example,\n```\nNestedInteger{_integer: 6, _list: []}\n```\n\nI want to focus on how we can sort data, so that\'s why I use simple numbers instead of NestedInteger\n\n---\n\n\n\n\nWe have two difficulties for this quesition\n\n---\n- How can we deal with eariler indices first?\n- How can we deal with nested list?\n---\n\n#### How can we deal with eariler indices first?\n\nThe first thing I came up with in my mind is to use `stack` because it is `Last In First Out` data structure, so it doesn\'t affect order of the other elements if we deal with only the last element in `stack`.\n\nIn that case, point is\n\n---\n\n\u2B50\uFE0F Points\n\nWe should put input list into `stack` with reverse order in the same level.\n\n---\n\nThat\'s because we want to deal with `3` at first, seems like it\'s easy if we have reverse order of input list in `stack`.\n\n### How can we deal with nested list? What is the same level?\n\nFirst of all, ignore the most outside open and close square bracket, so \n\n```\n[[3,2,[4,5]],1,6]\n\u2193\n[3,2,[4,5]],1,6\n```\nIn that case, single list is the same as a single integer.\n\n```\n[3,2,[4,5]],1,6\n\u2191 \u2191\n```\nWe can deal with this single list like `1` or `6`, because just iterating thorugh reversed list one by one then done.\n\nWhen we put the `[3,2,[4,5]],1,6` into `stack`, we should reverse them. In the end,\n\n```\n6,1,[3,2,[4,5]]\n```\n\nLet\'s focus on only `[3,2,[4,5]]`. Ignore the most outside open and close square bracket.\n\n```\n[3,2,[4,5]]\n\u2193\n3,2,[4,5]\n```\n\nThis is the same story. we can deal with `[4,5]` as the same level list `3` or `2`, so when we put the `3,2,[4,5]` into `stack`, we should reverse them.\n\nIn that case, we put like this.\n\n```\n[4,5],2,3\n```\n\nBut we have still list `[4,5]`, so when we find list, just reverse them before we put the list into stack.\n\n```\n5,4,2,3\n```\n\nIn the end, If we have all input numbers in `stack`, the order of the numbers should be\n\n```\n6,1,5,4,2,3\n```\n\nThat is completely opposite of output `[3,2,4,5,1,6]`. All we have to do is to pop numbers from the end by prepared function `getInteger() `.\n\n---\n\n\u2B50\uFE0F Points\n\n- Reverse input list and put them into stack\n- When we find the nested list, reverse them and put into stack\n\n---\n\n**Algorithm Overview:**\n\nThe code implements a nested list iterator using the provided `NestedInteger` class. The iterator is initialized with a nested list, and it provides two methods: `next` to retrieve the next integer in the flattened list, and `hasNext` to check if there are more integers to retrieve.\n\nThe code uses a stack to manage the elements in the nested list in a flattened order. The stack stores `NestedInteger` objects, and it follows a depth-first traversal of the nested structure.\n\n**Detailed Explanation:**\n\n1. Initialize an empty stack to hold `NestedInteger` objects.\n\n2. In the `__init__` constructor:\n - Iterate over the elements of the input `nestedList` in reverse order (from the last element to the first element).\n - For each element in `nestedList`:\n - Append the element to the `stack`. This order ensures that the first element in `nestedList` will be at the top of the stack.\n\n3. In the `next` method:\n - Pop the last `NestedInteger` object from the `stack`.\n - Call the `getInteger` method on the popped object to retrieve the integer value.\n - Return the integer value.\n\n4. In the `hasNext` method:\n - While the `stack` is not empty:\n - Get the last `NestedInteger` object from the `stack` (without removing it) and store it in the `current` variable.\n - Check if `current` is an integer using the `isInteger` method. If it is, return `True` because there is an integer to retrieve.\n - If `current` is not an integer, it\'s a nested list:\n - Pop `current` from the `stack`.\n - Get the nested list using the `getList` method on `current`.\n - Iterate over the elements of the nested list in reverse order and push them onto the `stack`. This ensures that the elements from the nested list will be processed before other elements.\n - If the `stack` becomes empty and no integer is found, return `False`.\n\n5. When you create a `NestedIterator` object and call its methods to retrieve elements, it will follow the logic above to flatten the nested list and return the elements in the correct order.\n\nThe key idea is to use a stack to manage the traversal of the nested list, pushing nested lists onto the stack and popping them when they are fully processed to ensure that elements are processed in the correct order during iteration.\n\n\n\n---\n\n\n\n\n# Complexity\n- Time complexity:\n - init: $$O(N)$$\n - initializes the iterator by adding all elements from the nestedList to the stack in reverse order. This operation takes $$O(N)$$ time, where N is the total number of elements in the nested list.\n - next: $$O(1)$$\n - hasNext: $$O(N)$$\n - The hasNext method involves a while loop that pops elements from the stack until an integer is found or the stack becomes empty. In the worst case, this could take $$O(N)$$ time, where N is the number of elements in the nested list.\n\n\n\n- Space complexity: $$O(N)$$\nIn the worst case, we have all numbers in `stack`\n\n\n```python []\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n self.stack = []\n # Add the nestedList to the stack in reverse order\n for i in range(len(nestedList) - 1, -1, -1):\n self.stack.append(nestedList[i]) \n \n def next(self) -> int:\n return self.stack.pop().getInteger() \n \n def hasNext(self) -> bool:\n # Flatten the list by popping elements from the stack until we find an integer\n while self.stack:\n current = self.stack[-1]\n if current.isInteger():\n return True\n\n # If it\'s a list, pop it and push its elements in reverse order\n self.stack.pop()\n nested_list = current.getList()\n for i in range(len(nested_list) - 1, -1, -1):\n self.stack.append(nested_list[i])\n\n return False \n```\n```javascript []\nclass NestedIterator {\n constructor(nestedList) {\n this.stack = [];\n for (let i = nestedList.length - 1; i >= 0; i--) {\n this.stack.push(nestedList[i]);\n }\n }\n\n next() {\n return this.stack.pop().getInteger();\n }\n\n hasNext() {\n while (this.stack.length > 0) {\n const current = this.stack[this.stack.length - 1];\n if (current.isInteger()) {\n return true;\n }\n this.stack.pop();\n const nestedList = current.getList();\n for (let i = nestedList.length - 1; i >= 0; i--) {\n this.stack.push(nestedList[i]);\n }\n }\n return false;\n }\n}\n```\n```java []\npublic class NestedIterator implements Iterator<Integer> {\n private Stack<NestedInteger> stack;\n \n public NestedIterator(List<NestedInteger> nestedList) {\n stack = new Stack<>();\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n stack.push(nestedList.get(i));\n } \n }\n\n @Override\n public Integer next() {\n return stack.pop().getInteger(); \n }\n\n @Override\n public boolean hasNext() {\n while (!stack.isEmpty()) {\n NestedInteger current = stack.peek();\n if (current.isInteger()) {\n return true;\n }\n stack.pop();\n List<NestedInteger> nestedList = current.getList();\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n stack.push(nestedList.get(i));\n }\n }\n return false; \n }\n}\n```\n```C++ []\nclass NestedIterator {\nprivate: \n stack<NestedInteger> stack;\n\npublic:\n NestedIterator(vector<NestedInteger> &nestedList) {\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n stack.push(nestedList[i]);\n } \n }\n \n int next() {\n int result = stack.top().getInteger();\n stack.pop();\n return result; \n }\n \n bool hasNext() {\n while (!stack.empty()) {\n NestedInteger current = stack.top();\n if (current.isInteger()) {\n return true;\n }\n stack.pop();\n vector<NestedInteger> nestedList = current.getList();\n for (int i = nestedList.size() - 1; i >= 0; i--) {\n stack.push(nestedList[i]);\n }\n }\n return false; \n }\n};\n```\n\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/constrained-subsequence-sum/solutions/4191844/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/KuMkwvvesgo\n\n\u25A0 Timeline of the video\n`0:04` Explain a few basic idea\n`3:21` What data we should put in deque?\n`5:10` Demonstrate how it works\n`13:27` Coding\n`16:03` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/backspace-string-compare/solutions/4184137/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/YBt2dPL6z5o\n\n\u25A0 Timeline of the video\n`0:04` Stack solution code\n`0:23` Explain key point with O(1) space\n`1:12` Consider 4 cases\n`3:14` Coding\n`7:20` Time Complexity and Space Complexity | 16 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Simple to understand Python Solution | flatten-nested-list-iterator | 0 | 1 | # Intuition\nRecursion(DFS) and keeping track of index in flattened list\n\n# Approach\n**1) Flatten part**\n->lets say we have flattened_list = []\nyou want to flatten [4,[1,2]]\nwe can see that 4 is not a list but an integer so we can simply\nappend it into flattened_list\n\n->Now we are left with [1,2] but [1,2] itself is a list so we need to flatten this further so now we recursively pass [1,2] into our flatten function(see my code) and do the same thing as we did before that is, we check each element of [1,2] and we see 1 is not a list so we add it in flattened_list and so on...\n\n**TIP** -> Try to visualise this using pen and paper to make it \n clear (maybe you want to try more examples)\n\n-> at the end the flattened_list will be as:\n[4,1,2] that is your answer\n\n->This was the core of this question.\n\n**2) Format of this problem**\n-> just look at my code and try to understand,at first i struggled to understand that what this problem is trying to do and how but after a while I got it worked\n\n\n\n\n# Complexity\n- Time complexity: **O(N)**\n-> As flatten function takes O(N) everything else takes\n O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(N)**\n-> 2 lists are used \n self.l = O(N) + self.x = O(N)\n \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# """\n# This is the interface that allows for creating nested lists.\n# You should not implement it, or speculate about its implementation\n# """\n#class NestedInteger:\n# def isInteger(self) -> bool:\n# """\n# @return True if this NestedInteger holds a single integer, rather than a nested list.\n# """\n#\n# def getInteger(self) -> int:\n# """\n# @return the single integer that this NestedInteger holds, if it holds a single integer\n# Return None if this NestedInteger holds a nested list\n# """\n#\n# def getList(self) -> [NestedInteger]:\n# """\n# @return the nested list that this NestedInteger holds, if it holds a nested list\n# Return None if this NestedInteger holds a single integer\n# """\n\nclass NestedIterator:\n\n def __init__(self, nestedList: [NestedInteger]):\n self.l = nestedList\n\n self.x = []\n self.flatten(self.l)\n self.n = len(self.x)\n self.idx = -1\n \n\n\n def flatten(self,z):\n for i in z:\n if i.isInteger():\n self.x.append(i.getInteger())\n\n else:\n self.flatten(i.getList())\n\n\n def next(self) -> int:\n if self.hasNext():\n a = self.x[self.idx + 1]\n self.idx += 1\n return a\n\n \n\n \n def hasNext(self) -> bool:\n return self.idx + 1 < self.n\n \n\n \n \n\n# Your NestedIterator object will be instantiated and called as such:\n# i, v = NestedIterator(nestedList), []\n# while i.hasNext(): v.append(i.next())\n```\nThis is my first solution post,I hope you guys understood it!\nKeep coding !!!! \n**THANK YOU**\n | 0 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Lazy Recursive Solution w/ Flat Generator | flatten-nested-list-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse generators to perform lazy flattening of a large and deep `nestedList`. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse `yield` to produce integers and `yield from` to produce integers from a nested generator. `yield from` is applied recursively, as it is yielding from the generator of the current list, which could be generating from another list. \n\nSince Python generators do not have an equivalent to `hasNext()` we instead check for the `StopIteration` error to determine if the generator has been exhausted.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$\\mathcal{O}(1)$$ as no iteration or traversal is done ahead of time. Obviously $$\\mathcal{O}(n)$$ to read and output all elements in the input. The main loop here is in `flat_generator` but when a `yield` occurs, Python blocks the loop until `next` is called at which point it will run until the next `yield`. This happpens recursively too, as `yield from` will go deeper into the nested generator. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$\\mathcal{O}(1)$$ as only a generator object and an integer are stored. The input list should not count as extra memory as we are only reading from it. \n\n# Code\n```\n# """\n# This is the interface that allows for creating nested lists.\n# You should not implement it, or speculate about its implementation\n# """\n#class NestedInteger:\n# def isInteger(self) -> bool:\n# """\n# @return True if this NestedInteger holds a single integer, rather than a nested list.\n# """\n#\n# def getInteger(self) -> int:\n# """\n# @return the single integer that this NestedInteger holds, if it holds a single integer\n# Return None if this NestedInteger holds a nested list\n# """\n#\n# def getList(self) -> [NestedInteger]:\n# """\n# @return the nested list that this NestedInteger holds, if it holds a nested list\n# Return None if this NestedInteger holds a single integer\n# """\n\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n def flat_generator(nL):\n for nI in nL:\n if nI.isInteger():\n yield nI.getInteger()\n else:\n yield from flat_generator(nI.getList())\n \n self.generator = flat_generator(nestedList)\n\n def next(self) -> int:\n return self.nextInteger\n \n def hasNext(self) -> bool:\n try:\n self.nextInteger = next(self.generator)\n return True\n except StopIteration:\n return False\n\n# Your NestedIterator object will be instantiated and called as such:\n# i, v = NestedIterator(nestedList), []\n# while i.hasNext(): v.append(i.next())\n``` | 0 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Cheat solution with Generators in Python | flatten-nested-list-iterator | 0 | 1 | # Intuition\nGenerators in Python itself works very similar to iterators, so one can just reuse it. In case of flatten list - just yield the elements from it, in case of nested structure - call the generator recursively.\nTo support hasNext method, one can take the next element in advance, to check if it exists.\n\n# Complexity\n- Time complexity:\n$$O(n)$$, each operation takes constant time, number of operations is linear\n\n- Space complexity:\n$$O(1)$$ in case of shallow nested list. $$O(n)$$ in case of deep nested structure (to maintain recursive call stack) \n\n# Code\n```\ndef make_gen(nestedList: [NestedInteger]):\n for elem in nestedList:\n if elem.isInteger():\n yield elem.getInteger()\n else:\n for sub_elem in make_gen(elem.getList()):\n yield sub_elem\n\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n self.gen = make_gen(nestedList)\n try:\n self.cur = next(self.gen)\n except:\n self.cur = None\n \n def next(self) -> int:\n result = self.cur\n try:\n self.cur = next(self.gen)\n except:\n self.cur = None\n return result\n \n def hasNext(self) -> bool:\n return self.cur is not None\n\n``` | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
341: Time 90.75%, Solution with step by step explanation | flatten-nested-list-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe NestedIterator class implements an iterator to flatten a nested list of integers. It has three methods:\n\n1. __init__(self, nestedList: List[NestedInteger]): Initializes the iterator with the nested list nestedList. It creates a deque to store the flattened integers, and calls the addInteger function to add integers to the deque.\n\n2. next(self) -> int: Returns the next integer in the nested list. It removes and returns the leftmost element from the deque using the popleft method.\n\n3. hasNext(self) -> bool: Returns true if there are still some integers in the nested list and false otherwise. It checks if the deque is not empty using the bool function.\n\n4. addInteger(self, nestedList: List[NestedInteger]) -> None: Adds integers to the deque. It takes a nested list as input, and iterates over its elements. If an element is an integer, it adds it to the deque using the append method. If an element is a list, it recursively calls the addInteger function to add integers to the deque.\n\n# Complexity\n- Time complexity:\n90.75%\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass NestedIterator:\n def __init__(self, nestedList: List[NestedInteger]):\n # Initialize a deque to store the flattened integers\n self.q = collections.deque()\n # Call the addInteger function to add integers to the deque\n self.addInteger(nestedList)\n\n def next(self) -> int:\n # Remove and return the leftmost element from the deque\n return self.q.popleft()\n\n def hasNext(self) -> bool:\n # Return True if the deque is not empty, False otherwise\n return bool(self.q)\n\n def addInteger(self, nestedList: List[NestedInteger]) -> None:\n # Iterate over the elements in the nestedList\n for ni in nestedList:\n # If the element is an integer, add it to the deque\n if ni.isInteger():\n self.q.append(ni.getInteger())\n # If the element is a list, recursively call the addInteger function to add integers to the deque\n else:\n self.addInteger(ni.getList())\n\n``` | 8 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
easy C++/Python recursion based on array vs queue|| 3ms Beats 94.83% | flatten-nested-list-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse recursion. Divide & conquer!\nFirst appeoach uses vector, second C++ solution uses queue.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet\'s see how the recursion flatten function `f` works. Consider the nestedList \n`[[],[1, [2,[3]]],[],[3]]` . There are some empty lists.\n```\nEnter the list\nEnter the list\nAdding int 1 to array\nEnter the list\nAdding int 2 to array\nEnter the list\nAdding int 3 to array\nEnter the list\nEnter the list\nAdding int 3 to array\n```\nAt final, `array=[1,2,3,3]`.\n\n1. The code begins with a comment block that describes the interface NestedInteger. It outlines the methods provided by the interface:\n\n `isInteger()`: Returns true if the NestedInteger holds a single integer, false if it holds a nested list.\n`getInteger()`: Returns the integer value if the NestedInteger holds a single integer (undefined behavior if it\'s a nested list).\n`getList()`: Returns a reference to the nested list if the NestedInteger holds a nested list (undefined behavior if it\'s a single integer).\n2. The `NestedIterator` class is defined:\n\nIt has a private member `array` of type `vector<int>` to store the flattened list of integers.\nIt has a private member `index` initialized to `-1` to keep track of the current position in the array.\n3. The class has a private member function `f` that is a recursive function to flatten the nested lists. It takes a reference to a vector of NestedInteger as an argument and processes each element:\n\nIf an element is an integer, it adds that integer to the array and prints a message indicating the addition.\nIf an element is a nested list, it calls itself recursively to process the nested list and prints a message indicating that it\'s entering the list.\n4. The class constructor `NestedIterator` takes a reference to a vector of `NestedInteger` called nestedList as its argument. It calls the `f` function to flatten the nested list and initializes `index` to 0, indicating that it\'s ready to iterate over the array.\n\n5. The `next` method returns the next integer from the `array` and increments the `index`.\n\n6. The `hasNext` method checks if there are more integers in the array by comparing the current `index` with the size of the array. It returns true if there are more integers and false if the end of the array has been reached.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`NestedIterator` class primarily depends on the recursive flattening process in the `f` function, which has a time complexity of $O(N)$. The next and hasNext methods have $O(1)$ time complexity \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(N)$\n# Code runtime 3ms Beats 94.83%\n```\n/**\n * // This is the interface that allows for creating nested lists.\n * // You should not implement it, or speculate about its implementation\n * class NestedInteger {\n * public:\n * // Return true if this NestedInteger holds a single integer, rather than a nested list.\n * bool isInteger() const;\n *\n * // Return the single integer that this NestedInteger holds, if it holds a single integer\n * // The result is undefined if this NestedInteger holds a nested list\n * int getInteger() const;\n *\n * // Return the nested list that this NestedInteger holds, if it holds a nested list\n * // The result is undefined if this NestedInteger holds a single integer\n * const vector<NestedInteger> &getList() const;\n * };\n */\n\nclass NestedIterator {\n vector<int> array;\n int index=-1;\n void f(const vector<NestedInteger> &nestedList){\n for(auto& L: nestedList){\n if (L.isInteger()) array.push_back(L.getInteger());\n else f(L.getList()); \n }\n }\npublic:\n NestedIterator(vector<NestedInteger> &nestedList) {\n f(nestedList);\n index=0;\n }\n \n int next() {\n return array[index++]; \n }\n \n bool hasNext() {\n return index<array.size();\n }\n};\n\n/**\n * Your NestedIterator object will be instantiated and called as such:\n * NestedIterator i(nestedList);\n * while (i.hasNext()) cout << i.next();\n */\n```\n# Python solution\n```\nlass NestedIterator:\n array=[]\n index=-1\n \n def __init__(self, nestedList: [NestedInteger]):\n def f(nestedList):\n for L in nestedList:\n if L.isInteger(): self.array.append(L.getInteger())\n else: f(L.getList())\n self.array.clear()\n f(nestedList)\n self.index=0\n \n def next(self) -> int:\n self.index+=1\n return self.array[self.index-1]\n \n def hasNext(self) -> bool:\n return self.index<len(self.array)\n```\n# C++ code using queue also runtime 3ms Beats 94.83%\n```\nclass NestedIterator {\npublic:\n queue<int> q;\n\n void f(const vector<NestedInteger> &nestedList){\n for(auto& L: nestedList){\n if (L.isInteger()) q.push(L.getInteger());\n else f(L.getList()); \n }\n }\n\n NestedIterator(vector<NestedInteger> &nestedList) {\n f(nestedList);\n }\n \n int next() {\n int x=q.front();\n q.pop();\n return x; \n }\n \n bool hasNext() {\n return !q.empty();\n }\n};\n``` | 7 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
[Python] Generator Solution with Explanation | flatten-nested-list-iterator | 0 | 1 | ### Introduction\n\nGiven an unknown implementation of a nested list structure containing integer values, design an iterator as a wrapper for the nested list structure which allows for 1) checking if a next value exists, and 2) obtaining of the next value in the iteration.\n\nI\'d just like to note that the type hinting for the Python version of the `NestedIterator` class (Py3 at least) isn\'t written very well; I had to resort to peeking at the data structure of the unknown `NestedInteger` class to get an idea of what we were dealing with behind the scenes. This is a big no-no for interviews especially since it\'s explicitly stated that the implementation of `NestedInteger` should remain unknown to us; however, this was the only way forward for me.\n\nI have re-written the type-hinting for `nestedList` in `__init__()` from `[NestedInteger]` to `List[NestedInteger]` (which btw makes no sense to me; why would you not wrap everything into one `NestedInteger` object and pass that to `NestedIterator` instead); hopefully this helps anyone who stumbles onto the same problem.\n\n---\n\n### Explanation\n\nThere are many possible solutions; generator objects are unique (I think) to Python so this is the implementation I am going with. The benefit of generator objects is that **we are not required to store the entire (nested) list in memory and access it index-wise**; rather, the generator object allows us to step through each object in the iteration manually. This **saves on memory without compromising the speed at which we are able to iterate through the nested list structure**.\n\nFor more information on generator objects, I think [this article](https://www.programiz.com/python-programming/generator) is a good start.\n\n---\n\n### Implementation\n\n```python\nclass NestedIterator:\n def __init__(self, nestedList: List[NestedInteger]):\n def get(currList: List[NestedInteger]) -> Generator[int, None, None]:\n """\n Generator function to iterate through all nested NestedInteger objects and return its integer value.\n :param currList: The current (nested) list of NestedIntegers to iterate through.\n :yields: The integer value of the current NestedInteger in the iteration.\n """\n for nestedInteger in currList:\n if nestedInteger.isInteger(): # nestedInteger has a single integer value\n yield nestedInteger.getInteger()\n else: # nestedInteger is a list of NestedIntegers\n yield from get(nestedInteger.getList())\n self.generator = get(nestedList) # Initialise the generator object with the given NestedInteger list\n self.nextInteger = next(self.generator, None) # Obtain the next (first) NestedInteger pre-emptively\n \n def next(self) -> int:\n result = self.nextInteger # store the current NestedInteger integer value\n self.nextInteger = next(self.generator, None) # Obtain the next NestedInteger pre-emptively\n return result\n \n def hasNext(self) -> bool:\n return self.nextInteger is not None\n```\n\n**TC: O(1)** for all functions, since we are stepping through the iteration manually.\n**SC: O(h)**, where `h` is the maximum depth of the nested list structure, due to implicit stack space used by the generator function.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 52 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Python 3 stack with memory-efficient iterator and lazy evaluation | flatten-nested-list-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nWe can use a stack to manage iterators for each level of nested lists. The `hasNext` method looks at the top iterator on the stack and tries to fetch the next element. If it\'s an integer, `hasNext` stores it for the next method to return. If it\'s another nested list, an iterator for that list is pushed onto the stack. If the iterator is exhausted, it\'s popped off the stack, effectively moving back to the parent list. This way, the nested list is "flattened" lazily, one element at a time, only when requested by the next method.\n\nWe\'ll use Python\'s iterator protocol which provides the following advantages: \n\n* Memory-efficient: Only flattens elements on-the-fly.\n* Lazy evaluation: Doesn\'t do any work until you ask for the next element.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* We maintain a stack of iterators. Each iterator corresponds to a level of nested lists.\n* In the `__init__()` method, we initialize the stack with the iterator for the outermost list.\n* In the `hasNext()` method, we loop through the stack to find the next integer. If we encounter a nested list, we put its iterator onto the stack and continue.\n* We use Python\'s `next()` function and handle the StopIteration exception to seamlessly iterate through each list.\n* We store the next integer value in `self.next_val` so that our `next()` method can return it later.\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(D)$$, where $$D$$ is the maximum depth of nested lists. This is because, at any one time, the stack only needs to store iterators for each level of nested lists, not for every individual element.\n\n# Code\n```\nclass NestedIterator:\n def __init__(self, nestedList: [NestedInteger]):\n self.stack = []\n self.stack.append(iter(nestedList))\n \n def next(self) -> int:\n # Should be called only if hasNext() is True\n return self.next_val\n \n def hasNext(self) -> bool:\n while self.stack:\n try:\n # Try to get the next element from the top iterator in the stack\n elem = next(self.stack[-1])\n except StopIteration:\n # The top iterator is exhausted, remove it from stack\n self.stack.pop()\n continue\n \n if elem.isInteger():\n self.next_val = elem.getInteger()\n return True\n else:\n self.stack.append(iter(elem.getList()))\n \n return False\n```\n### Additional explanation regarding how the iterator works: \n\nThe `StopIteration` exception is thrown when the `next()` function exhausts all the items in the iterator. In Python, an iterator object must implement two methods, `__iter__()` and `__next__()`. The `__next__()` method returns the next value from the iterator. When there are no more items to return, it should raise `StopIteration`.\n\nSo here\'s what happens: \n\n1. `self.stack[-1]` retrieves the iterator at the top of the stack, which is meant to traverse the current nested list being processed.\n\n2. `next(self.stack[-1])` attempts to fetch the next element from this iterator.\n\n3. If this iterator still has elements, `next(self.stack[-1])` will return the next element, and no exception is thrown.\n\n4. If the iterator has no more elements to return (i.e., we\'ve reached the end of the current nested list), `next(self.stack[-1])` will raise a `StopIteration` exception.\n\nWhen `StopIteration` is caught, the code removes the exhausted iterator from the stack (`self.stack.pop()`), essentially moving the focus back to the parent list (if any). The continue statement restarts the while-loop, allowing the algorithm to proceed with the next iterator in the stack.\n\n\n | 3 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
🔥 Optimizing Nested List Iteration: Three Approaches for Efficient Flattening || Mr. Robot | flatten-nested-list-iterator | 1 | 1 | \n# Flattening Nested Lists: Exploring the "NestedIterator" Class \u2753\n---\n## \uD83D\uDCA1Approach 1: Using Stack\n\n### \u2728Explanation\n\nThe `NestedIterator` class is a handy utility for dealing with nested lists in C++. This blog post dives into how this class can be used to efficiently flatten nested lists, making it easier to work with nested data structures.\n\nThe `NestedIterator` class is an excellent example of a practical data structure that simplifies working with nested lists of integers.\n\n### \uD83D\uDCDDDry Run\n\nTo illustrate the power of the `NestedIterator` class, let\'s consider an example:\n\nSuppose we have the following nested list:\n\n```\n[[1, 2], [3], [4, 5]]\n```\n\nThe `NestedIterator` class allows us to traverse this list and access each integer one by one.\n\n### \uD83D\uDD0DEdge Cases\n\nThe `NestedIterator` class can handle various scenarios involving nested lists, including cases with irregular nesting and empty lists.\n\n## \uD83D\uDD78\uFE0FComplexity Analysis\n\n- **Time Complexity**: Accessing the next integer is a constant-time operation, O(1), which is very efficient.\n- **Space Complexity**: The space complexity is O(n), where n is the total number of integers in the nested lists.\n\n## \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes \n```cpp []\n\nclass NestedIterator {\nprivate:\n stack<NestedInteger> nodes;\n\npublic:\n NestedIterator(vector<NestedInteger> &nestedList) {\n int size = nestedList.size();\n for (int i = size - 1; i >= 0; --i) {\n nodes.push(nestedList[i]);\n }\n }\n\n int next() {\n int result = nodes.top().getInteger();\n nodes.pop();\n return result;\n }\n\n bool hasNext() {\n while (!nodes.empty()) {\n NestedInteger curr = nodes.top();\n if (curr.isInteger()) {\n return true;\n }\n\n nodes.pop();\n vector<NestedInteger> &adjs = curr.getList();\n int size = adjs.size();\n for (int i = size - 1; i >= 0; --i) {\n nodes.push(adjs[i]);\n }\n }\n\n return false;\n }\n};\n```\n\n\n```java []\n\npublic class NestedIterator {\n private Stack<NestedInteger> nodes;\n\n public NestedIterator(List<NestedInteger> nestedList) {\n nodes = new Stack<>();\n int size = nestedList.size();\n for (int i = size - 1; i >= 0; i--) {\n nodes.push(nestedList.get(i));\n }\n }\n\n public int next() {\n NestedInteger current = nodes.pop();\n return current.getInteger();\n }\n\n public boolean hasNext() {\n while (!nodes.isEmpty()) {\n NestedInteger current = nodes.peek();\n if (current.isInteger()) {\n return true;\n }\n nodes.pop();\n List<NestedInteger> adjs = current.getList();\n int size = adjs.size();\n for (int i = size - 1; i >= 0; i--) {\n nodes.push(adjs.get(i));\n }\n }\n return false;\n }\n}\n```\n\n\n```python []\n\nclass NestedIterator:\n def __init__(self, nestedList: List[NestedInteger]):\n self.nodes = list(reversed(nestedList))\n \n def next(self) -> int:\n return self.nodes.pop().getInteger()\n\n def hasNext(self) -> bool:\n while self.nodes:\n curr = self.nodes[-1]\n if curr.isInteger():\n return True\n self.nodes.pop()\n self.nodes.extend(reversed(curr.getList()))\n return False\n```\n\n```csharp []\n\npublic class NestedIterator {\n private Stack<NestedInteger> nodes;\n\n public NestedIterator(IList<NestedInteger> nestedList) {\n nodes = new Stack<NestedInteger>();\n int size = nestedList.Count;\n for (int i = size - 1; i >= 0; i--) {\n nodes.Push(nestedList[i]);\n }\n }\n\n public int Next() {\n NestedInteger current = nodes.Pop();\n return current.GetInteger();\n }\n\n public bool HasNext() {\n while (nodes.Count > 0) {\n NestedInteger current = nodes.Peek();\n if (current.IsInteger()) {\n return true;\n }\n nodes.Pop();\n List<NestedInteger> adjs = new List<NestedInteger>(current.GetList()); // Explicit cast here\n int size = adjs.Count;\n for (int i = size - 1; i >= 0; i--) {\n nodes.Push(adjs[i]);\n }\n }\n return false;\n }\n}\n\n```\n\n```javascript []\n\nclass NestedIterator {\n constructor(nestedList) {\n this.nodes = [];\n for (let i = nestedList.length - 1; i >= 0; i--) {\n this.nodes.push(nestedList[i]);\n }\n }\n\n next() {\n return this.nodes.pop().getInteger();\n }\n\n hasNext() {\n while (this.nodes.length > 0) {\n const current = this.nodes[this.nodes.length - 1];\n if (current.isInteger()) {\n return true;\n }\n this.nodes.pop();\n const adjs = current.getList();\n for (let i = adjs.length - 1; i >= 0; i--) {\n this.nodes.push(adjs[i]);\n }\n }\n return false;\n }\n}\n```\n---\n\n## \uD83D\uDCA1Approach 2: Iterating with a Queue\n\n### \u2728Explanation\nIn this approach, we use a queue to efficiently traverse the nested list and extract integers when needed. The idea is to flatten the nested structure so that we can easily retrieve integers one by one.\n\n1. We initialize a queue, `qIntegers`, to store integers.\n\n2. In the constructor, we iterate through the input `nestedList`. For each element, we check whether it\'s an integer using `niIt.isInteger()`. If it\'s an integer, we push it onto the queue. If it\'s a nested list, we create a new `NestedIterator` for that nested list, effectively flattening it recursively.\n\n3. The `next` function simply dequeues the next integer from `qIntegers` and returns it.\n\n4. The `hasNext` function checks if there are any integers left in the queue, indicating whether there\'s more data to process.\n\nThis approach is memory-efficient as we don\'t immediately flatten the entire list, saving space by processing elements on-demand.\n\n### \uD83D\uDCDDDry Run\nLet\'s illustrate this approach with a dry run example:\n\nSuppose we have the following nested list: `[[1, 2], [3], [4, 5]]`.\n\n1. The `NestedIterator` constructor is called with this list. Initially, the `qIntegers` is empty.\n\n2. We start iterating through the nested list:\n - For the first nested list `[1, 2]`, we push `1` and `2` onto the `qIntegers`.\n - For the second list `[3]`, we push `3`.\n - For the third list `[4, 5]`, we push `4` and `5`.\n\n3. The `qIntegers` now contains `[1, 2, 3, 4, 5]`.\n\n4. Calling `next` will dequeue and return `1`, and so on.\n\n5. Calling `hasNext` will return `true` until all elements are processed.\n\n### \uD83D\uDD0DEdge Cases\nThis approach handles various nested structures, including empty lists and lists with both integers and nested lists.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: \n - The constructor takes O(N) time, where N is the total number of elements in the nested list.\n - The `next` and `hasNext` operations are O(1) since they involve dequeuing from the queue.\n- Space Complexity: O(N) for the `qIntegers` queue, where N is the total number of integers in the nested list.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes \n```cpp []\nqueue<int> qIntegers;\n\nclass NestedIterator {\npublic:\n NestedIterator(vector<NestedInteger> &nestedList) {\n for (auto& niIt : nestedList) {\n if (niIt.isInteger()) \n qIntegers.push(niIt.getInteger());\n else\n NestedIterator(niIt.getList());\n }\n }\n \n int next() {\n int nextInt = qIntegers.front();\n qIntegers.pop();\n return nextInt;\n }\n \n bool hasNext() {\n return !qIntegers.empty();\n }\n};\n```\n\n```java []\nimport java.util.LinkedList;\nimport java.util.List;\nimport java.util.Queue;\n\npublic class NestedIterator {\n private Queue<Integer> qIntegers = new LinkedList<>();\n\n public NestedIterator(List<NestedInteger> nestedList) {\n for (NestedInteger niIt : nestedList) {\n if (niIt.isInteger()) {\n qIntegers.offer(niIt.getInteger());\n } else {\n NestedIterator nested = new NestedIterator(niIt.getList());\n while (nested.hasNext()) {\n qIntegers.offer(nested.next());\n }\n }\n }\n }\n\n public Integer next() {\n return qIntegers.poll();\n }\n\n public boolean hasNext() {\n return !qIntegers.isEmpty();\n }\n}\n```\n\n\n```python []\nfrom collections import deque\n\nclass NestedIterator:\n def __init__(self, nestedList):\n self.qIntegers = deque()\n for niIt in nestedList:\n if niIt.isInteger():\n self.qIntegers.append(niIt.getInteger())\n else:\n nested = NestedIterator(niIt.getList())\n while nested.hasNext():\n self.qIntegers.append(nested.next())\n\n def next(self):\n return self.qIntegers.popleft()\n\n def hasNext(self):\n return len(self.qIntegers) > 0\n```\n\n\n```csharp []\nusing System.Collections.Generic;\n\npublic class NestedIterator {\n private Queue<int> qIntegers = new Queue<int>();\n\n public NestedIterator(IList<NestedInteger> nestedList) {\n foreach (var niIt in nestedList) {\n if (niIt.isInteger()) {\n qIntegers.Enqueue(niIt.getInteger());\n } else {\n NestedIterator nested = new NestedIterator(niIt.getList());\n while (nested.hasNext()) {\n qIntegers.Enqueue(nested.next());\n }\n }\n }\n }\n\n public int Next() {\n return qIntegers.Dequeue();\n }\n\n public bool HasNext() {\n return qIntegers.Count > 0;\n }\n}\n```\n\n\n```javascript []\nclass NestedIterator {\n constructor(nestedList) {\n this.qIntegers = [];\n for (const niIt of nestedList) {\n if (niIt.isInteger()) {\n this.qIntegers.push(niIt.getInteger());\n } else {\n const nested = new NestedIterator(niIt.getList());\n while (nested.hasNext()) {\n this.qIntegers.push(nested.next());\n }\n }\n }\n }\n\n next() {\n return this.qIntegers.shift();\n }\n\n hasNext() {\n return this.qIntegers.length > 0;\n }\n}\n```\n---\n\n# \uD83D\uDCA1 Approach 3: Recursive Depth-First Search (DFS)\n\n## \u2728 Explanation\nThis approach takes advantage of a recursive Depth-First Search (DFS) algorithm to flatten the nested list. It starts with an empty vector, and as it traverses the nested list recursively, it appends integers to the vector. The `next` and `hasNext` methods then operate on this vector.\n\n## \uD83D\uDCDD Dry Run\nLet\'s run a dry example to illustrate how this approach works. Consider the following nested list:\n```\n[[1, 2], 3, [4, [5, 6]], 7]\n```\n\nAs we apply the DFS algorithm, the `data` vector will store `[1, 2, 3, 4, 5, 6, 7]`, making it easy to retrieve the next integer.\n\n## \uD83D\uDD0D Edge Cases\nThis approach can handle nested lists of varying depths and sizes.\n\n## \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(N), where N is the total number of integers in the nested list.\n- Space Complexity: O(N), as we store all the integers in a vector.\n\n\n## \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Code\n\n```cpp []\nclass NestedIterator {\npublic:\n vector<int> data;\n int curr = 0, size;\n\n void DFS(vector<NestedInteger> &nestedList, vector<int> &data) {\n int i, n = nestedList.size();\n\n for (i = 0; i < n; i++) {\n if (nestedList[i].isInteger())\n this->data.push_back(nestedList[i].getInteger());\n else\n DFS(nestedList[i].getList(), this->data);\n }\n }\n\n NestedIterator(vector<NestedInteger> &nestedList) {\n DFS(nestedList, this->data);\n this->size = this->data.size();\n }\n\n int next() {\n int ans = this->data[curr];\n curr += 1;\n return ans;\n }\n\n bool hasNext() {\n if (this->curr == this->size)\n return false;\n return true;\n }\n};\n```\n\n```java []\nimport java.util.ArrayList;\nimport java.util.Iterator;\nimport java.util.List;\n\npublic class NestedIterator {\n private List<Integer> data;\n private int curr, size;\n\n private void dfs(List<NestedInteger> nestedList) {\n for (NestedInteger ni : nestedList) {\n if (ni.isInteger()) {\n data.add(ni.getInteger());\n } else {\n dfs(ni.getList());\n }\n }\n }\n\n public NestedIterator(List<NestedInteger> nestedList) {\n data = new ArrayList<>();\n dfs(nestedList);\n size = data.size();\n }\n\n public Integer next() {\n Integer ans = data.get(curr);\n curr++;\n return ans;\n }\n\n public boolean hasNext() {\n return curr < size;\n }\n}\n```\n\n```python []\nclass NestedIterator:\n def __init__(self, nestedList):\n self.data = []\n self.curr = 0\n\n def dfs(nestedList):\n for ni in nestedList:\n if ni.isInteger():\n self.data.append(ni.getInteger())\n else:\n dfs(ni.getList())\n\n dfs(nestedList)\n\n def next(self):\n ans = self.data[self.curr]\n self.curr += 1\n return ans\n\n def hasNext(self):\n return self.curr < len(self.data)\n```\n\n```csharp []\npublic class NestedIterator {\n private List<int> data;\n private int curr, size;\n\n private void DFS(IList<NestedInteger> nestedList) {\n foreach (var ni in nestedList) {\n if (ni.IsInteger()) {\n data.Add(ni.GetInteger());\n } else {\n DFS(ni.GetList());\n }\n }\n }\n\n public NestedIterator(IList<NestedInteger> nestedList) {\n data = new List<int>();\n DFS(nestedList);\n size = data.Count;\n }\n\n public int Next() {\n int ans = data[curr];\n curr++;\n return ans;\n }\n\n public bool HasNext() {\n return curr < size;\n }\n}\n```\n```javascript []\nclass NestedIterator {\n constructor(nestedList) {\n this.data = [];\n this.curr = 0;\n\n const dfs = (nestedList) => {\n for (const ni of nestedList) {\n if (ni.isInteger()) {\n this.data.push(ni.getInteger());\n } else {\n dfs(ni.getList());\n }\n }\n }\n\n dfs(nestedList);\n }\n\n next() {\n const ans = this.data[this.curr];\n this.curr++;\n return ans;\n }\n\n hasNext() {\n return this.curr < this.data.length;\n }\n}\n```\n\n---\n\n## \uD83D\uDCCA Analysis\n\n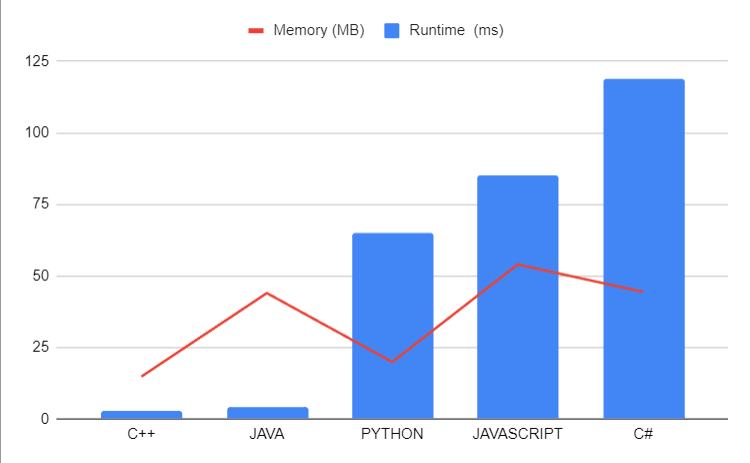\n\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|-------------|--------------|-------------|\n| C++ | 3 | 14.8 |\n| Java | 4 | 44 |\n| Python | 65 | 19.9 |\n| C# | 119 | 44.4 |\n| JavaScript | 85 | 54 |\n\n\n---\n\n## \uD83D\uDCAF Related Questions and Practice\n\n\n- [Flatten - 2D Vector](https://leetcode.com/problems/flatten-2d-vector/description/)\n- [zigzag-iterator](https://leetcode.com/problems/zigzag-iterator/description/)\n- [mini-parser](https://leetcode.com/problems/mini-parser/description/)\n\n---\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF* \n\n | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
Python short and clean. Functional programming. | flatten-nested-list-iterator | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is number of integers in the nested_list`.\n\n# Code\n```python\nclass NestedIterator:\n def __init__(self, nested_list: list[NestedInteger]):\n self.xs = flatten(nested_list)\n self.next_x = None\n \n def next(self) -> int:\n self.hasNext()\n x, self.next_x = self.next_x, None\n return x\n \n def hasNext(self) -> bool:\n self.next_x = next(self.xs, None) if self.next_x is None else self.next_x\n return self.next_x != None\n \ndef flatten(n_ints: list[NestedInteger]) -> Iterator[int]:\n yield from chain.from_iterable((x.getInteger(),) if x.isInteger() else flatten(x.getList()) for x in n_ints)\n\n\n``` | 1 | You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
Implement the `NestedIterator` class:
* `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
* `int next()` Returns the next integer in the nested list.
* `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = \[\]
while iterator.hasNext()
append iterator.next() to the end of res
return res
If `res` matches the expected flattened list, then your code will be judged as correct.
**Example 1:**
**Input:** nestedList = \[\[1,1\],2,\[1,1\]\]
**Output:** \[1,1,2,1,1\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,1,2,1,1\].
**Example 2:**
**Input:** nestedList = \[1,\[4,\[6\]\]\]
**Output:** \[1,4,6\]
**Explanation:** By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: \[1,4,6\].
**Constraints:**
* `1 <= nestedList.length <= 500`
* The values of the integers in the nested list is in the range `[-106, 106]`. | null |
【Video】Give me 3 minutes - without bitwise operations - Python, JavaScript, Java, C++ | power-of-four | 1 | 1 | # Intuition\nUse math.log function\n\n---\n\n# Solution Video\n\nhttps://youtu.be/dy_GA7sG22g\n\n\u25A0 Timeline of the video\n`0:05` Easy way to solve a constraint\n`0:03` Example code with Bitwise Operations\n`0:19` Solution with Build-in function\n`1:23` Coding with Build-in function\n`1:50` Time Complexity and Space Complexity with Build-in function\n`2:15` Coding without Build-in function\n`3:08` Time Complexity and Space Complexity without Build-in function\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,778\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nI think many posts use bitwise operations like this.\n\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and (n & (n - 1)) == 0 and (n & 0x55555555) != 0\n```\n\nThis is $$O(1)$$ time, but in real interviews, I\'ve never seen someone who solved questions with bitwise operations, so I\'ll show you another way.\n\n\n---\n\n\u2B50\uFE0F Points\n\nUse `math.log` function\n\n---\n\nI think each programming language has `math.log` function. We use it. For example, Python has `math.log(n, 4)` function. The `math.log(n, 4)` function in Python calculates the logarithm of `n to the base 4`. \n\nFor example,\n\n```\nmath.log(16, 4) == 2.0\nmath.log(15, 4) == 1.9534452978042594\n```\nbecause `4` raised to the power of `2` is `16`. In Python, we will get the answer with float(`2.0`). Simply, if the decimal part is `0`, we can return `True`, if not, return `False`. We can use `is_integer()` function to check it.\n\n\n---\n\n\n\n- Details of `is_integer()` ?\n\n`is_integer` is a method in Python for `float` objects (floating-point numbers) that is used to check whether the floating-point number is an integer. This method determines if a floating-point number consists of an integer part and a decimal part.\n\nSpecifically, the `is_integer` method checks if the floating-point number meets the following conditions:\n\n1. The floating-point number itself is accurately represented as an integer.\n2. The decimal part of the floating-point number is `0.0` (i.e., all decimal parts are zero).\n\nFor example, consider the following code:\n\n```python\nx = 10.0\ny = 10.5\n```\n\n`x` is an integer and has a decimal part of `0.0`, so `x.is_integer()` will return `True`. On the other hand, `y` is not an integer, and its decimal part is `0.5`, so `y.is_integer()` will return `False`.\n\nThis method can be useful in scenarios where you need to ensure that a floating-point number is an integer before performing certain operations.\n\n\n---\n\n\n\nLet\'s see a real algorithm!\n\n### Algorithm Overview:\nThis algorithm checks whether an input integer `n` is a power of 4.\n\n### Detailed Explanation:\n1. Check if `n` is less than or equal to 0.\n - If `n` is less than or equal to 0, return `False` because numbers less than or equal to 0 cannot be powers of 4.\n\n2. Calculate the logarithm of `n` to the base 4 using `math.log(n, 4)`.\n - The `math.log(n, 4)` function computes the logarithm of `n` to the base 4. This logarithm represents the exponent to which 4 must be raised to obtain `n`. For example, `math.log(16, 4)` would return 2 because 4^2 = 16.\n\n3. Check if the result from step 2 is an integer using `.is_integer()`.\n - The `.is_integer()` method checks whether the result of `math.log(n, 4)` is a whole number (integer). If it is, this means that `n` is a power of 4.\n - If the result is an integer, return `True`; otherwise, return `False`.\n\nIn summary, the algorithm first checks if the input is a non-positive integer (returning `False` if it is), then it calculates the logarithm of the input to the base 4 and checks if the result is an integer. If the result is an integer, the function returns `True`, indicating that the input is a power of 4; otherwise, it returns `False`.\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n \n return math.log(n, 4).is_integer()\n```\n```javascript []\nvar isPowerOfFour = function(n) {\n if (n <= 0) {\n return false;\n }\n return Number.isInteger(Math.log(n) / Math.log(4)); \n};\n```\n```java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n return Math.log(n) / Math.log(4) % 1 == 0; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n return fmod(log(n) / log(4), 1.0) == 0.0; \n }\n};\n```\n\n# Bonus Code\nIf you must write a solution code without build-in function in real interviews(ask interviewers), this is one of examples.\n\n```python []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n if n == 1:\n return True\n\n while n > 1:\n if n % 4 != 0:\n return False\n n //= 4\n\n return True \n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-largest-value-in-each-tree-row/solutions/4201364/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/0fnMZvFM4p8\n\n\u25A0 Timeline of the video\n`0:05` Two difficulties\n`0:29` How can you keep max value at a single level? (the first difficulty)\n`1:10` Points of the first difficulty\n`1:32` How can you keep nodes at the next down level (the second difficulty)\n`2:09` Demonstrate how it works\n`6:23` Points of the second difficulty\n`6:45` What if we use normal array instead of deque\n`7:35` Coding with BFS\n`9:31` Time Complexity and Space Complexity\n`10:25` Explain DFS solution briefly\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-score-of-a-good-subarray/solutions/4196248/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/ZiO47ctvu6w\n\n\u25A0 Timeline of the video\n`0:05` Easy way to solve a constraint\n`2:04` How we can move i and j pointers\n`3:59` candidates for minimum number and max score\n`4:29` Demonstrate how it works\n`8:25` Coding\n`11:04` Time Complexity and Space Complexity\n\n | 36 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Python3 Solution | power-of-four | 0 | 1 | \n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n<=0:\n return False\n return n>0 and log(n,4).is_integer() \n``` | 3 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Video Solution | Explaination With Drawings | In Depth | Java | C++ | Python 3 | power-of-four | 1 | 1 | # Intuition, approach, and complexity discussed in detail in video solution.\nhttps://youtu.be/GWcEoppPzBQ\n\n# Code\nC++\n```\n//TC : O(1)\n//SC : O(1)\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n return n > 0 && floor(log(n)/log(4)) == ceil(log(n)/log(4));\n }\n};\n```\nJava\n```\nclass Solution {\n public boolean isPowerOfFour(int n) {\n return n > 0 && Math.floor(Math.log(n)/Math.log(4)) == Math.ceil(Math.log(n)/Math.log(4));\n }\n}\n```\nPython 3\n```\nclass Solution:\n def isPowerOfFour(self, n):\n return n > 0 and math.floor(math.log(n)/math.log(4)) == math.ceil(math.log(n)/math.log(4))\n``` | 3 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
🚀 100% || Brute Force & Two Math Solutions || Explained Intuition 🚀 | power-of-four | 1 | 1 | # Problem Description\n\nGiven an integer `n`. The task is to determine whether `n` is a power of **four**. \nAn integer `n` is considered a power of **four** if there exists another integer `x` such that `n` is equal to `4` raised to the power of `x` (i.e., $n = 4^x$).\nReturn `true` if `n` is a power of **four**; otherwise, return `false`.\n\n- Constraints:\n - `-2e31 <= n <= 2e31 - 1`\n\n\n---\n\n# Intuition\n\nHi there, \n\nLet\'s dive deep \uD83E\uDD3F into today\'s interesting problem.\nThe problem says that we want to find if given number `n` is **power** of four $n = 4^x$ or not.\n\nSeems easy ?\uD83E\uDD14\nActually the first valid solution is **Brute Force**.\nWe can check all the **possible** power of fours and if our number is one of them then we return **true**.\nConcise and simple. \uD83D\uDC4C\nBut what is our **range**, how many number we will **check** ? \uD83E\uDD14\nour constraints are `2e31 <= n <= 2e31 - 1` so max number to check it power is `log(2e31) base 4` which is `15.5`.\nBut since this is the **maximum** value that **int** data type can hold so we will search maximum from `(0 -> 15)` because `4^16` will give us **integer** **overflow**.\n\nNow, this is the **Brute Force** solution with $O(log(N)^2)$ complexity, can we do **better**?\uD83E\uDD14\nActually, we can !\uD83E\uDD2F\nWe will have some help from **math** especially **Logarithms**.\u2797\u2795\nif we know that $n = 4^x$ then for sure `log(n) base 4` is an **integer** and if there is a **fraction** then `n` is not to the power of four.\n```\nEX1: n = 16\nn = 4 ^ 2 => power of four\nx = 2\n```\n```\nEX2: n = 256\nn = 4 ^ 4 => power of four\nx = 4\n```\n```\nEX3: n = 147\nn = 4 ^ 3.6 => not power of four\nx = 3.6\n```\n\nGreat ! but how will we get that `log base 4` since programming languages don\'t implement it !.\nHere comes the Logarithms properties. We have a rule called **Change of Base Rule**.\n\n\n\nMost of programming languages implements `log base 10` or `log base 2` or even `log base natural number e`.\n\nWe will **pick** one of these **implemented** logs and compute `log base 4` using them. and check if result if **integer** if not then it is not power of **four**.\n\nIs there another valid solution ?\uD83E\uDD14\nSay that I don\'t want to use this logarithmic **rule** and I am not good with it can I do something else? \uD83E\uDD28\n\nActually we can ! \uD83E\uDD2F\n\nLet\'s see this observation.\nn = $4 ^ x$\nn = $(2 * 2) ^ x$\nn = $2 ^ x$ * $2 ^ x$\nsqrt(n) = $2 ^ x$\nlog2(sqrt(n)) = x\n\nWhat is this ! \uD83E\uDD2F\nThis is the beauty of math. \uD83E\uDD29\nWe can get `x` without using change of base rule. since n = $4 ^ x$ so it is naturally **product** of two similar numbers then we can calculate its **square root**. then get its `log base 2` easily.\nmost programming languages implements `log base 2`. Sadly, except **Java** so we will go back to change of base rule.\nBut this also a valid solution if you are not using Java and don\'t want to calculate many logarithms.\uD83D\uDCAA\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Approach\n\n## Brute Force\n\n1. Start an iteration from `i` equal to 0 to 15, representing powers of `4` from `4^0` to `4^15` since the maximum value that **int** can hold is `4^(15.5)`.\n2. Calculate the `powerOfFour` by raising `4` to the power of `i`.\n3. if `powerOfFour` is equal to the input integer `n`. If they are equal, return `true` because `n` is a power of four.\n4. If `powerOfFour` becomes greater than `n`, there\'s no need to continue the loop, so return `false`.\n5. If none of the powers of `4` match `n` during the loop, return `false` to indicate that `n` is not a power of four.\n\n## Complexity\n- **Time complexity:** $O(log(N)^2)$\nSince we are iterating from `0` to `15` which `15` is `log(INT_MAX)` to the **base** of `4` and in each iteration we calculate the **power** of $4^i$ which is **logarithmic** operations so total complexity is `O(log(N)^2)`.\n- **Space complexity:** $O(1)$\nSince we are only storing constant variables.\n\n\n---\n\n\n\n\n## First Math Solution\n\n1. Check if the input integer `n` is equal to `1`. If it is, return **true** since `1` is a power of four.\n2. If `n` is **non-positive** (less than or equal to 0), return **false** since powers of four are **positive** integers.\n3. Calculate the logarithm of \'n\' with a base of 4 and store the result in the variable \'logarithmBase4.\'\n4. Check if \'logarithmBase4\' is an integer by comparing it to its integer cast. If they are equal, return `true`; otherwise, return `false`.\n\n## Complexity\n- **Time complexity:** $O(1)$\nSince we are only doing math operations without any loops or recursion.\n- **Space complexity:** $O(1)$\nSince we are only storing constant variables.\n\n\n---\n## Second Math Solution\n\n1. Check if the input integer `n` is equal to `1`. If it is, return **true** since `1` is a power of four.\n2. If `n` is **non-positive** (less than or equal to 0), return **false** since powers of four are **positive** integers.\n3. Calculate the square root of `n` and store it in the variable `sqrtN`.\n4. Compute the logarithm base `2` of `sqrtN` and store it in `log2SqrtN`.\n5. Check if `log2SqrtN` is an integer (i.e., it has no fractional part). If it is an integer, return **true**; otherwise, return **false**.\n\n## Complexity\n- **Time complexity:** $O(1)$\nSince we are only doing math operations without any loops or recursion.\n- **Space complexity:** $O(1)$\nSince we are only storing constant variables.\n\n\n\n\n---\n\n\n\n# Code\n\n## Brute Force\n\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n // Iterate through powers of 4 from 4^0 to 4^15\n for (int i = 0; i <= 15; i++) {\n int powerOfFour = pow(4, i);\n \n // If we find a power of four equal to \'n\', return true\n if (powerOfFour == n)\n return true;\n \n // If the current power of four is greater than \'n\', there\'s no need to continue\n if (powerOfFour > n)\n return false;\n }\n \n // \'n\' is not a power of four\n return false;\n }\n};\n\n```\n```Java []\npublic class Solution {\n public boolean isPowerOfFour(int n) {\n // Iterate through powers of 4 from 4^0 to 4^15\n for (int i = 0; i <= 15; i++) {\n int powerOfFour = (int) Math.pow(4, i);\n \n // If we find a power of four equal to \'n\', return true\n if (powerOfFour == n)\n return true;\n \n // If the current power of four is greater than \'n\', there\'s no need to continue\n if (powerOfFour > n)\n return false;\n }\n \n // \'n\' is not a power of four\n return false;\n }\n}\n```\n```Python []\nclass Solution:\n def isPowerOfFour(self, n):\n # Iterate through powers of 4 from 4^0 to 4^15\n for i in range(16):\n power_of_four = 4 ** i\n \n # If we find a power of four equal to \'n\', return True\n if power_of_four == n:\n return True\n \n # If the current power of four is greater than \'n\', there\'s no need to continue\n if power_of_four > n:\n return False\n \n # \'n\' is not a power of four\n return False\n\n```\n```C []\nbool isPowerOfFour(int n) {\n // Iterate through powers of 4 from 4^0 to 4^15\n for (int i = 0; i <= 15; i++) {\n int powerOfFour = pow(4, i);\n\n // If we find a power of four equal to \'n\', return true\n if (powerOfFour == n)\n return true;\n\n // If the current power of four is greater than \'n\', there\'s no need to continue\n if (powerOfFour > n)\n return false;\n }\n\n // \'n\' is not a power of four\n return false;\n}\n```\n\n\n\n---\n\n\n\n## First Math Solution\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n // If \'n\' is 1, it is a power of four\n if (n == 1)\n return true;\n \n // If \'n\' is non-positive, it cannot be a power of four\n if (n <= 0)\n return false; \n \n // Calculate the logarithm of \'n\' with base 4\n double logarithmBase4 = log(n) / log(4);\n \n // Check if the result of the logarithmic operation is an integer\n return (logarithmBase4 == (int)logarithmBase4);\n }\n};\n```\n```Java []\npublic class Solution {\n public boolean isPowerOfFour(int n) {\n // If \'n\' is 1, it is a power of four\n if (n == 1)\n return true;\n \n // If \'n\' is non-positive, it cannot be a power of four\n if (n <= 0)\n return false; \n \n // Calculate the logarithm of \'n\' with base 4\n double logarithmBase4 = Math.log(n) / Math.log(4);\n \n // Check if the result of the logarithmic operation is an integer\n return (logarithmBase4 == (int)logarithmBase4);\n }\n}\n```\n```Python []\nclass Solution:\n def isPowerOfFour(self, n):\n # If \'n\' is 1, it is a power of four\n if n == 1:\n return True\n \n # If \'n\' is non-positive, it cannot be a power of four\n if n <= 0:\n return False\n \n # Calculate the logarithm of \'n\' with base 4\n logarithm_base4 = math.log(n) / math.log(4)\n \n # Check if the result of the logarithmic operation is an integer\n return (logarithm_base4 == int(logarithm_base4))\n```\n```C []\nbool isPowerOfFour(int n) {\n // If \'n\' is 1, it is a power of four\n if (n == 1)\n return 1; // True in C is often represented as 1\n\n // If \'n\' is non-positive, it cannot be a power of four\n if (n <= 0)\n return 0; // False in C is often represented as 0\n\n // Calculate the logarithm of \'n\' with base 4\n double logarithmBase4 = log(n) / log(4);\n\n // Check if the result of the logarithmic operation is an integer\n return (logarithmBase4 == (int)logarithmBase4);\n}\n```\n\n\n---\n\n## Second Math Solution\n\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n // If \'n\' is 1, it is a power of four\n if (n == 1)\n return true;\n \n // If \'n\' is non-positive, it cannot be a power of four\n if (n <= 0)\n return false; \n \n // Calculate the square root of \'n\'\n double sqrtN = sqrt(n);\n\n // Take the logarithm base 2 of the square root\n double log2SqrtN = log2(sqrtN);\n \n // Check if the result of the logarithmic operation is an integer\n return (log2SqrtN == (int)log2SqrtN);\n }\n};\n```\n```Java []\npublic class Solution {\n public boolean isPowerOfFour(int n) {\n // If \'n\' is 1, it is a power of four\n if (n == 1)\n return true;\n\n // If \'n\' is non-positive, it cannot be a power of four\n if (n <= 0)\n return false;\n\n // Calculate the square root of \'n\'\n double sqrtN = Math.sqrt(n);\n\n // Take the logarithm base 2 of the square root\n double log2SqrtN = Math.log(sqrtN) / Math.log(2);\n\n // Check if the result of the logarithmic operation is an integer\n return (log2SqrtN == (int) log2SqrtN);\n }\n}\n```\n```Python []\nclass Solution:\n def isPowerOfFour(self, n):\n # If \'n\' is 1, it is a power of four\n if n == 1:\n return True\n\n # If \'n\' is non-positive, it cannot be a power of four\n if n <= 0:\n return False\n\n # Calculate the square root of \'n\'\n sqrtN = math.sqrt(n)\n\n # Take the logarithm base 2 of the square root\n log2SqrtN = math.log2(sqrtN)\n\n # Check if the result of the logarithmic operation is an integer\n return log2SqrtN == int(log2SqrtN)\n```\n```C []\nbool isPowerOfFour(int n) {\n // If \'n\' is 1, it is a power of four\n if (n == 1)\n return 1; // True in C is often represented as 1\n\n // If \'n\' is non-positive, it cannot be a power of four\n if (n <= 0)\n return 0; // False in C is often represented as 0\n\n // Calculate the square root of \'n\'\n double sqrtN = sqrt(n);\n\n // Take the logarithm base 2 of the square root\n double log2SqrtN = log2(sqrtN);\n\n // Check if the result of the logarithmic operation is an integer\n return (log2SqrtN == (int)log2SqrtN);\n}\n```\n\n\n\n\n\n\n\n | 107 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
🔥Shortest, Easiest 1 Line Solution | power-of-four | 0 | 1 | # Approach\nWe have to verify if an integer is a power of 4 by checking if it\'s both positive and if its logarithm with base 4 is an integer; if so, it\'s considered a power of 4.\n# Code\n```py\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n>0 and log(n,4).is_integer()\n```\n# Line by Line\n```py\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n # Check if n is positive\n is_positive = n > 0 # Check if n is positive\n \n # If n is positive, then check if its logarithm to base 4 is an integer\n if is_positive:\n is_log_integer = log(n, 4).is_integer() # Check if the logarithm is an integer\n return is_log_integer # Return True if the logarithm is an integer\n else:\n return False # Return False if n is not positive\n\n```\nplease upvote :D | 5 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || 1 line Code || 3 Approaches || EXPLAINED🔥 | power-of-four | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Brute force)***\n1. The `isPowerOfFour` function takes an integer `n` as input and returns a boolean (true or false) based on whether n is a power of four or not.\n\n1. It initializes a `for` loop that iterates from `i = 0` to `i = 15`. This range covers powers of 4 from 4^0 to 4^15.\n\n1. Inside the loop, it calculates the `powerOfFour` using the `pow` function, where `pow(4, i)` calculates 4^i for each iteration.\n\n1. It then compares `powerOfFour` to the input number `n`.\n\n1. If `powerOfFour` is equal to `n`, it means `n` is a power of four, so the function returns `true`.\n\n1. If `powerOfFour` becomes greater than `n`, there\'s no need to continue checking because we\'ve already passed the possible powers of four that could be equal to or less than `n`. In this case, the function returns `false`.\n\n1. If none of the powers of four matches `n` during the loop iterations, the function returns `false` outside the loop.\n\n\n# Complexity\n- *Time complexity:*\n $$O(1)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n // Iterate through powers of 4 from 4^0 to 4^15\n for (int i = 0; i <= 15; i++) {\n int powerOfFour = pow(4, i);\n \n // If we find a power of four equal to \'n\', return true\n if (powerOfFour == n)\n return true;\n \n // If the current power of four is greater than \'n\', there\'s no need to continue\n if (powerOfFour > n)\n return false;\n }\n \n // \'n\' is not a power of four\n return false;\n }\n};\n\n```\n\n```C []\nbool isPowerOfFour(int n) {\n // Iterate through powers of 4 from 4^0 to 4^15\n for (int i = 0; i <= 15; i++) {\n int powerOfFour = pow(4, i);\n\n // If we find a power of four equal to \'n\', return true\n if (powerOfFour == n)\n return true;\n\n // If the current power of four is greater than \'n\', there\'s no need to continue\n if (powerOfFour > n)\n return false;\n }\n\n // \'n\' is not a power of four\n return false;\n}\n\n```\n\n\n```Java []\npublic class Solution {\n public boolean isPowerOfFour(int n) {\n // Iterate through powers of 4 from 4^0 to 4^15\n for (int i = 0; i <= 15; i++) {\n int powerOfFour = (int) Math.pow(4, i);\n \n // If we find a power of four equal to \'n\', return true\n if (powerOfFour == n)\n return true;\n \n // If the current power of four is greater than \'n\', there\'s no need to continue\n if (powerOfFour > n)\n return false;\n }\n \n // \'n\' is not a power of four\n return false;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def isPowerOfFour(self, n):\n # Iterate through powers of 4 from 4^0 to 4^15\n for i in range(16):\n power_of_four = 4 ** i\n \n # If we find a power of four equal to \'n\', return True\n if power_of_four == n:\n return True\n \n # If the current power of four is greater than \'n\', there\'s no need to continue\n if power_of_four > n:\n return False\n \n # \'n\' is not a power of four\n return False\n\n\n```\n```javascript []\nvar isPowerOfFour = function(n) {\n for (var i = 0; i < 16; i++) {\n var powerOfFour = Math.pow(4, i);\n \n if (powerOfFour === n) {\n return true;\n }\n \n if (powerOfFour > n) {\n return false;\n }\n }\n \n return false;\n};\n\n```\n\n\n---\n\n#### ***Approach 2 (1st Math Solution)***\n1. The `isPowerOfFour` function takes an integer `n` as input and returns a boolean (true or false) based on whether `n` is a power of four or not.\n\n1. The first condition checks if `n` is greater than 0 and `(n & (n - 1)) == 0`. This is a common technique to check if a number is a power of 2. (`n & (n - 1)`) results in 0 if and only if `n` is a power of 2.\n\n1. If the first condition is satisfied, the code proceeds to check the second condition.\n\n1. The second condition checks whether `n - 1` is a multiple of 3. This is because powers of four (4^0, 4^1, 4^2, etc.) minus one are all divisible by 3. This property is used to distinguish powers of four from other powers of two.\n\n1. If both conditions are met, the function returns `true`, indicating that `n` is a power of four.\n\n1. If either of the conditions fails, the function returns `false`.\n\n\n# Complexity\n- *Time complexity:*\n $$O(1)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n if (n > 0 && (n & (n - 1)) == 0) {\n // Check if it\'s one more than a multiple of 3\n if((n - 1) % 3 == 0){\n\n\n return true; \n }\n }\n return false;\n\n }\n};\n\n```\n\n```C []\n\n\nbool isPowerOfFour(int n) {\n if (n > 0 && (n & (n - 1)) == 0) {\n // Check if it\'s one more than a multiple of 3\n if ((n - 1) % 3 == 0) {\n return true;\n }\n }\n return false;\n}\n\n\n```\n\n\n```Java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n if (n > 0 && (n & (n - 1)) == 0) {\n // Check if it\'s one more than a multiple of 3\n if ((n - 1) % 3 == 0) {\n return true;\n }\n }\n return false;\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n > 0 and (n & (n - 1)) == 0:\n # Check if it\'s one more than a multiple of 3\n if (n - 1) % 3 == 0:\n return True\n return False\n\n\n\n```\n```javascript []\nclass Solution {\n isPowerOfFour(n) {\n if (n > 0 && (n & (n - 1)) === 0) {\n // Check if it\'s one more than a multiple of 3\n if ((n - 1) % 3 === 0) {\n return true;\n }\n }\n return false;\n }\n}\n\n```\n\n\n---\n#### ***Approach 3 (2nd Math Solution)***\n1. **n > 0:** This condition checks that `n` is a positive integer. Powers of four are always positive, so negative numbers or zero are not considered.\n\n1. **(n & (n - 1)) == 0:** This condition checks if `n` is a power of two. It uses bitwise operations to determine if `n` contains only one \'1\' bit in its binary representation. If true, `n` is a power of two.\n\n1. **(n % 10 == 1 || n % 10 == 4 || n % 10 == 6):** This part checks whether `n` ends with one of the digits 1, 4, or 6. It uses the modulo operator `%`to get the last digit of `n` and compares it to the allowed digits.\n\n1. The function returns `true` if all these conditions are met; otherwise, it returns `false`.\n\n\n# Complexity\n- *Time complexity:*\n $$O(1)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n return n>0 && (n&(n-1))==0 && (n % 10 ==1|| n% 10==4|| n%10==6);\n } \n \n};\n\n```\n\n```C []\nbool isPowerOfFour(int n) {\n return n > 0 && (n & (n - 1)) == 0 && (n % 10 == 1 || n % 10 == 4 || n % 10 == 6);\n}\n\n\n```\n\n\n```Java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n return n > 0 && (n & (n - 1)) == 0 && (n % 10 == 1 || n % 10 == 4 || n % 10 == 6);\n }\n}\n\n\n```\n\n```python3 []\n\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and (n & (n - 1)) == 0 and (n % 10 == 1 or n % 10 == 4 or n % 10 == 6)\n\n\n```\n```javascript []\nvar isPowerOfFour = function(n) {\n return n > 0 && (n & (n - 1)) === 0 && (n % 10 === 1 || n % 10 === 4 || n % 10 === 6);\n};\n\n```\n\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Bitwise Solution | Python | power-of-four | 0 | 1 | # Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n.bit_count() == 1 and int(\'10\' * 16, 2) & n == 0\n``` | 1 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Python Solution Using Logarithms | power-of-four | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are dealing with powers of 4. We know that...\n4 ^ 0 = 1, \n4 ^ 1 = 4, \n4 ^ 2 = 16, etc.\nIn math, we use logarithms to find how many times the base number (in our case, 4) must be multiplied by itself to get some other particular number. \n```\nlog(base) (power of base) = (exponent)\n```\nThus,\nlog4 1 = 0,\nlog4 4 = 1,\nlog4 16 = 2, etc.\n\n**Logarithms cannot have a negative number, otherwise that would be undefined.**\nLorgatithms can also return exponents that are not integers: \nlog4 5 \u2248 1.1610\nlog4 9 \u2248 1.2075\nlog4 31 \u2248 2.4914\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPython comes with a built-in package called "math," which includes the logarithm function. So to begin, \n```\nimport math\n```\nThe method used is `math.log(power of base, base)`, which accepts two parameters, the number that we are finding the exponent of and the base. **This method will return the exponent**. Our base is `4`, and we are given a variable that is supposedly a power of `4`, `n`. So we get `math.log(n, 4)`. Now, this has to equal an integer if `n` is a power of `4`; we can use the `.is_integer()` function. So if `n` is a power of `4`, we return `True`. If it isn\'t, we return `False`.\n\nNow our code is:\n```\nimport Math\n\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if math.log(n, 4).is_integer() == True:\n return True\n return False\n```\n\nIf `n <= 0`, its logarithm will return a `ValueError`. Once we add this `if` statement in, we are all set.\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#Import logarithm package\nimport math\n\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n #n cannot be negative \n if n <= 0:\n return False\n #If log4 n == integer, n is a power of 4\n if math.log(n, 4).is_integer() == True:\n return True\n #If the program made it all the way over here, return False\n return False\n``` | 1 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Beginner-friendly || Loops and Math || Simple solution with Python3 / TypeScript | power-of-four | 0 | 1 | # Intuition\nLet\'s briefly explain what the problem is:\n- there\'s an integer `n`\n- our goal is to define, if this integer is a possible answer to `n = 4^x`\n\nThere\'re some solutions, including math and loops.\n\n# Complexity\n- Time complexity: **O(log N)** with loop solution, and **O(1)** - with logarithmic solution\n\n- Space complexity: **O(1)**, in both solutions.\n\n# Code in Python3\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and log(n, 4) % 1 == 0\n```\n\n# Code in TypeScript\n```\nfunction isPowerOfFour(n: number): boolean {\n if (n === 0) return false;\n\n while (n !== 1) {\n if (n % 4) return false;\n n = Math.floor(n / 4);\n }\n\n return true;\n}\n``` | 1 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
✅ One liner✅Beats 100%✅ easy and simple solution with explanation | power-of-four | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis code checks if a given number n is a power of four. In other words, it determines if n can be expressed as 4 raised to some non-negative integer (e.g., 1, 4, 16, 64, etc.).\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. It first checks if `n` is greater than 0, which ensures that we\'re dealing with a positive number.\n2. The code then checks if `n` is a power of 2 by using the expression `(n & (n - 1)) == 0`. If this condition is true, it means that `n` is a power of 2 because powers of 2 have only one \'1\' bit in their binary representation. For example, 4 in binary is 100, 8 is 1000, and so on.\n3. The last condition checks if `(n % 3 == 1)`. This is an additional check to ensure that the number is a power of four. It filters out numbers that are powers of 2 but not powers of 4.\n\nSo, the code combines these three conditions to determine if `n` is a power of four - it must be positive, a power of 2, and satisfy the modulo 3 condition to be considered a power of four.\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n return (n>0) && ((n&(n-1))==0) && ((n%3==1));\n }\n};\n```\n```python []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and n & (n - 1) == 0 and n % 3 == 1\n\n```\n```java []\npublic class Solution {\n public boolean isPowerOfFour(int n) {\n return n > 0 && (n & (n - 1)) == 0 && n % 3 == 1;\n }\n}\n\n```\n\n | 15 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
✅ 6 Different Methods || Beats 99.76% 🔥 || | power-of-four | 1 | 1 | ## This Solution took me a lot of time, so please UpVote\u2705 if you found this helpful :)\n# Approach 1: Iteration\n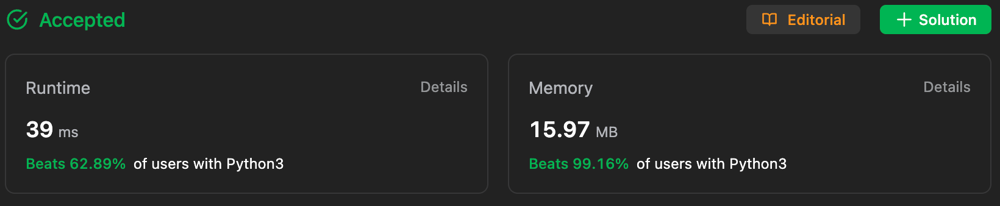\n\n# Intuition : \n**The idea is to keep dividing the number by 4, i.e, do n = n/4 iteratively. In any iteration, if n%4 becomes non-zero and n is not 1 then n is not a power of 4, otherwise n is a power of 4.**\n\n# Algorithm :\n1. If n is less than or equal to 0, return false.\n2. Otherwise, loop until n becomes 1 or n%4 becomes non-zero. In the loop, do n = n/4.\n3. After the loop, return true if n is 1, otherwise return false.\n\n# Complexity Analysis\n- Time complexity : ***O(log4n)***. In each iteration, we reduce the number by 4 times until it either becomes 1 or a number not divisible by 4.\n- Space complexity : ***O(1)***. We are not using any extra memory.\n\n\n\n\n# Code:\n\n``` Python []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n while n > 1:\n if n % 4 != 0:\n return False\n n //= 4\n return True\n```\n``` C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n while (n > 1) {\n if (n % 4 != 0) {\n return false;\n }\n n /= 4;\n }\n return true;\n }\n};\n\n```\n``` Java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n while (n > 1) {\n if (n % 4 != 0) {\n return false;\n }\n n /= 4;\n }\n return true;\n }\n}\n\n```\n# Approach 2: Bit Manipulation\n\n\n\n\n# Intuition :\nReturn true if n is a power of four. That is, return true if n is a power of 2 and its exponent is even. The second part of the condition can be checked by ensuring that n is not divisible by 3. If n is a power of 4, it is definitely a power of 2 since 4 is a power of 2. If n is a power of 2 but not a power of 4, its exponent must be odd. That is, if n is a power of 2, n%3 should be 1. Return true if n>0 and n is a power of 2 and n%3 is 1.\n\n# Algorithm :\n1. If n is less than or equal to 0, return false.\n2. Otherwise, check if n is a power of 2 by checking if n&(n-1) is 0. If not, return false.\n3. Finally, return true if n%3 is 1, otherwise return false.\n\n# Complexity Analysis\n- Time complexity : ***O(1)***. We are only doing one operation.\n- Space complexity : ***O(1)***. We are not using any extra memory.\n\n\n\n# Code:\n\n``` Python []\n\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and n & (n - 1) == 0 and n % 3 == 1\n \n```\n``` C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n return n > 0 && (n & (n - 1)) == 0 && n % 3 == 1;\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n return n > 0 && (n & (n - 1)) == 0 && n % 3 == 1;\n }\n}\n\n```\n\n\n# Approach 3: division\n\n\n\n# Intuition :\nThe idea is to keep dividing the number by 4, i.e, do n = n/4 iteratively. In any iteration, if n%4 becomes non-zero and n is not 1 then n is not a power of 4, otherwise n is a power of 4. \n\n# Algorithm :\n1. If n is less than or equal to 0, return false.\n2. Otherwise, loop until n becomes 1 or n%4 becomes non-zero. In the loop, do n = n/4.\n3. After the loop, return true if n is 1, otherwise return false.\n\n# Complexity Analysis\n- Time complexity : ***O(log4n)***. In each iteration, we reduce the number by 4 times until it either becomes 1 or a number not divisible by 4.\n- Space complexity : ***O(1)***. We are not using any extra memory.\n\n\n\n# Code:\n\n``` Python []\n\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n while n % 4 == 0:\n n //= 4\n return n == 1\n```\n``` C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n while (n % 4 == 0) {\n n /= 4;\n }\n return n == 1;\n }\n};\n\n```\n``` Java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n while (n % 4 == 0) {\n n /= 4;\n }\n return n == 1;\n }\n}\n\n```\n\n# Approach 4: Math\n\n\n\n# Intuition :\nIf n is a power of 4, it can be expressed as 4^a where a is an integer. If a is even, 4^a will be a power of 2. Otherwise, 4^a will not be a power of 2. We can use this fact to determine if n is a power of 4. First, we check that n is a power of 2. Then we check that the exponent a is even. Since a is an integer, a will be even only if a%2 is 0. In the case when n is a power of 2, a is n/2. Therefore, we check if n/2 is even or not. If n/2 is even, we return true. Otherwise, we return false.\n\n# Algorithm :\n1. If n is less than or equal to 0, return false.\n2. Otherwise, check if n is a power of 2 by checking if n&(n-1) is 0. If not, return false.\n3. Finally, return true if n/2 is even, otherwise return false.\n\n# Complexity Analysis\n- Time complexity : ***O(1)***. We are only doing one operation.\n- Space complexity : ***O(1)***. We are not using any extra memory.\n\n\n\n# Code:\n \n``` Python []\nimport math\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and math.log2(n) % 2 == 0\n \n```\n``` C++ []\n#include <cmath>\n\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n return n > 0 && fmod(log2(n), 2) == 0;\n }\n};\n```\n``` Java []\nimport java.lang.Math;\n\nclass Solution {\n public boolean isPowerOfFour(int n) {\n return n > 0 && Math.log(n) / Math.log(4) % 1 == 0;\n }\n}\n\n```\n\n\n# Approach 5: Recursive\n\n\n\n\n# Intuition :\nThe idea is to keep dividing the number by 4, i.e, do n = n/4 iteratively. In any iteration, if n%4 becomes non-zero and n is not 1 then n is not a power of 4, otherwise n is a power of 4. \n\n# Algorithm :\n1. If n is less than or equal to 0, return false.\n2. Otherwise, loop until n becomes 1 or n%4 becomes non-zero. In the loop, do n = n/4.\n3. After the loop, return true if n is 1, otherwise return false.\n\n# Complexity Analysis\n\n- Time complexity : ***O(log4n)***. In each iteration, we reduce the number by 4 times until it either becomes 1 or a number not divisible by 4.\n- Space complexity : ***O(1)***. We are not using any extra memory.\n\n\n\n# Code:\n \n``` Python []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n if n == 1:\n return True\n return n % 4 == 0 and self.isPowerOfFour(n // 4)\n \n```\n``` C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n if (n == 1) {\n return true;\n }\n return n % 4 == 0 && isPowerOfFour(n / 4);\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean isPowerOfFour(int n) {\n if (n <= 0) {\n return false;\n }\n if (n == 1) {\n return true;\n }\n return n % 4 == 0 && isPowerOfFour(n / 4);\n }\n}\n\n``` \n# Approach 6: Using Lookup Table\n\n\n\n\n# Intuition :\nWe can use a lookup table to check if n is a power of 4. The lookup table will contain all the powers of 4 that can be represented by a 32-bit signed integer. We can create the lookup table by calculating the powers of 4 until the maximum value of a 32-bit signed integer is reached. We can then check if n is present in the lookup table.\n\n# Algorithm :\n1. Create a lookup table that contains all the powers of 4 that can be represented by a 32-bit signed integer.\n2. Check if n is present in the lookup table.\n\n# Complexity Analysis\n- Time complexity : ***O(1)***. We are only doing one operation.\n- Space complexity : ***O(1)***. We are not using any extra memory.\n\n\n# Code:\n \n``` Python []\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n in [1, 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864, 268435456, 1073741824]\n \n```\n``` C++ []\nclass Solution {\npublic:\n bool isPowerOfFour(int n) {\n static const std::unordered_set<int> powersOfFour = {\n 1, 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144,\n 1048576, 4194304, 16777216, 67108864, 268435456, 1073741824\n };\n \n return powersOfFour.count(n) > 0;\n }\n};\n\n```\n``` Java []\nimport java.util.HashSet;\n\nclass Solution {\n private static final HashSet<Integer> powersOfFour = new HashSet<>() {\n {\n add(1);\n add(4);\n add(16);\n add(64);\n add(256);\n add(1024);\n add(4096);\n add(16384);\n add(65536);\n add(262144);\n add(1048576);\n add(4194304);\n add(16777216);\n add(67108864);\n add(268435456);\n add(1073741824);\n }\n };\n\n public boolean isPowerOfFour(int n) {\n return powersOfFour.contains(n);\n }\n}\n\n``` | 36 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Python 🐢 Slow and Fast 🐇 1 Lines without loops | power-of-four | 0 | 1 | # Target\nTo determine if an integer is a power of four, we examine its binary representation.\n\n# Approach\n- First, we ensure the input integer n is positive; negative numbers cannot be powers of four.\n- We check if there is only one set bit in n by verifying that n & (n - 1) equals zero. This condition ensures a single set bit.\n- We then check if this set bit is in an odd position by performing a bitwise AND operation between n and the mask 0x55555555, which has \'1\' bits at odd positions. If the result is non-zero, n is a power of four.\n\n## Slow Code:\n1. In the "Slow Code" approach, we check whether the given **integer n is a power of four by iteratively dividing it by 4.** We start by ensuring n is a positive integer. Then, in a **while loop**, we repeatedly divide n by 4 and check if it\'s divisible evenly. \n\n1. If at any point n is not divisible by 4, we return False. If the loop completes and n becomes 1, we return True, indicating that n is indeed a power of four.\n\n## Fast Code:\n1. The "Fast Code" approach offers a more efficient solution. It checks whether n is a power of four using bitwise operations and masks. First, **we verify that n is a positive power of 2 by checking if (n & (n - 1)) equals zero**. \n\n1. Then, we employ two masks, **0x55555555** and **0xAAAAAAAA**, to examine whether the set bit in n is at an odd position and if there are no set bits in even positions. If both conditions are met, we return True.\n\n# Complexity\n- Time complexity:\nO(1) as it involves a fixed number of operations.\n\n- Space complexity:\nO(1) since we use a constant amount of memory for variables and masks.\n\n# Slow Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n while n > 1:\n if n % 4 != 0:\n return False\n n /= 4\n return True\n\n```\n# Fast Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return n > 0 and (n & (n - 1)) == 0 and (n & 0x55555555) != 0\n#Update Eliminated redundancy**\n```\n\n### ****I look forward to assisting you with any other solutions in the near future. Until then, take care and goodbye for now!****\n---\n\n | 0 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
One liner Bitwise Manipulation | power-of-four | 0 | 1 | # Intuition\nThe problem requires us to check if a given integer is a power of 4. To understand whether a number is a power of 4, we can make use of bitwise operations. We know that a power of 4 is a positive integer with a binary representation that has only one set bit, and that set bit is at an odd position.\n# Approach\nCheck for Positivity: First, we check if the input integer n is greater than zero. Negative numbers and zero cannot be powers of 4.\n\nCheck for Being a Power of 2: We then check if n is a power of 2 by using the condition (n & (n - 1)) == 0. This condition checks if there\'s only one set bit in the binary representation of n. If there is, it could potentially be a power of 2.\n\nCheck for Odd Position Set Bit: To ensure it is a power of 4 and not just a power of 2, we use the condition (n & 0x55555555) != 0. The 0x55555555 value has a binary pattern where the set bit is at an odd position. If this condition is met, it means the set bit in n is at an odd position, indicating that it is a power of 4.\n# Complexity\nTime complexity:\n\nThe time complexity of this algorithm is O(1) because we are performing a fixed number of bitwise operations regardless of the size of the input integer n.\n\nSpace complexity:\n\nThe space complexity is O(1) as we are using a fixed amount of space to store constants and temporary variables.\n# Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return (n > 0) and (n & (n - 1) == 0) and (n & 0x55555555 != 0)\n``` | 2 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Easy. One Line Python Solution. Logarithm. | power-of-four | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse math\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse n logarithm to base 4.\n1. If n is negative return False.\n2. Check if the n logarithm to base 4 belongs to naturale numbers or not.\n$$log4(n)\u2208N$$\n# Complexity\n- Time complexity:$$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n return False if n < 1 or math.log(n, 4) % 1 != 0 else True\n \n``` | 0 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
1-liner | power-of-four | 0 | 1 | \n\n# Code\n```\ndef isPowerOfFour(self, n: int) -> bool:\n return n==1 if n<=1 else int(sqrt(n)) * int(sqrt(n)) == n and int(sqrt(n)).bit_count() == 1\n``` | 0 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.