title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python short and clean with explanation. SortedList (BST). | data-stream-as-disjoint-intervals | 0 | 1 | # Approach\nOverall algorithm:\n\n1. Initialize a `SortedList` of `intervals`, where an interval is of form `[a, b]`.\n\n2. Maintain the `non overlapping` invariant after each `addNum` operation. (Described below in `addNum` operation)\n\n3. In `getIntervals` operation, return the `intervals` list as is.\n\n\nOperation `addNum` algorithm:\n\n1. Binary search for the insertion point of `value` in the `intervals`, say index `i`.\n\n2. Let, `lt` be the left interval of `value`. i.e, `lt = intervals[i - 1]`.\n\n3. Let, `rt` be the right interval of `value`. i.e, `rt = intervals[i]`.\n\n4. Note that, `lt[1] <= value < rt[0]`.\n\n5. Now there are bunch of cases to handle:\n\n 1. `lt[0] <= value <= lt[1]`:\n Existing interval `lt` already covers `value`. No need to do anything.\n Ex: `lt = [2, 5], value = 4`.\n\n 2. `lt[1] + 1 == value` and `value == rt[0] - 1`:\n Both `lt` and `rt` can be merged using `value` as intermediate!\n Remove `lt` and `rt`. Add merged interval `[lt[0], rt[1]]`.\n Ex: `lt = [2, 5], value = 6, rt = [7, 9]` `=>` `..[2, 9]..`\n\n 3. `lt[1] + 1 == value` and `value != rt[0] - 1`:\n The `value` can be merged with `lt`.\n Remove `lt`. Add merged interval `[lt[0], value]`.\n Ex: `lt = [2, 5], value = 6, rt = [8, 9]` `=>` `..[2, 6],[8, 9]..`\n\n 4. `lt[1] + 1 != value` and `value == rt[0] - 1`:\n The `value` can be merged with `rt`.\n Remove `rt`. Add merged interval `[value, rt[1]]`.\n Ex: `lt = [2, 4], value = 6, rt = [7, 9]` `=>` `..[2, 4],[6, 9]..`\n\n 5. `lt[1] + 1 != value` and `value != rt[0] - 1`:\n The `value` can\'t be merged.\n Add standalone interval `[value, value]`.\n Ex: `lt = [2, 4], value = 6, rt = [8, 9]` `=>` `..[2, 4],[6, 6],[8, 9]..`\n\n6. Note: Below `code` compresses all the above cases into few conditions. But it\'s essentially doing the same.\n\n# Complexity\n- Time complexity:\n `addNum`: $$O(log(n))$$\n `getIntervals`: $$(1)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is min(number of intervals, number of values)`\n\n# Code\n```python\nfrom sortedcontainers import SortedList\n\nclass SummaryRanges:\n\n def __init__(self):\n self.intervals = SortedList()\n\n def addNum(self, value: int) -> None:\n n = len(self.intervals)\n i = self.intervals.bisect((value, math.inf))\n \n lt = self.intervals[i - 1] if 0 <= i - 1 < n else (-inf, -inf)\n rt = self.intervals[i ] if 0 <= i < n else ( inf, inf)\n \n if lt[0] <= value <= lt[1]: return\n\n a, b = value, value\n if lt[1] + 1 == value: self.intervals.remove(lt); a = lt[0]\n if value == rt[0] - 1: self.intervals.remove(rt); b = rt[1]\n\n self.intervals.add((a, b))\n\n def getIntervals(self) -> list[list[int]]:\n return self.intervals\n\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n\n``` | 6 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
python3 | binary search and merge or insert. | data-stream-as-disjoint-intervals | 0 | 1 | Consider ranges as a array maintained sorted. [(r1, r2), (r3,r4) .... ] => r1 < r2 < r3 < r4 ....\nThe above should also hold good after inserting a certain value.\n\nThe following are the cases to consider to insert a value into the range. The value ... \n1. is inside the current ranges ( can be eliminated during binary search of ranges )\n2. is connection point between two ranges\n3. extends an existing range\'s end\n4. extends an existing range\'s start\n5. Starts a new range at start, end or elsewhere.\n\nEx: 1 ranges = [1,4], [5,7], value = 6; => [1,4], [5,7]\nEx: 2 ranges = [1,2], [4,5], value = 3; => [1,5]\nEx: 3 ranges = [1,2], [6,7], value = 3; => [1,3], [6,7]\nEx: 4 ranges = [1,2], [6,7], value = 5; => [1,2], [5,7]\nEx: 5 ranges = [1,2], [6,7], value = 4; => [1,2], [4,4], [6,7]\n\n```\nclass SummaryRanges:\n\n def __init__(self):\n self.ranges = []\n\n def addNum(self, value: int) -> None: \n start, end, idx = 0, len(self.ranges), 0 \n \n # binary search the index where the value would end up if independent range.\n \n while start < end: \n pivot = (start+end)//2\n s,e = self.ranges[pivot]\n if value >= s and value <= e:\n return \n elif value > e:\n idx = start = pivot + 1\n elif value < s:\n idx = end = pivot\n \n if idx == len(self.ranges):\n \n\t\t\t# The value goes at the end, either merge with end range or open new one.\n \n\t\t\tif len(self.ranges) and self.ranges[-1][1] + 1 == value: \n self.ranges[-1][1] = value\n else: \n self.ranges.append([value, value])\n elif idx >= 0:\n if self.ranges[idx][0]-1 == value:\n \n # Merge value into the range at idx and check if we need to merge the range before. \n # Its a connection.\n \n self.ranges[idx][0] = value\n if idx and self.ranges[idx-1][1] + 1 == self.ranges[idx][0]:\n self.ranges[idx-1][1] = self.ranges[idx][1]\n \n # Delete range at idx if we merged the range with prev one.\n \n del self.ranges[idx]\n elif idx and self.ranges[idx-1][1]+1 == value: \n \n\t\t\t\t# value merges with the range before.\n \n self.ranges[idx-1][1] = value \n else:\n # open new range in middle.\n \n self.ranges.insert(idx, [value, value])\n\n def getIntervals(self) -> List[List[int]]:\n return self.ranges\n | 6 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Python LIS based approach | russian-doll-envelopes | 0 | 1 | The prerequisite for this problem is to understand and solve [Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/). So if you are familiar with LIS and have solved it, the difficulty of this problem is reduced.\n\nNow, before we can start implementing LIS for this problem, we need to determine the sort order of the input `envelopes`. You can read this post which explains how the sort order is determined -> [Explanation on which sort order to choose](https://leetcode.com/problems/russian-doll-envelopes/discuss/2071477/Best-Explanation-with-Pictures)\n\n**Time - O(nlogn)** - Time required for sorting and performing LIS\n**Space - O(n)** - space required for `res`.\n\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n \n res = []\t\t\n\t\t# Perform LIS\n for _, h in envelopes:\n l,r=0,len(res)-1\n\t\t\t# find the insertion point in the Sort order\n while l <= r:\n mid=(l+r)>>1\n if res[mid]>=h:\n r=mid-1\n else:\n l=mid+1 \n idx = l\n if idx == len(res):\n res.append(h)\n else:\n res[idx]=h\n return len(res)\n \n```\n\nWe can make the above code more concise by using a python library `bisect_left` to locate the insertion point in the sort order. \n\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1])) \n res = []\n for _, h in envelopes:\n idx = bisect_left(res, h)\n if idx == len(res):\n res.append(h)\n else:\n res[idx]=h\n return len(res) \n```\n\n---\n\n***Please upvote if you find it useful*** | 23 | You are given a 2D array of integers `envelopes` where `envelopes[i] = [wi, hi]` represents the width and the height of an envelope.
One envelope can fit into another if and only if both the width and height of one envelope are greater than the other envelope's width and height.
Return _the maximum number of envelopes you can Russian doll (i.e., put one inside the other)_.
**Note:** You cannot rotate an envelope.
**Example 1:**
**Input:** envelopes = \[\[5,4\],\[6,4\],\[6,7\],\[2,3\]\]
**Output:** 3
**Explanation:** The maximum number of envelopes you can Russian doll is `3` (\[2,3\] => \[5,4\] => \[6,7\]).
**Example 2:**
**Input:** envelopes = \[\[1,1\],\[1,1\],\[1,1\]\]
**Output:** 1
**Constraints:**
* `1 <= envelopes.length <= 105`
* `envelopes[i].length == 2`
* `1 <= wi, hi <= 105` | null |
354: Space 98.16%, Solution with step by step explanation | russian-doll-envelopes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We first sort the envelopes based on width in ascending order, and if the widths are equal, we sort them based on height in descending order. This is because when we are trying to find the maximum number of envelopes we can Russian doll, we only care about the heights of the envelopes that have the same width as the current envelope, and we want to sort them in descending order so that we can maintain the largest possible doll set.\n\n2. We then initialize an array called doll_set to store the heights of the envelopes in the Russian doll set.\n\n3. We iterate through each envelope in the sorted envelopes list.\n\n4. For each envelope, we get its height and use binary search to find the index where we can insert the current height to maintain the sorted order of the doll set.\n\n5. If the index is beyond the length of the doll set, we add the height to the end of the doll set.\n\n6. Otherwise, we replace the height at that index with the current height, since it can fit inside the previous envelope.\n\n7. After iterating through all the envelopes, the length of the doll_set array is the maximum number of envelopes we can Russian doll, so we return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n # Same as 300. Longest Increasing Subsequence\n ans = 0\n dp = [0] * len(envelopes)\n\n for _, h in envelopes:\n l = 0\n r = ans\n while l < r:\n m = (l + r) // 2\n if dp[m] >= h:\n r = m\n else:\n l = m + 1\n dp[l] = h\n if l == ans:\n ans += 1\n\n return ans\n\n``` | 7 | You are given a 2D array of integers `envelopes` where `envelopes[i] = [wi, hi]` represents the width and the height of an envelope.
One envelope can fit into another if and only if both the width and height of one envelope are greater than the other envelope's width and height.
Return _the maximum number of envelopes you can Russian doll (i.e., put one inside the other)_.
**Note:** You cannot rotate an envelope.
**Example 1:**
**Input:** envelopes = \[\[5,4\],\[6,4\],\[6,7\],\[2,3\]\]
**Output:** 3
**Explanation:** The maximum number of envelopes you can Russian doll is `3` (\[2,3\] => \[5,4\] => \[6,7\]).
**Example 2:**
**Input:** envelopes = \[\[1,1\],\[1,1\],\[1,1\]\]
**Output:** 1
**Constraints:**
* `1 <= envelopes.length <= 105`
* `envelopes[i].length == 2`
* `1 <= wi, hi <= 105` | null |
355: Time 94.7% and Space 95.87%, Solution with step by step explanation | design-twitter | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n94.7%\n\n- Space complexity:\n95.87%\n\n# Code\n```\nclass Twitter:\n def __init__(self):\n # Use itertools.count to generate a decreasing sequence of integers for tweets\n self.timer = itertools.count(step=-1)\n # Use defaultdict and deque to store tweets for each user\n self.tweets = collections.defaultdict(deque)\n # Use defaultdict and set to store followees for each user\n self.followees = collections.defaultdict(set)\n\n def postTweet(self, userId: int, tweetId: int) -> None:\n # Append the tweet to the left of the deque for the user, along with its timestamp\n self.tweets[userId].appendleft((next(self.timer), tweetId))\n # If the deque for the user has more than 10 tweets, remove the oldest tweet from the right\n if len(self.tweets[userId]) > 10:\n self.tweets[userId].pop()\n\n def getNewsFeed(self, userId: int) -> List[int]:\n # Merge the tweets of the user\'s followees (including the user) using heapq.merge\n tweets = list(heapq.merge(\n *(self.tweets[followee] for followee in self.followees[userId] | {userId})))\n # Return the tweet IDs of the 10 most recent tweets\n return [tweetId for _, tweetId in tweets[:10]]\n\n def follow(self, followerId: int, followeeId: int) -> None:\n # Add the followee to the set of followees for the follower\n self.followees[followerId].add(followeeId)\n\n def unfollow(self, followerId: int, followeeId: int) -> None:\n # Remove the followee from the set of followees for the follower (if the followee exists)\n self.followees[followerId].discard(followeeId)\n\n``` | 11 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
[Python] 12ms 99.1% better without heap and queue | design-twitter | 0 | 1 | \n```\nclass User:\n def __init__(self, userId):\n self.userId = userId\n self.tweets = {}\n self.followers = set()\n self.follows = set()\n\n\nclass Twitter(object):\n\n def __init__(self):\n self.users = {}\n self.time = 0\n\n def create(self, userid):\n \n if userid not in self.users:\n self.users[userid] = User(userid)\n\n def postTweet(self, userId, tweetId):\n """\n :type userId: int\n :type tweetId: int\n :rtype: None\n """\n self.create(userId)\n self.users[userId].tweets[tweetId] = self.time\n self.time += 1\n\n def getNewsFeed(self, userId):\n """\n :type userId: int\n :rtype: List[int]\n """\n feed = []\n temp = []\n self.create(userId)\n for i in self.users[userId].tweets:\n temp.append([i, self.users[userId].tweets[i]])\n for i in self.users[userId].follows:\n print(i.tweets)\n for j in i.tweets:\n temp.append([j, i.tweets[j]])\n temp.sort(key=lambda x:x[1], reverse=True)\n\n for i in temp:\n feed.append(i[0])\n return feed[:10]\n\n def follow(self, followerId, followeeId):\n """\n :type followerId: int\n :type followeeId: int\n :rtype: None\n """\n self.create(followerId)\n self.create(followeeId)\n self.users[followerId].follows.add(self.users[followeeId])\n self.users[followeeId].followers.add(self.users[followerId])\n\n def unfollow(self, followerId, followeeId):\n """\n :type followerId: int\n :type followeeId: int\n :rtype: None\n """\n self.create(followerId)\n self.create(followeeId)\n if self.users[followerId] in self.users[followeeId].followers:\n self.users[followeeId].followers.remove(self.users[followerId])\n self.users[followerId].follows.remove(self.users[followeeId])\n | 20 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
[ Python ] ✅✅ Simple Python Solution Using HashMap | Hash Table 🥳✌👍 | design-twitter | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 35 ms, faster than 47.64% of Python3 online submissions for Design Twitter.\n# Memory Usage: 14 MB, less than 95.67% of Python3 online submissions for Design Twitter.\n\n\tclass Twitter:\n\n\t\t\tdef __init__(self):\n\n\t\t\t\tself.followers = {}\n\t\t\t\tself.tweets = []\n\n\t\t\tdef postTweet(self, userId: int, tweetId: int) -> None:\n\n\t\t\t\tif not userId in self.followers:\n\t\t\t\t\tself.followers[userId] = [userId]\n\n\t\t\t\tself.tweets.append([userId, tweetId])\n\n\t\t\tdef getNewsFeed(self, userId: int) -> List[int]:\n\n\t\t\t\tresult = []\n\t\t\t\tcount = 1 \n\t\t\t\tindex = len(self.tweets) - 1\n\n\t\t\t\twhile count < 11 and index > -1:\n\n\t\t\t\t\tif self.tweets[index][0] in self.followers[userId]:\n\t\t\t\t\t\tresult.append(self.tweets[index][1])\n\t\t\t\t\t\tcount = count + 1\n\t\t\t\t\tindex = index - 1\n\n\t\t\t\treturn result\n\n\t\t\tdef follow(self, followerId: int, followeeId: int) -> None:\n\n\t\t\t\tif not followerId in self.followers:\n\t\t\t\t\tself.followers[followerId] = [followerId]\n\n\t\t\t\tself.followers[followerId].append(followeeId)\n\n\t\t\tdef unfollow(self, followerId: int, followeeId: int) -> None:\n\n\t\t\t\tif followeeId in self.followers[followerId]:\n\t\t\t\t\tself.followers[followerId].remove(followeeId)\n\n# Thank You So Much \uD83E\uDD73\u270C\uD83D\uDC4D | 1 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Simple Python Solution using Hashmap and Hashset with step-by-step explanation | design-twitter | 0 | 1 | \n```\nclass Twitter:\n def __init__(self):\n self.count = 0\n self.follows = collections.defaultdict(list)\n self.tweets = collections.defaultdict(list)\n self.time = collections.defaultdict(int)\n\n def postTweet(self, userId: int, tweetId: int) -> None:\n self.count += 1\n self.tweets[userId].append(tweetId)\n self.time[tweetId] = self.count\n\n def getNewsFeed(self, userId: int) -> List[int]:\n timeList = []\n totalTweets = []\n totalTweets += self.tweets[userId]\n for followee in self.follows[userId]:\n totalTweets.extend(self.tweets[followee])\n\n unique = set(totalTweets)\n for tweet in unique:\n timeList.append((tweet, self.time[tweet]))\n timeList.sort(key=lambda x:x[1], reverse=True)\n res = []\n for item, time in timeList:\n res.append(item)\n if len(res) > 10:\n return res[:10]\n return res\n\n def follow(self, followerId: int, followeeId: int) -> None:\n self.follows[followerId].append(followeeId)\n\n def unfollow(self, followerId: int, followeeId: int) -> None:\n l = self.follows[followerId]\n if followeeId in l:\n l.remove(followeeId)\n self.follows[followerId] = l\n```\n\n1. initiate class variables\n\tself.count -> to record the timestamps during running \n\tself.follows -> key:userId, value: a list of Ids that this user is following\n\tself.tweets -> key:userId, value: a list of tweet Ids that this user posted\n\tself.time -> key:tweetId, value: the timestamp that this tweet posted\n\n2. postTweets\n\teverytime post a tweet, we:\n\t1) increment the timestamp count by 1\n\t2) add this tweet to the according user\'s tweets list\n\t3) map the timestamp with according tweet\n\n3. getNewsFeed\n\twe get news feed from **user-self + user\'s followees**\n\t1) use the tweets hashmap to find all tweets we need\n\t2) use hashset to remove duplicates\n\t3) use the time hashmap to find post time for each tweet, store as a tuple\n\t4) sort the timeList of tuples by post time\n\t5) return the tweet only\n\t\n4. Follow\n\tsimply add the followeeId to according user\'s follow list\n\n5. Unfollow\n\tif followeeId not in the user\'s follow list -> do nothing\n\telse: remove it from the user\'s follow list and update the hashmap | 1 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Python solution with VERY detailed explanations | design-twitter | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are 3 entities/objects in this probelm: user, post, and the system. These entities have their own properties and ther are related in some ways. So I create the 3 classes for them.\nA user object has a unique UserId, a collection of the user\'s posts, and a list of ther user\'s followees. The post list is stored in a linkedlist where a post is a node. The newly created post will be insterted at the head of the linkedlist so the linkedlist is sorted by the timestamp. Why I use a linkedlist here is because I want to transform the getNewsFeed() into the *merge k sorted lists* problem. The user\'s followees are stored in a set, because doing intertions and deletions in a set takes O(1) time.\nA tweet(post) object has a unique postId, a timestamp, and a next pointer pointing to the next post object. \nInside the Twitter class, I create a global time variable which acts as a clock. Every time a function is called, the time would increment by 1. In this way every post can have a proper timestamp. I also create a hashmap(dictionary) to store the userID and the corresponding user object so that I can quickly retrieve the user object by the given userId.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWith the classes being set up, the algorithms get clear. The most complex one is getNewsFeed(). As I said before, I have degenerated it into the *merge k sorted lists* problem. More specifically, we need a heap(or priority queue), always push the heads of the linkedlists into the heap and pop out the 10 most recent posts (or less). \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\ngetNewsFeed(): O(10logN) where N is the maximum number of users a user can follow\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass User:\n def __init__(self, userId, next=None) -> None:\n self.id=userId\n self.posts=None ### a head node: post2 -> post1\n self.following={self}\n\nclass Tweet:\n def __init__(self, postId, time, next=None) -> None:\n self.id=postId\n self.timestamp=time\n self.next=None\n\nclass Twitter:\n\n def __init__(self):\n self.time=0\n self.users={} # {userId: User}\n\n def postTweet(self, userId: int, tweetId: int) -> None:\n self.time+=1\n self.users[userId] = self.users.get(userId, User(userId))\n user=self.users[userId]\n tweet = Tweet(tweetId, self.time)\n tweet.next=user.posts\n user.posts=tweet\n \n\n def getNewsFeed(self, userId: int) -> List[int]:\n self.time+=1\n self.users[userId] = self.users.get(userId, User(userId))\n user=self.users[userId]\n heap=[] # min heap\n for u in user.following:\n if u.posts:\n heapq.heappush(heap, (-u.posts.timestamp, u.posts))\n i=0\n res=[]\n while i<10 and heap:\n _, post=heapq.heappop(heap)\n res.append(post.id)\n if post.next:\n heapq.heappush(heap, (-post.next.timestamp, post.next))\n i+=1\n return res\n\n\n\n def follow(self, followerId: int, followeeId: int) -> None:\n self.time+=1\n self.users[followerId]=self.users.get(followerId, User(followerId))\n follower= self.users[followerId]\n self.users[followeeId]=self.users.get(followeeId, User(followeeId))\n followee= self.users[followeeId]\n follower.following.add(followee)\n\n\n def unfollow(self, followerId: int, followeeId: int) -> None:\n self.time+=1\n self.users[followerId]=self.users.get(followerId, User(followerId))\n follower= self.users[followerId]\n self.users[followeeId]=self.users.get(followeeId, User(followeeId))\n followee= self.users[followeeId]\n follower.following.discard(followee)\n\n\n# Your Twitter object will be instantiated and called as such:\n# obj = Twitter()\n# obj.postTweet(userId,tweetId)\n# param_2 = obj.getNewsFeed(userId)\n# obj.follow(followerId,followeeId)\n# obj.unfollow(followerId,followeeId)\n``` | 3 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Python3 super simple solution, faster than 94.61% | design-twitter | 0 | 1 | ```\nclass Twitter:\n\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.users=collections.defaultdict(list)\n self.time=1\n self.followers=collections.defaultdict(set)\n \n\n def postTweet(self, userId: int, tweetId: int) -> None:\n """\n Compose a new tweet.\n """\n self.users[userId].append((self.time,tweetId))\n self.time += 1 \n\n def getNewsFeed(self, userId: int) -> List[int]:\n """\n Retrieve the 10 most recent tweet ids in the user\'s news feed. Each item in the news feed must be posted by users who the user followed or by the user herself. Tweets must be ordered from most recent to least recent.\n """\n news=list(self.users[userId])\n for user in self.followers[userId]:\n news.extend(self.users[user])\n news.sort(reverse=True,key=lambda x:x[0])\n res=[]\n for i in range(len(news)):\n if i == 10: break\n res.append(news[i][1])\n return res\n\n def follow(self, followerId: int, followeeId: int) -> None:\n """\n Follower follows a followee. If the operation is invalid, it should be a no-op.\n """\n if followerId != followeeId:\n self.followers[followerId].add(followeeId)\n\n def unfollow(self, followerId: int, followeeId: int) -> None:\n """\n Follower unfollows a followee. If the operation is invalid, it should be a no-op.\n """\n if followeeId in self.followers[followerId]:\n self.followers[followerId].remove(followeeId)\n \n\n\n# Your Twitter object will be instantiated and called as such:\n# obj = Twitter()\n# obj.postTweet(userId,tweetId)\n# param_2 = obj.getNewsFeed(userId)\n# obj.follow(followerId,followeeId)\n# obj.unfollow(followerId,followeeId)\n``` | 13 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Simple Python two approaches: Sort naively or heapify | design-twitter | 0 | 1 | ```py\n# assign a timestamp to tweets and sort the tweets naively when you get feed \nclass Twitter:\n\n def __init__(self):\n self.user_to_tweets_map = collections.defaultdict(list) # userId -> list of [tweetIds]\n self.follower_to_followee_map = collections.defaultdict(set) # userId -> set of followeeId\n self.timestamp = 0\n \n def postTweet(self, userId: int, tweetId: int) -> None:\n self.user_to_tweets_map[userId].append((self.timestamp, tweetId))\n self.timestamp += 1\n\n def getNewsFeed(self, user_id: int) -> List[int]:\n tweet_candidates = self.user_to_tweets_map[user_id][::]\n for followee_id in self.follower_to_followee_map[user_id]:\n tweet_candidates.extend(self.user_to_tweets_map[followee_id]) \n \n tweet_candidates.sort(reverse=True) # most recent to least recent\n return [tweetId for timestamp, tweetId in tweet_candidates[:10]]\n \n def follow(self, follower_id: int, followee_id: int) -> None:\n self.follower_to_followee_map[follower_id].add(followee_id)\n \n def unfollow(self, follower_id: int, followee_id: int) -> None:\n self.follower_to_followee_map[follower_id].discard(followee_id)\n```\n\n```py\n# Use a heap to get most recent tweets. Python doesn\'t have max_heap so negate the timestamps and use min_heap\nmin_heap[0] gives the lowest timestamp. Timestamps go to negative, so most timestamp is the most negative one, i.e lowest value. min_heap[0] gives most recent timestamp.\nclass Twitter2:\n\n def __init__(self):\n self.user_to_tweets_map = collections.defaultdict(list) # userId -> list of (timestamp, tweetIds)\n self.follower_to_followee_map = collections.defaultdict(set) # userId -> set of followeeId\n self.timestamp = 0\n \n def postTweet(self, userId: int, tweetId: int) -> None:\n self.user_to_tweets_map[userId].append((self.timestamp, tweetId))\n self.timestamp -= 1\n\n def getNewsFeed(self, user_id: int) -> List[int]:\n news = []\n min_heap = [] # index 0 will give lowest timestamp, i.e. most recent tweet, because timestamp goies to negative\n for f_id in self.follower_to_followee_map[user_id] | {user_id}:\n if f_id in self.user_to_tweets_map: # has tweeted\n min_heap.extend(self.user_to_tweets_map[f_id])\n \n heapq.heapify(min_heap)\n while min_heap and len(news) < 10:\n timestamp, tweet_id = heapq.heappop(min_heap)\n news.append(tweet_id)\n return news\n \n def follow(self, follower_id: int, followee_id: int) -> None:\n self.follower_to_followee_map[follower_id].add(followee_id)\n \n def unfollow(self, follower_id: int, followee_id: int) -> None:\n self.follower_to_followee_map[follower_id].discard(followee_id)\n``` | 1 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Clean and simple Implementation || Heap || Hashmap | design-twitter | 0 | 1 | \n\n# Code\n```\nclass Twitter:\n\n def __init__(self):\n self.followMap = collections.defaultdict(set)\n self.postMap = collections.defaultdict(list)\n self.count = 0\n\n def postTweet(self, userId: int, tweetId: int) -> None:\n self.postMap[userId].append([self.count, tweetId])\n self.count-=1 #Just for creating the max-heap \n\n def getNewsFeed(self, userId: int) -> List[int]:\n res = []\n heap = []\n self.followMap[userId].add(userId)\n for user in self.followMap[userId]:\n for post in self.postMap[user][::-1]:\n heap.append(post)\n heapq.heapify(heap)\n while heap and len(res)<10:\n count, tweet = heapq.heappop(heap)\n res.append(tweet)\n return res\n\n def follow(self, followerId: int, followeeId: int) -> None:\n self.followMap[followerId].add(followeeId)\n \n def unfollow(self, followerId: int, followeeId: int) -> None:\n if followeeId in self.followMap[followerId]:\n self.followMap[followerId].remove(followeeId)\n\n \n# Your Twitter object will be instantiated and called as such:\n# obj = Twitter()\n# obj.postTweet(userId,tweetId)\n# param_2 = obj.getNewsFeed(userId)\n# obj.follow(followerId,followeeId)\n# obj.unfollow(followerId,followeeId)\n``` | 2 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Approach by storing posts separately. | design-twitter | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n postTweet: O(1)\n getNewsFeed: O(n) Where n is the total number of posts of all the users\n Follow: O(1)\n Unfollow: O(1)\n\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n- \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Twitter:\n\n def __init__(self):\n self.posts = []\n self.users = collections.defaultdict(set)\n\n def postTweet(self, userId: int, tweetId: int) -> None:\n self.posts.append((userId,tweetId))\n\n def getNewsFeed(self, userId: int) -> List[int]:\n followers = self.users[userId]\n followers.add(userId)\n feed = []\n for i in range(len(self.posts)-1,-1,-1):\n if self.posts[i][0] in followers:\n feed.append(self.posts[i][1])\n if len(feed) == 10:\n break\n\n return feed\n\n \n def follow(self, followerId: int, followeeId: int) -> None:\n self.users[followerId].add(followeeId)\n\n def unfollow(self, followerId: int, followeeId: int) -> None:\n try:\n self.users[followerId].remove(followeeId)\n except KeyError:\n pass\n \n\n\n# Your Twitter object will be instantiated and called as such:\n# obj = Twitter()\n# obj.postTweet(userId,tweetId)\n# param_2 = obj.getNewsFeed(userId)\n# obj.follow(followerId,followeeId)\n# obj.unfollow(followerId,followeeId)\n``` | 0 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
List and Dictionary Approach | design-twitter | 0 | 1 | # Intuition\nI first thought to use a heap but on later reflection ended up just using a list, since tweets are stored at the end of the list and so they are ordered in time anyways.\n\n# Approach\nThe provided code defines a Twitter class with methods to post tweets, get news feeds, follow users, and unfollow users. In the postTweet method, tweets are appended to the twitter list. The getNewsFeed method retrieves the news feed for a given user by considering the user\'s tweets and the tweets of the users they are following. The follow and unfollow methods allow users to follow or unfollow other users.\n\n# Complexity\n- Time complexity:\n\nPosting a tweet (postTweet): $$O(1)$$\nRetrieving news feed (getNewsFeed): $$O(n \\log n)$$ where n is the number of tweets in the twitter list\nFollowing a user (follow): $$O(1)$$\nUnfollowing a user (unfollow): $$O(m)$$ where m is the number of users the follower currently follows\n\n- Space complexity:\nThe space complexity for the twitter list is $$O(n)$$, where n is the number of tweets.\nThe space complexity for the follows dictionary is $$O(m)$$, where m is the number of unique users across all follow relationships.\n\n# Code\n```\nclass Twitter:\n\n def __init__(self):\n self.twitter = []\n self.follows = defaultdict(list)\n \n\n def postTweet(self, userId: int, tweetId: int) -> None:\n self.userId = userId\n self.tweetId = tweetId\n tweet = [tweetId, userId]\n self.twitter.append(tweet)\n\n def getNewsFeed(self, userId: int) -> List[int]:\n self.userId = userId\n self.newsfeed = []\n \n tweets = self.twitter[::-1] # Reverse the order to get the latest tweets first\n follows = set(self.follows[self.userId])\n follows.add(userId) # Include the user\'s own tweets in the newsfeed\n \n for tweet in tweets:\n if tweet[1] in follows:\n self.newsfeed.append(tweet[0])\n if len(self.newsfeed) == 10:\n break\n\n return self.newsfeed\n\n\n def follow(self, followerId: int, followeeId: int) -> None:\n self.followerId = followerId\n self.followeeId = followeeId\n self.follows[followerId].append(followeeId)\n\n def unfollow(self, followerId: int, followeeId: int) -> None:\n self.followerId = followerId\n self.followeeId = followeeId\n if followeeId in self.follows[followerId]:\n self.follows[followerId].remove(followeeId)\n \n\n\n# Your Twitter object will be instantiated and called as such:\n# obj = Twitter()\n# obj.postTweet(userId,tweetId)\n# param_2 = obj.getNewsFeed(userId)\n# obj.follow(followerId,followeeId)\n# obj.unfollow(followerId,followeeId)\n``` | 0 | Design a simplified version of Twitter where users can post tweets, follow/unfollow another user, and is able to see the `10` most recent tweets in the user's news feed.
Implement the `Twitter` class:
* `Twitter()` Initializes your twitter object.
* `void postTweet(int userId, int tweetId)` Composes a new tweet with ID `tweetId` by the user `userId`. Each call to this function will be made with a unique `tweetId`.
* `List getNewsFeed(int userId)` Retrieves the `10` most recent tweet IDs in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user themself. Tweets must be **ordered from most recent to least recent**.
* `void follow(int followerId, int followeeId)` The user with ID `followerId` started following the user with ID `followeeId`.
* `void unfollow(int followerId, int followeeId)` The user with ID `followerId` started unfollowing the user with ID `followeeId`.
**Example 1:**
**Input**
\[ "Twitter ", "postTweet ", "getNewsFeed ", "follow ", "postTweet ", "getNewsFeed ", "unfollow ", "getNewsFeed "\]
\[\[\], \[1, 5\], \[1\], \[1, 2\], \[2, 6\], \[1\], \[1, 2\], \[1\]\]
**Output**
\[null, null, \[5\], null, null, \[6, 5\], null, \[5\]\]
**Explanation**
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // User 1 posts a new tweet (id = 5).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\]. return \[5\]
twitter.follow(1, 2); // User 1 follows user 2.
twitter.postTweet(2, 6); // User 2 posts a new tweet (id = 6).
twitter.getNewsFeed(1); // User 1's news feed should return a list with 2 tweet ids -> \[6, 5\]. Tweet id 6 should precede tweet id 5 because it is posted after tweet id 5.
twitter.unfollow(1, 2); // User 1 unfollows user 2.
twitter.getNewsFeed(1); // User 1's news feed should return a list with 1 tweet id -> \[5\], since user 1 is no longer following user 2.
**Constraints:**
* `1 <= userId, followerId, followeeId <= 500`
* `0 <= tweetId <= 104`
* All the tweets have **unique** IDs.
* At most `3 * 104` calls will be made to `postTweet`, `getNewsFeed`, `follow`, and `unfollow`. | null |
Python | simple solution | Permutation | count-numbers-with-unique-digits | 0 | 1 | \tdef countNumbersWithUniqueDigits(self, n: int) -> int:\n ans = 1\n temp = 1\n for i in range(1,n+1):\n ans = 9*temp + ans\n temp = temp*(10-i)\n \n return ans | 3 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Python | Backtracking | slow but mine | count-numbers-with-unique-digits | 0 | 1 | \n\n# Approach\nUse backtracking and search for all possible results and increment count whenever we find the legal number.\nTip : look out for numbers involving 0\n\n\n# Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n self.count = 0\n if n == 0:\n return 1\n if n == 1:\n return 10\n \n searchSpace = [0,1,2,3,4,5,6,7,8,9]\n\n def backTrack(path):\n if len(path) <= n:\n if path:\n if path[0] != 0:\n self.count += 1\n else:\n return\n for num in searchSpace:\n if num not in path:\n path.append(num)\n backTrack(path)\n path.pop()\n\n backTrack([])\n return self.count + 1\n\n\n``` | 1 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
357: Time 95.29% and Space 94.84%, Solution with step by step explanation | count-numbers-with-unique-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if n is equal to 0. If it is, then there is only 1 possible number with unique digits, which is 0. Return 1 as the result.\n2. If n is greater than 10, then the count will be the same as countNumbersWithUniqueDigits(10) because for n > 10, there will be repetition, and the count will not change anymore. Therefore, set n to min(n, 10).\n3. Start with a base count of 10, since we can always have 0 to 9 as the first digit. We will add more numbers to this count as we go along.\n4. For the second digit, we can have 9 choices, since 0 is already used. For the third digit, we can have 9 choices again, since we cannot repeat the first or second digit. For the fourth digit, we can have 8 choices, and so on. The total count is the product of the number of choices for each digit.\n5. Therefore, for i from 2 to n, compute the number of choices for each digit and add it to the count.\n6. Return the count as the result.\n\n# Complexity\n- Time complexity:\n95.29%\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n if n == 0:\n return 1\n \n # The maximum number of unique digits we can have is 10, since we have 10 digits in base 10\n # For n > 10, there will be repetition, so the count will be the same as countNumbersWithUniqueDigits(10)\n n = min(n, 10)\n \n # Start with a base count of 10, since we can always have 0 to 9 as the first digit\n count = 10\n \n # For the second digit, we can have 9 choices, since 0 is already used\n # For the third digit, we can have 9 choices again, since we cannot repeat the first or second digit\n # For the fourth digit, we can have 8 choices, and so on\n # The total count is the product of the number of choices for each digit\n for i in range(2, n + 1):\n choices = 9\n for j in range(i - 1):\n choices *= 9 - j\n count += choices\n \n return count\n\n``` | 6 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Python O(1) 99.80% math with explanation | count-numbers-with-unique-digits | 0 | 1 | ```\nclass Solution(object):\n def countNumbersWithUniqueDigits(self, n):\n """\n :type n: int\n :rtype: int\n """\n def count(k):\n if k == max(10 - n, 0):\n return 0\n return k*(1 + count(k - 1))\n if n == 0:\n return 1\n return 9*count(9) + 10\n```\n\n\n | 23 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Python O(1) Solution both Math, DP explained | count-numbers-with-unique-digits | 0 | 1 | n = 2\nFrom 11 -> 20 => 11,22,33,..99 excluded. \nso ans = 10(for 1->10) + 9*9(as 1 element excluded in each 10 range). = 10 + 81 = 91\n\nn = 3\nfor 1 -> 100 => ans = 91\nFrom 101 -> 200 => (100,101), (110,112,113...119), (121,122),..(191,199) excluded.\nans(100, 199) = 8*9\nFrom 201 -> 300 => (200,202), (211,212), (220,221,222...229),..(292,299) excluded.\nans(200, 299) = 8*9\n.\n.\nans(100, 1000) = 8*9*9\nTotal ans = 10 + 8*9*9 = 739\n\nSo Pattern = ans + 9*(11-i) ans i = [2,n]\n\n```python\n# Math \n\nclass Solution:\n def countNumbersWithUniqueDigits(self, n):\n if n == 0: return 1\n if n == 1: return 10\n \n ans = 10\n tmp = 9\n for i in range(2, n+1):\n tmp *= (11 - i)\n ans += tmp\n \n return ans\n```\n\n```python\n# Dynamic Programming\n\nclass Solution:\n def countNumbersWithUniqueDigits(self, n):\n dp = [1, 10]\n for i in range(2, n+1):\n tmp = 81\n for j in range(1, i-1):\n tmp *= (9 - j)\n ans = dp[i-1] + tmp\n dp.append(ans)\n \n return dp[n]\n \n``` | 4 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Combinatorics | count-numbers-with-unique-digits | 0 | 1 | ```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n res = 10\n if n == 0:\n return 1\n if n == 1:\n return res\n def get_count_of_len_i(i):\n ans = 9\n for k in range(2, i+1):\n ans*=(9-k+2)\n return ans\n\n for i in range(2, n+1):\n f_i = get_count_of_len_i(i)\n res+=f_i\n return res \n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Python Simple Recursive Solution | count-numbers-with-unique-digits | 0 | 1 | Good explanation can be found here: https://youtu.be/nrDNGVW59c8?feature=shared\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n def numUnique(n):\n if n == 0:\n return 1\n else:\n tmp = n - 1\n res = 9\n choices = 9\n while tmp:\n res *= choices\n tmp -= 1\n choices -= 1\n return res + numUnique(n - 1)\n return numUnique(n)\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Just use math bro | count-numbers-with-unique-digits | 0 | 1 | # Intuition\nBase cases: \nn==0 return 1\nn == 1 return 10 (0-9)\n\nNow for case n == 2, for all 2 digit numbers:\nFirst digit: 9 possible digits can fill this spot (1-9)\nSecond digit: Still 9 possible digits (exclude first digit, but include 0)\n\nCombs = 9x9 + (combinations of 1 digit numbers)\n\nNow for case n == 3, for all 3 digit numbers:\nFirst digit: 9 possibilities\nSecond: 9 possibilities\nThird: 8 possibilities (0-9, exclude first and second digits)\n\nCombs = 9x9x8 + (combs of 2 digit numbers) + (combs of 1 digit numbers)\n\nAND SO ON..............\n\n\n# Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n if n == 0:\n return 1\n elif n == 1:\n return 10\n \n combs = 9\n mult = 9\n for i in range (n-1):\n combs *= mult\n mult -= 1\n\n return combs + self.countNumbersWithUniqueDigits(n-1)\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Python 3 || Solution | count-numbers-with-unique-digits | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n if n == 0:\n return 1\n if n == 1:\n return 10\n\n result = [10, 81]\n \n for i in range(n - 2):\n result.append(result[-1] * (8-i))\n\n return sum(result)\n \n\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
[Python3] Good enough | count-numbers-with-unique-digits | 0 | 1 | ``` Python3 []\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n unique = 0\n\n def helper(x, seen, digits):\n nonlocal unique\n unique += 1\n\n for y in range(10):\n if digits<n and not 2**y&seen and not(not x and not y):\n seen|=2**y\n helper(x*10+y, seen, digits+1)\n seen^=2**y\n\n helper(0, 0, 0)\n\n return unique\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Easy Python Solution | count-numbers-with-unique-digits | 0 | 1 | # Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n dp = [1 for _ in range(n + 1)]\n\n for i in range(len(dp)):\n if i == 0: \n dp[i] = 1\n\n elif i > 0:\n count = i - 1\n prod = 1\n mult = 9\n while count > 0:\n prod = prod * mult\n count = count - 1\n mult = mult - 1\n dp[i] = (9 * prod) + dp[i - 1]\n\n return dp[-1]\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
357. Count Numbers with Unique Digits | count-numbers-with-unique-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# class Solution:\n# def countNumbersWithUniqueDigits(self, n: int) -> int:\n# c = 0\n# for i in range(0,10**n):\n# if len(str(i)) == len(set(str(i))):\n# c += 1\n# return c\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n ans = 1\n temp = 1\n for i in range(1,n+1):\n ans = 9*temp + ans\n temp = temp*(10-i)\n \n return ans\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Python3 solution with Permutation, Explained | count-numbers-with-unique-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe solve this in a permutation approach, counting the number of unique values for each n. So for n = 3, we count the unique values between 0 - 9, 10 - 99, 100 - 999. Notice how for each of these, when we choose 1 digit (the leftmost), the next choice we have decreases by 1.\n\nn = 1\n_ 9 choices\n\nn = 2\n_ _ 9*9 choices\n\nn = 3\n_ _ _ 9*9*8 choices for digits.\n\nThe reason we do not immediately decrease the number of digits for the second digit is that we are given another option after the first digit: the second digit can also be 0.\n\nIf this doesn\'t make sense, let\'s take n = 3.\n- first digit we have 9 choices: {1,2,3,4,5,6,7,8,9} say we choose 9.\n- second digit we still have 9 choices: {0,1,2,3,4,5,6,7,8} say we choose 8.\n- third digit we have 8 choices: {0,1,2,3,4,5,6,7}\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1) since n is a number less than 8.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) since n is a number less than 8.\n\n# Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n if n == 0: return 1\n res = 0\n dig_unique = [9, 9] # idx = 0 is 1 dig, idx = 1 is 2 dig\n rolling = 9\n prev = 9 #after the first one, 0 is an option\n for i in range(n-1):\n rolling *= prev\n dig_unique.append(rolling)\n prev -= 1\n\n print(dig_unique)\n # res = 9\n # for i in range(1, n):\n # res += dig_unique[i]\n\n return 10+sum(dig_unique[2:])\n\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
Simple solution | count-numbers-with-unique-digits | 0 | 1 | ```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n if not n:\n return 1\n cnt_choice, total = 9, 10\n for i in range(9, 10-n, -1):\n cnt_choice *= i\n total += cnt_choice\n return total \n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
python solution ( constant time and space ) | count-numbers-with-unique-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def countNumbersWithUniqueDigits(self, n: int) -> int:\n if n == 8 : return 2345851\n if n == 7 : return 712891\n if n == 6 : return 168571\n if n == 5 : return 32491\n if n == 4 : return 5275\n if n == 3 : return 739\n if n == 2 : return 91\n if n == 1 : return 10\n if n == 0 : return 1\n``` | 0 | Given an integer `n`, return the count of all numbers with unique digits, `x`, where `0 <= x < 10n`.
**Example 1:**
**Input:** n = 2
**Output:** 91
**Explanation:** The answer should be the total numbers in the range of 0 <= x < 100, excluding 11,22,33,44,55,66,77,88,99
**Example 2:**
**Input:** n = 0
**Output:** 1
**Constraints:**
* `0 <= n <= 8` | A direct way is to use the backtracking approach. Backtracking should contains three states which are (the current number, number of steps to get that number and a bitmask which represent which number is marked as visited so far in the current number). Start with state (0,0,0) and count all valid number till we reach number of steps equals to 10n. This problem can also be solved using a dynamic programming approach and some knowledge of combinatorics. Let f(k) = count of numbers with unique digits with length equals k. f(1) = 10, ..., f(k) = 9 * 9 * 8 * ... (9 - k + 2) [The first factor is 9 because a number cannot start with 0]. |
363: Solution with step by step explanation | max-sum-of-rectangle-no-larger-than-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Firstly, iterate over all the columns starting from 0 to n. For each iteration, the sum of the values in the current column and all the previous columns will be stored in the list temp.\n2. Using the Kadane\'s algorithm, find the maximum sum of a subarray with a sum less than or equal to k in the list temp.\n3. Update the maximum sum of a subarray found so far.\n4. Return the maximum sum of a subarray found so far.\n\n\nThe problem asks us to find the maximum sum of a subrectangle in a given matrix matrix such that the sum is no larger than a given integer k.\n\nThe solution uses a nested loop to iterate over all the possible subrectangles in the matrix. The outer loop iterates over the left column index left, and the inner loop iterates over the right column index right that is to the right of left. This ensures that we are considering all possible subrectangles that start from column left and end at column right.\n\nFor each subrectangle, the solution calculates the sum of each row in the subrectangle by iterating over the rows of the matrix. The row sums are stored in the list temp.\n\nThe problem now reduces to finding the maximum sum of a subarray in temp such that the sum is no larger than k. The solution uses Kadane\'s algorithm to solve this subproblem. Kadane\'s algorithm is a dynamic programming algorithm that can be used to find the maximum subarray sum in a given array.\n\nThe solution maintains a list cum_sum_set that stores the cumulative sum of the elements in temp. For each cumulative sum cum_sum, the solution finds the largest cumulative sum cum_sum_prev in cum_sum_set such that cum_sum - cum_sum_prev is no larger than k. This is done using the bisect_left function from the bisect module.\n\nIf such a cum_sum_prev is found, the solution updates the maximum sum found so far as cum_sum - cum_sum_prev.\n\nFinally, the solution returns the maximum sum found over all subrectangles.\n# Complexity\n- Time complexity:\n75.76%\n\n- Space complexity:\n67.10%\n\n# Code\n```\nclass Solution:\n def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:\n \n # Getting the dimensions of the matrix\n m, n = len(matrix), len(matrix[0])\n \n # Initializing the maximum sum\n max_sum = -float(\'inf\')\n \n # Iterating over all the columns\n for left in range(n):\n \n # Initializing the temporary sum list\n temp = [0] * m\n \n # Iterating over all the columns to the right of left\n for right in range(left, n):\n \n # Adding the values of the current column to temp\n for i in range(m):\n temp[i] += matrix[i][right]\n \n # Kadane\'s algorithm to find the maximum sum of a subarray with sum less than or equal to k\n cum_sum = 0\n cum_sum_set = sorted([0])\n \n for t in temp:\n cum_sum += t\n it = bisect_left(cum_sum_set, cum_sum - k)\n if it != len(cum_sum_set):\n max_sum = max(max_sum, cum_sum - cum_sum_set[it])\n bisect.insort(cum_sum_set, cum_sum)\n \n # Returning the maximum sum found\n return max_sum\n\n``` | 2 | Given an `m x n` matrix `matrix` and an integer `k`, return _the max sum of a rectangle in the matrix such that its sum is no larger than_ `k`.
It is **guaranteed** that there will be a rectangle with a sum no larger than `k`.
**Example 1:**
**Input:** matrix = \[\[1,0,1\],\[0,-2,3\]\], k = 2
**Output:** 2
**Explanation:** Because the sum of the blue rectangle \[\[0, 1\], \[-2, 3\]\] is 2, and 2 is the max number no larger than k (k = 2).
**Example 2:**
**Input:** matrix = \[\[2,2,-1\]\], k = 3
**Output:** 3
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-100 <= matrix[i][j] <= 100`
* `-105 <= k <= 105`
**Follow up:** What if the number of rows is much larger than the number of columns? | null |
Solution In Python | max-sum-of-rectangle-no-larger-than-k | 0 | 1 | The bisect_left() method is provided by the bisect module, which returns the left-most index to insert the given element, while maintaining the sorted order.\nThe insort function is the second step that does the real insertion process. The function returns the list after the element has been inserted in the rightmost index without altering the sorted order.\n\n```\nclass Solution:\n def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:\n ans = float("-inf")\n m, n = len(matrix), len(matrix[0])\n for i in range(n):\n lstSum = [0] * m\n for j in range(i, n):\n currSum = 0\n curlstSum = [0]\n for t in range(m):\n lstSum[t] += matrix[t][j]\n currSum += lstSum[t]\n pos = bisect_left(curlstSum, currSum - k)\n if pos < len(curlstSum):\n if curlstSum[pos] == currSum - k:\n return k\n else:\n ans = max(ans, currSum - curlstSum[pos])\n insort(curlstSum, currSum)\n return ans\n\n``` | 9 | Given an `m x n` matrix `matrix` and an integer `k`, return _the max sum of a rectangle in the matrix such that its sum is no larger than_ `k`.
It is **guaranteed** that there will be a rectangle with a sum no larger than `k`.
**Example 1:**
**Input:** matrix = \[\[1,0,1\],\[0,-2,3\]\], k = 2
**Output:** 2
**Explanation:** Because the sum of the blue rectangle \[\[0, 1\], \[-2, 3\]\] is 2, and 2 is the max number no larger than k (k = 2).
**Example 2:**
**Input:** matrix = \[\[2,2,-1\]\], k = 3
**Output:** 3
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-100 <= matrix[i][j] <= 100`
* `-105 <= k <= 105`
**Follow up:** What if the number of rows is much larger than the number of columns? | null |
🔥[Python] DFS, BFS || Complexity analysis || Video explanation | water-and-jug-problem | 0 | 1 | # Approach\n- Keep tracking the total water of two jugs, ```total```\n- Four potiential operations: ```+jug1Capacity ```, ```-jug1Capacity ```, ```+jug2Capacity ```, ```-jug2Capacity ```\n- Use either DFS or BFS to search for ```total == targetCapacity ```\n - Creat ```set``` to track all ```seen``` total to avoid repeat\n - if ```total == targetCapacity ```, return ```True```\n - if ```total``` in seen, or ```total < 0 ``` or ```total > jug1Capacity + jug2Capacity ``` => return ```False```\n - Move to next step: ```total```+```jug1Capacity```, or ```total```-```jug1Capacity```, or ```total```+```jug2Capacity```, or ```total```-```jug2Capacity```\n\n# Complexity\n- Time complexity: $$O(jug1Capacity*jug2Capacity)$$\n\n- Space complexity: $$O(jug1Capacity+jug2Capacity)$$\n\n# Video explanation\nhttps://www.youtube.com/watch?v=0BgaoIN1VUQ&t=7s\n\n# Solution 1: DFS\n```\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n\n seen = set()\n\n def dfs(tot):\n if tot == targetCapacity:\n return True\n if tot in seen or tot < 0 or tot > jug1Capacity + jug2Capacity:\n return False\n \n seen.add(tot)\n\n return dfs(tot+jug1Capacity) or dfs(tot-jug1Capacity) or dfs(tot+jug2Capacity) or dfs(tot-jug2Capacity)\n \n return dfs(0)\n```\n\n# Solution 2: BFS\n```\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n \n q = deque([0])\n seen = set()\n steps = [jug1Capacity, -jug1Capacity, jug2Capacity, -jug2Capacity]\n\n while q:\n cur = q.popleft()\n for step in steps:\n tot = cur + step \n if tot == targetCapacity:\n return True\n if tot not in seen and 0 <= tot <= jug1Capacity + jug2Capacity:\n seen.add(tot)\n q.append(tot)\n return False\n``` \n\n# \uD83D\uDC4DPlease UPVOTE if you find it helpful. Thanks :)\n\n\n\n \n\n\n\n\n\n \n\n \n\n``` | 50 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Python Solution using BFS traversal | water-and-jug-problem | 0 | 1 | ```\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n edges=[jug1Capacity,jug2Capacity,abs(jug2Capacity-jug1Capacity)]\n lst=[0]\n mx=max(jug1Capacity,jug2Capacity,targetCapacity)\n visited=[0]*1000001\n if targetCapacity>(jug1Capacity+jug2Capacity):\n return False\n visited[0]=1\n while lst:\n x=lst.pop(0)\n if x==targetCapacity:\n return True\n for i in edges:\n if x+i<=mx and visited[x+i]==0:\n lst.append(x+i)\n visited[x+i]=1\n if x-i>=0 and visited[x-i]==0:\n lst.append(x-i)\n visited[x-i]=1\n return False\n``` | 2 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Use Breadth First search | Initial state (0, 0) | water-and-jug-problem | 0 | 1 | ```\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n """\n we can solve this problemm using simple bfs approach\n let the initial state be (0, 0), every time a state is dequeued, \n we can perform either of the following operations on that state\n\n pour from jug1 to jug2 (if there is water in jug1 and available capacity in jug2)\n pour from jug2 to jug1 (if there is water in jug2 and avaialable capacity in jug1)\n empty jug1 (if there is water present in jug 1)\n empty jug2 (if there is water present in jug2)\n completely fill jug1 (if there is avaialable capacity in jug1)\n completely fill jug2 (if there is avaialble capacity in jug2)\n\n if a state is already visited, then we won\'t be enqueuing that state again in the queue\n """\n visited = set()\n que = deque([(0, 0)])\n while len(que):\n a, b = que.popleft()\n if a + b == targetCapacity:\n return True\n\n if a and b < jug2Capacity:\n c = min(a, jug2Capacity - b)\n if (a-c, c+b) not in visited:\n visited.add((a-c, c+b))\n que.append((a-c, c+b))\n \n if b and a < jug1Capacity:\n c = min(b, jug1Capacity - a)\n if (a+c, b-c) not in visited:\n visited.add((a+c, b-c))\n que.append((a+c,b-c))\n \n if a and (0, b) not in visited:\n visited.add((0, b))\n que.append((0, b))\n \n if b and (a, 0) not in visited:\n visited.add((a, 0))\n que.append((a, 0))\n \n if a != jug1Capacity and (jug1Capacity, b) not in visited:\n visited.add((jug1Capacity, b))\n que.append((jug1Capacity, b))\n \n if b != jug2Capacity and (a, jug2Capacity) not in visited:\n visited.add((a, jug2Capacity))\n que.append((a, jug2Capacity))\n\n return False\n \n``` | 3 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Beats 100% | Simple Math | 0ms | 3 Lines of code 🔥🚀 | water-and-jug-problem | 1 | 1 | # Intuition\nUpvote if you find helpful!!\n\n\n# Approach\nJust do dry run on any example you will easily get the algorithm.\n\n# Complexity\n- Time complexity: O(logn)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n bool canMeasureWater(int x, int y, int z) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n if(x + y < z) \n return false;\n if(x == z or y == z or x + y == z)\n return true;\n \n // property of B\xE9zout\'s identity\n return (z % __gcd(x,y) == 0);\n }\n};\n``` | 4 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Easy python solution with 80% TC and 99% SC | water-and-jug-problem | 0 | 1 | ```\ndef canMeasureWater(self, jug1: int, jug2: int, tar: int) -> bool:\n\tif(jug1 + jug2 < tar):\n\t\treturn 0\n\treturn tar % math.gcd(jug1, jug2) == 0\n``` | 2 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
365: Solution with step by step explanation | water-and-jug-problem | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, we import the gcd function from the math module since we will need it later to compute the greatest common divisor of the jug capacities.\n\n2. We define a class called Solution and a method called canMeasureWater that takes three integer arguments: jug1Capacity, jug2Capacity, and targetCapacity. The method returns a boolean indicating whether or not it is possible to measure exactly targetCapacity liters using the two jugs.\n\n3. We start with a base case: if the target capacity is 0, then it is always possible to measure it, so we return True.\n\n4. Next, we check if the sum of the jug capacities is less than the target capacity. If it is, then it is impossible to measure the target capacity with the two jugs, so we return False.\n\n5. If neither of the above conditions is met, then we need to check if the target capacity is divisible by the greatest common divisor of the jug capacities. If it is, then it is possible to measure the target capacity using the jugs. If it isn\'t, then it is impossible to measure the target capacity using the jugs.\n\n6. We use the gcd function to compute the greatest common divisor of the jug capacities and then check if it divides the target capacity using the modulo operator (%).\n\n7. Finally, we return the boolean value indicating whether or not it is possible to measure the target capacity using the two jugs.\n\n# Complexity\n- Time complexity:\n87.44%\n\n- Space complexity:\n78.82%\n\n# Code\n```\nfrom math import gcd\n\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n # Base case: target capacity is 0\n if targetCapacity == 0:\n return True\n # If the sum of jug capacities is less than target capacity, it\'s impossible\n if jug1Capacity + jug2Capacity < targetCapacity:\n return False\n \n # Check if target capacity is divisible by the greatest common divisor of jug capacities\n return targetCapacity % gcd(jug1Capacity, jug2Capacity) == 0\n\n``` | 2 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Python - Math Solution | water-and-jug-problem | 0 | 1 | # Intuition\n For Example 1,\n\n I can take j1=3 pour to j2 and then take another j1=3 pour to j2, \n so I have j1=(3+3-5)=1 and j2=5 which I can throw away. so I have \n one unit of water between j1 & j2.\n in order to get to the target=4, I need to repeat this 4x(3+3-5) times.\n\n How many times I can do like this ? can I do till max capacity=8(j1+j2)\n after 3 times, 3x(3+3-5) leaves 3 units in j1\n\n 4th: j2=3, take j1=3 and pour to j2, so I have j1=(3+3-5) & j2=5, \n throw away j2 and transfer j1 to j2 (j2=1 & j1=0). take j1=3, so I \n have j1+j2=(3+1)=4\n summarize: start=3 (j1=3, j2=0) => 3+3-5 (+j1 twice & -j2 once) \n => end=4 (j1=3, j2=1)\n 5th: j2=4, j1=0; +j1,-j2 => j1=2,j2=0; j1->j2 and +j1 => j2=2,j1=3 (5)\n 6th: j2=5, j1=0; +j1,-j2 => j1=3,j2=0; j1->j2 and +j1 => j2=3,j1=3 (6)\n 7th: j2=5, j1=1; +j1,-j2 => j1=3,j2=1; j1->j2 and +j1 => j2=4,j1=3 (7)\n 8th: j2=5, j1=2; +j1,-j2 => j1=3,j2=2; j1->j2 and +j1 => j2=5,j1=3 (8)\n \n It looks like we can do it ? but why ? \n what we did effectively add j1 x times and subtract j2 y times to get \n to the target t\n => 3x + 5y = t, where x, y are integers and t >= 0\n => 3(2) + 5(-1) = 1\n => 3(4) + 5(-2) = 2 \n => t[3(2) + 5(-1)] = t => we can do t times to get to t\n => 3(2t) + 5(-1t) = t \n\n# Approach\n To generalize,\n given, ax + by = d where a, b are known and d is derived\n we can solve the equation ax\'+by\'=t only when t is multiple of d\n how do we derive d ? Based on Bezout\'s identity theorem \n d is the greatest common divisor of a and b \n i.e. ax + by = GCD(a, b) where x,y are integers\n\n in example1, a=3, b=5, d=1 (3 & 5 are coprime)\n => 3(x=2) + 5(y=-1) = 1\n as target=4 is multiple of 1 we can solve the equation\n 3x`+5y`=4\n\n in example2, a=2, b=6, d=2 (6%2=0, so 2 is GCD)\n => 2(x=3) + 6(y=-1) = 2\n as target=5 is not multiple of 2, we can\'t solve the equation\n 2x`+6y`!= 5\n\n in example3, a=1, b=2, d=1 (1 is GCD)\n => 1(x=2) + 2(y=-1) = 1\n as target=3 is a multiple of 1, we can solve the equation\n x`+2y`= 3\n\n So the solution is to get GCD(a, b) and check if GCD(a, b) divides \n target\n \n Note: edge case where target exceeds max capacity (a+b) then we can\'t \n solve it.\n\n# Complexity\n- Time complexity:\n$$O(logn)$$ - math.GCD take logx(n) times where n is max(j1, j2)\n\n- Space complexity:\n$$O(1)$$ - constant space\n\n# Code\n```\nimport math\n\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n if jug1Capacity+jug2Capacity < targetCapacity:\n return False\n\n gcd_of_j1_and_j2 = math.gcd(jug1Capacity, jug2Capacity)\n return targetCapacity % gcd_of_j1_and_j2 == 0\n``` | 2 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Simple GCD Solution - beats 80% | water-and-jug-problem | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n if jug1Capacity + jug2Capacity < targetCapacity:\n return False\n \n gcd = math.gcd(jug1Capacity, jug2Capacity)\n \n return targetCapacity % gcd == 0\n``` | 0 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Readable Python, BFS, no time to think | water-and-jug-problem | 0 | 1 | # Approach\nI use a standard BFS template and adapt it for the solution. We search a graph where the nodes represent the currently filled state of the jugs. The neighboring states occur due to pouring or filling of jugs. The termination criteria is when the the capacity of the jugs individually or in total meet the target.\n\nI\'ve noticed many solutions combine the state of the jugs together. In an interview setting, I probably won\'t take that leap until I\'ve already gone down the obvious solution path. The logic for filling puring one jug into the other does get a bit gnarly, though.\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def canMeasureWater(self, jug1Capacity: int, jug2Capacity: int, targetCapacity: int) -> bool:\n \n queue = deque([])\n queue.append((0, 0)) # empty (jug1, jug2)\n visited = set((0, 0))\n\n while queue:\n jug1, jug2 = queue.popleft()\n\n # termination criteria\n if (jug1 == targetCapacity) or (jug2 == targetCapacity) or (jug1 + jug2 == targetCapacity):\n return True\n\n # neighboring states are jug contents after doing some action\n for next_jugs in self.get_neighbors(jug1, jug2, jug1Capacity, jug2Capacity):\n if next_jugs not in visited:\n queue.append(next_jugs)\n visited.add(next_jugs)\n\n return False\n\n def get_neighbors(self, jug1, jug2, cap1, cap2):\n res = [\n (cap1, jug2), # fill jug1\n (jug1, cap2), # fill jug2\n (0, jug2), # empty jug1\n (jug1, 0), # empty jug2\n ]\n\n # this next part deals with some logic to pour one jug into the other\n\n jug1_space = cap1 - jug1\n jug2_space = cap2 - jug2\n\n # if there is space left in jug1 and jug2 has some water\n if jug1_space > 0 and jug2 > 0:\n if jug1_space >= jug2:\n # pur everything from jug2 to jug1\n foo = (jug1 + jug2, 0)\n else:\n # fill jug1 to capacity, some excess left over\n foo = (cap1, jug2 - jug1_space)\n res.append(foo)\n \n # if there is space left in jug2 and jug1 has some water\n if jug2_space > 0 and jug1 > 0:\n if jug2_space >= jug1:\n foo = (0, jug1 + jug2)\n else:\n foo = (jug1 - jug2_space, cap2)\n res.append(foo)\n\n return res\n``` | 0 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Simple logic - Python | water-and-jug-problem | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canMeasureWater(self, jug1: int, jug2: int, tar: int) -> bool:\n\t if(jug1 + jug2 < tar):\n\t\t return 0\n\t return tar % math.gcd(jug1, jug2) == 0\n\n``` | 0 | You are given two jugs with capacities `jug1Capacity` and `jug2Capacity` liters. There is an infinite amount of water supply available. Determine whether it is possible to measure exactly `targetCapacity` liters using these two jugs.
If `targetCapacity` liters of water are measurable, you must have `targetCapacity` liters of water contained **within one or both buckets** by the end.
Operations allowed:
* Fill any of the jugs with water.
* Empty any of the jugs.
* Pour water from one jug into another till the other jug is completely full, or the first jug itself is empty.
**Example 1:**
**Input:** jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
**Output:** true
**Explanation:** The famous [Die Hard](https://www.youtube.com/watch?v=BVtQNK_ZUJg&ab_channel=notnek01) example
**Example 2:**
**Input:** jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
**Output:** false
**Example 3:**
**Input:** jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
**Output:** true
**Constraints:**
* `1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106` | null |
Easy solution in Python3 | valid-perfect-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n if num > 0:\n root = int(num ** 0.5)\n return root * root == num\n \n``` | 1 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Without using SQRT( ) lib function | valid-perfect-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n s=int(num**0.5)\n return s*s==num\n\n\n``` | 1 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Python || 2 Approach || 85% beats | valid-perfect-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n if num == 1:\n return True\n\n half = num//2\n endpoint = half\n while half*half >= num:\n if half*half == num:\n # return half\n return True\n \n endpoint = half\n half = half//2\n\n for i in range(half,endpoint):\n if i*i == num:\n return True\n\n return False\n\n<!-- ========================================== -->\n# ------------------------2ND APPROACH---------------\n\n i = 1\n j = num\n while i <= j:\n mid_num = (i + j + 1) // 2\n val = mid_num ** 2\n if val < num:\n i = mid_num + 1\n elif val > num:\n j = mid_num - 1\n else:\n return True\n return False\n\n \n \n``` | 2 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Python3 || Beats 86.21%|| Beginner oneliner. | valid-perfect-square | 0 | 1 | # Please upvote if you find the solution helpful.\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n return sqrt(num) == floor(sqrt(num))\n\n``` | 1 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Python and CPP Solution in O(SQRT(NUM)) Time Complexity | valid-perfect-square | 0 | 1 | # Intuition\nnum = 16\n\ni = 1 , num/i = 16/1 = 16, 16>1 i.e. num/i > i\ni = 2 , num/i = 16/2 = 8, 8>2 i.e. num/i >i\ni = 3 , num/i = 16/3 = 5, 5>3 i.e. num/i > i\ni = 4 , num/i = 16/4 = 4, 4==4 i.e. num/i==i\ni = 5 , num/i = 16/5 = 3, 3<5 i.e. num/i<i\n\nSo here we can Observe a pattern, while finding for the square root of a number, if the quotient of the nums (divided by a number) is smaller than that number(which is dividing the nums) then we will not get the perfect square root of the given Number.\n\n# Approach\nwe will break the search loop as we will hit the above condition i.e. if num/i<i then break.\n\n\n# Complexity\n- Time complexity: O(SQRT(NUM))\n\n- Space complexity: O(1)\n\n# Code\nCOVERING OVERFLOW CONDITION (WHICH MAY ARISE IN C/C++/JAVA)\n\nSolution in CPP:\n```\nclass Solution1 {\npublic:\n bool isPerfectSquare(int num) {\n if (num==1){\n return true; }\n for(int i=2;i<=num/2;i++)\n {\n if (num%i==0 && num/i == i) return true;\n if (num/i < i) break;\n }\n return false;\n \n }\n};\n```\n\nSolution in Python:\n```\nclass Solution5:\n def isPerfectSquare(self, num: int) -> bool: \n if num==1:\n return True \n for i in range(2,num//2+1):\n if num/i < i:\n break\n if num/i == i:\n return True\n return False\n\n``` | 2 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
python | Binary Search | beats 99% | valid-perfect-square | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n if num == 1:\n return True\n lo = 2\n hi = num // 2\n while lo <= hi:\n mid = lo + (hi - lo) //2\n print(mid)\n if mid * mid == num:\n return True\n if mid * mid > num:\n hi = mid - 1\n else:\n lo = mid + 1\n return False\n\n``` | 1 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Binary Search and Linear Search Approach | valid-perfect-square | 0 | 1 | \n1.Binary Search Approach\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n left,right=1,num\n while left<=right:\n mid=(left+right)//2\n if mid*mid==num:\n return True\n elif (mid*mid)>num:\n right=mid-1\n else:\n left=mid+1\n return False\n #please upvote me it would encourage me alot\n\n```\n2. Linear search\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n for i in range(50000):\n if i*i==num:\n return True\n else:\n return False\n #please upvote me it would encourage me alot\n\n``` | 3 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
367: Solution with step by step explanation | valid-perfect-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses binary search to find the square root of the given number, which allows for a faster runtime compared to iterating through all possible squares.\n\nFirst, it checks if the given number is 1, which is considered a perfect square, and returns True if it is.\n\nNext, it initializes a binary search range for the possible square root values. The left bound is set to 1, since 1 is the smallest possible square root, and the right bound is set to the given number.\n\nIt then enters a while loop that continues until the left bound is greater than the right bound. In each iteration, it computes the middle value of the search range and squares it to check if it matches the given number. If it does, it returns True since the number is a perfect square. If the square of the middle value is less than the given number, it updates the left bound to be the middle value plus 1, since the square root must be greater than or equal to the middle value. If the square of the middle value is greater than the given number, it updates the right bound to be the middle value minus 1, since the square root must be less than or equal to the middle value.\n\nIf the while loop completes without finding the square root, it means the given number is not a perfect square, so it returns False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n # Base case: 1 is a perfect square\n if num == 1:\n return True\n \n # Binary search for the square root of the number\n left, right = 1, num\n while left <= right:\n mid = (left + right) // 2\n square = mid * mid\n if square == num:\n return True\n elif square < num:\n left = mid + 1\n else:\n right = mid - 1\n \n # If we haven\'t found the square root, the number is not a perfect square\n return False\n\n``` | 3 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Using Binary Search to Check for Perfect Squares | valid-perfect-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo check whether a number is a perfect square, we need to find the square root of the number. One way to do this is to use binary search. We can start by setting the left boundary to 1 and the right boundary to num. Then, we can repeatedly compute the middle point between the left and right boundaries and check whether its square is equal to num. If the middle point squared is greater than num, we can update the right boundary to be the middle point minus 1. Otherwise, we can update the left boundary to be the middle point plus 1. We repeat this process until we find the square root of num or we exhaust all possible values of the left and right boundaries.\n\n# Complexity\n- Time complexity: $$O(log n)$$, where $$ n$$ is the value of the input integer num. This is because we are using binary search to find the square root of num, and binary search has a time complexity of $$O(log n)$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$, since we are not using any extra data structures.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n left, right = 1, num\n while left <= right:\n mid = (left + right) // 2\n if mid * mid == num:\n return True\n elif mid * mid < num:\n left = mid + 1\n else:\n right = mid - 1\n return False\n``` | 15 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
Easy to Understand Python Solution using Binary Search! | valid-perfect-square | 0 | 1 | # Intuition\nUsing binary search to find if there is a sqrt of n that is an integer. \n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n # if using sqrt func\n # rounded_sqrt = round(sqrt(num))\n # return rounded_sqrt == num \n\n # without using sqrt func \n low = 1\n high = num\n \n while high >= low:\n middle = (high + low) // 2\n middle_sqrd = middle * middle\n if middle_sqrd == num:\n return True\n elif middle_sqrd < num:\n low = middle + 1\n # This could be else, but I thought this would be easier to understand.\n elif middle_sqrd > num:\n high = middle - 1\n \n return False\n``` | 2 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
📌 Python3 extension of binary search | valid-perfect-square | 0 | 1 | ```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n left,right = 1,num\n while left<=right:\n middle = (left+right)//2\n if middle**2==num:\n return True\n if middle**2>num:\n right = middle-1\n else:\n left = middle+1\n return False\n``` | 5 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
No brain Python solution | valid-perfect-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPerfectSquare(self, num: int) -> bool:\n return num in (i**2 for i in range(1, 46341))\n``` | 2 | Given a positive integer num, return `true` _if_ `num` _is a perfect square or_ `false` _otherwise_.
A **perfect square** is an integer that is the square of an integer. In other words, it is the product of some integer with itself.
You must not use any built-in library function, such as `sqrt`.
**Example 1:**
**Input:** num = 16
**Output:** true
**Explanation:** We return true because 4 \* 4 = 16 and 4 is an integer.
**Example 2:**
**Input:** num = 14
**Output:** false
**Explanation:** We return false because 3.742 \* 3.742 = 14 and 3.742 is not an integer.
**Constraints:**
* `1 <= num <= 231 - 1` | null |
SIMPLE PYTHON SOLUTION || BOTTOM-UP APPROACH | largest-divisible-subset | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(NlogN + N^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def largestDivisibleSubset(self, nums: List[int]) -> List[int]:\n nums.sort()\n n=len(nums)\n prev=[[] for i in range(n+1)]\n for i in range(1,n+1):\n curr=[[] for i in range(n+1)]\n for j in range(1,n+1):\n x=[]\n if (j-1)==0 or (nums[j-1]%nums[i-1]==0 or nums[i-1]%nums[j-1]==0):\n x=prev[i]+[nums[i-1]]\n y=prev[j]\n if len(y)>len(x):\n curr[j]=y[:]\n else:\n curr[j]=x[:]\n prev=curr[:]\n return prev[1]\n\n\n``` | 2 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
Python || 94.02% Faster || LIS Approach | largest-divisible-subset | 0 | 1 | **Since the list is sorted so if a element is divisible by previous element it means it also divisible by all the elements before that previous element because the list is sorted and it become similar to Longest Increasing Subsequence: https://leetcode.com/problems/longest-increasing-subsequence/**\n```\nclass Solution:\n def largestDivisibleSubset(self, nums: List[int]) -> List[int]:\n nums.sort() \n n=len(nums)\n dp=[1]*n\n dic=[i for i in range(n)]\n maxi=last_index=0\n for i in range(1,n):\n for prev in range(i):\n if nums[i]%nums[prev]==0 and dp[prev]+1>dp[i]:\n dp[i]=dp[prev]+1\n dic[i]=prev\n if maxi<dp[i]:\n maxi=dp[i]\n last_index=i\n ans=[nums[last_index]]\n while dic[last_index]!=last_index:\n last_index=dic[last_index]\n ans.append(nums[last_index])\n return ans[-1::-1]\n```\n**An upvote will be encouraging** | 1 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
[Python] Short, simple, Time-95%, Space-87%, Iterative | largest-divisible-subset | 0 | 1 | Please feel free to ask questions and give suggestions to improve. **Upvote** if you liked the solution.\n**Main Idea**: \n* If we traverse nums in ascending order and we need any 1 longest subset, we need to add exactly 1 new subset for each number. \n\t* If it\'s an extension of a subset we saw before, only 1 of the longest extensions need to be added. (Only the last value added in a subset matters (Anything divisible by the largest value will be divisible by the previously added smaller values (which are all factors of the largest value))\n\t* If it\'s not an extension, we build a new subset with just that value\n```\ndef largestDivisibleSubset(self, nums: List[int]) -> List[int]:\n\t# We\'ll traverse values in nums in ascending order\n\tnums.sort()\n\t# Ordered (by length) list of valid subsets that are largest subset candidates\n\tsubsets = []\n\t\n\t# Add max-length subset for each value\n\tfor i, num in enumerate(nums):\n\t\t# Find the biggest subset we can add num to, and add this new subset to subsets (maintaining order)\n\t\tfor j in range(i-1, -1, -1):\n\t\t\t# If satisfies divisibility, insert into subsets (as per size, 1 bigger than previous subset)\n\t\t\tif not num%subsets[j][-1]:\n\t\t\t\t# Location of where to insert new extended subset (Alt.: Could binary search for it)\n\t\t\t\tk = next(filter(lambda k: len(subsets[j])!=len(subsets[k]), range(j+1, i)), i)\n\t\t\t\tsubsets.insert(k, subsets[j]+[num])\n\t\t\t\tbreak\n\t\telse:\n\t\t\t# num can\'t be added as an extension to any subset, create a blank one for it\n\t\t\tsubsets.insert(0, [num])\n\n\treturn subsets[-1]\n``` | 4 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
✅ || python || clean solution | largest-divisible-subset | 0 | 1 | ```\nclass Solution:\n def largestDivisibleSubset(self, nums):\n \n \n n= len(nums)\n \n if n==0:return []\n \n nums.sort()\n \n dp=[ [i] for i in nums]\n \n for i in range(n):\n for j in range(i):\n \n if nums[i]%nums[j]==0 and len(dp[j])+1 > len(dp[i]):\n \n dp[i] = dp[j]+[nums[i]]\n \n return max(dp, key=len)\n``` | 9 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
Python DP solution | largest-divisible-subset | 0 | 1 | ```\nclass Solution:\n def largestDivisibleSubset(self, nums: List[int]) -> List[int]:\n n = len(nums)\n nums.sort()\n res = [[num] for num in nums] #contains sets starting with that number\n \n for i in range(n):\n for j in range(i):\n if (nums[i] % nums[j]) == 0 and len(res[i]) < len(res[j]) + 1: #to ensure the length of the set is maximal \n res[i] = res[j] + [nums[i]]\n \n return max(res, key=len) #return max length set\n \n``` | 5 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
368: Solution with step by step explanation | largest-divisible-subset | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis is a dynamic programming solution to find the largest divisible subset of a set of distinct positive integers.\n\nThe basic idea is to sort the input array so that we can process it in increasing order. We initialize two arrays: dp and prev. dp[i] stores the size of the largest divisible subset that ends with nums[i], while prev[i] stores the index of the previous element in the largest divisible subset that ends with nums[i].\n\nWe then iterate over the input array, and for each element nums[i], we check all previous elements nums[j] (j < i). If nums[i] is divisible by nums[j], and the size of the largest divisible subset that ends with nums[j] plus one is greater than the current size of dp[i], we update dp[i] and prev[i]. At the end of this process, we have computed the size of the largest divisible subset, which is stored in max_size, and the index of the last element in the largest divisible subset, which is stored in max_index.\n\nWe then use the prev array to backtrack from max_index to the first element in the largest divisible subset, appending each element to a result list. Finally, we return the result list in reverse order (since we built the list backwards during the backtracking process).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestDivisibleSubset(self, nums: List[int]) -> List[int]:\n if not nums:\n return []\n # Sort the input array\n nums.sort()\n \n # Initialize a dynamic programming table\n # dp[i] stores the size of the largest divisible subset that ends with nums[i]\n dp = [1] * len(nums)\n \n # Initialize a backtracking table\n # prev[i] stores the index of the previous element in the largest divisible subset that ends with nums[i]\n prev = [-1] * len(nums)\n \n # Find the largest divisible subset and its size\n max_size = 1\n max_index = 0\n for i in range(1, len(nums)):\n for j in range(i):\n if nums[i] % nums[j] == 0 and dp[j] + 1 > dp[i]:\n dp[i] = dp[j] + 1\n prev[i] = j\n if dp[i] > max_size:\n max_size = dp[i]\n max_index = i\n \n # Backtrack to find the largest divisible subset\n result = []\n while max_index != -1:\n result.append(nums[max_index])\n max_index = prev[max_index]\n \n return result[::-1]\n\n``` | 2 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
Easy Python Solution | largest-divisible-subset | 0 | 1 | # Code\n```\nclass Solution:\n def largestDivisibleSubset(self, nums: List[int]) -> List[int]:\n\n nums.sort()\n \n answer = [[nums[i]] for i in range(len(nums))]\n\n for i in range(1, len(nums)):\n subsets = []\n for j in range(i):\n last = answer[j][-1]\n if answer[i][0] % last == 0 or last % answer[i][0] == 0:\n subsets.append(answer[j] + answer[i])\n subsets.sort(key=len)\n if subsets: answer[i] = subsets[-1]\n\n answer.sort(key=len)\n\n return answer[-1]\n``` | 0 | Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
* `answer[i] % answer[j] == 0`, or
* `answer[j] % answer[i] == 0`
If there are multiple solutions, return any of them.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,2\]
**Explanation:** \[1,3\] is also accepted.
**Example 2:**
**Input:** nums = \[1,2,4,8\]
**Output:** \[1,2,4,8\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 2 * 109`
* All the integers in `nums` are **unique**. | null |
Read this if you want to learn about masks | sum-of-two-integers | 0 | 1 | In Python unlike other languages the range of bits for representing a value is not 32, its much much larger than that. This is great when dealing with non negative integers, however this becomes a big issue when dealing with negative numbers ( two\'s compliment) \n\nWhy ?\n\nLets have a look, say we are adding -2 and 3, which = 1\n\nIn Python this would be ( showing only 3 bits for clarity ) \n\n1 1 0 +\n0 1 1 \n\nUsing binary addition you would get\n\n0 0 1 \n\nThat seems fine but what happended to the extra carry bit ? ( 1 0 0 0 ), if you were doing this by hand you would simply ignore it, but Python does not, instead it continues \'adding\' that bit and continuing the sum. \n\n1 1 1 1 1 1 0 +\n0 0 0 0 0 1 1 \n0 0 0 1 0 0 0 + ( carry bit ) \n\nso this actually continues on forever unless ... \n\nMask ! \n\nThe logic behind a mask is really simple, you should know that x & 1 = x right, so using that simple principle,\n\nif we create a series of 4 1\'s and & them to any larger size series, we will get just that part of the series we want, so \n\n1 1 1 1 1 0 0 1\n0 0 0 0 1 1 1 1 &\n\n0 0 0 0 1 0 0 1 ( Important to note that using a mask removes the two\'s compliment) \n\nFor this question leetcode uses 32 bits, so you just need to create a 32 bit mask of 1\'s , the quickest way is to use hexadecimal and 0xffffffff, you can write the binary form if you prefer it will work the same. \n\nHere is my code ,\n\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n \n # 32 bit mask in hexadecimal\n mask = 0xffffffff\n \n # works both as while loop and single value check \n while (b & mask) > 0:\n \n carry = ( a & b ) << 1\n a = (a ^ b) \n b = carry\n \n # handles overflow\n return (a & mask) if b > 0 else a\n```\nNote the final check, if b = 0 that means the carry bit \'finished\', but when there is a negative number ( like -1), the carry bit will continue until it exceeds our 32 bit mask ( to end while loop ) it wont be 0 so in that case we use the mask. \n\nHope that helps, let me know if you have any further questions in comments. | 182 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
[Python3] Math solution with explanation | sum-of-two-integers | 0 | 1 | The main idea is the school formulas for the logarithm: \n1) 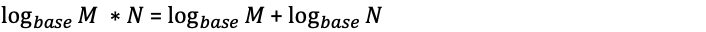\n2) \n\n\nThe first gives us the opportunity to get the sum of the logarithms of numbers, and the second to get the numbers themselves directly.\nmath.log(x) method returns the natural logarithm of a number, or the logarithm of number to base math.log(x, base).\nOnce there were about 15 testcases for this task and there were no problems with zeros. So now I had to add a couple of conditions for such cases.\n\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n if a == 0 and b != 0:\n return b\n elif b == 0 and a != 0:\n return a\n \n return int(log(exp(a) * exp(b)))\n```\n\nor even shorter:\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n return int(log(exp(a) * exp(b))) if a != 0 and b != 0 else a or b\n``` | 16 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
By Python using AND , XOR Logic also using Mask to tackle negative number testcases ! | sum-of-two-integers | 0 | 1 | We will do AND of A and B to get carry ,also XOR of A and B to get sum \n\nDo carry<<1 to shift the carry where it is to be added in sum ,then\nstore XOR of a and b again in \'a\' and carry again in \'b\' and repeat the process until carry is 0 !\n\nNow since Python cant handle negative numbers we must return the ans by converting it in a way that Python understands. \n\nTo explain, the hexadecimal number 0xffffffff is the same as the \nbinary number 0b1111111111111111111111111111111, containing 32 1\'s. (It\'s just easier to type lol.)\n\nIn order to make the code work like Java, we want to treat our numbers like they only have 32 bits. ANDing a number with the mask 0xffffffff, or 32 1\'s, basically turns all of a number\'s bits into 0\'s except for the rightmost 32. As a result, the number can be represented as if it only has 32 bits.\n\nUsing XOR for the sum and AND for the carry. We AND with the mask each time we set a and b in order to keep our numbers within 32 bits.\n\nAfter we exit the while loop, we have our answer a. If a is positive, then we can return it directly. However, in Python, negative numbers are represented in binary as having an unlimited number of leading 1\'s. The current answer would only have values in the rightmost 32 bits. Therefore, if the answer is negative, we need to convert it into Python\'s representation of negative numbers. \n\nFirst, we need to check if the answer is negative. We cannot just check to see if the answer is less than zero because our representation of the answer is not the same as Python\'s (since Python\'s have unlimited leading 1\'s). We are still treating our answer as if it only fits into 32 bits. \n\nA 32-bit signed integer is positive if the 32nd bit is a 0 and is negative if the 32nd bit is a 1. If we divide our mask (0xffffffff) by 2, we will get the binary number 0b0111111111111111111111111111111, which has 31 1\'s. This number is the greatest value we can have before the 32nd bit becomes a 1. Therefore, if our answer a > mask // 2, it is negative. Otherwise, it is positive and we can just return a itself.\n\nIf the number is negative, we then need to convert it into Python\'s representation of negative numbers. To do so, we can XOR with the mask of 32 1\'s in order to flip the rightmost 32 bits, since XORing a bit with 1 flips the bit. We can then NOT the number in order to turn all of the leading 0\'s into 1\'s. For example, say that the answer is -3, and (....0000000) or (....1111111) denote leading 0\'s or 1\'s until the 32nd bit:\n\nOur representation of -3 in 32 bits: (...0000000)11111111111111111111111111111101\nXOR with mask, aka flip rightmost 32 bits: (...0000000)00000000000000000000000000000010\nNOT, aka flipping all bits: (...1111111)1111111111111111111111111111101\nThe result is Python\'s representation of -3, including an unlimited number of leading 1\'s.\n\n# Code\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n mask = 0xffffffff\n while b!=0:\n temp = (a&b)<<1\n a =(a^b) & mask \n b = temp & mask \n\n if a > mask//2:\n #Negative number\n return ~(a^mask)\n else : \n return a\n```\nThis is not my logic ! Credits to sysy2152 in youtube comments for explaining this !\nRefer to - https://www.youtube.com/watch?v=gVUrDV4tZfY&t=3s for explanation \n | 3 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
(Python/C++/Java) Genius hack for similar questions | sum-of-two-integers | 0 | 1 | # Approach\nDo what they don\'t want you to. Question authority. Establish dominance.\n# Complexity\n- Time complexity:\nO(1)\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n return a+b\n``` | 3 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
One Liner || Python Solution | sum-of-two-integers | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n return sum([a,b])\n``` | 3 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
371: Solution with step by step explanation | sum-of-two-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution implements the bitwise operation approach to add two integers without using the + or - operators.\n\nThe algorithm starts by initializing a mask variable to 0xFFFFFFFF which is used to ensure that the result stays within the range of 32-bit integers.\n\nThen, using a while loop, the algorithm applies two bitwise operations on a and b until b becomes 0:\n\n1. (a ^ b) & mask: This operation performs the bitwise exclusive OR (^) operation on a and b and then bitwise ANDs (&) the result with the mask variable to ensure that the result stays within the range of 32-bit integers. The result is then stored in a.\n\n2. ((a & b) << 1) & mask: This operation performs the bitwise AND (&) operation on a and b, then left shifts the result by 1 bit (<< 1), and finally bitwise ANDs (&) the result with the mask variable to ensure that the result stays within the range of 32-bit integers. The result is then stored in b.\n\nThe above two operations are repeated until b becomes 0, at which point the value of a is returned as the sum of the original a and b values.\n\nFinally, the result is checked to ensure that it is within the range of 32-bit signed integers (0x7FFFFFFF or 2147483647 in decimal), and if it is greater than the maximum value, it is inverted and subtracted from the mask variable to get the correct negative value.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n mask = 0xFFFFFFFF\n \n while b:\n a, b = (a ^ b) & mask, ((a & b) << 1) & mask\n \n return a if a <= 0x7FFFFFFF else ~(a ^ mask)\n\n``` | 7 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
Python || 95.20% Faster || Bit Manipulation || O(1) Solution | sum-of-two-integers | 0 | 1 | ```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n f=0\n if a<0 and b<0:\n f=1\n mask=0xffffffff\n add=a^b\n carry=(a&b)<<1\n while carry!=0:\n add,carry=(add^carry)&mask,((add&carry)<<1)&mask\n if f:\n return ~(add^mask)\n return add \n```\n\n**An upvote will be encouraging** | 11 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
Marvelous Logic Python3,Java,Golang--->One Line | sum-of-two-integers | 1 | 1 | \n\n# One Line of Code Python3\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n return sum([a,b])\n```\n# 2. Python3---->Bit Manipulation\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n while b!=0:\n temp=(a&b)<<1\n a=a^b\n b=temp\n return a\n```\n# 3.Java Solution->Bit Manipulation\n```\nclass Solution {\n public int getSum(int a, int b) {\n int temp; \n while(b !=0 ) {\n temp = (a&b)<<1;\n a = a ^ b;\n b = temp;\n }\n return a;\n \n }\n}\n```\n# Golang Solution->Bit Manipulation\n```\nfunc getSum(a int, b int) int {\n for b!=0{\n temp:=a&b<<1\n a=a^b\n b=temp\n }\n return a\n}\n```\n# please upvote me it would encourage me alot\n | 7 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
Python | Recursive solution | Thought Process | sum-of-two-integers | 0 | 1 | **Prior Knowledge**\n\nYou guys should check out the top posts to understand the general solution of:\n\n```\ndef getSum(a, b):\n\tif b == 0: return a\n\treturn getSum(a ^ b, (a & b) << 1)\n```\n\nBut here\'s a quick summary:\n- Essentially, `a ^ b` add\'s binary numbers that do not require us to "carry" a "bit".\n- The (a & b) finds which bits need to be carried, and we simply bit shift to the left so the carried bit is in the right position. \n- By recursively calling `getSum` again, we will add the previous `a^b` result with the "carry" that needs to be accounted for to complete the add.\n\n**Python solution explanation**\n\nHowever, in python, integers can exceed 32 bits. This causes a problem for us! So to mitigate this, we have to:\n1. Make sure our integers are strictly 32 bits\n2. Juggle between 32 bit, two\'s complements.\n\nFirst, lets talk about the `mask` variable. Notice that it is equal to `0b11111111111111111111111111111111`. This is simply 32 bits of one\'s. This means any time the integer overflows to more than 32 bits, we do a `& mask` to set any bit greater than 32 to zero. This satifies our constraint #1 of making sure our intergers are strictly 32 bits.\n\nSecond, let\'s deal with the `MAX` variable. To understand the `MAX` variable, you must understand what is [two\'s complement](https://stackoverflow.com/questions/1049722/what-is-2s-complement). Ultimately, `MAX = 0b01111111111111111111111111111111` is the largest 32 bit integer that is "positve" under the "two\'s compelment" scheme. Thus, when we do `if a <= MAX` we are checking if `a` is positive. If `a` is greater than `MAX`, we have a "negative" number. *However, since python can deal with integers greater than 32 bits, python assumes this negative integer is positive*. Thus, `~(a ^ mask)` allows us to juggle from the positive number to the negative complement, ensuring we return the correct answer.\n\n```\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n\n mask = 0b11111111111111111111111111111111 \n MAX = 0b01111111111111111111111111111111\n \n if b == 0:\n return a if a <= MAX else ~(a ^ mask)\n \n return self.getSum(\n (a ^ b) & mask,\n ((a & b) << 1) & mask\n )\n```\n\nI hope this post has helped explain the python solution a tiny bit better!\n | 31 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
✅ Python one-line | sum-of-two-integers | 0 | 1 | Simply $$a + b = \\log_x(x^a * x^b)$$\n\n# Code\n```\nimport math\n\n\nclass Solution:\n def getSum(self, a: int, b: int) -> int:\n return int(math.log(2 ** a * 2 ** b, 2))\n``` | 7 | Given two integers `a` and `b`, return _the sum of the two integers without using the operators_ `+` _and_ `-`.
**Example 1:**
**Input:** a = 1, b = 2
**Output:** 3
**Example 2:**
**Input:** a = 2, b = 3
**Output:** 5
**Constraints:**
* `-1000 <= a, b <= 1000` | null |
C++uses Chinese Remainder& Fermat's Little Theorems Beats 99.6% | super-pow | 0 | 1 | # Intuition\nLike implementing RSA encryption\n\n# Approach\nUse least significant bit first/most significant bit first algorithm to compute the modular exponentiation. And use the Euler-Fermat Theorem to reduce exponent number modulo phi(n). \n**Euler-Fermat Theorem:**\n$$\na^{\\phi(n)}\\equiv 1 \\pmod{n}\n$$\nfor $\\gcd(a, n)=1$.\n\nIn this problem, \n$$n=1337=(191)(7), \\phi(n)=(191-1)(7-1)=(190)(6)=1140.$$\n\n What if $\\gcd(a, n)\\not=1$?\n That will be the boundary case. Try these 2 test cases: \n```\n7\n[1,1,4,0]\n191\n[1,1,4,0]\n```\nYou will find Euler-Fermat Theorem not enough! Suppose $\\gcd(a, p)=1$ & $\\gcd(a, q) \\not=1 $, one can still use $a^{p-1} \\equiv 1 \\pmod{p}$ to deal with. Then the Chinese Remainder Theorem comes to play.\n\nChinese Remainder says:\nLet $x\\equiv x_i \\pmod{n_i}$ with pairwise coprime $n_i$. Let $n=\\prod_i n_i$ Then \n$$\nx \\equiv \\sum_i x_iM_is_i \\pmod{n}\n$$\nwhere $M_i=n/n_i, s_i\\equiv M_i^{-1}\\pmod{n_i}$ \n\nIn our case:\n$$\n7^{-1}\\pmod{191}\\equiv 82, \\ 191^{-1}\\pmod{7}\\equiv 4\n$$\n\nIn fact Euler-Fermat Theorem is the basis for RSA. It can prove with the aid of Chinese Remainder the following theorem\n# Therem. If an postive integer a<n Then a^{k*phi(n)+1} =a (mod n) on matter what gcd(a, n) is.\n\nIn other word, the function $f(x)=a^x\\pmod{n}$ is a periodic function with $f(x)=f(x+k\\phi(n))$ which quarantees RSA works!\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n[Please turn on the English subtitles if necessary]\n[https://youtu.be/R3KdIxi0KLE](https://youtu.be/R3KdIxi0KLE)\n# Code\nC++ solution using Chinese Remainder.\n```\nint n=1337;\nint phi=1140;\nclass Solution {\npublic:\n int Chinese_Remainder(int a, int x, vector<int>& b){\n if (x==n) return 0;\n int p=n/x;\n int M;//modInverse i.e. x*M==1%p\n if (x==7) M=82;//can be computed by extended euclidean algorithm\n else M=4;\n \n int s=b.size();\n int exp=0;\n for(int i=0; i<s; i++)\n exp=(b[i]+10*exp)%(p-1);\n bitset<12> e(exp);\n int y=1;\n a%=n;\n for(int i=11; i>=0; i--){\n y=y*y%n;\n if (e[i]==1) y=y*a%n;\n }\n int ans=y*M*x%n;\n while( ans<0)\n ans+=n;\n // cout<<ans<<endl;\n return ans;//Chinese Remainder Theorem\n }\n int superPow(int a, vector<int>& b) {\n int g=gcd(a, n);\n // cout<<"gcd="<<g<<endl;\n if (g!=1) return Chinese_Remainder(a, g, b);\n int s=b.size();\n int exp=0;\n for(int i=0; i<s; i++)\n exp=(b[i]+10*exp)%phi;\n bitset<12> e(exp);\n int y=1;\n a%=n;\n for(int&& i=11; i>=0; i--){\n y=y*y%n;\n if (e[i]==1) y=y*a%n;\n }\n return y;\n }\n};\n```\n# Code using Chinese Remainder & Fermat\'s Little Theorem Beats 99.6%\n```\nclass Solution {\npublic:\n int n=1337;\n int phi=1140;\n int p2=7, p1=191;\n int xq=82; //7^{-1}%191=82\n long long modPow(int a, int exp, int p){//MSBF modular exponentiation algorithm\n a%=p;//mod p to make base smaller\n if (a==0) return 0; // gcd(a, n)!=1\n if (exp==0) return 1;\n if (exp==1) return a;\n int y=(exp%2==1)?a:1;\n return modPow( a*a%p , exp/2, p)*y%p;\n }\n\n long long Chinese_Remainder(int x1, int x2){\n long long num=xq*p2;// num%p1=1\n long long ans=(num*x1+(1-num)*x2)% n;\n while (ans<0) \n ans+=n;//ans>0\n return ans;\n }\n\n int superPow(int a, vector<int>& b) {\n int s=b.size();\n int exp=0, exp1=0, exp2=0;\n for(int i=0; i<s; i++)\n exp=(b[i]+10*exp)%phi;\n exp1=exp%(p1-1);\n exp2=exp%(p2-1); \n // cout<<exp1<<","<<exp2<<endl;\n // int gcd0=gcd(a, n);\n // cout<<gcd0<<endl;\n int x1=modPow(a, exp1, p1);//Fermat\'s Little Theorem\n int x2=modPow(a, exp2, p2);\n // cout<<"x1="<<x1<<", x2="<<x2<<endl;\n return Chinese_Remainder(x1, x2); \n }\n};\n```\n# Python solution dealing the boundary cases\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n exp=0\n for e in b:\n exp=e+10*exp\n exp%=1140\n if exp==0: exp=1140 #Add this line can save old solution\n return pow(a, exp, 1337)\n \n```\n | 5 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python Solution One Linear || easy to understand for begineers || pow function | super-pow | 0 | 1 | ```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n return pow(a,int(\'\'.join(map(str,b))),1337)\n``` | 1 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python3 (1 liner code) | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n return pow(a,int("".join(list(map(str,b)))),1337)\n``` | 8 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Easy Solution with explanation | super-pow | 0 | 1 | # Intuition\nGo digit by digit for b, starting from last digit.\n\n# Approach\n`x^(a+b) = (x^a)*(x^b)` ---(i)\n`x^(a*b) = (x^a)^b` ---(ii)\n\nlet `b = [x, y, z]`, here x, y, z are just digits, x00 means x\\*100, y0 means y\\*10.\n`b = xyz = x00 + y0 + z`\n`a^xyz = (a^x00) * (a^y0) * (a^z)` --- Using(i)\n`a^b = product(a^(b[n-i-1]*(10^i)) for i in [0..n-1])`\nLet `b[n-i-1] = x` for simplicity\n`a^(x*(10^i)) = a^((10^i)*x) = (a^(10^i))^x` --- Using(ii)\n\nWe are iterating from end of b, so i = [n-1..0], so replace b[n-i-1] with b[i] and 10^i with 10^(n-i-1).\n\n`a^b = product((a^(10^(n-i-1)))^b[i])`\n`(a^(10^(x+1))) = (a^((10^x)*10)) = (a^(10^x))^10` --- Using(ii)\n\nStore `a^(10^(n-i-1))` in variable `y`.\n`ans = product((a^(10^(n-i-1)))^b[i]) = product(y^b[i])` (But y will change at each iteration).\n\nUse the python inbuilt `pow(a, b, mod)` function that runs in logarithmic time.\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nmod = 1337\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n ans = 1\n i = len(b) - 1\n y = a\n while i >= 0:\n ans = (ans * pow(y, b[i], mod)) % mod\n y = pow(y, 10, mod)\n i -= 1\n return ans\n``` | 3 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
372: Time 100%, Solution with step by step explanation | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. The input a is a positive integer, and b is an array representing an extremely large positive integer.\n\n2. The first step is to compute a_mod, which is a modulo 1337. This is done because we need to return the final result modulo 1337.\n\n3. The second step is to compute n, which is the number represented by the array b. This is done using the reduce() function from the functools module, which applies a function to the elements of an iterable and reduces them to a single value. The lambda function lambda x, y: (x * 10 + y) % 1140 is applied to each digit of b in turn, starting with the first digit. The function takes two arguments x and y, which represent the running total and the next digit of b, respectively. It multiplies the running total by 10, adds the next digit y, and then takes the result modulo 1140. This is because 1140 is a multiple of 1337 (1140 = 2 x 2 x 3 x 5 x 19), so any number modulo 1140 is also modulo 1337.\n\n4. The third step is to compute result, which is initialized to 1. We then perform repeated squaring to compute a_mod raised to the power of n. This is done using a while loop that continues as long as n is greater than 0. If n is odd (i.e., n modulo 2 is 1), we multiply result by a_mod and take the result modulo 1337. We then update a_mod to be a_mod squared modulo 1337, and divide n by 2 using integer division (n //= 2). If n is even (i.e., n modulo 2 is 0), we simply update a_mod to be a_mod squared modulo 1337 and divide n by 2.\n\n5. Finally, we return the result modulo 1337.\n\n# Complexity\n- Time complexity:\n100%\n\n- Space complexity:\n47.88%\n\n# Code\n```\nfrom functools import reduce\n\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n # Compute a_mod = a mod 1337\n a_mod = a % 1337\n \n # Compute n, the number represented by the array b, using reduce()\n n = reduce(lambda x, y: (x * 10 + y) % 1140, b, 0)\n \n # Compute a_mod raised to the power of n using repeated squaring\n result = 1\n while n > 0:\n if n % 2 == 1:\n result = (result * a_mod) % 1337\n a_mod = (a_mod * a_mod) % 1337\n n //= 2\n \n # Return the result modulo 1337\n return result % 1337\n\n``` | 5 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python [EXPLAINED] | recursive | O(log(n)) | comparison with Pow(x, n) | super-pow | 0 | 1 | # Approach :\n- We can use recursive method.\n- when `n` will be even we can decrease the recursive calls by calculating it for `n/2` let\'s say `res` and return <sub>res</sub>2.\n- when `n` will be odd we just use previous step for calculating it for`(n-1)` as `res` and this time return x*(<sub>res</sub>2).\n\n\n\n# Complexity\n- Time complexity: O(log(n))\n- Space complexity: O(1)\n\n# Super-pow :\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n b = [str(i) for i in b]\n n = int("".join(b)) #converting list into integer\n def pow(x, n):\n if n == 0:\n return 1\n elif n%2==0:\n res = pow(x, n>>1)%1337\n return res**2\n else:\n res = pow(x, (n-1)>>1)%1337\n return x*(res**2)\n \n return pow(a, n)%1337\n \n```\n\n# Pow(x, n) :\n```\nclass Solution:\n def myPow(self, x: float, n: int) -> float:\n def pow(x, n):\n if n == 0:\n return 1\n elif n%2==0:\n res = pow(x, n/2)\n return res*res\n else:\n res = pow(x, (n-1)/2)\n return x*(res**2)\n \n if n>=0: \n return pow(x, n)\n else:\n return 1/pow(x, abs(n))\n\n```\n**Upvote the post if you find it helpful.\nHappy coding.**\n\n | 4 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Just Python Things | Easy | super-pow | 0 | 1 | If you are a **python** lover than this program is very easy for you as there is **no Integer Overflow**. So just covert the *power array to an integer* and calculate* a power b* with the given modulo.\n\n\n```\ndef superPow(self, a: int, b: List[int]) -> int:\n mod = 1337\n p = \'\'\n for i in b:\n p+=str(i)\n p=int(p)\n return pow(a,p,mod)\n```\n\n | 8 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
easiest python soln | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n number = \'\'\n for digit in b:\n number += str(digit)\n number = int(number)\n return pow(a, number, 1337) \n``` | 1 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python 3 (With Explanation) (Handles All Test Cases) (one line) (beats ~97%) | super-pow | 0 | 1 | _Explanation:_\n\nThis program is based on [Euler\'s Theorem](https://en.wikipedia.org/wiki/Euler%27s_theorem) which states that: a^( phi(n) ) = 1 (mod n), where phi(n) is Euler\'s Totient Function, provided that a and n are relatively prime (meaning they have no common factors). In our case, n = 1337, which has prime factorization 1337 = 7 x 191. We know that phi(p) = p - 1 when p is prime and also that phi(p x q) = phi(p) x phi(q). Thus it follows that phi(1337) = phi(7 x 191) = phi(7) x phi(191) = 6 x 190 = 1140. Thus, using Euler\'s Theorem it follows that a^1140 = 1 (mod 1337), provided that a and 1337 have no common factors. Since 1337 only has two factors, 7 and 191, it follows that a^1140 = 1 (mod 1337), provided that a is not divisible by 7 or 191. This makes sense intuitively because one can only find an inverse of a number (mod n), if the number is relatively prime to n. No multiple of 7 or 191 will ever be congruent to 1 mod 1337 because they are factors of 1337. The closest you can get to 1 mod 1337, is getting 0 mod 1337. For this reason, it is very important that we never allow 1 to be the answer in the case when a is divisible by 7 or 9 since that doesn\'t make sense.\n\nSince a^1140 = 1 (mod 1337), provided that a is not divisible by 7 or 191, it follows that if we write b = 1140q + r (where q is the quotient and r is the remainder after dividing b by 1140), then a^b = a^(1140q + r) = a^(1140q) x a^r = (a^1140)^q x a^r = 1^q x a^r = a^r (mod 1337). Thus if we reduce b (mod 1337) we can find the answer to a^b by instead just doing a^r (i.e. a^(b % 1337)). Furthermore since we want our answer mod 1337, it is wise to reduce a mod 1337 to keep the numbers smaller. Thus, provided that a is not divisible by 7 or 191, it follows by Euler\'s Theorem that a^b = (a %1337)^(b % 1140) % 1337.\n\nHowever, we must carefuly reflect on the case when a is divisible by 7 or 191. If it is divisible by both, then obviously a mod 1337 is 0 and our answer is 0. However, if it is divisisble by one of them and if b = 0 mod 1140 (i.e. b is a multiple of 1140), then our problem would reduce to (7n)^0 = 1 (mod 1337) or (191m)^0 = 1 (mod 1337). These are obviously wrong because a multiple of 7 or 191 can never be congruent to 1 mod 1337. They are also an impermissible application of Euler\'s Theorem because Euler\'s Theorem requires that a and n be relatively prime. The way around this issue is to be careful to not use r = 0, which will occur when b is divisible by 1140. Using r = 0 will lead to an incorrect result. What we will do in this case is if b mod 1140 = 0, then we will use b = 1140 instead. This will keep the 0 from being in the exponent. However, we do not have to check it with an if statement, we can simply always add 1140 to b mod 1140 for all cases. This will give us the correct result in the cases when a and b are not divisible by 7 or 191 but will also protect us for the case when they are divisible by 7 or 191.\n\nThe program then simply converts the list b to a string then a long int. It then reduces b mod 1140 and adds 1140 to that result so we never have to worry about getting a 0 in the exponent. The program finally evaluates (a % 1337)^(1140 + b % 1140) % 1337 which gives us the correct final answer.\n\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n return (a % 1337)**(1140 + int(\'\'.join(map(str, b))) % 1140) % 1337\n\t\t\n\t\t\n- Junaid Mansuri | 12 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
pow | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n p = ""\n for i in b:\n p += f"{i}"\n return pow(a,int(p),1337)\n \n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python 1 line solution | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDisclaimer : Joke solution, I find enjoyment cheesing LeetCode problems.\n\nThe inbuilt `pow()` function has this functionality already, we just need to convert `b` to a number\n\n# Code\n```\nclass Solution(object):\n def superPow(self, a, b):\n return pow(a,int("".join([str(i) for i in b])),1337)\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Easy and short Python solution base on the Multiplicative Order | super-pow | 0 | 1 | # Intuition\nWe try to find the [Multiplicative_order](https://en.wikipedia.org/wiki/Multiplicative_order) `r` (aka `len(cycle)`) and the next powers of `a` $(a^1, a^2 ..., a^{r-1})$ modulo `1337`. Because then $ a^b = a^{r*k + remainder} \\equiv a^{reminder} \\pmod{1337}$. Since from pigeonhole principle there there are at most 1337 values of remainder (In practise for this specific case there will be not as much because 1337 is not a prime number), we need to check a very limited subset of powers.\n\n# Approach\nCalculate the next modular powers of $a \\pmod{1337}$ until there is no cycle (`while ((temp * a) % mod) != cycle[0]`) and then take the position in array `cycle` which is the reminder of power and our multiplicative order. At the end we take `cycle[power-1]` because the first element (0th indexed) is `a` to the **first** power. \n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n mod = 1337\n temp = a % mod\n cycle = [temp]\n while ((temp * a) % mod) != cycle[0]:\n temp = (temp * a) % mod\n cycle.append(temp)\n \n power = int("".join(map(str, b))) % len(cycle)\n return cycle[power-1]\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Simple solution using Chinese remainder theorem with latex | super-pow | 0 | 1 | # Approach\nWe have $1337 = 7 \\cdot 191$, since $7$ and $191$ are coprime, by Chinese remainder theorem, the problem is equivalent to solving the following system of equations $\\begin{cases} x \\equiv a^b & \\pmod{7} \\\\ x \\equiv a^b & \\pmod{191} \\end{cases}$\n\nSince $7$ and $191$ are coprime, there exists two integers $m, n$ such that $7m + 191n = 1$. Then, by Chinese remainder theorem, the solution of the system of equations is $x\\equiv 7m\\cdot \\left(a^{b} \\text{ mod } 7\\right) + 191n\\cdot \\left(a^{b} \\text{ mod } 191\\right)\\pmod{1337}$.\n\nTo find $m, n$, we run the following simple function and get $m = -109$ and $n = 4$.\n```python\n# assume that a and b are positive integers and gcd(a, b) = 1.\ndef bezout(a: int, b: int) -> Tuple[int, int]:\n if a < b:\n x, y = bezout(b, a)\n return (y, x)\n\n q = a // b\n r = a % b\n\n if r == 0: # then b = 1 since gcd(a, b) = 1\n return (1, 1 - a) # 1 * a + (1 - a) * b = a + 1 - a = 1\n\n x, y = bezout(b, r) # we can call bezout(b, r) since gcd(b, r) = gcd(a, b) = 1\n # we have b * x + r * y = 1\n # since r = a - b * q, we have b * x + (a - b * q) * y = 1\n # equivalently, we have a * y + b * (x - q * y) = 1\n return (y, x - q * y) \n```\n\nIt\'s easy to calculate $a^b \\text{ mod } 7$ and $a^b \\text{ mod } 191$ by using Euler\'s theorem.\n\nTime coplexity: `O(b.length)`\nSpace complexity: `O(1)`\n\n# Code\n```python\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n x = a % 7\n y = a % 191\n\n p, q = 0, 0\n for d in b:\n p *= 10\n p += d\n p = p % 6\n\n q *= 10\n q += d\n q = q % 190\n \n X, Y = 1, 1\n if x == 0:\n X = 0\n else:\n for _ in range(p):\n X *= x\n X = X % 7\n if y == 0:\n Y = 0\n else:\n for _ in range(q):\n Y *= y\n Y = Y % 191\n\n return (X * 191 * 4 + Y * 7 * (-109)) % 1337\n\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
☑ 2 Liner using pow( ) ☑ | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n p = 0\n for i in b:\n p = (p * 10 + i)\n return pow(a, p, 1337)\n\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
best solution | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n s=0\n for i in b:\n s=s*10+i\n\n return pow(a,s,1337)\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Beats 74.25%of users --->Python3 | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n b=int("".join([str(i) for i in b]))\n return pow(a,b,1337)\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
simplepythoncode3 | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n s=\'\'.join(list(map(str,b)))\n s1=pow(a,int(s),1337)\n return s1\n \n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python easy solution | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n str_b = ""\n for i in b:\n str_b += str(i)\n int_b = int(str_b)\n\n return pow(a, int_b, 1337)\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Super pow | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n num=int("".join(list(map(str,b))))\n return pow(a,num,1337)\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Easy solution Python | super-pow | 0 | 1 | # Complexity\n- Time\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nRuntime : 79 ms 68.35%\n\nMemory : 13.3 MB 97.47%\n\n# Code\n```\nclass Solution(object):\n def superPow(self, a, b):\n B = map(str,b)\n B = int("".join(B))\n return pow(a,B,1337)\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
372. Super Pow [Code in Python] Full explanation using Fermat–Euler theorem | super-pow | 0 | 1 | ## Euler\'s theorem (a.k.a the Fermat\u2013Euler theorem or Euler\'s Totient theorem)\nIt states that if there are two co-prime number $$a$$, $$n$$\n$$a^{\\psi(n)}\\equiv 1$$ $$mod$$ $$n$$ \n$$a^{\\psi(n)}$$ $$mod$$ $$n$$ $$=1$$ \nGiven that $$gcd(a,n)=1$$, where $$\\psi(n)$$ is Euler\'s totient function\n\nThe problems requires to compute $$a^b$$ $$mod$$ $$1337$$, where b is a really huge number\nSince $$n = 1337$$ is a prime number, the $$gcd(a, n)= 1$$ is automatically satisfied.\nSince $$1337$$ can be written as $$1337 = 191 \\cdot 7$$\n>$$\\psi(1337) = (191-1)\\cdot(7 - 1) = 1140$$\n\nHence according to Fermat\u2013Euler theorem:\n>$$a^{1140}$$ $$mod$$ $$1337$$ = 1\n\nLet\'s assume that $$b$$ is a really huge integer instead of an array\n$$a^b$$ $$mod$$ $$1337$$\n$$(a^{b-1140}\\cdot a^{1140})$$ $$mod$$ $$1337$$\n$$(a^{b-1140}$$ $$mod$$ $$1337)$$ $$\\cdot$$ $$(a^{1140}$$ $$mod$$ $$1337)$$\n$$(a^{b-1140}$$ $$mod$$ $$1337)$$\nAfter n repetition: $$(a^{b-1140\\cdot n}$$ $$mod$$ $$1337)$$\nRepeat the above step until $$a^{b-1140\\cdot n}$$ reducess to its lowest form \ni.e. $$a^0$$ $$\\rightarrow$$ $$b - 1140\\cdot n=0$$\n$$n = \\lfloor\\frac{b}{1140}\\rfloor$$\n$$b - \\lfloor\\frac{b}{1140}\\rfloor\\cdot 1140 = b$$ $$mod$$ $$1140$$\n$$a^{b}$$ $$^{mod}$$ $$^{1140}$$ $$mod$$ $$1337)$$\n\nSo while converting $$b$$ from an array to integer apply the $$mod$$ $$1140$$ operation \nCheck the code for implementation\n\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n exp=0\n for e in b:\n exp=e+10*exp\n exp%=1140\n return pow(a, exp, 1337)\n \n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Easy Approach for Python Peeps: | super-pow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nPls upvote if useful, Ladies and Gentlemen\n# Code\n```\nclass Solution:\n def superPow(self, a: int, b: List[int]) -> int:\n st=""\n for i in b:\n st=st+str(i)\n num=int(st)\n return (pow(a,num,1337))\n``` | 0 | Your task is to calculate `ab` mod `1337` where `a` is a positive integer and `b` is an extremely large positive integer given in the form of an array.
**Example 1:**
**Input:** a = 2, b = \[3\]
**Output:** 8
**Example 2:**
**Input:** a = 2, b = \[1,0\]
**Output:** 1024
**Example 3:**
**Input:** a = 1, b = \[4,3,3,8,5,2\]
**Output:** 1
**Constraints:**
* `1 <= a <= 231 - 1`
* `1 <= b.length <= 2000`
* `0 <= b[i] <= 9`
* `b` does not contain leading zeros. | null |
Python Beginner || Solution using Heap 🐍🐍 | find-k-pairs-with-smallest-sums | 0 | 1 | # Code\n```\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n h = []; res = []\n for i in range(min(len(nums1), k)):\n tup = [nums1[i], nums2[0]]\n heapq.heappush(h, [sum(tup), tup, 0])\n while k>0 and len(h)>0:\n v = heapq.heappop(h)\n res.append(v[1])\n ind = v[2] + 1\n if ind != len(nums2):\n tup = [v[1][0], nums2[ind]]\n heapq.heappush(h, [sum(tup), tup, ind])\n k -= 1\n\n return res\n``` | 1 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
Python3 Solution | find-k-pairs-with-smallest-sums | 0 | 1 | \n```\nfrom heapq import *\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n heap=[]\n for i in range(min(k,len(nums1))):\n for j in range(min(k,len(nums2))):\n if len(heap)<k:\n heappush(heap,(-(nums1[i]+nums2[j]),nums1[i],nums2[j]))\n\n else:\n if nums1[i]+nums2[j]>-heap[0][0]:\n break\n\n else:\n heappushpop(heap,(-(nums1[i]+nums2[j]),nums1[i],nums2[j]))\n\n\n return [[first,second] for _,first,second in heap] \n``` | 1 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
From Dumb to Pro with Just One Visit - My Promise to You with Efficient Selection of k Smallest Pair | find-k-pairs-with-smallest-sums | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to find the k smallest pairs from two sorted arrays, `nums1` and `nums2`, based on their pair sums. The approach used in the code is optimized to avoid inserting all pairs into the priority queue, which would result in a time complexity of $O(N^2 log N^2)$ and lead to a Time Limit Exceeded (TLE) error.\n\nTo overcome this, the code follows a specific method to find the k smallest pairs efficiently. It starts by inserting the pair sums of each element from `nums1` and the first element of `nums2` into a priority queue. Since both arrays are sorted, the pair sums will be in increasing order.\n\nBy utilizing a priority queue, the smallest sum pair is always accessible at the top. The code then pops the smallest pair from the priority queue and adds it to the result vector. Next, it inserts the next pair, which consists of the same element from `nums1` but the next element from `nums2`.\n\nThe code repeats this process, gradually inserting pairs with increasing elements from `nums2`, until it has added k pairs to the result vector or the priority queue becomes empty (i.e., all pairs have been explored). This ensures that only the k smallest pairs are considered.\n\nFinally, the code returns the resulting vector containing the k smallest pairs.\n\nOverall, the approach intelligently uses the priority queue to avoid unnecessary computations, allowing for an optimized solution with a time complexity of $O(K log N)$, where N represents the size of `nums1` and K is the given parameter for the number of smallest pairs to find.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create an empty result vector `resV` to store the k smallest pairs.\n2. Create a priority queue `pq` to store pairs of elements from `nums1` and `nums2` with the smallest sums. The pairs are sorted by their sum in ascending order.\n3. Iterate through each element `x` in `nums1`.\n - Calculate the sum of `x` and the first element of `nums2` (since `nums2` is sorted, the first element has the smallest value).\n - Push the pair consisting of the sum and the index of the first element in `nums2` (which is 0) into the priority queue.\n4. While `k` is greater than 0 and the priority queue is not empty, perform the following steps:\n - Get the pair with the smallest sum from the top of the priority queue.\n - Extract the sum and the index from the pair.\n - Create a pair by subtracting the value of the second element in the pair from the sum and the value of the second element itself.\n - Add the created pair to the result vector `resV`.\n - Remove the pair from the priority queue.\n - If there are more elements in `nums2` (i.e., the index of the second element is less than the size of `nums2` minus 1), calculate the sum of the next pair by subtracting the current second element from the sum and adding the next element in `nums2`. Push this new pair into the priority queue.\n - Decrement `k` by 1.\n5. Return the resulting vector `resV` containing the k smallest pairs.\n\nThe approach essentially involves maintaining a priority queue to keep track of the smallest sums and their corresponding pairs. By iteratively extracting the smallest sum and updating the index of the second element from `nums2`, the code ensures that only the k smallest pairs are included in the result.\n\n# Complexity\n- Time Complexity:\n - The maximum size of the priority queue `pq` is `nums1.size()` (denoted as `n1`), as for each element in nums1, we push one element into the priority queue. The maximum number of iterations that can happen is `k`, as the loop runs until k smallest pairs are found or until the priority queue is empty.\n - **Therefore, the time complexity of the given code is $O(k * log (n1))$, where n1 is the size of nums1 and k is the desired number of smallest pairs to be found.**\n\n- Space Complexity:\n - The additional space used by the code includes the result vector `resV` and the priority queue `pq`.\n - The result vector `resV` will contain at most k pairs, so it occupies $O(k)$ space.\n - The priority queue `pq` can hold at most k pairs as well, resulting in $O(n1)$ space.\n - **Therefore, the overall space complexity is $O(n1 + k)$.**\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<vector<int>> resV; // Result vector to store the pairs\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;\n // Priority queue to store pairs with smallest sums, sorted by the sum\n\n // Push the initial pairs into the priority queue\n for(int x : nums1) {\n pq.push({x + nums2[0], 0}); // The sum and the index of the second element in nums2\n }\n\n // Pop the k smallest pairs from the priority queue\n while(k-- && !pq.empty()) {\n int sum = pq.top().first; // Get the smallest sum\n int pos = pq.top().second; // Get the index of the second element in nums2\n\n resV.push_back({sum - nums2[pos], nums2[pos]}); // Add the pair to the result vector\n pq.pop(); // Remove the pair from the priority queue\n\n // If there are more elements in nums2, push the next pair into the priority queue\n if(pos + 1 < nums2.size()) {\n pq.push({sum - nums2[pos] + nums2[pos + 1], pos + 1});\n }\n }\n\n return resV; // Return the k smallest pairs\n }\n};\n```\n```java []\nclass Solution {\n public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {\n List<List<Integer>> resV = new ArrayList<>(); // Result list to store the pairs\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);\n // Priority queue to store pairs with smallest sums, sorted by the sum\n\n // Push the initial pairs into the priority queue\n for (int x : nums1) {\n pq.offer(new int[]{x + nums2[0], 0}); // The sum and the index of the second element in nums2\n }\n\n // Pop the k smallest pairs from the priority queue\n while (k > 0 && !pq.isEmpty()) {\n int[] pair = pq.poll();\n int sum = pair[0]; // Get the smallest sum\n int pos = pair[1]; // Get the index of the second element in nums2\n\n List<Integer> currentPair = new ArrayList<>();\n currentPair.add(sum - nums2[pos]);\n currentPair.add(nums2[pos]);\n resV.add(currentPair); // Add the pair to the result list\n\n // If there are more elements in nums2, push the next pair into the priority queue\n if (pos + 1 < nums2.length) {\n pq.offer(new int[]{sum - nums2[pos] + nums2[pos + 1], pos + 1});\n }\n\n k--; // Decrement k\n }\n\n return resV; // Return the k smallest pairs\n }\n}\n```\n```python []\nclass Solution:\n def kSmallestPairs(self, nums1, nums2, k):\n resV = [] # Result list to store the pairs\n pq = [] # Priority queue to store pairs with smallest sums, sorted by the sum\n\n # Push the initial pairs into the priority queue\n for x in nums1:\n heapq.heappush(pq, [x + nums2[0], 0]) # The sum and the index of the second element in nums2\n\n # Pop the k smallest pairs from the priority queue\n while k > 0 and pq:\n pair = heapq.heappop(pq)\n s, pos = pair[0], pair[1] # Get the smallest sum and the index of the second element in nums2\n\n resV.append([s - nums2[pos], nums2[pos]]) # Add the pair to the result list\n\n # If there are more elements in nums2, push the next pair into the priority queue\n if pos + 1 < len(nums2):\n heapq.heappush(pq, [s - nums2[pos] + nums2[pos + 1], pos + 1])\n\n k -= 1 # Decrement k\n\n return resV # Return the k smallest pairs\n```\n*Thank you for taking the time to read my post in its entirety. I appreciate your attention and hope you found it informative and helpful.*\n\n**PLEASE UPVOTE THIS POST IF YOU FOUND IT HELPFUL** | 94 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
🔰Python 3 Solution with Explanation✌😀 | find-k-pairs-with-smallest-sums | 0 | 1 | # Approach\nTo solve this problem, we can utilize the concept of a priority queue or a min-heap. Here\'s a step-by-step explanation of the approach:\n\n- Create a min-heap or priority queue to store the pairs based on their sums.\n\n- Add elements of nums1 and add pairs (nums1[i], nums2[0]) to the min-heap, along with the indices i and 0.\n\n- While the min-heap is not empty and k is greater than 0:\na. Pop the pair with the smallest sum from the min-heap. Let\'s say the pair is (u, v) with indices i and j.\nb. Add the pair (u, v) to the result list.\nc. If j+1 is less than the length of nums2, add the pair (nums1[i], nums2[j+1]) to the min-heap with indices i and j+1.\nd. If i+1 is less than the length of nums1 and j is 0, add the pair (nums1[i+1], nums2[j]) to the min-heap with indices i+1 and j.\n\n- Return the result list containing the k pairs with the smallest sums.\n\n# Complexity\n- Time complexity:\nO min(k log k,nm log nm)\n\n- Space complexity:\nO min(k,nm)\n\n# Video Explanation\nhttps://www.youtube.com/watch?v=mP1e0aG7MOY\n\n# Code\n```\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n from heapq import heappush, heappop\n m = len(nums1)\n n = len(nums2)\n ans = []\n visited = set()\n minHeap = [(nums1[0] + nums2[0], (0,0))]\n visited.add((0,0))\n while k > 0 and minHeap:\n val, (i,j) = heappop(minHeap)\n ans.append([nums1[i],nums2[j]])\n if i+1 < m and (i+1,j) not in visited:\n heappush(minHeap, (nums1[i+1]+nums2[j],(i+1,j)))\n visited.add((i+1,j))\n if j+1 < n and (i,j+1) not in visited:\n heappush(minHeap, (nums1[i]+nums2[j+1],(i,j+1)))\n visited.add((i,j+1))\n k -= 1\n return ans\n```\n### If this Solution was helpful then, Upvote \uD83D\uDE00\uD83D\uDC4D\uD83C\uDFFB | 2 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
Priority Queue and Set | find-k-pairs-with-smallest-sums | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBasically the two pointer approach will not work for this problem ...\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe will be using a priority queue in order to actually tackle this kind of problem..\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n0(klogk)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int):\n heap=[]\n heapq.heappush(heap,(nums1[0]+nums2[0],0,0))\n visited=set()\n visited.add((0,0))\n output=[]\n while len(output)<k and heap:\n val=heapq.heappop(heap)\n output.append([nums1[val[1]],nums2[val[2]]])\n if(val[1]+1<len(nums1) and (val[1]+1,val[2]) not in visited):\n heapq.heappush(heap,(nums1[val[1]+1]+nums2[val[2]],val[1]+1,val[2]))\n visited.add((val[1]+1,val[2]))\n if(val[2]+1<len(nums2) and (val[1],val[2]+1) not in visited):\n heapq.heappush(heap,(nums1[val[1]]+nums2[val[2]+1],val[1],val[2]+1))\n visited.add((val[1],val[2]+1))\n return output\n``` | 1 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
🚀 Lightning Fast Solution: K Pairs with Smallest Sums | Python Coding with vanAmsen | find-k-pairs-with-smallest-sums | 0 | 1 | # Intuition\nWhen first encountering this problem, we might consider brute force - calculating the sum of all pairs, sorting them, and choosing the smallest k sums. However, this solution is not efficient and will exceed the time limit for large inputs. Observing that the arrays are sorted, we can leverage this property and use a heap data structure to optimize our solution. We can intelligently select and compare potential pairs rather than calculating all possible pairs, which will significantly increase the efficiency.\n\nhttps://youtu.be/ilK09wC4PQM\n\n# Approach\nOur approach involves using a min-heap data structure. Initially, we push the pair with the smallest sum (nums1[0], nums2[0]) into the heap. The heap will automatically arrange it based on the sum, which is the first element in the pair. To avoid processing duplicate pairs, we also maintain a visited set. Then, we start a while loop, continuing until we get k pairs or the heap is empty. In each iteration, we pop a pair from the heap, add it to the result list, and push the next potential pairs (nums1[i+1], nums2[j]) and (nums1[i], nums2[j+1]) into the heap. The heap and the visited set help us always pick the unvisited pair with the smallest sum. The process continues until we\'ve found our k pairs or exhausted all possible pairs.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(k log k) since we perform a heap push and pop operation up to k times, each operation has a log k complexity due to heap restructure.\n\n- Space complexity:\nThe space complexity of this solution is O(k) as we need to store the heap elements and visited pairs, the maximum of which can be k.\n\n\n# Code\n```\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n # Heap initialization \n queue = [] \n def push(i, j): \n # In Python heap is a min-heap \n # Therefore, we use a tuple, first element is a sum (the priority), then pair itself \n if i < len(nums1) and j < len(nums2): \n heapq.heappush(queue, [nums1[i] + nums2[j], i, j]) \n push(0, 0) \n # Set to keep track of pairs we have already pushed into the heap \n # It\'s needed because we are doing "push(i+1, j)" and "push(i, j+1)" separately \n # If not using this visited set, we will end up pushing many duplicate pairs into the heap \n visited = set() \n visited.add((0, 0)) \n result = [] \n while queue and len(result) < k: \n _, i, j = heapq.heappop(queue) \n result.append([nums1[i], nums2[j]]) \n if i+1 < len(nums1) and (i+1, j) not in visited: \n push(i+1, j) \n visited.add((i+1, j)) \n if j+1 < len(nums2) and (i, j+1) not in visited: \n push(i, j+1) \n visited.add((i, j+1)) \n return result \n \n``` | 2 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
373: Solution with step by step explanation | find-k-pairs-with-smallest-sums | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe problem asks to find the k pairs of numbers, one from nums1 and one from nums2, that have the smallest sum. The arrays nums1 and nums2 are sorted in ascending order.\n\nThe algorithm uses a heap to keep track of the smallest sums of pairs that haven\'t been added to the result list yet. The heap contains tuples of the form (sum, num1, num2, i, j), where sum is the sum of num1 and num2, i and j are the indices of num1 and num2 in their respective arrays, and num1 and num2 are the actual numbers in the pairs.\n\nThe algorithm starts by initializing the heap with the first pair, (nums1[0]+nums2[0], nums1[0], nums2[0], 0, 0), and marking (0, 0) as visited in a set.\n\nThen, the algorithm enters a loop that continues until either the heap is empty or k pairs have been added to the result list. In each iteration, the algorithm pops the smallest sum pair from the heap and adds it to the result list.\n\nThen, the algorithm checks if it can generate new pairs by incrementing either i or j. If i can be incremented (i.e. i < len(nums1)-1) and (i+1, j) hasn\'t been visited yet, then the algorithm generates a new pair with num1=nums1[i+1] and num2=nums2[j], adds it to the heap with the corresponding sum, and marks (i+1, j) as visited. If j can be incremented (i.e. j < len(nums2)-1) and (i, j+1) hasn\'t been visited yet, then the algorithm generates a new pair with num1=nums1[i] and num2=nums2[j+1], adds it to the heap with the corresponding sum, and marks (i, j+1) as visited.\n\nFinally, the algorithm returns the result list containing the k smallest sum pairs.\n\n# Complexity\n- Time complexity:\n81.2%\n\n- Space complexity:\n73.43%\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n heap = [(nums1[0] + nums2[0], nums1[0], nums2[0], 0, 0)]\n visited = set((0, 0))\n result = []\n \n while heap and len(result) < k:\n _, num1, num2, i, j = heapq.heappop(heap)\n result.append([num1, num2])\n \n if i < len(nums1) - 1 and (i+1, j) not in visited:\n heapq.heappush(heap, (nums1[i+1] + nums2[j], nums1[i+1], nums2[j], i+1, j))\n visited.add((i+1, j))\n \n if j < len(nums2) - 1 and (i, j+1) not in visited:\n heapq.heappush(heap, (nums1[i] + nums2[j+1], nums1[i], nums2[j+1], i, j+1))\n visited.add((i, j+1))\n \n return result\n\n``` | 6 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
Easy Heap solution || Beats 93% 🔥|| Python3, Java, C++ | find-k-pairs-with-smallest-sums | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe needed to find the K smallest pairs of numbers from two different sorted arrays. What better way than to use a heap (priority queue) to maintain the sorted order(to find the minimum) while also constantly changing the data structure.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe know that the two arrays are sorted, i.e, the smallest sum would for sure be nums1[0] + nums2[0], so we start with that. The next smallest sum would either be formed by the pair (nums1[1], nums2[0]) or (nums1[0], nums2[1]), so we keep adding these 2 possible pairs to the heap and every time we pop from the heap, the smallest sum would pop and we add that to our answer till either we find k pairs or our heap becomes empty.\nTo avoid the case of adding a pair of indices twice, we maintain a set named visited wherein everytime we visit(use in the answer) a pair of indices, we add it to the set so as to not add it again.\n\n# Python3 Code\n```\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n ans = []\n n1, n2 = len(nums1), len(nums2)\n visited = set()\n hp = []\n hp.append((nums1[0]+nums2[0],(0,0)))\n visited.add((0,0))\n count = 0\n while k and hp:\n val, (i,j) = heappop(hp)\n ans.append([nums1[i],nums2[j]])\n\n if i+1<n1 and (i+1,j) not in visited:\n heappush(hp, (nums1[i+1]+nums2[j],(i+1,j)))\n visited.add((i+1,j))\n\n if j+1<n2 and (i, j+1) not in visited:\n heappush(hp,(nums1[i]+nums2[j+1], (i,j+1)))\n visited.add((i,j+1))\n\n k -= 1\n\n return ans\n\n```\n# Java Code\n```\nclass Solution {\n public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {\n int m = nums1.length;\n int n = nums2.length;\n\n List<List<Integer>> ans = new ArrayList<>();\n Set<Pair<Integer, Integer>> visited = new HashSet<>();\n\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b)->(a[0] - b[0]));\n minHeap.offer(new int[]{nums1[0] + nums2[0], 0, 0});\n visited.add(new Pair<Integer, Integer>(0, 0));\n\n while (k-- > 0 && !minHeap.isEmpty()) {\n int[] top = minHeap.poll();\n int i = top[1];\n int j = top[2];\n\n ans.add(List.of(nums1[i], nums2[j]));\n\n if (i + 1 < m && !visited.contains(new Pair<Integer, Integer>(i + 1, j))) {\n minHeap.offer(new int[]{nums1[i + 1] + nums2[j], i + 1, j});\n visited.add(new Pair<Integer, Integer>(i + 1, j));\n }\n\n if (j + 1 < n && !visited.contains(new Pair<Integer, Integer>(i, j + 1))) {\n minHeap.offer(new int[]{nums1[i] + nums2[j + 1], i, j + 1});\n visited.add(new Pair<Integer, Integer>(i, j + 1));\n }\n }\n\n return ans;\n }\n}\n```\n# C++ Code\n```\nclass Solution {\npublic:\n vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {\n int m = nums1.size();\n int n = nums2.size();\n\n vector<vector<int>> ans;\n set<pair<int, int>> visited;\n\n priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>,\n greater<pair<int, pair<int, int>>>> minHeap;\n minHeap.push({nums1[0] + nums2[0], {0, 0}});\n visited.insert({0, 0});\n\n while (k-- && !minHeap.empty()) {\n auto top = minHeap.top();\n minHeap.pop();\n int i = top.second.first;\n int j = top.second.second;\n\n ans.push_back({nums1[i], nums2[j]});\n\n if (i + 1 < m && visited.find({i + 1, j}) == visited.end()) {\n minHeap.push({nums1[i + 1] + nums2[j], {i + 1, j}});\n visited.insert({i + 1, j});\n }\n\n if (j + 1 < n && visited.find({i, j + 1}) == visited.end()) {\n minHeap.push({nums1[i] + nums2[j + 1], {i, j + 1}});\n visited.insert({i, j + 1});\n }\n }\n\n return ans;\n }\n};\n``` | 8 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.