title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
🍀Easy Java 🔥| | Python 🔥| | C++ 🔥 | find-k-pairs-with-smallest-sums | 1 | 1 | # *Code*\n```java []\nclass Pair{\n int idx1 = 0;\n int idx2 = 0;\n int sum = 0;\n Pair(int idx1,int idx2,int sum)\n {\n this.idx1 = idx1;\n this.idx2 = idx2;\n this.sum = sum;\n }\n}\nclass Solution {\n public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {\n List<List<Integer>> result = new ArrayList<>();\n PriorityQueue<Pair> pq = new PriorityQueue<>((a,b)->a.sum-b.sum);\n for(int i = 0;i<nums1.length;i++)\n {\n pq.offer(new Pair(i,0,nums1[i]+nums2[0]));\n }\n while(pq.size() > 0 && result.size() < k)\n {\n int i = pq.peek().idx1;\n int j = pq.peek().idx2;\n pq.remove();\n result.add(Arrays.asList(nums1[i],nums2[j]));\n if(j < nums2.length-1)\n pq.offer(new Pair(i,j+1,nums1[i]+nums2[j+1]));\n }\n return result; \n }\n}\n```\n```python []\nimport heapq\n\nclass Pair:\n def __init__(self, idx1, idx2, sum):\n self.idx1 = idx1\n self.idx2 = idx2\n self.sum = sum\n\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n result = []\n pq = []\n heapq.heapify(pq)\n for i in range(len(nums1)):\n heapq.heappush(pq, Pair(i, 0, nums1[i]+nums2[0]))\n while pq and len(result) < k:\n p = heapq.heappop(pq)\n i = p.idx1\n j = p.idx2\n result.append([nums1[i], nums2[j]])\n if j < len(nums2)-1:\n heapq.heappush(pq, Pair(i, j+1, nums1[i]+nums2[j+1]))\n return result\n\n\n```\n```C++ []\nclass Pair{\n int idx1 = 0;\n int idx2 = 0;\n int sum = 0;\n Pair(int idx1,int idx2,int sum)\n {\n this->idx1 = idx1;\n this->idx2 = idx2;\n this->sum = sum;\n }\n};\nclass Solution {\npublic:\n vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<vector<int>> result;\n priority_queue<Pair, vector<Pair>, function<bool(Pair, Pair)>> pq([](Pair a, Pair b){return a.sum > b.sum;});\n for(int i = 0;i<nums1.size();i++)\n {\n pq.push(Pair(i,0,nums1[i]+nums2[0]));\n }\n while(pq.size() > 0 && result.size() < k)\n {\n int i = pq.top().idx1;\n int j = pq.top().idx2;\n pq.pop();\n result.push_back({nums1[i],nums2[j]});\n if(j < nums2.size()-1)\n pq.push(Pair(i,j+1,nums1[i]+nums2[j+1]));\n }\n return result; \n }\n};\n\n```\n---\n### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F\n | 6 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
Python BFS, beating 97%. 52 ms | find-k-pairs-with-smallest-sums | 0 | 1 | Use BFS with heap. In each iteration, we get the pair with minimal sum and then push its neighboring right and bottom (if exists) into the heap. Repeat `k` or at most `m*n` times of such iterations. Time complexity `O(k lg k)`. Space complexity `O(k)` for the heap.\n\n```\n\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n res = []\n from heapq import heappush, heappop\n m, n, visited = len(nums1), len(nums2), set()\n if m == 0 or n == 0: return [] \n h = [(nums1[0]+nums2[0], (0, 0))]\n for _ in range(min(k, (m*n))):\n val, (i, j) = heappop(h)\n res.append([nums1[i], nums2[j]])\n if i+1 < m and (i+1, j) not in visited:\n heappush(h, (nums1[i+1]+nums2[j], (i+1, j)))\n visited.add((i+1, j))\n if j+1 < n and (i, j+1) not in visited:\n heappush(h, (nums1[i]+nums2[j+1], (i, j+1)))\n visited.add((i, j+1))\n return res\n``` | 40 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
[Python] Simple heap solution explained | find-k-pairs-with-smallest-sums | 0 | 1 | ```\nclass Solution:\n def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:\n hq = []\n heapq.heapify(hq)\n \n # add all the pairs that we can form with\n # all the (first k) items in nums1 with the first\n # item in nums2\n for i in range(min(len(nums1), k)):\n heapq.heappush(hq, (nums1[i]+nums2[0], nums1[i], nums2[0], 0))\n\n # since the smallest pair will\n # be the first element from both nums1 and nums2. We\'ll\n # start with that and then subsequently, we\'ll pop it out\n # from the heap and also insert the pair of the current\n # element from nums1 with the next nums2 element\n out = []\n while k > 0 and hq:\n _, n1, n2, idx = heapq.heappop(hq)\n out.append((n1, n2))\n if idx + 1 < len(nums2):\n # the heap will ensure that the smallest element\n # based on the sum will remain on top and the\n # next iteration will give us the pair we require\n heapq.heappush(hq, (n1+nums2[idx+1], n1, nums2[idx+1], idx+1))\n k -= 1\n \n return out\n``` | 18 | You are given two integer arrays `nums1` and `nums2` sorted in **ascending order** and an integer `k`.
Define a pair `(u, v)` which consists of one element from the first array and one element from the second array.
Return _the_ `k` _pairs_ `(u1, v1), (u2, v2), ..., (uk, vk)` _with the smallest sums_.
**Example 1:**
**Input:** nums1 = \[1,7,11\], nums2 = \[2,4,6\], k = 3
**Output:** \[\[1,2\],\[1,4\],\[1,6\]\]
**Explanation:** The first 3 pairs are returned from the sequence: \[1,2\],\[1,4\],\[1,6\],\[7,2\],\[7,4\],\[11,2\],\[7,6\],\[11,4\],\[11,6\]
**Example 2:**
**Input:** nums1 = \[1,1,2\], nums2 = \[1,2,3\], k = 2
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The first 2 pairs are returned from the sequence: \[1,1\],\[1,1\],\[1,2\],\[2,1\],\[1,2\],\[2,2\],\[1,3\],\[1,3\],\[2,3\]
**Example 3:**
**Input:** nums1 = \[1,2\], nums2 = \[3\], k = 3
**Output:** \[\[1,3\],\[2,3\]\]
**Explanation:** All possible pairs are returned from the sequence: \[1,3\],\[2,3\]
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `-109 <= nums1[i], nums2[i] <= 109`
* `nums1` and `nums2` both are sorted in **ascending order**.
* `1 <= k <= 104` | null |
C++ || Binary Search || Easiest Beginner Friendly Sol | guess-number-higher-or-lower | 1 | 1 | # Intuition of this Problem:\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Initialize first to 1 and last to n.\n2. While first is less than or equal to last, do the following:\n a. Compute mid as first + (last - first) / 2.\n b. If guess(mid) returns 0, return mid.\n c. If guess(mid) returns -1, update last to mid - 1.\n d. If guess(mid) returns 1, update first to mid + 1.\n3. Return -1.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\n/** \n * Forward declaration of guess API.\n * @param num your guess\n * @return \t -1 if num is higher than the picked number\n *\t\t\t 1 if num is lower than the picked number\n * otherwise return 0\n * int guess(int num);\n */\n\nclass Solution {\npublic:\n int guessNumber(int n) {\n int first = 1, last = n;\n while (first <= last) {\n int mid = first + (last - first) / 2;\n if (guess(mid) == 0)\n return mid;\n else if (guess(mid) == -1)\n last = mid - 1;\n else\n first = mid + 1;\n }\n return -1;\n }\n};\n```\n```Java []\npublic class Solution extends GuessGame {\n public int guessNumber(int n) {\n int first = 1, last = n;\n while (first <= last) {\n int mid = first + (last - first) / 2;\n int res = guess(mid);\n if (res == 0) {\n return mid;\n } else if (res == -1) {\n last = mid - 1;\n } else {\n first = mid + 1;\n }\n }\n return -1;\n }\n}\n\n```\n```Python []\nclass Solution(GuessGame):\n def guessNumber(self, n: int) -> int:\n first, last = 1, n\n while first <= last:\n mid = first + (last - first) // 2\n res = self.guess(mid)\n if res == 0:\n return mid\n elif res == -1:\n last = mid - 1\n else:\n first = mid + 1\n return -1\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(logn)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 26 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
Python Easy Solution || 100% || Binary Search || | guess-number-higher-or-lower | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The guess API is already defined for you.\n# @param num, your guess\n# @return -1 if num is higher than the picked number\n# 1 if num is lower than the picked number\n# otherwise return 0\n# def guess(num: int) -> int:\n\nclass Solution:\n def guessNumber(self, n: int) -> int:\n l=0\n r=n\n while l<=r:\n m=(l+r)>>1\n if guess(m)==0:\n return m\n elif guess(m)==-1:\n r=m-1\n else:\n l=m+1\n \n``` | 2 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
📌 Python3 extension of Binary Search | guess-number-higher-or-lower | 0 | 1 | ```\nclass Solution:\n def guessNumber(self, n: int) -> int:\n low = 1\n high = n\n \n while low<=high:\n mid = (low+high)//2\n gussed = guess(mid)\n \n if gussed == 0:\n return mid\n if gussed<0:\n high = mid-1\n else:\n low = mid+1\n \n return low\n``` | 5 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
Easy Python Solution | guess-number-higher-or-lower | 0 | 1 | # Code\n```\nclass Solution:\n def guessNumber(self, n: int) -> int:\n low = 1\n high = n\n while low <= high:\n mid = (low + high)//2\n res = guess(mid)\n if res == 0 :\n return mid\n elif res == -1:\n high = mid - 1\n else:\n low = mid + 1\n``` | 4 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
Python: Beats 99% solutions O(log(n)) (w/ comments and using Walrus Operator) | guess-number-higher-or-lower | 0 | 1 | ```\ndef guessNumber(self, n: int) -> int:\n\tlowerBound, upperBound = 1, n\n\t# Binary division faster than (lowerBound + upperBound) //2\n\tmyGuess = (lowerBound+upperBound) >> 1\n\t# walrus operator \':=\' - assigns value of the function to the variable \'res\'\n\t# and then compare res with 0\n\twhile (res := guess(myGuess)) != 0:\n\t\tif res == 1:\n\t\t\tlowerBound = myGuess+1\n\t\telse:\n\t\t\tupperBound = myGuess-1\n\t\tmyGuess = (lowerBound+upperBound) >> 1\n\n\treturn myGuess\n``` | 42 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
ONE-LINER || Beats 92.63% 🔥 || SHORTEST POSSIBLE PYTHON EXPLAINED | guess-number-higher-or-lower | 0 | 1 | # \uD83D\uDD25 SOLUTION \uD83D\uDD25\n```\nclass Solution:\n def guessNumber(self, n: int) -> int:\n return bisect_left(range(n), 0, key=lambda num: -guess(num))\n \n```\n# STEP-BY-STEP\n\n- The bisect_left function is called with three arguments:\n1. The first argument is a range object created using the range function with n as the upper bound. This creates a sequence of numbers from 0 to n-1. bisect_left will search this sequence for the value 0.\n \n2. The second argument is the value 0, which is the target value that bisect_left will try to find within the sequence.\n\n3. The third argument is a key function that returns a value to be used for sorting the sequence. bisect_left assumes that the sequence is already sorted, so the key function is used to provide a way to compare values within the sequence that are not necessarily comparable with the standard less-than/greater-than operators. In this case, the key function is defined using a lambda function that takes a number num as input and returns the negative value of guess(num). guess is assumed to be a function that takes a number as input and returns a value indicating whether the guess is too high, too low, or correct. By negating the output of guess(num), the bisect_left function will effectively sort the sequence in descending order of how close each number is to the target value. | 1 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
Python binary search solution | guess-number-higher-or-lower | 0 | 1 | **Python :**\n\n```\ndef guessNumber(self, n: int) -> int:\n\tlow = 0\n\thigh = n\n\twhile low <= high:\n\t\tmid = (low + high ) // 2\n\t\tres = guess(mid)\n\t\tif res < 0:\n\t\t\thigh = mid - 1\n\n\t\telif res > 0:\n\t\t\tlow = mid + 1\n\n\t\telse:\n\t\t\treturn mid\n```\n\n**Like it ? please upvote !** | 27 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
374: Solution with step by step explanation | guess-number-higher-or-lower | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We initialize two variables left and right with 1 and n respectively, which represent the start and end points of our search range.\n\n2. We use a while loop to perform the binary search until we guess the correct number.\n\n3. In each iteration, we calculate the middle point of the search range using (left + right) // 2.\n\n4. We then use the guess function to check if the middle point is the correct number or not. If it is the correct number, we return it.\n\n5. If the guess is greater than the picked number, we update our search range to the left half by setting right = mid - 1.\n\n6. If the guess is smaller than the picked number, we update our search range to the right half by setting left = mid + 1.\n\n7. If we exhaust our search range and still haven\'t found the correct number, we return -1.\n\nNote: The guess function is not defined in the solution code because it is a pre-defined API function provided by the question prompt. We can assume that it takes an integer as input and returns 0 if the integer is the correct number, 1 if it is lower than the correct number, and -1 if it is greater than the correct number.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def guessNumber(self, n: int) -> int:\n left, right = 1, n\n \n while left <= right:\n mid = (left + right) // 2\n res = guess(mid)\n \n if res == 0:\n return mid\n elif res < 0:\n right = mid - 1\n else:\n left = mid + 1\n \n return -1\n\n``` | 10 | We are playing the Guess Game. The game is as follows:
I pick a number from `1` to `n`. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API `int guess(int num)`, which returns three possible results:
* `-1`: Your guess is higher than the number I picked (i.e. `num > pick`).
* `1`: Your guess is lower than the number I picked (i.e. `num < pick`).
* `0`: your guess is equal to the number I picked (i.e. `num == pick`).
Return _the number that I picked_.
**Example 1:**
**Input:** n = 10, pick = 6
**Output:** 6
**Example 2:**
**Input:** n = 1, pick = 1
**Output:** 1
**Example 3:**
**Input:** n = 2, pick = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 231 - 1`
* `1 <= pick <= n` | null |
Beats 84% | Easy To Understand 🚀🔥 | guess-number-higher-or-lower-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n // TC - O(Exponential) and SC - O(N)\n int getMoneyAmountRec(int start, int end)\n {\n if(start >= end)\n return 0;\n \n int ans = INT_MAX;\n\n for(int i = start; i <= end; i++)\n {\n ans = min(ans,i + max(getMoneyAmountRec(start,i-1),getMoneyAmountRec(i+1,end)));\n }\n\n return ans;\n }\n\n // TC - O(N*3) and SC - O(N*2)\n int getMoneyAmountMem(int start, int end, vector<vector<int>>& dp)\n {\n if(start >= end)\n return 0;\n if(dp[start][end] != -1)\n return dp[start][end];\n \n int ans = INT_MAX;\n\n for(int i = start; i <= end; i++)\n {\n ans = min(ans,i + max(getMoneyAmountMem(start,i-1,dp),getMoneyAmountMem(i+1,end,dp)));\n }\n\n dp[start][end] = ans;\n return dp[start][end];\n }\n\n // TC - O(N*3) and SC - O(N*2)\n int getMoneyAmountTab(int n)\n {\n vector<vector<int>> dp(n+2,vector<int>(n+2,0));\n\n for(int start = n; start >= 1; start--)\n {\n for(int end = 1; end <= n; end++)\n {\n if(start >= end)\n continue;\n \n int ans = INT_MAX;\n\n for(int i = start; i <= end; i++)\n {\n ans = min(ans,i + max(dp[start][i-1],dp[i+1][end]));\n }\n\n dp[start][end] = ans;\n }\n }\n return dp[1][n];\n }\n\n int getMoneyAmount(int n) {\n // 1. Recursion\n // return getMoneyAmountRec(1,n);\n\n // 2. Top Down Approach\n // vector<vector<int>> dp(n+1,vector<int>(n+1,-1));\n // return getMoneyAmountMem(1,n,dp);\n\n // 3. Bottom Up Approach\n return getMoneyAmountTab(n);\n }\n};\n``` | 2 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
[Python] DP, beat 97.52% in time, 99% in memory (with explanation) | guess-number-higher-or-lower-ii | 0 | 1 | **Appreciate if you could upvote this solution**\n\nCase 1: `n is odd`\nSelected nums = [2, 4, 6, ..., n-1]\n\nCase 2: `n is even`\nSelected nums = [1, 3, 5, ..., n-1]\n\nThe basic idea is that if we want to guess the right number, the maximum number of guessing time should be k = floor(n/2) which means we can find out the right number just using the k nums.\n\nFor example, \nWhen n = 5, k = floor(5/2) = 2\nwe can find out the right number by guessing 2 and 4 as 2 can classify [1, 2, 3] and 4 and classify [3, 4, 5]\n```\n1 2 3 4 5\n 2 4\n```\nWhen n = 6, k = floor(6/2) = 3\nwe can find out the right number by guessing 1, 3 and 5 as they can classify [1, 2], [2, 3, 4] and [4, 5, 6] respectively \n```\n1 2 3 4 5 6\n1 3 5\n```\n\nThus, we can use the selected nums to find out the minimum amount of money and the execution time will be reduced by half.\nIn the dp matrix, the row means the starting index and the col means the ending index.\nAt the beginning, the dp[i][i] is assignmed as selected_nums[i] because selected_nums[i] is the smallest cost to classify the nums in [selected_nums[i] - 1, selected_nums[i], selected_nums[i] + 1].\nAfter the initialization, the problem will become an easy dp question, just finding the optimal solution from length 2 to length k.\n\n```python\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n if n == 1:\n return 1\n starting_index = 1 if n % 2 == 0 else 2\n selected_nums = [i for i in range(starting_index, n, 2)]\n selected_nums_length = len(selected_nums)\n dp = [[0] * selected_nums_length for _ in range(selected_nums_length)]\n\n for i in range(selected_nums_length):\n dp[i][i] = selected_nums[i]\n\n for length in range(2, selected_nums_length + 1):\n for i in range(selected_nums_length - length + 1):\n j = i + length - 1\n dp[i][j] = float("inf")\n for k in range(i, j + 1):\n dp_left = dp[i][k - 1] if k != 0 else 0\n dp_right = dp[k + 1][j] if k != j else 0\n dp[i][j] = min(dp[i][j], selected_nums[k] + max(dp_left, dp_right))\n\n return dp[0][-1]\n``` | 33 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
✅ [Python] split into groups of 3 | guess-number-higher-or-lower-ii | 0 | 1 | The most economic way of guessing a number at the tail is to pick the middle one, e.g., `... 23 24 25` (choose `24`). But this means that a split should be done at `n-4` (i.e., `22` in the previous example). The same logic applies to every possible segment, thus, the split points are `n-3, n-7, n-11, ...`. \n\nThe minimum penalty for the interval `[l,r]` would be the minimum value among all split points for the sum of:\n1. The value at the split `m` itself, and\n2. The maximum of penalties for the left and right subintervals, `[l,m-1]` and `[m+1,l]`.\n\nAnswers for short subintervals are hardcoded.\n\n```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n \n @cache\n def dfs(l,r):\n if r-l == 4 : return 2*l + 4\n if r-l == 3 : return 2*l + 2\n if r-l == 2 : return l + 1\n if r-l == 1 : return l\n \n return min((m + max(dfs(l,m-1), dfs(m+1,r)) for m in range(r-3,l,-4)), default=0)\n\n if n <= 2 : return n-1\n if n == 3 : return 2\n \n return dfs(1,n)\n``` | 2 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
python dp approach | guess-number-higher-or-lower-ii | 0 | 1 | # Intuition\nLet `dp` is the minimum cost for make sure we win in range `[l, r]` (inclusive).\nIf we choose `i` and wrong, the correct answer should be in `[l, i - 1]` or `[i + 1, r]`. So if we choose `i` and wrong, we need to get maximum cost between this 2 cases + `i` for make sure we always win even the correct answer in `[l, i - 1]` or `[i + 1, r]`.\nSo minimum cost for make sure we win if we choose `i` and wrong is `i` + `max(dp(l, i - 1), dp(i + 1, r))`.\nTry all possible `i` in range `[l, r]` and find the minimum to get the minimum cost for make sure we win in range `[l, r]`.\n# Code\n```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n @lru_cache(None)\n def dp(l, r):\n if l >= r:\n return 0 \n ans = float(\'inf\') \n for i in range(l, r):\n ans = min(ans, max(dp(l, i - 1), dp(i + 1, r)) + i)\n return ans\n return dp(1, n)\n\n``` | 4 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
Python3 || dp, binSearch w/ explanation || T/M: 96%/ 47% | guess-number-higher-or-lower-ii | 0 | 1 | For an interval `[l,r]`, we choose a num, which if incorrect still allows us to know whether the secret is in either `[l,num-1]` or `[num+1,r]`. So, the worst-case (w-c) cost is num + max(w-c cost in`[l,num-1]`, w-c cost in `[num+1,r])`. We do this by recursion and binary search, starting with`[1,n]`.\n```\nclass Solution:\n def getMoneyAmount(self, n):\n\n @lru_cache(None) # <-- we cache function results to avoid recomputing them\n def dp(l = 1, r = n)-> int:\n if r-l < 1: return 0 # <-- base case for the recursion; one number in [l,r] \n ans = 1000 # <-- the answer for n = 200 is 952\n \n for choice in range((l+r)//2,r):\n ans = min(ans,choice+max(dp(l,choice-1),dp(choice+1,r)))\n\n return ans\n\n return dp()\n``` | 5 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
375: Solution with step by step explanation | guess-number-higher-or-lower-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses dynamic programming to solve the problem.\n\nFirst, we define a 2D array dp of size (n+2) x (n+2), where dp[i][j] represents the minimum amount of money needed to guarantee a win when guessing a number between i and j inclusive.\n\nThen, we iterate over all possible subranges of the range [1, n], which have lengths from 1 to n, using the outer loop with variable d and the inner loop with variable i. For each subrange [i, j], we need to find the minimum cost of guessing a number.\n\nTo find this minimum cost, we iterate over all possible guesses k between i and j, and compute the maximum cost between guessing k and the worst-case scenario for each of the two subranges [i, k-1] and [k+1, j]. The total cost of guessing k is the sum of k and the maximum cost of the two subranges.\n\nWe take the minimum cost over all possible guesses k and assign this value to dp[i][j].\n\nFinally, the minimum cost of guessing a number between 1 and n is stored in dp[1][n] and returned.\n\n# Complexity\n- Time complexity:\n63.66%\n\n- Space complexity:\n78.31%\n\n# Code\n```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n # dp[i][j] := min money you need to guarantee a win of picking i..j\n dp = [[0] * (n + 2) for _ in range(n + 2)]\n\n # iterate over all possible subranges of [1, n]\n for d in range(1, n + 1):\n for i in range(1, n - d + 1):\n j = i + d\n # initialize dp[i][j] to infinity\n dp[i][j] = math.inf\n # iterate over all possible guesses k between i and j\n for k in range(i, j + 1):\n # compute the maximum cost of guessing k and the worst-case scenario for each of the two subranges\n cost = max(dp[i][k-1], dp[k+1][j]) + k\n # take the minimum cost over all possible guesses k\n dp[i][j] = min(dp[i][j], cost)\n\n # the minimum cost of guessing a number between 1 and n is stored in dp[1][n]\n return dp[1][n]\n\n``` | 4 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
[Python] Very detailed explanation with examples | guess-number-higher-or-lower-ii | 0 | 1 | ```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n ## RC ##\n ## APPROACH : DP - MERGE INTERVALS PATTERN ##\n ## LOGIC - BOTTOM UP ##\n ## consider numbers 1,2,3,4 (here i = 1, j = 4) ## \n ## 1. we start by picking 2 or 3 ==> lets say we started by 2, player B says right side we pick 3 ==> so total = 5. or if player B says left side ? result will be 2 + 0 => 2. worst case scenarios is maximum of leftside and rightside. i.e for k=2 => max(5,2)\n ## 2. next if we start with 3 i.e k=3 ==> we can go left side or right side. for leftside ==> total = 3 + 1, for rightside total = 3 + 0. worst case is max(4,3) = 4\n ## In short, for start point k =2 in 1234, we need leftside [1,1] rightside[3,4] and pick worst\n ## for startpoint k = 3 in 1234, we need leftside [1,2] and rightside[4,4] and pick worst\n ## This is the reason why we need to have 2D DP matrix, to store left and right subproblems\n ## We need to return best of all worst cases, so res = minimum( worstcase( number + leftside sub problem, number + rightside subproblem ) ) \n ## ```dp[i][j] = min( dp[i][j], max( dp[i][k-1] + k, dp[k+1][j] + k ) )``` for all startpoints of k ( k lies between i and j)\n \n\t\t## TIME COMPLEXITY : O(N^2) ##\n\t\t## SPACE COMPLEXITY : O(N^2) ##\n\n ## EXAMPLE : 1 2 3 4 5 6 7 ##\n # [\n # [\'X\', \'X\', \'X\', \'X\', \'X\', \'X\', \'X\', \'X\'], \n # [\'X\', 0, 1, 2, 4, 6, 8, 10], \n # [\'X\', \'X\', 0, 2, 3, 6, 8, 10], \n # [\'X\', \'X\', \'X\', 0, 3, 4, 8, 10], \n # [\'X\', \'X\', \'X\', \'X\', 0, 4, 5, 10], \n # [\'X\', \'X\', \'X\', \'X\', \'X\', 0, 5, 6], \n # [\'X\', \'X\', \'X\', \'X\', \'X\', \'X\', 0, 6], \n # [\'X\', \'X\', \'X\', \'X\', \'X\', \'X\', \'X\', 0]\n # ]\n\n dp = [[ float(\'inf\') ] * (n+1) for _ in range(n+1)]\n for i in range(n, 0, -1):\n for j in range(i,n+1):\n if i == j :\n dp[i][j] = 0\n if j - i == 1:\n dp[i][j] = i\n for k in range(i+1, j):\n dp[i][j] = min( dp[i][j], max( dp[i][k-1] + k, dp[k+1][j] + k ) )\n # print(dp)\n return dp[1][-1]\n\n``` | 10 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
PYTHON 3, BOTTOM UP 2D, AND TOP DOWN W MEMOIZATION | guess-number-higher-or-lower-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst I solved using a top down with memoization approach. Then I used that to sold 2d dynamic programming approach. This made it more inuitive\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n\n dp = [[0]*(n+1) for _ in range(n+1)]\n #0123\n for length in range(1,n+1):\n for l in range(1,n+1-length):\n r = l+length\n res = float("inf")\n for piv in range((l+r)//2,r):\n gaur = piv + max(dp[l][piv-1],dp[piv+1][r])\n res = min(res,gaur)\n dp[l][r] = res\n return dp[1][n]\n\n\n #n^2 states with a o(n) in each state : n^3\n #dp[l][r] = min cost to gaurentee win btw l,r\n cache = {} #stores l,r \n def dfs(l,r):\n if l >=r:\n return 0 #at the last idx, dont need to take\n if (l,r) in cache:\n return cache[(l,r)]\n res = float("inf")\n for piv in range((r+l)//2,r):\n gaur = piv + max(dfs(l,piv-1),dfs(piv+1,r))\n res = min(res,gaur)\n cache[(l,r)] = res\n return res\n return dfs(1,n)\n``` | 0 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
Traditional dfs + cache solution. you will understand without explanation. | guess-number-higher-or-lower-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n h = {}\n\n def get_amount(l, r):\n \n if r - l == 2:\n return l + 1\n elif r - l == 1:\n return l\n elif r == l:\n return 0\n\n if (l, r) in h:\n return h[(l, r)]\n\n mini = float(\'inf\')\n for n in range(l+1, r):\n mid = n\n left = get_amount(l, n-1)\n right = get_amount(n+1, r)\n mini = min(mini, mid+max(left,right))\n\n h[(l, r)] = mini\n return mini\n \n res = get_amount(1, n)\n return res\n\n``` | 0 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
Three line python For fun | guess-number-higher-or-lower-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def getMoneyAmount(self,n): \n @cache \n def h(l,r):return 0 if r-l<1 else min([i+max(h(l,i-1),h(i+1,r)) for i in range((l+r)//2,r)])\n return h(1,n)\n``` | 0 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
Very intuitive explanation - recursive solution with Python (inefficient but helpful to understand) | guess-number-higher-or-lower-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nI really struggled to get the intuition as to how this problem can be divided into sub-problems. So if you have problems with that too, try thinking this way:\n\nWe have a range from 1 to n. Imagine that we chose some k in that range (say in the middle or smt). Now, think about how do we even evaluate this choice. There are three variants here:\n1. k hit the bull\'s eye so we don\'t need to spend any money - good, but doesn\'t give us the \'worst case\' estimate.\n2. k is **smaller** than the guessed number. In this case we definitely know that we pay k. But what else do we need? Right! - the estimate from the range of (k, n]. We need to know what is the most optimal solution for this range, and that would be our answer for this case. Hence we need to solve **the same** problem for the interval [k + 1, n] - here\'s our recursive relation.\n3. k is **bigger** than the guessed number. This is pretty much the same as variant 2 but the recursive interval is [1, k - 1].\n\nThat\'s why in recursion we just try all the different k-s between 1 and n, compute left-sided and right-sided score, and take the maximum of it - because that will guarantee us the find. We then just find the minimum of the scores for each k. Rinse and repeat for each subproblem. \n\nHope that helps! If not, really just sleep on it and let your brain settle with this problem. It helps a lot.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nThis is a pretty inefficient solution, but is great for gaining intuition about solving this problem. Other recursive solutions are bulkier and not as crisp.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMoneyAmount(self, n: int) -> int:\n \n @cache\n def dfs(i, j):\n if i >= j:\n return 0\n \n min_cost = float(\'+inf\')\n for k in range(i, j + 1):\n current_cost = max(dfs(i, k - 1) + k, k + dfs(k + 1, j))\n min_cost = min(min_cost, current_cost)\n \n return min_cost\n \n return dfs(1, n)\n``` | 0 | We are playing the Guessing Game. The game will work as follows:
1. I pick a number between `1` and `n`.
2. You guess a number.
3. If you guess the right number, **you win the game**.
4. If you guess the wrong number, then I will tell you whether the number I picked is **higher or lower**, and you will continue guessing.
5. Every time you guess a wrong number `x`, you will pay `x` dollars. If you run out of money, **you lose the game**.
Given a particular `n`, return _the minimum amount of money you need to **guarantee a win regardless of what number I pick**_.
**Example 1:**
**Input:** n = 10
**Output:** 16
**Explanation:** The winning strategy is as follows:
- The range is \[1,10\]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is \[8,10\]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is \[1,6\]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is \[4,6\]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is \[1,2\]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Explanation:** There is only one possible number, so you can guess 1 and not have to pay anything.
**Example 3:**
**Input:** n = 2
**Output:** 1
**Explanation:** There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
**Constraints:**
* `1 <= n <= 200` | The best strategy to play the game is to minimize the maximum loss you could possibly face. Another strategy is to minimize the expected loss. Here, we are interested in the first scenario. Take a small example (n = 3). What do you end up paying in the worst case? Check out this article if you're still stuck. The purely recursive implementation of minimax would be worthless for even a small n. You MUST use dynamic programming. As a follow-up, how would you modify your code to solve the problem of minimizing the expected loss, instead of the worst-case loss? |
376: Space 97.92%, Solution with step by step explanation | wiggle-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the length of the input list nums is less than 2. If yes, return the length of nums. This is because a sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.\n\n```\nn = len(nums)\nif n < 2:\n return n\n```\n2. Initialize two variables max_len and last_wiggle to keep track of the length of the longest wiggle subsequence and the last wiggle direction, respectively. Set max_len to 1 because the first element of the input list is always included in the wiggle subsequence.\n\n```\nmax_len = 1\nlast_wiggle = None\n```\n\n3. Loop through the input list nums starting from the second element (i = 1) until the end (i = n-1). For each iteration, calculate the difference between the current and previous element using the formula diff = nums[i] - nums[i-1].\n\n```\nfor i in range(1, n):\n diff = nums[i] - nums[i-1]\n```\n4. If the difference diff is positive and the last wiggle direction last_wiggle was negative, or if the difference diff is negative and the last wiggle direction last_wiggle was positive, then we\'ve found a new wiggle direction and can update the length of the longest wiggle subsequence max_len by adding 1. Update the last wiggle direction last_wiggle accordingly by setting it to 1 if diff is positive, and -1 otherwise.\n\n```\nif (diff > 0 and last_wiggle != 1) or (diff < 0 and last_wiggle != -1):\n max_len += 1\n last_wiggle = 1 if diff > 0 else -1\n```\n5. Return the final value of max_len as the length of the longest wiggle subsequence.\n\n```\nreturn max_len\n```\n\n# Complexity\n- Time complexity:\n74.22%\n\n- Space complexity:\n97.92%\n\n# Code\n```\nclass Solution:\n def wiggleMaxLength(self, nums: List[int]) -> int:\n n = len(nums)\n if n < 2:\n return n\n \n # Initialize variables to keep track of the length of the longest \n # wiggle subsequence and the last wiggle direction\n max_len = 1\n last_wiggle = None\n \n for i in range(1, n):\n # Calculate the difference between the current and previous element\n diff = nums[i] - nums[i-1]\n # If the difference is positive and the last wiggle direction was negative\n # or the difference is negative and the last wiggle direction was positive,\n # then we\'ve found a new wiggle direction and can update the length of the \n # longest wiggle subsequence\n if (diff > 0 and last_wiggle != 1) or (diff < 0 and last_wiggle != -1):\n max_len += 1\n # Update the last wiggle direction\n last_wiggle = 1 if diff > 0 else -1\n \n return max_len\n``` | 6 | A **wiggle sequence** is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.
* For example, `[1, 7, 4, 9, 2, 5]` is a **wiggle sequence** because the differences `(6, -3, 5, -7, 3)` alternate between positive and negative.
* In contrast, `[1, 4, 7, 2, 5]` and `[1, 7, 4, 5, 5]` are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.
A **subsequence** is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.
Given an integer array `nums`, return _the length of the longest **wiggle subsequence** of_ `nums`.
**Example 1:**
**Input:** nums = \[1,7,4,9,2,5\]
**Output:** 6
**Explanation:** The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).
**Example 2:**
**Input:** nums = \[1,17,5,10,13,15,10,5,16,8\]
**Output:** 7
**Explanation:** There are several subsequences that achieve this length.
One is \[1, 17, 10, 13, 10, 16, 8\] with differences (16, -7, 3, -3, 6, -8).
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6,7,8,9\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
**Follow up:** Could you solve this in `O(n)` time? | null |
Beats 73.3% - Simple Python Solution - Greedy | wiggle-subsequence | 0 | 1 | ```\nclass Solution:\n def wiggleMaxLength(self, nums: List[int]) -> int:\n length = 0\n curr = 0\n \n for i in range(len(nums) - 1):\n if curr == 0 and nums[i + 1] - nums[i] != 0:\n length += 1\n curr = nums[i + 1] - nums[i]\n \n if curr < 0 and nums[i + 1] - nums[i] > 0:\n length += 1\n curr = nums[i + 1] - nums[i]\n \n elif curr > 0 and nums[i + 1] - nums[i] < 0:\n length += 1\n curr = nums[i + 1] - nums[i]\n \n else:\n continue\n \n return length + 1\n``` | 3 | A **wiggle sequence** is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.
* For example, `[1, 7, 4, 9, 2, 5]` is a **wiggle sequence** because the differences `(6, -3, 5, -7, 3)` alternate between positive and negative.
* In contrast, `[1, 4, 7, 2, 5]` and `[1, 7, 4, 5, 5]` are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.
A **subsequence** is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.
Given an integer array `nums`, return _the length of the longest **wiggle subsequence** of_ `nums`.
**Example 1:**
**Input:** nums = \[1,7,4,9,2,5\]
**Output:** 6
**Explanation:** The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).
**Example 2:**
**Input:** nums = \[1,17,5,10,13,15,10,5,16,8\]
**Output:** 7
**Explanation:** There are several subsequences that achieve this length.
One is \[1, 17, 10, 13, 10, 16, 8\] with differences (16, -7, 3, -3, 6, -8).
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6,7,8,9\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
**Follow up:** Could you solve this in `O(n)` time? | null |
Python/JS/Java/Go/C++ O(n) DP [w/ State machine diagram] | wiggle-subsequence | 0 | 1 | **State machine diagram**\n\n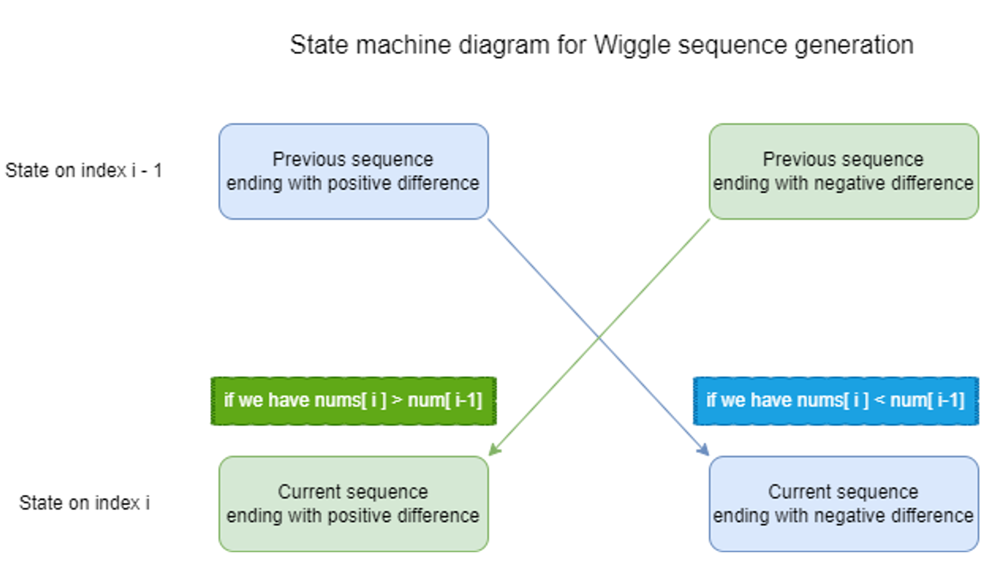\n\n\n---\n\nPython:\n\n```\nclass Solution(object):\n def wiggleMaxLength(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n \n n = len( nums )\n \n\t\t## Base case\n # length of wiggle sequence, ending in positive difference, negative difference\n positive, negative = 1, 1\n \n ## General cases:\n # scan from secnond number to last number\n for i in range(1, n):\n \n if nums[i] > nums[i-1]:\n \n # difference is positive, concatenated with negative prefix wiggle subsequence\n positive = negative + 1\n \n elif nums[i] < nums[i-1]:\n \n # differnce is negative, concatenated with positive prefix wiggle subsequence\n negative = positive + 1\n \n # compute the longest length of wiggle sequence \n return max(positive, negative)\n```\n\n---\n\nJava:\n\n```\nclass Solution {\n public int wiggleMaxLength(int[] nums) {\n \n final int n = nums.length;\n \n // Base case\n // length of wiggle sequence, ending in positive difference, negative difference\n int positive=1, negative = 1;\n \n // General cases:\n // scan from second number to last number\n for( int i = 1 ; i < n ; i++){\n \n if( nums[i] > nums[i-1] ){\n \n // difference is positive, concatednated with negative prefix wiggle subsequence\n positive = negative + 1;\n \n }else if( nums[i] < nums[i-1] ){\n \n // difference is negative, concatednated with positive prefix wiggle subsequence\n negative = positive + 1;\n } \n }\n \n // compute the longest length of wiggle sequence \n return Math.max(positive, negative);\n }\n}\n```\n\n---\n\nJavascript:\n\n```\nvar wiggleMaxLength = function(nums) {\n \n let n = nums.length;\n \n // Base case:\n // length of wiggle sequence, ending in positive difference, negative difference\n let [positive, negative] = [1, 1];\n \n \n // General cases:\n // scan from second number to last number\n for( let i = 1 ; i < n ; i++){\n \n if( nums[i] > nums[i-1] ){\n \n // difference is positive, concatenated with negative prefix wiggle sequence\n positive = negative + 1;\n \n }else if ( nums[i] < nums[i-1] ){\n \n // difference is negative, concatenated with positive prefix wiggle sequence\n negative = positive + 1;\n }\n \n }\n \n // compute the longest length of wiggle sequence \n return Math.max( positive, negative);\n \n};\n```\n\n---\n\nGo:\n\n```\nfunc max(x, y int) int {\n if x > y{\n return x\n }else{\n return y\n }\n}\n\n\nfunc wiggleMaxLength(nums []int) int {\n \n \n n := len( nums )\n \n\t// Base case:\n // length of wiggle sequence, ending in positive difference, negative difference\n positive, negative := 1, 1\n \n // General cases:\n // scan from second number to last number\n for i := 1; i < n; i++ {\n \n if nums[i] > nums[i-1]{\n \n // difference is positive, concatenated with negative prefix wiggle subsequence\n positive = negative + 1\n \n }else if nums[i] < nums[i-1]{\n \n // difference is negative, concatenated with positive prefix wiggle subsequence\n negative = positive + 1\n }\n \n }\n \n\t// compute the longest length of wiggle sequence \n return max(positive, negative)\n}\n```\n\n---\n\nC++\n\n\n```\nclass Solution {\npublic:\n int wiggleMaxLength(vector<int>& nums) {\n \n const int n = nums.size();\n \n // Base case\n // length of wiggle sequence, ending in positive difference, negative difference\n int positive=1, negative = 1;\n \n // General cases:\n // scan from second number to last number\n for( int i = 1 ; i < n ; i++){\n \n if( nums[i] > nums[i-1] ){\n \n // difference is positive, concatednated with negative prefix wiggle subsequence\n positive = negative + 1;\n \n }else if( nums[i] < nums[i-1] ){\n \n // difference is negative, concatednated with positive prefix wiggle subsequence\n negative = positive + 1;\n } \n }\n \n // compute the longest length of wiggle sequence \n return max(positive, negative);\n }\n};\n```\n\n---\n\n**Implementation** by Top-down DP\n\n```\nclass Solution:\n def wiggleMaxLength(self, nums: List[int]) -> int:\n \n def dp( i ):\n \n if i == 0:\n \n ## Bacse case:\n # Single number\n return 1, 1, nums[0]\n \n else:\n \n ## General cases:\n prev_positive, prev_negative, prev_num = dp(i-1)\n \n cur_positive, cur_negative = prev_positive, prev_negative\n diff = nums[i] - prev_num\n \n if diff> 0:\n cur_positive = prev_negative + 1\n \n elif diff < 0:\n cur_negative = prev_positive + 1\n \n return cur_positive, cur_negative, nums[i]\n \n # -----------------------------------------------------\n pos, neg, _ = dp( i = len(nums)-1)\n \n return max(pos, neg)\n``` | 10 | A **wiggle sequence** is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.
* For example, `[1, 7, 4, 9, 2, 5]` is a **wiggle sequence** because the differences `(6, -3, 5, -7, 3)` alternate between positive and negative.
* In contrast, `[1, 4, 7, 2, 5]` and `[1, 7, 4, 5, 5]` are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.
A **subsequence** is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.
Given an integer array `nums`, return _the length of the longest **wiggle subsequence** of_ `nums`.
**Example 1:**
**Input:** nums = \[1,7,4,9,2,5\]
**Output:** 6
**Explanation:** The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).
**Example 2:**
**Input:** nums = \[1,17,5,10,13,15,10,5,16,8\]
**Output:** 7
**Explanation:** There are several subsequences that achieve this length.
One is \[1, 17, 10, 13, 10, 16, 8\] with differences (16, -7, 3, -3, 6, -8).
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6,7,8,9\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
**Follow up:** Could you solve this in `O(n)` time? | null |
Simple O(n) Solution using Dynamic Programming | wiggle-subsequence | 0 | 1 | ```\n#####################################################################################################################\n# Problem: Wiggle Subsequence\n# Solution : Dynamic Programming\n# Time Complexity : O(n) \n# Space Complexity : O(1)\n#####################################################################################################################\n\nclass Solution:\n def wiggleMaxLength(self, nums: List[int]) -> int:\n \n positive, negative = 1, 1\n \n if len(nums) < 2:\n return len(nums)\n \n for i in range(1, len(nums)):\n if nums[i] > nums[i - 1]:\n positive = negative + 1\n elif nums[i] < nums[i - 1]:\n negative = positive + 1\n \n return max(positive, negative)\n``` | 1 | A **wiggle sequence** is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.
* For example, `[1, 7, 4, 9, 2, 5]` is a **wiggle sequence** because the differences `(6, -3, 5, -7, 3)` alternate between positive and negative.
* In contrast, `[1, 4, 7, 2, 5]` and `[1, 7, 4, 5, 5]` are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.
A **subsequence** is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.
Given an integer array `nums`, return _the length of the longest **wiggle subsequence** of_ `nums`.
**Example 1:**
**Input:** nums = \[1,7,4,9,2,5\]
**Output:** 6
**Explanation:** The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).
**Example 2:**
**Input:** nums = \[1,17,5,10,13,15,10,5,16,8\]
**Output:** 7
**Explanation:** There are several subsequences that achieve this length.
One is \[1, 17, 10, 13, 10, 16, 8\] with differences (16, -7, 3, -3, 6, -8).
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6,7,8,9\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 1000`
**Follow up:** Could you solve this in `O(n)` time? | null |
[ Python / Java / C++] 🔥100% | ✅ DP | combination-sum-iv | 1 | 1 | \n```Python []\nclass Solution:\n def combinationSum4(self, nums: List[int], t: int) -> int:\n self.dp=[-1]*(t+1)\n return self.solve(nums,t)\n\t\t\t\t\n def solve(self,nums,t):\n if t==0:\n return 1\n\n if self.dp[t]!=-1:\n return self.dp[t]\n\n res=0\n\n for i in nums:\n if t>=i:\n res+=self.solve(nums,t-i)\n self.dp[t]=res\n return res\n```\n```Java []\nclass Solution {\n int[] dp;\n public int combinationSum4(int[] nums, int t) {\n dp = new int[t+1];\n Arrays.fill(dp,-1);\n return dp(nums,t);\n }\n \n public int dp(int[] nums, int t){\n if(t==0) return 1;\n if(t<0) return 0;\n\n if(dp[t]!=-1) return dp[t];\n \n int temp = 0;\n for(int i=0;i<nums.length;i++){\n temp+=dp(nums,t-nums[i]);\n }\n dp[t] = temp;\n return temp;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n \n int solve(vector<int>&nums , int t , vector<int>&dp){\n if( t == 0) return 1;\n if( t < 0) return 0 ;\n\n if(dp[t] != -1) return dp[t];\n int temp = 0;\n\n for(int i =0 ; i< nums.size() ; i++){\n temp+= solve(nums , t - nums[i] ,dp);\n }\n return dp[t] = temp;;\n\n }\n int combinationSum4(vector<int>& nums, int target) {\n vector<int> dp( target+1 , -1);\n return solve( nums , target , dp);\n }\n};\n```\n\n\n | 2 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python3 Solution | combination-sum-iv | 0 | 1 | ```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n dp=[0]*(target+1)\n dp[0]=1\n for t in range(target+1):\n for num in nums:\n if num<=t:\n dp[t]+=dp[t-num]\n\n return dp[target] \n``` | 2 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Simple dp. Check for every sum till target | combination-sum-iv | 0 | 1 | \n# Code\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n nums.sort()\n dp = [0] * (target+1)\n for curr in range(target+1):\n for num in nums:\n if num > curr: continue\n elif num == curr: dp[curr] += 1\n else: dp[curr] += dp[curr - num]\n return dp[target]\n``` | 2 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
【Video】Beats 97.25% - Python, JavaScript, Java and C++ | combination-sum-iv | 1 | 1 | # Intuition\nUse Dynamic Programming. This Python solution beats 97.25% today.\n\n\n\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 257 videos as of September 9th, 2023.\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/uRHHc6hunls\nVolume of the video may be a little bit low. Please turn up the volume on your computer a bit. Thank you for your support.\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2263\nThank you for your support!\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n**1. Initialize the Dynamic Programming (DP) array**\n - Create a DP array `dp` of size `(target + 1)` and initialize all elements to 0.\n - Set `dp[0]` to 1 to represent that there is one way to make a sum of 0, which is by not selecting any number from `nums`.\n\n**2. Iterate through numbers from 1 to target**\n - Start a loop from `1` to `target` (inclusive).\n \n**3. Inner Loop through each number in the `nums` array**\n - Start another loop to iterate through each number `n` in the `nums` array.\n\n**4. Check if the current number `n` is less than or equal to the current target `i`**\n - Within the inner loop, check if the current number `n` is less than or equal to the current target `i`.\n\n**5. Update DP array**\n - If `n` is less than or equal to `i`, then update `dp[i]` by adding the value of `dp[i - n]`. This step accumulates the number of ways to reach the target `i` by considering the current number `n`.\n\n**6. Continue iterating**\n - Continue the outer loop, iterating through all possible target values from `1` to `target`, and for each target, iterate through the numbers in the `nums` array.\n\n**7. Return the result**\n - After completing both loops, return `dp[-1]`, which represents the total number of ways to make the target sum `target` using the numbers from the `nums` array.\n\nIn summary, this code uses dynamic programming to find the number of combinations that sum up to the target value using the given `nums` array. It builds up a DP array where each element represents the number of ways to reach a specific target value by considering all possible combinations of numbers from `nums`.\n\n# Complexity\nThis is based on Python Code. Other languages might be differnt.\n\n- Time complexity: O(TN)\nT is the target value and N is the length of the nums array. This is because we are iterating over all possible target values from 1 to T, and for each target value, we are iterating over all numbers in the nums array that are less than or equal to the current target value.\n\n- Space complexity: O(T)\nWe are creating a DP array of size T+1 to store the number of ways to make each target value. The rest of the variables used in the function are constant space, as they do not depend on the input size.\n\n\n```python []\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n dp = [0] * (target + 1)\n dp[0] = 1\n\n for i in range(1, target + 1):\n for n in nums:\n if n <= i:\n dp[i] += dp[i-n]\n \n return dp[-1]\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar combinationSum4 = function(nums, target) {\n const dp = new Array(target + 1).fill(0);\n dp[0] = 1;\n\n for (let i = 1; i <= target; i++) {\n for (const n of nums) {\n if (n <= i) {\n dp[i] += dp[i - n];\n }\n }\n }\n\n return dp[target]; \n};\n```\n```java []\nclass Solution {\n public int combinationSum4(int[] nums, int target) {\n int[] dp = new int[target + 1];\n dp[0] = 1;\n\n for (int i = 1; i <= target; i++) {\n for (int n : nums) {\n if (n <= i) {\n dp[i] += dp[i - n];\n }\n }\n }\n\n return dp[target]; \n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int combinationSum4(vector<int>& nums, int target) {\n vector<long long int>dp(target + 1, 0);\n dp[0] = 1;\n\n for(int i = 1; i <= target; i++){\n for(auto value : nums){\n if(i - value >= 0 && dp[i] <= INT_MAX)\n dp[i] += (long long int)dp[i - value]; \n }\n }\n \n return dp[target]; \n }\n};\n```\n\n\n---\n\n\nI started creating basic programming course with Python. This is the first video I created yesterday. Please check if you like.\n\nhttps://youtu.be/yb3_1LV5A0U\n\n## Thank you for reading the article! Have a nice day! | 29 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python 3 || 7 lines, recursion || T/S: 97% / 100% | combination-sum-iv | 0 | 1 | ```\nclass Solution:\n def combinationSum4(self, nums: list[int], target: int) -> int:\n \n @lru_cache(None)\n def dp(target: int, res = 0)->int:\n \n for n in nums:\n \n if n == target: res+= 1\n if n < target: res+= dp(target-n)\n\n return res \n\n return dp(target)\n```\n[https://leetcode.com/problems/combination-sum-iv/submissions/682887145/?envType=daily-question&envId=2023-09-09](http://)\n\nPython 3 || 5 lines, recursion || T/S: 97% / 100%\n\nI could be wrong, but I think that time complexity is *O*(*T*) and space complexity is *O*(*T*), in which *T* ~ `target`. (However, based on how the caching goes, both could be worst-case *O*(*NT*), in which *N* ~ `nums`.) | 3 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
✅ 98.22% Dynamic Programming & Recursion with Memoization | combination-sum-iv | 1 | 1 | # Comprehensive Guide to Solving "Combination Sum IV": Dynamic Programming and Memoization Approaches\n\n## Introduction & Problem Statement\n\nWelcome, fellow coders! Today, we\'ll dive deep into solving an intriguing combinatorial problem\u2014**Combination Sum IV**. This problem serves as a fantastic playground to explore some powerful algorithmic paradigms. Imagine you have an array of unique integers called `nums` and a `target` integer. Your mission, should you choose to accept it, is to find out how many distinct combinations of numbers from `nums` add up to `target`.\n\n## Key Concepts and Constraints\n\n### What Makes this Problem Unique?\n\n1. **Combination**: \n A combination here is a group of numbers taken from `nums` that, when summed up, equal `target`.\n\n2. **Order Matters**: \n Yes, you read that right! This isn\'t your typical combination problem where `[1, 2]` and `[2, 1]` would be considered the same. Here, the sequence matters, making each a distinct combination.\n\n3. **Constraints**: \n - The length of `nums` will be between 1 and 200.\n - Each integer in `nums` will be between 1 and 1000.\n - The `target` is also between 1 and 1000.\n\n---\n\n# Strategies to Tackle the Problem: A Two-Pronged Approach\n\n## Live Coding, Dynamic Programming & More\nhttps://youtu.be/BP09eTYEb64?si=NCbe-s7hT4Mha9Tj\n\n## Method 1: Dynamic Programming\n\n### The Ingenuity of Dynamic Programming\n\nDynamic Programming (DP) is a magical methodology that builds solutions from the ground up, much like constructing a pyramid. In this scenario, think of the `target` as the peak of your pyramid. You start with the foundational layer, which is your base case, and then build upon it, layer by layer, until you reach the apex. Each layer or block symbolizes a sub-problem that contributes to the solution of the overarching problem.\n\n### An In-Depth, Step-by-Step Guide\n\n1. **Initialization and Base Case**: \n - Create an array `dp` with `target + 1` slots, each initialized to zero. \n - This array will serve as our memory storage where `dp[i]` represents the number of combinations that can sum up to `i`.\n - Now, set `dp[0]` to 1. This serves as the base case, representing that there is one way to reach the target sum of zero: by using zero itself.\n\n2. **Filling up the DP Array (Iterative Computation)**: \n - Start iterating from 1 up to `target`. For each `i`, the aim is to fill `dp[i]` with the number of combinations that can make up that sum.\n - To find `dp[i]`, you need to look at the previously calculated `dp` values. How? For every number `num` in `nums`, you add `dp[i - num]` to `dp[i]` (given that `i - num >= 0`).\n - In simpler terms, for each `i`, you\'re summing up the number of ways to form `i` by looking at how you could have arrived at that sum using smaller numbers. \n\n3. **Reaching the Summit (Return the Result)**: \n - After the loop concludes, you\'ve successfully built your pyramid. At its peak, `dp[target]` will hold the total number of combinations that make up the target sum.\n\n### Nuances of Time and Space Complexity\n\n- **Time Complexity**: `O(N * target)`. The outer loop runs `target` times, and for each iteration, we potentially check all `N` numbers in `nums`.\n- **Space Complexity**: `O(target)`. The array `dp` will have `target + 1` elements, each requiring constant space. So the overall space complexity is linear in terms of the target value.\n\n## Code Dynamic Programming\n``` Python []\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n dp = [0] * (target + 1)\n dp[0] = 1\n \n for i in range(1, target + 1):\n for num in nums:\n if i - num >= 0:\n dp[i] += dp[i - num]\n \n return dp[target]\n```\n``` Go []\nfunc combinationSum4(nums []int, target int) int {\n dp := make([]int, target+1)\n dp[0] = 1\n \n for i := 1; i <= target; i++ {\n for _, num := range nums {\n if i - num >= 0 {\n dp[i] += dp[i - num]\n }\n }\n }\n \n return dp[target]\n}\n```\n``` Rust []\nimpl Solution {\n pub fn combination_sum4(nums: Vec<i32>, target: i32) -> i32 {\n let mut dp = vec![0; (target + 1) as usize];\n dp[0] = 1;\n \n for i in 1..=target as usize {\n for &num in &nums {\n if i as i32 - num >= 0 {\n dp[i] += dp[(i as i32 - num) as usize];\n }\n }\n }\n \n dp[target as usize]\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int combinationSum4(std::vector<int>& nums, int target) {\n std::vector<unsigned int> dp(target + 1, 0);\n dp[0] = 1;\n \n for (int i = 1; i <= target; ++i) {\n for (int num : nums) {\n if (i - num >= 0) {\n dp[i] += dp[i - num];\n }\n }\n }\n \n return dp[target];\n }\n};\n```\n``` Java []\npublic class Solution {\n public int combinationSum4(int[] nums, int target) {\n int[] dp = new int[target + 1];\n dp[0] = 1;\n \n for (int i = 1; i <= target; i++) {\n for (int num : nums) {\n if (i - num >= 0) {\n dp[i] += dp[i - num];\n }\n }\n }\n \n return dp[target];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar combinationSum4 = function(nums, target) {\n const dp = Array(target + 1).fill(0);\n dp[0] = 1;\n \n for (let i = 1; i <= target; i++) {\n for (const num of nums) {\n if (i - num >= 0) {\n dp[i] += dp[i - num];\n }\n }\n }\n \n return dp[target];\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @param Integer $target\n * @return Integer\n */\n function combinationSum4($nums, $target) {\n $dp = array_fill(0, $target + 1, 0);\n $dp[0] = 1;\n \n for ($i = 1; $i <= $target; $i++) {\n foreach ($nums as $num) {\n if ($i - $num >= 0) {\n $dp[$i] += $dp[$i - $num];\n }\n }\n }\n \n return $dp[$target];\n }\n}\n```\n``` C# []\npublic class Solution {\n public int CombinationSum4(int[] nums, int target) {\n int[] dp = new int[target + 1];\n dp[0] = 1;\n \n for (int i = 1; i <= target; i++) {\n foreach (int num in nums) {\n if (i - num >= 0) {\n dp[i] += dp[i - num];\n }\n }\n }\n \n return dp[target];\n }\n}\n```\n## Method 2: Memoization with Recursion\n\n### The Art of Memoization\n\nMemoization is an optimization technique that stores the results of expensive function calls and returns the cached result when the same inputs occur again. Think of it as a wise elder who recalls past tales to shed light on current challenges. In this context, we utilize memoization to remember the number of combinations for smaller targets, preventing the need for redundant, time-consuming recalculations.\n\n### A Detailed Walkthrough\n\n1. **Preprocessing**: \n - First and foremost, we sort the `nums` array. Why do we do this? Sorting allows us to iterate over the numbers in an ascending order. This order plays a crucial role in our early exit strategy during the recursive calls, ensuring we don\'t waste time on numbers that won\'t contribute to our solution.\n\n2. **Base Case and Early Exit**: \n - If `n = 0`, this means we\'ve successfully found a combination that sums up to the target. Hence, we return 1.\n - If `n < nums[0]`, given that `nums` is sorted, this means no combination can be formed to achieve the current `n`. So, we immediately return 0, optimizing our recursion.\n\n3. **The Recursive Magic**: \n - For each value of `n`, we delve into its past (i.e., make recursive calls) to uncover the pathways that led to `n`.\n - As we iterate over the sorted `nums`, if `n - num < 0`, we hit a break. This is because, with a sorted array, if the current number causes the difference to be negative, all subsequent numbers will do the same, making them irrelevant for the current `n`. Thus, we break out early, optimizing our process.\n\n4. **Memoization in Action**: \n - After calculating the number of combinations for a particular `n`, we store this value in a dictionary. This ensures that if we encounter the same `n` again, we can instantly retrieve its result rather than recalculating, saving precious time.\n\n5. **Returning the Final Verdict**: \n - Once all recursive calls are settled, the answer for our primary `target` will be waiting in our memoization dictionary, ready to be unveiled.\n\n### Delving into the Time and Space\n\n- **Time Complexity**: `O(N * target)`. Each unique `target` value is calculated once. For each calculation, we might iterate over all `N` numbers in `nums`.\n- **Space Complexity**: `O(target)`. This space is primarily used for our memoization dictionary, which can store up to `target` unique values.\n\n## Code Memoization with Recursion\n``` Python []\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n nums.sort() \n memo = {}\n \n def helper(n):\n if n in memo:\n return memo[n]\n if n == 0:\n return 1\n if n < nums[0]:\n return 0\n \n count = 0\n for num in nums:\n if n - num < 0:\n break \n count += helper(n - num)\n \n memo[n] = count\n return count\n \n return helper(target)\n```\n``` Go []\nimport "sort"\n\nfunc helper(nums []int, n int, memo map[int]int) int {\n if val, found := memo[n]; found {\n return val\n }\n if n == 0 {\n return 1\n }\n if n < nums[0] {\n return 0\n }\n \n count := 0\n for _, num := range nums {\n if n - num < 0 {\n break\n }\n count += helper(nums, n - num, memo)\n }\n \n memo[n] = count\n return count\n}\n\nfunc combinationSum4(nums []int, target int) int {\n sort.Ints(nums)\n memo := make(map[int]int)\n return helper(nums, target, memo)\n}\n```\n``` Rust []\nuse std::collections::HashMap;\n\nimpl Solution {\n pub fn combination_sum4(nums: Vec<i32>, target: i32) -> i32 {\n let mut nums = nums;\n nums.sort();\n let mut memo = HashMap::new();\n \n Self::helper(&nums, target, &mut memo)\n }\n \n fn helper(nums: &Vec<i32>, n: i32, memo: &mut HashMap<i32, i32>) -> i32 {\n if let Some(&count) = memo.get(&n) {\n return count;\n }\n if n == 0 {\n return 1;\n }\n if n < nums[0] {\n return 0;\n }\n \n let mut count = 0;\n for &num in nums {\n if n - num < 0 {\n break;\n }\n count += Self::helper(nums, n - num, memo);\n }\n \n memo.insert(n, count);\n count\n }\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) | Solution Type |\n|------------|-----------|-------------|---------------|\n| Rust | 0 ms | 2 MB | DP |\n| C++ | 0 ms | 6.6 MB | DP |\n| Go | 1 ms | 2 MB | DP |\n| Java | 1 ms | 39.6 MB | DP |\n| PHP | 6 ms | 19.2 MB | DP |\n| Python3 | 34 ms | 16.7 MB | Recursion |\n| Python3 | 36 ms | 16.2 MB | DP |\n| JavaScript | 56 ms | 44 MB | DP |\n| C# | 78 ms | 38.2 MB | DP |\n\n\n\n## Live Coding Memoization\nhttps://youtu.be/oHhmd5-IoM8?si=0yjXY02re64FJLaG\n\n## Code Highlights and Best Practices\n\n- Both Dynamic Programming and Memoization approaches build upon previous solutions, making them intuitive and efficient.\n- Dynamic Programming is more straightforward but iterates through the entire `nums` array for each `target`, making it slightly slower in practice.\n- Memoization with Recursion avoids redundant work, making it more efficient in practice.\n\nBy mastering these two approaches, you will be well-prepared to tackle similar combinatorial problems that involve finding the number of ways to reach a target sum. | 119 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python | Easy solution with Explanation | combination-sum-iv | 0 | 1 | # Intuition\nYou can solve this problem using dynamic programming. You\'ll create a table to keep track of the number of combinations for each possible target sum.\n\n# Approach\nIn this code, `dp[i]` represents the number of combinations to reach the target sum `i`. We initialize `dp[0]` to 1 because there is one way to make a sum of 0, which is by not selecting any element from `nums`.\n\nWe then iterate through all possible target sums from 1 to `target` and for each target sum, iterate through the elements in `nums`. If the current element is less than or equal to the current target sum, we add `dp[i - num]` to `dp[i]`, where `num` is the current element from `nums`. This step accumulates the number of combinations to reach the current target sum.\n\nFinally, `dp[target]` will contain the number of combinations to reach the target sum, which is returned as the result.\n\n# Complexity\n- Time complexity:\nO(target * len(nums))\n\n- Space complexity:\n O(target)\n\n# Code\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n\n dp=[0] * (target+1)\n dp[0]=1\n\n for i in range(target+1):\n for num in nums:\n if i >=num:\n dp[i]+=dp[i-num]\n return dp[target]\n\n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
[beast 99%] with BST + DP | Python | combination-sum-iv | 0 | 1 | I have used Binary search Tree to remove elements from nums greater than target which might make program faster at cost of `nums.sort()`\nwhich might slow the program lil bit.\n\n\n\nAlthough I didn\'t got this good score on first try, previous couple of try were >80%\n\nI won\u2019t be delving into the details of the dynamic programming portion of the code, as it has already been thoroughly explained by others in their solutions.\n\n# Code\n```python []\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n nums.sort()\n def BST_remove_ele_greater_target():\n """Removes numbers greater than target using Binary search approach"""\n lo, hi = 0, len(nums) \n while lo <= hi:\n mid = (lo + hi) // 2\n mid_num = nums[mid]\n if mid_num == target : return nums[:mid+1]\n elif mid_num > target: hi = mid - 1\n else : lo = mid + 1\n return nums[:mid+1]\n\n if nums[-1]>target: nums = BS_remove_ele_greater_target()\n\n dp = [1] + [0] * (target)\n\n for t in range(1, target + 1):\n for num in nums:\n if num <= t: dp[t] += dp[t - num]\n return dp[-1]\n\n``` | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python 1-liner. Recursion. Functional programming. | combination-sum-iv | 0 | 1 | # Approach\nThe number of `ways` to form target `k` is sum of `ways` of forming `k - x` after selecting a number `x` from `nums`. i.e,\n\n$$\nways(k) =\n\\begin{cases}\n 0 & \\text{if } k < 0 \\\\\n 1 & \\text{if } k = 0 \\\\\n \\sum_{x \\in nums} ways(k - x) & \\text{if } k > 0 \\\\\n\\end{cases}\n$$\n\n# Complexity\n- Time complexity: $$O(k \\cdot n)$$\n\n- Space complexity: $$O(k)$$\n\nwhere,\n`k = target`,\n`n = length of nums`.\n\n# Code\nFew-liner:\n```python\nclass Solution:\n def combinationSum4(self, nums: list[int], target: int) -> int:\n @cache\n def ways(k: int) -> int:\n return sum(ways(k - x) for x in nums) if k > 0 else k == 0\n \n return ways(target)\n\n\n```\n\n1-liner:\n```python\nclass Solution:\n def combinationSum4(self, nums: list[int], target: int) -> int:\n return (ways := cache(lambda k: sum(ways(k - x) for x in nums) if k > 0 else k == 0))(target)\n\n\n``` | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
99.10% Best Solution || DP | combination-sum-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n## Plss Up Vote for me\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n # first we define our cache memory to store every number of combination\n dp = { 0 : 1 }\n\n # Now let iterate 1 to target\n for total in range(1, target+1):\n # first initialise the dp[total] = 0\n dp[total] = 0\n\n # Now iterate in nums\n for num in nums:\n # Now getting the all combination and if combination in negative the assign 0\n dp[total] += dp.get(total - num, 0)\n \n # Now our work is complte so just return dp[target]\n return dp[target]\n``` | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
🚀100% || C++ || Java || Python || DP Recursive & Iterative || Commented Code🚀 | combination-sum-iv | 1 | 1 | # Problem Description\n- You are given an array of **distinct integers**, nums, and an integer **target**. \n- The **objective** is to determine the number of **possible combinations** that can be formed using elements from nums such that they add up to the given target. \n- Each element in nums can be **used multiple times in a combination**.\n- **Note** that [1,3] is a **different** solution than [3,1].\n\n- **Constraints:**\n - 1 <= nums.length <= 200\n - 1 <= nums[i] <= 1000\n - 1 <= target <= 1000\n - All the elements of nums are unique.\n\n\n---\n\n\n# Proposed Solutions\n## 1. Recursive Approach (Top-Down)\n### Intuation\nWe can think of Recursive Approach as **breaking** hard bricks into **small** rocks. but, how this apply to our problem ?\nWe can **break** our **complex problem** into **easier** ones and instead of finding the number of combinations for out **large target** we can find the solution for **(target - num)**, since we only need to add num to this smaller number then a **part** of our solution for target number is the solution for **(target - num)**.\n\n**As an example**, if we have target = 3 and nums = [1, 2]\nan obvious solution is equal to 3\n(1, 1, 1) , (1, 2) , (2, 1)\nlet\'s start breaking, we can think of 3 as sum of:\n- (3 - 2) -> 1 which has 1 solution.\n- (3 - 1) -> 2 which has 2 solutions.\n\nthen 3 has total of 3 solutions. \n\n### Approach\n1. Create an array **dp** to **cache** computed results for target values.\n\n2. Define a **recursive** function **countCombinations** that calculates combinations to reach a target sum:\n - **Base case**: If the target is 0, return 1.\n - **Base case**: If the target is negative, return 0.\n - **Check** if the result for the current remainingTarget is cached and **not equal to -1** ; if yes, return the cached result.\n - Initialize **currentCombinations** to 0.\n - **Iterate** through the numbers, recursively **calculate combinations** for the new target, and **add** them to currentCombinations.\n - **Cache** the result in the dp array for the current remainingTarget and **return currentCombinations**.\n\n3. In the **combinationSum4** function:\n - **Initialize** the dp array with **-1** for all possible target values.\n - Begin the combination count calculation by calling countCombinations with the given nums and target.\n\n### Complexity\n- **Time complexity:** $$O(N * T)$$\nSince, for each remaining number we have we try all the available numbers. so, time complexity is `O(N * T)` where `N` is `length` of nums and `T` is the value of `target`.\n\n- **Space complexity:** $$O(T)$$\nWe store only the `dp array` which has size of target then space complexity is `O(T)` where `T` is the value of `target`.\n\n\n## 2. Iterative Approach (Bottom-Up)\n### Intuation\nWe can think of Iterative Approach as **building** high building from small bricks. but, how this also apply to our problem ?\nWe can **solve** our **complex problem** by solving **easier** ones first and buil until we reach our complex problem and instead of finding the number of combinations for out **large target** we can **start** from 0 then 1 then 2 3 4 .... until we reach our large number.\n\n**As an example**, if we have target = 3 and nums = [1, 2]\nthe solution is equal to 3\n(1, 1, 1) , (1, 2) , (2, 1)\nlet\'s start building:\n- 0 -> **one** solution (empty)\n- 1 -> **one** solution (by adding num=1 to 0) => (solution of 0)\n- 2 -> **two** solutions (by adding num=1 to 1 / adding num=2 to 0) => (solution of 1 + solution of 0)\n- 3 -> **three** solutions (by adding num=1 to 2 / adding num=2 to 1) => (solution of 2 + solution of 1)\n\nthen 3 has total of 3 solutions. \n\n### Approach\n1. **Initialize** a **vector dp** where dp[i] represents the number of combinations to make the sum \'i\'. **Set all values to 0 initially**.\n\n2. Set **dp[0] to 1** because there is **one way to make a sum of 0**, which is by not selecting any number.\n \n3. **Iterate** through the possible target sums from 1 to target:\n - For **each target** sum currentSum, iterate through the given numbers in nums.\n - **Calculate currentNum** as the current number being considered from nums.\n - **Check if subtracting currentNum** from currentSum results in a non-negative value.\n - If yes, add the combination count at dp[currentSum - currentNum] to dp[currentSum]. This represents the number of combinations for the current sum using the current number.\n \n4. The final result, which represents the number of combinations to make the target sum, is stored in **dp[target]**.\n\n\n### Complexity\n- **Time complexity:** $$O(N * T)$$\nSince, for each number we reached have we try all the available numbers. so, time complexity is `O(N * T)` where `N` is `length` of nums and `T` is the value of `target`.\n\n- **Space complexity:** $$O(T)$$\nWe store only the `dp array` which has size of target then space complexity is `O(T)` where `T` is the value of `target`.\n\n---\n\n\n# Code\n## 1. Recursive Approach (Top-Down)\n```C++ []\nclass Solution {\npublic:\n static const int MAX_TARGET = 1010; // Maximum possible target value\n int dp[MAX_TARGET]; // Array to store computed results\n\n int countCombinations(vector<int> nums, int remainingTarget) {\n // If the remaining target is 0, there\'s one valid combination.\n if (remainingTarget == 0)\n return 1;\n \n // If the remaining target becomes negative, it\'s not possible to reach it.\n if (remainingTarget < 0)\n return 0;\n \n // If the result for \'remainingTarget\' is already computed, return it.\n if (~dp[remainingTarget])\n return dp[remainingTarget];\n \n int currentCombinations = 0;\n \n // Iterate through the numbers in \'nums\'.\n for (int i = 0; i < nums.size(); i++) {\n int currentNum = nums[i];\n // recursively calculate combinations for the new target.\n currentCombinations += countCombinations(nums, remainingTarget - currentNum);\n }\n \n // Store and return the computed result.\n return dp[remainingTarget] = currentCombinations;\n }\n\n int combinationSum4(vector<int>& nums, int target) {\n // Initialize the \'dp\' array with -1 to indicate uncomputed results.\n for (int i = 0; i < MAX_TARGET; i++) {\n dp[i] = -1;\n }\n \n // Start the combination count calculation.\n return countCombinations(nums, target);\n }\n};\n```\n```Java []\npublic class Solution {\n private static final int MAX_TARGET = 1010; // Maximum possible target value\n private int[] dp = new int[MAX_TARGET]; // Array to store computed results\n\n private int countCombinations(int[] nums, int remainingTarget) {\n // If the remaining target is 0, there\'s one valid combination.\n if (remainingTarget == 0)\n return 1;\n \n // If the remaining target becomes negative, it\'s not possible to reach it.\n if (remainingTarget < 0)\n return 0;\n \n // If the result for \'remainingTarget\' is already computed, return it.\n if (dp[remainingTarget] != -1)\n return dp[remainingTarget];\n \n int currentCombinations = 0;\n \n // Iterate through the numbers in \'nums\'.\n for (int i = 0; i < nums.length; i++) {\n int currentNum = nums[i];\n // Recursively calculate combinations for the new target.\n currentCombinations += countCombinations(nums, remainingTarget - currentNum);\n }\n \n // Store and return the computed result.\n return dp[remainingTarget] = currentCombinations;\n }\n\n public int combinationSum4(int[] nums, int target) {\n // Initialize the \'dp\' array with -1 to indicate uncomputed results.\n for (int i = 0; i < MAX_TARGET; i++) {\n dp[i] = -1;\n }\n \n // Start the combination count calculation.\n return countCombinations(nums, target);\n }\n}\n```\n```Python []\nclass Solution:\n MAX_TARGET = 1010 # Maximum possible target value\n\n def __init__(self):\n self.dp = [-1] * Solution.MAX_TARGET # Array to store computed results\n\n def countCombinations(self, nums, remainingTarget):\n # If the remaining target is 0, there\'s one valid combination.\n if remainingTarget == 0:\n return 1\n \n # If the remaining target becomes negative, it\'s not possible to reach it.\n if remainingTarget < 0:\n return 0\n \n # If the result for \'remainingTarget\' is already computed, return it.\n if self.dp[remainingTarget] != -1:\n return self.dp[remainingTarget]\n \n currentCombinations = 0\n \n # Iterate through the numbers in \'nums\'.\n for currentNum in nums:\n # Recursively calculate combinations for the new target.\n currentCombinations += self.countCombinations(nums, remainingTarget - currentNum)\n \n # Store and return the computed result.\n self.dp[remainingTarget] = currentCombinations\n return currentCombinations\n\n def combinationSum4(self, nums, target):\n # Start the combination count calculation.\n return self.countCombinations(nums, target)\n```\n\n## 2. Iterative Approach (Bottom-Up) \n```C++ []\nclass Solution {\npublic:\n int combinationSum4(vector<int>& nums, int target) {\n // dp[i] represents the number of combinations to make sum \'i\'\n vector<unsigned long long> dp(target + 1, 0);\n \n // There is one way to make sum 0, which is by not selecting any number.\n dp[0] = 1;\n \n for(int currentSum = 1; currentSum <= target; currentSum++) {\n for(int numIndex = 0; numIndex < nums.size(); numIndex++) {\n int currentNum = nums[numIndex];\n if(currentSum - currentNum >= 0) {\n // dp[i] can be achieved by adding the combination count at dp[i - currentNum]\n dp[currentSum] += dp[currentSum - currentNum];\n }\n }\n }\n \n // The final result is stored in dp[target]\n return dp[target];\n }\n};\n```\n```Java []\npublic class Solution {\n public int combinationSum4(int[] nums, int target) {\n // dp[i] represents the number of combinations to make sum \'i\'\n long[] dp = new long[target + 1];\n \n // There is one way to make sum 0, which is by not selecting any number.\n dp[0] = 1;\n \n for (int currentSum = 1; currentSum <= target; currentSum++) {\n for (int numIndex = 0; numIndex < nums.length; numIndex++) {\n int currentNum = nums[numIndex];\n if (currentSum - currentNum >= 0) {\n // dp[i] can be achieved by adding the combination count at dp[i - currentNum]\n dp[currentSum] += dp[currentSum - currentNum];\n }\n }\n }\n \n // The final result is stored in dp[target]\n return (int)dp[target];\n }\n}\n```\n```Python []\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n # Initialize an array dp where dp[i] represents the number of combinations to make sum \'i\'.\n dp = [0] * (target + 1)\n \n # There is one way to make sum 0, which is by not selecting any number.\n dp[0] = 1\n \n # Iterate through the possible target sums from 1 to target.\n for currentSum in range(1, target + 1):\n # Iterate through the given numbers in nums.\n for numIndex in range(0, len(nums)):\n currentNum = nums[numIndex]\n # Check if subtracting currentNum from currentSum results in a non-negative value.\n if currentSum - currentNum >= 0:\n # dp[i] can be achieved by adding the combination count at dp[i - currentNum].\n dp[currentSum] += dp[currentSum - currentNum]\n \n # The final result is stored in dp[target].\n return dp[target]\n```\n\n\n\n\n\n | 55 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
✔90.00% Beats C++✨ || DP || Memoization || Easy to Understand📈😇 || #Beginner😉😎 | combination-sum-iv | 1 | 1 | # Problem Understanding:\n- The code aims to solve the "Combination Sum IV" problem using dynamic programming. The problem statement can be summarized as follows:\n\n**Given:**\n\n- An array `nums` containing distinct positive integers.\n- A target integer `target`.\n\n**Task:**\nFind and return the number of possible combinations of numbers from the `nums` array that sum up to the given `target`. Each number from the `nums` array can be used an unlimited number of times.\n\n\n# Intuition\n- The code aims to solve the "Combination Sum IV" problem** using a recursive ****approach with memoization (dynamic programming). **\n- The problem is about finding the number of combinations that sum up to a given `target` using elements from the `nums` array, where elements from `nums` can be used an unlimited number of times.\n\n# Approach\n**1. Recursive Function (f):**\n- The recursive function `f` is designed to find the number of combinations to reach a specific `target` using elements from the `nums` array.\n- If the `target` becomes 0, it means we\'ve found a valid combination. In this case, the function returns 1.\n- If the `target` becomes negative, it means the current combination is not valid, so the function returns 0.\n- Memoization is used to store and reuse previously calculated results. If `dp[target]` is not equal to -1 (indicating it has already been computed), the function returns the cached `result`.\n- The `take` variable is used to accumulate the number of valid combinations for the current `target` value by considering all possible choices from the `nums` array.\n- The function recursively calls itself for each element in `nums`, subtracting the current element from the `target` and adding the result to `take`.\n\n1. **combinationSum4 Function:**\n\n- **This function serve**s as the entry point to the solution.\n- It initializes a vector `dp` of size `target+1` with all elements set to -1. This `dp` vector will be used for memoization to avoid redundant calculations.\n- It then calls the `f` function with the following arguments:\n - **`n:`** The size of the `nums` array (`nums.size()`).\n - **`nums:`** The array of positive integers.\n - **`target:`** The target value.\n - **`dp:`** The memoization vector.\n- Finally, it returns the result obtained from the `f` function, which represents the total number of combinations to reach the `target` using elements from the `nums` array.\n\n**In summary, this code solves the problem by recursively exploring** all possible combinations using elements from the `nums` array and memoizing the results to avoid redundant calculations. The final result is the number of valid combinations that sum up to the given `target`.\n\n\n\n\n\n\n\n# Complexity\n- Time complexity:\n **O(n^target)**\n\n- Space complexity:\n **O(target)**.\n\n# PLEASE UPVOTE\u2763\uD83D\uDE0D\n\n# Code\n```\nclass Solution {\npublic:\n // Recursive function to count combinations\n int f(int n, vector<int>& nums, int target, vector<int>& dp) {\n\n // If the target is reached, return 1 (one valid combination found)\n if (target == 0) {\n return 1;\n }\n // If the target becomes negative, it\'s not a valid combination\n if (target < 0) {\n return 0;\n }\n // If the result for the current target is already calculated, return it\n if (dp[target] != -1) {\n return dp[target];\n }\n int take = 0;\n\n // Iterate through the numbers and try taking each one to reach the target\n for (int j = 0; j < n; ++j) {\n take += f(n, nums, target - nums[j], dp); // Recursively count combinations\n }\n\n // Store the result in the DP table and return it\n return dp[target] = take;\n }\n \n int combinationSum4(vector<int>& nums, int target) {\n \n vector<int>dp(target+1,-1);\n return f(nums.size(),nums,target,dp);\n \n \n }\n};\n```\n# JAVA\n```\nimport java.util.Arrays;\n\npublic class Solution {\n public int f(int n, int[] nums, int target, int[] dp) {\n if (target == 0) {\n return 1;\n }\n if (target < 0) {\n return 0;\n }\n\n if (dp[target] != -1) {\n return dp[target];\n }\n\n int take = 0;\n\n for (int j = 0; j < n; ++j) {\n take += f(n, nums, target - nums[j], dp);\n }\n\n return dp[target] = take;\n }\n\n public int combinationSum4(int[] nums, int target) {\n int[] dp = new int[target + 1];\n Arrays.fill(dp, -1);\n return f(nums.length, nums, target, dp);\n }\n\n public static void main(String[] args) {\n Solution solution = new Solution();\n int[] nums = {1, 2, 3};\n int target = 4;\n int result = solution.combinationSum4(nums, target);\n System.out.println("Number of combinations: " + result);\n }\n}\n\n```\n# PYTHON\n```\nclass Solution:\n def f(self, n, nums, target, dp):\n if target == 0:\n return 1\n if target < 0:\n return 0\n\n if dp[target] != -1:\n return dp[target]\n\n take = 0\n\n for j in range(n):\n take += self.f(n, nums, target - nums[j], dp)\n\n dp[target] = take\n return take\n\n def combinationSum4(self, nums, target):\n dp = [-1] * (target + 1)\n return self.f(len(nums), nums, target, dp)\n\n# Example usage:\nsolution = Solution()\nnums = [1, 2, 3]\ntarget = 4\nresult = solution.combinationSum4(nums, target)\nprint("Number of combinations:", result)\n\n```\n# JAVASCRIPT\n```\nclass Solution {\n f(n, nums, target, dp) {\n if (target === 0) {\n return 1;\n }\n if (target < 0) {\n return 0;\n }\n\n if (dp[target] !== -1) {\n return dp[target];\n }\n\n let take = 0;\n\n for (let j = 0; j < n; ++j) {\n take += this.f(n, nums, target - nums[j], dp);\n }\n\n dp[target] = take;\n return take;\n }\n\n combinationSum4(nums, target) {\n const dp = Array(target + 1).fill(-1);\n return this.f(nums.length, nums, target, dp);\n }\n}\n\n// Example usage:\nconst solution = new Solution();\nconst nums = [1, 2, 3];\nconst target = 4;\nconst result = solution.combinationSum4(nums, target);\nconsole.log("Number of combinations:", result);\n\n```\n# GO\n```\npackage main\n\nimport "fmt"\n\ntype Solution struct{}\n\nfunc (s Solution) f(n int, nums []int, target int, dp []int) int {\n\tif target == 0 {\n\t\treturn 1\n\t}\n\tif target < 0 {\n\t\treturn 0\n\t}\n\n\tif dp[target] != -1 {\n\t\treturn dp[target]\n\t}\n\n\ttake := 0\n\n\tfor j := 0; j < n; j++ {\n\t\ttake += s.f(n, nums, target-nums[j], dp)\n\t}\n\n\tdp[target] = take\n\treturn take\n}\n\nfunc (s Solution) combinationSum4(nums []int, target int) int {\n\tdp := make([]int, target+1)\n\tfor i := 0; i <= target; i++ {\n\t\tdp[i] = -1\n\t}\n\treturn s.f(len(nums), nums, target, dp)\n}\n\nfunc main() {\n\tsolution := Solution{}\n\tnums := []int{1, 2, 3}\n\ttarget := 4\n\tresult := solution.combinationSum4(nums, target)\n\tfmt.Println("Number of combinations:", result)\n}\n\n```\n# PLEASE UPVOTE\u2763\uD83D\uDE0D\n | 12 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Solution with Top-Down Dynamic Programming in Python3 | combination-sum-iv | 0 | 1 | # Intuition\nThe task description is the following:\n- there\'s a list of unique `nums` and an integer `target`\n- our goal is find **how many** combinations of `nums` **sum up** to `target`\n\n```\n# Example\nnums = [1, 2], target = 3\n\n# Here\'s the list of possible combinations\n# [1, 1, 1], [1, 2], [2, 1]\n# For each number in a particular combination we need to\n# check the possible sum as diff = (sum - target) == 0, to be sure\n# this combination is valid, else if the diff < 0, this combination\n# is invalid one, otherwise continue to iterate over all nums\n```\nOne of the solutions is to **backtrack** all of the possible combinations, but we don\'t need to store them, because we\'re interested in **total count**, but we\'ll focus at [Dynamic Programming](https://en.wikipedia.org/wiki/Dynamic_programming) to define all of these combinations.\n\n**PS: Top-Down and Bottom-Up approaches for most cases are interplacable.**\n\n# Approach\n1. define a `cached` function `dp` with num state\n2. there\'re 2 base cases\n- if `num == 0`, this means we\'ve founded the right combination and return `1`\n- if `num < 0`, this combination is invalid one, so return `0`\n3. continue to iterate over all nums, using the **list comprehension** via **extracting** `num-x` at each new step\n4. return the same list comprehension, but with starting point as `target-num`.\n\n# Complexity\n- Time complexity: **O(n*m)**, where `n` is amount of nums and `m` eqauls to `target` times \n\n- Space complexity: **O(m)**, to store `target` `m` times.\n# Code\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n @cache\n def dp(num):\n if num == 0:\n return 1\n if num < 0:\n return 0\n \n return sum([dp(num - x) for x in nums])\n\n return sum([dp(target - num) for num in nums])\n``` | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python | Dynamic Programming | 98.87% | combination-sum-iv | 0 | 1 | # Python | Dynamic Programming | 98.87%\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n dp = [0] * (target + 1)\n dp[0] = 1\n \n for i in range(1, target + 1):\n for num in nums:\n if i - num >= 0:\n dp[i] += dp[i - num]\n \n return dp[target]\n``` | 28 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Fastest and shortest Solution Python | combination-sum-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Fastest Solution Code\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n count=[0]*2001\n count[0]=1\n nums.sort()\n for i in range(target):\n for j in nums:\n count[i+j]+=count[i]\n if i+j>target:\n break\n return count[target]\n\n```\n# Shortest Solution Code\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n count=[0]*2001\n count[0]=1\n for i in range(target):\n for j in nums:\n count[i+j]+=count[i]\n return count[target]\n\n``` | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python: easy to understand, straightforward, recursive + memo | combination-sum-iv | 0 | 1 | # Code\n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n \n @cache\n def rec(A, t):\n if t == 0:\n return 1\n res = 0\n for x in A:\n if x <= t:\n res += rec(A, t-x)\n return res\n \n return rec(tuple(nums), target)\n\n``` | 1 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
C++/Python recursive & iterative DP||Beats 100%||why signed not long long | combination-sum-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse DP to solve the problem, both of recursive version & iterative version.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n"different sequences are counted as different combinations."\nIt \'s not combination problem, but a problem for permutations.\n\nAccording to the description for example 1, this problem is a problem for permutations with repetition. Each element in the array nums can be chosen many times as you wish.\n\nA real hint for C/C++ users, use unsigned! Even using long long it overflows, very strange! But try unsigned, it will be fine.\n\nThough LC says "The test cases are generated so that the answer can fit in a 32-bit integer." It has no guarantees for intermediate values.\n\nOne useful testcase\n```\n[10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,220,230,240,250,260,270,280,290,300,310,320,330,340,350,360,370,380,390,400,410,420,430,440,450,460,470,480,490,500,510,520,530,540,550,560,570,580,590,600,610,620,630,640,650,660,670,680,690,700,710,720,730,740,750,760,770,780,790,800,810,820,830,840,850,860,870,880,890,900,910,920,930,940,950,960,970,980,990,111]\n999\n```\nUse unsigned, print the dp state array:\n \n\n\nA negative value is shown, strange! it overflows. Some of the intermediate values after that could be wrong. Using unsigned long long solves this problem.\n\n\n# why signed not long long\nDifferent type has different behavior. Signed integer (int or long long) in GCC will break as an error when overflowing. But unsigned integers will do the arithmetic as an modular operation (mod 4294967296=2^32) when overflowing. Since LC says "The test cases are generated so that the answer can fit in a 32-bit integer." the final is correct whereas the intermediate values can be treated as the computed values modulo 4294967296=2^32!\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n\\times target)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(target)$$ & stack need for recursive version at most $$O(n)$$\n# Code \n```\nclass Solution {\npublic:\n int combinationSum4(vector<int>& nums, int target) {\n vector<unsigned> dp(target+1, UINT_MAX);\n\n function<unsigned(unsigned)> f=[&](unsigned i)->unsigned\n {\n if (i==0) return 1;//base case\n if (dp[i]!=UINT_MAX) return dp[i];//Computed before\n unsigned ans=0;\n //Everything can be chosen, for permutations with repetition\n for(int x: nums)\n if (i>=x)\n ans+=f(i-x);//Recursion\n return dp[i]=ans; //Copy to dp array & return ans\n\n };\n \n return f(target);\n }\n};\n```\n# Code for iterative version Runtime 0 ms Beats 100%\n```\nclass Solution {\npublic:\n int combinationSum4(vector<int>& nums, int target) {\n vector<unsigned> dp(target+1, 0);//Must be unsigned\n dp[0]=1;\n for(int i=1; i<=target; i++){\n for (int x: nums){\n if (i>=x)\n dp[i]+=dp[i-x];\n }\n }\n return dp[target];\n }\n};\n```\n# Python Code \n```\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n dp=[0]*(target+1)\n dp[0]=1\n for i in range(1, target+1):\n for x in nums:\n if i>=x:\n dp[i]+=dp[i-x]\n return dp[-1]\n``` | 7 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Rust 0ms/Python 50ms. Dynamic programming with explanation | combination-sum-iv | 0 | 1 | # Intuition\n\nLets assume that we know the answer for every value below $t$ and it is stored in some some array `dp`. So `dp[0]` is 1 as you can reach the value 0 only with empty set and `dp[x]` is how many possible combinations needed to sum up to `x`.\n\nNow the question is how to many times to reach the sum of `t`. Lets move over all the values in `nums` and lets assume that now we are looking at `v`. So if we use this value, can find `dp[t - v]` ways to sum values to `t`. Doing this for all the values in the `nums` we get our answer.\n\nWhich gives us an easy solution where we slowly build our array `dp` one step at a time and start from `dp[0] = 1`\n\n\n# Complexity\n\nLet the size fo the `target` is `t` and the number of elements in array nums below the target is `n`, then\n\n- Time complexity: $O(n \\cdot t)$\n- Space complexity: $O(t)$\n\n# Code\n```Rust []\nimpl Solution {\n pub fn combination_sum4(mut nums: Vec<i32>, target: i32) -> i32 {\n let mut dp = vec![0; target as usize + 1];\n dp[0] = 1;\n\n nums.sort_unstable();\n for i in 1 ..= target {\n for j in 0 .. nums.len() {\n let p = i - nums[j];\n if p < 0 {\n break;\n }\n dp[i as usize] += dp[p as usize];\n }\n }\n\n return dp[dp.len() - 1];\n }\n}\n```\n```python []\nclass Solution:\n def combinationSum4(self, nums: List[int], target: int) -> int:\n data = set(nums)\n arr = [1]\n for num in range(1, target + 1):\n curr = 0\n for v in range(num):\n if num - v in data:\n curr += arr[v]\n arr.append(curr)\n \n return arr[-1]\n```\n | 2 | Given an array of **distinct** integers `nums` and a target integer `target`, return _the number of possible combinations that add up to_ `target`.
The test cases are generated so that the answer can fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\], target = 4
**Output:** 7
**Explanation:**
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
**Example 2:**
**Input:** nums = \[9\], target = 3
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 1000`
* All the elements of `nums` are **unique**.
* `1 <= target <= 1000`
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? | null |
Python solution beating 99.7% memory. Heapify the whole matrix inplace | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can use heap to find smallest element inside single row (`matrix[i]`) with $$O(1)$$ memory. Can we use the same approach for row?\n\n# Approach\n1. heapify each row in the matrix `heapq.heapify(matrix[i])`\n2. heapify columns so `matrix[0][0]` is always the smallest element in the whole matrix (`heapq.heapify(matrix)`)\n\n`While K:`\n1. Get `matrix[0][0]`\n2. `heappop` for `matrix[0]` to maintain heap properties of `matrix[0]`\n2. restore heap properties of `matrix`:\n 1. If `matrix[0]` is empty list \u2013 remove it from the "big" heap.\n 2. If `matrix[0]` is not empty \u2013 restore heap properties of "big" heap (`matrix`)\n4. decrement `K`\n\n\n\n# Complexity\n- Time complexity: $$N + Klog(N)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n # heapify everything\n for i in range(len(matrix)):\n heapq.heapify(matrix[i])\n\n heapq.heapify(matrix)\n\n while k > 0:\n res = matrix[0][0]\n heapq.heappop(matrix[0])\n\n if not len(matrix[0]):\n heapq.heappop(matrix)\n \n if len(matrix):\n # restore heap properties.\n # heappop() + heappush() is O(logN + logN)\n # not using heapq.heapify() because it is O(N)\n head = matrix[0]\n heapq.heappop(matrix)\n heapq.heappush(matrix, head)\n\n k -= 1\n\n return res\n``` | 1 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
Superb Solution in Python3 | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | \n\n# Solution in Python3\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n list1 = []\n for i in range(len(matrix)):\n for j in range(len(matrix)):\n list1.append(matrix[i][j])\n list1.sort()\n return list1[k-1]\n``` | 1 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
✅Python 85% Easy/Beginner Friendly [No BST/No Algo]✅ | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | # Intuition\n1) Basic Idea: The goal here is to combine all the sub-lists in the 2D array, and then find the k\'th smallest number as fast as possible. So, let\'s do that!\n\n# Approach\n1) Loop through the matrix and add each value into a new list\n2) Sort the list\n3) Return the [k-1] index of that list (Because indexes start at 0)\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n seen = [] \n for row in matrix:\n for value in row:\n seen.append(value)\n seen = sorted(seen)\n return seen[k-1]\n``` | 0 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
Python ✅✅✅|| Faster than 97.16% || Memory Beats 82.82% | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n flattened = []\n for row in matrix:\n for n in row:\n flattened.append(n)\n flattened.sort()\n return flattened[k-1]\n```\n\n\n\n\n | 1 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
kth Smallest Element in a sorted matrix | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nimport numpy as np\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n mat=np.array(matrix).flatten()\n mat.sort()\n return mat[k-1]\n``` | 1 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
378: Solution with step by step explanation | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo find the kth smallest element in a sorted matrix, we can use the binary search algorithm. First, we set the range of the search to be between the smallest element in the matrix and the largest element in the matrix. Then, we find the mid-point of the range and count the number of elements in the matrix that are less than or equal to the mid-point. If the count is less than k, then we know that the kth smallest element must be in the upper half of the range, so we update the range to be between the mid-point + 1 and the largest element in the matrix. If the count is greater than or equal to k, then we know that the kth smallest element must be in the lower half of the range, so we update the range to be between the smallest element in the matrix and the mid-point.\n\nWe repeat this process until we have narrowed down the range to a single element, which must be the kth smallest element.\n\n# Complexity\n- Time complexity:\n89.29%\n\n- Space complexity:\n71.50%\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n n = len(matrix)\n # Set the range of the search to be between the smallest element\n # and the largest element in the matrix\n left, right = matrix[0][0], matrix[n-1][n-1]\n \n # Binary search for the kth smallest element\n while left < right:\n mid = (left + right) // 2\n count = 0\n j = n - 1\n # Count the number of elements in the matrix that are less than or equal to mid\n for i in range(n):\n while j >= 0 and matrix[i][j] > mid:\n j -= 1\n count += j + 1\n # Update the range of the search\n if count < k:\n left = mid + 1\n else:\n right = mid\n \n return left\n\n``` | 14 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
faster than 98.81% using python3(5 lines) | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | ```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n temp_arr=[]\n for i in matrix:\n temp_arr.extend(i)\n temp_arr.sort()\n return temp_arr[k-1]\n``` | 3 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
Python Easy To Understand Solution || Beats 80.82% in Memory | kth-smallest-element-in-a-sorted-matrix | 0 | 1 | ```\nfrom itertools import chain\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int:\n flatten_list = list(chain.from_iterable(matrix))\n flatten_list.sort()\n return flatten_list[k-1]\n```\n**.\n.\n.\n<<< Please Up-Vote if find this useful >>>** | 2 | Given an `n x n` `matrix` where each of the rows and columns is sorted in ascending order, return _the_ `kth` _smallest element in the matrix_.
Note that it is the `kth` smallest element **in the sorted order**, not the `kth` **distinct** element.
You must find a solution with a memory complexity better than `O(n2)`.
**Example 1:**
**Input:** matrix = \[\[1,5,9\],\[10,11,13\],\[12,13,15\]\], k = 8
**Output:** 13
**Explanation:** The elements in the matrix are \[1,5,9,10,11,12,13,**13**,15\], and the 8th smallest number is 13
**Example 2:**
**Input:** matrix = \[\[-5\]\], k = 1
**Output:** -5
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 300`
* `-109 <= matrix[i][j] <= 109`
* All the rows and columns of `matrix` are **guaranteed** to be sorted in **non-decreasing order**.
* `1 <= k <= n2`
**Follow up:**
* Could you solve the problem with a constant memory (i.e., `O(1)` memory complexity)?
* Could you solve the problem in `O(n)` time complexity? The solution may be too advanced for an interview but you may find reading [this paper](http://www.cse.yorku.ca/~andy/pubs/X+Y.pdf) fun. | null |
Python | Super Efficient | Detailed Explanation | insert-delete-getrandom-o1 | 0 | 1 | In python, creating a simple api for a set() would be a perfect solution if not for the third operation, getRandom(). We know that we can retrieve an item from a set, and not know what that item will be, but that would not be actually random. (This is due to the way python implements sets. In python3, when using integers, elements are popped from the set in the order they appear in the underlying \nhashtable. Hence, not actually random.)\n\nA set is implemented essentially the same as a dict in python, so the time complexity of add / delete is on average O(1). When it comes to the random function, however, we run into the problem of needing to convert the data into a python list in order to return a random element. That conversion will add a significant overhead to getRandom, thus slowing the whole thing down.\n\nInstead of having to do that type conversion (set to list) we can take an approach that involves maintaining both a list and a dictionary side by side. That might look something like:\n\n```\ndata_map == {4: 0, 6: 1, 2: 2, 5: 3}\ndata == [4, 6, 2, 5]\n```\n\nNotice that the key in the `data_map` is the element in the list, and the value in the `data_map` is the index the element is at in the list. \n\nLet\'s look at the implementation:\n\n```python\nclass RandomizedSet:\n\n def __init__(self):\n self.data_map = {} # dictionary, aka map, aka hashtable, aka hashmap\n self.data = [] # list aka array\n\n def insert(self, val: int) -> bool:\n\n # the problem indicates we need to return False if the item \n # is already in the RandomizedSet---checking if it\'s in the\n # dictionary is on average O(1) where as\n # checking the array is on average O(n)\n if val in self.data_map:\n return False\n\n # add the element to the dictionary. Setting the value as the \n # length of the list will accurately point to the index of the \n # new element. (len(some_list) is equal to the index of the last item +1)\n self.data_map[val] = len(self.data)\n\n # add to the list\n self.data.append(val)\n \n return True\n\n def remove(self, val: int) -> bool:\n\n # again, if the item is not in the data_map, return False. \n # we check the dictionary instead of the list due to lookup complexity\n if not val in self.data_map:\n return False\n\n # essentially, we\'re going to move the last element in the list \n # into the location of the element we want to remove. \n # this is a significantly more efficient operation than the obvious \n # solution of removing the item and shifting the values of every item \n # in the dicitionary to match their new position in the list\n last_elem_in_list = self.data[-1]\n index_of_elem_to_remove = self.data_map[val]\n\n self.data_map[last_elem_in_list] = index_of_elem_to_remove\n self.data[index_of_elem_to_remove] = last_elem_in_list\n\n # change the last element in the list to now be the value of the element \n # we want to remove\n self.data[-1] = val\n\n # remove the last element in the list\n self.data.pop()\n\n # remove the element to be removed from the dictionary\n self.data_map.pop(val)\n return True\n\n def getRandom(self) -> int:\n # if running outside of leetcode, you need to `import random`.\n # random.choice will randomly select an element from the list of data.\n return random.choice(self.data)\n```\n\nNotes:\n\n1) this can be made more efficient by removing the variables `last_elem_in_list` and `index_of_elem_to_remove`. I have used this to aid in readability. \n2) the remove operation might appear complicated so here\'s a before and after of what the data looks like:\n\n```\nelement_to_remove = 7\n\nbefore: [4, 7, 9, 3, 5]\nafter: [4, 5, 9, 3]\n\nbefore: {4:0, 7:1, 9:2, 3:3, 5:4}\nafter: {4:0, 9:2, 3:3, 5:1}\n```\n\nAll we\'re doing is replacing the element in the list that needs to be removed with the last element in the list. And then we update the values in the dictionary to reflect that. | 296 | Implement the `RandomizedSet` class:
* `RandomizedSet()` Initializes the `RandomizedSet` object.
* `bool insert(int val)` Inserts an item `val` into the set if not present. Returns `true` if the item was not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the set if present. Returns `true` if the item was present, `false` otherwise.
* `int getRandom()` Returns a random element from the current set of elements (it's guaranteed that at least one element exists when this method is called). Each element must have the **same probability** of being returned.
You must implement the functions of the class such that each function works in **average** `O(1)` time complexity.
**Example 1:**
**Input**
\[ "RandomizedSet ", "insert ", "remove ", "insert ", "getRandom ", "remove ", "insert ", "getRandom "\]
\[\[\], \[1\], \[2\], \[2\], \[\], \[1\], \[2\], \[\]\]
**Output**
\[null, true, false, true, 2, true, false, 2\]
**Explanation**
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains \[1,2\].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains \[2\].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 *` `105` calls will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Using hashmap to track index and list to save number | insert-delete-getrandom-o1 | 0 | 1 | # Code\n```\nclass RandomizedSet:\n\n def __init__(self):\n # Dict to track index of nums in nums list \n self.toIndex = { }\n self.nums = collections.deque()\n\n def insert(self, val: int) -> bool:\n # If a number already exists then don\'t add it \n if val in self.toIndex: return False\n # Else add the number to nums and save its index in map\n self.nums.append(val)\n self.toIndex[val] = len(self.nums) - 1\n \n return True\n\n def remove(self, val: int) -> bool:\n # If number not in map then number does not exist \n if val not in self.toIndex: return False \n\n # Move the number to be removed to last index of nums so it \n # can be popped in O(1). \n # When we move number to be deleted to the end, we will also have to \n # update the index of the number that was origninally at the end \n oldIndex, numAtEnd = self.toIndex[val], self.nums[-1]\n # Swap num to be deleted with last number in list \n self.nums[oldIndex], self.nums[-1] = self.nums[-1], self.nums[oldIndex]\n # Update the index of number to be deleted (this also handles the situation\n # where deleted number already at end)\n self.toIndex[numAtEnd] = oldIndex \n # Remove last number in list and remove its entry from tha map \n self.nums.pop()\n del self.toIndex[val] \n\n return True \n\n def getRandom(self) -> int:\n # Choose a random index between 0 and len(list) and \n # then return a number at that index\n n = len(self.nums)\n randInd = random.randrange(0, n)\n return self.nums[randInd]\n\n\n# Your RandomizedSet object will be instantiated and called as such:\n# obj = RandomizedSet()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 1 | Implement the `RandomizedSet` class:
* `RandomizedSet()` Initializes the `RandomizedSet` object.
* `bool insert(int val)` Inserts an item `val` into the set if not present. Returns `true` if the item was not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the set if present. Returns `true` if the item was present, `false` otherwise.
* `int getRandom()` Returns a random element from the current set of elements (it's guaranteed that at least one element exists when this method is called). Each element must have the **same probability** of being returned.
You must implement the functions of the class such that each function works in **average** `O(1)` time complexity.
**Example 1:**
**Input**
\[ "RandomizedSet ", "insert ", "remove ", "insert ", "getRandom ", "remove ", "insert ", "getRandom "\]
\[\[\], \[1\], \[2\], \[2\], \[\], \[1\], \[2\], \[\]\]
**Output**
\[null, true, false, true, 2, true, false, 2\]
**Explanation**
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains \[1,2\].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains \[2\].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 *` `105` calls will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
For Best Space Complexity... | insert-delete-getrandom-o1 | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RandomizedSet:\n\n def __init__(self):\n self.data = []\n\n def insert(self, val: int) -> bool:\n if val not in self.data:\n self.data.append(val)\n return True\n else:\n return False\n\n def remove(self, val: int) -> bool:\n if val in self.data:\n self.data.remove(val)\n return True\n else:\n return False\n\n def getRandom(self) -> int:\n return random.choice(self.data)\n\n \n\n\n# Your RandomizedSet object will be instantiated and called as such:\n# obj = RandomizedSet()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 1 | Implement the `RandomizedSet` class:
* `RandomizedSet()` Initializes the `RandomizedSet` object.
* `bool insert(int val)` Inserts an item `val` into the set if not present. Returns `true` if the item was not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the set if present. Returns `true` if the item was present, `false` otherwise.
* `int getRandom()` Returns a random element from the current set of elements (it's guaranteed that at least one element exists when this method is called). Each element must have the **same probability** of being returned.
You must implement the functions of the class such that each function works in **average** `O(1)` time complexity.
**Example 1:**
**Input**
\[ "RandomizedSet ", "insert ", "remove ", "insert ", "getRandom ", "remove ", "insert ", "getRandom "\]
\[\[\], \[1\], \[2\], \[2\], \[\], \[1\], \[2\], \[\]\]
**Output**
\[null, true, false, true, 2, true, false, 2\]
**Explanation**
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains \[1,2\].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains \[2\].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 *` `105` calls will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
380: Solution with step by step explanation | insert-delete-getrandom-o1 | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe class RandomizedSet is implemented using a hash table and an array. The hash table stores the values and their indices in the array, while the array stores the actual values.\n\nThe insert method takes a value as input and adds it to the set if it does not already exist in the set. If the value already exists, it returns False to indicate that the operation was not successful. To check if the value exists in the set, the hash table is checked. If the value does not exist, the value is added to the end of the array, and the value-index pair is added to the hash table. The time complexity of this method is O(1) on average.\n\nThe remove method takes a value as input and removes it from the set if it exists in the set. If the value does not exist, it returns False to indicate that the operation was not successful. To check if the value exists in the set, the hash table is checked. If the value exists, the index of the value in the array is obtained from the hash table, and the last value in the array is obtained. The value at the index is replaced with the last value in the array, and the index of the last value in the hash table is updated. The last value in the array is then removed, and the value-index pair for the removed value is removed from the hash table. The time complexity of this method is O(1) on average.\n\nThe getRandom method returns a random value from the set. To do this, a random value is chosen from the array using the random.choice method. The time complexity of this method is O(1) on average.\n\nOverall, the time complexity of each method is O(1) on average since all operations involve constant time hash table and array operations. The space complexity of the class is O(n), where n is the number of values in the set, since it uses a hash table and an array to store the values.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RandomizedSet:\n\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.val_to_index = {} # Hash table to store values and their indices in the array\n self.vals = [] # Array to store the actual values\n\n def insert(self, val: int) -> bool:\n """\n Inserts a value to the set. Returns true if the set did not already contain the specified element.\n """\n if val in self.val_to_index: # If the value already exists in the hash table, return false\n return False\n self.val_to_index[val] = len(self.vals) # Add the value to the hash table with its index in the array\n self.vals.append(val) # Append the value to the end of the array\n return True # Return true to indicate success\n\n def remove(self, val: int) -> bool:\n """\n Removes a value from the set. Returns true if the set contained the specified element.\n """\n if val not in self.val_to_index: # If the value does not exist in the hash table, return false\n return False\n index = self.val_to_index[val] # Get the index of the value in the array\n last_val = self.vals[-1] # Get the last value in the array\n self.vals[index] = last_val # Swap the value at the index with the last value in the array\n self.val_to_index[last_val] = index # Update the index of the last value in the hash table\n self.vals.pop() # Remove the last value from the array\n del self.val_to_index[val] # Remove the removed value from the hash table\n return True # Return true to indicate success\n\n def getRandom(self) -> int:\n """\n Get a random element from the set.\n """\n return random.choice(self.vals) # Return a random value from the array\n\n``` | 6 | Implement the `RandomizedSet` class:
* `RandomizedSet()` Initializes the `RandomizedSet` object.
* `bool insert(int val)` Inserts an item `val` into the set if not present. Returns `true` if the item was not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the set if present. Returns `true` if the item was present, `false` otherwise.
* `int getRandom()` Returns a random element from the current set of elements (it's guaranteed that at least one element exists when this method is called). Each element must have the **same probability** of being returned.
You must implement the functions of the class such that each function works in **average** `O(1)` time complexity.
**Example 1:**
**Input**
\[ "RandomizedSet ", "insert ", "remove ", "insert ", "getRandom ", "remove ", "insert ", "getRandom "\]
\[\[\], \[1\], \[2\], \[2\], \[\], \[1\], \[2\], \[\]\]
**Output**
\[null, true, false, true, 2, true, false, 2\]
**Explanation**
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains \[1,2\].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains \[2\].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 *` `105` calls will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
in log(n) time | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:log(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\nimport random\nclass RandomizedCollection:\n\n def __init__(self):\n self.arr=SortedList([])\n self.dc=defaultdict(lambda:0)\n\n def insert(self, val: int) -> bool:\n self.arr.add(val)\n self.dc[val]+=1\n return self.dc[val]==1\n def remove(self, val: int) -> bool:\n if(self.dc[val]>0):\n self.arr.discard(val)\n self.dc[val]-=1\n return True\n return False\n \n\n def getRandom(self) -> int:\n return random.choice(self.arr)\n\n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 2 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
381: Time 92.67%, Solution with step by step explanation | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis is an implementation of the Randomized Collection data structure in Python, which supports the following operations:\n\n1. insert(val: int) -> bool: Inserts a value to the collection. Returns true if the collection did not already contain the specified element.\n\n2. remove(val: int) -> bool: Removes a value from the collection. Returns true if the collection contained the specified element.\n\n3. getRandom() -> int: Get a random element from the collection.\n\nThe implementation uses a list to store the values and a hash map to store the indices of each value in the list. The hash map is implemented using a dictionary data structure in Python.\n\n```\nimport random\n\nclass RandomizedCollection:\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.vals = [] # list to store values\n self.indices = {} # hash map to store indices of each value\n```\nThe __init__ method initializes the two data structures used by the RandomizedCollection class.\n\n```\n def insert(self, val: int) -> bool:\n """\n Inserts a value to the collection. Returns true if the collection did not already contain the specified element.\n """\n self.vals.append(val) # add value to end of list\n if val in self.indices: # if value already exists in hash map\n self.indices[val].add(len(self.vals)-1) # add index to set of indices\n return False\n else:\n self.indices[val] = {len(self.vals)-1} # create new set with index\n return True\n```\nThe insert method adds a value to the end of the vals list, and if the value already exists in the indices hash map, it adds the index of the new value to the set of indices for that value. If the value does not exist in the hash map, it creates a new set with the index of the new value and adds it to the hash map. It returns true if the collection did not already contain the specified element.\n\n```\n def remove(self, val: int) -> bool:\n """\n Removes a value from the collection. Returns true if the collection contained the specified element.\n """\n if val not in self.indices: # if value doesn\'t exist in hash map\n return False\n \n index = self.indices[val].pop() # get an index of the value and remove it from set\n last_val = self.vals[-1] # get the last value in list\n if index != len(self.vals)-1: # if index is not the last index\n self.vals[index] = last_val # replace value at index with last value\n self.indices[last_val].discard(len(self.vals)-1) # remove last index from set\n self.indices[last_val].add(index) # add index to set of last value\n \n self.vals.pop() # remove last value from list\n if not self.indices[val]: # if set of indices is empty\n del self.indices[val] # remove key from hash map\n \n return True\n```\nThe remove method removes a value from the collection. If the value does not exist in the indices hash map, it returns false. Otherwise, it gets an index of the value from the set of indices for that value and removes it from the set. It also gets the last value in the vals list and replaces the value at the given index with the last value if the index is not the last index in the list. It then removes the last value from the list and removes the key from the\n\n# Complexity\n- Time complexity:\n92.67%\n\n- Space complexity:\n13.13%\n\n# Code\n```\nclass RandomizedCollection:\n def __init__(self):\n """\n Initialize your data structure here.\n """\n self.vals = [] # list to store values\n self.indices = {} # hash map to store indices of each value\n\n def insert(self, val: int) -> bool:\n """\n Inserts a value to the collection. Returns true if the collection did not already contain the specified element.\n """\n self.vals.append(val) # add value to end of list\n if val in self.indices: # if value already exists in hash map\n self.indices[val].add(len(self.vals)-1) # add index to set of indices\n return False\n else:\n self.indices[val] = {len(self.vals)-1} # create new set with index\n return True\n\n def remove(self, val: int) -> bool:\n """\n Removes a value from the collection. Returns true if the collection contained the specified element.\n """\n if val not in self.indices: # if value doesn\'t exist in hash map\n return False\n \n index = self.indices[val].pop() # get an index of the value and remove it from set\n last_val = self.vals[-1] # get the last value in list\n if index != len(self.vals)-1: # if index is not the last index\n self.vals[index] = last_val # replace value at index with last value\n self.indices[last_val].discard(len(self.vals)-1) # remove last index from set\n self.indices[last_val].add(index) # add index to set of last value\n \n self.vals.pop() # remove last value from list\n if not self.indices[val]: # if set of indices is empty\n del self.indices[val] # remove key from hash map\n \n return True\n\n def getRandom(self) -> int:\n """\n Get a random element from the collection.\n """\n return random.choice(self.vals) # return a random value from the list\n\n``` | 5 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Python 3 || simple solution | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | \n```\nimport random\nfrom collections import defaultdict\n\nclass RandomizedCollection:\n\n def __init__(self):\n self.vals = []\n self.locs = defaultdict(set)\n\n def insert(self, val: int) -> bool:\n self.vals.append(val)\n self.locs[val].add(len(self.vals) - 1)\n return len(self.locs[val]) == 1\n\n def remove(self, val: int) -> bool:\n if not self.locs[val]:\n return False\n\n loc = self.locs[val].pop()\n last = self.vals[-1]\n\n self.vals[loc] = last\n self.locs[last].add(loc)\n self.locs[last].discard(len(self.vals) - 1)\n self.vals.pop()\n\n return True\n\n def getRandom(self) -> int:\n return random.choice(self.vals)\n\n``` | 1 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Simple Python easy to understand | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.d=defaultdict(int)\n self.li=[]\n \n\n def insert(self, val: int) -> bool:\n self.li.append(val)\n self.d[val]+=1\n if self.d[val]!=1:\n return False\n return True\n\n def remove(self, val: int) -> bool:\n if self.d[val]!=0:\n self.li.remove(val)\n self.d[val]-=1\n return True\n return False\n \n\n def getRandom(self) -> int:\n return random.choice(self.li)\n \n\n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
dict and list solution. beats 57% | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor list, you can only pop the last element, that is the key to solve the problem.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.nums = {}\n self.choices = []\n\n def insert(self, val: int) -> bool:\n idx = len(self.choices)\n\n if val in self.nums:\n self.nums[val].append(idx)\n self.choices.append([val, len(self.nums[val])-1])\n return False\n else:\n self.nums[val] = [idx]\n self.choices.append([val, len(self.nums[val])-1])\n return True\n\n def remove(self, val: int) -> bool:\n if val in self.nums:\n v, idx = self.choices[-1]\n idx2 = self.nums[val][-1]\n self.choices[idx2] = [v, idx]\n self.nums[v][idx] = idx2\n self.choices.pop()\n self.nums[val].pop()\n if len(self.nums[val]) == 0:\n del self.nums[val]\n return True\n else:\n return False\n\n def getRandom(self) -> int:\n return random.choice(self.choices)[0]\n\n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Solution | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport random\nclass RandomizedCollection:\n\n def __init__(self):\n self.collection = []\n\n def insert(self, val: int) -> bool:\n if val in self.collection:\n self.collection.append(val)\n return False\n else:\n self.collection.append(val)\n return True\n\n def remove(self, val: int) -> bool:\n if val not in self.collection:\n return False\n else:\n self.collection.remove(val)\n return True\n\n def getRandom(self) -> int:\n return random.choice(self.collection)\n\n\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Clear Code #Python | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Code\n```\nimport random\nclass RandomizedCollection:\n\n def __init__(self):\n self.arr = []\n self.s_arr = {}\n def insert(self, val: int) -> bool:\n self.arr.append(val)\n if val in self.s_arr and self.s_arr[val]>0:\n self.s_arr[val]+=1\n return False\n self.s_arr[val]=1\n return True \n\n def remove(self, val: int) -> bool:\n if val in self.s_arr and self.s_arr[val]>0:\n self.s_arr[val]-=1\n self.arr.remove(val)\n return True\n return False \n\n def getRandom(self) -> int:\n return random.choice(self.arr)\n \n\n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Java & Python Solution | Explained | insert-delete-getrandom-o1-duplicates-allowed | 1 | 1 | # Intuition - \n\nThe given code implements a data structure called `RandomizedCollection`, which is similar to a set but allows for duplicates and supports efficient random element retrieval. It allows inserting elements, removing elements (if they exist), and getting a random element.\n\n# Approach - \n\n1. `RandomizedCollection` uses two data structures:\n - `valueToIndices`: A dictionary (HashMap in Java) that maps a value to a list of indices in the `items` list where that value appears.\n - `items`: A list that stores instances of the `Item` class. Each `Item` object represents a value and its index in the `items` list.\n\n2. **Insertion (`insert` method):**\n - When inserting a value, we first check if it exists in the `valueToIndices` dictionary.\n - If it doesn\'t exist, we create an entry with an empty list as the value.\n - We add the current index of the `items` list to the corresponding list in `valueToIndices`, representing the index of the newly added value.\n - We create an `Item` object with the value and its index in the corresponding list.\n - We add this `Item` object to the `items` list.\n - If the size of the corresponding list in `valueToIndices` is 1, it means this is the first occurrence of the value, and we return `true`. Otherwise, we return `false`.\n\n3. **Removal (`remove` method):**\n - When removing a value, we first check if it exists in the `valueToIndices` dictionary.\n - If it doesn\'t exist, we return `false` as the value is not in the collection.\n - Otherwise, we retrieve the last index of the value from the corresponding list in `valueToIndices`.\n - We update the last `Item` in the `items` list with the value and index of the removed value.\n - We remove the last `Item` from the `items` list.\n - If the list of indices in `valueToIndices` becomes empty after removing the value, we remove the entry from the dictionary.\n - We return `true` to indicate successful removal.\n\n4. **Random Element Retrieval (`getRandom` method):**\n - We generate a random index within the range of valid indices in the `items` list.\n - We retrieve the `Item` object at that index and return its value.\n\n5. Helper methods:\n - `lastIndex`: Returns the last index in a list of indices.\n - `last`: Returns the last `Item` in a list of `Item` objects.\n\n# Complexity Analysis - \n - Time Complexity - (O(1))\n\n - Space Complexity - (O(N))\n\n\n# Code\n``` Java []\nclass Item {\n public int value;\n public int indexInMap;\n\n public Item(int value, int indexInMap) {\n this.value = value;\n this.indexInMap = indexInMap;\n }\n}\n\nclass RandomizedCollection {\n private Map<Integer, List<Integer>> valueToIndices = new HashMap<>();\n private List<Item> items = new ArrayList<>();\n private Random rand = new Random();\n\n public boolean insert(int value) {\n valueToIndices.putIfAbsent(value, new ArrayList<>());\n valueToIndices.get(value).add(items.size());\n items.add(new Item(value, valueToIndices.get(value).size() - 1));\n return valueToIndices.get(value).size() == 1;\n }\n\n public boolean remove(int value) {\n if (!valueToIndices.containsKey(value))\n return false;\n\n int index = lastIndex(valueToIndices.get(value));\n valueToIndices.get(last(items).value).set(last(items).indexInMap, index);\n int indicesSize = valueToIndices.get(value).size();\n valueToIndices.get(value).remove(indicesSize - 1);\n if (valueToIndices.get(value).isEmpty())\n valueToIndices.remove(value);\n items.set(index, last(items));\n items.remove(items.size() - 1);\n return true;\n }\n\n public int getRandom() {\n int index = rand.nextInt(items.size());\n return items.get(index).value;\n }\n\n private int lastIndex(List<Integer> indices) {\n return indices.get(indices.size() - 1);\n }\n\n private Item last(List<Item> items) {\n return items.get(items.size() - 1);\n }\n}\n\n```\n\n\n``` Python []\nimport random\n\nclass Item:\n def __init__(self, value, index_in_map):\n self.value = value\n self.index_in_map = index_in_map\n\nclass RandomizedCollection:\n def __init__(self):\n self.value_to_indices = {}\n self.items = []\n \n def insert(self, value):\n self.value_to_indices.setdefault(value, [])\n self.value_to_indices[value].append(len(self.items))\n self.items.append(Item(value, len(self.value_to_indices[value]) - 1))\n return len(self.value_to_indices[value]) == 1\n\n def remove(self, value):\n if value not in self.value_to_indices:\n return False\n\n index = self.value_to_indices[value].pop()\n last_item = self.items[-1]\n\n if index != len(self.items) - 1:\n self.value_to_indices[last_item.value][last_item.index_in_map] = index\n\n if not self.value_to_indices[value]:\n del self.value_to_indices[value]\n\n self.items[index] = last_item\n self.items.pop()\n return True\n\n def getRandom(self):\n index = random.randint(0, len(self.items) - 1)\n return self.items[index].value\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
@SunilKing55 | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.a = []\n\n def insert(self, val: int) -> bool:\n if val in self.a:\n self.a.append(val)\n return False\n else:\n self.a.append(val)\n return True\n \n def remove(self, val: int) -> bool:\n if val in self.a:\n self.a.remove(val)\n return True\n else:\n return False\n\n def getRandom(self) -> int:\n if len(self.a)>0:\n return random.choice(self.a)\n else:\n return -1\n \n\n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Python | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n list data structure\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(1)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.cache = []\n\n # O(1)\n def insert(self, val: int) -> bool:\n if val in self.cache:\n self.cache.append(val)\n return False\n\n self.cache.append(val)\n return True\n\n # O(1)\n def remove(self, val: int) -> bool:\n if val in self.cache:\n self.cache.remove(val)\n return True\n\n return False\n\n # O(1)\n def getRandom(self) -> int:\n return random.choice(self.cache)\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Simplest Python solution ever | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.stack = []\n \n\n def insert(self, val: int) -> bool:\n \n if val not in self.stack:\n self.stack.append(val)\n return True \n else: \n self.stack.append(val)\n return False\n \n \n\n def remove(self, val: int) -> bool:\n if val in self.stack:\n self.stack.remove(val)\n return True\n else:\n return False\n\n def getRandom(self) -> int:\n return random.choice(self.stack)\n \n\n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
commented O(1) solution with: dict(key - set()) for insert and remove, list() for random | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nsearch for all O(1) methods. look at insert, remove and random seperately.\nThen bridge them.\n\nall lines commented\n\n# Complexity\n\n- Time complexity:\nO(1) - all operations are constant in time\n\n\n- Space complexity:\nO(n) - linear for dict, set and list. No extra objects created\n\n\n\n# Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.item_dict = dict() # needed for O(1) insert and remove (values are the keys of dict())\n self.item_list = list() # needed for O(1) random selection\n\n def insert(self, val: int) -> bool:\n if val in self.item_dict: # O(1) if value present in dict (cant have 0 occurances)\n self.item_dict[val].add(len(self.item_list)) # O(1) store new list index of value\n self.item_list.append(val) # O(1) add value to list\n return False\n else:\n self.item_dict[val] = {len(self.item_list)} # O(1) k-v pair where v is set of indexes\n self.item_list.append(val) # O(1) add value to list\n return True\n\n def remove(self, val: int) -> bool:\n if val in self.item_dict:\n swap_val = self.item_list[-1] # O(1) take last val in list\n ind = self.item_dict[val].pop() # O(1) delete and assign an index from set of indexes\n self.item_list[ind] = swap_val # O(1) put swap_val in place of val\n self.item_list.pop() # O(1) remove last value from list\n self.item_dict[swap_val].add(ind) # O(1) add swap_val\'s new index to index set\n self.item_dict[swap_val].discard(len(self.item_list)) # O(1) remove index of poped val\n if len(self.item_dict[val]) == 0: # O(1) k-v pair has zero occurances\n del self.item_dict[val] # O(1) delete k-v pair\n return True\n else:\n return False\n\n def getRandom(self) -> int:\n item = random.choice(self.item_list) # O(1)\n return item\n \n\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Solution | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | \n# Code\n```\nimport random\n\nclass RandomizedCollection:\n def __init__(self):\n self.collection = []\n self.indices = {}\n\n def insert(self, val: int) -> bool:\n if val not in self.indices:\n self.indices[val] = set()\n self.indices[val].add(len(self.collection))\n self.collection.append(val)\n return len(self.indices[val]) == 1\n\n def remove(self, val: int) -> bool:\n if val in self.indices:\n index = self.indices[val].pop()\n last_element = self.collection[-1]\n if index != len(self.collection) - 1:\n self.collection[index] = last_element\n self.indices[last_element].remove(len(self.collection) - 1)\n self.indices[last_element].add(index)\n if not self.indices[val]:\n del self.indices[val]\n self.collection.pop()\n return True\n else:\n return False\n\n def getRandom(self) -> int:\n return random.choice(self.collection)\n\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Brute Fcking Force | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RandomizedCollection:\n\n def __init__(self):\n self.dic=dict()\n self.arr=[]\n def insert(self, val: int) -> bool:\n if self.dic.get(val)!=None:\n go=False\n self.dic[val].append(val)\n else:\n self.dic[val]=[val]\n go=True\n self.arr=[]\n for i in self.dic.values():\n self.arr+=i\n return go\n\n def remove(self, val: int) -> bool:\n if self.dic.get(val)!=None:\n go=True\n self.dic[val].pop()\n if len(self.dic[val])==0:self.dic.pop(val)\n else:go=False\n self.arr=[]\n for i in self.dic.values():\n self.arr+=i\n return go\n def getRandom(self) -> int:\n return random.choice(self.arr)\n# Your RandomizedCollection object will be instantiated and called as such:\n# obj = RandomizedCollection()\n# param_1 = obj.insert(val)\n# param_2 = obj.remove(val)\n# param_3 = obj.getRandom()\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
[Python] O(1) list and dictionary solution, beats 90% | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | ```\nclass RandomizedCollection:\n\n def __init__(self):\n self.list = []\n self.dict = defaultdict(set)\n\n def insert(self, val: int) -> bool:\n indices = self.dict[val]\n indices.add(len(self.list))\n self.list.append(val)\n return len(indices) == 1\n\n def remove(self, val: int) -> bool:\n val_indices = self.dict[val]\n if len(val_indices) == 0:\n return False\n moved_val = self.list[-1]\n moved_val_indices = self.dict[moved_val]\n i = val_indices.pop()\n self.list[i] = moved_val\n self.list.pop()\n moved_val_indices.add(i)\n moved_val_indices.remove(len(self.list))\n return True\n \n def getRandom(self) -> int:\n return choice(self.list)\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Python Solution that actually has O(1) for all operations | Faster than 99.8% | insert-delete-getrandom-o1-duplicates-allowed | 0 | 1 | # Intuition\nMy initial thought was to represent the set with a dictionary, with the key representing each unique item and the value acting as a counter for how many times it appears. This makes implementing insertion and removal relatively simple. For insertion you increment the counter, and for removal, you decrement it.\n\nGetRandom, however, is where this approach falls down: although we already have the weights for each item (weight = count), there is no $$O(1)$$ way to select a random item. \n\n# Approach\nTo solve the problem, we can use a combination of a dictionary and a list. The dictionary will store each unique item as a key and the list of indices where the item occurs in the list as the value. This way, we can efficiently insert and remove elements. Additionally, we maintain a list called available to store indices of empty spaces within the main list called pool. The pool list is used for the getRandom function, which allows us to randomly access an element with $$O(1)$$ time complexity.\n\n# Complexity\n- Time complexity: \n - Insert: $$O(1)$$\n - Remove: $$O(1)$$\n - GetRandom $$O(1)$$ (amortized, as multiple attempts might be required to find a non-empty index)\n- Space complexity: $$O(n)$$\n\n# Code\n```py\nfrom random import random\n\nclass RandomizedCollection:\n# contents: {val: [...]}, stores all indexes where the val occurs in the pool\n# available: this stores the index of any empty spaces within the pool\n# pool: this is a list of every value in the collection, for the getrandom function\n\n#Eg. contents = {1:[0,3], 2:[2]}\n# available = [1]\n# pool = [1,None,2,1]\n\n def __init__(self):\n self.contents = {} \n self.available=[]\n self.pool=[] \n\n def insert(self, val: int) -> bool:\n # set the output and initialise contents[val] if needed\n if val in self.contents:\n ret = False\n else:\n self.contents[val]=[]\n ret = True\n\n if self.available:\n # fill empty spaces if there are any\n loc = self.available.pop(0)\n self.pool[loc]=val\n self.contents[val].append(loc)\n else:\n # otherwise, add the value to the end of the pool\n self.pool.append(val)\n self.contents[val].append(len(self.pool)-1)\n return ret\n\n def remove(self, val: int) -> bool:\n if val not in self.contents:\n return False\n\n # removes the first index from contents[val], deleting it if it\'s the only one\n loc = self.contents[val].pop(0)\n if not self.contents[val]: del self.contents[val]\n\n # instead of removing/popping the value, it is replaced with an empty space and the location is stored\n # if it was removed, the indexes of all values proceeding it would change, breaking contents\n self.available.append(loc)\n self.pool[loc]=None\n \n return True\n \n\n def getRandom(self) -> int:\n while True:\n # generates a random index using a random float, if this index is empty it tries again\n index = int(random()*len(self.pool))\n if self.pool[index] is not None: return self.pool[index]\n``` | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Solution | insert-delete-getrandom-o1-duplicates-allowed | 1 | 1 | ```C++ []\nclass RandomizedCollection {\nprivate:\n unordered_map<int, vector<int>> m;\n vector<int> v;\npublic:\n RandomizedCollection() { \n }\n bool insert(int val) {\n v.push_back(val);\n bool ret = m.find(val) == m.end() ? true : false;\n m[val].push_back(v.size()-1);\n return ret;\n }\n bool remove(int val) {\n if(m.find(val) != m.end()) {\n int pos = m[val].back();\n m[val].pop_back();\n if(m[val].empty()) m.erase(val);\n if(m.find(v.back()) != m.end()) {\n for(int x = 0 ; x < m[v.back()].size() ; x++)\n if(m[v.back()][x] == v.size()-1) {\n m[v.back()][x] = pos;\n break;\n }\n }\n swap(v[pos], v[v.size()-1]);\n v.pop_back();\n return true;\n }\n return false;\n }\n int getRandom() {\n return v[rand()%v.size()];\n }\n};\n```\n\n```Python3 []\nclass RandomizedCollection:\n\n def __init__(self):\n self.nums = []\n self.d = defaultdict(set)\n \n def insert(self, val: int) -> bool:\n if val in self.d and len(self.d[val]) > 0:\n res = False\n else:\n res = True\n self.nums.append(val)\n self.d[val].add(len(self.nums)-1)\n return res\n \n def remove(self, val: int) -> bool:\n if val in self.d and len(self.d[val]) > 0:\n pos = self.d[val].pop() # element to remove position \n lpos = len(self.nums)-1 # last position\n lval = self.nums[lpos] # last val\n \n self.d[lval].add(pos) \n self.d[lval].remove(lpos)\n \n self.nums[pos], self.nums[lpos] = self.nums[lpos], self.nums[pos] \n \n self.nums.pop()\n return True\n return False\n \n def getRandom(self) -> int:\n size = len(self.nums)\n i = int(random.random()*size)\n return self.nums[i]\n```\n\n```Java []\nclass RandomizedCollection {\n\n private static final int INITIAL_CAPACITY = 500;\n private static final long CAPACITY_INCREMENT = 130; // 30%\n private final HashMap<Integer, Entry> map = new HashMap<>(INITIAL_CAPACITY);\n private int[] array;\n private int arraySize;\n\n private final Random random = new Random();\n\n private static class Entry {\n int val;\n HashMap<Integer, Integer> indexes;\n\n public Entry(int val) {\n this.val = val;\n indexes = new HashMap<>();\n }\n }\n public RandomizedCollection() {\n array = new int[INITIAL_CAPACITY];\n }\n public boolean insert(int val) {\n Entry entry = map.get(val);\n boolean returnValue = entry == null;\n if (entry == null) {\n entry = new Entry(val);\n map.put(val, entry);\n }\n entry.indexes.put(arraySize, 1);\n addValueToArray(val);\n return returnValue;\n }\n public boolean remove(int val) {\n Entry entry = map.get(val);\n if (entry == null) {\n return false;\n }\n int arrayIndex = entry.indexes.keySet().iterator().next();\n if (entry.indexes.size() == 1) {\n map.remove(val);\n } else {\n entry.indexes.remove(arrayIndex);\n }\n removeValueFromArray(arrayIndex);\n if (arrayIndex != arraySize) {\n Entry e = map.get(array[arrayIndex]);\n e.indexes.remove(arraySize);\n e.indexes.put(arrayIndex, 1);\n }\n return true;\n }\n public int getRandom() {\n return array[random.nextInt(arraySize)];\n }\n private void addValueToArray(int val) {\n if (arraySize == array.length) {\n long l = Math.min(CAPACITY_INCREMENT * array.length / 100, Integer.MAX_VALUE - 8);\n array = Arrays.copyOf(array, (int) l);\n }\n array[arraySize++] = val;\n }\n private void removeValueFromArray(int arrayIndex) {\n array[arrayIndex] = array[--arraySize];\n }\n}\n```\n | 0 | `RandomizedCollection` is a data structure that contains a collection of numbers, possibly duplicates (i.e., a multiset). It should support inserting and removing specific elements and also reporting a random element.
Implement the `RandomizedCollection` class:
* `RandomizedCollection()` Initializes the empty `RandomizedCollection` object.
* `bool insert(int val)` Inserts an item `val` into the multiset, even if the item is already present. Returns `true` if the item is not present, `false` otherwise.
* `bool remove(int val)` Removes an item `val` from the multiset if present. Returns `true` if the item is present, `false` otherwise. Note that if `val` has multiple occurrences in the multiset, we only remove one of them.
* `int getRandom()` Returns a random element from the current multiset of elements. The probability of each element being returned is **linearly related** to the number of the same values the multiset contains.
You must implement the functions of the class such that each function works on **average** `O(1)` time complexity.
**Note:** The test cases are generated such that `getRandom` will only be called if there is **at least one** item in the `RandomizedCollection`.
**Example 1:**
**Input**
\[ "RandomizedCollection ", "insert ", "insert ", "insert ", "getRandom ", "remove ", "getRandom "\]
\[\[\], \[1\], \[1\], \[2\], \[\], \[1\], \[\]\]
**Output**
\[null, true, false, true, 2, true, 1\]
**Explanation**
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return true since the collection does not contain 1.
// Inserts 1 into the collection.
randomizedCollection.insert(1); // return false since the collection contains 1.
// Inserts another 1 into the collection. Collection now contains \[1,1\].
randomizedCollection.insert(2); // return true since the collection does not contain 2.
// Inserts 2 into the collection. Collection now contains \[1,1,2\].
randomizedCollection.getRandom(); // getRandom should:
// - return 1 with probability 2/3, or
// - return 2 with probability 1/3.
randomizedCollection.remove(1); // return true since the collection contains 1.
// Removes 1 from the collection. Collection now contains \[1,2\].
randomizedCollection.getRandom(); // getRandom should return 1 or 2, both equally likely.
**Constraints:**
* `-231 <= val <= 231 - 1`
* At most `2 * 105` calls **in total** will be made to `insert`, `remove`, and `getRandom`.
* There will be **at least one** element in the data structure when `getRandom` is called. | null |
Easiest.py | linked-list-random-node | 0 | 1 | # Code\n```\nclass Solution:\n def __init__(self, head: Optional[ListNode]):\n self.ll=[]\n while head:\n self.ll.append(head.val)\n head=head.next\n def getRandom(self) -> int:\n return self.ll[randint(0, len(self.ll)-1)]\n``` | 5 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Python3 / Golang, 2 Easy and intuitive solutions | linked-list-random-node | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n## Version 1\n1. In `__init__` / constructor we initialize a list and append to it all the values from the single-linked list\n2. In `getRandom` return a random integer from the list \n\n# Complexity\n- Time complexity:\n`__init__` / constructor O(n)\n`getRandom` O(1)\n\n- Space complexity: O(n)\n\n\n\n#### Don\'t forget to Vote! :)\n\n# Code \n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.l = []\n \n curr = head\n while curr:\n self.l.append(curr.val)\n curr = curr.next\n \n def getRandom(self) -> int:\n return random.choice(self.l)\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n```\n```golang []\n/**\n * Definition for singly-linked list.\n * type ListNode struct {\n * Val int\n * Next *ListNode\n * }\n */\n\ntype Solution struct {\n Values []int\n}\n\n\nfunc Constructor(head *ListNode) Solution {\n values := []int{}\n curr := head\n for curr != nil {\n values = append(values, curr.Val)\n curr = curr.Next\n }\n\n return Solution{Values: values}\n}\n\n\nfunc (this *Solution) GetRandom() int {\n randInt := rand.Intn(len(this.Values))\n return this.Values[randInt]\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * obj := Constructor(head);\n * param_1 := obj.GetRandom();\n */\n```\n\n<!-- Describe your approach to solving the problem. -->\n## Version 2\n1. In `__init__` / constructor we only set the head field\n2. In `getRandom` iterate over the single-linked list, generate a random integer between 1 and counter that starts with 0, and if it is equal with 1 we set the node value. at the end we return the stored value. \n\n# Complexity\n- Time complexity:\n`__init__` / constructor O(1)\n`getRandom` O(n)\n\n- Space complexity: O(1)\n\n\n# Code \n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.h = head\n \n def getRandom(self) -> int:\n \n curr = self.h\n count = 0\n res = 0\n\n while curr:\n count += 1\n if randint(1, count) == 1:\n res = curr.val\n curr = curr.next\n \n return res\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n```\n```golang []\n/**\n * Definition for singly-linked list.\n * type ListNode struct {\n * Val int\n * Next *ListNode\n * }\n */\n\ntype Solution struct {\n Head *ListNode\n}\n\n\nfunc Constructor(head *ListNode) Solution {\n return Solution{Head: head}\n}\n\n\nfunc (this *Solution) GetRandom() int {\n \n curr := this.Head\n count := 0\n result := 0\n\n for curr != nil {\n \n count++ \n if (rand.Intn(count) + 1) == 1 {\n result = curr.Val\n }\n \n curr = curr.Next\n }\n return result\n}\n\n\n/**\n * Your Solution object will be instantiated and called as such:\n * obj := Constructor(head);\n * param_1 := obj.GetRandom();\n */\n```\n\n\n | 2 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
382: Solution with step by step explanation | linked-list-random-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis is an implementation of an algorithm to return a random node value from a linked list with each node having an equal probability of being chosen.\n\nThe class Solution is defined with an __init__ method that takes a singly linked list\'s head as input and initializes the object with it. The getRandom method of this class is responsible for choosing a node randomly from the list and returning its value.\n\nThe algorithm starts by initializing the reservoir with the value of the head node of the linked list. It also initializes the counter to 2 since we\'ve already processed the head node.\n\nThe loop starts from the second node in the linked list, and for each node, it calculates the probability of choosing that node using the formula 1/i, where i is the counter. If the randomly generated probability is less than this value, the reservoir value is replaced with the current node value.\n\nThe counter is then incremented by 1, and the loop continues with the next node in the linked list.\n\nFinally, the algorithm returns the final value of the reservoir, which will be the value of the node chosen randomly with equal probability from the linked list.\n\n# Complexity\n- Time complexity:\n70.70%\n\n- Space complexity:\n50.73%\n\n# Code\n```\nclass Solution:\n def __init__(self, head: Optional[ListNode]):\n self.head = head\n \n def getRandom(self) -> int:\n # Initialize the reservoir with the value of the head node\n reservoir = self.head.val\n \n # Initialize the counter to 2 since we\'ve already processed the head node\n i = 2\n \n # Loop through the linked list starting from the second node\n next = self.head.next\n while next:\n # With probability 1/i, replace the reservoir value with the value of the current node\n if random.random() < 1/i:\n reservoir = next.val\n \n # Increment the counter and move on to the next node\n i += 1\n next = next.next\n \n # Return the final reservoir value\n return reservoir\n\n``` | 2 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Easy Python3 | linked-list-random-node | 0 | 1 | # Code\n```\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.List = []\n\n while head:\n self.List.append(head.val)\n head = head.next\n \n\n def getRandom(self) -> int:\n return self.List[random.randrange(len(self.List))]\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Simple Easiest code in python3 | linked-list-random-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.head=head\n\n def getRandom(self) -> int:\n count,output=0,0\n curr=self.head\n while curr!=None:\n count+=1\n if random.randint(1,count)==1:\n output=curr.val\n curr=curr.next\n return output\n\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Python simple solution You will ever find. | linked-list-random-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.arr=[]\n curr=head\n while curr!=None:\n self.arr.append(curr.val)\n curr=curr.next\n\n def getRandom(self) -> int:\n return self.arr[random.randrange(len(self.arr))]\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Python3 | Faster Than 98.02% | linked-list-random-node | 0 | 1 | \n\n# Code\n```\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.lst=[]\n\n while(head):\n self.lst.append(head.val)\n head=head.next\n\n def getRandom(self) -> int:\n return random.choice(self.lst)\n\n\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Simple 🐍python solution👌 | linked-list-random-node | 0 | 1 | \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def __init__(self, head: ListNode):\n self.nodes = []\n while head:\n self.nodes.append(head.val)\n head = head.next\n\n def getRandom(self) -> int:\n ind = random.randint(0, len(self.nodes) - 1)\n return self.nodes[ind]\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Python3 || 97% fast || 2 methods || detailed explanation | linked-list-random-node | 0 | 1 | # Approach 1\n<!-- Describe your approach to solving the problem. -->\n- create array of nodes.\n- use random function to get random element from array.\n- return element.\n\n\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.head = head\n\n def getRandom(self) -> int:\n hmap = []\n head = self.head\n while head:\n hmap.append(head)\n head = head.next\n return random.choice(hmap).val\n```\n---\n# Approach 2\n- initialise result as first node.\n- maintain n for random value, now start n from 2.\n- now traverse from head.next, and get random value from 0 - n-1\n- if random value equals to 0 then update the result to current node.\n- every time increment further towards end of list.\n- when list ends return found result.\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n```\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.head = head\n\n def getRandom(self) -> int:\n result = self.head.val\n n = 2\n current = self.head.next\n while current:\n if random.randint(0,n-1) == 0:\n result = current.val\n current = current.next\n n += 1\n return result \n```\n # Please like and comment below :-) | 2 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Basic Probability to Advanced Random Sampling | linked-list-random-node | 1 | 1 | # Intuition\nA random node has to be returned everytime, with each node having an equal probability of getting selected. If we consider the length of the linked list, generate a number between it\'s length, and return the node at that position, we will have fulfilled all the constraints\n\n# Approach\nStore the list elements into an ArrayList for quick access, generate a random number and use it as the index.\n\n```\nint i = (int)(Math.random() * this.nodes.size());\n```\nSelf-explanatory step, generate the number i randomly, use it as index and return the node at that index.\n\n**Time:$$O(N)$$**\n**Space: $$O(N)$$**\nN-> Size of the list\n\n# Code\n\n\n\n```Java []\nclass Solution {\n ArrayList<Integer> nodes = new ArrayList<Integer>();\n public Solution(ListNode head) {\n while (head != null) {\n nodes.add(head.val);\n head = head.next;\n }\n }\n \n public int getRandom() {\n int i = (int)(Math.random() * this.nodes.size());\n return this.nodes.get(i);\n }\n}\n\n\n```\n```C++ []\nclass Solution {\n private:\n vector<int> nodes;\n public:\n Solution(ListNode* head) {\n while (head != nullptr) {\n nodes.push_back(head->val);\n head = head->next;\n }\n }\n \n int getRandom() {\n int i = rand() % nodes.size();\n return nodes[i];\n }\n};\n\n```\n```python []\n\nclass Solution:\n\n def __init__(self, head: ListNode):\n self.nodes = []\n while head:\n self.nodes.append(head.val)\n head = head.next\n\n def getRandom(self) -> int:\n i = random.randint(0, len(self.nodes) - 1)\n return self.nodes[i]\n\n```\n\n\n---\n\n\n\n\n\n\n# Advanced Approach\nTo select a random element from a data stream with unknown length, we use $$random$$ $$sampling$$. \n\n# Approach\nThink about reservior sampling as this lottery contest where everybody has equal chance of winning. How do we formulate such a method?\nLet\'s do with the basics:\n\n# Reservior Sampling:\n**The probability by which you decide if you should select the $$k-th$$ element or not is $$1/k$$. This ensures that everyone has the same probability of getting selected.**\n\nSuppose you have to select a random number between a,b,c,d,e.\n**Steps:**\n1. Start by selecting the first element, here $$a$$\n2. Iterate through the remaining elements. (say) For the $$4th$$ element, $$d$$, generate a number between $$1$$ and $$4$$. If you get $$1$$, discard the current alphabet you\'re holding and select $$d$$ instead.\n Why?\n The probability of selecting $$d$$ is $$1/4$$.\n $$success=[1]$$ \n$$samples=[1,2,3,4]$$\nOr $$1/4$$\n\n 3.Repeat the process until the end.\n\nThinking about this problem from the perspective of ***"Should I select the newest element or not"*** is intuitive. Next step is to breakdown how it ensures fairity. Let\'s get back to $$[a,b,c,d,e]$$\n\n- The probability of $$a$$ getting selected at the start is $$1$$`(1/k, where k=1)`\n- When we observe $$b$$, it is selected with a probability of $$1/2$$, that also means $$a$$ will be rejected when we observe $$b$$ with a probability of $$1/2$$. B or fairness. But doesn\'t that mean $$b$$ won\'t be selected with a probability of $$1/2$$ ? And $$a$$ will remain our choice with a 1/2 probability? Or fairness?\n- When we observe the next element $$c$$, it is either added to the reservoir with probability $$1/3$$. That means probability of $$c$$ not being selected is $$2/3$$\n- In the previous step, $$a$$ had a $$50$$ percent chance of remaining our selection. As our selections are independant, chances of $$\'a\'$$ remaining our selection are:\n$$50$$ % *of* $$2/3$$, or $$1/3$$\n- Same logic is followed for further steps.\n\n\n\n\n\n# Code\n```Java []\nclass Solution {\n private ListNode head;\n private Random rand;\n\n public Solution(ListNode head) {\n this.head = head;\n this.rand = new Random();\n }\n \n public int getRandom() {\n ListNode curr = this.head;\n int val = curr.val;\n for (int i = 1; curr.next != null; i++) {\n curr = curr.next;\n if (rand.nextInt(i + 1) == 1) {\n//generate a number between [0,i]. compare it with 1 \n//as test condition\n val = curr.val;\n }\n }\n return val;\n }\n}\n\n```\n```C++ []\nclass Solution {\nprivate:\n ListNode* head;\npublic:\n Solution(ListNode* head) {\n this->head = head;\n }\n \n int getRandom() {\n int count = 0, result;\n ListNode* curr = head;\n while (curr) {\n count++;\n if (rand() % count == 0) {\n result = curr->val;\n }\n curr = curr->next;\n }\n return result;\n }\n};\n\n```\n```Python3 []\nclass Solution:\n def __init__(self, head: ListNode):\n self.head = head\n \n def getRandom(self) -> int:\n curr = self.head\n val = curr.val\n i = 1\n while curr.next:\n curr = curr.next\n i += 1\n if random.randint(1, i) == 1:\n val = curr.val\n return val\n\n```\n | 24 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Easy python solution | linked-list-random-node | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nimport random\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.head = head \n self.arr = []\n\n def createList(self) : \n while self.head != None : \n self.arr.append(self.head.val)\n self.head = self.head.next \n\n def getRandom(self) -> int:\n if len(self.arr) == 0 : \n self.createList()\n\n index = random.randint(0, len(self.arr)-1)\n return self.arr[index]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
python3, using random.randrange() (70 ms, faster than 83.83%) | linked-list-random-node | 0 | 1 | Runtime: **70 ms, faster than 83.83%** of Python3 online submissions for Linked List Random Node. \nMemory Usage: 17.6 MB, less than 6.13% of Python3 online submissions for Linked List Random Node. \n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.length = 0\n self.head = head\n node = head\n while node:\n self.length += 1\n node = node.next\n\n def getRandom(self) -> int:\n p = randrange(self.length)\n node = self.head\n for _ in range(p):\n node = node.next\n return node.val\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n```\n\n**A large test case** \nhttps://leetcode.com/submissions/detail/912382970/testcase/ | 2 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
❤ [Python3] RESERVOIR SAMPLING ໒(^ᴥ^)७, Explained | linked-list-random-node | 0 | 1 | In the follow-up, the problem asks us to find an algorithm for an extremely large list and with no additional space. This immediately recalls us about reservoir sampling - an online algorithm for uniformly choosing `k` random elements from a stream. In our case, `k` is equal to 1 (we need to sample just one element). We create a reservoir and put there the first node. Then iterate over nodes and replace the node in the reservoir with the current one with probability `1/i`, where `i` is the index of the current node. In the end, we end up with the reservoir containing a node chosen with the uniform probability `1/n`, where `n` is the number of nodes.\n\n<img src="https://assets.leetcode.com/users/images/062defda-d542-4aec-9708-126a21f3fd26_1641516842.6092827.jpeg" width="500">\n\nWhy does it work? Intuitively we can see that elements from the start of the list can get to the reservoir relatively easily since the probability is pretty high at the beginning. But to stay there they have to survive the whole list of elements in front of them. The actual math proof can be found in this article https://florian.github.io/reservoir-sampling/\n\nTime: **O(n)** - scan\nSpace: **O(1)** - nothing is stored\n\nRuntime: 80 ms, faster than **71.58%** of Python3 online submissions for Linked List Random Node.\nMemory Usage: 17.2 MB, less than **85.41%** of Python3 online submissions for Linked List Random Node.\n\n```\nclass Solution:\n def __init__(self, head: Optional[ListNode]):\n self.head = head\n \n def getRandom(self) -> int:\n reservoir = self.head.val\n \n i = 2\n next = self.head.next\n while next:\n if random.random() < 1/i:\n reservoir = next.val\n \n i += 1\n next = next.next\n \n return reservoir\n``` | 42 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
easy python solution.91.90% faster..and very easy to understand. | linked-list-random-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfirst step->declare a list and append data through it.\nwhen you finished to do so.\nthe use this method random.choice(self.list)\nto select the random number from the list.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n def __init__(self, head: Optional[ListNode]):\n self.list=[]\n\n curr=head\n while curr is not None:\n self.list.append(curr.val)\n curr=curr.next\n \n\n def getRandom(self) -> int:\n return random.choice(self.list)\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(head)\n# param_1 = obj.getRandom()\n``` | 1 | Given a singly linked list, return a random node's value from the linked list. Each node must have the **same probability** of being chosen.
Implement the `Solution` class:
* `Solution(ListNode head)` Initializes the object with the head of the singly-linked list `head`.
* `int getRandom()` Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.
**Example 1:**
**Input**
\[ "Solution ", "getRandom ", "getRandom ", "getRandom ", "getRandom ", "getRandom "\]
\[\[\[1, 2, 3\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 1, 3, 2, 2, 3\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3\]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
**Constraints:**
* The number of nodes in the linked list will be in the range `[1, 104]`.
* `-104 <= Node.val <= 104`
* At most `104` calls will be made to `getRandom`.
**Follow up:**
* What if the linked list is extremely large and its length is unknown to you?
* Could you solve this efficiently without using extra space? | null |
Ransom Note | ransom-note | 0 | 1 | # 11/22\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n for i in range(len(magazine)):\n for j in range(len(ransomNote)):\n try:\n if magazine[i] == ransomNote[j]:\n ransomNote = ransomNote.replace(ransomNote[j], "",1)\n break\n except:\n pass\n return ransomNote == ""\n``` | 3 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Very Easy || 100% || Fully Explained || C++, Java, Python, Python3 | ransom-note | 1 | 1 | # **C++ Solution:**\n```\nclass Solution {\npublic:\n bool canConstruct(string ransomNote, string magazine) {\n // Initialize an array of count with the size 26...\n int counter[26] = {0};\n // Traverse a loop through the entire String of magazine where char ch stores the char at the index of magazine...\n for(char ch : magazine)\n counter[ch - \'a\']++;\n // Run another for loop for ransomNote...\n for(char ch : ransomNote)\n // If the charachter doesn\'t exists in magazine for ransomNote, we return false...\n if(counter[ch - \'a\']-- <= 0)\n return false;\n return true; // If nothing goes wrong, return true...\n }\n};\n```\n\n# **Java Solution:**\n```\nclass Solution {\n public boolean canConstruct(String ransomNote, String magazine) {\n // Initialize an array of count with the size 26...\n int[] counter = new int[128];\n // Traverse a loop through the entire String of magazine where char ch stores the char at the index of magazine...\n for (final char ch : magazine.toCharArray())\n ++counter[ch];\n // Run another for loop for ransomNote...\n for (final char ch : ransomNote.toCharArray())\n // If the charachter doesn\'t exists in magazine for ransomNote, we return false...\n if (--counter[ch] < 0)\n return false;\n return true; // If nothing goes wrong, return true...\n }\n}\n```\n\n# **Python/Python3 Solution:**\n```\nclass Solution(object):\n def canConstruct(self, ransomNote, magazine):\n st1, st2 = Counter(ransomNote), Counter(magazine)\n if st1 & st2 == st1:\n return True\n return False\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 234 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Solution Outperforms 93.93% of Users ! | ransom-note | 0 | 1 | \n\n# Approach\nThe code iterates through each character in the ransomNote. For each character, it checks if it is present in the magazine. If the character is not found in the magazine, the function immediately returns False, indicating that the ransom note cannot be constructed. If the character is found, it removes the first occurrence of that character from the magazine using the replace method.\n\nIf the loop completes without encountering any issues, it means that each character in the ransomNote has been found in the magazine, and the function returns True, indicating that the ransom note can be constructed.\n\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n for i in ransomNote :\n if i not in magazine :\n return False \n magazine = magazine.replace(i,\'\',1)\n return True \n``` | 3 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Python Find/Replace - Run Time: 47ms, Memory: 16.34MB | ransom-note | 0 | 1 | # Approach\nPython provides a string function to find the first index of a substring in an input string with str().find(). This returns -1 if the substring could not be found. Python also provides string function str().replace() with the 3rd argument being which match to replace if substring found. \n\nIf a letter from the ransomNote is found in the magazine, we replace a single instance of that letter from the magazine with an empty string. Otherwise the ransom letter does not correspond to the magazine and we short-circuit return False. If we make it through the whole ransom letter we will hit the final return True at the bottom. \n\n# Complexity\nNew to this type of description, but you loop through the entire ransomNote only once.\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n for abc in ransomNote:\n if magazine.find(abc) != -1:\n magazine = magazine.replace(abc, \'\', 1)\n else:\n return False\n return True\n``` | 0 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Easiest One Linear solution in Python3 | ransom-note | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n the given code to determine if you can construct a ransomNote from the characters in a magazine is as follows:\n\n1. First, a set of unique characters in the ransomNote is created using set(ransomNote). This is done to avoid unnecessary repetitions when iterating through characters.\n\n2. Then, a generator expression is used within the all function to iterate through each unique character c in the ransomNote.\n\n3. For each character c, it checks if the count of that character in the ransomNote (using ransomNote.count(c)) is less than or equal to the count of the same character in the magazine (using magazine.count(c)).\n\n4. If this condition holds true for all characters in the ransomNote, the all function returns True, indicating that you can construct the ransomNote from the characters in the magazine.\n\n5. If the condition fails for any character, the all function returns False, indicating that it\'s not possible to construct the ransomNote from the magazine.\n# Complexity\n- Time complexity: O(k * n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n return all(ransomNote.count(c) <= magazine.count(c) for c in set(ransomNote))\n\n```\n### One more complementary solution \n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n ransomNote = list(ransomNote)\n magazine = list(magazine)\n for char in ransomNote:\n if char in magazine:\n magazine.remove(char)\n else:\n return False\n return True\n``` | 11 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
🌟Hash-table 🌟O(mxn) 🌟 Easy solution 🌟Explained | ransom-note | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst count all the character int the `ransomNote` and then also check if the same numbers of characters are present in the `magazine` or not. If so, return `True` else `False`\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHashmaps or dictionary\n\n\n# Complexity\n- Time complexity: `O(mxn)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(m)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please UPVOTE my solution. It is a small gesture, but means a lot to me. Thanks \uD83D\uDE0A\uD83D\uDE4F\n```\nclass Solution(object):\n def canConstruct(self, ransomNote, magazine):\n \n chars = {}\n for char in magazine:\n if char not in chars: chars[char] = 1\n else: chars[char] += 1\n\n for char in ransomNote:\n if char in chars and chars[char] > 0: chars[char] -= 1\n else: return False\n \n return True\n``` | 13 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
383: Solution with step by step explanation | ransom-note | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We define a class Solution and a method canConstruct which takes two string arguments, ransomNote and magazine.\n\n2. We create Counter objects for both the ransomNote and magazine strings using the Counter() function from the collections module. Counter() returns a dictionary with the keys being the unique characters in the string and the values being the frequency of each character.\n\nFor example, Counter("aab") would return a dictionary {\'a\': 2, \'b\': 1}.\n\n3. We then check if the intersection of the note and mag Counter objects is equal to the note Counter object. We do this using the bitwise AND operator (&). The intersection of two Counter objects is another Counter object that contains the common keys and the minimum value from each object as the value for the key.\n\nFor example, if note = Counter("aab") and mag = Counter("abc"), note & mag would return a Counter object {\'a\': 1, \'b\': 1}.\n\n4. If the intersection of note and mag is equal to note, it means that all the letters in ransomNote can be formed using the letters in magazine. In this case, we return True, otherwise we return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n \n # Create Counter objects for the ransomNote and magazine strings\n note, mag = Counter(ransomNote), Counter(magazine)\n \n # Check if the intersection of note and mag Counter objects is equal to note Counter object\n # If it is, it means that all the letters in ransomNote can be formed using the letters in magazine\n if note & mag == note: return True\n return False\n``` | 52 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
4th | ransom-note | 0 | 1 | 4\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n for i in ransomNote:\n if i in magazine:\n magazine = magazine.replace(i, \'\', 1)\n ransomNote = ransomNote.replace(i, \'\', 1)\n return len(ransomNote) == 0\n``` | 2 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Easy Python code for Beginners | ransom-note | 0 | 1 | # Intuition\nThe intuition behind the given code is to check if we can construct the ransomNote string using the letters from the magazine string, while adhering to the constraint that each letter in magazine can only be used once.\n\nThe code accomplishes this by using two for loops to traverse the ransomNote and magazine strings.\n\n# Approach\nIn the first loop, we iterate over each character in the ransomNote string. For each character, we check if it is present in the magazine string. If the character is found, it means we can use it to construct the ransomNote, so we remove that character from the magazine string by calling magazine.remove(char).\n\nIf a character in ransomNote is not found in magazine, it means we cannot construct the ransomNote using the available characters, so we immediately return False.\n\nAfter iterating over all characters in ransomNote, if we have successfully removed each character from the magazine string, it means we can construct the ransomNote using the letters from magazine, while satisfying the constraint that each letter in magazine can only be used once. In this case, we return True.\n\nThe approach of converting the strings to lists allows us to manipulate the magazine string by removing characters as they are used, effectively ensuring that each letter in magazine is used only once.\n\n# Complexity\n- Time complexity: O(n*m)\n\n- Space complexity: O(n+m)\n\n# Code\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n ransomNote = list(ransomNote)\n magazine = list(magazine)\n for char in ransomNote:\n if char in magazine:\n magazine.remove(char)\n else:\n return False\n return True\n``` | 10 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Solution using python collections | ransom-note | 0 | 1 | ```\nfrom collections import defaultdict, Counter\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n d = dict(Counter(magazine))\n for x in ransomNote:\n if x not in d:\n return False\n else:\n d[x] -= 1\n if d[x] == 0:\n del d[x]\n return True\n | 3 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
One Line: understand set concept | ransom-note | 0 | 1 | \n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n return Counter(ransomNote)=Counter(magazine)\n #please upvote me it would encourage me alot\n\n \n```\n```\nclass Solution:\n def canConstruct(self, ransomNote: str, magazine: str) -> bool:\n return not Counter(ransomNote)-Counter(magazine)\n #please upvote me it would encourage me alot\n\n \n``` | 14 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Python3 95.20% O(N) Solution | Beginner Friendly | ransom-note | 0 | 1 | TC: O(N), N = max(len(a), len(b))\n\n```\nclass Solution:\n def canConstruct(self, a: str, b: str) -> bool:\n letter = [0 for _ in range(26)]\n \n for c in b:\n letter[ord(c) - 97] += 1\n \n for c in a:\n letter[ord(c) - 97] -= 1\n \n return not any((i < 0 for i in letter))\n \n \n``` | 3 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Python ||| Easy and Beginner Friendly Solution ||| | ransom-note | 0 | 1 | ```\ndef canConstruct(self, ransomNote: str, magazine: str) -> bool:\n\trn = Counter(ransomNote)\n\tmg = Counter(magazine)\n\tfor key in rn:\n\t\tif key not in mg:\n\t\t\treturn False\n\t\telse:\n\t\t\tif rn[key] > mg[key]:\n\t\t\t\treturn False\n\treturn True | 3 | Given two strings `ransomNote` and `magazine`, return `true` _if_ `ransomNote` _can be constructed by using the letters from_ `magazine` _and_ `false` _otherwise_.
Each letter in `magazine` can only be used once in `ransomNote`.
**Example 1:**
**Input:** ransomNote = "a", magazine = "b"
**Output:** false
**Example 2:**
**Input:** ransomNote = "aa", magazine = "ab"
**Output:** false
**Example 3:**
**Input:** ransomNote = "aa", magazine = "aab"
**Output:** true
**Constraints:**
* `1 <= ransomNote.length, magazine.length <= 105`
* `ransomNote` and `magazine` consist of lowercase English letters. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.