title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Constant time | Mathematical solution | power-of-four | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfind power of 4 of a given number if its whole number return `True`. if it has decimal number return `False`.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfew examples \n- log(16,4) => 2\n- log(17,4) => 2.0437 ( False)\n check if the log(n,4) value has digits after decimal (it is not power of 4)\n# Complexity\n- Time complexity: $$(constant)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$(constant)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n <= 0:\n return False\n\n float_val = math.log(abs(n),4)\n int_val = int(float_val)\n \n # check if there is any digits after decimal point\n if float_val - int_val != 0:\n return False\n\n return True\n\n \n``` | 0 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
Python code to return n if it's a power of 4 (TC&SC: O(1)) | power-of-four | 0 | 1 | \n\n# Approach\n\nThe isPowerOfFour function checks if the given integer n is a power of four. It does this by first checking if n is greater than zero and then comparing it to 4 raised to the power of the rounded logarithm of n to the base 4.\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def isPowerOfFour(self, n: int) -> bool:\n if n > 0:\n if 4**round(math.log(n,4),0) == n:\n return True\n``` | 2 | Given an integer `n`, return _`true` if it is a power of four. Otherwise, return `false`_.
An integer `n` is a power of four, if there exists an integer `x` such that `n == 4x`.
**Example 1:**
**Input:** n = 16
**Output:** true
**Example 2:**
**Input:** n = 5
**Output:** false
**Example 3:**
**Input:** n = 1
**Output:** true
**Constraints:**
* `-231 <= n <= 231 - 1`
**Follow up:** Could you solve it without loops/recursion? | null |
98.34 Beats 🔥, Easiest solution for beginners (O(1)) , Anyone can Understand. | integer-break | 0 | 1 | # Intuition\nBasically , I tried to find a pattern that would give the maximum product , I got to know that , this can only happen using prime numbers . From prime numbers i understood that any universal number can be written in 2\'s or 3\'s .\n\n# Approach\nChecking for the remainder of number and according to the remainders 0,1,2 there is a code given.\n1. For Remainder 0 : \n The highest product will be the product of all 3\'s.\n\n2. For Remainder 1:\n The highest product will be multiplying 4 with remaining threes .\n3. For Remainder 2 : \nThe highest product will be multiplying only 2 with remaining 3\'s.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\nclass Solution:\n def integerBreak(self, n: int) -> int:\n \n rem1 = n % 3 \n y = n//3\n if n ==1 or n==2 :\n return 1 \n elif n==3:\n return 2\n elif rem1 ==1 :\n s = pow(3,y-1)*4\n return s\n elif rem1==0:\n return pow(3,y)\n else:\n s = pow(3,y)*2\n return s \n \n \n\n\n\n \n``` | 6 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
C++/Python O(log n) Math & MSBF pow||0ms beats 100% | integer-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n6 is the number what is split into$2+2+2$ or $3+3$.... Which one is better?\nNote $2^3=8<9=3^2$, so $3+3$ is the most optimal. For integer $n>3$ it is considered $n=3*k+r$ where r=0, 2, 4\nthen compute\n$$\n3^k*f(r) \\ where \\ f(0)=1, f(2)=2, f(4)=4\n$$\n# Why not 2? Why not 4? Why not other p?\nConsider $n\\equiv 0\\pmod{6}$, observe $2^3=8<9=3^2$, for other $n\\equiv r\\pmod{6}$ is similar. So taking 3 is better than 2.\n\nConsider $n\\equiv 0\\pmod{12}$, observe $4^3=64<81=3^4$, for other $n\\equiv r\\pmod{12}$ is similar. So taking 3 is better than 4.\n\nWhy not other p? It suffices to prove that $$p^3<3^p$$ for $p\\not=3$ a natural number.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(\\log n)$$ pow(3, k) has TC O(log n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Custom pow using Most significant bit first Algorithm\n```\n int pow(int x, int k){\n int y=1;\n bitset<5> bk(k);\n #pragma unroll\n for(int i=4; i>=0; i--){\n y=y*y;\n if (bk[i]) y*=x;\n }\n return y; \n }\n```\n# Code\n```\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n<=3) return n-1;\n //Note 2^3=8<3^2, n=3*k+r where r=0, 2, 4\n auto [k, r]=div(n, 3);\n if (r==1){//Only this needs modification\n r=4, k--;\n }\n int ans=pow(3, k);\n if (r>0) ans*=r;\n return ans;\n }\n};\n\n```\n# Python code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n<=3: return n-1\n k,r=divmod(n,3)\n if r==1:\n r=4\n k-=1\n ans=3**k\n if r>0: ans*=r\n return ans\n \n``` | 8 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
🔥Easy explanation | Why 3s why not 4s?| 🚀Dynamic Programming Solution with Best Approach ✅✅✅✅✅ | integer-break | 1 | 1 | \n## Upvote if you like the eexplanation and solution \uD83D\uDD25\n\n---\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n We want to break the integer n into the sum of positive integers to maximize the product. By observation, it\'s more beneficial to use 3s instead of 4s because 3 * 3 > 4 * 4.\n\n\n---\n\n\n# Using 3s instead of 4s maximizes the product because:\n\n- 3 * 3 is greater than 4 * 4 (9 > 16).\n- When using 4s, we can always replace two 4s with three 3s, resulting in a larger product (4 * 4 = 16, but 3 * 3 * 3 > 4 * 4). This is why 3s are preferred.\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use dynamic programming to find the maximum product for each integer from 2 to n. We initialize the base cases for 2 and 3. Then, for each integer from 4 to n, we calculate the maximum product based on the previous results.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n The time complexity is O(n) because we iterate through all integers from 4 to n once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) due to the dynamic programming array dp.\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n <= 3) return n - 1;\n \n vector<int> dp(n + 1, 0);\n dp[2] = 2;\n dp[3] = 3;\n \n for (int i = 4; i <= n; ++i) {\n dp[i] = max(dp[i - 2] * 2, dp[i - 3] * 3);\n }\n \n return dp[n];\n }\n};\n\n``` | 4 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
easy solution | integer-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if(n<=3):\n return n-1\n n3=n//3\n r3=n%3\n if(r3==0):\n return 3**n3\n if(r3==1):\n r3=4\n n3-=1\n return r3*(3**n3)\n``` | 4 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
💯Faster✅💯 Lesser✅4 Methods🔥Simple Math🔥Dynamic Programming🔥Greedy Approach🔥Memoization | integer-break | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 4 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \n- The goal is to find the maximum product that can be obtained for any given positive integer n.\n\n- Here are some key points to understand about the problem:\n - You must break n into at least two parts, meaning that n itself cannot be one of the parts.\n - The parts into which n is broken must be positive integers, which means they are greater than zero.\n - The problem does not specify how many parts n should be broken into, but you need to determine the number and values of these parts to maximize their product.\n - You need to find an optimal strategy to break n into parts to maximize the product, and this often involves some mathematical analysis and dynamic programming techniques.\n - Solving this problem requires finding an algorithm or approach that determines the best way to break a given integer n into parts and calculates the maximum product efficiently. Various techniques, such as dynamic programming, mathematical analysis, and greedy algorithms, can be used to solve this problem, as described below.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering four different methods to solve this problem:\n1. Dynamic Programming (Bottom-Up)\n2. Dynamic Programming (Top-Down with Memoization)\n3. Greedy Approach\n4. Mathematical Approach\n\n# 1. Dynamic Programming (Bottom-Up): \n\n- Create an array dp of size n+1 to store the maximum product for each integer from 1 to n.\n- Initialize dp[1] = 1 since the maximum product for 1 is 1.\n- Iterate from i = 2 to n and for each i, iterate from j = 1 to i-1.\n- Calculate dp[i] as the maximum of dp[i], j * (i - j), and j * dp[i - j].\n- The final answer is dp[n].\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n^2)\n\n- \uD83D\uDE80 Space Complexity: O(n)\n\n# Code\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n dp = [0] * (n + 1)\n dp[1] = 1\n for i in range(2, n + 1):\n dp[i] = -float(\'inf\')\n for j in range(1, i):\n dp[i] = max(dp[i], j * (i - j), j * dp[i - j])\n return dp[n]\n```\n```Java []\nclass Solution {\n public int integerBreak(int n) {\n if (n <= 1) {\n return 0;\n }\n int[] dp = new int[n + 1];\n dp[1] = 1;\n for (int i = 2; i <= n; i++) {\n for (int j = 1; j < i; j++) {\n dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));\n }\n }\n return dp[n];\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n vector<int> dp(n + 1, 0);\n dp[1] = 1;\n for (int i = 2; i <= n; ++i) {\n for (int j = 1; j < i; ++j) {\n dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));\n }\n }\n return dp[n];\n }\n};\n```\n```C []\nint integerBreak(int n) {\n if (n < 2) {\n return 0;\n }\n int dp[n + 1];\n dp[1] = 1;\n for (int i = 2; i <= n; i++) {\n dp[i] = 0;\n for (int j = 1; j < i; j++) {\n dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));\n }\n }\n return dp[n];\n}\n```\n# 2. Dynamic Programming (Top-Down with Memoization):\n- Create a memoization table memo of size n+1 to store already computed values.\n- Create a recursive function maxProduct(n) to calculate the maximum product.\n- Inside the function, if n is in memo, return memo[n].\n- Otherwise, calculate memo[n] by iterating through possible splits and taking the maximum.\n- Return memo[n] as the result.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n^2)\n\n- \uD83D\uDE80 Space Complexity: O(n) (for the memoization table)\n\n# Code\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n memo = [-1] * (n + 1)\n def maxProduct(k):\n if memo[k] != -1:\n return memo[k]\n if k == 1:\n return 1\n result = -float(\'inf\')\n for i in range(1, k):\n result = max(result, i * maxProduct(k - i), i * (k - i))\n memo[k] = result\n return result\n return maxProduct(n)\n```\n```Java []\nclass Solution {\n public int integerBreak(int n) {\n if (n <= 1) {\n return 0;\n }\n int[] memo = new int[n + 1];\n return maxProduct(n, memo);\n }\n \n private int maxProduct(int n, int[] memo) {\n if (n == 2) {\n return 1;\n }\n if (memo[n] != 0) {\n return memo[n];\n }\n int max = 0;\n for (int i = 1; i < n; i++) {\n max = Math.max(max, Math.max(i * (n - i), i * maxProduct(n - i, memo)));\n }\n memo[n] = max;\n return max;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n vector<int> memo(n + 1, -1);\n return maxProduct(n, memo);\n }\n\nprivate:\n int maxProduct(int n, vector<int>& memo) {\n if (n == 1) return 1;\n if (memo[n] != -1) return memo[n];\n int maxProd = 0;\n for (int i = 1; i < n; ++i) {\n maxProd = max(maxProd, max(i * (n - i), i * maxProduct(n - i, memo)));\n }\n memo[n] = maxProd;\n return maxProd;\n }\n};\n```\n```C []\nint memo[101]; \n\nint maxProduct(int n) {\n if (n <= 2) {\n return 1;\n }\n if (memo[n] != 0) {\n return memo[n];\n }\n int max = 0;\n for (int i = 1; i <= n - 1; i++) {\n int product = i * (n - i);\n if (product > max) {\n max = product;\n }\n product = i * maxProduct(n - i);\n if (product > max) {\n max = product;\n }\n }\n memo[n] = max;\n return max;\n}\n\nint integerBreak(int n) {\n if (n < 2) {\n return 0;\n }\n for (int i = 0; i <= n; i++) {\n memo[i] = 0;\n }\n return maxProduct(n);\n}\n```\n# 3. Greedy Approach:\n - If n is less than or equal to 3, return n - 1 as the maximum product (special cases).\n- Initialize a variable result to 1.\n- While n is greater than 4:\n - Multiply result by 3.\n - Subtract 3 from n.\n- Multiply result by n to get the final result.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(1)\n\n- \uD83D\uDE80 Space Complexity: O(1)\n\n# Code\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n == 2:\n return 1\n if n == 3:\n return 2\n result = 1\n while n > 4:\n result *= 3\n n -= 3\n return result * n\n```\n```Java []\nclass Solution {\n public int integerBreak(int n) {\n if (n <= 1) {\n return 0; \n }\n if (n == 2) {\n return 1;\n }\n if (n == 3) {\n return 2;\n }\n int result = 1;\n while (n > 4) {\n result *= 3;\n n -= 3;\n }\n result *= n;\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n <= 3) {\n return n - 1;\n }\n int result = 1;\n while (n > 4) {\n result *= 3;\n n -= 3;\n }\n result *= n;\n return result;\n }\n};\n```\n```C []\nint integerBreak(int n) {\n if (n < 2) {\n return 0;\n }\n if (n == 2) {\n return 1;\n }\n if (n == 3) {\n return 2;\n }\n int product = 1;\n while (n > 4) {\n product *= 3;\n n -= 3;\n }\n product *= n;\n return product;\n}\n```\n# 4. Mathematical Approach:\n - If n is less than or equal to 3, return n - 1 as the maximum product (special cases).\n- Calculate the quotient q when dividing n by 3.\n- Calculate the remainder r when dividing n by 3.\n- If r is 0, return 3^q.\n- If r is 1, return (3^(q-1)) * 4.\n- If r is 2, return (3^q) * 2.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(1)\n\n- \uD83D\uDE80 Space Complexity: O(1)\n\n# Code\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n == 2:\n return 1\n if n == 3:\n return 2=\n q = n // 3\n r = n % 3\n if r == 0:\n return 3 ** q\n elif r == 1:\n return (3 ** (q - 1)) * 4\n else:\n return (3 ** q) * 2\n```\n```Java []\nclass Solution {\n public int integerBreak(int n) {\n if (n <= 1) {\n return 0;\n }\n if (n == 2) {\n return 1;\n }\n if (n == 3) {\n return 2;\n }\n int quotient = n / 3;\n int remainder = n % 3;\n if (remainder == 0) {\n return (int) Math.pow(3, quotient);3\n } else if (remainder == 1) {\n return (int) (Math.pow(3, quotient - 1) * 4);1\n } else {\n return (int) (Math.pow(3, quotient) * 2);\n }\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n <= 3) {\n return n - 1;\n }\n int quotient = n / 3;\n int remainder = n % 3;\n if (remainder == 0) {\n return pow(3, quotient);\n } else if (remainder == 1) {\n return pow(3, quotient - 1) * 4;\n } else {\n return pow(3, quotient) * 2;\n }\n }\n};\n\n```\n```C []\nint integerBreak(int n) {\n if (n < 2) {\n return 0;\n }\n if (n == 2) {\n return 1;\n }\n if (n == 3) {\n return 2; \n }\n int quotient = n / 3;\n int remainder = n % 3;\n if (remainder == 0) {\n return pow(3, quotient);\n } else if (remainder == 1) {\n return 4 * pow(3, quotient - 1);\n } else {\n return 2 * pow(3, quotient);\n }\n}\n```\n# \uD83C\uDFC6Conclusion: \nThe mathematical approach and the greedy approach are the most efficient in terms of time and space complexity. The mathematical approach is especially efficient as it doesn\'t require any loops or recursion and can directly compute the result based on the mathematical properties of the problem.\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 86 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
🚀 100% || DP Solution Then Math || Explained Intuition 🚀 | integer-break | 1 | 1 | # Problem Description\n\nGiven a positive integer `n`, the **task** is to break it into the sum of `k` positive integers, where $$k >= 2$$, in a way that **maximizes** their product. Return the **maximum** product achievable.\n\n- **Constraints:**\n - `2 <= n <= 58`\n\nSeem tough? \uD83E\uDD14\n\n---\n\n\n\n# Intuition\nHi there\uD83D\uDE03\n\nLet\'s take a look on today\'s problem.\uD83D\uDC40\nSimply, the task is to find maximum product for the number that sum up to `n`.\nActually, My team encountered this problem in **EgyptianCPC** **2022** **Qualifications** \uD83D\uDE02 \n\nHow can we think about a solution for this problem?\uD83E\uDD14\n- We can notice two things: \uD83E\uDD29\n - **First**, The **constraints** for the problem is not large its only `58`\n - **Second**, The task is to **maximize** some product. \u2197\n\nInteresting, I think it seems a task for our hero **Dynamic Programming**.\uD83E\uDDB8\u200D\u2642\uFE0F\nYES, **Dynamic Programming** can be used to **maximum** the desired product for the input number.\nIt has two methods **Top-Down** & **Bottom-Up**.\n\nToday, I only implemented **Bottom-Up** since anyone of them is easy to be implemented once you understood the other.\n\nAlright, Let\'s talk about some **implementation** details for **DP**.\n- **Base Cases** for **maximum** product?\n - if `n = 2` then maximum product is `1` which is `1 + 1`.\n - if `n = 3` then maximum product is `2` which is `2 + 1`.\n\n- **Base Cases** for **DP table**?\n - if `n = 1` then its entry is `1` since if the remaining in the sum is `1` then we will multiply by `1`.\n - if `n = 2` then its entry is `2` since if the remaining in the sum is `2` then we will multiply by `2`.\n - if `n = 3` then its entry is `3` since if the remaining in the sum is `3` then we will multiply by `3`.\n```\nEX: n = 5\nsum = 3 + 2 \nproduct = dp[3] * dp[2] = 6\n```\n\n- **Inner loop** for the DP solution ?\nAs we will see, we will loop from `1` to `num / 2`. Why not from `1` to `num`?\nsince any number after `num / 2` will be **redundant**.\n```\nEX: n = 10\n10 = 6 + 4 = 4 + 6\n10 = 7 + 3 = 3 + 7\n```\n\n**OKKKKKK**\n\nAfter seeing the **DP** Solution can we do **better** ?\uD83E\uDD14\nActually **YES** !\uD83E\uDD2F\uD83E\uDD2F\uD83E\uDD2F\nLet\'s look an **observation** from the DP Solution \uD83D\uDC40\n\n\n\nThis list is what I **printed** in my **CLion IDE** after implementing the **DP** Solution for number `20`.\nCan we see some pattern ?\nYES, the answer is always **utilizing** the number `3` but how?\nIt tries to multiply with `3s` always with taking into **considration** the remainder.\nAlso, How? \uD83D\uDE02\n\n**Case1:** For remainder `0`, The sum is only **sum** of `3s` and product is **product** of these `threes`\n```\nEX: n = 9\nsum = 3 + 3 + 3\nproduct = 27\n```\n```\nEX: n = 15\nsum = 3 + 3 + 3 + 3 + 3\nproduct = 243\n```\n\n**Case2:** For remainder `1`, Since there is a remainder we want to utilize it. **not** by summing all the `3s` we can, but we can let one of these `3s` **away** and **replace** it with `4`.\n```\nEX: n = 10\nsum = 3 + 3 + 4\nproduct = 36\n```\n```\nEX: n = 16\nsum = 3 + 3 + 3 + 3 + 4\nproduct = 324\n```\n\n**Case3:** For remainder `2`, Simply we can seek for the all numbers of `3s` we can then **multiply** by the remaining `2`.\n```\nEX: n = 11\nsum = 3 + 3 + 3 + 2\nproduct = 54\n```\n```\nEX: n = 17\nsum = 3 + 3 + 3 + 3 + 3 + 2\nproduct = 486\n```\n\nAnd this is simply the **Math** solution. The interesting thing that to fully understand it you must **pass** by the **DP** solution since we are sure that **DP** will give you the **optimal** answer.\n\n\n\n## **EDIT**\nThanks to [@lixx2100](/lixx2100), He added very interesting proof in the discussions section.\n\nAssuming we will break **n** into **(n / x)** x\'s then the product will be **x^(n / x)** and this is what we want to **maximize**.\nLet\'s take it\'s **derivative** and equal it to **zero** to find the value of **x** that **maximize** the equation.\n\nThe **derivative** will be **n * x^(n/x-2) * (1 - ln(x))**.\nequatin **n * x^(n/x-2) * (1 - ln(x)) = 0**. will eventually make us end with **x = e** (Euler\'s Number).\nWhich means that the result of the equation **x^(n / x)** will **increase** until **x** reaches **e** and there will be its **maximum** after that it will begin to **decrease**.\n\nSeems nice till now! But we need **x** to be an integer ?\nsince we have **2 < e < 3** then we have to options to use **2** or **3**. but since **3** is the **closer** number to **e** then we will use it since it will give it **greater** value than **2**.\n\nand of course there will be **corner cases** we discussed above considering the **remainder** of the required number to be handeled.\n\n\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n\n# Proposed Approaches\n## DP\n1. **Base Cases:**\n - If `n` is `2`, return `1`.\n - If `n` is `3`, return `2`.\n2. **Create** a DP table (array) called `maxProduct` of size `n + 1` to store the `maximum` products for each number up to `n`.\n3. **Base Cases For the Table:**\n - Set `maxProduct[1]` to 1.\n - Set `maxProduct[2]` to 2.\n - Set `maxProduct[3]` to 3.\n4. **DP Iteration:**\n - Iterate from `4` to `n`.\n - For each number `num` from `4` to `n`:\n - Initialize a variable `maxProductForNum` to `0`.\n - Iterate through smaller numbers from `1` to `num / 2`:\n - Calculate the product of the **smaller** number and its **complement** (difference from `num`).\n - Update `maxProductForNum` to be the **maximum** of the current value and the calculated product.\n - Update `maxProduct[num]` with `maxProductForNum`.\n5. Return `maxProduct[n]` as the maximum product achievable for the given `n`.\n\n## Complexity\n- **Time complexity:** $$O(N^2)$$\nSince we are using **nested** for loops **one** is iterating from `4` to `n` and the **inner** for loop is iterating from `1` to `num / 2` then complexity is `N * N / 2` which is `O(N^2)`.\n- **Space complexity:** $$O(N)$$\nSince we are an array to store the **best** solution for all number up to `N` then complexity is `O(N)`.\n\n---\n## Math\n1. **Base Cases:**\n - If `n` is less than 4, return `n - 1`.\n2. Calculate **Number of Threes** by Calculating the integer division of `n` by `3` and store it in `numOfThrees`.\n3. Calculate Initial Product by Initializing `productOfThrees` with the result of raising `3` to the power of `numOfThrees`.\n4. **Adjust Product Based on Remainder:**\n - If `n` modulo `3` equals `1`:\n - Update `productOfThrees` by **dividing** by `3` and then **multiplying** by `4`.\n - Else if `n` modulo `3` equals `2`:\n - Update `productOfThrees` by **multiplying** by `2`.\n5. Return the final value of `productOfThrees` as the **maximum** product achievable for the given `n`.\n\n## Complexity\n- **Time complexity:** $$O(log(N))$$\nSince we are calculating the power for the answer which is `O(log(N))` using **fast power algorithm** (I will put refrence for it in the comments).\n- **Space complexity:** $$O(1)$$\nSince we are only storing couple of constant variables.\n\n\n\n---\n\n\n\n# Code\n## DP\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n // handle base cases\n if (n == 2) return 1;\n if (n == 3) return 2;\n\n // Dynamic programming table to store maximum products\n vector<int> maxProduct(n + 1, 0);\n\n // Base cases for numbers 1, 2, and 3 -only for computing for rest of numbers-\n maxProduct[1] = 1;\n maxProduct[2] = 2;\n maxProduct[3] = 3;\n\n // Fill the dynamic programming table for larger numbers\n for (int num = 4; num <= n; ++num) {\n int maxProductForNum = 0;\n // Iterate through smaller numbers to calculate the maximum product\n for (int subNum = 1; subNum <= num / 2; ++subNum) {\n maxProductForNum = max(maxProductForNum, maxProduct[subNum] * maxProduct[num - subNum]);\n }\n // Update the maximum product for the current number\n maxProduct[num] = maxProductForNum;\n }\n\n return maxProduct[n];\n }\n};\n```\n```Java []\nclass Solution {\n public int integerBreak(int n) {\n // Handle base cases\n if (n == 2) return 1;\n if (n == 3) return 2;\n\n // Dynamic programming table to store maximum products\n int[] maxProduct = new int[n + 1];\n\n // Base cases for numbers 1, 2, and 3 -only for computing for the rest of the numbers-\n maxProduct[1] = 1;\n maxProduct[2] = 2;\n maxProduct[3] = 3;\n\n // Fill the dynamic programming table for larger numbers\n for (int num = 4; num <= n; ++num) {\n int maxProductForNum = 0;\n // Iterate through smaller numbers to calculate the maximum product\n for (int subNum = 1; subNum <= num / 2; ++subNum) {\n maxProductForNum = Math.max(maxProductForNum, maxProduct[subNum] * maxProduct[num - subNum]);\n }\n // Update the maximum product for the current number\n maxProduct[num] = maxProductForNum;\n }\n\n return maxProduct[n];\n }\n}\n```\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n # Handle base cases\n if n == 2:\n return 1\n if n == 3:\n return 2\n\n # Dynamic programming table to store maximum products\n max_product = [0] * (n + 1)\n\n # Base cases for numbers 1, 2, and 3 -only for computing for the rest of the numbers-\n max_product[1] = 1\n max_product[2] = 2\n max_product[3] = 3\n\n # Fill the dynamic programming table for larger numbers\n for num in range(4, n + 1):\n max_product_for_num = 0\n # Iterate through smaller numbers to calculate the maximum product\n for sub_num in range(1, num // 2 + 1):\n max_product_for_num = max(max_product_for_num, max_product[sub_num] * max_product[num - sub_num])\n # Update the maximum product for the current number\n max_product[num] = max_product_for_num\n\n return max_product[n]\n```\n\n\n---\n\n## Math\n\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n // Base cases: for n < 4, return n-1\n if (n < 4)\n return n - 1;\n\n // Calculate the number of times 3 can be multiplied\n int numOfThrees = n / 3;\n\n // Initialize the answer with the product of 3 raised to numOfThrees\n long long productOfThrees = pow(3, numOfThrees);\n\n // Adjust the product based on the remainder when divided by 3\n if (n % 3 == 1) {\n // If remainder is 1, you can multiply by 4 instead of 3\n productOfThrees /= 3;\n productOfThrees *= 4;\n } else if (n % 3 == 2) {\n // If remainder is 2, multiply by 2\n productOfThrees *= 2;\n }\n\n // Return the maximum product\n return productOfThrees;\n }\n};\n```\n```Java []\npublic class Solution {\n public int integerBreak(int n) {\n // Base cases: for n < 4, return n-1\n if (n < 4)\n return n - 1;\n\n // Calculate the number of times 3 can be multiplied\n int numOfThrees = n / 3;\n\n // Initialize the answer with the product of 3 raised to numOfThrees\n long productOfThrees = (long) Math.pow(3, numOfThrees);\n\n // Adjust the product based on the remainder when divided by 3\n if (n % 3 == 1) {\n // If remainder is 1, you can multiply by 4 instead of 3\n productOfThrees /= 3;\n productOfThrees *= 4;\n } else if (n % 3 == 2) {\n // If remainder is 2, multiply by 2\n productOfThrees *= 2;\n }\n\n // Return the maximum product\n return (int) productOfThrees;\n }\n}\n```\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n # Base cases: for n < 4, return n-1\n if n < 4:\n return n - 1\n\n # Calculate the number of times 3 can be multiplied\n num_of_threes = n // 3\n\n # Initialize the answer with the product of 3 raised to num_of_threes\n product_of_threes = 3 ** num_of_threes\n\n # Adjust the product based on the remainder when divided by 3\n if n % 3 == 1:\n # If remainder is 1, you can multiply by 4 instead of 3\n product_of_threes //= 3\n product_of_threes *= 4\n elif n % 3 == 2:\n # If remainder is 2, multiply by 2\n product_of_threes *= 2\n\n # Return the maximum product\n return product_of_threes\n```\n\n\n\n\n\n\n\n\n\n | 57 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
easy solution ✅ beats 93.57% ✅ python 3.0 ✅ hash map | integer-break | 0 | 1 | # Intuition\nwhat if we used a hashmap??\n\n# Approach\nimplement a hashmap!!\n\n# Complexity\n- Time complexity:\nidk\n\n- Space complexity:\nprobably pretty low\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n myDict = {\n 2:1,\n 3:2,\n 4:4,\n 5:6,\n 6:9,\n 7:12,\n 8:18,\n 9:27,\n 10:36,\n 11:54,\n 12:81,\n 13:108,\n 14:162,\n 15:243,\n 16:324,\n 17:486,\n 18:729,\n 19:972,\n 20:1458,\n 21:2187,\n 22:2916,\n 23:4374,\n 24:6561,\n 25:8748,\n 26:13122,\n 27:19683,\n 28:26244,\n 29:39366,\n 30:59049,\n 31:78732,\n 32:118098,\n 33:177147,\n 34:236196,\n 35:354294,\n 36:531441,\n 37:708588,\n 38:1062882,\n 39:1594323,\n 40:2125764,\n 41:3188646,\n 42:4782969,\n 43:6377292,\n 44:9565938,\n 45:14348907,\n 46:19131876,\n 47:28697814,\n 48:43046721,\n 49:57395628,\n 50:86093442,\n 51:129140163\n }\n\n return myDict[n]\n \n``` | 2 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
O(log n) time with O(1) space complexity, math solution with proofs (don't be afraid :D ) | integer-break | 0 | 1 | # Intuition\n\n1. **Small Numbers**: For small numbers like 2 and 3, breaking them up doesn\'t help, as $$ 2 = 1 + 1 \\rightarrow 1 \\times 1 = 1 $$ and $$ 3 = 1 + 2 \\rightarrow 1 \\times 2 = 2 $$, which don\'t yield a product greater than the numbers themselves.\n\n2. **Composite Numbers**: For composite numbers like 4, you can break it into $$ 2 + 2 \\rightarrow 2 \\times 2 $$, and the product becomes 4, which is the same as the original number. Similarly, 6 can be $$ 3 + 3 \\rightarrow 3 \\times 3 $$ or $$ 2+2+2 \\rightarrow 2 \\times 2 \\times 2 $$, yielding 9 vs 8, which is greater than 6.\n\n3. **Mathematical Insight**: When you break a number into its constituent parts, the product tends to be maximized when the parts are as equal as possible. This is a mathematical property and can be proven using calculus (e.g. the [Arithmetic Mean-Geometric Mean Inequality](https://www.wikiwand.com/en/AM-GM_Inequality)). See Extra Proof below.\n\n4. **Special Case for 3**: You\'ll find that breaking numbers into 3s (as much as possible) tends to give the maximum product. This is because $$ 3 \\times 3 > 2 \\times 2 \\times 2 $$. See Proof below.\n\n\n# Approach\n\nGiven the mathematical insights above, we can solve this problem more efficiently without using dynamic programming.\n\n1. If $$ n $$ is less than or equal to 3, return $$ n-1 $$ (because for these cases, $$ n-1 $$ will give the maximum product).\n \n2. Divide $$ n $$ by 3 as many times as possible until $$ n $$ is no longer divisible by 3 or is less than or equal to 4.\n\n3. Multiply the remaining number with the product of all the 3s.\n\n# Proof\n### Maximizing the Product\n\nSuppose you have a number $$ n $$ and you want to split it into $$ k $$ equal parts of $$ \\frac{n}{k} $$. The product of these $$ k $$ numbers would be $$ \\left(\\frac{n}{k}\\right)^k $$.\n\nTo maximize this product, we take the derivative with respect to $$ k $$ and set it to zero:\n\n$$\n\\begin{aligned}\nf(k) &= \\left(\\frac{n}{k}\\right)^k, \\\\\nf\'(k) &= 0.\n\\end{aligned}\n$$\n\n#### Differentiation\n\n1. Differentiate $$ f(k) = \\left(\\frac{n}{k}\\right)^k $$ with respect to $$ k $$ using logarithmic differentiation.\n\n$$\n\\begin{aligned}\n\\ln(f(k)) &= k \\ln\\left(\\frac{n}{k}\\right), \\\\\n\\frac{d\\ln(f(k))}{dk} &= \\ln\\left(\\frac{n}{k}\\right) + k \\left(-\\frac{1}{k}\\right), \\\\\n\\frac{1}{f(k)} \\frac{df(k)}{dk} &= \\ln\\left(\\frac{n}{k}\\right) - 1, \\\\\n\\frac{df(k)}{dk} &= \\left(\\frac{n}{k}\\right)^k (\\ln(n) - \\ln(k) - 1).\n\\end{aligned}\n$$\n\n2. To find the maximum, we set $$ \\frac{df(k)}{dk} = 0 $$:\n\n$$\n\\begin{aligned}\n\\ln(n) - \\ln(k) - 1 &= 0, \\\\\n\\ln\\left(\\frac{n}{k}\\right) &= 1, \\\\\n\\frac{n}{k} &= e, \\\\\nk &= \\frac{n}{e}.\n\\end{aligned}\n$$\n\n### Why 3 is Magical\n\nNow, it\'s not practical to break $$ n $$ into $$ \\frac{n}{e} $$ pieces unless $$ \\frac{n}{e} $$ is an integer. But this gives us an insight: breaking $$ n $$ into pieces of size around $$ e $$ (2.71828...) will yield a high product. Since we can only break $$ n $$ into integer pieces, the closest integers to $$ e $$ are 2 and 3.\n\nLet\'s compare:\n\n- $$ 2^2 = 4 $$\n- $$ 3^2 = 9 $$\n\nOr, for a larger value:\n\n- $$ 2^3 = 8 $$\n- $$ 3^3 = 27 $$\n\nIt\'s evident that 3 yields a larger product. Also, dividing by 3 reduces the number more slowly, allowing for more numbers in the product. Thus, 3 is the "magical" number that maximizes the product when an integer is broken down into $$ k $$ positive integers.\n\n\n# Complexity\n- Time complexity:\n$$O(log(n))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n <= 3:\n return n - 1\n \n product = 1\n while n > 4:\n product *= 3\n n -= 3\n \n product *= n\n \n return product\n```\n\n\n\n### Extra Proof: equal constitutent parts maximise the product\nSuppose you have a positive integer $$ n $$ that you want to divide into $$ k $$ parts $$ x_1, x_2, \\ldots, x_k $$ such that their sum is $$ n $$:\n\n$$\nx_1 + x_2 + \\ldots + x_k = n\n$$\n\nWe want to maximize the product $$ P = x_1 \\times x_2 \\times \\ldots \\times x_k $$.\n\nUsing the AM-GM inequality, we get:\n\n$$\n\\frac{x_1 + x_2 + \\ldots + x_k}{k} \\geq \\sqrt[k]{x_1 \\times x_2 \\times \\ldots \\times x_k}\n$$\n\n$$\n\\frac{n}{k} \\geq \\sqrt[k]{P}\n$$\n\n$$\nP \\leq \\left( \\frac{n}{k} \\right)^k\n$$\n\nThe inequality tells us that for a fixed $$ k $$, the maximum product $$ P $$ we can get is $$ \\left( \\frac{n}{k} \\right)^k $$, and this maximum is achieved when all $$ x_i $$ are equal, i.e., $$ x_i = \\frac{n}{k} $$ for all $$ i $$.\n\nTherefore, to maximize the product, it\'s best to divide $$ n $$ into $$ k $$ equal parts.\n\n | 24 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
✅ 93.65% Why 3s? | integer-break | 1 | 1 | # Intuition\nWhen given an integer `n`, our goal is to break it into sums of smaller integers such that their product is maximized. At first, it might seem that a brute-force approach of trying all combinations is the answer. However, a more in-depth analysis of the numbers reveals patterns that can be utilized to achieve the result more efficiently. \n\n## Live Coding & Expalin\nhttps://youtu.be/tDZAQM3VMu8?si=MIhHp-nL0EybsyOO\n\n# Approach\n1. **Why 3s?** By testing various numbers, it becomes evident that the number 3 plays a significant role in maximizing the product. For example:\n - `4 = 2 + 2` (product = 4)\n - `5 = 2 + 3` (product = 6)\n - `6 = 3 + 3` (product = 9)\n - `7 = 3 + 2 + 2` (product = 12)\n - `8 = 3 + 3 + 2` (product = 18)\n - `9 = 3 + 3 + 3` (product = 27)\n \n2. **Why not 4s?** Anytime we have a 4, we can always split it into two 2s, which will give a better or equal product.\n\n3. **Handling Remainders:** When `n` is divided by 3, the remainder can be 0, 1, or 2:\n - Remainder 0: `n` is a perfect multiple of 3. We break `n` entirely into 3s.\n - Remainder 1: It\'s better to take a 3 out and add a 4 (which is split as two 2s). This is because the product of three numbers, 3, 1, and `n-4`, is less than the product of the two numbers, 4 and `n-4`.\n - Remainder 2: We simply multiply the leftover 2 with the product of all 3s.\n\n# Complexity\n- **Time complexity:** `O(log n)`. This is because our primary operation involves raising 3 to the power of `count_of_3s` which, in Python, takes `O(log n)` time.\n \n- **Space complexity:** `O(1)`. We only use a constant amount of extra space regardless of the input size.\n\n# Code\n```Python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n == 2: return 1\n if n == 3: return 2\n \n count_of_3s, remainder = divmod(n, 3)\n \n if remainder == 0:\n return 3 ** count_of_3s\n elif remainder == 1:\n return 3 ** (count_of_3s - 1) * 4\n else: \n return 3 ** count_of_3s * 2\n```\n``` C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n == 2) return 1;\n if (n == 3) return 2;\n \n int count_of_3s = n / 3;\n int remainder = n % 3;\n \n if (remainder == 0) {\n return pow(3, count_of_3s);\n } else if (remainder == 1) {\n return pow(3, count_of_3s - 1) * 4;\n } else {\n return pow(3, count_of_3s) * 2;\n }\n }\n};\n```\n``` Java []\npublic class Solution {\n public int integerBreak(int n) {\n if (n == 2) return 1;\n if (n == 3) return 2;\n\n int count_of_3s = n / 3;\n int remainder = n % 3;\n\n if (remainder == 0) {\n return (int) Math.pow(3, count_of_3s);\n } else if (remainder == 1) {\n return (int) Math.pow(3, count_of_3s - 1) * 4;\n } else {\n return (int) Math.pow(3, count_of_3s) * 2;\n }\n }\n}\n```\n``` Go []\nfunc integerBreak(n int) int {\n if n == 2 { return 1 }\n if n == 3 { return 2 }\n \n count_of_3s := n / 3\n remainder := n % 3\n\n if remainder == 0 {\n return int(math.Pow(3, float64(count_of_3s)))\n } else if remainder == 1 {\n return int(math.Pow(3, float64(count_of_3s - 1))) * 4\n } else {\n return int(math.Pow(3, float64(count_of_3s))) * 2\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn integer_break(n: i32) -> i32 {\n if n == 2 { return 1; }\n if n == 3 { return 2; }\n\n let count_of_3s = n / 3;\n let remainder = n % 3;\n\n if remainder == 0 {\n return (3 as i32).pow(count_of_3s as u32);\n } else if remainder == 1 {\n return (3 as i32).pow((count_of_3s - 1) as u32) * 4;\n } else {\n return (3 as i32).pow(count_of_3s as u32) * 2;\n }\n }\n}\n```\n``` JavaScript []\nvar integerBreak = function(n) {\n if (n === 2) return 1;\n if (n === 3) return 2;\n\n let count_of_3s = Math.floor(n / 3);\n let remainder = n % 3;\n\n if (remainder === 0) {\n return 3 ** count_of_3s;\n } else if (remainder === 1) {\n return 3 ** (count_of_3s - 1) * 4;\n } else {\n return 3 ** count_of_3s * 2;\n }\n};\n```\n``` PHP []\nclass Solution {\n function integerBreak($n) {\n if ($n == 2) return 1;\n if ($n == 3) return 2;\n\n $count_of_3s = intdiv($n, 3);\n $remainder = $n % 3;\n\n if ($remainder == 0) {\n return pow(3, $count_of_3s);\n } elseif ($remainder == 1) {\n return pow(3, $count_of_3s - 1) * 4;\n } else {\n return pow(3, $count_of_3s) * 2;\n }\n }\n}\n```\n``` C# []\npublic class Solution {\n public int IntegerBreak(int n) {\n if (n == 2) return 1;\n if (n == 3) return 2;\n\n int count_of_3s = n / 3;\n int remainder = n % 3;\n\n if (remainder == 0) {\n return (int) Math.Pow(3, count_of_3s);\n } else if (remainder == 1) {\n return (int) Math.Pow(3, count_of_3s - 1) * 4;\n } else {\n return (int) Math.Pow(3, count_of_3s) * 2;\n }\n }\n}\n\n```\n\n# Why It Works?\nOur solution is based on the observation that breaking the number into as many 3s as possible (with exceptions mentioned above) gives the highest product. This is due to the mathematical properties of numbers and the product operation. When multiplying numbers, the more we can distribute the value equally among the multiplicands, the larger the product becomes. 3 is the optimal number for this task.\n\n# What We Learned?\nThis problem teaches us the importance of mathematical patterns and how they can be applied to derive an efficient solution. Instead of resorting to brute force or dynamic programming, sometimes a clever insight, based on the properties of numbers, can lead us to an elegant and optimal answer.\n\n# Performance\n\n| Language | Execution Time (ms) | Memory (MB) |\n|------------|---------------------|-------------|\n| Go | 0 ms | 1.9 MB |\n| Rust | 0 ms | 2.2 MB |\n| Java | 0 ms | 39.2 MB |\n| C++ | 0 ms | 6.5 MB |\n| PHP | 3 ms | 19.2 MB |\n| C# | 17 ms | 26.9 MB |\n| Python3 | 32 ms | 16.1 MB |\n| JavaScript | 43 ms | 41.5 MB |\n\n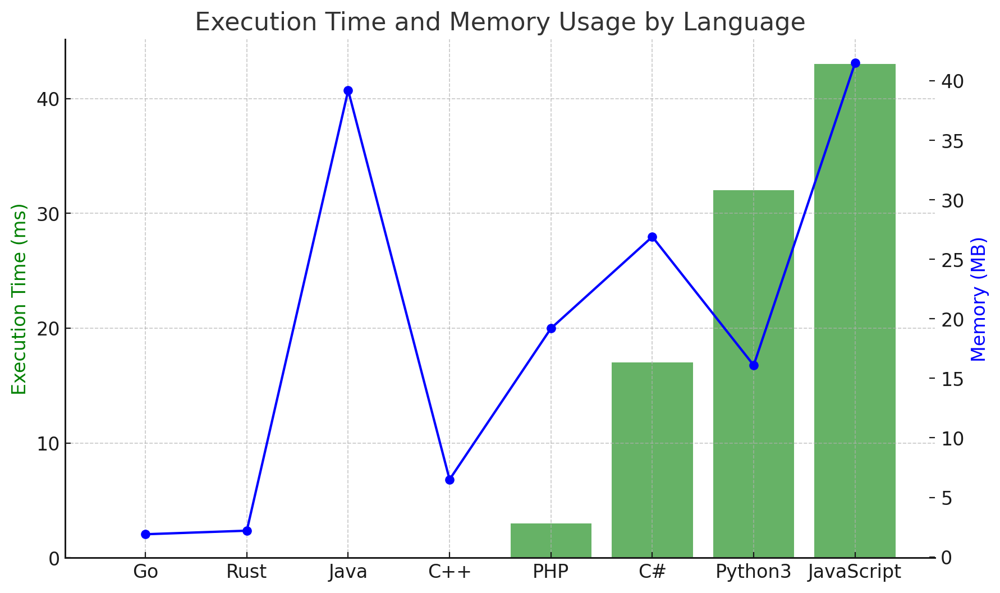\n | 68 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
【Video】Give me 10 minutes - How we think about a solution - No difficult mathematics | integer-break | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n\n# Intuition\nCreate 3 as many as possible.\n\n---\n\n# Solution Video\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\nhttps://youtu.be/q3EZpCSn6lY\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Integer Break\n`0:16` How we think about a solution\n`5:08` Demonstrate solution with an example\n`9:23` Coding\n`12:22` Time Complexity and Space Complexity\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,617\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution.\n\nWhen looks like we have a lot of answers, I always start with the simplest examples. Let\'s start from `n = 2 until 10` and `k >= 2`.\n\nWhen divided `2` into `1 + 1`, the product does not exceed `2`, so no further division is possible.\n\n```\n1 * 1 < 2\n```\n\nWhen divided `3` into `1 + 2`, the product does not exceed `3`, so no further division is possible.\n\n```\n1 * 1 * 1 < 3\n1 * 2 < 3\n```\n\n`4` can be divided into `2 + 2` (even though they are equal to `4`, we split for convenience).\n\n```\n1 * 1 * 1 * 1 < 4\n1 * 1 * 2 < 4\n2 * 2 = 4 \u2B50\uFE0F\n```\n\nSplitting `5` into `3 + 2` yields a higher product. `2` and `3` cannot be further divided based on the previous steps.\n\n```\n1 * 1 * 1 * 1 * 1 < 5\n1 * 1 * 1 * 2 < 5\n1 * 1 * 3 < 5\n1 * 2 * 2 < 5\n3 * 2 > 5 \u2B50\uFE0F\n4 * 1 < 5 (we can divide 4 into 2 * 2)\n```\n\nFrom examples above, we can divide the original numbers into small number from `4`.\n\nWhat is the biggest number after we break down the original number? It\'s `3` because It\'s the biggest and cannot be splitted into small numbers anymore.\n\nLet\'s comfirm with `6`. Focus on over `6` cases.\n```\n2 * 2 * 2 = 8\n3 * 3 = 9\n4 * 2 = 8 (= 2 * 2 * 2)\n```\n\nSplitting `6` into `3 + 3` yields a higher product.\n\n\n---\n\n\n\u2B50\uFE0F Points\n \nWe break down the original number because there is a pattern to get bigger number compared with the original number.\n\nFor example,\n```\nn = 5\n3 * 2 > 5\n\nLet\'s say we have another 2.\n6 * 2 > 5 * 2 (5 is original number)\n```\n\nThe biggest number which doesn\'t have the pattern to get bigger number by splitting is `3`. Look at case `3` above again.\n\nAs you can see, all the original numbers over 3 has the pattern. That\'s why we break down the original numbers and get `3` as many as possible.\n\nLook at more examples below.\n\n---\n\nFrom `7` to `10`,\n\nSplitting `7` into `3 + 2 + 2` yields a higher product. `3` and `2` cannot be further divided.\n\nSplitting `8` into `3 + 3 + 2` yields a higher product. `3` and `2` cannot be further divided.\n\nSplitting `9` into `3 + 3 + 3` yields a higher product. `3` cannot be further divided.\n\nSplitting `10` into `3 + 3 + 2 + 2` yields a higher product. `3` and `2` cannot be further divided.\n\n\n## How it works\n\nLet\'s see an example with `10`.\n\nWe try to create `3` as many as possible, so\n\n```\n10 // 3 = 3\n\nthrees: 3\nremainder: 1\n```\nEasy! Let\'s multiply all the numbers.\n```\n3 * 3 * 3 * 1 = 27 (1 is remainder)\n```\nWait! Description says when `n = 10`, output should be `36`.\n\nWhy this happened?\n\nWhen `n = 10`, output is `36`. but our answer is `27` which is `9 difference`. Let\'s simplify `3 * 3 * 3 * 1`.\n```\n9 * 3 * 1\n```\nLet\'s focus on `3 * 1` part. the reason why we get `27` is we have 3 nines right?\n```\n9 * 3 * 1\n\u2193\n9 * 3\n```\n\nBut what if we create `2 * 2` instead of `3 * 1`? we can do that because total of `2 + 2` and `3 + 1` is the same.\n\ntotal is the same but answer of multiplication is different `4` vs `3`.\n\nFrom the example, \n\n\n---\n\n\u2B50\uFE0F Points\n\nWhen we have `1` as a `remainder`, we will get bigger number if we borrow `1` from one of 3s and create `2 * 2` instead of `3 * 1`.\n\nSimply, we don\'t use `1` because `1` doesn\'t change an answer in multiplication. On the other hand, we know that `2` makes the number double.\n\n---\n\n\n\n---\n\n\n\u2B50\uFE0F In summary:\n\n1. Create as many threes as possible.\n2. When there\'s a remainder of 1, convert `3 * 1` to `2 * 2(or 4)`.\n\n\n---\n\nLet\'s see a real algorithm!\n\n\n**Algorithm Overview:**\n\n1. Check if n is 2 or 3 and return the appropriate value.\n2. Divide n into as many threes as possible and handle the remainder for maximizing the product.\n3. Multiply the result based on the division and the remainder.\n\n**Detailed Explanation:**\n\n1. **Check for n being 2 or 3:**\n - If \\(n\\) equals 2, return 1 (as specified in the problem).\n - If \\(n\\) equals 3, return 2 (as specified in the problem).\n\n2. **Divide n into as many threes as possible:**\n - Calculate the maximum number of threes that can be obtained from \\(n\\) using integer division (\\(n // 3\\)).\n - Calculate the remainder after dividing \\(n\\) by 3 (\\(n \\% 3\\)).\n\n3. **Handle remainder to maximize the product:**\n - If the remainder is 1:\n - Borrow one from a three to make two 2s by decrementing threes by 1 and setting remainder to 4.\n - If the remainder is 0:\n - Set remainder to 1 (no need to borrow).\n\n4. **Calculate the final product:**\n - Calculate the product by raising 3 to the power of threes (\\(3\\) raised to the power of \\(threes\\)) and multiplying by the remainder.\n\nHere\'s the provided code implementing the above steps:\n\n# Complexity\n- Time complexity:$$ O(log(threes))$$\n\nThe time complexity for raising a number to the power of another number depends on the method used for exponentiation. In the case of (3 ** threes), where threes is an integer, the time complexity is generally O(log(threes)) using the binary exponentiation (also known as exponentiation by squaring) algorithm.\n\nBinary exponentiation reduces the number of multiplications needed to compute an exponent by breaking down the exponent into a sum of powers of 2. This algorithm allows for more efficient calculations compared to a naive approach, which would require threes multiplications.\n\nHence, raising 3 to the power of threes (3 ** threes) typically has a time complexity of O(log(threes)) using efficient exponentiation algorithms.\n\n- Space complexity: $$O(1)$$\n\n```python []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n == 2:\n return 1\n if n == 3:\n return 2\n\n # Try to divide n into as many threes as possible\n threes = n // 3\n remainder = n % 3\n\n if remainder == 1:\n threes -= 1 # remove 3 * 1\n remainder = 4 # create 2 * 2\n elif remainder == 0:\n remainder = 1 # when remainder is 0, set 1 which doesn\'t affect your answer.\n\n return (3 ** threes) * remainder\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar integerBreak = function(n) {\n if (n === 2) {\n return 1;\n }\n if (n === 3) {\n return 2;\n }\n\n // Try to divide n into as many threes as possible\n let threes = Math.floor(n / 3);\n let remainder = n % 3;\n\n if (remainder === 1) {\n threes -= 1; // remove 3 * 1\n remainder = 4; // create 2 * 2\n } else if (remainder === 0) {\n remainder = 1; // when remainder is 0, set 1 which doesn\'t affect your answer.\n }\n\n return Math.pow(3, threes) * remainder; \n};\n```\n```java []\nclass Solution {\n public int integerBreak(int n) {\n if (n == 2) {\n return 1;\n }\n if (n == 3) {\n return 2;\n }\n\n // Try to divide n into as many threes as possible\n int threes = n / 3;\n int remainder = n % 3;\n\n if (remainder == 1) {\n threes -= 1; // remove 3 * 1\n remainder = 4; // create 2 * 2\n } else if (remainder == 0) {\n remainder = 1; // when remainder is 0, set 1 which doesn\'t affect your answer.\n }\n\n return (int) (Math.pow(3, threes) * remainder); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n == 2) {\n return 1;\n }\n if (n == 3) {\n return 2;\n }\n\n // Try to divide n into as many threes as possible\n int threes = n / 3;\n int remainder = n % 3;\n\n if (remainder == 1) {\n threes -= 1; // remove 3 * 1\n remainder = 4; // create 2 * 2\n } else if (remainder == 0) {\n remainder = 1; // when remainder is 0, set 1 which doesn\'t affect your answer.\n }\n\n return (int) (pow(3, threes) * remainder); \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge\nhttps://leetcode.com/problems/max-dot-product-of-two-subsequences/solutions/4143796/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n | 44 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Time - O(1) and no Extra space | Simple 1 line Solution | Beats 99% | 🔥🚀✅✅✅ | integer-break | 0 | 1 | # Code\n```C++ []\nclass Solution {\npublic:\n int integerBreak(int n) {\n return n == 2 ? 1 : n == 3 ? 2 : n % 3 == 0 ? pow(3, n / 3) : n % 3 == 1 ? 4 * pow(3, (int)(n / 3) - 1) : 2 * pow(3, (int)(n / 3));\n }\n};\n```\n```C []\nint integerBreak(int n) {\n return n == 2 ? 1 : n == 3 ? 2 : n % 3 == 0 ? pow(3, n / 3) : n % 3 == 1 ? 4 * pow(3, (int)(n / 3) - 1) : 2 * pow(3, (int)(n / 3));\n}\n```\n```python3 []\nclass Solution:\n def integerBreak(self, n: int) -> int:\n return 1 if n == 2 else 2 if n == 3 else 3 ** (n // 3) if not n % 3 else 4 * 3 ** (n // 3 - 1) if n % 3 == 1 else 2 * 3 ** (n // 3)\n```\n```Python []\nclass Solution(object):\n def integerBreak(self, n):\n return 1 if n == 2 else 2 if n == 3 else 3 ** (n // 3) if not n % 3 else 4 * 3 ** (n // 3 - 1) if n % 3 == 1 else 2 * 3 ** (n // 3)\n```\n | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Python Solution Beats 91% with Intuition | integer-break | 0 | 1 | # Intuition\nThe goal is the break the number into as many chunks as possible, the smallest 2 chunks are 2s and 3s, so we will try to break them down into chunks of 3s followed by whatever is remaining into chunks of 2s\n\nGoing by this approach we should stop with 3s chunks at 4 because inorder to break 4 we have 2 options -\n2x2 = 4\n3x1 = 3\nSo we should take the larger of the two.\n\n# Approach\nIf number if less than 4 we return `n-1`\n```\nif n < 4:\n return n-1\n```\n\nNow we will store our final value in `prod=1`.\n\nAt each iteration reduce n by 3 until as long as n > 4 and keep multiplying `prod` by 3.\n```\nwhile n > 4:\n prod *= 3\n n-=3\nreturn prod * n\n```\nFinally multiply `prod` with whatever n is left over.\n\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n < 4:\n return n-1\n prod = 1\n while n > 4:\n prod *= 3\n n-=3\n return prod * n\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
🔥 Easy solution | Python 3 🔥 | integer-break | 0 | 1 | # Intuition\nGiven a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a list dp of size n + 1 to store the maximum product for each integer from 1 to n. Set dp[1] to 1 since the maximum product for 1 is 1 (1 itself).\n\n1. Use a nested loop to iterate from 2 to n, representing the integers for which you want to find the maximum product.\n\n1. Inside the inner loop (from 1 to i - 1), consider different ways to break the integer i into smaller integers and calculate the product for each possibility.\n\n1. Update dp[i] with the maximum product found among the different possibilities. The formula used for this is max(j * (i - j), j * dp[i - j]), where j represents one of the integers being considered in the sum, and (i - j) represents the remaining part of the integer.\n\n1. After iterating through all possible values of j for a given i, you will have computed the maximum product for that integer.\n\n1. Continue this process for all integers from 2 to n.\n\n1. Finally, return dp[n], which contains the maximum product for the given integer n.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n dp = [0] * (n + 1)\n dp[1] = 1\n \n # Iterate from 2 to n\n for i in range(2, n + 1):\n # Iterate from 1 to i - 1\n for j in range(1, i):\n # Calculate the maximum product\n dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))\n \n # Return the maximum product\n return dp[n]\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
easy solution | integer-break | 0 | 1 | # Intuition\nhardcode\n\n# Approach\nlol\n\n# Complexity\n- Time complexity:\nO(logN) if i wasn\'t lazy i think\n\n- Space complexity:\nirrelevant\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n <=29:\n if n < 15:\n if n < 8:\n if n < 5:\n if (n == 2):\n return 1\n if (n == 3):\n return 2\n if (n == 4):\n return 4\n if (n == 5):\n return 6\n if n==6:\n return 9\n if n == 7:\n return 12\n if n==8:\n return 18\n if n ==9:\n return 27\n if n==10:\n return 36\n if n == 11:\n return 54\n if n==12:\n return 81\n if n==13:\n return 108\n if n==14:\n return 162\n if n==15:\n return 243\n if n==16:\n return 324\n if n==17:\n return 486\n if n==18:\n return 729\n if n==19:\n return 972\n if n ==20:\n return 1458\n if n==21:\n return 2187\n if n==22:\n return 2916\n if n==23:\n return 4374\n if n==24:\n return 6561\n if n==25:\n return 8748\n if n==26:\n return 13122\n if n==27:\n return 19683\n if n==28:\n return 26244\n if n==29:\n return 39366\n else:\n if n < 45:\n if n < 38:\n if n < 35:\n if n==30:\n return 59049\n if n==31:\n return 78732\n if n==32:\n return 118098\n if n==33:\n return 177147\n if n==34:\n return 236196\n if n==35:\n return 354294\n if n==36:\n return 531441\n if n==37:\n return 708588\n if n==38:\n return 1062882\n if n==39:\n return 1594323\n if n==40:\n return 2125764\n if n==41:\n return 3188646\n if n==42:\n return 4782969\n if n == 43:\n return 6377292\n if n== 44:\n return 9565938\n if n==45:\n return 14348907\n if n==46:\n return 19131876\n if n==47:\n return 28697814\n if n==48:\n return 43046721\n if n==49:\n return 57395628\n if n==50:\n return 86093442\n if n==51:\n return 129140163\n return 0\n \n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Python3 LogN solution | integer-break | 0 | 1 | - Time complexity: $$O(log N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n == 2:\n return 1\n if n == 3:\n return 2\n max_product = 1\n while n > 4:\n max_product *= 3\n n -= 3\n return max_product * n\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
✔️ Short easy solution with explanation || O(log n) time and constant space | integer-break | 0 | 1 | # Approach\nLet\'s say we divide a number n into k parts. It\'s easy to check that we can get the biggest product if we split n into k equal parts and share the remaining equally by adding `1` to the part of the numbers.\n`f.e. n = 10, k = 4 --> 10 // 4 = 2, 10 % 4 == 2 --> combination going to be 3 3 2 2 `\n\nNow all we need to know is k. We can find it by a binary search. At first, the product is growing with a growing number of k, but at some point, it starts to decrease, this point of inflection we are looking for.\n\n# Complexity\n- Time complexity: O(log n)\n\n- Space complexity: O(1)\n\nPlease upvote if you like the solution \uD83D\uDD96\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n def count_product(k: int) -> int:\n num, rem = divmod(n, k)\n return num ** (k - rem) * (num + 1) ** rem\n\n start, end = 2, n\n while start < end:\n midd = (start + end) // 2\n if count_product(midd) < count_product(midd + 1):\n start = midd + 1\n else:\n end = midd\n return count_product(start)\n\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Python and swift, bottoms up DP, intuitive, fun and detailed explanation. | integer-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLooking at the problem we get to know that there will be many cases if we try to brute force it. But if you have learnt DP before it is not a surprise that this can be solved using DP, this is just a typical 1D DP but with some additional step. \nBasically in this question we need to express a number in its **optimal form**, as I would like to call it. I you think about it a number can be expressed in its optimal form if its \'Components\' can be expressed in the same form too.(can you see where this is going...).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Define the base cases i.e, 1-1, 2-2 and 3-3.\n2. Next, since we use bottom up DP, we might need an array for memoization, so intialize an array for memoization (of length n+1).\n3. Set the base cases in the array. \n4. Now start using the base cases to contruct other solutions. \n - Starting with $4$, solve the problem for all numbers till $n$. (That\'s what the outer loop does)\n - Next, for a given number try including a number from $2$ to $n$ as one of its components and treat the expression of the remaining of the number as another subproblem(which we will have the answer to in the memoization array since it is bottom up DP)\n - Look which one has the maximum product, the number itself or the one which is brokern down to components.\n5. Finally return the last element of the memoization array which would be the solution of the problem.\n\n# Complexity\n- Time complexity:$O(\\log n)$\nThere are $O(n)$ possible states of num that $memo array$ can be called with. We only calculate each state once, as we calculate one state per outer for loop iteration. To calculate a state, we iterate from 2 until num, which costs up to $O(n)$. Thus, we have a time complexity of $O(n^2)$.\n\n(Layman\'s trick):- One for loop inside another thus $O(n^2)$.\n$^*$Might not work always, proceed with caution.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\nFor maintaining the memoization array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n# Code\n## Swift\n```\nclass Solution {\n func integerBreak(_ n: Int) -> Int {\n if n<=3{\n return n-1\n }\n\n //An array used for memoization for our DP approach\n var memo:[Int] = Array(repeating:0,count:n+1)\n\n //Setting the base case in the array\n for i in [1,2,3]{\n memo[i] = i\n }\n\n //Constructing the solution from the bottom up fashion\n for num in 4...n{\n var ans = num // This is the case where the number is not split at all.\n for i in 2..<num{\n ans = max(ans,i*memo[num-i])\n \n }\n memo[num] = ans\n }\n return memo[n]\n }\n\n}\n```\n\n## Python\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n <= 3:\n return n - 1\n \n dp = [0] * (n + 1)\n\n # Set base cases\n for i in [1, 2, 3]:\n dp[i] = i\n \n for num in range(4, n + 1):\n ans = num\n for i in range(2, num):\n ans = max(ans, i * dp[num - i])\n \n dp[num] = ans\n \n return dp[n]\n```\n\n\n### Please support me by giving an upvote\uD83D\uDE42 | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Python solution using DP with easy understanding with optimize solution | integer-break | 0 | 1 | \nEfficient solution for maximizing product when breaking n into positive integers. Employs dynamic programming, handles n=2, n=3, and iterates to optimize splits. Calculates and stores max product in dp[n].\nIf you find this solution helpful, please consider giving it a thumbs-up and sharing your thoughts in the comments. Your feedback is much appreciated! \uD83D\uDE4C\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find the maximum product when breaking down an integer n into the sum of positive integers, we should consider the factors that maximize the product. We need to use dynamic programming to store and calculate intermediate results, considering various cases.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We handle special cases where n is 2 or 3 directly, as these have different optimal solutions (2 = 1 + 1, 3 = 1 + 2, respectively).\n\n2. We create an array dp to store the maximum products for integers from 2 to n.\n\n3. Initialize the base cases:\n dp[2] = 2 because 2 can be broken down as 1 + 1.\n dp[3] = 3 because 3 can be broken down as 1 + 2.\n4. Iterate from i = 4 to n. For each i, we consider two possibilities:\n Breaking i into i - 2 and 2. In this case, the product is 2 * dp[i -2].\n Breaking i into i - 3 and 3. In this case, the product is 3 * dp[i -3].\nWe take the maximum of these two possibilities and assign it to dp[i].\n\nThe result is stored in dp[n], which represents the maximum product when breaking down n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n==0:\n return 0\n if n <= 2:\n return 1\n if n == 3:\n return 2\n dp = [0] * (n + 1)\n dp[2] = 2\n dp[3] = 3\n for i in range(4, n + 1):\n dp[i] = max(2 * dp[i - 2], 3 * dp[i - 3])\n return dp[n]\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
2ms Runtime TC O(1) SC O(1) | Easy to understand | Beginner Friendly Solution | integer-break | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers.\n\nReturn the maximum product you can get.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. If n is less than or equal to 3, return n - 1 as the maximum product (special cases).\n Calculate the quotient q when dividing n by 3.\n Calculate the remainder r when dividing n by 3.\n2. If r is 0, return 3^q.\n3. If r is 1, return (3^(q-1)) * 4.\n4. If r is 2, return (3^q) * 2.\n..\n..\nKindly upvote \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n <= 3) {\n return n - 1;\n }\n int quotient = n / 3;\n int remainder = n % 3;\n if (remainder == 0) {\n return pow(3, quotient);\n } else if (remainder == 1) {\n return pow(3, quotient - 1) * 4;\n } else {\n return pow(3, quotient) * 2;\n }\n }\n};\n```\n\n | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Easy to Understand. Beat 99% in Time Complexity | integer-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n res = 1\n if n == 2:\n return 1\n elif n == 3:\n return 2\n while n > 4:\n res = res * 3\n n-=3\n return res*n\n \n\n\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Python3 Solution | integer-break | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n==2:\n return 1\n if n==3:\n return 2\n ans=1\n while n>4:\n ans=ans*3\n n-=3\n return ans*n \n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
✅Beats 100% | O(n) Easy Solution🔥 | Why 3s why not 4s or else, explained in short and easy 🚀 | integer-break | 1 | 1 | # Do upvote if you like the solution and explanation please \uD83D\uDE80\n\n---\n\n\n# First Understand Why 3s why not 4s or else ?\n- The reason we use 3s instead of 4s is to maximize the product. When you break a number into smaller numbers, multiplying several smaller numbers together results in a larger product than multiplying larger numbers together.\n\n- Breaking a number into 3s is generally the best strategy because:\n\n- 2 * 2 * 2 < 3 * 3: Multiplying three 3s together is greater than multiplying three 2s together.\nUsing 4s is less efficient because 4 * 4 is equal to 2 * 2 * 2 * 2, which has the same product as four 2s. Therefore, breaking into 4s is less optimal in terms of maximizing the product.\nSo, we prefer breaking the number into as many 3s as possible, with possibly a few 2s left over. This is why we use 3s instead of 4s in the dynamic programming solution.\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to break an integer n into the sum of positive integers and maximize their product. To do this, we need to find a pattern that leads to the maximum product. We can observe that breaking n into as many 3s as possible will generally yield the maximum product. However, there are some exceptions when using 2s can be more beneficial.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. If n is less than or equal to 3, we return n - 1 because the maximum product for integers 2 and 3 is simply 2 and 3, respectively.\n\n2. For integers greater than 3, we use dynamic programming to calculate the maximum product. We initialize an array dp to store the maximum product for each integer from 2 to n.\n\n3. We loop through the integers from 4 to n and calculate the maximum product for each integer i by considering two options:\n\n4. Breaking i into i - 2 and multiplying it by 2.\nBreaking i into i - 3 and multiplying it by 3.\nWe take the maximum of these two options and store it in dp[i].\n\n5. Finally, we return dp[n], which contains the maximum product for integer n.\n\n---\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n) because we iterate through the integers from 4 to n once, and for each integer, we perform constant time operations.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) because we use an array dp of size n + 1 to store the maximum product for each integer from 2 to n.\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n int integerBreak(int n) {\n if (n <= 3) return n - 1;\n \n vector<int> dp(n + 1, 0);\n dp[2] = 2;\n dp[3] = 3;\n \n for (int i = 4; i <= n; ++i) {\n dp[i] = max(dp[i - 2] * 2, dp[i - 3] * 3);\n }\n \n return dp[n];\n }\n};\n\n``` | 9 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Simplest Solution in Python3 | integer-break | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. If n is less than or equal to 3, return n - 1 because for n <= 3, the maximum product can be achieved by breaking n into n - 1.\n\n2. Initialize res to 1. This variable will keep track of the maximum product.\n\n3. Use a while loop to iterate while n is greater than 4. Inside the loop, multiply res by 3 (to maximize the product) and subtract 3 from n. This step repeatedly breaks n into as many factors of 3 as possible while ensuring that n remains greater than 4.\n\n4. After the loop, n will be 2, 3, or 4. Multiply res by n to account for the remaining part.\n\n5. Return the final value of res, which represents the maximum product of integers that sum up to n.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n <= 3:\n return n - 1\n res = 1\n while n > 4:\n res *= 3\n n -= 3\n return res * n\n``` | 1 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Simple 99,8% 7 line Python solution | integer-break | 0 | 1 | # Code\n### \n```\nclass Solution:\n def integerBreak(self, n: int) -> int:\n if n < 4:\n n-=1 ## n2 = 1; n3 = 2\n ans = 1\n while n > 4:\n ans *= 3\n n -= 3\n return ans * n \n```\n\n | 2 | Given an integer `n`, break it into the sum of `k` **positive integers**, where `k >= 2`, and maximize the product of those integers.
Return _the maximum product you can get_.
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** 2 = 1 + 1, 1 \* 1 = 1.
**Example 2:**
**Input:** n = 10
**Output:** 36
**Explanation:** 10 = 3 + 3 + 4, 3 \* 3 \* 4 = 36.
**Constraints:**
* `2 <= n <= 58` | There is a simple O(n) solution to this problem. You may check the breaking results of n ranging from 7 to 10 to discover the regularities. |
Python 3 ~actually~ easiest solution | reverse-string | 0 | 1 | **It\'s so simiple, a caveman could do it**\n\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n s[:] = s[::-1]\n```\n\n**Note:**\n`s[:] = s[::-1]` is required **NOT** `s = s[::-1]` because you have to edit the list **inplace**. \nUnder the hood, `s[:] =` is editing the actual memory bytes s points to, and `s = ` points the variable name `s` to other bytes in the memory.\n\n(easiest except .reverse()) | 100 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
Python | faster than 93% | two pointer | reverse-string | 0 | 1 | ```\n"""https://leetcode.com/problems/reverse-string/"""\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n """\n Do not return anything, modify s in-place instead.\n """\n l=0\n r=len(s)-1\n while l<r:\n s[l],s[r]=s[r],s[l]\n l+=1\n r-=1\n \n# SUBMISSION REPORT:-\n # Runtime: 207 ms, faster than 93.06% of Python3 online submissions for Reverse String.\n # Memory Usage: 18.4 MB, less than 82.79% of Python3 online submissions for Reverse String.\n \n# EXPLANATION:-\n # We will use two pointers, one from start and one from end\n # We will swap the chars and increment the left and decrement the right\n``` | 11 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
Python 99 %beats 3 Approach || 1line code | reverse-string | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n\n3 Approachs , 2 are one line code and 3rd is by 2 pointer\n\n# Code\n```\n<!-- One Line Code -->\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n """\n Do not return anything, modify s in-place instead.\n """\n s.reverse()\n #OR\n s[:] = s[::-1]\n\n\n#=============================================================\n<!-- TWO Pointer -->\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n """\n Do not return anything, modify s in-place instead.\n """\n j = len(s)-1\n i = 0\n while i < j:\n s[i],s[j] = s[j], s[i]\n i += 1\n j -= 1\n``` | 5 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
Reverse String in Python | Faster than 99.33% | reverse-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nReversing a string means changing the order of its characters from the original sequence to the opposite sequence.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use the following method available for Python lists to reverse the elements of the input list in-place.\n\n> `list.reverse()`\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nIt iterates through the input list once, and the time it takes is directly proportional to the number of elements in the list, denoted as `n`.\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe are not using any extra memory to store the reversed string; we are modifying the input list in-place.\n\n# Code\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n s.reverse()\n``` | 4 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
[Python] - Two Pointer - Clean & Simple Solution | reverse-string | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n Loop goes until n/2 but we represent $$O(n/2)$$ to $$O(n)$$. \nHence TC is $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n # Two Pointer\n l, r =0, len(s) - 1\n while l < r:\n s[l], s[r] = s[r], s[l]\n l += 1\n r -= 1\n```\n\nSimply you can use for loop like below :\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n n = len(s)\n for i in range(n // 2):\n s[i], s[n - i - 1] = s[n - i - 1], s[i]\n \n``` | 16 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
Beginner friendly code in python | reverse-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n/2)-->O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n """\n Do not return anything, modify s in-place instead.\n """\n l=0\n r=len(s)-1\n while l<r:\n s[l],s[r]=s[r],s[l]\n l+=1\n r-=1\n return s\n``` | 2 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
Easy python solution | reverse-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(n)\n\n- Space complexity:0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n """\n Do not return anything, modify s in-place instead.\n """\n l = (len(s)//2)-1\n\n while l>-1:\n tmp = s[l]\n s[l] = s[len(s)-l-1]\n s[len(s)-l-1] = tmp\n l-=1\n\n # OR\n l,r = 0,len(s)-1\n while r > l:\n tmp = s[r]\n s[r] = s[l]\n s[l] = tmp\n l+=1\n r-=1 \n\n``` | 1 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
Python Solution || Super Easy | reverse-string | 0 | 1 | ```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n left, right = 0, len(s) - 1\n while (left < right):\n s[left], s[right] = s[right], s[left]\n left += 1\n right -= 1\n\n``` | 1 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
✅✅Python3 Two Word Answer not a single line beats 99.89% ✅✅ | reverse-string | 0 | 1 | # Intuition\njust make a copy of its own list\n# Approach\nReversing a list in place\n\n# Complexity\n- Time complexity:\nO[1]\n\n- Space complexity:\nO[1]\n\n# Code\n```\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n s[:] = s[::-1]\n``` | 3 | Write a function that reverses a string. The input string is given as an array of characters `s`.
You must do this by modifying the input array [in-place](https://en.wikipedia.org/wiki/In-place_algorithm) with `O(1)` extra memory.
**Example 1:**
**Input:** s = \["h","e","l","l","o"\]
**Output:** \["o","l","l","e","h"\]
**Example 2:**
**Input:** s = \["H","a","n","n","a","h"\]
**Output:** \["h","a","n","n","a","H"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is a [printable ascii character](https://en.wikipedia.org/wiki/ASCII#Printable_characters). | The entire logic for reversing a string is based on using the opposite directional two-pointer approach! |
2 pointer approach | reverse-vowels-of-a-string | 0 | 1 | # Approach\n<!-- 1.firstly we have make a string st containing all vowels\n2.Then by using two pointer approach we are swapping the vowels \n3.we are increasing e and b when they are not present in our string st containing all vowels -->\n\n# Complexity\n- Time complexity:\n<!-- with complexity O(n2)$$ -->\n\n- Space complexity:\n<!-- O(1)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n s=list(s)\n st="aeiouAEIOU"\n b=0\n e=len(s)-1\n while(b<e):\n while b<e and s[b] not in st:\n b=b+1\n continue\n while b<e and s[e] not in st:\n e=e-1\n continue\n s[b],s[e]=s[e],s[b]\n b=b+1\n e=e-1\n s=\'\'.join(s)\n return s\n\n``` | 3 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
SIMPLE EASY SOLUTION PYTHON JUST 3 FOR LOOPS | reverse-vowels-of-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n l=[]\n s=list(s)\n for i in range(len(s)):\n if s[i] in "aeiouAEIOU":\n l.append(s[i])\n s[i]="*"\n l=l[::-1]\n start=0\n for i in range(len(s)):\n if s[i]=="*" and start<len(l):\n s[i]=l[start]\n start+=1\n str1=""\n for i in s:\n str1+=i\n return str1\n\n\n\n``` | 1 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Easy Python Solution | reverse-vowels-of-a-string | 0 | 1 | # Intuition\nTwo pointer approach\n\n# Approach\nSwapping left and right if they are vowels.\n\n\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n s=list(s)\n n=len(s)\n left=0\n right=n-1\n vowels=set(\'AEIOUaeiou\')\n while left<right:\n while left<right and s[left] not in vowels:\n left+=1\n while left<right and s[right] not in vowels:\n right-=1\n s[left],s[right]=s[right],s[left]\n left+=1\n right-=1\n s=\'\'.join(s)\n return s\n\n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 38 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Easy solution 70% faster | reverse-vowels-of-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n output = ""\n vowels = []\n for c in s:\n if c in ["a", "e", "i", "o", "u", "A", "E", "I", "O", "U"]:\n vowels.append(c)\n for c in s:\n if c not in ["a", "e", "i", "o", "u", "A", "E", "I", "O", "U"]:\n output += c\n else:\n output += vowels[-1]\n vowels.pop()\n return output\n\n\n``` | 1 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Reverse Vowels of a String using python (simple solution) | reverse-vowels-of-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n j=0\n s1=[]\n for i in range(0,len(s)):\n if((s[i]==\'a\')or(s[i]==\'A\')or(s[i]==\'e\')or(s[i]==\'E\')or(s[i]==\'i\')or(s[i]==\'I\')or(s[i]==\'o\')or(s[i]==\'O\')or(s[i]==\'u\')or (s[i]==\'U\')): \n s1.append(s[i])\n s1.reverse()\n new=""\n for i in range(0,len(s1)):\n new+=s1[i]\n up=\'\'\n for i in u range(0,len(s)):\n if((s[i]==\'a\')or(s[i]==\'A\')or(s[i]==\'e\')or(s[i]==\'E\')or(s[i]==\'i\')or(s[i]==\'I\')or(s[i]==\'o\')or(s[i]==\'O\')or(s[i]==\'u\')or (s[i]==\'U\')):\n up+=new[j]\n j+=1\n else:\n up+=s[i]\n return up\n \n``` | 0 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Python - Beginner Friendly - O(N) | reverse-vowels-of-a-string | 0 | 1 | # Complexity\n- Time complexity: **O(N)** where **N** = *Length of the string*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(N)** where **N** = *Length of the string*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n result = []\n ans = ""\n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\', \'A\', \'E\', \'I\', \'O\', \'U\']\n for each in s:\n if each in vowels:\n result.append(each)\n for i in s:\n if i in vowels:\n ans += result.pop()\n else:\n ans += i\n return ans\n```\n | 2 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Time 'n', Space 'n' | reverse-vowels-of-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n\n\n v = {\'a\', \'e\', \'i\', \'o\', \'u\', \'A\', \'E\', \'I\', \'O\', \'U\'}\n\n a = [f for f in s[::-1] if f in v]\n\n n = \'\'\n\n j = 0 # Move this initialization of j outside of the loop\n\n for i in s:\n if i in v:\n n += a[j] # Append the corresponding vowel from a\n j += 1\n else:\n n += i\n\n return n\n``` | 2 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Python Easy Solution || Two Pointers | reverse-vowels-of-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n lis=[\'a\', \'e\', \'i\', \'o\',\'u\',\'A\',\'E\',\'I\',\'O\',\'U\']\n i=0\n j=len(s)-1\n s=list(s)\n while(i<j):\n if s[i] not in lis:\n i+=1\n if s[j] not in lis:\n j-=1\n if s[i] in lis and s[j] in lis:\n s[i],s[j]=s[j],s[i]\n i+=1\n j-=1\n s="".join(s)\n return s\n``` | 2 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Python3, simple solution | reverse-vowels-of-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo swap the positions, need to save the position and reverse the position list\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nval stores the value at the index and pos stores the position, next only one of the two lists is reversed. Next reconstruct the string.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAssume len(s) = n and len(val) = m\nthen time complexity:\n$$O(n+m)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nIDK\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n s = list(s)\n v = ["a","e","i","o","u"]\n val = []\n pos = []\n for i in range(len(s)):\n if s[i].lower() in v:\n val.append(s[i])\n pos.append(i)\n val = val[::-1]\n for i in range(len(pos)):\n s[pos[i]] = val[i] \n return \'\'.join(s)\n``` | 3 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
✅ Explained - Simple and Clear Python3 Code✅ | reverse-vowels-of-a-string | 0 | 1 | # Intuition\nThe given problem is to reverse only the vowels in a given string. The vowels are \'a\', \'e\', \'i\', \'o\', and \'u\', and they can appear in both lower and upper case.\n\n\n# Approach\nThe provided solution uses a two-pointer approach to reverse the vowels in the string. It initializes two pointers, start and end, at the beginning and end of the string, respectively. It also creates a list, vowels, that contains all the vowels (both lowercase and uppercase).\n\nThe solution converts the input string into a list, s, for easier manipulation. It then enters a while loop that continues until the start pointer surpasses the end pointer. Inside the loop, it checks if the character at s[start] is a vowel. If it is, it enters another nested while loop that moves the end pointer towards the start until it finds a vowel at s[end]. This helps in finding the corresponding vowel from the end of the string to swap with the vowel at the start.\n\nOnce a vowel is found at both the start and end pointers, the solution swaps them by using a temporary variable, aux. After the swap, both pointers are adjusted accordingly. The end pointer moves towards the start, and the start pointer moves towards the end.\n\nFinally, after the while loop, the solution reconstructs the modified list, s, into a string, res, by iterating over each character in s and appending it to res. This modified string is then returned as the output.\n\n\n\n# Complexity\n- Time complexity:\n The solution iterates through the string using two pointers, so the while loop runs until the pointers meet or cross each other. This takes O(n/2) time, where n is the length of the string. The process of swapping the vowels takes constant time. The reconstruction of the modified list into a string also takes O(n) time. Therefore, the overall time complexity of the solution is O(n).\n\n\n- Space complexity:\nThe solution uses additional space to store the modified list, s, and the final string, res. Both have a maximum size of n, where n is the length of the input string. Therefore, the space complexity is O(n).\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, word: str) -> str:\n start=0\n end=len(word)-1\n vowels= [\'a\', \'e\', \'i\', \'o\', \'u\',\'A\',\'E\',\'I\',\'O\',\'U\']\n s=[word[i] for i in range(len(word))]\n while start<end:\n if s[start] in vowels:\n while start<end and s[end] not in vowels:\n end-=1\n aux=s[start]\n s[start]=s[end]\n s[end]=aux\n end-=1\n start+=1\n res=""\n for i in s:\n res+=i\n return res\n\n\n``` | 9 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Easiest Two Pointer Approach to Reverse Vowels of a String | reverse-vowels-of-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution involves using a two-pointer approach to reverse the vowels in the given string. The idea is to find pairs of vowels from both ends of the string and swap them until the pointers meet in the middle. By swapping only the vowel characters, the non-vowel characters will remain in their original positions.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two pointers, l and r, pointing to the start and end of the string respectively.\n2. Create a list of vowel characters, both lowercase and uppercase.\n3. Convert the input string into a list of characters for ease of swapping.\n4. Iterate through the string using the two-pointer approach:\n - If the character at position l is not a vowel, increment l.\n - If the character at position r is not a vowel, decrement r.\n - If both characters at positions l and r are vowels, swap them and then increment l and decrement r.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe two-pointer approach iterates through the string once, so the time complexity is O(n), where n is the length of the input string.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe solution uses additional space to store the list of characters, which takes O(n) space, where n is the length of the input string.\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n l = 0\n r = len(s) - 1\n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\']\n s = list(s)\n while (l < r):\n if s[l].lower() not in vowels:\n l += 1\n elif s[r].lower() not in vowels:\n r -= 1\n else:\n s[l], s[r] = s[r], s[l]\n l += 1\n r -= 1\n return "".join(s)\n \n``` | 7 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Python solution beats 72.38% : 60ms | reverse-vowels-of-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe traverse the list from left and right till we find a vowel from both the directions \nthen we swap them and search for the next pair of vowels \nthis process repeats till left crosses right\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n left,right=0,len(s)-1\n v=\'aeiouAEIOU\'\n s=list(s)\n while left<right:\n if s[left] not in v:\n left+=1\n if s[right] not in v:\n right-=1 \n if s[left] in v and s[right] in v :\n s[left],s[right]=s[right],s[left]\n\n left+=1\n right-=1\n return \'\'.join(s) \n``` | 5 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Python Solution || 99.58% faster || 86.96% less memory | reverse-vowels-of-a-string | 0 | 1 | ```\nclass Solution:\n def reverseVowels(self, s: str) -> str:\n s = list(s)\n left = 0\n right = len(s) - 1\n m = \'aeiouAEIOU\'\n while left < right:\n if s[left] in m and s[right] in m:\n \n s[left], s[right] = s[right], s[left]\n \n left += 1; right -= 1\n \n elif s[left] not in m:\n left += 1\n \n elif s[right] not in m:\n right -= 1\n \n return \'\'.join(s)\n``` | 56 | Given a string `s`, reverse only all the vowels in the string and return it.
The vowels are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`, and they can appear in both lower and upper cases, more than once.
**Example 1:**
**Input:** s = "hello"
**Output:** "holle"
**Example 2:**
**Input:** s = "leetcode"
**Output:** "leotcede"
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consist of **printable ASCII** characters. | null |
Solution with FFT lol. | top-k-frequent-elements | 0 | 1 | ```py\nimport numpy as np\nfrom numpy.fft import fft, ifft\ndef solve(nums, k):\n n = len(nums)\n polynomial = np.zeros(n, dtype=complex)\n for num in nums:\n polynomial[num] += 1\n fft_result = fft(polynomial)\n topki = np.argpartition(np.abs(fft_result), -k)[-k:]\n inverted_fft = ifft(fft_result)\n topke = [\n (index, int(np.round(inverted_fft[index].real))) for index in topki\n ]\n topke.sort(key=lambda x: -x[1])\n return [element for element, _ in topke]\nnums = [3, 1, 1, 2, 2, 2, 3, 4, 4, 4]\nk = 2\nresult = solve(nums, k)\nprint(result)\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Quickselect approach O(n) | top-k-frequent-elements | 0 | 1 | # Intuition\nWe can do heap approach and bucket sort which is even better. But somewhere on internet i found that quick select by frequency is also nice linear solution for such type for problems.\n\n# Approach\nQuickselect by frequency. Partition method suffle elements in reverse order. Means that in the end of array we have low freq elements.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n cnt = collections.Counter(nums)\n unique = list(cnt.items()) # (number, frequency) pairs list\n\n self.quickselect(unique, 0, len(unique) - 1, k - 1)\n\n return [pair[0] for pair in unique[:k]]\n\n\n def quickselect(self, arr, low, high, k):\n if low == high:\n return arr[low]\n\n i = self.partition(arr, low, high)\n if k == i:\n return arr[k]\n elif k < i:\n return self.quickselect(arr, low, i - 1, k)\n else:\n return self.quickselect(arr, i + 1, high, k)\n\n\n def partition(self, arr, low, high):\n pivot = arr[high][1]\n i = low\n for j in range(low, high):\n if arr[j][1] > pivot:\n arr[i], arr[j] = arr[j], arr[i]\n i += 1\n\n arr[i], arr[high] = arr[high], arr[i]\n\n return i\n``` | 4 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
CodeDominar Solution | top-k-frequent-elements | 0 | 1 | # Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n ans=[]\n d = {}\n for ele in nums:\n d[ele] = d.get(ele,0)+1\n li = [k for k,v in sorted(d.items(), key=lambda item:item[1])]\n li = li[::-1] \n for i in range(k):\n ans.append(li[i])\n return ans\n \n \n``` | 3 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Easy Python Solution | top-k-frequent-elements | 0 | 1 | \n# Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n count, unique, c = [], [], []\n\n for i in nums:\n if i not in unique:\n unique.append(i)\n c.append(nums.count(i))\n\n for i in range(k):\n m=max(c)\n i=c.index(m)\n count.append(unique[i])\n c[i]=-1\n return count\n``` | 4 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
[ Python ] ✅✅ Simple Python Solution Using Dictionary ( HashMap ) ✌👍 | top-k-frequent-elements | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F \n# Runtime: 115 ms, faster than 46.79% of Python3 online submissions for Top K Frequent Elements.\n# Memory Usage: 21.1 MB, less than 41.02% of Python3 online submissions for Top K Frequent Elements.\n\n\tclass Solution:\n\t\tdef topKFrequent(self, nums: List[int], k: int) -> List[int]:\n\n\t\t\tfrequency = {}\n\n\t\t\tfor num in nums:\n\n\t\t\t\tif num not in frequency:\n\n\t\t\t\t\tfrequency[num] = 1\n\n\t\t\t\telse:\n\n\t\t\t\t\tfrequency[num] = frequency[num] + 1\n\n\t\t\tfrequency = dict(sorted(frequency.items(), key=lambda x: x[1], reverse=True))\n\n\t\t\tresult = list(frequency.keys())[:k]\n\n\t\t\treturn result\n\t\t\t\n\tTime Complexity : O(n * log(n))\n\tSpace Complexity : O(n)\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 62 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Python O(n) solution without sort, without heap | top-k-frequent-elements | 0 | 1 | \n\n\n\n\n# Code\n```\nclass Solution(object):\n def topKFrequent(self, nums, k):\n m = {}\n r = []\n for n in nums:\n if n in m:\n m[n] += 1\n else:\n m[n] = 1\n\n for j in range(k):\n max_freq = 0\n max_freq_num = 0\n for key, value in m.items():\n if value > max_freq:\n max_freq = value\n max_freq_num = key\n r.append(max_freq_num)\n m.pop(max_freq_num)\n\n return r\n\n``` | 5 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Easy Python Solution | top-k-frequent-elements | 0 | 1 | \n# Code\n```\nfrom collections import Counter\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n\n hm = dict(Counter(nums))\n hm = dict(sorted(hm.items(), key=lambda item: item[1], reverse = True))\n return list(hm)[:k]\n``` | 2 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Bucket Sort in Python | O(n) time complexity | top-k-frequent-elements | 0 | 1 | # Intuition\nInitially count the occurance using hash maps & sort them\nBut learning from neetcode the approach can be optimize using **Bucket Sort**\n\n# Approach\n1. Use Hash Maps to count number of instance\n2. Not using sort, but make an array with number of occurance as key, save the num as list\n\n# Complexity\n- Time complexity:\nO(n) since we only loop through the input, the dictionary maximum n times and no exponential aproach\n\n- Space complexity:\nO(n) since the dictionary & array sizes maximum is O(n + 2n)\n\n# Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n hashMaps = {}\n tabulationArr = [[] for i in range(len(nums) + 1)]\n result = []\n\n for idx, num in enumerate(nums):\n hashMaps[num] = (0 if hashMaps.get(num) is None else hashMaps[num]) + 1\n\n for key, val in hashMaps.items():\n # print(f\'Key {key} -> Val {val}\')\n tabulationArr[val].append(key)\n\n for i in range(len(nums), -1, -1):\n if(tabulationArr[i] == []):\n continue\n \n for num in tabulationArr[i]:\n result.append(num)\n if(len(result) == k):\n return result\n``` | 0 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
[Python3] BucketSort + Heap (2 lines) || beats 94% | top-k-frequent-elements | 0 | 1 | ### BucketSort approach:\n\n1. Count frequency for all numbers using Counter (or manually).\n2. Create buckets for grouping items by frequency. Buckets count is equal to number of nums. For example: ```nums[1,1,1,1,2,2,3,4] => buckets = [0:[], 1:[3,4], 2:[2], 3:[], 4:[1]]```. Instead of an array, you can use a dictionary for buckets, as some buckets may be empty.\n3. Group numbers by relevant bucket (according frequency).\n4. Now all values in buckets sorted by frequency in ascending order. Just return k most frequent values from the end.\n\nThe first approach is shorter, but slower (need time + space to reverse list to use chain).\n```python3 []\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n cnt = Counter(nums)\n buckets = [[] for _ in range(len(nums) + 1)]\n for val, freq in cnt.items():\n buckets[freq].append(val)\n \n return list(chain(*buckets[::-1]))[:k]\n```\n```python3 []\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n cnt = Counter(nums)\n buckets = [[] for _ in range(len(nums) + 1)]\n for val, freq in cnt.items():\n buckets[freq].append(val)\n \n res = []\n for bucket in reversed(buckets):\n for val in bucket:\n res.append(val)\n k -=1\n if k == 0:\n return res\n```\n### Heap using Counter approach:\nCounter.most_common method is just a shell over heapq.nlargest, see the [code](https://github.com/python/cpython/blob/1b85f4ec45a5d63188ee3866bd55eb29fdec7fbf/Lib/collections/__init__.py#L575)\n\n```python3 []\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n cnt = Counter(nums)\n return [val for val, _ in cnt.most_common(k)]\n```\n\n | 13 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Python Solution Using Heap | top-k-frequent-elements | 0 | 1 | # Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n ht = defaultdict(int)\n for num in nums:\n ht[num] += 1\n\n arr=[]\n heapify(arr)\n for num, freq in ht.items():\n heappush(arr, (freq, num))\n\n\n\n for _ in range(len(arr)-k):\n heappop(arr)\n\n for i in range(len(arr)):\n arr[i] = arr[i][1]\n \n return arr\n\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Powerful Heapmax and Hash Table | top-k-frequent-elements | 0 | 1 | \n# Heapmax and Hash Table\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n dic=Counter(nums)\n heapmax=[[-freq,num] for num,freq in dic.items()]\n heapq.heapify(heapmax)\n list1=[]\n for i in range(k):\n poping=heapq.heappop(heapmax)\n list1.append(poping[1])\n return list1\n\n\n```\n# please upvote me it would encourage me alot\n | 17 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
Python 3 simple code | top-k-frequent-elements | 0 | 1 | # Intuition\nSimple Python 3 code using dictionaries\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\no(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n dic={}\n for i in nums:\n dic[i]=dic.get(i,0)+1\n return sorted(dic,key=dic.get,reverse=True)[0:k] \n``` | 4 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
347: Time 91.58%, Solution with step by step explanation | top-k-frequent-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem can be solved by using a hash map to count the frequency of each element in the array. Then we can use a min-heap to store the top k frequent elements. The heap is ordered by the frequency of the elements, with the smallest frequency at the top of the heap. If we encounter an element with a frequency greater than the top of the heap, we remove the top element and insert the new element into the heap. Finally, we return the elements in the heap.\n\n# Complexity\n- Time complexity:\n91.58%, O(n log k), where n is the length of the input array and k is the number of unique elements in the array.\n\n- Space complexity:\n88.75%, O(n), where n is the length of the input array.\n\n# Code\n```\nclass Solution:\n def topKFrequent(self, nums: List[int], k: int) -> List[int]:\n # Step 1: Count the frequency of each element using a hash map\n freq = {}\n for num in nums:\n freq[num] = freq.get(num, 0) + 1\n \n # Step 2: Use a min-heap to store the top k frequent elements\n heap = []\n for num, count in freq.items():\n if len(heap) < k:\n heapq.heappush(heap, (count, num))\n elif count > heap[0][0]:\n heapq.heappop(heap)\n heapq.heappush(heap, (count, num))\n \n # Step 3: Return the elements in the heap\n return [num for count, num in heap]\n\n``` | 17 | Given an integer array `nums` and an integer `k`, return _the_ `k` _most frequent elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,1,1,2,2,3\], k = 2
**Output:** \[1,2\]
**Example 2:**
**Input:** nums = \[1\], k = 1
**Output:** \[1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `k` is in the range `[1, the number of unique elements in the array]`.
* It is **guaranteed** that the answer is **unique**.
**Follow up:** Your algorithm's time complexity must be better than `O(n log n)`, where n is the array's size. | null |
one string solution | intersection-of-two-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n return list((set(nums1) & set(nums2)))\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Two sets, without using built-in intersection function | intersection-of-two-arrays | 0 | 1 | # Approach\nRun through the first array, building a set with its values. Then run through the second array and built a new set only adding elements that are in the first set.\n\n# Complexity\n- Time complexity: O(N), as we are traversing nums1 first then nums2. Checking if an element of nums2 is in the set has time complexity of O(1), so it does not count as a nested loop.\n\n- Space complexity: O(N), as we have to store all unique elements from nums1 in a set.\n\n# Code\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n s1 = set()\n inter = set()\n for n in nums1:\n set.add(n)\n for n in nums2:\n if n in s1:\n inter.add(n)\n return inter\n```\nOr, using set comprehension:\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n s1 = set(n for n in nums1)\n return set(n for n in nums2 if n in s1)\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
easy soln | intersection-of-two-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n ans=[]\n dc=defaultdict(lambda:0)\n for a in nums1:\n dc[a]=1\n nums2=set(nums2)\n for a in nums2:\n if(dc[a]==1):\n ans.append(a)\n return ans\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Beats 96.07%of users with Python3 and Beats 96.71%of users with Python3 | intersection-of-two-arrays | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n nums1.sort()\n nums2.sort()\n ans = []\n def bs(i, nums2):\n start = 0\n finish = len(nums2)-1\n while start <= finish:\n mid = (start + finish) // 2\n values = nums2[mid]\n if values == i :\n ans.append(i)\n break\n if values > i:\n finish = mid -1\n else:\n start = mid + 1\n for i in set(nums1):\n bs(i,nums2)\n \n return ans\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
PYTHON3 Solution | intersection-of-two-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe map all the values in num1 and num2 in two hashmaps and store the values that are present in both these maps and return the answer\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n num1map={}\n num2map={}\n for num in nums1:\n if num in num1map:\n num1map[num]+=1\n else:\n num1map[num]=1\n for num in nums2:\n if num in num2map:\n num2map[num]+=1\n else:\n num2map[num]=1\n res=[]\n for num in num1map.keys():\n if num in num2map:\n res.append(num)\n return res\n \n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Easy solution in python with understandable explanation | intersection-of-two-arrays | 0 | 1 | # On my way of solving this problem: \n1. First we need an empty variable in type set.\n\n2. Secondly: we should change the list \'nums1\' as type set to save only unique numbers in it.\n\n3. After that we use loop for rotating \'nums1\' which we saved only unique numbers only and check if element is in \'nums2\' we add that element to variable \'v\' that we created as set.\n\n4. After all we just return v like list !!!\n\n**If it was useful and clear, Could you upvote me ? please.**\n\n# If you have any question about explanation or something isn\'t clear I wonder to know it, so you can ask me it in comments !\n\n\n# Code\n```\nclass Solution(object):\n def intersection(self, nums1, nums2):\n v = set()\n nums1 = set(nums1)\n for i in nums1:\n if i in nums2:\n v.add(i)\n return list(v)\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Single Line Code | intersection-of-two-arrays | 0 | 1 | \n# Super Logic Solution Using Python\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n return set(nums1) & set(nums2)\n``` | 5 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Awesome 2 Lines of Code | intersection-of-two-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)----->please upvote me\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)----->please upvote me\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n nums1,nums2=set(nums1),set(nums2)\n return nums1 & nums2\n``` | 3 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Python Solution || Hashtable | intersection-of-two-arrays | 0 | 1 | ```\nclass Solution:\n def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:\n \n d = {}\n if len(nums1) > len(nums2):\n nums1,nums2=nums2,nums1\n for i in nums1:\n d[i] = 0\n \n \n for i in nums2:\n if i not in d:\n continue\n else:\n d[i] = d[i]+1\n \n res = []\n for k,v in d.items():\n if v > 0:\n res.append(k)\n return res\n``` | 2 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must be **unique** and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[9,4\]
**Explanation:** \[4,9\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000` | null |
Very Easy || 100% || Fully Explained || Java, C++, Python, Python3 || HashMap & Two-Pointers | intersection-of-two-arrays-ii | 1 | 1 | # **Java Solution (Two-Pointers Approach):**\n```\n// Runtime: 1 ms, faster than 99.13% of Java online submissions for Intersection of Two Arrays II.\n// Memory Usage: 42.5 MB, less than 92.71% of Java online submissions for Intersection of Two Arrays II.\nclass Solution {\n public int[] intersect(int[] nums1, int[] nums2) {\n // Sort both the arrays first...\n Arrays.sort(nums1);\n Arrays.sort(nums2);\n // Create an array list...\n ArrayList<Integer> arr = new ArrayList<Integer>();\n // Use two pointers i and j for the two arrays and initialize both with zero.\n int i = 0, j = 0;\n while(i < nums1.length && j < nums2.length){\n // If nums1[i] is less than nums2[j]...\n // Leave the smaller element and go to next(greater) element in nums1...\n if(nums1[i] < nums2[j]) {\n i++;\n }\n // If nums1[i] is greater than nums2[j]...\n // Go to next(greater) element in nums2 array...\n else if(nums1[i] > nums2[j]){\n j++;\n }\n // If both the elements intersected...\n // Add this element to arr & increment both i and j.\n else{\n arr.add(nums1[i]);\n i++;\n j++;\n }\n }\n // Create a output list to store the output...\n int[] output = new int[arr.size()];\n int k = 0;\n while(k < arr.size()){\n output[k] = arr.get(k);\n k++;\n }\n return output;\n }\n}\n```\n\n# **C++ Solution (Using Hash map):**\n```\n// Runtime: 3 ms, faster than 96.43% of C++ online submissions for Intersection of Two Arrays II.\nclass Solution {\npublic:\n vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {\n // If the size of nums1 is greater than nums2, swap them...\n if(nums1.size() > nums2.size()) {\n swap(nums1, nums2);\n }\n // Create a hashmap to find out the intersection of two arrays...\n unordered_map<int,int> map;\n // Store the count of each element of one array using the Hash map...\n for(auto val: nums1) {\n map[val]++;\n }\n int idx = 0;\n // Traverse through the nums2 array....\n for(auto val: nums2) {\n // For each element in nums2, check if count of that element in nums1 is positive or not...\n // If count of nums2[idx] in array nums1 is positive, then add this element(nums2[idx]) in result array...\n if(map[val] > 0){\n nums1[idx++] = val;\n // Decrease the count of this element in Hash map.\n --map[val];\n }\n }\n return vector<int>(nums1.begin(), nums1.begin()+idx);\n }\n};\n```\n\n# **Python Solution (Two-Pointers Approach):**\n```\n# Runtime: 23 ms, faster than 89.65% of Python online submissions for Intersection of Two Arrays II.\n# Memory Usage: 11.4 MB, less than 87.45% of Python online submissions for Intersection of Two Arrays II.\nclass Solution(object):\n def intersect(self, nums1, nums2):\n # Sort both the arrays first...\n sortedArr1 = sorted(nums1)\n sortedArr2 = sorted(nums2)\n # Use two pointers i and j for the two arrays and initialize both with zero.\n i = 0\n j = 0\n # Create a output list to store the output...\n output = []\n while i < len(sortedArr1) and j < len(sortedArr2):\n # If sortedArr1[i] is less than sortedArr2[j]...\n # Leave the smaller element and go to next(greater) element in nums1...\n if sortedArr1[i] < sortedArr2[j]:\n i += 1\n # If sortedArr1[i] is greater than sortedArr2[j]...\n # Go to next(greater) element in nums2 array...\n elif sortedArr2[j] < sortedArr1[i]:\n j += 1\n # If both the elements intersected...\n # Add this element to output & increment both i and j.\n else:\n output.append(sortedArr1[i])\n i += 1\n j += 1\n return output # Return the output array...\n```\n \n# **Python3 Solution (Two-Pointers Approach):**\n```\n# Runtime: 51 ms, faster than 92.91% of Python3 online submissions for Intersection of Two Arrays II.\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n # Sort both the arrays first...\n sortedArr1 = sorted(nums1)\n sortedArr2 = sorted(nums2)\n # Use two pointers i and j for the two arrays and initialize both with zero.\n i = 0\n j = 0\n # Create a output list to store the output...\n output = []\n while i < len(sortedArr1) and j < len(sortedArr2):\n # If sortedArr1[i] is less than sortedArr2[j]...\n # Leave the smaller element and go to next(greater) element in nums1...\n if sortedArr1[i] < sortedArr2[j]:\n i += 1\n # If sortedArr1[i] is greater than sortedArr2[j]...\n # Go to next(greater) element in nums2 array...\n elif sortedArr2[j] < sortedArr1[i]:\n j += 1\n # If both the elements intersected...\n # Add this element to output & increment both i and j.\n else:\n output.append(sortedArr1[i])\n i += 1\n j += 1\n return output # Return the output array...\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 188 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Simple brute force that beats 100% | intersection-of-two-arrays-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n element_count_a = {}\n element_count_b = {}\n \n for num in nums1:\n element_count_a[num] = element_count_a.get(num, 0) + 1\n \n for num in nums2:\n element_count_b[num] = element_count_b.get(num, 0) + 1\n \n intersection = []\n for num in element_count_a:\n if num in element_count_b:\n min_occurrences = min(element_count_a[num], element_count_b[num])\n intersection.extend([num] * min_occurrences)\n \n return intersection\n \n\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
1 line code that beats 100% | intersection-of-two-arrays-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n return list((Counter(nums1) & Counter(nums2)).elements())\n \n\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Simple Python3 Solution || 🤖🧑💻💻|| Beats 97% | intersection-of-two-arrays-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n n1=len(nums1)\n n2=len(nums2)\n nums1.sort()\n nums2.sort()\n arr=[]\n i,j=0,0\n while(i<n1 and j<n2):\n if(nums1[i]==nums2[j]):\n arr.append(nums1[i])\n i+=1\n j+=1\n elif nums1[i]<nums2[j]:\n i+=1\n else:\n j+=1\n return arr\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
python solution with explanation | intersection-of-two-arrays-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitialize two empty dictionaries count1 and count2 to count the occurrences of each number in nums1 and nums2, respectively.\n\nLoop through each number in nums1 and increment its count in count1. The get() method is used to return the current count of the number if it is already in the dictionary, or 0 if it is not.\n\nLoop through each number in nums2 and increment its count in count2.\n\nInitialize an empty list arr to hold the intersection of the two arrays.\n\nLoop through each number in count1.\n\nIf the number is also in count2, then the minimum of the counts of the number in count1 and count2 is taken and the number is appended to arr that many times using the extend() method.\n\nReturn arr containing the intersection of the two arrays.\n\n# Complexity\n- Time complexity: The time complexity of this code is O(m + n), where m and n are the lengths of the two arrays nums1 and nums2, respectively. This is because the two for loops that count the occurrences of each number in the two arrays have a time complexity of O(m + n) in total, and the third loop that finds the intersection has a time complexity of O(min(m, n)) because it only iterates over the smaller dictionary.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity of this code is O(min(m, n)), because it uses two dictionaries count1 and count2 to count the occurrences of each number in the two arrays. The space complexity of the new list arr that holds the intersection of the two arrays is also O(min(m, n)), because it can hold at most min(m, n) elements.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n count1 = {}\n count2 = {}\n for num in nums1:\n count1[num] = count1.get(num, 0) + 1\n for num in nums2:\n count2[num] = count2.get(num, 0) + 1\n \n arr = []\n for num in count1:\n if num in count2:\n count = min(count1[num], count2[num])\n arr.extend([num] * count)\n \n return arr\n\n\n\n # arr = []\n # for i in nums1:\n # if i in nums2:\n # arr.append(i)\n # return arr\n# THIS SOLUTION FAILS FOR THIS TEST CASE - \n#Input\n# nums1 =\n# [1,2,2,1]\n# nums2 =\n# [2]\n# Output\n# [2,2]\n# Expected\n# [2]\n\n\n``` | 2 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
🔥[Python 3] 3 solutions: 1 line solution, Counters, 2 pointers 🥷🏼 | intersection-of-two-arrays-ii | 0 | 1 | ```python3 []\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n return (Counter(nums1) & Counter(nums2)).elements()\n```\n```python3 []\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n res, cnt1, cnt2 = [], Counter(nums1), Counter(nums2)\n for n, k in cnt1.items():\n if n in cnt2:\n res.extend([n]*min(k, cnt2[n]))\n return res\n```\n```python3 []\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n nums1.sort()\n nums2.sort()\n\n res = []\n i, j = 0, 0\n while i < len(nums1) and j < len(nums2):\n if nums1[i] < nums2[j]:\n i +=1\n elif nums1[i] > nums2[j]:\n j +=1\n else:\n res.append(nums1[i])\n i +=1\n j +=1\n\n return res\n```\n | 5 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
intersection-of-two-arrays-ii | intersection-of-two-arrays-ii | 0 | 1 | # Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n a = Counter(nums1)\n b = Counter(nums2)\n l = []\n for i in a:\n if b.get(i) is not None:\n l+=((min(b[i],a[i]))* [i])\n return l\n \n``` | 2 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
[Python] - clean & simple Solution | intersection-of-two-arrays-ii | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Here firstly we are sorting both of the list.\n- then we are adding infinity to end of the list in both.\n- Now we need to ust compare elements from start of both the list.\n- If both are same so move 1 ahead in both of the list and add it to our ans.\n- else check which one has smaller value move that list ahead by 1.\n\nI personally felt many problems you can solve easily if you are familier with merge sort application here by while loop of that is similar to that one.\n\n> so, if you can relate items than you can learn anything.\n\n# Complexity\n- Time complexity: $$O(max(mlogm, nlogn))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(min(m, n))$$ \nbecause we are keeping a list to store intersection so in worst case all elements can have same value.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n nums1.sort()\n nums2.sort()\n\n n1 = len(nums1)\n n2 = len(nums2)\n\n nums1.append(inf)\n nums2.append(inf)\n\n i = j = 0\n ans = []\n while i != n1 and j != n2:\n if nums1[i] == nums2[j]:\n ans.append(nums1[i])\n i += 1\n j += 1\n elif nums1[i] < nums2[j]:\n i += 1\n else:\n j+=1\n return ans\n``` | 5 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Simple Loop and if else solution #python3. | intersection-of-two-arrays-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n list1=[]\n if len(nums1)>len(nums2):\n for i in range(len(nums2)):\n if nums2[i] in nums1:\n nums1.remove(nums2[i])\n list1.append(nums2[i])\n else:\n for i in range(len(nums1)):\n if nums1[i] in nums2:\n nums2.remove(nums1[i])\n list1.append(nums1[i])\n return list1\n\n\n``` | 4 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Simple Python Solution | intersection-of-two-arrays-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n s = defaultdict(int)\n # if len()\n for i in nums1:\n s[i] +=1\n ans = []\n for i in nums2:\n if s[i]>0:\n ans.append(i)\n s[i] -=1\n\n return ans\n``` | 3 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Python3 | intersection-of-two-arrays-ii | 0 | 1 | # Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n l = []\n a = Counter(nums1)\n b = Counter(nums2)\n for i,j in a.items():\n if i in b:\n l+=[i]*min(j,b[i])\n return l\n\n``` | 6 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
📌 Python3 solution using counters faster than 90% | intersection-of-two-arrays-ii | 0 | 1 | ```\nfrom collections import Counter\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n counter = Counter(nums1)\n \n result = []\n for i in nums2:\n k = counter.get(i)\n if k!=None and k > 0:\n counter[i]-=1\n result.append(i)\n \n return result\n``` | 7 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Beginner friendly approach for finding the common elements between 2 arrays | intersection-of-two-arrays-ii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIterate through each element of list "nums1" and check if the element exists in list "nums2".\n\nIf the element exists in list "nums2", then append the element to another list and delete the element from the list "nums2" and return the resultant list\n\n# Complexity\n- Time complexity: O(len(nums1) * n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(len(nums1))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n res = []\n for i in nums1:\n if i in nums2:\n res.append(i)\n nums2.remove(i)\n return res \n\n\n \n``` | 3 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Python3 Easy Solution | intersection-of-two-arrays-ii | 0 | 1 | # Code\n```\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n n1,n2=Counter(nums1),Counter(nums2)\n ans=[]\n for i in n1.keys() and n2.keys():\n ans.extend([i]*min(n1[i],n2[i]))\n return ans\n``` | 2 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
✔Python - Simple approach using hashmap | intersection-of-two-arrays-ii | 0 | 1 | # Approach\nVery simple approach using python dictionary. Please let me know in the comment section if you have any doubts about the solution, and I\'ll be happy to clarify\uD83E\uDD17\n\n> ***And don\'t forget to upvote\u2B06 if you truly like my effort\'s !***\n\n\n\n# Code\n```\nfrom collections import Counter\nclass Solution:\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int] :\n result = []\n x = Counter(nums1) & Counter(nums2)\n for i, j in x.items() : \n result.extend([i] * j)\n return result\n``` | 1 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
Python code for reference | intersection-of-two-arrays-ii | 0 | 1 | \n# O(n) time and O(n) space \n```\n def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n hmap = defaultdict(int)\n res = []\n for val in nums1: hmap[val] += 1\n for val in nums2:\n if(hmap[val]>0):\n res.append(val);\n hmap[val]-=1\n return res;\n```\n\n# Follow up 1 : If Sorted \n```\ndef intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:\n nums1.sort()\n nums2.sort();\n res = []\n i,j=0,0\n while( i<len(nums1) and j<len(nums2)):\n if( nums1[i]==nums2[j]):\n res.append(nums1[i]);\n i+=1;\n j+=1;\n elif(nums1[i]<nums2[j]):\n i+=1\n elif(nums1[i]>nums2[j]):\n j+=1\n return res;\n```\nBetter to compare element wise\nO(n) time and O(1) space \n\n\n | 3 | Given two integer arrays `nums1` and `nums2`, return _an array of their intersection_. Each element in the result must appear as many times as it shows in both arrays and you may return the result in **any order**.
**Example 1:**
**Input:** nums1 = \[1,2,2,1\], nums2 = \[2,2\]
**Output:** \[2,2\]
**Example 2:**
**Input:** nums1 = \[4,9,5\], nums2 = \[9,4,9,8,4\]
**Output:** \[4,9\]
**Explanation:** \[9,4\] is also accepted.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 1000`
**Follow up:**
* What if the given array is already sorted? How would you optimize your algorithm?
* What if `nums1`'s size is small compared to `nums2`'s size? Which algorithm is better?
* What if elements of `nums2` are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once? | null |
📌📌Python3 || ⚡146 ms, faster than 99.33% of Python3 | data-stream-as-disjoint-intervals | 0 | 1 | ```\nclass SummaryRanges:\n\n def __init__(self):\n self.intervals = []\n\n def addNum(self, value: int) -> None:\n left, right = 0, len(self.intervals) - 1\n while left <= right:\n mid = (left + right) // 2\n e = self.intervals[mid]\n if e[0] <= value <= e[1]: return\n elif value < e[0]:right = mid - 1\n else:left = mid + 1\n pos = left\n self.intervals.insert(pos, [value, value])\n if pos + 1 < len(self.intervals) and value + 1 == self.intervals[pos+1][0]:\n self.intervals[pos][1] = self.intervals[pos+1][1]\n del self.intervals[pos+1]\n if pos - 1 >= 0 and value - 1 == self.intervals[pos-1][1]:\n self.intervals[pos-1][1] = self.intervals[pos][1]\n del self.intervals[pos]\n\n def getIntervals(self) -> List[List[int]]:\n return self.intervals\n\n``` | 2 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
352. Data Stream as Disjoint Intervals | Python (set) | data-stream-as-disjoint-intervals | 0 | 1 | # Code\n```\nclass SummaryRanges:\n def __init__(self):\n self.intervals = set()\n\n def addNum(self, value: int) -> None:\n self.intervals.add(value)\n\n def getIntervals(self) -> List[List[int]]:\n ans = []\n arr = sorted(self.intervals)\n start, end = arr[0], arr[0]\n for curr in arr[1:]:\n if end+1 == curr:\n end = curr\n else:\n ans.append([start, end])\n start, end = curr, curr\n ans.append([start, end])\n return ans\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
[Python] MinHeap + Hashset, Daily Challenge Jan., Day 28 | data-stream-as-disjoint-intervals | 0 | 1 | # Intuition\n\nfirst, think what kind of data structure do we need?\n1. need a sorted containers.\n2. need hashset to prevent duplicate\n\nfor a sorted containers, I think both of these should work:\n1. SortedList\n2. minHeap (lazy sorted)\n\nthen I choose minHeap and try to implement it\n\nit turns out the approach is straightforward:\n1. add `value` to min heap as single point `[value, value]`\n2. merge intervals at `def getIntervals()` and return merged result\n - merged intervals still a min heap!\n - we can directly update our minHeap with merged intervals and optimize time complexity of next call of `addNum` or `getIntervals`\n\n# Complexity\n- Time complexity:\n\naddNum: $$O(logn)$$\ngetIntervals: $$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass SummaryRanges(object):\n\n def __init__(self):\n self.intervals = []\n self.has = set()\n \n def addNum(self, val):\n if val in self.has: return\n self.has.add(val)\n heapq.heappush(self.intervals, [val, val])\n \n def getIntervals(self):\n res = []\n while self.intervals:\n start, end = heapq.heappop(self.intervals)\n if not res or start > res[-1][1]+1:\n res.append([start, end])\n else:\n res[-1][1] = max(res[-1][1], end)\n self.intervals = res\n return res\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
BUUM | data-stream-as-disjoint-intervals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SummaryRanges:\n\n def __init__(self):\n self.hashmap=set()\n def addNum(self, value: int) -> None:\n self.hashmap.add(value)\n\n def getIntervals(self) -> List[List[int]]:\n if len(self.hashmap)==0:return []\n arr=sorted(self.hashmap)\n res=[[arr[0],arr[0]]]\n for i in range(1,len(arr)):\n if arr[i]==res[-1][-1]+1:res[-1][-1]=arr[i]\n else:res.append([arr[i],arr[i]])\n return res\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | data-stream-as-disjoint-intervals | 0 | 1 | # Code\n```\nclass SummaryRanges:\n def __init__(self):\n self.intervals = []\n def addNum(self, val: int) -> None:\n left, right = 0, len(self.intervals) - 1\n while left <= right:\n mid = (left + right) // 2\n e = self.intervals[mid]\n if e[0] <= val <= e[1]: return\n elif val < e[0]:right = mid - 1\n else:left = mid + 1\n pos = left\n self.intervals.insert(pos, [val, val])\n if pos + 1 < len(self.intervals) and val + 1 == self.intervals[pos+1][0]:\n self.intervals[pos][1] = self.intervals[pos+1][1]\n del self.intervals[pos+1]\n if pos - 1 >= 0 and val - 1 == self.intervals[pos-1][1]:\n self.intervals[pos-1][1] = self.intervals[pos][1]\n del self.intervals[pos]\n\n def getIntervals(self) -> List[List[int]]:\n return self.intervals\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Stupid Desciption. Just expand the intervals . | data-stream-as-disjoint-intervals | 0 | 1 | # Intuition\n1. Sort all the incoming elements in the tree set.\n2. while implementing getIntervals() check for consecutives if elements are consecutive skip those elements\n3. else create a new interval\n\n# Approach\nI inserted elements into array at correct positions (by the help of lower_bound function)\nThen, created ranges[] list using simple O(N) traversal (skipping consequent equal values)\n\n# Complexity\nTc -> O(n.logn), SC -> O(n)\n\n# Code\n```\nclass SummaryRanges:\n def __init__(self):\n self.nums = set()\n\n def addNum(self, value: int) -> None:\n self.nums.add(value)\n\n def getIntervals(self) -> List[List[int]]:\n intervals = []\n seen = set()\n for num in self.nums:\n if num in seen: \n continue\n\n left = num\n while left - 1 in self.nums:\n left -= 1\n seen.add(left)\n\n right = num\n while right + 1 in self.nums:\n right += 1\n seen.add(right)\n \n intervals.append([left, right])\n return sorted(intervals)\n\n\n\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Using SortedList and Binary Search | data-stream-as-disjoint-intervals | 0 | 1 | # Intuition\nUsing Sorted Containers to maintain and update intervals for each new number and Binary Search to find where to insert the new number in out intervals list.\n\n# Approach\nFor each new number, find the index `idx` of where to insert the number.\nNow previous interval is `prev` which is `intervals[idx - 1]` \nAnd next interval is `nxt` which is `intervals[idx]`\n\nIf our number is already within `prev` or `nxt`, then no need to do anything. \nFor example if our `intervals = [[1, 4], [6,8]]` and our number is `3`, then no need to do anything as 3 is already part of `[1,4]`\n\nIf our number is one more than end of `prev` **AND** one less than start of `nxt`, then we can combine these two intervals \nFor example if our `intervals = [[1, 4], [6,8]]` and number is `5`, then we can write `intervals = [[1,8]]`\n\nIf our number is one more than end of `prev` **OR** one less than start of `nxt`, then we can merge it with `prev` or `nxt`\n\n# Complexity\n- Time complexity:\n For each addNum: Approximately $$O(logN)$$ (as we are using SortedList)\n For each getIntervals: $$O(1)$$\n\n- Space complexity: $$O(N)$$\n\n# Code\n```python\nfrom sortedcontainers import SortedList\n\nclass SummaryRanges:\n\n def __init__(self):\n self.intervals = SortedList()\n\n def addNum(self, value: int) -> None:\n INF = float(\'inf\')\n N = len(self.intervals)\n idx = self.intervals.bisect_left([value, value])\n\n pre_start, pre_end = self.intervals[idx - 1] if idx > 0 else [-INF, -INF]\n nxt_start, nxt_end = self.intervals[idx] if idx < N else [INF, INF]\n\n if pre_start <= value <= pre_end or nxt_start <= value <= nxt_end:\n # Eat 5 Star, Do nothing\n pass\n elif pre_end == value - 1 and nxt_start == value + 1:\n # Merge them\n self.intervals[idx - 1][1] = self.intervals[idx][1]\n self.intervals.pop(idx)\n elif pre_end == value - 1:\n # Merge with previous\n self.intervals[idx - 1][1] = value\n elif value + 1 == nxt_start:\n # Merge with next\n self.intervals[idx][0] = value\n else:\n # New interval entry\n self.intervals.add([value, value])\n\n def getIntervals(self) -> List[List[int]]:\n return self.intervals\n \n\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n```\n\nHope it helps :) | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
addNum O(log(n)) and getIntervals O(n) Solution | data-stream-as-disjoint-intervals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy original idea which is shown below was to add the elements to my sorted list using binary search(O(logn)) then to insert would be O(n). Thus this would take O(n*log(n)). \n\nThen iterate through the list in getIntervals and combined any numbers whose neighbors were 1 greater than them. This would take O(n). \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI wanted to optimize this approach, so I thought how I could insert and use binary search in log(n) time? I could use a binary search which is in python as SortDict. However, I would then need to turn it into a list. So I used the SortedList which is a binary search tree and linked list(under the hood). \n\nNow when I call getInterval, It will be O(n) to iterate through the list and use the same formula as above to calculate the intervals. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) - A List of n numbers\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(log(n)) - addNum\nO(n) - getIntervals\n\n# Code\n```\nfrom sortedcontainers import SortedDict, SortedSet, SortedList\nclass SummaryRanges:\n def __init__(self):\n self.sorted = SortedList([float(\'inf\')])\n self.seen = set()\n def addNum(self, value: int) -> None:\n if value not in self.seen:\n self.sorted.add(value)\n self.seen.add(value)\n \n \n def getIntervals(self) -> List[List[int]]:\n intervals = []\n length = 0\n front = self.sorted[0]\n for i in range(len(self.sorted)-1):\n back = self.sorted[i+1]\n length += 1\n if front + length != back:\n intervals.append([front, front + length - 1])\n front, length = back, 0\n return intervals\n \n\n\n """\n #Original Approach\n def __init__(self):\n self.numStream = [float(\'inf\')]\n self.nums = set()\n\n def addNum(self, value: int) -> None:\n if value not in self.nums:\n self.nums.add(value)\n insort(self.numStream, value)\n \n def getIntervals(self) -> List[List[int]]:\n intervals = []\n length = 0\n front = self.numStream[0]\n for i in range(len(self.numStream)-1):\n back = self.numStream[i+1]\n length += 1\n if front + length != back:\n intervals.append([front, front + length - 1])\n front, length = back, 0\n return intervals\n """\n \n\n\n\n \n\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
python solution native approach easy to understand | data-stream-as-disjoint-intervals | 0 | 1 | ```\nclass SummaryRanges:\n\n def __init__(self):\n\t\t# list to store values\n self.rtr = []\n\n def addNum(self, value: int) -> None:\n if not self.rtr:\n\t\t\t# if list is empty add the value\n self.rtr.append(value)\n else:\n\t\t\t# if value is already present just return\n if value in self.rtr:\n return\n f=False\n\t\t\t# traverse the list to find insert position for current elm -> you can use bisect module to do the same in logn time complexity.\n for index,elm in enumerate(self.rtr):\n if elm > value:\n f=True\n break\n if f:\n\t\t\t\t# inserting the element to its position so that the list is sorted\n self.rtr.insert(index,value)\n else:\n self.rtr.insert(index+1,value)\n\n def getIntervals(self) -> List[List[int]]:\n\t\t# default interval we\'ll update it inside loop of O(n) time complexity\n interval = [-2,-2]\n\t\t# parent will store all intervals\n parent = []\n\t\t# traversing the sorted elements list\n for num in self.rtr:\n\t\t\t# if no interval is available -> change the default interval to create one\n if interval[0]==-2:\n interval[0] = num\n interval[1] = num\n else:\n\t\t\t\t# otherwise check if the gap b/w them is 1 if it is update the intervals end with current number\n if interval[-1] + 1 == num:\n interval[-1] = num\n\t\t\t\t# otherwise append the current interval and create a new interval\n else:\n parent.append(list(interval))\n interval[0] = num\n interval[1] = num\n\t\t# if last interval is not been added to final list add the last one\n if interval[0]!=-2:\n parent.append(interval)\n # print(self.rtr,parent)\n return parent\n\n\'\'\'\n\tThanks For reading please upvote\n\tif you like :-)\n\'\'\'\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
[Python] Short O(nlogn) solution using SortedList (binary search tree) | data-stream-as-disjoint-intervals | 0 | 1 | Keep a sorted list of ranges, for each add operations, binary search the insert position, compare val with the previous and next ranges. \n\nThis can be implemented with a `list of ranges` but the complexity\'s gonna be `O(n)` for each addNum() since inserting into a list takes O(n) time. Instead, using a `SortedList of ranges` makes each addNum() `O(logn)` since SortedList is implemented with BST and BST insertion is O(logn).\n\n```\nfrom sortedcontainers import SortedList\nclass SummaryRanges:\n\n def __init__(self):\n self.sl = SortedList()\n\n def addNum(self, val: int) -> None:\n n = len(self.sl)\n i = self.sl.bisect_left([val, val])\n # val already added\n if i > 0 and self.sl[i-1][0] <= val <= self.sl[i-1][1] or i < n and self.sl[i][0] <= val <= self.sl[i][1]:\n pass\n # merge left & right\n elif 0 < i < n and self.sl[i-1][1] == val-1 and self.sl[i][0] == val+1:\n new = [self.sl[i-1][0], self.sl[i][1]]\n del self.sl[i]\n del self.sl[i-1]\n self.sl.add(new)\n # merge left only\n elif 0 < i and self.sl[i-1][1] == val-1:\n new = [self.sl[i-1][0], val]\n del self.sl[i-1]\n self.sl.add(new)\n # merge right only\n elif i < n and self.sl[i][0] == val+1:\n new = [val, self.sl[i][1]]\n del self.sl[i]\n self.sl.add(new)\n else:\n self.sl.add([val, val])\n\n def getIntervals(self) -> List[List[int]]:\n return self.sl\n \n``` | 20 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Python3 Beats 99.33% | data-stream-as-disjoint-intervals | 0 | 1 | \n\n# Code\n```\nclass SummaryRanges:\n\n def __init__(self):\n def cmp():\n return -1\n self.mp=defaultdict(cmp)\n self.a=[]\n \n\n def addNum(self, value: int) -> None:\n if self.mp[value]!=-1:\n return \n if self.mp[value-1]!=-1:\n self.a.remove([self.mp[value-1],value-1])\n \n self.mp[value]=self.mp[value-1]\n self.mp[self.mp[value-1]]=value\n self.a.append([self.mp[value],value])\n if self.mp[value+1]!=-1:\n self.a.remove([self.mp[value],value])\n self.a.remove([value+1,self.mp[value+1]])\n self.a.append([self.mp[value],self.mp[value+1]])\n self.mp[self.mp[value]]=self.mp[value+1]\n self.mp[self.mp[value+1]]=self.mp[value]\n \n elif self.mp[value+1]!=-1:\n self.a.remove([value+1,self.mp[value+1]])\n \n self.mp[value]=self.mp[value+1]\n self.mp[self.mp[value+1]]=value \n self.a.append([value,self.mp[value]]) \n \n if self.mp[value]==-1:\n self.mp[value]=value\n self.a.append([value,value])\n\n\n def getIntervals(self) -> List[List[int]]:\n return sorted(self.a)\n \n\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 14 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Python 3 || 4 lines, sets, zip || T/M: 100% / 100% | data-stream-as-disjoint-intervals | 0 | 1 | ```\nclass SummaryRanges:\n def __init__(self):\n self.stack = deque()\n \n def dfs(self, nums):\n return list(zip(sorted(set([n for n in nums if n-1 not in nums])),\n sorted(set([n for n in nums if n+1 not in nums]))))\n\n def addNum(self, val):\n self.stack.append(val)\n\n def getIntervals(self):\n return self.dfs(self.stack)\n```\n[https://leetcode.com/problems/data-stream-as-disjoint-intervals/submissions/906232980/](http://) | 4 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
python3 Solution | data-stream-as-disjoint-intervals | 0 | 1 | \n```\nclass SummaryRanges:\n\n def __init__(self):\n self.a=[]\n\n def addNum(self, val: int) -> None:\n a=self.a\n left=0\n right=len(a)-1\n while left<=right:\n mid=left+(right-left)//2\n if a[mid][0]<=val<=a[mid][1]:\n return\n if a[mid][1]<=val:\n left=mid+1\n \n else:\n right=mid-1\n \n i=left\n a.insert(i,[val,val])\n if i!=len(a)-1 and a[i+1][0]==val+1:\n a[i+1][0]=a[i][0]\n a.pop(i)\n \n if i!=0 and a[i-1][1]==val-1:\n a[i-1][1]=a[i][1]\n a.pop(i)\n\n def getIntervals(self) -> List[List[int]]:\n return self.a\n\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(val)\n# param_2 = obj.getIntervals()\n``` | 1 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Python simple approach. Expand around each number to find the interval | data-stream-as-disjoint-intervals | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nConstruct the interval by expanding around each of the added numbers. \n\n# Complexity\n- Time complexity: __O(N)__ for getIntervals, __O(1)__ for addNum\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: __O(N)__ for getIntervals, __O(1)__ for addNum\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SummaryRanges:\n\n def __init__(self):\n self.nums = set()\n\n def addNum(self, value: int) -> None:\n self.nums.add(value)\n\n def getIntervals(self) -> List[List[int]]:\n intervals = []\n seen = set()\n for num in self.nums:\n if num in seen: \n continue\n\n left = num\n while left - 1 in self.nums:\n left -= 1\n seen.add(left)\n\n right = num\n while right + 1 in self.nums:\n right += 1\n seen.add(right)\n \n intervals.append([left, right])\n return sorted(intervals)\n\n# Your SummaryRanges object will be instantiated and called as such:\n# obj = SummaryRanges()\n# obj.addNum(value)\n# param_2 = obj.getIntervals()\n``` | 19 | Given a data stream input of non-negative integers `a1, a2, ..., an`, summarize the numbers seen so far as a list of disjoint intervals.
Implement the `SummaryRanges` class:
* `SummaryRanges()` Initializes the object with an empty stream.
* `void addNum(int value)` Adds the integer `value` to the stream.
* `int[][] getIntervals()` Returns a summary of the integers in the stream currently as a list of disjoint intervals `[starti, endi]`. The answer should be sorted by `starti`.
**Example 1:**
**Input**
\[ "SummaryRanges ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals ", "addNum ", "getIntervals "\]
\[\[\], \[1\], \[\], \[3\], \[\], \[7\], \[\], \[2\], \[\], \[6\], \[\]\]
**Output**
\[null, null, \[\[1, 1\]\], null, \[\[1, 1\], \[3, 3\]\], null, \[\[1, 1\], \[3, 3\], \[7, 7\]\], null, \[\[1, 3\], \[7, 7\]\], null, \[\[1, 3\], \[6, 7\]\]\]
**Explanation**
SummaryRanges summaryRanges = new SummaryRanges();
summaryRanges.addNum(1); // arr = \[1\]
summaryRanges.getIntervals(); // return \[\[1, 1\]\]
summaryRanges.addNum(3); // arr = \[1, 3\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\]\]
summaryRanges.addNum(7); // arr = \[1, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 1\], \[3, 3\], \[7, 7\]\]
summaryRanges.addNum(2); // arr = \[1, 2, 3, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[7, 7\]\]
summaryRanges.addNum(6); // arr = \[1, 2, 3, 6, 7\]
summaryRanges.getIntervals(); // return \[\[1, 3\], \[6, 7\]\]
**Constraints:**
* `0 <= value <= 104`
* At most `3 * 104` calls will be made to `addNum` and `getIntervals`.
* At most `102` calls will be made to `getIntervals`.
**Follow up:** What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream? | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.