title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅👇3 Approach🔥||✅👇Transitioning from a 🔥brute-force to optimized ones✅👇 | find-the-duplicate-number | 1 | 1 | # Problem Understanding\nGiven an array of N + 1 integers where each element is between 1 and N, the task is to find the duplicate number efficiently.\n\n# Approach\n\n---\n\n**I have explored three different approaches to solve this problem, and I am gradually transitioning from a brute-force approach to more optimized ones.**\n\n---\n# Solution 1: Using Sorting\n**Approach:**\n\n1. **Sort** the given array in ascending order.\n2. **Iterate** through the sorted array.\n3. **Check if arr[i] is equal to arr[i+1].** If true, arr[i] is the duplicate number.\n\n**Intuition:**\nThe **idea** behind this approach is that **if there is a duplicate number in the array, it will be adjacent to another identical number** after sorting. Sorting the array allows us to find duplicates efficiently by comparing adjacent elements.\n\n# Solution 2: Using Frequency Array\n\n**Approach:**\n\n1. **Create a frequency array** of size N+1 and initialize it to all zeros.\n2. **Traverse** through the given array.\n3. **For each element arr[i], increment** the corresponding index in the frequency array by 1.\n4. **If you encounter an element with a frequency greater than 1, that element is the duplicate number.**\n\n**Intuition:**\n**This approach maintains a count of how many times each element appears in the array using a separate data structure** (the frequency array). When we encounter an element with a frequency greater than 1, we have found the duplicate element.\n\n\n# Solution 3: Linked List Cycle method\n**Step 1 (Phase 1 - Detect the Cycle):**\n<!-- Describe your approach to solving the problem. -->\n- **Initialize two pointers, slow and fast**, both initially pointing to the first element in the array.\n- **Use a loop to move slow one step at a time and fast two steps at a time.**\n- **Continue** this loop until slow and fast meet inside the cycle (i.e., slow == fast).\n\n**Step 2 (Phase 2 - Find the Entrance to the Cycle):**\n- **After detecting the cycle,** reset one of the pointers (in this case, we reset fast) to the beginning of the array (i.e., fast = nums[0]).\n- **Now, move both slow and fast one step at a time until they meet again.**\n- The point **where slow and fast meet** for the second time is the entrance to the cycle.\n\n**Step 3 (Return the Duplicate Number):**\n\n- Return either slow or fast because they both point to the entrance of the cycle, which corresponds to the duplicate number in the array.\n\n\n# Let\'s Dry run-\n**Step 1**: Consider the following array where each element\'s value indicates the next index to jump to.\n\n```\n[3,1,3,4,2]\n```\n\n**Step 2:** Initialize two pointers, slow and fast, both initially at the first element (index 0).\n```\nslow\n\u2193\n[3, 1, 3, 4, 2]\n\u2191\nfast\n```\n**Step 3:** Move the pointers. slow moves one step at a time, and fast moves two steps at a time.\n```\n slow\n \u2193\n[3, 1, 3, 4, 2]\n \u2191\n fast\n```\n**Step 4**: Continue moving the pointers.\n```\n slow\n \u2193\n[3, 1, 3, 4, 2]\n \u2191\n fast\n```\n\n**Step 5:** Continue moving the pointers one step at a time until they meet again. This meeting point will be the entrance to the cycle.\n```\n slow\n \u2193\n[3, 1, 3, 4, 2]\n \u2191\n fast\n```\n**Step 6:** Now Point out to slow at Start, then iterate it one step again. Until it does not meet up with fast. When they meet that\'s our duplicate Number.\n\n---\n# Time Complexity\n- Sorting-O(nlogn)\n- Map-O(n)\n- Linked List cycle-O(n)\n# Space Complexity\n- Sorting-O(1)\n- Map-O(n)\n- Linked List cycle-O(1)\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n# Code Using Sorting Method\n```C++ []\nclass Solution {\npublic:\n int findDuplicate(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n\n // Iterate through the sorted array\n for (int i = 1; i < nums.size(); i++) {\n // Check if adjacent elements are equal\n if (nums[i] == nums[i - 1]) {\n return nums[i]; // Found the duplicate number\n }\n }\n\n return -1; // No duplicate found (shouldn\'t happen for this problem)\n }\n};\n```\n```Java []\nimport java.util.Arrays;\n\npublic class Solution {\n public int findDuplicate(int[] nums) {\n Arrays.sort(nums); // Sort the array in ascending order\n\n // Iterate through the sorted array\n for (int i = 1; i < nums.length; i++) {\n // Check if adjacent elements are equal\n if (nums[i] == nums[i - 1]) {\n return nums[i]; // Found the duplicate number\n }\n }\n\n return -1; // No duplicate found (shouldn\'t happen for this problem)\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def findDuplicate(self, nums):\n nums.sort() # Sort the array in ascending order\n\n # Iterate through the sorted array\n for i in range(1, len(nums)):\n # Check if adjacent elements are equal\n if nums[i] == nums[i - 1]:\n return nums[i] # Found the duplicate number\n\n return -1 # No duplicate found (shouldn\'t happen for this problem)\n\n```\n\n# Code Using Map Method\n```C++ []\nclass Solution {\npublic:\n int findDuplicate(vector<int>& nums) {\n unordered_map<int, int> numCount; // Map to store the count of each number\n\n // Iterate through the array and count the occurrences of each number\n for (int num : nums) {\n if (numCount.find(num) != numCount.end()) {\n return num; // Found the duplicate number\n }\n numCount[num] = 1;\n }\n\n return -1; // No duplicate found (shouldn\'t happen for this problem) \n }\n};\n```\n```Java []\nimport java.util.HashMap;\nimport java.util.Map;\n\npublic class Solution {\n public int findDuplicate(int[] nums) {\n Map<Integer, Integer> numCount = new HashMap<>(); // Map to store the count of each number\n\n // Iterate through the array and count the occurrences of each number\n for (int num : nums) {\n if (numCount.containsKey(num)) {\n return num; // Found the duplicate number\n }\n numCount.put(num, 1);\n }\n\n return -1; // No duplicate found (shouldn\'t happen for this problem)\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def findDuplicate(self, nums):\n numCount = {} # Dictionary to store the count of each number\n\n # Iterate through the array and count the occurrences of each number\n for num in nums:\n if num in numCount:\n return num # Found the duplicate number\n numCount[num] = 1\n\n return -1 # No duplicate found (shouldn\'t happen for this problem)\n\n```\n\n# Code Using Linked-List cycle Method\n```C++ []\nclass Solution {\npublic:\n int findDuplicate(vector<int>& nums) {\n int slow = nums[0];\n int fast = nums[0];\n\n // Phase 1: Detect the cycle\n do {\n slow = nums[slow];\n fast = nums[nums[fast]];\n } while (slow != fast);\n\n // Phase 2: Find the entrance to the cycle\n slow = nums[0];\n while (slow != fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n\n return slow; // or fast, as they both point to the entrance of the cycle\n }\n};\n\n```\n```Java []\npublic class Solution {\n public int findDuplicate(int[] nums) {\n int slow = nums[0];\n int fast = nums[0];\n\n // Phase 1: Detect the cycle\n do {\n slow = nums[slow];\n fast = nums[nums[fast]];\n } while (slow != fast);\n\n // Phase 2: Find the entrance to the cycle\n slow = nums[0];\n while (slow != fast) {\n slow = nums[slow];\n fast = nums[fast];\n }\n\n return slow; // or fast, as they both point to the entrance of the cycle\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def findDuplicate(self, nums):\n slow = nums[0]\n fast = nums[0]\n\n # Phase 1: Detect the cycle\n while True:\n slow = nums[slow]\n fast = nums[nums[fast]]\n if slow == fast:\n break\n\n # Phase 2: Find the entrance to the cycle\n slow = nums[0]\n while slow != fast:\n slow = nums[slow]\n fast = nums[fast]\n\n return slow # or fast, as they both point to the entrance of the cycle\n\n```\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n\n | 60 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Easy python solution with O(n) time complexity with EXPLANANTION | find-the-duplicate-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is given that the array consists integers from 1 to n only. So our task is easy we can just have an array of size n intialized with zeros.\n\nNow we iterate with say i throughtout the list and increment the i^th index of the array.\n\nwhen the position of array gets equal to 2 we return the result.\n\nThis is how we solve this least time complexity possible.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n l=[0]*len(nums)\n for i in nums :\n l[i]+=1\n if l[i]==2 :\n return i\n \n \n``` | 0 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Find the duplicate number | find-the-duplicate-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n t=nums[0]\n h=nums[0]\n while True:\n t=nums[t]\n h=nums[nums[h]]\n if t==h:\n break\n t=nums[0]\n while t!=h:\n t=nums[t]\n h=nums[h]\n return t\n``` | 0 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
✅98.89%🔥Easy Solution🔥1 line code🔥 | find-the-duplicate-number | 0 | 1 | \n# Solution\n```\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n seen = set()\n return next(num for num in nums if num in seen or seen.add(num))\n\n\n``` | 19 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Easy & Fastest - slow and fast pointer approach | find-the-duplicate-number | 0 | 1 | \n# Code\n```\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n slow = nums[0]\n fast = nums[0]\n while True:\n slow = nums[slow]\n fast= nums[nums[fast]]\n if slow == fast: break\n \n fast = nums[0]\n while slow != fast:\n slow = nums[slow]\n fast = nums[fast]\n return slow\n``` | 5 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Python | Using two pointers | find-the-duplicate-number | 0 | 1 | # Intuition\nUsing Floyd\'s and Hare algorithm for cycle detection in a linked list using 2 pointers `slow` and `fast` pointers.\n\n# Approach\n\nThis algorithm works by first finding the intersection point of the two pointers within the cycle (Phase 1), and then finding the entrance to the cycle (Phase 2). The entrance to the cycle is the repeated number in the array.\n\n\n\n\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def findDuplicate(self, nums: List[int]) -> int:\n slow=nums[0]\n fast=nums[0]\n while True:\n slow=nums[slow]\n fast=nums[nums[fast]]\n if slow==fast:\n break\n slow=nums[0]\n while slow!=fast:\n slow=nums[slow]\n fast=nums[fast]\n return slow\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given an array of integers `nums` containing `n + 1` integers where each integer is in the range `[1, n]` inclusive.
There is only **one repeated number** in `nums`, return _this repeated number_.
You must solve the problem **without** modifying the array `nums` and uses only constant extra space.
**Example 1:**
**Input:** nums = \[1,3,4,2,2\]
**Output:** 2
**Example 2:**
**Input:** nums = \[3,1,3,4,2\]
**Output:** 3
**Constraints:**
* `1 <= n <= 105`
* `nums.length == n + 1`
* `1 <= nums[i] <= n`
* All the integers in `nums` appear only **once** except for **precisely one integer** which appears **two or more** times.
**Follow up:**
* How can we prove that at least one duplicate number must exist in `nums`?
* Can you solve the problem in linear runtime complexity? | null |
Using auxiliary board | Python | O(mn) | game-of-life | 0 | 1 | # Code\n```\nclass Solution:\n def gameOfLife(self, board: List[List[int]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n def withinbounds(a, b):\n if (a>=0 and a<=len(board)-1) and (b>=0 and b<=len(board[0])-1):\n return True\n return False\n\n def neighbours(i, j):\n # use offset to generate neighbours\n # check if neighbour is within matrix, and not the same element again\n n = []\n for a in range(-1, 2):\n for b in range(-1, 2):\n if a == 0 and b == 0:\n continue\n if withinbounds(i+a, j+b):\n n.append(board[i+a][j+b])\n return n\n\n # create auxiliary matrix with same size as board\n aux = [[0 for i in range(len(board[0]))]for j in range(len(board))]\n\n # fill aux with number of live neighbours\n for i in range(len(aux)):\n for j in range(len(aux[0])):\n n = sum(neighbours(i, j))\n aux[i][j] = n\n\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == 1:\n live = aux[i][j]\n if live < 2 or live > 3:\n board[i][j] = 0\n else:\n live = aux[i][j]\n if live == 3:\n board[i][j] = 1\n``` | 2 | According to [Wikipedia's article](https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life): "The **Game of Life**, also known simply as **Life**, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. "
The board is made up of an `m x n` grid of cells, where each cell has an initial state: **live** (represented by a `1`) or **dead** (represented by a `0`). Each cell interacts with its [eight neighbors](https://en.wikipedia.org/wiki/Moore_neighborhood) (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the `m x n` grid `board`, return _the next state_.
**Example 1:**
**Input:** board = \[\[0,1,0\],\[0,0,1\],\[1,1,1\],\[0,0,0\]\]
**Output:** \[\[0,0,0\],\[1,0,1\],\[0,1,1\],\[0,1,0\]\]
**Example 2:**
**Input:** board = \[\[1,1\],\[1,0\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 25`
* `board[i][j]` is `0` or `1`.
**Follow up:**
* Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
* In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems? | null |
289: Solution with step by step explanation | game-of-life | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe code implements the Game of Life, a cellular automaton, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). The function takes the current state of the board as input and returns the next state.\n\nThe algorithm works by iterating over each cell in the board and counting the number of live neighbors. It then applies the rules of the Game of Life to determine the state of the cell in the next generation.\n\nThe first for loop iterates over each row in the board, and the second for loop iterates over each cell in each row. For each cell, the algorithm counts the number of live neighbors by iterating over its 8 neighbors using two nested for loops. The max() and min() functions are used to handle the boundary cells.\n\nThe if statements apply the rules of the Game of Life. If a live cell has 2 or 3 live neighbors, it lives on to the next generation, and if a dead cell has exactly 3 live neighbors, it becomes a live cell. The |= operator is used to set the second bit to 1, which indicates the cell\'s state in the next generation.\n\nFinally, the second for loop is used to right-shift each cell\'s value by 1 to get the next state of the board.\n\nThe code uses bit manipulation to store the state of each cell in the current generation and the next generation. It updates the state of the current generation by setting the second bit to 1 and uses the first bit to store the state of the next generation. The right-shift operation is used to get the next generation\'s state by discarding the second bit.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def gameOfLife(self, board: List[List[int]]) -> None:\n m = len(board)\n n = len(board[0])\n\n for i in range(m):\n for j in range(n):\n ones = 0\n for x in range(max(0, i - 1), min(m, i + 2)):\n for y in range(max(0, j - 1), min(n, j + 2)):\n ones += board[x][y] & 1\n # Any live cell with 2 or 3 live neighbors\n # lives on to the next generation\n if board[i][j] == 1 and (ones == 3 or ones == 4):\n board[i][j] |= 0b10\n # Any dead cell with exactly 3 live neighbors\n # becomes a live cell, as if by reproduction\n if board[i][j] == 0 and ones == 3:\n board[i][j] |= 0b10\n\n for i in range(m):\n for j in range(n):\n board[i][j] >>= 1\n\n``` | 5 | According to [Wikipedia's article](https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life): "The **Game of Life**, also known simply as **Life**, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. "
The board is made up of an `m x n` grid of cells, where each cell has an initial state: **live** (represented by a `1`) or **dead** (represented by a `0`). Each cell interacts with its [eight neighbors](https://en.wikipedia.org/wiki/Moore_neighborhood) (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the `m x n` grid `board`, return _the next state_.
**Example 1:**
**Input:** board = \[\[0,1,0\],\[0,0,1\],\[1,1,1\],\[0,0,0\]\]
**Output:** \[\[0,0,0\],\[1,0,1\],\[0,1,1\],\[0,1,0\]\]
**Example 2:**
**Input:** board = \[\[1,1\],\[1,0\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 25`
* `board[i][j]` is `0` or `1`.
**Follow up:**
* Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
* In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems? | null |
[Python] Very Simple Solution with Explanation, No space used | game-of-life | 0 | 1 | ```\nclass Solution:\n def gameOfLife(self, board: List[List[int]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n ## RC ##\n ## APPRAOCH : IN-PLACE MANIPULATION ##\n # when the value needs to be updated, we donot just change 0 to 1 / 1 to 0 but we do in increments and decrements of 2. (table explains) \n ## previous value state change current state current value\n ## 0 no change dead 0\n ## 1 no change live 1\n ## 0 changed (+2) live 2\n ## 1 changed (-2) dead -1\n \n\t\t## TIME COMPLEXITY : O(MxN) ##\n\t\t## SPACE COMPLEXITY : O(1) ##\n\n directions = [(1,0), (1,-1), (0,-1), (-1,-1), (-1,0), (-1,1), (0,1), (1,1)]\n \n for i in range(len(board)):\n for j in range(len(board[0])):\n live = 0 # live neighbors count\n for x, y in directions: # check and count neighbors in all directions\n if ( i + x < len(board) and i + x >= 0 ) and ( j + y < len(board[0]) and j + y >=0 ) and abs(board[i + x][j + y]) == 1:\n live += 1\n if board[i][j] == 1 and (live < 2 or live > 3): # Rule 1 or Rule 3\n board[i][j] = -1\n if board[i][j] == 0 and live == 3: # Rule 4\n board[i][j] = 2\n for i in range(len(board)):\n for j in range(len(board[0])):\n board[i][j] = 1 if(board[i][j] > 0) else 0\n return board\n``` | 30 | According to [Wikipedia's article](https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life): "The **Game of Life**, also known simply as **Life**, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. "
The board is made up of an `m x n` grid of cells, where each cell has an initial state: **live** (represented by a `1`) or **dead** (represented by a `0`). Each cell interacts with its [eight neighbors](https://en.wikipedia.org/wiki/Moore_neighborhood) (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the `m x n` grid `board`, return _the next state_.
**Example 1:**
**Input:** board = \[\[0,1,0\],\[0,0,1\],\[1,1,1\],\[0,0,0\]\]
**Output:** \[\[0,0,0\],\[1,0,1\],\[0,1,1\],\[0,1,0\]\]
**Example 2:**
**Input:** board = \[\[1,1\],\[1,0\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 25`
* `board[i][j]` is `0` or `1`.
**Follow up:**
* Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
* In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems? | null |
C++ and Python Simple Solutions w/comments, O(nm) time, O(1) Space | game-of-life | 0 | 1 | **C++:**\n```\nclass Solution {\npublic:\n // Helper function to check validility of neighbor\n bool isValidNeighbor(int x, int y, vector<vector<int>>& board) {\n return (x >= 0 && x < board.size() && y >= 0 && y < board[0].size());\n }\n \n void gameOfLife(vector<vector<int>>& board) {\n // All directions of neighbors\n vector<int> ways_x = {0, 0, 1, 1, 1, -1, -1, -1};\n vector<int> ways_y = {1, -1, 1, -1, 0, 0, 1, -1};\n \n for (int row = 0; row < board.size(); row++) {\n for (int col = 0; col < board[0].size(); col++) {\n \n int count_live_neighbors = 0;\n \n // Loop to count all live neighbors\n for (int i = 0; i < 8; i++) {\n int curr_x = row + ways_x[i], curr_y = col + ways_y[i];\n if (isValidNeighbor(curr_x, curr_y, board) && abs(board[curr_x][curr_y]) == 1)\n count_live_neighbors++;\n }\n \n // Rules 1 and 3: -1 indicates a cell that was live but now is dead.\n if (board[row][col] == 1 && (count_live_neighbors < 2 || count_live_neighbors > 3))\n board[row][col] = -1;\n \n // Rule 4: 2 indicates a cell that was dead but now is live.\n if (board[row][col] == 0 && count_live_neighbors == 3)\n board[row][col] = 2;\n }\n }\n \n // Get the final board\n for (int row = 0; row < board.size(); row++) {\n for (int col = 0; col < board[0].size(); col++) {\n if (board[row][col] >= 1)\n board[row][col] = 1;\n else\n board[row][col] = 0;\n }\n }\n }\n};\n```\n**Python:**\n```\nclass Solution:\n def gameOfLife(self, board: List[List[int]]) -> None:\n # Helper function to check validility of neighbor\n def isValidNeighbor(x, y):\n return x < len(board) and x >= 0 and y < len(board[0]) and y >= 0\n\n # All directions of neighbors\n ways_x = [0, 0, 1, 1, 1, -1, -1, -1]\n ways_y = [1, -1, 1, -1, 0, 0, 1, -1]\n \n for row in range(len(board)):\n for col in range(len(board[0])):\n \n # Loop to count all live neighbors\n count_live_neighbors = 0\n for i in range(8):\n curr_x, curr_y = row + ways_x[i], col + ways_y[i]\n if isValidNeighbor(curr_x, curr_y) and abs(board[curr_x][curr_y]) == 1:\n count_live_neighbors+=1\n \n # Rules 1 and 3: -1 indicates a cell that was live but now is dead.\n if board[row][col] == 1 and (count_live_neighbors < 2 or count_live_neighbors > 3):\n board[row][col] = -1\n \n # Rule 4: 2 indicates a cell that was dead but now is live.\n if board[row][col] == 0 and count_live_neighbors == 3:\n board[row][col] = 2\n \n # Get the final board\n for row in range(len(board)):\n for col in range(len(board[0])):\n if board[row][col] >= 1:\n board[row][col] = 1\n else:\n board[row][col] = 0\n```\n**Like it? please upvote!!!\nHave any comments? I\'d love to hear...** | 18 | According to [Wikipedia's article](https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life): "The **Game of Life**, also known simply as **Life**, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. "
The board is made up of an `m x n` grid of cells, where each cell has an initial state: **live** (represented by a `1`) or **dead** (represented by a `0`). Each cell interacts with its [eight neighbors](https://en.wikipedia.org/wiki/Moore_neighborhood) (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the `m x n` grid `board`, return _the next state_.
**Example 1:**
**Input:** board = \[\[0,1,0\],\[0,0,1\],\[1,1,1\],\[0,0,0\]\]
**Output:** \[\[0,0,0\],\[1,0,1\],\[0,1,1\],\[0,1,0\]\]
**Example 2:**
**Input:** board = \[\[1,1\],\[1,0\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 25`
* `board[i][j]` is `0` or `1`.
**Follow up:**
* Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
* In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems? | null |
game of Life || Python3 || Arrays | game-of-life | 0 | 1 | ```\nclass Solution:\n def gameOfLife(self, board: List[List[int]]) -> None:\n """\n Do not return anything, modify board in-place instead.\n """\n dirs = [[1, 0], [0, 1], [-1, 0], [0, -1], [1, 1], [-1, -1], [1, -1], [-1, 1]]\n \n for i in range(0, len(board)):\n for j in range(0, len(board[0])):\n live_cells = self.count_live_cells(i, j, dirs, board)\n if(board[i][j] == 1 and (live_cells < 2 or live_cells > 3)):\n # Marking live cell now dead as -1\n board[i][j] = -1\n elif(board[i][j] == 0 and live_cells == 3):\n # Marking dead cells now live as 2\n board[i][j] = 2\n \n # Updating all values\n for i in range(0, len(board)):\n for j in range(0, len(board[0])):\n if(board[i][j] == -1):\n board[i][j] = 0\n elif(board[i][j] == 2):\n board[i][j] = 1\n return board\n \n \n def count_live_cells(self, i, j, dirs, board):\n # Get live neighbors for a cell from all 8 directions\n live_cells = 0\n for dx, dy in dirs:\n x = i + dx\n y = j + dy\n \n # Taking abs(board[x][y]) since -1 indicates live cell which is now dead\n if(x < 0 or y < 0 or x >= len(board) or y >= len(board[0]) or abs(board[x][y]) != 1):\n continue\n live_cells += 1\n return live_cells\n``` | 1 | According to [Wikipedia's article](https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life): "The **Game of Life**, also known simply as **Life**, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. "
The board is made up of an `m x n` grid of cells, where each cell has an initial state: **live** (represented by a `1`) or **dead** (represented by a `0`). Each cell interacts with its [eight neighbors](https://en.wikipedia.org/wiki/Moore_neighborhood) (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the `m x n` grid `board`, return _the next state_.
**Example 1:**
**Input:** board = \[\[0,1,0\],\[0,0,1\],\[1,1,1\],\[0,0,0\]\]
**Output:** \[\[0,0,0\],\[1,0,1\],\[0,1,1\],\[0,1,0\]\]
**Example 2:**
**Input:** board = \[\[1,1\],\[1,0\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m, n <= 25`
* `board[i][j]` is `0` or `1`.
**Follow up:**
* Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
* In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems? | null |
Python 3 || 2 lines, w/ explanation || T/M: 98% / 100% | word-pattern | 0 | 1 | A *bijection* is both *onto* and *one-to-one*. The figure below illustrates:\n- 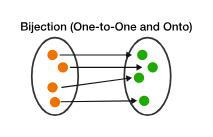\n\n\nThese conditions for bijectivity are satisfied if and only if the following is true:\n- The counts of distinct elements in two groups and the count of distinct mappings are all equal.\n\nIn terms of the figure, the count of the orange dots, the count of the green dots, and the count of arrows must all be equal. We can count the first two using `len(set())` and the third one by `len(set(zip_longest()))`.\n\n```\nclass Solution:\n def wordPattern(self, pattern: str, s: str) -> bool:\n\n s = s.split()\n\n return (len(set(pattern)) ==\n len(set(s)) ==\n len(set(zip_longest(pattern,s))))\n```\n[https://leetcode.com/problems/word-pattern/submissions/868765298/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 161 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
Python 3 lines. Check one to one relationship | word-pattern | 0 | 1 | # Complexity\n- Time complexity:\n $$O(n)$$\n- Space complexity:\n $$O(n)$$\n\n# Code\n```\nclass Solution:\n def wordPattern(self, pattern: str, s: str) -> bool:\n ls = s.split()\n k, v, p = Counter(pattern), Counter(ls), Counter(zip(pattern, ls))\n return len(k) == len(v) == len(p) and len(pattern) == len(ls)\n``` | 5 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
✔️ [Python3] SINGLE HASHMAP (•̀ᴗ•́)و, Explained | word-pattern | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nAt the first glance, the problem can be solved simply by using a hashmap `w_to_p` which maps words to letters from the pattern. But consider this example: `w = [\'dog\', \'cat\']` and `p = \'aa\'`. In this case, the hashmap doesn\'t allow us to verify whether we can assign the letter `a` as a value to the key `cat`. This case can be handled by comparing length of the unique letters from the pattern and unique words from the string.\n\nSpace: **O(n)** - scan\nTime: **O(n)** - for the hashmap\n\nRuntime: 28 ms, faster than **85.44%** of Python3 online submissions for Word Pattern.\nMemory Usage: 14 MB, less than **94.65%** of Python3 online submissions for Word Pattern.\n\n```\ndef wordPattern(self, p: str, s: str) -> bool:\n words, w_to_p = s.split(\' \'), dict()\n\n if len(p) != len(words): return False\n if len(set(p)) != len(set(words)): return False # for the case w = [\'dog\', \'cat\'] and p = \'aa\'\n\n for i in range(len(words)):\n if words[i] not in w_to_p: \n w_to_p[words[i]] = p[i]\n elif w_to_p[words[i]] != p[i]: \n return False\n\n return True\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 166 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
Solution with dict | word-pattern | 0 | 1 | \n# Code\n```\nclass Solution:\n def wordPattern(self, pattern: str, s: str) -> bool:\n res = {}\n s = s.split()\n if len(pattern) != len(s):\n return False\n for i in range(len(pattern)):\n if pattern[i] not in res.keys():\n if s[i] not in res.values():\n res[pattern[i]] = s[i]\n else:\n return False\n elif res[pattern[i]] != s[i]:\n return False\n return True\n\n``` | 1 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
Python | Easy Solution✅ | word-pattern | 0 | 1 | ```\ndef wordPattern(self, pattern: str, s: str) -> bool:\n arr = s.split()\n if len(arr) != len(pattern):\n return False\n \n for i in range(len(arr)):\n if pattern.find(pattern[i]) != arr.index(arr[i]):\n return False\n return True\n``` | 9 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
2 liners python solution which beats 98% submissions | word-pattern | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo split the string and map it to the pattern based on its indes.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wordPattern(self, pattern: str, str: str) -> bool:\n text = str.split()\n return [*map(pattern.index, pattern)] == [*map(text.index, text)]\n\n``` | 2 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
python solution, beats 97%, 10 ms | word-pattern | 0 | 1 | # Code\n```\nclass Solution(object):\n def wordPattern(self, pattern, s):\n l = s.split()\n if len(pattern) != len(l):\n return False\n hash = {}\n for key in range(len(pattern)):\n if pattern[key] not in hash and l[key] in hash.values():\n return False\n if pattern[key] not in hash:\n hash[pattern[key]] = l[key]\n elif hash[pattern[key]] != l[key]:\n return False\n return True\n```\n# HAPPY NEW YEAR LEETCODE!!!! | 3 | Given a `pattern` and a string `s`, find if `s` follows the same pattern.
Here **follow** means a full match, such that there is a bijection between a letter in `pattern` and a **non-empty** word in `s`.
**Example 1:**
**Input:** pattern = "abba ", s = "dog cat cat dog "
**Output:** true
**Example 2:**
**Input:** pattern = "abba ", s = "dog cat cat fish "
**Output:** false
**Example 3:**
**Input:** pattern = "aaaa ", s = "dog cat cat dog "
**Output:** false
**Constraints:**
* `1 <= pattern.length <= 300`
* `pattern` contains only lower-case English letters.
* `1 <= s.length <= 3000`
* `s` contains only lowercase English letters and spaces `' '`.
* `s` **does not contain** any leading or trailing spaces.
* All the words in `s` are separated by a **single space**. | null |
✅ EASIEST PYTHON ONE LINER SOLUTION ✅💯 | nim-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return False if n % 4 == 0 else True\n \n\n``` | 2 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
PYTHON | Simple Solution | DP & Memorization & Math | nim-game | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\ndef can_win(n: int, cache: dict[int, bool]) -> bool:\n if n in cache:\n return cache[n]\n cache[n - 1] = can_win(n - 1, cache)\n cache[n - 2] = can_win(n - 2, cache)\n cache[n - 3] = can_win(n - 3, cache)\n return not (cache[n - 1] and cache[n - 2] and cache[n - 3])\n\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n if n >= 134882061:\n return n % 4 != 0\n cache = {1: True, 2: True, 3: True, 4: False}\n return can_win(n, cache)\n```\n | 2 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Determining Winning Strategy in Nim Game using Game Theory. | nim-game | 0 | 1 | This is a classic example of a game theory problem where both players play optimally. The game\'s outcome depends on the number of stones in the heap. To determine whether you can win the game or not, we need to look at the number of stones in the heap and find a pattern.\n\nLet\'s consider the base cases first:\n\n- If there is only one stone, you can remove it and win the game.\n- If there are two stones, you can remove one stone and win the game.\n- If there are three stones, you can remove two stones and win the game.\n\nFor n=4, you cannot win the game, as you can remove at most three stones on your turn, and your friend can remove the remaining stones on their turn. Therefore, your friend will win the game.\n\nFor n=5,6,7, you can win the game. If there are 5 stones, you can remove one stone and reduce it to four stones, and your friend will be forced to remove one to three stones. In any case, you will be able to remove the last stone and win the game.\n\nSimilarly, if there are six stones, you can remove two stones, leaving four stones in the heap. Your friend will be forced to remove one to three stones, and you will be able to remove the last stone and win the game.\n\nIf there are seven stones, you can remove three stones, leaving four stones in the heap. Your friend will be forced to remove one to three stones, and you will be able to remove the last stone and win the game.\n\nWe can observe that for any n that is a multiple of four, you cannot win the game. For any other value of n, you can win the game.\n\nTherefore, to solve this problem, we need to check if n is a multiple of four or not. If it is, return false; otherwise, return true.\n\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n % 4 != 0\n``` | 13 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
python || simple solution || one-liner | nim-game | 0 | 1 | **time complexity:** o(1)\n\n**space complexity:** o(1)\n\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n # if n is not a multiple of 4, it is possible to win\n return n % 4\n```\n\n\uD83D\uDD3C please upvote if helpful \uD83D\uDD3C | 5 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
🎮Nim Game || ⚡Beats 90%⚡ || 🫱🏻🫲🏼Beginners Friendly... | nim-game | 0 | 1 | # KARRAR\n>Math...\n>>Brainteaser...\n>>>Game theory...\n>>>>Nim game...\n>>>>>Optimzed and generalized...\n>>>>>>Beginners friendly...\n>>>>>>>Enjoy LeetCode...\n- PLEASE UPVOTE...\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Take the mode of n by 4...\n Because the friend only when n is a divisor of 4...\n In other cases you can choose numbers like 1,2,3...\n If the result is 0, the answer is false...\n And true if it\'s not 0...\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Beats 90% (35 ms)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Beats 15% (16 MB)\n\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return True if n%4!=0 else False\n``` | 1 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
292: Time 99.68% and Space 90.42%, Solution with step by step explanation | nim-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution is similar to the previous one, but it is even more concise. Instead of using an if-else statement, it simply returns the result of the boolean expression n % 4 != 0. If n is divisible by 4, the expression will evaluate to False, meaning you cannot win. If n is not divisible by 4, the expression will evaluate to True, meaning you can win. This solution has the same time complexity of O(1) as the previous one.\n\n# Complexity\n- Time complexity:\n99.68%\n\n- Space complexity:\n90.42%\n\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n % 4 != 0\n``` | 7 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Easy one step python solution with explanation | nim-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nbasically me loses if the num becomes 4 \nwhen n is a multiple of 4 there a n/4 number of 4\'s\nso irrespective of what me chooses the other person can choose a number to fill it up to 4 this goes on and the other person wins\nexample:\n4\nme. other.\n1 3\n2 2\n3 1\n# Approach\n<!-- Describe your approach to solving the problem. -->\ncheck if n is a multiple of 4\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n%4!=0 \n \n``` | 4 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Simplest Python code!! | nim-game | 0 | 1 | <!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n%4\n``` | 3 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Python3 || 16ms, 99% faster|| one line | nim-game | 0 | 1 | ```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n % 4 != 0\n```\nif the value of n is divisible by 4 then only friend will win | 9 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Bottom-up DP python | nim-game | 0 | 1 | Using bottom-up programming: \nWe define function F(x): The capability of you winning the game with x stones on your first turn.\nIf you go first and n <= 3: you win.\nelse F(x) > 3 after your turn, it\'s your opponents turn\n\nWhich means if you go first and each of your three possible moves all land on F(X) => True for you, then it applies to your opponent as well. So F(X) = !F(x-1) and !F(x-2) and !F(x-3)\n\nT:O(N) S:O(N) Memory limit exceeded\n\nWe can reduce the space complexity by just updating an array of size 3, but an O(N) time is also unacceptable.\n\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool: \n if n <= 3:\n return True\n new_size = n + 1\n memo = [False] * (new_size)\n \n for i in range(4): \n memo[i] = True\n \n for i in range(4,new_size):\n for j in range(1,4):\n if memo[i] == True:\n break\n if memo[i-j] == True:\n memo[i] = False\n else:\n memo[i] = True\n \n return memo[n]\n``` | 14 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
24ms 97% beats in Python3 one-line | nim-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n We "75%" always win if we take 3 stones\n# Approach\n<!-- Describe your approach to solving the problem. -->\n play this game and you will understand\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n 24ms\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n 13.8 MB\n# Code\n\n\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return False if n%4==0 else True\n \n```\n | 3 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Python 1 line solution (BEATS 99.31%) | nim-game | 0 | 1 | # Intuition\nNotice that when we have a heap of 4 stones, we will lose. And similary, we will lose when we are left with a heap of 8 stones, because no matter you take 1,2, or 3 stones, your friend can always take 3, 2, or 1 stones. And now you are left with 4 stones. \n\n# Approach\nBased on the intuition, we simply check if the number of stones is a multiple of 4 or not.\n\n# Complexity\n- Time complexity:\nO(1)\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n % 4 != 0 \n``` | 0 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Beats 100.00% of users || 0ms || Dynamic Programming 😍 | nim-game | 1 | 1 | ## Intuition\nThe problem involves determining whether you can win the game of Nim given a certain number of stones. The game of Nim is a two-player game where players take turns removing stones from piles. The key to winning Nim is to leave your opponent with a pile that has a number of stones that is a multiple of 4.\n\n## Approach\nThe provided code checks if `n` is divisible by 4. If it is, the code returns `false`, indicating that the player cannot win Nim. If `n` is not divisible by 4, the code returns `true`, suggesting that the player can win Nim.\n\nThis solution relies on the observation that if you start with a pile of stones that is a multiple of 4, your opponent can always mirror your moves and leave you with a pile of 4 stones, which they can then win. Therefore, you want to force your opponent to start with a pile that is not a multiple of 4.\n\n## Complexity\n- Time complexity: O(1)\n - The time complexity is constant because the code performs a single arithmetic operation (`n % 4`) regardless of the input size.\n\n- Space complexity: O(1)\n - The space complexity is constant as the code uses a fixed amount of space for the integer variable `n`.\n# Code\n```\nclass Solution {\n public boolean canWinNim(int n) {\n if(n%4==0) return false;\n \n return true;\n }\n}\n```\n\n**JavaScript:**\n```javascript\nfunction canWinNim(n) {\n return n % 4 !== 0;\n}\n```\n\n**Python:**\n```python\ndef canWinNim(n):\n return n % 4 != 0\n```\n\n**Go:**\n```go\npackage main\n\nimport "fmt"\n\nfunc canWinNim(n int) bool {\n return n%4 != 0\n}\n\nfunc main() {\n fmt.Println(canWinNim(10))\n}\n```\n\n**Java:**\n```java\npublic class Solution {\n public boolean canWinNim(int n) {\n return n % 4 != 0;\n }\n}\n```\n\n**Kotlin:**\n```kotlin\nfun canWinNim(n: Int): Boolean {\n return n % 4 != 0\n}\n```\n\n**PHP:**\n```php\n<?php\n\nclass Solution {\n public function canWinNim($n) {\n return $n % 4 !== 0;\n }\n}\n\n$solution = new Solution();\necho $solution->canWinNim(10);\n```\n\n**C#:**\n```csharp\npublic class Solution {\n public bool CanWinNim(int n) {\n return n % 4 != 0;\n }\n}\n```\n\n**Swift:**\n```swift\nfunc canWinNim(_ n: Int) -> Bool {\n return n % 4 != 0\n}\n```\n\n**R:**\n```r\ncanWinNim <- function(n) {\n return n %% 4 != 0\n}\n```\n\n**Ruby:**\n```ruby\ndef can_win_nim(n)\n n % 4 != 0\nend\n```\n\n**C and C++:**\n```c\n#include <stdbool.h>\n\nbool canWinNim(int n) {\n return n % 4 != 0;\n}\n```\n\n**Matlab:**\n```matlab\nfunction result = canWinNim(n)\n result = mod(n, 4) ~= 0;\nend\n```\n\n**TypeScript:**\n```typescript\nfunction canWinNim(n: number): boolean {\n return n % 4 !== 0;\n}\n```\n\n**Scala:**\n```scala\nobject Solution {\n def canWinNim(n: Int): Boolean = {\n n % 4 != 0\n }\n}\n```\n\n**Rust:**\n```rust\npub fn can_win_nim(n: i32) -> bool {\n n % 4 != 0\n}\n```\n\n**Perl:**\n```perl\nsub canWinNim {\n my $n = shift;\n return $n % 4 != 0;\n}\n``` | 0 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Getting to `canWinNim = lambda n: n % 4 != 0` | nim-game | 0 | 1 | # Intuition\n\nWe can win if one of our moves puts our opponent in a losing position. This recursive description gives us an initial solution:\n\n```python\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n if n <= 3:\n return True\n else:\n return (\n not self.canWinNim(n - 1)\n or not self.canWinNim(n - 2)\n or not self.canWinNim(n - 3)\n )\n```\n\nWe use the above to create a table for small values of\n`Solution().canWinNim()`. Notice that we can win unless we start with a\nmultiple of four. Inductively, it\'s easy to see that `lambda n: n % 4 != 0`\nproduces the same result as the above recursion.\n\n# Complexity\n\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n\n```python\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n % 4 != 0\n```\n | 0 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
Explanation | nim-game | 0 | 1 | # Intuition\nWe find the pattern to win by listing first cases.\n\nLet denote **(n, r)** where **n** is the number of stones in the table and **r** be the result (win or lose) for the person who has a turn to remove these stones first.\n\n(1, win) (reason: remove 1 stone and win)\n(2, win) (remove 2 stones and win)\n(3, win) (remove 3 stones and win)\n(4, lose) (the current play can only remove the number of stones to 1 or 2 or 3 and the one who takes the next turn will win as indicated in the preceding cases)\n(5, win) (remove the stones to 4 and the next one will surely lose)\n(6, win) (remove the stones to 4 and the next one will surely lose)\n(7, win) (remove the stones to 4 and the next one will surely lose)\n(8, lose) (the current play can only remove the number of stones to 5 or 6 or 7 and let the next player win)\n\nSo we clearly spot the pattern here: if you take the number of stones which is divided by 4, then you lose; otherwise you win.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canWinNim(self, n: int) -> bool:\n return n % 4 != 0\n``` | 0 | You are playing the following Nim Game with your friend:
* Initially, there is a heap of stones on the table.
* You and your friend will alternate taking turns, and **you go first**.
* On each turn, the person whose turn it is will remove 1 to 3 stones from the heap.
* The one who removes the last stone is the winner.
Given `n`, the number of stones in the heap, return `true` _if you can win the game assuming both you and your friend play optimally, otherwise return_ `false`.
**Example 1:**
**Input:** n = 4
**Output:** false
**Explanation:** These are the possible outcomes:
1. You remove 1 stone. Your friend removes 3 stones, including the last stone. Your friend wins.
2. You remove 2 stones. Your friend removes 2 stones, including the last stone. Your friend wins.
3. You remove 3 stones. Your friend removes the last stone. Your friend wins.
In all outcomes, your friend wins.
**Example 2:**
**Input:** n = 1
**Output:** true
**Example 3:**
**Input:** n = 2
**Output:** true
**Constraints:**
* `1 <= n <= 231 - 1` | If there are 5 stones in the heap, could you figure out a way to remove the stones such that you will always be the winner? |
logn | find-median-from-data-stream | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(logn)\n- Space complexity:\nO(N)\n# Code\n```\nclass MedianFinder:\n\n def __init__(self):\n self.small,self.large = [],[]\n \n\n def addNum(self, num: int) -> None:\n if self.large and num > self.large[0]:\n heapq.heappush(self.large,num)\n else:\n heapq.heappush(self.small,-1*num)\n\n if len(self.small) > len(self.large)+1:\n val = -1* heapq.heappop(self.small)\n heapq.heappush(self.large,val)\n if len(self.large) > len(self.small)+1:\n val = heapq.heappop(self.large)\n heapq.heappush(self.small,-1*val)\n \n\n def findMedian(self) -> float:\n if len(self.small) > len(self.large):\n return -1*self.small[0]\n elif len(self.large) > len(self.small):\n return self.large[0]\n return (-1*self.small[0] + self.large[0])/2\n \n\n\n# Your MedianFinder object will be instantiated and called as such:\n# obj = MedianFinder()\n# obj.addNum(num)\n# param_2 = obj.findMedian()\n``` | 3 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
Python || Min and Max Heap Solution | find-median-from-data-stream | 0 | 1 | ```\nclass MedianFinder:\n\n def __init__(self):\n self.maxHeap=[]\n self.minHeap=[]\n\n def addNum(self, num: int) -> None:\n n1=len(self.maxHeap)\n n2=len(self.minHeap)\n if n1==n2:\n if num>self.findMedian():\n heappush(self.minHeap,num)\n else:\n heappush(self.maxHeap,-num)\n elif n1==n2-1:\n if num>self.findMedian():\n val=heappop(self.minHeap)\n heappush(self.maxHeap,-val)\n heappush(self.minHeap,num)\n else:\n heappush(self.maxHeap,-num)\n else:\n if num>self.findMedian():\n heappush(self.minHeap,num)\n else:\n val=-heappop(self.maxHeap)\n heappush(self.minHeap,val)\n heappush(self.maxHeap,-num)\n\n def findMedian(self) -> float:\n n1=len(self.maxHeap)\n n2=len(self.minHeap)\n if n1==n2-1:\n return self.minHeap[0]\n elif n2==n1-1:\n return -self.maxHeap[0]\n else:\n if n1==0 and n2==0:\n return 0\n return (-self.maxHeap[0]+self.minHeap[0])/2\n```\n**An upvote will be encouraging** | 2 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
using inbuilt functions easy | find-median-from-data-stream | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport statistics\nclass MedianFinder:\n\n def __init__(self):\n self.arr=[]\n\n def addNum(self, num: int) -> None:\n for i in range(len(self.arr)):\n if(num<=self.arr[i]):\n self.arr.insert(i,num)\n return \n self.arr.append(num)\n \n\n def findMedian(self) -> float:\n return statistics.median(self.arr)\n \n\n\n# Your MedianFinder object will be instantiated and called as such:\n# obj = MedianFinder()\n# obj.addNum(num)\n# param_2 = obj.findMedian()\n``` | 5 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
Using two heaps | find-median-from-data-stream | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBasically, you instantiate two heaps, a max heap to hold the first half of the numbers and a min_heap to hold the last half. Numbers will be added to the heaps in the sequence, max heap, min heap. When adding to the max_heap, you need to know if that number is not greater than any number in the min_heap before you add it to the max_heap, in the case where it is, we pop the min heap (taking the smallest number from the right half) and add that to the max heap, before putting our new number to the min heap, this is done to maintain the status quo of first half and last half. Returning the median becomes trivial and simply depends on whether the total number of digits are odd or even.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(log(N))\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass MedianFinder:\n\n def __init__(self):\n self.max_heap = []\n self.min_heap = []\n \n\n def addNum(self, num: int) -> None:\n if len(self.max_heap) == len(self.min_heap):\n if not len(self.max_heap) or num <= self.min_heap[0]:\n heapq.heappush(self.max_heap, -1 * num)\n else:\n heapq.heappush(self.max_heap, -1 * heapq.heappop(self.min_heap))\n heapq.heappush(self.min_heap, num)\n \n else:\n if num >= abs(self.max_heap[0]):\n heapq.heappush(self.min_heap, num)\n else:\n heapq.heappush(self.min_heap, -1 * heapq.heappop(self.max_heap))\n heapq.heappush(self.max_heap, -1 * num)\n\n \n\n def findMedian(self) -> float:\n size = len(self.max_heap) + len(self.min_heap)\n\n if size % 2:\n return float(-1 * self.max_heap[0])\n \n return (-1 * self.max_heap[0] + self.min_heap[0])/2\n\n \n\n\n# Your MedianFinder object will be instantiated and called as such:\n# obj = MedianFinder()\n# obj.addNum(num)\n# param_2 = obj.findMedian()\n``` | 2 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
Simple 3 liner Python code | find-median-from-data-stream | 0 | 1 | SortedList makes life easier.\n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass MedianFinder:\n\n def __init__(self):\n self.srt = SortedList()\n\n def addNum(self, num: int) -> None:\n self.srt.add(num)\n\n def findMedian(self) -> float:\n return median(self.srt)\n\n\n# Your MedianFinder object will be instantiated and called as such:\n# obj = MedianFinder()\n# obj.addNum(num)\n# param_2 = obj.findMedian()\n``` | 3 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
[Python] Logic Explained with 2 Heaps, Clean code. | find-median-from-data-stream | 0 | 1 | ```\n"""\n ## RC ##\n ## APPROACH : 2 HEAPS ##\n ## LOGIC ##\n ## One minheap to store low values and second maxheap to store max values, we keep track and update median every time after insertion ##\n \n\t\t## TIME COMPLEXITY : O(logN) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n ## EXAMPLE ##\n Adding number 41\n MaxHeap lo: [41] // MaxHeap stores the largest value at the top (index 0)\n MinHeap hi: [] // MinHeap stores the smallest value at the top (index 0)\n Median is 41\n =======================\n Adding number 35\n MaxHeap lo: [35] // max heap stores smaller half of nums\n MinHeap hi: [41] // min heap stores bigger half of nums\n Median is 38\n =======================\n Adding number 62\n MaxHeap lo: [41, 35]\n MinHeap hi: [62]\n Median is 41\n =======================\n Adding number 4\n MaxHeap lo: [35, 4]\n MinHeap hi: [41, 62]\n Median is 38\n =======================\n Adding number 97\n MaxHeap lo: [41, 35, 4]\n MinHeap hi: [62, 97]\n Median is 41\n =======================\n Adding number 108\n MaxHeap lo: [41, 35, 4]\n MinHeap hi: [62, 97, 108]\n Median is 51.5\n"""\n\nclass MedianFinder:\n def __init__(self):\n self.lo = [] \n self.hi = [] \n\n def addNum(self, num):\n heappush(self.lo, -num) # lo is maxheap, so -1 * num\n heappush(self.hi, -self.lo[0]) # hi is minheap\n heappop(self.lo)\n \n if len(self.lo) < len(self.hi):\n heappush(self.lo, -self.hi[0])\n heappop(self.hi)\n \n def findMedian(self):\n if len(self.lo) > len(self.hi):\n return -self.lo[0] \n else:\n return (self.hi[0] - self.lo[0]) / 2 # - as low has -ve values\n```\nPLEASE UPVOTE IF YOU LIKE MY SOLUTION | 79 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
2 Heaps easy to understand solution | find-median-from-data-stream | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince we need to find the median we are only concerened with the middle elements. We do not need to sort all the elements as we are worried about the elements other than the middle elements. THe question is how we can get the middle elements.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet say median of the data stream at any given moment is `m`. We will have two heaps. We will insert elements in the heaps such that one contaning all the elements less than `m` and other contaning all the elements greater than `m`. Make the difference between number of elements in both the heaps should not be more than `1`. First will be a max heap which will return an element that is largest of all the elements less than `m` and second will return smallest element greater than `m` when an element is popped out from them. We can then find what we want i.e the median of data stream which either mean of top of the elements of both the heaps or top element of min heap or max heap whichever you choose to have the more number of elements.\n\n# Complexity\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity:\nWe are inserting or removing an element an element from heap so its time complexity would be $$O(log n)$$\n\nSpace complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity:\nWe are storing all the elements in our heaps so space complexity would be $$O(n)$$\n\n# Code\n```\nclass MedianFinder:\n\n def __init__(self):\n self.minHeap = []\n heapq.heapify(self.minHeap)\n self.maxHeap = []\n heapq.heapify(self.maxHeap)\n\n def addNum(self, num: int) -> None:\n if len(self.minHeap) > 0 and num > -self.minHeap[0]:\n heapq.heappush(self.maxHeap, num)\n if len(self.maxHeap) > len(self.minHeap):\n item = heapq.heappop(self.maxHeap)\n heapq.heappush(self.minHeap, -item)\n else:\n heapq.heappush(self.minHeap, -num)\n if len(self.minHeap) - len(self.maxHeap) > 1:\n item = heapq.heappop(self.minHeap)\n heapq.heappush(self.maxHeap, -item)\n\n def findMedian(self) -> float:\n if len(self.minHeap) == len(self.maxHeap):\n return (-self.minHeap[0] + self.maxHeap[0]) / 2\n else:\n return -self.minHeap[0]\n\n\n\n# Your MedianFinder object will be instantiated and called as such:\n# obj = MedianFinder()\n# obj.addNum(num)\n# param_2 = obj.findMedian()\n``` | 2 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
295: Time 97.64%, Solution with step by step explanation | find-median-from-data-stream | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe MedianFinder class maintains two heaps: self.small (a max heap) and self.large (a min heap). The median is either the largest element in self.small, the smallest element in self.large, or the average of these two elements if the heaps have the same size.\n\nThe addNum method first pushes the new element onto self.small. If self.small becomes larger than self.large, the largest element in self.small is popped and pushed onto self.large. If self.large becomes larger than self.small, the smallest element in self.large is popped and pushed onto self.small.\n\nThe findMedian method returns the median as described above.\n\n# Complexity\n- Time complexity:\n97.64%\n\n- Space complexity:\n79.57%\n\n# Code\n```\nimport heapq\n\nclass MedianFinder:\n def __init__(self):\n """\n initialize your data structure here.\n """\n self.small = []\n self.large = []\n\n def addNum(self, num: int) -> None:\n if len(self.small) == len(self.large):\n heapq.heappush(self.large, -heapq.heappushpop(self.small, -num))\n else:\n heapq.heappush(self.small, -heapq.heappushpop(self.large, num))\n\n def findMedian(self) -> float:\n if len(self.small) == len(self.large):\n return (self.large[0] - self.small[0]) / 2.0\n else:\n return float(self.large[0])\n\n``` | 9 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
Simple Solution with Approach using Python Heap | find-median-from-data-stream | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create two heaps, such as mini and maxi.\n2. Mini would store smaller elements and maxi will store the larger elements following the max difference between their lengths should not exceed 1.\n3. In python, we only have min heap, in order to create a max heap, we need to negate the value before pushing it inside our heap (in our case it\'s done for mini).\n4. Following some, if else ladders, I\'ve inserted values in our heap.\n5. For findMedian function, we only need to check the current length of both heaps which are mini and maxi.\n6. If lengths are equal then pop values from mini and maxi and return their median.\n7. If lengths are different then pop value from mini and return.\n\n# Code\n```\nimport heapq\nclass MedianFinder:\n\n def __init__(self):\n self.mini = []\n self.maxi = []\n\n def addNum(self, num: int) -> None:\n if len(self.mini) == 0: \n heapq.heappush(self.mini, -num)\n elif len(self.mini) == len(self.maxi): \n x = self.maxi[0]\n if x < num:\n heapq.heappush(self.mini, -heapq.heappop(self.maxi))\n heapq.heappush(self.maxi, num)\n else:\n heapq.heappush(self.mini, -num)\n else:\n x = self.mini[0]\n if -x < num:\n heapq.heappush(self.maxi, num)\n else:\n heapq.heappush(self.maxi, -heapq.heappop(self.mini))\n heapq.heappush(self.mini, -num)\n return None\n\n def findMedian(self) -> float:\n if len(self.mini) == 0:\n return None\n if len(self.mini) > len(self.maxi):\n return -self.mini[0]\n else:\n return (-self.mini[0]+self.maxi[0])/2\n \n\n\n# Your MedianFinder object will be instantiated and called as such:\n# obj = MedianFinder()\n# obj.addNum(num)\n# param_2 = obj.findMedian()\n``` | 2 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
* For example, for `arr = [2,3,4]`, the median is `3`.
* For example, for `arr = [2,3]`, the median is `(2 + 3) / 2 = 2.5`.
Implement the MedianFinder class:
* `MedianFinder()` initializes the `MedianFinder` object.
* `void addNum(int num)` adds the integer `num` from the data stream to the data structure.
* `double findMedian()` returns the median of all elements so far. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input**
\[ "MedianFinder ", "addNum ", "addNum ", "findMedian ", "addNum ", "findMedian "\]
\[\[\], \[1\], \[2\], \[\], \[3\], \[\]\]
**Output**
\[null, null, null, 1.5, null, 2.0\]
**Explanation**
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = \[1\]
medianFinder.addNum(2); // arr = \[1, 2\]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3); // arr\[1, 2, 3\]
medianFinder.findMedian(); // return 2.0
**Constraints:**
* `-105 <= num <= 105`
* There will be at least one element in the data structure before calling `findMedian`.
* At most `5 * 104` calls will be made to `addNum` and `findMedian`.
**Follow up:**
* If all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution?
* If `99%` of all integer numbers from the stream are in the range `[0, 100]`, how would you optimize your solution? | null |
Recursive approach✅ | O( n)✅ | Python(Step by step explanation)✅ | serialize-and-deserialize-binary-tree | 0 | 1 | # Intuition\nThe problem involves serializing and deserializing a binary tree. Serialization is the process of converting a data structure into a string, and deserialization is the reverse process. The goal is to implement a `Codec` class that can serialize a binary tree into a string and deserialize the string back into a binary tree.\n\n# Approach\nThe approach is to perform a depth-first search (DFS) on the binary tree for both serialization and deserialization. During serialization, each node\'s value is added to a list, and "N" is used to represent null nodes. The list is then joined into a string separated by commas. For deserialization, the string is split into a list, and a recursive DFS function is used to reconstruct the binary tree.\n\n1. **Serialization Function (`serialize`)**\n - **DFS for Serialization**: Traverse the binary tree using DFS and append each node\'s value (or "N" for null) to a list.\n - **Reason**: DFS ensures a consistent order for serialization.\n - **List to String**: Join the list into a string using commas as separators.\n - **Reason**: This creates a string representation of the binary tree.\n\n2. **Deserialization Function (`deserialize`)**\n - **String Splitting**: Split the input string into a list of values.\n - **Reason**: The string contains the serialized representation of the binary tree.\n - **DFS for Deserialization**: Recursively reconstruct the binary tree from the list of values.\n - **Reason**: Recursion helps reconstruct the tree structure.\n\n3. **Serialization and Deserialization Components**\n - **List Usage for Serialization**: Utilize a list to store the serialized values during DFS.\n - **Reason**: Lists are mutable and easy to manipulate during DFS.\n - **String Splitting and Joining**: Use string splitting and joining operations to convert between strings and lists.\n - **Reason**: These operations simplify the conversion process.\n\n4. **Codec Class**\n - **DFS Helper Function for Serialization and Deserialization**: Implement a DFS helper function to traverse the binary tree during both serialization and deserialization.\n - **Reason**: Encapsulation of DFS logic for better code organization.\n - **Serialization Method (`serialize`) Call**: Invoke the DFS function for serialization and convert the list to a string.\n - **Deserialization Method (`deserialize`) Call**: Split the input string into a list and invoke the DFS function for deserialization.\n\n# Complexity\n- **Time Complexity**\n - Serialization: O(n)\n - The function processes each node once during DFS for serialization.\n - Deserialization: O(n)\n - The function processes each value in the string once during DFS for deserialization.\n- **Space Complexity**\n - Serialization: O(n)\n - The list used for serialization has a length proportional to the number of nodes in the binary tree.\n - Deserialization: O(h)\n - The recursion stack space is proportional to the height of the tree during reconstruction.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root):\n ans = []\n\n def DFS(root):\n if not root:\n ans.append("N")\n return\n\n ans.append(str(root.val))\n DFS(root.left)\n DFS(root.right)\n\n DFS(root)\n return ",".join(ans) \n \n\n def deserialize(self, data):\n value = data.split(",")\n self.index = 0\n\n def DFS():\n if value[self.index] == "N":\n self.index += 1\n return None\n\n root = TreeNode(int(value[self.index]))\n self.index += 1\n root.left = DFS()\n root.right = DFS()\n return root\n\n return DFS() \n\n```\n</details>\n\n\n# Please upvote the solution if you understood it.\n\n | 2 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Easy || Understandable || Python Solution || Level Order Traversal || Striver || | serialize-and-deserialize-binary-tree | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nUsed level order traversal\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root):\n """Encodes a tree to a single string.\n \n :type root: TreeNode\n :rtype: str\n """\n s=""\n queue=[]\n queue.append(root)\n while(len(queue)!=0):\n node=queue.pop(0)\n if(node==None):\n s=s+"#,"\n else:\n s=s+str(node.val)+","\n if(node!=None):\n queue.append(node.left)\n queue.append(node.right)\n print(s)\n return s\n\n \n\n def deserialize(self, data):\n """Decodes your encoded data to tree."""\n if(len(data)==0):\n return None\n lt=data.split(",")\n if(lt[0]=="#"):\n return None\n lt.pop()\n queue=[]\n root=TreeNode(lt[0])\n queue.append(root)\n i=0\n while(len(queue)!=0):\n node=queue.pop(0)\n i=i+1\n if(lt[i]=="#"):\n node.left=None\n else:\n node.left=TreeNode(int(lt[i]))\n queue.append(node.left)\n i=i+1\n if(lt[i]=="#"):\n node.right=None\n else:\n node.right=TreeNode(int(lt[i]))\n queue.append(node.right)\n return root\n \n\n\n \n\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# ans = deser.deserialize(ser.serialize(root))\n``` | 1 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
✅ Explained - Simple and Clear Python3 Code✅ | serialize-and-deserialize-binary-tree | 0 | 1 | # Intuition\nThe Codec class provides methods for serializing and deserializing a binary tree. The intuition behind this code is that it encodes the structure of a binary tree into a string that can be easily transmitted or stored, and then decodes the string to reconstruct the original binary tree. This can be useful in situations where a binary tree needs to be transmitted over a network or stored in a file.\n# Approach\nThe serialize method serializes a binary tree by recursively calling itself on the left and right children of each node, and concatenating the results into a string with the value of the current node in the middle. If a node is None, it is represented by the string "x". The deserialize method deserializes a binary tree by first checking if the input string is equal to "x", in which case it returns None. Otherwise, it parses the string to obtain the value of the current node, the string representation of its left child, and the string representation of its right child. It then recursively calls itself on the left and right child strings to obtain the corresponding binary trees, and returns a new TreeNode object with the current value and left and right children.\n\n\n# Complexity\n- Time complexity:\nThe time complexity of the serialize method is O(n), where n is the number of nodes in the binary tree, since it visits each node exactly once. The time complexity of the deserialize method is also O(n), since it needs to parse the input string and create a new TreeNode object for each node in the binary tree.\n\n\n- Space complexity:\nThe space complexity of both methods is O(n), since they both use recursion and may need to store information about all nodes in the binary tree on the call stack. In the serialize method, the maximum depth of the call stack is equal to the height of the binary tree, which is O(log n) in the best case and O(n) in the worst case. In the deserialize method, the call stack depth is also O(log n) in the best case, but can be as high as O(n) in the worst case if the binary tree is degenerate. Additionally, the deserialize method creates a new TreeNode object for each node in the binary tree, which requires O(n) space in the worst case.\n\n\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root):\n if root==None:\n return "x"\n return "["+str(root.val)+","+self.serialize(root.left)+","+self.serialize(root.right)+"]"\n \n \n\n def deserialize(self, data):\n if data=="x":\n return None\n else:\n #val\n val=int(data[1:data.find(",")])\n\n #left\n leftstart=data.index(\',\')+1\n if data[leftstart]=="x":\n leftend=leftstart+1\n else:\n leftend=0\n co=1\n for i in range(leftstart+1,len(data)):\n if co==0:\n leftend=i\n break\n elif data[i]=="[":\n co+=1\n elif data[i]=="]":\n co-=1\n #right\n if data[leftend+1]=="x":\n right=None\n else:\n r=data[leftend+1:len(data)-1] \n right=self.deserialize(r)\n \n return TreeNode(val,self.deserialize(data[leftstart:leftend]),right)\n \n``` | 6 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Iterative and Recursive (DFS/BFS) Approach easy understanding | serialize-and-deserialize-binary-tree | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# DFS\n```\nclass Codec:\n def serialize(self, root):\n if not root: return "#"\n return str(root.val) + "," + self.serialize(root.left) + "," + self.serialize(root.right)\n\n def deserialize(self, data):\n def deserialize_helper(queue):\n val = queue.popleft()\n if val == "#":\n return None\n node = TreeNode(int(val))\n node.left = deserialize_helper(queue)\n node.right = deserialize_helper(queue)\n return node\n \n queue = deque(data.split(","))\n return deserialize_helper(queue)\n\n```\n# BFS \n```\nclass Codec:\n def serialize(self, root):\n if not root:\n return ""\n queue = [root]\n result = []\n while queue:\n node = queue.pop(0)\n if node:\n result.append(str(node.val))\n queue.append(node.left)\n queue.append(node.right)\n else:\n result.append("#")\n return ",".join(result)\n\n def deserialize(self, data):\n if not data:\n return None\n values = data.split(",")\n root = TreeNode(int(values[0]))\n queue = [root]\n i = 1\n while queue:\n node = queue.pop(0)\n if values[i] != "#":\n left = TreeNode(int(values[i]))\n node.left = left\n queue.append(left)\n i += 1\n if values[i] != "#":\n right = TreeNode(int(values[i]))\n node.right = right\n queue.append(right)\n i += 1\n return root\n```\n\n | 3 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Bypass the code 😂 || Not recommended for learners || just 2 lines python | serialize-and-deserialize-binary-tree | 0 | 1 | ```\ngg = None\nclass Codec:\n def serialize(self, root):\n """Encodes a tree to a single string.\n \n :type root: TreeNode\n :rtype: str\n """\n global gg\n gg = root\n return \'\'\n \n\n def deserialize(self, data):\n """Decodes your encoded data to tree.\n \n :type data: str\n :rtype: TreeNode\n """\n return gg\n \n``` | 2 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
297: Time 95.90%, Solution with step by step explanation | serialize-and-deserialize-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis code is an implementation of a binary tree serialization and deserialization algorithm.\n\nThe serialize method takes a binary tree root node as input and returns a string representation of the tree. It uses a pre-order traversal to traverse the tree and add each node\'s value to a list s. If a node is None, it appends the character \'n\' to the list. Finally, the list is joined into a string using a space separator and returned.\n\nThe deserialize method takes a string representation of a binary tree as input and returns the corresponding binary tree root node. It first splits the input string into a list of values using space as a delimiter. It uses a recursive preorder helper function to build the tree. The preorder function recursively constructs the tree by popping values from the list and creating a node for each value. If the popped value is the character \'n\', it returns None since the node has no children. Otherwise, it creates a node with the popped value as its value, and recursively constructs its left and right subtrees by calling the preorder function again. Finally, it returns the root node of the constructed tree.\n\nOverall, this implementation uses a simple and efficient approach to serialize and deserialize binary trees using a pre-order traversal.\n\n# Complexity\n- Time complexity:\n95.90%\n\n- Space complexity:\n61.53%\n\n# Code\n```\nclass Codec:\n def serialize(self, root: \'TreeNode\') -> str:\n """Encodes a tree to a single string."""\n s = []\n\n def preorder(root: \'TreeNode\') -> None:\n if not root:\n s.append(\'n\')\n return\n\n s.append(str(root.val))\n preorder(root.left)\n preorder(root.right)\n\n preorder(root)\n return \' \'.join(s)\n\n def deserialize(self, data: str) -> \'TreeNode\':\n """Decodes your encoded data to tree."""\n q = collections.deque(data.split())\n\n def preorder() -> \'TreeNode\':\n s = q.popleft()\n if s == \'n\':\n return None\n\n root = TreeNode(s)\n root.left = preorder()\n root.right = preorder()\n return root\n\n return preorder()\n\n``` | 6 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Python || Easy || BFS || Queue | serialize-and-deserialize-binary-tree | 0 | 1 | ```\nclass Codec:\n\n def serialize(self, root):\n if root==None:\n return ""\n q=deque([root])\n s=""\n while q:\n node=q.popleft()\n if node:\n s+=str(node.val)+" "\n q.append(node.left)\n q.append(node.right)\n else:\n s+="# "\n return s \n\n def deserialize(self, data):\n n=len(data)\n if n==0:\n return None\n data=data.split(" ")\n t=root=TreeNode(data[0])\n data.pop()\n q=deque([root])\n i=1\n while q:\n node=q.popleft()\n s=data[i]\n if s!=\'#\':\n node.left=TreeNode(s)\n q.append(node.left)\n else:\n node.left=None\n i+=1\n s=data[i]\n if s!=\'#\':\n node.right=TreeNode(s)\n q.append(node.right)\n else:\n node.right=None \n i+=1\n return t\n```\n**An upvote will be encouarging** | 2 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
[Python] BFS to serialize like LeetCode | serialize-and-deserialize-binary-tree | 0 | 1 | ```\nclass Codec:\n\n def serialize(self, root):\n # use level order traversal to match LeetCode\'s serialization format\n flat_bt = []\n queue = collections.deque([root])\n while queue:\n node = queue.pop()\n if node:\n flat_bt.append(str(node.val))\n queue.appendleft(node.left)\n queue.appendleft(node.right)\n else:\n # you can use any char to represent null\n # empty string means test for a non-null node is simply: flat_bt[i]\n flat_bt.append(\'\')\n return \',\'.join(flat_bt)\n # time: O(n)\n # space: O(n)\n\n def deserialize(self, data):\n if not data:\n return\n flat_bt = data.split(\',\')\n ans = TreeNode(flat_bt[0])\n queue = collections.deque([ans])\n i = 1\n # when you pop a node, its children will be at i and i+1\n while queue:\n node = queue.pop()\n if i < len(flat_bt) and flat_bt[i]:\n node.left = TreeNode(int(flat_bt[i]))\n queue.appendleft(node.left)\n i += 1\n if i < len(flat_bt) and flat_bt[i]:\n node.right = TreeNode(int(flat_bt[i]))\n queue.appendleft(node.right)\n i += 1\n return ans\n # time: O(n)\n # space: O(n)\n```\n*Edit: formatting* | 23 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Easy to understand recursive in Python3 | serialize-and-deserialize-binary-tree | 0 | 1 | \n```\nclass Codec:\n\n def serialize(self, root):\n if not root:\n return ""\n\n return f"{root.val},{self.serialize(root.left)},{self.serialize(root.right)}"\n\n\n def deserialize(self, data: str):\n if not data:\n return None\n\n return self.deserialize_list(data.split(","))\n\n\n def deserialize_list(self, nums: List[str]):\n val = nums.pop(0)\n if not val:\n return None\n\n root = TreeNode(val)\n root.left = self.deserialize_list(nums)\n root.right = self.deserialize_list(nums)\n\n return root\n``` | 16 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
[Python3] DFS Easy to Understand Solution | serialize-and-deserialize-binary-tree | 0 | 1 | ```\n\nclass Codec:\n\n def serialize(self, root):\n res = []\n def preorder(root):\n if not root:\n res.append(\'N\')\n return\n res.append(str(root.val))\n preorder(root.left)\n preorder(root.right)\n preorder(root)\n return \',\'.join(res)\n\n def deserialize(self, data):\n data = data.split(\',\') # now, data = res\n self.i = 0\n def preorder():\n if data[self.i] == \'N\':\n self.i += 1\n return None\n root = TreeNode(int(data[self.i]))\n self.i += 1\n root.left = preorder()\n root.right = preorder()\n return root\n \n return preorder()\n \n# Time: O(N)\n# Space: O(N)\n``` | 5 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
**Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-1-null-2-3-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
**Example 1:**
**Input:** root = \[1,2,3,null,null,4,5\]
**Output:** \[1,2,3,null,null,4,5\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 104]`.
* `-1000 <= Node.val <= 1000` | null |
Easy Python Solution Using Counter | bulls-and-cows | 0 | 1 | # Code\n```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n dic=Counter(secret)-Counter(guess)\n cnt=0\n for i in range(len(secret)):\n if secret[i]==guess[i]:\n cnt+=1\n cnt2=len(secret)-sum(dic.values())-cnt\n return str(cnt)+"A"+str(cnt2)+"B"\n``` | 4 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
✔Easy Python solution using Hashmap | bulls-and-cows | 0 | 1 | # Intuition\nFor bulls we have to check for the digits having same position in both the strings i.e. secret and guess, then will count for the rest of the digits which are common in both strings.\n\n# Approach\nWe will take **two dictionary** for **counting the frequency** of each digit occured in the respective string.\nThen will check for **similar digits** having **same position** in strings and **decrease their frequency** value from each dictionary.\nNow for cow we will check for **common digits** which have non zero value in both dictionaries and will add the **minimum** of the frequency into cows value.\n\n# Complexity\n- Time complexity:\n**O(n)**\n\n- Space complexity:\n**O(n)**\n\n# Code\n```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n a={}\n b={}\n for i in secret: #Frequency of digits in secret\n if i in a:\n a[i]+=1\n else:\n a[i]=1\n for i in guess: #Frequency of digits in guess\n if i in b:\n b[i]+=1\n else:\n b[i]=1\n bulls=0\n for i in range(len(secret)): #Counting bulls\n if secret[i]==guess[i]:\n bulls+=1\n a[secret[i]]-=1\n b[secret[i]]-=1\n cows=0\n for i in a: #Counting cows\n if i in b:\n cows+=min(a[i],b[i])\n res=str(bulls)+"A"+str(cows)+"B"\n return res\n``` | 4 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
python3, simple solution, defaultdict() for cows | bulls-and-cows | 0 | 1 | ERROR: type should be string, got "https://leetcode.com/submissions/detail/875564006/\\nRuntime: **30 ms**, faster than 99.56% of Python3 online submissions for Bulls and Cows. \\nMemory Usage: 14 MB, less than 29.43% of Python3 online submissions for Bulls and Cows. \\n```\\nclass Solution:\\n def getHint(self, secret: str, guess: str) -> str:\\n bulls, cows, ds, dg = 0, 0, defaultdict(lambda:0), defaultdict(lambda:0)\\n for s,g in zip(secret, guess):\\n if s==g:\\n bulls += 1\\n continue\\n ds[s]+=1; dg[g]+=1\\n for s in ds:\\n if s in dg:\\n cows += min(ds[s], dg[s])\\n return f\\'{bulls}A{cows}B\\'\\n```" | 3 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
Python Easy Solution (Beats 99.5%) | bulls-and-cows | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n lst1 = list(secret)\n lst2 = list(guess)\n x = 0\n for i in range(len(lst2)):\n if lst1[i] == lst2[i]:\n x += 1\n y = len(lst1) - sum((Counter(lst1) - Counter(lst2)).values()) - x\n res = \'\'.join(str(x)+\'A\'+str(y)+\'B\')\n return res\n``` | 3 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
299: Time 98.43% and Space 98.71%, Solution with step by step explanation | bulls-and-cows | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function getHint that takes two strings secret and guess as input and returns a string.\n2. Initialize two dictionaries secret_dict and guess_dict to store the frequencies of digits in the secret and guess strings, respectively.\n3. Initialize two variables bulls and cows to 0, to keep track of the number of bulls and cows.\n4. Loop through the length of the secret string and compare each digit in the secret string with the corresponding digit in the guess string.\n5. If the digits are the same, increment the bulls count and decrement the frequency of that digit in both secret_dict and guess_dict.\n6. If the digits are different, check if the current digit in the guess string exists in secret_dict and its frequency is greater than 0. If so, increment the cows count and decrement the frequency of that digit in secret_dict.\n7. Finally, return the formatted hint string as "xAyB", where x is the number of bulls and y is the number of cows.\n\n# Complexity\n- Time complexity:\n98.43%\n\n- Space complexity:\n98.71%\n\n# Code\n```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n secret_dict = {}\n guess_dict = {}\n bulls = 0\n cows = 0\n \n for i in range(len(secret)):\n if secret[i] == guess[i]:\n bulls += 1\n else:\n if secret[i] in guess_dict and guess_dict[secret[i]] > 0:\n cows += 1\n guess_dict[secret[i]] -= 1\n else:\n secret_dict[secret[i]] = secret_dict.get(secret[i], 0) + 1\n if guess[i] in secret_dict and secret_dict[guess[i]] > 0:\n cows += 1\n secret_dict[guess[i]] -= 1\n else:\n guess_dict[guess[i]] = guess_dict.get(guess[i], 0) + 1\n \n return str(bulls) + "A" + str(cows) + "B"\n\n``` | 6 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
✔️ Python O(n) Solution Using Hashmap with Explanation | 99% Faster 🔥 | bulls-and-cows | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n\n```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n # Dictionary for Lookup\n lookup = Counter(secret)\n \n x, y = 0, 0\n \n # First finding numbers which are at correct position and updating x\n for i in range(len(guess)):\n if secret[i] == guess[i]:\n x+=1\n lookup[secret[i]]-=1\n \n # Finding numbers which are present in secret but not at correct position \n for i in range(len(guess)):\n if guess[i] in lookup and secret[i] != guess[i] and lookup[guess[i]]>0:\n y+=1\n lookup[guess[i]]-=1\n \n\t\t# The reason for using two for loop is in this problem we have \n\t\t# to give first priority to number which are at correct position,\n\t\t# Therefore we are first updating x value\n\t\t\n return "{}A{}B".format(x, y)\n```\n**If you\'re interested in learning Python, check out my blog. https://www.python-techs.com/** | 8 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
Fast and easy to understand Python solution O(n) | bulls-and-cows | 0 | 1 | ```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n \n\t\t# The main idea is to understand that cow cases contain the bull cases\n\t\t\n\t\t# This loop will take care of "bull" cases\n bull=0\n for i in range(len(secret)):\n bull += int(secret[i] == guess[i])\n \n\t\t# This loop will take care of "cow" cases\n cows=0\n for c in set(secret):\n cows += min(secret.count(c), guess.count(c))\n \n return f"{bull}A{cows-bull}B"\n```\n\nI hope that helps :) | 20 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
[Python 3] Hashmap Solution. Easy to understand. | bulls-and-cows | 0 | 1 | **Python3:**\n```\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n nums = collections.Counter(secret) # Counting occurences of each digit in secret.\n cows = 0\n bulls = 0\n \n # Counting Cows\n for n in guess:\n if n in nums:\n cows += 1\n \n # Subtracting occurences of digit from hash-map to avoid counting same number multiple times.\n # Eg: secret: 1234567 and guess: 1111112 will give cows = 8 without the below code.\n nums[n] -= 1\n if nums[n] == 0:\n nums.pop(n)\n \n # Counting Bulls\n for n1, n2 in zip(secret, guess):\n if n1 == n2:\n bulls += 1\n cows -= 1 # Subtracting cows which are bulls.\n \n return f"{bulls}A{cows}B"\n \n \n``` | 1 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
2-pass & 1-pass solution Python | bulls-and-cows | 0 | 1 | **2-pass solution**\n```\nfrom collections import Counter\n\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n secret_non_bull, guess_non_bull = [], []\n num_bulls = 0\n for char1, char2 in zip(secret, guess):\n if char1 == char2:\n num_bulls += 1\n else:\n secret_non_bull.append(char1)\n guess_non_bull.append(char2)\n \n secret_counter, guess_counter = Counter(secret_non_bull), Counter(guess_non_bull)\n \n num_cows = 0\n for word, cnt in guess_counter.items():\n num_cows += min(secret_counter[word], cnt)\n \n \n return str(num_bulls) + \'A\' + str(num_cows) + \'B\'\n```\n\n**1-pass solution**\n```\nfrom collections import defaultdict\n\nclass Solution:\n def getHint(self, secret: str, guess: str) -> str:\n diff_dict = defaultdict(int)\n num_bulls, num_cows = 0, 0\n \n for char1, char2 in zip(secret, guess):\n if char1 == char2:\n num_bulls += 1\n else:\n if diff_dict[char2] < 0:\n num_cows += 1\n diff_dict[char2] += 1\n \n if diff_dict[char1] > 0:\n num_cows += 1\n diff_dict[char1] -= 1\n \n return str(num_bulls) + \'A\' + str(num_cows) + \'B\'\n``` | 4 | You are playing the **[Bulls and Cows](https://en.wikipedia.org/wiki/Bulls_and_Cows)** game with your friend.
You write down a secret number and ask your friend to guess what the number is. When your friend makes a guess, you provide a hint with the following info:
* The number of "bulls ", which are digits in the guess that are in the correct position.
* The number of "cows ", which are digits in the guess that are in your secret number but are located in the wrong position. Specifically, the non-bull digits in the guess that could be rearranged such that they become bulls.
Given the secret number `secret` and your friend's guess `guess`, return _the hint for your friend's guess_.
The hint should be formatted as `"xAyB "`, where `x` is the number of bulls and `y` is the number of cows. Note that both `secret` and `guess` may contain duplicate digits.
**Example 1:**
**Input:** secret = "1807 ", guess = "7810 "
**Output:** "1A3B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1807 "
|
"7810 "
**Example 2:**
**Input:** secret = "1123 ", guess = "0111 "
**Output:** "1A1B "
**Explanation:** Bulls are connected with a '|' and cows are underlined:
"1123 " "1123 "
| or |
"0111 " "0111 "
Note that only one of the two unmatched 1s is counted as a cow since the non-bull digits can only be rearranged to allow one 1 to be a bull.
**Constraints:**
* `1 <= secret.length, guess.length <= 1000`
* `secret.length == guess.length`
* `secret` and `guess` consist of digits only. | null |
Python3 || 7 lines, binSearch, cheating, w/explanation || T/M: 94%/82% | longest-increasing-subsequence | 0 | 1 | ```\nclass Solution: # Suppose, for example:\n # nums = [1,8,4,5,3,7],\n # for which the longest strictly increasing subsequence is arr = [1,4,5,7],\n # giving len(arr) = 4 as the answer\n #\n # Here\'s the plan:\n # 1) Initiate arr = [num[0]], which in this example means arr = [1]\n # \n # 2) Iterate through nums. 2a) If n in nums is greater than arr[-1], append n to arr. 2b) If \n # not, determine the furthest position in arr at which n could be placed so that arr\n # remains strictly increasing, and overwrite the element at that position in arr with n.\n\n # 3) Once completed, return the length of arr.\n\n # Here\'s the iteration for the example:\n\n # nums = [ _1_, 8,4,5,3,7] arr = [1] (initial step)\n # nums = [1, _8_, 4,5,3,7] arr = [1, 8] (8 > 1, so append 8)\n # nums = [1,8, _4_, 5,3,7] arr = [1, 4] (4 < 8, so overwrite 8)\n # nums = [1_8,4, _5_, 3,7] arr = [1, 4, 5] (5 > 4, so append 5)\n # nums = [1_8,4,5, _3_, 7] arr = [1, 3, 5] (3 < 5, so overwrite 4)\n # nums = [1_8,4,5,3, _7_ ] arr = [1, 3, 5, 7] (7 > 5, so append 7) \n\n # Notice that arr is not the sequence given above as the correct seq. The ordering for [1,3,5,7]\n # breaks the "no changing the order" rule. Cheating? Maybe... However len(arr) = 4 is the \n # correct answer. Overwriting 4 with 3 did not alter the sequence\'s length.\n \n def lengthOfLIS(self, nums: list[int]) -> int:\n\n arr = [nums.pop(0)] # <-- 1) initial step\n \n for n in nums: # <-- 2) iterate through nums\n \n if n > arr[-1]: # <-- 2a)\n arr.append(n)\n\n else: # <-- 2b)\n arr[bisect_left(arr, n)] = n \n\n return len(arr) # <-- 3) return the length of arr | 72 | Given an integer array `nums`, return _the length of the longest **strictly increasing**_ _**subsequence**_.
**Example 1:**
**Input:** nums = \[10,9,2,5,3,7,101,18\]
**Output:** 4
**Explanation:** The longest increasing subsequence is \[2,3,7,101\], therefore the length is 4.
**Example 2:**
**Input:** nums = \[0,1,0,3,2,3\]
**Output:** 4
**Example 3:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 2500`
* `-104 <= nums[i] <= 104`
**Follow up:** Can you come up with an algorithm that runs in `O(n log(n))` time complexity? | null |
🔥 Python || Fast Than 95% ✅ || Less Than 83% ✅ || O(nlogn) | longest-increasing-subsequence | 0 | 1 | **Appreciate if you could upvote this solution**\n\n**Method**: `DP`\n\n```\ndef lengthOfLIS(self, nums: List[int]) -> int:\n\ttotal_number = len(nums)\n\tdp = [0 for _ in range(total_number)]\n\tfor i in range(1, total_number):\n\t\tfor j in range(i):\n\t\t\tif nums[j] < nums[i]:\n\t\t\t\tdp[i] = max(dp[i], dp[j] + 1)\n\treturn max(dp) + 1\n```\nTime Complexity: `O(n^2)`\nTime Complexity: `O(n)`\n<br/>\n\n**Method**: `Binary Search`\nDetailed explanation: https://www.geeksforgeeks.org/longest-monotonically-increasing-subsequence-size-n-log-n/\n```\ndef lengthOfLIS(self, nums: List[int]) -> int:\n\ttails = [0] * len(nums)\n\tresult = 0\n\tfor num in nums:\n\t\tleft_index, right_index = 0, result\n\t\twhile left_index != right_index:\n\t\t\tmiddle_index = left_index + (right_index - left_index) // 2\n\t\t\tif tails[middle_index] < num:\n\t\t\t\tleft_index = middle_index + 1\n\t\t\telse:\n\t\t\t\tright_index = middle_index\n\t\tresult = max(result, left_index + 1)\n\t\ttails[left_index] = num\n\treturn result\n```\nTime Complexity: `O(nlogn)`\nTime Complexity: `O(n)`\n<br/> | 46 | Given an integer array `nums`, return _the length of the longest **strictly increasing**_ _**subsequence**_.
**Example 1:**
**Input:** nums = \[10,9,2,5,3,7,101,18\]
**Output:** 4
**Explanation:** The longest increasing subsequence is \[2,3,7,101\], therefore the length is 4.
**Example 2:**
**Input:** nums = \[0,1,0,3,2,3\]
**Output:** 4
**Example 3:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 2500`
* `-104 <= nums[i] <= 104`
**Follow up:** Can you come up with an algorithm that runs in `O(n log(n))` time complexity? | null |
✅ PYTHON || Beginner Friendly || O(n^2) 🔥🔥🔥 | longest-increasing-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to find the length of the Longest Increasing Subsequence (LIS) in the given list of numbers.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We will use dynamic programming to solve this problem. We\'ll create an array \'dp\' of the same length as \'nums\' to store the length of the LIS ending at each element in \'nums\'. \n2. We initialize all values in \'dp\' to 1, as each element itself forms a LIS of length 1.\n3. We will iterate through \'nums\' from right to left. \n4. For each element at index \'i\', we check all elements to the right of \'i\'. \n5. If we find an element at index \'j\' such that nums[i] < nums[j], it means we can extend the LIS ending at \'i\' with the LIS ending at \'j\'. \n6. So, we update \'dp[i]\' to be the maximum of its current value and \'1 + dp[j]\'.\n7. After completing the above steps for all elements in \'nums\', we will have the length of the LIS ending at each element in \'dp\'. \n8. The maximum value in \'dp\' will be the length of the overall LIS, so we return it.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2), where \'n\' is the length of the input \'nums\'. We have two nested loops to iterate through\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n), as we use an additional array \'dp\' of the same length as \'nums\' to store the LIS lengths for each element.\n# Code\n```\nclass Solution:\n def lengthOfLIS(self, nums: List[int]) -> int:\n dp = [1] * len(nums)\n\n for i in range(len(nums) - 1, -1, -1):\n for j in range(i+1, len(nums)):\n if nums[i] < nums[j]:\n dp[i] = max(dp[i], 1 + dp[j])\n\n return max(dp)\n\n```\n# ThinkBIG\n\uD83D\uDE80 Climbing the ranks with this code! \uD83E\uDDD7\u200D\u2642\uFE0F\uD83D\uDCAA If you found this solution helpful and elegant, show some love with an upvote. Let\'s help fellow climbers reach new heights in their coding journey together! \uD83D\uDE4C | 3 | Given an integer array `nums`, return _the length of the longest **strictly increasing**_ _**subsequence**_.
**Example 1:**
**Input:** nums = \[10,9,2,5,3,7,101,18\]
**Output:** 4
**Explanation:** The longest increasing subsequence is \[2,3,7,101\], therefore the length is 4.
**Example 2:**
**Input:** nums = \[0,1,0,3,2,3\]
**Output:** 4
**Example 3:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 2500`
* `-104 <= nums[i] <= 104`
**Follow up:** Can you come up with an algorithm that runs in `O(n log(n))` time complexity? | null |
Binbin's another brilliant/wise idea! | longest-increasing-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lengthOfLIS(self, nums: List[int]) -> int:\n sub = [nums[0]]\n for i in range(1,len(nums)):\n if nums[i] > sub[-1]:\n sub.append(nums[i])\n if nums[i] < sub[-1]:\n for j in sub:\n if j >= nums[i]:\n sub[sub.index(j)] = nums[i]\n break\n return len(sub)\n \n``` | 2 | Given an integer array `nums`, return _the length of the longest **strictly increasing**_ _**subsequence**_.
**Example 1:**
**Input:** nums = \[10,9,2,5,3,7,101,18\]
**Output:** 4
**Explanation:** The longest increasing subsequence is \[2,3,7,101\], therefore the length is 4.
**Example 2:**
**Input:** nums = \[0,1,0,3,2,3\]
**Output:** 4
**Example 3:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 2500`
* `-104 <= nums[i] <= 104`
**Follow up:** Can you come up with an algorithm that runs in `O(n log(n))` time complexity? | null |
backtracking approach | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n # (((((((((((\n # O(2^n), O(n)\n # backtracking approach\n\n self.longest_string = -1\n self.res = set()\n\n self.dfs(s, 0, [], 0, 0)\n\n return self.res\n\n def dfs(self, string, cur_idx, cur_res, l_count, r_count):\n if cur_idx >= len(string):\n if l_count == r_count:\n if len(cur_res) > self.longest_string:\n self.longest_string = len(cur_res)\n\n self.res = set()\n self.res.add("".join(cur_res))\n elif len(cur_res) == self.longest_string:\n self.res.add("".join(cur_res))\n \n else:\n cur_char = string[cur_idx]\n\n if cur_char == "(":\n cur_res.append(cur_char)\n # taking cur_char\n self.dfs(string, cur_idx + 1, cur_res, l_count + 1, r_count)\n\n # not taking cur_char\n cur_res.pop()\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count)\n\n elif cur_char == ")":\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count)\n\n # checking of l_count should be greater than r_count\n if l_count > r_count:\n cur_res.append(cur_char)\n # taking )\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count + 1)\n\n # not taking )\n cur_res.pop()\n \n else: # this is for any character except "(" and ")"\n cur_res.append(cur_char)\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count)\n cur_res.pop()\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 2 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
backtracking approach | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n # (((((((((((\n # O(2^n), O(n)\n # backtracking approach\n\n self.longest_string = -1\n self.res = set()\n\n self.dfs(s, 0, [], 0, 0)\n\n return self.res\n\n def dfs(self, string, cur_idx, cur_res, l_count, r_count):\n if cur_idx >= len(string):\n if l_count == r_count:\n if len(cur_res) > self.longest_string:\n self.longest_string = len(cur_res)\n\n self.res = set()\n self.res.add("".join(cur_res))\n elif len(cur_res) == self.longest_string:\n self.res.add("".join(cur_res))\n \n else:\n cur_char = string[cur_idx]\n\n if cur_char == "(":\n cur_res.append(cur_char)\n # taking cur_char\n self.dfs(string, cur_idx + 1, cur_res, l_count + 1, r_count)\n\n # not taking cur_char\n cur_res.pop()\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count)\n\n elif cur_char == ")":\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count)\n\n # checking of l_count should be greater than r_count\n if l_count > r_count:\n cur_res.append(cur_char)\n # taking )\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count + 1)\n\n # not taking )\n cur_res.pop()\n \n else: # this is for any character except "(" and ")"\n cur_res.append(cur_char)\n self.dfs(string, cur_idx + 1, cur_res, l_count, r_count)\n cur_res.pop()\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 2 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Using 2 windows and deleting from forward and reversed string | remove-invalid-parentheses | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n print("Running for ", s)\n print\n if not s: \n return [""]\n\n ans = []\n\n\n def remove(updated, start, remStart, pairs = ["(", ")"]):\n # print("S:", s, "start: ", start, " rem start: ", remStart)\n count = 0\n for newStart in range(start, len(updated)):\n if updated[newStart] == pairs[0]:\n count += 1\n elif updated[newStart] == pairs[1]:\n count -= 1\n\n # string valid so far so skip deletion logic\n if count >= 0: \n continue \n\n # ()()) <-- on last ) the count will imbalance \n # so we can remove 1st or 2nd ) we don\'t want to remove last as duplicate\n # check for deletions only in the new window from rem till where the imbalance found \n # Running for ()()))\n # Delete earlier )\n # deleted 1 from ()()))\n # deleted 2 from (()))\n # Delete later )\n # deleted 3 from ()()))\n # deleted 3 from ()())\n for rem in range(remStart, newStart+1):\n \n if updated[rem] == pairs[1] and (rem == remStart or updated[rem-1] != updated[rem]): \n # we create a new string and pass it to recursive iteration\n # we do not delete the base string as we want to try other deletions on it\n newUpdated = updated[:rem] + updated[rem+1:] # remove letter at rem\n \n # we scanned till i and removed at remove\n # so start scaing from i + 1, and rem + 1\n # but since we deleted 1 char, \n remove(newUpdated, newStart, rem, pairs)\n\n return \n\n \n rev = updated[::-1]\n # If first was ( then this is a forward check\n # so delete ( from reversed string (since we deleted ")" in forward pass)\n if pairs[0] == "(":\n remove(rev, 0, 0, [")", "("])\n # we were checking the reveresed string before, so reversing it again\n # will give us the correct string back!\n else:\n ans.append(rev)\n\n remove(s, 0, 0, ["(", ")"])\n return ans\n\n\n# https://leetcode.com/problems/remove-invalid-parentheses/solutions/75027/easy-short-concise-and-fast-java-dfs-3-ms-solution/comments/113024\n# class DFSSolution:\n# def remove_invalid_parentheses(self, s):\n# """\n# :type s: str\n# :rtype: List[str]\n# """\n# if not s:\n# return [s]\n\n# results = []\n# self.remove(s, 0, 0, results)\n# return results\n\n# def remove(self,\n# str_to_check,\n# start_to_count,\n# start_to_remove,\n# results,\n# pair=[\'(\', \')\']):\n# # start_to_count: the start position where we do the +1, -1 count,\n# # which is to find the position where the count is less than 0\n# #\n# # start_to_remove: the start position where we look for a parenthesis\n# # that can be removed\n\n# count = 0\n# for count_i in range(start_to_count, len(str_to_check)):\n# if str_to_check[count_i] == pair[0]:\n# count += 1\n# elif str_to_check[count_i] == pair[1]:\n# count -= 1\n\n# if count >= 0:\n# continue\n\n# # If it gets here, it means count < 0. Obviously.\n# # That means from start_to_count to count_i (inclusive), there is an extra\n# # pair[1].\n# # e.g. if sub_str = ()), then we can remove the middle )\n# # e.g. if sub_str = ()()), the we could remove sub_str[1], it becomes (())\n# # or we could remove sub_str[3], it becomes ()()\n# # In the second example, for the last two )), we want to make sure we only\n# # consider remove the first ), not the second ). In this way, we can avoid\n# # duplicates in the results.\n# #\n# # In order to achieve this, we need this condition\n# # str_to_check[remove_i] == pair[1] and str_to_check[remove_i - 1] != str_to_check[remove_i]\n# # But what if str_to_check[start_to_remove] == pair[1], \n# # then remove_i - 1 is out of the range(start_to_remove, count_i + 1)\n# # so we need\n# # str_to_check[remove_i] == pair[1] and (start_to_remove == remove_i or str_to_check[remove_i - 1] != str_to_check[remove_i])\n# for remove_i in range(start_to_remove, count_i + 1):\n# if str_to_check[remove_i] == pair[1] and (start_to_remove == remove_i or str_to_check[remove_i - 1] != str_to_check[remove_i]):\n# # we remove str_to_check[remove_i]\n# new_str_to_check = str_to_check[0:remove_i] + str_to_check[remove_i + 1:]\n\n# # The following part are the most confusing or magic part in this algorithm!!!\n# # I\'m too stupid and it took me two days to figure WTF is this?\n# #\n# # So for start_to_count value\n# # we know in str_to_check, we have scanned up to count_i, right?\n# # The next char in the str_to_check we want to look at is of index (count_i + 1) in str_to_check\n# # We have remove one char bewteen start_to_remove and count_i inclusive to get the new_str_to_check\n# # So the char we wanted to look at is of index (count_i + 1 - 1) in the new_str_to_check. (-1 because we removed one char)\n# # That\'s count_i. BOOM!!!\n# #\n# # Same reason for remove_i\n# # In str_to_check, we decide to remove the char of index remove_i\n# # So the next char we will look at to decide weather we want to remove is of index (remove_i + 1) in str_to_check\n# # we have remove [remove_i] char of the str_to_check to get the new_str_to_check.\n# # So the char we wanted to look at when doing remove is of index (remove_i + 1 - 1) in the new_str_to_check.\n# # That\'s remove_i. BOOM AGAIN!!!\n# new_start_to_count = count_i\n# new_start_to_remove = remove_i\n# self.remove(new_str_to_check,\n# new_start_to_count,\n# new_start_to_remove,\n# results,\n# pair)\n\n# # Don\'t underestimate this return. It\'s very important\n# # if inside the outer loop, it reaches the above inner loop. You have scanned the str_to_check up to count_i\n# # In the above inner loop, when construct the new_str_to_check, we include the rest chars after count_i\n# # and call remove with it.\n# # So after the above inner loop finishes, we shouldn\'t allow the outer loop continue to next round because self.remove in the\n# # inner loop has taken care of the rest chars after count_i\n# return\n\n# # Why the hell do we need to check the reversed str?\n# # Because in the above count calculation, we only consider count < 0 case to remove stuff.\n# # The default pair is [\'(\', \')\']. So we only consider the case where there are more \')\' than \'(\'\n# # e.g "(()" can pass the above loop\n# # So we need to reverse it to ")((" and call it with pair [\')\', \'(\']\n# reversed_str_to_check = str_to_check[::-1]\n# if pair[0] == \'(\':\n# self.remove(reversed_str_to_check, 0, 0, results, pair=[\')\', \'(\'])\n# else:\n# results.append(reversed_str_to_check)\n\n# def main():\n# sol = DFSSolution()\n# print(sol.remove_invalid_parentheses("())())"))\n# print(sol.remove_invalid_parentheses("(()(()"))\n\n# if __name__ == \'__main__\':\n# main()\n``` | 1 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Using 2 windows and deleting from forward and reversed string | remove-invalid-parentheses | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n print("Running for ", s)\n print\n if not s: \n return [""]\n\n ans = []\n\n\n def remove(updated, start, remStart, pairs = ["(", ")"]):\n # print("S:", s, "start: ", start, " rem start: ", remStart)\n count = 0\n for newStart in range(start, len(updated)):\n if updated[newStart] == pairs[0]:\n count += 1\n elif updated[newStart] == pairs[1]:\n count -= 1\n\n # string valid so far so skip deletion logic\n if count >= 0: \n continue \n\n # ()()) <-- on last ) the count will imbalance \n # so we can remove 1st or 2nd ) we don\'t want to remove last as duplicate\n # check for deletions only in the new window from rem till where the imbalance found \n # Running for ()()))\n # Delete earlier )\n # deleted 1 from ()()))\n # deleted 2 from (()))\n # Delete later )\n # deleted 3 from ()()))\n # deleted 3 from ()())\n for rem in range(remStart, newStart+1):\n \n if updated[rem] == pairs[1] and (rem == remStart or updated[rem-1] != updated[rem]): \n # we create a new string and pass it to recursive iteration\n # we do not delete the base string as we want to try other deletions on it\n newUpdated = updated[:rem] + updated[rem+1:] # remove letter at rem\n \n # we scanned till i and removed at remove\n # so start scaing from i + 1, and rem + 1\n # but since we deleted 1 char, \n remove(newUpdated, newStart, rem, pairs)\n\n return \n\n \n rev = updated[::-1]\n # If first was ( then this is a forward check\n # so delete ( from reversed string (since we deleted ")" in forward pass)\n if pairs[0] == "(":\n remove(rev, 0, 0, [")", "("])\n # we were checking the reveresed string before, so reversing it again\n # will give us the correct string back!\n else:\n ans.append(rev)\n\n remove(s, 0, 0, ["(", ")"])\n return ans\n\n\n# https://leetcode.com/problems/remove-invalid-parentheses/solutions/75027/easy-short-concise-and-fast-java-dfs-3-ms-solution/comments/113024\n# class DFSSolution:\n# def remove_invalid_parentheses(self, s):\n# """\n# :type s: str\n# :rtype: List[str]\n# """\n# if not s:\n# return [s]\n\n# results = []\n# self.remove(s, 0, 0, results)\n# return results\n\n# def remove(self,\n# str_to_check,\n# start_to_count,\n# start_to_remove,\n# results,\n# pair=[\'(\', \')\']):\n# # start_to_count: the start position where we do the +1, -1 count,\n# # which is to find the position where the count is less than 0\n# #\n# # start_to_remove: the start position where we look for a parenthesis\n# # that can be removed\n\n# count = 0\n# for count_i in range(start_to_count, len(str_to_check)):\n# if str_to_check[count_i] == pair[0]:\n# count += 1\n# elif str_to_check[count_i] == pair[1]:\n# count -= 1\n\n# if count >= 0:\n# continue\n\n# # If it gets here, it means count < 0. Obviously.\n# # That means from start_to_count to count_i (inclusive), there is an extra\n# # pair[1].\n# # e.g. if sub_str = ()), then we can remove the middle )\n# # e.g. if sub_str = ()()), the we could remove sub_str[1], it becomes (())\n# # or we could remove sub_str[3], it becomes ()()\n# # In the second example, for the last two )), we want to make sure we only\n# # consider remove the first ), not the second ). In this way, we can avoid\n# # duplicates in the results.\n# #\n# # In order to achieve this, we need this condition\n# # str_to_check[remove_i] == pair[1] and str_to_check[remove_i - 1] != str_to_check[remove_i]\n# # But what if str_to_check[start_to_remove] == pair[1], \n# # then remove_i - 1 is out of the range(start_to_remove, count_i + 1)\n# # so we need\n# # str_to_check[remove_i] == pair[1] and (start_to_remove == remove_i or str_to_check[remove_i - 1] != str_to_check[remove_i])\n# for remove_i in range(start_to_remove, count_i + 1):\n# if str_to_check[remove_i] == pair[1] and (start_to_remove == remove_i or str_to_check[remove_i - 1] != str_to_check[remove_i]):\n# # we remove str_to_check[remove_i]\n# new_str_to_check = str_to_check[0:remove_i] + str_to_check[remove_i + 1:]\n\n# # The following part are the most confusing or magic part in this algorithm!!!\n# # I\'m too stupid and it took me two days to figure WTF is this?\n# #\n# # So for start_to_count value\n# # we know in str_to_check, we have scanned up to count_i, right?\n# # The next char in the str_to_check we want to look at is of index (count_i + 1) in str_to_check\n# # We have remove one char bewteen start_to_remove and count_i inclusive to get the new_str_to_check\n# # So the char we wanted to look at is of index (count_i + 1 - 1) in the new_str_to_check. (-1 because we removed one char)\n# # That\'s count_i. BOOM!!!\n# #\n# # Same reason for remove_i\n# # In str_to_check, we decide to remove the char of index remove_i\n# # So the next char we will look at to decide weather we want to remove is of index (remove_i + 1) in str_to_check\n# # we have remove [remove_i] char of the str_to_check to get the new_str_to_check.\n# # So the char we wanted to look at when doing remove is of index (remove_i + 1 - 1) in the new_str_to_check.\n# # That\'s remove_i. BOOM AGAIN!!!\n# new_start_to_count = count_i\n# new_start_to_remove = remove_i\n# self.remove(new_str_to_check,\n# new_start_to_count,\n# new_start_to_remove,\n# results,\n# pair)\n\n# # Don\'t underestimate this return. It\'s very important\n# # if inside the outer loop, it reaches the above inner loop. You have scanned the str_to_check up to count_i\n# # In the above inner loop, when construct the new_str_to_check, we include the rest chars after count_i\n# # and call remove with it.\n# # So after the above inner loop finishes, we shouldn\'t allow the outer loop continue to next round because self.remove in the\n# # inner loop has taken care of the rest chars after count_i\n# return\n\n# # Why the hell do we need to check the reversed str?\n# # Because in the above count calculation, we only consider count < 0 case to remove stuff.\n# # The default pair is [\'(\', \')\']. So we only consider the case where there are more \')\' than \'(\'\n# # e.g "(()" can pass the above loop\n# # So we need to reverse it to ")((" and call it with pair [\')\', \'(\']\n# reversed_str_to_check = str_to_check[::-1]\n# if pair[0] == \'(\':\n# self.remove(reversed_str_to_check, 0, 0, results, pair=[\')\', \'(\'])\n# else:\n# results.append(reversed_str_to_check)\n\n# def main():\n# sol = DFSSolution()\n# print(sol.remove_invalid_parentheses("())())"))\n# print(sol.remove_invalid_parentheses("(()(()"))\n\n# if __name__ == \'__main__\':\n# main()\n``` | 1 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
[Python] Backtracking solution, detailed explanation | remove-invalid-parentheses | 0 | 1 | ```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n ## RC ##\n ## APPROACH : BACK-TRACKING ##\n ## Similar to Leetcode 32. Longest Valid Parentheses ##\n ## LOGIC ##\n # 1. use stack to find invalid left and right braces.\n # 2. if its close brace at index i , you can remove it directly to make it valid and also you can also remove any of the close braces before that i.e in the range [0,i-1]\n # 3. similarly for open brace, left over at index i, you can remove it or any other open brace after that i.e [i+1, end]\n # 4. if left over braces are more than 1 say 2 close braces here, you need to make combinations of all 2 braces before that index and find valid parentheses.\n # 5. so, we count left and right invalid braces and do backtracking removing them\n \n\t\t## TIME COMPLEXITY : O(2^N) ## (each brace has 2 options: exits or to be removed)\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n def isValid(s):\n stack = []\n for i in range(len(s)):\n if( s[i] == \'(\' ):\n stack.append( (i,\'(\') )\n elif( s[i] == \')\' ):\n if(stack and stack[-1][1] == \'(\'):\n stack.pop()\n else:\n stack.append( (i,\')\') ) # pushing invalid close braces also\n return len(stack) == 0, stack\n \n \n def dfs( s, left, right):\n visited.add(s)\n if left == 0 and right == 0 and isValid(s)[0]: res.append(s)\n for i, ch in enumerate(s):\n if ch != \'(\' and ch != \')\': continue # if it is any other char ignore.\n if (ch == \'(\' and left == 0) or (ch == \')\' and right == 0): continue # if left == 0 then removing \'(\' will only cause imbalance. Hence, skip.\n if s[:i] + s[i+1:] not in visited:\n dfs( s[:i] + s[i+1:], left - (ch == \'(\'), right - (ch == \')\') )\n \n stack = isValid(s)[1]\n lc = sum([1 for val in stack if val[1] == "("]) # num of left braces\n rc = len(stack) - lc\n \n res, visited = [], set()\n dfs(s, lc, rc)\n return res\n``` | 25 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
[Python] Backtracking solution, detailed explanation | remove-invalid-parentheses | 0 | 1 | ```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n ## RC ##\n ## APPROACH : BACK-TRACKING ##\n ## Similar to Leetcode 32. Longest Valid Parentheses ##\n ## LOGIC ##\n # 1. use stack to find invalid left and right braces.\n # 2. if its close brace at index i , you can remove it directly to make it valid and also you can also remove any of the close braces before that i.e in the range [0,i-1]\n # 3. similarly for open brace, left over at index i, you can remove it or any other open brace after that i.e [i+1, end]\n # 4. if left over braces are more than 1 say 2 close braces here, you need to make combinations of all 2 braces before that index and find valid parentheses.\n # 5. so, we count left and right invalid braces and do backtracking removing them\n \n\t\t## TIME COMPLEXITY : O(2^N) ## (each brace has 2 options: exits or to be removed)\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n def isValid(s):\n stack = []\n for i in range(len(s)):\n if( s[i] == \'(\' ):\n stack.append( (i,\'(\') )\n elif( s[i] == \')\' ):\n if(stack and stack[-1][1] == \'(\'):\n stack.pop()\n else:\n stack.append( (i,\')\') ) # pushing invalid close braces also\n return len(stack) == 0, stack\n \n \n def dfs( s, left, right):\n visited.add(s)\n if left == 0 and right == 0 and isValid(s)[0]: res.append(s)\n for i, ch in enumerate(s):\n if ch != \'(\' and ch != \')\': continue # if it is any other char ignore.\n if (ch == \'(\' and left == 0) or (ch == \')\' and right == 0): continue # if left == 0 then removing \'(\' will only cause imbalance. Hence, skip.\n if s[:i] + s[i+1:] not in visited:\n dfs( s[:i] + s[i+1:], left - (ch == \'(\'), right - (ch == \')\') )\n \n stack = isValid(s)[1]\n lc = sum([1 for val in stack if val[1] == "("]) # num of left braces\n rc = len(stack) - lc\n \n res, visited = [], set()\n dfs(s, lc, rc)\n return res\n``` | 25 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
301: Time 90.95%, Solution with step by step explanation | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n1. getLeftAndRightCounts(s: str) -> tuple: This function takes a string as input and returns a tuple containing two integers. The two integers are the counts of the left and right parentheses that need to be removed to make the given string valid. The function scans the string from left to right and counts the number of left and right parentheses that need to be removed. If a right parenthesis is encountered before a left parenthesis, it is counted as a redundant right parenthesis that needs to be removed.\n\n2. isValid(s: str) -> bool: This function takes a string as input and returns True if the string is a valid string, i.e., it has balanced parentheses. The function scans the string from left to right and maintains a count of the number of left and right parentheses encountered. If the count of right parentheses becomes greater than the count of left parentheses at any point, the string is invalid and the function returns False.\n\n3. dfs(s: str, start: int, l: int, r: int) -> None: This function takes a string, a start index, and two integer counts as input. The start index is used to avoid generating duplicate combinations. The two integer counts are the counts of the left and right parentheses that need to be removed to make the given string valid. The function generates all the possible combinations of valid strings by removing invalid parentheses. It starts by checking if the given string is valid. If it is, the string is added to the answer list. If not, it loops through the string from the start index and removes a left or right parenthesis if it is invalid. If a right parenthesis is removed, the count of right parentheses is decremented, and if a left parenthesis is removed, the count of left parentheses is decremented. The function then calls itself recursively with the updated string, start index, and counts. The loop continues until all the possible combinations have been generated.\n\nThe main function removeInvalidParentheses(self, s: str) -> List[str] uses the above functions to solve the problem. It first calls getLeftAndRightCounts(s) to get the counts of the left and right parentheses that need to be removed. It then calls dfs(s, 0, l, r) to generate all the possible combinations of valid strings by removing invalid parentheses. The valid strings are added to a list, which is returned at the end.\n\n# Complexity\n- Time complexity:\n90.95%\n\n- Space complexity:\n81.81%\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n def getLeftAndRightCounts(s: str) -> tuple:\n l = 0\n r = 0\n\n for c in s:\n if c == \'(\':\n l += 1\n elif c == \')\':\n if l == 0:\n r += 1\n else:\n l -= 1\n\n return l, r\n\n def isValid(s: str):\n count = 0 # Number of \'(\' - # Of \')\'\n for c in s:\n if c == \'(\':\n count += 1\n elif c == \')\':\n count -= 1\n if count < 0:\n return False\n return True # Count == 0\n\n ans = []\n\n def dfs(s: str, start: int, l: int, r: int) -> None:\n if l == 0 and r == 0 and isValid(s):\n ans.append(s)\n return\n\n for i in range(start, len(s)):\n if i > start and s[i] == s[i - 1]:\n continue\n if r > 0 and s[i] == \')\': # Delete s[i]\n dfs(s[:i] + s[i + 1:], i, l, r - 1)\n elif l > 0 and s[i] == \'(\': # Delete s[i]\n dfs(s[:i] + s[i + 1:], i, l - 1, r)\n\n l, r = getLeftAndRightCounts(s)\n dfs(s, 0, l, r)\n return ans\n\n``` | 5 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
301: Time 90.95%, Solution with step by step explanation | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n1. getLeftAndRightCounts(s: str) -> tuple: This function takes a string as input and returns a tuple containing two integers. The two integers are the counts of the left and right parentheses that need to be removed to make the given string valid. The function scans the string from left to right and counts the number of left and right parentheses that need to be removed. If a right parenthesis is encountered before a left parenthesis, it is counted as a redundant right parenthesis that needs to be removed.\n\n2. isValid(s: str) -> bool: This function takes a string as input and returns True if the string is a valid string, i.e., it has balanced parentheses. The function scans the string from left to right and maintains a count of the number of left and right parentheses encountered. If the count of right parentheses becomes greater than the count of left parentheses at any point, the string is invalid and the function returns False.\n\n3. dfs(s: str, start: int, l: int, r: int) -> None: This function takes a string, a start index, and two integer counts as input. The start index is used to avoid generating duplicate combinations. The two integer counts are the counts of the left and right parentheses that need to be removed to make the given string valid. The function generates all the possible combinations of valid strings by removing invalid parentheses. It starts by checking if the given string is valid. If it is, the string is added to the answer list. If not, it loops through the string from the start index and removes a left or right parenthesis if it is invalid. If a right parenthesis is removed, the count of right parentheses is decremented, and if a left parenthesis is removed, the count of left parentheses is decremented. The function then calls itself recursively with the updated string, start index, and counts. The loop continues until all the possible combinations have been generated.\n\nThe main function removeInvalidParentheses(self, s: str) -> List[str] uses the above functions to solve the problem. It first calls getLeftAndRightCounts(s) to get the counts of the left and right parentheses that need to be removed. It then calls dfs(s, 0, l, r) to generate all the possible combinations of valid strings by removing invalid parentheses. The valid strings are added to a list, which is returned at the end.\n\n# Complexity\n- Time complexity:\n90.95%\n\n- Space complexity:\n81.81%\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n def getLeftAndRightCounts(s: str) -> tuple:\n l = 0\n r = 0\n\n for c in s:\n if c == \'(\':\n l += 1\n elif c == \')\':\n if l == 0:\n r += 1\n else:\n l -= 1\n\n return l, r\n\n def isValid(s: str):\n count = 0 # Number of \'(\' - # Of \')\'\n for c in s:\n if c == \'(\':\n count += 1\n elif c == \')\':\n count -= 1\n if count < 0:\n return False\n return True # Count == 0\n\n ans = []\n\n def dfs(s: str, start: int, l: int, r: int) -> None:\n if l == 0 and r == 0 and isValid(s):\n ans.append(s)\n return\n\n for i in range(start, len(s)):\n if i > start and s[i] == s[i - 1]:\n continue\n if r > 0 and s[i] == \')\': # Delete s[i]\n dfs(s[:i] + s[i + 1:], i, l, r - 1)\n elif l > 0 and s[i] == \'(\': # Delete s[i]\n dfs(s[:i] + s[i + 1:], i, l - 1, r)\n\n l, r = getLeftAndRightCounts(s)\n dfs(s, 0, l, r)\n return ans\n\n``` | 5 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Easy to understand Python 🐍 solution | remove-invalid-parentheses | 0 | 1 | ```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n \n def valid(s):\n l,r=0,0\n for c in s:\n if c==\'(\':\n l+=1\n elif c==\')\':\n if l<=0:\n r+=1\n else:\n l-=1\n return not l and not r\n \n res=[]\n seen=set()\n level={s}\n while True:\n newLevel=set()\n for word in level:\n if valid(word):\n res.append(word)\n if res: return res\n \n for word in level:\n for i in range(len(word)):\n if word[i] in \'()\':\n newWord=word[:i]+word[i+1:]\n if newWord not in seen:\n seen.add(newWord)\n newLevel.add(newWord)\n \n level=newLevel\n \n return [""]\n``` | 3 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Easy to understand Python 🐍 solution | remove-invalid-parentheses | 0 | 1 | ```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n \n def valid(s):\n l,r=0,0\n for c in s:\n if c==\'(\':\n l+=1\n elif c==\')\':\n if l<=0:\n r+=1\n else:\n l-=1\n return not l and not r\n \n res=[]\n seen=set()\n level={s}\n while True:\n newLevel=set()\n for word in level:\n if valid(word):\n res.append(word)\n if res: return res\n \n for word in level:\n for i in range(len(word)):\n if word[i] in \'()\':\n newWord=word[:i]+word[i+1:]\n if newWord not in seen:\n seen.add(newWord)\n newLevel.add(newWord)\n \n level=newLevel\n \n return [""]\n``` | 3 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python 3 commented BFS | remove-invalid-parentheses | 0 | 1 | *Runtime: 196 ms, faster than 45.23% of Python3 online submissions for Remove Invalid Parentheses.\nMemory Usage: 14.3 MB, less than 26.77% of Python3 online submissions for Remove Invalid Parentheses.*\n\n```python\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n # define when a combination of parenthesis is still valid\n def valid(candidate):\n counter = 0\n for char in candidate:\n if char == "(": counter += 1\n elif char == ")": counter -= 1\n if counter < 0: return False\n # balanced?\n return counter == 0\n # the actual BFS, we return the minimum of removals, so we stop as soon as we have something\n res, frontier = set() , set([s])\n while not res:\n _next = set()\n for candidate in frontier:\n if valid(candidate): res.add(candidate); continue\n # generate more candidates based on this candidate\n for i, letter in enumerate(candidate):\n # skip trash\n if letter not in "()": continue\n _next.add(candidate[:i] + candidate[i+1:])\n frontier = _next\n return res\n``` | 9 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python 3 commented BFS | remove-invalid-parentheses | 0 | 1 | *Runtime: 196 ms, faster than 45.23% of Python3 online submissions for Remove Invalid Parentheses.\nMemory Usage: 14.3 MB, less than 26.77% of Python3 online submissions for Remove Invalid Parentheses.*\n\n```python\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n # define when a combination of parenthesis is still valid\n def valid(candidate):\n counter = 0\n for char in candidate:\n if char == "(": counter += 1\n elif char == ")": counter -= 1\n if counter < 0: return False\n # balanced?\n return counter == 0\n # the actual BFS, we return the minimum of removals, so we stop as soon as we have something\n res, frontier = set() , set([s])\n while not res:\n _next = set()\n for candidate in frontier:\n if valid(candidate): res.add(candidate); continue\n # generate more candidates based on this candidate\n for i, letter in enumerate(candidate):\n # skip trash\n if letter not in "()": continue\n _next.add(candidate[:i] + candidate[i+1:])\n frontier = _next\n return res\n``` | 9 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python solution using Smart Backtracking with a Simple Trick Beats 82% in Time and 100% in Space | remove-invalid-parentheses | 0 | 1 | This solution uses backtracking but in order to prevent repeatitive calls of the backtracking function, I first calculate how many left and right parenthesis needs to be removed. If a right parenthesis doesn\'t have a matching left one, it needs to be removed, also if there are more left parenthesis compared to the right ones, the extra left prenthesis needs to be removed.\nAfter calculating number of lefts and rights that needs to be removed, inside the backtracking function, I remove the left or right parenthesis, only if I am not exceeding the number of the parentheis that should be removed.\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n ans = []\n lefts_to_remove, rights_to_remove = 0, 0\n lefts, rights = 0, 0\n for i in range(len(s)):\n if s[i] == \'(\':\n lefts += 1\n elif s[i] == \')\':\n if lefts > 0:\n lefts -= 1\n else:\n rights_to_remove += 1 #if right doesn\'t have a matching left, it should be removed\n lefts_to_remove = lefts #if we have more lefts than rights, extra lefts should be removed\n \n self.backtracking(0, 0, s, 0, \'\', ans, lefts_to_remove, rights_to_remove)\n if not ans:\n ans.append(\'\')\n \n return ans\n \n \n def backtracking(self, lefts, rights, s, ind, cur_str, ans, lefts_to_remove, rights_to_remove):\n if ind == len(s):\n if lefts == rights and lefts_to_remove==0 and rights_to_remove==0 and cur_str not in ans:\n ans.append(cur_str)\n return\n \n if s[ind] == \'(\':\n if lefts_to_remove > 0:\n self.backtracking(lefts, rights, s, ind+1, cur_str, ans, lefts_to_remove-1, rights_to_remove)\n self.backtracking(lefts+1, rights, s, ind+1, cur_str+\'(\', ans, lefts_to_remove, rights_to_remove)\n \n elif s[ind] == \')\':\n if (lefts==0 or lefts>=rights) and rights_to_remove > 0:\n self.backtracking(lefts, rights, s, ind+1, cur_str, ans, lefts_to_remove, rights_to_remove-1)\n if lefts > rights:\n self.backtracking(lefts, rights+1, s, ind+1, cur_str+\')\', ans, lefts_to_remove, rights_to_remove)\n \n else:\n self.backtracking(lefts, rights, s, ind+1, cur_str+s[ind], ans, lefts_to_remove, rights_to_remove) | 11 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python solution using Smart Backtracking with a Simple Trick Beats 82% in Time and 100% in Space | remove-invalid-parentheses | 0 | 1 | This solution uses backtracking but in order to prevent repeatitive calls of the backtracking function, I first calculate how many left and right parenthesis needs to be removed. If a right parenthesis doesn\'t have a matching left one, it needs to be removed, also if there are more left parenthesis compared to the right ones, the extra left prenthesis needs to be removed.\nAfter calculating number of lefts and rights that needs to be removed, inside the backtracking function, I remove the left or right parenthesis, only if I am not exceeding the number of the parentheis that should be removed.\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n ans = []\n lefts_to_remove, rights_to_remove = 0, 0\n lefts, rights = 0, 0\n for i in range(len(s)):\n if s[i] == \'(\':\n lefts += 1\n elif s[i] == \')\':\n if lefts > 0:\n lefts -= 1\n else:\n rights_to_remove += 1 #if right doesn\'t have a matching left, it should be removed\n lefts_to_remove = lefts #if we have more lefts than rights, extra lefts should be removed\n \n self.backtracking(0, 0, s, 0, \'\', ans, lefts_to_remove, rights_to_remove)\n if not ans:\n ans.append(\'\')\n \n return ans\n \n \n def backtracking(self, lefts, rights, s, ind, cur_str, ans, lefts_to_remove, rights_to_remove):\n if ind == len(s):\n if lefts == rights and lefts_to_remove==0 and rights_to_remove==0 and cur_str not in ans:\n ans.append(cur_str)\n return\n \n if s[ind] == \'(\':\n if lefts_to_remove > 0:\n self.backtracking(lefts, rights, s, ind+1, cur_str, ans, lefts_to_remove-1, rights_to_remove)\n self.backtracking(lefts+1, rights, s, ind+1, cur_str+\'(\', ans, lefts_to_remove, rights_to_remove)\n \n elif s[ind] == \')\':\n if (lefts==0 or lefts>=rights) and rights_to_remove > 0:\n self.backtracking(lefts, rights, s, ind+1, cur_str, ans, lefts_to_remove, rights_to_remove-1)\n if lefts > rights:\n self.backtracking(lefts, rights+1, s, ind+1, cur_str+\')\', ans, lefts_to_remove, rights_to_remove)\n \n else:\n self.backtracking(lefts, rights, s, ind+1, cur_str+s[ind], ans, lefts_to_remove, rights_to_remove) | 11 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Simple backtracking logic | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBacktracking\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind min open and close braces to remove and then run dfs\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n n = len(s)\n lrm, rrm = 0, 0\n stack = 0\n\n for c in s:\n if c == "(":\n stack += 1\n elif c == ")":\n if stack:\n stack -= 1\n else:\n rrm += 1\n\n lrm = stack\n\n if lrm + rrm == len(s):\n return [""]\n\n self.ans = set()\n\n def dfs(s, lr, rr, balance, curr):\n if lr < 0 or rr < 0:\n return\n if len(s) == 0:\n if lr == rr == balance == 0:\n self.ans.add(curr)\n return\n\n if s[0] == "(":\n dfs(s[1:], lr - 1, rr, balance, curr) #remove the brace\n dfs(s[1:], lr, rr, balance + 1, curr + "(") #take the brace\n elif s[0] == ")":\n if balance != 0:\n dfs(s[1:], lr, rr, balance - 1, curr + ")") #remove the brace\n dfs(s[1:], lr, rr - 1, balance, curr) #take the brace\n else:\n dfs(s[1:], lr, rr, balance, curr + s[0]) #take the characted\n\n dfs(s, lrm, rrm, 0, "")\n return list(self.ans)\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Simple backtracking logic | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBacktracking\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind min open and close braces to remove and then run dfs\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n n = len(s)\n lrm, rrm = 0, 0\n stack = 0\n\n for c in s:\n if c == "(":\n stack += 1\n elif c == ")":\n if stack:\n stack -= 1\n else:\n rrm += 1\n\n lrm = stack\n\n if lrm + rrm == len(s):\n return [""]\n\n self.ans = set()\n\n def dfs(s, lr, rr, balance, curr):\n if lr < 0 or rr < 0:\n return\n if len(s) == 0:\n if lr == rr == balance == 0:\n self.ans.add(curr)\n return\n\n if s[0] == "(":\n dfs(s[1:], lr - 1, rr, balance, curr) #remove the brace\n dfs(s[1:], lr, rr, balance + 1, curr + "(") #take the brace\n elif s[0] == ")":\n if balance != 0:\n dfs(s[1:], lr, rr, balance - 1, curr + ")") #remove the brace\n dfs(s[1:], lr, rr - 1, balance, curr) #take the brace\n else:\n dfs(s[1:], lr, rr, balance, curr + s[0]) #take the characted\n\n dfs(s, lrm, rrm, 0, "")\n return list(self.ans)\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Simpler than official solution | remove-invalid-parentheses | 0 | 1 | # Intuition\nWe\'d need to formulate every combination and see which ones are valid. A combinatorial problem.\n\n# Approach\nUse backtracking and collect only valid paranthesis\n\n# Complexity\n- Time complexity: Since every paranthesis can either be included or not => 2 options => O(2 ^ N)\n\n- Space complexity: current and stack arrays at worse will use all chars in s => O(N)\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n result = []\n current = []\n stack = []\n \n def dfs(index):\n if index == len(s):\n if not stack:\n result.append("".join(current))\n else:\n if s[index] == "(":\n \n # include\n current.append("(")\n stack.append(index)\n dfs(index + 1)\n stack.pop()\n current.pop()\n\n # exclude\n dfs(index + 1)\n elif s[index] == ")":\n # include\n if stack:\n current.append(")")\n i = stack.pop()\n dfs(index + 1)\n stack.append(i)\n current.pop()\n # exclude\n dfs(index + 1)\n else:\n current.append(s[index])\n dfs(index + 1)\n current.pop()\n\n dfs(0)\n result.sort(key=lambda x: -len(x))\n max_length = len(result[0])\n\n return [s for s in set(result) if len(s) == max_length]\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Simpler than official solution | remove-invalid-parentheses | 0 | 1 | # Intuition\nWe\'d need to formulate every combination and see which ones are valid. A combinatorial problem.\n\n# Approach\nUse backtracking and collect only valid paranthesis\n\n# Complexity\n- Time complexity: Since every paranthesis can either be included or not => 2 options => O(2 ^ N)\n\n- Space complexity: current and stack arrays at worse will use all chars in s => O(N)\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n result = []\n current = []\n stack = []\n \n def dfs(index):\n if index == len(s):\n if not stack:\n result.append("".join(current))\n else:\n if s[index] == "(":\n \n # include\n current.append("(")\n stack.append(index)\n dfs(index + 1)\n stack.pop()\n current.pop()\n\n # exclude\n dfs(index + 1)\n elif s[index] == ")":\n # include\n if stack:\n current.append(")")\n i = stack.pop()\n dfs(index + 1)\n stack.append(i)\n current.pop()\n # exclude\n dfs(index + 1)\n else:\n current.append(s[index])\n dfs(index + 1)\n current.pop()\n\n dfs(0)\n result.sort(key=lambda x: -len(x))\n max_length = len(result[0])\n\n return [s for s in set(result) if len(s) == max_length]\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python, beats 80% slightly different route | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n def transform(s):\n s = s.replace(")", "^")\n s = s.replace("(", ")")\n s = s.replace("^", "(")\n return s[::-1]\n\n ans = set()\n\n def correct(s, i, closed_indexes):\n nonlocal ans\n\n diff = 0\n\n while i < len(s):\n if s[i] == "(":\n diff += 1\n elif s[i] == ")":\n diff -= 1\n closed_indexes.append(i)\n if diff < 0:\n break\n\n i += 1 \n if diff >= 0:\n ans.add(s)\n else:\n for index in closed_indexes:\n temp = closed_indexes.copy()\n temp.remove(index)\n correct(s[:index] + "%" + s[index+1:], i + 1, temp)\n \n correct(s, 0, [])\n temp = ans.copy()\n ans = set()\n new_ans = []\n\n for x in temp:\n correct(transform(x), 0, [])\n for x in ans:\n new_ans.append(transform(x))\n\n res = set([s.replace("%", "") for s in new_ans])\n \n return list(res)\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python, beats 80% slightly different route | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n def transform(s):\n s = s.replace(")", "^")\n s = s.replace("(", ")")\n s = s.replace("^", "(")\n return s[::-1]\n\n ans = set()\n\n def correct(s, i, closed_indexes):\n nonlocal ans\n\n diff = 0\n\n while i < len(s):\n if s[i] == "(":\n diff += 1\n elif s[i] == ")":\n diff -= 1\n closed_indexes.append(i)\n if diff < 0:\n break\n\n i += 1 \n if diff >= 0:\n ans.add(s)\n else:\n for index in closed_indexes:\n temp = closed_indexes.copy()\n temp.remove(index)\n correct(s[:index] + "%" + s[index+1:], i + 1, temp)\n \n correct(s, 0, [])\n temp = ans.copy()\n ans = set()\n new_ans = []\n\n for x in temp:\n correct(transform(x), 0, [])\n for x in ans:\n new_ans.append(transform(x))\n\n res = set([s.replace("%", "") for s in new_ans])\n \n return list(res)\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Concise solution on python3 | remove-invalid-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n\n n = len(s)\n mx = 0\n ans = set()\n \n def go(pos, res, bal):\n nonlocal ans, mx\n\n if bal > 0:\n return\n\n if pos == n:\n if bal == 0:\n if len(res) > mx:\n mx = len(res)\n ans = set([res])\n elif len(res) == mx:\n ans.add(res)\n\n return\n \n if s[pos] not in \'()\':\n go(pos + 1, res + s[pos], bal)\n else:\n # try to remove\n go(pos + 1, res, bal)\n go(pos + 1, res + s[pos], bal - 1 if s[pos] == \'(\' else bal + 1)\n\n\n go(0, "", 0)\n return ans\n\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Concise solution on python3 | remove-invalid-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n\n n = len(s)\n mx = 0\n ans = set()\n \n def go(pos, res, bal):\n nonlocal ans, mx\n\n if bal > 0:\n return\n\n if pos == n:\n if bal == 0:\n if len(res) > mx:\n mx = len(res)\n ans = set([res])\n elif len(res) == mx:\n ans.add(res)\n\n return\n \n if s[pos] not in \'()\':\n go(pos + 1, res + s[pos], bal)\n else:\n # try to remove\n go(pos + 1, res, bal)\n go(pos + 1, res + s[pos], bal - 1 if s[pos] == \'(\' else bal + 1)\n\n\n go(0, "", 0)\n return ans\n\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
python3 solution | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n def valid(st):\n stack = []\n for char in st:\n if char == "(":\n stack.append(char)\n elif char == ")":\n if not stack or stack[-1] != "(":\n return False\n stack.pop()\n return not stack \n\n res = []\n @cache\n def dfs(i, curr):\n if i >= len(s):\n if valid(curr):\n res.append(curr)\n return \n # if s[i] == "(" or s[i] == ")":\n dfs(i+1, curr + s[i])\n dfs(i+1, curr)\n\n dfs(0, "")\n out = []\n res= list(set(res))\n for r in res:\n out.append([len(r), r])\n out.sort(reverse = True)\n x = out[0][0]\n ans = []\n for a, b in out:\n if a == x:\n ans.append(b)\n return ans\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
python3 solution | remove-invalid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n def valid(st):\n stack = []\n for char in st:\n if char == "(":\n stack.append(char)\n elif char == ")":\n if not stack or stack[-1] != "(":\n return False\n stack.pop()\n return not stack \n\n res = []\n @cache\n def dfs(i, curr):\n if i >= len(s):\n if valid(curr):\n res.append(curr)\n return \n # if s[i] == "(" or s[i] == ")":\n dfs(i+1, curr + s[i])\n dfs(i+1, curr)\n\n dfs(0, "")\n out = []\n res= list(set(res))\n for r in res:\n out.append([len(r), r])\n out.sort(reverse = True)\n x = out[0][0]\n ans = []\n for a, b in out:\n if a == x:\n ans.append(b)\n return ans\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python beats 99% solution | remove-invalid-parentheses | 0 | 1 | Not sure if it\'s because this question is too old to have enough Python submissions (very likely), and not sure if there are already similar or the same solutions. but I tried to digest the Editorial thoughts and convert it to code as concise/clear as possible.\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have done the easy version of this question, where we are already asked to tell the lease number of removals to make the string valid. So we use that to first calculate how many `\'(\'` and `\')\'` removals are needed to meet the string valid (variable `lrm` and `rrm` in the code). Then, we keep that in record when doing dfs in this question so that we never remove more than those two numbers. Meanwhile, we need to always keep the string so far valid, so I use another variable `stack` to count how many open `\'(\'` we have so far to determine if we are allowed to keep `\')\'` instead of removing it when we meet one.\nTherefore the key for dp memoization is `(i, lr, rr, stack)`, where `lr`, `rr` means number of remaining `\'(\'` and `\')\'` allowed to remove.\n\n# Complexity\n- Time complexity: 2^N \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: N^4 the worst case, imagine `)))(((`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n N = len(s)\n lrm = rrm = 0\n stack = 0\n for c in s:\n if c == \'(\':\n stack += 1\n elif c == \')\':\n if stack:\n stack -= 1\n else:\n rrm += 1\n lrm = stack\n\n @lru_cache(None)\n def dfs(i, lr, rr, stack):\n # list of returned strings without removing curent char\n ans = [] \n # list of returned strings need removing curent char\n rm_ans = []\n if i == N:\n if lr==rr==stack==0:\n return [""] # the previous removals result in valid result\n else:\n return [] # vice versa\n \n c = s[i]\n if c == \'(\':\n if lr>0:\n ret = dfs(i+1, lr-1, rr, stack)\n rm_ans.extend(ret)\n ret = dfs(i+1, lr, rr, stack+1)\n ans.extend(ret)\n elif c == \')\':\n if rr > 0:\n ret = dfs(i+1, lr, rr-1, stack)\n rm_ans.extend(ret)\n if stack > 0:\n ret = dfs(i+1, lr, rr, stack-1)\n ans.extend(ret)\n else:\n ret = dfs(i+1, lr, rr, stack)\n ans.extend(ret)\n res = [c+r for r in ans] + rm_ans\n return list(set(res)) # remove duplicates \n \n return dfs(0, lrm, rrm, 0)\n \n \n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python beats 99% solution | remove-invalid-parentheses | 0 | 1 | Not sure if it\'s because this question is too old to have enough Python submissions (very likely), and not sure if there are already similar or the same solutions. but I tried to digest the Editorial thoughts and convert it to code as concise/clear as possible.\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have done the easy version of this question, where we are already asked to tell the lease number of removals to make the string valid. So we use that to first calculate how many `\'(\'` and `\')\'` removals are needed to meet the string valid (variable `lrm` and `rrm` in the code). Then, we keep that in record when doing dfs in this question so that we never remove more than those two numbers. Meanwhile, we need to always keep the string so far valid, so I use another variable `stack` to count how many open `\'(\'` we have so far to determine if we are allowed to keep `\')\'` instead of removing it when we meet one.\nTherefore the key for dp memoization is `(i, lr, rr, stack)`, where `lr`, `rr` means number of remaining `\'(\'` and `\')\'` allowed to remove.\n\n# Complexity\n- Time complexity: 2^N \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: N^4 the worst case, imagine `)))(((`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n N = len(s)\n lrm = rrm = 0\n stack = 0\n for c in s:\n if c == \'(\':\n stack += 1\n elif c == \')\':\n if stack:\n stack -= 1\n else:\n rrm += 1\n lrm = stack\n\n @lru_cache(None)\n def dfs(i, lr, rr, stack):\n # list of returned strings without removing curent char\n ans = [] \n # list of returned strings need removing curent char\n rm_ans = []\n if i == N:\n if lr==rr==stack==0:\n return [""] # the previous removals result in valid result\n else:\n return [] # vice versa\n \n c = s[i]\n if c == \'(\':\n if lr>0:\n ret = dfs(i+1, lr-1, rr, stack)\n rm_ans.extend(ret)\n ret = dfs(i+1, lr, rr, stack+1)\n ans.extend(ret)\n elif c == \')\':\n if rr > 0:\n ret = dfs(i+1, lr, rr-1, stack)\n rm_ans.extend(ret)\n if stack > 0:\n ret = dfs(i+1, lr, rr, stack-1)\n ans.extend(ret)\n else:\n ret = dfs(i+1, lr, rr, stack)\n ans.extend(ret)\n res = [c+r for r in ans] + rm_ans\n return list(set(res)) # remove duplicates \n \n return dfs(0, lrm, rrm, 0)\n \n \n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
It ain't much but it's honest work. [Python][stack][DFS] | remove-invalid-parentheses | 0 | 1 | # Intuition\n- Break this down into two problems\n\n# Approach\nFor me, there are two parts to this problem\n- Find k: minimum number of invalid parentheses to remove [LC 1249](https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/description/)\n- Once you have k, it\'s a simple DFS: `dfs(index, k, path)`\n\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n if not s:\n return []\n \n \n def getInvalid(s):\n stack = []\n for x in s:\n if x == \')\':\n if stack and stack[-1] == \'(\':\n stack.pop()\n else:\n stack.append(x)\n if x == \'(\':\n stack.append(x)\n return len(stack)\n\n k = getInvalid(s)\n\n if not k: return [s]\n\n n = len(s)\n result= set()\n @cache\n def helper(index, k, path):\n nonlocal result\n\n if k < 0:\n return\n\n if index == n:\n if k == 0 and not getInvalid(path):\n result.add(path)\n return\n \n helper(index+1, k -1, path)\n helper(index+1, k, path + s[index])\n\n\n helper(0, k, \'\')\n return result\n \n\n \n\n\n\n\n \n \n\n \n\n \n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
It ain't much but it's honest work. [Python][stack][DFS] | remove-invalid-parentheses | 0 | 1 | # Intuition\n- Break this down into two problems\n\n# Approach\nFor me, there are two parts to this problem\n- Find k: minimum number of invalid parentheses to remove [LC 1249](https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/description/)\n- Once you have k, it\'s a simple DFS: `dfs(index, k, path)`\n\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n if not s:\n return []\n \n \n def getInvalid(s):\n stack = []\n for x in s:\n if x == \')\':\n if stack and stack[-1] == \'(\':\n stack.pop()\n else:\n stack.append(x)\n if x == \'(\':\n stack.append(x)\n return len(stack)\n\n k = getInvalid(s)\n\n if not k: return [s]\n\n n = len(s)\n result= set()\n @cache\n def helper(index, k, path):\n nonlocal result\n\n if k < 0:\n return\n\n if index == n:\n if k == 0 and not getInvalid(path):\n result.add(path)\n return\n \n helper(index+1, k -1, path)\n helper(index+1, k, path + s[index])\n\n\n helper(0, k, \'\')\n return result\n \n\n \n\n\n\n\n \n \n\n \n\n \n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
So many parameters | remove-invalid-parentheses | 0 | 1 | # Intuition\nWe only want to remove as many opening or closing parentheses as possible, to this end, we first find out how many of each we\'d need to remove, then run a recursive search to find all possible valid expressions.\n\n# Approach\n - First, find the number of closing or opening parentheses to be removed\n - Then, recursively build all possible expressions, removing parentheses as needed\n - If there are no more parentheses to be removed, add the expression to the result\n - If there are parentheses to be removed, remove them and continue building the expression\n - Return the result\n\n# Complexity\n- Time complexity: O(2^n)\n - We have to build all possible expressions, which is 2^n\n\n- Space complexity: O(2^n)\n - We have to store all possible expressions, which is 2^n\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n\n def toBeRemoved(s):\n openingToBeRemoved = 0\n closingToBeRemoved = 0\n for c in s:\n if c == \'(\':\n openingToBeRemoved += 1\n elif c == \')\':\n if openingToBeRemoved > 0:\n openingToBeRemoved -= 1\n else:\n closingToBeRemoved += 1\n return openingToBeRemoved, closingToBeRemoved\n \n def noneToBeRemoved(s):\n openingToBeRemoved, closingToBeRemoved = toBeRemoved(s)\n return not openingToBeRemoved and not closingToBeRemoved\n \n result = {}\n def buildRecursively(s, index, opening, closing, \n openingToBeRemoved, closingToBeRemoved, expressionSoFar):\n if index == len(s):\n if openingToBeRemoved == 0 and closingToBeRemoved == 0:\n ans = "".join(expressionSoFar)\n result[ans] = 1\n else:\n if ((s[index] == \'(\' and (openingToBeRemoved > 0)) or\n ((s[index] == \')\') and (closingToBeRemoved > 0))):\n buildRecursively(s, index + 1,\n opening, closing,\n openingToBeRemoved - (s[index] == \'(\'),\n closingToBeRemoved - (s[index] == \')\'),\n expressionSoFar)\n \n expressionSoFar.append(s[index])\n\n if s[index] != \'(\' and s[index] != \')\':\n buildRecursively(s, index + 1,\n opening, closing,\n openingToBeRemoved, closingToBeRemoved,\n expressionSoFar)\n elif s[index] == \'(\':\n buildRecursively(s, index + 1,\n opening + 1, closing,\n openingToBeRemoved, closingToBeRemoved,\n expressionSoFar)\n elif s[index] == \')\' and opening > closing:\n buildRecursively(s, index + 1,\n opening, closing + 1,\n openingToBeRemoved, closingToBeRemoved,\n expressionSoFar)\n \n expressionSoFar.pop()\n\n openingToBeRemoved, closingToBeRemoved = toBeRemoved(s)\n buildRecursively(s, 0, 0, 0, openingToBeRemoved, closingToBeRemoved, [])\n\n return list(result.keys())\n \n \n\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
So many parameters | remove-invalid-parentheses | 0 | 1 | # Intuition\nWe only want to remove as many opening or closing parentheses as possible, to this end, we first find out how many of each we\'d need to remove, then run a recursive search to find all possible valid expressions.\n\n# Approach\n - First, find the number of closing or opening parentheses to be removed\n - Then, recursively build all possible expressions, removing parentheses as needed\n - If there are no more parentheses to be removed, add the expression to the result\n - If there are parentheses to be removed, remove them and continue building the expression\n - Return the result\n\n# Complexity\n- Time complexity: O(2^n)\n - We have to build all possible expressions, which is 2^n\n\n- Space complexity: O(2^n)\n - We have to store all possible expressions, which is 2^n\n\n# Code\n```\nclass Solution:\n def removeInvalidParentheses(self, s: str) -> List[str]:\n\n def toBeRemoved(s):\n openingToBeRemoved = 0\n closingToBeRemoved = 0\n for c in s:\n if c == \'(\':\n openingToBeRemoved += 1\n elif c == \')\':\n if openingToBeRemoved > 0:\n openingToBeRemoved -= 1\n else:\n closingToBeRemoved += 1\n return openingToBeRemoved, closingToBeRemoved\n \n def noneToBeRemoved(s):\n openingToBeRemoved, closingToBeRemoved = toBeRemoved(s)\n return not openingToBeRemoved and not closingToBeRemoved\n \n result = {}\n def buildRecursively(s, index, opening, closing, \n openingToBeRemoved, closingToBeRemoved, expressionSoFar):\n if index == len(s):\n if openingToBeRemoved == 0 and closingToBeRemoved == 0:\n ans = "".join(expressionSoFar)\n result[ans] = 1\n else:\n if ((s[index] == \'(\' and (openingToBeRemoved > 0)) or\n ((s[index] == \')\') and (closingToBeRemoved > 0))):\n buildRecursively(s, index + 1,\n opening, closing,\n openingToBeRemoved - (s[index] == \'(\'),\n closingToBeRemoved - (s[index] == \')\'),\n expressionSoFar)\n \n expressionSoFar.append(s[index])\n\n if s[index] != \'(\' and s[index] != \')\':\n buildRecursively(s, index + 1,\n opening, closing,\n openingToBeRemoved, closingToBeRemoved,\n expressionSoFar)\n elif s[index] == \'(\':\n buildRecursively(s, index + 1,\n opening + 1, closing,\n openingToBeRemoved, closingToBeRemoved,\n expressionSoFar)\n elif s[index] == \')\' and opening > closing:\n buildRecursively(s, index + 1,\n opening, closing + 1,\n openingToBeRemoved, closingToBeRemoved,\n expressionSoFar)\n \n expressionSoFar.pop()\n\n openingToBeRemoved, closingToBeRemoved = toBeRemoved(s)\n buildRecursively(s, 0, 0, 0, openingToBeRemoved, closingToBeRemoved, [])\n\n return list(result.keys())\n \n \n\n``` | 0 | Given a string `s` that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return _a list of **unique strings** that are valid with the minimum number of removals_. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "()())() "
**Output:** \[ "(())() ", "()()() "\]
**Example 2:**
**Input:** s = "(a)())() "
**Output:** \[ "(a())() ", "(a)()() "\]
**Example 3:**
**Input:** s = ")( "
**Output:** \[ " "\]
**Constraints:**
* `1 <= s.length <= 25`
* `s` consists of lowercase English letters and parentheses `'('` and `')'`.
* There will be at most `20` parentheses in `s`. | Since we don't know which of the brackets can possibly be removed, we try out all the options! We can use recursion to try out all possibilities for the given expression. For each of the brackets, we have 2 options:
We keep the bracket and add it to the expression that we are building on the fly during recursion.
OR, we can discard the bracket and move on. The one thing all these valid expressions have in common is that they will all be of the same length i.e. as compared to the original expression, all of these expressions will have the same number of characters removed.
Can we somehow find the number of misplaced parentheses and use it in our solution? For every left parenthesis, we should have a corresponding right parenthesis. We can make use of two counters which keep track of misplaced left and right parenthesis and in one iteration we can find out these two values.
0 1 2 3 4 5 6 7
( ) ) ) ( ( ( )
i = 0, left = 1, right = 0
i = 1, left = 0, right = 0
i = 2, left = 0, right = 1
i = 3, left = 0, right = 2
i = 4, left = 1, right = 2
i = 5, left = 2, right = 2
i = 6, left = 3, right = 2
i = 7, left = 2, right = 2
We have 2 misplaced left and 2 misplaced right parentheses. We found out that the exact number of left and right parenthesis that has to be removed to get a valid expression. So, e.g. in a 1000 parentheses string, if there are 2 misplaced left and 2 misplaced right parentheses, after we are done discarding 2 left and 2 right parentheses, we will have only one option per remaining character in the expression i.e. to consider them. We can't discard them. |
Python O(1) solution, beats 97.85% | range-sum-query-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n arr = [nums[0]]\n for i in range(1,len(nums)):\n arr.append(arr[-1]+nums[i])\n self.arr = arr\n\n \n\n def sumRange(self, left: int, right: int) -> int:\n if left == 0:\n return self.arr[right]\n return self.arr[right] - self.arr[left - 1]\n \n\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# param_1 = obj.sumRange(left,right)\n\n\n\n"""\ngiven n>= j > i >0\nprefix_sum(i,j) = prefix_sum(0,j) - prefix_sum(0,i)\nwe need to itilaze a prefix_sum\n\n\n"""\n``` | 3 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
Easy to Understand | Faster | Simple | Python Solution | range-sum-query-immutable | 0 | 1 | ```\n def __init__(self, nums: List[int]):\n self.sum = []\n sum_till = 0\n for i in nums:\n sum_till += i\n self.sum.append(sum_till)\n\n def sumRange(self, i: int, j: int) -> int:\n if i > 0 and j > 0:\n return self.sum[j] - self.sum[i - 1]\n else:\n return self.sum[i or j]\n \n\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 43 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
PYTHON3 SINGLE LINE CODE ✅✅✅ | range-sum-query-immutable | 0 | 1 | \n\n# Code\n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n self.nums=nums\n\n def sumRange(self, left: int, right: int) -> int:\n return sum(self.nums[left:right+1])\n\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# param_1 = obj.sumRange(left,right)\n``` | 1 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
303: Solution with step by step explanation | range-sum-query-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- We define a NumArray class with two methods: __init__ and sumRange.\n- In __init__, we compute the prefix sums of the input nums array and store them in a prefix_sum list. We initialize the prefix_sum list with 0\'s and then loop through nums, adding each element to the corresponding index in prefix_sum. This gives us the cumulative sum up to each index in nums. Note that we add an extra 0 to the beginning of prefix_sum to simplify the code for sumRange.\n- In sumRange, we return the sum of the elements between left and right by subtracting the prefix sums at left and right+1. This is because prefix_sum[right+1] gives us the sum of the elements up to index right, while prefix_sum[left] gives us the sum of the elements up to index left-1. By subtracting these two values, we get the sum of the elements between left and right.\n\nThis solution has a time complexity of O(1) for each call to sumRange, since we only need to perform two constant-time operations: two lookups in the prefix_sum list and a subtraction. The space complexity is O(n), where n is the length of the input array, since we need to store the prefix_sum list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n self.prefix_sum = [0] * (len(nums) + 1)\n for i in range(len(nums)):\n self.prefix_sum[i + 1] = self.prefix_sum[i] + nums[i]\n\n def sumRange(self, left: int, right: int) -> int:\n return self.prefix_sum[right + 1] - self.prefix_sum[left]\n\n``` | 7 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
Efficient Range Sum Query using Prefix Sum Array | range-sum-query-immutable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to find the sum of the elements of nums between indices left and right inclusive. This can be achieved by creating a prefix sum array, which stores the sum of the elements up to that index. By subtracting the prefix sum of the left index - 1 from the prefix sum of the right index, we can obtain the sum of the elements between the two indices.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can initialize the prefix sum array with 0\'s, with a length of 1 greater than the length of the input array. We then iterate through the input array and store the cumulative sum up to that index in the prefix sum array.\n\nTo find the sum between the left and right indices, we return the difference between the prefix sum of the right index + 1 and the prefix sum of the left index.\n# Complexity\n- Time complexity: $$O(n)$$ for initializing the prefix sum array, where $$n$$ is the length of the input array. Each sumRange query can be answered in $$O(1)$$ time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$ O(n)$$ for storing the prefix sum array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass NumArray:\n\n def __init__(self, nums: List[int]):\n self.prefix_sum = [0] * (len(nums) + 1)\n for i in range(1, len(nums) + 1):\n self.prefix_sum[i] = self.prefix_sum[i-1] + nums[i-1]\n \n\n def sumRange(self, left: int, right: int) -> int:\n return self.prefix_sum[right+1] - self.prefix_sum[left]\n \n\n\n# Your NumArray object will be instantiated and called as such:\n# obj = NumArray(nums)\n# param_1 = obj.sumRange(left,right)\n``` | 5 | Given an integer array `nums`, handle multiple queries of the following type:
1. Calculate the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** where `left <= right`.
Implement the `NumArray` class:
* `NumArray(int[] nums)` Initializes the object with the integer array `nums`.
* `int sumRange(int left, int right)` Returns the **sum** of the elements of `nums` between indices `left` and `right` **inclusive** (i.e. `nums[left] + nums[left + 1] + ... + nums[right]`).
**Example 1:**
**Input**
\[ "NumArray ", "sumRange ", "sumRange ", "sumRange "\]
\[\[\[-2, 0, 3, -5, 2, -1\]\], \[0, 2\], \[2, 5\], \[0, 5\]\]
**Output**
\[null, 1, -1, -3\]
**Explanation**
NumArray numArray = new NumArray(\[-2, 0, 3, -5, 2, -1\]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3
**Constraints:**
* `1 <= nums.length <= 104`
* `-105 <= nums[i] <= 105`
* `0 <= left <= right < nums.length`
* At most `104` calls will be made to `sumRange`. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.