title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Tiny LL(1) Compiler in Python3 - Compiles expression to RPN and evaluate | basic-calculator | 0 | 1 | # Approach\nFirst generate AST (Abstract Syntax Tree) that contains the information needed to generate RPN, aka reverse polish notation, which is easy to evaluate on. Then doing tree traversal on AST to emit RPN. Finally evaluate the RPN.\n\nThe Backus\u2013Naur Form grammar: \n```\nexpr ::= base term\nterm ::= + base term | - base term | epsilon\nbase ::= [0-9] | ( expr )\n```\n\n# Code\n```\nimport ast\nimport re\nimport sys\nsys.setrecursionlimit(100000)\n\nclass ExprNode:\n def __init__(self, child1, child2):\n self.children = [child1, child2]\n def __str__(self):\n return("Expression")\n\nclass TermNode:\n def __init__(self, op, child1, child2):\n self.children = [child1, child2]\n self.op = op\n def __str__(self):\n if self.op == "+":\n return("Term PLUS")\n else:\n return("Term MINUS")\n\nclass BaseNode:\n def __init__(self, child, val=None):\n self.children = [child]\n self.val = val\n def __str__(self):\n if self.val == None:\n return("Parenthesis")\n else:\n return("Number " + str(self.val))\n\nclass Parser:\n def __init__(self, tokens):\n self.tokens = tokens\n self.cur = 0\n def expr(self):\n curtoken = self.tokens[self.cur]\n if curtoken.isdigit():\n self.cur += 1\n node = self.term()\n if not node:\n return BaseNode(None, int(curtoken))\n else:\n return ExprNode(BaseNode(None, int(curtoken)), node)\n else:\n # left parenthesis case\n b_node = self.base()\n t_node = self.term()\n return ExprNode(b_node, t_node)\n def term(self):\n if self.cur >= len(self.tokens) - 1:\n return None\n curtoken = self.tokens[self.cur]\n if curtoken in ["+", "-"]:\n self.cur += 1\n nexttoken = self.tokens[self.cur]\n if nexttoken.isdigit():\n self.cur += 1\n node = self.term()\n return TermNode(curtoken, BaseNode(None, int(nexttoken)), node)\n else:\n b_node = self.base()\n t_node = self.term()\n return TermNode(curtoken, b_node, t_node)\n else:\n return None\n\n # parses the parenthesis case only\n def base(self):\n if self.tokens[self.cur] == "(":\n self.cur += 1\n node = self.expr()\n if self.tokens[self.cur] != ")":\n print("Syntax Error: No matching right parenthesis")\n return None\n self.cur += 1\n return BaseNode(node)\n\nclass Solution:\n def calculate(self, s: str) -> int:\n def lexer(s):\n expression = re.sub(r\'\\s+\', "", s)\n expression = re.findall(r\'\\d+|[\\(\\)+-]\', expression)\n formatted = []\n for e in expression:\n if e == "-" and (not formatted or formatted[-1] == "("):\n formatted.append("0")\n formatted.append(e)\n return formatted\n def print_nodes(n, lvl=0):\n if not n:\n return\n print(" " * lvl, end="")\n print("|", end="")\n print("--" * lvl, end="")\n print(n)\n \n for c in n.children:\n print_nodes(c, lvl+1)\n \n rpn = []\n def emit_rpn(n):\n if not n:\n return\n if type(n) == TermNode:\n if n.children[0].val != None:\n rpn.append(n.children[0].val)\n rpn.append(n.op)\n else:\n emit_rpn(n.children[0])\n rpn.append(n.op)\n emit_rpn(n.children[1])\n\n\n elif type(n) == BaseNode:\n if n.val != None:\n rpn.append(n.val)\n else:\n emit_rpn(n.children[0])\n\n else:\n emit_rpn(n.children[0])\n emit_rpn(n.children[1])\n \n def evaluate_rpn(rpns):\n stack = []\n for token in rpns :\n if token == \'+\' :\n a , b = stack.pop() , stack.pop()\n stack.append( a + b ) \n elif token == \'-\':\n a , b = stack.pop() , stack.pop()\n stack.append( b - a ) \n else:\n stack.append(token) \n return stack.pop() \n \n ps = Parser(lexer(s))\n res = ps.expr()\n emit_rpn(res)\n return evaluate_rpn(rpn)\n``` | 1 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Shunting Yard Algorithm (Simple and Concise) | basic-calculator | 0 | 1 | # Intuition\nI was rather disappointed with this problem until I came across the really beautiful algorithm in Wikipedia.\n\nIt is hard to come up with a solution yourself if you are not familiar with [Shunting Yard Algorithm](https://en.wikipedia.org/wiki/Shunting_yard_algorithm) and [Polish Postfix Notation](https://en.wikipedia.org/wiki/Reverse_Polish_notation).\n\nI should say that this algorithm really impressed me with its beauty.\n\n# Approach\nThe main trouble are the uniray/binary dichotomy of `-` sign and abscence of external brackets. \n\nSo I decided to turn all minuses to binary. To do so, if we see `(` followed by `-`, we insert in every bracket `0` as a first term.\n\nTo avoid hustling with two cases: part without brackets and parts withtin brackets, the whole expression is wrapped in external brackets.\n\nThe solution is laconic and beatiful for my taste :)\n\nHere is the solution plan:\n1. remove spaces and add external brackets\n2. parse the tokens\n2. insert zeros where needed\n3. convert to Reverse Polish Notation using Shunting Yard\n4. solve Reverse Polish Notation using the approach in one of the previous tasks\n5. Enjoy the solution\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def parse(self, s):\n tokens = []\n index = 0\n while index < len(s):\n if s[index] <= \'9\' and s[index] >= \'0\':\n number = []\n while index < len(s) and s[index] <= \'9\' and s[index] >= \'0\':\n number.append(s[index])\n index += 1\n tokens.append(int(\'\'.join(number)))\n else:\n tokens.append(s[index])\n index += 1\n return tokens\n\n\n def insert_zero(self, tokens):\n res = []\n for index in range(len(tokens)):\n if tokens[index] == \'-\' and tokens[index - 1] == \'(\':\n res.append(0)\n res.append(tokens[index])\n\n return res\n\n def to_postfix(self, tokens):\n res = []\n num = []\n ops = []\n\n for t in tokens:\n if t in set([\'+\', \'-\']):\n while ops[-1] != \'(\':\n res.append(ops.pop())\n ops.append(t)\n\n elif t == \')\':\n while ops[-1] != \'(\':\n\n res.append(ops.pop())\n\n ops.pop()\n\n elif t == \'(\':\n ops.append(t)\n\n else:\n res.append(t)\n\n return res\n\n def solve_postfix(self, tokens):\n res = []\n\n for t in tokens:\n if t == \'+\':\n two = res.pop()\n one = res.pop()\n res.append(one + two)\n\n elif t == \'-\':\n two = res.pop()\n one = res.pop()\n res.append(one - two)\n\n else:\n res.append(t)\n\n return res[-1]\n\n\n def calculate(self, s: str) -> int:\n s = s.replace(\' \', \'\')\n s = \'(\' + s + \')\'\n\n tokens = self.parse(s)\n tokens = self.insert_zero(tokens)\n tokens = self.to_postfix(tokens)\n res = self.solve_postfix(tokens)\n\n return res \n``` | 1 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
[Python 3] Using recursion, without stack | basic-calculator | 0 | 1 | ```\nclass Solution:\n def calculate(self, s):\n def evaluate(i):\n res, digit, sign = 0, 0, 1\n \n while i < len(s):\n if s[i].isdigit():\n digit = digit * 10 + int(s[i])\n elif s[i] in \'+-\':\n res += digit * sign\n digit = 0\n sign = 1 if s[i] == \'+\' else -1\n elif s[i] == \'(\':\n subres, i = evaluate(i+1)\n res += sign * subres\n elif s[i] == \')\':\n res += digit * sign\n return res, i\n i += 1\n\n return res + digit * sign\n \n return evaluate(0)\n\n``` | 15 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
✅ Explained - Simple and Clear Python3 Code✅ | basic-calculator | 0 | 1 | The solution implements a basic calculator to evaluate a given expression string without using built-in functions like eval().\n\nThe evaluate_expression method handles the addition and subtraction operations within a given expression. It splits the expression at \'+\' characters and then further splits the resulting substrings at \'-\' characters. It keeps track of whether the first character of each substring is a \'-\' sign to indicate subtraction. It iterates over the substrings, converting them to integers and performing the necessary addition or subtraction. The results are stored in a list and then summed up to obtain the final result.\n\nThe calculate method handles the parentheses within the expression. It finds the outermost pair of parentheses, evaluates the expression inside them using evaluate_expression, and replaces the evaluated result back into the original string. This process is repeated until there are no more parentheses. Finally, it calls evaluate_expression with the modified string to calculate the overall result of the expression.\n\nThe solution provides a valid and accurate evaluation of the expression, taking into account the order of operations dictated by parentheses and the addition/subtraction operations.\n\n# Code\n```\nclass Solution:\n def evaluate_expression(self, expression: str) -> int:\n expression = expression.replace("--", "+")\n operands = expression.split("+")\n operands = [operand for operand in operands if operand != \'\']\n results = []\n\n for operand in operands:\n is_first_negative = False\n if operand[0] == "-":\n is_first_negative = True\n\n sub_operands = operand.split(\'-\')\n sub_operands = [sub_operand for sub_operand in sub_operands if sub_operand != \'\']\n subtotal = 0\n\n if is_first_negative:\n subtotal = -1 * int(sub_operands[0])\n else:\n subtotal = int(sub_operands[0])\n\n sub_operands.pop(0)\n\n for sub_operand in sub_operands:\n subtotal -= int(sub_operand)\n\n results.append(subtotal)\n\n total = 0\n\n for result in results:\n total += result\n\n return total\n\n def calculate(self, expression: str) -> int:\n expression = expression.replace(" ", "")\n open_parentheses = []\n end = 0\n i = 0\n\n while i < len(expression):\n if expression[i] == \'(\':\n open_parentheses.append(i)\n elif expression[i] == \')\':\n end = i\n start = open_parentheses[-1]\n sub_expression = expression[start + 1:end]\n evaluated_value = self.evaluate_expression(sub_expression)\n new_expression = expression[:start] + str(evaluated_value) + expression[end + 1:]\n open_parentheses.pop()\n expression = new_expression\n i = start - 1\n\n i += 1\n\n return self.evaluate_expression(expression)\n\n``` | 7 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
224: Time 93.3%, Solution with step by step explanation | basic-calculator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis code implements a basic calculator to evaluate a given expression represented as a string s.\n\nThe algorithm processes the string character by character and maintains three variables ans, num, and sign, and a stack stack.\n\nans stores the running total of the expression evaluated so far, num stores the currently processed number, and sign stores the sign of the current environment. The stack keeps track of nested environments by storing the sign of the previous environment.\n\nThe algorithm then iterates through each character c in the string s and does the following:\n\n- If c is a digit, it appends it to num.\n- If c is a left parenthesis (, it appends the current sign to the stack and sets sign to 1 (since the current environment is positive).\n- If c is a right parenthesis ), it pops the last sign from the stack and sets sign to it.\n- If c is a plus + or minus -, it updates the ans by adding the current sign * num to it, updates the sign to 1 or -1 depending on the current operator, and sets num to 0.\n\nFinally, the function returns the updated ans value plus the last sign * num.\n\nOverall, this algorithm works in linear time with respect to the length of the input string, since each character is processed once.\n\n# Complexity\n- Time complexity:\n93.3%\n\n- Space complexity:\n72.30%\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n ans = 0\n num = 0\n sign = 1\n stack = [sign] # stack[-1]: current env\'s sign\n\n for c in s:\n if c.isdigit():\n num = num * 10 + (ord(c) - ord(\'0\'))\n elif c == \'(\':\n stack.append(sign)\n elif c == \')\':\n stack.pop()\n elif c == \'+\' or c == \'-\':\n ans += sign * num\n sign = (1 if c == \'+\' else -1) * stack[-1]\n num = 0\n\n return ans + sign * num\n\n``` | 14 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Simple Python Solution using stack with explanation inline | basic-calculator | 0 | 1 | ```\n def calculate(self, s: str) -> int:\n """\n 1. Take 3 containers:\n num -> to store current num value only\n sign -> to store sign value, initially +1\n res -> to store sum\n When ( comes these containers used for calculate sum of intergers within () brackets.\n --------------------\n 2. When c is + or -\n Move num to res, because we need to empty num for next integer value.\n set num = 0\n sign = update with c\n --------------------\n 3. When c is \'(\'\n Here, we need num, res, sign to calculate sum of integers within ()\n So, move num and sign to stack => [num, sign]\n Now reset - res = 0, num = 0, sign = 1 (default)\n --------------------\n 4. When c is \')\' -> 2-(3+4), Here res=3, num=4, sign=1 stack [2, -] \n res +=sign*num -> calculate sum for num first, then pop items from stack, res=7\n res *=stack.pop() - > Pop sign(+ or -) to multiply with res, res = 7*(-1)\n res +=stack.pop() - > Pop integer and add with prev. sum, res = -7 + 2 - 5\n --------------------\n Simple Example: 2 - 3\n Initially res will have 2,i.e. res = 2\n then store \'-\' in sign. it will be used when 3 comes. ie. sign = -1\n Now 3 comes => res = res + num*sign\n Return statement: res+num*sign => res = 2 + 3(-1) = 2 - 3 = -1\n """\n num = 0\n sign = 1\n res = 0\n stack = []\n for i in range(len(s)): # iterate till last character\n c = s[i]\n if c.isdigit(): # process if there is digit\n num = num*10 + int(c) # for consecutive digits 98 => 9x10 + 8 = 98\n elif c in \'-+\': # check for - and +\n res += num*sign\n sign = -1 if c == \'-\' else 1\n num = 0\n elif c == \'(\':\n stack.append(res)\n stack.append(sign)\n res = 0\n sign = 1\n elif c == \')\':\n res +=sign*num\n res *=stack.pop()\n res +=stack.pop()\n num = 0\n return res + num*sign\n``` | 61 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Python (Faster than 98%) | O(N) stack solution | basic-calculator | 0 | 1 | \n\n\n\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n output, curr, sign, stack = 0, 0, 1, []\n for c in s:\n if c.isdigit():\n curr = (curr * 10) + int(c)\n \n elif c in \'+-\':\n output += curr * sign\n curr = 0\n if c == \'+\':\n sign = 1\n\n else:\n sign = -1\n \n elif c == \'(\':\n stack.append(output)\n stack.append(sign)\n sign = 1\n output = 0\n \n elif c == \')\':\n output += curr * sign\n output *= stack.pop() #sign\n output += stack.pop() #last output\n curr = 0\n\n return output + (curr * sign)\n```\n# Please upvote if you find this helpful. | 8 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Lexer, Parser, Interpreter | Abstraction | O(N) time and O(N) space | basic-calculator | 0 | 1 | # Intuition\nScanning a language and evaluating it\'s result in another language can be acheived with a lexer, parser, and interpreter.\n\nThis level of abstraction introduces overhead that affects performance, this is more of an exercise on interpreters than an optimized solution.\n\n# Approach\n- **Lexer**: Generates tokens from the input string, tokens are like the "words" of a language. In this case the "words" are the symbols `+`, `-`, `(`, and `)` as well as 32-bit unsigned integers. Lexers are commonly implemented as streams.\n- **Parser**: Generates a **parse tree** from the tokens generated by the lexer. The parse tree structure represents the higherarchy/order of operations of the arithmetic. In this case, parse trees are made up of parse nodes such as number, addition, subtraction, negation , and group (parenthesis) nodes.\n- **Interpreter**: Evaluates the parse tree generated by the parser. The interpreter collapses/folds the parse tree to evaluate its result.\n\n# Complexity\n- Time complexity: $$O(n)$$. We generate the tokens and parse nodes in $$O(n)$$ time then evaluate the parse tree in $$O(n)$$ time.\n\n- Space complexity: $$O(n)$$. We generate a proportion of $$n$$ parse nodes then evaluating the parse nodes consumes a proportion of $$n$$ stack frames due to recursion.\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n lexer = Lexer(s)\n parser = Parser(lexer)\n parse_tree = parser.parse(None)\n print(parse_tree)\n interpreter = Interpreter(parse_tree)\n return interpreter.eval()\n\nclass Lexer:\n def __init__(self, expr: str):\n self.expr = expr\n self.i = 0\n def parse_num(self) -> str:\n num = ""\n while self.i < len(self.expr) and self.expr[self.i].isdigit() :\n num += self.expr[self.i]\n self.i += 1\n return num\n def next_token(self) -> str:\n if self.i == len(self.expr):\n return ""\n\n ch = self.expr[self.i]\n if ch == " ":\n self.i += 1 ; return self.next_token()\n elif ch.isdigit():\n num = self.parse_num()\n return num\n elif ch in [\'+\', \'-\', \'(\', \')\']:\n self.i += 1 ; return ch\n\nclass num_node:\n def __init__(self, num):\n self.num = num\n def __repr__(self):\n return f\'{self.num}\'\nclass add_node:\n def __init__(self, left, right):\n self.left = left\n self.right = right\n def __repr__(self):\n return f\'{self.left}+{self.right}\'\nclass subtract_node:\n def __init__(self, left, right):\n self.left = left\n self.right = right\n def __repr__(self):\n return f\'{self.left}-{self.right}\'\nclass negate_node:\n def __init__(self, parse_tree):\n self.parse_tree = parse_tree\n def __repr__(self):\n return f\' -{self.parse_tree}\'\nclass group_node:\n def __init__(self, parse_tree):\n self.parse_tree = parse_tree\n def __repr__(self):\n return f\'({self.parse_tree})\'\nparse_node = num_node | add_node | subtract_node | negate_node | group_node\nclass Parser:\n def __init__(self, lexer):\n self.lexer = lexer\n def next_node(self, last_node) -> parse_node:\n token = self.lexer.next_token()\n if token == "":\n return None\n elif token == ")":\n return None\n elif token.isnumeric():\n return num_node(int(token))\n elif token == "+":\n return add_node(last_node, self.next_node(None))\n elif token == "-":\n if last_node is None:\n return negate_node(self.next_node(None))\n else:\n return subtract_node(last_node, self.next_node(None))\n elif token == "(":\n return group_node(self.parse(None))\n\n def parse(self, parse_tree: parse_node) -> parse_node:\n node = self.next_node(parse_tree)\n if node is None:\n return parse_tree\n else:\n return self.parse(node)\n \nclass Interpreter:\n def __init__(self, parse_tree):\n self.parse_tree = parse_tree\n def eval(self) -> int:\n return self.eval_pt(self.parse_tree)\n def eval_pt(self, parse_tree: parse_node) -> int:\n if isinstance(parse_tree, num_node):\n return parse_tree.num\n elif isinstance(parse_tree, add_node):\n return self.eval_pt(parse_tree.left) + self.eval_pt(parse_tree.right)\n elif isinstance(parse_tree, subtract_node):\n return self.eval_pt(parse_tree.left) - self.eval_pt(parse_tree.right)\n elif isinstance(parse_tree, negate_node):\n return -1 * self.eval_pt(parse_tree.parse_tree)\n elif isinstance(parse_tree, group_node):\n return self.eval_pt(parse_tree.parse_tree)\n``` | 2 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Binbin solved another hard question!!! very happy! | basic-calculator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n res = 0\n pre_op = "+"\n s += "+"\n num = 0\n stack = []\n for i in s:\n #print(i)\n #print(num,res,pre_op,stack)\n if i.isdigit():\n num = num*10 + int(i)\n elif i == " ":\n continue\n elif i in ["+","-"]:\n if pre_op == "+":\n res += num\n else:\n res -= num\n pre_op = i\n num = 0\n elif i == "(":\n stack.append(res)\n stack.append(pre_op)\n res = 0\n num = 0\n pre_op = "+"\n elif i == ")":\n if pre_op == "+":\n res += num\n else:\n res -= num\n if stack[-1] == "+":\n #res += num\n stack.pop()\n res += stack.pop()\n elif stack[-1] == "-":\n # res -= num\n stack.pop()\n res = stack.pop() - res\n num = 0\n pre_op = "+"\n return res \n\n``` | 2 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Python | O(n) | Recursive | Comments added | basic-calculator | 0 | 1 | \n```\nclass Solution:\n def calculate(self, expression: str) -> int:\n #recurse when brackets encountered\n def helper(s,index):\n result = 0\n sign = 1\n currnum = 0\n i = index\n while i<len(s):\n c = s[i]\n if c.isdigit():\n currnum = currnum*10+int(c)\n elif c in \'-+\': #update the sign\n result += sign*currnum\n sign = 1 if c==\'+\' else -1\n currnum = 0\n elif c == \'(\': #pause and call helper for the next section\n res, i = helper(s, i+1)\n result += sign*res\n elif c == \')\': #return results, index to resume to caller\n result += sign*currnum\n break\n i+=1\n #return result and current index\n return result, i\n \n if not expression:\n return 0\n #enclose input with brackets and call helper\n return helper(\'(\'+expression+\')\', 0)[0]\n\t\t | 1 | Given a string `s` representing a valid expression, implement a basic calculator to evaluate it, and return _the result of the evaluation_.
**Note:** You are **not** allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "1 + 1 "
**Output:** 2
**Example 2:**
**Input:** s = " 2-1 + 2 "
**Output:** 3
**Example 3:**
**Input:** s = "(1+(4+5+2)-3)+(6+8) "
**Output:** 23
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of digits, `'+'`, `'-'`, `'('`, `')'`, and `' '`.
* `s` represents a valid expression.
* `'+'` is **not** used as a unary operation (i.e., `"+1 "` and `"+(2 + 3) "` is invalid).
* `'-'` could be used as a unary operation (i.e., `"-1 "` and `"-(2 + 3) "` is valid).
* There will be no two consecutive operators in the input.
* Every number and running calculation will fit in a signed 32-bit integer. | null |
Beats 92% TC & 97% SC || Python Solution | implement-stack-using-queues | 0 | 1 | \n\n# Complexity\n- Time complexity:\n91.54%\n- Space complexity:\n97.2%\n# Code\n```\nclass MyStack:\n\n def __init__(self):\n self.queue = []\n\n def push(self, x: int) -> None:\n self.queue.append(x)\n\n def pop(self) -> int:\n return self.queue.pop()\n\n def top(self) -> int:\n return self.queue[-1]\n\n def empty(self) -> bool:\n return not self.queue\n\n\n# Your MyStack object will be instantiated and called as such:\n# obj = MyStack()\n# obj.push(x)\n# param_2 = obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.empty()\n``` | 1 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
Python3 Single queue operation easy understanding | implement-stack-using-queues | 0 | 1 | \n\n# Code\n```\nclass MyStack:\n\n def __init__(self):\n self.q = collections.deque()\n\n def push(self, x: int) -> None:\n self.q.append(x)\n\n def pop(self) -> int:\n for i in range(len(self.q) - 1):\n self.push(self.q.popleft())\n return self.q.popleft()\n\n def top(self) -> int:\n return self.q[-1]\n\n def empty(self) -> bool:\n return len(self.q) == 0\n\n\n# Your MyStack object will be instantiated and called as such:\n# obj = MyStack()\n# obj.push(x)\n# param_2 = obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.empty()\n``` | 1 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
✅ 99.74% One-Queue Approach | implement-stack-using-queues | 1 | 1 | # Interview Guide - Implement Stack using Queues:\n\n## Problem Understanding\n\n### **Description**: \nThe task is to implement a stack (Last In, First Out - LIFO) using queues. The stack should support the following functions: `push`, `pop`, `top`, and `empty`. These operations should behave just as they do in a typical stack data structure.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n- The stack must be implemented using only standard queue operations.\n- The integer values pushed onto the stack are between 1 and 9.\n- There will be at most 100 calls to each of the stack\'s functions (`push`, `pop`, `top`, and `empty`).\n- All calls to `pop` and `top` will be made when the stack is not empty.\n\n### 2. Approaches to Solve the Problem\n\n#### Two-Queue Approach\n- **How it Works**: Utilize two queues and move elements between them to mimic stack operations.\n- **Time Complexity**: $$O(n)$$ for `pop` and `top`, $$O(1)$$ for `push` and `empty`.\n- **When to Use**: Choose this approach when the frequency of `push` and `empty` operations is higher than `pop` and `top`.\n\n#### One-Queue Approach\n- **How it Works**: Use a single queue and reorganize (rotate) its elements when pushing a new element.\n- **Time Complexity**: $$O(n)$$ for `push`, $$O(1)$$ for `pop`, `top`, and `empty`.\n- **When to Use**: Choose this approach when you expect `pop` and `top` operations to be more frequent than `push`.\n\n### 4. Thought Process\n- The two-queue approach is more straightforward but involves more element transfers for `pop` and `top`.\n- The one-queue approach requires more work during the `push` operation but makes `pop` and `top` more efficient.\n \n## Conclusion\nThe problem is a good exercise in understanding how one data structure can be implemented using another while maintaining its essential characteristics with both one-queue and two-queue approaches.\n\n---\n\n# Live Coding in Python\nhttps://youtu.be/8cwvQWfsPfs?si=KDUxRZDvlPSljfM8\n\n---\n\n# Approach: Two-Queue Approach\n\n## Key Data Structures\n- Two queues, often implemented using Python\'s `deque` from the `collections` library.\n\n## Enhanced Breakdown\n\n### 1. Initialization:\n- Create two empty queues, referred to as `q1` and `q2`. `q1` will serve as the main queue where new elements are pushed, while `q2` will serve as an auxiliary queue for temporary operations.\n\n### 2. Base Cases:\n- For the `empty` function, directly check the length or size of `q1`. If it\'s empty, return `True`, otherwise return `False`.\n\n### 3. Main Algorithm:\n\n#### Push Operation\n- For the `push` operation, simply add the new element to the back (enqueue) of `q1`.\n\n#### Pop Operation\n- For the `pop` operation, you need to access the last element pushed into `q1`, which is at the back.\n- To do this, dequeue from `q1` and enqueue into `q2` until only one element remains in `q1`.\n- The remaining element is the one to be popped. Dequeue it from `q1`.\n\n#### Top Operation\n- Similar to the `pop` operation, but after accessing the last element, it should be enqueued back into `q2`.\n\n### 4. Wrap-up:\n- After each `pop` and `top` operation, swap `q1` and `q2` to make `q2` the new main queue and `q1` the new auxiliary queue.\n\n## Complexity\n### Time Complexity:\n- $$O(n)$$ for the `pop` and `top` operations as you have to move $$n-1$$ elements between the two queues.\n- $$O(1)$$ for the `push` and `empty` operations as they are direct enqueue and length check operations.\n\n### Space Complexity:\n- $$O(n)$$ for storing the elements in the queues.\n\n---\n\n# Approach: One-Queue Approach\n\n## Key Data Structures\n- A single queue, again best implemented using Python\'s `deque` from the `collections` library.\n\n## Enhanced Breakdown\n\n### 1. Initialization:\n- Create a single empty queue, referred to as `q`.\n\n### 2. Base Cases:\n- Similar to the Two-Queue Approach, directly check if the queue `q` is empty for the `empty` operation.\n\n### 3. Main Algorithm:\n\n#### Push Operation\n- Enqueue the new element at the back of `q`.\n- To ensure that the last element can be accessed from the front, rotate the queue by dequeueing and enqueuing each element except the newly pushed element.\n\n#### Pop and Top Operations\n- Simply dequeue from the front for `pop` and peek at the front for `top`.\n\n### 4. Wrap-up:\n- There\'s no need to swap or move elements for `pop` and `top`, making these operations faster compared to the Two-Queue Approach.\n\n## Complexity\n### Time Complexity:\n- $$O(n)$$ for the `push` operation due to the rotation required to bring the last element to the front.\n- $$O(1)$$ for the `pop`, `top`, and `empty` operations.\n\n### Space Complexity:\n- $$O(n)$$ for storing the elements in the queue.\n---\n\n# Performance\n\n| Language | Approach | Runtime (ms) | Memory (MB) |\n|-----------|----------|--------------|-------------|\n| Rust | 1Q | 0 ms | 2.2 MB |\n| Go | 1Q | 1 ms | 2 MB |\n| C++ | 1Q | 0 ms | 6.7 MB |\n| Java | 1Q | 0 ms | 40.5 MB |\n| PHP | 1Q | 0 ms | 18.8 MB |\n| Python3 | 1Q | 24 ms | 16.5 MB |\n| Python3 | 2Q | 40 ms | 16.4 MB |\n| JavaScript| 1Q | 45 ms | 41.6 MB |\n| C# | 1Q | 105 ms | 40.7 MB |\n\n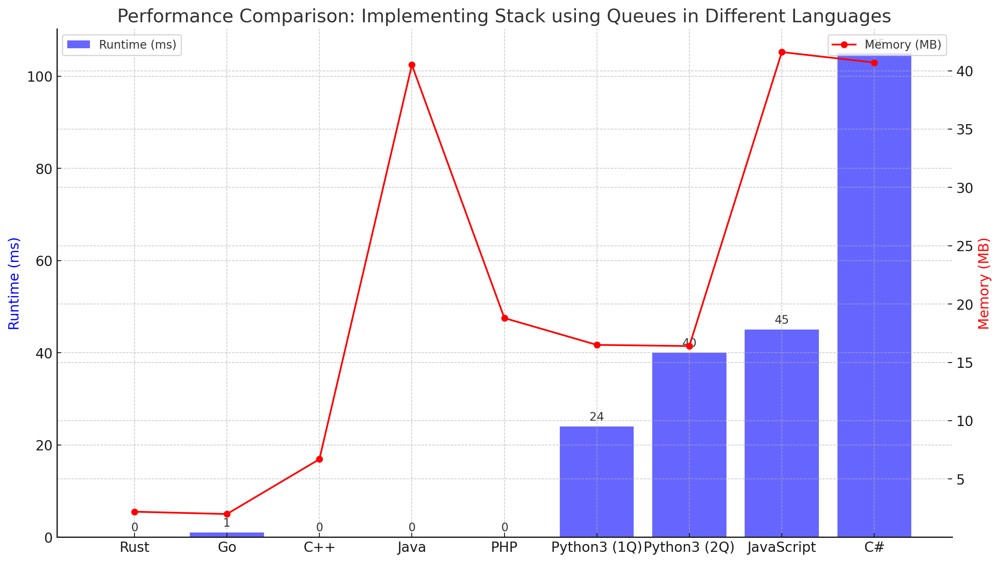\n\n---\n\n# Code One-Queue\n``` Python []\nclass MyStack:\n\n def __init__(self):\n self.q = deque()\n\n def push(self, x: int) -> None:\n self.q.append(x)\n for _ in range(len(self.q) - 1):\n self.q.append(self.q.popleft())\n\n def pop(self) -> int:\n return self.q.popleft()\n\n def top(self) -> int:\n return self.q[0]\n\n def empty(self) -> bool:\n return len(self.q) == 0\n```\n``` C++ []\n#include <queue>\n\nclass MyStack {\nprivate:\n std::queue<int> q;\n\npublic:\n MyStack() {}\n\n void push(int x) {\n q.push(x);\n for (int i = 0; i < q.size() - 1; ++i) {\n q.push(q.front());\n q.pop();\n }\n }\n\n int pop() {\n int val = q.front();\n q.pop();\n return val;\n }\n\n int top() {\n return q.front();\n }\n\n bool empty() {\n return q.empty();\n }\n};\n```\n``` Go []\ntype MyStack struct {\n q []int\n}\n\nfunc Constructor() MyStack {\n return MyStack{}\n}\n\nfunc (this *MyStack) Push(x int) {\n this.q = append(this.q, x)\n for i := 0; i < len(this.q)-1; i++ {\n this.q = append(this.q, this.q[0])\n this.q = this.q[1:]\n }\n}\n\nfunc (this *MyStack) Pop() int {\n val := this.q[0]\n this.q = this.q[1:]\n return val\n}\n\nfunc (this *MyStack) Top() int {\n return this.q[0]\n}\n\nfunc (this *MyStack) Empty() bool {\n return len(this.q) == 0\n}\n```\n``` Rust []\nuse std::collections::VecDeque;\n\npub struct MyStack {\n q: VecDeque<i32>,\n}\n\nimpl MyStack {\n pub fn new() -> Self {\n MyStack { q: VecDeque::new() }\n }\n\n pub fn push(&mut self, x: i32) {\n self.q.push_back(x);\n for _ in 0..self.q.len() - 1 {\n let val = self.q.pop_front().unwrap();\n self.q.push_back(val);\n }\n }\n\n pub fn pop(&mut self) -> i32 {\n self.q.pop_front().unwrap()\n }\n\n pub fn top(&self) -> i32 {\n *self.q.front().unwrap()\n }\n\n pub fn empty(&self) -> bool {\n self.q.is_empty()\n }\n}\n```\n``` Java []\npublic class MyStack {\n private Queue<Integer> q;\n\n public MyStack() {\n q = new LinkedList<>();\n }\n\n public void push(int x) {\n q.add(x);\n for (int i = 1; i < q.size(); i++) {\n q.add(q.remove());\n }\n }\n\n public int pop() {\n return q.remove();\n }\n\n public int top() {\n return q.peek();\n }\n\n public boolean empty() {\n return q.isEmpty();\n }\n}\n```\n``` JavaScript []\nclass MyStack {\n constructor() {\n this.q = [];\n }\n\n push(x) {\n this.q.push(x);\n for (let i = 0; i < this.q.length - 1; i++) {\n this.q.push(this.q.shift());\n }\n }\n\n pop() {\n return this.q.shift();\n }\n\n top() {\n return this.q[0];\n }\n\n empty() {\n return this.q.length === 0;\n }\n}\n```\n``` PHP []\n\nclass MyStack {\n private $q = [];\n\n public function push($x) {\n array_push($this->q, $x);\n for ($i = 0; $i < count($this->q) - 1; $i++) {\n array_push($this->q, array_shift($this->q));\n }\n }\n\n public function pop() {\n return array_shift($this->q);\n }\n\n public function top() {\n return $this->q[0];\n }\n\n public function empty() {\n return empty($this->q);\n }\n}\n\n```\n``` C# []\npublic class MyStack {\n private Queue<int> q;\n\n public MyStack() {\n q = new Queue<int>();\n }\n\n public void Push(int x) {\n q.Enqueue(x);\n for (int i = 0; i < q.Count - 1; i++) {\n q.Enqueue(q.Dequeue());\n }\n }\n\n public int Pop() {\n return q.Dequeue();\n }\n\n public int Top() {\n return q.Peek();\n }\n\n public bool Empty() {\n return q.Count == 0;\n }\n}\n```\n\n# Code Two-Queue\n``` Python []\nclass MyStack:\n\n def __init__(self):\n self.q1 = deque()\n self.q2 = deque()\n\n def push(self, x: int) -> None:\n self.q1.append(x)\n\n def pop(self) -> int:\n while len(self.q1) > 1:\n self.q2.append(self.q1.popleft())\n \n popped_element = self.q1.popleft()\n \n # Swap q1 and q2\n self.q1, self.q2 = self.q2, self.q1\n \n return popped_element\n\n def top(self) -> int:\n while len(self.q1) > 1:\n self.q2.append(self.q1.popleft())\n \n top_element = self.q1[0]\n \n self.q2.append(self.q1.popleft())\n \n # Swap q1 and q2\n self.q1, self.q2 = self.q2, self.q1\n \n return top_element\n\n def empty(self) -> bool:\n return len(self.q1) == 0\n```\n\nThis exercise challenges you to think critically about basic data structures like stacks and queues. Implementing a stack using queues not only tests your understanding of these structures but also your ability to creatively use one to emulate the other. The multiple approaches available serve as a lesson in computational trade-offs, essential knowledge for technical interviews and real-world problem-solving. Dive in and explore these solutions, as each has its unique learning points. Happy coding! \uD83D\uDE80\uD83D\uDCA1\uD83C\uDF1F | 70 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
✅Easy Solution🔥Python3/C#/C++/Java🔥With🗺️Image🗺️ | implement-stack-using-queues | 1 | 1 | \n\n```Python3 []\nclass MyStack(object):\n\n def __init__(self):\n self.q = deque()\n\n def push(self, x):\n self.q.append(x)\n \n\n def pop(self):\n for i in range(len(self.q) - 1):\n self.push(self.q.popleft())\n return self.q.popleft()\n \n\n def top(self):\n return self.q[-1]\n \n\n def empty(self):\n return len(self.q) == 0\n \n```\n```python []\nclass MyStack(object):\n\n def __init__(self):\n self.q = deque()\n\n def push(self, x):\n self.q.append(x)\n \n\n def pop(self):\n for i in range(len(self.q) - 1):\n self.push(self.q.popleft())\n return self.q.popleft()\n \n\n def top(self):\n return self.q[-1]\n \n\n def empty(self):\n return len(self.q) == 0\n \n```\n```C# []\nclass MyStack\n{\n private Queue<int> q = new Queue<int>();\n\n public void Push(int x)\n {\n q.Enqueue(x);\n }\n\n public int Pop()\n {\n int count = q.Count;\n for (int i = 0; i < count - 1; i++)\n {\n Push(q.Dequeue());\n }\n return q.Dequeue();\n }\n\n public int Top()\n {\n return q.Last();\n }\n\n public bool Empty()\n {\n return q.Count == 0;\n }\n}\n```\n```C++ []\nclass MyStack {\nprivate:\n std::queue<int> q;\n\npublic:\n void push(int x) {\n q.push(x);\n }\n\n int pop() {\n int count = q.size();\n for (int i = 0; i < count - 1; i++) {\n push(q.front());\n q.pop();\n }\n int topValue = q.front();\n q.pop();\n return topValue;\n }\n\n int top() {\n return q.back();\n }\n\n bool empty() {\n return q.empty();\n }\n};\n```\n```Java []\nclass MyStack {\n private Queue<Integer> q = new LinkedList<>();\n\n public void push(int x) {\n q.add(x);\n }\n\n public int pop() {\n int size = q.size();\n for (int i = 0; i < size - 1; i++) {\n push(q.remove());\n }\n return q.remove();\n }\n\n public int top() {\n int size = q.size();\n for (int i = 0; i < size - 1; i++) {\n push(q.remove());\n }\n int topValue = q.remove();\n push(topValue);\n return topValue;\n }\n\n public boolean empty() {\n return q.isEmpty();\n }\n}\n```\n | 23 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | implement-stack-using-queues | 1 | 1 | # Intuition\nIn my opinion, solution with two queues is more complicated than solution with one queue.\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 250 videos as of August 28th, 2023.\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/wWnUeY1XkQg\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n---\n\n# Approach with one queue\nThis is based on Python. Other might be different a bit.\n\n**`__init__` Method:**\n\n- Initialize a new instance of the `MyStack` class.\n- Create an empty deque named `q` to store the stack elements.\n\n**`push` Method:**\n\n- Accept an integer `x` as input.\n- Append the input integer `x` to the right end of the deque `q`.\n- Loop for the number of times equal to the length of the deque minus one (length - 1).\n - In each iteration, remove an element from the left end of the deque (`popleft`) and immediately append it back to the right end.\n- This loop ensures that the last added element is at the front of the deque, simulating the behavior of a stack.\n\n**`pop` Method:**\n\n\n- Remove and return the element from the left end of the deque `q`.\n- This operation effectively mimics the behavior of popping an element off the stack.\n\n**`top` Method:**\n\n- Return the element at the left end of the deque `q` without removing it.\n- This operation provides the top element of the stack without altering the stack itself.\n\n**`empty` Method:**\n\n- Check if the length of the deque `q` is equal to 0.\n- If the length is 0, the stack is empty, so return `True`; otherwise, return `False`.\n\n\n# Complexity\n- Time complexity:\npop, top and empty are O(1), push is O(n)\n\n- Space complexity: O(n)\n\n```python []\nclass MyStack:\n\n def __init__(self):\n self.q = deque()\n\n def push(self, x: int) -> None:\n self.q.append(x)\n for _ in range(len(self.q) - 1):\n self.q.append(self.q.popleft())\n\n def pop(self) -> int:\n return self.q.popleft()\n \n def top(self) -> int:\n return self.q[0]\n\n def empty(self) -> bool:\n return len(self.q) == 0\n```\n```javascript []\nclass MyStack {\n constructor() {\n this.q = [];\n }\n\n push(x) {\n this.q.push(x);\n for (let i = 0; i < this.q.length - 1; i++) {\n this.q.push(this.q.shift());\n }\n }\n\n pop() {\n return this.q.shift();\n }\n\n top() {\n return this.q[0];\n }\n\n empty() {\n return this.q.length === 0;\n }\n}\n```\n```java []\nclass MyStack {\n\n private Queue<Integer> q;\n\n public MyStack() {\n q = new LinkedList<>();\n }\n\n public void push(int x) {\n q.add(x);\n for (int i = 0; i < q.size() - 1; i++) {\n q.add(q.poll());\n }\n }\n\n public int pop() {\n return q.poll();\n }\n\n public int top() {\n return q.peek();\n }\n\n public boolean empty() {\n return q.isEmpty();\n }\n}\n```\n```C++ []\nclass MyStack {\nprivate:\n std::queue<int> q;\n\npublic:\n MyStack() {}\n\n void push(int x) {\n q.push(x);\n for (int i = 0; i < q.size() - 1; i++) {\n q.push(q.front());\n q.pop();\n }\n }\n\n int pop() {\n int top = q.front();\n q.pop();\n return top;\n }\n\n int top() {\n return q.front();\n }\n\n bool empty() {\n return q.empty();\n }\n};\n```\n\n# Approach with two queues\n\nCertainly! Here\'s the step-by-step algorithmic explanation for each method in the given Python code:\n\n**`__init__` Method:**\n\n- Initialize a new instance of the `MyStack` class.\n- Create two empty deques: `q1` and `q2` to store the stack elements and assist in simulating stack operations.\n\n**`push` Method:**\n\n- Accept an integer `x` as input.\n- Append the input integer `x` to the right end of the deque `q1`.\n\n**`pop` Method:**\n\n- While the length of `q1` is greater than 1:\n - Remove an element from the left end of the deque `q1` (popleft operation).\n - Append the removed element to the right end of the deque `q2`.\n- Remove and return the leftmost (front) element of the deque `q1`, which effectively simulates popping an element from the stack.\n- Swap the contents of `q1` and `q2`, making `q2` ready for future operations.\n\n**`top` Method:**\n\n- While the length of `q1` is greater than 1:\n - Remove an element from the left end of the deque `q1` (popleft operation).\n - Append the removed element to the right end of the deque `q2`.\n- Retrieve and store the leftmost (front) element of the deque `q1`, which corresponds to the top element of the stack.\n- Remove the top element from `q1` and immediately append it to the right end of `q2`.\n- Swap the contents of `q1` and `q2`, restoring the original state of the deques.\n\n**`empty` Method:**\n\n- Check if the length of the deque `q1` is equal to 0.\n- If the length is 0, the stack is empty, so return `True`; otherwise, return `False`.\n\n# Complexity\n- Time complexity:\npush and empty are O(1), pop and top are O(n)\n\n- Space complexity: O(n)\n\n```python []\nclass MyStack:\n\n def __init__(self):\n self.q1 = deque()\n self.q2 = deque()\n\n def push(self, x: int) -> None:\n self.q1.append(x)\n\n def pop(self) -> int:\n while len(self.q1) > 1:\n self.q2.append(self.q1.popleft())\n\n popped_val = self.q1.popleft()\n self.q1, self.q2 = self.q2, self.q1\n\n return popped_val\n \n def top(self) -> int:\n while len(self.q1) > 1:\n self.q2.append(self.q1.popleft())\n\n top_val = self.q1[0]\n self.q2.append(self.q1.popleft())\n self.q1, self.q2 = self.q2, self.q1\n\n return top_val\n\n def empty(self) -> bool:\n return len(self.q1) == 0\n```\n```javascript []\nclass MyStack {\n constructor() {\n this.q1 = [];\n this.q2 = [];\n }\n\n push(x) {\n this.q1.push(x);\n }\n\n pop() {\n while (this.q1.length > 1) {\n this.q2.push(this.q1.shift());\n }\n\n const poppedVal = this.q1.shift();\n [this.q1, this.q2] = [this.q2, this.q1];\n\n return poppedVal;\n }\n\n top() {\n while (this.q1.length > 1) {\n this.q2.push(this.q1.shift());\n }\n\n const topVal = this.q1[0];\n this.q2.push(this.q1.shift());\n [this.q1, this.q2] = [this.q2, this.q1];\n\n return topVal;\n }\n\n empty() {\n return this.q1.length === 0;\n }\n}\n```\n```java []\nclass MyStack {\n\n private Queue<Integer> q1;\n private Queue<Integer> q2;\n\n public MyStack() {\n q1 = new ArrayDeque<>();\n q2 = new ArrayDeque<>();\n }\n\n public void push(int x) {\n q1.add(x);\n }\n\n public int pop() {\n while (q1.size() > 1) {\n q2.add(q1.poll());\n }\n\n int poppedVal = q1.poll();\n Queue<Integer> temp = q1;\n q1 = q2;\n q2 = temp;\n\n return poppedVal;\n }\n\n public int top() {\n while (q1.size() > 1) {\n q2.add(q1.poll());\n }\n\n int topVal = q1.peek();\n q2.add(q1.poll());\n Queue<Integer> temp = q1;\n q1 = q2;\n q2 = temp;\n\n return topVal;\n }\n\n public boolean empty() {\n return q1.isEmpty();\n }\n}\n\n```\n```C++ []\nclass MyStack {\nprivate:\n std::queue<int> q1;\n std::queue<int> q2;\n\npublic:\n MyStack() {}\n\n void push(int x) {\n q1.push(x);\n }\n\n int pop() {\n while (q1.size() > 1) {\n q2.push(q1.front());\n q1.pop();\n }\n\n int poppedVal = q1.front();\n q1.pop();\n std::swap(q1, q2);\n\n return poppedVal;\n }\n\n int top() {\n while (q1.size() > 1) {\n q2.push(q1.front());\n q1.pop();\n }\n\n int topVal = q1.front();\n q2.push(q1.front());\n q1.pop();\n std::swap(q1, q2);\n\n return topVal;\n }\n\n bool empty() {\n return q1.empty();\n }\n};\n```\n\n | 24 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
🟢 Implementing a Stack Using a Single Queue || Full Explanation || Mr. Robot | implement-stack-using-queues | 1 | 1 | ---\n\n## Implementing a Stack Using a Single Queue in C++\n\n**Introduction:**\nStacks are fundamental data structures used in programming for managing data in a last-in, first-out (LIFO) manner. In this blog post, we\'ll delve into an interesting challenge: implementing a stack using just a single queue. We\'ll explore an ingenious approach that leverages the power of rotations to achieve this feat.\n\n**Problem Statement:**\nThe challenge is to create a stack data structure that supports the basic stack operations (`push`, `pop`, `top`, and `empty`) using only a single queue. This might sound counterintuitive, but with the right strategy, it\'s definitely possible.\n\n**Approach Overview:**\nOur approach involves simulating the stack behavior by manipulating the queue through rotations. We\'ll maintain the top element of the stack in a separate variable and use rotations to ensure that the top element is always at the front of the queue.\n\n**Implementation Walkthrough:**\nLet\'s dive into the implementation details of each method in the `MyStack` class:\n\n1. **Constructor (`MyStack() {}`):**\n - Initialize an empty queue (`q`) to store the stack elements.\n\n2. **`push(int x)`:**\n - Enqueue element `x` into the queue.\n - Update the `topp` variable to hold the value of the newly pushed element.\n - Perform a rotation of the queue by dequeuing elements from the front and enqueuing them back. This ensures that the newly pushed element becomes the front element.\n\n3. **`pop()`:**\n - Dequeue the front element of the queue and store it in the `remo` variable.\n - If the queue is not empty, update the `topp` variable with the new front element.\n - Return the removed element.\n\n4. **`top()`:**\n - Return the value of the `topp` variable, which holds the top element of the stack.\n\n5. **`empty()`:**\n - Check if the queue is empty using the `empty()` method of the queue.\n\n**Algorithm Analysis:**\nThe time complexity of the `push`, `pop`, `top`, and `empty` operations is O(n) in the worst case, where n is the number of elements in the queue. This approach is slightly less efficient than traditional stack implementations but offers a unique perspective on data manipulation.\n\n**Advantages and Limitations:**\n- Advantages: This approach utilizes a single queue and is simple to understand and implement.\n- Limitations: It might not be the most efficient solution for large queues due to the rotation process, which takes linear time.\n\n**Comparisons with Other Approaches:**\nComparing this approach with the standard stack and two-queue approaches, our implementation sacrifices some efficiency for simplicity and an interesting use of rotations.\n\n**Use Cases and Examples:**\nThis implementation can be useful in scenarios where you want to explore unique stack implementations. Let\'s look at some examples:\n\n```cpp\nMyStack stack;\nstack.push(5);\nstack.push(10);\ncout << stack.top() << endl; // Output: 10\nstack.pop();\ncout << stack.top() << endl; // Output: 5\ncout << stack.empty() << endl; // Output: 0 (false)\n```\n\n**Conclusion:**\nImplementing a stack using a single queue is a fascinating exercise that demonstrates the power of creative problem-solving. While this approach might not be the most efficient, it showcases how rotations can be used to achieve stack behavior using a unique twist on a classic data structure.\n\nExperiment with the code, run your own test cases, and consider how this approach aligns with different programming challenges. This implementation serves as a valuable addition to your arsenal of programming techniques.\n\n---\n\n# Code \n```C++ []\n#include <queue>\n\nclass MyStack {\npublic:\n queue<int> q;\n int topp = -1;\n\n MyStack() {}\n\n void push(int x) {\n q.push(x);\n topp = x;\n int size = q.size();\n while (size > 1) {\n int front = q.front();\n q.pop();\n q.push(front);\n size--;\n }\n }\n\n int pop() {\n int remo = q.front();\n q.pop();\n if (!q.empty()) {\n topp = q.front();\n }\n return remo;\n }\n\n int top() {\n return topp;\n }\n\n bool empty() {\n return q.empty();\n }\n};\n```\n```python []\nfrom queue import Queue\n\nclass MyStack:\n def __init__(self):\n self.q = Queue()\n self.topp = -1\n\n def push(self, x):\n self.q.put(x)\n self.topp = x\n size = self.q.qsize()\n while size > 1:\n front = self.q.get()\n self.q.put(front)\n size -= 1\n\n def pop(self):\n remo = self.q.get()\n if not self.q.empty():\n self.topp = self.q.queue[0]\n return remo\n\n def top(self):\n return self.topp\n\n def empty(self):\n return self.q.empty()\n\n# Example usage\n#stack = MyStack()\n#stack.push(5)\n#stack.push(10)\n#print(stack.top()) # Output: 10\n#stack.pop()\n#print(stack.top()) # Output: 5\n#print(stack.empty()) # Output: False\n\n```\n```java []\nimport java.util.LinkedList;\nimport java.util.Queue;\n\nclass MyStack {\n private Queue<Integer> q = new LinkedList<>();\n private int topp = -1;\n\n public void push(int x) {\n q.offer(x);\n topp = x;\n int size = q.size();\n while (size > 1) {\n int front = q.poll();\n q.offer(front);\n size--;\n }\n }\n\n public int pop() {\n int remo = q.poll();\n if (!q.isEmpty()) {\n topp = q.peek();\n }\n return remo;\n }\n\n public int top() {\n return topp;\n }\n\n public boolean empty() {\n return q.isEmpty();\n }\n}\n\n// Example usage\n//MyStack stack = new MyStack();\n//stack.push(5);\n//stack.push(10);\n//System.out.println(stack.top()); // Output: 10\n//stack.pop();\n//System.out.println(stack.top()); // Output: 5\n//System.out.println(stack.empty()); // Output: false\n\n```\n``` ruby []\nclass MyStack\n def initialize\n @q = []\n @topp = -1\n end\n\n def push(x)\n @q.push(x)\n @topp = x\n (@q.length - 1).times { @q.push(@q.shift) }\n end\n\n def pop\n remo = @q.shift\n @topp = @q[0] || -1\n remo\n end\n\n def top\n @topp\n end\n\n def empty\n @q.empty?\n end\nend\n\n# Example usage\n# stack = MyStack.new\n# stack.push(5)\n# stack.push(10)\n# puts stack.top # Output: 10\n# stack.pop\n# puts stack.top # Output: 5\n# puts stack.empty # Output: false\n```\n``` Javascript []\nclass MyStack {\n constructor() {\n this.q = [];\n this.topp = -1;\n }\n\n push(x) {\n this.q.push(x);\n this.topp = x;\n for (let i = 0; i < this.q.length - 1; i++) {\n this.q.push(this.q.shift());\n }\n }\n\n pop() {\n const remo = this.q.shift();\n if (this.q.length > 0) {\n this.topp = this.q[0];\n }\n return remo;\n }\n\n top() {\n return this.topp;\n }\n\n empty() {\n return this.q.length === 0;\n }\n}\n\n// Example usage\n// const stack = new MyStack();\n// stack.push(5);\n// stack.push(10);\n// console.log(stack.top()); // Output: 10\n// stack.pop();\n// console.log(stack.top()); // Output: 5\n// console.log(stack.empty()); // Output: false\n\n```\n```C# []\nusing System;\nusing System.Collections.Generic;\n\nclass MyStack\n{\n private Queue<int> q = new Queue<int>();\n private int topp = -1;\n\n public void Push(int x)\n {\n q.Enqueue(x);\n topp = x;\n int size = q.Count;\n while (size > 1)\n {\n int front = q.Dequeue();\n q.Enqueue(front);\n size--;\n }\n }\n\n public int Pop()\n {\n int remo = q.Dequeue();\n if (q.Count > 0)\n {\n topp = q.Peek();\n }\n return remo;\n }\n\n public int Top()\n {\n return topp;\n }\n\n public bool Empty()\n {\n return q.Count == 0;\n }\n}\n\n// Example usage\n// MyStack stack = new MyStack();\n// stack.Push(5);\n// stack.Push(10);\n// Console.WriteLine(stack.Top()); // Output: 10\n// stack.Pop();\n// Console.WriteLine(stack.Top()); // Output: 5\n// Console.WriteLine(stack.Empty()); // Output: False\n\n```\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF* | 2 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
Python || One Queue || Two Approaches || Easy | implement-stack-using-queues | 0 | 1 | ```\nfrom queue import Queue\n\nclass MyStack: # Using One Queue\n\n def __init__(self):\n self.q=Queue()\n\n def push(self, x: int) -> None:\n self.q.put(x)\n for i in range(self.q.qsize()-1):\n self.q.put(self.q.get())\n\n def pop(self) -> int:\n return self.q.get()\n\n def top(self) -> int:\n return self.q.queue[0]\n\n def empty(self) -> bool:\n return self.q.empty()\n```\n\t\t\n```\nclass MyStack: # Using Two Queues\n\n def __init__(self):\n self.q1=Queue()\n self.q2=Queue()\n\n def push(self, x: int) -> None:\n self.q2.put(x)\n while not self.q1.empty():\n self.q2.put(self.q1.get())\n self.q1,self.q2=self.q2,self.q1\n\n def pop(self) -> int:\n return self.q1.get()\n\n def top(self) -> int:\n return self.q1.queue[0]\n\n def empty(self) -> bool:\n return self.q1.empty()\n```\n**An upvote will be encouraging** | 2 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
Python short and clean. Functional programming. | implement-stack-using-queues | 0 | 1 | # Approach\nIn every `push(x)` create a new queue with `x` and nest the existing queue as second element.\n\nIn `pop()`, unpack the existing queue and return the top value.\n\n# Complexity\n- Time complexity: $$O(1)$$ for all methods.\n\n- Space complexity: $$O(1)$$ for all methods.\n\n# Code\n```python\nclass MyStack:\n\n def __init__(self):\n self.queue = deque()\n\n def push(self, x: int) -> None:\n self.queue = deque((x, self.queue))\n\n def pop(self) -> int:\n value, self.queue = self.queue\n return value\n\n def top(self) -> int:\n return self.queue[0]\n\n def empty(self) -> bool:\n return not self.queue\n\n\n``` | 1 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
Simple solution | implement-stack-using-queues | 0 | 1 | \n\n# Complexity\n- Time complexity: $$\u041E(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$\u041E(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyStack:\n\n def __init__(self):\n self.q = deque()\n\n def push(self, x: int) -> None:\n self.q.append(x)\n \n\n def pop(self) -> int:\n return self.q.pop()\n\n def top(self) -> int:\n a = self.q.pop()\n self.q.append(a)\n return a\n\n def empty(self) -> bool:\n return len(self.q) == 0\n\n``` | 1 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
Simple Python solution Beats 80% run time | implement-stack-using-queues | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MyStack:\n\n def __init__(self):\n self.container=[]\n \n\n def push(self, x: int) -> None:\n self.container.append(x)\n def pop(self) -> int:\n return self.container.pop()\n\n def top(self) -> int:\n return self.container[-1]\n\n def empty(self) -> bool:\n return len(self.container)==0\n\n\n# Your MyStack object will be instantiated and called as such:\n# obj = MyStack()\n# obj.push(x)\n# param_2 = obj.pop()\n# param_3 = obj.top()\n# param_4 = obj.empty()\n``` | 3 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
225: Solution with step by step explanation | implement-stack-using-queues | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution also uses a deque from the collections module, but instead of using two queues, it only uses one queue. The trick is to use the push operation to move the newly added element to the front of the queue, effectively making it the top element of the stack.\n\nHere\'s a step-by-step explanation of the code:\n\n1. The constructor initializes an empty deque.\n\n2. The push operation adds the element to the end of the deque and then moves it to the front by dequeuing and enqueuing all the other elements in the deque. This makes the newly added element the first element in the deque, which is the top of the stack.\n\n3. The pop operation simply dequeues the first element in the deque, which is the top of the stack.\n\n4. The top operation returns the first element in the deque, which is the top of the stack.\n\n5. The empty operation checks if the deque is empty and returns True or False accordingly.\n\nThis solution has a time complexity of O(n) for the push operation and O(1) for the pop, top, and empty operations, where n is the size of the deque. The space complexity is O(n) to store the deque.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n\nclass MyStack:\n\n def __init__(self):\n self.q = deque()\n\n def push(self, x: int) -> None:\n self.q.append(x)\n # Move the newly added element to the front\n for _ in range(len(self.q) - 1):\n self.q.append(self.q.popleft())\n\n def pop(self) -> int:\n return self.q.popleft()\n\n def top(self) -> int:\n return self.q[0]\n\n def empty(self) -> bool:\n return len(self.q) == 0\n\n``` | 10 | Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (`push`, `top`, `pop`, and `empty`).
Implement the `MyStack` class:
* `void push(int x)` Pushes element x to the top of the stack.
* `int pop()` Removes the element on the top of the stack and returns it.
* `int top()` Returns the element on the top of the stack.
* `boolean empty()` Returns `true` if the stack is empty, `false` otherwise.
**Notes:**
* You must use **only** standard operations of a queue, which means that only `push to back`, `peek/pop from front`, `size` and `is empty` operations are valid.
* Depending on your language, the queue may not be supported natively. You may simulate a queue using a list or deque (double-ended queue) as long as you use only a queue's standard operations.
**Example 1:**
**Input**
\[ "MyStack ", "push ", "push ", "top ", "pop ", "empty "\]
\[\[\], \[1\], \[2\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, 2, 2, false\]
**Explanation**
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False
**Constraints:**
* `1 <= x <= 9`
* At most `100` calls will be made to `push`, `pop`, `top`, and `empty`.
* All the calls to `pop` and `top` are valid.
**Follow-up:** Can you implement the stack using only one queue? | null |
🔥0 ms🔥|🚀Simplest Solution🚀||🔥Full Explanation||🔥C++🔥|| Python3 | invert-binary-tree | 0 | 1 | # Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful\n```\n# Intuition\nIn this question we have to **Invert the binary tree**.\nSo we use **Post Order Treversal** in which first we go in **Left subtree** and then in **Right subtree** then we return back to **Parent node**.\nWhen we come back to the parent node we **swap** it\'s **Left subtree** and **Right subtree**.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n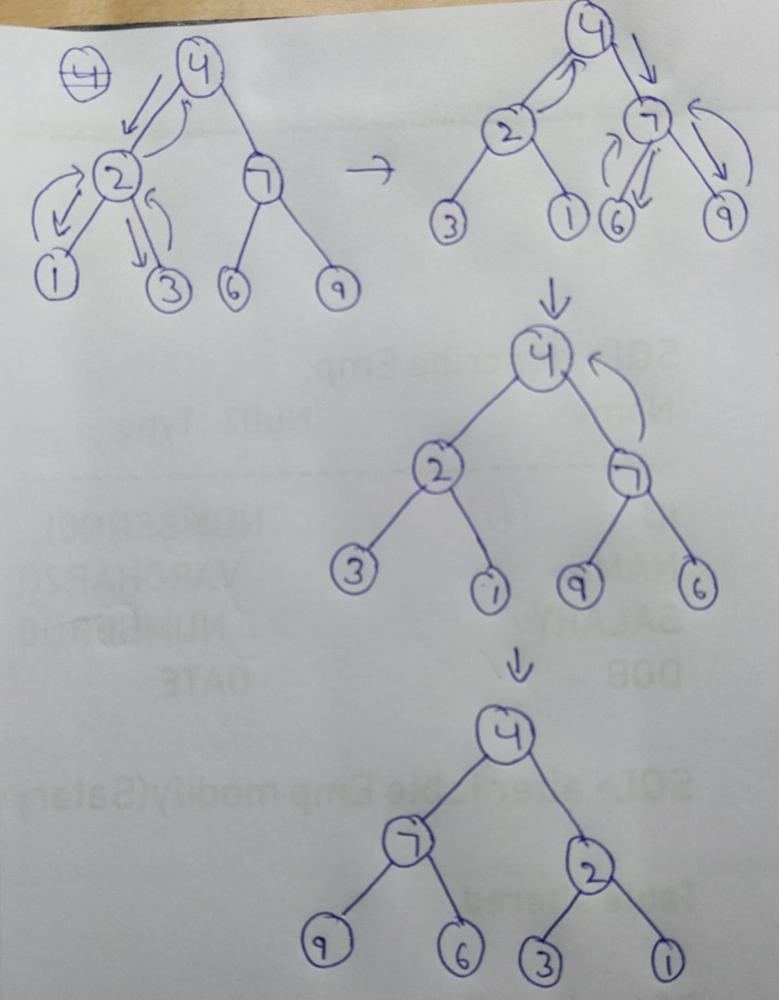\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N) Recursive stack space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n TreeNode* invertTree(TreeNode* root) {\n // Base Case\n if(root==NULL)\n return NULL;\n invertTree(root->left); //Call the left substree\n invertTree(root->right); //Call the right substree\n // Swap the nodes\n TreeNode* temp = root->left;\n root->left = root->right;\n root->right = temp;\n return root; // Return the root\n }\n};\n```\n```python []\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n if not root: #Base Case\n return root\n self.invertTree(root.left) #Call the left substree\n self.invertTree(root.right) #Call the right substree\n # Swap the nodes\n root.left, root.right = root.right, root.left\n return root # Return the root\n```\n\n\n```\n Give a \uD83D\uDC4D. It motivates me alot\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/) | 331 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Easy || 100% || Fully Explained || Java, C++, Python, JS, C, Python3 || Recursive & Iterative | invert-binary-tree | 1 | 1 | # **Java Solution (Recursive & Iterative Approach):**\n```\n/** Recursive Approach:**/\n// Runtime: 0 ms, faster than 100.00% of Java online submissions for Invert Binary Tree.\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\n public TreeNode invertTree(TreeNode root) {\n // Base case: if the tree is empty...\n if(root == null){\n return root;\n }\n // Call the function recursively for the left subtree...\n invertTree(root.left);\n // Call the function recursively for the right subtree...\n invertTree(root.right);\n // Swapping process...\n TreeNode curr = root.left;\n root.left = root.right;\n root.right = curr;\n return root; // Return the root...\n }\n}\n--------------------------------------------------------------------------------------------------------------------------------------------------------\n/**Iterative Approach:**/\n// Runtime: 1 ms, faster than 90.96% of Java online submissions for Invert Binary Tree.\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\n public TreeNode invertTree(TreeNode root) {\n LinkedList<TreeNode> q = new LinkedList<TreeNode>();\n // Base case: if the tree is empty...\n if(root != null){\n // Push the root node...\n q.add(root);\n }\n // Loop till queue is empty...\n while(!q.isEmpty()){\n // Dequeue front node...\n TreeNode temp = q.poll();\n // Enqueue left child of the popped node...\n if(temp.left != null)\n q.add(temp.left);\n // Enqueue right child of the popped node\n if(temp.right != null)\n q.add(temp.right);\n // Swapping process...\n TreeNode curr = temp.left;\n temp.left = temp.right;\n temp.right = curr;\n }\n return root; // Return the root...\n }\n}\n```\n\n# **C++ Solution (Recursive Approach):**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\npublic:\n TreeNode* invertTree(TreeNode* root) {\n // Base case...\n if(root == NULL){\n return root;\n }\n // Call the function recursively for the left subtree...\n invertTree(root->left);\n // Call the function recursively for the right subtree...\n invertTree(root->right);\n // swapping process...\n TreeNode* curr = root->left;\n root->left = root->right;\n root->right = curr;\n return root; // Return the root...\n }\n};\n```\n\n# **Python / Python3 Solution (Recursive Approach):**\n```\nclass Solution(object):\n def invertTree(self, root):\n # Base case...\n if root == None:\n return root\n # swapping process...\n root.left, root.right = root.right, root.left\n # Call the function recursively for the left subtree...\n self.invertTree(root.left)\n # Call the function recursively for the right subtree...\n self.invertTree(root.right)\n return root # Return the root...\n```\n \n# **JavaScript Solution (Recursive Approach):**\n```\n// Runtime: 64 ms, faster than 92.88% of JavaScript online submissions for Invert Binary Tree.\nvar invertTree = function(root) {\n // Base case...\n if(root == null){\n return root\n }\n // Call the function recursively for the left subtree...\n invertTree(root.left)\n // Call the function recursively for the right subtree...\n invertTree(root.right)\n // swapping process...\n const curr = root.left\n root.left = root.right\n root.right = curr\n return root // Return the root... \n};\n```\n\n# **C Language (Recursive Approach):**\n```\nstruct TreeNode* invertTree(struct TreeNode* root){\n // Base case...\n if(root == NULL){\n return root;\n }\n // Call the function recursively for the left subtree...\n invertTree(root->left);\n // Call the function recursively for the right subtree...\n invertTree(root->right);\n // swapping process...\n struct TreeNode* curr = root->left;\n root->left = root->right;\n root->right = curr;\n return root; // Return the root...\n}\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 185 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Simplest Python Recursive! O(N) Time | invert-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe main intuition is to swap the left child of the root with the right child. This process of swapping should occur in each sub tree recursively.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis is a recurse approach. In the base case we check if the root is null or not, if not null then calling the recursive function to invert the left child and right child after that we are swapping the right child with the left child \n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n if not root: return root\n self.invertTree(root.left)\n self.invertTree(root.right)\n temp = root.left \n root.left = root.right\n root.right = temp\n return root\n \n``` | 1 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
if i made it then you also can do it . just simple solution | invert-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n if root==None:\n return \n t=root.left\n root.left=root.right\n root.right=t\n self.invertTree(root.left)\n self.invertTree(root.right)\n return root\n``` | 0 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
✅Easy Solution🔥Python/C/C#/C++/Java🔥WTF⁉️1 Line Code⁉️ | invert-binary-tree | 1 | 1 | \n\n\n```python3 []\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n return root and TreeNode(root.val, self.invertTree(root.right), self.invertTree(root.left))\n```\n```Python []\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n return root and TreeNode(root.val, self.invertTree(root.right), self.invertTree(root.left))\n```\n```C# []\npublic class Solution {\n public TreeNode InvertTree(TreeNode root) {\n if (root == null) {\n return null;\n }\n \n TreeNode temp = root.left;\n root.left = InvertTree(root.right);\n root.right = InvertTree(temp);\n \n return root;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n TreeNode* invertTree(TreeNode* root) {\n if (root == nullptr) {\n return nullptr;\n }\n \n std::swap(root->left, root->right);\n invertTree(root->left);\n invertTree(root->right);\n \n return root;\n }\n};\n```\n```Java []\nclass Solution {\n public TreeNode invertTree(TreeNode root) {\n if (root == null) {\n return null;\n }\n \n TreeNode temp = root.left;\n root.left = invertTree(root.right);\n root.right = invertTree(temp);\n \n return root;\n }\n}\n`\n``\n | 21 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Binbin's very fast solution | invert-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n stack = [root]\n while stack:\n node = stack.pop()\n if node:\n node.left,node.right = node.right, node.left\n stack.append(node.left)\n stack.append(node.right)\n return root\n \n``` | 1 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
✅Python3 easy solution 30ms 🔥🔥🔥 | invert-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Travelling tree with changing left right node.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- If current node is not None, then travel further.\n- while travelling change left node with right node.\n- now travel left and right node doing same thing.\n- that\'s it we inverted tree.\n- return treeRoot\n\n# Complexity\n- Time complexity: O(tree height)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n def firstPass(curr = root):\n if curr != None:\n curr.left, curr.right = curr.right, curr.left\n firstPass(curr.left)\n firstPass(curr.right)\n return\n firstPass()\n return root\n```\n# Please Like and Comment below.\n# (\u0254\u25D4\u203F\u25D4)\u0254 \u2665 | 4 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
Solution | invert-binary-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* invertTree(TreeNode* root) {\n if(root==NULL){\n return NULL;\n }\n invertTree(root->left);\n invertTree(root->right);\n TreeNode* temp=root->right;\n root->right=root->left;\n root->left=temp;\n return root;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n if root:\n root.left, root.right = root.right, root.left\n self.invertTree(root.left)\n self.invertTree(root.right)\n return root\n```\n\n```Java []\nclass Solution {\n public TreeNode invertTree(TreeNode root) {\n if (root == null)\n return null;\n\n TreeNode left = root.left;\n TreeNode right = root.right;\n root.left = invertTree(right);\n root.right = invertTree(left);\n return root;\n }\n}\n```\n | 19 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
🔥🔥|| 1 Line Code || 🔥🔥 | invert-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n if root is None:\n return None\n\n # Swap the left and right subtrees recursively using self.invertTree\n root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)\n\n return root\n\n``` | 3 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
One-Liner.py 🐍 | invert-binary-tree | 0 | 1 | # Code\n```\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n return TreeNode(root.val, self.invertTree(root.right), self.invertTree(root.left)) if root else None\n```\n<h1>Upvote if you like this...</h1>\n<br>\n\n\n | 17 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
[Python] - DFS (Recursion) - Clean & Simple - 21ms | invert-binary-tree | 0 | 1 | \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n For Recursive call Stack Space used at max can be $$O(n)$$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nUsing Another function for Recursive Calls\n```Python [1]\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n def fun(root):\n if root:\n root.left, root.right = root.right, root.left\n fun(root.left)\n fun(root.right)\n \n fun(root)\n return root \n```\nUsing Same Function for Recursive Calls\n```Python [2]\nclass Solution:\n def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:\n if root:\n root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)\n return root \n``` | 3 | Given the `root` of a binary tree, invert the tree, and return _its root_.
**Example 1:**
**Input:** root = \[4,2,7,1,3,6,9\]
**Output:** \[4,7,2,9,6,3,1\]
**Example 2:**
**Input:** root = \[2,1,3\]
**Output:** \[2,3,1\]
**Example 3:**
**Input:** root = \[\]
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100` | null |
py clean & short sol. using stack | basic-calculator-ii | 0 | 1 | \n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n n = len(s)\n if s == \'0\':\n return 0\n num, sign, stack = 0, \'+\', []\n for i, ch in enumerate(s):\n if ch.isdigit():\n num = num * 10 + ord(ch) - ord(\'0\')\n if (not ch.isdigit() and ch != \' \' ) or i == n-1:\n if sign == \'+\':\n stack.append(num)\n elif sign == \'-\':\n stack.append(-num)\n elif sign == \'*\':\n stack.append(stack.pop()*num)\n else:\n tmp = stack.pop()\n if tmp//num < 0 and tmp%num != 0:\n stack.append(tmp//num+1)\n else:\n stack.append(tmp//num)\n sign = ch\n num = 0\n return sum(stack)\n``` | 4 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Single Pass | Stack Postfix conversion solution | basic-calculator-ii | 0 | 1 | # Complexity\n- Time complexity:\n O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n s=s.replace(" ","")\n N=len(s)\n precedence={\'/\':2,\'*\':2,\'+\':1,\'-\':1}#higher val higher precedence\n operators_stack=[]\n operands_stack=[]\n i=0\n while i<N:\n temp=s[i]\n j=i+1\n while j<N and s[j] not in precedence:\n temp+=s[j]\n j+=1\n \n operand=int(temp)\n operands_stack.append(operand)\n if j==N:\n break\n operator=s[j]\n i=j+1\n # empty stack \n if (not operators_stack) :\n operators_stack.append(operator)\n else:\n top=operators_stack[-1]\n # current precedence > top precedence\n if precedence[operator]>precedence[top]:\n operators_stack.append(operator)\n # current precedence <= top precedence\n else:\n while operators_stack and precedence[operators_stack[-1]]>=precedence[operator]:\n top=operators_stack.pop()\n b=int(operands_stack.pop())\n a=int(operands_stack.pop())\n result=0\n if top == \'+\':\n result = a+b\n elif top == \'-\':\n result =a-b\n elif top == \'*\':\n result =a*b\n elif top == \'/\':\n result =a//b \n operands_stack.append(result)\n operators_stack.append(operator)\n while operators_stack :\n top=operators_stack.pop()\n b=int(operands_stack.pop())\n a=int(operands_stack.pop())\n result=0\n if top == \'+\':\n result = a+b\n elif top == \'-\':\n result =a-b\n elif top == \'*\':\n result =a*b\n elif top == \'/\':\n result =a//b \n operands_stack.append(result)\n return int(operands_stack[0])\n```\nAll suggestions are welcome.\nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\nHappy Learning, Cheers Guys \uD83D\uDE0A\n | 1 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
python stack | basic-calculator-ii | 0 | 1 | \n\n```\ndef calculate(self, s: str) -> int:\n num = 0\n res = 0\n pre_op = \'+\'\n s+=\'+\'\n stack = []\n for c in s:\n if c.isdigit():\n num = num*10 + int(c)\n elif c == \' \':\n pass\n else:\n if pre_op == \'+\':\n stack.append(num)\n elif pre_op == \'-\':\n stack.append(-num)\n elif pre_op == \'*\':\n operant = stack.pop()\n stack.append((operant*num))\n elif pre_op == \'/\':\n operant = stack.pop()\n stack.append(math.trunc(operant/num))\n num = 0\n pre_op = c\n return sum(stack)\n```\n | 61 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
227: Time 91.15%, Solution with step by step explanation | basic-calculator-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses a stack to evaluate the expression. The stack variable stores the intermediate results and the cur variable stores the current operand. The op variable stores the current operator and is initialized with +.\n\nThe input string is traversed character by character in a for loop. If the current character is a space, the loop continues to the next iteration. If the current character is a digit, the cur variable is updated by multiplying it by 10 and adding the integer value of the current digit.\n\nIf the current character is an operator or the end of the string is reached, the current operand is added to the stack according to the current operator. If the current operator is -, the negative of the current operand is added to the stack. If the current operator is *, the top of the stack is popped and multiplied by the current operand, and the result is added to the stack. If the current operator is /, the top of the stack is popped, divided by the current operand (integer division), and the result is added to the stack. Finally, the cur variable is reset to 0 and the op variable is updated to the current character.\n\nAfter traversing the string, the sum of the stack is returned as the final result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n stack, cur, op = [], 0, \'+\'\n for c in s + \'+\':\n if c == " ":\n continue\n elif c.isdigit():\n cur = (cur * 10) + int(c)\n else:\n if op == \'-\':\n stack.append(-cur)\n elif op == \'+\':\n stack.append(cur)\n elif op == \'*\':\n stack.append(stack.pop() * cur)\n elif op == \'/\':\n stack.append(int(stack.pop() / cur))\n cur, op = 0, c\n return sum(stack)\n``` | 13 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Very detailed explanation, no stack needed! | basic-calculator-ii | 0 | 1 | # Intuition\nYou can think of an expression as multiple sections divided by + or -. For example, \n```\n1 + 2 * 3 * 4 + 2 / 2\n```\nhas 3 sections, each section is numbers connected with * or /. \n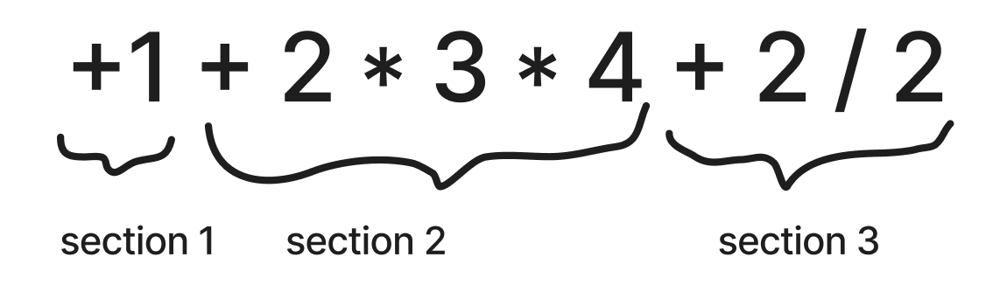\nWe will need four variables\nfinal_result: stores the result of the expresion that has processed so far\nsection_result: stores the result of the current section under processing\ncurr_num: stores the current number\nprev_op: stores the previous operator\nThe most important decision to make is we check prev_op,\n- if prev_op in \'+-\', you can add section_result to final_result since you are done with the current section\n- if prev_op in \'*/\', you need to apply prev_op on section_result and curr_num and assign the result back to section_result\nHere is an illustration of what happens when prev_op is * and + respectively. \n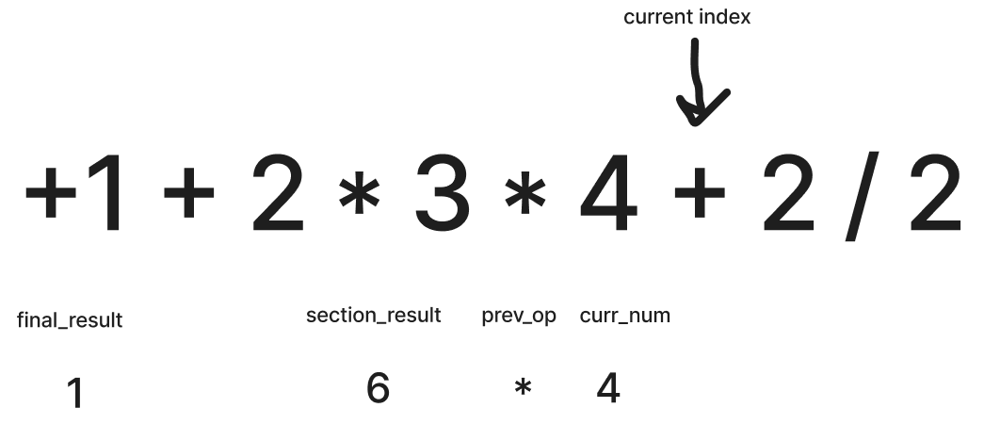\nAt this point, you know that 6 and 4 belong to the same section, so you apply prev_op on them and assign the result back to section_result.\n\nAt this point, 24 is in its own section, so you add 24 to final_result and assign curr_num to section_result.\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n operator_to_evaluate, curr_num, accu, result = \'+\', 0, 0, 0\n for c in s+\'#\':\n if c == \' \':\n continue\n elif c.isdigit():\n curr_num = curr_num*10 + int(c)\n else:\n if operator_to_evaluate == \'+\':\n result += accu\n accu = curr_num\n elif operator_to_evaluate == \'-\':\n result += accu\n accu = -curr_num\n elif operator_to_evaluate == \'*\':\n accu = accu * curr_num\n elif operator_to_evaluate == \'/\':\n accu = int(accu / curr_num)\n\n operator_to_evaluate = c\n curr_num = 0\n\n if c == \'#\':\n result += accu\n return result\n\n \n\n\n\n\n \n``` | 0 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
python - without any stack and beat 99% | basic-calculator-ii | 0 | 1 | ```\nclass Solution:\n def calculate(self, s: str) -> int:\n curr_res = 0\n res = 0\n num = 0\n op = "+" # keep the last operator we have seen\n \n\t\t# append a "+" sign at the end because we can catch the very last item\n for ch in s + "+":\n if ch.isdigit():\n num = 10 * num + int(ch)\n\n # if we have a symbol, we would start to calculate the previous part.\n # note that we have to catch the last chracter since there will no sign afterwards to trigger calculation\n if ch in ("+", "-", "*", "/"):\n if op == "+":\n curr_res += num\n elif op == "-":\n curr_res -= num\n elif op == "*":\n curr_res *= num\n elif op == "/":\n # in python if there is a negative number, we should alway use int() instead of //\n curr_res = int(curr_res / num)\n \n # if the chracter is "+" or "-", we do not need to worry about\n # the priority so that we can add the curr_res to the eventual res\n if ch in ("+", "-"):\n res += curr_res\n curr_res = 0\n \n op = ch\n num = 0\n \n return res\n | 24 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Binbin learned this brillian solution today | basic-calculator-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n num = 0\n pre_op = \'+\'\n s+=\'+\'\n stack = []\n for c in s:\n if c.isdigit():\n num = num*10 + int(c)\n elif c == \' \':\n continue\n else:\n if pre_op == \'+\':\n stack.append(num)\n elif pre_op == \'-\':\n stack.append(-num)\n elif pre_op == \'*\':\n operant = stack.pop()\n stack.append((operant*num))\n elif pre_op == \'/\':\n operant = stack.pop()\n stack.append(int(operant/num))\n num = 0\n pre_op = c\n return sum(stack)\n``` | 2 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Python (Simple Stack) | basic-calculator-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculate(self, s):\n i, num, stack, sign = 0, 0, [], "+"\n s += \' \'\n while i < len(s):\n if s[i].isdigit():\n num = num*10 + int(s[i])\n elif s[i] in \'+-*/\' or i == len(s)-1:\n if sign == \'+\':\n stack.append(num)\n elif sign == \'-\':\n stack.append(-num)\n elif sign == \'*\':\n stack.append(stack.pop()*num)\n else:\n stack.append(int(stack.pop()/num))\n\n num = 0\n sign = s[i]\n i += 1\n\n return sum(stack)\n\n \n \n \n \n \n \n``` | 0 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Python3: O(1) space-complexity approach (no stack) | basic-calculator-ii | 0 | 1 | ```\nclass Solution:\n\n def calculate(self, s: str) -> int:\n # Edge cases\n if len(s) == 0: # empty string\n return 0\n \n # remove all spaces\n s = s.replace(" ", "")\n \n\t\t# Initialization \n curr_number = prev_number = result = 0 \n operation = "+" # intitialize the current operation to be "addition"\n \n i = 0 # initialize i\n while i < len(s): # len(s) is the length of the string\n char = s[i] # parsing ghe current currecter\n # if the character is digit\n if char.isdigit(): # current character is digit\n while i < len(s) and s[i].isdigit():\n curr_number = curr_number * 10 + int(s[i]) # forming the number (112 for example)\n i += 1 # increment i by 1 if s[i] is still a digit\n i -= 1 # decrement i by 1 to go back to the location immediately before the current operation\n \n if operation == "+": \n result += curr_number # add the curr_number to the result\n prev_number = curr_number # update the previous number\n \n elif operation == "-": \n result -= curr_number # subtract the curr_number from the result\n prev_number = -curr_number # update the previous number\n \n elif operation == "*":\n result -= prev_number # subtract the previous number first\n result += prev_number * curr_number # add the result of multiplication\n prev_number = prev_number * curr_number # update the previous number\n \n elif operation == "/":\n result -= prev_number # subtract the previous number first\n result += int(prev_number/curr_number) # add the result of division\n prev_number = int(prev_number/curr_number) # update the previous number\n \n curr_number = 0 # reset the current number\n # if the character is an operation\n else:\n operation = char\n \n i += 1 # increment i by 1\n return result\n``` | 3 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Python clean stack solution (easy understanding) | basic-calculator-ii | 0 | 1 | ```\nclass Solution:\n def calculate(self, s: str) -> int:\n num, ope, stack = 0, \'+\', []\n \n for cnt, i in enumerate(s):\n if i.isnumeric():\n num = num * 10 + int(i)\n if i in \'+-*/\' or cnt == len(s) - 1:\n if ope == \'+\':\n stack.append(num)\n elif ope == \'-\':\n stack.append(-num)\n elif ope == \'*\':\n j = stack.pop() * num\n stack.append(j)\n elif ope == \'/\':\n j = int(stack.pop() / num)\n stack.append(j)\n \n ope = i\n num = 0\n \n return sum(stack)\n``` | 10 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
✔️ [Python3] GENERATOR, O(1) Space ฅ^•ﻌ•^ฅ, , Explained | basic-calculator-ii | 0 | 1 | We can create a helper function that would return us the term for addition and substraction. Inside the function we would handle terms that fromed by multiplication and division. In helper we simply iterate over characthers and accumulate substring that form the integer. As soon as we meet any terminate symbol for current term (`+/-`), we yield the result. For `/` and `*` we remember current sign and calculate a term until meet the terminate charater.\n\nTime: **O(n)** - scan\nSpace: **O(1)** - nothing stored\n\nRuntime: 76 ms, faster than **84.36%** of Python3 online submissions for Basic Calculator II.\nMemory Usage: 15.3 MB, less than **90.98%** of Python3 online submissions for Basic Calculator II.\n\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n\n def get_term():\n terminate = {\'+\', \'-\', \'|\'}\n\n term, sign = None, None\n cur = \'\'\n\n for ch in s + \'|\':\n if ch == \' \': continue\n \n if ch.isdigit():\n cur += ch\n continue\n\n if sign:\n if sign == \'*\':\n term *= int(cur)\n else:\n term //= int(cur)\n else:\n term = int(cur)\n \n sign = ch\n \n if ch in terminate:\n yield (term, ch)\n term, sign = None, None\n \n cur = \'\'\n \n res = 0\n prevSign = None\n \n for term, sign in get_term():\n if not prevSign or prevSign == \'+\':\n res += term\n else:\n res -= term\n\n prevSign = sign\n \n return res\n``` | 4 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Python 3, Runtime 76ms, Stack Approach | basic-calculator-ii | 0 | 1 | ```\nclass Solution:\n def calculate(self, s: str) -> int:\n num, presign, stack=0, "+", []\n for i in s+\'+\':\n if i.isdigit():\n num = num*10 +int(i)\n elif i in \'+-*/\':\n if presign ==\'+\':\n stack.append(num)\n if presign ==\'-\':\n stack.append(-num)\n if presign ==\'*\':\n stack.append(stack.pop()*num)\n if presign == \'/\':\n stack.append(math.trunc(stack.pop()/num))\n presign = i\n num = 0\n return sum(stack)\n``` | 16 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
✅ [Python] Simple Solutions Stack [ 98%] | basic-calculator-ii | 0 | 1 | \u2714\uFE0F Complexity\nNow time complexity it is O(n), space is still O(n).\n\n```\nclass Solution:\n def calculate(self, s: str) -> int:\n stack, p, sign, total = [], 0, 1, 0\n s = s.replace(" ","")\n while p < len(s):\n char = s[p]\n if char.isdigit():\n num = ""\n while p < len(s) and s[p].isdigit():\n num += s[p]\n p += 1\n p -= 1\n num = int(num) *sign\n total += num\n sign = 1\n elif char in [\'+\', \'-\']:\n if stack:\n total *= stack.pop()\n total += stack.pop()\n if char == \'-\':\n sign = -1\n stack.append(total)\n stack.append(sign)\n total, sign = 0, 1\n elif char in [\'*\', \'/\']:\n p += 1\n num = ""\n while p < len(s) and s[p].isdigit():\n num += s[p]\n p += 1\n p -= 1\n if char == \'*\':\n total *= int(num)\n else:\n total /= int(num)\n total = int(total)\n p += 1\n if len(stack) == 2:\n total *= stack.pop()\n total += stack.pop()\n return int(total)\n```\n\n\n# ****UP VOTE IF HELPFUL | 4 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Python easy to read and understand | stack | basic-calculator-ii | 0 | 1 | ```\nclass Solution:\n def update(self, sign, num, stack):\n if sign == "+": stack.append(num)\n if sign == "-": stack.append(-num)\n if sign == "*": stack.append(stack.pop()*num)\n if sign == "/": stack.append(int(stack.pop()/num))\n return stack\n \n def solve(self, i, s):\n stack, num, sign = [], 0, "+"\n while i < len(s):\n if s[i].isdigit():\n num = num*10 + int(s[i])\n elif s[i] in ["+", "-", "*", "/"]:\n stack = self.update(sign, num, stack)\n num, sign = 0, s[i]\n elif s[i] == "(":\n num, i = self.solve(i+1, s)\n elif s[i] == ")":\n stack = self.update(sign, num, stack)\n return sum(stack), i\n i += 1\n #print(num, sign)\n stack = self.update(sign, num, stack)\n return sum(stack)\n \n def calculate(self, s: str) -> int:\n return self.solve(0, s)\n | 2 | Given a string `s` which represents an expression, _evaluate this expression and return its value_.
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of `[-231, 231 - 1]`.
**Note:** You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as `eval()`.
**Example 1:**
**Input:** s = "3+2\*2"
**Output:** 7
**Example 2:**
**Input:** s = " 3/2 "
**Output:** 1
**Example 3:**
**Input:** s = " 3+5 / 2 "
**Output:** 5
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists of integers and operators `('+', '-', '*', '/')` separated by some number of spaces.
* `s` represents **a valid expression**.
* All the integers in the expression are non-negative integers in the range `[0, 231 - 1]`.
* The answer is **guaranteed** to fit in a **32-bit integer**. | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | summary-ranges | 1 | 1 | # An Upvote will be encouraging \uD83D\uDC4D\n\n# Approach and Intuition\n\n- First, we check if the input list nums is empty. If it is, we return an empty list since there are no ranges to summarize.\n\n- Initialize an empty list called ranges to store the summarized ranges.\n\n- Set the start variable to the first element of the nums list. This will be the starting point of the current range.\n\n- Iterate over the nums list starting from the second element (index 1) using a for loop.\n\n- For each iteration, compare the current element nums[i] with the previous element nums[i-1]. If they are not consecutive (i.e., nums[i] is not equal to nums[i-1] + 1), it means the current range has ended.\n\n- In this case, we need to add the summarized range to the ranges list. We check if the start value is equal to the previous element (nums[i-1]). If they are equal, it means the range consists of only one number. So we append the string representation of start to the ranges list.\n\n- If the start value is different from the previous element, it means the range has more than one number. In this case, we append the string representation of start concatenated with "->" and the string representation of the previous element (nums[i-1]) to the ranges list.\n\n- After adding the summarized range, we update the start variable to the current element (nums[i]) since it will be the starting point of the next range.\n\n- After the loop, we need to handle the last range. We check if the start value is equal to the last element of nums (nums[-1]). If they are equal, it means the last range consists of only one number. So we append the string representation of start to the ranges list.\n\n- If the start value is different from the last element, it means the last range has more than one number. In this case, we append the string representation of start concatenated with "->" and the string representation of the last element (nums[-1]) to the ranges list.\n\n- Finally, we return the ranges list, which contains the summarized ranges as strings.\n\nThe intuition behind this approach is to iterate over the nums list and identify consecutive sequences of numbers. Whenever a sequence is interrupted, we add the summarized range to the ranges list. By keeping track of the starting point of each range (start variable), we can determine whether a range consists of a single number or multiple numbers. The code handles the first and last ranges separately to ensure all ranges are summarized correctly.\n\n```Python []\nclass Solution:\n def summaryRanges(self, nums):\n if not nums:\n return []\n\n ranges = []\n start = nums[0]\n\n for i in range(1, len(nums)):\n if nums[i] != nums[i-1] + 1:\n if start == nums[i-1]:\n ranges.append(str(start))\n else:\n ranges.append(str(start) + "->" + str(nums[i-1]))\n start = nums[i]\n\n # Handle the last range\n if start == nums[-1]:\n ranges.append(str(start))\n else:\n ranges.append(str(start) + "->" + str(nums[-1]))\n\n return ranges\n```\n```Java []\n\nclass Solution {\n public List<String> summaryRanges(int[] nums) {\n if (nums == null || nums.length == 0) {\n return new ArrayList<>();\n }\n\n List<String> ranges = new ArrayList<>();\n int start = nums[0];\n\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] != nums[i - 1] + 1) {\n if (start == nums[i - 1]) {\n ranges.add(Integer.toString(start));\n } else {\n ranges.add(start + "->" + nums[i - 1]);\n }\n start = nums[i];\n }\n }\n\n // Handle the last range\n if (start == nums[nums.length - 1]) {\n ranges.add(Integer.toString(start));\n } else {\n ranges.add(start + "->" + nums[nums.length - 1]);\n }\n\n return ranges;\n }\n}\n\n```\n```C++ []\n\nclass Solution {\npublic:\n std::vector<std::string> summaryRanges(std::vector<int>& nums) {\n if (nums.empty()) {\n return {};\n }\n\n std::vector<std::string> ranges;\n int start = nums[0];\n\n for (int i = 1; i < nums.size(); i++) {\n if (nums[i] != nums[i - 1] + 1) {\n if (start == nums[i - 1]) {\n ranges.push_back(std::to_string(start));\n } else {\n ranges.push_back(std::to_string(start) + "->" + std::to_string(nums[i - 1]));\n }\n start = nums[i];\n }\n }\n\n // Handle the last range\n if (start == nums.back()) {\n ranges.push_back(std::to_string(start));\n } else {\n ranges.push_back(std::to_string(start) + "->" + std::to_string(nums.back()));\n }\n\n return ranges;\n }\n};\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 47 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Simple solution using a simple interval | summary-ranges | 0 | 1 | # Intuition\nTreat the values in the list like an interval. Then return their formatted result per the format required for the problem.\n\n# Approach\nBut each entry in the interval by updating the range when the value is consecutive to the start value in the interval. When the value is not, start another interval.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n if len(nums) == 0:\n return []\n # looks like interval problem\n subArrays = [[]]\n \n # initialize the first subArray\n subArrays.append([nums[0]])\n for i in range(1, len(nums)):\n if nums[i] > nums[i - 1] + 1:\n # is the current number more than one greater\n # create a new subArray\n subArrays.append([nums[i]])\n else:\n # if the value is only one value greater\n if len(subArrays[-1]) == 1:\n subArrays[-1].append(nums[i])\n else:\n subArrays[-1][1] = nums[i] \n \n # now create an array with the values\n result = []\n for subArray in subArrays:\n if len(subArray) == 0:\n continue\n elif len(subArray) == 1:\n result.append(str(subArray[0]))\n elif len(subArray) == 2:\n result.append(str(subArray[0]) + "->" + str(subArray[1])) \n return result\n``` | 0 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Easiest python O(n) solution clearly explained | summary-ranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires summarizing consecutive ranges of numbers in a given list. We can iterate through the list and identify the start and end of each range by checking if the numbers are consecutive.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck if the input list is empty. If it is, return an empty list as there are no ranges to summarize.\n1.Initialize an empty list to store the summary ranges.\n\n2.Initialize variables start and end to the first element of the list.\n\n3.Iterate through the numbers starting from the second element.\n\n4.If the current number is consecutive to the previous number, update the end of the range.\n\n5.If the current number is not consecutive, add the current range to the result list.\n\n6.Reset the start and end variables to the current number.\n\n7.After the loop, add the last range to the result list.\nReturn the list of summary ranges.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n \n # Check if the input list is empty\n if nums == []:\n return []\n \n # Initialize the list to store the summary ranges\n ranges = []\n \n # Initialize variables for the start and end of the range\n start = nums[0]\n end = nums[0]\n\n # Iterate through the numbers starting from the second element\n for num in nums[1:]:\n if num == end + 1:\n # The number is consecutive, update the end of the range\n end = num\n else:\n # The number is not consecutive, add the current range to the result list\n if start == end:\n ranges.append(str(start))\n else:\n ranges.append(f"{start}->{end}")\n \n # Reset the start and end to the current number\n start = num\n end = num\n\n # Add the last range to the result list\n if start == end:\n ranges.append(str(start))\n else:\n ranges.append(f"{start}->{end}")\n \n return ranges\n\n``` | 6 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
[Python 3] Find ranges x->y and return formatted result || beats 97% || 27ms | summary-ranges | 0 | 1 | ```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n ranges = [] # [start, end] or [x, y]\n for n in nums:\n if ranges and ranges[-1][1] == n-1:\n ranges[-1][1] = n\n else:\n ranges.append([n, n])\n\n return [f\'{x}->{y}\' if x != y else f\'{x}\' for x, y in ranges]\n```\n\n | 35 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
python simple code | summary-ranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n ranges = [] # [start, end] or [x, y]\n for i, n in enumerate(nums):\n if ranges and ranges[-1][1] == n-1:\n ranges[-1][1] = n\n else:\n ranges.append([n, n])\n\n return [f\'{x}->{y}\' if x != y else f\'{x}\' for x, y in ranges]\n``` | 2 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
228: Solution with step by step explanation | summary-ranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis code implements the solution to the problem of finding the summary ranges for a given sorted unique integer array nums. The main idea is to iterate through nums and find the beginning and ending of each range.\n\nThe function summaryRanges takes a list of integers nums as input and returns a list of strings ans.\n\nThe variable ans is initialized as an empty list to store the final summary ranges.\n\nThe variable i is initialized to 0, which is used as the index to iterate through nums.\n\nIn the while loop, we first find the beginning of the range by assigning the value of nums[i] to the variable begin.\n\nThen we check if the current element and the next element form a range by checking if nums[i] is equal to nums[i+1] - 1. If they do form a range, we keep incrementing i until we reach the end of the range. We update the value of end to nums[i] once we reach the end of the range.\n\nNext, we check if the range contains only one element, i.e., begin is equal to end. If it does, we append the string representation of begin to ans. If not, we append the string representation of begin concatenated with "->" and the string representation of end to ans.\n\nFinally, we increment i by 1 to move to the next element in nums.\n\nOnce the loop is done, we return ans, which contains the summary ranges.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n ans = []\n\n i = 0\n while i < len(nums):\n begin = nums[i]\n while i < len(nums) - 1 and nums[i] == nums[i + 1] - 1:\n i += 1\n end = nums[i]\n if begin == end:\n ans.append(str(begin))\n else:\n ans.append(str(begin) + "->" + str(end))\n i += 1\n\n return ans\n\n``` | 12 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Python short and clean 1-liner. Functional programming. | summary-ranges | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$, including output.\n\nwhere, `n is length of nums.`\n\n# Code\nImperative:\n```python\nclass Solution:\n def summaryRanges(self, nums: list[int]) -> list[str]:\n ranges = [[-inf, -inf]]\n for x in nums:\n if x == ranges[-1][1] + 1: ranges[-1][1] = x\n else: ranges.append([x, x])\n\n return [f\'{a}\' if a == b else f\'{a}->{b}\' for a, b in islice(ranges, 1, None)]\n\n\n```\n\nFunctional (multiline for readability):\n```python\nclass Solution:\n def summaryRanges(self, nums: list[int]) -> list[str]:\n make_range = lambda a, x: (setitem(a[-1], 1, x) if x == a[-1][1] + 1 else a.append([x, x])) or a\n ranges = reduce(make_range, nums, [[-inf, -inf]])\n return [f\'{a}\' if a == b else f\'{a}->{b}\' for a, b in islice(ranges, 1, None)]\n\n\n```\n\nFunctional (1-liner, less readable):\n```python\nclass Solution:\n def summaryRanges(self, nums: list[int]) -> list[str]:\n return [f\'{a}\' if a == b else f\'{a}->{b}\' for a, b in islice(reduce(lambda a, x: (setitem(a[-1], 1, x) if x == a[-1][1] + 1 else a.append([x, x])) or a, nums, [[-inf, -inf]]), 1, None)]\n\n\n``` | 3 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Beats 100% O(N) 🔥| 2 Pointer 🔥Approach | Full Optmized Code 🔥 | summary-ranges | 1 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n- **Its Very Simple LOOK !!**\n- Set to pointer start and end \n- Start to set at the starting of the range and end for the end of the range \n- if they are in continous range means next number is +1 , then end++ till you find the out of range is not +1.\n- At last push the element to vector;\n- To handle to overflow caused by i+1 ,handle the last element sepeartly in the last !! \n- Doone !!\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution {\npublic:\n vector<string> summaryRanges(vector<int>& nums) {\n vector<string>jat;\n if(nums.size()==0) return jat;\n long long start=0,end=0;\n for(int i=0;i<nums.size()-1;i++)\n {\n \n if((nums[i]+1)==nums[i+1])\n {\n end++;\n }\n else\n {\n if(start==end)\n jat.push_back(to_string(nums[start]));\n else\n {\n string s=to_string(nums[start]);\n string e=to_string(nums[end]);\n string final=s+"->"+e;\n jat.push_back(final);\n }\n start=end+1;\n end+=1;\n }\n }\n if(start==end)\n jat.push_back(to_string(nums[start]));\n else\n {\n string s=to_string(nums[start]);\n string e=to_string(nums[end]);\n string final=s+"->"+e;\n jat.push_back(final);\n }\n\n return jat;\n \n }\n};\n```\n\n | 5 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
[ Python ] ✅✅ Simple Python Solution Using Iterative Approach || O(n) 🔥✌ | summary-ranges | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 34 ms, faster than 71.53% of Python3 online submissions for Summary Ranges.\n# Memory Usage: 13.8 MB, less than 88.25% of Python3 online submissions for Summary Ranges.\n# Time Complexity : - O(n)\n\n\tclass Solution:\n\t\tdef summaryRanges(self, nums: List[int]) -> List[str]:\n\n\t\t\tresult = []\n\n\t\t\tstart , end = 0 , 0\n\n\t\t\twhile start < len(nums) and end < len(nums):\n\n\t\t\t\tif (end + 1) < len(nums) and nums[end] + 1 == nums[end + 1]:\n\t\t\t\t\tend = end + 1\n\t\t\t\telse:\n\n\t\t\t\t\tif nums[start] == nums[end]:\n\t\t\t\t\t\tresult.append(str(nums[start]))\n\t\t\t\t\t\tstart = start + 1\n\t\t\t\t\t\tend = end + 1\n\n\t\t\t\t\telse:\n\t\t\t\t\t\tresult.append(str(nums[start]) + \'->\' + str(nums[end]))\n\t\t\t\t\t\tend = end + 1\n\t\t\t\t\t\tstart = end\n\n\t\t\treturn result\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D\n | 44 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Python Simple Solution! Beats 93%! TC- O(n) | summary-ranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is sorted and in a range the element next to "n" has to be \n"n+1". it can be used to derive a simple solution to this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTake a variable to keep the starting point of the range and an other variable to keep the current or last of the range.\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n ans = []\n if not len(nums):\n return ans\n num = nums[0]\n temp = nums[0]\n \n\n for i in range(1,len(nums)):\n if nums[i] == temp+1:\n temp = nums[i]\n else:\n if (temp - num) >= 1:\n ans.append(f"{num}->{temp}")\n else:\n ans.append(str(num))\n num = nums[i]\n temp = nums[i]\n\n # to add the last elements in the list.\n if (temp - num) >= 1: \n ans.append(f"{num}->{temp}")\n else:\n ans.append(str(num))\n\n return ans\n\n\n\n``` | 2 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Easy.py | summary-ranges | 0 | 1 | # Code\n```\nclass Solution:\n def summaryRanges(self, nums: List[int]) -> List[str]:\n if len(nums)==0:return []\n ans,i=[],0\n st=nums[0]\n for i in range(1,len(nums)):\n if nums[i]!=nums[i-1]+1:\n if st==nums[i-1]:\n ans.append(str(st))\n else:\n ans.append(str(st)+"->"+str(nums[i-1]))\n st=nums[i]\n if st==nums[-1]:\n ans.append(str(st))\n else:\n ans.append(str(st)+"->"+str(nums[len(nums)-1]))\n return ans\n``` | 3 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
python3 Solution | summary-ranges | 0 | 1 | \n# Code\n```\nclass Solution:\n def summaryRanges(self,nums:List[int])->List[int]:\n if not nums:\n return None\n\n ans=[]\n j=0\n for i in range(len(nums)):\n if i+1==len(nums) or nums[i]+1!=nums[i+1]:\n if j==i:\n ans.append(str(nums[i]))\n\n else:\n ans.append(str(nums[j])+"->"+str(nums[i]))\n j=i+1\n\n return ans \n``` | 8 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
Very Easy || 100% || Fully Explained || Java, C++, Python, Javascript, Python3 | summary-ranges | 1 | 1 | # **Java Solution:**\n```\n// Runtime: 3 ms, faster than 92.99% of Java online submissions for Summary Ranges.\n// Time Complexity : O(N)\n// Space Complexity : O(1)\nclass Solution {\n public List<String> summaryRanges(int[] nums) {\n // Create a list of string to store the output result...\n List<String> output = new ArrayList<String>();\n // Start traversing the array from idx = 0 till idx < sizeofarray in a while loop.\n int idx = 0;\n while(idx < nums.length) {\n // Initialize beg and last index for identifying the continuous element in the array...\n int beg, last;\n // Mark the number at current index as beginning element of the range...\n beg = nums[idx];\n // Traverse the array beggining from current index & find the last element whose difference from previous element is exactly 1, i.e. nums[idx + 1] == nums[idx] + 1...\n while(idx+1 < nums.length && nums[idx+1] == nums[idx] + 1) \n idx++;\n // Set this element as last element of the range...\n last = nums[idx];\n // If continuous element isn\'t present...\n if(beg == last)\n output.add(beg + "");\n // If present...\n else\n output.add( beg + "->" + last );\n idx++; \n }\n return output; // Return the output result list...\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Runtime: 2 ms, faster than 81.97% of C++ online submissions for Summary Ranges.\n// Time Complexity : O(N)\n// Space Complexity : O(1)\nclass Solution {\npublic:\n vector<string> summaryRanges(vector<int>& nums) {\n // Create a list of string to store the output result...\n vector<string> output;\n // Start traversing the array from idx = 0 till idx < sizeofarray in a while loop.\n int idx = 0;\n while(idx < nums.size()) {\n // Initialize beg and last index for identifying the continuous element in the array...\n int beg, last;\n // Mark the number at current index as beginning element of the range...\n beg = nums[idx];\n // Traverse the array beggining from current index & find the last element whose difference from previous element is exactly 1, i.e. nums[idx + 1] == nums[idx] + 1...\n while(idx+1 < nums.size() && nums[idx+1] == nums[idx] + 1)\n idx++;\n // Set this element as last element of the range...\n last = nums[idx];\n // If continuous element isn\'t present...\n if(beg == last)\n output.push_back(to_string(beg));\n // If present...\n else\n output.push_back(to_string(beg) + "->" + to_string(last));\n idx++;\n }\n return output; // Return the output result list\n }\n};\n```\n\n# **Python/Python3 Solution:**\n```\n# Runtime: 11 ms, faster than 98.68% of Python online submissions for Summary Ranges.\n# Memory Usage: 13.4 MB, less than 82.54% of Python online submissions for Summary Ranges.\n# Time Complexity : O(N)\n# Space Complexity : O(1)\nclass Solution(object):\n def summaryRanges(self, nums):\n # Create a list of string to store the output result...\n output = []\n # Start traversing the array from idx = 0 till idx < sizeofarray in a while loop.\n idx = 0\n while idx < len(nums):\n # Mark the number at current index as beginning element of the range...\n beg = nums[idx]\n # Traverse the array beggining from current index & find the last element whose difference from previous element is exactly 1, i.e. nums[idx + 1] == nums[idx] + 1...\n while idx+1 < len(nums) and nums[idx+1] == nums[idx] + 1:\n idx += 1\n # Set this element as last element of the range...\n last = nums[idx]\n # If continuous element isn\'t present...\n if beg == last:\n output.append(str(beg))\n # If present...\n else:\n output.append(str(beg) + "->" + str(last))\n idx += 1\n return output; # Return the output result list...\n```\n \n# **JavaScript Solution:**\n```\n// Runtime: 46 ms, faster than 86.21% of JavaScript online submissions for Summary Ranges.\n// Time Complexity : O(N)\n// Space Complexity : O(1)\nvar summaryRanges = function(nums) {\n // Create a list of string to store the output result...\n const output = [];\n // Start traversing the array from idx = 0 till idx < sizeofarray in a while loop.\n let idx = 0;\n while(idx < nums.length) {\n // Initialize beg and last index for identifying the continuous element in the array...\n let beg, last;\n // Mark the number at current index as beginning element of the range...\n beg = nums[idx];\n // Traverse the array beggining from current index & find the last element whose difference from previous element is exactly 1, i.e. nums[idx + 1] == nums[idx] + 1...\n while(idx+1 < nums.length && nums[idx+1] == nums[idx] + 1) \n idx++;\n // Set this element as last element of the range...\n last = nums[idx];\n // If continuous element isn\'t present...\n if(beg == last)\n output.push(beg + "");\n // If present...\n else\n output.push( beg + "->" + last );\n idx++; \n }\n return output; // Return the output result list...\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 22 | You are given a **sorted unique** integer array `nums`.
A **range** `[a,b]` is the set of all integers from `a` to `b` (inclusive).
Return _the **smallest sorted** list of ranges that **cover all the numbers in the array exactly**_. That is, each element of `nums` is covered by exactly one of the ranges, and there is no integer `x` such that `x` is in one of the ranges but not in `nums`.
Each range `[a,b]` in the list should be output as:
* `"a->b "` if `a != b`
* `"a "` if `a == b`
**Example 1:**
**Input:** nums = \[0,1,2,4,5,7\]
**Output:** \[ "0->2 ", "4->5 ", "7 "\]
**Explanation:** The ranges are:
\[0,2\] --> "0->2 "
\[4,5\] --> "4->5 "
\[7,7\] --> "7 "
**Example 2:**
**Input:** nums = \[0,2,3,4,6,8,9\]
**Output:** \[ "0 ", "2->4 ", "6 ", "8->9 "\]
**Explanation:** The ranges are:
\[0,0\] --> "0 "
\[2,4\] --> "2->4 "
\[6,6\] --> "6 "
\[8,9\] --> "8->9 "
**Constraints:**
* `0 <= nums.length <= 20`
* `-231 <= nums[i] <= 231 - 1`
* All the values of `nums` are **unique**.
* `nums` is sorted in ascending order. | null |
🚀 99.7% || HashMap & Boyer-Moore Majority Voting || Explained Intuition 🚀 | majority-element-ii | 1 | 1 | # Problem Description\nThe problem is to **identify** elements in an integer array, `nums`, of size `n`, that appear more than `\u230An/3\u230B` times and **return** them as an output.\n\n- **Constraints:**\n - `1 <= nums.length <= 5 * 10e4`\n - `-10e9 <= nums[i] <= 10e9`\n\nSeems Easy! \uD83D\uDE03\n\n---\n\n\n# Intuition\n\nHi there everyone \uD83D\uDE03,\n\nLet\'s see our today interesting problem, We are required to return the number that has appeared **more** than `\u230An/3\u230B` times in our array.\uD83E\uDD14\nSeems Interesting.\uD83E\uDD29\n\nWe know that we need something here, **count** the number of **occurencies** and **store** them somewhere and then return the required elements.\uD83D\uDE03\n\nIt\'s a job for **HASHMAPS** !!\uD83E\uDDB8\u200D\u2642\uFE0F\uD83E\uDDB8\u200D\u2642\uFE0F\nOur hero today is the `HashMap` since, we can **store** the number of occurencies for each unique element and then return the elements that have appeared more than `\u230An/3\u230B` times.\uD83D\uDE80\uD83D\uDE80\n\nIt is an easy solution. Can we do better ?\uD83E\uDD14\nActually, We can \uD83E\uDD2F\uD83E\uDD2F\nThere is an interesting observation we want to look at.\uD83D\uDC40\n\n```\nEX1 : Array = [1, 2, 2, 4, 4, 4]\nAnswer = [4]\n```\n```\nEX2 : Array = [1, 2, 2, 2, 4, 4, 4]\nAnswer = [2, 4]\n```\n```\nEX3 : Array = [1, 1, 2, 2, 2, 4, 4, 4]\nAnswer = [2, 4]\n```\n```\nEX4 : Array = [1, 1, 1, 2, 2, 2, 4, 4, 4]\nAnswer = []\n```\n\nI think we have something here.\uD83E\uDD14\nSince we are required to return elements that appeared more than `\u230An/3\u230B` times then we have atmost **two elements** that we can return.\uD83D\uDCAA\n\nBut how two elements ???\uD83E\uDD2F\uD83E\uDD2F\uD83E\uDD2F\uD83E\uDD2F\nSince we want to return elements that appeared more than `\u230An/3\u230B` times then atleast it must have appeared `\u230An/3\u230B + 1` times.\n`\u230An/3\u230B + 1` is greater than the **third** of the array so \n```\n`\u230An/3\u230B + 1` * 3 > array size\n```\nSo, it is impossible to return more than two elements.\uD83D\uDE14\n\nHow can we **utilize** a great observation like this?\uD83E\uDD14\nInstead of **storing** the occurencies of all elements, We can only **track** the **two highest elements** that have appeared in our array and return them!\uD83E\uDD29\nAnd there is algorithm for that. It is called **Boyer-Moore Majority Voting Algorithm**.\n\nThis algorithm can be used to return the highest `K` elements that appeared in the array more than `array_size/(K+1)` times. In our case, `K = 2`.\n\n- The major **Intuition** behind this algorithm is that **maintaining** voting variable for the **candidates**:\n - **Increase** the variable if you faced the candidate in your iteration.\n - **Decrease** the variable if you faced another element.\n - If the variable reaches `0`, look for **another** promising candidate.\n\nWhy this work?\uD83E\uDD14\nAssume we are searching for the element that appeared **more** than `array_size / 2` times, then we are sure that the voting variable can has value `array_size / 2 + 1` and if we **decreased** it for all other elements in the array it will also stay **positive** enough to tell us the **desired** candidate.\n\nThis is small image illustrating the algorithm for `K=1` and the major element is the red square.\n\n\n\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n---\n\n\n# Proposed Approaches\n## 1. HashMap Solution\n1. **Create** an `HashMap` to store the **count** of each element.\n2. **Iterate** through the input array and **increment** the **count** for each element in the `HashMap`.\n3. **Create** a vector to store the result and **Calculate** the `threshold` count (1/3 of the array size).\n5. **Iterate** through the `HashMap` and for each element:\n - Check if the **element count** is **greater** than the `threshold`.\n - If **yes**, **add** the element to the result vector.\n6. **Return** the **vector** containing the identified majority elements.\n\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are **iterating** over the array then it\'s a **linear** complexity and we are **iterating** over the `HashMap` that also can be **linear** complexity, then the total complexity is `2 * N` which is `O(N)`\n- **Space complexity:** $$O(N)$$\nSince we are storing the **count** of occurencies for each **unique** element in the nums array and the array\'s elements can **all** be unique then it is **linear** complexity which is `O(N)`.\n\n---\n\n## 1. Boyer-Moore Majority Voting Solution\n1. Create **variables** to **track** counts and candidates for potential majority elements.\n2. **First Pass** - Find **Potential** Majority Elements:\n - **Iterate** through the input array and **identify** potential majority element candidates.\n - **Update** the candidates based on **specific** conditions.\n - **Maintain** counts for each candidate.\n3. **Second Pass** - **Count** Occurrences:\n - Iterate through the input array again to **count** the occurrences of the **potential** majority elements.\n4. **Compare** the counts with a threshold to **determine** the majority elements.\n5. **Return** Majority Elements.\n\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over the array in **two** passes then the complexity is `2 * N` which is `O(N)`.\n- **Space complexity:** $$O(1)$$\nSince we are only storing **constant** variables then the complexity is `O(1)`.\n\n\n---\n\n\n\n# Code\n## HashMap Solution\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n // Create a frequency map to store the count of each element\n unordered_map<int, int> elementCountMap;\n \n // Iterate through the input array to count element occurrences\n for(int i = 0; i < nums.size(); i++) {\n elementCountMap[nums[i]]++;\n }\n \n vector<int> majorityElements;\n int threshold = nums.size() / 3;\n \n // Iterate through the frequency map to identify majority elements\n for(auto elementCountPair : elementCountMap) {\n int element = elementCountPair.first;\n int count = elementCountPair.second;\n \n // Check if the element count is greater than the threshold\n if(count > threshold) {\n majorityElements.push_back(element);\n }\n }\n \n return majorityElements; \n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n // Create a frequency map to store the count of each element\n Map<Integer, Integer> elementCountMap = new HashMap<>();\n \n // Iterate through the input array to count element occurrences\n for (int i = 0; i < nums.length; i++) {\n elementCountMap.put(nums[i], elementCountMap.getOrDefault(nums[i], 0) + 1);\n }\n \n List<Integer> majorityElements = new ArrayList<>();\n int threshold = nums.length / 3;\n \n // Iterate through the frequency map to identify majority elements\n for (Map.Entry<Integer, Integer> entry : elementCountMap.entrySet()) {\n int element = entry.getKey();\n int count = entry.getValue();\n \n // Check if the element count is greater than the threshold\n if (count > threshold) {\n majorityElements.add(element);\n }\n }\n \n return majorityElements;\n }\n}\n```\n```Python []\nclass Solution:\n def majorityElement(self, nums: list[int]) -> list[int]:\n # Create a Counter to store the count of each element\n element_count = Counter(nums)\n \n majority_elements = []\n threshold = len(nums) // 3\n \n # Iterate through the element count to identify majority elements\n for element, count in element_count.items():\n # Check if the element count is greater than the threshold\n if count > threshold:\n majority_elements.append(element)\n \n return majority_elements\n```\n\n\n---\n\n## Boyer-Moore Majority Voting Solution\n\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int count1 = 0, count2 = 0; // Counters for the potential majority elements\n int candidate1 = 0, candidate2 = 0; // Potential majority element candidates\n\n // First pass to find potential majority elements.\n for (int i = 0; i < nums.size(); i++) {\n // If count1 is 0 and the current number is not equal to candidate2, update candidate1.\n if (count1 == 0 && nums[i] != candidate2) {\n count1 = 1;\n candidate1 = nums[i];\n } \n // If count2 is 0 and the current number is not equal to candidate1, update candidate2.\n else if (count2 == 0 && nums[i] != candidate1) {\n count2 = 1;\n candidate2 = nums[i];\n } \n // Update counts for candidate1 and candidate2.\n else if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n } \n // If the current number is different from both candidates, decrement their counts.\n else {\n count1--;\n count2--;\n }\n }\n\n vector<int> result;\n int threshold = nums.size() / 3; // Threshold for majority element\n\n // Second pass to count occurrences of the potential majority elements.\n count1 = 0, count2 = 0;\n for (int i = 0; i < nums.size(); i++) {\n if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n }\n }\n\n // Check if the counts of potential majority elements are greater than n/3 and add them to the result.\n if (count1 > threshold) {\n result.push_back(candidate1);\n }\n if (count2 > threshold) {\n result.push_back(candidate2);\n }\n\n return result;\n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n int count1 = 0, count2 = 0; // Counters for the potential majority elements\n int candidate1 = 0, candidate2 = 0; // Potential majority element candidates\n\n // First pass to find potential majority elements.\n for (int i = 0; i < nums.length; i++) {\n // If count1 is 0 and the current number is not equal to candidate2, update candidate1.\n if (count1 == 0 && nums[i] != candidate2) {\n count1 = 1;\n candidate1 = nums[i];\n } \n // If count2 is 0 and the current number is not equal to candidate1, update candidate2.\n else if (count2 == 0 && nums[i] != candidate1) {\n count2 = 1;\n candidate2 = nums[i];\n } \n // Update counts for candidate1 and candidate2.\n else if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n } \n // If the current number is different from both candidates, decrement their counts.\n else {\n count1--;\n count2--;\n }\n }\n\n List<Integer> result = new ArrayList<>();\n int threshold = nums.length / 3; // Threshold for majority element\n\n // Second pass to count occurrences of the potential majority elements.\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < nums.length; i++) {\n if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n }\n }\n\n // Check if the counts of potential majority elements are greater than n/3 and add them to the result.\n if (count1 > threshold) {\n result.add(candidate1);\n }\n if (count2 > threshold) {\n result.add(candidate2);\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def majorityElement(self, nums: list[int]) -> list[int]:\n # Counters for the potential majority elements\n count1 = count2 = 0 \n # Potential majority element candidates\n candidate1 = candidate2 = 0\n\n # First pass to find potential majority elements.\n for num in nums:\n # If count1 is 0 and the current number is not equal to candidate2, update candidate1.\n if count1 == 0 and num != candidate2:\n count1 = 1\n candidate1 = num\n\n # If count2 is 0 and the current number is not equal to candidate1, update candidate2.\n elif count2 == 0 and num != candidate1:\n count2 = 1\n candidate2 = num\n \n # Update counts for candidate1 and candidate2.\n elif candidate1 == num:\n count1 += 1\n elif candidate2 == num:\n count2 += 1\n\n # If the current number is different from both candidates, decrement their counts.\n else:\n count1 -= 1\n count2 -= 1\n\n result = []\n threshold = len(nums) // 3 # Threshold for majority element\n\n # Second pass to count occurrences of the potential majority elements.\n count1 = count2 = 0\n for num in nums:\n if candidate1 == num:\n count1 += 1\n elif candidate2 == num:\n count2 += 1\n\n # Check if the counts of potential majority elements are greater than n/3 and add them to the result.\n if count1 > threshold:\n result.append(candidate1)\n if count2 > threshold:\n result.append(candidate2)\n\n return result\n\n```\n\n\n\n\n\n | 234 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
🚀 99.7% || HashMap & Boyer-Moore Majority Voting || Explained Intuition 🚀 | majority-element-ii | 1 | 1 | # Problem Description\nThe problem is to **identify** elements in an integer array, `nums`, of size `n`, that appear more than `\u230An/3\u230B` times and **return** them as an output.\n\n- **Constraints:**\n - `1 <= nums.length <= 5 * 10e4`\n - `-10e9 <= nums[i] <= 10e9`\n\nSeems Easy! \uD83D\uDE03\n\n---\n\n\n# Intuition\n\nHi there everyone \uD83D\uDE03,\n\nLet\'s see our today interesting problem, We are required to return the number that has appeared **more** than `\u230An/3\u230B` times in our array.\uD83E\uDD14\nSeems Interesting.\uD83E\uDD29\n\nWe know that we need something here, **count** the number of **occurencies** and **store** them somewhere and then return the required elements.\uD83D\uDE03\n\nIt\'s a job for **HASHMAPS** !!\uD83E\uDDB8\u200D\u2642\uFE0F\uD83E\uDDB8\u200D\u2642\uFE0F\nOur hero today is the `HashMap` since, we can **store** the number of occurencies for each unique element and then return the elements that have appeared more than `\u230An/3\u230B` times.\uD83D\uDE80\uD83D\uDE80\n\nIt is an easy solution. Can we do better ?\uD83E\uDD14\nActually, We can \uD83E\uDD2F\uD83E\uDD2F\nThere is an interesting observation we want to look at.\uD83D\uDC40\n\n```\nEX1 : Array = [1, 2, 2, 4, 4, 4]\nAnswer = [4]\n```\n```\nEX2 : Array = [1, 2, 2, 2, 4, 4, 4]\nAnswer = [2, 4]\n```\n```\nEX3 : Array = [1, 1, 2, 2, 2, 4, 4, 4]\nAnswer = [2, 4]\n```\n```\nEX4 : Array = [1, 1, 1, 2, 2, 2, 4, 4, 4]\nAnswer = []\n```\n\nI think we have something here.\uD83E\uDD14\nSince we are required to return elements that appeared more than `\u230An/3\u230B` times then we have atmost **two elements** that we can return.\uD83D\uDCAA\n\nBut how two elements ???\uD83E\uDD2F\uD83E\uDD2F\uD83E\uDD2F\uD83E\uDD2F\nSince we want to return elements that appeared more than `\u230An/3\u230B` times then atleast it must have appeared `\u230An/3\u230B + 1` times.\n`\u230An/3\u230B + 1` is greater than the **third** of the array so \n```\n`\u230An/3\u230B + 1` * 3 > array size\n```\nSo, it is impossible to return more than two elements.\uD83D\uDE14\n\nHow can we **utilize** a great observation like this?\uD83E\uDD14\nInstead of **storing** the occurencies of all elements, We can only **track** the **two highest elements** that have appeared in our array and return them!\uD83E\uDD29\nAnd there is algorithm for that. It is called **Boyer-Moore Majority Voting Algorithm**.\n\nThis algorithm can be used to return the highest `K` elements that appeared in the array more than `array_size/(K+1)` times. In our case, `K = 2`.\n\n- The major **Intuition** behind this algorithm is that **maintaining** voting variable for the **candidates**:\n - **Increase** the variable if you faced the candidate in your iteration.\n - **Decrease** the variable if you faced another element.\n - If the variable reaches `0`, look for **another** promising candidate.\n\nWhy this work?\uD83E\uDD14\nAssume we are searching for the element that appeared **more** than `array_size / 2` times, then we are sure that the voting variable can has value `array_size / 2 + 1` and if we **decreased** it for all other elements in the array it will also stay **positive** enough to tell us the **desired** candidate.\n\nThis is small image illustrating the algorithm for `K=1` and the major element is the red square.\n\n\n\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n---\n\n\n# Proposed Approaches\n## 1. HashMap Solution\n1. **Create** an `HashMap` to store the **count** of each element.\n2. **Iterate** through the input array and **increment** the **count** for each element in the `HashMap`.\n3. **Create** a vector to store the result and **Calculate** the `threshold` count (1/3 of the array size).\n5. **Iterate** through the `HashMap` and for each element:\n - Check if the **element count** is **greater** than the `threshold`.\n - If **yes**, **add** the element to the result vector.\n6. **Return** the **vector** containing the identified majority elements.\n\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are **iterating** over the array then it\'s a **linear** complexity and we are **iterating** over the `HashMap` that also can be **linear** complexity, then the total complexity is `2 * N` which is `O(N)`\n- **Space complexity:** $$O(N)$$\nSince we are storing the **count** of occurencies for each **unique** element in the nums array and the array\'s elements can **all** be unique then it is **linear** complexity which is `O(N)`.\n\n---\n\n## 1. Boyer-Moore Majority Voting Solution\n1. Create **variables** to **track** counts and candidates for potential majority elements.\n2. **First Pass** - Find **Potential** Majority Elements:\n - **Iterate** through the input array and **identify** potential majority element candidates.\n - **Update** the candidates based on **specific** conditions.\n - **Maintain** counts for each candidate.\n3. **Second Pass** - **Count** Occurrences:\n - Iterate through the input array again to **count** the occurrences of the **potential** majority elements.\n4. **Compare** the counts with a threshold to **determine** the majority elements.\n5. **Return** Majority Elements.\n\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over the array in **two** passes then the complexity is `2 * N` which is `O(N)`.\n- **Space complexity:** $$O(1)$$\nSince we are only storing **constant** variables then the complexity is `O(1)`.\n\n\n---\n\n\n\n# Code\n## HashMap Solution\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n // Create a frequency map to store the count of each element\n unordered_map<int, int> elementCountMap;\n \n // Iterate through the input array to count element occurrences\n for(int i = 0; i < nums.size(); i++) {\n elementCountMap[nums[i]]++;\n }\n \n vector<int> majorityElements;\n int threshold = nums.size() / 3;\n \n // Iterate through the frequency map to identify majority elements\n for(auto elementCountPair : elementCountMap) {\n int element = elementCountPair.first;\n int count = elementCountPair.second;\n \n // Check if the element count is greater than the threshold\n if(count > threshold) {\n majorityElements.push_back(element);\n }\n }\n \n return majorityElements; \n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n // Create a frequency map to store the count of each element\n Map<Integer, Integer> elementCountMap = new HashMap<>();\n \n // Iterate through the input array to count element occurrences\n for (int i = 0; i < nums.length; i++) {\n elementCountMap.put(nums[i], elementCountMap.getOrDefault(nums[i], 0) + 1);\n }\n \n List<Integer> majorityElements = new ArrayList<>();\n int threshold = nums.length / 3;\n \n // Iterate through the frequency map to identify majority elements\n for (Map.Entry<Integer, Integer> entry : elementCountMap.entrySet()) {\n int element = entry.getKey();\n int count = entry.getValue();\n \n // Check if the element count is greater than the threshold\n if (count > threshold) {\n majorityElements.add(element);\n }\n }\n \n return majorityElements;\n }\n}\n```\n```Python []\nclass Solution:\n def majorityElement(self, nums: list[int]) -> list[int]:\n # Create a Counter to store the count of each element\n element_count = Counter(nums)\n \n majority_elements = []\n threshold = len(nums) // 3\n \n # Iterate through the element count to identify majority elements\n for element, count in element_count.items():\n # Check if the element count is greater than the threshold\n if count > threshold:\n majority_elements.append(element)\n \n return majority_elements\n```\n\n\n---\n\n## Boyer-Moore Majority Voting Solution\n\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int count1 = 0, count2 = 0; // Counters for the potential majority elements\n int candidate1 = 0, candidate2 = 0; // Potential majority element candidates\n\n // First pass to find potential majority elements.\n for (int i = 0; i < nums.size(); i++) {\n // If count1 is 0 and the current number is not equal to candidate2, update candidate1.\n if (count1 == 0 && nums[i] != candidate2) {\n count1 = 1;\n candidate1 = nums[i];\n } \n // If count2 is 0 and the current number is not equal to candidate1, update candidate2.\n else if (count2 == 0 && nums[i] != candidate1) {\n count2 = 1;\n candidate2 = nums[i];\n } \n // Update counts for candidate1 and candidate2.\n else if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n } \n // If the current number is different from both candidates, decrement their counts.\n else {\n count1--;\n count2--;\n }\n }\n\n vector<int> result;\n int threshold = nums.size() / 3; // Threshold for majority element\n\n // Second pass to count occurrences of the potential majority elements.\n count1 = 0, count2 = 0;\n for (int i = 0; i < nums.size(); i++) {\n if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n }\n }\n\n // Check if the counts of potential majority elements are greater than n/3 and add them to the result.\n if (count1 > threshold) {\n result.push_back(candidate1);\n }\n if (count2 > threshold) {\n result.push_back(candidate2);\n }\n\n return result;\n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n int count1 = 0, count2 = 0; // Counters for the potential majority elements\n int candidate1 = 0, candidate2 = 0; // Potential majority element candidates\n\n // First pass to find potential majority elements.\n for (int i = 0; i < nums.length; i++) {\n // If count1 is 0 and the current number is not equal to candidate2, update candidate1.\n if (count1 == 0 && nums[i] != candidate2) {\n count1 = 1;\n candidate1 = nums[i];\n } \n // If count2 is 0 and the current number is not equal to candidate1, update candidate2.\n else if (count2 == 0 && nums[i] != candidate1) {\n count2 = 1;\n candidate2 = nums[i];\n } \n // Update counts for candidate1 and candidate2.\n else if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n } \n // If the current number is different from both candidates, decrement their counts.\n else {\n count1--;\n count2--;\n }\n }\n\n List<Integer> result = new ArrayList<>();\n int threshold = nums.length / 3; // Threshold for majority element\n\n // Second pass to count occurrences of the potential majority elements.\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < nums.length; i++) {\n if (candidate1 == nums[i]) {\n count1++;\n } else if (candidate2 == nums[i]) {\n count2++;\n }\n }\n\n // Check if the counts of potential majority elements are greater than n/3 and add them to the result.\n if (count1 > threshold) {\n result.add(candidate1);\n }\n if (count2 > threshold) {\n result.add(candidate2);\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def majorityElement(self, nums: list[int]) -> list[int]:\n # Counters for the potential majority elements\n count1 = count2 = 0 \n # Potential majority element candidates\n candidate1 = candidate2 = 0\n\n # First pass to find potential majority elements.\n for num in nums:\n # If count1 is 0 and the current number is not equal to candidate2, update candidate1.\n if count1 == 0 and num != candidate2:\n count1 = 1\n candidate1 = num\n\n # If count2 is 0 and the current number is not equal to candidate1, update candidate2.\n elif count2 == 0 and num != candidate1:\n count2 = 1\n candidate2 = num\n \n # Update counts for candidate1 and candidate2.\n elif candidate1 == num:\n count1 += 1\n elif candidate2 == num:\n count2 += 1\n\n # If the current number is different from both candidates, decrement their counts.\n else:\n count1 -= 1\n count2 -= 1\n\n result = []\n threshold = len(nums) // 3 # Threshold for majority element\n\n # Second pass to count occurrences of the potential majority elements.\n count1 = count2 = 0\n for num in nums:\n if candidate1 == num:\n count1 += 1\n elif candidate2 == num:\n count2 += 1\n\n # Check if the counts of potential majority elements are greater than n/3 and add them to the result.\n if count1 > threshold:\n result.append(candidate1)\n if count2 > threshold:\n result.append(candidate2)\n\n return result\n\n```\n\n\n\n\n\n | 234 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Video Solution | Explanation With Drawings | In Depth | C++ | Java | Python 3 | majority-element-ii | 1 | 1 | # Intuition and approach discussed in detail in video solution\nhttps://youtu.be/l4wooU0Tgws\n# Code\nC++\n```\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int freq1 = 0, freq2 = 0;\n int cand1 = 23, cand2 = 0;\n for(auto & num : nums){\n if(num == cand1)freq1++;\n else if(num == cand2)freq2++;\n else if(freq1 == 0){\n freq1 = 1;\n cand1 = num;\n }\n else if(freq2 == 0){\n freq2 = 1;\n cand2 = num;\n }else{\n freq1--;\n freq2--;\n }\n }\n freq1 = freq2 = 0;\n for(auto num : nums){\n if(num == cand2)freq2++;\n else if(num == cand1)freq1++;\n }\n vector<int> res;\n int sz = nums.size();\n if(sz / 3 < freq1)res.push_back(cand1);\n if(sz / 3 < freq2)res.push_back(cand2);\n \n return res;\n }\n};\n```\nJava\n```\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n int freq1 = 0, freq2 = 0;\n int cand1 = 23, cand2 = 0;\n for(var num : nums){\n if(num == cand1)freq1++;\n else if(num == cand2)freq2++;\n else if(freq1 == 0){\n freq1 = 1;\n cand1 = num;\n }\n else if(freq2 == 0){\n freq2 = 1;\n cand2 = num;\n }else{\n freq1--;\n freq2--;\n }\n }\n freq1 = freq2 = 0;\n for(var num : nums){\n if(num == cand2)freq2++;\n else if(num == cand1)freq1++;\n }\n List<Integer> res = new ArrayList<>();\n int sz = nums.length;\n if(sz / 3 < freq1)res.add(cand1);\n if(sz / 3 < freq2)res.add(cand2);\n \n return res;\n }\n}\n```\nPython 3\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n freq1, freq2 = 0, 0\n cand1, cand2 = 0, 0\n \n for num in nums:\n if num == cand1:\n freq1 += 1\n elif num == cand2:\n freq2 += 1\n elif freq1 == 0:\n freq1 = 1\n cand1 = num\n elif freq2 == 0:\n freq2 = 1\n cand2 = num\n else:\n freq1 -= 1\n freq2 -= 1\n freq1, freq2 = 0, 0\n for num in nums:\n if num == cand2:\n freq2 += 1\n elif num == cand1:\n freq1 += 1\n \n res = []\n sz = len(nums)\n if sz // 3 < freq1:\n res.append(cand1)\n if sz // 3 < freq2:\n res.append(cand2)\n \n return res\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Video Solution | Explanation With Drawings | In Depth | C++ | Java | Python 3 | majority-element-ii | 1 | 1 | # Intuition and approach discussed in detail in video solution\nhttps://youtu.be/l4wooU0Tgws\n# Code\nC++\n```\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int freq1 = 0, freq2 = 0;\n int cand1 = 23, cand2 = 0;\n for(auto & num : nums){\n if(num == cand1)freq1++;\n else if(num == cand2)freq2++;\n else if(freq1 == 0){\n freq1 = 1;\n cand1 = num;\n }\n else if(freq2 == 0){\n freq2 = 1;\n cand2 = num;\n }else{\n freq1--;\n freq2--;\n }\n }\n freq1 = freq2 = 0;\n for(auto num : nums){\n if(num == cand2)freq2++;\n else if(num == cand1)freq1++;\n }\n vector<int> res;\n int sz = nums.size();\n if(sz / 3 < freq1)res.push_back(cand1);\n if(sz / 3 < freq2)res.push_back(cand2);\n \n return res;\n }\n};\n```\nJava\n```\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n int freq1 = 0, freq2 = 0;\n int cand1 = 23, cand2 = 0;\n for(var num : nums){\n if(num == cand1)freq1++;\n else if(num == cand2)freq2++;\n else if(freq1 == 0){\n freq1 = 1;\n cand1 = num;\n }\n else if(freq2 == 0){\n freq2 = 1;\n cand2 = num;\n }else{\n freq1--;\n freq2--;\n }\n }\n freq1 = freq2 = 0;\n for(var num : nums){\n if(num == cand2)freq2++;\n else if(num == cand1)freq1++;\n }\n List<Integer> res = new ArrayList<>();\n int sz = nums.length;\n if(sz / 3 < freq1)res.add(cand1);\n if(sz / 3 < freq2)res.add(cand2);\n \n return res;\n }\n}\n```\nPython 3\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n freq1, freq2 = 0, 0\n cand1, cand2 = 0, 0\n \n for num in nums:\n if num == cand1:\n freq1 += 1\n elif num == cand2:\n freq2 += 1\n elif freq1 == 0:\n freq1 = 1\n cand1 = num\n elif freq2 == 0:\n freq2 = 1\n cand2 = num\n else:\n freq1 -= 1\n freq2 -= 1\n freq1, freq2 = 0, 0\n for num in nums:\n if num == cand2:\n freq2 += 1\n elif num == cand1:\n freq1 += 1\n \n res = []\n sz = len(nums)\n if sz // 3 < freq1:\n res.append(cand1)\n if sz // 3 < freq2:\n res.append(cand2)\n \n return res\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Python3 Solution | majority-element-ii | 0 | 1 | \n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n count=Counter(nums)\n ans=[]\n n=len(nums)\n for key,value in count.items():\n if value>(n//3):\n ans.append(key)\n return ans \n \n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Python3 Solution | majority-element-ii | 0 | 1 | \n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n count=Counter(nums)\n ans=[]\n n=len(nums)\n for key,value in count.items():\n if value>(n//3):\n ans.append(key)\n return ans \n \n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
🧠 >99% Python One-liner | majority-element-ii | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return [ k for k, v in Counter(nums).items() if v > len(nums) // 3 ]\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
🧠 >99% Python One-liner | majority-element-ii | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return [ k for k, v in Counter(nums).items() if v > len(nums) // 3 ]\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅97.21%🔥Easy Solution🔥1 line code🔥 | majority-element-ii | 1 | 1 | # Problem\n#### The problem you\'re describing is about finding elements in an integer array that appear more than a third of the total number of elements in the array. The task is to return all such elements.\n---\n# python Solution\n\n##### 1. Defining the majorityElement method: This method takes one argument, nums, which is the input integer array.\n\n##### 2. Using Counter to count occurrences: Counter(nums) is used to create a dictionary-like object where keys are elements from the nums array, and values are their respective counts.\n\n##### 3. List comprehension: The code uses a list comprehension to iterate over the items (key-value pairs) in the Counter(nums).items() dictionary-like object.\n\n##### 4. Filtering elements: For each item (num, count) in the dictionary, it checks if the count is greater than len(nums) // 3. If it is, the element num is included in the result list.\n\n##### 5. Returning the result: The list comprehension generates a list of elements that meet the condition (appearing more than a third of the total count), and this list is returned as the result of the majorityElement method.\n---\n# Code\n```python []\nclass Solution:\n def majorityElement(self, nums):\n return [num for num, count in Counter(nums).items() if count > len(nums) // 3]\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int candidate1 = 0, candidate2 = 1, count1 = 0, count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) count1++;\n else if (num == candidate2) count2++;\n else if (count1 == 0) candidate1 = num, count1 = 1;\n else if (count2 == 0) candidate2 = num, count2 = 1;\n else count1--, count2--;\n }\n\n count1 = count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) count1++;\n if (num == candidate2) count2++;\n }\n\n if (count1 > nums.size() / 3) result.push_back(candidate1);\n if (count2 > nums.size() / 3) result.push_back(candidate2);\n\n return result;\n }\n};\n\n```\n```C []\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int* result = NULL;\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n int threshold = numsSize / 3;\n\n for (int i = 0; i < numsSize; i++) {\n int num = nums[i];\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = count2 = 0;\n\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n\n int resultSize = 0;\n if (count1 > threshold) {\n result = (int*)malloc(sizeof(int));\n result[resultSize++] = candidate1;\n }\n if (count2 > threshold) {\n if (result == NULL) {\n result = (int*)malloc(sizeof(int));\n } else {\n result = (int*)realloc(result, 2 * sizeof(int));\n }\n result[resultSize++] = candidate2;\n }\n\n *returnSize = resultSize;\n return result;\n}\n\n```\n```javascript []\nvar majorityElement = function(nums) {\n let candidate1 = null, candidate2 = null, count1 = 0, count2 = 0;\n \n for (let num of nums) {\n if (num === candidate1) {\n count1++;\n } else if (num === candidate2) {\n count2++;\n } else if (count1 === 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 === 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n \n count1 = count2 = 0;\n \n for (let num of nums) {\n if (num === candidate1) count1++;\n else if (num === candidate2) count2++;\n }\n \n const threshold = Math.floor(nums.length / 3);\n const result = [];\n \n if (count1 > threshold) result.push(candidate1);\n if (count2 > threshold) result.push(candidate2);\n \n return result;\n};\n\n```\n```C# []\npublic class Solution {\n public IList<int> MajorityElement(int[] nums) {\n IList<int> result = new List<int>();\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n\n foreach (int num in nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = count2 = 0;\n foreach (int num in nums) {\n if (num == candidate1) count1++;\n if (num == candidate2) count2++;\n }\n\n int threshold = nums.Length / 3;\n\n if (count1 > threshold) result.Add(candidate1);\n if (count2 > threshold && candidate1 != candidate2) result.Add(candidate2);\n\n return result;\n }\n}\n\n```\n```Java []\npublic class Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n Map<Integer, Integer> counts = new HashMap<>();\n int n = nums.length;\n int threshold = n / 3;\n\n for (int num : nums) {\n counts.put(num, counts.getOrDefault(num, 0) + 1);\n }\n\n for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {\n if (entry.getValue() > threshold) {\n result.add(entry.getKey());\n }\n }\n\n return result;\n }\n}\n```\n```PHP []\nclass Solution {\n function majorityElement($nums) {\n $candidate1 = null;\n $candidate2 = null;\n $count1 = 0;\n $count2 = 0;\n \n foreach ($nums as $num) {\n if ($num === $candidate1) {\n $count1++;\n } elseif ($num === $candidate2) {\n $count2++;\n } elseif ($count1 === 0) {\n $candidate1 = $num;\n $count1 = 1;\n } elseif ($count2 === 0) {\n $candidate2 = $num;\n $count2 = 1;\n } else {\n $count1--;\n $count2--;\n }\n }\n \n $count1 = 0;\n $count2 = 0;\n \n foreach ($nums as $num) {\n if ($num === $candidate1) {\n $count1++;\n } elseif ($num === $candidate2) {\n $count2++;\n }\n }\n \n $threshold = floor(count($nums) / 3);\n $result = [];\n \n if ($count1 > $threshold) {\n $result[] = $candidate1;\n }\n if ($count2 > $threshold) {\n $result[] = $candidate2;\n }\n \n return $result;\n }\n}\n\n```\n---\n\n | 29 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅97.21%🔥Easy Solution🔥1 line code🔥 | majority-element-ii | 1 | 1 | # Problem\n#### The problem you\'re describing is about finding elements in an integer array that appear more than a third of the total number of elements in the array. The task is to return all such elements.\n---\n# python Solution\n\n##### 1. Defining the majorityElement method: This method takes one argument, nums, which is the input integer array.\n\n##### 2. Using Counter to count occurrences: Counter(nums) is used to create a dictionary-like object where keys are elements from the nums array, and values are their respective counts.\n\n##### 3. List comprehension: The code uses a list comprehension to iterate over the items (key-value pairs) in the Counter(nums).items() dictionary-like object.\n\n##### 4. Filtering elements: For each item (num, count) in the dictionary, it checks if the count is greater than len(nums) // 3. If it is, the element num is included in the result list.\n\n##### 5. Returning the result: The list comprehension generates a list of elements that meet the condition (appearing more than a third of the total count), and this list is returned as the result of the majorityElement method.\n---\n# Code\n```python []\nclass Solution:\n def majorityElement(self, nums):\n return [num for num, count in Counter(nums).items() if count > len(nums) // 3]\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int candidate1 = 0, candidate2 = 1, count1 = 0, count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) count1++;\n else if (num == candidate2) count2++;\n else if (count1 == 0) candidate1 = num, count1 = 1;\n else if (count2 == 0) candidate2 = num, count2 = 1;\n else count1--, count2--;\n }\n\n count1 = count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) count1++;\n if (num == candidate2) count2++;\n }\n\n if (count1 > nums.size() / 3) result.push_back(candidate1);\n if (count2 > nums.size() / 3) result.push_back(candidate2);\n\n return result;\n }\n};\n\n```\n```C []\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int* result = NULL;\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n int threshold = numsSize / 3;\n\n for (int i = 0; i < numsSize; i++) {\n int num = nums[i];\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = count2 = 0;\n\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n\n int resultSize = 0;\n if (count1 > threshold) {\n result = (int*)malloc(sizeof(int));\n result[resultSize++] = candidate1;\n }\n if (count2 > threshold) {\n if (result == NULL) {\n result = (int*)malloc(sizeof(int));\n } else {\n result = (int*)realloc(result, 2 * sizeof(int));\n }\n result[resultSize++] = candidate2;\n }\n\n *returnSize = resultSize;\n return result;\n}\n\n```\n```javascript []\nvar majorityElement = function(nums) {\n let candidate1 = null, candidate2 = null, count1 = 0, count2 = 0;\n \n for (let num of nums) {\n if (num === candidate1) {\n count1++;\n } else if (num === candidate2) {\n count2++;\n } else if (count1 === 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 === 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n \n count1 = count2 = 0;\n \n for (let num of nums) {\n if (num === candidate1) count1++;\n else if (num === candidate2) count2++;\n }\n \n const threshold = Math.floor(nums.length / 3);\n const result = [];\n \n if (count1 > threshold) result.push(candidate1);\n if (count2 > threshold) result.push(candidate2);\n \n return result;\n};\n\n```\n```C# []\npublic class Solution {\n public IList<int> MajorityElement(int[] nums) {\n IList<int> result = new List<int>();\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n\n foreach (int num in nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = count2 = 0;\n foreach (int num in nums) {\n if (num == candidate1) count1++;\n if (num == candidate2) count2++;\n }\n\n int threshold = nums.Length / 3;\n\n if (count1 > threshold) result.Add(candidate1);\n if (count2 > threshold && candidate1 != candidate2) result.Add(candidate2);\n\n return result;\n }\n}\n\n```\n```Java []\npublic class Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n Map<Integer, Integer> counts = new HashMap<>();\n int n = nums.length;\n int threshold = n / 3;\n\n for (int num : nums) {\n counts.put(num, counts.getOrDefault(num, 0) + 1);\n }\n\n for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {\n if (entry.getValue() > threshold) {\n result.add(entry.getKey());\n }\n }\n\n return result;\n }\n}\n```\n```PHP []\nclass Solution {\n function majorityElement($nums) {\n $candidate1 = null;\n $candidate2 = null;\n $count1 = 0;\n $count2 = 0;\n \n foreach ($nums as $num) {\n if ($num === $candidate1) {\n $count1++;\n } elseif ($num === $candidate2) {\n $count2++;\n } elseif ($count1 === 0) {\n $candidate1 = $num;\n $count1 = 1;\n } elseif ($count2 === 0) {\n $candidate2 = $num;\n $count2 = 1;\n } else {\n $count1--;\n $count2--;\n }\n }\n \n $count1 = 0;\n $count2 = 0;\n \n foreach ($nums as $num) {\n if ($num === $candidate1) {\n $count1++;\n } elseif ($num === $candidate2) {\n $count2++;\n }\n }\n \n $threshold = floor(count($nums) / 3);\n $result = [];\n \n if ($count1 > $threshold) {\n $result[] = $candidate1;\n }\n if ($count2 > $threshold) {\n $result[] = $candidate2;\n }\n \n return $result;\n }\n}\n\n```\n---\n\n | 29 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅ One Line Python || BEATS 5% ✅ | majority-element-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n***If you can do it in many lines... you can do it in one!***\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return list(set(i for i in nums if nums.count(i) > len(nums)// 3))\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅ One Line Python || BEATS 5% ✅ | majority-element-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n***If you can do it in many lines... you can do it in one!***\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return list(set(i for i in nums if nums.count(i) > len(nums)// 3))\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Easy Python Solution | majority-element-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n count = len(nums)//3\n ans = []\n hashmap = {}\n for n in nums:\n hashmap[n] = 1 + hashmap.get(n, 0)\n for key in hashmap:\n if hashmap[key] > count:\n ans.append(key)\n return ans\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Easy Python Solution | majority-element-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n count = len(nums)//3\n ans = []\n hashmap = {}\n for n in nums:\n hashmap[n] = 1 + hashmap.get(n, 0)\n for key in hashmap:\n if hashmap[key] > count:\n ans.append(key)\n return ans\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Two appoarches (TypeScript / Python3) || Simple solution with HashMap DS | majority-element-ii | 0 | 1 | # Intuition\nHere\'s a brief explanation of the problem:\n- there\'s a list of `nums`\n- our goal is to define such nums, that fits the next constraint\n```\nfreqOfNum > nums.length / 3\n```\n\nThis approach is using a [HashMap DS](https://en.wikipedia.org/wiki/Hash_table) to store frequencies of integers, and next iterating with checking the constraint **above**.\n\n# Approach\n1. declare an empty frequency `map`\n2. fill the `map` by iterating over `nums`\n3. define `ans` and `threshold = nums.length / 3`\n4. iterate over `map` and check the constraint\n5. if the constraint **is fitted**, add this num to the `ans`\n6. return `ans`\n\n# Complexity\n- Time complexity: **O(n)**, for twice iterating over `nums` and `map`, respectively.\n\n- Space complexity: **O(n)**, to store `nums` in `map`, since all of the `nums` could be **unique**.\n\n# Code in Python3 (using list comprehension)\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return [k for k, v in Counter(nums).items() if v > len(nums) / 3]\n};\n```\n# Code in TypeScript\n```\nfunction majorityElement(nums: number[]): number[] {\n const map = new Map()\n\n for (let i = 0; i < nums.length; i++) {\n map.set(nums[i], (map.get(nums[i]) || 0) + 1)\n }\n\n const ans = []\n const threshold = nums.length / 3\n\n for (const [k, v] of map.entries()) {\n if (v > threshold) {\n ans.push(k)\n }\n }\n\n return ans\n};\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Two appoarches (TypeScript / Python3) || Simple solution with HashMap DS | majority-element-ii | 0 | 1 | # Intuition\nHere\'s a brief explanation of the problem:\n- there\'s a list of `nums`\n- our goal is to define such nums, that fits the next constraint\n```\nfreqOfNum > nums.length / 3\n```\n\nThis approach is using a [HashMap DS](https://en.wikipedia.org/wiki/Hash_table) to store frequencies of integers, and next iterating with checking the constraint **above**.\n\n# Approach\n1. declare an empty frequency `map`\n2. fill the `map` by iterating over `nums`\n3. define `ans` and `threshold = nums.length / 3`\n4. iterate over `map` and check the constraint\n5. if the constraint **is fitted**, add this num to the `ans`\n6. return `ans`\n\n# Complexity\n- Time complexity: **O(n)**, for twice iterating over `nums` and `map`, respectively.\n\n- Space complexity: **O(n)**, to store `nums` in `map`, since all of the `nums` could be **unique**.\n\n# Code in Python3 (using list comprehension)\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return [k for k, v in Counter(nums).items() if v > len(nums) / 3]\n};\n```\n# Code in TypeScript\n```\nfunction majorityElement(nums: number[]): number[] {\n const map = new Map()\n\n for (let i = 0; i < nums.length; i++) {\n map.set(nums[i], (map.get(nums[i]) || 0) + 1)\n }\n\n const ans = []\n const threshold = nums.length / 3\n\n for (const [k, v] of map.entries()) {\n if (v > threshold) {\n ans.push(k)\n }\n }\n\n return ans\n};\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Beginner's friendly Solution using Hashmap | majority-element-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n freq={}\n ans=[]\n for i in range(0,len(nums)):\n if(nums[i] in freq):\n freq[nums[i]]+=1\n else:\n freq[nums[i]]=0\n for i in freq:\n if freq[i]>=len(nums)//3:\n ans.append(i)\n return ans\n\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Beginner's friendly Solution using Hashmap | majority-element-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n freq={}\n ans=[]\n for i in range(0,len(nums)):\n if(nums[i] in freq):\n freq[nums[i]]+=1\n else:\n freq[nums[i]]=0\n for i in freq:\n if freq[i]>=len(nums)//3:\n ans.append(i)\n return ans\n\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅ 92.99% Boyer-Moore Voting Algorithm | majority-element-ii | 1 | 1 | # Intuition\nWhen faced with the problem of finding elements that appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times, our initial thought may lean towards using a hash map to count the occurrences of each element. However, the problem challenges us to think beyond this obvious solution, specifically hinting at a linear time and O(1) space complexity solution.\n\nThe Boyer-Moore Voting Algorithm, which efficiently finds a majority element in an array, can be extended to this problem. At most, only two numbers can appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times. Keeping this fact in mind can guide our approach.\n\n## Live Coding & Explain\nhttps://youtu.be/j30EwQrrnUk?si=j9kDquWuj_UOd5Ay\n\n# Approach\n1. **Initialization**: We initiate two candidate variables and their respective counters. These candidates will represent potential elements that could appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times.\n \n2. **Voting Mechanism**: As we traverse through the array:\n - If we find a number equal to either of our candidates, we increment the respective counter.\n - If one of the counters is zero, we replace the respective candidate with the current number and reset the counter.\n - If the current number doesn\'t match either candidate, both counters are decremented.\n \n3. **Verification**: The two candidates selected might not actually be numbers that appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times. So, we need to traverse the array again to count and verify their occurrences.\n\n# Why It Works?\nThe Boyer-Moore Voting Algorithm leverages the fact that any number that appears more than $$ \\left\\lfloor \\frac{n}{k} \\right\\rfloor $$ times will have at most $$ k-1 $$ such numbers. By generalizing the algorithm to maintain two candidates and counters, we can handle the $$ k=3 $$ case for this problem. The decrementing of counters ensures that if a number truly appears more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times, it will survive till the end.\n\n# What We Have Learned?\nThis problem teaches us the power of algorithm generalization and thinking beyond straightforward hash map solutions. The Boyer-Moore Voting Algorithm\'s extension showcases the importance of understanding underlying principles and insights of algorithms, enabling us to apply them in varied scenarios.\n\n# Complexity\n- **Time complexity**: $$O(n)$$. We go through the list thrice: once for voting and twice for counting.\n- **Space complexity**: $$O(1)$$. Only a constant amount of extra space is used, irrespective of the input size.\n\n\n# Code\n``` Python []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n if not nums:\n return []\n \n candidate1, candidate2, count1, count2 = 0, 1, 0, 0\n \n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n elif count1 == 0:\n candidate1, count1 = num, 1\n elif count2 == 0:\n candidate2, count2 = num, 1\n else:\n count1 -= 1\n count2 -= 1\n \n return [num for num in (candidate1, candidate2) if nums.count(num) > len(nums) // 3]\n\n```\n``` Go []\nfunc majorityElement(nums []int) []int {\n var candidate1, candidate2, count1, count2 int = 0, 1, 0, 0\n \n for _, num := range nums {\n if num == candidate1 {\n count1++\n } else if num == candidate2 {\n count2++\n } else if count1 == 0 {\n candidate1 = num\n count1 = 1\n } else if count2 == 0 {\n candidate2 = num\n count2 = 1\n } else {\n count1--\n count2--\n }\n }\n\n count1, count2 = 0, 0\n for _, num := range nums {\n if num == candidate1 {\n count1++\n } else if num == candidate2 {\n count2++\n }\n }\n\n var result []int\n if count1 > len(nums)/3 {\n result = append(result, candidate1)\n }\n if count2 > len(nums)/3 {\n result = append(result, candidate2)\n }\n return result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn majority_element(nums: Vec<i32>) -> Vec<i32> {\n let (mut candidate1, mut candidate2, mut count1, mut count2) = (0, 1, 0, 0);\n for &num in &nums {\n if num == candidate1 {\n count1 += 1;\n } else if num == candidate2 {\n count2 += 1;\n } else if count1 == 0 {\n candidate1 = num;\n count1 = 1;\n } else if count2 == 0 {\n candidate2 = num;\n count2 = 1;\n } else {\n count1 -= 1;\n count2 -= 1;\n }\n }\n\n let mut result = Vec::new();\n if nums.iter().filter(|&&x| x == candidate1).count() > nums.len() / 3 {\n result.push(candidate1);\n }\n if nums.iter().filter(|&&x| x == candidate2).count() > nums.len() / 3 {\n result.push(candidate2);\n }\n result\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> majorityElement(std::vector<int>& nums) {\n int candidate1 = 0, candidate2 = 1, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n \n std::vector<int> result;\n if (std::count(nums.begin(), nums.end(), candidate1) > nums.size() / 3) result.push_back(candidate1);\n if (std::count(nums.begin(), nums.end(), candidate2) > nums.size() / 3) result.push_back(candidate2);\n return result;\n }\n};\n```\n``` Java []\nimport java.util.*;\n\npublic class Solution {\n public List<Integer> majorityElement(int[] nums) {\n Integer candidate1 = null, candidate2 = null;\n int count1 = 0, count2 = 0;\n for (int num : nums) {\n if (candidate1 != null && num == candidate1.intValue()) {\n count1++;\n } else if (candidate2 != null && num == candidate2.intValue()) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (candidate1 != null && num == candidate1.intValue()) {\n count1++;\n } \n if (candidate2 != null && num == candidate2.intValue()) {\n count2++;\n }\n }\n\n List<Integer> result = new ArrayList<>();\n if (count1 > nums.length / 3) result.add(candidate1);\n if (count2 > nums.length / 3) result.add(candidate2);\n return result;\n }\n}\n```\n``` JavaScript []\nvar majorityElement = function(nums) {\n let candidate1 = 0, candidate2 = 1, count1 = 0, count2 = 0;\n\n for (let num of nums) {\n if (num === candidate1) {\n count1++;\n } else if (num === candidate2) {\n count2++;\n } else if (count1 === 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 === 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n let result = [];\n if (nums.filter(n => n === candidate1).length > nums.length / 3) result.push(candidate1);\n if (nums.filter(n => n === candidate2).length > nums.length / 3) result.push(candidate2);\n return result;\n};\n```\n``` PHP []\nclass Solution {\n\n function majorityElement($nums) {\n $candidate1 = 0;\n $candidate2 = 1;\n $count1 = 0;\n $count2 = 0;\n\n foreach ($nums as $num) {\n if ($num == $candidate1) {\n $count1++;\n } elseif ($num == $candidate2) {\n $count2++;\n } elseif ($count1 == 0) {\n $candidate1 = $num;\n $count1 = 1;\n } elseif ($count2 == 0) {\n $candidate2 = $num;\n $count2 = 1;\n } else {\n $count1--;\n $count2--;\n }\n }\n\n $result = [];\n if (count(array_filter($nums, function($n) use ($candidate1) { return $n == $candidate1; })) > count($nums) / 3) {\n $result[] = $candidate1;\n }\n if (count(array_filter($nums, function($n) use ($candidate2) { return $n == $candidate2; })) > count($nums) / 3) {\n $result[] = $candidate2;\n }\n return $result;\n }\n}\n```\n``` C# []\npublic class Solution {\n public IList<int> MajorityElement(int[] nums) {\n int? candidate1 = null, candidate2 = null, count1 = 0, count2 = 0;\n foreach (int num in nums) {\n if (candidate1.HasValue && num == candidate1) {\n count1++;\n } else if (candidate2.HasValue && num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n \n var result = new List<int>();\n if (nums.Count(n => n == candidate1) > nums.Length / 3) result.Add(candidate1.Value);\n if (nums.Count(n => n == candidate2) > nums.Length / 3) result.Add(candidate2.Value);\n return result;\n }\n}\n```\n\n## Performance\n| Language | Execution Time (ms) | Memory Usage |\n|------------|---------------------|----------------|\n| Rust | 1 | 2.3 MB |\n| Java | 4 | 47.3 MB |\n| C++ | 9 | 16.3 MB |\n| Go | 11 | 5 MB |\n| PHP | 32 | 23.3 MB |\n| JavaScript | 66 | 48.5 MB |\n| Python3 | 102 | 17.8 MB |\n| C# | 145 | 46.4 MB |\n\n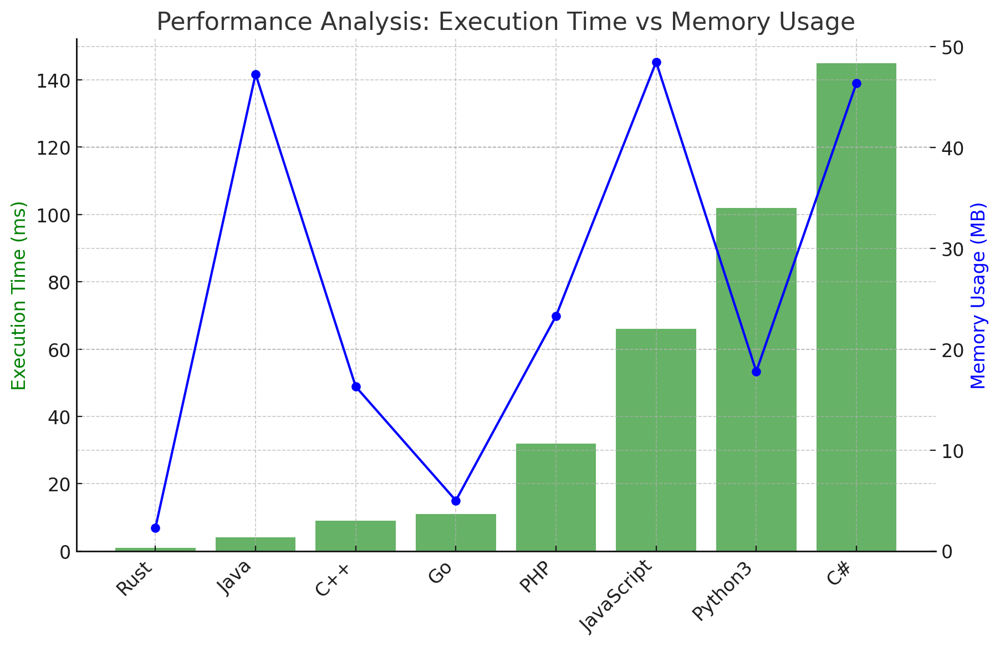\n\n | 50 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅ 92.99% Boyer-Moore Voting Algorithm | majority-element-ii | 1 | 1 | # Intuition\nWhen faced with the problem of finding elements that appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times, our initial thought may lean towards using a hash map to count the occurrences of each element. However, the problem challenges us to think beyond this obvious solution, specifically hinting at a linear time and O(1) space complexity solution.\n\nThe Boyer-Moore Voting Algorithm, which efficiently finds a majority element in an array, can be extended to this problem. At most, only two numbers can appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times. Keeping this fact in mind can guide our approach.\n\n## Live Coding & Explain\nhttps://youtu.be/j30EwQrrnUk?si=j9kDquWuj_UOd5Ay\n\n# Approach\n1. **Initialization**: We initiate two candidate variables and their respective counters. These candidates will represent potential elements that could appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times.\n \n2. **Voting Mechanism**: As we traverse through the array:\n - If we find a number equal to either of our candidates, we increment the respective counter.\n - If one of the counters is zero, we replace the respective candidate with the current number and reset the counter.\n - If the current number doesn\'t match either candidate, both counters are decremented.\n \n3. **Verification**: The two candidates selected might not actually be numbers that appear more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times. So, we need to traverse the array again to count and verify their occurrences.\n\n# Why It Works?\nThe Boyer-Moore Voting Algorithm leverages the fact that any number that appears more than $$ \\left\\lfloor \\frac{n}{k} \\right\\rfloor $$ times will have at most $$ k-1 $$ such numbers. By generalizing the algorithm to maintain two candidates and counters, we can handle the $$ k=3 $$ case for this problem. The decrementing of counters ensures that if a number truly appears more than $$ \\left\\lfloor \\frac{n}{3} \\right\\rfloor $$ times, it will survive till the end.\n\n# What We Have Learned?\nThis problem teaches us the power of algorithm generalization and thinking beyond straightforward hash map solutions. The Boyer-Moore Voting Algorithm\'s extension showcases the importance of understanding underlying principles and insights of algorithms, enabling us to apply them in varied scenarios.\n\n# Complexity\n- **Time complexity**: $$O(n)$$. We go through the list thrice: once for voting and twice for counting.\n- **Space complexity**: $$O(1)$$. Only a constant amount of extra space is used, irrespective of the input size.\n\n\n# Code\n``` Python []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n if not nums:\n return []\n \n candidate1, candidate2, count1, count2 = 0, 1, 0, 0\n \n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n elif count1 == 0:\n candidate1, count1 = num, 1\n elif count2 == 0:\n candidate2, count2 = num, 1\n else:\n count1 -= 1\n count2 -= 1\n \n return [num for num in (candidate1, candidate2) if nums.count(num) > len(nums) // 3]\n\n```\n``` Go []\nfunc majorityElement(nums []int) []int {\n var candidate1, candidate2, count1, count2 int = 0, 1, 0, 0\n \n for _, num := range nums {\n if num == candidate1 {\n count1++\n } else if num == candidate2 {\n count2++\n } else if count1 == 0 {\n candidate1 = num\n count1 = 1\n } else if count2 == 0 {\n candidate2 = num\n count2 = 1\n } else {\n count1--\n count2--\n }\n }\n\n count1, count2 = 0, 0\n for _, num := range nums {\n if num == candidate1 {\n count1++\n } else if num == candidate2 {\n count2++\n }\n }\n\n var result []int\n if count1 > len(nums)/3 {\n result = append(result, candidate1)\n }\n if count2 > len(nums)/3 {\n result = append(result, candidate2)\n }\n return result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn majority_element(nums: Vec<i32>) -> Vec<i32> {\n let (mut candidate1, mut candidate2, mut count1, mut count2) = (0, 1, 0, 0);\n for &num in &nums {\n if num == candidate1 {\n count1 += 1;\n } else if num == candidate2 {\n count2 += 1;\n } else if count1 == 0 {\n candidate1 = num;\n count1 = 1;\n } else if count2 == 0 {\n candidate2 = num;\n count2 = 1;\n } else {\n count1 -= 1;\n count2 -= 1;\n }\n }\n\n let mut result = Vec::new();\n if nums.iter().filter(|&&x| x == candidate1).count() > nums.len() / 3 {\n result.push(candidate1);\n }\n if nums.iter().filter(|&&x| x == candidate2).count() > nums.len() / 3 {\n result.push(candidate2);\n }\n result\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> majorityElement(std::vector<int>& nums) {\n int candidate1 = 0, candidate2 = 1, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n \n std::vector<int> result;\n if (std::count(nums.begin(), nums.end(), candidate1) > nums.size() / 3) result.push_back(candidate1);\n if (std::count(nums.begin(), nums.end(), candidate2) > nums.size() / 3) result.push_back(candidate2);\n return result;\n }\n};\n```\n``` Java []\nimport java.util.*;\n\npublic class Solution {\n public List<Integer> majorityElement(int[] nums) {\n Integer candidate1 = null, candidate2 = null;\n int count1 = 0, count2 = 0;\n for (int num : nums) {\n if (candidate1 != null && num == candidate1.intValue()) {\n count1++;\n } else if (candidate2 != null && num == candidate2.intValue()) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (candidate1 != null && num == candidate1.intValue()) {\n count1++;\n } \n if (candidate2 != null && num == candidate2.intValue()) {\n count2++;\n }\n }\n\n List<Integer> result = new ArrayList<>();\n if (count1 > nums.length / 3) result.add(candidate1);\n if (count2 > nums.length / 3) result.add(candidate2);\n return result;\n }\n}\n```\n``` JavaScript []\nvar majorityElement = function(nums) {\n let candidate1 = 0, candidate2 = 1, count1 = 0, count2 = 0;\n\n for (let num of nums) {\n if (num === candidate1) {\n count1++;\n } else if (num === candidate2) {\n count2++;\n } else if (count1 === 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 === 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n let result = [];\n if (nums.filter(n => n === candidate1).length > nums.length / 3) result.push(candidate1);\n if (nums.filter(n => n === candidate2).length > nums.length / 3) result.push(candidate2);\n return result;\n};\n```\n``` PHP []\nclass Solution {\n\n function majorityElement($nums) {\n $candidate1 = 0;\n $candidate2 = 1;\n $count1 = 0;\n $count2 = 0;\n\n foreach ($nums as $num) {\n if ($num == $candidate1) {\n $count1++;\n } elseif ($num == $candidate2) {\n $count2++;\n } elseif ($count1 == 0) {\n $candidate1 = $num;\n $count1 = 1;\n } elseif ($count2 == 0) {\n $candidate2 = $num;\n $count2 = 1;\n } else {\n $count1--;\n $count2--;\n }\n }\n\n $result = [];\n if (count(array_filter($nums, function($n) use ($candidate1) { return $n == $candidate1; })) > count($nums) / 3) {\n $result[] = $candidate1;\n }\n if (count(array_filter($nums, function($n) use ($candidate2) { return $n == $candidate2; })) > count($nums) / 3) {\n $result[] = $candidate2;\n }\n return $result;\n }\n}\n```\n``` C# []\npublic class Solution {\n public IList<int> MajorityElement(int[] nums) {\n int? candidate1 = null, candidate2 = null, count1 = 0, count2 = 0;\n foreach (int num in nums) {\n if (candidate1.HasValue && num == candidate1) {\n count1++;\n } else if (candidate2.HasValue && num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n \n var result = new List<int>();\n if (nums.Count(n => n == candidate1) > nums.Length / 3) result.Add(candidate1.Value);\n if (nums.Count(n => n == candidate2) > nums.Length / 3) result.Add(candidate2.Value);\n return result;\n }\n}\n```\n\n## Performance\n| Language | Execution Time (ms) | Memory Usage |\n|------------|---------------------|----------------|\n| Rust | 1 | 2.3 MB |\n| Java | 4 | 47.3 MB |\n| C++ | 9 | 16.3 MB |\n| Go | 11 | 5 MB |\n| PHP | 32 | 23.3 MB |\n| JavaScript | 66 | 48.5 MB |\n| Python3 | 102 | 17.8 MB |\n| C# | 145 | 46.4 MB |\n\n\n\n | 50 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Solved using 2 Approaches | majority-element-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1st intuition was to use dictionary, will iterate through the array and store the integer in the dictionary and update its count as the integer is encountered again\n# Approach 1\n<!-- Describe your approach to solving the problem. -->\nAs per intuition, the implementation is straight forward, simply declare an empty dictionary `mydict`.\nIf the current integer is not in `mydict.keys()` we will insert the integer as key and its value as 1 (here 1 denotes the count) .\nBut if the current integer is in `mydict.keys()`we will increment the its count value.\nAfter the iteration is complete, we will iterate through dictionary and the key whose value is greater than \u230A n/3 \u230B will be added in the result array.\nAfter that iteration is over, we will simply return that array.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n m = len(nums) // 3\n mydict = {}\n for i in range(len(nums)):\n if nums[i] in mydict.keys():\n mydict[nums[i]] +=1\n else:\n mydict.update({nums[i] : 1})\n nums = []\n for i,j in mydict.items():\n if j > m:\n nums.append(i)\n return nums\n```\nit can also be coded as:\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return [k for k,v in Counter(nums).items() if v > len(nums)//3]\n```\n# Approach 2\n<!-- Describe your approach to solving the problem. -->\nAnother way I thought is to 1st sort the given `nums` array, this way we will have same integers clustered together. Now we will iterate through 1st index (considering it is 0-index array) till the end. If the current integer is similar to previous integer then we will increment the `count` of that variable else we will check if value of count is greater than \u230A n/3 \u230B, if yes we will store the current element in a seperate array `ans` (which will be our result array) , then restore count to 1 and if value of count is not greater than \u230A n/3 \u230B we simply restore count to 1.\nAfter the iteration is complete we still need to check if count is greater than \u230A n/3 \u230B one last time so that we dont miss to check the count of last cluster of integers. After that simply return the `ans` array\n# Complexity\n- Time complexity:$$ O(n log n) $$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n nums.sort()\n ans = []\n count = 1\n m = len(nums)//3\n for i in range(1,len(nums)):\n if nums[i] == nums[i-1]:\n count += 1\n else:\n if count > m:\n print(count)\n ans.append(nums[i-1])\n count = 1\n if count > m:\n ans.append(nums[-1])\n return ans\n```\n\n\nOverall as per time complexity Approach 1 is better!\nUpvote if you like :) | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Solved using 2 Approaches | majority-element-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1st intuition was to use dictionary, will iterate through the array and store the integer in the dictionary and update its count as the integer is encountered again\n# Approach 1\n<!-- Describe your approach to solving the problem. -->\nAs per intuition, the implementation is straight forward, simply declare an empty dictionary `mydict`.\nIf the current integer is not in `mydict.keys()` we will insert the integer as key and its value as 1 (here 1 denotes the count) .\nBut if the current integer is in `mydict.keys()`we will increment the its count value.\nAfter the iteration is complete, we will iterate through dictionary and the key whose value is greater than \u230A n/3 \u230B will be added in the result array.\nAfter that iteration is over, we will simply return that array.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n m = len(nums) // 3\n mydict = {}\n for i in range(len(nums)):\n if nums[i] in mydict.keys():\n mydict[nums[i]] +=1\n else:\n mydict.update({nums[i] : 1})\n nums = []\n for i,j in mydict.items():\n if j > m:\n nums.append(i)\n return nums\n```\nit can also be coded as:\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n return [k for k,v in Counter(nums).items() if v > len(nums)//3]\n```\n# Approach 2\n<!-- Describe your approach to solving the problem. -->\nAnother way I thought is to 1st sort the given `nums` array, this way we will have same integers clustered together. Now we will iterate through 1st index (considering it is 0-index array) till the end. If the current integer is similar to previous integer then we will increment the `count` of that variable else we will check if value of count is greater than \u230A n/3 \u230B, if yes we will store the current element in a seperate array `ans` (which will be our result array) , then restore count to 1 and if value of count is not greater than \u230A n/3 \u230B we simply restore count to 1.\nAfter the iteration is complete we still need to check if count is greater than \u230A n/3 \u230B one last time so that we dont miss to check the count of last cluster of integers. After that simply return the `ans` array\n# Complexity\n- Time complexity:$$ O(n log n) $$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n nums.sort()\n ans = []\n count = 1\n m = len(nums)//3\n for i in range(1,len(nums)):\n if nums[i] == nums[i-1]:\n count += 1\n else:\n if count > m:\n print(count)\n ans.append(nums[i-1])\n count = 1\n if count > m:\n ans.append(nums[-1])\n return ans\n```\n\n\nOverall as per time complexity Approach 1 is better!\nUpvote if you like :) | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
💯Faster✅💯 Lesser✅5 Methods🔥Simple Counting🔥Hashmap🔥Moore Voting Algorithm🔥Boyer-Moore Voting | majority-element-ii | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 5 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe "Majority Element II" problem is a well-known problem in computer science and data analysis. It\'s a variation of the more common "Majority Element" problem, which asks you to find an element in an array that appears more than half of the time. In the "Majority Element II" problem, the requirement is a bit stricter: we are tasked with finding all elements that appear more than \u230An/3\u230B times in an array of integers, where n is the length of the array.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering four different methods to solve this problem:\n1. Simple Counting\n2. Boyer-Moore Voting Algorithm\n3. Hash Map\n4. Sorting\n5. Moore Voting Algorithm\n\n# 1. Simple Counting: \n\n- Initialize an empty list result to store the majority elements.\n- Iterate through the unique elements in the input list nums using set(nums). This ensures that we examine each unique element only once.\n- For each unique element num in the set:\n - Count the number of occurrences of num in the original nums list using nums.count(num).\n - Check if the count is greater than \u230An/3\u230B, where n is the length of the nums list.\n - If the count meets the majority criteria, append num to the result list.\n- After iterating through all unique elements, return the result list containing the majority elements.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n^2) in the worst case.\n\n- \uD83D\uDE80 Space Complexity: O(k), where k is the number of unique elements in the nums.\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n res = []\n for i in set(nums):\n if nums.count(i) > len(nums) // 3:\n res.append(i)\n return res\n```\n```Java []\npublic class Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n Set<Integer> uniqueNums = new HashSet<>();\n for (int num : nums) {\n uniqueNums.add(num);\n }\n for (int num : uniqueNums) {\n int count = 0;\n for (int n : nums) {\n if (n == num) {\n count++;\n }\n }\n if (count > nums.length / 3) {\n result.add(num);\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n std::vector<int> majorityElement(std::vector<int>& nums) {\n std::vector<int> result; \n std::unordered_set<int> uniqueNums;\n for (int num : nums) {\n uniqueNums.insert(num);\n } \n for (int num : uniqueNums) {\n int count = 0;\n for (int n : nums) {\n if (n == num) {\n count++;\n }\n }\n if (count > nums.size() / 3) {\n result.push_back(num);\n }\n } \n return result;\n }\n};\n```\n```C []\nint cmpfunc(const void *a, const void *b) {\n return (*(int *)a - *(int *)b);\n}\n\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int* result = (int*)malloc(2 * sizeof(int));\n if (result == NULL) {\n *returnSize = 0;\n return NULL;\n }\n qsort(nums, numsSize, sizeof(int), cmpfunc);\n int candidate1 = nums[0];\n int candidate2 = nums[0];\n int count1 = 0;\n int count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = nums[i];\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = nums[i];\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n int resultSize = 0;\n if (count1 > numsSize / 3) {\n result[resultSize++] = candidate1;\n }\n if (count2 > numsSize / 3) {\n result[resultSize++] = candidate2;\n }\n *returnSize = resultSize;\n return result;\n}\n```\n# 2. Boyer-Moore Voting Algorithm:\n- Initialize two variables candidate1 and candidate2 to None, and two counters count1 and count2 to 0.\n- Iterate through the array.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n - If count1 is 0, set num as candidate1 and increment count1.\n - If count2 is 0, set num as candidate2 and increment count2.\n - If neither of the above conditions is met, decrement count1 and count2.\n- Initialize count1 and count2 to 0.\n- Iterate through the array again.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n- Check if count1 and count2 are greater than \u230An/3\u230B. If they are, both candidates are potential majority elements.\n- Iterate through the array again and count the occurrences of candidate1 and candidate2.\n- Return the candidates that meet the majority criteria.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n) - This algorithm makes three passes through the array.\n\n- \uD83D\uDE80 Space Complexity: O(1) - Constant extra space is used.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n candidate1, candidate2 = None, None\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n elif count1 == 0:\n candidate1 = num\n count1 = 1\n elif count2 == 0:\n candidate2 = num\n count2 = 1\n else:\n count1 -= 1\n count2 -= 1\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n result = []\n if count1 > len(nums) // 3:\n result.append(candidate1)\n if count2 > len(nums) // 3:\n result.append(candidate2)\n return result\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1++;\n } else if (count2 == 0) {\n candidate2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n if (count1 > nums.length / 3) {\n result.add(candidate1);\n }\n if (count2 > nums.length / 3) {\n result.add(candidate2);\n }\n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n int n = nums.size();\n if (count1 > n / 3) {\n result.push_back(candidate1);\n }\n if (count2 > n / 3) {\n result.push_back(candidate2);\n }\n return result;\n }\n};\n```\n```C []\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int candidate1 = 0, candidate2 = 0;\n int count1 = 0, count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = nums[i];\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = nums[i];\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n int* result = NULL;\n *returnSize = 0;\n \n if (count1 > numsSize / 3) {\n result = (int*)realloc(result, sizeof(int) * ((*returnSize) + 1));\n result[(*returnSize)++] = candidate1;\n }\n if (count2 > numsSize / 3) {\n result = (int*)realloc(result, sizeof(int) * ((*returnSize) + 1));\n result[(*returnSize)++] = candidate2;\n }\n return result;\n}\n```\n# 3. Hash Map:\n - Initialize an empty dictionary count_dict.\n- Iterate through the array.\n- For each element num in the array, increment its count in count_dict.\n- Iterate through the keys in count_dict.\n- Check if the count of each key is greater than \u230An/3\u230B.\n- Return the keys that meet the majority criteria.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n) - This algorithm makes a single pass through the array.\n\n- \uD83D\uDE80 Space Complexity: O(n) - Extra space is used to store counts in the dictionary.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n\n count_dict = Counter(nums)\n result = [num for num, count in count_dict.items() if count > len(nums) // 3]\n return result\n\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n Map<Integer, Integer> countMap = new HashMap<>();\n for (int num : nums) {\n countMap.put(num, countMap.getOrDefault(num, 0) + 1);\n }\n for (Map.Entry<Integer, Integer> entry : countMap.entrySet()) {\n if (entry.getValue() > nums.length / 3) {\n result.add(entry.getKey());\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n unordered_map<int, int> count_dict;\n vector<int> result;\n for (int num : nums) {\n count_dict[num]++;\n }\n int n = nums.size();\n for (auto& entry : count_dict) {\n if (entry.second > n / 3) {\n result.push_back(entry.first);\n }\n }\n return result;\n }\n};\n```\n```C []\nstruct Entry {\n int value;\n int count;\n};\n\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int mapSize = 2; \n struct Entry* hashMap = (struct Entry*)malloc(sizeof(struct Entry) * mapSize);\n if (hashMap == NULL) {\n perror("Memory allocation failed");\n exit(EXIT_FAILURE);\n }\n for (int i = 0; i < mapSize; i++) {\n hashMap[i].value = 0;\n hashMap[i].count = 0;\n }\n for (int i = 0; i < numsSize; i++) {\n bool found = false;\n for (int j = 0; j < mapSize; j++) {\n if (hashMap[j].count > 0 && hashMap[j].value == nums[i]) {\n hashMap[j].count++;\n found = true;\n break;\n }\n }\n if (!found) {\n bool inserted = false;\n for (int j = 0; j < mapSize; j++) {\n if (hashMap[j].count == 0) {\n hashMap[j].value = nums[i];\n hashMap[j].count = 1;\n inserted = true;\n break;\n }\n }\n if (!inserted) {\n mapSize *= 2;\n hashMap = (struct Entry*)realloc(hashMap, sizeof(struct Entry) * mapSize);\n if (hashMap == NULL) {\n perror("Memory allocation failed");\n exit(EXIT_FAILURE);\n }\n for (int j = mapSize / 2; j < mapSize; j++) {\n hashMap[j].value = 0;\n hashMap[j].count = 0;\n }\n i--;\n }\n }\n }\n int* result = (int*)malloc(sizeof(int) * mapSize);\n if (result == NULL) {\n perror("Memory allocation failed");\n exit(EXIT_FAILURE);\n }\n *returnSize = 0;\n for (int i = 0; i < mapSize; i++) {\n if (hashMap[i].count > numsSize / 3) {\n result[(*returnSize)++] = hashMap[i].value;\n }\n }\n free(hashMap);\n return result;\n}\n\n```\n# 4. Sorting:\n - Sort the input array.\n- Initialize an empty list result.\n- Initialize a variable count to 1.\n- Iterate through the sorted array, starting from the second element.\n- For each element num in the array:\n - If num is equal to the previous element, increment count.\n - If num is different from the previous element, check if count is greater than \u230An/3\u230B.\n - If count is greater, append the previous element to result.\n- Reset count to 1.\n- After the loop, check if the last element has a count greater than \u230An/3\u230B and append it to result.\nReturn result.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n log n) - This algorithm sorts the array.\n\n- \uD83D\uDE80 Space Complexity: O(1) - Constant extra space is used.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n nums.sort()\n result = []\n count = 1\n for i in range(1, len(nums)):\n if nums[i] == nums[i - 1]:\n count += 1\n else:\n if count > len(nums) // 3:\n result.append(nums[i - 1])\n count = 1\n if count > len(nums) // 3:\n result.append(nums[-1])\n return result\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n Arrays.sort(nums);\n int n = nums.length;\n int count = 1;\n for (int i = 1; i < n; i++) {\n if (nums[i] == nums[i - 1]) {\n count++;\n } else {\n if (count > n / 3) {\n result.add(nums[i - 1]);\n }\n count = 1;\n }\n }\n if (count > n / 3) {\n result.add(nums[n - 1]);\n }\n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int n = nums.size();\n sort(nums.begin(), nums.end());\n int count = 1;\n for (int i = 1; i < n; i++) {\n if (nums[i] == nums[i - 1]) {\n count++;\n } else {\n if (count > n / 3) {\n result.push_back(nums[i - 1]);\n }\n count = 1;\n }\n }\n if (count > n / 3) {\n result.push_back(nums[n - 1]);\n }\n return result;\n }\n};\n\n```\n```C []\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n qsort(nums, numsSize, sizeof(int), compare);\n int* result = (int*)malloc(sizeof(int) * 2); // At most 2 majority elements\n *returnSize = 0;\n int count = 1;\n for (int i = 1; i < numsSize; i++) {\n if (nums[i] == nums[i - 1]) {\n count++;\n } else {\n if (count > numsSize / 3) {\n result[(*returnSize)++] = nums[i - 1];\n }\n count = 1;\n }\n }\n if (count > numsSize / 3) {\n result[(*returnSize)++] = nums[numsSize - 1];\n }\n return result;\n}\n```\n# 5. Moore Voting Algorithm:\n - Initialize two variables candidate1 and candidate2 to None, and two counters count1 and count2 to 0.\n- Iterate through the array.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n - If count1 is 0, set num as candidate1 and increment count1.\n - If count2 is 0, set num as candidate2 and increment count2.\n - If neither of the above conditions is met, decrement count1 and count2.\n- Initialize count1 and count2 to 0.\n- Iterate through the array again.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n- Initialize two variables freq1 and freq2 to 0.\n- Iterate through the array.\n- For each element num in the array:\n - If num is equal to candidate1, increment freq1.\n - If num is equal to candidate2, increment freq2.\n- Check if freq1 and freq2 are greater than \u230An/3\u230B. If they are, both candidates are potential majority elements.\n- Return the candidates that meet the majority criteria.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n) - This algorithm makes three passes through the array.\n\n- \uD83D\uDE80 Space Complexity: O(1) - Constant extra space is used.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n candidate1, candidate2 = None, None\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n elif count1 == 0:\n candidate1 = num\n count1 = 1\n elif count2 == 0:\n candidate2 = num\n count2 = 1\n else:\n count1 -= 1\n count2 -= 1\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n result = []\n if count1 > len(nums) // 3:\n result.append(candidate1)\n if count2 > len(nums) // 3:\n result.append(candidate2)\n return result\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1++;\n } else if (count2 == 0) {\n candidate2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n \n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n if (count1 > nums.length / 3) {\n result.add(candidate1);\n }\n if (count2 > nums.length / 3) {\n result.add(candidate2);\n }\n \n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n int n = nums.size();\n if (count1 > n / 3) {\n result.push_back(candidate1);\n }\n if (count2 > n / 3) {\n result.push_back(candidate2);\n }\n\n return result;\n }\n};\n\n```\n```C []\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int candidate1 = 0, candidate2 = 0;\n int count1 = 0, count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = nums[i];\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = nums[i];\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n int* result = (int*)malloc(sizeof(int) * 2); // At most 2 majority elements\n *returnSize = 0;\n if (count1 > numsSize / 3) {\n result[(*returnSize)++] = candidate1;\n }\n if (count2 > numsSize / 3) {\n result[(*returnSize)++] = candidate2;\n }\n return result;\n}\n```\n# \uD83C\uDFC6Conclusion: \nThe Boyer-Moore Voting Algorithm and Moore Voting Algorithm are particularly efficient with O(1) space complexity.\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 46 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
💯Faster✅💯 Lesser✅5 Methods🔥Simple Counting🔥Hashmap🔥Moore Voting Algorithm🔥Boyer-Moore Voting | majority-element-ii | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 5 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe "Majority Element II" problem is a well-known problem in computer science and data analysis. It\'s a variation of the more common "Majority Element" problem, which asks you to find an element in an array that appears more than half of the time. In the "Majority Element II" problem, the requirement is a bit stricter: we are tasked with finding all elements that appear more than \u230An/3\u230B times in an array of integers, where n is the length of the array.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering four different methods to solve this problem:\n1. Simple Counting\n2. Boyer-Moore Voting Algorithm\n3. Hash Map\n4. Sorting\n5. Moore Voting Algorithm\n\n# 1. Simple Counting: \n\n- Initialize an empty list result to store the majority elements.\n- Iterate through the unique elements in the input list nums using set(nums). This ensures that we examine each unique element only once.\n- For each unique element num in the set:\n - Count the number of occurrences of num in the original nums list using nums.count(num).\n - Check if the count is greater than \u230An/3\u230B, where n is the length of the nums list.\n - If the count meets the majority criteria, append num to the result list.\n- After iterating through all unique elements, return the result list containing the majority elements.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n^2) in the worst case.\n\n- \uD83D\uDE80 Space Complexity: O(k), where k is the number of unique elements in the nums.\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n res = []\n for i in set(nums):\n if nums.count(i) > len(nums) // 3:\n res.append(i)\n return res\n```\n```Java []\npublic class Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n Set<Integer> uniqueNums = new HashSet<>();\n for (int num : nums) {\n uniqueNums.add(num);\n }\n for (int num : uniqueNums) {\n int count = 0;\n for (int n : nums) {\n if (n == num) {\n count++;\n }\n }\n if (count > nums.length / 3) {\n result.add(num);\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n std::vector<int> majorityElement(std::vector<int>& nums) {\n std::vector<int> result; \n std::unordered_set<int> uniqueNums;\n for (int num : nums) {\n uniqueNums.insert(num);\n } \n for (int num : uniqueNums) {\n int count = 0;\n for (int n : nums) {\n if (n == num) {\n count++;\n }\n }\n if (count > nums.size() / 3) {\n result.push_back(num);\n }\n } \n return result;\n }\n};\n```\n```C []\nint cmpfunc(const void *a, const void *b) {\n return (*(int *)a - *(int *)b);\n}\n\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int* result = (int*)malloc(2 * sizeof(int));\n if (result == NULL) {\n *returnSize = 0;\n return NULL;\n }\n qsort(nums, numsSize, sizeof(int), cmpfunc);\n int candidate1 = nums[0];\n int candidate2 = nums[0];\n int count1 = 0;\n int count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = nums[i];\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = nums[i];\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n int resultSize = 0;\n if (count1 > numsSize / 3) {\n result[resultSize++] = candidate1;\n }\n if (count2 > numsSize / 3) {\n result[resultSize++] = candidate2;\n }\n *returnSize = resultSize;\n return result;\n}\n```\n# 2. Boyer-Moore Voting Algorithm:\n- Initialize two variables candidate1 and candidate2 to None, and two counters count1 and count2 to 0.\n- Iterate through the array.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n - If count1 is 0, set num as candidate1 and increment count1.\n - If count2 is 0, set num as candidate2 and increment count2.\n - If neither of the above conditions is met, decrement count1 and count2.\n- Initialize count1 and count2 to 0.\n- Iterate through the array again.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n- Check if count1 and count2 are greater than \u230An/3\u230B. If they are, both candidates are potential majority elements.\n- Iterate through the array again and count the occurrences of candidate1 and candidate2.\n- Return the candidates that meet the majority criteria.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n) - This algorithm makes three passes through the array.\n\n- \uD83D\uDE80 Space Complexity: O(1) - Constant extra space is used.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n candidate1, candidate2 = None, None\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n elif count1 == 0:\n candidate1 = num\n count1 = 1\n elif count2 == 0:\n candidate2 = num\n count2 = 1\n else:\n count1 -= 1\n count2 -= 1\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n result = []\n if count1 > len(nums) // 3:\n result.append(candidate1)\n if count2 > len(nums) // 3:\n result.append(candidate2)\n return result\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1++;\n } else if (count2 == 0) {\n candidate2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n if (count1 > nums.length / 3) {\n result.add(candidate1);\n }\n if (count2 > nums.length / 3) {\n result.add(candidate2);\n }\n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n int n = nums.size();\n if (count1 > n / 3) {\n result.push_back(candidate1);\n }\n if (count2 > n / 3) {\n result.push_back(candidate2);\n }\n return result;\n }\n};\n```\n```C []\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int candidate1 = 0, candidate2 = 0;\n int count1 = 0, count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = nums[i];\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = nums[i];\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n int* result = NULL;\n *returnSize = 0;\n \n if (count1 > numsSize / 3) {\n result = (int*)realloc(result, sizeof(int) * ((*returnSize) + 1));\n result[(*returnSize)++] = candidate1;\n }\n if (count2 > numsSize / 3) {\n result = (int*)realloc(result, sizeof(int) * ((*returnSize) + 1));\n result[(*returnSize)++] = candidate2;\n }\n return result;\n}\n```\n# 3. Hash Map:\n - Initialize an empty dictionary count_dict.\n- Iterate through the array.\n- For each element num in the array, increment its count in count_dict.\n- Iterate through the keys in count_dict.\n- Check if the count of each key is greater than \u230An/3\u230B.\n- Return the keys that meet the majority criteria.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n) - This algorithm makes a single pass through the array.\n\n- \uD83D\uDE80 Space Complexity: O(n) - Extra space is used to store counts in the dictionary.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n\n count_dict = Counter(nums)\n result = [num for num, count in count_dict.items() if count > len(nums) // 3]\n return result\n\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n Map<Integer, Integer> countMap = new HashMap<>();\n for (int num : nums) {\n countMap.put(num, countMap.getOrDefault(num, 0) + 1);\n }\n for (Map.Entry<Integer, Integer> entry : countMap.entrySet()) {\n if (entry.getValue() > nums.length / 3) {\n result.add(entry.getKey());\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n unordered_map<int, int> count_dict;\n vector<int> result;\n for (int num : nums) {\n count_dict[num]++;\n }\n int n = nums.size();\n for (auto& entry : count_dict) {\n if (entry.second > n / 3) {\n result.push_back(entry.first);\n }\n }\n return result;\n }\n};\n```\n```C []\nstruct Entry {\n int value;\n int count;\n};\n\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int mapSize = 2; \n struct Entry* hashMap = (struct Entry*)malloc(sizeof(struct Entry) * mapSize);\n if (hashMap == NULL) {\n perror("Memory allocation failed");\n exit(EXIT_FAILURE);\n }\n for (int i = 0; i < mapSize; i++) {\n hashMap[i].value = 0;\n hashMap[i].count = 0;\n }\n for (int i = 0; i < numsSize; i++) {\n bool found = false;\n for (int j = 0; j < mapSize; j++) {\n if (hashMap[j].count > 0 && hashMap[j].value == nums[i]) {\n hashMap[j].count++;\n found = true;\n break;\n }\n }\n if (!found) {\n bool inserted = false;\n for (int j = 0; j < mapSize; j++) {\n if (hashMap[j].count == 0) {\n hashMap[j].value = nums[i];\n hashMap[j].count = 1;\n inserted = true;\n break;\n }\n }\n if (!inserted) {\n mapSize *= 2;\n hashMap = (struct Entry*)realloc(hashMap, sizeof(struct Entry) * mapSize);\n if (hashMap == NULL) {\n perror("Memory allocation failed");\n exit(EXIT_FAILURE);\n }\n for (int j = mapSize / 2; j < mapSize; j++) {\n hashMap[j].value = 0;\n hashMap[j].count = 0;\n }\n i--;\n }\n }\n }\n int* result = (int*)malloc(sizeof(int) * mapSize);\n if (result == NULL) {\n perror("Memory allocation failed");\n exit(EXIT_FAILURE);\n }\n *returnSize = 0;\n for (int i = 0; i < mapSize; i++) {\n if (hashMap[i].count > numsSize / 3) {\n result[(*returnSize)++] = hashMap[i].value;\n }\n }\n free(hashMap);\n return result;\n}\n\n```\n# 4. Sorting:\n - Sort the input array.\n- Initialize an empty list result.\n- Initialize a variable count to 1.\n- Iterate through the sorted array, starting from the second element.\n- For each element num in the array:\n - If num is equal to the previous element, increment count.\n - If num is different from the previous element, check if count is greater than \u230An/3\u230B.\n - If count is greater, append the previous element to result.\n- Reset count to 1.\n- After the loop, check if the last element has a count greater than \u230An/3\u230B and append it to result.\nReturn result.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n log n) - This algorithm sorts the array.\n\n- \uD83D\uDE80 Space Complexity: O(1) - Constant extra space is used.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n nums.sort()\n result = []\n count = 1\n for i in range(1, len(nums)):\n if nums[i] == nums[i - 1]:\n count += 1\n else:\n if count > len(nums) // 3:\n result.append(nums[i - 1])\n count = 1\n if count > len(nums) // 3:\n result.append(nums[-1])\n return result\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n Arrays.sort(nums);\n int n = nums.length;\n int count = 1;\n for (int i = 1; i < n; i++) {\n if (nums[i] == nums[i - 1]) {\n count++;\n } else {\n if (count > n / 3) {\n result.add(nums[i - 1]);\n }\n count = 1;\n }\n }\n if (count > n / 3) {\n result.add(nums[n - 1]);\n }\n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int n = nums.size();\n sort(nums.begin(), nums.end());\n int count = 1;\n for (int i = 1; i < n; i++) {\n if (nums[i] == nums[i - 1]) {\n count++;\n } else {\n if (count > n / 3) {\n result.push_back(nums[i - 1]);\n }\n count = 1;\n }\n }\n if (count > n / 3) {\n result.push_back(nums[n - 1]);\n }\n return result;\n }\n};\n\n```\n```C []\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n qsort(nums, numsSize, sizeof(int), compare);\n int* result = (int*)malloc(sizeof(int) * 2); // At most 2 majority elements\n *returnSize = 0;\n int count = 1;\n for (int i = 1; i < numsSize; i++) {\n if (nums[i] == nums[i - 1]) {\n count++;\n } else {\n if (count > numsSize / 3) {\n result[(*returnSize)++] = nums[i - 1];\n }\n count = 1;\n }\n }\n if (count > numsSize / 3) {\n result[(*returnSize)++] = nums[numsSize - 1];\n }\n return result;\n}\n```\n# 5. Moore Voting Algorithm:\n - Initialize two variables candidate1 and candidate2 to None, and two counters count1 and count2 to 0.\n- Iterate through the array.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n - If count1 is 0, set num as candidate1 and increment count1.\n - If count2 is 0, set num as candidate2 and increment count2.\n - If neither of the above conditions is met, decrement count1 and count2.\n- Initialize count1 and count2 to 0.\n- Iterate through the array again.\n- For each element num in the array:\n - If num is equal to candidate1, increment count1.\n - If num is equal to candidate2, increment count2.\n- Initialize two variables freq1 and freq2 to 0.\n- Iterate through the array.\n- For each element num in the array:\n - If num is equal to candidate1, increment freq1.\n - If num is equal to candidate2, increment freq2.\n- Check if freq1 and freq2 are greater than \u230An/3\u230B. If they are, both candidates are potential majority elements.\n- Return the candidates that meet the majority criteria.\n# Complexity\n- \u23F1\uFE0F Time Complexity: O(n) - This algorithm makes three passes through the array.\n\n- \uD83D\uDE80 Space Complexity: O(1) - Constant extra space is used.\n\n# Code\n```Python []\nclass Solution:\n def majorityElement(self, nums):\n candidate1, candidate2 = None, None\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n elif count1 == 0:\n candidate1 = num\n count1 = 1\n elif count2 == 0:\n candidate2 = num\n count2 = 1\n else:\n count1 -= 1\n count2 -= 1\n count1, count2 = 0, 0\n for num in nums:\n if num == candidate1:\n count1 += 1\n elif num == candidate2:\n count2 += 1\n result = []\n if count1 > len(nums) // 3:\n result.append(candidate1)\n if count2 > len(nums) // 3:\n result.append(candidate2)\n return result\n```\n```Java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n List<Integer> result = new ArrayList<>();\n if (nums == null || nums.length == 0) {\n return result;\n }\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1++;\n } else if (count2 == 0) {\n candidate2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n \n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n if (count1 > nums.length / 3) {\n result.add(candidate1);\n }\n if (count2 > nums.length / 3) {\n result.add(candidate2);\n }\n \n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n vector<int> result;\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n int n = nums.size();\n if (count1 > n / 3) {\n result.push_back(candidate1);\n }\n if (count2 > n / 3) {\n result.push_back(candidate2);\n }\n\n return result;\n }\n};\n\n```\n```C []\nint* majorityElement(int* nums, int numsSize, int* returnSize) {\n int candidate1 = 0, candidate2 = 0;\n int count1 = 0, count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = nums[i];\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = nums[i];\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n count1 = 0;\n count2 = 0;\n for (int i = 0; i < numsSize; i++) {\n if (nums[i] == candidate1) {\n count1++;\n } else if (nums[i] == candidate2) {\n count2++;\n }\n }\n int* result = (int*)malloc(sizeof(int) * 2); // At most 2 majority elements\n *returnSize = 0;\n if (count1 > numsSize / 3) {\n result[(*returnSize)++] = candidate1;\n }\n if (count2 > numsSize / 3) {\n result[(*returnSize)++] = candidate2;\n }\n return result;\n}\n```\n# \uD83C\uDFC6Conclusion: \nThe Boyer-Moore Voting Algorithm and Moore Voting Algorithm are particularly efficient with O(1) space complexity.\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 46 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
【Video】How we think about a solution - Boyer-Moore Majority Vote Algorithm | majority-element-ii | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\nFind two majority candidates at first.\n\n# Approach\n\n---\n\n# Solution Video\n\nhttps://youtu.be/KzJHu5sWLKE\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Majority Element II\n`1:03` How we think about a solution\n`3:47` Demonstrate solution with an example\n`5:42` Explain Boyer-Moore Majority Vote Algorithm with visualization\n`9:19` Coding\n`12:49` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,607\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n### How we think about a solution\n\nSimply, we can solve the question like this.\n\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n counts = {}\n for num in nums:\n counts[num] = counts.get(num, 0) + 1\n\n # Find all elements in the hash table that have a count greater than n/3.\n result = []\n for num, count in counts.items():\n if count > len(nums) // 3:\n result.append(num)\n\n return result\n```\n\nBut there is a constraint saying "Could you solve the problem in linear time and in $$O(1)$$ space?" That solution should be $$O(n)$$ space.\n\nLet\'s think about $$O(1)$$ space. we have a hint to solve the question. The description says "more than n/3 times".\n\nLet\'s start with the simplest case.\n```\n[1,2,3]\n```\n In this case, `n/3 is 1` and occurence of all numbers are `1`, so we don\'t find majority numbers.\n```\n[1,2,1]\n```\nIn this case, `n/3 is 1` and occurence of `1` is `2`, so we find 1 majority number.\n```\n[1,2,1,2]\n```\nIn this case, `n/3 is 1.333...` and occurence of `1` and `2` are both `2`, so we find 2 majority numbers.\n```\n[1,2,1,2,3]\n```\nIn this case, `n/3 is 1.666...` occurence of `1` and `2` are both are `2`, so we find 2 majority numbers.\n\n```\n[1,2,1,2,3,3]\n```\nIn this case, `n/3 is 2` all numbers are `2`, so we don\'t find majority numbers.\n\n---\n\u2B50\uFE0F Points\n\nFrom exmaples above, We can find **2 majority numbers at most**.\n\nTo prove that, we can calculate like this.\n\nFrom `[1,2,3]` and `[1,2,1]` cases, to make some number majority element, we need n/3 + 1 of some number. If we multiply 3 with n/3 + 1, the answer is definitely longer than length of original input array. That\'s why we can\'t create 3 majority elements.\n```\n(n/3 + 1) * 3 > input array\n```\n```\nn = 6\n\ncase * 3\n(6/3 + 1) * 3 > 6\n\ncase * 2 , both sides are equal.\n(6/3 + 1) * 2 == 6\n```\n\nThat\'s why we can find **2 majority numbers at most**.\n\n---\n\nBut there is an case where we find 1 majority number, we are not sure we have 1 or 2 majority numbers.\n\nThat\'s why at first, it\'s good idea to find `two majority candidates` in the array whether they are more than `n/3 or not`.\n\nLet\'s see this input.\n\n```\nInput: [1,4,6,3,10,4,4,3,4]\n```\nIterate through the input array and it turns out two majority candidates are `4` and `3`. Let me explain how we find the two majority candidates later.\n\nThen, we iterate through the input array again to count occurence of `4` and `3`.\n```\n4: 4 times\n3: 2 times\n```\nAt last, if occurence of `4` and `3` is more than len(input) // 3, then we find majority numbers.\n\n```\nlen(input) // 3 = 3\noccurence of 4 is more than 3? Yes\noccurence of 3 is more than 3? No\n```\n\n```\nOutput: [4]\n```\n\n- **How can we find majority candidates?**\n\nSince we can\'t use data structure like `HashMap`, simply we use two variables for majority candidates and two `counts` variables.\n\nBut let\'s simplify the question. try to find 1 majority number.\n```\n[1,1,2,2,2,1,1]\nmajority = 0\ncount = 0\n```\nIterate through one by one\n```\nAt index 0. find 1\nmajority = 1\ncount = 1\n```\n```\nAt index 1. find 1\nmajority = 1\ncount = 2\n```\n```\nAt index 2. find 2\nmajority = 1\ncount = 1\n```\nIn this case, we find `2`, add `-1` to `count` which is number of occurence of `1`, but still `1` is a majority number.\n```\nAt index 3. find 2\nmajority = 1\ncount = 0\n```\nAgain, add `-1` to `count` which is number of occurence of `1`. Now `count` is `0` which means `next number should will be majority number`. \n\nIn early index, we just found `1` twice. That\'s why `1` is majority number `so far`, but from index `2`, we found `2` twice. Now occurence of `1` and `2` is the same. \n```\nAt index 4. find 2\nmajority = 2\ncount = 1\n```\nNow `count` means occurence of `2` instead of `1`, because at index 4, `2` is majority number so far.\n```\nAt index 5. find 1\nmajority = 2\ncount = 0\n```\nNow `count` is `0`, so next number will be a majority number. \n```\nAt index 6. find 1\nmajority = 1\ncount = 1\n```\n```\nOutput: Majority number is 1\n```\nActually, I use the same algorithm for majority number \u2160. I solved it about a year ago.\n\nhttps://youtu.be/sBuRjHqDTzY\n\n\n---\n\n# Boyer-Moore Majority Vote Algorithm\n\nThe algorithm above is known as Boyer-Moore Majority Vote Algorithm.\n\nThe Boyer-Moore Majority Vote Algorithm is an efficient algorithm used to find the majority element (an element that appears more than half of the time) in a given array. This algorithm operates in linear time and requires O(1) additional space.\n\nHere are the basic steps of the Boyer-Moore Majority Vote Algorithm:\n\n1. **Candidate Element Selection**: Choose the first element of the array as the candidate element and initialize a counter.\n\n2. **Element Counting**: Traverse through the array. If the current element matches the candidate element, increment the counter. If they don\'t match, decrement the counter.\n\n3. **Check Counter**: If the counter becomes zero, choose the current element as the new candidate element and reset the counter to one.\n\n4. **Final Candidate Verification**: After these steps, verify if the selected candidate is indeed the majority element.\n\nBy following these steps, the algorithm efficiently identifies the most frequently occurring element, if one exists, in linear time O(n) in the worst case. This efficiency is achieved by carefully selecting candidate elements and comparing them against other elements.\n\n\n---\n\n\n\nWe use this idea for two majority candidates. Let\'s see real algorithm!\n\n### Algorithm Overview:\n\n1. Initialize `majority1`, `majority2`, `count1`, and `count2` to track the majority elements and their counts.\n2. Iterate through the input list `nums` to find the two majority elements.\n3. Iterate through `nums` again to verify the counts of the two majority elements.\n4. Return a list of majority elements that appear more than `len(nums) // 3` times.\n\n### Detailed Explanation:\n\n1. **Initialization:**\n - Initialize `majority1`, `majority2`, `count1`, and `count2` to 0. These variables will be used to keep track of the majority elements and their counts.\n\n2. **First Iteration to Find Majority Elements:**\n - Iterate through the input list `nums`.\n - If the current number is equal to `majority1`, increment `count1`.\n - If the current number is equal to `majority2`, increment `count2`.\n - If `count1` is 0, update `majority1` to the current number and increment `count1`.\n - If `count2` is 0, update `majority2` to the current number and increment `count2`.\n - If both `count1` and `count2` are non-zero and the current number is not equal to either majority, decrement `count1` and `count2`.\n\n3. **Second Iteration to Verify Counts:**\n - Reset `count1` and `count2` to 0.\n - Iterate through `nums` again.\n - Count the occurrences of `majority1` and `majority2` by incrementing `count1` and `count2` accordingly.\n\n4. **Result Generation:**\n - Create an empty list `res` to store the majority elements.\n - If `count1` is greater than `len(nums) // 3`, add `majority1` to `res`.\n - If `count2` is greater than `len(nums) // 3`, add `majority2` to `res`.\n - Return the list `res` containing the majority elements that appear more than `len(nums) // 3` times.\n\nThe algorithm uses the Boyer-Moore Majority Vote algorithm to find the majority elements in `nums` efficiently and then verifies their counts to ensure they appear more than `len(nums) // 3` times before returning the result.\n\n\n---\n\n\n# Complexity\n- Time complexity: O(n)\n\n\n- Space complexity: O(1)\n\n\n```python []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n majority1 = majority2 = count1 = count2 = 0\n\n for num in nums:\n if num == majority1:\n count1 += 1\n elif num == majority2:\n count2 += 1\n elif count1 == 0:\n majority1 = num\n count1 += 1\n elif count2 == 0:\n majority2 = num\n count2 += 1\n else:\n count1 -= 1\n count2 -= 1\n\n # Verify that majority1 and majority2 appear more than n/3 times.\n count1, count2 = 0, 0\n\n for num in nums:\n if num == majority1:\n count1 += 1\n elif num == majority2:\n count2 += 1\n\n res = []\n if count1 > len(nums) // 3:\n res.append(majority1)\n if count2 > len(nums) // 3:\n res.append(majority2)\n\n return res\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar majorityElement = function(nums) {\n let majority1 = 0;\n let majority2 = 0;\n let count1 = 0;\n let count2 = 0;\n\n for (const num of nums) {\n if (num === majority1) {\n count1++;\n } else if (num === majority2) {\n count2++;\n } else if (count1 === 0) {\n majority1 = num;\n count1++;\n } else if (count2 === 0) {\n majority2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n\n for (const num of nums) {\n if (num === majority1) {\n count1++;\n } else if (num === majority2) {\n count2++;\n }\n }\n\n const res = [];\n const n = nums.length;\n\n if (count1 > Math.floor(n / 3)) {\n res.push(majority1);\n }\n if (count2 > Math.floor(n / 3)) {\n res.push(majority2);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n Integer majority1 = 0;\n Integer majority2 = 0;\n int count1 = 0;\n int count2 = 0;\n\n for (int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n } else if (count1 == 0) {\n majority1 = num;\n count1++;\n } else if (count2 == 0) {\n majority2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n\n for (int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n }\n }\n\n List<Integer> res = new ArrayList<>();\n int n = nums.length;\n\n if (count1 > n / 3) {\n res.add(majority1);\n }\n if (count2 > n / 3) {\n res.add(majority2);\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int majority1 = 0;\n int majority2 = 0;\n int count1 = 0;\n int count2 = 0;\n\n for (const int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n } else if (count1 == 0) {\n majority1 = num;\n count1++;\n } else if (count2 == 0) {\n majority2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n\n for (const int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n }\n }\n\n std::vector<int> res;\n\n if (count1 > nums.size() / 3) {\n res.push_back(majority1);\n }\n if (count2 > nums.size() / 3) {\n res.push_back(majority2);\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Oct 6th, 2023\nhttps://leetcode.com/problems/integer-break/solutions/4137225/how-we-think-about-a-solution-no-difficult-mathematics-python-javascript-java-c/\n | 33 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
【Video】How we think about a solution - Boyer-Moore Majority Vote Algorithm | majority-element-ii | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\nFind two majority candidates at first.\n\n# Approach\n\n---\n\n# Solution Video\n\nhttps://youtu.be/KzJHu5sWLKE\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Majority Element II\n`1:03` How we think about a solution\n`3:47` Demonstrate solution with an example\n`5:42` Explain Boyer-Moore Majority Vote Algorithm with visualization\n`9:19` Coding\n`12:49` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,607\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n### How we think about a solution\n\nSimply, we can solve the question like this.\n\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n counts = {}\n for num in nums:\n counts[num] = counts.get(num, 0) + 1\n\n # Find all elements in the hash table that have a count greater than n/3.\n result = []\n for num, count in counts.items():\n if count > len(nums) // 3:\n result.append(num)\n\n return result\n```\n\nBut there is a constraint saying "Could you solve the problem in linear time and in $$O(1)$$ space?" That solution should be $$O(n)$$ space.\n\nLet\'s think about $$O(1)$$ space. we have a hint to solve the question. The description says "more than n/3 times".\n\nLet\'s start with the simplest case.\n```\n[1,2,3]\n```\n In this case, `n/3 is 1` and occurence of all numbers are `1`, so we don\'t find majority numbers.\n```\n[1,2,1]\n```\nIn this case, `n/3 is 1` and occurence of `1` is `2`, so we find 1 majority number.\n```\n[1,2,1,2]\n```\nIn this case, `n/3 is 1.333...` and occurence of `1` and `2` are both `2`, so we find 2 majority numbers.\n```\n[1,2,1,2,3]\n```\nIn this case, `n/3 is 1.666...` occurence of `1` and `2` are both are `2`, so we find 2 majority numbers.\n\n```\n[1,2,1,2,3,3]\n```\nIn this case, `n/3 is 2` all numbers are `2`, so we don\'t find majority numbers.\n\n---\n\u2B50\uFE0F Points\n\nFrom exmaples above, We can find **2 majority numbers at most**.\n\nTo prove that, we can calculate like this.\n\nFrom `[1,2,3]` and `[1,2,1]` cases, to make some number majority element, we need n/3 + 1 of some number. If we multiply 3 with n/3 + 1, the answer is definitely longer than length of original input array. That\'s why we can\'t create 3 majority elements.\n```\n(n/3 + 1) * 3 > input array\n```\n```\nn = 6\n\ncase * 3\n(6/3 + 1) * 3 > 6\n\ncase * 2 , both sides are equal.\n(6/3 + 1) * 2 == 6\n```\n\nThat\'s why we can find **2 majority numbers at most**.\n\n---\n\nBut there is an case where we find 1 majority number, we are not sure we have 1 or 2 majority numbers.\n\nThat\'s why at first, it\'s good idea to find `two majority candidates` in the array whether they are more than `n/3 or not`.\n\nLet\'s see this input.\n\n```\nInput: [1,4,6,3,10,4,4,3,4]\n```\nIterate through the input array and it turns out two majority candidates are `4` and `3`. Let me explain how we find the two majority candidates later.\n\nThen, we iterate through the input array again to count occurence of `4` and `3`.\n```\n4: 4 times\n3: 2 times\n```\nAt last, if occurence of `4` and `3` is more than len(input) // 3, then we find majority numbers.\n\n```\nlen(input) // 3 = 3\noccurence of 4 is more than 3? Yes\noccurence of 3 is more than 3? No\n```\n\n```\nOutput: [4]\n```\n\n- **How can we find majority candidates?**\n\nSince we can\'t use data structure like `HashMap`, simply we use two variables for majority candidates and two `counts` variables.\n\nBut let\'s simplify the question. try to find 1 majority number.\n```\n[1,1,2,2,2,1,1]\nmajority = 0\ncount = 0\n```\nIterate through one by one\n```\nAt index 0. find 1\nmajority = 1\ncount = 1\n```\n```\nAt index 1. find 1\nmajority = 1\ncount = 2\n```\n```\nAt index 2. find 2\nmajority = 1\ncount = 1\n```\nIn this case, we find `2`, add `-1` to `count` which is number of occurence of `1`, but still `1` is a majority number.\n```\nAt index 3. find 2\nmajority = 1\ncount = 0\n```\nAgain, add `-1` to `count` which is number of occurence of `1`. Now `count` is `0` which means `next number should will be majority number`. \n\nIn early index, we just found `1` twice. That\'s why `1` is majority number `so far`, but from index `2`, we found `2` twice. Now occurence of `1` and `2` is the same. \n```\nAt index 4. find 2\nmajority = 2\ncount = 1\n```\nNow `count` means occurence of `2` instead of `1`, because at index 4, `2` is majority number so far.\n```\nAt index 5. find 1\nmajority = 2\ncount = 0\n```\nNow `count` is `0`, so next number will be a majority number. \n```\nAt index 6. find 1\nmajority = 1\ncount = 1\n```\n```\nOutput: Majority number is 1\n```\nActually, I use the same algorithm for majority number \u2160. I solved it about a year ago.\n\nhttps://youtu.be/sBuRjHqDTzY\n\n\n---\n\n# Boyer-Moore Majority Vote Algorithm\n\nThe algorithm above is known as Boyer-Moore Majority Vote Algorithm.\n\nThe Boyer-Moore Majority Vote Algorithm is an efficient algorithm used to find the majority element (an element that appears more than half of the time) in a given array. This algorithm operates in linear time and requires O(1) additional space.\n\nHere are the basic steps of the Boyer-Moore Majority Vote Algorithm:\n\n1. **Candidate Element Selection**: Choose the first element of the array as the candidate element and initialize a counter.\n\n2. **Element Counting**: Traverse through the array. If the current element matches the candidate element, increment the counter. If they don\'t match, decrement the counter.\n\n3. **Check Counter**: If the counter becomes zero, choose the current element as the new candidate element and reset the counter to one.\n\n4. **Final Candidate Verification**: After these steps, verify if the selected candidate is indeed the majority element.\n\nBy following these steps, the algorithm efficiently identifies the most frequently occurring element, if one exists, in linear time O(n) in the worst case. This efficiency is achieved by carefully selecting candidate elements and comparing them against other elements.\n\n\n---\n\n\n\nWe use this idea for two majority candidates. Let\'s see real algorithm!\n\n### Algorithm Overview:\n\n1. Initialize `majority1`, `majority2`, `count1`, and `count2` to track the majority elements and their counts.\n2. Iterate through the input list `nums` to find the two majority elements.\n3. Iterate through `nums` again to verify the counts of the two majority elements.\n4. Return a list of majority elements that appear more than `len(nums) // 3` times.\n\n### Detailed Explanation:\n\n1. **Initialization:**\n - Initialize `majority1`, `majority2`, `count1`, and `count2` to 0. These variables will be used to keep track of the majority elements and their counts.\n\n2. **First Iteration to Find Majority Elements:**\n - Iterate through the input list `nums`.\n - If the current number is equal to `majority1`, increment `count1`.\n - If the current number is equal to `majority2`, increment `count2`.\n - If `count1` is 0, update `majority1` to the current number and increment `count1`.\n - If `count2` is 0, update `majority2` to the current number and increment `count2`.\n - If both `count1` and `count2` are non-zero and the current number is not equal to either majority, decrement `count1` and `count2`.\n\n3. **Second Iteration to Verify Counts:**\n - Reset `count1` and `count2` to 0.\n - Iterate through `nums` again.\n - Count the occurrences of `majority1` and `majority2` by incrementing `count1` and `count2` accordingly.\n\n4. **Result Generation:**\n - Create an empty list `res` to store the majority elements.\n - If `count1` is greater than `len(nums) // 3`, add `majority1` to `res`.\n - If `count2` is greater than `len(nums) // 3`, add `majority2` to `res`.\n - Return the list `res` containing the majority elements that appear more than `len(nums) // 3` times.\n\nThe algorithm uses the Boyer-Moore Majority Vote algorithm to find the majority elements in `nums` efficiently and then verifies their counts to ensure they appear more than `len(nums) // 3` times before returning the result.\n\n\n---\n\n\n# Complexity\n- Time complexity: O(n)\n\n\n- Space complexity: O(1)\n\n\n```python []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n majority1 = majority2 = count1 = count2 = 0\n\n for num in nums:\n if num == majority1:\n count1 += 1\n elif num == majority2:\n count2 += 1\n elif count1 == 0:\n majority1 = num\n count1 += 1\n elif count2 == 0:\n majority2 = num\n count2 += 1\n else:\n count1 -= 1\n count2 -= 1\n\n # Verify that majority1 and majority2 appear more than n/3 times.\n count1, count2 = 0, 0\n\n for num in nums:\n if num == majority1:\n count1 += 1\n elif num == majority2:\n count2 += 1\n\n res = []\n if count1 > len(nums) // 3:\n res.append(majority1)\n if count2 > len(nums) // 3:\n res.append(majority2)\n\n return res\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar majorityElement = function(nums) {\n let majority1 = 0;\n let majority2 = 0;\n let count1 = 0;\n let count2 = 0;\n\n for (const num of nums) {\n if (num === majority1) {\n count1++;\n } else if (num === majority2) {\n count2++;\n } else if (count1 === 0) {\n majority1 = num;\n count1++;\n } else if (count2 === 0) {\n majority2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n\n for (const num of nums) {\n if (num === majority1) {\n count1++;\n } else if (num === majority2) {\n count2++;\n }\n }\n\n const res = [];\n const n = nums.length;\n\n if (count1 > Math.floor(n / 3)) {\n res.push(majority1);\n }\n if (count2 > Math.floor(n / 3)) {\n res.push(majority2);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public List<Integer> majorityElement(int[] nums) {\n Integer majority1 = 0;\n Integer majority2 = 0;\n int count1 = 0;\n int count2 = 0;\n\n for (int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n } else if (count1 == 0) {\n majority1 = num;\n count1++;\n } else if (count2 == 0) {\n majority2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n\n for (int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n }\n }\n\n List<Integer> res = new ArrayList<>();\n int n = nums.length;\n\n if (count1 > n / 3) {\n res.add(majority1);\n }\n if (count2 > n / 3) {\n res.add(majority2);\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int majority1 = 0;\n int majority2 = 0;\n int count1 = 0;\n int count2 = 0;\n\n for (const int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n } else if (count1 == 0) {\n majority1 = num;\n count1++;\n } else if (count2 == 0) {\n majority2 = num;\n count2++;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = 0;\n count2 = 0;\n\n for (const int num : nums) {\n if (num == majority1) {\n count1++;\n } else if (num == majority2) {\n count2++;\n }\n }\n\n std::vector<int> res;\n\n if (count1 > nums.size() / 3) {\n res.push_back(majority1);\n }\n if (count2 > nums.size() / 3) {\n res.push_back(majority2);\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Oct 6th, 2023\nhttps://leetcode.com/problems/integer-break/solutions/4137225/how-we-think-about-a-solution-no-difficult-mathematics-python-javascript-java-c/\n | 33 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Beats 94.15% solution, PYTHON easy!! | majority-element-ii | 0 | 1 | # Intuition\nThe Question gives us an array called nums, and it wants us to return all the elements the occur more than len(nums)/3 times.\nSo, if the length of our nums array is 6, then **6/3 = 2**, we need to return all the elements that occur **more than 2 times**.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- To solve this question, we need the count of elements in our nums array, there are many ways to find this, but for simplicity we can use the "Counter" method in the collections library.\n ```\nnums = [1,6,6,6,2,5]\ncountMap = Counter(nums)\n// {1:1,6:3,2:1,5:1}\n```\n- Then we iterate through the countMap array to find counts that are greater than len(nums)/2,and if we find any element , we append it to our return array.\n\n \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\nO(2 * n) is the time complexity as we traverse the nums array twice.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\nAs we are using a hashmap, so the space complexity is equal to the length of nums array\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n minCount = int(len(nums)/3)\n ret = []\n countMap = Counter(nums)\n for i in countMap:\n if countMap[i] > minCount:\n ret.append(i)\n return ret\n\n\n\n \n``` | 0 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Beats 94.15% solution, PYTHON easy!! | majority-element-ii | 0 | 1 | # Intuition\nThe Question gives us an array called nums, and it wants us to return all the elements the occur more than len(nums)/3 times.\nSo, if the length of our nums array is 6, then **6/3 = 2**, we need to return all the elements that occur **more than 2 times**.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- To solve this question, we need the count of elements in our nums array, there are many ways to find this, but for simplicity we can use the "Counter" method in the collections library.\n ```\nnums = [1,6,6,6,2,5]\ncountMap = Counter(nums)\n// {1:1,6:3,2:1,5:1}\n```\n- Then we iterate through the countMap array to find counts that are greater than len(nums)/2,and if we find any element , we append it to our return array.\n\n \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\nO(2 * n) is the time complexity as we traverse the nums array twice.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\nAs we are using a hashmap, so the space complexity is equal to the length of nums array\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n minCount = int(len(nums)/3)\n ret = []\n countMap = Counter(nums)\n for i in countMap:\n if countMap[i] > minCount:\n ret.append(i)\n return ret\n\n\n\n \n``` | 0 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
BEGINNER FRIENDLY - 100% - ONE LINE TRAVERSAL IN C++/JAVA/PYTHON(TIME - O(N),PSACE-O(1)) | majority-element-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n If the array contains the majority of elements, their occurrence must be greater than the floor(N/3). Now, we can say that the count of minority elements and majority elements is equal up to a certain point in the array. So when we traverse through the array we try to keep track of the counts of elements and the elements themselves for which we are tracking the counts. \n\nAfter traversing the whole array, we will check the elements stored in the variables. Then we need to check if the stored elements are the majority elements or not by manually checking their counts.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis C++ code implements an algorithm to find the majority elements in an array. A majority element is an element that appears more than n/3 times in the array, where n is the size of the array. Here\'s a breakdown of the approach used in the code:\n\n Initialization:\n Initialize counters (cnt1 and cnt2) and elements (el1 and el2) to keep track of the potential majority elements.\n\n First Pass:\n Iterate through the input array, updating the counters and elements based on the encountered elements.\n If cnt1 is zero and the current element is not equal to el2, update cnt1 and el1.\n If cnt2 is zero and the current element is not equal to el1, update cnt2 and el2.\n If the current element is equal to el1, increment cnt1.\n If the current element is equal to el2, increment cnt2.\n If the current element is different from both el1 and el2, decrement cnt1 and cnt2.\n\n Second Pass:\n Count the occurrences of el1 and el2 in the array.\n\n Final Result:\n If the count of el1 is greater than or equal to n/3, add el1 to the result vector.\n If the count of el2 is greater than or equal to n/3, add el2 to the result vector.\n Return the result vector containing the majority elements.\n\nThe code ensures that it finds and returns the majority elements based on the specified conditions and the majority element definition.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N) + O(N),\n where N = size of the given array.\nReason: The first O(N) is to calculate the counts and find the expected majority elements. The second one is to check if the calculated elements are the majority ones or not.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1) as we are only using a list that stores a maximum of 2 elements. The space used is so small that it can be considered constant.\n\n# Code\n\n```c++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int n = nums.size(); \n\n int cnt1 = 0, cnt2 = 0; \n int el1 = INT_MIN; \n int el2 = INT_MIN; \n\n for (int i = 0; i < n; i++) {\n if (cnt1 == 0 && el2 != nums[i]) {\n cnt1 = 1;\n el1 = nums[i];\n }\n else if (cnt2 == 0 && el1 != nums[i]) {\n cnt2 = 1;\n el2 = nums[i];\n }\n else if (nums[i] == el1) cnt1++;\n else if (nums[i] == el2) cnt2++;\n else {\n cnt1--, cnt2--;\n }\n }\n\n vector<int> ls; \n\n cnt1 = 0, cnt2 = 0;\n\n for (int i = 0; i < n; i++) {\n if (nums[i] == el1) cnt1++;\n if (nums[i] == el2) cnt2++;\n }\n\n int mini = int(n / 3) + 1;\n if (cnt1 >= mini) ls.push_back(el1);\n if (cnt2 >= mini) ls.push_back(el2);\n\n return ls;\n }\n};\n```\n```java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<Integer> majorityElement(int[] nums){\n int n = nums.length;\n int cnt1 = 0, cnt2 = 0;\n int el1 = Integer.MIN_VALUE;\n int el2 = Integer.MIN_VALUE;\n for (int i = 0; i < n; i++) {\n if (cnt1 == 0 && el2 != nums[i]) {\n cnt1 = 1;\n el1 = nums[i];\n } else if (cnt2 == 0 && el1 != nums[i]) {\n cnt2 = 1;\n el2 = nums[i];\n } else if (nums[i] == el1) {\n cnt1++;\n } else if (nums[i] == el2) {\n cnt2++;\n } else {\n cnt1--;\n cnt2--;\n }\n }\n List<Integer> ls = new ArrayList<>();\n cnt1 = 0;\n cnt2 = 0;\n for (int i = 0; i < n; i++) {\n if (nums[i] == el1) {\n cnt1++;\n }\n if (nums[i] == el2) {\n cnt2++;\n }\n }\n int mini = n / 3 + 1;\n if (cnt1 >= mini) {\n ls.add(el1);\n }\n if (cnt2 >= mini) {\n ls.add(el2);\n }\n return ls;\n }\n}\n```\n```python []\nclass Solution:\n def majorityElement(self, nums):\n n = len(nums)\n cnt1 = 0\n cnt2 = 0\n el1 = float(\'-inf\')\n el2 = float(\'-inf\')\n for i in range(n):\n if cnt1 == 0 and el2 != nums[i]:\n cnt1 = 1\n el1 = nums[i]\n elif cnt2 == 0 and el1 != nums[i]:\n cnt2 = 1\n el2 = nums[i]\n elif nums[i] == el1:\n cnt1 += 1\n elif nums[i] == el2:\n cnt2 += 1\n else:\n cnt1 -= 1\n cnt2 -= 1\n ls = []\n cnt1 = 0\n cnt2 = 0\n for i in range(n):\n if nums[i] == el1:\n cnt1 += 1\n if nums[i] == el2:\n cnt2 += 1\n mini = n // 3 + 1\n if cnt1 >= mini:\n ls.append(el1)\n if cnt2 >= mini:\n ls.append(el2)\n return ls\n```\n# ***PLEASE UPVOTE THIS CODE*** | 0 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
BEGINNER FRIENDLY - 100% - ONE LINE TRAVERSAL IN C++/JAVA/PYTHON(TIME - O(N),PSACE-O(1)) | majority-element-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n If the array contains the majority of elements, their occurrence must be greater than the floor(N/3). Now, we can say that the count of minority elements and majority elements is equal up to a certain point in the array. So when we traverse through the array we try to keep track of the counts of elements and the elements themselves for which we are tracking the counts. \n\nAfter traversing the whole array, we will check the elements stored in the variables. Then we need to check if the stored elements are the majority elements or not by manually checking their counts.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis C++ code implements an algorithm to find the majority elements in an array. A majority element is an element that appears more than n/3 times in the array, where n is the size of the array. Here\'s a breakdown of the approach used in the code:\n\n Initialization:\n Initialize counters (cnt1 and cnt2) and elements (el1 and el2) to keep track of the potential majority elements.\n\n First Pass:\n Iterate through the input array, updating the counters and elements based on the encountered elements.\n If cnt1 is zero and the current element is not equal to el2, update cnt1 and el1.\n If cnt2 is zero and the current element is not equal to el1, update cnt2 and el2.\n If the current element is equal to el1, increment cnt1.\n If the current element is equal to el2, increment cnt2.\n If the current element is different from both el1 and el2, decrement cnt1 and cnt2.\n\n Second Pass:\n Count the occurrences of el1 and el2 in the array.\n\n Final Result:\n If the count of el1 is greater than or equal to n/3, add el1 to the result vector.\n If the count of el2 is greater than or equal to n/3, add el2 to the result vector.\n Return the result vector containing the majority elements.\n\nThe code ensures that it finds and returns the majority elements based on the specified conditions and the majority element definition.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N) + O(N),\n where N = size of the given array.\nReason: The first O(N) is to calculate the counts and find the expected majority elements. The second one is to check if the calculated elements are the majority ones or not.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1) as we are only using a list that stores a maximum of 2 elements. The space used is so small that it can be considered constant.\n\n# Code\n\n```c++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int n = nums.size(); \n\n int cnt1 = 0, cnt2 = 0; \n int el1 = INT_MIN; \n int el2 = INT_MIN; \n\n for (int i = 0; i < n; i++) {\n if (cnt1 == 0 && el2 != nums[i]) {\n cnt1 = 1;\n el1 = nums[i];\n }\n else if (cnt2 == 0 && el1 != nums[i]) {\n cnt2 = 1;\n el2 = nums[i];\n }\n else if (nums[i] == el1) cnt1++;\n else if (nums[i] == el2) cnt2++;\n else {\n cnt1--, cnt2--;\n }\n }\n\n vector<int> ls; \n\n cnt1 = 0, cnt2 = 0;\n\n for (int i = 0; i < n; i++) {\n if (nums[i] == el1) cnt1++;\n if (nums[i] == el2) cnt2++;\n }\n\n int mini = int(n / 3) + 1;\n if (cnt1 >= mini) ls.push_back(el1);\n if (cnt2 >= mini) ls.push_back(el2);\n\n return ls;\n }\n};\n```\n```java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<Integer> majorityElement(int[] nums){\n int n = nums.length;\n int cnt1 = 0, cnt2 = 0;\n int el1 = Integer.MIN_VALUE;\n int el2 = Integer.MIN_VALUE;\n for (int i = 0; i < n; i++) {\n if (cnt1 == 0 && el2 != nums[i]) {\n cnt1 = 1;\n el1 = nums[i];\n } else if (cnt2 == 0 && el1 != nums[i]) {\n cnt2 = 1;\n el2 = nums[i];\n } else if (nums[i] == el1) {\n cnt1++;\n } else if (nums[i] == el2) {\n cnt2++;\n } else {\n cnt1--;\n cnt2--;\n }\n }\n List<Integer> ls = new ArrayList<>();\n cnt1 = 0;\n cnt2 = 0;\n for (int i = 0; i < n; i++) {\n if (nums[i] == el1) {\n cnt1++;\n }\n if (nums[i] == el2) {\n cnt2++;\n }\n }\n int mini = n / 3 + 1;\n if (cnt1 >= mini) {\n ls.add(el1);\n }\n if (cnt2 >= mini) {\n ls.add(el2);\n }\n return ls;\n }\n}\n```\n```python []\nclass Solution:\n def majorityElement(self, nums):\n n = len(nums)\n cnt1 = 0\n cnt2 = 0\n el1 = float(\'-inf\')\n el2 = float(\'-inf\')\n for i in range(n):\n if cnt1 == 0 and el2 != nums[i]:\n cnt1 = 1\n el1 = nums[i]\n elif cnt2 == 0 and el1 != nums[i]:\n cnt2 = 1\n el2 = nums[i]\n elif nums[i] == el1:\n cnt1 += 1\n elif nums[i] == el2:\n cnt2 += 1\n else:\n cnt1 -= 1\n cnt2 -= 1\n ls = []\n cnt1 = 0\n cnt2 = 0\n for i in range(n):\n if nums[i] == el1:\n cnt1 += 1\n if nums[i] == el2:\n cnt2 += 1\n mini = n // 3 + 1\n if cnt1 >= mini:\n ls.append(el1)\n if cnt2 >= mini:\n ls.append(el2)\n return ls\n```\n# ***PLEASE UPVOTE THIS CODE*** | 0 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
[C++] [Python] Brute Force Approach || Too Easy || Fully Explained | majority-element-ii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nSuppose the input vector `nums` is `{3, 2, 3, 3, 1, 2, 2}`.\n\n1. Create an empty unordered map `mp` to store the frequency count of each element.\n2. Create an empty vector `ans` to store the elements that occur more than `n = nums.size() / 3` times, where `n` is the majority element threshold.\n3. Begin the loop to traverse each element of `nums`:\n - First iteration (it = 3):\n - Increment the count of 3 in the `mp` map. Now `mp` contains `{3: 1}`.\n - Second iteration (it = 2):\n - Increment the count of 2 in the `mp` map. Now `mp` contains `{3: 1, 2: 1}`.\n - Third iteration (it = 3):\n - Increment the count of 3 in the `mp` map. Now `mp` contains `{3: 2, 2: 1}`.\n - Fourth iteration (it = 3):\n - Increment the count of 3 in the `mp` map. Now `mp` contains `{3: 3, 2: 1}`.\n - Fifth iteration (it = 1):\n - Increment the count of 1 in the `mp` map. Now `mp` contains `{3: 3, 2: 1, 1: 1}`.\n - Sixth iteration (it = 2):\n - Increment the count of 2 in the `mp` map. Now `mp` contains `{3: 3, 2: 2, 1: 1}`.\n - Seventh iteration (it = 2):\n - Increment the count of 2 in the `mp` map. Now `mp` contains `{3: 3, 2: 3, 1: 1}`.\n\n4. Calculate the majority element threshold `n` as `nums.size() / 3`. For our example, `n = 7 / 3 = 2`.\n5. Begin the second loop to traverse the elements and their counts in the `mp` map:\n - First iteration (it = {3, 3}):\n - The count of 3 is greater than `n`, which is 2. So, add 3 to the `ans` vector. Now `ans` contains `{3}`.\n - Second iteration (it = {2, 3}):\n - The count of 2 is greater than `n`, which is 2. So, add 2 to the `ans` vector. Now `ans` contains `{3, 2}`.\n - Third iteration (it = {1, 1}):\n - The count of 1 is not greater than `n`, which is 2. So, skip this element.\n\n6. The second loop ends.\n7. Return the `ans` vector, which contains the majority elements that appear more than `n = 2` times in the `nums` vector. In our example, the `ans` vector will be `{3, 2}`.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n unordered_map<int,int>mp;\n vector<int> ans;\n for(auto it:nums){\n mp[it]++;\n }\n int n = nums.size() / 3;\n for(auto it:mp){\n if(it.second > n){\n ans.push_back(it.first);\n }\n }\n return ans;\n }\n};\n```\n``` Python []\nfrom collections import Counter\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n num = list(set(nums))\n ls = []\n for i in num:\n d = nums.count(i)\n if d > len(nums) // 3:\n ls.append(i)\n return ls\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
[C++] [Python] Brute Force Approach || Too Easy || Fully Explained | majority-element-ii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nSuppose the input vector `nums` is `{3, 2, 3, 3, 1, 2, 2}`.\n\n1. Create an empty unordered map `mp` to store the frequency count of each element.\n2. Create an empty vector `ans` to store the elements that occur more than `n = nums.size() / 3` times, where `n` is the majority element threshold.\n3. Begin the loop to traverse each element of `nums`:\n - First iteration (it = 3):\n - Increment the count of 3 in the `mp` map. Now `mp` contains `{3: 1}`.\n - Second iteration (it = 2):\n - Increment the count of 2 in the `mp` map. Now `mp` contains `{3: 1, 2: 1}`.\n - Third iteration (it = 3):\n - Increment the count of 3 in the `mp` map. Now `mp` contains `{3: 2, 2: 1}`.\n - Fourth iteration (it = 3):\n - Increment the count of 3 in the `mp` map. Now `mp` contains `{3: 3, 2: 1}`.\n - Fifth iteration (it = 1):\n - Increment the count of 1 in the `mp` map. Now `mp` contains `{3: 3, 2: 1, 1: 1}`.\n - Sixth iteration (it = 2):\n - Increment the count of 2 in the `mp` map. Now `mp` contains `{3: 3, 2: 2, 1: 1}`.\n - Seventh iteration (it = 2):\n - Increment the count of 2 in the `mp` map. Now `mp` contains `{3: 3, 2: 3, 1: 1}`.\n\n4. Calculate the majority element threshold `n` as `nums.size() / 3`. For our example, `n = 7 / 3 = 2`.\n5. Begin the second loop to traverse the elements and their counts in the `mp` map:\n - First iteration (it = {3, 3}):\n - The count of 3 is greater than `n`, which is 2. So, add 3 to the `ans` vector. Now `ans` contains `{3}`.\n - Second iteration (it = {2, 3}):\n - The count of 2 is greater than `n`, which is 2. So, add 2 to the `ans` vector. Now `ans` contains `{3, 2}`.\n - Third iteration (it = {1, 1}):\n - The count of 1 is not greater than `n`, which is 2. So, skip this element.\n\n6. The second loop ends.\n7. Return the `ans` vector, which contains the majority elements that appear more than `n = 2` times in the `nums` vector. In our example, the `ans` vector will be `{3, 2}`.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n unordered_map<int,int>mp;\n vector<int> ans;\n for(auto it:nums){\n mp[it]++;\n }\n int n = nums.size() / 3;\n for(auto it:mp){\n if(it.second > n){\n ans.push_back(it.first);\n }\n }\n return ans;\n }\n};\n```\n``` Python []\nfrom collections import Counter\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n num = list(set(nums))\n ls = []\n for i in num:\n d = nums.count(i)\n if d > len(nums) // 3:\n ls.append(i)\n return ls\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Easiest Approach to solve this Question in Python3 | majority-element-ii | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code\'s approach:\n\n1. element_count = Counter(nums): This line creates a dictionary-like object element_count using Python\'s Counter class. It counts the occurrences of each unique element in the nums list. The keys of element_count are the elements in nums, and the values are the counts of each element.\n\n2. majority_elements = []: This initializes an empty list majority_elements to store the majority elements found in the list.\n\n3. threshold = len(nums) // 3: This calculates the threshold value. It\'s equal to one-third of the length of the input list nums. Any element that appears more than this threshold times is considered a majority element.\n\n4. The code then iterates through the items (element, count) in the element_count dictionary:\n\n- - if count > threshold:: If the count of a particular element is greater than the threshold, it means that this element is a majority element.\n\n- - majority_elements.append(element): The majority element is added to the majority_elements list.\n\n5. Finally, the code returns the majority_elements list, which contains all the majority elements in the input list nums.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: list[int]) -> list[int]:\n element_count = Counter(nums)\n majority_elements = []\n threshold = len(nums) // 3\n \n for element, count in element_count.items():\n if count > threshold:\n majority_elements.append(element)\n return majority_elements\n```\n\n### Also One Liner \n```\nclass Solution:\n def majorityElement(self, nums):\n return [num for num, count in Counter(nums).items() if count > len(nums) // 3]\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Easiest Approach to solve this Question in Python3 | majority-element-ii | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code\'s approach:\n\n1. element_count = Counter(nums): This line creates a dictionary-like object element_count using Python\'s Counter class. It counts the occurrences of each unique element in the nums list. The keys of element_count are the elements in nums, and the values are the counts of each element.\n\n2. majority_elements = []: This initializes an empty list majority_elements to store the majority elements found in the list.\n\n3. threshold = len(nums) // 3: This calculates the threshold value. It\'s equal to one-third of the length of the input list nums. Any element that appears more than this threshold times is considered a majority element.\n\n4. The code then iterates through the items (element, count) in the element_count dictionary:\n\n- - if count > threshold:: If the count of a particular element is greater than the threshold, it means that this element is a majority element.\n\n- - majority_elements.append(element): The majority element is added to the majority_elements list.\n\n5. Finally, the code returns the majority_elements list, which contains all the majority elements in the input list nums.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: list[int]) -> list[int]:\n element_count = Counter(nums)\n majority_elements = []\n threshold = len(nums) // 3\n \n for element, count in element_count.items():\n if count > threshold:\n majority_elements.append(element)\n return majority_elements\n```\n\n### Also One Liner \n```\nclass Solution:\n def majorityElement(self, nums):\n return [num for num, count in Counter(nums).items() if count > len(nums) // 3]\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Python || 99.90 beats || Simple Code || 2 Approach (HashMap and set , count ,list) | majority-element-ii | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n# Code\n**1st Approach -> Set, Count, List (Beats 99.90)**\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n d = []\n for i in set(nums):\n if nums.count(i) > len(nums) / 3:\n d.append(i)\n return d\n\n```\n.\n**2nd Approach -> HashMap (Beats 98.6% )**\n```\n \nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n\n n = len(nums) // 3\n d = {}\n for ele in nums:\n d[ele] = d.get(ele,0) + 1\n\n maxe = [ele for ele in d if d[ele] > n]\n return maxe\n # OR\n return [ele for ele in d if d[ele] > n]\n\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Python || 99.90 beats || Simple Code || 2 Approach (HashMap and set , count ,list) | majority-element-ii | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n# Code\n**1st Approach -> Set, Count, List (Beats 99.90)**\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n d = []\n for i in set(nums):\n if nums.count(i) > len(nums) / 3:\n d.append(i)\n return d\n\n```\n.\n**2nd Approach -> HashMap (Beats 98.6% )**\n```\n \nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n\n n = len(nums) // 3\n d = {}\n for ele in nums:\n d[ele] = d.get(ele,0) + 1\n\n maxe = [ele for ele in d if d[ele] > n]\n return maxe\n # OR\n return [ele for ele in d if d[ele] > n]\n\n``` | 2 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅ Python 🔥|| Beats 99%🚀|| Beginner Friendly ✔️🔥 | majority-element-ii | 0 | 1 | # Intuition\n\nThis algorithm efficiently tracks two potential majority elements while traversing the array twice. It cancels out non-majority elements and validates the candidates\' counts to determine the final result. This approach provides a **linear time solution** with **minimal space usage**, making it effective for solving problems involving finding elements with a certain frequency threshold.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n * Create a list containing **distinct elements** of nums.\n * Calculate len(nums)//3 and initialize resultant list, res.\n * loop through the list and if **count** of the element is more than the length of nums divided by 3, append it to the res list.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n<sup>2</sup>)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n n = list(set(nums))\n l = len(nums)//3\n res = []\n\n for i in n:\n if nums.count(i) > l:\n res.append(i)\n \n return res\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
✅ Python 🔥|| Beats 99%🚀|| Beginner Friendly ✔️🔥 | majority-element-ii | 0 | 1 | # Intuition\n\nThis algorithm efficiently tracks two potential majority elements while traversing the array twice. It cancels out non-majority elements and validates the candidates\' counts to determine the final result. This approach provides a **linear time solution** with **minimal space usage**, making it effective for solving problems involving finding elements with a certain frequency threshold.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n * Create a list containing **distinct elements** of nums.\n * Calculate len(nums)//3 and initialize resultant list, res.\n * loop through the list and if **count** of the element is more than the length of nums divided by 3, append it to the res list.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n<sup>2</sup>)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n n = list(set(nums))\n l = len(nums)//3\n res = []\n\n for i in n:\n if nums.count(i) > l:\n res.append(i)\n \n return res\n``` | 1 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
🚩Beats 99.07% | Solution Using Boyer-Moore Majority Vote algorithm | 📈O(n) Solution | majority-element-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to find all elements that appear more than \u230A n/3 \u230B times in a given integer array. To solve this efficiently, we can adapt the Boyer-Moore Majority Vote algorithm to find at most two candidates that might fulfill this condition. Then, we verify the actual occurrences of these candidates and return the ones that meet the requirement.\n\n---\n\n\n# Do upvote if you like the solution and explanation please \uD83D\uDEA9\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize four variables: candidate1, candidate2, count1, and count2 to keep track of the two potential candidates and their respective counts.\n\n2. Iterate through the nums array:\n\n- If the current number is equal to candidate1, increment count1.\n- Else if the current number is equal to candidate2, increment count2.\n- Else if count1 is 0, update candidate1 to the current number and set count1 to 1.\n- Else if count2 is 0, update candidate2 to the current number and set count2 to 1.\n3. Otherwise, decrement both count1 and count2.\nAfter the first pass, we have two potential candidates, but we need to verify their actual occurrences in the array. Reset count1 and count2 to 0.\n\n4. Iterate through the nums array again:\n\n- If the current number is equal to candidate1, increment count1.\n- Else if the current number is equal to candidate2, increment count2.\n5. Finally, check if count1 and count2 are greater than \u230A n/3 \u230B, and if so, add the corresponding candidates to the result vector.\n\n6. Return the result vector containing elements that appear more than \u230A n/3 \u230B times.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe algorithm makes two passes through the nums array, each taking O(n) time, where n is the size of the input array. Therefore, the time complexity of this algorithm is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe algorithm uses a constant amount of extra space, primarily for the candidate1, candidate2, count1, count2, and result variables. Hence, the space complexity is O(1).\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n\n vector<int> result;\n\n if (count1 > nums.size() / 3) {\n result.push_back(candidate1);\n }\n if (count2 > nums.size() / 3) {\n result.push_back(candidate2);\n }\n\n return result;\n }\n};\n\n``` | 6 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
🚩Beats 99.07% | Solution Using Boyer-Moore Majority Vote algorithm | 📈O(n) Solution | majority-element-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to find all elements that appear more than \u230A n/3 \u230B times in a given integer array. To solve this efficiently, we can adapt the Boyer-Moore Majority Vote algorithm to find at most two candidates that might fulfill this condition. Then, we verify the actual occurrences of these candidates and return the ones that meet the requirement.\n\n---\n\n\n# Do upvote if you like the solution and explanation please \uD83D\uDEA9\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize four variables: candidate1, candidate2, count1, and count2 to keep track of the two potential candidates and their respective counts.\n\n2. Iterate through the nums array:\n\n- If the current number is equal to candidate1, increment count1.\n- Else if the current number is equal to candidate2, increment count2.\n- Else if count1 is 0, update candidate1 to the current number and set count1 to 1.\n- Else if count2 is 0, update candidate2 to the current number and set count2 to 1.\n3. Otherwise, decrement both count1 and count2.\nAfter the first pass, we have two potential candidates, but we need to verify their actual occurrences in the array. Reset count1 and count2 to 0.\n\n4. Iterate through the nums array again:\n\n- If the current number is equal to candidate1, increment count1.\n- Else if the current number is equal to candidate2, increment count2.\n5. Finally, check if count1 and count2 are greater than \u230A n/3 \u230B, and if so, add the corresponding candidates to the result vector.\n\n6. Return the result vector containing elements that appear more than \u230A n/3 \u230B times.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe algorithm makes two passes through the nums array, each taking O(n) time, where n is the size of the input array. Therefore, the time complexity of this algorithm is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe algorithm uses a constant amount of extra space, primarily for the candidate1, candidate2, count1, count2, and result variables. Hence, the space complexity is O(1).\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> majorityElement(vector<int>& nums) {\n int candidate1 = 0, candidate2 = 0, count1 = 0, count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n } else if (count1 == 0) {\n candidate1 = num;\n count1 = 1;\n } else if (count2 == 0) {\n candidate2 = num;\n count2 = 1;\n } else {\n count1--;\n count2--;\n }\n }\n\n count1 = count2 = 0;\n\n for (int num : nums) {\n if (num == candidate1) {\n count1++;\n } else if (num == candidate2) {\n count2++;\n }\n }\n\n vector<int> result;\n\n if (count1 > nums.size() / 3) {\n result.push_back(candidate1);\n }\n if (count2 > nums.size() / 3) {\n result.push_back(candidate2);\n }\n\n return result;\n }\n};\n\n``` | 6 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Simple Python3 Solution || 1 Line Code O(n) || Upto 98 % Space Saver O(1) | majority-element-ii | 0 | 1 | # Intuition\nWe use Counter to generate a Dictionary of nums and count of each distint number. Using this we filter the only the ones that are repeated more than n/3 times where n is the lenght of nums.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> List[int]:\n \n \n return [k for k,v in Counter(nums).items() if v > int(len(nums)/3)]\n``` | 0 | Given an integer array of size `n`, find all elements that appear more than `⌊ n/3 ⌋` times.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** \[3\]
**Example 2:**
**Input:** nums = \[1\]
**Output:** \[1\]
**Example 3:**
**Input:** nums = \[1,2\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow up:** Could you solve the problem in linear time and in `O(1)` space? | How many majority elements could it possibly have?
Do you have a better hint? Suggest it! |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.