title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python3 | two-sum-ii-input-array-is-sorted | 0 | 1 | \nO(n)\n# Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n left, right = 0, len(numbers) - 1 # Initialize two pointers, left and right, pointing to the start and end of the list respectively.\n\n while left < right: # Continue the loop until the pointers meet or cross each other.\n if numbers[left] + numbers[right] == target: # If the sum of the numbers at the left and right pointers is equal to the target:\n return [left + 1, right + 1] # Return the indices (1-based) of the two numbers that add up to the target.\n \n if numbers[left] + numbers[right] < target: # If the sum is less than the target:\n left += 1 # Move the left pointer to the right, increasing its index.\n else: # If the sum is greater than the target:\n right -= 1 # Move the right pointer to the left, decreasing its index.\n\n``` | 4 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
clean Python3 code using two pointers technique | two-sum-ii-input-array-is-sorted | 0 | 1 | # Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n l,r=0,len(numbers)-1\n while(l<r):\n sum=numbers[l]+numbers[r]\n if(sum==target):return [l+1,r+1]\n elif sum>target:r-=1\n else:l+=1\n``` | 3 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
UNIQUE TWO POINTER SOLUTION | Visual Explanation | two-sum-ii-input-array-is-sorted | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate two pointers where one points at the first index in the array and the other points at the second index. \n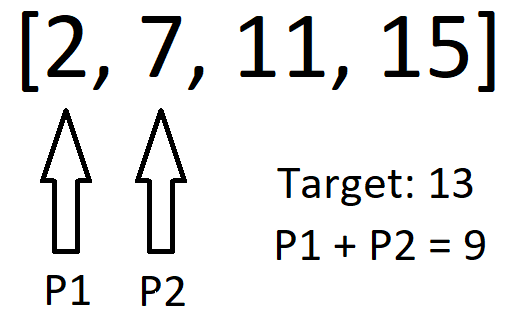\n\nIf the sum of the values at the pointers is less than the target, shift both pointers over one. \n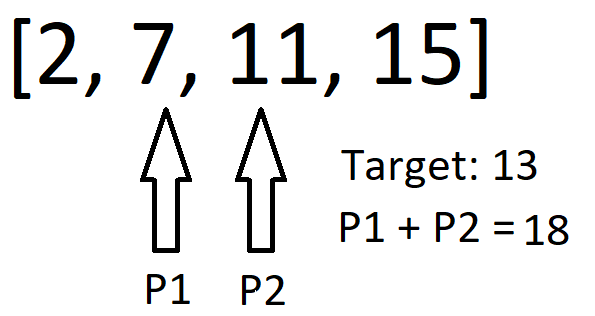\n\nIf the values summed are greater, shift the first pointer left one. \n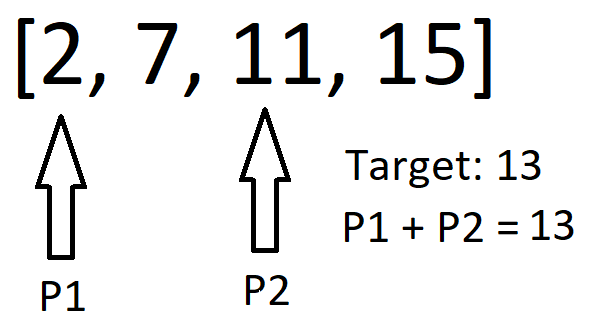\n\n# Complexity\n- Time complexity: O(n)\n\n\n# Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n p1, p2 = 0, 1;\n while not (numbers[p1] + numbers[p2] == target):\n if numbers[p1] + numbers[p2] < target:\n p2+=1;\n p1+=1;\n else:\n p1-=1; \n return [p1+1, p2+1]\n``` | 7 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
167. Two pointer technique | no nested loops | two-sum-ii-input-array-is-sorted | 0 | 1 | # Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n left, right = 0, len(numbers)-1\n while left < right:\n tot = numbers[left] + numbers[right]\n if tot< target: \n left += 1\n elif tot > target:\n right -= 1\n else: \n return left + 1, right + 1\n\n``` | 1 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
Easy and Detailed solution with 8 lines of Python Code | two-sum-ii-input-array-is-sorted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst of all I have written down the problem description in a simpler way, then I thought about having two pointers, one at the begining of the list, and the other pointing at the last element in the list, then we should repeat the process until we can get the target, as it is gaurenteed to have a solution. \n\nAfter that I thought, what if we have added the numbes which the pointers points at together. then the trick will depend on the result of their summation.\n\nif the summation was greater than our target, then sure we need to decrease the value which we already have. \n\nAnd since the given list is already sorted in a non decreasing way. \n\nHence we have to take a smaller value than what we already have, so we should move the pointer which at the end of the list, one position to the left and repeat the process. \n\nwhile if the summation was smaller than our target, then we have to increase our result by moving the pointer at the begining of the list one place to the right. \n\nand we should repeat this process until we can get the correct answer. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nSimply I used two integers as reference for the elements indicies. Initially the left pointer is called **bgn** and it starts from zero (when we want to get the correct result we will add one to it), and the other pointer is called **lst**, and it points to the last element which exist in the index = length of the given array - 1. \n\nThen we should repeat for ever until we get the correct answer so I used while true. \n\nand simply applied the logic using if else conditions. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe complexity of my algorithm even with the exist of while true in the code, but it does not exceed O(n) that is because actually the maximum time it can take is n/2 + 1 because we move the pointers in each step, and the two pointers will never meet each other, so for finding the upper bound it will be O(n), where n is the length of the given list. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nsince I have not used any extra lists, so it will be O(n) where n is the size of the given list. \n> Note that we do not count the size of the defined integers, as they are not defined in side a loop, so we assume that their complexity is O(1). \n# Code\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n bgn, lst = 0, len(numbers) - 1\n while(True):\n if(numbers[lst] + numbers[bgn] > target):\n lst -= 1\n elif (numbers[lst] + numbers[bgn] < target):\n bgn += 1\n else:\n return [bgn + 1, lst + 1]\n \n``` | 3 | Given a **1-indexed** array of integers `numbers` that is already **_sorted in non-decreasing order_**, find two numbers such that they add up to a specific `target` number. Let these two numbers be `numbers[index1]` and `numbers[index2]` where `1 <= index1 < index2 <= numbers.length`.
Return _the indices of the two numbers,_ `index1` _and_ `index2`_, **added by one** as an integer array_ `[index1, index2]` _of length 2._
The tests are generated such that there is **exactly one solution**. You **may not** use the same element twice.
Your solution must use only constant extra space.
**Example 1:**
**Input:** numbers = \[2,7,11,15\], target = 9
**Output:** \[1,2\]
**Explanation:** The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return \[1, 2\].
**Example 2:**
**Input:** numbers = \[2,3,4\], target = 6
**Output:** \[1,3\]
**Explanation:** The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return \[1, 3\].
**Example 3:**
**Input:** numbers = \[\-1,0\], target = -1
**Output:** \[1,2\]
**Explanation:** The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return \[1, 2\].
**Constraints:**
* `2 <= numbers.length <= 3 * 104`
* `-1000 <= numbers[i] <= 1000`
* `numbers` is sorted in **non-decreasing order**.
* `-1000 <= target <= 1000`
* The tests are generated such that there is **exactly one solution**. | null |
✅ 100% Recursive & Iterative 2-Approaches | excel-sheet-column-title | 1 | 1 | # Problem Understanding\n\nIn the "Excel Sheet Column Title" problem, we are given an integer representing a column number. The task is to return its corresponding column title as it appears in an Excel sheet, where the letters range from A to Z for the numbers 1 to 26, and then AA to AZ, BA to BZ, and so on.\n\nFor instance, given the input 28, the output should be "AB".\n\n**Input**: columnNumber = 28\n**Output**: "AB"\n\n---\n\n# Live Coding Iterative & Recursive:\nhttps://youtu.be/Vlu300w6HbY\n\n- [Coding in Python \uD83D\uDC0D](https://youtu.be/Vlu300w6HbY)\n- [Coding in Rust \uD83E\uDD80](https://youtu.be/nutdEPmd3kM)\n\n---\n\n# Approach 1: Iterative\n\nTo solve the "Excel Sheet Column Title" problem using the iterative approach, we continuously divide the given number by 26 and determine the remainder. This remainder gives us the current character of the Excel title, starting from the least significant character.\n\n## Key Data Structures:\n- **List (result)**: Used to store the characters of the Excel title.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Create an empty list named `result`.\n \n2. **Processing Each Number**:\n - While `columnNumber` is not zero:\n - Use the `divmod` function to get the quotient and remainder of `columnNumber` when divided by 26.\n - Decrement the `columnNumber` by 1 and append the corresponding character to the `result` list.\n \n3. **Wrap-up**:\n - Reverse the `result` list and join the characters to form the final Excel title.\n\n## Example:\n\nGiven the input 701:\n\n**Iterative Approach:**\n\n- First iteration: remainder = 24, quotient = 26; result = ["Y"]\n- Second iteration: remainder = 25, quotient = 0; result = ["Y", "Z"]\n- No further iterations since quotient is now 0; final result = "ZY"\n\n---\n\n# Approach 2: Recursive\n\nTo tackle this problem recursively, we adopt a top-down approach, determining the most significant character first and then recursively determining the rest.\n\n## Key Data Structures:\n- **String**: As this is a recursive approach, we construct the Excel title directly as a string.\n\n## Enhanced Breakdown:\n\n1. **Base Case**:\n - If `columnNumber` is zero, return an empty string.\n \n2. **Recursive Call**:\n - Use the `divmod` function to determine the quotient and remainder of `columnNumber` divided by 26.\n - Construct the current character of the Excel title using the remainder.\n - Recursively call the function with the quotient to determine the preceding characters of the Excel title.\n\n3. **Wrap-up**:\n - Concatenate the result of the recursive call with the current character to form the current state of the Excel title.\n\n## Example:\n\nGiven the input 701:\n\n**Recursive Approach:**\n\n- First call: remainder = 24, quotient = 26; current character = "Y"\n- Second call: remainder = 25, quotient = 0; current character = "Z"\n- No further recursive calls as quotient is now 0; final result = "ZY"\n\n(Note: The order of the recursive approach\'s results is due to the nature of recursion, where the deeper levels of recursion resolve first.)\n\n---\n\n# Complexity:\n\n**Time Complexity for Both Approaches:** \n- The time complexity is $$O(\\log_{26} n)$$ for both methods, where $$n$$ is the given `columnNumber`. This is because we\'re continuously dividing the number by 26 until it becomes zero.\n\n**Space Complexity for Iterative Approach:** \n- The space complexity is $$O(\\log_{26} n)$$ due to the list we use to store the Excel title characters.\n\n**Space Complexity for Recursive Approach:** \n- The space complexity is also $$O(\\log_{26} n)$$ due to the recursive call stack.\n\n---\n\n# Performance:\n\n**Iterative Approach:**\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Rust | 0 ms | 100% | 2 MB | 86.84% |\n| Java | 0 ms | 100% | 39.7 MB | 61.65% |\n| Go | 1 ms | 74.84% | 1.9 MB | 94.34% |\n| C++ | 2 ms | 49.78% | 6 MB | 37.93% |\n| Python3 | 32 ms | 93.98% | 16.3 MB | 23.11% |\n| JavaScript | 44 ms | 93.13% | 42.1 MB | 11.16% |\n| C# | 55 ms | 97.28% | 36.8 MB | 15.65% |\n\n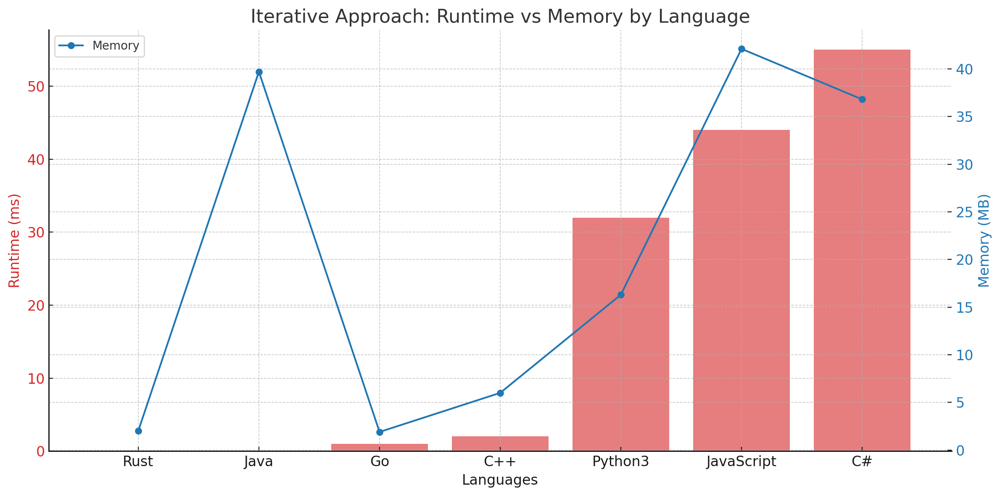\n\n\n**Recursive Approach:**\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Rust | 0 ms | 100% | 2.2 MB | 23.68% |\n| C++ | 0 ms | 100% | 5.9 MB | 37.93% |\n| Go | 1 ms | 74.84% | 1.9 MB | 94.34% |\n| Java | 6 ms | 34.8% | 40.6 MB | 5.65% |\n| Python3 | 34 ms | 88.27% | 16.4 MB | 23.11% |\n| JavaScript | 42 ms | 96.14% | 41.3 MB | 86.70% |\n| C# | 69 ms | 51.2% | 36.8 MB | 15.65% |\n\n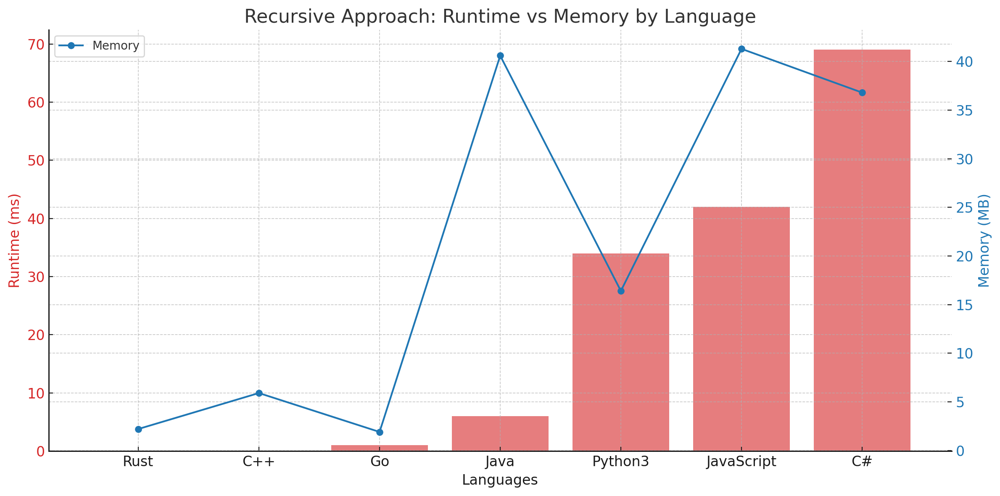\n\n\n---\n\n# Code Iterative\n``` Python []\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n result = []\n while columnNumber:\n columnNumber, remainder = divmod(columnNumber - 1, 26)\n result.append(chr(65 + remainder))\n return \'\'.join(reversed(result))\n```\n``` C++ []\nclass Solution {\npublic:\n string convertToTitle(int columnNumber) {\n string result = "";\n while (columnNumber) {\n columnNumber--;\n char c = \'A\' + columnNumber % 26;\n result = c + result;\n columnNumber /= 26;\n }\n return result;\n }\n};\n```\n``` Rust []\nimpl Solution {\n pub fn convert_to_title(column_number: i32) -> String {\n let mut result = String::new();\n let mut number = column_number;\n while number > 0 {\n number -= 1;\n let char_code = ((number % 26) as u8) + b\'A\';\n result.insert(0, char_code as char);\n number /= 26;\n }\n result\n }\n}\n```\n``` Go []\nfunc convertToTitle(columnNumber int) string {\n var result string\n for columnNumber > 0 {\n columnNumber--\n charCode := \'A\' + rune(columnNumber % 26)\n result = string(charCode) + result\n columnNumber /= 26\n }\n return result\n}\n```\n``` Java []\npublic class Solution {\n public String convertToTitle(int columnNumber) {\n StringBuilder result = new StringBuilder();\n while (columnNumber > 0) {\n columnNumber--;\n char c = (char) (\'A\' + columnNumber % 26);\n result.insert(0, c);\n columnNumber /= 26;\n }\n return result.toString();\n }\n}\n```\n``` C# []\npublic class Solution {\n public string ConvertToTitle(int columnNumber) {\n string result = "";\n while (columnNumber > 0) {\n columnNumber--;\n char c = (char) (\'A\' + columnNumber % 26);\n result = c + result;\n columnNumber /= 26;\n }\n return result;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} columnNumber\n * @return {string}\n */\nvar convertToTitle = function(columnNumber) {\n let result = "";\n while (columnNumber > 0) {\n columnNumber--;\n let charCode = \'A\'.charCodeAt(0) + columnNumber % 26;\n result = String.fromCharCode(charCode) + result;\n columnNumber = Math.floor(columnNumber / 26);\n }\n return result;\n};\n```\n\n# Code Recusrive\n``` Python []\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n if not columnNumber:\n return ""\n columnNumber, remainder = divmod(columnNumber - 1, 26)\n return self.convertToTitle(columnNumber) + chr(65 + remainder)\n```\n``` C++ []\nclass Solution {\npublic:\n string convertToTitle(int columnNumber) {\n if (columnNumber == 0) return "";\n columnNumber--;\n char c = \'A\' + columnNumber % 26;\n return convertToTitle(columnNumber / 26) + c;\n }\n};\n```\n``` Rust []\nimpl Solution {\n pub fn convert_to_title(column_number: i32) -> String {\n if column_number == 0 {\n return String::new();\n }\n let mut number = column_number;\n number -= 1;\n let char_code = ((number % 26) as u8) + b\'A\';\n let prev = Self::convert_to_title(number / 26);\n return format!("{}{}", prev, char_code as char);\n }\n}\n```\n``` Go []\nfunc convertToTitle(columnNumber int) string {\n if columnNumber == 0 {\n return ""\n }\n columnNumber--\n charCode := \'A\' + rune(columnNumber%26)\n return convertToTitle(columnNumber/26) + string(charCode)\n}\n```\n``` Java []\npublic class Solution {\n public String convertToTitle(int columnNumber) {\n if (columnNumber == 0) return "";\n columnNumber--;\n char c = (char) (\'A\' + columnNumber % 26);\n return convertToTitle(columnNumber / 26) + c;\n }\n}\n```\n``` C# []\npublic class Solution {\n public string ConvertToTitle(int columnNumber) {\n if (columnNumber == 0) return "";\n columnNumber--;\n char c = (char) (\'A\' + columnNumber % 26);\n return ConvertToTitle(columnNumber / 26) + c;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} columnNumber\n * @return {string}\n */\nvar convertToTitle = function(columnNumber) {\n if (columnNumber === 0) return "";\n columnNumber--;\n let charCode = \'A\'.charCodeAt(0) + columnNumber % 26;\n return convertToTitle(Math.floor(columnNumber / 26)) + String.fromCharCode(charCode);\n};\n```\n\n# Live Coding in Rust:\nhttps://youtu.be/nutdEPmd3kM\n\nThis problem provides an elegant demonstration of how to convert base-10 numbers to another base, in this case, base-26. It\'s a great reminder that sometimes algorithmic problems can be rooted in simple number base conversions. \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB | 56 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Easy || 0 ms || 100% || Fully Explained (Java, C++, Python, Python3) | excel-sheet-column-title | 1 | 1 | # **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Excel Sheet Column Title.\n```\nclass Solution {\n public String convertToTitle(int columnNumber) {\n // Create an empty string for storing the characters...\n StringBuilder output = new StringBuilder();\n // Run a while loop while columnNumber is positive...\n while(columnNumber > 0){\n // Subtract 1 from columnNumber...\n columnNumber--;\n // Get current character by doing modulo of columnNumber by 26...\n char c = (char) (columnNumber % 26 + \'A\');\n // Divide columnNumber by 26...\n columnNumber /= 26;\n // Append the character into output...\n output.append(c);\n }\n // Reverse the output string...\n // Bcause we have found characters from right to left...\n output.reverse();\n // Return the reversed string.\n return output.toString();\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n string convertToTitle(int columnNumber) {\n // Create an empty string for storing the characters...\n string output;\n // Run a while loop while columnNumber is positive...\n while(columnNumber > 0){\n // Subtract 1 from columnNumber...\n columnNumber--;\n // Get current character by doing modulo of columnNumber by 26...\n int m = columnNumber % 26;\n // Divide columnNumber by 26...\n columnNumber /= 26;\n output += \'A\' + m;\n }\n // Reverse the output string...\n // Bcause we have found characters from right to left...\n reverse(output.begin(),output.end());\n // Return the reversed string.\n return output;\n }\n};\n```\n\n# **Python / Python3 Solution:**\n```\nclass Solution(object):\n def convertToTitle(self, columnNumber):\n # Create an empty string for storing the characters...\n output = ""\n # Run a while loop while columnNumber is positive...\n while columnNumber > 0:\n # Subtract 1 from columnNumber and get current character by doing modulo of columnNumber by 26...\n output = chr(ord(\'A\') + (columnNumber - 1) % 26) + output\n # Divide columnNumber by 26...\n columnNumber = (columnNumber - 1) // 26\n # Return the output string.\n return output\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 90 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Simplest Python solution. Divide by 26 | excel-sheet-column-title | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def convertToTitle(self, n: int) -> str:\n res = ""\n while n > 0:\n r = (n-1) % 26\n n = (n-1)// 26\n res += chr(ord("A")+r)\n return res[::-1]\n``` | 4 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | excel-sheet-column-title | 1 | 1 | # Intuition\nConvert to base 26 system.\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 246 videos as of August 22nd.\n\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/q8DkXSns3Xk\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n**Initialization:**\n- Initialize an empty string `res` to store the resulting column title.\n\n**Conversion Loop:**\n- Enter a loop while `columnNumber` is greater than 0.\n - Decrement `columnNumber` by 1 to account for 1-based indexing in column titles.\n - Calculate the remainder of `columnNumber` divided by 26. This remainder will represent the position of the current letter in the alphabet (0 to 25).\n - Convert the calculated remainder to its corresponding uppercase letter using `chr((columnNumber % 26) + ord("A"))`.\n - Add the calculated letter to the beginning of the `res` string.\n - Update `columnNumber` by performing integer division (floor division) by 26. This shifts to the next position in the column title.\n\n**Return:**\n- Return the final `res` string, which represents the column title in Excel sheet notation.\n\nThis algorithm processes a given column number and converts it into its corresponding column title using a base-26 numbering system.\n\n# Complexity\n- Time complexity:O(log26 n)\nn is a given column number.\n\n- Space complexity: O(log26 n)\n\n```python []\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n res = ""\n\n while columnNumber > 0:\n columnNumber -= 1\n res = chr((columnNumber % 26) + ord("A")) + res\n columnNumber //= 26\n \n return res\n```\n```javascript []\n/**\n * @param {number} columnNumber\n * @return {string}\n */\nvar convertToTitle = function(columnNumber) {\n let res = "";\n\n while (columnNumber > 0) {\n columnNumber--;\n res = String.fromCharCode((columnNumber % 26) + "A".charCodeAt(0)) + res;\n columnNumber = Math.floor(columnNumber / 26);\n }\n \n return res; \n};\n```\n```java []\nclass Solution {\n public String convertToTitle(int columnNumber) {\n StringBuilder res = new StringBuilder();\n\n while (columnNumber > 0) {\n columnNumber--;\n res.insert(0, (char) ((columnNumber % 26) + \'A\'));\n columnNumber /= 26;\n }\n \n return res.toString(); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string convertToTitle(int columnNumber) {\n string res = "";\n\n while (columnNumber > 0) {\n columnNumber--;\n res = char((columnNumber % 26) + \'A\') + res;\n columnNumber /= 26;\n }\n \n return res; \n }\n};\n```\n | 9 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Python 3 || 6 lines, rotated string || T/M: 100% / 100% | excel-sheet-column-title | 0 | 1 | ```\nclass Solution:\n def convertToTitle(self, n: int) -> str:\n\n alpha, ans = \'Z\'+ ascii_uppercase, ""\n\n while n:\n n, r = divmod(n,26)\n ans = alpha[r] + ans\n if not r: n-= 1\n return ans\n```\n[https://leetcode.com/problems/excel-sheet-column-title/submissions/611614578/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(log*N*) and space complexity is *O*(1), in which *N* ~ `n`. | 5 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Python easy solution. | excel-sheet-column-title | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n result = ""\n while columnNumber > 0:\n columnNumber, remainder = divmod(columnNumber - 1, 26)\n result = chr(65 + remainder) + result\n return result\n\n``` | 2 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Converting Column Number to Column Title in Excel Sheet using Base-26 System | excel-sheet-column-title | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to convert a given column number into the corresponding column title in an Excel sheet. We can use the ASCII codes of the capital letters to represent the column titles.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use the algorithm mentioned earlier to convert the column number to its corresponding title. We start by initializing an empty string to store the column title. We then use a while loop to iterate over the column number until it becomes zero. Within the loop, we subtract 1 from the column number to account for 0-based indexing, and then compute the remainder of the column number when divided by 26. We add this remainder to the ASCII code of \'A\' to get the corresponding capital letter, which we then append to the beginning of the column title string. Finally, we divide the column number by 26 and update its value for the next iteration. We continue this process until the column number becomes zero, and then return the column title string.\n# Complexity\n- Time complexity:The time complexity of the algorithm is $$O(log N)$$, where N is the given column number. This is because we divide the column number by 26 in each iteration of the loop, which reduces its value by a factor of 26. Since the number of digits in the base 26 representation of N is $$log(N)$$, the number of iterations required to reduce N to zero is $$log(N)$$ The time complexity of the chr() and ord() functions used to convert between ASCII codes and characters is $$O(1)$$, so they do not affect the overall time complexity of the algorithm.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity of the algorithm is also $$O(log N$$), since the size of the column title string is proportional to the number of iterations of the loop.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n## Summary -\nThis algorithm converts a given column number to its corresponding column title in an Excel sheet using the base-26 system and ASCII codes of capital letters. It works by iterating over the column number, computing the remainder when divided by 26, and adding the corresponding letter to the beginning of the column title. It then updates the column number and continues the process until the column number becomes zero. The time complexity of the algorithm is $$O(log N)$$, and the space complexity is also $$O(log N)$$ where N is the given column number.\n# Code\n```\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n title = ""\n while columnNumber > 0:\n columnNumber -= 1\n letter = chr(columnNumber % 26 + ord(\'A\'))\n title = letter + title\n columnNumber //= 26\n return title\n\n``` | 3 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Python3 Solution | excel-sheet-column-title | 0 | 1 | \n```\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str: \n ans="" \n while columnNumber>0:\n c=chr(ord(\'A\')+(columnNumber-1)%26)\n ans=c+ans\n columnNumber=(columnNumber-1)//26 \n return ans \n``` | 7 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Easy.py | excel-sheet-column-title | 0 | 1 | # Code\n```\nclass Solution:\n def convertToTitle(self, n: int) -> str:\n if n<27:\n return chr(ord(\'A\')+(n-1)%26)\n ans=""\n while n>0:\n if n%26==0:\n ans+=chr(ord(\'A\')+25)\n n-=1\n else:\n ans+=chr(ord(\'A\')+n%26-1)\n n//=26\n return ans[::-1]\n``` | 2 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Excel Sheet Column Title in Python | excel-sheet-column-title | 0 | 1 | # Intuition\nAssign characters as per unicode values, keeping in mind the values that go beyond the 26 letters of the alphabet.\n\n# Approach\nAssign the value of `columnNumber` to a variable `n`. Initialize a blank string `res`. Initialize a while loop with the condition `n > 0`. \nInside the `while loop`:\nDecrement the value of `n` by 1, to fit the number system starting with `0` instead of `1`. Calculate the modulus of `n` when divided by `26`, to get the value by which the number is exceeding the 26 letters of the alphabet. Add this value to the unicode value of `A`, to get the unicode value of the letter. Apply the `chr` function with this value as the input, to get the letter. Concatenate this with the string `res`. Calculate the value of the floor division of `n` by 26, to move on to the next value for consideration in the loop.\n\n**Let us understand this with the help of an example:**\n\nSuppose, `columnNumber` is given as 27.\nWe assign this value to `n`.\nThen initialize the empty string `res`.\nCheck the while loop codition, which is passed. So, we enter the loop. \nDecrement `n` by 1, so we get 26. \nNext, the modulus of `n` when divided by 26 is calculated as 0. We add this to the unicode value of `A`, which gives us 65. \nThe `chr` function returns `A` for this value. \nWe concatenate `A` with res, to get `A`.\nFloor division of `n` by 26 gives 1.\nThis value goes back into the loop. \nThe condition is passed, so we wnter the loop and `n` is decremented to 0. \nThe modulus is still 0, so the output of `chr` function is `A`, which is concatenated with the previous value of `res`, which is `A`.\nFloor division of `n` by 26 now gives 0, which fails the loop condition, so we exit.\nFinally, we return the value of `res` as `AA`.\n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:\n\n\n# Code\n```\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n n = columnNumber\n res = ""\n while n > 0:\n n -= 1\n res = chr(n % 26 + ord(\'A\')) + res\n n //= 26\n return res\n\n``` | 3 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Python Easy Solution | excel-sheet-column-title | 0 | 1 | # Code\n```\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n res=""\n while(columnNumber>0):\n columnNumber-=1\n i=columnNumber%26\n res+=chr(65+i)\n columnNumber=columnNumber//26\n return res[::-1]\n```\n\n***Please Upvote*** | 3 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Python | Fastest | Easy to Understand | Optimal Solution | excel-sheet-column-title | 0 | 1 | # Python | Fastest | Easy to Understand | Optimal Solution\n```\nclass Solution:\n def convertToTitle(self, n: int) -> str:\n ans = []\n while(n > 0):\n n -= 1\n curr = n % 26\n n = int(n / 26)\n ans.append(chr(curr + ord(\'A\')))\n \n return \'\'.join(ans[::-1])\n``` | 5 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Simple 3 lines code, beats 100% || C++ || Java || Python | excel-sheet-column-title | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust take out the last element from columnNumber smaller than or equal to 26 (%26) and put the equivalent character from capital letters in the string and reduce the columnNumber to the reminder by using (/26). Reverse the string finally to get the final answer.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```C++ []\nclass Solution {\npublic:\n string convertToTitle(int columnNumber) {\n string ans;\n \n while (columnNumber) {\n columnNumber--;\n // Get the last character and append it at the end of string.\n ans = ans + (char)((columnNumber) % 26 + \'A\');\n columnNumber = (columnNumber) / 26;\n }\n \n // Reverse it, as we appended characters in reverse order.\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```\n```java []\nclass Solution {\npublic:\n string convertToTitle(int columnNumber) {\n string ans;\n \n while (columnNumber) {\n columnNumber--;\n // Get the last character and append it at the end of string.\n ans = ans + (char)((columnNumber) % 26 + \'A\');\n columnNumber = (columnNumber) / 26;\n }\n \n // Reverse it, as we appended characters in reverse order.\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```\n```Python []\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n ans = ""\n \n while columnNumber > 0:\n columnNumber -= 1\n # Get the last character and append it at the end of the string.\n ans += chr(columnNumber % 26 + ord(\'A\'))\n columnNumber //= 26\n \n # Reverse it, as we appended characters in reverse order.\n ans = ans[::-1]\n return ans\n```\nPlease upvote :)\n | 2 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Python Easy to Understand Solution | excel-sheet-column-title | 0 | 1 | Please upvote if you like it.\n```\nclass Solution:\n def convertToTitle(self, num: int) -> str:\n ans=""\n while num > 0:\n num -= 1\n ans = chr(num % 26 + 65) + ans\n num //= 26\n return ans | 6 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
Excel sheet column Title using Python3 | excel-sheet-column-title | 0 | 1 | # Code\n```\nclass Solution:\n def convertToTitle(self, columnNumber: int) -> str:\n s=\'\'\n while columnNumber > 0:\n d = (columnNumber - 1) % 26\n s += chr(d + ord(\'A\'))\n columnNumber = (columnNumber - 1) // 26\n return s[::-1] \n\n\n\n``` | 1 | Given an integer `columnNumber`, return _its corresponding column title as it appears in an Excel sheet_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnNumber = 1
**Output:** "A "
**Example 2:**
**Input:** columnNumber = 28
**Output:** "AB "
**Example 3:**
**Input:** columnNumber = 701
**Output:** "ZY "
**Constraints:**
* `1 <= columnNumber <= 231 - 1` | null |
✅3 Method's || Beats 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | majority-element | 1 | 1 | # Approach 1: Sorting\n\n# Intuition:\nThe intuition behind this approach is that if an element occurs more than n/2 times in the array (where n is the size of the array), it will always occupy the middle position when the array is sorted. Therefore, we can sort the array and return the element at index n/2.\n\n# Explanation:\n1. The code begins by sorting the array `nums` in non-decreasing order using the `sort` function from the C++ Standard Library. This rearranges the elements such that identical elements are grouped together.\n2. Once the array is sorted, the majority element will always be present at index `n/2`, where `n` is the size of the array.\n - This is because the majority element occurs more than n/2 times, and when the array is sorted, it will occupy the middle position.\n3. The code returns the element at index `n/2` as the majority element.\n\nThe time complexity of this approach is O(n log n) since sorting an array of size n takes O(n log n) time.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int majorityElement(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n return nums[n/2];\n }\n};\n```\n```Java []\nclass Solution {\n public int majorityElement(int[] nums) {\n Arrays.sort(nums);\n int n = nums.length;\n return nums[n/2];\n }\n}\n```\n```Python3 []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> int:\n nums.sort()\n n = len(nums)\n return nums[n//2]\n```\n\n\n# Approach 2: Hash Map\n\n# Intuition:\nThe intuition behind using a hash map is to count the occurrences of each element in the array and then identify the element that occurs more than n/2 times. By storing the counts in a hash map, we can efficiently keep track of the occurrences of each element.\n\nExplanation:\n1. The code begins by initializing a hash map `m` to store the count of occurrences of each element.\n2. It then iterates through the array `nums` using a for loop.\n3. For each element `nums[i]`, it increments its count in the hash map `m` by using the line `m[nums[i]]++;`.\n - If `nums[i]` is encountered for the first time, it will be added to the hash map with a count of 1.\n - If `nums[i]` has been encountered before, its count in the hash map will be incremented by 1.\n4. After counting the occurrences of each element, the code updates `n` to be `n/2`, where `n` is the size of the array. This is done to check if an element occurs more than n/2 times, which is the criteria for being the majority element.\n5. The code then iterates through the key-value pairs in the hash map using a range-based for loop.\n - For each key-value pair `(x.first, x.second)`, it checks if the count `x.second` is greater than `n`.\n - If the count is greater than `n`, it means that `x.first` occurs more than n/2 times, so it returns `x.first` as the majority element.\n6. If no majority element is found in the hash map, the code returns 0 as the default value.\n - Note that this will only occur if the input array `nums` is empty or does not have a majority element.\n\nThe time complexity of this approach is O(n) because it iterates through the array once to count the occurrences and then iterates through the hash map, which has a maximum size of the number of distinct elements in the array.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int majorityElement(vector<int>& nums) {\n int n = nums.size();\n unordered_map<int, int> m;\n \n for(int i = 0; i < n; i++){\n m[nums[i]]++;\n }\n n = n/2;\n for(auto x: m){\n if(x.second > n){\n return x.first;\n }\n }\n return 0;\n }\n};\n```\n```Java []\nclass Solution {\n public int majorityElement(int[] nums) {\n int n = nums.length;\n Map<Integer, Integer> map = new HashMap<>();\n \n for (int i = 0; i < n; i++) {\n map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);\n }\n \n n = n / 2;\n for (Map.Entry<Integer, Integer> entry : map.entrySet()) {\n if (entry.getValue() > n) {\n return entry.getKey();\n }\n }\n \n return 0;\n }\n}\n```\n```Python3 []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> int:\n n = len(nums)\n m = defaultdict(int)\n \n for num in nums:\n m[num] += 1\n \n n = n // 2\n for key, value in m.items():\n if value > n:\n return key\n \n return 0\n```\n\n# Approach 3: Moore Voting Algorithm\n\n# Intuition:\nThe intuition behind the Moore\'s Voting Algorithm is based on the fact that if there is a majority element in an array, it will always remain in the lead, even after encountering other elements.\n\n# Explanation:\n\n**Algorithm:**\n1. Initialize two variables: `count` and `candidate`. Set `count` to 0 and `candidate` to an arbitrary value.\n2. Iterate through the array `nums`:\n a. If `count` is 0, assign the current element as the new `candidate` and increment `count` by 1.\n b. If the current element is the same as the `candidate`, increment `count` by 1.\n c. If the current element is different from the `candidate`, decrement `count` by 1.\n3. After the iteration, the `candidate` variable will hold the majority element.\n\n**Explanation:**\n1. The algorithm starts by assuming the first element as the majority candidate and sets the count to 1.\n2. As it iterates through the array, it compares each element with the candidate:\n a. If the current element matches the candidate, it suggests that it reinforces the majority element because it appears again. Therefore, the count is incremented by 1.\n b. If the current element is different from the candidate, it suggests that there might be an equal number of occurrences of the majority element and other elements. Therefore, the count is decremented by 1.\n - Note that decrementing the count doesn\'t change the fact that the majority element occurs more than n/2 times.\n3. If the count becomes 0, it means that the current candidate is no longer a potential majority element. In this case, a new candidate is chosen from the remaining elements.\n4. The algorithm continues this process until it has traversed the entire array.\n5. The final value of the `candidate` variable will hold the majority element.\n\n**Explanation of Correctness:**\nThe algorithm works on the basis of the assumption that the majority element occurs more than n/2 times in the array. This assumption guarantees that even if the count is reset to 0 by other elements, the majority element will eventually regain the lead.\n\nLet\'s consider two cases:\n1. If the majority element has more than n/2 occurrences:\n - The algorithm will ensure that the count remains positive for the majority element throughout the traversal, guaranteeing that it will be selected as the final candidate.\n\n2. If the majority element has exactly n/2 occurrences:\n - In this case, there will be an equal number of occurrences for the majority element and the remaining elements combined.\n - However, the majority element will still be selected as the final candidate because it will always have a lead over any other element.\n\nIn both cases, the algorithm will correctly identify the majority element.\n\nThe time complexity of the Moore\'s Voting Algorithm is O(n) since it traverses the array once.\n\nThis approach is efficient compared to sorting as it requires only a single pass through the array and does not change the original order of the elements.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int majorityElement(vector<int>& nums) {\n int count = 0;\n int candidate = 0;\n \n for (int num : nums) {\n if (count == 0) {\n candidate = num;\n }\n \n if (num == candidate) {\n count++;\n } else {\n count--;\n }\n }\n \n return candidate;\n }\n};\n```\n```Java []\nclass Solution {\n public int majorityElement(int[] nums) {\n int count = 0;\n int candidate = 0;\n \n for (int num : nums) {\n if (count == 0) {\n candidate = num;\n }\n \n if (num == candidate) {\n count++;\n } else {\n count--;\n }\n }\n \n return candidate;\n }\n}\n```\n```Python3 []\nclass Solution:\n def majorityElement(self, nums: List[int]) -> int:\n count = 0\n candidate = 0\n \n for num in nums:\n if count == 0:\n candidate = num\n \n if num == candidate:\n count += 1\n else:\n count -= 1\n \n return candidate\n```\n\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. **Practice them in a row for better understanding and please Upvote the post for more questions.**\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 1,271 | Given an array `nums` of size `n`, return _the majority element_.
The majority element is the element that appears more than `⌊n / 2⌋` times. You may assume that the majority element always exists in the array.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,2,1,1,1,2,2\]
**Output:** 2
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you solve the problem in linear time and in `O(1)` space? | null |
Solution | majority-element | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int majorityElement(vector<int>& nums) {\n \n int n = nums.size();\n int k = ceil(n/2);\n\n unordered_map<int,int>m1;\n for(int i=0;i<nums.size();i++){\n m1[nums[i]]++;\n }\n int g=0;\n for(auto it:m1){\n if(it.second > k){\n g=it.first;\n } \n }\n return g;\n }\n};\n```\n\n```Python3 []\nimport statistics\nf = open("user.out", \'w\')\nfor line in stdin:\n l = sorted(map(int, line.rstrip()[1:-1].split(\',\')))\n print(l[len(l) // 2], file=f)\nexit(0)\n```\n\n```Java []\nclass Solution {\n public static int majorityElement(int[] nums) {\n return helper(nums,0,nums[0]);\n }static int helper(int[] nums, int si, int ref){\n int c=0;\n for(int i=si;i<nums.length;i++){\n if(nums[i]==ref)\n c++;\n else\n c--;\n if(c==-1)\n return helper(nums,i,nums[i]);\n }return ref;\n }\n public static void main(String[] args)throws Exception{\n BufferedReader br=new BufferedReader(new InputStreamReader(System.in));\n String[] s=br.readLine().split(" ");\n int[] nums=new int[s.length];\n for(int i=0;i<s.length;i++){\n nums[i]=Integer.parseInt(s[i]);\n }majorityElement(nums);\n }\n}\n```\n | 204 | Given an array `nums` of size `n`, return _the majority element_.
The majority element is the element that appears more than `⌊n / 2⌋` times. You may assume that the majority element always exists in the array.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,2,1,1,1,2,2\]
**Output:** 2
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you solve the problem in linear time and in `O(1)` space? | null |
O( n*log(n) )✅ | Python (Step by step explanation)✅ | majority-element | 0 | 1 | # Intuition\n<!-- Your intuition or thoughts about solving the problem -->\nMy intuition is to use Python\'s `statistics.mode` function to directly find the majority element in the list.\n\n# Approach\n<!-- Describe your approach to solving the problem -->\n1. Utilize the `statistics.mode` function, which returns the mode (majority element) of the given list.\n2. Return the result obtained from `statistics.mode` as the majority element.\n\n# Complexity\n- Time complexity:\n - The `statistics.mode` function calculates the mode in a list. Its time complexity depends on the algorithm used by the implementation but is typically efficient and is often close to O(n).\n - The overall time complexity depends on the specific implementation of `statistics.mode`, which may vary, but it is generally efficient.\n\n- Space complexity:\n - Your code doesn\'t use additional data structures that depend on the input size, so the space complexity is typically O(1),\n\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> int:\n mode = statistics.mode(nums)\n return mode\n\n```\n\n# Please upvote the solution if you understood it.\n\n | 2 | Given an array `nums` of size `n`, return _the majority element_.
The majority element is the element that appears more than `⌊n / 2⌋` times. You may assume that the majority element always exists in the array.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,2,1,1,1,2,2\]
**Output:** 2
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you solve the problem in linear time and in `O(1)` space? | null |
Python3: O(N) time, O(1) space; Boyer-Moore's majority voting algo with link to easy explanation | majority-element | 0 | 1 | # Intuition\nTo solve it in $O(N)$ time and $O(1)$ space, we canot use a hashmap ($O(N)$ space) or sort the array in-place ($O(NlogN)$ time). Therefore, we have to use Boyer-Moore\u2019s majority voting algorithm which does the trick.\n\n# Approach\nTo understand how the algorithm works, see [C++|| Moore\'s Voting Algorithm Explained in Super Simple Fast Way!!!](https://leetcode.com/problems/majority-element/solutions/3015428/c-moore-s-voting-algorithm-explained-in-super-simple-fast-way/)\n\n# Complexity\n- Time complexity: $O(N)$\n\n- Space complexity: $O(1)$\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> int:\n result = 0\n count = 0\n\n for num in nums:\n if count == 0:\n result = num\n \n if num == result:\n count += 1\n else:\n count -= 1\n \n return result\n\n``` | 0 | Given an array `nums` of size `n`, return _the majority element_.
The majority element is the element that appears more than `⌊n / 2⌋` times. You may assume that the majority element always exists in the array.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,2,1,1,1,2,2\]
**Output:** 2
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you solve the problem in linear time and in `O(1)` space? | null |
Beats 85.08% of users with Python3 | majority-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def majorityElement(self, nums: List[int]) -> int:\n set_nums = set(nums)\n for i in set_nums:\n if nums.count(i)>len(nums)/2:\n return i\n``` | 0 | Given an array `nums` of size `n`, return _the majority element_.
The majority element is the element that appears more than `⌊n / 2⌋` times. You may assume that the majority element always exists in the array.
**Example 1:**
**Input:** nums = \[3,2,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,2,1,1,1,2,2\]
**Output:** 2
**Constraints:**
* `n == nums.length`
* `1 <= n <= 5 * 104`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you solve the problem in linear time and in `O(1)` space? | null |
✔️ [Python3] CLEAN SOLUTION (๑❛ꆚ❛๑), Explained | excel-sheet-column-number | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nEssentially, what we asked to do here is to convert a number in the base 26 numeral system to a decimal number. This is a standard algorithm, where we iterate over the digits from right to left and multiply them by the base to the power of the position of the digit. To translate a letter to a number we use the Python method `ord` which returns the Unicode code of the letter. By subtracting the code by 64, we can map letters to the numbers from 1 to 26.\n\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n ans, pos = 0, 0\n for letter in reversed(columnTitle):\n digit = ord(letter)-64\n ans += digit * 26**pos\n pos += 1\n \n return ans\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 160 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
[Python] | Simple & Clean code | excel-sheet-column-number | 0 | 1 | # Code\n```\nclass Solution:\n def titleToNumber(self, s: str) -> int:\n n = len(s)\n cnt = [0] * 7\n p = 0\n for i in range(n -1, -1, -1):\n cnt[i] = (ord(s[i]) - ord(\'A\') + 1) * 26 ** p\n p += 1\n return sum(cnt)\n``` | 2 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Simple Question with best appoarch | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n number=0\n for alpha in columnTitle:\n number=number*26+(ord(alpha)-64)\n return number\n\n\n``` | 1 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Beats : 7.07% [23/145 Top Interview Question] | excel-sheet-column-number | 0 | 1 | # Intuition\n*exponential value*\n\n# Approach\nThis code defines a class called `Solution` with a method called `titleToNumber` that takes a string `columnTitle` as input and returns an integer value that represents the column number corresponding to the given column title in an Excel spreadsheet.\n\nThe variables used in the code are:\n- `columnTitle`: A string that represents the title of the column in an Excel spreadsheet.\n- `result`: A variable that stores the final computed column number value.\n- `multiplier`: A variable that keeps track of the value to multiply the current digit with.\n\nThe algorithm used in this method is based on the fact that each column in an Excel spreadsheet is represented by a string title. These titles can be converted to corresponding column numbers using the following formula:\n- For each character in the title, we first calculate its corresponding number value by subtracting the ASCII value of `\'A\'` from its own ASCII value and adding 1 (since column A corresponds to the number 1).\n- We then multiply this number value with the appropriate power of 26 and add it to the result variable.\n- Finally, we update the `multiplier` variable to be the next power of 26 that we need to multiply with.\n\nThe algorithm iterates over the characters of the `columnTitle` string from right to left (i.e., from the least significant digit to the most significant digit), computes the corresponding number value of each character using the formula described above, and updates the `result` variable accordingly. It also updates the `multiplier` variable to keep track of the current power of 26 that needs to be multiplied with.\n\nAfter iterating through all the characters of the `columnTitle` string, the method returns the final value of the `result` variable, which represents the corresponding column number for the given column title.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\nThe `time complexity` of this algorithm is `O(n)`, where n is the length of the input string `columnTitle`. This is because the algorithm performs a single pass through the input string, and the time taken to execute each iteration of the loop is constant.\n\nThe `space complexity` of this algorithm is also `O(1)`, because the algorithm only uses a constant amount of extra space to store the variables `result` and `multiplier`. This space usage does not depend on the size of the input string, so the algorithm is said to have a `space complexity` of `O(1)` or `constant space complexity`.\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n result = 0\n multiplier = 1\n for i in range(len(columnTitle)-1 , -1, -1):\n num = ord(columnTitle[i]) - 64\n result = result + ( num * multiplier)\n multiplier = multiplier * 26\n return result\n``` | 1 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Python 1 Line Solution | excel-sheet-column-number | 0 | 1 | # Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n cnt=0\n for i in range(len(columnTitle)):\n cnt+=(26**(len(columnTitle)-i-1))*(ord(columnTitle[i])-64)\n return cnt\n```\n\n***Please Upvote*** | 1 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Simple Approach. | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n number=0\n for alpha in columnTitle:\n number=number*26 + (ord(alpha)-64)\n return number\n``` | 2 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Converting Excel column title to column number using positional value of letters. | excel-sheet-column-number | 0 | 1 | # Intuition\n To convert a column title to a corresponding column number in Excel, we need to understand the positional value of each letter in the title. Each letter in the title represents a value that is a power of 26, where the letter \'A\' represents the zeroth power of 26, \'B\' represents the first power of 26, and so on. We can start from the rightmost letter of the title and work our way left, accumulating the corresponding values using the formula (value = (letter value) * (26 ^ position)). Once we have computed the values for each letter in the title, we can add them up to get the final column number. \n\n# Approach\nThe approach I used is to iterate through each character in the input string and convert it to its corresponding column value by subtracting the ASCII value of \'A\' and adding 1. We use a variable to keep track of the positional value of the letter and calculate the corresponding value using the formula mentioned earlier. Finally, we add up all the values to get the final result.\n\n# Complexity\n- Time complexity:\n The time complexity of this approach is$$ O(n),$$ where n is the length of the input string. This is because we need to iterate over each character in the string once to compute its corresponding column value. \n\n- Space complexity:\n The space complexity of this approach is $$O(1)$$, as we are only using a constant amount of extra space to store variables such as the result and positional value.\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n result = 0\n for i in range(len(columnTitle)):\n letter_value = ord(columnTitle[i]) - ord(\'A\') + 1\n position = len(columnTitle) - i - 1\n result += letter_value * (26 ** position)\n return result\n\n``` | 3 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Python: the only explanation that is understandable and makes sense to those who just start | excel-sheet-column-number | 0 | 1 | **Disclaimer**: I hate when the "Discussion" session has tons of posts that contain just a few lines of code with indecipherable variables and an impossible-to-follow logic. For this question, I haven\'t found a single solution that a novice user can follow and understand. ```ord()``` is everywhere, etc. \n\n**Explanation:**\nIt\'s easier to start with a different and, probably, easier problem. How to convert a string of digits to a number. Let\'s say, you\'re given \'67\' and you want to return 67. Sure you can do \n``` return int(s)``` \nbut if you are here for this, you don\'t want to be here. Let\'s assume, to make the explanation shorter, you can apply ```int()``` only to single digits but not to the whole number.\nYou\'re given \'67.\'\nLet\'s start reading this line element by element and initialise a variable ```res = 0``` that will contain the final result.\nWe will put the integer value of the first string\'s element to ```res```. Now ```res``` contains 6. Are we done with the string? No. Let\'s read the next character.\nThe next character is 7. If we just add 7 to ```res```, we will get 13. It\'s not what we want. We want to take whatever is stored in ```res``` already, multiply it by ten and add seven. This way we will take six, turn it into 60, add 7, and resave into ```res```. Are we done with the line? Yes. Then just return ```res```.\n\nHere is the whole thing encoded:\n```\ndef str2num(s):\n res = 0\n for digit in s:\n res = res * 10 + int(digit)\n return res\n```\n\nBy the way, you can also do it recursively:\n```\ndef str2num_recursively(s):\n def _helper(s, res):\n if not s: return res\n return _helper(s[1:], res * 10 + int(s[0]))\n return _helper(s, 0)\n```\nBut the secret is: **NEVER USE RECURSION UNLESS IT\'S A DFS PROBLEM**. **In real life**, once you finally get that fat FAANG job, **NEVER USE RECURSION**.\n\nLet\'s get back to 171. The idea here is the same with two differences:\n1) We will use a dictionary to create a mapping "character: number." \n2) We will use 26 instead of 10\n\n```\ndef titleToNumber(s):\n res = 0\n val = [i for i in range(1, 27)]\n letters = list("ABCDEFGHIJKLMNOPQRSTUVWXYZ")\n d = dict(zip(letters, val))\n for ch in s:\n res = res * 26 + d[ch]\n return res\n```\nAs you can see, res is calculated exactly the same way as in the first portion of code above. We just use 26 instead of 10, and ```d[ch]``` instead of ```int(s[0])```.\n\nAnd for those who don\'t listen to good advices, the recursive implementation:\n```\ndef titleToNumber_recur(s):\n val = [i for i in range(1, 27)]\n letters = list("ABCDEFGHIJKLMNOPQRSTUVWXYZ")\n d = dict(zip(letters, val))\n def _helper(s, res, d):\n if not s: return res\n res = res * 26 + d[s[0]]\n return _helper(s[1:], res, d)\n return _helper(s, 0, d)\n```\n | 96 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Easy || 100% || Explained || Java || C++|| Python (1 Line) || C || Python3 | excel-sheet-column-number | 1 | 1 | **Problem Statement:**\nGiven a string columnTitle that represents the column title as appears in an Excel sheet, return its corresponding column number.\n**For example:**\n\n\t\t\t\t\t\tA -> 1\n\t\t\t\t\t\tB -> 2\n\t\t\t\t\t\tC -> 3\n\t\t\t\t\t\t............\n\t\t\t\t\t\tZ -> 26\n\t\t\t\t\t\tAA -> 27\n\t\t\t\t\t\tAB -> 28 \n\t\t\t\t\t\t..................\n\n \n\n# **Java Solution:**\nRuntime: 1 ms, faster than 93.25% of Java online submissions for Excel Sheet Column Number.\nMemory Usage: 42.4 MB, less than 81.68% of Java online submissions for Excel Sheet Column Number.\n```\nclass Solution {\n public int titleToNumber(String columnTitle) {\n // Initialize the output result...\n int output = 0;\n // Traverse the whole list through the loop...\n for(int i = 0; i < columnTitle.length(); i++){\n // Process to get the excel sheet column number...\n output = output * 26 + (columnTitle.charAt(i) - \'A\' + 1);\n }\n return output; // Return the output...\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n int titleToNumber(string columnTitle) {\n // Initialize the output result...\n int output = 0;\n // Traverse the whole list through the loop...\n for(auto c: columnTitle) {\n // Process to get the excel sheet column number...\n output = output * 26 + (c - \'A\' + 1); \n }\n return output; // Return the output... \n }\n};\n```\n\n# **Python Solution:**\nRuntime: 22 ms, faster than 83.54% of Python online submissions for Excel Sheet Column Number.\n```\nclass Solution(object):\n def titleToNumber(self, columnTitle):\n s = columnTitle[::-1]\n return sum([(ord(s[i]) - 64) * (26 ** i) for i in range(len(s))])\n```\n \n# **C Language:**\n```\nint titleToNumber(char * columnTitle){\n int output = 0;\n for(int i = 0; i < strlen(columnTitle); i++){\n output *= 26;\n output += (columnTitle[i] - \'A\' + 1);\n }\n return output;\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n s = columnTitle[::-1]\n return sum([(ord(s[i]) - 64) * (26 ** i) for i in range(len(s))])\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 15 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Python Smallest Easiest Solution | excel-sheet-column-number | 0 | 1 | \n\n# Code\n```\nclass Solution(object):\n def titleToNumber(self, columnTitle):\n """\n :type columnTitle: str\n :rtype: int\n """\n s = 0\n for jj in columnTitle:\n s = s * 26 + ord(jj) - ord(\'A\') + 1\n return s\n\'\'\'Please Upvote\'\'\'\n``` | 4 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
✅ Python easy one liner | Explaination | excel-sheet-column-number | 0 | 1 | **How to form a number using a list of digits?**\n1. We take a variable ```ans``` and initialize it with 0 \n2. We traverse through the list and update the variable as ```ans = ans * 10 + currDigit ```\n\nIn this question we need to do the same but we multiply it with 26 instead of 10\n```ans = ans * 26 + currDigit```\n\n\nNow we need to think how we will get the ```currDigit``` out of Characters.\nwe will use ascii value of the characters\n\n```ord(i) - ord(\'A\') + 1 #ord will return the ascii value of the character```\n```\n A = 1 | ord(\'A\') - ord(\'A\') + 1 = 1\n B = 2 | ord(\'B\') - ord(\'A\') + 1 = 2\n C = 3 | ord(\'C\') - ord(\'A\') + 1 = 3\n```\n\nLet\'s code this in a simple way.\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n ans = 0\n for i in columnTitle:\n ans = ans * 26 + ord(i) - ord(\'A\') + 1\n return ans\n```\n\nNow If you are in love with python, you might be wondering how we will reduce the line of code to one.\nSo here is one liner solution.\n```\nclass Solution:\n def titleToNumber(self, title: str) -> int:\n return reduce(lambda x,y: x * 26 + y, map(lambda x: ord(x)-ord(\'A\')+1,title))\n```\n\n***If you have any questions or If you have a much shorter code please comment down below***\n | 20 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
best python solution beaten 98% codes in TC | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI have iterated the given input string from the end and multiplied the index of the character with 26 power of k value , which is intialized to zero.\nk=indicates the length from the end\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n str="ABCDEFGHIJKLMNOPQRSTUVWXYZ"\n k=0\n res=0\n for i in range(len(columnTitle)-1,-1,-1):\n p=str.index(columnTitle[i])\n res+=(p+1)*(26**k)\n k+=1\n return res\n\n\n``` | 5 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
best approach | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n number=0\n for alpha in columnTitle:\n number=number*26 + (ord(alpha)-64)\n return number\n``` | 1 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
171: Solution with step by step explanation | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe are given a string columnTitle representing the column title as appears in an Excel sheet. We are supposed to return its corresponding column number.\n\nOne way to solve the problem is by traversing the string columnTitle and for each character, we multiply the result so far by 26 and add the value corresponding to the current character.\n\nFor example, if columnTitle is "AB", then the corresponding column number is 1*26 + 2 = 28. Here, we start with 0, and multiply the result by 26 (which is the number of alphabets), and then add the value of the first character which is 1, which corresponds to the letter \'A\'. Then we multiply the result by 26 again, and add the value of the second character which is 2, corresponding to the letter \'B\'. This gives us the final result of 28.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n result = 0\n for ch in columnTitle:\n result = result*26 + ord(ch)-ord(\'A\')+1\n return result\n\n```\nIn the above code, we first initialize the result variable to 0. We then traverse the string columnTitle character by character. For each character, we multiply the result by 26 and add the value of the current character (after converting it to its corresponding integer value). Finally, we return the result.\n\nNote that we subtract ord(\'A\')-1 from the integer value of the character ch to get its corresponding value. We add 1 to it to get the actual value of the character (since \'A\' corresponds to 1 and not 0). | 7 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Python 3 : Super Easy To Understand With Explanation | excel-sheet-column-number | 0 | 1 | ```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n \n p = 1\n summ = 0\n for i in columnTitle[::-1] :\n summ += p*(ord(i)-64) # -ord(A)+1\n p*= 26\n \n return summ\n \n```\n* \'\'\'\n\t\tA.....to......Z = 26 elements\n\t\tAA.....to......ZZ = 26*26 elements\n\t\tAAA...to.....ZZZ = 26^3 elements\n\t\tso on.....\n\t\t\n\t\ttherefore for eg : ABCD\n\n ABCD = [(A)*26^3] + [(B)*26^2] + [(C)*26^1] + [(D)] \n \n where (A) = 1,(B) = 2 ......(AA) = 27....\n \'\'\'\n* eg : **"ZY"** --->\n* --first Y , ord(Y) = 89,-->89-64=25(value of Y in the first 26 elements),therefore its excel sheet value will be = [(26^0)*25] == 25\n* --second Z, ord(Z) = 90,-->90-64=26(value of Z in the first 26 elements) ,therefore its excel sheet value will be = [(26^1)*26] == 656\n* taking summ of them gives "ZY"\'s column number i.e, 656 + 25 = 701\n\n***please upvote if you like : )*** | 13 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
DUMBEST WAY TO SOLVE THE PROBLEM :) !!! | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n alpha = {\n \'A\': 1,\n \'B\': 2,\n \'C\': 3,\n \'D\': 4,\n \'E\': 5,\n \'F\': 6,\n \'G\': 7,\n \'H\': 8,\n \'I\': 9,\n \'J\': 10,\n \'K\': 11,\n \'L\': 12,\n \'M\': 13,\n \'N\': 14,\n \'O\': 15,\n \'P\': 16,\n \'Q\': 17,\n \'R\': 18,\n \'S\': 19,\n \'T\': 20,\n \'U\': 21,\n \'V\': 22,\n \'W\': 23,\n \'X\': 24,\n \'Y\': 25,\n \'Z\': 26\n }\n sno = 0\n columnTitle = columnTitle[::-1]\n for i in range(0,len(columnTitle)):\n sno += (alpha[columnTitle[i]]*(26**i))\n return sno\n\n``` | 1 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
[Python] Intuitive Straightforward Beginner-friendly Mathematical Solution Using Dictionary | excel-sheet-column-number | 0 | 1 | ## Step 1:\nTo start, when seeing the 26 English alphabets are used to represent numbers, the first intuition is to use a dictionary to pair 1-26 and A-Z, before considering the calculation in detials.\n* Method 1: \nUsing zip()\n```\nalphabet = \'ABCDEFGHIJKLMNOPQRSTUVWXYZ\'\nnums = range(1,27)\nalpha_dict = dict(zip(alphabet, nums))\nprint(alpha_dict)\n```\n\n* Method 2:\nComprehension\n```\nalpha_dict = {alphabet[i]: nums[i] for i in range(len(alphabet))}\nprint(alpha_dict)\n```\n\n## Step 2:\nWith this dictionary in mind, write down a few examples, a formula will soon pop up clearly:\n* AA -> 26 * 1 + 1 \n* AB -> 26 * 1 + 2\n* ZZ -> 26 * 26 + 26\n* ABC -> 26^2 * 1 + 26 * 2 + 3\nThat is:\n* AA -> 26^1 * A + 26^0 * A \n* AB -> 26^1 * A + 26^0 * B\n* ZZ -> 26^1 * Z + 26^0 * Z\n* ABC -> 26^2 * A + 26^1 * B + 26^0 * C\n\n\nSo the formula is:\n\n26^largest_digit_value * Letter_on_digit + ... + 26^0 * Letter_on_digit\n\n\n## Translate above intuition into code:\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n\t\n\t\t# Use dictionary to map alphabets A to Z one-on-one to integer 1 to 26:\n alphabet = \'ABCDEFGHIJKLMNOPQRSTUVWXYZ\'\n nums = range(1,27)\n alpha_to_nums = {alphabet[i]: nums[i] for i in range(len(alphabet))}\n\t\t\n\t\t# Express the formula above in a simple for loop, iterating from the last digit:\n column_number = 0\n for pos, letter in enumerate (reversed(columnTitle)):\n column_number += 26**(pos) * alpha_to_nums[letter] \n\t\t\t\n return column_number\n``` | 7 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Easy to understand Python solution || Runtime: 27ms Faster than 96% of other solution | excel-sheet-column-number | 0 | 1 | Please Upvote if you like the solution.\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n a = 0\n for i in columnTitle:\n a = a * 26 + ord(i) - ord(\'A\') + 1\n return a | 4 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Short and Simple Python solution | excel-sheet-column-number | 0 | 1 | # Intuition\nEach character is mapped to its positional value in the alphabet, and the title\'s characters are iterated through to calculate the numeric representation.\n# Approach\nIterate through each character in the column title, calculate its positional value using the formula 26^(n-i-1) * (ASCII_value - 64), and accumulate the sum.\n\n# Complexity\n- Time complexity:\nO(n), where n is the length of the columnTitle.\n\n- Space complexity:\nO(1), as only a few variables are used regardless of the input size.\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n n = len(columnTitle);sum = 0\n for i in range(n):\n sum += 26**(n-i-1)*(ord(columnTitle[i])-64)\n return sum\n\n\n \n``` | 0 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Python 3 Solution | O(n) | excel-sheet-column-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def titleToNumber(self, columnTitle: str) -> int:\n out = 0\n\n for letter in columnTitle:\n v = ord(letter) - ord(\'A\') + 1\n out = out * 26 + v \n\n return out\n``` | 1 | Given a string `columnTitle` that represents the column title as appears in an Excel sheet, return _its corresponding column number_.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
**Example 1:**
**Input:** columnTitle = "A "
**Output:** 1
**Example 2:**
**Input:** columnTitle = "AB "
**Output:** 28
**Example 3:**
**Input:** columnTitle = "ZY "
**Output:** 701
**Constraints:**
* `1 <= columnTitle.length <= 7`
* `columnTitle` consists only of uppercase English letters.
* `columnTitle` is in the range `[ "A ", "FXSHRXW "]`. | null |
Very Easy O(log₅n) Solution 0ms Beats 100%| Explanation | factorial-trailing-zeroes | 0 | 1 | \n\n# Intuition\nTo determine the number of trailing zeros in 152 factorial (152!), it\'s essential to understand that trailing zeros result from the multiplication of multiples of 5 and 2. The key is to count the number of 5\'s and 2\'s in the multiplication process.\n\nFirstly, let\'s count the 5\'s: 5, 10, 15, 20, 25, and so on, totaling 20 occurrences. However, since numbers like 25, 50, 75, and 100 have two 5\'s each, we need to count them twice, resulting in a total of 24 occurrences.\n\nMoving on to count the 2\'s: 2, 4, 6, 8, 10, and so forth. There are 50 multiples of 2, 25 multiples of 4 (counted once more), 12 multiples of 8 (counted once more), and so on. The grand total of 2\'s is 97 occurrences.\n\nSince each pair of 2 and 5 contributes to a trailing zero, and we have 24 5\'s, we can form only 24 pairs of 2\'s and 5\'s. Thus, the number of trailing zeros in 152 factorial is 24.\n\nIn a more general formula, the number of trailing zeros in any factorial (x!) can be expressed as min(\u2211na=1x5a).\n\n# Approach\n\nLet, N = 152!\n\nFor those who don\u2019t know what factorial is, 100! = 100 * 99 * 98 * \u2026 * 2 * 1\n\nWe have to find how many zeroes are there at the end of this number N. To deduce this, we have to know how trailing zeros are formed in the first place. A trailing zero is formed when a multiple of 5 is multiplied with a multiple of 2. Now, all we have to do is count the number of 5\u2019s and 2\u2019s in the multiplication.\n\nLet\u2019s count the 5\u2019s first. 5, 10, 15, 20, 25 and so on making a total of 20. However, there is more to this. Since 25, 50, 75 and 100 have two 5\u2019s in each of them (25 = 5 * 5, 50 = 2 * 5 * 5, \u2026), you have to count them twice. This makes the grand total of 24. For people who like to look at it from a formula point of view\n\nNumber of 5\u2019s = 100/5 + 100/25 + 100/125 + \u2026 = 24 (Integer values only)\n\nMoving on to count the number of 2\u2019s. 2, 4, 6, 8, 10 and so on. Total of 50 multiples of 2\u2019s, 25 multiples of 4\u2019s (count these once more), 12 multiples of 8\u2019s (count these once more) and so on\u2026 The grand total comes out to\n\nNumber of 2\u2019s = 100/2 + 100/4 + 100/8 + 100/16 + 100/32 + 100/64 + 100/128 + \u2026 = 97 (Integer values only)\n\nEach pair of 2 and 5 will cause a trailing zero. Since we have only 24 5\u2019s, we can only make 24 pairs of 2\u2019s and 5\u2019s thus the number of trailing zeros in 100 factorial is 24.\n\nAs we have seen from the above example, the number of 5\u2019s are the limiting factor for the no of zeroes in this case and decides the number of trailing zeroes for the factorial. So, we don\u2019t need to calculate no of 2\u2019s.\n\nNumber of zeroes for any given factorial (x!)\n can be expressed as min(\u2211na=1x5a)\n \n\nSo, the number of zeroes at the end of 152! will be,\n\nmin(15251)+min(15252)+min(15253)+min(15254)+....\n \n\n=min(1525)+min(15225)+min(152125)+min(152625)+....\n \n\n=30+6+1+0+...\n \n\n=37\n \n\nSo, there are a total of 37 zeroes at the end of 152!\n\nThanks for reading my answer. Hope this helps. If so, please consider upvoting.\n\n# Complexity\n- Time complexity: The time complexity to determine the number of trailing zeros in a factorial is approximately O(log\u2085n), where n is the input value (152 in this case). This is because we are counting the number of multiples of 5 in the factorial.\n\n- Space complexity: The space complexity is O(1) since the algorithm uses a constant amount of space regardless of the input size. We are not using any additional data structures that depend on the input.\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int trailingZeroes(int n) {\n long long powerOfFive = 5;\n long long countOfZero = 0;\n\n while(n/five)\n {\n countOfZero+=n/powerOfFive;\n powerOfFive*=5;\n }\n return countOfZero;\n }\n};\n```\n\n```Python []\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n countOfZero = 0\n powerOfFive = 5\n\n while n//powerOfFive:\n countOfZero+=n//powerOfFive\n powerOfFive*=5\n return countOfZero\n``` | 8 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
python simplest solution✅✅ | factorial-trailing-zeroes | 0 | 1 | \n\n\n\n# Time complexity:\nThe time complexity of this approach is O(log n) because the while loop runs until \'5^a\' is less than or equal to \'n\'. As we multiply \'b\' by 5 in each iteration, the loop will run approximately log base 5 of \'n\' times.\n\n# Space complexity:\nThe space complexity of this approach is O(1) because we are using only a constant amount of space to store the variables \'a\', \'b\', and \'c\'.\n\n\n\n# Code\n```\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n a=1\n b=5\n c=0\n while (5**a)<=n:\n c+=n//b\n a+=1\n b=b*5\n return c\n\n``` | 6 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
172. Factorial Trailing Zeroes | Python3 Solution | Brute Force Approach | factorial-trailing-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimply Apply Brute Force Method\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First find factorial of a number.\n2. converted into string.\n3. converted into list and reverse it list.\n4. Find the frequency of zero\'s using for loop and if the zero is not come then break the loop.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport sys\nsys.set_int_max_str_digits(0)\n\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n prod = 1\n count = 0\n num = n\n\n if n == 0:\n return 0\n\n else:\n for i in range (n):\n nu = num - i\n prod = prod*nu\n\n str_prod = str(prod)\n prod_list = []\n\n for i in range (len(str_prod)):\n prod_list.append(int(str_prod[i]))\n\n \n size = len(prod_list)\n prod_list.reverse()\n\n if size == 1:\n return count\n else:\n for i in range (size):\n if prod_list[i] != 0:\n break\n elif prod_list[i] == 0:\n count = count + 1\n return count \n\n \n\n \n\n``` | 1 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Python Log(n) Loop | 100% Speed | factorial-trailing-zeroes | 0 | 1 | **Python Log(n) Loop | 100% Speed**\n\nThe code below presents an Easy Python solution with clear syntax. The algorithm works as follows:\n\n1. The numbers of "zeros" in "n!" can be traced by decomposing the multiplication "n * (n-1) * ..." into a prime factorization with the format:\n * n! = 2^a * 3^b * 5^c, ...\n\n2. In this factorization, the number of "zeros" in "n!" would correspond to the highest number of "10\'s" that we can form. Since "10 = 5 * 2", the number of zeros would be "10\'s = min(a,c) ". \n\n3. While we should consider tracking 2^a and 5^c separately, we can note that 50% of integer numbers are even (multiples of 2), whereas only 20% are multiples of 5.\n\n4. As a result, we can conclude that we add a zero to our factorial every time we multiply by 5...\n\n5. Some numbers can multiply by 5 more than once, such as 5^2 = 25 or 5^3 = 125. We can consider these cases by adding a loop to account for all multiples of 5^x. Since 5^x grows exponentially, we achieve an algorithm with Log(n) time complexity.\n\nI hope the explanation was helpful. This is a very interesting problem.\n\nCheers,\n\n```\nclass Solution:\n def trailingZeroes(self, n):\n x = 5\n res = 0\n while x <= n:\n res += n//x\n x *= 5\n return res\n``` | 35 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
172: Solution with step by step explanation | factorial-trailing-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo compute the number of trailing zeroes in n!, we need to count the number of factors of 10 in n!. Notice that 10 can only be formed by multiplying 2 and 5, and we can always find more factors of 2 than factors of 5 in n!. Therefore, it suffices to count the number of factors of 5 in n! to determine the number of trailing zeroes.\n\nLet count = 0 be the variable that keeps track of the number of factors of 5. We can count the factors of 5 in n! by computing n/5 + n/25 + n/125 + ... until the quotient becomes 0. Each term in the sum corresponds to the number of multiples of 5, 25, 125, ..., that are less than or equal to n.\n\nThe final value of count will be the number of trailing zeroes in n!.\n# Complexity\n- Time complexity:\nO(log n) - we keep dividing n by 5 in each iteration until n becomes 0.\n\n- Space complexity:\nO(1) - we only use a constant amount of extra space to store the variable count.\n\n# Code\n```\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n count = 0\n while n > 0:\n count += n // 5\n n //= 5\n return count\n\n``` | 8 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Easiest Python Solution | factorial-trailing-zeroes | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n co = 0\n while n > 0:\n co+= n // 5\n n //= 5\n return co\n``` | 3 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Clear explanation of the solution since I didn't find an adequate one | factorial-trailing-zeroes | 0 | 1 | This problem is difficult mainly because you must reach the insight that __it is a multiple of 5 and an even number that leads to a trailing zero__ and since there are on average 4 times as many even numbers as 5s (from 1-9 for example 2,4,6,8), the limiting factor for the number of trailing zeros are the number of 5s that will be multiplied. Hence, you count them and you\'re good.\n\nTake for example 5! (5 factorial). It is `5 x 4 x 3 x 2 x 1`. It can be written either as `20 x 6` or `10 x 12` in both cases the mutiplication of 5 either with 4 or 2 being the factor that causes the single trailing zero in the final answer 120.\n\nSo for n = 25, the factorial:\n`25 x 24 x 23 x 22 x 21 x 20 x 19 x 18 x 17 x 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1`\n\nSo the number of 5s here are 5, 10 (5 x 2), 15 (5 x 3), 20 (5 x 4), and two 5s in 25 (5 x 5). So in total 6 fives. So we should expect 6 trailing zeros.\n\nAnd indeed it is the case: 15511210043330985984**000000**\n\nHow to get them? Do integer division!\n\nFirst `25 // 5 -> 5`. Then `5 // 5 -> 1` (stopping here since `1 // 5 -> 0` so ignoring that). So we would expect 5 + 1 trailing zeros.\n\nThe code below is from another post. Purpose of the post was to give the intuition of what\'s happening below.\n```python\ndef trailingZeroes(n: int) -> int:\n cnt = 0\n while n != 0:\n n = n // 5\n cnt = cnt + n # NOT incremented by 1. Incremented by n.\n return cnt\n``` | 32 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Python | factorial-trailing-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n count = 0\n while (n >0):\n n= n// 5\n count += n\n return count\n``` | 1 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Python3 O(log(n)) time, O(1) space. Explanation | factorial-trailing-zeroes | 0 | 1 | To help this intution stick let\'s work with an example, say 60! I can tell you that 60! has 14 trailing zeros.\n\nLet\'s begin by understanding how a trailing zero is created. The simplest way to create a trailing zero is to multiply a given number by 10. Now, every number has at least two factors, namely itself and 1, however these are the trivial factors that every number has. Excluding these trivial factors 10 can be factored as 2 x 5. We can therefore deduce that the number of trailing zeros will be dictated by the smaller of the count of factor 2 and the count of factor 5 in 60!\n\n60! can be divided by 2, 52 times and divided by 5, 14 times. As multiples of 2 occur more frequently than multiples of 5 in the natural numbers, the number of trailing zeros will be dictated by the number of times 60! can be divided by 5.\n\nWhich of the natural numbers up to 60 have at least one factor of 5?\nThere are 12, (5, 10, 15, 20, 35, 30, 35, 40, 45, 50, 55, 60), which can be found by 60 / 5\n\nSo we\'ve found the number of natural numbers up to 60 that have at least a factor of 5 but you may notice that 25 and 50 can be factored as 5x5 and 5x5x2 and so we\'ll have to account for the fact that there are some numbers that will have more than one factor of 5.\n\n60 // 5 + 60 // 25 = 12 + 2 which gives us our answer.\n\nTo find the general solution to this problem we can factor our previous equation as follows:\nquotient = 60 // 5\nans = quotient + quotient // 5\n\nThis can be applied in a recursive way to account for increasingly many numbers with increasing factors of 5.\n\n```\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n quotient = n // 5\n return quotient + self.trailingZeroes(quotient) if quotient >= 5 else quotient\n``` | 12 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Very Easy || 100% || Fully Explained || Java || C++|| Python || JS || C || Python3 | factorial-trailing-zeroes | 1 | 1 | # **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Factorial Trailing Zeroes.\n\n```\nclass Solution {\n public int trailingZeroes(int n) {\n // Negative Number Edge Case...\n if (n < 0)\n\t\t return -1;\n // Initialize the output result i.e., the number of trailing zeroes...\n\t int output = 0;\n // Count number of 5s in prime factors of n!\n\t for (long idx = 5; n/idx >= 1; idx *= 5) {\n\t\t output += n/idx;\n\t }\n // Return the number of trailing zeroes...\n return output;\n }\n}\n/**\n**The following example helps you to understand the code...**\nLet, n = 25\nInitialize the output as 0...\n\nAfter first pass,\n\t\t\t\tloop for idx = 5; n / idx >= 1\n\t\t\t\t25 / 5 >= 1 or, 5 >= 1... It\'s true...\n\t\t\t\toutput = output + n / idx = 0 + 25/5 = 0 + 5 = 5\n\t\t\t\tand, idx *= 5 i.e., idx = 5 * 5 = 25\n\nAfter second pass,\n\t\t\t\tn / idx >= 1 or, 25 / 25 >= 1 or, 1 >= 1... It\'s true...\n\t\t\t\toutput = output + n / idx = 5 + 25/25 = 5 + 1 = 6\n\t\t\t\tnow, idx *= 5 i.e., idx = 25 * 5 = 125\n\t\t\t\t\nAgain,\n\t\t\t\tn / idx >= 1\n\t\t\t\t28 / 125 >= 1 or, 0 >= 1... It\'s false\n\t\t\t\t\n**So we return the output as 6...**\n**/\n```\n\n\n# **C++ / C Solution:**\n```\nclass Solution {\npublic:\n int trailingZeroes(int n) {\n int output = 0;\n for(int idx = 5; idx <= n; idx += 5) {\n int x = idx;\n while(x > 0 && x % 5 == 0) {\n ++output;\n x /= 5;\n }\n }\n return output;\n }\n};\n/**\nTotal number of trailing zeroes will be equal to count of how many times 10 is factor of that number.\nAnd every 10 is formed of the product of two prime numbers 2 and 5.\nSo if we find out how many factors of 2\u2019s are there in the number. Similarly how many factors of 5\u2019s are there. Then we can say that each of these will combine to make product equal to 10.\nTherefore total number of trailing zeroes will be equal to minimum( count of 2\u2019s , count of 5\u2019s).\n**/\n```\n\n# **Python/Python3 Solution:**\n```\nclass Solution(object):\n def trailingZeroes(self, n):\n # Negative Number Edge Case\n if(n < 0):\n return -1\n # Initialize output...\n output = 0\n # Keep dividing n by 5 & update output...\n while(n >= 5):\n n //= 5\n output += n\n return output # Return the output...\n```\n \n# **JavaScript Solution:**\n```\nvar trailingZeroes = function(n) {\n // Negative Number Edge Case...\n if (n < 0) return -1;\n // Initialize the output result i.e., the number of trailing zeroes...\n\tlet output = 0;\n // Count number of 5s in prime factors of n!\n\tfor (let idx = 5; n/idx >= 1; idx *= 5) {\n\t\toutput += Math.floor(n/idx);\n\t}\n // Return the number of trailing zeroes...\n return output;\n};\n``` | 7 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Python beats 99.43% | factorial-trailing-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(log(n))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution:\n def trailingZeroes(self, n: int) -> int:\n count = 0\n log = 5\n while n >= log:\n count += n//log\n log *= 5\n return count\n \n``` | 2 | Given an integer `n`, return _the number of trailing zeroes in_ `n!`.
Note that `n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1`.
**Example 1:**
**Input:** n = 3
**Output:** 0
**Explanation:** 3! = 6, no trailing zero.
**Example 2:**
**Input:** n = 5
**Output:** 1
**Explanation:** 5! = 120, one trailing zero.
**Example 3:**
**Input:** n = 0
**Output:** 0
**Constraints:**
* `0 <= n <= 104`
**Follow up:** Could you write a solution that works in logarithmic time complexity? | null |
Simple solution with In-order Traversal in Binary Tree (Python3 / TypeScript) | binary-search-tree-iterator | 0 | 1 | # Intuition\nHere we have:\n- **Binary Search Tree** as `root`\n- our goal is to implement **an iterator** over this tree\n\nWe\'re going to **imitate** an iterator as **traversing** the whole tree **before** extracting.\nWe should store a **pointer**, that represent a current node inside of a `root`.\n\n# Approach\n1. declare `idx` as pointer\n2. traverse over `root` by **in-order traversal** and collect all the nodes values\n3. implement `next` method by shifting `idx` pointer and extracting a value of a particular node\n4. implement `hasNext` as checking, if iterator **is done** as `idx < count of values`\n\n# Complexity\n- Time complexity: **O(N)** to iterate over `root`\n\n- Space complexity: **O(N)**, the same for storing\n\n# Code in Python3\n```\nclass BSTIterator:\n\n def __init__(self, root: Optional[TreeNode]):\n self.idx = 0\n self.values = self.getValues(root)\n \n def getValues(self, root: Optional[TreeNode]):\n values = []\n\n def dfs(node):\n if node:\n dfs(node.left)\n values.append(node.val)\n dfs(node.right)\n\n dfs(root)\n\n return values\n\n\n def next(self) -> int:\n node = self.values[self.idx]\n self.idx += 1\n\n return node\n\n def hasNext(self) -> bool:\n return self.idx < len(self.values)\n```\n# Code in TypeScript\n```\nclass BSTIterator {\n idx = 0\n values: number[]\n\n constructor(root: TreeNode | null) {\n this.values = this.getValues(root)\n }\n\n getValues(root: TreeNode | null) {\n const values = []\n\n const dfs = (node: TreeNode | null) => {\n if (node) {\n dfs(node.left)\n values.push(node.val)\n dfs(node.right)\n }\n }\n\n dfs(root)\n\n return values\n }\n\n next(): number {\n return this.values[this.idx++]\n }\n\n hasNext(): boolean {\n return this.idx < this.values.length\n }\n}\n``` | 1 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
[Python] TC O(1) SC O(h) Generator Solution | binary-search-tree-iterator | 0 | 1 | ### Explanation\n\nOne way to only use O(h) space is to utilise a generator for our inorder traversal. We can implement it as such:\n\n```python\ndef inorder(node: Optional[TreeNode]) -> Generator[int, None, None]:\n """\n Generator function that takes the root node of a binary tree\n and iterates through the nodes of the tree via inorder traversal.\n @param node - The root node of the binary tree.\n """\n if node:\n yield from inorder(node.left)\n yield node.val\n yield from inorder(node.right)\n```\n\nSince a generator does not store the entire inorder traversal in memory, the only space used is effectively the implicit stack used when making recursive calls to the function, which has a maximum recursion depth of `h` (where `h` is the maximum height of the tree).\n\nHowever, using a generator object alone will not allow us to know whether some nodes in the inorder traversal remain to be traversed (i.e., the `hasNext()` function), since generator objects do not have this functionality. We can overcome this by pre-emptively obtaining and storing the next value in the inorder traversal. Then, `hasNext()` will check whether the next value is valid, whereas `next()` will return the stored value before the *next next* value is obtained.\n\n---\n\n### Solution\n\n```python\nclass BSTIterator:\n def __init__(self, root: Optional[TreeNode]):\n self.iter = self._inorder(root)\n self.nxt = next(self.iter, None)\n \n def _inorder(self, node: Optional[TreeNode]) -> Generator[int, None, None]:\n if node:\n yield from self._inorder(node.left)\n yield node.val\n yield from self._inorder(node.right)\n\n def next(self) -> int:\n res, self.nxt = self.nxt, next(self.iter, None)\n return res\n\n def hasNext(self) -> bool:\n return self.nxt is not None\n```\n\n**TC: O(1)**, since the generator object handles everything for us.\nEDIT: Amortised O(1), see [this comment](https://leetcode.com/problems/binary-search-tree-iterator/discuss/1965156/Python-TC-O(1)-SC-O(h)-Generator-Solution/1358785) for a simple explanation.\n**SC: O(h)**, due to the implicit recursive call stack used by the generator function.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 50 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
[python] 3 different approaches and step by step optimisation [faster than 98%, 88% less space ] | binary-search-tree-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince we have to do the in-order tranversal and print the next node in in-order. We can do it in 3 different ways\n1. Create an inorder array inside class constructor recursively and maintain an index to track current element \n2. Maintain a stack of elements\n3. [Most efficient] Scroll down and see this one. \n\n# Approach 1 [Accepted] : create array in constructor\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) -> using recursion + storing in array\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass BSTIterator:\n\n def __init__(self, root: Optional[TreeNode]):\n self.arr = []\n self.curr_index = 0\n self.in_order(root)\n print(self.arr)\n \n def in_order(self, root):\n if not root:\n return\n self.in_order(root.left)\n self.arr.append(root.val)\n self.in_order(root.right)\n\n def next(self) -> int:\n val = self.arr[self.curr_index]\n self.curr_index+=1\n return val\n \n\n def hasNext(self) -> bool:\n return self.curr_index<=len(self.arr)-1\n\n\n# Your BSTIterator object will be instantiated and called as such:\n# obj = BSTIterator(root)\n# param_1 = obj.next()\n# param_2 = obj.hasNext()\n```\n## problem with above approach\nWe are creating the whole in-order array in constructor, which is waste of computation and resource. We should do it on demand when methods are called. \n\n----\n# Approach 2 [Accepted]: Use stack + on-the-go push and pop \nHere instead of creating the whole array in constructor, we use stack to maintain the part we have not traversed yet. As `next` is called, we will keep `poping` from stack. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) -> using stack\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code \n```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass BSTIterator(object):\n\n def __init__(self, root):\n """\n :type root: TreeNode\n """\n self.stack = []\n while root:\n self.stack.append(root)\n root = root.left\n \n\n def next(self):\n """\n :rtype: int\n """\n node=self.stack.pop()\n r = node.right\n while r:\n self.stack.append(r)\n r = r.left\n return node.val\n \n\n def hasNext(self):\n """\n :rtype: bool\n """\n return self.stack\n\n\n# Your BSTIterator object will be instantiated and called as such:\n# obj = BSTIterator(root)\n# param_1 = obj.next()\n# param_2 = obj.hasNext()\n```\n## Problem/Drawback\nUsing a stack make space complexity `O(n)`. it would be great if we can get rid of it. \n\n# Approach 3: Using Morris Inorder traversal\nWe all know the [moris in-order traversal](https://www.youtube.com/watch?v=wGXB9OWhPTg&t=632s&ab_channel=TusharRoy-CodingMadeSimple), keep track of right unvisited node by making a tempraroy right pointer to current. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass BSTIterator:\n\n def __init__(self, root: Optional[TreeNode]):\n self.curr = root\n\n def next(self) -> int:\n while self.curr:\n if not self.curr.left:\n val = self.curr.val\n self.curr = self.curr.right\n return val\n else:\n pred = self.curr.left\n while pred.right and pred.right!=self.curr:\n pred = pred.right\n if pred.right==self.curr:\n pred.right=None\n val = self.curr.val\n self.curr= self.curr.right\n return val\n else:\n pred.right = self.curr\n self.curr = self.curr.left\n\n \n\n def hasNext(self) -> bool:\n return self.curr is not None\n\n\n# Your BSTIterator object will be instantiated and called as such:\n# obj = BSTIterator(root)\n# param_1 = obj.next()\n# param_2 = obj.hasNext()\n```\n\n\n | 7 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
173: Solution with step by step explanation | binary-search-tree-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe main idea behind this solution is to implement an iterator that returns the nodes in the in-order traversal of the binary search tree. We can use a stack to keep track of the nodes we need to visit.\n\n- In the constructor of the BSTIterator class, we initialize the stack with the leftmost path of the root node. We do this by adding all the left children of the root to the stack.\n- hasNext() method returns true if the stack is not empty, which means that there are more nodes to be visited.\n- next() method pops the top node from the stack, and if the popped node has a right child, we add all its left children to the stack.\n\n# Complexity\n- Time complexity:\nThe constructor will take O(h) time where h is the height of the tree. The hasNext() and next() method will take O(1) time.\n\n- Space complexity:\nThe space required by the stack is O(h).\n\n# Code\n```\nclass BSTIterator:\n def __init__(self, root: TreeNode):\n self.stack = []\n while root:\n self.stack.append(root)\n root = root.left\n \n def next(self) -> int:\n node = self.stack.pop()\n if node.right:\n current = node.right\n while current:\n self.stack.append(current)\n current = current.left\n return node.val\n \n def hasNext(self) -> bool:\n return len(self.stack) > 0\n\n``` | 10 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
Python || 94.82% Faster || Easy || Iterative Solution | binary-search-tree-iterator | 0 | 1 | ```\nclass BSTIterator:\n st=[]\n def __init__(self, root: Optional[TreeNode]):\n self.pushall(root)\n\n def next(self) -> int:\n temp=self.st.pop()\n self.pushall(temp.right)\n return temp.val\n\n def hasNext(self) -> bool:\n return True if len(self.st)>0 else False\n\n def pushall(self,root):\n while root:\n self.st.append(root)\n root=root.left\n```\n**An upvote will be encouraging** | 5 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
Python 96% faster | binary-search-tree-iterator | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass BSTIterator:\n\n def __init__(self, root: Optional[TreeNode]):\n self.stack = []\n cur = root\n while root:\n self.stack.append(root)\n root = root.left\n \n\n def next(self) -> int:\n res = self.stack.pop()\n cur = res.right\n while cur:\n self.stack.append(cur)\n cur = cur.left\n return res.val\n\n def hasNext(self) -> bool:\n return self.stack!=[]\n \n\n\n# Your BSTIterator object will be instantiated and called as such:\n# obj = BSTIterator(root)\n# param_1 = obj.next()\n# param_2 = obj.hasNext()\n``` | 2 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
Python3 solution | Iterative inorder traversal | binary-search-tree-iterator | 0 | 1 | ```\nclass BSTIterator:\n def __init__(self, root: Optional[TreeNode]):\n self.root = root\n self.iter = iter(self.iterativeInorder())\n self.nextValue = -1\n\n def iterativeInorder(self) :\n stack = []\n curr = self.root\n while True :\n if curr is not None :\n stack.append(curr)\n curr = curr.left\n\n elif stack :\n curr = stack.pop()\n yield curr.val\n curr = curr.right\n\n else :\n break\n\n return -1\n\n def next(self) -> int:\n if self.nextValue >= 0 :\n res = self.nextValue\n self.nextValue = -1\n return res \n\n else :\n return next(self.iter)\n\n def hasNext(self) -> bool:\n if self.nextValue >= 0 : return True\n try :\n self.nextValue = next(self.iter)\n return True\n except StopIteration :\n return False\n\n``` | 1 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
Python3 O(H) solution with stacks. | binary-search-tree-iterator | 0 | 1 | ```\nclass BSTIterator:\n\n def __init__(self, root: Optional[TreeNode]):\n self.root = root\n self.stack = []\n while root:\n self.stack.append(root)\n root = root.left\n \n\n def next(self) -> int:\n if self.stack:\n x = self.stack[-1]\n z = self.stack.pop()\n \n if z.right:\n z = z.right\n while z:\n self.stack.append(z)\n z = z.left\n return x.val\n def hasNext(self) -> bool:\n if self.stack:\n return True\n return False\n\n``` | 1 | Implement the `BSTIterator` class that represents an iterator over the **[in-order traversal](https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR))** of a binary search tree (BST):
* `BSTIterator(TreeNode root)` Initializes an object of the `BSTIterator` class. The `root` of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
* `boolean hasNext()` Returns `true` if there exists a number in the traversal to the right of the pointer, otherwise returns `false`.
* `int next()` Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to `next()` will return the smallest element in the BST.
You may assume that `next()` calls will always be valid. That is, there will be at least a next number in the in-order traversal when `next()` is called.
**Example 1:**
**Input**
\[ "BSTIterator ", "next ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[\[7, 3, 15, null, null, 9, 20\]\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, 3, 7, true, 9, true, 15, true, 20, false\]
**Explanation**
BSTIterator bSTIterator = new BSTIterator(\[7, 3, 15, null, null, 9, 20\]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `0 <= Node.val <= 106`
* At most `105` calls will be made to `hasNext`, and `next`.
**Follow up:**
* Could you implement `next()` and `hasNext()` to run in average `O(1)` time and use `O(h)` memory, where `h` is the height of the tree? | null |
python3 + binary search and dp | dungeon-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:\n r = len(dungeon)\n c = len(dungeon[0])\n\n def possible(n):\n mat = [[-math.inf for x in range(c)] for _ in range(r)]\n mat[0][0] = n+dungeon[0][0]\n for row in range(r):\n for col in range(c):\n if row==0 and col==0:\n continue\n up,left = -math.inf,-math.inf\n if row-1>=0:\n up = mat[row-1][col]\n if col-1>=0:\n left = mat[row][col-1]\n mat[row][col] = dungeon[row][col] + max(up,left)\n if mat[row][col] <=0:\n mat[row][col] = -math.inf\n return mat[-1][-1] > 0\n\n \n l = 1 if dungeon[0][0] >=0 else abs(dungeon[0][0])+1\n h=int(3e5)\n while l<=h:\n mid = (l+h)//2\n if possible(mid):\n h=mid-1\n else:\n l=mid+1\n\n return l\n \n``` | 0 | The demons had captured the princess and imprisoned her in **the bottom-right corner** of a `dungeon`. The `dungeon` consists of `m x n` rooms laid out in a 2D grid. Our valiant knight was initially positioned in **the top-left room** and must fight his way through `dungeon` to rescue the princess.
The knight has an initial health point represented by a positive integer. If at any point his health point drops to `0` or below, he dies immediately.
Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).
To reach the princess as quickly as possible, the knight decides to move only **rightward** or **downward** in each step.
Return _the knight's minimum initial health so that he can rescue the princess_.
**Note** that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.
**Example 1:**
**Input:** dungeon = \[\[-2,-3,3\],\[-5,-10,1\],\[10,30,-5\]\]
**Output:** 7
**Explanation:** The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.
**Example 2:**
**Input:** dungeon = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == dungeon.length`
* `n == dungeon[i].length`
* `1 <= m, n <= 200`
* `-1000 <= dungeon[i][j] <= 1000` | null |
Python DP Solution | dungeon-game | 0 | 1 | # Intuition\nWhen tackling DP problems, remember to first figure out the underlying state transfer equation. \n\nIn this question, it is not simply the shortest path question, since we only care about the minimum starting HP. Hence to find out the initial HP needed at pos (i, j), we need to find out how much HP do we need at pos (i + 1, j) and (i, j + 1). \n\nAnother important point to notice is that the equation should only worry about the minimum HP, hence when any of the dp(i + 1, j) or dp(i, j + 1) is greater or equal to 0 we set memo[i][j] to be 1.\n\n# Code\n```\nclass Solution:\n def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:\n n = len(dungeon)\n m = len(dungeon[0])\n memo = [[-1] * m for _ in range(n)]\n\n # From (i, j) to bottom right corner what is the min HP needed\n def dp(grid, i, j):\n # Base case\n if i == n - 1 and j == m - 1:\n return 1 if grid[i][j] >= 0 else -grid[i][j] + 1\n if i >= n or j >= m:\n return math.inf\n # Memoization\n if memo[i][j] != -1:\n return memo[i][j]\n # State transfer\n res = grid[i][j] - min(\n dp(grid, i + 1, j),\n dp(grid, i, j + 1)\n )\n\n memo[i][j] = 1 if res >= 0 else -res \n return memo[i][j]\n\n return dp(dungeon, 0, 0)\n \n``` | 1 | The demons had captured the princess and imprisoned her in **the bottom-right corner** of a `dungeon`. The `dungeon` consists of `m x n` rooms laid out in a 2D grid. Our valiant knight was initially positioned in **the top-left room** and must fight his way through `dungeon` to rescue the princess.
The knight has an initial health point represented by a positive integer. If at any point his health point drops to `0` or below, he dies immediately.
Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).
To reach the princess as quickly as possible, the knight decides to move only **rightward** or **downward** in each step.
Return _the knight's minimum initial health so that he can rescue the princess_.
**Note** that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.
**Example 1:**
**Input:** dungeon = \[\[-2,-3,3\],\[-5,-10,1\],\[10,30,-5\]\]
**Output:** 7
**Explanation:** The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.
**Example 2:**
**Input:** dungeon = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == dungeon.length`
* `n == dungeon[i].length`
* `1 <= m, n <= 200`
* `-1000 <= dungeon[i][j] <= 1000` | null |
DYNAMIC PROGRAMMING | dungeon-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to use dynamic programming to store the minimum health required to reach each cell in a 2D array, and then calculate the minimum health required to reach each cell by taking the minimum of the health required to reach the cell on the right and the cell below, and then subtracting the health change of the current cell. This allows us to calculate the minimum health required to reach each cell starting from the bottom-right cell and working our way towards the top-left cell. By doing this, we ensure that the minimum health required to reach each cell is calculated based on the minimum health required to reach the cells that can be reached from that cell, so we are able to find the minimum initial health required to reach the top-left cell.\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis solution uses dynamic programming to store the minimum health required to reach each cell in a 2D array, and then calculates the minimum health required to reach each cell by taking the minimum of the health required to reach the cell on the right and the cell below, and then subtracting the health change of the current cell. It initializes the minimum health required to reach the bottom-right cell to 1, and then iterates over the cells in the dungeon in reverse order to calculate the minimum health required to reach each cell\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(m * n), where m and n are the number of rows and columns in the dungeon. This is because the solution iterates over all the cells in the dungeon to calculate the minimum health required to reach each cell. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is also O(m * n) because it stores the minimum health required to reach each cell in a 2D array.\n\n# Code\n```\nclass Solution:\n def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:\n # Get the number of rows and columns in the dungeon\n m, n = len(dungeon), len(dungeon[0])\n \n # Create a 2D array to store the minimum health required to reach each cell\n dp = [[float(\'inf\')] * (n + 1) for _ in range(m + 1)]\n \n # Set the minimum health required to reach the bottom-right cell to 1\n dp[m][n - 1] = dp[m - 1][n] = 1\n \n # Iterate over the cells in the dungeon in reverse order\n for i in range(m - 1, -1, -1):\n for j in range(n - 1, -1, -1):\n # Calculate the minimum health required to reach the current cell\n # by taking the minimum of the health required to reach the cell on the right\n # and the cell below, and then subtracting the health change of the current cell\n dp[i][j] = max(1, min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j])\n \n # Return the minimum health required to reach the top-left cell\n return dp[0][0]\n``` | 1 | The demons had captured the princess and imprisoned her in **the bottom-right corner** of a `dungeon`. The `dungeon` consists of `m x n` rooms laid out in a 2D grid. Our valiant knight was initially positioned in **the top-left room** and must fight his way through `dungeon` to rescue the princess.
The knight has an initial health point represented by a positive integer. If at any point his health point drops to `0` or below, he dies immediately.
Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).
To reach the princess as quickly as possible, the knight decides to move only **rightward** or **downward** in each step.
Return _the knight's minimum initial health so that he can rescue the princess_.
**Note** that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.
**Example 1:**
**Input:** dungeon = \[\[-2,-3,3\],\[-5,-10,1\],\[10,30,-5\]\]
**Output:** 7
**Explanation:** The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.
**Example 2:**
**Input:** dungeon = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == dungeon.length`
* `n == dungeon[i].length`
* `1 <= m, n <= 200`
* `-1000 <= dungeon[i][j] <= 1000` | null |
174: Solution with step by step explanation | dungeon-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses dynamic programming to solve the problem. The main idea is to build a 2D array dp to store the minimum initial health required at each position to reach the bottom-right corner. We start from the bottom-right corner and work our way backwards to the top-left corner.\n\nAt each position, we take the minimum of the minimum initial health required at the position below and the position to the right, and subtract the dungeon value at the current position. If the result is less than or equal to 0, we set it to 1 (since the knight needs to have at least 1 health point to be alive). Finally, we return the value at the top-left corner of the dp array.\n\nTo handle the boundary cases, we add an extra row and an extra column to the dp array, and set them all to infinity except for dp[m-1][n] and dp[m][n-1], which are set to 1.\n\nThis solution has a time complexity of O(mn) and a space complexity of O(mn).\n\n# Complexity\n- Time complexity:\nBeats\n68.28%\n\n- Space complexity:\nBeats\n97.32%\n\n# Code\n```\nclass Solution:\n def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:\n m, n = len(dungeon), len(dungeon[0])\n dp = [[float(\'inf\')] * (n+1) for _ in range(m+1)]\n dp[m-1][n] = dp[m][n-1] = 1\n for i in range(m-1, -1, -1):\n for j in range(n-1, -1, -1):\n dp[i][j] = max(min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j], 1)\n return dp[0][0]\n\n``` | 3 | The demons had captured the princess and imprisoned her in **the bottom-right corner** of a `dungeon`. The `dungeon` consists of `m x n` rooms laid out in a 2D grid. Our valiant knight was initially positioned in **the top-left room** and must fight his way through `dungeon` to rescue the princess.
The knight has an initial health point represented by a positive integer. If at any point his health point drops to `0` or below, he dies immediately.
Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).
To reach the princess as quickly as possible, the knight decides to move only **rightward** or **downward** in each step.
Return _the knight's minimum initial health so that he can rescue the princess_.
**Note** that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.
**Example 1:**
**Input:** dungeon = \[\[-2,-3,3\],\[-5,-10,1\],\[10,30,-5\]\]
**Output:** 7
**Explanation:** The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.
**Example 2:**
**Input:** dungeon = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == dungeon.length`
* `n == dungeon[i].length`
* `1 <= m, n <= 200`
* `-1000 <= dungeon[i][j] <= 1000` | null |
Easy Python3 solution | dungeon-game | 0 | 1 | Not pretending for unique solution, but I hope that my code will be easy to understand.\n\nThe main idea is that we go reversed and compare ``max(1, min(previous_cells_values))``. That\'s the key. \n\nWhy do we compare max with 1? Because we don\'t need extra 30 hp, only 1 to be alive.\n\n\n```\nclass Solution:\n def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:\n \n rows, columns = len(dungeon), len(dungeon[0])\n hp = [[0]*columns for i in range(rows)]\n \n \n # We will start at endpoint:\n hp[-1][-1] = max(1, 1-dungeon[-1][-1]) # in example we will need 6 HP to cover -5 loss\n \n # Completing the border lines. Excluding endpoint everywhere\n for i in range(rows-2, -1,-1):\n hp[i][-1] = max(1, \n hp[i+1][-1] - dungeon[i][-1]) \n for j in range(columns-2, -1, -1): \n hp[-1][j] = max(1, \n hp[-1][j+1] - dungeon[-1][j])\n \n # print(hp) to see our HealthPoint table\n \n\t\t\n # Next we complete the remaining table\n for i in range(rows-2, -1, -1):\n for j in range(columns-2, -1, -1): \n hp[i][j] = max(1, min(hp[i+1][j] - dungeon[i][j], \n hp[i][j+1] - dungeon[i][j]) )\n \n return hp[0][0]\n```\n\nRuntime: 80 ms, faster than 89.23% of Python3 online submissions for Dungeon Game.\nMemory Usage: 15 MB, less than 11.11% of Python3 online submissions for Dungeon Game. | 20 | The demons had captured the princess and imprisoned her in **the bottom-right corner** of a `dungeon`. The `dungeon` consists of `m x n` rooms laid out in a 2D grid. Our valiant knight was initially positioned in **the top-left room** and must fight his way through `dungeon` to rescue the princess.
The knight has an initial health point represented by a positive integer. If at any point his health point drops to `0` or below, he dies immediately.
Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).
To reach the princess as quickly as possible, the knight decides to move only **rightward** or **downward** in each step.
Return _the knight's minimum initial health so that he can rescue the princess_.
**Note** that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.
**Example 1:**
**Input:** dungeon = \[\[-2,-3,3\],\[-5,-10,1\],\[10,30,-5\]\]
**Output:** 7
**Explanation:** The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.
**Example 2:**
**Input:** dungeon = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == dungeon.length`
* `n == dungeon[i].length`
* `1 <= m, n <= 200`
* `-1000 <= dungeon[i][j] <= 1000` | null |
Easy Solution Using Functools | largest-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n def compare(x, y):\n return int(str(y) + str(x)) - int(str(x) + str(y))\n \n sorted_numbers = sorted(nums, key=cmp_to_key(compare))\n ans = \'\'.join(str(i) for i in sorted_numbers)\n return ans if ans[0] != \'0\' else \'0\'\n\n``` | 2 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
179: Solution with step by step explanation | largest-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo solve this problem, we need to sort the given list of numbers such that they form the largest possible number. To do this, we need to create a custom sorting function that compares two numbers at a time and concatenates them in different orders to see which order forms the larger number. Once we have sorted the numbers, we can concatenate them to form the final result.\n\n# Complexity\n- Time complexity:\nBeats\n56.81%\n\n- Space complexity:\nBeats\n95.75%\n\n# Code\n```\nclass LargerNumKey(str):\n def __lt__(x, y):\n # Compare x+y with y+x in reverse order to get descending order\n return x+y > y+x\n\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n # Convert the list of numbers to list of strings\n nums = [str(num) for num in nums]\n \n # Sort the list of strings using our custom sorting function\n nums.sort(key=LargerNumKey)\n \n # Join the sorted list of strings to form the final result\n largest_num = \'\'.join(nums)\n \n # If the largest number is 0, return "0"\n # Otherwise, return the largest number\n return "0" if largest_num[0] == "0" else largest_num\n\n```\nThe LargerNumKey class is a subclass of the built-in str class that overrides the less than operator (<) to compare two strings in a special way. The __lt__ method is called when we use the less than operator to compare two strings. We define the method to compare two strings x and y in the following way:\n\n1. Concatenate x and y in reverse order: x+y.\n2. Concatenate y and x in reverse order: y+x.\n3. Compare the two concatenated strings in reverse order to get descending order. That is, if x+y is greater than y+x, we return True. Otherwise, we return False.\n\nIn the largestNumber method, we first convert the list of numbers to a list of strings. We then sort the list of strings using our custom sorting function. Finally, we join the sorted list of strings to form the largest number.\n\nNote that if the largest number is 0, we return "0" instead of the actual largest number. This is because "0" is the only case where the leading digit is "0". | 20 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
Simple solution using Sort and String Comparison , Python | largest-number | 0 | 1 | # Code\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n lst = []\n\n for ele in nums:\n lst += [str(ele)]\n \n n = len(lst)\n\n for i in range(n):\n for j in range(i+1 , n):\n \n if str(lst[i]) + str(lst[j]) > str(lst[j]) + str(lst[i]):\n # if current order is greatest value .. continue\n continue\n else:\n # else swap the values ..!!!\n lst[i] , lst[j] = lst[j] , lst[i]\n \n \n ans = \'\'.join(lst)\n\n if int(ans) == 0:\n return "0"\n \n return ans\n\n """\n A = str(lst[i])\n B = str(lst[j])\n\n if AB > BA:\n continue\n else:\n str(lst[i]) = B\n str(lst[j]) = A\n # to make the order as BA\n """\n``` | 9 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
[Python] Proper Python 3 without Resorting to cmp_to_key(), The Best | largest-number | 0 | 1 | # Complexity\n- Time complexity: $$O(n\\log n\\log N)$$\n- Space complexity: $$O(n\\log N)$$\n\nThe Best!\n\n# Code\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n nums[:] = map(str, nums)\n nums.sort(key=NumCompare, reverse=True)\n return \'\'.join(nums).lstrip(\'0\') or \'0\'\n\nclass NumCompare:\n def __init__(self, s: str):\n self.s = s\n def __lt__(self, other: str) -> bool:\n return self.s + other.s < other.s + self.s\n``` | 2 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
python easy custom sort solution!!!!!!! | largest-number | 0 | 1 | My solution is based on this obvious math inference:\nx: n digit; y: m digit\nif xy > yx,\nthen 10^m * x + y > 10^n * y + x\nthen x / (10^n - 1) > y / (10^m - 1)\nso we could use this method to make a sorting custom key.\n\n\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n nums = sorted(nums,key=lambda x:x / (10 ** len(str(x)) - 1 ), reverse=True)\n str_nums = [str(num) for num in nums]\n res = \'\'.join(str_nums)\n res = str(int(res))\n return res\n \n | 22 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
Python 3 Simple Solution Explained (video + code) | largest-number | 0 | 1 | [](https://www.youtube.com/watch?v=xH3fgc8Q7Xc)\nhttps://www.youtube.com/watch?v=xH3fgc8Q7Xc\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n if not any(map(bool, nums)):\n return \'0\'\n \n nums = list(map(str, nums))\n if len(nums) < 2:\n return "".join(nums)\n \n def compare(x, y):\n return (int(nums[x]+nums[y])) > (int(nums[y]+nums[x]))\n \n for x in range(len(nums) - 1):\n y = x + 1\n while x < len(nums) and y < (len(nums)):\n if not compare(x,y):\n nums[y], nums[x] = nums[x], nums[y]\n y+=1\n\n return "".join(nums) \n``` | 28 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
[Python] Detailed Explanation with comparator | largest-number | 0 | 1 | ```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n ## RC ##\n ## APPROACH : CUSTOM SORTING WITH COMPARATOR ##\n ## MAIN IDEA : It\'s all about comparison . We define a func that compares two strings a ,b. we consider a bigger than b if a+b > b+a . then we sort the numbers and concatenate them .\n ## a-> 3, b-> 30 => 330 > 303\n ## Things to note : Your comparator is supposed to return negative/zero/positive, not a boolean. ##\n \n ## ALSO : We can use any type of sort, while sorting instead of comparing two numbers directly, we can use the current comparator logic to compare and swap elements accordingly.\n \n ## Edge case : o/p -> "00" expected:"0"\n \n\t\t## TIME COMPLEXITY : O(NlogN) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n import functools\n def comparator(s1, s2):\n if int(s1+s2) < int(s2+s1):\n return -1\n if int(s1+s2) > int(s2+s1):\n return 1\n return 0\n \n nums = [str(num) for num in nums]\n nums = sorted(nums, key = functools.cmp_to_key(comparator), reverse = True)\n ans = \'0\' if nums[0] == \'0\' else \'\'.join(nums) # if the biggest number after sorting is 0 in first position, then rest all will also be 0\'s so return 0\n return ans\n``` | 27 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
Beating 94.90% Shortest and Easiest Python Solution | largest-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n a = \'\'.join(sorted([str(a) for a in nums], \n key=lambda a: ((str(a)*9)[:9],a), \n reverse=True))\n return str(int(a))\n``` | 1 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
Python Solution | largest-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestNumber(self, nums: List[int]) -> str:\n res=""\n for i in nums:\n i=str(i)\n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if str(nums[i])+str(nums[j]) > str(nums[j])+str(nums[i]): #comparing xy and yx\n continue\n else:\n nums[i],nums[j]=nums[j],nums[i] #swap \n res=\'\'.join(str(i) for i in nums) #joining list\n if int(res)==0:\n return "0"\n return res\n``` | 2 | Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
Since the result may be very large, so you need to return a string instead of an integer.
**Example 1:**
**Input:** nums = \[10,2\]
**Output:** "210 "
**Example 2:**
**Input:** nums = \[3,30,34,5,9\]
**Output:** "9534330 "
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 109` | null |
Brute Force solution in Python | repeated-dna-sequences | 0 | 1 | # Intuition\nWe just need to return a list of substrings which appeared more than once.\n\n# Approach\nIf length of string is less than or equal to 10, no substring could be repeated so an empty list is returned. Else, starting from 0th index, substrings of length 10 are stored in list1. If a substring is already present in list1; it is added to list2 (storing repeated substrings). List2 is returned.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n list1 = set()\n list2 = set()\n l = len(s)\n if l<=10:\n return list(list1)\n for i in range(0, l-9):\n stri = s[i:i+10]\n if stri in list1 and stri not in list2:\n list2.add(stri)\n elif stri not in list1:\n list1.add(stri)\n return list(list2)\n``` | 1 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
187: Solution with step by step explanation | repeated-dna-sequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nStep-by-step explanation:\n\n1. Define a class named Solution that will contain the method to solve the problem.\n\n2. Define a method named findRepeatedDnaSequences that takes in a string s representing a DNA sequence and returns a list of all the 10-letter-long substrings that occur more than once in the sequence.\n\n3. Initialize an empty dictionary named freq that will store the frequency of each 10-letter-long substring in the DNA sequence.\n\n4. Iterate over each 10-letter-long substring in the DNA sequence by using a for loop that runs from the first index to the index of the last 10-letter-long substring in the sequence. The index of the last 10-letter-long substring is len(s) - 9, because we want to extract substrings of length 10.\n\n5. Within the for loop, extract the current 10-letter-long substring using string slicing by specifying the starting index as i and the ending index as i + 10.\n\n6. Update the frequency count of the current substring in the freq dictionary by using the get() method to retrieve the current count (or 0 if it doesn\'t exist) and adding 1 to it.\n\n7. After the for loop, filter out the substrings that occur less than twice by using a list comprehension that iterates over the keys in the freq dictionary and only includes the keys (i.e., the substrings) that have a value (i.e., the frequency count) greater than 1.\n\n8. Return the list of filtered substrings as the final result of the method.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n # initialize a dictionary to store the frequency of each 10-letter-long substring\n freq = {}\n # iterate over each 10-letter-long substring in the DNA sequence\n for i in range(len(s) - 9):\n # extract the current 10-letter-long substring\n substring = s[i:i+10]\n # update the frequency count of the current substring in the dictionary\n freq[substring] = freq.get(substring, 0) + 1\n # filter out the substrings that occur less than twice and return the list of the remaining substrings\n return [substring for substring in freq if freq[substring] > 1]\n\n``` | 5 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
O(n) time | O(n) space | solution explained | repeated-dna-sequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse a hashset and search for repeated sequences (10-size substring). Add the repeated sequences to the result.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- set res = a hash set to store the repeated sequences and avoid duplicates\n- set seen = a hash set to track the repeated sequences\n- traverse the string. loop size - 9 times to keep index inbound\n - get current sequence/substring of size 10\n - if the sequence is in the seen hashmap, it is a repeated sequence, add it to the result\n - add the sequence to the hashset\n- return res as a list \n\n# Complexity\n- Time complexity: O(string traversal * substring creation) \u2192 O(n - 9 * k) \u2192 O(n - 9 * 10) \u2192 O(n)\n - iterations = n - 9\n - substring size = k = 10\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(seen hashset + result hashset + substring) \u2192 O(n-9 + n/10 + k) \u2192 O(n + n + 10) \u2192 O(n)\n - if every sequence is unique, the seen hashset will contain n-9 sequences because total iterations are n - 9 and in each iteration, a sequence is added\n - if every sequence is repeated twice, the result hashset will contain n/10 sequences\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n res = set()\n seen = set()\n for i in range(len(s) - 9):\n seq = s[i:i+10]\n if seq in seen:\n res.add(seq)\n seen.add(seq)\n return list(res)\n \n``` | 2 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Simple 🐍 python solution✔ | repeated-dna-sequences | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n visited = {}\n res = []\n for i in range(len(s) - 9):\n sequence = s[i:i+10]\n if sequence in visited:\n if not visited[sequence]:\n visited[sequence] = True\n res.append(sequence)\n else:\n visited[sequence] = False \n return res\n``` | 2 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Python || Easy for Beginners || O(N) | repeated-dna-sequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n###### We can use the ***dictionary*** to solve this problem easily. \n\n# Approach\n1. Find the length of the string. if ***length is less than or equal to 10***, return ***empty list***.\n2. Using ***dictionary*** to get the count of the substring of the string.\n3. If the ***value of the dictionary is more than 1***, we have to **append it to the list**.\n\n# Complexity\n- Time complexity: **O(N)** where **N** = *Length of the string*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(N)** where **N** = *Length of the string*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n n = len(s)\n # step 1:\n if n <= 10:\n return []\n # step 2:\n d = dict()\n for i in range(n-9):\n key = s[i:i+10]\n if key not in d:\n d[key] = 1\n else:\n d[key] += 1\n # step 3:\n return [key for key in d.keys() if d[key] > 1]\n``` | 4 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Simple Python Code | repeated-dna-sequences | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n l=[]\n seen=set()\n dna=\'\'\n if len(s)>=10:\n for i in range(len(s)):\n dna=s[i:i+10]\n if dna in seen:\n if dna not in l:\n l.append(dna)\n seen.add(dna)\n return l\n``` | 2 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Python || Simple | repeated-dna-sequences | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n res=set()\n seen=set()\n for i in range(len(s)-9):\n curr=s[i:i+10]\n if curr in seen:\n res.add(curr)\n seen.add(curr)\n return list(res)\n\n``` | 2 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
[Python] 2 solutions - HashTable & Rolling Hash - Clean & Concise | repeated-dna-sequences | 0 | 1 | **\u2714\uFE0F Solution 1: Hashtable**\n```python3\nclass Solution(object):\n def findRepeatedDnaSequences(self, s):\n n = len(s)\n cnt = defaultdict(int)\n ans = []\n\n for i in range(n - 9):\n dna = s[i:i+10]\n cnt[dna] += 1\n if cnt[dna] == 2:\n ans.append(dna)\n\n return ans\n```\n\n**Complexity**\n- Time & Space: `O(10*N)`\n\n----\n**\u2714\uFE0F Solution 2: Hashtable + Rolling Hash**\n```python3\nclass Solution(object):\n def getVal(self, c):\n if c == \'A\': return 0\n if c == \'C\': return 1\n if c == \'G\': return 2\n return 3\n\n def findRepeatedDnaSequences(self, s):\n n = len(s)\n cnt = defaultdict(int)\n ans = []\n \n dnaHash = 0\n POWN1 = 4 ** 9\n for i in range(n):\n dnaHash = dnaHash * 4 + self.getVal(s[i])\n if i >= 9:\n cnt[dnaHash] += 1\n if cnt[dnaHash] == 2:\n ans.append(s[i-9:i+1])\n\n dnaHash -= POWN1 * self.getVal(s[i-9])\n\n return ans\n```\n**Complexity**\n- Time & Space: `O(10*N)` (in worst case) | 32 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Easy Python3 Sliding Window Hashmap/Set Solution | repeated-dna-sequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n myMap = {}\n mySet = set()\n\n for i in range(len(s) - 9):\n if s[i:i+10] in myMap:\n mySet.add(s[i:i+10])\n else:\n myMap[s[i:i+10]] = 1\n \n return mySet\n``` | 3 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Python3 Rabin-Karp | repeated-dna-sequences | 0 | 1 | # Intuition\nUse bitmasking rolling hash procedure to produce hash of each 10-character sequence so we don\'t have to create a new substring just to check if the substring has been visited before.\n\n# Approach\nAssign each of the four possible characters a unique binary number\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n if len(s) < 10:\n return []\n res = []\n # assign each of the four possible letters to the first four binary numbers\n letterToBin = {\'A\':0b00, \'C\':0b01, \'G\':0b10, \'T\':0b11}\n currHash = letterToBin[s[0]]\n for i in range(1,10):\n currHash <<= 2\n binOfLetter = letterToBin[s[i]]\n currHash |= binOfLetter\n\n seenHashBefore = {}\n seenHashBefore[currHash] = False\n le=1\n for ri in range(10,len(s)):\n currLetter = s[ri]\n binOfLetter = letterToBin[currLetter]\n currHash <<= 2\n currHash &= ~(0b11 << 2*10)\n currHash |= binOfLetter\n if currHash in seenHashBefore and not seenHashBefore[currHash]:\n seenHashBefore[currHash] = True\n res.append(s[le:ri+1])\n # either currHash not in seenHashBefore or seenHashBefore[currHash]\n elif currHash not in seenHashBefore:\n seenHashBefore[currHash] = False\n le+=1\n return res\n # time = O(n)\n # memory = O(n)\n\n \n``` | 1 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Easy python solution | repeated-dna-sequences | 0 | 1 | \n# Code\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n lst=[]\n set1=set()\n for i in range(0,len(s)-9):\n tmp=s[i:i+10]\n if tmp not in set1:\n set1.add(tmp)\n else:\n lst.append(tmp)\n return list(set(lst))\n``` | 2 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
Python O(n) by set and iteration [w/ Comment] | repeated-dna-sequences | 0 | 1 | Python O(n) by set and iteration\n\n---\n\n**Implementation** by set and iteration\n\n```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n \n # set for sequence\n sequence = set()\n \n # set for sequence with repetition\n repeated = set()\n \n for i in range( len(s)-9 ):\n \n # make current sequence for i to i+10\n cur_seq = s[i:i+10]\n \n if cur_seq in sequence:\n # check for repetition\n repeated.add( cur_seq )\n \n # add to sequence set\n sequence.add( cur_seq )\n \n return [ *repeated ]\n``` | 16 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
python 3 || simple hash map solution | repeated-dna-sequences | 0 | 1 | ```\nclass Solution:\n def findRepeatedDnaSequences(self, s: str) -> List[str]:\n seen = {}\n res = []\n \n for i in range(len(s) - 9):\n sequence = s[i:i+10]\n if sequence in seen:\n if not seen[sequence]:\n seen[sequence] = True\n res.append(sequence)\n else:\n seen[sequence] = False\n \n return res | 2 | The **DNA sequence** is composed of a series of nucleotides abbreviated as `'A'`, `'C'`, `'G'`, and `'T'`.
* For example, `"ACGAATTCCG "` is a **DNA sequence**.
When studying **DNA**, it is useful to identify repeated sequences within the DNA.
Given a string `s` that represents a **DNA sequence**, return all the **`10`\-letter-long** sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in **any order**.
**Example 1:**
**Input:** s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
**Output:** \["AAAAACCCCC","CCCCCAAAAA"\]
**Example 2:**
**Input:** s = "AAAAAAAAAAAAA"
**Output:** \["AAAAAAAAAA"\]
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'A'`, `'C'`, `'G'`, or `'T'`. | null |
3-D Bottom-Up Dynamic Programming Solution Python3 | best-time-to-buy-and-sell-stock-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nuse dp to find out the max profit for all days using t transactions while keeping track of having the stock or not\n\nonly selling counts as an extra transaction\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ndp[i][0][t] = max profit using first i prices, not having the stock on day i with at most t transactions\n\ndp[i][1][t] = max profit using first i prices, having the stock on day i with at most t transactions\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n n = len(prices)\n O(n*k)\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n n = len(prices)\n O(n*k)\n\n# Code\n```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n dp = [[[float(\'-inf\')]*(k+1) for i in range(2)] for j in range(len(prices))]\n\n for i in range(len(prices)):\n dp[i][0][0] = 0\n dp[0][1][0] = -prices[0]\n\n for t in range(k+1):\n for i in range(1,len(prices)):\n dp[i][1][t] = max(dp[i-1][0][t]-prices[i], dp[i-1][1][t])\n dp[i][0][t] = max(dp[i-1][0][t], dp[i-1][1][t-1] + prices[i])\n \n return max(dp[len(prices)-1][0])\n``` | 1 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Solution | best-time-to-buy-and-sell-stock-iv | 1 | 1 | ```C++ []\n#include <stack>\n#include <vector>\n#include <utility>\n#include <algorithm>\n#include <numeric>\nusing std::stack;\nusing std::pair;\nusing std::vector;\nusing std::nth_element;\nusing std::accumulate;\n\nclass Solution {\n\npublic:\n int maxProfit(int k, const vector<int>& prices) {\n vector<int> profits;\n stack<pair<int, int>> vps;\n int v = 0;\n int p = -1;\n \n const int n = prices.size();\n for (;;) {\n for (v = p + 1; (v + 1) < n && prices[v] >= prices[v + 1]; ++v);\n for (p = v; (p + 1) < n && prices[p] <= prices[p + 1]; ++p);\n if (p == v) break;\n \n while (!vps.empty() && prices[vps.top().first] >= prices[v]) {\n auto vp = vps.top();\n profits.push_back(prices[vp.second] - prices[vp.first]);\n vps.pop();\n }\n while (!vps.empty() && prices[vps.top().second] <= prices[p]) {\n profits.push_back(prices[vps.top().second] - prices[v]);\n v = vps.top().first; // (v1, p2)\n vps.pop();\n }\n vps.emplace(v, p);\n }\n while (!vps.empty()) {\n auto vp = vps.top(); vps.pop();\n profits.push_back(prices[vp.second] - prices[vp.first]);\n }\n if (k >= profits.size()) {\n return accumulate(profits.begin(), profits.end(), 0);\n } else {\n nth_element(profits.begin(), profits.end() - k, profits.end());\n return accumulate(profits.end() - k, profits.end(), 0);\n }\n }\n};\n```\n\n```Python3 []\nclass DoubleLinkListNode:\n def __init__(self, ind, pre = None, next = None):\n self.ind = ind\n self.pre = pre if pre else self\n self.next = next if next else self\n\nclass Solution:\n def MinMaxList(self, arr: List[int]) -> List[int]:\n n = len(arr)\n if n == 0:\n return []\n sign = -1\n res = [9999]\n for num in arr:\n if num * sign > res[-1] * sign:\n res[-1] = num\n else:\n res.append(num)\n sign *= -1\n if len(res) & 1:\n res.pop()\n return res\n def maxProfit(self, k: int, prices: List[int]) -> int:\n newP = self.MinMaxList(prices)\n n = len(newP)\n m = n // 2\n res = 0\n for i in range(m):\n res += newP[i*2+1] - newP[i*2]\n if m <= k:\n return res\n head, tail = DoubleLinkListNode(-1), DoubleLinkListNode(-1)\n NodeList = [DoubleLinkListNode(0, head)]\n for i in range(1, n):\n NodeList.append(DoubleLinkListNode(i, NodeList[-1]))\n NodeList[i-1].next = NodeList[i]\n NodeList[n-1].next = tail\n head.next, tail.pre = NodeList[0], NodeList[n-1]\n heap = []\n for i in range(n-1):\n if i&1:\n heappush(heap, [newP[i] - newP[i+1], i, i+1, 0])\n else:\n heappush(heap, [newP[i+1] - newP[i], i, i+1, 1])\n while m > k:\n loss, i, j, t = heappop(heap)\n if NodeList[i] == None or NodeList[j] == None: continue\n m -= 1\n res -= loss\n nodei, nodej = NodeList[i], NodeList[j]\n nodel, noder = nodei.pre, nodej.next\n l, r = nodel.ind, noder.ind\n valL, valR = newP[l], newP[r]\n noder.pre, nodel.next = nodel, noder\n NodeList[i], NodeList[j] = None, None\n if t == 0:\n heappush(heap, [valR - valL, l, r, 1])\n elif l != -1 and r != -1:\n heappush(heap, [valL - valR, l, r, 0])\n return res\n```\n\n```Java []\nclass Solution {\n static int solveTab(int[] prices,int k){\n int n=prices.length;\n\n int [][] curr = new int[2][k+2];\n int [][] next = new int[2][k+2];\n\n for(int index=n-1;index>=0;index--){\n for(int buy=1;buy>=0;buy--){\n for(int limit=1;limit<=k;limit++){\n int profit=0;\n if(buy==1){\n int salekaro=prices[index]+next[0][limit-1];\n int skipkaro=0+next[1][limit];\n profit+=Math.max(salekaro,skipkaro);\n }\n else{\n int buykaro=-prices[index]+next[1][limit];\n int skipkaro=0+next[0][limit];\n profit+=Math.max(buykaro,skipkaro);\n }\n curr[buy][limit]=profit;\n }\n }\n next=curr;\n }\n return next[0][k];\n }\n public int maxProfit(int k, int[] prices) {\n return solveTab(prices,k);\n }\n}\n```\n | 206 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Dynamic programming with iterations notebook - Best time to buy and sell stock problem | best-time-to-buy-and-sell-stock-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is Markov: we only care how much cash we have in hand and if stock is head. The state variables should be therefore `(time=i, stock_held=0 or 1)`; the state transition function:\n `dp[i][0] = max(dp[i-1][0],\n dp[i-1][1]+prices[i]) # doing nothing or sell`\n `dp[i][1] = max(dp[i-1][0]-prices[i],\n dp[i-1][1]) # buying, or doing nothing`\n\nHowever we have ignored in the above formulae `k`, the maximal number of transactions allowed. Expanding the state variableas to a triple `(time=i, number_of_transactions_done=t, stock_held=0 or 1)`,\nWe have the following state transitions:\n For `t = 0`:\n `dp[i][t=0][0] = 0 # trivial: no sales done`\n `dp[i][t=0][1] = max(dp[i-1][t=0][1], -prices[i]) # for the best deal`\n\n For all possible `t>=1; t = number of transactions done`:\n `dp[i][t][0] = max(dp[i-1][t][0], \n dp[i-1][t-1][1]+prices[i]) # doing nothing or sell`\n `dp[i][t][1] = max(dp[i-1][t][0]-prices[i],\n dp[i-1][t][1]) # buying, or doing nothing`\n\n \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`O(n * min(k, n/2))`\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`O(n * min(k, n//2))`\n# Code\n```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n """\n setup:\n n = len(prices)\n state = (current time, holding or not)\n trans = number of transactions done;\n adjusted at the closing of a sale\n dp[i, trans, h] = max cash up to current time, given the holding condition,\n\n to calculate: dp[n-1,:, 0]\n """\n n = len(prices)\n maxT = min(n//2, k)\n dp = [[[0, -9999] for u in range(maxT+1)] for _ in range(n)]\n for t in range(maxT+1): # max k =100\n dp[0][t][0] = 0\n dp[0][t][1] = -prices[0] \n #print(0, prices[0])\n for i in range(1, n):\n dp[i][0][0] = 0 # no transactions done\n dp[i][0][1] = max(dp[i-1][0][1], -prices[i])\n\n for t in range(1, maxT+1):\n dp[i][t][0] = max(dp[i-1][t][0],\n dp[i-1][t-1][1] + prices[i])\n dp[i][t][1] = max(dp[i-1][t][1],\n dp[i-1][t][0] - prices[i])\n\n #print(i, prices[i], dp[i])\n return max(dp[n-1][t][0] for t in range(maxT+1))\n``` | 0 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Python3 / Rust / Java/ JavaScript - Dynamic Programming | best-time-to-buy-and-sell-stock-iv | 1 | 1 | # Intuition\nThe given code solves the problem of finding the maximum profit achievable by making at most $$k$$ transactions in a given $$prices$$ list.\n\n# Approach\n1. The code initializes a 2D list $$transactions$$, where each row represents a transaction, and the columns represent the minimum buying price and maximum profit for that transaction.\n2. It iterates through the given prices and updates the transactions list for each transaction.\n3. It uses a nested loop to iterate through each transaction, updating the minimum buying price and maximum profit based on the current stock price and the previous profit.\n4. Finally, it returns the maximum profit from the last transaction.\n\n# Complexity\n- Time complexity: $$O(k\u22C5n)$$, where $$k$$ is the maximum number of transactions allowed, and $$n$$ is the length of the $$prices$$ list. The nested loop iterates over the transactions and prices.\n\n- Space complexity: $$O(k)$$ for storing the $$transactions$$ list.\n\n# Code\n``` python []\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n transactions = [[1000, 0] for i in range(k)]\n\n for price in prices:\n prev_profit = 0\n for i in range(k):\n transactions[i][0] = min(transactions[i][0], price - prev_profit)\n transactions[i][1] = max(transactions[i][1], price - transactions[i][0])\n prev_profit = transactions[i][1]\n\n return transactions[k-1][1]\n```\n``` rust []\nimpl Solution {\n pub fn max_profit(k: i32, prices: Vec<i32>) -> i32 {\n let k: usize = k as usize;\n let mut transactions: Vec<[i32; 2]> = vec![[1000, 0]; k];\n let mut prev_profit: i32 = 0;\n\n for price in prices {\n prev_profit = 0;\n for i in 0..k {\n transactions[i][0] = transactions[i][0].min(price - prev_profit);\n transactions[i][1] = transactions[i][1].max(price - transactions[i][0]);\n prev_profit = transactions[i][1];\n }\n }\n\n transactions[k-1][1]\n }\n}\n```\n``` java []\nclass Solution {\n public int maxProfit(int k, int[] prices) {\n int[][] transactions = new int[k][2];\n for (int i = 0; i < k; i++) {\n transactions[i][0] = 1000;\n transactions[i][1] = 0;\n }\n\n int prevProfit = 0;\n\n for (int i = 0; i < prices.length; i++) {\n prevProfit = 0;\n for (int j = 0; j < k; j++) {\n transactions[j][0] = Math.min(transactions[j][0], prices[i] - prevProfit);\n transactions[j][1] = Math.max(transactions[j][1], prices[i] - transactions[j][0]);\n prevProfit = transactions[j][1];\n }\n }\n\n return transactions[k-1][1];\n }\n}\n\n```\n``` javascript []\n/**\n * @param {number} k\n * @param {number[]} prices\n * @return {number}\n */\nvar maxProfit = function(k, prices) {\n let transactions = Array.from({ length: k }, () => [1000, 0]);\n let prev_profit = 0;\n\n for (let i = 0; i < prices.length; i++) {\n prev_profit = 0;\n for (let j = 0; j < k; j++) {\n transactions[j][0] = Math.min(transactions[j][0], prices[i] - prev_profit);\n transactions[j][1] = Math.max(transactions[j][1], prices[i] - transactions[j][0]);\n prev_profit = transactions[j][1];\n }\n }\n\n return transactions[k-1][1];\n};\n``` | 1 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
🔥 [LeetCode The Hard Way] 🔥 7 Lines | Line By Line Explanation | best-time-to-buy-and-sell-stock-iv | 0 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\nI\'d suggest to finish the previous problems first.\n\n- [121. Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock/)\n- [122. Best Time to Buy and Sell Stock II](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/)\n- [123. Best Time to Buy and Sell Stock III](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/)\n\n**C++**\n\n```cpp\nclass Solution {\npublic:\n int maxProfit(int k, vector<int>& prices) {\n // no transaction, no profit\n if (k == 0) return 0;\n // dp[k][0] = min cost you need to spend at most k transactions\n // dp[k][1] = max profit you can achieve at most k transactions\n vector<vector<int>> dp(k + 1, vector<int>(2));\n for (int i = 0; i <= k; i++) dp[i][0] = INT_MAX;\n for (auto& price : prices) {\n for (int i = 1; i <= k; i++) {\n // price - dp[i - 1][1] is how much you need to spend\n // i.e use the profit you earned from previous transaction to buy the stock\n // we want to minimize it\n dp[i][0] = min(dp[i][0], price - dp[i - 1][1]);\n // price - dp[i][0] is how much you can achieve from previous min cost\n // we want to maximize it\n dp[i][1] = max(dp[i][1], price - dp[i][0]);\n }\n }\n // return max profit at most k transactions\n // or you can use `return dp.back()[1];`\n return dp[k][1];\n }\n};\n```\n\n**Python**\n\n```py\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n # no transaction, no profit\n if k == 0: return 0\n # dp[k][0] = min cost you need to spend at most k transactions\n # dp[k][1] = max profit you can achieve at most k transactions\n dp = [[1000, 0] for _ in range(k + 1)]\n for price in prices:\n for i in range(1, k + 1):\n # price - dp[i - 1][1] is how much you need to spend\n # i.e use the profit you earned from previous transaction to buy the stock\n # we want to minimize it\n dp[i][0] = min(dp[i][0], price - dp[i - 1][1])\n # price - dp[i][0] is how much you can achieve from previous min cost\n # we want to maximize it\n dp[i][1] = max(dp[i][1], price - dp[i][0])\n # return max profit at most k transactions\n\t\t# or you can write `return dp[-1][1]`\n return dp[k][1]\n```\n\n**Java**\n\n```java\nclass Solution {\n public int maxProfit(int k, int[] prices) {\n // no transaction, no profit\n if (k == 0) return 0;\n // dp[k][0] = min cost you need to spend at most k transactions\n // dp[k][1] = max profit you can achieve at most k transactions\n int [][] dp = new int[k + 1][2];\n for (int i = 0; i <= k; i++) dp[i][0] = 1000;\n for (int i = 0; i < prices.length; i++) {\n for (int j = 1; j <= k; j++) {\n // price - dp[i - 1][1] is how much you need to spend\n // i.e use the profit you earned from previous transaction to buy the stock\n // we want to minimize it\n dp[j][0] = Math.min(dp[j][0], prices[i] - dp[j - 1][1]);\n // price - dp[i][0] is how much you can achieve from previous min cost\n // we want to maximize it\n dp[j][1] = Math.max(dp[j][1], prices[i] - dp[j][0]);\n }\n }\n // return max profit at most k transactions\n return dp[k][1];\n }\n}\n``` | 83 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Easy python 15 line DP solution | best-time-to-buy-and-sell-stock-iv | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n def func(i,buy,prices,ct,dic):\n if i>=len(prices) or ct==0:\n return 0\n if (i,buy,ct) in dic:\n return dic[(i,buy,ct)]\n x,y,a,b=0,0,0,0\n if buy:\n x=-prices[i]+func(i+1,False,prices,ct,dic)\n y=0+func(i+1,buy,prices,ct,dic)\n else:\n a=prices[i]+func(i+1,True,prices,ct-1,dic)\n b=0+func(i+1,buy,prices,ct,dic)\n dic[(i,buy,ct)]=max(a,b,x,y)\n return max(a,b,x,y)\n return func(0,True,prices,k,{})\n``` | 4 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Python Solution || Faster Than 98.22% Of Python Submissions || Easy To Read | best-time-to-buy-and-sell-stock-iv | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n buy = [inf for _ in range(k+1)]\n profit = [0 for _ in range(k+1)]\n for currPrice in prices:\n for i in range(1, k+1):\n buy[i] = min(buy[i], currPrice - profit[i-1])\n profit[i] = max(profit[i], currPrice - buy[i])\n\n return profit[k]\n``` | 1 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Simple Dp Solution using Python | best-time-to-buy-and-sell-stock-iv | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxProfit(self, k: int, prices: List[int]) -> int:\n # Similar to 123. Best Time to Buy and Sell Stock III\n \n n = len(prices)\n dp = [[[0 for m in range(k+1)] for i in range(3)] for j in range(n+1)]\n\n # Tabulation ..!!!!\n \n for ind in range(n-1 , -1 , -1):\n for buy in range(2):\n for days in range(k):\n if buy:\n take = -prices[ind] + dp[ind+1][0][days]\n not_take = 0 + dp[ind+1][1][days]\n \n else:\n take = prices[ind] + dp[ind+1][1][days-1]\n not_take = 0 + dp[ind+1][0][days]\n \n dp[ind][buy][days] = max(take , not_take)\n \n return dp[0][1][k-1]\n \n\n # Memoization .. !!!\n \n """\n def solve(ind , buy , days):\n if ind >= n or days <= 0: return 0\n\n if dp[ind][buy][days] != -1: return dp[ind][buy][days]\n\n if buy:\n take = -prices[ind] + solve(ind+1 , 0 , days)\n not_take = 0 + solve(ind+1 , 1 , days)\n \n else:\n take = prices[ind] + solve(ind+1 , 1 , days-1)\n not_take = 0 + solve(ind+1 , 0 , days)\n \n dp[ind][buy][days] = max(take , not_take)\n return dp[ind][buy][days]\n\n return solve(0 , 1 , k)\n """\n``` | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Python Striver Solution O(N*K) Easy Solution ✔ | best-time-to-buy-and-sell-stock-iv | 0 | 1 | # Recursive :\n```\n\nclass Solution:\n def f(self,ind,transNo,n,k,price):\n if ind==n or transNo==2*k:\n return 0\n\n if transNo%2==0: #buy\n profit=max(-price[ind] + self.f(ind+1,transNo+1,n,k,price),\n 0 + self.f(ind+1,transNo,n,k,price))\n else:\n profit=max(price[ind] + self.f(ind+1,transNo+1,n,k,price),\n 0 + self.f(ind+1,transNo,n,k,price))\n\n return profit\n \n def maxProfit(self, k: int, prices: List[int]) -> int:\n n=len(prices)\n return self.f(0,0,n,k,prices)\n```\n# Memoisation :\n\n```\n\n\nclass Solution:\n def f(self,ind,transNo,n,k,price,dp):\n if ind==n or transNo==2*k:\n return 0\n if dp[ind][transNo]!=-1:\n return dp[ind][transNo]\n if transNo%2==0: #buy\n profit=max(-price[ind] + self.f(ind+1,transNo+1,n,k,price,dp),\n 0 + self.f(ind+1,transNo,n,k,price,dp))\n else:\n profit=max(price[ind] + self.f(ind+1,transNo+1,n,k,price,dp),\n 0 + self.f(ind+1,transNo,n,k,price,dp))\n dp[ind][transNo]= profit\n return dp[ind][transNo]\n \n def maxProfit(self, k: int, prices: List[int]) -> int:\n n=len(prices)\n dp=[[-1 for i in range(2*k)]for j in range(n)]\n return self.f(0,0,n,k,prices,dp)\n```\n# Tabulation :\n def maxProfit(self, k: int, prices: List[int]) -> int:\n n=len(prices)\n dp=[[0 for i in range(2*k+1)]for j in range(n+1)]\n \n for ind in range(n-1,-1,-1):\n for transNo in range(2*k-1,-1,-1):\n if transNo%2==0: # buy\n profit=max(-prices[ind] + dp[ind+1][transNo+1],\n 0 + dp[ind+1][transNo])\n else:\n profit=max(prices[ind] + dp[ind+1][transNo+1],\n 0 + dp[ind+1][transNo])\n dp[ind][transNo]=profit\n \n return dp[0][0]\n# Space Optimisation : ) --> O(2K)\n```\n def maxProfit(self, k: int, prices: List[int]) -> int:\n n=len(prices)\n\n after=[0]*(2*k+1)\n curr=[0]*(2*k+1)\n \n for ind in range(n-1,-1,-1):\n for transNo in range(2*k-1,-1,-1):\n if transNo%2==0: # buy\n profit=max(-prices[ind] + after[transNo+1],\n 0 + after[transNo])\n else:\n profit=max(prices[ind] + after[transNo+1],\n 0 + after[transNo])\n curr[transNo]=profit\n after=curr\n \n return after[0]\n```\n | 4 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day, and an integer `k`.
Find the maximum profit you can achieve. You may complete at most `k` transactions: i.e. you may buy at most `k` times and sell at most `k` times.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** k = 2, prices = \[2,4,1\]
**Output:** 2
**Explanation:** Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.
**Example 2:**
**Input:** k = 2, prices = \[3,2,6,5,0,3\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
**Constraints:**
* `1 <= k <= 100`
* `1 <= prices.length <= 1000`
* `0 <= prices[i] <= 1000` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.