title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅ 99.53% Recursion & Math & Dynamic Programming | pascals-triangle | 1 | 1 | # Comprehensive Guide to Generating Pascal\'s Triangle: A Three-Pronged Approach for Programmers\n\n## Introduction & Problem Statement\n\nWelcome to this in-depth guide on generating Pascal\'s Triangle up to a given number of rows. Pascal\'s Triangle is a mathematical concept that finds applications in various domains, including combinatorics, probability theory, and computer science. In this guide, we will explore three distinct methods to solve this problem: Dynamic Programming, Recursion, and Math (Combinatorics).\n\n## Key Concepts and Constraints\n\n1. **Row Anatomy**: \n In Pascal\'s Triangle, each row starts and ends with 1. Each inner element is the sum of the two elements directly above it in the previous row.\n\n2. **Row Generation**: \n Our primary task is to generate the first `numRows` of Pascal\'s Triangle.\n\n3. **Constraints**: \n 1 <= `numRows` <= 30. The constraint allows us to generate up to 30 rows of Pascal\'s Triangle.\n\n---\n\n# Strategies to Tackle the Problem: A Three-Pronged Approach\n\n### Live Coding Dynamic Programming\nhttps://youtu.be/g1QAZX8MLWo?si=eeIe-f-Hi4PJfipl\n\n## Method 1. Dynamic Programming\n\n### Intuition and Logic Behind the Solution\n\nIn Dynamic Programming, we use the concept of "building upon previous solutions" to solve the problem. We start with the first row and iteratively generate each subsequent row based on the row above it.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Start with a list containing the first row `[1]`.\n\n2. **Iterative Row Generation**: \n - For each subsequent row, generate it based on the last row in the list. Start and end each row with 1 and fill the middle elements according to Pascal\'s rule.\n\n3. **Return the Triangle**: \n - After generating the required number of rows, return the triangle.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$O(n^2)$$ \u2014 Each row takes $$O(n)$$ time to generate.\n- **Space Complexity**: $$O(n^2)$$ \u2014 Storing the triangle takes $$O(n^2)$$ space.\n\n## Code Dynamic Programming \n``` Python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 0:\n return []\n \n triangle = [[1]]\n \n for i in range(1, numRows):\n prev_row = triangle[-1]\n new_row = [1]\n \n for j in range(1, len(prev_row)):\n new_row.append(prev_row[j-1] + prev_row[j])\n \n new_row.append(1)\n triangle.append(new_row)\n \n return triangle\n```\n``` Go []\nfunc generate(numRows int) [][]int {\n\tvar triangle [][]int\n\tif numRows == 0 {\n\t\treturn triangle\n\t}\n\n\ttriangle = append(triangle, []int{1})\n\n\tfor i := 1; i < numRows; i++ {\n\t\tprevRow := triangle[i-1]\n\t\tvar newRow []int\n\t\tnewRow = append(newRow, 1)\n\n\t\tfor j := 1; j < len(prevRow); j++ {\n\t\t\tnewRow = append(newRow, prevRow[j-1]+prevRow[j])\n\t\t}\n\n\t\tnewRow = append(newRow, 1)\n\t\ttriangle = append(triangle, newRow)\n\t}\n\n\treturn triangle\n}\n```\n``` Rust []\nimpl Solution {\n pub fn generate(num_rows: i32) -> Vec<Vec<i32>> {\n let mut triangle = Vec::new();\n if num_rows == 0 {\n return triangle;\n }\n\n triangle.push(vec![1]);\n\n for _ in 1..num_rows {\n let prev_row = triangle.last().unwrap();\n let mut new_row = vec![1];\n\n for j in 1..prev_row.len() {\n new_row.push(prev_row[j-1] + prev_row[j]);\n }\n\n new_row.push(1);\n triangle.push(new_row);\n }\n\n triangle\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> triangle;\n if (numRows == 0) return triangle;\n\n triangle.push_back({1});\n\n for (int i = 1; i < numRows; ++i) {\n vector<int> prev_row = triangle.back();\n vector<int> new_row = {1};\n\n for (int j = 1; j < prev_row.size(); ++j) {\n new_row.push_back(prev_row[j-1] + prev_row[j]);\n }\n\n new_row.push_back(1);\n triangle.push_back(new_row);\n }\n\n return triangle;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> triangle = new ArrayList<>();\n if (numRows == 0) return triangle;\n\n triangle.add(new ArrayList<>());\n triangle.get(0).add(1);\n\n for (int i = 1; i < numRows; i++) {\n List<Integer> prev_row = triangle.get(i - 1);\n List<Integer> new_row = new ArrayList<>();\n new_row.add(1);\n\n for (int j = 1; j < prev_row.size(); j++) {\n new_row.add(prev_row.get(j - 1) + prev_row.get(j));\n }\n\n new_row.add(1);\n triangle.add(new_row);\n }\n\n return triangle;\n }\n}\n```\n``` C# []\nclass Solution {\n public IList<IList<int>> Generate(int numRows) {\n List<IList<int>> triangle = new List<IList<int>>();\n if (numRows == 0) return triangle;\n\n triangle.Add(new List<int>() { 1 });\n\n for (int i = 1; i < numRows; i++) {\n List<int> prevRow = (List<int>)triangle[i - 1];\n List<int> newRow = new List<int> { 1 };\n\n for (int j = 1; j < prevRow.Count; j++) {\n newRow.Add(prevRow[j - 1] + prevRow[j]);\n }\n\n newRow.Add(1);\n triangle.Add(newRow);\n }\n\n return triangle;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} numRows\n * @return {number[][]}\n */\nvar generate = function(numRows) {\n let triangle = [];\n if (numRows === 0) return triangle;\n\n triangle.push([1]);\n\n for (let i = 1; i < numRows; i++) {\n let prevRow = triangle[i - 1];\n let newRow = [1];\n\n for (let j = 1; j < prevRow.length; j++) {\n newRow.push(prevRow[j - 1] + prevRow[j]);\n }\n\n newRow.push(1);\n triangle.push(newRow);\n }\n\n return triangle;\n};\n```\n``` PHP []\nclass Solution {\n function generate($numRows) {\n $triangle = [];\n if ($numRows == 0) return $triangle;\n\n $triangle[] = [1];\n\n for ($i = 1; $i < $numRows; $i++) {\n $prevRow = end($triangle);\n $newRow = [1];\n\n for ($j = 1; $j < count($prevRow); $j++) {\n $newRow[] = $prevRow[$j - 1] + $prevRow[$j];\n }\n\n $newRow[] = 1;\n $triangle[] = $newRow;\n }\n\n return $triangle;\n}\n}\n```\n\n---\n\n## Method 2. Recursion\n\n### Intuition and Logic Behind the Solution\n\nThe Recursive approach generates Pascal\'s Triangle by making recursive calls to generate the previous rows and then building upon that to generate the current row.\n\n### Step-by-step Explanation\n\n1. **Base Case**: \n - If `numRows` is 1, return `[[1]]`.\n\n2. **Recursive Row Generation**: \n - Make a recursive call to generate the first `numRows - 1` rows.\n - Generate the `numRows`-th row based on the last row in the list.\n\n3. **Return the Triangle**: \n - Return the triangle after adding the new row.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$O(n^2)$$\n- **Space Complexity**: $$O(n^2)$$\n\n## Code Recursion\n``` Python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 1:\n return [[1]]\n \n triangle = self.generate(numRows - 1)\n \n prev_row = triangle[-1]\n new_row = [1]\n \n for i in range(1, len(prev_row)):\n new_row.append(prev_row[i-1] + prev_row[i])\n \n new_row.append(1)\n triangle.append(new_row)\n \n return triangle\n```\n``` Go []\nfunc generate(numRows int) [][]int {\n if numRows == 1 {\n return [][]int{{1}}\n }\n\n triangle := generate(numRows - 1)\n prevRow := triangle[len(triangle) - 1]\n var newRow []int\n newRow = append(newRow, 1)\n\n for i := 1; i < len(prevRow); i++ {\n newRow = append(newRow, prevRow[i-1] + prevRow[i])\n }\n\n newRow = append(newRow, 1)\n triangle = append(triangle, newRow)\n\n return triangle\n}\n\n```\n\n---\n\n## Method 3. Math (Combinatorics)\n\n### Intuition and Logic Behind the Solution\n\nThis method uses the mathematical formula for combinations to directly compute the elements of Pascal\'s Triangle without relying on previous rows. This formula is $$ \\binom{n}{k} $$.\n\n### Step-by-step Explanation\n\n1. **Define the Combination Function**: \n - Use `math.comb()` or a custom function to calculate $$ \\binom{n}{k} $$.\n\n2. **Direct Row Generation**: \n - For each row $$ n $$ and each index $$ k $$ in that row, directly compute the element using $$ \\binom{n}{k} $$.\n\n3. **Return the Triangle**: \n - Return the generated triangle.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$O(n^2)$$\n- **Space Complexity**: $$O(n^2)$$\n\n## Code Math\n``` Python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n import math\n\n triangle = []\n \n for n in range(numRows):\n row = []\n for k in range(n+1):\n row.append(math.comb(n, k))\n triangle.append(row)\n \n return triangle\n```\n\n## Performance\n\n| Language | Method | Execution Time (ms) | Memory (MB) |\n|--------------|-------------|---------------------|-------------|\n| Go | Recursion | 0 | 2.5 |\n| Rust | DP | 1 | 2.0 |\n| Java | DP | 1 | 41.2 |\n| Go | DP | 2 | 2.4 |\n| PHP | DP | 3 | 19 |\n| C++ | DP | 4 | 6.8 |\n| Python3 | Recursion | 27 | 16.3 |\n| Python3 | Math | 35 | 16.2 |\n| Python3 | DP | 40 | 16.3 |\n| JavaScript | DP | 48 | 42.1 |\n| C# | DP | 76 | 36.9 |\n\n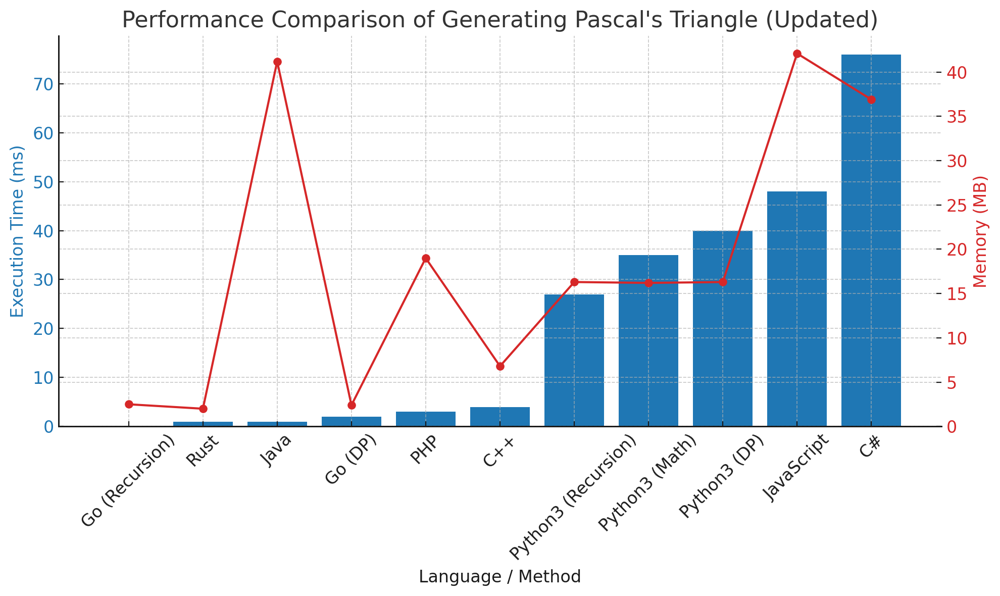\n\n\n## Live Coding Recursion\nhttps://youtu.be/DW5CiB4WBu0?si=Hg1oI3_R6BlA6_X5\n\n\n## Code Highlights and Best Practices\n\n- In the Dynamic Programming and Recursion approaches, we build upon previous solutions, making them more intuitive but dependent on previous rows.\n- The Math approach directly computes each element, making it independent of previous rows but less intuitive.\n- The Dynamic Programming approach is often the most straightforward and easy to implement.\n\nBy understanding these three approaches, you\'ll be well-equipped to tackle problems that involve generating Pascal\'s Triangle or similar combinatorial constructs. | 74 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Python3 Code: | pascals-triangle | 0 | 1 | \n# Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n triangle = [[1]] #creating a new row, as it always begins with one, initialising that alone\n for i in range(1,numRows): #for loop for the range of 1 to the num of rows given\n prev_row = triangle[-1] #assign the previous row in the triangle to a variable\n new_row = [1] #as all the rows begins with 1, create a list with 1 as the starting value\n for j in range(1,i): #for loop for the inner range 1 to i\n new_ele = prev_row[j-1] + prev_row[j] #add the two values (say if n=3, on 3rd iteration of i, this loop will execute twice and add the values 1+2 = 3, 2+1=3)\n new_row.append(new_ele) #now append the added element to the new row\n new_row.append(1) #now append the 1 to the end of the row because all rows ends with one\n triangle.append(new_row) #append the newly formed row to the triangle\n return triangle\n``` | 1 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Brute-force Approach (Runtime - beats 93.54%) | Simple Straightforward Solution | pascals-triangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to generate Pascal\'s Triangle up to the specified number of rows. Pascal\'s Triangle is a triangular array of numbers in which each number is the sum of the two numbers directly above it. The first and last values in each row are always 1.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The code initializes an empty list `output` to store the rows of Pascal\'s Triangle.\n- It handles the base cases for `numRows` 0 and 1 by returning an empty list and a list with a single element `[1]`, respectively.\n- For each row from 2 to `numRows - 1`, the code appends a list of ones to `output` (representing the first and last values of each row).\n- It then modifies the elements in the rows starting from the third row (index 2) onward. Specifically, it sets the second element in each row (index 1) to 2.\n- Finally, for rows starting from the fourth row (index 3) onward, it calculates the values of the elements in the row using the values from the previous row.\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 0:\n return []\n if numRows == 1:\n return [[1]]\n output = []\n for i in range(numRows):\n output.append([1]*(i+1))\n \n if len(output) >= 3:\n output[2][1] = 2\n for j in range(3, numRows):\n for k in range(1, j):\n output[j][k] = output[j-1][k-1] + output[j-1][k]\n\n return output\n``` | 1 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Beginner Friendly Python Solution | pascals-triangle | 0 | 1 | # Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n triangle = []\n for i in range(numRows):\n row = [1] * (i + 1)\n for j in range(1, i):\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]\n triangle.append(row)\n return triangle\n``` | 1 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
[ Java / Python / C++] 🔥100% | ✅EASY | pascals-triangle | 1 | 1 | \n``` java []\nclass Solution {\n public List<List<Integer>> generate(int n) {\n List<List<Integer>> dp = new ArrayList<>();\n\n for (int i = 0; i < n; ++i) {\n Integer[] temp = new Integer[i + 1];\n Arrays.fill(temp, 1);\n dp.add(Arrays.asList(temp));\n }\n\n for (int i = 2; i < n; ++i)\n for (int j = 1; j < dp.get(i).size() - 1; ++j)\n dp.get(i).set(j, dp.get(i - 1).get(j - 1) + dp.get(i - 1).get(j));\n\n return dp;\n }\n}\n```\n```python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n ans=[]\n ans.append([1])\n for i in range(numRows-1):\n temp=[1]\n for j in range(i):\n temp.append(ans[i][j]+ans[i][j+1])\n temp.append(1)\n ans.append(temp)\n return ans\n \n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int n) {\n vector<vector<int>> dp;\n\n for(int i =0 ; i<n ; i++){\n dp.push_back( vector<int>(i+1 , 1));\n }\n\n for(int i = 2 ; i< n ; i++ ){\n for(int j = 1 ; j< dp[i].size()-1 ; j++){\n dp[i][j] = dp[i-1][j] + dp[i-1][j-1];\n }\n }\n\n return dp;\n }\n};\n```\n\n\n | 2 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Generating Pascal's Triangle in C++, Python, and Dart 😃 | pascals-triangle | 0 | 1 | # Intuition\nMy initial thoughts on solving this problem revolve around traversing through the array and keeping track of the maximum sum obtained so far. I might consider using Kadane\'s algorithm, which efficiently finds the maximum subarray sum in a single traversal.\n\n# Approach\n1. Initialize variables: max_sum to store the maximum sum found so far, and current_sum to keep track of the current sum.\n2. Start iterating through the array from the first element.\n3. At each iteration, update current_sum by adding the current element or starting a new subarray if the current element itself is larger than the sum of the previous subarray.\n4. Update max_sum if current_sum exceeds it.\n5. Continue iterating through the array and repeat steps 3-4.\n6. Finally, return the max_sum obtained, which represents the maximum sum of a subarray.\n\n# Complexity\n- Time complexity:\n O(n) - We traverse the array only once.\n\n- Space complexity:\nO(1) - We use a constant amount of extra space for variables max_sum and current_sum regardless of the input size.\n\n# Code\n``` C++ []\nclass Solution {\n List<List<int>> generate(int numRows) {\n List<List<int>> triangle = [];\n\n if (numRows <= 0) {\n return triangle;\n }\n\n for (int i = 0; i < numRows; i++) {\n List<int> row = List.filled(i + 1, 1);\n\n if (i >= 2) {\n for (int j = 1; j < i; j++) {\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j];\n }\n }\n\n triangle.add(row);\n }\n\n return triangle;\n }\n}\n\n```\n``` Python []\nclass Solution(object):\n def generate(self, numRows):\n if numRows <= 0:\n return []\n \n triangle = []\n \n for i in range(numRows):\n row = [1] * (i + 1)\n \n if i >= 2:\n for j in range(1, i):\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]\n \n triangle.append(row)\n \n return triangle\n\n```\n``` Dart []\nclass Solution {\n List<List<int>> generate(int numRows) {\n List<List<int>> triangle = [];\n\n if (numRows <= 0) {\n return triangle;\n }\n\n for (int i = 0; i < numRows; i++) {\n List<int> row = List.filled(i + 1, 1);\n\n if (i >= 2) {\n for (int j = 1; j < i; j++) {\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j];\n }\n }\n\n triangle.add(row);\n }\n\n return triangle;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows <= 0:\n return []\n \n triangle = []\n \n for i in range(numRows):\n row = [1] * (i + 1)\n \n if i >= 2:\n for j in range(1, i):\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]\n \n triangle.append(row)\n \n return triangle\n``` | 6 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
【Video】Beats 97.21% - Python, JavaScript, Java, C++ | pascals-triangle | 1 | 1 | # Main point of the Solution\n\nThe main point of this solution is to generate Pascal\'s triangle, up to a specified number of rows, by iteratively constructing each row based on the previous one. It initializes with the first row containing a single "1," then iterates through the desired number of rows, creating each row by adding zeros at both ends of the previous row, and calculating the inner values as sums of adjacent elements.\n\nThis Python solution beats 97.61%\n\n\n\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 257 videos as of September 8th, 2023.\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/oiO0ov9SSF8\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2253\nThank you for your support!\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize the result list `res` with a single row containing the value 1.\n - Explanation: The `res` list will store the generated Pascal\'s triangle.\n\n2. Use a for loop to iterate `numRows - 1` times.\n - Explanation: We need to generate a total of `numRows` rows in Pascal\'s triangle, so we start with one row already added in `res`.\n\n3. Create a `dummy_row` by adding a 0 at the beginning and end of the last row in `res`.\n - Explanation: In Pascal\'s triangle, each row begins and ends with a 1, so we add a 0 on both sides of the previous row to calculate the values for the current row.\n\n4. Initialize an empty list `row` to store the values of the current row.\n\n5. Use a for loop to iterate over the indices of `dummy_row`.\n - Explanation: We iterate through `dummy_row` to calculate the values of the current row by adding pairs of adjacent values from `dummy_row`.\n\n6. Inside the loop, calculate the sum of `dummy_row[i]` and `dummy_row[i+1]` and append it to the `row` list.\n - Explanation: Each value in the current row is the sum of the two values directly above it in the `dummy_row`.\n\n7. After the loop completes, append the `row` list to the `res` list.\n - Explanation: The calculated values for the current row are added to the `res` list.\n\n8. Repeat steps 3-7 for a total of `numRows - 1` times to generate the required number of rows.\n\n9. Once the loop finishes, return the `res` list containing Pascal\'s triangle.\n\nIn summary, this code generates Pascal\'s triangle up to the specified number of rows by iteratively calculating each row based on the previous row using the principle that each value in a row is the sum of the two values directly above it.\n\n# Complexity\n- **Time complexity: O(n^2)** where n is numRows\n\n - The outer for loop iterates numRows - 1 times.\n - Inside the loop, we perform operations that depend on the length of the current row (which increases with each iteration).\n - The inner loop iterates over the elements of the `dummy_row`, which has a length equal to the length of the last row in `res` plus 2 (due to the added zeros at both ends).\n - In the worst case, the length of the last row in `res` would be numRows - 1 (e.g., for the 5th row, it would be [1, 4, 6, 4, 1]).\n - So, the inner loop runs a number of times proportional to numRows.\n\nConsidering the outer and inner loops, the overall time complexity is O(numRows^2).\n\n- **Space complexity: O(n^2)**, where n is numRows\n\n - The `res` list stores the entire Pascal\'s triangle, which has numRows rows and a total of (numRows^2)/2 elements (since each row has an increasing number of elements).\n - The `dummy_row` list is created in each iteration of the loop and has a length equal to the length of the last row in `res` plus 2.\n - The `row` list is created in each iteration and has a length equal to the length of the current `dummy_row`.\n\n Considering the space used by `res`, `dummy_row`, and `row`, the space complexity is O(numRows^2).\n\n\nIn summary, both the time and space complexity of this code are O(n^2), meaning they grow quadratically with the input parameter `numRows`.\n\n\n```python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n res = [[1]]\n\n for _ in range(numRows - 1):\n dummy_row = [0] + res[-1] + [0]\n row = []\n\n for i in range(len(res[-1]) + 1):\n row.append(dummy_row[i] + dummy_row[i+1])\n res.append(row)\n \n return res\n```\n```javascript []\n/**\n * @param {number} numRows\n * @return {number[][]}\n */\nvar generate = function(numRows) {\n const res = [[1]];\n\n for (let i = 0; i < numRows - 1; i++) {\n const dummyRow = [0, ...res[res.length - 1], 0];\n const row = [];\n\n for (let j = 0; j < dummyRow.length - 1; j++) {\n row.push(dummyRow[j] + dummyRow[j + 1]);\n }\n\n res.push(row);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> res = new ArrayList<>();\n res.add(List.of(1));\n\n for (int i = 0; i < numRows - 1; i++) {\n List<Integer> dummyRow = new ArrayList<>();\n dummyRow.add(0);\n dummyRow.addAll(res.get(res.size() - 1));\n dummyRow.add(0);\n List<Integer> row = new ArrayList<>();\n\n for (int j = 0; j < dummyRow.size() - 1; j++) {\n row.add(dummyRow.get(j) + dummyRow.get(j + 1));\n }\n\n res.add(row);\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n std::vector<std::vector<int>> res;\n res.push_back({1});\n\n for (int i = 0; i < numRows - 1; i++) {\n std::vector<int> dummyRow = {0};\n dummyRow.insert(dummyRow.end(), res.back().begin(), res.back().end());\n dummyRow.push_back(0);\n std::vector<int> row;\n\n for (int j = 0; j < dummyRow.size() - 1; j++) {\n row.push_back(dummyRow[j] + dummyRow[j + 1]);\n }\n\n res.push_back(row);\n }\n\n return res; \n }\n};\n```\n | 24 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Python | Easy to Understand | Fast | pascals-triangle | 0 | 1 | # Python | Easy to Understand | Fast\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n finalNums=[]\n finalNums.append([1])\n for i in range(numRows-1):\n newRow=[1]\n for j in range(i):\n newRow.append(finalNums[i][j]+finalNums[i][j+1])\n newRow.append(1)\n finalNums.append(newRow)\n return finalNums\n``` | 17 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
🚀 C++beats 100% 0ms || Java || Python || DP & Combinatorics || Commented Code 🚀 | pascals-triangle | 1 | 1 | # Problem Description\nGiven an integer numRows, return the first `numRows` of **Pascal\'s triangle**.\n\nIn **Pascal\'s triangle**, each number is the sum of the two numbers directly above it as shown:\n\n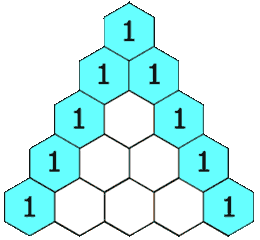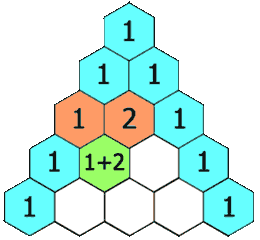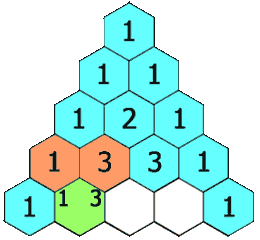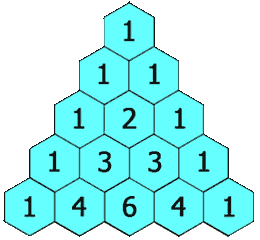\n\n- **Constraints:**\n - `1 <= numRows <= 30`\n\n---\n\n\n# Proposed Solutions\n## 1. Dynamic Programming\n\n### Approach\n1. **Initialize 2D Vector**: Create a 2D vector pascalTriangle with numRows rows to represent Pascal\'s Triangle.\n2. **Generate Rows**: Generate first row seperately then Loop through each row from 1 to numRows - 1.\n3. **Set First and Last Elements**: Set the first and last elements of each row to 1.\n4. **Calculate Middle Elements**: For each row, calculate and append the middle elements by adding the corresponding elements from the previous row.\n5. **Return** Pascal\'s Triangle.\n\n### Complexity\n- **Time complexity:**\nWe have two for-loops each of max size of `n`, then time complexity is `O(N^2)`.\n- **Space complexity:**\n`O(N^2)`, Since we are storing the triangle.\n\n\n## 2. Combinatorics \n\n### Approach\n1. **Initialize 2D Vector**: Create a 2D vector pascalTriangle with numRows rows to represent Pascal\'s Triangle.\n2. **Generate Rows**: Loop through each row from 0 to numRows-1.\n3. **Calculate Middle Elements**: For each row, calculate and append the row elements by calculating combinatorics like the picture below :\n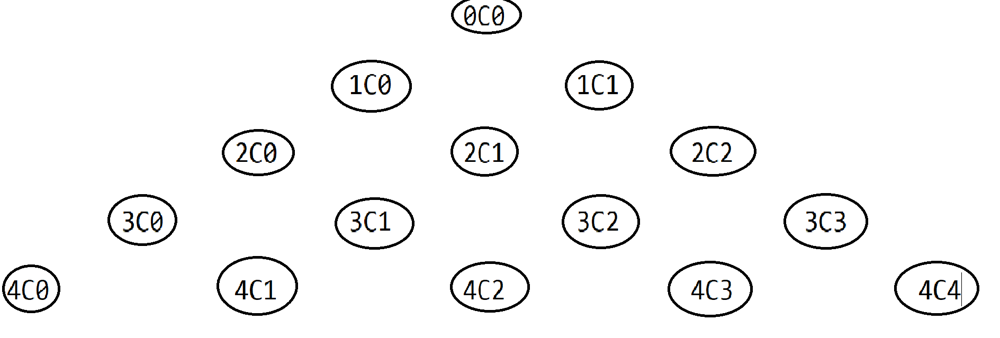\n\n\n4. **Return** Pascal\'s Triangle.\n\n\n### Complexity\n- **Time complexity:**\nWe have two for-loops each of max size of `n` and we have the for loop that generates the combinatorics, then time complexity is `O(N^3)`.\nBut it won\'t make any difference since `1 <= N <= 30`.\n- **Space complexity:**\n`O(N^2)`, Since we are storing the triangle.\n\n---\n\n\n# Code\n## 1. Dynamic Programming\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n // Initialize a 2D vector to represent Pascal\'s Triangle\n vector<vector<int>> pascalTriangle(numRows);\n\n // Initialize the first row with a single element \'1\'\n pascalTriangle[0].push_back(1);\n\n // Generate the rest of the rows\n for (int currentRow = 1; currentRow < numRows; currentRow++) {\n // The first element of each row is always \'1\'\n pascalTriangle[currentRow].push_back(1);\n\n // Get a reference to the current row and the previous row\n vector<int>& currentRowList = pascalTriangle[currentRow];\n const vector<int>& previousRowList = pascalTriangle[currentRow - 1];\n\n // Calculate and populate the middle elements of the row\n for (int j = 1; j < previousRowList.size(); j++) {\n int sum = previousRowList[j] + previousRowList[j - 1];\n currentRowList.push_back(sum);\n }\n\n // The last element of each row is also \'1\'\n currentRowList.push_back(1);\n }\n\n return pascalTriangle;\n }\n};\n```\n```Java []\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n // Initialize the result as a list of lists\n List<List<Integer>> pascalTriangle = new ArrayList<>();\n\n // Initialize the first row with a single element \'1\'\n pascalTriangle.add(new ArrayList<>());\n pascalTriangle.get(0).add(1);\n\n // Generate the rest of the rows\n for (int currentRow = 1; currentRow < numRows; currentRow++) {\n // Create a new row for the current level\n pascalTriangle.add(new ArrayList<>());\n\n // Get references to the current and previous rows\n List<Integer> currentRowList = pascalTriangle.get(currentRow);\n List<Integer> previousRowList = pascalTriangle.get(currentRow - 1);\n\n // The first element of each row is always \'1\'\n currentRowList.add(1);\n\n // Calculate and populate the middle elements of the row\n for (int j = 1; j < previousRowList.size(); j++) {\n int sum = previousRowList.get(j) + previousRowList.get(j - 1);\n currentRowList.add(sum);\n }\n\n // The last element of each row is also \'1\'\n currentRowList.add(1);\n }\n\n return pascalTriangle;\n }\n}\n```\n```Python []\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n """\n Generates Pascal\'s Triangle up to the specified number of rows.\n :param numRows: The number of rows to generate in Pascal\'s Triangle.\n :return: A list of lists representing Pascal\'s Triangle.\n """\n # Initialize Pascal\'s Triangle with empty lists\n pascal_triangle = [[] for _ in range(numRows)]\n\n # Set the first element of the first row to 1\n pascal_triangle[0].append(1)\n\n # Generate the rest of the rows\n for i in range(1, numRows):\n current_row = pascal_triangle[i]\n prev_row = pascal_triangle[i - 1]\n\n # The first element of each row is always 1\n current_row.append(1)\n\n # Calculate and populate the middle elements of the row\n for j in range(1, len(prev_row)):\n element_sum = prev_row[j] + prev_row[j - 1]\n current_row.append(element_sum)\n\n # The last element of each row is also 1\n current_row.append(1)\n\n return pascal_triangle\n\n```\n\n## 2. Combinatorics\n```C++ []\nclass Solution {\npublic:\n // Calculate n choose r (nCr) using a loop\n int calculateCombination(int n, int r) {\n int result = 1;\n for (int i = 0; i < r; i++) {\n result = result * (n - i) / (i + 1);\n }\n return result;\n }\n\n // Generate Pascal\'s Triangle with \'numRows\' rows\n vector<vector<int>> generate(int numRows) {\n // Initialize a 2D vector to represent Pascal\'s Triangle\n vector<vector<int>> pascalTriangle(numRows);\n\n for (int i = 0; i < numRows; i++) {\n for (int j = 0; j <= i; j++) {\n // Calculate and insert the binomial coefficient (nCr) into the current row\n pascalTriangle[i].push_back(calculateCombination(i, j));\n }\n }\n return pascalTriangle;\n }\n};\n```\n```Java []\nclass Solution {\n // Calculate n choose r (nCr) using a loop\n public int calculateCombination(int n, int r) {\n int result = 1;\n for (int i = 0; i < r; i++) {\n result = result * (n - i) / (i + 1);\n }\n return result;\n }\n\n // Generate Pascal\'s Triangle with \'numRows\' rows\n public List<List<Integer>> generate(int numRows) {\n // Initialize a list of lists to represent Pascal\'s Triangle\n List<List<Integer>> pascalTriangle = new ArrayList<>();\n\n for (int i = 0; i < numRows; i++) {\n pascalTriangle.add(new ArrayList<>());\n List<Integer> currentRow = pascalTriangle.get(i);\n\n for (int j = 0; j <= i; j++) {\n // Calculate and insert the binomial coefficient (nCr) into the current row\n currentRow.add(calculateCombination(i, j));\n }\n }\n return pascalTriangle;\n }\n}\n```\n```Python []\nclass Solution:\n\n def calculate_combination(self, n: int, r: int) -> int:\n """\n Calculate the combination (n choose r) using the formula C(n, r) = n! / (r! * (n - r)!).\n :param n: Total number of items.\n :param r: Number of items to choose.\n :return: The combination value C(n, r).\n """\n result = 1\n for i in range(r):\n result = result * (n - i) // (i + 1) # Use integer division to ensure an integer result\n return result\n\n def generate(self, numRows: int) -> List[List[int]]:\n """\n Generate Pascal\'s Triangle up to a given number of rows.\n :param numRows: The number of rows in the Pascal\'s Triangle.\n :return: A list of lists representing Pascal\'s Triangle.\n """\n pascal_triangle = [[] for _ in range(numRows)]\n\n for i in range(numRows):\n for j in range(i + 1):\n pascal_triangle[i].append(self.calculate_combination(i, j))\n\n return pascal_triangle\n```\n\n | 11 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
✔📈100.00% Beats C++✨ || Easy to understand 😇|| C++|| Python||JavaScript || Java||Go| #Beginner😉😎 | pascals-triangle | 1 | 1 | # Objective:\n - The code aims to generate a Pascal\'s Triangle up to a specified number of rows (`numRows`).\n\n# Strategies to Tackle the Problem:\n1. **Understand the Goal**: First, understand that the code\'s goal is to generate Pascal\'s Triangle up to a specified number of rows (`numRows`).\n\n1. **Visualize Pascal\'s Triangle:** It\'s helpful to visualize Pascal\'s Triangle to see the pattern of numbers.\n\n1. **Step Through the Code:** Go through the code step by step, keeping track of the ans vector and how each row is generated.\n\n**Use Test Cases:** Try running the code with different values of `numRows` to see the generated Pascal\'s Triangles and observe how they change.\n\n1. **Check the Math:** Understand that each number in a row is the sum of the two numbers directly above it.\n\n1. **Look for Optimization:** Consider how the code could be optimized or improved for efficiency.\n\n# Intuition\n- **The code generates each row of Pascal\'s Triangle** iteratively, starting with the first row (which contains only 1) and using the values from the previous row to **calculate the values of the current row.** \n-** The inner loop calculates the non-edge **values by adding two values from the previous row. \n- **This process continues** until all rows up to `numRows` are generated.\n\n# Approach\n1. Initialize an empty vector `ans` to store the rows of Pascal\'s Triangle.\n\n1. For each row from `i = 0` to `i = numRows - 1`:\na. Initialize a vector `row` with `i + 1` elements, all set to `1`.\nb. For each element in `row` from `j = 1` to `j = i - 1`, calculate its value by adding two values from the previous row (`ans[i - 1][j]` and `ans[i - 1][j - 1`]).\nc. Add the completed `row` to the `ans` vector.\n\n1. Return the ans vector containing the Pascal\'s Triangle up to numRows.\n\nThis approach builds Pascal\'s Triangle row by row, and the final result is a 2D vector representing the complete triangle.\n\n# Code Explanation:\n1. `vector<vector<int>> ans;`: Initialize an empty 2D vector `ans` to store the rows of Pascal\'s Triangle.\n\n1. `for (int i = 0; i < numRows; i++) {`: Start a loop that iterates from `i = 0` to `i = numRows - 1`. This loop will generate each row of Pascal\'s Triangle.\n\n1. `vector<int> row(i + 1, 1);`: Initialize a vector `row` with `i + 1` elements, all initialized to `1`. This represents the current row being generated.\n\n1. `for (int j = 1; j < i; j++) {`: Start a nested loop that iterates from `j = 1` to `j = i - 1`. This loop fills in the values of `row` between the first and last `1` of the row.\n\n1. `row[j] = ans[i - 1][j] + ans[i - 1][j - 1];`: Calculate the value at position `row[j]` by adding the values from the previous row (`ans[i - 1][j]` and `ans[i - 1][j - 1]`) and assign it to `row[j]`.\n\n1. `ans.push_back(row);`: Add the completed row to the ans vector, representing the current row of Pascal\'s Triangle.\n\n1. Repeat steps 3-6 for each row from `i = 0` to `i = numRows - 1`.\n\n1. Finally, return the ans vector containing the complete Pascal\'s Triangle.\n\n# Comlexity\n**Time Complexity:** `O(numRows^2)`\n**Space Complexity:** `O(numRows^2)`\n\n\n\n# Complexity Explanation:\n**- Time complexity:**\nThe time complexity of the code is` O(numRows^2),` where `numRows` is the `input argument` specifying how many rows of Pascal\'s Triangle to generate.\n\n- `**The outer loop runs for numRows iterations**`, and for each iteration, it performs operations proportional to the current row number (i).\n\n- `The inner loop runs for i - 1 iterations` (excluding the first and last elements of each row), and within the inner loop, there are constant time operations (addition and assignment).\n\n**Therefore, the overall time complexity is determined by the sum of operations for each row, which is roughly 1 + 2 + 3 + ... + numRows. This sum is proportional to numRows^2/2**, resulting in a `time complexity of O(numRows^2)`.\n\n**- Space complexity:**\n\n\n- The space complexity of the code is `O(numRows^2) `as well.\n\n- **The main space usage comes from the ans vector,** which stores the entire Pascal\'s Triangle. \n- **The number of rows in the triangle is equal to numRows,** and for each row, there are on average numRows/2 elements (since the number of elements increases linearly with the row number). \n- Therefore, the space complexity is `O(numRows * numRows/2)`, which simplifies to O(numRows^2).\n\n- Additionally, t**here\'s a constant amount of space used for integer variables i, j, and the temporary row vector.**\n\n- In summary,** both the time and space complexity of the code are O(numRows^2) with respect to the input argument numRows.**\n\n# PLEASE UPVOTE\u2763\uD83D\uDE0D\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> ans;\n for (int i = 0; i < numRows; i++) {\n vector<int> row(i + 1, 1);\n for (int j = 1; j < i; j++) {\n row[j] = ans[i - 1][j] + ans[i - 1][j - 1];\n }\n ans.push_back(row);\n }\n return ans;\n }\n};\n```\n# JAVA\n```\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> ans = new ArrayList<>();\n for (int i = 0; i < numRows; i++) {\n List<Integer> row = new ArrayList<>();\n for (int j = 0; j <= i; j++) {\n if (j == 0 || j == i) {\n row.add(1);\n } else {\n int val = ans.get(i - 1).get(j - 1) + ans.get(i - 1).get(j);\n row.add(val);\n }\n }\n ans.add(row);\n }\n return ans;\n }\n}\n\n```\n# PYTHON3\n```\nclass Solution:\n def generate(self, numRows):\n ans = []\n for i in range(numRows):\n row = [1] * (i + 1)\n for j in range(1, i):\n row[j] = ans[i - 1][j] + ans[i - 1][j - 1]\n ans.append(row)\n return ans\n\n```\n# JAVASCRIPT\n```\nvar generate = function(numRows) {\n let ans = [];\n for (let i = 0; i < numRows; i++) {\n let row = new Array(i + 1).fill(1);\n for (let j = 1; j < i; j++) {\n row[j] = ans[i - 1][j] + ans[i - 1][j - 1];\n }\n ans.push(row);\n }\n return ans;\n};\n\n```\n# GO\n```\npackage main\n\nimport "fmt"\n\nfunc generate(numRows int) [][]int {\n ans := make([][]int, numRows)\n for i := 0; i < numRows; i++ {\n row := make([]int, i+1)\n for j := 1; j < i; j++ {\n row[j] = ans[i-1][j] + ans[i-1][j-1]\n }\n row[0], row[i] = 1, 1\n ans[i] = row\n }\n return ans\n}\n\nfunc main() {\n numRows := 5 // You can change this value as needed\n result := generate(numRows)\n \n for _, row := range result {\n fmt.Println(row)\n }\n}\n\n```\n# PLEASE UPVOTE\u2763\uD83D\uDE0D | 7 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Simple recursion Python | pascals-triangle | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n if numRows == 1:\n return [[1]]\n prev = self.generate(numRows - 1)\n fin = prev[-1]\n now = [1]\n for i in range(len(fin)-1):\n now.append(fin[i] + fin[i+1])\n now.append(1)\n prev.append(now)\n return prev\n``` | 4 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Easy || 0 ms || 100% || Fully Explained || Java, C++, Python, JavaScript, Python3 || DP | pascals-triangle | 1 | 1 | # **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Pascal\'s Triangle.\n```\nclass Solution {\n public List<List<Integer>> generate(int numRows) {\n // Create an array list to store the output result...\n List<List<Integer>> output = new ArrayList<List<Integer>>();\n // Base cases...\n\t if (numRows <= 0) return output;\n // Create an array list to store the prev triangle value for further addition...\n\t ArrayList<Integer> prev = new ArrayList<Integer>();\n // Inserting for the first row & store the prev array to the output array...\n\t prev.add(1);\n\t output.add(prev);\n // For rest of the rows, Traverse all elements through a for loop...\n\t for (int i = 2; i <= numRows; i++) {\n // Create another array to store the current triangle value...\n\t\t ArrayList<Integer> curr = new ArrayList<Integer>();\n\t\t curr.add(1); //first\n // Calculate for each of the next values...\n\t\t for (int j = 0; j < prev.size() - 1; j++) {\n // Inserting the addition of the prev arry two values...\n\t\t\t curr.add(prev.get(j) + prev.get(j + 1)); //middle\n\t\t }\n // Store the number 1...\n\t\t curr.add(1); //last\n // Store the value in the Output array...\n\t\t output.add(curr);\n // Set prev is equal to curr...\n\t\t prev = curr;\n\t }\n\t return output; // Return the output list of pascal values...\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> output;\n // Base cases...\n if(numRows == 0) return output;\n // Traverse all the elements through a loop\n for(int i=0; i<numRows; i++)\n output.push_back(vector<int>(i + 1, 1)); // Initialize the first row of the pascal triangle as {1}.\n // For generating each row of the triangle...\n for (int i = 2; i < numRows; ++i)\n // Run an inner loop from j = 1 to j = {previous row size} for calculating element of each row of the triangle.\n for (int j = 1; j < output[i].size() - 1; ++j)\n // Calculate the elements of a row, add each pair of adjacent elements of the previous row in each step of the inner loop.\n output[i][j] = output[i - 1][j - 1] + output[i - 1][j];\n return output; // After the inner loop gets over, simply output the row generated.\n }\n};\n```\n\n# **Python/Python3 Solution:**\n```\nclass Solution(object):\n def generate(self, numRows):\n # Create an array list to store the output result...\n output = []\n for i in range(numRows):\n if(i == 0):\n # Create a list to store the prev triangle value for further addition...\n # Inserting for the first row & store the prev array to the output array...\n prev = [1]\n output.append(prev)\n else:\n curr = [1]\n j = 1\n # Calculate for each of the next values...\n while(j < i):\n # Inserting the addition of the prev arry two values...\n curr.append(prev[j-1] + prev[j])\n j+=1\n # Store the number 1...\n curr.append(1)\n # Store the value in the Output array...\n output.append(curr)\n # Set prev is equal to curr...\n prev = curr\n return output # Return the output list of pascal values...\n```\n \n# **JavaScript Solution:**\n```\nvar generate = function(numRows) {\n var i = 0;\n var j = 0;\n // Create an array list to store the output result...\n var res = [];\n // For generating each row of the triangle...\n for (i = 0; i < numRows; i++) {\n res.push(Array(i + 1)); // Initialize the first row of the pascal triangle as {1}...\n for (j = 0; j <= i; j++) {\n // Primary...\n if (j === 0 || j === i) {\n res[i][j] = 1;\n }\n else {\n // Calculate the elements of a row, add each pair of adjacent elements of the previous row in each step of the inner loop.\n res[i][j] = res[i - 1][j - 1] + res[i - 1][j];\n }\n }\n }\n return res; // Return the output list of pascal values...\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 217 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Bottom-up tabulation (Dynamic Programming) in Python3 | pascals-triangle | 0 | 1 | # Intuition\nThe problem description is the following:\n- we have an integer `numRows`\n- our goal is to recreate the **Pascal\'s triangle (PT)**\n\n\n---\n\nIf you want to know more about [PT](https://en.wikipedia.org/wiki/Pascal%27s_triangle), follow the link.\n\n```\n# Example\nnumRows = 4\n\n# The first level is always going to be [1]\n# And all of the other levels will consist according to the sum\n# of indexes of two nums, whose are\nprevAbove = j - 1\nnextAbove = j \n\n# Any level starts and ends with 1-s and the visual representation\n# can look like this\n\n# [1] <= 1 lvl\n# [1, 1] <= 2 lvl\n# [1, 2, 1] <= 3 lvl\n# [1, 3, 3, 1] <= 4 lvl\n\n# If you break down the next level after the first (let\'s consider\n# the second), you\'ll see the pattern of creating this triangle \n\n# for i, that more than one\n# for j, that more or equals to one\n# each row[j] = prevRow[j - 1] + prevRow[j]\n```\n\n# Approach\n1. initialize an `ans` variable with the first level of triangle\n2. iterate in range `[1, numRows)`\n3. at each step create a new `row`, and fill it with `1`- s\n4. fill the row, according to the schema above\n5. push the `row` into triangle `ans`\n6. return the `ans`\n\n# Complexity\n- Time complexity: **O(n^2)**, because the number of iterations grows for `numRows` as `numRows * (numRows + 1) / 2` \n\n- Space complexity: **O(n^2)**, the same, because of storing triangle\n# Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n ans = [[1]]\n\n for i in range(1, numRows):\n row = [1] * (i + 1)\n\n for j in range(1, len(row) - 1):\n row[j] = ans[i - 1][j - 1] + ans[i - 1][j]\n\n ans.append(row)\n\n return ans\n``` | 1 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Beats 100%||C/C++/Python iterative DP||Math Explain | pascals-triangle | 0 | 1 | # Intuition\nHere is a real C solution provided which is really very rare.\n\nSolution via Pascal\'s identity $$C^i_j=C^{i-1}_{j-1}+C^{i-1}_{j}$$& $$C^i_j=C^i_{i-j}$$\n\nDon\'t use the built-in function comb(i, j) to compute, because it is very time consuming.\n\nIt is also not suggested direct to use the defintion to compute:\n$$\nC^i_j=\\frac{i!}{j!(i-j)!}\n$$\nwhere the compting for factorial $i!$ is very slow $O(i)$& will overflow when $i$ is more than 12 for 32-bit int. Pascal triangle is a theorem for computing binomial coefficients!\n$$\n(x+y)^i=\\sum_{j=0}^i C^i_jx^{i-j}y^j\n$$\n# Use binomial coefficients to prove Pascal\'s triangle:\n$$\n(x+y)^i=\\sum_{j=0}^i C^i_jx^{i-j}y^j\\\\\n=(x+y)^{i-1}(x+y)\\\\\n=\\sum_{j=1}^i C^{i-1}_{j-1}x^ {i-j-1}y^j(x+y)\\\\\n=\\sum_{j=1}^i C^{i-1}_{j-1}x^ {i-j}y^j+\\sum_{j=0}^{i-1} C^{i-1}_{j}x^ {i-j}y^j\n$$\nCompare the coefficients for term $x^{i-j}y^j$, one obtain \n$$C^i_j=C^{i-1}_{j-1}+C^{i-1}_{j}$$ QED.\n# Approach\nIterative DP uses double for loop.\n\n[Please turn English subtitles if neccessary]\n[https://www.youtube.com/watch?v=paoJGMYEEhA](https://www.youtube.com/watch?v=paoJGMYEEhA)\n# Complexity\n- Time complexity:\n $$O(n^2)$$\n\n- Space complexity:\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n $$O(n^2)$$ for returning answer. $$O(1)$$ for extra need.\n\n\n# Code Runtime 0ms Beats 100%\n```\nclass Solution {\npublic:\n vector<vector<int>> generate(int numRows) {\n vector<vector<int>> a(numRows);\n for(int&& i=0; i<numRows; i++){\n a[i].assign(i+1, 1);// exact allocation once\n for(int&& j=1; j<=i/2; j++){\n a[i][i-j]=a[i][j]=a[i-1][j-1]+a[i-1][j];\n \n } \n }\n return a;\n }\n};\n\n```\n# C code\n```\n/**\n * Return an array of arrays of size *returnSize.\n * The sizes of the arrays are returned as *returnColumnSizes array.\n * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().\n */\nint** generate(int numRows, int* returnSize, int** returnColumnSizes) {\n int** a = (int**)malloc(sizeof(int*) * numRows);\n *returnSize = numRows;\n *returnColumnSizes=(int*)malloc(sizeof(int)*numRows); //Allocate for column sizes array\n\n for (register int i=0; i<numRows; i++) {\n (*returnColumnSizes)[i] =i+1; // Set the size of each row in column sizes array\n a[i] = (int*)malloc(sizeof(int)*(i+1));\n\n a[i][0] = a[i][i] = 1;\n for (register int j=1; j<=i/2; j++) {\n a[i][j]=a[i][i-j]= a[i-1][j-1]+a[i-1][j];\n }\n }\n return a;\n}\n```\n# Python solution\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n a=[[]]*numRows\n for i in range(numRows):\n a[i]=[1]*(i+1)\n for j in range(1,i//2+1):\n a[i][i-j]=a[i][j]=a[i-1][j-1]+a[i-1][j]\n return a\n```\n# Python code using lambda function\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n a = [[1]]\n for i in range(1, numRows):\n a += [list(map(lambda x, y: x+y, a[-1] + [0], [0] + a[-1]))]\n return a[:numRows]\n```\n# Pascal Traingle can solve [62. Unique Paths](https://leetcode.com/problems/unique-paths/solutions/3994527/c-python-math-pascal-triangle-dp-beats-100/)\n[Please turn on English subtitles if necessary]\n[https://youtu.be/sgRvG0rhWGI?si=N7nEiMEw70QCsnLx](https://youtu.be/sgRvG0rhWGI?si=N7nEiMEw70QCsnLx) | 10 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Pascals Traingle (simple Maths) | pascals-triangle | 0 | 1 | # Intuition\n<!-- Describe your first- thoughts on how to solve this problem. -->\nUsing the for loops and just iterating through it..\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\njust observe the pattern and see for every row the leading and ending 1\'s are in commmon..\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n**2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def generate(self, n: int) -> List[List[int]]:\n dp=[]\n for i in range(1,n+1):\n dp.append([0]*i)\n for i in range(0,n):\n for j in range(0,i+1):\n if(j==0 or j==i):\n #For leading and trailing of the row the 1 should be appended....\n dp[i][j]=1\n else:\n #The previous values both are added together\n dp[i][j]=dp[i-1][j-1]+dp[i-1][j]\n return dp\n \n``` | 5 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
👹 easy simple solution, python & java 🐍☕ | pascals-triangle | 1 | 1 | # Intuition\nstarts with 1, then goes down a level and sums the two values and puts in after the first one, and incremends for each row\n\n# Approach\nfirst row is always 1\ngo row by columns, ie: nested for loop\n1. for i in range (from 1 to rowsnumber):\'\n inside the loop add a 1 as the first elem in the first col, then calculate the sum and add to value\n2. for j in range 1 to nummber of current row(we add values depending on row number)\n3. value is going to be = triangle[current row-1][current col-1]+triangle[current row-1][current col]\n\n***simpler*:** \n go to prev row, sum left elem of prev row, and right elem of prev row, get sum and post as value after first 1, and before last 1, increment the number of values that are needed based on which row your\'e at and create more values based on which col your\'e at as well\nmore cols and rows = more values of summs\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n^2)\n\n# PYTHON\n```\nclass Solution(object):\n def generate(self, numRows):\n if numRows == 0:\n return []\n\n triangle = [[1]] #first row\n\n for i in range(1,numRows):\n row = [1]\n for j in range(1,i):\n value = triangle[i-1][j-1]+triangle[i-1][j]\n row.append(value)\n row.append(1)\n triangle.append(row) \n return triangle\n```\n# JAVA\n```\nimport java.util.ArrayList;\nimport java.util.List;\n\npublic class Solution {\n public List<List<Integer>> generate(int numRows) {\n List<List<Integer>> triangle = new ArrayList<>();\n\n if (numRows == 0) {\n return triangle;\n }\n\n List<Integer> firstRow = new ArrayList<>();\n firstRow.add(1);\n triangle.add(firstRow);\n\n for (int i = 1; i < numRows; i++) {\n List<Integer> row = new ArrayList<>();\n row.add(1);\n \n for (int j = 1; j < i; j++) {\n int value = triangle.get(i - 1).get(j - 1) + triangle.get(i - 1).get(j);\n row.add(value);\n }\n \n row.add(1);\n triangle.add(row);\n }\n \n return triangle;\n }\n}\n\n```\n\n | 3 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Easy Python Solution With Briefly Explanation ✅✅ | pascals-triangle | 0 | 1 | # Approach\nLet\'s break down the given Python code step by step. This code defines a class `Solution` with a method `generate` that generates Pascal\'s triangle up to a specified number of rows.\n\n```python\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n```\n\nThis line defines a class called `Solution` with a method `generate`. This method takes an integer `numRows` as an argument and is expected to return a list of lists of integers.\n\n```python\n res = [[1]]\n```\n\nHere, we initialize a list `res` with a single row, which contains only a single element, the number 1. This represents the first row of Pascal\'s triangle.\n\n```python\n for i in range(numRows - 1):\n```\n\nThis for loop runs for `numRows - 1` iterations. It\'s important to note that we already initialized `res` with the first row, so we start generating additional rows.\n\n```python\n temp = [0] + res[-1] + [0]\n```\n\nIn each iteration, we create a new list `temp`. This list is constructed by adding a 0 at the beginning and end of the last row in `res`. This is because Pascal\'s triangle has 1s at its edges, and we\'re preparing `temp` to calculate the values in the next row.\n\n```python\n row = []\n```\n\nWe initialize an empty list `row` to store the elements of the current row we\'re generating.\n\n```python\n for j in range(len(res[-1]) + 1):\n```\n\nThis inner for loop runs for the length of the last row in `res` plus 1. This is because we want to generate one more element than the previous row had.\n\n```python\n row.append(temp[j] + temp[j+1])\n```\n\nIn this line, we calculate each element of the current row by adding the corresponding elements from `temp` and `temp` shifted one position to the right. This is how the values in Pascal\'s triangle are calculated, as each element is the sum of the two elements above it.\n\n```python\n res.append(row)\n```\n\nOnce we have generated the current row (`row`), we append it to the `res` list, which stores all the rows of Pascal\'s triangle.\n\nFinally, after all iterations are complete, we return the `res` list, which contains the Pascal\'s triangle up to the specified number of rows.\n\nIn summary, this code generates Pascal\'s triangle up to the specified number of rows by iteratively calculating each row based on the previous row and appending it to a list of rows (`res`).\n\n# Python Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]: \n res = [[1]]\n for i in range(numRows-1):\n temp = [0]+res[-1]+[0]\n row = []\n\n for j in range(len(res[-1])+1):\n row.append(temp[j] + temp[j+1])\n res.append(row)\n\n return res\n\n```\n\n**Please upvote if you like the solution.\nHappy Coding! \uD83D\uDE0A**\n | 5 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
NOOB CODE | pascals-triangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initializes lists a1, a2, and an with the first three rows of Pascal\'s Triangle.\n2. Sets p to an to track the previous row.\n3. Creates an empty list f to store the entire Pascal\'s Triangle.\n4. Appends the first two rows (a1 and a2) to f.\n5. If numRows is 1, returns [[1]] (the first row).\n6. Otherwise, iterates from k = 2 to numRows - 1.\n7. In each iteration, calculates the values of the current row (an) based on the previous row (p) by summing adjacent elements.\n8. Appends the current row (an) to f, updates p to an, and resets an to [1, 1].\n9. The loop continues until all numRows rows are generated.\n10. Finally, returns f, containing Pascal\'s Triangle.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: **o(n^2)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **o(n^2)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def generate(self, numRows: int) -> List[List[int]]:\n a1=[1]\n a2=[1,1]\n an=[1,1]\n p=an\n f=[]\n f.append(a1)\n f.append(a2)\n if numRows==1:\n f=[[1]]\n else:\n for k in range (2,numRows):\n for i in range(1,k):\n an.insert(i,p[i]+p[i-1])\n f.append(an)\n p=an\n an=[1,1]\n return(f)\n``` | 3 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Pascals Traingle (simple Maths) | pascals-triangle | 0 | 1 | # Intuition\n<!-- Describe your first- thoughts on how to solve this problem. -->\nUsing the for loops and just iterating through it..\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\njust observe the pattern and see for every row the leading and ending 1\'s are in commmon..\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n**2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def generate(self, n: int) -> List[List[int]]:\n dp=[]\n for i in range(1,n+1):\n dp.append([0]*i)\n for i in range(0,n):\n for j in range(0,i+1):\n if(j==0 or j==i):\n #For leading and trailing of the row the 1 should be appended....\n dp[i][j]=1\n else:\n #The previous values both are added together\n dp[i][j]=dp[i-1][j-1]+dp[i-1][j]\n return dp\n \n``` | 1 | Given an integer `numRows`, return the first numRows of **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** numRows = 5
**Output:** \[\[1\],\[1,1\],\[1,2,1\],\[1,3,3,1\],\[1,4,6,4,1\]\]
**Example 2:**
**Input:** numRows = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= numRows <= 30` | null |
Python3 Solution | pascals-triangle-ii | 0 | 1 | \n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n ans=[1]\n for i in range(1,rowIndex+1):\n ans.append(1)\n for j in range(len(ans)-2,0,-1):\n ans[j]+=ans[j-1]\n\n return ans\n``` | 3 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
【Video】Give me 10 minutes - How we think about a solution - Python JavaScript, Java, C++ | pascals-triangle-ii | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\nadd left number and right number in a previous row\n\n---\n\n# Solution Video\n\nhttps://youtu.be/1162hVzZ3sM\n\n\u25A0 Timeline of the video\n`0:04` Key point to solve this question\n`0:05` Two key points to solve this question\n`0:16` Actually there is a formula for Pascal\'s Triangle\n`0:32` Explain basic idea and the key point\n`2:38` Demonstrate real algorithms\n`6:39` Coding\n`7:43` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,720\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution.\n\nFirst of all there is formula for Pascal\'s Triangle Recurrence Relation.\n\n\n```\nnext_element = previous element\xD7(rowIndex\u2212position+1) / position\n```\n\nBased on the formula, you can implement solution code like this.\n\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n row = [1]\n\n for i in range(1, rowIndex + 1):\n next_element = row[i - 1] * (rowIndex - i + 1) // i\n row.append(next_element)\n\n return row\n```\n\nBut in real interview, it\'s hard to come up with the formula, so I don\'t use this solution.\n\nWe know that we add left and right numbers in above row, then create a current row.\n\u200B\nso we iterate the same two rows at the same time but add `[0]` to the first position for one row and add `[0]` to the last position for the other row.\n\nThis idea comes from Pascal Tringle \u2160. I have a video here.\n\nhttps://youtu.be/oiO0ov9SSF8\n\n\n---\n\n\u2B50\uFE0F Points\n\nAdd `[0]` to the first position for one row and add `[0]` to the last position for the other row, because we can prevent out of bounds when we iterate thorugh each row and we can create order of left number and order of right number.\n\nWhat I\'m trying to do is for example, when we create the second row, we need to add left and right number in the first row `[1]`. But how?\n\nWhen we create the `index 0` number in the second row, left number in the first row is out of bounds.\n\nThat\'s why we add `0` to the first and the last position of the first row.\n\n`[0,1,0]`\n\nso we can calulcate 0 + 1 for `index 0` in the second row.\nwe can calulcate 1 + 0 for `index 1` in the second row.\n\nin the end, we have `[1,1]`\n\n`0` doesn\'t afffect result of calculation.\n\nWe use this basic idea to this problem.\n\n---\n\nLet\'s see an example.\n\n```\nInput: rowIndex = 3\n```\n\nFirst of all, we initialize `row = [1]`, because the frist row in the triangle row is `1`.\n\nAfter that, we add `[0]` to the first position and the last position respectively.\n\nNow we have\n\n```\n[0,1] (order of left number)\n[1,0] (order of right number)\n\nPascal Triangle I, I created [0,1,0] for the first row.\n\norder of left number is the first two numbers [0,1] in [0,1,0]\norder of right number is the last two numbers [1,0] in [0,1,0]\n```\n\nAdd each position. In the end we have\n```\n[1,1]\n```\n\nNext, add `[0]` to the first and the last.\n```\n[0,1,1] (order of left number)\n[1,1,0] (order of right number)\n\nPascal Triangle I, I created [0,1,1,0] for the second row.\n\norder of left number is the first three numbers [0,1,1] in [0,1,1,0]\norder of right number is the last three numbers [1,1,0] in [0,1,1,0]\n```\n \nAdd each position. In the end we have\n```\n[1,2,1]\n```\n\nNext, add `[0]` to the first and the last.\n```\n[0,1,2,1] (order of left number)\n[1,2,1,0] (order of right number)\n\nPascal Triangle I, I created [0,1,2,1,0] for the third row.\n\norder of left number is the first four numbers [0,1,2,1] in [0,1,2,1,0]\norder of right number is the last four numbers [1,2,1,0] in [0,1,2,1,0]\n```\n\nAdd each position. In the end we have\n```\nOutput: [1,3,3,1]\n```\n\nLet\'s see real algorithm!\n\n### Algorithm Overview:\n1. Initialize a list `row` with a single element, which is 1.\n2. Iterate `rowIndex` times, each time calculating the next row using the binomial coefficient recurrence relation and updating the `row`.\n3. Return the generated row.\n\n### Detailed Explanation:\n1. Start with an initial row containing a single element: [1]. This is the 0th row (rowIndex = 0).\n\n2. For each iteration from 0 to `rowIndex` (exclusive):\n a. Calculate each element of the new row using binomial coefficients.\n b. The element at index `i` in the new row is the sum of the element at index `i` and the element at index `i-1` in the previous row.\n c. Update `row` with the new row for the next iteration.\n\n3. After all iterations, return the `row` which represents the `rowIndex`-th row of Pascal\'s Triangle.\n\n# Complexity\n- Time complexity: $$O(rowIndex^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(rowIndex)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution(object):\n def getRow(self, rowIndex):\n row = [1]\n\n for _ in range(rowIndex):\n row = [left + right for left, right in zip([0]+row, row+[0])]\n \n return row \n```\n```javascript []\n/**\n * @param {number} rowIndex\n * @return {number[]}\n */\nvar getRow = function(rowIndex) {\n let row = [1];\n\n for (let i = 0; i < rowIndex; i++) {\n row = row.map((val, index) => (row[index - 1] || 0) + (row[index] || 0));\n row.push(1);\n }\n\n return row; \n};\n```\n```java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> row = new ArrayList<>();\n row.add(1);\n\n for (int i = 0; i < rowIndex; i++) {\n List<Integer> newRow = new ArrayList<>();\n newRow.add(1);\n for (int j = 1; j < row.size(); j++) {\n newRow.add(row.get(j - 1) + row.get(j));\n }\n newRow.add(1);\n row = newRow;\n }\n\n return row; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> row(1, 1);\n\n for (int i = 0; i < rowIndex; i++) {\n vector<int> newRow;\n newRow.push_back(1);\n for (int j = 1; j < row.size(); j++) {\n newRow.push_back(row[j - 1] + row[j]);\n }\n newRow.push_back(1);\n row = newRow;\n }\n\n return row; \n }\n};\n```\n\n\n---\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/parallel-courses-iii/solutions/4180474/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/PWorxtrU6hY\n\n\u25A0 Timeline of the video\n`0:04` Key point to solve this question\n`0:23` Explain the first key point\n`1:12` Explain the second key point\n`1:39` Demonstrate real algorithms\n`6:36` Coding\n`10:33` Time Complexity and Space Complexity\n\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/number-of-ways-to-stay-in-the-same-place-after-some-steps/solutions/4169623/video-give-me-10-minutes-how-we-think-abou-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/uC0nI4E7ozw\n\n\u25A0 Timeline of the video\n`0:04` How we think about a solution\n`0:05` Two key points to solve this question\n`0:21` Explain the first key point\n`1:28` Explain the second key point\n`2:36` Break down and explain real algorithms\n`6:09` Demonstrate how it works\n`10:17` Coding\n`12:58` Time Complexity and Space Complexity\n | 40 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
✅ 100% Easy Optimized | pascals-triangle-ii | 1 | 1 | # Intuition\nWhen faced with Pascal\'s Triangle, a fundamental pattern that stands out is the binomial coefficient. The elements of each row in Pascal\'s Triangle can be represented as combinations. Recognizing this mathematical property offers a direct route to the solution without the need to iterate through all the preceding rows.\n\n## Live Coding + Explaining\nhttps://youtu.be/BY95fxcrjag?si=d2BKTlF0FCIhLjoU\n\n# Approach\nEach row of Pascal\'s Triangle can be represented using the sequence of combinations:\n$$ C(r, 0), C(r, 1), C(r, 2), \\ldots, C(r, r) $$\nwhere $$ C(n, k) $$ is the binomial coefficient, defined as:\n$$ C(n, k) = \\frac{n!}{k!(n-k)!} $$\n\nThe row\'s first element is always 1. Given the previous element in the row (`prev`), the next element can be calculated using:\n$$ \\text{next\\_val} = \\text{prev} \\times \\frac{\\text{rowIndex} - k + 1}{k} $$\nThis formula is derived from the relationship between consecutive binomial coefficients in the same row.\n\nIterating from `k = 1` to `k = rowIndex`, we can directly generate the elements for the desired row without building the entire triangle.\n\n# Complexity\n- Time complexity: $$O(\\text{rowIndex})$$\nThis is because we are directly computing the rowIndex-th row without iterating through all previous rows.\n\n- Space complexity: $O(\\text{rowIndex})$\nThe only significant space used is for the result list, which has a length of rowIndex + 1.\n\n# Code\n``` Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n res = [1]\n prev = 1\n for k in range(1, rowIndex + 1):\n next_val = prev * (rowIndex - k + 1) // k\n res.append(next_val)\n prev = next_val\n return res\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> getRow(int rowIndex) {\n std::vector<int> res(1, 1);\n long long prev = 1;\n for(int k = 1; k <= rowIndex; k++) {\n long long next_val = prev * (rowIndex - k + 1) / k;\n res.push_back(next_val);\n prev = next_val;\n }\n return res;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> res = new ArrayList<>();\n res.add(1);\n long prev = 1;\n for (int k = 1; k <= rowIndex; k++) {\n long next_val = prev * (rowIndex - k + 1) / k;\n res.add((int) next_val);\n prev = next_val;\n }\n return res;\n }\n}\n```\n``` Go []\nfunc getRow(rowIndex int) []int {\n res := []int{1}\n prev := 1\n for k := 1; k <= rowIndex; k++ {\n next_val := prev * (rowIndex - k + 1) / k\n res = append(res, next_val)\n prev = next_val\n }\n return res\n}\n```\n``` Rust []\nimpl Solution {\n pub fn get_row(row_index: i32) -> Vec<i32> {\n let mut res = vec![1];\n let mut prev: i64 = 1; // use i64 for the calculations\n for k in 1..=row_index {\n let next_val = prev * (row_index - k + 1) as i64 / k as i64;\n res.push(next_val as i32);\n prev = next_val;\n }\n res\n }\n}\n```\n``` PHP []\nclass Solution {\n function getRow($rowIndex) {\n $res = [1];\n $prev = 1;\n for($k = 1; $k <= $rowIndex; $k++) {\n $next_val = $prev * ($rowIndex - $k + 1) / $k;\n $res[] = $next_val;\n $prev = $next_val;\n }\n return $res;\n }\n}\n```\n``` JavaScript []\nvar getRow = function(rowIndex) {\n let res = [1];\n let prev = 1;\n for(let k = 1; k <= rowIndex; k++) {\n let next_val = prev * (rowIndex - k + 1) / k;\n res.push(next_val);\n prev = next_val;\n }\n return res;\n};\n```\n``` C# []\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> res = new List<int> {1};\n long prev = 1;\n for (int k = 1; k <= rowIndex; k++) {\n long next_val = prev * (rowIndex - k + 1) / k;\n res.Add((int)next_val);\n prev = next_val;\n }\n return res;\n }\n}\n```\n\n\n## Performance\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| Rust | 0 ms | 2 MB |\n| Java | 0 ms | 39.8 MB |\n| C++ | 0 ms | 6.9 MB |\n| Go | 1 ms | 1.9 MB |\n| PHP | 3 ms | 19.1 MB |\n| Python3 | 36 ms | 16.2 MB |\n| JavaScript | 45 ms | 42 MB |\n| C# | 83 ms | 35.8 MB |\n\n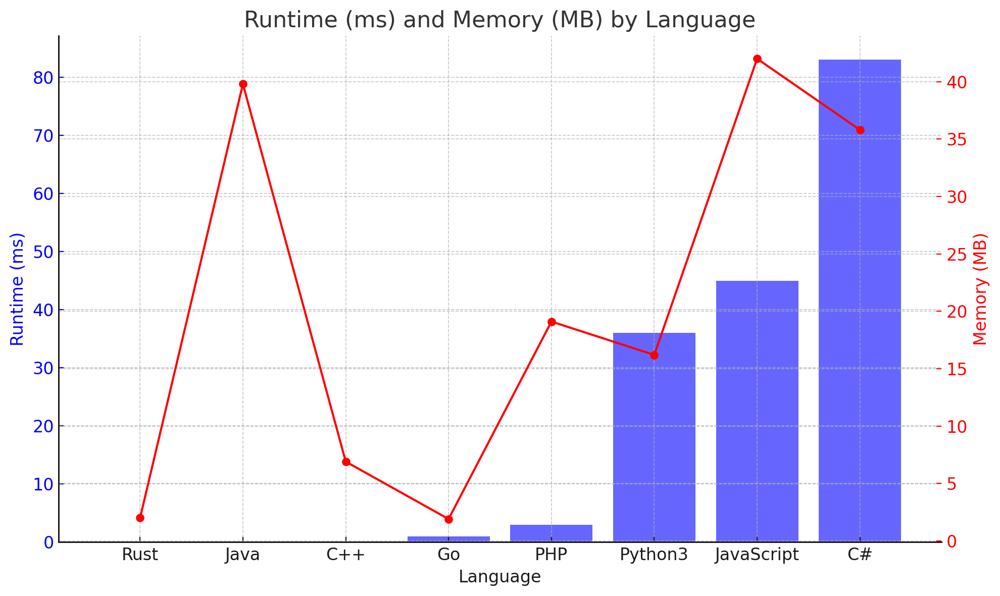\n\n\n# What have we learned?\nThis problem teaches us the importance of recognizing patterns and mathematical properties in data. Rather than relying on a brute-force approach (i.e., building the entire Pascal\'s Triangle up to the desired row), we leveraged the properties of binomial coefficients to directly compute the required row. This understanding reduces both the time and space complexity of our solution. The logic behind this solution is the inherent mathematical relationship between consecutive binomial coefficients in Pascal\'s Triangle, which allows us to compute the next coefficient given the previous one. This is a testament to the power of mathematical insight in algorithm design. | 72 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
📢-: The Magic of Pascal's Triangle: Generating Rows with Ease || Mr. Robot | pascals-triangle-ii | 1 | 1 | # Efficiently Generating Pascal\'s Triangle Row\n\n## Introduction\n\nIn the world of combinatorics, Pascal\'s Triangle is a true gem. It\'s a triangular array of numbers where each number is the sum of the two numbers directly above it. In this blog post, we\'ll explore an efficient C++ code that generates the `rowIndex`-th row of Pascal\'s Triangle using dynamic programming. \n\n## The Challenge\n\nLeetCode offers a problem that asks us to find the `rowIndex`-th row of Pascal\'s Triangle. Given an integer `rowIndex`, we want to return the `rowIndex`-th row of the Pascal\'s Triangle.\n\n## The Approach\n\nTo efficiently generate the `rowIndex`-th row of Pascal\'s Triangle, we\'ll use dynamic programming. In particular, we\'ll calculate binomial coefficients using the recurrence relation: `C(n, r) = C(n-1, r) + C(n-1, r-1)` with some base cases.\n\n\n**Dry Run:**\n\nLet\'s say we want to find the 4th row of Pascal\'s Triangle, i.e., `rowIndex = 3`.\n\n1. We initialize `ans` as an empty vector to store our result.\n2. We create a 2D vector `dp` of size `4x4` and initialize it with -1.\n\n ```cpp\n dp = {\n {-1, -1, -1, -1},\n {-1, -1, -1, -1},\n {-1, -1, -1, -1},\n {-1, -1, -1, -1}\n }\n ```\n\n3. We enter a loop from `i = 0` to `3`, where `i` represents the current index within the row.\n\n - For `i = 0`, we calculate `ans[0]` by calling `ncr(3, 0, dp)`. This, in turn, computes binomial coefficient C(3, 0) and sets `ans[0] = 1`.\n\n - For `i = 1`, we calculate `ans[1]` by calling `ncr(3, 1, dp)`. This computes C(3, 1) and sets `ans[1] = 3`.\n\n - For `i = 2`, we calculate `ans[2]` by calling `ncr(3, 2, dp)`. This computes C(3, 2) and sets `ans[2] = 3`.\n\n - For `i = 3`, we calculate `ans[3]` by calling `ncr(3, 3, dp)`. This computes C(3, 3) and sets `ans[3] = 1`.\n\n4. The loop ends, and `ans` now contains the 4th row of Pascal\'s Triangle: `[1, 3, 3, 1]`.\n\n5. The function returns `ans`.\n\n**Edge Case:**\n\nLet\'s consider an edge case where `rowIndex` is set to `0`, i.e., we want to find the 1st row of Pascal\'s Triangle.\n\n- In this case, `ans` will be an empty vector, as the loop won\'t execute since `i` goes from `0` to `0`.\n\n- The function will return an empty vector, indicating that the 1st row of Pascal\'s Triangle is `[1]`.\n\n\n**Time Complexity:**\nThe time complexity of this code can be analyzed as follows:\n\n1. Computing `nCr` values involves two recursive calls for each pair `(n, r)` where `r` is not 0 or `n`. This leads to a binary tree-like structure of recursive calls, with a maximum depth of `n`. In each recursive call, we are doing constant-time operations. Therefore, the time complexity for computing `nCr` for a given `(n, r)` pair is O(n) since there are O(n) unique `(n, r)` pairs.\n\n2. We are iterating through each value from `0` to `rowIndex` and calling `ncr` for each of these values. So, the overall time complexity of the `getRow` function is O(rowIndex).\n\n3. In summary, the code\'s time complexity is O(rowIndex * n).\n\n**Space Complexity:**\nThe space complexity of this code is determined by the auxiliary space used for memoization and the space used for the `ans` vector.\n\n1. The `dp` 2D vector is used for memoization. It has a size of `(rowIndex + 1) x (rowIndex + 1)`, which is O(rowIndex^2) in terms of space.\n\n2. The `ans` vector stores the final result, which is also of size `rowIndex + 1`, leading to O(rowIndex) space.\n\n3. Therefore, the overall space complexity of the code is O(rowIndex^2 + rowIndex), which can be simplified to O(rowIndex^2) since the dominating term is the memoization table.\n\n- It\'s important to note that while this code provides an `easy-to-understand way` to compute the k-th row of Pascal\'s Triangle, it `may not be the most efficient in terms of space`. There are more memory-efficient algorithms to calculate the same result, but this `code focuses on readability and clarity`.\n\n**C++**\n```cpp []\nclass Solution {\npublic:\n int ncr(int n, int r, vector<vector<int>>& dp) {\n if (r == 0 || r == n) return 1;\n if (r == 1 || r == n - 1) return n;\n if (dp[n][r] != -1) return dp[n][r];\n return dp[n][r] = ncr(n - 1, r, dp) + ncr(n - 1, r - 1, dp);\n }\n\n vector<int> getRow(int rowIndex) {\n vector<int> ans;\n vector<vector<int>> dp(rowIndex + 1, vector<int>(rowIndex + 1, -1));\n for (int i = 0; i <= rowIndex; i++) {\n ans.push_back(ncr(rowIndex, i, dp));\n }\n return ans;\n }\n};\n```\n\n\n**Java:**\n\n```java\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public int ncr(int n, int r, List<List<Integer>> dp) {\n if (r == 0 || r == n)\n return 1;\n if (r == 1 || r == n - 1)\n return n;\n if (dp.get(n).get(r) != -1)\n return dp.get(n).get(r);\n int result = ncr(n - 1, r, dp) + ncr(n - 1, r - 1, dp);\n dp.get(n).set(r, result);\n return result;\n }\n\n public List<Integer> getRow(int rowIndex) {\n List<Integer> ans = new ArrayList<>();\n List<List<Integer>> dp = new ArrayList<>();\n for (int i = 0; i <= rowIndex; i++) {\n dp.add(new ArrayList<>());\n for (int j = 0; j <= rowIndex; j++) {\n dp.get(i).add(-1);\n }\n }\n for (int i = 0; i <= rowIndex; i++) {\n ans.add(ncr(rowIndex, i, dp));\n }\n return ans;\n }\n}\n```\n\n**Python:**\n\n```python\nclass Solution:\n def ncr(self, n, r, dp):\n if r == 0 or r == n:\n return 1\n if r == 1 or r == n - 1:\n return n\n if dp[n][r] != -1:\n return dp[n][r]\n dp[n][r] = self.ncr(n - 1, r, dp) + self.ncr(n - 1, r - 1, dp)\n return dp[n][r]\n\n def getRow(self, rowIndex):\n ans = []\n dp = [[-1] * (rowIndex + 1) for _ in range(rowIndex + 1)]\n for i in range(rowIndex + 1):\n ans.append(self.ncr(rowIndex, i, dp))\n return ans\n```\n\n**JavaScript:**\n\n```javascript []\n var ncr= function(n, r, dp) {\n if (r === 0 || r === n) return 1;\n if (r === 1 || r === n - 1) return n;\n if (dp[n][r] !== -1) return dp[n][r];\n dp[n][r] = ncr(n - 1, r, dp) + ncr(n - 1, r - 1, dp);\n return dp[n][r];\n }\n\n var getRow = function(rowIndex) {\n const ans = [];\n const dp = new Array(rowIndex + 1).fill(-1).map(() => new Array(rowIndex + 1).fill(-1));\n for (let i = 0; i <= rowIndex; i++) {\n ans.push( ncr(rowIndex, i, dp));\n }\n return ans;\n }\n```\n\n**C#:**\n\n```csharp\npublic class Solution {\n public int Ncr(int n, int r, int[][] dp) {\n if (r == 0 || r == n) return 1;\n if (r == 1 || r == n - 1) return n;\n if (dp[n][r] != -1) return dp[n][r];\n dp[n][r] = Ncr(n - 1, r, dp) + Ncr(n - 1, r - 1, dp);\n return dp[n][r];\n }\n\n public int[] GetRow(int rowIndex) {\n int[] ans = new int[rowIndex + 1];\n int[][] dp = new int[rowIndex + 1][];\n for (int i = 0; i <= rowIndex; i++) {\n dp[i] = new int[rowIndex + 1];\n for (int j = 0; j <= rowIndex; j++) {\n dp[i][j] = -1;\n }\n }\n for (int i = 0; i <= rowIndex; i++) {\n ans[i] = Ncr(rowIndex, i, dp);\n }\n return ans;\n }\n}\n```\n\n**Ruby:**\n\n```ruby []\n\n def ncr(n, r, dp)\n return 1 if r == 0 || r == n\n return n if r == 1 || r == n - 1\n return dp[n][r] if dp[n][r] != -1\n\n dp[n][r] = ncr(n - 1, r, dp) + ncr(n - 1, r - 1, dp)\n dp[n][r]\n end\n\n def get_row(row_index)\n ans = []\n dp = Array.new(row_index + 1) { Array.new(row_index + 1, -1) }\n (0..row_index).each do |i|\n ans << ncr(row_index, i, dp)\n end\n ans\n end\n```\n\n---\n**Approach 2 : Efficiently Generating Pascal\'s Triangle**\n\n\n\n**Understanding Pascal\'s Triangle:**\n\nBefore delving into the details of Approach 2, let\'s briefly recap Pascal\'s Triangle. It starts with a 1 at the apex and then continues with rows of numbers. The first few rows look like this:\n\n```\n 1\n 1 1\n 1 2 1\n 1 3 3 1\n 1 4 6 4 1\n```\n\nEach number in the triangle is the sum of the two numbers directly above it. For example, in the fourth row, the middle number \'3\' is the sum of \'1\' and \'2\' from the row above it.\n\n## **Approach 2: Efficient Row Generation**\n\nIn Approach 2, we will use an efficient algorithm to generate the k-th row of Pascal\'s Triangle. The key idea behind this approach is to maintain a single array, `A`, of size `k+1`, where each element of the array represents a number in the k-th row.\n\nHere\'s a step-by-step breakdown of Approach 2:\n\n1. Initialize an array `A` of size `k+1` and set the first element, `A[0]`, to 1. This is because the first element of every row in Pascal\'s Triangle is always 1.\n\n2. Use a nested loop to iterate through the remaining elements of `A`. The outer loop runs from `i = 1` to `k`, representing each row, and the inner loop starts from the current value of `i` and goes down to `1`.\n\n3. In each iteration of the inner loop, update the `j`-th element of `A` by adding the values of `A[j]` and `A[j-1]`. This step follows the fundamental property of Pascal\'s Triangle, where each number is the sum of the two numbers directly above it.\n\n4. After completing the loops, the array `A` contains the k-th row of Pascal\'s Triangle.\n\nCertainly, let\'s analyze the time and space complexity of the given code.\n\n**Time Complexity:**\nThe time complexity of this code can be analyzed as follows:\n\n1. The code uses two nested loops. The outer loop runs from `i = 1` to `rowIndex`, and the inner loop runs from `j = i` to `1`. \n\n2. In each iteration of the inner loop, there is a constant-time operation, which is adding `A[j-1]` to `A[j]`.\n\n3. The number of iterations in the inner loop decreases with each iteration of the outer loop. In the first outer loop iteration, the inner loop runs `i` times. In the second iteration, it runs `i-1` times, and so on.\n\n4. Therefore, the total number of operations can be computed as the sum of the first `rowIndex` natural numbers, which is O(rowIndex^2).\n\n5. In summary, the time complexity of this code is O(rowIndex^2) due to the nested loops.\n\n**Space Complexity:**\nThe space complexity of this code is determined by the auxiliary space used for the `A` vector, which stores the result.\n\n1. The `A` vector is of size `rowIndex + 1`, so it requires O(rowIndex) space.\n\n2. The space required for variables like `i`, `j`, and other constants is negligible and does not contribute significantly to the space complexity.\n\n3. Therefore, the overall space complexity of the code is O(rowIndex).\n\n\n\n```cpp []\nvector<int> getRow(int rowIndex) {\n vector<int> A(rowIndex+1, 0);\n A[0] = 1;\n for(int i=1; i<rowIndex+1; i++)\n for(int j=i; j>=1; j--)\n A[j] += A[j-1];\n return A;\n}\n```\n\n\n```java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> A = new ArrayList<>(rowIndex + 1);\n A.add(1);\n for (int i = 1; i <= rowIndex; i++) {\n for (int j = i; j >= 1; j--) {\n if (j == A.size()) {\n A.add(A.get(j - 1));\n } else {\n A.set(j, A.get(j) + A.get(j - 1));\n }\n }\n }\n return A;\n }\n}\n```\n\n\n```python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n A = [0] * (rowIndex + 1)\n A[0] = 1\n for i in range(1, rowIndex + 1):\n for j in range(i, 0, -1):\n A[j] += A[j - 1]\n return A\n```\n\n```javascript []\nvar getRow = function(rowIndex) {\n let A = new Array(rowIndex + 1).fill(0);\n A[0] = 1;\n for (let i = 1; i <= rowIndex; i++) {\n for (let j = i; j >= 1; j--) {\n A[j] += A[j - 1];\n }\n }\n return A;\n};\n```\n\n\n```csharp []\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> A = new List<int>(rowIndex + 1);\n A.Add(1);\n for (int i = 1; i <= rowIndex; i++) {\n for (int j = i; j >= 1; j--) {\n if (j == A.Count) {\n A.Add(A[j - 1]);\n } else {\n A[j] += A[j - 1];\n }\n }\n }\n return A;\n }\n}\n```\n\n```ruby []\n# @param {Integer} row_index\n# @return {Integer[]}\ndef get_row(row_index)\n a = Array.new(row_index + 1, 0)\n a[0] = 1\n (1..row_index).each do |i|\n i.downto(1) do |j|\n a[j] += a[j - 1]\n end\n end\n a\nend\n```\n\nThese code snippets in different languages implement "Approach 2" to efficiently generate the k-th row of Pascal\'s Triangle, as described in the previous blog post.\n\nThe result will be `[1, 4, 6, 4, 1]`, which is indeed the 5th row of Pascal\'s Triangle.\n\n---\n# Analysis\n\n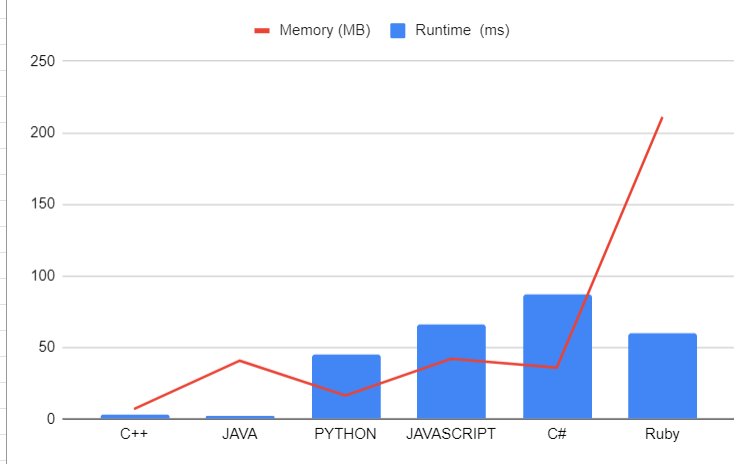\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|-------------|--------------|-------------|\n| C++ | 3 | 6.9 |\n| Java | 2 | 40.7 |\n| Python | 45 | 16.4 |\n| JavaScript | 66 | 42.1 |\n| C# | 87 | 35.9 |\n| Ruby | 60 | 211.1 |\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n\n\n\n | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Video Solution | Explanation With Drawings | In Depth | C++ | Java | Python 3 | pascals-triangle-ii | 1 | 1 | # Intuition and approach discussed in detail in video solution\nhttps://youtu.be/r-7NUInsUjA\n# Code\nC++\n```\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<vector<int>> tria (rowIndex + 1);\n int colNum = 1;\n for(int r = 0; r <= rowIndex; r++){\n \n vector<int> row(colNum, 1);\n \n tria[r] = row;\n \n for(int c = 1; c < colNum-1; c++){\n tria[r][c] = tria[r-1][c-1] + tria[r-1][c];\n }\n colNum++;\n } \n return tria[rowIndex];\n }\n};\n```\nJava\n```\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<List<Integer>> tria = new ArrayList<>(rowIndex + 1);\n int colNum = 1;\n for (int r = 0; r <= rowIndex; r++) {\n List<Integer> row = new ArrayList<>(colNum);\n for (int i = 0; i < colNum; i++) {\n row.add(1);\n }\n tria.add(row);\n for (int c = 1; c < colNum - 1; c++) {\n tria.get(r).set(c, tria.get(r - 1).get(c - 1) + tria.get(r - 1).get(c));\n }\n colNum++;\n }\n return tria.get(rowIndex);\n }\n}\n```\nPython 3\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n tria = [[] for _ in range(rowIndex + 1)]\n colNum = 1\n for r in range(rowIndex + 1):\n row = [1] * colNum\n tria[r] = row\n for c in range(1, colNum - 1):\n tria[r][c] = tria[r - 1][c - 1] + tria[r - 1][c]\n colNum += 1\n return tria[rowIndex]\n \n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Pascal’s Triangle Solution in python with explanation | pascals-triangle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n##### Points to remember after reading the problem:\n1. Every row depends on previous row.\n2. First two rows are [1] and [1,1]\n3. They asked only the particular row to return, so we will go through iteration for every row until given index.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Take list of [1], [1,1] in one list as "pas".\n2. first for loop to get every row until givrn rowIndex\n3. lets take current row as curr and append 1 to it because for every row 1st element is 1 after that adding above two elements will be the answer for current row.\n4. Take previous row as **last** from **pas**\n5. now again use for loop to add every two elements and append it to **curr**\n6. Finally append 1 to curr and after that append that whole curr row to pas before it going to another loop.(so that when we take last row from pas then for next iteration the last will be the updated row.)\n7. Now they ask only the particular row,so return pas[rowIndex] to get the result.\n\n\n# Complexity\n- Time complexity:O(rowIndex * (rowIndex -1)) --> O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n pas=[[1],[1,1]] # Pas means Pascal\'s Triangle\n if rowIndex>1:\n for i in range(rowIndex-1):\n curr=[1] #curr means current row\n last=pas[-1] # last means previous row \n for i in range(len(last)-1):\n curr.append(last[i]+last[i+1])\n curr.append(1)\n pas.append(curr)\n return pas[rowIndex]\n\n\n\n \n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Easy Python3 solution | pascals-triangle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe know that first and last value in any row is 1, then we can build\nthe tree till the rowIndex by iterating over previous res row and\nappend to new row created everytime as \'g\', the middle values of g[1:-1], are depend on current res row and [j-1] and [j] column.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n if rowIndex==0:\n return [1]\n elif rowIndex==1:\n return [1,1]\n \n res=[[1],[1,1]]\n \n \n for i in range(1,rowIndex):\n g=[0]*(len(res[i])+1)\n \n g[0],g[-1]=1,1\n for j in range(1,len(g)-1):\n g[j]=res[i][j-1]+res[i][j]\n res.append(g)\n \n return res[-1]\n \n \n \n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
This is the Best Approch To Find The Solution In the Best Time Complexity..... | pascals-triangle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n res = [1]\n prev = 1\n for k in range(1,rowIndex+1):\n next_val = prev * ( rowIndex - k + 1) // k\n res.append(next_val)\n prev = next_val\n return res\n\n \n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
4 line using math | pascals-triangle-ii | 0 | 1 | # Formula\n$$ans[0] = 1$$\n$$k = 1 \\,\\to\\, n$$\n$$ans[k]=ans[k-1]\xD7 \\frac{n\u2212k+1}k\\\n\n\u200B\t\n $$\n# Code\n```py\nclass Solution:\n def getRow(self, n: int) -> List[int]:\n ans = [1]\n for k in range(1, n + 1):\n ans.append(ans[k-1] * (n - k + 1) // k)\n return ans\n```\n\n\u200B\t\n | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Beginner-friendly || Simple solution with Dynamic Programming in Python3 / TypeScript | pascals-triangle-ii | 0 | 1 | # Intuition\nLet\'s briefly explain what the problem is:\n- there\'s a `rowIndex` of **Pascal\'s Triangle**\n- our goal is to extract a particular row by `rowIndex`\n\nTo be short, [Pascal\'s Triangle](https://en.wikipedia.org/wiki/Pascal%27s_triangle) is a matrix of rows, whose elements follow the next formula.\n\n```\nfor i >= 2 in row:\n each col >= 1 and col < row.count - 1:\n row[col] = prevRow[i - 1][j - 1] + prevRow[i - 1][j]\n\n# Example\nrowIndex = 3\n\n# The triangle will look like this\n# [\n# [1]\n# [1, 1]\n# [1, 2, 1]\n# [1, 3, 3, 1]\n# ] \n\n# The first two rows has only the elements, that\'re 1-s.\n# At row i >= 2, the formula is applied.\n```\n\n# Approach\n1. declare `triangle` with first **two rows**\n2. iterate over range `[i, rowIndex]`\n3. declare `row` to store `1-s` for a particular row\n4. fill the `row` with formula above\n5. return `triangle[rowIndex]`, that represent a particular answer row\n\n# Complexity\n- Time complexity: **O(N^2)**, there\'re **two nested loops**\n\n- Space complexity: **O(N^2)**, the same for storing a matrix `triangle`\n\n# Code in Python3\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n triangle = [[1], [1, 1]]\n\n for i in range(2, rowIndex + 1):\n row = [1] * (i + 1)\n\n for j in range(1, len(row) - 1):\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]\n\n triangle.append(row)\n\n return triangle[rowIndex]\n\n```\n# Code in TypeScript\n```\nfunction getRow(rowIndex: number): number[] {\n const triangle = [[1], [1, 1]];\n\n for (let i = 2; i < rowIndex + 1; i++) {\n const row = Array(i + 1).fill(1);\n\n for (let j = 1; j < row.length - 1; j++) {\n row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j];\n }\n\n triangle.push(row);\n }\n\n return triangle[rowIndex];\n}\n\n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Quick & Easy Python Solution | pascals-triangle-ii | 0 | 1 | \n# Python solution\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n results=[1]\n last=1\n for i in range(1,rowIndex+1):\n next_value=last * (rowIndex - i + 1) // i\n results.append(next_value)\n last=next_value\n return results\n```\n\n | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
✅ Beats 98.39% 🔥 within 4 Lines || Easiest Solution 2 Approaches || | pascals-triangle-ii | 1 | 1 | \n\n\n# Intuition\n1. We know that the pascal triangle is a triangle of binomial coefficients.\n2. We know that the binomial coefficients can be calculated using the formula nCr = n!/(r!*(n-r)!)\n3. We know that the binomial coefficients are symmetric, i.e. nCr = nC(n-r) \n4. We know that the binomial coefficients can be calculated using the previous row of the pascal triangle. \n5. We know that the first and last element of each row is 1.\n6. We know that the number of elements in each row is equal to the row number.\n7. We know that the row number starts from 0.\n8. We know that the first row is [1].\n9. Now, we can use the above information to calculate the pascal triangle.\n\n# Approach 1 : Dynamic Programming \n## (Least Optimized)\n###### This Approach if least optimized but for beginners who are facing difficulty with DP , in this solution dp is elaborated very well.\n1. Create a list of list called triangle and initialize it with [[1]].\n2. Iterate from 0 to rowIndex-1.\n3. Get the last row of the triangle and store it in last_row.\n4. Create a new list called new_row and initialize it with [1].\n5. Iterate from 1 to len(last_row)-1.\n6. Append the sum of last_row[j-1] and last_row[j] to new_row.\n7. Append 1 to new_row.\n8. Append new_row to triangle.\n9. Return the last row of the triangle.\n\n# Complexity\n- Time complexity : $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n if rowIndex==0:\n return [1]\n \n triangle=[[1]]\n\n for i in range(rowIndex):\n last_row=triangle[-1]\n new_row=[1]\n\n for j in range(1,len(last_row)):\n new_row.append(last_row[j-1]+last_row[j])\n \n new_row.append(1)\n triangle.append(new_row)\n \n return triangle[-1]\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n if (rowIndex == 0)\n return {1};\n \n vector<vector<int>> triangle{{1}};\n\n for (int i = 0; i < rowIndex; ++i) {\n vector<int>& last_row = triangle.back();\n vector<int> new_row{1};\n\n for (int j = 1; j < last_row.size(); ++j) {\n new_row.push_back(last_row[j-1] + last_row[j]);\n }\n\n new_row.push_back(1);\n triangle.push_back(new_row);\n }\n \n return triangle.back();\n }\n};\n\n```\n``` Java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n if (rowIndex == 0) {\n return Arrays.asList(1);\n }\n\n List<List<Integer>> triangle = new ArrayList<>();\n triangle.add(Arrays.asList(1));\n\n for (int i = 0; i < rowIndex; i++) {\n List<Integer> lastRow = triangle.get(triangle.size() - 1);\n List<Integer> newRow = new ArrayList<>();\n newRow.add(1);\n\n for (int j = 1; j < lastRow.size(); j++) {\n newRow.add(lastRow.get(j - 1) + lastRow.get(j));\n }\n\n newRow.add(1);\n triangle.add(newRow);\n }\n\n return triangle.get(triangle.size() - 1);\n }\n}\n\n```\n``` JavaScript []\n/**\n * @param {number} rowIndex\n * @return {number[]}\n */\nvar getRow = function(rowIndex) {\n if (rowIndex === 0) {\n return [1];\n }\n\n let triangle = [[1]];\n\n for (let i = 0; i < rowIndex; i++) {\n let lastRow = triangle[triangle.length - 1];\n let newRow = [1];\n\n for (let j = 1; j < lastRow.length; j++) {\n newRow.push(lastRow[j - 1] + lastRow[j]);\n }\n\n newRow.push(1);\n triangle.push(newRow);\n }\n\n return triangle[triangle.length - 1];\n};\n```\n``` TypeScript []\nfunction getRow(rowIndex: number): number[] {\nif (rowIndex === 0) {\n return [1];\n }\n\n let triangle: number[][] = [[1]];\n\n for (let i = 0; i < rowIndex; i++) {\n let lastRow: number[] = triangle[triangle.length - 1];\n let newRow: number[] = [1];\n\n for (let j = 1; j < lastRow.length; j++) {\n newRow.push(lastRow[j - 1] + lastRow[j]);\n }\n\n newRow.push(1);\n triangle.push(newRow);\n }\n\n return triangle[triangle.length - 1];\n };\n```\n``` C# []\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n if (rowIndex == 0) {\n return new int[] { 1 };\n }\n\n List<List<int>> triangle = new List<List<int>>();\n triangle.Add(new List<int> { 1 });\n\n for (int i = 0; i < rowIndex; i++) {\n List<int> lastRow = triangle[triangle.Count - 1];\n List<int> newRow = new List<int>();\n newRow.Add(1);\n\n for (int j = 1; j < lastRow.Count; j++) {\n newRow.Add(lastRow[j - 1] + lastRow[j]);\n }\n\n newRow.Add(1);\n triangle.Add(newRow);\n }\n\n return triangle[triangle.Count - 1].ToArray();\n }\n }\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $rowIndex\n * @return Integer[]\n */\n function getRow($rowIndex) {\n if ($rowIndex === 0) {\n return [1];\n }\n\n $triangle = [[1]];\n\n for ($i = 0; $i < $rowIndex; $i++) {\n $lastRow = $triangle[count($triangle) - 1];\n $newRow = [1];\n\n for ($j = 1; $j < count($lastRow); $j++) {\n array_push($newRow, $lastRow[$j - 1] + $lastRow[$j]);\n }\n\n array_push($newRow, 1);\n array_push($triangle, $newRow);\n }\n\n return $triangle[count($triangle) - 1];\n }\n }\n```\n``` Kotlin []\nclass Solution {\n fun getRow(rowIndex: Int): List<Int> {\n if (rowIndex == 0) {\n return listOf(1)\n }\n\n val triangle = mutableListOf(listOf(1))\n\n for (i in 0 until rowIndex) {\n val lastRow = triangle.last()\n val newRow = mutableListOf(1)\n\n for (j in 1 until lastRow.size) {\n newRow.add(lastRow[j - 1] + lastRow[j])\n }\n\n newRow.add(1)\n triangle.add(newRow)\n }\n\n return triangle.last()\n }\n }\n```\n# Intuition :\n\n###### Here, we will use the formula nCr = n!/(r!*(n-r)!) to calculate the binomial coefficients.\n\n# Approach 2 : Using Combinatorics\n### This Approach is well Optimized.\n\n### Algorithm :\n1. Create a list called row and initialize it with 1.\n2. Iterate from 1 to rowIndex.\n3. Update the value of row[i] to row[i-1]*(rowIndex-i+1)/i.\n4. Return row.\n\n# Complexity\n- Time Complexity : $$O(n)$$ \n- Space Complexity : $$O(n)$$ \n\n# Code\n``` Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n row=[1]\n for i in range(1,rowIndex+1):\n row.append(int(row[i-1]*(rowIndex-i+1)/i))\n return row\n```\n``` C+ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> row = {1};\n for (int i = 1; i <= rowIndex; ++i) {\n row.push_back(static_cast<int>(row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n }\n};\n```\n``` Java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> row = new ArrayList<>();\n row.add(1);\n for (int i = 1; i <= rowIndex; ++i) {\n row.add((int)((long)row.get(i - 1) * (rowIndex - i + 1) / i));\n }\n return row;\n }\n}\n```\n``` JavaScript []\nvar getRow = function(rowIndex) {\n const row = [1];\n for (let i = 1; i <= rowIndex; ++i) {\n row.push(Math.floor(row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n};\n```\n``` TypeScript []\nfunction getRow(rowIndex: number): number[] {\nconst row: number[] = [1];\n for (let i = 1; i <= rowIndex; ++i) {\n row.push(Math.floor(row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n };\n```\n``` C# []\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> row = new List<int> { 1 };\n for (int i = 1; i <= rowIndex; ++i) {\n row.Add((int)((long)row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n }\n}\n```\n``` PHP []\nclass Solution {\n function getRow($rowIndex) {\n $row = [1];\n for ($i = 1; $i <= $rowIndex; ++$i) {\n $row[] = intval($row[$i - 1] * ($rowIndex - $i + 1) / $i);\n }\n return $row;\n }\n}\n```\n``` Kotlin []\nclass Solution {\n fun getRow(rowIndex: Int): List<Int> {\n val row = mutableListOf(1)\n for (i in 1..rowIndex) {\n row.add((row[i - 1].toLong() * (rowIndex - i + 1) / i).toInt())\n }\n return row\n }\n}\n```\n\n\n | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
🚀 100 % || DP & Combinatorics then Optimized Space || Commented Code 🚀 | pascals-triangle-ii | 1 | 1 | # Problem Description\nGiven an integer rowIndex, return the `rowIndexth` (0-indexed) row of the **Pascal\'s triangle**.\n\nIn **Pascal\'s triangle**, each number is the sum of the two numbers directly above it as shown:\n\n\n\n- **Constraints:**\n - `0 <= rowIndex <= 33`\n\n\n---\n\n\n# Proposed Solutions\n## 1. Dynamic Programming\n\n### Approach\n1. **Initialize 2D Vector**: Create a 2D vector pascalTriangle with numRows rows to represent Pascal\'s Triangle.\n2. **Generate Rows**: Generate first row seperately then Loop through each row from 1 to numRows (inclusive).\n3. **Set First and Last Elements**: Set the first and last elements of each row to 1.\n4. **Calculate Middle Elements**: For each row, calculate and append the middle elements by adding the corresponding elements from the previous row.\n5. **Return** Last computed row.\n\n### Complexity\n- **Time complexity:**\nWe have two for-loops each of max size of `n`, then time complexity is `O(N^2)`.\n- **Space complexity:**\n`O(N^2)`, Since we are storing the triangle.\n\n\n---\n\n## 2. Dynamic Programming Optimized Space\n\n### Approach\n1. **Initialize 2D Vector**: Create a 2D vector pascalTriangle with only two rows to represent last two rows of our Pascal\'s Triangle.\n2. **Generate Rows**: Generate first row seperately then Loop through each row from 1 to numRows (inclusive).\n3. **Set First and Last Elements**: Set the first and last elements of each row to 1.\n4. **Calculate Middle Elements**: For each row, calculate and append the middle elements by adding the corresponding elements from the previous row.\n5. **Change Rows**: After each iteration, switch the last computed row with the first row then deleted its vector.\n6. **Return** Last computed row.\n\n### Complexity\n- **Time complexity:**\nWe have two for-loops each of max size of `n`, then time complexity is `O(N^2)`.\n- **Space complexity:**\n`O(N)`, Since we are storing only two rows each iteration.\n\n\n\n---\n\n\n\n## 3. Combinatorics \n\n**Note: For this solution, it can be done in one for loop but I wanted to write the whole function of calculateCombination to show you how to calculate combinatorics generally.**\n\n### Approach\n1. **Initialize Vector**: Create a vector lastRow with that represents the last row.\n2. **Generate Row**: Loop through each element in the last row.\n3. **Calculate Middle Elements**: For each element, calculate and append them by using combinatorics like the picture below :\n\n\n4. **Return** Last computed row.\n\n\n### Complexity\n- **Time complexity:**\nWe have one for-loops of max size of `n` and we have the for loop that generates the combinatorics, then time complexity is `O(N^2)`.\n- **Space complexity:**\n`O(N)`, Since we are storing only the last row.\n\n\n\n\n\n---\n\n\n# Code\n## 1. Dynamic Programming\n```C++ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n // Initialize a 2D vector to represent Pascal\'s Triangle\n vector<vector<int>> pascalTriangle(rowIndex + 1);\n\n // Initialize the first row with a single element \'1\'\n pascalTriangle[0].push_back(1);\n\n // Generate the rest of the rows\n for (int currentRow = 1; currentRow <= rowIndex; currentRow++) {\n // The first element of each row is always \'1\'\n pascalTriangle[currentRow].push_back(1);\n\n // Get a reference to the current row and the previous row\n vector<int>& currentRowList = pascalTriangle[currentRow];\n vector<int>& previousRowList = pascalTriangle[currentRow - 1];\n\n // Calculate and populate the middle elements of the row\n for (int j = 1; j < previousRowList.size(); j++) {\n int sum = previousRowList[j] + previousRowList[j - 1];\n currentRowList.push_back(sum);\n }\n\n // The last element of each row is also \'1\'\n currentRowList.push_back(1);\n }\n\n return pascalTriangle[rowIndex];\n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n // Initialize a 2D list to represent Pascal\'s Triangle\n List<List<Integer>> pascalTriangle = new ArrayList<>();\n \n // Generate the rows\n for (int i = 0; i <= rowIndex; i++) {\n List<Integer> currentRow = new ArrayList<>();\n \n // The first element of each row is always \'1\'\n currentRow.add(1);\n \n if (i > 0) {\n // Get a reference to the previous row\n List<Integer> previousRow = pascalTriangle.get(i - 1);\n \n // Calculate and populate the middle elements of the row\n for (int j = 1; j < previousRow.size(); j++) {\n int sum = previousRow.get(j) + previousRow.get(j - 1);\n currentRow.add(sum);\n }\n \n // The last element of each row is also \'1\'\n currentRow.add(1);\n }\n \n pascalTriangle.add(currentRow);\n }\n \n return pascalTriangle.get(rowIndex);\n }\n}\n```\n```Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n # Initialize a list of lists to represent Pascal\'s Triangle\n pascal_triangle = [[] for _ in range(rowIndex + 1)]\n \n # Initialize the first row with a single element \'1\'\n pascal_triangle[0].append(1)\n \n # Generate the rest of the rows\n for current_row in range(1, rowIndex + 1):\n # The first element of each row is always \'1\'\n pascal_triangle[current_row].append(1)\n \n # Calculate and populate the middle elements of the row\n for j in range(1, len(pascal_triangle[current_row - 1])):\n sum_val = pascal_triangle[current_row - 1][j] + pascal_triangle[current_row - 1][j - 1]\n pascal_triangle[current_row].append(sum_val)\n \n # The last element of each row is also \'1\'\n pascal_triangle[current_row].append(1)\n \n return pascal_triangle[rowIndex]\n\n```\n``` C []\nint* getRow(int rowIndex, int* returnSize) {\n // Initialize a 2D array to represent Pascal\'s Triangle\n int** pascalTriangle = (int**)malloc((rowIndex + 1) * sizeof(int*));\n \n for (int i = 0; i <= rowIndex; i++) {\n pascalTriangle[i] = (int*)malloc((i + 1) * sizeof(int));\n }\n \n // Generate the rows\n for (int currentRow = 0; currentRow <= rowIndex; currentRow++) {\n pascalTriangle[currentRow][0] = 1; // The first element of each row is always \'1\'\n \n if (currentRow > 0) {\n int* previousRow = pascalTriangle[currentRow - 1];\n \n // Calculate and populate the middle elements of the row\n for (int j = 1; j < currentRow; j++) {\n pascalTriangle[currentRow][j] = previousRow[j] + previousRow[j - 1];\n }\n \n pascalTriangle[currentRow][currentRow] = 1; // The last element of each row is also \'1\'\n }\n }\n \n // Set the return size\n *returnSize = rowIndex + 1;\n \n // Copy the row to a 1D array\n int* resultRow = (int*)malloc((rowIndex + 1) * sizeof(int));\n for (int i = 0; i <= rowIndex; i++) {\n resultRow[i] = pascalTriangle[rowIndex][i];\n }\n \n return resultRow;\n}\n```\n\n---\n\n\n## 2. Dynamic Programming Optimized Space\n\n```C++ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n // Initialize a 2D vector to represent Pascal\'s Triangle\n vector<vector<int>> pascalTriangle(2);\n\n // Initialize the first row with a single element \'1\'\n pascalTriangle[0].push_back(1);\n\n // Generate the rest of the rows\n for (int currentRow = 1; currentRow <= rowIndex; currentRow++) {\n // The first element of each row is always \'1\'\n pascalTriangle[1].push_back(1);\n\n // Get a reference to the current row and the previous row\n vector<int>& currentRowList = pascalTriangle[1];\n vector<int>& previousRowList = pascalTriangle[0];\n\n // Calculate and populate the middle elements of the row\n for (int j = 1; j < previousRowList.size(); j++) {\n int sum = previousRowList[j] + previousRowList[j - 1];\n currentRowList.push_back(sum);\n }\n\n // The last element of each row is also \'1\'\n currentRowList.push_back(1);\n\n // Switch rows\n pascalTriangle[0] = pascalTriangle[1] ;\n pascalTriangle[1].clear() ;\n }\n\n return pascalTriangle[0];\n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<List<Integer>> pascalTriangle = new ArrayList<>();\n pascalTriangle.add(new ArrayList<>());\n pascalTriangle.add(new ArrayList<>());\n\n // Initialize the first row with a single element \'1\'\n pascalTriangle.get(0).add(1);\n\n // Generate the rest of the rows\n for (int currentRow = 1; currentRow <= rowIndex; currentRow++) {\n // The first element of each row is always \'1\'\n pascalTriangle.get(1).add(1);\n\n List<Integer> currentRowList = pascalTriangle.get(1);\n List<Integer> previousRowList = pascalTriangle.get(0);\n\n // Calculate and populate the middle elements of the row\n for (int j = 1; j < previousRowList.size(); j++) {\n int sum = previousRowList.get(j) + previousRowList.get(j - 1);\n currentRowList.add(sum);\n }\n\n // The last element of each row is also \'1\'\n currentRowList.add(1);\n\n // Switch rows\n pascalTriangle.set(0, new ArrayList<>(pascalTriangle.get(1)));\n pascalTriangle.get(1).clear();\n }\n\n return pascalTriangle.get(0);\n }\n}\n```\n```Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n pascal_triangle = [[1], []]\n\n for currentRow in range(1, rowIndex + 1):\n # The first element of each row is always \'1\'\n pascal_triangle[1].append(1)\n\n currentRowList = pascal_triangle[1]\n previousRowList = pascal_triangle[0]\n\n # Calculate and populate the middle elements of the row\n for j in range(1, len(previousRowList)):\n sum_val = previousRowList[j] + previousRowList[j - 1]\n currentRowList.append(sum_val)\n\n # The last element of each row is also \'1\'\n currentRowList.append(1)\n\n # Switch rows\n pascal_triangle[0] = pascal_triangle[1][:]\n pascal_triangle[1] = []\n\n return pascal_triangle[0]\n```\n``` C []\nint* getRow(int rowIndex, int* returnSize) {\n // Initialize a 2D array to represent Pascal\'s Triangle\n int** pascalTriangle = (int**)malloc(2 * sizeof(int*));\n for (int i = 0; i < 2; i++) {\n pascalTriangle[i] = (int*)malloc((rowIndex + 1) * sizeof(int));\n }\n\n // Initialize the first row with a single element \'1\'\n pascalTriangle[0][0] = 1;\n int currentRow = 1;\n\n // Generate the rest of the rows\n for (int i = 1; i <= rowIndex; i++) {\n // The first element of each row is always \'1\'\n pascalTriangle[currentRow][0] = 1;\n\n // Calculate and populate the middle elements of the row\n for (int j = 1; j < i; j++) {\n pascalTriangle[currentRow][j] = pascalTriangle[1 - currentRow][j] + pascalTriangle[1 - currentRow][j - 1];\n }\n\n // The last element of each row is also \'1\'\n pascalTriangle[currentRow][i] = 1;\n\n // Switch rows\n currentRow = 1 - currentRow;\n }\n\n *returnSize = rowIndex + 1;\n\n // Copy the row to a 1D array\n int* resultRow = (int*)malloc((rowIndex + 1) * sizeof(int));\n for (int i = 0; i <= rowIndex; i++) {\n resultRow[i] = pascalTriangle[1 - currentRow][i];\n }\n\n return resultRow;\n}\n```\n\n---\n\n\n## 3. Combinatorics\n```C++ []\nclass Solution {\npublic:\n // Calculate n choose r (nCr) using a loop\n int calculateCombination(int n, int r) {\n long long result = 1;\n for (int i = 0; i < r; i++) {\n result = result * (n - i) / (i + 1);\n }\n return result;\n }\n\n vector<int> getRow(int rowIndex) {\n // Initialize a vector to represent The last Row\n vector<int> lastRow;\n\n for (int j = 0; j <= rowIndex; j++) {\n // Calculate and insert the binomial coefficient (nCr) into the row\n lastRow.push_back(calculateCombination(rowIndex, j));\n }\n \n return lastRow;\n }\n};\n```\n```Java []\nclass Solution {\n // Calculate n choose r (nCr) using a loop\n private long calculateCombination(int n, int r) {\n long result = 1;\n for (int i = 0; i < r; i++) {\n result = result * (n - i) / (i + 1);\n }\n return result;\n }\n\n public List<Integer> getRow(int rowIndex) {\n // Initialize a list to represent the last row\n List<Integer> lastRow = new ArrayList<>();\n\n for (int j = 0; j <= rowIndex; j++) {\n // Calculate and insert the binomial coefficient (nCr) into the row\n lastRow.add((int) calculateCombination(rowIndex, j));\n }\n\n return lastRow;\n }\n}\n```\n```Python []\nclass Solution:\n def calculateCombination(self, n: int, r: int) -> int:\n result = 1\n for i in range(r):\n result = result * (n - i) // (i + 1)\n return result\n\n def getRow(self, rowIndex: int) -> list[int]:\n last_row = []\n\n for j in range(rowIndex + 1):\n # Calculate and append the binomial coefficient (nCr) into the row\n last_row.append(self.calculateCombination(rowIndex, j))\n\n return last_row\n```\n```C []\nlong long calculateCombination(int n, int r) {\n long long result = 1;\n for (int i = 0; i < r; i++) {\n result = result * (n - i) / (i + 1);\n }\n return result;\n}\n\nint* getRow(int rowIndex, int* returnSize) {\n // Initialize an array to represent the last row\n int* lastRow = (int*)malloc((rowIndex + 1) * sizeof(int));\n\n for (int j = 0; j <= rowIndex; j++) {\n // Calculate and insert the binomial coefficient (nCr) into the row\n lastRow[j] = (int)calculateCombination(rowIndex, j);\n }\n\n *returnSize = rowIndex + 1;\n\n return lastRow;\n}\n```\n\n\n\n\n\n | 39 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Beats 100% | Optimised Solution Using Combinations | pascals-triangle-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this solution, we use the concept of combinations (n choose k) to calculate each element of the Pascal\'s Triangle\'s row. We start with a value of 1 and update it in each step by multiplying by the relevant factor to get the next value in the row. By leveraging the mathematical properties of combinations, we can efficiently compute the row.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty vector `result` to store the row.\n\n2. Initialize a variable `val` to 1, which represents the current value.\nIterate from 0 to `rowIndex`:\n\n- Set the current value in the `result` vector at index `i` to `val`.\n- Update `val` by multiplying it with `(rowIndex - i) / (i + 1)`. This step calculates the next value based on combinations.\n\n3. After the loop, `result` contains the row of Pascal\'s Triangle at the given `rowIndex`.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is `O(rowIndex)` because we iterate through rowIndex elements, performing constant time operations for each element.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(rowIndex) because we store the row in the `result` vector, which has `rowIndex + 1` elements. The `val` variable is of constant space.\n# Code\n```\n/* class Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> prevRow(rowIndex + 1, 1);\n vector<int> currentRow(rowIndex + 1, 1);\n \n for (int i = 1; i <= rowIndex; i++) {\n for (int j = 1; j < i; j++) {\n currentRow[j] = prevRow[j - 1] + prevRow[j];\n }\n swap(prevRow, currentRow);\n }\n \n return prevRow;\n }\n};\n//using two array and swapping */\n\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> result(rowIndex + 1);\n long long val = 1;\n \n for (int i = 0; i <= rowIndex; i++) {\n result[i] = val;\n val = val * (rowIndex - i) / (i + 1);\n }\n \n return result;\n }\n};\n\n```\n\n# \uD83D\uDCA1If you come this far, then i would like to request you to please upvote this solution so that it could reach out to another one \u2763\uFE0F\uD83D\uDCA1 | 6 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
🔥5 - Approaches 🚀| Java | C++ | Python | JavaScript | C# | | pascals-triangle-ii | 1 | 1 | Here\'s the problem statement:\n\nGiven an integer `k`, return the `k`-th row of the Pascal\'s triangle.\n\nNow, let\'s discuss the approaches to solve this problem from naive to efficient:\n\n## 1. Naive Approach: 79% Beats\uD83D\uDE80\n - Generate Pascal\'s triangle up to the `k`-th row and return the `k`-th row.\n - This approach involves generating all the rows up to the `k`-th row and then returning the desired row.\n### \uD83D\uDEA9Time complexity: O(k^2) as you need to generate all previous rows.\n### \uD83D\uDEA9Space complexity: O(k^2) to store all rows.\n\n``` Java []\n// 79% Beats\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<List<Integer>> triangle = new ArrayList<>();\n\n for (int i = 0; i <= rowIndex; i++) {\n List<Integer> row = new ArrayList<>();\n for (int j = 0; j <= i; j++) {\n if (j == 0 || j == i) {\n row.add(1); // The first and last elements in each row are 1.\n } else {\n int prevRow = i - 1;\n int leftVal = triangle.get(prevRow).get(j - 1);\n int rightVal = triangle.get(prevRow).get(j);\n row.add(leftVal + rightVal); // Sum of the two numbers above.\n }\n }\n triangle.add(row);\n }\n\n return triangle.get(rowIndex);\n }\n}\n```\n``` C++ []\n// 60% Beast\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n std::vector<std::vector<int>> triangle;\n\n for (int i = 0; i <= rowIndex; i++) {\n std::vector<int> row(i + 1);\n for (int j = 0; j <= i; j++) {\n if (j == 0 || j == i) {\n row[j] = 1; // The first and last elements in each row are 1.\n } else {\n int prevRow = i - 1;\n int leftVal = triangle[prevRow][j - 1];\n int rightVal = triangle[prevRow][j];\n row[j] = leftVal + rightVal; // Sum of the two numbers above.\n }\n }\n triangle.push_back(row);\n }\n\n return triangle[rowIndex];\n }\n};\n```\n``` Python []\n# 88% Beats\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n triangle = []\n\n for i in range(rowIndex + 1):\n row = []\n for j in range(i + 1):\n if j == 0 or j == i:\n row.append(1) # The first and last elements in each row are 1.\n else:\n prevRow = i - 1\n leftVal = triangle[prevRow][j - 1]\n rightVal = triangle[prevRow][j]\n row.append(leftVal + rightVal) # Sum of the two numbers above.\n\n triangle.append(row)\n\n return triangle[rowIndex]\n\n```\n``` JavaScript []\n// 87% Beast\nvar getRow = function(rowIndex) {\n let triangle = [];\n\n for (let i = 0; i <= rowIndex; i++) {\n let row = [];\n for (let j = 0; j <= i; j++) {\n if (j === 0 || j === i) {\n row.push(1); // The first and last elements in each row are 1.\n } else {\n let prevRow = i - 1;\n let leftVal = triangle[prevRow][j - 1];\n let rightVal = triangle[prevRow][j];\n row.push(leftVal + rightVal); // Sum of the two numbers above.\n }\n }\n triangle.push(row);\n }\n\n return triangle[rowIndex];\n};\n```\n``` C# []\n// 50% Beats\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<List<int>> triangle = new List<List<int>>();\n\n for (int i = 0; i <= rowIndex; i++)\n {\n List<int> row = new List<int>();\n for (int j = 0; j <= i; j++)\n {\n if (j == 0 || j == i)\n {\n row.Add(1); // The first and last elements in each row are 1.\n }\n else\n {\n int prevRow = i - 1;\n int leftVal = triangle[prevRow][j - 1];\n int rightVal = triangle[prevRow][j];\n row.Add(leftVal + rightVal); // Sum of the two numbers above.\n }\n }\n triangle.Add(row);\n }\n\n return triangle[rowIndex]; \n }\n}\n```\n\n\n---\n## 2. Combinatorial Approach: 100% Beats\uD83D\uDE80\n - Utilize the combinatorial properties of Pascal\'s triangle.\n - Use the binomial coefficient formula to directly compute the `k`-th row.\n#### \uD83D\uDEA9Time complexity: O(k).\n#### \uD83D\uDEA9Space complexity: O(k) for storing the result.\n``` Java []\n// 100% Beats\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> result = new ArrayList<>();\n\n // Initialize the first element of the row to 1.\n result.add(1);\n\n // Calculate each element in the row using the binomial coefficient formula.\n for (int i = 1; i <= rowIndex; i++) {\n long prevElement = (long) result.get(i - 1);\n // Use the formula C(rowIndex, i) = C(rowIndex, i-1) * (rowIndex - i + 1) / i\n long currentElement = prevElement * (rowIndex - i + 1) / i;\n result.add((int) currentElement);\n }\n\n return result;\n }\n}\n```\n``` C++ []\n// 100% Beats\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n std::vector<int> result;\n\n // Initialize the first element of the row to 1.\n result.push_back(1);\n\n // Calculate each element in the row using the binomial coefficient formula.\n for (int i = 1; i <= rowIndex; i++) {\n long prevElement = result[i - 1];\n // Use the formula C(r, i) = C(r, i-1) * (r - i + 1) / i\n long currentElement = prevElement * (rowIndex - i + 1) / i;\n result.push_back(static_cast<int>(currentElement));\n }\n\n return result;\n }\n};\n```\n``` Python []\n# 25% Beats\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n result = [1]\n\n for i in range(1, rowIndex + 1):\n prevElement = result[i - 1]\n # Use the formula C(r, i) = C(r, i-1) * (r - i + 1) / i\n currentElement = prevElement * (rowIndex - i + 1) // i\n result.append(currentElement)\n\n return result\n\n```\n``` JavaScript []\n// 93% Beats\nvar getRow = function(rowIndex) {\n let result = [1];\n\n for (let i = 1; i <= rowIndex; i++) {\n let prevElement = result[i - 1];\n // Use the formula C(r, i) = C(r, i-1) * (r - i + 1) / i\n let currentElement = (prevElement * (rowIndex - i + 1)) / i;\n result.push(currentElement);\n }\n\n return result;\n};\n```\n``` C# []\n// 30% Beats\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> result = new List<int>();\n\n // Initialize the first element of the row to 1.\n result.Add(1);\n\n // Calculate each element in the row using the binomial coefficient formula.\n for (int i = 1; i <= rowIndex; i++)\n {\n long prevElement = result[i - 1];\n // Use the formula C(r, i) = C(r, i-1) * (r - i + 1) / i\n long currentElement = prevElement * (rowIndex - i + 1) / i;\n result.Add((int)currentElement);\n }\n\n return result;\n }\n}\n```\n\n\n---\n## 3. Dynamic Programming Approach: 79% Beats\uD83D\uDE80\n - Calculate the `k`-th row using a dynamic programming approach.\n - Initialize an array to store the current row and use the values from the previous row to compute the current row.\n#### \uD83D\uDEA9Time complexity: O(k^2) (less efficient than the combinatorial approach).\n#### \uD83D\uDEA9Space complexity: O(k) for storing the current row.\n``` Java []\n// 79% Beats\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> currentRow = new ArrayList<Integer>();\n\n // Base case: The first row is always [1].\n currentRow.add(1);\n\n for (int i = 1; i <= rowIndex; i++) {\n List<Integer> newRow = new ArrayList<Integer>();\n \n // The first element of each row is always 1.\n newRow.add(1);\n\n // Calculate the middle elements using the values from the previous row.\n for (int j = 1; j < i; j++) {\n int sum = currentRow.get(j - 1) + currentRow.get(j);\n newRow.add(sum);\n }\n\n // The last element of each row is always 1.\n newRow.add(1);\n\n // Update the current row with the newly calculated row.\n currentRow = newRow;\n }\n \n return currentRow;\n }\n}\n```\n``` C++ []\n// 100% Beats\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n std::vector<int> currentRow;\n\n // Base case: The first row is always [1].\n currentRow.push_back(1);\n\n for (int i = 1; i <= rowIndex; i++) {\n std::vector<int> newRow;\n \n // The first element of each row is always 1.\n newRow.push_back(1);\n\n // Calculate the middle elements using the values from the previous row.\n for (int j = 1; j < i; j++) {\n int sum = currentRow[j - 1] + currentRow[j];\n newRow.push_back(sum);\n }\n\n // The last element of each row is always 1.\n newRow.push_back(1);\n\n // Update the current row with the newly calculated row.\n currentRow = newRow;\n }\n \n return currentRow;\n }\n};\n```\n``` Python []\n# 50% Beats\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n currentRow = []\n\n # Base case: The first row is always [1].\n currentRow.append(1)\n\n for i in range(1, rowIndex + 1):\n newRow = []\n \n # The first element of each row is always 1.\n newRow.append(1)\n\n # Calculate the middle elements using the values from the previous row.\n for j in range(1, i):\n sum_val = currentRow[j - 1] + currentRow[j]\n newRow.append(sum_val)\n\n # The last element of each row is always 1.\n newRow.append(1)\n\n # Update the current row with the newly calculated row.\n currentRow = newRow\n \n return currentRow\n\n```\n``` JavaScript []\n// 73% Beats\nvar getRow = function(rowIndex) {\n let currentRow = [];\n\n // Base case: The first row is always [1].\n currentRow.push(1);\n\n for (let i = 1; i <= rowIndex; i++) {\n let newRow = [];\n \n // The first element of each row is always 1.\n newRow.push(1);\n\n // Calculate the middle elements using the values from the previous row.\n for (let j = 1; j < i; j++) {\n let sum = currentRow[j - 1] + currentRow[j];\n newRow.push(sum);\n }\n\n // The last element of each row is always 1.\n newRow.push(1);\n\n // Update the current row with the newly calculated row.\n currentRow = newRow;\n }\n \n return currentRow;\n};\n```\n``` C# []\n// 55% Beats\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> currentRow = new List<int>();\n\n // Base case: The first row is always [1].\n currentRow.Add(1);\n\n for (int i = 1; i <= rowIndex; i++){\n List<int> newRow = new List<int>();\n \n // The first element of each row is always 1.\n newRow.Add(1);\n\n // Calculate the middle elements using the values from the previous row.\n for (int j = 1; j < i; j++)\n {\n int sum = currentRow[j - 1] + currentRow[j];\n newRow.Add(sum);\n }\n\n // The last element of each row is always 1.\n newRow.Add(1);\n\n // Update the current row with the newly calculated row.\n currentRow = newRow;\n }\n \n return currentRow;\n }\n}\n```\n\n\n---\n## 4. Efficient Space Dynamic Programming Approach: 80% Beats\uD83D\uDE80\n - You can optimize the dynamic programming approach by using two arrays to represent the current and previous rows.\n - This reduces the space complexity\n#### \uD83D\uDEA9while maintaining the time complexity of O(k^2).\n#### \uD83D\uDEA9space complexity to O(k) \n``` Java []\n// 80% Beats\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> currentRow = new ArrayList<>();\n List<Integer> previousRow = new ArrayList<>();\n\n for (int i = 0; i <= rowIndex; i++) {\n currentRow = new ArrayList<>();\n for (int j = 0; j <= i; j++) {\n if (j == 0 || j == i) {\n currentRow.add(1); // The first and last elements are always 1.\n } else {\n int sum = previousRow.get(j - 1) + previousRow.get(j);\n currentRow.add(sum);\n }\n }\n\n previousRow = new ArrayList<>(currentRow);\n }\n\n return currentRow;\n }\n}\n```\n``` C++ []\n// 100% Beats\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n std::vector<int> currentRow, previousRow;\n\n for (int i = 0; i <= rowIndex; i++) {\n currentRow.clear();\n for (int j = 0; j <= i; j++) {\n if (j == 0 || j == i) {\n currentRow.push_back(1); // The first and last elements are always 1.\n } else {\n int sum = previousRow[j - 1] + previousRow[j];\n currentRow.push_back(sum);\n }\n }\n\n previousRow = currentRow;\n }\n\n return currentRow;\n }\n};\n```\n``` Python []\n# 50% Beats\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n currentRow, previousRow = [], []\n\n for i in range(rowIndex + 1):\n currentRow.clear()\n for j in range(i + 1):\n if j == 0 or j == i:\n currentRow.append(1) # The first and last elements are always 1.\n else:\n currentRow.append(previousRow[j - 1] + previousRow[j])\n\n previousRow = currentRow[:]\n\n return currentRow\n```\n``` JavaScript []\n// 95% Beats\nvar getRow = function(rowIndex) {\n let currentRow = [];\n let previousRow = [];\n\n for (let i = 0; i <= rowIndex; i++) {\n currentRow = [];\n for (let j = 0; j <= i; j++) {\n if (j === 0 || j === i) {\n currentRow.push(1); // The first and last elements are always 1.\n } else {\n currentRow.push(previousRow[j - 1] + previousRow[j]);\n }\n }\n\n previousRow = currentRow.slice();\n }\n\n return currentRow;\n};\n```\n``` C# []\n// 80% Beats\npublic class Solution {\n public List<int> GetRow(int rowIndex) {\n List<int> currentRow = new List<int>();\n List<int> previousRow = new List<int>();\n\n for (int i = 0; i <= rowIndex; i++) {\n currentRow.Clear();\n for (int j = 0; j <= i; j++) {\n if (j == 0 || j == i) {\n currentRow.Add(1); // The first and last elements are always 1.\n } else {\n int sum = previousRow[j - 1] + previousRow[j];\n currentRow.Add(sum);\n }\n }\n\n previousRow = new List<int>(currentRow);\n }\n\n return currentRow;\n }\n}\n```\n\n\n---\n## 5. Mathematical Optimization: 100% Beats\uD83D\uDE80\n - Utilize the properties of binomial coefficients to calculate each element in the `k`-th row directly.\n - This approach is mathematically optimized for efficiency.\n#### \uD83D\uDEA9Time complexity: O(k).\n#### \uD83D\uDEA9Space complexity: O(k) for storing the result.\n``` Java []\n// 100% Beats\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> result = new ArrayList<>();\n\n // Initialize the first element of the row to 1.\n result.add(1);\n\n // Calculate the `k`-th row using binomial coefficient formula.\n for (int i = 1; i <= rowIndex; i++) {\n // Use the previous element to calculate the current element.\n long currentElement = (long) result.get(i - 1) * (rowIndex - i + 1) / i;\n result.add((int) currentElement);\n }\n\n return result;\n }\n}\n```\n``` C++ []\n// 100% Beats\nclass Solution {\npublic:\n std::vector<int> getRow(int rowIndex) {\n std::vector<int> result;\n \n // Initialize the first element of the row to 1.\n result.push_back(1);\n \n // Calculate the `k`-th row using binomial coefficient formula.\n for (int i = 1; i <= rowIndex; i++) {\n // Use the previous element to calculate the current element.\n long long currentElement = static_cast<long long>(result[i - 1]) * (rowIndex - i + 1) / i;\n result.push_back(static_cast<int>(currentElement));\n }\n \n return result;\n }\n};\n```\n``` Python []\n# 55% Beats\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n result = [1]\n\n for i in range(1, rowIndex + 1):\n # Use the previous element to calculate the current element.\n current_element = result[i - 1] * (rowIndex - i + 1) // i\n result.append(current_element)\n\n return result\n\n```\n``` JavaScript []\n// 95% Beats\nvar getRow = function(rowIndex) {\n let result = [1];\n\n for (let i = 1; i <= rowIndex; i++) {\n // Use the previous element to calculate the current element.\n let currentElement = result[i - 1] * (rowIndex - i + 1) / i;\n result.push(Math.round(currentElement));\n }\n\n return result;\n};\n```\n``` C# []\n// 100% Beats\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> result = new List<int>();\n\n // Initialize the first element of the row to 1.\n result.Add(1);\n\n // Calculate the `k`-th row using binomial coefficient formula.\n for (int i = 1; i <= rowIndex; i++) {\n // Use the previous element to calculate the current element.\n long currentElement = (long)result[i - 1] * (rowIndex - i + 1) / i;\n result.Add((int)currentElement);\n }\n\n return result;\n }\n}\n```\n\n**The most efficient approach is the mathematical optimization method, followed by the combinatorial approach. The naive approach is the least efficient as it generates the entire Pascal\'s triangle up to the `k`-th row. Depending on the constraints and your goals, you can choose the most appropriate approach for solving this problem.**\n\n\n# Up Vote Guys\n | 33 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Solution of pascal's triangle II problem | pascals-triangle-ii | 0 | 1 | # Approach\nSolved using dynamic programming\n- Step one: append 1 to list\n- Step two: from the end of the row construct a row for Pascal\'s triangle \n- Step three: continue until `len(triangle) != idx + 1`\n# Complexity\n- Time complexity:\n$$O(rowIndex)$$ - as we use extra space for answer equal to a constant\n\n- Space complexity:\n$$O(rowIndex^2)$$ - as dynamic programming takes $$O(rowIndex)$$ time and it repeats rowIndex times --> $$O(rowIndex * rowIndex)$$ = $$O(rowIndex^2)$$\n\n# Dynamic programming Code \n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n def pascal(idx, triangle):\n if len(triangle) == idx + 1:\n return triangle\n triangle.append(1)\n for i in range(len(triangle) - 2, 0, -1):\n triangle[i] = triangle[i] + triangle[i-1]\n return pascal(idx, triangle)\n return pascal(rowIndex, [])\n \n```\n# Extra solution\n- Use math to find pascal triangle: $$C(n,k) =$$ $$k!(n\u2212k)!/n!$$\nfor each element in the row\n- The row\'s first element is always 1. Given the previous element in the row, the next element can be calculated using:\n$$(previuos * (rowIndex \u2212 k + 1)) // k$$\n\n# Gigachad Code solution\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n answer = [1]\n prev = answer[-1]\n for k in range(1, rowIndex + 1):\n next_val = prev * (rowIndex - k + 1) // k\n answer.append(next_val)\n prev = answer[-1]\n return answer\n```\n\n | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
100% Acceptance | Optimised Solution Using a single array with reduced calculations | pascals-triangle-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt aims to optimize the generation of the `rowIndex`-th row of Pascal\'s Triangle by using a single array and a middle-out approach. By calculating elements from the center outwards, it reduces the number of calculations and minimizes memory usage.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a vector `result` of size `rowIndex + 1` and fill it with 1s to represent the first half of the row, which is always symmetrical in Pascal\'s Triangle.\n\n2. Iterate from `1` to `rowIndex / 2` to calculate the elements in the second half of the row. For each element at index `i`, calculate the value based on the previous element (at index `i - 1`) using integer division and the symmetry property of Pascal\'s Triangle.\n\n3. Update the corresponding element in the first half of the row with the calculated value to maintain symmetry.\n\n4. Continue the iteration until the entire row is constructed.\n\n5. Return the `result` vector, which represents the `rowIndex`-th row of Pascal\'s Triangle.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(rowIndex), where rowIndex is the input. The loop iterates from `1` to `rowIndex / 2`, and each iteration performs a constant amount of work\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(rowIndex) as we store the `result` vector of size rowIndex + 1 to represent the entire row of Pascal\'s Triangle. The space used for variables and loop control is negligible compared to the size of the result vector.\n# Code\n```\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> result(rowIndex + 1, 1);\n \n for (int i = 1; i <= rowIndex / 2; i++) {\n result[i] = (long long)result[i - 1] * (rowIndex - i + 1) / i;\n result[rowIndex - i] = result[i];\n }\n \n return result;\n }\n};\n\n```\n\n\n# \uD83D\uDCA1If you come this far, then i would like to request you to please upvote this solution so that it could reach out to another one \u2763\uFE0F\uD83D\uDCA1 | 6 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
✔️ Python Solution with Briefly Explanation 🔥🔥 | pascals-triangle-ii | 0 | 1 | # Explanation\nLet\'s break down the given code step by step.\n\n```python\ndef getRow(self, rowIndex: int) -> List[int]:\n res = [[1]]\n```\n- This function is defined as a method within a class, as it has `self` as its first parameter. It takes an integer `rowIndex` as input and is expected to return a list of integers.\n- `res` is initialized as a list containing a single list with the value `[1]`. This list represents the first row of Pascal\'s Triangle.\n\n```python\n for i in range(rowIndex):\n temp = [0] + res[-1] + [0]\n row = []\n```\n- A loop is set up to iterate from 0 to `rowIndex - 1`. This loop is used to calculate the subsequent rows of Pascal\'s Triangle.\n- `temp` is initialized as a new list, which is formed by adding `0` at the beginning and end of the last row in `res`. This is done to create a buffer of zeros around the row to calculate the next row.\n- `row` is initialized as an empty list. This list will store the values of the current row being calculated.\n\n```python\n for j in range(len(res[-1])+1):\n row.append(temp[j] + temp[j+1])\n```\n- Another nested loop is set up to iterate over the elements of `temp` and calculate the values of the current row.\n- For each element at index `j` in `temp`, it adds the value at index `j` and the value at index `j+1` and appends the result to the `row` list.\n\n```python\n res.append(row)\n```\n- After calculating all the values for the current row, the `row` list is appended to the `res` list. This adds a new row to the list, representing the current row of Pascal\'s Triangle.\n\n```python\n return res[-1]\n```\n- After the loop completes (i.e., all rows up to `rowIndex` have been calculated and added to `res`), the function returns the last row of `res`, which corresponds to the row at index `rowIndex` in Pascal\'s Triangle.\n\nIn summary, this code calculates and returns the `rowIndex`-th row of Pascal\'s Triangle using a list-based approach, where each row is calculated based on the previous row. It builds up the rows one by one, starting with the first row as `[1]` and using the values from the previous row to calculate the next row.\n\n# Python Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n res = [[1]]\n \n for i in range(rowIndex):\n temp = [0] + res[-1] + [0]\n row = []\n\n for j in range(len(res[-1])+1):\n row.append(temp[j] + temp[j+1])\n res.append(row)\n\n return res[-1]\n```\n**Please upvote if you like the solution & feel free to give your opinion. \nHappy Coding! \uD83D\uDE0A** | 5 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
three liner || code || python || super easy approach | pascals-triangle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def getRow(self, rowIndex):\n row = [1]\n\n for _ in range(rowIndex):\n row = [left + right for left, right in zip([0]+row, row+[0])]\n \n return row \n``` | 0 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
🚀🚩Beats 100%🧭 | Easy and Optimised Solution🚀 Using a single array with less divisions🔥 | pascals-triangle-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is an optimized approach to generate the `rowIndex`-th row of Pascal\'s Triangle. It utilizes a single array to store the values of each element in the row while minimizing calculations and avoiding overflow by using `long long` data types.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create a vector named `result` of size `rowIndex + 1` and initialize all elements to 1, as the first and last elements of each row in Pascal\'s Triangle are always 1.\n\n2. Initialize a variable `val` to 1, which will be used to compute the next element in the row.\n\n3. Loop from `i = 1` to `i = rowIndex`. In each iteration:\n\n- Update `val` by multiplying it with `(rowIndex - i + 1) / i`. This step calculates the next element in the row efficiently, taking advantage of the fact that each element is obtained by multiplying the previous element by `(rowIndex - i + 1)` and dividing by `i`.\n\n- Set `result[i]` to the computed `val`. This stores the element in the row.\n\n4. After the loop, the `result` vector contains the `rowIndex-th` row of Pascal\'s Triangle.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(rowIndex) because it iterates through the row once, performing constant-time operations for each element.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(rowIndex) because we are using a single vector of size `rowIndex + 1` to store the row\'s elements. The space required is proportional to the size of the row you want to generate.\n\n---\n\n\n# \uD83D\uDCA1If you come this far, then i would like to request you to please upvote this solution so that it could reach out to another one \u2763\uFE0F\uD83D\uDCA1\n\n\n---\n\n\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> result(rowIndex + 1, 1);\n long long val = 1;\n \n for (int i = 1; i <= rowIndex; i++) {\n val = val * (rowIndex - i + 1) / i;\n result[i] = val;\n }\n \n return result;\n }\n};\n\n``` | 5 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
The Finest solution | pascals-triangle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n l=[[1]]\n for i in range(rowIndex):\n t=[0]+l[-1]+[0]\n l1=[]\n for j in range(len(l[-1])+1):\n l1.append(t[j]+t[j+1])\n l.append(l1)\n return l[rowIndex]\n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Python 99.1% beats 7lines code || Simple and easy approach | pascals-triangle-ii | 0 | 1 | **If you got help from this,... Plz Upvote .. it encourage me**\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n prev = []\n for i in range(rowIndex+1):\n temp = [1]*(i+1)\n for j in range(1,i):\n temp[j] = prev[j] + prev[j-1]\n prev = temp\n \n return temp\n``` | 3 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
🚀📈Beats 100%🧭🚩 | 🔥Easy O(rowIndex) Solution 🚀| Optimised Solution 🚩 | pascals-triangle-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this optimized code is to calculate the `rowIndex-th` row of Pascal\'s Triangle efficiently. Instead of constructing the entire triangle, we can iteratively calculate each element of the row in place.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a vector `result` of size `rowIndex + 1`, with all elements set to 1. This is the initial state of the `rowIndex-th` row with 1s at the beginning and end.\n\n2. Iterate over the rows from 1 to `rowIndex` (inclusive).\n\n3. For each row, we start from the second element (index 1) and go up to the second-to-last element (index `i - 1`) because the first and last elements are always 1.\n\n4. Inside the inner loop, we maintain a variable `prev` to keep track of the value at the previous index. We calculate the value for the current index by adding the previous value `(prev)` to the current value at index `j`.\n\n5. We also store the original value at index `j` in a temporary variable `temp` to be used in the next iteration.\n\n6. After completing the inner loop, we return the `result` vector, which now contains the `rowIndex-th` row of Pascal\'s Triangle.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this optimized solution is O(rowIndex) since we only need to perform a constant number of operations for each row up to the desired `rowIndex`.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(rowIndex) because we are using a vector of size `rowIndex + 1` to store the row values in Pascal\'s Triangle.\n# Code\n```\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> result(rowIndex + 1, 1); // Initialize the row with all 1s\n \n for (int i = 1; i <= rowIndex; i++) {\n int prev = 1;\n for (int j = 1; j < i; j++) {\n int temp = result[j]; // Store the current value to update it in the next iteration\n result[j] = prev + result[j];\n prev = temp; // Update prev for the next iteration\n }\n }\n \n return result;\n }\n};\n\n``` | 4 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Python Easy Solution || Beginner Friendly | pascals-triangle-ii | 0 | 1 | # Code\n```\nclass Solution:\n def pascal(self, lis: list,k: int)-> List:\n res=[0]*(k+1)\n res[0]=1\n res[k]=1\n for i in range(1,len(res)-1):\n res[i]=lis[i-1]+lis[i]\n return res\n\n def getRow(self, rowIndex: int) -> List[int]:\n prev=[1]\n for i in range(rowIndex):\n prev=Solution.pascal(self,prev,i+1)\n return prev\n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
✅ Beats 98.39% 🔥 | 2 Approaches Detailed Explanation | Beginner Friendly Code | | pascals-triangle-ii | 1 | 1 | \n\n\n# Intuition\n1. We know that the pascal triangle is a triangle of binomial coefficients.\n2. We know that the binomial coefficients can be calculated using the formula nCr = n!/(r!*(n-r)!)\n3. We know that the binomial coefficients are symmetric, i.e. nCr = nC(n-r) \n4. We know that the binomial coefficients can be calculated using the previous row of the pascal triangle. \n5. We know that the first and last element of each row is 1.\n6. We know that the number of elements in each row is equal to the row number.\n7. We know that the row number starts from 0.\n8. We know that the first row is [1].\n9. Now, we can use the above information to calculate the pascal triangle.\n\n# Approach 1 : Dynamic Programming \n## (Least Optimized)\n###### This Approach if least optimized but for beginners who are facing difficulty with DP , in this solution dp is elaborated very well.\n1. Create a list of list called triangle and initialize it with [[1]].\n2. Iterate from 0 to rowIndex-1.\n3. Get the last row of the triangle and store it in last_row.\n4. Create a new list called new_row and initialize it with [1].\n5. Iterate from 1 to len(last_row)-1.\n6. Append the sum of last_row[j-1] and last_row[j] to new_row.\n7. Append 1 to new_row.\n8. Append new_row to triangle.\n9. Return the last row of the triangle.\n\n# Complexity\n- Time complexity : $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n if rowIndex==0:\n return [1]\n \n triangle=[[1]]\n\n for i in range(rowIndex):\n last_row=triangle[-1]\n new_row=[1]\n\n for j in range(1,len(last_row)):\n new_row.append(last_row[j-1]+last_row[j])\n \n new_row.append(1)\n triangle.append(new_row)\n \n return triangle[-1]\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n if (rowIndex == 0)\n return {1};\n \n vector<vector<int>> triangle{{1}};\n\n for (int i = 0; i < rowIndex; ++i) {\n vector<int>& last_row = triangle.back();\n vector<int> new_row{1};\n\n for (int j = 1; j < last_row.size(); ++j) {\n new_row.push_back(last_row[j-1] + last_row[j]);\n }\n\n new_row.push_back(1);\n triangle.push_back(new_row);\n }\n \n return triangle.back();\n }\n};\n\n```\n``` Java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n if (rowIndex == 0) {\n return Arrays.asList(1);\n }\n\n List<List<Integer>> triangle = new ArrayList<>();\n triangle.add(Arrays.asList(1));\n\n for (int i = 0; i < rowIndex; i++) {\n List<Integer> lastRow = triangle.get(triangle.size() - 1);\n List<Integer> newRow = new ArrayList<>();\n newRow.add(1);\n\n for (int j = 1; j < lastRow.size(); j++) {\n newRow.add(lastRow.get(j - 1) + lastRow.get(j));\n }\n\n newRow.add(1);\n triangle.add(newRow);\n }\n\n return triangle.get(triangle.size() - 1);\n }\n}\n\n```\n``` JavaScript []\n/**\n * @param {number} rowIndex\n * @return {number[]}\n */\nvar getRow = function(rowIndex) {\n if (rowIndex === 0) {\n return [1];\n }\n\n let triangle = [[1]];\n\n for (let i = 0; i < rowIndex; i++) {\n let lastRow = triangle[triangle.length - 1];\n let newRow = [1];\n\n for (let j = 1; j < lastRow.length; j++) {\n newRow.push(lastRow[j - 1] + lastRow[j]);\n }\n\n newRow.push(1);\n triangle.push(newRow);\n }\n\n return triangle[triangle.length - 1];\n};\n```\n``` TypeScript []\nfunction getRow(rowIndex: number): number[] {\nif (rowIndex === 0) {\n return [1];\n }\n\n let triangle: number[][] = [[1]];\n\n for (let i = 0; i < rowIndex; i++) {\n let lastRow: number[] = triangle[triangle.length - 1];\n let newRow: number[] = [1];\n\n for (let j = 1; j < lastRow.length; j++) {\n newRow.push(lastRow[j - 1] + lastRow[j]);\n }\n\n newRow.push(1);\n triangle.push(newRow);\n }\n\n return triangle[triangle.length - 1];\n };\n```\n``` C# []\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n if (rowIndex == 0) {\n return new int[] { 1 };\n }\n\n List<List<int>> triangle = new List<List<int>>();\n triangle.Add(new List<int> { 1 });\n\n for (int i = 0; i < rowIndex; i++) {\n List<int> lastRow = triangle[triangle.Count - 1];\n List<int> newRow = new List<int>();\n newRow.Add(1);\n\n for (int j = 1; j < lastRow.Count; j++) {\n newRow.Add(lastRow[j - 1] + lastRow[j]);\n }\n\n newRow.Add(1);\n triangle.Add(newRow);\n }\n\n return triangle[triangle.Count - 1].ToArray();\n }\n }\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $rowIndex\n * @return Integer[]\n */\n function getRow($rowIndex) {\n if ($rowIndex === 0) {\n return [1];\n }\n\n $triangle = [[1]];\n\n for ($i = 0; $i < $rowIndex; $i++) {\n $lastRow = $triangle[count($triangle) - 1];\n $newRow = [1];\n\n for ($j = 1; $j < count($lastRow); $j++) {\n array_push($newRow, $lastRow[$j - 1] + $lastRow[$j]);\n }\n\n array_push($newRow, 1);\n array_push($triangle, $newRow);\n }\n\n return $triangle[count($triangle) - 1];\n }\n }\n```\n``` Kotlin []\nclass Solution {\n fun getRow(rowIndex: Int): List<Int> {\n if (rowIndex == 0) {\n return listOf(1)\n }\n\n val triangle = mutableListOf(listOf(1))\n\n for (i in 0 until rowIndex) {\n val lastRow = triangle.last()\n val newRow = mutableListOf(1)\n\n for (j in 1 until lastRow.size) {\n newRow.add(lastRow[j - 1] + lastRow[j])\n }\n\n newRow.add(1)\n triangle.add(newRow)\n }\n\n return triangle.last()\n }\n }\n```\n# Intuition :\n\n###### Here, we will use the formula nCr = n!/(r!*(n-r)!) to calculate the binomial coefficients.\n\n# Approach 2 : Using Combinatorics\n### This Approach is well Optimized.\n\n### Algorithm :\n1. Create a list called row and initialize it with 1.\n2. Iterate from 1 to rowIndex.\n3. Update the value of row[i] to row[i-1]*(rowIndex-i+1)/i.\n4. Return row.\n\n# Code\n``` Python []\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n row=[1]\n for i in range(1,rowIndex+1):\n row.append(int(row[i-1]*(rowIndex-i+1)/i))\n return row\n```\n``` C+ []\nclass Solution {\npublic:\n vector<int> getRow(int rowIndex) {\n vector<int> row = {1};\n for (int i = 1; i <= rowIndex; ++i) {\n row.push_back(static_cast<int>(row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n }\n};\n```\n``` Java []\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n List<Integer> row = new ArrayList<>();\n row.add(1);\n for (int i = 1; i <= rowIndex; ++i) {\n row.add((int)((long)row.get(i - 1) * (rowIndex - i + 1) / i));\n }\n return row;\n }\n}\n```\n``` JavaScript []\nvar getRow = function(rowIndex) {\n const row = [1];\n for (let i = 1; i <= rowIndex; ++i) {\n row.push(Math.floor(row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n};\n```\n``` TypeScript []\nfunction getRow(rowIndex: number): number[] {\nconst row: number[] = [1];\n for (let i = 1; i <= rowIndex; ++i) {\n row.push(Math.floor(row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n };\n```\n``` C# []\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n List<int> row = new List<int> { 1 };\n for (int i = 1; i <= rowIndex; ++i) {\n row.Add((int)((long)row[i - 1] * (rowIndex - i + 1) / i));\n }\n return row;\n }\n}\n```\n``` PHP []\nclass Solution {\n function getRow($rowIndex) {\n $row = [1];\n for ($i = 1; $i <= $rowIndex; ++$i) {\n $row[] = intval($row[$i - 1] * ($rowIndex - $i + 1) / $i);\n }\n return $row;\n }\n}\n```\n``` Kotlin []\nclass Solution {\n fun getRow(rowIndex: Int): List<Int> {\n val row = mutableListOf(1)\n for (i in 1..rowIndex) {\n row.add((row[i - 1].toLong() * (rowIndex - i + 1) / i).toInt())\n }\n return row\n }\n}\n```\n\n\n | 3 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Approach made Easier ! | pascals-triangle-ii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# ****Read the Approach : Looks long But it\'s easy ! :****\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nAs you see :\n```***********\n\n# Step 1 :\n\nfor row 0 : we have 1 elements ;\n\nand for row 1 : we have 2 elements ;\n \nand for row 2 : we have 3 elements ;\n\nso , for nth row we\'ll have n+1 elements ;\n\nso i initiallized the array a with n+1 elements size ;\n\n\n\n\n# Step 2 :\n\nNow fill the arrays with complete 0\'s ;\n\nLet me consider that n=3; // (rowindex or size)\n\nif n==3 than a.length==4 // ---> (from step 1)\n\nAnd our array will be like [0,0,0,0] ; // ---> from step 2;\n\nNow initialize a[0]=1 ;\n\nAfter it our array will be [1,0,0,0]\n\n\n\n\n# Step 3 : Looping\n\n for (int i=1;i<=rowIndex;i++){\n for (int j=i;j>0;j--){\n a[j]=a[j]+a[j-1];\n }\n }\n\nHere i starts from 1 and inner loop j starts with i ;\n\nfor iteration 1 : i=1 and j=1 :\n\nAfter the iteration : a=[1,1,0,0]\n\nfor iteration 2 : i=2 and j=2 :\n\nAfter the iteration : a=[1,1,1,0]\n\nNow at j=1 and i=2 (j-- ) : After the iteration : a=[1,2,1,0]\n\n\nfor iteration 3 : i=3 and j=3 :\n\nAfter the iteration : a=[1,2,1,1]\n\nNow at j=2 and i=3 (j-- ) : After the iteration : a=[1,2,3,1]\n\nNow at j=1 and i=3 (j-- ) : After the iteration : a=[1,3,3,1]\n\nUprove Amigos :)\n\n```\n\n\n# Complexity\n- Time complexity: 1 ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 40 mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```Java []\n\nclass Solution {\n public List<Integer> getRow(int rowIndex) {\n \n Integer[] a=new Integer[rowIndex+1];\n \n Arrays.fill(a,0);\n \n a[0]=1;\n \n for (int i=1;i<=rowIndex;i++)\n {\n for (int j=i;j>0;j--){\n a[j]=a[j]+a[j-1];\n }\n }\n\n \n return Arrays.asList(a);\n\n }\n //uprove :)\n }\n\n```\n```javascript []\n\nclass Solution {\n getRow(rowIndex) {\n const a = new Array(rowIndex + 1).fill(0);\n a[0] = 1;\n\n for (let i = 1; i <= rowIndex; i++) {\n for (let j = i; j > 0; j--) {\n a[j] = a[j] + a[j - 1];\n }\n }\n\n return a;\n }\n}\n\n```\n```python []\n\nclass Solution:\n def getRow(self, rowIndex):\n a = [0] * (rowIndex + 1)\n a[0] = 1\n\n for i in range(1, rowIndex + 1):\n for j in range(i, 0, -1):\n a[j] = a[j] + a[j - 1]\n\n return a\n\n```\n```ruby []\nclass Solution\n def get_row(row_index)\n a = Array.new(row_index + 1, 0)\n a[0] = 1\n\n (1..row_index).each do |i|\n i.downto(1) do |j|\n a[j] = a[j] + a[j - 1]\n end\n end\n\n a\n end\nend\n\n```\n```C++ []\n\nclass Solution {\n\nstd::vector<int> getRow(int rowIndex) {\n std::vector<int> a(rowIndex + 1, 0);\n a[0] = 1;\n\n for (int i = 1; i <= rowIndex; i++) {\n for (int j = i; j > 0; j--) {\n a[j] = a[j] + a[j - 1];\n }\n }\n\n return a;\n}\n\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\nint* getRow(int rowIndex, int* returnSize) {\n int* a = (int*)malloc((rowIndex + 1) * sizeof(int));\n for (int i = 0; i <= rowIndex; i++) {\n a[i] = 0;\n }\n a[0] = 1;\n\n for (int i = 1; i <= rowIndex; i++) {\n for (int j = i; j > 0; j--) {\n a[j] = a[j] + a[j - 1];\n }\n }\n\n *returnSize = rowIndex + 1;\n return a;\n}\n\n\n```\n```C# []\n\npublic class Solution {\n public IList<int> GetRow(int rowIndex) {\n int[] a = new int[rowIndex + 1];\n for (int i = 0; i <= rowIndex; i++) {\n a[i] = 0;\n }\n a[0] = 1;\n\n for (int i = 1; i <= rowIndex; i++) {\n for (int j = i; j > 0; j--) {\n a[j] = a[j] + a[j - 1];\n }\n }\n\n return a;\n }\n}\n\n\n```\n | 4 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Normal Math Approach Two Approches --->Python3 | pascals-triangle-ii | 0 | 1 | \n# Brute Force\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n list1=[]\n for i in range(rowIndex+1):\n level=[]\n for j in range(i+1):\n if j==0 or j==i:\n level.append(1)\n else:\n level.append(list1[i-1][j-1]+list1[i-1][j])\n list1.append(level)\n return list1[-1]\n```\n# Smart Approches\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n def value(numRows,col):\n ans=1\n for i in range(col):\n ans=ans*(numRows-i)\n ans=ans//(i+1)\n return ans\n res=[]\n for k in range(1,rowIndex+):\n res.append(value(rowIndex,k-1))\n return res\n \n ```\n # please upvote me it would encourage me alot\n | 3 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
My first solution in Python. | pascals-triangle-ii | 0 | 1 | Here is my successfully uploaded solution of today\'s problem in Python language.\n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n def insum(L):\n l=[1]\n for i in range(0,len(L)-1):\n l.append(L[i]+L[i+1])\n l.append(1)\n return l\n if rowIndex==0:\n return[1]\n elif rowIndex==1:\n return[1,1]\n else:\n L=[1,1]\n for i in range(rowIndex-1):\n L=insum(L)\n return L\n``` | 2 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
8 lines dp solution python3 | pascals-triangle-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n res=[[1]]\n for i in range(rowIndex):\n temp=[0]+res[-1]+[0]\n row=[]\n for j in range(len(res[-1])+1):\n row.append(temp[j]+temp[j+1])\n res.append(row)\n return res[-1]\n```\n# plz consider upvoting\n\n\n | 7 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Python easy recursion | 9 Line | 40 ms | pascals-triangle-ii | 0 | 1 | # Intuition\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(k^2)$$ where k is lengt of array with result\n- Space complexity:\n$$O(k)$$ \n\n# Code\n```\nclass Solution:\n def getRow(self, rowIndex: int) -> List[int]:\n if rowIndex == 0:\n return [1]\n \n prevIndex = self.getRow(rowIndex - 1)\n res = [1]*(len(prevIndex)+1)\n for i in range(1,len(res)-1):\n res[i] = prevIndex[i-1]+prevIndex[i]\n \n return res\n \n \n``` | 1 | Given an integer `rowIndex`, return the `rowIndexth` (**0-indexed**) row of the **Pascal's triangle**.
In **Pascal's triangle**, each number is the sum of the two numbers directly above it as shown:
**Example 1:**
**Input:** rowIndex = 3
**Output:** \[1,3,3,1\]
**Example 2:**
**Input:** rowIndex = 0
**Output:** \[1\]
**Example 3:**
**Input:** rowIndex = 1
**Output:** \[1,1\]
**Constraints:**
* `0 <= rowIndex <= 33`
**Follow up:** Could you optimize your algorithm to use only `O(rowIndex)` extra space? | null |
Triangle-(python easy to understand) | triangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nNo extra space is required\nO(1)\n\n# Code\n```\nclass Solution:\n def minimumTotal(self, triangle: List[List[int]]) -> int:\n for i in range(len(triangle)-2,-1,-1):\n for j in range(0,len(triangle[i])):\n triangle[i][j]+=min(triangle[i+1][j+1],triangle[i+1][j])\n return triangle[0][0]\n``` | 1 | Given a `triangle` array, return _the minimum path sum from top to bottom_.
For each step, you may move to an adjacent number of the row below. More formally, if you are on index `i` on the current row, you may move to either index `i` or index `i + 1` on the next row.
**Example 1:**
**Input:** triangle = \[\[2\],\[3,4\],\[6,5,7\],\[4,1,8,3\]\]
**Output:** 11
**Explanation:** The triangle looks like:
2
3 4
6 5 7
4 1 8 3
The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).
**Example 2:**
**Input:** triangle = \[\[-10\]\]
**Output:** -10
**Constraints:**
* `1 <= triangle.length <= 200`
* `triangle[0].length == 1`
* `triangle[i].length == triangle[i - 1].length + 1`
* `-104 <= triangle[i][j] <= 104`
**Follow up:** Could you do this using only `O(n)` extra space, where `n` is the total number of rows in the triangle? | null |
Python 3 Solutions | triangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nRecursive Solution --> TLE\n\nclass Solution:\n def solve(self,i,j,triangle,n):\n if i== n-1:\n return triangle[i][j]\n\n down = triangle[i][j] + self.solve(i+1,j,triangle,n)\n diagonal = triangle[i][j] + self.solve(i+1,j+1,triangle,n)\n return min(down,diagonal)\n def minimumTotal(self, triangle: List[List[int]]) -> int:\n n = len(triangle)\n if n == 1:\n return triangle[0][0]\n return self.solve(0,0,triangle,n)\n```\n```\nMemoization --> TLE\nclass Solution:\n def solve(self,i,j,triangle,n):\n t = [[-1 for _ in range(n)] for _ in range(n)]\n if i== n-1:\n return triangle[i][j]\n if t[i][j] != -1:\n return t[i][j]\n down = triangle[i][j] + self.solve(i+1,j,triangle,n)\n diagonal = triangle[i][j] + self.solve(i+1,j+1,triangle,n)\n t[i][j] = min(down,diagonal)\n return t[i][j]\n def minimumTotal(self, triangle: List[List[int]]) -> int:\n n = len(triangle)\n if n == 1:\n return triangle[0][0]\n return self.solve(0,0,triangle,n)\n```\n```\nTabulation \nclass Solution:\n def minimumTotal(self, triangle: List[List[int]]) -> int:\n \n n = len(triangle)\n t = [[-1 for _ in range(n)] for _ in range(n)]\n for j in range(n):\n t[n-1][j] = triangle[n-1][j]\n \n for i in range(n-2,-1,-1):\n for j in range(i,-1,-1):\n down = triangle[i][j] + t[i+1][j]\n diagonal = triangle[i][j] + t[i+1][j+1]\n t[i][j] = min(down,diagonal)\n return t[0][0]\n``` | 1 | Given a `triangle` array, return _the minimum path sum from top to bottom_.
For each step, you may move to an adjacent number of the row below. More formally, if you are on index `i` on the current row, you may move to either index `i` or index `i + 1` on the next row.
**Example 1:**
**Input:** triangle = \[\[2\],\[3,4\],\[6,5,7\],\[4,1,8,3\]\]
**Output:** 11
**Explanation:** The triangle looks like:
2
3 4
6 5 7
4 1 8 3
The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).
**Example 2:**
**Input:** triangle = \[\[-10\]\]
**Output:** -10
**Constraints:**
* `1 <= triangle.length <= 200`
* `triangle[0].length == 1`
* `triangle[i].length == triangle[i - 1].length + 1`
* `-104 <= triangle[i][j] <= 104`
**Follow up:** Could you do this using only `O(n)` extra space, where `n` is the total number of rows in the triangle? | null |
[Python] In-place DP with Explanation | triangle | 0 | 1 | ### Intuition\n\nWe can use the ```triangle``` array to perform our DP. This allows us to use O(1) auxiliary space. Why?\n\n- For any given coordinate in the triangle ```(x, y)``` where ```0 <= x < len(triangle)``` and ```0 <= y < len(triangle[x])```, the minimum path sum of the path that ends up on ```(x, y)``` is given by **```triangle[x][y]``` plus the minimum path sum of the previous coordinate**.\n- Once we compute the minimum path sum at ```(x, y)```, we **no longer require the standalone value for ```(x, y)``` to perform any calculation**. Instead, per above, we will use the minimum sum.\n\nWhich coordinates are considered "previous" to any given coordinate ```(x, y)```? Since from any ```(x, y)``` in the ```triangle``` we can move to ```(x+1, y)``` or ```(x+1, y+1)```, we can use this information in reverse: **For any given coordinate ```(x, y)```, its "previous" coordinates are either ```(x-1, y-1)``` or ```(x-1, y)```**.\n\n---\n\n### Approach 1: Top-Down Approach\n\nFrom the discussion above, we can implement a top-down DP using the following pseudocode:\n\n- For each row in the ```triangle```, calculate the minimum sum at each element.\n- After all computation is complete, return the minimum sum from the last row (i.e. ```min(triangle[-1])```).\n\n```python\nclass Solution:\n def minimumTotal(self, triangle: List[List[int]]) -> int:\n for i in range(1, len(triangle)): # for each row in triangle (skipping the first),\n for j in range(i+1): # loop through each element in the row\n triangle[i][j] += min(triangle[i-1][j-(j==i)], # minimum sum from coordinate (x-1, y)\n triangle[i-1][j-(j>0)]) # minimum sum from coordinate (x-1, y-1)\n return min(triangle[-1]) # obtain minimum sum from last row\n```\n\n**TC: O(n<sup>2</sup>)**, since we visit each element in the array\n**SC: O(1)**, as discussed above.\n\n---\n\n### Approach 2: Bottom-Up Approach\n\nWe can use the same pseudocode but implement it in reverse. This saves on the min check at the end (which runs in O(n) time), since we know that **the last element for a bottom-up approach has to be `triangle[0][0]`, and therefore that is where our answer is stored**.\n\n```python\nclass Solution:\n def minimumTotal(self, triangle: List[List[int]]) -> int:\n for i in range(len(triangle)-2, -1, -1): # for each row in triangle (skipping the last),\n for j in range(i+1): # loop through each element in the row\n triangle[i][j] += min(triangle[i+1][j], # minimum sum from coordinate (x+1, y)\n triangle[i+1][j+1]) # minimum sum from coordinate (x+1, y+1)\n return triangle[0][0]\n```\n\n**TC: O(n<sup>2</sup>)**, as discussed above.\n**SC: O(1)**, as discussed above.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 26 | Given a `triangle` array, return _the minimum path sum from top to bottom_.
For each step, you may move to an adjacent number of the row below. More formally, if you are on index `i` on the current row, you may move to either index `i` or index `i + 1` on the next row.
**Example 1:**
**Input:** triangle = \[\[2\],\[3,4\],\[6,5,7\],\[4,1,8,3\]\]
**Output:** 11
**Explanation:** The triangle looks like:
2
3 4
6 5 7
4 1 8 3
The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).
**Example 2:**
**Input:** triangle = \[\[-10\]\]
**Output:** -10
**Constraints:**
* `1 <= triangle.length <= 200`
* `triangle[0].length == 1`
* `triangle[i].length == triangle[i - 1].length + 1`
* `-104 <= triangle[i][j] <= 104`
**Follow up:** Could you do this using only `O(n)` extra space, where `n` is the total number of rows in the triangle? | null |
Most optimized solution, easy to understand || C++ || JAVA || Python | best-time-to-buy-and-sell-stock | 1 | 1 | # Approach\nTo solve this problem, I employed a straightforward approach that iterates through the array of stock prices. At each step, I kept track of the minimum stock price seen so far (`min_price`) and calculated the potential profit that could be obtained by selling at the current price (`prices[i] - min_price`). I updated the `maxprof` (maximum profit) variable with the maximum of its current value and the calculated profit. Additionally, I updated the `min_price` to be the minimum of the current stock price and the previously seen minimum.\n\n# Complexity\n- Time complexity: $$O(n)$$\nThe algorithm iterates through the array of stock prices once, performing constant-time operations at each step. Therefore, the time complexity is linear in the size of the input array.\n\n- Space complexity: $$O(1)$$\nThe algorithm uses a constant amount of extra space to store variables like `min_price` and `maxprof`. The space complexity remains constant regardless of the size of the input array.\n\n\n# Code\n``` cpp []\nclass Solution {\npublic:\n int maxProfit(vector<int>& prices) {\n int min_price = prices[0];\n int maxprof = 0;\n\n for(int i=1;i<prices.size();i++){\n maxprof = max(maxprof,prices[i]-min_price);\n min_price = min(prices[i],min_price);\n }\n\n return maxprof;\n }\n};\n```\n\n``` java []\nclass Solution {\n public int maxProfit(int[] prices) {\n int min_price = prices[0];\n int maxprof = 0;\n\n for(int i=1;i<prices.length;i++){\n maxprof = Math.max(maxprof,prices[i]-min_price);\n min_price = Math.min(prices[i],min_price);\n }\n\n return maxprof;\n }\n}\n```\n\n``` python3 []\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n min_price = prices[0]\n max_profit = 0\n \n for price in prices[1:]:\n max_profit = max(max_profit, price - min_price)\n min_price = min(min_price, price)\n \n return max_profit\n```\n\nHope you liked the Solution,\nIf you have any questions or suggestions, feel free to share \u2013 happy coding!\n\n---\n\n\n\n | 250 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
O(n) | best-time-to-buy-and-sell-stock | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n m=prices[0]\n d=0\n c=0\n for i in range(1,len(prices)):\n m=min(m,prices[i])\n if prices[i]<prices[i-1]:\n c+=1 \n else:\n diff=prices[i]-m\n d=max(d,diff)\n \n if c==len(prices):\n return 0\n else:\n return d\n \n``` | 1 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Simplest solution using two pointers | best-time-to-buy-and-sell-stock | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n l,r=0,1\n maxP=0\n\n while r<len(prices):\n if prices[l]<prices[r]:\n profit=prices[r]-prices[l]\n maxP=max(maxP,profit)\n else:\n l=r\n r+=1\n return maxP\n\n``` | 1 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Day 56 || O(n) time and O(1) space || Easiest Beginner Friendly Sol | best-time-to-buy-and-sell-stock | 1 | 1 | # Intuition of this Problem:\nThe intuition behind the code is to keep track of the minimum stock value seen so far while traversing the array from left to right. At each step, if the current stock value is greater than the minimum value seen so far, we calculate the profit that can be earned by selling the stock at the current value and buying at the minimum value seen so far, and update the maximum profit seen so far accordingly.\n\nBy keeping track of the minimum stock value and the maximum profit seen so far, we can solve the problem in a single pass over the array, without needing to consider all possible pairs of buy-sell transactions. This makes the code efficient and easy to implement.\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Initialize a variable n to the size of the input vector prices.\n2. Initialize variables maximumProfit and minStockVal to 0 and INT_MAX respectively.\n3. Initialize a loop variable i to 0.\n4. While i is less than n, do the following:\n - a. Set minStockVal to the minimum value between minStockVal and the value of prices at index i.\n - b. If minStockVal is less than or equal to the value of prices at index i, set maximumProfit to the maximum value between maximumProfit and the difference between prices at index i and minStockVal.\n - c. Increment i by 1.\n1. Return maximumProfit.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int maxProfit(vector<int>& prices) {\n int n = prices.size();\n int maximumProfit = 0, minStockVal = INT_MAX;\n int i = 0;\n while (i < n) {\n minStockVal = min(minStockVal, prices[i]);\n // whenever the price of current stock is greater then then the stock value which we bought then only we will sell the stock \n if (prices[i] >= minStockVal)\n maximumProfit = max(maximumProfit, prices[i] - minStockVal);\n i++;\n }\n return maximumProfit;\n }\n};\n```\n```Java []\nclass Solution {\n public int maxProfit(int[] prices) {\n int n = prices.length;\n int maximumProfit = 0, minStockVal = Integer.MAX_VALUE;\n int i = 0;\n while (i < n) {\n minStockVal = Math.min(minStockVal, prices[i]);\n // whenever the price of current stock is greater then then the stock value which we bought then only we will sell the stock \n if (prices[i] >= minStockVal)\n maximumProfit = Math.max(maximumProfit, prices[i] - minStockVal);\n i++;\n }\n return maximumProfit;\n }\n}\n\n```\n```Python []\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n n = len(prices)\n maximumProfit, minStockVal = 0, float(\'inf\')\n i = 0\n while i < n:\n minStockVal = min(minStockVal, prices[i])\n if prices[i] >= minStockVal:\n maximumProfit = max(maximumProfit, prices[i] - minStockVal)\n i += 1\n return maximumProfit\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the size of the input vector prices.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**, as we are only using constant extra space for variables.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 93 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
[VIDEO] Intuitive Visualization and Proof of O(n) Solution | best-time-to-buy-and-sell-stock | 0 | 1 | https://www.youtube.com/watch?v=ioFPBdChabY\n\nA brute force approach would calculate every possible buy-sell combination and would run in O(n^2), but we can reduce this to O(n) by avoiding unncessary computations. The strategy below iterates once for every sell date, and handles two cases:\n1. If buy price < sell price, calculate the profit and compare it to the max profit so far. If it is greater than the max profit, replace it. Also, there is no need to go back and calculate profits using this <i>sell</i> date as a buy date, since we can always achieve a higher profit from using the original buy date (which is at a lower price).\n2. If sell price <= buy date, simply update the buy date to be the current sell date, since we have found a lower price to buy from.\n\nAt the end, return `profit`, which will contain the maximum profit achievable.\n\n# Code\n```\nclass Solution(object):\n def maxProfit(self, prices):\n profit = 0\n buy = prices[0]\n for sell in prices[1:]:\n if sell > buy:\n profit = max(profit, sell - buy)\n else:\n buy = sell\n \n return profit\n``` | 6 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Easy || 100% || Kadane's Algorithm (Java, C++, Python, JS, Python3) || Min so far | best-time-to-buy-and-sell-stock | 1 | 1 | Given an array prices where prices[i] is the price of a given stock on the ith day.\nmaximize our profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.\nReturn the maximum profit achieve from this transaction. If you cannot achieve any profit, return 0\n\n**Example:**\nInput: prices = [7,1,5,3,6,4]\nOutput: 5\n**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.\n**Note that, buying on day 2 and selling on day 1 is not allowed because we must buy before sell.**\n# **Java Solution:**\nRuntime: 1 ms, faster than 98.59% of Java online submissions for Best Time to Buy and Sell Stock.\n```\nclass Solution {\n public int maxProfit(int[] prices) {\n // Base case...\n // If the array is empty or its length <= 1, return 0...\n if(prices == null || prices.length <= 1) return 0;\n // Initialize the minimum price to buy...\n int minBuy = prices[0];\n // Initialize the maximum profit...\n int profit = 0;\n // Traverse all elements through a for loop...\n for(int i = 1; i < prices.length; i++) {\n // Get the minimum price to buy...\n minBuy = Math.min(minBuy, prices[i]);\n // Get maximum profit...\n profit = Math.max(profit, prices[i] - minBuy);\n }\n return profit; //return the maximum profit...\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n int maxProfit(vector<int>& prices) {\n if(prices.size() == 0) return 0;\n int profit = 0;\n int low = prices[0], high = prices[0];\n for(int i = 0; i < prices.size(); i++){\n if(prices[i] < low){\n profit = max(profit, high - low);\n low = prices[i];\n high = prices[i];\n }else{\n high = max(high, prices[i]);\n }\n }\n profit = max(profit, high - low);\n return profit;\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def maxProfit(self, prices):\n if len(prices) == 0: return 0\n else:\n profit = 0\n minBuy = prices[0]\n for i in range(len(prices)):\n profit = max(prices[i] - minBuy, profit)\n minBuy = min(minBuy, prices[i])\n return profit\n```\n \n# **JavaScript Solution:**\n```\nvar maxProfit = function(prices) {\n if(prices == null || prices.length <= 1) return 0;\n let minBuy = prices[0];\n let profit = 0;\n for(let i = 1; i < prices.length; i++) {\n minBuy = Math.min(minBuy, prices[i]);\n profit = Math.max(profit, prices[i] - minBuy);\n }\n return profit;\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n if len(prices) == 0: return 0\n else:\n profit = 0\n minBuy = prices[0]\n for i in range(len(prices)):\n profit = max(prices[i] - minBuy, profit)\n minBuy = min(minBuy, prices[i])\n return profit\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 133 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Python 3 -> Very simple solution. Explanation added | best-time-to-buy-and-sell-stock | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\nWe might think about using sliding window technique, but obviously we don\'t need subarray here. We just need one value from the given input list. So, this technique is not useful.\n\n**Solution:**\nWe always need to know what is the maxProfit we can make if we sell the stock on i-th day. So, keep track of maxProfit.\nThere might be a scenario where if stock bought on i-th day is minimum and we sell it on (i + k)th day. So, keep track of minPurchase as well.\n\n```\ndef maxProfit(self, prices: List[int]) -> int:\n\tif not prices:\n\t\treturn 0\n\n\tmaxProfit = 0\n\tminPurchase = prices[0]\n\tfor i in range(1, len(prices)):\t\t\n\t\tmaxProfit = max(maxProfit, prices[i] - minPurchase)\n\t\tminPurchase = min(minPurchase, prices[i])\n\treturn maxProfit\n```\n\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 308 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Buy and sell Stocks in Python | best-time-to-buy-and-sell-stock | 0 | 1 | # Intuition\nJust observe your daily stock buy and sell process\n\n# Approach\nwe start from the beginning of list and if any day we see the price has gone down then we take hold i.e. we buy at that price and if the price if higher we just compute the last max profit and store it\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices):\n max_profit = 0\n\n buy = prices[0]\n\n for sell in prices[1:]:\n if sell > buy:\n max_profit = max(sell-buy, max_profit)\n else:\n buy=sell\n\n return max_profit\n\n``` | 0 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
basic o(n) solution .not higly optimised. Only for your reference. :p | best-time-to-buy-and-sell-stock | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProfit(self, a: List[int]) -> int:\n n=len(a)\n m=0\n t=a[0]\n for j in range(0,n):\n if t-a[j]>0:\n t=a[j]\n print(t,end=" ")\n else:\n m=max(m,abs(t-a[j]))\n return m\n``` | 0 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Easiest One Linear Solution in Python3 | best-time-to-buy-and-sell-stock | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s the approach used in this code:\n\n1. The accumulate function is used from the itertools library. It calculates the cumulative sums of the input list prices. For example, if prices is [7, 1, 5, 3, 6, 4], then accumulate(prices) will yield [7, 8, 13, 16, 22, 26]. These cumulative sums represent the potential profit if you sell the stock at each corresponding day.\n\n2. min(prices) is used to find the minimum stock price in the given list. This represents the lowest possible buying price.\n\n3. The zip(prices, accumulate(prices, min)) construct pairs each day\'s stock price with the corresponding minimum buying price. For example, with prices = [7, 1, 5, 3, 6, 4] and min(prices) = 1, the zip operation would yield [(7, 1), (1, 1), (5, 1), (3, 1), (6, 1), (4, 1)]. This represents the potential profit on each day if you buy at the minimum price and sell at the current day\'s price.\n\n4. The generator expression j - k for j, k in zip(prices, accumulate(prices, min)) calculates the profit for each day by subtracting the buying price (k) from the current day\'s price (j).\n\n5. max(j - k for j, k in ...) finds the maximum profit among all the potential profits calculated in step 4. This maximum profit represents the best profit you can obtain by buying and selling the stock multiple times.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n return max(j - k for j,k in zip(prices, accumulate(prices,min)))\n``` | 4 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Python || 99.54% Faster || T.C. O(n) S.C. O(1) | best-time-to-buy-and-sell-stock | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n m1=prices[0]\n m2=0\n for i in range(1,n):\n if m1>prices[i]:\n m1=prices[i]\n if m2<(prices[i]-m1):\n m2=prices[i]-m1\n return m2 \n``` | 3 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
best-time-to-buy-and-sell-stock | best-time-to-buy-and-sell-stock | 0 | 1 | # Code\n```\nclass Solution:\n def maxProfit(self, nums: List[int]) -> int:\n l = [nums[-1]]\n for i in range(len(nums)-2,-1,-1):\n if nums[i]>l[-1]:\n l.append(nums[i])\n else:\n l.append(l[-1])\n l = l[::-1]\n b = 0\n for i,j in zip(nums,l):\n b = max(b,j - i)\n return b\n\n\n\n \n``` | 1 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Python3 Easy Solution | best-time-to-buy-and-sell-stock | 0 | 1 | \n# Complexity\n- Time complexity:\n0(N)\n\n- Space complexity:\n0(1)\n\n# Code\n```\nclass Solution:\n def maxProfit(self, arr: List[int]) -> int:\n minSoFar=float(\'inf\')\n maxProfit=0\n for i in range(len(arr)):\n minSoFar=min(minSoFar,arr[i])\n maxProfit=max(maxProfit,arr[i]-minSoFar)\n return maxProfit\n``` | 1 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
You want to maximize your profit by choosing a **single day** to buy one stock and choosing a **different day in the future** to sell that stock.
Return _the maximum profit you can achieve from this transaction_. If you cannot achieve any profit, return `0`.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 5
**Explanation:** Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
**Example 2:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transactions are done and the max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 104` | null |
Python/JS/Java/Go/C++ O(n) by DP // Greedy [+ Visualization] | best-time-to-buy-and-sell-stock-ii | 1 | 1 | Method_#1\nO(n) sol by DP + state machine\n\nDefine "**Hold**" as the state of **holding stock**. (\u6301\u6709\u80A1\u7968)\nDefine "**NotHold**" as the state of **keep cash**. (\u6301\u6709\u73FE\u91D1)\n\nGeneral rule aka recursive relationship.\n\n```\nDP[Hold] \n= max(keep holding stock, or just buy stock & hold today)\n= max( DP[Previous Hold], DP[previous NotHold] - stock price)\n```\n---\n\n```\nDP[NotHold] \n= max(keep cash, or just sell out stock today)\n= max( DP[Previous NotHold], DP[previous Hold] + stock price)\n```\n\n---\n\n**State machine diagram**:\n\n<img src="https://assets.leetcode.com/users/images/62d26ff8-bba1-497c-b429-702e002a05d1_1684081274.8362317.png" width="1000" height="600">\n\n---\n\n**Implementation** by botoom-up DP + iteration:\n<iframe src="https://leetcode.com/playground/J7fnkkAb/shared" frameBorder="0" width="1000" height="600"></iframe>\n\nTime Complexity: O(n), for single level for loop\nSpace Complexity: O(1), for fixed size of temporary variables\n\n---\n\n**Implementation** with Top down DP + recursion \n<iframe src="https://leetcode.com/playground/2zaLvs2H/shared" frameBorder="0" width="1000" height="600"></iframe>\n\nTime Complexity: O(n), for single level for loop\nSpace Complexity: O(n), for 1D DP recursion call depth\n\n---\n\nMethod_#2\nO(n) sol by Greedy\n\nShare another O(n) solution by price gain collection with **greedy** value taking concept.\n\nMax profit with [long position](https://en.wikipedia.org/wiki/Long_(finance)) ,\'\u505A\u591A\' in chinese, is met by **collecting all price gain** in the stock price sequence.\n\nTake care that holding **multiple position at the same time is NOT allowed** by [description](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/).\n\n---\n\n**Visualization**:\n\n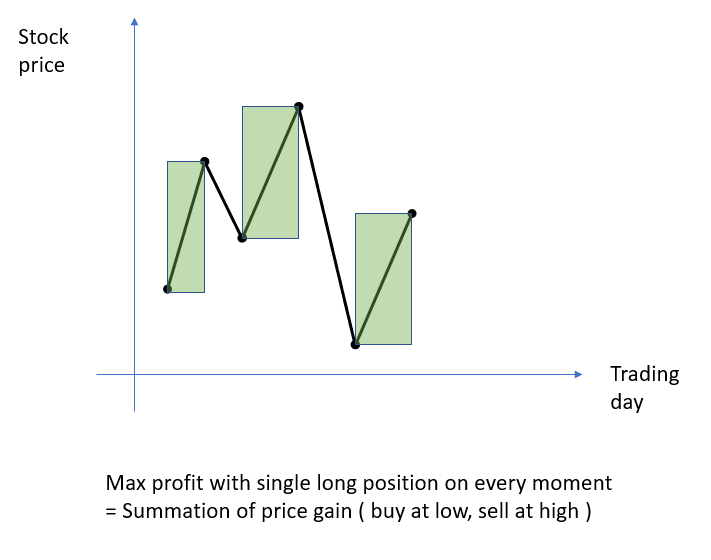\n\n---\n\n**Implementation** based on container and summation function:\n\n\n```python []\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n\n price_gain = []\n \n for idx in range( len(prices)-1 ):\n \n if prices[idx] < prices[idx+1]:\n \n price_gain.append( prices[idx+1]- prices[idx])\n \n return sum( price_gain )\n```\n```Java []\nclass Solution {\n \n \n public int maxProfit(int[] prices) {\n\n ArrayList<Integer> priceGain = new ArrayList<Integer>();\n \n for(int idx = 0 ; idx < prices.length-1; idx++){\n \n if( prices[idx] < prices[idx+1] ){\n priceGain.add( prices[idx+1]- prices[idx]);\n }\n \n }\n return priceGain.stream().mapToInt(n->n).sum();\n \n }\n}\n```\n```Javascript []\nconst accumulate = ( (prev, cur) => (prev + cur) );\n\nvar maxProfit = function(prices) {\n \n let profit = new Array();\n \n for( let i = 0 ; i < prices.length-1 ; i++ ){\n \n if( prices[i] < prices[i+1] ){\n profit.push( prices[i+1] - prices[i] );\n }\n }\n return profit.reduce(accumulate, 0);\n}\n```\n```Go []\nfunc Accumulate(elements ...int) int { \n sum := 0 \n for _, elem := range elements { \n sum += elem \n } \n return sum \n} \n\n\nfunc maxProfit(prices []int) int {\n \n profit := make([]int, 0)\n \n for i := 0 ; i < len(prices)-1 ; i++{\n \n if( prices[i] < prices[i+1] ){\n profit = append(profit, ( prices[i+1] - prices[i] ))\n }\n }\n\n return Accumulate(profit...)\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProfit(vector<int>& prices) {\n \n vector<int> profit;\n \n for( size_t i = 0 ; i < prices.size()-1 ; i++ ){\n \n if( prices[i] < prices[i+1] ){\n profit.push_back( prices[i+1] - prices[i] );\n }\n \n }\n return accumulate( profit.begin(), profit.end(), 0);\n }\n};\n```\n\nTime Complexity: O(n), for single level for loop\nSpace Complexity: O(n), for array storage sapce\n\n\n---\n\n**Implementation** based on generator expression and sum( ... ):\n\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n\n return sum( ( prices[idx+1]-prices[idx] ) for idx in range(len(prices)-1) if prices[idx] < prices[idx+1] )\n```\n\n---\n\n**Implementation** based on O(1) aux space:\n\n```python []\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n \n profit_from_price_gain = 0\n for idx in range( len(prices)-1 ):\n \n if prices[idx] < prices[idx+1]:\n profit_from_price_gain += ( prices[idx+1] - prices[idx])\n \n return profit_from_price_gain\n```\n```Javascript []\nvar maxProfit = function(prices) {\n \n let profitFromPriceGain = 0;\n \n for( let i = 0 ; i < prices.length-1 ; i++ ){\n \n if( prices[i] < prices[i+1] ){\n profitFromPriceGain += ( prices[i+1] - prices[i] );\n }\n }\n \n return profitFromPriceGain;\n}\n```\n```Java []\nclass Solution {\n public int maxProfit(int[] prices) { \n int profitFromPriceGain = 0;\n \n for( int i = 0 ; i < prices.length-1 ; i++ ){\n \n if( prices[i] < prices[i+1] ){\n profitFromPriceGain += ( prices[i+1] - prices[i] );\n }\n }\n \n return profitFromPriceGain;\n }\n}\n```\n```Go []\nfunc maxProfit(prices []int) int {\n \n profitFromPriceGain := 0\n \n for i := 0 ; i < len(prices)-1 ; i++{\n \n if( prices[i] < prices[i+1] ){\n profitFromPriceGain += ( prices[i+1] - prices[i] )\n }\n }\n\n return profitFromPriceGain\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProfit(vector<int>& prices) {\n \n int profitFromPriceGain = 0;\n \n for( size_t i = 0 ; i < prices.size()-1 ; i++ ){\n \n if( prices[i] < prices[i+1] ){\n profitFromPriceGain += ( prices[i+1] - prices[i] );\n }\n \n }\n return profitFromPriceGain;\n }\n};\n```\n\nTime Complexity: O(n), for single level for loop\nSpace Complexity: O(1), for fixed size of temporary variables\n\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #121 Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock)\n\n[Leetcode #123 Best Time to Buy and Sell Stock III ](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii)\n\n[Leetcode #188 Best Time to Buy and Sell Stock IV ](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv)\n\n[Leetcode #309 Best Time to Buy and Sell Stock with Cooldown](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown)\n\n[Leetcode #714 Best Time to Buy and Sell Stock with Transaction Fee ](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee) \n\n---\n\nReference:\n\n[1] [Python official docs about generator expression](https://www.python.org/dev/peps/pep-0289/)\n\n[2] [Python official docs about sum( ... )](https://docs.python.org/3/library/functions.html#sum) | 655 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
python + easy_sol + 95% | best-time-to-buy-and-sell-stock-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n def back(x):\n while x < len(prices) - 1 and prices[x] < prices[x + 1]:\n x += 1\n return x\n mx = j = i = 0\n while i < len(prices) - 1:\n p = 0\n if prices[i] < prices[i + 1]:\n j = back(i)\n mx += prices[j] - prices[i]\n i = j\n if j >= len(prices) - 1:\n break\n i += 1\n \n return mx\n``` | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
✅Python3✅ Greedy | best-time-to-buy-and-sell-stock-ii | 0 | 1 | # Please Upvote \uD83D\uDE07\n\n## Python3\n```\nclass Solution:\n def maxProfit(self, a: List[int]) -> int:\n ans=0\n x=a[0]\n for i in range(1,len(a)):\n if(x>a[i]):\n x=a[i]\n else:\n ans+=a[i]-x\n x=a[i]\n return ans\n\n \n``` | 34 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
best time to buy and sell stock 2 - python with description | best-time-to-buy-and-sell-stock-ii | 0 | 1 | # Intuition\nIf we can buy and sell on any day, then all we need to check is day i and day i - 1 to see if buying/selling the next day gives us a profit. If it does, do it. Otherwise don\'t.\n\n# Approach\n1. inizialize profit to 0\n2. iterate through prices starting at 2nd value (so we can i-1)\n3. if the ith price is greater than the i-1th price, then add the difference\n4. return profit\n\n# Complexity\n- Time complexity:\nO(n) - single pass\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n profit = 0\n\n for i in range(1, len(prices)):\n # we make profit today, so buy and sell\n if prices[i] > prices[i - 1]:\n profit += (prices[i] - prices[i - 1])\n\n return profit\n\n``` | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
Fantastic Logic----->Python3 | best-time-to-buy-and-sell-stock-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n maxprofit=0\n for i in range(len(prices)-1):\n if prices[i+1]>prices[i]:\n maxprofit+=prices[i+1]-prices[i]\n return maxprofit\n #please upvote me it would encourage me alot\n\n``` | 26 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
DETAILED EXPLANATION STOCK-II and STOCK-FEE in Python | best-time-to-buy-and-sell-stock-ii | 0 | 1 | \n# Approach\nIn stock related problems, it is very important to grasp some concepts related to how we can maximize our total profit. Let me state a few obvious points:\n1. We need the minimum possible buying price of that stock\n2. We need the maximum possible sell price of that stock\n\nKeeping these two obvious points in mind, we can make a few notes:\n1. Buy something cheaper and assign the buy variable as price - sell.\n\n `buy = price - sell`\n\n2. Then sell something to make an actual profit and assign the sell variable as price - buy.\n\n`sell = price - buy`\n\nAfter iterations, we will have the result in the sell variable.\n\n---\n\nNow since we are comparing the buy to find the minimum buying price possible, we will compare it with the initial of b as something really big so that we can take: \n\n`min(buy, price - sell)`\n\nObviously we cannot take the value of buy to be something small like 0. Luckily we do not really have to guess what the upper limit of "buy" we need to assume since in python we can just declare it as `float(\'inf\')`\n\n---\nNow for the sell variable, we need something bigger as out sell price hence we will be comparing it with 0. Obviously our sell will be greater than that since we need to make a profit. So we just declare it as `0`.\n\n---\n\nNow coming to the final part which is related to Stock-III problem. It basically is Stock-II but with a transaction fee involved for each transaction committed. For this we just need subtract the transaction fee from sell variable at each step. Hence the code will look like:\n\n `sell = max(sell, p - buy - fee)`\n\n\n# Code for STOCK - II\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n buy = float(\'inf\')\n sell = 0\n for p in prices:\n buy = min(buy, p - sell)\n sell = max(sell, p - buy)\n return sell\n```\n# Code for STOCK - FEE\n```\nclass Solution:\n def maxProfit(self, prices: List[int], fee: int) -> int:\n buy = float(\'inf\')\n sell = 0\n for p in prices:\n buy = min(buy, p - sell)\n sell = max(sell, p - buy - fee)\n return sell\n``` | 2 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
Simple Python Solution with 99%beats | best-time-to-buy-and-sell-stock-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:99.76%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:72.54%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n res=0\n for i in range(len(prices)-1):\n if prices[i]<prices[i+1]:\n res+=prices[i+1]-prices[i]\n return res\n``` | 1 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
Python short 1-liner. Functional programming. | best-time-to-buy-and-sell-stock-ii | 0 | 1 | # Approach\n1. For every day $$d_i$$, if $$prices[d_i] < prices[d_{i + 1}]$$ then buy the stock on $$d_i$$ and sell it on $$d_{i + 1}$$ else do nothing.\n\n2. Continue this for each day and return the `sum` of all the profits.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is length of prices`.\n\n# Code\n```python\nclass Solution:\n def maxProfit(self, prices: list[int]) -> int:\n return sum(max(b - a, 0) for a, b in pairwise(prices))\n\n\n``` | 5 | You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
On each day, you may decide to buy and/or sell the stock. You can only hold **at most one** share of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
Find and return _the **maximum** profit you can achieve_.
**Example 1:**
**Input:** prices = \[7,1,5,3,6,4\]
**Output:** 7
**Explanation:** Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.
**Constraints:**
* `1 <= prices.length <= 3 * 104`
* `0 <= prices[i] <= 104` | null |
with step by step explanation | best-time-to-buy-and-sell-stock-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe basic idea is to iterate over the array of stock prices and update four variables:\n\nbuy1 - the minimum price seen so far for the first transaction\nsell1 - the maximum profit seen so far for the first transaction\nbuy2 - the minimum price seen so far for the second transaction, taking into account the profit from the first transaction\nsell2 - the maximum profit seen so far for the second transaction\nAt the end of the iteration, the value of sell2 is returned as the maximum profit achievable with two transactions.\n\nThe if not prices check is included to handle the edge case where the input array is empty.\n\nHere\'s how the algorithm works step by step for the input [3,3,5,0,0,3,1,4]:\n\n1. Initialize buy1, buy2, sell1, and sell2 to inf, inf, 0, and 0, respectively.\n2. For the first price of 3, update buy1 to 3, sell1 to 0, buy2 to -3, and sell2 to 0.\n3. For the second price of 3, update buy1 to 3, sell1 to 0, buy2 to -3, and sell2 to 0 (no change).\n4. For the third price of 5, update buy1 to 3, sell1 to 2, buy2 to -1, and sell2 to 2.\n5. For the fourth price of 0, update buy1 to 0, sell1 to 2, buy2 to -1, and sell2 to 2 (no change).\n6. For the fifth price of 0, update buy1 to 0, sell1 to 2, buy2 to -2, and sell2 to 2 (no change).\n7. For the sixth price of 3, update buy1 to 0, sell1 to 3, buy2 to 0, and sell2 to 3.\n8. For the seventh price of 1, update buy1 to 0, sell1 to 3, buy2 to -3, and sell2 to 3 (no change).\n9. For the eighth price of 4, update buy1 to 0, sell1 to 4, buy2 to 0, and sell2 to 4\n# Complexity\n- Time complexity:\nBeats\n88.20%\n\n- Space complexity:\nBeats\n91.19%\n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n if not prices:\n return 0\n\n # initialize variables for first buy, first sell, second buy, and second sell\n buy1, buy2 = float(\'inf\'), float(\'inf\')\n sell1, sell2 = 0, 0\n\n # iterate over prices to update buy and sell values\n for price in prices:\n # update first buy and sell values\n buy1 = min(buy1, price)\n sell1 = max(sell1, price - buy1)\n # update second buy and sell values\n buy2 = min(buy2, price - sell1)\n sell2 = max(sell2, price - buy2)\n\n return sell2\n\n``` | 29 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
Superb Dynamic Logic | best-time-to-buy-and-sell-stock-iii | 0 | 1 | # Dynamic programming\n```\nclass Solution:\n def maxProfit(self, A: List[int]) -> int:\n N=len(A)\n sell=[0]*N\n for _ in range(2):\n buy=-A[0]\n profit=0\n for i in range(1,N):\n buy=max(buy,sell[i]-A[i])\n profit=max(profit,A[i]+buy)\n sell[i]=profit\n return sell[-1]\n```\n# please upvote me it would encourage me alot\n | 7 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
O(n)time/BEATS 99.97% MEMORY/SPEED 0ms MAY 2022 | best-time-to-buy-and-sell-stock-iii | 1 | 1 | ```\n```\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* ***Java***\n```\nclass Solution {\n public int maxProfit(int[] prices) {\n if(prices == null || prices.length < 1) return 0;\n int buy1 = -prices[0], sell1 = 0, buy2 = -prices[0], sell2 = 0;\n for(int i = 1; i < prices.length; i++) {\n buy1 = Math.max(buy1, -prices[i]);\n sell1 = Math.max(sell1, buy1 + prices[i]);\n buy2 = Math.max(buy2, sell1 - prices[i]);\n sell2 = Math.max(sell2, buy2 + prices[i]);\n }\n return sell2;\n }\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 7.0MB*** (beats 100.00% / 100.00%).\n* ***C++***\n```\nclass Solution {\npublic:\n \n int solve(vector<int>&prices, int day, int transactionsLeft){\n \n if(day == prices.size()){\n return 0;\n }\n \n if(transactionsLeft == 0){\n return 0;\n }\n \n // choice 1\n // no transaction today\n int ans1 = solve(prices, day + 1, transactionsLeft);\n \n \n // choice 2\n // doing the possible transaction today \n int ans2 = 0;\n bool buy = (transactionsLeft % 2 == 0);\n \n if(buy == true){ // buy\n ans2 = -prices[day] + solve(prices, day + 1, transactionsLeft - 1);\n }else{ // sell\n ans2 = prices[day] + solve(prices, day + 1, transactionsLeft - 1);\n }\n \n return max(ans1, ans2);\n \n \n }\n \n \n int maxProfit(vector<int>& prices) {\n \n int ans = solve(prices, 0, 4); // starting with day 0 and max 4 transactions can be done\n return ans;\n \n }\n};\n```\n\n```\n```\n\n```\n```\n\n\nThe best result for the code below is ***26ms / 12.2MB*** (beats 95.42% / 82.32%).\n* ***Python***\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n buy, sell = [inf]*2, [0]*2\n for x in prices:\n for i in range(2): \n if i: buy[i] = min(buy[i], x - sell[i-1])\n else: buy[i] = min(buy[i], x)\n sell[i] = max(sell[i], x - buy[i])\n return sell[1]\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***51ms / 34.2MB*** (beats 100.00% / 84.12%).\n* ***JavaScript***\n```\nvar maxProfit = function(prices) {\n if(prices.length == 0) return 0\n \n let dp = new Array(prices.length).fill(0);\n let min = prices[0];\n let max = 0;\n for (let i = 1; i < prices.length; i++) {\n min = Math.min(min, prices[i]); // or Math.min(min, prices[i] - dp[i]) , FYI: dp[i] is 0\n max = Math.max(max, prices[i] - min);\n dp[i] = max;\n }\n \n // 1st run dp = [0,0,2,2,2,3,3,4];\n \n min = prices[0];\n max = 0;\n for (let i = 1; i < prices.length; i++) {\n min = Math.min(min, prices[i] - dp[i]); // substract dp[i] = current price - what profit we made during 1st run.\n max = Math.max(max, prices[i] - min);\n dp[i] = max;\n }\n \n // 2nd run dp = [0,0,2,2,2,5,5,6];\n \n return dp.pop();\n};\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***68ms / 44.2MB*** (beats 100.00% / 45.25%).\n* ***C***\n```\nint maxProfit(int* prices, int pricesSize){\n int *s1 = (int *)malloc(sizeof(int) * pricesSize);\n int *s2 = (int *)malloc(sizeof(int) * pricesSize);\n \n memset(s1, 0, sizeof(int) * pricesSize);\n memset(s2, 0, sizeof(int) * pricesSize);\n \n int max = INT_MIN, min= prices[0];\n\n for(int i=1; i<pricesSize-1; i++){\n if(min > prices[i]) min = prices[i]; \n \n if(max < (prices[i]- min)) max = prices[i] - min;\n s1[i] = max;\n }//for i\n \n min= INT_MIN, max=prices[pricesSize-1];\n s2[pricesSize-1] = 0;\n\n for(int i=pricesSize-2; i>=0; i--){\n if(prices[i] > max) max = prices[i]; \n if(min < (max- prices[i])) min = max - prices[i];\n \n s2[i] = min;\n }//for i\n \n max=INT_MIN;\n for(int i=0;i<pricesSize;i++){\n max = max < (s1[i] + s2[i]) ? (s1[i] + s2[i]) : max;\n }\n\n return max;\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***12ms / 32.2MB*** (beats 95% / 84%).\n* ***Swift***\n```\nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the length of the prices.\n // - space: O(1), only constant space is used.\n\n func maxProfit(_ prices: [Int]) -> Int {\n var buy1 = Int.max\n var buy2 = Int.max\n var sell1 = 0\n var sell2 = 0\n\n for price in prices {\n buy1 = min(buy1, price)\n sell1 = max(sell1, price - buy1)\n\n buy2 = min(buy2, price - sell1)\n sell2 = max(sell2, price - buy2)\n }\n\n return sell2\n }\n\n}\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC*** | 26 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
🔥Mastering Buying and Selling Stocks || From Recursion To DP || Complete Guide By Mr. Robot | best-time-to-buy-and-sell-stock-iii | 1 | 1 | # \u2753 Buying and Selling Stocks with K Transactions \u2753\n\n\n## \uD83D\uDCA1 Approach 1: Recursive Approach\n\n### \u2728 Explanation\nThe logic and approach for this solution involve recursively exploring the possibilities of buying and selling stocks with a given number of transactions. The function `Recursive` takes as input the stock prices, the current index (`ind`), a boolean flag (`b` for buy or sell), and the remaining transactions `k`. It returns the maximum profit that can be obtained. The function considers two options at each step: either buying or not buying the stock (if `b` is `true`), or selling or holding the stock (if `b` is `false`). It recursively explores these options to find the maximum profit.\n\n### \uD83D\uDCDD Dry Run\nLet\'s dry run the `Recursive` function with an example:\n- Input: `prices = [3, 2, 6, 5, 0, 3], k = 2`\n- Start with index 0, `b` is `true`, and `k` is 2.\n- At index 0, we can buy the stock, so we explore two options: \n 1. Buy it and move to index 1 (profit: -3), or\n 2. Leave it and move to index 1 (profit: 0).\n- We choose the first option (buy), and the function moves to index 1 with `k` reduced by 1.\n- This process continues, and we explore all possible options until we reach the end. The function returns the maximum profit.\n\n### \uD83D\uDD0D Edge Cases\n- The `Recursive` function handles cases where the number of transactions is limited.\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(2^n), where n is the number of stock prices. The function explores all possible combinations.\n- Space Complexity: O(n), for the function call stack.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Codes\n```cpp []\nclass Solution {\npublic:\n int Recursive(vector<int> &p, int ind, bool b, int k) {\n if (ind >= p.size() || k <= 0) return 0;\n int ans = 0;\n \n if (b) {\n return max(-p[ind] + Recursive(p, ind + 1, !b, k), Recursive(p, ind + 1, b, k));\n } else {\n return max({ p[ind] + Recursive(p, ind + 1, !b, k - 1), Recursive(p, ind + 1, b, k) });\n }\n }\n\n int maxProfit(int k, vector<int> &prices) {\n return Recursive(prices, 0, true, k);\n }\n};\n```\n\n```python []\nclass Solution:\n def recursive(self, p, ind, b, k):\n if ind >= len(p) or k <= 0:\n return 0\n\n if b:\n return max(-p[ind] + self.recursive(p, ind + 1, not b, k), self.recursive(p, ind + 1, b, k))\n else:\n return max(p[ind] + self.recursive(p, ind + 1, not b, k - 1), self.recursive(p, ind + 1, b, k))\n\n def maxProfit(self, k, prices):\n return self.recursive(prices, 0, True, k)\n```\n\n\n```java []\nclass Solution {\n public int recursive(int[] p, int ind, boolean b, int k) {\n if (ind >= p.length || k <= 0)\n return 0;\n\n int ans = 0;\n\n if (b) {\n return Math.max(-p[ind] + recursive(p, ind + 1, !b, k), recursive(p, ind + 1, b, k));\n } else {\n return Math.max(p[ind] + recursive(p, ind + 1, !b, k - 1), recursive(p, ind + 1, b, k));\n }\n }\n\n public int maxProfit(int k, int[] prices) {\n return recursive(prices, 0, true, k);\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public int Recursive(int[] p, int ind, bool b, int k) {\n if (ind >= p.Length || k <= 0)\n return 0;\n\n int ans = 0;\n\n if (b) {\n return Math.Max(-p[ind] + Recursive(p, ind + 1, !b, k), Recursive(p, ind + 1, b, k));\n } else {\n return Math.Max(p[ind] + Recursive(p, ind + 1, !b, k - 1), Recursive(p, ind + 1, b, k));\n }\n }\n\n public int MaxProfit(int k, int[] prices) {\n return Recursive(prices, 0, true, k);\n }\n}\n```\n\n\n```javascript []\nclass Solution {\n recursive(p, ind, b, k) {\n if (ind >= p.length || k <= 0)\n return 0;\n\n if (b) {\n return Math.max(-p[ind] + this.recursive(p, ind + 1, !b, k), this.recursive(p, ind + 1, b, k));\n } else {\n return Math.max(p[ind] + this.recursive(p, ind + 1, !b, k - 1), this.recursive(p, ind + 1, b, k));\n }\n }\n\n maxProfit(k, prices) {\n return this.recursive(prices, 0, true, k);\n }\n}\n```\n\n\n\n\n\n---\n\n## \uD83D\uDCA1 Approach 2: Dynamic Programming\n\n### \u2728 Explanation\nThe dynamic programming approach optimizes the previous solution by using memoization to store previously computed results. The function `RecursionWithMemoisation` is similar to the `Recursive` function but with memoization to avoid redundant calculations.\n\n### \uD83D\uDCDD Dry Run\nThe `RecursionWithMemoisation` function follows the same logic as the recursive approach but uses a memoization table to store and reuse intermediate results. This significantly improves the efficiency of the algorithm.\n\n### \uD83D\uDD0D Edge Cases\n- The `RecursionWithMemoisation` function handles cases where the number of transactions is limited.\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(n * k), where n is the number of stock prices, and k is the maximum number of transactions allowed.\n- Space Complexity: O(n * k), for the memoization table.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Codes\n```cpp []\nclass Solution {\npublic:\n int RecursionWithMemoisation(vector<int> &p, int ind, bool canBuy, int k, vector<vector<vector<int>>> &dp) {\n if (ind >= p.size() || k <= 0) return 0;\n \n if (dp[ind][canBuy][k] != -1) return dp[ind][canBuy][k];\n \n if (canBuy) {\n dp[ind][canBuy][k] = max(-p[ind] + RecursionWithMemoisation(p, ind + 1, !canBuy, k, dp), RecursionWithMemoisation(p, ind + 1, canBuy, k, dp));\n } else {\n dp[ind][canBuy][k] = max({ p[ind] + RecursionWithMemoisation(p, ind + 1, !canBuy, k - 1, dp), RecursionWithMemoisation(p, ind + 1, canBuy, k, dp) });\n }\n \n return dp[ind][canBuy][k];\n }\n \n int maxProfit(vector<int> &prices) {\n int k = 2; // change the value of k as per the question \n vector<vector<vector<int>>> dp(prices.size() + 1, vector<vector<int>>(3,vector<int>(k+1,-1)));\n return RecursionWithMemoisation(prices, 0, true, 2, dp);\n }\n};\n```\n```python []\nclass Solution:\n def recursion_with_memoization(self, p, ind, can_buy, k, dp):\n if ind >= len(p) or k <= 0:\n return 0\n\n if dp[ind][can_buy][k] != -1:\n return dp[ind][can_buy][k]\n\n if can_buy:\n dp[ind][can_buy][k] = max(-p[ind] + self.recursion_with_memoization(p, ind + 1, not can_buy, k, dp), self.recursion_with_memoization(p, ind + 1, can_buy, k, dp))\n else:\n dp[ind][can_buy][k] = max(p[ind] + self.recursion_with_memoization(p, ind + 1, not can_buy, k - 1, dp), self.recursion_with_memoization(p, ind + 1, can_buy, k, dp))\n\n return dp[ind][can_buy][k]\n\n def max_profit(self, prices):\n k = 2 # change the value of k as per the question\n dp = [[[[-1 for _ in range(k + 1)] for _ in range(3)] for _ in range(len(prices) + 1)]\n return self.recursion_with_memoization(prices, 0, True, k, dp)\n```\n\n```java []\nclass Solution {\n public int recursionWithMemoization(int[] p, int ind, boolean canBuy, int k, int[][][] dp) {\n if (ind >= p.length || k <= 0)\n return 0;\n\n if (dp[ind][canBuy ? 1 : 0][k] != -1)\n return dp[ind][canBuy ? 1 : 0][k];\n\n int maxProfit;\n if (canBuy) {\n maxProfit = Math.max(-p[ind] + recursionWithMemoization(p, ind + 1, false, k, dp), recursionWithMemoization(p, ind + 1, true, k, dp));\n } else {\n maxProfit = Math.max(p[ind] + recursionWithMemoization(p, ind + 1, false, k - 1, dp), recursionWithMemoization(p, ind + 1, true, k, dp));\n }\n\n dp[ind][canBuy ? 1 : 0][k] = maxProfit;\n return maxProfit;\n }\n\n public int maxProfit(int[] prices) {\n int k = 2; // change the value of k as per the question\n int[][][] dp = new int[prices.length + 1][3][k + 1];\n for (int i = 0; i <= prices.length; i++) {\n for (int j = 0; j < 3; j++) {\n Arrays.fill(dp[i][j], -1);\n }\n }\n return recursionWithMemoization(prices, 0, true, k, dp);\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public int RecursionWithMemoization(int[] p, int ind, bool canBuy, int k, int[][][] dp) {\n if (ind >= p.Length || k <= 0)\n return 0;\n\n if (dp[ind][canBuy ? 1 : 0][k] != -1)\n return dp[ind][canBuy ? 1 : 0][k];\n\n int maxProfit;\n if (canBuy) {\n maxProfit = Math.Max(-p[ind] + RecursionWithMemoization(p, ind + 1, false, k, dp), RecursionWithMemoization(p, ind + 1, true, k, dp));\n } else {\n maxProfit = Math.Max(p[ind] + RecursionWithMemoization(p, ind + 1, false, k - 1, dp), RecursionWithMemoization(p, ind + 1, true, k, dp));\n }\n\n dp[ind][canBuy ? 1 : 0][k] = maxProfit;\n return maxProfit;\n }\n\n public int MaxProfit(int[] prices) {\n int k = 2; // change the value of k as per the question\n int[][][] dp = new int[prices.Length + 1][][];\n for (int i = 0; i <= prices.Length; i++) {\n dp[i] = new int[3][];\n for (int j = 0; j < 3; j++) {\n dp[i][j] = new int[k + 1];\n for (int l = 0; l <= k; l++) {\n dp[i][j][l] = -1;\n }\n }\n }\n return RecursionWithMemoization(prices, 0, true, k, dp);\n }\n}\n```\n\n\n\n\n\n---\n\n## \uD83D\uDCA1 Approach 3: Bottom-Up Dynamic Programming\n\n### \u2728 Explanation\nThe bottom-up dynamic programming approach solves the problem by iteratively calculating the maximum profit for each possible state. The function `bottomup` uses a 3D DP array to store results and iterates through the stock prices, transactions, and buying/selling states.\n\n### \uD83D\uDCDD Dry Run\nThe `bottomup` function iterates through the stock prices, transactions, and buying/selling states, filling in the DP table with the maximum profit at each state. It starts from the last day and works backward to compute the final result.\n\n### \uD83D\uDD0D Edge Cases\n- The `bottomup` function handles cases where the number of transactions is limited.\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n- Time Complexity: O(n * K), where n is the number of stock prices, and K is the maximum number of transactions allowed.\n- Space Complexity: O(n * 2 * K), for the 3D DP table.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBB Codes\n```cpp []\nclass Solution {\npublic:\n int bottomup(int K, vector<int> &p) {\n vector<vector<vector<int> > > dp(p.size() + 1, vector<vector<int>>(3, vector<int>(K + 1, 0)));\n \n for (int ind = p.size() - 1; ind >= 0; ind--) {\n for (int b = 0; b <= 1; b++) {\n for (int k = 1; k <= K;\n\n k++) {\n if (b) {\n dp[ind][b][k] = max(-p[ind] + dp[ind + 1][!b][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = max(p[ind] + dp[ind + 1][!b][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n int maxProfit(int k, vector<int> &prices) {\n return bottomup(k, prices);\n }\n};\n```\n\n\n```python []\nclass Solution:\n def bottomup(self, K, p):\n dp = [[[0 for _ in range(K + 1)] for _ in range(3)] for _ in range(len(p) + 1)]\n \n for ind in range(len(p) - 1, -1, -1):\n for b in range(2):\n for k in range(1, K + 1):\n if b:\n dp[ind][b][k] = max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k])\n else:\n dp[ind][b][k] = max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k])\n \n return dp[0][1][K]\n\n def maxProfit(self, k, prices):\n return self.bottomup(k, prices)\n```\n\n\n```java []\nclass Solution {\n public int bottomup(int K, int[] p) {\n int[][][] dp = new int[p.length + 1][3][K + 1];\n \n for (int ind = p.length - 1; ind >= 0; ind--) {\n for (int b = 0; b <= 1; b++) {\n for (int k = 1; k <= K; k++) {\n if (b == 1) {\n dp[ind][b][k] = Math.max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = Math.max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n public int maxProfit(int k, int[] prices) {\n return bottomup(k, prices);\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public int BottomUp(int K, int[] p) {\n int[][][] dp = new int[p.Length + 1][][];\n for (int i = 0; i <= p.Length; i++) {\n dp[i] = new int[3][];\n for (int j = 0; j < 3; j++) {\n dp[i][j] = new int[K + 1];\n }\n }\n \n for (int ind = p.Length - 1; ind >= 0; ind--) {\n for (int b = 0; b <= 1; b++) {\n for (int k = 1; k <= K; k++) {\n if (b == 1) {\n dp[ind][b][k] = Math.Max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = Math.Max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n public int MaxProfit(int k, int[] prices) {\n return BottomUp(k, prices);\n }\n}\n```\n\n```javascript []\nclass Solution {\n bottomUp(K, p) {\n const dp = new Array(p.length + 1);\n for (let i = 0; i <= p.length; i++) {\n dp[i] = new Array(3);\n for (let j = 0; j < 3; j++) {\n dp[i][j] = new Array(K + 1).fill(0);\n }\n }\n\n for (let ind = p.length - 1; ind >= 0; ind--) {\n for (let b = 0; b <= 1; b++) {\n for (let k = 1; k <= K; k++) {\n if (b === 1) {\n dp[ind][b][k] = Math.max(-p[ind] + dp[ind + 1][0][k], dp[ind + 1][b][k]);\n } else {\n dp[ind][b][k] = Math.max(p[ind] + dp[ind + 1][1][k - 1], dp[ind + 1][b][k]);\n }\n }\n }\n }\n return dp[0][1][K];\n }\n\n maxProfit(k, prices) {\n return this.bottomUp(k, prices);\n }\n}\n```\n\n---\n\n#\n\n---\n\n## \uD83D\uDCAF Related Questions and Practice\nHere are some related questions and practice problems to further enhance your coding skills:\n\n1. [Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock/)\n2. [Best Time to Buy and Sell Stock II](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/)\n3. [Best Time to Buy and Sell Stock III](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/)\n4. [Best Time to Buy and Sell Stock IV](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/)\n\nFeel free to explore these problems to gain more experience and understanding of similar concepts.\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n-- *MR. ROBOT SIGNING OFF*\n\n---\n | 1 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
Python || DP || Recursion->Space Optimization | best-time-to-buy-and-sell-stock-iii | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(2^n)\n#Space Complexity: O(n)\nclass Solution1:\n def maxProfit(self, prices: List[int]) -> int:\n def solve(ind,buy,cap):\n if ind==n or c==0:\n return 0\n profit=0\n if buy==0: # buy a stock\n take=-prices[ind]+solve(ind+1,1,cap)\n not_take=0+solve(ind+1,0,cap)\n profit=max(take,not_take)\n else: # sell a stock\n take=prices[ind]+solve(ind+1,0,cap-1)\n not_take=0+solve(ind+1,1,cap)\n profit=max(take,not_take)\n return profit\n n=len(prices)\n return solve(0,0,2)\n\n#Memoization (Top-Down)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n*2*3) + O(n)\nclass Solution2:\n def maxProfit(self, prices: List[int]) -> int:\n def solve(ind,buy,cap):\n if ind==n or cap==0:\n return 0\n if dp[ind][buy][cap]!=-1:\n return dp[ind][buy][cap]\n profit=0\n if buy==0:\n take=-prices[ind]+solve(ind+1,1,cap)\n not_take=0+solve(ind+1,0,cap)\n profit=max(take,not_take)\n else:\n take=prices[ind]+solve(ind+1,0,cap-1)\n not_take=0+solve(ind+1,1,cap)\n profit=max(take,not_take)\n dp[ind][buy][cap]=profit\n return dp[ind][buy][cap]\n n=len(prices)\n dp=[[[ -1 for _ in range(3)] for _ in range(2)] for _ in range(n)]\n return solve(0,0,2)\n \n#Tabulation (Bottom-Up)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n*2*3)\nclass Solution3:\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n dp=[[[0 for _ in range(3)] for _ in range(2)] for _ in range(n+1)]\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n for cap in range(1,3):\n profit=0\n if buy==0:\n take=-prices[ind]+dp[ind+1][1][cap]\n not_take=0+dp[ind+1][0][cap]\n profit=max(take,not_take)\n else:\n take=prices[ind]+dp[ind+1][0][cap-1]\n not_take=0+dp[ind+1][1][cap]\n profit=max(take,not_take)\n dp[ind][buy][cap]=profit\n return dp[0][0][2]\n\n#Space Optimization\n#Time Complexity: O(n^2)\n#Space Complexity: O(1)\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n ahead=[[0]*3 for _ in range(2)]\n curr=[[0]*3 for _ in range(2)]\n for ind in range(n-1,-1,-1):\n for buy in range(2):\n for cap in range(1,3):\n profit=0\n if buy==0:\n take=-prices[ind]+ahead[1][cap]\n not_take=0+ahead[0][cap]\n profit=max(take,not_take)\n else:\n take=prices[ind]+ahead[0][cap-1]\n not_take=0+ahead[1][cap]\n profit=max(take,not_take)\n curr[buy][cap]=profit\n ahead=curr[:]\n return curr[0][2]\n```\n**An upvote will be encouraging** | 3 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
Python O(n) by DP // Reduction [w/ Visualization] | best-time-to-buy-and-sell-stock-iii | 0 | 1 | Python sol by DP and state machine\n\n---\n\n**State machine diagram**\n\n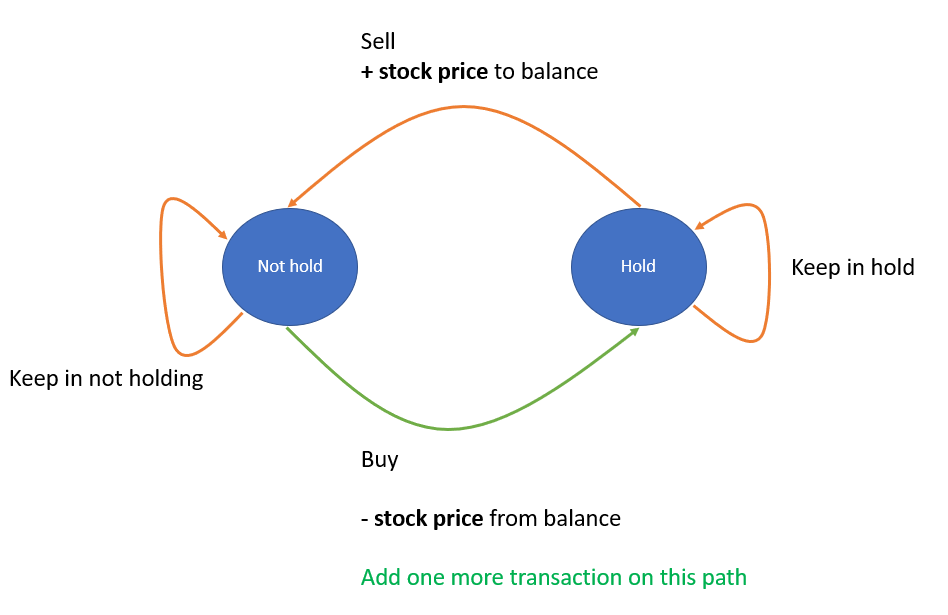\n\n---\n\n**Implementation** by DP:\n\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n \n\t\t\'\'\'\n\t\tdp_2_hold: max profit with 2 transactions, and in hold state\n\t\tdp_2_not_hold: max profit with 2 transactions, and not in hold state\n \n\t\tdp_1_hold: max profit with 1 transaction, and in hold state\n\t\tdp_1_not_hold: max profit with 1 transaction, and not in hold state\n\t\t\n\t\tNote: it is impossible to have stock in hand and sell on first day, therefore -infinity is set as initial profit value for hold state\n\t\t\'\'\'\n\t\t\n\t\tdp_2_hold, dp_2_not_hold = -float(\'inf\'), 0\n dp_1_hold, dp_1_not_hold = -float(\'inf\'), 0\n \n for stock_price in prices:\n \n\t\t\t# either keep being in not-hold state, or sell with stock price today\n dp_2_not_hold = max( dp_2_not_hold, dp_2_hold + stock_price )\n\t\t\t\n\t\t\t# either keep being in hold state, or just buy with stock price today ( add one more transaction )\n dp_2_hold = max( dp_2_hold, dp_1_not_hold - stock_price )\n \n\t\t\t# either keep being in not-hold state, or sell with stock price today\n dp_1_not_hold = max( dp_1_not_hold, dp_1_hold + stock_price )\n\t\t\t\n\t\t\t# either keep being in hold state, or just buy with stock price today ( add one more transaction )\n dp_1_hold = max( dp_1_hold, 0 - stock_price )\n \n \n return dp_2_not_hold\n```\n\n---\n\nor, we can use **reduction** from ( general template Leetcode #188 ) **Trade at most k times** with k=2 to solve this problem.\n\nReduction from [Leetcode #188 Best Time to Buy and Sell Stock IV](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/)\n<details>\n<summary>Click to show source code</summary>\n\n```\nclass Solution:\n\tdef maxProfit(self, prices: List[int]) -> int:\n\t\t\n\t\t# Reduction from Leetcode #188 Best Time to Buy and Sell Stock IV\n\t\tdef trade_at_most_k_times( k: int, prices: List[int]) -> int:\n\n\t\t\tn = len(prices)\n\n\t\t\tif n == 0:\n\n\t\t\t\t## Base case:\n\t\t\t\t# Price sequence is empty, we can do nothing : )\n\t\t\t\treturn 0\n\n\n\t\t\t## General case:\n\n\t\t\t# DP[ k ][ d ] = max profit on k, d\n\t\t\t# where k stands for k-th transaction, d stands for d-th trading day.\n\t\t\tdp = [ [ 0 for _ in range(n)] for _ in range(k+1) ]\n\n\n\t\t\t# Update by each transction as well as each trading day\n\t\t\tfor trans_k in range(1, k+1):\n\n\t\t\t\t# Balance before 1st transaction must be zero\n\t\t\t\t# Buy stock on first day means -prices[0]\n\t\t\t\tcur_balance_with_buy = 0 - prices[0]\n\n\t\t\t\tfor day_d in range(1, n):\n\n\t\t\t\t\t# Either we have finished all k transactions before, or just finished k-th transaction today\n\t\t\t\t\tdp[trans_k][day_d] = max( dp[trans_k][day_d-1], cur_balance_with_buy + prices[day_d] )\n\n\t\t\t\t\t# Either keep holding the stock we bought before, or just buy in today\n\t\t\t\t\tcur_balance_with_buy = max(cur_balance_with_buy, dp[trans_k-1][day_d-1] - prices[day_d] )\n\n\t\t\treturn dp[k][n-1]\n\t\t# --------------------------------------------\n\t\treturn trade_at_most_k_times(k=2, prices=prices)\n```\n</br>\n</details>\n\n\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #121 Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock)\n\n[Leetcode #122 Best Time to Buy and Sell Stock II](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii)\n\n[Leetcode #123 Best Time to Buy and Sell Stock III ](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii)\n\n[Leetcode #188 Best Time to Buy and Sell Stock IV ](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv)\n\n[Leetcode #309 Best Time to Buy and Sell Stock with Cooldown](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown)\n\n[Leetcode #714 Best Time to Buy and Sell Stock with Transaction Fee ](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee) \n\n--- | 41 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
Easy O(n) solution, no DP, Python | best-time-to-buy-and-sell-stock-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe first split the question to 3 parts: at most 2 trades == max(0 trade, 1 trade, 2 trades)\n\nmaximum profit for doing exactly 0 trade is easy (it will be 0)\nmaximum profit for doing exactly 1 trade is easy (can be calculate in linear time)\n\nFor doing exactly 2 trades, we first iterate through the `prices` array in reverse, calculate and stores the maximum obtainable profit from day `i` to day `n` where `n` is the last day.\n\nAfter we obtain this result, we again iterate through `prices` in normal order calculating the maximum obtainable profit from day `0` to day `i`, and since we have the maximum profit from day `i+1` to the last day already, the profit of doing 2 trades will simply be the sum of that.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPlease see comments for the detailed implementation.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n n = len(prices)\n\n # Profit if do **exactly** 1 transaction\n def maxOneProfit():\n curMin = prices[0]\n profit = -float("inf")\n for i in range(1, n):\n profit = max(profit, prices[i] - curMin)\n curMin = min(curMin, prices[i])\n return profit\n\n # If only 1 price, we cannot do any trade\n if len(prices) == 1:\n return 0\n\n # If less than 4 prices, we can only do 1 or 0 trade\n if len(prices) < 4:\n return max(0, maxOneProfit())\n\n\n\n #### Code for **exactly** 2 transactions ####\n\n # back[i] means maximum obtainable possible profit from day i to day n\n # here we use a reversed logic compared to maxOneProfit()\n back = [-1] * n\n curMax = prices[-1]\n profit = -float("inf")\n for i in range(n-2, -1, -1):\n profit = max(profit, curMax - prices[i])\n curMax = max(curMax, prices[i])\n back[i] = profit\n \n # Now we iterate from day 1, calculate maximum obtainable profit from day 0 to day i\n curMin = prices[0]\n profit = -float("inf")\n result = -float("inf")\n for i in range(1, n-2):\n profit = max(profit, prices[i] - curMin)\n result = max(result, profit + back[i+1]) # result stores the sum of two maximum obtainable profit (day 0-i, day (i+1)-n)\n curMin = min(curMin, prices[i])\n\n #### Code for **exactly** 2 transactions ####\n\n\n # At the end we return the max of {0 trade, 1 trade and 2 trade}\n return max(0, maxOneProfit(), result)\n\n``` | 3 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
[Python 3] Most Intuitive Approach | best-time-to-buy-and-sell-stock-iii | 0 | 1 | # Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n initial = 0\n bought1 = -inf\n sold1 = 0\n bought2 = -inf\n sold2 = 0\n for x in prices:\n sold2 = max(bought2 + x, sold2)\n bought2 = max(sold1 - x, bought2)\n sold1 = max(bought1 + x, sold1)\n bought1 = max(initial - x, bought1)\n return sold2\n\n```\n\n# Complexity\n- Time complexity: $O(N)$\n\n- Space complexity: $O(1)$\n | 3 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
Python3 Easy Solution with Comments | best-time-to-buy-and-sell-stock-iii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxProfit(self, prices: List[int]) -> int:\n buy1 = buy2 = float("inf")\n profit1 = profit2 = 0\n \n # Iterate through the prices and update the maximum profits\n for price in prices:\n # Update the price at which we should buy the first stock\n buy1 = min(buy1, price)\n # Update the profit we can make if we sell the first stock at this price\n profit1 = max(profit1, price - buy1)\n # Update the price at which we should buy the second stock\n buy2 = min(buy2, price - profit1)\n # Update the profit we can make if we sell the second stock at this price\n profit2 = max(profit2, price - buy2)\n \n # Return the maximum profit we can achieve after the second transaction\n return profit2\n\n\n\n\n\n``` | 4 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
MOST OPTIMIZED PYTHON SOLUTION | best-time-to-buy-and-sell-stock-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N*2*3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N*2*3)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # def dp(self,i,buy,tq,prices,n,dct):\n # if i==n:\n # return 0\n # if tq==0:\n # return 0\n # if (i,buy,tq) in dct:\n # return dct[(i,buy,tq)]\n # if buy:\n # x=max(self.dp(i+1,buy,tq,prices,n,dct),self.dp(i+1,0,tq,prices,n,dct)-prices[i])\n # else:\n # x=max(self.dp(i+1,buy,tq,prices,n,dct),self.dp(i+1,1,tq-1,prices,n,dct)+prices[i])\n # dct[(i,buy,tq)]=x\n # return x\n \n def maxProfit(self, prices: List[int]) -> int:\n n=len(prices)\n # dp=[[[0]*3 for _ in range(2)] for _ in range(n+1)]\n ahd=[[0]*3 for _ in range(2)]\n for i in range(n-1,-1,-1):\n curr=[[0]*3 for _ in range(2)] \n for j in range(1,-1,-1):\n for k in range(1,3):\n if j:\n curr[j][k]=max(ahd[j][k],ahd[0][k]-prices[i])\n else:\n curr[j][k]=max(ahd[j][k],ahd[1][k-1]+prices[i])\n ahd=curr\n # print(dp)\n return ahd[1][2]\n\n\n\n\n\n # return self.dp(0,1,2,prices,n,{})\n \n``` | 2 | You are given an array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
Find the maximum profit you can achieve. You may complete **at most two transactions**.
**Note:** You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
**Example 1:**
**Input:** prices = \[3,3,5,0,0,3,1,4\]
**Output:** 6
**Explanation:** Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** 4
**Explanation:** Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.
**Example 3:**
**Input:** prices = \[7,6,4,3,1\]
**Output:** 0
**Explanation:** In this case, no transaction is done, i.e. max profit = 0.
**Constraints:**
* `1 <= prices.length <= 105`
* `0 <= prices[i] <= 105` | null |
A very concise python3 solution | binary-tree-maximum-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n self.ans = float("-inf")\n def dfs(node):\n if node:\n if not node.left and not node.right:\n self.ans = max(self.ans, node.val)\n return node.val if node.val > 0 else 0\n ls = dfs(node.left)\n rs = dfs(node.right)\n self.ans = max(self.ans, ls + node.val + rs, ls + node.val, rs + node.val, node.val)\n if ls > rs and ls > 0:\n return ls + node.val\n elif ls <= rs and rs > 0:\n return rs + node.val\n else:\n return node.val if node.val > 0 else 0\n else:\n return 0\n dfs(root)\n\n return self.ans\n``` | 1 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
CodeDominar solution | binary-tree-maximum-path-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int: \n max_ans = float(\'-inf\')\n def helper(root):\n nonlocal max_ans\n if not root:\n return 0\n l = helper(root.left)\n r = helper(root.right)\n max_ans = max(max_ans,root.val,root.val+l,root.val+r,root.val+l+r)\n return max(root.val,root.val+l,root.val+r)\n helper(root)\n return max_ans\n\n\n \n``` | 2 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
Recursive approach✅ | O( n)✅ | Python and C++(Step by step explanation)✅ | binary-tree-maximum-path-sum | 0 | 1 | # Intuition\nThe problem involves finding the maximum path sum in a binary tree. A path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections.\n\n# Approach\nThe approach is to perform a Depth-First Search (DFS) traversal of the binary tree. At each node, calculate the maximum path sum that includes the current node. Update the global maximum path sum if needed. The DFS function returns the maximum path sum that extends from the current node to its parent.\n\n1. **DFS Function**: Implement a recursive DFS function that calculates the maximum path sum at each node.\n\n **Reason**: Recursive DFS is a natural fit for exploring the tree and updating the maximum path sum.\n\n2. **Base Case**: Check for the base case where the current node is `None`. If true, return `0`.\n\n **Reason**: A `None` node contributes zero to the path sum.\n\n3. **Recursive Calls**: Recursively calculate the maximum path sum for the left and right subtrees.\n\n **Reason**: To explore the entire tree and compute the maximum path sum.\n\n4. **Update Global Maximum**: Update the global maximum path sum considering the current node.\n\n **Reason**: The maximum path sum may include the current node and its left and right subtrees.\n\n5. **Return Maximum Path Sum**: Return the maximum path sum that extends from the current node to its parent.\n\n **Reason**: The DFS function should provide the maximum path sum that includes the current node.\n\n6. **Initial Call**: Perform the initial call to the DFS function with the root of the tree.\n\n **Reason**: Start the DFS traversal from the root.\n\n7. **Return Result**: Return the final result, which represents the maximum path sum in the entire binary tree.\n\n **Reason**: The result should reflect the maximum path sum in the binary tree.\n\n# Complexity\n- **Time complexity**: O(n)\n - The algorithm processes each node once.\n- **Space complexity**: O(h)\n - The recursion stack space is proportional to the height of the tree, where h is the height.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n ans = [root.val]\n\n def DFS(root):\n if root == None:\n return 0\n\n lmax = DFS(root.left)\n rmax = DFS(root.right)\n lmax = 0 if lmax < 0 else lmax\n rmax = 0 if rmax < 0 else rmax\n\n ans[0] = max(ans[0] , root.val + lmax + rmax)\n\n return root.val + max(lmax , rmax) \n\n DFS(root) \n return ans[0] \n \n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n int maxPathSum(TreeNode* root) {\n int maxPath = INT_MIN;\n DFS(root, maxPath);\n return maxPath;\n }\nprivate:\n int DFS(TreeNode* root, int& maxPath) {\n if (root == NULL) {\n return 0;\n }\n \n int lmax = max(DFS(root->left, maxPath), 0);\n int rmax = max(DFS(root->right, maxPath), 0);\n \n maxPath = max(maxPath, root->val + lmax + rmax);\n \n return root->val + max(lmax, rmax);\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n\n | 5 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
Self-Explanatory Python Code, Check Concise Version In The Comment! | binary-tree-maximum-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nmaxlen gives return the max length from the node down to leaves\n\nnodeMax is the max length joining two branches from left and right, and has to include the current node.val. Basically, the path is like this ^\n\ndfs is just looping throught the tree and at each node, it uses the side effect to update the max for rs\n\nPretty self explanatory, the concise code is just to incorporate this thought into one recursive function that uses side effect to update the rs and return what maxlen returns\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: linear\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: linear\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n @cache\n def maxlen(node):\n if not node: return 0\n return max([maxlen(node.left), maxlen(node.right), 0])+node.val\n \n @cache\n def nodeMax(node):\n if not node: return 0\n return max(0, maxlen(node.left))+max(0, maxlen(node.right))+node.val\n\n # if not root: return 0\n rs = -float(\'inf\')\n @cache\n def dfs(node):\n nonlocal rs\n if not node: return\n rs=max(rs, nodeMax(node))\n dfs(node.left)\n dfs(node.right)\n\n dfs(root)\n return rs\n\n\n\n \n``` | 0 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
Recursive O(n) solution | binary-tree-maximum-path-sum | 0 | 1 | # Intuition\r\nThe first thing tha comes to mind is using recursion. This is correct but we must be careful. \r\n\r\n# Approach\r\nEach node has its best path, that will be passed up to the father, thanks to recursion. But what are the best path starting from node?\r\n\r\nThere are three possibilities:\r\n\r\n- **value** of root + best path for the **left** child\r\n- **value** of root + best path for the **right** child\r\n- **value** of root\r\n\r\nNotice how we consider that the children\'s path could be terrible so the best path is the root only.\r\n\r\nThese are the best paths specifically if we start from the root node. But we cannot assume that the result of the aglorithm starting from the root path is the correct answer\r\n\r\nMaybe the best path start\'s from an internal node. For this reason, at every iteration we change the real answer, which is passed by parameter.\r\nIn particular, in each iteration we have that the solution is equal to the max value from:\r\n\r\n- itself\r\n- **left** + **right** + value of **root**\r\n- the **best path** starting from **this node**\r\n\r\nThe second option is something we have to consider for the final solution, however see how it cannot be a valid result to pass to the father node.\r\n\r\n# Complexity\r\n- Time complexity: O(n), each node is visited once\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity: O(n), in the worst case, from the root we have n recursive calls \r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```python\r\nclass TreeNode:\r\n def __init__(self, val=0, left=None, right=None):\r\n self.val = val\r\n self.left = left\r\n self.right = right\r\n\r\ndef maxPathSum(root: TreeNode, m: list[int]) -> int:\r\n res = 0\r\n if root:\r\n left = maxPathSum(root.left, m)\r\n right = maxPathSum(root.right, m)\r\n res = max(left+root.val, right+root.val, root.val)\r\n m[0] = max(m[0], left+right+root.val, res)\r\n return res\r\n\r\nclass Solution:\r\n def maxPathSum(self, root: TreeNode) -> int:\r\n m = [-1001]\r\n maxPathSum(root, m)\r\n return m[0]\r\n \r\n``` | 2 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
Easy Python Recursion with Explanation | Beats 92% | binary-tree-maximum-path-sum | 0 | 1 | # Intuition\nAt each node either that (node) or (node + left subtree) or (node + right subtree) or (left subtree + node + rightsubtree) is the maximum that we can get.\n\nBut, if we reach that node either we can stay ther, or go to left side or right side, we can not come from some other node and then traverse the complete subtree from that node.\nThat is why we return maximum of (node) or (node +left) or (node + right).\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(V+E)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(h)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n ans = float(\'-inf\') \n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n def dfs(root) :\n if root:\n lmax = dfs(root.left)\n rmax = dfs(root.right) \n curr = root.val\n cmax = max(curr,curr+lmax,curr+rmax,lmax+curr+rmax)\n if cmax > self.ans :\n self.ans = cmax \n return max(curr,curr+lmax,curr+rmax)\n else:\n return 0\n dfs(root)\n return self.ans\n \n``` | 2 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
Most effective and simple recursive solution with explanation | binary-tree-maximum-path-sum | 1 | 1 | \n\n# Approach\n- **Recursive Function (findMaxPathSum):** For each node, calculate the maximum path sum that includes the current node. This sum is the maximum of either the left subtree\'s sum or the right subtree\'s sum, plus the current node\'s value. Update maxi with the maximum of the current maxi value and the sum of left subtree, right subtree, and the current node\'s value.\n\n- **Base Case:** If the node is NULL, return 0, indicating an empty path.\n\n- **maxPathSum Function:** Initialize maxi to negative infinity. Call the findMaxPathSum function to calculate the maximum path sum, and then return the final maxi value.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n```C++ []\nclass Solution {\npublic:\n int findMaxPathSum(TreeNode* node, int & maxi) {\n if (node== NULL) return 0;\n int left= max(0, findMaxPathSum(node-> left, maxi));\n int right = max(0, findMaxPathSum(node-> right, maxi));\n maxi = max(maxi, (left + right) +node->val);\n return max(left, right) +node->val;\n}\n int maxPathSum(TreeNode* root) {\n int maxi = INT_MIN;\n findMaxPathSum(root, maxi);\n return maxi;\n }\n};\n```\n```python3 []\nclass Solution:\n def maxPathSum(self, root: TreeNode) -> int:\n def findMaxPathSum(node):\n nonlocal maxi\n if not node:\n return 0\n left = max(findMaxPathSum(node.left), 0)\n right = max(findMaxPathSum(node.right), 0)\n maxi = max(maxi, left + right + node.val)\n return max(left, right) + node.val\n \n maxi = float(\'-inf\')\n findMaxPathSum(root)\n return maxi\n```\n```Java []\npublic class Solution {\n public int maxPathSum(TreeNode root) {\n int[] maxi = {Integer.MIN_VALUE}; // Using an array to store the max value\n findMaxPathSum(root, maxi);\n return maxi[0];\n }\n \n private int findMaxPathSum(TreeNode node, int[] maxi) {\n if (node == null) return 0;\n int left = Math.max(0, findMaxPathSum(node.left, maxi));\n int right = Math.max(0, findMaxPathSum(node.right, maxi));\n maxi[0] = Math.max(maxi[0], left + right + node.val);\n return Math.max(left, right) + node.val;\n }\n}\n```\n | 1 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
Solution | binary-tree-maximum-path-sum | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxPathSum(TreeNode* root) {\n int res = INT_MIN;\n find_max(root, res);\n return res;\n }\n\n int find_max(TreeNode* root, int& res) {\n if (root == nullptr) return 0;\n\n int left_max = find_max(root->left, res);\n int right_max = find_max(root->right, res);\n\n int sum = root->val;\n if (left_max > 0) sum += left_max;\n if (right_max > 0) sum += right_max;\n if (sum > res) res = sum;\n\n int root_max = root->val;\n root_max += max(0, max(left_max, right_max));\n return root_max;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n self.sum = root.val\n def maxHelper( root: Optional[TreeNode]) -> int:\n l, r = 0, 0\n if root.left != None:\n l += maxHelper(root.left)\n if root.right != None:\n r += maxHelper(root.right)\n\n sum1, sum2 = root.val, root.val\n if l > 0:\n sum1 += l\n if r > 0:\n sum1 += r\n \n if l > 0 or r > 0:\n sum2 += l if l > r else r\n\n self.sum = sum2 if self.sum < sum2 else self.sum\n self.sum = sum1 if self.sum < sum1 else self.sum\n return sum2\n if root:\n maxHelper(root)\n return self.sum\n```\n\n```Java []\nclass Solution {\n\n int ans = Integer.MIN_VALUE;\n\n public int maxPathSum(TreeNode root) {\n maxPathSumHelper(root);\n return ans;\n }\n\n public int maxPathSumHelper(TreeNode root) {\n\n if(root == null) return 0;\n int left = maxPathSumHelper(root.left);\n int right = maxPathSumHelper(root.right);\n int max = Math.max(root.val, Math.max(Math.max(root.val+left, root.val+right), root.val+left+right)); \n ans = Math.max(ans, max);\n return Math.max(root.val, Math.max(root.val+left, root.val+right));\n }\n}\n```\n | 4 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
✅ Explained - Simple and Clear Python3 Code✅ | binary-tree-maximum-path-sum | 0 | 1 | The logic for finding the maximum path sum in a binary tree involves traversing the tree in a post-order manner.\n\nAt each node, we consider three scenarios: \n1. the maximum path sum passing through the current node and including its left child\n2. the maximum path sum passing through the current node and including its right child\n3. the maximum path sum being just the value of the current node itself.\n\nWe update the value of each node to represent the maximum path sum possible from that node. \n\nThroughout the traversal, we keep track of the overall maximum path sum found so far and return it as the result.\n\n\n\n\n\n\n# Code\n```\n\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n self.res=root.val\n def traverse_leaf_to_root(root):\n if root is None:\n return\n\n if root.left is None and root.right is None:\n self.res=max(self.res,root.val)\n return\n\n traverse_leaf_to_root(root.left)\n traverse_leaf_to_root(root.right)\n\n vals=[root.val,root.val,root.val]\n cp=root.val\n if root.left:\n vals[1]+=root.left.val\n cp+=root.left.val\n if root.right:\n vals[2]+=root.right.val\n cp+=root.right.val\n root.val=max(vals)\n self.res=max(self.res,max(root.val,cp))\n\n res=root.val\n traverse_leaf_to_root(root)\n return self.res\n\n \n``` | 7 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
O(n)time/BEATS 99.97% MEMORY/SPEED 0ms MAY 2022 | binary-tree-maximum-path-sum | 1 | 1 | ```\n```\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* ***Java***\n```\n// just returns the nodes in post-order\npublic Iterable<TreeNode> topSort(TreeNode root) {\n Deque<TreeNode> result = new LinkedList<>();\n if (root != null) {\n Deque<TreeNode> stack = new LinkedList<>();\n stack.push(root);\n while (!stack.isEmpty()) {\n TreeNode curr = stack.pop();\n result.push(curr);\n if (curr.right != null) stack.push(curr.right);\n if (curr.left != null) stack.push(curr.left);\n }\n }\n return result;\n}\n\npublic int maxPathSum(TreeNode root) {\n int result = Integer.MIN_VALUE;\n Map<TreeNode, Integer> maxRootPath = new HashMap<>(); // cache\n maxRootPath.put(null, 0); // for simplicity we want to handle null nodes\n for (TreeNode node : topSort(root)) {\n // as we process nodes in post-order their children are already cached\n int left = Math.max(maxRootPath.get(node.left), 0);\n int right = Math.max(maxRootPath.get(node.right), 0); \n maxRootPath.put(node, Math.max(left, right) + node.val);\n result = Math.max(left + right + node.val, result);\n }\n return result;\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 7.0MB*** (beats 100.00% / 100.00%).\n* ***C++***\n```\nint maxSum(TreeNode* root, int& ans) {\n /* This function return the Branch Sum......\n So if the node is NULL then it won\'t have a branch....so the branch sum will be 0.\n */\n //Base Case\n if(root == NULL){\n return 0;\n }\n \n //Recursive Case \n //BS = Branch Sum\n int leftBS = root->val + maxSum( root->left , ans );\n int rightBS = root->val + maxSum( root->right , ans );\n \n ans = max({\n ans, //we may have found the maximum ans already\n root->val, //may be the current root val is the maximum sum possible\n leftBS, //may be the answer contain root->val + left branch value\n rightBS, //may be the answer contain root->val + right branch value\n leftBS + rightBS - root->val // may be ans conatin left branch + right branch + root->val\n // Since the root val is added twice from leftBS and rightBS so we are sunstracting it.\n });\n \n //Return the max branch Sum\n return max({ leftBS , rightBS , root->val });\n}\n\nint maxPathSum(TreeNode* root) {\n int ans = INT_MIN;\n maxSum(root, ans);\n return ans;\n}\n```\n\n```\n```\n\n```\n```\n\n\nThe best result for the code below is ***26ms / 12.2MB*** (beats 95.42% / 82.32%).\n* ***Python***\n```\nclass Solution:\n def __init__(self):\n self.maxSum = float(\'-inf\')\n def maxPathSum(self, root: TreeNode) -> int:\n def traverse(root):\n if root:\n left = traverse(root.left)\n right = traverse(root.right)\n self.maxSum = max(self.maxSum,root.val, root.val + left, root.val + right, root.val + left + right)\n return max(root.val,root.val + left,root.val + right)\n else:\n return 0\n traverse(root)\n return self.maxSum\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***51ms / 34.2MB*** (beats 100.00% / 84.12%).\n* ***JavaScript***\n```\nvar maxPathSum = function(root) {\n var max = -Number.MAX_VALUE;\n getMaxSum(root);\n return max;\n function getMaxSum(node) {\n if (!node) return 0;\n var leftSum = getMaxSum(node.left);\n var rightSum = getMaxSum(node.right);\n max = Math.max(max, node.val + leftSum + rightSum);\n return Math.max(0, node.val + leftSum, node.val + rightSum);\n }\n};\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***68ms / 44.2MB*** (beats 100.00% / 45.25%).\n* ***Kotlin***\n```\nclass Solution {\n fun maxPathSum(root: TreeNode?) = postorder(root).maxSum\n\n private fun postorder(node: TreeNode?): Res {\n if (node == null)\n return Res(Int.MIN_VALUE, 0)\n\n val (leftMaxSum, leftPathSum) = postorder(node.left)\n val (rightMaxSum, rightPathSum) = postorder(node.right)\n\n val value = node.`val`\n val sum = leftPathSum + rightPathSum + value\n\n return Res(maxOf(leftMaxSum, rightMaxSum, sum), maxOf(0, value + maxOf(leftPathSum, rightPathSum)))\n }\n\n private data class Res(val maxSum: Int, val pathSum: Int)\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***12ms / 32.2MB*** (beats 95% / 84%).\n* ***Swift***\n```\nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the number of nodes in binary tree.\n // - space: O(n), where n is the number of nodes in binary tree.\n \n func maxPathSum(_ root: TreeNode?) -> Int {\n guard let root = root else { return 0 }\n var currMaxSum = Int.min\n return max(maxPathSum(root, currMaxSum: &currMaxSum), currMaxSum)\n }\n\n \n private func maxPathSum(_ currNode: TreeNode?, currMaxSum: inout Int) -> Int {\n guard let currNode = currNode else { return 0 }\n\n let leftSum = max(maxPathSum(currNode.left, currMaxSum: &currMaxSum), 0)\n let rightSum = max(maxPathSum(currNode.right, currMaxSum: &currMaxSum), 0)\n\n currMaxSum = max(currNode.val + leftSum + rightSum, currMaxSum)\n return max(leftSum, rightSum) + currNode.val\n }\n\n}\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC*** | 20 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
DFS - Fast and Easy Solution O(N) | binary-tree-maximum-path-sum | 0 | 1 | \n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxPathSum(self, root: Optional[TreeNode]) -> int:\n self.max_path_sum = root.val\n if not root:\n return 0\n \n def DFS(root):\n if not root:\n return 0\n \n left_path_sum = max(DFS(root.left), 0)\n right_path_sum = max(DFS(root.right), 0)\n\n self.max_path_sum = max(self.max_path_sum, left_path_sum + right_path_sum + root.val)\n\n return max(left_path_sum, right_path_sum) + root.val\n\n DFS(root)\n return self.max_path_sum\n\n``` | 2 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
The **path sum** of a path is the sum of the node's values in the path.
Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.
**Example 1:**
**Input:** root = \[1,2,3\]
**Output:** 6
**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
**Example 2:**
**Input:** root = \[-10,9,20,null,null,15,7\]
**Output:** 42
**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3 * 104]`.
* `-1000 <= Node.val <= 1000` | null |
[VIDEO] Step-by-Step Visualization of Two Pointer Solution | valid-palindrome | 0 | 1 | https://www.youtube.com/watch?v=4rzENqwlVU8\n\nTo test if a string is a palindrome, we\'ll use a two pointer approach that starts at the ends of the string. At each step, if the characters at the two pointers are equal, then we\'ll move both pointers inwards and compare the next set of characters. Since a palindrome reads the same forwards and backwards, each pair of characters should be equal at each step.\n\nHowever, for this problem, we also need to ignore non-alphanumeric characters and ignore case. To do this, we\'ll use two Python string methods:\n\nThe `.isalnum()` method returns true if a string is alphanumeric, and returns false otherwise. The `.lower()` method converts the entire string into lowercase characters and returns the result.\n\nSo inside of the `while` loop, we check if the characters at index `l` and `r` are alphanumeric. If they are not, then we skip that character by moving that pointer inwards. Once both characters are alphanumeric, we convert both characters to lowercase and check for equality.\n\nIf both characters are equal to each other, then we can move on to the next set of characters by moving both pointers inwards. If, at this point, they are not equal to each other, then that means that the string is not a palindrome, so we go into the `else` block and just return false immediately.\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n l = 0\n r = len(s) - 1\n while l < r:\n if not s[l].isalnum():\n l += 1\n elif not s[r].isalnum():\n r -= 1\n elif s[l].lower() == s[r].lower():\n l += 1\n r -= 1\n else:\n return False\n\n return True\n \n``` | 8 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Easy Python Solution || Valid Palindrome? Let's Find it out..... | valid-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this function is to determine whether a given string s is a palindrome or not. A palindrome is a string that reads the same backward as forward, ignoring spaces, punctuation, and capitalization.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The function iterates through each character in the input string s.\n- It checks if each character is alphanumeric using the isalnum() method.\n- If a character is alphanumeric, it is converted to lowercase and appended to the string.\n- The resulting modified string is then compared with its reverse to check for palindromic properties.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nLet n be the length of the input string s. The time complexity of this solution is O(n) because it iterates through each character in the string once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is also O(n), where n is the length of the input string. This is because the string variable stores the alphanumeric characters, and in the worst case, it could be as long as the input string.\n\n---\n# I hope you understood the explanation. If it hlped you, please do upvote me...!!!\n\n---\n\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n # Initialize an empty string to store alphanumeric characters\n string = \'\'\n \n # Iterate through each character in the input string\n for i in s:\n # Check if the character is alphanumeric\n if i.isalnum() == True:\n # If alphanumeric, convert to lowercase and append to the \'string\'\n string += i.lower()\n \n # Check if the modified string is a palindrome\n return string == string[::-1]\n\n``` | 4 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Valid Palindrome in Python3 | valid-palindrome | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n#### Here\'s a breakdown of how the method works:\n\n1. new = ("".join(i for i in s if i.isalnum())).lower(): This line of code takes the input string s and performs the following operations:\n\n- It iterates through each character in the input string s.\n- Using a generator expression (i for i in s if i.isalnum()), it filters out non-alphanumeric characters (removes spaces, punctuation, etc.) from the input string.\n- The resulting characters are joined together using "".join(...).\n- The resulting string is then converted to lowercase using .lower(). This step ensures that the comparison for palindrome checking is case-insensitive.\n2. return new == new[::-1]: This line of code checks whether the modified string new is equal to its reverse. If new is equal to its reverse, it means that the original input string s is a palindrome, and the method returns True. Otherwise, it returns False.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n new=("".join(i for i in s if i.isalnum())).lower()\n return new==new[::-1]\n \n``` | 2 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
[Python 3] Two solutions || beats 99% || 33ms 🥷🏼 | valid-palindrome | 0 | 1 | ```python3 []\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n s = [c.lower() for c in s if c.isalnum()]\n return all (s[i] == s[~i] for i in range(len(s)//2))\n```\n```python3 []\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n i, j = 0, len(s) - 1\n while i < j:\n while i < j and not s[i].isalnum(): i += 1\n while i < j and not s[j].isalnum(): j -= 1\n\n if s[i].lower() != s[j].lower(): return False\n i += 1\n j -= 1\n\n return True\n```\nOperator **~** is the bitwise NOT operator (`~x == -x-1` => `~0 == -1` => `~1 == -2` and etc). It performs [logical negation](https://en.wikipedia.org/wiki/Negation) on a given number by flipping all of its bits:\n\n\n\n\n### Bonus: problems to practise using operator ~\n[344. Reverse String](https://leetcode.com/problems/reverse-string/description/)\n```python3 []\nclass Solution:\n def reverseString(self, s: List[str]) -> None:\n for i in range(len(s)//2):\n s[i], s[~i] = s[~i], s[i]\n```\n[1572. Matrix Diagonal Sum](https://leetcode.com/problems/matrix-diagonal-sum/description/)\n~ using to traverse by matrix antidiagonal (the second diagonal)\n```python3 []\nclass Solution:\n def diagonalSum(self, mat: List[List[int]]) -> int:\n res = 0\n for i in range(len(mat)):\n res = res + mat[i][i] + mat[i][~i]\n\n if (len(mat)) % 2:\n mid = len(mat)//2\n res -= mat[mid][mid]\n \n return res\n```\n\n\n | 39 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Python || 98% Beats ||| Simple code | valid-palindrome | 0 | 1 | # Your upvote is my motivation!\n\n\n# Code\n```\n<!-- Optimize Code -->\n\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n s1 = \'\'\n for c in s.lower():\n if c.isalnum():\n s1 += c\n\n return True if s1==s1[::-1] else False\n\n============================================================\n<!-- # Practice Code Understand -->\n============================================================\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n s1 = \'\'\n for c in s.lower():\n if c.isalpha() or c.isnumeric():\n s1 += c\n print(s1)\n\n s = s1[::-1]\n return True if s1==s else False\n``` | 20 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
2 Simple Python Solutions (Two Pointers approach (Beats 99.99%)) | valid-palindrome | 0 | 1 | # Intuition\nThe code aims to determine whether a given string is a palindrome or not. A palindrome is a string that reads the same forwards and backwards. The code uses two pointers, l and r, to traverse the string from the beginning and end simultaneously. It skips non-alphanumeric characters and compares the corresponding characters at l and r positions. If at any point the characters are not equal, the string is not a palindrome. If the pointers meet or cross each other, the string is a palindrome.\n\n# Approach\n1. Initialize l and r as the left and right pointers.\n2. While l is less than r:\n 1. Increment l until it points to an alphanumeric character.\n 2. Decrement r until it points to an alphanumeric character.\n 3. If l becomes greater than r, return True as the string is a palindrome.\n 4. Compare characters at l and r (case-insensitive):\n 1. If they are not equal, return False as the string is not a palindrome.\n 2. If they are equal, increment l and decrement r.\n3. Return True if the loop completes without finding any mismatch.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n\nSolution 1: (Two Pointers | Beats 99.99%)\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n l = 0\n r = len(s) - 1\n \n while l < r:\n \n while l < r and s[l].isalnum() == False: \n l += 1\n while r > l and s[r].isalnum() == False: \n r -= 1\n if l > r or s[l].lower() != s[r].lower():\n return False\n else:\n l += 1\n r -= 1\n return True\n \n```\n\nSolution 2: (Simple two liner)\n```\nclass Solution:\n def isPalindrome(self, s: str) -> bool:\n s = [char.lower() for char in s if char.isalnum()]\n return s == s[::-1]\n```\n\nPlease "Upvote" if you find it useful. | 39 | A phrase is a **palindrome** if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
Given a string `s`, return `true` _if it is a **palindrome**, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "A man, a plan, a canal: Panama "
**Output:** true
**Explanation:** "amanaplanacanalpanama " is a palindrome.
**Example 2:**
**Input:** s = "race a car "
**Output:** false
**Explanation:** "raceacar " is not a palindrome.
**Example 3:**
**Input:** s = " "
**Output:** true
**Explanation:** s is an empty string " " after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s` consists only of printable ASCII characters. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.