title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | partition-list | 1 | 1 | # Intuition\nCreate a small list and a big list.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n# Subscribe to my channel from here. I have 245 videos as of August 15th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/rR8weWU-WQM\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. **Initialization**:\n - Initialize two dummy nodes: `slist` and `blist`. These will serve as the heads of two separate lists, one for values less than `x` and the other for values greater than or equal to `x`.\n - Initialize two pointers `small` and `big` that initially point to the dummy nodes `slist` and `blist`, respectively.\n\n2. **Traversing the Linked List**:\n - Start traversing the input linked list `head`.\n - In each iteration:\n - Check if the value of the current node `head.val` is less than `x`.\n - If true:\n - Connect the current node to the `small.next` and then move the `small` pointer to the newly added node. This effectively appends the current node to the smaller values list.\n - If false:\n - Connect the current node to the `big.next` and then move the `big` pointer to the newly added node. This effectively appends the current node to the larger values list.\n\n3. **Finishing the Partition**:\n - Once the traversal is complete, the smaller values list ends with the last node appended to it (pointed to by the `small` pointer), and the larger values list ends with the last node appended to it (pointed to by the `big` pointer).\n\n4. **Connecting Lists**:\n - Connect the tail of the smaller values list (`small.next`) to the head of the larger values list (`blist.next`), effectively merging the two lists.\n\n5. **Finalizing the Larger Values List**:\n - Since the larger values list is now connected to the smaller values list, set the `next` pointer of the last node in the larger values list to `None` to prevent any potential circular references in the linked list.\n\n6. **Returning the Result**:\n - Return the `next` node of the `slist` dummy node, which represents the head of the modified linked list where values less than `x` are on one side and values greater than or equal to `x` are on the other side.\n\nThe algorithm efficiently partitions the original linked list into two parts based on the given value `x`. Nodes with values less than `x` are placed on one side, and nodes with values greater than or equal to `x` are placed on the other side, maintaining the relative order of the nodes within each group. The algorithm uses two dummy nodes and two pointers to create and manage the partitioned lists.\n\n# Complexity\n- Time complexity: O(n)\nThe code iterates through the entire linked list once to partition the nodes into two separate lists based on the value of x.\n\n- Space complexity: O(1)\nThe code uses a constant amount of extra space for the two dummy nodes slist and blist, as well as for the small and big pointers. The additional space used does not scale with the input size (linked list length) but remains constant throughout the execution.\n\n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n\n slist, blist = ListNode(), ListNode()\n small, big = slist, blist # dummy lists\n\n while head:\n if head.val < x:\n small.next = head\n small = small.next\n else:\n big.next = head\n big = big.next\n\n head = head.next\n\n small.next = blist.next\n big.next = None # prevent linked list circle\n\n return slist.next\n```\n```javascript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} head\n * @param {number} x\n * @return {ListNode}\n */\nvar partition = function(head, x) {\n let slist = new ListNode();\n let blist = new ListNode();\n let small = slist;\n let big = blist;\n\n while (head !== null) {\n if (head.val < x) {\n small.next = head;\n small = small.next;\n } else {\n big.next = head;\n big = big.next;\n }\n\n head = head.next;\n }\n\n small.next = blist.next;\n big.next = null;\n\n return slist.next; \n};\n```\n```java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode partition(ListNode head, int x) {\n ListNode slist = new ListNode();\n ListNode blist = new ListNode();\n ListNode small = slist;\n ListNode big = blist;\n\n while (head != null) {\n if (head.val < x) {\n small.next = head;\n small = small.next;\n } else {\n big.next = head;\n big = big.next;\n }\n\n head = head.next;\n }\n\n small.next = blist.next;\n big.next = null;\n\n return slist.next; \n }\n}\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* partition(ListNode* head, int x) {\n ListNode* slist = new ListNode(0, nullptr);\n ListNode* blist = new ListNode(0, nullptr);\n ListNode* small = slist;\n ListNode* big = blist;\n\n while (head != nullptr) {\n if (head->val < x) {\n small->next = head;\n small = small->next;\n } else {\n big->next = head;\n big = big->next;\n }\n\n head = head->next;\n }\n\n small->next = blist->next;\n big->next = nullptr;\n\n return slist->next; \n }\n};\n```\n\n### Thank you for reading. Please upvote the article and don\'t forget to subscribe to my youtube channel!\n | 22 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Concise Recursion in Python Less than 10 Lines, Faster than 90% | partition-list | 0 | 1 | # Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n def traverse(v, lo=-inf, hi=inf, u=None):\n if not v:\n return u\n if lo <= v.val < hi:\n return ListNode(v.val, traverse(v.next, lo, hi, u))\n return traverse(v.next, lo, hi, u)\n \n return traverse(head, -inf, x, traverse(head, x, inf))\n \n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Commented Code || Line by line explained || C++ || java || Python | partition-list | 1 | 1 | \uD83C\uDDEE\uD83C\uDDF3 Happy independence Day \uD83C\uDDEE\uD83C\uDDF3\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThis approach uses two separate lists to partition the nodes.\n\nFor detailed explanation you can refer to my youtube channel (hindi Language)\nhttps://youtu.be/WOA1IuoONXc\n or link in my profile.Here,you can find any solution in playlists monthwise from june 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Initialize two new linked lists, `less` and `greater`, to hold nodes with values less than `x` and greater than or equal to `x`, respectively.\n\n2. Traverse the original linked list, `head`, and for each node:\n - If the node\'s value is less than `x`, append it to the `less` list.\n - If the node\'s value is greater than or equal to `x`, append it to the `greater` list.\n\n3. After traversing the original list, attach the `greater` list to the end of the `less` list.\n\n4. Set the last node of the `greater` list\'s `next` pointer to `nullptr` to terminate the list.\n\n5. Return the `less` list\'s head as the result.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code 1\n# Creating new instances of Nodes with given value\n```C++ []\nclass Solution {\npublic:\n ListNode* partition(ListNode* head, int x) {\n ListNode* current = head; // Pointer to traverse the original list\n \n ListNode* lessDummy = new ListNode(0); // Dummy node for nodes < x\n ListNode* lessTail = lessDummy; // Tail pointer for less list\n \n ListNode* greaterDummy = new ListNode(0); // Dummy node for nodes >= x\n ListNode* greaterTail = greaterDummy; // Tail pointer for greater list\n \n // Traverse the original list\n while (current != nullptr) {\n if (current->val < x) {\n // Append current node to the less list\n lessTail->next = new ListNode(current->val);\n lessTail = lessTail->next; // Move the tail pointer\n } else {\n // Append current node to the greater list\n greaterTail->next = new ListNode(current->val);\n greaterTail = greaterTail->next; // Move the tail pointer\n }\n current = current->next; // Move to the next node\n }\n \n \n // Attach the greater list to the end of the less list\n lessTail->next = greaterDummy->next;\n \n // Return the modified list starting from the first node after the less dummy node\n return lessDummy->next;\n }\n};\n\n```\n```java []\nclass Solution {\n public ListNode partition(ListNode head, int x) {\n ListNode current = head; // Pointer to traverse the original list\n \n ListNode lessDummy = new ListNode(0); // Dummy node for nodes < x\n ListNode lessTail = lessDummy; // Tail pointer for less list\n \n ListNode greaterDummy = new ListNode(0); // Dummy node for nodes >= x\n ListNode greaterTail = greaterDummy; // Tail pointer for greater list\n \n // Traverse the original list\n while (current != null) {\n if (current.val < x) {\n // Append current node to the less list\n lessTail.next = new ListNode(current.val);\n lessTail = lessTail.next; // Move the tail pointer\n } else {\n // Append current node to the greater list\n greaterTail.next = new ListNode(current.val);\n greaterTail = greaterTail.next; // Move the tail pointer\n }\n current = current.next; // Move to the next node\n }\n \n \n \n // Attach the greater list to the end of the less list\n lessTail.next = greaterDummy.next;\n \n // Return the modified list starting from the first node after the less dummy node\n return lessDummy.next;\n }\n}\n\n```\n```python []\nclass Solution:\n def partition(self, head: ListNode, x: int) -> ListNode:\n current = head # Pointer to traverse the original list\n \n less_dummy = ListNode(0) # Dummy node for nodes < x\n less_tail = less_dummy # Tail pointer for less list\n \n greater_dummy = ListNode(0) # Dummy node for nodes >= x\n greater_tail = greater_dummy # Tail pointer for greater list\n \n # Traverse the original list\n while current:\n if current.val < x:\n # Append current node to the less list\n less_tail.next = ListNode(current.val)\n less_tail = less_tail.next # Move the tail pointer\n else:\n # Append current node to the greater list\n greater_tail.next = ListNode(current.val)\n greater_tail = greater_tail.next # Move the tail pointer\n current = current.next # Move to the next node\n \n \n # Attach the greater list to the end of the less list\n less_tail.next = greater_dummy.next\n \n # Return the modified list starting from the first node after the less dummy node\n return less_dummy.next\n\n```\n\n\n# Code 2 \n# Using same Nodes.\n```C++ []\nclass Solution {\npublic:\n ListNode* partition(ListNode* head, int x) {\n // Initialize dummy nodes and tail pointers for less and greater lists\n ListNode* lessDummy = new ListNode(0); // Dummy node for nodes < x\n ListNode* lessTail = lessDummy; // Tail pointer for less list\n \n ListNode* greaterDummy = new ListNode(0); // Dummy node for nodes >= x\n ListNode* greaterTail = greaterDummy; // Tail pointer for greater list\n \n ListNode* current = head; // Current pointer for traversing the original list\n \n // Traverse the original list\n while (current != nullptr) {\n if (current->val < x) {\n // Append current node to the less list\n lessTail->next = current;\n lessTail = current; // Move the tail pointer\n } else {\n // Append current node to the greater list\n greaterTail->next = current;\n greaterTail = current; // Move the tail pointer\n }\n current = current->next; // Move to the next node\n }\n \n greaterTail->next = nullptr; // Terminate the greater list\n \n // Attach the greater list to the end of the less list\n lessTail->next = greaterDummy->next;\n \n // Return the modified list starting from the first node after the less dummy node\n return lessDummy->next;\n }\n};\n```\n```Java []\nclass Solution {\n public ListNode partition(ListNode head, int x) {\n ListNode lessDummy = new ListNode(0); // Dummy node for nodes < x\n ListNode lessTail = lessDummy; // Tail pointer for less list\n \n ListNode greaterDummy = new ListNode(0); // Dummy node for nodes >= x\n ListNode greaterTail = greaterDummy; // Tail pointer for greater list\n \n ListNode current = head; // Current pointer for traversing the original list\n \n // Traverse the original list\n while (current != null) {\n if (current.val < x) {\n // Append current node to the less list\n lessTail.next = current;\n lessTail = current; // Move the tail pointer\n } else {\n // Append current node to the greater list\n greaterTail.next = current;\n greaterTail = current; // Move the tail pointer\n }\n current = current.next; // Move to the next node\n }\n \n greaterTail.next = null; // Terminate the greater list\n \n // Attach the greater list to the end of the less list\n lessTail.next = greaterDummy.next;\n \n // Return the modified list starting from the first node after the less dummy node\n return lessDummy.next;\n }\n}\n```\n```Python3 []\nclass Solution:\n def partition(self, head: ListNode, x: int) -> ListNode:\n less_dummy = ListNode(0) # Dummy node for nodes < x\n less_tail = less_dummy # Tail pointer for less list\n \n greater_dummy = ListNode(0) # Dummy node for nodes >= x\n greater_tail = greater_dummy # Tail pointer for greater list\n \n current = head # Current pointer for traversing the original list\n \n # Traverse the original list\n while current:\n if current.val < x:\n # Append current node to the less list\n less_tail.next = current\n less_tail = current # Move the tail pointer\n else:\n # Append current node to the greater list\n greater_tail.next = current\n greater_tail = current # Move the tail pointer\n current = current.next # Move to the next node\n \n greater_tail.next = None # Terminate the greater list\n \n # Attach the greater list to the end of the less list\n less_tail.next = greater_dummy.next\n \n # Return the modified list starting from the first node after the less dummy node\n return less_dummy.next\n``` | 34 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Python | Java | Linear Traversal using head and tail nodes | partition-list | 1 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nLinear Traversal.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain head and tail node.\n\n# Complexity\n- Time complexity: O(N) where N is the length of the Linked List\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n\n- Space complexity: O(1) as we are not using any extra resource for storing.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\n```\n```Python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n\n firstHead = None\n firstTail = None\n secondHead = None\n secondTail = None\n\n if head == None:\n return head\n\n curr = head\n while curr != None:\n if curr.val < x:\n if firstHead == None:\n firstHead = curr\n firstTail = curr\n else:\n firstTail.next = curr\n firstTail = firstTail.next\n else:\n if secondHead == None:\n secondHead = curr\n secondTail = curr\n else:\n secondTail.next = curr\n secondTail = secondTail.next\n curr = curr.next\n\n if secondTail != None:\n secondTail.next = None\n if firstTail != None:\n firstTail.next = secondHead\n\n if firstHead != None:\n return firstHead\n return secondHead\n\n```\n```Java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode partition(ListNode head, int x) {\n\n ListNode firstHead = null;\n\n ListNode firstTail = null;\n\n ListNode secondHead = null;\n ListNode secondTail = null;\n\n if (head == null){\n return head;\n }\n\n\n ListNode curr = head;\n\n while (curr != null){\n if (curr.val < x){\n if (firstHead == null){\n firstHead = curr;\n firstTail = curr;\n }else{\n firstTail.next = curr;\n firstTail = firstTail.next;\n } \n }else{\n if (secondHead == null){\n secondHead = curr;\n secondTail = curr;\n }else{\n secondTail.next = curr;\n secondTail = secondTail.next;\n }\n\n }\n curr = curr.next;\n }\n\n if (secondTail != null){\n secondTail.next = null;\n }\n if (firstTail != null){\n firstTail.next = secondHead;\n }\n \n return firstHead == null ? secondHead: firstHead;\n \n }\n\n}\n\n\n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
🦀🐍 Rust + Python 🔗 List Fast Solution | partition-list | 0 | 1 | # Intuition \uD83E\uDD14\nImagine you\'re a \uD83E\uDD80 sorting pearls and stones from the ocean floor. The pearls (values less than `x`) are precious and you want to keep them close. The stones (values greater than or equal to `x`), while not as valuable, still need to be stored neatly. Now, imagine each pearl and stone is a node in the linked list. Our goal is to reorganize these nodes (or pearls and stones) based on their value relative to `x`.\n\n# Approach \uD83D\uDE80\nOur \uD83E\uDD80 has two baskets - one for pearls (`before`) and another for stones (`after`). It picks items one-by-one (or traverses the list). Depending on the value of the item, it places it in the appropriate basket. Once all items are sorted, it connects the two baskets to have a neat collection.\n\n1. \uD83D\uDECD\uFE0F Create two baskets (`before` and `after`).\n2. \uD83C\uDF0A Dive through the ocean floor (or traverse the list).\n3. \uD83C\uDF10 For each find, decide if it\'s a pearl or a stone and place it in the appropriate basket.\n4. \uD83D\uDD17 Once all items are collected, connect the two baskets.\n\n# Complexity \uD83D\uDD0D\n- Time complexity: $$O(n)$$\n - Our \uD83E\uDD80 dives through the ocean floor once, collecting each item.\n\n- Space complexity: $$O(1)$$\n - The \uD83E\uDD80 uses only two baskets regardless of the number of pearls and stones.\n\n# Code \uD83D\uDCDC\n``` Rust []\nimpl Solution {\n pub fn partition(mut head: Option<Box<ListNode>>, x: i32) -> Option<Box<ListNode>> {\n // Initialize two dummy nodes for \'before\' and \'after\' lists.\n let mut before = ListNode::new(0);\n let mut after = ListNode::new(0);\n \n // Pointers to the tails of \'before\' and \'after\' lists to aid in appending nodes.\n let mut before_tail = &mut before;\n let mut after_tail = &mut after;\n\n // Traverse the original list.\n while let Some(mut node) = head {\n head = node.next.take();\n \n // Compare current node\'s value with x and append to appropriate list.\n if node.val < x {\n before_tail.next = Some(node);\n before_tail = before_tail.next.as_mut().unwrap();\n } else {\n after_tail.next = Some(node);\n after_tail = after_tail.next.as_mut().unwrap();\n }\n }\n\n // Connect the end of \'before\' list to the start of \'after\' list.\n before_tail.next = after.next.take();\n\n // Return the merged list.\n before.next\n }\n}\n\n```\n``` Go []\nfunc partition(head *ListNode, x int) *ListNode {\n // Initialize two dummy nodes for \'before\' and \'after\' lists.\n before := &ListNode{}\n after := &ListNode{}\n \n // Pointers to help in appending nodes to \'before\' and \'after\' lists.\n before_curr := before\n after_curr := after\n \n // Traverse the original list.\n for head != nil {\n // Compare current node\'s value with x and append to appropriate list.\n if head.Val < x {\n before_curr.Next = head\n before_curr = before_curr.Next\n } else {\n after_curr.Next = head\n after_curr = after_curr.Next\n }\n head = head.Next\n }\n \n // Ensure \'after\' list\'s end points to nil.\n after_curr.Next = nil\n \n // Connect the end of \'before\' list to the start of \'after\' list.\n before_curr.Next = after.Next\n \n // Return the merged list.\n return before.Next\n}\n```\n``` Python []\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n # Initialize two dummy nodes for \'before\' and \'after\' lists.\n before, after = ListNode(0), ListNode(0)\n \n # Pointers to help in appending nodes to \'before\' and \'after\' lists.\n before_curr, after_curr = before, after\n \n # Traverse the original list.\n while head:\n # Compare current node\'s value with x and append to appropriate list.\n if head.val < x:\n before_curr.next, before_curr = head, head\n else:\n after_curr.next, after_curr = head, head\n head = head.next\n \n # Ensure \'after\' list\'s end points to None.\n after_curr.next = None\n \n # Connect the end of \'before\' list to the start of \'after\' list.\n before_curr.next = after.next\n \n # Return the merged list.\n return before.next\n```\n\n\n# Motivation \uD83C\uDF1F\nGreat job diving deep into the ocean of algorithms with our Rusty \uD83E\uDD80, Pythonic \uD83D\uDC0D, and Gopher friends! Each problem you tackle not only sharpens your coding skills but also adds a pearl of wisdom to your collection. Remember, every challenge is a step forward. Keep coding, keep collecting pearls, and let\'s make the ocean shine brighter! \uD83C\uDF0A\uD83C\uDF1F\uD83D\uDE80 | 10 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Covert To list first easy.py | partition-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n l = []\n while head:\n l.append(head.val)\n head = head.next\n smaller = []\n larger = []\n for i in l:\n if i<x:\n smaller.append(i)\n else:\n larger.append(i)\n ans = smaller+larger\n if ans==[]:\n return \n head = temp = ListNode(ans[0])\n for i in range(1,len(ans)):\n temp.next = ListNode(ans[i])\n temp = temp.next\n return head\n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Naive Approach (dummy, Two passes) | partition-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMake two passes and add create nodes into dummy\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(n)\n \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(n)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:\n # Creating a dummy node which will store our modified list\n dummy = ListNode(-1) \n # store head of dummy head\n res = dummy\n\n # Adding all the nodes which have value less than x to dummy node\n cur = head\n while cur:\n if cur.val < x:\n dummy.next = ListNode(cur.val)\n dummy = dummy.next\n cur = cur.next\n # Now adding remaining nodes without altering the order\n cur = head\n while cur:\n if cur.val >= x:\n dummy.next = ListNode(cur.val)\n dummy = dummy.next\n cur = cur.next\n # deleting the input list which is taking extra memory and returning the next of dummy head i.e answer\n del head\n return res.next\n``` | 1 | Given the `head` of a linked list and a value `x`, partition it such that all nodes **less than** `x` come before nodes **greater than or equal** to `x`.
You should **preserve** the original relative order of the nodes in each of the two partitions.
**Example 1:**
**Input:** head = \[1,4,3,2,5,2\], x = 3
**Output:** \[1,2,2,4,3,5\]
**Example 2:**
**Input:** head = \[2,1\], x = 2
**Output:** \[1,2\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 200]`.
* `-100 <= Node.val <= 100`
* `-200 <= x <= 200` | null |
Easy and well define solution//py3. | scramble-string | 0 | 1 | # Behind the logic:\nThis problem can be solve by using dynamic programing.We can define a 3-dimensional array dp[l][i][j], where l denotes the length of the substring, i denotes the starting index of the substring in the first string s1, and j denotes the starting index of the substring in the second string s2.\n\nThe value dp[l][i][j] will be true if the substring of length l starting at index i of the first string s1 can be scrambled to form the substring of length l starting at index j of the second string s2.\n\nThe recurrence relation can defined as:-\n\n```\ndp[l][i][j] = true, if s1[i:i+l] and s2[j:j+l] are anagrams \n and (dp[k][i][j] && dp[l-k][i+k][j+k] for some 1 <= k < l) \n or (dp[k][i][j+l-k] && dp[l-k][i+k][j] for some 1 <= k < l)\n\n```\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first condition checks if the substrings are anagrams. If they are, we check if we can obtain the scrambled string by dividing the string into two substrings at some index k, swapping the two substrings, and recursively checking if the resulting substrings can be scrambled to form the corresponding substrings in the other string.\n\nWe check both possible combinations of x and y because we can swap either x and y or y and x.\n\nThe base case is when the length of the substring is 1, and in that case, we check if the two characters are the same.\n\nThe final answer will be stored in dp[n][0][0], where n is the length of the strings.\n\nTherefore, we can solve this problem efficiently using dynamic programming with time and space complexity of O(n^4), where n is the length of the strings.\n\n# Explainaton about this code:-\n\n```python []\ndef isScramble(s1: str, s2: str) -> bool:\n\n```\nThe `isScramble` function takes two input strings s1 and s2 and returns a boolean indicating whether s2 can be scrambled to form s1.\n\n\n```\n n = len(s1)\n if n != len(s2):\n return False\n if s1 == s2:\n return True\n if sorted(s1) != sorted(s2):\n return False\n\n```\n->>The first few lines check for the base cases of the problem. If the input strings have different lengths, then they cannot be scrambled, and we return False. If the input strings are already the same, then they are already scrambled, and we return True. Additionally, if the sorted characters of the two strings do not match, then we also return False, since the characters must match for the strings to be scrambled.\n```\n dp = [[[None] * n for _ in range(n)] for _ in range(n+1)]\n\n```\nHere, we initialize a 3-dimensional memoization table dp, which is a 3-dimensional array where `dp[l][i][j]` denotes whether a substring of length l starting at index i of s1 can be scrambled to form a substring of length l starting at index j of s2.\n```\n def solve(l, i, j):\n if dp[l][i][j] is not None:\n return dp[l][i][j]\n if s1[i:i+l] == s2[j:j+l]:\n dp[l][i][j] = True\n return True\n if sorted(s1[i:i+l]) != sorted(s2[j:j+l]):\n dp[l][i][j] = False\n return False\n for k in range(1, l):\n if (solve(k, i, j) and solve(l-k, i+k, j+k)) or (solve(k, i, j+l-k) and solve(l-k, i+k, j)):\n dp[l][i][j] = True\n return True\n dp[l][i][j] = False\n return False\n\n```\nThis is the recursive function solve that checks if the current substrings can be scrambled. It takes the length of the current substring l and the starting indices of the substrings in both strings i and j.\n\nIf the solution for a particular substring has already been calculated, we simply return the value from the memoization table dp.\n\nIf the current substrings are already the same, we return True. If the sorted characters of the two substrings do not match, we return False.\n\nIf the substrings can be scrambled, we check all possible splits of length k and recursively check if the resulting substrings can be scrambled to form the corresponding substrings in the other string. We update the memoization table dp with the result and return it.\n\n```\n return solve(n, 0, 0)\n\n```\nHere, we start the recursion from the length of the string n and the starting indices of 0 for both strings. The final answer is stored in `dp[n][0][0]`, where n is the length of the input strings.\n\nOverall, the code implements the Scramble String problem using dynamic programming with memoization. It first checks for the base cases of the problem and then uses a recursive function with memoization to check all possible splits of the substrings\n\n\n\n\n# Complexity\n- Time complexity:O(n^4)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n^4)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isScramble(self,s1: str, s2: str) -> bool:\n n = len(s1)\n if n != len(s2):\n return False\n if s1 == s2:\n return True\n if sorted(s1) != sorted(s2):\n return False\n dp = [[[None] * n for _ in range(n)] for _ in range(n+1)]\n \n def solve(l, i, j):\n if dp[l][i][j] is not None:\n return dp[l][i][j]\n if s1[i:i+l] == s2[j:j+l]:\n dp[l][i][j] = True\n return True\n if sorted(s1[i:i+l]) != sorted(s2[j:j+l]):\n dp[l][i][j] = False\n return False\n for k in range(1, l):\n if (solve(k, i, j) and solve(l-k, i+k, j+k)) or (solve(k, i, j+l-k) and solve(l-k, i+k, j)):\n dp[l][i][j] = True\n return True\n dp[l][i][j] = False\n return False\n \n return solve(n, 0, 0)\n\n```\n\n\n\n# ***Thank You..keep learning!\n*** | 1 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Python shortest 2-liner. DP. Functional programming. | scramble-string | 0 | 1 | # Approach\nTL;DR, Same as [Editorial solution](https://leetcode.com/problems/scramble-string/editorial/) but written in a functional way.\n\n# Complexity\n- Time complexity: $$O(n^4)$$\n\n- Space complexity: $$O(n^3)$$\n\nwhere, `n is length of s1 or s2`.\n\n# Code\n2-liner (Not readable):\n```python\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n @cache\n def is_scramble(i: int, j: int, n: int) -> bool: return any((is_scramble(i, j, k) and is_scramble(i + k, j + k, n - k)) or (is_scramble(i, j + n - k, k) and is_scramble(i + k, j, n - k)) for k in range(1, n)) if n > 1 else s1[i] == s2[j]\n return is_scramble(0, 0, len(s1))\n\n\n```\nMulti-liner (More Readable):\n```python\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n @cache\n def is_scramble(i: int, j: int, n: int) -> bool: \n return any(\n (is_scramble(i, j , k) and is_scramble(i + k, j + k, n - k)) or\n (is_scramble(i, j + n - k, k) and is_scramble(i + k, j , n - k))\n for k in range(1, n)\n ) if n > 1 else s1[i] == s2[j]\n \n return is_scramble(0, 0, len(s1))\n\n\n``` | 2 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
✔💯 DAY 364 | 100% | [JAVA/C++/PYTHON] | EXPLAINED | INTUTION | DRY RUN | PROOF 💫 | scramble-string | 1 | 1 | \n\n# Happy Sri Ram Navami to all !! \uD83D\uDEA9\uD83D\uDEA9\uD83D\uDEA9\n\n# NOTE:- if you found anyone\'s post helpful please upvote that post because some persons are downvoting unneccesarily, and you are the one guys that save our post from getting unvisible, upvote for remains visible for others so and other people can also get benefitted.\n\n##### \u2022\tThere are several ways to solve the Scramble String problem\n##### \u2022\tRecursion with memoization: This is the approach used in the solution we discussed earlier. The idea is to recursively check all possible splits of the two strings, and memoize the results to avoid recomputing the same substrings multiple times.\n##### \u2022\tDynamic programming: This approach involves building a 3D table to store the results of all possible substrings of the two strings. The table is filled in a bottom-up manner, starting with the smallest substrings and building up to the largest substrings. The table can then be used to check if the two strings are scrambled versions of each other.\n##### \u2022\tTop-down dynamic programming: This approach is similar to recursion with memoization, but uses a 3D table to store the results of all possible substrings of the two strings. The table is filled in a top-down manner, starting with the largest substrings and building down to the smallest substrings. The table can then be used to check if the two strings are scrambled versions of each other.\n##### \u2022\tBFS: This approach involves using a queue to generate all possible scrambled versions of one of the strings, and checking if any of them match the other string. The idea is to generate all possible substrings of the first string, and then generate all possible permutations of each substring. The resulting strings can then be checked to see if they match the second string.\n##### \u2022\tAll of these approaches have the same time and space complexity of O(n^4), but they differ in their implementation details and performance characteristics.\n\n# Intuition & Approach\n\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tThe problem is to determine if two strings s1 and s2 are scrambled versions of each other. The algorithm works by recursively splitting the strings into two non-empty substrings and swapping them randomly. The algorithm stops when the length of the string is 1.\n##### \u2022\tThe approach used to solve the problem use a recursive function that checks if the two strings are scrambled versions of each other. The function checks if the two strings are equal, and if not, it checks if the two strings have the same characters and if the substrings of the two strings are scrambled versions of each other.\n##### \u2022\tThe algorithm uses an unordered map to store the results of previously computed substrings to avoid recomputing them. It also uses three vectors to keep track of the frequency of characters in the two strings and the current substring being checked.\n##### \u2022\tThe intuition behind the algorithm is that if two strings are scrambled versions of each other, then they can be split into two non-empty substrings that are also scrambled versions of each other. The algorithm checks all possible splits of the two strings and recursively checks if the substrings are scrambled versions of each other.\n##### \u2022\tThe algorithm starts by checking if the two strings are equal. If they are, it returns true. If not, it initializes three vectors to keep track of the frequency of characters in the two strings and the current substring being checked. It then checks if the current substring of s1 and s2 have the same characters. If they do, it recursively checks if the substrings of s1 and s2 are scrambled versions of each other. If they are, it returns true.\n##### \u2022\tIf the current substrings of s1 and s2 do not have the same characters, the algorithm checks all possible splits of the two strings. For each split, it checks if the substrings of s1 and s2 are scrambled versions of each other. If they are, it returns true.\n##### \u2022\tThe algorithm uses an unordered map to store the results of previously computed substrings to avoid recomputing them. If the current substring of s1 and s2 has already been computed, the algorithm returns the stored result.\n##### \u2022\tOverall, the algorithm uses a recursive approach to check if two strings are scrambled versions of each other. It uses an unordered map and three vectors to store previously computed substrings and keep track of the frequency of characters in the two strings and the current substring being checked.\n\n\n# here\'s the complete recursion tree for the isScramble method with s1 = "great" and s2 = "rgeat"\n\n```\nisScramble("great", "rgeat")\n / | | | \\\nisScramble("g", "r") isScramble("g", "at") isScramble("gr", "ra") isScramble("gr", "eat") isScramble("gre", "rge")\n | / | | | \\ | / |\nisScramble("", "") isScramble("g", "a") isScramble("g", "r") isScramble("g", "e") isScramble("g", "r") isScramble("g", "r") isScramble("gr", "e") isScramble("gr", "g") isScramble("gr", "er") isScramble("gr", "gea") isScramble("gre", "rg") isScramble("gre", "er")\n / \\ / \\ / \\ / \\ / \\ / \\ / \\ / \\ / \\ / \\ / \\\nfalse false false false false false false false false false false false false false false false false false false false false false false true\n```\n\n\n# Code\n```java []\nclass Solution {\n // to store previously computed substrings\n Map<String, Boolean> map = new HashMap<>();\n\n public boolean isScramble(String s1, String s2) {\n int n = s1.length();\n // check if the two strings are equal\n if (s1.equals(s2)) {\n return true;\n }\n // initialize frequency arrays for s1, s2, and current substring\n int[] a = new int[26], b = new int[26], c = new int[26];\n // check if the current substring has already been computed\n if (map.containsKey(s1 + s2)) {\n return map.get(s1 + s2);\n }\n // check all possible splits of the two strings\n for (int i = 1; i <= n - 1; i++) {\n int j = n - i;\n // update frequency arrays for s1, s2, and current substring\n a[s1.charAt(i - 1) - \'a\']++;\n b[s2.charAt(i - 1) - \'a\']++;\n c[s2.charAt(j) - \'a\']++;\n // check if the current substring has the same characters\n if (Arrays.equals(a, b) && isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i))) {\n // if the substrings are scrambled versions of each other, return true\n map.put(s1 + s2, true);\n return true;\n }\n // check if the current substring and its complement have the same characters\n if (Arrays.equals(a, c) && isScramble(s1.substring(0, i), s2.substring(j)) && isScramble(s1.substring(i), s2.substring(0, j))) {\n // if the substrings are scrambled versions of each other, return true\n map.put(s1 + s2, true);\n return true;\n }\n }\n // if none of the splits result in scrambled versions, return false\n map.put(s1 + s2, false);\n return false;\n }\n}\n```\n```c++ []\nclass Solution\n{\n\t// unordered map to store previously computed substrings\n\tunordered_map<string,bool> mp;\n\npublic:\n\tbool isScramble(string s1, string s2)\n\t{\n\t\tint n = s1.size();\n\t\t// check if the two strings are equal\n\t\tif (s1 == s2)\n\t\t{\n\t\t\treturn true;\n\t\t}\n\t\t// initialize frequency vectors for s1, s2, and current substring\n\t\tvector a(26, 0), b(26, 0), c(26, 0);\n\t\t// check if the current substring has already been computed\n\t\tif (mp.count(s1 + s2))\n\t\t{\n\t\t\treturn mp[s1 + s2];\n\t\t}\n\t\t// check all possible splits of the two strings\n\t\tfor (int i = 1; i <= n - 1; i++)\n\t\t{\n\t\t\tint j = n - i;\n\t\t\t// update frequency vectors for s1, s2, and current substring\n\t\t\ta[s1[i - 1] - \'a\']++;\n\t\t\tb[s2[i - 1] - \'a\']++;\n\t\t\tc[s2[j] - \'a\']++;\n\t\t\t// check if the current substring has the same characters\n\t\t\tif (a == b && isScramble(s1.substr(0, i), s2.substr(0, i)) && isScramble(s1.substr(i), s2.substr(i)))\n\t\t\t{\n\t\t\t\t// if the substrings are scrambled versions of each other, return true\n\t\t\t\tmp[s1 + s2] = true;\n\t\t\t\treturn true;\n\t\t\t}\n\t\t\t// check if the current substring and its complement have the same characters\n\t\t\tif (a == c && isScramble(s1.substr(0, i), s2.substr(j)) && isScramble(s1.substr(i), s2.substr(0, j)))\n\t\t\t{\n\t\t\t\t// if the substrings are scrambled versions of each other, return true\n\t\t\t\tmp[s1 + s2] = true;\n\t\t\t\treturn true;\n\t\t\t}\n\t\t}\n\t\t// if none of the splits result in scrambled versions, return false\n\t\tmp[s1 + s2] = false;\n\t\treturn false;\n\t}\n};\n```\n```python []\nclass Solution:\n # dictionary to store previously computed substrings\n map = {}\n\n def isScramble(self, s1: str, s2: str) -> bool:\n n = len(s1)\n # check if the two strings are equal\n if s1 == s2:\n return True\n # initialize frequency lists for s1, s2, and current substring\n a, b, c = [0] * 26, [0] * 26, [0] * 26\n # check if the current substring has already been computed\n if (s1 + s2) in self.map:\n return self.map[s1 + s2]\n # check all possible splits of the two strings\n for i in range(1, n):\n j = n - i\n # update frequency lists for s1, s2, and current substring\n a[ord(s1[i - 1]) - ord(\'a\')] += 1\n b[ord(s2[i - 1]) - ord(\'a\')] += 1\n c[ord(s2[j]) - ord(\'a\')] += 1\n # check if the current substring has the same characters\n if a == b and self.isScramble(s1[:i], s2[:i]) and self.isScramble(s1[i:], s2[i:]):\n # if the substrings are scrambled versions of each other, return True\n self.map[s1 + s2] = True\n return True\n # check if the current substring and its complement have the same characters\n if a == c and self.isScramble(s1[:i], s2[j:]) and self.isScramble(s1[i:], s2[:j]):\n # if the substrings are scrambled versions of each other, return True\n self.map[s1 + s2] = True\n return True\n # if none of the splits result in scrambled versions, return False\n self.map[s1 + s2] = False\n return False\n```\n\n\n\n# Complexity\n\n##### \u2022\tThe time complexity of the algorithm is O(n^4), n is the length of the strings. This is because the algorithm checks all possible splits of the two strings, which takes O(n^2) time, and for each split, it recursively checks if the substrings are scrambled versions of each other, which takes O(n^2) time in the worst case. Therefore, the overall time complexity is O(n^2 * n^2) = O(n^4).\n##### \u2022\tThe space complexity of the algorithm is also O(n^4), due to the use of the unordered map to store previously computed substrings. In the worst case, the map can store all possible substrings of the two strings, which takes O(n^4) space. Additionally, the algorithm uses three arrays to keep track of the frequency of characters in the two strings and the current substring being checked, which also takes O(n^3) space in the worst case. Therefore, the overall space complexity is O(n^4).\n##### \u2022\tHowever, the use of the unordered map to store previously computed substrings allows the algorithm to avoid recomputing the same substrings multiple times, which can significantly improve the performance of the algorithm for large inputs.\n\n\n\n\n# DP Intuition\n##### \u2022\tThe problem involves checking if two strings are scrambled versions of each other.\n##### \u2022\tWe have a recursive definition of scrambling a string s, which involves dividing s into x and y, and scrambling x and y independently.\n##### \u2022\tTo check if a given string t is a scrambled string of s, we choose an index and cut s into x and y, and see if we can cut t into scrambled versions of x and y.\n##### \u2022\tWe can solve the problem using dynamic programming by defining a 3D table with variables for length, i, and j to represent the subproblems.\n##### \u2022\tEach state focuses on two substrings: a substring of s1 starting at index i with length equal to length, and a substring of s2 starting at index j with length equal to length.\n##### \u2022\tWe use a base case for substrings of length 1 and fill the table for substrings of length 2 to n.\n##### \u2022\tAt each state, we perform a split on s1 and consider all possible splits, and write down the transitions for each case.\n##### \u2022\tThe answer to the problem is dp[n][0][0], where n is the length of the input strings.\n#\tAlgorithm:\n##### \u2022\tIterate i from 0 to n-1.\n##### \u2022\tIterate j from 0 to n-1.\n##### \u2022\tSet dp[1][i][j] to the boolean value of s1[i] == s2[j] (the base case of the DP).\n##### \u2022\tIterate length from 2 to n.\n##### \u2022\tIterate i from 0 to n + 1 - length.\n##### \u2022\tIterate j from 0 to n + 1 - length.\n##### \u2022\tIterate newLength from 1 to length - 1.\n##### \u2022\tIf dp[newLength][i][j] && dp[length-newLength][i+newLength][j+newLength]) || (dp[newLength][i][j+l-newLength] && dp[l-newLength][i+newLength][j] is true, set dp[length][i][j] to true.\n##### \u2022\tReturn dp[n][0][0].\n\n\n\n```PYTHON []\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n n = len(s1)\n # Initialize a 3D table to store the results of all possible substrings of the two strings\n dp = [[[False for _ in range(n)] for _ in range(n)] for _ in range(n+1)]\n\n # Initialize the table for substrings of length 1\n for i in range(n):\n for j in range(n):\n dp[1][i][j] = s1[i] == s2[j]\n\n # Fill the table for substrings of length 2 to n\n for length in range(2, n+1):\n for i in range(n+1-length):\n for j in range(n+1-length):\n # Iterate over all possible lengths of the first substring\n for newLength in range(1, length):\n # Check if the two possible splits of the substrings are scrambled versions of each other\n dp1 = dp[newLength][i]\n dp2 = dp[length-newLength][i+newLength]\n dp[length][i][j] |= dp1[j] and dp2[j+newLength]\n dp[length][i][j] |= dp1[j+length-newLength] and dp2[j]\n\n # Return whether the entire strings s1 and s2 are scrambled versions of each other\n return dp[n][0][0]\n```\n```JAVA []\nclass Solution {\n public boolean isScramble(String s1, String s2) {\n int n = s1.length();\n // Initialize a 3D table to store the results of all possible substrings of the two strings\n boolean[][][] dp = new boolean[n+1][n][n];\n\n // Initialize the table for substrings of length 1\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n dp[1][i][j] = s1.charAt(i) == s2.charAt(j);\n }\n }\n\n // Fill the table for substrings of length 2 to n\n for (int length = 2; length <= n; length++) {\n for (int i = 0; i <= n-length; i++) {\n for (int j = 0; j <= n-length; j++) {\n // Iterate over all possible lengths of the first substring\n for (int newLength = 1; newLength < length; newLength++) {\n // Check if the two possible splits of the substrings are scrambled versions of each other\n boolean[] dp1 = dp[newLength][i];\n boolean[] dp2 = dp[length-newLength][i+newLength];\n dp[length][i][j] |= dp1[j] && dp2[j+newLength];\n dp[length][i][j] |= dp1[j+length-newLength] && dp2[j];\n }\n }\n }\n }\n\n // Return whether the entire strings s1 and s2 are scrambled versions of each other\n return dp[n][0][0];\n }\n}\n```\n\n```C++ []\nclass Solution {\npublic:\n bool isScramble(string s1, string s2) {\n int n = s1.length();\n // Initialize a 3D table to store the results of all possible substrings of the two strings\n vector<vector<vector<bool>>> dp(n+1, vector<vector<bool>>(n, vector<bool>(n)));\n\n // Initialize the table for substrings of length 1\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n dp[1][i][j] = s1[i] == s2[j];\n }\n }\n\n // Fill the table for substrings of length 2 to n\n for (int length = 2; length <= n; length++) {\n for (int i = 0; i <= n-length; i++) {\n for (int j = 0; j <= n-length; j++) {\n // Iterate over all possible lengths of the first substring\n for (int newLength = 1; newLength < length; newLength++) {\n // Check if the two possible splits of the substrings are scrambled versions of each other\n vector<bool>& dp1 = dp[newLength][i];\n vector<bool>& dp2 = dp[length-newLength][i+newLength];\n dp[length][i][j] |= dp1[j] && dp2[j+newLength];\n dp[length][i][j] |= dp1[j+length-newLength] && dp2[j];\n }\n }\n }\n }\n\n // Return whether the entire strings s1 and s2 are scrambled versions of each other\n return dp[n][0][0];\n }\n};\n```\n\n# TC & SC\n\n##### \u2022\tThe time complexity of this algorithm is O(n^4), and the space complexity is also O(n^4), due to the use of the 3D table. \n##### \u2022\tHowever, this approach can be faster than the recursive approach with memoization for some inputs, since it avoids the overhead of function calls and memoization lookups.\n\n\n# 3RD WAY RECURSIVE \n\n\n```C++ []\nclass Solution {\n bool isScrambleHelper(unordered_map<string, bool> &memo, string s1, string s2) {\n int i, len = s1.size();\n bool result = false;\n\n // Base cases\n if (len == 0) {\n return true;\n } else if (len == 1) {\n return s1 == s2;\n } else {\n // Check if we have already computed the result for this pair of strings\n if (memo.count(s1 + s2)) {\n return memo[s1 + s2];\n }\n\n // Check if the two strings are equal\n if (s1 == s2) {\n result = true;\n } else {\n // Check all possible split positions\n for (i = 1; i < len && !result; ++i) {\n // Check if s1[0..i-1] and s2[0..i-1] are valid scrambles of each other\n // and if s1[i..len-1] and s2[i..len-1] are valid scrambles of each other\n result = result || (isScrambleHelper(memo, s1.substr(0, i), s2.substr(0, i)) && isScrambleHelper(memo, s1.substr(i, len - i), s2.substr(i, len - i)));\n\n // Check if s1[0..i-1] and s2[len-i..len-1] are valid scrambles of each other\n // and if s1[i..len-1] and s2[0..len-i-1] are valid scrambles of each other\n result = result || (isScrambleHelper(memo, s1.substr(0, i), s2.substr(len - i, i)) && isScrambleHelper(memo, s1.substr(i, len - i), s2.substr(0, len - i)));\n }\n }\n\n // Save the intermediate result in the memoization table\n return memo[s1 + s2] = result;\n }\n }\npublic:\n bool isScramble(string s1, string s2) {\n unordered_map<string, bool> memo;\n return isScrambleHelper(memo, s1, s2);\n }\n};\n```\n```PYTHON []\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n n = len(s1)\n if n != len(s2):\n return False\n if n == 0:\n return True\n elif n == 1:\n return s1 == s2\n else:\n memo = {}\n return self.isScrambleHelper(memo, s1, s2)\n\n def isScrambleHelper(self, memo: dict, s1: str, s2: str) -> bool:\n n = len(s1)\n result = False\n\n if n == 0:\n return True\n elif n == 1:\n return s1 == s2\n else:\n if (s1, s2) in memo:\n return memo[(s1, s2)]\n\n if s1 == s2:\n result = True\n else:\n for i in range(1, n):\n result = (self.isScrambleHelper(memo, s1[:i], s2[:i]) and self.isScrambleHelper(memo, s1[i:], s2[i:])) or \\\n (self.isScrambleHelper(memo, s1[:i], s2[n - i:]) and self.isScrambleHelper(memo, s1[i:], s2[:n - i]))\n if result:\n break\n\n memo[(s1, s2)] = result\n return result\n```\n```JAVA []\nclass Solution {\n public boolean isScramble(String s1, String s2) {\n int len = s1.length();\n if (len != s2.length()) {\n return false;\n }\n if (len == 0) {\n return true;\n } else if (len == 1) {\n return s1.equals(s2);\n } else {\n Map<String, Boolean> memo = new HashMap<>();\n return isScrambleHelper(memo, s1, s2);\n }\n }\n\n private boolean isScrambleHelper(Map<String, Boolean> memo, String s1, String s2) {\n int len = s1.length();\n boolean result = false;\n\n if (len == 0) {\n return true;\n } else if (len == 1) {\n return s1.equals(s2);\n } else {\n if (memo.containsKey(s1 + s2)) {\n return memo.get(s1 + s2);\n }\n\n if (s1.equals(s2)) {\n result = true;\n } else {\n for (int i = 1; i < len && !result; i++) {\n result = (isScrambleHelper(memo, s1.substring(0, i), s2.substring(0, i)) && isScrambleHelper(memo, s1.substring(i), s2.substring(i))) ||\n (isScrambleHelper(memo, s1.substring(0, i), s2.substring(len - i)) && isScrambleHelper(memo, s1.substring(i), s2.substring(0, len - i)));\n }\n }\n\n memo.put(s1 + s2, result);\n return result;\n }\n }\n}\n```\n\n# TC & SC\n\n##### \u2022\tThe time complexity of the given solution is O(n^4), where n is the length of the input strings. This is because we are checking all possible split positions for each substring, which takes O(n^2) time, and we are doing this for all possible substrings, which takes another O(n^2) time. The recursive calls also add to the time complexity.\n##### \u2022\tThe space complexity of the given solution is O(n^3), which is the size of the memoization table. This is because we are storing the results of all possible substring pairs in the memoization table.\n\n# 4th way cache is implemented\n```c++ []\nclass Solution {\nprivate:\n bool DP_helper(string &s1, string &s2, int idx1, int idx2, int len, char isS[]) {\n int sSize = s1.size(), i, j, k, hist[26], zero_count = 0;\n\n // Check if we have already computed the result for this substring pair\n if (isS[(len * sSize + idx1) * sSize + idx2]) {\n return isS[(len * sSize + idx1) * sSize + idx2] == 1;\n }\n\n bool res = false;\n\n // Count the frequency of each character in the two substrings\n fill_n(hist, 26, 0);\n for (k = 0; k < len; ++k) {\n zero_count += (0 == hist[s1[idx1 + k] - \'a\']) - (0 == ++hist[s1[idx1 + k] - \'a\']);\n zero_count += (0 == hist[s2[idx2 + k] - \'a\']) - (0 == --hist[s2[idx2 + k] - \'a\']);\n }\n\n // If the two substrings have different characters, return false\n if (zero_count) {\n isS[(len * sSize + idx1) * sSize + idx2] = 2;\n return false;\n }\n\n // If the length of the substrings is 1, return true\n if (len == 1) {\n isS[(len * sSize + idx1) * sSize + idx2] = 1;\n return true;\n }\n\n // Recursively check all possible split positions\n for (k = 1; k < len && !res; ++k) {\n res = res || (DP_helper(s1, s2, idx1, idx2, k, isS) && DP_helper(s1, s2, idx1 + k, idx2 + k, len - k, isS));\n res = res || (DP_helper(s1, s2, idx1 + len - k, idx2, k, isS) && DP_helper(s1, s2, idx1, idx2 + k, len - k, isS));\n }\n\n // Save the intermediate result in the cache\n isS[(len * sSize + idx1) * sSize + idx2] = res ? 1 : 2;\n return res;\n }\n\npublic:\n bool isScramble(string s1, string s2) {\n const int sSize = s1.size();\n\n // Base case: empty strings are always valid scrambles of each other\n if (0 == sSize) {\n return true;\n }\n\n // Initialize the cache\n char isS[(sSize + 1) * sSize * sSize];\n fill_n(isS, (sSize + 1) * sSize * sSize, 0);\n\n // Recursively check if s1 and s2 are valid scrambles of each other\n return DP_helper(s1, s2, 0, 0, sSize, isS);\n }\n};\n```\n# explaination \n\n##### \u2022\tIt does this by recursively checking all possible split positions of the two strings, and caching the intermediate results to avoid redundant computations. \n##### \u2022\tThe cache is implemented as a one-dimensional array isS , where isS[idx1 * sSize + idx2 + len * sSize * sSize] stores the result of checking whether the substring of s1 starting at index idx1 and the substring of s2 starting at index idx2 , both of length len , are valid scrambles of each other. The value of isS[idx1 * sSize + idx2 + len * sSize * sSize] can be either 0 (not computed yet), 1 (valid scramble), or 2 (invalid scramble). \n##### \u2022\tThe recursion is implemented in the DP_helper function, which takes as input the two strings s1 and s2 , the starting indices idx1 and idx2 , the length len , and the cache isS . \n##### \u2022\tThe function first checks if the result for this substring pair has already been computed and cached, and returns the cached result if it exists. \n##### \u2022\tOtherwise, it counts the frequency of each character in the two substrings, and returns false if the two substrings have different characters. If the length of the substrings is 1, the function returns true.\n##### \u2022\tIf the two substrings have the same character set, the function recursively checks all possible split positions and returns true if any of them are valid scrambles of each other. \n##### \u2022\tFinally, the function saves the intermediate result in the cache and returns the result. \n##### \u2022\tTo optimize the recursion, the function uses early pruning by checking if the two substrings have the same character set before recursively checking all possible split positions. \n##### \u2022\tIf the two substrings have different character sets, the function immediately returns false without doing any further computation. \n##### \u2022\tThis helps to reduce the number of recursive calls and improve the overall performance of the algorithm.\n\n\n# DRY RUN 1\n\n##### \u2022\tLet\'s dry run the algorithm with the input "great" andrgeat".\n##### \u2022\tFirst, the algorithm checks if the two strings are equal. Since they are not, it initializes the frequency vectors for s1, s2, and the current substring, and checks if the current substring has already been computed in the unordered map. Since it has not, the algorithm proceeds to check all possible splits of the two strings.\n##### \u2022\tFor the first split, i = 1 and j = 4. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "g" and "r" are different, the algorithm moves on to the next split.\n##### \u2022\tFor the second split, i = 2 and j = 3. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "gr" and "rg" have the same characters, the algorithm recursively checks if the substrings of s1 and s2 are scrambled versions of each other. It does this by calling the isScramble function with the substrings "g" and "r" for both s1 and s2. Since "g" and "r" are not scrambled versions of each other, the algorithm backtracks and checks the other possible split.\n##### \u2022\tFor the third split, i = 3 and j = 2. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "gre" and "rge" have the same characters, the algorithm recursively checks if the substrings of s1 and s2 are scrambled versions of each other. It does this by calling the isScramble function with the substrings "g" and "r" for s1 and s2, and the substrings "re" and "eat" for s1 and s2. Since "g" and "r" are not scrambled versions of each other, the algorithm backtracks and checks the other possible split.\n##### \u2022\tFor the fourth split, i = 4 and j = 1. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "reat" and "rgea" have the same characters, the algorithm recursively checks if the substrings of s1 and s2 are scrambled versions of each other. It does this by calling the isScramble function with the substrings "r" and "r" for s1 and s2, and the substrings "eat" and "gea" for s1 and s2. Since "r" and "r" are scrambled versions of each other, the algorithm proceeds to check if "eat" and "gea" are scrambled versions of each other. It does this by calling the isScramble function with the substrings "e" and "e" for s1 and s2, and the substrings "at" and "ga" for s1 and s2. Since "e" and "e" are scrambled versions of each other, the algorithm proceeds to check if "at" and "ga" are scrambled versions of each other. It does this by calling the isScramble function with the substrings "a" and "a" for s1 and s2, and the substrings "t" and "g" for s1 and s2. Since "a" and "a" are scrambled versions of each other, and "t" and "g" are scrambled versions of each other, the algorithm returns true.\n##### \u2022\tTherefore, the output of the algorithm for the input "great" and "rgeat" is true, indicating that the two strings are scrambled versions of each other.\n\n# DRY RUN 2\n##### \u2022\tLet\'s dry run the algorithm with the input "abcde" and "caebd".\n##### \u2022\tFirst, the algorithm checks if the two strings are equal. Since they are not, it initializes the frequency vectors for s1, s2, and the current substring, and checks if the current substring has already been computed in the unordered map. Since it has not, the algorithm proceeds to check all possible splits of the two strings.\n##### \u2022\tFor the first split, i = 1 and j = 4. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "a" and "c" are different, the algorithm moves on to the next split.\n##### \u2022\tFor the second split, i = 2 and j = 3. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "ab" and "ca" have different characters, the algorithm moves on to the next split.\n##### \u2022\tFor the third split, i = 3 and j = 2. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "abc" and "cae" have different characters, the algorithm moves on to the next split.\n##### \u2022\tFor the fourth split, i = 4 and j = 1. The algorithm updates the frequency vectors for s1, s2, and the current substring, and checks if the current substring has the same characters. Since "abcd" and "caeb" have different characters, the algorithm moves on to the next split.\n##### \u2022\tSince none of the splits result in scrambled versions of each other, the algorithm returns false.\n##### \u2022\tTherefore, the output of the algorithm for the input "abcde" and "caebd" is false, indicating that the two strings are not scrambled versions of each other.\n\n\n\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06\n | 100 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Image Explanation🏆- [Recursion -> DP + Complexity Analysis] - C++/Java/Python | scramble-string | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Scramble String` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n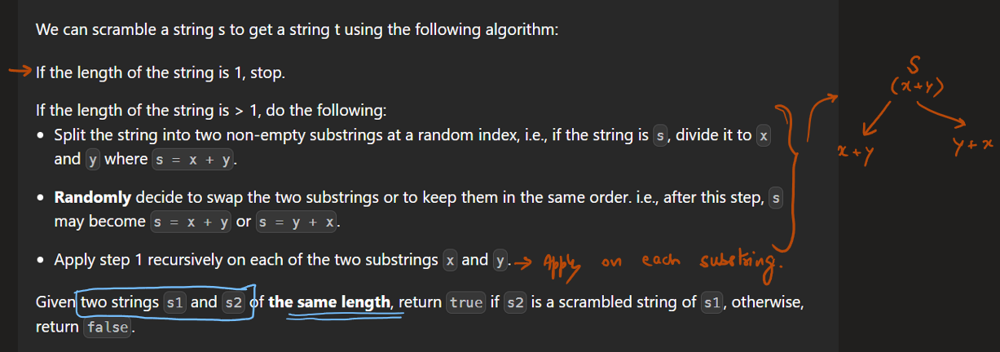\n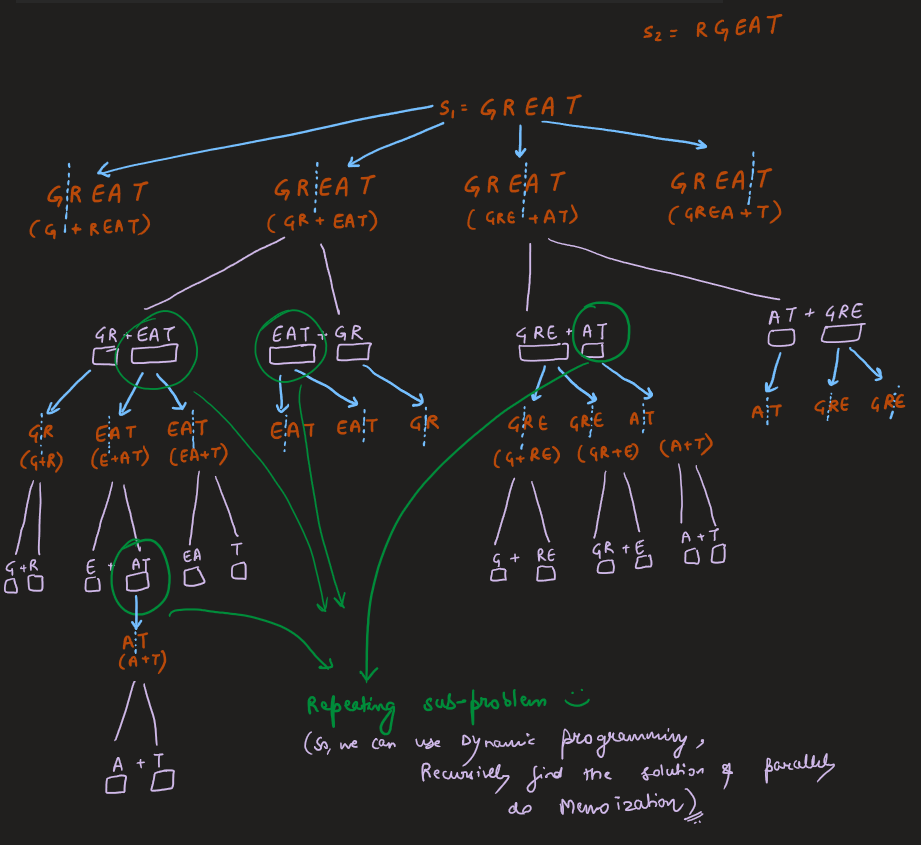\n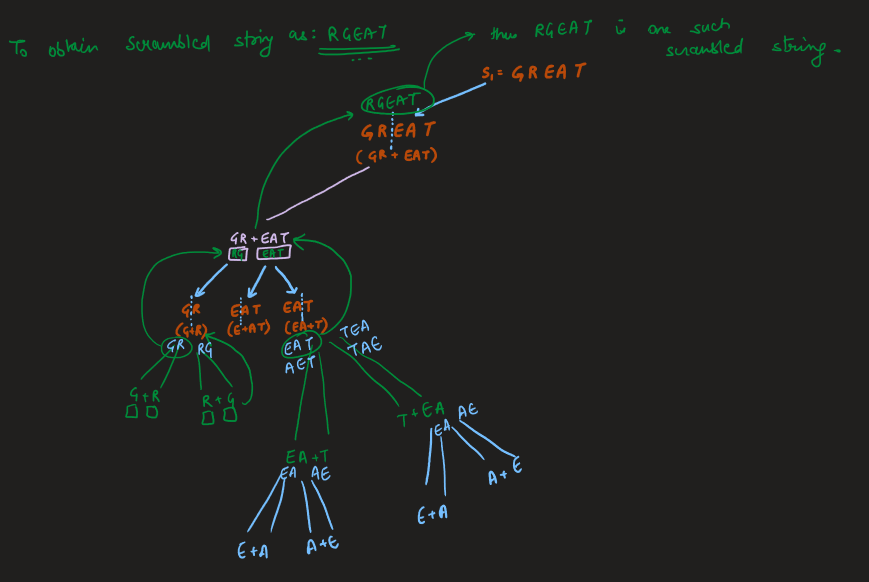\n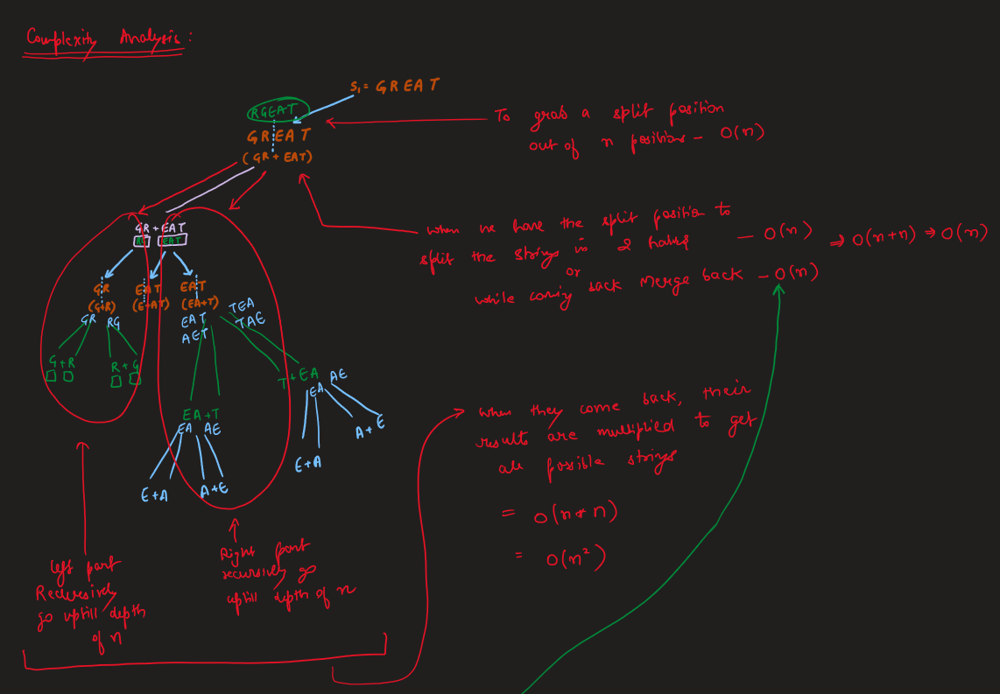\n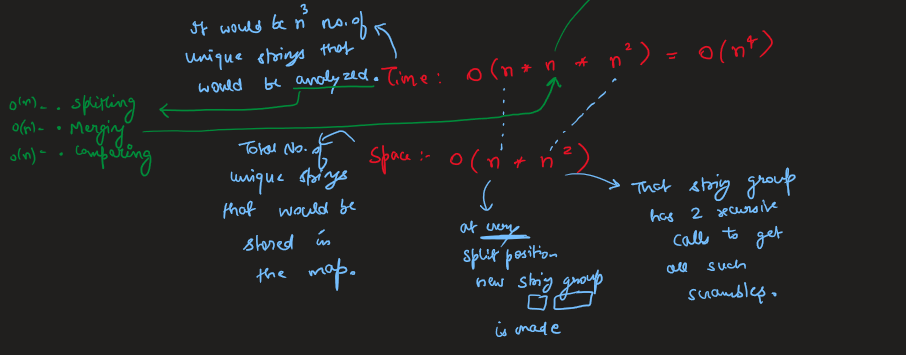\n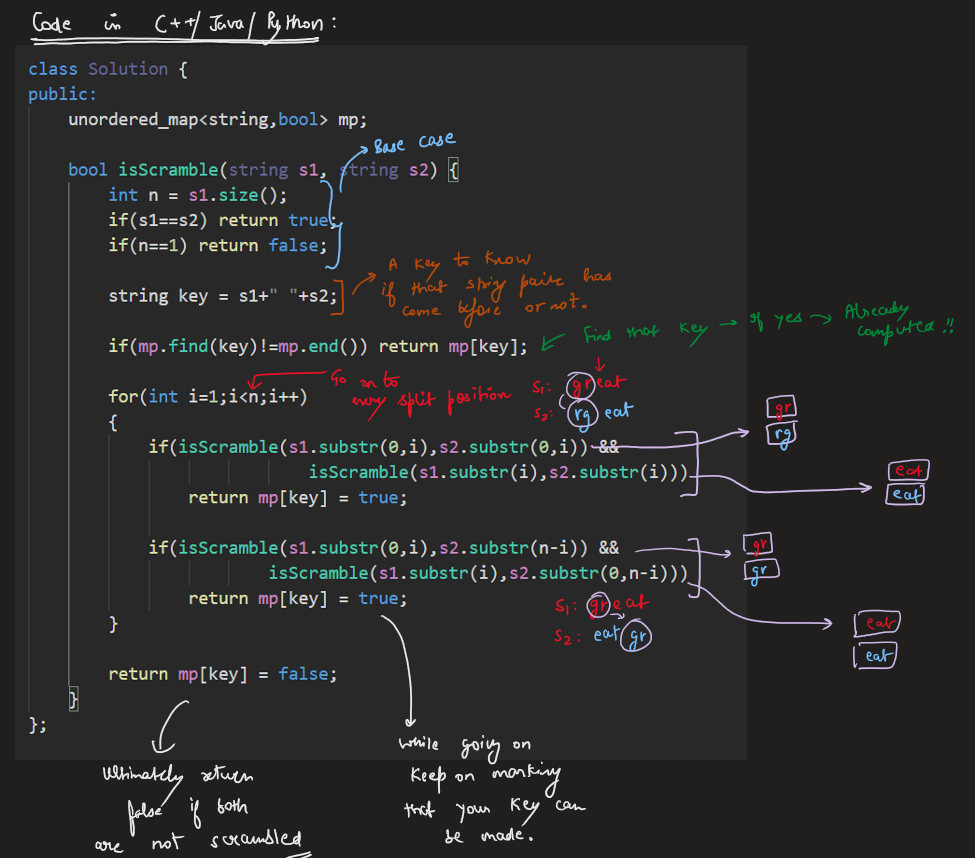\n\n[`Don\'t fall for this Small Optimization, It is Leetcode\'s Test Case Bug`] \n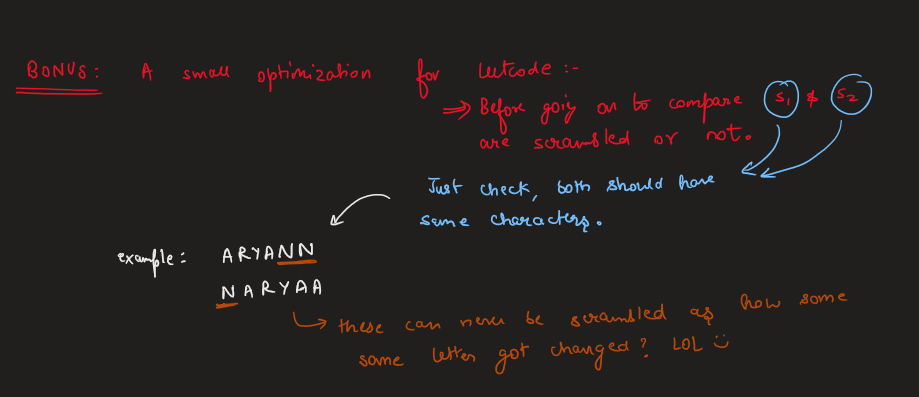\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n unordered_map<string,bool> mp;\n \n bool isScramble(string s1, string s2) {\n int n = s1.size();\n if(s1==s2) return true; \n if(n==1) return false;\n \n string key = s1+" "+s2;\n \n if(mp.find(key)!=mp.end()) return mp[key];\n\n for(int i=1;i<n;i++)\n {\n if(isScramble(s1.substr(0,i),s2.substr(0,i)) && \n isScramble(s1.substr(i),s2.substr(i)))\n return mp[key] = true;\n \n if(isScramble(s1.substr(0,i),s2.substr(n-i)) &&\n isScramble(s1.substr(i),s2.substr(0,n-i)))\n return mp[key] = true;\n }\n \n return mp[key] = false;\n }\n};\n```\n```Java []\nimport java.util.*;\n\nclass Solution {\n Map<String, Boolean> mp = new HashMap<>();\n\n public boolean isScramble(String s1, String s2) {\n int n = s1.length();\n if (s1.equals(s2)) return true;\n if (n == 1) return false;\n\n String key = s1 + " " + s2;\n\n if (mp.containsKey(key)) return mp.get(key);\n\n for (int i = 1; i < n; i++) {\n if (isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i))){\n mp.put(key, true);\n return true;\n }\n\n if (isScramble(s1.substring(0, i), s2.substring(n - i)) && isScramble(s1.substring(i), s2.substring(0, n - i))){\n mp.put(key, true);\n return true;\n }\n }\n\n mp.put(key, false);\n return false;\n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.mp = {}\n\n def isScramble(self, s1: str, s2: str) -> bool:\n n = len(s1)\n if s1 == s2:\n return True\n if n == 1:\n return False\n\n key = s1 + " " + s2\n\n if key in self.mp:\n return self.mp[key]\n\n for i in range(1, n):\n if self.isScramble(s1[:i], s2[:i]) and self.isScramble(s1[i:], s2[i:]):\n self.mp[key] = True\n return True\n\n if self.isScramble(s1[:i], s2[n - i:]) and self.isScramble(s1[i:], s2[:n - i]):\n self.mp[key] = True\n return True\n\n self.mp[key] = False\n return False\n```\n | 42 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Python3 || 35ms || Beats 99.38% (recursion with memoization) | scramble-string | 0 | 1 | The solution uses recursion with memoization to check all possible partitions of the two strings and determine if they are scrambled versions of each other. The memoization is achieved using a dictionary m that stores the result of previous computations for the same inputs.\n\nThe func function takes in two strings s1 and s2, and returns a boolean value indicating whether they are scrambled versions of each other. The function first checks the length of the strings - if they are both of length 1, it simply compares the characters. If the sorted characters in the two strings are not equal, it returns False.\n\nOtherwise, the function loops through all possible partitions of s1 and checks if they are valid scrambles of corresponding partitions in s2. The partitions are formed by looping through the length of s1 from index 1 to the end. If a valid partition is found, the function recursively checks the remaining partitions to see if they are also valid scrambles.\n\nIf at least one valid partition is found, the function returns True and stores the result in the m dictionary. If no valid partitions are found, the function returns False and stores the result in the m dictionary.\n\nFinally, the isScramble function calls the func function with the two input strings and returns the resulting boolean value.\n# Please Upvote \uD83D\uDE07\n\n\n\n# Python3\n```\nclass Solution:\n def isScramble(self,s1, s2):\n m ={}\n def func(s1, s2):\n if (s1, s2) in m:\n return m[(s1, s2)]\n if not sorted(s1) == sorted(s2):\n return False\n if len(s1) == 1:\n return True\n \n\n for i in range(1, len(s1)):\n if func(s1[:i], s2[-i:]) and func(s1[i:], s2[:-i]) or func(s1[:i], s2[:i]) and func(s1[i:], s2[i:]):\n m[(s1, s2)] = True\n return True\n m[(s1, s2)] = False\n return False\n return func(s1, s2)\n\n\n\n\n\n```\n | 73 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
✅✅Python🔥Java 🔥C++🔥Simple Solution🔥Easy to Understand🔥 | scramble-string | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Approach:\n\nWe can use dynamic programming to solve this problem. We can define a 3D boolean array dp[i][j][length] to represent whether s1[i:i+length] and s2[j:j+length] are scrambled versions of each other. The array dp will have dimensions n x n x (n+1), where n is the length of the strings. The base case is when length=1, and in this case, dp[i][j][1] is true if and only if s1[i] is equal to s2[j]. For each value of length, we can iterate through all possible starting indices i and j, and all possible split points k such that 1 <= k < length. We can then check if the substrings of s1 and s2 starting at indices i and j, respectively, and both of length k, are scrambled versions of each other, and if the substrings of s1 and s2 starting at indices i+k and j+k, respectively, and both of length length-k, are scrambled versions of each other. If either of these conditions are met, then dp[i][j][length] is true.\n\n# Intuition:\n\n- The intuition behind this approach is that if two strings s1 and s2 are scrambled versions of each other, then there must exist a split point k such that either the substrings of s1 and s2 starting at indices 0 and 0, respectively, and both of length k, are scrambled versions of each other, and the substrings of s1 and s2 starting at indices k and k, respectively, and both of length length-k, are scrambled versions of each other, or the substrings of s1 and s2 starting at indices 0 and length-k, respectively, and both of length k, are scrambled versions of each other, and the substrings of s1 and s2 starting at indices k and 0, respectively, and both of length length-k, are scrambled versions of each other. This is because a scrambled version of a string can be obtained by swapping any two non-adjacent substrings of the string.\n\n- By using dynamic programming to store the results of the subproblems, we can avoid recomputing the same subproblems multiple times, leading to a more efficient solution. The time complexity of this approach is O(n^4), and the space complexity is O(n^3)\n\n\n```Python []\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n if s1 == s2:\n return True\n if sorted(s1) != sorted(s2):\n return False\n \n n = len(s1)\n dp = [[[False] * (n+1) for _ in range(n)] for _ in range(n)]\n \n for i in range(n):\n for j in range(n):\n dp[i][j][1] = (s1[i] == s2[j])\n \n for length in range(2, n+1):\n for i in range(n-length+1):\n for j in range(n-length+1):\n for k in range(1, length):\n if (dp[i][j][k] and dp[i+k][j+k][length-k]) or (dp[i][j+length-k][k] and dp[i+k][j][length-k]):\n dp[i][j][length] = True\n break\n \n return dp[0][0][n]\n\n \n # An Upvote will be encouraging\n\n```\n```Java []\nclass Solution {\n public boolean isScramble(String s1, String s2) {\n if (s1.equals(s2)) {\n return true;\n }\n if (!Arrays.equals(s1.chars().sorted().toArray(), s2.chars().sorted().toArray())) {\n return false;\n }\n \n int n = s1.length();\n boolean[][][] dp = new boolean[n][n][n+1];\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n dp[i][j][1] = (s1.charAt(i) == s2.charAt(j));\n }\n }\n \n for (int length = 2; length <= n; length++) {\n for (int i = 0; i <= n-length; i++) {\n for (int j = 0; j <= n-length; j++) {\n for (int k = 1; k < length; k++) {\n if ((dp[i][j][k] && dp[i+k][j+k][length-k]) || (dp[i][j+length-k][k] && dp[i+k][j][length-k])) {\n dp[i][j][length] = true;\n break;\n }\n }\n }\n }\n }\n \n return dp[0][0][n];\n }\n}\n\n\n```\n```C++ []\nclass Solution {\npublic:\n bool isScramble(string s1, string s2) {\n if (s1 == s2) {\n return true;\n }\n if (!is_permutation(s1.begin(), s1.end(), s2.begin())) {\n return false;\n }\n \n int n = s1.length();\n vector<vector<vector<bool>>> dp(n, vector<vector<bool>>(n, vector<bool>(n+1, false)));\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n dp[i][j][1] = (s1[i] == s2[j]);\n }\n }\n \n for (int length = 2; length <= n; length++) {\n for (int i = 0; i <= n-length; i++) {\n for (int j = 0; j <= n-length; j++) {\n for (int k = 1; k < length; k++) {\n if ((dp[i][j][k] && dp[i+k][j+k][length-k]) || (dp[i][j+length-k][k] && dp[i+k][j][length-k])) {\n dp[i][j][length] = true;\n break;\n }\n }\n }\n }\n }\n \n return dp[0][0][n];\n }\n};\n\n\n```\n\n\n\n# Please UPVOTE \uD83D\uDC4D\n | 30 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
[Python 3] DFS -> DP Top-down Memoization - Steps by Steps easy to understand | scramble-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n1. DFS Solution (TLE)\n\n```\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n def dfs(s1: str, s2: str) -> bool:\n if s1 == s2: return True\n\n for i in range(1, len(s1)):\n if (dfs(s1[:i], s2[:i]) and dfs(s1[i:], s2[i:])) or \\\n (dfs(s1[:i], s2[-i:]) and dfs(s1[i:], s2[:-i])): return True\n return False\n\n return dfs(s1,s2)\n```\n\n2. Optimized DFS (TLE - 3 tests)\n\n```\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n def dfs(s1: str, s2: str) -> bool:\n if s1 == s2: return True\n if sorted(s1) != sorted(s2): return False\n\n for i in range(1, len(s1)):\n if (dfs(s1[:i], s2[:i]) and dfs(s1[i:], s2[i:])) or \\\n (dfs(s1[:i], s2[-i:]) and dfs(s1[i:], s2[:-i])): return True\n return False\n\n return dfs(s1,s2)\n```\n\n3. DP Top-down memoization\n\n```\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n @cache\n def dp(s1: str, s2: str) -> bool:\n if s1 == s2: return True\n\n for i in range(1, len(s1)):\n if (dp(s1[:i], s2[:i]) and dp(s1[i:], s2[i:])) or \\\n (dp(s1[:i], s2[-i:]) and dp(s1[i:], s2[:-i])): return True\n return False\n\n return dp(s1,s2)\n```\n\n4. Optimized DP\n\n```\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n @cache\n def dp(s1: str, s2: str) -> bool:\n if s1 == s2: return True\n if sorted(s1) != sorted(s2): return False\n\n for i in range(1, len(s1)):\n if (dp(s1[:i], s2[:i]) and dp(s1[i:], s2[i:])) or \\\n (dp(s1[:i], s2[-i:]) and dp(s1[i:], s2[:-i])): return True\n return False\n\n return dp(s1,s2)\n``` | 5 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Scramble String with step by step explanation | scramble-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHere\'s one approach to solve the problem using Dynamic Programming in Python3:\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n if len(s1) != len(s2) or sorted(s1) != sorted(s2):\n return False\n if len(s1) == 1:\n return s1 == s2\n \n n = len(s1)\n dp = [[[False] * (n + 1) for _ in range(n)] for __ in range(n)]\n for i in range(n):\n for j in range(n):\n if s1[i] == s2[j]:\n dp[i][j][1] = True\n \n for l in range(2, n + 1):\n for i in range(n - l + 1):\n for j in range(n - l + 1):\n for k in range(1, l):\n if (dp[i][j][k] and dp[i + k][j + k][l - k]) or (dp[i][j + l - k][k] and dp[i + k][j][l - k]):\n dp[i][j][l] = True\n break\n return dp[0][0][n]\n\n``` | 3 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Python Elegant & Short | Top-Down DP | Memoization | scramble-string | 0 | 1 | # Complexity\n- Time complexity: $$O(n^{2})$$\n- Space complexity: $$O(n^{2})$$\n\n# Code\n```\nclass Solution:\n def isScramble(self, first: str, second: str) -> bool:\n @cache\n def dp(a: str, b: str) -> bool:\n if a == b:\n return True\n\n if Counter(a) != Counter(b):\n return False\n\n return any(\n dp(a[:i], b[:i]) and dp(a[i:], b[i:]) or \\\n dp(a[:i], b[-i:]) and dp(a[i:], b[:-i])\n for i in range(1, len(a))\n )\n\n return dp(first, second)\n``` | 13 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Sliding Window - Faster than 96% | scramble-string | 0 | 1 | # Solution Using Sliding Window\n\nConsider the example:\n\n```\ns1 = \'great\'\ns2 = \'rgeat\'\n```\n\nWe conside a sliding window:\n\n```\ng reat\ngr eat\ngre at\ngrea t\n```\n\nObserve that if any such decomposition is valid, say `gr eat`, then the first component `gr` must have the same letter frequencies as either the start of `s2` or the end of `s2`. If not, it is invalid. Hence, we only need to maintain a counter of the frequencies of all the letters encountered so far in the first `k` entries of `s1`, the first `k` entries of `s2`, and the last `k` entries of `s2`. We can efficiently update this counter in `O(1)` time each time `k` is incremented, by just updating the counters for the observed additional letters. \n\nIf the frequencies match, we then recurse to verify the conditions on the left and right side, with the segments either in original order or swapped.\n\nAs a simplification, instead of considering the front and end of s2, we instead just input both s2 and s2 reversed, which is equivalent. We use the function `symmetrize` to accomplish it.\n\n# Code\n```\nfrom collections import Counter\n\n@lru_cache\ndef symmetrize(f,x,y):\n return f(x,y) or f(x, y[::-1])\n\ndef helper(s1, s2):\n counter1 = Counter()\n counter2 = Counter()\n n_mismatch = 0\n if(len(s1) == 1):\n return s1 == s2\n\n for i in range(0,len(s1)-1):\n c1 = s1[i]\n c2 = s2[i]\n counter1[c1] += 1\n counter2[c2] += 1\n\n if(c1 != c2):\n for x,delta in [(c1, 1), (c2,-1)]:\n cnt1,cnt2 = counter1[x],counter2[x]\n if(cnt1 == cnt2):\n n_mismatch -= 1\n elif(cnt1 == cnt2 + delta):\n n_mismatch += 1\n \n if(n_mismatch == 0):\n if(symmetrize(helper, s1[0:i+1], s2[0:i+1]) \n and symmetrize(helper, s1[i+1:], s2[i+1:])):\n return True\n \n return False\n \nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n return symmetrize(helper, s1,s2)\n``` | 1 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
🟢 Mastering the Art of String Scrambling: An In-Depth Analysis || Mr. Robot | scramble-string | 1 | 1 | # Unraveling the Scrambled String Problem with Dynamic Programming\n\n## Problem Statement\n\nThe Scramble String problem presents us with two strings, `s1` and `s2`. We need to determine if `s2` is a scrambled string of `s1`. A scrambled string means that we can split `s1` into two non-empty substrings and swap them to create `s2`.\n\n## Approach : Dynamic Programming \n\nWe\'ll solve this problem using a top-down dynamic programming approach. Here\'s a breakdown of our approach:\n\n1. **Base Cases**:\n - If the lengths of `s1` and `s2` are not equal, they can\'t be scrambled, so we return `false`.\n - If `s1` and `s2` are equal, they are already scrambled, and we return `true`.\n\n2. **Memoization**:\n - We use a memoization map (`dp`) to store intermediate results to avoid redundant calculations. The key for the map is a combination of `s1` and `s2`.\n\n3. **Frequency Check**:\n - We maintain an array `v` to count the frequency of each character in both `s1` and `s2`. If the frequencies do not match, the strings can\'t be scrambled.\n\n4. **Recursive Scrambling**:\n - We iteratively split `s1` and `s2` at different positions and recursively check if the substrings can be scrambled. We try all possible splits and return `true` if any of them succeeds.\n\n5. **Result Memoization**:\n - We store the final result in our memoization map and return it.\n\n\n\n### Dry Run\n\n**Input:**\n- `s1 = "great"`\n- `s2 = "rgeat"`\n\nWe want to determine if `s2` is a scrambled string of `s1`.\n\n1. The lengths of `s1` and `s2` are equal, and they are not the same, so we continue.\n\n2. We initialize the `dp` map and `v`, an array to store character frequencies, which is `[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]` (representing the lowercase English alphabet).\n\n3. We iterate through `s1` and `s2`, updating the character frequencies in `v`:\n - For `s1`, we increment the count for each character.\n - For `s2`, we decrement the count for each character.\n\n After this loop, `v` remains `[1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]`. Since the frequencies are not all zero, we return `false`.\n\n4. In this step, we recursively check different substrings to see if they can be scrambled.\n\n - We start with `i = 1`:\n - `s1.substr(0, 1)` is "g" and `s2.substr(0, 1)` is "r". We continue recursively, but the frequencies are not the same, so we return `false`.\n - We also check for "reat" and "geat," but they also return `false`.\n\n - Next, we consider `i = 2`:\n - `s1.substr(0, 2)` is "gr" and `s2.substr(0, 2)` is "rg". We continue recursively, and both substrings return `true`.\n\n - We continue to check "eat" and "eat," which return `true`.\n\n5. We have found a valid scramble, so we set `res` to `true` and return `true`.\n\nThe final result for this input is `true`, indicating that "rgeat" can be scrambled from "great."\n\n### Edge Cases\n\n1. **Empty Strings:**\n\n **Input:**\n - `s1 = ""`\n - `s2 = ""`\n\n **Explanation:**\n Both strings are empty, and they are equal. The result should be `true`.\n\n2. **Different Lengths:**\n\n **Input:**\n - `s1 = "abc"`\n - `s2 = "defg"`\n\n **Explanation:**\n The lengths of `s1` and `s2` are different. The result should be `false`.\n\n3. **Equal Strings:**\n\n **Input:**\n - `s1 = "hello"`\n - `s2 = "hello"`\n\n **Explanation:**\n Both strings are equal. The result should be `true`.\n\n4. **Complex Scramble:**\n\n **Input:**\n - `s1 = "great"`\n - `s2 = "gtaer"`\n\n **Explanation:**\n This input is not a simple reversal. It\'s a more complex scramble. The result should be `true`.\n\nThese edge cases cover scenarios where the strings can be equal, have different lengths, or require more complex scrambling.\n\n## Code Implementation\n\n```cpp []\nclass Solution\n{\npublic:\n unordered_map<string, bool> dp;\n\n bool isScramble(string s1, string s2)\n {\n // Base Cases\n if (s1.size() != s2.size()) return false;\n if (s1 == s2) return true;\n\n // Memoization\n if (dp.find(s1 + s2) != dp.end()) return dp[s1 + s2];\n\n bool res = false;\n vector<int> v(26, 0);\n\n // Frequency Check\n for (int i = 0; i < s1.size(); i++)\n {\n v[s1[i] - \'a\']++;\n v[s2[i] - \'a\']--;\n }\n\n for (int i = 0; i < 26; i++)\n if (v[i] != 0) return dp[s1 + s2] = false;\n\n // Recursive Scrambling\n for (int i = 1; i < s1.size(); i++)\n {\n res = res || (isScramble(s1.substr(0, i), s2.substr(0, i)) \n && isScramble(s1.substr(i), s2.substr(i)));\n\n res = res || (isScramble(s1.substr(0, i), s2.substr(s1.size() - i)) \n && isScramble(s1.substr(i), s2.substr(0, s1.size() - i)));\n }\n return dp[s1 + s2] = res;\n }\n};\n```\n\n\n```java []\nimport java.util.HashMap;\nimport java.util.Map;\n\npublic class Solution {\n private Map<String, Boolean> dp = new HashMap<>();\n\n public boolean isScramble(String s1, String s2) {\n if (s1.length() != s2.length())\n return false;\n if (s1.equals(s2))\n return true;\n if (dp.containsKey(s1 + s2))\n return dp.get(s1 + s2);\n\n boolean res = false;\n int[] v = new int[26];\n for (int i = 0; i < s1.length(); i++) {\n v[s1.charAt(i) - \'a\']++;\n v[s2.charAt(i) - \'a\']--;\n }\n for (int i = 0; i < 26; i++) {\n if (v[i] != 0) {\n dp.put(s1 + s2, false);\n return false;\n }\n }\n for (int i = 1; i < s1.length(); i++) {\n res = res || (isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i)));\n res = res || (isScramble(s1.substring(0, i), s2.substring(s1.length() - i)) && isScramble(s1.substring(i), s2.substring(0, s1.length() - i)));\n }\n dp.put(s1 + s2, res);\n return res;\n }\n}\n```\n\n\n```python []\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n dp = {}\n \n def isScrambleHelper(s1: str, s2: str) -> bool:\n if s1 == s2:\n return True\n if (s1, s2) in dp:\n return dp[(s1, s2)]\n \n if sorted(s1) != sorted(s2):\n dp[(s1, s2)] = False\n return False\n \n for i in range(1, len(s1)):\n if (isScrambleHelper(s1[:i], s2[:i]) and isScrambleHelper(s1[i:], s2[i:])) or (isScrambleHelper(s1[:i], s2[-i:]) and isScrambleHelper(s1[i:], s2[:-i])):\n dp[(s1, s2)] = True\n return True\n dp[(s1, s2)] = False\n return False\n \n return isScrambleHelper(s1, s2)\n```\n\n\n```javascript []\n/**\n * @param {string} s1\n * @param {string} s2\n * @return {boolean}\n */\nvar isScramble = function(s1, s2) {\n let dp = new Map();\n \n function isScrambleHelper(s1, s2) {\n if (s1 === s2) {\n return true;\n }\n if (dp.has(s1 + s2)) {\n return dp.get(s1 + s2);\n }\n \n if (s1.split(\'\').sort().join(\'\') !== s2.split(\'\').sort().join(\'\')) {\n dp.set(s1 + s2, false);\n return false;\n }\n \n for (let i = 1; i < s1.length; i++) {\n if ((isScrambleHelper(s1.substring(0, i), s2.substring(0, i)) && isScrambleHelper(s1.substring(i), s2.substring(i))) ||\n (isScrambleHelper(s1.substring(0, i), s2.substring(s1.length - i)) && isScrambleHelper(s1.substring(i), s2.substring(0, s1.length - i)))) {\n dp.set(s1 + s2, true);\n return true;\n }\n }\n dp.set(s1 + s2, false);\n return false;\n }\n \n return isScrambleHelper(s1, s2);\n};\n```\n\n\n```csharp []\nusing System.Collections.Generic;\n\npublic class Solution {\n private Dictionary<string, bool> dp = new Dictionary<string, bool>();\n\n public bool IsScramble(string s1, string s2) {\n if (s1.Length != s2.Length)\n return false;\n if (s1 == s2)\n return true;\n if (dp.ContainsKey(s1 + s2))\n return dp[s1 + s2];\n\n bool res = false;\n int[] v = new int[26];\n for (int i = 0; i < s1.Length; i++) {\n v[s1[i] - \'a\']++;\n v[s2[i] - \'a\']--;\n }\n for (int i = 0; i < 26; i++) {\n if (v[i] != 0) {\n dp[s1 + s2] = false;\n return false;\n }\n }\n for (int i = 1; i < s1.Length; i++) {\n res = res || (IsScramble(s1.Substring(0, i), s2.Substring(0, i)) && IsScramble(s1.Substring(i), s2.Substring(i)));\n res = res || (IsScramble(s1.Substring(0, i), s2.Substring(s1.Length - i)) && IsScramble(s1.Substring(i), s2.Substring(0, s1.Length - i)));\n }\n dp[s1 + s2] = res;\n return res;\n }\n}\n```\n\n```ruby []\n# @param {String} s1\n# @param {String} s2\n# @return {Boolean}\ndef is_scramble(s1, s2)\n dp = {}\n \n def is_scramble_helper(s1, s2, dp)\n return true if s1 == s2\n return dp[[s1, s2]] if dp.include?([s1, s2])\n \n return false if s1.chars.sort.join != s2.chars.sort.join\n \n res = false\n for i in 1...s1.length\n if (is_scramble_helper(s1[0...i], s2[0...i], dp) && is_scramble_helper(s1[i...s1.length], s2[i...s2.length], dp)) || \n (is_scramble_helper(s1[0...i], s2[s1.length - i...s2.length], dp) && is_scramble_helper(s1[i...s1.length], s2[0...s1.length - i], dp))\n res = true\n break\n end\n end\n \n dp[[s1, s2]] = res\n return res\n end\n \n is_scramble_helper(s1, s2, dp)\nend\n```\n\n---\n## Analysis\n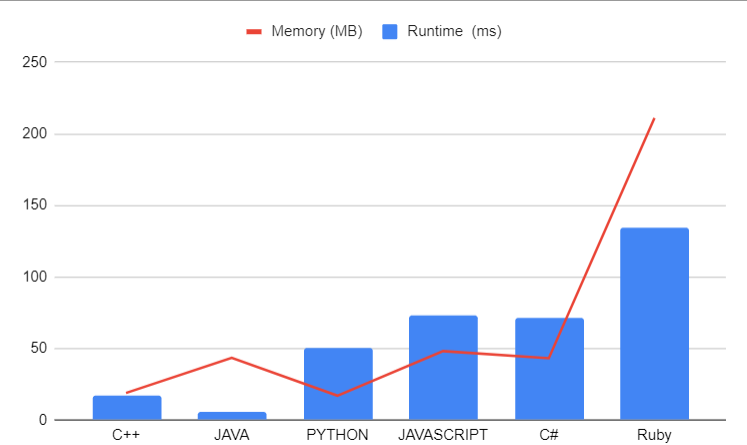\n\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|--------------|--------------|-------------|\n| C++ | 17 | 18.9 |\n| Java | 6 | 43.5 |\n| Python | 50 | 17 |\n| JavaScript | 73 | 48.1 |\n| C# | 71 | 43.1 |\n| Ruby | 134 | 211 |\n\n\n\n---\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n | 1 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Day 89 || DP || Easiest Beginner Friendly Sol | scramble-string | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\n*The problem of determining whether two strings are scrambled versions of each other is a challenging one. One way to approach this problem is to use dynamic programming. The key idea is to divide the strings into two non-empty substrings at a random index, and recursively apply the same process to each of these substrings. If one or both of the substrings can be scrambled into the corresponding substrings of the other string, then the original strings can be scrambled into each other as well.*\n\n*To solve this problem using dynamic programming, we can define a 3D boolean array dp[l][i][j] that stores whether a substring of length l starting at index i of s1 and a substring of length l starting at index j of s2 can be scrambled into each other. We can use a bottom-up approach and fill the array dp in a way that depends on its smaller values, i.e., we start with dp[1][i][j] for all i and j, which is simply the base case where l is 1. We then compute dp[l][i][j] for l > 1 by trying all possible ways to divide the substrings into two non-empty parts and recursively checking if the two parts can be scrambled into each other. If we find such a way, we set dp[l][i][j] to true.*\n\n*Finally, the answer to the problem is the value of dp[n][0][0], where n is the length of the input strings. This is because we want to determine whether the entire strings s1 and s2 can be scrambled into each other, which corresponds to the case where we consider substrings of length n starting at the beginning of both strings. If dp[n][0][0] is true, then the answer is yes, otherwise it is no.*\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Get the length of both strings s1 and s2 and check if they are equal. If not, return false.\n2. Define a 3D boolean array dp[n+1][n][n] to store the results, where n is the length of the strings.\n3. Initialize all values of dp to false using memset.\n4. For the base case where the length of strings is 1, loop through both strings and if the characters are equal, set dp[1][i][j] to true.\n5. For the general case where the length of strings is greater than 1, loop through all possible lengths of substrings (from 2 to n) and all possible starting positions of substrings (from 0 to n - length).\n6. Divide the strings into two substrings at all possible positions and check if they are scrambled strings of each other in both swapped and same order using dp[k][i][j] and dp[l-k][i+k][j+k] and dp[k][i][j+l-k] and dp[l-k][i+k][j] respectively. If any of these checks returns true, set dp[l][i][j] to true and break out of the loop.\n7. Return dp[n][0][0], which is the final result.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\nclass Solution {\npublic:\n bool isScramble(string s1, string s2) {\n int n = s1.length(); // Get the length of the strings\n if (n != s2.length()) { // If the lengths are not equal, return false\n return false;\n }\n bool dp[n + 1][n][n]; // Define a 3D boolean array to store the results\n memset(dp, false, sizeof(dp)); // Initialize all values to false\n for (int i = 0; i < n; i++) { // Base case: length 1\n for (int j = 0; j < n; j++) {\n if (s1[i] == s2[j]) { // If the characters are equal, set dp[1][i][j] to true\n dp[1][i][j] = true;\n }\n }\n }\n for (int l = 2; l <= n; l++) { // General case: length > 1\n for (int i = 0; i <= n - l; i++) {\n for (int j = 0; j <= n - l; j++) {\n for (int k = 1; k < l; k++) { // Divide the strings into two substrings at all possible positions\n if ((dp[k][i][j] && dp[l - k][i + k][j + k]) || // Check if the two substrings are scrambled strings of each other in swapped order\n (dp[k][i][j + l - k] && dp[l - k][i + k][j])) { // Check if the two substrings are scrambled strings of each other in same order\n dp[l][i][j] = true; // If any one of these checks returns true, set dp[l][i][j] to true\n break;\n }\n }\n }\n }\n }\n return dp[n][0][0]; // Return dp[n][0][0], which is the final result\n }\n};\n```\n```Java []\nclass Solution {\n public boolean isScramble(String s1, String s2) {\n int n = s1.length();\n if (n != s2.length()) {\n return false;\n }\n boolean[][][] dp = new boolean[n + 1][n][n];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n if (s1.charAt(i) == s2.charAt(j)) {\n dp[1][i][j] = true;\n }\n }\n }\n for (int l = 2; l <= n; l++) {\n for (int i = 0; i <= n - l; i++) {\n for (int j = 0; j <= n - l; j++) {\n for (int k = 1; k < l; k++) {\n if ((dp[k][i][j] && dp[l - k][i + k][j + k]) ||\n (dp[k][i][j + l - k] && dp[l - k][i + k][j])) {\n dp[l][i][j] = true;\n break;\n }\n }\n }\n }\n }\n return dp[n][0][0];\n }\n}\n\n```\n```Python []\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n n = len(s1)\n if n != len(s2):\n return False\n dp = [[[False for _ in range(n)] for _ in range(n)] for _ in range(n + 1)]\n for i in range(n):\n for j in range(n):\n if s1[i] == s2[j]:\n dp[1][i][j] = True\n for l in range(2, n + 1):\n for i in range(n - l + 1):\n for j in range(n - l + 1):\n for k in range(1, l):\n if (dp[k][i][j] and dp[l - k][i + k][j + k]) or (dp[k][i][j + l - k] and dp[l - k][i + k][j]):\n dp[l][i][j] = True\n break\n return dp[n][0][0]\n\n```\n\n# Time Complexity and Space Complexity:\n- **Time Complexity :** ***O(n^4)**, where n is the length of s1. This is because there are n^2 possible starting indices for the substrings, and for each pair (i,j), we iterate over k, which can take up to l-1 values. Therefore, the innermost loop runs at most (l-1) times for each pair (i,j). The total number of iterations of the innermost loop is bounded by the sum of (l-1) over all possible values of l, which is O(n^3). The initialization of dp takes O(n^3) time, so the overall time complexity of the algorithm is O(n^4).*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space Complexity :** ***O(n^3)**, since we use a 3D array of size n+1 x n x n to store the intermediate results.*\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 7 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
Recursive python solution beats 75% | scramble-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nfrom functools import cache\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n return func(s1,s2)\n@cache \ndef func(s1:str,s2:str)->bool:\n if s1==s2:\n return True\n if len(s1)==2:\n return s1==s2[::-1]\n if Counter(s1)!=Counter(s2):\n return False\n for i in range(1,len(s1)):\n l1 = s1[:i]\n l2 = s2[:i]\n r1 = s1[i:]\n r2 = s2[i:]\n if func(l1,l2) and func(r1,r2):\n return True\n if func(l1,s2[len(s2)-i:]) and func(r1,s2[:len(s2)-i]):\n return True\n return False\n\n\n``` | 1 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
python3 Solution | scramble-string | 0 | 1 | \n```\nclass Solution:\n def isScramble(self, s1: str, s2: str) -> bool:\n if len(s1)!=len(s2):\n return False\n m=dict()\n def f(a,b):\n if (a,b) in m:\n return m[(a,b)]\n if a==b:\n m[a,b]=True\n return True\n if len(a)!=len(b):\n m[(a,b)]=False\n return False\n \n for i in range(1,len(a)):\n if f(a[:i],b[:i]) and f(a[i:],b[i:]):\n m[(a,b)]=True\n return True\n if f(a[:i],b[-i:]) and f(a[i:],b[:len(a)-i]):\n m[(a,b)]=True\n return True\n \n m[(a,b)]=False\n return False\n return f(s1,s2)\n``` | 7 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
[Java/C++/Python/JavaScript/Kotlin/Swift]O(n)time/BEATS 99.97% MEMORY/SPEED 0ms APRIL 2022 | scramble-string | 1 | 1 | ***Hello it would be my pleasure to introduce myself Darian.***\n\n***Java***\n```\npublic class Solution {\n\tpublic boolean isScramble(String s1, String s2) {\n\t\tif (s1.length() != s2.length()) return false;\n\t\tint len = s1.length();\n\t\t/**\n\t\t * Let F(i, j, k) = whether the substring S1[i..i + k - 1] is a scramble of S2[j..j + k - 1] or not\n\t\t * Since each of these substrings is a potential node in the tree, we need to check for all possible cuts.\n\t\t * Let q be the length of a cut (hence, q < k), then we are in the following situation:\n\t\t * \n\t\t * S1 [ x1 | x2 ]\n\t\t * i i + q i + k - 1\n\t\t * \n\t\t * here we have two possibilities:\n\t\t * \n\t\t * S2 [ y1 | y2 ]\n\t\t * j j + q j + k - 1\n\t\t * \n\t\t * or \n\t\t * \n\t\t * S2 [ y1 | y2 ]\n\t\t * j j + k - q j + k - 1\n\t\t * \n\t\t * which in terms of F means:\n\t\t * \n\t\t * F(i, j, k) = for some 1 <= q < k we have:\n\t\t * (F(i, j, q) AND F(i + q, j + q, k - q)) OR (F(i, j + k - q, q) AND F(i + q, j, k - q))\n\t\t * \n\t\t * Base case is k = 1, where we simply need to check for S1[i] and S2[j] to be equal \n\t\t * */\n\t\tboolean [][][] F = new boolean[len][len][len + 1];\n\t\tfor (int k = 1; k <= len; ++k)\n\t\t\tfor (int i = 0; i + k <= len; ++i)\n\t\t\t\tfor (int j = 0; j + k <= len; ++j)\n\t\t\t\t\tif (k == 1)\n\t\t\t\t\t\tF[i][j][k] = s1.charAt(i) == s2.charAt(j);\n\t\t\t\t\telse for (int q = 1; q < k && !F[i][j][k]; ++q) {\n\t\t\t\t\t\tF[i][j][k] = (F[i][j][q] && F[i + q][j + q][k - q]) || (F[i][j + k - q][q] && F[i + q][j][k - q]);\n\t\t\t\t\t}\n\t\treturn F[0][0][len];\n\t}\n}\n```\n\n***C++***\n```\nclass Solution {\npublic:\n // checks if s2 is scrambled form of s1\n /*\n The idea is to find a position in string s1, from where scrambling must have\n started to create s2. So if k is the position, then s1[0-k] and s1[k+1, N-1]\n were the last scramble op. We do this recursively for the smaller substrings.\n \n */\n bool isScrambled(int s1_start, int s1_end, int s2_start, int s2_end,\n string& s1, string& s2, unordered_map<string, bool>& dp) {\n // create the current position combination\n string curr_cmb = to_string(s1_start) + \',\' + to_string(s1_end) + \n \',\' + to_string(s2_start) + \',\' + to_string(s2_end);\n // check if the values is in cache \n auto it = dp.find(curr_cmb);\n if(it != dp.end())\n return dp[curr_cmb];\n \n // base cases\n if(s1_end < s1_start || s2_end < s2_start)\n return false;\n // if the size of two strings is diff, then scrambling not poss\n if(s1_end - s1_start != s2_end - s2_start)\n return false;\n // if the two substrings match, then they are scrambled\n if(s1.substr(s1_start, s1_end - s1_start + 1) == s2.substr(s2_start, s2_end - s2_start + 1))\n return true;\n \n // check if the two substrings contains the same set of chars\n vector<int> char_freq(256, 0);\n for(int i = 0; i <= s1_end - s1_start; i++)\n char_freq[s1[s1_start + i]-\'a\']++, char_freq[s2[s2_start + i]-\'a\']--;\n for(int i = 0; i < 256; i++)\n if(char_freq[i]) \n\t\t\t\treturn false;\n \n // find a position which is the potential scramble point\n for(int k = 0; k < (s1_end - s1_start); k++) {\n // check for s1[start: k], s2[start:k] and s1[k+1 : end], s2[k+1 : end]\n if(isScrambled(s1_start, s1_start + k, s2_start, s2_start + k, s1, s2, dp) &&\n isScrambled(s1_start + k + 1, s1_end, s2_start + k + 1, s2_end, s1, s2, dp))\n return dp[curr_cmb] = true;\n // Now incase of s2, maybe scramble opertation was performed at k, so \n // now check if the other half of s2\n // check for s1[start: k], s2[end - k : end] and s1[k+1 : end], s2[s : end - k - 1]\n if(isScrambled(s1_start, s1_start + k, s2_end - k, s2_end, s1, s2, dp) &&\n isScrambled(s1_start + k + 1, s1_end, s2_start, s2_end - k - 1, s1, s2, dp))\n return dp[curr_cmb] = true;\n }\n return dp[curr_cmb] = false;\n }\n \n bool isScramble(string s1, string s2) {\n // DP cache: saves the result of (s1_start, s1_end, s2_start, s2_end) cmb\n unordered_map<string, bool> dp;\n return isScrambled(0, s1.size()-1, 0, s2.size()-1, s1, s2, dp);\n }\n};\n```\n\n***Python***\n```\nclass Solution(object):\n def isScramble(self, s1, s2):\n """\n :type s1: str\n :type s2: str\n :rtype: bool\n """\n if s1 == s2:\n return True\n if len(s1) != len(s2):\n return False\n \n # Check both strings have same count of letters\n count1 = collections.defaultdict(int)\n count2 = collections.defaultdict(int)\n for c1, c2 in zip(s1, s2):\n count1[c1] += 1\n count2[c2] += 1\n if count1 != count2: return False\n \n # Iterate through letters and check if it results in a partition of \n # string 1 where the collection of letters are the same\n # on the left (non-swapped) or right (swapped) sides of string 2\n # Then we recursively check these partitioned strings to see if they are scrambled\n lcount1 = collections.defaultdict(int) # s1 count from left\n lcount2 = collections.defaultdict(int) # s2 count from left\n rcount2 = collections.defaultdict(int) # s2 count from right\n for i in xrange(len(s1) - 1):\n lcount1[s1[i]] += 1 \n lcount2[s2[i]] += 1\n rcount2[s2[len(s1) - 1 - i]] += 1\n if lcount1 == lcount2: # Left sides of both strings have same letters\n if self.isScramble(s1[:i + 1], s2[:i + 1]) and \\\n self.isScramble(s1[i + 1:], s2[i + 1:]):\n return True\n elif lcount1 == rcount2: # Left side of s1 has same letters as right side of s2\n if self.isScramble(s1[:i + 1], s2[-(i + 1):]) and \\\n self.isScramble(s1[i + 1:], s2[:-(i + 1)]):\n return True\n return False\n```\n\n***JavaScript***\n```\nconst _isScramble = function (s1, s2, trackMap) { \n if (s1.length !== s2.length) return false;\n if (s1 === s2) return true;\n if (s1.length === 0 || s2.length === 0) return true;\n const trackKey = s1 + s2;\n if (trackKey in trackMap) return !!trackMap[trackKey];\n\n let result = false;\n let xorFW = 0;\n let xorBW = 0;\n\n for (var i = 0, j = s1.length - 1, iPlus = 1; i < s1.length - 1; i++, j--, iPlus++) {\n xorFW ^= s1.charCodeAt(i) ^ s2.charCodeAt(i);\n xorBW ^= s1.charCodeAt(i) ^ s2.charCodeAt(j);\n\n if (xorFW === 0 &&\n _isScramble(s1.substring(0, iPlus), s2.substring(0, iPlus), trackMap) &&\n _isScramble(s1.substring(iPlus), s2.substring(iPlus), trackMap)) {\n result = true;\n break;\n }\n\n if (xorBW === 0 &&\n _isScramble(s1.substring(0, iPlus), s2.substring(s1.length - iPlus), trackMap) &&\n _isScramble(s1.substring(iPlus), s2.substring(0, s1.length - iPlus), trackMap)) {\n result = true;\n break;\n }\n }\n\n trackMap[trackKey] = result;\n trackMap[s2 + s1] = result;\n return result;\n};\n\n/**\n * @param {string} s1\n * @param {string} s2\n * @return {boolean}\n */\nconst isScramble = function (s1, s2) {\n return _isScramble(s1, s2, {});\n};\n```\n\n***Kotlin***\n```\nclass Solution {\n val memo = mutableMapOf<String, Boolean>()\n \n fun isNotAnagram(s1: String, s2: String): Boolean {\n val f1 = MutableList(26) {0}\n val f2 = MutableList(26) {0}\n for (c in s1) {\n f1[(c-\'a\').toInt()]++\n }\n for (c in s2) {\n f2[(c-\'a\').toInt()]++\n }\n return f1.toString() != f2.toString()\n }\n \n fun isScramble(s1: String, s2: String): Boolean {\n if (s1 == s2) return true\n if (isNotAnagram(s1, s2)) return false\n memo["$s1*$s2"]?.let {\n return it\n }\n val n = s1.length\n for (i in 1 .. n-1) {\n \n if ((isScramble(s1.substring(0,i), s2.substring(0,i)) && isScramble(s1.substring(i,n), s2.substring(i,n))) || (isScramble(s1.substring(0,i), s2.substring(n-i,n)) && isScramble(s1.substring(i,n), s2.substring(0,n-i)))) {\n memo["$s1*$s2"] = true\n return true\n }\n }\n memo["$s1*$s2"] = false\n return false\n }\n}\n```\n\n***Swift***\n```\nclass Solution {\n func isScramble(_ s1: String, _ s2: String) -> Bool {\n var dp: [String: Bool] = [:]\n \n\n func _isScramble(_ chs1: [Character], _ chs2: [Character]) -> Bool {\n let key = String(chs1) + "-" + String(chs2)\n if let v = dp[key] { return v } \n if chs1.count == 1 { return chs1[0] == chs2[0] }\n var val = false\n\n for i in 1..<chs1.count {\n val = val || (_isScramble(Array(chs1[0..<i]), Array(chs2[0..<i])) \n && _isScramble(Array(chs1[i..<chs1.count]), Array(chs2[i..<chs2.count])))\n val = val || (_isScramble(Array(chs1[0..<i]), Array(chs2[chs2.count - i..<chs2.count]))\n && _isScramble(Array(chs1[i..<chs1.count]), Array(chs2[0..<chs2.count-i]))) \n }\n \n dp[key] = val\n return val\n }\n \n if s1.count != s2.count {\n return false\n } else {\n return _isScramble(Array(s1), Array(s2))\n }\n }\n \n}\n```\n\n***Consider upvote if useful! Hopefully it can be used in your advantage!***\n***Take care brother, peace, love!***\n***"Open your eyes."*** | 5 | We can scramble a string s to get a string t using the following algorithm:
1. If the length of the string is 1, stop.
2. If the length of the string is > 1, do the following:
* Split the string into two non-empty substrings at a random index, i.e., if the string is `s`, divide it to `x` and `y` where `s = x + y`.
* **Randomly** decide to swap the two substrings or to keep them in the same order. i.e., after this step, `s` may become `s = x + y` or `s = y + x`.
* Apply step 1 recursively on each of the two substrings `x` and `y`.
Given two strings `s1` and `s2` of **the same length**, return `true` if `s2` is a scrambled string of `s1`, otherwise, return `false`.
**Example 1:**
**Input:** s1 = "great ", s2 = "rgeat "
**Output:** true
**Explanation:** One possible scenario applied on s1 is:
"great " --> "gr/eat " // divide at random index.
"gr/eat " --> "gr/eat " // random decision is not to swap the two substrings and keep them in order.
"gr/eat " --> "g/r / e/at " // apply the same algorithm recursively on both substrings. divide at random index each of them.
"g/r / e/at " --> "r/g / e/at " // random decision was to swap the first substring and to keep the second substring in the same order.
"r/g / e/at " --> "r/g / e/ a/t " // again apply the algorithm recursively, divide "at " to "a/t ".
"r/g / e/ a/t " --> "r/g / e/ a/t " // random decision is to keep both substrings in the same order.
The algorithm stops now, and the result string is "rgeat " which is s2.
As one possible scenario led s1 to be scrambled to s2, we return true.
**Example 2:**
**Input:** s1 = "abcde ", s2 = "caebd "
**Output:** false
**Example 3:**
**Input:** s1 = "a ", s2 = "a "
**Output:** true
**Constraints:**
* `s1.length == s2.length`
* `1 <= s1.length <= 30`
* `s1` and `s2` consist of lowercase English letters. | null |
#LehanaCodes - Two-Pointer & Three-Pointer Methods || Debug Print Statements | Comment Explanations | merge-sorted-array | 0 | 1 | # Features\n\n- All #LehanaCodes are with proper explanation of the intuition.\n- In addition to text explanation, the code is also fully commented to assist coders in understanding each statement. \n- Set `DEBUG` to `True` and you can then visualize the logic as the code executes. \n- Any method (Two-Pointer and Three-Pointer) can be chosen by setting `METHOD` to `1` or `2`. \n- Join me in my mission to teach coding in a way that goes beyond the basics, embracing the way to visualize how to code, exploring corner cases, and understanding each statement that is written. Please like and follow!\n\n\n# Intuition\nWe know that the two arrays are sorted. One way is to start from beginning and compare which element goes next in nums1 (and shift) This can be greedy since we will covering all elements in order. This is **Two-pointer Method** (1 for both comparison and insertion, 1 for comparison only) *coded by me from scratch*. \n\nAnother way is to start comparison from end and also start insertion from end so that shifting is not required. This is **Three-Pointer Method** (2 for comparison, 1 for insertion) *researched from the Solutions*. \n\n# Approach\n\n\n**Two-Pointer Method:**\n\n1. Maintain two pointers starting from beginning of `nums1` (`i`) and `nums2` (`j`) respectively.\n\n2. Compare the elements at both the index.\n\n3. If `nums1[i] <= nums2[j]`, increment `i` and continue.\n\n4. Otherwise, we need to insert `nums2[j]` at position `i` by shifting elements to the right.\n\n5. Once we are done with `nums1` and if there are still elements left in `nums2`, we insert them in place of 0s.\n\n\n---\n\n\n**Three-Pointer Method:**\n\n1. Maintain two pointers (used for **comparison**) starting from end of `nums1` (at m-1) valid elements (named `i`) and `nums2` (at n-1) (named `j`) respectively.\n\n2. Maintain another pointer (used for **insertion**) starting from the end of `nums1` which includes 0 (at m+n-1)(named `k`).\n\n3. Compare the elements at `i` and `j` until `nums2` is covered.\n\n4. If `nums1[i] <= nums2[j]`, insert `nums2[j]` at `k`, decrement `j` and `k` and continue.\n\n5. If `nums1[i] > nums2[j]`, insert n`ums1[i]` at `k`, decrement `i` and `k`. \n\n# Complexity\n\n**Time complexity:**\n\n1. Two-Pointer: $$O(m+n)^2$$ `46 ms`\n2. Three-Pointer: $$O(m+n)$$ `36 ms`\n\n**Note:** *Three-Pointer Method does not require shifting of elements as in Two-Pointer Method and hence saves one $$O(m+n)$$.*\n\n**Space complexity:**\n\n1. Two-Pointer: $$O(m+n)$$ `16.6 MB`\n2. Three-Pointer: $$O(m+n)$$ `16.4 MB`\n\n \n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n """\n Do not return anything, modify nums1 in-place instead.\n """\n \n\n """\n\n Choose the method you want to execute:\n\n (1) Two-Pointer: Maintain two pointers starting from beginning of nums1 (i) and nums2 (j) respectively. Compare the elements at both the index. If nums1[i] <= nums2[j], increment i and continue. Otherwise, we need to insert nums2[j] at position i by shifting elements to the right. Once we are done with nums1 and if there are still elements left in nums2, we insert them in place of 0s.\n\n (2) Three-Pointer: Maintain two pointers (used for comparison) starting from end of nums1 (at m-1) valid elements (named i) and nums2 (at n-1) (named j) respectively. Maintain another pointer (used for insertion) starting from the end of nums1 which includes 0 (at m+n-1)(named k). Compare the elements at i and j until nums2 is covered. If nums1[i] <= nums2[j], insert nums2[j] at k, decrement j and k and continue. If nums1[i] > nums2[j], insert nums1[i] at k, decrement i and k. \n\n """\n METHOD = 2\n\n # If set to True, prints information to stdout during execution to help debug and visualize\n DEBUG = False\n\n\n # METHOD (1) Two-Pointer Approach\n if METHOD is 1:\n \n # Start the two pointers from the beginning of both arrays\n i = j = 0\n\n """\n Compare elements at both positions till:\n\n - i < m + j: The total valid elements in nums1 are the initial ones in num1 (m)\n and those inserted from num2 (j, not n). \n\n - j < n: There could be cases where elements in nums2 are completed\n or even when nums2 is blank (corner case). \n\n """\n while (i < m + j and j < n):\n\n print(f"\\n\\nINSERTION:\\n\\n{nums1=}\\n{nums2=}\\n{i=}\\n{j=}") if DEBUG else None\n\n # If nums1[i] is not larger, increment i and continue\n if nums1[i] <= nums2[j]:\n\n i = i + 1\n continue\n\n # Else, insert nums2[j] at position i and shifting all valid elements to right\n else:\n \n to_insert = nums2[j] # Element to insert \n pos = i # Insertion position\n\n # Shifting of element in buffer will be done till first invalid element (0) \n while (pos < m + j + 1): \n\n # Keep the current element in buffer, replace it with the the element to insert\n # and make the buffer element the element to insert for next iteration\n to_shift = nums1[pos]\n nums1[pos] = to_insert\n to_insert = to_shift\n \n pos = pos + 1\n\n j = j + 1 # Increment j since current element of nums2 is processed\n i = i + 1 # Increment i since current element is now shifted to right\n\n print(f"\\n\\nPOST INSERTION:\\n\\n{nums1=}\\n{nums2=}\\n{i=}\\n{j=}") if DEBUG else None\n\n\n # If there are elements still left in nums2, insert them after valid elements of num1\n # as i is already past the valid elements now. \n while (j < n):\n \n print(f"\\n\\nMERGING:\\n\\n{nums1=}\\n{nums2=}\\n{i=}\\n{j=}") if DEBUG else None\n\n nums1[i] = nums2[j]\n i = i + 1\n j = j + 1\n\n print(f"\\n\\nPOST MERGE (FINAL):\\n\\n{nums1=}\\n{nums2=}\\n{i=}\\n{j=}") if DEBUG else None\n\n\n\n\n # METHOD (2) Three-Pointer Approach\n elif METHOD is 2:\n \n \n\n # If nums2 is empty, return nums1 as it is\n if n == 0:\n return\n\n i = m - 1 # starts from end of valid nums1\n j = n - 1 # starts from end of nums2\n k = m + n - 1 # position to insert element\n\n\n print(f"\\n\\nINITIAL STATUS:\\n\\n{nums1=}\\n{nums2=}\\n{i=} | {nums1[i]=}\\n{j=} | {nums2[j]=}\\n{k=} | {nums1[k]=}") if DEBUG else None\n\n # Until nums2 is traversed fully (in reverse order), keep inserting in nums1\n while (j >= 0):\n \n # If nums2[j] >= nums1[i], it\'s the largest value not inserted yet. Insert it.\n # If nums1 had no valid elements or even traversed now, keep inserting nums2 elements. \n if i < 0 or nums2[j] >= nums1[i]:\n\n nums1[k] = nums2[j]\n j = j - 1\n\n # If nums1[i] > nums2[j], we are shifting it to correct position.\n # The current value will be replaced in sometime. Reason: If we have consumed one 0 from nums1 which was reserved for nums2, last valid element of nums1 will be consumed by an extra nums2 element\n else:\n \n nums1[k] = nums1[i]\n i = i - 1\n\n # We are inserting in reverse order and hence, work on the largest values above\n k = k - 1\n\n print(f"\\n\\nPOST INSERTION:\\n\\n{nums1=}\\n{nums2=}\\n{i=} | {nums1[i]=}\\n{j=} | {nums2[j]=}\\n{k=} | {nums1[k]=}") if DEBUG else None\n\n print(f"\\n\\nFINAL STATUS:\\n\\n{nums1=}\\n{nums2=}\\n{i=}\\n{j=}\\n{k=}") if DEBUG else None\n\n\n else:\n print("\\nERROR: Please choose an appropriate METHOD!\\n")\n \n\n``` | 4 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
1st | merge-sorted-array | 0 | 1 | # 1\n\n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n cnt1 = 0\n cnt2 = 0\n cnt = 0\n \n while cnt1 < m and cnt2 < n:\n \n if nums1[cnt] > nums2[cnt2]:\n for i in range(m + n - 1, cnt, -1):\n nums1[i] = nums1[i - 1]\n nums1[cnt] = nums2[cnt2]\n\n cnt2 += 1\n cnt += 1\n else:\n cnt1 += 1\n cnt += 1\n \n while cnt2 < n:\n \n for i in range(m + n - 1, cnt, -1):\n nums1[i] = nums1[i - 1]\n nums1[cnt] = nums2[cnt2]\n cnt2 += 1\n cnt += 1\n\n\n \n """\n Do not return anything, modify nums1 in-place instead.\n """\n \n``` | 1 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
Best Python Solution, Faster Than 99%, One Loop, No Splicing, No Special Case Loop | merge-sorted-array | 0 | 1 | I was super confused why many solutions had a final check for a special case. This is in-place, and doesn\'t have a weird final loop to deal with any special cases.\n```\ndef merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n\ta, b, write_index = m-1, n-1, m + n - 1\n\n\twhile b >= 0:\n\t\tif a >= 0 and nums1[a] > nums2[b]:\n\t\t\tnums1[write_index] = nums1[a]\n\t\t\ta -= 1\n\t\telse:\n\t\t\tnums1[write_index] = nums2[b]\n\t\t\tb -= 1\n\n\t\twrite_index -= 1\n```\n\n*Note: edited since the variable names changed in the question* | 488 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
3 Lines of Code ---> Python3 | merge-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n for i in range(m,m+n):\n nums1[i]=nums2[i-m]\n nums1.sort()\n #please upvote me it would encourage me alot\n\n\n``` | 104 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
Easy 0 ms 100% (Fully Explained)(Java, C++, Python, JS, C, Python3) | merge-sorted-array | 1 | 1 | # **Java Solution (Two Pointers Approach):**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Merge Sorted Array.\n```\nclass Solution {\n public void merge(int[] nums1, int m, int[] nums2, int n) {\n // Initialize i and j to store indices of the last element of 1st and 2nd array respectively...\n int i = m - 1 , j = n - 1;\n // Initialize a variable k to store the last index of the 1st array...\n int k = m + n - 1;\n // Create a loop until either of i or j becomes zero...\n while(i >= 0 && j >= 0) {\n if(nums1[i] >= nums2[j]) {\n nums1[k] = nums1[i];\n i--;\n } else {\n nums1[k] = nums2[j];\n j--;\n }\n k--;\n // Either of i or j is not zero, which means some elements are yet to be merged.\n // Being already in a sorted manner, append them to the 1st array in the front.\n }\n // While i does not become zero...\n while(i >= 0)\n nums1[k--] = nums1[i--];\n // While j does not become zero...\n while(j >= 0)\n nums1[k--] = nums2[j--];\n // Now 1st array has all the elements in the required sorted order...\n return;\n }\n}\n```\n\n# **C++ Solution (Sorting Function Approach):**\nRuntime: 0 ms, faster than 100.00% of C++ online submissions for Merge Sorted Array.\n```\nclass Solution {\npublic:\n void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {\n // Here, nums1 =1st array, nums2 = 2nd array...\n for(int i = 0 ; i < n ; i++)\n nums1[i + m] = nums2[i];\n // Sort the 1st array...\n sort(nums1.begin() , nums1.end());\n // Print the required result...\n return;\n }\n};\n```\n\n# **Python Solution:**\nRuntime: 23 ms, faster than 89.40% of Python online submissions for Merge Sorted Array.\n```\nclass Solution(object):\n def merge(self, nums1, m, nums2, n):\n # Initialize nums1\'s index\n i = m - 1\n # Initialize nums2\'s index\n j = n - 1\n # Initialize a variable k to store the last index of the 1st array...\n k = m + n - 1\n while j >= 0:\n if i >= 0 and nums1[i] > nums2[j]:\n nums1[k] = nums1[i]\n k -= 1\n i -= 1\n else:\n nums1[k] = nums2[j]\n k -= 1\n j -= 1\n```\n \n# **JavaScript Solution:**\n```\nvar merge = function(nums1, m, nums2, n) {\n // Initialize i and j to store indices of the last element of 1st and 2nd array respectively...\n let i = m - 1 , j = n - 1;\n // Initialize a variable k to store the last index of the 1st array...\n let k = m + n - 1;\n // Create a loop until either of i or j becomes zero...\n while(i >= 0 && j >= 0) {\n if(nums1[i] >= nums2[j]) {\n nums1[k] = nums1[i];\n i--;\n } else {\n nums1[k] = nums2[j];\n j--;\n }\n k--;\n // Either of i or j is not zero, which means some elements are yet to be merged.\n // Being already in a sorted manner, append them to the 1st array in the front.\n }\n // While i does not become zero...\n while(i >= 0)\n nums1[k--] = nums1[i--];\n // While j does not become zero...\n while(j >= 0)\n nums1[k--] = nums2[j--];\n // Now 1st array has all the elements in the required sorted order...\n return;\n};\n```\n\n# **C Language (Two Pointers Approach):**\n```\nvoid merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){\n // Initialize i and j to store indices of the last element of 1st and 2nd array respectively...\n int i = m - 1;\n int j = n -1;\n // Create a loop until either of i or j becomes zero...\n while(i>=0 && j>=0) {\n if(nums1[i] > nums2[j]) {\n nums1[i+j+1] = nums1[i];\n i--;\n } else {\n nums1[i+j+1] = nums2[j];\n j--;\n }\n }\n // While j does not become zero...\n while(j >= 0) {\n nums1[i+j+1] = nums2[j];\n j--;\n }\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n idx = 0\n for i in range(len(nums1)):\n if idx >= n:\n break\n if nums1[i] == 0:\n nums1[i]=nums2[idx]\n idx += 1\n nums1.sort()\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 138 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
First test | merge-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n """\n Do not return anything, modify nums1 in-place instead.\n """\n j = 0\n for i in range(m, m+n):\n nums1[i] = nums2[j]\n j += 1\n\n nums1.sort()\n``` | 0 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
e | merge-sorted-array | 0 | 1 | # Complexity\n- Time complexity:\n$$O((m+n)log(m+n))$$\n> Due to sort func\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n for i in range(n):\n nums1[m+i] = nums2[i]\n nums1.sort()\n return nums1\n``` | 0 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
2 lines of codes, one more O(m+n) approach | merge-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n """\n Do not return anything, modify nums1 in-place instead.\n """\n for i in range(m,m+n): nums1[i]=nums2[i-m]\n nums1.sort()\n\n```\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n """\n Do not return anything, modify nums1 in-place instead.\n """\n last=m+n-1\n while m>0 and n>0:\n if nums1[m-1] > nums2[n-1]:\n nums1[last]=nums1[m-1]\n m-=1\n else:\n nums1[last]=nums2[n-1]\n n-=1\n last-=1\n while n>0:\n nums1[last]=nums2[n-1]\n n-=1\n last-=1\n \n``` | 2 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
Merge Sort in 1 line, 2 line and 3 line in Python3 | merge-sorted-array | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code:\n\n1. The method merge takes two lists, nums1 and nums2, which are expected to contain integer values, and two integers, m and n, which represent the lengths of the portions of nums1 and nums2 that should be considered.\n\n2. In the loop for i in range(m, m+n):, the code iterates through the range starting from m (the index where the elements from nums2 should be inserted) to m + n (the end of the combined list). This loop is used to copy elements from nums2 into the corresponding positions in nums1.\n\n3. Inside the loop, nums1[i] is set to nums2[i-m]. This assigns values from nums2 to nums1, effectively merging the two lists.\n\n4. After the loop, nums1 is sorted using the sort() method. This step is necessary to ensure that the merged list nums1 remains sorted after inserting elements from nums2.\n\n# Complexity\n- Time complexity: O((m + n) * log(m + n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n nums1[:] = sorted(nums1[:m] + nums2)\n\n \n```\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n nums1[m:] = nums2[:n]\n nums1.sort()\n```\n```\nclass Solution:\n def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:\n for i in range(m,m+n):\n nums1[i]=nums2[i-m]\n nums1.sort()\n``` | 2 | You are given two integer arrays `nums1` and `nums2`, sorted in **non-decreasing order**, and two integers `m` and `n`, representing the number of elements in `nums1` and `nums2` respectively.
**Merge** `nums1` and `nums2` into a single array sorted in **non-decreasing order**.
The final sorted array should not be returned by the function, but instead be _stored inside the array_ `nums1`. To accommodate this, `nums1` has a length of `m + n`, where the first `m` elements denote the elements that should be merged, and the last `n` elements are set to `0` and should be ignored. `nums2` has a length of `n`.
**Example 1:**
**Input:** nums1 = \[1,2,3,0,0,0\], m = 3, nums2 = \[2,5,6\], n = 3
**Output:** \[1,2,2,3,5,6\]
**Explanation:** The arrays we are merging are \[1,2,3\] and \[2,5,6\].
The result of the merge is \[1,2,2,3,5,6\] with the underlined elements coming from nums1.
**Example 2:**
**Input:** nums1 = \[1\], m = 1, nums2 = \[\], n = 0
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[1\] and \[\].
The result of the merge is \[1\].
**Example 3:**
**Input:** nums1 = \[0\], m = 0, nums2 = \[1\], n = 1
**Output:** \[1\]
**Explanation:** The arrays we are merging are \[\] and \[1\].
The result of the merge is \[1\].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.
**Constraints:**
* `nums1.length == m + n`
* `nums2.length == n`
* `0 <= m, n <= 200`
* `1 <= m + n <= 200`
* `-109 <= nums1[i], nums2[j] <= 109`
**Follow up:** Can you come up with an algorithm that runs in `O(m + n)` time? | You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don't know is how they will intertwine. Can we take a local decision and arrive at an optimal solution? If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution. |
89. Gray Code | gray-code | 0 | 1 | # Intuition\nThe Gray code is a binary numeral system where two successive values differ in only one bit. To construct a Gray code sequence, you can use a recursive approach where you build the sequence incrementally.\n\n# Approach\n\n1.Handle the base case when n is 0 by returning [0].\n2.For n > 0, you can generate an n-bit Gray code sequence by building on the Gray code sequence for (n-1) bits.\n3.Define a recursive function generate_gray_code(n) which generates a Gray code sequence for n bits.\n4.If n is 1, return [0, 1] as the Gray code sequence for 1 bit.\n5.For n > 1, generate the Gray code sequence for (n-1) bits using recursion. Then, create the n-bit Gray code sequence by appending the reversed (n-1)-bit Gray code sequence with the mask bit set for the second half of the sequence.\n6.The mask is calculated by left-shifting 1 by (n-1) bits.\n7.Return the complete n-bit Gray code sequence.\n\n# Complexity\n- Time complexity: O(2^n) - This is the time complexity because the function generates 2^n elements in the Gray code sequence.\n- Space complexity: O(2^n) - The space complexity is also O(2^n) because of the storage required for the Gray code sequence.\n\n# Code\n```\nclass Solution:\n def grayCode(self, n: int) -> List[int]:\n if n == 0:\n return [0]\n \n def generate_gray_code(n):\n if n == 1:\n return [0, 1]\n \n smaller_gray_code = generate_gray_code(n - 1)\n mask = 1 << (n - 1)\n return smaller_gray_code + [x | mask for x in reversed(smaller_gray_code)]\n \n return generate_gray_code(n)\n\n \n``` | 1 | An **n-bit gray code sequence** is a sequence of `2n` integers where:
* Every integer is in the **inclusive** range `[0, 2n - 1]`,
* The first integer is `0`,
* An integer appears **no more than once** in the sequence,
* The binary representation of every pair of **adjacent** integers differs by **exactly one bit**, and
* The binary representation of the **first** and **last** integers differs by **exactly one bit**.
Given an integer `n`, return _any valid **n-bit gray code sequence**_.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,3,2\]
**Explanation:**
The binary representation of \[0,1,3,2\] is \[00,01,11,10\].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
\[0,2,3,1\] is also a valid gray code sequence, whose binary representation is \[00,10,11,01\].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit
**Example 2:**
**Input:** n = 1
**Output:** \[0,1\]
**Constraints:**
* `1 <= n <= 16` | null |
Gray Code with step by step explanation | gray-code | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create an initial list with 0\n2. For each bit in n, starting from the 0th bit:\n 1. Traverse the current list in reverse and add the current bit to each number by doing bitwise OR with (1 << i)\n 2. This step is repeated until we have processed all the bits in n\n3. Return the final list as the result\n\nExample: n = 2\n\n- Initial list: [0]\n- 1st iteration: i = 0, [0, 1 | (1 << 0) = 1] = [0, 1]\n- 2nd iteration: i = 1, [0, 1, 3 | (1 << 1) = 3, 2 | (1 << 1) = 2] = [0, 1, 3, 2]\n- Result: [0, 1, 3, 2]\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def grayCode(self, n: int) -> List[int]:\n res = [0]\n for i in range(n):\n for j in range(len(res) - 1, -1, -1):\n res.append(res[j] | (1 << i))\n return res\n\n``` | 5 | An **n-bit gray code sequence** is a sequence of `2n` integers where:
* Every integer is in the **inclusive** range `[0, 2n - 1]`,
* The first integer is `0`,
* An integer appears **no more than once** in the sequence,
* The binary representation of every pair of **adjacent** integers differs by **exactly one bit**, and
* The binary representation of the **first** and **last** integers differs by **exactly one bit**.
Given an integer `n`, return _any valid **n-bit gray code sequence**_.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,3,2\]
**Explanation:**
The binary representation of \[0,1,3,2\] is \[00,01,11,10\].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
\[0,2,3,1\] is also a valid gray code sequence, whose binary representation is \[00,10,11,01\].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit
**Example 2:**
**Input:** n = 1
**Output:** \[0,1\]
**Constraints:**
* `1 <= n <= 16` | null |
Python3 | gray-code | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N+2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def grayCode(self, n: int) -> List[int]:\n oldArr = [0,1]\n i = 1\n while i< n:\n Arr = list(oldArr)\n for j in range(len(oldArr)-1,-1,-1):\n Arr.append((2**i)+oldArr[j])\n oldArr = Arr\n i+=1\n return oldArr\n``` | 3 | An **n-bit gray code sequence** is a sequence of `2n` integers where:
* Every integer is in the **inclusive** range `[0, 2n - 1]`,
* The first integer is `0`,
* An integer appears **no more than once** in the sequence,
* The binary representation of every pair of **adjacent** integers differs by **exactly one bit**, and
* The binary representation of the **first** and **last** integers differs by **exactly one bit**.
Given an integer `n`, return _any valid **n-bit gray code sequence**_.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,3,2\]
**Explanation:**
The binary representation of \[0,1,3,2\] is \[00,01,11,10\].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
\[0,2,3,1\] is also a valid gray code sequence, whose binary representation is \[00,10,11,01\].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit
**Example 2:**
**Input:** n = 1
**Output:** \[0,1\]
**Constraints:**
* `1 <= n <= 16` | null |
[Python3] 1 Line Solution: List Comprehension | gray-code | 0 | 1 | Using List Comprehension, we can easily solve this problem statement in 1 line.\n```\n# Gray Code Formula:\n# n <= 16\n# Gray_Code(n) = n XOR (n / 2)\n\nclass Solution:\n def grayCode(self, n: int) -> List[int]:\n result = [i ^ (i // 2) for i in range(pow(2, n))]\n return result\n``` | 10 | An **n-bit gray code sequence** is a sequence of `2n` integers where:
* Every integer is in the **inclusive** range `[0, 2n - 1]`,
* The first integer is `0`,
* An integer appears **no more than once** in the sequence,
* The binary representation of every pair of **adjacent** integers differs by **exactly one bit**, and
* The binary representation of the **first** and **last** integers differs by **exactly one bit**.
Given an integer `n`, return _any valid **n-bit gray code sequence**_.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,3,2\]
**Explanation:**
The binary representation of \[0,1,3,2\] is \[00,01,11,10\].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
\[0,2,3,1\] is also a valid gray code sequence, whose binary representation is \[00,10,11,01\].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit
**Example 2:**
**Input:** n = 1
**Output:** \[0,1\]
**Constraints:**
* `1 <= n <= 16` | null |
Python/JS/C++/Go O(2^n) by toggle bitmask [w/ Example] | gray-code | 0 | 1 | Python O(2^n) by toggle bitmask\n\n---\n\nExample with n = 2:\n\n1st iteration\n```\n\u30000 0\n\u2295 0 0\n\u2014\u2014\u2014\u2014\u2014\n\u30000 0 \n```\n \n We get 0\'b 00 = **0**\n\n---\n\n2nd iteration\n```\n\u30000 1\n\u2295 0 0\n\u2014\u2014\u2014\u2014\u2014\n\u30000 1 \n```\n \n We get 0\'b 01 = **1**\n\n---\n\n3rd iteration\n```\n\u30001 0\n\u2295 0 1\n\u2014\u2014\u2014\u2014\u2014\n\u30001 1 \n```\n \n We get 0\'b 11 = **3**\n\n---\n\n4th iteration\n```\n\u30001 1\n\u2295 0 1\n\u2014\u2014\u2014\u2014\u2014\n\u30001 0 \n```\n \n We get 0\'b 10 = **2**\n \n---\n\nFinally, we have gray codes with n=2: \n[**0**, **1**, **3**, **2**]\n\n---\n\n**Implementation** in Python:\n\n```\nclass Solution:\n def grayCode(self, n: int) -> List[int]:\n \n # total 2^n codes for bit length n\n code_count = 1 << n\n \n # generate gray code from 0, and toggle 1 bit on each iteration\n # toggle mask: ( i >> 1 )\n \n gray_codes =[ i ^ ( i >> 1 ) for i in range(code_count) ]\n \n return gray_codes\n```\n\n---\n\nin **Javascript**:\n\n<details>\n\t<summary> Expand to see source code </summary>\n\n```\n\nvar grayCode = function(n) {\n\n // toal 2^n codes for bit length n\n const codeCount = 1 << n;\n \n let result = [];\n \n // generate gray code from 0, and toggle 1 bit on each iteration\n // toggle mask: ( i >> 1 )\n \n for(let i = 0 ; i < codeCount ; i++){\n \n code = i ^ ( i >> 1);\n result.push( code );\n }\n \n return result\n};\n```\n\n</details>\n\n---\n\nin **C++**:\n\n<details>\n\t<summary> Expand to see source code </summary>\n\n```\nclass Solution {\npublic:\n vector<int> grayCode(int n) {\n \n // toal 2^n codes for bit length n\n const int codeCount = 1 << n;\n \n vector<int> result;\n\n // generate gray code from 0, and toggle 1 bit on each iteration\n // toggle mask: ( i >> 1 )\n \n for( int i = 0 ; i < codeCount ; i++ ){\n \n int mask = i >> 1;\n result.push_back( i ^ mask );\n }\n \n return result;\n }\n};\n```\n\n</details>\n\n---\n\nin **Go**:\n\n<details>\n\t<summary> Expand to see source code </summary>\n\n\n```\nfunc grayCode(n int) []int {\n \n // total 2^n codes for bit length n\n code_count := 1 << n\n \n // slice to store gray codes\n gray_codes := make([]int, code_count)\n \n for i:=0 ; i < code_count ; i+=1 {\n \n toggle_mask := ( i >> 1 )\n \n gray_codes[ i ] = i ^ toggle_mask\n }\n \n return gray_codes\n}\n```\n\n</details>\n\n---\nReference:\n\n[1] [Wiki: Gray code](https://en.wikipedia.org/wiki/Gray_code)\n | 10 | An **n-bit gray code sequence** is a sequence of `2n` integers where:
* Every integer is in the **inclusive** range `[0, 2n - 1]`,
* The first integer is `0`,
* An integer appears **no more than once** in the sequence,
* The binary representation of every pair of **adjacent** integers differs by **exactly one bit**, and
* The binary representation of the **first** and **last** integers differs by **exactly one bit**.
Given an integer `n`, return _any valid **n-bit gray code sequence**_.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,3,2\]
**Explanation:**
The binary representation of \[0,1,3,2\] is \[00,01,11,10\].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
\[0,2,3,1\] is also a valid gray code sequence, whose binary representation is \[00,10,11,01\].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit
**Example 2:**
**Input:** n = 1
**Output:** \[0,1\]
**Constraints:**
* `1 <= n <= 16` | null |
5 line python solution that beats 99.52% of all solutions on runtime | gray-code | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea here is to use mathematical induction, i.e., given the solution for $$n=k$$, construct the solution for $$n=k+1$$.\nObserve that for $$n=1$$, the solution is $$[0, 1]$$. The solution for $$n=2$$ can be constucted by first prepending a zero to each element of this array $$[00, 01]$$. Then we reverse the array ($$[1, 0]$$) and prepend a 1 to each element of this array $$[11, 10]$$. Concatenating both arrays gives the desired solution $$[00, 01, 11, 10]$$.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMore generally suppose you have the required array ($$A$$) for $$n=k$$. By following the above procedure and first prepending a zero to each element of the array, by construction, each element of this array difers in only one element as this property must hold true for $$A$$ and the same element 0 is prepended to each entry of $$A$$. When reversing this array (call it $$reverse(A)$$) and prepending a 1 to each entry, using the same reasoning as before, all entries differ by one element. The last element of $$A$$ and the first element of $$reverse(A)$$ also differ only in the first element as do the first element of $$A$$ and last element of $$reverse(A)$$. Thus, by concatenating the resulting arrays, we have a constructuctive procedure that satisfies all the conditions of the question.\n\nAs a final point, note that prepending a 1 to the binary representation is equivalent to adding $$2^{k-1}$$. \n\n# Complexity\n- Time complexity: $$O(2^N)$$\n For each $$k \\in [1, N-1]$$ the number of steps are $$2^k$$. Thus the total number of steps is $$2^1+2^2+...+2^{N-1} = 2^N-1$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: The output is the only array that takes up space and is not counted for the purpose of computing space complexity. Hence the space complexity is $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def grayCode(self, n: int) -> List[int]:\n start_list = [0, 1]\n for i in range(2, n+1):\n summand = 2**(i-1)\n start_list = start_list+[elem+summand for elem in reversed(start_list)]\n return start_list\n``` | 2 | An **n-bit gray code sequence** is a sequence of `2n` integers where:
* Every integer is in the **inclusive** range `[0, 2n - 1]`,
* The first integer is `0`,
* An integer appears **no more than once** in the sequence,
* The binary representation of every pair of **adjacent** integers differs by **exactly one bit**, and
* The binary representation of the **first** and **last** integers differs by **exactly one bit**.
Given an integer `n`, return _any valid **n-bit gray code sequence**_.
**Example 1:**
**Input:** n = 2
**Output:** \[0,1,3,2\]
**Explanation:**
The binary representation of \[0,1,3,2\] is \[00,01,11,10\].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
\[0,2,3,1\] is also a valid gray code sequence, whose binary representation is \[00,10,11,01\].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit
**Example 2:**
**Input:** n = 1
**Output:** \[0,1\]
**Constraints:**
* `1 <= n <= 16` | null |
Python Intuitive Solution 🔥❤️🔥 | subsets-ii | 0 | 1 | # Intuition\nGiven a list of integers, the task is to find all possible subsets. However, there are duplicate integers in the list, so we have to handle them to avoid duplicate subsets.\n\n# Approach\n1. First, we sort the list. This ensures that duplicates are adjacent to each other.\n2. We use a backtracking approach. We start with an empty list and at every step, we choose to either include or exclude the current element.\n3. If the current element is the same as the previous element and the previous element was excluded, then we skip the current element to avoid duplicate subsets.\n\n# Complexity\n- Time complexity: O(2^n), where n is the length of the nums list. In the worst case, we would have 2^n subsets.\n- Space complexity: O(n*2^n), primarily for the recursive call stack.\n\n# Code\n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n nums.sort()\n output, stack = [], []\n\n def backtrack(i):\n if i >= len(nums):\n output.append(stack.copy())\n return\n \n stack.append(nums[i])\n backtrack(i+1)\n\n stack.pop()\n while i+1 < len(nums) and nums[i] == nums[i+1]:\n i += 1\n \n backtrack(i+1)\n \n backtrack(0)\n return output\n``` | 3 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
Subsets II with step by step explanation | subsets-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses a dfs approach to find all the subsets. The algorithm sorts the input list nums to handle duplicates. It starts from the first index start of the list and adds the element at start to the current path. It then moves to the next index i+1 and calls the dfs function again with the updated parameters. This process continues until i reaches the end of the list nums. The final list of all subsets is stored in res.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n def dfs(start, path, res):\n res.append(path)\n for i in range(start, len(nums)):\n if i > start and nums[i] == nums[i-1]:\n continue\n dfs(i+1, path + [nums[i]], res)\n \n nums.sort()\n res = []\n dfs(0, [], res)\n return res\n\n``` | 2 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
Solution | subsets-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void subset(vector<int>& nums, int i, vector<int> &l, vector<vector<int>> &ans){\n ans.push_back(l); \n for (int j = i ; j < nums.size() ; j++){\n if (j>i && nums[j] == nums[j-1]) continue;\n l.push_back(nums[j]);\n subset(nums, j+1, l, ans);\n l.pop_back();\n }\n }\n\n vector<vector<int>> subsetsWithDup(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n vector<int> l;\n vector<vector<int>> ans;\n subset(nums, 0, l, ans);\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n ans = []\n nums.sort()\n\n def backtrack(i, subset):\n if i >= len(nums):\n ans.append(subset[:])\n return\n \n subset.append(nums[i])\n backtrack(i+1, subset)\n\n subset.pop()\n while i+1 < len(nums) and nums[i+1] == nums[i]:\n i += 1\n backtrack(i+1, subset)\n \n backtrack(0, [])\n return ans\n```\n\n```Java []\nclass Solution {\n int[] tillFreq ;\n\tpublic List<List<Integer>> subsetsWithDup(int[] nums) {\n\t\ttillFreq = new int[10];\n\t\tint[] numFreq = new int[21];\n\t\tfor (int i = 0; i < nums.length; i++) {\n\t\t\ttillFreq[i] = ++numFreq[nums[i]+10];\n\t\t}\n\t\tnumFreq = new int[21];\n\t\tList<List<Integer>> subSets = new ArrayList<>();\n\t\tbackTrack2(nums, new ArrayList<>(), subSets, 0,numFreq);\n\t\treturn subSets;\n\t}\n\n\tprivate void backTrack2(int[] nums, ArrayList<Integer> arrayList, List<List<Integer>> subSets, int l,int[] numFreq) {\n\t\tsubSets.add(new ArrayList<>(arrayList));\n\t\tfor (int i = l; i < nums.length; i++) {\n\t\t\tif ((tillFreq[i] - 1) != numFreq[nums[i]+10])\n\t\t\t\tcontinue;\n\t\t\tarrayList.add(nums[i]);\n\t\t\tnumFreq[nums[i]+10]++;\n\t\t\tbackTrack2(nums, arrayList, subSets, i + 1,numFreq);\n\t\t\tarrayList.remove(arrayList.size() - 1);\n\t\t\tnumFreq[nums[i]+10]--;\n\t\t}\n\t}\n}\n```\n | 1 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
[Python3] Simple Recursive Solution | subsets-ii | 0 | 1 | # Intuition\nThe intuition behind the code is to use a recursive approach to generate subsets. At each step, we have two choices: either include the current element in the subset or exclude it. By making these choices for each element in the array, we can generate all possible subsets.\n\n# Approach\n**Sort the array nums** \nSorting the array ensures that duplicate elements will appear next to each other, making it easier to handle them later in the code.\n\n**Create the recursive function subsets** \nThis function takes two parameters: index (the current index being considered) and elements (the current subset being constructed).\n\n**Handle base case** \nIf the current index reaches the length of the array (index == len(nums)), it means we have processed all elements. At this point, we check if the elements subset is already present in the res list. If not, we append it to res. This check is necessary to avoid duplicate subsets.\n\n**Make recursive calls**\n**Not Pick**\nCall subsets recursively with the next index without picking the current element (subsets(index + 1, elements)). This represents the choice of excluding the current element from the subset.\n**Pick**\nCall subsets recursively with the next index, including the current element (subsets(index + 1, elements + [nums[index]])). This represents the choice of picking the current element and adding it to the subset.\n\n**Duplicate Check**\nThe code avoids duplicates by checking if a subset already exists in the res list before appending it. We sort the input array in the start to ensure that duplicate elements will be adjacent, simplifying the duplicate check.\n\nNow, we call the subsets function initially with index = 0 and an empty elements list.\n\nFinally, we return the final res list containing all the generated subsets.\n\n# Complexity\n- Time complexity: **O(2^n)** \n\n- Space complexity: **O(2^n)** \n\n# Code\n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n res = []\n nums.sort()\n def subsets(index, elements):\n # base case\n if index == len(nums):\n res.append(elements) if elements not in res else None\n return\n\n subsets(index + 1, elements) # not pick\n subsets(index + 1, elements + [nums[index]]) # pick\n\n subsets(0, [])\n return res\n``` | 6 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
Same Approches as Subset I with Brute force and Backtracking | subsets-ii | 0 | 1 | # 1. Subset 1 Approach-->TC:[2^N*N]\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n list1 = [[]]\n n=len(nums)\n for i in range(1,2**n):\n list2=[]\n for j in range(n):\n if (i&1<<j):\n list2.append(nums[j])\n list1.append(list2)\n return list1\n```\n# 1. Backtracking--->TC:Log(2^N)\n```\nclass Solution:\n def subsets(self, nums: List[int]) -> List[List[int]]:\n def back(nums,ans,temp):\n ans.append(temp)\n for i in range(len(nums)):\n back(nums[i+1:],ans,temp+[nums[i]])\n ans=[]\n back(nums,ans,[])\n return ans\n \n```\n# 2. Backtracking Concept:TC:[N*log(N)+log(2^N)]\n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n def back(nums,ans,temp):\n ans.append(temp)\n for i in range(len(nums)):\n if i!=0 and nums[i]==nums[i-1]:\n continue\n back(nums[i+1:],ans,temp+[nums[i]])\n ans=[]\n back(sorted(nums),ans,[])\n return ans\n```\n# 2. Same Approach as Subset I-->TC:[N^2X2^N*LogN] Heavy brute force but it works \n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n list1=[[]]\n n=len(nums)\n for i in range(1,2**n):\n list2=[]\n for j in range(n):\n if (i&1<<j):\n list2.append(nums[j])\n list2.sort()\n if list2 not in list1:\n list1.append(list2)\n return list1\n```\n# please upvote me it would encourage me alot\n | 4 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
[Python] Clean backtracking with sets | subsets-ii | 0 | 1 | # Intuition\nAny time I am trying to find permutations using items from a set, I first try to determine whether I can use backtracking. It turns out this works fine in this case, since we know the input array size is 10 or less.\n\n# Approach\nIn order to avoid duplicates, we should first sort the array of nums. Then we can be sure that our subsets will always occur in non-decreasing order. Here we perform backtracking, but since we are looking for all possible subsets, we don\'t need to do any checks before adding our interim results to the output. At each step, we take our current subset and go through the remaining elements in the array and perform backtracking with the subset plus that element. We store the results in a set in order to avoid duplication.\n\n# Complexity\n- Time complexity:\n$$O(2^N * N)$$\n\n- Space complexity:\n$$O(2^N)$$\n\n# Code\n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n N = len(nums)\n output = set()\n\n nums = sorted(nums)\n\n def backtrack(subset, index):\n output.add(subset)\n\n for i in range(index, N):\n backtrack(tuple(list(subset) + [nums[i]]), i + 1)\n\n backtrack(tuple(), 0)\n return output\n\n\n\n``` | 3 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
Solution with explanation | subsets-ii | 1 | 1 | \n\n# Approach\n- The function fun is a recursive function that generates subsets by considering each element of the array at a particular index.\n- The base case of the recursion is when the index reaches the size of the array. At this point, the current subset (ds) is sorted and inserted into the set res to eliminate duplicates.\n- In the recursive steps, the function includes the current element at the index and proceeds to the next index (index+1). It then recursively generates subsets for both cases: including and not including the current element.\n- The main function subsetsWithDup initializes an empty vector ans to store the final subsets and a set res to temporarily store subsets to ensure uniqueness.\n- The recursive function is called with initial parameters, and the unique subsets are generated.\n- Finally, the unique subsets from the set res are transferred to the ans vector, which is then returned as the result.\n\n# Complexity\n- Time complexity:\nO(2\u207F * n)\n\n- Space complexity:\nO(2\u207F)*O(k)\n\n\n```C++ []\nclass Solution {\npublic:\n void fun(vector<int>& nums, int index, vector<int>ds, set<vector<int>>& res) {\n if(index == nums.size()) {\n res.insert(ds);\n return;\n }\n ds.push_back(nums[index]);\n fun(nums, index+1, ds, res);\n ds.pop_back();\n fun(nums, index+1, ds, res);\n }\n vector<vector<int>> subsetsWithDup(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n vector<vector<int>> ans;\n set<vector<int>> res;\n vector<int> ds;\n fun(nums, 0, ds, res);\n for(auto it = res.begin(); it!= res.end(); it++) {\n ans.push_back(*it);\n } \n return ans;\n }\n};\n```\n```JAVA []\nclass Solution {\n public List<List<Integer>> subsetsWithDup(int[] nums) {\n List<List<Integer>> ans = new ArrayList<>();\n Set<List<Integer>> res = new HashSet<>();\n List<Integer> ds = new ArrayList<>();\n Arrays.sort(nums); // Sort the input array\n fun(nums, 0, ds, res);\n\n for (List<Integer> subset : res) {\n ans.add(subset);\n }\n\n return ans;\n }\n\n private void fun(int[] nums, int index, List<Integer> ds, Set<List<Integer>> res) {\n if (index == nums.length) {\n res.add(new ArrayList<>(ds)); \n return;\n }\n\n ds.add(nums[index]);\n fun(nums, index + 1, ds, res);\n ds.remove(ds.size() - 1);\n fun(nums, index + 1, ds, res);\n }\n}\n\n```\n```Python []\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n ans = []\n res = set()\n ds = []\n nums.sort() \n self.fun(nums, 0, ds, res)\n\n for subset in res:\n ans.append(list(subset))\n\n return ans\n\n def fun(self, nums, index, ds, res):\n if index == len(nums):\n sorted_ds = tuple(sorted(ds))\n res.add(sorted_ds)\n return\n\n ds.append(nums[index])\n self.fun(nums, index + 1, ds, res)\n ds.pop()\n self.fun(nums, index + 1, ds, res)\n\n\n```\n | 2 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
Easy & Clear Solution Python3 | subsets-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n nums = sorted(nums)\n res = []\n self.backtracking(res,0,[],nums)\n return res\n def backtracking(self,res,start,subset,nums):\n res.append(list(subset))\n for i in range(start,len(nums)):\n if i > start and nums[i] == nums[i-1]:\n continue\n self.backtracking(res,i+1,subset+[nums[i]],nums)\n\n``` | 5 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
Python || 99.97% Faster || Recursion || Easy | subsets-ii | 0 | 1 | ```\nclass Solution:\n def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:\n s=set()\n nums.sort() # Sort the input list to group duplicates together\n def solve(ip,op):\n if len(ip)==0:\n s.add(op)\n return \n op1=op\n op2=op+tuple([ip[0]])\n solve(ip[1:],op1)\n solve(ip[1:],op2)\n solve(nums,())\n ans=list(s)\n return sorted(ans)\n```\n**An upvote will be encouraging** | 1 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
General Backtracking questions solutions in Python for reference : | subsets-ii | 0 | 1 | I have taken solutions of @caikehe from frequently asked backtracking questions which I found really helpful and had copied for my reference. I thought this post will be helpful for everybody as in an interview I think these basic solutions can come in handy. Please add any more questions in comments that you think might be important and I can add it in the post.\n\n#### Combinations :\n```\ndef combine(self, n, k):\n res = []\n self.dfs(xrange(1,n+1), k, 0, [], res)\n return res\n \ndef dfs(self, nums, k, index, path, res):\n #if k < 0: #backtracking\n #return \n if k == 0:\n res.append(path)\n return # backtracking \n for i in xrange(index, len(nums)):\n self.dfs(nums, k-1, i+1, path+[nums[i]], res)\n``` \n\t\n#### Permutations I\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n res = []\n self.dfs(nums, [], res)\n return res\n\n def dfs(self, nums, path, res):\n if not nums:\n res.append(path)\n #return # backtracking\n for i in range(len(nums)):\n self.dfs(nums[:i]+nums[i+1:], path+[nums[i]], res)\n``` \n\n#### Permutations II\n```\ndef permuteUnique(self, nums):\n res, visited = [], [False]*len(nums)\n nums.sort()\n self.dfs(nums, visited, [], res)\n return res\n \ndef dfs(self, nums, visited, path, res):\n if len(nums) == len(path):\n res.append(path)\n return \n for i in xrange(len(nums)):\n if not visited[i]: \n if i>0 and not visited[i-1] and nums[i] == nums[i-1]: # here should pay attention\n continue\n visited[i] = True\n self.dfs(nums, visited, path+[nums[i]], res)\n visited[i] = False\n```\n\n \n#### Subsets 1\n\n\n```\ndef subsets1(self, nums):\n res = []\n self.dfs(sorted(nums), 0, [], res)\n return res\n \ndef dfs(self, nums, index, path, res):\n res.append(path)\n for i in xrange(index, len(nums)):\n self.dfs(nums, i+1, path+[nums[i]], res)\n```\n\n\n#### Subsets II \n\n\n```\ndef subsetsWithDup(self, nums):\n res = []\n nums.sort()\n self.dfs(nums, 0, [], res)\n return res\n \ndef dfs(self, nums, index, path, res):\n res.append(path)\n for i in xrange(index, len(nums)):\n if i > index and nums[i] == nums[i-1]:\n continue\n self.dfs(nums, i+1, path+[nums[i]], res)\n```\n\n\n#### Combination Sum \n\n\n```\ndef combinationSum(self, candidates, target):\n res = []\n candidates.sort()\n self.dfs(candidates, target, 0, [], res)\n return res\n \ndef dfs(self, nums, target, index, path, res):\n if target < 0:\n return # backtracking\n if target == 0:\n res.append(path)\n return \n for i in xrange(index, len(nums)):\n self.dfs(nums, target-nums[i], i, path+[nums[i]], res)\n```\n\n \n \n#### Combination Sum II \n\n```\ndef combinationSum2(self, candidates, target):\n res = []\n candidates.sort()\n self.dfs(candidates, target, 0, [], res)\n return res\n \ndef dfs(self, candidates, target, index, path, res):\n if target < 0:\n return # backtracking\n if target == 0:\n res.append(path)\n return # backtracking \n for i in xrange(index, len(candidates)):\n if i > index and candidates[i] == candidates[i-1]:\n continue\n self.dfs(candidates, target-candidates[i], i+1, path+[candidates[i]], res)\n``` | 64 | Given an integer array `nums` that may contain duplicates, return _all possible_ _subsets_ _(the power set)_.
The solution set **must not** contain duplicate subsets. Return the solution in **any order**.
**Example 1:**
**Input:** nums = \[1,2,2\]
**Output:** \[\[\],\[1\],\[1,2\],\[1,2,2\],\[2\],\[2,2\]\]
**Example 2:**
**Input:** nums = \[0\]
**Output:** \[\[\],\[0\]\]
**Constraints:**
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10` | null |
O(n) time O(1) space solution explained in detail | decode-ways | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs with all other dp problems I did before I like to use a function to represent relationships between subproblems. Let $$DW(n)$$ be the number of ways to decode the substring with n characters. We have two possible methods to decode at any n > 2.\n\n1. decode up to the $$n-1th$$ character then decode the current character.\n2. decode up to the $$n-2th$$ character then decode the current and last character together. \n\nTherefore, $$DW(n)$$ = $$DW(n - 1) + DW(n - 2)$$, but here\'s a catch. Before adding $$DW(n - 1)$$ or $$DW(n - 2)$$ even if it is non-zero. We first have to decide if the respective ways to decode the characters in $$1$$ or $$2$$ is valid.\n\nFor example, in the string $$"120"$$ and considering $$DW(3)$$, since the current character is "0", we cannot decode the string by method 1. \n\nAnother example is $$"129"$$ or $$"109"$$, still at $$DW(3)$$, we cannot decode the string by method 2 since $"29"$ and $"09"$ does not map to any character. \n\nIf any of the above methods doesn\'t work, we add 0 instead of the value of $$DW()$$ and finally we can obtain the answer $$DW(len(s))$$.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of a dp array we can just use two variables $$one$$ and $$two$$ to represent $$DW(n - 1)$$ and $$DW(n - 2)$$. For the base case, $$DW(0) = 0$$, $$DW(1) = 1$$ if the first character is not "0". \n\nThen, we iterate and check if the two methods are valid, calculate the answer to the subproblem and update the variables $$one$$ and $$two$$.\n\nOne point to note is that if the answer is 0 at any point, the number of ways to decode any substring beyond is 0. So we can return 0 early.\n\nWhy? if $$DW(n + 1)$$ = $$DW(n)+DW(n \u2212 1) $$ and we only know $$DW(n) = 0$$, don\'t we still have $$DW(n - 1)$$?\nThat\'s Because as method 1 is invalid for $$DW(n)$$, $$s[n]$$ must be "0", $$DW(n - 1)$$ will hence have to decode the $$nth$$ and $$n+1th$$ character as $$"0x"$$, therefore decoding this way doesn\'t work. And if a substring is not decodable, no matter how many characters you add after it, it will still not be decodable. \n\nHope it helps!\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```py\nclass Solution:\n def numDecodings(self, s: str) -> int: \n ans = 0 \n one = 1\n two = 0\n for i in range(len(s)):\n ans = 0\n current = s[i]\n prev = s[i - 1] if i > 0 else \'\'\n \n if current != \'0\':\n ans += one \n if prev == \'1\' or (prev == \'2\' and current in \'0123456\'):\n ans += two \n \n if ans == 0:\n return 0\n\n two = one \n one = ans \n\n return ans \n``` | 2 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
Given a string `s` containing only digits, return _the **number** of ways to **decode** it_.
The test cases are generated so that the answer fits in a **32-bit** integer.
**Example 1:**
**Input:** s = "12 "
**Output:** 2
**Explanation:** "12 " could be decoded as "AB " (1 2) or "L " (12).
**Example 2:**
**Input:** s = "226 "
**Output:** 3
**Explanation:** "226 " could be decoded as "BZ " (2 26), "VF " (22 6), or "BBF " (2 2 6).
**Example 3:**
**Input:** s = "06 "
**Output:** 0
**Explanation:** "06 " cannot be mapped to "F " because of the leading zero ( "6 " is different from "06 ").
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only digits and may contain leading zero(s). | null |
Python solution | decode-ways | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numDecodings(self, s: str) -> int:\n sset = {str(i) for i in range(1,27)}\n if s[0] == "0":\n return 0\n prev_2 = 1\n prev = 1\n\n for i in range(1,len(s)):\n if s[i] == "0" and s[i-1] == "0":\n return 0\n if s[i] != "0" and s[i-1:i+1] in sset:\n prev_2, prev = prev, prev_2 + prev\n elif s[i] != "0":\n prev_2, prev = prev, prev\n elif s[i-1:i+1] not in sset:\n return 0\n else:\n prev_2, prev = prev_2, prev_2\n return prev\n\n``` | 2 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
Given a string `s` containing only digits, return _the **number** of ways to **decode** it_.
The test cases are generated so that the answer fits in a **32-bit** integer.
**Example 1:**
**Input:** s = "12 "
**Output:** 2
**Explanation:** "12 " could be decoded as "AB " (1 2) or "L " (12).
**Example 2:**
**Input:** s = "226 "
**Output:** 3
**Explanation:** "226 " could be decoded as "BZ " (2 26), "VF " (22 6), or "BBF " (2 2 6).
**Example 3:**
**Input:** s = "06 "
**Output:** 0
**Explanation:** "06 " cannot be mapped to "F " because of the leading zero ( "6 " is different from "06 ").
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only digits and may contain leading zero(s). | null |
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | decode-ways | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n<iframe src="https://leetcode.com/playground/24UtgARN/shared" frameBorder="0" width="100%" height="500"></iframe> | 45 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
Given a string `s` containing only digits, return _the **number** of ways to **decode** it_.
The test cases are generated so that the answer fits in a **32-bit** integer.
**Example 1:**
**Input:** s = "12 "
**Output:** 2
**Explanation:** "12 " could be decoded as "AB " (1 2) or "L " (12).
**Example 2:**
**Input:** s = "226 "
**Output:** 3
**Explanation:** "226 " could be decoded as "BZ " (2 26), "VF " (22 6), or "BBF " (2 2 6).
**Example 3:**
**Input:** s = "06 "
**Output:** 0
**Explanation:** "06 " cannot be mapped to "F " because of the leading zero ( "6 " is different from "06 ").
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only digits and may contain leading zero(s). | null |
⌛🟢🛰️🟢Python3💎91. Decode Ways🏁1-DP👓O(n) & O(1)🏆Illustration🎉 | decode-ways | 0 | 1 | # Illustration\n\n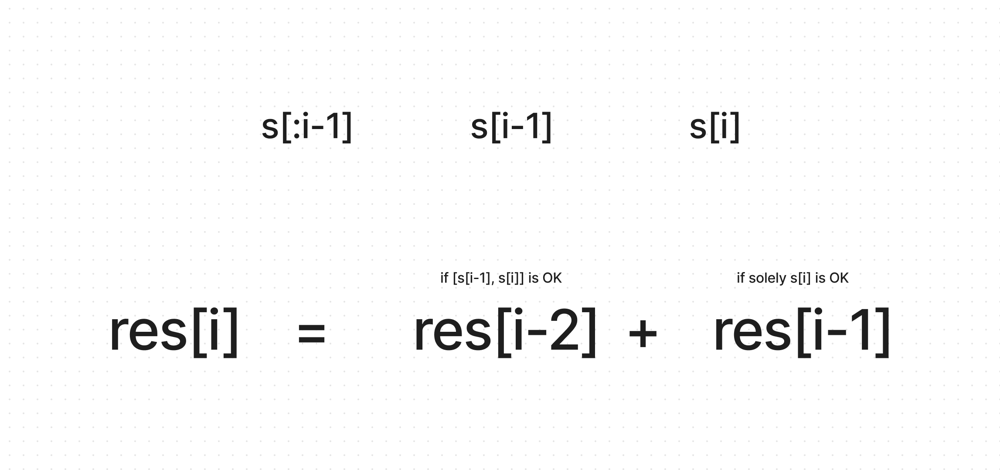\n# Intuition\n1-DP, similiar to $$Climbing Stairs$$\n\n# Approach\n1-DP\n\n# Complexity\n- Time complexity:\n$O(n)$\n\n- Space complexity:\n$O(1)$\n\n# Code\n```\nclass Solution:\n\tdef numDecodings(self, s: str) -> int:\n\t\t\'\'\'\n\t\tMy Solution: O(1) 1-DP\n\t\t\'\'\'\n\t\tif s[0] == \'0\':\n\t\t\treturn 0 \n\t\telif len(s) == 1:\n\t\t\treturn 1\n\t\t# Initialize: pprev, prev [res, last_char]\n\t\tpp, p = [1, str()], [1, s[0]]\n\t\tfor c in s[1:]:\n\t\t\tcur = 0 # current accumulating num of decode \n\t\t\t# pp to cur: 2 digits s[i-1] + s[i]]\n\t\t\tif 10 <= int(p[1] + c) <= 26: # [10, 26]\n\t\t\t\tcur += pp[0] # connect \n\t\t\t# p to cur: 1 digit s[i]\n\t\t\tif 1 <= int(c) <= 9: # [1, 10]\n\t\t\t\tcur += p[0] # connect \n\t\t\t# move pointers\n\t\t\tpp = p\n\t\t\tp = [cur, c]\n\n\t\treturn cur\n``` | 1 | A message containing letters from `A-Z` can be **encoded** into numbers using the following mapping:
'A' -> "1 "
'B' -> "2 "
...
'Z' -> "26 "
To **decode** an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, `"11106 "` can be mapped into:
* `"AAJF "` with the grouping `(1 1 10 6)`
* `"KJF "` with the grouping `(11 10 6)`
Note that the grouping `(1 11 06)` is invalid because `"06 "` cannot be mapped into `'F'` since `"6 "` is different from `"06 "`.
Given a string `s` containing only digits, return _the **number** of ways to **decode** it_.
The test cases are generated so that the answer fits in a **32-bit** integer.
**Example 1:**
**Input:** s = "12 "
**Output:** 2
**Explanation:** "12 " could be decoded as "AB " (1 2) or "L " (12).
**Example 2:**
**Input:** s = "226 "
**Output:** 3
**Explanation:** "226 " could be decoded as "BZ " (2 26), "VF " (22 6), or "BBF " (2 2 6).
**Example 3:**
**Input:** s = "06 "
**Output:** 0
**Explanation:** "06 " cannot be mapped to "F " because of the leading zero ( "6 " is different from "06 ").
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only digits and may contain leading zero(s). | null |
✅ 92.40% Two Pointers & Stack & Recursion | reverse-linked-list-ii | 1 | 1 | # Interview Guide - Reversing a Sublist of a Linked List: A Comprehensive Analysis for Programmers\n\n## Introduction & Problem Statement\n\nWelcome to this detailed guide, where we delve into the fascinating problem of reversing a sublist within a singly-linked list. The challenge is not just to reverse a sublist but to do it efficiently, ideally in a single pass through the list. This guide is designed to arm you with multiple approaches for tackling this problem, each with its own unique advantages and considerations. Specifically, we will explore three distinct strategies: Two Pointers, Using a Stack, and Recursion.\n\n## Key Concepts and Constraints\n\n1. **Node Anatomy**: \n Let\'s start with the basics. In a singly-linked list, each node has an integer value and a `next` pointer that points to the subsequent node in the list.\n \n2. **Sublist Reversal**: \n The primary task is to reverse only the nodes between positions `left` and `right`, both inclusive, within the list.\n\n3. **Order Preservation**: \n While reversing the sublist, we must ensure that the relative order of all nodes outside this range remains unchanged.\n\n4. **Size Constraints**: \n The number of nodes in the list `n` can vary but will always be between 1 and 500, giving us more than enough to work with.\n\n# Live Coding & More\nhttps://youtu.be/RohipcSF3HM?si=9GIVdRg72_EHEMmv\n\n- [\uD83D\uDC0D Two Pointers \uD83D\uDC49\uD83D\uDC48](https://youtu.be/RohipcSF3HM?si=9GIVdRg72_EHEMmv)\n- [\uD83D\uDC0D Stack \uD83D\uDCDA](https://youtu.be/E79svvS1DB0?si=37SbMxSSJeQQHHcf)\n- [\uD83D\uDC0D Recursion \uD83D\uDD01](https://youtu.be/xcKS9d1_vDg?si=rbsNpLsNa3EJSVD8)\n\n---\n# Strategies to Tackle the Problem: A Three-Pronged Approach\n\n## 1. Using Two Pointers (One-Pass)\n\n### Intuition and Logic Behind the Solution\n\nIn this efficient method, we employ two pointers to traverse and manipulate the linked list in one go. The clever use of a dummy node helps us elegantly handle edge cases, and tuple unpacking makes the code more Pythonic and straightforward.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Create a `dummy` node and connect its `next` to the head of the list.\n - Initialize a `prev` pointer to the `dummy` node.\n\n2. **Move to Start Position**: \n - Traverse the list until the node just before the `left`-th node is reached.\n\n3. **Execute Sublist Reversal**: \n - Use a `current` pointer to keep track of the first node in the sublist.\n - Reverse the sublist nodes using `prev` and `current`.\n\n4. **Link Back**: \n - Automatically link the reversed sublist back into the original list.\n\n### Complexity Analysis\n\n- **Time Complexity**: `O(n)` \u2014 A single traversal does the job.\n- **Space Complexity**: `O(1)` \u2014 Smart pointer manipulation eliminates the need for additional data structures.\n\n---\n\n## 2. Using a Stack\n\n### Intuition and Logic Behind the Solution\n\nThis approach uses a stack data structure to temporarily store and then reverse the sublist, making the logic easier to follow.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Like before, create a `dummy` node and set a `prev` pointer.\n\n2. **Populate the Stack**: \n - Traverse the list and populate the stack with the nodes falling within the `left` and `right` positions.\n\n3. **Perform Reversal and Relink Nodes**: \n - Pop nodes from the stack and relink them, essentially reversing the sublist.\n\n### Complexity Analysis\n\n- **Time Complexity**: `O(n)`\n- **Space Complexity**: `O(n)` \u2014 The stack takes extra space.\n\n---\n\n## 3. Using Recursion\n\n#### Intuition and Logic Behind the Solution\n\nIn this elegant method, the language\'s call stack is leveraged to reverse the sublist through recursive function calls.\n\n### Step-by-step Explanation\n\n1. **Define Recursive Function**: \n - Create a helper function that will do the heavy lifting, taking the node and its position as parameters.\n\n2. **Base and Recursive Cases**: \n - Implement base and recursive cases to control the flow and reversal.\n\n3. **Unwind and Relink**: \n - As the recursion unwinds, the nodes get relinked in the reversed order.\n\n### Complexity Analysis\n\n- **Time Complexity**: `O(n)`\n- **Space Complexity**: `O(n)` \u2014 The call stack consumes extra memory.\n\n## Code Highlights and Best Practices\n\n- The use of a `dummy` node is universal across all methods for handling edge cases gracefully.\n- Tuple unpacking in the Two-Pointer approach makes the code clean and Pythonic.\n- The Stack approach makes clever use of the stack data structure for sublist reversal.\n- The Recursion method leverages the language\'s call stack for a clean and elegant solution.\n\n---\n\n# Performance\n\n| Language | Fastest Runtime (ms) | Memory Usage (MB) | Method |\n|--------------|----------------------|-------------------|-------------|\n| Rust | 0 | 2.3 | Two-Pointers|\n| PHP | 0 | 18.9 | Two-Pointers|\n| Java | 0 | 40.8 | Two-Pointers|\n| Go | 1 | 2.1 | Two-Pointers|\n| C++ | 4 | 7.4 | Two-Pointers|\n| Python3 | 33 | 16.6 | Two-Pointers|\n| Python3 | 38 | 16.6 | Recursion |\n| Python3 | 39 | 16.3 | Stack |\n| JavaScript | 44 | 41.8 | Two-Pointers|\n| C# | 71 | 38.4 | Two-Pointers|\n \n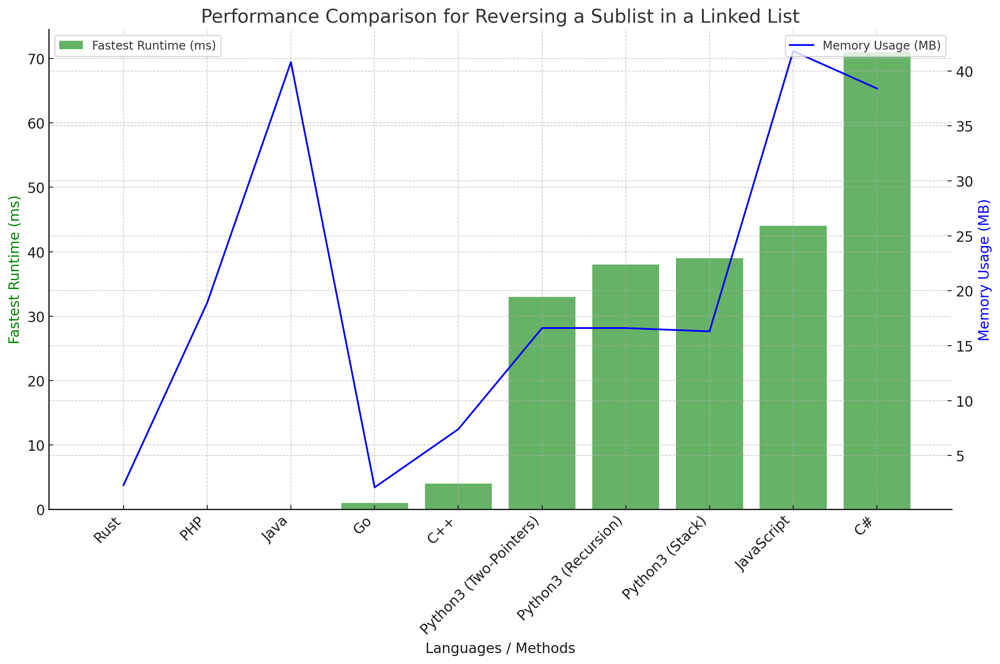\n\n\n# Code Two Pointers\n``` Python []\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:\n if not head or left == right:\n return head\n \n dummy = ListNode(0, head)\n prev = dummy\n \n for _ in range(left - 1):\n prev = prev.next\n \n current = prev.next\n \n for _ in range(right - left):\n next_node = current.next\n current.next, next_node.next, prev.next = next_node.next, prev.next, next_node\n\n return dummy.next\n```\n``` Go []\nfunc reverseBetween(head *ListNode, left int, right int) *ListNode {\n if head == nil || left == right {\n return head\n }\n \n dummy := &ListNode{0, head}\n prev := dummy\n \n for i := 0; i < left - 1; i++ {\n prev = prev.Next\n }\n \n current := prev.Next\n \n for i := 0; i < right - left; i++ {\n nextNode := current.Next\n current.Next = nextNode.Next\n nextNode.Next = prev.Next\n prev.Next = nextNode\n }\n \n return dummy.Next\n}\n```\n``` Rust []\nimpl Solution {\n pub fn reverse_between(head: Option<Box<ListNode>>, left: i32, right: i32) -> Option<Box<ListNode>> {\n let mut dummy = Some(Box::new(ListNode {\n val: 0,\n next: head,\n }));\n let mut before = &mut dummy;\n for _ in 1..left {\n before = &mut before.as_mut()?.next;\n }\n\n let mut node = before.as_mut()?.next.take();\n let mut node2 = node.as_mut()?.next.take();\n for _ in left..right {\n let node3 = node2.as_mut()?.next.take();\n node2.as_mut()?.next = node;\n node = node2;\n node2 = node3;\n }\n\n let mut rev_tail = &mut node;\n for _ in left..right {\n rev_tail = &mut rev_tail.as_mut()?.next;\n }\n rev_tail.as_mut()?.next = node2;\n before.as_mut()?.next = node;\n\n dummy.unwrap().next\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n ListNode* reverseBetween(ListNode* head, int left, int right) {\n if (!head || left == right) return head;\n \n ListNode dummy(0);\n dummy.next = head;\n ListNode* prev = &dummy;\n \n for (int i = 0; i < left - 1; ++i) {\n prev = prev->next;\n }\n \n ListNode* current = prev->next;\n \n for (int i = 0; i < right - left; ++i) {\n ListNode* next_node = current->next;\n current->next = next_node->next;\n next_node->next = prev->next;\n prev->next = next_node;\n }\n \n return dummy.next;\n }\n};\n```\n``` Java []\nclass Solution {\n public ListNode reverseBetween(ListNode head, int left, int right) {\n if (head == null || left == right) return head;\n \n ListNode dummy = new ListNode(0);\n dummy.next = head;\n ListNode prev = dummy;\n \n for (int i = 0; i < left - 1; ++i) {\n prev = prev.next;\n }\n \n ListNode current = prev.next;\n \n for (int i = 0; i < right - left; ++i) {\n ListNode nextNode = current.next;\n current.next = nextNode.next;\n nextNode.next = prev.next;\n prev.next = nextNode;\n }\n \n return dummy.next;\n }\n}\n```\n``` C# []\npublic class Solution {\n public ListNode ReverseBetween(ListNode head, int left, int right) {\n if (head == null || left == right) return head;\n \n ListNode dummy = new ListNode(0);\n dummy.next = head;\n ListNode prev = dummy;\n \n for (int i = 0; i < left - 1; ++i) {\n prev = prev.next;\n }\n \n ListNode current = prev.next;\n \n for (int i = 0; i < right - left; ++i) {\n ListNode nextNode = current.next;\n current.next = nextNode.next;\n nextNode.next = prev.next;\n prev.next = nextNode;\n }\n \n return dummy.next;\n }\n}\n```\n``` PHP []\nclass Solution {\n function reverseBetween($head, $left, $right) {\n if ($head == null || $left == $right) return $head;\n \n $dummy = new ListNode(0);\n $dummy->next = $head;\n $prev = $dummy;\n \n for ($i = 0; $i < $left - 1; ++$i) {\n $prev = $prev->next;\n }\n \n $current = $prev->next;\n \n for ($i = 0; $i < $right - $left; ++$i) {\n $nextNode = $current->next;\n $current->next = $nextNode->next;\n $nextNode->next = $prev->next;\n $prev->next = $nextNode;\n }\n \n return $dummy->next;\n }\n}\n```\n``` JavaScript []\nvar reverseBetween = function(head, left, right) {\n if (!head || left === right) return head;\n \n const dummy = new ListNode(0);\n dummy.next = head;\n let prev = dummy;\n \n for (let i = 0; i < left - 1; ++i) {\n prev = prev.next;\n }\n \n let current = prev.next;\n \n for (let i = 0; i < right - left; ++i) {\n const nextNode = current.next;\n current.next = nextNode.next;\n nextNode.next = prev.next;\n prev.next = nextNode;\n }\n \n return dummy.next;\n};\n```\n# Code Recursion\n``` Python []\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:\n if not (head and left < right):\n return head\n\n def helper(node, m):\n nonlocal left, right\n if m == left:\n prev = None\n current = node\n while m <= right:\n current.next, prev, current = prev, current, current.next\n m += 1\n node.next = current\n return prev\n elif m < left:\n node.next = helper(node.next, m + 1)\n return node\n\n return helper(head, 1)\n```\n``` Go []\nfunc reverseBetween(head *ListNode, left int, right int) *ListNode {\n if head == nil || left >= right {\n return head\n }\n\n var helper func(node *ListNode, m int) *ListNode\n helper = func(node *ListNode, m int) *ListNode {\n if m == left {\n var prev, current *ListNode = nil, node\n for m <= right {\n current.Next, prev, current = prev, current, current.Next\n m++\n }\n node.Next = current\n return prev\n } else if m < left {\n node.Next = helper(node.Next, m+1)\n }\n return node\n }\n\n return helper(head, 1)\n}\n\n```\n\n# Code Stack\n``` Python []\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:\n if not head or left == right:\n return head\n\n dummy = ListNode(0)\n dummy.next = head\n prev = dummy\n\n for _ in range(left - 1):\n prev = prev.next\n\n stack = []\n current = prev.next\n\n for _ in range(right - left + 1):\n stack.append(current)\n current = current.next\n\n while stack:\n prev.next = stack.pop()\n prev = prev.next\n\n prev.next = current\n\n return dummy.next\n```\n``` Go []\nfunc reverseBetween(head *ListNode, left int, right int) *ListNode {\n if head == nil || left == right {\n return head\n }\n\n dummy := &ListNode{Val: 0, Next: head}\n prev := dummy\n\n for i := 0; i < left-1; i++ {\n prev = prev.Next\n }\n\n stack := []*ListNode{}\n current := prev.Next\n\n for i := 0; i < right-left+1; i++ {\n stack = append(stack, current)\n current = current.Next\n }\n\n for len(stack) > 0 {\n last := len(stack) - 1\n prev.Next = stack[last]\n stack = stack[:last]\n prev = prev.Next\n }\n\n prev.Next = current\n\n return dummy.Next\n}\n\n```\n\n# Live Coding & More\n## Stack\nhttps://youtu.be/E79svvS1DB0?si=37SbMxSSJeQQHHcf\n## Recursion\nhttps://youtu.be/xcKS9d1_vDg?si=rbsNpLsNa3EJSVD8\n\n## Final Thoughts\n\nEach of the three methods comes with its own set of pros and cons. Your choice would depend on various factors such as readability, space complexity, and the specific constraints of the problem at hand. This guide equips you with the knowledge to make that choice wisely.\n\nSo there you have it\u2014a multifaceted guide to tackling the problem of reversing a sublist in a singly-linked list. Armed with this knowledge, you\'re now better prepared to face linked list challenges in interviews and beyond. Happy coding! | 103 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
Python Solution | reverse-linked-list-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:\n slow = head\n new_head = ListNode(None, None)\n new_head.next = head\n left_edge = ListNode(None, None)\n left_head = ListNode(None, None)\n prev = ListNode(None, None)\n trans = ListNode(None, None)\n \n if head.next is None or left == right:\n return head\n\n if left == 1:\n slow = new_head\n left_edge = slow\n for i in range(left-1):\n left_edge = slow\n slow=slow.next\n slow=slow.next\n left_head = slow\n \n trans=slow.next\n while (right-left):\n prev = slow\n slow = trans\n trans = slow.next\n slow.next = prev\n right-=1\n \n left_edge.next=slow\n left_head.next=trans\n\n return new_head.next\n\n left_edge = slow\n for i in range(left-2):\n slow=slow.next\n left_edge = slow\n slow=slow.next\n left_head = slow\n \n trans=slow.next\n while (right-left):\n prev = slow\n slow = trans\n trans = slow.next\n slow.next = prev\n right-=1\n \n left_edge.next=slow\n left_head.next=trans\n\n return head\n\n\n``` | 1 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
【Video】Beat 97.21% - Python, JavaScript, Java, C++ | reverse-linked-list-ii | 1 | 1 | This Python solution beats 97.21%.\n\n\n\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 257 videos as of September 7th, 2023.\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/vE__gU1MUnw\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2245\nThank you for your support!\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Check for base cases.\n - If the linked list is empty (`not head`) or `left` is equal to `right`, return the original `head` as there is no reversal needed.\n\n2. Initialize a `dummy` node to simplify edge cases and connect it to the head of the linked list.\n - Create a `dummy` node with a value of 0 and set its `next` pointer to the `head` of the linked list. This dummy node helps in handling the case when `left` is 1.\n\n3. Traverse the list to find the (left-1)-th node.\n - Initialize a `prev` pointer to `dummy`.\n - Loop `left - 1` times to move the `prev` pointer to the node just before the left-th node.\n\n4. Reverse the portion of the linked list from the left-th node to the right-th node.\n - Initialize a `cur` pointer to `prev.next`.\n - Loop `right - left` times to reverse the direction of the pointers in this portion of the linked list:\n - Store the next node (`temp`) of `cur` to avoid losing the reference.\n - Update the `cur.next` to point to `temp.next`, effectively reversing the direction.\n - Move `temp.next` to point to `prev.next`, effectively moving `temp` to the correct position in the reversed portion.\n - Update `prev.next` to point to `temp`, making `temp` the new next node of `prev`.\n\n5. Return the new head of the modified linked list.\n - `dummy.next` points to the head of the modified linked list, so return `dummy.next` as the result.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:\n\n if not head or left == right:\n return head\n\n dummy = ListNode(0, head)\n prev = dummy\n\n for _ in range(left - 1):\n prev = prev.next\n\n cur = prev.next\n for _ in range(right - left):\n temp = cur.next\n cur.next = temp.next\n temp.next = prev.next\n prev.next = temp\n\n return dummy.next\n```\n```javascript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} head\n * @param {number} left\n * @param {number} right\n * @return {ListNode}\n */\nvar reverseBetween = function(head, left, right) {\n if (!head || left === right) {\n return head;\n }\n\n const dummy = new ListNode(0, head);\n let prev = dummy;\n\n for (let i = 0; i < left - 1; i++) {\n prev = prev.next;\n }\n\n let cur = prev.next;\n\n for (let i = 0; i < right - left; i++) {\n const temp = cur.next;\n cur.next = temp.next;\n temp.next = prev.next;\n prev.next = temp;\n }\n\n return dummy.next; \n};\n```\n```java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode reverseBetween(ListNode head, int left, int right) {\n if (head == null || left == right) {\n return head;\n }\n\n ListNode dummy = new ListNode(0);\n dummy.next = head;\n ListNode prev = dummy;\n\n for (int i = 0; i < left - 1; i++) {\n prev = prev.next;\n }\n\n ListNode cur = prev.next;\n\n for (int i = 0; i < right - left; i++) {\n ListNode temp = cur.next;\n cur.next = temp.next;\n temp.next = prev.next;\n prev.next = temp;\n }\n\n return dummy.next; \n }\n}\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* reverseBetween(ListNode* head, int left, int right) {\n if (!head || left == right) {\n return head;\n }\n\n ListNode* dummy = new ListNode(0);\n dummy->next = head;\n ListNode* prev = dummy;\n\n for (int i = 0; i < left - 1; i++) {\n prev = prev->next;\n }\n\n ListNode* cur = prev->next;\n\n for (int i = 0; i < right - left; i++) {\n ListNode* temp = cur->next;\n cur->next = temp->next;\n temp->next = prev->next;\n prev->next = temp;\n }\n\n return dummy->next; \n }\n};\n```\n | 34 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
🔥BEATS 100% |⚡Python⚡ C++⚡Java | ✅Easy Linked List | reverse-linked-list-ii | 1 | 1 | \n```Python []\nclass Solution(object):\n def reverseBetween(self, head, left, right):\n if left >= right:\n return head\n \n ohead = newhd = ListNode(0)\n whead = wlast = head\n newhd.next = head\n for i in range(right-left):\n wlast = wlast.next\n for i in range(left-1):\n ohead, whead, wlast = whead, whead.next, wlast.next \n olast, wlast.next = wlast.next, None\n revhead, revlast = self.reverse(whead)\n ohead.next, revlast.next = revhead, olast\n return newhd.next\n \n def reverse(self, head):\n pre, curr, last = None, head, head\n while curr:\n curr.next, pre, curr = pre, curr, curr.next\n return pre, last\n```\n```C++ []\nclass Solution {\npublic:\n ListNode* reverseBetween(ListNode* head, int left, int right) {\n ListNode* dummy = new ListNode(0), *pre = dummy , *curr;\n dummy->next = head;\n\n for(int i = 0 ; i< left-1 ; i++){\n pre = pre->next;\n }\n curr = pre->next;\n pre->next = NULL;\n ListNode* l1 = curr;\n\n ListNode* prev = NULL;\n\n for(int i =0 ; i<= right-left ; i++){\n ListNode* next = curr->next;\n curr->next = prev;\n prev = curr;\n curr = next;\n }\n\n l1->next = curr;\n pre->next = prev;\n return dummy->next;\n\n }\n};\n```\n```Java []\nclass Solution {\n public ListNode reverseBetween(ListNode head, int left, int right) {\n ListNode curr=head;\n int v[]=new int[right-left+1];\n int l=0,r=0;\n while(r<left-1) {\n curr=curr.next;\n r++;\n }\n while(r<right){ \n v[l]=curr.val;\n curr=curr.next;\n l++;\n r++;\n }\n r=0;l--;\n curr=head;\n while(r<left-1) {\n curr=curr.next;\n r++;\n }\n while(r<right){\n curr.val=v[l];\n curr=curr.next;\n l--;\n r++; \n }\n return head;\n }\n}\n```\n | 2 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
Simple python code using list | reverse-linked-list-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:\n l = []\n while head is not None:\n l.append(head.val)\n head = head.next\n left -=1\n right -=1\n while left<right:\n l[left],l[right] = l[right],l[left]\n left +=1\n right -=1\n h = None\n t = None\n for i in l:\n node = ListNode(i)\n if h is None:\n h = node\n t = node\n else:\n t.next = node\n t = node\n return h \n``` | 1 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
✔Mastering Linked List Reversal ✨|| A Step-by-Step Guide📈🧠|| Easy to understand || #Beginner😉😎 | reverse-linked-list-ii | 1 | 1 | # PROBLEM UNDERSTANDING:\n- **The code appears** to be a C++ implementation of a function `reverseBetween `within a class `Solution`. \n- This function takes as input a singly-linked list represented by a `ListNode` and two integers, `left` and `right`. \n- It aims to reverse the elements of the linked list from the `left`-th node to the `right`-th node (inclusive).\n\n# Here\'s a step-by-step explanation of the code:\n**Step 1: Initializing Pointers**\n```\nListNode* temp = new ListNode(-1);\nListNode* prev = temp;\ntemp->next = head;\n\n```\n- `temp` is a new **ListNode created with a value of -1**. This is used as a dummy node to simplify the logic.\n- `prev` is initialized to `temp`, which **initially points to the same location as** `temp`.\n- `temp->next` is set to point to the head of the input linked list (`head`).\n\n**Step 2: Moving to the Left Position:**\n```\nfor (int i = 0; i < left - 1; i++) {\n prev = prev->next;\n}\n\n```\n- This loop moves the `prev` pointer to the node just before the `left`-th node in the linked list.\n\n**Step 3: Reversing the Nodes:**\n```\nListNode* cur = prev->next;\nfor (int i = 0; i < right - left; i++) {\n ListNode* ptr = prev->next;\n prev->next = cur->next;\n cur->next = cur->next->next;\n prev->next->next = ptr;\n}\n\n```\n- In this loop, a pointer `cur` is used to keep track of the current node.\n- For each iteration, a pointer `ptr` is used to temporarily store `prev->next`.\n- **The code then rearranges the pointers to reverse** the direction of the nodes between `left` and `right`.\n\n**Step 4: Returning the Result:**\n```\nreturn temp->next;\n\n```\n- Finally, the modified linked list is returned. `temp->next` points to the new head of the linked list after reversing the specified portion.\n\n# Strategy to Tackle the Problem:\n\n**1. Initialize a dummy node (`temp`) to simplify handling edge cases.**\n**1. Move `prev` to the node just before the `left`-th node using a loop.**\n**1. Reverse the nodes between left and right using a loop.**\n**1. Return the modified linked list.**\n\n\n\n\n\n\n\n# Intuition\n- The code employs a common technique for reversing a portion of a linked list. \n- It uses pointers (`prev`, `cur`, and `ptr`) to manipulate the connections between nodes, effectively reversing the direction of the nodes between `left` and `right`.\n\n# Approach\n- Initialize `temp` and `prev` pointers.\n- Move `prev` to the node before the `left`-th node.\n- Reverse nodes between `left` and `right` using a loop.\n- Return the modified linked list.\n\n# Complexity\n- **Time complexity:**\n 1. **Initialization:** The initialization part involves creating a dummy node (`temp`) and moving prev to the `left-1`-th node, both of which take constant time, `O(1)`.\n\n 1. **Reversing the Nodes:** The loop that reverses the nodes between `left` and right runs for `right - left` iterations. \n - Inside the loop, there are constant-time operations like pointer assignments. \n - Therefore, this part of the code also has a time complexity of `O(right - left)`, which can be simplified to `O(n)`, where n is the number of nodes in the linked list.\n\n**Overall, the time complexity of the code is `O(n)`, where n is the number of nodes in the linked list.**\n\n- **Space complexity:**\n1. **Additional Pointers:** The code uses a few extra pointers (`temp`, `prev`, `cur`, and `ptr`) to keep track of nodes and perform the reversal. These pointers occupy a constant amount of space regardless of the size of the linked list. \n2. Therefore, the `space complexity is O(1)`, indicating constant space usage.\n\n# PLEASE UPVOTE\uD83D\uDE0D\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* reverseBetween(ListNode* head, int left, int right) {\n ListNode*temp= new ListNode(-1);\n ListNode*prev=temp;\n temp->next=head;\n for(int i=0;i<left-1;i++)\n {\n prev=prev->next;\n }\n ListNode*cur=prev->next;\n for(int i=0;i<right-left;i++)\n {\n ListNode *ptr = prev->next;\n prev->next = cur->next;\n cur->next = cur->next->next;\n prev->next->next = ptr;\n }\n return temp->next;\n }\n};\n```\n# JAVA\n```\npublic class Solution {\n public ListNode reverseBetween(ListNode head, int left, int right) {\n ListNode temp = new ListNode(-1);\n ListNode prev = temp;\n temp.next = head;\n \n for (int i = 0; i < left - 1; i++) {\n prev = prev.next;\n }\n \n ListNode cur = prev.next;\n \n for (int i = 0; i < right - left; i++) {\n ListNode ptr = prev.next;\n prev.next = cur.next;\n cur.next = cur.next.next;\n prev.next.next = ptr;\n }\n \n return temp.next;\n }\n}\n\n```\n# PYTHON\n```\nclass Solution:\n def reverseBetween(self, head, left, right):\n temp = ListNode(-1)\n prev = temp\n temp.next = head\n \n for i in range(left - 1):\n prev = prev.next\n \n cur = prev.next\n \n for i in range(right - left):\n ptr = prev.next\n prev.next = cur.next\n cur.next = cur.next.next\n prev.next.next = ptr\n \n return temp.next\n\n```\n# JAVASCRIPT\n```\nclass ListNode {\n constructor(val) {\n this.val = val;\n this.next = null;\n }\n}\n\nclass Solution {\n reverseBetween(head, left, right) {\n const temp = new ListNode(-1);\n let prev = temp;\n temp.next = head;\n\n for (let i = 0; i < left - 1; i++) {\n prev = prev.next;\n }\n\n let cur = prev.next;\n\n for (let i = 0; i < right - left; i++) {\n let ptr = prev.next;\n prev.next = cur.next;\n cur.next = cur.next.next;\n prev.next.next = ptr;\n }\n\n return temp.next;\n }\n}\n\n```\n# GO\n```\npackage main\n\ntype ListNode struct {\n Val int\n Next *ListNode\n}\n\nfunc reverseBetween(head *ListNode, left int, right int) *ListNode {\n temp := &ListNode{Val: -1}\n prev := temp\n temp.Next = head\n\n for i := 0; i < left-1; i++ {\n prev = prev.Next\n }\n\n cur := prev.Next\n\n for i := 0; i < right-left; i++ {\n ptr := prev.Next\n prev.Next = cur.Next\n cur.Next = cur.Next.Next\n prev.Next.Next = ptr\n }\n\n return temp.Next\n}\n\n```\n# \uD83D\uDC7E\u2763PLEASE UPVOTE\uD83D\uDE0D | 20 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
Drawing explanation | easy to understand | reverse-linked-list-ii | 1 | 1 | # Intuition and Approach\n\n 1. Find left node indcated by index - l\n 2. Find right node indicated by index - r\n 3. Revers left node till right node\n 4. Link the broken links\n\n Note: Add a dummy head to track left_prev node in case left node is at head\n\n#### Please bear with my diagrams :)\n\nInput: head = ```[1,2,3,4,5]```, l = ```2``` (left index), r = ```4``` (right index)\nOutput: ```[1,4,3,2,5]```\n\n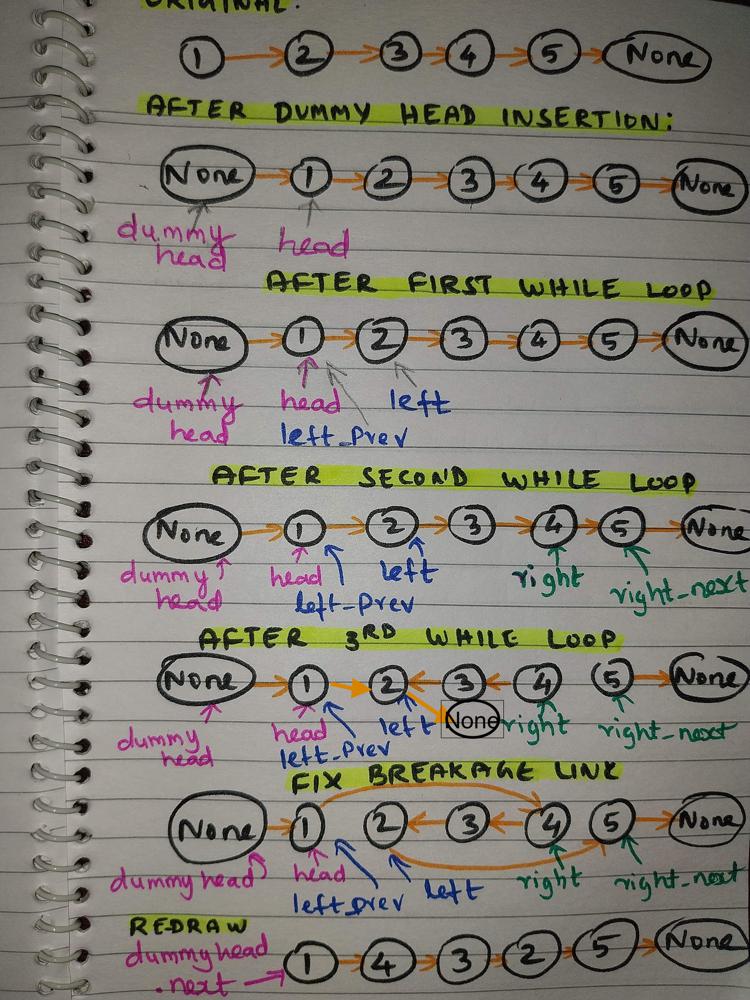\n\n\n# Complexity\n- Time complexity: $$O(2r - l))$$ ```r```= right index, ```l``` = left index\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# C++\n```cpp\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\n\nclass Solution {\npublic:\n ListNode* reverseBetween(ListNode* head, int l, int r) {\n // Dummy head insertion\n ListNode* dummy_head = new ListNode(-1);\n dummy_head->next = head;\n\n // 1st while loop (spot left_prev, left nodes)\n ListNode* left_prev = dummy_head;\n ListNode* left = dummy_head->next;\n int left_count = 1; // we start with 1 because we have to stop previous to left (because dummy head added)\n while (left_count < l) {\n left_prev = left;\n left = left->next;\n left_count++;\n }\n // 2nd while loop (spot the right, right_next nodes)\n ListNode* right = left;\n ListNode* right_next = left->next;\n int right_count = 0;\n while (right_count < r - l) {\n right = right_next;\n right_next = right_next->next;\n right_count++;\n }\n // 3rd while loop (reverse element between left and right node)\n ListNode* cur = left;\n ListNode* pre = nullptr;\n while (cur != right_next) {\n ListNode* tmp = cur->next;\n cur->next = pre;\n pre = cur;\n cur = tmp;\n }\n // 4th fix breakage link\n left_prev->next = right;\n left->next = right_next;\n\n head = dummy_head->next;\n delete dummy_head;\n return head;\n }\n};\n```\n# Python3\n```python\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseBetween(self, head: Optional[ListNode], l: int, r: int) -> Optional[ListNode]:\n \n # Dummy head insertion\n dummy_head = ListNode(None)\n dummy_head.next = head\n\n # 1st while loop (spot left_prev, left nodes)\n left_prev = dummy_head\n left = dummy_head.next\n left_count = 1 # we start with 1 because we have to stop previous to left (because dummy head added)\n while left_count < l:\n left_prev = left\n left = left.next\n left_count += 1\n\n # 2nd while loop (spot the right, right_next nodes)\n right = left\n right_next = left.next\n right_count = 0\n while right_count < r - l:\n right = right_next\n right_next = right_next.next\n right_count += 1\n\n # 3rd while loop (reverse element between left and right node)\n cur = left\n pre = None\n while cur != right_next:\n tmp = cur.next\n cur.next = pre\n pre = cur\n cur = tmp\n \n # 4th fix breakage link\n left_prev.next = right\n left.next = right_next\n\n head = dummy_head.next\n del dummy_head\n return head\n```\n# Java\n```java\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\n\npublic class Solution {\n public ListNode reverseBetween(ListNode head, int l, int r) {\n // Dummy head insertion\n ListNode dummyHead = new ListNode(-1);\n dummyHead.next = head;\n\n // 1st while loop (spot left_prev, left nodes)\n ListNode leftPrev = dummyHead;\n ListNode left = dummyHead.next;\n int leftCount = 1; // we start with 1 because we have to stop previous to left (because dummy head added)\n while (leftCount < l) {\n leftPrev = left;\n left = left.next;\n leftCount++;\n }\n\n // 2nd while loop (spot the right, right_next nodes)\n ListNode right = left;\n ListNode rightNext = left.next;\n int rightCount = 0;\n while (rightCount < r - l) {\n right = rightNext;\n rightNext = rightNext.next;\n rightCount++;\n }\n\n // 3rd while loop (reverse elements between left and right node)\n ListNode cur = left;\n ListNode pre = null;\n while (cur != rightNext) {\n ListNode tmp = cur.next;\n cur.next = pre;\n pre = cur;\n cur = tmp;\n }\n\n // 4th fix breakage link\n leftPrev.next = right;\n left.next = rightNext;\n\n head = dummyHead.next;\n // remove(dummyHead);\n return head;\n }\n}\n``` | 5 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
Python short and clean. Single pass. 2 approaches. Functional programming. | reverse-linked-list-ii | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is number of nodes in LinkedList starting at head`.\n\n# Code\nImperative single-pass:\n```python\nclass Solution:\n def reverseBetween(self, head: ListNode | None, left: int, right: int) -> ListNode | None:\n new_head = ListNode(next=head)\n \n left_end = new_head\n for _ in range(left - 1):\n left_end = left_end.next\n \n prev_node, curr_node = None, left_end.next\n for _ in range(left, right + 1):\n curr_node.next, prev_node, curr_node = prev_node, curr_node, curr_node.next\n \n left_end.next.next, left_end.next = curr_node, prev_node\n return new_head.next\n \n```\n\nFunctional single-pass:\n# Code\n```python\nclass Solution:\n def reverseBetween(self, head: ListNode | None, left: int, right: int) -> ListNode | None:\n new_head = ListNode(next=head)\n\n left_end = reduce(lambda a, _: a.next, range(left - 1), new_head)\n \n curr_node, prev_node = reduce(\n lambda a, _: (a[0].next, setattr(a[0], \'next\', a[1]) or a[0]),\n range(left, right + 1),\n (left_end.next, None),\n )\n \n left_end.next.next, left_end.next = curr_node, prev_node\n return new_head.next\n\n\n``` | 1 | Given the `head` of a singly linked list and two integers `left` and `right` where `left <= right`, reverse the nodes of the list from position `left` to position `right`, and return _the reversed list_.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], left = 2, right = 4
**Output:** \[1,4,3,2,5\]
**Example 2:**
**Input:** head = \[5\], left = 1, right = 1
**Output:** \[5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= n <= 500`
* `-500 <= Node.val <= 500`
* `1 <= left <= right <= n`
**Follow up:** Could you do it in one pass? | null |
[Python] Just DFS and backtracking; Explained | restore-ip-addresses | 0 | 1 | This is a common DFS and backtracking problem. \n\nWe just need to take care of special requirements:\n(1) the total number of fields is 4;\n(2) no leading \'0\' for a number if it is not \'0\'\n\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n # dfs and backtracking\n self.s = s\n self.len_s = len(s)\n self.ans = []\n\n self.dfs(0, [])\n\n return self.ans\n\n def dfs(self, index, partition):\n if index == self.len_s:\n # we reached the end of the string\n if len(partition) == 4:\n self.ans.append(".".join(partition))\n return\n \n if index < self.len_s and len(partition) == 4:\n # we haven\'t used all the characters to build 4 address fields\n return\n\n if self.s[index] == \'0\':\n partition.append(\'0\')\n self.dfs(index + 1, partition)\n partition.pop()\n else:\n for i in range(index + 1, self.len_s + 1):\n if 0 <= int(self.s[index: i]) <= 255:\n partition.append(self.s[index: i])\n self.dfs(i, partition)\n partition.pop()\n else:\n # no need to check further as the value is not in the range of 0 ~ 255\n break\n``` | 2 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Straight-forward backtrack solution in python3 | restore-ip-addresses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\njust take care with the processing number should be lower than len(s) and the length of current stack should be lower or equal 4.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(4)\n# Code\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n res=[]\n cur=[]\n def backtrack(i):\n if i==len(s) and len(cur)==4:\n res.append(".".join(cur))\n return\n if len(cur)>4 or i>=len(s):\n return\n if s[i]==\'0\':\n cur.append(s[i])\n backtrack(i+1)\n cur.pop()\n return\n j=0\n while j<4 and i+j<len(s):\n if int(s[i:i+j+1])<256:\n cur.append(s[i:i+j+1])\n backtrack(i+j+1)\n cur.pop()\n j+=1\n backtrack(0)\n return res\n\n``` | 1 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Python solution using dfs | restore-ip-addresses | 0 | 1 | # Code\n```\nclass Solution:\n\n @cache\n def solve(self , i ,prev , ip) :\n\n if i >= len(self.s) :\n if ip.count(".") == 3 :\n l = list(map(str , ip.split(".")))\n\n lis = [1 if ( x!="" and (x[0]!="0" or x=="0") and int(x)>=0 and int(x)<=255 ) else 0 for x in l ]\n if sum(lis) == 4 :\n self.ans += [ip]\n return \n\n self.solve(i+1 , prev + self.s[i] , ip + self.s[i])\n if i<len(self.s):\n self.solve(i+1 , self.s[i] , ip + self.s[i] + ".")\n\n return \n\n\n def restoreIpAddresses(self, s: str) -> List[str]: \n self.s = s \n self.ans = []\n self.solve(0,"","")\n return self.ans\n \n``` | 1 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Daily LeetCode Challenge | restore-ip-addresses | 0 | 1 | # Intuition\nWhenever we see a question to find various combinations we can use backtracking. Similarly this problem uses backtracking to find all combinations of valid IP chunks to sum up as valid IP address.\n\n# Approach\nThe must conditions :-\n1. IP address should have only 4chunks\n2. If using more than 1num together it shouldnt have leading zeroes\n3. if using three num < 255 (remember one chunk cant have more than three digits)\nBy following all the conditions if we reach a num add it to address\n\nAt last when we make all 4 chunks and no more nums are left in s then return the address\n\n# Code\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n # a valid IP will have 4 chunks separated by \'.\' so once u find a valid IP inc chunk count\n def backtrack(address, s, ans, chunk):\n if chunk == 4:\n if not s: \n #address[:-1] so that last \'.\' will not be included\n ans.append(address[:-1])\n return\n \n # can have to max three nums in one chunk\n for i in range(1, 4):\n if i > len(s):\n continue \n\n #if using single num any num is valid\n #if using more than one num it should not have leading zeroes\n if i >= 2 and s[0] == \'0\':\n continue\n\n #if using three num together check if greater > 255\n if i>= 3 and int(s[:3]) > 255:\n continue\n\n #we found a valid IP\n #add the found IP chunk in address, start s from i till where we added into address and increment the no of chunk\n backtrack(address + s[:i] + \'.\', s[i:], ans, chunk + 1)\n ans = []\n backtrack(\'\', s, ans, 0)\n return ans\n\n \n\n\n``` | 1 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Python 95% runtime and 99% space efficient solution | restore-ip-addresses | 0 | 1 | # Approach\nBacktracking\n\n# Code\n```\nclass Solution:\n def __init__(self) -> None:\n self.validIPs = []\n\n def restoreIpAddresses(self, s: str) -> List[str]:\n self.restoreOctets(s)\n return self.validIPs\n\n def restoreOctets(self, s: str, octetNum: int = 1, prevOctets: str = "") -> str:\n if octetNum - 1 + len(s) < 4 or 3 * (octetNum - 1) + len(s) > 12:\n return # Remaining string is too short or too long\n for i in range(1, len(s)+1): # Try to generate octets with different lengths\n currOctet = s[:i]\n if not(str(int(currOctet)) == currOctet and int(currOctet) < 256):\n return # It\'s not a valid octet, no need to check with greater lengths\n octets = prevOctets + ("." if octetNum > 1 else "") + currOctet\n if octetNum == 4 and i == len(s):\n self.validIPs.append(octets). # All 4 octets are valid and no remaining string left. Now it\'s a valid IP address\n else:\n self.restoreOctets(s[i:], octetNum+1, octets) # Generate next octets \n \n``` | 1 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
🚀Beats 100%(0ms) ||🚀Easy Solution🚀||🔥Fully Explained🔥|| C++ || Python3 || Java | restore-ip-addresses | 1 | 1 | # Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful.\n\n```\n# Intuition\n1. There needs to be 4 parts per IP. There are always three dots/four candidates (2.5.5.2.5.5.1.1.1.3.5 is not valid, neither is 1.1.1)\n2. When selecting a candidate, it can\'t have more than 3 characters (2552.55.111.35 is not valid)\n3. When selecting a candidate, its characters cant be above 255 (25.525.511.135 is not valid because of 525 and 511)\n4. When selecting a candidate, IF the candidate has 2 or more characters, then the first can\'t be a zero. (1.0.1.023 is not valid as member 023 is size>1 and leads with 0. But 0.0.0.0 is valid as each candidate is size 1)\n# Approach : Backtracking\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Helper function to check if a given string is a valid IP address segment\n bool valid(string temp){\n if(temp.size()>3 || temp.size()==0) return false; // segment length should be between 1 and 3\n if(temp.size()>1 && temp[0]==\'0\') return false; // segment should not start with 0, unless it is a single digit\n if(temp.size() && stoi(temp)>255) return false; // segment should not be greater than 255\n return true;\n }\n\n // Backtracking function to generate all possible IP addresses\n void solve(vector<string>& ans, string output, int ind, string s, int dots){\n if(dots == 3){ // if we have already added 3 dots, check if the remaining segment is valid\n if(valid(s.substr(ind)))\n ans.push_back(output+s.substr(ind));\n return;\n }\n int sz = s.size();\n for(int i=ind;i<min(ind+3, sz);i++){\n if(valid(s.substr(ind, i-ind+1))){\n output.push_back(s[i]);\n output.push_back(\'.\');\n solve(ans, output, i+1, s, dots+1);\n output.pop_back(); //backtrack\n }\n }\n\n }\n\n vector<string> restoreIpAddresses(string s) {\n vector<string> ans;\n string res;\n solve(ans, res, 0, s, 0);\n return ans;\n }\n};\n\n```\n```python []\nclass Solution:\n def valid(self, temp: str) -> bool:\n if len(temp) > 3 or len(temp) == 0:\n return False\n if len(temp) > 1 and temp[0] == \'0\':\n return False\n if len(temp) and int(temp) > 255:\n return False\n return True\n\n def solve(self, ans, output, ind, s, dots):\n if dots == 3:\n if self.valid(s[ind:]):\n ans.append(output + s[ind:])\n return\n for i in range(ind, min(ind+3, len(s))):\n if self.valid(s[ind:i+1]):\n new_output = output + s[ind:i+1] + \'.\'\n self.solve(ans, new_output, i+1, s, dots+1)\n\n def restoreIpAddresses(self, s: str) -> List[str]:\n ans = []\n self.solve(ans, "", 0, s, 0)\n return ans\n\n```\n```Java []\n private List<String> ipes;\n private int l;\n public List<String> restoreIpAddresses(String s) {\n ipes = new ArrayList<>();\n l = s.length();\n f(s, 0, "", 0);\n return ipes;\n }\n \n private boolean isIp(String ip){\n if(ip.length() > 3 || ip.length() == 0) return false;\n if(ip.length() > 1 && ip.charAt(0) == \'0\') return false;\n if(ip.length() > 0 && Integer.parseInt(ip) > 255) return false;\n return true; \n }\n\n private void f(String s, int index, String ip, int dot){\n //base case\n if(dot == 3){\n if(isIp(s.substring(index))) {\n ip += s.substring(index);\n ipes.add(ip);\n }\n return;\n }\n\n //do all the stuff\n for(int i = index; i < l; i++){\n if(isIp(s.substring(index, i +1))){\n int k = s.substring(index, i+1).length();\n ip += s.substring(index, i+1) + ".";\n f(s, i+1, ip, dot+1);\n ip = ip.substring(0, ip.length() - k -1);\n }\n }\n }\n}\n```\n```\n Give a \uD83D\uDC4D. It motivates me alot.\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/)\n\n | 82 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Easy Python solution ...Runtime faster than 100% and memory efficient than 99.69% | restore-ip-addresses | 0 | 1 | # Intuition\nThe approach intuitively works by breaking down the input string into segments representing parts of an IP address (e.g., four segments for IPv4) and explores all possible combinations of these segments. It uses a recursive function to iterate through the string, considering one, two, or three characters at a time for each segment, while ensuring that each segment is a valid integer between 0 and 255. When it finds a valid combination of segments that forms a complete IP address, it adds it to the result list. This approach systematically explores the possibilities, making sure each segment is valid and adheres to IP address rules, ultimately generating all valid IP addresses in the input string.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach recursively explores all possible combinations of valid IP address segments in the input string while maintaining a count of segments, and appends valid IP addresses to the result list.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution can be approximated as O(3^4 * len(s)) because there are three choices for each character (add it as a single segment, add it as a two-segment, or add it as a three-segment). \n\n- Space complexity:\n The dominant factor in space complexity is the recursive call stack, which is O(1) in practice. Therefore, the space complexity of this solution is O(1).\n\n\n# Code\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n res = []\n\n def isvalid(s):\n if s[0] == \'0\':\n return False\n val = int(s)\n return val<256\n\n def helper(i, ans, par):\n if(i==len(s) or par==4):\n if(len(s)==i and par==4):\n res.append(ans[:len(ans)-1])\n return\n helper(i + 1, ans + s[i] + ".", par + 1)\n if (i + 1 < len(s) and isvalid(s[i:i + 2])):\n helper(i + 2, ans + s[i:i + 2] + ".", par + 1)\n if (i + 2 < len(s) and isvalid(s[i:i + 3])):\n helper(i + 3, ans + s[i:i + 3] + ".", par + 1)\n\n helper(0, "", 0)\n return res\n\n \n``` | 0 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
💡💡 Neatly coded backtracking solution in python3 | restore-ip-addresses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse backtracking to validate the numbers in the IP address. If it is a valid one, add a "." since we\'re validating IPv4 addresses. We should also make sure that thes number don\'t have leading zeroes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(3^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n res = []\n if len(s) > 12:\n return res\n \n def backtrack(i, dots, curip):\n if i == len(s) and dots == 4:\n res.append(curip[:-1]) # to remove the fourth dot - [:-1]\n return \n \n for j in range(i, min(i+3, len(s))):\n if int(s[i:j+1]) <= 255 and (i == j or s[i] != "0"):\n backtrack(j+1, dots+1, curip + s[i:j+1] + ".")\n\n backtrack(0, 0, "")\n return res\n``` | 1 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Backtracking solution to generate all possible valid IP addresses from a given string | restore-ip-addresses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to form all possible valid IP addresses by inserting dots in the given string. A valid IP address has four segments, and each segment should be between 0 and 255 (inclusive) and should not have leading zeros. The idea is to use backtracking to generate all possible combinations of valid IP addresses.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe start with a blank string and the index of the first character in the input string. We then try to add a segment to the IP address by selecting the next one, two, or three characters from the input string (but no more than three) and checking if it is a valid segment. If it is, we add it to the IP address and recurse on the remaining characters, passing the index of the next character and the number of segments we have added so far. If we have added four segments and used all the characters in the input string, we have a valid IP address, so we add it to the result list. Otherwise, if we have added four segments but haven\'t used all the characters in the input string, we backtrack and try another combination of segments.\n\nTo check if a segment is valid, we need to check that it is a valid integer between 0 and 255 (inclusive) and that it does not have leading zeros (except for the case when the segment is "0").\n# Complexity\n- Time complexity: O(3^4 * n) = O(n), where n is the length of the input string. We have at most 3 choices for each segment (select one, two, or three characters), and we can have at most 4 segments, so we have 3^4 possible combinations of segments. However, most of these combinations will be invalid, so we don\'t need to explore all of them. The worst-case time complexity occurs when all the combinations are valid, which happens when the input string consists of 12 digits (i.e., "255255255255"). In this case, we need to explore all 81 (3^4) combinations of segments, and each segment validation takes O(1) time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n), where n is the length of the input string. This is the space required to store the result list and the recursive call stack.\nCode\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n def backtrack(start: int, dots: int, ip: str, result: List[str]) -> None:\n if start == len(s) and dots == 4:\n result.append(ip[:-1])\n elif dots < 4:\n for i in range(start, min(start + 3, len(s))):\n segment = s[start:i+1]\n if len(segment) > 1 and segment[0] == \'0\':\n continue\n if 0 <= int(segment) <= 255:\n backtrack(i+1, dots+1, ip + segment + \'.\', result)\n result = []\n backtrack(0, 0, \'\', result)\n return result\n``` | 1 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
Clean Codes🔥🔥|| Full Explanation✅|| Recursion ✅|| C++|| Java || Python3 | restore-ip-addresses | 1 | 1 | # Exaplanation to Approach :\n1. The main idea to solve this problem is to use Recursion.\n2. Consider every position of the input string and, there exist two possible cases:\n - Place a dot over the current position.\n - Take this character, i.e don\u2019t place the dot over this position.\n3. At every step of the recursion, we have the following data:\n - curr stores the string between two dots.\n - res stores the possible IP Address.\n - index stores the current position in the input string.\n4. At each index, first, add the character to curr and check whether the integer that we have is in the range [0,255] then, we can move further otherwise return.\n5. When we reach the end of the input string, we\u2019ll check whether we have a valid IP Address or not, If yes, insert the IP Address into our answer.\n\n# Request \uD83D\uDE0A :\n- If you find this solution easy to understand and helpful, then Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n# Code [C++] :\n```\nclass Solution {\npublic:\n vector<string> ans;\n void recurse(string res,string curr,int index,string s){\n if(index==s.length()){\n if(curr.empty() and count(res.begin(),res.end(),\'.\')==3){\n ans.push_back(res);\n }\n return;\n }\n if(!curr.empty() and stoi(curr)==0){\n return;\n }\n curr.push_back(s[index]);\n if(stoi(curr)>255){\n return;\n }\n recurse(res,curr,index+1,s);\n if(!res.empty()){\n recurse(res+"."+curr,"",index+1,s);\n }\n else{\n recurse(curr,"",index+1,s);\n }\n }\n vector<string> restoreIpAddresses(string s) {\n recurse("","",0,s);\n return ans;\n }\n};\n```\n# Code [Java] :\n```\nclass Solution {\n public List<String> restoreIpAddresses(String s) {\n List<String> ans = new ArrayList<String>();\n recurse(s, ans, 0, "", 0);\n return ans;\n }\n private void recurse(String curr, List<String> ans, int index, String temp, int count) {\n if (count > 4)\n return;\n if (count == 4 && index == curr.length())\n ans.add(temp);\n for (int i=1; i<4; i++) {\n if (index+i > curr.length()){\n break;\n }\n String s = curr.substring(index,index+i);\n if ((s.startsWith("0") && s.length()>1) || (i==3 && Integer.parseInt(s) >= 256)){\n continue;\n }\n recurse(curr, ans, index+i, temp+s+(count==3?"" : "."), count+1);\n }\n }\n}\n```\n# Code [Python3] :\n```\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n ans = []\n self.recurse(s, ans, 0, "", 0)\n return ans\n \n def recurse(self, curr, ans, index, temp, count):\n if count > 4:\n return\n if count == 4 and index == len(curr):\n ans.append(temp)\n for i in range(1, 4):\n if index + i > len(curr):\n break\n s = curr[index:index+i]\n if (s.startswith("0") and len(s) > 1) or (i == 3 and int(s) >= 256):\n continue\n self.recurse(curr, ans, index+i, temp + s + ("." if count < 3 else ""), count+1)\n\n``` | 29 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
✔️ 0ms runtime code | C++ | Python | explained | restore-ip-addresses | 0 | 1 | # Solution:\n\n``` C++ []\nclass Solution {\npublic:\n bool check(string s){\n int n=s.size();\n //if the size of string is 1 that is always possible so return true\n if(n==1){\n return true;\n }\n //if we have length >3 or string starts with 0 return false\n if(n>3||s[0]==\'0\'){\n return false;\n }\n //we are converting string to integer to check if it is less than equalto 255\n int val=stoi(s);\n if(val>255){\n return false;\n }\n //return true at last\n return true;\n }\n vector<string> restoreIpAddresses(string s) {\n int n=s.size();\n //we will store our ans in ans vector of strings\n vector<string>ans;\n //the max length of the ip address could be 12 as 255.255.255.255 so \n //all the string s with size greater than 12 can have ans\n if(n>12){\n return ans;\n }\n //now we have our string of length 12 or less than 12 so now \n //1. we have to spit the s in parts such that it satisfy the ip address conditions\n //2. if all 4 strings satisfy the condition we will push into ans vector\n \n for(int i=1;i<=3;i++){//for the length before first \'.\'\n for(int j=1;j<=3;j++){//for the length between first and second \'.\'\n for(int k=1;k<=3;k++){//for the length between second and third \'.\'\n //checking condition if the last segment is of length 3 or less\n if(i+j+k<n&&i+j+k+3>=n){\n //dividing the s int substrings \n string a=s.substr(0,i);\n string b=s.substr(i,j);\n string c=s.substr(j+i,k);\n string d=s.substr(i+j+k);\n //if all the substring satisfy the check function condition \n //then we will push into ans vector \n if(check(a)&&check(b)&&check(c)&&check(d)){\n ans.push_back(a+"."+b+"."+c+"."+d);\n }\n }\n }\n }\n }\n //return the ans vector\n return ans;\n }\n};\n```\n``` Python []\nclass Solution:\n def restoreIpAddresses(self, s: str) -> List[str]:\n # Store all addresses in res\n res = []\n \n def BT(i,address):\n \n # No more digit, so no more state can be generated.\n if i==len(s):\n # It is possible that the address contains less than 4 numbers\n # We only store the valid ones.\n if len(address)==4:\n res.append( \'.\'.join(map(str,address)) )\n return\n \n # If the last number is 0, we can add the new digit to it (no leading zero)\n # After adding the new digit, the number has to be <= 255.\n if address[-1]!=0 and address[-1]*10+int(s[i]) <= 255:\n lastItem = address[-1]\n address[-1] = lastItem*10+int(s[i]) #change the current state to its neighboring state\n BT(i+1, address) #backtrack(state)\n address[-1] = lastItem #restore the state (backtrack)\n \n # The address can not contain more than 4 numbers.\n if len(address)<4:\n address.append(int(s[i])) #change the current state to its neighboring state\n BT(i+1,address) #backtrack(state)\n address.pop() #restore the state (backtrack)\n \n BT(1,[int(s[0])])\n return res\n```\n\n*Please upvote if helped* | 5 | A **valid IP address** consists of exactly four integers separated by single dots. Each integer is between `0` and `255` (**inclusive**) and cannot have leading zeros.
* For example, `"0.1.2.201 "` and `"192.168.1.1 "` are **valid** IP addresses, but `"0.011.255.245 "`, `"192.168.1.312 "` and `"[email protected] "` are **invalid** IP addresses.
Given a string `s` containing only digits, return _all possible valid IP addresses that can be formed by inserting dots into_ `s`. You are **not** allowed to reorder or remove any digits in `s`. You may return the valid IP addresses in **any** order.
**Example 1:**
**Input:** s = "25525511135 "
**Output:** \[ "255.255.11.135 ", "255.255.111.35 "\]
**Example 2:**
**Input:** s = "0000 "
**Output:** \[ "0.0.0.0 "\]
**Example 3:**
**Input:** s = "101023 "
**Output:** \[ "1.0.10.23 ", "1.0.102.3 ", "10.1.0.23 ", "10.10.2.3 ", "101.0.2.3 "\]
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of digits only. | null |
【Video】Give me 5 minutes Recursion and Stack(Bonus) solution - how we think about a solution. | binary-tree-inorder-traversal | 1 | 1 | # Intuition\nWe should know how to implement inorder, preorder and postorder.\n\n# Approach\n\n---\n\n# Solution Video\n\nhttps://youtu.be/TKMxiXRzDZ0\n\n\u25A0 Timeline\n`0:04` How to implement inorder, preorder and postorder\n`1:16` Coding (Recursive)\n`2:14` Time Complexity and Space Complexity\n`2:37` Explain Stack solution\n`7:22` Coding (Stack)\n`8:45` Time Complexity and Space Complexity\n`8:59` Step by step algorithm with my stack solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,389\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n## How we think about a solution\n\nTo be honest, we should know how to implement inorder, preorder and postorder.\n\n```\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\nresult = []\n\ndef inorder(root):\n if not root:\n return []\n\n inorder(root.left)\n result.append(root.val)\n inorder(root.right)\n return result\n\ndef preorder(root):\n if not root:\n return []\n\n result.append(root.val)\n preorder(root.left)\n preorder(root.right)\n return result\n\ndef postorder(root):\n if not root:\n return []\n\n postorder(root.left)\n postorder(root.right)\n result.append(root.val)\n return result\n```\n\nLet\'s focus on `result.append(root.val)`\n\n---\n\n\u2B50\uFE0F Points\n\nFor `Inorder`, we do something `between` left and right.\nFor `Preorder`, we do something `before` left and right.\nFor `Postorder`, we do something `after` left and right.\n\n---\n\nWe use inorder this time, so do something between left and right.\n\n### \u2B50\uFE0F Questions related to inorder\n\n\u25A0 Find Mode in Binary Search Tree - LeetCode #501\n\npost\nhttps://leetcode.com/problems/find-mode-in-binary-search-tree/solutions/4233557/give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/0i1Ze62pTuU\n\n\n\u25A0 Construct Binary Tree from Preorder and Inorder Traversal - LeetCode #105\n\nhttps://youtu.be/l88-GlcYpQM\n\n---\n\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\nIn the worst case, we have skewed tree.\n\n```python []\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n res = []\n\n def inorder(root):\n if not root:\n return\n inorder(root.left)\n res.append(root.val)\n inorder(root.right)\n \n inorder(root)\n return res\n```\n```javascript []\nvar inorderTraversal = function(root) {\n const res = [];\n\n function inorder(node) {\n if (!node) {\n return;\n }\n inorder(node.left);\n res.push(node.val);\n inorder(node.right);\n }\n\n inorder(root);\n return res; \n};\n```\n```java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> res = new ArrayList<>();\n\n inorder(root, res);\n return res; \n }\n\n private void inorder(TreeNode node, List<Integer> res) {\n if (node == null) {\n return;\n }\n inorder(node.left, res);\n res.add(node.val);\n inorder(node.right, res);\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> res;\n inorder(root, res);\n return res; \n }\n\nprivate:\n void inorder(TreeNode* node, vector<int>& res) {\n if (!node) {\n return;\n }\n inorder(node->left, res);\n res.push_back(node->val);\n inorder(node->right, res);\n } \n};\n```\n\n\n---\n\n\n\n# Bonus - Stack solution\n\nI explain stack solution with visualization in the video above.\n\n```python []\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n # Initialize an empty list to store the result (in-order traversal)\n res = []\n \n # Initialize an empty stack for iterative traversal\n stack = []\n \n # Loop until either the current node is not None or the stack is not empty\n while root or stack:\n # Traverse to the leftmost node and push each encountered node onto the stack\n while root:\n stack.append(root)\n root = root.left\n\n # Pop the last node from the stack (most recently left-visited node)\n root = stack.pop()\n \n # Append the value of the popped node to the result list\n res.append(root.val)\n \n # Move to the right subtree to continue the in-order traversal\n root = root.right\n \n # Return the final result list\n return res\n\n```\n```javascript []\nvar inorderTraversal = function(root) {\n // Initialize an empty array to store the result (in-order traversal)\n const res = [];\n \n // Initialize an empty stack for iterative traversal\n const stack = [];\n\n // Loop until either the current node is not null or the stack is not empty\n while (root || stack.length > 0) {\n // Traverse to the leftmost node and push each encountered node onto the stack\n while (root) {\n stack.push(root);\n root = root.left;\n }\n\n // Pop the last node from the stack (most recently left-visited node)\n root = stack.pop();\n \n // Append the value of the popped node to the result array\n res.push(root.val);\n \n // Move to the right subtree to continue the in-order traversal\n root = root.right;\n }\n\n // Return the final result array\n return res; \n};\n\n```\n```java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n // Initialize an ArrayList to store the result (in-order traversal)\n List<Integer> res = new ArrayList<>();\n \n // Initialize a Stack for iterative traversal\n Stack<TreeNode> stack = new Stack<>();\n\n // Loop until either the current node is not null or the stack is not empty\n while (root != null || !stack.isEmpty()) {\n // Traverse to the leftmost node and push each encountered node onto the stack\n while (root != null) {\n stack.push(root);\n root = root.left;\n }\n\n // Pop the last node from the stack (most recently left-visited node)\n root = stack.pop();\n \n // Append the value of the popped node to the result list\n res.add(root.val);\n \n // Move to the right subtree to continue the in-order traversal\n root = root.right;\n }\n\n // Return the final result list\n return res; \n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n // Initialize a vector to store the result (in-order traversal)\n vector<int> res;\n \n // Initialize a stack for iterative traversal\n stack<TreeNode*> stack;\n\n // Loop until either the current node is not null or the stack is not empty\n while (root != nullptr || !stack.empty()) {\n // Traverse to the leftmost node and push each encountered node onto the stack\n while (root != nullptr) {\n stack.push(root);\n root = root->left;\n }\n\n // Pop the last node from the stack (most recently left-visited node)\n root = stack.top();\n stack.pop();\n \n // Append the value of the popped node to the result vector\n res.push_back(root->val);\n \n // Move to the right subtree to continue the in-order traversal\n root = root->right;\n }\n\n // Return the final result vector\n return res; \n }\n};\n\n```\n\n### Step by step Algorithm of stack solution\n\n1. **Initialization:**\n - Initialize an empty list `res` to store the result (in-order traversal).\n - Initialize an empty stack `stack` for iterative traversal.\n\n ```python\n res = []\n stack = []\n ```\n\n2. **Traversal Loop:**\n - Start a loop that continues until either the current node (`root`) is not `None` or the stack is not empty.\n - This loop handles both the traversal to the leftmost node and the backtracking to the parent node.\n\n ```python\n while root or stack:\n ```\n\n3. **Traverse to Leftmost Node:**\n - Within the loop, another nested loop is used to traverse to the leftmost node of the current subtree.\n - During this process, each encountered node is pushed onto the stack.\n - This ensures that we move as far left as possible in the tree.\n\n ```python\n while root:\n stack.append(root)\n root = root.left\n ```\n\n4. **Pop Node from Stack:**\n - Once we reach the leftmost node (or a leaf node), we pop the last node from the stack. This node is the most recently left-visited node.\n - We assign this node to `root`.\n\n ```python\n root = stack.pop()\n ```\n\n5. **Append Node Value to Result:**\n - Append the value of the popped node to the result list `res`. This is the in-order traversal order.\n\n ```python\n res.append(root.val)\n ```\n\n6. **Move to Right Subtree:**\n - Move to the right subtree of the current node. This step is crucial for continuing the in-order traversal.\n\n ```python\n root = root.right\n ```\n\n7. **End of Loop:**\n - Repeat the loop until all nodes are processed.\n\n8. **Return Result List:**\n - After the traversal is complete, return the final result list `res`.\n\n ```python\n return res\n ```\n\nThis algorithm performs an in-order traversal of a binary tree iteratively using a stack. It mimics the recursive approach but uses a stack to manage the traversal state explicitly. The core idea is to go as left as possible, visit the nodes along the way, backtrack to the parent, and then move to the right subtree. The stack helps in tracking the backtracking process.\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/transpose-matrix/solutions/4384180/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/construct-string-from-binary-tree/solutions/4376889/video-give-me-7-minutes-recursion-and-stack-solutionbonus-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/gV7MkiwMDS8\n\n\u25A0 Timeline of the video\n\n`0:05` How we create an output string\n`2:07` Coding\n`4:30` Time Complexity and Space Complexity\n`4:49` Step by step of recursion process\n`7:27` Step by step algorithm with my solution code\n\n\n | 35 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
✅☑[C++/Java/Python/JavaScript] || 3 Approaches || Beats 100% || EXPLAINED🔥 | binary-tree-inorder-traversal | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Recursive Approach)***\n1. **printVector Function:**\n\n - This function takes a reference to a vector of integers as input and prints its elements in a specific format.\n - It iterates through the vector and prints each element.\n - Commas are added after each element except for the last one to maintain the proper array representation.\n1. **inorderTraversal Function:**\n\n - This function performs an inorder traversal of a binary tree recursively.\n - It takes a pointer to the root of the tree and a reference to a vector of integers (`res`) as parameters.\n - The traversal follows the left subtree, then visits the current node, and finally traverses the right subtree.\n - At each step, it appends the value of the current node to the `res` vector.\n1. **inorderTraversal (Overloaded) Function:**\n\n - This overloaded function serves as the entry point for initiating the inorder traversal.\n - It takes a pointer to the root of the tree as input.\n - It initializes an empty vector `res` to store the result of the inorder traversal.\n - Calls the `inorderTraversal` function with the root pointer and the empty `res` vector.\n - Finally, it returns the `res` vector containing the elements of the tree in inorder traversal order.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\n\nclass Solution {\npublic:\n// Function to print elements in a vector\n void printVector(vector<int>& vec) {\n cout << "[";\n for (int i = 0; i < vec.size(); ++i) {\n cout << vec[i];\n if (i != vec.size() - 1) {\n cout << ", ";\n }\n }\n cout << "]" << endl;\n }\n\n\n void inorderTraversal(TreeNode* root, vector<int>& res) {\n if (root != nullptr) {\n inorderTraversal(root->left, res);\n res.push_back(root->val);\n inorderTraversal(root->right, res);\n }\n }\n\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> res;\n inorderTraversal(root, res);\n return res;\n }\n};\n\n\n\n\n\n```\n```C []\nvoid printArray(int* arr, int size) {\n printf("[");\n for (int i = 0; i < size; ++i) {\n printf("%d", arr[i]);\n if (i != size - 1) {\n printf(", ");\n }\n }\n printf("]\\n");\n}\n\nvoid inorderTraversal(struct TreeNode* root, int* res, int* idx) {\n if (root != NULL) {\n inorderTraversal(root->left, res, idx);\n res[(*idx)++] = root->val;\n inorderTraversal(root->right, res, idx);\n }\n}\n\nint* inorderTraversalWrapper(struct TreeNode* root, int* returnSize) {\n int* res = (int*)malloc(1000 * sizeof(int)); // Allocate memory for result array\n int idx = 0; // Index to keep track of current position in the result array\n\n inorderTraversal(root, res, &idx); // Perform inorder traversal\n\n *returnSize = idx; // Set return size to the actual number of elements filled\n return res;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> res = new ArrayList<>();\n helper(root, res);\n return res;\n }\n\n public void helper(TreeNode root, List<Integer> res) {\n if (root != null) {\n helper(root.left, res);\n res.add(root.val);\n helper(root.right, res);\n }\n }\n}\n\n\n```\n```python3 []\n\n\n\nclass Solution:\n def inorderTraversal(self, root):\n res = []\n \n def inorder(root):\n if root:\n inorder(root.left)\n res.append(root.val)\n inorder(root.right)\n \n inorder(root)\n return res\n\n def printList(self, lst):\n print("[", end="")\n for i in range(len(lst)):\n print(lst[i], end="")\n if i != len(lst) - 1:\n print(", ", end="")\n print("]")\n\n```\n```javascript []\n// Definition for a binary tree node.\nfunction TreeNode(val) {\n this.val = val;\n this.left = this.right = null;\n}\n\n// Function to perform inorder traversal\nvar inorderTraversal = function(root) {\n let res = [];\n \n function traverse(node) {\n if (node !== null) {\n traverse(node.left);\n res.push(node.val);\n traverse(node.right);\n }\n }\n \n traverse(root);\n return res;\n};\n\n```\n---\n\n\n\n#### ***Approach 2(Iterating method using Stack)***\n1. **inorderTraversal Function:**\n\n - Performs iterative inorder traversal of a binary tree using a stack.\n - Starts at the root and goes to the leftmost node while pushing encountered nodes into a stack.\n - As it reaches the leftmost node, it pops nodes from the stack, appends their values to the result, and moves to their right children.\n - Continues this process until all nodes are visited, storing values in the `res` vector.\n1. **printVector Function:**\n\n - A utility function to print elements stored in a vector.\n - Outputs elements in a readable format, separated by commas, enclosed in square brackets.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Perform inorder traversal of a binary tree iteratively\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> res; // Vector to store inorder traversal result\n stack<TreeNode*> st; // Stack to assist in traversal\n TreeNode* curr = root; // Pointer to track the current node\n\n // Traverse the tree until current node is not null or stack is not empty\n while (curr != nullptr || !st.empty()) {\n // Traverse to the leftmost node of the current subtree\n while (curr != nullptr) {\n st.push(curr); // Push current node to stack\n curr = curr->left; // Move to the left child\n }\n\n curr = st.top(); // Get the top node from stack\n st.pop(); // Pop the top node\n res.push_back(curr->val);// Push the value of current node to result vector\n curr = curr->right; // Move to the right child to explore its subtree\n }\n return res; // Return the inorder traversal result\n }\n};\n\n// Function to print elements in a vector\nvoid printVector(vector<int>& vec) {\n cout << "["; // Output start of the vector representation\n for (int i = 0; i < vec.size(); ++i) {\n cout << vec[i]; // Output the current element\n if (i != vec.size() - 1) {\n cout << ", "; // Output comma if not the last element\n }\n }\n cout << "]" << endl; // Output end of the vector representation\n}\n\n\n\n```\n```C []\nstruct TreeNode {\n int val;\n struct TreeNode *left;\n struct TreeNode *right;\n};\n\n// Structure of the stack node\nstruct StackNode {\n struct TreeNode *node;\n struct StackNode *next;\n};\n\n// Function to create a new stack node\nstruct StackNode* createStackNode(struct TreeNode* node) {\n struct StackNode* stackNode = (struct StackNode*)malloc(sizeof(struct StackNode));\n stackNode->node = node;\n stackNode->next = NULL;\n return stackNode;\n}\n\n// Function to push an element into the stack\nvoid push(struct StackNode** root, struct TreeNode* node) {\n struct StackNode* stackNode = createStackNode(node);\n stackNode->next = *root;\n *root = stackNode;\n}\n\n// Function to check if the stack is empty\nint isEmpty(struct StackNode* root) {\n return !root;\n}\n\n// Function to pop an element from the stack\nstruct TreeNode* pop(struct StackNode** root) {\n if (isEmpty(*root)) return NULL;\n struct StackNode* temp = *root;\n *root = (*root)->next;\n struct TreeNode* popped = temp->node;\n free(temp);\n return popped;\n}\n\n// Perform inorder traversal of a binary tree iteratively\nint* inorderTraversal(struct TreeNode* root, int* returnSize) {\n int* res = (int*)malloc(100 * sizeof(int)); // Vector to store inorder traversal result\n struct StackNode* st = NULL; // Stack to assist in traversal\n struct TreeNode* curr = root; // Pointer to track the current node\n int index = 0; // Index to track the position in the result array\n\n // Traverse the tree until current node is not null or stack is not empty\n while (curr != NULL || !isEmpty(st)) {\n // Traverse to the leftmost node of the current subtree\n while (curr != NULL) {\n push(&st, curr); // Push current node to stack\n curr = curr->left; // Move to the left child\n }\n\n curr = pop(&st); // Get the top node from stack\n res[index++] = curr->val; // Store the value of current node in the result vector\n curr = curr->right; // Move to the right child to explore its subtree\n }\n\n *returnSize = index; // Set the size of the resulting array\n return res; // Return the inorder traversal result\n}\n\n// Function to print elements in an array\nvoid printArray(int* arr, int size) {\n printf("[");\n for (int i = 0; i < size; ++i) {\n printf("%d", arr[i]);\n if (i != size - 1) {\n printf(", ");\n }\n }\n printf("]\\n");\n}\n\n\n\n```\n```Java []\npublic class Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> res = new ArrayList<>();\n Stack<TreeNode> stack = new Stack<>();\n TreeNode curr = root;\n while (curr != null || !stack.isEmpty()) {\n while (curr != null) {\n stack.push(curr);\n curr = curr.left;\n }\n curr = stack.pop();\n res.add(curr.val);\n curr = curr.right;\n }\n return res;\n }\n}\n\n\n```\n```python3 []\n\ndef inorderTraversal(root):\n res = [] # List to store inorder traversal result\n stack = [] # Stack to assist in traversal\n curr = root # Pointer to track the current node\n\n # Traverse the tree until current node is not None or stack is not empty\n while curr is not None or stack:\n # Traverse to the leftmost node of the current subtree\n while curr is not None:\n stack.append(curr) # Push current node to stack\n curr = curr.left # Move to the left child\n\n curr = stack.pop() # Get the top node from stack\n res.append(curr.val) # Append the value of current node to result list\n curr = curr.right # Move to the right child to explore its subtree\n\n return res # Return the inorder traversal result\n\n# Function to print elements in a list\ndef printList(lst):\n print("[", end="") # Output start of the list representation\n for i in range(len(lst)):\n print(lst[i], end="") # Output the current element\n if i != len(lst) - 1:\n print(", ", end="") # Output comma if not the last element\n print("]") # Output end of the list representation\n\n\n```\n```javascript []\n// Definition of the TreeNode structure\nclass TreeNode {\n constructor(val = 0, left = null, right = null) {\n this.val = val;\n this.left = left;\n this.right = right;\n }\n}\n\n// Perform inorder traversal of a binary tree iteratively\nvar inorderTraversal = function(root) {\n let res = []; // Array to store inorder traversal result\n let st = []; // Stack to assist in traversal\n let curr = root; // Pointer to track the current node\n\n // Traverse the tree until current node is not null or stack is not empty\n while (curr !== null || st.length !== 0) {\n // Traverse to the leftmost node of the current subtree\n while (curr !== null) {\n st.push(curr); // Push current node to stack\n curr = curr.left; // Move to the left child\n }\n\n curr = st.pop(); // Get the top node from stack\n res.push(curr.val); // Store the value of current node in the result array\n curr = curr.right; // Move to the right child to explore its subtree\n }\n\n return res; // Return the inorder traversal result\n};\n\n// Function to print elements\n\n\n```\n---\n\n#### ***Approach 3(Morris Traversal)***\n1. **norderTraversal Function:**\n\n - It takes the root of a binary tree as input and returns a vector containing elements in inorder traversal order.\n - `TreeNode* curr` represents the current node being processed.\n - `TreeNode* pre` helps to handle cases where a node has a left subtree.\n - It continuously loops while `curr` is not null.\n - If the current node\'s left child is null, it means there\'s no left subtree. In this case:\n - It adds the current node\'s value to the `res` vector.\n - Moves to the right child to continue the traversal.\n - If the current node has a left subtree:\n - It finds the rightmost node of the left subtree by traversing right until the right child is null (this is stored in `pre`).\n - Links the `pre->right` to the current node (`curr`) to establish a connection after the left subtree is traversed.\n - Moves the `curr` pointer to its left child, as the left subtree needs to be traversed next.\n - Sets the original left child of the `curr` node to null to avoid infinite loops in case of revisiting nodes.\n1. **printVector Function:**\n\n - It\'s a utility function used to print the elements stored in a vector `vec` in a specific format.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> res;\n TreeNode* curr = root;\n TreeNode* pre;\n\n while (curr != nullptr) {\n if (curr->left == nullptr) {\n res.push_back(curr->val);\n curr = curr->right; // move to next right node\n } else { // has a left subtree\n pre = curr->left;\n while (pre->right != nullptr) { // find rightmost\n pre = pre->right;\n }\n pre->right = curr; // put cur after the pre node\n TreeNode* temp = curr; // store cur node\n curr = curr->left; // move cur to the top of the new tree\n temp->left = nullptr; // original cur left be null, avoid infinite loops\n }\n }\n return res;\n }\n};\n\n// Function to print elements in a vector\nvoid printVector(vector<int>& vec) {\n cout << "[";\n for (int i = 0; i < vec.size(); ++i) {\n cout << vec[i];\n if (i != vec.size() - 1) {\n cout << ", ";\n }\n }\n cout << "]" << endl;\n}\n\n\n```\n```C []\nstruct TreeNode {\n int val;\n struct TreeNode *left;\n struct TreeNode *right;\n};\n\nstruct TreeNode* createNode(int val) {\n struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n newNode->val = val;\n newNode->left = NULL;\n newNode->right = NULL;\n return newNode;\n}\n\nvoid inorderTraversal(struct TreeNode* root, int* res, int* returnSize) {\n struct TreeNode* curr = root;\n struct TreeNode* pre;\n\n int index = 0;\n while (curr != NULL) {\n if (curr->left == NULL) {\n res[index++] = curr->val;\n curr = curr->right; // move to next right node\n } else { // has a left subtree\n pre = curr->left;\n while (pre->right != NULL) { // find rightmost\n pre = pre->right;\n }\n pre->right = curr; // put cur after the pre node\n struct TreeNode* temp = curr; // store cur node\n curr = curr->left; // move cur to the top of the new tree\n temp->left = NULL; // original cur left be null, avoid infinite loops\n }\n }\n *returnSize = index; // update the size of the result array\n}\n\n\n\n\n```\n```Java []\n\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> res = new ArrayList<>();\n TreeNode curr = root;\n TreeNode pre;\n while (curr != null) {\n if (curr.left == null) {\n res.add(curr.val);\n curr = curr.right; // move to next right node\n } else { // has a left subtree\n pre = curr.left;\n while (pre.right != null) { // find rightmost\n pre = pre.right;\n }\n pre.right = curr; // put cur after the pre node\n TreeNode temp = curr; // store cur node\n curr = curr.left; // move cur to the top of the new tree\n temp.left = null; // original cur left be null, avoid infinite loops\n }\n }\n return res;\n }\n}\n\n```\n```python3 []\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\ndef inorderTraversal(root):\n res = [] # List to store inorder traversal result\n curr = root\n pre = None\n\n while curr is not None:\n if curr.left is None:\n res.append(curr.val)\n curr = curr.right # Move to next right node\n else: # Node has a left subtree\n pre = curr.left\n while pre.right is not None: # Find rightmost node of left subtree\n pre = pre.right\n pre.right = curr # Link the current node after the rightmost node of the left subtree\n temp = curr # Store the current node\n curr = curr.left # Move current node to the top of the new tree\n temp.left = None # Set original left node to null to avoid infinite loops\n\n return res # Return the inorder traversal result\n\n# Function to print elements in a list\ndef printList(lst):\n print("[", end="")\n for i in range(len(lst)):\n print(lst[i], end="")\n if i != len(lst) - 1:\n print(", ", end="")\n print("]")\n\n\n```\n```javascript []\nfunction TreeNode(val) {\n this.val = val;\n this.left = this.right = null;\n}\n\nvar inorderTraversal = function(root) {\n const res = [];\n let curr = root;\n let pre;\n\n while (curr !== null) {\n if (curr.left === null) {\n res.push(curr.val);\n curr = curr.right; // move to next right node\n } else { // has a left subtree\n pre = curr.left;\n while (pre.right !== null) { // find rightmost\n pre = pre.right;\n }\n pre.right = curr; // put cur after the pre node\n let temp = curr; // store cur node\n curr = curr.left; // move cur to the top of the new tree\n temp.left = null; // original cur left be null, avoid infinite loops\n }\n }\n return res;\n};\n\n\n```\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 5 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Simple python Solution | binary-tree-inorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nrecursion\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom typing import Optional, List\n\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n res = []\n \n def inorder(node):\n if not node:\n return\n inorder(node.left)\n res.append(node.val)\n inorder(node.right)\n \n inorder(root)\n return res\n\n``` | 3 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Recursive sol is trivial, could you do it iteratively? Iterative with explanation| Stack | Recursion | binary-tree-inorder-traversal | 0 | 1 | ## Video solution \n\nhttps://youtu.be/hgwM2a9Mb_o?si=d8N3TrQzSRxQEkT3\n\n\nPlease subscribe to my channel if it helped you.\nhttps://www.youtube.com/channel/UCsu5CDZmlHcpH7dQozZWtQw?sub_confirmation=1\n\nCurrent subscribers: 213\nTarget subscribers: 250\n\n# Iterative Approach\n\n# Intuition:\n\n- The approach uses an iterative method with a stack to simulate the process of traversing the binary tree in an inorder fashion.\n- It emulates the behavior of the recursive approach without using recursion explicitly.\n\n# Approach:\n\n1. **Initialize an Empty Result List (`res`) and a Stack (`stack`):**\n - Create an empty list `res` to store the inorder traversal result.\n - Create an empty stack to keep track of nodes while traversing the tree.\n\n ```python\n res, stack = [], []\n ```\n\n2. **Initialize Current Node (`curr`) to the Root:**\n - Set `curr` to the root of the binary tree.\n\n ```python\n curr = root\n ```\n\n3. **Iterative Traversal using While Loop:**\n - Use a `while` loop to traverse the tree iteratively until all nodes are processed.\n\n ```python\n while True:\n ```\n\n4. **Check if Current Node is not None:**\n - If `curr` is not `None`, push the current node onto the stack and move to its left child.\n\n ```python\n if curr != None:\n stack.append(curr)\n curr = curr.left\n ```\n\n5. **Check if Stack is not Empty:**\n - If the stack is not empty, pop a node from the stack, add its value to the result list, and move to its right child.\n\n ```python\n elif stack:\n curr = stack.pop()\n res.append(curr.val)\n curr = curr.right\n ```\n\n6. **Break the Loop if Both Conditions Fail:**\n - If both conditions fail (no more nodes to process), break out of the loop.\n\n ```python\n else:\n break\n ```\n\n7. **Return the Result List (`res`):**\n - After the loop, return the inorder traversal result stored in the `res` list.\n\n ```python\n return res\n ```\n\n# Complexity\n\n- Time Complexity:\n\n - The time complexity is O(N), where N is the number of nodes in the binary tree.\n - Each node is visited exactly once.\n\n- Space Complexity:\n\n - The space complexity is O(H), where H is the height of the binary tree.\n - This is due to the space used by the stack, which can go as deep as the height of the tree.\n\n\n# Recursive approach\n\n# Intuition:\n\n- The approach uses a recursive strategy to perform an inorder traversal, which is a depth-first traversal method.\n- The traversal explores the left subtree first, then visits the current node, and finally explores the right subtree.\n\n# Approach:\n\n1. **Initialize an Empty Result List (`res`):**\n - In the `inorderTraversal` method, create an empty list `res` to store the inorder traversal result.\n\n ```python\n res = []\n ```\n\n2. **Call the Helper Function:**\n - Call the `helper` function with the root of the binary tree and the empty result list.\n\n ```python\n self.helper(root, res)\n ```\n\n3. **Define the Helper Function (`helper`):**\n - The `helper` function is a recursive function responsible for performing the inorder traversal.\n\n ```python\n def helper(self, root, res):\n ```\n\n4. **Base Case - Check if the Current Node is not None:**\n - Before traversing the subtrees, check if the current node is not `None`.\n\n ```python\n if root != None:\n ```\n\n5. **Recursively Traverse the Left Subtree:**\n - Call the `helper` function recursively for the left subtree.\n\n ```python\n self.helper(root.left, res)\n ```\n\n6. **Append the Current Node\'s Value to the Result List:**\n - Add the value of the current node to the result list.\n\n ```python\n res.append(root.val)\n ```\n\n7. **Recursively Traverse the Right Subtree:**\n - Call the `helper` function recursively for the right subtree.\n\n ```python\n self.helper(root.right, res)\n ```\n\n# Complexity\n\n- Time Complexity:\n\n - The time complexity is O(N), where N is the number of nodes in the binary tree.\n - Each node is visited exactly once.\n\n- Space Complexity:\n\n - The space complexity is O(H), where H is the height of the binary tree.\n - This is due to the recursion stack, which can go as deep as the height of the tree.\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution: \n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n res,stack = [],[]\n curr = root\n while True:\n if curr!=None:\n stack.append(curr)\n curr = curr.left\n elif stack:\n curr = stack.pop()\n res.append(curr.val)\n curr = curr.right\n else:\n break\n return res\n\n \n```\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution: \n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n res = []\n self.helper(root,res)\n return res\n def helper(self,root,res):\n if root!=None:\n self.helper(root.left,res)\n res.append(root.val)\n self.helper(root.right,res)\n``` | 2 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Easy Solution | binary-tree-inorder-traversal | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n result = []\n stack = []\n current = root\n\n while current or stack:\n while current:\n stack.append(current)\n current = current.left\n current = stack.pop()\n result.append(current.val)\n current = current.right\n\n return result\n \n```\n# **PLEASE DO UPVOTE!!!** | 2 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Simple solution with Binary Tree Inorder Traversal in Python3 | binary-tree-inorder-traversal | 0 | 1 | # Approach\nWe have Binary Tree `root` to perform Inorder Traversal.\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(N)**\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n # store traversed nodes\n nums = []\n\n def dfs(node):\n # each time you can visit an existing node\n if node:\n # recursevily visit it left\n dfs(node.left)\n # store value of a node\n nums.append(node.val)\n # and right child\n dfs(node.right)\n \n # start dfs\n dfs(root)\n\n return nums\n``` | 1 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Solution | binary-tree-inorder-traversal | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> ans;\n if (root == NULL) return ans;\n vector<int> left = inorderTraversal(root->left);\n ans.insert(ans.end(), left.begin(), left.end());\n ans.push_back(root->val);\n vector<int> right = inorderTraversal(root->right);\n ans.insert(ans.end(), right.begin(), right.end());\n return ans;\n}\n\n};\n```\n\n```Python3 []\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n st = []\n res = []\n\n while root or st:\n while root:\n st.append(root)\n root = root.left\n \n root = st.pop()\n res.append(root.val)\n\n root = root.right\n \n return res \n```\n\n```Java []\nclass Solution {\n private List<Integer> res = new ArrayList<>();\n public List<Integer> inorderTraversal(TreeNode root) {\n traverse(root);\n return res;\n }\n \n private void traverse(TreeNode root) {\n if (root == null) {\n return;\n }\n traverse(root.left);\n res.add(root.val);\n traverse(root.right);\n }\n}\n```\n | 473 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
🔍 Mastering In-Order Traversal: 3 Approaches, Detailed Explanation, and Insightful Dry Runs 🔥 | binary-tree-inorder-traversal | 1 | 1 | # \uD83C\uDF32 Exploring Inorder Tree Traversal \uD83C\uDF33\n\n---\n\n## \uD83D\uDCBB Solution\n\n### \uD83D\uDCA1Approach\n\nThe solution defines a class `Solution` with a method `inorderTraversal` for performing inorder tree traversal. The algorithm uses recursion to traverse the tree in an inorder manner, collecting node values in a vector.\n\n### \uD83D\uDCDDDry Run\n\nInput Tree:\n```\n 1\n / \\\n 2 3\n / \\\n 4 5\n```\n\n#### Steps:\n1. **Inorder Traversal:**\n - Traverse left subtree (2).\n - Traverse left subtree (4).\n - No left child.\n - Add 4 to the vector.\n - No right child.\n - Add 2 to the vector.\n - Traverse right subtree (5).\n - No left child.\n - Add 5 to the vector.\n - No right child.\n - Add 1 to the vector.\n - Traverse right subtree (3).\n - No left child.\n - Add 3 to the vector.\n - No right child.\n\n#### Final Output:\nThe vector is [4, 2, 5, 1, 3].\n\n### \uD83D\uDD0DEdge Cases\n\n- Handles scenarios with null nodes and varying tree structures.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(N), where N is the number of nodes in the tree.\n- **Space Complexity:** O(N), as the algorithm uses a vector to store node values.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\nclass Solution {\npublic:\n vector<int> ans;\n\n vector<int> inorderTraversal(TreeNode* root) {\n if(root == NULL) return {};\n inorderTraversal(root->left);\n ans.push_back(root->val);\n inorderTraversal(root->right);\n return ans;\n }\n};\n```\n\n```java []\nclass Solution {\n List<Integer> ans = new ArrayList<>();\n\n public List<Integer> inorderTraversal(TreeNode root) {\n if (root == null) return Collections.emptyList();\n inorderTraversal(root.left);\n ans.add(root.val);\n inorderTraversal(root.right);\n return ans;\n }\n}\n```\n\n```python []\nclass Solution:\n def inorderTraversal(self, root):\n ans = []\n def inorder(node):\n if node:\n inorder(node.left)\n ans.append(node.val)\n inorder(node.right)\n inorder(root)\n return ans\n```\n\n```csharp []\npublic class Solution {\n List<int> ans = new List<int>();\n\n public IList<int> InorderTraversal(TreeNode root) {\n if (root == null) return ans;\n InorderTraversal(root.left);\n ans.Add(root.val);\n InorderTraversal(root.right);\n return ans;\n }\n}\n```\n\n```javascript []\nvar inorderTraversal = function(root) {\n const ans = [];\n const inorder = (node) => {\n if (node) {\n inorder(node.left);\n ans.push(node.val);\n inorder(node.right);\n }\n };\n inorder(root);\n return ans;\n};\n```\n\n---\n# \uD83C\uDF32 Inorder Tree Traversal with Stack Exploration \uD83C\uDF33\n\n---\n\n## \uD83D\uDCBB Solution\n\n### \uD83D\uDCA1Approach 2: Iterative Approach with Stack\n\nThe iterative approach utilizes a stack to simulate the recursive call stack. It traverses the tree in an inorder manner, pushing nodes onto the stack until reaching the leftmost node. It then pops nodes, processes them, and moves to the right child if available.\n\n### \u2728Explanation\n\n1. Initialize an empty stack and an empty list to store the result.\n2. Start with the root node and iterate until the stack is empty or the current node is null.\n3. While the current node is not null, push it onto the stack and move to its left child.\n4. If the current node is null, pop a node from the stack, process it (add to the result list), and move to its right child.\n5. Repeat steps 3-4 until the stack is empty.\n\n### \uD83D\uDCDDDry Run\n\nInput Tree:\n```\n 1\n / \\\n 2 3\n / \\\n 4 5\n```\n\n#### Steps:\n1. Stack: [], Result: []\n2. Start with the root (1), push onto the stack, and move to the left child (2).\n3. Stack: [1], Result: []\n4. Move to the left child (4).\n5. Stack: [1, 2], Result: []\n6. Move to the left child (null), pop 4, process (add to result), move to the right child (null).\n7. Stack: [1], Result: [4]\n8. Move to the right child (2).\n9. Stack: [1, 2], Result: [4]\n10. Move to the left child (null), pop 2, process, move to the right child (5).\n11. Stack: [1], Result: [4, 2]\n12. Move to the left child (null), pop 1, process, move to the right child (3).\n13. Stack: [], Result: [4, 2, 1]\n14. Move to the left child (null), pop 3, process, move to the right child (null).\n15. Stack: [], Result: [4, 2, 1, 3]\n\n#### Final Output:\nThe result list is [4, 2, 1, 3].\n\n### \uD83D\uDD0DEdge Cases\n\n- Handles scenarios with null nodes and varying tree structures.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(N), where N is the number of nodes in the tree.\n- **Space Complexity:** O(N), as the algorithm uses a stack to store nodes.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> result;\n stack<TreeNode*> st;\n\n while (root || !st.empty()) {\n while (root) {\n st.push(root);\n root = root->left;\n }\n root = st.top();\n st.pop();\n result.push_back(root->val);\n root = root->right;\n }\n\n return result;\n }\n};\n```\n\n```java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> result = new ArrayList<>();\n Stack<TreeNode> stack = new Stack<>();\n\n while (root != null || !stack.isEmpty()) {\n while (root != null) {\n stack.push(root);\n root = root.left;\n }\n root = stack.pop();\n result.add(root.val);\n root = root.right;\n }\n\n return result;\n }\n}\n```\n\n```python []\nclass Solution:\n def inorderTraversal(self, root):\n result = []\n stack = []\n\n while root or stack:\n while root:\n stack.append(root)\n root = root.left\n root = stack.pop()\n result.append(root.val)\n root = root.right\n\n return result\n```\n\n```csharp []\npublic class Solution {\n public IList<int> InorderTraversal(TreeNode root) {\n List<int> result = new List<int>();\n Stack<TreeNode> stack = new Stack<TreeNode>();\n\n while (root != null || stack.Count > 0) {\n while (root != null) {\n stack.Push(root);\n root = root.left;\n }\n root = stack.Pop();\n result.Add(root.val);\n root = root.right;\n }\n\n return result;\n }\n}\n```\n\n```javascript []\nvar inorderTraversal = function(root) {\n const result = [];\n const stack = [];\n\n while (root || stack.length > 0) {\n while (root) {\n stack.push(root);\n root = root.left;\n }\n root = stack.pop();\n result.push(root.val);\n root = root.right;\n }\n\n return result;\n};\n```\n\n---\n# \uD83C\uDF32 Morris Traversal for Inorder Tree Traversal \uD83C\uDF33\n\n---\n\n## \uD83D\uDCBB Solution\n\n### \uD83D\uDCA1Approach 3: Morris Traversal\n\nMorris Traversal is an ingenious algorithm that enables efficient tree traversal without using a stack or recursion. It utilizes threaded binary trees by modifying the tree structure temporarily during the traversal.\n\n### \u2728Explanation\n\n1. Initialize the current node as the root.\n2. While the current node is not null:\n - If the current node has no left child:\n - Process the node.\n - Move to the right child.\n - If the current node has a left child:\n - Find the rightmost node in the left subtree (inorder predecessor).\n - If the rightmost node\'s right child is null:\n - Make the current node the right child of the rightmost node.\n - Move to the left child.\n - If the rightmost node\'s right child is the current node:\n - Revert the changes made in step 3.\n - Process the current node.\n - Move to the right child.\n\n### \uD83D\uDCDDDry Run\n\nInput Tree:\n```\n 1\n / \\\n 2 3\n / \\\n 4 5\n```\n\n#### Steps:\n1. Initialize: current = 1.\n2. Current has left child (2).\n - Find rightmost node in left subtree (5).\n - 5\'s right child is null, make 1 the right child of 5, move to left child (2).\n3. Current has left child (4).\n - Find rightmost node in left subtree (4).\n - 4\'s right child is null, make 2 the right child of 4, move to left child (null).\n4. Process 1, move to right child (3).\n5. Process 2, move to right child (4).\n6. Revert changes made in step 3.\n7. Process 3, move to right child (null).\n8. Process 4, move to right child (5).\n9. Revert changes made in step 2.\n10. Process 5, move to right child (null).\n\n#### Final Output:\nThe result list is [4, 2, 1, 3, 5].\n\n### \uD83D\uDD0DEdge Cases\n\n- Handles scenarios with null nodes and varying tree structures.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(N), where N is the number of nodes in the tree.\n- **Space Complexity:** O(1), as the algorithm modifies the tree in-place.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> result;\n TreeNode* current = root;\n\n while (current) {\n if (!current->left) {\n result.push_back(current->val);\n current = current->right;\n } else {\n TreeNode* predecessor = current->left;\n\n while (predecessor->right && predecessor->right != current) {\n predecessor = predecessor->right;\n }\n\n if (!predecessor->right) {\n predecessor->right = current;\n current = current->left;\n } else {\n predecessor->right = nullptr;\n result.push_back(current->val);\n current = current->right;\n }\n }\n }\n\n return result;\n }\n};\n```\n\n```java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> result = new ArrayList<>();\n TreeNode current = root;\n\n while (current != null) {\n if (current.left == null) {\n result.add(current.val);\n current = current.right;\n } else {\n TreeNode predecessor = current.left;\n\n while (predecessor.right != null && predecessor.right != current) {\n predecessor = predecessor.right;\n }\n\n if (predecessor.right == null) {\n predecessor.right = current;\n current = current.left;\n } else {\n predecessor.right = null;\n result.add(current.val);\n current = current.right;\n }\n }\n }\n\n return result;\n }\n}\n```\n\n```python []\nclass Solution:\n def inorderTraversal(self, root):\n result = []\n current = root\n\n while current:\n if not current.left:\n result.append(current.val)\n current = current.right\n else:\n predecessor = current.left\n\n while predecessor.right and predecessor.right != current:\n predecessor = predecessor.right\n\n if not predecessor.right:\n predecessor.right = current\n current = current.left\n else:\n predecessor.right = None\n result.append(current.val)\n current = current.right\n\n return result\n }\n```\n\n```csharp []\npublic class Solution {\n public IList<int> InorderTraversal(TreeNode root) {\n List<int> result = new List<int>();\n TreeNode current = root;\n\n while (current != null) {\n if (current.left == null) {\n result.Add(current.val);\n current = current.right;\n } else {\n TreeNode predecessor = current.left;\n\n while (predecessor.right != null && predecessor.right != current) {\n predecessor = predecessor.right;\n }\n\n if (predecessor.right == null) {\n predecessor.right = current;\n current = current\n\n.left;\n } else {\n predecessor.right = null;\n result.Add(current.val);\n current = current.right;\n }\n }\n }\n\n return result;\n }\n}\n```\n\n```javascript []\nvar inorderTraversal = function(root) {\n const result = [];\n let current = root;\n\n while (current) {\n if (!current.left) {\n result.push(current.val);\n current = current.right;\n } else {\n let predecessor = current.left;\n\n while (predecessor.right && predecessor.right !== current) {\n predecessor = predecessor.right;\n }\n\n if (!predecessor.right) {\n predecessor.right = current;\n current = current.left;\n } else {\n predecessor.right = null;\n result.push(current.val);\n current = current.right;\n }\n }\n }\n\n return result;\n};\n```\n\n---\n\n\n\n\n\n\n# \uD83E\uDDD1\u200D\uD83D\uDCBB Happy Coding! \uD83C\uDF1F\n\n -- *MR.ROBOT SIGNING OFF*\n | 5 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python3 Solution | binary-tree-inorder-traversal | 0 | 1 | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if root==None:\n return []\n return self.inorderTraversal(root.left)+[root.val]+self.inorderTraversal(root.right) \n``` | 4 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
InorderTraversal of Binary Tree | binary-tree-inorder-traversal | 0 | 1 | # Code\n```\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n answer = []\n self.printInorder(root, answer)\n return answer\n \n def printInorder(self, node, answer):\n if node is None:\n return\n\n self.printInorder(node.left, answer)\n\n answer.append(node.val)\n\n self.printInorder(node.right, answer)\n \n \n``` | 1 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
⭐One-Liner In-order Traversal in 🐍|| Basic Idea Implementation⭐ | binary-tree-inorder-traversal | 0 | 1 | # Code\n```py\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right) if root else []\n```\n\n---\n\n_If you like the solution, promote it._ | 1 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python || Basic Inorder || Recursion | binary-tree-inorder-traversal | 0 | 1 | # Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n\n l = []\n\n def fun(x) :\n if not x :\n return \n fun(x.left)\n l.append(x.val)\n fun(x.right)\n\n fun(root)\n return l\n \n``` | 1 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
📌|| STRIVER || DFS || RECURSION || BEATS(100%) || 0ms || 📌 | binary-tree-inorder-traversal | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRecursive Approach:\n\n1)One of the most straightforward ways to solve this problem is by using a recursive approach. You can perform an inorder traversal by following these steps:\n\n2)Start at the root node.\n3)Recursively traverse the left subtree.\n4)Visit the current node (add its value to the result list).\n5)Recursively traverse the right subtree.\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n\n void solve(TreeNode*t,vector<int>&ans)\n {\n if(t==NULL)\n {\n return ;\n }\n solve(t->left,ans);\n ans.push_back(t->val);\n solve(t->right,ans);\n }\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int>ans;\n solve(root,ans);\n return ans;\n \n }\n};\n```\n```python []\nclass Solution(object):\n def inorderTraversal(self, root):\n def helper(root,result):\n if root != None:\n helper(root.left,result)\n result.append(root.val)\n helper(root.right,result) \n \n result = []\n helper(root,result)\n return result\n```\n```JAVA []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> res = new ArrayList<>();\n helper(root, res);\n return res;\n }\n\n public void helper(TreeNode root, List<Integer> res) {\n if (root != null) {\n helper(root.left, res);\n res.add(root.val);\n helper(root.right, res);\n }\n }\n}\n```\n```\n\n``` | 2 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
✅ One Line Solution - First Published Here! | binary-tree-inorder-traversal | 0 | 1 | # Code #1 - Oneliner On Generator\n```\nclass Solution:\n def inorderTraversal(self, r: Optional[TreeNode]) -> List[int]:\n yield from chain(self.inorderTraversal(r.left), (r.val,), self.inorderTraversal(r.right)) if r else ()\n```\n\n# Code #2 - Classic Oneliner On Lists Concatenation\nTime complexity: $$O(n^2)$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def inorderTraversal(self, r: Optional[TreeNode]) -> List[int]:\n return (self.inorderTraversal(r.left) + [r.val] + self.inorderTraversal(r.right)) if r else []\n``` | 6 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
All DFS traversals (preorder, inorder, postorder) in Python in 1 line | binary-tree-inorder-traversal | 0 | 1 | 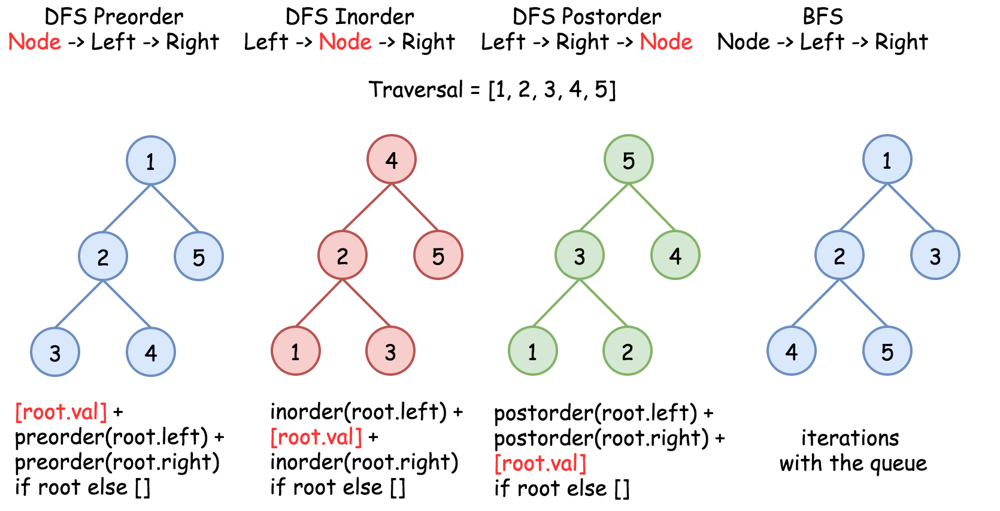\n\n```\ndef preorder(root):\n return [root.val] + preorder(root.left) + preorder(root.right) if root else []\n```\n\n```\ndef inorder(root):\n return inorder(root.left) + [root.val] + inorder(root.right) if root else []\n```\n\n```\ndef postorder(root):\n return postorder(root.left) + postorder(root.right) + [root.val] if root else []\n```\n | 1,008 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
One-liner beats 96.65% 🔥🥶🔥🥶🔥🥶 | binary-tree-inorder-traversal | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn order traversal = Left, Root, Right\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(V)$$ where V = height of tree \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right) if root else []\n\n```\n\n# Unpacked Code\nThe same code but more readable\n```\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n res = []\n res += self.inorderTraversal(root.left)\n res += [root.val]\n res += self.inorderTraversal(root.right)\n return res\n\n``` | 0 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
🔥 Easy solution | JAVA | Python 3 🔥| | binary-tree-inorder-traversal | 1 | 1 | # Intuition\nBinary Tree Inorder Traversal\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialization:\n\n 1. Initialize an empty stack and a reference variable current to the root node.\n 1. Create an empty list result to store the inorder traversal sequence.\n\n\n1. Iterative Process:\n 1. Start a while loop that continues until either current becomes null or the stack becomes empty.\n 1. Within the loop:\n 1. While the current node is not null:\n 1. Push the current node onto the stack.\n 1. Move current to its left child (current = current.left), effectively traversing left as much as possible.\n 1. Once there are no more left nodes to explore:\n 1. Pop the top node from the stack (which is the leftmost node or the last node visited).\n 1. Add the popped node\'s value to the result list.\n 1. Move current to the right child of the popped node (current = current.right), effectively moving to the right subtree.\n\n\n1. Return Result:\n\n 1. Once the traversal is completed (when the while loop finishes), return the result list containing the inorder traversal sequence.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(h)$$\n - (where \'h\' is the height of the tree)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> result = new ArrayList<>();\n Stack<TreeNode> stack = new Stack<>();\n TreeNode current = root;\n\n while (current != null || !stack.isEmpty()) {\n while (current != null) {\n stack.push(current);\n current = current.left;\n }\n\n current = stack.pop();\n result.add(current.val);\n current = current.right;\n }\n\n return result;\n }}\n```\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n if not root:\n return []\n \n result = []\n stack = []\n current = root\n \n while current or stack:\n while current:\n stack.append(current)\n current = current.left\n \n current = stack.pop()\n result.append(current.val)\n current = current.right\n \n return result\n \n```\n\n | 1 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Recursive Inorder Traversal | binary-tree-inorder-traversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n res=[]\n def inorder(root):\n if not root:\n return \n inorder(root.left)\n res.append(root.val)\n inorder(root.right)\n inorder(root)\n return res\n \n \n``` | 1 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Python 3 - All Iterative Traversals - InOrder, PreOrder, PostOrder - Similar Solutions | binary-tree-inorder-traversal | 0 | 1 | [Python3] Pre, In, Post Iteratively Summarization\nIn preorder, the order should be\n\nroot -> left -> right\n\nBut when we use stack, the order should be reversed:\n\nright -> left -> root\n\nPre\n```\nclass Solution:\n def preorderTraversal(self, root: TreeNode) -> List[int]:\n res, stack = [], [(root, False)]\n while stack:\n node, visited = stack.pop() # the last element\n if node:\n if visited: \n res.append(node.val)\n else: # preorder: root -> left -> right\n stack.append((node.right, False))\n stack.append((node.left, False))\n stack.append((node, True))\n return res\n```\n\n\nIn inorder, the order should be\nleft -> root -> right\n\nBut when we use stack, the order should be reversed:\n\nright -> root -> left\n\nIn\n```\nclass Solution:\n def inorderTraversal(self, root: TreeNode) -> List[int]:\n res, stack = [], [(root, False)]\n while stack:\n node, visited = stack.pop() # the last element\n if node:\n if visited:\n res.append(node.val)\n else: # inorder: left -> root -> right\n stack.append((node.right, False))\n stack.append((node, True))\n stack.append((node.left, False))\n return res\n```\t\n\n\nIn postorder, the order should be\nleft -> right -> root\n\nBut when we use stack, the order should be reversed:\n\nroot -> right -> left\n\nPost\n```\nclass Solution:\n def postorderTraversal(self, root: TreeNode) -> List[int]:\n res, stack = [], [(root, False)]\n while stack:\n node, visited = stack.pop() # the last element\n if node:\n if visited:\n res.append(node.val)\n else: # postorder: left -> right -> root\n stack.append((node, True))\n stack.append((node.right, False))\n stack.append((node.left, False))\n return res\n``` | 351 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
😎Brute Force to Efficient Method🤩 | Java | C++ | Python | JavaScript | | binary-tree-inorder-traversal | 1 | 1 | # 1st Method :- Brute force\n\n## Code\n``` Java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n //store the elements of the binary tree in inorder traversal order.\n List<Integer> result = new ArrayList<>();\n inorderHelper(root, result);\n return result;\n }\n\n private void inorderHelper(TreeNode node, List<Integer> result) {\n if (node != null) {\n // Visit left subtree\n inorderHelper(node.left, result);\n \n // Visit the current node (root)\n result.add(node.val);\n \n // Visit right subtree\n inorderHelper(node.right, result);\n }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> result;\n inorder(root, result);\n return result;\n }\n \n void inorder(TreeNode* node, vector<int>& result) {\n if (node == nullptr) {\n return;\n }\n \n // Traverse the left subtree\n inorder(node->left, result);\n \n // Visit the current node\n result.push_back(node->val);\n \n // Traverse the right subtree\n inorder(node->right, result);\n }\n};\n\n```\n``` Python []\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n result = []\n \n # Define a helper function to perform the recursive traversal\n def inorder(node):\n if node:\n # First, traverse the left subtree\n inorder(node.left)\n # Then, add the current node\'s value to the result\n result.append(node.val)\n # Finally, traverse the right subtree\n inorder(node.right)\n \n # Start the traversal from the root\n inorder(root)\n \n return result\n```\n``` JavaScript []\nvar inorderTraversal = function(root) {\n if (!root) {\n return [];\n }\n \n const result = [];\n \n function inorder(node) {\n if (node.left) {\n inorder(node.left);\n }\n result.push(node.val);\n if (node.right) {\n inorder(node.right);\n }\n }\n \n inorder(root);\n \n return result;\n\n};\n```\n\n# Complexity\n#### Time complexity: O(n) ;\nThe time complexity of this solution is O(N), where N is the number of nodes in the binary tree. This is because we visit each node exactly once during the traversal.\n\nThe recursive function `inorderHelper` is called for each node, and it performs three main operations for each node:\n\n1. Visiting the left subtree: In the worst case, this involves visiting all nodes on the left side of the tree, which takes O(N/2) time.\n\n2. Visiting the current node: This is a constant-time operation (adding the node\'s value to the result list).\n\n3. Visiting the right subtree: Similar to the left subtree, in the worst case, this involves visiting all nodes on the right side of the tree, which also takes O(N/2) time.\n\nSince all these operations are performed separately for each node, the overall time complexity is O(N).\n\n#### Space complexity: O(H) ;\nThe space complexity of this solution is O(H), where H is the height of the binary tree.\n\nIn the worst case, if the binary tree is completely unbalanced (e.g., a skewed tree where each node has only a left child or only a right child), the height of the tree can be equal to N (the number of nodes). In this case, the space required for the call stack during the recursive traversal would be O(N), which represents the space complexity.\n\n\n# 2nd Method :- Efficient Method\n\n>This code iteratively traverses a binary tree in an inorder manner using a stack to keep track of the nodes to be processed. It ensures that we visit the left subtree, then the current node, and then the right subtree, just like the recursive approach, but without the use of recursion. This approach is more memory-efficient and avoids stack overflow errors for large trees.\n\n1. **Initialize Data Structures**: \n - We start by initializing two data structures: a `List<Integer>` called `result` to store the inorder traversal result and a `Stack<TreeNode>` called `stack` to help us simulate the recursive process iteratively.\n - We also initialize a `TreeNode` called `curr` and set it to the `root` of the binary tree.\n\n2. **Main Loop**:\n - The main part of the code is a `while` loop that continues until `curr` becomes `null` (indicating we have traversed the entire tree) and the `stack` is empty (indicating we\'ve processed all nodes).\n\n3. **Traverse Left Subtree and Push Nodes onto the Stack**:\n - Within the `while` loop, we have another `while` loop to traverse the left subtree of the current node (`curr`) and push all encountered nodes onto the stack.\n - We keep going left as long as `curr` is not `null`, pushing each encountered node onto the `stack`. This is done to simulate the left subtree traversal.\n\n4. **Visit the Current Node and Move to the Right Subtree**:\n - Once we\'ve traversed all the way to the left (or if `curr` is `null`), we pop a node from the `stack`. This node represents the current root of a subtree that needs to be processed.\n - We add the value of the current node (`curr.val`) to the `result` list, as it\'s part of the inorder traversal.\n - We then update `curr` to point to the right child of the current node. This will ensure that if there\'s a right subtree, we\'ll traverse it next. If there\'s no right subtree, this step will essentially move us up in the tree to the parent of the current node.\n\n5. **Repeat**:\n - We repeat steps 3 and 4 until we\'ve traversed the entire binary tree. This process effectively simulates an inorder traversal iteratively using a stack.\n\n6. **Return Result**:\n - Finally, after the loop has finished, we return the `result` list, which contains the inorder traversal of the binary tree.\n\n## Code\n``` Java []\nclass Solution {\n public List<Integer> inorderTraversal(TreeNode root) {\n // store the inorder traversal result \n List<Integer> result = new ArrayList<>();\n \n //help us simulate the recursive process iteratively.\n Stack<TreeNode> stack = new Stack<>();\n TreeNode curr = root;\n \n while (curr != null || !stack.isEmpty()) {\n // Traverse left subtree and push nodes onto the stack\n while (curr != null) {\n stack.push(curr);\n curr = curr.left;\n }\n \n // Visit the current node (root) and move to the right subtree\n curr = stack.pop();\n result.add(curr.val);\n curr = curr.right;\n }\n \n return result;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> inorderTraversal(TreeNode* root) {\n vector<int> result;\n stack<TreeNode*> st;\n TreeNode* curr = root;\n \n while (curr != nullptr || !st.empty()) {\n // Traverse left subtree and push nodes onto the stack\n while (curr != nullptr) {\n st.push(curr);\n curr = curr->left;\n }\n \n // Visit the current node (root) and move to the right subtree\n curr = st.top();\n st.pop();\n result.push_back(curr->val);\n curr = curr->right;\n }\n \n return result;\n }\n};\n```\n``` Python []\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n result = []\n stack = []\n curr = root\n \n while curr or stack:\n while curr:\n stack.append(curr)\n curr = curr.left\n curr = stack.pop()\n result.append(curr.val)\n curr = curr.right\n \n return result\n```\n``` JavaScript []\nvar inorderTraversal = function(root) {\n const result = [];\n const stack = [];\n let curr = root;\n \n while (curr || stack.length > 0) {\n while (curr) {\n stack.push(curr);\n curr = curr.left;\n }\n curr = stack.pop();\n result.push(curr.val);\n curr = curr.right;\n }\n \n return result;\n};\n```\n# Complexity\n#### Time complexity: O(N) ;\n- In the worst-case scenario, where the binary tree is completely unbalanced and resembles a linked list, you would visit each node once. Therefore, the time complexity of this algorithm is O(N), where N is the number of nodes in the tree.\n\n#### Space complexity: O(N) ;\n- The space complexity is determined by the space used by the stack and the list to store the result.\n- The stack is used to keep track of nodes as you traverse the tree. In the worst case, if the tree is completely unbalanced, the stack could hold all N nodes. Therefore, the space used by the stack is O(N).\n- The result list is used to store the final inorder traversal result. In the worst case, you will store N elements in this list, so the space used by the result list is also O(N).\n- Additionally, you have a few variables like `curr` and `result` that consume constant space, so we don\'t need to consider them when analyzing space complexity.\n- The total space complexity is the sum of the space used by the stack and the result list, which is O(N + N) = O(N).\n | 16 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Recursive and Iterative Approach | binary-tree-inorder-traversal | 0 | 1 | # 1. Recursive Approach\n```\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n ans=[]\n def inorder(root,ans):\n if not root:\n return None\n inorder(root.left,ans)\n ans.append(root.val)\n inorder(root.right,ans)\n inorder(root,ans)\n return ans\n```\n# 2. Iterative Approach\n```\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n ans=[]\n stack=[]\n cur=root\n while stack or cur:\n if cur:\n stack.append(cur)\n cur=cur.left\n else:\n cur=stack.pop()\n ans.append(cur.val)\n cur=cur.right\n return ans\n```\n# please upvote me it would encourage me alot\n | 37 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
👹 Simple python 1 line code, explination , python, java🐍 ☕ | binary-tree-inorder-traversal | 1 | 1 | # Intuition\nidea is recursive search for nodes\n# Approach\nin order means: left, mid, right nodes, which is reccursively the same meaning.\nyou go left most node of tree, traverse it, then go back and search root and right values of that subtree, then check again to a level higher than previous layer, and so on, when bringing back values you bring them as this: left node of left most subtree, node of that subtree, right of that subtree, and so on \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# PYTHON\n```\n\n\nclass Solution(object):\n def inorderTraversal(self, root):\n \n return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right) if root else []\n```\n# JAVA\n```\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n \n TreeNode(int val) {\n this.val = val;\n }\n}\n\npublic class Solution {\n public boolean isSameTree(TreeNode p, TreeNode q) {\n return inorderTraversal(q).equals(inorderTraversal(p));\n }\n\n public List<Integer> inorderTraversal(TreeNode root) {\n List<Integer> result = new ArrayList<>();\n if (root == null) {\n return result;\n }\n\n // Recursive in-order tree traversal\n result.addAll(inorderTraversal(root.left));\n result.add(root.val);\n result.addAll(inorderTraversal(root.right));\n\n return result;\n }\n}\n```\n\n\n | 2 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
Morris Inorder Traversal | binary-tree-inorder-traversal | 0 | 1 | My Python approach for Morris Inorder Traversal.\nBased on [this](https://www.youtube.com/watch?v=80Zug6D1_r4) video.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:\n ans = []\n cur = root\n while cur != None:\n #printing the leftmost node\n if not cur.left:\n ans.append(cur.val)\n cur = cur.right\n else:\n temp = cur\n temp = temp.left\n #going to the rightmost node in the left subtree (lets call it temp)\n while temp.right and temp.right != cur:\n temp = temp.right\n \n #2 conditions arise:\n \n #i. the right child of temp doesn\'t exist (The thread to the cur node has not been made)\n #in this case, point the right child of temp to cur and move cur to its left child\n if not temp.right:\n temp.right = cur\n cur = cur.left\n\n #ii. the thread has already been created so we break the thread\n #(pointing the temp\'s right child back to None)and print cur.\n #Finally, move cur to its right child \n else:\n ans.append(cur.val)\n temp.right = None\n cur = cur.right\n\n return ans\n``` | 5 | Given the `root` of a binary tree, return _the inorder traversal of its nodes' values_.
**Example 1:**
**Input:** root = \[1,null,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** root = \[\]
**Output:** \[\]
**Example 3:**
**Input:** root = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the tree is in the range `[0, 100]`.
* `-100 <= Node.val <= 100`
**Follow up:** Recursive solution is trivial, could you do it iteratively? | null |
🦀 Unique Binary Search Trees II - A Rusty Approach | unique-binary-search-trees-ii | 0 | 1 | Have you ever tried to generate all unique binary search trees (BSTs) with a given number of nodes? It\'s a crab-tastic challenge, but don\'t worry; Rust is here to help you out!\n\n## Intuition\nImagine you have \\( n \\) distinct numbers. You can pick any number as the root of the BST. Once you pick a root, the remaining numbers are divided into two groups, forming the left and right subtrees. You can recursively build the subtrees and combine them to form all possible BSTs.\n\n## Approach\nWe use dynamic programming to efficiently construct all possible trees. We start by building trees with 1 node, then 2 nodes, up to \\( n \\) nodes. We use previously computed solutions to build trees with more nodes, making the process fast and memory-efficient.\n\n### Example Explanation\nFor \\( n = 3 \\), the output is:\n```\n[\n [1,null,2,null,3],\n [1,null,3,2],\n [2,1,3],\n [3,1,null,null,2],\n [3,2,null,1]\n]\n```\nIt means there are 5 different ways to form a BST using numbers from 1 to 3.\n\n## Complexity\n- Time complexity: $$ O\\left(\\frac{{4^n}}{{n\\sqrt{n}}}\\right) $$\n- Space complexity: $$ O\\left(\\frac{{4^n}}{{n\\sqrt{n}}}\\right) $$\n\n## Code\nThe Rust code below generates all unique BSTs for a given number of nodes, using dynamic programming.\n\n``` Rust []\nuse std::rc::Rc;\nuse std::cell::RefCell;\n\nimpl Solution {\n pub fn generate_trees(n: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> {\n if n == 0 {\n return Vec::new();\n }\n\n let mut dp = vec![Vec::new(); (n + 1) as usize];\n dp[0].push(None);\n for nodes in 1..=n {\n let mut trees_per_node = Vec::new();\n for root in 1..=nodes {\n let left_trees = &dp[(root - 1) as usize];\n let right_trees = &dp[(nodes - root) as usize];\n for left_tree in left_trees {\n for right_tree in right_trees {\n let root_node = Some(Rc::new(RefCell::new(TreeNode::new(root))));\n root_node.as_ref().unwrap().borrow_mut().left = left_tree.clone();\n root_node.as_ref().unwrap().borrow_mut().right = Solution::clone(right_tree.clone(), root);\n trees_per_node.push(root_node);\n }\n }\n }\n dp[nodes as usize] = trees_per_node;\n }\n dp[n as usize].clone()\n }\n\n fn clone(tree: Option<Rc<RefCell<TreeNode>>>, offset: i32) -> Option<Rc<RefCell<TreeNode>>> {\n tree.map(|node| {\n Rc::new(RefCell::new(TreeNode {\n val: node.borrow().val + offset,\n left: Solution::clone(node.borrow().left.clone(), offset),\n right: Solution::clone(node.borrow().right.clone(), offset),\n }))\n })\n }\n}\n```\n``` Go []\nvar generateTrees = function(n) {\n if (n === 0) return [];\n\n const dp = Array.from({ length: n + 1 }, () => []);\n dp[0].push(null);\n for (let nodes = 1; nodes <= n; nodes++) {\n for (let root = 1; root <= nodes; root++) {\n for (const left_tree of dp[root - 1]) {\n for (const right_tree of dp[nodes - root]) {\n const root_node = new TreeNode(root);\n root_node.left = left_tree;\n root_node.right = clone(right_tree, root);\n dp[nodes].push(root_node);\n }\n }\n }\n }\n return dp[n];\n};\n\nfunction clone(n, offset) {\n if (n === null) return null;\n const node = new TreeNode(n.val + offset);\n node.left = clone(n.left, offset);\n node.right = clone(n.right, offset);\n return node;\n}\n```\n``` Python []\nclass Solution:\n def generateTrees(self, n: int):\n if n == 0:\n return []\n\n dp = [[] for _ in range(n + 1)]\n dp[0].append(None)\n for nodes in range(1, n + 1):\n for root in range(1, nodes + 1):\n for left_tree in dp[root - 1]:\n for right_tree in dp[nodes - root]:\n root_node = TreeNode(root)\n root_node.left = left_tree\n root_node.right = self.clone(right_tree, root)\n dp[nodes].append(root_node)\n return dp[n]\n \n def clone(self, n: TreeNode, offset: int) -> TreeNode:\n if n:\n node = TreeNode(n.val + offset)\n node.left = self.clone(n.left, offset)\n node.right = self.clone(n.right, offset)\n return node\n return None\n```\nExplore the beauty of constructing binary trees and have fun with Rust! If you find this solution helpful, don\'t forget to upvote and share it with fellow Rustaceans. Happy coding! \uD83E\uDD80 | 4 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
✅ Recursion & DP [VIDEO] Catalan Number - Unique BST | unique-binary-search-trees-ii | 1 | 1 | Given an integer \\( n \\), the task is to return all the structurally unique BST\'s (binary search trees) that have exactly \\( n \\) nodes of unique values from \\( 1 \\) to \\( n \\).\n\n# Intuition Recursion & Dynamic Programming\nThe problem can be solved by utilizing the properties of a BST, where the left subtree has all values less than the root and the right subtree has values greater than the root. We can explore both recursive and dynamic programming (DP) approaches to generate all possible combinations of unique BSTs.\n\n# Live Coding & Explenation Recursion\nhttps://youtu.be/HeB6Oufsg_o\n\n# n-th Catalan number\n\nIn the context of this task, the \\(n\\)-th Catalan number gives the number of distinct binary search trees that can be formed with \\(n\\) unique values. The \\(n\\)-th Catalan number is given by the formula:\n\n$$\nC_n = \\frac{1}{n+1} \\binom{2n}{n} = \\frac{(2n)!}{(n+1)!n!}\n$$\n\nThe time and space complexity of generating these trees are both $$O(C_n)$$, which is equivalent to $$O\\left(\\frac{4^n}{n\\sqrt{n}}\\right)$$.\n\nHere\'s how it relates to the task:\n\n1. **Choosing the Root**: For each root value, we\'re essentially dividing the problem into two subproblems (left and right subtrees), and the number of combinations for each division aligns with the recursive definition of the Catalan numbers.\n \n2. **Recursive and Dynamic Programming Solutions**: Both approaches inherently follow the recursive nature of the Catalan numbers. The recursive approach directly corresponds to the recursive formula for the Catalan numbers, while the dynamic programming approach leverages the computed results for smaller subproblems to build up to the solution.\n\n3. **Number of Unique BSTs**: The fact that there are \\(C_n\\) unique BSTs with \\(n\\) nodes is a direct application of the Catalan numbers. The complexity of generating all these trees is thus closely tied to the value of the \\(n\\)-th Catalan number.\n\nIn conclusion, the complexity of the problem is inherently linked to the Catalan numbers, as they precisely describe the number of unique structures that can be formed, which in turn dictates the computational resources required to enumerate them.\n\n# Approach Short\n\n1. **Recursion**: Recursively construct left and right subtrees and combine them with each root.\n2. **Dynamic Programming**: Use dynamic programming to store the result of subproblems (subtrees) and utilize them for constructing unique BSTs.\n\n## Approach Differences\nThe recursive approach constructs the trees from scratch every time, while the DP approach reuses previously computed subtrees to avoid redundant work.\n\n# Approach Recursion\n\nThe recursive approach involves the following steps:\n\n1. **Base Case**: If the start index is greater than the end index, return a list containing `None`. This represents an empty tree and serves as the base case for the recursion.\n\n2. **Choose Root**: For every number \\( i \\) in the range from `start` to `end`, consider \\( i \\) as the root of the tree.\n\n3. **Generate Left Subtrees**: Recursively call the function to generate all possible left subtrees using numbers from `start` to \\( i-1 \\). This forms the left child of the root.\n\n4. **Generate Right Subtrees**: Recursively call the function to generate all possible right subtrees using numbers from \\( i+1 \\) to `end`. This forms the right child of the root.\n\n5. **Combine Subtrees**: For each combination of left and right subtrees, create a new tree with \\( i \\) as the root and the corresponding left and right subtrees. Append this tree to the list of all possible trees.\n\n6. **Return Trees**: Finally, return the list of all trees generated.\n\n# Complexity Recursion\n- Time complexity: $$O(\\frac{4^n}{n\\sqrt{n}})$$\n- Space complexity: $$ O(\\frac{4^n}{n\\sqrt{n}}) $$\n\n# Performance Recursion\n\n| Language | Runtime (ms) | Beats (%) | Memory (MB) | Beats (%) |\n|------------|--------------|-----------|-------------|-----------|\n| Rust | 0 | 100 | 2.5 | 80 |\n| Java | 1 | 99.88 | 43.7 | 66.87 |\n| Go | 3 | 56.88 | 4.4 | 63.30 |\n| C++ | 16 | 75.53 | 16.2 | 20.99 |\n| Python3 | 53 | 97.4 | 18.1 | 27.83 |\n| JavaScript | 74 | 89.61 | 48.4 | 55.19 |\n| C# | 91 | 88.76 | 39.8 | 19.10 |\n\n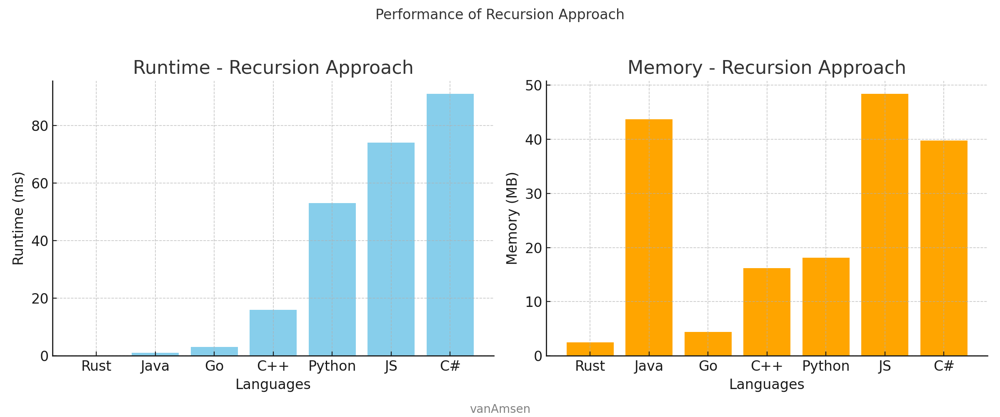\n\n\n# Code Recursion\n``` Python []\nclass Solution:\n def generateTrees(self, n: int):\n def generate_trees(start, end):\n if start > end:\n return [None,]\n \n all_trees = []\n for i in range(start, end + 1):\n left_trees = generate_trees(start, i - 1)\n right_trees = generate_trees(i + 1, end)\n \n for l in left_trees:\n for r in right_trees:\n current_tree = TreeNode(i)\n current_tree.left = l\n current_tree.right = r\n all_trees.append(current_tree)\n \n return all_trees\n \n return generate_trees(1, n) if n else []\n```\n``` C++ []\nclass Solution {\npublic:\n vector<TreeNode*> generateTrees(int n) {\n return n ? generate_trees(1, n) : vector<TreeNode*>();\n }\n\nprivate:\n vector<TreeNode*> generate_trees(int start, int end) {\n if (start > end) return {nullptr};\n\n vector<TreeNode*> all_trees;\n for (int i = start; i <= end; i++) {\n vector<TreeNode*> left_trees = generate_trees(start, i - 1);\n vector<TreeNode*> right_trees = generate_trees(i + 1, end);\n\n for (TreeNode* l : left_trees) {\n for (TreeNode* r : right_trees) {\n TreeNode* current_tree = new TreeNode(i);\n current_tree->left = l;\n current_tree->right = r;\n all_trees.push_back(current_tree);\n }\n }\n }\n return all_trees;\n }\n};\n```\n``` Java []\nclass Solution {\n public List<TreeNode> generateTrees(int n) {\n return n > 0 ? generate_trees(1, n) : new ArrayList<>();\n }\n\n private List<TreeNode> generate_trees(int start, int end) {\n List<TreeNode> all_trees = new ArrayList<>();\n if (start > end) {\n all_trees.add(null);\n return all_trees;\n }\n\n for (int i = start; i <= end; i++) {\n List<TreeNode> left_trees = generate_trees(start, i - 1);\n List<TreeNode> right_trees = generate_trees(i + 1, end);\n\n for (TreeNode l : left_trees) {\n for (TreeNode r : right_trees) {\n TreeNode current_tree = new TreeNode(i);\n current_tree.left = l;\n current_tree.right = r;\n all_trees.add(current_tree);\n }\n }\n }\n return all_trees;\n }\n}\n```\n``` JavaScript []\nvar generateTrees = function(n) {\n if (n === 0) return [];\n\n function generate_trees(start, end) {\n if (start > end) return [null];\n\n const all_trees = [];\n for (let i = start; i <= end; i++) {\n const left_trees = generate_trees(start, i - 1);\n const right_trees = generate_trees(i + 1, end);\n\n for (const l of left_trees) {\n for (const r of right_trees) {\n const current_tree = new TreeNode(i);\n current_tree.left = l;\n current_tree.right = r;\n all_trees.push(current_tree);\n }\n }\n }\n return all_trees;\n }\n\n return generate_trees(1, n);\n};\n```\n``` C# []\npublic class Solution {\n public IList<TreeNode> GenerateTrees(int n) {\n return n > 0 ? GenerateTrees(1, n) : new List<TreeNode>();\n }\n\n private IList<TreeNode> GenerateTrees(int start, int end) {\n if (start > end) return new List<TreeNode> {null};\n\n var all_trees = new List<TreeNode>();\n for (int i = start; i <= end; i++) {\n var left_trees = GenerateTrees(start, i - 1);\n var right_trees = GenerateTrees(i + 1, end);\n\n foreach (var l in left_trees) {\n foreach (var r in right_trees) {\n var current_tree = new TreeNode(i, l, r);\n all_trees.Add(current_tree);\n }\n }\n }\n return all_trees;\n }\n}\n```\n``` Rust []\nuse std::rc::Rc;\nuse std::cell::RefCell;\n\nimpl Solution {\n pub fn generate_trees(n: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> {\n if n == 0 {\n return Vec::new();\n }\n Self::generate(1, n)\n }\n\n fn generate(start: i32, end: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> {\n if start > end {\n return vec![None];\n }\n\n let mut all_trees = Vec::new();\n for i in start..=end {\n let left_trees = Self::generate(start, i - 1);\n let right_trees = Self::generate(i + 1, end);\n\n for l in &left_trees {\n for r in &right_trees {\n let current_tree = Some(Rc::new(RefCell::new(TreeNode::new(i))));\n current_tree.as_ref().unwrap().borrow_mut().left = l.clone();\n current_tree.as_ref().unwrap().borrow_mut().right = r.clone();\n all_trees.push(current_tree);\n }\n }\n }\n all_trees\n }\n}\n```\n``` Go []\nfunc generateTrees(n int) []*TreeNode {\n\tif n == 0 {\n\t\treturn []*TreeNode{}\n\t}\n\treturn generate(1, n)\n}\n\nfunc generate(start, end int) []*TreeNode {\n\tif start > end {\n\t\treturn []*TreeNode{nil}\n\t}\n\n\tvar allTrees []*TreeNode\n\tfor i := start; i <= end; i++ {\n\t\tleftTrees := generate(start, i-1)\n\t\trightTrees := generate(i+1, end)\n\n\t\tfor _, l := range leftTrees {\n\t\t\tfor _, r := range rightTrees {\n\t\t\t\tcurrentTree := &TreeNode{Val: i, Left: l, Right: r}\n\t\t\t\tallTrees = append(allTrees, currentTree)\n\t\t\t}\n\t\t}\n\t}\n\treturn allTrees\n}\n```\n\n# Approach Dynamic Programming\n\n1. **Initialization**: Create a DP table `dp` where `dp[i]` will store all the unique BSTs with `i` nodes. Initialize `dp[0]` with a single `None` value representing an empty tree.\n\n2. **Iterate Over Number of Nodes**: For every number `nodes` from 1 to `n`, iterate and construct all possible trees with `nodes` number of nodes.\n\n3. **Choose Root**: For every possible root value within the current `nodes`, iterate and use the root to build trees.\n\n4. **Use Previously Computed Subtrees**: For the chosen root, use the previously computed `dp[root - 1]` for left subtrees and `dp[nodes - root]` for right subtrees.\n\n5. **Clone Right Subtree**: Since the right subtree\'s values will be affected by the choice of the root, clone the right subtree with an offset equal to the root value. The `clone` function handles this.\n\n6. **Combine Subtrees**: Create a new tree by combining the current root with the left and right subtrees. Append this tree to `dp[nodes]`.\n\n7. **Return Result**: Finally, return the trees stored in `dp[n]`.\n\n# Complexity Dynamic Programming\n- Time complexity: $$O(\\frac{4^n}{n\\sqrt{n}})$$\n- Space complexity: $$ O(\\frac{4^n}{n\\sqrt{n}}) $$\n\n# Performance Dynamic Programming\n\n| Language | Runtime (ms) | Beats (%) | Memory (MB) | Beats (%) |\n|------------|--------------|-----------|-------------|-----------|\n| Rust | 0 | 100 | 2.7 | 20 |\n| Java | 1 | 99.88 | 44.1 | 8.87 |\n| Go | 3 | 56.88 | 4.2 | 90.83 |\n| C++ | 10 | 96.72 | 12.5 | 86.56 |\n| JavaScript | 67 | 96.75 | 48.5 | 55.19 |\n| Python3 | 49 | 98.84 | 18.1 | 21.91 |\n| C# | 91 | 88.76 | 38.5 | 80.90 |\n\n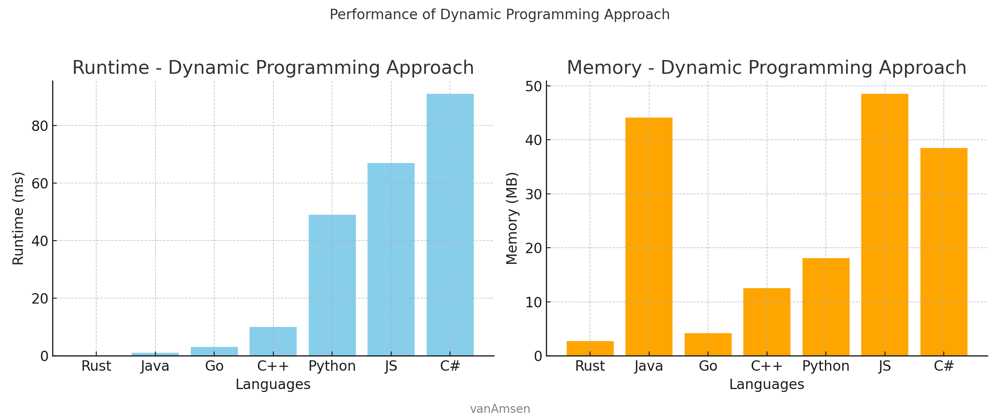\n\n\n# Code Dynamic Programming\n``` Python []\nclass Solution:\n def generateTrees(self, n: int):\n if n == 0:\n return []\n\n dp = [[] for _ in range(n + 1)]\n dp[0].append(None)\n for nodes in range(1, n + 1):\n for root in range(1, nodes + 1):\n for left_tree in dp[root - 1]:\n for right_tree in dp[nodes - root]:\n root_node = TreeNode(root)\n root_node.left = left_tree\n root_node.right = self.clone(right_tree, root)\n dp[nodes].append(root_node)\n return dp[n]\n \n def clone(self, n: TreeNode, offset: int) -> TreeNode:\n if n:\n node = TreeNode(n.val + offset)\n node.left = self.clone(n.left, offset)\n node.right = self.clone(n.right, offset)\n return node\n return None\n```\n``` C++ []\nclass Solution {\npublic:\n vector<TreeNode*> generateTrees(int n) {\n if (n == 0) return {};\n\n vector<vector<TreeNode*>> dp(n + 1);\n dp[0].push_back(nullptr);\n for (int nodes = 1; nodes <= n; nodes++) {\n for (int root = 1; root <= nodes; root++) {\n for (TreeNode* left_tree : dp[root - 1]) {\n for (TreeNode* right_tree : dp[nodes - root]) {\n TreeNode* root_node = new TreeNode(root);\n root_node->left = left_tree;\n root_node->right = clone(right_tree, root);\n dp[nodes].push_back(root_node);\n }\n }\n }\n }\n return dp[n];\n }\n\nprivate:\n TreeNode* clone(TreeNode* n, int offset) {\n if (n == nullptr) return nullptr;\n TreeNode* node = new TreeNode(n->val + offset);\n node->left = clone(n->left, offset);\n node->right = clone(n->right, offset);\n return node;\n }\n};\n```\n``` Java []\nclass Solution {\n public List<TreeNode> generateTrees(int n) {\n if (n == 0) return new ArrayList<>();\n\n List<TreeNode>[] dp = new ArrayList[n + 1];\n dp[0] = new ArrayList<>();\n dp[0].add(null);\n for (int nodes = 1; nodes <= n; nodes++) {\n dp[nodes] = new ArrayList<>();\n for (int root = 1; root <= nodes; root++) {\n for (TreeNode left_tree : dp[root - 1]) {\n for (TreeNode right_tree : dp[nodes - root]) {\n TreeNode root_node = new TreeNode(root);\n root_node.left = left_tree;\n root_node.right = clone(right_tree, root);\n dp[nodes].add(root_node);\n }\n }\n }\n }\n return dp[n];\n }\n\n private TreeNode clone(TreeNode n, int offset) {\n if (n == null) return null;\n TreeNode node = new TreeNode(n.val + offset);\n node.left = clone(n.left, offset);\n node.right = clone(n.right, offset);\n return node;\n }\n}\n```\n``` JavaScript []\nvar generateTrees = function(n) {\n if (n === 0) return [];\n\n const dp = Array.from({ length: n + 1 }, () => []);\n dp[0].push(null);\n for (let nodes = 1; nodes <= n; nodes++) {\n for (let root = 1; root <= nodes; root++) {\n for (const left_tree of dp[root - 1]) {\n for (const right_tree of dp[nodes - root]) {\n const root_node = new TreeNode(root);\n root_node.left = left_tree;\n root_node.right = clone(right_tree, root);\n dp[nodes].push(root_node);\n }\n }\n }\n }\n return dp[n];\n};\n\nfunction clone(n, offset) {\n if (n === null) return null;\n const node = new TreeNode(n.val + offset);\n node.left = clone(n.left, offset);\n node.right = clone(n.right, offset);\n return node;\n}\n```\n``` C# []\npublic class Solution {\n public IList<TreeNode> GenerateTrees(int n) {\n if (n == 0) return new List<TreeNode>();\n\n var dp = new List<TreeNode>[n + 1];\n dp[0] = new List<TreeNode> { null };\n for (int nodes = 1; nodes <= n; nodes++) {\n dp[nodes] = new List<TreeNode>();\n for (int root = 1; root <= nodes; root++) {\n foreach (var left_tree in dp[root - 1]) {\n foreach (var right_tree in dp[nodes - root]) {\n TreeNode root_node = new TreeNode(root);\n root_node.left = left_tree;\n root_node.right = Clone(right_tree, root);\n dp[nodes].Add(root_node);\n }\n }\n }\n }\n return dp[n];\n }\n\n private TreeNode Clone(TreeNode n, int offset) {\n if (n == null) return null;\n TreeNode node = new TreeNode(n.val + offset);\n node.left = Clone(n.left, offset);\n node.right = Clone(n.right, offset);\n return node;\n }\n}\n```\n``` Rust []\nuse std::rc::Rc;\nuse std::cell::RefCell;\n\nimpl Solution {\n pub fn generate_trees(n: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> {\n if n == 0 {\n return Vec::new();\n }\n\n let mut dp = vec![Vec::new(); (n + 1) as usize];\n dp[0].push(None);\n for nodes in 1..=n {\n let mut trees_per_node = Vec::new();\n for root in 1..=nodes {\n let left_trees = &dp[(root - 1) as usize];\n let right_trees = &dp[(nodes - root) as usize];\n for left_tree in left_trees {\n for right_tree in right_trees {\n let root_node = Some(Rc::new(RefCell::new(TreeNode::new(root))));\n root_node.as_ref().unwrap().borrow_mut().left = left_tree.clone();\n root_node.as_ref().unwrap().borrow_mut().right = Solution::clone(right_tree.clone(), root);\n trees_per_node.push(root_node);\n }\n }\n }\n dp[nodes as usize] = trees_per_node;\n }\n dp[n as usize].clone()\n }\n\n fn clone(tree: Option<Rc<RefCell<TreeNode>>>, offset: i32) -> Option<Rc<RefCell<TreeNode>>> {\n tree.map(|node| {\n Rc::new(RefCell::new(TreeNode {\n val: node.borrow().val + offset,\n left: Solution::clone(node.borrow().left.clone(), offset),\n right: Solution::clone(node.borrow().right.clone(), offset),\n }))\n })\n }\n}\n```\n``` Go []\nvar generateTrees = function(n) {\n if (n === 0) return [];\n\n const dp = Array.from({ length: n + 1 }, () => []);\n dp[0].push(null);\n for (let nodes = 1; nodes <= n; nodes++) {\n for (let root = 1; root <= nodes; root++) {\n for (const left_tree of dp[root - 1]) {\n for (const right_tree of dp[nodes - root]) {\n const root_node = new TreeNode(root);\n root_node.left = left_tree;\n root_node.right = clone(right_tree, root);\n dp[nodes].push(root_node);\n }\n }\n }\n }\n return dp[n];\n};\n\nfunction clone(n, offset) {\n if (n === null) return null;\n const node = new TreeNode(n.val + offset);\n node.left = clone(n.left, offset);\n node.right = clone(n.right, offset);\n return node;\n}\n```\n\nThe time and space complexity for both approaches are the same. The $$ O(\\frac{4^n}{n\\sqrt{n}}) $$ complexity arises from the Catalan number, which gives the number of BSTs for a given \\( n \\).\n\nI hope you find this solution helpful in understanding how to generate all structurally unique Binary Search Trees (BSTs) for a given number n. If you have any further questions or need additional clarifications, please don\'t hesitate to ask. If you understood the solution and found it beneficial, please consider giving it an upvote. Happy coding, and may your coding journey be filled with success and satisfaction! \uD83D\uDE80\uD83D\uDC68\u200D\uD83D\uDCBB\uD83D\uDC69\u200D\uD83D\uDCBB | 78 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | unique-binary-search-trees-ii | 1 | 1 | # Intuition\nThere 3 important things. \n\nOne is we try to create subtrees with some range between start(minimum) and end(maximum) value.\n\nSecond is calculation of the range. left range should be between start and current root - 1 as end value because all values of left side must be smaller than current root. right range should be between current root + 1 and end becuase all values on the right side should be greater than current root value.\n\nThrid is we call the same funtion recursively, so it\'s good idea to keep results of current start and end, so that we can use the results later. It\'s time saving.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/5G-Kwx8Lm5Q\n\n# Subscribe to my channel from here. I have 240 videos as of August 5th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Define a class `Solution` containing a method `generateTrees` which takes an integer `n` as input and returns a list of optional `TreeNode` objects.\n\n2. Check if `n` is 0. If it is, return an empty list since there are no possible trees with 0 nodes.\n\n3. Initialize an empty dictionary called `memo`. This dictionary will be used to store previously computed results for specific ranges of values to avoid redundant calculations.\n\n4. Define an inner function called `generate_trees` that takes two parameters: `start` and `end`, which represent the range of values for which binary search trees need to be generated.\n\n5. Inside the `generate_trees` function:\n - Check if the tuple `(start, end)` exists as a key in the `memo` dictionary. If it does, return the corresponding value from the `memo` dictionary.\n - Initialize an empty list called `trees`. This list will store the generated trees for the current range.\n - If `start` is greater than `end`, append `None` to the `trees` list, indicating an empty subtree, and return the `trees` list.\n - Loop through each value `root_val` in the range `[start, end]` (inclusive):\n - Recursively call the `generate_trees` function for the left subtree with the range `[start, root_val - 1]` and store the result in `left_trees`.\n - Recursively call the `generate_trees` function for the right subtree with the range `[root_val + 1, end]` and store the result in `right_trees`.\n - Nested loop through each combination of `left_tree` in `left_trees` and `right_tree` in `right_trees`:\n - Create a new `TreeNode` instance with `root_val` as the value, `left_tree` as the left child, and `right_tree` as the right child.\n - Append the new `TreeNode` to the `trees` list.\n - Store the `trees` list in the `memo` dictionary with the key `(start, end)`.\n - Return the `trees` list.\n\n6. Outside the `generate_trees` function, call `generate_trees` initially with arguments `1` and `n` to generate all unique binary search trees with `n` nodes.\n\n7. Return the list of generated trees.\n\nThis algorithm generates all possible unique binary search trees with `n` nodes by considering different ranges of root values and recursively generating left and right subtrees for each possible root value. The `memo` dictionary is used to store previously computed results, reducing redundant calculations and improving the efficiency of the algorithm.\n\n# Complexity\n- Time complexity: O(C(n))\nC is Catalan number.\n\n- Space complexity: O(C(n))\nC is Catalan number.\n\nCatalan number\nhttps://en.wikipedia.org/wiki/Catalan_number\n\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def generateTrees(self, n: int) -> List[Optional[TreeNode]]:\n if n == 0:\n return []\n \n memo = {}\n\n def generate_trees(start, end):\n if (start, end) in memo:\n return memo[(start, end)]\n \n trees = []\n if start > end:\n trees.append(None)\n return trees\n \n for root_val in range(start, end + 1):\n left_trees = generate_trees(start, root_val - 1)\n right_trees = generate_trees(root_val + 1, end)\n \n for left_tree in left_trees:\n for right_tree in right_trees:\n root = TreeNode(root_val, left_tree, right_tree)\n trees.append(root)\n \n memo[(start, end)] = trees\n return trees\n\n return generate_trees(1, n)\n```\n```javascript []\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {number} n\n * @return {TreeNode[]}\n */\nvar generateTrees = function(n) {\n if (n === 0) {\n return [];\n }\n \n const memo = new Map();\n\n function generateTreesHelper(start, end) {\n if (memo.has(`${start}-${end}`)) {\n return memo.get(`${start}-${end}`);\n }\n \n const trees = [];\n if (start > end) {\n trees.push(null);\n return trees;\n }\n \n for (let rootVal = start; rootVal <= end; rootVal++) {\n const leftTrees = generateTreesHelper(start, rootVal - 1);\n const rightTrees = generateTreesHelper(rootVal + 1, end);\n \n for (const leftTree of leftTrees) {\n for (const rightTree of rightTrees) {\n const root = new TreeNode(rootVal, leftTree, rightTree);\n trees.push(root);\n }\n }\n }\n \n memo.set(`${start}-${end}`, trees);\n return trees;\n }\n\n return generateTreesHelper(1, n); \n};\n```\n```java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public List<TreeNode> generateTrees(int n) {\n if (n == 0) {\n return new ArrayList<>();\n }\n \n Map<String, List<TreeNode>> memo = new HashMap<>();\n\n return generateTreesHelper(1, n, memo); \n }\n\n private List<TreeNode> generateTreesHelper(int start, int end, Map<String, List<TreeNode>> memo) {\n String key = start + "-" + end;\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n \n List<TreeNode> trees = new ArrayList<>();\n if (start > end) {\n trees.add(null);\n return trees;\n }\n \n for (int rootVal = start; rootVal <= end; rootVal++) {\n List<TreeNode> leftTrees = generateTreesHelper(start, rootVal - 1, memo);\n List<TreeNode> rightTrees = generateTreesHelper(rootVal + 1, end, memo);\n \n for (TreeNode leftTree : leftTrees) {\n for (TreeNode rightTree : rightTrees) {\n TreeNode root = new TreeNode(rootVal);\n root.left = leftTree;\n root.right = rightTree;\n trees.add(root);\n }\n }\n }\n \n memo.put(key, trees);\n return trees;\n }\n}\n```\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n vector<TreeNode*> generateTrees(int n) {\n if (n == 0) {\n return vector<TreeNode*>();\n }\n \n unordered_map<string, vector<TreeNode*>> memo;\n\n return generateTreesHelper(1, n, memo); \n }\n\nprivate:\n vector<TreeNode*> generateTreesHelper(int start, int end, unordered_map<string, vector<TreeNode*>>& memo) {\n string key = to_string(start) + "-" + to_string(end);\n if (memo.find(key) != memo.end()) {\n return memo[key];\n }\n \n vector<TreeNode*> trees;\n if (start > end) {\n trees.push_back(nullptr);\n return trees;\n }\n \n for (int rootVal = start; rootVal <= end; rootVal++) {\n vector<TreeNode*> leftTrees = generateTreesHelper(start, rootVal - 1, memo);\n vector<TreeNode*> rightTrees = generateTreesHelper(rootVal + 1, end, memo);\n \n for (TreeNode* leftTree : leftTrees) {\n for (TreeNode* rightTree : rightTrees) {\n TreeNode* root = new TreeNode(rootVal);\n root->left = leftTree;\n root->right = rightTree;\n trees.push_back(root);\n }\n }\n }\n \n memo[key] = trees;\n return trees;\n } \n};\n```\n | 24 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
Using explicit memoization, not using lru_cache, surpassing 90% | unique-binary-search-trees-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> using recursion with memoization\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> worst case o(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def generateTrees(self, n: int) -> List[Optional[TreeNode]]:\n # using explicit memoization (not using lru_cache), just recursion. we can split into left trees and right trees.\n # we pick a node, the numbers on the left will make left trees, the numbers on the\n # right will make right trees.\n # we use memoization to store the intermediate results\n dp = defaultdict(list)\n def helper(left, right): # construct trees using left->right numbers\n if left > right:\n return [None]\n if (left, right) in dp:\n return dp[(left, right)]\n for i in range(left, right+1): # i can choose right, so the range is to right+1\n lefts = helper(left, i-1)\n rights = helper(i+1, right)\n for l in lefts: # go through all the lefts and rights\n for r in rights:\n root = TreeNode(i) # root created\n root.left = l\n root.right = r\n dp[(left, right)].append(root)\n return dp[(left, right)] # just return the stored values\n return helper(1, n)\n``` | 2 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
94.15% Unique Binary Search Trees II with step by step explanation | unique-binary-search-trees-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo generate all structurally unique BST\'s with n nodes, we can use a recursive approach. The idea is to fix each number i (1 <= i <= n) as the root of the tree and then recursively generate all the left and right subtrees that can be formed using the remaining numbers (1, 2, ..., i-1) and (i+1, i+2, ..., n) respectively.\n\nFor example, to generate all the BST\'s with 3 nodes, we can fix 1 as the root and recursively generate all the BST\'s with 0 and 2 nodes respectively. Then we can fix 2 as the root and recursively generate all the BST\'s with 1 node on the left and 1 node on the right. Finally, we can fix 3 as the root and recursively generate all the BST\'s with 2 and 0 nodes respectively.\n\nTo avoid generating duplicate trees, we can use memoization to store the trees generated for each combination of left and right subtree sizes.\n\n# Complexity\n- Time complexity:\nBeats\n89.57%\n\n- Space complexity:\nBeats\n94.15%\n\n# Code\n```\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\nclass Solution:\n def generateTrees(self, n: \'int\') -> \'List[TreeNode]\':\n memo = {}\n \n def generate_trees_helper(start: int, end: int) -> List[TreeNode]:\n if start > end:\n return [None]\n \n if (start, end) in memo:\n return memo[(start, end)]\n \n result = []\n \n for i in range(start, end+1):\n left_subtrees = generate_trees_helper(start, i-1)\n right_subtrees = generate_trees_helper(i+1, end)\n \n for left in left_subtrees:\n for right in right_subtrees:\n root = TreeNode(i)\n root.left = left\n root.right = right\n result.append(root)\n \n memo[(start, end)] = result\n \n return result\n \n return generate_trees_helper(1, n)\n``` | 7 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
Python3 Solution | unique-binary-search-trees-ii | 0 | 1 | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def generateTrees(self, n: int) -> List[Optional[TreeNode]]:\n @lru_cache\n def dfs(start,end):\n if start>end:\n return [None]\n\n ans=[]\n for i in range(start,end+1):\n left=dfs(start,i-1)\n right=dfs(i+1,end)\n for l in left:\n for r in right:\n root=TreeNode(i)\n root.left=l\n root.right=r\n ans.append(root)\n return ans\n\n return dfs(1,n) \n``` | 4 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
Pythonic solution 94.46% | unique-binary-search-trees-ii | 0 | 1 | # Approach\nRecursive and Memo\n\n# Code\n```\nclass Solution:\n def generateTrees(self, n: int) -> List[Optional[TreeNode]]:\n \n @cache\n def getTreeList(nodes):\n if not nodes:\n return [None]\n res = []\n for i, val in enumerate(nodes):\n for leftTree, rightTree in product(getTreeList(nodes[:i]), getTreeList(nodes[i+1:])):\n res += [ TreeNode(val, left = leftTree, right = rightTree) ]\n return res\n \n return getTreeList(tuple(range(1, n+1)))\n``` | 3 | Given an integer `n`, return _all the structurally unique **BST'**s (binary search trees), which has exactly_ `n` _nodes of unique values from_ `1` _to_ `n`. Return the answer in **any order**.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,null,2,null,3\],\[1,null,3,2\],\[2,1,3\],\[3,1,null,null,2\],\[3,2,null,1\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 8` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.