title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Image Explanation🏆- [Simple, Easy & Concise - Stack] - C++/Java/Python | simplify-path | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Simplify Path` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n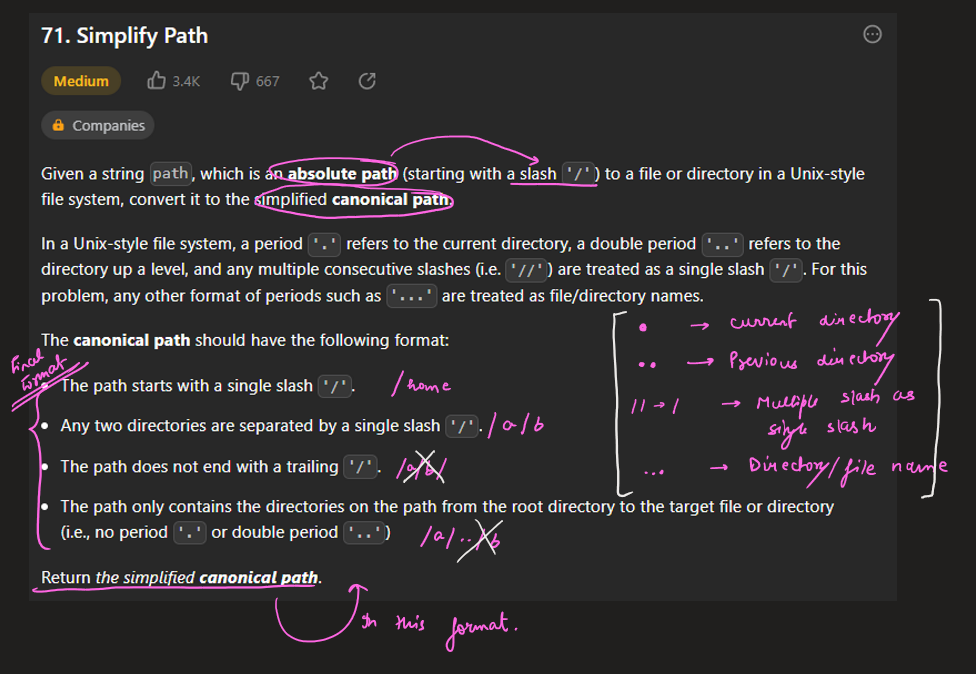\n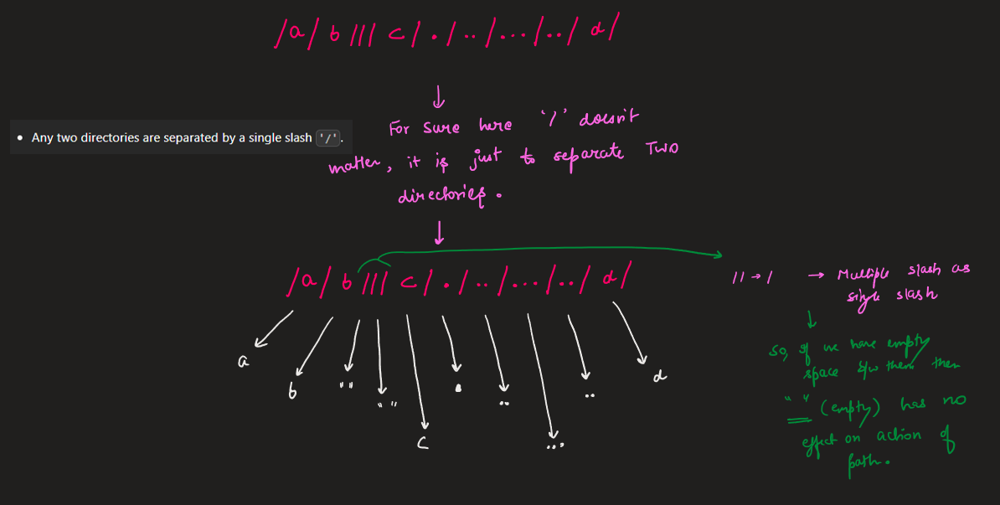\n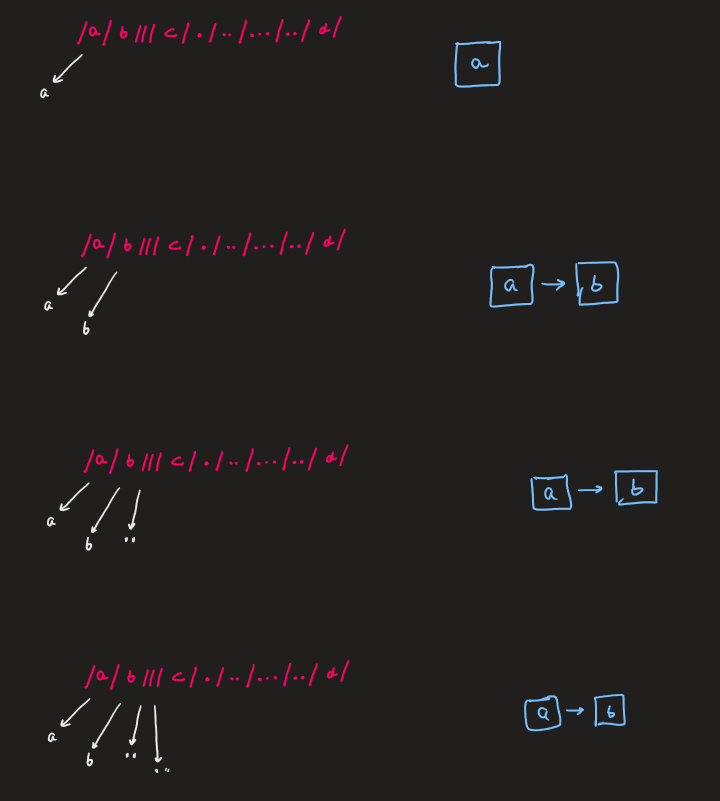\n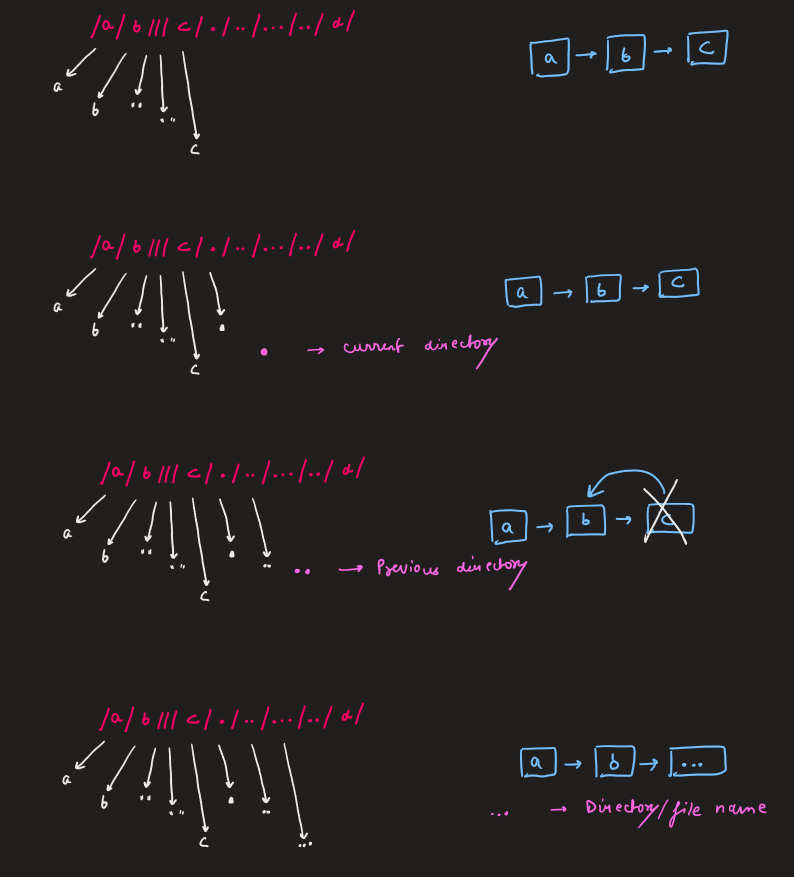\n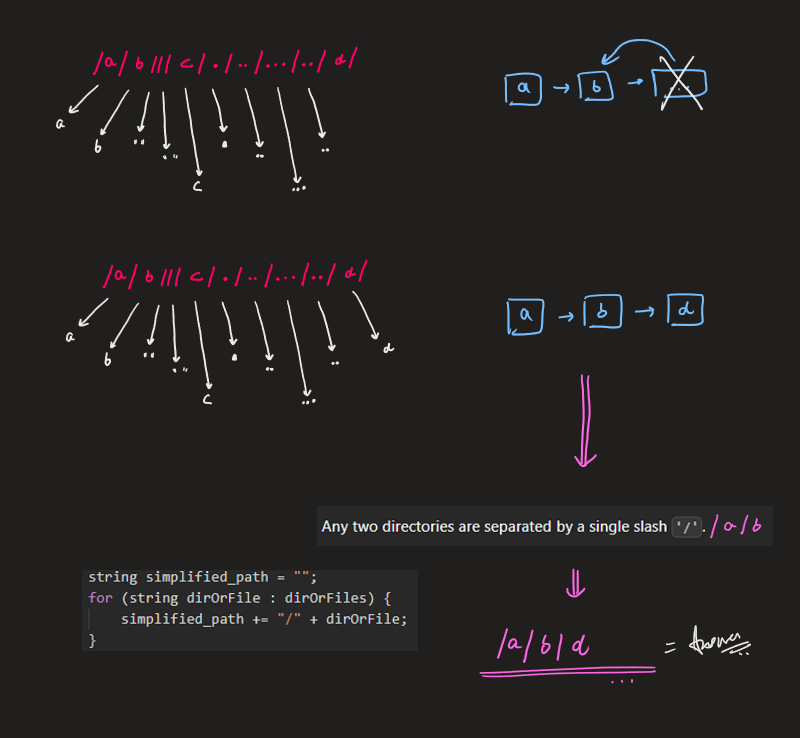\n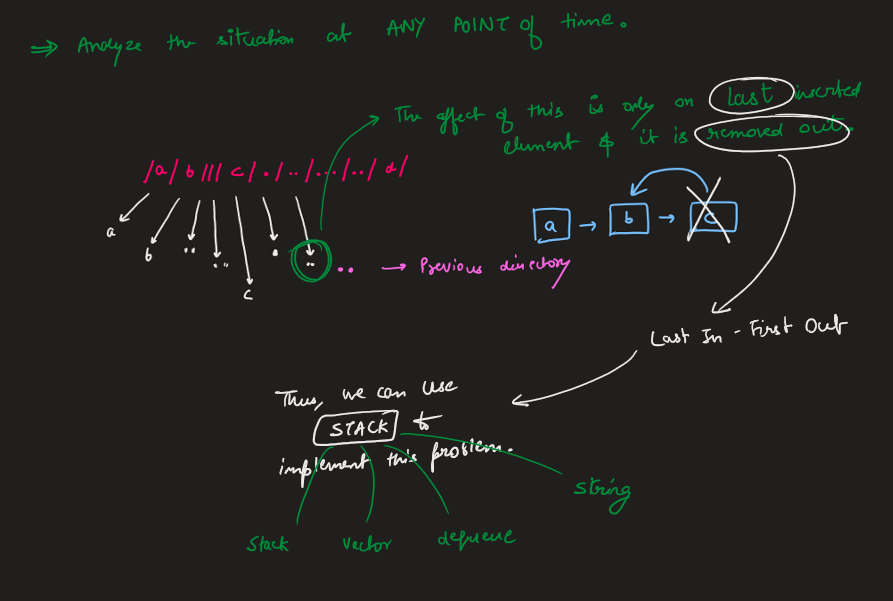\n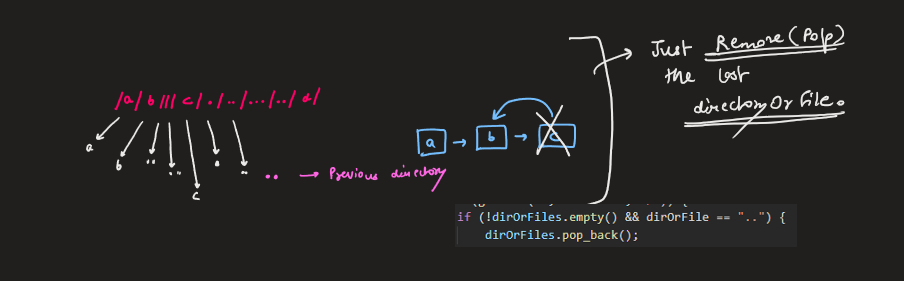\n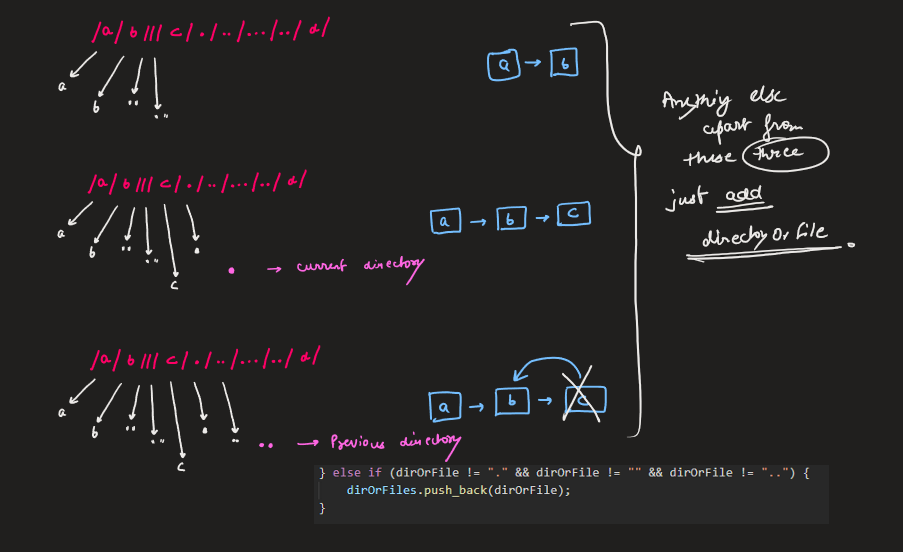\n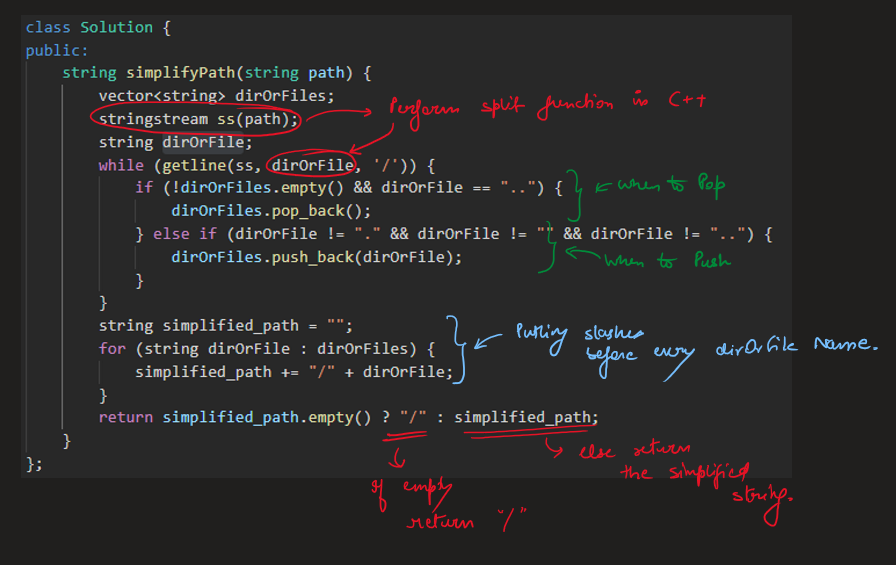\n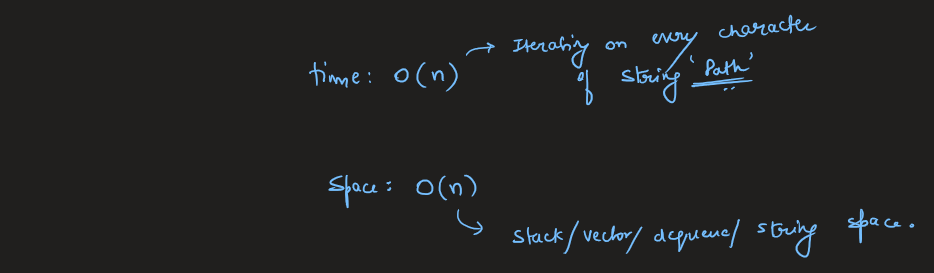\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n string simplifyPath(string path) {\n vector<string> dirOrFiles;\n stringstream ss(path);\n string dirOrFile;\n while (getline(ss, dirOrFile, \'/\')) {\n if (!dirOrFiles.empty() && dirOrFile == "..") {\n dirOrFiles.pop_back();\n } else if (dirOrFile != "." && dirOrFile != "" && dirOrFile != "..") {\n dirOrFiles.push_back(dirOrFile);\n }\n }\n string simplified_path = "";\n for (string dirOrFile : dirOrFiles) {\n simplified_path += "/" + dirOrFile;\n }\n return simplified_path.empty() ? "/" : simplified_path;\n }\n};\n```\n```Java []\nclass Solution {\n public String simplifyPath(String path) {\n Deque<String> dirOrFiles = new ArrayDeque<>();\n for (String dirOrFile : path.split("/")) {\n if (!dirOrFiles.isEmpty() && dirOrFile.equals("..")) {\n dirOrFiles.removeLast();\n } else if (!dirOrFile.equals(".") && !dirOrFile.equals("") && !dirOrFile.equals("..")) {\n dirOrFiles.addLast(dirOrFile);\n }\n }\n StringBuilder simplified_path = new StringBuilder();\n for (String dirOrFile : dirOrFiles) {\n simplified_path.append("/").append(dirOrFile);\n }\n return simplified_path.length() == 0 ? "/" : simplified_path.toString();\n }\n}\n```\n```Python []\nclass Solution:\n def simplifyPath(self, path):\n dirOrFiles = []\n path = path.split("/")\n for elem in path:\n if dirOrFiles and elem == "..":\n dirOrFiles.pop()\n elif elem not in [".", "", ".."]:\n dirOrFiles.append(elem)\n \n return "/" + "/".join(dirOrFiles)\n```\n | 74 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Python faster than 99.8% super simple solution | simplify-path | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThink of it as a filesytem path and split it into folders, forget the "/"\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n path_arr = path.split(\'/\')\n new_path = []\n for folder in path_arr:\n if folder == ".." and len(new_path) > 0:\n new_path.pop(-1)\n elif folder != "." and folder != "" and folder != "..":\n new_path.append(folder)\n return "/" + "/".join(new_path)\n\n``` | 0 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
🐍 python solution using stack; O(N) faster than 99.92% | simplify-path | 0 | 1 | # Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n new_path = []\n for folder in path.split(\'/\'):\n if folder!=\'\' and folder!=\'.\' and folder!=\'..\':\n new_path.append(folder) \n elif folder==\'..\' and len(new_path)>0:\n new_path.pop() \n return \'/\'+ (\'/\').join(new_path)\n```\n\n\n | 1 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
✅✅Python🔥Java 🔥C++🔥Simple Solution🔥🔥Easy to Understand🔥🔥 | simplify-path | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am Giving away my premium content videos related to computer science and data science and also will be sharing well-structured assignments and study materials to clear interviews at top companies to my first 10,000 Subscribers. So, **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\n# Video Solution\n\n**Search \uD83D\uDC49 `Simplify Path by Tech Wired` on YouTube**\n\n\n\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Approach:\n\n- Initialize an empty stack to hold the directories in the simplified path.\n- Split the input path string into individual directories using the forward slash ("/") as a separator.\nFor each directory:\n- If the directory is a parent directory reference ("..") and the stack is non-empty, pop the last directory off the stack to remove the preceding directory.\n- If the directory is not a special directory reference (i.e. neither ".", "" nor ".."), append it to the stack.\n- Construct the simplified path by joining the directories in the stack with forward slashes ("/") and adding a leading forward slash ("/").\n\n\n# Intuition:\nThe problem asks us to simplify a path in the Unix-style directory format, which consists of a sequence of directory names separated by forward slashes. The path may contain special directory references, such as "." (current directory), "" (empty directory), and ".." (parent directory). We need to remove any redundant directories and parent directory references to simplify the path.\n\nTo solve the problem, we can use a stack to keep track of the directories in the simplified path. We iterate over each directory in the input path and perform the following actions:\n\n- If the directory is a parent directory reference ("..") and the stack is non-empty, we pop the last directory off the stack to remove the preceding directory.\n- If the directory is not a special directory reference, we append it to the stack.\n- We then construct the simplified path by joining the directories in the stack with forward slashes and adding a leading forward slash.\n- Using a stack allows us to keep track of the directories in the path in a last-in-first-out (LIFO) order, which is convenient for removing parent directory references. By only appending non-special directories to the stack, we can ensure that the simplified path does not contain any redundant directories or empty directory references. - Finally, joining the directories in the stack with forward slashes gives us the simplified path in the correct format.\n\n\n```Python []\nclass Solution:\n def simplifyPath(self, path):\n dir_stack = []\n path = path.split("/")\n for elem in path:\n if dir_stack and elem == "..":\n dir_stack.pop()\n elif elem not in [".", "", ".."]:\n dir_stack.append(elem)\n \n return "/" + "/".join(dir_stack)\n\n```\n```Java []\nclass Solution {\n public String simplifyPath(String path) {\n Deque<String> dir_stack = new ArrayDeque<>();\n for (String dir : path.split("/")) {\n if (!dir_stack.isEmpty() && dir.equals("..")) {\n dir_stack.removeLast();\n } else if (!dir.equals(".") && !dir.equals("") && !dir.equals("..")) {\n dir_stack.addLast(dir);\n }\n }\n StringBuilder simplified_path = new StringBuilder();\n for (String dir : dir_stack) {\n simplified_path.append("/").append(dir);\n }\n return simplified_path.length() == 0 ? "/" : simplified_path.toString();\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n string simplifyPath(string path) {\n vector<string> dir_stack;\n stringstream ss(path);\n string dir;\n while (getline(ss, dir, \'/\')) {\n if (!dir_stack.empty() && dir == "..") {\n dir_stack.pop_back();\n } else if (dir != "." && dir != "" && dir != "..") {\n dir_stack.push_back(dir);\n }\n }\n string simplified_path = "";\n for (string dir : dir_stack) {\n simplified_path += "/" + dir;\n }\n return simplified_path.empty() ? "/" : simplified_path;\n }\n};\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D\n\n | 45 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Python- More example Testcases + Easily explained solution | simplify-path | 0 | 1 | # Example test cases\nSimplify the directory path (Unix like)\nGiven an absolute path for a file (Unix-style), simplify it. Note that absolute path always begin with \u2018/\u2019 ( root directory ), a dot in path represent current directory and double dot represents parent directory.\n\nExamples:\n\n"/a/./" --> means stay at the current directory \'a\'\n"/a/b/.." --> means jump to the parent directory\nfrom \'b\' to \'a\'\n"////" --> consecutive multiple \'/\' are a valid\npath, they are equivalent to single "/".\n\nInput : /home/\nOutput : /home\n\nInput : /a/./b/../../c/\nOutput : /c\n\nInput : /a/..\nOutput : /\n\nInput : /a/../\nOuput : /\n\nInput : /../../../../../a\nOuput : /a\n\nInput : /a/./b/./c/./d/\nOuput : /a/b/c/d\n\nInput : /a/../.././../../.\nOuput : /\n\nInput : /a//b//c//////d\nOuput : /a/b/c/d\n\nCredit for testcases: https://leetcode.com/noobie@work/\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have to solve 3 cases in order to solve the problem, that is if current directory is \n1) ..\n2) .\n3) //\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSolving (..):\n.. implies go to the parent directory from the most recent directory.\nthat is if we keep storing the directories we have travelled through in a stack, we have to pop an element.\n\nSolving(.):\n. implies go to the current directory . if we keep storing directories we have travelled through in a stack, we just have to do nothing\n\nSolving (/):\nignore more than one / , can be done easily by having a count variable or using str.split("/") in python.\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n), stack\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n #.. implies go a directory before, or pop.\n #. implies continue or do nothing\n #"" implies it was a trailing /, which means we have to do nothing\n # anything other is a directory, so we append it\n stack=[]\n path=path.split("/")\n for i in path:\n if(i=="" or i=="."):\n continue\n elif(i==".."):\n if(len(stack)>0):\n stack.pop()\n else:\n continue\n else:\n stack.append("/"+i)\n if(len(stack)==0):\n return "/"\n return "".join(stack)\n\n``` | 1 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Easy solution Python | using split :D | simplify-path | 0 | 1 | # Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n cadenas = path.split(\'/\')\n arr = []\n for s in cadenas:\n if s != \'.\' and s != \'..\' and s:\n arr.append(s)\n elif s == "..":\n if arr:\n arr.pop()\n\n return \'/\' + \'/\'.join(arr)\n\n``` | 1 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
One line solution | simplify-path | 0 | 1 | # Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n return __import__(\'os\').path.abspath(path)\n``` | 5 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Line by line explanation | Beats 100% Time and space, [Python], | simplify-path | 0 | 1 | Here is Line by line code in \n**Python :**\n```\ndef simplify_path(path):\n # Split path into a list of directory names\n dirs = path.split(\'/\')\n # Initialize the stack of directories\n stack = []\n # Iterate through the directories\n for d in dirs:\n # Ignore double slashes\n if d == \'\':\n continue\n # If it\'s a double period, pop the top directory from the stack\n elif d == \'..\':\n if stack:\n stack.pop()\n # If it\'s a single period or a regular directory name, add it to the stack\n elif d != \'.\':\n stack.append(d)\n # Construct the simplified canonical path\n simplified_path = \'/\' + \'/\'.join(stack)\n return simplified_path\n```\nUpvote if you find it useful | 10 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Python Simple solution using Stack | simplify-path | 0 | 1 | \n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n stack = []\n\n # different directories present in the string\n temp = path.split(\'/\') \n\n for i in temp:\n if i != \'.\' and i != \'\' and i != \'..\':\n stack.append(i) # add if it is directory\n\n # move to back directory if \'..\'\n elif i == \'..\':\n if stack:\n stack.pop()\n \n return \'/\' + \'/\'.join(stack)\n``` | 5 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Simple python solution | simplify-path | 0 | 1 | # Complexity\n- Time complexity: Given `n = len(path)` then complexity is `O(n)`\n\n- Space complexity: Given `n = len(path)` then complexity is `O(n)`\n\n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n levels, stack = path.split("/"), []\n\n for l in levels:\n if len(l)>0 and l != \'.\':\n if l == \'..\' and stack:\n stack.pop()\n else if != \'..\':\n stack.append(l)\n \n return "/"+"/".join(stack)\n``` | 2 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Simple Python Solution using stack | simplify-path | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n```\nStep 1 : spliting with respect to "/"\nStep 2 : if ".." (parent directory) so pop the current dirctory ie top one in the stack\n if "." (current directory) so dont add to stack\n if null then dont add\n if not null add to stack\nStep 3 : now join every one in the stack separated by /\n```\n\n\n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n\n st = []\n l = list(path.split("/"))\n i = 0\n while(i<len(l)) :\n if l[i] == ".." :\n if len(st)>0 :\n st.pop()\n elif l[i] == "." or l[i]=="":\n pass\n else :\n st += [l[i]]\n i += 1\n\n news = "/"\n for i in range(0,len(st)) :\n if st[i] != "" :\n news += st[i]\n news += "/"\n\n if news == "/" :\n return news\n return news[:-1] \n``` | 1 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
python3 solution | simplify-path | 0 | 1 | \n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n \n stack=[]\n for a in path.split(\'/\'):\n if a==\'..\':\n if stack:\n stack.pop()\n\n elif a not in (\'\',\'.\'):\n stack.append(a)\n\n\n return "/"+"/".join(stack) \n``` | 4 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Easy Python Solution Using Stacks | Easy to Understand | simplify-path | 0 | 1 | \n# Complexity\n- Time complexity: $$ O(n) $$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$ O(n) $$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def simplifyPath(self, path: str) -> str:\n paths = path.split(\'/\')\n st = []\n for path in paths:\n if path != "" and path != ".." and path !=".":\n st.append(path)\n if path == ".." and len(st) > 0:\n st.pop()\n print(st)\n return "/"+"/".join(st)\n\n\n\n``` | 3 | Given a string `path`, which is an **absolute path** (starting with a slash `'/'`) to a file or directory in a Unix-style file system, convert it to the simplified **canonical path**.
In a Unix-style file system, a period `'.'` refers to the current directory, a double period `'..'` refers to the directory up a level, and any multiple consecutive slashes (i.e. `'//'`) are treated as a single slash `'/'`. For this problem, any other format of periods such as `'...'` are treated as file/directory names.
The **canonical path** should have the following format:
* The path starts with a single slash `'/'`.
* Any two directories are separated by a single slash `'/'`.
* The path does not end with a trailing `'/'`.
* The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period `'.'` or double period `'..'`)
Return _the simplified **canonical path**_.
**Example 1:**
**Input:** path = "/home/ "
**Output:** "/home "
**Explanation:** Note that there is no trailing slash after the last directory name.
**Example 2:**
**Input:** path = "/../ "
**Output:** "/ "
**Explanation:** Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
**Example 3:**
**Input:** path = "/home//foo/ "
**Output:** "/home/foo "
**Explanation:** In the canonical path, multiple consecutive slashes are replaced by a single one.
**Constraints:**
* `1 <= path.length <= 3000`
* `path` consists of English letters, digits, period `'.'`, slash `'/'` or `'_'`.
* `path` is a valid absolute Unix path. | null |
Clean Codes🔥🔥|| Full Explanation✅|| Dynamic Programming✅|| C++|| Java|| Python3 | edit-distance | 1 | 1 | # Intuition :\n- Here we have to find the minimum edit distance problem between two strings word1 and word2. \n- The minimum edit distance is defined as the minimum number of operations required to transform one string into another.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- The approach here that I am using is dynamic programming. The idea is to build a 2D matrix dp where `dp[i][j] `represents the minimum number of operations required to transform the substring `word1[0...i-1]` into the substring `word2[0...j-1].`\n# How is Matrix built :\n- The matrix is built iteratively using the following recurrence relation:\n1. If `word1[i-1] == word2[j-1]`, then `dp[i][j] = dp[i-1][j-1]`. That is, no operation is required because the characters at positions `i-1` and `j-1` are already the same.\n2. Otherwise, `dp[i][j]` is the minimum of the following three values:\n- `dp[i-1][j-1] + 1`: replace the character at position `i-1` in `word1` with the character at position `j-1` in` word2`.\n- `dp[i-1][j] + 1`: delete the character at position `i-1` in `word1.`\n- `dp[i][j-1] + 1`: insert the character at position `j-1` in `word2` into `word1` at position `i`.\n# The base cases are:\n- `dp[i][0] = i`: transforming `word1[0...i-1]` into an empty string requires `i` deletions.\n- `dp[0][j] = j`: transforming an empty string into `word2[0...j-1] `requires `j` insertions.\n<!-- Describe your approach to solving the problem. -->\n# Final Step :\n- Finally, return `dp[m][n]`, which represents the minimum number of operations required to transform `word1 `into `word2`, where `m` is the length of `word1` and `n` is the length of `word2`.\n\n# Complexity\n- Time complexity : O(mn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(mn)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] : With Comments\n```C++ []\nclass Solution {\n public:\n int minDistance(string word1, string word2) {\n const int m = word1.length();//first word length\n const int n = word2.length();//second word length\n // dp[i][j] := min # of operations to convert word1[0..i) to word2[0..j)\n vector<vector<int>> dp(m + 1, vector<int>(n + 1));\n\n for (int i = 1; i <= m; ++i)\n dp[i][0] = i;\n\n for (int j = 1; j <= n; ++j)\n dp[0][j] = j;\n\n for (int i = 1; i <= m; ++i)\n for (int j = 1; j <= n; ++j)\n if (word1[i - 1] == word2[j - 1])//same characters\n dp[i][j] = dp[i - 1][j - 1];//no operation\n else\n dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;\n //replace //delete //insert\n return dp[m][n];\n }\n};\n```\n```Java []\nclass Solution {\n public int minDistance(String word1, String word2) {\n final int m = word1.length();//first word length\n final int n = word2.length();///second word length\n // dp[i][j] := min # of operations to convert word1[0..i) to word2[0..j)\n int[][] dp = new int[m + 1][n + 1];\n\n for (int i = 1; i <= m; ++i)\n dp[i][0] = i;\n\n for (int j = 1; j <= n; ++j)\n dp[0][j] = j;\n\n for (int i = 1; i <= m; ++i)\n for (int j = 1; j <= n; ++j)\n if (word1.charAt(i - 1) == word2.charAt(j - 1))//same characters\n dp[i][j] = dp[i - 1][j - 1];//no operation\n else\n dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1; //replace //delete //insert\n\n return dp[m][n];\n }\n}\n\n```\n```Python []\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n m = len(word1)\n n = len(word2)\n # dp[i][j] := min # Of operations to convert word1[0..i) to word2[0..j)\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n\n for i in range(1, m + 1):\n dp[i][0] = i\n\n for j in range(1, n + 1):\n dp[0][j] = j\n\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if word1[i - 1] == word2[j - 1]:\n dp[i][j] = dp[i - 1][j - 1]\n else:\n dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1\n\n return dp[m][n]\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 322 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Bottom up DP | edit-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n # dynamic programming, bottom up\n cache = [[float("inf")]* (len(word2)+1) for _ in range(len(word1)+1)]\n # fill in the bottom row\n for col in range(len(word2)+1): \n cache[len(word1)][col] = len(word2) - col # base case when word 1 is empty\n # fill in the last column\n for row in range(len(word1)+1): \n cache[row][len(word2)] = len(word1) - row # base case when word 2 is empty\n for i in range(len(word1) - 1, -1, -1):\n for j in range(len(word2)-1,-1,-1):\n if word1[i] == word2[j]: # char is equal\n cache[i][j] = cache[i+1][j+1]\n else: # char is not equal\n cache[i][j] = min(cache[i+1][j],cache[i][j+1],cache[i+1][j+1])+1 # check insert, delete, replace, all there directions in the 2d cache array\n\n return cache[0][0]\n\n\n``` | 1 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Python easy to understand | Dynamic Programming | Tabulation (Bottom-Up Approach) | edit-distance | 0 | 1 | # Complexity\n- Time complexity: $$O(m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n m, n = len(word1), len(word2)\n if not m or not n: return max(m, n)\n\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n for j in range(n + 1):\n dp[m][j] = n - j\n for i in range(m + 1):\n dp[i][n] = m - i\n \n for i in range(m - 1, -1, -1):\n for j in range(n - 1, -1, -1):\n if word1[i] == word2[j]:\n dp[i][j] = dp[i + 1][j + 1]\n else:\n dp[i][j] = min(dp[i][j + 1], dp[i + 1][j], dp[i + 1][j + 1]) + 1\n return dp[0][0]\n``` | 1 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Simple DP Solution with Comments | edit-distance | 0 | 1 | # Code\n```\nclass Solution:\n def fun(self, word1, word2, dp):\n\n # check if the result is already present in the dp table\n if dp[len(word2)][len(word1)] != -1:\n return dp[len(word2)][len(word1)] \n\n # if both words are empty, then the number of operations required is 0\n if len(word1) == 0 and len(word2) == 0:\n return 0\n\n # if one of the words is empty, then the number of operations required is the length of the other word\n if len(word2) == 0:\n return len(word1)\n\n if len(word1) == 0:\n return len(word2)\n\n # add: insert a character in word1 to match word2\n add = self.fun(word1, word2[1:], dp) + 1\n\n # delete: delete a character in word1 to match word2\n delete = self.fun(word1[1:], word2, dp) + 1\n\n # replace: replace a character in word1 to match word2\n if word1[0] == word2[0]:\n # if the firsr character is same, then the number of operations will not increase\n replace = self.fun(word1[1:], word2[1:], dp)\n else:\n # else, the number of operations will increase\n replace = self.fun(word1[1:], word2[1:], dp) + 1\n \n # take the minimum of the three recursive calls and store in the dp table\n dp[len(word2)][len(word1)] = min(min(add, delete), replace)\n\n # return the result\n return dp[len(word2)][len(word1)]\n \n\n def minDistance(self, word1: str, word2: str) -> int:\n # create the dp table with -1 as initial values\n dp = [[-1 for i in range(len(word1)+1)] for j in range(len(word2)+1)]\n\n # call the recursive function and return the result\n return self.fun(word1, word2, dp)\n\n\n``` | 1 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
DP || Tabulation || Commented line by line | edit-distance | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n #In tabulation method, we\'ll assign rows and columns\n #wih length of given words\n len1=len(word1)+1\n len2=len(word2)+1\n dp=[[-1 for j in range(len2)] for j in range(len1)]\n #if i become 0 then return j\n #if j become 0 then return i \n for i in range(len1):\n for j in range(len2):\n if i==0:\n dp[i][j]=j\n elif j==0:\n dp[i][j]=i\n #if there is a match between them\n #return the diagonal element\n elif word1[i-1]==word2[j-1]:\n dp[i][j]=dp[i-1][j-1]\n else:\n #otherwise take min of diagnol,upper and left element \n #and add 1 to it\n dp[i][j]=1+min(dp[i-1][j],min(dp[i-1][j-1],dp[i][j-1]))\n return dp[len1-1][len2-1]\n``` | 1 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Solution | edit-distance | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> dp;\n \n int solve(int i, int j, string &s, string &t){\n if(i<0 && j<0)\n return 0;\n \n if(i < 0 && j>=0){\n return j+1;\n }\n \n if(i>=0 && j<0){\n return i+1;\n }\n \n if(dp[i][j] != -1)\n return dp[i][j];\n \n int l = 1000, r = 1000, z = 1000, p = 1000;\n if(s[i] == t[j]){\n l = solve(i-1,j-1,s,t);\n }\n else{\n r = 1 + solve(i-1,j,s,t);\n z = 1 + solve(i-1,j-1,s,t);\n p = 1 + solve(i,j-1,s,t);\n }\n \n return dp[i][j] = min(l,min(r,min(z,p)));\n }\n \n \n int minDistance(string s, string t) {\n dp.resize(s.size()+1,vector<int>(t.size()+1,-1));\n return solve(s.size(),t.size(),s,t);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n n = len(word1)\n m = len(word2)\n \n to_visit = [(0, 0)]\n visited = set()\n dist = 0\n while to_visit:\n nxt_lvl = []\n while to_visit:\n i, j = to_visit.pop()\n if (i, j) in visited:\n continue\n while i < n and j < m and word1[i] == word2[j]:\n i += 1\n j += 1\n if i == n and j == m:\n return dist\n if (i, j + 1) not in visited:\n nxt_lvl.append((i, j + 1))\n if (i + 1, j) not in visited:\n nxt_lvl.append((i + 1, j))\n if (i + 1, j + 1) not in visited:\n nxt_lvl.append((i + 1, j + 1))\n visited.add((i, j))\n dist += 1\n to_visit = nxt_lvl\n```\n\n```Java []\nclass Solution {\n public int minDistance(String word1, String word2) {\n if (word1.length() < word2.length()) {\n return minDistance(word2, word1);\n }\n char[] w1 = word1.toCharArray(), w2 = word2.toCharArray();\n int[] dp = new int[w2.length];\n int last = 0;\n int diag = 0;\n for (int i = 0; i < dp.length; i++) {\n dp[i] = dp.length - i;\n }\n for (int i = w1.length - 1; i > -1; i--) {\n last = w1.length - i;\n diag = w1.length - 1 - i;\n for (int j = w2.length - 1; j > -1; j--) {\n int tmp = dp[j];\n if (w1[i] == w2[j]) {\n last = dp[j] = diag;\n } else {\n last = dp[j] = Math.min(diag, Math.min(dp[j], last)) + 1;\n }\n diag = tmp;\n }\n }\n return last;\n }\n}\n```\n | 26 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
🥳【Python3】🔥 Easy Solution | edit-distance | 0 | 1 | **Python3 Solution**\n```python\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n m, n = len(word1), len(word2)\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n # base case - i steps away\n for i in range(1, m + 1):\n dp[i][0] = i\n for j in range(1, n + 1):\n dp[0][j] = j\n # each step has four possibilities\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n # same character, i and j move ahead together\n if word1[i - 1] == word2[j - 1]:\n dp[i][j] = dp[i - 1][j - 1]\n # find min of insert, replace, remove a character\n else:\n dp[i][j] = min(\n dp[i - 1][j] + 1,\n dp[i][j - 1] + 1,\n dp[i - 1][j - 1] + 1\n )\n \n return dp[m][n]\n``` | 8 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Very Simple Dp solution | edit-distance | 0 | 1 | \n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n n, m = len(word1), len(word2)\n inf = int(1e9+90)\n \n dp = [[inf for _ in range(m+1)] for _ in range(n+1)]\n \n for i in range(m+1):\n dp[n][i] = m - i\n \n for i in range(n+1):\n dp[i][m] = n - i\n \n for i in range(n-1,-1,-1):\n for j in range(m-1,-1,-1):\n dp[i][j] = min(\n dp[i+1][j] + 1,\n dp[i][j+1] + 1,\n dp[i+1][j+1] + (word1[i] != word2[j])\n )\n \n return dp[0][0]\n``` | 1 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
100 % SPACE OPTIMIZED SOLUTION || DP | edit-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(N*M)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(M)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n n=len(word1)\n m=len(word2)\n # dp=[[0]*(m+1) for i in range(n+1)]\n # for i in range(n+1):\n # dp[i][0]=i\n # for j in range(m+1):\n # dp[0][j]=j\n prev=[i for i in range(m+1)]\n \n for i in range(1,n+1):\n curr=[0]*(m+1)\n curr[0]=i\n for j in range(1,m+1):\n if word1[i-1]==word2[j-1]:\n curr[j]=prev[j-1]\n else:\n curr[j]=min(prev[j],curr[j-1],prev[j-1])+1\n prev=curr\n return prev[-1]\n\n # return self.dp(n,m,word1,word2,{})\n``` | 2 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Python || 91.89% Faster || DP || Memoization+Tabulation | edit-distance | 0 | 1 | ```\n\'\'\'\nExample: s1: \'horse\'\n s2: \'ros\'\n\nCase1: Inserting a Character\n\nNow if we have to match the strings by insertions, what would we do?: \n\nWe would have placed an \u2018s\u2019 at index 5 of S1.\nSuppose i now point to s at index 5 of S1 and j points are already pointing to s at index j of S2.\nNow, we hit the condition, where characters do match. (as mentioned in case 1).\nTherefore, we will decrement i and j by 1. They will now point to index 4 and 1 respectively.\n\nNow, the number of operations we did were only 1 (inserting s at index 5) but do we need to really insert the \u2018s\u2019 at index 5 and modify the string? The answer is simply NO. As we see that inserting a character (here \u2018s\u2019 at index 5), we will eventually get to the third step. So we can just return 1+ f(i,j-1) as i remains there only after insertion and j decrements by 1. We can say that we have hypothetically inserted character s.\n\nCase 2: Deleting a character \n\nConsider the same example,\n\nWe can simply delete the character at index 4 and check from the next index.\n\nNow, j remains at its original index and we decrement i by 1. We perform 1 operation, therefore we will recursively call 1+f(i-1,j).\n\nCase3: Replacing a character \n\nConsider the same example,\n\n\nIf we replace the character \u2018e\u2019 at index 4 of S1 with \u2018s\u2019, we have matched both the characters ourselves. We again hit the case of character matching, therefore we decrement both i and j by 1. As the number of operations performed is 1, we will return 1+f(i-1,j-1).\n\nTo summarise, these are the three choices we have in case characters don\u2019t match:\n\nreturn 1+f(i-1,j) // Insertion of character.\nreturn 1+f(i,j-1) // Deletion of character.\nreturn 1+f(i-1,j-1) // Replacement of character.\n\'\'\'\n\n#Recursion \n#Time Complexity: O(2^(m+n))\n#Space Complexity: O(m+n)\nclass Solution1:\n def minDistance(self, word1: str, word2: str) -> int:\n def solve(i,j):\n if i==0:\n return j\n if j==0:\n return i\n if word1[i-1]==word2[j-1]:\n return solve(i-1,j-1)\n else:\n return 1 + min(solve(i,j-1),solve(i-1,j),solve(i-1,j-1))\n m,n=len(word1),len(word2)\n return solve(m,n)\n \n#Memoization (Top-Down)\n#Time Complexity: O(m*n)\n#Space Complexity: O(m+n) + O(m*n)\nclass Solution2:\n def minDistance(self, word1: str, word2: str) -> int:\n def solve(i,j):\n if i==0:\n return j\n if j==0:\n return i\n if dp[i][j]!=-1:\n return dp[i][j]\n if word1[i-1]==word2[j-1]:\n dp[i][j]=solve(i-1,j-1)\n return dp[i][j]\n else:\n dp[i][j]=1 + min(solve(i,j-1),solve(i-1,j),solve(i-1,j-1))\n return dp[i][j]\n m,n=len(word1),len(word2)\n dp=[[-1 for j in range(n+1)] for i in range(m+1)]\n return solve(m,n)\n \nclass Solution3:\n def minDistance(self, word1: str, word2: str) -> int:\n m,n = len(word1),len(word2)\n dp = [[0 for j in range(n+1)] for i in range(m+1)]\n for i in range(m+1):\n dp[i][0] = i\n for j in range(n+1):\n dp[0][j] = j\n for i in range(1,m+1):\n for j in range(1,n+1):\n if word1[i-1] == word2[j-1]:\n dp[i][j] = dp[i-1][j-1]\n else:\n dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])\n return dp[m][n]\n \n#Space Optimization\n#Time Complexity: O(m*n)\n#Space Complexity: O(n)\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n m,n = len(word1),len(word2)\n prev=[0]*(n+1)\n curr=[0]*(n+1)\n for j in range(n+1):\n prev[j]=j\n for i in range(1,m+1):\n curr[0]=i\n for j in range(1,n+1):\n if word1[i-1] == word2[j-1]:\n curr[j] = prev[j-1]\n else:\n curr[j] = 1 + min(prev[j-1], prev[j], curr[j-1])\n prev=curr[:]\n return prev[n]\n```\n**An upovte will be encouraging** | 3 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Python 3 || 8 lines, w/ comments || T/M: 100% / 78% | edit-distance | 0 | 1 | ```\nclass Solution:\n def minDistance(self, word1: str, word2: str) -> int:\n\n w1, w2 = len(word1), len(word2)\n \n @lru_cache(None)\n def dp(i, j):\n\n if i >= w1 : return w2-j # word1 used up, so all inserts\n if j >= w2 : return w1-i # word2 used up, so all deletes\n if word1[i] == word2[j]: return dp(i+1, j+1) # letters match, so no operation\n\n return min(dp(i,j+1), dp(i+1,j), dp(i+1,j+1)) + 1 # insert, delete, replace\n\n return dp(0,0)\n```\n[https://leetcode.com/problems/edit-distance/submissions/905093377/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*MN*) and space complexity is *O*(*MN*), in which *M, N* ~ `len(word1),len(word2)`.\n | 18 | Given two strings `word1` and `word2`, return _the minimum number of operations required to convert `word1` to `word2`_.
You have the following three operations permitted on a word:
* Insert a character
* Delete a character
* Replace a character
**Example 1:**
**Input:** word1 = "horse ", word2 = "ros "
**Output:** 3
**Explanation:**
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
**Example 2:**
**Input:** word1 = "intention ", word2 = "execution "
**Output:** 5
**Explanation:**
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
**Constraints:**
* `0 <= word1.length, word2.length <= 500`
* `word1` and `word2` consist of lowercase English letters. | null |
Helper Function (Beats 90% and 99%) | set-matrix-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n visited = []\n def helper(row,col):\n for i in range(0,len(matrix[0])):\n matrix[row][i] = 0\n for j in range(0,len(matrix)):\n matrix[j][col] = 0\n \n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n if matrix[i][j]==0:\n visited.append((i,j))\n\n for i,j in visited:\n helper(i,j)\n \n \n \n```\n\n**Please UpVote if you find Helpful** | 3 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Helper Function (Beats 90% and 99%) | set-matrix-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n visited = []\n def helper(row,col):\n for i in range(0,len(matrix[0])):\n matrix[row][i] = 0\n for j in range(0,len(matrix)):\n matrix[j][col] = 0\n \n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n if matrix[i][j]==0:\n visited.append((i,j))\n\n for i,j in visited:\n helper(i,j)\n \n \n \n```\n\n**Please UpVote if you find Helpful** | 3 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Python Solution w/ approach explanation & readable with space progression from: O(m+n) & O(1) | set-matrix-zeroes | 0 | 1 | Note: m = number of rows, n = number of cols\n\n**Brute force using O(m*n) space:** The initial approach is to start with creating another matrix to store the result. From doing that, you\'ll notice that we want a way to know when each row and col should be changed to zero. We don\'t want to prematurely change the values in the matrix to zero because as we go through it, we might change a row to 0 because of the new value. \n\n**More optimized using O(m + n) space:** To do better, we want O(m + n). How do we go about that? Well, we really just need a way to track if any row or any col has a zero, because then that means the entire row or col has to be zero. Ok, well, then we can use an array to track the zeroes for the row and zeros for the col. Whenever we see a zero, just set that row or col to be True.\n\nSpace: O(m + n) for the zeroes_row and zeroes_col array \n``` Python\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n # input validation\n if not matrix:\n return []\n\n m = len(matrix)\n n = len(matrix[0])\n\n zeroes_row = [False] * m\n zeroes_col = [False] * n\n for row in range(m):\n for col in range(n):\n if matrix[row][col] == 0:\n zeroes_row[row] = True\n zeroes_col[col] = True\n\n for row in range(m):\n for col in range(n):\n if zeroes_row[row] or zeroes_col[col]:\n matrix[row][col] = 0\n```\n\n**Most optimized using O(1) space:** But, we can do even better, O(1) - initial ask of the problem. What if instead of having a separate array to track the zeroes, we simply use the first row or col to track them and then go back to update the first row and col with zeroes after we\'re done replacing it? The approach to get constant space is to use first row and first col of the matrix as a tracker. \n* At each row or col, if you see a zero, then mark the first row or first col as zero with the current row and col. \n* Then iterate through the array again to see where the first row and col were marked as zero and then set that row/col as 0. \n* After doing that, you\'ll need to traverse through the first row and/or first col if there were any zeroes there to begin with and set everything to be equal to 0 in the first row and/or first col. \n\nTime complexity for all three progression is O(m * n).\n\n\n\n**Space:** O(1) for modification in place and using the first row and first col to keep track of zeros instead of zeroes_row and zeroes_col\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n\n m = len(matrix)\n n = len(matrix[0])\n\t\t\n first_row_has_zero = False\n first_col_has_zero = False\n \n # iterate through matrix to mark the zero row and cols\n for row in range(m):\n for col in range(n):\n if matrix[row][col] == 0:\n if row == 0:\n first_row_has_zero = True\n if col == 0:\n first_col_has_zero = True\n matrix[row][0] = matrix[0][col] = 0\n \n # iterate through matrix to update the cell to be zero if it\'s in a zero row or col\n for row in range(1, m):\n for col in range(1, n):\n matrix[row][col] = 0 if matrix[0][col] == 0 or matrix[row][0] == 0 else matrix[row][col]\n \n # update the first row and col if they\'re zero\n if first_row_has_zero:\n for col in range(n):\n matrix[0][col] = 0\n \n if first_col_has_zero:\n for row in range(m):\n matrix[row][0] = 0\n \n``` | 195 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Python Solution w/ approach explanation & readable with space progression from: O(m+n) & O(1) | set-matrix-zeroes | 0 | 1 | Note: m = number of rows, n = number of cols\n\n**Brute force using O(m*n) space:** The initial approach is to start with creating another matrix to store the result. From doing that, you\'ll notice that we want a way to know when each row and col should be changed to zero. We don\'t want to prematurely change the values in the matrix to zero because as we go through it, we might change a row to 0 because of the new value. \n\n**More optimized using O(m + n) space:** To do better, we want O(m + n). How do we go about that? Well, we really just need a way to track if any row or any col has a zero, because then that means the entire row or col has to be zero. Ok, well, then we can use an array to track the zeroes for the row and zeros for the col. Whenever we see a zero, just set that row or col to be True.\n\nSpace: O(m + n) for the zeroes_row and zeroes_col array \n``` Python\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n # input validation\n if not matrix:\n return []\n\n m = len(matrix)\n n = len(matrix[0])\n\n zeroes_row = [False] * m\n zeroes_col = [False] * n\n for row in range(m):\n for col in range(n):\n if matrix[row][col] == 0:\n zeroes_row[row] = True\n zeroes_col[col] = True\n\n for row in range(m):\n for col in range(n):\n if zeroes_row[row] or zeroes_col[col]:\n matrix[row][col] = 0\n```\n\n**Most optimized using O(1) space:** But, we can do even better, O(1) - initial ask of the problem. What if instead of having a separate array to track the zeroes, we simply use the first row or col to track them and then go back to update the first row and col with zeroes after we\'re done replacing it? The approach to get constant space is to use first row and first col of the matrix as a tracker. \n* At each row or col, if you see a zero, then mark the first row or first col as zero with the current row and col. \n* Then iterate through the array again to see where the first row and col were marked as zero and then set that row/col as 0. \n* After doing that, you\'ll need to traverse through the first row and/or first col if there were any zeroes there to begin with and set everything to be equal to 0 in the first row and/or first col. \n\nTime complexity for all three progression is O(m * n).\n\n\n\n**Space:** O(1) for modification in place and using the first row and first col to keep track of zeros instead of zeroes_row and zeroes_col\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n\n m = len(matrix)\n n = len(matrix[0])\n\t\t\n first_row_has_zero = False\n first_col_has_zero = False\n \n # iterate through matrix to mark the zero row and cols\n for row in range(m):\n for col in range(n):\n if matrix[row][col] == 0:\n if row == 0:\n first_row_has_zero = True\n if col == 0:\n first_col_has_zero = True\n matrix[row][0] = matrix[0][col] = 0\n \n # iterate through matrix to update the cell to be zero if it\'s in a zero row or col\n for row in range(1, m):\n for col in range(1, n):\n matrix[row][col] = 0 if matrix[0][col] == 0 or matrix[row][0] == 0 else matrix[row][col]\n \n # update the first row and col if they\'re zero\n if first_row_has_zero:\n for col in range(n):\n matrix[0][col] = 0\n \n if first_col_has_zero:\n for row in range(m):\n matrix[row][0] = 0\n \n``` | 195 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Two Different Approaches | set-matrix-zeroes | 0 | 1 | # without Space ---->O(1)\n# Time complexity ------>O(N^3)\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n m=len(matrix)\n n=len(matrix[0])\n for i in range(m):\n for j in range(n):\n if matrix[i][j]==0:\n for row in range(n):\n if matrix[i][row]!=0:\n matrix[i][row]=-2**32\n for col in range(m):\n if matrix[col][j]!=0:\n matrix[col][j]=-2**32\n\n for i in range(m):\n for j in range(n):\n if matrix[i][j]==(-2**32):\n matrix[i][j]=0\n```\n# with space Complexity:O(2*k) \n# Time Complexity--->O(N^2)\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n m=len(matrix)\n n=len(matrix[0])\n arr=[]\n for i in range(m):\n for j in range(n):\n if matrix[i][j]==0:\n arr.append([i,j])\n \n for k,l in arr:\n for row in range(n):\n matrix[k][row]=0\n for col in range(m):\n matrix[col][l]=0\n ```\n # please upvote me it would encourage me alot\n\n\n \n\n\n \n \n | 13 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Two Different Approaches | set-matrix-zeroes | 0 | 1 | # without Space ---->O(1)\n# Time complexity ------>O(N^3)\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n m=len(matrix)\n n=len(matrix[0])\n for i in range(m):\n for j in range(n):\n if matrix[i][j]==0:\n for row in range(n):\n if matrix[i][row]!=0:\n matrix[i][row]=-2**32\n for col in range(m):\n if matrix[col][j]!=0:\n matrix[col][j]=-2**32\n\n for i in range(m):\n for j in range(n):\n if matrix[i][j]==(-2**32):\n matrix[i][j]=0\n```\n# with space Complexity:O(2*k) \n# Time Complexity--->O(N^2)\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n m=len(matrix)\n n=len(matrix[0])\n arr=[]\n for i in range(m):\n for j in range(n):\n if matrix[i][j]==0:\n arr.append([i,j])\n \n for k,l in arr:\n for row in range(n):\n matrix[k][row]=0\n for col in range(m):\n matrix[col][l]=0\n ```\n # please upvote me it would encourage me alot\n\n\n \n\n\n \n \n | 13 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
🔥[Python3] O(1) with reverse traversal | set-matrix-zeroes | 0 | 1 | ```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n firstRowVal, R, C = 1, len(matrix), len(matrix[0])\n\n for i in range(R):\n for j in range(C):\n if matrix[i][j] == 0:\n matrix[0][j] = 0 # mark column\n if i != 0: \n matrix[i][0] = 0\n else:\n firstRowVal = 0\n \n for i in reversed(range(R)):\n for j in reversed(range(C)):\n if i == 0:\n matrix[i][j] *= firstRowVal\n elif matrix[0][j] == 0 or matrix[i][0] == 0:\n matrix[i][j] = 0\n``` | 12 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
🔥[Python3] O(1) with reverse traversal | set-matrix-zeroes | 0 | 1 | ```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n firstRowVal, R, C = 1, len(matrix), len(matrix[0])\n\n for i in range(R):\n for j in range(C):\n if matrix[i][j] == 0:\n matrix[0][j] = 0 # mark column\n if i != 0: \n matrix[i][0] = 0\n else:\n firstRowVal = 0\n \n for i in reversed(range(R)):\n for j in reversed(range(C)):\n if i == 0:\n matrix[i][j] *= firstRowVal\n elif matrix[0][j] == 0 or matrix[i][0] == 0:\n matrix[i][j] = 0\n``` | 12 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Solution | set-matrix-zeroes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void setZeroes(vector<vector<int>>& mat) {\n int row=mat.size(),col=mat[0].size();\n int c=1;\n for(int i=0;i<row;i++){\n if(mat[i][0]==0)\n c=0;\n for(int j=1;j<col;j++){\n if(mat[i][j]==0){\n mat[0][j]=0;\n mat[i][0]=0;\n }\n }\n }\n for(int i=row-1;i>=0;i--){\n for(int j=col-1;j>0;j--)\n if(mat[i][0]==0||mat[0][j]==0)\n mat[i][j]=0;\n if(c==0)\n mat[i][0]=0;\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n zeroRowIndexes = set()\n zeroColIndexes = set()\n m = len(matrix)\n n = len(matrix[0])\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == 0:\n zeroRowIndexes.add(i)\n zeroColIndexes.add(j)\n for i in range(m):\n for j in range(n):\n if i in zeroRowIndexes or j in zeroColIndexes:\n matrix[i][j] = 0\n```\n\n```Java []\nclass Solution {\n public void setZeroes(int[][] matrix) {\n int col0 = 1, rows = matrix.length, cols = matrix[0].length;\n \n for(int i = 0; i < rows; i++){\n if(matrix[i][0] == 0) col0 = 0;\n for(int j = 1; j < cols; j++)\n if (matrix[i][j] == 0)\n matrix[i][0] = matrix[0][j] = 0;\n }\n \n for(int i = rows - 1; i >= 0; i--){\n for(int j = cols - 1; j >= 1; j --)\n if (matrix[i][0] == 0 || matrix[0][j] == 0)\n matrix[i][j] = 0;\n if (col0 == 0) matrix[i][0] = 0;\n }\n }\n}\n```\n | 4 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Solution | set-matrix-zeroes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void setZeroes(vector<vector<int>>& mat) {\n int row=mat.size(),col=mat[0].size();\n int c=1;\n for(int i=0;i<row;i++){\n if(mat[i][0]==0)\n c=0;\n for(int j=1;j<col;j++){\n if(mat[i][j]==0){\n mat[0][j]=0;\n mat[i][0]=0;\n }\n }\n }\n for(int i=row-1;i>=0;i--){\n for(int j=col-1;j>0;j--)\n if(mat[i][0]==0||mat[0][j]==0)\n mat[i][j]=0;\n if(c==0)\n mat[i][0]=0;\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n zeroRowIndexes = set()\n zeroColIndexes = set()\n m = len(matrix)\n n = len(matrix[0])\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == 0:\n zeroRowIndexes.add(i)\n zeroColIndexes.add(j)\n for i in range(m):\n for j in range(n):\n if i in zeroRowIndexes or j in zeroColIndexes:\n matrix[i][j] = 0\n```\n\n```Java []\nclass Solution {\n public void setZeroes(int[][] matrix) {\n int col0 = 1, rows = matrix.length, cols = matrix[0].length;\n \n for(int i = 0; i < rows; i++){\n if(matrix[i][0] == 0) col0 = 0;\n for(int j = 1; j < cols; j++)\n if (matrix[i][j] == 0)\n matrix[i][0] = matrix[0][j] = 0;\n }\n \n for(int i = rows - 1; i >= 0; i--){\n for(int j = cols - 1; j >= 1; j --)\n if (matrix[i][0] == 0 || matrix[0][j] == 0)\n matrix[i][j] = 0;\n if (col0 == 0) matrix[i][0] = 0;\n }\n }\n}\n```\n | 4 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Beats 99.93% users on Leetcode 🔥🔥 | set-matrix-zeroes | 0 | 1 | # Intuition\nFind Address of All Zeroes and then all element respect the address becomes zero.\n\n# Approach\nstep 1 : First i create two lists:- row,col in which i stored the rows and colums where zero is present.\n\nstep 2 : go in evey row and change element to value zero\n\nstep 3 : go in evey coloumn and change element to value zero\n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:\n\n\n# Code\n```\nclass Solution:\n def setZeroes(self, mat: List[List[int]]) -> None:\n n = len(mat)\n m = len(mat[0])\n\n rows = []\n col = []\n x = 0\n for i in range(n):\n if x in (mat[i]):\n rows.append(i)\n for j in range(m):\n if mat[i][j] == 0:\n col.append(j)\n \n for i in rows:\n for j in range(m):\n mat[i][j] = 0\n \n for j in col:\n for i in range(n):\n mat[i][j] = 0\n # print(rows,col)\n \n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Beats 99.93% users on Leetcode 🔥🔥 | set-matrix-zeroes | 0 | 1 | # Intuition\nFind Address of All Zeroes and then all element respect the address becomes zero.\n\n# Approach\nstep 1 : First i create two lists:- row,col in which i stored the rows and colums where zero is present.\n\nstep 2 : go in evey row and change element to value zero\n\nstep 3 : go in evey coloumn and change element to value zero\n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:\n\n\n# Code\n```\nclass Solution:\n def setZeroes(self, mat: List[List[int]]) -> None:\n n = len(mat)\n m = len(mat[0])\n\n rows = []\n col = []\n x = 0\n for i in range(n):\n if x in (mat[i]):\n rows.append(i)\n for j in range(m):\n if mat[i][j] == 0:\n col.append(j)\n \n for i in rows:\n for j in range(m):\n mat[i][j] = 0\n \n for j in col:\n for i in range(n):\n mat[i][j] = 0\n # print(rows,col)\n \n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Basic logic easy Code Python 3 | set-matrix-zeroes | 0 | 1 | # Intuition\nIdentify which columns and rows that we need to make 0\n\n# Approach\nRows and Cols lists store the row no and col no which needs to be made 0\nUsing a for loop we check for the condition if the element is 0\nif it is we push its column and row number to the respective lists\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n m = len(matrix)\n n = len(matrix[0])\n cols = []\n rows = []\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == 0:\n if i not in rows:\n rows.append(i)\n if j not in cols:\n cols.append(j)\n for i in rows:\n for j in range(n):\n matrix[i][j] = 0\n for i in cols:\n for j in range(m):\n matrix[j][i] = 0\n \n\n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Basic logic easy Code Python 3 | set-matrix-zeroes | 0 | 1 | # Intuition\nIdentify which columns and rows that we need to make 0\n\n# Approach\nRows and Cols lists store the row no and col no which needs to be made 0\nUsing a for loop we check for the condition if the element is 0\nif it is we push its column and row number to the respective lists\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n m = len(matrix)\n n = len(matrix[0])\n cols = []\n rows = []\n for i in range(m):\n for j in range(n):\n if matrix[i][j] == 0:\n if i not in rows:\n rows.append(i)\n if j not in cols:\n cols.append(j)\n for i in rows:\n for j in range(n):\n matrix[i][j] = 0\n for i in cols:\n for j in range(m):\n matrix[j][i] = 0\n \n\n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Python thought process | set-matrix-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nuse special char to notate zero and mark them as zero in 2nd pass\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(mn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Constant\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n m, n = len(matrix), len(matrix[0])\n\n for r in range(m):\n for c in range(n):\n if matrix[r][c] == 0:\n for i in range(n):\n if matrix[r][i] != 0:\n matrix[r][i] = \'*\'\n\n for i in range(m):\n if matrix[i][c] != 0:\n matrix[i][c] = \'*\'\n\n for r in range(m):\n for c in range(n):\n if matrix[r][c] == \'*\':\n matrix[r][c] = 0\n\n\n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Python thought process | set-matrix-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nuse special char to notate zero and mark them as zero in 2nd pass\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(mn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Constant\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n m, n = len(matrix), len(matrix[0])\n\n for r in range(m):\n for c in range(n):\n if matrix[r][c] == 0:\n for i in range(n):\n if matrix[r][i] != 0:\n matrix[r][i] = \'*\'\n\n for i in range(m):\n if matrix[i][c] != 0:\n matrix[i][c] = \'*\'\n\n for r in range(m):\n for c in range(n):\n if matrix[r][c] == \'*\':\n matrix[r][c] = 0\n\n\n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Intuitive Python Solution - Constant Space | Beats 100% | set-matrix-zeroes | 0 | 1 | # Intuition\nThe first issue one runs into when solving this problem is figuring out how to not accidentally "override" the next row or column you wish to change to 0\'s. For example, If one were to look at the rows, and finds a 0, they could go through the row and change all the numbers to 0, but they might lose track of other 0\'s that were in the matrix to begin with.\n\nTo solve this problem with non-constant space we can instead pass through the array twice. Once to fill a list with all the current spots with 0, and the second time to actually convert all necessary rows and columns to 0.\n\nHowever this problem then asks us to solve with constant space, meaning we can only use either what\'s given to us, or use other variables that do not grow in size when n and m grow.\n\n# Approach\nI feel the need to say my approach may be a bit cheaty all things considered, as I\'m taking advantage of what an int array can contain. \n\nSince the matrix can contain every int, we need to find another placeholder for our 0\'s, so instead we are going to use None (NULL in non-pythonic languages). Since we know that no value in the matrix will be None, we can use the state of None as a placeholder for filling in our rows and colums with 0\'s, so we do two passes.\n\nThe first pass we check if any values are 0:\n`if matrix[i][j] == 0:`\nAt this point, we want to stop, go back to the start of this row, and start changing non-0\'s to 0, and if we find a 0, then we change it to None:\n```\nfor k in range(col):\n if matrix[i][k] == 0:\n matrix[i][k] = None\n else:\n matrix[i][k] = 0\n```\nTo optimize, we can break from the current row check loop, since we already did that.\n\nThe Second pass we now replace all columns that contain None with 0, note that we are now traversing columns first, so we can break and optimize time:\n```\nif matrix[j][i] == None:\n for k in range(row):\n matrix[k][i] = 0\n break\n```\n\n# Complexity\n- Time complexity:\nSince we run two passes only, the time complexity is:\n**O(2nm), linear, or O(N)**\n\n- Space complexity:\nWe aren\'t making any new variables, and only utilizing what the problem gives us. The space complexity is:\n**O(1), or constant**\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n row, col = len(matrix), len(matrix[0])\n \n # rows, prepping cols\n for i in range(row):\n for j in range(col):\n if matrix[i][j] == 0:\n for k in range(col):\n if matrix[i][k] == 0:\n matrix[i][k] = None\n else:\n matrix[i][k] = 0\n break\n \n # doing cols\n for i in range(col):\n for j in range(row):\n if matrix[j][i] == None:\n for k in range(row):\n matrix[k][i] = 0\n break\n \n```\n\nThanks for reading! | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Intuitive Python Solution - Constant Space | Beats 100% | set-matrix-zeroes | 0 | 1 | # Intuition\nThe first issue one runs into when solving this problem is figuring out how to not accidentally "override" the next row or column you wish to change to 0\'s. For example, If one were to look at the rows, and finds a 0, they could go through the row and change all the numbers to 0, but they might lose track of other 0\'s that were in the matrix to begin with.\n\nTo solve this problem with non-constant space we can instead pass through the array twice. Once to fill a list with all the current spots with 0, and the second time to actually convert all necessary rows and columns to 0.\n\nHowever this problem then asks us to solve with constant space, meaning we can only use either what\'s given to us, or use other variables that do not grow in size when n and m grow.\n\n# Approach\nI feel the need to say my approach may be a bit cheaty all things considered, as I\'m taking advantage of what an int array can contain. \n\nSince the matrix can contain every int, we need to find another placeholder for our 0\'s, so instead we are going to use None (NULL in non-pythonic languages). Since we know that no value in the matrix will be None, we can use the state of None as a placeholder for filling in our rows and colums with 0\'s, so we do two passes.\n\nThe first pass we check if any values are 0:\n`if matrix[i][j] == 0:`\nAt this point, we want to stop, go back to the start of this row, and start changing non-0\'s to 0, and if we find a 0, then we change it to None:\n```\nfor k in range(col):\n if matrix[i][k] == 0:\n matrix[i][k] = None\n else:\n matrix[i][k] = 0\n```\nTo optimize, we can break from the current row check loop, since we already did that.\n\nThe Second pass we now replace all columns that contain None with 0, note that we are now traversing columns first, so we can break and optimize time:\n```\nif matrix[j][i] == None:\n for k in range(row):\n matrix[k][i] = 0\n break\n```\n\n# Complexity\n- Time complexity:\nSince we run two passes only, the time complexity is:\n**O(2nm), linear, or O(N)**\n\n- Space complexity:\nWe aren\'t making any new variables, and only utilizing what the problem gives us. The space complexity is:\n**O(1), or constant**\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n row, col = len(matrix), len(matrix[0])\n \n # rows, prepping cols\n for i in range(row):\n for j in range(col):\n if matrix[i][j] == 0:\n for k in range(col):\n if matrix[i][k] == 0:\n matrix[i][k] = None\n else:\n matrix[i][k] = 0\n break\n \n # doing cols\n for i in range(col):\n for j in range(row):\n if matrix[j][i] == None:\n for k in range(row):\n matrix[k][i] = 0\n break\n \n```\n\nThanks for reading! | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
🐍3 || FAST BEATS 96.44%🍔 || HALF MEMORY BEATS 56.23% 🧠 | set-matrix-zeroes | 0 | 1 | # Explanation\nFirst, you want to find the coordinates where there are zeroes.\nThen, you want to change the rows and colums with the items at those coordinates\n\n# Code\n```\nclass Solution:\n def getChanges(self, mat):\n changePositions = []\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 0:\n changePositions.append((i, j))\n return changePositions\n def setZeroes(self, matrix) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n changes = self.getChanges(matrix)\n m = len(matrix)\n n = len(matrix[0])\n for coor in changes:\n for i in range(m):\n matrix[i][coor[1]] = 0\n for j in range(n):\n matrix[coor[0]][j] = 0\n```\n\n\n\n\n | 2 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
🐍3 || FAST BEATS 96.44%🍔 || HALF MEMORY BEATS 56.23% 🧠 | set-matrix-zeroes | 0 | 1 | # Explanation\nFirst, you want to find the coordinates where there are zeroes.\nThen, you want to change the rows and colums with the items at those coordinates\n\n# Code\n```\nclass Solution:\n def getChanges(self, mat):\n changePositions = []\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 0:\n changePositions.append((i, j))\n return changePositions\n def setZeroes(self, matrix) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n changes = self.getChanges(matrix)\n m = len(matrix)\n n = len(matrix[0])\n for coor in changes:\n for i in range(m):\n matrix[i][coor[1]] = 0\n for j in range(n):\n matrix[coor[0]][j] = 0\n```\n\n\n\n\n | 2 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Python easy solution with clear explanation with example | set-matrix-zeroes | 0 | 1 | # Intuition\nHere, our intuition is to make every row and column zero if there is a zero present in that row. To accomplish this, we need to follow these steps:\n\n# Approach\n\nStep 1: Append the indices to a list where there is a zero.\nFor example, given the list [[0,1,2,0],[3,4,5,2],[1,3,1,5]], the list of indices would be [0, 3].\n\nThis list is created because:\ni) If there is a zero in a nested list, we make the entire list zero.\nii) If a zero is not present in a row, but it is present in another row in the same column, we make that column zero for every nested list.\n\nTo perform this, we use two separate for loops:\n- The first loop is used to get the indices of the zeros in the nested list and store them in `zero_cols`.\n- The second loop is used to update the values to zero based on the conditions mentioned above.\n\n\n\n# **Kindly do a upvote if you find it usefull and a comment if found any mistake\uD83D\uDE4F\uD83C\uDFFB\uD83D\uDE4F\uD83C\uDFFB\uD83E\uDEC2**\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n l_c = []\n\n for i in range(len(matrix)):\n for j in range(len(matrix[i])):\n if matrix[i][j] == 0:\n l_c.append(j)\n\n for i in range(len(matrix)):\n if 0 in matrix[i]:\n for ii in range(len(matrix[i])):\n matrix[i][ii] = 0\n else:\n for _ in l_c:\n matrix[i][_] = 0\n return matrix\n\n\n\n``` | 4 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Python easy solution with clear explanation with example | set-matrix-zeroes | 0 | 1 | # Intuition\nHere, our intuition is to make every row and column zero if there is a zero present in that row. To accomplish this, we need to follow these steps:\n\n# Approach\n\nStep 1: Append the indices to a list where there is a zero.\nFor example, given the list [[0,1,2,0],[3,4,5,2],[1,3,1,5]], the list of indices would be [0, 3].\n\nThis list is created because:\ni) If there is a zero in a nested list, we make the entire list zero.\nii) If a zero is not present in a row, but it is present in another row in the same column, we make that column zero for every nested list.\n\nTo perform this, we use two separate for loops:\n- The first loop is used to get the indices of the zeros in the nested list and store them in `zero_cols`.\n- The second loop is used to update the values to zero based on the conditions mentioned above.\n\n\n\n# **Kindly do a upvote if you find it usefull and a comment if found any mistake\uD83D\uDE4F\uD83C\uDFFB\uD83D\uDE4F\uD83C\uDFFB\uD83E\uDEC2**\n\n# Code\n```\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n l_c = []\n\n for i in range(len(matrix)):\n for j in range(len(matrix[i])):\n if matrix[i][j] == 0:\n l_c.append(j)\n\n for i in range(len(matrix)):\n if 0 in matrix[i]:\n for ii in range(len(matrix[i])):\n matrix[i][ii] = 0\n else:\n for _ in l_c:\n matrix[i][_] = 0\n return matrix\n\n\n\n``` | 4 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Detailed solution in Python3/Go/TypeScript with O(mn) time and O(1) space complexity | set-matrix-zeroes | 0 | 1 | # Intuition\nWe can save space by simply marking the first row with zeroes at the columns for which we find zeroes on any row and doing the same for the first column.\n\nHowever, we will have a common cell at `[0][0]` that will then act as a marker for both, so we will let that act as an indicator for column and use an extra variable for the rows instead.\n\n# Approach\n## Determine which rows and columns need to be zeroes\nTraverse through the entire `matrix` from top-left to bottom-right. Whenever a zero is found mark its **topmost** cell as zero and its **leftmost** cell as zero, too. \n\n>If it is the first row however, use an extra variable to mark for the first row instead of the leftmost cell on the first row, as we will be using it for the column indicator already.\n\nTraverse through every cell on the `matrix` again except the first row and the first column and assign zeroes wherever we find the first row or the first column to contain a zero after our first traversal.\n\nAs we skipped the first column earlier, now traverse through the first column and set all of it to zero if the **topmost** cell on the first column is zero.\n\nIf our extra variable contains `true`, traverse through the first row and set it all to zero as well.\n\n# Complexity\n- Time complexity: $$O(mn)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python []\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n # Get the dimensions of the matrix\n rows, cols = len(matrix), len(matrix[0])\n \n # Set a flag that would indicate if the \n # first row needs to be zero or not\n rowZero = False\n\n # Determine which rows and columns need to be zeroes\n for row in range(rows):\n for col in range(cols):\n if matrix[row][col] == 0:\n # Place marker on first row for the column\n matrix[0][col] = 0\n\n # Place marker on first column of the row\n # if it is not the first row in which case\n # we mark using the flag we set up already\n if row > 0: matrix[row][0] = 0\n else: rowZero = True\n\n # Convert all rows except the first\n # and all columns except the first\n # to zero if they are marked as zero\n # in the first column and the first row\n for row in range(1, rows):\n for col in range(1, cols):\n if matrix[0][col] == 0 or matrix[row][0] == 0:\n matrix[row][col] = 0\n\n # Handle the first column as \n # tbe previous loop skipped it\n if matrix[0][0] == 0:\n for row in range(rows):\n matrix[row][0] = 0\n\n # Handle the first row as\n # the previous loop skipped it\n if rowZero:\n for col in range(cols):\n matrix[0][col] = 0\n\n```\n```golang []\nfunc setZeroes(matrix [][]int) {\n // Get the dimensions of the matrix\n rows, cols := len(matrix), len(matrix[0])\n \n // Set a flag that would indicate if the \n // first row needs to be zero or not\n rowZero := false\n\n // Determine which rows and columns need to be zeroes\n for row := 0; row < rows; row ++ {\n for col := 0; col < cols; col++ {\n if matrix[row][col] == 0 {\n // Place marker on first row for the column\n matrix[0][col] = 0\n\n // Place marker on first column of the row\n // if it is not the first row in which case\n // we mark using the flag we set up already\n if row > 0 {\n matrix[row][0] = 0\n } else {\n rowZero = true\n }\n }\n }\n }\n\n // Convert all rows except the first\n // and all columns except the first\n // to zero if they are marked as zero\n // in the first column and the first row\n for row := 1; row < rows; row ++ {\n for col := 1; col < cols; col++ {\n if matrix[0][col] == 0 || matrix[row][0] == 0 {\n matrix[row][col] = 0\n }\n }\n }\n\n // Handle the first column as \n // tbe previous loop skipped it\n if matrix[0][0] == 0 {\n for row := 0; row < rows; row ++ {\n matrix[row][0] = 0\n }\n }\n\n // Handle the first row as\n // the previous loop skipped it\n if rowZero {\n for col := 0; col < cols; col++ {\n matrix[0][col] = 0\n }\n }\n}\n```\n```typescript []\nfunction setZeroes(matrix: number[][]): void {\n // Get the dimensions of the matrix\n const rows = matrix.length, cols = matrix[0].length;\n \n // Set a flag that would indicate if the \n // first row needs to be zero or not\n let rowZero = false;\n\n // Determine which rows and columns need to be zeroes\n for (let row = 0; row < rows; row ++) {\n for (let col = 0; col < cols; col++) {\n if (matrix[row][col] == 0) {\n // Place marker on first row for the column\n matrix[0][col] = 0;\n\n // Place marker on first column of the row\n // if it is not the first row in which case\n // we mark using the flag we set up already\n if (row > 0) \n matrix[row][0] = 0;\n else\n rowZero = true;\n }\n }\n }\n\n // Convert all rows except the first\n // and all columns except the first\n // to zero if they are marked as zero\n // in the first column and the first row\n for (let row = 1; row < rows; row ++)\n for (let col = 1; col < cols; col++)\n if (matrix[0][col] == 0 || matrix[row][0] == 0)\n matrix[row][col] = 0;\n\n // Handle the first column as \n // tbe previous loop skipped it\n if (matrix[0][0] == 0)\n for (let row = 0; row < rows; row ++)\n matrix[row][0] = 0;\n\n // Handle the first row as\n // the previous loop skipped it\n if (rowZero)\n for (let col = 0; col < cols; col++)\n matrix[0][col] = 0;\n};\n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Detailed solution in Python3/Go/TypeScript with O(mn) time and O(1) space complexity | set-matrix-zeroes | 0 | 1 | # Intuition\nWe can save space by simply marking the first row with zeroes at the columns for which we find zeroes on any row and doing the same for the first column.\n\nHowever, we will have a common cell at `[0][0]` that will then act as a marker for both, so we will let that act as an indicator for column and use an extra variable for the rows instead.\n\n# Approach\n## Determine which rows and columns need to be zeroes\nTraverse through the entire `matrix` from top-left to bottom-right. Whenever a zero is found mark its **topmost** cell as zero and its **leftmost** cell as zero, too. \n\n>If it is the first row however, use an extra variable to mark for the first row instead of the leftmost cell on the first row, as we will be using it for the column indicator already.\n\nTraverse through every cell on the `matrix` again except the first row and the first column and assign zeroes wherever we find the first row or the first column to contain a zero after our first traversal.\n\nAs we skipped the first column earlier, now traverse through the first column and set all of it to zero if the **topmost** cell on the first column is zero.\n\nIf our extra variable contains `true`, traverse through the first row and set it all to zero as well.\n\n# Complexity\n- Time complexity: $$O(mn)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python []\nclass Solution:\n def setZeroes(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n # Get the dimensions of the matrix\n rows, cols = len(matrix), len(matrix[0])\n \n # Set a flag that would indicate if the \n # first row needs to be zero or not\n rowZero = False\n\n # Determine which rows and columns need to be zeroes\n for row in range(rows):\n for col in range(cols):\n if matrix[row][col] == 0:\n # Place marker on first row for the column\n matrix[0][col] = 0\n\n # Place marker on first column of the row\n # if it is not the first row in which case\n # we mark using the flag we set up already\n if row > 0: matrix[row][0] = 0\n else: rowZero = True\n\n # Convert all rows except the first\n # and all columns except the first\n # to zero if they are marked as zero\n # in the first column and the first row\n for row in range(1, rows):\n for col in range(1, cols):\n if matrix[0][col] == 0 or matrix[row][0] == 0:\n matrix[row][col] = 0\n\n # Handle the first column as \n # tbe previous loop skipped it\n if matrix[0][0] == 0:\n for row in range(rows):\n matrix[row][0] = 0\n\n # Handle the first row as\n # the previous loop skipped it\n if rowZero:\n for col in range(cols):\n matrix[0][col] = 0\n\n```\n```golang []\nfunc setZeroes(matrix [][]int) {\n // Get the dimensions of the matrix\n rows, cols := len(matrix), len(matrix[0])\n \n // Set a flag that would indicate if the \n // first row needs to be zero or not\n rowZero := false\n\n // Determine which rows and columns need to be zeroes\n for row := 0; row < rows; row ++ {\n for col := 0; col < cols; col++ {\n if matrix[row][col] == 0 {\n // Place marker on first row for the column\n matrix[0][col] = 0\n\n // Place marker on first column of the row\n // if it is not the first row in which case\n // we mark using the flag we set up already\n if row > 0 {\n matrix[row][0] = 0\n } else {\n rowZero = true\n }\n }\n }\n }\n\n // Convert all rows except the first\n // and all columns except the first\n // to zero if they are marked as zero\n // in the first column and the first row\n for row := 1; row < rows; row ++ {\n for col := 1; col < cols; col++ {\n if matrix[0][col] == 0 || matrix[row][0] == 0 {\n matrix[row][col] = 0\n }\n }\n }\n\n // Handle the first column as \n // tbe previous loop skipped it\n if matrix[0][0] == 0 {\n for row := 0; row < rows; row ++ {\n matrix[row][0] = 0\n }\n }\n\n // Handle the first row as\n // the previous loop skipped it\n if rowZero {\n for col := 0; col < cols; col++ {\n matrix[0][col] = 0\n }\n }\n}\n```\n```typescript []\nfunction setZeroes(matrix: number[][]): void {\n // Get the dimensions of the matrix\n const rows = matrix.length, cols = matrix[0].length;\n \n // Set a flag that would indicate if the \n // first row needs to be zero or not\n let rowZero = false;\n\n // Determine which rows and columns need to be zeroes\n for (let row = 0; row < rows; row ++) {\n for (let col = 0; col < cols; col++) {\n if (matrix[row][col] == 0) {\n // Place marker on first row for the column\n matrix[0][col] = 0;\n\n // Place marker on first column of the row\n // if it is not the first row in which case\n // we mark using the flag we set up already\n if (row > 0) \n matrix[row][0] = 0;\n else\n rowZero = true;\n }\n }\n }\n\n // Convert all rows except the first\n // and all columns except the first\n // to zero if they are marked as zero\n // in the first column and the first row\n for (let row = 1; row < rows; row ++)\n for (let col = 1; col < cols; col++)\n if (matrix[0][col] == 0 || matrix[row][0] == 0)\n matrix[row][col] = 0;\n\n // Handle the first column as \n // tbe previous loop skipped it\n if (matrix[0][0] == 0)\n for (let row = 0; row < rows; row ++)\n matrix[row][0] = 0;\n\n // Handle the first row as\n // the previous loop skipped it\n if (rowZero)\n for (let col = 0; col < cols; col++)\n matrix[0][col] = 0;\n};\n``` | 1 | Given an `m x n` integer matrix `matrix`, if an element is `0`, set its entire row and column to `0`'s.
You must do it [in place](https://en.wikipedia.org/wiki/In-place_algorithm).
**Example 1:**
**Input:** matrix = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** \[\[1,0,1\],\[0,0,0\],\[1,0,1\]\]
**Example 2:**
**Input:** matrix = \[\[0,1,2,0\],\[3,4,5,2\],\[1,3,1,5\]\]
**Output:** \[\[0,0,0,0\],\[0,4,5,0\],\[0,3,1,0\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[0].length`
* `1 <= m, n <= 200`
* `-231 <= matrix[i][j] <= 231 - 1`
**Follow up:**
* A straightforward solution using `O(mn)` space is probably a bad idea.
* A simple improvement uses `O(m + n)` space, but still not the best solution.
* Could you devise a constant space solution? | If any cell of the matrix has a zero we can record its row and column number using additional memory.
But if you don't want to use extra memory then you can manipulate the array instead. i.e. simulating exactly what the question says. Setting cell values to zero on the fly while iterating might lead to discrepancies. What if you use some other integer value as your marker?
There is still a better approach for this problem with 0(1) space. We could have used 2 sets to keep a record of rows/columns which need to be set to zero. But for an O(1) space solution, you can use one of the rows and and one of the columns to keep track of this information. We can use the first cell of every row and column as a flag. This flag would determine whether a row or column has been set to zero. |
Search a 2D Matrix | Binary Search | Telugu | Python | Amazon | Microsoft | Adobe | Paytm | search-a-2d-matrix | 0 | 1 | \n# Video Explanation : \n[https://youtu.be/5lgoHAKlBNo?si=p5wDI_E8Iw7o1305]()\n# Please Subscribe \uD83D\uDE0A\n\n\n\n# Complexity\n- Time complexity:$$O(log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n rows=len(matrix)\n cols=len(matrix[0])\n top=0\n bottom=rows-1\n requiredRow=-1\n while top<=bottom:\n midRow= (top+bottom)//2\n if matrix[midRow][0]<=target and matrix[midRow][cols-1]>=target:\n requiredRow=midRow\n break\n elif matrix[midRow][0]>target:\n bottom=midRow-1\n elif matrix[midRow][cols-1]<target:\n top=midRow+1\n if requiredRow==-1:\n return False\n \n left=0\n right=cols-1\n while left<=right:\n mid = (left+right)//2\n if matrix[requiredRow][mid]==target:\n return True\n elif matrix[requiredRow][mid]>target:\n right=mid-1\n else:\n left=mid+1\n return False\n\n```\n | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
Python3 Solution | search-a-2d-matrix | 0 | 1 | \n```\nclass Solution:\n def searchMatrix(self,matrix:List[List[int]],target:int)->bool:\n n=len(matrix)\n m=len(matrix[0])\n for i in range(n):\n for j in range(m):\n if matrix[i][j]==target:\n return True\n\n return False \n``` | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
BEATS 99.92%. PYTHON SIMPLE BINARY SEARCH | search-a-2d-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n def BinarySearch(resCol, low, high, target):\n while low <= high:\n mid = (low+high) // 2\n if resCol[mid] == target:\n return True\n elif resCol[mid] > target:\n high = mid -1\n else:\n low = mid + 1\n return False\n\n l, r = 0, len(matrix) - 1\n while l <= r:\n mid = (l+r) // 2\n if matrix[mid][0] <= target and matrix[mid][-1] >= target:\n resCol = matrix[mid]\n return BinarySearch(resCol, 0, len(resCol), target)\n elif matrix[mid][0] > target:\n r = mid - 1\n else:\n l = mid + 1\n return False\n\n \n \n``` | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
Python3 Binary Search Solution | search-a-2d-matrix | 0 | 1 | # Intuition\nBinary Search\n\n# Approach\nBinary Search\n# Complexity\n- Time complexity:\nOlog(n*m)\n\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n left = 0\n right = len(matrix)-1\n while left<=right:\n mid = (left+right)//2\n if target>=matrix[mid][0] and target<=matrix[mid][-1]:\n break\n elif target>matrix[mid][-1]:\n left = mid + 1\n else:\n right = mid-1\n\n left = 0\n new_list = matrix[mid]\n right = len(new_list)-1\n \n while left<=right:\n mid = (left+right)//2\n if target == new_list[mid]:\n return True\n elif target>new_list[mid]:\n left = mid + 1\n\n else:\n right = mid-1\n\n return False\n\n\n\n``` | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
✅ 100% Binary Search [VIDEO] - Simple Solution | search-a-2d-matrix | 1 | 1 | # Problem Understanding\nThe task is to find a target integer in a 2D matrix with the following properties: \n1. Each row is sorted in non-decreasing order.\n2. The first integer of each row is greater than the last integer of the previous row.\n\nThe challenge is to determine if the target integer exists within the matrix.\n\n# Approach\nGiven the problem, it may be tempting to perform a linear search through the entire matrix, but this would result in a time complexity of $$O(m \\times n)$$, which is not acceptable given the problem\'s constraint of $$O(\\log(m \\times n))$$.\n\nInstead, we can leverage the fact that the matrix is sorted both row-wise and column-wise, and apply a binary search to find the target.\n\n# Live Coding & Explenation\nhttps://youtu.be/ePF8QegEy-8\n\n## Treating the Matrix as a 1-Dimensional Array\nTo apply binary search, we need a one-dimensional array. We can treat our 2-D matrix as a one-dimensional array because of the matrix\'s sorted property. The first integer of each row is greater than the last integer of the previous row, so we can think of the rows as being appended one after the other to form a single sorted array.\n\n## Binary Search\nBinary search is a search algorithm that finds the position of a target value within a sorted array. It compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated, and the search continues on the remaining half until it is successful or the remaining half is empty.\n\n## Initialization\nBefore we start the binary search, we need to initialize two pointers:\n\n1. `left` - This represents the start of the array. We set this to 0 (the index of the first element).\n2. `right` - This represents the end of the array. We set this to `m * n - 1` (the index of the last element), where `m` and `n` are the number of rows and columns in the matrix, respectively.\n\n## Iterative Binary Search\nWe perform a binary search iteratively within a while loop until `left` exceeds `right`. In each iteration, we calculate the midpoint between `left` and `right`.\n\nTo get the row and column of the midpoint in the matrix, we use the `divmod` function with `mid` and `n`. The `divmod` function takes two numbers and returns a pair of numbers (a tuple) consisting of their quotient and remainder.\n\nWe then compare the value at the midpoint with the target:\n\n1. If the midpoint value is equal to the target, we have found the target in the matrix, and we return `True`.\n2. If the midpoint value is less than the target, this means the target must be in the right half of the array. So, we adjust `left` to be `mid + 1`.\n3. If the midpoint value is greater than the target, this means the target must be in the left half of the array. So, we adjust `right` to be `mid - 1`.\n\nIf we exit the while loop, that means we did not find the target in the matrix, so we return `False`.\n\n# Complexity\n## Time Complexity\nThe time complexity is $$O(\\log(m \\times n))$$, since we\'re effectively performing a binary search over the $$m \\times n$$ elements of the matrix.\n\n## Space Complexity\nThe space complexity is $$O(1)$$ because we only use a constant amount of space to store our variables (`left`, `right`, `mid`, `mid_value`), regardless of the size of the input matrix.\n\n# Performance\nThe performance of this solution is optimal given the problem constraints. Since the matrix is sorted and the problem requires us to find an element, binary search is the best possible approach.\n\nCertainly, here\'s the table sorted by runtime (ms) and then by memory usage (MB):\n\n| Programming Language | Runtime (ms) | Beats (%) | Memory (MB) | Beats (%) |\n|---|---|---|---|---|\n| Rust | 0 | 100 | 2.2 | 28.37 |\n| Java | 0 | 100 | 41.6 | 9.3 |\n| C++ | 3 | 82.89 | 9.5 | 19.73 |\n| Go | 3 | 58.16 | 2.7 | 98.33 |\n| JavaScript | 48 | 92.89 | 42.3 | 28.19 |\n| Python3 | 49 | 90.75 | 16.8 | 64.57 |\n| C# | 82 | 99.1 | 40.9 | 35.48 |\n\n\n\n\n# Code\n```Python []\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n if not matrix:\n return False\n m, n = len(matrix), len(matrix[0])\n left, right = 0, m * n - 1\n\n while left <= right:\n mid = (left + right) // 2\n mid_row, mid_col = divmod(mid, n)\n\n if matrix[mid_row][mid_col] == target:\n return True\n elif matrix[mid_row][mid_col] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return False\n```\n``` C++ []\nclass Solution {\npublic:\n bool searchMatrix(vector<vector<int>>& matrix, int target) {\n int m = matrix.size();\n int n = matrix[0].size();\n int left = 0, right = m * n - 1;\n\n while (left <= right) {\n int mid = left + (right - left) / 2;\n int mid_val = matrix[mid / n][mid % n];\n\n if (mid_val == target)\n return true;\n else if (mid_val < target)\n left = mid + 1;\n else\n right = mid - 1;\n }\n return false;\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean searchMatrix(int[][] matrix, int target) {\n int m = matrix.length;\n int n = matrix[0].length;\n int left = 0, right = m * n - 1;\n\n while (left <= right) {\n int mid = left + (right - left) / 2;\n int mid_val = matrix[mid / n][mid % n];\n\n if (mid_val == target)\n return true;\n else if (mid_val < target)\n left = mid + 1;\n else\n right = mid - 1;\n }\n return false;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[][]} matrix\n * @param {number} target\n * @return {boolean}\n */\nvar searchMatrix = function(matrix, target) {\n let m = matrix.length;\n let n = matrix[0].length;\n let left = 0, right = m * n - 1;\n\n while (left <= right) {\n let mid = Math.floor((left + right) / 2);\n let mid_val = matrix[Math.floor(mid / n)][mid % n];\n\n if (mid_val === target)\n return true;\n else if (mid_val < target)\n left = mid + 1;\n else\n right = mid - 1;\n }\n return false;\n};\n```\n``` C# []\npublic class Solution {\n public bool SearchMatrix(int[][] matrix, int target) {\n int m = matrix.Length;\n int n = matrix[0].Length;\n int left = 0, right = m * n - 1;\n\n while (left <= right) {\n int mid = left + (right - left) / 2;\n int mid_val = matrix[mid / n][mid % n];\n\n if (mid_val == target)\n return true;\n else if (mid_val < target)\n left = mid + 1;\n else\n right = mid - 1;\n }\n return false;\n }\n}\n```\n``` Go []\nfunc searchMatrix(matrix [][]int, target int) bool {\n m := len(matrix)\n n := len(matrix[0])\n left, right := 0, m*n-1\n\n for left <= right {\n mid := left + (right-left)/2\n mid_val := matrix[mid/n][mid%n]\n\n if mid_val == target {\n return true\n } else if mid_val < target {\n left = mid + 1\n } else {\n right = mid - 1\n }\n }\n return false\n}\n```\n``` Rust []\nimpl Solution {\n pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {\n let rows = matrix.len() as i32;\n let cols = matrix[0].len() as i32;\n\n let mut start = 0;\n let mut end = rows * cols - 1;\n\n while start <= end {\n let mid = start + (end - start) / 2;\n let mid_value = matrix[(mid / cols) as usize][(mid % cols) as usize];\n\n if mid_value == target {\n return true;\n } else if mid_value < target {\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n\n false\n }\n}\n```\n\n# Live Coding + Explenation in Go\nhttps://youtu.be/edGrFBOtnc4\n\nI hope you find this solution helpful in understanding how to solve the "Search a 2D Matrix" problem. If you have any further questions or need additional clarifications, please don\'t hesitate to ask. If you understood the solution and found it beneficial, please consider giving it an upvote. Happy coding, and may your coding journey be filled with success and satisfaction! \uD83D\uDE80\uD83D\uDC68\u200D\uD83D\uDCBB\uD83D\uDC69\u200D\uD83D\uDCBB | 98 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
One Liner Hack in 🐍 | 🔥Beats 86%🔥 | search-a-2d-matrix | 0 | 1 | \n\n\n---\n# Complexity\n- Time complexity: $$O(m * n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m * n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n return target in list(chain.from_iterable(matrix))\n```\n---\n# **An upvote would be encouraging...** | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
Python | Easy Solution | Beats 90% | search-a-2d-matrix | 0 | 1 | # Intuition\nWe are applying Binary Search here.\n\n# Approach\nSame as binary search but in 2D.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nfrom typing import List\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n low=0\n m=len(matrix[0])\n n=len(matrix)\n if not matrix:\n return False\n high=n*m-1\n while low<=high:\n mid=(high+low)//2\n row,col= mid//m, mid%m\n if matrix[row][col] == target:\n return True\n elif matrix[row][col] > target:\n high=mid-1\n else:\n low=mid+1\n return False\n \n```\n# **Please Do Upvote!!!\uD83E\uDD79** | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
[Python3] ✅: Binary Search | search-a-2d-matrix | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem statement basically gives the solution away. The problem statement made some very particular descriptions about the relationship [in terms of magnitude] between the first and last numbers of each row of the matrix. If you evaluate the implication of such relationship, you can deduce that the matrix is basically a non-decreasing collection of numbers from left to right, top to bottom. \n\nWe can now easily see the matrix as an array [if we combine the all the rows one after another from top to bottom. Now we simply need a system/method of knowing if a value is in the matrix. Since binary search requires that the input array is sorted, we can treat the matrix [in our heads] as an array with values in ascending order. \n\n# Complexity\n- Time complexity:\n$$O(n + m)$$ Where n = number of rows, m = number of columns\n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n # Binary Search\n nr, nc = len(matrix), len(matrix[0])\n length = nr * nc\n\n def val(index: int):\n """\n Given an integer index which serves as the index of a value in the \n matrx (assuming we took the entire matrix as on array), return the element\n at that index.\n\n Example:\n 1 3 5 7\n \xA0 \xA0 \xA0 \xA0 \xA0 \xA019 11 16 60\n\n The above grid is equivalent to\n 1 3 5 7 19 11 16 60\n\n And thus we can consider that as an array of non-decreasing integers\n\n val(0) -> 1\n val(3) -> 7\n val(6) -> 16\n """\n return matrix[math.floor(index / nc)][index % nc]\n\n def bin_search(n: int) -> bool:\n """\n Given an integer n, return true if it\'s in the matrix, else false\n """\n l, r = 0, length - 1\n while l <= r:\n mid = (l + r) // 2\n if val(mid) == n: return True\n if val(mid) > n:\n r = mid - 1\n else:\n l = mid + 1\n \n return False\n\n return bin_search(target)\n```\n\nRemember to upvote if you liked this solution \uD83D\uDE42 | 1 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
Binary Search Logic Easy | search-a-2d-matrix | 0 | 1 | \n# Binary Search Approach---->O(LogN) \n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> \n row,col=len(matrix),len(matrix[0])\n left,right=0,row*col-1\n while left<=right:\n mid=(left+right)//2\n num=matrix[mid//col][mid%col]\n if num==target:\n return True\n if num>target:\n right=mid-1\n else:\n left=mid+1\n return False\n```\n# Binary Search Approach---->O(N+LogN)\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n list1=[]\n for row in matrix:\n if row[-1]>=target:\n list1=row\n break\n left,right=0,len(list1)-1\n while left<=right:\n mid=(right+left)//2\n if list1[mid]==target:\n return True\n elif list1[mid]>target:\n right=mid-1\n else:\n left=mid+1\n return False\n //please upvote me it would encourage me alot\n \n```\n# 3 Lines Of Code ---->O(N^2)\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n for row in matrix:\n if row[-1] >= target:\n return target in row\n\n# please upvote me it would encourage me alot\n```\n# please upvote me it would encourage me alot\n\n | 39 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
Simple easy python solution using binary search!! beginner's friendly. 🙂🔥 | search-a-2d-matrix | 1 | 1 | p# Code\n```\nclass Solution:\n def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:\n rows,columns=len(matrix),len(matrix[0])\n top,bottom=0,rows-1\n while top<=bottom:\n row=(top+bottom)//2\n if target<matrix[row][0]:\n bottom=row-1\n elif target>matrix[row][-1]:\n top=row+1\n else:\n break\n row=(top+bottom)//2\n l,r=0,columns-1\n while l<=r:\n mid=(l+r)//2\n if target<matrix[row][mid]:\n r=mid-1\n elif target>matrix[row][mid]:\n l=mid+1\n else:\n return True\n return False\n``` | 4 | You are given an `m x n` integer matrix `matrix` with the following two properties:
* Each row is sorted in non-decreasing order.
* The first integer of each row is greater than the last integer of the previous row.
Given an integer `target`, return `true` _if_ `target` _is in_ `matrix` _or_ `false` _otherwise_.
You must write a solution in `O(log(m * n))` time complexity.
**Example 1:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 3
**Output:** true
**Example 2:**
**Input:** matrix = \[\[1,3,5,7\],\[10,11,16,20\],\[23,30,34,60\]\], target = 13
**Output:** false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104` | null |
Solution | sort-colors | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void sortColors(vector<int>& nums) {\n int l = 0;\n int m = 0;\n int h = nums.size()-1;\n\n while(m<=h){\n if(nums[m]==0){\n swap(nums[l], nums[m]);\n l++;\n m++;\n }\n else if(nums[m]==1){\n m++;\n }\n else if(nums[m]==2){\n swap(nums[m], nums[h]);\n h--;\n }\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def sortColors(self, nums: List[int]) -> None:\n\n red, white, blue = 0, 0, len(nums) - 1\n\n while white <= blue:\n if nums[white] == 0:\n nums[white], nums[red] = nums[red], nums[white]\n red += 1\n white += 1\n elif nums[white] == 1:\n white += 1\n else:\n nums[white], nums[blue] = nums[blue], nums[white]\n blue -= 1\n```\n\n```Java []\nclass Solution {\n public void sortColors(int[] nums) {\n int l = 0;\n int r = nums.length - 1;\n\n for (int i = 0; i <= r;)\n if (nums[i] == 0)\n swap(nums, i++, l++);\n else if (nums[i] == 1)\n ++i;\n else\n swap(nums, i, r--);\n }\n\n private void swap(int[] nums, int i, int j) {\n final int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n}\n```\n | 465 | Given an array `nums` with `n` objects colored red, white, or blue, sort them **[in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
We will use the integers `0`, `1`, and `2` to represent the color red, white, and blue, respectively.
You must solve this problem without using the library's sort function.
**Example 1:**
**Input:** nums = \[2,0,2,1,1,0\]
**Output:** \[0,0,1,1,2,2\]
**Example 2:**
**Input:** nums = \[2,0,1\]
**Output:** \[0,1,2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `nums[i]` is either `0`, `1`, or `2`.
**Follow up:** Could you come up with a one-pass algorithm using only constant extra space? | A rather straight forward solution is a two-pass algorithm using counting sort. Iterate the array counting number of 0's, 1's, and 2's. Overwrite array with the total number of 0's, then 1's and followed by 2's. |
0ms Solution Beats 100.00% C++ | sort-colors | 0 | 1 | # Intuition\nThis is a similar problem to Move Zeroes to the end.\nWe just need to move the colors 1 and 2 at the end and 0 at the starting of the list\n\n# Approach\n1. Initialize two variables k1 and k2 as -1 and 0 respectively.\nHere, k1 is the left most index of 1 and k2 is the left most index of 2.\n2. Iterate through the list and check if current number is 0 then it needs to be moved just before k1 wherever the first \'1\' is present or just before k2 i.e. \'2\' if 1 is not present.\n3. If 1 is present, then we need to swap 0 with 1 and then if required/possible move swap 1 with 2 as we need to put 0 before 1 and 1 before 2.\n4. Repeating the above steps, we can guarantee that 0 comes before 1 and 1 before 2 automatically.\n\n# Complexity\n- Time complexity:\nO(N) : as we are iterating through the array/list in a single pass\n\n- Space complexity:\nO(1) : as we are not using any extra space.\n\n# C++ Code\n```\nclass Solution {\npublic:\n void sortColors(vector<int>& nums) {\n int k1=-1,k2=0,n=nums.size();\n for(int i=0;i<n;i++){\n if(nums[i]==0){\n if(k1!=-1 && k1<n) swap(nums[k1++],nums[i]);\n if(k2<n) swap(nums[k2++],nums[i]);\n }\n else if(nums[i]==1){\n if(k1==-1) k1=k2;\n if(k2<n) swap(nums[k2++],nums[i]);\n }\n }\n }\n};\n```\n\n\n# Python Code\n```\nclass Solution:\n def sortColors(self, nums: List[int]) -> None:\n k1 = -1\n k2 = 0\n n = len(nums)\n for i in range(n):\n if nums[i] == 0:\n if k1 != -1 and k1 < n:\n nums[k1], nums[i] = nums[i], nums[k1]\n k1 += 1\n if k2 < n:\n nums[k2], nums[i] = nums[i], nums[k2]\n k2 += 1\n elif nums[i] == 1:\n if k1 == -1:\n k1 = k2\n if k2 < n:\n nums[k2], nums[i] = nums[i], nums[k2]\n k2 += 1\n\n```\n\n\n# Kotlin Code\n```\nclass Solution {\n fun sortColors(nums: IntArray): Unit {\n var k1=-1\n var k2=0\n val n = nums.size\n for(i in 0..n-1){\n if(nums[i]==0){\n if(k1!=-1 && k1<n){\n val temp = nums[k1]\n nums[k1] = nums[i]\n nums[i] = temp\n k1++\n }\n if(k2<n){\n val temp = nums[k2]\n nums[k2] = nums[i]\n nums[i] = temp\n k2++\n }\n }\n else if(nums[i]==1){\n if(k1==-1) k1=k2;\n if(k2<n){\n val temp = nums[k2]\n nums[k2] = nums[i]\n nums[i] = temp\n k2++\n }\n }\n }\n }\n}\n```\n | 2 | Given an array `nums` with `n` objects colored red, white, or blue, sort them **[in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
We will use the integers `0`, `1`, and `2` to represent the color red, white, and blue, respectively.
You must solve this problem without using the library's sort function.
**Example 1:**
**Input:** nums = \[2,0,2,1,1,0\]
**Output:** \[0,0,1,1,2,2\]
**Example 2:**
**Input:** nums = \[2,0,1\]
**Output:** \[0,1,2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `nums[i]` is either `0`, `1`, or `2`.
**Follow up:** Could you come up with a one-pass algorithm using only constant extra space? | A rather straight forward solution is a two-pass algorithm using counting sort. Iterate the array counting number of 0's, 1's, and 2's. Overwrite array with the total number of 0's, then 1's and followed by 2's. |
Dutch Flag algorithm python | sort-colors | 0 | 1 | Simple implementation of Dutch flag algorithm in python\n\n# Complexity\n- Time complexity: O(n)\n\n# Code\n```\nclass Solution:\n def sortColors(self, arr: List[int]) -> None:\n n = len(arr)\n low = 0\n high = n - 1\n i = 0\n\n while i <= high:\n \n if arr[i] == 0:\n arr[i], arr[low] = arr[low], arr[i]\n low += 1\n \n elif arr[i] == 2:\n arr[i], arr[high] = arr[high], arr[i]\n high -= 1\n i -= 1\n i += 1\n``` | 2 | Given an array `nums` with `n` objects colored red, white, or blue, sort them **[in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
We will use the integers `0`, `1`, and `2` to represent the color red, white, and blue, respectively.
You must solve this problem without using the library's sort function.
**Example 1:**
**Input:** nums = \[2,0,2,1,1,0\]
**Output:** \[0,0,1,1,2,2\]
**Example 2:**
**Input:** nums = \[2,0,1\]
**Output:** \[0,1,2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `nums[i]` is either `0`, `1`, or `2`.
**Follow up:** Could you come up with a one-pass algorithm using only constant extra space? | A rather straight forward solution is a two-pass algorithm using counting sort. Iterate the array counting number of 0's, 1's, and 2's. Overwrite array with the total number of 0's, then 1's and followed by 2's. |
Beginner-friendly || Simple solution with HashMap+Prefix Sum in Python3 / TypeScript | sort-colors | 0 | 1 | # Intuition\nLet\'s briefly explain, what the problem is:\n- there a list of `nums`, it consists **only** with `0, 1`\'s and `2`\'s\n- our goal is to **sort** `nums` in **ascending order in-place**\n\nThe simplest approach we could use is to **apply built-in** sorting methods, but they\'re **not allowed**.\n\nSo, what if we count **frequencies of integers?** We will get a **frequency map**.\nSince we know, that all of the integers **must be sorted** like `[0,0,1,2]` we will **map** frequency of each integer to **a particular index** with using **intervals**.\n\n```\n# Example\nnums = [1,1,0,0,2]\nmap = {0: 2, 1: 2, 2: 1}\n\n# To be more specific, let me introduce a temporary array with \n# indexes of a particular interval with starting and ending points.\ninterval = [\n {start: 0, end: 1}, \n {start: 2, end: 3}, \n {start: 4, end: 4}\n]\n\n# To build an interval, you should have a pointer to the last\n# interval and add an amount of a particular integer from map.\n```\n\n# Approach\n1. declare `prefix` array to map frequencies to a particular integer\n2. iterate over `nums` and build `prefix`\n3. iterate over **each interval** from `map` and add to `prefix` the last frequency for integers `1` and `2`\n\n# Complexity\n- Time complexity: **O(N)**, since we iterate over `nums`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space, except `prefix`, but it stores only **constant amount** of integers, while having a maximum size as `3`\n\n# Code in Python3\n```\nclass Solution:\n def sortColors(self, nums: List[int]) -> None:\n prefix = Counter(nums)\n\n for i in range(prefix[0]): nums[i] = 0\n\n prefix[1] += prefix[0]\n\n for i in range(prefix[0], prefix[1]): nums[i] = 1\n\n prefix[2] += prefix[1]\n\n for i in range(prefix[1], prefix[2]): nums[i] = 2\n \n```\n# Code in TypeScript\n```\nfunction sortColors(nums: number[]): void {\n const prefix = Array(3).fill(0)\n\n for (let i = 0; i < nums.length; i++) {\n prefix[nums[i]]++\n }\n\n for (let i = 0; i < prefix[0]; i++) {\n nums[i] = 0\n }\n\n prefix[1] += prefix[0]\n\n for (let i = prefix[0]; i < prefix[1]; i++) {\n nums[i] = 1\n }\n\n prefix[2] += prefix[1]\n\n for (let i = prefix[1]; i < prefix[2]; i++) {\n nums[i] = 2\n }\n}\n``` | 3 | Given an array `nums` with `n` objects colored red, white, or blue, sort them **[in-place](https://en.wikipedia.org/wiki/In-place_algorithm)** so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
We will use the integers `0`, `1`, and `2` to represent the color red, white, and blue, respectively.
You must solve this problem without using the library's sort function.
**Example 1:**
**Input:** nums = \[2,0,2,1,1,0\]
**Output:** \[0,0,1,1,2,2\]
**Example 2:**
**Input:** nums = \[2,0,1\]
**Output:** \[0,1,2\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 300`
* `nums[i]` is either `0`, `1`, or `2`.
**Follow up:** Could you come up with a one-pass algorithm using only constant extra space? | A rather straight forward solution is a two-pass algorithm using counting sort. Iterate the array counting number of 0's, 1's, and 2's. Overwrite array with the total number of 0's, then 1's and followed by 2's. |
Solution | minimum-window-substring | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string minWindow(string s, string t) {\n vector<int> map(128,0);\n for (char c : t) {\n map[c]++;\n }\n\n int counter = t.size(), begin = 0, end = 0, d = INT_MAX, head = 0;\n while (end < s.size()){\n if (map[s[end++]]-- > 0) {\n counter--;\n }\n while (counter == 0) {\n if (end - begin < d) {\n head = begin;\n d = end - head;\n }\n if (map[s[begin++]]++ == 0) {\n counter++;\n }\n } \n }\n return d == INT_MAX ? "" : s.substr(head, d);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if len(s) < len(t):\n return ""\n needstr = collections.defaultdict(int)\n for ch in t:\n needstr[ch] += 1\n needcnt = len(t)\n res = (0, float(\'inf\'))\n start = 0\n for end, ch in enumerate(s):\n if needstr[ch] > 0:\n needcnt -= 1\n needstr[ch] -= 1\n if needcnt == 0:\n while True:\n tmp = s[start]\n if needstr[tmp] == 0:\n break\n needstr[tmp] += 1\n start += 1\n if end - start < res[1] - res[0]:\n res = (start, end)\n needstr[s[start]] += 1\n needcnt += 1\n start += 1\n return \'\' if res[1] > len(s) else s[res[0]:res[1]+1]\n```\n\n```Java []\nclass Solution {\n public String minWindow(String s, String t) {\n if (s == null || t == null || s.length() ==0 || t.length() == 0 ||\n s.length() < t.length()) {\n return new String();\n }\n int[] map = new int[128];\n int count = t.length();\n int start = 0, end = 0, minLen = Integer.MAX_VALUE,startIndex =0;\n for (char c :t.toCharArray()) {\n map[c]++;\n }\n char[] chS = s.toCharArray();\n while (end < chS.length) {\n if (map[chS[end++]]-- >0) {\n count--;\n }\n while (count == 0) {\n if (end - start < minLen) {\n startIndex = start;\n minLen = end - start;\n }\n if (map[chS[start++]]++ == 0) {\n count++;\n }\n }\n }\n\n return minLen == Integer.MAX_VALUE? new String():\n new String(chS,startIndex,minLen);\n }\n}\n```\n | 477 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Solution | minimum-window-substring | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string minWindow(string s, string t) {\n vector<int> map(128,0);\n for (char c : t) {\n map[c]++;\n }\n\n int counter = t.size(), begin = 0, end = 0, d = INT_MAX, head = 0;\n while (end < s.size()){\n if (map[s[end++]]-- > 0) {\n counter--;\n }\n while (counter == 0) {\n if (end - begin < d) {\n head = begin;\n d = end - head;\n }\n if (map[s[begin++]]++ == 0) {\n counter++;\n }\n } \n }\n return d == INT_MAX ? "" : s.substr(head, d);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if len(s) < len(t):\n return ""\n needstr = collections.defaultdict(int)\n for ch in t:\n needstr[ch] += 1\n needcnt = len(t)\n res = (0, float(\'inf\'))\n start = 0\n for end, ch in enumerate(s):\n if needstr[ch] > 0:\n needcnt -= 1\n needstr[ch] -= 1\n if needcnt == 0:\n while True:\n tmp = s[start]\n if needstr[tmp] == 0:\n break\n needstr[tmp] += 1\n start += 1\n if end - start < res[1] - res[0]:\n res = (start, end)\n needstr[s[start]] += 1\n needcnt += 1\n start += 1\n return \'\' if res[1] > len(s) else s[res[0]:res[1]+1]\n```\n\n```Java []\nclass Solution {\n public String minWindow(String s, String t) {\n if (s == null || t == null || s.length() ==0 || t.length() == 0 ||\n s.length() < t.length()) {\n return new String();\n }\n int[] map = new int[128];\n int count = t.length();\n int start = 0, end = 0, minLen = Integer.MAX_VALUE,startIndex =0;\n for (char c :t.toCharArray()) {\n map[c]++;\n }\n char[] chS = s.toCharArray();\n while (end < chS.length) {\n if (map[chS[end++]]-- >0) {\n count--;\n }\n while (count == 0) {\n if (end - start < minLen) {\n startIndex = start;\n minLen = end - start;\n }\n if (map[chS[start++]]++ == 0) {\n count++;\n }\n }\n }\n\n return minLen == Integer.MAX_VALUE? new String():\n new String(chS,startIndex,minLen);\n }\n}\n```\n | 477 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
[Python3] Sliding window O(N+M) | minimum-window-substring | 0 | 1 | \n# Approach\nThis problem follows the Sliding Window pattern and has a lot of similarities with [567 Permutation in a String](https://leetcode.com/problems/permutation-in-string/description/) with one difference. In this problem, we need to find a substring having all characters of the pattern which means that the required substring can have some additional characters and doesn\u2019t need to be a permutation of the pattern. Here is how we will manage these differences:\n\n1. We will keep a running count of every matching instance of a character.\n2. Whenever we have matched all the characters, we will try to shrink the window from the beginning, keeping track of the smallest substring that has all the matching characters.\n3. We will stop the shrinking process as soon as we remove a matched character from the sliding window. One thing to note here is that we could have redundant matching characters, e.g., we might have two \u2018a\u2019 in the sliding window when we only need one \u2018a\u2019. In that case, when we encounter the first \u2018a\u2019, we will simply shrink the window without decrementing the matched count. We will decrement the matched count when the second \u2018a\u2019 goes out of the window.\n\n# Complexity\n- Time complexity:\nThe time complexity of the above algorithm will be O(N+M) where \u2018N\u2019 and \u2018M\u2019 are the number of characters in the input string and the pattern respectively.\n\n- Space complexity:\nThe space complexity of the algorithm is O(M) since in the worst case, the whole pattern can have distinct characters which will go into the HashMap. In the worst case, we also need O(N) space for the resulting substring, which will happen when the input string is a permutation of the pattern.\n\n# Code\n```python3 []\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if len(s) < len(t): return \'\'\n \n need, match, l, start, windowLen = Counter(t), 0, 0, 0, len(s) + 1\n \n for r, ch in enumerate(s):\n if ch in need:\n need[ch] -= 1\n match += need[ch] == 0\n\n while match == len(need):\n if windowLen > r - l + 1:\n start, windowLen = l, r - l + 1\n \n removeCh = s[l]\n l += 1 \n if removeCh in need:\n match -= need[removeCh] == 0\n need[removeCh] += 1\n\n return s[start:start + windowLen] if windowLen <= len(s) else \'\'\n``` | 5 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
[Python3] Sliding window O(N+M) | minimum-window-substring | 0 | 1 | \n# Approach\nThis problem follows the Sliding Window pattern and has a lot of similarities with [567 Permutation in a String](https://leetcode.com/problems/permutation-in-string/description/) with one difference. In this problem, we need to find a substring having all characters of the pattern which means that the required substring can have some additional characters and doesn\u2019t need to be a permutation of the pattern. Here is how we will manage these differences:\n\n1. We will keep a running count of every matching instance of a character.\n2. Whenever we have matched all the characters, we will try to shrink the window from the beginning, keeping track of the smallest substring that has all the matching characters.\n3. We will stop the shrinking process as soon as we remove a matched character from the sliding window. One thing to note here is that we could have redundant matching characters, e.g., we might have two \u2018a\u2019 in the sliding window when we only need one \u2018a\u2019. In that case, when we encounter the first \u2018a\u2019, we will simply shrink the window without decrementing the matched count. We will decrement the matched count when the second \u2018a\u2019 goes out of the window.\n\n# Complexity\n- Time complexity:\nThe time complexity of the above algorithm will be O(N+M) where \u2018N\u2019 and \u2018M\u2019 are the number of characters in the input string and the pattern respectively.\n\n- Space complexity:\nThe space complexity of the algorithm is O(M) since in the worst case, the whole pattern can have distinct characters which will go into the HashMap. In the worst case, we also need O(N) space for the resulting substring, which will happen when the input string is a permutation of the pattern.\n\n# Code\n```python3 []\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if len(s) < len(t): return \'\'\n \n need, match, l, start, windowLen = Counter(t), 0, 0, 0, len(s) + 1\n \n for r, ch in enumerate(s):\n if ch in need:\n need[ch] -= 1\n match += need[ch] == 0\n\n while match == len(need):\n if windowLen > r - l + 1:\n start, windowLen = l, r - l + 1\n \n removeCh = s[l]\n l += 1 \n if removeCh in need:\n match -= need[removeCh] == 0\n need[removeCh] += 1\n\n return s[start:start + windowLen] if windowLen <= len(s) else \'\'\n``` | 5 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
✅ Explained - Simple and Clear Python3 Code✅ | minimum-window-substring | 0 | 1 | \n# Approach\n\nThe solution utilizes a sliding window approach to find the minimum window substring in string s that includes all characters from string t.\n\nInitially, the algorithm initializes the necessary data structures to keep track of character counts. It iterates through s to identify the leftmost character in s that is also present in t, which becomes the starting point of the window.\n\nAs the algorithm progresses, it moves the right pointer to expand the window, incrementing the count of characters from t encountered along the way. Whenever the current window contains all the required characters from t, it checks if it is the smallest window encountered so far and updates the result accordingly.\n\nTo find the next potential window, the algorithm shifts the left pointer while maintaining the validity of the window. It decrements the count of the character at the left pointer and moves the left pointer to the next valid position until the condition of including all characters from t is no longer satisfied.\n\nThe process continues until the right pointer reaches the end of s. Finally, the algorithm returns the result, which represents the minimum window substring containing all characters from t. If no such substring is found, an empty string is returned.\n\n\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n ans=""\n occ = collections.Counter(t)\n track = dict()\n\n def test():\n for key, val in occ.items():\n if val >track[key]:\n return False\n return True\n\n #init\n for k in occ.keys():\n track.update({k : 0})\n #first look\n left=0\n right=0\n for i in range(len(s)):\n if s[i] in occ.keys():\n left=i\n break\n \n for i in range(left,len(s)):\n \n #move right\n right=i\n if s[i] in occ.keys():\n track.update({s[i]:track[s[i]]+1})\n while test():\n w=s[left:right+1]\n if ans=="" or len(w)<len(ans):\n ans=w\n #move left\n track.update({s[left]:track[s[left]]-1})\n\n for j in range(left+1,right+1):\n if s[j] in occ.keys():\n left=j\n break\n if (test()):\n if ans=="" or len(w)<len(ans):\n ans=w\n return ans\n\n\n``` | 6 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
✅ Explained - Simple and Clear Python3 Code✅ | minimum-window-substring | 0 | 1 | \n# Approach\n\nThe solution utilizes a sliding window approach to find the minimum window substring in string s that includes all characters from string t.\n\nInitially, the algorithm initializes the necessary data structures to keep track of character counts. It iterates through s to identify the leftmost character in s that is also present in t, which becomes the starting point of the window.\n\nAs the algorithm progresses, it moves the right pointer to expand the window, incrementing the count of characters from t encountered along the way. Whenever the current window contains all the required characters from t, it checks if it is the smallest window encountered so far and updates the result accordingly.\n\nTo find the next potential window, the algorithm shifts the left pointer while maintaining the validity of the window. It decrements the count of the character at the left pointer and moves the left pointer to the next valid position until the condition of including all characters from t is no longer satisfied.\n\nThe process continues until the right pointer reaches the end of s. Finally, the algorithm returns the result, which represents the minimum window substring containing all characters from t. If no such substring is found, an empty string is returned.\n\n\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n ans=""\n occ = collections.Counter(t)\n track = dict()\n\n def test():\n for key, val in occ.items():\n if val >track[key]:\n return False\n return True\n\n #init\n for k in occ.keys():\n track.update({k : 0})\n #first look\n left=0\n right=0\n for i in range(len(s)):\n if s[i] in occ.keys():\n left=i\n break\n \n for i in range(left,len(s)):\n \n #move right\n right=i\n if s[i] in occ.keys():\n track.update({s[i]:track[s[i]]+1})\n while test():\n w=s[left:right+1]\n if ans=="" or len(w)<len(ans):\n ans=w\n #move left\n track.update({s[left]:track[s[left]]-1})\n\n for j in range(left+1,right+1):\n if s[j] in occ.keys():\n left=j\n break\n if (test()):\n if ans=="" or len(w)<len(ans):\n ans=w\n return ans\n\n\n``` | 6 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Min Window Substring, let me know if something is missing. | minimum-window-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem seems to be about finding the minimum window in string `str1` that contains all characters of string `str2`. The idea is to use a sliding window approach, maintaining counts of characters in both strings and adjusting the window based on these counts.\n\nCredit goes to Neetcode.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two hashmaps, `countT` and `window`, to store the counts of characters in `str2` and the current window of characters in `str1`.\n2. Iterate through `str2` and count the occurrences of each character, storing the counts in `countT`.\n3. Initialize variables `result` to store the result window indices, `resLen` to store the length of the minimum window, and `have` and `need` to keep track of the characters needed and found in the current window.\n4. Use two pointers, `l` and `r`, to represent the left and right boundaries of the window.\n5. Iterate through `str1` using the right pointer `r`, updating the counts in the `window` hashmap.\n6. Check if the current character at `r` is in `countT`, and if its count in the `window` matches the count in `countT`. If so, increment the `have` count.\n7. Check if `have` is equal to `need`. If true, it means all characters from `str2` are found in the current window, so we try to minimize the window by moving the left pointer `l` until the window no longer contains all characters from `str2`.\n8. Update the result and `resLen` if the current window is smaller than the previously stored minimum window.\n9. Repeat steps 5-8 until the right pointer `r` reaches the end of `str1`.\n10. Finally, return the minimum window substring using the indices stored in the `result` variable.\n\n\n# Complexity\n- Time complexity: O(n), where n is the length of `str1`. Both the left and right pointers traverse the string once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n\n- Space complexity: O(n), where n is the number of characters in str2. The space is used for the two hashmaps (countT and window).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minWindow(self, str1: str, str2: str) -> str:\n if len(str1) < len(str2):\n return ""\n\n # using hashmaps\n countT, window = {}, {}\n\n for c in str2:\n countT[c] = 1 + countT.get(c, 0)\n # counting chars in str2 \n\n result = [-1,-1] # this is to save the result pointers\n resLen = float("infinity")\n have , need = 0 , len(countT)\n # these variable are used to check if met the result or not \n\n l = 0 # left pointer, r is right pointer \n for r in range(len(str1)):\n chr = str1[r] # character from str1 \n # add this in hashmap ie window\n window[chr] = 1 + window.get(chr, 0)\n\n if chr in countT and window[chr] == countT[chr]:\n have += 1\n \n # now if have == need means we got the result then we \n # start decreasing the result to get min from left side of result\n\n while have == need:\n # update the result \n if (r - l + 1) < resLen:\n result = [l, r]\n resLen = (r - l + 1)\n \n # decrease the length of the result, also we use while above \n # if after decreasing the length of result from left side and have is same \n # as need then we can update the result as we have to return min length\n\n window[str1[l]] -= 1\n\n # now checking if the character we removed is in need too\n # then we have decrease the count of have as well to maintain it\n\n if str1[l] in countT and window[str1[l]] < countT[str1[l]]:\n have -= 1\n l += 1\n \n l, r = result\n return str1[l:r+1] if resLen != float("infinity") else ""\n\n\n\n\n``` | 0 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Min Window Substring, let me know if something is missing. | minimum-window-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem seems to be about finding the minimum window in string `str1` that contains all characters of string `str2`. The idea is to use a sliding window approach, maintaining counts of characters in both strings and adjusting the window based on these counts.\n\nCredit goes to Neetcode.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two hashmaps, `countT` and `window`, to store the counts of characters in `str2` and the current window of characters in `str1`.\n2. Iterate through `str2` and count the occurrences of each character, storing the counts in `countT`.\n3. Initialize variables `result` to store the result window indices, `resLen` to store the length of the minimum window, and `have` and `need` to keep track of the characters needed and found in the current window.\n4. Use two pointers, `l` and `r`, to represent the left and right boundaries of the window.\n5. Iterate through `str1` using the right pointer `r`, updating the counts in the `window` hashmap.\n6. Check if the current character at `r` is in `countT`, and if its count in the `window` matches the count in `countT`. If so, increment the `have` count.\n7. Check if `have` is equal to `need`. If true, it means all characters from `str2` are found in the current window, so we try to minimize the window by moving the left pointer `l` until the window no longer contains all characters from `str2`.\n8. Update the result and `resLen` if the current window is smaller than the previously stored minimum window.\n9. Repeat steps 5-8 until the right pointer `r` reaches the end of `str1`.\n10. Finally, return the minimum window substring using the indices stored in the `result` variable.\n\n\n# Complexity\n- Time complexity: O(n), where n is the length of `str1`. Both the left and right pointers traverse the string once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n\n- Space complexity: O(n), where n is the number of characters in str2. The space is used for the two hashmaps (countT and window).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minWindow(self, str1: str, str2: str) -> str:\n if len(str1) < len(str2):\n return ""\n\n # using hashmaps\n countT, window = {}, {}\n\n for c in str2:\n countT[c] = 1 + countT.get(c, 0)\n # counting chars in str2 \n\n result = [-1,-1] # this is to save the result pointers\n resLen = float("infinity")\n have , need = 0 , len(countT)\n # these variable are used to check if met the result or not \n\n l = 0 # left pointer, r is right pointer \n for r in range(len(str1)):\n chr = str1[r] # character from str1 \n # add this in hashmap ie window\n window[chr] = 1 + window.get(chr, 0)\n\n if chr in countT and window[chr] == countT[chr]:\n have += 1\n \n # now if have == need means we got the result then we \n # start decreasing the result to get min from left side of result\n\n while have == need:\n # update the result \n if (r - l + 1) < resLen:\n result = [l, r]\n resLen = (r - l + 1)\n \n # decrease the length of the result, also we use while above \n # if after decreasing the length of result from left side and have is same \n # as need then we can update the result as we have to return min length\n\n window[str1[l]] -= 1\n\n # now checking if the character we removed is in need too\n # then we have decrease the count of have as well to maintain it\n\n if str1[l] in countT and window[str1[l]] < countT[str1[l]]:\n have -= 1\n l += 1\n \n l, r = result\n return str1[l:r+1] if resLen != float("infinity") else ""\n\n\n\n\n``` | 0 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
O( n )✅ | Python (Step by step explanation)✅ | minimum-window-substring | 0 | 1 | # Intuition\nThe problem requires finding the minimum window in string \'s\' that contains all characters from string \'t\'. We can use a sliding window approach to solve this problem efficiently.\n\n# Approach\n1. First, we handle the edge case: if \'t\' is an empty string, we return an empty string as the result.\n\n2. We initialize two dictionaries, \'t_counter\' and \'window\', to keep track of character counts in \'t\' and the current window, respectively.\n\n3. We populate \'t_counter\' by iterating through the characters of \'t\' and incrementing their counts. It helps us keep track of the characters we need to match in \'s\'.\n\n4. We define \'have\' to track how many required characters we have in our current window and \'need\' to represent the total number of characters required. We also initialize \'ans\' and \'ans_size\' to store the minimum window and its size. \'ans\' starts as [-1, -1] to represent an invalid window, and \'ans_size\' starts as positive infinity.\n\n5. We set \'left\' to 0 as the start of our sliding window.\n\n6. We iterate through \'s\' using a \'right\' pointer to expand the window:\n - Update \'window\' to keep track of character counts in the current window.\n - If the character at \'right\' is in \'t_counter\' and its count in \'window\' matches its count in \'t_counter\', we increment \'have\'.\n\n7. We enter a while loop as long as we have all required characters in our window:\n - If the current window size is smaller than \'ans_size\', we update \'ans\' and \'ans_size\' to record this as a potential minimum window.\n - We decrement the count of the character at \'left\' in \'window\'.\n - If the character at \'left\' is in \'t_counter\' and its count in \'window\' is less than its count in \'t_counter\', we decrement \'have\'.\n - We move \'left\' to the right to shrink the window.\n\n8. After the loop, we have found the minimum window. We return the substring of \'s\' from \'ans[0]\' to \'ans[1]\' if \'ans_size\' is not still equal to positive infinity. Otherwise, we return an empty string.\n\n# Complexity\n- Time complexity: O(s + t), where \'s\' is the length of string \'s\' and \'t\' is the length of string \'t\'.\n- Space complexity: O(s + t) due to the dictionaries \'t_counter\' and \'window\'.\n\n\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if t=="" : return ""\n\n t_counter , window = {} , {}\n\n for x in t:\n t_counter[x] = 1 + t_counter.get(x , 0)\n\n have , need = 0 , len(t_counter)\n ans , ans_size = [-1 , -1] , float("infinity") \n left = 0\n\n for right in range(len(s)):\n window[s[right]] = 1 + window.get(s[right] , 0)\n\n if s[right] in t_counter and window[s[right]] == t_counter[s[right]] :\n have += 1\n\n while have == need :\n if (right - left + 1) < ans_size:\n ans = [left , right] \n ans_size = (right - left + 1)\n\n window[s[left]] -= 1\n if s[left] in t_counter and window[s[left]] < t_counter[s[left]] :\n have -= 1\n left += 1\n\n return s[ans[0] : ans[1]+1] if ans_size != float("infinity") else "" \n \n```\n\n# Please upvote the solution if you understood it.\n\n | 3 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
O( n )✅ | Python (Step by step explanation)✅ | minimum-window-substring | 0 | 1 | # Intuition\nThe problem requires finding the minimum window in string \'s\' that contains all characters from string \'t\'. We can use a sliding window approach to solve this problem efficiently.\n\n# Approach\n1. First, we handle the edge case: if \'t\' is an empty string, we return an empty string as the result.\n\n2. We initialize two dictionaries, \'t_counter\' and \'window\', to keep track of character counts in \'t\' and the current window, respectively.\n\n3. We populate \'t_counter\' by iterating through the characters of \'t\' and incrementing their counts. It helps us keep track of the characters we need to match in \'s\'.\n\n4. We define \'have\' to track how many required characters we have in our current window and \'need\' to represent the total number of characters required. We also initialize \'ans\' and \'ans_size\' to store the minimum window and its size. \'ans\' starts as [-1, -1] to represent an invalid window, and \'ans_size\' starts as positive infinity.\n\n5. We set \'left\' to 0 as the start of our sliding window.\n\n6. We iterate through \'s\' using a \'right\' pointer to expand the window:\n - Update \'window\' to keep track of character counts in the current window.\n - If the character at \'right\' is in \'t_counter\' and its count in \'window\' matches its count in \'t_counter\', we increment \'have\'.\n\n7. We enter a while loop as long as we have all required characters in our window:\n - If the current window size is smaller than \'ans_size\', we update \'ans\' and \'ans_size\' to record this as a potential minimum window.\n - We decrement the count of the character at \'left\' in \'window\'.\n - If the character at \'left\' is in \'t_counter\' and its count in \'window\' is less than its count in \'t_counter\', we decrement \'have\'.\n - We move \'left\' to the right to shrink the window.\n\n8. After the loop, we have found the minimum window. We return the substring of \'s\' from \'ans[0]\' to \'ans[1]\' if \'ans_size\' is not still equal to positive infinity. Otherwise, we return an empty string.\n\n# Complexity\n- Time complexity: O(s + t), where \'s\' is the length of string \'s\' and \'t\' is the length of string \'t\'.\n- Space complexity: O(s + t) due to the dictionaries \'t_counter\' and \'window\'.\n\n\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if t=="" : return ""\n\n t_counter , window = {} , {}\n\n for x in t:\n t_counter[x] = 1 + t_counter.get(x , 0)\n\n have , need = 0 , len(t_counter)\n ans , ans_size = [-1 , -1] , float("infinity") \n left = 0\n\n for right in range(len(s)):\n window[s[right]] = 1 + window.get(s[right] , 0)\n\n if s[right] in t_counter and window[s[right]] == t_counter[s[right]] :\n have += 1\n\n while have == need :\n if (right - left + 1) < ans_size:\n ans = [left , right] \n ans_size = (right - left + 1)\n\n window[s[left]] -= 1\n if s[left] in t_counter and window[s[left]] < t_counter[s[left]] :\n have -= 1\n left += 1\n\n return s[ans[0] : ans[1]+1] if ans_size != float("infinity") else "" \n \n```\n\n# Please upvote the solution if you understood it.\n\n | 3 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Step by step solution with O(N) time and O(1) space complexity | minimum-window-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe most obvious way to do it is brute force with sliding window where we can check if all characters of t is present in a given window of string s where we slide the window on s , however we can optimize the solution using two hashmaps and checking how manys keys of s\'s hashmap meets that of t\'s hashmap and update two variables **have** and **need** . We can check if the given window of s has all chars of t if need == have \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Return empty string if len(s) < len(t) || len(t) = 0 \n2) Intialize needmap() for s and havemap() for t\n3) add all chars along with their count to needmap and update havemap with 0 values for all char in t \n4) Intialize res and len(res) = \'inf\' ,have = 0 , need = len(havemap)\n5) Iterate through the array with r , check if s[r] is a key in needmap , increment havemap[s[r]] with 1\n6) Check if havemap[s[r]] == needmap[s[r]]\n then increment have by 1\n7) Use a while loop to update the left pointer when need == have\n8) if window length is less than resLen , then update resLen and res \n9) Check if s[l] is in havemap then decrement havemap[s[l]] -= 1 \n10) Check if needmap[s[l]] > havemap[s[l]] then decrement have by 1\n11) Finally Increment the left pointer \n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(52) = O(1) $$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n # base case \n if t =="" or len(s) < len(t): return ""\n\n # Intialize and set needmap(string t) and havemap(window)\n needmap , havemap = {} , {} \n for c in t:\n needmap[c] = needmap.get(c,0) + 1 # t char count \n havemap[c] = 0 # intialize with t chars and 0 as value for all keys\n \n need , have = len(needmap) , 0 \n l = 0 \n res , resLen = "" , float("infinity")\n for r in range(len(s)):\n if s[r] in needmap: # check if it is a char in t \n havemap[s[r]] += 1 # update count in window \n if havemap[s[r]] == needmap[s[r]] : # compare the count of window and t\'s counter \n have += 1 \n while(have == need) : # to reduce window size to optimal value until valid \n if resLen > r-l+1:\n resLen = r-l+1 # update results \n res = s[l:r+1]\n if s[l] in havemap :\n havemap[s[l]] -= 1 # update window counter \n if needmap[s[l]] > havemap[s[l]] : \n have -= 1\n l+=1 # increment left pointer of the window \n return res \n \n\n\n``` | 2 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Step by step solution with O(N) time and O(1) space complexity | minimum-window-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe most obvious way to do it is brute force with sliding window where we can check if all characters of t is present in a given window of string s where we slide the window on s , however we can optimize the solution using two hashmaps and checking how manys keys of s\'s hashmap meets that of t\'s hashmap and update two variables **have** and **need** . We can check if the given window of s has all chars of t if need == have \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Return empty string if len(s) < len(t) || len(t) = 0 \n2) Intialize needmap() for s and havemap() for t\n3) add all chars along with their count to needmap and update havemap with 0 values for all char in t \n4) Intialize res and len(res) = \'inf\' ,have = 0 , need = len(havemap)\n5) Iterate through the array with r , check if s[r] is a key in needmap , increment havemap[s[r]] with 1\n6) Check if havemap[s[r]] == needmap[s[r]]\n then increment have by 1\n7) Use a while loop to update the left pointer when need == have\n8) if window length is less than resLen , then update resLen and res \n9) Check if s[l] is in havemap then decrement havemap[s[l]] -= 1 \n10) Check if needmap[s[l]] > havemap[s[l]] then decrement have by 1\n11) Finally Increment the left pointer \n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(52) = O(1) $$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n # base case \n if t =="" or len(s) < len(t): return ""\n\n # Intialize and set needmap(string t) and havemap(window)\n needmap , havemap = {} , {} \n for c in t:\n needmap[c] = needmap.get(c,0) + 1 # t char count \n havemap[c] = 0 # intialize with t chars and 0 as value for all keys\n \n need , have = len(needmap) , 0 \n l = 0 \n res , resLen = "" , float("infinity")\n for r in range(len(s)):\n if s[r] in needmap: # check if it is a char in t \n havemap[s[r]] += 1 # update count in window \n if havemap[s[r]] == needmap[s[r]] : # compare the count of window and t\'s counter \n have += 1 \n while(have == need) : # to reduce window size to optimal value until valid \n if resLen > r-l+1:\n resLen = r-l+1 # update results \n res = s[l:r+1]\n if s[l] in havemap :\n havemap[s[l]] -= 1 # update window counter \n if needmap[s[l]] > havemap[s[l]] : \n have -= 1\n l+=1 # increment left pointer of the window \n return res \n \n\n\n``` | 2 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Simple Python sliding window solution with detailed explanation | minimum-window-substring | 0 | 1 | ```\nfrom collections import Counter\n\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n \'\'\'\n Keep t_counter of char counts in t\n \n We make a sliding window across s, tracking the char counts in s_counter\n We keep track of matches, the number of chars with matching counts in s_counter and t_counter\n Increment or decrement matches based on how the sliding window changes\n When matches == len(t_counter.keys()), we have a valid window. Update the answer accordingly\n \n How we slide the window:\n Extend when matches < chars, because we can only get a valid window by adding more.\n Contract when matches == chars, because we could possibly do better than the current window.\n \n How we update matches:\n This only applies if t_counter[x] > 0.\n If s_counter[x] is increased to match t_counter[x], matches += 1\n If s_counter[x] is increased to be more than t_counter[x], do nothing\n If s_counter[x] is decreased to be t_counter[x] - 1, matches -= 1\n If s_counter[x] is decreased to be less than t_counter[x] - 1, do nothing\n \n Analysis:\n O(s + t) time: O(t) to build t_counter, then O(s) to move our sliding window across s. Each index is only visited twice.\n O(s + t) space: O(t) space for t_counter and O(s) space for s_counter\n \'\'\'\n \n if not s or not t or len(s) < len(t):\n return \'\'\n \n t_counter = Counter(t)\n chars = len(t_counter.keys())\n \n s_counter = Counter()\n matches = 0\n \n answer = \'\'\n \n i = 0\n j = -1 # make j = -1 to start, so we can move it forward and put s[0] in s_counter in the extend phase \n \n while i < len(s):\n \n # extend\n if matches < chars:\n \n # since we don\'t have enough matches and j is at the end of the string, we have no way to increase matches\n if j == len(s) - 1:\n return answer\n \n j += 1\n s_counter[s[j]] += 1\n if t_counter[s[j]] > 0 and s_counter[s[j]] == t_counter[s[j]]:\n matches += 1\n\n # contract\n else:\n s_counter[s[i]] -= 1\n if t_counter[s[i]] > 0 and s_counter[s[i]] == t_counter[s[i]] - 1:\n matches -= 1\n i += 1\n \n # update answer\n if matches == chars:\n if not answer:\n answer = s[i:j+1]\n elif (j - i + 1) < len(answer):\n answer = s[i:j+1]\n \n return answer\n``` | 111 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Simple Python sliding window solution with detailed explanation | minimum-window-substring | 0 | 1 | ```\nfrom collections import Counter\n\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n \'\'\'\n Keep t_counter of char counts in t\n \n We make a sliding window across s, tracking the char counts in s_counter\n We keep track of matches, the number of chars with matching counts in s_counter and t_counter\n Increment or decrement matches based on how the sliding window changes\n When matches == len(t_counter.keys()), we have a valid window. Update the answer accordingly\n \n How we slide the window:\n Extend when matches < chars, because we can only get a valid window by adding more.\n Contract when matches == chars, because we could possibly do better than the current window.\n \n How we update matches:\n This only applies if t_counter[x] > 0.\n If s_counter[x] is increased to match t_counter[x], matches += 1\n If s_counter[x] is increased to be more than t_counter[x], do nothing\n If s_counter[x] is decreased to be t_counter[x] - 1, matches -= 1\n If s_counter[x] is decreased to be less than t_counter[x] - 1, do nothing\n \n Analysis:\n O(s + t) time: O(t) to build t_counter, then O(s) to move our sliding window across s. Each index is only visited twice.\n O(s + t) space: O(t) space for t_counter and O(s) space for s_counter\n \'\'\'\n \n if not s or not t or len(s) < len(t):\n return \'\'\n \n t_counter = Counter(t)\n chars = len(t_counter.keys())\n \n s_counter = Counter()\n matches = 0\n \n answer = \'\'\n \n i = 0\n j = -1 # make j = -1 to start, so we can move it forward and put s[0] in s_counter in the extend phase \n \n while i < len(s):\n \n # extend\n if matches < chars:\n \n # since we don\'t have enough matches and j is at the end of the string, we have no way to increase matches\n if j == len(s) - 1:\n return answer\n \n j += 1\n s_counter[s[j]] += 1\n if t_counter[s[j]] > 0 and s_counter[s[j]] == t_counter[s[j]]:\n matches += 1\n\n # contract\n else:\n s_counter[s[i]] -= 1\n if t_counter[s[i]] > 0 and s_counter[s[i]] == t_counter[s[i]] - 1:\n matches -= 1\n i += 1\n \n # update answer\n if matches == chars:\n if not answer:\n answer = s[i:j+1]\n elif (j - i + 1) < len(answer):\n answer = s[i:j+1]\n \n return answer\n``` | 111 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
✅🔥Sliding Window Approach with Explanation - C++/Java/Python | minimum-window-substring | 1 | 1 | \n# Intuition\nIn this problem, we need to find the minimum window substring of string `s` that contains all characters from string `t`. We can use a sliding window approach to find the minimum window substring efficiently.\n\n# Approach 01\n1. Create an unordered_map `mp` to store the count of characters in string `t`.\n2. Initialize variables `ans`, `start`, and `count`.\n3. Use pointers `i` and `j` to iterate through string `s`.\n4. Decrement count of the current character in the map; if it becomes 0, decrement the `count` variable.\n5. Move pointer `i` to check if it is possible to remove more characters and get smaller substrings.\n6. Store the smaller length in `ans` and update the `start` variable.\n7. Add the current element to the map and increment the count if it becomes greater than 0.\n8. If `ans` has a length other than `INT_MAX`, return the substring from the `start` index to the length of `ans`; otherwise, return an empty string.\n\n# Complexity\n\n- Time complexity: The time complexity of this solution is O(m), where \'m\' is the length of string \'s\'. The algorithm iterates through the string once, and each iteration involves constant time operations.\n\n- Space complexity: The space complexity is O(n), where \'n\' is the length of string \'t\'. We use additional space for the unordered_map to store characters from \'t\'.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n string minWindow(string s, string t) {\n int m = s.size(), n = t.size();\n unordered_map<char, int> mp;\n\n int ans = INT_MAX;\n int start = 0;\n\n for (auto x : t)\n mp[x]++;\n\n int count = mp.size();\n\n int i = 0, j = 0;\n\n while (j < s.length()) {\n mp[s[j]]--;\n if (mp[s[j]] == 0)\n count--;\n\n if (count == 0) {\n while (count == 0) {\n if (ans > j - i + 1) {\n ans = j - i + 1;\n start = i;\n }\n mp[s[i]]++;\n if (mp[s[i]] > 0)\n count++;\n\n i++;\n }\n }\n j++;\n }\n if (ans != INT_MAX)\n return s.substr(start, ans);\n else\n return "";\n }\n};\n```\n```Java []\nclass Solution {\n public String minWindow(String s, String t) {\n int m = s.length(), n = t.length();\n HashMap<Character, Integer> mp = new HashMap<>();\n\n int ans = Integer.MAX_VALUE;\n int start = 0;\n\n for (char x : t.toCharArray())\n mp.put(x, mp.getOrDefault(x, 0) + 1);\n\n int count = mp.size();\n\n int i = 0, j = 0;\n\n while (j < s.length()) {\n mp.put(s.charAt(j), mp.getOrDefault(s.charAt(j), 0) - 1);\n if (mp.get(s.charAt(j)) == 0)\n count--;\n\n if (count == 0) {\n while (count == 0) {\n if (ans > j - i + 1) {\n ans = j - i + 1;\n start = i;\n }\n mp.put(s.charAt(i), mp.getOrDefault(s.charAt(i), 0) + 1);\n if (mp.get(s.charAt(i)) > 0)\n count++;\n\n i++;\n }\n }\n j++;\n }\n if (ans != Integer.MAX_VALUE)\n return s.substring(start, start + ans);\n else\n return "";\n }\n}\n```\n```python []\nclass Solution(object):\n def minWindow(self, s, t):\n m, n = len(s), len(t)\n mp = {}\n\n ans = float(\'inf\')\n start = 0\n\n for x in t:\n mp[x] = mp.get(x, 0) + 1\n\n count = len(mp)\n\n i = 0\n j = 0\n\n while j < len(s):\n mp[s[j]] = mp.get(s[j], 0) - 1\n if mp[s[j]] == 0:\n count -= 1\n\n if count == 0:\n while count == 0:\n if ans > j - i + 1:\n ans = j - i + 1\n start = i\n mp[s[i]] = mp.get(s[i], 0) + 1\n if mp[s[i]] > 0:\n count += 1\n\n i += 1\n j += 1\n\n if ans != float(\'inf\'):\n return s[start:start + ans]\n else:\n return ""\n```\n\n\n---\n\n> **Please upvote this solution**\n> | 57 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
✅🔥Sliding Window Approach with Explanation - C++/Java/Python | minimum-window-substring | 1 | 1 | \n# Intuition\nIn this problem, we need to find the minimum window substring of string `s` that contains all characters from string `t`. We can use a sliding window approach to find the minimum window substring efficiently.\n\n# Approach 01\n1. Create an unordered_map `mp` to store the count of characters in string `t`.\n2. Initialize variables `ans`, `start`, and `count`.\n3. Use pointers `i` and `j` to iterate through string `s`.\n4. Decrement count of the current character in the map; if it becomes 0, decrement the `count` variable.\n5. Move pointer `i` to check if it is possible to remove more characters and get smaller substrings.\n6. Store the smaller length in `ans` and update the `start` variable.\n7. Add the current element to the map and increment the count if it becomes greater than 0.\n8. If `ans` has a length other than `INT_MAX`, return the substring from the `start` index to the length of `ans`; otherwise, return an empty string.\n\n# Complexity\n\n- Time complexity: The time complexity of this solution is O(m), where \'m\' is the length of string \'s\'. The algorithm iterates through the string once, and each iteration involves constant time operations.\n\n- Space complexity: The space complexity is O(n), where \'n\' is the length of string \'t\'. We use additional space for the unordered_map to store characters from \'t\'.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n string minWindow(string s, string t) {\n int m = s.size(), n = t.size();\n unordered_map<char, int> mp;\n\n int ans = INT_MAX;\n int start = 0;\n\n for (auto x : t)\n mp[x]++;\n\n int count = mp.size();\n\n int i = 0, j = 0;\n\n while (j < s.length()) {\n mp[s[j]]--;\n if (mp[s[j]] == 0)\n count--;\n\n if (count == 0) {\n while (count == 0) {\n if (ans > j - i + 1) {\n ans = j - i + 1;\n start = i;\n }\n mp[s[i]]++;\n if (mp[s[i]] > 0)\n count++;\n\n i++;\n }\n }\n j++;\n }\n if (ans != INT_MAX)\n return s.substr(start, ans);\n else\n return "";\n }\n};\n```\n```Java []\nclass Solution {\n public String minWindow(String s, String t) {\n int m = s.length(), n = t.length();\n HashMap<Character, Integer> mp = new HashMap<>();\n\n int ans = Integer.MAX_VALUE;\n int start = 0;\n\n for (char x : t.toCharArray())\n mp.put(x, mp.getOrDefault(x, 0) + 1);\n\n int count = mp.size();\n\n int i = 0, j = 0;\n\n while (j < s.length()) {\n mp.put(s.charAt(j), mp.getOrDefault(s.charAt(j), 0) - 1);\n if (mp.get(s.charAt(j)) == 0)\n count--;\n\n if (count == 0) {\n while (count == 0) {\n if (ans > j - i + 1) {\n ans = j - i + 1;\n start = i;\n }\n mp.put(s.charAt(i), mp.getOrDefault(s.charAt(i), 0) + 1);\n if (mp.get(s.charAt(i)) > 0)\n count++;\n\n i++;\n }\n }\n j++;\n }\n if (ans != Integer.MAX_VALUE)\n return s.substring(start, start + ans);\n else\n return "";\n }\n}\n```\n```python []\nclass Solution(object):\n def minWindow(self, s, t):\n m, n = len(s), len(t)\n mp = {}\n\n ans = float(\'inf\')\n start = 0\n\n for x in t:\n mp[x] = mp.get(x, 0) + 1\n\n count = len(mp)\n\n i = 0\n j = 0\n\n while j < len(s):\n mp[s[j]] = mp.get(s[j], 0) - 1\n if mp[s[j]] == 0:\n count -= 1\n\n if count == 0:\n while count == 0:\n if ans > j - i + 1:\n ans = j - i + 1\n start = i\n mp[s[i]] = mp.get(s[i], 0) + 1\n if mp[s[i]] > 0:\n count += 1\n\n i += 1\n j += 1\n\n if ans != float(\'inf\'):\n return s[start:start + ans]\n else:\n return ""\n```\n\n\n---\n\n> **Please upvote this solution**\n> | 57 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Simple python solution using two hash maps, beginner's friendly!! 💖🔥 | minimum-window-substring | 0 | 1 | \n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if t=="":\n return ""\n countT,hm={},{}\n for c in t:\n countT[c]=1+countT.get(c,0)\n \n have,need=0,len(countT)\n res=[-1,-1]\n reslen=float(\'infinity\')\n l=0\n for r in range(len(s)):\n c=s[r]\n hm[c]=1+hm.get(c,0)\n\n if c in countT and hm[c]==countT[c]:\n have+=1\n\n while have==need:\n if r-l+1 <reslen:\n res=[l,r]\n reslen=r-l+1\n\n hm[s[l]]-=1\n if s[l] in countT and hm[s[l]]<countT[s[l]]:\n have-=1\n l+=1\n l,r=res\n return s[l:r+1] if reslen != float(\'infinity\') else ""\n\n\n``` | 2 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Simple python solution using two hash maps, beginner's friendly!! 💖🔥 | minimum-window-substring | 0 | 1 | \n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n if t=="":\n return ""\n countT,hm={},{}\n for c in t:\n countT[c]=1+countT.get(c,0)\n \n have,need=0,len(countT)\n res=[-1,-1]\n reslen=float(\'infinity\')\n l=0\n for r in range(len(s)):\n c=s[r]\n hm[c]=1+hm.get(c,0)\n\n if c in countT and hm[c]==countT[c]:\n have+=1\n\n while have==need:\n if r-l+1 <reslen:\n res=[l,r]\n reslen=r-l+1\n\n hm[s[l]]-=1\n if s[l] in countT and hm[s[l]]<countT[s[l]]:\n have-=1\n l+=1\n l,r=res\n return s[l:r+1] if reslen != float(\'infinity\') else ""\n\n\n``` | 2 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
C++ - Easiest Beginner Friendly Sol || Sliding window | minimum-window-substring | 1 | 1 | # Intuition of this Problem:\nReference - https://leetcode.com/problems/minimum-window-substring/solutions/26808/here-is-a-10-line-template-that-can-solve-most-substring-problems/?orderBy=hot\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create a vector of size 128, m, to store the count of characters in string t.\n2. Initialize start and end pointers, counter and variables minStart and minLen to store the starting position and length of the minimum window substring.\n3. Traverse the string s from the end pointer and increase the end pointer until you find a valid window:\n4. If the current character in s exists in t, decrease the counter.\n5. Decrease the value of the current character in m.\n6. If a valid window is found, move the start pointer to find a smaller window:\n7. If the current window size is smaller than the minimum length found so far, update the minimum length and start position.\n8. Increase the value of the current character in m.\n9. If the current character exists in t, increase the counter.\n10. Repeat steps 3 and 4 until the end pointer reaches the end of the string s.\n11. If the minimum length is not equal to INT_MAX, return the minimum window substring, otherwise return an empty string.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n string minWindow(string s, string t) {\n\t vector<int> m(128, 0);\n\t // Statistic for count of char in t\n\t for (auto c : t) \n m[c]++;\n\t // counter represents the number of chars of t to be found in s.\n\t int start = 0, end = 0, counter = t.size(), minStart = 0, minLen = INT_MAX;\n\t int size = s.size();\n\t\n\t // Move end to find a valid window.\n\t while (end < size) {\n\t\t // If char in s exists in t, decrease counter\n\t\t if (m[s[end]] > 0)\n\t\t\t counter--;\n\t\t // Decrease m[s[end]]. If char does not exist in t, m[s[end]] will be negative.\n\t\t m[s[end]]--;\n\t\t end++;\n\t\t // When we found a valid window, move start to find smaller window.\n\t\t while (counter == 0) {\n\t\t\t if (end - start < minLen) {\n\t\t\t\t minStart = start;\n\t\t\t\t minLen = end - start;\n\t\t\t }\n\t\t\t m[s[start]]++;\n\t\t\t // When char exists in t, increase counter.\n\t\t\t if (m[s[start]] > 0)\n\t\t\t\t counter++;\n\t\t\t start++;\n\t\t }\n\t }\n\t if (minLen != INT_MAX)\n\t\t return s.substr(minStart, minLen);\n\t return "";\n }\n};\n```\n```Java []\nclass Solution {\n public String minWindow(String s, String t) {\n int[] m = new int[128];\n for (char c : t.toCharArray()) \n m[c]++;\n int start = 0, end = 0, counter = t.length(), minStart = 0, minLen = Integer.MAX_VALUE;\n int size = s.length();\n while (end < size) {\n if (m[s.charAt(end++)]-- > 0) \n counter--;\n while (counter == 0) {\n if (end - start < minLen) {\n minStart = start;\n minLen = end - start;\n }\n if (m[s.charAt(start++)]++ == 0) \n counter++;\n }\n }\n return minLen == Integer.MAX_VALUE ? "" : s.substring(minStart, minStart + minLen);\n }\n}\n\n```\n```Python []\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n m = [0] * 128\n for c in t:\n m[ord(c)] += 1\n start = 0\n end = 0\n counter = len(t)\n minStart = 0\n minLen = float(\'inf\')\n size = len(s)\n while end < size:\n if m[ord(s[end])] > 0:\n counter -= 1\n m[ord(s[end])] -= 1\n end += 1\n while counter == 0:\n if end - start < minLen:\n minStart = start\n minLen = end - start\n m[ord(s[start])] += 1\n if m[ord(s[start])] > 0:\n counter\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the length of the input string s. This is because the while loop runs at most 2n times in the worst case (when all characters of s are different from t).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**, as the size of the frequency vector is fixed at 128. This is because the ASCII character set has only 128 characters. The size of other variables used in the algorithm is constant and does not grow with the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 12 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
C++ - Easiest Beginner Friendly Sol || Sliding window | minimum-window-substring | 1 | 1 | # Intuition of this Problem:\nReference - https://leetcode.com/problems/minimum-window-substring/solutions/26808/here-is-a-10-line-template-that-can-solve-most-substring-problems/?orderBy=hot\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create a vector of size 128, m, to store the count of characters in string t.\n2. Initialize start and end pointers, counter and variables minStart and minLen to store the starting position and length of the minimum window substring.\n3. Traverse the string s from the end pointer and increase the end pointer until you find a valid window:\n4. If the current character in s exists in t, decrease the counter.\n5. Decrease the value of the current character in m.\n6. If a valid window is found, move the start pointer to find a smaller window:\n7. If the current window size is smaller than the minimum length found so far, update the minimum length and start position.\n8. Increase the value of the current character in m.\n9. If the current character exists in t, increase the counter.\n10. Repeat steps 3 and 4 until the end pointer reaches the end of the string s.\n11. If the minimum length is not equal to INT_MAX, return the minimum window substring, otherwise return an empty string.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n string minWindow(string s, string t) {\n\t vector<int> m(128, 0);\n\t // Statistic for count of char in t\n\t for (auto c : t) \n m[c]++;\n\t // counter represents the number of chars of t to be found in s.\n\t int start = 0, end = 0, counter = t.size(), minStart = 0, minLen = INT_MAX;\n\t int size = s.size();\n\t\n\t // Move end to find a valid window.\n\t while (end < size) {\n\t\t // If char in s exists in t, decrease counter\n\t\t if (m[s[end]] > 0)\n\t\t\t counter--;\n\t\t // Decrease m[s[end]]. If char does not exist in t, m[s[end]] will be negative.\n\t\t m[s[end]]--;\n\t\t end++;\n\t\t // When we found a valid window, move start to find smaller window.\n\t\t while (counter == 0) {\n\t\t\t if (end - start < minLen) {\n\t\t\t\t minStart = start;\n\t\t\t\t minLen = end - start;\n\t\t\t }\n\t\t\t m[s[start]]++;\n\t\t\t // When char exists in t, increase counter.\n\t\t\t if (m[s[start]] > 0)\n\t\t\t\t counter++;\n\t\t\t start++;\n\t\t }\n\t }\n\t if (minLen != INT_MAX)\n\t\t return s.substr(minStart, minLen);\n\t return "";\n }\n};\n```\n```Java []\nclass Solution {\n public String minWindow(String s, String t) {\n int[] m = new int[128];\n for (char c : t.toCharArray()) \n m[c]++;\n int start = 0, end = 0, counter = t.length(), minStart = 0, minLen = Integer.MAX_VALUE;\n int size = s.length();\n while (end < size) {\n if (m[s.charAt(end++)]-- > 0) \n counter--;\n while (counter == 0) {\n if (end - start < minLen) {\n minStart = start;\n minLen = end - start;\n }\n if (m[s.charAt(start++)]++ == 0) \n counter++;\n }\n }\n return minLen == Integer.MAX_VALUE ? "" : s.substring(minStart, minStart + minLen);\n }\n}\n\n```\n```Python []\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n m = [0] * 128\n for c in t:\n m[ord(c)] += 1\n start = 0\n end = 0\n counter = len(t)\n minStart = 0\n minLen = float(\'inf\')\n size = len(s)\n while end < size:\n if m[ord(s[end])] > 0:\n counter -= 1\n m[ord(s[end])] -= 1\n end += 1\n while counter == 0:\n if end - start < minLen:\n minStart = start\n minLen = end - start\n m[ord(s[start])] += 1\n if m[ord(s[start])] > 0:\n counter\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the length of the input string s. This is because the while loop runs at most 2n times in the worst case (when all characters of s are different from t).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**, as the size of the frequency vector is fixed at 128. This is because the ASCII character set has only 128 characters. The size of other variables used in the algorithm is constant and does not grow with the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 12 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python | My advice | minimum-window-substring | 0 | 1 | My advice for solving this problem is to:\n* Understand the intuition and what to do at a high level\n* Try to implement your own solution WITHOUT copying anyone elses\n* This is how you will learn\n* You will remember high level concepts, but never line for line code\n\nIntuition:\n* Two pointers, left and right\n* Both start from 0,0\n* Increase right pointer until valid window is found\n* Decrease left pointer until window is no longer valid\n* Add the minimum length window you\'ve found to your results\n* Continue increasing right pointer, pretty much repeating what we did above\n* Return the minimum length of your results\n\n\nMy code is AC but definitely not optimal, so I have some more learning & practice to do. I just wanted to share that by trying to implement & solve most of the problem yourself (after learning the high level concept), your learning is massive.\n\n\n```python\nfrom collections import Counter\n\n\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n \n # Define variables\n s_count, t_count = Counter(), Counter(t)\n \n l, r = 0, 0\n \n results = []\n \n while r <= len(s)-1:\n \n # Find valid window\n s_count[s[r]] += 1 \n r += 1\n if s_count & t_count != t_count:\n continue\n \n # Minimize this window\n while l < r:\n s_count[s[l]] -= 1 \n l += 1\n if s_count & t_count == t_count:\n continue\n results.append(s[l-1:r])\n break\n \n \n # Return result\n if not results:\n return "" \n return min(results, key=len)\n``` | 62 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python | My advice | minimum-window-substring | 0 | 1 | My advice for solving this problem is to:\n* Understand the intuition and what to do at a high level\n* Try to implement your own solution WITHOUT copying anyone elses\n* This is how you will learn\n* You will remember high level concepts, but never line for line code\n\nIntuition:\n* Two pointers, left and right\n* Both start from 0,0\n* Increase right pointer until valid window is found\n* Decrease left pointer until window is no longer valid\n* Add the minimum length window you\'ve found to your results\n* Continue increasing right pointer, pretty much repeating what we did above\n* Return the minimum length of your results\n\n\nMy code is AC but definitely not optimal, so I have some more learning & practice to do. I just wanted to share that by trying to implement & solve most of the problem yourself (after learning the high level concept), your learning is massive.\n\n\n```python\nfrom collections import Counter\n\n\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n \n # Define variables\n s_count, t_count = Counter(), Counter(t)\n \n l, r = 0, 0\n \n results = []\n \n while r <= len(s)-1:\n \n # Find valid window\n s_count[s[r]] += 1 \n r += 1\n if s_count & t_count != t_count:\n continue\n \n # Minimize this window\n while l < r:\n s_count[s[l]] -= 1 \n l += 1\n if s_count & t_count == t_count:\n continue\n results.append(s[l-1:r])\n break\n \n \n # Return result\n if not results:\n return "" \n return min(results, key=len)\n``` | 62 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python || Hashmap || Beats 98 % || Easy to understand | minimum-window-substring | 0 | 1 | # Approach\nFirst we will check the corner edge condititon. now create two hashmaps one that we need and one that we have and create one variable is to store window size and one list to store the window information. count the frequency of all the character that we need. we will also initalise a variable **have** as 0 and **need** as length of needmap and we will intialise one pointer l as 0 and iterate using other pointer. first store the character at current iteration in the havemap. check if it is in t and if it\'s frequency is equal to what we needed. if it is equal than increment **have** variable. check if **have** is equal to **need** that means we found the substring that contains all the character that we wanted. now we will check if it is minimum and we will also shrink the window. first we will check if the window size is less than what we had, if it is than we will store this window size and its info. After that we will shrink the window from left side, first we will remove it\'s freq from havemap then we will check if it is a part of **t** and if removing it will dissatisfy the condition, if it is then we will decrement the have variable and we will now increment the left pointer to shrink the window. \nIt can be possible that the string doesn\'t even exist. In that case we will return empty string.\n\n# Complexity\n- Time complexity:$$O(n)$$\n\n- Space complexity:$$O(n)$$\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n\n if t=="": return ""\n\n have = 0\n needmap = {}\n havemap = {}\n\n res = float(\'inf\')\n resl = [0,len(s)]\n\n for i in t:\n needmap[i] = 1 + needmap.get(i,0)\n\n need = len(needmap) \n\n l = 0 \n\n for r in range(len(s)):\n\n havemap[s[r]] = 1 + havemap.get(s[r],0)\n\n if s[r] in needmap and havemap[s[r]]==needmap[s[r]]:\n have+=1\n\n while have==need:\n \n if (r-l+1)<res:\n res = r-l+1\n resl = [l,r]\n\n havemap[s[l]]-=1 \n\n if s[l] in needmap and havemap[s[l]]<needmap[s[l]]:\n have-=1\n\n l+=1 \n\n l,r = resl\n\n return s[l:r+1] if res!=float(\'inf\') else ""\n\n``` | 3 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python || Hashmap || Beats 98 % || Easy to understand | minimum-window-substring | 0 | 1 | # Approach\nFirst we will check the corner edge condititon. now create two hashmaps one that we need and one that we have and create one variable is to store window size and one list to store the window information. count the frequency of all the character that we need. we will also initalise a variable **have** as 0 and **need** as length of needmap and we will intialise one pointer l as 0 and iterate using other pointer. first store the character at current iteration in the havemap. check if it is in t and if it\'s frequency is equal to what we needed. if it is equal than increment **have** variable. check if **have** is equal to **need** that means we found the substring that contains all the character that we wanted. now we will check if it is minimum and we will also shrink the window. first we will check if the window size is less than what we had, if it is than we will store this window size and its info. After that we will shrink the window from left side, first we will remove it\'s freq from havemap then we will check if it is a part of **t** and if removing it will dissatisfy the condition, if it is then we will decrement the have variable and we will now increment the left pointer to shrink the window. \nIt can be possible that the string doesn\'t even exist. In that case we will return empty string.\n\n# Complexity\n- Time complexity:$$O(n)$$\n\n- Space complexity:$$O(n)$$\n# Code\n```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n\n if t=="": return ""\n\n have = 0\n needmap = {}\n havemap = {}\n\n res = float(\'inf\')\n resl = [0,len(s)]\n\n for i in t:\n needmap[i] = 1 + needmap.get(i,0)\n\n need = len(needmap) \n\n l = 0 \n\n for r in range(len(s)):\n\n havemap[s[r]] = 1 + havemap.get(s[r],0)\n\n if s[r] in needmap and havemap[s[r]]==needmap[s[r]]:\n have+=1\n\n while have==need:\n \n if (r-l+1)<res:\n res = r-l+1\n resl = [l,r]\n\n havemap[s[l]]-=1 \n\n if s[l] in needmap and havemap[s[l]]<needmap[s[l]]:\n have-=1\n\n l+=1 \n\n l,r = resl\n\n return s[l:r+1] if res!=float(\'inf\') else ""\n\n``` | 3 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python || Easy || Sliding Window || Dictionary | minimum-window-substring | 0 | 1 | ```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n d=Counter(t)\n c=len(d)\n i=start=0\n n=len(s)\n ans=n+1\n for j in range(n):\n if s[j] in d:\n d[s[j]]-=1\n if d[s[j]]==0:\n c-=1 \n while c==0:\n if ans>j-i+1:\n ans=j-i+1\n start=i\n if s[i] in d:\n d[s[i]]+=1\n if d[s[i]]>0:\n c+=1\n i+=1\n if ans>n:\n return ""\n return s[start:start+ans]\n```\n\n**An upvote will be encouraging** | 4 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python || Easy || Sliding Window || Dictionary | minimum-window-substring | 0 | 1 | ```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n d=Counter(t)\n c=len(d)\n i=start=0\n n=len(s)\n ans=n+1\n for j in range(n):\n if s[j] in d:\n d[s[j]]-=1\n if d[s[j]]==0:\n c-=1 \n while c==0:\n if ans>j-i+1:\n ans=j-i+1\n start=i\n if s[i] in d:\n d[s[i]]+=1\n if d[s[i]]>0:\n c+=1\n i+=1\n if ans>n:\n return ""\n return s[start:start+ans]\n```\n\n**An upvote will be encouraging** | 4 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python | Sliding Window | With Explanation | Easy to Understand | minimum-window-substring | 0 | 1 | ```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n target_counter = Counter(t)\n left = 0\n min_length = float(\'inf\')\n substring = ""\n target_length = len(t)\n \n for right in range(len(s)):\n # if we find a letter in t\n if target_counter[s[right]] > 0:\n target_length -= 1\n \n target_counter[s[right]] -= 1\n \n # if the sliding window is valid, i.e. we find all letters in t\n while target_length == 0:\n len_window = right - left + 1\n \n if not substring or len(substring) > len_window:\n substring = s[left: right + 1]\n \n # move the window one step to the right\n target_counter[s[left]] += 1\n \n # if s[left] is a letter in t\n # we need to break the while loop\n if target_counter[s[left]] > 0:\n target_length += 1\n \n left += 1\n \n return substring | 2 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python | Sliding Window | With Explanation | Easy to Understand | minimum-window-substring | 0 | 1 | ```\nclass Solution:\n def minWindow(self, s: str, t: str) -> str:\n target_counter = Counter(t)\n left = 0\n min_length = float(\'inf\')\n substring = ""\n target_length = len(t)\n \n for right in range(len(s)):\n # if we find a letter in t\n if target_counter[s[right]] > 0:\n target_length -= 1\n \n target_counter[s[right]] -= 1\n \n # if the sliding window is valid, i.e. we find all letters in t\n while target_length == 0:\n len_window = right - left + 1\n \n if not substring or len(substring) > len_window:\n substring = s[left: right + 1]\n \n # move the window one step to the right\n target_counter[s[left]] += 1\n \n # if s[left] is a letter in t\n # we need to break the while loop\n if target_counter[s[left]] > 0:\n target_length += 1\n \n left += 1\n \n return substring | 2 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Easy Approach with Explanation: 97.81% faster than others | minimum-window-substring | 0 | 1 | Step 1: Create a Counter Dictionary{name: countT} for Substring t\nStep 2: Define have = 0, need=len(t)\nStep 3: Create a Hash Map(Dictionary){name: window} and Traverse String s and a left ptr l = 0.\n ->when countT[char] == window[char]: have += 1\n \n ->when have == need: {we got a subtring in a string}\n if len(currentstr) < len(res): res = currentstr\n\t\t\t - ->increment left ptr l and decrement window[s[l]] in windows dictionary\n\t\t\t and if window[s[l]] < countT[s[l]]: have -= 1\n\t\t\t \nDefined res = [-1,-1] and reslen = infinity as we want minimum length of substring in string. \n\n\n\n def minWindow(self, s: str, t: str) -> str:\n if t=="" or len(t) > len(s):\n return ""\n \n res, reslen = [-1,-1], float("inf")\n countT = {}\n for c in t:\n countT[c] = countT.get(c, 0) + 1\n \n have, need = 0, len(countT)\n \n window = {}\n l = 0\n for r in range(len(s)):\n ch = s[r]\n window[ch] = window.get(ch, 0) + 1\n \n if ch in countT and window[ch] == countT[ch]:\n have += 1\n \n while have == need:\n if (r-l+1) < reslen:\n res = [l, r]\n reslen = r-l+1\n \n window[s[l]] -= 1\n \n if s[l] in countT and window[s[l]] < countT[s[l]]:\n have -= 1\n l+=1\n \n l,r = res\n return s[l:r+1] if reslen != float("inf") else ""\n\n\n \n \n \n | 3 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Easy Approach with Explanation: 97.81% faster than others | minimum-window-substring | 0 | 1 | Step 1: Create a Counter Dictionary{name: countT} for Substring t\nStep 2: Define have = 0, need=len(t)\nStep 3: Create a Hash Map(Dictionary){name: window} and Traverse String s and a left ptr l = 0.\n ->when countT[char] == window[char]: have += 1\n \n ->when have == need: {we got a subtring in a string}\n if len(currentstr) < len(res): res = currentstr\n\t\t\t - ->increment left ptr l and decrement window[s[l]] in windows dictionary\n\t\t\t and if window[s[l]] < countT[s[l]]: have -= 1\n\t\t\t \nDefined res = [-1,-1] and reslen = infinity as we want minimum length of substring in string. \n\n\n\n def minWindow(self, s: str, t: str) -> str:\n if t=="" or len(t) > len(s):\n return ""\n \n res, reslen = [-1,-1], float("inf")\n countT = {}\n for c in t:\n countT[c] = countT.get(c, 0) + 1\n \n have, need = 0, len(countT)\n \n window = {}\n l = 0\n for r in range(len(s)):\n ch = s[r]\n window[ch] = window.get(ch, 0) + 1\n \n if ch in countT and window[ch] == countT[ch]:\n have += 1\n \n while have == need:\n if (r-l+1) < reslen:\n res = [l, r]\n reslen = r-l+1\n \n window[s[l]] -= 1\n \n if s[l] in countT and window[s[l]] < countT[s[l]]:\n have -= 1\n l+=1\n \n l,r = res\n return s[l:r+1] if reslen != float("inf") else ""\n\n\n \n \n \n | 3 | Given two strings `s` and `t` of lengths `m` and `n` respectively, return _the **minimum window**_ **_substring_** _of_ `s` _such that every character in_ `t` _(**including duplicates**) is included in the window_. If there is no such substring, return _the empty string_ `" "`.
The testcases will be generated such that the answer is **unique**.
**Example 1:**
**Input:** s = "ADOBECODEBANC ", t = "ABC "
**Output:** "BANC "
**Explanation:** The minimum window substring "BANC " includes 'A', 'B', and 'C' from string t.
**Example 2:**
**Input:** s = "a ", t = "a "
**Output:** "a "
**Explanation:** The entire string s is the minimum window.
**Example 3:**
**Input:** s = "a ", t = "aa "
**Output:** " "
**Explanation:** Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.
**Constraints:**
* `m == s.length`
* `n == t.length`
* `1 <= m, n <= 105`
* `s` and `t` consist of uppercase and lowercase English letters.
**Follow up:** Could you find an algorithm that runs in `O(m + n)` time? | Use two pointers to create a window of letters in S, which would have all the characters from T. Since you have to find the minimum window in S which has all the characters from T, you need to expand and contract the window using the two pointers and keep checking the window for all the characters. This approach is also called Sliding Window Approach.
L ------------------------ R , Suppose this is the window that contains all characters of T
L----------------- R , this is the contracted window. We found a smaller window that still contains all the characters in T
When the window is no longer valid, start expanding again using the right pointer. |
Python easy solutions || time & memory efficient | combinations | 0 | 1 | # Intuition\nThe problem requires generating all combinations of length k from the integers from 1 to n. To achieve this, we can use the itertools.combinations function, which will efficiently generate all possible combinations for us.\n\n# Approach\nWe will use the itertools.combinations function from the Python standard library. This function will take a sequence of integers from 1 to n (inclusive) and generate all combinations of length k. By utilizing this function, we can obtain the desired combinations without having to write a custom algorithm.\n\n# Complexity\n- Time complexity:\nO(n^k)\n\n- Space complexity:\nO(n^k)\n\n# Code\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return list(combinations(range(1, n + 1), k))\n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Python 1 line, use the tool you have | combinations | 0 | 1 | # Code\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return list(combinations(range(1, n+1), k))\n```\n\n# Code (For interview)\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n pool = tuple(range(1, n+1))\n n = len(pool)\n indices = list(range(k))\n res = [tuple(pool[i] for i in indices)]\n while True:\n for i in reversed(range(k)):\n # - Select i if i is not at its maximum\n if indices[i] != i + n - k:\n break\n else: # Reach the last combination\n return res\n indices[i] += 1\n # - Align the indices after i \n for j in range(i+1, k):\n indices[j] = indices[j-1] + 1\n res.append(tuple(pool[i] for i in indices))\n```\n\n# Reference: \nhttps://docs.python.org/3/library/itertools.html#itertools.combinations | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
✔️Python||C||C++🔥99%✅Backtrack with graph explained || Beginner-friendly ^_^ | combinations | 0 | 1 | # Intuition\nThis is a backtracking problem.\nWe made a recursion function, and get all combinations by take or not take specific number.\n\n# Approach\n## variables\n`nums` is the current combination.\n`pos` is the current position in `nums`\n`cur` is the current number\n\nIn the function `backtrack`:\nIf `pos == k`, we know that we got one of the combination.\nIf `pos != k`, we can try every possible number to fit in the current position, then we call `backtrack` again.\n\n## Here is a graph for better understand\n\n\n\n# Code\n<iframe src="https://leetcode.com/playground/LchAVxik/shared" frameBorder="0" width="1500" height="800"></iframe>\n\n# Please UPVOTE if this helps you!!\n\n\n\n | 16 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
🧩 Iterative & Backtracking [VIDEO] 100% Efficient Combinatorial Generation | combinations | 1 | 1 | # Intuition\nGiven two integers `n` and `k`, the task is to generate all possible combinations of `k` numbers from the range `[1, n]`. The initial intuition to solve this problem is to leverage the concept of combination generation, where we iteratively choose `k` numbers from `n` numbers without any repetition. However, there are multiple approaches to achieve this, and in this analysis, we\'ll be comparing two of them: **backtracking** and **iterative** generation. \n\n# Video - Backtracking\nhttps://youtu.be/aXgNccfxlkA\n\n# Video - Iterative\nhttps://youtu.be/7Ocr2RXNIC4\n\n# Approaches - Summary\nWe\'ll tackle this problem using two distinct methods. The first method utilizes a classic backtracking algorithm, which involves building up a solution incrementally. The second method employs an iterative algorithm, which efficiently generates combinations in lexicographical order. While both methods aim to generate all possible combinations of `k` numbers out of `n`, the iterative approach has been found to be faster for the given test cases. \n\n1. **Backtracking Approach**: This approach involves a recursive function, `backtrack`, that generates all combinations of `k` numbers. We iterate over all numbers from `first` to `n`. For each number `i`, we add it to the current combination and then recursively generate all the combinations of the next numbers. After that, we remove `i` from the current combination to backtrack and try the next number.\n\n2. **Iterative Approach**: This approach uses an iterative algorithm to generate combinations. It maintains a list of current indices and generates the next combination from the current one by incrementing the rightmost element that hasn\'t reached its maximum value yet.\n\n# Approach - Backtracking\n\nOur approach specifically involves a recursive function, `backtrack`, that generates all combinations of \\(k\\) numbers. Here\'s a step-by-step walkthrough of the process:\n\n1. **Initialization**: We define an empty list, `output`, to store all our valid combinations. We also initialize our `backtrack` function, which takes as input parameters the first number to add to the current combination (`first`) and the current combination itself (`curr`).\n\n2. **Base case for recursion**: Within the `backtrack` function, we first check if the length of the current combination (`curr`) is equal to \\(k\\). If it is, we have a valid combination and add a copy of it to our `output` list.\n\n3. **Loop through the numbers**: For each number \\(i\\) in the range from `first` to \\(n\\), we add \\(i\\) to the current combination (`curr`).\n\n4. **Recursive call**: We then make a recursive call to `backtrack`, incrementing the value of `first` by 1 for the next iteration and passing the current combination as parameters. This step allows us to generate all combinations of the remaining numbers.\n\n5. **Backtrack**: After exploring all combinations with \\(i\\) included, we need to remove \\(i\\) from the current combination. This allows us to backtrack and explore the combinations involving the next number. This is done using the `pop()` method, which removes the last element from the list.\n\n6. **Return the result**: Finally, after all recursive calls and backtracking, the `backtrack` function will have filled our `output` list with all valid combinations of \\(k\\) numbers. We return this list as our final result.\n\n# Approach - Iterative\n\nThe approach taken to solve this problem involves the use of function calls to generate all possible combinations. Here is a more detailed step-by-step breakdown of the approach:\n\n1. **Define the `generate_combinations` function:** This function takes in two parameters: `elems` (the range of numbers to choose from) and `num` (the number of elements in each combination). It begins by converting `elems` to a tuple (`elems_tuple`) for efficient indexing. It then checks if `num` is greater than the total number of elements; if it is, the function returns as it\'s impossible to select more elements than exist in the range.\n\n2. **Initialize indices:** An array `curr_indices` is initialized with the first `num` indices. This will represent the indices in `elems_tuple` that we are currently considering for our combination.\n\n3. **Generate combinations:** The function enters a loop. In each iteration, it first generates a combination by picking elements from `elems_tuple` using the indices in `curr_indices` and yields it. This is done using a tuple comprehension.\n\n4. **Update indices:** Next, the function attempts to update `curr_indices` to represent the next combination. It starts from the end of `curr_indices` and moves towards the start, looking for an index that hasn\'t reached its maximum value (which is its position from the end of `elems_tuple`). When it finds such an index, it increments it and sets all subsequent indices to be one greater than their previous index. This ensures that we generate combinations in increasing order. If it doesn\'t find any index to increment (meaning we have generated all combinations), it breaks out of the loop and the function returns.\n\n5. **Call the `generate_combinations` function:** In the `combine` method, the `generate_combinations` function is called with the range `[1, n+1]` and `k` as arguments. The returned combinations are tuples, so a list comprehension is used to convert each combination into a list.\n\n# Complexity - Iterative\n\n- **Time complexity:** The time complexity is \\(O(C(n, k))\\), where \\(n\\) is the total number of elements and \\(k\\) is the number of elements in each combination. This is because the function generates each combination once. Here, \\(C(n, k)\\) denotes the number of ways to choose \\(k\\) elements from \\(n\\) elements without regard to the order of selection, also known as "n choose k".\n\n- **Space complexity:** The space complexity is also \\(O(C(n, k))\\) as we store all combinations in a list. \n\n\n# Complexity - Backtracking\n- **Time complexity:** The time complexity of this approach is (O(C(n, k)*k)). This is because in the worst-case scenario, we would need to explore all combinations of \\(k\\) out of \\(n\\) (which is C(n, k) and for each combination, it takes \\(O(k)\\) time to make a copy of it.\n- **Space complexity:** The space complexity is \\(O(k)\\). This is because, in the worst case, if we consider the function call stack size in a depth-first search traversal, we could end up going as deep as \\(k\\) levels.\n\n# Code - Iterative\n```Python []\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n def generate_combinations(elems, num):\n elems_tuple = tuple(elems)\n total = len(elems_tuple)\n if num > total:\n return\n curr_indices = list(range(num))\n while True:\n yield tuple(elems_tuple[i] for i in curr_indices)\n for idx in reversed(range(num)):\n if curr_indices[idx] != idx + total - num:\n break\n else:\n return\n curr_indices[idx] += 1\n for j in range(idx+1, num):\n curr_indices[j] = curr_indices[j-1] + 1\n\n return [list(combination) for combination in generate_combinations(range(1, n+1), k)]\n```\n``` Java []\nclass Solution {\n public List<List<Integer>> combine(int n, int k) {\n List<List<Integer>> result = new ArrayList<>();\n generateCombinations(1, n, k, new ArrayList<Integer>(), result);\n return result;\n }\n\n private void generateCombinations(int start, int n, int k, List<Integer> combination, List<List<Integer>> result) {\n if (k == 0) {\n result.add(new ArrayList<>(combination));\n return;\n }\n for (int i = start; i <= n - k + 1; i++) {\n combination.add(i);\n generateCombinations(i + 1, n, k - 1, combination, result);\n combination.remove(combination.size() - 1);\n }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<vector<int>> combine(int n, int k) {\n vector<vector<int>> result;\n vector<int> combination(k);\n generateCombinations(1, n, k, combination, result);\n return result;\n }\n\nprivate:\n void generateCombinations(int start, int n, int k, vector<int> &combination, vector<vector<int>> &result) {\n if (k == 0) {\n result.push_back(combination);\n return;\n }\n for (int i = start; i <= n; ++i) {\n combination[combination.size() - k] = i;\n generateCombinations(i + 1, n, k - 1, combination, result);\n }\n }\n};\n```\n``` C# []\npublic class Solution {\n public IList<IList<int>> Combine(int n, int k) {\n var result = new List<IList<int>>();\n GenerateCombinations(1, n, k, new List<int>(), result);\n return result;\n }\n \n private void GenerateCombinations(int start, int n, int k, List<int> combination, IList<IList<int>> result) {\n if (k == 0) {\n result.Add(new List<int>(combination));\n return;\n }\n for (var i = start; i <= n; ++i) {\n combination.Add(i);\n GenerateCombinations(i + 1, n, k - 1, combination, result);\n combination.RemoveAt(combination.Count - 1);\n }\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number} k\n * @return {number[][]}\n */\nvar combine = function(n, k) {\n const result = [];\n generateCombinations(1, n, k, [], result);\n return result;\n};\n\nfunction generateCombinations(start, n, k, combination, result) {\n if (k === 0) {\n result.push([...combination]);\n return;\n }\n for (let i = start; i <= n; ++i) {\n combination.push(i);\n generateCombinations(i + 1, n, k - 1, combination, result);\n combination.pop();\n }\n}\n```\n\n# Code - Backtracking\n``` Python []\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n def backtrack(first = 1, curr = []):\n if len(curr) == k:\n output.append(curr[:])\n return\n for i in range(first, n + 1):\n curr.append(i)\n backtrack(i + 1, curr)\n curr.pop()\n output = []\n backtrack()\n return output\n```\n``` C++ []\nclass Solution {\npublic:\n vector<vector<int>> combine(int n, int k) {\n vector<vector<int>> result;\n vector<int> combination;\n backtrack(n, k, 1, combination, result);\n return result;\n }\n\nprivate:\n void backtrack(int n, int k, int start, vector<int>& combination, vector<vector<int>>& result) {\n if (combination.size() == k) {\n result.push_back(combination);\n return;\n }\n for (int i = start; i <= n; i++) {\n combination.push_back(i);\n backtrack(n, k, i + 1, combination, result);\n combination.pop_back();\n }\n }\n};\n```\n``` Java []\nclass Solution {\n public List<List<Integer>> combine(int n, int k) {\n List<List<Integer>> result = new ArrayList<>();\n backtrack(n, k, 1, new ArrayList<>(), result);\n return result;\n }\n\n private void backtrack(int n, int k, int start, List<Integer> combination, List<List<Integer>> result) {\n if (combination.size() == k) {\n result.add(new ArrayList<>(combination));\n return;\n }\n for (int i = start; i <= n; i++) {\n combination.add(i);\n backtrack(n, k, i + 1, combination, result);\n combination.remove(combination.size() - 1);\n }\n }\n}\n```\n``` JavaScript []\nvar combine = function(n, k) {\n const result = [];\n backtrack(n, k, 1, [], result);\n return result;\n};\n\nfunction backtrack(n, k, start, combination, result) {\n if (combination.length === k) {\n result.push([...combination]);\n return;\n }\n for (let i = start; i <= n; i++) {\n combination.push(i);\n backtrack(n, k, i + 1, combination, result);\n combination.pop();\n }\n}\n```\n``` C# []\npublic class Solution {\n public IList<IList<int>> Combine(int n, int k) {\n IList<IList<int>> result = new List<IList<int>>();\n Backtrack(n, k, 1, new List<int>(), result);\n return result;\n }\n\n private void Backtrack(int n, int k, int start, IList<int> combination, IList<IList<int>> result) {\n if (combination.Count == k) {\n result.Add(new List<int>(combination));\n return;\n }\n for (int i = start; i <= n; i++) {\n combination.Add(i);\n Backtrack(n, k, i + 1, combination, result);\n combination.RemoveAt(combination.Count - 1);\n }\n }\n}\n```\n\n## Performances - Iterative\n| Language | Runtime | Rank | Memory |\n|----------|---------|------|--------|\n| Java | 1 ms | 100% | 45.3 MB|\n| C++ | 14 ms | 90.1%| 9.2 MB |\n| Python3 | 68 ms | 99.72%| 18.8 MB|\n| JavaScript | 79 ms | 99.84%| 48.6 MB|\n| C# | 101 ms | 93.1%| 44.1 MB|\n\n## Performances - Backtracking\n| Language | Runtime | Beats | Memory |\n|----------|---------|-------|--------|\n| Java | 17 ms | 75.30%| 44.5 MB|\n| C++ | 21 ms | 85.40%| 9.1 MB |\n| JavaScript | 86 ms | 97.78%| 48 MB |\n| C# | 105 ms | 88.60%| 44.4 MB|\n| Python3 | 286 ms | 78.68%| 18.2 MB|\n\nI hope you found this solution helpful! If so, please consider giving it an upvote. If you have any questions or suggestions for improving the solution, don\'t hesitate to leave a comment. Your feedback not only helps me improve my answers, but it also helps other users who might be facing similar problems. Thank you for your support!\n | 83 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Three Optimal Solutions (Python) | combinations | 0 | 1 | Each of these solutions defines `solution.combine` as a generator instead of having it return a list. This approach is accepted, it\'s a bit cleaner, and it\'s probably a little bit faster.\n##### Recursive:\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n if k == 0:\n yield []\n else:\n for hi in range(k, n+1):\n for comb in self.combine(hi-1, k-1):\n yield comb + [hi]\n```\n##### Iterative:\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n comb = list(range(1, k+1))\n yield list(comb)\n while comb[0] != n-k+1:\n d = k-1\n while comb[d] == n-k+1+d:\n d -= 1\n\n comb[d] += 1\n for d2 in range(d+1, k):\n comb[d2] = comb[d]+d2-d\n\n yield list(comb)\n```\n##### One-liner using `itertools.combinations`:\n```\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return combinations(range(1, n+1), k)\n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Python Code 🐍(Only 1 Line😮😮😮) Beats 99.89%🤩 | combinations | 0 | 1 | \n\n# Code\n```\nfrom itertools import combinations\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n return list(combinations(range(1, n+1), k))\n\n```\n# ***Upvote my Solution if u learned something new today*** | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Python Easy Solution || 100% || | combinations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport itertools\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n arr = [i for i in range(1,n+1)]\n res = []\n if n==1:\n return [[1]]\n else:\n perm_set = itertools.combinations(arr,k)\n for i in perm_set:\n res.append(i)\n return res\n``` | 1 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | combinations | 1 | 1 | # Intuition\nUsing backtracking to create all possible combinations.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/oDn_6n0ahkM\n\n# Subscribe to my channel from here. I have 237 videos as of August 1st\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Create an empty list `res` to store the final combinations and an empty list `comb` to store the current combination being formed.\n\n2. Define a recursive function `backtrack(start)`, which will generate all possible combinations of size `k` from the numbers starting from `start` up to `n`.\n\n3. In the `backtrack` function:\n - If the length of `comb` becomes equal to `k`, it means we have formed a valid combination, so we append a copy of the current `comb` list to the `res` list. We use `comb[:]` to create a copy of the list since lists are mutable in Python, and we want to preserve the combination at this point without being modified later.\n\n - If the length of `comb` is not equal to `k`, we continue the recursion.\n \n4. Within the `backtrack` function, use a loop to iterate over the numbers starting from `start` up to `n`.\n - For each number `num` in the range, add it to the current `comb` list to form the combination.\n \n - Make a recursive call to `backtrack` with `start` incremented by 1. This ensures that each number can only be used once in each combination, avoiding duplicate combinations.\n\n - After the recursive call, remove the last added number from the `comb` list using `comb.pop()`. This allows us to backtrack and try other numbers for the current position in the combination.\n\n5. Start the recursion by calling `backtrack(1)` with `start` initially set to 1, as we want to start forming combinations with the numbers from 1 to `n`.\n\n6. After the recursion is complete, the `res` list will contain all the valid combinations of size `k` formed from the numbers 1 to `n`. Return `res` as the final result.\n\nThe code uses a recursive backtracking approach to generate all the combinations efficiently. It explores all possible combinations, avoiding duplicates and forming valid combinations of size `k`. The result `res` will contain all such combinations at the end.\n\n# Complexity\n- Time complexity: O(n * k)\nn is the number of elements and k is the size of the subset. The backtrack function is called n times, because there are n possible starting points for the subset. For each starting point, the backtrack function iterates through all k elements. This is because the comb list must contain all k elements in order for it to be a valid subset.\n\n- Space complexity: O(k)\nThe comb list stores at most k elements. This is because the backtrack function only adds elements to the comb list when the subset is not yet complete.\n\n```python []\nclass Solution:\n def combine(self, n: int, k: int) -> List[List[int]]:\n res = []\n comb = []\n\n def backtrack(start):\n if len(comb) == k:\n res.append(comb[:])\n return\n \n for num in range(start, n + 1):\n comb.append(num)\n backtrack(num + 1)\n comb.pop()\n\n backtrack(1)\n return res\n```\n```javascript []\n/**\n * @param {number} n\n * @param {number} k\n * @return {number[][]}\n */\nvar combine = function(n, k) {\n const res = [];\n const comb = [];\n\n function backtrack(start) {\n if (comb.length === k) {\n res.push([...comb]);\n return;\n }\n\n for (let num = start; num <= n; num++) {\n comb.push(num);\n backtrack(num + 1);\n comb.pop();\n }\n }\n\n backtrack(1);\n return res; \n};\n```\n```java []\nclass Solution {\n public List<List<Integer>> combine(int n, int k) {\n List<List<Integer>> res = new ArrayList<>();\n List<Integer> comb = new ArrayList<>();\n\n backtrack(1, comb, res, n, k);\n return res;\n }\n\n private void backtrack(int start, List<Integer> comb, List<List<Integer>> res, int n, int k) {\n if (comb.size() == k) {\n res.add(new ArrayList<>(comb));\n return;\n }\n\n for (int num = start; num <= n; num++) {\n comb.add(num);\n backtrack(num + 1, comb, res, n, k);\n comb.remove(comb.size() - 1);\n }\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> combine(int n, int k) {\n std::vector<std::vector<int>> res;\n std::vector<int> comb;\n\n backtrack(1, comb, res, n, k);\n return res; \n }\n\nprivate:\n void backtrack(int start, std::vector<int>& comb, std::vector<std::vector<int>>& res, int n, int k) {\n if (comb.size() == k) {\n res.push_back(comb);\n return;\n }\n\n for (int num = start; num <= n; num++) {\n comb.push_back(num);\n backtrack(num + 1, comb, res, n, k);\n comb.pop_back();\n }\n } \n};\n```\n | 15 | Given two integers `n` and `k`, return _all possible combinations of_ `k` _numbers chosen from the range_ `[1, n]`.
You may return the answer in **any order**.
**Example 1:**
**Input:** n = 4, k = 2
**Output:** \[\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Explanation:** There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., \[1,2\] and \[2,1\] are considered to be the same combination.
**Example 2:**
**Input:** n = 1, k = 1
**Output:** \[\[1\]\]
**Explanation:** There is 1 choose 1 = 1 total combination.
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= n` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.