title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python3 Solution | unique-paths-ii | 0 | 1 | \n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n dp=[[0 for _ in range(n)] for _ in range(m)]\n for col in range(n):\n if obstacleGrid[0][col]==1:\n break\n dp[0][col]=1\n for row in range(m):\n if obstacleGrid[row][0]==1:\n break\n\n dp[row][0]=1\n\n for row in range(1,m):\n for col in range(1,n):\n if obstacleGrid[row][col]==1:\n continue\n\n dp[row][col]=dp[row-1][col]+dp[row][col-1]\n\n return dp[-1][-1] \n``` | 3 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Well Explained , Slow ass DFS | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use recursive DFS with memoization (2D array) and initialize with setting the destination value to 1\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck out the Populated grid here :\n\n[7, 3, 3, 1]\n[4, 0, 2, 1]\n[4, 2, 1, 1]\n[2, 1, 0, 1]\n[1, 1, 1, 1]\n\nThis is for input\n[0,0,0,0]\n[0,1,0,0]\n[0,0,0,0]\n[0,0,1,0]\n[0,0,0,0]\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mxn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(mxn)\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n \n \n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n dfsStack = []\n\n\n direction = [(1,0) , (0,1) ]\n \n if obstacleGrid[m-1][n-1] == 1 or obstacleGrid[0][0]:\n return 0\n\n\n memo = [[0 for _ in range(n)] for _ in range(m)] \n\n # inititalise the memo for the dest\n memo[m-1][n-1]=1\n\n\n def recurDFS(i,j):\n \n if obstacleGrid[i][j]==1:\n return 0\n\n if memo[i][j] !=0:\n return memo[i][j]\n\n for x,y in direction:\n # print(x,y)\n dx = i+x\n dy = j+y\n \n\n if 0<=dx<m and 0<=dy<n :\n # print(">",dx,dy)\n memo[i][j] += recurDFS(dx,dy)\n\n return memo[i][j]\n\n recurDFS(0,0)\n for i in range(m):\n print(memo[i])\n return memo[0][0]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Well Explained , Slow ass DFS | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use recursive DFS with memoization (2D array) and initialize with setting the destination value to 1\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck out the Populated grid here :\n\n[7, 3, 3, 1]\n[4, 0, 2, 1]\n[4, 2, 1, 1]\n[2, 1, 0, 1]\n[1, 1, 1, 1]\n\nThis is for input\n[0,0,0,0]\n[0,1,0,0]\n[0,0,0,0]\n[0,0,1,0]\n[0,0,0,0]\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mxn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(mxn)\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n \n \n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n dfsStack = []\n\n\n direction = [(1,0) , (0,1) ]\n \n if obstacleGrid[m-1][n-1] == 1 or obstacleGrid[0][0]:\n return 0\n\n\n memo = [[0 for _ in range(n)] for _ in range(m)] \n\n # inititalise the memo for the dest\n memo[m-1][n-1]=1\n\n\n def recurDFS(i,j):\n \n if obstacleGrid[i][j]==1:\n return 0\n\n if memo[i][j] !=0:\n return memo[i][j]\n\n for x,y in direction:\n # print(x,y)\n dx = i+x\n dy = j+y\n \n\n if 0<=dx<m and 0<=dy<n :\n # print(">",dx,dy)\n memo[i][j] += recurDFS(dx,dy)\n\n return memo[i][j]\n\n recurDFS(0,0)\n for i in range(m):\n print(memo[i])\n return memo[0][0]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Less no of line code with python | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n if obstacleGrid[0][0]: return 0\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1\n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j] or (i == 0 and j == 0): continue\n dp[i][j] = (dp[i-1][j] if i else 0) + (dp[i][j-1] if j else 0)\n return dp[m-1][n-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Less no of line code with python | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n if obstacleGrid[0][0]: return 0\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1\n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j] or (i == 0 and j == 0): continue\n dp[i][j] = (dp[i-1][j] if i else 0) + (dp[i][j-1] if j else 0)\n return dp[m-1][n-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python 13 lines | unique-paths-ii | 0 | 1 | # Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, A: List[List[int]]) -> int:\n if A[0][0] or A[-1][-1]:\n return 0\n rangeN, rangeM, source = range(len(A)), range(len(A[0])), [(-1, 0), (0, -1)]\n A[0][0] = -1\n for i, j, (_i, _j) in product(rangeN, rangeM, source):\n if A[i][j] == 1:\n continue\n try:\n if i+_i != -1 and j+_j != -1 and A[i+_i][j+_j] != 1:\n A[i][j] += A[i+_i][j+_j]\n except:\n pass\n return -A[-1][-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python 13 lines | unique-paths-ii | 0 | 1 | # Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, A: List[List[int]]) -> int:\n if A[0][0] or A[-1][-1]:\n return 0\n rangeN, rangeM, source = range(len(A)), range(len(A[0])), [(-1, 0), (0, -1)]\n A[0][0] = -1\n for i, j, (_i, _j) in product(rangeN, rangeM, source):\n if A[i][j] == 1:\n continue\n try:\n if i+_i != -1 and j+_j != -1 and A[i+_i][j+_j] != 1:\n A[i][j] += A[i+_i][j+_j]\n except:\n pass\n return -A[-1][-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
PYTHON CODE || using MEMOIZATION | unique-paths-ii | 0 | 1 | \n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n memo={}\n def uniquePathsWithObstacleHelper(i,j,obstacleGrid):\n if i==len(obstacleGrid)-1 and j==len(obstacleGrid[0])-1 and obstacleGrid[i][j]==1:\n return 0\n if i==len(obstacleGrid)-1 and j==len(obstacleGrid[0])-1:\n return 1\n if i>len(obstacleGrid)-1 or j>len(obstacleGrid[0])-1 or obstacleGrid[i][j]==1:\n return 0\n if (i,j) in memo:\n return memo[(i,j)]\n memo[(i,j)]=uniquePathsWithObstacleHelper(i+1,j,obstacleGrid)+uniquePathsWithObstacleHelper(i,j+1,obstacleGrid)\n return memo[(i,j)]\n return uniquePathsWithObstacleHelper(0,0,obstacleGrid)\n \n\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
PYTHON CODE || using MEMOIZATION | unique-paths-ii | 0 | 1 | \n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n memo={}\n def uniquePathsWithObstacleHelper(i,j,obstacleGrid):\n if i==len(obstacleGrid)-1 and j==len(obstacleGrid[0])-1 and obstacleGrid[i][j]==1:\n return 0\n if i==len(obstacleGrid)-1 and j==len(obstacleGrid[0])-1:\n return 1\n if i>len(obstacleGrid)-1 or j>len(obstacleGrid[0])-1 or obstacleGrid[i][j]==1:\n return 0\n if (i,j) in memo:\n return memo[(i,j)]\n memo[(i,j)]=uniquePathsWithObstacleHelper(i+1,j,obstacleGrid)+uniquePathsWithObstacleHelper(i,j+1,obstacleGrid)\n return memo[(i,j)]\n return uniquePathsWithObstacleHelper(0,0,obstacleGrid)\n \n\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Binbin is undefeatable! | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n\n if m == 1 or n == 1:\n if any(1 in row for row in obstacleGrid):\n return 0\n else:\n return 1\n\n L=[[0 for _ in range(n)] for _ in range(m)]\n \n temp_x=obstacleGrid[0]\n if temp_x[0] == 1: \n return 0\n else:\n for t in range(0,n):\n if temp_x[t] == 0:\n L[0][t]=1\n if temp_x[t] == 1:\n for i in range (t,n):\n L[0][t]=0\n break\n \n \n temp_y=[]\n for i in range(1,m):\n temp_y.append(obstacleGrid[i][0])\n \n for t in range(0,m-1):\n if temp_y[t] == 0:\n L[t+1][0]=1\n elif temp_y[t] == 1:\n for i in range (t,m-1):\n L[i+1][0]=0\n break\n # print(L)\n\n for i in range(1,m):\n for j in range(1,n):\n if obstacleGrid[i][j]==1:\n L[i][j] =0\n elif obstacleGrid[i][j]==0:\n L[i][j]= L[i][j-1]+L[i-1][j]\n # print(L) \n return L[-1][-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Binbin is undefeatable! | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n\n if m == 1 or n == 1:\n if any(1 in row for row in obstacleGrid):\n return 0\n else:\n return 1\n\n L=[[0 for _ in range(n)] for _ in range(m)]\n \n temp_x=obstacleGrid[0]\n if temp_x[0] == 1: \n return 0\n else:\n for t in range(0,n):\n if temp_x[t] == 0:\n L[0][t]=1\n if temp_x[t] == 1:\n for i in range (t,n):\n L[0][t]=0\n break\n \n \n temp_y=[]\n for i in range(1,m):\n temp_y.append(obstacleGrid[i][0])\n \n for t in range(0,m-1):\n if temp_y[t] == 0:\n L[t+1][0]=1\n elif temp_y[t] == 1:\n for i in range (t,m-1):\n L[i+1][0]=0\n break\n # print(L)\n\n for i in range(1,m):\n for j in range(1,n):\n if obstacleGrid[i][j]==1:\n L[i][j] =0\n elif obstacleGrid[i][j]==0:\n L[i][j]= L[i][j-1]+L[i-1][j]\n # print(L) \n return L[-1][-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | unique-paths-ii | 1 | 1 | # Intuition\nMain goal is to determine the count of unique paths from the top-left corner to the bottom-right corner of a grid while accounting for obstacles in the grid. It uses dynamic programming to iteratively calculate the paths, avoiding obstacles and utilizing previously computed values to efficiently arrive at the final count.\n\nThis python solution beats 96%.\n\n\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n# Subscribe to my channel from here. I have 244 videos as of August 12th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/-nVmLvqo5qc\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Define the class `Solution` which contains the method `uniquePathsWithObstacles` that takes `obstacleGrid` as input and returns the number of unique paths.\n\n2. Check if `obstacleGrid` is empty or if the starting cell (0, 0) is an obstacle (marked as 1). If either of these conditions is met, return 0, as there is no way to reach the destination.\n\n3. Get the number of rows and columns in the `obstacleGrid` and store them in `rows` and `cols` variables, respectively.\n\n4. Create an array `dp` of size `cols` to store the number of unique paths for each column. Initialize all values in `dp` to 0.\n\n5. Set `dp[0]` to 1, representing the number of ways to reach the starting cell (0, 0).\n\n6. Iterate through each row (`r`) in the `obstacleGrid`:\n\n a. For each row, iterate through each column (`c`) in the `obstacleGrid`:\n\n - If the current cell (`obstacleGrid[r][c]`) contains an obstacle (marked as 1), set `dp[c]` to 0, indicating that there are no paths to reach this obstacle cell.\n\n - Otherwise, if the current cell is not an obstacle:\n\n - Check if `c` is greater than 0 (i.e., not in the leftmost column). If true, update `dp[c]` by adding the value of `dp[c - 1]`. This accounts for the paths coming from the cell above (`dp[c]`) and the cell to the left (`dp[c - 1]`).\n\n7. After iterating through all the cells in the grid, return the value of `dp[cols - 1]`, which represents the number of unique paths to reach the bottom-right cell (rows - 1, cols - 1).\n\nIn summary, this algorithm uses dynamic programming to calculate the number of unique paths from the top-left corner to the bottom-right corner of the grid while avoiding obstacles. The `dp` array is updated iteratively, taking into account the paths from the cell above and the cell to the left.\n\n# How solution code works\n`[0, 0, 0]`\n`[0, 1, 0]`\n`[0, 0, 0]`\n\nBefore starting nested loop, `dp` is `[1, 0, 0]`.\n\n1. iterating the first row and using `[1, 0, 0]`(previous result). In the end dp should be `[1, 1, 1]`\n - check `uniquePathsWithObstacles[0][0]` \u2192 `dp = [1, 0, 0]`\n - check `uniquePathsWithObstacles[0][1]` \u2192 `dp = [1, 1, 0]`\n - check `uniquePathsWithObstacles[0][2]` \u2192 `dp = [1, 1, 1]`\n\n2. iterating the second row and using `[1, 1, 1]`(previous result). In the end dp should be `[1, 0, 1]`\n - check `uniquePathsWithObstacles[1][0]` \u2192 `dp = [1, 1, 1]`\n - check `uniquePathsWithObstacles[1][1]` \u2192 `dp = [1, 0, 1]`\n - check `uniquePathsWithObstacles[1][2]` \u2192 `dp = [1, 0, 1]`\n\n3. iterating the thrid row and using `[1, 0, 1]`(previous result). In the end dp should be `[1, 1, 2]`\n - check `uniquePathsWithObstacles[2][0]` \u2192 `dp = [1, 0, 1]`\n - check `uniquePathsWithObstacles[2][1]` \u2192 `dp = [1, 1, 1]`\n - check `uniquePathsWithObstacles[2][2]` \u2192 `dp = [1, 1, 2]` \n\nOutput should be `2`.\n\n# Complexity\n- Time complexity: O(rows * cols)\n\n- Space complexity: O(cols)\n\n```python []\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n if not obstacleGrid or obstacleGrid[0][0] == 1:\n return 0\n\n rows, cols = len(obstacleGrid), len(obstacleGrid[0])\n dp = [0] * cols\n dp[0] = 1\n\n for r in range(rows):\n for c in range(cols):\n if obstacleGrid[r][c] == 1:\n dp[c] = 0\n else:\n if c > 0:\n dp[c] += dp[c - 1]\n\n return dp[cols - 1] \n```\n```javascript []\n/**\n * @param {number[][]} obstacleGrid\n * @return {number}\n */\nvar uniquePathsWithObstacles = function(obstacleGrid) {\n if (!obstacleGrid || obstacleGrid[0][0] === 1) {\n return 0;\n }\n\n const rows = obstacleGrid.length;\n const cols = obstacleGrid[0].length;\n const dp = new Array(cols).fill(0);\n dp[0] = 1;\n\n for (let r = 0; r < rows; r++) {\n for (let c = 0; c < cols; c++) {\n if (obstacleGrid[r][c] === 1) {\n dp[c] = 0;\n } else {\n if (c > 0) {\n dp[c] += dp[c - 1];\n }\n }\n }\n }\n\n return dp[cols - 1]; \n};\n```\n```java []\nclass Solution {\n public int uniquePathsWithObstacles(int[][] obstacleGrid) {\n if (obstacleGrid == null || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int rows = obstacleGrid.length;\n int cols = obstacleGrid[0].length;\n int[] dp = new int[cols];\n dp[0] = 1;\n\n for (int r = 0; r < rows; r++) {\n for (int c = 0; c < cols; c++) {\n if (obstacleGrid[r][c] == 1) {\n dp[c] = 0;\n } else {\n if (c > 0) {\n dp[c] += dp[c - 1];\n }\n }\n }\n }\n\n return dp[cols - 1]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {\n if (obstacleGrid.empty() || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int rows = obstacleGrid.size();\n int cols = obstacleGrid[0].size();\n vector<int> dp(cols, 0);\n dp[0] = 1;\n\n for (int r = 0; r < rows; r++) {\n for (int c = 0; c < cols; c++) {\n if (obstacleGrid[r][c] == 1) {\n dp[c] = 0;\n } else {\n if (c > 0) {\n dp[c] += dp[c - 1];\n }\n }\n }\n }\n\n return dp[cols - 1]; \n }\n};\n```\n\n# Related video\nI have an video for Unique Path I. Please check if you like.\n\nhttps://youtu.be/6NorAYw7NMU\n\nThank you for reading. Please upvote this article and don\'t forget to subscribe to my youtube channel!\n | 15 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | unique-paths-ii | 1 | 1 | # Intuition\nMain goal is to determine the count of unique paths from the top-left corner to the bottom-right corner of a grid while accounting for obstacles in the grid. It uses dynamic programming to iteratively calculate the paths, avoiding obstacles and utilizing previously computed values to efficiently arrive at the final count.\n\nThis python solution beats 96%.\n\n\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n# Subscribe to my channel from here. I have 244 videos as of August 12th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/-nVmLvqo5qc\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Define the class `Solution` which contains the method `uniquePathsWithObstacles` that takes `obstacleGrid` as input and returns the number of unique paths.\n\n2. Check if `obstacleGrid` is empty or if the starting cell (0, 0) is an obstacle (marked as 1). If either of these conditions is met, return 0, as there is no way to reach the destination.\n\n3. Get the number of rows and columns in the `obstacleGrid` and store them in `rows` and `cols` variables, respectively.\n\n4. Create an array `dp` of size `cols` to store the number of unique paths for each column. Initialize all values in `dp` to 0.\n\n5. Set `dp[0]` to 1, representing the number of ways to reach the starting cell (0, 0).\n\n6. Iterate through each row (`r`) in the `obstacleGrid`:\n\n a. For each row, iterate through each column (`c`) in the `obstacleGrid`:\n\n - If the current cell (`obstacleGrid[r][c]`) contains an obstacle (marked as 1), set `dp[c]` to 0, indicating that there are no paths to reach this obstacle cell.\n\n - Otherwise, if the current cell is not an obstacle:\n\n - Check if `c` is greater than 0 (i.e., not in the leftmost column). If true, update `dp[c]` by adding the value of `dp[c - 1]`. This accounts for the paths coming from the cell above (`dp[c]`) and the cell to the left (`dp[c - 1]`).\n\n7. After iterating through all the cells in the grid, return the value of `dp[cols - 1]`, which represents the number of unique paths to reach the bottom-right cell (rows - 1, cols - 1).\n\nIn summary, this algorithm uses dynamic programming to calculate the number of unique paths from the top-left corner to the bottom-right corner of the grid while avoiding obstacles. The `dp` array is updated iteratively, taking into account the paths from the cell above and the cell to the left.\n\n# How solution code works\n`[0, 0, 0]`\n`[0, 1, 0]`\n`[0, 0, 0]`\n\nBefore starting nested loop, `dp` is `[1, 0, 0]`.\n\n1. iterating the first row and using `[1, 0, 0]`(previous result). In the end dp should be `[1, 1, 1]`\n - check `uniquePathsWithObstacles[0][0]` \u2192 `dp = [1, 0, 0]`\n - check `uniquePathsWithObstacles[0][1]` \u2192 `dp = [1, 1, 0]`\n - check `uniquePathsWithObstacles[0][2]` \u2192 `dp = [1, 1, 1]`\n\n2. iterating the second row and using `[1, 1, 1]`(previous result). In the end dp should be `[1, 0, 1]`\n - check `uniquePathsWithObstacles[1][0]` \u2192 `dp = [1, 1, 1]`\n - check `uniquePathsWithObstacles[1][1]` \u2192 `dp = [1, 0, 1]`\n - check `uniquePathsWithObstacles[1][2]` \u2192 `dp = [1, 0, 1]`\n\n3. iterating the thrid row and using `[1, 0, 1]`(previous result). In the end dp should be `[1, 1, 2]`\n - check `uniquePathsWithObstacles[2][0]` \u2192 `dp = [1, 0, 1]`\n - check `uniquePathsWithObstacles[2][1]` \u2192 `dp = [1, 1, 1]`\n - check `uniquePathsWithObstacles[2][2]` \u2192 `dp = [1, 1, 2]` \n\nOutput should be `2`.\n\n# Complexity\n- Time complexity: O(rows * cols)\n\n- Space complexity: O(cols)\n\n```python []\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n if not obstacleGrid or obstacleGrid[0][0] == 1:\n return 0\n\n rows, cols = len(obstacleGrid), len(obstacleGrid[0])\n dp = [0] * cols\n dp[0] = 1\n\n for r in range(rows):\n for c in range(cols):\n if obstacleGrid[r][c] == 1:\n dp[c] = 0\n else:\n if c > 0:\n dp[c] += dp[c - 1]\n\n return dp[cols - 1] \n```\n```javascript []\n/**\n * @param {number[][]} obstacleGrid\n * @return {number}\n */\nvar uniquePathsWithObstacles = function(obstacleGrid) {\n if (!obstacleGrid || obstacleGrid[0][0] === 1) {\n return 0;\n }\n\n const rows = obstacleGrid.length;\n const cols = obstacleGrid[0].length;\n const dp = new Array(cols).fill(0);\n dp[0] = 1;\n\n for (let r = 0; r < rows; r++) {\n for (let c = 0; c < cols; c++) {\n if (obstacleGrid[r][c] === 1) {\n dp[c] = 0;\n } else {\n if (c > 0) {\n dp[c] += dp[c - 1];\n }\n }\n }\n }\n\n return dp[cols - 1]; \n};\n```\n```java []\nclass Solution {\n public int uniquePathsWithObstacles(int[][] obstacleGrid) {\n if (obstacleGrid == null || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int rows = obstacleGrid.length;\n int cols = obstacleGrid[0].length;\n int[] dp = new int[cols];\n dp[0] = 1;\n\n for (int r = 0; r < rows; r++) {\n for (int c = 0; c < cols; c++) {\n if (obstacleGrid[r][c] == 1) {\n dp[c] = 0;\n } else {\n if (c > 0) {\n dp[c] += dp[c - 1];\n }\n }\n }\n }\n\n return dp[cols - 1]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {\n if (obstacleGrid.empty() || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int rows = obstacleGrid.size();\n int cols = obstacleGrid[0].size();\n vector<int> dp(cols, 0);\n dp[0] = 1;\n\n for (int r = 0; r < rows; r++) {\n for (int c = 0; c < cols; c++) {\n if (obstacleGrid[r][c] == 1) {\n dp[c] = 0;\n } else {\n if (c > 0) {\n dp[c] += dp[c - 1];\n }\n }\n }\n }\n\n return dp[cols - 1]; \n }\n};\n```\n\n# Related video\nI have an video for Unique Path I. Please check if you like.\n\nhttps://youtu.be/6NorAYw7NMU\n\nThank you for reading. Please upvote this article and don\'t forget to subscribe to my youtube channel!\n | 15 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
✅ 100% Dynamic Programming [VIDEO] - Optimal Solution | unique-paths-ii | 1 | 1 | # Problem Understanding\n\nIn the "Unique Paths II" problem, we are presented with a grid filled with obstacles and open paths. Starting from the top-left corner, the goal is to find the number of unique paths that lead to the bottom-right corner. We can only move right or down at any point in time. If a cell has an obstacle, we cannot pass through it.\n\nFor example, consider the following grid:\n\n$$\n\\begin{array}{ccc}\n0 & 0 & 0 \\\\\n0 & 1 & 0 \\\\\n0 & 0 & 0 \\\\\n\\end{array}\n$$\n\n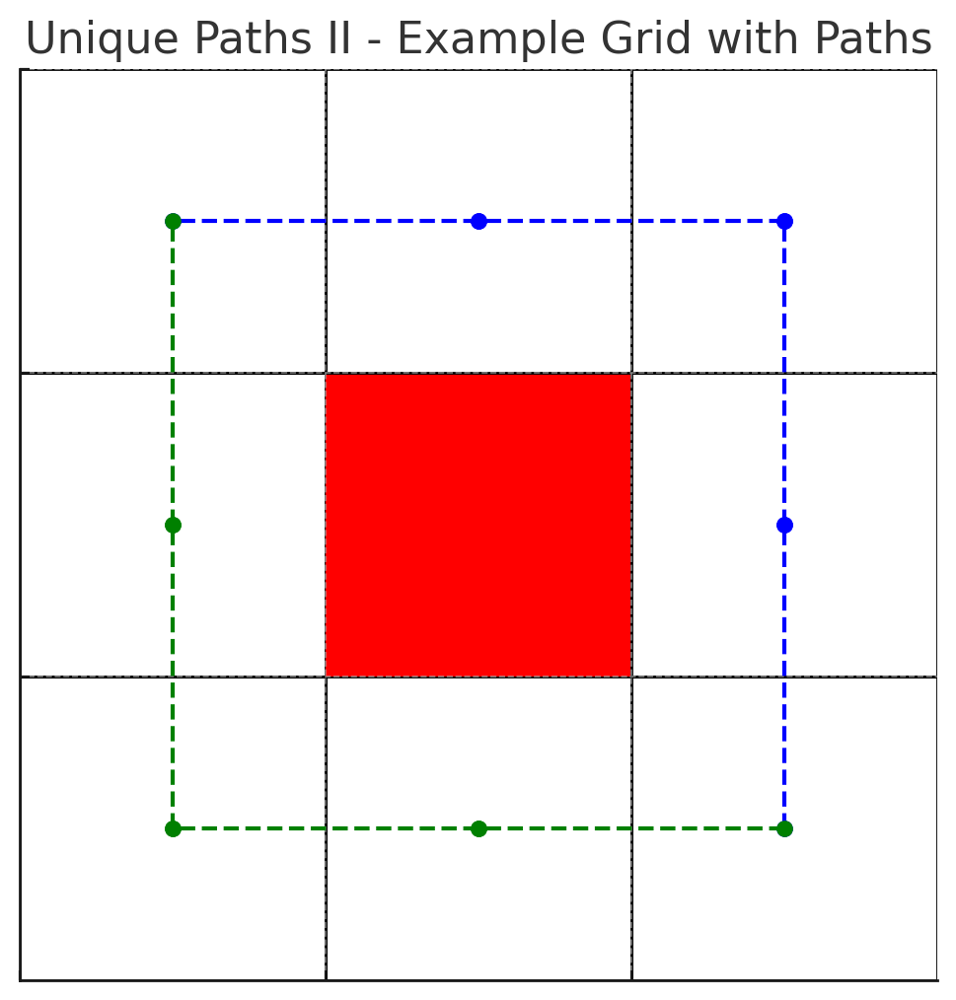\n\n\n- The grid cells with obstacles are colored in red.\n- The two unique paths from the top-left to the bottom-right corner are represented by the blue and green dashed lines.\n\nFrom the plot, you can see the two possible routes:\n\n- The blue path goes Right -> Right -> Down -> Down.\n- The green path goes Down -> Down -> Right -> Right.\n\n---\n\n# Live Coding\nhttps://youtu.be/pJ40_FmXAfo\n\n- [in Python \uD83D\uDC0D](https://youtu.be/pJ40_FmXAfo)\n- [in Rust \uD83E\uDD80](https://youtu.be/xt_1OzCH_NA)\n\n# Approach\n\n## The Basic Idea\n\nThe underlying concept is rooted in dynamic programming. Essentially, for any cell `(i, j)`, the number of ways you can reach it is the sum of the ways you can reach the cell directly above it `(i-1, j)` and the cell directly to its left `(i, j-1)`. However, this is only true if the cell `(i, j)` does not have an obstacle. If it does, then the number of ways to reach this cell is 0 because it\'s inaccessible.\n\n### 2D Transition:\nIn a 2D dynamic programming approach, you would have a `dp` array of size `m x n`, where ` dp[i][j] ` represents the number of ways to reach cell ` (i, j) `.\n\nThe transition formula would be:\n$$ dp[i][j] = \n\\begin{cases} \n0 & \\text{if } obstacleGrid[i][j] = 1 \\\\\ndp[i-1][j] + dp[i][j-1] & \\text{otherwise}\n\\end{cases}\n$$\n\nSo, for each cell ` (i, j) `, if there\'s no obstacle, its value would be the sum of the cell above it and the cell to its left.\n\n### Translation to 1D:\n\nNow, given the 2D transition, notice how for any cell \\( (i, j) \\), we only need values from the current row and the previous row. This observation allows us to reduce our 2D `dp` array to two 1D arrays, `previous` and `current`.\n\nThe transition formula in 1D would be analogous to the 2D version but slightly adjusted:\n\nFor the first column (`j = 0`):\n$$ current[0] = \n\\begin{cases} \n0 & \\text{if } obstacleGrid[i][0] = 1 \\\\\nprevious[0] & \\text{otherwise}\n\\end{cases}\n$$\n\nFor other columns:\n$$ current[j] = \n\\begin{cases} \n0 & \\text{if } obstacleGrid[i][j] = 1 \\\\\nprevious[j] + current[j-1] & \\text{otherwise}\n\\end{cases}\n$$\n\nHere, `previous` is analogous to `dp[i-1]` and `current` is analogous to `dp[i]` from our 2D approach. After processing each row, we\'ll swap `previous` and `current` to roll over to the next iteration.\n\nThe transition remains conceptually the same between the 2D and 1D versions. The 1D optimization simply leverages the observation that for each cell, we only need data from the current and previous rows. This reduces space complexity from $$ O(m \\times n) $$ to $$ O(n) $$.\n\nThis rolling array technique is a common optimization strategy in dynamic programming problems involving grids.\n\n### Step-by-step Breakdown:\n\n1. **Initialization**:\n - We initialize the `previous` array with zeros. This array represents the number of ways to reach each cell in the previous row.\n - We set `previous[0]` to 1 because there\'s only one way to get to the starting cell (by starting there!).\n \n2. **Iterate through the Grid**:\n - For each row, we consider each cell:\n - If the cell has an obstacle, it\'s unreachable, so the number of ways to get there (`current[j]`) is 0.\n - Otherwise, the number of ways to reach the cell is the sum of the ways to reach the cell above and the cell to the left. This translates to `current[j-1] + previous[j]`.\n - Once we\'ve processed a row, we set `previous` to `current`, preparing for the next iteration.\n\n3. **Result**:\n - Once we\'ve processed all rows, `previous[n-1]` gives us the number of unique paths to the bottom-right corner of the grid.\n\n## Example\n\nUsing the earlier example:\n\n$$\n\\begin{array}{ccc}\n0 & 0 & 0 \\\\\n0 & 1 & 0 \\\\\n0 & 0 & 0 \\\\\n\\end{array}\n$$\n\nHere\'s how the `previous` and `current` arrays evolve:\n\nThe function\'s output matches the example description:\n\n**Initial State**:\n- `previous`: $$[1, 0, 0]$$\n- `current`: $$[0, 0, 0]$$\n\n**After processing row 0**:\n- `previous`: $$[1, 0, 0]$$\n- `current`: $$[1, 1, 1]$$\n\n**After processing row 1**:\n- `previous`: $$[1, 1, 1]$$\n- `current`: $$[1, 0, 1]$$\n\n**After processing row 2**:\n- `previous`: $$[1, 0, 1]$$\n- `current`: $$[1, 1, 2]$$\n\nFrom the final state of the `previous` array, we can infer that there are 2 unique paths from the top-left to the bottom-right corner, avoiding obstacles. This matches the expected result.\n\n# Complexity\n\n**Time Complexity:** $$O(m \\times n)$$\n**Space Complexity:** $$O(n)$$\n\nThis solution is optimal in terms of both time and space complexity. It efficiently computes the number of unique paths by building upon previous calculations.\n\n# Performance\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|-------------|--------------|------------------|-------------|-----------------|\n| Go | 0 | 100% | 2.4 | 71.38% |\n| C++ | 0 | 100% | 7.6 | 81.25% |\n| Java | 0 | 100% | 40.5 | 72.53% |\n| Rust | 1 | 85% | 2 | 87.50% |\n| Python3 | 38 | 99.30% | 16.3 | 82.98% |\n| JavaScript | 47 | 97.40% | 41.6 | 97.86% |\n| C# | 81 | 80.72% | 38.7 | 63.25% |\n\n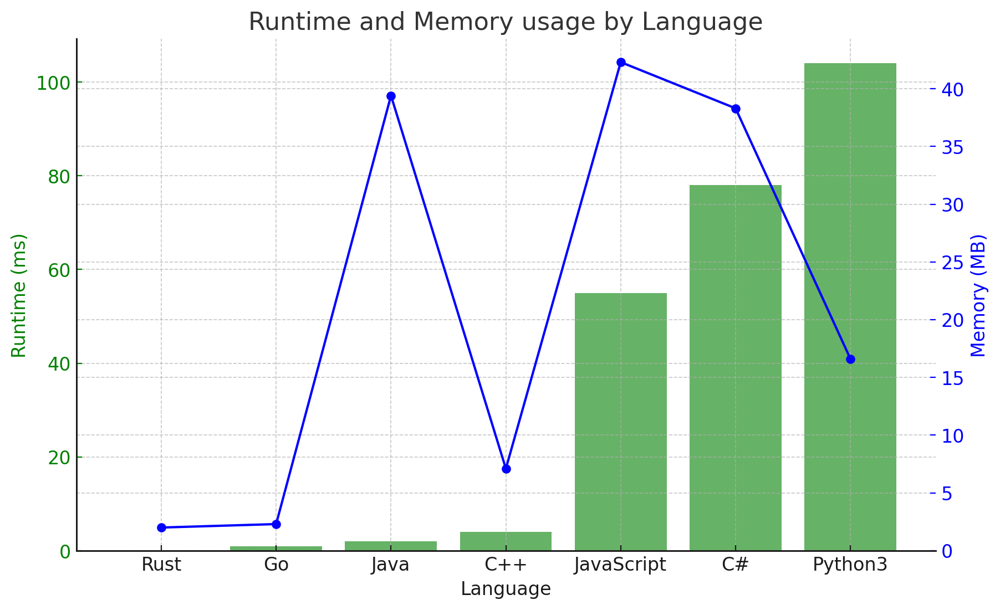\n\n\n---\n\n# Code\n\n``` Python []\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n if not obstacleGrid or not obstacleGrid[0] or obstacleGrid[0][0] == 1:\n return 0\n \n m, n = len(obstacleGrid), len(obstacleGrid[0])\n \n previous = [0] * n\n current = [0] * n\n previous[0] = 1\n \n for i in range(m):\n current[0] = 0 if obstacleGrid[i][0] == 1 else previous[0]\n for j in range(1, n):\n current[j] = 0 if obstacleGrid[i][j] == 1 else current[j-1] + previous[j]\n previous[:] = current\n \n return previous[n-1]\n```\n``` C++ []\nclass Solution {\npublic:\n int uniquePathsWithObstacles(std::vector<std::vector<int>>& obstacleGrid) {\n if (obstacleGrid.empty() || obstacleGrid[0].empty() || obstacleGrid[0][0] == 1) {\n return 0;\n }\n \n int m = obstacleGrid.size();\n int n = obstacleGrid[0].size();\n \n std::vector<int> previous(n, 0);\n std::vector<int> current(n, 0);\n previous[0] = 1;\n \n for (int i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] == 1 ? 0 : previous[0];\n for (int j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] == 1 ? 0 : current[j-1] + previous[j];\n }\n previous = current;\n }\n \n return previous[n-1];\n }\n};\n```\n``` Go []\nfunc uniquePathsWithObstacles(obstacleGrid [][]int) int {\n if len(obstacleGrid) == 0 || len(obstacleGrid[0]) == 0 || obstacleGrid[0][0] == 1 {\n return 0\n }\n\n m := len(obstacleGrid)\n n := len(obstacleGrid[0])\n\n previous := make([]int, n)\n current := make([]int, n)\n previous[0] = 1\n\n for i := 0; i < m; i++ {\n if obstacleGrid[i][0] == 1 {\n current[0] = 0\n } else {\n current[0] = previous[0]\n }\n \n for j := 1; j < n; j++ {\n if obstacleGrid[i][j] == 1 {\n current[j] = 0\n } else {\n current[j] = current[j-1] + previous[j]\n }\n }\n previous, current = current, previous\n }\n return previous[n-1]\n}\n```\n``` Rust []\nimpl Solution {\n pub fn unique_paths_with_obstacles(obstacleGrid: Vec<Vec<i32>>) -> i32 {\n if obstacleGrid.is_empty() || obstacleGrid[0].is_empty() || obstacleGrid[0][0] == 1 {\n return 0;\n }\n \n let m = obstacleGrid.len();\n let n = obstacleGrid[0].len();\n \n let mut previous = vec![0; n];\n let mut current = vec![0; n];\n previous[0] = 1;\n \n for row in &obstacleGrid {\n current[0] = if row[0] == 1 { 0 } else { previous[0] };\n for j in 1..n {\n if row[j] == 1 {\n current[j] = 0;\n } else {\n current[j] = current[j-1] + previous[j];\n }\n }\n std::mem::swap(&mut previous, &mut current);\n }\n \n previous[n-1]\n }\n}\n```\n``` Java []\npublic class Solution {\n public int uniquePathsWithObstacles(int[][] obstacleGrid) {\n if (obstacleGrid == null || obstacleGrid.length == 0 || obstacleGrid[0].length == 0 || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int m = obstacleGrid.length;\n int n = obstacleGrid[0].length;\n\n int[] previous = new int[n];\n int[] current = new int[n];\n previous[0] = 1;\n\n for (int i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] == 1 ? 0 : previous[0];\n for (int j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] == 1 ? 0 : current[j-1] + previous[j];\n }\n System.arraycopy(current, 0, previous, 0, n);\n }\n\n return previous[n-1];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[][]} obstacleGrid\n * @return {number}\n */\nvar uniquePathsWithObstacles = function(obstacleGrid) {\n if (!obstacleGrid.length || !obstacleGrid[0].length || obstacleGrid[0][0] === 1) {\n return 0;\n }\n\n let m = obstacleGrid.length;\n let n = obstacleGrid[0].length;\n\n let previous = new Array(n).fill(0);\n let current = new Array(n).fill(0);\n previous[0] = 1;\n\n for (let i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] === 1 ? 0 : previous[0];\n for (let j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] === 1 ? 0 : current[j-1] + previous[j];\n }\n previous = [...current];\n }\n\n return previous[n-1];\n};\n```\n``` C# []\npublic class Solution {\n public int UniquePathsWithObstacles(int[][] obstacleGrid) {\n if (obstacleGrid == null || obstacleGrid.Length == 0 || obstacleGrid[0].Length == 0 || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int m = obstacleGrid.Length;\n int n = obstacleGrid[0].Length;\n\n int[] previous = new int[n];\n int[] current = new int[n];\n previous[0] = 1;\n\n for (int i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] == 1 ? 0 : previous[0];\n for (int j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] == 1 ? 0 : current[j-1] + previous[j];\n }\n Array.Copy(current, previous, n);\n }\n\n return previous[n-1];\n }\n}\n```\n\n# Conclusion\n\nThe "Unique Paths II" problem showcases how dynamic programming can help find solutions to combinatorial problems in a structured and efficient manner. By understanding the relationship between subproblems, we can incrementally build the solution and avoid redundant computations. \n\nAs with any algorithmic challenge, practice and understanding the underlying principles are key. Don\'t hesitate to tweak, optimize, and experiment with the solution to deepen your understanding!\n\n# Live Coding in Rust\nhttps://youtu.be/xt_1OzCH_NA | 50 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
✅ 100% Dynamic Programming [VIDEO] - Optimal Solution | unique-paths-ii | 1 | 1 | # Problem Understanding\n\nIn the "Unique Paths II" problem, we are presented with a grid filled with obstacles and open paths. Starting from the top-left corner, the goal is to find the number of unique paths that lead to the bottom-right corner. We can only move right or down at any point in time. If a cell has an obstacle, we cannot pass through it.\n\nFor example, consider the following grid:\n\n$$\n\\begin{array}{ccc}\n0 & 0 & 0 \\\\\n0 & 1 & 0 \\\\\n0 & 0 & 0 \\\\\n\\end{array}\n$$\n\n\n\n\n- The grid cells with obstacles are colored in red.\n- The two unique paths from the top-left to the bottom-right corner are represented by the blue and green dashed lines.\n\nFrom the plot, you can see the two possible routes:\n\n- The blue path goes Right -> Right -> Down -> Down.\n- The green path goes Down -> Down -> Right -> Right.\n\n---\n\n# Live Coding\nhttps://youtu.be/pJ40_FmXAfo\n\n- [in Python \uD83D\uDC0D](https://youtu.be/pJ40_FmXAfo)\n- [in Rust \uD83E\uDD80](https://youtu.be/xt_1OzCH_NA)\n\n# Approach\n\n## The Basic Idea\n\nThe underlying concept is rooted in dynamic programming. Essentially, for any cell `(i, j)`, the number of ways you can reach it is the sum of the ways you can reach the cell directly above it `(i-1, j)` and the cell directly to its left `(i, j-1)`. However, this is only true if the cell `(i, j)` does not have an obstacle. If it does, then the number of ways to reach this cell is 0 because it\'s inaccessible.\n\n### 2D Transition:\nIn a 2D dynamic programming approach, you would have a `dp` array of size `m x n`, where ` dp[i][j] ` represents the number of ways to reach cell ` (i, j) `.\n\nThe transition formula would be:\n$$ dp[i][j] = \n\\begin{cases} \n0 & \\text{if } obstacleGrid[i][j] = 1 \\\\\ndp[i-1][j] + dp[i][j-1] & \\text{otherwise}\n\\end{cases}\n$$\n\nSo, for each cell ` (i, j) `, if there\'s no obstacle, its value would be the sum of the cell above it and the cell to its left.\n\n### Translation to 1D:\n\nNow, given the 2D transition, notice how for any cell \\( (i, j) \\), we only need values from the current row and the previous row. This observation allows us to reduce our 2D `dp` array to two 1D arrays, `previous` and `current`.\n\nThe transition formula in 1D would be analogous to the 2D version but slightly adjusted:\n\nFor the first column (`j = 0`):\n$$ current[0] = \n\\begin{cases} \n0 & \\text{if } obstacleGrid[i][0] = 1 \\\\\nprevious[0] & \\text{otherwise}\n\\end{cases}\n$$\n\nFor other columns:\n$$ current[j] = \n\\begin{cases} \n0 & \\text{if } obstacleGrid[i][j] = 1 \\\\\nprevious[j] + current[j-1] & \\text{otherwise}\n\\end{cases}\n$$\n\nHere, `previous` is analogous to `dp[i-1]` and `current` is analogous to `dp[i]` from our 2D approach. After processing each row, we\'ll swap `previous` and `current` to roll over to the next iteration.\n\nThe transition remains conceptually the same between the 2D and 1D versions. The 1D optimization simply leverages the observation that for each cell, we only need data from the current and previous rows. This reduces space complexity from $$ O(m \\times n) $$ to $$ O(n) $$.\n\nThis rolling array technique is a common optimization strategy in dynamic programming problems involving grids.\n\n### Step-by-step Breakdown:\n\n1. **Initialization**:\n - We initialize the `previous` array with zeros. This array represents the number of ways to reach each cell in the previous row.\n - We set `previous[0]` to 1 because there\'s only one way to get to the starting cell (by starting there!).\n \n2. **Iterate through the Grid**:\n - For each row, we consider each cell:\n - If the cell has an obstacle, it\'s unreachable, so the number of ways to get there (`current[j]`) is 0.\n - Otherwise, the number of ways to reach the cell is the sum of the ways to reach the cell above and the cell to the left. This translates to `current[j-1] + previous[j]`.\n - Once we\'ve processed a row, we set `previous` to `current`, preparing for the next iteration.\n\n3. **Result**:\n - Once we\'ve processed all rows, `previous[n-1]` gives us the number of unique paths to the bottom-right corner of the grid.\n\n## Example\n\nUsing the earlier example:\n\n$$\n\\begin{array}{ccc}\n0 & 0 & 0 \\\\\n0 & 1 & 0 \\\\\n0 & 0 & 0 \\\\\n\\end{array}\n$$\n\nHere\'s how the `previous` and `current` arrays evolve:\n\nThe function\'s output matches the example description:\n\n**Initial State**:\n- `previous`: $$[1, 0, 0]$$\n- `current`: $$[0, 0, 0]$$\n\n**After processing row 0**:\n- `previous`: $$[1, 0, 0]$$\n- `current`: $$[1, 1, 1]$$\n\n**After processing row 1**:\n- `previous`: $$[1, 1, 1]$$\n- `current`: $$[1, 0, 1]$$\n\n**After processing row 2**:\n- `previous`: $$[1, 0, 1]$$\n- `current`: $$[1, 1, 2]$$\n\nFrom the final state of the `previous` array, we can infer that there are 2 unique paths from the top-left to the bottom-right corner, avoiding obstacles. This matches the expected result.\n\n# Complexity\n\n**Time Complexity:** $$O(m \\times n)$$\n**Space Complexity:** $$O(n)$$\n\nThis solution is optimal in terms of both time and space complexity. It efficiently computes the number of unique paths by building upon previous calculations.\n\n# Performance\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|-------------|--------------|------------------|-------------|-----------------|\n| Go | 0 | 100% | 2.4 | 71.38% |\n| C++ | 0 | 100% | 7.6 | 81.25% |\n| Java | 0 | 100% | 40.5 | 72.53% |\n| Rust | 1 | 85% | 2 | 87.50% |\n| Python3 | 38 | 99.30% | 16.3 | 82.98% |\n| JavaScript | 47 | 97.40% | 41.6 | 97.86% |\n| C# | 81 | 80.72% | 38.7 | 63.25% |\n\n\n\n\n---\n\n# Code\n\n``` Python []\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n if not obstacleGrid or not obstacleGrid[0] or obstacleGrid[0][0] == 1:\n return 0\n \n m, n = len(obstacleGrid), len(obstacleGrid[0])\n \n previous = [0] * n\n current = [0] * n\n previous[0] = 1\n \n for i in range(m):\n current[0] = 0 if obstacleGrid[i][0] == 1 else previous[0]\n for j in range(1, n):\n current[j] = 0 if obstacleGrid[i][j] == 1 else current[j-1] + previous[j]\n previous[:] = current\n \n return previous[n-1]\n```\n``` C++ []\nclass Solution {\npublic:\n int uniquePathsWithObstacles(std::vector<std::vector<int>>& obstacleGrid) {\n if (obstacleGrid.empty() || obstacleGrid[0].empty() || obstacleGrid[0][0] == 1) {\n return 0;\n }\n \n int m = obstacleGrid.size();\n int n = obstacleGrid[0].size();\n \n std::vector<int> previous(n, 0);\n std::vector<int> current(n, 0);\n previous[0] = 1;\n \n for (int i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] == 1 ? 0 : previous[0];\n for (int j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] == 1 ? 0 : current[j-1] + previous[j];\n }\n previous = current;\n }\n \n return previous[n-1];\n }\n};\n```\n``` Go []\nfunc uniquePathsWithObstacles(obstacleGrid [][]int) int {\n if len(obstacleGrid) == 0 || len(obstacleGrid[0]) == 0 || obstacleGrid[0][0] == 1 {\n return 0\n }\n\n m := len(obstacleGrid)\n n := len(obstacleGrid[0])\n\n previous := make([]int, n)\n current := make([]int, n)\n previous[0] = 1\n\n for i := 0; i < m; i++ {\n if obstacleGrid[i][0] == 1 {\n current[0] = 0\n } else {\n current[0] = previous[0]\n }\n \n for j := 1; j < n; j++ {\n if obstacleGrid[i][j] == 1 {\n current[j] = 0\n } else {\n current[j] = current[j-1] + previous[j]\n }\n }\n previous, current = current, previous\n }\n return previous[n-1]\n}\n```\n``` Rust []\nimpl Solution {\n pub fn unique_paths_with_obstacles(obstacleGrid: Vec<Vec<i32>>) -> i32 {\n if obstacleGrid.is_empty() || obstacleGrid[0].is_empty() || obstacleGrid[0][0] == 1 {\n return 0;\n }\n \n let m = obstacleGrid.len();\n let n = obstacleGrid[0].len();\n \n let mut previous = vec![0; n];\n let mut current = vec![0; n];\n previous[0] = 1;\n \n for row in &obstacleGrid {\n current[0] = if row[0] == 1 { 0 } else { previous[0] };\n for j in 1..n {\n if row[j] == 1 {\n current[j] = 0;\n } else {\n current[j] = current[j-1] + previous[j];\n }\n }\n std::mem::swap(&mut previous, &mut current);\n }\n \n previous[n-1]\n }\n}\n```\n``` Java []\npublic class Solution {\n public int uniquePathsWithObstacles(int[][] obstacleGrid) {\n if (obstacleGrid == null || obstacleGrid.length == 0 || obstacleGrid[0].length == 0 || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int m = obstacleGrid.length;\n int n = obstacleGrid[0].length;\n\n int[] previous = new int[n];\n int[] current = new int[n];\n previous[0] = 1;\n\n for (int i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] == 1 ? 0 : previous[0];\n for (int j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] == 1 ? 0 : current[j-1] + previous[j];\n }\n System.arraycopy(current, 0, previous, 0, n);\n }\n\n return previous[n-1];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[][]} obstacleGrid\n * @return {number}\n */\nvar uniquePathsWithObstacles = function(obstacleGrid) {\n if (!obstacleGrid.length || !obstacleGrid[0].length || obstacleGrid[0][0] === 1) {\n return 0;\n }\n\n let m = obstacleGrid.length;\n let n = obstacleGrid[0].length;\n\n let previous = new Array(n).fill(0);\n let current = new Array(n).fill(0);\n previous[0] = 1;\n\n for (let i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] === 1 ? 0 : previous[0];\n for (let j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] === 1 ? 0 : current[j-1] + previous[j];\n }\n previous = [...current];\n }\n\n return previous[n-1];\n};\n```\n``` C# []\npublic class Solution {\n public int UniquePathsWithObstacles(int[][] obstacleGrid) {\n if (obstacleGrid == null || obstacleGrid.Length == 0 || obstacleGrid[0].Length == 0 || obstacleGrid[0][0] == 1) {\n return 0;\n }\n\n int m = obstacleGrid.Length;\n int n = obstacleGrid[0].Length;\n\n int[] previous = new int[n];\n int[] current = new int[n];\n previous[0] = 1;\n\n for (int i = 0; i < m; i++) {\n current[0] = obstacleGrid[i][0] == 1 ? 0 : previous[0];\n for (int j = 1; j < n; j++) {\n current[j] = obstacleGrid[i][j] == 1 ? 0 : current[j-1] + previous[j];\n }\n Array.Copy(current, previous, n);\n }\n\n return previous[n-1];\n }\n}\n```\n\n# Conclusion\n\nThe "Unique Paths II" problem showcases how dynamic programming can help find solutions to combinatorial problems in a structured and efficient manner. By understanding the relationship between subproblems, we can incrementally build the solution and avoid redundant computations. \n\nAs with any algorithmic challenge, practice and understanding the underlying principles are key. Don\'t hesitate to tweak, optimize, and experiment with the solution to deepen your understanding!\n\n# Live Coding in Rust\nhttps://youtu.be/xt_1OzCH_NA | 50 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python easy solutions | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSame as unique path solution. But we do just one thing that, where the obstacle is there we assign it to zero and calculate further. \n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n # m, n = len(obstacleGrid), len(obstacleGrid[0])\n # dp = {(m-1, n-1): 1}\n\n # def dfs(r, c):\n # if r==m or c==n or obstacleGrid[r][c]:\n # return 0\n # if (r, c) in dp:\n # return dp[(r, c)]\n # dp[(r, c)] = dfs(r+1, c) + dfs(r, c+1)\n # return dp[(r, c)]\n # return dfs(0, 0)\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n \n if obstacleGrid[m-1][n-1] == 1: \n return 0\n else:\n dp = [0]*n\n dp[n-1] = 1\n\n for i in reversed(range(m)):\n for j in reversed(range(n)):\n if obstacleGrid[i][j]:\n dp[j] = 0\n elif j+1 < n:\n dp[j] = dp[j] + dp[j+1]\n\n return dp[0]\n``` | 2 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python easy solutions | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSame as unique path solution. But we do just one thing that, where the obstacle is there we assign it to zero and calculate further. \n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n # m, n = len(obstacleGrid), len(obstacleGrid[0])\n # dp = {(m-1, n-1): 1}\n\n # def dfs(r, c):\n # if r==m or c==n or obstacleGrid[r][c]:\n # return 0\n # if (r, c) in dp:\n # return dp[(r, c)]\n # dp[(r, c)] = dfs(r+1, c) + dfs(r, c+1)\n # return dp[(r, c)]\n # return dfs(0, 0)\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n \n if obstacleGrid[m-1][n-1] == 1: \n return 0\n else:\n dp = [0]*n\n dp[n-1] = 1\n\n for i in reversed(range(m)):\n for j in reversed(range(n)):\n if obstacleGrid[i][j]:\n dp[j] = 0\n elif j+1 < n:\n dp[j] = dp[j] + dp[j+1]\n\n return dp[0]\n``` | 2 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python DP + Memo | unique-paths-ii | 0 | 1 | ## Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n dp=[[0 for _ in range(n)] for _ in range(m)]\n dp[0][0]=1 - obstacleGrid[0][0]\n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j]==0:\n if j+1<n and obstacleGrid[i][j+1]!=1:\n dp[i][j+1]+=dp[i][j]\n if i+1<m and obstacleGrid[i+1][j]!=1:\n dp[i+1][j]+=dp[i][j]\n \n return dp[m-1][n-1]\n``` | 2 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python DP + Memo | unique-paths-ii | 0 | 1 | ## Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n dp=[[0 for _ in range(n)] for _ in range(m)]\n dp[0][0]=1 - obstacleGrid[0][0]\n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j]==0:\n if j+1<n and obstacleGrid[i][j+1]!=1:\n dp[i][j+1]+=dp[i][j]\n if i+1<m and obstacleGrid[i+1][j]!=1:\n dp[i+1][j]+=dp[i][j]\n \n return dp[m-1][n-1]\n``` | 2 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python short and clean. Multiple solutions. | unique-paths-ii | 0 | 1 | # Approach 1: Top-Down DP\n\n# Complexity\n- Time complexity: $$O(m \\cdot n)$$\n\n- Space complexity: $$O(m \\cdot n)$$\n\n# Code\n```python\nclass Solution:\n def uniquePathsWithObstacles(self, grid: list[list[int]]) -> int:\n m, n = len(grid), len(grid[0])\n end = (m - 1, n - 1)\n\n @cache\n def npaths(i: int, j: int) -> int:\n return (i < m and j < n and grid[i][j] == 0) and (\n (i, j) == end or npaths(i + 1, j) + npaths(i, j + 1)\n )\n\n return npaths(0, 0)\n\n\n```\n\n---\n# Approach 2: Bottom-Up DP\n\n# Complexity\n- Time complexity: $$O(m \\cdot n)$$\n\n- Space complexity: $$O(m \\cdot n)$$\n\n# Code\n```python\nclass Solution:\n def uniquePathsWithObstacles(self, grid: list[list[int]]) -> int:\n m, n = len(grid), len(grid[0])\n\n npaths = [[0] * (n + 1) for _ in range(m + 1)]\n npaths[0][1] = 1\n\n for i, j in product(range(m), range(n)):\n npaths[i + 1][j + 1] = 0 if grid[i][j] else npaths[i][j + 1] + npaths[i + 1][j]\n \n return npaths[-1][-1]\n\n\n```\n\n---\n# Approach 3: Space optimized Bottom-Up DP\n\n# Complexity\n- Time complexity: $$O(m \\cdot n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def uniquePathsWithObstacles(self, grid: list[list[int]]) -> int:\n m, n = len(grid), len(grid[0])\n\n npaths = [0] * (n + 1)\n npaths[1] = 1\n\n for i, j in product(range(m), range(n)):\n npaths[j + 1] = 0 if grid[i][j] else npaths[j + 1] + npaths[j]\n \n return npaths[-1]\n\n\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python short and clean. Multiple solutions. | unique-paths-ii | 0 | 1 | # Approach 1: Top-Down DP\n\n# Complexity\n- Time complexity: $$O(m \\cdot n)$$\n\n- Space complexity: $$O(m \\cdot n)$$\n\n# Code\n```python\nclass Solution:\n def uniquePathsWithObstacles(self, grid: list[list[int]]) -> int:\n m, n = len(grid), len(grid[0])\n end = (m - 1, n - 1)\n\n @cache\n def npaths(i: int, j: int) -> int:\n return (i < m and j < n and grid[i][j] == 0) and (\n (i, j) == end or npaths(i + 1, j) + npaths(i, j + 1)\n )\n\n return npaths(0, 0)\n\n\n```\n\n---\n# Approach 2: Bottom-Up DP\n\n# Complexity\n- Time complexity: $$O(m \\cdot n)$$\n\n- Space complexity: $$O(m \\cdot n)$$\n\n# Code\n```python\nclass Solution:\n def uniquePathsWithObstacles(self, grid: list[list[int]]) -> int:\n m, n = len(grid), len(grid[0])\n\n npaths = [[0] * (n + 1) for _ in range(m + 1)]\n npaths[0][1] = 1\n\n for i, j in product(range(m), range(n)):\n npaths[i + 1][j + 1] = 0 if grid[i][j] else npaths[i][j + 1] + npaths[i + 1][j]\n \n return npaths[-1][-1]\n\n\n```\n\n---\n# Approach 3: Space optimized Bottom-Up DP\n\n# Complexity\n- Time complexity: $$O(m \\cdot n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def uniquePathsWithObstacles(self, grid: list[list[int]]) -> int:\n m, n = len(grid), len(grid[0])\n\n npaths = [0] * (n + 1)\n npaths[1] = 1\n\n for i, j in product(range(m), range(n)):\n npaths[j + 1] = 0 if grid[i][j] else npaths[j + 1] + npaths[j]\n \n return npaths[-1]\n\n\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Beats 90.79% 63. Unique Paths II with step by step explanation | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a 2D dp list with the size of m+1 x n+1, with all elements initialized as 0.\n2. Set dp[0][1] to 1 as it is the starting point for the robot.\n3. Loop through the grid, if the current element is not an obstacle (obstacleGrid[i-1][j-1] == 0), calculate the number of possible paths to reach the current cell by adding the number of paths from the cell above and the cell on the left (dp[i][j] = dp[i-1][j] + dp[i][j-1]).\n4. Return the number of paths to reach the bottom-right corner (dp[m][n]).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n dp[0][1] = 1\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if obstacleGrid[i - 1][j - 1] == 0:\n dp[i][j] = dp[i - 1][j] + dp[i][j - 1]\n return dp[m][n]\n\n``` | 3 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Beats 90.79% 63. Unique Paths II with step by step explanation | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a 2D dp list with the size of m+1 x n+1, with all elements initialized as 0.\n2. Set dp[0][1] to 1 as it is the starting point for the robot.\n3. Loop through the grid, if the current element is not an obstacle (obstacleGrid[i-1][j-1] == 0), calculate the number of possible paths to reach the current cell by adding the number of paths from the cell above and the cell on the left (dp[i][j] = dp[i-1][j] + dp[i][j-1]).\n4. Return the number of paths to reach the bottom-right corner (dp[m][n]).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n dp[0][1] = 1\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if obstacleGrid[i - 1][j - 1] == 0:\n dp[i][j] = dp[i - 1][j] + dp[i][j - 1]\n return dp[m][n]\n\n``` | 3 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Finding Unique Paths in a Grid with Obstacles: A Dynamic Programming Approach | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to find the number of unique paths from the top-left corner of a matrix to the bottom-right corner. The matrix contains obstacles which are represented by 1 and free spaces represented by 0. If there is an obstacle at a cell, we cannot go through that cell. Our intuition should be to use Dynamic Programming (DP) to solve this problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a DP matrix `dp` of the same size as the input `obstacleGrid`. The value of `dp[i][j]` represents the number of unique paths to reach the cell at `(i, j)` in `obstacleGrid`.\n\nWe can initialize the `dp` matrix with `0`s. For the top-left corner of `obstacleGrid`, if there is an obstacle, then there are no unique paths to reach that cell. Hence, we set `dp[0][0]` to `0`. Otherwise, there is only one unique path to reach that cell, so we set `dp[0][0]` to `1`.\n\nNext, we can consider the first row and first column of `obstacleGrid`. If there is an obstacle in any cell in the first row or first column, we cannot move right or down, respectively. Hence, we set the corresponding `dp` value to `0`. Otherwise, we can only move either right or down in these cells, and hence there is only one unique path to reach these cells. We set the corresponding `dp` value to `1`.\n\nWe then iterate over the remaining cells in `obstacleGrid`, and for each cell, we check if there is an obstacle in that cell. If there is an obstacle, we set the corresponding dp value to 0, as we cannot go through that cell. Otherwise, the number of unique paths to reach that cell is the sum of the number of unique paths to reach the cell above it and the cell to the left of it. Hence, we set `dp[i][j] = dp[i-1][j] + dp[i][j-1]`.\n\nFinally, the number of unique paths to reach the bottom-right corner of `obstacleGrid` is `dp[m-1][n-1]`, where `m` and `n` are the number of rows and columns in `obstacleGrid`, respectively.\n# Complexity\n- Time complexity: The algorithm iterates over each cell in `obstacleGrid` exactly once, and for each cell, it performs a constant number of operations. Hence, the time complexity of this algorithm is $$O(mn)$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The algorithm uses a DP matrix `dp` of size `m` x `n`, which requires $$O(mn)$$ space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0\n for i in range(1, m):\n if obstacleGrid[i][0] == 0:\n dp[i][0] = dp[i-1][0]\n for j in range(1, n):\n if obstacleGrid[0][j] == 0:\n dp[0][j] = dp[0][j-1]\n for i in range(1, m):\n for j in range(1, n):\n if obstacleGrid[i][j] == 0:\n dp[i][j] = dp[i-1][j] + dp[i][j-1]\n return dp[m-1][n-1]\n``` | 15 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Finding Unique Paths in a Grid with Obstacles: A Dynamic Programming Approach | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to find the number of unique paths from the top-left corner of a matrix to the bottom-right corner. The matrix contains obstacles which are represented by 1 and free spaces represented by 0. If there is an obstacle at a cell, we cannot go through that cell. Our intuition should be to use Dynamic Programming (DP) to solve this problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a DP matrix `dp` of the same size as the input `obstacleGrid`. The value of `dp[i][j]` represents the number of unique paths to reach the cell at `(i, j)` in `obstacleGrid`.\n\nWe can initialize the `dp` matrix with `0`s. For the top-left corner of `obstacleGrid`, if there is an obstacle, then there are no unique paths to reach that cell. Hence, we set `dp[0][0]` to `0`. Otherwise, there is only one unique path to reach that cell, so we set `dp[0][0]` to `1`.\n\nNext, we can consider the first row and first column of `obstacleGrid`. If there is an obstacle in any cell in the first row or first column, we cannot move right or down, respectively. Hence, we set the corresponding `dp` value to `0`. Otherwise, we can only move either right or down in these cells, and hence there is only one unique path to reach these cells. We set the corresponding `dp` value to `1`.\n\nWe then iterate over the remaining cells in `obstacleGrid`, and for each cell, we check if there is an obstacle in that cell. If there is an obstacle, we set the corresponding dp value to 0, as we cannot go through that cell. Otherwise, the number of unique paths to reach that cell is the sum of the number of unique paths to reach the cell above it and the cell to the left of it. Hence, we set `dp[i][j] = dp[i-1][j] + dp[i][j-1]`.\n\nFinally, the number of unique paths to reach the bottom-right corner of `obstacleGrid` is `dp[m-1][n-1]`, where `m` and `n` are the number of rows and columns in `obstacleGrid`, respectively.\n# Complexity\n- Time complexity: The algorithm iterates over each cell in `obstacleGrid` exactly once, and for each cell, it performs a constant number of operations. Hence, the time complexity of this algorithm is $$O(mn)$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The algorithm uses a DP matrix `dp` of size `m` x `n`, which requires $$O(mn)$$ space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m, n = len(obstacleGrid), len(obstacleGrid[0])\n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0\n for i in range(1, m):\n if obstacleGrid[i][0] == 0:\n dp[i][0] = dp[i-1][0]\n for j in range(1, n):\n if obstacleGrid[0][j] == 0:\n dp[0][j] = dp[0][j-1]\n for i in range(1, m):\n for j in range(1, n):\n if obstacleGrid[i][j] == 0:\n dp[i][j] = dp[i-1][j] + dp[i][j-1]\n return dp[m-1][n-1]\n``` | 15 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python || 99.01% Faster || DP || Memoization+Tabulation | unique-paths-ii | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(2^(m+n))\n#Space Complexity: O(n)\nclass Solution1: \n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n def solve(i,j):\n if obstacleGrid[i][j]:\n return 0\n if i==0 and j==0:\n return 1\n if i<0 or j<0:\n return 0\n up=solve(i-1,j)\n left=solve(i,j-1)\n return up+left\n \n m,n=len(obstacleGrid),len(obstacleGrid[0])\n return solve(m-1,n-1)\n \n#Memoization (Top-Down)\n#Time Complexity: O(m*n)\n#Space Complexity: O(m+n) + O(m*n)\nclass Solution2:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n def solve(i,j):\n if obstacleGrid[i][j]:\n return 0\n if i==0 and j==0:\n return 1\n if i<0 or j<0:\n return 0\n if dp[i][j]!=-1:\n return dp[i][j]\n up=solve(i-1,j)\n left=solve(i,j-1)\n dp[i][j]=up+left\n return dp[i][j]\n \n m,n=len(obstacleGrid),len(obstacleGrid[0])\n dp=[[-1 for j in range(n)] for i in range(m)]\n return solve(m-1,n-1) \n\n#Tabulation (Bottom-Up)\n#Time Complexity: O(m*n)\n#Space Complexity: O(m*n)\nclass Solution3:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m,n=len(obstacleGrid),len(obstacleGrid[0])\n if obstacleGrid[0][0] or obstacleGrid[m-1][n-1]:\n return 0\n dp=[[-1 for j in range(n)] for i in range(m)]\n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j]:\n dp[i][j]=0\n continue\n if i==0 and j==0:\n dp[i][j]=1\n continue\n up=left=0\n left=0\n if i>0:\n up=dp[i-1][j]\n if j>0:\n left=dp[i][j-1]\n dp[i][j]=up+left\n return dp[m-1][n-1]\n\n#Space Optimization\n#Time Complexity: O(m*n)\n#Space Complexity: O(n)\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m,n=len(obstacleGrid),len(obstacleGrid[0])\n if obstacleGrid[0][0] or obstacleGrid[m-1][n-1]:\n return 0\n prev=[0]*n\n for i in range(m):\n temp=[0]*n\n for j in range(n):\n if obstacleGrid[i][j]:\n prev[j]=0\n continue\n if i==0 and j==0:\n temp[j]=1\n continue\n up=left=0\n if i>0:\n up=prev[j]\n if j>0:\n left=temp[j-1]\n temp[j]=up+left\n prev=temp\n return prev[n-1]\n```\n**An upvote will be encouraging** | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Python || 99.01% Faster || DP || Memoization+Tabulation | unique-paths-ii | 0 | 1 | ```\n#Recursion \n#Time Complexity: O(2^(m+n))\n#Space Complexity: O(n)\nclass Solution1: \n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n def solve(i,j):\n if obstacleGrid[i][j]:\n return 0\n if i==0 and j==0:\n return 1\n if i<0 or j<0:\n return 0\n up=solve(i-1,j)\n left=solve(i,j-1)\n return up+left\n \n m,n=len(obstacleGrid),len(obstacleGrid[0])\n return solve(m-1,n-1)\n \n#Memoization (Top-Down)\n#Time Complexity: O(m*n)\n#Space Complexity: O(m+n) + O(m*n)\nclass Solution2:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n def solve(i,j):\n if obstacleGrid[i][j]:\n return 0\n if i==0 and j==0:\n return 1\n if i<0 or j<0:\n return 0\n if dp[i][j]!=-1:\n return dp[i][j]\n up=solve(i-1,j)\n left=solve(i,j-1)\n dp[i][j]=up+left\n return dp[i][j]\n \n m,n=len(obstacleGrid),len(obstacleGrid[0])\n dp=[[-1 for j in range(n)] for i in range(m)]\n return solve(m-1,n-1) \n\n#Tabulation (Bottom-Up)\n#Time Complexity: O(m*n)\n#Space Complexity: O(m*n)\nclass Solution3:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m,n=len(obstacleGrid),len(obstacleGrid[0])\n if obstacleGrid[0][0] or obstacleGrid[m-1][n-1]:\n return 0\n dp=[[-1 for j in range(n)] for i in range(m)]\n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j]:\n dp[i][j]=0\n continue\n if i==0 and j==0:\n dp[i][j]=1\n continue\n up=left=0\n left=0\n if i>0:\n up=dp[i-1][j]\n if j>0:\n left=dp[i][j-1]\n dp[i][j]=up+left\n return dp[m-1][n-1]\n\n#Space Optimization\n#Time Complexity: O(m*n)\n#Space Complexity: O(n)\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m,n=len(obstacleGrid),len(obstacleGrid[0])\n if obstacleGrid[0][0] or obstacleGrid[m-1][n-1]:\n return 0\n prev=[0]*n\n for i in range(m):\n temp=[0]*n\n for j in range(n):\n if obstacleGrid[i][j]:\n prev[j]=0\n continue\n if i==0 and j==0:\n temp[j]=1\n continue\n up=left=0\n if i>0:\n up=prev[j]\n if j>0:\n left=temp[j-1]\n temp[j]=up+left\n prev=temp\n return prev[n-1]\n```\n**An upvote will be encouraging** | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Simple solution using dp | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m = len(obstacleGrid)\n n = len(obstacleGrid[0])\n \n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0\n \n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j] == 1:\n continue\n if i > 0:\n dp[i][j] += dp[i-1][j]\n if j > 0:\n dp[i][j] += dp[i][j-1]\n \n return dp[m-1][n-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Simple solution using dp | unique-paths-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m = len(obstacleGrid)\n n = len(obstacleGrid[0])\n \n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0\n \n for i in range(m):\n for j in range(n):\n if obstacleGrid[i][j] == 1:\n continue\n if i > 0:\n dp[i][j] += dp[i-1][j]\n if j > 0:\n dp[i][j] += dp[i][j-1]\n \n return dp[m-1][n-1]\n``` | 1 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
✅✅Python🔥Java 🔥C++🔥Simple Solution🔥Easy to Understand🔥 | minimum-path-sum | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n\n# Video Solution\n**Search \uD83D\uDC49 `Minimum Path Sum by Tech Wired` on YouTube**\n\n\n\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Approach:\n\n- The code implements a dynamic programming approach to find the minimum path sum in a grid.\n\n- The algorithm uses a 2D array to store the minimum path sum to reach each position (i, j) in the grid, where i represents the row and j represents the column.\n\n- The minimum path sum to reach each position (i, j) is computed by taking the minimum of the path sum to reach the position above (i-1, j) and the position to the left (i, j-1), and adding the cost of the current position (i, j).\n\n- The minimum path sum to reach the bottom-right corner of the grid is stored in the last element of the array (grid[m-1][n-1]), where m is the number of rows and n is the number of columns in the grid.\n\n# Intuition:\n\n- The intuition behind the dynamic programming approach is that the minimum path sum to reach a position (i, j) in the grid can be computed by considering the minimum path sum to reach the positions (i-1, j) and (i, j-1).\n\n- This is because the only two possible ways to reach the position (i, j) are either by moving down from (i-1, j) or moving right from (i, j-1).\n\n- By computing the minimum path sum to reach each position in the grid, the algorithm can find the minimum path sum to reach the bottom-right corner of the grid by simply looking at the last element of the array (grid[m-1][n-1]).\n\n\n```Python []\nclass Solution:\n def minPathSum(self, grid: List[List[int]]) -> int:\n \n \n m, n = len(grid), len(grid[0])\n \n for i in range(1, m):\n grid[i][0] += grid[i-1][0]\n \n for i in range(1, n):\n grid[0][i] += grid[0][i-1]\n \n for i in range(1, m):\n for j in range(1, n):\n grid[i][j] += min(grid[i-1][j], grid[i][j-1])\n \n return grid[-1][-1]\n \n # An Upvote will be encouraging\n\n```\n```Java []\nclass Solution {\n public int minPathSum(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n \n for (int i = 1; i < m; i++) {\n grid[i][0] += grid[i-1][0];\n }\n \n for (int j = 1; j < n; j++) {\n grid[0][j] += grid[0][j-1];\n }\n \n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n grid[i][j] += Math.min(grid[i-1][j], grid[i][j-1]);\n }\n }\n \n return grid[m-1][n-1];\n }\n}\n\n\n```\n```C++ []\nclass Solution {\npublic:\n int minPathSum(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n \n for (int i = 1; i < m; i++) {\n grid[i][0] += grid[i-1][0];\n }\n \n for (int j = 1; j < n; j++) {\n grid[0][j] += grid[0][j-1];\n }\n \n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n grid[i][j] += min(grid[i-1][j], grid[i][j-1]);\n }\n }\n \n return grid[m-1][n-1];\n }\n};\n\n\n```\n\n\n\n# Please UPVOTE \uD83D\uDC4D | 288 | Given a `m x n` `grid` filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
**Note:** You can only move either down or right at any point in time.
**Example 1:**
**Input:** grid = \[\[1,3,1\],\[1,5,1\],\[4,2,1\]\]
**Output:** 7
**Explanation:** Because the path 1 -> 3 -> 1 -> 1 -> 1 minimizes the sum.
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\]\]
**Output:** 12
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `0 <= grid[i][j] <= 100` | null |
Python Dijikstra Algo | O(n*m*log(n*m) | Code for reference | minimum-path-sum | 0 | 1 | \n```\n def minPathSum(self, grid: List[List[int]]) -> int:\n direc = [[1,0],[0,1]] # only down and right\n n,m = len(grid),len(grid[0])\n dist = [ [n*m*100 for _ in range(0,m)] for _ in range(0,n) ]\n dist[0][0] = grid[0][0]\n heap = [ [grid[0][0],0,0] ] #dist,point\n\n while(len(heap)>0):\n dis,i,j=heapq.heappop(heap)\n for dir in direc:\n x = i+dir[0]\n y = j+dir[1]\n if(x<n and y<m and grid[x][y]+dis < dist[x][y] ):\n dist[x][y] = grid[x][y]+dis\n heapq.heappush(heap,[dist[x][y],x,y])\n \n return dist[n-1][m-1]\n\n\n\n\n``` | 1 | Given a `m x n` `grid` filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
**Note:** You can only move either down or right at any point in time.
**Example 1:**
**Input:** grid = \[\[1,3,1\],\[1,5,1\],\[4,2,1\]\]
**Output:** 7
**Explanation:** Because the path 1 -> 3 -> 1 -> 1 -> 1 minimizes the sum.
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\]\]
**Output:** 12
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `0 <= grid[i][j] <= 100` | null |
Dynamic Programming: Finding the Minimum Path Sum in a Grid | minimum-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe problem asks to find the minimum sum of a path from the top-left corner to the bottom-right corner of a grid. Since we are only allowed to move right and down, the possible paths we can take are limited. Hence, we can use dynamic programming to solve this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can create a 2D array `dp` that stores the minimum sum of a path from the top-left corner to the current cell (i, j). We can initialize `dp[0][0]` as the first element of the grid. We can then populate the first row and column of the `dp` array by adding the current element of the grid to the previous element in the row/column.\n\nAfter initializing the first row and column, we can iterate through the rest of the `dp` array and calculate the minimum sum of the path to the current cell (i, j). We can calculate this by taking the minimum of the previous minimum path sum of the cell above (i-1, j) and the cell to the left (i, j-1). We then add the current element of the grid to the minimum sum.\n\nThe minimum sum of the path from the top-left corner to the bottom-right corner of the grid will be stored in `dp[m-1][n-1]`, where `m` and `n` are the dimensions of the grid.\n# Complexity\n- Time complexity: $$O(mn)$$, where m and n are the dimensions of the grid. We iterate through each cell in the `dp` array exactly once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(mn)$$, where m and n are the dimensions of the grid. We create a 2D array of size m x n to store the minimum path sum to each cell.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPathSum(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n dp = [[0] * n for _ in range(m)]\n dp[0][0] = grid[0][0]\n for i in range(1, m):\n dp[i][0] = dp[i-1][0] + grid[i][0]\n for j in range(1, n):\n dp[0][j] = dp[0][j-1] + grid[0][j]\n for i in range(1, m):\n for j in range(1, n):\n dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]\n return dp[m-1][n-1]\n``` | 9 | Given a `m x n` `grid` filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
**Note:** You can only move either down or right at any point in time.
**Example 1:**
**Input:** grid = \[\[1,3,1\],\[1,5,1\],\[4,2,1\]\]
**Output:** 7
**Explanation:** Because the path 1 -> 3 -> 1 -> 1 -> 1 minimizes the sum.
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\]\]
**Output:** 12
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `0 <= grid[i][j] <= 100` | null |
python top down and bottom up approach with explanation | minimum-path-sum | 0 | 1 | \n## Intuition\nThink of how to solve this problem using recursion. if your current position is x, y ; you can go either x+1, y or x, y+1. you need to take the minimum sum of these 2 traversals\n\n## Top down Approach\n<!-- Describe your approach to solving the problem. -->\nIn Top down approach, as explained in intuition we need to write a recursive solution. you can use a 2d array or map to store your answer. if your answer is already memoized, return the answer. The tricky part here is `memo[(x,y)] = ans - cur_sum`. `memo[(x,y)]` needs to store the sum of the path from (x,y) to (m,n) only. That is the reason `cur_sum` is being subtracted from the answer.\n\n\n## Bottom up Approach\n\nIn Bottom up approach, we construct the dp equation by understanding the following concept. we can reach a point (x,y) either from (x-1,y) or (x,y-1). so, if we know the min path sum of (x-1,y) and (x, y -1), we would choose the minimum of these two paths\n\n`dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]`\n\n# Code\n```\nclass Solution:\n def minPathSum(self, grid: List[List[int]]) -> int:\n m = len(grid) \n n = len(grid[0]) \n memo = {}\n def top_down(x, y, cur_sum = 0):\n # print(f"{x}, {y}, {cur_sum}, {grid[x][y]}")\n if x == m-1 and y == n-1:\n return cur_sum + grid[x][y]\n ans = -1\n if (x,y) in memo:\n return memo[(x,y)] + cur_sum\n elif x + 1 < m and y+1 < n:\n ans = min(top_down(x+1,y, cur_sum + grid[x][y]) , \n top_down(x,y+1, cur_sum + grid[x][y]))\n elif x+1 < m:\n ans = top_down(x+1, y, cur_sum + grid[x][y]) \n elif y+1 < n:\n ans = top_down(x, y+1, cur_sum + grid[x][y]) \n memo[(x,y)] = ans - cur_sum\n return ans\n \n def bottom_up():\n dp = [[ math.inf] * n for i in range(m)]\n dp[0][0] = grid[0][0]\n for i in range(1,n):\n dp[0][i] = dp[0][i-1] + grid[0][i]\n\n for i in range(1,m):\n for j in range(0,n):\n if j-1 >= 0:\n dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]\n else:\n dp[i][j] = dp[i-1][j] + grid[i][j]\n return dp[m-1][n-1]\n\n\n return bottom_up()\n return top_down(0 , 0)\n \n\n``` | 2 | Given a `m x n` `grid` filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
**Note:** You can only move either down or right at any point in time.
**Example 1:**
**Input:** grid = \[\[1,3,1\],\[1,5,1\],\[4,2,1\]\]
**Output:** 7
**Explanation:** Because the path 1 -> 3 -> 1 -> 1 -> 1 minimizes the sum.
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\]\]
**Output:** 12
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `0 <= grid[i][j] <= 100` | null |
✅Python3 || C++✅ DP ( 91 ms || Beats 94.21%) | minimum-path-sum | 0 | 1 | This code is an implementation of the minimum path sum problem on a 2D grid. The problem requires finding the minimum sum of numbers along a path from the top-left corner to the bottom-right corner of the grid.\n\nThe function takes a 2D list of integers grid as input, which represents the values in the grid. The function uses dynamic programming approach to solve the problem.\n\nFirst, the function determines the dimensions of the grid using the len() function. Then, it iterates over the grid using two nested for loops to check each cell of the grid.\n\nFor each cell, the function checks if it is on the top row or the leftmost column of the grid. If the cell is on the top row, the function adds the value of the cell to the value of the cell immediately to its left. Similarly, if the cell is on the leftmost column, the function adds the value of the cell to the value of the cell immediately above it.\n\nFor all other cells, the function adds the value of the cell to the minimum value of the cells directly above and directly to the left of the current cell.\n\nFinally, the function returns the value in the bottom-right corner of the grid, which represents the minimum path sum.\n\n# Please Upvote \uD83D\uDE07\n\n## Python3\n```\nclass Solution:\n def minPathSum(self, grid: List[List[int]]) -> int:\n n=len(grid)\n m=len(grid[0])\n for i in range(n):\n for j in range(m):\n if i==0:\n if j!=0:\n grid[i][j]+=grid[i][j-1]\n elif j==0:\n if i!=0:\n grid[i][j]+=grid[i-1][j]\n else:\n grid[i][j]+=min(grid[i-1][j],grid[i][j-1])\n return grid[n-1][m-1]\n```\n# C++\n```\nclass Solution {\npublic:\n int minPathSum(vector<vector<int>>& grid) {\n int n=grid.size(),m=grid[0].size();\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(i==0 and j!=0) grid[i][j]+=grid[i][j-1];\n if(j==0 and i!=0) grid[i][j]+=grid[i-1][j];\n if(i!=0 and j!=0) grid[i][j]+=min(grid[i-1][j],grid[i][j-1]);\n }\n }\n return grid[n-1][m-1];\n }\n};\n```\n\n | 51 | Given a `m x n` `grid` filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
**Note:** You can only move either down or right at any point in time.
**Example 1:**
**Input:** grid = \[\[1,3,1\],\[1,5,1\],\[4,2,1\]\]
**Output:** 7
**Explanation:** Because the path 1 -> 3 -> 1 -> 1 -> 1 minimizes the sum.
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\]\]
**Output:** 12
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `0 <= grid[i][j] <= 100` | null |
Image Explanation🏆- [Recursion - DP (4 Methods)] - C++/Java/Python | minimum-path-sum | 1 | 1 | # Video Solution (`Aryan Mittal`)\n`Minimum Path Sum` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n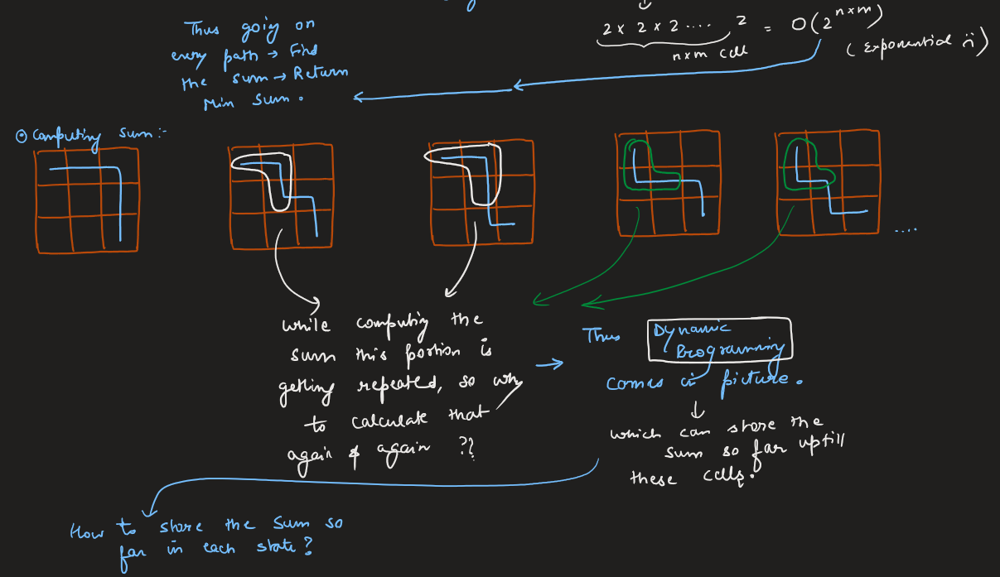\n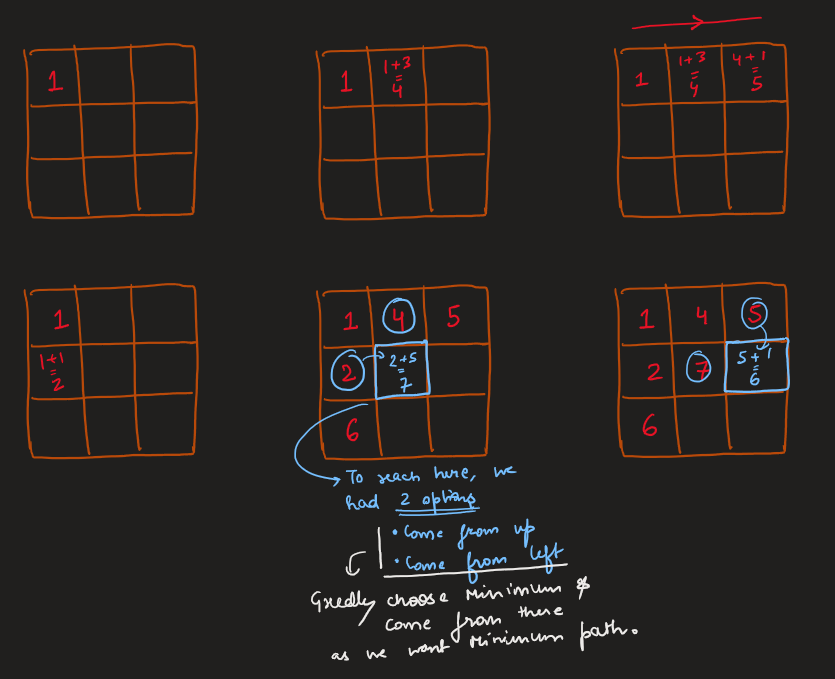\n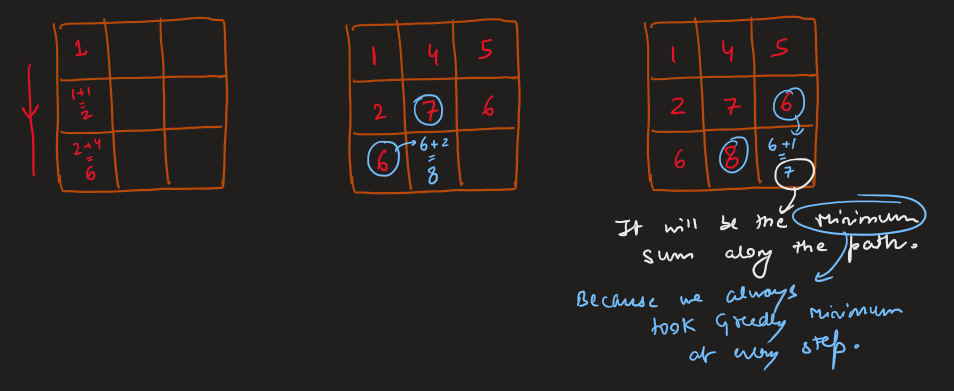\n\n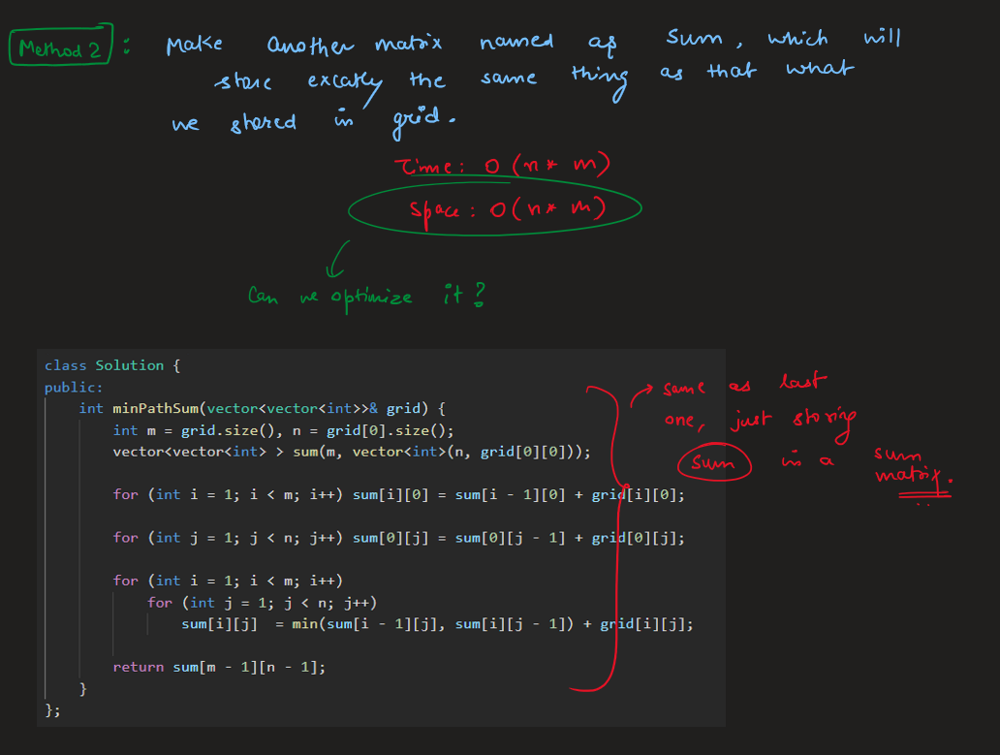\n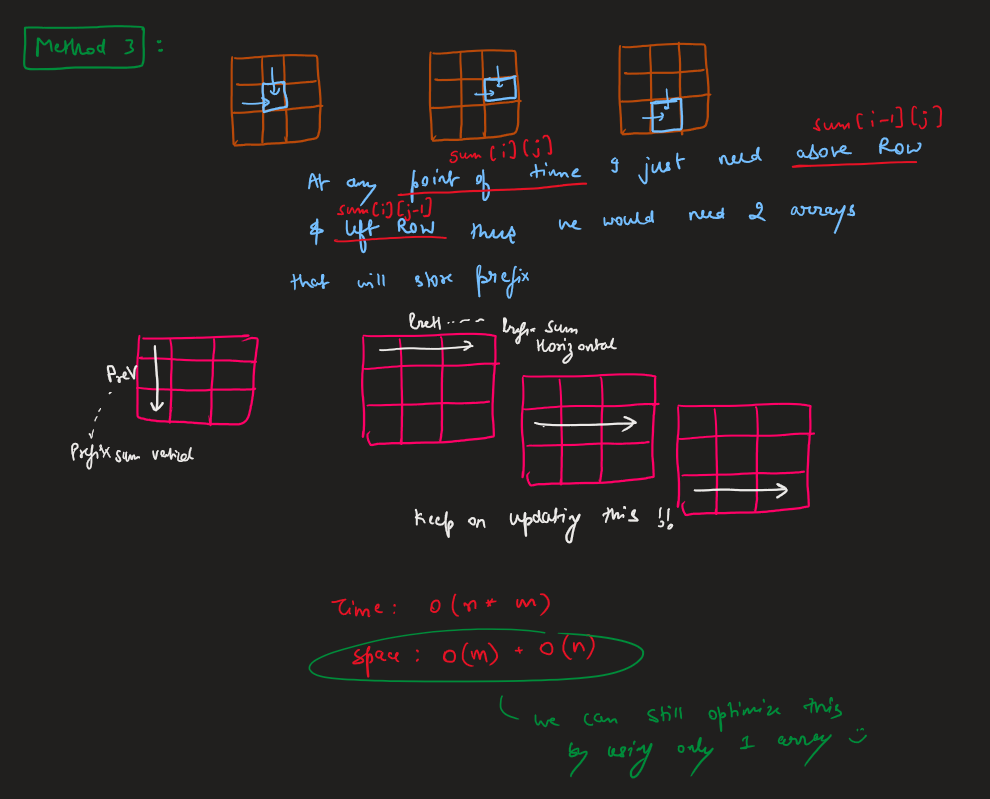\n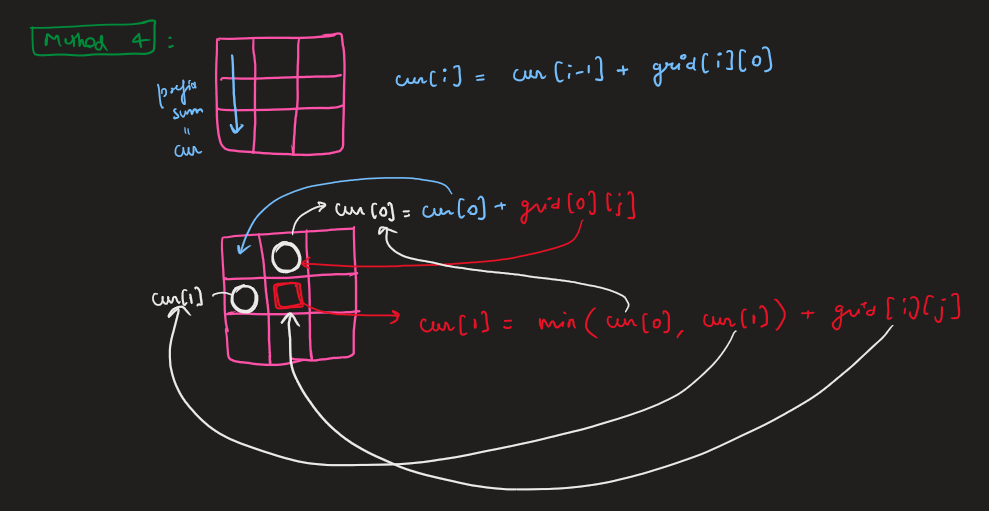\n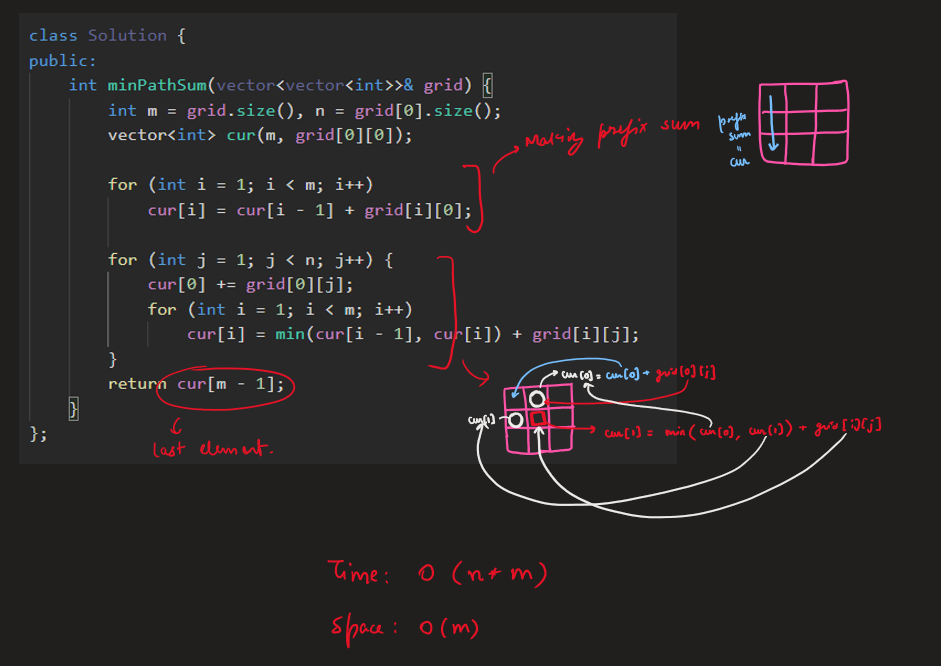\n\n\n\n# Method1 Code: By Modifying the Grid O(1) Space\n```C++ []\nclass Solution {\npublic:\n int minPathSum(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n \n for (int i = 1; i < m; i++) grid[i][0] += grid[i-1][0];\n \n for (int j = 1; j < n; j++) grid[0][j] += grid[0][j-1];\n \n for (int i = 1; i < m; i++)\n for (int j = 1; j < n; j++)\n grid[i][j] += min(grid[i-1][j], grid[i][j-1]);\n \n return grid[m-1][n-1];\n }\n};\n```\n```Java []\nclass Solution {\n public int minPathSum(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n \n for (int i = 1; i < m; i++) grid[i][0] += grid[i-1][0];\n \n for (int j = 1; j < n; j++) grid[0][j] += grid[0][j-1];\n \n for (int i = 1; i < m; i++)\n for (int j = 1; j < n; j++)\n grid[i][j] += Math.min(grid[i-1][j], grid[i][j-1]);\n \n return grid[m-1][n-1];\n }\n}\n```\n```Python []\nclass Solution:\n def minPathSum(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n for i in range(1, m):\n grid[i][0] += grid[i-1][0]\n \n for i in range(1, n):\n grid[0][i] += grid[0][i-1]\n \n for i in range(1, m):\n for j in range(1, n):\n grid[i][j] += min(grid[i-1][j], grid[i][j-1])\n \n return grid[-1][-1]\n```\n\n# Method4 Code: Without Modifying the Grid O(m) Space\n```C++ []\nclass Solution {\npublic:\n int minPathSum(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n vector<int> cur(m, grid[0][0]);\n \n for (int i = 1; i < m; i++)\n cur[i] = cur[i - 1] + grid[i][0]; \n \n for (int j = 1; j < n; j++) {\n cur[0] += grid[0][j]; \n for (int i = 1; i < m; i++)\n cur[i] = min(cur[i - 1], cur[i]) + grid[i][j];\n }\n return cur[m - 1];\n }\n};\n```\n```Java []\nclass Solution {\n public int minPathSum(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[] cur = new int[m];\n cur[0] = grid[0][0];\n \n for (int i = 1; i < m; i++)\n cur[i] = cur[i - 1] + grid[i][0];\n \n for (int j = 1; j < n; j++) {\n cur[0] += grid[0][j];\n for (int i = 1; i < m; i++)\n cur[i] = Math.min(cur[i - 1], cur[i]) + grid[i][j];\n }\n return cur[m - 1];\n }\n}\n```\n```Python []\nclass Solution:\n def minPathSum(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n cur = [grid[0][0]] * m\n \n for i in range(1, m):\n cur[i] = cur[i - 1] + grid[i][0]\n \n for j in range(1, n):\n cur[0] += grid[0][j]\n for i in range(1, m):\n cur[i] = min(cur[i - 1], cur[i]) + grid[i][j]\n \n return cur[m - 1]\n```\n | 40 | Given a `m x n` `grid` filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
**Note:** You can only move either down or right at any point in time.
**Example 1:**
**Input:** grid = \[\[1,3,1\],\[1,5,1\],\[4,2,1\]\]
**Output:** 7
**Explanation:** Because the path 1 -> 3 -> 1 -> 1 -> 1 minimizes the sum.
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\]\]
**Output:** 12
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `0 <= grid[i][j] <= 100` | null |
Solution | valid-number | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isNumber(string s) {\n return is_valid_number(s);\n }\n\nbool is_valid_number(const std::string& s) {\n if (s.empty()) return false;\n\n size_t i = 0;\n if (s[i] == \'+\' || s[i] == \'-\') i++;\n\n bool has_integer_part = false;\n while (i < s.size() && isdigit(s[i])) {\n has_integer_part = true;\n i++;\n }\n\n bool has_decimal_part = false;\n if (i < s.size() && s[i] == \'.\') {\n i++;\n while (i < s.size() && isdigit(s[i])) {\n has_decimal_part = true;\n i++;\n }\n }\n\n if (i < s.size() && (s[i] == \'e\' || s[i] == \'E\')) {\n i++;\n\n if (i < s.size() && (s[i] == \'+\' || s[i] == \'-\')) i++;\n\n if (i == s.size() || !isdigit(s[i])) {\n return false;\n }\n while (i < s.size() && isdigit(s[i])) {\n i++;\n }\n }\n return i == s.size() && (has_integer_part || has_decimal_part);\n}\n};\n```\n\n```Python3 []\nclass Solution:\n r\n def is_uinteger(self, st):\n if st=="": return False\n return set(st).issubset("0123456789")\n def is_integer(self,st):\n if st=="": return False\n if st[0] in "+-":\n return self.is_uinteger(st[1:])\n return self.is_uinteger(st)\n def is_decimal(self,st):\n if st=="": return False\n for c,ss in enumerate(st):\n if ss==".": break \n else: \n return self.is_integer(st) \n left = st[:c]\n right = st[c+1:]\n return (((left in "+-") and self.is_uinteger(right)) or\n ((self.is_integer(left) and (self.is_uinteger(right) or right==""))))\n def isNumber(self, s: str) -> bool:\n for c,ss in enumerate(s):\n if ss in "eE":\n break \n else:\n return self.is_decimal(s) or self.is_integer(s)\n return self.is_decimal(s[:c]) & self.is_integer(s[c+1:])\n```\n\n```Java []\nclass Solution {\n public boolean isNumber(String S) {\n boolean num = false, exp = false, sign = false, dec = false;\n for (int i = 0; i < S.length(); i++) {\n char c = S.charAt(i);\n if (c >= \'0\' && c <= \'9\') num = true ; \n else if (c == \'e\' || c == \'E\')\n if (exp || !num) return false;\n else {\n exp = true;\n sign = false;\n num = false;\n dec = false;\n }\n else if (c == \'+\' || c == \'-\')\n if (sign || num || dec) return false;\n else sign = true;\n else if (c == \'.\')\n if (dec || exp) return false;\n else dec = true;\n else return false;\n }\n return num;\n }\n}\n```\n | 13 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Python Simple Solution Beats 100% | valid-number | 0 | 1 | # Intuition\nUsed try and except method.\n\n# Approach\nSimply used except block when getting error in try block while typecasting string to integer\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n try:\n if s == "inf" or s == "-inf" or s == "+inf" or s =="Infinity" or s == "infinity" or s=="+Infinity" or s == "-Infinity" or s == "+infinity" or s == "-infinity" or s == "nan":\n return 0\n num = float(s)\n return 1\n except:\n return 0\n``` | 5 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Python 3 Regex with example | valid-number | 0 | 1 | If you want to practice regex, regex101.com is a good site\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n\t\t#Example: +- 1 or 1. or 1.2 or .2 e or E +- 1 \n engine = re.compile(r"^[+-]?((\\d+\\.?\\d*)|(\\d*\\.?\\d+))([eE][+-]?\\d+)?$")\n return engine.match(s.strip(" ")) # i prefer this over putting more things (\\S*) in regex\n```\nPlease leave a like if you find this helpful.\n\nAs @nwiger pointed out, the new testcase consists of "E" as well, so it should be `"^[+-]?((\\d+\\.?\\d*)|(\\d*\\.?\\d+))([eE][+-]?\\d+)?$"` (extra `E`)\n\nThanks,\nJummyEgg | 67 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Very fast and easy to understand solution (without python built-in tools) | valid-number | 0 | 1 | ```\nclass Solution:\n r"""\n Idea: split the input by the e or E and follow the validation rule"""\n def is_uinteger(self, st):\n if st=="": return False\n return set(st).issubset("0123456789")\n def is_integer(self,st):\n if st=="": return False\n if st[0] in "+-":\n return self.is_uinteger(st[1:])\n return self.is_uinteger(st)\n def is_decimal(self,st):\n if st=="": return False\n for c,ss in enumerate(st):\n if ss==".": break \n else: \n return self.is_integer(st) \n left = st[:c]\n right = st[c+1:]\n # first operand : rule 1 and 2.3 \n # second operand: rule 2.1 and 2.2\n return (((left in "+-") and self.is_uinteger(right)) or\n ((self.is_integer(left) and (self.is_uinteger(right) or right==""))))\n \n def isNumber(self, s: str) -> bool:\n for c,ss in enumerate(s):\n if ss in "eE":\n break \n else:\n return self.is_decimal(s) or self.is_integer(s)\n return self.is_decimal(s[:c]) & self.is_integer(s[c+1:])\n```\nPlease upvote :) | 5 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
28ms Beats 98.80% | O(n) |Explanation | valid-number | 0 | 1 | # Intuition\nThe code is designed to determine whether a given string represents a valid numeric value according to certain rules. The primary components to consider are the part before \'e\' (if present), the part after \'e\' (if present), the presence of a sign (\'+\' or \'-\') at the beginning, and the use of a decimal point. The code goes through these components, character by character, to validate the string.\n\n# Approach\nThe code starts by defining a helper function isValid to validate a given substring according to the rules.\n\nInside isValid, it splits the input string into two parts: before and after \'e\' (if \'e\' or \'E\' exists in the string). The before \'e\' part is further checked for signs, digits, and the decimal point, and the after \'e\' part is checked for valid integer conversion.\n\nIf both the before \'e\' and after \'e\' parts are valid, the function returns True, indicating that the input string is a valid numeric value. If any part is invalid, the function returns False.\n\nThe main isNumber function calls isValid on the input string s and returns the result.\n# Complexity\n- Time Complexity: The code iterates through the characters of the input string s once. For each character, it performs checks, conversions, and comparisons. The time complexity of the code is O(n), where \'n\' is the length of the input string.\n\n- Space Complexity: The code uses a few variables to store intermediate results, such as beforeE, afterE, sign, dot, ans, and the flags beforeEValid and afterEValid. The space complexity of the code is O(1), as the space used is constant and does not depend on the input size.\n# Code\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n # Helper function to check the validity of a substring\n def isValid(s):\n beforeE = None # Stores characters before \'e\' or \'E\'\n afterE = None # Stores characters after \'e\' or \'E\'\n\n afterEValid = 0 # Flag to check if characters after \'e\' are valid\n beforeEValid = 0 # Flag to check if characters before \'e\' are valid\n\n # Iterate through the string to find \'e\' or \'E\'\n for index, char in enumerate(s):\n if char == \'e\' or char == \'E\':\n beforeE = s[0:index] # Characters before \'e\'\n afterE = s[index + 1:] # Characters after \'e\'\n break\n\n if beforeE is None:\n beforeE = s # If \'e\' or \'E\' is not present, consider the whole string\n if len(beforeE) == 0:\n return 0 # If there are no characters before \'e\', it\'s not valid\n if afterE is None:\n afterEValid = 1 # If there are no characters after \'e\', it\'s considered valid\n elif len(afterE) == 0:\n return 0 # If there are no characters after \'e\', it\'s not valid\n else:\n try:\n val = int(afterE) # Attempt to convert the characters after \'e\' to an integer\n afterEValid = 1\n except:\n afterEValid = 0 # If conversion to integer fails, it\'s not valid\n\n sign = None # Stores the sign character (+ or -)\n dot = 0 # Counts the number of decimal points\n ans = 0 # Stores the sum of digits before \'e\'\n\n if beforeE[0] == \'-\' or beforeE[0] == \'+\':\n sign = beforeE[0] # If there\'s a sign character, store it\n beforeE = beforeE[1:] # Remove the sign character from consideration\n\n for val in beforeE:\n if val in [\'+\',\'-\']:\n return 0 # If there\'s a sign character other than the first position, it\'s not valid\n elif val in [\'1\',\'2\',\'3\',\'4\',\'5\',\'6\',\'7\',\'8\',\'9\',\'0\']:\n beforeEValid = 1 # If the character is a digit, it\'s valid\n ans += int(val) # Add the digit to the sum\n elif val == \'.\':\n dot += 1\n if dot > 1:\n return 0 # If there are more than one decimal points, it\'s not valid\n else:\n return 0 # If there\'s any other character, it\'s not valid\n\n # The result is valid if both parts (before \'e\' and after \'e) are valid\n return beforeEValid and afterEValid\n\n # Call the isValid function and return its result\n return isValid(s)\n\n \n``` | 1 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Beats 98% in runtime & 100% in memory | valid-number | 0 | 1 | \nPlease !!!!!!!!!!!!!!\n\n\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n if s==\'inf\' or s==\'-inf\' or s==\'+inf\' or s==\'Infinity\' or s==\'+Infinity\' or s==\'-Infinity\' or s==\'nan\':return False\n try:num=float(s);return True\n except:return False\n``` | 3 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
python3 Very easy Solution | valid-number | 0 | 1 | \n```\nclass Solution:\n def isNumber(self,s:str)->bool:\n try:\n float(s)\n except:\n return False\n\n return "inf" not in s.lower() \n``` | 3 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Python3 DFA | valid-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse DFA\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n\n# Code\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n currState = 0\n dfa = [\n { \'digit\': 1, \'dot\': 5, \'sign\': 6 },\n { \'digit\': 1, \'dot\': 2, \'eE\': 3 },\n { \'digit\': 2, \'eE\': 3 },\n { \'sign\': 7, \'digit\': 8 },\n { \'digit\': 4, \'eE\': 3 },\n { \'digit\': 4 },\n { \'dot\': 5, \'digit\': 1 },\n { \'digit\': 8 },\n { \'digit\': 8 }\n ]\n\n for c in s:\n # print(c)\n if c <= "9" and c >= "0":\n c = \'digit\'\n elif c == "e" or c == "E":\n c = \'eE\'\n elif c == ".":\n c = \'dot\'\n elif c == "-" or c == "+":\n c = \'sign\'\n # print(c)\n # print(currState)\n if c in dfa[currState]:\n # print(currState)\n currState = dfa[currState][c]\n # print(currState)\n else:\n return False\n\n # print(currState)\n return currState in (1,2,4,8)\n``` | 4 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
65. Valid Number | valid-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses a simple approach to keep track of different components of the number and validate each one according to the rules mentioned in the problem statement. The time complexity of this solution is O(n) where n is the length of the input string.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n s = s.strip()\n if not s: return False\n \n dot_seen = False\n e_seen = False\n num_seen = False\n num_after_e = False\n \n for i, char in enumerate(s):\n if char == \'+\' or char == \'-\':\n if i > 0 and s[i - 1] != \'e\' and s[i - 1] != \'E\':\n return False\n if i == len(s) - 1:\n return False\n elif char.isdigit():\n num_seen = True\n num_after_e = True\n elif char == \'.\':\n if dot_seen or e_seen:\n return False\n dot_seen = True\n if i == len(s) - 1:\n return num_seen\n elif char == \'e\' or char == \'E\':\n if e_seen or not num_seen:\n return False\n e_seen = True\n num_after_e = False\n if i == len(s) - 1:\n return False\n else:\n return False\n return num_seen and num_after_e\n\n``` | 3 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Python3 beating 94.83% Easiest Smallest Understandable Solution | valid-number | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def isNumber(self,s:str)->bool:\n try:\n float(s)\n except:\n return False\n return "inf" not in s.lower() \n``` | 2 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
[Python3] dfa | valid-number | 0 | 1 | This solution is based on [this thread](https://leetcode.com/problems/valid-number/discuss/23728/A-simple-solution-in-Python-based-on-DFA) which is by far the most inspirational solution that I\'ve found on LC. Please upvote that thread if you like this implementation. \n\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n dfa = [{\'space\': 0, \'sign\': 1, \'digit\': 2, \'.\': 3}, #state 0 - leading space\n {\'digit\': 2, \'.\': 3}, #state 1 - sign\n {\'digit\': 2, \'.\': 4, \'e\': 5, \'space\': 8}, #state 2 - digit (terminal)\n {\'digit\': 4}, #state 3 - dot\n {\'digit\': 4, \'e\': 5, \'space\': 8}, #state 4 - digit post dot (terminal)\n {\'sign\': 6, \'digit\': 7}, #state 5 - exponential \n {\'digit\': 7}, #state 6 - sign post exponential \n {\'digit\': 7, \'space\': 8}, #state 7 - digit post exponential (terminal)\n {\'space\': 8} #state 8 - trailing space (terminal)\n ]\n \n state = 0\n for c in s.lower(): \n if c in "0123456789": c = "digit"\n elif c == " ": c = "space"\n elif c in "+-": c = "sign"\n if c not in dfa[state]: return False \n state = dfa[state][c]\n return state in [2, 4, 7, 8]\n``` | 11 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Simple Python Solution (faster than 95%) (4 lines) | valid-number | 0 | 1 | Using try and except block in the question makes it extremely simple to handle.\nBasically, **just return True if float of the string exists, else the compiler will throw an error which will be caught by the except block, where we can return False.**\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n try:\n if \'inf\' in s.lower() or s.isalpha():\n return False\n if float(s) or float(s) >= 0:\n return True\n except:\n return False\n```\nTime Complexity: O(n) where n -> Length of the string\nSpace Complexity: O(1) | 8 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
[Python3] Solutions with explanation | valid-number | 0 | 1 | Initialize the flags **dot**, **exp** and **digit** to keep track of whether the current token being parsed is a decimal point, exponent, or digit, respectively. Then loop over the each character in the input string s and check the conditions from the **task description**.\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n dot, exp, digit = False, False, False\n\n for idx, char in enumerate(s):\n if char in [\'+\', \'-\']:\n if idx > 0 and s[idx - 1] != \'e\' and s[idx - 1] != \'E\':\n return False\n\n elif char == \'.\':\n if dot or exp:\n return False\n\n dot = True\n\n elif char == \'e\' or char == \'E\':\n if exp or not digit:\n return False\n\n exp, digit = True, False\n\n elif char.isdigit():\n digit = True\n else:\n return False\n\n return digit\n```\nSame solution using **regular expressions**:\nFirst regex pattern matches a string that starts with an optional **\'+\'** or **\'-\'** sign, (? quantifier makes the preceding \'+\' lazily match, meaning it will stop matching digits as soon as it encounters a non-digit character, this corresponds to the **mantissa**), optionally including a radix point, and ending with an optional **exponent** part, preceded by **\'+\'** or **\'-\'** sign. Second regex pattern matches a string starts with an optional **\'+\'** or **\'-\'** sign, followed by either the word **\'inf\'** or the word **\'Infinity\'**.\n\nFirst we check our string using the second pattern (**infinity check**). If the string matches, then we return **False**.\nAfter we try to convert the string to a **float** number. If it works, return **True**, otherwise go to the next check. \nNow we check if the string not matches the first pattern (**digits and exponent check**) or the first character is not **\'+\'** or **\'-\'** (after trying to convert string into float number).\nFinally, we check possible combinations of adjacent characters for the **correct record of the exponent** (as they said in description: (Optional) An \'e\' or \'E\', followed by an integer).\n```\nclass Solution:\n def isNumber(self, s: str) -> bool:\n regex = r"^[-+]?(\\d+?)([eE][-+]?\\d+)?$"\n inf_regex = r"^[-+]?(inf|Infinity|nan)"\n \n if re.match(inf_regex, s):\n return False\n\n try:\n float(s)\n return True\n except:\n pass\n \n if not re.match(regex, s) or s[0] not in ["-", "+"]:\n return False\n\n for idx, char in enumerate(s):\n if char == "." and (s[0] == "-" and s[idx - 1] == "e" or s[0] == "+" and s[idx - 1] == "E"):\n return False\n\n return True\n``` | 2 | A **valid number** can be split up into these components (in order):
1. A **decimal number** or an **integer**.
2. (Optional) An `'e'` or `'E'`, followed by an **integer**.
A **decimal number** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One of the following formats:
1. One or more digits, followed by a dot `'.'`.
2. One or more digits, followed by a dot `'.'`, followed by one or more digits.
3. A dot `'.'`, followed by one or more digits.
An **integer** can be split up into these components (in order):
1. (Optional) A sign character (either `'+'` or `'-'`).
2. One or more digits.
For example, all the following are valid numbers: `[ "2 ", "0089 ", "-0.1 ", "+3.14 ", "4. ", "-.9 ", "2e10 ", "-90E3 ", "3e+7 ", "+6e-1 ", "53.5e93 ", "-123.456e789 "]`, while the following are not valid numbers: `[ "abc ", "1a ", "1e ", "e3 ", "99e2.5 ", "--6 ", "-+3 ", "95a54e53 "]`.
Given a string `s`, return `true` _if_ `s` _is a **valid number**_.
**Example 1:**
**Input:** s = "0 "
**Output:** true
**Example 2:**
**Input:** s = "e "
**Output:** false
**Example 3:**
**Input:** s = ". "
**Output:** false
**Constraints:**
* `1 <= s.length <= 20`
* `s` consists of only English letters (both uppercase and lowercase), digits (`0-9`), plus `'+'`, minus `'-'`, or dot `'.'`. | null |
Python 98.30 % beats || 2 Approachs || Simple Code | plus-one | 0 | 1 | # Your upvote is my motivation!\n\n# Code\n# Approach 1 (Array) -> 98.30 % beats\n```\nclass Solution:\n def plusOne(self, digits: List[int]) -> List[int]:\n\n for i in range(len(digits)-1, -1, -1):\n if digits[i] == 9:\n digits[i] = 0\n else:\n digits[i] = digits[i] + 1\n return digits\n return [1] + digits \n\n \n```\n\n# Approach 2 (Convert list -> Number :: -> Addition +1 :: -> Number -> List\n```\nclass Solution:\n def plusOne(self, digits: List[int]) -> List[int]:\n # List -> Number\n n = 0\n for ele in digits:\n n = (n*10) + ele\n \n n = n+1\n \n # Number -> List\n digits = []\n while n > 0:\n digits.insert(0, n % 10) \n n //= 10 \n return digits\n``` | 38 | You are given a **large integer** represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.
Increment the large integer by one and return _the resulting array of digits_.
**Example 1:**
**Input:** digits = \[1,2,3\]
**Output:** \[1,2,4\]
**Explanation:** The array represents the integer 123.
Incrementing by one gives 123 + 1 = 124.
Thus, the result should be \[1,2,4\].
**Example 2:**
**Input:** digits = \[4,3,2,1\]
**Output:** \[4,3,2,2\]
**Explanation:** The array represents the integer 4321.
Incrementing by one gives 4321 + 1 = 4322.
Thus, the result should be \[4,3,2,2\].
**Example 3:**
**Input:** digits = \[9\]
**Output:** \[1,0\]
**Explanation:** The array represents the integer 9.
Incrementing by one gives 9 + 1 = 10.
Thus, the result should be \[1,0\].
**Constraints:**
* `1 <= digits.length <= 100`
* `0 <= digits[i] <= 9`
* `digits` does not contain any leading `0`'s. | null |
On Fire Python Solution! | plus-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n converting into string and int and so\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n iterated over list and calculate edge cases \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n# Code\n```\nclass Solution:\n def plusOne(self, digits: List[int]) -> List[int]:\n i = len(digits)-1\n flag = False \n while digits[i] == 9: \n digits[i] = 0\n if i == 0:\n v = (digits[0]+1)%9\n digits = [0]*(len(digits)+1)\n digits[0] = v\n flag = True \n break\n i -= 1\n if not flag:\n digits[i] += 1 \n\n return digits\n\n\n \n``` | 0 | You are given a **large integer** represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.
Increment the large integer by one and return _the resulting array of digits_.
**Example 1:**
**Input:** digits = \[1,2,3\]
**Output:** \[1,2,4\]
**Explanation:** The array represents the integer 123.
Incrementing by one gives 123 + 1 = 124.
Thus, the result should be \[1,2,4\].
**Example 2:**
**Input:** digits = \[4,3,2,1\]
**Output:** \[4,3,2,2\]
**Explanation:** The array represents the integer 4321.
Incrementing by one gives 4321 + 1 = 4322.
Thus, the result should be \[4,3,2,2\].
**Example 3:**
**Input:** digits = \[9\]
**Output:** \[1,0\]
**Explanation:** The array represents the integer 9.
Incrementing by one gives 9 + 1 = 10.
Thus, the result should be \[1,0\].
**Constraints:**
* `1 <= digits.length <= 100`
* `0 <= digits[i] <= 9`
* `digits` does not contain any leading `0`'s. | null |
One `for` loop beats 93% | plus-one | 0 | 1 | # Code\n```\nclass Solution:\n def plusOne(self, digits: List[int]) -> List[int]:\n\n for i in range(len(digits)-1,-1,-1):\n if digits[i]==9:\n digits[i]=0\n else:\n digits[i]+=1\n return digits\n return [1]+digits\n``` | 27 | You are given a **large integer** represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.
Increment the large integer by one and return _the resulting array of digits_.
**Example 1:**
**Input:** digits = \[1,2,3\]
**Output:** \[1,2,4\]
**Explanation:** The array represents the integer 123.
Incrementing by one gives 123 + 1 = 124.
Thus, the result should be \[1,2,4\].
**Example 2:**
**Input:** digits = \[4,3,2,1\]
**Output:** \[4,3,2,2\]
**Explanation:** The array represents the integer 4321.
Incrementing by one gives 4321 + 1 = 4322.
Thus, the result should be \[4,3,2,2\].
**Example 3:**
**Input:** digits = \[9\]
**Output:** \[1,0\]
**Explanation:** The array represents the integer 9.
Incrementing by one gives 9 + 1 = 10.
Thus, the result should be \[1,0\].
**Constraints:**
* `1 <= digits.length <= 100`
* `0 <= digits[i] <= 9`
* `digits` does not contain any leading `0`'s. | null |
Simplest Python Approach - Beats 99.5% | plus-one | 0 | 1 | # Intuition\nOften the obvious approach is among the best. If you just convert to an integer and add one, it beats 98% of solutions.\n\n# Approach\nInstead of looping across the list and accounting for random 9s, just convert to an integer and add one. Then convert back to a list.\n\n# Complexity\nThe time complexity is O(n) because we have to traverse the list exactly once then convert back to a list.\n\n# Code\n```\nclass Solution:\n def plusOne(self, digits):\n strings = ""\n for number in digits:\n strings += str(number)\n\n temp = str(int(strings) +1)\n\n return [int(temp[i]) for i in range(len(temp))]\n\n\n``` | 40 | You are given a **large integer** represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.
Increment the large integer by one and return _the resulting array of digits_.
**Example 1:**
**Input:** digits = \[1,2,3\]
**Output:** \[1,2,4\]
**Explanation:** The array represents the integer 123.
Incrementing by one gives 123 + 1 = 124.
Thus, the result should be \[1,2,4\].
**Example 2:**
**Input:** digits = \[4,3,2,1\]
**Output:** \[4,3,2,2\]
**Explanation:** The array represents the integer 4321.
Incrementing by one gives 4321 + 1 = 4322.
Thus, the result should be \[4,3,2,2\].
**Example 3:**
**Input:** digits = \[9\]
**Output:** \[1,0\]
**Explanation:** The array represents the integer 9.
Incrementing by one gives 9 + 1 = 10.
Thus, the result should be \[1,0\].
**Constraints:**
* `1 <= digits.length <= 100`
* `0 <= digits[i] <= 9`
* `digits` does not contain any leading `0`'s. | null |
✅ Python || Time Complexity O(n) || Beats 98.26% in Python3 || Using Iteration ✔ | plus-one | 0 | 1 | # Intuition\nUsing Iteration form n-1 to 0\n\nWe have to add 1 in given digit ( given array ) , so we simple iterate form last index (n-1) to first index (0) and will check if we add (+1) or not , ( (if(digits[i] == 9)) if current element is 9 then we can\'t add directly )\n\nif not (means digits[i] == 9 ) then we make current element 0 (digits[i] = 0) and move to its previous element and we perform this step until we reach to element which is less then 9 , if we reach to (0) index and it is still (digits[0] == 9 , means all element of array is 9 [9,9,9,9,9,9] ) then at the end we insert new element (1) at zero index [1,0,0,0,0,0,0]\n digits.insert(0 , 1)\n return digits\n\nif (digits[i] != 9) then add 1 ,and after adding we break the loop \n digits[i] = digits[i] + 1\n return digits\n\nTime Complexity is O(N) and Space Complexity is O(1)\n\n\n\n\n\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n\n* If this was helpful, please upvote so that others can see this solution too.\n\n# Code\n```\nclass Solution:\n def plusOne(self, digits: List[int]) -> List[int]:\n n = len(digits)\n\n for i in range(n-1 , -1 , -1):\n if(digits[i] == 9):\n digits[i] = 0 \n else:\n digits[i] = digits[i] + 1\n return digits\n \n digits.insert(0 , 1)\n return digits\n``` | 6 | You are given a **large integer** represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.
Increment the large integer by one and return _the resulting array of digits_.
**Example 1:**
**Input:** digits = \[1,2,3\]
**Output:** \[1,2,4\]
**Explanation:** The array represents the integer 123.
Incrementing by one gives 123 + 1 = 124.
Thus, the result should be \[1,2,4\].
**Example 2:**
**Input:** digits = \[4,3,2,1\]
**Output:** \[4,3,2,2\]
**Explanation:** The array represents the integer 4321.
Incrementing by one gives 4321 + 1 = 4322.
Thus, the result should be \[4,3,2,2\].
**Example 3:**
**Input:** digits = \[9\]
**Output:** \[1,0\]
**Explanation:** The array represents the integer 9.
Incrementing by one gives 9 + 1 = 10.
Thus, the result should be \[1,0\].
**Constraints:**
* `1 <= digits.length <= 100`
* `0 <= digits[i] <= 9`
* `digits` does not contain any leading `0`'s. | null |
Simple easy Solution in Python3 | plus-one | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def plusOne(self, digits: List[int]) -> List[int]:\n s= \'\'.join(map(str,digits))\n i=int(s)+1\n li=list(map(int,str(i))) \n return li\n``` | 5 | You are given a **large integer** represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.
Increment the large integer by one and return _the resulting array of digits_.
**Example 1:**
**Input:** digits = \[1,2,3\]
**Output:** \[1,2,4\]
**Explanation:** The array represents the integer 123.
Incrementing by one gives 123 + 1 = 124.
Thus, the result should be \[1,2,4\].
**Example 2:**
**Input:** digits = \[4,3,2,1\]
**Output:** \[4,3,2,2\]
**Explanation:** The array represents the integer 4321.
Incrementing by one gives 4321 + 1 = 4322.
Thus, the result should be \[4,3,2,2\].
**Example 3:**
**Input:** digits = \[9\]
**Output:** \[1,0\]
**Explanation:** The array represents the integer 9.
Incrementing by one gives 9 + 1 = 10.
Thus, the result should be \[1,0\].
**Constraints:**
* `1 <= digits.length <= 100`
* `0 <= digits[i] <= 9`
* `digits` does not contain any leading `0`'s. | null |
1ms (Beats 100%)🔥🔥|| Full Explanation✅|| Append & Reverse✅|| C++|| Java|| Python3 | add-binary | 1 | 1 | # Intuition :\n- We have to add two binary numbers (made up of 0\'s and 1\'s) and returns the result in binary.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- We start at the right end of each binary number, adding the digits and any carry-over value, and storing the result in a new string. \n- Now we move to the next digit on the left and repeats the process until it has gone through all the digits in both binary numbers.\n- If there is any carry-over value after adding all the digits, append it to the end of the new string. \n- Finally, the new string is reversed and returned as the sum of the two binary numbers.\n<!-- Describe your approach to solving the problem. -->\n# Explanation to Approach :\n- Suppose we want to add two binary numbers - "1010" and "1101". \n- To add these two numbers, we can use the given function as follows:\n- First, we initialize a StringBuilder object to store the sum and two integer variables \'carry\' and \'i\' to keep track of the carry-over value and the current position in the first binary number (a), respectively. \n- We also initialize another integer variable \'j\' to keep track of the current position in the second binary number (b). Here is how the code initializes these variables:\n```\nStringBuilder sb = new StringBuilder();\nint carry = 0;\nint i = a.length() - 1;\nint j = b.length() - 1;\n\n```\n- Next, we enter a while loop that iterates until we have processed all digits in both binary numbers and there is no more carry-over value left. In each iteration, we add the digits from both numbers at the current position and the carry-over value (if any), and append the result to the StringBuilder object. \n- We also update the carry-over value based on the sum of the digits. Here is the code for this step:\n```\nwhile (i >= 0 || j >= 0 || carry == 1) {\n if (i >= 0) {\n carry += a.charAt(i--) - \'0\';\n }\n if (j >= 0) {\n carry += b.charAt(j--) - \'0\';\n }\n sb.append(carry % 2);\n carry /= 2;\n}\n\n```\n- In each iteration, the current position in each binary number is moved one digit to the left (if there are any digits left to process) by decrementing the value of i and j. \n- If there is a carry-over value from the previous iteration or the addition of the two digits produces a carry-over value, we set the value of \'carry\' to 1; otherwise, we set it to 0. \n- We also append the sum of the digits to the StringBuilder object by computing the remainder of \'carry\' divided by 2 (which is either 0 or 1). \n- Finally, we update the value of \'carry\' by dividing it by 2 (which gives either 0 or 1) so that we can carry over any remaining value to the next iteration.\n- After the while loop completes, we reverse the StringBuilder object and convert it to a string using the toString() method. \n- This gives us the sum of the two binary numbers in binary format. Here is the final code:\n```\nreturn sb.reverse().toString();\n\n```\n# Example : the sum of "1010" and "1101\n```\n 1010\n +1101\n ______\n 10111\n```\n\n# Complexity\n- Time complexity : O(max|a|,|b|)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(max|a|,|b|)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] \n```C++ []\nclass Solution {\n public:\n string addBinary(string a, string b) {\n string ans;\n int carry = 0;\n int i = a.length() - 1;\n int j = b.length() - 1;\n\n while (i >= 0 || j >= 0 || carry) {\n if (i >= 0)\n carry += a[i--] - \'0\';\n if (j >= 0)\n carry += b[j--] - \'0\';\n ans += carry % 2 + \'0\';\n carry /= 2;\n }\n\n reverse(begin(ans), end(ans));\n return ans;\n }\n};\n```\n```Java []\nclass Solution \n{\n public String addBinary(String a, String b) \n {\n StringBuilder sb = new StringBuilder();\n int carry = 0;\n int i = a.length() - 1;\n int j = b.length() - 1;\n\n while (i >= 0 || j >= 0 || carry == 1) \n {\n if(i >= 0)\n carry += a.charAt(i--) - \'0\';\n if(j >= 0)\n carry += b.charAt(j--) - \'0\';\n sb.append(carry % 2);\n carry /= 2;\n }\n return sb.reverse().toString();\n }\n}\n```\n```Python3 []\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n s = []\n carry = 0\n i = len(a) - 1\n j = len(b) - 1\n\n while i >= 0 or j >= 0 or carry:\n if i >= 0:\n carry += int(a[i])\n i -= 1\n if j >= 0:\n carry += int(b[j])\n j -= 1\n s.append(str(carry % 2))\n carry //= 2\n\n return \'\'.join(reversed(s))\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 487 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
one liner beats 85% | add-binary | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n return bin(int(a, 2) + int(b, 2))[2:]\n``` | 1 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
🔥🚀Super Easy Solution🚀||🔥Full Explanation||🔥C++🔥|| Python3 || Java || Commented | add-binary | 1 | 1 | # Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful\n```\n# Intuition\nLet\'s understand with an example : Addition of 1 and 1 will lead to carry 1 and print 0 , Addition of 1 and 0 give us 1 as carry will lead print 0 , Addition of last remaning carry 1 with no body will lead to print 1 , So, we get something like "1 0 0" as answer\nOne key point total addition will be 3 then print 1 and carry will remain 1.\n\n**Adding 2 binary bits :**\n 0 + 0 = 0\n 1 + 0 = 1\n 0 + 1 = 1\n 1 + 1 = 10\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**Example :**\n- So, what\'s going in diagram is intially **carry is "0"** we **add 1 + 1** we **get 2** which is **more then 1**, so there is a **carry of 1 and result is 0**. Now we have **carry of 1, again 1 + 1 is 0**, and **still left with carry of 1**. And the last carry one will be **return as it is**.\n- So, if you see this binary number it is **[2^2 * 1 + 2^1 * 0 + 2^0 * 0]** and this is the decimal coversion of **[1 0 0] which is 4.**\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(max(n, m))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(max(n, m))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Consider\uD83D\uDC4D\n Thanks for visiting\uD83D\uDE0A\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to add two binary numbers represented as strings\n string addBinary(string a, string b) {\n // Initialize two pointers to traverse the binary strings from right to left\n int i = a.length()-1;\n int j = b.length()-1;\n string ans;\n int carry = 0;\n \n // Loop until both pointers have reached the beginning of their respective strings and there is no carry-over value left\n while(i >= 0 || j >= 0 || carry) {\n // Add the current binary digit in string a, if the pointer is still within bounds\n if(i >= 0) {\n carry += a[i] - \'0\';\n i--;\n }\n \n // Add the current binary digit in string b, if the pointer is still within bounds\n if(j >= 0) {\n carry += b[j] - \'0\';\n j--;\n }\n \n // Calculate the next binary digit in the result by taking the remainder of the sum divided by 2\n ans += (carry % 2 + \'0\');\n \n // Calculate the next carry-over value by dividing the sum by 2\n carry = carry / 2;\n }\n \n // Reverse the result and return it as a string\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n\n```\n```python []\nclass Solution:\n \n # Function to add two binary numbers represented as strings\n def addBinary(self, a, b):\n # List to store the result\n result = []\n # Variable to store the carry-over value\n carry = 0\n \n # Initialize two pointers to traverse the binary strings from right to left\n i, j = len(a)-1, len(b)-1\n \n # Loop until both pointers have reached the beginning of their respective strings and there is no carry-over value left\n while i >= 0 or j >= 0 or carry:\n total = carry\n \n # Add the current binary digit in string a, if the pointer is still within bounds\n if i >= 0:\n total += int(a[i])\n i -= 1\n \n # Add the current binary digit in string b, if the pointer is still within bounds\n if j >= 0:\n total += int(b[j])\n j -= 1\n \n # Calculate the next binary digit in the result by taking the remainder of the sum divided by 2\n result.append(str(total % 2))\n \n # Calculate the next carry-over value by dividing the sum by 2\n carry = total // 2\n \n # Reverse the result and join the elements to form a single string\n return \'\'.join(reversed(result))\n\n```\n```Java []\nclass Solution {\n // Function to add two binary numbers represented as strings\n public String addBinary(String a, String b) {\n // Initialize two pointers to traverse the binary strings from right to left\n int i = a.length() - 1;\n int j = b.length() - 1;\n StringBuilder ans = new StringBuilder();\n int carry = 0;\n \n // Loop until both pointers have reached the beginning of their respective strings and there is no carry-over value left\n while (i >= 0 || j >= 0 || carry != 0) {\n // Add the current binary digit in string a, if the pointer is still within bounds\n if (i >= 0) {\n carry += a.charAt(i) - \'0\';\n i--;\n }\n \n // Add the current binary digit in string b, if the pointer is still within bounds\n if (j >= 0) {\n carry += b.charAt(j) - \'0\';\n j--;\n }\n \n // Calculate the next binary digit in the result by taking the remainder of the sum divided by 2\n ans.append(carry % 2);\n \n // Calculate the next carry-over value by dividing the sum by 2\n carry = carry / 2;\n }\n \n // Reverse the result and return it as a string\n return ans.reverse().toString();\n }\n}\n\n```\n\n```\n Give a \uD83D\uDC4D. It motivates me alot\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/) | 85 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
29 ms python solution( beats 97.90%) | add-binary | 0 | 1 | The function called addBinary takes in two strings, a and b, which represent binary numbers. The function then performs a series of operations to add these two binary numbers together and returns the result as a string.\n\nTo do this, the code first initializes a carry variable to 0, which will be used to store any carry over from one bit to the next as the numbers are added together. The function then loops over the bits of the two numbers from the most significant bit (MSB) to the least significant bit (LSB). For each bit, the code extracts the corresponding bits from a and b and adds them together along with the current carry value. If the sum of these three values is greater than or equal to 2, it means that there is a carry over to the next bit, so the code sets the carry value to 1 and reduces the sum by 2. Otherwise, the carry value is set to 0.\n\nAfter each iteration of the loop, the code appends the current sum to a string called result, which will be used to store the final result of the addition. At the end of the loop, the code checks if there is a final carry value of 1 and, if so, appends a 1 to the beginning of the result string. Finally, the addBinary function returns the result string.\n\nI hope this helps! Let me know if you have any other questions about the code.\n\n# Time Complexity:\nO(max(N,M)) \nLet N equal the size of the string a and M the size of the string b\n\n# Code\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n carry = 0\n result=""\n for i in range( max(len(a),len(b))):\n aBit = int( a[len(a)-1-i] ) if len(a)-1-i >=0 else 0\n bBit = int( b[len(b)-1-i] ) if len(b)-1-i >=0 else 0\n sum = aBit + bBit + carry\n if sum >=2:\n carry = 1\n sum = (sum)%2\n else:\n carry =0\n result = str(sum) + result\n if carry:return "1"+result\n return result\n \n``` | 1 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
Python 3 || One lines of code || Time 95 % O(1) | add-binary | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis code is a simple implementation of converting binary numbers to integers, adding them, and then converting the sum back to binary. The conversion of binary to integer is done using the int() method with a base of 2, which means that it will treat the string as a binary number and return the equivalent integer. After adding the integers,\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n return bin(int(a , 2) + int(b,2))[2:]\n``` | 13 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
STRIVER || C++ || SIGMA || BEGGINER FRIENDLY|| | add-binary | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string addBinary(string a, string b) {\n \n string ans="";\n int i=a.size()-1;\n int j=b.size()-1;\n int value=0;\n int carry=0;\n\n while(i>=0 || j>=0 || value)\n\n {\n if(i>=0)\n {\n value+=a[i]-\'0\';\n i--;\n }\n if(j>=0)\n {\n value+=b[j]-\'0\';\n j--;\n\n }\n\n ans+=value%2+\'0\';\n value=value/2;\n }\n\nreverse(ans.begin(),ans.end());\nreturn ans;\n }\n};\n``` | 1 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
🔥1 Line using Built-In Functions, With Explanation | add-binary | 0 | 1 | \n# Code\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n return bin(int(a, 2) + int(b, 2))[2:]\n\n```\n\n# Explanation\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n # Convert binary string \'a\' to an integer.\n int_a = int(a, 2)\n \n # Convert binary string \'b\' to an integer.\n int_b = int(b, 2)\n \n # Calculate the sum of the two integers.\n sum_int = int_a + int_b\n \n # Convert the sum back to a binary string.\n binary_sum = bin(sum_int)\n \n # Remove the \'0b\' prefix from the binary string.\n binary_sum_str = binary_sum[2:]\n \n # Return the binary sum as a string.\n return binary_sum_str\n\n``` | 2 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
📌📌Python3 || ⚡28 ms, faster than 93.95% of Python3 | add-binary | 0 | 1 | \n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n res = []\n carry = 0\n i, j = len(a) - 1, len(b) - 1\n while i >= 0 or j >= 0:\n sum = carry\n if i >= 0:\n sum += int(a[i])\n i -= 1\n if j >= 0:\n sum += int(b[j])\n j -= 1\n carry = sum >> 1\n res.append(str(sum & 1))\n if carry:\n res.append(str(carry))\n return "".join(res[::-1])\n```\nThe program implements the binary addition of two strings a and b. Here\'s a step by step description of the code:\n1. Initialize a list res to store the binary sum, a variable carry to store the carry from the previous addition, and two variables i and j to keep track of the indices of the binary strings a and b.\n1. Start a while loop that continues until both indices i and j are less than zero.\n1. Inside the while loop, initialize a variable sum to the current value of the carry variable.\n1. If i is greater than or equal to zero, add the integer value of the i-th character of a to sum. Then decrement i by 1.\n1. If j is greater than or equal to zero, add the integer value of the j-th character of b to sum. Then decrement j by 1.\n1. Calculate the carry from the current addition by shifting the sum one bit to the right. Assign the result to the carry variable.\n1. Append the result of the current addition modulo 2 to the res list.\n1. If carry is not equal to zero, append the carry value as a string to the res list.\n1. Return the concatenation of the res list in reverse order, joined as a string. | 3 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
sol using python - just 2 line | add-binary | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n res = str(bin(int(a, 2) + int(b, 2)))\n return res[2:]\n \n\n\n``` | 6 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
👹 Super Simple Solution, PYTHON🐍 | add-binary | 0 | 1 | # Intuition\nconvert to int, add, back to binary return\n\n\n# Complexity\n- Time complexity:\n O(log n).\n\n- Space complexity:\n O(log n).\n\n# Code\n```\nclass Solution:\n def addBinary(self, a: str, b: str) -> str:\n int_sum = int(a, 2) + int(b, 2)\n binary_sum = bin(int_sum)[2:] #to remove 0b prefix that shows sting is binary\n return binary_sum\n\n```\n\n | 2 | Given two binary strings `a` and `b`, return _their sum as a binary string_.
**Example 1:**
**Input:** a = "11", b = "1"
**Output:** "100"
**Example 2:**
**Input:** a = "1010", b = "1011"
**Output:** "10101"
**Constraints:**
* `1 <= a.length, b.length <= 104`
* `a` and `b` consist only of `'0'` or `'1'` characters.
* Each string does not contain leading zeros except for the zero itself. | null |
✅ 94.14% 2-Approaches Greedy | text-justification | 1 | 1 | # Interview Problem Understanding\n\nIn interviews, understanding the problem at hand is half the battle. Let\'s break down the "Text Justification" challenge:\n\n**The Scenario**: Imagine you\'re building a word processor, and you need to implement the "Justify" alignment feature. This means that when a user selects a group of words and chooses the "Justify" option, the text is adjusted so that each line spans the entire width of the available space. Words are spaced out, and additional spaces are added between them to achieve this uniform width.\n\n**The Challenge**: Given an array of strings (or words) and a defined maximum width for each line:\n- Your task is to format the text such that each line is exactly the specified maximum width.\n- Each line should be both left and right justified. This means the words on each line are separated by one or more spaces to ensure the line extends from the very left to the very right.\n- There\'s a catch, though. For lines that aren\'t the last, if the spaces don\'t divide evenly, the leftmost gaps get more spaces. For the very last line or a line with a single word, it should be left-justified, and the extra spaces are added to the end.\n\n**Example**:\nSuppose you\'re given the words `["This", "is", "an", "example", "of", "text", "justification."]` and a `maxWidth` of 16. This means each line of the output can only be 16 characters wide. Your output should resemble:\n\n```\n[\n "This is an",\n "example of text",\n "justification. "\n]\n```\n\n**Input/Output**:\n- **Input**: You\'re provided with an array of words and a maximum width for each line.\n- **Output**: Your goal is to return a list of strings, where each string is a line of text that adheres to the justification rules.\n\n---\n\n# Live Coding + Explenation Modulo-based\nhttps://youtu.be/KGfXrj7G0W0?si=VmyOm2RqX6yfMm9w\n\n---\n\n## Approach 1: Modulo-based Space Distribution\n\nTo solve the "Text Justification" problem using this approach, we pack words into each line using a greedy strategy. We then distribute spaces among the words on each line, using modulo arithmetic to decide where to place the extra spaces.\n\n### Key Data Structures:\n- **List**: To store the current words for a line and the result.\n\n### Enhanced Breakdown:\n\n1. **Initialization**:\n - We start by initializing empty lists for the result and the current line words.\n - A counter is also initialized to keep track of the total length of words in the current line.\n \n2. **Processing Each Word**:\n - For each word, we check if adding the next word to the current line would make it exceed the maximum width.\n - If it does, we proceed to justify the current line. This involves distributing spaces among the words. The modulo arithmetic is handy here, ensuring that extra spaces are evenly spread among the words.\n - Once the line is justified, we reset the lists and counter for the next line.\n - A special case is the last line, where we simply left-justify the words.\n\n3. **Wrap-up**:\n - Once all the words are processed and lines are justified, we return the result list.\n\n## Example:\n\nGiven the `words = ["This", "is", "an", "example"]` and `maxWidth = 16`:\n\n- The word "This" is added to the current line.\n- The word "is" is added to the current line.\n- The word "an" is added to the current line, completing it with the string "This is an".\n- The word "example" starts a new line.\n\n---\n\n## Approach 2: Gap-based Space Distribution\n\nIn this method, the way we pack words into each line remains similar to the first approach. However, when it comes to distributing spaces, the logic is a tad different. Instead of using modulo arithmetic directly, we compute the number of gaps between words and then decide how many spaces to put in each gap. This makes the logic more intuitive.\n\n### Key Data Structures:\n- **List**: To store the current words for a line and the result.\n\n### Enhanced Breakdown:\n\n1. **Initialization**:\n - As before, we initialize empty lists for the result and the current line words.\n - A counter keeps track of the total length of words in the current line.\n \n2. **Processing Each Word**:\n - For every word, we check if adding it to the current line would cross the maximum width.\n - If yes, we justify the current line. This time, we compute the total number of spaces required for the current line. This is based on the maximum width and the length of words on the line.\n - We then determine how many gaps exist between the words and compute the number of spaces that can be evenly distributed across these gaps.\n - Any extra spaces that can\'t be evenly distributed are then added to the gaps from left to right.\n - The last line is handled specially, where we left-justify the words.\n\n3. **Wrap-up**:\n - After processing all the words and justifying the lines, we return the result list.\n\n---\n\n# Complexity:\n\n**Time Complexity:** Both approaches process each word once and have a time complexity of $$O(n)$$, where $$n$$ is the number of words.\n\n**Space Complexity:** The space complexity for both methods is $$O(n \\times m)$$, where $$n$$ is the number of words and $$m$$ is the average length of the words.\n\n---\n\n# Performance:\n\n| Language | Runtime (ms) | Memory (MB) |\n|-------------|--------------|-------------|\n| Rust | 1 ms | 2.1 MB |\n| Go | 1 ms | 2.1 MB |\n| Java | 1 ms | 40.7 MB |\n| C++ | 4 ms | 7.6 MB |\n| Python3 (v2)| 34 ms | 16.3 MB |\n| Python3 (v1)| 34 ms | 16.1 MB |\n| JavaScript | 55 ms | 42.2 MB |\n| C# | 139 ms | 43.7 MB |\n\n\n\n# Code Modulo-based\n``` Python []\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n res, line, width = [], [], 0\n\n for w in words:\n if width + len(w) + len(line) > maxWidth:\n for i in range(maxWidth - width): line[i % (len(line) - 1 or 1)] += \' \'\n res, line, width = res + [\'\'.join(line)], [], 0\n line += [w]\n width += len(w)\n\n return res + [\' \'.join(line).ljust(maxWidth)]\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<std::string> fullJustify(std::vector<std::string>& words, int maxWidth) {\n std::vector<std::string> res;\n std::vector<std::string> cur;\n int num_of_letters = 0;\n\n for (std::string word : words) {\n if (word.size() + cur.size() + num_of_letters > maxWidth) {\n for (int i = 0; i < maxWidth - num_of_letters; i++) {\n cur[i % (cur.size() - 1 ? cur.size() - 1 : 1)] += \' \';\n }\n res.push_back("");\n for (std::string s : cur) res.back() += s;\n cur.clear();\n num_of_letters = 0;\n }\n cur.push_back(word);\n num_of_letters += word.size();\n }\n\n std::string last_line = "";\n for (std::string s : cur) last_line += s + \' \';\n last_line = last_line.substr(0, last_line.size()-1); // remove trailing space\n while (last_line.size() < maxWidth) last_line += \' \';\n res.push_back(last_line);\n\n return res;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<String> fullJustify(String[] words, int maxWidth) {\n List<String> res = new ArrayList<>();\n List<String> cur = new ArrayList<>();\n int num_of_letters = 0;\n\n for (String word : words) {\n if (word.length() + cur.size() + num_of_letters > maxWidth) {\n for (int i = 0; i < maxWidth - num_of_letters; i++) {\n cur.set(i % (cur.size() - 1 > 0 ? cur.size() - 1 : 1), cur.get(i % (cur.size() - 1 > 0 ? cur.size() - 1 : 1)) + " ");\n }\n StringBuilder sb = new StringBuilder();\n for (String s : cur) sb.append(s);\n res.add(sb.toString());\n cur.clear();\n num_of_letters = 0;\n }\n cur.add(word);\n num_of_letters += word.length();\n }\n\n StringBuilder lastLine = new StringBuilder();\n for (int i = 0; i < cur.size(); i++) {\n lastLine.append(cur.get(i));\n if (i != cur.size() - 1) lastLine.append(" ");\n }\n while (lastLine.length() < maxWidth) lastLine.append(" ");\n res.add(lastLine.toString());\n\n return res;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string[]} words\n * @param {number} maxWidth\n * @return {string[]}\n */\nvar fullJustify = function(words, maxWidth) {\n let res = [];\n let cur = [];\n let num_of_letters = 0;\n\n for (let word of words) {\n if (word.length + cur.length + num_of_letters > maxWidth) {\n for (let i = 0; i < maxWidth - num_of_letters; i++) {\n cur[i % (cur.length - 1 || 1)] += \' \';\n }\n res.push(cur.join(\'\'));\n cur = [];\n num_of_letters = 0;\n }\n cur.push(word);\n num_of_letters += word.length;\n }\n\n let lastLine = cur.join(\' \');\n while (lastLine.length < maxWidth) lastLine += \' \';\n res.push(lastLine);\n\n return res;\n }\n```\n``` C# []\npublic class Solution {\n public IList<string> FullJustify(string[] words, int maxWidth) {\n var res = new List<string>();\n var cur = new List<string>();\n int num_of_letters = 0;\n\n foreach (var word in words) {\n if (word.Length + cur.Count + num_of_letters > maxWidth) {\n for (int i = 0; i < maxWidth - num_of_letters; i++) {\n cur[i % (cur.Count - 1 > 0 ? cur.Count - 1 : 1)] += " ";\n }\n res.Add(string.Join("", cur));\n cur.Clear();\n num_of_letters = 0;\n }\n cur.Add(word);\n num_of_letters += word.Length;\n }\n\n string lastLine = string.Join(" ", cur);\n while (lastLine.Length < maxWidth) lastLine += " ";\n res.Add(lastLine);\n\n return res;\n }\n}\n```\n``` Go []\nfunc fullJustify(words []string, maxWidth int) []string {\n var res []string\n var cur []string\n num_of_letters := 0\n\n for _, word := range words {\n if len(word) + len(cur) + num_of_letters > maxWidth {\n for i := 0; i < maxWidth - num_of_letters; i++ {\n cur[i % max(1, len(cur) - 1)] += " "\n }\n res = append(res, strings.Join(cur, ""))\n cur = cur[:0]\n num_of_letters = 0\n }\n cur = append(cur, word)\n num_of_letters += len(word)\n }\n\n lastLine := strings.Join(cur, " ")\n for len(lastLine) < maxWidth {\n lastLine += " "\n }\n res = append(res, lastLine)\n\n return res\n}\n\n// Helper function to get the maximum of two integers\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` Rust []\nimpl Solution {\n pub fn full_justify(words: Vec<String>, max_width: i32) -> Vec<String> {\n let mut res = Vec::new();\n let mut cur = Vec::new();\n let mut num_of_letters: i32 = 0;\n\n for word in &words {\n if word.len() as i32 + cur.len() as i32 + num_of_letters > max_width {\n for i in 0..(max_width - num_of_letters) {\n let idx = i as usize % (if cur.len() > 1 { cur.len() - 1 } else { cur.len() });\n cur[idx] = format!("{} ", cur[idx]);\n }\n res.push(cur.join(""));\n cur.clear();\n num_of_letters = 0;\n }\n cur.push(word.clone());\n num_of_letters += word.len() as i32;\n }\n\n let last_line = cur.join(" ");\n res.push(format!("{:<width$}", last_line, width=max_width as usize));\n\n res\n }\n}\n```\n\n# Code Gap-based\n``` Python []\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n res, cur_words, cur_len = [], [], 0\n\n for word in words:\n if cur_len + len(word) + len(cur_words) > maxWidth:\n total_spaces = maxWidth - cur_len\n gaps = len(cur_words) - 1\n if gaps == 0:\n res.append(cur_words[0] + \' \' * total_spaces)\n else:\n space_per_gap = total_spaces // gaps\n extra_spaces = total_spaces % gaps\n line = \'\'\n for i, w in enumerate(cur_words):\n line += w\n if i < gaps:\n line += \' \' * space_per_gap\n if i < extra_spaces:\n line += \' \'\n res.append(line)\n cur_words, cur_len = [], 0\n cur_words.append(word)\n cur_len += len(word)\n\n last_line = \' \'.join(cur_words)\n remaining_spaces = maxWidth - len(last_line)\n res.append(last_line + \' \' * remaining_spaces)\n\n return res\n\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<std::string> fullJustify(std::vector<std::string>& words, int maxWidth) {\n std::vector<std::string> res, cur_words;\n int cur_len = 0;\n\n for (const std::string& word : words) {\n if (cur_len + word.length() + cur_words.size() > maxWidth) {\n int total_spaces = maxWidth - cur_len;\n int gaps = cur_words.size() - 1;\n if (gaps == 0) {\n res.push_back(cur_words[0] + std::string(total_spaces, \' \'));\n } else {\n int space_per_gap = total_spaces / gaps;\n int extra_spaces = total_spaces % gaps;\n std::string line = "";\n for (int i = 0; i < cur_words.size(); ++i) {\n line += cur_words[i];\n if (i < gaps) {\n line += std::string(space_per_gap, \' \');\n if (i < extra_spaces) {\n line += \' \';\n }\n }\n }\n res.push_back(line);\n }\n cur_words.clear();\n cur_len = 0;\n }\n cur_words.push_back(word);\n cur_len += word.length();\n }\n\n std::string last_line = "";\n for (const std::string& word : cur_words) {\n if (!last_line.empty()) {\n last_line += \' \';\n }\n last_line += word;\n }\n last_line += std::string(maxWidth - last_line.length(), \' \');\n res.push_back(last_line);\n\n return res;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<String> fullJustify(String[] words, int maxWidth) {\n List<String> res = new ArrayList<>();\n List<String> curWords = new ArrayList<>();\n int curLen = 0;\n\n for (String word : words) {\n if (curLen + word.length() + curWords.size() > maxWidth) {\n int totalSpaces = maxWidth - curLen;\n int gaps = curWords.size() - 1;\n if (gaps == 0) {\n res.add(curWords.get(0) + " ".repeat(totalSpaces));\n } else {\n int spacePerGap = totalSpaces / gaps;\n int extraSpaces = totalSpaces % gaps;\n StringBuilder line = new StringBuilder();\n for (int i = 0; i < curWords.size(); i++) {\n line.append(curWords.get(i));\n if (i < gaps) {\n line.append(" ".repeat(spacePerGap));\n if (i < extraSpaces) {\n line.append(\' \');\n }\n }\n }\n res.add(line.toString());\n }\n curWords.clear();\n curLen = 0;\n }\n curWords.add(word);\n curLen += word.length();\n }\n\n StringBuilder lastLine = new StringBuilder(String.join(" ", curWords));\n while (lastLine.length() < maxWidth) {\n lastLine.append(\' \');\n }\n res.add(lastLine.toString());\n\n return res;\n }\n}\n```\n``` C# []\npublic class Solution {\n public IList<string> FullJustify(string[] words, int maxWidth) {\n List<string> res = new List<string>();\n List<string> curWords = new List<string>();\n int curLen = 0;\n\n foreach (string word in words) {\n if (curLen + word.Length + curWords.Count > maxWidth) {\n int totalSpaces = maxWidth - curLen;\n int gaps = curWords.Count - 1;\n if (gaps == 0) {\n res.Add(curWords[0] + new string(\' \', totalSpaces));\n } else {\n int spacePerGap = totalSpaces / gaps;\n int extraSpaces = totalSpaces % gaps;\n StringBuilder line = new StringBuilder();\n for (int i = 0; i < curWords.Count; i++) {\n line.Append(curWords[i]);\n if (i < gaps) {\n line.Append(new string(\' \', spacePerGap));\n if (i < extraSpaces) {\n line.Append(\' \');\n }\n }\n }\n res.Add(line.ToString());\n }\n curWords.Clear();\n curLen = 0;\n }\n curWords.Add(word);\n curLen += word.Length;\n }\n\n string lastLine = string.Join(" ", curWords);\n while (lastLine.Length < maxWidth) {\n lastLine += \' \';\n }\n res.Add(lastLine);\n\n return res;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string[]} words\n * @param {number} maxWidth\n * @return {string[]}\n */\nvar fullJustify = function(words, maxWidth) {\n let res = [];\n let curWords = [];\n let curLen = 0;\n\n for (let word of words) {\n if (curLen + word.length + curWords.length > maxWidth) {\n let totalSpaces = maxWidth - curLen;\n let gaps = curWords.length - 1;\n if (gaps === 0) {\n res.push(curWords[0] + \' \'.repeat(totalSpaces));\n } else {\n let spacePerGap = Math.floor(totalSpaces / gaps);\n let extraSpaces = totalSpaces % gaps;\n let line = \'\';\n for (let i = 0; i < curWords.length; i++) {\n line += curWords[i];\n if (i < gaps) {\n line += \' \'.repeat(spacePerGap);\n if (i < extraSpaces) {\n line += \' \';\n }\n }\n }\n res.push(line);\n }\n curWords = [];\n curLen = 0;\n }\n curWords.push(word);\n curLen += word.length;\n }\n\n let lastLine = curWords.join(\' \');\n while (lastLine.length < maxWidth) {\n lastLine += \' \';\n }\n res.push(lastLine);\n\n return res;\n }\n```\n\nThe choice between the two methods will depend on the specific use-case and the preference for clarity vs. conciseness. Both approaches offer an efficient way to tackle the problem of text justification. \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB | 65 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
spaghetti | text-justification | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n arr,res,total,size=[],[],0,len(words)\n for i in range(size):\n if total+len(words[i])+len(arr)<=maxWidth:\n total+=(len(words[i]))\n arr.append(words[i])\n if i==size-1:\n line=""\n for j in range(len(arr)):\n line+=arr[j]\n if j!=len(arr)-1:line+=" "\n line+=" "*(maxWidth-len(line))\n res.append(line)\n else:\n line=""\n arrSize=len(arr)\n spaces=maxWidth-total\n if arrSize==1:line=arr[0]+" "*spaces\n else:\n space1=int(spaces/(arrSize-1))\n spaceX=spaces%(arrSize-1)\n for j in range(arrSize):\n if j!=arrSize-1:\n line+=arr[j]\n if j<spaceX:line+=" "*(space1+1)\n else :line+=" "*(space1)\n else:line+=arr[j]\n res.append(line)\n line=""\n arr=[words[i]]\n total=len(words[i])\n if i==size-1:\n line=arr[0]+" "*(maxWidth-len(arr[0]))\n res.append(line)\n return res\n \n``` | 1 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | text-justification | 1 | 1 | # Intuition\nThe algorithm justifies a given list of words into lines with a specified maximum width. It iterates through the words, adding them to a line if they fit within the width limit, or starts a new line if not. After splitting the text into lines, it evenly distributes extra spaces among words to justify the lines, ensuring the last line is left-justified. The final justified lines are returned as a result.\n\n---\n\n\n# Solution Video\nUsually, I put a video to visualize solution but today I have to go on business trip and come back at late night. Please subscribe to my channel from URL below and don\'t miss my latest solution videos in the future.\n\nI have 247 videos as of August 24th, 2023. Currently there are 2,071 subscribers.\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. **Initialization of Variables:**\n - Initialize an empty list `result` to store the final justified lines.\n - Initialize an empty list `line` to temporarily store words for the current line being processed.\n - Initialize an integer variable `line_length` to track the length of words in the current line.\n\n2. **Loop through Words:**\n - Loop through each word in the `words` list.\n - Check if adding the current `word` to the current line would exceed the `maxWidth` for the line.\n - If the addition doesn\'t exceed, append the `word` to the `line` and update the `line_length` accordingly.\n - If the addition exceeds, append the current `line` to the `result`, start a new line with the current `word`, and update `line_length`.\n\n3. **Append Last Line:**\n - Append the last `line` to the `result`.\n\n4. **Initialization for Justified Lines:**\n - Initialize an empty list `justified_lines` to store the lines after justification.\n\n5. **Loop through Lines for Justification:**\n - Loop through each line in `result` except the last one (from 0 to `len(result) - 2`).\n - Get the current `line` from the `result`.\n - Calculate the total number of words in the `line` as `num_words`.\n - Calculate the total number of spaces available for justification as `num_spaces` by subtracting the sum of lengths of words in the line from `maxWidth`.\n\n6. **Handle Zero Space Gaps:**\n - Calculate the number of space gaps (`space_gaps`) by taking the maximum of `num_words - 1` and 1 (to ensure there\'s at least one gap).\n\n7. **Calculate Spaces per Gap:**\n - Calculate the number of spaces per gap (`spaces_per_gap`) by performing integer division `num_spaces // space_gaps`.\n\n8. **Calculate Extra Spaces:**\n - Calculate the remaining extra spaces (`extra_spaces`) after distributing spaces evenly among gaps using modulo `num_spaces % space_gaps`.\n\n9. **Building Justified Line:**\n - Initialize an empty string `justified_line` to build the justified line.\n - Iterate through each `word` in the `line`.\n - Concatenate the `word` to the `justified_line`.\n - Check if there are more spaces to distribute (`space_gaps > 0`).\n - If yes, calculate the number of spaces to add (`spaces_to_add`) by adding `spaces_per_gap` and an extra space if `extra_spaces` is greater than 0.\n - Concatenate the calculated number of spaces to the `justified_line`.\n - Decrement `extra_spaces` and `space_gaps`.\n\n10. **Append Justified Line:**\n - Append the `justified_line` to the `justified_lines` list.\n\n11. **Construct the Last Line:**\n - Join the words in the last `result` line with a single space to form the `last_line`.\n - Add the required number of spaces at the end to make the total length `maxWidth`.\n\n12. **Append Last Line to Justified Lines:**\n - Append the `last_line` to the `justified_lines` list.\n\n13. **Return Justified Lines:**\n - Return the list of `justified_lines`.\n\n```python []\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n result = [] # To store the final justified lines\n line = [] # To temporarily store words for current line\n line_length = 0 # To track the length of the words in the current line\n \n # Loop through each word in the input words list\n for word in words:\n # Check if adding the current word exceeds the maxWidth for the line\n if line_length + len(line) + len(word) <= maxWidth:\n line.append(word) # Add the word to the line\n line_length += len(word) # Update the line length\n else:\n result.append(line) # Add the words in the line to the result\n line = [word] # Start a new line with the current word\n line_length = len(word) # Set the line length to the word\'s length\n \n result.append(line) # Append the last line to the result\n \n justified_lines = []\n \n # Loop through each line except the last one\n for i in range(len(result) - 1):\n line = result[i]\n num_words = len(line)\n num_spaces = maxWidth - sum(len(word) for word in line)\n \n # Handle the case when space_gaps is zero\n space_gaps = max(num_words - 1, 1)\n \n spaces_per_gap = num_spaces // space_gaps\n extra_spaces = num_spaces % space_gaps\n\n justified_line = ""\n \n # Iterate through each word in the line\n for word in line:\n justified_line += word\n \n # Check if there are more spaces to distribute\n if space_gaps > 0:\n spaces_to_add = spaces_per_gap + (1 if extra_spaces > 0 else 0)\n justified_line += " " * spaces_to_add\n extra_spaces -= 1\n space_gaps -= 1\n\n justified_lines.append(justified_line)\n\n last_line = " ".join(result[-1])\n last_line += " " * (maxWidth - len(last_line))\n justified_lines.append(last_line)\n\n return justified_lines\n```\n```javascript []\n/**\n * @param {string[]} words\n * @param {number} maxWidth\n * @return {string[]}\n */\nvar fullJustify = function(words, maxWidth) {\n const result = [];\n let line = [];\n let lineLength = 0;\n\n for (const word of words) {\n if (lineLength + line.length + word.length <= maxWidth) {\n line.push(word);\n lineLength += word.length;\n } else {\n result.push(line);\n line = [word];\n lineLength = word.length;\n }\n }\n\n result.push(line);\n\n const justifiedLines = [];\n for (let i = 0; i < result.length - 1; i++) {\n line = result[i];\n const numWords = line.length;\n const numSpaces = maxWidth - line.reduce((acc, word) => acc + word.length, 0);\n\n let spaceGaps = Math.max(numWords - 1, 1);\n const spacesPerGap = Math.floor(numSpaces / spaceGaps);\n let extraSpaces = numSpaces % spaceGaps;\n\n let justifiedLine = "";\n for (const word of line) {\n justifiedLine += word;\n\n if (spaceGaps > 0) {\n const spacesToAdd = spacesPerGap + (extraSpaces > 0 ? 1 : 0);\n justifiedLine += " ".repeat(spacesToAdd);\n extraSpaces -= 1;\n spaceGaps -= 1;\n }\n }\n\n justifiedLines.push(justifiedLine);\n }\n\n const lastLine = result[result.length - 1].join(" ");\n justifiedLines.push(lastLine + " ".repeat(maxWidth - lastLine.length));\n\n return justifiedLines; \n};\n```\n```java []\nclass Solution {\n public List<String> fullJustify(String[] words, int maxWidth) {\n List<List<String>> result = new ArrayList<>();\n List<String> line = new ArrayList<>();\n int lineLength = 0;\n\n for (String word : words) {\n if (lineLength + line.size() + word.length() <= maxWidth) {\n line.add(word);\n lineLength += word.length();\n } else {\n result.add(line);\n line = new ArrayList<>();\n line.add(word);\n lineLength = word.length();\n }\n }\n\n result.add(line);\n\n List<String> justifiedLines = new ArrayList<>();\n for (int i = 0; i < result.size() - 1; i++) {\n line = result.get(i);\n int numWords = line.size();\n int numSpaces = maxWidth - line.stream().mapToInt(String::length).sum();\n\n int spaceGaps = Math.max(numWords - 1, 1);\n int spacesPerGap = numSpaces / spaceGaps;\n int extraSpaces = numSpaces % spaceGaps;\n\n StringBuilder justifiedLine = new StringBuilder();\n for (String word : line) {\n justifiedLine.append(word);\n\n if (spaceGaps > 0) {\n int spacesToAdd = spacesPerGap + (extraSpaces > 0 ? 1 : 0);\n justifiedLine.append(" ".repeat(spacesToAdd));\n extraSpaces -= 1;\n spaceGaps -= 1;\n }\n }\n\n justifiedLines.add(justifiedLine.toString());\n }\n\n StringBuilder lastLine = new StringBuilder(String.join(" ", result.get(result.size() - 1)));\n lastLine.append(" ".repeat(maxWidth - lastLine.length()));\n justifiedLines.add(lastLine.toString());\n\n return justifiedLines; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<string> fullJustify(vector<string>& words, int maxWidth) {\n std::vector<std::vector<std::string>> result;\n std::vector<std::string> line;\n int lineLength = 0;\n\n for (const std::string& word : words) {\n if (lineLength + line.size() + word.length() <= maxWidth) {\n line.push_back(word);\n lineLength += word.length();\n } else {\n result.push_back(line);\n line.clear();\n line.push_back(word);\n lineLength = word.length();\n }\n }\n\n result.push_back(line);\n\n std::vector<std::string> justifiedLines;\n for (int i = 0; i < result.size() - 1; i++) {\n line = result[i];\n int numWords = line.size();\n int numSpaces = maxWidth;\n for (const std::string& word : line) {\n numSpaces -= word.length();\n }\n\n int spaceGaps = std::max(numWords - 1, 1);\n int spacesPerGap = numSpaces / spaceGaps;\n int extraSpaces = numSpaces % spaceGaps;\n\n std::string justifiedLine = "";\n for (const std::string& word : line) {\n justifiedLine += word;\n\n if (spaceGaps > 0) {\n int spacesToAdd = spacesPerGap + (extraSpaces > 0 ? 1 : 0);\n justifiedLine += std::string(spacesToAdd, \' \');\n extraSpaces -= 1;\n spaceGaps -= 1;\n }\n }\n\n justifiedLines.push_back(justifiedLine);\n }\n\n std::string lastLine = "";\n for (const std::string& word : result[result.size() - 1]) {\n lastLine += word + " ";\n }\n lastLine.pop_back();\n lastLine += std::string(maxWidth - lastLine.length(), \' \');\n justifiedLines.push_back(lastLine);\n\n return justifiedLines; \n }\n};\n```\n | 12 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Concise python solution, 10 lines. | text-justification | 0 | 1 | --------------------------------------------\n\n def fullJustify(self, words, maxWidth):\n res, cur, num_of_letters = [], [], 0\n for w in words:\n if num_of_letters + len(w) + len(cur) > maxWidth:\n for i in range(maxWidth - num_of_letters):\n cur[i%(len(cur)-1 or 1)] += \' \'\n res.append(\'\'.join(cur))\n cur, num_of_letters = [], 0\n cur += [w]\n num_of_letters += len(w)\n return res + [\' \'.join(cur).ljust(maxWidth)]\n\nHow does it work? Well in the question statement, the sentence "Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line do not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right" was just a really long and awkward way to say *round robin*. The following line implements the round robin logic: \n\n for i in range(maxWidth - num_of_letters):\n cur[i%(len(cur)-1 or 1)] += \' \'\n\nWhat does this line do? Once you determine that there are only k words that can fit on a given line, you know what the total length of those words is num_of_letters. Then the rest are spaces, and there are (maxWidth - num_of_letters) of spaces. The "or 1" part is for dealing with the edge case len(cur) == 1.\n\n###### Note: I found that this problem & solution is directly being used in the "Elements of Programming Interviews in Python" book. Cool I guess, but the book should include an acknowledgement or link to this source.\n--------------------------------------------\n\nThe following is my older solution for reference, longer and less clear. The idea is the same, but I did not figure out the nice way to distribute the space at the time.\n\n def fullJustify(self, words, maxWidth):\n res, cur, num_of_letters = [], [], 0\n for w in words:\n if num_of_letters + len(w) + len(cur) > maxWidth:\n if len(cur) == 1:\n res.append( cur[0] + \' \'*(maxWidth - num_of_letters) )\n else:\n num_spaces = maxWidth - num_of_letters\n space_between_words, num_extra_spaces = divmod( num_spaces, len(cur)-1)\n for i in range(num_extra_spaces):\n cur[i] += \' \'\n res.append( (\' \'*space_between_words).join(cur) )\n cur, num_of_letters = [], 0\n cur += [w]\n num_of_letters += len(w)\n res.append( \' \'.join(cur) + \' \'*(maxWidth - num_of_letters - len(cur) + 1) )\n return res | 565 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Python🔥Java🔥C++🔥Simple Solution | text-justification | 1 | 1 | # ANNOUNCEMENT:\n**Join the discord and don\'t forget to Subscribe the youtube channel to access the premium content materials related to computer science and data science in the discord. (For Only first 10,000 Subscribers)**\n\n**Happy Learning, Cheers Guys \uD83D\uDE0A**\n\n# Click the Link in my Profile to Subscribe\n\n# An UPVOTE will be encouraging \uD83D\uDC4D\n\n#Intuition\n\n- Initialize an empty result list to store the justified lines, an empty current line (cur), and a variable to keep track of the total number of letters in the current line (numOfLetters).\n\n- Iterate through the list of words one by one.\n\nFor each word:\n\n- Check if adding the word to the current line would exceed the maximum width. If it would, it\'s time to justify the current line.\n- Calculate the number of spaces that need to be added to distribute them evenly. This is done by finding the difference between the maximum width and the total number of letters in the current line.\n- Distribute these spaces evenly among the words in the current line. The modulo operator is used to ensure that spaces are distributed evenly, even if there are more words than spaces.\n- Add the justified line to the result list.\n- Clear the current line and reset the numOfLetters counter.\n- Continue adding words to the current line until you reach a point where adding the next word would exceed the maximum width.\n\n- For the last line of text, left-justify it by adding spaces between words. Ensure that the total width of the line matches the maximum width.\n\n- Return the list of justified lines as the final result.\n\n```Python []\nclass Solution:\n def fullJustify(self, words, maxWidth):\n result, cur, num_of_letters = [], [], 0\n\n for word in words:\n if num_of_letters + len(word) + len(cur) > maxWidth:\n for i in range(maxWidth - num_of_letters):\n cur[i % (len(cur) - 1 or 1)] += \' \'\n result.append(\'\'.join(cur))\n cur, num_of_letters = [], 0\n\n cur += [word]\n num_of_letters += len(word)\n\n return result + [\' \'.join(cur).ljust(maxWidth)]\n```\n```Java []\n\npublic class TextJustification {\n public List<String> fullJustify(String[] words, int maxWidth) {\n List<String> result = new ArrayList<>();\n List<String> cur = new ArrayList<>();\n int numOfLetters = 0;\n\n for (String word : words) {\n if (numOfLetters + word.length() + cur.size() > maxWidth) {\n int spacesToAdd = maxWidth - numOfLetters;\n for (int i = 0; i < spacesToAdd; i++) {\n cur.set(i % (cur.size() - 1), cur.get(i % (cur.size() - 1)) + " ");\n }\n result.add(String.join("", cur));\n cur.clear();\n numOfLetters = 0;\n }\n\n cur.add(word);\n numOfLetters += word.length();\n }\n\n result.add(String.join(" ", cur) + " ".repeat(maxWidth - numOfLetters - cur.size() + 1));\n\n return result;\n }\n}\n\n```\n```C++ []\n\nclass TextJustification {\npublic:\n vector<string> fullJustify(vector<string>& words, int maxWidth) {\n vector<string> result;\n vector<string> cur;\n int numOfLetters = 0;\n\n for (const string& word : words) {\n if (numOfLetters + word.length() + cur.size() > maxWidth) {\n int spacesToAdd = maxWidth - numOfLetters;\n for (int i = 0; i < spacesToAdd; i++) {\n cur[i % (cur.size() - 1)] += \' \';\n }\n result.push_back(accumulate(cur.begin(), cur.end(), string("")));\n cur.clear();\n numOfLetters = 0;\n }\n\n cur.push_back(word);\n numOfLetters += word.length();\n }\n\n string lastLine = accumulate(cur.begin(), cur.end(), string(" "));\n lastLine += string(maxWidth - numOfLetters - cur.size() + 1, \' \');\n result.push_back(lastLine);\n\n return result;\n }\n};\n\n```\n | 10 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
🔥🔥🔥🔥🔥Beats 100% | JS | TS | Java | C++ | C# | C | Python | python3 | Kotlin | PHP 🔥🔥🔥🔥🔥 | text-justification | 1 | 1 | ---\n\n\n---\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n#include <string.h>\n\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nchar ** fullJustify(char ** words, int wordsSize, int maxWidth, int* returnSize) {\n char **result = (char **)malloc(sizeof(char *) * wordsSize);\n *returnSize = 0;\n \n int start = 0; // Index of the first word in the current line.\n \n while (start < wordsSize) {\n int end = start; // Index of the last word in the current line.\n int lineLength = 0; // Length of the words and spaces in the current line.\n \n // Calculate the number of words and total length that can fit in the current line.\n while (end < wordsSize && lineLength + strlen(words[end]) + end - start <= maxWidth) {\n lineLength += strlen(words[end]);\n end++;\n }\n \n // Calculate the total number of spaces needed in the line.\n int totalSpaces = maxWidth - lineLength;\n \n // If it\'s the last line or only one word in the line, left-justify.\n if (end == wordsSize || end - start == 1) {\n result[*returnSize] = (char *)malloc(sizeof(char) * (maxWidth + 1));\n int idx = 0;\n for (int i = start; i < end; i++) {\n strcpy(result[*returnSize] + idx, words[i]);\n idx += strlen(words[i]);\n if (i != end - 1) {\n result[*returnSize][idx++] = \' \';\n }\n }\n while (idx < maxWidth) {\n result[*returnSize][idx++] = \' \';\n }\n result[*returnSize][maxWidth] = \'\\0\';\n } else {\n int spaceBetweenWords = totalSpaces / (end - start - 1);\n int extraSpaces = totalSpaces % (end - start - 1);\n \n result[*returnSize] = (char *)malloc(sizeof(char) * (maxWidth + 1));\n int idx = 0;\n for (int i = start; i < end; i++) {\n strcpy(result[*returnSize] + idx, words[i]);\n idx += strlen(words[i]);\n if (i != end - 1) {\n int spaces = spaceBetweenWords + (extraSpaces > 0 ? 1 : 0);\n extraSpaces--;\n for (int j = 0; j < spaces; j++) {\n result[*returnSize][idx++] = \' \';\n }\n }\n }\n result[*returnSize][maxWidth] = \'\\0\';\n }\n \n (*returnSize)++;\n start = end;\n }\n \n return result;\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<string> fullJustify(vector<string>& words, int maxWidth) {\n vector<string> result;\n int i = 0;\n \n while (i < words.size()) {\n int lineLen = words[i].size();\n int j = i + 1;\n \n // Find the words that can fit in the current line\n while (j < words.size() && lineLen + 1 + words[j].size() <= maxWidth) {\n lineLen += 1 + words[j].size();\n j++;\n }\n \n int numWords = j - i;\n int totalSpaces = maxWidth - lineLen + numWords - 1;\n \n // Construct the formatted line\n string line = words[i];\n if (numWords == 1 || j == words.size()) { // Left-justify\n for (int k = i + 1; k < j; k++) {\n line += " " + words[k];\n }\n line += string(maxWidth - line.size(), \' \'); // Pad with spaces\n } else { // Fully justify\n int spacesBetweenWords = totalSpaces / (numWords - 1);\n int extraSpaces = totalSpaces % (numWords - 1);\n for (int k = i + 1; k < j; k++) {\n int spaces = k - i <= extraSpaces ? spacesBetweenWords + 1 : spacesBetweenWords;\n line += string(spaces, \' \') + words[k];\n }\n }\n \n result.push_back(line);\n i = j;\n }\n \n return result;\n }\n};\n```\n```Typescript []\nfunction fullJustify(words: string[], maxWidth: number): string[] {\n let res = [], str = "", i = 0, n = words.length, x = 0;\n while( i < n ){\n if( (str + words[i]).length === maxWidth ){\n str += words[i++];\n res.push(str);\n str = "";\n x = i;\n }\n else if( (str + words[i]).length > maxWidth ){\n let j = x, cnt = maxWidth - (str.length - 1);\n while( cnt > 0 && j < i - 1 ){\n words[j++] += " ";\n cnt--;\n if( j === i - 1 && cnt > 0 )j = x\n }\n let tempStr = ""; j = x;\n while( j < i )tempStr += j < i - 1 ? words[j++] + " " : words[j++];\n while( tempStr.length < maxWidth )tempStr += " "\n res.push(tempStr);\n str = "";\n x = i;\n }\n else str += words[i++] + " ";\n }\n if( str.length > 0 ){\n let cnt = maxWidth - str.length;\n while( cnt > 0 ){\n str += " ";\n cnt--;\n }\n res.push(str)\n }\n return res\n};\n```\n```Java []\nclass Solution {\n public List<String> fullJustify(String[] words, int maxWidth) {\n List<String> result = new ArrayList<>();\n int index = 0;\n\n while (index < words.length) {\n int lineStart = index;\n int lineLength = words[index].length();\n index++;\n\n while (index < words.length && lineLength + words[index].length() + (index - lineStart) <= maxWidth) {\n lineLength += words[index].length();\n index++;\n }\n\n int totalSpaces = maxWidth - lineLength;\n int numWords = index - lineStart;\n\n StringBuilder line = new StringBuilder(words[lineStart]);\n \n if (numWords == 1 || index == words.length) { // Left-justify last line or single-word lines\n for (int i = lineStart + 1; i < index; i++) {\n line.append(\' \').append(words[i]);\n }\n line.append(String.valueOf(\' \').repeat(maxWidth - line.length())); // Add extra spaces at the end\n } else {\n int spacesBetweenWords = totalSpaces / (numWords - 1);\n int extraSpaces = totalSpaces % (numWords - 1);\n \n for (int i = lineStart + 1; i < index; i++) {\n int spaces = spacesBetweenWords + (extraSpaces-- > 0 ? 1 : 0);\n line.append(String.valueOf(\' \').repeat(spaces)).append(words[i]);\n }\n }\n\n result.add(line.toString());\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution(object):\n def fullJustify(self, words, maxWidth):\n result = []\n line = []\n line_length = 0\n \n for word in words:\n if line_length + len(line) + len(word) > maxWidth:\n # Justify the current line\n spaces_to_add = maxWidth - line_length\n if len(line) == 1:\n result.append(line[0] + \' \' * spaces_to_add)\n else:\n num_gaps = len(line) - 1\n spaces_per_gap = spaces_to_add // num_gaps\n extra_spaces = spaces_to_add % num_gaps\n justified_line = line[0]\n for i in range(1, len(line)):\n spaces = spaces_per_gap + (1 if i <= extra_spaces else 0)\n justified_line += \' \' * spaces + line[i]\n result.append(justified_line)\n \n # Reset line and line_length\n line = []\n line_length = 0\n \n line.append(word)\n line_length += len(word)\n \n # Left-justify the last line\n last_line = \' \'.join(line)\n last_line += \' \' * (maxWidth - len(last_line))\n result.append(last_line)\n \n return result\n```\n```Python3 []\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n result = []\n line = [] # Stores words for the current line\n line_length = 0\n \n for word in words:\n # Check if adding the current word to the line exceeds the maxWidth\n if line_length + len(line) + len(word) > maxWidth:\n # Distribute extra spaces between words\n num_words = len(line)\n total_spaces = maxWidth - line_length\n \n if num_words == 1:\n # Left-justify if there\'s only one word in the line\n result.append(line[0] + \' \' * (maxWidth - len(line[0])))\n else:\n # Calculate even and extra spaces\n spaces_per_word = total_spaces // (num_words - 1)\n extra_spaces = total_spaces % (num_words - 1)\n \n # Create the justified line\n justified_line = ""\n for i in range(num_words - 1):\n justified_line += line[i] + \' \' * spaces_per_word\n if extra_spaces > 0:\n justified_line += \' \'\n extra_spaces -= 1\n justified_line += line[num_words - 1]\n result.append(justified_line)\n \n # Reset line variables for the next line\n line = []\n line_length = 0\n \n line.append(word)\n line_length += len(word)\n \n # Last line: left-justify and no extra spaces\n result.append(\' \'.join(line) + \' \' * (maxWidth - line_length - len(line) + 1))\n \n return result\n```\n```C# []\npublic class Solution {\n public IList<string> FullJustify(string[] words, int maxWidth) {\n List<string> result = new List<string>();\n int startIndex = 0;\n\n while (startIndex < words.Length) {\n int endIndex = startIndex;\n int lineLength = 0;\n\n // Find the range of words that can fit in the current line\n while (endIndex < words.Length && lineLength + words[endIndex].Length + (endIndex - startIndex) <= maxWidth) {\n lineLength += words[endIndex].Length;\n endIndex++;\n }\n\n // Calculate the number of total spaces and gaps between words\n int totalSpaces = maxWidth - lineLength;\n int totalGaps = endIndex - startIndex - 1;\n \n StringBuilder lineBuilder = new StringBuilder();\n\n // If it\'s the last line or only one word in the line, left-justify\n if (endIndex == words.Length || totalGaps == 0) {\n for (int i = startIndex; i < endIndex; i++) {\n lineBuilder.Append(words[i]);\n if (i < endIndex - 1) {\n lineBuilder.Append(\' \');\n }\n }\n while (lineBuilder.Length < maxWidth) {\n lineBuilder.Append(\' \');\n }\n } else {\n int spacesPerGap = totalSpaces / totalGaps;\n int extraSpaces = totalSpaces % totalGaps;\n\n for (int i = startIndex; i < endIndex; i++) {\n lineBuilder.Append(words[i]);\n if (i < endIndex - 1) {\n int spacesToAdd = spacesPerGap + (i - startIndex < extraSpaces ? 1 : 0);\n lineBuilder.Append(\' \', spacesToAdd);\n }\n }\n }\n\n result.Add(lineBuilder.ToString());\n startIndex = endIndex;\n }\n\n return result;\n }\n}\n```\n```Javascript []\nvar fullJustify = function(words, maxWidth) {\n let result = [];\n \n let line = [];\n let lineLength = 0;\n \n for(let i = 0; i < words.length; i++) {\n let w = words[i];\n \n if(lineLength === 0 && w.length <= maxWidth) {\n\t\t\t// Note: We add first word assuming no space will be added after it. As we know this is not the case. \n\t\t\t// The space for first word will be accounted for by our last word in the line & \n\t\t\t// the lack of space after last word is accounted for by this first word.\n line.push(w);\n lineLength += w.length;\n } else if(lineLength + w.length + 1 <= maxWidth){\n\t\t\t// we add word and consider it\'s length plus a space following it\n line.push(w);\n lineLength += (w.length + 1);\n } else {\n\t\t\t//OUR LINE IS FULL AND SHOULD BE ADDED TO THE RESULT\n\t\t\t\n // add the required single space after each word except last one\n line = addMinSpace(line);\n \n // find remaining space to distribute\n let remainingSpace = maxWidth - lineLength;\n \n // add remaining space to each word expect last one\n line = distributeSpaces(line, remainingSpace);\n\n // turn array into a single string\n let temp = line.join("")\n \n // If the line only had one large word, we add remaining spaces to it\'s end just like how we would later do for last line\n if(line.length === 1) temp = addRemainingSpaces(temp, remainingSpace)\n \n result.push(temp);\n \n // reset the line and it\'s length\n line = [];\n lineLength = 0;\n \n // add this new word like it\'s the first one\n line.push(w);\n lineLength += w.length;\n }\n }\n \n \n // pad our final line\n line = addMinSpace(line);\n \n // create final string\n let temp = line.join("")\n \n // find remaining padding \n let remainingSpace = maxWidth - lineLength;\n \n // add remaining padding to end of our final line\n temp = addRemainingSpaces(temp, remainingSpace)\n \n // add final line to result\n result.push(temp);\n \n // return result\n return result;\n \n\t// Adds single space after each word except last one\n function addMinSpace(line) {\n for(let i = 0; i < line.length - 1; i++) line[i] += " ";\n return line;\n }\n \n\t// add remaining spaces to end of line\n function addRemainingSpaces(line, spaces) {\n while(spaces > 0) {\n line += " ";\n spaces--;\n }\n return line;\n }\n \n\t// distribute remaining spaces from left to right\n function distributeSpaces(arr, spaces) {\n while(spaces > 0 && arr.length > 1) {\n for(let i = 0; i < arr.length - 1; i++) {\n if(spaces <= 0) break;\n arr[i] = arr[i] + " ";\n spaces --;\n } \n }\n return arr;\n }\n};\n```\n```Kotlin []\nclass Solution {\n fun fullJustify(words: Array<String>, maxWidth: Int): List<String> {\n val result = mutableListOf<String>()\n var lineWords = mutableListOf<String>()\n var lineLength = 0\n \n for (word in words) {\n if (lineLength + lineWords.size + word.length <= maxWidth) {\n lineWords.add(word)\n lineLength += word.length\n } else {\n result.add(constructLine(lineWords, maxWidth, lineLength))\n lineWords.clear()\n lineWords.add(word)\n lineLength = word.length\n }\n }\n \n // Last line\n if (lineWords.isNotEmpty()) {\n val lastLine = lineWords.joinToString(" ")\n result.add(lastLine.padEnd(maxWidth))\n }\n \n return result\n }\n \n private fun constructLine(words: List<String>, maxWidth: Int, lineLength: Int): String {\n val numWords = words.size\n if (numWords == 1) {\n return words[0].padEnd(maxWidth)\n }\n \n val totalSpaces = maxWidth - lineLength\n val spaceSlots = numWords - 1\n val baseSpace = totalSpaces / spaceSlots\n val extraSpaceSlots = totalSpaces % spaceSlots\n \n val lineBuilder = StringBuilder()\n for (i in 0 until numWords - 1) {\n lineBuilder.append(words[i])\n lineBuilder.append(" ".repeat(baseSpace))\n if (i < extraSpaceSlots) {\n lineBuilder.append(" ")\n }\n }\n lineBuilder.append(words.last())\n \n return lineBuilder.toString()\n }\n}\n```\n```PHP []\nclass Solution {\n /**\n * @param String[] $words\n * @param Integer $maxWidth\n * @return String[]\n */\n function fullJustify($words, $maxWidth) {\n $result = [];\n $line = [];\n $lineWidth = 0;\n \n foreach ($words as $word) {\n // Check if adding the next word exceeds maxWidth\n if ($lineWidth + count($line) + strlen($word) > $maxWidth) {\n $formattedLine = $this->formatLine($line, $lineWidth, $maxWidth);\n $result[] = $formattedLine;\n \n $line = [];\n $lineWidth = 0;\n }\n \n $line[] = $word;\n $lineWidth += strlen($word);\n }\n \n // Handle the last line\n $lastLine = implode(\' \', $line);\n $lastLine .= str_repeat(\' \', $maxWidth - strlen($lastLine));\n $result[] = $lastLine;\n \n return $result;\n }\n \n // Helper function to format a line\n private function formatLine($line, $lineWidth, $maxWidth) {\n $numWords = count($line);\n $numSpaces = $maxWidth - $lineWidth;\n \n if ($numWords === 1) {\n return $line[0] . str_repeat(\' \', $numSpaces);\n }\n \n $avgSpaces = floor($numSpaces / ($numWords - 1));\n $extraSpaces = $numSpaces % ($numWords - 1);\n \n $formattedLine = $line[0];\n \n for ($i = 1; $i < $numWords; $i++) {\n $numPaddingSpaces = $avgSpaces + ($i <= $extraSpaces ? 1 : 0);\n $formattedLine .= str_repeat(\' \', $numPaddingSpaces) . $line[$i];\n }\n \n return $formattedLine;\n }\n}\n```\n\n\n---\n\n\n--- | 9 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
One pass, easy to understand with comments | O(n) | text-justification | 0 | 1 | We\'ll build the result array line by line while iterating over words in the input. Whenever the current line gets too big, we\'ll appropriately format it and proceed with the next line until for loop is over. Last but not least, we\'ll need to left-justify the last line.\n\nTime complexity is **O(n)**:\nThere is just one for loop, which iterates over words provided as input.\nSpace complexity: **O(n + l)**\nWhere **n** is lenght of words, and **l** max length of words in one line. Worst case scenario **l = n**, which will add up to **O(2n)** but in asymptotic analysis we don\'t care about constants so final complexity is linear: **O(n)**\n\n```\nclass Solution:\n\t# Why slots: https://docs.python.org/3/reference/datamodel.html#slots\n # TLDR: 1. faster attribute access. 2. space savings in memory.\n # For letcode problems this can save ~ 0.1MB of memory <insert is something meme>\n __slots__ = ()\n\t\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n\t # Init return array in which, we\'ll store justified lines\n lines = []\n\t\t# current line width\n width = 0\n\t\t# current line words\n line = []\n \n for word in words:\n\t\t\t# Gather as many words that will fit under maxWidth restrictions.\n\t\t\t# Line length is a sum of:\n\t\t\t# 1) Current word length\n\t\t\t# 2) Sum of words already in the current line\n\t\t\t# 3) Number of spaces (each word needs to be separated by at least one space)\n if (len(word) + width + len(line)) <= maxWidth:\n width += len(word)\n line.append(word)\n continue\n \n\t\t\t# If the current line only contains one word, fill the remaining string with spaces.\n if len(line) == 1:\n\t\t\t\t# Use the format function to fill the remaining string with spaces easily and readable.\n\t\t\t\t# For letcode police, yes you could do something like:\n\t\t\t\t# line = " ".join(line)\n\t\t\t\t# line += " " * (maxWidth - len(line))\n\t\t\t\t# lines.append(line)\n\t\t\t\t# to be more "raw", but I see no point in that.\n lines.append(\n "{0: <{width}}".format( " ".join(line), width=maxWidth)\n )\n else:\n\t\t\t # Else calculate how many common spaces and extra spaces are there for the current line.\n\t\t\t\t# Example:\n # line = [\'a\', \'computer.\', \'Art\', \'is\']\n\t\t\t\t# width left in line equals to: maxWidth - width: 20 - 15 = 5\n\t\t\t\t# len(line) - 1 because to the last word, we aren\'t adding any spaces\n\t\t\t\t# Now divmod will give us how many spaces are for all words and how many extra to distribute.\n\t\t\t\t# divmod(5, 3) = 1, 2\n\t\t\t\t# This means there should be one common space for each word, and for the first two, add one extra space.\n space, extra = divmod(\n maxWidth - width,\n len(line) - 1\n )\n \n i = 0\n\t\t\t\t# Distribute extra spaces first\n\t\t\t\t# There cannot be a case where extra spaces count is greater or equal to number words in the current line.\n while extra > 0:\n line[i] += " "\n extra -= 1\n i += 1\n \n\t\t\t\t# Join line array into a string by common spaces, and append to justified lines.\n lines.append(\n (" " * space).join(line)\n )\n \n\t\t\t# Create new line array with the current word in iteration, and reset current line width as well.\n line = [word]\n width = len(word)\n \n\t\t# Last but not least format last line to be left-justified with no extra space inserted between words.\n\t\t# No matter the input, there always be the last line at the end of for loop, which makes things even easier considering the requirement.\n lines.append(\n "{0: <{width}}".format(" ".join(line), width=maxWidth)\n )\n \n return lines\n``` | 47 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Python3 Solution | text-justification | 0 | 1 | \n```\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n n=len(words)\n ans=[]\n i=0\n while i<n:\n temp=[]\n seen=0\n cur=""\n while i<n and seen+len(words[i])+len(temp)<=maxWidth:\n temp.append(words[i])\n seen+=len(words[i])\n i+=1\n\n m=len(temp)\n if (m-1)!=0 and i!=n:\n q,r=divmod(maxWidth-seen,(m-1))\n sp=[q+(1 if j<r else 0) for j in range(m-1)]\n for j in range(m-1):\n cur+=temp[j]+\' \'*sp[j]\n cur+=temp[-1]\n\n else:\n for j in range(m-1):\n cur+=temp[j]+\' \'\n cur+=temp[-1]\n cur+=\' \'*(maxWidth-len(cur))\n\n ans.append(cur)\n return ans \n``` | 3 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Python | Easy to Understand | Fastest | Fully Explained | Concise Solution | text-justification | 0 | 1 | # Python | Easy to Understand | Fastest | Fully Explained | Concise Solution\n```\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n \n result, current_list, num_of_letters = [],[], 0\n # result -> stores final result output\n # current_list -> stores list of words which are traversed but not yet added to result\n # num_of_letters -> stores number of chars corresponding to words in current_list\n \n for word in words:\n \n # total no. of chars in current_list + total no. of chars in current word\n # + total no. of words ~= min. number of spaces between words\n if num_of_letters + len(word) + len(current_list) > maxWidth:\n # size will be used for module "magic" for round robin\n # we use max. 1 because atleast one word would be there and to avoid modulo by 0\n size = max(1, len(current_list)-1)\n \n for i in range(maxWidth-num_of_letters):\n # add space to each word in round robin fashion\n index = i%size\n current_list[index] += \' \' \n \n # add current line of words to the output\n result.append("".join(current_list))\n current_list, num_of_letters = [], 0\n \n # add current word to the list and add length to char count\n current_list.append(word)\n num_of_letters += len(word)\n \n # form last line by join with space and left justify to maxWidth using ljust (python method)\n # that means pad additional spaces to the right to make string length equal to maxWidth\n result.append(" ".join(current_list).ljust(maxWidth))\n \n return result\n``` | 2 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Pox | text-justification | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n res = []\n\n i = 0\n width = 0\n cur_line = []\n\n while i < len(words):\n cur_word = words[i]\n\n if width + len(cur_word) <= maxWidth:\n cur_line.append(cur_word)\n width += len(cur_word) + 1\n i += 1\n else:\n spaces = maxWidth - width + len(cur_line)\n\n added = 0\n j = 0\n\n while added < spaces:\n if j >= len(cur_line) - 1:\n j = 0\n\n cur_line[j] += " "\n\n added += 1\n j += 1\n\n res.append("".join(cur_line))\n\n cur_line = []\n\n width = 0\n \n for word in range(len(cur_line) - 1):\n cur_line[word] += " "\n cur_line[-1] += " " * (maxWidth - width + 1)\n\n res.append("".join(cur_line))\n\n return res\n``` | 1 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
68. Text Justification with step by step explanation | text-justification | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n res = []\n i = 0\n while i < len(words):\n j, total_len = i, 0\n while j < len(words) and total_len + len(words[j]) + j - i <= maxWidth:\n total_len += len(words[j])\n j += 1\n if j == len(words):\n res.append(" ".join(words[i:j]) + " " * (maxWidth - total_len - (j - i - 1)))\n else:\n spaces = maxWidth - total_len\n slots = j - i - 1\n if slots == 0:\n res.append(words[i] + " " * spaces)\n else:\n spaces_per_slot = spaces // slots\n extra_spaces = spaces % slots\n line = words[i]\n for k in range(i + 1, j):\n line += " " * (spaces_per_slot + (1 if extra_spaces > 0 else 0))\n extra_spaces -= 1\n line += words[k]\n res.append(line)\n i = j\n return res\n\n``````\n```\nclass Solution:\n def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:\n # list to store the justified lines\n justified_lines = []\n # list to store the current line of words\n line = []\n # length of the current line\n line_length = 0\n # loop through all words\n for word in words:\n # if adding the current word to the line and a space would exceed the maxWidth\n if line_length + len(word) + len(line) > maxWidth:\n # calculate the number of spaces needed to be added to the line\n spaces = maxWidth - line_length\n # distribute the spaces as evenly as possible between the words\n for i in range(spaces):\n line[i % (len(line) - 1 or 1)] += \' \'\n # add the line to the justified_lines list\n justified_lines.append(\'\'.join(line))\n # reset line and line_length for the next line\n line = []\n line_length = 0\n # add the current word to the line\n line.append(word)\n line_length += len(word)\n # handle the last line, which is left-justified\n last_line = \' \'.join(line)\n last_line += \' \' * (maxWidth - len(last_line))\n justified_lines.append(last_line)\n return justified_lines\n\n```\n``` | 3 | Given an array of strings `words` and a width `maxWidth`, format the text such that each line has exactly `maxWidth` characters and is fully (left and right) justified.
You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces `' '` when necessary so that each line has exactly `maxWidth` characters.
Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.
For the last line of text, it should be left-justified, and no extra space is inserted between words.
**Note:**
* A word is defined as a character sequence consisting of non-space characters only.
* Each word's length is guaranteed to be greater than `0` and not exceed `maxWidth`.
* The input array `words` contains at least one word.
**Example 1:**
**Input:** words = \[ "This ", "is ", "an ", "example ", "of ", "text ", "justification. "\], maxWidth = 16
**Output:**
\[
"This is an ",
"example of text ",
"justification. "
\]
**Example 2:**
**Input:** words = \[ "What ", "must ", "be ", "acknowledgment ", "shall ", "be "\], maxWidth = 16
**Output:**
\[
"What must be ",
"acknowledgment ",
"shall be "
\]
**Explanation:** Note that the last line is "shall be " instead of "shall be ", because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
**Example 3:**
**Input:** words = \[ "Science ", "is ", "what ", "we ", "understand ", "well ", "enough ", "to ", "explain ", "to ", "a ", "computer. ", "Art ", "is ", "everything ", "else ", "we ", "do "\], maxWidth = 20
**Output:**
\[
"Science is what we ",
"understand well ",
"enough to explain to ",
"a computer. Art is ",
"everything else we ",
"do "
\]
**Constraints:**
* `1 <= words.length <= 300`
* `1 <= words[i].length <= 20`
* `words[i]` consists of only English letters and symbols.
* `1 <= maxWidth <= 100`
* `words[i].length <= maxWidth` | null |
Fastest solution | sqrtx | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst thing that came to my mind was math module present in Python.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI imported math module and used its isqrt() function. What it does is basically the calculation of square root of the integer given to it and also converting the float to integer.\n\n# Complexity\n- Time complexity: Not sure\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Not sure\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mySqrt(self, x: int) -> int:\n import math\n return(math.isqrt(x))\n``` | 1 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
C++ || Binary Search || Easiest Beginner Friendly Sol | sqrtx | 1 | 1 | # Intuition of this Problem:\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. If x is 0, return 0.\n2. Initialize first to 1 and last to x.\n3. While first is less than or equal to last, do the following:\n a. Compute mid as first + (last - first) / 2.\n b. If mid * mid equals x, return mid.\n c. If mid * mid is greater than x, update last to mid - 1.\n d. If mid * mid is less than x, update first to mid + 1.\n4. Return last.\n\n<!-- Describe your approach to solving the problem. -->\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int mySqrt(int x) {\n if (x == 0)\n return x;\n int first = 1, last = x;\n while (first <= last) {\n int mid = first + (last - first) / 2;\n // mid * mid == x gives runtime error\n if (mid == x / mid)\n return mid;\n else if (mid > x / mid) {\n last = mid - 1;\n }\n else {\n first = mid + 1;\n }\n }\n return last;\n }\n};\n```\n```Java []\nclass Solution {\n public int mySqrt(int x) {\n if (x == 0) {\n return 0;\n }\n int first = 1, last = x;\n while (first <= last) {\n int mid = first + (last - first) / 2;\n if (mid == x / mid) {\n return mid;\n } else if (mid > x / mid) {\n last = mid - 1;\n } else {\n first = mid + 1;\n }\n }\n return last;\n }\n}\n\n```\n```Python []\nclass Solution:\n def mySqrt(self, x: int) -> int:\n if x == 0:\n return 0\n first, last = 1, x\n while first <= last:\n mid = first + (last - first) // 2\n if mid == x // mid:\n return mid\n elif mid > x // mid:\n last = mid - 1\n else:\n first = mid + 1\n return last\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(logn)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 265 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
[VIDEO] Step-by-Step Visualization of Binary Search Solution | sqrtx | 0 | 1 | https://youtu.be/1_4xlky3Y2Y?si=6ycdxyKdrj3Zy31b\n\nOne way to solve this would be to check every number starting from 0. Since we could stop once we reach the square root of x, this would run in O(sqrt(n)) time. However, binary search runs in O(log n) time, which, as you can see from the graph below, is superior to O(sqrt n) time.\n\n\n\nNow, why does binary search run in O(log n) time? Well, with each iteration, we eliminate around half of the array. So now the question is: how many iterations does it take to converge on a single element? In other words, how many times do we need to divide\xA0n\xA0by 2 until we reach 1?\n\nIf\xA0**k**\xA0is the number of times we need to divide\xA0n\xA0by 2 to reach 1, then the equation is:\n\nn / 2<sup>k</sup>\xA0= 1\n\nn = 2<sup>k</sup>\xA0\xA0\xA0(multiply both sides by 2k)\n\nlog<sub>2</sub>n = k \xA0\xA0(definition of logarithms)\n\nSo we know that it takes log<sub>2</sub>n steps in the worst case to find the element. But in Big O notation, we ignore the base, so this ends up running in O(log n) time.\n\n# Code\n```\nclass Solution:\n def mySqrt(self, x: int) -> int:\n left = 0\n right = x\n while left <= right:\n mid = (left + right) // 2\n if mid * mid < x:\n left = mid + 1\n elif mid * mid > x:\n right = mid -1\n else:\n return mid\n \n return right\n``` | 9 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
4 Lines of Code--->Binary Search Approach and Normal Approach | sqrtx | 0 | 1 | \n\n# 1. Normal Math Approach\n```\nclass Solution:\n def mySqrt(self, x: int) -> int:\n number=1\n while number*number<=x:\n number+=1\n return number\n\n```\n# Binary Search Approach\n```\n\nclass Solution:\n def mySqrt(self, x: int) -> int:\n left,right=1,x\n while left<=right:\n mid=(left+right)//2\n if mid*mid==x:\n return mid\n if mid*mid>x:\n right=mid-1\n else:\n left=mid+1\n return right\n \n\n```\n# please upvote me it would encourage me alot\n\n | 51 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
Easy to understand and also Beats 93.18%of users with Python3. | sqrtx | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mySqrt(self, x: int) -> int:\n return(int(math.sqrt(x)))\n \n``` | 0 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
Easy python if else solution | sqrtx | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mySqrt(self, s: int) -> int:\n x=sqrt(s)\n if x%1<0.5:\n return round(x)\n else:\n return round(x-0.5)\n``` | 1 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
Python Easy Solution || Binary Search || 100% || | sqrtx | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity \n- Time complexity: $$O(logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mySqrt(self, x: int) -> int:\n l=1\n r=x\n while l<=r:\n mid=(l+r)>>1\n if mid*mid==x:\n return mid\n elif mid*mid<x:\n l=mid+1\n else:\n r=mid-1\n return l-1\n``` | 2 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
sqrtx | sqrtx | 0 | 1 | # Intuition\nBeats 99.99% more then any Antiseptic strength to kill germs\n\n\n\n# Code\n```\nclass Solution:\n <!-- def mySqrt(self, x: int) -> int:\n return int(x**0.5) -->\n def mySqrt(self, x: int) -> int:\n left=0\n right=10000000\n mid=(left+right)//2\n while(True):\n temp=mid\n if mid*mid>x:\n right=mid+1\n else:\n left=mid\n mid=(left+right)//2\n if temp==mid:\n break\n return left\n``` | 2 | Given a non-negative integer `x`, return _the square root of_ `x` _rounded down to the nearest integer_. The returned integer should be **non-negative** as well.
You **must not use** any built-in exponent function or operator.
* For example, do not use `pow(x, 0.5)` in c++ or `x ** 0.5` in python.
**Example 1:**
**Input:** x = 4
**Output:** 2
**Explanation:** The square root of 4 is 2, so we return 2.
**Example 2:**
**Input:** x = 8
**Output:** 2
**Explanation:** The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
**Constraints:**
* `0 <= x <= 231 - 1` | Try exploring all integers. (Credits: @annujoshi) Use the sorted property of integers to reduced the search space. (Credits: @annujoshi) |
✅4 Method's 🤯 || Beat's 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | climbing-stairs | 1 | 1 | # Intuition:\nTo calculate the number of ways to climb the stairs, we can observe that when we are on the nth stair, \nwe have two options: \n1. either we climbed one stair from the (n-1)th stair or \n2. we climbed two stairs from the (n-2)th stair. \n\nBy leveraging this observation, we can break down the problem into smaller subproblems and apply the concept of the Fibonacci series. \nThe base cases are when we are on the 1st stair (only one way to reach it) and the 2nd stair (two ways to reach it). \nBy summing up the number of ways to reach the (n-1)th and (n-2)th stairs, we can compute the total number of ways to climb the stairs. This allows us to solve the problem efficiently using various dynamic programming techniques such as recursion, memoization, tabulation, or space optimization.\n\n# Approach 1: Recursion ```\u274C TLE \u274C```\n**Explanation**: The recursive solution uses the concept of Fibonacci numbers to solve the problem. It calculates the number of ways to climb the stairs by recursively calling the `climbStairs` function for (n-1) and (n-2) steps. However, this solution has exponential time complexity (O(2^n)) due to redundant calculations.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int climbStairs(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n return climbStairs(n-1) + climbStairs(n-2);\n }\n};\n```\n```Java []\nclass Solution {\n public int climbStairs(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n return climbStairs(n-1) + climbStairs(n-2);\n }\n}\n```\n```Python3 []\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n == 0 or n == 1:\n return 1\n return self.climbStairs(n-1) + self.climbStairs(n-2)\n```\n\n# Approach 2: Memoization\n**Explanation**: The memoization solution improves the recursive solution by introducing memoization, which avoids redundant calculations. We use an unordered map (`memo`) to store the already computed results for each step `n`. Before making a recursive call, we check if the result for the given `n` exists in the memo. If it does, we return the stored value; otherwise, we compute the result recursively and store it in the memo for future reference.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int climbStairs(int n, unordered_map<int, int>& memo) {\n if (n == 0 || n == 1) {\n return 1;\n }\n if (memo.find(n) == memo.end()) {\n memo[n] = climbStairs(n-1, memo) + climbStairs(n-2, memo);\n }\n return memo[n];\n }\n\n int climbStairs(int n) {\n unordered_map<int, int> memo;\n return climbStairs(n, memo);\n }\n};\n```\n```Java []\nclass Solution {\n public int climbStairs(int n) {\n Map<Integer, Integer> memo = new HashMap<>();\n return climbStairs(n, memo);\n }\n \n private int climbStairs(int n, Map<Integer, Integer> memo) {\n if (n == 0 || n == 1) {\n return 1;\n }\n if (!memo.containsKey(n)) {\n memo.put(n, climbStairs(n-1, memo) + climbStairs(n-2, memo));\n }\n return memo.get(n);\n }\n}\n```\n```Python3 []\nclass Solution:\n def climbStairs(self, n: int) -> int:\n memo = {}\n return self.helper(n, memo)\n \n def helper(self, n: int, memo: dict[int, int]) -> int:\n if n == 0 or n == 1:\n return 1\n if n not in memo:\n memo[n] = self.helper(n-1, memo) + self.helper(n-2, memo)\n return memo[n]\n```\n\n# Approach 3: Tabulation\n**Explanation**: The tabulation solution eliminates recursion and uses a bottom-up approach to solve the problem iteratively. It creates a DP table (`dp`) of size n+1 to store the number of ways to reach each step. The base cases (0 and 1 steps) are initialized to 1 since there is only one way to reach them. Then, it iterates from 2 to n, filling in the DP table by summing up the values for the previous two steps. Finally, it returns the value in the last cell of the DP table, which represents the total number of ways to reach the top.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int climbStairs(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n\n vector<int> dp(n+1);\n dp[0] = dp[1] = 1;\n \n for (int i = 2; i <= n; i++) {\n dp[i] = dp[i-1] + dp[i-2];\n }\n return dp[n];\n }\n};\n```\n```Java []\nclass Solution {\n public int climbStairs(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n\n int[] dp = new int[n+1];\n dp[0] = dp[1] = 1;\n \n for (int i = 2; i <= n; i++) {\n dp[i] = dp[i-1] + dp[i-2];\n }\n return dp[n];\n }\n}\n```\n```Python3 []\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n == 0 or n == 1:\n return 1\n\n dp = [0] * (n+1)\n dp[0] = dp[1] = 1\n \n for i in range(2, n+1):\n dp[i] = dp[i-1] + dp[i-2]\n return dp[n]\n```\n\n# Approach 4: Space Optimization\n**Explanation**: The space-optimized solution further reduces the space complexity by using only two variables (`prev` and `curr`) instead of an entire DP table. It initializes `prev` and `curr` to 1 since there is only one way to reach the base cases (0 and 1 steps). Then, in each iteration, it updates `prev` and `curr` by shifting their values. `curr` becomes the sum of the previous two values, and `prev` stores the previous value of `curr`.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int climbStairs(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n int prev = 1, curr = 1;\n for (int i = 2; i <= n; i++) {\n int temp = curr;\n curr = prev + curr;\n prev = temp;\n }\n return curr;\n }\n};\n```\n```Java []\nclass Solution {\n public int climbStairs(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n int prev = 1, curr = 1;\n for (int i = 2; i <= n; i++) {\n int temp = curr;\n curr = prev + curr;\n prev = temp;\n }\n return curr;\n }\n}\n```\n```Python3 []\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n == 0 or n == 1:\n return 1\n prev, curr = 1, 1\n for i in range(2, n+1):\n temp = curr\n curr = prev + curr\n prev = temp\n return curr\n```\n\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 1,005 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
C++ || Python || Beats 100% || Using DP || 2 ways (Recursion + memorization , Tabulation, Space Opt) | climbing-stairs | 0 | 1 | # Intuition\nUsing Top - Down Approach -> Recursion + Memorization.\n\n# Approach\nStoring the values of overlapping sub - problems in a vector.\n\n# Complexity\n- Time complexity:\nO(n) -> As we are visiting all values of n atleast 1 time.\n\n- Space complexity:\nO(n) + O(n) - > (Recursive calls + Array of size n)\n\n# Code\n```\nclass Solution {\npublic:\n int solve(int n,vector<int> &dp){\n //base case\n if(n<=2)\n return n;\n \n if(dp[n]!=-1) \n return dp[n]; \n \n dp[n]=solve(n-1,dp)+solve(n-2,dp);\n return dp[n];\n }\n int climbStairs(int n) {\n if(n<=2)\n return n;\n vector<int> dp(n+1,-1);\n return solve(n,dp);\n }\n};\n```\n\n# Intuition\nUsing Bottom - up Approach -> Tabulation.\n\n# Approach\nStoring the values of overlapping sub - problems in a vector.\n\n# Complexity\n- Time complexity:\nO(n) -> As we are traversing the vector atleast 1 time.\n\n- Space complexity:\nO(n) - > (Array of size n)\n\n# Code\n```\nclass Solution {\npublic:\n int climbStairs(int n) {\n if(n<=2)\n return n;\n vector<int> dp(n+1);\n dp[0]=0;\n dp[1]=1;\n dp[2]=2;\n for(int i=3;i<=n;i++)\n dp[i]=dp[i-1]+dp[i-2];\n \n return dp[n];\n }\n};\n```\n\n# Python Code :\nContributed by : Aarya_R\n\n# Complexity\n- Time complexity:\nO(n) -> As we are traversing the vector atleast 1 time.\n\n- Space complexity:\nO(1) \n```\ndef climbStairs(self, n):\n prev = 1\n prev2 = 0\n for i in range(1, n+1):\n curi = prev + prev2\n prev2 = prev\n prev = curi\n return prev \n```\n\n\n | 421 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
7 lines of code beats 99.41% very easy solution | climbing-stairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n <= 1:\n return 1\n dp = [0] * (n + 1)\n dp[0], dp[1] = 1, 1\n for i in range(2, n + 1):\n dp[i] = dp[i - 1] + dp[i - 2]\n return dp[n]\n``` | 1 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Python :Detail explanation (3 solutions easy to difficult) : Recursion, dictionary & DP | climbing-stairs | 0 | 1 | #####\n### General inutution\n##### \t-> Intution : the next distinict way of climbing stairs is euqal to the sum of the last two distinict way of climbing\n##### \t\tdistinct(n) = distinict(n-1) + distinict(n-2)\n##### This intution can be applied using the following three approach --> ordered from easy to difficult approach\n#####\n##### \n##### \n#### Idea 1 : pure recursive (Can\'t pass the test case :does not work for big number, result time-exced limit)\n##### \t- The base case will be when only 1 or 2 steps left\n##### \t- Result time-exced limit\n##### \n \n\n```\nclass Solution(object):\n def climbStairs(self, n):\n """\n :type n: int\n :rtype: int\n """\n def climb(n):\n if n==1: #only one step option is availble\n return 1\n if n ==2: # two options are possible : to take two 1-stpes or to only take one 2-steps\n return 2\n return climb(n-1) + climb(n-2)\n return climb(n)\n \n```\n##### \n##### \'\'\'\n#### Idea 2 : use dictionary (look-up table) to memorize repeating recursion\n##### - The memory start with the base case and recored every recurssion\n##### \'\'\'\n```\nclass Solution(object):\n def climbStairs(self, n):\n """\n :type n: int\n :rtype: int\n """\n memo ={}\n memo[1] = 1\n memo[2] = 2\n \n def climb(n):\n if n in memo: # if the recurssion already done before first take a look-up in the look-up table\n return memo[n]\n else: # Store the recurssion function in the look-up table and reuturn the stored look-up table function\n memo[n] = climb(n-1) + climb(n-2)\n return memo[n]\n \n return climb(n)\n```\n \n##### \'\'\'\n### Idea 3 : Dynamic programming \n##### --> store the distinct ways in a dynamic table\n##### climb = [climb(0), climb(1), climb(2)=climb(0)+climb(1), climb(3)=climb(2)+climb(1),......climb(n)=climb(n-1)+climb(n-2)]\n##### dp = [ 0, 1, 2, 3, 5, dp(i-1)+dp(i-2])]\n##### return dp[n]\n##### \'\'\'\n\tdef climb(n):\n #edge cases\n if n==0: return 0\n if n==1: return 1\n if n==2: return 2\n dp = [0]*(n+1) # considering zero steps we need n+1 places\n dp[1]= 1\n dp[2] = 2\n for i in range(3,n+1):\n dp[i] = dp[i-1] +dp[i-2]\n print(dp)\n return dp[n]\n\t\t\t\n### ****** upvote as a sign of appriatation ***** | 672 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Python3 solution beats 82% (recursion & memoization) | climbing-stairs | 0 | 1 | # Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n @cache\n def count(n):\n return 1 if n == 1 else 2 if n == 2 else count(n-1) + count(n-2)\n return count(n)\n\n \n``` | 1 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Python easy solution | climbing-stairs | 0 | 1 | # Intuition\nFibonacci Series\n\n# Approach\nPriorly just apply bruteforce method to solve, but get the fibonacci series as a result. So at the end just apply the concept of fibonacci series.\n\nStairs: 1 2 3 4 5 6....\nSteps : 1 2 5 8 13 21...\n\nHere, we see that for climb stair 1 or 2 we have same n numbers of steps. But after that if we see that add the current no. of steps and previous that is for 3 it will be (2+1) and so on. So this is the concept of fibonacci series.\n\n# Complexity\n- Time complexity:\nO(2^n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n<=2: return n\n\n p1 = 1\n p2 = 2\n current = 0\n\n for i in range (2, n):\n current = p1+p2\n p1=p2\n p2=current\n return current\n``` | 1 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Beats 100%. Easiest 1 min explanation in JAVA and Python | climbing-stairs | 1 | 1 | # Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal here is to find the number of distinct ways to climb to the top of a staircase with n steps. You can take either one step or two steps at a time.\n\nThe intuition behind this solution is to use dynamic programming to efficiently calculate the number of ways to climb the stairs. Here\'s how it works:\n\n1. We use three variables:\n - `climbSecondLastStair`: This variable keeps track of the number of ways to climb the second-to-last stair.\n - `climbLastStair`: This variable keeps track of the number of ways to climb the last stair.\n - `climbCurrentStair`: This variable is used to calculate the number of ways to climb the current stair.\n\n2. We start iterating from the first stair (i = 1) up to the nth stair. For each stair, we calculate the number of ways to reach that stair using the following logic:\n - `climbCurrentStair` is calculated as the sum of `climbSecondLastStair` and `climbLastStair`. This is because you can either reach the current stair from the stair before it (if you take one step) or from the stair before the previous one (if you take two steps).\n - Then, we update `climbSecondLastStair` to be equal to `climbLastStair`, and `climbLastStair` to be equal to `climbCurrentStair`. This prepares the variables for the next iteration.\n\n3. By the end of the loop, `climbCurrentStair` contains the number of ways to climb the nth stair, which is the answer we need.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\nBecause we iterate over one loop for n times.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\nBecause we do not use any extra space. Generally people use an array to store the count. We have avoided that to further optimize space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` java []\nclass Solution {\n public int climbStairs(int n) {\n int climbSecondLastStair = 0;\n int climbLastStair = 1;\n int climbCurrentStair = 1;\n for(int i = 1; i <= n; i++) {\n climbCurrentStair = climbSecondLastStair + climbLastStair;\n climbSecondLastStair = climbLastStair;\n climbLastStair = climbCurrentStair;\n }\n return climbCurrentStair;\n }\n}\n```\n``` python3 []\nclass Solution:\n def climbStairs(self, n: int) -> int:\n last = 1\n sec_last = 0\n for i in range(n):\n ways = last + sec_last\n sec_last = last\n last = ways\n return ways\n #because to reach nth step, we can jump 1 step from (n-1)th step or 2 steps from (n-2)th step\n```\n***Please give an upvote if you understood my solution in optimal time :)*** | 4 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Dynamic Programming Python3 | climbing-stairs | 0 | 1 | ```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n dp=[-1]*(n+2)\n def solve(i):\n if i==0 or i==1:\n return 1\n if dp[i]!=-1:\n return dp[i]\n left=solve(i-1)\n right=solve(i-2)\n dp[i]=left+right\n return left+right\n return solve(n)\n```\n\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n one,two=1,1\n for i in range(n-1):\n temp=one+two\n one=two\n two=temp\n return two\n #please upvote me it would encourage me alot\n\n\n``` | 99 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
BEATS 98.5% OF PYTHON SOLUTIONS!!!!! ✅✔☑🔥✅✔☑🔥✅✔☑🔥 | climbing-stairs | 0 | 1 | # Approach\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nusing basic aptitute we can approach this problem by finding the sum of fibonacci series of the given number (n) + 1. To find the total number of ways to climb the stairs.\n\n\n\n# Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n \n fib_series = [0, 1]\n while len(fib_series) < n:\n fib_series.append(fib_series[-1] + fib_series[-2])\n if n==1:\n return 1 \n return sum(fib_series)+1\n\n```\n\n# Proof:\n\n\n\n\n# Please upvote me\n\n\n\n# co-partner: isolve\n | 2 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Climbing stairs solved through recursion. | climbing-stairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def climbStairs(self, n: int, memo = {}) -> int:\n if n in memo:\n return memo[n]\n if n==0:\n return 1\n elif n<0:\n return 0\n else:\n memo[n] = self.climbStairs(n-1)+self.climbStairs(n-2)\n return memo[n]\n \n``` | 1 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Using Fibonnaci Approach || Climbing Stairs | climbing-stairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n==0 or n==1:\n return 1\n a=1\n b=1\n for i in range(2,n+1):\n c=a+b\n a=b\n b=c\n return b\n``` | 3 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Python Easy Solution || 100 % || | climbing-stairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind the relation with fibonacci Series.\n\n\nThink it as Fibonacci series.\nLet think about 4 steps.\nAt step 4 we have two option either take 1 step or Two step.\n - If take 1 then remaining 3 steps\n - If take 2 then remaining 2 steps\nsimilarlry for step 3 we can take either 1 step or 2 step\nyou can easly get it from the figure.\nfrom figure we can see that\nfor 1 step - 1 Way\n 2 Step - 2 Way\n 3 Step - 3 Way\n 4 Step - 5 Way (3 Step + 2 Step)\n 5 Step - 8 Way (4 Step + 3 Step)\n 6 Step - 13 Way (5 Step + 4 Step)\nclearly we can see this is forming a Fibonacci Series with first and second values as 1 and 2 respectively.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere as we can see this one is recursive oin nature, SO we will use either Recurssion or for better time complexity will use DP\n\n\n# Complexity\n- Time complexity: $$O(log (n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def memo(self,n, arr):\n if n<=1:\n return 1\n if arr[n]!=-1:\n return arr[n]\n sm = self.memo(n-1, arr)+self.memo(n-2, arr)\n arr[n]=sm\n return arr[n]\n def climbStairs(self, n: int) -> int:\n dp = [-1]*(n+2)\n return self.memo(n, dp)\n\n``` | 1 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
🎯Optimizing Stair Climbing: From Recursion 🔄 to Dynamic Programming 📊 | climbing-stairs | 0 | 1 | # Intuition \uD83E\uDD14\nThe problem seems similar to the Fibonacci series, where the number of ways to reach the nth stair is the sum of ways to reach the (n-1)th and (n-2)th stair. A naive recursive solution might have a large number of overlapping computations. Thus, dynamic programming principles come into play to optimize our approach.\n\n# Approach \uD83D\uDE80\n1.Recursive Solution:\n\nIf n == 0 or n == 1, there\'s only one way to climb, so return 1.\nFor other values of n, the result is climbStairs(n-1) + climbStairs(n-2).\n\n2.Memoization (Top-down):\n\nCreate a dp array of size n+1 initialized with -1 to store the results.\nModify the recursive function to check the dp array before recursive calls. If a result is already present for a particular n, use it instead of recalculating.\nStore the result of each computation in the dp array to reuse it later.\n\n3.Tabulation (Bottom-up):\n\nIterate from 0 to n using a loop.\nFor the base cases (n == 0 and n == 1), fill in the value 1.\nFor other values, calculate the result using values already present in the dp array (dp[i-1] + dp[i-2]).\nStore the result in the current dp array index.\n\n# Video \uD83D\uDCE3\nFor those looking to dive deeper into the topic or get a visual representation, check out this fantastic YouTube playlist,\n[https://youtu.be/3ewW2lsX7Ug?si=yBH4-63fSBXXHDpl]() \n\n# Complexity\n- Time complexity:\n$$Recursive: O(2^n)$$(due to overlapping computations)\n$$Memoization: O(n)$$ (since each computation is stored and reused)\n$$Tabulation: O(n)$$ (since the solution is built iteratively)\n\n- Space complexity:\n $$Recursive: O(n)$$(due to recursion stack)\n$$Memoization: O(n)$$ (due to the dp array and recursion stack))\n$$Tabulation: O(n)$$ (only the dp array)\n# Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n # if n==1: return 1\n # if n==0: return 1\n # n1 = self.climbStairs(n-1)\n # n2 = self.climbStairs(n-2)\n # return n1+n2\n #for Recur to Memo\n \n #1. dp of n+1 init wih 0 or 1 \n # dp=[-1]*(n+1)\n # 2. replcae recur function with dp and store final ans in dp\n # def memo(n,dp):\n # if n==0: return 1\n # if n==1: return 1\n # #return dp if has value!\n # if dp[n]!=-1:\n # return dp[n]\n \n # f1 = memo(n-1,dp)\n # f2 = memo(n-2,dp)\n \n # dp[n]=f1+f2\n # return dp[n]\n # return memo(n,dp) \n \n \n # #1. start a loop from a base case or n+1\n # #2. Copy all Memo Code\n # #3. Insted of return statement, save value in dp and write continue\n dp=[-1]*(n+1)\n def tab(n,dp):\n for i in range(0,n+1):\n if i==0: \n dp[i]=1\n continue\n #return 1\n if i==1: \n dp[i]=1\n continue\n #return 1\n #return dp if has value!\n if dp[i]!=-1:\n return dp[i]\n #4. At place of recursie call , acces dp \n f1 =dp[i-1]\n f2 =dp[i-2]\n \n dp[i]=f1+f2\n return dp[n]\n return tab(n,dp)\n \n \n\n```\n\n**Hey there,** \uD83C\uDF1F Did this solution just make our connection a bit stronger? If you felt that spark, why not hit that upvote button? After all, who can resist a little mutual appreciation, right? \uD83D\uDE09\uD83D\uDCA1 But remember, it\'s all in good fun. Stay awesome, you coding rockstar! \uD83D\uDE80\uD83C\uDFB8 | 2 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Simplest Python DP code. Its basically Fibonacci | climbing-stairs | 0 | 1 | \n# Code\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n dp = [0] * (n+1)\n dp[0], dp[1] = 1, 1\n \n for i in range(2, n+1):\n dp[i] = dp[i-1] + dp[i-2]\n \n return dp[n]\n\n``` | 2 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
[VIDEO] Visualization of Bottom-Up Dynamic Programming Approach | climbing-stairs | 0 | 1 | https://www.youtube.com/watch?v=4ikxUxiEB10\n\nSince you can only take 1 step or 2 steps, the total number of ways to climb `n` steps can be defined recursively as: the total number of ways to climb `n-1` stairs + the total number of ways to climb `n-2` stairs. Below is the recursive code:\n\n## Recursive Solution\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n == 1:\n return 1\n if n == 2:\n return 2\n return self.climbStairs(n-1) + self.climbStairs(n-2)\n```\n\nThis works, but the problem is that we make many of the same function calls over and over again, and the algorithm ends up running in O(2<sup>n</sup>) time. So instead, the bottom-up dynamic programming approach calculates the number of ways to climb a certain number of stairs <i>only once</i>, and reuses previous values to build up to the solution. For a visualization, please see the video, but because each calculation only needs to be done once, the runtime is reduced to O(n) time.\n\nWe start by calculating the number of ways to climb 2 steps. `one_before` is the number of ways to climb 1 step, and `two_before` is the number of ways to climb 0 steps (you could argue this should be 0, not 1, but for this problem we need to start with 1). So following the recursive defintion, we know that the number of ways to climb 2 steps is `one_before` + `two_before`. Then we update those two variables and continue building our solution until we reach `n`.\n\n# Dynammic Programming Solution\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n == 1:\n return 1\n\n one_before = 1\n two_before = 1\n total = 0\n\n for i in range(n-1):\n total = one_before + two_before\n two_before = one_before\n one_before = total\n\n return total\n``` | 12 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Python | C++ | Easy to Understand | Fastest Solution | C++ runtime - 3ms. | climbing-stairs | 0 | 1 | # *Approach*\n<!-- Describe your approach to solving the problem. -->\n- *When employing dynamic programming, we only need to keep track of the prior and the prior of the prior; otherwise, dp of size n is worthless for further steps.*\n\n# *Complexity*\n- *Time complexity: **O(n)***\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- *Space complexity: **O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# *Code*\n### *Python*\n```\nclass Solution:\n def climbStairs(self, n: int) -> int:\n if n == 1:\n return 1\n prev_prev = prev = 1 \n curr = 0 \n for i in range(2, n+1):\n curr = prev + prev_prev\n prev_prev = prev\n prev = curr\n return curr\n```\n### *C++*\n- *Since using that much space is pointless, the above solution is the most effective one. However, you may also consider this dp, which is also allowed.*\n- *You can also see a commented chunk of code that states that Dynamic Programming is utilised because **TIME LIMIT EXCEEDED** owing to Overlapping Sub-Problems.*\n```\nclass Solution {\npublic:\n int climbStairs(int n) {\n int dp[n+1];\n dp[0]=1;\n dp[1]=1;\n for(int i=2;i<n+1;i++){\n dp[i]=dp[i-1]+dp[i-2];\n }\n return dp[n];\n }\n}; \n// Recursion gives TLE \n// if(n==0) return 1;\n// if(n<0) return 0;\n \n// return climbStairs(n-1)+climbStairs(n-2);\n\n``` | 2 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Beats 70% solution, easy mathematical approach | climbing-stairs | 0 | 1 | # Intuition\niterates from max nums of 2 steps, and min nums of 1 steps\n\n- Time complexity:\n O(n/2 * n/2!)\n- Space complexity:\n O(n)\n\n# Code\n```\nimport operator\nfrom collections import Counter\nfrom math import factorial\n\nclass Solution:\n def climbStairs(self, n: int) -> int:\n #bucket of 1,2 = factorial(num of steps)/(factorial(num of 1) * factorial(num of 2)\n #(n/2, n) range of bucket\n\n step_2 = n // 2\n\n if n % 2 == 0:\n step_1 = 0\n count = 1\n else:\n step_1 = 1\n count = 0\n\n for i in range(n//2,n):\n count += math.factorial(step_2+step_1)//(math.factorial(step_1) * math.factorial(step_2))\n step_2 -= 1\n step_1 += 2\n\n return count\n``` | 4 | You are climbing a staircase. It takes `n` steps to reach the top.
Each time you can either climb `1` or `2` steps. In how many distinct ways can you climb to the top?
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
**Example 2:**
**Input:** n = 3
**Output:** 3
**Explanation:** There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
**Constraints:**
* `1 <= n <= 45` | To reach nth step, what could have been your previous steps? (Think about the step sizes) |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.