title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Java/C++/Python/JavaScript/Kotlin/Swift]O(n)time/BEATS 99.97% MEMORY/SPEED 0ms APRIL 2022 | multiply-strings | 1 | 1 | ***Hello it would be my pleasure to introduce myself Darian.***\n\n***Java***\n```\npublic String multiply(String num1, String num2) {\n int m = num1.length(), n = num2.length();\n int[] pos = new int[m + n];\n \n for(int i = m - 1; i >= 0; i--) {\n for(int j = n - 1; j >= 0; j--) {\n int mul = (num1.charAt(i) - \'0\') * (num2.charAt(j) - \'0\'); \n int p1 = i + j, p2 = i + j + 1;\n int sum = mul + pos[p2];\n\n pos[p1] += sum / 10;\n pos[p2] = (sum) % 10;\n }\n } \n \n StringBuilder sb = new StringBuilder();\n for(int p : pos) if(!(sb.length() == 0 && p == 0)) sb.append(p);\n return sb.length() == 0 ? "0" : sb.toString();\n}\n```\n\n***C++***\n```\nclass Solution {\npublic:\n string multiply(string num1, string num2) {\n // handle edge-case where the product is 0\n if (num1 == "0" || num2 == "0") return "0";\n \n // num1.size() + num2.size() == max no. of digits\n vector<int> num(num1.size() + num2.size(), 0);\n \n // build the number by multiplying one digit at the time\n for (int i = num1.size() - 1; i >= 0; --i) {\n for (int j = num2.size() - 1; j >= 0; --j) {\n num[i + j + 1] += (num1[i] - \'0\') * (num2[j] - \'0\');\n num[i + j] += num[i + j + 1] / 10;\n num[i + j + 1] %= 10;\n }\n }\n \n // skip leading 0\'s\n int i = 0;\n while (i < num.size() && num[i] == 0) ++i;\n \n // transofrm the vector to a string\n string res = "";\n while (i < num.size()) res.push_back(num[i++] + \'0\');\n \n return res;\n }\n};\n```\n\n***Python***\n```\nclass Solution:\n def multiply(self, num1: str, num2: str) -> str:\n return str(self.strint(num1)*self.strint(num2))\n def strint(self,n):\n result=0\n for i in range(len(n)):\n result = result*10 + ord(n[i])-ord(\'0\')\n return result\n```\n\n***JavaScript***\n```\nconst multiply = function(num1, num2) {\n const dp = [...Array(num1.length+num2.length)].fill(0); \n for(let i = num1.length-1; i >= 0; i--){\n for(let j = num2.length-1; j >= 0; j--){\n\t \n\t //Define\n\t\tconst prevRemainder = dp[i+j+1] \n const product = num1[i]*num2[j]+prevRemainder\n const unitsDigit = product%10\n const carryOver = Math.floor(product/10)\n\t\t\t\n\t\t//Update\n dp[i+j+1] = unitsDigit;\n\t\tdp[i+j] += carryOver\n }\n }\n \n //Delete leading-zeroes\n let idx = 0\n while(dp[idx] === 0) dp.shift()\n if(!dp.length) return "0"\n return dp.join("") \n};\n```\n\n***Kotlin***\n```\nfun multiply(num1: String, num2: String): String {\n if (num1 == "0" || num2 == "0") return "0"\n \n val num1 = StringBuilder(num1).reversed().toString()\n val num2 = StringBuilder(num2).reversed().toString()\n val len1 = num1.length; val len2 = num2.length\n \n val sums = IntArray(len1 + len2)\n \n for (i in 0..len1 - 1) {\n val a = num1[i] - \'0\'\n for (j in 0..len2 - 1) {\n val b = num2[j] - \'0\'\n sums[i + j] += a * b\n }\n }\n\n val res = StringBuilder()\n var carry = 0\n \n for (sum in sums) {\n val num = (sum + carry) % 10\n carry = (sum + carry) / 10\n res.append(num)\n }\n\n if (res.last() == \'0\') res.deleteCharAt(res.length - 1)\n return res.reversed().toString()\n}\n```\n\n***Swift***\n```\nclass Solution {\n func multiply(_ num1: String, _ num2: String) -> String {\n\t\tif (num1 == "0" || num2 == "0") { return "0"}\n\t\tlet list1 = convertString(num1)\n\t\tlet list2 = convertString(num2)\n\t\tvar tmp1 = list1\n\t\tvar tmp2 = list2\n\t\tvar lists: [ListNode?] = []\n\t\tvar index = 0\n\n\t\twhile tmp1 != nil {\n\t\t\tvar list: ListNode? = nil\n\t\t\tvar current = list\n\t\t\tvar add = 0\n\t\t\tfor _ in 0..<index {\n\t\t\t\tlet node = ListNode(0)\n\t\t\t\tif list == nil { list = node }\n\t\t\t\tcurrent?.next = node\n\t\t\t\tcurrent = node\n\t\t\t}\n\t\t\twhile tmp2 != nil {\n\t\t\t\tlet val = tmp1!.val * tmp2!.val + add\n\t\t\t\tlet node = ListNode(val % 10)\n\t\t\t\tadd = val / 10\n\t\t\t\tif list == nil { list = node }\n\t\t\t\tcurrent?.next = node\n\t\t\t\tcurrent = node\n\t\t\t\ttmp2 = tmp2?.next\n\t\t\t}\n\t\t\tif add > 0 {\n\t\t\t\tcurrent?.next = ListNode(add)\n\t\t\t}\n\t\t\ttmp1 = tmp1?.next\n\t\t\ttmp2 = list2\n\t\t\tlists.append(list)\n\t\t\tindex += 1\n\t\t}\n\t\tlet res = addLists(lists)\n return convertListNode(res)\n }\n\n\n\tfunc convertString(_ num: String) -> ListNode? {\n\t\tvar list: ListNode? = nil\n\t\tvar current = list\n\t\t\n\t\tfor i in num.reversed() {\n\t\t\tlet node = ListNode(Int(String(i)) ?? 0)\n\t\t\tif current != nil {\n\t\t\t\tcurrent?.next = node\n\t\t\t} else {\n\t\t\t\tlist = node\n\t\t\t}\n\t\t\tcurrent = node\n\t\t}\n\t\treturn list\n\t}\n\n\n\tfunc convertListNode(_ list: ListNode?) -> String {\n\t\tvar tmp = list\n\t\tvar string = ""\n\t\twhile tmp != nil {\n\t\t\tstring = "\\(tmp!.val)\\(string)"\n\t\t\ttmp = tmp!.next;\n\t\t}\n\t\treturn string\n\t}\n\n\n\tfunc addTwoNumbers(_ l1: ListNode?, _ l2: ListNode?) -> ListNode? {\n var add = 0\n var _l1 = l1\n var _l2 = l2\n var list: [ListNode] = []\n while _l1 != nil || _l2 != nil {\n let _l1_val = _l1?.val ?? 0\n let _l2_val = _l2?.val ?? 0\n let val = _l1_val + _l2_val + add\n let num = val % 10\n add = val / 10\n list.append(ListNode(num))\n _l1 = _l1?.next\n _l2 = _l2?.next\n }\n if (add == 1) {\n list.append(ListNode(1))\n }\n var head: ListNode?\n for node in list.reversed() {\n node.next = head\n head = node\n }\n return head\n }\n\n\n\tfunc addLists(_ lists: [ListNode?]) -> ListNode? {\n\t\tif lists.count == 1 {\n\t\t\treturn lists[0]\n\t\t} else {\n\t\t\tvar tmp = lists[0]\n\t\t\tfor (i, list) in lists.enumerated() {\n\t\t\t\tif i > 0 {\n\t\t\t\t\ttmp = addTwoNumbers(tmp, list)\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn tmp\n\t\t}\n\t}\n\n}\n```\n\n***Consider upvote if useful! Hopefully it can be used in your advantage!***\n***Take care brother, peace, love!***\n***"Open your eyes."*** | 4 | Given two non-negative integers `num1` and `num2` represented as strings, return the product of `num1` and `num2`, also represented as a string.
**Note:** You must not use any built-in BigInteger library or convert the inputs to integer directly.
**Example 1:**
**Input:** num1 = "2", num2 = "3"
**Output:** "6"
**Example 2:**
**Input:** num1 = "123", num2 = "456"
**Output:** "56088"
**Constraints:**
* `1 <= num1.length, num2.length <= 200`
* `num1` and `num2` consist of digits only.
* Both `num1` and `num2` do not contain any leading zero, except the number `0` itself. | null |
Bijil Boby | wildcard-matching | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n i,j,si,m=0,0,-1,0\n while i<len(s):\n if j<len(p) and (s[i]==p[j] or p[j]==\'?\'):\n j+=1\n i+=1\n elif j<len(p) and p[j]==\'*\':\n si=j\n m=i\n j+=1\n elif si!=-1:\n j=si+1\n m+=1\n i=m\n else:\n return False\n while j<len(p) and p[j]==\'*\':\n j+=1\n return j==len(p)\n \n``` | 0 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Easy To understand | wildcard-matching | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n i, j = 0, 0\n last_match, star = 0, -1\n\n while i < len(s):\n if j < len(p) and (s[i] == p[j] or p[j] == \'?\'):\n i += 1\n j += 1\n elif j < len(p) and p[j] == \'*\':\n last_match = i\n star = j\n j += 1\n elif star != -1:\n j = star + 1\n i = last_match + 1\n last_match += 1\n else:\n return False\n\n while j < len(p) and p[j] == \'*\':\n j += 1\n\n return j == len(p)\n ##Upvote me If it helps\n\n``` | 3 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Python3 || DP space optimized | wildcard-matching | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(mn)$$ where m, n are the length of s and p, respectively\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n\n m, n = len(s), len(p)\n\n dp_ip1 = [True] * (n + 1)\n for j in range(n-1, -1, -1):\n dp_ip1[j] = p[j] == \'*\' and dp_ip1[j+1]\n \n for i in range(m-1, -1, -1):\n dp_i = [False] * (n+1)\n for j in range(n-1, -1, -1):\n if s[i] == p[j] or p[j] == \'?\':\n dp_i[j] = dp_ip1[j+1]\n elif p[j] == \'*\':\n dp_i[j] = dp_ip1[j] or dp_i[j+1]\n else:\n dp_i[j] = False\n dp_ip1 = dp_i\n return dp_ip1[0]\n\n``` | 1 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
✨💯💥Linear Time Solution | Detailed Explanation | Images | Visualisations💥💯✨ | wildcard-matching | 0 | 1 | # Intuition\nI solved this problem using dynamic programming .Its time complexity was $$O(len(s)*len(p))$$. However this post doesn\'t explain that solution. I am sure there are many more posts to explain that.\n\nThereafter I found a solution in linear time using 2 pointer approach. I have made some visualisations using python to understand this solution. Here is the link to the blog post for this solution by [Yu](https://yucoding.blogspot.com/2013/02/leetcode-question-123-wildcard-matching.html):\n\n---\n\n\n\n# Approach\n1. Start by setting up some placeholders: We set up some variables that keep track of positions and states (s_cur, p_cur, match, star) as we move through the string and pattern.\n2. (Loop) While we haven\'t reached the end of the string, we check the following:\n 1. If the current character in the pattern matches the current character in the string or if the pattern character is a question mark, we move forward in both the string and pattern.\n 1. If we encounter a \'*\' in the pattern, we note down the current positions in the string and pattern and move the pattern position forward.\n 1. If none of the above conditions are met, but we have seen a \'\' before, we reset the pattern position after the \'\' to the next character, increment the match counter, and move the string position to the new match.\n 1. If none of the conditions are met mainly (p_cur reaches the end) and we have no \'*\' to fall back on, we know the pattern doesn\'t match the string, so we return False.\n3. After going through the string, we check if there are any \'*\' characters left in the pattern. If there are, we move the pattern position forward.\n4. Finally, if we\'ve reached the end of the pattern at this point, we know the pattern matches the string, so we return True. Otherwise, we return False.\n<!-- Describe your approach to solving the problem. -->\n\n---\n\n\n# Complexity\n- Average Time complexity: $$O(n)$$\n- Worst Case Time complexity: $$O(mn)$$ (Eg String (s): "aaaaaaaaaaab"\nPattern (p): "*aab")\n- Space complexity: $$O(1)$$\n\n\n---\n\n\n# Dry Run with Visualisation \nThe yellow highlighted cells represent s_cur and p_cur respectively\n$$\ns =\nabcabczzzde\n$$\n$$\np =\n*abc???de*\n$$\n\n\n\nWorst Case Example\n$$\ns =\naaaaaaab\n$$\n$$\np =\n*aab\n$$\n\n$$\ns =\nabxbcbgh\n$$\n$$\np =\na*c*h\n$$\n\n\n\n\n---\n\n\n\n# Code\n```\nclass Solution:\n def isMatch(self, s, p):\n s_cur = 0\n p_cur= 0\n match = 0\n star = -1\n while s_cur<len(s):\n if p_cur<len(p):\n print("Pattern Char",p[p_cur])\n if p_cur< len(p) and (s[s_cur]==p[p_cur] or p[p_cur]==\'?\'):\n s_cur = s_cur + 1\n p_cur = p_cur + 1\n elif p_cur<len(p) and p[p_cur]==\'*\':\n match = s_cur\n star = p_cur\n p_cur = p_cur+1\n elif (star!=-1):\n p_cur = star+1\n match = match+1\n s_cur = match\n else:\n return False\n while p_cur<len(p) and p[p_cur]==\'*\':\n p_cur = p_cur+1\n \n if p_cur==len(p):\n return True\n else:\n return False\n```\n\n---\n\nAll suggestions are welcome.\nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\nHappy Learning, Cheers Guys \uD83D\uDE0A\nKeep Grinding \uD83D\uDE00\uD83D\uDE00\n | 5 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
BEATS 95% OF THE USERS IN PYTHON3 O(n^2) DYNAMIC PROGRAMMING SOLUTION | wildcard-matching | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport copy\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n if p=="":\n if s=="":\n return True\n else:\n return False\n if s=="":\n if p=="" or p=="*"*len(p):\n return True\n else:\n return False\n \n \n \n\n \n i=0\n l=[]\n prev=[]\n while(i<len(p)):\n #print(p[i])\n if i==0:\n if p[0]=="*":\n while(i<len(p) and p[i]=="*"):\n i+=1\n if i>=len(p):\n return True\n if p[i]=="?":\n for j in range(len(s)):\n l.append(j)\n else:\n for j in range(len(s)):\n if p[i]==s[j]:\n l.append(j)\n elif p[0]=="?" or p[0]==s[0]:\n l.append(0)\n else:\n if p[i]=="*":\n while(i<len(p) and p[i]=="*"):\n i+=1\n if i>=len(p):\n return True\n if p[i]=="?":\n for j in range(prev[0]+1,len(s)):\n l.append(j)\n else:\n for j in range(len(s)):\n if p[i]==s[j] and j>prev[0]:\n l.append(j)\n elif p[i]=="?":\n for j in range(len(prev)):\n if (prev[j]+1)<len(s):\n l.append(prev[j]+1)\n else:\n for j in range(len(prev)):\n if prev[j]+1<len(s) and s[prev[j]+1]==p[i]:\n l.append(prev[j]+1)\n #print(prev)\n #print(l)\n if l==[]:\n return False\n \n prev=copy.copy(l)\n l=[]\n i+=1\n \n if len(s)-1 in prev:\n return True\n else:\n return False\n\n\n \n \n \n``` | 2 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Python || faster than 90% || Explained with comments | wildcard-matching | 0 | 1 | # Complexity\n- Time complexity:\nBetter than 90%\n\n- Space complexity:\nBetter than 90%\n\n# Code\n```\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n # Initialize the pointers for the input string and the pattern\n i = 0\n j = 0\n \n # Initialize the pointers for the last character matched and the last\n # \'*\' encountered in the pattern\n last_match = 0\n star = -1\n \n # Loop through the input string and the pattern\n while i < len(s):\n # Check if the current characters in the input string and the pattern\n # match, or if the pattern character is a \'?\'\n if j < len(p) and (s[i] == p[j] or p[j] == \'?\'):\n # Move the pointers for the input string and the pattern forward\n i += 1\n j += 1\n # Check if the current pattern character is a \'*\'\n elif j < len(p) and p[j] == \'*\':\n # Store the current positions of the pointers for the input string\n # and the pattern\n last_match = i\n star = j\n # Move the pointer for the pattern forward\n j += 1\n # If none of the above conditions are met, check if we have encountered\n # a \'*\' in the pattern previously\n elif star != -1:\n # Move the pointer for the pattern back to the last \'*\'\n j = star + 1\n # Move the pointer for the input string to the next character\n # after the last character matched\n i = last_match + 1\n # Move the pointer for the last character matched forward\n last_match += 1\n # If none of the above conditions are met, the input string and the\n # pattern do not match\n else:\n return False\n \n # Loop through the remaining characters in the pattern and check if they\n # are all \'*\' characters\n while j < len(p) and p[j] == \'*\':\n j += 1\n \n # Return True if all the characters in the pattern have been processed,\n # False otherwise\n return j == len(p)\n \n``` | 18 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Wildcard Matching with step by step explanation | wildcard-matching | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a 2D boolean array dp with m + 1 rows and n + 1 columns, where m is the length of string s and n is the length of string p.\n2. Set dp[0][0] to True, which means an empty string matches an empty pattern.\n3. For each column in the first row, if the corresponding character in p is \'*\', set the value in the same column of the first row to the value in the previous column. This is because \'*\' matches any sequence of characters.\n4. For each row from 1 to m, and each column from 1 to n:\nIf the corresponding character in p is \'*\', set the value in dp[i][j] to the OR of the values in dp[i][j - 1] and dp[i - 1][j]. This means \'*\' matches any sequence of characters, including the empty sequence.\nIf the corresponding character in p is \'?\' or the same as the corresponding character in s, set the value in dp[i][j] to the value in dp[i - 1][j - 1]. This means \'?\' matches any single character, and a character in s matches the same character in p.\n5. Return dp[m][n], which is the result of matching the entire input string s with the entire pattern p.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n m, n = len(s), len(p)\n dp = [[False] * (n + 1) for _ in range(m + 1)]\n dp[0][0] = True\n for j in range(1, n + 1):\n if p[j - 1] == \'*\':\n dp[0][j] = dp[0][j - 1]\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if p[j - 1] == \'*\':\n dp[i][j] = dp[i][j - 1] or dp[i - 1][j]\n elif p[j - 1] == \'?\' or s[i - 1] == p[j - 1]:\n dp[i][j] = dp[i - 1][j - 1]\n return dp[m][n]\n\n``` | 4 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Simple Backtracking with DP | wildcard-matching | 0 | 1 | # Intuition\n- The problem can be classified as Backtracking but to optimize it, we can add memoization to eliminate repeat recursions when computing \'*\'s.\n\n# Approach\n - Backtracking with Dynamic Programming (memoization)\n\n# Code\n```\nclass Solution:\n\n def isMatch(self, s: str, p: str) -> bool:\n memo = {}\n\n def recur(i, j):\n if (i, j) in memo:\n return memo[(i, j)]\n\n if i >= len(s) and j >= len(p):\n memo[(i, j)] = True\n elif j >= len(p):\n memo[(i, j)] = False\n elif i >= len(s):\n if p[j] == \'*\':\n memo[(i, j)] = recur(i, j + 1)\n else:\n memo[(i, j)] = False\n elif p[j] == \'*\':\n memo[(i, j)] = recur(i + 1, j + 1) or recur(i, j + 1) or recur(i + 1, j)\n elif p[j] == \'?\' or p[j] == s[i]:\n memo[(i, j)] = recur(i + 1, j + 1)\n else:\n memo[(i, j)] = False\n\n return memo[(i, j)]\n\n return recur(0, 0)\n\n\n``` | 2 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Python Bottom up dp solution | wildcard-matching | 0 | 1 | \n# Code\n```\n def isMatch(self, s: str, p: str) -> bool:\n n = len(s);\n m = len(p);\n dp = [[0]*(m+1) for _ in range(0,n+1)]\n\n dp[0][0] = 1\n for j in range(1,m+1):\n if(p[j-1] == \'*\' ): dp[0][j] = dp[0][j-1];\n\n for i in range(1,n+1):\n for j in range(1,m+1):\n if(s[i-1] == p[j-1] or p[j-1] == \'?\' ): dp[i][j] = dp[i-1][j-1]\n elif( p[j-1] == \'*\' ):\n # did we match without the chracter in s or did we match with the character before \'*\' in p\n dp[i][j] = dp[i-1][j] or dp[i][j-1]\n\n return dp[-1][-1]\n \n \n``` | 5 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Python Solution Recursion Memo , tabulation, Space Optimization | wildcard-matching | 0 | 1 | \n# Code\n```\nclass Solution:\n def isallstar(self,p,i) -> bool:\n for ii in range (1,i+1):\n if (p[ii-1]!="*"):\n return False\n return True\n\n def memo(self,p,s,i,j,dp):\n if (i<0 and j<0):\n return True\n if (i<0 and j>=0):\n return False\n if (j<0 and i>=0):\n for ii in range (i+1):\n if p[ii]!="*":\n return False\n else:\n return True\n \n if dp[i][j]!=-1:\n return dp[i][j]\n if (p[i]==s[j] or p[i]=="?"):\n dp[i][j]= self.memo(p,s,i-1,j-1,dp) \n \n elif (p[i]=="*"):\n dp[i][j]= (self.memo(p,s,i-1,j,dp) or self.memo(p,s,i,j-1,dp))\n else:\n dp[i][j]= False\n return dp[i][j]\n \n def tabulation(self,p,s,n,m):\n dp=[[0 for i in range (m+1)] for j in range (n+1)]\n dp[0][0]=True\n for j in range (1,m+1):\n dp[0][j]=False\n \n for i in range (1,n+1):\n dp[i][0]=self.isallstar(p,i)\n \n for i in range (1,n+1):\n for j in range (1,m+1):\n if (p[i-1]==s[j-1] or p[i-1]=="?"):\n dp[i][j]= dp[i-1][j-1] \n \n elif (p[i-1]=="*"):\n dp[i][j]= (dp[i-1][j] or dp[i][j-1])\n else:\n dp[i][j]= False\n return dp[n][m]\n \n def spaceOptimization(self,s,p,n,m):\n prev=[0 for i in range (m+1)]\n curr=[0 for i in range (m+1)]\n prev[0]=True\n for i in range (1,n+1):\n curr[0]=self.isallstar(p,i)\n for j in range (1,m+1):\n if (p[i-1]==s[j-1] or p[i-1]=="?"):\n curr[j]= prev[j-1] \n elif (p[i-1]=="*"):\n curr[j]= (prev[j] or curr[j-1])\n else:\n curr[j]= False\n prev=[val for val in curr]\n return prev[m]\n \n \n def isMatch(self, s: str, p: str) -> bool:\n n=len(p)\n m=len(s)\n dp=[[-1 for i in range (m+1)] for j in range (n+1)]\n # return self.memo(p,s,n-1,m-1,dp)\n # return self.tabulation(p,s,n,m)\n return self.spaceOptimization(s,p,n,m)\n\n\n\n```\n\n\nhttps://youtu.be/ZmlQ3vgAOMo | 2 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
💡💡 Neatly coded recursion with memoization in python3 | wildcard-matching | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimilar to LCS, difference in the conditions. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nConditions:\n1. If the characters match or the char in pattern is "?": we decremet both i and j by 1\n2. If the char in pattern in "*": we have a choice to match it with s from 0 characters to the entire string. So, we consider 0, decrement j by 1 and also consider it, decrement i by 1 and perform OR on both of them.\n3. If the characters, don\'t match, return False\n\nBase conditions:\n1. If both i and j are 0, we return True since we\'re using 1 based indexing.\n2. If only p has been exhausted, we return False\n3. If only s has been exhausted, we iterate over p ot check if there are any "*" or "?" remaining, if not we return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m*n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m*n)\n\n# Code\n```\nclass Solution:\n def isMatch(self, s: str, p: str) -> bool:\n\n def recurs(i, j):\n if i == 0 and j == 0:\n t[i][j] = True\n return True\n elif i == 0 and j > 0:\n for k in range(0, j):\n if p[k] != "*":\n t[i][j] = False\n return False\n t[i][j] = True\n return True\n elif j == 0 and i > 0:\n t[i][j] = False\n return False\n elif t[i][j] != -1:\n return t[i][j]\n elif s[i-1] == p[j-1] or p[j-1] == "?":\n t[i][j] = recurs(i-1, j-1)\n return t[i][j]\n elif p[j-1] == "*":\n nottake = recurs(i, j-1)\n take = recurs(i-1, j)\n t[i][j] = nottake or take\n return t[i][j]\n else:\n t[i][j] = False\n return False\n \n\n t = []\n m = len(s)\n n = len(p)\n for i in range(m+1):\n row = [-1] * (n+1)\n t.append(row)\n res = recurs(m, n)\n return res\n \n``` | 1 | Given an input string (`s`) and a pattern (`p`), implement wildcard pattern matching with support for `'?'` and `'*'` where:
* `'?'` Matches any single character.
* `'*'` Matches any sequence of characters (including the empty sequence).
The matching should cover the **entire** input string (not partial).
**Example 1:**
**Input:** s = "aa ", p = "a "
**Output:** false
**Explanation:** "a " does not match the entire string "aa ".
**Example 2:**
**Input:** s = "aa ", p = "\* "
**Output:** true
**Explanation:** '\*' matches any sequence.
**Example 3:**
**Input:** s = "cb ", p = "?a "
**Output:** false
**Explanation:** '?' matches 'c', but the second letter is 'a', which does not match 'b'.
**Constraints:**
* `0 <= s.length, p.length <= 2000`
* `s` contains only lowercase English letters.
* `p` contains only lowercase English letters, `'?'` or `'*'`. | null |
Clean Codes🔥🔥|| Full Explanation✅|| Implicit BFS✅|| C++|| Java|| Python3 | jump-game-ii | 1 | 1 | # Intuition :\n- We have to find the minimum number of jumps required to reach the end of a given array of non-negative integers i.e the shortest number of jumps needed to reach the end of an array of numbers.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Explanation to Approach :\n- We are using a search algorithm that works by moving forward in steps and counting each step as a jump. \n- The algorithm keeps track of the farthest reachable position at each step and updates the number of jumps needed to reach that farthest position. \n- The algorithm returns the minimum number of jumps needed to reach the end of the array.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity :\n- Time complexity : O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n\n# Codes [C++ |Java |Python3] with Comments :\n```C++ []\nclass Solution {\n public:\n int jump(vector<int>& nums) {\n int ans = 0;\n int end = 0;\n int farthest = 0;\n\n // Implicit BFS\n for (int i = 0; i < nums.size() - 1; ++i) {\n farthest = max(farthest, i + nums[i]);\n if (farthest >= nums.size() - 1) {\n ++ans;\n break;\n }\n if (i == end) { // Visited all the items on the current level\n ++ans; // Increment the level\n end = farthest; // Make the queue size for the next level\n }\n }\n\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int jump(int[] nums) {\n int ans = 0;\n int end = 0;\n int farthest = 0;\n\n // Implicit BFS\n for (int i = 0; i < nums.length - 1; ++i) {\n farthest = Math.max(farthest, i + nums[i]);\n if (farthest >= nums.length - 1) {\n ++ans;\n break;\n }\n if (i == end) { // Visited all the items on the current level\n ++ans; // Increment the level\n end = farthest; // Make the queue size for the next level\n }\n }\n\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def jump(self, nums: List[int]) -> int:\n ans = 0\n end = 0\n farthest = 0\n\n # Implicit BFS\n for i in range(len(nums) - 1):\n farthest = max(farthest, i + nums[i])\n if farthest >= len(nums) - 1:\n ans += 1\n break\n if i == end: # Visited all the items on the current level\n ans += 1 # Increment the level\n end = farthest # Make the queue size for the next level\n\n return ans\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n | 194 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
Jiraiya's Barrier technique || Linear solution || intuitive explanation | jump-game-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about finding the minimum number of jumps to reach the end of the array. We can think of this problem as Jiraiya(A popular character from Naruto Universe) trying to detect an enemy at the n-1th position using his barrier arts technique. The furthest distance he can jump from his current position is given by the value at the current index in the array.\n\n\nWe start from the first index and keep track of the farthest position we can reach from the current position. We also keep a barrier that indicates the end of the current jump. When we reach the barrier, we increase the jump count and update the barrier to the farthest position we can reach. We repeat this process until we reach or cross the end of the array.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nEach jump Jiraiya makes is equivalent to a loop iteration in the code. The farthest variable represents the furthest position Jiraiya can reach with his current jump, and barrier represents the end of the current jump. When Jiraiya reaches the end of his current jump (i.e., when he reaches the barrier), he makes another jump, which is represented by incrementing res in the code. This process continues until Jiraiya reaches or crosses the enemy\u2019s position (i.e., the end of the array).\n\n\n# Complexity\n- Time complexity:\nThe time complexity is O(n)\nbecause we are visiting each element in the array once.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nThe space complexity is O(1) because we are not using any extra space that scales with the input size.\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def jump(self, nums: List[int]) -> int:\n n = len(nums)\n if n==1:\n return 0\n res = 0\n curr = 0\n farthest = nums[curr]\n barrier = 0\n while True:\n for positions in range(curr,barrier+1):\n farthest = max(farthest, positions+nums[positions])\n if farthest>=n-1:\n return res+1\n curr = barrier+1\n barrier = farthest\n res+=1\n```\n\nif you think the explanation was great, please consider upvoting the solution!!\n\n | 8 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
🚀Super Easy Solution🚀||🔥Fully Explained🔥|| C++ || Python || Commented | jump-game-ii | 0 | 1 | # Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful\n```\n\n# Intuition\nIn this question we have to find the minimum number of jumps to reach the last index.\nSo, we calculate the maximum index we can reach from the current index.\nIf our pointer `i` reaches the last index that can be reached with current number of jumps then we have to make a jumps.\nSo, we increase the `count`. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Greedy Approach\n Example\n nums = [2,3,1,1,4]\n Here at index `0` reach become 2 and `i` == `last`. \n So increase the `count`(1)\n At index `1` `reach` becomes `4`.\n So, when `i` becomes `2` it becomes equal to last.\n We update last with current maximum jump(`reach`) last = 4.\n And increase `count`.\n So, answer = 2.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int jump(vector<int>& nums) {\n int reach=0, count=0, last=0; // reach: maximum reachable index from current position\n // count: number of jumps made so far\n // last: rightmost index that has been reached so far\n for(int i=0;i<nums.size()-1;i++){ // loop through the array excluding the last element\n reach = max(reach, i+nums[i]); // update reach to the maximum between reach and i+nums[i]\n if(i==last){ // if i has reached the last index that can be reached with the current number of jumps\n last = reach; // update last to the new maximum reachable index\n count++; // increment the number of jumps made so far\n }\n }\n return count; // return the minimum number of jumps required\n }\n};\n\n```\n```python []\nclass Solution:\n def jump(self, nums):\n # Initialize reach (maximum reachable index), count (number of jumps), and last (rightmost index reached)\n reach, count, last = 0, 0, 0\n \n # Loop through the array excluding the last element\n for i in range(len(nums)-1): \n # Update reach to the maximum between reach and i + nums[i]\n reach = max(reach, i + nums[i])\n \n # If i has reached the last index that can be reached with the current number of jumps\n if i == last:\n # Update last to the new maximum reachable index\n last = reach\n # Increment the number of jumps made so far\n count += 1\n \n # Return the minimum number of jumps required\n return count\n\n```\n\n```\n Give a \uD83D\uDC4D. It motivates me alot\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/) | 66 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
Python DP + Memo solution | jump-game-ii | 0 | 1 | # Approach\nCreate an array containing minimum steps you need to take to get to the i-th position.\nWe can simply go through all elements of the array and then iterate over all possible jump lengths updating information in our array.\nWe can either jump from our current position, or some other position that we considered earlier. Take the minimum of these two and you will get an answer.\n\n# Complexity\n- Time complexity: $$O(nk)$$, where k is a sum of all jumps (sum of nums array)\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def jump(self, nums: List[int]) -> int:\n n=len(nums)\n dp=[float(\'inf\') for _ in range(n)]\n dp[0]=0\n for i in range(n):\n for j in range(1,nums[i]+1):\n if i+j<n:\n dp[i+j]=min(dp[i+j],dp[i]+1)\n return dp[n-1]\n``` | 5 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
Python | jump-game-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nGreedy Approach\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def jump(self, a: List[int]) -> int:\n jump, currEnd, nextEnd = 0, 0, 0\n for i in range(len(a)-1):\n nextEnd = max(nextEnd, i + a[i])\n if currEnd == i:\n currEnd = nextEnd\n jump += 1\n return jump\n``` | 1 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
Easy & Clear Solution Python3 | jump-game-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def jump(self, nums: List[int]) -> int:\n n=len(nums)\n dp=[-1 for _ in range(n-1)]\n dp+=[0]\n for i in range(n-2,-1,-1):\n for j in range(i+1,min(n,i+nums[i]+1)):\n if dp[j]!=-1:\n if dp[i]==-1:\n dp[i]=dp[j]+1\n else:\n dp[i]=min(dp[i],dp[j]+1)\n return dp[0]\n``` | 6 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
PYTHON | BEATS 99.99% | EASY-SOLUTION | jump-game-ii | 0 | 1 | ```\nclass Solution:\n def jump(self, nums: List[int]) -> int:\n\n x = [nums[i]+i for i in range(len(nums))] \n # each element in this represent max index that can be reached from the current index \n\n l,r,jumps = 0,0,0\n\n while r < len(nums)-1 :\n jumps += 1\n l,r = r+1,max(x[l:r+1]) \n\n return jumps\n``` | 8 | You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
* `0 <= j <= nums[i]` and
* `i + j < n`
Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** 2
**Explanation:** The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[2,3,0,1,4\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 1000`
* It's guaranteed that you can reach `nums[n - 1]`. | null |
🔐 [VIDEO] 100% Unlocking Recursive & Backtracking for Permutations | permutations | 1 | 1 | # Intuition\nWhen I first looked at this problem, I realized it was a classic case of generating all possible permutations of a given list of numbers. My initial thought was to use a recursive approach to solve it. Recursive algorithms, especially backtracking, often provide a clean and efficient solution for generating permutations. I implemented two different versions of the solution in Python, both capitalizing on recursion and backtracking.\n\nBoth versions achieve the same result, but v2 provides more granular control over the recursive process. Version 1 has also been implemented in other programming languages including C++, JavaScript, C#, Java, Rust, Swift, and Go, demonstrating the versatility and applicability of the recursive backtracking approach across different coding environments.\n\nhttps://youtu.be/Jlw0sIGdS_4\n\n# Approach\nThe main approach here is to use recursion (a form of backtracking) to generate all permutations of the input list. Here\'s a detailed step-by-step guide:\n\n1. **Initialize Result**: Create an empty list, `result`, to store the final permutations.\n\n2. **Define Backtracking Function**: Define a recursive helper function `backtrack`, which takes the remaining numbers to be permuted (`nums`) and the current permutation (`path`) as parameters.\n \n a. **Base Case**: If there are no numbers left to permute (`nums` is empty), we have a complete permutation, and we add the current `path` to the `result`.\n \n b. **Recursive Case**: For each number in `nums`, we perform the following steps:\n i. Add the current number to `path`.\n ii. Remove the current number from `nums`.\n iii. Recursively call `backtrack` with the updated `nums` and `path`.\n iv. Since we are using slicing to create new lists, there is no need to revert the changes to `nums` and `path` after the recursive call.\n\n3. **Start Recursion**: Call the `backtrack` function with the original `nums` and an empty `path` to start the process.\n\n4. **Return Result**: Return the `result` list, which will contain all the permutations.\n\nBy iteratively choosing one element and recursively calling the function on the remaining elements, this approach ensures that all permutations are explored.\n\n# Complexity\n- Time complexity: O(n*n!) \n This is because for generating permutations, we perform n! operations (since there are n! permutations for n numbers) and for each operation, we spend O(n) time for slicing the list in our recursive call.\n\n- Space complexity: O(n*n!) \n This is due to the number of solutions. In the worst case, if we have \'n\' distinct numbers, there would be n! permutations. Since each permutation is a list of \'n\' numbers, the space complexity is O(n*n!).\n\n# Code\n``` Python []\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n def backtrack(nums, path): \n if not nums: \n result.append(path) \n return \n for i in range(len(nums)): \n backtrack(nums[:i] + nums[i+1:], path + [nums[i]]) \n result = [] \n backtrack(nums, []) \n return result \n```\n``` C++ []\nclass Solution {\npublic:\n void permuteRec(vector<int>& nums, int begin, vector<vector<int>>& result) { \n if (begin == nums.size()) { \n result.push_back(nums); \n return; \n } \n for (int i = begin; i < nums.size(); i++) { \n swap(nums[begin], nums[i]); \n permuteRec(nums, begin + 1, result); \n swap(nums[begin], nums[i]); \n } \n } \n \n vector<vector<int>> permute(vector<int>& nums) {\n vector<vector<int>> result; \n permuteRec(nums, 0, result); \n return result; \n \n }\n};\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @return {number[][]}\n */\nvar permute = function(nums) {\n const result = [];\n const backtrack = (nums, path) => {\n if (nums.length === 0) {\n result.push(path);\n return;\n }\n for (let i = 0; i < nums.length; i++) {\n backtrack([...nums.slice(0, i), ...nums.slice(i + 1)], [...path, nums[i]]);\n }\n };\n backtrack(nums, []);\n return result;\n};\n```\n``` C# []\npublic class Solution {\n public IList<IList<int>> Permute(int[] nums) {\n IList<IList<int>> result = new List<IList<int>>();\n Backtrack(nums, new List<int>(), result);\n return result;\n }\n\n private void Backtrack(int[] nums, List<int> path, IList<IList<int>> result) {\n if (path.Count == nums.Length) {\n result.Add(new List<int>(path));\n return;\n }\n foreach (int num in nums) {\n if (path.Contains(num)) continue;\n path.Add(num);\n Backtrack(nums, path, result);\n path.RemoveAt(path.Count - 1);\n }\n }\n}\n```\n``` Java []\npublic class Solution {\n public void permuteRec(int[] nums, int begin, List<List<Integer>> result) {\n if (begin == nums.length) {\n List<Integer> temp = new ArrayList<Integer>();\n for (int num : nums) temp.add(num);\n result.add(temp);\n return;\n }\n for (int i = begin; i < nums.length; i++) {\n // Swap\n int temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n \n permuteRec(nums, begin + 1, result);\n \n // Swap back\n temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n }\n }\n \n public List<List<Integer>> permute(int[] nums) {\n List<List<Integer>> result = new ArrayList<List<Integer>>();\n permuteRec(nums, 0, result);\n return result;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn permute(nums: Vec<i32>) -> Vec<Vec<i32>> {\n let mut result = Vec::new();\n Self::backtrack(nums, vec![], &mut result);\n result\n }\n\n fn backtrack(nums: Vec<i32>, path: Vec<i32>, result: &mut Vec<Vec<i32>>) {\n if nums.is_empty() {\n result.push(path);\n return;\n }\n for i in 0..nums.len() {\n let mut new_nums = nums.clone();\n new_nums.remove(i);\n let mut new_path = path.clone();\n new_path.push(nums[i]);\n Self::backtrack(new_nums, new_path, result);\n }\n }\n}\n```\n``` Swift []\nclass Solution {\n func permute(_ nums: [Int]) -> [[Int]] {\n var result: [[Int]] = []\n \n func backtrack(_ nums: [Int], _ path: [Int]) {\n if nums.isEmpty {\n result.append(path)\n return\n }\n for i in 0..<nums.count {\n var newNums = nums\n newNums.remove(at: i)\n backtrack(newNums, path + [nums[i]])\n }\n }\n \n backtrack(nums, [])\n return result\n }\n}\n```\n``` Go []\nfunc permute(nums []int) [][]int {\n var result [][]int\n \n var backtrack func([]int, []int)\n backtrack = func(nums []int, path []int) {\n if len(nums) == 0 {\n result = append(result, append([]int(nil), path...))\n return\n }\n for i := 0; i < len(nums); i++ {\n newNums := append([]int(nil), nums[:i]...)\n newNums = append(newNums, nums[i+1:]...)\n newPath := append([]int(nil), path...)\n newPath = append(newPath, nums[i])\n backtrack(newNums, newPath)\n }\n }\n \n backtrack(nums, []int{})\n return result\n}\n```\n\n# Video for Python v2\nhttps://youtu.be/jTCdBWNaLe8\n\n# Code v2\n``` Python \nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n def dfs(path, used): \n if len(path) == len(nums): \n result.append(path[:]) \n return \n for i in range(len(nums)): \n if not used[i]: \n path.append(nums[i]) \n used[i] = True \n dfs(path, used) \n path.pop() \n used[i] = False \n result = [] \n dfs([], [False] * len(nums)) \n return result \n```\n\n## Performance \n| Language | Runtime | Beats | Memory |\n|------------|---------|---------|---------|\n| C++ | 0 ms | 100% | 7.5 MB |\n| Java | 1 ms | 98.58% | 44.1 MB |\n| Rust | 1 ms | 87.70% | 2.3 MB |\n| Go | 2 ms | 61.28% | 3.1 MB |\n| Swift | 8 ms | 91.96% | 14.4 MB |\n| Python3 v2 | 36 ms | 99.39% | 16.5 MB |\n| Python3 | 39 ms | 98.74% | 16.7 MB |\n| JavaScript | 72 ms | 55% | 44.1 MB |\n| C# | 131 ms | 94.50% | 43.4 MB |\n\nThis sorted table provides a quick comparison of the runtime performance across different programming languages for the given problem. | 51 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Python Solution Using Backtracking | permutations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n n = len(nums)\n ans = []\n def backtrack(start):\n if start == n:\n ans.append(nums[:]) \n return\n for i in range(start, n):\n nums[start], nums[i] = nums[i], nums[start] \n backtrack(start + 1) \n nums[start], nums[i] = nums[i], nums[start] \n \n backtrack(0)\n return ans\n\n``` | 1 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
One Liner.Built In Function | permutations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n return permutations(nums)\n``` | 1 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
ONE LINER 96% BEATS | permutations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:12MS\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:14 MB\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import permutations\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n return list(permutations(nums))\n``` | 2 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Permutation.py | permutations | 0 | 1 | # Code\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n temp,ans=[],[]\n def param(i,nums):\n if i==len(nums):\n ans.append(nums.copy())\n return\n for j in range(i,len(nums)):\n nums[i],nums[j]=nums[j],nums[i]\n param(i+1,nums)\n nums[i],nums[j]=nums[j],nums[i]\n param(0,nums)\n return ans\n``` | 4 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
✔️C++||Python||C🔥0ms✅Backtrack with graph explained || Beginner-friendly ^_^ | permutations | 0 | 1 | # Approach\nUse a recursive function `backtrack`, in the function, we pass in a index.\nIn the function, we use a for loop swap `nums[index]` with different numbers in `nums`.\nAfter each swap, call `backtrack` again with `index+1`.\nThen swap back the values, so that we can get every permutations as the graph shown below.\n\nIf `index` reach `n-1`, we kwon that we get one of the premutations.\nSo just add `nums` into `arr`.\nAfter all the recursion, we get our answer.\n \n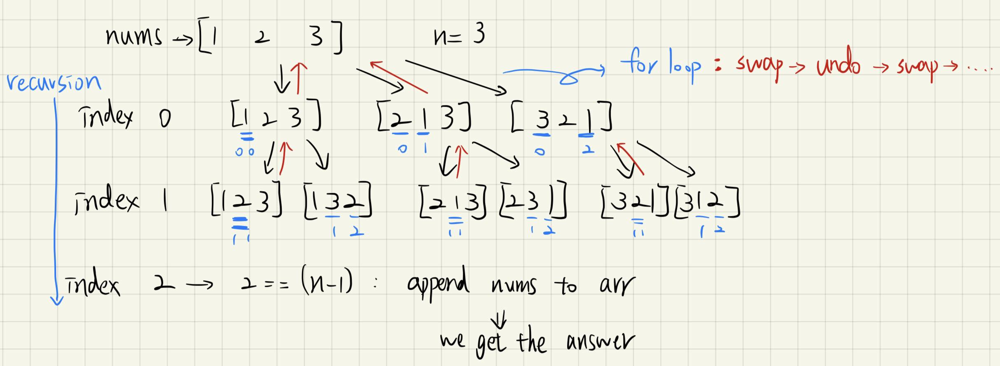\n\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> arr;\n void backtrack(vector<int>& nums, int n, int index){\n if(index == n - 1){\n arr.push_back(nums);\n return;\n }\n for(int i=index; i<n; i++){\n swap(nums[index], nums[i]);\n backtrack(nums, n, index+1);\n swap(nums[index], nums[i]);\n }\n }\n vector<vector<int>> permute(vector<int>& nums) {\n int n = nums.size();\n backtrack(nums, n, 0);\n return arr;\n }\n};\n```\n```c []\n void swap(int* a, int* b){\n int temp = *a;\n *a = *b;\n *b = temp;\n }\n\n void backtrack(int* nums, int numsSize, int*** arr, int* returnSize, int** returnColumnSizes, int index){\n if(index == numsSize - 1){\n (*returnSize)++;\n *arr = (int**)realloc(*arr, sizeof(int*) * (*returnSize));\n (*returnColumnSizes)[*returnSize - 1] = numsSize;\n (*arr)[*returnSize - 1] = (int*)malloc(sizeof(int) * numsSize);\n for(int i=0; i<numsSize; i++){\n (*arr)[*returnSize - 1][i] = nums[i];\n }\n return;\n }\n for(int i=index; i<numsSize; i++){\n swap(nums+index, nums+i);\n backtrack(nums, numsSize, arr, returnSize, returnColumnSizes, index + 1);\n swap(nums+index, nums+i);\n }\n }\n\nint** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){\n *returnSize = 1;\n for(int i=1; i<=numsSize; i++) (*returnSize) *= i;\n *returnColumnSizes = (int*)malloc(*returnSize * sizeof(int)); \n *returnSize = 0;\n int **arr = (int**)malloc(sizeof(int*));\n backtrack(nums, numsSize, &arr, returnSize, returnColumnSizes, 0);\n return arr;\n}\n\n```\n```Python []\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n n = len(nums)\n arr = []\n\n def backtrack(index):\n if(index == n):\n arr.append(nums[:])\n return\n for i in range(index, n):\n nums[index], nums[i] = nums[i], nums[index] # swap\n backtrack(index + 1)\n nums[index], nums[i] = nums[i], nums[index] # swap back\n \n backtrack(0)\n return arr\n```\n# Please UPVOTE if this helps\n\n\n\n | 23 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
DFS/backtracking - Python/Java/Javascript, PICTURE | permutations | 1 | 1 | Classic combinatorial search problem, we can solve it using 3-step system \n\n1. Identify states\nWhat state do we need to know whether we have reached a solution (and using it to construct a solution if the problem asks for it).\nWe need a state to keep track of the list of letters we have chosen for the current permutation\n\nWhat state do we need to decide which child nodes should be visited next and which ones should be pruned?\nWe have to know what are the letters left that we can still use (since each letter can only be used once).\n\n2. Draw the State-space Tree\n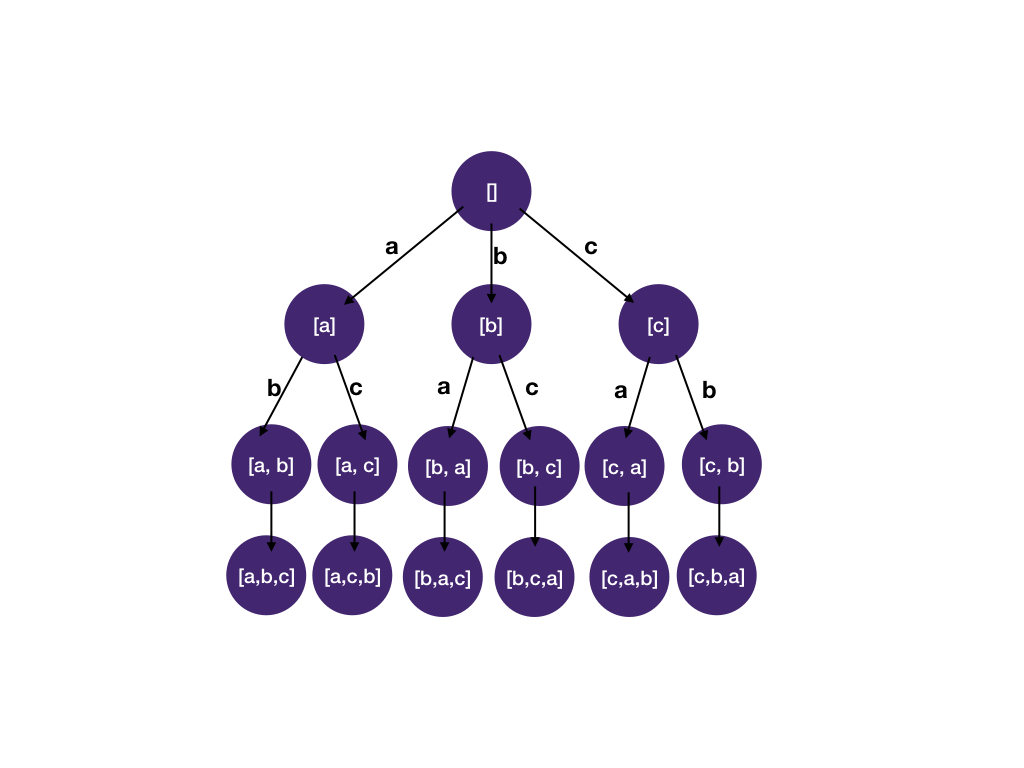\n\n3. DFS on the State-space tree\nUsing the [backtracking template](https://algo.monster/problems/backtracking) as basis, we add the two states we identified in step 1:\n\nA list to represent permutation constructed so far, path\nA list to record which letters are already used, used, used[i] == true means ith letter in the origin list has been used.\n\nImplementation in 3 languages:\n\nPython\n```\nclass Solution:\n def permute(self, l: List[int]) -> List[List[int]]:\n def dfs(path, used, res):\n if len(path) == len(l):\n res.append(path[:]) # note [:] make a deep copy since otherwise we\'d be append the same list over and over\n return\n\n for i, letter in enumerate(l):\n # skip used letters\n if used[i]:\n continue\n # add letter to permutation, mark letter as used\n path.append(letter)\n used[i] = True\n dfs(path, used, res)\n # remove letter from permutation, mark letter as unused\n path.pop()\n used[i] = False\n \n res = []\n dfs([], [False] * len(l), res)\n return res\n```\n\nJava\n```\nclass Solution {\n public List<List<Integer>> permute(int[] letters) {\n List<List<Integer>> res = new ArrayList<>();\n dfs(new ArrayList<>(), new boolean[letters.length], res, letters);\n return res;\n }\n\n private static void dfs(List<Integer> path, boolean[] used, List<List<Integer>> res, int[] letters) {\n if (path.size() == used.length) {\n // make a deep copy since otherwise we\'d be append the same list over and over\n res.add(new ArrayList<Integer>(path));\n return;\n }\n\n for (int i = 0; i < used.length; i++) {\n // skip used letters\n if (used[i]) continue;\n // add letter to permutation, mark letter as used\n path.add(letters[i]);\n used[i] = true;\n dfs(path, used, res, letters);\n // remove letter from permutation, mark letter as unused\n path.remove(path.size() - 1);\n used[i] = false;\n }\n } \n}\n```\n\nJavascript\n```\nvar permute = function(letters) {\n let res = [];\n dfs(letters, [], Array(letters.length).fill(false), res);\n return res;\n}\n\nfunction dfs(letters, path, used, res) {\n if (path.length == letters.length) {\n // make a deep copy since otherwise we\'d be append the same list over and over\n res.push(Array.from(path));\n return;\n }\n for (let i = 0; i < letters.length; i++) {\n // skip used letters\n if (used[i]) continue;\n // add letter to permutation, mark letter as used\n path.push(letters[i]);\n used[i] = true;\n dfs(letters, path, used, res);\n // remove letter from permutation, mark letter as unused\n path.pop();\n used[i] = false;\n }\n}\n```\n\nPlease upvote if you find it useful. And learn more about backtracking/dfs here https://algo.monster/problems/backtracking | 244 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
🔥 100% Backtracking / Recursive Approach - Unlocking Permutations | permutations | 1 | 1 | # Intuition\nThe problem requires generating all possible permutations of a given array of distinct integers. A clear and intuitive understanding of the recursive approach can be achieved by watching vanAmsen\'s video explanation, where the permutations are constructed by choosing one element at a time and recursively calling the function on the remaining elements. The video thoroughly explains the underlying logic and how to implement it in code. Special thanks to vanAmsen for the insightful explanation! [Watch the video here](https://youtu.be/Jlw0sIGdS_4).\n\n\n# Approach\n1. We define a recursive function `backtrack` that takes the current numbers and the path of the permutation being constructed.\n2. In the base case, if there are no numbers left, we append the current path to the result list.\n3. We iterate through the numbers, and for each number, we add it to the current path and recursively call `backtrack` with the remaining numbers (excluding the current number).\n4. We initialize an empty result list and call the `backtrack` function with the original numbers and an empty path to start the process.\n5. The result list will contain all the permutations, and we return it.\n\n# Complexity\n- Time complexity: \\(O(n!)\\)\n - We generate \\(n!\\) permutations, where \\(n\\) is the length of the input list.\n\n- Space complexity: \\(O(n)\\)\n - The maximum depth of the recursion is \\(n\\), and we use additional space for the current path and slicing operations.\n\n# Code\n``` Python []\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n def backtrack(nums, path): \n if not nums: \n result.append(path) \n return \n for i in range(len(nums)): \n backtrack(nums[:i] + nums[i+1:], path + [nums[i]]) \n result = [] \n backtrack(nums, []) \n return result \n```\n``` C++ []\nclass Solution {\npublic:\n void permuteRec(vector<int>& nums, int begin, vector<vector<int>>& result) { \n if (begin == nums.size()) { \n result.push_back(nums); \n return; \n } \n for (int i = begin; i < nums.size(); i++) { \n swap(nums[begin], nums[i]); \n permuteRec(nums, begin + 1, result); \n swap(nums[begin], nums[i]); \n } \n } \n \n vector<vector<int>> permute(vector<int>& nums) {\n vector<vector<int>> result; \n permuteRec(nums, 0, result); \n return result; \n \n }\n};\n```\n``` JavaScript []\nvar permute = function(nums) {\n let result = []; \n permuteRec(nums, 0, result); \n return result; \n \n};\n\nfunction permuteRec(nums, begin, result) { \n if (begin === nums.length) { \n result.push(nums.slice()); \n return; \n } \n for (let i = begin; i < nums.length; i++) { \n [nums[begin], nums[i]] = [nums[i], nums[begin]]; \n permuteRec(nums, begin + 1, result); \n [nums[begin], nums[i]] = [nums[i], nums[begin]]; \n } \n} \n```\n``` C# []\npublic class Solution {\n public void PermuteRec(int[] nums, int begin, IList<IList<int>> result) {\n if (begin == nums.Length) {\n var temp = new List<int>(nums);\n result.Add(temp);\n return;\n }\n for (int i = begin; i < nums.Length; i++) {\n // Swap\n int temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n \n PermuteRec(nums, begin + 1, result);\n \n // Swap back\n temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n }\n }\n \n public IList<IList<int>> Permute(int[] nums) {\n IList<IList<int>> result = new List<IList<int>>();\n PermuteRec(nums, 0, result);\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public void permuteRec(int[] nums, int begin, List<List<Integer>> result) {\n if (begin == nums.length) {\n List<Integer> temp = new ArrayList<Integer>();\n for (int num : nums) temp.add(num);\n result.add(temp);\n return;\n }\n for (int i = begin; i < nums.length; i++) {\n // Swap\n int temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n \n permuteRec(nums, begin + 1, result);\n \n // Swap back\n temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n }\n }\n \n public List<List<Integer>> permute(int[] nums) {\n List<List<Integer>> result = new ArrayList<List<Integer>>();\n permuteRec(nums, 0, result);\n return result;\n }\n}\n``` | 10 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | permutations | 1 | 1 | # Intuition\nUsing backtracking to create all possible combinations\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/J7m7W7P6e3s\n\n# Subscribe to my channel from here. I have 238 videos as of August 2nd\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python solution. Other might be different a bit.\n\n1. The function `permute` takes a list of integers `nums` as input and aims to generate all possible permutations of the elements in the input list.\n\n2. The base case is checked: if the length of the `nums` list is 1, then it means there\'s only one element left to permute, and at this point, a list containing that single element is returned as a permutation.\n\n3. If the `nums` list has more than one element, the algorithm proceeds with permutation generation.\n\n4. Initialize an empty list `res` to store the permutations.\n\n5. Iterate over each element in the `nums` list (using `_` as a placeholder for the loop variable). In each iteration, pop the first element `n` from the `nums` list.\n\n6. Recursively call the `permute` function on the remaining elements in `nums` after removing the first element. This generates all possible permutations of the remaining elements.\n\n7. For each permutation `p` generated in the recursive call, append the previously removed element `n` to it.\n\n8. Extend the `res` list with the permutations generated in the recursive calls, each with the element `n` appended.\n\n9. After the loop completes, add the removed element `n` back to the end of the `nums` list, restoring the original state for the next iteration.\n\n10. Finally, return the list `res` containing all the generated permutations.\n\nIn summary, this code uses a recursive approach to generate all possible permutations of the input list `nums`. It removes one element at a time, generates permutations for the remaining elements, appends the removed element to those permutations, and collects all permutations in the `res` list. The recursion continues until only one element is left in the list, at which point a permutation containing that single element is returned. \n\n# Complexity\n- Time complexity: O(n * n!)\n\n - Recursive Calls: The permute function is called recursively, and each time it generates permutations for a smaller list by removing one element. In the worst case, the recursion depth is equal to the length of the input list nums, which is n.\n\n - Permutation Generation: For each index, we are generating permutations for the remaining elements and appending the removed element at the end. This involves recursive calls and list manipulations. In general time complexity of permutation should be O(n!)\n\n- Space complexity: O(n)\n - Recursion Depth: The depth of recursion goes up to the number of elements in the input list. So, the maximum recursion depth is O(n).\n - Additional Memory: The additional memory usage includes the res list, the n variable, and the space used in each recursive call.\n\n Considering these factors, the space complexity is O(n)\n\n\n```python []\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n if len(nums) == 1:\n return [nums[:]]\n \n res = []\n\n for _ in range(len(nums)):\n n = nums.pop(0)\n perms = self.permute(nums)\n\n for p in perms:\n p.append(n)\n \n res.extend(perms)\n nums.append(n)\n \n return res\n \n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number[][]}\n */\nvar permute = function(nums) {\n if (nums.length === 1) {\n return [nums.slice()];\n }\n \n var res = [];\n\n for (var i = 0; i < nums.length; i++) {\n var n = nums.shift();\n var perms = permute(nums.slice());\n\n for (var p of perms) {\n p.push(n);\n }\n \n res.push(...perms);\n nums.push(n);\n }\n \n return res; \n};\n```\n```java []\nclass Solution {\n public List<List<Integer>> permute(int[] nums) {\n List<List<Integer>> res = new ArrayList<>();\n if (nums.length == 1) {\n List<Integer> singleList = new ArrayList<>();\n singleList.add(nums[0]);\n res.add(singleList);\n return res;\n }\n\n for (int i = 0; i < nums.length; i++) {\n int n = nums[i];\n int[] remainingNums = new int[nums.length - 1];\n int index = 0;\n for (int j = 0; j < nums.length; j++) {\n if (j != i) {\n remainingNums[index] = nums[j];\n index++;\n }\n }\n \n List<List<Integer>> perms = permute(remainingNums);\n for (List<Integer> p : perms) {\n p.add(n);\n }\n \n res.addAll(perms);\n }\n \n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> permute(vector<int>& nums) {\n vector<vector<int>> res;\n if (nums.size() == 1) {\n vector<int> singleList;\n singleList.push_back(nums[0]);\n res.push_back(singleList);\n return res;\n }\n\n for (int i = 0; i < nums.size(); i++) {\n int n = nums[i];\n vector<int> remainingNums;\n for (int j = 0; j < nums.size(); j++) {\n if (j != i) {\n remainingNums.push_back(nums[j]);\n }\n }\n \n vector<vector<int>> perms = permute(remainingNums);\n for (vector<int> p : perms) {\n p.insert(p.begin(), n); // Insert n at the beginning of the permutation\n res.push_back(p); // Append the modified permutation to the result\n }\n }\n \n return res; \n }\n};\n```\n\n- This is bonus codes I don\'t explain in the article.\n\n```python []\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n\n def backtrack(start):\n if start == len(nums):\n res.append(nums[:])\n return\n \n for i in range(start, len(nums)):\n nums[start], nums[i] = nums[i], nums[start]\n backtrack(start + 1)\n nums[start], nums[i] = nums[i], nums[start]\n\n res = []\n backtrack(0)\n return res\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number[][]}\n */\nvar permute = function(nums) {\n const backtrack = (start) => {\n if (start === nums.length) {\n res.push([...nums]);\n return;\n }\n \n for (let i = start; i < nums.length; i++) {\n [nums[start], nums[i]] = [nums[i], nums[start]];\n backtrack(start + 1);\n [nums[start], nums[i]] = [nums[i], nums[start]];\n }\n };\n\n const res = [];\n backtrack(0);\n return res; \n};\n```\n```java []\nclass Solution {\n public List<List<Integer>> permute(int[] nums) {\n List<List<Integer>> res = new ArrayList<>();\n backtrack(nums, 0, res);\n return res; \n }\n\n private void backtrack(int[] nums, int start, List<List<Integer>> res) {\n if (start == nums.length) {\n res.add(arrayToList(nums));\n return;\n }\n\n for (int i = start; i < nums.length; i++) {\n swap(nums, start, i);\n backtrack(nums, start + 1, res);\n swap(nums, start, i);\n }\n }\n \n private List<Integer> arrayToList(int[] arr) {\n List<Integer> list = new ArrayList<>();\n for (int num : arr) {\n list.add(num);\n }\n return list;\n }\n \n private void swap(int[] nums, int i, int j) {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> permute(vector<int>& nums) {\n vector<vector<int>> res;\n backtrack(nums, 0, res);\n return res;\n }\n\n void backtrack(vector<int>& nums, int start, vector<vector<int>>& res) {\n if (start == nums.size()) {\n res.push_back(nums);\n return;\n }\n\n for (int i = start; i < nums.size(); i++) {\n swap(nums[start], nums[i]);\n backtrack(nums, start + 1, res);\n swap(nums[start], nums[i]);\n }\n }\n \n void swap(int& a, int& b) {\n int temp = a;\n a = b;\n b = temp;\n } \n};\n```\n\n\n\n\n | 18 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Python short and clean. Generic solution. Functional programming. | permutations | 0 | 1 | # Approach\n\n# Complexity\n- Time complexity: $$O(n!)$$\n\n- Space complexity: $$O(n!)$$\n\n# Code\n```python\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n T = TypeVar(\'T\')\n def permutations(pool: Iterable[T], r: int = None) -> Iterator[Iterator[T]]:\n pool = tuple(pool)\n r = len(pool) if r is None else r\n\n yield from (\n (x,) + p\n for i, x in enumerate(pool)\n for p in permutations(pool[:i] + pool[i + 1:], r - 1)\n ) if pool and r else ((),)\n \n return list(permutations(nums))\n\n\n``` | 1 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
ONE LINER 97% Beats | permutations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:47ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:16mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import permutations\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n return list(permutations(nums))\n``` | 1 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Python easy solutions || time & memory efficient | permutations | 0 | 1 | # Intuition\nThe problem requires generating all possible permutations of a given array of distinct integers. One intuitive approach to achieve this is by using the itertools.permutations function, which provides a straightforward way to generate all permutations of a sequence.\n\n# Approach\nThe solution makes use of the itertools.permutations function to generate all permutations of the input array nums. It utilizes the Solution class and the permute method to encapsulate the functionality and make it reusable.\n\n# Complexity\n- Time complexity:\nO(n!)\n\n- Space complexity:\nO(n!)\n\n# Code\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n # Use itertools.permutations to generate all permutations\n return list(itertools.permutations(nums))\n``` | 2 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Very simple[C,C++,Java,python3 codes] Easy to understand Approach. | permutations | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to generate all possible permutations of a given array of distinct integers. A permutation is an arrangement of elements in a specific order. For example, given the array [1, 2, 3], the permutations are [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 2, 1], [3, 1, 2]].\n\nTo solve this problem, we can use a recursive approach known as backtracking. The intuition behind the backtracking approach is to try out all possible combinations by swapping elements to find the different arrangements.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create a helper function that takes the current index as a parameter and generates permutations for the remaining elements.\n- The base case for recursion is when the current index reaches the end of the array. At this point, we have a valid permutation, so we add it to the result list.\n- For each index from the current position, swap the element at the current index with the element at the current position, and then recursively generate permutations for the rest of the array.\n- After the recursive call, swap the elements back to their original positions to restore the original array for further exploration.\n\n# Complexity\n- Time complexity: **O(n!)** We have to generate all possible permutations, and there are n! permutations for an array of size n.\n\n- Space complexity:**O(n)** The space required for recursion depth and the result list\n\n# Code\n## C++\n```\nclass Solution {\npublic:\n vector<vector<int>> permute(vector<int>& nums) {\n vector<vector<int>> result;\n generatePermutations(nums, 0, result);\n return result;\n }\n\nprivate:\n void generatePermutations(vector<int>& nums, int index, vector<vector<int>>& result) {\n if (index == nums.size()) {\n result.push_back(nums);\n return;\n }\n\n for (int i = index; i < nums.size(); ++i) {\n swap(nums[index], nums[i]);\n generatePermutations(nums, index + 1, result);\n swap(nums[index], nums[i]); // Backtrack\n }\n }\n};\n```\n## Java\n```\nclass Solution {\n public List<List<Integer>> permute(int[] nums) {\n List<List<Integer>> result = new ArrayList<>();\n generatePermutations(nums, 0, result);\n return result;\n }\n\n private void generatePermutations(int[] nums, int index, List<List<Integer>> result) {\n if (index == nums.length) {\n List<Integer> currentPerm = new ArrayList<>();\n for (int num : nums) {\n currentPerm.add(num);\n }\n result.add(currentPerm);\n return;\n }\n\n for (int i = index; i < nums.length; i++) {\n swap(nums, index, i);\n generatePermutations(nums, index + 1, result);\n swap(nums, index, i); // Backtrack\n }\n }\n\n private void swap(int[] nums, int i, int j) {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n}\n```\n## Python3\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n def generate_permutations(index):\n if index == len(nums):\n result.append(nums.copy())\n return\n \n for i in range(index, len(nums)):\n nums[index], nums[i] = nums[i], nums[index]\n generate_permutations(index + 1)\n nums[index], nums[i] = nums[i], nums[index] # Backtrack\n \n result = []\n generate_permutations(0)\n return result\n```\n## C\n```\nvoid swap(int* nums, int i, int j) {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n}\n\nvoid generatePermutations(int* nums, int numsSize, int index, int** result, int* returnSize, int** returnColumnSizes) {\n if (index == numsSize) {\n result[*returnSize] = malloc(numsSize * sizeof(int));\n memcpy(result[*returnSize], nums, numsSize * sizeof(int));\n (*returnColumnSizes)[*returnSize] = numsSize;\n (*returnSize)++;\n return;\n }\n\n for (int i = index; i < numsSize; i++) {\n swap(nums, index, i);\n generatePermutations(nums, numsSize, index + 1, result, returnSize, returnColumnSizes);\n swap(nums, index, i); // Backtrack\n }\n}\n\nint** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) {\n int totalPermutations = 1;\n for (int i = 1; i <= numsSize; i++) {\n totalPermutations *= i;\n }\n\n int** result = (int**)malloc(totalPermutations * sizeof(int*));\n *returnColumnSizes = (int*)malloc(totalPermutations * sizeof(int));\n *returnSize = 0;\n\n generatePermutations(nums, numsSize, 0, result, returnSize, returnColumnSizes);\n return result;\n}\n```\n\n\n | 11 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Short straight forward solution in Python | permutations | 0 | 1 | # Intuition\n\n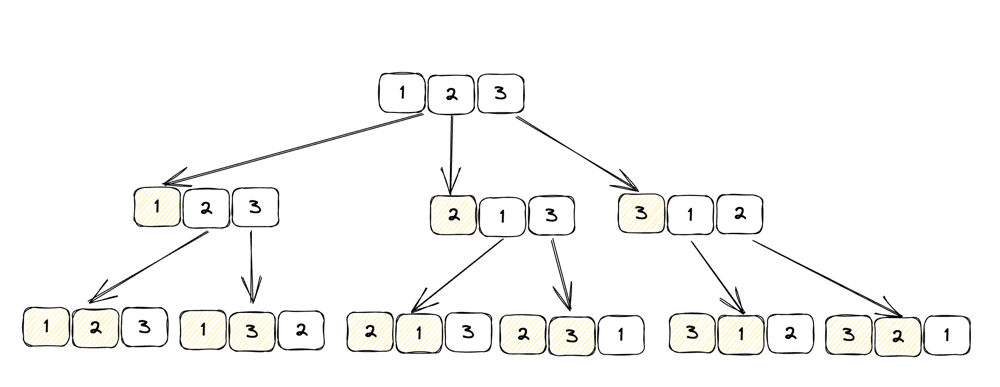\n\n\n# Approach\nDirectly implement as is shown on the image using recursion \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n lon(n))$$ -->\n$$O(n!)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n!)$$\n\n# Code\n```\nclass Solution:\n def permute(self, nums):\n if len(nums) == 1:\n return [nums]\n result = []\n for i, num in enumerate(nums):\n # Use slices to select other items\n for r in self.permute(nums[:i]+nums[i+1:]):\n result.append([num]+r)\n return result\n``` | 2 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Python3 | Easy to understand + simple recursive approach | Beats 85% | permutations | 0 | 1 | # Approach\nRecursive call tries to add a number that was not used earlier (not in the list). If the list gains the right length it goes to the result. The process repeats with each num as a first element.\n# Code\n```re\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n res = []\n def solve(s=[], nums=[]):\n if len(s) == len(nums):\n res.append(s)\n return\n for i in range(len(nums)):\n if nums[i] not in s:\n solve(s + [nums[i]], nums)\n solve([], nums)\n return res\n\n```\n\n\n## UPVOTE makes me happy --> (o\u02D8\u25E1\u02D8o) | 6 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Layman's Code in 🐍 | One Liner Hack | 🔥Beats 99.9%🔥 | permutations | 0 | 1 | ---\n\n\n---\n\n# Complexity\n- Time complexity: $$O(n!)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n!)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n---\n\n# Code\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n return list(itertools.permutations(nums))\n```\n---\n# _**An upvote would be encouraging...**_ | 1 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
🔥PYTHON🔥 Seriously 1 Liner 😱😱 | permutations | 0 | 1 | \n# Code\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n return list(itertools.permutations(nums,len(nums)))\n``` | 7 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
🚀 [VIDEO] Backtracking 100% - Unlocking Permutations | permutations | 0 | 1 | # Intuition\nUpon encountering this problem, I was immediately struck by its resemblance to a well-known puzzle: generating all possible permutations of a given sequence. It\'s like holding a Rubik\'s Cube of numbers and twisting it to discover every conceivable arrangement. With the challenge laid out, my mind gravitated towards the elegant world of recursion, an approach that often weaves simplicity with efficiency. In particular, the concept of backtracking emerged as a promising path. Imagine walking through a maze of numbers, exploring every turn and alley, but with the magical ability to step back and try a different route whenever needed. That\'s the beauty of backtracking in recursion. It\'s not just about finding a solution; it\'s about crafting an adventure through the mathematical landscape, one permutation at a time.\n\nhttps://youtu.be/Jlw0sIGdS_4\n\n# Approach\nThe solution to this problem is elegantly found through recursion, a form of backtracking. The approach begins by initializing an empty list, `result`, to store the final permutations. Then, a recursive helper function `backtrack` is defined, which takes the remaining numbers (`nums`) and the current permutation (`path`) as parameters. The base case is reached when there are no numbers left to permute; at this point, the current `path` is added to the `result`. In the recursive case, for each number in `nums`, the following steps are performed: (i) add the current number to `path`, (ii) remove the current number from `nums`, (iii) recursively call `backtrack` with the updated `nums` and `path`, and (iv) proceed without needing to revert the changes to `nums` and `path` due to the use of list slicing. Finally, the `backtrack` function is called with the original `nums` and an empty `path` to start the process, and the `result` list containing all the permutations is returned. This method ensures that all permutations are explored by iteratively choosing one element and recursively calling the function on the remaining elements.\n\n# Complexity\n- Time complexity: O(n*n!) \n This is because for generating permutations, we perform n! operations (since there are n! permutations for n numbers) and for each operation, we spend O(n) time for slicing the list in our recursive call.\n\n- Space complexity: O(n*n!) \n This is due to the number of solutions. In the worst case, if we have \'n\' distinct numbers, there would be n! permutations. Since each permutation is a list of \'n\' numbers, the space complexity is O(n*n!).\n\n# Code\n``` Python []\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n def backtrack(nums, path): \n if not nums: \n result.append(path) \n return \n for i in range(len(nums)): \n backtrack(nums[:i] + nums[i+1:], path + [nums[i]]) \n result = [] \n backtrack(nums, []) \n return result \n```\n``` C++ []\nclass Solution {\npublic:\n void permuteRec(vector<int>& nums, int begin, vector<vector<int>>& result) { \n if (begin == nums.size()) { \n result.push_back(nums); \n return; \n } \n for (int i = begin; i < nums.size(); i++) { \n swap(nums[begin], nums[i]); \n permuteRec(nums, begin + 1, result); \n swap(nums[begin], nums[i]); \n } \n } \n \n vector<vector<int>> permute(vector<int>& nums) {\n vector<vector<int>> result; \n permuteRec(nums, 0, result); \n return result; \n \n }\n};\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @return {number[][]}\n */\nvar permute = function(nums) {\n const result = [];\n const backtrack = (nums, path) => {\n if (nums.length === 0) {\n result.push(path);\n return;\n }\n for (let i = 0; i < nums.length; i++) {\n backtrack([...nums.slice(0, i), ...nums.slice(i + 1)], [...path, nums[i]]);\n }\n };\n backtrack(nums, []);\n return result;\n};\n```\n``` C# []\npublic class Solution {\n public IList<IList<int>> Permute(int[] nums) {\n IList<IList<int>> result = new List<IList<int>>();\n Backtrack(nums, new List<int>(), result);\n return result;\n }\n\n private void Backtrack(int[] nums, List<int> path, IList<IList<int>> result) {\n if (path.Count == nums.Length) {\n result.Add(new List<int>(path));\n return;\n }\n foreach (int num in nums) {\n if (path.Contains(num)) continue;\n path.Add(num);\n Backtrack(nums, path, result);\n path.RemoveAt(path.Count - 1);\n }\n }\n}\n```\n``` Java []\npublic class Solution {\n public void permuteRec(int[] nums, int begin, List<List<Integer>> result) {\n if (begin == nums.length) {\n List<Integer> temp = new ArrayList<Integer>();\n for (int num : nums) temp.add(num);\n result.add(temp);\n return;\n }\n for (int i = begin; i < nums.length; i++) {\n // Swap\n int temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n \n permuteRec(nums, begin + 1, result);\n \n // Swap back\n temp = nums[begin];\n nums[begin] = nums[i];\n nums[i] = temp;\n }\n }\n \n public List<List<Integer>> permute(int[] nums) {\n List<List<Integer>> result = new ArrayList<List<Integer>>();\n permuteRec(nums, 0, result);\n return result;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn permute(nums: Vec<i32>) -> Vec<Vec<i32>> {\n let mut result = Vec::new();\n Self::backtrack(nums, vec![], &mut result);\n result\n }\n\n fn backtrack(nums: Vec<i32>, path: Vec<i32>, result: &mut Vec<Vec<i32>>) {\n if nums.is_empty() {\n result.push(path);\n return;\n }\n for i in 0..nums.len() {\n let mut new_nums = nums.clone();\n new_nums.remove(i);\n let mut new_path = path.clone();\n new_path.push(nums[i]);\n Self::backtrack(new_nums, new_path, result);\n }\n }\n}\n```\n``` Swift []\nclass Solution {\n func permute(_ nums: [Int]) -> [[Int]] {\n var result: [[Int]] = []\n \n func backtrack(_ nums: [Int], _ path: [Int]) {\n if nums.isEmpty {\n result.append(path)\n return\n }\n for i in 0..<nums.count {\n var newNums = nums\n newNums.remove(at: i)\n backtrack(newNums, path + [nums[i]])\n }\n }\n \n backtrack(nums, [])\n return result\n }\n}\n```\n``` Go []\nfunc permute(nums []int) [][]int {\n var result [][]int\n \n var backtrack func([]int, []int)\n backtrack = func(nums []int, path []int) {\n if len(nums) == 0 {\n result = append(result, append([]int(nil), path...))\n return\n }\n for i := 0; i < len(nums); i++ {\n newNums := append([]int(nil), nums[:i]...)\n newNums = append(newNums, nums[i+1:]...)\n newPath := append([]int(nil), path...)\n newPath = append(newPath, nums[i])\n backtrack(newNums, newPath)\n }\n }\n \n backtrack(nums, []int{})\n return result\n}\n```\n## Performance \n| Language | Runtime | Beats | Memory |\n|------------|---------|---------|---------|\n| C++ | 0 ms | 100% | 7.5 MB |\n| Java | 1 ms | 98.58% | 44.1 MB |\n| Rust | 1 ms | 87.70% | 2.3 MB |\n| Go | 2 ms | 61.28% | 3.1 MB |\n| Swift | 8 ms | 91.96% | 14.4 MB |\n| Python3 | 39 ms | 98.74% | 16.7 MB |\n| JavaScript | 72 ms | 55% | 44.1 MB |\n| C# | 131 ms | 94.50% | 43.4 MB |\n\n\nThis sorted table provides a quick comparison of the runtime performance across different programming languages for the given problem. | 9 | Given an array `nums` of distinct integers, return _all the possible permutations_. You can return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** \[\[0,1\],\[1,0\]\]
**Example 3:**
**Input:** nums = \[1\]
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
* All the integers of `nums` are **unique**. | null |
Python || Recursive Code Slight Modification || SubSequence Method 🔥 | permutations-ii | 0 | 1 | # Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n ans = []\n nums.sort()\n def subset(p, up):\n if len(up) == 0:\n if p not in ans:\n ans.append(p)\n return \n ch = up[0]\n for i in range(len(p) + 1):\n subset(p[0:i] + [ch] + p[i:], up[1:])\n subset([], nums)\n return ans\n``` | 1 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
✅ Python Simple Backtrack - Beats ~90% | permutations-ii | 0 | 1 | The problem is solved using a backtracking approach. For this particular case, as we have duplicates in input, we can track the count of each number. Python provides a built-in lib `Counter` which I will be using for this problem. As the order of output results doesn\'t matter, we can use this `Counter` variable to track visited elements in the exploration path\n\nThe solution Tree for this problem for an input `[1,1,2]` would look like this:\n\n<img width="400" src="https://assets.leetcode.com/users/images/c7ae7036-ae8b-4d79-aca7-8950a2750a27_1652316056.5212104.jpeg">\n\nBelow is the code that will represent the above solution tree\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n \n permutations = []\n counter = Counter(nums)\n def findAllPermutations(res):\n if len(res) == len(nums):\n permutations.append(res)\n return \n \n for key in counter:\n if counter[key]:\n counter[key]-=1 # decrement visited key\n findAllPermutations(res + [key]) \n counter[key]+=1 # restore the state of visited key to find the next path\n \n findAllPermutations([])\n return permutations\n```\n**Space** - `O(N)` - Each call stack depth would be `N` where `N` is the length of input list.\n**Time** - `O(n * \u03A3(P(N, k)))` - In worst case, all numbers in the input array will be unique. In this case, each path will go upto `N` depth in solution tree. At each level, the branching factor is reduced by `1` so it will go like `N, N-1, N-2...1` starting from root. (Time complexity shared by [@AntonBelski](https://leetcode.com/AntonBelski/))\n\n\n---\n\n***Please upvote if you find it useful*** | 44 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Beats 99.70% Permutations II | permutations-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n ans = []\n used = [False] * len(nums)\n\n def dfs(path: List[int]) -> None:\n if len(path) == len(nums):\n ans.append(path.copy())\n return\n\n for i, num in enumerate(nums):\n if used[i]:\n continue\n if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:\n continue\n used[i] = True\n path.append(num)\n dfs(path)\n path.pop()\n used[i] = False\n\n nums.sort()\n dfs([])\n return ans\n\n``` | 2 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Python | 80% Faster Code | Backtracking | permutations-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**Backtracking**\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n def backtrack(arr, ds, res, hashmap):\n if len(ds) == len(arr):\n if ds[:] not in res:\n res.append(ds[:])\n return\n\n for i in range(len(arr)):\n if hashmap[i] == 1:\n continue\n hashmap[i] = 1\n ds.append(arr[i])\n backtrack(arr, ds, res, hashmap)\n ds.pop()\n hashmap[i] = 0\n\n res = []\n hashmap = [0]*len(nums)\n backtrack(nums, [], res, hashmap)\n return res\n\n``` | 1 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
A simple code with built-in functions. Life is beautiful don't make it complex by backtracking. | permutations-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n f= list(permutations(nums))\n f=list(set(f))\n return f\n``` | 2 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Backtracking / Recursion - Beat 99.61% in runtime. | permutations-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn each recursion, only fill a position in a new list. Assume the exsit *n* non-repeated elements in each recursion, so the position has *n* candidates.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the list: nums.\n2. In each recursive, place an element in a new list.\n3. For avoiding duplicates, same element only can be concatenated with the new list once.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n ans = []\n def permute(res, nums):\n if len(nums) == 0:\n ans.append(res) \n for i in range(len(nums)):\n if i > 0 and nums[i] == nums[i-1]:\n continue\n permute(res+[nums[i]], nums[:i]+nums[i+1:])\n nums.sort()\n permute([], nums)\n return ans\n``` | 2 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Backtracking concept | permutations-ii | 0 | 1 | # Backtracking concept\n```\nclass Solution:\n def permute(self, nums: List[int]) -> List[List[int]]:\n def back(nums,ans,temp):\n if len(nums)==0:\n ans.append(temp)\n return \n for i in range(len(nums)):\n back(nums[:i]+nums[i+1:],ans,temp+[nums[i]])\n ans=[]\n back(nums,ans,[])\n return ans\n```\n# please upvote me it would encourage me alot\n | 3 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Cheat one-liner in Python using in-built permutations method | permutations-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n return set(permutations(nums)) \n``` | 5 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Recursive,Intutive ,using Set to optimize search | permutations-ii | 0 | 1 | \n\n# Approach\n<!--ma -->\nmaintaining a set of un-visited indexes of *nums* for every permutation along with a dictionary to check whether the value has already been used at the position ,the variable "*lv*" is indicating the postion till which numbers have been filled \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n!)\nAdd your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n l=len(nums)\n se=set(range(l))\n final=[]\n \n def ite(se_,a_,k_,lv):\n if lv==l:\n ma.append(a_)\n else:\n se=se_.copy()\n a=a_.copy()\n k=k_.copy()\n for i in se:\n if nums[i] in k:\n pass\n else:\n k[nums[i]]=1\n ite(se-{i},a+[nums[i]],{},lv+1)\n ite(se,[],{},0)\n return final\n\n\n``` | 1 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
ONE LINER 97.93% Beats | permutations-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:12ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:11mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import permutations\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n return set(list(permutations(nums)))\n``` | 3 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Easy and Clear Solution Python 3 | permutations-ii | 0 | 1 | ```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n res=set()\n def per(nm: List[int],x: List[int]) -> None:\n if nm ==[]:\n aa=""\n for i in x:\n aa+=str(i)+"*"\n res.add(aa)\n else:\n for i in range(len(nm)): \n nmc=nm[:i]+nm[i+1:]\n xx=x.copy()\n xx.append(nm[i])\n per(nmc,xx)\n per(nums,[])\n r=[]\n for i in res:\n a=i.split(\'*\')\n a.pop()\n b=[]\n for j in a:\n b.append(int(j))\n r.append(b)\n return r\n``` | 3 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
BEATS 90% SUBMISSIONS || EASIEST || BACKTRACKING || HASHMAP | permutations-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRECURSIVE APPROACH USING A HASHMAP.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBACKTRACKING AFTER APPENDING THE ELEMENTS TO THE LIST WHILE USING A HASHMAP WHICH STORES THE COUNT OF THE ELEMENTS PRESENT IN THE LIST.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N * 2^N)\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n res=[]\n perm=[]\n count={n:0 for n in nums}\n for n in nums:\n count[n] +=1 \n def dfs():\n if len(perm)==len(nums):\n res.append(perm.copy())\n return\n for n in count:\n if count[n]>0:\n perm.append(n)\n count[n] -=1\n dfs()\n count[n]+=1\n perm.pop()\n dfs()\n return res\n``` | 1 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Python3 || Beats 94.85% ||simple beginner solution. | permutations-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def permuteUnique(self, nums: List[int]) -> List[List[int]]:\n per = permutations(nums)\n l = []\n for i in per:\n if i not in l:\n l.append(i)\n return l \n```\n# **Please upvote if you find the solution helpful.** | 2 | Given a collection of numbers, `nums`, that might contain duplicates, return _all possible unique permutations **in any order**._
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:**
\[\[1,1,2\],
\[1,2,1\],
\[2,1,1\]\]
**Example 2:**
**Input:** nums = \[1,2,3\]
**Output:** \[\[1,2,3\],\[1,3,2\],\[2,1,3\],\[2,3,1\],\[3,1,2\],\[3,2,1\]\]
**Constraints:**
* `1 <= nums.length <= 8`
* `-10 <= nums[i] <= 10` | null |
Rotating 2-D visualization and Python solution | rotate-image | 0 | 1 | # Intuition\nThink like concentric circles and moving around in the direction from outwards to inwards. You can use it vice versa also i.e. from inwards to outwards. So, the total number of concentric cicles would be total_rows/2. \n##### Q. Why total number of concentric circles would be total_rows/2?\n##### A. Becuase each circle covers the top part and the bottom part also. e.g. 4x4 matrix could be covered with 2 concentric circles. See the image below.\n\n# Approach\n\n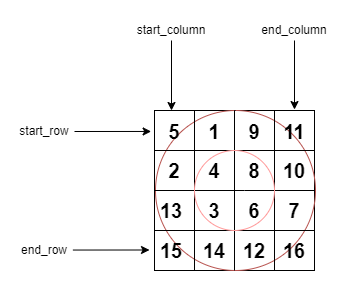\n\n\nKeep moving around the concentric circles in clockwise/anticlock-wise manner using a loop iterator. For every iteration of loop, fix your start_row, start_column, end_row and end_column. These concentric circles are called layers.\n\nNote that, blue is are the items to be swapped.\n\nSwapping would visually look like:\n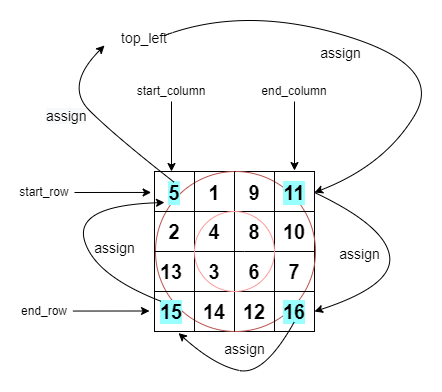\n\nAfter swapping, the 2-D array looks like:\n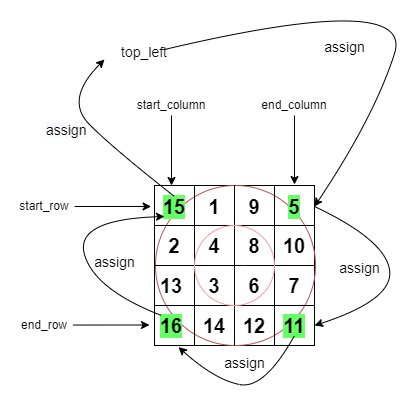\n\n\nNote that the swaps which were performed in current or the previous steps are marked with Green.\n\nStart by iterating columns of the start_row and then keep swapping. Pay special attention to the loop iterator. In every line, for every swap, wherever the iterator j is involved, it has the offset in the form:\n1. For rows- `end_row - j + start_row`\n2. For columns - `end_columns - j + start_column`\n\nWith the iterator `j` taking the next value, the swapping could be visualized as:\n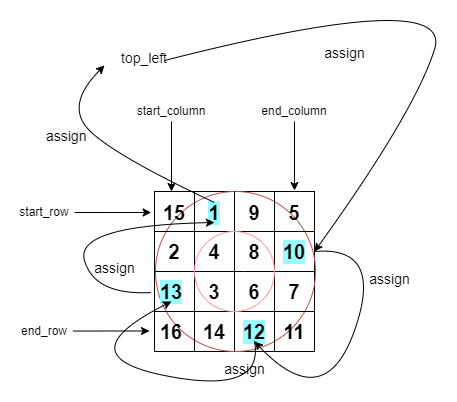\n \nAfter performing the swap, the 2-D array would look like:\n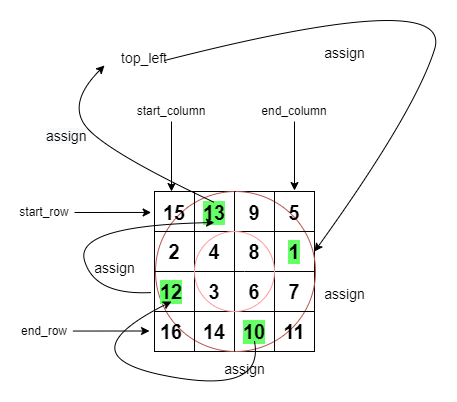\n\nAfter every layer, we would increment start_row and start_column and decrease end_row and end_column. These start_row, start_column, end_row and end_columns help in visualizing the concentric circles we would work on.\nSimilarly at the end of 1st layer of swapping we would have, the following 2-D array:\n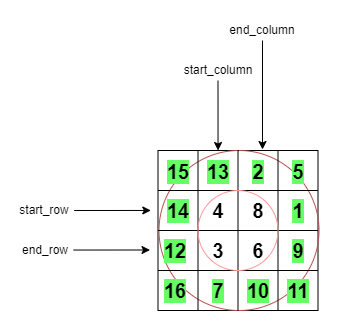\n\n\nNow we can think how the loop on the second layer/circle would look like:\n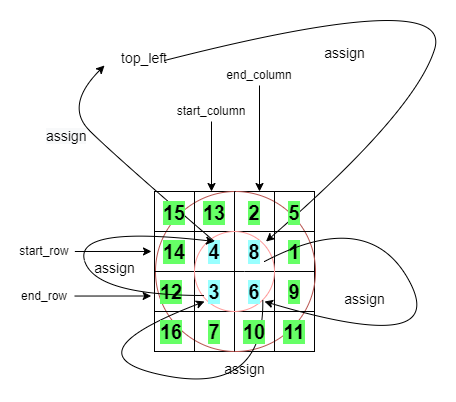\n\nNow after the loop in the second layer ends, the 2-D array looks like:\n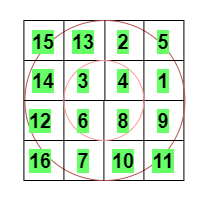\n\nThere are no more concentric circles left to process, so we end here and this is our solution.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ - We are traversing through all the elements of the 2-D array.\n\n- Space complexity:\n$$O(1)$$ - We are taking only definite set of variables for storage and loop iterators.\n\n# Code\n```\nclass Solution:\n def rotate(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n layers = int(len(matrix)/2)\n rows = columns = len(matrix)\n start_row = start_column = 0\n end_row = end_column = rows-1\n for l in range(0, layers):\n i = start_row\n for j in range(start_column, end_column):\n left_top = matrix[i][j]\n matrix[i][j] = matrix[end_row-j+start_row][start_column]\n matrix[end_row-j+start_row][start_column] = matrix[end_row][end_column + start_column - j]\n matrix[end_row][end_column + start_column - j] = matrix[j][end_column]\n matrix[j][end_column] = left_top\n start_row += 1\n start_column += 1\n end_row -= 1\n end_column -= 1\n``` | 1 | You are given an `n x n` 2D `matrix` representing an image, rotate the image by **90** degrees (clockwise).
You have to rotate the image [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm), which means you have to modify the input 2D matrix directly. **DO NOT** allocate another 2D matrix and do the rotation.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[7,4,1\],\[8,5,2\],\[9,6,3\]\]
**Example 2:**
**Input:** matrix = \[\[5,1,9,11\],\[2,4,8,10\],\[13,3,6,7\],\[15,14,12,16\]\]
**Output:** \[\[15,13,2,5\],\[14,3,4,1\],\[12,6,8,9\],\[16,7,10,11\]\]
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 20`
* `-1000 <= matrix[i][j] <= 1000` | null |
Easy Python from scratch (2 Steps) | rotate-image | 0 | 1 | \t# reverse\n\tl = 0\n\tr = len(matrix) -1\n\twhile l < r:\n\t\tmatrix[l], matrix[r] = matrix[r], matrix[l]\n\t\tl += 1\n\t\tr -= 1\n\t# transpose \n\tfor i in range(len(matrix)):\n\t\tfor j in range(i):\n\t\t\tmatrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]\n\t\t\t\nWe want to rotate\n[1,2,3],\n[4,5,6],\n[7,8,9]\n->\n[7,4,1],\n[8,5,2],\n[9,6,3]]\n\nWe can do this in two steps.\nReversing the matrix does this:\n[1,2,3],\n[4,5,6],\n[7,8,9]] \n-> \n[7, 8, 9],\n[4, 5, 6], \n[1, 2, 3]\n\nTransposing means: rows become columns, columns become rows.\n\n[7, 8, 9], \n[4, 5, 6], \n[1, 2, 3]\n ->\n[7,4,1],\n[8,5,2],\n[9,6,3]\nIf you like this explanation, please consider giving it a star on my [github](https://github.com/bwiens/leetcode-python). Means a lot to me. | 310 | You are given an `n x n` 2D `matrix` representing an image, rotate the image by **90** degrees (clockwise).
You have to rotate the image [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm), which means you have to modify the input 2D matrix directly. **DO NOT** allocate another 2D matrix and do the rotation.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[7,4,1\],\[8,5,2\],\[9,6,3\]\]
**Example 2:**
**Input:** matrix = \[\[5,1,9,11\],\[2,4,8,10\],\[13,3,6,7\],\[15,14,12,16\]\]
**Output:** \[\[15,13,2,5\],\[14,3,4,1\],\[12,6,8,9\],\[16,7,10,11\]\]
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 20`
* `-1000 <= matrix[i][j] <= 1000` | null |
Easiest python solution with step-by-step explanation beats 61% python solution👨🏾💻💥🚀 | rotate-image | 0 | 1 | # Intuition\n`matrix = [[1, 2, 3],\n [4, 5, 6],\n [7, 8, 9]]`\n\n```\n[1] [2] [3]\n[4] [5] [6]\n[7] [8] [9]\n```\n\nIf we take the each column and reverse it and put it horizontally , we get:\n\n```\n[7] [4] [1]\n[8] [5] [2]\n[9] [6] [3]\n```\n# Approach\n\n---\n\n\n\n**Step 1:** Copy the matrix into a `new_lis` since we need to update the original `matrix` itself, so we will clear it.\n\n```python []\nnew_lis = matrix.copy()\nmatrix.clear()\n```\n\n---\n\n\n\n**Step 2:** Create a nested list that contains $$empty$$ $$lists$$ with the same length as the `new_lis`.\n```python []\nfor _ in range(len(new_lis)):\n matrix.append([])\n```\n\n---\n\n\n**Step 3:** Create two nested loops, one to iterate over the length of the `matrix` and the other to iterate inside the $$nested$$ $$list$$.\n```python []\nfor i in range(len(new_lis)):\n for j in range(len(new_lis[0])):\n```\n\n---\n\n\n**Step 4:** Use "`div_ = j % len(new_lis[0])`" to store the index of the element that we are going to insert in the `matrix`.\n```python []\ndiv_ = j % len(new_lis[0])\n```\n\n***note :***\n"`div_`" will always have a value between 0 and the length of the nested list to prevent `Index errors`.\n\n---\n\n\n\n**Step 5:** Now we just need to insert the element at the $$0th$$ $$index$$ since it\'s difficult for us to go in *reverse loop*, which makes our task easier.\n```python []\nmatrix[j].insert(0, new_lis[i][div_])\n```\n\n---\n\n\n***I hope this clarifies the steps for you! Let me know if you have any further questions.***\n- Time complexity:\n$$O(m*n)$$\n\n- Space complexity:\n$$O(m*n)$$\n\n# Code\n```\nclass Solution:\n def rotate(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n new_lis = matrix.copy()\n matrix.clear()\n\n for _ in range(len(new_lis)):\n matrix.append([])\n for i in range(len(new_lis)):\n for j in range(len(new_lis[0])):\n # print(l[j][0])\n div_ = j % len(new_lis[0])\n matrix[j].insert(0, new_lis[i][div_])\n\n\n return(matrix)\n``` | 2 | You are given an `n x n` 2D `matrix` representing an image, rotate the image by **90** degrees (clockwise).
You have to rotate the image [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm), which means you have to modify the input 2D matrix directly. **DO NOT** allocate another 2D matrix and do the rotation.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[7,4,1\],\[8,5,2\],\[9,6,3\]\]
**Example 2:**
**Input:** matrix = \[\[5,1,9,11\],\[2,4,8,10\],\[13,3,6,7\],\[15,14,12,16\]\]
**Output:** \[\[15,13,2,5\],\[14,3,4,1\],\[12,6,8,9\],\[16,7,10,11\]\]
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 20`
* `-1000 <= matrix[i][j] <= 1000` | null |
Simplest Solution in 2 steps | rotate-image | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nFor Rotating matrix 90 degree clockwise we need to do this simple steps:\n1. Transpose of Matrix\n2. Reverse each rows\n\nThat\'s all now our matrix will be rotated by 90 degree clockwise.\n\n# Complexity\n- Time complexity: O(m * n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code \n``` python [0]\nclass Solution:\n def rotate(self, matrix: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n for i in range(1, len(matrix)):\n for j in range(i):\n matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]\n \n for i in range(len(matrix)):\n matrix[i] = matrix[i][::-1]\n \n```\n | 3 | You are given an `n x n` 2D `matrix` representing an image, rotate the image by **90** degrees (clockwise).
You have to rotate the image [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm), which means you have to modify the input 2D matrix directly. **DO NOT** allocate another 2D matrix and do the rotation.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[7,4,1\],\[8,5,2\],\[9,6,3\]\]
**Example 2:**
**Input:** matrix = \[\[5,1,9,11\],\[2,4,8,10\],\[13,3,6,7\],\[15,14,12,16\]\]
**Output:** \[\[15,13,2,5\],\[14,3,4,1\],\[12,6,8,9\],\[16,7,10,11\]\]
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 20`
* `-1000 <= matrix[i][j] <= 1000` | null |
2 Simple Solutions | 10ms | 🚀🚀Accepted🔥 | rotate-image | 0 | 1 | # Code\n```\nclass Solution:\n def rotate(self, x: List[List[int]]) -> None:\n """\n Do not return anything, modify matrix in-place instead.\n """\n for i in range(len(x)):\n for j in range(i,len(x)):\n x[i][j],x[j][i]=x[j][i],x[i][j]\n for i in range(len(x)):\n x[i]=x[i][::-1]\n```\n\n```\nclass Solution:\n def rotate(self, x: List[List[int]]) -> None:\n x[:]=[i[::-1] for i in zip(*x)]\n\n``` | 3 | You are given an `n x n` 2D `matrix` representing an image, rotate the image by **90** degrees (clockwise).
You have to rotate the image [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm), which means you have to modify the input 2D matrix directly. **DO NOT** allocate another 2D matrix and do the rotation.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[7,4,1\],\[8,5,2\],\[9,6,3\]\]
**Example 2:**
**Input:** matrix = \[\[5,1,9,11\],\[2,4,8,10\],\[13,3,6,7\],\[15,14,12,16\]\]
**Output:** \[\[15,13,2,5\],\[14,3,4,1\],\[12,6,8,9\],\[16,7,10,11\]\]
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 20`
* `-1000 <= matrix[i][j] <= 1000` | null |
✅Beats 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | group-anagrams | 1 | 1 | \n# Intuition:\n\nThe intuition is to group words that are anagrams of each other together. Anagrams are words that have the `same` characters but in a `different` order.\n\n# Explanation:\n\nLet\'s go through the code step by step using the example input `["eat","tea","tan","ate","nat","bat"]` to understand how it works.\n\n1. **Initializing Variables**\n - We start by initializing an empty unordered map called `mp` (short for map), which will store the groups of anagrams.\n\n2. **Grouping Anagrams**\nWe iterate through each word in the input vector `strs`. Let\'s take the first word, "eat", as an example.\n\n - **Sorting the Word**\nWe create a string variable called `word` and assign it the value of the current word ("eat" in this case). \n\n Next, we sort the characters in `word` using the `sort()` function. After sorting, `word` becomes "aet". \n\n - **Grouping the Anagram**\nWe insert `word` as the key into the `mp` unordered map using `mp[word]`, and we push the original word ("eat") into the vector associated with that key using `mp[word].push_back(x)`, where `x` is the current word.\n\n Since "aet" is a unique sorted representation of all the anagrams, it serves as the key in the `mp` map, and the associated vector holds all the anagrams. \n\nFor the given example, the `mp` map would look like this after processing all the words:\n```\n{\n "aet": ["eat", "tea", "ate"],\n "ant": ["tan", "nat"],\n "abt": ["bat"]\n}\n```\n\n3. **Creating the Result**\nWe initialize an empty vector called `ans` (short for answer) to store the final result.\n\n - We iterate through each key-value pair in the `mp` map using a range-based for loop. For each pair, we push the vector of anagrams (`x.second`) into the `ans` vector.\n\nFor the given example, the `ans` vector would look like this:\n```\n[\n ["eat", "tea", "ate"],\n ["tan", "nat"],\n ["bat"]\n]\n```\n\n4. **Returning the Result**\nWe return the `ans` vector, which contains the groups of anagrams.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<string>> groupAnagrams(vector<string>& strs) {\n unordered_map<string, vector<string>> mp;\n \n for(auto x: strs){\n string word = x;\n sort(word.begin(), word.end());\n mp[word].push_back(x);\n }\n \n vector<vector<string>> ans;\n for(auto x: mp){\n ans.push_back(x.second);\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public List<List<String>> groupAnagrams(String[] strs) {\n Map<String, List<String>> map = new HashMap<>();\n \n for (String word : strs) {\n char[] chars = word.toCharArray();\n Arrays.sort(chars);\n String sortedWord = new String(chars);\n \n if (!map.containsKey(sortedWord)) {\n map.put(sortedWord, new ArrayList<>());\n }\n \n map.get(sortedWord).add(word);\n }\n \n return new ArrayList<>(map.values());\n }\n}\n```\n```Python3 []\nclass Solution:\n def groupAnagrams(self, strs):\n anagram_map = defaultdict(list)\n \n for word in strs:\n sorted_word = \'\'.join(sorted(word))\n anagram_map[sorted_word].append(word)\n \n return list(anagram_map.values())\n```\n\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. [Valid Anagram](https://leetcode.com/problems/valid-anagram/solutions/3687854/3-methods-c-java-python-beginner-friendly/)\n11. [Group Anagrams](https://leetcode.com/problems/group-anagrams/solutions/3687735/beats-100-c-java-python-beginner-friendly/)\n12. **Practice them in a row for better understanding and please Upvote for more questions.**\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 822 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
🔥Python || Easily Understood ✅ || Hash Table || Fast || Simple | group-anagrams | 0 | 1 | **Appreciate if you could upvote this solution**\n\n\nMethod: `Hash Table`\n\nSince the output needs to group the anagrams, it is suitable to use `dict` to store the different anagrams.\nThus, we need to find a common `key` for those anagrams.\nAnd one of the best choices is the `sorted string` as all the anagrams have the same anagrams.\n\n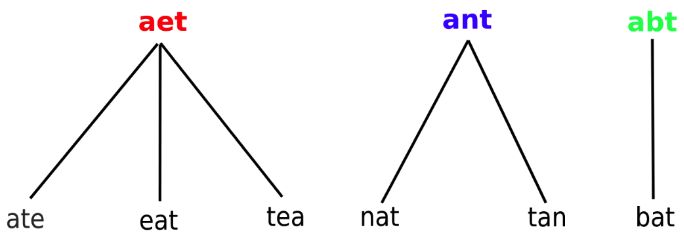\n\n\n\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n strs_table = {}\n\n for string in strs:\n sorted_string = \'\'.join(sorted(string))\n\n if sorted_string not in strs_table:\n strs_table[sorted_string] = []\n\n strs_table[sorted_string].append(string)\n\n return list(strs_table.values())\n```\nTime complexity: `O(m*nlogn))`\nSpace complexity: `O(n)`\n<br/> | 163 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
An odd solution using a Counter | group-anagrams | 0 | 1 | # Intuition\nMy first thought was that all anagrams have identical counts of letters, so immediately thought of using a Counter().\n\n# Approach\nI keep a dict of Counters and check if the counter is already a key. The problem I ran into is that the Counter class is not a hashable object. So I created a hashable version. I\'m not happy with just using the hash of a string consisting of an alphabetical concatenation of key value pairs. But it works for this purpose. Not the best solution (in terms of the below), but I thought it was interesting enough to share.\n\n# Complexity\n- Time complexity:\nIt is $$O(n)$$, but is not very fast (high constants I assume).\n\n- Space complexity:\nShould be $$O(n)$$, but agion with not great contstants compared with other designs.\n\n# Code\n```\nfrom collections import Counter\n\nclass HashableCounter(Counter):\n def __hash__(self):\n hash_str = ""\n for c in sorted(self.keys()):\n hash_str += f"{c}{self[c]}"\n return hash(hash_str)\n def __eq__(self, other):\n return self.items() == other.items()\n\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n anagrams_dict = {}\n \n output = []\n for word in strs:\n cw = HashableCounter(word)\n if cw in anagrams_dict:\n anagrams_dict[cw].append(word)\n else:\n word_list = [word]\n output.append(word_list)\n anagrams_dict[cw] = word_list\n return output\n \n``` | 0 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
using Hashtable Easy to understand | group-anagrams | 0 | 1 | \n\n# Python Solution\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n dic={}\n for word in strs:\n sorted_word="".join(sorted(word))\n if sorted_word not in dic:\n dic[sorted_word]=[word]\n else:\n dic[sorted_word].append(word)\n return dic.values()\n```\n# please upvote me it would encourage me alot\n | 38 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Easy Python Solution 👨💻 || Briefly Explained ✅✅ | group-anagrams | 0 | 1 | # Code Explanation\nThe provided Python code defines a class `Solution` with a method `groupAnagrams`. This method takes a list of strings `strs` as input and is supposed to group the anagrams from the input list into lists of lists, where each inner list contains words that are anagrams of each other. Anagrams are words or phrases formed by rearranging the letters of another, such as "listen" and "silent."\n\nLet\'s break down the code step by step:\n\n1. **Initialize a Dictionary**: The code starts by initializing an empty dictionary called `ans`. This dictionary will be used to store groups of anagrams, with the keys being the character counts of the letters in the anagrams and the values being lists of strings that belong to each group.\n\n ```python\n ans = collections.defaultdict(list)\n ```\n\n Here, `collections.defaultdict(list)` creates a dictionary where the default value for each key is an empty list.\n\n2. **Iterate Through the Input List**: The code then enters a loop to iterate through each string `s` in the input list `strs`.\n\n ```python\n for s in strs:\n ```\n\n3. **Initialize a Character Count List**: Inside the loop, a list called `count` is initialized with 26 zeros. This list will be used to count the occurrences of each letter in the current string `s`. Each index in the `count` list corresponds to a letter in the lowercase English alphabet.\n\n ```python\n count = [0] * 26\n ```\n\n4. **Count the Occurrence of Letters in the String**: The code then enters another loop to iterate through each character `c` in the current string `s`.\n\n ```python\n for c in s:\n ```\n\n5. **Increment the Count for Each Letter**: Inside the inner loop, the code calculates the position of the character `c` in the alphabet (by subtracting the ASCII value of \'a\' from the ASCII value of `c`) and increments the corresponding element in the `count` list. This effectively counts the occurrence of each letter in the current string `s`.\n\n ```python\n count[ord(c) - ord("a")] += 1\n ```\n\n6. **Group Anagrams Using Character Counts as Keys**: After counting the occurrences of letters in the current string `s`, the code converts the `count` list into a tuple. This tuple is used as a key in the `ans` dictionary. The value associated with this key is a list, and the current string `s` is appended to this list. This step groups strings with the same character count together.\n\n ```python\n ans[tuple(count)].append(s)\n ```\n\n7. **Return Grouped Anagrams**: After processing all strings in the input list `strs`, the code returns the values of the `ans` dictionary. These values are lists of grouped anagrams.\n\n ```python\n return ans.values()\n ```\n\nSo, in summary, this code efficiently groups anagrams by counting the occurrences of each letter in each string and using these counts as keys in a dictionary. It ensures that anagrams with the same character counts are grouped together, and it returns these groups as a list of lists.\n\n# Python Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n ans = collections.defaultdict(list)\n\n for s in strs:\n count = [0] * 26\n for c in s:\n count[ord(c) - ord("a")] += 1 \n ans[tuple(count)].append(s)\n\n return ans.values()\n\n```\n\n**Please upvote if you like the solution.\nHappy Coding! \uD83D\uDE0A**\n | 13 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Solution | group-anagrams | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<string>> groupAnagrams(vector<string>& strs) {\n unordered_map<string,vector<string>>mp;\n vector<vector<string>>ans;\n for(int i=0;i<strs.size();i++){\n string t=strs[i];\n sort(t.begin(),t.end());\n mp[t].push_back(strs[i]);\n \n }\n for(auto it=mp.begin();it!=mp.end();it++){\n ans.push_back(it->second);\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nf = open(\'user.out\', \'w\'); [print(json.dumps(list(reduce(lambda res, s: res[str(sorted(s))].append(s) or res, json.loads(line.rstrip()), defaultdict(list)).values())), file=f) for line in stdin];exit(); \n\nf = open("user.out", "w");[print(json.dumps(list(reduce(lambda res, s: res[str(sorted(s))].append(s) or res, json.loads(line.rstrip()), defaultdict(list)).values())), file=f) for line in stdin];exit()\n```\n\n```Java []\nimport java.util.AbstractList;\nclass Solution {\n public List<List<String>> groupAnagrams(String[] strs) {\n \n Map<String, List<String>> map = new HashMap<>();\n \n return new AbstractList<List<String>>(){\n \n List<List<String>> result;\n public List<String> get(int index) {\n if (result == null) init();\n return result.get(index);\n }\n\n public int size() {\n if (result == null) init();\n return result.size();\n }\n\n private void init() {\n for (String s: strs) {\n char[] keys = new char[26];\n for (int i = 0; i < s.length(); i++)\n keys[s.charAt(i) - \'a\']++;\n\n String key = new String(keys);\n System.out.println(key);\n List<String> list = map.get(key);\n if (list == null) map.put(key, new ArrayList<>());\n map.get(key).add(s);\n }\n result = new ArrayList<>(map.values());\n }\n };\n \n }\n}\n```\n | 6 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
🔥🔥Python3 Beats 96% With explanation🔥🔥 | group-anagrams | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n$$Solution$$ $$above$$ $$code.$$\n\n\n\n\n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n #create a hashmap, itterate through strs and create a new variable\n #for each word in strs but sorted. Check if that word is in the hashmap\n #if it is, append the current word in strs to the key value array.\n #if it is not, add the sorted word as the key and the current value as the array value\n myMap = {}\n for word in strs:\n temp = \'\'.join(sorted(word))\n if temp in myMap:\n myMap[temp].append(word)\n else:\n myMap[temp] = [word]\n return myMap.values()\n\n \n``` | 4 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Simple and clever solution for Python3 | group-anagrams | 0 | 1 | # Intuition\nTo solve the problem of grouping anagrams, one common method is to represent each word by a unique signature. Since anagrams have the same letters, just rearranged, their signatures will be the same. One way to create such a signature is by counting the frequency of each letter in the word.\n\n# Approach\nFor each word in the list strs, we count the occurrence of each letter (from \'a\' to \'z\') and store this in the chr list. We then use this list (converted to a tuple since lists can\'t be dictionary keys) as a key in our solution dictionary. The value for each key in the dictionary is a list of words (anagrams) that match the signature. By iterating through the entire list of strs, we effectively group all anagrams together.\n\n# Complexity\n- Time complexity:\nThe time complexity is O(nk), where n is the number of words in strs and k is the maximum length of a word in strs. This is because for each word, we are counting its letters which takes O(k) time.\n- Space complexity:\nThe space complexity is O(nk), where n is the number of words and k is the maximum length of a word. This is because we store each word and its signature in the solution dictionary.\n\n# Tips\n\n- I utilized defaultdict(list) to ensure that the default value for each key in the dictionary is a list. This allows me to group multiple values under a single key, producing a structure like {"dog": ["Matilda", "Sparky", "John"]}\n\n- The ord function returns the Unicode value of a character. By performing the calculation ord(k) - ord("a"), I can map characters "a" through "z" to indices 0 through 25, respectively. For instance, \'a\' maps to 0, \'b\' to 1, and so forth.\n\n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n from collections import defaultdict\n\n solution=defaultdict(list)\n\n for i in strs:\n chr=[0]*26 # from a to z\n for k in i:\n chr[ord(k)-ord("a")]+=1\n solution[tuple(chr)].append(i)\n return solution.values()\n \n\n``` | 5 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Python O(N) Solution | group-anagrams | 0 | 1 | # Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nSorted anagrams string will always be equal.\nHence, create a hash_map where key will the sorted string.\nAdd current string if its key is present, other wise create a new entry.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\nAs, first we are traversing over the given list.\nFor each list sorting and join operation will take constant time as its given string size will be max of 100 characters.\n\n- Space complexity:\n$$O(n)$$\nAs, in worst case all unique string in given list. \n\n\n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n # Hash Map\n hash_map = {}\n # Iterate over each string in given list\n for s in strs:\n # Hash function to get key\n key = \'\'.join(sorted(s))\n # CASE: If key is in hash map\n if key in hash_map:\n hash_map[key].append(s)\n # CASE: If key is not in hash map\n else:\n hash_map[key] = [s]\n return list(hash_map.values())\n``` | 6 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
95.28% Beats Python || Beginner Friendly || Code Explained | group-anagrams | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We will use a hashmap to associate anagrams (words formed by using same letters).\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create a hashmap/dictionary `d`.\n\n2. Iterate through the given list `strs`.\n\n3. Create a variable `temp` to store the sorted form of the word.\n This `temp` variable becomes the **key** in our hashmap/dictionary `d`.\n\n4. If `temp` is not present in `d`, then we add a new key-value pair.\n **key** ->`temp` and **value** -> `[word]` (word as list).\n\n5. If `temp` is present, then we append `word` to the values list.\n\n6. Return `d.values()`. The **values()** method returns a list of all the values in the hashmap/dictionary.\n\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n d = {}\n\n for word in strs:\n temp = \'\'.join(sorted(word))\n\n if temp not in d:\n d[temp] = [word]\n else:\n d[temp].append(word)\n return d.values()\n\n``` | 3 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Python || Beats 99.38% | group-anagrams | 0 | 1 | \n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n answer = defaultdict(list)\n for word in strs:\n answer["".join(sorted(word))].append(word)\n return list(answer.values())\n\n\n``` | 6 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
100 % Animation to the Hard Solution and Easy Solution Explained | group-anagrams | 1 | 1 | [https://youtu.be/3cAxlUsBfas]()\n | 30 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Python 3 solution; detailed explanation; faster than 97.5% | group-anagrams | 0 | 1 | ```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n h = {}\n for word in strs:\n sortedWord = \'\'.join(sorted(word))\n if sortedWord not in h:\n h[sortedWord] = [word]\n else:\n h[sortedWord].append(word)\n final = []\n for value in h.values():\n final.append(value)\n return final\n```\nWe recall that anagrams are strings which have identical counts of characters. So anagrams, when sorted, result in the same string. We take advantage of this last property.\n\nWe create a dictionary and for each word in the input array, we add a key to the dictionary if the **sorted version of the word** doesn\'t already exist in the list of keys. The key then becomes the sorted version of the word, and the value for the key is an array that stores each anagram of the key. i.e. for every next word that is an anagram, **we would sort the word, find the key that is equal to the sorted form, and add the original word to the list of values for the key**.\n\nAt the end of it, we just add every value in the dictionary to the final array. | 124 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Dictionary | Sorting | Python easy solution with explanation | group-anagrams | 0 | 1 | # Intuition\n**Find a way to associate similar words together.** \nWe can utilize the **wo**rd **co**unt **ap**proach but I preferred the approach where you **so**rt the **wo**rd. This allows **an**agrams to be **so**rted and we can then **ma**tch the **wo**rds. \nFor example, \n\n`\'tan\' and \'nat\' when sorted would become \'ant\' and \'ant\'`\n\n\n\n# Approach\n1. Iterate over the \'strs\' and sort each word.\n2. Check if the sorted word exists as key in the dictionary/hashmap\n3. Because we are going to use the original word in the returned output,create a temp variable to store the sorted word.\n4. Now check if the temporary sorted word exists in the dictionary/hashmap\n5. If yes, append the word to the values list.\n6. If no, add a new key-value pair in the dictionary/hashmap.\n\n\n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n # Create a dictionary to act as hashmap\n res = {}\n for word in strs:\n # We want to retain the original word to add to the dictionary\n # Therefore, create a temporary variable with the sorted word\n temp = \'\'.join(sorted(word))\n # If the sorted word exists in the dictionary, \n # append to the values list\n if temp in res:\n res[temp].append(word)\n # Else, add a new key-value pair to the dictionary\n else:\n res[temp] = [word]\n # We only require the values list to be returned\n return res.values()\n\n```\n<br><br>\nPlease **up**vote if you find the approach and **ex**planation **us**eful!\n<br> | 19 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Prime | group-anagrams | 0 | 1 | Use prime to make a unique key for each anagram \n\n# Code\n```\nclass Solution:\n def groupAnagrams(self, strs: List[str]) -> List[List[str]]:\n anagrams: dict[int, int] = dict()\n i = 0\n # first 26 prime numbers\n primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29,\n 31, 37, 41, 43, 47, 53, 59, 61, 67,\n 71, 73, 79, 83, 89, 97, 101]\n while i < len(strs):\n s = strs[i]\n f = 1\n for c in s:\n f *= primes[ord(c) - 97]\n if f in anagrams:\n strs[anagrams[f]].append(s)\n strs.pop(i)\n else:\n anagrams[f] = i\n strs[i] = [s]\n i += 1\n return strs\n``` | 1 | Given an array of strings `strs`, group **the anagrams** together. You can return the answer in **any order**.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
**Example 1:**
**Input:** strs = \["eat","tea","tan","ate","nat","bat"\]
**Output:** \[\["bat"\],\["nat","tan"\],\["ate","eat","tea"\]\]
**Example 2:**
**Input:** strs = \[""\]
**Output:** \[\[""\]\]
**Example 3:**
**Input:** strs = \["a"\]
**Output:** \[\["a"\]\]
**Constraints:**
* `1 <= strs.length <= 104`
* `0 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Python Simple Recursive | powx-n | 0 | 1 | # Intuition\n\nDivide and Conquer\n\nTake $x^{10}$ and as example\n\n$x^{10} = x^5 * x^5 * x^0$\n$x^5 = x^2 * x^2 * x^1$\n$x^2 = x^1 * x^1 * x^0$\n\n# Complexity\n- Time complexity: $$O(logN)$$\n\n- Space complexity: $$O(logN)$$\n\n# Code\n```\nclass Solution:\n @cache\n def myPow(self, x: float, n: int) -> float:\n if n == 0:\n return 1\n elif n == 1:\n return x\n elif n == -1:\n return 1/x\n return self.myPow(x, n//2) * self.myPow(x, n//2) * self.myPow(x, n%2)\n```\n\n# Note\n`@cache` stores the results of an immutable input function and its respective outcomes. To illustrate, after executing self.myPow(x, 5) and obtaining the results, any subsequent calls to self.myPow(x, 5) will reference a hash table to swiftly retrieve the stored value, thus preventing unnecessary recomputation. While this approach does consume additional memory, it offers significant convenience.\n\n\n\n\n | 19 | Implement [pow(x, n)](http://www.cplusplus.com/reference/valarray/pow/), which calculates `x` raised to the power `n` (i.e., `xn`).
**Example 1:**
**Input:** x = 2.00000, n = 10
**Output:** 1024.00000
**Example 2:**
**Input:** x = 2.10000, n = 3
**Output:** 9.26100
**Example 3:**
**Input:** x = 2.00000, n = -2
**Output:** 0.25000
**Explanation:** 2\-2 = 1/22 = 1/4 = 0.25
**Constraints:**
* `-100.0 < x < 100.0`
* `-231 <= n <= 231-1`
* `n` is an integer.
* `-104 <= xn <= 104` | null |
Python3 Beats 95% runtime Recursion Short Answer | powx-n | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: logn\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: logn\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def myPow(self, x: float, n: int) -> float:\n def helper(n, p):\n if p==0 or n==1: return 1\n if p<0: return 1/helper(n, -p)\n rs = helper(n*n, p//2)\n return rs * n if p&1 else rs\n return helper(x, n)\n \n \n \n \n \n \n``` | 1 | Implement [pow(x, n)](http://www.cplusplus.com/reference/valarray/pow/), which calculates `x` raised to the power `n` (i.e., `xn`).
**Example 1:**
**Input:** x = 2.00000, n = 10
**Output:** 1024.00000
**Example 2:**
**Input:** x = 2.10000, n = 3
**Output:** 9.26100
**Example 3:**
**Input:** x = 2.00000, n = -2
**Output:** 0.25000
**Explanation:** 2\-2 = 1/22 = 1/4 = 0.25
**Constraints:**
* `-100.0 < x < 100.0`
* `-231 <= n <= 231-1`
* `n` is an integer.
* `-104 <= xn <= 104` | null |
Python Recursive Solution - Faster than 99 % | powx-n | 0 | 1 | 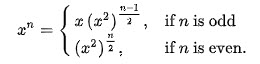\n```\nclass Solution:\n def myPow(self, x: float, n: int) -> float:\n\n def function(base=x, exponent=abs(n)):\n if exponent == 0:\n return 1\n elif exponent % 2 == 0:\n return function(base * base, exponent // 2)\n else:\n return base * function(base * base, (exponent - 1) // 2)\n\n f = function()\n \n return float(f) if n >= 0 else 1/f\n``` | 147 | Implement [pow(x, n)](http://www.cplusplus.com/reference/valarray/pow/), which calculates `x` raised to the power `n` (i.e., `xn`).
**Example 1:**
**Input:** x = 2.00000, n = 10
**Output:** 1024.00000
**Example 2:**
**Input:** x = 2.10000, n = 3
**Output:** 9.26100
**Example 3:**
**Input:** x = 2.00000, n = -2
**Output:** 0.25000
**Explanation:** 2\-2 = 1/22 = 1/4 = 0.25
**Constraints:**
* `-100.0 < x < 100.0`
* `-231 <= n <= 231-1`
* `n` is an integer.
* `-104 <= xn <= 104` | null |
50. Pow(x, n) Solution in Python | powx-n | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nSure, let me explain the code in a more understandable way.\n\nThis code defines a Python class called "Solution" with a method (function) called "myPow." The purpose of this method is to calculate the result of raising a given number \'x\' to a certain power \'n\' and return the result as a floating-point number.\n\nHere\'s a step-by-step breakdown of what the code does:\n1. class Solution:: This line declares a class named "Solution." In Python, a class is like a blueprint for creating objects with specific behaviors and attributes.\n\n2. def myPow(self, x: float, n: int) -> float:: This line defines a method named "myPow" within the "Solution" class. This method takes two parameters:\n\n- self: This is a reference to the instance of the class and is used to access its attributes and methods (though it\'s not used in this particular method).\n- x: This is a floating-point number, and it represents the base value that we want to raise to a power.\n- n: This is an integer, and it represents the exponent to which we want to raise \'x.\'\n3. return pow(x, n): This line contains the core logic of the method. It uses the built-in Python function pow() to calculate \'x\' raised to the power of \'n.\' The result is then returned as a floating-point number.\n\nIn simpler terms, this code defines a method that calculates \'x\' raised to the power of \'n\' and returns the result. It does this by using the built-in pow() function, which is a convenient way to perform exponentiation in Python.\n\n# Complexity\n- Time complexity: O(log|n|)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def myPow(self, x: float, n: int) -> float:\n return pow(x,n)\n \n``` | 3 | Implement [pow(x, n)](http://www.cplusplus.com/reference/valarray/pow/), which calculates `x` raised to the power `n` (i.e., `xn`).
**Example 1:**
**Input:** x = 2.00000, n = 10
**Output:** 1024.00000
**Example 2:**
**Input:** x = 2.10000, n = 3
**Output:** 9.26100
**Example 3:**
**Input:** x = 2.00000, n = -2
**Output:** 0.25000
**Explanation:** 2\-2 = 1/22 = 1/4 = 0.25
**Constraints:**
* `-100.0 < x < 100.0`
* `-231 <= n <= 231-1`
* `n` is an integer.
* `-104 <= xn <= 104` | null |
Easy to understanable soltuion | n-queens | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def solveNQueens(self, n: int) -> List[List[str]]:\n res = []\n def initialize(n):\n for key in [\'queen\', \'row\', \'col\', \'nwtose\', \'swtone\']:\n board[key] = {}\n for i in range(n):\n board[\'queen\'][i] = -1\n board[\'row\'][i] = 0\n board[\'col\'][i] = 0\n for i in range(-(n - 1), n):\n board[\'nwtose\'][i] = 0\n for i in range(2 * n - 1):\n board[\'swtone\'][i] = 0\n\n\n def printboard(n):\n ans = []\n s = []\n for col in range(n):\n s.append(".")\n for row in sorted(board[\'queen\'].keys()):\n x=board[\'queen\'][row]\n s[x]="Q"\n ans.append("".join(s))\n s[x]="."\n return ans\n\n\n def free(i, j):\n return (board[\'row\'][i] == 0 and board[\'col\'][j] == 0 and\n board[\'nwtose\'][j - i] == 0 and board[\'swtone\'][j + i] == 0)\n\n\n def addqueen(i, j):\n board[\'queen\'][i] = j\n board[\'row\'][i] = 1\n board[\'col\'][j] = 1\n board[\'nwtose\'][j - i] = 1\n board[\'swtone\'][j + i] = 1\n\n\n def undoqueen(i, j):\n board[\'queen\'][i] = -1\n board[\'row\'][i] = 0\n board[\'col\'][j] = 0\n board[\'nwtose\'][j - i] = 0\n board[\'swtone\'][j + i] = 0\n\n\n def placequeen(i):\n n = len(board[\'queen\'].keys())\n for j in range(n):\n if free(i, j):\n addqueen(i, j)\n if i == n - 1:\n res.append(printboard(n))\n else:\n placequeen(i + 1)\n undoqueen(i, j)\n\n\n board = {}\n \n initialize(n)\n placequeen(0)\n return res\n\n \n \n \n \n\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Easy To Understand || Beats 99%|| | n-queens | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n state = [["."] * n for _ in range(n)] # Start with an empty board\n res = []\n\n visited_cols = set()\n visited_diagonals = set()\n visited_antidiagonals = set()\n\n def backtrack(row):\n if row == n:\n res.append(["".join(row) for row in state])\n return\n\n for col in range(n):\n diagonal_difference = row - col\n diagonal_sum = row + col\n\n if not (col in visited_cols or\n diagonal_difference in visited_diagonals or\n diagonal_sum in visited_antidiagonals):\n\n visited_cols.add(col)\n visited_diagonals.add(diagonal_difference)\n visited_antidiagonals.add(diagonal_sum)\n state[row][col] = \'Q\'\n backtrack(row + 1)\n\n visited_cols.remove(col)\n visited_diagonals.remove(diagonal_difference)\n visited_antidiagonals.remove(diagonal_sum)\n state[row][col] = \'.\'\n\n backtrack(0)\n return res\n # Please Upvote me \n\n``` | 2 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
🔥 [Python3] Easy backtracking with 1 hash | n-queens | 0 | 1 | ```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n d, boards = set(), []\n\n def backtracking(row, leaft, board):\n if not leaft:\n boards.append([\'\'.join(row )for row in board])\n return\n\n line = [\'.\' for _ in range(n)]\n for col in range(n): #process all columns in current row\n colKey = f\'col_{col}\'\n majorDiagKey = f\'d1_{row-col}\'\n subDiagKey = f\'d2_{row+col}\'\n local_d = set([colKey, majorDiagKey, subDiagKey])\n\n if local_d & d: continue #has intersection (collision)\n \n line[col] = \'Q\'\n board.append(line)\n d.update(local_d)\n \n backtracking(row+1, leaft-1, board)\n \n #return data to previously state\n line[col] = \'.\' \n board.pop() \n d.difference_update(local_d) \n\n backtracking(0, n, [])\n \n return boards\n``` | 8 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
O(1) solution 220 IQ moment | n-queens | 0 | 1 | # Intuition\ncommon sense\n\n# Approach\nFind answer of each from test case then copy-paste the results.\nBy writing 9 if conditions.\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n return [] | 2 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Most efficient solution with complete explanation | n-queens | 1 | 1 | \n\n# Approach\n**solveNQueens Function Setup:**\n\n- Initialize an empty vector of vector of strings named ans to store the solutions.\n- Create a vector of strings named board to represent the current state of the chessboard. Initialize each string with N \'.\' characters.\n - Create three vectors of integers:\n - lr (leftrow): To keep track of whether a row is occupied or not.\n - ud (upperDiagonal): To keep track of whether an upper diagonal is occupied or not.\n - ld (lowerDiagonal): To keep track of whether a lower diagonal is occupied or not.\n- Call the solve function with appropriate parameters to start solving the puzzle.\n\n**solve Function:**\n\n- The solve function is a recursive backtracking function that tries to place queens column by column.\n- The base case is when col reaches N. This means all columns have been successfully filled with queens, so the current board configuration is added to the ans vector.\n- For each row in the current column (col), the function checks if the current cell can be a valid position for a queen. It checks if the corresponding row, upper diagonal, and lower diagonal are unoccupied.\n- If the position is valid, it places a queen in that cell, updates the tracking vectors (lr, ud, ld), and proceeds to the next column by making a recursive call.\n- After exploring all possible placements for the current column, it backtracks by removing the queen from the cell and resetting the tracking vectors.\n\n\n\n```C++ []\nclass Solution {\npublic:\n void solve(int col, vector<string>& board, vector<vector<string>>& ans, vector<int>& lr, vector<int>& ud, vector<int>& ld, int n) {\n if (col == n) {\n ans.push_back(board);\n return;\n }\n for (int row = 0; row < n; row++) {\n if (lr[row] == 0 && ld[row + col] == 0 && ud[n - 1 + col - row] == 0) {\n board[row][col] = \'Q\';\n lr[row] = 1;\n ld[row + col] = 1;\n ud[n - 1 + col - row] = 1;\n \n solve(col + 1, board, ans, lr, ud, ld, n);\n \n board[row][col] = \'.\';\n lr[row] = 0;\n ld[row + col] = 0;\n ud[n - 1 + col - row] = 0;\n }\n }\n }\n\npublic:\n vector<vector<string>> solveNQueens(int n) {\n vector<vector<string>> ans;\n vector<string> board(n);\n string s(n, \'.\');\n for (int i = 0; i < n; i++) {\n board[i] = s;\n }\n vector<int> leftrow(n, 0), upperDiagonal(2 * n - 1, 0), lowerDiagonal(2 * n - 1, 0);\n \n solve(0, board, ans, leftrow, upperDiagonal, lowerDiagonal, n);\n \n return ans;\n }\n};\n\n```\n```JAVA []\nclass Solution {\n public List<List<String>> solveNQueens(int n) {\n List<List<String>> ans = new ArrayList<>();\n String[] board = new String[n];\n Arrays.fill(board, ".".repeat(n));\n int[] leftrow = new int[n];\n int[] upperDiagonal = new int[2 * n - 1];\n int[] lowerDiagonal = new int[2 * n - 1];\n solve(0, board, ans, leftrow, upperDiagonal, lowerDiagonal, n);\n return ans;\n }\n\n private void solve(int col, String[] board, List<List<String>> ans, int[] lr, int[] ud, int[] ld, int n) {\n if (col == n) {\n ans.add(new ArrayList<>(Arrays.asList(board)));\n return;\n }\n for (int row = 0; row < n; row++) {\n if (lr[row] == 0 && ld[row + col] == 0 && ud[n - 1 + col - row] == 0) {\n char[] charArray = board[row].toCharArray();\n charArray[col] = \'Q\';\n board[row] = new String(charArray);\n lr[row] = 1;\n ld[row + col] = 1;\n ud[n - 1 + col - row] = 1;\n \n solve(col + 1, board, ans, lr, ud, ld, n);\n \n charArray[col] = \'.\';\n board[row] = new String(charArray);\n lr[row] = 0;\n ld[row + col] = 0;\n ud[n - 1 + col - row] = 0;\n }\n }\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n def solve(col, board, ans, lr, ud, ld, n):\n if col == n:\n ans.append([\'\'.join(row) for row in board])\n return\n for row in range(n):\n if lr[row] == 0 and ld[row - col] == 0 and ud[row + col] == 0:\n board[row][col] = \'Q\'\n lr[row] = 1\n ld[row - col] = 1\n ud[row + col] = 1\n \n solve(col + 1, board, ans, lr, ud, ld, n)\n \n board[row][col] = \'.\'\n lr[row] = 0\n ld[row - col] = 0\n ud[row + col] = 0\n \n ans = []\n board = [[\'.\' for _ in range(n)] for _ in range(n)]\n leftrow = [0] * n\n upperDiagonal = [0] * (2 * n - 1)\n lowerDiagonal = [0] * (2 * n - 1)\n solve(0, board, ans, leftrow, upperDiagonal, lowerDiagonal, n)\n return ans\n\n\n```\n | 4 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
✅ Python Solution with Explanation | n-queens | 0 | 1 | The approach that we will be using is backtracking. I have added comments in the code to help understand better.\n\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n state= [["."] * n for _ in range(n)] # start with empty board\n res=[]\n \n # for tracking the columns which already have a queen\n visited_cols=set()\n \n # This will hold the difference of row and col\n # This is required to identify diagonals\n # specifically for diagonals with increasing row and increasing col pattern\n # example: square (1,0) = 1-0 = 1\n # squares in same diagonals will have same difference\n # example: squares (0,0) and (8,8) are in the same diagonal\n # as both have same difference which is `0`\n \n visited_diagonals=set()\n \n # This will hold the sum of row and col\n # This is required to identify antidiagonals.\n # specifically for diagonals with increasing row and decreasing col pattern\n # the squares in same diagonal won\'t have the same difference.\n # example: square (1,0) = 1-0 = 1\n # squares in same diagonals will have same difference\n # example: squares (0,7) and (1,6) are in the same diagonal\n # as both have same sum which is `7`\n visited_antidiagonals=set()\n \n def backtrack(r):\n if r==n: \n res.append(["".join(row) for row in state])\n return\n \n for c in range(n):\n diff=r-c\n _sum=r+c\n \n # If the current square doesn\'t have another queen in same column and diagonal.\n if not (c in visited_cols or diff in visited_diagonals or _sum in visited_antidiagonals): \n visited_cols.add(c)\n visited_diagonals.add(diff)\n visited_antidiagonals.add(_sum)\n state[r][c]=\'Q\' # place the queen\n backtrack(r+1) \n\n # reset the path\n visited_cols.remove(c)\n visited_diagonals.remove(diff)\n visited_antidiagonals.remove(_sum)\n state[r][c]=\'.\' \n\n backtrack(0)\n return res\n```\n\n**Time - O(N!)** - In the solution tree, number of valid exploration paths from a node reduces by 2 at each level. In first level, we have N columns options to place the queen i.e N paths from the root node. In the next level, we have max N-2 options available because we can\'t place the queen in same column and same diagonal as previous queen. In the next level, it will be N-4 because of two columns and two diagonals occupied by previous two queens. This will continue and give us a `O(N!)`Time. (Let me know if you think otherwise :) )\n\n**Space - O(N^2)** - recursive call stack to explore all possible solutions\n\n---\n\n***Please upvote if you find it useful*** | 46 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Python backtracking solution | n-queens | 0 | 1 | # Intuition\nUsing backtracking, we\'ll add combinations of Qs to an empty n * n board conditional upon visited sets marking columns, bottom right diagonals, and bottom left diagonals, while iterating by a row-by-row basis. Upon iterating our row to n, append to our answer array.\n# Approach\n1. We first declare our sets such that each Queen, alone, occupies its own column (j), bottom-left diagonal(j + i), and bottom-right diagonal(i - j). \n2. Backtrack for each row i. Iterate through throughout the columns of row i until a open spot is available which does not occupy any previous row or diagonal previously marked within our set.\n3. Once our row increment i, reaches n, we append a string[] copy of board to our answer array as our base case.\n# Complexity\n- Time complexity:\nWorst case: we\'ll explore every possible placement of Q on each row.\n*O(n!)*\n\n- Space complexity:\nsize of board + n-sized max depth of call stack for each row\n*O(n^2)*\n# Code\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n cols = set()\n diagsr = set()\n diagsl = set()\n board = [[\'.\'] * n for _ in range(n)]\n\n def addToAns(b):\n temp = []\n for l in b:\n temp.append(\'\'.join(l))\n ans.append(temp)\n\n def backtrack(i):\n if i >= n:\n addToAns(board)\n return\n for j in range(n):\n if j not in cols and i - j not in diagsr and j + i not in diagsl:\n cols.add(j)\n diagsr.add(i - j)\n diagsl.add(j + i)\n board[i][j] = \'Q\'\n backtrack(i + 1)\n cols.remove(j)\n diagsr.remove(i - j)\n diagsl.remove(j + i)\n board[i][j] = \'.\'\n return\n\n ans = []\n backtrack(0)\n return ans\n``` | 3 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Python3 || Backtracking || Language Independent Approach | n-queens | 0 | 1 | ```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n def issafe(r,c):\n n = len(board)\n for i in range(n):\n if board[i][c] == \'Q\':\n return False\n if r - i >= 0 and c - i >= 0 and board[r-i][c-i] == \'Q\':\n return False\n if r - i >= 0 and c + i < n and board[r-i][c+i] == \'Q\':\n return False\n return True\n \n def solve(r):\n n = len(board)\n if r == n:\n print(board)\n ans.append(["".join(i) for i in board])\n return \n for c in range(0,n):\n if issafe(r,c):\n board[r][c] = \'Q\'\n solve(r+1)\n board[r][c] = \'.\'\n board = [[\'.\']*n for i in range(n)]\n ans =[]\n solve(0) \n return ans\n# Please upvote if you understand the solution | 21 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Backtracking Logic Solution | n-queens | 0 | 1 | \n# 1. BackTracking Solution\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n board=[]\n ans=[]\n lrow=[0]*n\n upperd=[0]*(2*n-1)\n lowerd=[0]*(2*n-1)\n self.solve(0,board,ans,lrow,lowerd,upperd,n)\n return ans\n def solve(self,col,board,ans,lrow,lowerd,upperd,n):\n if col==n:\n ans.append(board[::])\n return\n for row in range(n):\n if lrow[row]==0 and upperd[n-1+col-row]==0 and lowerd[row+col]==0:\n board.append("."*(row)+"Q"+"."*(n-row-1))\n lrow[row]=1\n upperd[n-1+col-row]=1\n lowerd[row+col]=1\n self.solve(col+1,board,ans,lrow,lowerd,upperd,n)\n board.pop()\n lrow[row]=0\n upperd[n-1+col-row]=0\n lowerd[row+col]=0\n\n```\n# please upvote me it would encourage me alot\n | 4 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
EFFICIENT PYTHON SOLUTION-EASY TO UNDERSTAND | n-queens | 0 | 1 | \n# Approach\nUsed Hashing to check ifSafe to place the Queen without attack\n\n\n# Code\n```\nclass Solution:\n def solve(self,col,board,ans,n,leftrow,upperdia,lowerdia):\n if(col==n):\n ans.append(board.copy())\n return\n for row in range(n):\n if(leftrow[row]==0 and lowerdia[col+row]==0 and upperdia[n-1+col-row]==0):\n board[row]=board[row][:col]+\'Q\'+board[row][col+1:]\n leftrow[row]=1\n upperdia[n-1+col-row]=1\n lowerdia[row+col]=1\n self.solve(col+1,board,ans,n,leftrow,upperdia,lowerdia)\n leftrow[row]=0\n upperdia[n-1+col-row]=0\n lowerdia[row+col]=0\n board[row]=board[row][:col]+\'.\'+board[row][col+1:]\n\n \n def solveNQueens(self, n: int) -> List[List[str]]:\n board=[\'.\' * n ] * n\n ans=list()\n leftrow=[0]*n\n upperdia=[0]*(2*n-1)\n lowerdia=[0]*(2*n-1)\n self.solve(0,board,ans,n,leftrow,upperdia,lowerdia)\n return ans \n \n``` | 2 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Easy Understanding Python Solution || Beats 97% of other solutions | n-queens | 0 | 1 | Please Upvote if you like it.\n\nPython Code:\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n def b(a):\n if a == n:\n ans.append(["".join(a) for a in c])\n return\n for i in range(n):\n if not e[i] and not d[a+i] and not rev[a-i]:\n c[a][i] = \'Q\'\n e[i], d[a+i], rev[a-i] = True, True, True\n b(a+1)\n c[a][i] = \'.\'\n e[i], d[a+i], rev[a-i] = False, False, False\n \n c= [[\'.\' for j in range(n)] for j in range(n)]\n e, d, rev = [False]*n, [False]*(2*n), [False]*(2*n-1)\n ans = []\n b(0)\n return ans | 3 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Python Easy Solution||Beats 98.41% Solutions||Backtracking | n-queens | 0 | 1 | # Python Solution\n\n# Beats 98.41% Solutions\n\n# Approach\nBackTracking Approach\n\n\n# Code\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n ############## Diagonal = row-col AntiDiagonal = row+col ##########\n\n def solver(row):\n if row == n:\n ans.append(["".join(i) for i in res])\n return\n for curr_col in range(n):\n curr_diag=row-curr_col\n curr_antiDiag=row+curr_col\n if curr_col not in col and curr_diag not in diag and curr_antiDiag not in antiDiag:\n col.add(curr_col)\n diag.add(curr_diag)\n antiDiag.add(curr_antiDiag)\n res[row][curr_col]="Q"\n\n solver(row+1)\n\n ####### Backtracking ########\n\n col.remove(curr_col)\n diag.remove(curr_diag)\n antiDiag.remove(curr_antiDiag)\n res[row][curr_col]="."\n\n\n\n\n res=[["." for i in range(n)] for i in range(n)]\n col=set()\n diag=set()\n antiDiag=set()\n ans=[]\n solver(0)\n return ans\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
✔️ ||BACKTRACKING EXPLAINED || ✔️ | n-queens | 0 | 1 | We first create a **( n X n )** chess board and assign **0** to every index.\nWhenever a queen will be placed, index will be made **1**.\n\nIn this approach , we fill queens **column-wise** starting from left side.\n\nWhenever a queen is placed, at first it is checked if it satisfies the conditions given that it is not under attack.\n\n**validMove** function.\nFirst it check there are no other queen in row the queen is filled.\nAs we are putting queen column wise so no need to check for column.\nThen there are two diagonals to check for.\n* Only left part of the diagonals are checked as positions to the right of the present column are still unfilled.\n\nIf conditions satisfied, Queen is placed and we move to next column.\nIf no queen satisfy the problem, we backtrack and try to change the position of previous queen.\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n \n def validMove(board,row,col):\n \n # check for queens in same row\n i=col\n while i>=0:\n if board[row][i]:\n return False\n i-=1\n \n #check for diagonal that goes toward top-left\n i=row\n j=col\n while (i>=0 and j>=0):\n if board[i][j]:\n return False\n i-=1\n j-=1\n \n # check for diagonal that goes towards bottom-left\n i=row\n j=col\n while (i<n and j>=0):\n if board[i][j]:\n return False\n i+=1\n j-=1\n return True\n \n\n def solve(board,col):\n\n \t# if solution found i.e. all places filled\n if (col==n):\n res.append([])\n for i in range(n):\n res[-1].append("")\n for j in range(n):\n if board[i][j]:\n res[-1][-1]+="Q"\n else:\n res[-1][-1]+="."\n return\n \n # try for all row values of that column\n for i in range(n):\n if validMove(board,i,col):\n board[i][col]=1\n solve(board,col+1)\n board[i][col]=0\n return\n \n res=[] # to store answers\n board=[] # create the chess board\n for i in range(n):\n board.append([])\n for j in range(n):\n board[-1].append(0)\n solve(board,0)\n board.clear()\n return res\n```\n\n | 4 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
✔️ PYTHON || ✔️ EXPLAINED || ; ] | n-queens | 0 | 1 | We first create a **( n X n )** chess board and assign **0** to every index.\nWhenever a queen will be placed, index will be made **1**.\n\nIn this approach , we fill queens **column-wise** starting from left side.\n\nWhenever a queen is placed, at first it is checked if it satisfies the conditions given that it is not under attack.\n\n**validMove** function.\nFirst it check there are no other queen in row the queen is filled.\nAs we are putting queen column wise so no need to check for column.\nThen there are two diagonals to check for.\n* Only left part of the diagonals are checked as positions to the right of the present column are still unfilled.\n\nIf conditions satisfied, Queen is placed and we move to next column.\nIf no queen satisfy the problem, we backtrack and try to change the position of previous queen.\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n \n def validMove(board,row,col):\n \n # check for queens in same row\n i=col\n while i>=0:\n if board[row][i]:\n return False\n i-=1\n \n #check for diagonal that goes toward top-left\n i=row\n j=col\n while (i>=0 and j>=0):\n if board[i][j]:\n return False\n i-=1\n j-=1\n \n # check for diagonal that goes towards bottom-left\n i=row\n j=col\n while (i<n and j>=0):\n if board[i][j]:\n return False\n i+=1\n j-=1\n return True\n \n\n def solve(board,col):\n\n \t# if solution found i.e. all places filled\n if (col==n):\n res.append([])\n for i in range(n):\n res[-1].append("")\n for j in range(n):\n if board[i][j]:\n res[-1][-1]+="Q"\n else:\n res[-1][-1]+="."\n return\n \n # try for all row values of that column\n for i in range(n):\n if validMove(board,i,col):\n board[i][col]=1\n solve(board,col+1)\n board[i][col]=0\n return\n \n res=[] # to store answers\n board=[] # create the chess board\n for i in range(n):\n board.append([])\n for j in range(n):\n board[-1].append(0)\n solve(board,0)\n board.clear()\n return res\n```\n\n | 4 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _all distinct solutions to the **n-queens puzzle**_. You may return the answer in **any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
**Example 1:**
**Input:** n = 4
**Output:** \[\[ ".Q.. ", "...Q ", "Q... ", "..Q. "\],\[ "..Q. ", "Q... ", "...Q ", ".Q.. "\]\]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above
**Example 2:**
**Input:** n = 1
**Output:** \[\[ "Q "\]\]
**Constraints:**
* `1 <= n <= 9` | null |
Python fast backtracking + horizontal symmetry [97.39%] | n-queens-ii | 0 | 1 | # Intuition\nTry to check all possible combinations with backtracking.\nE.g.\nFind a row where you can put a queen in the first column. \nFind a row where you can put a queen in the second column.\n...\nIf it\'s not last column, but you can\'t put queen. Then go back to the previous column and find the next row where you can put queen.\n... \nIf it\'s a last column and you found a row where you can put queen - you have plus one possible solution.\n\n# Approach\n\nNaive aproach would be to store state of a board in an array of arrays, where `False` empty cell and `True` is a cell with a queen. However, in this case you would need to check all placed queens, to verify position of the next queen.\n\nIt easier and more effective to store ocupied rows and diagonals separatly. Columns are not stored as backtracking goes from 1st to n-th one by one.\n\nThe easiest logical optimization would be to find solutions with a queen in the first column and first half or rows. For the second half of rows solutions are horizontaly symetric. And don\'t forget about midde row. It would make any solution almost 2 times faster.\nYou can go further and think of vertical symetry, and rotation symetry.\n\n# Code\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n rows = [0 for _ in range(n)]\n ldiags = [0 for _ in range(2 * n + 1)]\n rdiags = [0 for _ in range(2 * n + 1)]\n total = 0\n\n def backtrack(i, j_range=None):\n nonlocal rows\n nonlocal ldiags\n nonlocal rdiags\n nonlocal total\n\n for j in range(*j_range) if j_range else range(n):\n if not (\n rows[j] or rdiags[(r := i + j)] or ldiags[(l := i - j + n - 1)]\n ):\n if i + 1 == n:\n total += 1\n else:\n rows[j] = 1\n ldiags[l] = 1\n rdiags[r] = 1\n backtrack(i + 1)\n rows[j] = 0\n ldiags[l] = 0\n rdiags[r] = 0\n\n backtrack(0, (0, n // 2))\n total *= 2\n if n % 2:\n backtrack(0, (n // 2, n // 2 + 1))\n\n return total\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Python || Recursive BackTracking || Just Print the length 🔥 | n-queens-ii | 0 | 1 | # Code\n```\nclass Solution:\n def IsSafe(self,row,column,n,board):\n for i in range(column):\n if board[row][i] == "Q":\n return False\n i,j = row,column\n while(i>=0 and j>=0):\n if(board[i][j] == "Q"):\n return False\n i -= 1\n j -= 1\n i,j = row,column\n while(i<n and j>=0):\n if(board[i][j] == "Q"):\n return False\n i += 1\n j -= 1\n return True\n def solveQueens(self,column,n,board,result):\n if column == n:\n result.append(["".join(i) for i in board])\n return\n for row in range(n):\n if(self.IsSafe(row,column,n,board)):\n board[row][column] = "Q"\n self.solveQueens(column+1,n,board,result)\n board[row][column] = "."\n return\n def totalNQueens(self, n: int) -> int:\n board = [["." for i in range(n)] for i in range(n)]\n result = []\n self.solveQueens(0,n,board,result)\n return len(result)\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Python3 Backtracking Easy solution beats 98% | n-queens-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n ans=0\n left,upleft,lowleft=[0]*n,[0]*(2*n-1),[0]*(2*n-1)\n def solve(col,board):\n nonlocal ans\n if col==n:\n ans+=1\n return \n for row in range(n):\n if not left[row] and not upleft[row+col] and not lowleft[n-1+row-col]:\n board[row][col]="Q"\n left[row],upleft[row+col],lowleft[n-1+row-col]=1,1,1\n solve(col+1,board)\n board[row][col]="."\n left[row],upleft[row+col],lowleft[n-1+row-col]=0,0,0\n board=[["." for i in range(n)] for _ in range(n)]\n solve(0,board)\n return ans\n``` | 2 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Python || 96.52% Faster || Two Approaches | n-queens-ii | 0 | 1 | **Brute Force Approch:**\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n def safe(row,col,board):\n i,j=row,col\n while i>=0 and j>=0: # for diagonaly upwards direction in left\n if board[i][j]==\'Q\':\n return False\n i-=1\n j-=1\n i,j=row,col\n while i<n and j>=0: # for diagonaly downwards direction in left\n if board[i][j]==\'Q\':\n return False\n i+=1\n j-=1\n while col>=0: # for checking the same column\n if board[row][col]==\'Q\':\n return False\n col-=1\n return True\n \n def solve(c,board):\n if c==n:\n ans.append(board[:])\n return \n for i in range(n):\n if safe(i,c,board):\n board[i]=board[i][:c]+\'Q\'+board[i][c+1:]\n solve(c+1,board)\n board[i]=board[i][:c]+\'.\'+board[i][c+1:]\n \n board=[\'.\'*n for _ in range(n)]\n ans=[]\n solve(0,board)\n return len(ans) \n```\n**Optimized Approach:**\n```\nclass Solution:\n def solveNQueens(self, n: int) -> List[List[str]]:\n def safe(row,col,same_row,left_up,left_down):\n if row in same_row:\n return False\n if (n-1+col-row) in left_up:\n return False\n if (row+col) in left_down:\n return False\n return True\n \n def solve(c,board,same_row,left_up,left_down):\n if c==n:\n ans.append(board[:])\n return \n for i in range(n):\n if safe(i,c,same_row,left_up,left_down):\n board[i]=board[i][:c]+\'Q\'+board[i][c+1:]\n same_row.add(i)\n left_up.add(n-1+c-i)\n left_down.add(i+c)\n solve(c+1,board,same_row,left_up,left_down)\n same_row.remove(i)\n left_up.remove(n-1+c-i)\n left_down.remove(i+c)\n board[i]=board[i][:c]+\'.\'+board[i][c+1:]\n \n board=[\'.\'*n for _ in range(n)]\n same_row=set()\n left_up=set()\n left_down=set()\n ans=[]\n solve(0,board,same_row,left_up,left_down)\n return len(ans)\n```\n**An upovte will be encouraging** | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
BackTracking Logic Solution | n-queens-ii | 0 | 1 | \n\n# 1. BackTracking Logic Solution\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n def addans(board,ans):\n temp=[]\n for row in board:\n for j in range(len(row)):\n if row[j]=="Q":\n temp.append(j+1)\n ans.append(temp)\n def solve(col,board,low,upper,lower,ans,n):\n if col==n:\n addans(board,ans)\n return \n for row in range(n):\n if low[row]==0 and upper[n-1+col-row]==0 and lower[row+col]==0:\n board[row][col]="Q"\n low[row]=1\n upper[n-1+col-row]=1\n lower[row+col]=1\n solve(col+1,board,low,upper,lower,ans,n)\n low[row]=0\n upper[n-1+col-row]=0\n lower[row+col]=0\n ans=[] \n board=[[0]*n for i in range(n)]\n low=[0]*n\n upper=[0]*(2*n-1)\n lower=[0]*(2*n-1)\n solve(0,board,low,upper,lower,ans,n)\n return len(ans)\n```\n # please upvote me it would encourage me alot\n\n\n\n | 4 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
✅ Python Solution with Explanation | n-queens-ii | 0 | 1 | This problem is an extension on the yesterday\'s daily challenge problem [N-Queens](https://leetcode.com/problems/n-queens/discuss/2107719/python-solution-with-explanation). Please refer the link to understand how **N-Queens** is implemented. \n\n\nThe below code is just a slight modification on yesterday\'s [solution](https://leetcode.com/problems/n-queens/discuss/2107719/python-solution-with-explanation) that I had posted. In this, instead of returning the list of valid solutions, I am returning the count of number of valid solutions.\n\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n state=[[\'.\'] * n for _ in range(n)]\n\t\t\n\t\t# for tracking the columns which already have a queen\n visited_cols=set()\n\t\t\n\t\t# This will hold the difference of row and col\n # This is required to identify diagonals\n # specifically for diagonals with increasing row and increasing col pattern\n # example: square (1,0) = 1-0 = 1\n # squares in same diagonals will have same difference\n # example: squares (0,0) and (8,8) are in the same diagonal\n # as both have same difference which is `0`\n visited_diagonals=set()\n\t\t\n\t\t # This will hold the sum of row and col\n # This is required to identify antidiagonals.\n # specifically for diagonals with increasing row and decreasing col pattern\n # the squares in same diagonal won\'t have the same difference.\n # example: square (1,0) = 1-0 = 1\n # squares in same diagonals will have same difference\n # example: squares (0,7) and (1,6) are in the same diagonal\n # as both have same sum which is `7`\n visited_antidiagonals=set()\n \n res=set()\n def backtrack(r):\n if r==n:\n res.add(map(\'#\'.join, map(\'\'.join, state))) # add a valid solution\n return\n \n for c in range(n):\n\t\t\t # If the current square doesn\'t have another queen in same column and diagonal.\n if not(c in visited_cols or (r-c) in visited_diagonals or (r+c) in visited_antidiagonals):\n visited_cols.add(c)\n visited_diagonals.add(r-c)\n visited_antidiagonals.add(r+c)\n state[r][c]=\'Q\'\n backtrack(r+1)\n \n\t\t\t\t\t# reset the exploration path for backtracking\n visited_cols.remove(c)\n visited_diagonals.remove(r-c)\n visited_antidiagonals.remove(r+c)\n state[r][c]=\'.\'\n \n backtrack(0)\n return len(res)\n\n```\n\nBut sometimes while building a solution for a problem that is an extension or similar to another problem, we might end up with similar solution with slight change. This is what I did in my above approach. We were already tracking valid solutions in [N-Queens](https://leetcode.com/problems/n-queens/discuss/2107719/python-solution-with-explanation). So instead of returning the list of valid solutions, I am returning count of the number of solutions in the list.\n\nIf you observe the exploration path that solution tree takes, you would notice that it starts at a different row each time. Each path it takes is unique. So instead of tracking the valid solutions. We can just track the count of valid solutions. Whenever we hit the required number of queens, we just add that path to overall tally.\n\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int: \n visited_cols=set()\n visited_diagonals=set()\n visited_antidiagonals=set()\n \n res=set()\n def backtrack(r):\n if r==n: # valid solution state \n return 1\n \n cnt=0\n for c in range(n):\n if not(c in visited_cols or (r-c) in visited_diagonals or (r+c) in visited_antidiagonals):\n visited_cols.add(c)\n visited_diagonals.add(r-c)\n visited_antidiagonals.add(r+c) \n cnt+=backtrack(r+1) # count the overall tally from this current state\n \n visited_cols.remove(c)\n visited_diagonals.remove(r-c)\n visited_antidiagonals.remove(r+c) \n \n return cnt\n \n return backtrack(0)\n\n```\n\n**Time - O(N!)** - In the solution tree, number of valid exploration paths from a node reduces by 2 at each level. In first level, we have `N` columns options to place the queen i.e `N` paths from the root node. In the next level, we have max `N-2` options available because we can\'t place the queen in same column and same diagonal as previous queen. In the next level, it will be `N-4` because of two columns and two diagonals occupied by previous two queens. This will continue and give us a `O(N!)`Time. (Let me know if you think otherwise :) )\n\n**Space - O(N^2)** - recursive call stack to explore all possible solutions\n\n---\n\n***Please upvote if you find it useful*** | 22 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
52. N-Queens II with step by step explanation | n-queens-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- In this solution, we use depth first search (dfs) to find all solutions to the N-Queens problem\n- The queens list keeps track of the row number for each column, where queens[i] represents the row number for the ith column.\n- The dif list keeps track of the difference between the row number and the column number, where dif[i] = p - q and p is the row number and q is the column number.\n- The sum list keeps track of the sum of the row number and the column number, where sum[i] = p + q and p is the row number and q is the column number.\n- For each iteration, we check if the column q has not been used in the current solution and if the diagonal represented by dif[i] and the diagonal represented by sum[i] have not been used. If both conditions are met, we add q to the current solution and continue the search.\n- If the length of the queens list is equal to n, it means we have found a solution and we increment the result by 1.\n- Finally, we return the result which represents the number of solutions to the N-Queens problem.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n def dfs(queens, dif, sum):\n p = len(queens)\n if p == n:\n self.result += 1\n return None\n for q in range(n):\n if q not in queens and p-q not in dif and p+q not in sum:\n dfs(queens+[q], dif+[p-q], sum+[p+q])\n \n self.result = 0\n dfs([],[],[])\n return self.result\n\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
BackTracking Logic Solution | n-queens-ii | 0 | 1 | \n\n# 1. BackTracking Logic Solution\n\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n res,col,pos,neg=0,set(),set(),set()\n def backtracking(r):\n if n==r:\n nonlocal res\n res+=1\n for c in range(n):\n if c in col or (c+r) in pos or (r-c) in neg:\n continue\n col.add(c)\n pos.add(c+r)\n neg.add(r-c)\n backtracking(r+1)\n col.remove(c)\n pos.remove(c+r)\n neg.remove(r-c)\n backtracking(0)\n return res\n #please upvote me it would encourage me alot\n\n\n```\n\n# please upvote me it would encourage me alot\n | 5 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Easiest Python Solution Beating 81.66% | n-queens-ii | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n def search(queens, dif, sum):\n l = len(queens)\n if l == n:\n self.ans += 1\n return None\n for q in range(n):\n if q not in queens and l-q not in dif and l+q not in sum:\n search(queens+[q], dif+[l-q], sum+[l+q])\n \n self.ans = 0\n search([],[],[])\n return self.ans\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Easiest solution you will ever see! | n-queens-ii | 0 | 1 | Placing a queen at [r, c] imposes 4 bans on further placements.\n1. Can\'t place another queen in row r.\n2. Can\'t place another queen in col c.\n3. Can\'t place another queen in [r\',c\'] where r\'+c\' == r+c (same diagonal, lets call it sum diagonal).\n4. Can\'t place another queen in [r\',c\'] where r\'-c\' == r-c (same diagonal, lets call it diff diagonal).\n\nTo take care of these 4 bans\n1. Let\'s iterate from row 0 to row n-1\n2. Keep a set of banned cols\n3. Keep a set of banned sum diagonals\n4. Keep a set of banned diff diagonals\n\nwe will place a Queen at [row,col] only when it is not banned. Code is pretty self explainatory.\n\n\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n \n def helper(row, banned_cols, banned_diag_sum, banned_diag_diff):\n ans = 0\n if row==n:\n # means we have placed n queens as we are using 0 based index\n return 1\n for col in range(n):\n # can we place a queen given our banned columns and diagonals due to previous placements?\n can_place_at_row_col = (col not in banned_cols) and \\\n (row+col not in banned_diag_sum) and \\\n (row-col not in banned_diag_diff)\n # if yes, we move to next row, update the bans and see the possibility if it can lead to a valid board or not and we add up all possibility\n if can_place_at_row_col:\n ans+=helper(row+1, \n banned_cols.union({col}), \n banned_diag_sum.union({row+col}), \n banned_diag_diff.union({row-col}))\n return ans\n \n # initially nothing is banned\n return helper(0, set(), set(), set())\n\t\t\n\t\t\n | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Beats 99.20% (32ms) clean recursive solution in Python | n-queens-ii | 0 | 1 | This solution is basically the same as the solution introduced in the article, but I condensed it into 10 lines of code to look more compact.\n\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int: \n def rec(col, horizontal, diag, anti_diag):\n if col == n: return 1\n res = 0\n for row in range(n):\n if row not in horizontal and (row + col) not in diag and (row - col) not in anti_diag:\n horizontal[row] = True; diag[row + col] = True; anti_diag[row - col] = True;\n res += rec(col + 1, horizontal, diag, anti_diag)\n del horizontal[row]; del diag[row + col]; del anti_diag[row - col];\n return res\n return rec(0, {}, {}, {})\n``` | 5 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
python3- Simple | n-queens-ii | 0 | 1 | Simple understanding\n```\nclass Solution:\n def totalNQueens(self, n: int) -> int:\n def verify(r,c,board):\n for i in range(n):\n for j in range(n):\n if (i==r and j!=c) or (j==c and i!=r) or abs(r-i)==abs(c-j):\n if board[i][j]=="Q":\n return False\n return True\n def stri(l):\n a=[]\n for i in range(n):\n s=\'\'\n for j in range(n):\n s+=l[i][j]\n a.append(s)\n return a\n def lst(n):\n a=[]\n for i in range(n):\n l1=[]\n for j in range(n):\n l1.append(".")\n a.append(l1)\n return a\n def chakri(c,board):\n if c==n:\n res.append(stri(board))\n return\n for i in range(n):\n if verify(i,c,board):\n board[i][c]="Q"\n chakri(c+1,board)\n board[i][c]=\'.\'\n \n board=lst(n)\n res=[]\n a=chakri(0,board)\n return len(res)\n#print(board)\n#board[3][1]="Q"\n#print(verify(0,1,board))\n\n``` | 1 | The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
Given an integer `n`, return _the number of distinct solutions to the **n-queens puzzle**_.
**Example 1:**
**Input:** n = 4
**Output:** 2
**Explanation:** There are two distinct solutions to the 4-queens puzzle as shown.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 9` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.