title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Problems with Python3 and Multiple Solutions | merge-k-sorted-lists | 0 | 1 | **Python 2 Solution:**\n```\ndef mergeKLists_Python2(self, lists):\n\th = []\n\thead = tail = ListNode(0)\n\tfor i in lists:\n\t\tif i:\n\t\t\theapq.heappush(h, (i.val, i))\n\n\twhile h:\n\t\tnode = heapq.heappop(h)[1]\n\t\ttail.next = node\n\t\ttail = tail.next\n\t\tif node.next:\n\t\t\theapq.heappush(h, (node.next.val, node.next))\n\n\treturn head.next\n```\n\n**Python 3:** \nThe above solution works fine with Python 2.However, with Python3 it gives Type Error:\nTypeError: \'<\' not supported between instances of \'ListNode\' and \'ListNode\'\n**This error occurs because the cmp() special method is no longer honored in Python 3**\n\nHere are the two ways we can solve this problem:\n**a) Implement eq, lt methods** \n\t\nOne of the solution would be to provide `__eq__ and __lt__` method implementation to `ListNode` class\n```\ndef mergeKLists_Python3(self, lists):\n\tListNode.__eq__ = lambda self, other: self.val == other.val\n\tListNode.__lt__ = lambda self, other: self.val < other.val\n\th = []\n\thead = tail = ListNode(0)\n\tfor i in lists:\n\t\tif i:\n\t\t\theapq.heappush(h, (i.val, i))\n\n\twhile h:\n\t\tnode = heapq.heappop(h)[1]\n\t\ttail.next = node\n\t\ttail = tail.next\n\t\tif node.next:\n\t\t\theapq.heappush(h, (node.next.val, node.next))\n\n\treturn head.next\n```\n\n**b) Fix heapq** \n\nThe problem while adding `ListNode` objects as tasks is that the Tuple comparison breaks for (priority, task) pairs if the priorities are equal and the tasks do not have a default comparison order. The solution is to store entries as 3-element list including the priority, an entry count, and the task.\nThe entry count serves as a tie-breaker so that two tasks with the same priority are returned in the order they were added.\nAnd since no two entry counts are the same, the tuple comparison will never attempt to directly compare two tasks.\n\n```\ndef mergeKLists_heapq(self, lists):\n\th = []\n\thead = tail = ListNode(0)\n\tfor i in range(len(lists)):\n\t\theapq.heappush(h, (lists[i].val, i, lists[i]))\n\n\twhile h:\n\t\tnode = heapq.heappop(h)\n\t\tnode = node[2]\n\t\ttail.next = node\n\t\ttail = tail.next\n\t\tif node.next:\n\t\t\ti+=1\n\t\t\theapq.heappush(h, (node.next.val, i, node.next))\n\n\treturn head.next\n```\n\t | 168 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Python solution | heap 96%faster | merge-k-sorted-lists | 0 | 1 | # Code\n```\nclass Solution:\n def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n if not lists:\n return\n\n heap = []\n cur = ListNode()\n dummy = cur\n\n for node in lists:\n while node:\n heapq.heappush(heap, node.val)\n node = node.next\n \n while heap:\n cur.next = ListNode(heapq.heappop(heap))\n cur = cur.next\n \n return dummy.next\n``` | 2 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Solution | merge-k-sorted-lists | 1 | 1 | ```C++ []\nofstream ans("user.out");\nint main() {\n vector<int> v;\n v.reserve(1e4);\n string s;\n while (getline(cin, s)) {\n s.erase(remove(begin(s), end(s), \'[\'), end(s));\n s.erase(remove(begin(s), end(s), \']\'), end(s));\n for (auto &i: s) if (i == \',\') i = \' \';\n istringstream iss(s);\n int temp;\n v.clear();\n while (iss >> temp) v.push_back(temp);\n sort(v.begin(), v.end());\n ans << \'[\';\n for (int i = 0; i < v.size(); ++i) {\n if (i) ans << \',\';\n ans << v[i];\n }\n ans << "]\\n";\n }\n}\nclass Solution {\npublic:\n ListNode* mergeKLists(vector<ListNode*>& lists) {\n return nullptr;\n }\n};\n```\n\n```Python3 []\nf = open("user.out", \'w\')\nfor s in sys.stdin:\n print(\'[\', \',\'.join(\n map(str, sorted(int(v) for v in s.rstrip().replace(\'[\', \',\').replace(\']\', \',\').split(\',\') if v))), \']\', sep=\'\',\n file=f)\nexit(0)\n```\n\n```Java []\nclass Solution {\n\n ListNode merge(ListNode list1, ListNode list2) {\n\n if (list1 == null) {\n return list2;\n } else if (list2 == null) {\n return list1;\n }\n\n ListNode head = null, curr = head;\n ListNode curr1 = list1, curr2 = list2;\n while (curr1 != null && curr2 != null) {\n\n ListNode minNode = null;\n if (curr1.val < curr2.val) {\n minNode = curr1;\n curr1 = curr1.next;\n } else {\n minNode = curr2;\n curr2 = curr2.next;\n }\n\n if (head == null) {\n curr = head = minNode;\n } else {\n curr.next = minNode;\n curr = curr.next;\n }\n }\n\n if (curr1 != null) {\n curr.next = curr1;\n } else if (curr2 != null) {\n curr.next = curr2;\n }\n\n return head;\n }\n\n ListNode mergeSort(ListNode[] lists, int beg, int end) {\n\n if (beg == end) {\n return lists[beg];\n }\n\n int mid = (beg + end) / 2;\n ListNode list1 = mergeSort(lists, beg, mid);\n ListNode list2 = mergeSort(lists, mid + 1, end);\n ListNode head = merge(list1, list2);\n return head;\n }\n\n public ListNode mergeKLists(ListNode[] lists) {\n\n if (lists.length == 0) {\n return null;\n }\n return mergeSort(lists, 0, lists.length - 1);\n }\n}\n```\n | 27 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Python || Using While Loop || Easy To Understand 🔥 | merge-k-sorted-lists | 0 | 1 | # Code\n```\nclass Solution:\n def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n def mergeTwoLists(left, right) -> Optional[ListNode]:\n if left == None:\n return right\n if right == None:\n return left\n ans = ListNode(-1, None)\n temp = ans\n while left and right:\n if left.val < right.val:\n temp.next = left\n temp = left\n left = left.next\n else:\n temp.next = right\n temp = right\n right = right.next\n if left:\n temp.next = left\n if right:\n temp.next = right\n return ans.next\n h = ListNode(0)\n if len(lists) == 0: return None \n if len(lists) == 1: return lists[0]\n if len(lists) < 2: return lists\n newHead = mergeTwoLists(lists[0], lists[1])\n i = 2\n while i < len(lists):\n head1 = lists[i]\n i += 1\n newHead = mergeTwoLists(head1, newHead)\n return newHead\n``` | 2 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Easy Python Solution [Bruteforce] | merge-k-sorted-lists | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n test = ListNode(0)\n tail = test\n\n while list1 and list2:\n if list1.val <= list2.val:\n tail.next = list1\n list1 = list1.next\n else:\n tail.next = list2\n list2 = list2.next\n tail = tail.next\n\n if list1:\n tail.next = list1\n elif list2:\n tail.next = list2\n\n return test.next\n\n def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n if not lists:\n return None\n\n temp = [lists[0]]\n for i in range(len(lists) - 1):\n x = self.mergeTwoLists(temp[i], lists[i + 1])\n temp.append(x)\n return temp[-1]\n\n``` | 3 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Python || Double Recursion || Clean Code | merge-k-sorted-lists | 0 | 1 | # Intuition + Approach\nThe Solution class has two methods: merge and mergeKLists. The first method, merge, takes two sorted linked lists and merges them into a single sorted linked list in descending order. The second method, mergeKLists, takes a list of k sorted linked lists and recursively divides this list into smaller problems. It then calls the merge method on the sub-problems to combine the sorted linked lists until the final result, a sorted linked list in descending order, emerges.\n\nThe code sorts k given sorted linked lists into a single sorted linked list in descending order, effectively addressing the problem statement.\n\n# Complexity\n- Time complexity: nLog(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def merge(self, left, right):\n dummy = ListNode()\n current = dummy\n\n while left is not None and right is not None:\n if left.val < right.val:\n current.next = left\n left = left.next\n else:\n current.next = right\n right = right.next\n current = current.next\n\n if left is not None:\n current.next = left\n else:\n current.next = right\n\n return dummy.next\n \n def mergeKLists(self, lists: List[ListNode]) -> ListNode:\n if len(lists) == 0:\n return None\n if len(lists) == 1:\n return lists[0]\n mid = len(lists) // 2\n left = self.mergeKLists(lists[:mid])\n right = self.mergeKLists(lists[mid:])\n return self.merge(left, right)\n``` | 1 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
✔️ [Python3] PRIORITY QUEUE ೭੧(❛▿❛✿)੭೨, Explained | merge-k-sorted-lists | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe main challenge in the problem is the fact that the number of lists `k` can be huge and iterating over list heads every time attaching a new node to the result would be time-consuming. Essentially what is important to know on every merging step is what is the smallest node among all list heads. We can utilize the priority queue to fast access the current smallest node. \n\nFirst, we form the initial heap with tuples containing val and node itself. Notice that in Python implementation of the heap, the first element of the tuple is considered as a priority. In case the heap already has an element with the same priority, the Python compares the next element of the tuple. That is why we need index `i` in the second place.\n\nThen we run a cycle until the heap is empty. On every step, we pop out the smallest node and attach it to the result. Right away we push to the heap the next node.\n\nTime: **O(k * n * log(k))** - scan and manipulation with heap\nSpace: **O(k)** - for the heap\n\nRuntime: 96 ms, faster than **93.66%** of Python3 online submissions for Merge k Sorted Lists.\nMemory Usage: 17.9 MB, less than **61.96%** of Python3 online submissions for Merge k Sorted Lists.\n\n```\ndef mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n\theap, res = [], ListNode()\n\tfor i, list in enumerate(lists):\n\t\tif list: \n\t\t\theappush(heap, (list.val, i, list))\n\n\tcur = res\n\twhile heap:\n\t\t_, i, list = heappop(heap)\n\t\tif list.next:\n\t\t\theappush(heap, (list.next.val, i, list.next))\n\n\t\tcur.next, cur = list, list\n\n\treturn res.next\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 44 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
✔️ [Python3] I HATE LINKED LISTS, щ(゚Д゚щ), Not Explained | swap-nodes-in-pairs | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38-_-\'), If you have any question, feel free to ask.**\n\nJust a bunch of placeholders, edge cases, and strange errors about a cycle meanwhile :(\n\nprev cur cur porev next cur prev pasdfaslfjgnzdsf;ljgfsdaz;lkjkfgn\n\nTime: **O(n)** - iterate\nSpace: **O(1)**\n\n```\ndef swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\tif not head: return head\n\n\tprev, cur, ans = None, head, head.next\n\twhile cur and cur.next:\n\t\tadj = cur.next\n\t\tif prev: prev.next = adj\n\n\t\tcur.next, adj.next = adj.next, cur\n\t\tprev, cur = cur, cur.next\n\n\treturn ans or head\n```\n\n**UPVOTE if you like (\uD83C\uDF38-_-\'), If you have any question, feel free to ask.** | 174 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | swap-nodes-in-pairs | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution\n\n# Search \uD83D\uDC49 `Swap Nodes in Pairs by Tech Wired`\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\nThe approach used in the code is to traverse the linked list and swap adjacent pairs of nodes. This is done iteratively by maintaining a current pointer that points to the previous node before the pair to be swapped. The swapping is done by modifying the next pointers of the nodes.\n\n# Intuition:\nThe intuition behind the code is to break down the problem into smaller subproblems. By swapping two nodes at a time, we can gradually swap adjacent pairs throughout the linked list. This is achieved by manipulating the next pointers of the nodes.\n\nThe use of a dummy node helps in handling the edge case where the head of the list needs to be swapped. It serves as a placeholder for the new head of the modified list.\n\nThe while loop iterates as long as there are at least two nodes remaining in the list. In each iteration, the current pair of nodes is swapped by adjusting the next pointers accordingly.\n\n\n\n```Python []\nclass Solution:\n def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\n if not head or not head.next: return head\n\n dummy = ListNode(0)\n dummy.next = head\n curr = dummy\n\n while curr.next and curr.next.next:\n first = curr.next\n second = curr.next.next\n curr.next = second\n first.next = second.next\n second.next = first\n curr = curr.next.next\n \n return dummy.next\n```\n```Java []\nclass Solution {\n public ListNode swapPairs(ListNode head) {\n if (head == null || head.next == null) {\n return head;\n }\n \n ListNode dummy = new ListNode(0);\n dummy.next = head;\n ListNode curr = dummy;\n \n while (curr.next != null && curr.next.next != null) {\n ListNode first = curr.next;\n ListNode second = curr.next.next;\n curr.next = second;\n first.next = second.next;\n second.next = first;\n curr = curr.next.next;\n }\n \n return dummy.next;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n ListNode* swapPairs(ListNode* head) {\n if (head == nullptr || head->next == nullptr) {\n return head;\n }\n \n ListNode* dummy = new ListNode(0);\n dummy->next = head;\n ListNode* curr = dummy;\n \n while (curr->next != nullptr && curr->next->next != nullptr) {\n ListNode* first = curr->next;\n ListNode* second = curr->next->next;\n curr->next = second;\n first->next = second->next;\n second->next = first;\n curr = curr->next->next;\n }\n \n return dummy->next;\n }\n};\n```\n# An Upvote will be encouraging \uD83D\uDC4D\n\n | 54 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
Python 4-line iterative || Crazy NEXTs | swap-nodes-in-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust for fun. It works.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n head = node = ListNode(0, head)\n while node.next and node.next.next: \n node.next.next.next, node.next.next, node.next, node =\\\n node.next, node.next.next.next, node.next.next, node.next\n return head.next\n``` | 0 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
Easy Python Solution || using lists||runtime 97% | swap-nodes-in-pairs | 0 | 1 | \n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n lst=[]\n while head:\n lst.append(head.val)\n head=head.next\n ans=[]\n for i in range(0,len(lst),2):\n val=lst[i:i+2]\n ans+=val[::-1]\n final=ListNode(0)\n tmp=final\n for i in ans:\n tmp.next=ListNode(i)\n tmp=tmp.next\n return final.next\n``` | 4 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
5 lines of code python O(n) time and space compelxity | swap-nodes-in-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe plan is to traverse the list by taking two steps at a time.\n\nOn each step, you\'ll swap the node value and till you get to the end of the list. \n\nThis will ignore cases of node that cannot form a pair like [2,3,4], where 4 which is the last node will be ignored according to the condition.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n h = head\n\n\n while h and h.next:\n h.val, h.next.val = h.next.val, h.val\n \n h = h.next.next\n \n return head\n``` | 1 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
Easy Solution | Beginner Friendly | Easy to Understand | Beats 100% | JAVA | PYTHON 3 |C ++| JS | C# | swap-nodes-in-pairs | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTraverse the list and swap pairs of nodes one by one.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The node "ans" is to point to the head of the original list. It then uses a "curr" node to traverse the list and swap pairs of nodes. The loop continues as long as there are at least two more nodes to swap.\n\n- Inside the loop, the solution uses two temporary nodes, "t1" and "t2", to hold the first and second nodes of the pair. Then, it updates the pointers to swap the nodes, and moves "curr" two nodes ahead. At the end, it returns the modified list starting from the next node of the "ans" node.\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode swapPairs(ListNode head) {\n if (head == null || head.next == null) {\n return head;\n }\n ListNode ans =new ListNode(0);\n ans.next=head;\n ListNode curr=ans;\n while (curr.next != null && curr.next.next != null) {\n ListNode t1 = curr.next;\n ListNode t2 = curr.next.next;\n curr.next = t2;\n t1.next = t2.next;\n t2.next = t1;\n curr = curr.next.next;\n } \n return ans.next;\n }\n}\n```\n```python []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if not head or not head.next:\n return head\n \n ans = ListNode(0)\n ans.next = head\n curr = ans\n \n while curr.next and curr.next.next:\n t1 = curr.next\n t2 = curr.next.next\n curr.next = t2\n t1.next = t2.next\n t2.next = t1\n curr = curr.next.next\n \n return ans.next\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* swapPairs(ListNode* head) {\n if (head == NULL || head->next == NULL) {\n return head;\n }\n struct ListNode* ans = (struct ListNode*) malloc(sizeof(struct ListNode));\n ans->next = head;\n struct ListNode* curr = ans;\n while (curr->next != NULL && curr->next->next != NULL) {\n struct ListNode* t1 = curr->next;\n struct ListNode* t2 = curr->next->next;\n curr->next = t2;\n t1->next = t2->next;\n t2->next = t1;\n curr = curr->next->next;\n }\n return ans->next;\n }\n};\n```\n```Javascript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} head\n * @return {ListNode}\n */\nvar swapPairs = function(head) {\n if (head == null || head.next == null) {\n return head;\n }\n let ans = new ListNode(0);\n ans.next = head;\n let curr = ans;\n while (curr.next != null && curr.next.next != null) {\n let t1 = curr.next;\n let t2 = curr.next.next;\n curr.next = t2;\n t1.next = t2.next;\n t2.next = t1;\n curr = curr.next.next;\n }\n return ans.next;\n};\n```\n```C# []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * public int val;\n * public ListNode next;\n * public ListNode(int val=0, ListNode next=null) {\n * this.val = val;\n * this.next = next;\n * }\n * }\n */\npublic class Solution {\n public ListNode SwapPairs(ListNode head) {\n if (head == null || head.next == null) {\n return head;\n }\n ListNode ans = new ListNode(0);\n ans.next = head;\n ListNode curr = ans;\n while (curr.next != null && curr.next.next != null) {\n ListNode t1 = curr.next;\n ListNode t2 = curr.next.next;\n curr.next = t2;\n t1.next = t2.next;\n t2.next = t1;\n curr = curr.next.next;\n }\n return ans.next; \n }\n}\n```\n```Kotlin []\n/**\n * Example:\n * var li = ListNode(5)\n * var v = li.`val`\n * Definition for singly-linked list.\n * class ListNode(var `val`: Int) {\n * var next: ListNode? = null\n * }\n */\nclass Solution {\n fun swapPairs(head: ListNode?): ListNode? {\n if (head == null || head.next == null) {\n return head\n }\n val ans = ListNode(0)\n ans.next = head\n var curr: ListNode? = ans\n while (curr?.next != null && curr.next?.next != null) {\n val t1 = curr.next\n val t2 = curr.next?.next\n curr.next = t2\n t1.next = t2?.next\n t2?.next = t1\n curr = curr.next?.next\n }\n return ans.next\n }\n}\n```\n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\nstruct ListNode* swapPairs(struct ListNode* head){\n if (head == NULL || head->next == NULL) {\n return head;\n }\n struct ListNode* ans = (struct ListNode*) malloc(sizeof(struct ListNode));\n ans->next = head;\n struct ListNode* curr = ans;\n while (curr->next != NULL && curr->next->next != NULL) {\n struct ListNode* t1 = curr->next;\n struct ListNode* t2 = curr->next->next;\n curr->next = t2;\n t1->next = t2->next;\n t2->next = t1;\n curr = curr->next->next;\n }\n return ans->next;\n}\n```\n\nUPVOTES ARE ENCOURAGING! | 24 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
✔💯 DAY 411 | BRUTE=>BETTER=>OPTIMAL | 100% | | [PYTHON/JAVA/C++] | EXPLAINED 🆙🆙🆙 | swap-nodes-in-pairs | 1 | 1 | \n\n\n\n# BRUTE\n```JAVA []\npublic ListNode swapPairs(ListNode head) {\n List<ListNode> list = new ArrayList<>();\n ListNode temNode = head;\n while (temNode != null) {\n list.add(temNode);\n temNode = temNode.next;\n }\n for (int i = 0; i < list.size() - 1; i += 2) {\n int swapElement = list.get(i).val;\n list.get(i).val = list.get(i + 1).val;\n list.get(i + 1).val = swapElement;\n }\n return head;\n}\n```\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\nwe first check if the input head is null or has only one node. If so, we return the head as it is. Otherwise, we create two nodes first and second and set them to the first and second nodes of the linked list, respectively. We then recursively call the swapPairs function on the next of the second node and set the next of the first node to the result. We then swap the next pointers of the first and second nodes and return the second node.\n\n# BETTER\n```JAVA []\npublic ListNode swapPairs(ListNode head) {\n if (head == null || head.next == null) {\n return head;\n }\n ListNode first = head;\n ListNode second = head.next;\n first.next = swapPairs(second.next);\n second.next = first;\n return second;\n}\n```\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(LOG(N))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# OPTIMAL\nWe create a dummy node and set its next to the head. We then create a current node and initialize it to the dummy node. We use a single loop to swap every two adjacent nodes. We do this by creating two nodes first and second and swapping their next pointers. We then update the current node to point to the second node and continue the loop. Finally, we return the next of the dummy node.The time complexity of this solution is O(n) as we need to traverse the entire linked list once.\n```JAVA []\npublic ListNode swapPairs(ListNode head) {\n if (head == null || head.next == null) {\n return head;\n }\n ListNode dummy = new ListNode(0);\n dummy.next = head;\n ListNode current = dummy;\n while (current.next != null && current.next.next != null) {\n ListNode first = current.next;\n ListNode second = current.next.next;\n first.next = second.next;\n second.next = first;\n current.next = second;\n current = current.next.next;\n }\n return dummy.next;\n}\n```\n```c++ []\nListNode* swapPairs(ListNode* head) {\n ListNode* dummy = new ListNode(0);\n dummy->next = head;\n ListNode* current = dummy;\n while (current->next != NULL && current->next->next != NULL) {\n ListNode* first = current->next;\n ListNode* second = current->next->next;\n first->next = second->next;\n second->next = first;\n current->next = second;\n current = current->next->next;\n }\n return dummy->next;\n}\n```\n```python []\ndef swapPairs(self, head: ListNode) -> ListNode:\n dummy = ListNode(0)\n dummy.next = head\n current = dummy\n while current.next and current.next.next:\n first = current.next\n second = current.next.next\n first.next = second.next\n second.next = first\n current.next = second\n current = current.next.next\n return dummy.next\n```\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \u2B06 \n | 12 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
Python3|| Easy solution || Linkedlist-List. | swap-nodes-in-pairs | 0 | 1 | # Please upvote if you find the solution helful.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:\n lst = []\n while head:\n lst.append(head.val)\n head = head.next\n for i in range(0,len(lst)-1,2):\n lst[i],lst[i+1]=lst[i+1],lst[i]\n a = ListNode(0)\n temp = a\n for i in lst:\n temp.next = ListNode(i)\n temp = temp.next\n return a.next\n\n \n``` | 1 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
5 Lines😎|| 0ms ✅|| Easy Approach🔥|| Beasts 100%👌|| Stepped Explanation 😍 | swap-nodes-in-pairs | 1 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere we are using a very simple and easy ***recursive*** approach to solve this\n\n\n**Steps:**\n\n1. At first we will check, if head value is null we will return null.\n\n `if(head==null) return null;`\n2. Then we check, if next head value is null we will return current head.\n\n `if (head.next == null) return head;`\n3. Later we will swap the 2 value of by creating a temp variable & recursively swapping the values.\n \n - Storing the next head to a temp ListNode that we will return at last. `ListNode temp = head.next;`\n - Then we get the call the function recursively for next head. \n `head.next = swapPairs(temp.next);`\n - Then we swap value next temp with the head.\n `temp.next = head;`\n4. At last we will return the temp ListNode we created .\n \n `return temp;`\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n\n```\nclass Solution {\n public ListNode swapPairs(ListNode head) {\n \n if(head==null) return null;\n if (head.next == null) return head;\n\n ListNode temp = head.next;\n head.next = swapPairs(temp.next);\n temp.next = head;\n\n return temp;\n }\n}\n```\n\n<!-- ---\n**Iterative** \n```\npublic ListNode swapPairs1(ListNode head) {\n if (head == null || head.next == null) {\n return head;\n }\n ListNode pre = new ListNode(0), p = head, ret = head.next;\n while (p != null && p.next != null) {\n ListNode nxt = p.next;\n p.next = nxt.next;\n nxt.next = p;\n pre.next = nxt;\n pre = p;\n p = p.next;\n }\n return ret;\n}\n``` -->\n\n\n\n\n\n\n | 7 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
✅ C++ | | Python | | Recursive Solution | | Beginners Friendly ✅ | swap-nodes-in-pairs | 0 | 1 | \n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++\n```\nclass Solution {\npublic:\n ListNode* swapPairs(ListNode* head) {\n\n if(head == NULL) return NULL;\n ListNode* curr = head;\n ListNode* nn = NULL;\n ListNode* prev = NULL;\n\n int ct = 0;\n while(curr != NULL && ct < 2){\n nn = curr->next;\n curr->next = prev;\n prev = curr;\n curr = nn;\n ct++;\n }\n\n head->next = swapPairs(nn); // 3 pass to recursion\n return prev; // return pointer which return to 2\n\n }\n};\n```\n\n# Python\n\n```\nclass Solution:\n def swapPairs(self, head: ListNode) -> ListNode:\n if head is None:\n return None\n curr = head\n nn = None\n prev = None\n ct = 0\n while curr is not None and ct < 2:\n nn = curr.next\n curr.next = prev\n prev = curr\n curr = nn\n ct += 1\n head.next = self.swapPairs(nn)\n return prev\n``` | 3 | Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
**Example 1:**
**Input:** head = \[1,2,3,4\]
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** head = \[\]
**Output:** \[\]
**Example 3:**
**Input:** head = \[1\]
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 100]`.
* `0 <= Node.val <= 100` | null |
Easy Solution | reverse-nodes-in-k-group | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reverseKGroup(self, head: ListNode, k: int) -> ListNode:\n # Check if there are at least k nodes remaining\n count = 0\n curr = head\n while curr and count < k:\n curr = curr.next\n count += 1\n\n # If there are fewer than k nodes, no need to reverse\n if count < k:\n return head\n\n # Reverse the group (basic way to reverse linked list)\n prev, curr = None, head\n for _ in range(k):\n nxt = curr.next\n curr.next = prev\n prev = curr\n curr = nxt\n\n # Recursively reverse the remaining groups\n head.next = self.reverseKGroup(curr, k)\n return prev\n\n``` | 3 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
Python solution using list | reverse-nodes-in-k-group | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:88%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n lst=[]\n tmp=head\n while tmp:\n lst.append(tmp.val)\n tmp=tmp.next\n res=[]\n for i in range(0,len(lst),k):\n t=lst[i:i+k]\n if len(t)==k:\n res+=t[::-1]\n else:\n res+=t\n dummy=ListNode(0)\n temp=dummy\n while len(res)!=0:\n temp.next=ListNode(res.pop(0))\n temp=temp.next\n return dummy.next\n``` | 1 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
Python Iterative Solution with Constant Space Complexity | reverse-nodes-in-k-group | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can reverse the one-way nodes using several pointers.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, we will count the total length of the list.\nSecond, we can now calculate how many groups we should reverse. (name it `repeat`)\nThird, we will iterate `repeat` times for reversing one group.\nFourth, in the iteration I mentioned right before, we will iterate `k - 1` times for manipulating the nodes.\n\n# Complexity\n- Time complexity: O(N), but it will be less or equal to N\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(1), we are using constant number of pointers.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def count(self, root: Optional[ListNode]) -> int:\n res = 0\n while root:\n res += 1\n root = root.next\n return res\n\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n n = self.count(head)\n\n repeat = n // k\n\n root = ListNode()\n\n root.next = head\n\n tmp_head = root\n node = head\n for _i in range(repeat):\n for _j in range(k - 1):\n next_node = node.next\n next_next_node = node.next.next\n\n node.next = next_next_node\n next_node.next = tmp_head.next\n tmp_head.next = next_node\n \n tmp_head = node\n node = tmp_head.next\n \n return root.next\n``` | 1 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
Python || 97.85% Faster || T.C. O(n) and S.C. O(1) | reverse-nodes-in-k-group | 0 | 1 | ```\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n count=0\n temp=head\n while temp:\n temp=temp.next\n count+=1\n n=count//k #No. of groups to be reversed\n prev=dummy=ListNode()\n dummy.next=head\n while n:\n curr=prev.next\n nex=curr.next\n for i in range(1,k): #If we have to reverse k nodes then k-1 links will be reversed\n curr.next=nex.next\n nex.next=prev.next\n prev.next=nex\n nex=curr.next\n prev=curr\n n-=1\n return dummy.next\n```\n**An upvote will be encouraging** | 11 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
Clean and Readable Python code | reverse-nodes-in-k-group | 0 | 1 | \n# Code\n```\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n \n dummy = ListNode(0, head)\n currGroup = dummy\n\n while True:\n kth = self.getKth(currGroup, k)\n if not kth:\n break\n nextGroup = kth.next\n\n # reverse the currGroup\n prev, curr = kth.next, currGroup.next\n while curr != nextGroup:\n tmp = curr.next\n curr.next = prev\n prev = curr\n curr = tmp\n\n currGroup.next, currGroup = kth, currGroup.next\n\n return dummy.next\n\n\n def getKth(self, node, k):\n while node and k:\n node = node.next\n k -= 1\n return node\n\n``` | 3 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
[Python3] Iterative + recursive solutions || beats 98%🥷🏼 | reverse-nodes-in-k-group | 0 | 1 | # Iterative solution:\n```python3 []\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n def getGroupEnd(cur, k):\n while k > 1 and cur.next:\n cur = cur.next \n k-=1\n return cur if k == 1 else None\n\n def reverseGroup(start, end):\n prev, cur, new_group_start = None, start, end.next\n while cur != new_group_start:\n cur.next, cur, prev = prev, cur.next, cur \n\n dummy = ListNode()\n prev_group = dummy\n while head:\n group_start = head\n group_end = getGroupEnd(head, k)\n if not group_end: break # not enough todes to make a new group\n next_group_start = group_end.next # save link to the next group start\n reverseGroup(group_start, group_end) # reverse the current group\n prev_group.next = group_end # group_end is the start of the reversed group\n prev_group = group_start # group_start is the end of the reversed group\n group_start.next = next_group_start # link current reversed group with the next group\n head = next_group_start # move current point to the start of the next group\n\n return dummy.next \n```\n```python3 []\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n dummy = ListNode()\n prev_group = dummy\n while head:\n j, group_end = 1, head #start of group = end after reverse\n while j < k and head.next:\n head = head.next \n j+=1\n group_start = head #end of group = start after reverse\n next_group = head = head.next #start of next group\n\n if j != k: #don\'t need reverse (not enough nodes)\n break\n #reverse current group without links to prev and next groups\n prev, cur = None, group_end\n while cur != next_group:\n cur.next, cur, prev = prev, cur.next, cur \n\n prev_group.next = group_start\n prev_group = group_end\n group_end.next = next_group\n\n return dummy.next \n```\n\n# Recursive solution:\n```python3 []\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if not head: return\n start, end = head, head\n for _ in range(k):\n if not end: return head\n end = end.next\n \n # reverse diapason [start:end)\n def reverse(start, end):\n prev = None\n while start != end:\n start.next, start, prev = prev, start.next, start\n return prev # return head node of the reversed group\n \n newHead = reverse(start, end)\n start.next = self.reverseKGroup(end, k)\n\n return newHead\n```\n\n\n | 15 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
My Solution using Reverse And Link | reverse-nodes-in-k-group | 0 | 1 | \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def link(self,a,b):\n r=a\n while a.next:\n a=a.next\n a.next=b\n\n def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:\n h=head\n nh=head\n if head == None:\n return None\n while h.next!=None:\n second=nh\n nh=h.next \n h.next=nh.next\n nh.next=second \n return nh\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n heads=[]\n count=0\n x=head\n while x:\n if count%k==0:\n heads.append(x)\n x=x.next\n count+=1\n last=None\n if count%k!=0:\n last=heads.pop()\n newheads=[]\n for i in heads:\n c=0\n t=i\n while c<k-1:\n i=i.next\n c+=1\n i.next=None\n newheads.append(t)\n reverse=[]\n for i in newheads:\n reverse.append(self.reverseList(i))\n print(reverse)\n self.link(reverse[-1],last)\n for i in range(len(reverse)-2,-1,-1):\n self.link(reverse[i],reverse[i+1])\n return reverse[0]\n``` | 4 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
python3 easy recursion solution | reverse-nodes-in-k-group | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def reverseKGroup(self, head: ListNode, k: int) -> ListNode: \n # Check if we need to reverse the group\n curr = head\n for _ in range(k):\n if not curr: return head\n curr = curr.next\n\t\t \n\t\t\t\t\n # Reverse the group (basic way to reverse linked list)\n prev = None\n curr = head\n for _ in range(k):\n nxt = curr.next\n curr.next = prev\n prev = curr\n curr = nxt\n \n\t\t\n # After reverse, we know that `head` is the tail of the group.\n\t\t# And `curr` is the next pointer in original linked list order\n head.next = self.reverseKGroup(curr, k)\n return prev\n ``` | 93 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
Python solution easy to understand || O(k) space complexity || O(N) time complexity | reverse-nodes-in-k-group | 0 | 1 | ```\nclass Solution:\n def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n nodes = []\n cnt = 0\n cpy = head\n while head:\n nodes.append(head)\n head = head.next\n cnt += 1\n if cnt == k:\n cnt = 0\n m,n = 0,k-1\n while m<n:\n nodes[m].val,nodes[n].val = nodes[n].val,nodes[m].val\n m,n = m+1,n-1\n nodes = []\n return cpy\n``` | 1 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
✅ C++ | | Python | | Recursive Solution | | Beginners Friendly ✅ | reverse-nodes-in-k-group | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: if(recursion stack): O(n) else: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++\n```\nclass Solution {\nprivate:\n int length(ListNode* head){\n int size = 0;\n ListNode* ptr = head;\n while(ptr){\n ptr = ptr->next;\n size++;\n }\n return size;\n }\npublic:\n ListNode* solve(ListNode* head,int &k,int size){\n if(size < k){\n return head;\n }\n if(head == NULL){\n return NULL;\n }\n\n ListNode* curr = head,*nn = NULL,*prev = NULL;\n int ct = 0;\n while(curr != NULL && ct < k){\n nn = curr->next;\n curr->next = prev;\n prev = curr;\n curr = nn;\n ct++;\n }\n\n head->next = solve(nn,k,size - k);\n return prev;\n }\n\n ListNode* reverseKGroup(ListNode* head, int k) {\n int n = length(head);\n return solve(head,k,n);\n }\n};\n```\n\n# Python\n```\nclass Solution:\n def length(self, head):\n size = 0\n ptr = head\n while ptr:\n ptr = ptr.next\n size += 1\n return size\n \n def solve(self, head, k, size):\n if size < k:\n return head\n if head is None:\n return None\n curr = head\n nn = None\n prev = None\n ct = 0\n while curr is not None and ct < k:\n nn = curr.next\n curr.next = prev\n prev = curr\n curr = nn\n ct += 1\n head.next = self.solve(nn, k, size - k)\n return prev\n \n def reverseKGroup(self, head, k):\n n = self.length(head)\n return self.solve(head, k, n)\n\n``` | 2 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return _the modified list_.
`k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[2,1,4,3,5\]
**Example 2:**
**Input:** head = \[1,2,3,4,5\], k = 3
**Output:** \[3,2,1,4,5\]
**Constraints:**
* The number of nodes in the list is `n`.
* `1 <= k <= n <= 5000`
* `0 <= Node.val <= 1000`
**Follow-up:** Can you solve the problem in `O(1)` extra memory space? | null |
✅Best Method 🔥|| 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | remove-duplicates-from-sorted-array | 1 | 1 | # Intuition:\nThe Intuition is to use two pointers, `i` and `j`, to iterate through the array. The variable `j` is used to keep track of the current index where a unique element should be placed. The initial value of `j` is 1 since the first element in the array is always unique and doesn\'t need to be changed.\n\n# Explanation:\nThe code starts iterating from `i = 1` because we need to compare each element with its previous element to check for duplicates.\n\nThe main logic is inside the `for` loop:\n1. If the current element `nums[i]` is not equal to the previous element `nums[i - 1]`, it means we have encountered a new unique element.\n2. In that case, we update `nums[j]` with the value of the unique element at `nums[i]`, and then increment `j` by 1 to mark the next position for a new unique element.\n3. By doing this, we effectively overwrite any duplicates in the array and only keep the unique elements.\n\nOnce the loop finishes, the value of `j` represents the length of the resulting array with duplicates removed.\n\nFinally, we return `j` as the desired result.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int removeDuplicates(vector<int>& nums) {\n int j = 1;\n for(int i = 1; i < nums.size(); i++){\n if(nums[i] != nums[i - 1]){\n nums[j] = nums[i];\n j++;\n }\n }\n return j;\n }\n};\n```\n```Java []\nclass Solution {\n public int removeDuplicates(int[] nums) {\n int j = 1;\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] != nums[i - 1]) {\n nums[j] = nums[i];\n j++;\n }\n }\n return j;\n }\n}\n```\n```Python3 []\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n j = 1\n for i in range(1, len(nums)):\n if nums[i] != nums[i - 1]:\n nums[j] = nums[i]\n j += 1\n return j\n```\n\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. **Practice them in a row for better understanding and please Upvote the post for more questions.**\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 1,168 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
[Py]All 4 Methods: Intuitions Walk-through Wrong answer explanations for Beginners [Python]] | remove-duplicates-from-sorted-array | 0 | 1 | \n## \u2705 Method 1: sort in place using `[:]`\n```\n\tdef removeDuplicates(self, nums: List[int]) -> int:\n\t\tnums[:] = sorted(set(nums))\n\t\treturn len(nums)\n```\n\n\n**Time Complexity:** `O(n)`\n**Space Complexity:** `O(1)`\n\n\n### \u274C Common Wrong Answers:\n```\n\tnums = sorted(set(nums))\n\treturn len(nums)\n```\n\xA0`nums =`\xA0 doesn\'t replace elements in the original list.\n `nums[:] =`\xA0replaces element in place\n\nIn short, without `[:]`, we\'re creating a new list object, which is against what this problem is asking for:\n"Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory."\n\n-----------------------\n## \u2705 Method 2: Two-pointers\n### \uD83E\uDD14 Initial Intuition:\nUse a `slow` pointer to "lock" the "wanted" element, and use a `fast` pointer to move forward along the list and look for new unique elements in the list.\nOr, in other words, the current `slow` pointer is used to locate the latest unique number for the results, and `fast` is used for iterating and discovery.\n\nHave `fast` advanced in every iteration, but `slow` is only advanced when two pointers are onto two different elements. \n\nThat means, the elements after `nums[slow]` and before `nums[fast]` are numbers we\'ve **seen** before and don\'t need anymore (one copy of these numbers is already saved before the current `slow` (inclusive)). \n\nTherefore, in order to have this newly discovered (unseen) number pointed by the current `fast` to the front of the array for the final answer, we just need to swap this newly discovered number to the location that follows the current `slow` pointer, with one of the **seen** numbers (we don\'t need it for the answer regardlessly), and then advance the `slow` in the same iteration to lock this new number.\n\n```\n\tdef removeDuplicates(self, nums: List[int]) -> int:\n\t\tslow, fast = 0, 1\n\t\twhile fast in range(len(nums)):\n\t\t\tif nums[slow] == nums[fast]:\n\t\t\t\tfast += 1\n\t\t\telse:\n\t\t\t\tnums[slow+1] = nums[fast]\n\t\t\t\tfast += 1\n\t\t\t\tslow += 1\n\n\t\treturn slow + 1\n```\n\n### \u2747\uFE0F Simplified two-pointers with for loops:\n\uD83D\uDCA1 However, observe, `fast` pointer is simply incremented in every iteration regardless of the conditions, that\'s just a typical for loop\'s job. Therefore, we can simplify this "two-pointers" system as follows:\n```\n\tdef removeDuplicates(self, nums: List[int]) -> int:\n\t\tj = 0\n\t\tfor i in range(1, len(nums)):\n\t\t\tif nums[j] != nums[i]:\n\t\t\t\tj += 1\n\t\t\t\tnums[j] = nums[i]\n\t\treturn j + 1\n```\n\n**Time Complexity:** `O(n)`\n**Space Complexity:** `O(1)`\n\n-----------------------\n## Method 3: Using `.pop()`\n```\n\tdef removeDuplicates(self, nums: List[int]) -> int:\n\t\ti = 1\n\t\twhile i < len(nums):\n\t\t\tif nums[i] == nums[i - 1]:\n\t\t\t\tnums.pop(i)\n\t\t\telse:\n\t\t\t\ti += 1\n\t\treturn len(nums)\n```\n-----------------------\n## Method 4: Using `OrderedDict.fromkeys()`\n```\nfrom collections import OrderedDict\nclass Solution(object):\n def removeDuplicates(self, nums):\n nums[:] = OrderedDict.fromkeys(nums)\n return len(nums)\n```\n-------------------\n-----------------------\nAs a total beginner, I am writing these all out to help myself, and hopefully also help anyone out there who is like me at the same time.\n\nPlease upvote\u2B06\uFE0F if you find this helpful or worth-reading for beginners in anyway.\nYour upvote is much more than just supportive to me. \uD83D\uDE33\uD83E\uDD13\uD83E\uDD70\n\nIf you find this is not helpful, needs improvement, or is questionable, would you please leave a quick comment below to point out the problem before you decide to downvote? It will be very helpful for me (maybe also others) to learn as a beginner.\n\nThank you very much either way \uD83E\uDD13. | 575 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
[VIDEO] Visualization of O(n) Solution | remove-duplicates-from-sorted-array | 0 | 1 | https://www.youtube.com/watch?v=oMr9lehS7Us\n\nOne option is to use the pop() method to pop any duplicates that are detected, but using pop() is actually very inefficient because if we pop an element near the start of the array, we now have to shift all the other elements back 1 space. So each pop() runs in O(n) time, and in the worst case, we\'d have to pop n-1 elements, so the algorithm would run in O(n<sup>2</sup>) time.\n\nInstead, we\'ll use an O(n) 2-pointer approach. One pointer, `replace`, will keep track of which element we need to overwrite/replace. The other one, loop variable `i`, will traverse the entire array and detect duplicates. Since we know the array is already sorted, we can detect duplicates by comparing each element to the one before it. If they\'re the same, then we\'ve found a duplicate.\n\nIf a duplicate is found, we just keep incrementing `i` while keeping `replace` at the same spot. Basically, we keep searching for the next unique element. Once a unique element is found, we overwrite the element at the `replace`index with the unique one we just found. Then we increment `replace` so that it\'s ready to write at the next slot.\n\nAt the end, we can just return `replace` since it\'s been keeping track of the index of the last unique element written.\n\n# Code\n```\nclass Solution(object):\n def removeDuplicates(self, nums):\n replace = 1\n for i in range(1, len(nums)):\n if nums[i-1] != nums[i]:\n nums[replace] = nums[i]\n replace += 1\n return replace\n``` | 10 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
🔥Beats 100% | C++ | Java | Python | Javascript | Ruby | C | O(n) Solution ❣️| Detailed Explanation | remove-duplicates-from-sorted-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to remove duplicates from a sorted integer array nums while keeping track of the number of unique elements. The function should return the count of unique elements and modify the input array in-place to contain only the unique elements at the beginning in the same order.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First, we check if the input vector nums is empty. If it is empty, there are no unique elements, so we return 0.\n\n2. We initialize a variable k to 1. This variable will keep track of the count of unique elements in the modified nums array.\n\n3. We iterate through the input vector nums starting from the second element (index 1) using a for loop.\n\n4. Inside the loop, we compare the current element nums[i] with the previous unique element nums[k - 1]. If they are not equal, it means we have encountered a new unique element. In this case, we update the nums[k] position with the current element to keep it in place. We then increment k to indicate that we have found one more unique element.\n\n5. After the loop completes, k contains the count of unique elements, and the first k elements of the nums vector contain the unique elements in the same order they appeared in the input.\n\n6. We return the value of k as the final count of unique elements.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this algorithm is O(n), where n is the number of elements in the input vector nums. This is because we iterate through the input vector once, and each iteration takes constant time.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this algorithm is O(1) because it modifies the input array in-place without using any additional data structures that depend on the size of the input.\n\n---\n\n# \uD83D\uDCA1"If you have advanced to this point, I kindly request that you consider upvoting this solution to broaden its reach among others."\u2763\uFE0F\uD83D\uDCA1\n\n---\n\n```C++ []\nclass Solution {\npublic:\n int removeDuplicates(vector<int>& nums) {\n if (nums.empty()) {\n return 0;\n }\n\n int k = 1; // Initialize the count of unique elements to 1\n for (int i = 1; i < nums.size(); i++) {\n if (nums[i] != nums[i - 1]) {\n nums[k] = nums[i]; // Overwrite the next unique element\n k++;\n }\n }\n \n return k;\n }\n};\n\n```\n```Java []\npublic class Solution {\n public int removeDuplicates(int[] nums) {\n if (nums.length == 0) {\n return 0;\n }\n\n int k = 1; // Initialize the count of unique elements to 1\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] != nums[k - 1]) {\n nums[k] = nums[i]; // Overwrite the next unique element\n k++;\n }\n }\n \n return k;\n }\n}\n\n```\n```Python []\nclass Solution:\n def removeDuplicates(self, nums):\n if not nums:\n return 0\n \n k = 1 # Initialize the count of unique elements to 1\n for i in range(1, len(nums)):\n if nums[i] != nums[i - 1]:\n nums[k] = nums[i] # Overwrite the next unique element\n k += 1\n \n return k\n\n```\n```Javascript []\nfunction removeDuplicates(nums) {\n if (nums.length === 0) {\n return 0;\n }\n\n let k = 1; // Initialize the count of unique elements to 1\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] !== nums[k - 1]) {\n nums[k] = nums[i]; // Overwrite the next unique element\n k++;\n }\n }\n\n return k;\n}\n\n```\n```C []\nint removeDuplicates(int* nums, int numsSize) {\n if (numsSize == 0) {\n return 0;\n }\n\n int k = 1; // Initialize the count of unique elements to 1\n for (int i = 1; i < numsSize; i++) {\n if (nums[i] != nums[k - 1]) {\n nums[k] = nums[i]; // Overwrite the next unique element\n k++;\n }\n }\n\n return k;\n}\n\n```\n```Ruby []\nclass Solution\n def remove_duplicates(nums)\n return 0 if nums.empty?\n\n k = 1 # Initialize the count of unique elements to 1\n (1...nums.size).each do |i|\n if nums[i] != nums[k - 1]\n nums[k] = nums[i] # Overwrite the next unique element\n k += 1\n end\n end\n\n k\n end\nend\n\n```\n\n# Do Upvote if you like the solution and Explanation please \u2763\uFE0F | 43 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
8 lines two pointer in #python | remove-duplicates-from-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n i,j=0,1\n while i<=j and j<len(nums):\n if nums[i]==nums[j]:\n j+=1\n else:\n nums[i+1]=nums[j]\n i+=1\n return i+1\n\n\n \n```\n# Consider upvoting if found helpul\n \n\n | 169 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
Beats 97.98% | Remove Duplicates from Sorted Array...... | remove-duplicates-from-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The idea is to use two pointers, one (i) to keep track of the position of the last unique element in the modified array, and another (j) to iterate through the array.\n- When a different element is found, update the modified array by moving the pointer (i) and copying the unique element to the new position.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Use two pointers, i and j, to iterate through the array.\n- Compare elements at positions j and i. If they are different, update i and copy the unique element to position i.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe program iterates through the array once, so the time complexity is O(n), where n is the length of the input array. So, it has linear time complexity\n\n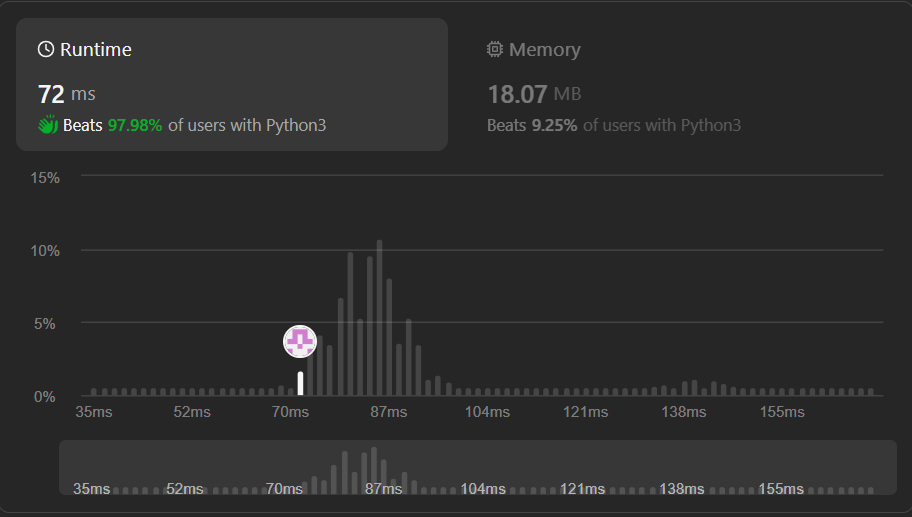\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe algorithm modifies the input array in-place, so the space complexity is O(1), indicating constant space usage regardless of the input size.\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n # Initialize a pointer i at the beginning of the array\n i = 0\n\n # Iterate through the array starting from the second element (j = 1)\n for j in range(1, len(nums)):\n # If the current element is different from the previous element\n if nums[j] != nums[i]:\n # Increment i to move to the next unique element\n i += 1\n # Update the current position (i) with the unique element (nums[j])\n nums[i] = nums[j]\n\n # Return the length of the modified array (i + 1)\n return i + 1\n\n``` | 4 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
Two Pointer | remove-duplicates-from-sorted-array | 0 | 1 | \n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n\n i,j=0,1\n while i<=j and j<len(nums):\n if nums[i]==nums[j]:\n j+=1\n\n else:\n nums[i+1]=nums[j]\n i+=1\n\n return i+1\n``` | 2 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
help me modify my code to decrease the runtime | remove-duplicates-from-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ni am a beginner and when solving i did use the prebuilt function count() in python to know the number of occurances of the item in the array \n# Approach\n<!-- Describe your approach to solving the problem. -->\ni made use of the count() function in python to solve the problem \n\n# Complexity\n- Time complexity:O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n for i in nums:\n if nums.count(i)==1:\n continue\n elif nums.count(i)>1:\n for j in range(nums.count(i)-1):\n nums.remove(i)\n \n``` | 0 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
Python Easy Solution || 100% | remove-duplicates-from-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n if len(set(nums))==len(nums):\n return len(nums)\n else:\n res=[]\n i=0\n while nums[i]!="_":\n if nums[i] in set(res):\n nums.pop(i)\n nums.append(\'_\')\n else:\n res.append(nums[i])\n i+=1\n return len(res)\n``` | 1 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
EASY PYTHON SOLUTION | remove-duplicates-from-sorted-array | 0 | 1 | ```\nclass Solution:\n def removeDuplicates(self, nums: List[int]) -> int:\n if len(nums)==1:\n return 1\n x=nums[0]\n i=0\n while i<len(nums)-1:\n if x==nums[1+i]:\n del nums[1+i]\n else:\n x=nums[1+i]\n i+=1\n return i+1\n``` | 8 | Given an integer array `nums` sorted in **non-decreasing order**, remove the duplicates [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm) such that each unique element appears only **once**. The **relative order** of the elements should be kept the **same**. Then return _the number of unique elements in_ `nums`.
Consider the number of unique elements of `nums` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the unique elements in the order they were present in `nums` initially. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int\[\] expectedNums = \[...\]; // The expected answer with correct length
int k = removeDuplicates(nums); // Calls your implementation
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** 2, nums = \[1,2,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,0,1,1,1,2,2,3,3,4\]
**Output:** 5, nums = \[0,1,2,3,4,\_,\_,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-100 <= nums[i] <= 100`
* `nums` is sorted in **non-decreasing** order. | In this problem, the key point to focus on is the input array being sorted. As far as duplicate elements are concerned, what is their positioning in the array when the given array is sorted? Look at the image above for the answer. If we know the position of one of the elements, do we also know the positioning of all the duplicate elements? We need to modify the array in-place and the size of the final array would potentially be smaller than the size of the input array. So, we ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements. Essentially, once an element is encountered, you simply need to bypass its duplicates and move on to the next unique element. |
✅Best 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | remove-element | 1 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nThe intuition behind this solution is to iterate through the array and keep track of two pointers: `index` and `i`. The `index` pointer represents the position where the next non-target element should be placed, while the `i` pointer iterates through the array elements. By overwriting the target elements with non-target elements, the solution effectively removes all occurrences of the target value from the array.\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n1. Initialize `index` to 0, which represents the current position for the next non-target element.\r\n2. Iterate through each element of the input array using the `i` pointer.\r\n3. For each element `nums[i]`, check if it is equal to the target value.\r\n - If `nums[i]` is not equal to `val`, it means it is a non-target element.\r\n - Set `nums[index]` to `nums[i]` to store the non-target element at the current `index` position.\r\n - Increment `index` by 1 to move to the next position for the next non-target element.\r\n4. Continue this process until all elements in the array have been processed.\r\n5. Finally, return the value of `index`, which represents the length of the modified array.\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n$$ O(n) $$\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n$$ O(1) $$\r\n\r\n# Code\r\n```C++ []\r\nclass Solution {\r\npublic:\r\n int removeElement(vector<int>& nums, int val) {\r\n int index = 0;\r\n for(int i = 0; i< nums.size(); i++){\r\n if(nums[i] != val){\r\n nums[index] = nums[i];\r\n index++;\r\n }\r\n }\r\n return index;\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n public int removeElement(int[] nums, int val) {\r\n int index = 0;\r\n for (int i = 0; i < nums.length; i++) {\r\n if (nums[i] != val) {\r\n nums[index] = nums[i];\r\n index++;\r\n }\r\n }\r\n return index;\r\n }\r\n}\r\n```\r\n```Python3 []\r\nclass Solution:\r\n def removeElement(self, nums: List[int], val: int) -> int:\r\n index = 0\r\n for i in range(len(nums)):\r\n if nums[i] != val:\r\n nums[index] = nums[i]\r\n index += 1\r\n return index\r\n```\r\n\r\n\r\n\r\n\r\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\r\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\r\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\r\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\r\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\r\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\r\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\r\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\r\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\r\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\r\n10. **Practice them in a row for better understanding and please Upvote for more questions.**\r\n\r\n\r\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\r\n | 1,020 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
2nd | remove-element | 0 | 1 | 2\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n k = len(nums)\n i = 0\n while i < k:\n if nums[i] == val:\n nums[i] = nums[k-1]\n nums[k-1] = \'_\'\n k -= 1\n i -= 1\n i += 1\n return k\n \n\n``` | 1 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
[VIDEO] Clear Visualization of O(n) Solution | remove-element | 0 | 1 | https://youtu.be/pGKDzt0gk-A\n\nOne way to do this is to check every element of `nums`, and if an element is equal to `val`, then we use the pop method to pop it off. This works, but the problem is that the pop method is very inefficient because if we pop an element near the start of the array, all the other elements have to be shifted back one spot. Each shift runs in O(n) time, and in the worst case, we\'d have to do n shifts, so this algorithm ends up running in O(n<sup>2</sup>) time.\n\nInstead, we can use a two pointer approach that overwrites the first `k` elements of the array, where `k` is the number of elements that are not equal to `val`. The index variable `i` keeps track of the next spot to overwrite in the array, and we use `x` to check the value of each element and compare it to `val`.\n\nIf an element is equal to `val`, we just move on and don\'t do anything. Basically, we keep searching until we find an element that is not equal to `val`. Once we do find an element not equal to `val`, we write it to the array at index `i`, then increment `i` so that it\'s ready to write at the next spot.\n\nAt the end, we can just return `i` since it has been incremented exactly once for each element found that is not equal to `val`.\n\n```\nclass Solution(object):\n def removeElement(self, nums, val):\n i = 0\n for x in nums:\n if x != val:\n nums[i] = x\n i += 1\n return i\n``` | 12 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
2 Lines of Code Python3 | remove-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n while val in nums:\n nums.remove(val)\n#please upvote me it would encourage me alot\n\n``` | 117 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
✔️💯% || Easy explanation || Beginner Friendly🔥🔥 | remove-element | 1 | 1 | # Intuition\nThe problem asks to remove all occurrences of a specific value (val) in the given array (nums) in-place. Additionally, it requires returning the count of elements in the modified array that are not equal to the given value. The order of the elements may change after the removal.\n\n# Approach\nWe can solve this problem efficiently by using a two-pointer approach. The basic idea is to maintain two pointers, one for iterating through the array (i), and another for updating the modified array without the specified value (k).\n\n**Here are the steps:**\n\n***Initialize Pointers:***\n\nInitialize two pointers, i and k, both starting from index 0.\n\n***Iterate Through the Array:***\nIterate through the array using the i pointer.\nIf the current element is not equal to the specified value (val), update the array at the k index with the current element and increment k.\nContinue this process until the end of the array.\n\n***Return Result:***\nThe value of k represents the count of elements in the modified array that are not equal to the specified value.\n\n***Modify the Original Array:***\nAfter determining the count, we can modify the original array by copying the first k elements from the modified array back to the original array.\nReturn the Count:\n\nReturn the value of k.\n\n# Code\n\n```c++ []\nclass Solution {\npublic:\n int removeElement(vector<int>& nums, int val) {\n int k = 0;\n for(int i = 0; i< nums.size(); i++){\n if(nums[i] != val){\n nums[k] = nums[i];\n k++;\n }\n }\n return k;\n }\n};\n```\n```java []\nclass Solution {\n public int removeElement(int[] nums, int val) {\n int k = 0;\n for (int i = 0; i < nums.length; i++) {\n if (nums[i] != val) {\n nums[k] = nums[i];\n k++;\n }\n }\n return k;\n }\n}\n```\n```python []\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n k = 0\n for i in range(len(nums)):\n if nums[i] != val:\n nums[k] = nums[i]\n k += 1\n return k\n```\n```javascript []\nfunction removeElement(nums, val) {\n let k = 0;\n for (let i = 0; i < nums.length; i++) {\n if (nums[i] !== val) {\n nums[k] = nums[i];\n k++;\n }\n }\n return k;\n}\n```\n\n\n# Explanation\n\nIn Example 1,\n val = 3. We iterate through the array, and when nums[i] is not equal to val, we update nums[k] with that value and increment k. After the iteration, the modified array becomes [2, 2, _, _], and k is 2.\n\nIn Example 2, \nval = 2. After the iteration, the modified array becomes [0, 1, 4, 0, 3, _, _, _], and k is 5.\n\nThe modified array is sorted and contains the first k elements not equal to val. The final count k is returned as the result.\n\nThis approach modifies the array in-place without using extra space and efficiently returns the count of elements not equal to the specified value. | 3 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
simple easy solution ||beats 93% 🤖💻🧑💻 | remove-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n ind=0\n for i in range(len(nums)):\n if val!=nums[i]:\n nums[ind]=nums[i]\n ind+=1\n \n \n return ind\n\n``` | 2 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Python two pointer| Beats 99% | remove-element | 0 | 1 | ```\nGiven : val = 2\n1 2 2 2 5 2 5 \ni j\nFirst Start from the far end \n1 2 2 2 5 2 5 \n i j\nwhen nums[i] == val , nums[i] = nums[j]\n1 2 2 2 5 2 5 \n i j \nif(num[j]) is also val then move it left till its not\n1 5 5 2 2 2 5 \n i j \nwhen i==j.. stop\n1 5 5 2 2 2 5 \n i,j\nyou see that i can still be val, \nso we check before returning the answer \n\n\n\n```\n\n\n```\n def removeElement(self, nums: List[int], val: int) -> int:\n\n i,j=0,len(nums)-1;\n if(j==-1): return 0\n while(i<j):\n if(nums[i]==val):\n while(i<j and nums[j]==val): \n j-=1\n nums[i]=nums[j];\n j-=1\n continue;\n i+=1\n return i+1 if nums[i]!=val else i\n\n``` | 8 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Two approach for easy understanding in Python | With and Without python functions | remove-element | 0 | 1 | # Approach1\n## Time complexity: O(nlogn)\n## Space Complexity = O(1)\n\n# Approach2\n## Time complexity: O(n)\n## Space Complexity = O(1)\n\n# Code\n``` Approach1 []\n\n# Iterate linearly over the nums array.\n# Find the nums with val and replace it with something else.\n# Sort the elements and return the count \n\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n count = 0\n for i in range(len(nums)):\n if nums[i] == val:\n nums[i] = 51\n count += 1\n \n nums[:] = sorted(nums)\n\n return len(nums) - count\n```\n```Approach2 []\n\n# Iterate linearly over the nums array\n# Maintain a count of unique numbers\n# If you encounter a unique number, move it to nums[count]\n# Return the count of unique elements\n\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n ind = 0\n for num in nums:\n if num != val:\n nums[ind] = num\n ind += 1\n \n return ind\n\n``` | 2 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
a brilliant solution from an outstanding and gorgeous scientist | remove-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n j = len(nums)-1\n i = 0\n\n while j -i >= 1:\n if nums[j] == val:\n j = j-1\n \n else:\n if nums[i] == val:\n nums[i] = nums[j]\n nums[j] = val\n j = j-1\n i += 1\n if nums[i] != val:\n i += 1\n if i == j :\n if nums[j]==val:\n \n return i\n else: \n return i+1\n if i-j ==1:\n return i\n\n``` | 2 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Removing by sorting (welcome to ask questions :)) | remove-element | 0 | 1 | # Intuition\nSort elemts that are equal to val and remove them\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSort elements that are equal to val and leave that are not equal\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n nums[:] = [x for x in nums if x != val]\n return len(nums)\n \n``` | 3 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
[ PYTHON ] Simple Two Pointer Solution Beats 95% || | remove-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n if not nums:\n return 0\n\n left = 0 \n right = len(nums) - 1 \n\n while left <= right:\n if nums[left] == val:\n nums[left], nums[right] = nums[right], nums[left] \n right -= 1 \n else:\n left += 1\n \n return left\n``` | 5 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Beat 100% Python One Line, Most Pythonic and List Comprehension No While Loops | remove-element | 0 | 1 | # Intuition\nSeems like any other pythonic list comprehension problem. Only hurdle is that it has to be in place\n# Approach\nBy using nums[:] you can make it in place\n# Complexity\n- Time complexity:\n\n- Space complexity:\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n\n nums[:] = [num for num in nums if num != val]\n \n return len(nums)\n``` | 8 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Two-Pointer In-Place Removal Solution. | remove-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this approach is to iterate through the `nums` array and keep track of the number of elements not equal to `val`. We will move the elements not equal to `val` to the front of the array and update the count accordingly.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe main idea is to maintain **two pointers** - one to iterate through the `nums` array `indx`, and another to track the next available position for elements not equal to `val` - `num_of_nums`. \nWhenever we encounter an element that is not equal to `val`, we move it to the front of the array by assigning it to `nums[num_of_nums]`. We then increment `num_of_nums` to indicate the addition of a new element to the modified array.\n1. Initialize a variable `num_of_nums` to keep track of the number of elements not equal to `val`.\n2. Iterate through each element in the `nums` array using a `for` loop.\n3. Check if the current element `nums[indx]` is not equal to `val`.\n- If it is not equal, it means it should be included in the modified array. We move this element to the front of the array by assigning it to `nums[num_of_nums]`, where `num_of_nums` is the index of the next available position in the modified array.\n- Increment `num_of_nums` by 1 to reflect the addition of a new element to the modified array.\n4. After processing all the elements in the `nums` array, the modified array will contain the elements not equal to `val` in the first `num_of_nums` positions.\n5. Return `num_of_nums`, which represents the number of elements not equal to `val`.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this approach is $$O(n)$$, where $$n$$ is the length of the `nums` array. This is because we iterate through each element in the array once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(1)$$ since we are modifying the `nums` array in-place and using a constant amount of extra space to store the `num_of_nums` variable.\n\n# Runtime & Memory\n\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n num_of_nums = 0\n for indx in range(len(nums)):\n if nums[indx] != val:\n nums[num_of_nums] = nums[indx]\n num_of_nums += 1\n return num_of_nums\n\n``` | 1 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Python - Remove Element - just 6 lines of code | remove-element | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeElement(self, nums: List[int], val: int) -> int:\n n = 0\n for i in range(len(nums)):\n if nums[i] == val: \n nums[i] = float(\'inf\') \n n += 1\n nums.sort()\n return(len(nums) - n)\n``` | 1 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
⭐C#, Java, Python3,JavaScript Solution (Faster than 90~100%) | remove-element | 1 | 1 | \nSee the code : **\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-27-remove-element-from-sorted-array-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-27-remove-element-from-sorted-array-solution-and-explanation-en/)\u2B50**\n\n**Submissioon detail**\n\n\n\n\n\n**\uD83E\uDDE1See more LeetCode solution : [Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)** | 8 | Given an integer array `nums` and an integer `val`, remove all occurrences of `val` in `nums` [**in-place**](https://en.wikipedia.org/wiki/In-place_algorithm). The order of the elements may be changed. Then return _the number of elements in_ `nums` _which are not equal to_ `val`.
Consider the number of elements in `nums` which are not equal to `val` be `k`, to get accepted, you need to do the following things:
* Change the array `nums` such that the first `k` elements of `nums` contain the elements which are not equal to `val`. The remaining elements of `nums` are not important as well as the size of `nums`.
* Return `k`.
**Custom Judge:**
The judge will test your solution with the following code:
int\[\] nums = \[...\]; // Input array
int val = ...; // Value to remove
int\[\] expectedNums = \[...\]; // The expected answer with correct length.
// It is sorted with no values equaling val.
int k = removeElement(nums, val); // Calls your implementation
assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
assert nums\[i\] == expectedNums\[i\];
}
If all assertions pass, then your solution will be **accepted**.
**Example 1:**
**Input:** nums = \[3,2,2,3\], val = 3
**Output:** 2, nums = \[2,2,\_,\_\]
**Explanation:** Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Example 2:**
**Input:** nums = \[0,1,2,2,3,0,4,2\], val = 2
**Output:** 5, nums = \[0,1,4,0,3,\_,\_,\_\]
**Explanation:** Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).
**Constraints:**
* `0 <= nums.length <= 100`
* `0 <= nums[i] <= 50`
* `0 <= val <= 100` | The problem statement clearly asks us to modify the array in-place and it also says that the element beyond the new length of the array can be anything. Given an element, we need to remove all the occurrences of it from the array. We don't technically need to remove that element per-say, right? We can move all the occurrences of this element to the end of the array. Use two pointers! Yet another direction of thought is to consider the elements to be removed as non-existent. In a single pass, if we keep copying the visible elements in-place, that should also solve this problem for us. |
Simple and Easy Solution🔥🔥|| Explained for finding first occurrence of string ||Beats 100%🔥🔥 | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | # Intuition\nThe problem calls for finding the first occurrence of a substring (needle) within another string (haystack). If the needle is not present in the haystack, the function should return -1.\n# Approach\n1. Initialization: Get lengths of needle (m) and haystack (n).\n2. Equal Strings Check: If haystack equals needle, return 0.\n3. Substring Search: Iterate through possible starting positions (i) where remaining haystack length is enough.\n4. Character Comparison: For each starting position, compare characters with needle. If a mismatch is found, break out.\n5. Return Position if Match: If complete match found, return the starting position.\n6. Return -1 if No Match: If no match found, return -1.\n# Complexity\n- Time complexity:\nO(n * m), where n is the length of the haystack and m is the length of the needle. In the worst case, the algorithm checks each possible starting position and compares up to m characters.\n- Space complexity:\nO(1), as the algorithm uses a constant amount of space regardless of the input size.\n# Code\n```C++ []\nclass Solution {\npublic:\n int strStr(string haystack, string needle) {\n int m = needle.length();\n int n = haystack.length();\n\n // Check if both strings are equal\n if (haystack == needle) {\n return 0;\n }\n\n // If lengths are different, perform substring search\n for (int i = 0; i <= n - m; i++) {\n int j;\n for (j = 0; j < m; j++) {\n if (haystack[i + j] != needle[j]) {\n break;\n }\n }\n if (j == m) {\n return i;\n }\n }\n\n return -1;\n }\n};\n```\n\n```python []\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n m = len(needle)\n n = len(haystack)\n\n # Check if both strings are equal\n if haystack == needle:\n return 0\n\n # If lengths are different, perform substring search\n for i in range(n - m + 1):\n for j in range(m):\n if haystack[i + j] != needle[j]:\n break\n else:\n return i\n\n return -1\n\n# Example usage:\n# solution = Solution()\n# result = solution.strStr("hello", "ll")\n# print(result)\n\n | 2 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
[VIDEO] Visualization of O(n) KMP Algorithm | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | https://youtu.be/0iDiUuHZE_g\n\nThe KMP algorithm improves the brute force algorithm from O(m*n) to O(m+n) and consists of two parts. The first part is the preprocessing step, where we find the length of "the longest proper prefix that is also a suffix" for every prefix in `needle`.\n\nThe second part is the main algorithm, where we compare `needle` and `haystack` letter-by-letter. If two characters match, we move both pointers up and see how far we can keep going. If they don\'t match, then we use the array created in the preprocessing step to determine how far to move up `needle` to compare the next characters. For a detailed explanation, please see the video - it\'s very difficult to explain without visuals. But the idea is that when traversing `needle` and hitting a mismatch, we know that any proper prefixes that are also a suffix will overlap, so we can skip those characters.\n```\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n lps = [0] * len(needle)\n\n # Preprocessing\n pre = 0\n for i in range(1, len(needle)):\n while pre > 0 and needle[i] != needle[pre]:\n pre = lps[pre-1]\n if needle[pre] == needle[i]:\n pre += 1\n lps[i] = pre\n\n # Main algorithm\n n = 0 #needle index\n for h in range(len(haystack)):\n while n > 0 and needle[n] != haystack[h]:\n n = lps[n-1]\n if needle[n] == haystack[h]:\n n += 1\n if n == len(needle):\n return h - n + 1\n\n return -1\n``` | 15 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
Easiest, Big IQ, fast solution | Beats 97% of solutions | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | \n# Code\n```\nclass Solution(object):\n def strStr(self, haystack, needle):\n # makes sure we don\'t iterate through a substring that is shorter than needle\n for i in range(len(haystack) - len(needle) + 1):\n # check if any substring of haystack with the same length as needle is equal to needle\n if haystack[i : i+len(needle)] == needle:\n # if yes, we return the first index of that substring\n return i\n # if we exit the loop, return -1 \n return -1\n```\n\n\n\n | 28 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
one line code using python ( TC: O(N) | SC: O(1)) | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | # Intuition\nThe intuition behind this approach is to use the built-in find() function in Python to find the index of the first occurrence of the needle string within the haystack string. If the needle is not found, it returns -1.\n# Approach\nThe approach is simple and straightforward. We can directly use the find() function on the haystack string and pass the needle string as the argument. The find() function returns the index of the first occurrence of the needle string in the haystack string, or -1 if it is not found.\n\n\n# Complexity\n- Time complexity:\nThe find() function has a time complexity of O(n), where n is the length of the haystack string.\n- Space complexity:\nThe space complexity is O(1) since no extra space is used.\n\n# Code\n```\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n return haystack.find(needle)\n```\n##### reach me to discuss any problems - https://www.linkedin.com/in/naveen-kumar-g-500469210/\n#\n#\n\n\n | 47 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
Find the Index of the First Occurrence in a String - 3 | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n try: \n index = haystack.find(needle)\n return index\n except ValueError:\n return -1\n``` | 0 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
EASIEST PYTHON SOLUTION BEATS 99.6% MEMORY | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n try: return haystack.find(needle) \n except: return -1\n``` | 1 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
Python String Search | ".find" & ".index" | find-the-index-of-the-first-occurrence-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to find the index of the first occurrence of the target string in the given input string if it is a substring.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nString search logic:\n1. Check if the target string is a substring of the input string.\n2. If it is a substring, return the index of its first occurrence.\n3. If the target string is not a substring, return -1.\n\nBoth of the following approaches share the same logic of finding the first occurrence of the target string. However, they differ in implementation:\n\n- `.find` method performs the search logic automatically (with no error)\n- `.index` method requires additional code for handling exceptions when the target is not found\n\n## Approach 1: Using `.find()` method\n\n> `str.find(target)` \u2192 it finds the first occurrence of the target value\n\nThis method **returns -1** if the value is not found.\n\n## Approach 2: Using `.index()` method\n\n> `str.index(target)` \u2192 it finds the first occurrence of the target value\n\nThis method **raises an exception** if the value is not found.\n\n# Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`n` is the length of the input string we are going through to find the target string. Both methods have linear time complexity because their performance scales proportionally with the length of the input string, examining each character in the worst case.\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of both methods is constant because they do not use additional data structures whose size depends on the input length; instead, they use a fixed amount of memory to store variables and control flow.\n\n# Code\n### Approach 1 Solution:\n```\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n return haystack.find(needle)\n```\n\n### Approach 2 Solution:\n````\nclass Solution:\n def strStr(self, haystack: str, needle: str) -> int:\n if needle in haystack:\n return haystack.index(needle)\n return -1\n```` | 3 | Given two strings `needle` and `haystack`, return the index of the first occurrence of `needle` in `haystack`, or `-1` if `needle` is not part of `haystack`.
**Example 1:**
**Input:** haystack = "sadbutsad ", needle = "sad "
**Output:** 0
**Explanation:** "sad " occurs at index 0 and 6.
The first occurrence is at index 0, so we return 0.
**Example 2:**
**Input:** haystack = "leetcode ", needle = "leeto "
**Output:** -1
**Explanation:** "leeto " did not occur in "leetcode ", so we return -1.
**Constraints:**
* `1 <= haystack.length, needle.length <= 104`
* `haystack` and `needle` consist of only lowercase English characters. | null |
Easy Solution in Python3 | divide-two-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def divide(self, dividend: int, divisor: int) -> int:\n if dividend == -2147483648 and divisor == -1:\n return 2147483647\n else:\n division = dividend/divisor\n if division > 0:\n return floor(division)\n return ceil(division)\n\n\n \n``` | 2 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
Python3 - easiest solution | divide-two-integers | 0 | 1 | 1) Define the result\'s sign and operate with positive dividend and divisor.\n2) Calculate the result using the length of range.\n3) Apply the sign.\n4) Apply the 32-bit integer limitations.\n\nNo multiplication, division, or mod used.\n\n\n```\nclass Solution:\n def divide(self, dividend: int, divisor: int) -> int:\n sign = -1 if (dividend >= 0 and divisor < 0) or (dividend < 0 and divisor >= 0) else 1\n dividend = abs(dividend)\n divisor = abs(divisor)\n result = len(range(0, dividend-divisor+1, divisor))\n if sign == -1:\n result = -result\n minus_limit = -(2**31)\n plus_limit = (2**31 - 1)\n result = min(max(result, minus_limit), plus_limit)\n return result\n\n | 41 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
Bits of Python | divide-two-integers | 0 | 1 | \n# Code\n```\nclass Solution:\n def divide(self, dividend: int, divisor: int) -> int:\n sign = -1 if (dividend >= 0 and divisor < 0) or (dividend < 0 and divisor >= 0) else 1\n dividend = abs(dividend)\n divisor = abs(divisor)\n result = len(range(0, dividend-divisor+1, divisor))\n if sign == -1:\n result = -result\n minus_limit = -(2**31)\n plus_limit = (2**31 - 1)\n result = min(max(result, minus_limit), plus_limit)\n return result\n``` | 4 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
Efficient Bit Manipulation Algorithm for Integer Division without Multiplication or Mod Operator. | divide-two-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to divide two integers, `dividend` and `divisor`, and return the quotient without using multiplication, division, and mod operator.\n\nWe can solve this problem using bit manipulation and binary search. We can find the largest multiple of the divisor that is less than or equal to the dividend using bit manipulation. Then we can perform division using binary search.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Handle division by zero: If the divisor is 0, return `2**31 - 1`.\n\n- Handle overflow case: If the dividend is `-2**31` and divisor is `-1`, return `2**31 - 1`.\n\n- Get the sign of the result: If both dividend and divisor are negative or positive, the sign of the result will be positive. If either dividend or divisor is negative, the sign of the result will be negative.\n\n- Find the largest multiple of the divisor that is less than or equal to the dividend using bit manipulation. We can do this by left-shifting the divisor and multiple by 1 until the left-shifted divisor is greater than the dividend.\n\n- Perform division using binary search. We can do this by right-shifting the divisor and multiple by 1 until multiple is 0. If the dividend is greater than or equal to the divisor, subtract the divisor from the dividend and add the multiple to the quotient. Repeat until multiple is 0.\n\n- Apply the sign to the quotient and return it.\n\n# Complexity\n- Time complexity: The time complexity of this solution is $$O(log(dividend))$$.\n\nFinding the largest multiple of the divisor that is less than or equal to the dividend takes `log(dividend)` iterations. Performing division using binary search takes `log(dividend) `iterations as well.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity of this solution is `O(1)`.\n\nWe only use a constant amount of extra space to store variables.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code Explanation\n\nThe code is an implementation of the binary division algorithm. The algorithm is used to divide two integers (dividend and divisor) and return the quotient (integer division result). Here is how the code works:\n\n- The function accepts two integer parameters, dividend and divisor, and returns an integer (quotient).\n- The function first checks if the divisor is zero. If it is, it returns the maximum 32-bit integer value (2^31 - 1). This is because dividing by zero is not possible, and we need to handle this edge case.\n- The function then checks for an overflow case where the dividend is the minimum 32-bit integer value (-2^31) and the divisor is -1. In this case, the quotient is the maximum 32-bit integer value (2^31 - 1) since dividing the minimum value by -1 would result in an overflow error.\n- The function determines the sign of the result by checking the signs of the dividend and divisor. If both are negative or both are positive, the sign is positive. Otherwise, the sign is negative, and we make both values positive for the next step.\n- The function then finds the largest multiple of the divisor that is less than or equal to the dividend. It does this by left-shifting the divisor and multiple variables (initially set to 1) until the shifted divisor is greater than the dividend. At this point, the last multiple that was less than or equal to the dividend is the largest multiple we need to find. The function keeps track of this multiple value and the divisor value for the next step.\n- The function then performs the division using binary search. It does this by right-shifting the divisor and multiple variables until multiple is zero. At each step, it checks if the dividend is greater than or equal to the divisor. If it is, it subtracts the divisor from the dividend, adds the multiple to the quotient, and continues the loop. Otherwise, it right-shifts the divisor and multiple variables to check for the next value. At the end of this step, the quotient variable contains the integer division result.\n- Finally, the function applies the sign to the result and returns it.\n\n\nOverall, the binary division algorithm is an efficient way to perform integer division using bit manipulation. The code handles edge cases such as division by zero and overflow and returns the correct result with the correct sign.\n\n\n\n\n\n\n```\nclass Solution:\n def divide(self, dividend: int, divisor: int) -> int:\n # Handle division by zero\n if divisor == 0:\n return 2**31 - 1\n \n # Handle overflow case\n if dividend == -2**31 and divisor == -1:\n return 2**31 - 1\n \n # Get the sign of the result\n sign = 1\n if dividend < 0:\n dividend = -dividend\n sign = -sign\n if divisor < 0:\n divisor = -divisor\n sign = -sign\n \n # Find the largest multiple of the divisor that is less than or equal to the dividend\n multiple = 1\n while dividend >= (divisor << 1):\n divisor <<= 1\n multiple <<= 1\n \n # Perform division using binary search\n quotient = 0\n while multiple > 0:\n if dividend >= divisor:\n dividend -= divisor\n quotient += multiple\n divisor >>= 1\n multiple >>= 1\n \n # Apply the sign to the result\n return sign * quotient\n\n``` | 17 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
My solution for this problem | divide-two-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# Complexity\n- Time complexity:O[log(y)]\n<!-- Add your time complexity here , e.g. $$O(n)$$ -->\n\n- Space complexity:O[1]\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def divide(self, dividend: int, divisor: int) -> int:\n x=abs(dividend)\n y=abs(divisor)\n a=x//y\n if (dividend<0 and divisor<0) or(dividend>0 and divisor>0):\n return min(2**31-1,a)\n else:\n return max(-(2**31),-a)\n\n \n\n \n``` | 0 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
Python fast code with detailed explanation | divide-two-integers | 0 | 1 | I took the code of [@tusizi](https://leetcode.com/problems/divide-two-integers/discuss/13403/Clear-python-code) and made it easier to understand by changing variable names, and adding a detailed explanation for each line. I\'m also not experienced myself and whatever I right here comes from discussion forums and googling. The high level idea is that you substract `dividend` by `divisor` until `dividend` is less than `divisor`. Also, the solution has two `while` loops. The inner `while` loop tries to substract `divisor`, `2*divisor`, `4*divisor` and so on, until `dividend` is less than `divisor` where it starts over the outer `while` loop. \n\n```\nclass Solution:\n# @return an integer\ndef divide(self, dividend, divisor):\n positive = (dividend < 0) is (divisor < 0) # 1\n dividend, divisor = abs(dividend), abs(divisor) # 2\n res = 0 # 3\n while dividend >= divisor: # 4\n curr_divisor, num_divisors = divisor, 1 # 5\n while dividend >= curr_divisor: # 6\n dividend -= curr_divisor # 7\n res += num_divisors # 8\n \n curr_divisor = curr_divisor << 1 # 9\n num_divisors = num_divisors << 1 # 10\n\t\t\t\t\n if not positive: # 11\n res = -res # 12\n\t\t\n return min(max(-2147483648, res), 2147483647) # 13\n```\n\n`#1`: `is` operator is similar to `==` operator except that it compares that whether both the operands refer to the same object or not. check [this](https://www.***.org/difference-operator-python/).\nSo here, if both of `dividend` and `divisor` have similar sign, it returns `True`. Otherwise, `False`. This will be used in line `#11` when we check if the `positive` variable is `True` or `False`. And, if it\'s not `True` (meaning if they don\'t have similar signs, we add a `-` to the output (`#12`). Note that in this example `==` works just fine as `is`. \n\n`#2`: No that we decided on the sign in line `#1`, we can use absolute values of `dividend` and `divisor`. That\'s what\'s being done here. \n\n`#3`: Initiating the output by setting it to zero. \n\n`#4`: So the high level idea is that we substract `divisor` from `dividend` until we can\'t substract anymore. Imagine you want to divide 7 by 2. 7-2 =5, 5-2=3, 3-2 = 1 ! You can\'t substract anymore. Them the `while` loope stops. \n\n`#5`: Now, we enter the main (tricky, challenging, confusing) part of the code. This line is not complicated. It simply initilize some values, meaning `curr_divisor` and `num_divisors\' with `divisor` and `1`, recpectively. This means we assume `curr_divisor = divisor` and `num_divisor = 1`, initially. \n\n`#7` and `#8`: These two lines are updating `dividend` and `res`. When you substract `dividend` by `curr_divisor`, you\'re basically saying if I was going to calculating the quotient of division, I could still cut another piece with the size of `divisor` from `dividend`, and that\'s why you update the `res` variable by num_divisor (`res += num_divisors` means `res = res + num_divisors`). \n\n`#9` and `#10`: `currdivisor = currdivisor << 1` is the same as `currdivisor = currdivisor 2`, and `numdivisors = numdivisors << 1`, is the same as`numdivisors = numdivisors2`. This is called bitwise operation. Check [this](https://wiki.python.org/moin/BitwiseOperators). `<<` sign is left-shifting bitwise operator which shift bits in binary of a number by one to the left. Imaging you have number 4, (`bin(4) = 0b100`)! doing `4 >> 1` make the new binary `1000` (shifted to the left by 1 and added a zero to the rightmost bit) which is the binary for 8. The reason it tries to do the multiplicaion is to fasten the process. From [here](https://leetcode.com/problems/divide-two-integers/discuss/13403/Clear-python-code/329694), A naive method here is to repeatedly subtract divisor from dividend, until there is none enough left. Then the count of subtractions will be the answer. Yet this takes linear time and is thus slow. A better method is to subtract divisor in a more efficient way. We can subtract divisor, 2divisor, 4divisor, 8*divisor... as is implemented above. .It will go to the outer loop once it cannot substract anymore of `curr_divisor` from `dividend`, and set the `curr_divisor = divisor` and tries the actual divisor (no 2 multiplications). \n\n`#13`: We are told by problem statement to limit the output to 32-bit integers, meaning the `res` parameter fall in the [-2^31, 2*^31-1] range. Here, the line has two components. First, it compares output (`res`) with -2^31 value and return the max of the two since we don\'t want values less than -2^31. Next, it compares the value from `max(-2147483648, res)` with the maximum allowable value (meaning 2^31). So, if we put `a = max(-2147483648, res)`, then it does `min(a, 2147483647)` and return the min of two since we\'re not allowed to go above 2^31 = 2147483647 number. \n\n=========================================\n\nFinal note: In order to fully understand the code, I suggest to grab a piece of paper and pen (or write on a notepad or something similar in out laptop/pc) and write a simple example and try to pass through the algorithm by hand. Here is an example from [this](https://leetcode.com/problems/divide-two-integers/discuss/13403/Clear-python-code/144026). \n\nLet\'s take an example: `50 / 4`\nAt the start,\n`curr_divisor, num_divisors = divisor, 1` # dividend = 50, curr_divisor = 4, num_divisors = 1\n`dividend -= curr_divisor` # dividend = 46, curr_divisor = 4 ,num_divisors = 1\n`res += num_divisors` # res = 1\n`num_divisors <<= 1 ` # dividend = 46, curr_divisor = 4 , num_divisors = 2\n`curr_divisor <<= 1` # dividend = 46, curr_divisor = 8 , num_divisors = 2\n\nSecond iteration:\n`dividend -= curr_divisor` # dividend = 38, curr_divisor = 8 , num_divisors= 2\n`res += num_divisors` # res = 3\n`num_divisors <<= 1` # dividend = 38, curr_divisor = 8 , num_divisors = 3\n`curr_divisor <<= 1` # dividend = 38, curr_divisor = 12 , num_divisors = 3\n\nand so on, when `dividend > curr_divisor`, we start over again with `curr_divisor = 4`, and `num_divisors = 1`\n\n\n===========================================================================\nFinal note 2: Since I believe if I could explain something to others in a simple manner, it would be helpful to me, I try to add more posts like this as I move forward through my leetcode journey. \n\nFinal note 3: There might be some typos in the writing above!! | 42 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
Python Subtraction O(logN) | divide-two-integers | 0 | 1 | You can refer to this [video solution](https://www.youtube.com/watch?v=xefkgtd44hg&ab_channel=CheatCodeNinja) \n\nHere we are doubling the divisor everytime and hence compressing the total number of subtraction operations. \nIf the doubled divisor is greater than the dividend, we reset our divisor to its initial value and try again.\n\nAt the end, we make sure that the output is within the given range and avoid an overflow.\n\n```\nclass Solution:\n def divide(self, dividend: int, divisor: int) -> int:\n a = abs(dividend)\n b=abs(divisor)\n \n negative = (dividend<0 and divisor>=0) or (dividend>=0 and divisor<0)\n \n output = 0\n \n while a>=b:\n counter = 1\n decrement = b\n \n while a>=decrement:\n a-=decrement\n \n output+=counter\n counter+=counter\n decrement+=decrement\n \n output = output if not negative else -output\n \n return min(max(-2147483648, output), 2147483647)\n | 12 | Given two integers `dividend` and `divisor`, divide two integers **without** using multiplication, division, and mod operator.
The integer division should truncate toward zero, which means losing its fractional part. For example, `8.345` would be truncated to `8`, and `-2.7335` would be truncated to `-2`.
Return _the **quotient** after dividing_ `dividend` _by_ `divisor`.
**Note:** Assume we are dealing with an environment that could only store integers within the **32-bit** signed integer range: `[-231, 231 - 1]`. For this problem, if the quotient is **strictly greater than** `231 - 1`, then return `231 - 1`, and if the quotient is **strictly less than** `-231`, then return `-231`.
**Example 1:**
**Input:** dividend = 10, divisor = 3
**Output:** 3
**Explanation:** 10/3 = 3.33333.. which is truncated to 3.
**Example 2:**
**Input:** dividend = 7, divisor = -3
**Output:** -2
**Explanation:** 7/-3 = -2.33333.. which is truncated to -2.
**Constraints:**
* `-231 <= dividend, divisor <= 231 - 1`
* `divisor != 0` | null |
Python solution using hash map | substring-with-concatenation-of-all-words | 0 | 1 | \n# Code\n```\nclass Solution:\n\n def calc(self ,i):\n\n cnt = 0\n ind = i\n while (ind < i+self.pl):\n news = self.s[ind : ind + self.n]\n if news in self.dic :\n self.dic[news] -= 1 \n if self.dic[news] == 0 :\n cnt += 1 \n ind += self.n\n else :\n return False \n if cnt == len(self.dic) :\n return True \n else :\n return False\n\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n self.s = s \n self.n = len(words[0])\n\n d = {}\n for x in words :\n if x in d :\n d[x] += 1 \n else :\n d[x] = 1 \n\n self.pl = len(words)*len(words[0])\n ans = []\n i = 0\n while(i< len(s) - self.pl + 1):\n self.dic = {x : d[x] for x in d}\n if self.calc(i) :\n ans += [i]\n i += 1\n else :\n i += 1\n \n return ans \n\n\n\n\n \n``` | 1 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
Simple sliding window solution (beats 99% for time) | substring-with-concatenation-of-all-words | 0 | 1 | \n\n# Approach\nTo solve this problem, we can use a sliding window approach combined with a hashmap to keep track of the word counts. The steps are as follows:\n\n1. Calculate Word Lengths and Total Length: Since all words in words are of the same length, calculate the length of each word and the total length of the concatenated substring.\n\n2. Create a Frequency Map for words: Map each word to its frequency in the words list.\n\n3. Sliding Window: Move a sliding window of the total length of the concatenated substring across s. In each window, break the window into substrings of the word\'s length and check if these substrings form a permutation of words.\n\n4. Track Word Counts: Use a hashmap to track the counts of words in the current window. If the count of a word exceeds its count in the words frequency map, it\'s not a valid window.\n\n5. Check for Valid Concatenation: If the hashmap of the current window matches the frequency map of words, then the current window is a valid concatenated substring. Add the start index of this window to the result.\n\n6. Return Indices: Return the starting indices of all valid windows.\n\n# Complexity\n- Time complexity:\n$$O(N\xD7K/L+M)$$\n\n- Space complexity:\n$$O(N\xD7K/L)$$\n\n# Code\n```\nclass Solution:\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n if not words or not s:\n return []\n\n word_length = len(words[0])\n total_length = word_length * len(words)\n word_count = {}\n\n # Create a frequency map for words\n for word in words:\n if word in word_count:\n word_count[word] += 1\n else:\n word_count[word] = 1\n\n result = []\n\n # Check each possible window in the string\n for i in range(word_length):\n left = i\n count = 0\n temp_word_count = {}\n\n for j in range(i, len(s) - word_length + 1, word_length):\n word = s[j:j + word_length]\n if word in word_count:\n temp_word_count[word] = temp_word_count.get(word, 0) + 1\n count += 1\n\n while temp_word_count[word] > word_count[word]:\n left_word = s[left:left + word_length]\n temp_word_count[left_word] -= 1\n left += word_length\n count -= 1\n\n if count == len(words):\n result.append(left)\n else:\n temp_word_count.clear()\n count = 0\n left = j + word_length\n\n return result\n``` | 2 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
Solution | substring-with-concatenation-of-all-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n\tstruct matcher {\n\t\tstruct info { int mtindex, count; };\n\t\tunordered_map<string_view, info>dict;\n\t\tint different_word_count;\n\n\t\tvector<int>slot;\n\t\tint maching_slot_count;\n\n\t\tmatcher(const vector<string>& words) {\n\t\t\tint mtind = 0;\n\t\t\tfor (auto& word : words) {\n\t\t\t\tauto find = dict.find(word);\n\t\t\t\tif (find != dict.end()) {\n\t\t\t\t\t++find->second.count;\n\t\t\t\t}\n\t\t\t\telse { dict[word] = { mtind++,1 }; }\n\t\t\t}\n\t\t\tdifferent_word_count = mtind;\n\t\t\tslot = vector<int>(different_word_count, 0);\n\t\t\tmaching_slot_count = 0;\n\t\t}\n\n\t\tvoid reset() {\n\t\t\tfor (auto& i : slot) { i = 0; }\n\t\t\tmaching_slot_count = 0;\n\t\t}\n\t\tbool match() {\n\t\t\treturn maching_slot_count == different_word_count;\n\t\t}\n\t\tvoid push(string_view sv) {\n\t\t\tauto find = dict.find(sv);\n\t\t\tif (find == dict.end())return;\n\t\t\tif (++slot[find->second.mtindex] == find->second.count) {\n\t\t\t\t++maching_slot_count;\n\t\t\t}\n\t\t}\n\t\tvoid pop(string_view sv) {\n\t\t\tauto find = dict.find(sv);\n\t\t\tif (find == dict.end())return;\n\t\t\tif (--slot[find->second.mtindex] == find->second.count - 1) {\n\t\t\t\t--maching_slot_count;\n\t\t\t}\n\t\t}\n\t};\n\tvector<int> findSubstring(string s, const vector<string>& words) {\n\t\tint word_count = words.size();\n\t\tint word_len = words[0].size();\n\n\t\tmatcher matcher(words);\n\n\t\tconst char* str = s.c_str();\n\t\tint len = s.size();\n\t\tvector<int> ret;\n\n\t\tfor (int off = 0; off < word_len; off++) {\n\t\t\tconst char* beg = str + off, * end = str + len;\n\t\t\tif (beg + word_len * word_count <= end) {\n\t\t\t\tmatcher.reset();\n\t\t\t\tfor (int i = 0; i < word_count; i++) {\n\t\t\t\t\tstring_view sv(beg + i * word_len, word_len);\n\t\t\t\t\tmatcher.push(sv);\n\t\t\t\t}\n\t\t\t\tif (matcher.match()) {\n\t\t\t\t\tret.push_back(beg - str);\n\t\t\t\t}\n\t\t\t\tconst char* pos = beg + word_len * word_count;\n\t\t\t\twhile (pos + word_len <= end) {\n\t\t\t\t\tstring_view del(beg, word_len);\n\t\t\t\t\tstring_view add(pos, word_len);\n\t\t\t\t\tbeg += word_len;\n\t\t\t\t\tpos += word_len;\n\t\t\t\t\tmatcher.pop(del);\n\t\t\t\t\tmatcher.push(add);\n\t\t\t\t\tif (matcher.match()) {\n\t\t\t\t\t\tret.push_back(beg - str);\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn ret;\n\t}\n};\n```\n\n```Python3 []\nclass Solution:\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n n_word = len(words)\n n_char = len(words[0])\n word2freq = {}\n for word in words:\n if word in word2freq:\n word2freq[word] += 1\n else:\n word2freq[word] = 1\n\n all_start_ind = []\n for start_ind in range(n_char):\n curr_map = {}\n curr_total = 0\n excessive = False\n for i in range(start_ind, len(s), n_char):\n word = s[i:i+n_char]\n if word in word2freq: # a valid word for permutation \n curr_total += 1\n if word in curr_map: # found valid word\n curr_map[word] += 1\n if curr_map[word] > word2freq[word]: \n excessive = word\n else:\n curr_map[word] = 1\n\n earliest_ind = i - (curr_total-1)*n_char\n while excessive:\n earliest_word = s[earliest_ind: earliest_ind+n_char]\n curr_map[earliest_word] -= 1\n curr_total -= 1\n if earliest_word == excessive:\n excessive = False\n break\n earliest_ind += n_char\n if curr_total == n_word:\n earliest_ind = i - (n_word-1)*n_char\n\n all_start_ind.append(earliest_ind)\n\n earliest_word = s[earliest_ind: earliest_ind+n_char]\n curr_total -= 1\n curr_map[earliest_word] -= 1\n else:\n curr_total = 0\n curr_map = {}\n return all_start_ind\n \n def check_map_equal(self, curr_map, ref_map) -> bool:\n for word, freq in curr_map.items():\n if word not in ref_map or freq != ref_map[word]:\n return False\n return True\n```\n\n```Java []\nclass Solution {\n public List<Integer> findSubstring(String s, String[] words) {\n int wordLength = words[0].length();\n int totalWordsLength = wordLength * words.length;\n Map<String, Integer> hash = new HashMap<>();\n List<Integer> ans = new ArrayList<>();\n char[] s2 = s.toCharArray();\n for (String value : words) {\n hash.putIfAbsent(value, hash.size());\n }\n int[] count = new int[hash.size()];\n for (String word : words) {\n count[hash.get(word)]++;\n }\n for (int i = 0; i < wordLength; i++) {\n for (int j = i; j <= s.length() - totalWordsLength; j += wordLength) {\n int[] localCount = new int[hash.size()];\n for (int k = j + totalWordsLength - wordLength; k >= j; k -= wordLength) {\n String str = new String(s2, k, wordLength); // [ k, k+wordLength )\n Integer key = hash.get(str);\n if (!(key != null && count[key] >= ++localCount[key])) {\n j = k;\n break;\n }\n if (j == k) {\n ans.add(j);\n }\n }\n }\n }\n return ans;\n }\n}\n```\n | 28 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
✅ Explained - Simple and Clear Python3 Code✅ | substring-with-concatenation-of-all-words | 0 | 1 | \n# Approach\n\nThe solution iterates through possible starting points in the given string and checks if the substring starting from each point forms a concatenated substring. It maintains a dictionary to track the occurrences of words encountered and compares it with the expected occurrences. By updating the counts while scanning the string, it identifies valid concatenated substrings and records their starting indices. The solution effectively ensures that all the words in any permutation of the input words array are present in the substring, returning the starting indices of all such valid substrings.\n\n# Code\n```\nclass Solution:\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n wlen= len(words[0])\n slen= wlen*len(words)\n track=dict()\n \n occ = collections.Counter(words)\n\n def test():\n for key, val in track.items():\n if val !=occ[key]:\n return False\n return True\n res=[]\n #first look\n\n for k in range(wlen):\n for i in words:\n track.update({i : 0})\n for i in range(k,slen+k,wlen):\n w=s[i:i+wlen]\n if w in words:\n track.update({w: track[w]+1})\n if test():\n res.append(k)\n #complete\n for i in range(wlen+k, len(s)-slen+1,wlen):\n \n nw=s[i+slen-wlen:i+slen]\n pw=s[i-wlen:i]\n if nw in words:\n track.update({nw: track[nw]+1})\n if pw in words:\n track.update({pw: track[pw]-1})\n if test():\n res.append(i)\n return res\n\n \n``` | 6 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
Substring with Concatenation of All Words with step by step explanation, | substring-with-concatenation-of-all-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nOne approach to solve this problem is using a sliding window technique.\n\nStep 1: Calculate the length of each word and the total length of words.\n\nStep 2: Create a dictionary to store the frequency of each word in words.\n\nStep 3: Iterate through the string s with a sliding window of the length of words, and keep a count of each word in the current window.\n\nStep 4: If the count of each word in the current window is the same as in the dictionary, add the starting index of the window to the result.\n\nStep 5: Move the sliding window to the right by one character and repeat from step 3.\n\nStep 6: Return the result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n if not s or not words:\n return []\n \n word_len = len(words[0])\n total_len = word_len * len(words)\n result = []\n word_dict = {}\n \n for word in words:\n word_dict[word] = word_dict.get(word, 0) + 1\n \n for i in range(len(s) - total_len + 1):\n window = {}\n j = 0\n while j < total_len:\n word = s[i + j:i + j + word_len]\n if word in word_dict:\n window[word] = window.get(word, 0) + 1\n if window[word] > word_dict[word]:\n break\n else:\n break\n j += word_len\n if j == total_len:\n result.append(i)\n \n return result\n\n``` | 1 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
Python Elegant & Short | Sliding window | 98.89% faster | substring-with-concatenation-of-all-words | 0 | 1 | \n\n```\nfrom collections import Counter, defaultdict\n\n\nclass Solution:\n\t"""\n\tTime: O(n*k), n = length of s, k = length of each word\n\tMemory: O(m*k), m = length of words, k = length of each word\n\t"""\n\n\tdef findSubstring(self, s: str, words: List[str]) -> List[int]:\n\t\tlength = len(words[0])\n\t\tword_count = Counter(words)\n\t\tindexes = []\n\n\t\tfor i in range(length):\n\t\t\tstart = i\n\t\t\twindow = defaultdict(int)\n\t\t\twords_used = 0\n\n\t\t\tfor j in range(i, len(s) - length + 1, length):\n\t\t\t\tword = s[j:j + length]\n\n\t\t\t\tif word not in word_count:\n\t\t\t\t\tstart = j + length\n\t\t\t\t\twindow = defaultdict(int)\n\t\t\t\t\twords_used = 0\n\t\t\t\t\tcontinue\n\n\t\t\t\twords_used += 1\n\t\t\t\twindow[word] += 1\n\n\t\t\t\twhile window[word] > word_count[word]:\n\t\t\t\t\twindow[s[start:start + length]] -= 1\n\t\t\t\t\tstart += length\n\t\t\t\t\twords_used -= 1\n\n\t\t\t\tif words_used == len(words):\n\t\t\t\t\tindexes.append(start)\n\n\t\treturn indexes\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n\n | 16 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
SUBSTRING WITH CONCATENATION of all words | substring-with-concatenation-of-all-words | 0 | 1 | [https://leetcode.com/problems/substring-with-concatenation-of-all-words/description/]()\n[https://www.linkedin.com/in/shivansh-srivastava-cs/]()\n# DO UPVOTE IF YOU FIND IT SUITABLE AND HELPFUL AND FOR ANY DOUBTS COMMENT.\n# DO LIKE AS EACH VOTE COUNTS\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Refer and take the refernce from the find all anagrams and permutations in a string question of leetcode 438.\n\n# Approach\n<!-- Describe your approach to solving the problem. --> Sliding window + hashtable for each word in words list and then inside nested loop use substrcount each time new and compare for equivalence\\.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->The first for-loop iterates over all words in the input list words and takes O(N) time where N is the number of words in the list.\nThe second for-loop iterates over all substrings of length len(words)*len(words[0]) in the input string s. The number of substrings will be O(M) where M is the length of the input string. For each substring, the code creates a new dictionary substrcount and iterates over all words of length len(words[0]) in the substring. This takes O(len(substr)/len(words[0])) time for each substring. Therefore, the overall time complexity of the second for-loop is O(M * len(substr)/len(words[0])) = O(M*N), where N and M are defined as before.\nThe dictionary operations (insertion, lookup) in the code take O(1) time.\nThus, the overall time complexity of the code is O(M*N), where N is the number of words in the input list and M is the length of the input string.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->The code uses two dictionaries, wordcount and substrcount, to store word frequencies. The maximum size of each dictionary is N (the number of words in the input list).\nThe code stores the input string s, which takes O(M) space.\nThe code stores the result list result, which can take up to O(M/N) space in the worst case (when all substrings are valid).\nThus, the overall space complexity of the code is O(M + N).\n\nIn summary, the time complexity of the given code is O(M*N) and the space complexity is O(M + N), where N is the number of words in the input list and M is the length of the input string.\n\n\n\n\n# Code\n```\nclass Solution:\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n wordcount={}\n for word in words:\n wordcount[word]=1+wordcount.get(word,0)\n result=[]\n substringlength=len(words)*len(words[0])\n for i in range(len(s)-substringlength+1):\n substr=s[i:i+substringlength]\n substrcount={}\n for j in range(0,len(substr),len(words[0])):\n word=substr[j:j+len(words[0])]\n substrcount[word]=1+substrcount.get(word,0)\n if substrcount==wordcount:\n result.append(i)\n return result\n\n# m=\'\'.join(words)\n# pcount=dict()\n# scount=dict()\n# if len(m)>len(s):\n# print([])\n# for i in range(len(m)):\n# pcount[m[i]]=1+pcount.get(m[i],0)\n# scount[s[i]]=1+scount.get(s[i],0)\n# # print(pcount)\n# # print(scount)\n# res=[0]if pcount==scount else []\n# l=0\n# for i in range(len(m),len(s),1):\n# scount[s[i]]=1+scount.get(s[i],0)\n# scount[s[l]]-=1 \n# if scount[s[l]]==0:\n# del scount[s[l]]\n# l+=1 \n# if scount==pcount:\n# res.append(l)\n# #@print(res)\n# return res\n \n``` | 6 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
Simple python solution | substring-with-concatenation-of-all-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubstring(self, s: str, words: List[str]) -> List[int]:\n output = []\n d = {}\n for word in words:\n if word in d:\n d[word] +=1\n else:\n d[word] = 1\n \n i = 0\n j = len(words[0])*len(words) - 1\n\n while j < len(s):\n tmp = {}\n a = i\n b = i+len(words[0])-1\n\n while b <= j:\n cur = s[a:b+1]\n if cur in tmp:\n tmp[cur] +=1\n else:\n tmp[cur] = 1\n a = b+1\n b = b+len(words[0])\n \n if tmp == d:\n output.append(i)\n i+=1\n j+=1\n \n return output\n``` | 1 | You are given a string `s` and an array of strings `words`. All the strings of `words` are of **the same length**.
A **concatenated substring** in `s` is a substring that contains all the strings of any permutation of `words` concatenated.
* For example, if `words = [ "ab ", "cd ", "ef "]`, then `"abcdef "`, `"abefcd "`, `"cdabef "`, `"cdefab "`, `"efabcd "`, and `"efcdab "` are all concatenated strings. `"acdbef "` is not a concatenated substring because it is not the concatenation of any permutation of `words`.
Return _the starting indices of all the concatenated substrings in_ `s`. You can return the answer in **any order**.
**Example 1:**
**Input:** s = "barfoothefoobarman ", words = \[ "foo ", "bar "\]
**Output:** \[0,9\]
**Explanation:** Since words.length == 2 and words\[i\].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo ". It is the concatenation of \[ "bar ", "foo "\] which is a permutation of words.
The substring starting at 9 is "foobar ". It is the concatenation of \[ "foo ", "bar "\] which is a permutation of words.
The output order does not matter. Returning \[9,0\] is fine too.
**Example 2:**
**Input:** s = "wordgoodgoodgoodbestword ", words = \[ "word ", "good ", "best ", "word "\]
**Output:** \[\]
**Explanation:** Since words.length == 4 and words\[i\].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.
**Example 3:**
**Input:** s = "barfoofoobarthefoobarman ", words = \[ "bar ", "foo ", "the "\]
**Output:** \[6,9,12\]
**Explanation:** Since words.length == 3 and words\[i\].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe ". It is the concatenation of \[ "foo ", "bar ", "the "\] which is a permutation of words.
The substring starting at 9 is "barthefoo ". It is the concatenation of \[ "bar ", "the ", "foo "\] which is a permutation of words.
The substring starting at 12 is "thefoobar ". It is the concatenation of \[ "the ", "foo ", "bar "\] which is a permutation of words.
**Constraints:**
* `1 <= s.length <= 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 30`
* `s` and `words[i]` consist of lowercase English letters. | null |
Python full two step easy explanation with examples | next-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLike Djikstra algorithm, finding the next permutation is something that its better to just know the steps. Knowing the steps is key which I illustrated in the comments. Now I think the challenge is if the interviewer told you the solution to this problem, coding it is not that easy if you have not done enough practice with coding in arrays. I suggest to memorise the algorithm solution and practice it to solve it under 10 minutes or less after not coding this exercise for a while. It has a lot of array manipulation and it can be done in different ways so that is that. As many comments discussed in leetcode, most interviewers avoid asking this problem as even giving the answer in full is still challenging to code, but perfect to practice your array skills once you know the solution. The idea is you can translate complex steps into code, then medium/easy steps would be easier when you have to code.\n\nIf you fond this on Striver DSE is because it was expected you could get the next permutation from the built-in libraries. This is as complex as creating your own sort function rather than using the ones in built-in libraries.\n\n\n# Approach\nBefore implementation, the idea is to come up with the solution\nThe solution to find the next palindrome is:\n* 1. Starting from the end to the start as the index order: \n* 1a. Find the index where the number is smaller than its previous index. In DSA, this is called the "break point".\n* 1b. If none is found, there is no next palindrome as its the max palindrome\n* 1b. to get the min palindrome from max palindrome, just reverse the array and skip step 2.\n\n* 2. Starting from the end to the index of step 1: \n* 2a. Continue iterating until the current index finds a number that is greater than index 1a value.\n* 2b. If have not found one before exhausting end of index, its the last index to swap. \n* 2b. Swap that index with what was found on 1a.\n* 2c. Reverse the subarray between the index of 1a+1 and end of index.\nThe examples in exercise are not helpful, get a large complex example to think ALL use cases.\n\nFor example (example descriptions indexes are zero index and start from the beginning)\n```158476531```\n* 1a: Starting from end, we find number "4" is smaller than "7" at index 3 and 4 correspondingly.\n* 1b: This is not the max palindrome, so we still continue.\n* 2a: Starting from end of index, we find that there is a number greater than 4.\n* 2b. The number is "5" at index 6. We swap the "5" we found at index 6 from "1a" and we get:\n```158576431```\n* 2c. We Reverse between index "4" and the end. That is, `76431` is reversed to `13467`. \n```158513467```\n\nWhat are we doing here?\n```\nFinding a number that is out of order incrementally\nSo we could correct it and reverse it.\nThat is how to get the next palindrome mathematically.\n```\nSecond example:\n```677877777```\n* From (1a) the index is 3 at value 8 (so this is not a max palindrome). \n* (2a) We can\'t find anything greater than 8, so we swap the last index\n```677777778```\n* (2c) We reverse the 77778 to 87777\n```677787777```\n\nThird example:\n```999998654```\n* After doing (1a), we could not find a smaller number than its previous index. That means its the max palindrome. So just get the min palindrome in that use case as instructed by the exercise. \n* To get the min palindrome from the max palindrome, (1b) `just reverse it`. That is how it works mathematically.\n```456899999```\n\nSo repeat after me:\n* 1a. From end to start, find index where value of index is smaller than the index we scanned before.\n* 1b. If none is found, this is the max palindrome. Return the reverse of it to get min palindrome.\n* 2a. Otherwise, from end until index of step 1, find the index where value is greater than the value of the index found on step 1. If none is found, set it as the last index of the array.\n* 2b. Swap the indexes you found from step 1 and 2.\n* 2c. Reverse the index between the ranges of index found on step 1 until the end of the index.\nThat is it. Now you know the next palindrome in 2 steps.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nIts O(N) after removing the constants.\n\n\nO(3N) = One loop for Finding breakbpoint, another loop to find value greater than the value from breakpoint index. One to do the reverse the values from breakpoint index and onwards. I don\'t think we need to state O(A+B+C) as the work is iterated on the same array and the worst cae complexity will always end up the same, that is, if A = B = C = N, then just 3N will do.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1). Only very few variables stored for later use (break point index, index to swap with break point, size array) so its constant.\n# Code\n```\n \nclass Solution:\n def nextPermutation(self, nums: List[int]) -> None:\n size_array = len(nums)\n # 1(a)\n index_for_out_of_order_number = -1\n for i in range(size_array-2,-1,-1):\n if nums[i] < nums[i+1]:\n index_for_out_of_order_number = i\n break\n # 1(b)\n if index_for_out_of_order_number == -1:\n nums.reverse()\n else:\n # 2(a)\n # default if none is found\n index_to_swap_with = size_array-1\n for i in range(size_array-1,index_for_out_of_order_number,-1):\n if nums[i] > nums[index_for_out_of_order_number]:\n index_to_swap_with = i\n break\n # 2(b)\n nums[index_for_out_of_order_number], nums[index_to_swap_with] = nums[index_to_swap_with],nums[index_for_out_of_order_number]\n # 2(c)\n nums[index_for_out_of_order_number + 1:] = reversed(nums[index_for_out_of_order_number + 1:])\n``` | 3 | A **permutation** of an array of integers is an arrangement of its members into a sequence or linear order.
* For example, for `arr = [1,2,3]`, the following are all the permutations of `arr`: `[1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1]`.
The **next permutation** of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the **next permutation** of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
* For example, the next permutation of `arr = [1,2,3]` is `[1,3,2]`.
* Similarly, the next permutation of `arr = [2,3,1]` is `[3,1,2]`.
* While the next permutation of `arr = [3,2,1]` is `[1,2,3]` because `[3,2,1]` does not have a lexicographical larger rearrangement.
Given an array of integers `nums`, _find the next permutation of_ `nums`.
The replacement must be **[in place](http://en.wikipedia.org/wiki/In-place_algorithm)** and use only constant extra memory.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[1,2,3\]
**Example 3:**
**Input:** nums = \[1,1,5\]
**Output:** \[1,5,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Python3 | O(n) | next-permutation | 0 | 1 | ```\nclass Solution:\n def nextPermutation(self, nums: List[int]) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n for curr in reversed(range(0, len(nums) - 1)):\n if nums[curr] >= nums[curr + 1]:\n continue;\n \n next = curr + 1;\n while next < len(nums) and nums[next] > nums[curr]:\n next += 1;\n \n nums[curr], nums[next - 1] = nums[next - 1], nums[curr];\n \n nums[curr+1:] = reversed(nums[curr+1:])\n \n return nums;\n \n return nums.sort();\n``` | 2 | A **permutation** of an array of integers is an arrangement of its members into a sequence or linear order.
* For example, for `arr = [1,2,3]`, the following are all the permutations of `arr`: `[1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1]`.
The **next permutation** of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the **next permutation** of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
* For example, the next permutation of `arr = [1,2,3]` is `[1,3,2]`.
* Similarly, the next permutation of `arr = [2,3,1]` is `[3,1,2]`.
* While the next permutation of `arr = [3,2,1]` is `[1,2,3]` because `[3,2,1]` does not have a lexicographical larger rearrangement.
Given an array of integers `nums`, _find the next permutation of_ `nums`.
The replacement must be **[in place](http://en.wikipedia.org/wiki/In-place_algorithm)** and use only constant extra memory.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[1,2,3\]
**Example 3:**
**Input:** nums = \[1,1,5\]
**Output:** \[1,5,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Python 3 Solution beats 96.6% | next-permutation | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nAlgorithm / Intuition\nThe steps are the following:\n\n1.) Find the break-point, i: Break-point means the first index i from the back of the given array where arr[i] becomes smaller than arr[i+1].\nFor example, if the given array is {2,1,5,4,3,0,0}, the break-point will be index 1(0-based indexing). Here from the back of the array, index 1 is the first index where arr[1] i.e. 1 is smaller than arr[i+1] i.e. 5.\nTo find the break-point, using a loop we will traverse the array backward and store the index i where arr[i] is less than the value at index (i+1) i.e. arr[i+1].\n\n2.) If such a break-point does not exist i.e. if the array is sorted in decreasing order, the given permutation is the last one in the sorted order of all possible permutations. So, the next permutation must be the first i.e. the permutation in increasing order.\nSo, in this case, we will reverse the whole array and will return it as our answer.\n\n3.) If a break-point exists:\nFind the smallest number i.e. > arr[i] and in the right half of index i(i.e. from index i+1 to n-1) and swap it with arr[i].\nReverse the entire right half(i.e. from index i+1 to n-1) of index i. And finally, return the array.\n\n# Complexity\n- Time complexity:\n\nFinding the break-point, finding the next greater element, and reversal at the end takes O(N) for each, where N is the number of elements in the input array. Hence, O(N) is the time complexity of this algorithm.\n\n- Space complexity:\n\nSince no extra storage is required. Thus, its space complexity is O(1).\n\n# Code\n```\nclass Solution:\n def nextPermutation(self, nums: List[int]) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n n=len(nums)\n ind=-1\n for i in range(n-2,-1,-1):\n if nums[i]<nums[i+1]:\n ind=i\n break\n print(ind)\n if ind==-1:\n return nums.reverse()\n \n for i in range(n-1,ind,-1):\n if nums[i]>nums[ind]:\n nums[i],nums[ind]=nums[ind],nums[i]\n break\n \n nums[ind+1:]=reversed(nums[ind+1:])\n return nums\n \n\n\n \n``` | 2 | A **permutation** of an array of integers is an arrangement of its members into a sequence or linear order.
* For example, for `arr = [1,2,3]`, the following are all the permutations of `arr`: `[1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1]`.
The **next permutation** of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the **next permutation** of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
* For example, the next permutation of `arr = [1,2,3]` is `[1,3,2]`.
* Similarly, the next permutation of `arr = [2,3,1]` is `[3,1,2]`.
* While the next permutation of `arr = [3,2,1]` is `[1,2,3]` because `[3,2,1]` does not have a lexicographical larger rearrangement.
Given an array of integers `nums`, _find the next permutation of_ `nums`.
The replacement must be **[in place](http://en.wikipedia.org/wiki/In-place_algorithm)** and use only constant extra memory.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[1,2,3\]
**Example 3:**
**Input:** nums = \[1,1,5\]
**Output:** \[1,5,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Great Python Solution! Using 'Sort' and 'UpperBound' | O(NlogN) Time complexity | O(1) Space | next-permutation | 0 | 1 | # Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have to find the first index where the ascending starts Ex. in 2,1,3,2 element at index 2 is greater than element at index 1 hence index 1 is the target index. Now we have to replace that index with the upper bound of the element(For lexicographically next value) using our custom function then sort it from index 2 till the end using sort function and return it\n\nif the given array has no ascending index then just sort and return\n\n# Complexity\n- Time complexity: O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def upper(self,start,end,nums,target):\n res = start\n while start<=end:\n mid = (start+end)//2\n if nums[mid]>target:\n res = mid\n start = mid+1\n else:\n end = mid-1\n return res\n def nextPermutation(self, nums: List[int]) -> None:\n if len(nums)==1:\n return\n i = len(nums)-2\n j = i+1\n while i>=0:\n if nums[i]<nums[j]:\n up = self.upper(j,len(nums)-1,nums,nums[i])\n nums[i],nums[up]=nums[up],nums[i]\n nums[j:] = sorted(nums[j:])\n return\n i-=1\n j-=1\n nums.sort()\n return\n \n\n \n``` | 3 | A **permutation** of an array of integers is an arrangement of its members into a sequence or linear order.
* For example, for `arr = [1,2,3]`, the following are all the permutations of `arr`: `[1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1]`.
The **next permutation** of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the **next permutation** of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
* For example, the next permutation of `arr = [1,2,3]` is `[1,3,2]`.
* Similarly, the next permutation of `arr = [2,3,1]` is `[3,1,2]`.
* While the next permutation of `arr = [3,2,1]` is `[1,2,3]` because `[3,2,1]` does not have a lexicographical larger rearrangement.
Given an array of integers `nums`, _find the next permutation of_ `nums`.
The replacement must be **[in place](http://en.wikipedia.org/wiki/In-place_algorithm)** and use only constant extra memory.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[1,2,3\]
**Example 3:**
**Input:** nums = \[1,1,5\]
**Output:** \[1,5,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Python Solution with easy understanding and comments. (Bonus: Related links) | next-permutation | 0 | 1 | ```\nclass Solution:\n def nextPermutation(self, nums: List[int]) -> None:\n """\n Do not return anything, modify nums in-place instead.\n """\n # To find next permutations, we\'ll start from the end\n i = j = len(nums)-1\n # First we\'ll find the first non-increasing element starting from the end\n while i > 0 and nums[i-1] >= nums[i]:\n i -= 1\n # After completion of the first loop, there will be two cases\n # 1. Our i becomes zero (This will happen if the given array is sorted decreasingly). In this case, we\'ll simply reverse the sequence and will return \n if i == 0:\n nums.reverse()\n return \n # 2. If it\'s not zero then we\'ll find the first number grater then nums[i-1] starting from end\n while nums[j] <= nums[i-1]:\n j -= 1\n # Now out pointer is pointing at two different positions\n # i. first non-assending number from end\n # j. first number greater than nums[i-1]\n \n # We\'ll swap these two numbers\n nums[i-1], nums[j] = nums[j], nums[i-1]\n \n # We\'ll reverse a sequence strating from i to end\n nums[i:]= nums[len(nums)-1:i-1:-1]\n # We don\'t need to return anything as we\'ve modified nums in-place\n \'\'\'\n Dhruval\n \'\'\'\n```\n\nTake an example from this site and try to re-run above code manually. This will better help to understand the code\nhttps://www.nayuki.io/page/next-lexicographical-permutation-algorithm\n\nRelated Link: \nhttps://www.nayuki.io/res/next-lexicographical-permutation-algorithm/nextperm.py\nhttps://en.wikipedia.org/wiki/Lexicographic_order | 88 | A **permutation** of an array of integers is an arrangement of its members into a sequence or linear order.
* For example, for `arr = [1,2,3]`, the following are all the permutations of `arr`: `[1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1]`.
The **next permutation** of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the **next permutation** of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
* For example, the next permutation of `arr = [1,2,3]` is `[1,3,2]`.
* Similarly, the next permutation of `arr = [2,3,1]` is `[3,1,2]`.
* While the next permutation of `arr = [3,2,1]` is `[1,2,3]` because `[3,2,1]` does not have a lexicographical larger rearrangement.
Given an array of integers `nums`, _find the next permutation of_ `nums`.
The replacement must be **[in place](http://en.wikipedia.org/wiki/In-place_algorithm)** and use only constant extra memory.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** \[1,3,2\]
**Example 2:**
**Input:** nums = \[3,2,1\]
**Output:** \[1,2,3\]
**Example 3:**
**Input:** nums = \[1,1,5\]
**Output:** \[1,5,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Easy To Understand | longest-valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n max_length = 0\n stack = [-1] # Initialize with a start index\n\n for i in range(len(s)):\n if s[i] == \'(\':\n stack.append(i)\n else:\n stack.pop()\n if not stack:\n stack.append(i) # If popped -1, add a new start index\n else:\n # Update the length of the valid substring\n max_length = max(max_length, i - stack[-1])\n\n return max_length\n\n``` | 4 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Python Easy 2 approaches - Space O(n) and O(1) | longest-valid-parentheses | 0 | 1 | The time complexity for both the approaches is `O(len(s)`.\n\n 1. ##### **Space - O(len(s))**\n\nThis approach solves the problem in similar way as https://leetcode.com/problems/valid-parentheses/ using `Stack`. The stack is used to track indices of `(`. So whenever we hit a `)`, we pop the pair from stack and update the length of valid substring.\n\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n max_length = 0\n stck=[-1] # initialize with a start index\n for i in range(len(s)):\n if s[i] == \'(\':\n stck.append(i)\n else:\n stck.pop()\n if not stck: # if popped -1, add a new start index\n stck.append(i)\n else:\n max_length=max(max_length, i-stck[-1]) # update the length of the valid substring\n return max_length\n```\n\n2. ##### **Space - O(1)**\nThe valid parantheses problem can also be solved using a counter variable. Below implementation modifies this approach a bit and uses two counters:`left` and `right` for `(` and `)` respectively. \n\nThe pseudo code for this approach:\n1. Increment `left` on hitting `(`.\n2. Increment `right` on hitting `)`.\n3. If `left=right`, then calculate the current substring length and update the `max_length`\n4. If `right>left`, then it means it\'s an invalid substring. So reset both `left` and `right` to `0`.\n\nPerform the above algorithm once on original `s` and then on the reversed `s`.\n\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n max_length = 0\n \n l,r=0,0 \n # traverse the string from left to right\n for i in range(len(s)):\n if s[i] == \'(\':\n l+=1\n else:\n r+=1 \n if l == r:# valid balanced parantheses substring \n max_length=max(max_length, l*2)\n elif r>l: # invalid case as \')\' is more\n l=r=0\n \n l,r=0,0 \n # traverse the string from right to left\n for i in range(len(s)-1,-1,-1):\n if s[i] == \'(\':\n l+=1\n else:\n r+=1 \n if l == r:# valid balanced parantheses substring \n max_length=max(max_length, l*2)\n elif l>r: # invalid case as \'(\' is more\n l=r=0\n return max_length\n```\n\n---\n\n***Please upvote if you find it useful*** | 61 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Python 56ms Solution | longest-valid-parentheses | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Firstly determine which of the consecutive parentheses are valid and create a duplicate list of the given string where each bracket is a different element i.e.\nif $$givenstring="( ( )"$$\ncreate list =list(given_string) which will result in$$ [ " ( " , " ( " , " ) " ] $$\n\n2. Now iterate through the list and check for each element if their exists any closing stack bracket further in the list\nI\'ve done this by keeping an the element\'s opening character and its index and if I found its complement i would turn its value to True\n\n3. After 1st for loop iteration we have the values of each element whether its complement exists (means if its closing bracket exists in the list or not) and if it does we replace the index value with True else False\n4. Then we count the most consecutive number of True occuring in our list\nwhich will be our answer\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(2*n)$$ which is when\n if there are only opening brackets in the given string\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Variables \n1. list1 : To convert the given string into a list\n\n2. stack : using stack data structure to add on the TOS the opening bracket and popping the TOS if we encounter any closing bracket\nIts first element will contain the opening character and second value will contain the index i.e\n$$stack=["(",index]$$\n\n3. max1 :contains the longest consecutive True occurences\n4. ctr : contains current number of consecutive True occurences\n\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack=[]\n list1=list(s)\n for i in range(len(s)):\n if(len(stack)==0):stack.append([s[i],i])\n elif(stack[-1][0]=="(" and s[i]==")"):\n list1[stack[-1][1]]=True\n list1[i]=True\n stack.pop()\n else:stack.append([s[i],i])\n ctr,max1=0,0\n for i in list1:\n if i==True:\n ctr+=1\n max1=max(max1,ctr)\n else:ctr=0\n return max1\n\n \n``` | 1 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
✅Python3 Beats 99.80% Solution with Detailed Explanation✅ | longest-valid-parentheses | 0 | 1 | # Approach\n1. Initiate stack [-1] (Must be -1 !!)\n2. If you cannot understand why it must be -1, consider the case "(()())"\n3. The -1 is to get the correct current position in case there is nothing to pop in the stack\n4. For every element, if it is "(", we append the current index\n5. *Append index to keep track of the longest substring!\n6. Else, we pop the stack and update the current longest substring\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack = [-1] # Mystery!!! To get the current length of the string: Consider case "(()())"\n longest = 0\n for i, n in enumerate(s):\n if n == "(":\n stack.append(i)\n else:\n stack.pop()\n if stack:\n longest = max(longest, i - stack[-1])\n else:\n stack.append(i)\n\n return longest\n``` | 1 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Dynamic Programming Approach to Longest Valid Parentheses Substring | longest-valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, we can use dynamic programming. Let dp[i] be the length of the longest valid parentheses substring ending at index i. We can observe the following:\n\n1. If s[i] = \'(\', there can be no valid substring ending at index i, so dp[i] = 0.\n2. If s[i] = \')\', we have two cases:\na. If s[i-1] = \'(\', then dp[i] = dp[i-2] + 2.\nb. If s[i-1] = \')\' and s[i-dp[i-1]-1] = \'(\', then dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2.\n\nIn case (2a), we add 2 to dp[i-2] because we have a matching pair of parentheses at indices i-1 and i, and we can extend the valid substring ending at index i-2 (if there is one) to include this pair.\n\nIn case (2b), we add dp[i-1] to account for the length of the valid substring ending at index i-1, and dp[i-dp[i-1]-2] to account for any valid substring that starts before the opening bracket of the current substring. For example, consider the string "(()())". When we reach the second closing bracket at index 5, we can extend the valid substring ending at index 4 (which has length 2) to include the current pair of parentheses, giving us a length of 4. However, we also need to account for the valid substring that starts before the opening bracket of this substring, which is the substring that ends at index 1 (which has length 2).\n\nFinally, the length of the longest valid parentheses substring is the maximum value in the dp array.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize the dp array with zeros, and the maximum length variable max_len with 0.\n- Iterate over the indices of the input string from left to right.\n- If s[i] = \')\', check if the previous character s[i-1] is \'(\'. If it is, set dp[i] = dp[i-2] + 2.\n- Otherwise, check if s[i-dp[i-1]-1] is \'(\'. If it is, set dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2.\n- Update max_len with the maximum value in the dp array.\n- Return max_len.\n# Complexity\n- Time complexity: O(n), where n is the length of the input string.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n), where n is the length of the input string.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack = [-1]\n max_len = 0\n for i in range(len(s)):\n if s[i] == \'(\':\n stack.append(i)\n else:\n stack.pop()\n if not stack:\n stack.append(i)\n else:\n max_len = max(max_len, i - stack[-1])\n return max_len\n``` | 4 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Longest Valid Parenthesesis (Valid Parenthesesis) | longest-valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is similar to the valid parenthesesis but there we check the validity condition but in this we need to find the length of the longest valid parenthesis so inorder to find the length we needed to store the index of the brackets and traverse along the way...\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStore the indexes now when ever we encounter the closing bracket(")") then we must and should check for the recent opening bracket and update the maximum length so far in the varaible....\n\n For better understading go through the explaination of valid parenthesesis....\n\n https://leetcode.com/problems/valid-parentheses/solutions/3187475/valid-parenthesis-python3-solution/\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack=[-1]\n maxi=0\n for i in range(0,len(s)):\n char=s[i]\n if char=="(":\n stack.append(i)\n else:\n index=stack.pop()\n if stack:\n #update the length \n maxi=max(maxi,i-stack[-1])\n else:\n #push the value in the stack\n stack.append(i)\n return maxi\n\n``` | 2 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Easiest Python3 Solution [ Beats 97.40% ] 🔥🔥 | longest-valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The intuition behind solving this problem is to use a stack data structure to keep track of the indices of opening parentheses \'(\' in the input string. By doing this, we can identify valid pairs of parentheses and calculate their lengths to find the longest valid parentheses substring.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- This solution uses a stack to keep track of the indices of opening parentheses \'(\' in the string.\n- When a closing parentheses \')\' is encountered, we pop the top of the stack, which represents the last unmatched opening parentheses.\n- The length of the valid parentheses substring is calculated as the difference between the current index and the index at the top of the stack.\n- We update `max_so_far` with this length whenever a valid substring is found.\n- The stack is initialized with -1 to handle edge cases where there are no matching parentheses at the start of the string.\n\n# Complexity\n- Time complexity: O(n), where n is the length of the input string `s`.\n- Space complexity: O(n), as we use a stack to store the indices of opening parentheses.\n\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack = [-1]\n max_so_far = 0\n for i in range(len(s)):\n if s[i] == \'(\':\n stack.append(i)\n else:\n stack.pop()\n if not stack:\n stack.append(i)\n else:\n max_so_far = max(max_so_far,i - stack[-1])\n return max_so_far\n``` | 2 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Stack Approach .. Using Python | longest-valid-parentheses | 0 | 1 | # Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n n = len(s)\n stack = []\n\n stack += [["first_node" , -1]]\n \n for i in range(n):\n if s[i] == "(": \n stack += [["(" , i]]\n \n else: # s[i] == ")"\n if stack[-1][0] == "(":\n stack.pop()\n else:\n stack += [[")" , i]]\n \n stack += [["last_node" , n]]\n\n ans = 0\n for i in range( 1 , len(stack) ):\n ans = max( ans , (stack[i][1] - stack[i-1][1]) - 1)\n \n return ans\n\n """\n Check each element .. if valid parentheses then pop .. else push to stack\n \n at the end .. stack contains only the invalid elements of s \n and all elements within the range of consecutive elements in the stack are valid ..@2 \n """\n``` | 2 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Python3 Simple Solution | longest-valid-parentheses | 0 | 1 | ```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n \n maxi = 0\n stack = [-1]\n \n for i in range(len(s)) :\n if s[i] == "(" : stack.append(i)\n else :\n stack.pop()\n if len(stack) == 0 : stack.append(i)\n else : maxi = max(maxi, i - stack[-1])\n \n return maxi\n``` | 4 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
[Python 93%] Easy explained short solution with stack | longest-valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhile iterating through the string, we can use a stack to keep track of the indices of the opening parentheses that have not yet been matched with a closing parenthesis. When we encounter a closing parenthesis, we pop the last element off the stack. The difference between the current index and the last element in the stack gives the length of the valid substring that starts at the last element in the stack.\n\n# Detailed approach\n<!-- Describe your approach to solving the problem. -->\nIf the current character is an opening parenthesis, its index is added to the `stack`. \nIf it is a closing parenthesis, the last element in the `stack` is removed. \nIf the `stack` is not empty, the current length of the valid substring is calculated by subtracting the current index from the last index in the stack (i.e. `stack[-1]`), and the `max_length` is updated if the current length is greater than the previous `max_length`. \nIf the `stack` is empty after popping a element, we set a new starting index by adding current index to the `stack`.\n\n# Python Code\n\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack = [-1]\n max_length = 0\n for i in range(len(s)):\n if s[i] == \'(\':\n stack.append(i)\n else:\n stack.pop()\n if stack:\n max_length = max(max_length, i - stack[-1])\n else:\n stack.append(i)\n return max_length\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nThe Time complexity of this approach is `O(n)`, where n is the length of the input string. We are iterating through the string once and in worst case we may push and pop all the elements from the stack. So the space complexity is also `O(n)`. | 1 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Easy Python Code | longest-valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack = [-1] # Initialize stack with -1 to handle edge case of starting with \')\'\n ans = 0\n for i in range(len(s)):\n if s[i] == \'(\':\n stack.append(i)\n else:\n stack.pop()\n if not stack: # If the stack is empty, push current index as a starting point\n stack.append(i)\n else: # If the stack is not empty, update the maximum length\n ans = max(ans, i - stack[-1])\n return ans\n\n``` | 0 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Two Approaches Using Stack and without space | longest-valid-parentheses | 0 | 1 | # Using Stack:\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n stack=[]\n stack.append(-1)\n ans=0\n for i in range(len(s)):\n if s[i]==\'(\':\n stack.append(i)\n else:\n stack.pop()\n if len(stack)==0:\n stack.append(i)\n ans=max(ans,i-stack[-1])\n return ans\n```\n# without Space complexity:\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n open,close,ans=0,0,0\n for i in s:\n if i=="(":\n open+=1\n else:\n close+=1\n if close==open:\n ans=max(ans,close+open)\n elif close>open:\n open=close=0\n open=close=0\n for i in range(len(s)-1,-1,-1):\n if "("==s[i]:\n open+=1\n else:\n close+=1\n if close==open:\n ans=max(ans,close+open)\n elif open>close:\n open=close=0\n return ans\n``` | 7 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
Python || 97.04% Faster || Two Approaches || O(1) and o(n) Space | longest-valid-parentheses | 0 | 1 | **Brute Force O(n) Space:**\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n st=[-1]\n m=0\n for i in range(len(s)):\n if s[i]==\'(\':\n st.append(i)\n else:\n st.pop()\n if not st: #if -1 is popped\n st.append(i)\n else:\n m=max(m,i-st[-1])\n return m\n```\n**Optimized Solution O(1) Space:**\n```\nclass Solution:\n def longestValidParentheses(self, s: str) -> int:\n l=r=m=0\n for i in range(len(s)):\n if s[i]==\'(\':\n l+=1\n else:\n r+=1\n if l==r: #for balanced parantheses\n m=max(m,l+r)\n elif r>l: #invalid case\n l=r=0\n l=r=0\n# We are traversing right to left for the test case where opening brackets are more than closing brackets. eg: s = "(()"\n for i in range(len(s)-1,-1,-1):\n if s[i]==\'(\':\n l+=1\n else:\n r+=1\n if l==r: #for balanced parantheses\n m=max(m,l+r)\n elif l>r: #invalid case\n l=r=0 \n return m\n```\n**An upvote will be encouraging** | 5 | Given a string containing just the characters `'('` and `')'`, return _the length of the longest valid (well-formed) parentheses_ _substring_.
**Example 1:**
**Input:** s = "(() "
**Output:** 2
**Explanation:** The longest valid parentheses substring is "() ".
**Example 2:**
**Input:** s = ")()()) "
**Output:** 4
**Explanation:** The longest valid parentheses substring is "()() ".
**Example 3:**
**Input:** s = " "
**Output:** 0
**Constraints:**
* `0 <= s.length <= 3 * 104`
* `s[i]` is `'('`, or `')'`. | null |
✅ 100% Binary Search Easy [VIDEO] O(log(n)) Optimal Solution | search-in-rotated-sorted-array | 1 | 1 | # Problem Understanding\n\nThe task is to search for a target integer in a sorted array that has been rotated at an unknown pivot. \n\nFor instance, the array $$[0,1,2,4,5,6,7]$$ could be rotated at the 4th position to give $$[4,5,6,7,0,1,2]$$. The challenge is to find the position of the target integer in this rotated array. \n\n\n\n- The top section shows the `nums` array with a red rectangle highlighting the current "mid" value being considered in each step.\n- The bottom section displays a table that presents the steps of the binary search. Each row corresponds to a step, detailing:\n - The step number.\n - The indices of the low (L), mid (M), and high (R) pointers.\n - The values at the low (L), mid (M), and high (R) positions.\n\n# Live Coding & Explenation\nhttps://youtu.be/hywGbVJldj0\n\n# Approach\n\nGiven the properties of the array, it\'s tempting to perform a linear search. However, that would result in a time complexity of $$O(n)$$. Instead, we can use the properties of the array to our advantage and apply a binary search to find the target with time complexity of $$ O(\\log n) $$ only.\n\n## Treating the Rotated Array\n\nAlthough the array is rotated, it retains some properties of sorted arrays that we can leverage. Specifically, one half of the array (either the left or the right) will always be sorted. This means we can still apply binary search by determining which half of our array is sorted and whether the target lies within it.\n\n## Binary Search\n\nBinary search is an efficient algorithm for finding a target value within a sorted list. It works by repeatedly dividing the search interval in half. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. Otherwise, narrow it to the upper half. Repeatedly check until the value is found or the interval is empty.\n\n## Initialization\n\nWe start with two pointers:\n\n- $$ \\text{left} $$ - This represents the beginning of the array. We initialize it to 0, the index of the first element.\n- $$ \\text{right} $$ - This represents the end of the array. It\'s set to $$ n - 1 $$, the index of the last element, where $$ n $$ is the length of the array.\n\n## Iterative Binary Search\n\nWe perform the binary search within a while loop until $$ \\text{left} $$ exceeds $$ \\text{right} $$. In each iteration, we calculate the midpoint between $$ \\text{left} $$ and $$ \\text{right} $$.\n\n### Deciding the Sorted Half:\n\nAt any point during the search in the rotated array, one half (either the left or the right) will always be sorted. Determining which half is sorted is crucial for our modified binary search. \n\n- **If left half $$[low...mid]$$ is sorted**: We know this if the element at $$ \\text{low} $$ is less than or equal to the element at $$ \\text{mid} $$. In a normally sorted array, if the start is less than or equal to the midpoint, it means all elements till the midpoint are in the correct increasing order.\n\n - **If the target lies within this sorted left half**: We know this if the target is greater than or equal to the element at $$ \\text{low} $$ and less than the element at $$ \\text{mid} $$. If this is the case, we then move our search to this half, meaning, we update $$ \\text{high} $$ to $$ \\text{mid} - 1 $$.\n\n - **Otherwise**: The target must be in the right half. So, we update $$ \\text{low} $$ to $$ \\text{mid} + 1 $$.\n\n- **If right half $$[mid...high]$$ is sorted**: This is the else part. If the left half isn\'t sorted, the right half must be!\n\n - **If the target lies within this sorted right half**: We know this if the target is greater than the element at $$ \\text{mid} $$ and less than or equal to the element at $$ \\text{high} $$. If so, we move our search to this half by updating $$ \\text{low} $$ to $$ \\text{mid} + 1 $$.\n\n - **Otherwise**: The target must be in the left half. So, we update $$ \\text{high} $$ to $$ \\text{mid} - 1 $$.\n\n### Rationale:\n\nThe beauty of this approach lies in its ability to determine with certainty which half of the array to look in, even though the array is rotated. By checking which half of the array is sorted and then using the sorted property to determine if the target lies in that half, we can effectively eliminate half of the array from consideration at each step, maintaining the $$ O(\\log n) $$ time complexity of the binary search.\n\n## Complexity\n\n**Time Complexity**: The time complexity is $$ O(\\log n) $$ since we\'re performing a binary search over the elements of the array.\n\n**Space Complexity**: The space complexity is $$ O(1) $$ because we only use a constant amount of space to store our variables ($$ \\text{left} $$, $$\\text{right} $$, $$ \\text{mid} $$), regardless of the size of the input array.\n\n# Performance\n\n\n\n\n# Code\n\n``` Python []\nclass Solution:\n def search(self, nums: List[int], target: int) -> int:\n left, right = 0, len(nums) - 1\n\n while left <= right:\n mid = (left + right) // 2\n\n if nums[mid] == target:\n return mid\n\n # Check if left half is sorted\n if nums[left] <= nums[mid]:\n if nums[left] <= target < nums[mid]:\n right = mid - 1\n else:\n left = mid + 1\n # Otherwise, right half is sorted\n else:\n if nums[mid] < target <= nums[right]:\n left = mid + 1\n else:\n right = mid - 1\n\n return -1\n```\n``` C++ []\nclass Solution {\npublic:\n int search(std::vector<int>& nums, int target) {\n int low = 0, high = nums.size() - 1;\n\n while (low <= high) {\n int mid = (low + high) / 2;\n\n if (nums[mid] == target) {\n return mid;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target < nums[mid]) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[high]) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n }\n\n return -1;\n }\n};\n```\n``` Go []\nfunc search(nums []int, target int) int {\n low, high := 0, len(nums) - 1\n\n for low <= high {\n mid := (low + high) / 2\n\n if nums[mid] == target {\n return mid\n }\n\n if nums[low] <= nums[mid] {\n if nums[low] <= target && target < nums[mid] {\n high = mid - 1\n } else {\n low = mid + 1\n }\n } else {\n if nums[mid] < target && target <= nums[high] {\n low = mid + 1\n } else {\n high = mid - 1\n }\n }\n }\n\n return -1\n}\n```\n``` Rust []\nimpl Solution {\n pub fn search(nums: Vec<i32>, target: i32) -> i32 {\n let mut low = 0;\n let mut high = nums.len() as i32 - 1;\n\n while low <= high {\n let mid = (low + high) / 2;\n\n if nums[mid as usize] == target {\n return mid;\n }\n\n if nums[low as usize] <= nums[mid as usize] {\n if nums[low as usize] <= target && target < nums[mid as usize] {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n } else {\n if nums[mid as usize] < target && target <= nums[high as usize] {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n }\n\n -1\n }\n}\n```\n``` Java []\nclass Solution {\n public int search(int[] nums, int target) {\n int low = 0, high = nums.length - 1;\n\n while (low <= high) {\n int mid = (low + high) / 2;\n\n if (nums[mid] == target) {\n return mid;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target < nums[mid]) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[high]) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n }\n\n return -1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar search = function(nums, target) {\n let low = 0, high = nums.length - 1;\n\n while (low <= high) {\n let mid = Math.floor((low + high) / 2);\n\n if (nums[mid] === target) {\n return mid;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target < nums[mid]) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[high]) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n }\n\n return -1;\n};\n```\n``` C# []\npublic class Solution {\n public int Search(int[] nums, int target) {\n int low = 0, high = nums.Length - 1;\n\n while (low <= high) {\n int mid = (low + high) / 2;\n\n if (nums[mid] == target) {\n return mid;\n }\n\n if (nums[low] <= nums[mid]) {\n if (nums[low] <= target && target < nums[mid]) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n } else {\n if (nums[mid] < target && target <= nums[high]) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n }\n\n return -1;\n }\n}\n```\n\nI hope this explanation provides clarity on the "Search in Rotated Sorted Array" problem. If you have any more questions, feel free to ask! If you found this helpful, consider giving it a thumbs up. Happy coding! \uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDE80\uD83D\uDC68\u200D\uD83D\uDCBB | 262 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
Python short and clean. Single Binary-Search 2 solutions. | search-in-rotated-sorted-array | 0 | 1 | # Approach 1\nTL;DR, Similar to [Editorial solution Approach 3](https://leetcode.com/problems/search-in-rotated-sorted-array/editorial/) but shorter and cleaner.\ni.e Compares subarray limits first and then the target.\n\n# Complexity\n- Time complexity: $$O(log_2(n))$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution:\n def search(self, nums: list[int], target: int) -> int:\n l, r = 0, len(nums) - 1\n\n while l <= r:\n m = (l + r) // 2\n\n if nums[m] == target: return m\n elif nums[l] <= nums[m]:\n l, r = (l, m - 1) if nums[l] <= target < nums[m] else (m + 1, r)\n else:\n l, r = (m + 1, r) if nums[m] < target <= nums[r] else (l, m - 1)\n \n return -1\n\n\n```\n\n---\n\n# Approach 2\nSimilar to Approach 1 above, but compares target first and then the subarray limits.\n\n# Complexity\n- Time complexity: $$O(log_2(n))$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution:\n def search(self, nums: list[int], target: int) -> int:\n l, r = 0, len(nums) - 1\n\n while l <= r:\n m = (l + r) // 2\n\n if target < nums[m]:\n l, r = (l, m - 1) if target >= nums[l] or nums[l] > nums[m] else (m + 1, r)\n elif target > nums[m]:\n l, r = (m + 1, r) if target <= nums[r] or nums[r] < nums[m] else (l, m - 1)\n else: return m\n \n return -1\n\n\n``` | 1 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
three lines of python | search-in-rotated-sorted-array | 0 | 1 | If I were writing real code, then for the sake of clarity I would (at the very least) expand the second line into an if-else block. But it\'s still fun to solve in as few lines as possible.\n\n# Complexity\n- Time complexity: O(log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) additional space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom bisect import bisect_left\n\nclass Solution:\n def search(self, nums: List[int], target: int) -> int:\n rotation = bisect_left(nums[:-1], True, key=lambda n: n < nums[-1])\n idx = bisect_left(nums, target, **{\'lo\' if target <= nums[-1] else \'hi\': rotation})\n\n return idx if nums[idx] == target else -1\n``` | 1 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
Python 3 || 7 lines, binary searches, w/ explanation || T/M: 92% / 94% | search-in-rotated-sorted-array | 0 | 1 | Here\'s the intuition:\n\n1. If we can determine`k`, the so-called *unknown pivot index*, the solution becomes easier. The key is that `nums[k]` is the first element in `nums` that is strictly less than `nums[0]`, so we can find it in *O*(log*N*) time with a boolean binary search.\n\n1. We now have the two subrrays, `nums[:k]` and `nums[k:]`, and we easily deduce in which subarray `target` must lie (if it indeed does lie in`nums`) by comparing `target` to `nums[0]`.\n\n1. We perform a numerical binary search on the appropriate subarray, return the index if we find`target`, otherwise we return`-1`.\n\n\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> int:\n\n k = bisect_left(nums, True, key = lambda x: x < nums[0]) # <-- 1\n \n if target >= nums[0]: # <-- 2\n \n left = bisect_left(nums, target, hi = k-1) # \n return left if nums[left] == target else -1 #\n # <-- 3\n rght = bisect_left(nums, target, lo = k) #\n return rght if rght < len(nums # (this line to avoid index out of range)\n ) and nums[rght] == target else -1 #\n```\n[https://leetcode.com/problems/search-in-rotated-sorted-array/submissions/1015192078/](http://)\n\nI could be wrong, but I think that time complexity is *O*(log*N*) and space complexity is *O*(1), in which *N* ~ `len(nums)`. | 5 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
easy by Binary search.... | search-in-rotated-sorted-array | 0 | 1 | #first find the index of minimum number\n#split the array into two halfs\n#apply Binary search on both the arrays \n\nclass Solution:\n def search(self, nums: List[int], target: int) -> int:\n l=0\n l3=[]\n h=len(nums)-1\n mi=-1\n#Binary seaarch to first find the index of minimum number\n while(l<=h):\n mid=(l+h)//2\n prev=(mid+len(nums)-1)%len(nums)\n if nums[mid]<=nums[prev]:\n mi=mid\n break\n if nums[l]<=nums[h]:\n mi=l\n break\n elif nums[l]<=nums[mid]:\n l=mid+1\n elif nums[mid]<=nums[h]:\n h=mid-1\n#split the array into two halfs\n l1=nums[:mi]\n l2=nums[mi:]\n#apply Binary search on both the arrays \n low1=0\n high1=len(l1)-1\n low2=0\n high2=len(l2)-1\n while(low1<=high1):\n mid=(low1+high1)//2\n if l1[mid]==target:\n l3.append(mid)\n break\n elif l1[mid]<target:\n low1=mid+1\n else:\n high1=mid-1\n while(low2<=high2):\n mid=(low2+high2)//2\n if l2[mid]==target:\n l3.append(mid+len(l1))\n break\n elif l2[mid]<target:\n low2=mid+1\n else:\n high2=mid-1\n if l3:\n return l3[0]\n return -1\n``` | 1 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
Easiest Solution | Binary Search | search-in-rotated-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(logn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def search(self, nums: List[int], target: int) -> int:\n left, right = 0, len(nums) - 1\n while left <= right:\n middle = (left + right) // 2\n if nums[middle] == target:\n return middle\n break\n if nums[left] <= nums[middle]:\n if target > nums[middle] or target < nums[left]:\n left = middle + 1\n else:\n right = middle - 1\n else:\n if target < nums[middle] or target > nums[right]:\n right = middle - 1\n else:\n left = middle + 1\n return -1\n``` | 1 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
C++ simple solution 15 lines binary search | search-in-rotated-sorted-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(log N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int search(vector<int>& arr, int k) {\n int low=0,hi=arr.size()-1;\n int l=-1,f=-1;\n int n=arr.size();\n while(low<=hi){\n int mid=low+(hi-low)/2;\n if(arr[mid]==k) return mid;\n else if(arr[mid]>=arr[low]){\n if(k>=arr[low] && k<arr[mid]) hi=mid-1;\n else low=mid+1;\n }else{\n if(k>arr[mid] && k<=arr[hi]){\n low=mid+1;\n }else hi=mid-1;\n }\n \n }\n return -1;\n }\n};\n``` | 1 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
C++/Python binary search|| beats 100% | search-in-rotated-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is solved by using binary search several times.\nFirstly, it is suggested to find the location for the peak which can be done by binary search.\nSecondly, using binary search to find location for the target which is possible before the peak or after the peak.\n\nBe careful for the boundary cases when n=1 and n=2.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo find the location for the peak, it needs to build a binary searching function for this special purpose. Once the location of the peak is sure, then use the built-in C++ lower_bound to find the target.\n\nThe python solution uses bisect_left.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n $$O(\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n $$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n int n;\n vector<int> x;\n int findK() {\n if (n==1) return 0;\n if (n==2) return (x[0]<x[1])?1:0;\n int l=0, r=n, m;\n while(l<r){\n m=(r+l)/2;\n if (m==n-1 || x[m]>x[m+1]) return m;\n if (x[m]>x[l]) l=m;\n else r=m; \n }\n return m;\n }\n int search(vector<int>& nums, int target) {\n x=nums;\n n=nums.size();\n int k=findK();\n // cout<<"k="<<k<<endl;\n auto it=x.begin();\n if (target>=x[0] || k==n-1){\n int i=lower_bound(it,it+k+1,target)-it;\n if (i == k+1 || x[i] != target) return -1;\n return i;\n } \n else{\n int i=lower_bound(it+k+1,it+n,target)-it;\n if (i == n || x[i] != target) return -1;\n return i;\n }\n }\n};\n```\n# Python solution\n```\nclass Solution:\n def search(self, x: List[int], target: int) -> int:\n n = len(x)\n \n def findK():\n if n == 1:\n return 0\n if n==2:\n if x[0]<x[1]: return 1\n else: return 0\n l=0\n r=n\n while l < r:\n m = (r + l) // 2\n if m==n-1 or x[m]>x[m+1]: return m\n if x[m]>x[l]: l=m\n else: r=m\n return m\n \n k=findK()\n \n if target >= x[0]:\n i = bisect_left(x, target, hi=k)\n if i<n and x[i] == target:\n return i\n return -1\n else:\n i = bisect_left(x, target, lo=k+1)\n if i<n and x[i] == target:\n return i\n return -1\n```\n# findK() uses bisect_right()\n```\ndef findK():\n if n == 1:\n return 0\n return bisect_right(x, False, key=lambda y: y < x[0])\n``` | 6 | There is an integer array `nums` sorted in ascending order (with **distinct** values).
Prior to being passed to your function, `nums` is **possibly rotated** at an unknown pivot index `k` (`1 <= k < nums.length`) such that the resulting array is `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]` (**0-indexed**). For example, `[0,1,2,4,5,6,7]` might be rotated at pivot index `3` and become `[4,5,6,7,0,1,2]`.
Given the array `nums` **after** the possible rotation and an integer `target`, return _the index of_ `target` _if it is in_ `nums`_, or_ `-1` _if it is not in_ `nums`.
You must write an algorithm with `O(log n)` runtime complexity.
**Example 1:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 0
**Output:** 4
**Example 2:**
**Input:** nums = \[4,5,6,7,0,1,2\], target = 3
**Output:** -1
**Example 3:**
**Input:** nums = \[1\], target = 0
**Output:** -1
**Constraints:**
* `1 <= nums.length <= 5000`
* `-104 <= nums[i] <= 104`
* All values of `nums` are **unique**.
* `nums` is an ascending array that is possibly rotated.
* `-104 <= target <= 104` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.