title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
398: Solution with step by step explanation | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo solve this problem, we can create a dictionary to store the indices of each target number. Then, when we need to pick a random index, we can use the random module to generate a random index from the list of indices associated with the target number.\n\n1. Create a dictionary to store the indices of each target number.\n\n2. Iterate through the array nums and add the index i to the list of indices associated with nums[i].\n\n3. When pick(target) is called, get the list of indices associated with the target number from the dictionary.\n\n4. Use the random module to generate a random index from the list of indices.\n\n5. Return the random index.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def __init__(self, nums: List[int]):\n # Create a dictionary to store the indices of each target number\n self.indices = {}\n # Iterate through the array nums and add the index i to the list of indices associated with nums[i]\n for i, num in enumerate(nums):\n if num not in self.indices:\n self.indices[num] = [i]\n else:\n self.indices[num].append(i)\n\n def pick(self, target: int) -> int:\n # Get the list of indices associated with the target number from the dictionary\n indices = self.indices[target]\n # Use the random module to generate a random index from the list of indices\n return random.choice(indices)\n\n``` | 3 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python simplest 4-line solution | random-pick-index | 0 | 1 | **Like it? please upvote...**\n```\nclass Solution:\n def __init__(self, nums: List[int]):\n self.index_dict = defaultdict(list)\n for i in range(len(nums)):\n self.index_dict[nums[i]].append(i)\n\n def pick(self, target: int) -> int:\n return random.choice(self.index_dict[target])\n``` | 8 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Solution | random-pick-index | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> arr;\n Solution(vector<int>& nums) {\n arr = nums; \n }\n int pick(int target) {\n int len = arr.size();\n int random = 0 + (rand() % len);\n while(arr[random] != target)\n random = 0 + (rand() % len);\n return random;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.nums = nums\n\n def pick(self, target: int) -> int:\n while True:\n i = int(random.random()*len(self.nums))\n if self.nums[i] == target:\n return i\n```\n\n```Java []\nclass Solution {\n private Random rmd;\n private int[] nums;\n public Solution(int[] nums) {\n this.rmd = new Random();\n this.nums = nums;\n }\n public int pick(int target) {\n while (true) {\n int index = rmd.nextInt(nums.length);\n if (nums[index] == target) {\n return index;\n }\n }\n }\n}\n```\n | 1 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Succinct solution | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nimport random \n\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.val_to_index = defaultdict(list)\n\n for idx,val in enumerate(nums):\n self.val_to_index[val].append(idx)\n \n \n def pick(self, target: int) -> int:\n return random.choice(self.val_to_index[target])\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python: simple and clear solution (Hashmap) | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n random.seed(127)\n self.m = collections.defaultdict(list)\n for i, v in enumerate(nums):\n self.m[v].append(i)\n \n\n def pick(self, target: int) -> int:\n bucket = self.m.get(target)\n if bucket:\n return bucket[int(random.random() * len(bucket))]\n return None\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python | Combining dictionary and reservoir sampling to beat TLE | random-pick-index | 0 | 1 | I wasn\'t able to avoid TLE with either reservoir sampling or the simple hash map strategy (even copying other listed solutions).\n\nIn the end, I was only able to avoid TLE by combining the two approaches. Instead of building up the dictionary of index lists (from which we randomly sample) in the initializer, we instead perform reservoir sampling in the first call to `pick` while saving all indices seen in the same loop. Subsequent calls to `pick` then just randomly select from the saved list.\n\n# Code\n```\nfrom random import randint\n\nclass Solution:\n def __init__(self, nums: List[int]):\n # save nums array for reservoir sampling for the first\n # call to pick\n self.nums = nums\n # save lists of indices to skip reservoir sampling\n # after we\'ve done one pick\n self.indices = defaultdict(list)\n\n def pick(self, target: int) -> int:\n # if we\'ve already called pick, just randomly select\n # from the saved index list\n if target in self.indices:\n return self.indices[target][\n randint(0, len(self.indices[target])-1)\n ]\n \n # otherwise, iterate through the whole list for reservoir\n # sampling\n r = None\n count = 0\n\n for i, n in enumerate(self.nums):\n if n == target:\n if r is None or randint(0, count) == 0:\n r = i\n count += 1\n\n # build up lists of indices\n self.indices[n].append(i)\n return r\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python3 || Simple || Hash Table || Random.randrange | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nGroup all numbers in the nums array and save all of their indexes. Generate a random number in the range of the size of the index list that has already been calculated. \n\n# Complexity\n- Time complexity: Constant\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n lookup = defaultdict(list)\n\n def __init__(self, nums: List[int]):\n\n # leetcode is flaky and state of this variable would persist across test cases if not cleared\n self.lookup.clear() \n\n for index, num in enumerate(nums):\n self.lookup[num].append(index)\n\n def pick(self, target: int) -> int:\n if len(self.lookup[target]) == 1:\n return self.lookup[target][0]\n \n random_index = randrange(len(self.lookup[target]))\n return self.lookup[target][random_index]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python3 Solution without using random module | random-pick-index | 0 | 1 | \n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n \n self.nums=nums\n self.d=defaultdict(list)\n for i,val in enumerate(nums):\n self.d[val].append(i)\n \n\n def pick(self, target: int) -> int:\n indices=self.d[target]\n ans=indices[0]\n self.d[target]=indices[1:]+indices[:1]\n return ans\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python | Simple intuitive Solution using hash_map | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.hash_map = {}\n\n for index, item in enumerate(nums):\n if item not in self.hash_map:\n self.hash_map[item] = []\n self.hash_map[item].append(index)\n print(self.hash_map)\n self.total = len(nums)-1\n\n def pick(self, target: int) -> int:\n index_list = self.hash_map[target]\n random_num = random.randint(0, len(index_list)-1)\n\n return index_list[random_num]\n\n\n\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Easy Python Solution | random-pick-index | 0 | 1 | # Code\n```\nfrom collections import Counter\nimport random\n\nclass Solution:\n def __init__(self, nums: List[int]):\n self.dict = {}\n for i in range(len(nums)):\n if nums[i] in self.dict: self.dict[nums[i]].append(i)\n else: self.dict[nums[i]] = [i]\n\n def pick(self, target: int) -> int:\n return self.dict[target][random.randint(0, len(self.dict[target]) - 1)]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
super short python solution using random.choice | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, nums: List[int]):\n self.d = defaultdict(list)\n for i, n in enumerate(nums):\n self.d[n].append(i)\n \n\n\n def pick(self, target: int) -> int:\n if target in self.d and len(self.d[target]) > 1:\n return random.choice(self.d[target])\n \n return self.d[target][0]\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Easy Python Solution ✅ | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Store all the values of nums as HASHMAP Keys\n- All the corresponding indices as HASHMAP Values\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, nums: List[int]):\n self.hashMap = {}\n for idx, i in enumerate(nums):\n if i not in self.hashMap:\n self.hashMap[i] = []\n\n self.hashMap[i].append(idx)\n\n def pick(self, target: int) -> int:\n idx_list = self.hashMap[target]\n return choice(idx_list)\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Preprocess the data and make the pick fast | random-pick-index | 0 | 1 | # Intuition\nFirst pre-process the data to make the read faster.\n# Approach\n1. Compute indices for each number\n2. Randomly choose indices\n\nStep 1. is going to take more space.\n# Complexity\n- Time complexity:\nO(1) to generate random index and fetch from list.\n\n- Space complexity:\nO(N) - Each entry can be unique and have an index.\n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.container = collections.defaultdict(list)\n for i, n in enumerate(nums):\n self.container[n].append(i)\n \n\n def pick(self, target: int) -> int:\n return random.choice(self.container[target])\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Pythonic - easy and quick | random-pick-index | 0 | 1 | # Intuition\n\nCreate a dictionary of all the indices then sample the indices\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom random import choice\n\nclass Solution:\n\n def __init__(self, nums: List[int]):\n data = {}\n for i, val in enumerate(nums):\n tmp = data.get(val, [])\n tmp.append(i) # update the indices list\n data[val] = tmp\n self.data = data\n \n def pick(self, target: int) -> int:\n indices = self.data[target]\n return choice(indices)\n \n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Simple using map | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.m = defaultdict(list)\n for i, e in enumerate(nums):\n self.m[e].append(i)\n \n def pick(self, target: int) -> int:\n ls = self.m[target]\n return ls[randrange(len(ls))]\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
python | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # (1) store each value index in a defaultdict list\n # (2) pick random from it\n\n # time complexity: O(n) for init, as we traverse all nodes; O(1) for pick()\n # space complexity: O(n), as we use extra space\n def __init__(self, nums: List[int]):\n self.mapper = defaultdict(list)\n for i in range(len(nums)):\n self.mapper[nums[i]].append(i)\n\n def pick(self, target: int) -> int:\n target_list = self.mapper[target]\n length = len(target_list)\n\n random_int = random.randint(0, length - 1)\n return target_list[random_int]\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python | random-pick-index | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n Hash Table\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```\nclass Solution:\n\n # O(n)\n def __init__(self, nums: List[int]):\n d = {}\n for i, num in enumerate(nums):\n d[num] = d.get(num, [])\n d[num].append(i)\n\n self.d = d\n\n # O(1)\n def pick(self, target: int) -> int:\n return random.choice(self.d[target])\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
[Python3] Beats 100% runtime and 100% memory | random-pick-index | 0 | 1 | # Code\n```\nclass Solution:\n def __init__(self, nums: List[int]):\n self.nums = nums\n self.map = {}\n\n def pick(self, target: int) -> int:\n if target not in self.map:\n temp = [i for i, n in enumerate(self.nums) if n == target]\n self.map[target] = temp\n return random.choice(temp)\n else:\n return random.choice(self.map[target])\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Python3 Dictionary+Dictionary | random-pick-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse two dictionaries one for storing all the indexes and for storing last used index.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.d={}\n for i,number in enumerate(nums):\n if number in self.d.keys():\n self.d[number].append(i)\n else:\n self.d[number]=[i]\n self.uniform={}\n for k in self.d.keys():\n self.uniform[k]=0\n\n def pick(self, target: int) -> int:\n index=self.uniform[target]\n index+=1\n if index>=len(self.d[target]):\n index=0\n self.uniform[target]=index\n return self.d[target][index]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
3 liner python solution | random-pick-index | 0 | 1 | \n# Code\n```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.a = nums\n\n def pick(self, target: int) -> int:\n self.i = [i for i, num in enumerate(self.a) if num == target]\n return random.choice(self.i)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Hash map based approach | random-pick-index | 0 | 1 | ```\nclass Solution:\n\n def __init__(self, nums: List[int]):\n self.hash_map = defaultdict(list)\n for i, num in enumerate(nums):\n self.hash_map[num].append(i)\n\n def pick(self, target: int) -> int:\n s = self.hash_map[target]\n index = random.randint(0, len(s)-1)\n return s[index]\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(nums)\n# param_1 = obj.pick(target)\n``` | 0 | Given an integer array `nums` with possible **duplicates**, randomly output the index of a given `target` number. You can assume that the given target number must exist in the array.
Implement the `Solution` class:
* `Solution(int[] nums)` Initializes the object with the array `nums`.
* `int pick(int target)` Picks a random index `i` from `nums` where `nums[i] == target`. If there are multiple valid i's, then each index should have an equal probability of returning.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick "\]
\[\[\[1, 2, 3, 3, 3\]\], \[3\], \[1\], \[3\]\]
**Output**
\[null, 4, 0, 2\]
**Explanation**
Solution solution = new Solution(\[1, 2, 3, 3, 3\]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums\[0\] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `-231 <= nums[i] <= 231 - 1`
* `target` is an integer from `nums`.
* At most `104` calls will be made to `pick`. | null |
Image Explanation🏆- [Easiest, Concise & Complete Intuition] - C++/Java/Python | evaluate-division | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Evaluate Division` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n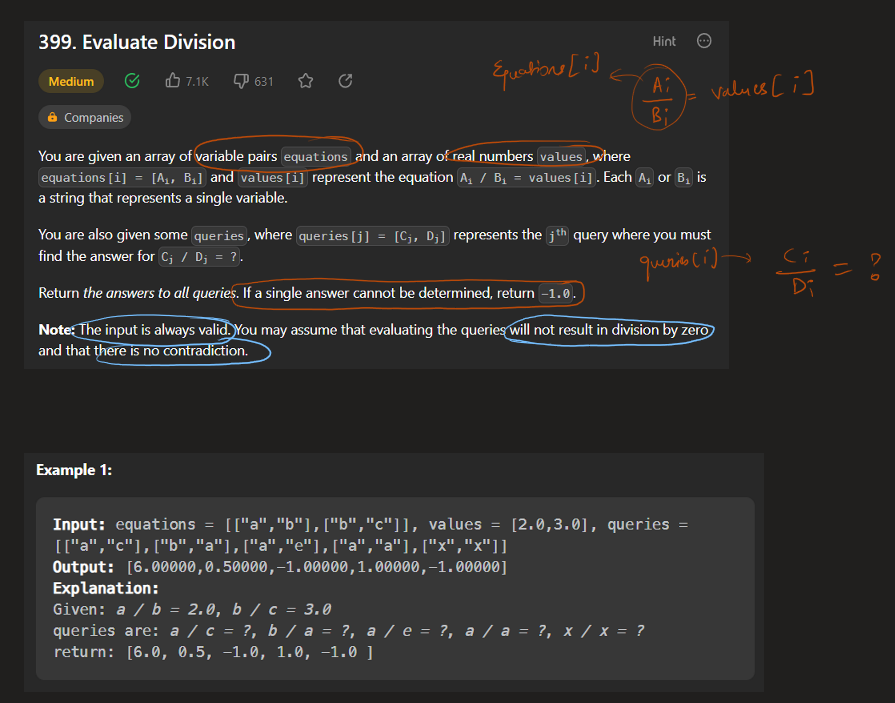\n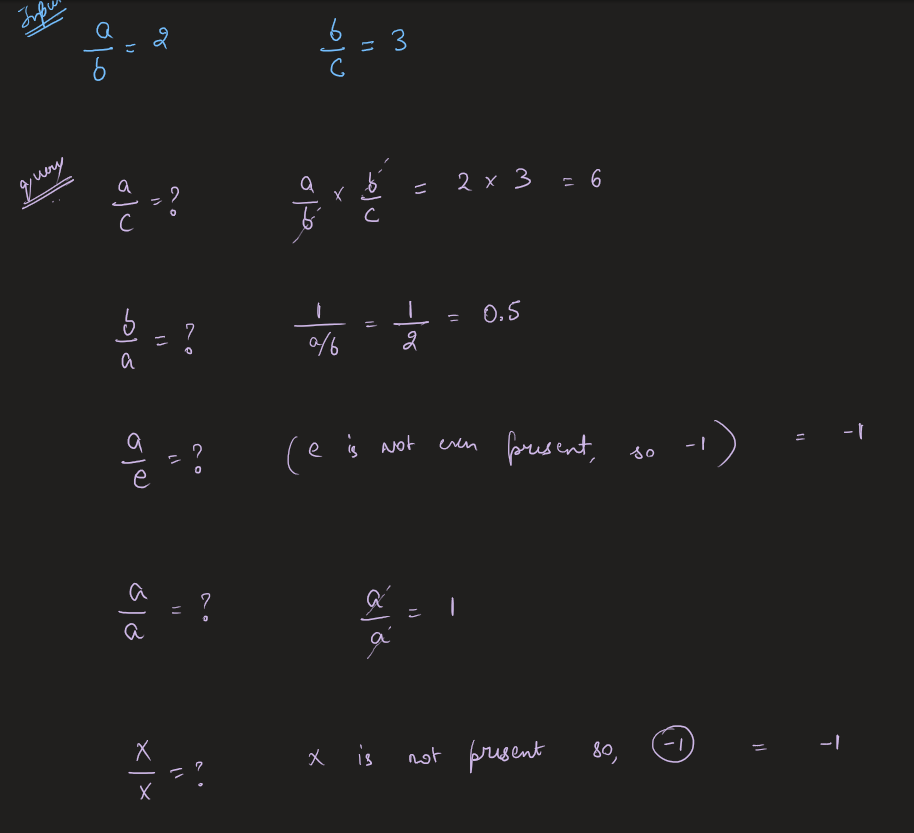\n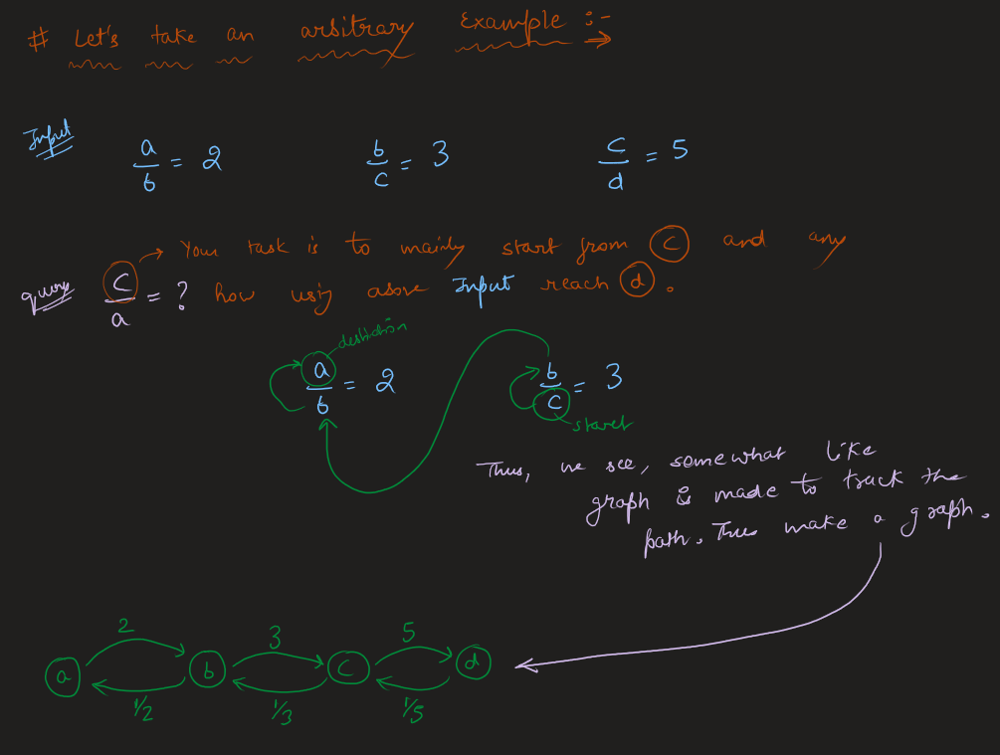\n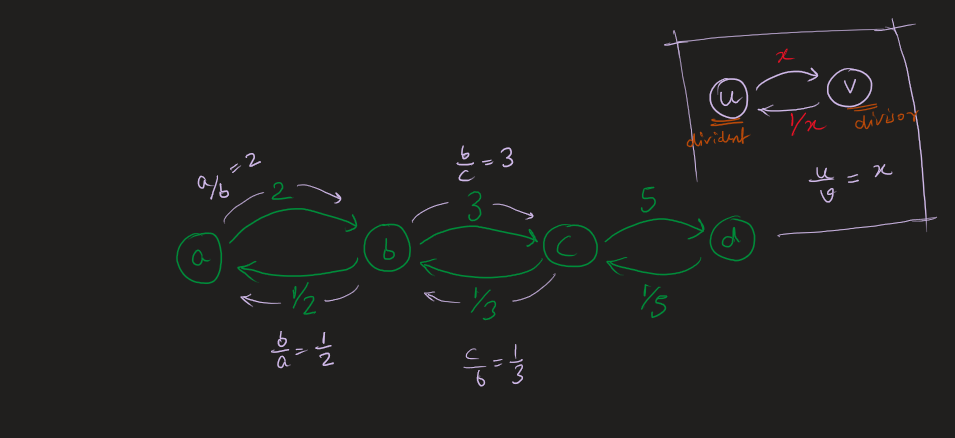\n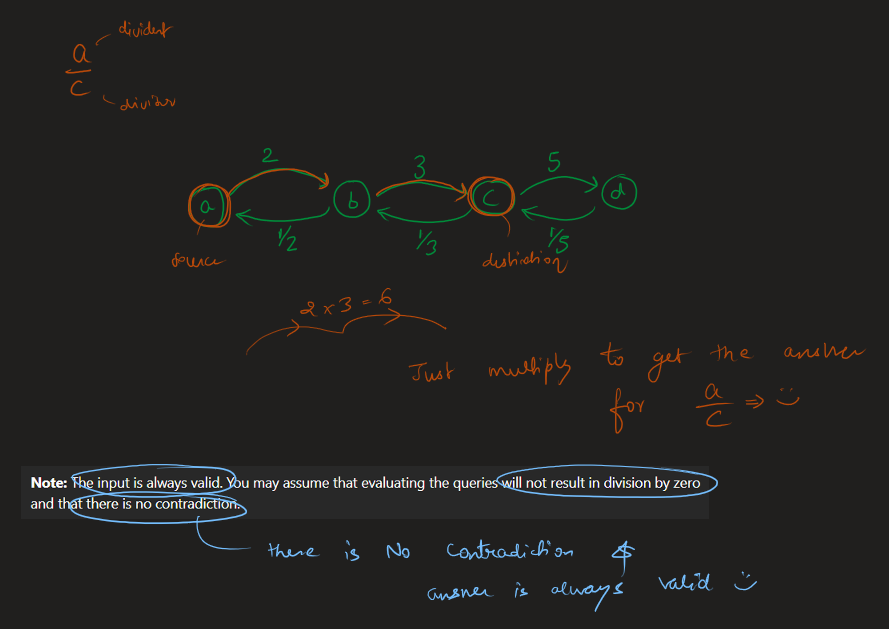\n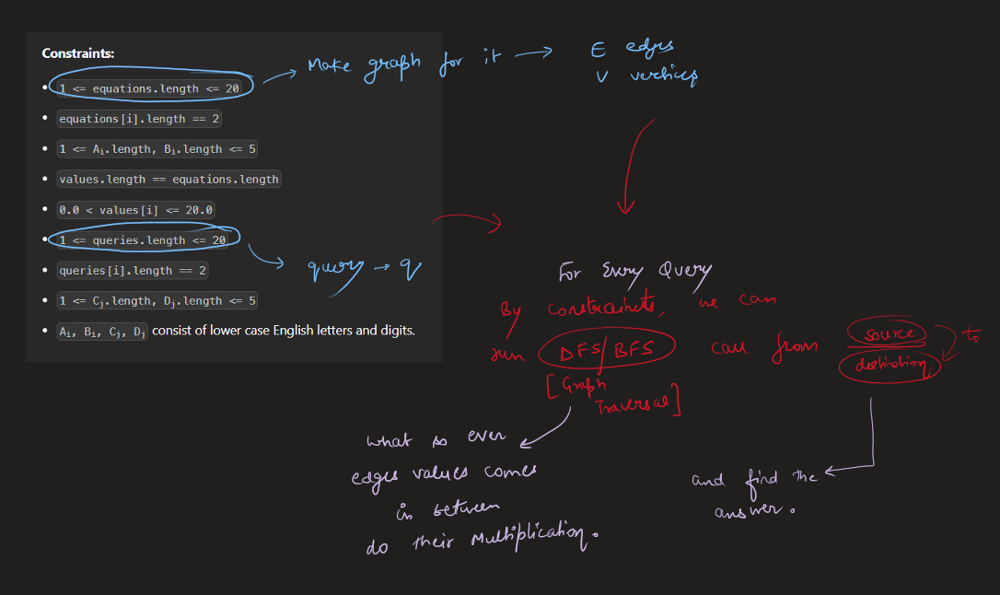\n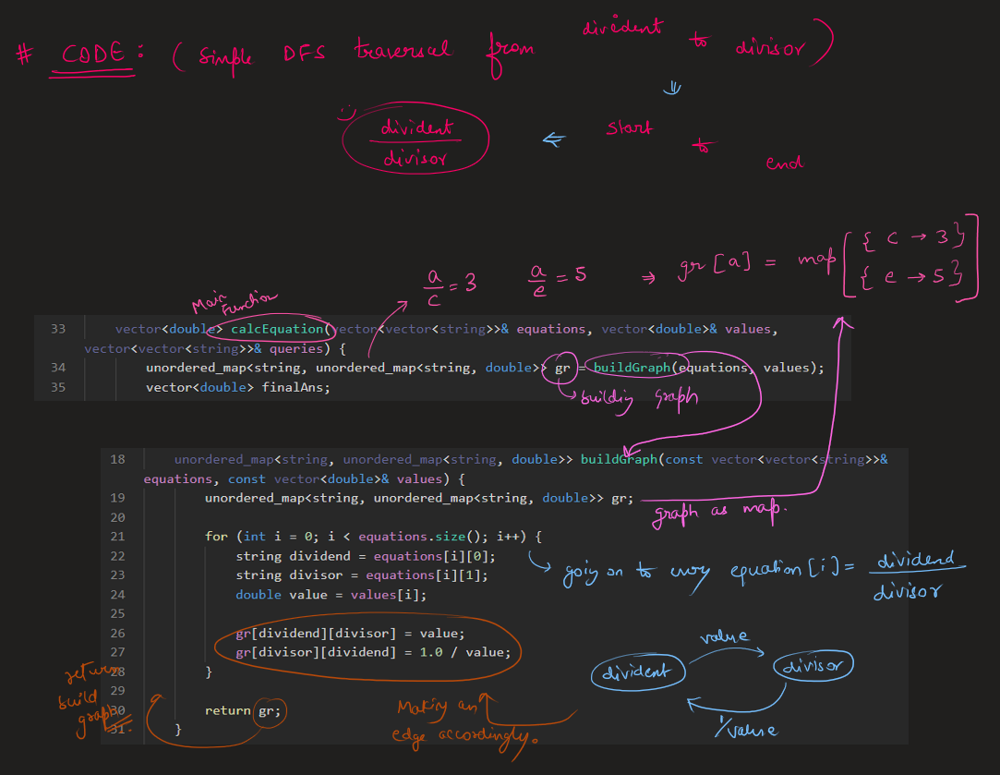\n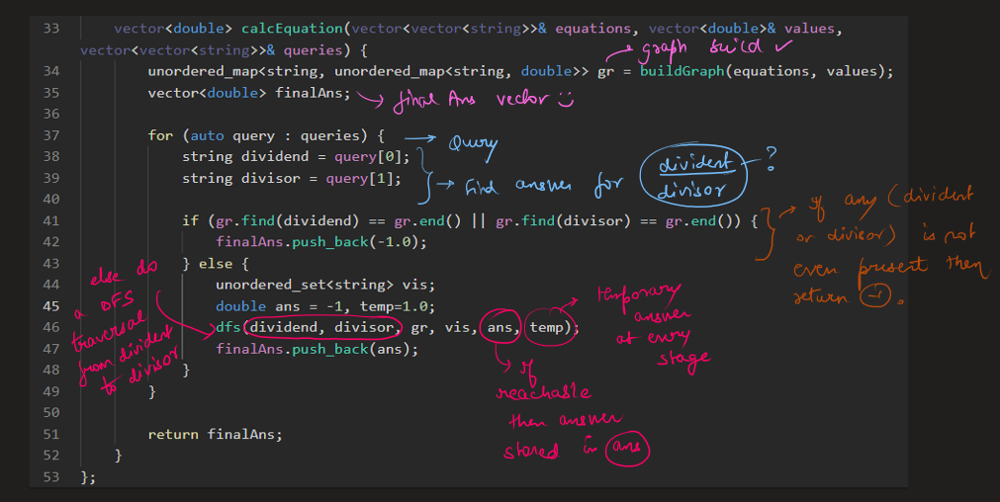\n\n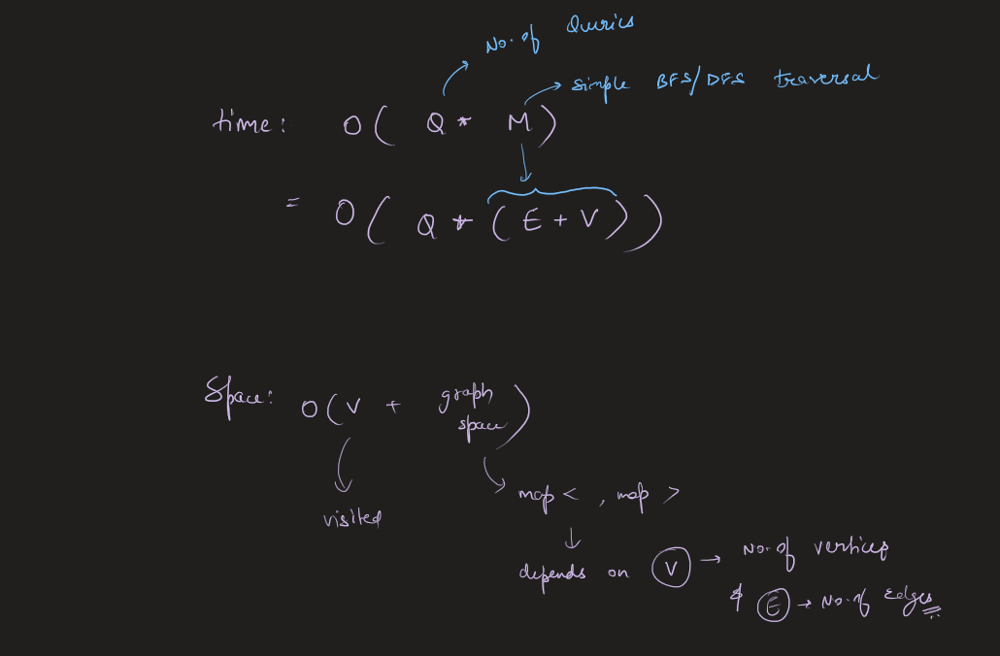\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n\n void dfs(string node, string& dest, unordered_map<string, unordered_map<string, double>>& gr, unordered_set<string>& vis, double& ans, double temp) {\n if(vis.find(node) != vis.end()) return;\n\n vis.insert(node);\n if(node == dest){\n ans = temp;\n return;\n }\n\n for(auto ne : gr[node]){\n dfs(ne.first, dest, gr, vis, ans, temp * ne.second);\n }\n }\n\n unordered_map<string, unordered_map<string, double>> buildGraph(const vector<vector<string>>& equations, const vector<double>& values) {\n unordered_map<string, unordered_map<string, double>> gr;\n\n for (int i = 0; i < equations.size(); i++) {\n string dividend = equations[i][0];\n string divisor = equations[i][1];\n double value = values[i];\n\n gr[dividend][divisor] = value;\n gr[divisor][dividend] = 1.0 / value;\n }\n\n return gr;\n }\n\n vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {\n unordered_map<string, unordered_map<string, double>> gr = buildGraph(equations, values);\n vector<double> finalAns;\n\n for (auto query : queries) {\n string dividend = query[0];\n string divisor = query[1];\n\n if (gr.find(dividend) == gr.end() || gr.find(divisor) == gr.end()) {\n finalAns.push_back(-1.0);\n } else {\n unordered_set<string> vis;\n double ans = -1, temp=1.0;\n dfs(dividend, divisor, gr, vis, ans, temp);\n finalAns.push_back(ans);\n }\n }\n\n return finalAns;\n }\n};\n```\n```Java []\nclass Solution {\n public void dfs(String node, String dest, HashMap<String, HashMap<String, Double>> gr, HashSet<String> vis, double[] ans, double temp) {\n if (vis.contains(node))\n return;\n\n vis.add(node);\n if (node.equals(dest)) {\n ans[0] = temp;\n return;\n }\n\n for (Map.Entry<String, Double> entry : gr.get(node).entrySet()) {\n String ne = entry.getKey();\n double val = entry.getValue();\n dfs(ne, dest, gr, vis, ans, temp * val);\n }\n }\n\n public HashMap<String, HashMap<String, Double>> buildGraph(List<List<String>> equations, double[] values) {\n HashMap<String, HashMap<String, Double>> gr = new HashMap<>();\n\n for (int i = 0; i < equations.size(); i++) {\n String dividend = equations.get(i).get(0);\n String divisor = equations.get(i).get(1);\n double value = values[i];\n\n gr.putIfAbsent(dividend, new HashMap<>());\n gr.putIfAbsent(divisor, new HashMap<>());\n\n gr.get(dividend).put(divisor, value);\n gr.get(divisor).put(dividend, 1.0 / value);\n }\n\n return gr;\n }\n\n public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {\n HashMap<String, HashMap<String, Double>> gr = buildGraph(equations, values);\n double[] finalAns = new double[queries.size()];\n\n for (int i = 0; i < queries.size(); i++) {\n String dividend = queries.get(i).get(0);\n String divisor = queries.get(i).get(1);\n\n if (!gr.containsKey(dividend) || !gr.containsKey(divisor)) {\n finalAns[i] = -1.0;\n } else {\n HashSet<String> vis = new HashSet<>();\n double[] ans = {-1.0};\n double temp = 1.0;\n dfs(dividend, divisor, gr, vis, ans, temp);\n finalAns[i] = ans[0];\n }\n }\n\n return finalAns;\n }\n}\n```\n```Python []\nfrom typing import List\n\nclass Solution:\n def dfs(self, node: str, dest: str, gr: dict, vis: set, ans: List[float], temp: float) -> None:\n if node in vis:\n return\n\n vis.add(node)\n if node == dest:\n ans[0] = temp\n return\n\n for ne, val in gr[node].items():\n self.dfs(ne, dest, gr, vis, ans, temp * val)\n\n def buildGraph(self, equations: List[List[str]], values: List[float]) -> dict:\n gr = {}\n\n for i in range(len(equations)):\n dividend, divisor = equations[i]\n value = values[i]\n\n if dividend not in gr:\n gr[dividend] = {}\n if divisor not in gr:\n gr[divisor] = {}\n\n gr[dividend][divisor] = value\n gr[divisor][dividend] = 1.0 / value\n\n return gr\n\n def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:\n gr = self.buildGraph(equations, values)\n finalAns = []\n\n for query in queries:\n dividend, divisor = query\n\n if dividend not in gr or divisor not in gr:\n finalAns.append(-1.0)\n else:\n vis = set()\n ans = [-1.0]\n temp = 1.0\n self.dfs(dividend, divisor, gr, vis, ans, temp)\n finalAns.append(ans[0])\n\n return finalAns\n\n``` | 94 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | evaluate-division | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n\n# or\n\n\n# Click the Link in my Profile\n\n# Approach:\n\nThe problem can be solved using graph traversal, specifically breadth-first search (BFS). We can represent the given equations as a graph, where each variable is a node, and the values represent the edges between the nodes. The division result between two variables can be found by traversing from the dividend node to the divisor node and multiplying the edge values encountered along the path.\n\n- Build the graph: Iterate through the given equations and values, and construct an adjacency map that represents the graph. For each equation (a / b = k), add edges (a, b) and (b, a) to the graph with edge values k and 1/k, respectively.\n\n- Evaluate queries: For each query (x, y), perform a BFS starting from node x and searching for node y. During the BFS traversal, keep track of the product of the edge values encountered. If y is reached, return the product as the division result. If y is not reached or either x or y is not present in the graph, return -1.\n\n# Intuition:\n\nThe problem can be viewed as finding a path in a graph from the dividend node to the divisor node while keeping track of the product of the edge values. Each node represents a variable, and the edge values represent the division results between variables. By performing a BFS, we can explore all possible paths and find the division result if it exists.\n\nBy building the graph and using BFS, we can efficiently evaluate the division queries by traversing the graph and multiplying the edge values encountered along the way. If the query variables are not present in the graph or if the destination variable is not reachable from the source variable, we return -1 to indicate that the division result is not possible.\n\nOverall, the approach leverages graph traversal and the properties of division to evaluate the division results efficiently.\n\n\n\n\n\n\n```Python []\nfrom collections import defaultdict, deque\n\nclass Solution:\n def calcEquation(self, equations, values, queries):\n graph = self.buildGraph(equations, values)\n results = []\n \n for dividend, divisor in queries:\n if dividend not in graph or divisor not in graph:\n results.append(-1.0)\n else:\n result = self.bfs(dividend, divisor, graph)\n results.append(result)\n \n return results\n \n def buildGraph(self, equations, values):\n graph = defaultdict(dict)\n \n for (dividend, divisor), value in zip(equations, values):\n graph[dividend][divisor] = value\n graph[divisor][dividend] = 1.0 / value\n \n return graph\n \n def bfs(self, start, end, graph):\n queue = deque([(start, 1.0)])\n visited = set()\n \n while queue:\n node, value = queue.popleft()\n \n if node == end:\n return value\n \n visited.add(node)\n \n for neighbor, weight in graph[node].items():\n if neighbor not in visited:\n queue.append((neighbor, value * weight))\n \n return -1.0\n\n```\n```Java []\n\nclass Solution {\n public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {\n Map<String, Map<String, Double>> graph = buildGraph(equations, values);\n double[] results = new double[queries.size()];\n\n for (int i = 0; i < queries.size(); i++) {\n List<String> query = queries.get(i);\n String dividend = query.get(0);\n String divisor = query.get(1);\n\n if (!graph.containsKey(dividend) || !graph.containsKey(divisor)) {\n results[i] = -1.0;\n } else {\n results[i] = bfs(dividend, divisor, graph);\n }\n }\n\n return results;\n }\n\n private Map<String, Map<String, Double>> buildGraph(List<List<String>> equations, double[] values) {\n Map<String, Map<String, Double>> graph = new HashMap<>();\n\n for (int i = 0; i < equations.size(); i++) {\n List<String> equation = equations.get(i);\n String dividend = equation.get(0);\n String divisor = equation.get(1);\n double value = values[i];\n\n graph.putIfAbsent(dividend, new HashMap<>());\n graph.putIfAbsent(divisor, new HashMap<>());\n graph.get(dividend).put(divisor, value);\n graph.get(divisor).put(dividend, 1.0 / value);\n }\n\n return graph;\n }\n\n private double bfs(String start, String end, Map<String, Map<String, Double>> graph) {\n Queue<Pair<String, Double>> queue = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n queue.offer(new Pair<>(start, 1.0));\n\n while (!queue.isEmpty()) {\n Pair<String, Double> pair = queue.poll();\n String node = pair.getKey();\n double value = pair.getValue();\n\n if (node.equals(end)) {\n return value;\n }\n\n visited.add(node);\n\n for (Map.Entry<String, Double> neighbor : graph.get(node).entrySet()) {\n String neighborNode = neighbor.getKey();\n double neighborValue = neighbor.getValue();\n\n if (!visited.contains(neighborNode)) {\n queue.offer(new Pair<>(neighborNode, value * neighborValue));\n }\n }\n }\n\n return -1.0;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {\n unordered_map<string, unordered_map<string, double>> graph = buildGraph(equations, values);\n vector<double> results;\n\n for (const auto& query : queries) {\n const string& dividend = query[0];\n const string& divisor = query[1];\n\n if (graph.find(dividend) == graph.end() || graph.find(divisor) == graph.end()) {\n results.push_back(-1.0);\n } else {\n results.push_back(bfs(dividend, divisor, graph));\n }\n }\n\n return results;\n }\n\nprivate:\n unordered_map<string, unordered_map<string, double>> buildGraph(const vector<vector<string>>& equations, const vector<double>& values) {\n unordered_map<string, unordered_map<string, double>> graph;\n\n for (int i = 0; i < equations.size(); i++) {\n const string& dividend = equations[i][0];\n const string& divisor = equations[i][1];\n double value = values[i];\n\n graph[dividend][divisor] = value;\n graph[divisor][dividend] = 1.0 / value;\n }\n\n return graph;\n }\n\n double bfs(const string& start, const string& end, unordered_map<string, unordered_map<string, double>>& graph) {\n queue<pair<string, double>> q;\n unordered_set<string> visited;\n q.push({start, 1.0});\n\n while (!q.empty()) {\n string node = q.front().first;\n double value = q.front().second;\n q.pop();\n\n if (node == end) {\n return value;\n }\n\n visited.insert(node);\n\n for (const auto& neighbor : graph[node]) {\n const string& neighborNode = neighbor.first;\n double neighborValue = neighbor.second;\n\n if (visited.find(neighborNode) == visited.end()) {\n q.push({neighborNode, value * neighborValue});\n }\n }\n }\n\n return -1.0;\n }\n};\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 22 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
Python Elegant & Short | Floyd–Warshall | evaluate-division | 0 | 1 | # Complexity\n- Time complexity: $$O(n^3)$$\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:\n graph = defaultdict(dict)\n\n for (u, v), val in zip(equations, values):\n graph[u][u] = graph[v][v] = 1\n graph[u][v] = val\n graph[v][u] = 1 / val\n\n for k in graph:\n for i in graph[k]:\n for j in graph[k]:\n graph[i][j] = graph[i][k] * graph[k][j]\n\n return [graph[u].get(v, -1) for u, v in queries]\n``` | 18 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
EASY PYTHON SOLUTION USING BFS | evaluate-division | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N * E)\n- N is number of queries\n- E is number of edges or simple number of equations\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:\n\n # No division by zero\n adjacencyList = collections.defaultdict(list) # A defaultdict is a dictionary-like object that automatically initializes values for nonexistent keys\n\n for i,eq in enumerate(equations):\n a,b = eq # Each equation has two values\n adjacencyList[a].append([b,values[i]]) # Append [b,value(a/b)]\n adjacencyList[b].append([a,1/values[i]]) # b/a will be equal to 1 / (a/b)\n\n print(adjacencyList)\n def bfs(src,trg):\n if src not in adjacencyList or trg not in adjacencyList:\n return -1\n \n q = deque()\n visited = set()\n\n q.append([src,1]) # I\'ll append a node with the weight upto that node\n visited.add(src)\n \n while q:\n n , w = q.popleft() # Neighbor, Weight\n\n if n == trg:\n return w\n\n for neighbor,weight in adjacencyList[n]: # Iterating over the adjacency List of that particular node\n if neighbor not in visited:\n q.append([neighbor, w * weight])\n visited.add(n)\n\n return -1\n\n return [bfs(query[0],query[1]) for query in queries]\n \n\n``` | 1 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
DFS Approach | Python | Golang | C++ | evaluate-division | 0 | 1 | # Code\n``` Go []\nfunc calcEquation(equations [][]string, values []float64, queries [][]string) []float64 {\n graph := make(map[string]map[string]float64)\n\tseen := make(map[string]bool)\n\n\tfor i := 0; i < len(equations); i++ {\n\t\ta, b := equations[i][0], equations[i][1]\n\n\t\tif _, ok := graph[a]; !ok {\n\t\t\tgraph[a] = make(map[string]float64)\n\t\t}\n\t\tgraph[a][b] = values[i]\n\n\t\tif _, ok := graph[b]; !ok {\n\t\t\tgraph[b] = make(map[string]float64)\n\t\t}\n\t\tgraph[b][a] = 1 / values[i]\n\t}\n\n\tvar divide func(string, string) float64\n\tdivide = func(a, b string) float64 {\n\t\tif a == b {\n\t\t\treturn 1.00000\n\t\t}\n\n\t\tseen[a] = true\n\t\tfor key, value := range graph[a] {\n\t\t\tif seen[key] {\n\t\t\t\tcontinue\n\t\t\t}\n\n\t\t\tres := divide(key, b)\n\t\t\tif res > 0 {\n\t\t\t\treturn res * value\n\t\t\t}\n\t\t}\n\t\treturn -1.000\n\t}\n\n var isExists func(string, string) bool\n isExists = func(a, b string) bool {\n if _, ok := graph[a]; !ok {\n return false\n }\n\n if _, ok := graph[b]; !ok {\n return false\n }\n\n return true\n }\n\n\tans := make([]float64, 0)\n\tfor _, q := range queries {\n\t\ta, b := q[0], q[1]\n\n\t\tif !isExists(a, b) {\n\t\t\tans = append(ans, -1.000)\n\t\t\tcontinue\n\t\t}\n\n\t\tseen = make(map[string]bool)\n\t\tans = append(ans, divide(a, b))\n\t}\n\n\treturn ans\n}\n```\n``` Python []\nfrom collections import defaultdict\n\nclass Solution:\n def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:\n graph = defaultdict(dict)\n seen = set()\n\n for i in range(len(equations)):\n a, b = equations[i][0], equations[i][1]\n graph[a][b] = values[i]\n graph[b][a] = 1 / values[i]\n\n\n def divide(a, b):\n if a == b:\n return 1.00000\n\n seen.add(a)\n for key, value in graph[a].items():\n if key in seen:\n continue\n\n res = divide(key, b)\n if res > 0:\n return float(res * value)\n return -1.000\n\n ans = []\n for q in queries:\n a, b = q[0], q[1]\n\n if a not in graph or b not in graph:\n ans.append(-1.000)\n continue\n\n seen = set()\n ans.append(divide(a, b))\n\n return ans\n```\n```C++ []\n#define pb push_back\n\nclass Solution {\npublic:\n unordered_map<string , unordered_map<string , double>> graph;\n unordered_set<string> seen;\n vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {\n vector<double>ans;\n \n for(int i=0;i<equations.size();i++){\n const string& A = equations[i][0];\n const string& B = equations[i][1];\n \n graph[A][B] = values[i];\n graph[B][A] = 1/ values[i];\n }\n \n for(const auto&q : queries){\n const string& C = q[0];\n const string& D = q[1];\n \n if(!graph.count(C) || !graph.count(D)) {ans.pb(-1) ; continue;}\n ans.pb(divide(C , D ));\n seen.clear();\n }\n \n return ans;\n }\n \nprivate:\n double divide(const string& A ,const string& C){\n if(A==C) return 1;\n seen.insert(A);\n \n for(const auto& i:graph[A]){\n string B = i.first;\n double value = i.second;\n if(seen.count(B)) continue;\n const double res = divide(B , C);\n if(res > 0) return res * value;\n }\n \n return -1;\n }\n};\n``` | 4 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
399: Solution with step by step explanation | evaluate-division | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe solution uses a graph data structure to represent the equations, with each variable as a node and the value of the edge between two nodes representing the ratio of their values. The graph is built by iterating through the given equations and values and adding the appropriate edges to the graph using a defaultdict.\n\nThe solution then uses a depth-first search (DFS) algorithm to find the value of the query for each given pair of variables. The DFS function takes as input the starting node, ending node, and a set of visited nodes, and recursively traverses the graph to find the path value between the starting and ending nodes. The visited set is used to avoid visiting nodes that have already been visited in the current path, which prevents infinite loops in cyclic graphs. If the path value is found, the DFS function returns the product of the current edge value and the path value. If the path value is not found, the DFS function returns -1.0 to indicate that the query cannot be evaluated.\n\nFinally, the solution iterates through the given queries, performs the DFS algorithm for each query, and appends the resulting value to the output list.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(N*M), where N is the number of equations and M is the length of the longest path in the graph, since the DFS algorithm is called once for each query and may visit each node in the graph at most once.\n\n- Space complexity:\nThe space complexity is O(N), since the graph is represented using a defaultdict that may have at most N keys.\n\n# Code\n```\nclass Solution:\n def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:\n # Build the graph\n graph = defaultdict(dict)\n for i in range(len(equations)):\n u, v = equations[i]\n graph[u][v] = values[i]\n graph[v][u] = 1 / values[i]\n \n # Helper function to perform DFS and find the path value\n def dfs(start, end, visited):\n # If we have already visited this node or it doesn\'t exist in the graph, return -1.0\n if start in visited or start not in graph:\n return -1.0\n # If we have reached the end node, return the path value\n if start == end:\n return 1.0\n # Mark the current node as visited\n visited.add(start)\n # Traverse the neighbors and find the path value recursively\n for neighbor, value in graph[start].items():\n path_value = dfs(neighbor, end, visited)\n # If we have found a valid path, return the product of the current value and path value\n if path_value != -1.0:\n return value * path_value\n # If we haven\'t found a valid path, return -1.0\n return -1.0\n \n # Calculate the answer for each query\n result = []\n for query in queries:\n start, end = query\n # Perform DFS to find the path value\n result.append(dfs(start, end, set()))\n \n return result\n\n``` | 8 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
Python DFS solution Explained (video + code) | evaluate-division | 0 | 1 | [](https://www.youtube.com/watch?v=EfkvVigVou0)\nhttps://www.youtube.com/watch?v=EfkvVigVou0\n```\nclass Solution:\n def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:\n # Step 1. Build the Graph\n graph = collections.defaultdict(dict)\n for (x, y), val in zip(equations,values):\n graph[x][y] = val\n graph[y][x] = 1.0 / val\n print(graph)\n \n # Step 2. DFS function\n def dfs(x, y, visited):\n # neither x not y exists\n if x not in graph or y not in graph:\n return -1.0\n \n # x points to y\n if y in graph[x]:\n return graph[x][y]\n \n # x maybe connected to y through other nodes\n # use dfs to see if there is a path from x to y\n for i in graph[x]:\n if i not in visited:\n visited.add(i)\n temp = dfs(i, y, visited)\n if temp == -1:\n continue\n else:\n return graph[x][i] * temp\n return -1\n \n # go through each of the queries and find the value\n res = []\n for query in queries:\n res.append(dfs(query[0], query[1], set()))\n return res\n``` | 40 | You are given an array of variable pairs `equations` and an array of real numbers `values`, where `equations[i] = [Ai, Bi]` and `values[i]` represent the equation `Ai / Bi = values[i]`. Each `Ai` or `Bi` is a string that represents a single variable.
You are also given some `queries`, where `queries[j] = [Cj, Dj]` represents the `jth` query where you must find the answer for `Cj / Dj = ?`.
Return _the answers to all queries_. If a single answer cannot be determined, return `-1.0`.
**Note:** The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
**Example 1:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\]\], values = \[2.0,3.0\], queries = \[\[ "a ", "c "\],\[ "b ", "a "\],\[ "a ", "e "\],\[ "a ", "a "\],\[ "x ", "x "\]\]
**Output:** \[6.00000,0.50000,-1.00000,1.00000,-1.00000\]
**Explanation:**
Given: _a / b = 2.0_, _b / c = 3.0_
queries are: _a / c = ?_, _b / a = ?_, _a / e = ?_, _a / a = ?_, _x / x = ?_
return: \[6.0, 0.5, -1.0, 1.0, -1.0 \]
**Example 2:**
**Input:** equations = \[\[ "a ", "b "\],\[ "b ", "c "\],\[ "bc ", "cd "\]\], values = \[1.5,2.5,5.0\], queries = \[\[ "a ", "c "\],\[ "c ", "b "\],\[ "bc ", "cd "\],\[ "cd ", "bc "\]\]
**Output:** \[3.75000,0.40000,5.00000,0.20000\]
**Example 3:**
**Input:** equations = \[\[ "a ", "b "\]\], values = \[0.5\], queries = \[\[ "a ", "b "\],\[ "b ", "a "\],\[ "a ", "c "\],\[ "x ", "y "\]\]
**Output:** \[0.50000,2.00000,-1.00000,-1.00000\]
**Constraints:**
* `1 <= equations.length <= 20`
* `equations[i].length == 2`
* `1 <= Ai.length, Bi.length <= 5`
* `values.length == equations.length`
* `0.0 < values[i] <= 20.0`
* `1 <= queries.length <= 20`
* `queries[i].length == 2`
* `1 <= Cj.length, Dj.length <= 5`
* `Ai, Bi, Cj, Dj` consist of lower case English letters and digits. | Do you recognize this as a graph problem? |
5 liner code | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n x,y,q=1,1,10\n while q<n:\n x,y=q,y+1,\n q=x+9*y*(10**(y-1))\n return int(str((10**(y-1))+((n-x)//(y)))[(n-x)%(y)])\n``` | 6 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
[Python3] O(logN) solution | nth-digit | 0 | 1 | Observe that there are 9 numbers with 1 digit, 90 numbers with 2 digits, 900 numbers with 3 digits, ... A `O(logN)` solution can be derived from it. \n\n```\n 1-9 | 9\n 10-99 | 90\n 100-999 | 900 \n 1000-9999 | 9000 \n10000-99999 | 90000\n```\n\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n digit = base = 1 # starting from 1 digit\n while n > 9*base*digit: # upper limit of d digits \n n -= 9*base*digit\n digit += 1\n base *= 10 \n q, r = divmod(n-1, digit)\n return int(str(base + q)[r])\n``` | 36 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
400: Solution with step by step explanation | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if n is a single digit number, return n if true.\n2. Set the base value for the digit count to 9 and the initial number of digits to 1.\n3. Use a while loop to iterate as long as n is greater than the product of the base and digits.\n4. Inside the loop, subtract the count of digits from n, increase the base value by a factor of 10, and increase the number of digits by 1.\n5. Calculate the number where the nth digit is located by using the formula: num = 10 ** (digits - 1) + (n - 1) // digits.\n6. Calculate the index of the nth digit in the number by using the formula: idx = (n - 1) % digits.\n7. Return the nth digit as an integer by converting the character at the calculated index to an integer.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n if n <= 9: # If n is a single digit, return n\n return n\n \n base = 9 # Set the base value for the digit count\n digits = 1 # Set the initial number of digits to 1\n while n > base * digits:\n n -= base * digits # Subtract the count of digits from n\n base *= 10 # Increase the base value by a factor of 10\n digits += 1 # Increase the number of digits by 1\n \n num = 10 ** (digits - 1) + (n - 1) // digits # Calculate the number where the nth digit is located\n idx = (n - 1) % digits # Calculate the index of the nth digit in the number\n \n return int(str(num)[idx]) # Return the nth digit as an integer\n\n``` | 7 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
python clean & simple solution ✅ | | beats 94% in runtime | nth-digit | 0 | 1 | *Straight forward way to solve the problem in 3 steps:*\n\n*1. find the length of the number where the nth digit is from*\n*2. find the actual number where the nth digit is from*\n*3. find the nth digit and return*\n# *Code*\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n digit = 1\n cnt = 9\n st = 1\n while cnt*digit < n:\n n -= cnt*digit\n digit += 1\n cnt *= 10\n st *= 10\n\n st += (n- 1)/digit\n st = str(st)\n return int(st[(n-1)%digit])\n``` | 4 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python3 with math | nth-digit | 0 | 1 | ```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n """\n imagine the number you need to find have 4 digit\n so you need to go throught all num have 1 digit, 2 digit, 3 digit\n number have 1 digit: 10 ** 1 - 1 = 9 => 9 * 1 = 9 digit\n number have 2 digit: 10 ** 2 - 1 = 90 => 90 * 2 = 180 digit\n number have 3 digit: 10 ** 3 - 1 = 900 => 900 * 3 = 2700 digit\n ...\n just subtract until you find how many digit of the number you need to find\n when you got the number of digit \n """\n if n < 10:\n return n\n \n number_of_digit = 0 # check how many digit of the number you need to find\n while n > 0:\n number_of_digit += 1\n n -= 9 * 10 ** ((number_of_digit - 1)) * number_of_digit\n n += 9 * 10 ** ((number_of_digit - 1)) * number_of_digit\n \n """ \n print(n , number_of_digit) if you dont understand \n after subtract you will find number of digit\n all you need to do now is find exactly number by just a little bit of math\n """ \n tmp_num = 0\n \n if n % number_of_digit == 0:\n n //= number_of_digit \n tmp_num += 10 ** ((number_of_digit - 1)) - 1\n return int(str(tmp_num + n)[-1])\n else:\n n /= number_of_digit\n digit = int((n * number_of_digit) % number_of_digit)\n tmp_num += 10 ** ((number_of_digit - 1)) - 1\n return int(str(int(tmp_num + n) + 1)[digit - 1])\n \n``` | 3 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
80% TC and 89% SC easy python solution | nth-digit | 0 | 1 | ```\ndef findNthDigit(self, n: int) -> int:\n\ttemp = 0\n\ti = 1\n\twhile(temp + i*(10**i - 10**(i-1)) < n):\n\t\ttemp += i*(10**i - 10**(i-1))\n\t\ti += 1\n\td = i\n\tn -= temp\n\tnum = n//d\n\tdone = str(10**(d-1)-1 + num + int(n%d > 0))\n\tif(n % d):\n\t\treturn done[n%d - 1]\n\treturn done[-1]\n``` | 1 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Full math solution | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n cur = 0\n seed = 9\n bits = 1\n while cur + seed * bits < n:\n cur += seed * bits\n seed *= 10\n bits += 1\n\n needs = (n-cur) // bits \n bit = (n-cur) % bits\n num = 10**(bits-1) + needs\n if bit:\n return int(str(num)[bit-1]) \n else:\n num -= 1\n return int(str(num)[-1])\n \n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Time complexity: O(log(N)) , Space complexity: O(log(N)) | nth-digit | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nCalculate Interval (inte): Divide n by 9 to determine the interval of numbers with a certain length.\n\nFind Length (indes): Convert inte to a string (le) and iterate through possible lengths (j). Find the length indes such that the cumulative count of numbers with lengths less than or equal to indes is greater than inte.\n\nCalculate Starting Number (num): Iterate through lengths up to indes - 1 and calculate the cumulative count of numbers with those lengths (num). This gives the starting number for the length indes.\n\nAdjust n: Subtract the cumulative count of numbers with lengths less than indes from n.\n\nCalculate Actual Number (result): Determine the actual number based on the length indes and the adjusted n.\n\nCalculate Digit Position (m): Calculate the position of the digit within the number by taking the remainder of the adjusted n divided by indes.\n\nRetrieve Digit (results): If m is greater than 0, retrieve the digit at position m - 1 in the string representation of result + 1. Otherwise, retrieve the last digit of the string representation of result.\n\nReturn Result: Return the final digit.\n# Complexity\n- Time complexity: O(log(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(log(N))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n inte = n // 9\n le = str(inte)\n indes = 0\n num = 0\n for j in range(1,len(le)+2):\n num = num + j*10**(j-1)\n if inte < num:\n indes = j\n break\n num = 0\n for k in range(1,indes):\n num = num + k*9*10**(k-1)\n n = n - num \n result = 10**(indes-1) - 1 + n // indes\n m = int(n % indes)\n if m > 0:\n results = int(str(result+1)[m-1])\n else:\n results = int(str(result)[-1])\n return results\n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
[Python] Intution, Drawing Explanation and Code for my Math Solution. | nth-digit | 0 | 1 | ## Intuition and Drawing Explanation\n\n\nWe can simply keep subtracting from n and get the range. Code is as follows\n\n```\nnumbers_with_i_digits = 9\npower = 1\ndigits = n\nfor i in range(1,10):\n if(digits < numbers_with_i_digits * i):\n power = i - 1\n break\n digits -= numbers_with_i_digits * i\n numbers_with_i_digits *= 10\n```\n**power** represents lower range as 10^power and 10^(power + 1) (for example, if power is 2, the numbers is between 10 and 100)\n\n\n\nIn my code since I am adding digits/(power + 1) to number at start of range, I have to calculate it as (digits - 1)// (power + 1). Since 3rd and 4th digit both would be give 1, in our case ( // represents integer division)\n\n```\n# Suppose its between 10 and 99. We need to check for (digits)th digit \nstart_of_range = pow(10,power)\nat_which_number = (digits - 1)//(power + 1)\nat_which_index = (digits - 1) % (power + 1)\nreturn int(str(start_of_range + at_which_number)[at_which_index])\n```\nThis code doesn\'t have a case covered, what if digits == 0. It simply means, it\'s the 9th digit or (9 + 90*2 = 189)th digit, which is in fact just 9!\n\n## Code\n\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n # 9 numbers with 1 digit, 90 numbers with 2 digits, 900 numbers with 3 digits, etc.\n numbers_with_i_digits = 9\n power = 1\n digits = n\n for i in range(1,10):\n if(digits < numbers_with_i_digits * i):\n power = i - 1\n break\n digits -= numbers_with_i_digits * i\n numbers_with_i_digits *= 10\n\n if (digits == 0):\n return 9\n \n # Suppose its between 10 and 99. We need to check for (temp)th digit \n start_of_range = pow(10,power)\n at_which_number = (digits - 1)//(power + 1)\n at_which_index = (digits - 1) % (power + 1)\n return int(str(start_of_range + at_which_number)[at_which_index])\n```\n\nThere maybe a lot of optimisations that can be done here, to make it even more faster, by making the code shorter, but logic remains same. The above solution is faster than 82% | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Beginner Friendly Solution | nth-digit | 0 | 1 | # Complexity\n- Time complexity:$$O(logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n num,digit = 1,1\n count = 9\n\n while(n > digit * count):\n n -= digit * count\n digit +=1\n count *= 10\n num *=10\n\n num += (n-1)//digit\n index = (n-1)%digit\n s = str(num)\n return int(s[index])\n\n \n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python solution | runtime - 32 ms beats - 90% ✅✅ | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n x,y,q=1,1,10\n while q<n:\n x,y=q,y+1,\n q=x+9*y*(10**(y-1))\n return int(str((10**(y-1))+((n-x)//(y)))[(n-x)%(y)])\n \n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python O(log(n)) | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLook at the number of digits:\n1. 1*9: 1~9;\n2. 2*90: 10~99;\n3. 3*900: 100~999;\n4. 4*9000:1000~9999\n5. ....\n\nEach step can take 9, 90, 900, 9000...\nSo the intuition is to subtract number of digits denoted by n_digits * step and when n <= n_digits * step, we stop the loop and try to calculate the actual number in which the N-th digit lies and the corresponding index/position of the N-th digit.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe while loop can take O(log(n)).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code 1\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n if n <= 9:\n return n\n n_digits = 1\n base = 1\n while n >= 9 * base * n_digits:\n n -= 9 * base * n_digits\n n_digits += 1\n base *= 10\n \n if n == 0:\n return 9\n\n number = base + (n-1) // n_digits\n idx = (n-1) % n_digits\n return int(str(number)[idx])\n```\n# Code 2\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n n_digits = 1\n base = 1\n while n > 9 * base * n_digits:\n n -= 9 * base * n_digits\n n_digits += 1\n base *= 10\n \n number = base + (n-1) // n_digits\n idx = (n-1) % n_digits\n return int(str(number)[idx])\n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Simple brute force that beats 100% in o(logn) | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n# **O**(logn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# **O**(1)\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n if n < 10:\n return n\n\n group = 1\n group_size = 9\n while n > group_size * group:\n n -= group_size * group\n group += 1\n group_size *= 10\n\n num_in_group = 10 ** (group - 1) + (n - 1) // group\n digit_index = (n - 1) % group\n\n return int(str(num_in_group)[digit_index])\n \n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Binary search | nth-digit | 0 | 1 | let f(x) = how many digits in sequence [1,x]\n\nbinary search with this f \n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n def f(bound):\n if (bound <=0):return 0\n digits = int(math.log10(bound))+1\n result =0 \n c = 9\n\n for i in range(1, digits):\n \n result += 9 * (10**(i - 1)) *i\n # print(9 * (10**(i - 1)) *i)\n\n # [1*00(digits), bound]\n result += (bound - ((10**(digits - 1))-1)) * digits\n # print((bound - (10**(digits - 1))) * digits)\n return result\n\n left = 1\n right = n\n\n while left <=right:\n mid = (left+ right) // 2\n if f(mid - 1) <= n and f(mid) >=n:\n start = f(mid-1)\n end = f(mid)\n for i in range(0, len(str(mid))):\n start += 1\n if start == n:\n return int(str(mid)[i])\n\n if f(mid) >= n:\n right = mid - 1\n elif f(mid) <= n:\n left = mid + 1\n \n\n\n\n return 0\n \n\n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python || Binary Search | nth-digit | 0 | 1 | # Intuition\n- We have a search space that is from 1 to n and we will need to find where is the number that we are looking for. Hence binary search\n\n# Approach\n- Binary search\n\n# Complexity\n- Time complexity:\n- O(logN)\n\n- Space complexity:\n- O(1)\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n l = 1\n r = n\n total = 0\n mid = -1\n while l<=r:\n mid = (l+r)//2\n curr = 9\n count = 1\n numbers = 0\n total = 0\n while numbers < mid:\n if numbers+curr > mid:\n total+=((mid-numbers)*count)\n numbers = n\n else:\n total+=curr*count\n numbers+=curr\n count+=1 \n curr*=10\n if total==n:\n return mid%10\n elif total < n:\n l=mid+1\n else:\n r=mid-1\n if total > n:\n str_mid = str(mid)\n gap = total-n\n for i in range(len(str_mid)-1,-1,-1):\n if gap == 0:\n return int(str_mid[i])\n gap-=1\n elif total < n:\n gap = n-total\n str_mid = str(l)\n for i in range(0,len(str_mid)):\n gap-=1\n if gap == 0:\n return int(str_mid[i])\n \n\n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
[Python3] Straightforward Solution | nth-digit | 0 | 1 | # Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n lst = []\n cnt = 1\n cur = 9\n for i in range(30):\n lst.append(cnt*cur)\n cnt+=1\n cur*=10\n if cnt*cur > pow(2, 31)-1:\n break\n \n cur = 0\n idx = 0\n for i in range(len(lst)):\n cur += lst[i]\n if cur >= n:\n idx = i\n break\n\n prev = sum(lst[:idx])\n offset = n-prev\n\n start = pow(10, idx)\n nTh = idx+1\n \n skip = offset//nTh - 1\n if skip > 0:\n start += skip\n offset = offset - skip*nTh\n\n s = ""\n for i in range(start, start+offset+1):\n s += str(i)\n \n return int(s[offset-1])\n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python Solution | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n d = b = 1\n \n while n> 9* b*d:\n n -= 9 *b*d\n d += 1\n b *=10\n q,r = divmod(n-1, d)\n return int(str(b + q)[r])\n \n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Pattern of Number of Values | Explained and Commented | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst thing to notice is the pattern of the number of digits in set ranges \nIn 1 -> 10 : 9 values \nIn 10 -> 100 : 90 values \nIn 100 -> 1000 : 900 values \n\nThis shows that the difference of the current and prior power of 10 is the number of values in a given range. \n\nThis gives us the total number of values, but not the total number of string indices. To get that, we need to then multiply this difference by the length of a power of 10 at the current power. Once we do, we then know how many are in a range \n\nIn 1 -> 10 : indices 0 - 9\nIn 10 -> 100 : indices 10 -> 189\nIn 100 -> 1000 : indices 190 -> 2889 \n\nThis now lets us have our while loop, so that we can capture the point at which n, afte rbeing reduced by the size of the last range, is not greater than or equal to the current range of indices \n\nHowever, even though it\'s in range, we still need to find out how much of it is left over. Due to the offset of 1 for indice 0, we need to reduce n by 1. Then, based on how many digits are in the current power of 10, we can divide n - 1 by that, and get the remainder of n-1 % number of digits. \n\nThe n-1 divided by number of digits gives us the remaining n not yet accounted for. \n\nThe n-1 modulo number of digits gives us the index of the nth digit. \n\nThen, we need to figure out the final value. \n\nThe final value should start at the value of 10 to the power of the number of digits - 1. This is because 10^0 is 1, so we do need to reduce by 1. \n\nWe also add to this the remaining n by the division above. \n\nThen, we need to go to the index of the nth digit within that value. \n\nThis is our final integer value. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIf n is less than 10, return it (edge case) \n\nOtherwise, we start with the number of digits in our current value being 1, and the base of that value being 9 \n\nSo long as the product of the number of digits and base of that value is strictly less than n, we do the following \n- decrement n by the product of the base of the value and number of digits\n- increment number of digits by 1 \n- multiply base of value by 10 \n\nWhen done, we can calculate the remaining value of n, and the index of the nth digit using a divmod of n-1 and the number of digits after the loop \n\nOur final value is 10 ** number of digits - 1 (offset for initial value) plus any remaining value of n \n\nWe then return the int cast of the character in the final value at the index of the nth digit \n\n# Complexity\n- Time complexity: O(max(L + log n))\n - We use steps of approximately 10* every loop iteration \n - This means we do log base 10 of n work to get to n\'s stopping point\n - All other operations can be said to take O(1) time most often \n - We do need to build a string out of an integer, which takes O(L) time\n - Overall O(max(L + log n)) \n\n- Space complexity: O(1)\n - In the return statement, a string is generated but the memory is not kept. So, we can safely say O(1) \n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n # base case \n if n < 10 : \n return n \n # start with 1 number of digits \n number_of_digits = 1 \n # using a base value of 9 \n base_of_value = 9 \n # while n is greater than base * number of digits \n while n > base_of_value * number_of_digits : \n # decrement n by the value of their combinations \n n -= (base_of_value * number_of_digits)\n # number of digits goes up by 1, base of value goes up by 10 \n # number_of_digits -> 1, 2, 3, 4 ... \n # base of value -> 9, 90, 900, 9000, ... \n # combined value goes -> 9, 180, 2700, 36000\n number_of_digits += 1 \n base_of_value *= 10\n # get any remaining n and the index offset using n-1 and number of digits \n remaining_n, index_of_nth_digit = divmod((n-1), number_of_digits)\n # final value is at 10^number of digits - 1 to deal with base 9 shenanigans \n # it is incremented by any remaining n not captured in the while loop \n final_value = 10**(number_of_digits - 1) + remaining_n \n # return the final values nth digit \n return int(str(final_value)[index_of_nth_digit])\n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python Solution | nth-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n if n <= 9:\n return n\n\n base = 9\n digits = 1\n\n while n > base * digits:\n n -= base * digits\n base *= 10\n digits += 1\n \n num = 10 ** (digits - 1) + (n-1)//digits\n idx = (n-1 ) % digits \n return int(str(num)[idx])\n\n \n``` | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Solution | nth-digit | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int findNthDigit(int n) {\n int digitSize = 1;\n int startNum = 1;\n long count = 9;\n\n while (digitSize * count < n) {\n n -= digitSize * count;\n ++digitSize;\n startNum *= 10;\n count *= 10;\n }\n const int targetNum = startNum + (n - 1) / digitSize;\n const int index = (n - 1) % digitSize;\n return to_string(targetNum)[index] - \'0\';\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findNthDigit(self, n: int) -> int:\n start = 1\n count = 9\n length = 1\n while n > length*count:\n n = n - length*count\n start *= 10\n count *= 10\n length += 1\n count, num = divmod(n-1, length)\n number = start + count\n return int(str(number)[num])\n```\n\n```Java []\nclass Solution {\n public int findNthDigit(int n) \n {\n if(n<=9)\n return n;\n long x=9;\n int d=1,p=n,num=0;\n do\n { \n p-=x*d;\n num+=x;\n x=x*10;\n d++;\n }while(p>(x*d));\n num+=p/d;\n if(p%d==0)\n return num%10;\n else\n {\n num++;\n p=p%d;\n x=(int)Math.pow(10,(d-p));\n num/=x;\n return num%10;\n }\n }\n}\n```\n | 0 | Given an integer `n`, return the `nth` digit of the infinite integer sequence `[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]`.
**Example 1:**
**Input:** n = 3
**Output:** 3
**Example 2:**
**Input:** n = 11
**Output:** 0
**Explanation:** The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
401: Solution with step by step explanation | binary-watch | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize an empty list to store the output.\n2. Loop through all possible combinations of hours and minutes from 0 to 11 and 0 to 59 respectively.\n3. For each combination, count the number of set bits in the binary representation of hours and minutes by using the count() method of the string representation of the binary number.\n4. Check if the total number of set bits equals the input parameter turnedOn.\n5. If it does, format the hours and minutes into a string with the required format of "HH:MM" and append it to the output list.\n6. Return the output list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n output = []\n # Loop through all possible combinations of hours and minutes and count the number of set bits\n for h in range(12):\n for m in range(60):\n if bin(h).count(\'1\') + bin(m).count(\'1\') == turnedOn: # Check if the number of set bits in hours and minutes equals the target number\n output.append(f"{h}:{m:02d}") # Add the valid combination of hours and minutes to the output list\n return output\n\n``` | 14 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Decode the Binary Watch: Find All Possible Times with a Given Number of LEDs On | binary-watch | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOne way to solve this problem is to generate all possible times that can be represented by a binary watch and check how many LEDs are turned on. If the number of turned-on LEDs matches the given input "turnedOn", we add the time to the result list. Since there are only 10 LEDs on the watch, we can iterate through all possible combinations using bit manipulation.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo implement the above intuition, we can start by iterating through all possible values of the hours (0-11) and minutes (0-59) and check how many LEDs are turned on in the binary representation of the hours and minutes. We can do this using the `bin()` function, which converts an integer to its binary representation as a string. Then, we can count the number of 1s in the binary string using the `count()` method of the `str` object. If the sum of the number of turned-on LEDs in the hours and minutes is equal to the given input "turnedOn", we can add the corresponding time to our output list.\n# Complexity\n- Time complexity: The time complexity of this approach is O(1) since we are iterating through a constant number of possible values of the hours (0-11) and minutes (0-59), which is 12 and 60, respectively. Counting the number of set bits in a binary string takes O(log n) time, which is negligible compared to the overall time complexity.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity of this approach is O(1) since we are not using any extra space to store intermediate results. The output list has a maximum size of 1024, which is the total number of possible combinations of turned-on LEDs.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n res = []\n for h in range(12):\n for m in range(60):\n if bin(h).count(\'1\') + bin(m).count(\'1\') == turnedOn:\n res.append(f"{h}:{m:02d}")\n return res\n```\n\nIn the code above, we use the `bin()` function to convert the integer hours and minutes to their binary representation. We use the `count()` method of the `str` object to count the number of set bits in the binary representation of the hours and minutes. We also use the f-string notation to format the output string with leading zero if necessary. | 7 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Very simple python solution | binary-watch | 0 | 1 | ```python\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n # for example:\n # 2 1 (3 min) - two leds on, bin: 11 \n # 2 (2 min) - one led on, bin: 10\n # 1 (1 min) - one led on, bin: 1\n \n def bit_counter(n):\n s = bin(n)[2:]\n temp = 0\n for i in s:\n if i == \'1\':\n temp += 1\n return temp\n \n result = []\n \n for h in range(12):\n for m in range(60):\n if bit_counter(h) + bit_counter(m) == turnedOn:\n result.append(f\'{h}:{m:02}\')\n \n return result\n``` | 1 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Python3 simple solution "One-liner" | binary-watch | 0 | 1 | ```\nclass Solution:\n def readBinaryWatch(self, turnedOn):\n return [\'{}:{}\'.format(i,str(j).zfill(2)) for i in range(12) for j in range(60) if bin(i)[2:].count(\'1\') + bin(j)[2:].count(\'1\') == turnedOn]\n```\n**If you like this solution, please upvote for this** | 5 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Solution in Python 3 (beats ~98%) (one line) | binary-watch | 0 | 1 | _Check All Possible Times:_\n```\nclass Solution:\n def readBinaryWatch(self, n: int) -> List[str]:\n \treturn [str(h)+\':\'+\'0\'*(m<10)+str(m) for h in range(12) for m in range(60) if (bin(m)+bin(h)).count(\'1\') == n]\n\n\n\n```\n_Check All Possible Combinations of LEDs:_\n```\nfrom itertools import combinations\n\nclass Solution:\n def readBinaryWatch(self, n: int) -> List[str]:\n \tT, m = [], [480,240,120,60,32,16,8,4,2,1]\n \tfor i in combinations(m,n):\n \t\tif 32 in i and 16 in i and 8 in i and 4 in i: continue\n \t\th, m = divmod(sum(i),60)\n \t\tif h > 11: continue\n \t\tT.append(str(h)+\':\'+\'0\'*(m < 10)+str(m))\n \treturn T\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com | 10 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Easy solution with full explanation : ) | binary-watch | 1 | 1 | Let\'s break down the problem and the code using the first example:\n\n**Example:**\n```plaintext\nInput: turnedOn = 1\nOutput: ["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"]\n```\n\n**Problem Explanation:**\nYou are given an integer `turnedOn` representing the number of LEDs that are currently on on a binary watch. The watch has 4 LEDs on top to represent the hours (0-11) and 6 LEDs on the bottom to represent the minutes (0-59). The task is to return all possible times the watch could represent given the number of LEDs that are turned on.\n\n**Step-by-Step Explanation (using the given code in C++):**\n\n1. **Define the Function:**\n ```cpp\n vector<string> readBinaryWatch(int turnedOn) {\n ```\n This line declares a function named `readBinaryWatch` that takes an integer `turnedOn` as input and returns a vector of strings.\n\n2. **Initialize Result Vector:**\n ```cpp\n vector<string> result;\n ```\n This line declares a vector of strings named `result` to store the output.\n\n3. **Loop through Hours and Minutes:**\n ```cpp\n for (int h = 0; h < 12; ++h) {\n for (int m = 0; m < 60; ++m) {\n ```\n These nested loops iterate through all possible combinations of hours (0 to 11) and minutes (0 to 59).\n\n4. **Count Turned On LEDs:**\n ```cpp\n if (bitset<4>(h).count() + bitset<6>(m).count() == turnedOn) {\n ```\n This line uses `bitset` to convert the integer values `h` and `m` into binary representation and counts the number of turned-on LEDs in both the hours and minutes. If the sum is equal to `turnedOn`, it means the current combination is valid.\n\n5. **Add Valid Time to Result:**\n ```cpp\n result.push_back(to_string(h) + (m < 10 ? ":0" : ":") + to_string(m));\n ```\n If the combination is valid, the time is formatted as a string (hour:minute) and added to the `result` vector.\n\n6. **Return the Result:**\n ```cpp\n return result;\n ```\n The final vector of valid times is returned.\n\n**Applying the Code to the Example:**\n- For the input `turnedOn = 1`, the loops iterate through all possible combinations of hours and minutes.\n- For each combination, it checks if the sum of turned-on LEDs in hours and minutes is equal to 1.\n- If true, it adds the formatted time to the result vector.\n- The final result is `["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"]`.\n\nThis logic is implemented similarly in Java and Python. The key is to iterate through all possible combinations, count the turned-on LEDs, and add the valid times to the result.\n\n```java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<String> readBinaryWatch(int turnedOn) {\n List<String> result = new ArrayList<>();\n for (int h = 0; h < 12; ++h) {\n for (int m = 0; m < 60; ++m) {\n if (Integer.bitCount(h) + Integer.bitCount(m) == turnedOn) {\n result.add(String.format("%d:%02d", h, m));\n }\n }\n }\n return result;\n }\n}\n```\n```python []\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n result = []\n for h in range(12):\n for m in range(60):\n if bin(h).count(\'1\') + bin(m).count(\'1\') == turnedOn:\n result.append(f"{h}:{m:02d}")\n return result\n```\n```C++ []\nclass Solution {\npublic:\n vector<string> readBinaryWatch(int turnedOn) {\n vector<string> result;\n for (int h = 0; h < 12; ++h) {\n for (int m = 0; m < 60; ++m) {\n if (bitset<4>(h).count() + bitset<6>(m).count() == turnedOn) {\n result.push_back(to_string(h) + (m < 10 ? ":0" : ":") + to_string(m));\n }\n }\n }\n return result;\n }\n};\n```\n | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Easy to understand, but terrible performance (beats 5%) | binary-watch | 0 | 1 | \n```\nclass Solution:\n def convertBitsToTime(self, bits):\n hour_bits = bits[:4]\n minute_bits = bits[4:]\n hour = 0\n minutes = 0\n for i in range(len(hour_bits)):\n hour += hour_bits[len(hour_bits) - 1 - i] * (2 ** i)\n for i in range(len(minute_bits)):\n minutes += minute_bits[len(minute_bits) - 1 - i] * (2 ** i)\n\n if hour >= 12 or minutes >= 60:\n return None\n\n hour = str(hour)\n minutes = str(minutes)\n if len(minutes) == 1:\n minutes = \'0\' + minutes\n\n return hour + \':\' + minutes\n\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n if turnedOn >= 9:\n return []\n \n bits = [0] * 10\n possibleBits = []\n visited = set()\n times = []\n\n def dfs():\n if tuple(bits) in visited:\n return\n visited.add(tuple(bits))\n if sum(bits) == turnedOn:\n possibleBits.append(bits.copy())\n \n for i in range(10):\n if not bits[i]:\n bits[i] = 1\n dfs()\n bits[i] = 0\n \n dfs()\n for p in possibleBits:\n r = self.convertBitsToTime(p)\n if r:\n times.append(r)\n\n return times\n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
This problem is really hard. used itertools.combinations. beats 88% | binary-watch | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n if turnedOn > 10:\n return []\n\n table = [1,2,4,8,1,2,4,8,16,32]\n output = []\n for idxs in itertools.combinations(range(10), turnedOn):\n h = sum(table[x] for x in idxs if x < 4)\n m = sum(table[x] for x in idxs if x > 3)\n if h >= 12 or m >= 60:\n continue\n adding = f"{h}:{m}" if m > 9 else f"{h}:0{m}"\n output.append(adding)\n\n return output\n\n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
[Python] Beats 100% in time, Combination problem | binary-watch | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nA simple and tuitive combination problem.\r\n\r\n# Code\r\n```\r\nHOURS = [8, 4, 2, 1]\r\nMINUTES = [32, 16, 8, 4, 2, 1]\r\nclass Solution:\r\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\r\n res = []\r\n for t in range(turnedOn+1):\r\n h_selected = min(t, 4)\r\n m_selected = turnedOn - h_selected\r\n\r\n for h_comb in combinations(HOURS, h_selected):\r\n for m_comb in combinations(MINUTES, m_selected):\r\n h_total = sum(h_comb)\r\n if h_total > 11:\r\n continue\r\n m_total = sum(m_comb)\r\n if m_total > 59:\r\n continue\r\n res.append(f\'{h_total}:{m_total:02}\')\r\n return res\r\n```\r\n\r\n | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
python3 enumerate and backtracking solution | binary-watch | 0 | 1 | \n# Code\nenumerate solution \n```\nclass Solution:\n def hanming_distance(self, num):\n count = 0\n while num:\n num &= num - 1\n count += 1\n return count\n\n def get_num_map(self):\n num_map = [0] * 60\n for i in range(60):\n num_map[i] = self.hanming_distance(i)\n return num_map\n\n def get_time_str(self, hour, minutes):\n time = str(hour) + ":"\n m = str(minutes)\n if len(m) == 1:\n time += "0" + m\n else:\n time += m\n return time\n\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n num_map = self.get_num_map()\n time = []\n for i in range(12):\n for j in range(60):\n if num_map[i] + num_map[j] == turnedOn:\n time.append(self.get_time_str(i, j))\n return time\n```\n\nbacktracking\n```\nclass Solution:\n\n def __init__(self):\n self.hash_map = (8, 4, 2, 1, 16, 32, 8, 4, 2, 1)\n\n def get_time_str(self, hour, minutes):\n time = str(hour) + ":"\n m = str(minutes)\n if len(m) == 1:\n time += "0" + m\n else:\n time += m\n return time\n\n def backtracking(self, turnedOn, startIndex, hour, minute, result):\n if turnedOn == 0:\n if hour > 11 or minute > 59: return \n result.append(self.get_time_str(hour, minute))\n return\n\n for i in range(startIndex, len(self.hash_map)):\n if i < 4: \n hour += self.hash_map[i]\n else:\n minute += self.hash_map[i]\n self.backtracking(turnedOn - 1, i + 1, hour, minute, result)\n if i < 4: \n hour -= self.hash_map[i]\n else:\n minute -= self.hash_map[i]\n\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n result = []\n self.backtracking(turnedOn, 0, 0, 0, result)\n return result\n \n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Python Medium | binary-watch | 0 | 1 | ```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n \'\'\'\n hours 0 - 11\n 1111\n\n\n 6 leds for minutes\n 111111\n\n\n \'\'\'\n\n self.ans = []\n\n def backTrack(curHours, curMinutes, turnedOn):\n if len(curHours) == 4 and len(curMinutes) == 6:\n\n if turnedOn != 0:\n return\n\n i = 3\n hours = 0\n\n for num in curHours:\n if num == "1":\n hours += 2 ** i\n\n\n i -= 1\n\n \n j = 5\n minutes = 0\n\n for num in curMinutes:\n if num == "1":\n \n minutes += 2 ** j\n\n j -= 1\n\n \n if not (0 <= minutes < 60) or not (0 <= hours < 12):\n return\n\n\n sHours = str(hours)\n sMinutes = str(minutes)\n\n temp = ""\n\n if len(sHours) == 2:\n temp += sHours\n temp += ":"\n\n else:\n temp += sHours\n temp += ":"\n\n\n if len(sMinutes) == 2:\n temp += sMinutes\n\n\n else:\n temp += "0"\n temp += sMinutes\n\n self.ans.append(temp)\n return \n \n\n\n\n if len(curHours) == 4:\n backTrack(curHours, curMinutes + "1", turnedOn - 1)\n backTrack(curHours, curMinutes + "0", turnedOn)\n\n else:\n backTrack(curHours + "1", curMinutes, turnedOn - 1)\n backTrack(curHours + "0", curMinutes, turnedOn)\n\n\n\n\n\n backTrack("", "", turnedOn)\n\n\n return self.ans\n \n \n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Using recursion. Real problem solving ;) | binary-watch | 0 | 1 | # Code\n```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n\n # UNDERSTANDING\n # 4 LEDs to show hours\n # 6 LEDs to show minutes\n\n # turnedOn give us the count of LED(s) turnedOn as the name suggestes\n\n # need to return all the possible times the LED(s) can show\n\n # can we use more than 1 LEDs for showing the hour?\n # yes we can as shown in example "10:02", which can only done using "8" and "2" LEDs\n\n # can we represent "12:00" ?\n # No, as the clock doesn\'t represent 24 hrs. 12:00 will be 00:00.\n # STEP ONE COMPLETED ////////////////////////////////////////////////////////////////////\n\n # BREAKING THE PROBLEM (SOLVING THE SUB-PROBLEM)\n # How we get the values of the LEDs?\n # Returning all the feasible cases?\n # Return only one answer using using input as 1?\n # I think we store them in an array or hashmap\n\n # using list\n # hours = [8, 4, 2, 1]\n # minutes = [32, 16, 8, 4, 2, 1]\n\n # using hashmap\n # hours_dt = {8 : 1, 4 : 1, 2 : 1, 1 : 1} \n # minutes_dt = {32 : 1, 16 : 1, 8 : 1, 4 : 1, 2 : 1, 1 : 1} \n\n # How to return the ans in string?\n # ans = []\n # for x in hours:\n # ans.append(f"{x}:00")\n\n # for x in minutes:\n # if len(str(x)) > 1:\n # ans.append(f"0:{x}")\n # else:\n # ans.append(f"0:0{x}")\n\n # return ans \n\n output = []\n\n hoursList = [8, 4, 2, 1]\n minutesList = [32, 16, 8, 4, 2, 1]\n\n # how can I use both of the array at the same time and create a solution using both of them?\n # I can use take and notTake to form multiple feasible solutions\n def watchHelper(led, hIdx, mIdx, hours, minutes):\n\n if led < 0 or hours > 11 or minutes > 59:\n return\n\n if led == 0:\n if minutes > 9:\n output.append(f"{hours}:{minutes}")\n else:\n output.append(f"{hours}:0{minutes}")\n return\n\n # After the previous index values being checked\n if hIdx >= len(hoursList) and mIdx >= len(minutesList):\n return \n\n # taking both\n if hIdx < len(hoursList) and mIdx < len(minutesList):\n watchHelper(led - 2, hIdx + 1, mIdx + 1, hours + hoursList[hIdx], minutes + minutesList[mIdx])\n\n # taking hours or minutes\n if hIdx < len(hoursList):\n watchHelper(led - 1, hIdx + 1, mIdx + 1, hours + hoursList[hIdx], minutes)\n \n if mIdx < len(minutesList):\n watchHelper(led - 1, hIdx + 1, mIdx + 1, hours, minutes + minutesList[mIdx]) \n\n # not taking both \n watchHelper(led, hIdx + 1, mIdx + 1, hours, minutes) \n\n\n watchHelper(turnedOn, 0, 0, 0, 0)\n return output \n\n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Time Traveler's Guide: Finding All Possible Binary Watch Times | binary-watch | 0 | 1 | # Intuition\nThe problem involves finding all valid times on a binary watch given the number of "1" bits (turnedOn). To tackle this problem, we can systematically iterate through all possible combinations of hours (0-11) and minutes (0-59). For each combination, we check if the total count of "1" bits in the binary representations of the hour and minute equals the specified turnedOn. If they match, we add that combination to the list of valid times.\n\n# Approach\n1. We initialize an empty list, output, to store the valid times.\n2. We use two nested loops to iterate through all possible combinations of hours and minutes:\n - The outer loop (for hour in range(12)) iterates through possible values for the hours (0-11).\n - The inner loop (for minute in range(60)) iterates through possible values for the minutes (0-59).\n3. For each combination of hours and minutes, we calculate the number of "1" bits in the binary representations of both the hour and the minute. This is done using the bin function, which converts a decimal number to its binary representation, and the count method to count the number of "1" bits.\n4. If the sum of the "1" bits in the hour and minute binary representations equals the given turnedOn value, it means this combination represents a valid time. We format this combination as a string (f"{hour}:{minute:02d}") and add it to the output list.\n5. Finally, we return the output list, which contains all the valid times that satisfy the condition.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(1) since we systematically iterate through all possible combinations of hours (12 possibilities) and minutes (60 possibilities), resulting in a constant number of operations. The time complexity is not dependent on the value of turnedOn.\n\n- Space complexity: The space complexity is O(1) as we use a fixed amount of additional space to store the output list and temporary variables for hours and minutes.\n\n# Code\n```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n output = []\n\n for hour in range(12):\n for minute in range(60):\n if bin(hour).count("1") + bin(minute).count("1") == turnedOn:\n output.append(f"{hour}:{minute:02d}")\n return output\n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
Easy to Understand Brute Force + Recursion Solution | 32ms Runtime | binary-watch | 0 | 1 | Brute force solution, 32ms runtime 16.1MB memory utilization, not sure why but runtime is inconsistent, this is the fastest I got.\n\n# Code\n```\nclass Solution:\n def readBinaryWatch(self, turnedOn: int) -> List[str]:\n def solve(i,index, s, r, ti, lis, t):\n if i>=ti:\n r.append(s)\n return r\n while index<len(lis):\n if (t == "hr" and s+lis[index] <= 11) or (t == "mi" and s+lis[index] <= 59):\n r=solve(i+1, index+1, s+lis[index], r, ti, lis, t)\n index+=1\n return r\n\n h=[8,4,2,1]\n m=[32,16,8,4,2,1]\n if turnedOn==0:\n return ["0:00"]\n elif turnedOn>8:\n return []\n else:\n res=[]\n for i in range(0, turnedOn+1):\n if turnedOn-i<6 and i<4:\n hr=i\n mi=turnedOn-i\n hr_lis = solve(0,0, 0, [], hr, h, "hr")\n mi_lis=solve(0,0, 0, [], mi, m, "mi")\n for h_i in hr_lis:\n for m_i in mi_lis:\n res.append(f\'{h_i}:{str(m_i).rjust(2,"0")}\')\n return res\n \n``` | 0 | A binary watch has 4 LEDs on the top to represent the hours (0-11), and 6 LEDs on the bottom to represent the minutes (0-59). Each LED represents a zero or one, with the least significant bit on the right.
* For example, the below binary watch reads `"4:51 "`.
Given an integer `turnedOn` which represents the number of LEDs that are currently on (ignoring the PM), return _all possible times the watch could represent_. You may return the answer in **any order**.
The hour must not contain a leading zero.
* For example, `"01:00 "` is not valid. It should be `"1:00 "`.
The minute must be consist of two digits and may contain a leading zero.
* For example, `"10:2 "` is not valid. It should be `"10:02 "`.
**Example 1:**
**Input:** turnedOn = 1
**Output:** \["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"\]
**Example 2:**
**Input:** turnedOn = 9
**Output:** \[\]
**Constraints:**
* `0 <= turnedOn <= 10` | Simplify by seeking for solutions that involve comparing bit counts. Consider calculating all possible times for comparison purposes. |
✔️ [Python3] MONOTONIC STACK (o^^o)♪, Explained | remove-k-digits | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nIn order to get the smallest possible number, we have to get rid of as many as possible big digits in the most significant places on the left. We can use a monotonically increasing stack to help us remove those big digits. When adding a new digit, we check whether the previous one is bigger than the current and pop it out. In the end, we concatenate the remaining elements from the stack and return the result.\n\nTime: **O(n)** - iteration\nSpace: **O(n)** - stack\n\nRuntime: 43 ms, faster than **77.80%** of Python3 online submissions for Remove K Digits.\nMemory Usage: 14.2 MB, less than **81.82%** of Python3 online submissions for Remove K Digits.\n\n```\nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n st = list()\n for n in num:\n while st and k and st[-1] > n:\n st.pop()\n k -= 1\n \n if st or n is not \'0\': # prevent leading zeros\n st.append(n)\n \n if k: # not fully spent\n\t\t\tst = st[0:-k]\n \n return \'\'.join(st) or \'0\'\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 154 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
[Python] Very detail explanation with examples using stack | remove-k-digits | 0 | 1 | ```\nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n ## RC ##\n\t\t## APPROACH : STACK ##\n ## IDEA : 1234, k= 2 => when numbers are in increasing order we need to delete last digits \n ## 4321 , k = 2 ==> when numbers are in decreasing order, we need to delete first digits\n ## so, we need to preserve increasing sequence and remove decreasing sequence ##\n\t\t## LOGIC ##\n\t\t#\t1. First think in terms of stack\n\t\t#\t2. push num into stack IF num it is greater than top of stack\n\t\t#\t3. ELSE pop all elements less than num\n\t\t\n ## TIME COMPLEXICITY : O(N) ##\n\t\t## SPACE COMPLEXICITY : O(N) ##\n\t \n stack = []\n for n in num:\n while( stack and int(stack[-1]) > int(n) and k):\n stack.pop()\n k -= 1\n stack.append(str(n))\n \n # If no elements are removed, pop last elements, (increasing order)\n while(k):\n stack.pop()\n k -= 1\n\n # removing leading zeros\n i = 0\n while( i <len(stack) and stack[i] == "0" ):\n i += 1\n \n return \'\'.join(stack[i:]) if (len(stack[i:]) > 0) else "0" \n \n```\nIF YOU LIKE MY SOLUTION, PLEASE UPVOTE. | 90 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Monostonic Stack Logic Python3 | remove-k-digits | 0 | 1 | # 1. Monostonic Stack concept:\n```\nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n stack = []\n for n in num:\n while stack and k>0 and stack[-1] > n:\n stack.pop()\n k -= 1\n if stack or n is not \'0\': \n stack.append(n) \n if k:\n stack=stack[0:-k] \n return \'\'.join(stack) or \'0\'\n``` | 5 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
402: Solution with step by step explanation | remove-k-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe algorithm uses a stack to keep track of the digits. It loops through each digit in num, and for each digit, it pops digits from the stack until either the top digit is smaller than the current digit or k becomes 0. Then it appends the current digit to the stack. After looping through all digits in num, if there are still digits to be removed (i.e., k > 0), it pops digits from the stack until k becomes 0.\n\nFinally, it converts the remaining digits in the stack to a string and removes any leading zeroes, then returns the resulting string. If there are no remaining digits, it returns the string "0".\n\nOverall, the algorithm has a time complexity of O(n), where n is the length of num, and a space complexity of O(n), as the stack can store up to all n digits of num.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n stack = [] # Use a stack to keep track of the digits\n for digit in num:\n while k > 0 and stack and stack[-1] > digit: # Pop digits from the stack until the top digit is smaller than the current digit or k becomes 0\n stack.pop()\n k -= 1\n stack.append(digit) # Append the current digit to the stack\n while k > 0: # If there are still digits to be removed, pop them from the stack\n stack.pop()\n k -= 1\n result = "".join(stack).lstrip("0") # Convert the remaining digits to a string and remove any leading zeroes\n return result if result else "0" # Return the resulting string, or "0" if there are no remaining digits\n\n``` | 4 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Python Solution || Monotonic Stack || O(n) time | remove-k-digits | 0 | 1 | \n\n```\nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n st = []\n for i in num:\n while k and len(st) > 0 and st[-1] > i:\n k -= 1\n st.pop()\n st.append(i)\n while k:\n k -= 1\n st.pop()\n st = "".join(st).lstrip("0")\n return st if st else "0"\n```\n\n**Please upvote if you find the solution helpful and interesting!!!\nThank you.** | 11 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
📍 ✔Python3 || Using Stack || faster solution | remove-k-digits | 0 | 1 | ```\nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n stack = ["0"]\n if len(num)==k:\n return "0"\n for i in range(len(num)):\n while stack[-1] > num[i] and k > 0:\n stack.pop()\n k=k-1\n stack.append(num[i])\n while k>0:\n stack.pop()\n k-=1\n while stack[0] == "0" and len(stack)>1:\n stack.pop(0)\n return "".join(stack)\n``` | 6 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Explanation for beginners like me | remove-k-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwhen the input str is monotonically increasing like "**12345**" k=2 , we remove "45" turn it into "**123**".\nwhen the input array is monotonically decreasing like "**54321**", k=2, we remove "45" turn it into "**321**".\nDoes this mean we just remove the larger digits and ignore the whether it is in tens\' digit or hundreds\' digit? No!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nnums="1999" k=1 we remove "9" no matter which 9 is same and turn it into "199"\nnums="9119" k=1 we also remove "9", but when we remove the first 9, it is "119"; when we remove the second "9", it is "911". \n1. we prefer to remove the left one when the number is bigger.\n\nnums="**54989**" k=2, do we just remove "9" and "9" and turn it into "**548**"? \nwe should remove the "5" and "9" to "**489**\u201C.\n\n2. thus we can initialize a stack , and append number to it and compare the current number with the former one, **when the former is larger we just pop it and decrement k by one**, after the loop, we will get a monotonically increasing stack. \n3. we should check whether the stack\'s length is equal to the demanded "len(num)-k". Because our stack after iteration is monotonically increasing, we just **slice the index 0 to index "len(stack)-k**(k is changed after the iteration)".\nfor example, **nums="54989" k=3**, after iteration **k=1 **and the stack is ```[4,8,9]```, then we slice it into stack[:(3-1)] becomes **[4,8]**\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeKdigits(self, nums: str, k: int) -> str:\n stack=[]\n for i in range(len(nums)):\n while k>0 and stack and stack[-1]>nums[i]:\n stack.pop()\n k-=1\n stack.append(nums[i])\n stack=stack[:len(stack)-k]\n result="".join(stack).lstrip("0") \n return result if result else "0"\n\n``` | 2 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Python3 "ValueError: Exceeds the limit (4300)..." error | remove-k-digits | 0 | 1 | Python 3.11.4 released on June 14, 2023.\n\nCPython introduced limiting conversion size up to 4300 to mitigate DOS attack (CVE-2020-10735)\n\nHowever, since the test case exceeds 4300 characters, an error occurs.\n\nWorkaround: Add below line on your solution\n```\nimport sys\nsys.set_int_max_str_digits(0) \n``` | 2 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
I bet you will Understand!!! Peak and Valley Python 3 | remove-k-digits | 0 | 1 | \nThis question can be analyzed as a series of peaks and valleys\nwe have to delete all **starting point of valleys** till attempts(k) are left!!\n\nfor ex - test case [1,4,3,2,2,1,9]\n\n**Elements inside [ ] are starting point of valleys which we have to delete**\n\n```\n 9\n /\n [4] /\n / \\ /\n / [3] /\n / \\ /\n / 2__[2] /\n/ \\ / \n1 1\n```\n\n\n**We can delete valleys untils we can afford to delete it i.e(k>0)**\n_____\n**Case 1: valley>k**\n_____\nSupoose total valley\'s starting point in our test case is 5 but we can delete only 3 elements i.e k=3 in this case we will delete first 3 valley which will give our ans \n____\n**Case 2: valley<k**\n____\nSuppose there is a testcase where valley = 2 and k = 5 so after deleting all the valley still we have to delete so we pop remaining k from our stack\n\n\njust delete the valleys until k>=0 each time we delete a valley we do k--\n. we do a check before returning ans if k>0 simply start \npopping from last of stack \n\nP.S - Try drawing valley and peak sketch for other test cases same as above\ni bet you will understand till the core!!!\n\n\n```\nclass Solution:\n\n # O(N) O(N)\n def removeKdigits(self, nums: str, k: int) -> str:\n\n if len(nums)==1: # if only 1 digit we can only get 0 \n return "0"\n\n stack = []\n \n for num in nums:\n # k--> no of deletion\n # len(nums)-k --> len of our answer --> len of stack at last\n while stack and stack[-1]>num and k>0:\n stack.pop()\n k-=1\n stack.append(num)\n\n # a case like [112] k = 1 no deletion will happen because there is no valley\n # so we pop k elements from last\n while k>0 and stack:\n stack.pop()\n k-=1\n \n return \'\'.join(stack).lstrip("0") or "0" # lstrip is for removal of cases where stack is 000200\n\t\t\n\t\t# but our ans should be 200\n\t\t\n``` | 6 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Standard Greedy Approach | remove-k-digits | 0 | 1 | Our appraoch is to remove the decreasing sequence and how can we remove the decreasing sequence, well it is by removing the first digit of the decreasing sequence and we will continue to do so till the time our k becomes zero\n\nif there is no decreasing sequence that means it has increasing sequence, in this case we will remove the digits from last\n\nThis is the catch of this problem.\nI hope it makes sense to the reader\n\n\tclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n stack = []\n \n for n in num:\n while(stack and int(stack[-1])>int(n) and k):\n k-=1\n stack.pop()\n stack.append(n)\n \n while(k):\n stack.pop()\n k-=1\n \n if len(stack)==0:\n return "0"\n s=\'\'\n for i in range(len(stack)):\n s+=stack[i]\n \n return str(int(s))\n\t\t\n\t\n | 1 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
65% Tc and 55% Sc easy python solution | remove-k-digits | 0 | 1 | ```\ndef removeKdigits(self, num: str, k: int) -> str:\n l = len(num)\n if(l == k): return \'0\'\n ans = []\n for i in num:\n while(len(ans) and k > 0 and ans[-1] > i):\n ans.pop()\n k -= 1\n ans.append(i)\n if(k > 0): ans = ans[:-k]\n return str(int(\'\'.join(ans)))\n``` | 1 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Faster than 98% and less space than 100 % with just a little change | remove-k-digits | 0 | 1 | \nclass Solution:\n def removeKdigits(self, num: str, k: int) -> str:\n \n res = []\n counter = 0\n n = len(num)\n \n if n == k: return "0"\n \n for i in range(n):\n while k and res and res[-1] > num[i]:\n res.pop()\n k -= 1\n res.append(num[i])\n\n \n while k:\n res.pop()\n k -= 1\n \n return "".join(res).lstrip(\'0\') or "0"\n \n | 11 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Python solution with explanation | Stack | Similar to problem 1673 | remove-k-digits | 0 | 1 | The question asks us to remove k digits so that the resulting number is the smallest. Instead of approaching the problem with the mantality of removing k digits, think of the it from another perspective: if the len of the string is N, the question can be re-phrased as:\n\nFind the smallest number with length of N - k. \n\nThis is exactly the same as the problem [Find the Most Competitive Subsequence](https://leetcode.com/problems/find-the-most-competitive-subsequence/), with very minor changes. These 2 problems follow the exact same pattern, and the only way to recognize the pattern is, you guess it, do a lot of problems.\n\nHere are the solutions to both:\n\n**Find the most competitive subsequence**\n```\nresult = []\nfor i in range(len(nums)):\n\tcurr = nums[i]\n\twhile len(result) and result[-1] > curr and len(result) - 1 + len(nums) - i >= k:\n\t\tresult.pop()\n\tif len(result) < k:\n\t\tresult.append(curr) \nreturn result\n```\n\n\n**Remove K digits**\n```\nif len(num) == k:\n\t\treturn "0"\nnumLen = len(num) - k\nresult = []\nfor i in range(len(num)):\n\tcurr = num[i]\n\twhile len(result) and result[-1] > curr and len(result) - 1 + len(num) - i >= numLen:\n\t\tresult.pop()\n\tif len(result) < numLen:\n\t\tresult.append(curr)\ni = 0\nfor i in range(len(result)):\n\tif result[i] != "0":\n\t\tbreak\nif i >= len(result):\n\treturn "0"\nreturn "".join(result[i:])\n```\n\nNotice that the for loop is exactly the same for both problems. The main idea here is: as long as we have enough digits to construct the subsequence (len(result) - 1 + len(nums) - i >= k), and the last number in the stack is greater than the current number (result[-1] > curr), we pop from the stack. After the while loop, if the len of the stack is less than the number of elements we need in the final result, we add the current number to the stack. I won\'t go into more details on how the core stack logic works as there are many great explanations in the discussion.\n\nFor this problem, after getting the resulting array, we need to perform one more step, which is to elimate the leading zeroes from the final result. And that is it! | 6 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
python | beats 98% | simple | remove-k-digits | 0 | 1 | ```\nif len(nums)==k:\n return "0"\n stack=[]\n count=0\n stack.append(nums[0])\n for i in range(1,len(nums)):\n while(stack and stack[-1]>nums[i]):\n stack.pop()\n count+=1\n if count==k:\n if stack:\n return str(int("".join(stack)))+"".join(nums[i:])\n else:\n return str(int("".join(nums[i:])))\n stack.append(nums[i])\n while (stack and count<k):\n stack.pop()\n count+=1\n return str(int("".join(stack))) | 5 | Given string num representing a non-negative integer `num`, and an integer `k`, return _the smallest possible integer after removing_ `k` _digits from_ `num`.
**Example 1:**
**Input:** num = "1432219 ", k = 3
**Output:** "1219 "
**Explanation:** Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.
**Example 2:**
**Input:** num = "10200 ", k = 1
**Output:** "200 "
**Explanation:** Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.
**Example 3:**
**Input:** num = "10 ", k = 2
**Output:** "0 "
**Explanation:** Remove all the digits from the number and it is left with nothing which is 0.
**Constraints:**
* `1 <= k <= num.length <= 105`
* `num` consists of only digits.
* `num` does not have any leading zeros except for the zero itself. | null |
Simple brute force without dp that beats 100% | frog-jump | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n**2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n if not stones:\n return False\n n = len(stones)\n stack = [(0, 0)]\n visited = set()\n while stack:\n stone, jump = stack.pop()\n for j in [jump-1, jump, jump+1]:\n if j <= 0:\n continue\n next_stone = stone + j\n if next_stone == stones[-1]:\n return True\n if next_stone in stones:\n if (next_stone, j) not in visited:\n stack.append((next_stone, j))\n visited.add((next_stone, j))\n return False\n``` | 3 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Bottom-up Dynamic Programming (memoization), beats 97% / 29% | frog-jump | 0 | 1 | # Intuition\nThe problem description tell us about the steps - **HOW** we can choose the **NEXT** stone for the frog jump.\n\n```\n# The frog can jump at each new step with K-previous step.\n# Following to the description there\'re 3 possible movements\nfirstStep = prevStep - 1\nmiddleStep = prevStep\nlastStep = prevStep + 1\n\n# Lets consider an example\nstones = [0, 1, 2, 3, 7]\n\n# we can jump from \n# 0 => 1\n# 1 => 2 or 1 => 3\n# 2 => 3\n# but we can\'t jump for the fifth stone, because we don\'t have\n# too much steps \n```\nThus, the way to determine if a frog **can jump to the last stone** is to iterate over all possible stones, that\'s leading us to the **DP**.\n\n# Approach\n1. save the last stone into a variable\n2. convert **stones** into a Set for better lookup\n3. create dp-function, use a cache, and start from ```dp(0, 0)```\n4. the state for dp is current stone and previous step\n5. the recurrence relation is to provide three steps, that\'re declared in the description\n6. at each step we\'re only take care about **"if the frog can jump to the last stone"**\n\n# Complexity\n- Time complexity: **O(n^2)**, because of iterating all combinations ```cur``` and ```step```\n\n- Space complexity: **O(n^2)**, the same explanation as in TC.\n\n# Code\n```\nclass Solution:\n def canCross(self, stones: list[int]) -> bool:\n # save the last stone\n last = stones[-1]\n # optimize look up by converting stones into a Set\n stones = set(stones)\n\n @cache\n def dp(cur, step):\n if cur == last:\n return True\n \n nextStep = cur + step \n\n if nextStep in stones and nextStep != cur:\n if dp(nextStep, step):\n return True\n\n if nextStep - 1 in stones and nextStep - 1 != cur:\n if dp(nextStep - 1, step - 1):\n return True\n\n if nextStep + 1 in stones:\n if dp(nextStep + 1, step + 1):\n return True\n\n return False \n\n return dp(0, 0)\n\n\n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python BS + DP. Beats 100%. Explained | frog-jump | 0 | 1 | # Intuition\nThe problem is a DP problem where each state can be represented as (index, prev_jump). Since we are using dfs any state that we encounter again means its false. So use a simple hashmap to store the states. For traversal make use of a for loop to search all positions from prev-1, prev, prev+1, check if stones[idx] + the jump value is in the stones array using binary search. If it exists and then dfs of new index and jump is true, return true\n\n# Complexity\n- Time complexity:\nO(n*n)\n\n- Space complexity:\nO(n*n)\n\n# Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n visited = set()\n def dfs(idx, prev):\n if idx == len(stones) - 1:\n return True\n if (idx, prev) in visited:\n return False\n visited.add((idx, prev))\n for j in range(max(prev-1, 0), prev+2):\n if stones[idx] + j <= stones[-1]:\n i = bisect_left(stones, stones[idx] + j)\n if stones[i] == stones[idx] + j and dfs(i, j):\n return True\n return False\n if len(stones) == 1:\n return True\n if stones[1] == 1:\n return dfs(1, 1)\n return False\n\n \n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python 9 lines 96.65% | frog-jump | 0 | 1 | # Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n t = stones[-1]\n stones = set(stones)\n @cache\n def rec(loc, j):\n nonlocal stones, t\n if loc not in stones or j == 0:\n return False\n return (loc == t) or rec(loc+j-1, j-1) or rec(loc+j, j) or rec(loc+j+1, j+1)\n \n return rec(1, 1)\n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Simple Solution in Python: Just Ask the Right Questions | frog-jump | 0 | 1 | # Code (See below for line-by-line breakdown)\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n s = set(stones)\n end = stones[-1]\n\n @cache\n def jump(current: int, k: int):\n if k <= 0:\n # Jumping backwards or in-place.\n return False\n elif current not in s:\n # Jumped into the water.\n return False\n if current == end:\n # Made it to the last stone!\n return True\n if current > end:\n # Jumped over the last stone.\n return False\n\n return jump(current + k - 1, k - 1) \\\n or jump(current + k, k) \\\n or jump(current + k + 1, k + 1)\n \n return jump(1, 1)\n```\n\n\n# Complexity\n- Time complexity:\nO(N^2) (remember to memoize or cache)\n\n- Space complexity:\nO(N^2) (remember to memoize or cache)\n\n# Intuition\n- What can the frog do?\n - It can jump _forward_.\n\n- What does the frog need to know?\n - It\'s current position: `current`.\n - The size of it\'s last jump: `k`.\n\n- We can represent this action with a function.\n\n ```python\n def jump(current: int, k: int) -> bool:\n ```\n\n- What can happen to the frog when it jumps?\n - It can try to jump a distance <= 0 --> False\n - It can jump into the water --> False\n - It can reach the end --> True\n - It can jump too far and miss the last stone --> False\n - It can jump onto a stone --> Continue\n\n This gives us our base cases.\n ```python\n s = set(stones)\n end = stones[-1]\n\n def jump(current: int, k: int):\n if k <= 0:\n # Jumping backwards or in-place.\n return False\n elif current not in s:\n # Jumped into the water.\n return False\n if current == end:\n # Made it to the last stone!\n return True\n if current > end:\n # Jumped over the last stone.\n return False\n\n # Continue\n ```\n\n- We know our Frog may jump `k - 1`, `k`, or `k + 1`\n ```\n ...\n #Continue\n return jump(current + k - 1, k - 1) \\\n or jump(current + k, k) \\\n or jump(current + k + 1, k + 1)\n ```\n\n- Our first jump is of size 1, to get to square 1 so...\n```python\n return jump(1, 1)\n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python3 | DFS | Memoization | frog-jump | 0 | 1 | # Complexity\n- Time complexity:\nO($$n.k$$)\n- Space complexity:\nO($$n.k$$)\n\nhere k can go upto n so O($$n^2$$)\n\n# Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n\n if stones[1] != 1:\n return False\n\n def dfs(i, k):\n if i == len(stones) - 1:\n return True\n\n if (i, k) in dp:\n return dp[(i, k)]\n\n res = False\n for j in range(i + 1, len(stones)):\n if stones[i] + k == stones[j]:\n res = res or dfs(j, k)\n if stones[i] + k + 1 == stones[j]:\n res = res or dfs(j, k + 1)\n if stones[i] + k - 1 == stones[j]:\n res = res or dfs(j, k - 1)\n\n dp[(i, k)] = res\n return res\n \n dp = {}\n return dfs(1, 1)\n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Graph || BFS || Commented line by line | frog-jump | 0 | 1 | # Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n #destination is a variable which stores the \n #position of last stone where frog need to reach\n destination=stones[len(stones)-1]\n #it may happen that elements can be repeated so to avoid that\n #associate a set for every stone in stones array\n #make a hash map of stones along with set()\n #for eg.1 : \n #stones = [0,1,3,5,6,8,12,17]\n #hash_map={0: set(), 1: set(), 3: set(), 5: set(), 6: set(), 8: set(), 12: set(), 17: set()}\n hash_map=dict()\n #in hash map , key will be stone and value will be set()\n for stone in stones:\n hash_map[stone]=set()\n #it is given that the initial jump of frog is 1\n hash_map[stones[0]].add(1)\n #jumps is a set of particular position of stones \n #for every position of stone in stones\n #find out the new position while iterating over set of jumps\n for position in stones:\n jumps=hash_map[position]\n for j in jumps:\n #calculate newposition by adding position with j \n new_pos=position+j\n #check whether the new_pos is our target destination or not\n if new_pos==destination:\n return True\n #check whether the new position is available in hash map\n #if yes ,perform the below operation\n if new_pos in hash_map:\n #if j-1 > 0 then add j-1 to the new position in hashmap\n if (j-1)>0:\n hash_map[new_pos].add(j-1)\n #add j to the new position in hashmap\n hash_map[new_pos].add(j)\n #add j+1 to the new position in hashmap\n hash_map[new_pos].add(j+1)\n #else return false\n return False\n\n \n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Top Down DP with Memoization Solution | frog-jump | 0 | 1 | # Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n if stones[1] - stones[0] != 1:\n return False\n \n stone_ind = {s: i for i, s in enumerate(stones)}\n\n @cache\n def dp(i, lastj):\n if i == len(stones) - 1:\n return True\n \n curr_at = stones[i]\n \n k_minus_1 = False\n if lastj > 1 and curr_at + lastj - 1 in stone_ind:\n k_minus_1 = dp(stone_ind[curr_at + lastj - 1], lastj - 1)\n \n k = False\n if curr_at + lastj in stone_ind:\n k = dp(stone_ind[curr_at + lastj], lastj)\n \n k_plus_1 = False\n if curr_at + lastj + 1 in stone_ind:\n k_plus_1 = dp(stone_ind[curr_at + lastj + 1], lastj + 1)\n \n return k_plus_1 or k or k_minus_1\n \n return dp(1, 1)\n \n``` | 2 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | frog-jump | 1 | 1 | # Intuition\nUse dynamic programming to keep the last jump and I thought why the frog can\'t jump into the water.\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 249 videos as of August 28th, 2023.\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/dvoouRUguvw\n\n## In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. **Initialization and Base Case Setup:**\n Initialize a dictionary `dp` where keys represent the positions of stones, and values are sets to store possible jump distances for each stone. Initialize the stone at position 0 with a set containing only the jump distance 0.\n\n **Explanation:** At the start, we create a dictionary to keep track of the possible jump distances for each stone. Since the frog starts at position 0, we initialize the set for the stone at position 0 with a jump distance of 0, indicating that it\'s the starting point.\n\n2. **Iterating Through Stones:**\n Iterate through each stone in the list `stones`.\n\n a. **Loop Through Jump Distances of Current Stone:**\n For the current stone\'s position, loop through the possible jump distances stored in `dp[stone]`.\n\n b. **Considering Different Jump Distances:**\n For each jump distance, consider three potential jump distances: `jump - 1`, `jump`, and `jump + 1`.\n\n c. **Checking and Updating Valid Jumps:**\n Check if the calculated `jump_distance` is greater than 0 and if the resulting position (`stone + jump_distance`) is present in the `dp` dictionary. If both conditions are met, add the current `jump_distance` to the set of possible jump distances for the next stone\'s position (`stone + jump_distance`).\n\n **Explanation:** This nested loop structure is crucial for exploring the different jump distances the frog can take and updating the `dp` dictionary with valid jump possibilities.\n\n3. **Checking if Frog Can Reach the Last Stone:**\n After processing all stones and their respective jump distances:\n\n a. **Checking Last Stone\'s Jump Distances:**\n Check if the last stone\'s position (`stones[-1]`) has any possible jump distances greater than 0 in the `dp` dictionary.\n\n b. **Returning the Result:**\n If there are any valid jump distances for the last stone, return `True` to indicate that the frog can successfully cross the river. Otherwise, return `False` to indicate that the frog cannot cross the river.\n\n **Explanation:** This step is the final determination of whether the frog can cross the river based on the calculated jump possibilities for each stone.\n\n# Complexity\n- Time complexity: O(n^2)\n\n- Space complexity: O(n^2)\n\n```python []\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n dp = {stone : set() for stone in stones}\n dp[0] = {0}\n\n for stone in stones:\n for jump in dp[stone]:\n for jump_distance in [jump - 1, jump, jump + 1]:\n if jump_distance > 0 and stone + jump_distance in dp:\n dp[stone + jump_distance].add(jump_distance)\n \n return len(dp[stones[-1]]) > 0\n```\n```javascript []\n/**\n * @param {number[]} stones\n * @return {boolean}\n */\nvar canCross = function(stones) {\n const dp = new Map();\n stones.forEach(stone => dp.set(stone, new Set()));\n dp.get(0).add(0);\n\n for (const stone of stones) {\n for (const jump of dp.get(stone)) {\n for (const jumpDistance of [jump - 1, jump, jump + 1]) {\n if (jumpDistance > 0 && dp.has(stone + jumpDistance)) {\n dp.get(stone + jumpDistance).add(jumpDistance);\n }\n }\n }\n }\n\n return dp.get(stones[stones.length - 1]).size > 0; \n};\n```\n```java []\nclass Solution {\n public boolean canCross(int[] stones) {\n Map<Integer, Set<Integer>> dp = new HashMap<>();\n for (int stone : stones) {\n dp.put(stone, new HashSet<>());\n }\n dp.get(0).add(0);\n\n for (int stone : stones) {\n for (int jump : dp.get(stone)) {\n for (int jumpDistance : new int[] {jump - 1, jump, jump + 1}) {\n if (jumpDistance > 0 && dp.containsKey(stone + jumpDistance)) {\n dp.get(stone + jumpDistance).add(jumpDistance);\n }\n }\n }\n }\n\n return !dp.get(stones[stones.length - 1]).isEmpty(); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool canCross(vector<int>& stones) {\n std::unordered_map<int, std::unordered_set<int>> dp;\n for (int stone : stones) {\n dp[stone] = std::unordered_set<int>();\n }\n dp[0].insert(0);\n\n for (int stone : stones) {\n for (int jump : dp[stone]) {\n for (int jumpDistance : {jump - 1, jump, jump + 1}) {\n if (jumpDistance > 0 && dp.find(stone + jumpDistance) != dp.end()) {\n dp[stone + jumpDistance].insert(jumpDistance);\n }\n }\n }\n }\n\n return !dp[stones.back()].empty(); \n }\n};\n```\n | 21 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python3 Solution | frog-jump | 0 | 1 | \n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n n=len(stones)\n dp={stone:set() for stone in stones}\n dp[0].add(0)\n for i in range(n):\n for k in dp[stones[i]]:\n for step in range(k-1,k+2):\n if step and stones[i]+step in dp:\n dp[stones[i]+step].add(step)\n\n return len(dp[stones[-1]])>0 \n``` | 7 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
C++/Python 2d DP||binary Search vs Hash table||Beats 98.48% | frog-jump | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse recursion with meomory to solve. That is DP. Since stones is in ascending order, one approach is using binary search to find the next stone for frog jump. 2nd approach a hash table is established without BS.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn English subtitles if neccessary]\n[https://youtu.be/IkUmZHbsyl0?si=pAF9VqtXj8ordm2t](https://youtu.be/IkUmZHbsyl0?si=pAF9VqtXj8ordm2t)\nThe code uses DP approach to solve the frog river crossing problem. \n\nThe 2D dp[i][k] matrix is indexed by (index for stone, jump units).\nIt maintains a 2D dp matrix to store results. The recursive function f explores possible jump units and uses binary search to find the next stone the frog can jump to. Consider dp[next][jump] where stones[next]=stones[i]+jump & jump=k-1, k, k+1.\n\nThe results of subproblems are memoized in the dp matrix to avoid redundant calculations. \n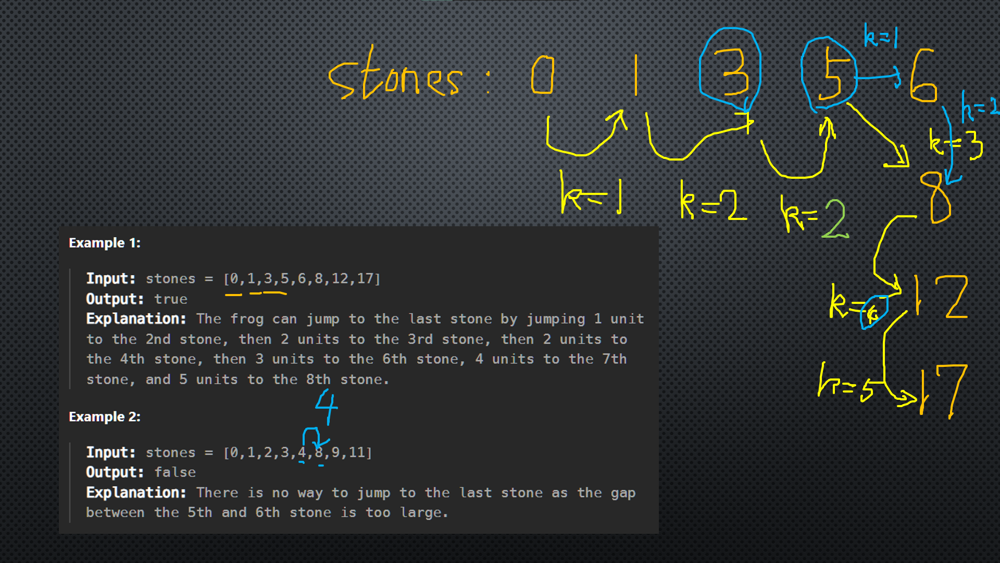\n\n2 approaches have the similar speed behaviors, although the code using hash table has smaller time complexity!\n\n# Code using binary search Runtime 36 ms Beats 98.48%\n```\nclass Solution {\npublic:\n int n;\n vector<vector<int>> dp; //2D dp matrix (index for stone, jump units)\n bool f(vector<int>& stones, int i, int k){\n if (i==n-1) return 1;\n if (dp[i][k]!=-1) return dp[i][k];\n bool ans=0;\n for(int jump: {k-1, k, k+1}){//possible jump units: k-1, k, k+1\n if (jump==0) continue;\n //Use binary search, since stones[i] is ascending\n int next=lower_bound(stones.begin()+(i+1), stones.end(), stones[i]+jump)\n -stones.begin();\n if (next==n || stones[next]!=stones[i]+jump) continue; // not found\n ans=ans||f(stones, next, jump);\n }\n return dp[i][k]=ans;\n }\n\n bool canCross(vector<int>& stones) {\n n=stones.size();\n dp.assign(n+1, vector<int>(n+1, -1));\n return f(stones, 0, 0); \n }\n};\n```\n# Code using Hash table without binary Search 49ms Beats 94.53%\n\n```\nclass Solution {\npublic:\n int n;\n vector<vector<int>> dp; //2D dp matrix (index for stone, jump units)\n unordered_map<int, int> stone2i; // Save Binary search\n bool f(vector<int>& stones, int i, int k){\n if (i==n-1) return 1;\n if (dp[i][k]!=-1) return dp[i][k];\n bool ans=0;\n for(int jump: {k-1, k, k+1}){//possible jump units: k-1, k, k+1\n if (jump==0) continue;\n //See whether stones[i]+jump in the hashTable stone2i\n if (stone2i.count(stones[i]+jump)==0) continue; // not found\n int next=stone2i[stones[i]+jump];\n ans=ans||f(stones, next, jump);\n }\n return dp[i][k]=ans;\n }\n\n bool canCross(vector<int>& stones) {\n n=stones.size();\n dp.assign(n+1, vector<int>(n+1, -1));\n for(int i=0; i<n; i++)\n stone2i[stones[i]]=i;\n return f(stones, 0, 0); \n }\n};\n\n```\n# Python solution using 1st approach\n\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n n=len(stones)\n\n @cache\n def f(i, k):\n if i==n-1: return True\n ans=False\n for jump in [k-1, k, k+1]:\n if jump==0: continue\n next= bisect_left(stones[i+1:], stones[i]+jump)+(i+1)\n if next==n or stones[next]!=stones[i]+jump: continue\n ans = ans or f(next, jump)\n return ans\n \n return f(0, 0)\n``` | 6 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python short and clean. Functional programming. | frog-jump | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution. Approach 1](https://leetcode.com/problems/frog-jump/editorial/) but shorter and functional.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is number of stones`.\n\n# Code\n```python\nclass Solution:\n def canCross(self, stones: list[int]) -> bool:\n stones_set = set(stones)\n\n @cache\n def can_jump(i: int, k: int) -> bool:\n return i == stones[-1] or any(\n x and x + i in stones_set and can_jump(i + x, x)\n for x in range(k - 1, k + 2)\n )\n \n return can_jump(stones[0], 0)\n\n\n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python | Depth-First-Search | Easy to Understand | Fastest | frog-jump | 0 | 1 | # Python | Depth-First-Search | Easy to Understand | Fastest\n```\nclass Solution(object):\n def canCross(self, stones):\n self.memo = set()\n target = stones[-1]\n stones = set(stones)\n\n res = self.bt(stones, 1, 1, target)\n return res\n\n def bt(self, stones, cur, speed, target):\n # check memo\n if (cur, speed) in self.memo:\n return False\n\n if cur==target:\n return True\n \n if cur>target or cur<0 or speed<=0 or cur not in stones:\n return False\n # dfs\n candidate = [speed-1, speed, speed+1]\n for c in candidate:\n if (cur + c) in stones:\n if self.bt(stones, cur+c, c, target):\n return True\n\n self.memo.add((cur,speed))\n return False\n``` | 2 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python solution with Top Down Dynamic programming | frog-jump | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nAs the frist jump can only be 1 unit. If `stones[1] != 1`, we know the frog cannot jump across. Then we start from `stones[1]` and treat the following postions. We define a function `dp(i, k)`, which means whether the frog can jump to position `i` with `k` jumps from the previous position. If `i == len(stones) - 1`, we know the frog can cross the river.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nUse top-down dynamic programming (DP) to check if the frog can reach the following positions recursively. The key point is the frog can potentially jump to all the following stones instead of only the next one. So we use a for loop to check the remaining stones. As the positions in the stones are increasing sorted, we can break the loop if the current position cannot be reached with `k + 1` jump.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n$$O(N^2)$$, with N the length of `stones`.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n$$O(N)$$. For each position in stones, we have at most three states (`k - 1`, `k`, `k + 1`)\n\n# Code\n```\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n\n if stones[1] != 1: return False\n\n mem = {}\n def dp(i, k):\n\n if (i, k) in mem:\n return mem[i, k]\n\n if i == len(stones) - 1: return True\n\n res = False\n for step in range(1, len(stones) - i):\n if stones[i + step] == stones[i] + k:\n res = res or dp(i + step, k)\n elif stones[i + step] == stones[i] + k - 1:\n res = res or dp(i + step, k - 1)\n elif stones[i + step] == stones[i] + k + 1:\n res = res or dp(i + step, k + 1)\n elif stones[i + step] > stones[i] + k + 1:\n break\n\n mem[i, k] = res\n\n return res\n\n return dp(1, 1)\n\n\n``` | 1 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
🔥🔥🔥🔥🔥Beats 100% | JS | TS | Java | C++ | C# | Python | python3 | Kotlin | 🔥🔥🔥🔥🔥 | frog-jump | 1 | 1 | ---\n\n\n---\n\n```C++ []\nclass Solution {\npublic:\n bool canCross(vector<int>& stones) {\n // Create a hashmap to store possible jump sizes for each stone position\n // Key: Stone position, Value: Set of valid jump sizes from that position\n unordered_map<int, unordered_set<int>> hashMap;\n\n // Initialize the first stone\'s jump sizes. Since the frog starts at position 0,\n // it can only jump 1 unit to reach the first stone.\n hashMap[stones[0] + 1] = {1};\n\n // Iterate through the stones starting from the second stone\n for (int i = 1; i < stones.size(); ++i) {\n int position = stones[i]; // Current stone\'s position\n\n // Iterate through the possible jump sizes for the current stone\'s position\n for (auto it : hashMap[position]) {\n // For each valid jump size \'it\', update the jump sizes for the next stones\n \n // Jump to the next stone with the same jump size \'it\'\n hashMap[position + it].insert(it);\n\n // Jump to the next stone with jump size \'it + 1\'\n hashMap[position + it + 1].insert(it + 1);\n\n // Jump to the next stone with jump size \'it - 1\'\n hashMap[position + it - 1].insert(it - 1);\n }\n }\n \n // If the last stone\'s position has any valid jump sizes, it means the frog can cross\n // the river and reach the last stone\n return hashMap[stones.back()].size() != 0;\n }\n};\n```\n```Typescript []\nfunction canCross(stones: number[]): boolean {\n const jumpMap: Map<number, Set<number>> = new Map();\n\n // Initialize the jumpMap with stone positions\n for (const stone of stones) {\n jumpMap.set(stone, new Set());\n }\n jumpMap.get(0).add(0); // The frog starts at position 0 with jump size 0\n\n for (const stone of stones) {\n const jumpSizes = jumpMap.get(stone);\n \n for (const jumpSize of jumpSizes) {\n for (let nextJumpSize = jumpSize - 1; nextJumpSize <= jumpSize + 1; nextJumpSize++) {\n if (nextJumpSize > 0 && jumpMap.has(stone + nextJumpSize)) {\n jumpMap.get(stone + nextJumpSize).add(nextJumpSize);\n }\n }\n }\n }\n\n return jumpMap.get(stones[stones.length - 1]).size > 0;\n}\n```\n```Java []\nimport java.util.*;\n\nclass Solution {\n public boolean canCross(int[] stones) {\n // Create a hashmap to store jump distances for each stone position\n HashMap<Integer, HashSet<Integer>> jumpMap = new HashMap<>();\n \n // Initialize the hashmap with the first stone\n jumpMap.put(0, new HashSet<>());\n jumpMap.get(0).add(1); // Frog can jump 1 unit from the first stone\n \n // Populate the jumpMap for each stone\n for (int i = 1; i < stones.length; i++) {\n jumpMap.put(stones[i], new HashSet<>());\n }\n \n // Iterate through stones and update jump distances\n for (int i = 0; i < stones.length - 1; i++) {\n int stonePos = stones[i];\n HashSet<Integer> jumpDistances = jumpMap.get(stonePos);\n \n for (int jumpDistance : jumpDistances) {\n int nextPos = stonePos + jumpDistance;\n if (nextPos == stones[stones.length - 1]) {\n return true; // Frog can reach the last stone\n }\n \n HashSet<Integer> nextJumpDistances = jumpMap.get(nextPos);\n if (nextJumpDistances != null) {\n nextJumpDistances.add(jumpDistance);\n if (jumpDistance > 1) {\n nextJumpDistances.add(jumpDistance - 1);\n }\n nextJumpDistances.add(jumpDistance + 1);\n }\n }\n }\n \n return false; // Frog cannot reach the last stone\n }\n}\n```\n```Python []\nclass Solution(object):\n def canCross(self, stones):\n n = len(stones)\n # Create a dictionary to store the possible jump sizes at each stone.\n dp = {stone: set() for stone in stones}\n dp[0].add(0) # The frog starts at the first stone with a jump size of 0.\n\n for stone in stones:\n # Iterate through all possible jump sizes at the current stone.\n for jump_size in dp[stone]:\n # Try the next possible jump sizes for the next stone.\n for step in range(jump_size - 1, jump_size + 2):\n if step > 0 and stone + step in dp:\n dp[stone + step].add(step)\n\n # If the last stone has any valid jump sizes, then the frog can cross the river.\n return len(dp[stones[-1]]) > 0\n```\n```Python3 []\nclass Solution:\n def canCross(self, stones: List[int]) -> bool:\n n = len(stones)\n \n # Create a dictionary to store possible jump lengths at each stone.\n # The key is the stone position, and the value is a set of possible jump lengths.\n jump_lengths = {stone: set() for stone in stones}\n jump_lengths[0].add(0) # Initial jump\n \n for stone in stones:\n for jump in jump_lengths[stone]:\n for next_jump in [jump - 1, jump, jump + 1]:\n if next_jump > 0 and stone + next_jump in jump_lengths:\n jump_lengths[stone + next_jump].add(next_jump)\n \n # If the last stone has any possible jump lengths, then the frog can cross.\n return len(jump_lengths[stones[-1]]) > 0\n```\n```C# []\npublic class Solution {\n HashSet<int> lookup; // HashSet to quickly check if a stone exists at a certain unit\n Dictionary<string, bool> dp; // Memoization dictionary to store computed results\n\n public bool CanCross(int[] stones) {\n if (stones[1] != 1)\n return false; // If the second stone is not at position 1, the frog can\'t jump to it\n\n lookup = new HashSet<int>();\n dp = new Dictionary<string, bool>();\n\n // Adding stone positions to the lookup HashSet for quick lookup\n for (int i = 0; i < stones.Length; i++)\n lookup.Add(stones[i]);\n\n // Start the recursive process from the first stone (position 1) with a step of 1\n return DetermineCanCross(1, 1, stones[stones.Length - 1]);\n }\n\n private bool DetermineCanCross(int reachedUnits, int lastStep, int destination) {\n if (!lookup.Contains(reachedUnits))\n return false; // If the frog can\'t land at the reachedUnits, return false\n\n if (reachedUnits == destination)\n return true; // If the frog reaches the destination, return true\n\n string localLookup = reachedUnits + "~" + lastStep;\n if (dp.ContainsKey(localLookup))\n return dp[localLookup]; // If the result for this combination of reachedUnits and lastStep is already computed, return it from the memoization dictionary\n\n if (lastStep == 0) {\n // The frog can only jump to the next stone with a step of 1\n bool computedResult = DetermineCanCross(reachedUnits + 1, 1, destination);\n dp.Add(localLookup, computedResult); // Store the computed result in the memoization dictionary\n return computedResult;\n } else if (lastStep == 1) {\n // The frog can jump to the next stone with a step of 1 or 2\n bool computedResult = DetermineCanCross(reachedUnits + 1, 1, destination) ||\n DetermineCanCross(reachedUnits + 2, 2, destination);\n dp.Add(localLookup, computedResult);\n return computedResult;\n } else {\n // The frog can jump to the next stone with a step of lastStep - 1, lastStep, or lastStep + 1\n bool computedResult = DetermineCanCross(reachedUnits + lastStep - 1, lastStep - 1, destination) ||\n DetermineCanCross(reachedUnits + lastStep, lastStep, destination) ||\n DetermineCanCross(reachedUnits + lastStep + 1, lastStep + 1, destination);\n dp.Add(localLookup, computedResult);\n return computedResult;\n }\n }\n}\n```\n```Javascript []\nvar canCross = function(stones) {\n const n = stones.length;\n \n // Create a map to store possible jump lengths at each stone\n const jumpMap = new Map();\n for (const stone of stones) {\n jumpMap.set(stone, new Set());\n }\n jumpMap.get(0).add(0); // The frog starts at the first stone\n \n // Iterate through each stone and update possible jump lengths\n for (let i = 0; i < n; i++) {\n const stone = stones[i];\n for (const jumpLength of jumpMap.get(stone)) {\n for (let k = jumpLength - 1; k <= jumpLength + 1; k++) {\n if (k > 0 && jumpMap.has(stone + k)) {\n jumpMap.get(stone + k).add(k);\n }\n }\n }\n }\n \n // Check if the last stone has any valid jump lengths\n return jumpMap.get(stones[n - 1]).size > 0;\n};\n```\n```Kotlin []\nclass Solution {\n fun canCross(stones: IntArray): Boolean {\n val jumpMap = mutableMapOf<Int, HashSet<Int>>()\n \n for (stone in stones) {\n jumpMap[stone] = HashSet()\n }\n \n jumpMap[0]?.add(0) // The frog starts at position 0 with a jump of size 0\n \n for (i in stones.indices) {\n val currentStone = stones[i]\n for (jumpSize in jumpMap[currentStone]!!) {\n for (step in -1..1) {\n val nextJumpSize = jumpSize + step\n if (nextJumpSize > 0 && jumpMap.containsKey(currentStone + nextJumpSize)) {\n jumpMap[currentStone + nextJumpSize]?.add(nextJumpSize)\n }\n }\n }\n }\n \n return jumpMap[stones.last()]?.isNotEmpty() ?: false\n }\n}\n```\n\n\n---\n\n\n--- | 3 | A frog is crossing a river. The river is divided into some number of units, and at each unit, there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of `stones`' positions (in units) in sorted **ascending order**, determine if the frog can cross the river by landing on the last stone. Initially, the frog is on the first stone and assumes the first jump must be `1` unit.
If the frog's last jump was `k` units, its next jump must be either `k - 1`, `k`, or `k + 1` units. The frog can only jump in the forward direction.
**Example 1:**
**Input:** stones = \[0,1,3,5,6,8,12,17\]
**Output:** true
**Explanation:** The frog can jump to the last stone by jumping 1 unit to the 2nd stone, then 2 units to the 3rd stone, then 2 units to the 4th stone, then 3 units to the 6th stone, 4 units to the 7th stone, and 5 units to the 8th stone.
**Example 2:**
**Input:** stones = \[0,1,2,3,4,8,9,11\]
**Output:** false
**Explanation:** There is no way to jump to the last stone as the gap between the 5th and 6th stone is too large.
**Constraints:**
* `2 <= stones.length <= 2000`
* `0 <= stones[i] <= 231 - 1`
* `stones[0] == 0`
* `stones` is sorted in a strictly increasing order. | null |
Python DFS/Recursion Easy + Intuitive | sum-of-left-leaves | 0 | 1 | At any node, check if the left child is a leaf.\nif yes -> return the left leaf child\'s value + any left leaf children in the right sub-tree\nif no -> bummer. gotta check in the right sub-tree for any left leaf children\n\nAlso, we cannot enter a node and then determine whether it was a left child. For this, one may want to pass a flag variable. If we want to avoid any passing of variables, we need to look down from a parent node at its children node. \n\nTherefore our smallest unit for consideration becomes a node and its immediate children.\n\n\n\n```\nclass Solution:\n def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n\n # does this node have a left child which is a leaf?\n if root.left and not root.left.left and not root.left.right:\n\t\t\t# gotcha\n return root.left.val + self.sumOfLeftLeaves(root.right)\n\n # no it does not have a left child or it\'s not a leaf\n else:\n\t\t\t# bummer\n return self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)\n \n``` | 50 | Given the `root` of a binary tree, return _the sum of all left leaves._
A **leaf** is a node with no children. A **left leaf** is a leaf that is the left child of another node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 24
**Explanation:** There are two left leaves in the binary tree, with values 9 and 15 respectively.
**Example 2:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-1000 <= Node.val <= 1000` | null |
C++ / Python simple and short solutions | sum-of-left-leaves | 0 | 1 | **C++ :**\n\n```\nint sumOfLeftLeaves(TreeNode* root) {\n\tif(!root) return 0;\n\n\tif(root -> left && !root -> left -> left && !root -> left -> right)\n\t\treturn root -> left -> val + sumOfLeftLeaves(root -> right);\n\n\treturn sumOfLeftLeaves(root -> left) + sumOfLeftLeaves(root -> right); \n}\n```\n\n**Python :**\n\n```\ndef sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:\n\tif not root:\n\t\treturn 0\n\n\tif root.left and not root.left.left and not root.left.right:\n\t\treturn root.left.val + self.sumOfLeftLeaves(root.right)\n\n\treturn self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)\n```\n\n**Like it ? please upvote !** | 16 | Given the `root` of a binary tree, return _the sum of all left leaves._
A **leaf** is a node with no children. A **left leaf** is a leaf that is the left child of another node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 24
**Explanation:** There are two left leaves in the binary tree, with values 9 and 15 respectively.
**Example 2:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-1000 <= Node.val <= 1000` | null |
404: Time 98.99%, Solution with step by step explanation | sum-of-left-leaves | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe algorithm works by recursively traversing the binary tree and checking if each node is a left child and a leaf node. If so, it adds the value of the node to the sum of left leaves. Otherwise, it recursively traverses the left and right subtrees and adds their results.\n\nThe algorithm uses a helper function called traverse, which takes two arguments: the current node being traversed and a boolean value indicating if the current node is a left child. The function returns the sum of left leaves of the subtree rooted at the current node.\n\nThe main function sumOfLeftLeaves calls the helper function with the root node and False to indicate that the root is not a left child. It returns the result of the helper function.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfLeftLeaves(self, root: TreeNode) -> int:\n # Define a helper function to recursively traverse the tree and compute the sum of left leaves\n def traverse(node, is_left):\n # If the current node is None, return 0\n if not node:\n return 0\n \n # If the current node is a leaf node and is a left child, return its value\n if not node.left and not node.right and is_left:\n return node.val\n \n # Recursively traverse the left and right subtrees\n left_sum = traverse(node.left, True)\n right_sum = traverse(node.right, False)\n \n return left_sum + right_sum\n \n # Call the helper function with the root node and False to indicate that the root is not a left child\n return traverse(root, False)\n\n``` | 8 | Given the `root` of a binary tree, return _the sum of all left leaves._
A **leaf** is a node with no children. A **left leaf** is a leaf that is the left child of another node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 24
**Explanation:** There are two left leaves in the binary tree, with values 9 and 15 respectively.
**Example 2:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-1000 <= Node.val <= 1000` | null |
Python iterative solution, beats 100% | sum-of-left-leaves | 0 | 1 | For those who were also confused if root node with no leaves count as left leaf - it is not.\nJust go through all the elements using DFS with stack and remember if it is left or right child.\n\n```\nclass Solution:\n def sumOfLeftLeaves(self, root: TreeNode) -> int:\n result = 0\n stack = [(root, False)]\n while stack:\n curr, is_left = stack.pop()\n if not curr:\n continue\n if not curr.left and not curr.right:\n if is_left:\n result += curr.val\n else:\n stack.append((curr.left, True))\n stack.append((curr.right, False))\n return result\n``` | 36 | Given the `root` of a binary tree, return _the sum of all left leaves._
A **leaf** is a node with no children. A **left leaf** is a leaf that is the left child of another node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 24
**Explanation:** There are two left leaves in the binary tree, with values 9 and 15 respectively.
**Example 2:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-1000 <= Node.val <= 1000` | null |
✅|| Easiest Way|| Python|| 38ms | sum-of-left-leaves | 0 | 1 | We can easily the reach the leaf nodes, the problem to tackle here is how to know wheather the given node is a left leaf node or not. \n\nTo solve this what I have done is on every recursive call I sent one extra Boolean Variable which was ```True``` when ever I was sending a left node and ```False``` everytime the node was a right node.\n\nNow how would this work? Let\'s assume we have reached the last node of the given test case \n\n\nHere when we reach 9 , it won\'t have a left node or a right node so hence it qualifies to be a leaf node. \nNow because our recursive calls runs with the check variable whose value in this case is true hence this value is added to the variable ```ans``` and this process repeats.\n\nNow let\'s say we have reached 7 this time. It also qualifies as leaf node, but it won\'t qualify as left leaf because the check variable is False\n\nHere is the code:-\n```\nclass Solution:\n def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:\n ans=[0]\n def finder(node,ans,check):\n if not node:\n return\n if not node.left and not node.right and check:\n # print(node.val)\n ans[0]+=node.val\n return\n finder(node.left,ans,True)\n finder(node.right,ans,False)\n return\n finder(root,ans,False)\n return ans[0]\n```\n\nIf you like this please **UPVOTE**.\n\n\n\n | 3 | Given the `root` of a binary tree, return _the sum of all left leaves._
A **leaf** is a node with no children. A **left leaf** is a leaf that is the left child of another node.
**Example 1:**
**Input:** root = \[3,9,20,null,null,15,7\]
**Output:** 24
**Explanation:** There are two left leaves in the binary tree, with values 9 and 15 respectively.
**Example 2:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `-1000 <= Node.val <= 1000` | null |
405: Solution with step by step explanation | convert-a-number-to-hexadecimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function toHex that takes an integer num as input and returns a string representing its hexadecimal representation.\n2. Check if the input number is zero. If so, return \'0\' as its hexadecimal representation.\n3. If the input number is negative, convert it to its corresponding positive value using two\'s complement. This is achieved by adding 2^32 to the input number, since we are dealing with 32-bit integers.\n4. Define the string hex_digits that contains the hexadecimal digits from \'0\' to \'f\'.\n5. Initialize an empty string hex_num to store the hexadecimal representation of the input number.\n6. Repeatedly divide the input number by 16 and convert the remainder to its corresponding hexadecimal digit until the quotient becomes zero. We can use integer division // to obtain the quotient.\n7. For each remainder obtained in step 6, convert it to its corresponding hexadecimal digit using the hex_digits string and add it to the beginning of the hex_num string using string concatenation.\n8. Return the hex_num string as the hexadecimal representation of the input number.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n # If the input number is zero, return \'0\'\n if num == 0:\n return \'0\'\n # If the input number is negative, convert it to its corresponding positive value using two\'s complement\n if num < 0:\n num = (1 << 32) + num\n \n hex_digits = \'0123456789abcdef\' # The hexadecimal digits\n \n hex_num = \'\' # Initialize an empty string to store the hexadecimal representation of the input number\n \n # Repeatedly divide the input number by 16 and convert the remainder to its corresponding hexadecimal digit until the quotient becomes zero\n while num > 0:\n digit = num % 16 # Get the remainder of dividing the input number by 16\n hex_digit = hex_digits[digit] # Convert the remainder to its corresponding hexadecimal digit\n hex_num = hex_digit + hex_num # Add the hexadecimal digit to the beginning of the hexadecimal representation\n num //= 16 # Update the input number by dividing it by 16\n \n return hex_num\n\n``` | 15 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
using binary code logic || Easily Understandable || | convert-a-number-to-hexadecimal | 0 | 1 | - if you find it usefull please vote it so it can reach maximum people.\n# Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n d = {10:\'a\',11:\'b\',12:\'c\',13:\'d\',14:\'e\',15:\'f\'}\n res = ""\n if num == 0:\n return "0"\n if num<0:\n num = (1<<32)+num\n while num>0:\n if num%16<10:\n res+=str(num%16)\n else:\n res+=str(d[num%16])\n num=num//16\n return res[::-1]\n``` | 6 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
convert to hexadecimal number | convert-a-number-to-hexadecimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n if num == 0:\n return "0"\n\n hex_chars = "0123456789abcdef" # List of hexadecimal characters\n result = [] # Initialize an empty list to store the hexadecimal digits\n \n # Convert negative numbers using two\'s complement\n if num < 0:\n num += 2 ** 32 # Convert negative number to its positive equivalent\n \n while num > 0:\n digit = num % 16 # Extract the remainder when divided by 16\n result.append(hex_chars[digit]) # Append the corresponding hex character to the result list\n num //= 16 # Divide the number by 16 for the next iteration\n \n return \'\'.join(result[::-1]) # Reverse the list and join the elements to form the hexadecimal representation\n\n``` | 3 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
easy solution with explanation | convert-a-number-to-hexadecimal | 0 | 1 | * if you find it usefull please vote it so it can reach maximum people.\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n hex="0123456789abcdef" #created string for reference\n ot="" # created a string variable to store and update output string\n if num==0:\n return "0"\n elif num<0:\n num+=2**32\n while num:\n ot=hex[num%16]+ot # we update the output string with the reminder of num/16 , 16 because we are dealing with hex.\n num//=16 # now we are updating num by dividing it by 16 ***// operator used for floor division , means division will be always integer not float.\n return ot # then we simply return ot\n```\n* if you have any doubts ask in comments section. | 12 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.