title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Easiest Python Solution | convert-a-number-to-hexadecimal | 0 | 1 | ```\ndef toHex(self, num: int) -> str:\n\tif num == 0: return \'0\'\n\tmap = \'0123456789abcdef\'\n\tresult = \'\'\n\t#if negative (two\'s compliment)\n\tif num<0: num += 2 ** 32\n\twhile num > 0:\n\t\tdigit = num % 16\n\t\tnum = (num-digit) // 16\n\t\tresult += str(map[digit])\n\treturn result[::-1]\n```\nIf you like this solution please consider giving it a star on my [github](https://github.com/bwiens/leetcode-python). Means a lot to me. | 19 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
O(1) Python solution | convert-a-number-to-hexadecimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is that this problem can be solved by converting the decimal number to its hexadecimal representation. I can achieve this by using bit manipulation and a lookup table to convert the last 4 bits of the decimal number to its corresponding hexadecimal representation.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach to solving this problem is to first check if the input number is equal to 0, in which case the function returns "0". A lookup table of hexadecimal characters is created. A variable ans is used to store the final hexadecimal representation. The function uses a while loop to iterate until the number is not 0 and the length of the hexadecimal representation is less than 8. The function uses bit manipulation to obtain the last 4 bits of the decimal number and uses the lookup table to convert it to its corresponding hexadecimal representation. The resulting hexadecimal character is added to the ans variable. The number is then shifted 4 bits to the right to obtain the next 4 bits. The function returns the final hexadecimal representation.\n\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n if num == 0:\n return "0"\n hexa = "0123456789abcdef"\n ans = ""\n while num != 0 and len(ans) < 8:\n ans = hexa[num & 15] + ans\n num >>= 4\n return ans\n\n``` | 4 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
[Python3] One line | convert-a-number-to-hexadecimal | 0 | 1 | Using **str.format()** method we can convert to **hexadecimal** format. This option is also aviable for **binary**, **octal** and **decimal** representation with \'b\', \'o\', \'d\' case respectively.\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n return "{0:x}".format(num) if num >= 0 else "{0:x}".format(num + 2 ** 32)\n``` | 4 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
4-Lines Python Solution || 98% Faster (24ms) || Memory less than 76% | convert-a-number-to-hexadecimal | 0 | 1 | ```\nclass Solution:\n def toHex(self, num: int) -> str:\n Hex=\'0123456789abcdef\' ; ans=\'\'\n if num<0: num+=2**32\n while num>0: ans=Hex[num%16]+ans ; num//=16\n return ans if ans else \'0\'\n```\n-------------------\n***----- Taha Choura -----***\n*[email protected]* | 2 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
Python : 🐍 Only 2 Line❗️Easy❗️ | convert-a-number-to-hexadecimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n \n**If you think this is easy, Please Vote for everyone !**\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n if num<0: num+=2**32\n ans=("%x"% num)\n return ans\n``` | 2 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
Easy Solution with simple explanation : ) | convert-a-number-to-hexadecimal | 1 | 1 | Let\'s break down the problem and the provided code in simpler terms:\n\n### Problem Explanation:\nThe task is to convert an integer `num` into its hexadecimal representation. The hexadecimal system uses base-16, where each digit can be one of 16 values (0-9 and A-F). For negative numbers, a method called two\'s complement is used.\n\n### Approach:\nThe code uses bitwise operations to extract the last 4 bits of the number at a time. It then converts these 4 bits to a hexadecimal digit and adds it to the result. This process is repeated until all 32 bits of the number are processed (8 groups of 4 bits).\n\n### Code Explanation (Java):\n```java\nclass Solution {\n public String toHex(int num) {\n // Check if the number is zero, return "0" in that case\n if (num == 0) {\n return "0";\n }\n\n // Using StringBuilder to efficiently build the hexadecimal representation\n StringBuilder result = new StringBuilder();\n \n // Process 32 bits (4 hex digits) at a time\n for (int i = 0; num != 0 && i < 8; i++) {\n int hexDigit = num & 0xF; // Extract the last 4 bits\n result.insert(0, Integer.toHexString(hexDigit));\n num >>>= 4; // Right shift by 4 bits\n }\n\n return result.toString();\n }\n}\n```\n\n### Example:\nLet\'s take an example:\n```java\nInput: num = 26\n```\nBinary representation of 26: `0000 0000 0000 0000 0000 0000 0001 1010`\n\nNow, process 4 bits at a time:\n1. Last 4 bits: `1010` (in decimal, 10) \u2192 Hexadecimal digit: `a`\n2. Next 4 bits: `0001` (in decimal, 1) \u2192 Hexadecimal digit: `1`\n\nCombine the digits: `1a`, which is the expected output.\n\n### Explanation (Step by Step):\n1. Initialize a StringBuilder to store the result.\n2. Process the number 4 bits at a time (hexadecimal digit).\n3. Extract the last 4 bits using bitwise AND with `0xF` (binary `1111`).\n4. Convert the 4 bits to a hexadecimal digit using `Integer.toHexString`.\n5. Insert the digit at the beginning of the result (to maintain order).\n6. Right shift the number by 4 bits to process the next group.\n7. Repeat steps 3-6 until all 32 bits are processed or until `num` becomes 0.\n8. Return the final result.\n\n### Note:\n- `>>>` is the unsigned right shift operator in Java, which fills the leftmost bits with zeros.\n\nThis process is similar for the Python and C++ implementations, with slight syntax differences. The key idea is to break down the number into 4-bit groups and convert them to hexadecimal digits.\n\n```java []\nclass Solution {\n public String toHex(int num) {\n if (num == 0) {\n return "0";\n }\n\n // Using StringBuilder to efficiently build the hexadecimal representation\n StringBuilder result = new StringBuilder();\n \n // Process 32 bits (4 hex digits) at a time\n for (int i = 0; num != 0 && i < 8; i++) {\n int hexDigit = num & 0xF; // Extract the last 4 bits\n result.insert(0, Integer.toHexString(hexDigit));\n num >>>= 4; // Right shift by 4 bits\n }\n\n return result.toString();\n }\n}\n```\n```python []\nclass Solution:\n def toHex(self, num: int) -> str:\n if num == 0:\n return "0"\n\n result = []\n # Process 32 bits (4 hex digits) at a time\n for _ in range(8):\n hex_digit = num & 0xF # Extract the last 4 bits\n result.insert(0, hex(hex_digit)[2:]) # Convert to hexadecimal and add to the front\n num >>= 4 # Right shift by 4 bits\n\n return \'\'.join(result)\n```\n```C++ []\nclass Solution {\npublic:\n string toHex(int num) {\n if (num == 0) {\n return "0";\n }\n\n // Using stringstream to efficiently build the hexadecimal representation\n stringstream result;\n\n // Process 32 bits (4 hex digits) at a time\n for (int i = 0; num != 0 && i < 8; i++) {\n int hexDigit = num & 0xF; // Extract the last 4 bits\n result << hex << hexDigit; // Convert to hexadecimal and add to the stringstream\n num >>= 4; // Right shift by 4 bits\n }\n\n return result.str();\n }\n};\n```\n | 0 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
Hexadecimal Conversion with Two's Complement | convert-a-number-to-hexadecimal | 0 | 1 | # Intuition\nUse the two\'s complement method to convert integers to their hexadecimal representation.\n\n# Approach\nIterate through 8 groups of 4 bits in the 32-bit integer, extract each group\'s value, and convert it to hexadecimal. Remove leading zeros.\n\n# Complexity\n- Time complexity: O(1)\n- Space complexity: O(1)\n\n# Code\n```python\nclass Solution:\n def toHex(self, num: int) -> str:\n if num == 0:\n return \'0\'\n hex_map = \'0123456789abcdef\'\n result = \'\'\n for i in range(8):\n group_value = (num >> (4 * i)) & 0xf\n result = hex_map[group_value] + result\n return result.lstrip(\'0\')\n | 0 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
easy python soultion | convert-a-number-to-hexadecimal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n map="0123456789abcdefg"\n res=""\n if num<0:\n num+=(1<<32) #or 2**32\n elif num==0:\n return "0"\n while num>0:\n num,rem=divmod(num,16)\n res+=str(map[rem])\n return res[::-1]\n``` | 0 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
Python | 3 lines | Build in functions | convert-a-number-to-hexadecimal | 0 | 1 | # Code\n```\nclass Solution:\n def toHex(self, num: int) -> str:\n if num < 0:\n num = 2**32 + num\n return hex(num)[2:]\n\n``` | 0 | Given an integer `num`, return _a string representing its hexadecimal representation_. For negative integers, [two's complement](https://en.wikipedia.org/wiki/Two%27s_complement) method is used.
All the letters in the answer string should be lowercase characters, and there should not be any leading zeros in the answer except for the zero itself.
**Note:** You are not allowed to use any built-in library method to directly solve this problem.
**Example 1:**
**Input:** num = 26
**Output:** "1a"
**Example 2:**
**Input:** num = -1
**Output:** "ffffffff"
**Constraints:**
* `-231 <= num <= 231 - 1` | null |
Trivial solution with Sorting in Python3 | queue-reconstruction-by-height | 0 | 1 | # Intuition\nHere we have:\n- `people`, that is tuple `[height, pos]`\n- our goal is to reconstruct a Queue\n\nTo reconstruct this Queue, the only thing we should do is to insert a particular `people[i]` into `pos`, after sorting people by height in **descending** order. \n\n# Approach\n1. define `ans` as **deque**\n2. sort `people` by `[-x[0], x[1]]`\n3. iterate over `people`\n4. insert them at `pos` position\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N log N)**\n\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def reconstructQueue(self, people: list[list[int]]) -> list[list[int]]:\n ans = deque()\n people.sort(key = lambda x: (-x[0], x[1]))\n\n for person in people:\n ans.insert(person[1], person)\n\n return ans\n``` | 1 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Trivial solution with Sorting in Python3 | queue-reconstruction-by-height | 0 | 1 | # Intuition\nHere we have:\n- `people`, that is tuple `[height, pos]`\n- our goal is to reconstruct a Queue\n\nTo reconstruct this Queue, the only thing we should do is to insert a particular `people[i]` into `pos`, after sorting people by height in **descending** order. \n\n# Approach\n1. define `ans` as **deque**\n2. sort `people` by `[-x[0], x[1]]`\n3. iterate over `people`\n4. insert them at `pos` position\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N log N)**\n\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def reconstructQueue(self, people: list[list[int]]) -> list[list[int]]:\n ans = deque()\n people.sort(key = lambda x: (-x[0], x[1]))\n\n for person in people:\n ans.insert(person[1], person)\n\n return ans\n``` | 1 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Python Easy Greedy O(1) Space approach | queue-reconstruction-by-height | 0 | 1 | ```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n output=[] \n \n # sort the array in decreasing order of height \n # within the same height group, you would sort it in increasing order of k\n # eg: Input : [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]\n # after sorting: [[7,0],[7,1],[6,1],[5,0],[5,2],[4,4]]\n people.sort(key=lambda x: (-x[0], x[1])) \n for a in people:\n # Now let\'s start the greedy here\n # We insert the entry in the output array based on the k value\n # k will act as a position within the array\n output.insert(a[1], a)\n \n return output \n```\n\n**Time - O(nlogn + n * n)** - We sort the array in **O(nlogn)** and the greedy algorithm loop takes **O(n * n)** because of array insert operation.\n**Space - O(1)** - If you exclude the output array.\n\n\n---\n\n***Please upvote if you find it useful*** | 91 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Python Easy Greedy O(1) Space approach | queue-reconstruction-by-height | 0 | 1 | ```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n output=[] \n \n # sort the array in decreasing order of height \n # within the same height group, you would sort it in increasing order of k\n # eg: Input : [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]\n # after sorting: [[7,0],[7,1],[6,1],[5,0],[5,2],[4,4]]\n people.sort(key=lambda x: (-x[0], x[1])) \n for a in people:\n # Now let\'s start the greedy here\n # We insert the entry in the output array based on the k value\n # k will act as a position within the array\n output.insert(a[1], a)\n \n return output \n```\n\n**Time - O(nlogn + n * n)** - We sort the array in **O(nlogn)** and the greedy algorithm loop takes **O(n * n)** because of array insert operation.\n**Space - O(1)** - If you exclude the output array.\n\n\n---\n\n***Please upvote if you find it useful*** | 91 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
📌 Python3 naive solution: Insert into result array | queue-reconstruction-by-height | 0 | 1 | ```\nfrom bisect import insort\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n dic = {}\n heights = []\n result = []\n for height, peopleAhead in people:\n if height in dic:\n insort(dic[height],peopleAhead)\n else:\n dic[height] = [peopleAhead]\n insort(heights,height)\n \n heights = heights[::-1]\n index = 0\n length = len(heights)\n \n while index < length:\n height = heights[index]\n if len(dic[height]) <=0:\n index+=1\n else:\n temp = dic[height].pop(0)\n peopleAhead = temp\n j = 0\n while j < len(result):\n if peopleAhead == 0:\n break\n if result[j][0] >= height:\n peopleAhead-=1\n j+=1\n result.insert(j, [height, temp])\n return result\n``` | 6 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
📌 Python3 naive solution: Insert into result array | queue-reconstruction-by-height | 0 | 1 | ```\nfrom bisect import insort\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n dic = {}\n heights = []\n result = []\n for height, peopleAhead in people:\n if height in dic:\n insort(dic[height],peopleAhead)\n else:\n dic[height] = [peopleAhead]\n insort(heights,height)\n \n heights = heights[::-1]\n index = 0\n length = len(heights)\n \n while index < length:\n height = heights[index]\n if len(dic[height]) <=0:\n index+=1\n else:\n temp = dic[height].pop(0)\n peopleAhead = temp\n j = 0\n while j < len(result):\n if peopleAhead == 0:\n break\n if result[j][0] >= height:\n peopleAhead-=1\n j+=1\n result.insert(j, [height, temp])\n return result\n``` | 6 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Python 96% Fast and 93% space efficient solution | queue-reconstruction-by-height | 0 | 1 | optimal best solution:\n\n\n\tclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n people.sort(key = lambda x: (-x[0], x[1]))\n queue = []\n for p in people:\n queue.insert(p[1], p) \n return queue\n\t\t\n\t\t\naverage time solution:\n\t\n\tclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n ans = []\n for p in sorted(people, key=lambda p: (-1 * p[0], p[1])):\n ans.insert(p[1], p)\n return ans | 2 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Python 96% Fast and 93% space efficient solution | queue-reconstruction-by-height | 0 | 1 | optimal best solution:\n\n\n\tclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n people.sort(key = lambda x: (-x[0], x[1]))\n queue = []\n for p in people:\n queue.insert(p[1], p) \n return queue\n\t\t\n\t\t\naverage time solution:\n\t\n\tclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n ans = []\n for p in sorted(people, key=lambda p: (-1 * p[0], p[1])):\n ans.insert(p[1], p)\n return ans | 2 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
[Python] O(NlogN) Solution using SortedList | queue-reconstruction-by-height | 0 | 1 | The `O(N^2)` solution is well explained by others. Here we present an `O(NlogN)` solution using Python\'s SortedList (or other similar data structures, e.g. binary indexed tree).\n```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n from sortedcontainers import SortedList\n n = len(people)\n people.sort()\n ans = [None] * n\n ans[people[0][1]] = people[0]\n sl = SortedList(range(n))\n toRemove = [people[0][1]]\n for i in range(1, n):\n if people[i][0] != people[i - 1][0]:\n for index in toRemove:\n sl.remove(index)\n toRemove = []\n ans[sl[people[i][1]]] = people[i]\n toRemove.append(sl[people[i][1]])\n return ans\n``` | 3 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
[Python] O(NlogN) Solution using SortedList | queue-reconstruction-by-height | 0 | 1 | The `O(N^2)` solution is well explained by others. Here we present an `O(NlogN)` solution using Python\'s SortedList (or other similar data structures, e.g. binary indexed tree).\n```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n from sortedcontainers import SortedList\n n = len(people)\n people.sort()\n ans = [None] * n\n ans[people[0][1]] = people[0]\n sl = SortedList(range(n))\n toRemove = [people[0][1]]\n for i in range(1, n):\n if people[i][0] != people[i - 1][0]:\n for index in toRemove:\n sl.remove(index)\n toRemove = []\n ans[sl[people[i][1]]] = people[i]\n toRemove.append(sl[people[i][1]])\n return ans\n``` | 3 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
406: Solution with step by step explanation | queue-reconstruction-by-height | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, sort the input list people in decreasing order by height (hi). If multiple people have the same height, they should be sorted in increasing order by the number of people in front of them (ki). This can be achieved using a lambda function as the key for the sort() method.\n\n2. Initialize an empty list result to store the reconstructed queue.\n\n3. Iterate through each person in the sorted people list.\n\n4. For each person, insert them into the result list at the index ki, which represents the number of people in front of them who are taller or the same height.\n\n5. After iterating through all people, the result list will contain the reconstructed queue in the correct order.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n # Step 1: Sort the input list in decreasing order by height and increasing order by the number of people in front\n people.sort(key=lambda x: (-x[0], x[1]))\n \n # Step 2: Initialize an empty list to store the reconstructed queue\n result = []\n \n # Step 3: Iterate through each person in the sorted list\n for person in people:\n # Step 4: Insert the person into the result list at the index ki\n result.insert(person[1], person)\n \n # Step 5: Return the reconstructed queue\n return result\n\n``` | 5 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
406: Solution with step by step explanation | queue-reconstruction-by-height | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, sort the input list people in decreasing order by height (hi). If multiple people have the same height, they should be sorted in increasing order by the number of people in front of them (ki). This can be achieved using a lambda function as the key for the sort() method.\n\n2. Initialize an empty list result to store the reconstructed queue.\n\n3. Iterate through each person in the sorted people list.\n\n4. For each person, insert them into the result list at the index ki, which represents the number of people in front of them who are taller or the same height.\n\n5. After iterating through all people, the result list will contain the reconstructed queue in the correct order.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n # Step 1: Sort the input list in decreasing order by height and increasing order by the number of people in front\n people.sort(key=lambda x: (-x[0], x[1]))\n \n # Step 2: Initialize an empty list to store the reconstructed queue\n result = []\n \n # Step 3: Iterate through each person in the sorted list\n for person in people:\n # Step 4: Insert the person into the result list at the index ki\n result.insert(person[1], person)\n \n # Step 5: Return the reconstructed queue\n return result\n\n``` | 5 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Python 3 simple solution with explanation | queue-reconstruction-by-height | 0 | 1 | **Idea**\nIn order to achieve the requested output order, a sorted input list can be processed by inserting the new value at index=`k`. In the given example, sort the input by `h` in decreasing order and by `k` in increasing order:\n```\n[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] -> [[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]]\n```\nThe iterate over the values and add the new value at the index `k`:\n```\nEmpty list: []\n[7,0] -> Add 7 at index 0: [[7,0]]\n[7,1] -> Add 7 at index 1: [[7,0], [7,1]]\n[6,1] -> Add 6 at index 1: [[7, 0], [6, 1], [7, 1]] \n[5,0] -> Add 5 at index 0: [[5, 0], [7, 0], [6, 1], [7, 1]] \n[5,2] -> Add 5 at index 2: [[5, 0], [7, 0], [5, 2], [6, 1], [7, 1]] \n[4,4] -> Add 4 at index 4: [[5, 0], [7, 0], [5, 2], [6, 1], [4, 4], [7, 1]]\n```\n\n**Implementation**\n```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n result = []\n for h, k in sorted(people, key=lambda x: (-x[0], x[1])):\n result.insert(k, [h, k])\n return result\n``` | 30 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Python 3 simple solution with explanation | queue-reconstruction-by-height | 0 | 1 | **Idea**\nIn order to achieve the requested output order, a sorted input list can be processed by inserting the new value at index=`k`. In the given example, sort the input by `h` in decreasing order and by `k` in increasing order:\n```\n[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] -> [[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]]\n```\nThe iterate over the values and add the new value at the index `k`:\n```\nEmpty list: []\n[7,0] -> Add 7 at index 0: [[7,0]]\n[7,1] -> Add 7 at index 1: [[7,0], [7,1]]\n[6,1] -> Add 6 at index 1: [[7, 0], [6, 1], [7, 1]] \n[5,0] -> Add 5 at index 0: [[5, 0], [7, 0], [6, 1], [7, 1]] \n[5,2] -> Add 5 at index 2: [[5, 0], [7, 0], [5, 2], [6, 1], [7, 1]] \n[4,4] -> Add 4 at index 4: [[5, 0], [7, 0], [5, 2], [6, 1], [4, 4], [7, 1]]\n```\n\n**Implementation**\n```\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n result = []\n for h, k in sorted(people, key=lambda x: (-x[0], x[1])):\n result.insert(k, [h, k])\n return result\n``` | 30 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Solution.py | queue-reconstruction-by-height | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\n\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n people.sort(key=lambda x: (-x[0], x[1]))\n ans = []\n \n for person in people:\n ans.insert(person[1], person)\n \n return ans\n\n``` | 2 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
Solution.py | queue-reconstruction-by-height | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\n\nclass Solution:\n def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n people.sort(key=lambda x: (-x[0], x[1]))\n ans = []\n \n for person in people:\n ans.insert(person[1], person)\n \n return ans\n\n``` | 2 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
easy peasy python solution | queue-reconstruction-by-height | 0 | 1 | \tdef reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n ln = len(people)\n if ln == 0:\n return []\n \n people = sorted(people, key = lambda x: (-x[0], x[1]))\n \n ls = []\n for pep in people:\n ls.insert(pep[1], pep)\n \n return ls | 13 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
easy peasy python solution | queue-reconstruction-by-height | 0 | 1 | \tdef reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:\n ln = len(people)\n if ln == 0:\n return []\n \n people = sorted(people, key = lambda x: (-x[0], x[1]))\n \n ls = []\n for pep in people:\n ls.insert(pep[1], pep)\n \n return ls | 13 | You are given an array of people, `people`, which are the attributes of some people in a queue (not necessarily in order). Each `people[i] = [hi, ki]` represents the `ith` person of height `hi` with **exactly** `ki` other people in front who have a height greater than or equal to `hi`.
Reconstruct and return _the queue that is represented by the input array_ `people`. The returned queue should be formatted as an array `queue`, where `queue[j] = [hj, kj]` is the attributes of the `jth` person in the queue (`queue[0]` is the person at the front of the queue).
**Example 1:**
**Input:** people = \[\[7,0\],\[4,4\],\[7,1\],\[5,0\],\[6,1\],\[5,2\]\]
**Output:** \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\]
**Explanation:**
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence \[\[5,0\],\[7,0\],\[5,2\],\[6,1\],\[4,4\],\[7,1\]\] is the reconstructed queue.
**Example 2:**
**Input:** people = \[\[6,0\],\[5,0\],\[4,0\],\[3,2\],\[2,2\],\[1,4\]\]
**Output:** \[\[4,0\],\[5,0\],\[2,2\],\[3,2\],\[1,4\],\[6,0\]\]
**Constraints:**
* `1 <= people.length <= 2000`
* `0 <= hi <= 106`
* `0 <= ki < people.length`
* It is guaranteed that the queue can be reconstructed. | What can you say about the position of the shortest person?
If the position of the shortest person is i, how many people would be in front of the shortest person? Once you fix the position of the shortest person, what can you say about the position of the second shortest person? |
[Python3][Visualization] BFS Solution With Explanation | trapping-rain-water-ii | 0 | 1 | Cells which can trap the rain water, must be surrounded by cells with higher heights. We can maintain a `level` and increases1 by 1 from 0. At the same time, use BFS with a Min-Heap to iterate each cell. \n<br/>\n\n# Graph\n<ins>**Green**</ins>: The cell added in the heap\n<ins>**Yellow**</ins>: The current cell\n<ins>**Blue**</ins>: The cell is connecting to the current cell and is added to the heap\n<ins>**Red**</ins>: The cell popped out from the heap\n<ins>**White**</ins>: The cell has not been visited yet\n\n<br/>\n\n# Initial \n\n\nCells which can trap the rain water, must be surrounded by cells with higher heights, so board cells cannot trap the water. Let\'s add those cells to the heap first (Sorted by height).\n\n<br/>\n\n# Level 1\n\n\nCells with the lowest height will be popped out. In this case, there are 3 cells with height 1 will be popped out. The Order doesn\'t matter. \n\n## Graph 1.1\nCell[0,0] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 1.2\nCell[0,3] is popped out from the heap. Cell[1,3] height is larger than level(1). Added Cell[1,3] to the heap.\n\n## Graph 1.3\nCell[2,5] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n<br/>\n\n# Level 2\n\n\nThere is no level 1 cell in the heap, so set level = 2. There are 3 cells with height 2 will be popped out. The Order doesn\'t matter. \n\n## Graph 2.1\nCell[2,0] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 2.2\nCell[0,5] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 2.3\nCell[2,3] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n<br/>\n\n# Level 3\n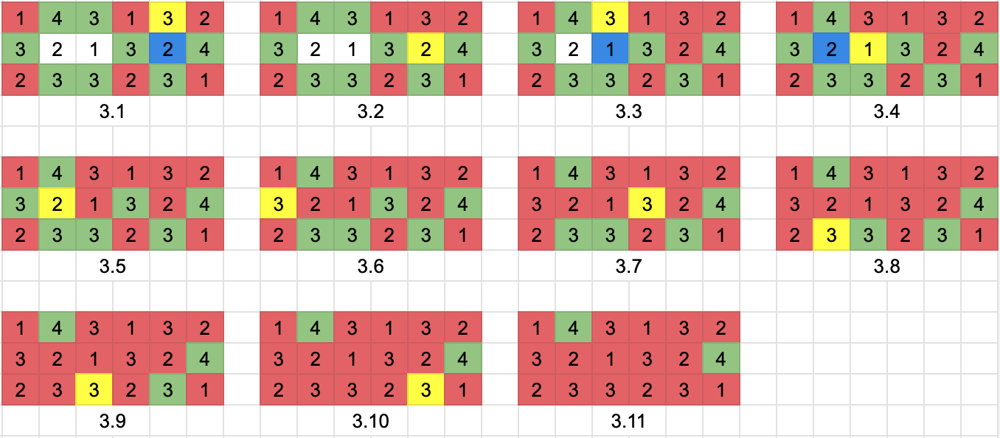\n\nThere is no level 2 cell in the heap, so set level = 3. There are 7 cells with height 3 will be popped out. The Order doesn\'t matter. \n\n## Graph 3.1\nCell[0,4] is popped out from the heap. Cell[1,4] height is smaller than level(3). <ins>**Cell[1,4] can trap rain water: Level(3) - Cell[1,4] height(2) = 1**</ins>. Added Cell[1,4] to the heap.\n\n## Graph 3.2\nCell[1,4] is popped out from the heap, since it has the lowest height 2. There is no non-visited cells connecting to it.\n\n## Graph 3.3\nCell[0,2] is popped out from the heap. Cell[1,2] height is smaller than level(3). <ins>**Cell[1,2] can trap rain water: Level(3) - Cell[1,2] height(1) = 2**</ins>. Added Cell[1,2] to the heap.\n\n## Graph 3.4\nCell[1,2] is popped out from the heap, since it has the lowest height 1. Cell[1,1] height is smaller than level(3). <ins>**Cell[1,1] can trap rain water: Level(3) - Cell[1,1] height(2) = 1**</ins>. Added Cell[1,1] to the heap.\n\n## Graph 3.5\nCell[1,1] is popped out from the heap, since it has the lowest height 2. There is no non-visited cells connecting to it.\n\n## Graph 3.6\nCell[1,0] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 3.7\nCell[1,3] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 3.8\nCell[2,1] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 3.9\nCell[2,2] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 3.10\nCell[2,4] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n<br/>\n\n# Level 4\n\n\nThere is no level 3 cell in the heap, so set level = 4. There are 2 cells with height 4 will be popped out. The Order doesn\'t matter. \n\n## Graph 4.1\nCell[0,1] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n## Graph 4.2\nCell[1,5] is popped out from the heap, and there is no non-visited cells connecting to it.\n\n<br/>\n\n# Summary\n<ins>**Volume of water**</ins>: 1 + 2 + 1 = 4\n\n<br/>\n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n if not heightMap or not heightMap[0]:\n return 0\n\t\t\t\n\t\t\t\n\t\t# Initial\n\t\t# Board cells cannot trap the water\n m, n = len(heightMap), len(heightMap[0])\n if m < 3 or n < 3:\n return 0\n\t\t\t\n\t\t\t\n\t\t# Add Board cells first\n heap = []\n for i in range(m):\n for j in range(n):\n if i == 0 or i == m - 1 or j == 0 or j == n - 1:\n heapq.heappush(heap, (heightMap[i][j], i, j))\n heightMap[i][j] = -1\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t# Start from level 0\n level, res = 0, 0\n \n\t\twhile heap:\n height, x, y = heapq.heappop(heap)\n level = max(height, level)\n\n for i, j in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:\n if 0 <= i < m and 0 <= j < n and heightMap[i][j] != -1:\n heapq.heappush(heap, (heightMap[i][j], i, j))\n\t\t\t\t\t\n\t\t\t\t\t# If cell\'s height smaller than the level, then it can trap the rain water\n if heightMap[i][j] < level:\n res += level - heightMap[i][j]\n\t\t\t\t\t\t\n\t\t\t\t\t# Set the height to -1 if the cell is visited\n heightMap[i][j] = -1\n\n return res\n```\n\n\n\nAll good? ^v^ Now you can try a smiliar quesion: [778. Swim in Rising Water](https://leetcode.com/problems/swim-in-rising-water/) | 309 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
407: Time 96.51%, Solution with step by step explanation | trapping-rain-water-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check for edge cases\nThe function starts by checking if the input height map is empty or has no columns, in which case there is no water that can be trapped and the function returns 0.\n\n2. Initialize variables\nThe function initializes some variables, including the size of the height map (m and n), a visited matrix to keep track of which cells have been processed, an empty heap, and a variable to store the amount of water trapped.\n\n3. Add border cells to heap\nNext, the function adds all the border cells to the heap, along with their heights and coordinates. These are the cells that will be processed first, as they are the ones that can potentially trap water.\n\n4. Process cells in heap\nThe function then enters a loop that processes cells in the heap until there are no more cells left. The loop works as follows:\n\n - Pop the cell with the lowest height from the heap\n - Check its neighbors (up, down, left, right) to see if they can be processed\n - If a neighbor is within the bounds of the height map and has not been visited before, calculate the amount of water that can be trapped in it based on the current highest boundary and the height of the cell, and add it to the total amount of trapped water\n - Add the neighbor to the heap, with its height updated to the maximum of its original height and the current highest boundary\n - Mark the neighbor as visited\n\n5. Return amount of trapped water\nOnce all cells in the heap have been processed, the function returns the total amount of trapped water.\n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n if not heightMap or not heightMap[0]:\n return 0\n \n m, n = len(heightMap), len(heightMap[0])\n visited = [[False]*n for _ in range(m)]\n heap = []\n water_trapped = 0\n \n # Add all the border cells to the heap\n for i in range(m):\n heapq.heappush(heap, (heightMap[i][0], i, 0))\n heapq.heappush(heap, (heightMap[i][n-1], i, n-1))\n visited[i][0] = visited[i][n-1] = True\n \n for j in range(1, n-1):\n heapq.heappush(heap, (heightMap[0][j], 0, j))\n heapq.heappush(heap, (heightMap[m-1][j], m-1, j))\n visited[0][j] = visited[m-1][j] = True\n \n # Process cells in the heap\n while heap:\n height, i, j = heapq.heappop(heap)\n for di, dj in [(-1, 0), (1, 0), (0, -1), (0, 1)]:\n ni, nj = i+di, j+dj\n if ni >= 0 and ni < m and nj >= 0 and nj < n and not visited[ni][nj]:\n visited[ni][nj] = True\n water = max(0, height - heightMap[ni][nj])\n water_trapped += water\n heapq.heappush(heap, (max(heightMap[ni][nj], height), ni, nj))\n \n return water_trapped\n\n``` | 3 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Python 3 || 15 lines, heap || T/M: 85%/24% | trapping-rain-water-ii | 0 | 1 | ```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n \n m, n = len(heightMap), len(heightMap[0])\n M, N = range(m), range(n)\n\n border = set().union({(i,0) for i in M}, {(i,n-1) for i in M},\n {(0,j) for j in N}, {(m-1,j) for j in N})\n\n seen, ans, di, dj = border, 0, 1, 0 \n \n heap = [(heightMap[i][j], i, j) for i,j in border]\n heapify(heap)\n \n while heap:\n h, i, j = heappop(heap)\n\n for _ in range(4):\n I, J, di, dj = i+di, j+dj, -dj, di\n\n if I in M and J in N and (I,J) not in seen:\n \n ans+= max(0, h - heightMap[I][J])\n\n heappush(heap, (max(h, heightMap[I][J]), I, J))\n seen.add((I,J))\n\n return ans\n\n```\n\n\n | 5 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Python solution beats 99% | trapping-rain-water-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition is to use a heap to keep track of the lowest points in the grid and use Dijkstra\'s algorithm to traverse the grid and fill the trapped water.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach is to first initialize a heap with the outermost points of the grid, and a visited 2D array to mark the cells that have been visited. Then I use a while loop to iterate through the heap. For each cell, I check its neighbors and calculate the trapped water by subtracting the current cell height with the neighbor\'s height. If the neighbor is higher, I add it to the heap and mark it as visited. I continue this process until the heap is empty.\n\n\n# Complexity\n- Time complexity: $$O(mnlog(m*n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n if not heightMap or not heightMap[0]:\n return 0\n m, n = len(heightMap), len(heightMap[0])\n heap = []\n visited = [[False] * n for _ in range(m)]\n for i in range(m):\n heapq.heappush(heap, (heightMap[i][0], i, 0))\n heapq.heappush(heap, (heightMap[i][n - 1], i, n - 1))\n visited[i][0] = True\n visited[i][n - 1] = True\n for j in range(n):\n heapq.heappush(heap, (heightMap[0][j], 0, j))\n heapq.heappush(heap, (heightMap[m - 1][j], m - 1, j))\n visited[0][j] = True\n visited[m - 1][j] = True\n res = 0\n while heap:\n h, i, j = heapq.heappop(heap)\n for di, dj in ((0, 1), (0, -1), (1, 0), (-1, 0)):\n ni, nj = i + di, j + dj\n if 0 <= ni < m and 0 <= nj < n and not visited[ni][nj]:\n res += max(0, h - heightMap[ni][nj])\n heapq.heappush(heap, (max(h, heightMap[ni][nj]), ni, nj))\n visited[ni][nj] = True\n return res\n``` | 2 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Share my novel solution with horizontal scanning (No heap used) | trapping-rain-water-ii | 0 | 1 | I didn\'t check other posts when first solving this problem. After my solution got AC, I checked the discussions and found no similar solution (most people use heap). This approach is quite intuitive. After a few optimization, it can beat 90%.\n\n**Intuition**\nThe basic idea is to horizontally scan the whole building blocks, from the bottom to the top. At each scan, we compute the area that can hold water. Then step by step, the total volumn accumulates by `area*(h - h_prev)`, where `h`is the current height and `h_prev`is previous height which is a bit lower.\n\nNow the difficult part would be how to compute the area with water at each level. My solution is to use DFS (BFS also works, we only care about reachability). From each edge cell, spreading through the map to see whether an inner cell is reachable from the outside. If an inner cell is horizontally reachable from the edge, it certainlly cannot hold water.\n\n**Implementation details**\nI first sort all the heights, so that we can scan bottom-top. Then we maintain a `m x n` matrix named`level`, which is the scanned profile at a certain height. There are 3 distinct values in `level`: `1` means that this cell is concrete (for current height); `0` means that this cell can hold water; `-1` means that this cell can only hold air (that water would leak from here). And `area` would be the number of `0`s at each level.\n\nOn the ground level, certainly there are only `1` in `level`, and that is how we initialize. As the height gradually rising, `0` occurs. However, if this `0` is at edge or is adjacent to another known leaking cell, it should also be marked `-1`. Further more, other cells that previously can hold water may no longer hold water at this height, so we should DFS to find all leaking cells. Once a position is marked "leaking", it will always "leak" at a higher height. When we reach the top, there are only `-1` in `level`.\n\n**Complexity Analysis**\nTime complexity would be *O*(*mn*log(*mn*)) for the sorting. The iteration would cost *O*(*mn*) since DFS would only visit each cell once (or checking maximum 4 times from adjacent cells) and accumulating volumn costs constant at each level (*mn* levels in total). Space complexity would be *O*(*mn*).\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n m, n = len(heightMap), len(heightMap[0])\n if m < 3 or n < 3: return 0\n # to simplify the code\n def adjacent(i,j):\n return [(i-1,j), (i+1,j), (i,j-1), (i,j+1)]\n \n # first we sort all heights from the matrix and store their corresponding positions\n # heights will be [(h1,[p1, p2,...]), (h2,[p1, p2, ...]), ...]\n d = defaultdict(list)\n for i in range(m):\n for j in range(n):\n d[heightMap[i][j]].append((i,j))\n heights = sorted(d.items())\n # initialization\n volumn, area, h_lower = 0, 0, heights[0][0]\n level = [[1 for j in range(n)] for i in range(m)]\n for h, positions in heights:\n volumn += area*(h-h_lower)\n h_lower = h\n leak = []\n for i, j in positions:\n # due to height rising, now this position may hold water\n level[i][j] = 0\n area += 1\n if i == 0 or i == m-1 or j == 0 or j == n-1 or any([level[a][b] == -1 for a, b in adjacent(i,j)]):\n # this position is reachable from outside, therefore cannot hold water\n leak.append((i,j))\n level[i][j] = -1\n area -= 1\n while leak:\n i, j = leak.pop()\n for a, b in adjacent(i,j):\n if 0 <= a < m and 0 <= b < n and not level[a][b]:\n # new leaking position found through DFS\n leak.append((a,b))\n level[a][b] = -1\n area -= 1\n\n return volumn\n \n```\nPlease upvote if you like.:-) | 5 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Python BFS + Minheap with explanation | trapping-rain-water-ii | 0 | 1 | ```\n# Solution Logic: MinHeap+BFS\n# 1. Start from the boundary elements\n# 2. Maintain a minheap of heights \n# 3. Maintain a a set of visited elements\n# 4. push all outer boundary elements to the minheap\n# 5. while minheap is not empty:\n# pop the element from minheap\n# check all 4 neighbors \n# check if neoighbor is in bounds of the grid i.e isValid and check if it is not visited\n# calculate if element height is greater than the neighbor\n# if yes, add the diff to result and ADD THE NEIGHBOR WITH UPDATED HEIGHT EQUAL TO CURRENT ELEMENT HEIGHT TO MINHEAP\n# else ADD THE NEIGHBOR TO MINHEAP with no change in its height\n# mark the neighbor as visited by adding it to the visited set\n \n# NOTE: few important points:\n# 1. why we use minheap: because we need to process low heights first as they will be able to make water flow out of the grid. if we start with max ones, then we might have wrong result coz the neighbors will be reached in incorrect order.\n# 2. why BFS: layer by layer exploration of neighbors helps get optimal answer\n\n\nimport heapq\nclass Solution:\n def trapRainWater(self, h: List[List[int]]) -> int:\n \n q=[]\n heapq.heapify(q)\n visited=set()\n \n def isValid(m,n):\n if 0<=m<r and 0<=n<c:\n return True\n return False\n \n r=len(h)\n c=len(h[0])\n \n for i in range(r):\n for j in range(c):\n if i==0 or i==r-1 or j==0 or j==c-1:\n heapq.heappush(q,(h[i][j],i,j))\n visited.add((i,j))\n res=0\n while q:\n cur=heapq.heappop(q)\n \n for d in [(-1,0),(1,0),(0,-1),(0,1)]:\n new_i=cur[1]+d[0]\n new_j = cur[2]+d[1]\n if isValid(new_i, new_j) and (new_i, new_j) not in visited:\n h_inc=max(0,cur[0]-h[new_i][new_j])\n res+=h_inc\n if h_inc>0:\n heapq.heappush(q,(cur[0],new_i, new_j))\n else:\n heapq.heappush(q,(h[new_i][new_j],new_i, new_j))\n visited.add((new_i, new_j))\n return res\n\n``` | 3 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Going up step by step | trapping-rain-water-ii | 0 | 1 | # Code\n```\nclass Solution:\n def trapRainWater(self, ht: List[List[int]]) -> int:\n m,n = len(ht),len(ht[0])\n m1,n1 = m-1,n-1\n hp = []\n for i in range(m):\n heappush(hp,(ht[i][0],i,0))\n heappush(hp,(ht[i][-1],i,n1))\n ht[i][0] = -1\n ht[i][-1] = -1\n for j in range(1,n1):\n heappush(hp,(ht[0][j],0,j))\n heappush(hp,(ht[m1][j],m1,j))\n ht[0][j] = -1\n ht[m1][j] = -1\n\n step = 0\n ans = 0\n dirs = [(-1,0),(1,0),(0,1),(0,-1)]\n \n while hp:\n dep,i,j = heappop(hp)\n if dep < step:\n ans += step - dep\n elif dep > step:\n step = dep\n for x,y in dirs:\n i1,j1 = i + x, j + y\n if not (0 <= i1 < m and 0 <= j1 < n):\n continue\n if ht[i1][j1] > -1:\n heappush(hp,(ht[i1][j1],i1,j1))\n ht[i1][j1] = -1\n return ans\n\n\n``` | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Iterative solution to find the maximum height of water. | trapping-rain-water-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTaking inspiration from the 1D problem, I first tried to solve by finding the max height on either of the four sides but realised after submitting that this will fail as the limiting factor for the height either of the sides could be another of their adjacent heights and not the immediate neighbour\'s height.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo we create a matrix of maximum height of the water starting from the edges, finding the minimum height among the four sides. We do this iteratively until ultimately we have no more changes in the max height matrix.\n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n m = len(heightMap);\n n = len(heightMap[0]);\n maxHeight = [];\n totalSum = 0;\n for i in range(0, m):\n maxHeight.append([-1]*n);\n \n for k in range(0,30):\n hasChanged = False;\n for i in range(0, m):\n for j in range(0, n):\n lbounds = [];\n rbounds = [];\n if(i-1 >= 0):\n lbounds.append(max(heightMap[i-1][j], maxHeight[i-1][j]));\n else:\n lbounds.append(0);\n if(j-1 >= 0):\n lbounds.append(max(heightMap[i][j-1], maxHeight[i][j-1]))\n else:\n lbounds.append(0);\n if(maxHeight[i][j] != -1):\n lbounds.append(maxHeight[i][j]);\n newVal = min(lbounds);\n if((not(hasChanged)) and (newVal != maxHeight[i][j])):\n hasChanged = True;\n maxHeight[i][j] = newVal;\n \n if(m-1-i+1 < m):\n rbounds.append(max(heightMap[m-1-i+1][n-j-1], maxHeight[m-1-i+1][n-j-1]));\n else:\n rbounds.append(0);\n if(n-1-j+1 < n):\n rbounds.append(max(heightMap[m-i-1][n-1-j+1], maxHeight[m-1-i][n-1-j+1]));\n else:\n rbounds.append(0);\n if(maxHeight[m-1-i][n-1-j] != -1):\n rbounds.append(maxHeight[m-1-i][n-1-j]);\n newVal = min(rbounds);\n if((not(hasChanged)) and (newVal != maxHeight[m-1-i][n-1-j])):\n hasChanged = True;\n maxHeight[m-1-i][n-1-j] = newVal;\n if(not hasChanged):\n break\n\n for i in range(1, m-1):\n for j in range(1, n-1):\n if(maxHeight[i][j] > heightMap[i][j]):\n totalSum += maxHeight[i][j] - heightMap[i][j];\n\n return totalSum\n\n\n``` | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Python Easy Solution | trapping-rain-water-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n ans = 0\n m = len(heightMap)\n n = len(heightMap[0])\n visited = [[False]*n for _ in range(m)]\n heap = []\n\n for i in range(m):\n for j in range(n):\n if i == 0 or i == m-1 or j == 0 or j == n-1:\n visited[i][j] = True\n heapq.heappush(heap,(heightMap[i][j],i,j))\n\n while len(heap) != 0:\n h,i,j = heapq.heappop(heap)\n\n for x,y in [(i-1,j),(i,j-1),(i+1,j),(i,j+1)]:\n if 0 <= x < m and 0 <= y < n and not visited[x][y]:\n visited[x][y] = True\n if heightMap[x][y] < h:\n ans += h - heightMap[x][y]\n heapq.heappush(heap,(h,x,y))\n else:\n heapq.heappush(heap,(heightMap[x][y],x,y))\n\n return ans\n\n\n\n\n\n\n``` | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Priority Queue | trapping-rain-water-ii | 0 | 1 | # Code\n```\nimport heapq\nfrom typing import List\n\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n if not heightMap:\n return 0\n \n m, n = len(heightMap), len(heightMap[0])\n pq = []\n visited = set()\n water_volume = 0\n max_height = float("-inf")\n \n # Add all border cells to the priority queue and mark them as visited\n for i in range(m):\n for j in range(n):\n if i == 0 or i == m - 1 or j == 0 or j == n - 1:\n heapq.heappush(pq, (heightMap[i][j], i, j))\n visited.add((i, j))\n \n # Process cells in the priority queue\n while pq:\n height, row, col = heapq.heappop(pq)\n max_height = max(max_height, height)\n \n # Check neighbors\n for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n new_row, new_col = row + dx, col + dy\n \n if 0 <= new_row < m and 0 <= new_col < n and (new_row, new_col) not in visited:\n visited.add((new_row, new_col))\n \n if heightMap[new_row][new_col] < max_height:\n water_volume += max_height - heightMap[new_row][new_col]\n \n heapq.heappush(pq, (heightMap[new_row][new_col], new_row, new_col))\n \n return water_volume\n\n``` | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Trapping Rain Water II using Python3 | trapping-rain-water-ii | 0 | 1 | # Intuition\nThe problem asks us to find the amount of water that can be trapped between the blocks in a 2D elevation map after raining. To solve this problem, we can make use of the concept of BFS (Breadth-First Search) and Heap (Priority Queue).\n\n# Approach\nOne approach to solve this problem is to use the concept of BFS with priority queue.\n\nFirst, we can add all the border cells to a priority queue with their height as the priority. Then, we can do a BFS traversal starting from the cell with the smallest height and visit its neighbors.\n\nFor each neighbor, we can calculate the water trapped by taking the difference between the neighbor\'s height and the maximum height we have seen so far (which is the maximum height of all the cells visited so far).\n\nIf the neighbor\'s height is greater than or equal to the maximum height seen so far, we can add it to the priority queue. Otherwise, we can add the current maximum height to the neighbor\'s height and add it to the priority queue with the new height as the priority.\n\nWe keep doing this until the priority queue is empty. The total water trapped is the sum of the water trapped at each cell.\n\n# Complexity\n- Time complexity:\n$$O(mn log(mn))$$\n\n- Space complexity:\n$$O(mn)$$ \n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n if not heightMap or not heightMap[0]:\n return 0\n \n m, n = len(heightMap), len(heightMap[0])\n visited = [[False] * n for _ in range(m)]\n pq = []\n water = 0\n \n # add all the border cells to the priority queue\n for i in range(m):\n for j in range(n):\n if i == 0 or i == m-1 or j == 0 or j == n-1:\n heapq.heappush(pq, (heightMap[i][j], i, j))\n visited[i][j] = True\n \n while pq:\n h, i, j = heapq.heappop(pq)\n \n # visit the neighbors\n for x, y in [(i+1,j), (i-1,j), (i,j+1), (i,j-1)]:\n if 0 <= x < m and 0 <= y < n and not visited[x][y]:\n visited[x][y] = True\n if heightMap[x][y] < h:\n water += h - heightMap[x][y]\n heapq.heappush(pq, (h, x, y))\n else:\n heapq.heappush(pq, (heightMap[x][y], x, y))\n \n return water\n``` | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Solution using priority queue | trapping-rain-water-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a heap to store the cells on the boundary of the height map along with their corresponding heights. Mark these cells as visited.\n2. Iterate over the height map and push the cells on the boundary (top, bottom, left, and right) into the heap with their heights. Mark these cells as visited.\n3. Use a heap-based approach to process the cells in the heap. Pop the cell with the lowest height from the heap.\n4. For the popped cell, check its neighboring cells (top, bottom, left, and right).\n5. If the neighboring cell has not been visited, update its height to the maximum of its current height and the height of the popped cell. Add the updated neighboring cell to the heap and mark it as visited. Also, calculate and accumulate the trapped water by taking the difference between the updated neighboring cell\'s height and its original height.\n6. Repeat steps 3-5 until the heap is empty, which means all cells in the height map have been processed.\n7. Return the accumulated trapped water as the result.\n\n# Note: \nThe approach aims to raise the height of the lower cells to the level of the higher cells, simulating the trapping of rainwater in valleys formed by higher cells. The heap is used to efficiently process the cells in the order of their heights. However, there are some issues in the code that may cause errors and need to be addressed, as mentioned in the previous response.\n\n\n\n\n\n\n\n# Complexity\n- Time complexity:$$O(m*n log m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n m = len(heightMap); n = len(heightMap[0]); water = 0\n visit = [[False]*n for i in range(m)]\n heap = []\n for i in range(n):\n heapq.heappush(heap,[heightMap[0][i],0,i]); visit[0][i] = True\n heapq.heappush(heap,[heightMap[m-1][i],m-1,i]); visit[m-1][i] = True\n\n for j in range(m):\n heapq.heappush(heap,[heightMap[j][0],j,0]); visit[j][0] = True\n heapq.heappush(heap,[heightMap[j][n-1],j,n-1]); visit[j][n-1] = True\n\n # print(heap)\n\n dir = [[0,1],[1,0],[-1,0],[0,-1]]\n while heap:\n val,r,c = heapq.heappop(heap)\n # print(val,r,c)\n \n for x,y in dir:\n ro = r+x; co = c+y\n if ro >= m or co >= n or visit[ro][co] == True:\n continue\n # print(ro,co,x,y)\n if heightMap[ro][co] < val:\n # print(val,ro,co,heightMap[ro][co])\n water+= val-heightMap[ro][co]\n heightMap[ro][co] = val \n\n heapq.heappush(heap,[heightMap[ro][co],ro,co]); visit[ro][co] = True\n \n return water\n\n``` | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Solution | trapping-rain-water-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n struct val {\n int _height;\n int16_t _x;\n int16_t _y;\n bool operator> (val const & v) const {\n return _height > v._height;\n }\n };\n int trapRainWater(vector<vector<int>>& heightMap) {\n ios_base::sync_with_stdio(0);\n cin.tie(0); cout.tie(0);\n int maxx = heightMap.size();\n int maxy = heightMap[0].size(); \n if(maxx < 3 || maxy < 3) \n return 0;\n priority_queue<val, vector<val>, greater<val>> pq;\n bool visited[200][200] = {0}; \n for(int16_t x = 0; x < maxx; x++) {\n for(int16_t y = 0; y < maxy; y++) {\n if(!(x == 0 || x == maxx - 1 || y == 0 || y == maxy - 1)) \n continue;\n pq.push({heightMap[x][y], x, y});\n visited[x][y] = true;\n }\n }\n array<int, 5> dir = {0, 1, 0, -1, 0};\n int H = INT_MIN;\n int res = 0;\n while(!pq.empty()) {\n auto [height, x, y] = pq.top();\n pq.pop();\n H = max(H, height);\n for (int d = 0; d < 4; d++) {\n\n int16_t nextx = x + dir[d];\n int16_t nexty = y + dir[d+1];\n if(nextx < 0 || nextx >= maxx || nexty < 0 || nexty >= maxy || visited[nextx][nexty]) \n continue;\n visited[nextx][nexty] = true;\n int diff = H - heightMap[nextx][nexty];\n if(diff > 0) \n res += diff;\n pq.push({heightMap[nextx][nexty], nextx, nexty});\n }\n }\n return res;\n } \n};\n```\n\n```Python3 []\nfrom typing import List\nimport heapq\n\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n m = len(heightMap)\n if m < 3:\n return 0\n n = len(heightMap[0])\n if n < 3:\n return 0\n state=[[0]*n for _ in range(m)]\n mq = []\n for i in range(m):\n heapq.heappush(mq, (heightMap[i][0],i,0))\n state[i][0]=1\n heapq.heappush(mq, (heightMap[i][n-1],i,n-1))\n state[i][n-1]=1\n for j in range(n):\n heapq.heappush(mq, (heightMap[0][j],0,j))\n state[0][j]=1\n heapq.heappush(mq, (heightMap[m-1][j],m-1,j))\n state[m-1][j]=1\n ret = 0 \n while mq:\n val,i,j = heapq.heappop(mq)\n if i > 0 and state[i-1][j] == 0:\n ret += max(0, val - heightMap[i-1][j])\n state[i-1][j]=1\n heapq.heappush(mq,(max(val,heightMap[i-1][j]),i-1,j))\n if i < m-1 and state[i+1][j] == 0:\n ret += max(0, val - heightMap[i+1][j])\n state[i+1][j]=1\n heapq.heappush(mq,(max(val,heightMap[i+1][j]),i+1,j))\n if j > 0 and state[i][j-1] == 0:\n ret += max(0, val - heightMap[i][j-1])\n state[i][j-1]=1\n heapq.heappush(mq,(max(val,heightMap[i][j-1]),i,j-1))\n if j < n-1 and state[i][j+1] == 0:\n ret += max(0, val - heightMap[i][j+1])\n state[i][j+1]=1\n heapq.heappush(mq,(max(val,heightMap[i][j+1]),i,j+1))\n return ret \n```\n\n```Java []\nclass Solution {\n public int trapRainWater(int[][] heightMap) {\n int trappedWater = 0;\n int[][] waterLevelMap = new int[heightMap.length][heightMap[0].length];\n\n for (int i = 1; i < heightMap.length-1; i++) {\n waterLevelMap[i][0] = heightMap[i][0];\n for (int j = 1; j < heightMap[i].length-1; j++) {\n waterLevelMap[i][j] = 20_000;\n }\n waterLevelMap[i][heightMap[i].length-1] = heightMap[i][heightMap[i].length-1];\n }\n for (int i = 0; i < heightMap[0].length; i++) {\n waterLevelMap[0][i] = heightMap[0][i];\n waterLevelMap[heightMap.length-1][i] = heightMap[heightMap.length-1][i];\n }\n\n boolean drain = true;\n while (drain) {\n drain = false;\n for (int i = 1; i < heightMap[0].length-1; i++) {\n for (int j = 1; j < heightMap.length-1; j++) {\n if (waterLevelMap[j][i] > heightMap[j][i]) {\n if (waterLevelMap[j][i] > waterLevelMap[j][i-1])\n waterLevelMap[j][i] = Integer.max(waterLevelMap[j][i-1], heightMap[j][i]);\n if (waterLevelMap[j][i] > waterLevelMap[j-1][i])\n waterLevelMap[j][i] = Integer.max(waterLevelMap[j-1][i], heightMap[j][i]);\n }\n }\n }\n for (int i = heightMap[0].length-2; i > 0; i--) {\n for (int j = heightMap.length-2; j > 0; j--) {\n if (waterLevelMap[j][i] > heightMap[j][i]) {\n if (waterLevelMap[j][i] > waterLevelMap[j][i+1])\n waterLevelMap[j][i] = Integer.max(waterLevelMap[j][i+1], heightMap[j][i]);\n if (waterLevelMap[j][i] > waterLevelMap[j+1][i])\n waterLevelMap[j][i] = Integer.max(waterLevelMap[j+1][i], heightMap[j][i]);\n if (waterLevelMap[j][i] < waterLevelMap[j][i+1] && waterLevelMap[j][i+1] > heightMap[j][i+1]\n || waterLevelMap[j][i] < waterLevelMap[j+1][i] && waterLevelMap[j+1][i] > heightMap[j+1][i])\n drain = true;\n }\n }\n }\n }\n for (int i = 1; i < waterLevelMap.length-1; i++) {\n for (int j = 1; j < waterLevelMap[i].length-1; j++) {\n trappedWater += waterLevelMap[i][j] - heightMap[i][j];\n }\n }\n return trappedWater;\n }\n}\n```\n | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
Heap BFS + DFS for a more convincing explanation | trapping-rain-water-ii | 0 | 1 | I didn\'t found the explanation for BFS with heap solutions convincing enough.\n**Here is my intuition for this problem**:\n`Since the water level (not depth) must remain the same across every connected point. If a point in the matrix is connected to a corner point then the maximum water level can be at max the value of that corner point else it will spil over. It is possible that there are some islands inside the matrix which are not connected to any corner point but we can consider those islands as a separate matrix and still apply the intuition.`\n\n**Definition for connection to a root**: `A point is connected to the root of dfs if its value is less than the value of root and it was first discovered by the same root`\n\n**Steps:**\n`1. We go through every corner point and put it in a min-heap according to their value in heightMap.`\n`2. We pick the lowest height point from the min-heap and do a dfs to discover all the points connected to it.`\n`3. If we encounter a yet undiscovered point with height >= the root, we push it into the min-heap. These will serve as the wall of the islands.`\n`4. For the remaining points we sum the water contained in every column over the point (i,j) discovered during dfs, with contribution of a single point = heightOfRoot - heightOfPoint(i,j) and also keep discovering that point\'s children using dfs`. **We do not push these points to the min-heap.**\n\n\n\n```\nclass Solution:\n def trapRainWater(self, heightMap: List[List[int]]) -> int:\n n, m, ans = len(heightMap), len(heightMap[0]), 0\n visit, pos,q = [[False for j in range(m)] for i in range(n)], [[0,1], [-1,0], [1,0], [0,-1]], []\n \n \n for i in range(n):\n for j in range(m):\n if i == 0 or j == 0 or i == n-1 or j == m - 1:\n heappush(q, (heightMap[i][j], i, j)) # insert the initial candidate roots for dfs\n visit[i][j] = True # a node will be pushed into the min-heap at max once\n \n def dfs(i, j, rootHeight):\n ans = rootHeight - heightMap[i][j]\n \n for pi, pj in pos:\n newI, newJ = pi + i,pj + j\n if min(newI, newJ) >=0 and newI < n and newJ < m and not visit[newI][newJ]: # for every not yet discovered node \n visit[newI][newJ] = True\n if heightMap[newI][newJ] >= rootHeight: # add this node as a root candidate for dfs, will be traversed later\n heappush(q, (heightMap[newI][newJ], newI, newJ))\n else:\n ans += dfs(newI, newJ, rootHeight) # traverse this node get the sum of all its children\n\t\t\t\t\t\t\n return ans # returns the sum of water-level for all node visited by this node and its children\n \n ans = 0\n while q:\n val, i, j = heappop(q)\n ans += dfs(i, j, val)\n \n \n return ans\n \n```\n | 0 | Given an `m x n` integer matrix `heightMap` representing the height of each unit cell in a 2D elevation map, return _the volume of water it can trap after raining_.
**Example 1:**
**Input:** heightMap = \[\[1,4,3,1,3,2\],\[3,2,1,3,2,4\],\[2,3,3,2,3,1\]\]
**Output:** 4
**Explanation:** After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.
**Example 2:**
**Input:** heightMap = \[\[3,3,3,3,3\],\[3,2,2,2,3\],\[3,2,1,2,3\],\[3,2,2,2,3\],\[3,3,3,3,3\]\]
**Output:** 10
**Constraints:**
* `m == heightMap.length`
* `n == heightMap[i].length`
* `1 <= m, n <= 200`
* `0 <= heightMap[i][j] <= 2 * 104` | null |
C++ - Easiest Beginner Friendly Sol || O(n) time and O(128) = O(1) space | longest-palindrome | 1 | 1 | # Intuition of this Problem:\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Initialize two variables, oddCount to store the number of characters with an odd count of occurrences and an unordered map ump to store the count of each character in the string.\n2. Iterate through the string and for each character ch, increment the count of that character in the unordered map.\n3. If the count of the current character ch is odd, increment oddCount. If the count is even, decrement oddCount.\n4. If oddCount is greater than 1, return s.length() - oddCount + 1, which is the maximum length of a palindrome that can be formed by using all but one character with an odd count of occurrences.\n5. If oddCount is not greater than 1, return s.length(), which is the length of the original string, as all characters can be used to form a palindrome.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int longestPalindrome(string s) {\n int oddCount = 0;\n unordered_map<char, int> ump;\n for(char ch : s) {\n ump[ch]++;\n if (ump[ch] % 2 == 1)\n oddCount++;\n else \n oddCount--;\n }\n if (oddCount > 1)\n return s.length() - oddCount + 1;\n return s.length();\n }\n};\n```\n```Java []\nclass Solution {\n public int longestPalindrome(String s) {\n int oddCount = 0;\n Map<Character, Integer> map = new HashMap<>();\n for (char ch : s.toCharArray()) {\n map.put(ch, map.getOrDefault(ch, 0) + 1);\n if (map.get(ch) % 2 == 1)\n oddCount++;\n else\n oddCount--;\n }\n if (oddCount > 1)\n return s.length() - oddCount + 1;\n return s.length();\n }\n}\n\n```\n```Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n odd_count = 0\n d = {}\n for ch in s:\n if ch in d:\n d[ch] += 1\n else:\n d[ch] = 1\n if d[ch] % 2 == 1:\n odd_count += 1\n else:\n odd_count -= 1\n if odd_count > 1:\n return len(s) - odd_count + 1\n return len(s)\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the length of the string s. This is because we are iterating through the string only once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(m)**, where m is the number of unique characters in the string. This is because we are using an unordered map to store the count of each character.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 243 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
Simple python solution | longest-palindrome | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n arr=[x for x in s]\n frq=Counter(arr)\n count=list(frq.values())\n res=0\n for i in range(len(count)):\n if count[i]%2==0:\n res+=count[i]\n else:\n res+=count[i]-1\n return res if len(arr)==res else res+1\n``` | 2 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
Python 3 solution using Set() | longest-palindrome | 0 | 1 | **Idea**:\nStart adding letters to a set. If a given letter not in the set, add it. If the given letter is already in the set, remove it from the set. \nIf the set isn\'t empty, you need to return length of the string minus length of the set plus 1.\nOtherwise, you return the length of the string (example \'bb.\' Your set is empty, you just return 2).\n\nEssentially, your set contains non-paired letters. It\'s one of those bad questions where you need to go over all possible cases and somehow fit them into the solution. \n\n```\ndef longestPalindrome_set(s):\n ss = set()\n for letter in s:\n if letter not in ss:\n ss.add(letter)\n else:\n ss.remove(letter)\n if len(ss) != 0:\n return len(s) - len(ss) + 1\n else:\n return len(s)\n``` | 111 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
Make all Odds as Even || Example and Comments || Python | longest-palindrome | 0 | 1 | # Intuition\nA palindrome repeats itself from the middle this means for making longest palindrome we need as many even count of chars.\nBut in a palindrome you can adjust "at most" one odd count char\neg => bbbabbb , bbbcccbbb ....\nSo to maximize the length of palindrome add the count of all even char + 1 odd char count + make other odd count char as even\neg => bbbcccabbb is not a palindrome\nb : 6, c : 3, a : 1 \nso make \'c\' count as even (3-1 = 2)\nres => b : 6 a : 1 c : 2 \nstring as palindrome => bbbcacbbb\n\n\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n #take all even count + 1 odd count + make other odds as even\n count = Counter(s)\n oddFlag = True\n c = 0 \n for v in count.values():\n if v % 2 == 0:\n c += v\n #take first odd as it is\n elif v % 2 != 0 and oddFlag:\n c += v\n oddFlag = False\n #make other odds as even as it can be made palindrome\n elif v % 2 != 0 and not oddFlag:\n c += (v - 1)\n return c\n``` | 1 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
Python Easy Solution || Hashmap | longest-palindrome | 0 | 1 | # Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n dic={}\n tot=0\n flg=0\n for i in s:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n for i in dic:\n if dic[i]%2==0:\n tot+=dic[i]\n else:\n flg=1\n tot+=dic[i]-1\n if flg==1:\n return tot+1\n return tot\n``` | 2 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
[Python] Hash Table faster than 99.88% | longest-palindrome | 0 | 1 | Upvote If you like it \uFF1A\uFF09\n\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n count = {} # Hash Table \n ans = [] # every word\'s frequency \n odd= 0 # store an odd number\'s frequency \n for word in s:\n if word not in count:\n count[word] = 1\n else:\n count[word] += 1\n for times in count.values():\n ans.append(times)\n if times % 2 != 0:\n odd += 1 # calculate an odd number\'s frequency\n if odd != 0:\n return sum(ans) - odd + 1 \n elif odd == 0:\n return sum(ans) - odd\n```\n\n | 12 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
409: Solution with step by step explanation | longest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize an empty dictionary freq_dict to store the frequency of each character in the string s.\n2. Iterate over each character char in the string s and add it to the dictionary freq_dict if it doesn\'t exist, or increment its frequency by 1 if it does.\n3. Initialize a variable length to 0, which will store the length of the longest palindrome.\n4. Iterate over each frequency freq in the values of the dictionary freq_dict and add up the length of all even-frequency characters by computing freq // 2 * 2 and adding it to the variable length.\n5. Check if there are any characters whose frequency is odd by using the any function on a generator expression that checks if the frequency is odd (freq % 2 == 1). If there are any such characters, add one of them to the length by incrementing length by 1.\n6. Return the variable length as the answer.\n\nThe algorithm works by observing that any palindrome can be constructed by pairing up characters with even frequencies, and adding a single character with an odd frequency if one exists. By iterating over the frequencies of each character and adding up the length of all even-frequency characters, and then adding one odd-frequency character (if any exist), we obtain the length of the longest possible palindrome that can be constructed from the characters in the input string.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n # Initialize a dictionary to store the frequency of each character in the string\n freq_dict = {}\n for char in s:\n freq_dict[char] = freq_dict.get(char, 0) + 1\n \n # Initialize a variable \'length\' to 0, which will store the length of the longest palindrome\n length = 0\n \n # Iterate through the dictionary and add up the length of all even-frequency characters\n for freq in freq_dict.values():\n length += freq // 2 * 2\n \n # Check if there are any characters whose frequency is odd. If yes, add one of them to the length\n if any(freq % 2 == 1 for freq in freq_dict.values()):\n length += 1\n \n # Return the length as the answer\n return length\n\n``` | 9 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
Easiest python solution | longest-palindrome | 0 | 1 | class Solution:\n1. def longestPalindrome(self, s: str) -> int:\n c=Counter(s)\n count=0\n p=0\n for a in c:\n if c[a]%2==0:\n count+=c[a]\n if c[a]%2==1:\n count+=c[a]-1\n p=1\n if p==1:\n return count+1\n return count\n | 2 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
python3 easy to understand solution 98.12% beats with froop | longest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nPlease Upvote !!!!!!!!!!!\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> int:\n set_=set()\n for character in s:\n if character not in set_:set_.add(character)\n else:set_.remove(character)\n if len(set_) != 0:return len(s)-len(set_)+1\n else:return len(s)\n``` | 5 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
Hindi + English easy Python solution | longest-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf number of repeated letters is even, there will not be any single central letter. But if there are any single letters (not repeated), then maximum one can be in the centre of the palindrome.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLets consider the input string as \'shabd\'. \nIt is made up of different letters called \'akshar\'. \nFirst, we will make the set of single elements and call it \'akele\'.\nThen we will traverse through the shabd and add elements in the set \'akele\'. \nIf an element is already in \'akele\' and we find another same element, it is not akela anymore so we remove it from the set and add both of them to the final palindrome. \nAt the end, if there is any element in the set \'akele\' then our final palindrome will have odd element in the centre so we add 1 to the palindrome length. \nIf \'akele\' is empty then it means the palindrome will have only pairs and so we don\'t need to add anything :)\n\n# Complexity\n- Time complexity: O(n), since we iterate over each character in the string\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1), since the only extra storage we use is the counter for palindrome length and a set that is at most the size of our character set.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, shabd: str) -> int:\n akele = set()\n lengthpal = 0\n\n for akshar in shabd:\n if akshar in akele:\n akele.remove(akshar)\n lengthpal += 2\n else:\n akele.add(akshar)\n \n if len(akele) > 0:\n lengthpal += 1\n \n return lengthpal\n``` | 3 | Given a string `s` which consists of lowercase or uppercase letters, return _the length of the **longest palindrome**_ that can be built with those letters.
Letters are **case sensitive**, for example, `"Aa "` is not considered a palindrome here.
**Example 1:**
**Input:** s = "abccccdd "
**Output:** 7
**Explanation:** One longest palindrome that can be built is "dccaccd ", whose length is 7.
**Example 2:**
**Input:** s = "a "
**Output:** 1
**Explanation:** The longest palindrome that can be built is "a ", whose length is 1.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists of lowercase **and/or** uppercase English letters only. | null |
BINARY SEARCH SOLUTION ✅💯 | split-array-largest-sum | 0 | 1 | # Intuition\nUse **Binary Search**\n# Approach\nUse Binary Search\n# Complexity\n- Time complexity:\n**O(nlogm)**\n\n- Space complexity:\n**O(1)**\n\n# Code\n```\nclass Solution:\n def splitArray(self, nums: List[int], k: int) -> int:\n def check(arr, guess, k):\n total = 0\n count = 1\n for i in arr:\n if total + i > guess:\n total = 0\n count += 1\n total += i\n return count > k\n \n\n left = max(nums)\n right = sum(nums)\n\n while left<right:\n mid = (left+right)//2\n if check(nums, mid, k):\n left = mid + 1\n else:\n right = mid\n\n return left\n\n\n\n\n\n\n``` | 1 | Given an integer array `nums` and an integer `k`, split `nums` into `k` non-empty subarrays such that the largest sum of any subarray is **minimized**.
Return _the minimized largest sum of the split_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[7,2,5,10,8\], k = 2
**Output:** 18
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[7,2,5\] and \[10,8\], where the largest sum among the two subarrays is only 18.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 9
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[1,2,3\] and \[4,5\], where the largest sum among the two subarrays is only 9.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 106`
* `1 <= k <= min(50, nums.length)` | null |
Most optimal solution using binary search with explanation | split-array-largest-sum | 1 | 1 | \n\n# Approach\nThe countPartitions function takes an array and a maximum sum as input and returns the number of partitions needed to ensure that no subarray\'s sum exceeds the maximum sum. It iterates through the array, keeping track of a running sum (subSum). If adding the current element to subSum keeps it within the maximum sum limit, the element is included in the current partition. If adding the current element would exceed the maximum sum, a new partition is started, and the current element becomes the start of the new partition. The function returns the total number of partitions.\n\nThe splitArray function uses binary search to find the optimal value for the minimum maximum sum. It initializes low as the maximum element in the array (as any subarray\'s sum must be at least that) and high as the sum of all elements in the array. It then performs binary search in the range [low, high]. For each mid-point value, it calculates the number of partitions using the countPartitions function. If the number of partitions exceeds \'K\', it means the maximum sum is too small, so the binary search narrows the range to the upper half. If the number of partitions is less than or equal to \'K\', it means the maximum sum is achievable, and the binary search narrows the range to the lower half. Finally, when the binary search converges, it returns the optimal minimum maximum sum.\n\n# Complexity\n- Time complexity:\nO(log(sum-max+1)*n)\n\n- Space complexity:\nO(1)\n\n```C++ []\nclass Solution {\npublic:\n int countPartitions(vector<int> nums, int maxSum) {\n int partitions = 1;\n long long subSum = 0;\n for(int i = 0; i< nums.size(); i++) {\n if(subSum + nums[i] <= maxSum) subSum += nums[i];\n else {\n partitions++;\n subSum = nums[i];\n }\n }\n return partitions;\n }\n\n int splitArray(vector<int>& nums, int k) {\n int low = *max_element(nums.begin(), nums.end());\n int high = accumulate(nums.begin(), nums.end(), 0);\n while(low <= high) {\n int mid = (low+high)/2;\n int partitions = countPartitions(nums, mid);\n if(partitions >k ) low = mid+1;\n else high = mid-1;\n }\n return low;\n }\n};\n```\n```JAVA []\nclass Solution {\n public int countPartitions(int[] nums, int maxSum) {\n int partitions = 1;\n long subSum = 0;\n for (int num : nums) {\n if (subSum + num <= maxSum) {\n subSum += num;\n } else {\n partitions++;\n subSum = num;\n }\n }\n return partitions;\n }\n\n public int splitArray(int[] nums, int k) {\n int low = Arrays.stream(nums).max().getAsInt();\n int high = Arrays.stream(nums).sum();\n while (low <= high) {\n int mid = (low + high) / 2;\n int partitions = countPartitions(nums, mid);\n if (partitions > k) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n return low;\n }\n}\n\n```\n```Python []\nclass Solution:\n def countPartitions(self, nums, maxSum):\n partitions = 1\n subSum = 0\n for num in nums:\n if subSum + num <= maxSum:\n subSum += num\n else:\n partitions += 1\n subSum = num\n return partitions\n\n def splitArray(self, nums: List[int], k: int) -> int:\n low = max(nums)\n high = sum(nums)\n while low <= high:\n mid = (low + high) // 2\n partitions = self.countPartitions(nums, mid)\n if partitions > k:\n low = mid + 1\n else:\n high = mid - 1\n return low\n\n```\n | 2 | Given an integer array `nums` and an integer `k`, split `nums` into `k` non-empty subarrays such that the largest sum of any subarray is **minimized**.
Return _the minimized largest sum of the split_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[7,2,5,10,8\], k = 2
**Output:** 18
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[7,2,5\] and \[10,8\], where the largest sum among the two subarrays is only 18.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 9
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[1,2,3\] and \[4,5\], where the largest sum among the two subarrays is only 9.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 106`
* `1 <= k <= min(50, nums.length)` | null |
Python Binary Search. Readable code | split-array-largest-sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def splitArray(self, nums: List[int], k: int) -> int:\n def check(x):\n splits = 1\n n = 0\n for num in nums:\n n += num\n if n > x:\n n = num\n splits += 1\n if splits > k:\n return False\n return True\n l = max(nums)\n r = sum(nums)\n while l < r:\n mid = (l+r) >> 1\n if not check(mid):\n l=mid+1\n else:\n r=mid\n return l\n \n``` | 2 | Given an integer array `nums` and an integer `k`, split `nums` into `k` non-empty subarrays such that the largest sum of any subarray is **minimized**.
Return _the minimized largest sum of the split_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[7,2,5,10,8\], k = 2
**Output:** 18
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[7,2,5\] and \[10,8\], where the largest sum among the two subarrays is only 18.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 9
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[1,2,3\] and \[4,5\], where the largest sum among the two subarrays is only 9.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 106`
* `1 <= k <= min(50, nums.length)` | null |
THE ONLY PYTHON SOLUTION WITH DP + MEMOIZATION | split-array-largest-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def splitArray(self, nums: List[int], k: int) -> int:\n x = nums.count(0)\n if x>k:\n nums.sort()\n while(nums.count(0)!=k):\n nums.pop(0)\n \n\n\n \n ind = 0\n dp = {}\n return self.splitAray(nums,ind,k,dp)\n\n \n def splitAray(self,nums,ind,k,dp):\n if k==1:\n return sum(nums[ind:len(nums)])\n \n\n if (ind,k) in dp:\n return dp[(ind,k)]\n\n ans = 1e9\n sumi = 0\n for i in range(ind,len(nums)):\n sumi +=nums[i]\n ans = min(ans, max(sumi , self.splitAray(nums,i+1,k-1,dp)))\n dp[(ind,k)] = ans\n return ans\n``` | 4 | Given an integer array `nums` and an integer `k`, split `nums` into `k` non-empty subarrays such that the largest sum of any subarray is **minimized**.
Return _the minimized largest sum of the split_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[7,2,5,10,8\], k = 2
**Output:** 18
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[7,2,5\] and \[10,8\], where the largest sum among the two subarrays is only 18.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 9
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[1,2,3\] and \[4,5\], where the largest sum among the two subarrays is only 9.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 106`
* `1 <= k <= min(50, nums.length)` | null |
410: Solution with step by step explanation | split-array-largest-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, we define the range for our binary search. The minimum value can be the maximum value in the array since we cannot have a subarray with a sum greater than the maximum value. The maximum value can be the sum of all elements in the array since we can have k subarrays with each subarray having a sum of at least 1 element.\n2. We define a helper function \'is_possible\' to check if it is possible to split the array into k subarrays such that the maximum sum of any subarray is less than or equal to \'mid\'.\n3. Inside the \'is_possible\' function, we iterate through the array and keep adding the current element to a running sum \'curr_sum\'. If \'curr_sum\' becomes greater than \'mid\', we increment our \'count\' variable and reset \'curr_sum\' to the current element. If \'count\' becomes greater than \'k\', it means that it is not possible to split the array into k subarrays such that the maximum sum of any subarray is less than or equal to \'mid\', so we return False.\n4. If we have successfully iterated through the entire array and \'count\' is less than or equal to \'k\', it means that it is possible to split the array into k subarrays such that the maximum sum of any subarray is less than or equal to \'mid\', so we return True.\n5. We then perform binary search on the range defined in step 1. If \'is_possible(mid)\' returns True, it means that it is possible to split the array into k subarrays such that the maximum sum of any subarray is less than or equal to \'mid\', so we narrow down the search range to the left half. Otherwise, we increase the search range to the right half.\n6. We continue the binary search until the search range is reduced to a single value. This value is the answer.\n7. We return the answer.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitArray(self, nums: List[int], k: int) -> int:\n # Define the binary search range\n left = max(nums)\n right = sum(nums)\n \n # Define a helper function to check if it\'s possible to split the array into k subarrays\n def is_possible(mid):\n count = 1\n curr_sum = 0\n for num in nums:\n curr_sum += num\n if curr_sum > mid:\n count += 1\n curr_sum = num\n if count > k:\n return False\n return True\n \n # Binary search\n while left < right:\n mid = (left + right) // 2\n if is_possible(mid):\n right = mid\n else:\n left = mid + 1\n \n # Return the answer\n return left\n\n``` | 5 | Given an integer array `nums` and an integer `k`, split `nums` into `k` non-empty subarrays such that the largest sum of any subarray is **minimized**.
Return _the minimized largest sum of the split_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[7,2,5,10,8\], k = 2
**Output:** 18
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[7,2,5\] and \[10,8\], where the largest sum among the two subarrays is only 18.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 9
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[1,2,3\] and \[4,5\], where the largest sum among the two subarrays is only 9.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 106`
* `1 <= k <= min(50, nums.length)` | null |
✅ Python Short and Simple NLogSum | split-array-largest-sum | 0 | 1 | ```\nclass Solution:\n def splitArray(self, nums: List[int], m: int) -> int:\n def isPossible(maxSum):\n curr = count = 0\n for i in nums:\n count += (i + curr > maxSum)\n curr = curr + i if i + curr <= maxSum else i\n return count + 1 <= m\n \n lo, hi = max(nums), sum(nums)\n while lo <= hi:\n mid = (lo + hi) // 2\n if isPossible(mid): hi = mid - 1\n else: lo = mid + 1\n return lo\n```\n***\n```Time complexity: N * Log(max+sum)```\n```N``` for checking isPossible function and ```Log(max+sum)``` for selecting each mid(maxSum) using binary search.\n*** | 3 | Given an integer array `nums` and an integer `k`, split `nums` into `k` non-empty subarrays such that the largest sum of any subarray is **minimized**.
Return _the minimized largest sum of the split_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[7,2,5,10,8\], k = 2
**Output:** 18
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[7,2,5\] and \[10,8\], where the largest sum among the two subarrays is only 18.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 9
**Explanation:** There are four ways to split nums into two subarrays.
The best way is to split it into \[1,2,3\] and \[4,5\], where the largest sum among the two subarrays is only 9.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 106`
* `1 <= k <= min(50, nums.length)` | null |
43sec & 17.3MB in python | fizz-buzz | 0 | 1 | **Bold**# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n return ["Fizz"*(d%3==0)+"Buzz"*(d%5==0) or f"{d}" for d in range(1,n+1)]\n \n \n``` | 0 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
i am a new learner. any tips would be great | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n answer = []\n for x in range(1,n+1):\n if x % 5 == 0 and x % 3 == 0:\n answer.append("FizzBuzz") \n elif x % 5 == 0 :\n answer.append("Buzz") \n elif x % 3 == 0 :\n answer.append("Fizz") \n else:\n answer.append(str(x))\n return answer\n\n``` | 1 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
simple solution in python | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n arr=[]\n for i in range(1,n+1):\n if i % 3==0 and i % 5==0 :\n arr.append("FizzBuzz")\n elif i % 3==0:\n arr.append("Fizz")\n elif i % 5==0 :\n arr.append("Buzz")\n \n else:\n arr.append(str(i))\n return(arr)\n``` | 3 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Python beats 83% | fizz-buzz | 0 | 1 | # Intuition\nWe could use a for loop to iterate through list and if statements to check.\n\n# Approach\nFirst I made a list that will return at the end.\n\nSecond I created a for loop with range of n + 1 and I started it at index 1 since we didnt need to look at zero.\n\nThe if statements were pretty simple and explained clearly which gave us the statements we needed. If an if statement was true I would append "FizzBuss", "Fizz" or "Buzz" to the end of my empty list called return_list. If none of the if statements were true then it qould goto my else statement, which would append the current index as a string to return_list.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n return_list = []\n for i in range(1, n + 1):\n if i % 3 == 0 and i % 5 == 0:\n return_list.append("FizzBuzz")\n elif i % 3 == 0:\n return_list.append("Fizz")\n elif i % 5 == 0:\n return_list.append("Buzz")\n else:\n return_list.append(str(i))\n return return_list\n\n``` | 0 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Easy Solution | Beats : 88.23% | fizz-buzz | 0 | 1 | \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n ans = []\n for i in range(1,n+1):\n if i%3==0 and i%5==0:\n ans.append("FizzBuzz")\n elif i%3==0:\n ans.append("Fizz")\n elif i%5==0:\n ans.append("Buzz")\n else:\n ans.append(str(i))\n return ans\n\n \n``` | 2 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Python one-line solution beats 82% | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nList comprehension\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n return ("FizzBuzz" if not(i%3) and not(i%5) else "Fizz" if not(i%3) else "Buzz" if not(i%5) else str(i) for i in range(1, n + 1))\n\n \n``` | 2 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Python3 readable solution using for and if | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n answer = []\n \n for num in range(1, n+1):\n if num % 3 == 0 and num % 5 == 0:\n answer.append("FizzBuzz")\n elif num % 3 == 0:\n answer.append("Fizz")\n elif num % 5 == 0:\n answer.append("Buzz")\n else:\n answer.append(str(num))\n return answer\n``` | 4 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Python 3 Beats 100.0% Simple | fizz-buzz | 0 | 1 | This solution beats 100% both experimentally and should a lot run faster than the average solution theoretically too.\n\nHere\'s the "average" solution:\n```\n def fizzBuzz(self, n: int) -> List[str]:\n arr = []\n\t\t\n for x in range(1, n + 1):\n if x % 15 == 0:\n arr.append(\'FizzBuzz\')\n elif x % 3 == 0:\n arr.append(\'Fizz\')\n elif x % 5 == 0:\n arr.append(\'Buzz\')\n else:\n arr.append(str(x))\n\t\t\t\n return arr\n```\nHowever, this is slow for many reasons. First, the % operator is costly. It\'s a lot slower than most people would expect it to be. Second, the "average" case where it\'s just a normal integer that you add to the list, you have to go through 4 % operators. This is extremely unnecessary.\n\nNow, here\'s an improved code:\n```\n def fizzBuzz(self, n: int) -> List[str]:\n f, b, fb = \'Fizz\', \'Buzz\', \'FizzBuzz\'\n arr = [str(x + 1) for x in range(n)]\n \n for i in range(2, n, 3):\n arr[i] = f\n \n for i in range(4, n, 5):\n arr[i] = b\n \n for i in range(14, n, 15):\n arr[i] = fb\n \n return arr\n```\n\nNow, instead of the average case having to go through 4 % operators, it just has to be initiated once. There are no % operators *or* if else\'s, making it extremely fast. | 57 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Simple Solution with python with best space and time complexity. | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n arr=[]\n for i in range(1,n+1):\n if i%3==0 and i%5==0:\n arr.append("FizzBuzz")\n elif i%3==0:\n arr.append("Fizz")\n elif i%5==0:\n arr.append("Buzz")\n else:\n arr.append(str(i))\n return arr\n\n\n``` | 2 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Python3 most easy solution | fizz-buzz | 0 | 1 | Code:\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n l=[]\n for i in range(1,n+1):\n if i%3==0 and i%5==0:\n l.append("FizzBuzz")\n elif i%3==0:\n l.append("Fizz")\n elif i%5==0:\n l.append("Buzz")\n else:\n l.append(str(i))\n return l\n``` | 1 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Oneliner! | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n return [[str(i), \'Fizz\', \'Buzz\', \'FizzBuzz\'][(i%3==0)+(i%5==0)*2] for i in range(1, n+1)]\n``` | 16 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Simple solution with time complexity O(n) | fizz-buzz | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n result=[]\n for i in range(1,n+1):\n if(i%3==0 and i%5==0):\n result.append("FizzBuzz")\n elif(i%3==0):\n result.append("Fizz")\n elif(i%5==0):\n result.append("Buzz")\n else:\n result.append(str(i))\n return result\n``` | 2 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
Beats : 86.83% [37/145 Top Interview Question] | fizz-buzz | 0 | 1 | # Intuition\n*When seeing the FizzBuzz problem for the first time, my intuition would be to use a loop to iterate from 1 to n, and for each number, check if it is divisible by both 3 and 5, only 3, only 5, or neither. Based on the divisibility, we would append the corresponding string to a result list. At the end of the loop, we would return the result list.*\n\n*The FizzBuzz problem is a simple one, so it can be solved in many ways, including using conditional statements or a switch statement. My primary focus would be on finding a clean and efficient solution that is easy to read and understand.*\n\n# Approach\nThis code is a Python implementation of the FizzBuzz problem. The `Solution` class has a method called `fizzBuzz` that takes a single integer argument `n` and returns a list of strings.\n\nThe method first initializes an empty list `result` to store the FizzBuzz output. It then uses a `for` loop to iterate from 1 to `n`. For each number, the method checks if it is divisible by both 3 and 5, only 3, only 5, or neither. \n\nIf the number is not divisible by either 3 or 5, the method appends the string representation of the number to the `result` list. If the number is divisible by 3, the string "Fizz" is added to the `res` variable. If the number is divisible by 5, the string "Buzz" is added to the `res` variable. If the number is divisible by both 3 and 5, both "Fizz" and "Buzz" are added to the `res` variable.\n\nAfter each iteration, the `res` variable is appended to the `result` list. Finally, the method returns the `result` list.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\nThe `time complexity` of the `fizzBuzz` method is `O(n)`, where n is the input integer, because the method iterates through each number from `1 to n`. \nThe `space complexity` is also `O(n)`, because the `result` list can contain up to n elements.\n# Code\n```\nclass Solution:\n def fizzBuzz(self, n: int) -> List[str]:\n result = []\n for i in range(1, n+1):\n res = ""\n if i % 5 != 0 and i % 3 != 0:\n res = str(i)\n else:\n if i % 3 == 0:\n res += "Fizz" \n if i % 5 == 0:\n res += "Buzz" \n result.append(res)\n return result\n``` | 3 | Given an integer `n`, return _a string array_ `answer` _(**1-indexed**) where_:
* `answer[i] == "FizzBuzz "` if `i` is divisible by `3` and `5`.
* `answer[i] == "Fizz "` if `i` is divisible by `3`.
* `answer[i] == "Buzz "` if `i` is divisible by `5`.
* `answer[i] == i` (as a string) if none of the above conditions are true.
**Example 1:**
**Input:** n = 3
**Output:** \["1","2","Fizz"\]
**Example 2:**
**Input:** n = 5
**Output:** \["1","2","Fizz","4","Buzz"\]
**Example 3:**
**Input:** n = 15
**Output:** \["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"\]
**Constraints:**
* `1 <= n <= 104` | null |
413: Solution with step by step explanation | arithmetic-slices | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We define a class Solution with a function numberOfArithmeticSlices that takes in an integer list nums and returns an integer representing the number of arithmetic slices in nums.\n\n2. We initialize a counter variable count to 0. This variable will keep track of the total number of arithmetic slices in nums.\n\n3. We also initialize a variable curr to 0. This variable will keep track of the current length of the arithmetic slice that we are checking.\n\n4. We iterate through the list nums starting from the third element, since we need at least three elements to form an arithmetic slice.\n\n5. For each element nums[i], we check if it is part of an arithmetic slice by comparing its difference with the previous element\'s difference. If the difference is the same, then we know that the current element is part of an arithmetic slice.\n\n6. If the current element is part of an arithmetic slice, we increment the curr variable by 1, which represents the length of the current arithmetic slice.\n\n7. We also add the curr variable to the count variable to keep track of the total number of arithmetic slices.\n\n8. If the current element is not part of an arithmetic slice, we reset the curr variable to 0 since we are no longer in an arithmetic slice.\n\n9. After iterating through the entire list, we return the count variable, which represents the total number of arithmetic slices in the list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n count = 0 # Initialize a counter for the number of arithmetic slices\n curr = 0 # Initialize a variable for the current length of the arithmetic slice\n \n for i in range(2, len(nums)):\n if nums[i] - nums[i-1] == nums[i-1] - nums[i-2]:\n curr += 1 # Increase the current length of the arithmetic slice\n count += curr # Add the current length to the total count of arithmetic slices\n else:\n curr = 0 # Reset the current length to 0 if the slice is not arithmetic\n \n return count # Return the total count of arithmetic slices\n\n``` | 2 | An integer array is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1,3,5,7,9]`, `[7,7,7,7]`, and `[3,-1,-5,-9]` are arithmetic sequences.
Given an integer array `nums`, return _the number of arithmetic **subarrays** of_ `nums`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We have 3 arithmetic slices in nums: \[1, 2, 3\], \[2, 3, 4\] and \[1,2,3,4\] itself.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000` | null |
Python || O(n) | arithmetic-slices | 0 | 1 | # Intuition\nI thought about dp and math in my high school\n\n# Approach\nIf the length of the input list is less than or equal to 2, there are no arithmetic slices, so we return 0.\n\n\n\n\n\n\n1.We create a list dp of length n (the length of the input list) and initialize all its elements to 0. This list will store the number of arithmetic slices ending at each index.\n\n2.We set k to the difference between the last two elements of the input list, since any arithmetic slice must have this common difference.\nWe iterate backwards through the input list, starting from the second to last element.\n\n3.For each element at index i, we check if the element and the element k positions ahead (i + 2) form an arithmetic slice with the element at index i + 1. If they do, we set dp[i] to dp[i + 1] + 1, since the number of arithmetic slices ending at index i is equal to the number ending at index i + 1 plus the new slice we just found.\n\n4.We update k to be the difference between the current element and the next element (nums[i + 1] - nums[i]), since this will be the common difference for the next arithmetic slice we might find.\n\n5.We return the sum of all the elements in dp, which gives us the total number of arithmetic slices in the input list.\n\n\n\n# Complexity\n- Time complexity:\nO(n) # we iterate through the list once\n\n- Space complexity:\nO(n) # The "dp" list takes up O(n) space in memory\n\n# Code\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n if len(nums) <= 2:\n return 0\n dp = [0] * len(nums)\n k = nums[-1] - nums[-2] # "k" represents the common difference in the arithmetic progression formed by the input array\n\n \n\n for i in range(len(nums) -3, -1,-1):\n if nums[i] + k == nums[i + 1] == nums[i + 2] - k: \n dp[i] = dp[i + 1] + 1\n k = nums[i + 1] - nums[i]\n return sum(dp)\n``` | 2 | An integer array is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1,3,5,7,9]`, `[7,7,7,7]`, and `[3,-1,-5,-9]` are arithmetic sequences.
Given an integer array `nums`, return _the number of arithmetic **subarrays** of_ `nums`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We have 3 arithmetic slices in nums: \[1, 2, 3\], \[2, 3, 4\] and \[1,2,3,4\] itself.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000` | null |
Faster than 99.44% PYTHON 3 Simple solution | arithmetic-slices | 0 | 1 | \n\n\n**-->** Create an array of size le (le=len(A))\n\n**-->** as given \'\'A sequence of numbers is called arithmetic if it consists of at **least three elements**\'\', start for loop from 2 to le.(**because first two elements(index 0 and 1) will never from a sequence as minimum length of a sequence is 3**)\n\n**-->** it is also given that \'\'A sequence of numbers is called arithmetic if it consists of at least three elements and **if the difference between any two consecutive elements is the same.**\'\'\nhere i is current element ,if A[i]-A[i-1] == A[i-1]-A[i-2] then **sequence length for current element i.e l[i] will be 1+sequence length of previous element(l[i-1)**\n\nTO return the total number of arithmetic slices in the array A **return Caluculated Sum of array l**\n\n```\nclass Solution:\n def numberOfArithmeticSlices(self, A: List[int]) -> int:\n le=len(A)\n l=[0]*(le)\n for i in range(2,le):\n if A[i]-A[i-1] == A[i-1]-A[i-2]:\n l[i]=1+l[i-1]\n return sum(l)\n\n | 72 | An integer array is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1,3,5,7,9]`, `[7,7,7,7]`, and `[3,-1,-5,-9]` are arithmetic sequences.
Given an integer array `nums`, return _the number of arithmetic **subarrays** of_ `nums`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We have 3 arithmetic slices in nums: \[1, 2, 3\], \[2, 3, 4\] and \[1,2,3,4\] itself.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000` | null |
Clean, Fast Python3 | O(n) Time, O(1) Space | arithmetic-slices | 0 | 1 | Please upvote if it helps! :)\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n n, subs = len(nums), 0\n last_diff, count = None, 0\n for i in range(1, n):\n this_diff = nums[i] - nums[i - 1]\n if this_diff == last_diff:\n subs += count\n count += 1\n else:\n last_diff = this_diff\n count = 1\n return subs | 1 | An integer array is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1,3,5,7,9]`, `[7,7,7,7]`, and `[3,-1,-5,-9]` are arithmetic sequences.
Given an integer array `nums`, return _the number of arithmetic **subarrays** of_ `nums`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We have 3 arithmetic slices in nums: \[1, 2, 3\], \[2, 3, 4\] and \[1,2,3,4\] itself.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000` | null |
beginners solution, Easy to understand | arithmetic-slices | 0 | 1 | 93.60% Faster\n```\nclass Solution:\n def numberOfArithmeticSlices(self, nums: List[int]) -> int:\n count = 0\n for i in range(len(nums)-2):\n j = i+1\n while(j<len(nums)-1):\n if nums[j]-nums[j-1] == nums[j+1]-nums[j]:\n count += 1\n j += 1\n else:\n break\n return count\n```\n\n\n \n | 3 | An integer array is called arithmetic if it consists of **at least three elements** and if the difference between any two consecutive elements is the same.
* For example, `[1,3,5,7,9]`, `[7,7,7,7]`, and `[3,-1,-5,-9]` are arithmetic sequences.
Given an integer array `nums`, return _the number of arithmetic **subarrays** of_ `nums`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We have 3 arithmetic slices in nums: \[1, 2, 3\], \[2, 3, 4\] and \[1,2,3,4\] itself.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000` | null |
Python | 99% Faster | Easy Solution✅ | third-maximum-number | 0 | 1 | ```\ndef thirdMax(self, nums: List[int]) -> int:\n nums = sorted(list(set(nums)))\n if len(nums) > 2:\n return nums[-3]\n return nums[-1]\n```\n\n | 12 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
Awesome Code Python3 | third-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n if len(set(nums))<3:\n return max(nums)\n return sorted((set(nums)),reverse=True)[2]\n#please upvote me it would encourage me alot\n \n\n \n``` | 5 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
one liner . easy to understand.beginner solution | third-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n return max(list(set(nums))) if len(list(set(nums)))<3 else sorted(list(set(nums)))[-3]\n``` | 7 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
Python easy soln using set() fn. | third-maximum-number | 0 | 1 | # Intuition\nsorted the array in descending order to get the 3rd max number\n\n# Approach\ncreated new array (res) to remove duplicates from \'nums\'\nthen applied the conditon to return the index \'2\' where the array of lenght is more than \'3\'\nfor less than \'3\' use max(nums)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n res = list(set(nums))\n res.sort(reverse = True)\n if len(res) >= 3:\n return res[2]\n return max(res)\n\n \n\n``` | 1 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
Easy Python solution | third-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n return sorted(set(nums))[-3] if len(set(nums))>2 else max(sorted(set(nums)))\n``` | 1 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
414: Time 93.15%, Solution with step by step explanation | third-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Eliminate duplicates: First, eliminate duplicates from the input list nums using the set() method and convert it back to a list.\n2. Handle edge cases: If the length of the modified nums list is less than 3, then return the maximum element from the list.\n3. Sort in decreasing order: Sort the nums list in descending order using the sorted() method with the reverse=True argument.\n4. Find the third maximum: Loop through the sorted nums list, and count the number of times a new distinct element is encountered by comparing it with the previous element. If the count is equal to 3, return the current element.\n5. Return the maximum element: If the loop completes without finding the third maximum element, return the first element of the nums list, which is the maximum element.\n\n# Complexity\n- Time complexity:\nO(n log n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n nums = list(set(nums)) # Eliminate duplicates\n if len(nums) < 3:\n return max(nums)\n nums = sorted(nums, reverse=True) # Sort in decreasing order\n count = 1\n for i in range(1, len(nums)):\n if nums[i] < nums[i-1]:\n count += 1\n if count == 3:\n return nums[i]\n return nums[0] # Return the maximum element\n\n``` | 3 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
O(N) Time complexity python3 | third-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n nums=set(nums)\n if len(nums)<3:\n return max(nums)\n else:\n nums.remove(max(nums))\n nums.remove(max(nums))\n return max(nums)\n\n\n \n\n \n``` | 6 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
using Heapq Solution | third-maximum-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thirdMax(self, nums: List[int]) -> int:\n nums=list(set(nums))\n if len(nums)<3:\n return max(nums)\n n=[-i for i in nums]\n heapq.heapify(n)\n for i in range(3):\n poping=heapq.heappop(n)\n if i==2:\n return -(poping)\n \n\n \n``` | 4 | Given an integer array `nums`, return _the **third distinct maximum** number in this array. If the third maximum does not exist, return the **maximum** number_.
**Example 1:**
**Input:** nums = \[3,2,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2.
The third distinct maximum is 1.
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 2
**Explanation:**
The first distinct maximum is 2.
The second distinct maximum is 1.
The third distinct maximum does not exist, so the maximum (2) is returned instead.
**Example 3:**
**Input:** nums = \[2,2,3,1\]
**Output:** 1
**Explanation:**
The first distinct maximum is 3.
The second distinct maximum is 2 (both 2's are counted together since they have the same value).
The third distinct maximum is 1.
**Constraints:**
* `1 <= nums.length <= 104`
* `-231 <= nums[i] <= 231 - 1`
**Follow up:** Can you find an `O(n)` solution? | null |
Easiest Solution using unecessary variables | add-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n sys.set_int_max_str_digits(10000)\n nattu = int(num1)\n babu = int(num2)\n result = str(nattu+babu)\n return result\n\n``` | 2 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
Easy Solution in Python3 | add-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport sys\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n sys.set_int_max_str_digits(10000)\n n1,n2=int(num1),int(num2)\n return str(n1+n2)\n``` | 1 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
LeetCode 415 | Using String Operations Only !!! | Python3 Solution | ✅ | add-strings | 0 | 1 | # Intuition\nThis approach just does addition like humans do.\n\n# Approach\n1. **Patiently** list all possibility of the addition. (It\'s stupid, but that\'s it. `:))`)\n2. Fill the leading zero to the shorter number string.\n3. Initial the carry as `0`.\n4. Iterate from the lowest digit to the highest digit.\n5. Check if there is carry after the end of the loop.\n\n# Complexity\n- Time complexity: $$O(max(n_1, n_2))$$ which $$n_i$$ means the length of the number string.\n- Space complexity: $$O(max(n_1, n_2))$$ which $$n_i$$ means the length of the number string.\n\n# Code\n```python\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n length = max(len(num1), len(num2))\n answer = ""\n carry = "0"\n for digit_1, digit_2 in zip(num1.zfill(length)[::-1], num2.zfill(length)[::-1]):\n carry, digit = self.add_digit(digit_1, digit_2, carry)\n answer += digit\n if carry != "0":\n answer += carry\n return answer[::-1]\n\n def add_digit(self, digit_1: str = "0", digit_2: str = "0", carry: str = "0") -> str:\n match digit_1 + digit_2 + carry:\n case "000":\n return "0", "0"\n case "010" | "100" | "001":\n return "0", "1"\n case "020" | "110" | "200" | "011" | "101":\n return "0", "2"\n case "030" | "120" | "210" | "300" | "021" | "111" | "201":\n return "0", "3"\n case "040" | "130" | "220" | "310" | "400" | "031" | "121" | "211" | "301":\n return "0", "4"\n case "050" | "140" | "230" | "320" | "410" | "500" | "041" | "131" | "221" | "311" | "401":\n return "0", "5"\n case "060" | "150" | "240" | "330" | "420" | "510" | "600" | "051" | "141" | "231" | "321" | "411" | "501":\n return "0", "6"\n case "070" | "160" | "250" | "340" | "430" | "520" | "610" | "700" | "061" | "151" | "241" | "331" | "421" | "511" | "601":\n return "0", "7"\n case "080" | "170" | "260" | "350" | "440" | "530" | "620" | "710" | "800" | "071" | "161" | "251" | "341" | "431" | "521" | "611" | "701":\n return "0", "8"\n case "090" | "180" | "270" | "360" | "450" | "540" | "630" | "720" | "810" | "900" | "081" | "171" | "261" | "351" | "441" | "531" | "621" | "711" | "801":\n return "0", "9"\n case "190" | "280" | "370" | "460" | "550" | "640" | "730" | "820" | "910" | "091" | "181" | "271" | "361" | "451" | "541" | "631" | "721" | "811" | "901":\n return "1", "0"\n case "290" | "380" | "470" | "560" | "650" | "740" | "830" | "920" | "191" | "281" | "371" | "461" | "551" | "641" | "731" | "821" | "911":\n return "1", "1"\n case "390" | "480" | "570" | "660" | "750" | "840" | "930" | "291" | "381" | "471" | "561" | "651" | "741" | "831" | "921":\n return "1", "2"\n case "490" | "580" | "670" | "760" | "850" | "940" | "391" | "481" | "571" | "661" | "751" | "841" | "931":\n return "1", "3"\n case "590" | "680" | "770" | "860" | "950" | "491" | "581" | "671" | "761" | "851" | "941":\n return "1", "4"\n case "690" | "780" | "870" | "960" | "591" | "681" | "771" | "861" | "951":\n return "1", "5"\n case "790" | "880" | "970" | "691" | "781" | "871" | "961":\n return "1", "6"\n case "890" | "980" | "791" | "881" | "971":\n return "1", "7"\n case "990" | "891" | "981":\n return "1", "8"\n case "991":\n return "1", "9"\n case _:\n raise NotImplementedError\n\n``` | 1 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
Non-effective Python solution | add-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n a = 0\n b = 0\n count = 0\n for indi, i in enumerate(num1):\n while str(count) != i:\n count += 1\n a += count*10**(len(num1)-1-indi)\n count = 0\n for indd, d in enumerate(num2):\n while str(count) != d:\n count += 1\n b += count*10**(len(num2)-1-indd)\n count = 0 \n return str(a+b)\n``` | 1 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
Simple python solution | add-strings | 0 | 1 | **Method 1:**\nUse of dictionary\n```\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n \n def str2int(num):\n numDict = {\'0\' : 0, \'1\' : 1, \'2\' : 2, \'3\' : 3, \'4\' : 4, \'5\' : 5,\n \'6\' : 6, \'7\' : 7, \'8\' : 8, \'9\' : 9}\n output = 0\n for d in num:\n output = output * 10 + numDict[d]\n return output\n \n return str(str2int(num1) + str2int(num2)) \n```\n\n**Method 2**\nUse of unicode\n```\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n def str2int(num):\n result = 0\n for n in num:\n result = result * 10 + ord(n) - ord(\'0\')\n return result\n return str(str2int(num1) + str2int(num2))\n``` | 77 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
Python ||Simple Code || Optimize code beats 89.6% || 2 Different way - same approach | add-strings | 0 | 1 | Approach Same but Differnent Way\nLong way -> To understand\nShort way -> To optimize \n\n# Code\n```\n<!-- Long Way -->\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n # As we can\'nt use any built-in library and also not to convert input to int. So we Create Dict to handle this Prob.\n dic = {\'0\':0, \'1\':1, \'2\':2, \'3\':3, \'4\':4, \'5\':5, \'6\':6, \'7\':7, \'8\':8, \'9\':9 }\n\n ans = \'\'\n c = 0\n\n while num1 or num2 or c:\n s = 0\n if num1:\n digit1 = dic[num1[-1]]\n num1 = num1[:-1]\n s += digit1\n if num2:\n digit2 = dic[num2[-1]]\n num2 = num2[:-1]\n s += digit2\n \n s += c\n d = s %10\n c = s // 10\n\n ans = str(d) + ans\n\n return ans\n```\n\n```\n<!-- Short Way :: Optimize -->\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n # As we can\'nt use any built-in library and also not to convert input to int. So we Create Dict to handle this Prob.\n dic = {\'0\':0, \'1\':1, \'2\':2, \'3\':3, \'4\':4, \'5\':5, \'6\':6, \'7\':7, \'8\':8, \'9\':9 }\n\n ans = \'\'\n c = 0\n\n while num1 or num2 or c:\n s = c\n if num1:\n s += dic[num1[-1]]\n num1 = num1[:-1]\n if num2:\n s += dic[num2[-1]]\n num2 = num2[:-1]\n \n c = s // 10\n ans = str(s %10) + ans\n\n return ans\n\n``` | 2 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
415: Solution with step by step explanation | add-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Reverse the input strings num1 and num2 so that we start adding from the least significant digits.\n\n2. Pad the shorter input string with zeros so that both strings are the same length.\n\n3. Initialize an empty string result to store the sum of the two input strings and a variable carry to 0.\n\n4. Loop through both strings, starting from the least significant digits, and add the corresponding digits of num1 and num2.\n\n5. If there is a carry from the previous iteration, add it to the sum.\n\n6. If the sum is greater than or equal to 10, set carry to 1 and subtract 10 from the sum. Otherwise, set carry to 0.\n\n7. Append the least significant digit of the sum to the result string.\n\n8. If there is a carry after the last iteration, append it to the result string.\n\n9. Reverse the result string to obtain the final sum.\n\n10. Return the final sum as a string.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n # Reverse the input strings to start adding from the least significant digits\n num1 = num1[::-1]\n num2 = num2[::-1]\n # Pad the shorter input string with zeros\n if len(num1) < len(num2):\n num1 += \'0\' * (len(num2) - len(num1))\n else:\n num2 += \'0\' * (len(num1) - len(num2))\n \n result = \'\'\n carry = 0\n \n # Loop through both strings, starting from the least significant digits\n for i in range(len(num1)):\n # Convert the current digit in each string to an integer and add them together\n digit_sum = int(num1[i]) + int(num2[i]) + carry\n # Determine the carry for the next iteration, if any\n carry = digit_sum // 10\n # Append the least significant digit of the sum to the result string\n result += str(digit_sum % 10)\n \n # If there is a carry after the last iteration, append it to the result string\n if carry > 0:\n result += str(carry)\n \n # Reverse the result string to obtain the final sum\n return result[::-1]\n\n``` | 14 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
Single line Python Solution | add-strings | 0 | 1 | \n\n# Code\n```\nclass Solution(object):\n def addStrings(self, num1, num2):\n """\n :type num1: str\n :type num2: str\n :rtype: str\n """\n return str(int(num1)+int(num2))\n \n``` | 1 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
🔥Easy way using python🔥 | add-strings | 0 | 1 | # Intuition\nEasy way using python inbuilt functions\n\n# Approach\nconverting strings to int solve it and again convert to string\n\n# Complexity\n- Time complexity:\n- Space complexity:\n# Code\n```\nclass Solution:\n def addStrings(self, num1: str, num2: str) -> str:\n sys.set_int_max_str_digits(10000)\n n=int(num1)\n n1=int(num2)\n n2=n+n1\n return str(n2)\n``` | 4 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
[Python3] Easy Code with One Loop; guides provided | add-strings | 0 | 1 | # Approach:\nThis code uses similar logic explained in solution for question #[2 Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solution/). Make sure to read that. The only difference is that here we are dealing with strings and not linked lists. The algorithm is the same as adding two numbers on a piece of paper we learned in Elementary School. Therefore, only one loop is enough.\n\n# Note:\nBased on the rules in the question: "You must not convert the inputs to integer directly", I think it is permitted to use int and str functions as long as you convert only one character. Since you are not converting the inputs directly, it should be acceptable.\n\n# Python3 Code:\n```\n def addStrings(self, num1: str, num2: str) -> str:\n num1, num2 = num1[::-1], num2[::-1]\n num3 = \'\'\n carry = i = 0\n l1, l2 = len(num1), len(num2)\n l3 = max(l1, l2)\n while i < l3 or carry:\n dig1 = int(num1[i]) if i < l1 else 0\n dig2 = int(num2[i]) if i < l2 else 0\n dig3 = (dig1 + dig2 + carry) % 10\n carry = (dig1 + dig2 + carry) // 10\n num3 += str(dig3)\n i += 1\n return num3[::-1]\n``` | 29 | Given two non-negative integers, `num1` and `num2` represented as string, return _the sum of_ `num1` _and_ `num2` _as a string_.
You must solve the problem without using any built-in library for handling large integers (such as `BigInteger`). You must also not convert the inputs to integers directly.
**Example 1:**
**Input:** num1 = "11 ", num2 = "123 "
**Output:** "134 "
**Example 2:**
**Input:** num1 = "456 ", num2 = "77 "
**Output:** "533 "
**Example 3:**
**Input:** num1 = "0 ", num2 = "0 "
**Output:** "0 "
**Constraints:**
* `1 <= num1.length, num2.length <= 104`
* `num1` and `num2` consist of only digits.
* `num1` and `num2` don't have any leading zeros except for the zero itself. | null |
Python Top Down memoization solution for reference | partition-equal-subset-sum | 0 | 1 | ```\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n def rec(i,rsum ):\n if(rsum==0): return True\n if(i==len(nums) or rsum < 0): return False \n elif(self.dp[i][rsum] != -1 ):\n return self.dp[i][rsum]\n self.dp[i][rsum]= rec(i+1,rsum-nums[i]) or rec(i+1,rsum)\n return self.dp[i][rsum]\n \n \n totalsum = sum(nums)\n if(totalsum%2): return False \n else: \n self.dp = [ [-1]*((totalsum//2)+1) for _ in range(len(nums))]\n return rec(0,totalsum//2)\n``` | 1 | Given an integer array `nums`, return `true` _if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,5,11,5\]
**Output:** true
**Explanation:** The array can be partitioned as \[1, 5, 5\] and \[11\].
**Example 2:**
**Input:** nums = \[1,2,3,5\]
**Output:** false
**Explanation:** The array cannot be partitioned into equal sum subsets.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100` | null |
Python || DP || Memoization+Tabulation || Space Optimization | partition-equal-subset-sum | 0 | 1 | ```\n#Memoization (Top-Down)\n#Time Complexity: O(n*k)\n#Space Complexity: O(n) + O(n*k)\nclass Solution1:\n def canPartition(self, arr: List[int]) -> bool:\n def solve(ind,target):\n if target==0:\n return True\n if ind==0:\n return arr[ind]==target\n if dp[ind][target]!=-1:\n return dp[ind][target]\n not_pick=solve(ind-1,target)\n pick=False\n if target>=arr[ind]:\n pick=solve(ind-1,target-arr[ind])\n dp[ind][target]=pick or not_pick\n return dp[ind][target]\n s=sum(arr)\n if s%2!=0:\n return False\n s//=2\n n=len(arr)\n dp=[[-1 for j in range(s+1)] for i in range(n)]\n return solve(n-1,s)\n\n#Tabulation (Bottom-Up)\n#Time Complexity: O(n*k)\n#Space Complexity: O(n*k)\nclass Solution2:\n def canPartition(self, arr: List[int]) -> bool:\n n=len(arr)\n s=sum(arr)\n if s%2!=0:\n return False\n k=s//2\n dp=[[False for j in range(k+1)] for i in range(n)]\n for i in range(n):\n dp[i][0] = True\n if arr[0] <= k:\n dp[0][arr[0]] = True\n for ind in range(1,n):\n for target in range(1,k+1):\n not_pick=dp[ind-1][target]\n pick=False\n if target>=arr[ind]:\n pick=dp[ind-1][target-arr[ind]]\n dp[ind][target]= pick or not_pick \n return dp[n-1][k]\n\n#Space Optimization\n#Time Complexity: O(n*k)\n#Space Complexity: O(k)\nclass Solution:\n def canPartition(self, arr: List[int]) -> bool:\n n=len(arr)\n s=sum(arr)\n if s%2!=0:\n return False\n k=s//2\n prev=[False]*(k+1)\n for i in range(n):\n prev[0] = True\n if arr[0] <= k:\n prev[arr[0]] = True\n for ind in range(1,n):\n curr=[False]*(k+1)\n for target in range(1,k+1):\n curr[0]=True\n not_pick=prev[target]\n pick=False\n if target>=arr[ind]:\n pick=prev[target-arr[ind]]\n curr[target]= pick or not_pick \n prev=curr[:]\n return prev[k]\n```\n**An upvote will be encouraging** | 2 | Given an integer array `nums`, return `true` _if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,5,11,5\]
**Output:** true
**Explanation:** The array can be partitioned as \[1, 5, 5\] and \[11\].
**Example 2:**
**Input:** nums = \[1,2,3,5\]
**Output:** false
**Explanation:** The array cannot be partitioned into equal sum subsets.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100` | null |
416: Space 99.79%, Solution with step by step explanation | partition-equal-subset-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We calculate the total sum of the input array and store it in a variable called total_sum.\n2. If the total sum is odd, we cannot partition the array into two equal sum subsets, so we return False.\n3. Otherwise, we calculate the target sum for each subset by dividing the total sum by 2 and storing it in a variable called target_sum.\n4. We initialize a boolean list called dp of size target_sum+1 to keep track of whether a sum can be formed using the input array. We initialize all elements in the list to False.\n5. We can always form a sum of 0 using the input array, so we set dp[0] = True.\n6. We loop through each element in the input array using a for loop.\n7. Starting from the target sum, we loop backwards through the dp list using another for loop. We use a range function to specify the range of indices to loop through. We start at target_sum and end at num-1, and we step backwards by 1 each time. This loop is responsible for updating the dp list to reflect whether or not we can form each possible sum using the current element and the previous elements in the input array.\n8. For each iteration of the inner loop, we check whether we can form a sum of j-num using the previous elements in the input array. If we can, then we can also form a sum of j using the current element. We update the dp list accordingly.\n9. After both loops have finished executing, we return whether or not we can form a sum of target_sum using the input array by returning dp[target_sum].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n # Calculate the total sum of the input array\n total_sum = sum(nums)\n \n # If the total sum is odd, we cannot partition the array into two equal sum subsets\n if total_sum % 2 == 1:\n return False\n \n # Calculate the target sum for each subset\n target_sum = total_sum // 2\n \n # Initialize a boolean list of size target_sum+1 to keep track of whether a sum can be formed using the input array\n dp = [False] * (target_sum+1)\n \n # We can always form a sum of 0 using the input array\n dp[0] = True\n \n # Loop through each element in the input array\n for num in nums:\n # Starting from the target sum, loop backwards through the dp list\n for j in range(target_sum, num-1, -1):\n # If we can form a sum j-num using the previous elements in the input array,\n # we can also form a sum j using the current element\n dp[j] = dp[j] or dp[j-num]\n \n # Return whether or not we can form a sum of target_sum using the input array\n return dp[target_sum]\n\n``` | 22 | Given an integer array `nums`, return `true` _if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,5,11,5\]
**Output:** true
**Explanation:** The array can be partitioned as \[1, 5, 5\] and \[11\].
**Example 2:**
**Input:** nums = \[1,2,3,5\]
**Output:** false
**Explanation:** The array cannot be partitioned into equal sum subsets.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100` | null |
[Python] DP & DFS Solutions - Easy-to-understand with Explanation | partition-equal-subset-sum | 0 | 1 | ### Introduction\n\nWe want to partition `nums` into two subsets such that their sums are equal. Intuitively, we can establish that the total sum of the elements in `nums` **has to be an even number** for this to be possible:\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n\t if sum(nums)%2: # or if sum(nums)&1\n\t\t return False\n\t\t# main logic here\n```\n\n---\n\n### Approach 1: DP (0/1 Knapsack Problem)\n\nThis problem is a variant of the famous [Knapsack problem](https://en.wikipedia.org/wiki/Knapsack_problem). Essentially, if we were able to pick certain elements from `nums` to create one of the two subsets, which elements would we pick? This involves looping through combinations of elements to find one possible combination that satisfies our criteria, namely, that partitions `nums` such that their sums are equal.\n\nWe can perform this iteration on each element in `nums`. Since there only exists two choices - to select the current element or not - we can compute and store the obtained total sum for each case into an array.\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n s = sum(nums)\n if s&1:\n return False\n """\n The dp array stores the total obtained sums we have come across so far.\n Notice that dp[0] = True; if we never select any element, the total sum is 0.\n """\n dp = [True]+[False]*s\n # Now, loop through each element\n for num in nums:\n for curr in range(s, num-1, -1): # avoid going out-of-bounds\n """\n Case 1: The current sum (curr) has been seen before.\n Then, if we don\'t select the current element, the sum will not change.\n\t\t\t\t\t\tSo, this total sum will still exist, and its dp value remains True.\n\t\t\t\t\n\t\t\t\tCase 2: The current sum (curr) has not been seen before,\n\t\t\t\t but it can be obtained by selecting the current element.\n\t\t\t\t\t\tThis means that dp[curr-num] = True, and thus dp[curr] now becomes True.\n\t\t\t\t\n\t\t\t\tCase 3: The current sum (curr) has not been seen before,\n\t\t\t\t and it cannot be obtained by selecting the current element.\n\t\t\t\t\t\tSo, this total sum will still not exist, and its dp value remains False.\n """\n dp[curr] = dp[curr] or dp[curr-num]\n # Finally, we want to obtain the target sum\n return dp[s//2] # or dp[s>>1]\n```\n\nWe can further optimise this implementation by discarding all obtained sums that are greater than the target sum.\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n s = sum(nums)\n if s&1:\n return False\n dp = [True]+[False]*(s>>1)\n for num in nums:\n for curr in range(s>>1, num-1, -1):\n dp[curr] = dp[curr] or dp[curr-num]\n return dp[-1]\n```\n\nWe can also replace the `dp` array with a `set()` instead, so that we don\'t need to store `False` for a value that has not yet been obtained.\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n dp, s = set([0]), sum(nums)\n if s&1:\n return False\n for num in nums:\n for curr in range(s>>1, num-1, -1):\n if curr not in dp and curr-num in dp:\n if curr == s>>1:\n return True\n dp.add(curr)\n return False\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(nW)" title="O(nW)" />**, where `n` is the number of elements in `nums` and `W` is `sum(nums)`, due to the nested for loop. It should be noted that <img src="https://latex.codecogs.com/png.image?\\dpi{110}&space;O(n^{2})\\leq&space;TC<&space;O(2^{n})" title="O(n^{2})\\leq TC<O(2^{n})" />, which is a large range, but it\'s the best estimate of the TC that I have so far (comment down below if you have a more reasonable one).\n**SC: <img src="https://latex.codecogs.com/png.image?\\dpi{110}&space;O(\\frac{W}{2})" title="O(\\frac{W}{2})" />**, for the `dp` array / set.\n\nFinally, we can do away with having to loop through the range of possible total sums (credit to [@archit91](https://leetcode.com/archit91/) for the suggestion). From the set implementation, all we need to do is iterate through each sum that has already been obtained, and add the element\'s value to it. Our previous optimisation of limiting the obtained sum to the target sum (which is half of the total sum of elements in `nums`) now serves the purpose of preventing the set from growing exponentially.\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n dp, s = set([0]), sum(nums)\n if s&1:\n return False\n for num in nums:\n dp.update([v+num for v in dp if v+num <= s>>1])\n return s>>1 in dp\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(n^{2})\\leq&space;TC<&space;O(nW)" title="O(n^{2})\\leq TC< O(nW)" />**. It is still very difficult to pinpoint the exact time complexity, although it will definitely be much closer to <img src="https://latex.codecogs.com/svg.image?O(n^{2})" title="O(n^{2})" /> than the previous implementation.\n**SC: <img src="https://latex.codecogs.com/svg.image?SC\\leq&space;O(\\frac{W}{2})" title="SC\\leq O(\\frac{W}{2})" />**, due to the space optimisations as discussed above.\n\n---\n\n### Approach 2: DFS (Backtracking)\n\nAnother way to approach this problem is to select each element in `nums` until the target sum is reached / exceeded. If we exceed the target sum, then we remove the previously-selected element and mark it as unselected before trying the next element. This continues until we either reach the target sum or until we have iterated through all possible combinations.\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n l, s = len(nums), sum(nums)\n @cache # this is important to avoid unnecessary recursion\n def dfs(curr: int, idx: int) -> bool:\n """\n Select elements and check if nums can be partitioned.\n :param curr: The current sum of the elements in the subset.\n :param idx: The index of the current element in nums.\n :return: True if nums can be partitioned, False otherwise.\n """\n if idx == l: # we have reached the end of the array\n return curr == s>>1\n elif curr+nums[idx] == s>>1 or \\ # target sum obtained\n (curr+nums[idx] < s>>1 and \\\n dfs(curr+nums[idx], idx+1)): # or, target sum will be reached by selecting this element\n return True\n return dfs(curr, idx+1) # else, don\'t select this element, continue\n return False if s&1 else dfs(0, 0)\n```\n\nYou could compress the code if you wanted, though I would not recommend doing so.\n\n```python\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n l, s = len(nums), sum(nums)\n @cache\n def dfs(curr: int, idx: int) -> bool:\n\t\t return curr == s>>1 if idx == l else True if curr+nums[idx] == s>>1 or \\\n\t\t\t\t(curr+nums[idx] < s>>1 and dfs(curr+nums[idx], idx+1)) else dfs(curr, idx+1)\n return False if s&1 else dfs(0, 0)\n```\n\n**TC: <img src="https://latex.codecogs.com/svg.image?O(n^{2})\\leq&space;TC<&space;O(nW)" title="O(n^{2})\\leq TC< O(nW)" />**. <code lang=python>dfs(curr+nums[idx], idx+1)</code> acts as a nested for loop since when it fails, it calls <code lang=python>dfs(curr, idx+1)</code>.\n**SC: <img src="https://latex.codecogs.com/svg.image?SC\\leq&space;O(\\frac{W}{2})" title="SC\\leq O(\\frac{W}{2})" />**. The `cache` will most likely have to store each of the obtained sums, which will perform on par with the DP approach as discussed above.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 58 | Given an integer array `nums`, return `true` _if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,5,11,5\]
**Output:** true
**Explanation:** The array can be partitioned as \[1, 5, 5\] and \[11\].
**Example 2:**
**Input:** nums = \[1,2,3,5\]
**Output:** false
**Explanation:** The array cannot be partitioned into equal sum subsets.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100` | null |
Easy To Undestand | DP 🚀🚀 | partition-equal-subset-sum | 1 | 1 | # Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // 1. Using Recursion\n // TC - O(Exponential)\n bool canPartitionRec(int index, vector<int>& nums, int target)\n {\n // Base Case\n if(index >= nums.size())\n return 0;\n if(target < 0)\n return 0;\n if(target == 0)\n return 1;\n \n int include = canPartitionRec(index + 1, nums, target - nums[index]);\n int exclude = canPartitionRec(index + 1, nums, target);\n\n return (include or exclude);\n }\n\n // 2. Top Down Approach\n // TC and SC -- O(N * M)\n bool canPartitionMemo(int index, vector<int>& nums, int target, vector<vector<int>>& dp)\n {\n // Base Case\n if(index >= nums.size())\n return 0;\n if(target < 0)\n return 0;\n if(target == 0)\n return 1;\n if(dp[index][target] != -1)\n return dp[index][target];\n \n int include = canPartitionMemo(index + 1, nums, target - nums[index], dp);\n int exclude = canPartitionMemo(index + 1, nums, target, dp);\n\n dp[index][target] = (include or exclude);\n return dp[index][target];\n }\n\n // 3. Bottom Up Approach\n // TC and SC -- O(N * M)\n bool canPartitionTab(vector<int> nums, int target)\n {\n int n = nums.size();\n vector<vector<int>> dp(n+1,vector<int>(target+1,0));\n\n for(int i = 0; i < n; i++)\n dp[i][0] = 1;\n \n for(int index = n - 1; index >= 0; index--)\n {\n for(int t = 1; t <= target; t++)\n {\n int include = 0;\n if(t - nums[index] >= 0)\n include = dp[index + 1][t - nums[index]];\n int exclude = dp[index + 1][t];\n\n dp[index][t] = (include or exclude);\n }\n }\n return dp[0][target];\n }\n\n // 4. Space Optimization\n // TC -- O(N * M) and SC -- O(N)\n bool canPartitionSO(vector<int> nums, int target)\n {\n int n = nums.size();\n vector<int> curr(target+1,0);\n vector<int> next(target+1,0);\n\n for(int i = 0; i < n; i++)\n curr[0] = 1;\n \n for(int index = n - 1; index >= 0; index--)\n {\n for(int t = 1; t <= target; t++)\n {\n int include = 0;\n if(t - nums[index] >= 0)\n include = next[t - nums[index]];\n int exclude = next[t];\n\n curr[t] = (include or exclude);\n }\n // Shift\n next = curr;\n }\n return curr[target];\n }\n\n bool canPartition(vector<int>& nums) {\n int sum = accumulate(nums.begin(),nums.end(),0);\n cout << sum << endl;\n\n // We cannot divide odd number into two equal halves\n if(sum & 1) return false;\n\n int target = sum / 2;\n\n // return canPartitionRec(0,nums,target);\n\n // 2. Top Down\n // vector<vector<int>> dp(nums.size(),vector<int>(target+1,-1));\n // return canPartitionMemo(0,nums,target,dp);\n\n // 3. Bottom Up\n // return canPartitionTab(nums,target);\n\n // 4. Space Optimization\n return canPartitionSO(nums,target);\n }\n};\n``` | 2 | Given an integer array `nums`, return `true` _if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,5,11,5\]
**Output:** true
**Explanation:** The array can be partitioned as \[1, 5, 5\] and \[11\].
**Example 2:**
**Input:** nums = \[1,2,3,5\]
**Output:** false
**Explanation:** The array cannot be partitioned into equal sum subsets.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100` | null |
✅ Dynamic Programming Top Down Approach | partition-equal-subset-sum | 0 | 1 | # Complexity\n- Time complexity: $$O(n*sum)$$.\n\n- Space complexity: $$O(n*sum)$$.\n\n# Code\n```\nclass Solution:\n def canPartition(self, nums: List[int]) -> bool:\n summ = sum(nums)\n if summ%2:\n return False\n\n self.cache = {}\n \n return self.check(nums, 0, summ//2)\n \n\n def check(self, nums, i, target):\n if (i, target) in self.cache:\n return self.cache[(i, target)]\n\n if nums[i] == target:\n return True\n if target < 0 or i == len(nums)-1:\n return False\n \n result = self.check(nums, i+1, target - nums[i]) or self.check(nums, i+1, target)\n self.cache[(i, target)] = result\n\n return result\n``` | 10 | Given an integer array `nums`, return `true` _if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,5,11,5\]
**Output:** true
**Explanation:** The array can be partitioned as \[1, 5, 5\] and \[11\].
**Example 2:**
**Input:** nums = \[1,2,3,5\]
**Output:** false
**Explanation:** The array cannot be partitioned into equal sum subsets.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100` | null |
Cleaned up public solution | pacific-atlantic-water-flow | 0 | 1 | # Desription\nCleaned up public solution https://leetcode.com/problems/pacific-atlantic-water-flow/solutions/4187974/python-bfs/\nThank you @nanzhuangdalao\n\n# Code\n```\nclass Solution:\n\n def __init__(self):\n\n self.heights = None\n self.row_l = None\n self.row_r = None\n self.directions = ((1, 0), (-1, 0), (0, 1), (0, -1))\n\n def bfs(self, queue: Deque) -> Set:\n\n seen = set()\n\n while queue:\n\n x, y = queue.popleft()\n\n seen.add((x,y))\n\n for dx, dy in self.directions:\n\n new_x = x + dx\n new_y = y + dy\n\n if (0 <= new_x < self.row_l) and (0 <= new_y < self.col_l) and (self.heights[new_x][new_y] >= self.heights[x][y]):\n\n if (new_x, new_y) not in seen:\n queue.append((new_x, new_y))\n\n return seen\n\n\n def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:\n \n self.heights = heights\n self.row_l = len(heights)\n self.col_l = len(heights[0])\n\n p = deque() # pacific\n a = deque() # atlantic\n\n for i in range(self.row_l):\n p.append((i, 0))\n a.append((i, self.col_l - 1))\n \n for j in range(self.col_l):\n p.append((0, j))\n a.append((self.row_l - 1, j))\n\n to_pacific = self.bfs(p)\n to_atlantic = self.bfs(a)\n\n return list(to_pacific.intersection(to_atlantic))\n\n\n \n``` | 1 | There is an `m x n` rectangular island that borders both the **Pacific Ocean** and **Atlantic Ocean**. The **Pacific Ocean** touches the island's left and top edges, and the **Atlantic Ocean** touches the island's right and bottom edges.
The island is partitioned into a grid of square cells. You are given an `m x n` integer matrix `heights` where `heights[r][c]` represents the **height above sea level** of the cell at coordinate `(r, c)`.
The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is **less than or equal to** the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.
Return _a **2D list** of grid coordinates_ `result` _where_ `result[i] = [ri, ci]` _denotes that rain water can flow from cell_ `(ri, ci)` _to **both** the Pacific and Atlantic oceans_.
**Example 1:**
**Input:** heights = \[\[1,2,2,3,5\],\[3,2,3,4,4\],\[2,4,5,3,1\],\[6,7,1,4,5\],\[5,1,1,2,4\]\]
**Output:** \[\[0,4\],\[1,3\],\[1,4\],\[2,2\],\[3,0\],\[3,1\],\[4,0\]\]
**Explanation:** The following cells can flow to the Pacific and Atlantic oceans, as shown below:
\[0,4\]: \[0,4\] -> Pacific Ocean
\[0,4\] -> Atlantic Ocean
\[1,3\]: \[1,3\] -> \[0,3\] -> Pacific Ocean
\[1,3\] -> \[1,4\] -> Atlantic Ocean
\[1,4\]: \[1,4\] -> \[1,3\] -> \[0,3\] -> Pacific Ocean
\[1,4\] -> Atlantic Ocean
\[2,2\]: \[2,2\] -> \[1,2\] -> \[0,2\] -> Pacific Ocean
\[2,2\] -> \[2,3\] -> \[2,4\] -> Atlantic Ocean
\[3,0\]: \[3,0\] -> Pacific Ocean
\[3,0\] -> \[4,0\] -> Atlantic Ocean
\[3,1\]: \[3,1\] -> \[3,0\] -> Pacific Ocean
\[3,1\] -> \[4,1\] -> Atlantic Ocean
\[4,0\]: \[4,0\] -> Pacific Ocean
\[4,0\] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.
**Example 2:**
**Input:** heights = \[\[1\]\]
**Output:** \[\[0,0\]\]
**Explanation:** The water can flow from the only cell to the Pacific and Atlantic oceans.
**Constraints:**
* `m == heights.length`
* `n == heights[r].length`
* `1 <= m, n <= 200`
* `0 <= heights[r][c] <= 105` | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.