title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python3 Beats 94% | most-visited-sector-in-a-circular-track | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mostVisited(self, n: int, rounds: List[int]) -> List[int]:\n if rounds[0]<=rounds[-1]:\n return list(range(rounds[0],rounds[-1]+1))\n else:\n return list(range(1,rounds[-1]+1))+list(range(rounds[0],n+1))\n``` | 0 | Given an integer `n` and an integer array `rounds`. We have a circular track which consists of `n` sectors labeled from `1` to `n`. A marathon will be held on this track, the marathon consists of `m` rounds. The `ith` round starts at sector `rounds[i - 1]` and ends at sector `rounds[i]`. For example, round 1 starts at sector `rounds[0]` and ends at sector `rounds[1]`
Return _an array of the most visited sectors_ sorted in **ascending** order.
Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).
**Example 1:**
**Input:** n = 4, rounds = \[1,3,1,2\]
**Output:** \[1,2\]
**Explanation:** The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.
**Example 2:**
**Input:** n = 2, rounds = \[2,1,2,1,2,1,2,1,2\]
**Output:** \[2\]
**Example 3:**
**Input:** n = 7, rounds = \[1,3,5,7\]
**Output:** \[1,2,3,4,5,6,7\]
**Constraints:**
* `2 <= n <= 100`
* `1 <= m <= 100`
* `rounds.length == m + 1`
* `1 <= rounds[i] <= n`
* `rounds[i] != rounds[i + 1]` for `0 <= i < m` | Imagine that startTime[i] and endTime[i] form an interval (i.e. [startTime[i], endTime[i]]). The answer is how many times the queryTime laid in those mentioned intervals. |
C++/Java Frequency Count O(n+m) vs Python sort 1 line||3ms Beats 100% | maximum-number-of-coins-you-can-get | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse frequency count instead of sorting.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince you can decide each turn for which triple are choosen.\nLet Bob pick the min n/3 piles. Alice & you choose the max 2n/3 piles alternatively according to the descending order.\n\nLet me explain by using test case `piles=[9,8,7,6,5,1,2,3,4]`.\n\nLet Bob pick the min 3 piles `[1,2,3]`. The rest of piles is in descending order \n```\n[9,8,7,6,5,4]\n```\nAlice & you pick piles in alternative way. So,\n`ans=8+6+4=18`\n\nFor comparion, an implementation using sort also done which is easy to understand. The python 1 line code is also provided in the same way. Since Python has a very slow loop speed, it is not suggested to use frequency count method; sort method is suitable for Python users!!!!!\n\n|C++ implementation|Freq count| Sort |\n|---|---|---|\n|Elapsed time|32ms|102ms |\n|Time complexity|$O(n+m)$|$O(n \\log n)$\n\nFor curiosity, I implement the same algorithm in Java. It took only 3ms. Leetcode\'s C/ C++ is much slower.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n+m)$$ where $m=\\max(piles)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(10001)$$\n# C++ 32 ms Beats 100.00%|| Java 3ms Beats 100.00%\n```C++ []\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n int n=piles.size(), M=0;\n int freq[10001]={0};\n #pragma unroll\n for(int x: piles){\n freq[x]++;\n M=max(M, x);\n }\n // cout<<M<<endl;\n int ans=0, count=0, x;\n bool alice=0;\n #pragma unroll\n for(x=M; count<n/3; x--){\n if (freq[x]>0){\n int f=freq[x]+alice;\n int f0=f>>1;\n count+=f0;\n ans+=f0*x;\n alice=(f&1)?1:0;//Last one taken by Alice or you\n }\n }\n ans-=(count-n/3)*(x+1);//if count>n/3 subtract some piles\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n```Java []\nclass Solution {\n public int maxCoins(int[] piles) {\n int n=piles.length, M=0;\n int [] freq=new int[10001];\n // Arrays.fill(freq, 0);\n for (int x : piles){\n freq[x]++;\n M=Math.max(M, x);\n }\n int ans=0, count=0, x=0, alice=0, k=n/3;\n for(x=M; count<k; x--){\n if (freq[x]>0){\n int f=freq[x]+alice;\n int f0=f>>1;\n count+=f0;\n ans+=f0*x;\n alice=(f%2==1)?1:0;\n }\n }\n ans-=(count-k)*(x+1);//if count>n/3 subtract some piles\n return ans;\n }\n}\n```\n\n\n\n```\n# code using sort||Python 503ms Beats 94.16%\n```Python []\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n return sum(sorted(piles, reverse=True)[1:len(piles)*2//3:2])\n \n```\n```C++ []\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n int n=piles.size();\n sort(piles.rbegin(), piles.rend());\n int ans=0;\n int k=n/3*2;\n #pragma unroll\n for(int i=1; i<k; i+=2)\n ans+=piles[i];\n return ans;\n }\n};\n```\n | 11 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
😎🚀 Beats 98% | Detailed Explaination 🔥🦅 | C++ | JAVA | PYTHON | JS | maximum-number-of-coins-you-can-get | 1 | 1 | # Intuition\nUPVOTE IF YOU FOUND THIS HELPFUL !!!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. SORT THE PILES VECTOR IN DECREASING ORDER.\n2. WE CAN TAKE ANY THREE NO.S SO HERE WE TAKE TWO LARGE NUMBERS FOR ALICE AND YOU, AND 1 SMALL NUMBER FOR BOB WHICH IS FROM ENDPOINT OF PILES VECTOR.\n3. FOR ALICE, JUST MOVE FORWARD THE POINTER i BY 1\n4. FOR YOU, ADD THE VALUE TO ANSWER\n5. FOR BOB , DO j--\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n int ans = 0;\n sort(piles.begin(),piles.end(),greater<int>());\n\n int i = 0, j = piles.size() - 1;\n while(i < j)\n {\n i++; // Alice\n ans += piles[i++]; // You\n j--; // Bob\n }\n return ans;\n }\n};\n``` | 3 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
【Video】Give me 4 minutes - How we think about a solution | maximum-number-of-coins-you-can-get | 1 | 1 | # Intuition\nSort input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/HPzfCHfWPlY\n\n\u25A0 Timeline\u3000of the video\n`0:04` Two key points to solve this question\n`1:46` Demonstrate how it works\n`3:17` Coding\n`4:14` Time Complexity and Space Complexity\n`4:33` Summary of the algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,196\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n## How we think about a solution\n\nKey points to solve this question are as follows:\n\n---\n\n\u2B50\uFE0F Points\n\n- piles.length % 3 == 0\n- Bob will get all coins from index 0 to total number of piles / 3\n\n---\n- piles.length % 3 == 0\n\nThis means we can divide total piles of coins by `3`.\n\n- Bob will get all coins from index 0 to total number of piles / 3\n\nLet\'s say\n\n```\nInput = [1,2,3,4,5,6,7,8,9]\n```\nEveryone has `3` chances to get coins, because total number of piles is `9` and every time `3` piles are taken. \n\nAnd the description says\n\n---\n- Alice will pick the pile with the maximum number of coins.\n- You will pick the next pile with the maximum number of coins.\n- Bob will pick the last pile.\n\n---\nTo get maximum number of coins, we should choose `2` piles from the last and `1` pile from the beginning, so that you will get the maximum number of coins with following the rules.\n\nThe first round should be\n```\n[1,8,9]\n\nAlice will get 9\nYou will get 8\nBob will get 1\n```\nBob will not take `7`, because if he takes `7`, Alice will get `6` and you will get `5` in the second around which is not maximum number of coins. \n\nLook at the second round case where Bob doesn\'t take `7`. You will get `6` instead of `5`.\n\nThe second round should be\n```\n[2,6,7]\n\n\nAlice will get 7\nYou will get 6\nBob will get 2\n```\nThe third round should be\n```\n[3,4,5]\n\nAlice will get 5\nYou will get 4\nBob will get 3\n```\n\nYou will get\n```\nOuput: 18 (= 8 + 6 + 4) \n```\nBob will get `1`, `2` and `3` coins.\n\nFrom the idea above, in the solution code, we can start from index `3`(in this case) which is `4` coins and every time we increment the index by `2` on each iteration. Because we know that Bob will get `1`,`2` and `3` coins, so from coin `4` to coin `9`, Alice will get the maximum number of coins and you will get the second maximum number of coins in every two pair `[4,5]`, `[6,7]`, `[8,9]`.\n\nThis is an image of iteration in the solution code. Start from `index 3` in this case.\n```\n[1,2,3,4,5,6,7,8,9] (The first round)\n b b b \u2191 a\n[1,2,3,4,5,6,7,8,9] (The second round)\n b b b y a \u2191 a \n[1,2,3,4,5,6,7,8,9] (The third round)\n b b b y a y a \u2191 a\n\na: Alice\ny: You\nb: Bob \n\u2191: a current number you get\n```\nThe last important thing is that we should sort input array, so that we can easily take the maximum number of coins and minimum number of coins from input array.\n\n---\n\n\u2B50\uFE0F Points\n\nSort input array before interation\n\n---\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n### Algorithm Overview\n\n1. Sort input array\n2. Start index from `len(piles) // 3` and increment index number by `2`\n\n### Detailed Explanation:\n\n**1. Sort the input list**\n```python\npiles.sort()\n```\n\n**Explanation:**\nThis line sorts the `piles` list in ascending order. Sorting is necessary to ensure that the piles with the highest number of coins are considered later in the iteration.\n\n**2. Initialize the result variable**\n```python\nres = 0\n```\n\n**Explanation:**\nHere, a variable `res` is initialized to zero. This variable will be used to keep track of the total sum of coins.\n\n**3. Iterate through piles starting from one-third of the length**\n```python\nfor i in range(len(piles) // 3, len(piles), 2):\n res += piles[i]\n```\n\n**Explanation:**\nThis `for` loop is used to iterate through the `piles` list. It starts from the index corresponding to one-third of the length of the list (`len(piles) // 3`). The loop increments the index by `2` in each iteration, effectively selecting every second pile.\n\nIn each iteration of the loop, the value at the current index (`piles[i]`) is added to the `res` variable. This is done to accumulate the total sum of coins from the selected piles.\n\n**4. Return the final result**\n```python\nreturn res\n```\n\n**Explanation:**\nFinally, the function returns the total sum of coins (`res`) as the result.\n\nIn summary, the algorithm first sorts the `piles` list, then iterates through a subset of the sorted list (every second element starting from one-third of the way through), adding the values at each selected index to the result. The final result is the total sum of coins from the selected piles.\n\n\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log n)$$ or $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n res = 0\n\n for i in range(len(piles) // 3, len(piles), 2):\n res += piles[i]\n \n return res\n```\n```javascript []\nvar maxCoins = function(piles) {\n piles.sort((a, b) => a - b);\n let res = 0;\n\n for (let i = Math.floor(piles.length / 3); i < piles.length; i += 2) {\n res += piles[i];\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int maxCoins(int[] piles) {\n Arrays.sort(piles);\n int res = 0;\n\n for (int i = piles.length / 3; i < piles.length; i += 2) {\n res += piles[i];\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n sort(piles.begin(), piles.end());\n int res = 0;\n\n for (int i = piles.size() / 3; i < piles.size(); i += 2) {\n res += piles[i];\n }\n\n return res; \n }\n};\n```\n\n\n---\n\n# Bonus code\n\nYou can solve this question with `deque`. `pop` is to get the largest number in input array and `popleft` is to get the smallest number in input array.\n\nThe first `pop` is for Alice and the second `pop` is for you. `popleft` is for Bob.\n\nTime compelxity is $$O(nlogn)$$\nSapce compelxity is $$O(n)$$\n\n```python []\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n q = deque(piles)\n res = 0\n\n while q:\n q.pop() # For Alice\n res += q.pop() # For you\n q.popleft() # For Bob\n \n return res\n```\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/sum-of-absolute-differences-in-a-sorted-array/solutions/4329227/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bwQh44GWME8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve this question\n`1:56` Calculate left total\n`6:32` Calculate right total\n`11:12` Create answers\n`11:51` Coding\n`14:14` Time Complexity and Space Complexity\n`14:39` Summary of the algorithm with my solution code\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/arithmetic-subarrays/solutions/4321453/video-give-me-6-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bE6YT9q16K8\n\n\u25A0 Timeline of the video\n\n`0:04` What does the formula mean?\n`1:46` Demonstrate how it works\n`3:39` Coding\n`5:40` Time Complexity and Space Complexity\n`6:06` Summary of the algorithm with my solution code\n | 42 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
Simple Python implementation | maximum-number-of-coins-you-can-get | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to get the sum of coins that we can pick\nFor each Iteration, we get 1 min pile and 2 max piles to maximize the coins that we pick. \n\n# Approach\n1. Sort the piles array\n2. Create a subarray of all the coins that we can pick\n3. Start picking coins from the 2nd last coin pile (2nd largest coin pile)\n4. Keep picking the 2nd largest coin pile with a step of -2\n5. Ignore the coins that Bob will pick. (N//3)\n6. The picking process will end when there are no more piles to pick. \n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n return sum(piles[-2:(len(piles)//3)-1:-2])\n \n``` | 3 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
python3 Solution | maximum-number-of-coins-you-can-get | 0 | 1 | \n```\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n q=collections.deque(piles)\n ans=0\n while len(q)>0:\n q.popleft()\n q.pop()\n ans+=q[-1]\n q.pop()\n return ans \n``` | 3 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | maximum-number-of-coins-you-can-get | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Greedy Simulation with Deque)***\n1. Sort the `piles` in ascending order as we want to optimize the number of coins we can get.\n1. Utilize a deque (double-ended queue) for efficient removal of the maximum and minimum elements.\n1. Transfer elements from `piles` to the deque.\n1. During the picking process:\n - Alice always picks the maximum (from the back of deque) and discards it.\n - \'Us\' (the algorithm) pick the maximum from the remaining elements and accumulate coins.\n - Bob always picks the minimum (from the front of deque) and discards it.\n - Accumulate the total coins we obtained while following this strategy.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n sort(piles.begin(), piles.end()); // Sort the piles in ascending order\n deque<int> queue;\n \n // Push elements from piles to a deque for easy front and back access\n for (int num : piles) {\n queue.push_back(num);\n }\n \n int ans = 0;\n while (!queue.empty()) {\n queue.pop_back(); // Alice picks the maximum (back of deque)\n ans += queue.back(); // We (as \'us\') pick the maximum from the remaining elements\n queue.pop_back(); // Remove the maximum element after picking it\n queue.pop_front(); // Bob picks the minimum (front of deque)\n }\n \n return ans; // Return the total coins we accumulated\n }\n};\n\n\n\n```\n```C []\nvoid sort(int arr[], int n) {\n // Sort the array in ascending order\n // Implementation of sorting algorithm here\n}\n\nint maxCoins(int piles[], int n) {\n sort(piles, n);\n\n // Initializing pointers for Alice, Bob, and us\n int i = n - 2; // Alice\n int j = 0; // Bob\n int k = n - 1; // Us\n\n int ans = 0;\n while (i > j) {\n ans += piles[k]; // Collecting coins for us\n k -= 2;\n i--;\n j++;\n }\n\n return ans;\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int maxCoins(int[] piles) {\n Arrays.sort(piles);\n ArrayDeque<Integer> queue = new ArrayDeque();\n for (int num : piles) {\n queue.addLast(num);\n }\n \n int ans = 0;\n while (!queue.isEmpty()) {\n queue.removeLast(); // alice\n ans += queue.removeLast(); // us\n queue.removeFirst(); // bob\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n queue = deque(piles)\n ans = 0\n while queue:\n queue.pop() # alice\n ans += queue.pop() # us\n queue.popleft() # bob\n\n return ans\n\n\n```\n```javascript []\nvar maxCoins = function(piles) {\n piles.sort((a, b) => a - b);\n let queue = [];\n piles.forEach(num => {\n queue.push(num);\n });\n \n let ans = 0;\n while (queue.length > 0) {\n queue.pop(); // Alice\n ans += queue[queue.length - 1]; // Us\n queue.pop();\n queue.shift(); // Bob\n }\n \n return ans;\n};\n\n```\n\n---\n\n\n#### ***Approach 2(Sort)***\n1. **Sorting:**\n - The `piles` vector is sorted in ascending order, which allows for an optimal selection strategy.\n1. **Iteration and Accumulation:**\n - The loop starts from the index that represents 1/3rd of the total elements in the piles. This point ensures Alice gets the optimal selection.\n - It continues till the end of the piles, considering every alternate 2nd element.\n - The coins from the selected piles are accumulated in the `ans` variable.\n1. **Return:**\n - The accumulated sum of coins (`ans`) is returned as the final result.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or $$O(logn)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to calculate the maximum number of coins that can be obtained\n int maxCoins(vector<int>& piles) {\n // Sort the piles in ascending order to get the optimal selection pattern\n sort(piles.begin(), piles.end());\n int ans = 0; // Initialize the answer variable\n \n // Start from the index which is 1/3rd of the total elements until the end of the piles\n // Increment the index by 2 in each iteration to consider every alternate 2nd element\n for (int i = piles.size() / 3; i < piles.size(); i += 2) {\n ans += piles[i]; // Accumulate the coins from the selected piles\n }\n \n return ans; // Return the total number of collected coins\n }\n};\n\n\n\n```\n```C []\nint maxCoins(int* piles, int pilesSize) {\n // Sort the piles in ascending order to get the optimal selection pattern\n qsort(piles, pilesSize, sizeof(int), compare);\n int ans = 0; // Initialize the answer variable\n\n // Start from the index which is 1/3rd of the total elements until the end of the piles\n // Increment the index by 2 in each iteration to consider every alternate 2nd element\n for (int i = pilesSize / 3; i < pilesSize; i += 2) {\n ans += piles[i]; // Accumulate the coins from the selected piles\n }\n\n return ans; // Return the total number of collected coins\n}\n\n// Function to compare elements for sorting\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int maxCoins(int[] piles) {\n Arrays.sort(piles);\n int ans = 0;\n \n for (int i = piles.length / 3; i < piles.length; i += 2) {\n ans += piles[i];\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n ans = 0\n \n for i in range(len(piles) // 3, len(piles), 2):\n ans += piles[i]\n \n return ans\n\n\n```\n```javascript []\nvar maxCoins = function(piles) {\n piles.sort((a, b) => a - b); // Sort the piles in ascending order\n let ans = 0; // Initialize the answer variable\n\n // Start from the index which is 1/3rd of the total elements until the end of the piles\n // Increment the index by 2 in each iteration to consider every alternate 2nd element\n for (let i = Math.floor(piles.length / 3); i < piles.length; i += 2) {\n ans += piles[i]; // Accumulate the coins from the selected piles\n }\n\n return ans; // Return the total number of collected coins\n};\n\n\n```\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
Linear Solution in Python3, using counting sort | maximum-number-of-coins-you-can-get | 0 | 1 | # Approach\nThe optimal for *us* could be the sum of **the second most coins of each run**, thus using greedy.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(m)$$, where $$m$$ is `max(piles)`\n\n# Code\n```\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n cnt = [0] * (max(piles) + 1)\n s, ans = len(piles), 0\n # count pile of coins\n for p in piles:\n cnt[p] += 1\n i, j = 0, len(cnt) - 1\n while s:\n # find the next available pile for the most and the least, repectively\n while not cnt[j]:\n j -= 1\n while not cnt[i]:\n i += 1\n if cnt[j] >= 2:\n # there are 2 piles of max coins, grab it as Alice does since the second most is also there\n ans += j\n cnt[j] -= 2\n elif cnt[j] == 1:\n # there\'s only 1 pile of max coins which belongs to Alice, proceed to find the second most\n cnt[j] -= 1\n while not cnt[j]:\n j -= 1\n ans += j\n cnt[j] -= 1\n # i, as the minimum coins, is always for Bob\n cnt[i] -= 1\n s -= 3\n\n return ans\n``` | 2 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
Simple python solution | maximum-number-of-coins-you-can-get | 0 | 1 | # Code\n```\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n sum=0\n piles.sort()\n for i in range(len(piles)//3):\n sum+=piles[-i*2-2]\n return sum\n``` | 2 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
Easy Code to Understand | maximum-number-of-coins-you-can-get | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo maximize the sum of the trio of numbers - the greatest, second greatest, and smallest, we need to sort the piles. Assume Alice takes the greatest number, you take the second greatest, and Bob is left with the smallest.\n\nIn other words, we aim to exploit Bob by giving him the smallest piles possible. The order in which we pick the piles doesn\'t matter, as per the question.\n\nConsider the example with piles = [9, 8, 7, 6, 5, 1, 2, 3, 4]:\nAfter sorting, [1, 2, 3, 4, 5, 6, 7, 8, 9], and n/3 is 3.\n\nThe optimal pattern is:\nBob(Smallest): 1 2 3\nAlice(Largest): 5 7 9\nYou(Second Largest): 4 6 8 => Your total = 18 (answer)\n\nThe pattern is based on n/3, where \'S\' denotes the smallest, \'M\' denotes the second smallest, and \'L\' denotes the largest. The sequence is S S S M L M L M L, as this arrangement yields the maximum value for your coin pile.\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(1)\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n sort(piles.begin(), piles.end());\n int sum=0;\n int pair= piles.size()/3;\n for(int i=pair;i<piles.size();i+=2)\n {\n sum+=piles[i];\n }\n return sum;\n }\n};\n```\n```python []\nclass Solution:\n def maxCoins(self, piles):\n piles.sort()\n total_coins = 0\n pair = len(piles) // 3\n for i in range(pair, len(piles), 2):\n total_coins += piles[i]\n return total_coins\n\n```\n```java []\npublic class Solution {\n public int maxCoins(int[] piles) {\n Arrays.sort(piles);\n int totalCoins = 0;\n int pair = piles.length / 3;\n for (int i = pair; i < piles.length; i += 2) {\n totalCoins += piles[i];\n }\n return totalCoins;\n }\n}\n\n```\n\n\n | 16 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
Clean and beginner-friendly 6 line greedy solution | maximum-number-of-coins-you-can-get | 0 | 1 | # Intuition\nNotice that Bob would only take the smallest amount of coins.\nSo after sorting, the first n piles of coins would be taken by Bob.\nWe can then simplify the problem, as the other piles of coins are only shared between Amy and us.\nSince Amy always gets the most coins, we could only get the second-largest piles in every duplet.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn), sorting is used\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1), no extra space used\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n piles.sort()\n bob = len(piles)//3\n res = 0\n for x in range(bob, len(piles), 2):\n res += piles[x]\n return res\n``` | 1 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
🤦♂️Shortest Code simple approach... check it...🤦♂️... | maximum-number-of-coins-you-can-get | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxCoins(vector<int>& piles) {\n sort(piles.begin(),piles.end());\n int i=0,j=piles.size()-1;\n int sum=0;\n while(i<j)\n {\n sum=sum+piles[j-1];\n j=j-2;\n i++;\n }\n return sum;\n \n }\n};\n``` | 1 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
faster than 99% of python solutions||sorting||greedy||array|| | maximum-number-of-coins-you-can-get | 0 | 1 | **Problem:**\n\nYou are playing a game with your friends Alice and Bob. There are 3n piles of coins of varying size. In each step of the game, you will choose any 3 piles of coins. Alice will then pick the pile with the maximum number of coins, you will pick the next pile with the maximum number of coins, and Bob will pick the last pile. This process will continue until there are no more piles of coins left. Your goal is to maximize the number of coins you can collect.\n\n**Intuition:**\n\nThe key insight to this problem is that you can always choose the three piles with the largest number of coins. This is because Alice will always pick the pile with the largest number of coins, so you don\'t need to worry about her taking one of the other piles.\n\n**Approach:**\n\nTo solve this problem, we can sort the piles of coins in descending order. Then, we can iterate through the piles in pairs, picking the two piles with the largest number of coins. This will ensure that we always pick the three piles with the largest number of coins, and we will therefore maximize the number of coins we can collect.\n\n**Complexity:**\n\nThe time complexity of this solution is O(n log n), where n is the number of piles of coins. This is because we need to sort the piles of coins, and sorting takes O(n log n) time. The space complexity of this solution is O(1), where n is the number of piles of coins. This is because we do not need to allocate any additional memory besides the memory needed to store the input array.\n\n**Code:**\n\nThe provided code implements the described approach. It first sorts the piles of coins in descending order using the `sort()` method. Then, it iterates through the piles in pairs and adds the value of the second pile to a running total. Finally, it returns the running total.\n\nI hope this explanation is helpful. Please let me know if you have any other questions.\n\n```\nclass Solution:\n def maxCoins(self, piles: List[int]) -> int:\n \n piles.sort()\n i = 0\n k = len(piles) - 2\n total = 0\n while(i < k): \n total += piles[k]\n i += 1\n k -= 2\n return total\n \n \n```\n\n\n\n | 1 | There are `3n` piles of coins of varying size, you and your friends will take piles of coins as follows:
* In each step, you will choose **any** `3` piles of coins (not necessarily consecutive).
* Of your choice, Alice will pick the pile with the maximum number of coins.
* You will pick the next pile with the maximum number of coins.
* Your friend Bob will pick the last pile.
* Repeat until there are no more piles of coins.
Given an array of integers `piles` where `piles[i]` is the number of coins in the `ith` pile.
Return the maximum number of coins that you can have.
**Example 1:**
**Input:** piles = \[2,4,1,2,7,8\]
**Output:** 9
**Explanation:** Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with **7** coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with **2** coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, **2**, 8), (2, **4**, 7) you only get 2 + 4 = 6 coins which is not optimal.
**Example 2:**
**Input:** piles = \[2,4,5\]
**Output:** 4
**Example 3:**
**Input:** piles = \[9,8,7,6,5,1,2,3,4\]
**Output:** 18
**Constraints:**
* `3 <= piles.length <= 105`
* `piles.length % 3 == 0`
* `1 <= piles[i] <= 104` | Store each word and their relative position. Then, sort them by length of words in case of tie by their original order. |
Ranges Accounting | find-latest-group-of-size-m | 0 | 1 | # Approach\nFirst of all we make the task opposite - we assume having string of ones and go through ```arr``` from back to begin.\nWe have ```ranges```, firstly consisted of one range [1, n], representing ranges of ones. \nThen step by step we put zeros in our string which split ranges of ones into slaller ranges. After each split/reduction we calculate length of new ranges and compare with ```m```.\n\n# Complexity\n- Time complexity: $$O(n*log(n))$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nBEGIN = 0\nEND = 1\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n n = len(arr)\n if m == n:\n return n\n\n ranges = [[1, n]]\n for i in range(-1, -n-1, -1):\n rangeInd = None\n lInd, rInd = 0, len(ranges)-1\n while lInd <= rInd:\n mInd = lInd + (rInd-lInd)//2\n if ranges[mInd][BEGIN] <= arr[i]:\n rangeInd = mInd\n lInd = mInd + 1\n else:\n rInd = mInd - 1\n\n if arr[i] == ranges[rangeInd][BEGIN] == ranges[rangeInd][END]:\n del ranges[rangeInd]\n elif arr[i] == ranges[rangeInd][BEGIN]:\n ranges[rangeInd][BEGIN] += 1\n if ranges[rangeInd][END] - ranges[rangeInd][BEGIN] + 1 == m:\n return n - abs(i)\n elif arr[i] == ranges[rangeInd][END]:\n ranges[rangeInd][END] -= 1\n if ranges[rangeInd][END] - ranges[rangeInd][BEGIN] + 1 == m:\n return n - abs(i)\n else:\n end = ranges[rangeInd][END]\n ranges[rangeInd][END] = arr[i]-1\n ranges.insert(rangeInd+1, [arr[i]+1, end])\n if ranges[rangeInd][END] - ranges[rangeInd][BEGIN] + 1 == m or \\\n ranges[rangeInd+1][END] - ranges[rangeInd+1][BEGIN] + 1 == m:\n return n - abs(i)\n \n return -1\n``` | 1 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
Ranges Accounting | find-latest-group-of-size-m | 0 | 1 | # Approach\nFirst of all we make the task opposite - we assume having string of ones and go through ```arr``` from back to begin.\nWe have ```ranges```, firstly consisted of one range [1, n], representing ranges of ones. \nThen step by step we put zeros in our string which split ranges of ones into slaller ranges. After each split/reduction we calculate length of new ranges and compare with ```m```.\n\n# Complexity\n- Time complexity: $$O(n*log(n))$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nBEGIN = 0\nEND = 1\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n n = len(arr)\n if m == n:\n return n\n\n ranges = [[1, n]]\n for i in range(-1, -n-1, -1):\n rangeInd = None\n lInd, rInd = 0, len(ranges)-1\n while lInd <= rInd:\n mInd = lInd + (rInd-lInd)//2\n if ranges[mInd][BEGIN] <= arr[i]:\n rangeInd = mInd\n lInd = mInd + 1\n else:\n rInd = mInd - 1\n\n if arr[i] == ranges[rangeInd][BEGIN] == ranges[rangeInd][END]:\n del ranges[rangeInd]\n elif arr[i] == ranges[rangeInd][BEGIN]:\n ranges[rangeInd][BEGIN] += 1\n if ranges[rangeInd][END] - ranges[rangeInd][BEGIN] + 1 == m:\n return n - abs(i)\n elif arr[i] == ranges[rangeInd][END]:\n ranges[rangeInd][END] -= 1\n if ranges[rangeInd][END] - ranges[rangeInd][BEGIN] + 1 == m:\n return n - abs(i)\n else:\n end = ranges[rangeInd][END]\n ranges[rangeInd][END] = arr[i]-1\n ranges.insert(rangeInd+1, [arr[i]+1, end])\n if ranges[rangeInd][END] - ranges[rangeInd][BEGIN] + 1 == m or \\\n ranges[rangeInd+1][END] - ranges[rangeInd+1][BEGIN] + 1 == m:\n return n - abs(i)\n \n return -1\n``` | 1 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
Union Find || Python | find-latest-group-of-size-m | 0 | 1 | ```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n n = len(arr)\n parent = {index:index for index in range(1, n+ 1)}\n explored,size = [0]*(n + 1), [0]*(n+1)\n ans, self.cnt = -1, 0\n def find(x):\n if x == parent[x]:return x\n parent[x] = find(parent[x])\n return parent[x]\n \n def union(a, b):\n v,u = find(b),find(a)\n if u != v:\n self.cnt -= size[v] == m\n parent[u] = v\n size[v] += size[u]\n \n for index in range(n):\n size[arr[index]], explored[arr[index]] = 1, 1\n if arr[index] - 1 > 0 and explored[arr[index]-1]:union(arr[index], arr[index]-1)\n if arr[index] + 1 <= n and explored[arr[index]+1]:union(arr[index], arr[index] + 1) \n u = find(arr[index])\n self.cnt += size[u] == m\n ans = index + 1 if self.cnt >= 1 else ans\n \n return ans\n \n \n \n \n \n``` | 0 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
Union Find || Python | find-latest-group-of-size-m | 0 | 1 | ```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n n = len(arr)\n parent = {index:index for index in range(1, n+ 1)}\n explored,size = [0]*(n + 1), [0]*(n+1)\n ans, self.cnt = -1, 0\n def find(x):\n if x == parent[x]:return x\n parent[x] = find(parent[x])\n return parent[x]\n \n def union(a, b):\n v,u = find(b),find(a)\n if u != v:\n self.cnt -= size[v] == m\n parent[u] = v\n size[v] += size[u]\n \n for index in range(n):\n size[arr[index]], explored[arr[index]] = 1, 1\n if arr[index] - 1 > 0 and explored[arr[index]-1]:union(arr[index], arr[index]-1)\n if arr[index] + 1 <= n and explored[arr[index]+1]:union(arr[index], arr[index] + 1) \n u = find(arr[index])\n self.cnt += size[u] == m\n ans = index + 1 if self.cnt >= 1 else ans\n \n return ans\n \n \n \n \n \n``` | 0 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
Python, no fancy techniques, simply dictionary. | find-latest-group-of-size-m | 0 | 1 | # Code\n```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n\n # Let\'s put all the seen intervals into a dict. \n # We put both ways of an interval into the dict so we can\n # find the intervals from both end in O(1) time. \n # We keep track of how many intervals have length m \n # separately.\n\n ms = 0 # number of intervals with length m\n ans = -1\n intervals = {} # we store intervals in both direction,\n # e.g., to store interval [1,3], \n # we set "intervals[1] = 3, intervals[3] = 1"\n for i, num in enumerate(arr):\n # update adjacent intervals\n if num - 1 not in intervals and num + 1 not in intervals:\n # create new interval\n intervals[num] = num\n length = 1\n elif num - 1 not in intervals: # num + (num+1:)\n r = intervals[num+1]\n intervals[num] = r\n intervals[r] = num\n if m == r - num:\n ms -= 1\n length = r - num + 1\n elif num + 1 not in intervals: # (:num-1) + num\n l = intervals[num-1]\n intervals[num] = l\n intervals[l] = num\n if m == num - l:\n ms -= 1\n length = num - l + 1\n else: # (:num-1) + num + (num+1:)\n l = intervals[num-1]\n r = intervals[num+1]\n intervals[l] = r\n intervals[r] = l\n if m == r - num:\n ms -= 1\n if m == num - l:\n ms -= 1\n length = r - l + 1\n # update ms\n if length == m:\n ms += 1\n if ms > 0:\n ans = i + 1\n return ans\n \n\n\n\n \n\n \n \n\n\n``` | 0 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
Python, no fancy techniques, simply dictionary. | find-latest-group-of-size-m | 0 | 1 | # Code\n```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n\n # Let\'s put all the seen intervals into a dict. \n # We put both ways of an interval into the dict so we can\n # find the intervals from both end in O(1) time. \n # We keep track of how many intervals have length m \n # separately.\n\n ms = 0 # number of intervals with length m\n ans = -1\n intervals = {} # we store intervals in both direction,\n # e.g., to store interval [1,3], \n # we set "intervals[1] = 3, intervals[3] = 1"\n for i, num in enumerate(arr):\n # update adjacent intervals\n if num - 1 not in intervals and num + 1 not in intervals:\n # create new interval\n intervals[num] = num\n length = 1\n elif num - 1 not in intervals: # num + (num+1:)\n r = intervals[num+1]\n intervals[num] = r\n intervals[r] = num\n if m == r - num:\n ms -= 1\n length = r - num + 1\n elif num + 1 not in intervals: # (:num-1) + num\n l = intervals[num-1]\n intervals[num] = l\n intervals[l] = num\n if m == num - l:\n ms -= 1\n length = num - l + 1\n else: # (:num-1) + num + (num+1:)\n l = intervals[num-1]\n r = intervals[num+1]\n intervals[l] = r\n intervals[r] = l\n if m == r - num:\n ms -= 1\n if m == num - l:\n ms -= 1\n length = r - l + 1\n # update ms\n if length == m:\n ms += 1\n if ms > 0:\n ans = i + 1\n return ans\n \n\n\n\n \n\n \n \n\n\n``` | 0 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
Python Recursion | find-latest-group-of-size-m | 0 | 1 | In this approach algorithm starts from the end - binary string is full of ones. Iterating over list from the last index sets bit to 0 and divide binary string into two parts. Alghorithm checks length of these parts and if they are m length return current step. In the other case continues recurrence call.\n\n\n# Code\n\n class Solution:\n def __init__(self):\n self.arr = []\n self.m = 0\n\n def check(self, l, p, i):\n p_res = -1\n l_res = -1\n if l <= p:\n if self.arr[i] >= l and self.arr[i] <= p:\n left = self.arr[i] - l\n right = p - self.arr[i]\n if (left == self.m or right == self.m):\n return i\n if left > self.m:\n l_res = self.check(l, self.arr[i] - 1, i - 1)\n if right > self.m:\n p_res = self.check(self.arr[i] + 1, p, i - 1)\n if l_res or p_res:\n return p_res if p_res > l_res else l_res\n else:\n l_res = self.check(l, p, i - 1)\n if l_res != -1:\n return l_res\n\n return -1\n\n def findLatestStep(self, arr, m):\n self.arr = arr\n self.m = m\n if m == len(arr):\n return len(arr)\n res = self.check(1, len(arr), len(arr) - 1)\n return res\n``` | 0 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
Python Recursion | find-latest-group-of-size-m | 0 | 1 | In this approach algorithm starts from the end - binary string is full of ones. Iterating over list from the last index sets bit to 0 and divide binary string into two parts. Alghorithm checks length of these parts and if they are m length return current step. In the other case continues recurrence call.\n\n\n# Code\n\n class Solution:\n def __init__(self):\n self.arr = []\n self.m = 0\n\n def check(self, l, p, i):\n p_res = -1\n l_res = -1\n if l <= p:\n if self.arr[i] >= l and self.arr[i] <= p:\n left = self.arr[i] - l\n right = p - self.arr[i]\n if (left == self.m or right == self.m):\n return i\n if left > self.m:\n l_res = self.check(l, self.arr[i] - 1, i - 1)\n if right > self.m:\n p_res = self.check(self.arr[i] + 1, p, i - 1)\n if l_res or p_res:\n return p_res if p_res > l_res else l_res\n else:\n l_res = self.check(l, p, i - 1)\n if l_res != -1:\n return l_res\n\n return -1\n\n def findLatestStep(self, arr, m):\n self.arr = arr\n self.m = m\n if m == len(arr):\n return len(arr)\n res = self.check(1, len(arr), len(arr) - 1)\n return res\n``` | 0 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
Python Greedy Solution | find-latest-group-of-size-m | 0 | 1 | ```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n cur = [0] * len(arr)\n right = [-1] * len(arr)\n left = [-1] * len(arr)\n groups = [0] * len(arr)\n res = -1\n\n for i in range(len(arr)):\n cur[arr[i]-1] = 1\n \n if arr[i]-2 >= 0 and cur[arr[i]-2] == 1:\n left[arr[i]-1] = left[arr[i]-2]\n groups[right[arr[i]-2] - left[arr[i]-2]] -= 1\n else:\n left[arr[i]-1] = arr[i]-1\n \n if arr[i] < len(arr) and cur[arr[i]] == 1:\n right[arr[i]-1] = right[arr[i]]\n groups[right[arr[i]] - left[arr[i]]] -= 1\n else:\n right[arr[i]-1] = arr[i]-1\n \n if arr[i]-2 >= 0 and cur[arr[i]-2] == 1:\n right[left[arr[i]-2]] = right[arr[i]-1]\n\n if arr[i] < len(arr) and cur[arr[i]] == 1: \n left[right[arr[i]]] = left[arr[i]-1]\n \n groups[right[arr[i]-1] - left[arr[i]-1]] += 1\n \n if groups[m-1] > 0:res = i+1\n \n return res\n``` | 0 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
Python Greedy Solution | find-latest-group-of-size-m | 0 | 1 | ```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n cur = [0] * len(arr)\n right = [-1] * len(arr)\n left = [-1] * len(arr)\n groups = [0] * len(arr)\n res = -1\n\n for i in range(len(arr)):\n cur[arr[i]-1] = 1\n \n if arr[i]-2 >= 0 and cur[arr[i]-2] == 1:\n left[arr[i]-1] = left[arr[i]-2]\n groups[right[arr[i]-2] - left[arr[i]-2]] -= 1\n else:\n left[arr[i]-1] = arr[i]-1\n \n if arr[i] < len(arr) and cur[arr[i]] == 1:\n right[arr[i]-1] = right[arr[i]]\n groups[right[arr[i]] - left[arr[i]]] -= 1\n else:\n right[arr[i]-1] = arr[i]-1\n \n if arr[i]-2 >= 0 and cur[arr[i]-2] == 1:\n right[left[arr[i]-2]] = right[arr[i]-1]\n\n if arr[i] < len(arr) and cur[arr[i]] == 1: \n left[right[arr[i]]] = left[arr[i]-1]\n \n groups[right[arr[i]-1] - left[arr[i]-1]] += 1\n \n if groups[m-1] > 0:res = i+1\n \n return res\n``` | 0 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
Python3 DP solution. | find-latest-group-of-size-m | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is to keep track of the positions of the 1s in the array and the length of the consecutive 1s to the left and right of them. If the length of left or right is equal to m, we have found the latest step. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe will use a dynamic programming approach. We use an array l to store the length of consecutive 1s to the left and right of the current 1 in the array. We iterate through the array and calculate the length of left and right 1s. The length of left and right 1s is updated in the array l. If the length of left or right is equal to m, we have found the latest step. \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nWe iterate through the array which has a length of n. The time complexity is therefore O(n). \n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe use an array l of length n + 2 to store the length of consecutive 1s to the left and right of the current 1 in the array. The space complexity is therefore O(n).\n# Code\n```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n if m == len(arr):\n return m\n l = [0] * (len(arr) + 2)\n res = -1\n for i, a in enumerate(arr):\n left = l[a - 1]\n right = l[a + 1]\n l[a - left] = l[a + right] = left + right + 1\n if left == m or right == m:\n res = i\n return res\n``` | 1 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
Python3 DP solution. | find-latest-group-of-size-m | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is to keep track of the positions of the 1s in the array and the length of the consecutive 1s to the left and right of them. If the length of left or right is equal to m, we have found the latest step. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe will use a dynamic programming approach. We use an array l to store the length of consecutive 1s to the left and right of the current 1 in the array. We iterate through the array and calculate the length of left and right 1s. The length of left and right 1s is updated in the array l. If the length of left or right is equal to m, we have found the latest step. \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nWe iterate through the array which has a length of n. The time complexity is therefore O(n). \n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe use an array l of length n + 2 to store the length of consecutive 1s to the left and right of the current 1 in the array. The space complexity is therefore O(n).\n# Code\n```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n if m == len(arr):\n return m\n l = [0] * (len(arr) + 2)\n res = -1\n for i, a in enumerate(arr):\n left = l[a - 1]\n right = l[a + 1]\n l[a - left] = l[a + right] = left + right + 1\n if left == m or right == m:\n res = i\n return res\n``` | 1 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
✅ || tried my best to explain O(n) solution || python || | find-latest-group-of-size-m | 0 | 1 | ```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n \n \n if m == len(arr): # if the length of group we want is equal to length of arr than in the end eventually we are getting the group of length == m and latest step will be the last step\n \n return m\n \n abhi = [0]*(len(arr)+2)\n \n res = -1\n \n for i , a in enumerate(arr):\n \n left , right = abhi[a-1] , abhi[a+1] # now we are storing the curr length of the right group and left group if exist . the right group and left group means the right and left of current element\n \n if left == m or right == m:\n \n res = i # if any on the above two groups having length of m than the latest step will be i , and result will be updated . \n \n abhi[a-left] = abhi[a+right] = left + right +1 # and in the final step we have to merge the left group and right group if it makes the contigeous substring of 1\'s , basically we are increasing the length of group because finally we want to deal with the length of groups . this step is kind of similiar to the step which we do in sub array sum equal to k problem . \n \n return res\n \n \n \n \n \n \n \n \n``` | 4 | Given an array `arr` that represents a permutation of numbers from `1` to `n`.
You have a binary string of size `n` that initially has all its bits set to zero. At each step `i` (assuming both the binary string and `arr` are 1-indexed) from `1` to `n`, the bit at position `arr[i]` is set to `1`.
You are also given an integer `m`. Find the latest step at which there exists a group of ones of length `m`. A group of ones is a contiguous substring of `1`'s such that it cannot be extended in either direction.
Return _the latest step at which there exists a group of ones of length **exactly**_ `m`. _If no such group exists, return_ `-1`.
**Example 1:**
**Input:** arr = \[3,5,1,2,4\], m = 1
**Output:** 4
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "00101 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "11101 ", groups: \[ "111 ", "1 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
The latest step at which there exists a group of size 1 is step 4.
**Example 2:**
**Input:** arr = \[3,1,5,4,2\], m = 2
**Output:** -1
**Explanation:**
Step 1: "00100 ", groups: \[ "1 "\]
Step 2: "10100 ", groups: \[ "1 ", "1 "\]
Step 3: "10101 ", groups: \[ "1 ", "1 ", "1 "\]
Step 4: "10111 ", groups: \[ "1 ", "111 "\]
Step 5: "11111 ", groups: \[ "11111 "\]
No group of size 2 exists during any step.
**Constraints:**
* `n == arr.length`
* `1 <= m <= n <= 105`
* `1 <= arr[i] <= n`
* All integers in `arr` are **distinct**. | Use hashing to convert company names in numbers and then for each list check if this is a subset of any other list. In order to check if a list is a subset of another list, use two pointers technique to get a linear solution for this task. The total complexity will be O(n^2 * m) where n is the number of lists and m is the maximum number of elements in a list. |
✅ || tried my best to explain O(n) solution || python || | find-latest-group-of-size-m | 0 | 1 | ```\nclass Solution:\n def findLatestStep(self, arr: List[int], m: int) -> int:\n \n \n if m == len(arr): # if the length of group we want is equal to length of arr than in the end eventually we are getting the group of length == m and latest step will be the last step\n \n return m\n \n abhi = [0]*(len(arr)+2)\n \n res = -1\n \n for i , a in enumerate(arr):\n \n left , right = abhi[a-1] , abhi[a+1] # now we are storing the curr length of the right group and left group if exist . the right group and left group means the right and left of current element\n \n if left == m or right == m:\n \n res = i # if any on the above two groups having length of m than the latest step will be i , and result will be updated . \n \n abhi[a-left] = abhi[a+right] = left + right +1 # and in the final step we have to merge the left group and right group if it makes the contigeous substring of 1\'s , basically we are increasing the length of group because finally we want to deal with the length of groups . this step is kind of similiar to the step which we do in sub array sum equal to k problem . \n \n return res\n \n \n \n \n \n \n \n \n``` | 4 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current “1” groups. At each step (going backwards) you need to split one group and update the map. |
[Python / Golang] Simple DP Solution with a Trick for Python | stone-game-v | 0 | 1 | **Idea**\nThe idea is straight forward. we just try out all the possibilities to find the answer. Naive brute force solution will lead to O(n!) complexity, so we need to store the interim results to improve the complexity to O(n^3).\n\n**A trick for slower languages**\nSince I got TLE for the O(n^3) solution in Python. I add a shortcut for a special case when all the elements within a specific range are the same. In this special case, we can get the results in O(logn) complexity.\n\n**Complexity**\nTime: O(n^3)\nSpace: O(n^2)\n\nPlease do not downvote unless you find it necessary. Please bro.\n\n**Python**\n```\nfrom functools import lru_cache\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n presum = [0]\n for s in stoneValue:\n presum += presum[-1] + s,\n \n def sm(i, j):\n return presum[j + 1] - presum[i]\n \n @lru_cache(None)\n def helper(i, j):\n if i == j: return 0\n \n if all(stoneValue[k] == stoneValue[j] for k in range(i, j)):\n cnt = 0\n l = j - i + 1\n while l > 1:\n l //= 2\n cnt += l\n return cnt * stoneValue[j] \n \n res = 0\n for k in range(i, j):\n if sm(i, k) < sm(k + 1, j):\n score = helper(i, k) + sm(i, k)\n elif sm(i, k) > sm(k + 1, j):\n score = sm(k + 1, j) + helper(k + 1, j)\n else: \n score = max(helper(i, k) + sm(i, k), sm(k + 1, j) + helper(k + 1, j))\n res = max(res, score)\n return res \n \n return helper(0, len(stoneValue) - 1)\n```\n\n\n**Golang**\n```\nfunc stoneGameV(stoneValue []int) int {\n n := len(stoneValue)\n memo := make([][]int, n)\n for i := range memo {\n memo[i] = make([]int, n)\n }\n presum := make([]int, n + 1)\n for i := 1; i <= n; i++ {\n presum[i] = presum[i - 1] + stoneValue[i - 1]\n }\n sum := func(i, j int) int {return presum[j + 1] - presum[i]}\n \n \n for l := 2; l <= n; l++ { // l mean length\n for i := 0; i < n - l + 1; i++ {\n j := i + l - 1\n score := 0\n for k := i; k < j; k++ {\n switch {\n case sum(i, k) > sum(k + 1, j):\n score = max(score, memo[k + 1][j] + sum(k + 1, j))\n case sum(i, k) < sum(k + 1, j):\n score = max(score, memo[i][k] + sum(i, k))\n default:\n tmp := max(memo[i][k] + sum(i, k), memo[k + 1][j] + sum(k + 1, j))\n score = max(score, tmp)\n }\n }\n memo[i][j] = score\n }\n }\n return memo[0][n - 1]\n}\n\nfunc max(i, j int) int {\n if i < j {\n return j\n }\n return i\n}\n``` | 13 | There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
In each round of the game, Alice divides the row into **two non-empty rows** (i.e. left row and right row), then Bob calculates the value of each row which is the sum of the values of all the stones in this row. Bob throws away the row which has the maximum value, and Alice's score increases by the value of the remaining row. If the value of the two rows are equal, Bob lets Alice decide which row will be thrown away. The next round starts with the remaining row.
The game ends when there is only **one stone remaining**. Alice's is initially **zero**.
Return _the maximum score that Alice can obtain_.
**Example 1:**
**Input:** stoneValue = \[6,2,3,4,5,5\]
**Output:** 18
**Explanation:** In the first round, Alice divides the row to \[6,2,3\], \[4,5,5\]. The left row has the value 11 and the right row has value 14. Bob throws away the right row and Alice's score is now 11.
In the second round Alice divides the row to \[6\], \[2,3\]. This time Bob throws away the left row and Alice's score becomes 16 (11 + 5).
The last round Alice has only one choice to divide the row which is \[2\], \[3\]. Bob throws away the right row and Alice's score is now 18 (16 + 2). The game ends because only one stone is remaining in the row.
**Example 2:**
**Input:** stoneValue = \[7,7,7,7,7,7,7\]
**Output:** 28
**Example 3:**
**Input:** stoneValue = \[4\]
**Output:** 0
**Constraints:**
* `1 <= stoneValue.length <= 500`
* `1 <= stoneValue[i] <= 106` | If there is an optimal solution, you can always move the circle so that two points lie on the boundary of the circle. When the radius is fixed, you can find either 0 or 1 or 2 circles that pass two given points at the same time. Loop for each pair of points and find the center of the circle, after that count the number of points inside the circle. |
[Python / Golang] Simple DP Solution with a Trick for Python | stone-game-v | 0 | 1 | **Idea**\nThe idea is straight forward. we just try out all the possibilities to find the answer. Naive brute force solution will lead to O(n!) complexity, so we need to store the interim results to improve the complexity to O(n^3).\n\n**A trick for slower languages**\nSince I got TLE for the O(n^3) solution in Python. I add a shortcut for a special case when all the elements within a specific range are the same. In this special case, we can get the results in O(logn) complexity.\n\n**Complexity**\nTime: O(n^3)\nSpace: O(n^2)\n\nPlease do not downvote unless you find it necessary. Please bro.\n\n**Python**\n```\nfrom functools import lru_cache\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n presum = [0]\n for s in stoneValue:\n presum += presum[-1] + s,\n \n def sm(i, j):\n return presum[j + 1] - presum[i]\n \n @lru_cache(None)\n def helper(i, j):\n if i == j: return 0\n \n if all(stoneValue[k] == stoneValue[j] for k in range(i, j)):\n cnt = 0\n l = j - i + 1\n while l > 1:\n l //= 2\n cnt += l\n return cnt * stoneValue[j] \n \n res = 0\n for k in range(i, j):\n if sm(i, k) < sm(k + 1, j):\n score = helper(i, k) + sm(i, k)\n elif sm(i, k) > sm(k + 1, j):\n score = sm(k + 1, j) + helper(k + 1, j)\n else: \n score = max(helper(i, k) + sm(i, k), sm(k + 1, j) + helper(k + 1, j))\n res = max(res, score)\n return res \n \n return helper(0, len(stoneValue) - 1)\n```\n\n\n**Golang**\n```\nfunc stoneGameV(stoneValue []int) int {\n n := len(stoneValue)\n memo := make([][]int, n)\n for i := range memo {\n memo[i] = make([]int, n)\n }\n presum := make([]int, n + 1)\n for i := 1; i <= n; i++ {\n presum[i] = presum[i - 1] + stoneValue[i - 1]\n }\n sum := func(i, j int) int {return presum[j + 1] - presum[i]}\n \n \n for l := 2; l <= n; l++ { // l mean length\n for i := 0; i < n - l + 1; i++ {\n j := i + l - 1\n score := 0\n for k := i; k < j; k++ {\n switch {\n case sum(i, k) > sum(k + 1, j):\n score = max(score, memo[k + 1][j] + sum(k + 1, j))\n case sum(i, k) < sum(k + 1, j):\n score = max(score, memo[i][k] + sum(i, k))\n default:\n tmp := max(memo[i][k] + sum(i, k), memo[k + 1][j] + sum(k + 1, j))\n score = max(score, tmp)\n }\n }\n memo[i][j] = score\n }\n }\n return memo[0][n - 1]\n}\n\nfunc max(i, j int) int {\n if i < j {\n return j\n }\n return i\n}\n``` | 13 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Python O(n^2) optimized solution. O(n^3) cannot pass. | stone-game-v | 0 | 1 | Python is slow sometimes!\n\nTraditional DP: \n```\nfor i in (0, length): \n\tfor j in (0, length): \n\t\tfor k in (i, j): \n\t\t\tdp[i][j] = dp[i][k] + s[i][k]] or dp[k+1][j] + s[k+1][j]\n```\n\nThe hardest thing for us to optimize the O(n^3) is finding a way to reduce the innest loop for k in (i, j), but it\'s not sorted and no way to find which one is best, totaly irregular?\n**However**, the lowest bound and hight bound of the cut index in (i, j) comes from the best cut in (i+1, j) and (i, j-1), **BECAUSE**\n\n**`best_cut[i][j-1] - 1 <= best_cut[i][j] <= best_cut[i+1][j] + 1`** \n\nYou can prove it by yourself.\n\nAdd a best cut array to optimize the O(n^3) solution, to make it **ALMOST O(n^2)**, the number of k from bestcut[i][j-1] to bestcut[i+1][j] is ***almost a constant value averagly*** (depends on the values in list).\n\n\n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n length = len(stoneValue)\n if length == 1:\n return 0\n \n\t\t# Calculate sum\n s = [0 for _ in range(length)]\n s[0] = stoneValue[0]\n for i in range(1, length):\n s[i] = s[i-1] + stoneValue[i]\n\t\t\n\t\t# dp for best value, best_cut for where is the cut in (i, j), i, j inclusive\n dp = [[0 for _ in range(length)] for _ in range(length)]\n best_cut = [[0 for _ in range(length)] for _ in range(length)]\n \n for i in range(0, length-1):\n dp[i][i+1] = min(stoneValue[i], stoneValue[i+1])\n best_cut[i][i+1] = i\n \n for t in range(2, length):\n for i in range(0, length-t):\n tmp_dp = 0\n tmp_cut = 0\n left_bound = best_cut[i][i+t-1]\n if left_bound > i:\n left_bound -= 1\n right_bound = best_cut[i+1][i+t]\n if right_bound < i+t-1:\n right_bound += 1\n \n for k in range(left_bound, 1+right_bound):\n s1 = s[k] - s[i-1] if i > 0 else s[k]\n s2 = s[i+t] - s[k]\n if s1 < s2:\n tmp = s1 + dp[i][k]\n if tmp > tmp_dp:\n tmp_dp = tmp\n tmp_cut = k\n elif s1 > s2:\n tmp = s2 + dp[k+1][i+t]\n if tmp > tmp_dp:\n tmp_dp = tmp\n tmp_cut = k\n else:\n tmp1 = s1 + dp[i][k]\n tmp2 = s2 + dp[k+1][i+t]\n if tmp1 > tmp_dp:\n tmp_dp = tmp1\n tmp_cut = k\n if tmp2 > tmp_dp:\n tmp_dp = tmp2\n tmp_cut = k\n \n dp[i][i+t] = tmp_dp\n best_cut[i][i+t] = tmp_cut\n \n return dp[0][length-1]\n``` | 6 | There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
In each round of the game, Alice divides the row into **two non-empty rows** (i.e. left row and right row), then Bob calculates the value of each row which is the sum of the values of all the stones in this row. Bob throws away the row which has the maximum value, and Alice's score increases by the value of the remaining row. If the value of the two rows are equal, Bob lets Alice decide which row will be thrown away. The next round starts with the remaining row.
The game ends when there is only **one stone remaining**. Alice's is initially **zero**.
Return _the maximum score that Alice can obtain_.
**Example 1:**
**Input:** stoneValue = \[6,2,3,4,5,5\]
**Output:** 18
**Explanation:** In the first round, Alice divides the row to \[6,2,3\], \[4,5,5\]. The left row has the value 11 and the right row has value 14. Bob throws away the right row and Alice's score is now 11.
In the second round Alice divides the row to \[6\], \[2,3\]. This time Bob throws away the left row and Alice's score becomes 16 (11 + 5).
The last round Alice has only one choice to divide the row which is \[2\], \[3\]. Bob throws away the right row and Alice's score is now 18 (16 + 2). The game ends because only one stone is remaining in the row.
**Example 2:**
**Input:** stoneValue = \[7,7,7,7,7,7,7\]
**Output:** 28
**Example 3:**
**Input:** stoneValue = \[4\]
**Output:** 0
**Constraints:**
* `1 <= stoneValue.length <= 500`
* `1 <= stoneValue[i] <= 106` | If there is an optimal solution, you can always move the circle so that two points lie on the boundary of the circle. When the radius is fixed, you can find either 0 or 1 or 2 circles that pass two given points at the same time. Loop for each pair of points and find the center of the circle, after that count the number of points inside the circle. |
Python O(n^2) optimized solution. O(n^3) cannot pass. | stone-game-v | 0 | 1 | Python is slow sometimes!\n\nTraditional DP: \n```\nfor i in (0, length): \n\tfor j in (0, length): \n\t\tfor k in (i, j): \n\t\t\tdp[i][j] = dp[i][k] + s[i][k]] or dp[k+1][j] + s[k+1][j]\n```\n\nThe hardest thing for us to optimize the O(n^3) is finding a way to reduce the innest loop for k in (i, j), but it\'s not sorted and no way to find which one is best, totaly irregular?\n**However**, the lowest bound and hight bound of the cut index in (i, j) comes from the best cut in (i+1, j) and (i, j-1), **BECAUSE**\n\n**`best_cut[i][j-1] - 1 <= best_cut[i][j] <= best_cut[i+1][j] + 1`** \n\nYou can prove it by yourself.\n\nAdd a best cut array to optimize the O(n^3) solution, to make it **ALMOST O(n^2)**, the number of k from bestcut[i][j-1] to bestcut[i+1][j] is ***almost a constant value averagly*** (depends on the values in list).\n\n\n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n length = len(stoneValue)\n if length == 1:\n return 0\n \n\t\t# Calculate sum\n s = [0 for _ in range(length)]\n s[0] = stoneValue[0]\n for i in range(1, length):\n s[i] = s[i-1] + stoneValue[i]\n\t\t\n\t\t# dp for best value, best_cut for where is the cut in (i, j), i, j inclusive\n dp = [[0 for _ in range(length)] for _ in range(length)]\n best_cut = [[0 for _ in range(length)] for _ in range(length)]\n \n for i in range(0, length-1):\n dp[i][i+1] = min(stoneValue[i], stoneValue[i+1])\n best_cut[i][i+1] = i\n \n for t in range(2, length):\n for i in range(0, length-t):\n tmp_dp = 0\n tmp_cut = 0\n left_bound = best_cut[i][i+t-1]\n if left_bound > i:\n left_bound -= 1\n right_bound = best_cut[i+1][i+t]\n if right_bound < i+t-1:\n right_bound += 1\n \n for k in range(left_bound, 1+right_bound):\n s1 = s[k] - s[i-1] if i > 0 else s[k]\n s2 = s[i+t] - s[k]\n if s1 < s2:\n tmp = s1 + dp[i][k]\n if tmp > tmp_dp:\n tmp_dp = tmp\n tmp_cut = k\n elif s1 > s2:\n tmp = s2 + dp[k+1][i+t]\n if tmp > tmp_dp:\n tmp_dp = tmp\n tmp_cut = k\n else:\n tmp1 = s1 + dp[i][k]\n tmp2 = s2 + dp[k+1][i+t]\n if tmp1 > tmp_dp:\n tmp_dp = tmp1\n tmp_cut = k\n if tmp2 > tmp_dp:\n tmp_dp = tmp2\n tmp_cut = k\n \n dp[i][i+t] = tmp_dp\n best_cut[i][i+t] = tmp_cut\n \n return dp[0][length-1]\n``` | 6 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Python3 Iterative Solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | ```python\ndef containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n\ti = 0\n\twhile i <= len(arr)-1:\n\t\tp = arr[i:i+m]\n\t\tif p * k == arr[i:i+m*k]:\n\t\t\treturn True\n\n\t\ti += 1\n\n\treturn False\n```\n\ntrungnguyen276\'s solution (optimized)\n\n```python\ndef containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n streak = 0\n for i in range(len(arr)-m):\n streak = streak + 1 if arr[i] == arr[i+m] else 0\n if streak == (k-1)*m: return True\n return False\n``` | 56 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Python3 Iterative Solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | ```python\ndef containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n\ti = 0\n\twhile i <= len(arr)-1:\n\t\tp = arr[i:i+m]\n\t\tif p * k == arr[i:i+m*k]:\n\t\t\treturn True\n\n\t\ti += 1\n\n\treturn False\n```\n\ntrungnguyen276\'s solution (optimized)\n\n```python\ndef containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n streak = 0\n for i in range(len(arr)-m):\n streak = streak + 1 if arr[i] == arr[i+m] else 0\n if streak == (k-1)*m: return True\n return False\n``` | 56 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
[Python3] O(n) time O(m) space (With explanation) | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | **Just as the hint mentioned, a few key points:**\n1) The pattern must appear consecutively.\n2) No need to loop till the end\n\n**Code:**\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n = len(arr)\n max_start_point = n - m * k\n\t\t# If there is an answer, it must be m*k length,\n\t\t# so we just need to loop until max_start_point\n\t\t\n for i in range(max_start_point+1):\n count = 1\n curr = i + m\n patt = arr[i:curr]\n\t\t\t# set subarray starting from this point as pattern\n \n while curr <= n-m: \n\t\t\t\t# compare every following subarray with pattern\n if arr[curr:curr+m] == patt: \n curr += m\n count += 1\n if count == k: return True\n else:\n break \n\t\t\t\t\t# not consecutive, therefore not the answer\n \n return False\n```\n\n**Time and space complexity:**\nWorst case scenario is to search every starting point until the max_start_point, and for each starting point the while loop will break when:\n1. We found the answer after comparing k times. **OR**\n2. We found out that current pattern is not consecutive. (Comparing less than k times)\n\nWorst case scenario takes O(k(n-mk)) time, and therefore this is a O(n) solution.\nWe use list to store pattern, and therefore O(m) space.\n\nI am a beginner. Not the best solution. Feel free to give upvotes and any advice. Thanks! | 5 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
[Python3] O(n) time O(m) space (With explanation) | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | **Just as the hint mentioned, a few key points:**\n1) The pattern must appear consecutively.\n2) No need to loop till the end\n\n**Code:**\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n = len(arr)\n max_start_point = n - m * k\n\t\t# If there is an answer, it must be m*k length,\n\t\t# so we just need to loop until max_start_point\n\t\t\n for i in range(max_start_point+1):\n count = 1\n curr = i + m\n patt = arr[i:curr]\n\t\t\t# set subarray starting from this point as pattern\n \n while curr <= n-m: \n\t\t\t\t# compare every following subarray with pattern\n if arr[curr:curr+m] == patt: \n curr += m\n count += 1\n if count == k: return True\n else:\n break \n\t\t\t\t\t# not consecutive, therefore not the answer\n \n return False\n```\n\n**Time and space complexity:**\nWorst case scenario is to search every starting point until the max_start_point, and for each starting point the while loop will break when:\n1. We found the answer after comparing k times. **OR**\n2. We found out that current pattern is not consecutive. (Comparing less than k times)\n\nWorst case scenario takes O(k(n-mk)) time, and therefore this is a O(n) solution.\nWe use list to store pattern, and therefore O(m) space.\n\nI am a beginner. Not the best solution. Feel free to give upvotes and any advice. Thanks! | 5 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
[Python3] Sliding Window | Iterative | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | Check for each subarray of size m if it consecutively exists and the frequency matches to k\n\n```\ndef containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n = len(arr)\n for i in range(n-m+1):\n j = i + m\n pat = arr[i: j]\n # freq = 0\n start = 0\n for e in range(n-m+1):\n start = e\n freq = 0\n while start <= n-m:\n end = start + m\n if (arr[start: end] == pat):\n freq += 1\n start += m\n else:\n freq = 0\n start += 1\n if freq == k:\n return True\n return False\n``` | 5 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
[Python3] Sliding Window | Iterative | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | Check for each subarray of size m if it consecutively exists and the frequency matches to k\n\n```\ndef containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n = len(arr)\n for i in range(n-m+1):\n j = i + m\n pat = arr[i: j]\n # freq = 0\n start = 0\n for e in range(n-m+1):\n start = e\n freq = 0\n while start <= n-m:\n end = start + m\n if (arr[start: end] == pat):\n freq += 1\n start += m\n else:\n freq = 0\n start += 1\n if freq == k:\n return True\n return False\n``` | 5 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Beats 97.14% of users with Python3 | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int, start: int = 0) -> bool:\n # bruteforce solution\n # 34ms\n # Beats 93.65% of users with Python3\n prev, temp = None, []\n for i in range(start, len(arr), m):\n val = arr[i:i+m]\n if len(val) < m:\n break\n \n if len(temp) == 0:\n temp = [val]\n prev = val\n continue\n \n if temp[-1] == val:\n temp.append(val)\n if len(temp) == k:\n return True\n else:\n temp = [val]\n \n prev = val\n \n if start == m:\n return False\n \n return self.containsPattern(arr, m, k, start+1)\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Beats 97.14% of users with Python3 | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int, start: int = 0) -> bool:\n # bruteforce solution\n # 34ms\n # Beats 93.65% of users with Python3\n prev, temp = None, []\n for i in range(start, len(arr), m):\n val = arr[i:i+m]\n if len(val) < m:\n break\n \n if len(temp) == 0:\n temp = [val]\n prev = val\n continue\n \n if temp[-1] == val:\n temp.append(val)\n if len(temp) == k:\n return True\n else:\n temp = [val]\n \n prev = val\n \n if start == m:\n return False\n \n return self.containsPattern(arr, m, k, start+1)\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
HashMap solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe keep track of the last previous index the pattern was found, see if it is consecutive with the previous index , add one or set it as latest in different cases. We also keep track of the maximum values obtained by each pattern consecutively. We will be using this to return our answer. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n mapper={}\n maxValue={}\n for i in range(len(arr)-m+1):\n \n temp=[]\n for j in range(i,i+m):\n temp.append(arr[j])\n if tuple(temp) not in mapper.keys():\n mapper[tuple(temp)]=(1,i)\n maxValue[tuple(temp)]=1\n elif i-mapper[tuple(temp)][1]==m:\n mapper[tuple(temp)]=(mapper[tuple(temp)][0]+1,i)\n maxValue[tuple(temp)]=max(maxValue[tuple(temp)],mapper[tuple(temp)][0])\n \n elif i-mapper[tuple(temp)][1]>m: \n mapper[tuple(temp)]=(1,i)\n print(f\'Mapper:{mapper}\')\n print(f\'MaxValue:{maxValue}\')\n\n\n\n\n print(mapper)\n return any(c>=k for c in maxValue.values())\n\n \n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
HashMap solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe keep track of the last previous index the pattern was found, see if it is consecutive with the previous index , add one or set it as latest in different cases. We also keep track of the maximum values obtained by each pattern consecutively. We will be using this to return our answer. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n mapper={}\n maxValue={}\n for i in range(len(arr)-m+1):\n \n temp=[]\n for j in range(i,i+m):\n temp.append(arr[j])\n if tuple(temp) not in mapper.keys():\n mapper[tuple(temp)]=(1,i)\n maxValue[tuple(temp)]=1\n elif i-mapper[tuple(temp)][1]==m:\n mapper[tuple(temp)]=(mapper[tuple(temp)][0]+1,i)\n maxValue[tuple(temp)]=max(maxValue[tuple(temp)],mapper[tuple(temp)][0])\n \n elif i-mapper[tuple(temp)][1]>m: \n mapper[tuple(temp)]=(1,i)\n print(f\'Mapper:{mapper}\')\n print(f\'MaxValue:{maxValue}\')\n\n\n\n\n print(mapper)\n return any(c>=k for c in maxValue.values())\n\n \n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Python one-line solution beats 65% | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCompare all sublists of length m multiplied by number of occurrences k and see if the concatenated sublist exists in the array\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Not sure\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n return any([arr[i:i + m * k] == arr[i:i + m] * k for i in range(len(arr)-m)])\n \n```\nHere is the same solution below in multiple lines for extra clarity\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n for i in range(len(arr) - m):\n if arr[i:i + m * k] == arr[i:i + m] * k:\n return True\n return False\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Python one-line solution beats 65% | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCompare all sublists of length m multiplied by number of occurrences k and see if the concatenated sublist exists in the array\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Not sure\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n return any([arr[i:i + m * k] == arr[i:i + m] * k for i in range(len(arr)-m)])\n \n```\nHere is the same solution below in multiple lines for extra clarity\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n for i in range(len(arr) - m):\n if arr[i:i + m * k] == arr[i:i + m] * k:\n return True\n return False\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Easy to understand Python3 solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n l = 0\n r = l + m\n\n while r < len(arr):\n count = 1\n current_window = arr[l:r]\n\n for i in range(r, len(arr), m):\n if current_window == arr[i:i+m]:\n count += 1\n else:\n break\n if count >= k:\n return True\n l += 1\n r = l + m\n \n return False\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Easy to understand Python3 solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n l = 0\n r = l + m\n\n while r < len(arr):\n count = 1\n current_window = arr[l:r]\n\n for i in range(r, len(arr), m):\n if current_window == arr[i:i+m]:\n count += 1\n else:\n break\n if count >= k:\n return True\n l += 1\n r = l + m\n \n return False\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
easy python3 solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | \n# Complexity\n- Time complexity:\n- O(N*M^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n=len(arr)\n for i in range(0,n-m):\n x=arr[i:i+m]\n c=1\n for j in range(i+m,n-m+1):\n if(x==arr[j:j+m]):\n c=c+1\n else:\n break\n if(c>=k):\n return True\n return False\n \n\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
easy python3 solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | \n# Complexity\n- Time complexity:\n- O(N*M^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n=len(arr)\n for i in range(0,n-m):\n x=arr[i:i+m]\n c=1\n for j in range(i+m,n-m+1):\n if(x==arr[j:j+m]):\n c=c+1\n else:\n break\n if(c>=k):\n return True\n return False\n \n\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Solution by Python | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n = len(arr)\n \n # Helper function to check if two subarrays are equal\n def are_subarrays_equal(start1, end1, start2, end2):\n return all(arr[i] == arr[j] for i, j in zip(range(start1, end1), range(start2, end2)))\n \n for i in range(n - m * k + 1):\n # Check if the subarray of length m is repeated k or more times\n repeated = True\n for j in range(1, k):\n if not are_subarrays_equal(i, i + m, i + j * m, i + (j + 1) * m):\n repeated = False\n break\n if repeated:\n return True\n \n return False\n\n\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Solution by Python | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n n = len(arr)\n \n # Helper function to check if two subarrays are equal\n def are_subarrays_equal(start1, end1, start2, end2):\n return all(arr[i] == arr[j] for i, j in zip(range(start1, end1), range(start2, end2)))\n \n for i in range(n - m * k + 1):\n # Check if the subarray of length m is repeated k or more times\n repeated = True\n for j in range(1, k):\n if not are_subarrays_equal(i, i + m, i + j * m, i + (j + 1) * m):\n repeated = False\n break\n if repeated:\n return True\n \n return False\n\n\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
easy solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n for i in range(len(arr) - m):\n match = arr[i:i + m]\n if match * k == arr[i:i + m * k]:\n return True\n return False\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
easy solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n for i in range(len(arr) - m):\n match = arr[i:i + m]\n if match * k == arr[i:i + m * k]:\n return True\n return False\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Straightforward Python Solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n i = 0\n while i < len(arr)-1:\n p = arr[i:i+m]\n if p*k == arr[i:i+m*k]:\n return True\n i += 1\n return False\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Straightforward Python Solution | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n i = 0\n while i < len(arr)-1:\n p = arr[i:i+m]\n if p*k == arr[i:i+m*k]:\n return True\n i += 1\n return False\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Python easy solution via classic for loop | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code iterates through the given array arr and checks for patterns of length m that are repeated k or more times consecutively. It compares each element at index i with the element at index i + m to identify patterns.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a variable consecutive to keep track of the consecutive occurrences of the pattern.\n2. Iterate through the array arr from index 0 to len(arr) - m - 1.\n3. At each iteration, compare the element at index i with the element at index i + m.\n4. If they are equal, increment the consecutive counter by 1.\n5. Check if the consecutive counter has reached (k - 1) * m. If so, a pattern of length m has been repeated k or more times consecutively, and we return True.\n6. If the elements are not equal, reset the consecutive counter to 0.\n7. After the loop ends, if no pattern is found, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the array arr once, resulting in a time complexity of O(n), where n is the length of the array arr.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe code uses a constant amount of extra space, resulting in a space complexity of O(1).\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n consecutive = 0\n for i in range(len(arr) - m):\n if arr[i] == arr[i + m]:\n consecutive += 1\n if consecutive == (k - 1) * m:\n return True\n else:\n consecutive = 0\n return False\n\n\n``` | 0 | Given an array of positive integers `arr`, find a pattern of length `m` that is repeated `k` or more times.
A **pattern** is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times **consecutively** without overlapping. A pattern is defined by its length and the number of repetitions.
Return `true` _if there exists a pattern of length_ `m` _that is repeated_ `k` _or more times, otherwise return_ `false`.
**Example 1:**
**Input:** arr = \[1,2,4,4,4,4\], m = 1, k = 3
**Output:** true
**Explanation:** The pattern **(4)** of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.
**Example 2:**
**Input:** arr = \[1,2,1,2,1,1,1,3\], m = 2, k = 2
**Output:** true
**Explanation:** The pattern **(1,2)** of length 2 is repeated 2 consecutive times. Another valid pattern **(2,1) is** also repeated 2 times.
**Example 3:**
**Input:** arr = \[1,2,1,2,1,3\], m = 2, k = 3
**Output:** false
**Explanation:** The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.
**Constraints:**
* `2 <= arr.length <= 100`
* `1 <= arr[i] <= 100`
* `1 <= m <= 100`
* `2 <= k <= 100` | First extract the words of the sentence. Check for each word if searchWord occurs at index 0, if so return the index of this word (1-indexed) If searchWord doesn't exist as a prefix of any word return the default value (-1). |
Python easy solution via classic for loop | detect-pattern-of-length-m-repeated-k-or-more-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code iterates through the given array arr and checks for patterns of length m that are repeated k or more times consecutively. It compares each element at index i with the element at index i + m to identify patterns.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a variable consecutive to keep track of the consecutive occurrences of the pattern.\n2. Iterate through the array arr from index 0 to len(arr) - m - 1.\n3. At each iteration, compare the element at index i with the element at index i + m.\n4. If they are equal, increment the consecutive counter by 1.\n5. Check if the consecutive counter has reached (k - 1) * m. If so, a pattern of length m has been repeated k or more times consecutively, and we return True.\n6. If the elements are not equal, reset the consecutive counter to 0.\n7. After the loop ends, if no pattern is found, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the array arr once, resulting in a time complexity of O(n), where n is the length of the array arr.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe code uses a constant amount of extra space, resulting in a space complexity of O(1).\n\n# Code\n```\nclass Solution:\n def containsPattern(self, arr: List[int], m: int, k: int) -> bool:\n consecutive = 0\n for i in range(len(arr) - m):\n if arr[i] == arr[i + m]:\n consecutive += 1\n if consecutive == (k - 1) * m:\n return True\n else:\n consecutive = 0\n return False\n\n\n``` | 0 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
[Python3/Go/Java] Dynamic Programming O(N) time O(1) space | maximum-length-of-subarray-with-positive-product | 0 | 1 | ### Explanation\n"pos[i]", "neg[i]" represent longest consecutive numbers ending with nums[i] forming a positive/negative product.\n\n#### Complexity\n`time`: O(N)\n`space`: O(N)\n\n#### Python3:\n\n```python\ndef getMaxLen(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tpos, neg = [0] * n, [0] * n\n\tif nums[0] > 0: pos[0] = 1\n\tif nums[0] < 0: neg[0] = 1\n\tans = pos[0]\n\tfor i in range(1, n):\n\t\tif nums[i] > 0:\n\t\t\tpos[i] = 1 + pos[i - 1]\n\t\t\tneg[i] = 1 + neg[i - 1] if neg[i - 1] > 0 else 0\n\t\telif nums[i] < 0:\n\t\t\tpos[i] = 1 + neg[i - 1] if neg[i - 1] > 0 else 0\n\t\t\tneg[i] = 1 + pos[i - 1]\n\t\tans = max(ans, pos[i])\n\treturn ans\n```\n\n\n#### Golang:\n\n```Golang\nfunc getMaxLen(nums []int) int {\n n := len(nums)\n pos := make([]int, n)\n neg := make([]int, n)\n if nums[0] > 0 {\n pos[0] = 1\n } else if nums[0] < 0 {\n neg[0] = 1\n }\n ans := pos[0]\n for i := 1; i < n; i++ {\n if nums[i] > 0 {\n pos[i] = 1 + pos[i - 1]\n if neg[i - 1] > 0 {\n neg[i] = 1 + neg[i - 1]\n } else {\n neg[i] = 0\n }\n } else if nums[i] < 0 {\n if neg[i - 1] > 0 {\n pos[i] = 1 + neg[i - 1]\n } else {\n pos[i] = 0\n }\n neg[i] = 1 + pos[i - 1]\n }\n ans = Max(ans, pos[i])\n }\n return ans\n}\n\nfunc Max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n\n\n#### Java:\n\n```Java\npublic int getMaxLen(int[] nums) {\n\tint n = nums.length;\n\tint[] pos = new int[n];\n\tint[] neg = new int[n];\n\tif (nums[0] > 0) pos[0] = 1;\n\tif (nums[0] < 0) neg[0] = 1;\n\tint ans = pos[0];\n\tfor (int i = 1; i < n; i++) {\n\t\tif (nums[i] > 0) {\n\t\t\tpos[i] = 1 + pos[i - 1];\n\t\t\tneg[i] = neg[i - 1] > 0 ? 1 + neg[i - 1]:0;\n\t\t} else if (nums[i] < 0) {\n\t\t\tpos[i] = neg[i - 1] > 0 ? 1 + neg[i - 1]:0;\n\t\t\tneg[i] = 1 + pos[i - 1];\n\t\t}\n\t\tans = Math.max(ans, pos[i]);\n\t}\n\treturn ans;\n}\n```\n\n\n### Space Optimization\n\n### Complexity\n`time`: O(N)\n`space`: O(1)\n\nThanks @Spin0za for pointing out.\nSince only the previous one value of pos/neg is used, we can use 2 variables instead of 2 lists.\n\n#### Python3\n```python\ndef getMaxLen(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tpos, neg = 0, 0\n\tif nums[0] > 0: pos = 1\n\tif nums[0] < 0: neg = 1\n\tans = pos\n\tfor i in range(1, n):\n\t\tif nums[i] > 0:\n\t\t\tpos = 1 + pos\n\t\t\tneg = 1 + neg if neg > 0 else 0\n\t\telif nums[i] < 0:\n\t\t\tpos, neg = 1 + neg if neg > 0 else 0, 1 + pos\n\t\telse:\n\t\t\tpos, neg = 0, 0\n\t\tans = max(ans, pos)\n\treturn ans\n``` | 142 | Given an array of integers `nums`, find the maximum length of a subarray where the product of all its elements is positive.
A subarray of an array is a consecutive sequence of zero or more values taken out of that array.
Return _the maximum length of a subarray with positive product_.
**Example 1:**
**Input:** nums = \[1,-2,-3,4\]
**Output:** 4
**Explanation:** The array nums already has a positive product of 24.
**Example 2:**
**Input:** nums = \[0,1,-2,-3,-4\]
**Output:** 3
**Explanation:** The longest subarray with positive product is \[1,-2,-3\] which has a product of 6.
Notice that we cannot include 0 in the subarray since that'll make the product 0 which is not positive.
**Example 3:**
**Input:** nums = \[-1,-2,-3,0,1\]
**Output:** 2
**Explanation:** The longest subarray with positive product is \[-1,-2\] or \[-2,-3\].
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | Keep a window of size k and maintain the number of vowels in it. Keep moving the window and update the number of vowels while moving. Answer is max number of vowels of any window. |
[Python3/Go/Java] Dynamic Programming O(N) time O(1) space | maximum-length-of-subarray-with-positive-product | 0 | 1 | ### Explanation\n"pos[i]", "neg[i]" represent longest consecutive numbers ending with nums[i] forming a positive/negative product.\n\n#### Complexity\n`time`: O(N)\n`space`: O(N)\n\n#### Python3:\n\n```python\ndef getMaxLen(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tpos, neg = [0] * n, [0] * n\n\tif nums[0] > 0: pos[0] = 1\n\tif nums[0] < 0: neg[0] = 1\n\tans = pos[0]\n\tfor i in range(1, n):\n\t\tif nums[i] > 0:\n\t\t\tpos[i] = 1 + pos[i - 1]\n\t\t\tneg[i] = 1 + neg[i - 1] if neg[i - 1] > 0 else 0\n\t\telif nums[i] < 0:\n\t\t\tpos[i] = 1 + neg[i - 1] if neg[i - 1] > 0 else 0\n\t\t\tneg[i] = 1 + pos[i - 1]\n\t\tans = max(ans, pos[i])\n\treturn ans\n```\n\n\n#### Golang:\n\n```Golang\nfunc getMaxLen(nums []int) int {\n n := len(nums)\n pos := make([]int, n)\n neg := make([]int, n)\n if nums[0] > 0 {\n pos[0] = 1\n } else if nums[0] < 0 {\n neg[0] = 1\n }\n ans := pos[0]\n for i := 1; i < n; i++ {\n if nums[i] > 0 {\n pos[i] = 1 + pos[i - 1]\n if neg[i - 1] > 0 {\n neg[i] = 1 + neg[i - 1]\n } else {\n neg[i] = 0\n }\n } else if nums[i] < 0 {\n if neg[i - 1] > 0 {\n pos[i] = 1 + neg[i - 1]\n } else {\n pos[i] = 0\n }\n neg[i] = 1 + pos[i - 1]\n }\n ans = Max(ans, pos[i])\n }\n return ans\n}\n\nfunc Max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n\n\n#### Java:\n\n```Java\npublic int getMaxLen(int[] nums) {\n\tint n = nums.length;\n\tint[] pos = new int[n];\n\tint[] neg = new int[n];\n\tif (nums[0] > 0) pos[0] = 1;\n\tif (nums[0] < 0) neg[0] = 1;\n\tint ans = pos[0];\n\tfor (int i = 1; i < n; i++) {\n\t\tif (nums[i] > 0) {\n\t\t\tpos[i] = 1 + pos[i - 1];\n\t\t\tneg[i] = neg[i - 1] > 0 ? 1 + neg[i - 1]:0;\n\t\t} else if (nums[i] < 0) {\n\t\t\tpos[i] = neg[i - 1] > 0 ? 1 + neg[i - 1]:0;\n\t\t\tneg[i] = 1 + pos[i - 1];\n\t\t}\n\t\tans = Math.max(ans, pos[i]);\n\t}\n\treturn ans;\n}\n```\n\n\n### Space Optimization\n\n### Complexity\n`time`: O(N)\n`space`: O(1)\n\nThanks @Spin0za for pointing out.\nSince only the previous one value of pos/neg is used, we can use 2 variables instead of 2 lists.\n\n#### Python3\n```python\ndef getMaxLen(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tpos, neg = 0, 0\n\tif nums[0] > 0: pos = 1\n\tif nums[0] < 0: neg = 1\n\tans = pos\n\tfor i in range(1, n):\n\t\tif nums[i] > 0:\n\t\t\tpos = 1 + pos\n\t\t\tneg = 1 + neg if neg > 0 else 0\n\t\telif nums[i] < 0:\n\t\t\tpos, neg = 1 + neg if neg > 0 else 0, 1 + pos\n\t\telse:\n\t\t\tpos, neg = 0, 0\n\t\tans = max(ans, pos)\n\treturn ans\n``` | 142 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
[Python3] 7-line O(N) time & O(1) space | maximum-length-of-subarray-with-positive-product | 0 | 1 | Define two counters `pos` and `neg` as the length of positive and negative products ending at current element. \n\n```\nclass Solution:\n def getMaxLen(self, nums: List[int]) -> int:\n ans = pos = neg = 0\n for x in nums: \n if x > 0: pos, neg = 1 + pos, 1 + neg if neg else 0\n elif x < 0: pos, neg = 1 + neg if neg else 0, 1 + pos\n else: pos = neg = 0 # reset \n ans = max(ans, pos)\n return ans \n``` | 68 | Given an array of integers `nums`, find the maximum length of a subarray where the product of all its elements is positive.
A subarray of an array is a consecutive sequence of zero or more values taken out of that array.
Return _the maximum length of a subarray with positive product_.
**Example 1:**
**Input:** nums = \[1,-2,-3,4\]
**Output:** 4
**Explanation:** The array nums already has a positive product of 24.
**Example 2:**
**Input:** nums = \[0,1,-2,-3,-4\]
**Output:** 3
**Explanation:** The longest subarray with positive product is \[1,-2,-3\] which has a product of 6.
Notice that we cannot include 0 in the subarray since that'll make the product 0 which is not positive.
**Example 3:**
**Input:** nums = \[-1,-2,-3,0,1\]
**Output:** 2
**Explanation:** The longest subarray with positive product is \[-1,-2\] or \[-2,-3\].
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | Keep a window of size k and maintain the number of vowels in it. Keep moving the window and update the number of vowels while moving. Answer is max number of vowels of any window. |
[Python3] 7-line O(N) time & O(1) space | maximum-length-of-subarray-with-positive-product | 0 | 1 | Define two counters `pos` and `neg` as the length of positive and negative products ending at current element. \n\n```\nclass Solution:\n def getMaxLen(self, nums: List[int]) -> int:\n ans = pos = neg = 0\n for x in nums: \n if x > 0: pos, neg = 1 + pos, 1 + neg if neg else 0\n elif x < 0: pos, neg = 1 + neg if neg else 0, 1 + pos\n else: pos = neg = 0 # reset \n ans = max(ans, pos)\n return ans \n``` | 68 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
Easy Java Solution 🚀 Clean Code . . . | minimum-number-of-days-to-disconnect-island | 1 | 1 | # Java Code\n---\n> #### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F\n---\n```\nclass Solution {\n int[] xDir = {0,0,-1,1};\n int[] yDir = {-1,1,0,0};\n public boolean isSafe(int[][] grid,int i,int j,boolean[][] visited)\n {\n return(i>=0 && j>=0 && i<grid.length && j<grid[0].length && visited[i][j] == false && grid[i][j] == 1);\n }\n public void islandCount(int[][] grid,int i,int j,boolean[][] visited)\n {\n visited[i][j] = true;\n for(int k = 0;k<4;k++)\n {\n int newRow = i+xDir[k];\n int newCol = j+yDir[k];\n if(isSafe(grid,newRow,newCol,visited))\n {\n islandCount(grid,newRow,newCol,visited);\n }\n }\n }\n public int CountLand(int[][] grid,boolean[][] visited)\n {\n int count = 0;\n for(int i = 0;i<grid.length;i++)\n {\n for(int j = 0;j<grid[0].length;j++)\n {\n if(grid[i][j] == 1 && visited[i][j] == false)\n {\n islandCount(grid,i,j,visited);\n count++;\n }\n }\n }\n return count;\n }\n public int minDays(int[][] grid) {\n int rows = grid.length;\n int cols = grid[0].length;\n boolean[][] visited = new boolean[rows][cols];\n int count = CountLand(grid,visited);\n if(count > 1 || count == 0) return 0;\n for(int i = 0;i<rows;i++)\n {\n for(int j = 0;j<cols;j++)\n {\n if(grid[i][j] == 1)\n {\n grid[i][j] = 0;\n boolean[][] mat = new boolean[rows][cols];\n int count2 = CountLand(grid,mat);\n grid[i][j] = 1;\n if(count2 > 1 || count2 == 0)\n {\n return 1; \n }\n }\n }\n }\n return 2;\n }\n}\n```\n---\n | 6 | You are given an `m x n` binary grid `grid` where `1` represents land and `0` represents water. An **island** is a maximal **4-directionally** (horizontal or vertical) connected group of `1`'s.
The grid is said to be **connected** if we have **exactly one island**, otherwise is said **disconnected**.
In one day, we are allowed to change **any** single land cell `(1)` into a water cell `(0)`.
Return _the minimum number of days to disconnect the grid_.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,0,0,0\]\]
**Output:** 2
**Explanation:** We need at least 2 days to get a disconnected grid.
Change land grid\[1\]\[1\] and grid\[0\]\[2\] to water and get 2 disconnected island.
**Example 2:**
**Input:** grid = \[\[1,1\]\]
**Output:** 2
**Explanation:** Grid of full water is also disconnected (\[\[1,1\]\] -> \[\[0,0\]\]), 0 islands.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either `0` or `1`. | Note that the node values of a path form a palindrome if at most one digit has an odd frequency (parity). Use a Depth First Search (DFS) keeping the frequency (parity) of the digits. Once you are in a leaf node check if at most one digit has an odd frequency (parity). |
python3 solution | minimum-number-of-days-to-disconnect-island | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : DFS\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, grid: List[List[int]]) -> int:\n R = len(grid)\n C = len(grid[0])\n directions = [[1, 0], [0, 1], [-1, 0], [0, -1]]\n\n def dfs(r, c, visit):\n if r < 0 or c < 0 or c >= C or r >= R or (r, c) in visit or grid[r][c] == 0:\n return\n visit.add((r, c))\n for dr, dc in directions:\n dfs(r + dr, c + dc, visit)\n\n def count_islands():\n islands = 0\n visited = set()\n for r in range(R):\n for c in range(C):\n if grid[r][c] == 1 and (r, c) not in visited:\n islands += 1\n dfs(r, c, visited)\n return islands\n\n islands = count_islands()\n if islands != 1:\n return 0\n\n for r in range(R):\n for c in range(C):\n if grid[r][c] == 1:\n grid[r][c] = 0\n islands = count_islands()\n if islands != 1:\n return 1\n grid[r][c] = 1\n return 2\n\n``` | 0 | You are given an `m x n` binary grid `grid` where `1` represents land and `0` represents water. An **island** is a maximal **4-directionally** (horizontal or vertical) connected group of `1`'s.
The grid is said to be **connected** if we have **exactly one island**, otherwise is said **disconnected**.
In one day, we are allowed to change **any** single land cell `(1)` into a water cell `(0)`.
Return _the minimum number of days to disconnect the grid_.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,0,0,0\]\]
**Output:** 2
**Explanation:** We need at least 2 days to get a disconnected grid.
Change land grid\[1\]\[1\] and grid\[0\]\[2\] to water and get 2 disconnected island.
**Example 2:**
**Input:** grid = \[\[1,1\]\]
**Output:** 2
**Explanation:** Grid of full water is also disconnected (\[\[1,1\]\] -> \[\[0,0\]\]), 0 islands.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either `0` or `1`. | Note that the node values of a path form a palindrome if at most one digit has an odd frequency (parity). Use a Depth First Search (DFS) keeping the frequency (parity) of the digits. Once you are in a leaf node check if at most one digit has an odd frequency (parity). |
[Python] Tarjan's Algorithm + Articulation Point detection = at most 2 days of flipping 1s to 0s | minimum-number-of-days-to-disconnect-island | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a haaaard problem if you don\'t know that we can take at most 2 days to separate a given island. We solve this using SCCs concept + articulation point detection.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use Tarjan\'s algorithm with articulation point detection. This enables us to calculate the number of islands (strongly connected components) in our grid. Moreover, we detect if we have an articulation point -> a node/point, if remove, will disconnect our SCC breaking it to separate SCCs\n2. Handle edge cases. If we have more than 1 SCCs, return 0. If we have an articulation point, return 1. Otherwise, check if we actually have islands in the grid. If no islands, return 0. If we have a single 1, return 1.\n3. Finally, if any of the above did not happen, return 2. Imagine a board full of 1. At the minimum, how many 1 should we erase to have two separate islands?\n\n# Complexity\n- Time complexity: $$O(m * n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m * n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, grid: List[List[int]]) -> int:\n rows, cols = len(grid), len(grid[0])\n\n disc_time = [[-1 for _ in range(cols)] for _ in range(rows)]\n low_value = [[-1 for _ in range(cols)] for _ in range(rows)]\n parents = [[(-1, -1) for _ in range(cols)] for _ in range(rows)]\n is_ap = [[False for _ in range(cols)] for _ in range(rows)]\n dirs = [(1, 0), (0, 1), (-1, 0), (0, -1)]\n\n time = 0\n has_ap = False\n def dfs(i, j):\n if grid[i][j] == 0:\n return\n nonlocal time\n nonlocal has_ap\n disc_time[i][j] = time\n low_value[i][j] = time\n time += 1\n\n child = 0\n for di, dj in dirs:\n ni, nj = i + di, j + dj\n if not (0 <= ni < rows) or not (0 <= nj < cols):\n continue\n if grid[ni][nj] != 1:\n continue\n\n if disc_time[ni][nj] == -1: # not visited\n child += 1\n parents[ni][nj] = (i, j)\n dfs(ni, nj)\n low_value[i][j] = min(low_value[i][j], low_value[ni][nj])\n\n if parents[i][j] == (-1, -1) and child > 1:\n is_ap[i][j] = True\n has_ap = True\n\n if parents[i][j] != (-1, -1) and low_value[ni][nj] >= disc_time[i][j]:\n is_ap[i][j] = True\n has_ap = True\n elif (ni, nj) != parents[i][j]:\n low_value[i][j] = min(low_value[i][j], disc_time[ni][nj])\n\n sccs = 0\n num_ones = 0\n for i in range(rows):\n for j in range(cols):\n if grid[i][j] == 1:\n num_ones += 1\n if disc_time[i][j] == -1 and grid[i][j] == 1:\n dfs(i, j)\n sccs += 1\n\n\n if sccs > 1:\n return 0\n elif has_ap:\n return 1\n else:\n if num_ones == 1:\n return 1\n elif num_ones == 0:\n return 0\n return 2\n\n\n``` | 0 | You are given an `m x n` binary grid `grid` where `1` represents land and `0` represents water. An **island** is a maximal **4-directionally** (horizontal or vertical) connected group of `1`'s.
The grid is said to be **connected** if we have **exactly one island**, otherwise is said **disconnected**.
In one day, we are allowed to change **any** single land cell `(1)` into a water cell `(0)`.
Return _the minimum number of days to disconnect the grid_.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,0,0,0\]\]
**Output:** 2
**Explanation:** We need at least 2 days to get a disconnected grid.
Change land grid\[1\]\[1\] and grid\[0\]\[2\] to water and get 2 disconnected island.
**Example 2:**
**Input:** grid = \[\[1,1\]\]
**Output:** 2
**Explanation:** Grid of full water is also disconnected (\[\[1,1\]\] -> \[\[0,0\]\]), 0 islands.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either `0` or `1`. | Note that the node values of a path form a palindrome if at most one digit has an odd frequency (parity). Use a Depth First Search (DFS) keeping the frequency (parity) of the digits. Once you are in a leaf node check if at most one digit has an odd frequency (parity). |
Not an optimized approach but good to know it. | minimum-number-of-days-to-disconnect-island | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, grid: List[List[int]]) -> int:\n\n def numIslands(grid):\n ans=0\n n=len(grid)\n m=len(grid[0])\n def dfs(i,j,visited):\n if (i,j) in visited:\n return\n if grid[i][j]==0:\n visited.add((i,j))\n return\n visited.add((i,j))\n A=[(-1,0),(1,0),(0,-1),(0,1)]\n for dx,dy in A:\n if 0<=i+dx<=n-1 and 0<=j+dy<=m-1 and grid[i+dx][j+dy]==1:\n dfs(i+dx,j+dy,visited)\n visited=set()\n for i in range(n):\n for j in range(m):\n if grid[i][j]==1 and (i,j) not in visited:\n dfs(i,j,visited)\n ans+=1\n return ans\n \n if numIslands(grid)!=1:\n return 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j]==1:\n grid[i][j]=0\n \n if numIslands(grid)!=1:\n return 1\n else:\n grid[i][j]=1\n return 2\n \n``` | 0 | You are given an `m x n` binary grid `grid` where `1` represents land and `0` represents water. An **island** is a maximal **4-directionally** (horizontal or vertical) connected group of `1`'s.
The grid is said to be **connected** if we have **exactly one island**, otherwise is said **disconnected**.
In one day, we are allowed to change **any** single land cell `(1)` into a water cell `(0)`.
Return _the minimum number of days to disconnect the grid_.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,0,0,0\]\]
**Output:** 2
**Explanation:** We need at least 2 days to get a disconnected grid.
Change land grid\[1\]\[1\] and grid\[0\]\[2\] to water and get 2 disconnected island.
**Example 2:**
**Input:** grid = \[\[1,1\]\]
**Output:** 2
**Explanation:** Grid of full water is also disconnected (\[\[1,1\]\] -> \[\[0,0\]\]), 0 islands.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either `0` or `1`. | Note that the node values of a path form a palindrome if at most one digit has an odd frequency (parity). Use a Depth First Search (DFS) keeping the frequency (parity) of the digits. Once you are in a leaf node check if at most one digit has an odd frequency (parity). |
max 2 days | Easy solution | minimum-number-of-days-to-disconnect-island | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n num_1s = abs(sum(sum(row) for row in grid))\n\n @cache\n def get_rc():\n for r in range(m):\n for c in range(n):\n if grid[r][c]:\n yield r, c\n\n # mul = 1\n # def set_dist(r, c, dist):\n # if r < 0 or r>= m or c < 0 or c >= n:\n # return\n # if grid[r][c] != 1 and grid[r][c] <= dist:\n # return\n # grid[r][c] = dist\n \n # set_dist(r-1, c, dist + 1)\n # set_dist(r+1, c, dist + 1)\n # set_dist(r, c-1, dist + 1)\n # set_dist(r, c+1, dist + 1)\n \n island = 1\n def is_connected():\n nonlocal island\n def count(r, c):\n if r < 0 or r>= m or c < 0 or c >= n: return 0\n if grid[r][c] != island: return 0\n grid[r][c] = -island\n total = 1\n total += count(r-1, c)\n total += count(r+1, c)\n total += count(r, c-1)\n total += count(r, c+1)\n return total\n r, c = first_rc\n if not grid[r][c]:\n r, c = second_rc\n conn = count(r, c)\n island = -island\n return conn == num_1s\n\n if num_1s == 0:\n return 0\n elif num_1s == 1:\n return 1\n \n \n g = get_rc()\n first_rc = next(g)\n second_rc = next(g)\n\n if not is_connected():\n return 0\n elif num_1s == 2:\n return 2\n \n\n # skip = True\n num_1s -= 1\n for r in range(m):\n for c in range(n):\n if grid[r][c] == 0:\n continue\n # if skip:\n # skip = False\n # continue\n grid[r][c] = 0\n if not is_connected():\n # print(f"Choke at {r}, {c}")\n return 1\n grid[r][c] = island\n \n \n return 2\n\n\n``` | 0 | You are given an `m x n` binary grid `grid` where `1` represents land and `0` represents water. An **island** is a maximal **4-directionally** (horizontal or vertical) connected group of `1`'s.
The grid is said to be **connected** if we have **exactly one island**, otherwise is said **disconnected**.
In one day, we are allowed to change **any** single land cell `(1)` into a water cell `(0)`.
Return _the minimum number of days to disconnect the grid_.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,0,0,0\]\]
**Output:** 2
**Explanation:** We need at least 2 days to get a disconnected grid.
Change land grid\[1\]\[1\] and grid\[0\]\[2\] to water and get 2 disconnected island.
**Example 2:**
**Input:** grid = \[\[1,1\]\]
**Output:** 2
**Explanation:** Grid of full water is also disconnected (\[\[1,1\]\] -> \[\[0,0\]\]), 0 islands.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either `0` or `1`. | Note that the node values of a path form a palindrome if at most one digit has an odd frequency (parity). Use a Depth First Search (DFS) keeping the frequency (parity) of the digits. Once you are in a leaf node check if at most one digit has an odd frequency (parity). |
Python 3 || 9 lines, recursion || T/M: 95% / 80% | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | ```\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n\n def dp(nums: List[int]) -> int:\n\n n = len(nums)\n if n < 3: return 1\n root, left, right = nums[0], [], []\n\n for x in nums:\n if x < root: left .append(x)\n elif x > root: right.append(x)\n\n return dp(left) * dp(right) * comb(n-1, len(left))\n\n return (dp(nums)-1) %1000000007\n```\n[https://leetcode.com/problems/number-of-ways-to-reorder-array-to-get-same-bst/submissions/972434217/](http://)\n\n | 4 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
w Explanation||C++/Python using Math Pascal's triangle/comb Beats 96.74% | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first element in array must be the root. Then divide the array into left subtree and right subtree! \n\nUse recursion, if the subproblems for left subtree and right subtree are solved, with the returning number l and r, Use the following formula:\n$$\nTotalNumber=l\\times r\\times C^{N-1}_{Len(left\\_subtree)}-1\n$$\nto solve the problem! Remember modulo 10**9+7 \n\nPlease turn on the English subtitles if neccessary!\n[https://youtu.be/eS-Po5QJE24](https://youtu.be/eS-Po5QJE24)\n# Why multiplication? The fundamental principle of counting/rule of product or multiplication principle says:\n> if there are a ways of doing something and b ways of doing another thing, then there are a \xB7 b ways of performing both actions.\n\n# Why the binomial number $C^{N-1}_{Len(left\\_subtree)}$?\nQ: Let N = len(nums). The position for the root is always at index 0. While you can change the positions of elements in the left and right subtrees, you need to maintain the orderings within each subtree. Therefore, there are N-1 available places to position either the left or right subtree. The count of possible arrangements is exactly given by $C^{N-1}_{Len(left\\_subtree)}$!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe computation for the binomial number $C^n_k$ from n choose k is using [Pascal\'s triangle](https://leetcode.com/problems/pascals-triangle/solutions/3201092/best-c-solution-via-pascal-s-identity-c-i-j-c-i-i-j-beats-100/)!\n\nThis test case makes using direct method computing $C^{N-1}_{Len(left\\_subtree)}$ impossible in C++, even using unsigned long long! But in python there is a function comb. \n```\n[74,24,70,11,6,4,59,9,36,82,80,30,46,31,22,34,8,69,32,57,18,21,37,83,55,38,41,72,48,65,27,60,73,58,68,50,16,77,75,20,81,3,61,13,10,29,62,49,12,66,39,45,28,40,42,52,78,56,44,17,14,67,35,26,19,5,63,51,43,23,79,2,54,47,76,53,7,25,64,33,1,15,71]\n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code with Explanation in comments\n```\nclass Solution {\npublic:\n long Mod = 1e9 + 7;\n // Calculate C_{n} choose k using Pascal\'s equation\n vector<vector<long>> C; // Matrix to store calculated binomial coefficients\n \n long compute_C_N_choose_K(int N, int K) {\n if (K > N / 2)\n K = N - K; // C_N choose K = C_N choose N-K\n \n C.assign(N + 1, vector<long>(K + 1, 0)); \n // Initialize the matrix with zeros\n \n for (int i = 0; i <= N; i++) {\n C[i][0] = 1; // Set the first column of each row to 1\n \n for (int j = 1; j <= min(i, K); j++)\n C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % Mod; \n // Calculate binomial coefficient using Pascal\'s equation\n }\n \n return C[N][K]; // Return the computed binomial coefficient\n }\n\n long Subproblem(vector<int>& nums) {\n int n = nums.size();\n \n if (n <= 2)\n return 1; \n// Base case: If the number of elements is less than or equal to 2, \n//there is only one way to split\n \n vector<int> left, right;\n int root = nums[0]; // Choose the first element as the root\n \n // Split the remaining elements into left and \n //right parts based on their values compared to the root\n for (int i = 1; i < n; i++) {\n if (root < nums[i])\n right.push_back(nums[i]); \n// Add the element to the right part if it is greater than the root\n\n else\n left.push_back(nums[i]); \n// Add the element to the left part if \n//it is less than or equal to the root\n }\n \n long r = Subproblem(right) % Mod; \n// Recursively calculate the number of ways for the right part\n\n long l = Subproblem(left) % Mod; \n// Recursively calculate the number of ways for the left part\n \n return compute_C_N_choose_K(n - 1, left.size()) * r % Mod * l % Mod; \n// Compute the total number of ways based on binomial coefficients \n// and the number of ways for left and right parts\n }\n\n int numOfWays(vector<int>& nums) {\n return Subproblem(nums); \n// Start the recursive computation by calling the Subproblem function\n }\n};\n\n```\n# 2nd Solution w SC O(N) & twice faster than 1st one\n```\nclass Solution {\npublic:\n int Mod=1e9+7;\n //Calcute C_{n} choose k by Pascal\'s equation\n \n int compute_C_N_choose_K(int N, int K){\n if (K>N/2) K=N-K;//C_N choose K =C_N choose N-K\n vector<int> C_N(K+1, 0), prevC(K+1, 0);\n for(int i=0; i<=N; i++){\n C_N[0]=1;\n for(int j=1; j<=min(i, K);j++){\n C_N[j]=((long)prevC[j-1]+prevC[j])%Mod; \n }\n prevC=C_N; \n }\n return C_N[K];\n }\n\n long Subproblem(vector<int>& nums){\n int n=nums.size();\n if (n<=2) return 1;\n vector<int> left, right;\n int root=nums[0];\n for (int i=1; i<n; i++){\n if (root<nums[i]) right.push_back(nums[i]);\n else left.push_back(nums[i]);\n }\n long r=Subproblem(right), l=Subproblem(left);\n return compute_C_N_choose_K(n-1, left.size())*r%Mod*l%Mod;\n\n }\n int numOfWays(vector<int>& nums) {\n return (Subproblem(nums)-1)%Mod;\n }\n};\n```\n# Python solution Runtime 155 ms Beats 96.74%\n```\nclass Solution: \n def numOfWays(self, nums: List[int]) -> int:\n Mod=10**9+7\n import math\n def Subproblem(nums: List[int]):\n n=len(nums)\n if n<=2: return 1\n root=nums[0]\n left=[]\n right=[]\n for y in nums[1:]:\n if y<root: left.append(y)\n else: right.append(y)\n return Subproblem(right)*Subproblem(left)%Mod*math.comb(len(nums)-1, len(left))%Mod\n return int((Subproblem(nums)-1)%Mod)\n``` | 3 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Python short and clean. | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/number-of-ways-to-reorder-array-to-get-same-bst/editorial/).\n\n# Complexity\n- Time complexity: $$O(n ^ 2)$$\n\n- Space complexity: $$O(n ^ 2)$$\n\n# Code\n```python\nclass Solution:\n def numOfWays(self, nums: list[int]) -> int:\n M = 1_000_000_007\n\n def num_ways(bst: Sequence[int]) -> int:\n if len(bst) <= 2: return 1\n lefts, rights = [x for x in bst if x < bst[0]], [x for x in bst if x > bst[0]]\n return num_ways(lefts) * num_ways(rights) * comb(len(lefts) + len(rights), len(lefts)) % M\n \n return (num_ways(nums) - 1) % M\n\n\n``` | 2 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Fastest Solution Yet | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Intuition\nGiven an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.\n\nThe code works as follows:\n1. It first defines a function ```cnr()``` that calculates the combination of two numbers. This function is used later in the code to calculate the number of ways to split a range of numbers into two smaller ranges.\n\n2. It then defines two arrays, ```leng``` and ```cnt```, which store the length and count of each range of numbers, respectively.\n\n3. It then iterates through the array ```nums``` in reverse order. For each number ```p```, it calculates the length of the range of numbers to the left of ```p``` (stored in ```h```) and the length of the range of numbers to the right of ```p``` (stored in ```k```).\n\n4. It then calculates the number of ways to split the range of numbers from ```p-h``` to ```p+k``` into two smaller ranges (left sub-tree and right sub-tree). This is done by multiplying the count of the range of numbers to the left of ```p``` (stored in ```cnt[p-1]```), the count of the range of numbers to the right of ```p``` (stored in ```cnt[p+1]```), and the combination of ```h+k``` and ```h```.\n\n5. It then updates the length and count of the range of numbers from ```p-h``` to ```p+k``` to be ```h+k+1``` and ```t```, respectively.\n\n6. It repeats steps 3-5 for each number in ```nums```.\n\n7. It then returns the count of the range of numbers from ```1 to n```, which is stored in ```cnt[1]```.\n\n\n\n\n# Approach\nUse bottom-up recursion with merge interval.\n\n# Complexity\n- Time complexity:$$O(n^2)$$. This is because the code iterates through the array nums once, and for each number in the array, it calculates the length and count of the range of numbers to the left and right of the number. The space complexity of the code is O(n), because it stores the arrays leng and cnt.\n\n- Space complexity:$$O(n^2)$$. This is because the two arrays leng and cnt both have a size of n+2, and each element in the arrays takes up constant space. Therefore, the total space complexity is O(n^2).\n\nHere is a breakdown of the space complexity of each of the two arrays:\n\n - leng: This array stores the lengths of the intervals that have been processed so far. The size of this array is n+2 because we need to store the lengths of all intervals, including the empty interval at the beginning and end.\n \n - cnt: This array stores the number of ways to partition the intervals that have been processed so far. The size of this array is also n+2 because we need to store the number of ways to partition all intervals, including the empty partition at the beginning and end.\n\n\nThe total space complexity is then the sum of the space complexities of the two arrays, which is O(n^2).\n\n\n\n# Code\n```\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n mod = 1000000007\n n = len(nums)\n\n\n # stores the length of each range of numbers, respectively.\n leng = [0]*(n+2) \n\n # stores the count of each range of numbers, respectively.\n cnt = [1]*(n+2) \n\n # Iterate the array in reverse order\n for p in nums[::-1]: \n # k consecutive values larger than p (on the left) are already in BST if leng[p+1] > 0 indicates that. Length [p+1] and h are the respective integers in the right child BST of p.\n h,k = leng[p-1],leng[p+1] \n\n # The size of the BST rooted at p should be used to update the lengths at the rightmost and leftmost numbers in the BST (consecutive intervals). Because it won\'t be needed in the subsequent computation of length and cnt, the numbers in between (p-h, p+k) don\'t need to be updated.\n leng[p-h]=leng[p+k]=h+k+1 \n\n # The number of permutated arrays that can construct the BST of the left child and the right child of p is given by dp(BST rooted at p) = dp(left(p-1))*dp(right(p+1))*C(left+right,right).\n t = (cnt[p-1]*cnt[p+1]%mod)*comb(h+k,h)%mod \n\n # Only the cnt\'s rightmost and leftmost elements should be updated because those two numbers will be the only ones used in the next merge interval.\n cnt[p-h]=cnt[p+k]=t \n\n # return the number of ways to reorder nums\n return (cnt[1]-1)%mod \n``` | 2 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Best Solution 😎💪🏼 | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Approach\nThe approach used in the code involves a depth-first search (DFS) algorithm. The dfs function takes three parameters: i represents the current index, l represents the lower bound, and h represents the upper bound.\n\nThe function checks if the upper bound h is one greater than the lower bound l. If so, it means there are no more elements to consider, and the function returns 1.\n\nOtherwise, the function checks if the value at index i is between l and h. If it is, it recursively calls dfs twice: once with the left subarray (from l to A[i]) and once with the right subarray (from A[i] to h). It also calculates the number of combinations between the left and right subarrays using math.comb and multiplies it with the recursive results.\n\nIf the value at index i is not between l and h, the function makes a recursive call with the same index but updates only the upper bound.\n\nFinally, the function returns the result of the recursive calls subtracted by 1.\n\nThe numOfWays function initializes some variables and then calls dfs with the initial parameters.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: The time complexity depends on the number of recursive calls made. Each recursive call reduces the problem size, so the time complexity can be expressed as O(2^n), where n is the length of the input list A.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is determined by the depth of the recursive calls, which can go up to n. Therefore, the space complexity is O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfWays(self, A):\n n = len(A)\n mod = 10 ** 9 + 7\n\n def dfs(i, l, h):\n if h == l + 1:\n return 1\n if l < A[i] < h:\n return (dfs(i + 1, l, A[i]) * dfs(i + 1, A[i], h) * math.comb(h - l - 2, A[i] - l - 1)) % mod\n return dfs(i + 1, l, h)\n \n return dfs(0, 0, n + 1) - 1\n\n```\n\n### *Kindly Upvote\u270C\uD83C\uDFFC* | 4 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Python3 Solution | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | \n```\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n mod=10**9+7\n \n def f(nums):\n n=len(nums)\n if n<=1:\n return len(nums) \n\n left=[i for i in nums if i<nums[0]]\n right=[i for i in nums if i>nums[0]]\n\n Left=f(left)\n Right=f(right)\n\n if not Left or not Right :\n return Left or Right\n ans=comb(len(right)+len(left),len(right))\n return ans*Left*Right\n\n return (f(nums)-1)%mod \n\n return (f(nums)-1)%mod \n``` | 1 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Finding topological sorts (clean code + explanation) | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Intuition\nThis problem can be rephrased as finding the number of ways to topological sort the BST. We are given one, which can be used to build a tree, and the task is to find the rest.\n\n# Approach\nAfter building our tree, define a helper function `h(x)` that returns the number of topological sortings for the tree node `x`. If number of nodes in the subtree `x` is less than or equal to 1, then `h(x) = 1` (Base case).\n\nFor an arbitrary tree node, the goal is to work out how many ways there are of interleaving the topological sorts of the left and right subtrees. For the time being, lets assume that both the left and right subtrees have exactly one topological sort each, and lengths `m` and `n` respectively (like example 2 in the problem where `x` is the root). Assume these sequences are $l=(l_1, l_2, ..., l_m)$ and $r=(r_1, r_2, ..., r_n)$.\n\nWe know the total length of the ordering is $m + n$, and if we can figure out where all of the values from $l$ go, those for $r$ will fall out. In other words, we need to choose $m$ indices from $m + n$; therefore the answer is $\\frac{(m + n)!}{m! n!}$ (combination formula).\n\nWhen there are more than 1 topological sorts for each subtree, we have to multiply the above formula by the product of these values (since the orderings are independent of each other... different subtrees):\n$$ \\frac{(m +n)!}{m!n!}\\times h(x_{left}) \\times h(x_{right}) $$.\n\n# Code\n```\nclass Node:\n def __init__(self, val):\n self.val = val\n self.left = None\n self.right = None\n self.size = 1\n\n def insert(self, x):\n self.size += 1\n if x < self.val:\n if self.left: self.left.insert(x)\n else: self.left = Node(x)\n else:\n if self.right: self.right.insert(x)\n else: self.right = Node(x)\n\n\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n root = Node(nums[0])\n for i in range(1, len(nums)):\n # Insert\n root.insert(nums[i])\n\n # Return num topsorts\n def h(root):\n if not node or (not root.left and not root.right): return 1\n L = h(root.left)\n R = h(root.right)\n return math.comb(root.size - 1, root.left.size if root.left else 0) * L * R\n\n return (h(root) - 1) % 1_000_000_007\n\n```\n\n# References\n\n- https://cs.stackexchange.com/questions/12713/find-the-number-of-topological-sorts-in-a-tree\n- https://cs.stackexchange.com/questions/12713/find-the-number-of-topological-sorts-in-a-tree | 2 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Python 🐍 Easy & Fast Solution | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nHere are my initial thoughts on how to solve this problem:\n\n- The base case of the recursive function f is when the length of the input list nums is less than or equal to 2, in which case there is only one way to arrange the numbers. This is returned as 1.\n\n- The recursive case involves splitting the list nums into two sublists: left and right. The left sublist contains numbers smaller than the first element of nums, while the right sublist contains numbers greater than the first element.\n\n- The number of ways to arrange the numbers in nums is calculated as the product of three factors:\n\n- The number of ways to choose the positions for the right sublist among the total number of positions (i.e., combinations of the lengths of left and right).\n- The number of ways to arrange the numbers in the left sublist.\n- The number of ways to arrange the numbers in the right sublist.\n\n- The recursive calls to f are made on the left and right sublists to compute the number of ways to arrange their respective numbers.\n\n- Finally, the result is obtained by subtracting 1 from the total number of ways and taking the modulus with (10**9 + 7).\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nThe numOfWays function calculates the number of ways to arrange the given list of numbers by recursively calling the helper function f.\n\nThe recursive function f performs the following steps:\n\n- It checks for the base case: if the length of the input list nums is less than or equal to 2, indicating that there is only one way to arrange the numbers, it returns 1.\n\n- For the recursive case, the function splits the input list nums into two sublists: left and right. The left sublist contains all the numbers smaller than the first element of nums, while the right sublist contains all the numbers greater than the first element.\n\n- The number of ways to arrange the numbers in nums is calculated as follows:\n\n- Determine the number of positions available for the right sublist by combining the lengths of the left and right sublists using the comb function from the math module.\n\n- Multiply the above value by the number of ways to arrange the numbers in the left sublist (by making a recursive call to f).\n\n- Multiply the result by the number of ways to arrange the numbers in the right sublist (also by making a recursive call to f).\n\n- The final result is obtained by subtracting 1 from the total number of ways calculated and taking the modulus with (10**9 + 7).\n\n## To improve the code:\n\nImport the comb function from the math module.\nUse proper formatting and indentation to enhance code readability.\nTesting the code with different inputs and comparing the results against expected outcomes would be crucial to ensure the correctness of the implementation.\n\n\n# Complexity\n- Time complexity:$$O(2^n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import comb\nfrom typing import List\n\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n def f(nums):\n if len(nums) <= 2:\n return 1\n left = [v for v in nums if v < nums[0]]\n right = [v for v in nums if v > nums[0]]\n return comb(len(left) + len(right), len(right)) * f(left) * f(right)\n \n return (f(nums) - 1) % (10**9 + 7)\n\n```\n\n\n | 63 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Clear Explanation of an Easy Recursive Combinatorics Solution | number-of-ways-to-reorder-array-to-get-same-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs with most tree problems, we repeatedly explore the left and right subtrees of the tree to arrive at our solution. In this case, we look at how many permutations of a subtree array correspond to the same subtree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAfter noting that the first element in the array is the root of the (sub)tree, we can also conclude that all the elements in num[1:] which are smaller than the root will be in the left subtree and all the elements in nums[1:] which are greater than the root will be in the right subtree. \n\nFor example, if the BST array is [3, 2, 1, 4, 5], then the root is 3 and the left subtree is [2, 1] with root node 2 and the right subtree is [4, 5] with root node 4. Notice that the subarray [2, 3] can be permuted in any position in nums[1:] as along as their relative permutation to each other is the same. For example, the array [3, 4, 2, 5, 1] will also give us the left subtree [2, 1] and the right subtree [4, 5]. Let $m$ be the length of the array, and let $k$ be the number of nodes in the left subtree. We need to choose $k$ spots out of $m-1$ positions to place our left subtree nodes in the array. This can done in $\\binom{m-1}{k}$ ways where $\\binom{x}{y}$ is the binomial coefficient which is equal to $\\frac{x!}{y!(x-y!)}$. \n\nHowever, our final answer is not $\\binom{m-1}{k}$. This only tells us the number of ways the children of the current root node can be permuted in the array. It does not tell us about the children nodes of the current root node\'s children i.e. it does not tell us about deeper subtrees. For example, consider the BST array [3, 1, 5, 2, 4, 7]. The left subtree here is [1, 2] and the right subtree is [5, 4, 7]. Notice how the right subtree can be [5, 7, 4] or [5, 4, 7] and still correspond to the same BST. This implies that we must traverse each subtree and calculate the valid permutations for its children node as well. The final answer will be the valid permutation of the left subtree multiplied by the valid permutations of the right subtree multiplied by the valid permutations of the current tree. \n\n# Complexity\n- Time complexity: $O(n^2)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThis is because we are calling the dfs function twice for each node in the tree. \n\n- Space complexity:$O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nFirst, we are storing the left and right subtrees which have linear space. Next, our recursive call stack can have at most $n-1$ calls.\n\n# Code\n```\n\nclass Solution:\n\tdef numOfWays(self, nums: List[int]) -> int:\n\t\t"""\n\t\tCalculates the number of ways an array can be rearranged and\n\t\tstill correspond to the same BST. \n\n\t\tArgs:\n\t\t\tnums: List[int] = array of integers which correspond to a BST \n\n\t\tReturns:\n\t\t\tcount: int = number of ways the array can be rearranged and \n\t\t\t\t\t\t still correspond to the same BST\n\t\t"""\n\n\t\t# Since the answer might be very large, we return it modulo 10**9 + 7\n\t\tmod = 10 ** 9 + 7 \n\n\t\t# define a recursive function which repeatedly calculates the answer\n\t\t# for each level of the binary search tree\n\n\t\tdef dfs(arr):\n\n\t\t\t# if the length of the current subtree is less than or equal to\n\t\t\t# two, then we can\'t rearrange the array in more ways since the \n\t\t\t# first element is the root of the subtree\n\n\t\t\tlength = len(arr)\n\t\t\tif length <= 2:\n\t\t\t\treturn 1 \n\n\t\t\t# we collect the array representation of the left subtree and the\n\t\t\t# right subtree\n\t\t\tleft_nodes = [num for num in arr if num < arr[0]]\n\t\t\tright_nodes = [num for num in arr if num > arr[0]]\n\n\t\t\t# at this current level, we can permute the left and right subtree\n\t\t\t# nodes by choosing len(left_nodes) spots from the arr[1:]\n\t\t\tcurrent_level_permutation = comb(length-1, len(left_nodes))\n\n\t\t\t# we have calculated the permutations for the current level of the BST,\n\t\t\t# we need to calculate the permutations for the left subtree and the right\n\t\t\t# subtree. We multiply all the factors together and return the final answer.\n\t\t\treturn dfs(left_nodes) * dfs(right_nodes) *current_level_permutation\n\n\t\t# we call the function for the BST, subtract one since the argument passed in is\n\t\t# not considered, and return the answer modulo 10 ** 9 + 7\n\t\treturn (dfs(nums) - 1) % mod \n``` | 1 | Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.
* For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.
Return _the number of ways to reorder_ `nums` _such that the BST formed is identical to the original BST formed from_ `nums`.
Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 1
**Explanation:** We can reorder nums to be \[2,3,1\] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
**Example 2:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** 5
**Explanation:** The following 5 arrays will yield the same BST:
\[3,1,2,4,5\]
\[3,1,4,2,5\]
\[3,1,4,5,2\]
\[3,4,1,2,5\]
\[3,4,1,5,2\]
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** There are no other orderings of nums that will yield the same BST.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**. | Use dynamic programming, define DP[i][j] as the maximum dot product of two subsequences starting in the position i of nums1 and position j of nums2. |
Python3 Easiest solution || 2 methods | matrix-diagonal-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Simple logic**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- traverse primary diagonal and add elements.\n- while travesing put 0 as diagonal element, indicating we traversed it.\n- now traverse secondary diagonal and add elements.\n- return answer\n\n# Complexity\n- Time complexity: O(2N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def diagonalSum(self, mat: List[List[int]]) -> int:\n ans = 0\n i, j = 0, 0\n def isValid(i, j): # to check co-ordinates\n return 0 <= i < len(mat) and 0 <= j < len(mat[0])\n\n while isValid(i, j): # traverse primary diagonal\n ans += mat[i][j]\n mat[i][j] = 0 # replace element with 0 to identify\n i += 1\n j += 1\n \n i, j = len(mat) - 1, 0\n \n while isValid(i, j): # secondary diagonal\n ans += mat[i][j]\n i -= 1\n j += 1\n\n return ans\n```\n---\n# Approach\n- same as above but here we do primary and secondary in one loop ending up in o(N) time\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n# Code\n```\nclass Solution:\n def diagonalSum(self, mat: List[List[int]]) -> int:\n ans = 0\n i, j, k = 0, 0, len(mat) - 1\n def isValid(i, j):\n return 0 <= i < len(mat) and 0 <= j < len(mat[0])\n\n while isValid(i, j): # primary and secondary diagonal adding in same loop\n ans += mat[i][j]\n mat[i][j] = 0 # making 0 to make sure we don\'t add again\n ans += mat[k][j]\n i += 1\n j += 1\n k -= 1\n\n return ans\n```\n# Please like and comment below | 1 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
Check indices of count of 1. Simple Python implementation | number-of-ways-to-split-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n MOD = 10 ** 9 + 7\n N = len(s)\n c1 = s.count(\'1\')\n if not c1:\n return (((N-1)*(N-2))//2) % MOD\n if c1 % 3:\n return 0\n idx1, idx2, idx3, idx4 = 0, 0, 0, 0\n cnt = 0\n cnt1 = 0\n for i in range(N):\n if s[i] == \'1\':\n cnt += 1\n if cnt == c1//3:\n idx1 = i\n break\n for i in range(idx1+1,N):\n if s[i] == \'1\':\n idx2 = i\n break\n for i in range(N-1,-1,-1):\n if s[i] == \'1\':\n cnt1 += 1\n if cnt1 == c1//3:\n idx4 = i\n break\n for i in range(idx4-1,-1,-1):\n if s[i] == \'1\':\n idx3 = i\n break\n return ((idx2-idx1) * (idx4-idx3)) % MOD\n``` | 2 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Check indices of count of 1. Simple Python implementation | number-of-ways-to-split-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n MOD = 10 ** 9 + 7\n N = len(s)\n c1 = s.count(\'1\')\n if not c1:\n return (((N-1)*(N-2))//2) % MOD\n if c1 % 3:\n return 0\n idx1, idx2, idx3, idx4 = 0, 0, 0, 0\n cnt = 0\n cnt1 = 0\n for i in range(N):\n if s[i] == \'1\':\n cnt += 1\n if cnt == c1//3:\n idx1 = i\n break\n for i in range(idx1+1,N):\n if s[i] == \'1\':\n idx2 = i\n break\n for i in range(N-1,-1,-1):\n if s[i] == \'1\':\n cnt1 += 1\n if cnt1 == c1//3:\n idx4 = i\n break\n for i in range(idx4-1,-1,-1):\n if s[i] == \'1\':\n idx3 = i\n break\n return ((idx2-idx1) * (idx4-idx3)) % MOD\n``` | 2 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
[Java/Python 3] Multiplication of the ways of 1st and 2nd cuts w/ explanation and analysis. | number-of-ways-to-split-a-string | 1 | 1 | Please refer to the outstanding elaboration from `@lionkingeatapple`, who deserves more upvotes than me:\n\n----\n\nWe have three different scenarios.\n\n`scenarios_1:` If the total number of ones in the input string is not the multiple of three, there is no way we can cut the string into three blocks with an equal number of ones. `=> Count the total number of the 1s, if not divisible by 3, then return 0;`\n\n`scenarios_2:` If give input string are all zeros, it doesn\'t matter how you want to cut, and each block will have the same number of ones. In other words, the number of ones equals zero in each block. Therefore, the total number of ways to cut the input string is `(n - 2) + (n - 3) + ... + 2 + 1 = (n - 2) * (n - 1) / 2`. (Please reference the proof from @rock explanation).\n\n`scenarios_3:` This is a more general situation. First, think about it, in order to cut the input string to three parts, we need only two cuts, so we can get three blocks. Let\'s say these three blocks are `b1, b2, b3`. Now, we want the number of ones to be equal for all three blocks and the number of ones we need for each block is `total number of ones / 3`. The questions now become where we need to do our cut, remember we need to only two cuts to make three blocks, so we need to decide where we need to do our first cut, and where we can do our second cut, with all of these we can know our final answer.\n\n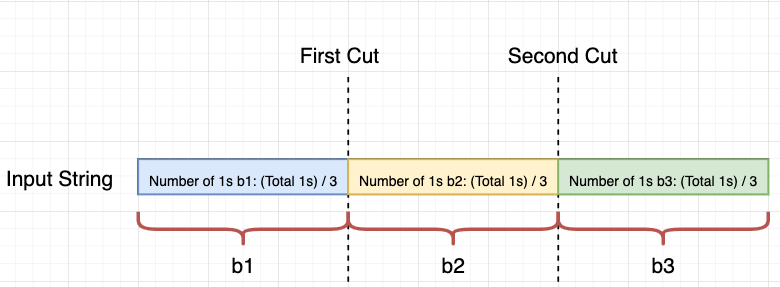\n\n\n\nStarts from begin of the input string, we can not cut until the number of ones in the substring is less than `total number of ones / 3`. If the number of ones in the substring is equal to `total number of ones / 3`, then that is our place to do the first cut. For example, we have an input string 100100010100110. The number of ones for each block will be `total number of ones / 3 = 6 / 3 = 2`. The first cut place can be either after index `3,4,5 and 6` because of those substrings `( substring(0, 4), substring(0, 5), substring(0, 6), substring(0, 7)` will have the same number of ones, which is `2` and the number of ways to cut at first place is `4` (see diagram below).\n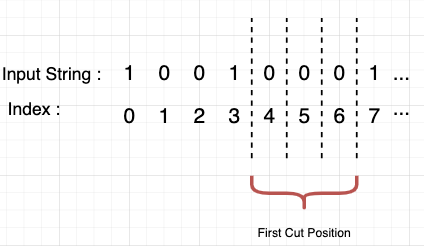\n\n**Our first block (b1) could be either one of them below:**\n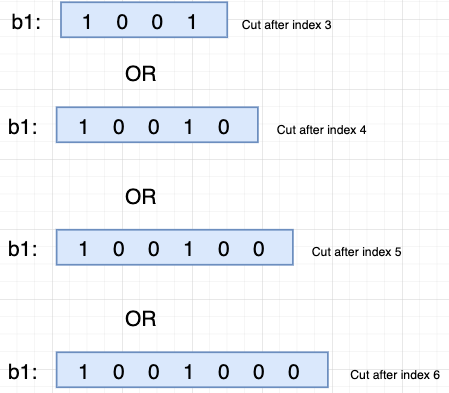\n\n\n\nAfter, we know about our first places to cut the input string, we need to know the second place to cut. When it comes to the second block, the number of ones we want are `the number of ones in the first block + the number of ones in the second block = 1s in b1 + 1s in b2.` Based on the example above, `1s in b1 + 1s in b2 = 2 + 2 = 4`, since the ones between blocks are equal, we can also simply do `2 * (number of ones each block) = 2 * 2 = 4`. Therefore, we need to find the substring with the total number of ones is equal to `4`. Those substrings are `substring(0, 10), substring(0, 11), substring(0, 12)` and our second cut places can be either after index `9, 10, 11` and the number of ways to cut at second place is `3`. (see diagram below)\n\n\n\n\n\nFinally, after two cuts, we got our `3 blocks` and we have known all the places we can do these two cuts, so we can calculate the total ways of cutting are `number of ways to cut at first place x number of ways to cut at second place = 4 x 3 = 12`.\n\n**Follow up question**\n`Return number of ways split input string s into N non-empty strings, each string has an equal number of ones. (2 < N < length of input string)`\n\nThinking:\nIn order to have `N` substrings, we need to cut input string `N - 1` times, so we will have `N - 1` blocks. Then, we have `b1, b2, b3, b4, ... ...b(n-1)`. Each of the blocks needs to have `number of ones = total number of ones / N`. And let\'s assume the number of ways to split string for each cut is `Wi`, so the total number of ways to cut will be `W1 x W2 x W3 x ... ...x Wn-1`. I didn\'t code this yet. I think you guys are smart enough to get an answer.\n\n----\n\n1. Count the total number of the `1`s, if not divisible by `3`, then return `0`;\n2. If the count is `0`, then we can choose 1st `0` as our 1st cut, correspondingly, the 2nd cut between the other `2` non-empty subarrays will have `n - 2` options, where `n = s.length()`; Similarly, we can also choose 2nd `0` as 1st cut, then we have `n - 3` options for the 2nd cut, ..., etc, totally, the result is `(n - 2) + (n - 3) + ... + 2 + 1 = (n - 2) * (n - 1) / 2`;\n3. Otherwise, traverse the input array: count the `1`s again, if the count reaches the `1 / 3` of the totoal number of `1`s, we begin to accumulate the number of the ways of the 1st cut, until the count is greater than `1 / 3 * total ones`; when the count reaches the `2 / 3` of the total number of the `1`s, start to accumulate the number of the ways of the 2nd cut, until the count is greater than `2 / 3 * total ones`;\n4. Multification of the numbers of the ways of 1st and 2nd cuts is the result..\n\n```java\n private static final int m = 1_000_000_007;\n public int numWays(String s) {\n int ones = 0, n = s.length();\n for (int i = 0; i < n; ++i) {\n ones += s.charAt(i) - \'0\';\n }\n if (ones == 0) {\n return (int)((n - 2L) * (n - 1L) / 2 % m);\n }\n if (ones % 3 != 0) {\n return 0;\n }\n int onesInEachSplitedBlock = ones / 3;\n long waysOfFirstCut = 0, waysOfSecondCut = 0;\n for (int i = 0, count = 0; i < n; ++i) {\n count += s.charAt(i) - \'0\';\n if (count == onesInEachSplitedBlock) {\n ++waysOfFirstCut;\n }else if (count == 2 * onesInEachSplitedBlock) {\n ++waysOfSecondCut;\n }\n }\n return (int)(waysOfFirstCut * waysOfSecondCut % m); \n```\n```python\n def numWays(self, s: str) -> int:\n ones, n, m = s.count(\'1\'), len(s), 10 ** 9 + 7\n if ones == 0:\n return (n - 2) * (n - 1) // 2 % m\n if ones % 3 != 0:\n return 0\n ones_in_each_splited_block = ones // 3\n count = ways_of_first_cut = ways_of_second_cut = 0\n for char in s:\n if char == \'1\':\n count += 1\n if count == ones_in_each_splited_block:\n ways_of_first_cut += 1\n elif count == 2 * ones_in_each_splited_block:\n ways_of_second_cut += 1\n return ways_of_first_cut * ways_of_second_cut % m \n```\n**Analysis:**\n\nTwo Pass.\n\nTime: O(n), space: O(1), where n = s.length(). | 205 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
[Java/Python 3] Multiplication of the ways of 1st and 2nd cuts w/ explanation and analysis. | number-of-ways-to-split-a-string | 1 | 1 | Please refer to the outstanding elaboration from `@lionkingeatapple`, who deserves more upvotes than me:\n\n----\n\nWe have three different scenarios.\n\n`scenarios_1:` If the total number of ones in the input string is not the multiple of three, there is no way we can cut the string into three blocks with an equal number of ones. `=> Count the total number of the 1s, if not divisible by 3, then return 0;`\n\n`scenarios_2:` If give input string are all zeros, it doesn\'t matter how you want to cut, and each block will have the same number of ones. In other words, the number of ones equals zero in each block. Therefore, the total number of ways to cut the input string is `(n - 2) + (n - 3) + ... + 2 + 1 = (n - 2) * (n - 1) / 2`. (Please reference the proof from @rock explanation).\n\n`scenarios_3:` This is a more general situation. First, think about it, in order to cut the input string to three parts, we need only two cuts, so we can get three blocks. Let\'s say these three blocks are `b1, b2, b3`. Now, we want the number of ones to be equal for all three blocks and the number of ones we need for each block is `total number of ones / 3`. The questions now become where we need to do our cut, remember we need to only two cuts to make three blocks, so we need to decide where we need to do our first cut, and where we can do our second cut, with all of these we can know our final answer.\n\n\n\n\n\nStarts from begin of the input string, we can not cut until the number of ones in the substring is less than `total number of ones / 3`. If the number of ones in the substring is equal to `total number of ones / 3`, then that is our place to do the first cut. For example, we have an input string 100100010100110. The number of ones for each block will be `total number of ones / 3 = 6 / 3 = 2`. The first cut place can be either after index `3,4,5 and 6` because of those substrings `( substring(0, 4), substring(0, 5), substring(0, 6), substring(0, 7)` will have the same number of ones, which is `2` and the number of ways to cut at first place is `4` (see diagram below).\n\n\n**Our first block (b1) could be either one of them below:**\n\n\n\n\nAfter, we know about our first places to cut the input string, we need to know the second place to cut. When it comes to the second block, the number of ones we want are `the number of ones in the first block + the number of ones in the second block = 1s in b1 + 1s in b2.` Based on the example above, `1s in b1 + 1s in b2 = 2 + 2 = 4`, since the ones between blocks are equal, we can also simply do `2 * (number of ones each block) = 2 * 2 = 4`. Therefore, we need to find the substring with the total number of ones is equal to `4`. Those substrings are `substring(0, 10), substring(0, 11), substring(0, 12)` and our second cut places can be either after index `9, 10, 11` and the number of ways to cut at second place is `3`. (see diagram below)\n\n\n\n\n\nFinally, after two cuts, we got our `3 blocks` and we have known all the places we can do these two cuts, so we can calculate the total ways of cutting are `number of ways to cut at first place x number of ways to cut at second place = 4 x 3 = 12`.\n\n**Follow up question**\n`Return number of ways split input string s into N non-empty strings, each string has an equal number of ones. (2 < N < length of input string)`\n\nThinking:\nIn order to have `N` substrings, we need to cut input string `N - 1` times, so we will have `N - 1` blocks. Then, we have `b1, b2, b3, b4, ... ...b(n-1)`. Each of the blocks needs to have `number of ones = total number of ones / N`. And let\'s assume the number of ways to split string for each cut is `Wi`, so the total number of ways to cut will be `W1 x W2 x W3 x ... ...x Wn-1`. I didn\'t code this yet. I think you guys are smart enough to get an answer.\n\n----\n\n1. Count the total number of the `1`s, if not divisible by `3`, then return `0`;\n2. If the count is `0`, then we can choose 1st `0` as our 1st cut, correspondingly, the 2nd cut between the other `2` non-empty subarrays will have `n - 2` options, where `n = s.length()`; Similarly, we can also choose 2nd `0` as 1st cut, then we have `n - 3` options for the 2nd cut, ..., etc, totally, the result is `(n - 2) + (n - 3) + ... + 2 + 1 = (n - 2) * (n - 1) / 2`;\n3. Otherwise, traverse the input array: count the `1`s again, if the count reaches the `1 / 3` of the totoal number of `1`s, we begin to accumulate the number of the ways of the 1st cut, until the count is greater than `1 / 3 * total ones`; when the count reaches the `2 / 3` of the total number of the `1`s, start to accumulate the number of the ways of the 2nd cut, until the count is greater than `2 / 3 * total ones`;\n4. Multification of the numbers of the ways of 1st and 2nd cuts is the result..\n\n```java\n private static final int m = 1_000_000_007;\n public int numWays(String s) {\n int ones = 0, n = s.length();\n for (int i = 0; i < n; ++i) {\n ones += s.charAt(i) - \'0\';\n }\n if (ones == 0) {\n return (int)((n - 2L) * (n - 1L) / 2 % m);\n }\n if (ones % 3 != 0) {\n return 0;\n }\n int onesInEachSplitedBlock = ones / 3;\n long waysOfFirstCut = 0, waysOfSecondCut = 0;\n for (int i = 0, count = 0; i < n; ++i) {\n count += s.charAt(i) - \'0\';\n if (count == onesInEachSplitedBlock) {\n ++waysOfFirstCut;\n }else if (count == 2 * onesInEachSplitedBlock) {\n ++waysOfSecondCut;\n }\n }\n return (int)(waysOfFirstCut * waysOfSecondCut % m); \n```\n```python\n def numWays(self, s: str) -> int:\n ones, n, m = s.count(\'1\'), len(s), 10 ** 9 + 7\n if ones == 0:\n return (n - 2) * (n - 1) // 2 % m\n if ones % 3 != 0:\n return 0\n ones_in_each_splited_block = ones // 3\n count = ways_of_first_cut = ways_of_second_cut = 0\n for char in s:\n if char == \'1\':\n count += 1\n if count == ones_in_each_splited_block:\n ways_of_first_cut += 1\n elif count == 2 * ones_in_each_splited_block:\n ways_of_second_cut += 1\n return ways_of_first_cut * ways_of_second_cut % m \n```\n**Analysis:**\n\nTwo Pass.\n\nTime: O(n), space: O(1), where n = s.length(). | 205 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Python | One-pass | Explained & Visualised | number-of-ways-to-split-a-string | 0 | 1 | Scan ```s``` to record positions for ```\'1\'```. After checking the edge cases, the result is simply a combination of choices.\n\n\n```Python\nclass Solution:\n def numWays(self, s: str) -> int:\n n,ones = len(s),[]\n for i,val in enumerate(s):\n if val == \'1\':\n ones.append(i)\n total = len(ones)\n if total == 0:\n\t\t # ref: https://en.wikipedia.org/wiki/Combination\n\t\t\t# combination of selecting 2 places to split the string out of n-1 places\n return ((n-1)*(n-2)//2) % (10**9+7) \n if total % 3 != 0:\n return 0\n target = total // 3\n return (ones[target]-ones[target-1])*(ones[target*2]-ones[target*2-1])%(10**9+7)\n``` | 87 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Python | One-pass | Explained & Visualised | number-of-ways-to-split-a-string | 0 | 1 | Scan ```s``` to record positions for ```\'1\'```. After checking the edge cases, the result is simply a combination of choices.\n\n\n```Python\nclass Solution:\n def numWays(self, s: str) -> int:\n n,ones = len(s),[]\n for i,val in enumerate(s):\n if val == \'1\':\n ones.append(i)\n total = len(ones)\n if total == 0:\n\t\t # ref: https://en.wikipedia.org/wiki/Combination\n\t\t\t# combination of selecting 2 places to split the string out of n-1 places\n return ((n-1)*(n-2)//2) % (10**9+7) \n if total % 3 != 0:\n return 0\n target = total // 3\n return (ones[target]-ones[target-1])*(ones[target*2]-ones[target*2-1])%(10**9+7)\n``` | 87 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Python | Combination concept Mathematics | Explained with Concept and Code | Easy Solution | number-of-ways-to-split-a-string | 0 | 1 | <h1>There are two most important part of the solution</h1>\n\n### Basic Observation\n- The only part that matters are zeroes that lies on the borders\n- Borders are the places from where the string is split, it is **2** here\n### 1. When there are only zeroes\n- Let\'s us understand this in terms of following details\n- We have n zeroes and we have to place two borders\nIf we make an observation we can find:\nfor zeroes = 3: "000", we have ```4 or n + 1 ``` possible places for borders\n```\n| 0 | 0 | 0 |\n```\nfor zeroes = 4: "0000", we have ```5 or n + 1 ``` possible places for borders\n```\n| 0 | 0 | 0 | 0 |\n```\nfor zeroes = 5: "00000", we have ```6 or n + 1 ``` possible places for borders\n```\n| 0 | 0 | 0 | 0 | 0 |\n```\nBut in every case we can find that, the borders in the extreme left and extreme right are not valid,\nSo the valid number of choices will be ```n + 1 - 2 = n - 1```\n\nNow we have total valid choices as : ```n - 1```\n\nSo ways of selecting two borders from ```n - 1``` valid choices can be given as\n\n<sup>(n - 1)</sup>C<sub>r</sub>, where r = 2\nSo it will be <sup>(n - 1)</sup>C<sub>2</sub>\n\nwhich can be simplified as \n```((n - 1) * (n - 2)) / 2```\n\nSo few examples for the different values of n\n3: 1, 4: 3, 5: 6, 6: 10, 7: 15\n\n### 2. When we have valid number of zeroes on the both borders \nlet\'s take an example: s = ```"100100010100110"```\nUpon splitting, such that first and third doesn\'t have any extra zeroes\n```\n1001 | 00010100 | 110\n```\n- Let\'s think of the middle group ie., ```00010100```, it has ```3 zeroes in the left and 2 zeroes in the right```\n- Now the solution will revolve around different combinations of zeroes in the middle group\n> We are not focussing on the left and right because that will automatically be validated if we \n> validate the middle one as if we have two choices and if we select one the other one gets \n> selected automatically\n- So now we have 3 zeroes in the left but 4 choices as 3 choices are the 3 zeroes but one choice \nis phi ie., zero isn\'t present in the left side of the middle group so ```4 choices``` in the left\n- And similarly we have ```3 choices ``` in the right\n- Now this has become the question of combination, And we have to select one out of 4 choices for\n the left side of middle group and one out of 3 choices for the right side of the middle group\n \n> We can also think it as the number of places where we can put the border, in that case we will have \n4 places on the left side to put the borders and 3 places on the right side to put the border. and we \nwill have to select one out of these choices\n> Both these ways of attempting the problem will lead to the solution\n> \n\n- so ways of selecting zeroes can be given as\n\n\t<h1><b><sup>n</sup>C<sub>r</sub></b></h1>\n\t\n\twhere **n is the number of choices** and\n\t**r is 1 here as we have to chose one among n**\n\t\n - For left\n - n = 4 and r = 1\n - val = <sup>4</sup>C<sub>1</sub> = 4\n - For right\n - n = 3 and r = 1\n - val = <sup>3</sup>C<sub>1</sub> = 3\n \n### Important\n**Multiplication rule**: Let an event occurs in two stage A and B.If the stage A can occurs in \u2018M\' \nways and stage B can occurs in \u2019N\' ways,where A and B are independent of each other,then event \ncan occur in ( M\xD7N )ways\n\n**Addition rule**: Let A and B be two disjoint event ( they never occur together). If A occur in \u2018M\'\n ways and B occur in \u2019N\' ways , then exactly one of the event can occur in (M+N) ways\n\n- Both the actions are independent of each other and can occur simultaneously here so we will have to find the product.\n- Hence, the solution will be ```4 * 3 = 12```\n\n> Please solve the problem now, before looking at the code, this will help you understand the actual logic of the problem. \n\n\n# Solution\n\n```python\nclass Solution:\n def numWays(self, s: str) -> int:\n ones = 0\n\n # Count number of Ones\n for char in s:\n if char == "1":\n ones += 1\n\n # Can\'t be grouped equally if the ones are not divisible by 3\n if ones > 0 and ones % 3 != 0:\n return 0\n\n # Ways of selecting two dividers from n - 1 dividers \n if ones == 0:\n n = len(s)\n\t\t\t# n = {3: 1, 4: 3, 5: 6, 6: 10, 7: 15 ... }\n return (((n - 1) * (n - 2)) // 2) % ((10 ** 9) + 7)\n\n # Number of ones in each group\n ones_interval = ones // 3\n\n # Number of zeroes which lie on the borders\n left, right = 0, 0\n\n # Iterator\n i = 0\n temp = 0\n\n # Finding the zeroes on the left and right border\n while i < len(s):\n temp += int(s[i]) & 1\n if temp == ones_interval:\n if s[i] == \'0\':\n left += 1\n if temp == 2 * ones_interval:\n if s[i] == \'0\':\n right += 1\n i += 1\n \n # The result is the product of number of (left + 1) and (right + 1)\n # Because let\'s assume it as we only want to fill up the middle group\n # The solution would be if we have zero then there might be a zero in the middle\n # Or there might not be the zero, so this might case is added and then\n\t\t# the events are independent so product of both the events\n return ((left + 1) * (right + 1)) % ((10 ** 9) + 7)\n\n```\n\n\nI am building different Solutions in different languages of different topics of Data Structures and \nAlgorithms, So if you want to contribute or want to refer it visit the link given below\n\n**Data Structures and Algorithms:** https://github.com/ramanaditya/data-structure-and-algorithms\n**Interview Docs:** http://interview-docs.readthedocs.io/\n\n**GItHub :** https://github.com/ramanaditya\n**LinkedIn :** https://www.linkedin.com/in/ramanaditya/\n**Twitter :** https://twitter.com/_adityaraman\n | 22 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Python | Combination concept Mathematics | Explained with Concept and Code | Easy Solution | number-of-ways-to-split-a-string | 0 | 1 | <h1>There are two most important part of the solution</h1>\n\n### Basic Observation\n- The only part that matters are zeroes that lies on the borders\n- Borders are the places from where the string is split, it is **2** here\n### 1. When there are only zeroes\n- Let\'s us understand this in terms of following details\n- We have n zeroes and we have to place two borders\nIf we make an observation we can find:\nfor zeroes = 3: "000", we have ```4 or n + 1 ``` possible places for borders\n```\n| 0 | 0 | 0 |\n```\nfor zeroes = 4: "0000", we have ```5 or n + 1 ``` possible places for borders\n```\n| 0 | 0 | 0 | 0 |\n```\nfor zeroes = 5: "00000", we have ```6 or n + 1 ``` possible places for borders\n```\n| 0 | 0 | 0 | 0 | 0 |\n```\nBut in every case we can find that, the borders in the extreme left and extreme right are not valid,\nSo the valid number of choices will be ```n + 1 - 2 = n - 1```\n\nNow we have total valid choices as : ```n - 1```\n\nSo ways of selecting two borders from ```n - 1``` valid choices can be given as\n\n<sup>(n - 1)</sup>C<sub>r</sub>, where r = 2\nSo it will be <sup>(n - 1)</sup>C<sub>2</sub>\n\nwhich can be simplified as \n```((n - 1) * (n - 2)) / 2```\n\nSo few examples for the different values of n\n3: 1, 4: 3, 5: 6, 6: 10, 7: 15\n\n### 2. When we have valid number of zeroes on the both borders \nlet\'s take an example: s = ```"100100010100110"```\nUpon splitting, such that first and third doesn\'t have any extra zeroes\n```\n1001 | 00010100 | 110\n```\n- Let\'s think of the middle group ie., ```00010100```, it has ```3 zeroes in the left and 2 zeroes in the right```\n- Now the solution will revolve around different combinations of zeroes in the middle group\n> We are not focussing on the left and right because that will automatically be validated if we \n> validate the middle one as if we have two choices and if we select one the other one gets \n> selected automatically\n- So now we have 3 zeroes in the left but 4 choices as 3 choices are the 3 zeroes but one choice \nis phi ie., zero isn\'t present in the left side of the middle group so ```4 choices``` in the left\n- And similarly we have ```3 choices ``` in the right\n- Now this has become the question of combination, And we have to select one out of 4 choices for\n the left side of middle group and one out of 3 choices for the right side of the middle group\n \n> We can also think it as the number of places where we can put the border, in that case we will have \n4 places on the left side to put the borders and 3 places on the right side to put the border. and we \nwill have to select one out of these choices\n> Both these ways of attempting the problem will lead to the solution\n> \n\n- so ways of selecting zeroes can be given as\n\n\t<h1><b><sup>n</sup>C<sub>r</sub></b></h1>\n\t\n\twhere **n is the number of choices** and\n\t**r is 1 here as we have to chose one among n**\n\t\n - For left\n - n = 4 and r = 1\n - val = <sup>4</sup>C<sub>1</sub> = 4\n - For right\n - n = 3 and r = 1\n - val = <sup>3</sup>C<sub>1</sub> = 3\n \n### Important\n**Multiplication rule**: Let an event occurs in two stage A and B.If the stage A can occurs in \u2018M\' \nways and stage B can occurs in \u2019N\' ways,where A and B are independent of each other,then event \ncan occur in ( M\xD7N )ways\n\n**Addition rule**: Let A and B be two disjoint event ( they never occur together). If A occur in \u2018M\'\n ways and B occur in \u2019N\' ways , then exactly one of the event can occur in (M+N) ways\n\n- Both the actions are independent of each other and can occur simultaneously here so we will have to find the product.\n- Hence, the solution will be ```4 * 3 = 12```\n\n> Please solve the problem now, before looking at the code, this will help you understand the actual logic of the problem. \n\n\n# Solution\n\n```python\nclass Solution:\n def numWays(self, s: str) -> int:\n ones = 0\n\n # Count number of Ones\n for char in s:\n if char == "1":\n ones += 1\n\n # Can\'t be grouped equally if the ones are not divisible by 3\n if ones > 0 and ones % 3 != 0:\n return 0\n\n # Ways of selecting two dividers from n - 1 dividers \n if ones == 0:\n n = len(s)\n\t\t\t# n = {3: 1, 4: 3, 5: 6, 6: 10, 7: 15 ... }\n return (((n - 1) * (n - 2)) // 2) % ((10 ** 9) + 7)\n\n # Number of ones in each group\n ones_interval = ones // 3\n\n # Number of zeroes which lie on the borders\n left, right = 0, 0\n\n # Iterator\n i = 0\n temp = 0\n\n # Finding the zeroes on the left and right border\n while i < len(s):\n temp += int(s[i]) & 1\n if temp == ones_interval:\n if s[i] == \'0\':\n left += 1\n if temp == 2 * ones_interval:\n if s[i] == \'0\':\n right += 1\n i += 1\n \n # The result is the product of number of (left + 1) and (right + 1)\n # Because let\'s assume it as we only want to fill up the middle group\n # The solution would be if we have zero then there might be a zero in the middle\n # Or there might not be the zero, so this might case is added and then\n\t\t# the events are independent so product of both the events\n return ((left + 1) * (right + 1)) % ((10 ** 9) + 7)\n\n```\n\n\nI am building different Solutions in different languages of different topics of Data Structures and \nAlgorithms, So if you want to contribute or want to refer it visit the link given below\n\n**Data Structures and Algorithms:** https://github.com/ramanaditya/data-structure-and-algorithms\n**Interview Docs:** http://interview-docs.readthedocs.io/\n\n**GItHub :** https://github.com/ramanaditya\n**LinkedIn :** https://www.linkedin.com/in/ramanaditya/\n**Twitter :** https://twitter.com/_adityaraman\n | 22 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Python O(n) + Explanation | number-of-ways-to-split-a-string | 0 | 1 | First count 1\'s in given string. ```cnt = s.count(\'1\')```\n**if cnt == 0:** special case: ```return (len(s)-1)*(len(s)-2)//2```\n**elif cnt is not divisible by 3:** ```return 0```\n**else:**\nkeep track of indices of 1\'s in ones list:\nfor exaple: s = \'100100010100110\'\nones = [0,3,7,9,12,13]\nwe need to devide this list into 3parts: \n\'1001\' + {0\'s here} + \'101\' + {0\'s here }+ \'110\'\n```result = x * y ```\n*x = number of 0\'s between first and second part + 1*\n*y = number of 0\'s between second and third part + 1*\nto find x and y:\n```x = ones[cnt//3] - ones[cnt//3-1] ```\n```y = ones[2*cnt//3] - ones[2*cnt//3-1]```\n\n\n\n```\ndef numWays(self, s):\n\tmod = 10**9+7\n\tcnt = s.count(\'1\')\n\tif cnt == 0: return (len(s)-1)*(len(s)-2)//2 % mod\n\tif cnt % 3 != 0: return 0\n\tones = []\n\tfor i,x in enumerate(s):\n\t\tif x == \'1\': ones.append(i)\n\treturn (ones[cnt//3] - ones[cnt//3-1]) * (ones[2*cnt//3]- ones[2*cnt//3-1]) % mod\n``` | 13 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Python O(n) + Explanation | number-of-ways-to-split-a-string | 0 | 1 | First count 1\'s in given string. ```cnt = s.count(\'1\')```\n**if cnt == 0:** special case: ```return (len(s)-1)*(len(s)-2)//2```\n**elif cnt is not divisible by 3:** ```return 0```\n**else:**\nkeep track of indices of 1\'s in ones list:\nfor exaple: s = \'100100010100110\'\nones = [0,3,7,9,12,13]\nwe need to devide this list into 3parts: \n\'1001\' + {0\'s here} + \'101\' + {0\'s here }+ \'110\'\n```result = x * y ```\n*x = number of 0\'s between first and second part + 1*\n*y = number of 0\'s between second and third part + 1*\nto find x and y:\n```x = ones[cnt//3] - ones[cnt//3-1] ```\n```y = ones[2*cnt//3] - ones[2*cnt//3-1]```\n\n\n\n```\ndef numWays(self, s):\n\tmod = 10**9+7\n\tcnt = s.count(\'1\')\n\tif cnt == 0: return (len(s)-1)*(len(s)-2)//2 % mod\n\tif cnt % 3 != 0: return 0\n\tones = []\n\tfor i,x in enumerate(s):\n\t\tif x == \'1\': ones.append(i)\n\treturn (ones[cnt//3] - ones[cnt//3-1]) * (ones[2*cnt//3]- ones[2*cnt//3-1]) % mod\n``` | 13 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Permutation solution | number-of-ways-to-split-a-string | 0 | 1 | # Intuition\nSplit the string into 3 piece, in other words, need to selet two position r index to cut over \n\n# Approach\nuse index_1, index_2, index_3, index_4 to mark the two position\'s range\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n\n MOD = 10**9+7 \n\n count = s.count("1")\n N = len(s)\n\n if not count:\n return (((N-1)*(N-2))//2) % MOD\n\n if count % 3:\n return 0\n\n index_1, index_2, index_3, index_4 = None, None, None, None \n\n cnt = 0 \n\n for index, item in enumerate(s):\n if item == "1":\n cnt += 1 \n\n if cnt == count//3 and index_1 is None:\n index_1 = index\n \n if cnt == count//3+1 and index_2 is None:\n index_2 = index\n \n if cnt == 2*count//3 and index_3 is None:\n index_3 = index \n if cnt == 2*count//3+1 and index_4 is None:\n index_4 = index \n \n return ((index_2-index_1)*(index_4-index_3)) % MOD\n \n \n\n \n``` | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Permutation solution | number-of-ways-to-split-a-string | 0 | 1 | # Intuition\nSplit the string into 3 piece, in other words, need to selet two position r index to cut over \n\n# Approach\nuse index_1, index_2, index_3, index_4 to mark the two position\'s range\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n\n MOD = 10**9+7 \n\n count = s.count("1")\n N = len(s)\n\n if not count:\n return (((N-1)*(N-2))//2) % MOD\n\n if count % 3:\n return 0\n\n index_1, index_2, index_3, index_4 = None, None, None, None \n\n cnt = 0 \n\n for index, item in enumerate(s):\n if item == "1":\n cnt += 1 \n\n if cnt == count//3 and index_1 is None:\n index_1 = index\n \n if cnt == count//3+1 and index_2 is None:\n index_2 = index\n \n if cnt == 2*count//3 and index_3 is None:\n index_3 = index \n if cnt == 2*count//3+1 and index_4 is None:\n index_4 = index \n \n return ((index_2-index_1)*(index_4-index_3)) % MOD\n \n \n\n \n``` | 0 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Trash problem | number-of-ways-to-split-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n \n MOD = 10**9 + 7\n\n # Count the total number of ones in the string\n total_ones = s.count(\'1\')\n\n # If the total number of ones is not divisible by 3, return 0\n if total_ones % 3 != 0:\n return 0\n\n # If there are no ones in the string, calculate the number of ways to split\n if total_ones == 0:\n n = len(s)\n return ((n - 1) * (n - 2) // 2) % MOD\n\n # Calculate the target number of ones per substring\n ones_per_substring = total_ones // 3\n\n # Initialize variables\n count = 0\n prefix_zeros = 0\n suffix_zeros = 0\n\n # Iterate through the string to find the number of ways to split\n for char in s:\n if char == \'1\':\n count += 1\n\n if count == ones_per_substring:\n prefix_zeros += 1\n elif count == 2 * ones_per_substring:\n suffix_zeros += 1\n\n return (prefix_zeros * suffix_zeros) % MOD\n\n``` | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Trash problem | number-of-ways-to-split-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n \n MOD = 10**9 + 7\n\n # Count the total number of ones in the string\n total_ones = s.count(\'1\')\n\n # If the total number of ones is not divisible by 3, return 0\n if total_ones % 3 != 0:\n return 0\n\n # If there are no ones in the string, calculate the number of ways to split\n if total_ones == 0:\n n = len(s)\n return ((n - 1) * (n - 2) // 2) % MOD\n\n # Calculate the target number of ones per substring\n ones_per_substring = total_ones // 3\n\n # Initialize variables\n count = 0\n prefix_zeros = 0\n suffix_zeros = 0\n\n # Iterate through the string to find the number of ways to split\n for char in s:\n if char == \'1\':\n count += 1\n\n if count == ones_per_substring:\n prefix_zeros += 1\n elif count == 2 * ones_per_substring:\n suffix_zeros += 1\n\n return (prefix_zeros * suffix_zeros) % MOD\n\n``` | 0 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Probably the easiest and most intuitive method one can come up with with O(n) time and O(1) space | number-of-ways-to-split-a-string | 0 | 1 | # Intuition\nwe start by creating boundaries i imagined them as blocks \nhow many ways can one can create three seprations that is going to be\nto cut it from 2 different places \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is pretty simple when you get the idea and jusr find the flexible area in which you can place your 2 seprators or positions\n\n# Complexity\n- Time complexity:\nO(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nO(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n mod = 10 ** 9 + 7\n n = len(s)\n #A shorter method in python \n count_1 = s.count(\'1\')\n if not count_1:\n #we are unable to find any ones we could place boudaries everywhere\n return (((n-1)*(n-2))//2) % mod\n if count_1%3!=0:\n return 0\n #unable to divide the 1\'s in pairs of 3\n first_block=0 # to mark index of 1st block\n sub_block_1=0 # to count 1s in that sub block\n for i in range(n):\n if s[i] == \'1\':\n sub_block_1 += 1\n if sub_block_1 == count_1//3:\n first_block = i\n break\n open_area_front=-1\n for i in range(first_block+1,n):\n if s[i] == \'1\':\n open_area_front=i-first_block\n break\n last_block=n\n sub_block_1=0\n for i in range(n-1,-1,-1):\n if s[i] == \'1\':\n sub_block_1+=1\n if sub_block_1 == count_1//3:\n last_block = i\n break\n open_area_back=n\n for i in range(last_block-1,-1,-1):\n if s[i] == \'1\':\n open_area_back = last_block-i\n break\n return (open_area_front*open_area_back)%mod\n``` | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Probably the easiest and most intuitive method one can come up with with O(n) time and O(1) space | number-of-ways-to-split-a-string | 0 | 1 | # Intuition\nwe start by creating boundaries i imagined them as blocks \nhow many ways can one can create three seprations that is going to be\nto cut it from 2 different places \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is pretty simple when you get the idea and jusr find the flexible area in which you can place your 2 seprators or positions\n\n# Complexity\n- Time complexity:\nO(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nO(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWays(self, s: str) -> int:\n mod = 10 ** 9 + 7\n n = len(s)\n #A shorter method in python \n count_1 = s.count(\'1\')\n if not count_1:\n #we are unable to find any ones we could place boudaries everywhere\n return (((n-1)*(n-2))//2) % mod\n if count_1%3!=0:\n return 0\n #unable to divide the 1\'s in pairs of 3\n first_block=0 # to mark index of 1st block\n sub_block_1=0 # to count 1s in that sub block\n for i in range(n):\n if s[i] == \'1\':\n sub_block_1 += 1\n if sub_block_1 == count_1//3:\n first_block = i\n break\n open_area_front=-1\n for i in range(first_block+1,n):\n if s[i] == \'1\':\n open_area_front=i-first_block\n break\n last_block=n\n sub_block_1=0\n for i in range(n-1,-1,-1):\n if s[i] == \'1\':\n sub_block_1+=1\n if sub_block_1 == count_1//3:\n last_block = i\n break\n open_area_back=n\n for i in range(last_block-1,-1,-1):\n if s[i] == \'1\':\n open_area_back = last_block-i\n break\n return (open_area_front*open_area_back)%mod\n``` | 0 | You own a **Goal Parser** that can interpret a string `command`. The `command` consists of an alphabet of `"G "`, `"() "` and/or `"(al) "` in some order. The Goal Parser will interpret `"G "` as the string `"G "`, `"() "` as the string `"o "`, and `"(al) "` as the string `"al "`. The interpreted strings are then concatenated in the original order.
Given the string `command`, return _the **Goal Parser**'s interpretation of_ `command`.
**Example 1:**
**Input:** command = "G()(al) "
**Output:** "Goal "
**Explanation:** The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal ".
**Example 2:**
**Input:** command = "G()()()()(al) "
**Output:** "Gooooal "
**Example 3:**
**Input:** command = "(al)G(al)()()G "
**Output:** "alGalooG "
**Constraints:**
* `1 <= command.length <= 100`
* `command` consists of `"G "`, `"() "`, and/or `"(al) "` in some order. | There is no way if the sum (number of '1's) is not divisible by the number of splits. So sum%3 should be 0. Preffix s1 , and suffix s3 should have sum/3 characters '1'. Follow up: Can you generalize the problem with numbers between [-10^9, 10^9] such the sum between subarrays s1, s2, s3 are the same? |
Python3 | O(n) Time complexity | Two pointers | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | Cases:\n1. Remove left side:\n\t- eg. nums = [5,1, 3, 6] -> Remove nums[0:1] = [5]\n2. Remove right side:\n\t- eg. nums = [5, 6, 1, 0] -> Remove nums[2:] = [1, 0]\n3. Remove middle:\n - eg. nums = [1, 2, 3, 6, 4, 5] -> Remove nums[3:4] = [6]\n4. Remove nothing:\n\t- eg. nums = [1,2,3] -> Remove nothing\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n # sentinel\n arr.append(float("inf"))\n arr.insert(0, 0)\n \n left = 0\n right = len(arr) - 1\n shortest = float("inf")\n # find longest ascending array at left side.\n while left < len(arr) - 2 and arr[left] <= arr[left + 1]:\n left += 1\n \n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \n # left \n \n # move right pointer while moving left pointer.\n while left >= 0:\n while right - 1 > left and arr[right - 1] >= arr[left] and arr[right] >= arr[right - 1]:\n right -= 1\n shortest = min(shortest, right - left - 1)\n left -= 1\n \n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 4\n # \n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 3\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 3\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 3\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 4\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 5\n \n return shortest\n \n``` | 6 | Given an integer array `arr`, remove a subarray (can be empty) from `arr` such that the remaining elements in `arr` are **non-decreasing**.
Return _the length of the shortest subarray to remove_.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,2,3,10,4,2,3,5\]
**Output:** 3
**Explanation:** The shortest subarray we can remove is \[10,4,2\] of length 3. The remaining elements after that will be \[1,2,3,3,5\] which are sorted.
Another correct solution is to remove the subarray \[3,10,4\].
**Example 2:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 4
**Explanation:** Since the array is strictly decreasing, we can only keep a single element. Therefore we need to remove a subarray of length 4, either \[5,4,3,2\] or \[4,3,2,1\].
**Example 3:**
**Input:** arr = \[1,2,3\]
**Output:** 0
**Explanation:** The array is already non-decreasing. We do not need to remove any elements.
**Constraints:**
* `1 <= arr.length <= 105`
* `0 <= arr[i] <= 109` | Use brute force: two loops to select i and j, then select the maximum value of (nums[i]-1)*(nums[j]-1). |
Python3 | O(n) Time complexity | Two pointers | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | Cases:\n1. Remove left side:\n\t- eg. nums = [5,1, 3, 6] -> Remove nums[0:1] = [5]\n2. Remove right side:\n\t- eg. nums = [5, 6, 1, 0] -> Remove nums[2:] = [1, 0]\n3. Remove middle:\n - eg. nums = [1, 2, 3, 6, 4, 5] -> Remove nums[3:4] = [6]\n4. Remove nothing:\n\t- eg. nums = [1,2,3] -> Remove nothing\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n # sentinel\n arr.append(float("inf"))\n arr.insert(0, 0)\n \n left = 0\n right = len(arr) - 1\n shortest = float("inf")\n # find longest ascending array at left side.\n while left < len(arr) - 2 and arr[left] <= arr[left + 1]:\n left += 1\n \n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \n # left \n \n # move right pointer while moving left pointer.\n while left >= 0:\n while right - 1 > left and arr[right - 1] >= arr[left] and arr[right] >= arr[right - 1]:\n right -= 1\n shortest = min(shortest, right - left - 1)\n left -= 1\n \n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 4\n # \n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 3\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 3\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 3\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 4\n #\n # [0, 1, 2, 3, 10, 4, 2, 3, 5, \u221E]\n # \u2191 \u2191\n # left right -> length = 5\n \n return shortest\n \n``` | 6 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
Break the array and binary search | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfind the left part and right part that is non-decreasing.\nFor each value `arr[i]` in left part, find the first value in right part >= `arr[i]`\nFor each value `arr[i]` in right part, find the last value in left part <= `arr[i]`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(Nlog(N))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n\n left, right = 0, len(arr) - 1\n while left < len(arr) - 1 and arr[left] <= arr[left + 1]:\n left += 1\n if left == right: return 0\n\n while right > 0 and arr[right] >= arr[right - 1]:\n right -= 1\n\n res = inf\n for i in range(left + 1):\n if arr[-1] < arr[i]:\n res = min(res, len(arr) - i - 1)\n continue\n\n lo, hi = right, len(arr) - 1\n while lo < hi:\n mid = lo + (hi - lo) // 2\n if arr[mid] >= arr[i]:\n hi = mid\n else:\n lo = mid + 1\n res = min(res, hi - i - 1)\n\n for i in range(right, len(arr)):\n if arr[0] > arr[i]:\n res = min(res, right)\n continue\n\n lo, hi = 0, left\n while lo < hi:\n mid = lo + (hi - lo + 1) // 2\n if arr[mid] <= arr[i]:\n lo = mid\n else:\n hi = mid - 1\n res = min(res, i - lo - 1)\n\n return res\n\n \n \n\n``` | 1 | Given an integer array `arr`, remove a subarray (can be empty) from `arr` such that the remaining elements in `arr` are **non-decreasing**.
Return _the length of the shortest subarray to remove_.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,2,3,10,4,2,3,5\]
**Output:** 3
**Explanation:** The shortest subarray we can remove is \[10,4,2\] of length 3. The remaining elements after that will be \[1,2,3,3,5\] which are sorted.
Another correct solution is to remove the subarray \[3,10,4\].
**Example 2:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 4
**Explanation:** Since the array is strictly decreasing, we can only keep a single element. Therefore we need to remove a subarray of length 4, either \[5,4,3,2\] or \[4,3,2,1\].
**Example 3:**
**Input:** arr = \[1,2,3\]
**Output:** 0
**Explanation:** The array is already non-decreasing. We do not need to remove any elements.
**Constraints:**
* `1 <= arr.length <= 105`
* `0 <= arr[i] <= 109` | Use brute force: two loops to select i and j, then select the maximum value of (nums[i]-1)*(nums[j]-1). |
Break the array and binary search | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfind the left part and right part that is non-decreasing.\nFor each value `arr[i]` in left part, find the first value in right part >= `arr[i]`\nFor each value `arr[i]` in right part, find the last value in left part <= `arr[i]`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(Nlog(N))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n\n left, right = 0, len(arr) - 1\n while left < len(arr) - 1 and arr[left] <= arr[left + 1]:\n left += 1\n if left == right: return 0\n\n while right > 0 and arr[right] >= arr[right - 1]:\n right -= 1\n\n res = inf\n for i in range(left + 1):\n if arr[-1] < arr[i]:\n res = min(res, len(arr) - i - 1)\n continue\n\n lo, hi = right, len(arr) - 1\n while lo < hi:\n mid = lo + (hi - lo) // 2\n if arr[mid] >= arr[i]:\n hi = mid\n else:\n lo = mid + 1\n res = min(res, hi - i - 1)\n\n for i in range(right, len(arr)):\n if arr[0] > arr[i]:\n res = min(res, right)\n continue\n\n lo, hi = 0, left\n while lo < hi:\n mid = lo + (hi - lo + 1) // 2\n if arr[mid] <= arr[i]:\n lo = mid\n else:\n hi = mid - 1\n res = min(res, i - lo - 1)\n\n return res\n\n \n \n\n``` | 1 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
Beats 96.93% || Basic Two Pointer Approach | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | # Intuition\nWhen I saw that the constraints are of the range 10^5, I decided to use a Two Pointer approach.Then I thought that if it is a subarray it should be increasing that means of we remove some elements from middle, then definitely the first subarray should be increasing and the second subarray should be increasinh. Here you go :).\n\n# Approach\nI need to find the index upto which from the 0th index is a valid increasing subarray(Let this be i).I also need to find the index from the last which is a valid increasing subarray(Let this be j).See the below image to understand about i and j.\n\n\n\n\nNow we divide the given array into two increasing subarrays.Our increasing subarray is a part of this two subarrays.We start iterating through first subarray and check if the element is <= the element in the second subarray if it is then we know that (elements upto this first element in the first subarray and all the elements in the second subarray from the second subarray element) then increment to next element of the first subarray, else if it is > increment to next element of the second subarray.Use a maxi variable to store the maximum length of the subarray that is possible.\n\nFinally, check the max value in between the maxi,length of first subarray, length of second subarray. Removing this value from total elements gives us the minimum number of elements that are to be removed from the subarray.\n\n# Sorry if my english/explaination is not good, you can once try out the testcase in the image to actually know my approach :).\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n n=len(arr)\n i,j=0,n-1\n while i<n-1:\n if arr[i]>arr[i+1]:\n break\n i+=1\n if i==j:\n return 0\n while j>0:\n if arr[j-1]>arr[j]:\n break\n j-=1\n l,r,maxi=0,j,1\n while l<=i and r<n:\n if arr[l]<=arr[r]:\n maxi=max(maxi,(l+1+n-r))\n print(maxi)\n l+=1\n else:\n r+=1\n return n-max(maxi,i+1,n-j)\n``` | 0 | Given an integer array `arr`, remove a subarray (can be empty) from `arr` such that the remaining elements in `arr` are **non-decreasing**.
Return _the length of the shortest subarray to remove_.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,2,3,10,4,2,3,5\]
**Output:** 3
**Explanation:** The shortest subarray we can remove is \[10,4,2\] of length 3. The remaining elements after that will be \[1,2,3,3,5\] which are sorted.
Another correct solution is to remove the subarray \[3,10,4\].
**Example 2:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 4
**Explanation:** Since the array is strictly decreasing, we can only keep a single element. Therefore we need to remove a subarray of length 4, either \[5,4,3,2\] or \[4,3,2,1\].
**Example 3:**
**Input:** arr = \[1,2,3\]
**Output:** 0
**Explanation:** The array is already non-decreasing. We do not need to remove any elements.
**Constraints:**
* `1 <= arr.length <= 105`
* `0 <= arr[i] <= 109` | Use brute force: two loops to select i and j, then select the maximum value of (nums[i]-1)*(nums[j]-1). |
Beats 96.93% || Basic Two Pointer Approach | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | # Intuition\nWhen I saw that the constraints are of the range 10^5, I decided to use a Two Pointer approach.Then I thought that if it is a subarray it should be increasing that means of we remove some elements from middle, then definitely the first subarray should be increasing and the second subarray should be increasinh. Here you go :).\n\n# Approach\nI need to find the index upto which from the 0th index is a valid increasing subarray(Let this be i).I also need to find the index from the last which is a valid increasing subarray(Let this be j).See the below image to understand about i and j.\n\n\n\n\nNow we divide the given array into two increasing subarrays.Our increasing subarray is a part of this two subarrays.We start iterating through first subarray and check if the element is <= the element in the second subarray if it is then we know that (elements upto this first element in the first subarray and all the elements in the second subarray from the second subarray element) then increment to next element of the first subarray, else if it is > increment to next element of the second subarray.Use a maxi variable to store the maximum length of the subarray that is possible.\n\nFinally, check the max value in between the maxi,length of first subarray, length of second subarray. Removing this value from total elements gives us the minimum number of elements that are to be removed from the subarray.\n\n# Sorry if my english/explaination is not good, you can once try out the testcase in the image to actually know my approach :).\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n n=len(arr)\n i,j=0,n-1\n while i<n-1:\n if arr[i]>arr[i+1]:\n break\n i+=1\n if i==j:\n return 0\n while j>0:\n if arr[j-1]>arr[j]:\n break\n j-=1\n l,r,maxi=0,j,1\n while l<=i and r<n:\n if arr[l]<=arr[r]:\n maxi=max(maxi,(l+1+n-r))\n print(maxi)\n l+=1\n else:\n r+=1\n return n-max(maxi,i+1,n-j)\n``` | 0 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
Python Simple linear time Solution | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | # Intuition\nThe question asks us to make the array sorted by removing a subarray. So we can boil down the solution to three steps :-\n\n1. Find the non decreasing subarray from start=0 and remove all part of array after that.\n1. Find the non increasing subarray from end=len(arr)-1 and remove all part of the array before that.\n1. Try to merge the arrays found from start and end and find the maximum increasing subarray. For this we can use two pointer technique.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Code\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n st = 0\n end = len(arr) - 1\n prev = None\n \n st = Solution.find_end_subarray(arr=arr, st=0, inc_flag=True)\n end = Solution.find_end_subarray(arr=arr, st=len(arr)-1, inc_flag=False)\n\n merge_length = Solution.merge(st-1, end+1, arr)\n take_first = len(arr) - st\n take_end = end + 1\n take_merged = len(arr) - merge_length\n return min(take_first, min(take_end, take_merged))\n \n @staticmethod\n def find_end_subarray(arr, st, inc_flag, prev=None):\n while(st < len(arr) if inc_flag else st >= 0):\n if prev is None or (arr[st] >= prev if inc_flag else arr[st] <= prev):\n prev = arr[st]\n st = st + 1 if inc_flag else st - 1\n else:\n break\n return st\n \n @staticmethod\n def merge(first_arr_end, second_arr_st, arr):\n ans = 0\n first_arr_st = 0\n while(first_arr_st <= first_arr_end and second_arr_st < len(arr)):\n if arr[first_arr_st] <= arr[second_arr_st]:\n if first_arr_st >= second_arr_st:\n ans = max(ans, len(arr) - 1)\n break\n else:\n ans = max(ans, first_arr_st + len(arr) - second_arr_st + 1)\n first_arr_st += 1\n else:\n second_arr_st += 1\n return ans \n``` | 0 | Given an integer array `arr`, remove a subarray (can be empty) from `arr` such that the remaining elements in `arr` are **non-decreasing**.
Return _the length of the shortest subarray to remove_.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,2,3,10,4,2,3,5\]
**Output:** 3
**Explanation:** The shortest subarray we can remove is \[10,4,2\] of length 3. The remaining elements after that will be \[1,2,3,3,5\] which are sorted.
Another correct solution is to remove the subarray \[3,10,4\].
**Example 2:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 4
**Explanation:** Since the array is strictly decreasing, we can only keep a single element. Therefore we need to remove a subarray of length 4, either \[5,4,3,2\] or \[4,3,2,1\].
**Example 3:**
**Input:** arr = \[1,2,3\]
**Output:** 0
**Explanation:** The array is already non-decreasing. We do not need to remove any elements.
**Constraints:**
* `1 <= arr.length <= 105`
* `0 <= arr[i] <= 109` | Use brute force: two loops to select i and j, then select the maximum value of (nums[i]-1)*(nums[j]-1). |
Python Simple linear time Solution | shortest-subarray-to-be-removed-to-make-array-sorted | 0 | 1 | # Intuition\nThe question asks us to make the array sorted by removing a subarray. So we can boil down the solution to three steps :-\n\n1. Find the non decreasing subarray from start=0 and remove all part of array after that.\n1. Find the non increasing subarray from end=len(arr)-1 and remove all part of the array before that.\n1. Try to merge the arrays found from start and end and find the maximum increasing subarray. For this we can use two pointer technique.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Code\n```\nclass Solution:\n def findLengthOfShortestSubarray(self, arr: List[int]) -> int:\n st = 0\n end = len(arr) - 1\n prev = None\n \n st = Solution.find_end_subarray(arr=arr, st=0, inc_flag=True)\n end = Solution.find_end_subarray(arr=arr, st=len(arr)-1, inc_flag=False)\n\n merge_length = Solution.merge(st-1, end+1, arr)\n take_first = len(arr) - st\n take_end = end + 1\n take_merged = len(arr) - merge_length\n return min(take_first, min(take_end, take_merged))\n \n @staticmethod\n def find_end_subarray(arr, st, inc_flag, prev=None):\n while(st < len(arr) if inc_flag else st >= 0):\n if prev is None or (arr[st] >= prev if inc_flag else arr[st] <= prev):\n prev = arr[st]\n st = st + 1 if inc_flag else st - 1\n else:\n break\n return st\n \n @staticmethod\n def merge(first_arr_end, second_arr_st, arr):\n ans = 0\n first_arr_st = 0\n while(first_arr_st <= first_arr_end and second_arr_st < len(arr)):\n if arr[first_arr_st] <= arr[second_arr_st]:\n if first_arr_st >= second_arr_st:\n ans = max(ans, len(arr) - 1)\n break\n else:\n ans = max(ans, first_arr_st + len(arr) - second_arr_st + 1)\n first_arr_st += 1\n else:\n second_arr_st += 1\n return ans \n``` | 0 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
easy C++/Python dfs DP solutions | count-all-possible-routes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse DFS and DP. Set dp[i][fuel] as the state for the city i and with fuel=fuel.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe given code counts the number of routes from a start to a finish location within a fuel limit. It uses dynamic programming with a recursive function. The code initializes a 2D list to store route counts. The dfs function recursively explores routes, incrementing the count for valid routes. It memoizes the counts to avoid redundant calculations. The function returns the count of routes from start to finish with the given fuel. The code improves efficiency by reusing intermediate results, enhancing performance compared to naive recursive approaches.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(n^2 * fuel)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(n * fuel)$\n# Code\n\n```C++ []\nclass Solution {\npublic:\n const int Mod=1e9+7;\n \n int countRoutes(vector<int>& locations, int start, int finish, int fuel) {\n int n=locations.size();\n vector<vector<int>> dp(n, vector(fuel+1, -1));\n\n function<int(int, int, int)> dfs=[&](int i, int finish, int fuel)->int{\n if (fuel<0) return 0;\n if (dp[i][fuel]!=-1) return dp[i][fuel];\n int ans=0;\n if (i==finish) ans++;\n for(int j=0; j<n; j++){\n if (j==i) continue;\n ans=(ans+dfs(j, finish, fuel-abs(locations[i]-locations[j])))%Mod;\n }\n return dp[i][fuel]=ans;\n };\n\n return dfs(start, finish, fuel);\n }\n};\n```\n```python []\nclass Solution:\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n Mod=10**9+7\n n=len(locations)\n row=[-1]*(fuel+1)\n dp=[row[:] for _ in range(n)]\n\n def dfs(i, finish, fuel):\n if fuel<0: return 0\n if dp[i][fuel]!=-1: return dp[i][fuel]\n ans=0\n if i==finish: ans+=1\n for j in range(n):\n if j==i: continue\n ans=(ans+dfs(j, finish, fuel-abs(locations[i]-locations[j])))%Mod\n dp[i][fuel]=ans\n return ans\n\n return dfs(start, finish, fuel)\n```\n | 4 | You are given an array of **distinct** positive integers locations where `locations[i]` represents the position of city `i`. You are also given integers `start`, `finish` and `fuel` representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city `i`, you can pick any city `j` such that `j != i` and `0 <= j < locations.length` and move to city `j`. Moving from city `i` to city `j` reduces the amount of fuel you have by `|locations[i] - locations[j]|`. Please notice that `|x|` denotes the absolute value of `x`.
Notice that `fuel` **cannot** become negative at any point in time, and that you are **allowed** to visit any city more than once (including `start` and `finish`).
Return _the count of all possible routes from_ `start` _to_ `finish`. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** locations = \[2,3,6,8,4\], start = 1, finish = 3, fuel = 5
**Output:** 4
**Explanation:** The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
**Example 2:**
**Input:** locations = \[4,3,1\], start = 1, finish = 0, fuel = 6
**Output:** 5
**Explanation:** The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5
**Example 3:**
**Input:** locations = \[5,2,1\], start = 0, finish = 2, fuel = 3
**Output:** 0
**Explanation:** It is impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.
**Constraints:**
* `2 <= locations.length <= 100`
* `1 <= locations[i] <= 109`
* All integers in `locations` are **distinct**.
* `0 <= start, finish < locations.length`
* `1 <= fuel <= 200` | Sort the arrays, then compute the maximum difference between two consecutive elements for horizontal cuts and vertical cuts. The answer is the product of these maximum values in horizontal cuts and vertical cuts. |
easy C++/Python dfs DP solutions | count-all-possible-routes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse DFS and DP. Set dp[i][fuel] as the state for the city i and with fuel=fuel.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe given code counts the number of routes from a start to a finish location within a fuel limit. It uses dynamic programming with a recursive function. The code initializes a 2D list to store route counts. The dfs function recursively explores routes, incrementing the count for valid routes. It memoizes the counts to avoid redundant calculations. The function returns the count of routes from start to finish with the given fuel. The code improves efficiency by reusing intermediate results, enhancing performance compared to naive recursive approaches.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(n^2 * fuel)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(n * fuel)$\n# Code\n\n```C++ []\nclass Solution {\npublic:\n const int Mod=1e9+7;\n \n int countRoutes(vector<int>& locations, int start, int finish, int fuel) {\n int n=locations.size();\n vector<vector<int>> dp(n, vector(fuel+1, -1));\n\n function<int(int, int, int)> dfs=[&](int i, int finish, int fuel)->int{\n if (fuel<0) return 0;\n if (dp[i][fuel]!=-1) return dp[i][fuel];\n int ans=0;\n if (i==finish) ans++;\n for(int j=0; j<n; j++){\n if (j==i) continue;\n ans=(ans+dfs(j, finish, fuel-abs(locations[i]-locations[j])))%Mod;\n }\n return dp[i][fuel]=ans;\n };\n\n return dfs(start, finish, fuel);\n }\n};\n```\n```python []\nclass Solution:\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n Mod=10**9+7\n n=len(locations)\n row=[-1]*(fuel+1)\n dp=[row[:] for _ in range(n)]\n\n def dfs(i, finish, fuel):\n if fuel<0: return 0\n if dp[i][fuel]!=-1: return dp[i][fuel]\n ans=0\n if i==finish: ans+=1\n for j in range(n):\n if j==i: continue\n ans=(ans+dfs(j, finish, fuel-abs(locations[i]-locations[j])))%Mod\n dp[i][fuel]=ans\n return ans\n\n return dfs(start, finish, fuel)\n```\n | 4 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.