title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Image Explanation🏆- [Recursion -> Memo(4 states - 2 states) -> Bottom Up] - C++/Java/Python | minimum-cost-to-cut-a-stick | 1 | 1 | \n\n# Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Minimum Cost to Cut a Stick` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n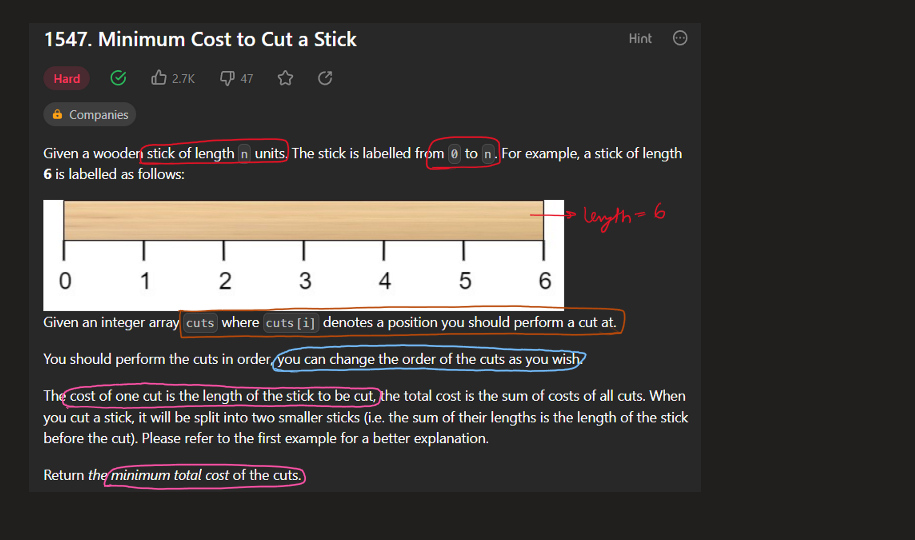\n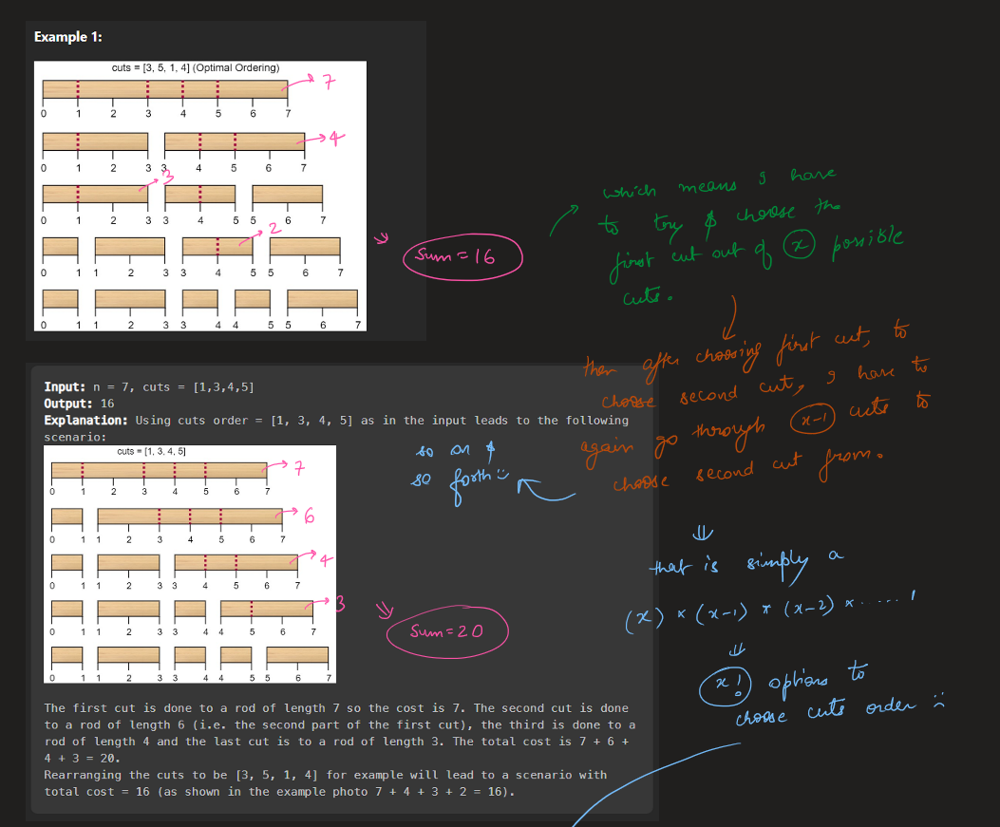\n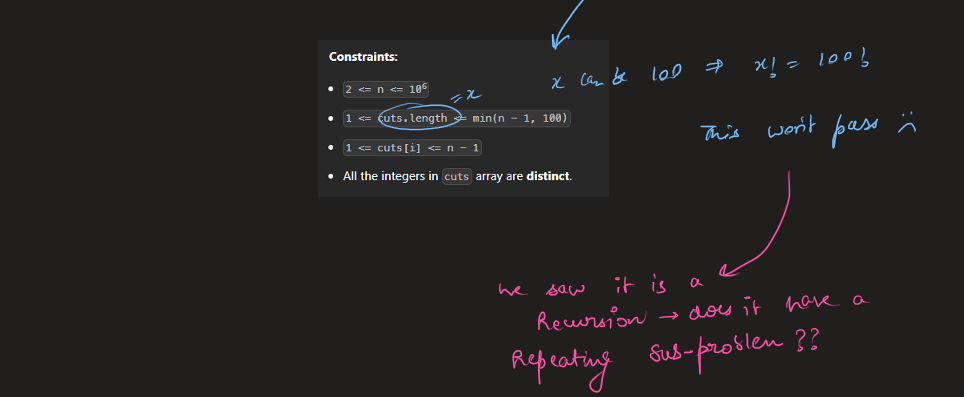\n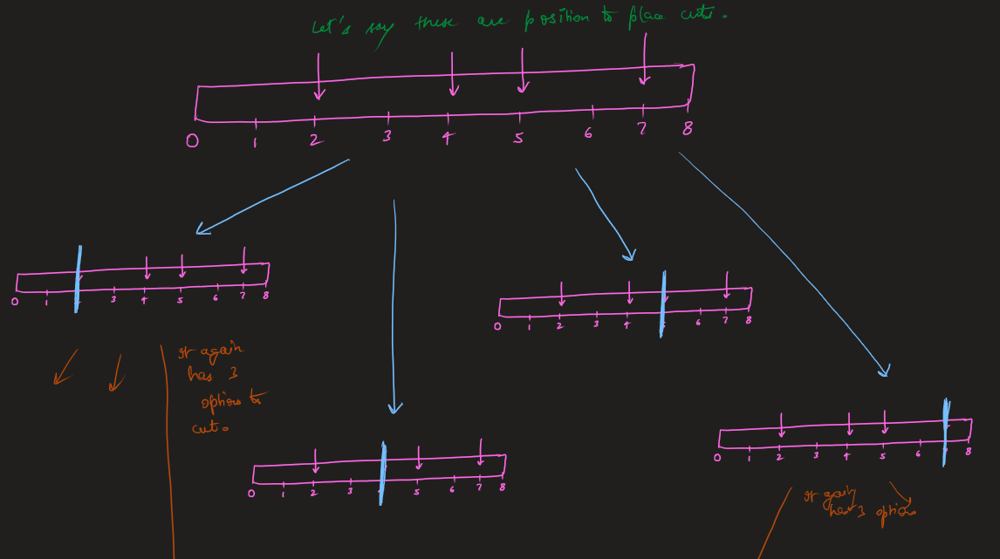\n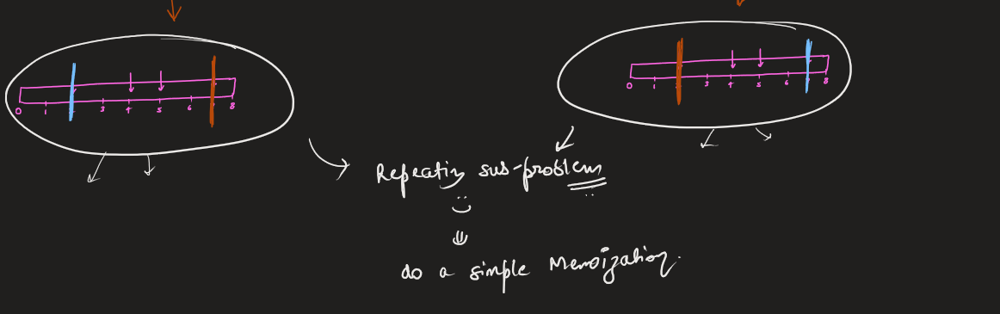\n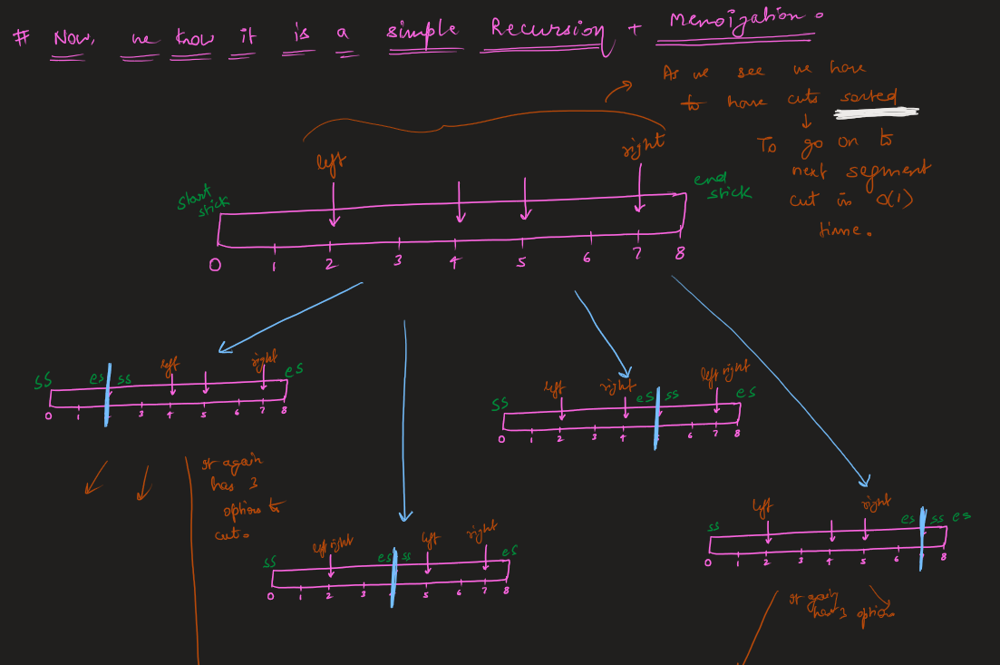\n\n\n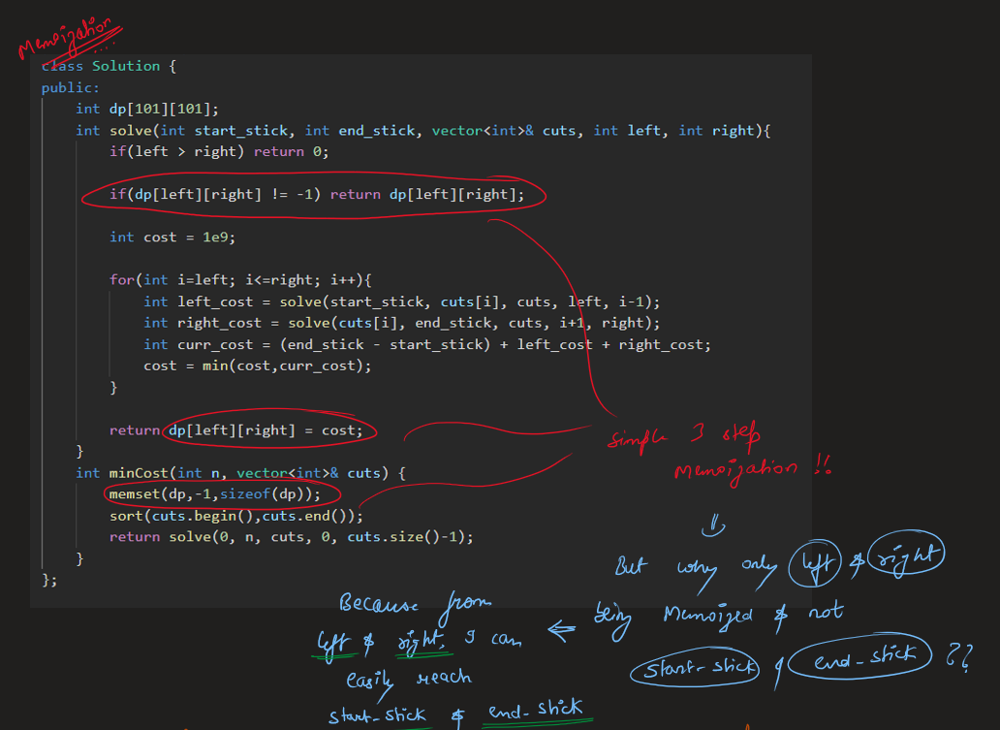\n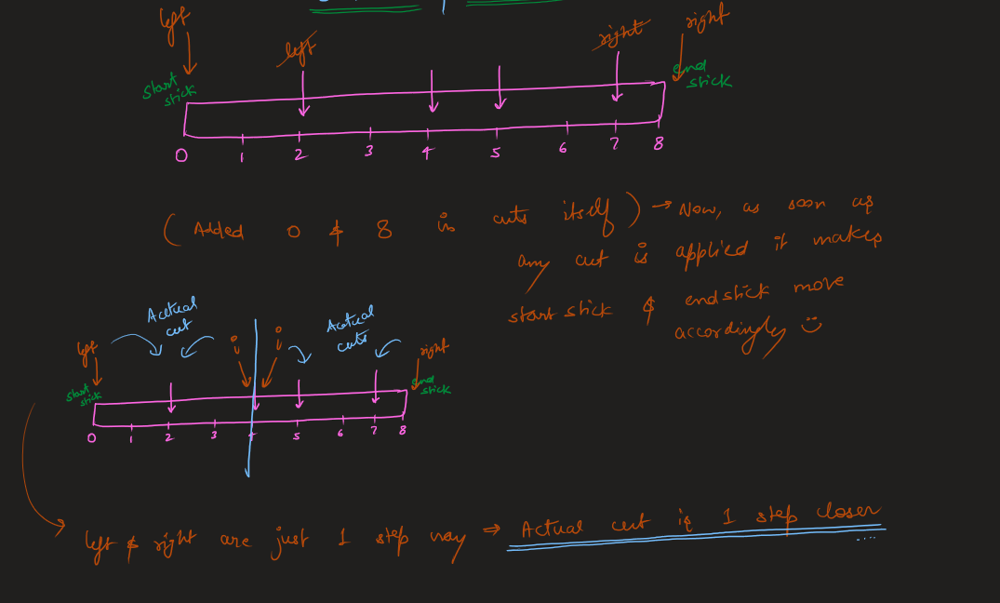\n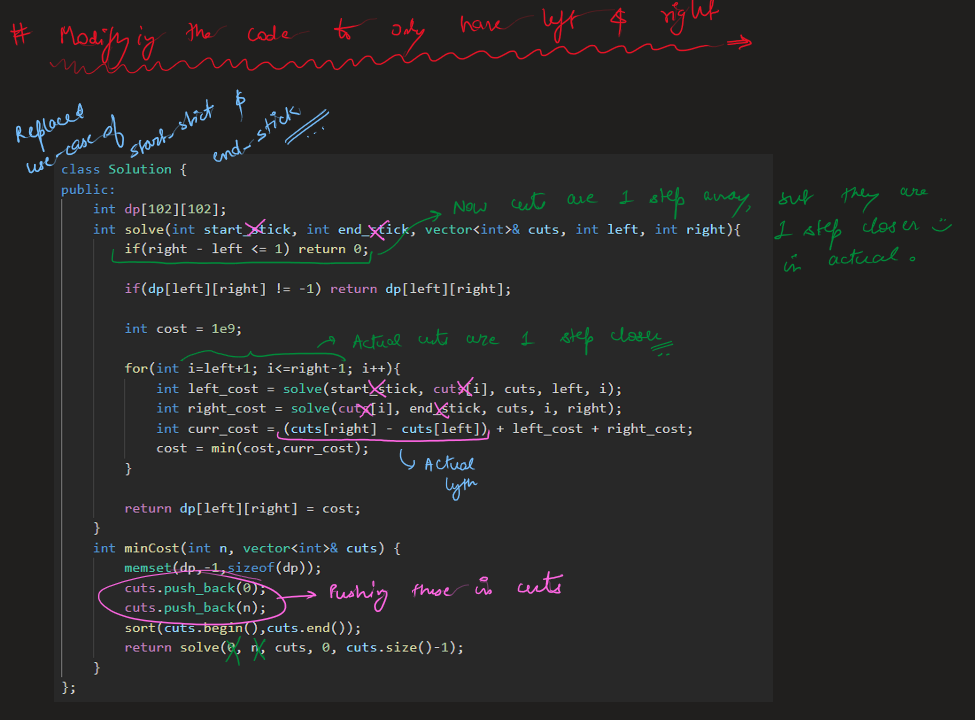\n\n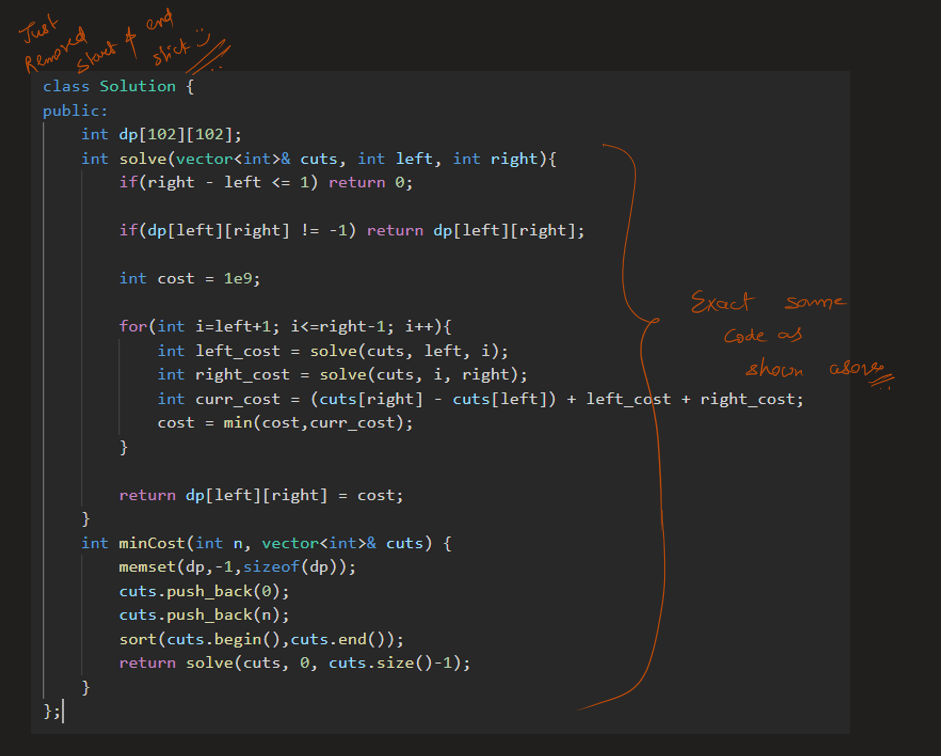\n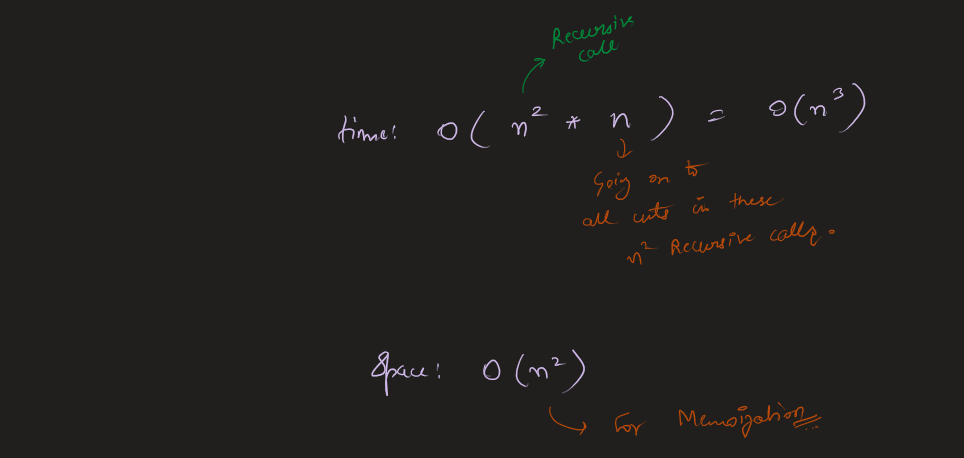\nHere the above n - represents the cuts.size(), you can also take it as m^3 also for time & m^2 for space.\n\n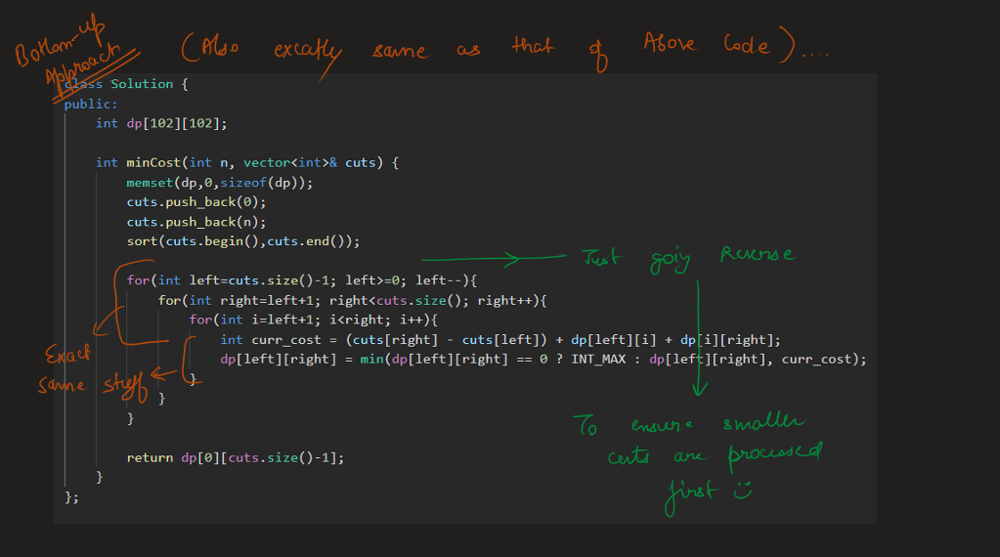\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int dp[101][101];\n int solve(int start_stick, int end_stick, vector<int>& cuts, int left, int right){\n if(left > right) return 0;\n \n if(dp[left][right] != -1) return dp[left][right];\n \n int cost = 1e9;\n \n for(int i=left; i<=right; i++){\n int left_cost = solve(start_stick, cuts[i], cuts, left, i-1);\n int right_cost = solve(cuts[i], end_stick, cuts, i+1, right);\n int curr_cost = (end_stick - start_stick) + left_cost + right_cost;\n cost = min(cost,curr_cost);\n }\n \n return dp[left][right] = cost;\n }\n int minCost(int n, vector<int>& cuts) {\n memset(dp,-1,sizeof(dp));\n sort(cuts.begin(),cuts.end());\n return solve(0, n, cuts, 0, cuts.size()-1);\n }\n};\n```\n```Java []\nclass Solution {\n int[][] dp;\n \n int solve(int start_stick, int end_stick, int[] cuts, int left, int right) {\n if (left > right) return 0;\n\n if (dp[left][right] != -1) return dp[left][right];\n\n int cost = Integer.MAX_VALUE;\n\n for (int i = left; i <= right; i++) {\n int left_cost = solve(start_stick, cuts[i], cuts, left, i - 1);\n int right_cost = solve(cuts[i], end_stick, cuts, i + 1, right);\n int curr_cost = (end_stick - start_stick) + left_cost + right_cost;\n cost = Math.min(cost, curr_cost);\n }\n\n return dp[left][right] = cost;\n }\n \n int minCost(int n, int[] cuts) {\n dp = new int[cuts.length][cuts.length];\n for (int[] row : dp) {\n Arrays.fill(row, -1);\n }\n \n Arrays.sort(cuts);\n return solve(0, n, cuts, 0, cuts.length - 1);\n }\n}\n```\n```Python []\nclass Solution:\n def solve(self, start_stick, end_stick, cuts, left, right, dp):\n if left > right:\n return 0\n\n if dp[left][right] != -1:\n return dp[left][right]\n\n cost = float(\'inf\')\n\n for i in range(left, right + 1):\n left_cost = self.solve(start_stick, cuts[i], cuts, left, i - 1, dp)\n right_cost = self.solve(cuts[i], end_stick, cuts, i + 1, right, dp)\n curr_cost = (end_stick - start_stick) + left_cost + right_cost\n cost = min(cost, curr_cost)\n\n dp[left][right] = cost\n return cost\n\n def minCost(self, n, cuts):\n dp = [[-1] * len(cuts) for _ in range(len(cuts))]\n cuts.sort()\n return self.solve(0, n, cuts, 0, len(cuts) - 1, dp)\n``` | 77 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Python short and clean. Functional programming. | minimum-cost-to-cut-a-stick | 0 | 1 | # Complexity\n- Time complexity: $$O(m ^ 3)$$\n\n- Space complexity: $$O(m ^ 2)$$\n\nwhere, `m is the number of cuts`.\n\n# Code\n```python\nclass Solution:\n def minCost(self, n: int, cuts: list[int]) -> int:\n s_cuts = sorted(chain(cuts, (0, n)))\n\n @cache\n def min_cost(i: int, j: int) -> int:\n return (cost := s_cuts[j] - s_cuts[i]) + min((min_cost(i, k) + min_cost(k, j) for k in range(i + 1, j)), default=-cost)\n \n return min_cost(0, len(s_cuts) - 1)\n\n\n``` | 2 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Python short and clean. Functional programming. | minimum-cost-to-cut-a-stick | 0 | 1 | # Complexity\n- Time complexity: $$O(m ^ 3)$$\n\n- Space complexity: $$O(m ^ 2)$$\n\nwhere, `m is the number of cuts`.\n\n# Code\n```python\nclass Solution:\n def minCost(self, n: int, cuts: list[int]) -> int:\n s_cuts = sorted(chain(cuts, (0, n)))\n\n @cache\n def min_cost(i: int, j: int) -> int:\n return (cost := s_cuts[j] - s_cuts[i]) + min((min_cost(i, k) + min_cost(k, j) for k in range(i + 1, j)), default=-cost)\n \n return min_cost(0, len(s_cuts) - 1)\n\n\n``` | 2 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | minimum-cost-to-cut-a-stick | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n\n# Approach:\n\n- Sort the cuts in ascending order.\n- Create a 2D array dp of size (m+2) x (m+2) (where m is the number of cuts) to store the minimum cost for each subinterval.\n- Iterate over the lengths l from 2 to m+1.\n- For each length l, iterate over the starting indices i from 0 to m+1-l.\n- Calculate the ending index j as i + l.\n- Initialize dp[i][j] with a maximum value.\n- Iterate over the cutting points k from i+1 to j-1.\n- Calculate the cost of cutting the interval [cuts[i-1], cuts[j-1]] at point cuts[k-1].\n- Update dp[i][j] by taking the minimum between the current value and the cost of the new cut.\n- Calculate the left and right lengths of the interval before and after the cuts using the indices i and j.\n- Update dp[i][j] by adding the length of the interval [cuts[i-1], cuts[j-1]].\n- Repeat steps 3-9 until all subintervals of different lengths are processed.\n- Return dp[0][m+1] as the minimum cost to cut the stick.\n# Intuition:\nThe problem can be solved using dynamic programming. We want to find the minimum cost to cut the stick into smaller segments at the given cutting points. By considering subintervals of different lengths, we can break down the problem into smaller subproblems.\n\nWe use a bottom-up approach, starting from the smallest subintervals and gradually building up to the larger ones. We maintain a 2D array dp to store the minimum cost for each subinterval. The value at dp[i][j] represents the minimum cost to cut the interval [cuts[i-1], cuts[j-1]] into smaller segments.\n\nTo calculate the minimum cost for a subinterval, we iterate over all possible cutting points within that interval. For each cutting point, we calculate the cost of making the cut and update the minimum cost if necessary.\n\nWe also keep track of the lengths of the interval before and after the cut. By considering the left and right lengths, we can calculate the cost of cutting the stick at a particular point. We update the dp array by adding the cost of the cut and the lengths of the left and right segments.\n\nBy repeating this process for all subintervals of different lengths, we can determine the minimum cost to cut the stick. Finally, the value at dp[0][m+1] represents the minimum cost to cut the entire stick.\n\n```Python []\nclass Solution:\n def minCost(self, n, cuts):\n cuts.append(0)\n cuts.append(n)\n cuts.sort()\n m = len(cuts)\n dp = [[0] * m for _ in range(m)]\n\n for l in range(2, m):\n for i in range(m - l):\n j = i + l\n dp[i][j] = float(\'inf\')\n for k in range(i + 1, j):\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])\n\n return dp[0][m - 1]\n\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int minCost(int n, int[] cuts) {\n Arrays.sort(cuts);\n int m = cuts.length;\n int[][] dp = new int[m + 2][m + 2];\n\n for (int l = 2; l <= m + 1; l++) {\n for (int i = 0; i + l <= m + 1; i++) {\n int j = i + l;\n dp[i][j] = Integer.MAX_VALUE;\n for (int k = i + 1; k < j; k++) {\n dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);\n }\n int left = (i == 0) ? 0 : cuts[i - 1];\n int right = (j == m + 1) ? n : cuts[j - 1];\n dp[i][j] += right - left;\n }\n }\n\n return dp[0][m + 1];\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minCost(int n, std::vector<int>& cuts) {\n std::sort(cuts.begin(), cuts.end());\n int m = cuts.size();\n std::vector<std::vector<int>> dp(m + 2, std::vector<int>(m + 2, 0));\n\n for (int l = 2; l <= m + 1; l++) {\n for (int i = 0; i + l <= m + 1; i++) {\n int j = i + l;\n dp[i][j] = INT_MAX;\n for (int k = i + 1; k < j; k++) {\n dp[i][j] = std::min(dp[i][j], dp[i][k] + dp[k][j]);\n }\n int left = (i == 0) ? 0 : cuts[i - 1];\n int right = (j == m + 1) ? n : cuts[j - 1];\n dp[i][j] += right - left;\n }\n }\n\n return dp[0][m + 1];\n }\n};\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 18 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | minimum-cost-to-cut-a-stick | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n\n# Approach:\n\n- Sort the cuts in ascending order.\n- Create a 2D array dp of size (m+2) x (m+2) (where m is the number of cuts) to store the minimum cost for each subinterval.\n- Iterate over the lengths l from 2 to m+1.\n- For each length l, iterate over the starting indices i from 0 to m+1-l.\n- Calculate the ending index j as i + l.\n- Initialize dp[i][j] with a maximum value.\n- Iterate over the cutting points k from i+1 to j-1.\n- Calculate the cost of cutting the interval [cuts[i-1], cuts[j-1]] at point cuts[k-1].\n- Update dp[i][j] by taking the minimum between the current value and the cost of the new cut.\n- Calculate the left and right lengths of the interval before and after the cuts using the indices i and j.\n- Update dp[i][j] by adding the length of the interval [cuts[i-1], cuts[j-1]].\n- Repeat steps 3-9 until all subintervals of different lengths are processed.\n- Return dp[0][m+1] as the minimum cost to cut the stick.\n# Intuition:\nThe problem can be solved using dynamic programming. We want to find the minimum cost to cut the stick into smaller segments at the given cutting points. By considering subintervals of different lengths, we can break down the problem into smaller subproblems.\n\nWe use a bottom-up approach, starting from the smallest subintervals and gradually building up to the larger ones. We maintain a 2D array dp to store the minimum cost for each subinterval. The value at dp[i][j] represents the minimum cost to cut the interval [cuts[i-1], cuts[j-1]] into smaller segments.\n\nTo calculate the minimum cost for a subinterval, we iterate over all possible cutting points within that interval. For each cutting point, we calculate the cost of making the cut and update the minimum cost if necessary.\n\nWe also keep track of the lengths of the interval before and after the cut. By considering the left and right lengths, we can calculate the cost of cutting the stick at a particular point. We update the dp array by adding the cost of the cut and the lengths of the left and right segments.\n\nBy repeating this process for all subintervals of different lengths, we can determine the minimum cost to cut the stick. Finally, the value at dp[0][m+1] represents the minimum cost to cut the entire stick.\n\n```Python []\nclass Solution:\n def minCost(self, n, cuts):\n cuts.append(0)\n cuts.append(n)\n cuts.sort()\n m = len(cuts)\n dp = [[0] * m for _ in range(m)]\n\n for l in range(2, m):\n for i in range(m - l):\n j = i + l\n dp[i][j] = float(\'inf\')\n for k in range(i + 1, j):\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])\n\n return dp[0][m - 1]\n\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int minCost(int n, int[] cuts) {\n Arrays.sort(cuts);\n int m = cuts.length;\n int[][] dp = new int[m + 2][m + 2];\n\n for (int l = 2; l <= m + 1; l++) {\n for (int i = 0; i + l <= m + 1; i++) {\n int j = i + l;\n dp[i][j] = Integer.MAX_VALUE;\n for (int k = i + 1; k < j; k++) {\n dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);\n }\n int left = (i == 0) ? 0 : cuts[i - 1];\n int right = (j == m + 1) ? n : cuts[j - 1];\n dp[i][j] += right - left;\n }\n }\n\n return dp[0][m + 1];\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minCost(int n, std::vector<int>& cuts) {\n std::sort(cuts.begin(), cuts.end());\n int m = cuts.size();\n std::vector<std::vector<int>> dp(m + 2, std::vector<int>(m + 2, 0));\n\n for (int l = 2; l <= m + 1; l++) {\n for (int i = 0; i + l <= m + 1; i++) {\n int j = i + l;\n dp[i][j] = INT_MAX;\n for (int k = i + 1; k < j; k++) {\n dp[i][j] = std::min(dp[i][j], dp[i][k] + dp[k][j]);\n }\n int left = (i == 0) ? 0 : cuts[i - 1];\n int right = (j == m + 1) ? n : cuts[j - 1];\n dp[i][j] += right - left;\n }\n }\n\n return dp[0][m + 1];\n }\n};\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 18 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Tabulation (Bottom up) | Python / JS Solution | minimum-cost-to-cut-a-stick | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we a given a wooden stick of length `n` units, where the stick is labelled from `0` to `n` and array `cuts` where `cuts[i]` denotes a position you should perform a cut at. \n\nPerforming the cuts in order with the cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut).\n\nWe want to return the `minimum total cost` of the cuts\n\n### Explanation\n\nOur main goal is to determine the minimum total cost to perform a series of cuts on the given wooden stick denoted in the `cuts` array. \n\nThe `cuts` array contains positions where the cuts should be made and the order of the cuts can be changed. For each cut, it will have the cost equal to the length of the stick being cut at that current position. The total cost will then be the sum of the cost of all the cuts. \n\nSince, we are trying to find the `minimum total cost` to perform a `series` of cuts, we can use `Dynamic Programming Tabulation (Bottom up)` approach to help us simulate the `series` of cuts as we find the `minimum total cost`\n\n\nTo ensure we perform each cut in order, we should `sort` cuts in ascending order. \n\nOnce sorted, we can create a new `cuts` array and add a `0` to the beginning and our given `n` to the end. The new `cuts` array will represent the position at which cuts will be made as it will include the starting and ending position of the wooden stick. \n\nSince we are using `Tabulation (Bottom up)` approach, we will use a `2D` table represented as `dp` with the dimensions of `length of cuts * length of cuts`.\n\nUsing our `2D`table, we will store the minimum cost needed to cut the stick between position `cut[i]` and `cuts[j]` later on\n\n### Base case\n\nAs the problem using `Tabulation (Bottom up)` our base case is predefined in ` dp = [[0]* stick_len for _ in range(stick_len)]`, representing as when no cuts are needed the cost of those cuts are `0`\n\n### Recurrence relation\n\nFor the recurrence relation, when `i < k < j` we will be calculating the cost of cutting the sticks between positions `cuts[i]` and `cuts[j]`, while we also consider the potential cut needed at position `cuts[k]`\n\n`cuts[j]` and `cuts[i]` represents the length of the stick being cut at positions `cuts[i]` and `cuts[j]` as we also accounts for the cost of the current cut being considered\n\n`dp[i][k]` represents the minimum cost of cutting the stick between positions `cuts[i]` and `cuts[k]`. `dp[i][k]` will be obtained from the previous computed subproblems, which represents the minimum cost for the left wooden stick\n\n`dp[k][j]` represents the minimum cost of cutting the stick between positions `cuts[k]` and `cuts[j]`. `dp[k][j]` will be obtained from the previous computed subproblems, which represents the minimum cost for the right wooden stick\n\n`min_cost` is used to keep track of the minimum cost encountered among all potential cuts `k` within the range of `i < k < j` to ensure the minimum cost will be found among all different combinations of cuts being made\n\n`dp[i][j]` is then updated with `min_cost` to ensure we properly store the minimum cost needed for the current range of cuts for `i` to `j`\n\nPutting it all together, we have a recurrence relation denoted as follows:\n\n `cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n min_cost = min(min_cost, cost)\n dp[i][j] = min_cost`\n \nNow, create an outer loop to iterate over cuts array in reverse order starting from the second-to-last cut moving towards the first cut. Instead of `length - 1`, we will perform `length - 2` to ensure we consider all subproblem.\n\nInitialize `min_cost`\n\nInside the inner loop, we now also iterate cuts array from `k + 1` to the end of the array `j` to find the potential position to make cuts between `cuts[i]` and `cuts[j]`. So, iterate over `i + 1` to `j` to find all possible positions for making cuts between the indices `i` and `j` and perform our recurrence relation of `cost` and `min_cost`\n\nUpdate `dp[i][j]` after the inner loop \n\nThe minimum total cost of the cuts will then be stored in `dp[0][stick_len - 1]` in the first row last element \n\n\n# Code\n**Python**\n```\n def minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n cuts = [0] + cuts + [n]\n\n stick_len = len(cuts)\n\n dp = [[0]* stick_len for _ in range(stick_len)]\n\n for i in range(stick_len - 2, -1, -1):\n for j in range(i + 2, stick_len):\n min_cost = float("inf")\n for k in range(i + 1, j):\n cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n min_cost = min(min_cost, cost)\n dp[i][j] = min_cost\n\n return dp[0][stick_len - 1]\n```\n\n**JavaScript**\n```\n/**\n * @param {number} n\n * @param {number[]} cuts\n * @return {number}\n */\nvar minCost = function(n, cuts) {\n cuts.sort((a, b) => a - b)\n cuts = [0, ...cuts, n]\n\n const stickLen = cuts.length\n\n const dp = Array(stickLen).fill(0).map(() => Array(stickLen).fill(0))\n\n for (let i = stickLen - 2; i >= 0; i--){\n for (let j = i + 2; j < stickLen; j++){\n let minCost = Infinity\n for (let k = i + 1; k < j; k++){\n const cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n minCost = Math.min(minCost, cost)\n }\n\n dp[i][j] = minCost\n }\n }\n return dp[0][stickLen - 1]\n};\n```\n### Time Complexity: O(n^3 + n logn )\n### Space Complexity: O(n^2)\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n | 5 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Tabulation (Bottom up) | Python / JS Solution | minimum-cost-to-cut-a-stick | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we a given a wooden stick of length `n` units, where the stick is labelled from `0` to `n` and array `cuts` where `cuts[i]` denotes a position you should perform a cut at. \n\nPerforming the cuts in order with the cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut).\n\nWe want to return the `minimum total cost` of the cuts\n\n### Explanation\n\nOur main goal is to determine the minimum total cost to perform a series of cuts on the given wooden stick denoted in the `cuts` array. \n\nThe `cuts` array contains positions where the cuts should be made and the order of the cuts can be changed. For each cut, it will have the cost equal to the length of the stick being cut at that current position. The total cost will then be the sum of the cost of all the cuts. \n\nSince, we are trying to find the `minimum total cost` to perform a `series` of cuts, we can use `Dynamic Programming Tabulation (Bottom up)` approach to help us simulate the `series` of cuts as we find the `minimum total cost`\n\n\nTo ensure we perform each cut in order, we should `sort` cuts in ascending order. \n\nOnce sorted, we can create a new `cuts` array and add a `0` to the beginning and our given `n` to the end. The new `cuts` array will represent the position at which cuts will be made as it will include the starting and ending position of the wooden stick. \n\nSince we are using `Tabulation (Bottom up)` approach, we will use a `2D` table represented as `dp` with the dimensions of `length of cuts * length of cuts`.\n\nUsing our `2D`table, we will store the minimum cost needed to cut the stick between position `cut[i]` and `cuts[j]` later on\n\n### Base case\n\nAs the problem using `Tabulation (Bottom up)` our base case is predefined in ` dp = [[0]* stick_len for _ in range(stick_len)]`, representing as when no cuts are needed the cost of those cuts are `0`\n\n### Recurrence relation\n\nFor the recurrence relation, when `i < k < j` we will be calculating the cost of cutting the sticks between positions `cuts[i]` and `cuts[j]`, while we also consider the potential cut needed at position `cuts[k]`\n\n`cuts[j]` and `cuts[i]` represents the length of the stick being cut at positions `cuts[i]` and `cuts[j]` as we also accounts for the cost of the current cut being considered\n\n`dp[i][k]` represents the minimum cost of cutting the stick between positions `cuts[i]` and `cuts[k]`. `dp[i][k]` will be obtained from the previous computed subproblems, which represents the minimum cost for the left wooden stick\n\n`dp[k][j]` represents the minimum cost of cutting the stick between positions `cuts[k]` and `cuts[j]`. `dp[k][j]` will be obtained from the previous computed subproblems, which represents the minimum cost for the right wooden stick\n\n`min_cost` is used to keep track of the minimum cost encountered among all potential cuts `k` within the range of `i < k < j` to ensure the minimum cost will be found among all different combinations of cuts being made\n\n`dp[i][j]` is then updated with `min_cost` to ensure we properly store the minimum cost needed for the current range of cuts for `i` to `j`\n\nPutting it all together, we have a recurrence relation denoted as follows:\n\n `cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n min_cost = min(min_cost, cost)\n dp[i][j] = min_cost`\n \nNow, create an outer loop to iterate over cuts array in reverse order starting from the second-to-last cut moving towards the first cut. Instead of `length - 1`, we will perform `length - 2` to ensure we consider all subproblem.\n\nInitialize `min_cost`\n\nInside the inner loop, we now also iterate cuts array from `k + 1` to the end of the array `j` to find the potential position to make cuts between `cuts[i]` and `cuts[j]`. So, iterate over `i + 1` to `j` to find all possible positions for making cuts between the indices `i` and `j` and perform our recurrence relation of `cost` and `min_cost`\n\nUpdate `dp[i][j]` after the inner loop \n\nThe minimum total cost of the cuts will then be stored in `dp[0][stick_len - 1]` in the first row last element \n\n\n# Code\n**Python**\n```\n def minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n cuts = [0] + cuts + [n]\n\n stick_len = len(cuts)\n\n dp = [[0]* stick_len for _ in range(stick_len)]\n\n for i in range(stick_len - 2, -1, -1):\n for j in range(i + 2, stick_len):\n min_cost = float("inf")\n for k in range(i + 1, j):\n cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n min_cost = min(min_cost, cost)\n dp[i][j] = min_cost\n\n return dp[0][stick_len - 1]\n```\n\n**JavaScript**\n```\n/**\n * @param {number} n\n * @param {number[]} cuts\n * @return {number}\n */\nvar minCost = function(n, cuts) {\n cuts.sort((a, b) => a - b)\n cuts = [0, ...cuts, n]\n\n const stickLen = cuts.length\n\n const dp = Array(stickLen).fill(0).map(() => Array(stickLen).fill(0))\n\n for (let i = stickLen - 2; i >= 0; i--){\n for (let j = i + 2; j < stickLen; j++){\n let minCost = Infinity\n for (let k = i + 1; k < j; k++){\n const cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n minCost = Math.min(minCost, cost)\n }\n\n dp[i][j] = minCost\n }\n }\n return dp[0][stickLen - 1]\n};\n```\n### Time Complexity: O(n^3 + n logn )\n### Space Complexity: O(n^2)\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n | 5 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Python || Bottom Up DP || Easy To Understand 🔥 | minimum-cost-to-cut-a-stick | 0 | 1 | # Code\n```\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n cuts = [0] + cuts + [n]\n m = len(cuts)\n dp = [[0] * m for _ in range(m)]\n for i in range(m - 2, -1, -1):\n for j in range(i + 2, m):\n mini = float(\'inf\')\n for k in range(i + 1, j):\n cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n mini = min(mini, cost)\n dp[i][j] = mini\n return dp[0][m - 1]\n``` | 2 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Python || Bottom Up DP || Easy To Understand 🔥 | minimum-cost-to-cut-a-stick | 0 | 1 | # Code\n```\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n cuts = [0] + cuts + [n]\n m = len(cuts)\n dp = [[0] * m for _ in range(m)]\n for i in range(m - 2, -1, -1):\n for j in range(i + 2, m):\n mini = float(\'inf\')\n for k in range(i + 1, j):\n cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]\n mini = min(mini, cost)\n dp[i][j] = mini\n return dp[0][m - 1]\n``` | 2 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Python easy to understand | three-consecutive-odds | 0 | 1 | ```\ndef threeConsecutiveOdds(self, arr: List[int]) -> bool:\n count = 0\n for num in arr:\n if num % 2 != 0:\n count += 1\n if count == 3:\n return True\n else:\n count = 0\n return False | 1 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python easy to understand | three-consecutive-odds | 0 | 1 | ```\ndef threeConsecutiveOdds(self, arr: List[int]) -> bool:\n count = 0\n for num in arr:\n if num % 2 != 0:\n count += 1\n if count == 3:\n return True\n else:\n count = 0\n return False | 1 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Python beats 99%, use string | three-consecutive-odds | 0 | 1 | ```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n return "111" in "".join([str(i%2) for i in arr])\n``` | 41 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python beats 99%, use string | three-consecutive-odds | 0 | 1 | ```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n return "111" in "".join([str(i%2) for i in arr])\n``` | 41 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Python Easy Solution | three-consecutive-odds | 0 | 1 | # Code\n```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n if len(arr)<3:\n return 0\n window=[arr[0]%2,arr[1]%2,arr[2]%2]\n if window==[1,1,1]:\n return 1\n for i in range(3,len(arr)):\n window.pop(0)\n window.append(arr[i]%2)\n if window==[1,1,1]:\n return 1\n``` | 2 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python Easy Solution | three-consecutive-odds | 0 | 1 | # Code\n```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n if len(arr)<3:\n return 0\n window=[arr[0]%2,arr[1]%2,arr[2]%2]\n if window==[1,1,1]:\n return 1\n for i in range(3,len(arr)):\n window.pop(0)\n window.append(arr[i]%2)\n if window==[1,1,1]:\n return 1\n``` | 2 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Simple loop python | three-consecutive-odds | 0 | 1 | ```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n c=0\n for i in arr:\n if i%2==0:\n c=0\n else:\n c+=1\n if c==3:\n return True\n return False\n``` | 2 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Simple loop python | three-consecutive-odds | 0 | 1 | ```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n c=0\n for i in arr:\n if i%2==0:\n c=0\n else:\n c+=1\n if c==3:\n return True\n return False\n``` | 2 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Python3 straight forward solution | three-consecutive-odds | 0 | 1 | ```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n count = 0\n \n for i in range(0, len(arr)):\n if arr[i] %2 != 0:\n count += 1\n if count == 3:\n return True\n else:\n count = 0\n return False\n``` | 21 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python3 straight forward solution | three-consecutive-odds | 0 | 1 | ```\nclass Solution:\n def threeConsecutiveOdds(self, arr: List[int]) -> bool:\n count = 0\n \n for i in range(0, len(arr)):\n if arr[i] %2 != 0:\n count += 1\n if count == 3:\n return True\n else:\n count = 0\n return False\n``` | 21 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Most easiest python code✅✅ | minimum-operations-to-make-array-equal | 0 | 1 | \n\n# Approach\nIF LENGTH OF str = even \nwe need to sum first n//2 odd numbers\nwhich n//2 square\nand vice versa\n\n# Complexity\n- Time complexity:\nI think it will be o(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, n: int) -> int:\n if n%2==1:\n return (n//2)*(n//2+1)\n else:\n return (n//2)**2\n``` | 2 | You have an array `arr` of length `n` where `arr[i] = (2 * i) + 1` for all valid values of `i` (i.e., `0 <= i < n`).
In one operation, you can select two indices `x` and `y` where `0 <= x, y < n` and subtract `1` from `arr[x]` and add `1` to `arr[y]` (i.e., perform `arr[x] -=1` and `arr[y] += 1`). The goal is to make all the elements of the array **equal**. It is **guaranteed** that all the elements of the array can be made equal using some operations.
Given an integer `n`, the length of the array, return _the minimum number of operations_ needed to make all the elements of arr equal.
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** arr = \[1, 3, 5\]
First operation choose x = 2 and y = 0, this leads arr to be \[2, 3, 4\]
In the second operation choose x = 2 and y = 0 again, thus arr = \[3, 3, 3\].
**Example 2:**
**Input:** n = 6
**Output:** 9
**Constraints:**
* `1 <= n <= 104` | null |
Most easiest python code✅✅ | minimum-operations-to-make-array-equal | 0 | 1 | \n\n# Approach\nIF LENGTH OF str = even \nwe need to sum first n//2 odd numbers\nwhich n//2 square\nand vice versa\n\n# Complexity\n- Time complexity:\nI think it will be o(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, n: int) -> int:\n if n%2==1:\n return (n//2)*(n//2+1)\n else:\n return (n//2)**2\n``` | 2 | You are given an integer array `nums` of **even** length `n` and an integer `limit`. In one move, you can replace any integer from `nums` with another integer between `1` and `limit`, inclusive.
The array `nums` is **complementary** if for all indices `i` (**0-indexed**), `nums[i] + nums[n - 1 - i]` equals the same number. For example, the array `[1,2,3,4]` is complementary because for all indices `i`, `nums[i] + nums[n - 1 - i] = 5`.
Return the _**minimum** number of moves required to make_ `nums` _**complementary**_.
**Example 1:**
**Input:** nums = \[1,2,4,3\], limit = 4
**Output:** 1
**Explanation:** In 1 move, you can change nums to \[1,2,2,3\] (underlined elements are changed).
nums\[0\] + nums\[3\] = 1 + 3 = 4.
nums\[1\] + nums\[2\] = 2 + 2 = 4.
nums\[2\] + nums\[1\] = 2 + 2 = 4.
nums\[3\] + nums\[0\] = 3 + 1 = 4.
Therefore, nums\[i\] + nums\[n-1-i\] = 4 for every i, so nums is complementary.
**Example 2:**
**Input:** nums = \[1,2,2,1\], limit = 2
**Output:** 2
**Explanation:** In 2 moves, you can change nums to \[2,2,2,2\]. You cannot change any number to 3 since 3 > limit.
**Example 3:**
**Input:** nums = \[1,2,1,2\], limit = 2
**Output:** 0
**Explanation:** nums is already complementary.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `1 <= nums[i] <= limit <= 105`
* `n` is even. | Build the array arr using the given formula, define target = sum(arr) / n What is the number of operations needed to convert arr so that all elements equal target ? |
[Python] O(1) solution using math | minimum-operations-to-make-array-equal | 0 | 1 | # Code\n```python []\nclass Solution:\n def minOperations(self, n: int) -> int:\n return (n ** 2) // 4\n```\n# Approach\nIf we look attentively, we\'ll discover that the array arr is a sequence of odd numbers.\nFirst, I tried to find any rule or regularity in answers, and I nociced that we should do all operations and as a result bring all numbers to a single one (for ex. if n = 3: arr = [1, 3, 5], we make arr = [3, 3, 3], we bring all numbers to 3; if n = 4: arr = [1, 3, 5, 7] and we bring all numbers to 4: arr becomes [4, 4, 4, 4] etc.). And as you can notice if n is odd (in this ex. 3) this resulting number is n itself (3). If n is even (4 in this ex.) the resulting number is also n itself (4). So that means we need to bring all numbers to n by using operations. But how to calculate the minimum number of operations? Let\'s again look at the previous example. \nIf n = 4 (n is even): arr = [1, 3, 5, 7]. \nFirst, we make 3 and 5 become 4 by one opeartion (3 += 1 and 5 -= 1), then 1 and 7 become 4 by three operations (just do 1 += 1 and 7 -= 1 three times). So we have total 1 + 3 (**it\'s an arithmetic sequence with step 2 starting with 1**) operations.\nFor ex. if n = 5 (n is odd): arr = [1, 3, 5, 7, 9].\nSince 5 is already there we move on and make 3 and 7 become 5 by two operations (3 += 1 and 7 -= 1 two times). Then 1 and 9 become 5 by four operations (1 += 1 and 9 -= 1 four times). So we get in total 2 + 4 operations (**also arithmetic sequence with also step 2, but starting with 2**.)\nWe see the regularity: \n1) **If n is odd we should calculate the sum of arithmetic sequence with the step 2 and which starts with 2 upto n - 1 (arithmetic sequence = [2, 4, 6, 8, ..., n - 1]).** \n2) **If n is even we should calculate the sum of arithmetic sequence with the step 2 and which starts with 1 upto n - 1 (arithmetic sequence = [1, 3, 5, 7, ..., n - 1]).**\n \nWe can simply calculate those sums by using formula for finding the sum of arithmetic sequence:\n\n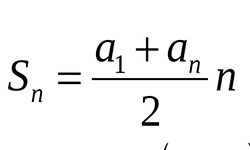, where a1 - first element, an - last element, n - quantity of elements. \nSo for the case when n is odd: \na1 = 2, \nan = n - 1,\nn = n // 2 (since the sequence has the step 2)\n\nAnd for the case when n is even:\na1 = 1, \nan = n - 1, \nn = n // 2 (since the sequence also has the step 2). \n\nTherefore if n is odd: result1 = (2 + (n - 1)) * (n // 2) / 2; \nand if n is even: result2 = (1 + (n - 1) * (n // 2) / 2. \nBy simplifying we get: result1 = (n + 1) * (n // 2) / 2, result2 = n * (n // 2) / 2. We could stop here but let\'s try to think more.\nWe can notice that if n is odd then n // 2 = (n - 1) / 2 therefore result1 = (n + 1) * (n - 1) / 2 / 2. By simplifying we get result1 = (n ** 2 - 1) / 4. \nThen we can notice that if n is even then n // 2 = n / 2 therefore also by simplifying result2 we get: result2 = (n ** 2) / 4. We can see that if n is odd then n ** 2 is also odd therefore n ** 2 will not be divided wholly by 4 and that\'s why we subtract one from it, but since we just need the whole part we can simply get: result1 = (n ** 2) // 4. By the same logic we get result2 = (n ** 2) // 4. So in both cases the answer is the same so we just return (n ** 2) // 4.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1) | 10 | You have an array `arr` of length `n` where `arr[i] = (2 * i) + 1` for all valid values of `i` (i.e., `0 <= i < n`).
In one operation, you can select two indices `x` and `y` where `0 <= x, y < n` and subtract `1` from `arr[x]` and add `1` to `arr[y]` (i.e., perform `arr[x] -=1` and `arr[y] += 1`). The goal is to make all the elements of the array **equal**. It is **guaranteed** that all the elements of the array can be made equal using some operations.
Given an integer `n`, the length of the array, return _the minimum number of operations_ needed to make all the elements of arr equal.
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** arr = \[1, 3, 5\]
First operation choose x = 2 and y = 0, this leads arr to be \[2, 3, 4\]
In the second operation choose x = 2 and y = 0 again, thus arr = \[3, 3, 3\].
**Example 2:**
**Input:** n = 6
**Output:** 9
**Constraints:**
* `1 <= n <= 104` | null |
[Python] O(1) solution using math | minimum-operations-to-make-array-equal | 0 | 1 | # Code\n```python []\nclass Solution:\n def minOperations(self, n: int) -> int:\n return (n ** 2) // 4\n```\n# Approach\nIf we look attentively, we\'ll discover that the array arr is a sequence of odd numbers.\nFirst, I tried to find any rule or regularity in answers, and I nociced that we should do all operations and as a result bring all numbers to a single one (for ex. if n = 3: arr = [1, 3, 5], we make arr = [3, 3, 3], we bring all numbers to 3; if n = 4: arr = [1, 3, 5, 7] and we bring all numbers to 4: arr becomes [4, 4, 4, 4] etc.). And as you can notice if n is odd (in this ex. 3) this resulting number is n itself (3). If n is even (4 in this ex.) the resulting number is also n itself (4). So that means we need to bring all numbers to n by using operations. But how to calculate the minimum number of operations? Let\'s again look at the previous example. \nIf n = 4 (n is even): arr = [1, 3, 5, 7]. \nFirst, we make 3 and 5 become 4 by one opeartion (3 += 1 and 5 -= 1), then 1 and 7 become 4 by three operations (just do 1 += 1 and 7 -= 1 three times). So we have total 1 + 3 (**it\'s an arithmetic sequence with step 2 starting with 1**) operations.\nFor ex. if n = 5 (n is odd): arr = [1, 3, 5, 7, 9].\nSince 5 is already there we move on and make 3 and 7 become 5 by two operations (3 += 1 and 7 -= 1 two times). Then 1 and 9 become 5 by four operations (1 += 1 and 9 -= 1 four times). So we get in total 2 + 4 operations (**also arithmetic sequence with also step 2, but starting with 2**.)\nWe see the regularity: \n1) **If n is odd we should calculate the sum of arithmetic sequence with the step 2 and which starts with 2 upto n - 1 (arithmetic sequence = [2, 4, 6, 8, ..., n - 1]).** \n2) **If n is even we should calculate the sum of arithmetic sequence with the step 2 and which starts with 1 upto n - 1 (arithmetic sequence = [1, 3, 5, 7, ..., n - 1]).**\n \nWe can simply calculate those sums by using formula for finding the sum of arithmetic sequence:\n\n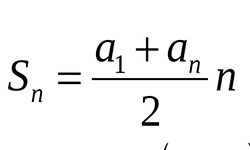, where a1 - first element, an - last element, n - quantity of elements. \nSo for the case when n is odd: \na1 = 2, \nan = n - 1,\nn = n // 2 (since the sequence has the step 2)\n\nAnd for the case when n is even:\na1 = 1, \nan = n - 1, \nn = n // 2 (since the sequence also has the step 2). \n\nTherefore if n is odd: result1 = (2 + (n - 1)) * (n // 2) / 2; \nand if n is even: result2 = (1 + (n - 1) * (n // 2) / 2. \nBy simplifying we get: result1 = (n + 1) * (n // 2) / 2, result2 = n * (n // 2) / 2. We could stop here but let\'s try to think more.\nWe can notice that if n is odd then n // 2 = (n - 1) / 2 therefore result1 = (n + 1) * (n - 1) / 2 / 2. By simplifying we get result1 = (n ** 2 - 1) / 4. \nThen we can notice that if n is even then n // 2 = n / 2 therefore also by simplifying result2 we get: result2 = (n ** 2) / 4. We can see that if n is odd then n ** 2 is also odd therefore n ** 2 will not be divided wholly by 4 and that\'s why we subtract one from it, but since we just need the whole part we can simply get: result1 = (n ** 2) // 4. By the same logic we get result2 = (n ** 2) // 4. So in both cases the answer is the same so we just return (n ** 2) // 4.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1) | 10 | You are given an integer array `nums` of **even** length `n` and an integer `limit`. In one move, you can replace any integer from `nums` with another integer between `1` and `limit`, inclusive.
The array `nums` is **complementary** if for all indices `i` (**0-indexed**), `nums[i] + nums[n - 1 - i]` equals the same number. For example, the array `[1,2,3,4]` is complementary because for all indices `i`, `nums[i] + nums[n - 1 - i] = 5`.
Return the _**minimum** number of moves required to make_ `nums` _**complementary**_.
**Example 1:**
**Input:** nums = \[1,2,4,3\], limit = 4
**Output:** 1
**Explanation:** In 1 move, you can change nums to \[1,2,2,3\] (underlined elements are changed).
nums\[0\] + nums\[3\] = 1 + 3 = 4.
nums\[1\] + nums\[2\] = 2 + 2 = 4.
nums\[2\] + nums\[1\] = 2 + 2 = 4.
nums\[3\] + nums\[0\] = 3 + 1 = 4.
Therefore, nums\[i\] + nums\[n-1-i\] = 4 for every i, so nums is complementary.
**Example 2:**
**Input:** nums = \[1,2,2,1\], limit = 2
**Output:** 2
**Explanation:** In 2 moves, you can change nums to \[2,2,2,2\]. You cannot change any number to 3 since 3 > limit.
**Example 3:**
**Input:** nums = \[1,2,1,2\], limit = 2
**Output:** 0
**Explanation:** nums is already complementary.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `1 <= nums[i] <= limit <= 105`
* `n` is even. | Build the array arr using the given formula, define target = sum(arr) / n What is the number of operations needed to convert arr so that all elements equal target ? |
Binary search approach with explanation | magnetic-force-between-two-balls | 0 | 1 | Please upvote if you like my solution. Let me know in the comments if you have any suggestions to increase performance or readability.\n# Code\n```\nclass Solution:\n def maxDistance(self, position: List[int], m: int) -> int:\n # Sort the position array in ascending order\n position.sort()\n \n # Set the left and right bounds for the binary search\n left, right = 1, position[-1] - position[0]\n\n # Perform binary search to find the maximum possible minimum magnetic force\n while left <= right:\n # Calculate the midpoint of the search range\n mid = (left + right) // 2\n \n # Initialize variables for tracking the number of balls placed and the previous position\n balls_placed, prev_pos = 1, position[0]\n\n # Iterate through the remaining baskets and check if we can place the remaining balls\n for i in range(1, len(position)):\n if position[i] - prev_pos >= mid:\n # If the current basket is far enough from the previous one, place a ball\n balls_placed += 1\n prev_pos = position[i]\n\n # If we can place all the balls with the given magnetic force, increase the force\n if balls_placed >= m:\n left = mid + 1\n max_force = mid\n # Otherwise, decrease the force\n else:\n right = mid - 1\n\n # Return the maximum possible minimum magnetic force\n return max_force\n```\nIn conclusion:\nI\'m sure there are many more approaches. I\'m interested in the thoughts people have on which is best in an interview!\nHappy coding!\n | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
Binary search approach with explanation | magnetic-force-between-two-balls | 0 | 1 | Please upvote if you like my solution. Let me know in the comments if you have any suggestions to increase performance or readability.\n# Code\n```\nclass Solution:\n def maxDistance(self, position: List[int], m: int) -> int:\n # Sort the position array in ascending order\n position.sort()\n \n # Set the left and right bounds for the binary search\n left, right = 1, position[-1] - position[0]\n\n # Perform binary search to find the maximum possible minimum magnetic force\n while left <= right:\n # Calculate the midpoint of the search range\n mid = (left + right) // 2\n \n # Initialize variables for tracking the number of balls placed and the previous position\n balls_placed, prev_pos = 1, position[0]\n\n # Iterate through the remaining baskets and check if we can place the remaining balls\n for i in range(1, len(position)):\n if position[i] - prev_pos >= mid:\n # If the current basket is far enough from the previous one, place a ball\n balls_placed += 1\n prev_pos = position[i]\n\n # If we can place all the balls with the given magnetic force, increase the force\n if balls_placed >= m:\n left = mid + 1\n max_force = mid\n # Otherwise, decrease the force\n else:\n right = mid - 1\n\n # Return the maximum possible minimum magnetic force\n return max_force\n```\nIn conclusion:\nI\'m sure there are many more approaches. I\'m interested in the thoughts people have on which is best in an interview!\nHappy coding!\n | 1 | You are given an array `nums` of `n` positive integers.
You can perform two types of operations on any element of the array any number of times:
* If the element is **even**, **divide** it by `2`.
* For example, if the array is `[1,2,3,4]`, then you can do this operation on the last element, and the array will be `[1,2,3,2].`
* If the element is **odd**, **multiply** it by `2`.
* For example, if the array is `[1,2,3,4]`, then you can do this operation on the first element, and the array will be `[2,2,3,4].`
The **deviation** of the array is the **maximum difference** between any two elements in the array.
Return _the **minimum deviation** the array can have after performing some number of operations._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 1
**Explanation:** You can transform the array to \[1,2,3,2\], then to \[2,2,3,2\], then the deviation will be 3 - 2 = 1.
**Example 2:**
**Input:** nums = \[4,1,5,20,3\]
**Output:** 3
**Explanation:** You can transform the array after two operations to \[4,2,5,5,3\], then the deviation will be 5 - 2 = 3.
**Example 3:**
**Input:** nums = \[2,10,8\]
**Output:** 3
**Constraints:**
* `n == nums.length`
* `2 <= n <= 5 * 104`
* `1 <= nums[i] <= 109` | If you can place balls such that the answer is x then you can do it for y where y < x. Similarly if you cannot place balls such that the answer is x then you can do it for y where y > x. Binary search on the answer and greedily see if it is possible. |
Python binary search with Explanation. | magnetic-force-between-two-balls | 0 | 1 | # Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxDistance(self, position: List[int], m: int) -> int:\n position.sort()\n\n # To check whether or not m balls could be distributed into the baskets \n def feasible(force: int) -> bool:\n x, k = 0, m\n for i in range(len(position)):\n if position[i] >= x:\n x, k = position[i] + force, k - 1\n if k == 0:\n return True\n return False\n\n # search space of minimum magnetic force\n # from 1 to max of minimum magnetic force\n l, r = 1, (position[-1] - position[0]) // (m - 1)\n\n # When breaking the loop, l will be the maximal number satisfying the feasible function;\n # It means that l is the answer.\n while l < r:\n mid = l + (r - l + 1) // 2\n if feasible(mid):\n l = mid\n else:\n r = mid - 1\n return l\n``` | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
Python binary search with Explanation. | magnetic-force-between-two-balls | 0 | 1 | # Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxDistance(self, position: List[int], m: int) -> int:\n position.sort()\n\n # To check whether or not m balls could be distributed into the baskets \n def feasible(force: int) -> bool:\n x, k = 0, m\n for i in range(len(position)):\n if position[i] >= x:\n x, k = position[i] + force, k - 1\n if k == 0:\n return True\n return False\n\n # search space of minimum magnetic force\n # from 1 to max of minimum magnetic force\n l, r = 1, (position[-1] - position[0]) // (m - 1)\n\n # When breaking the loop, l will be the maximal number satisfying the feasible function;\n # It means that l is the answer.\n while l < r:\n mid = l + (r - l + 1) // 2\n if feasible(mid):\n l = mid\n else:\n r = mid - 1\n return l\n``` | 1 | You are given an array `nums` of `n` positive integers.
You can perform two types of operations on any element of the array any number of times:
* If the element is **even**, **divide** it by `2`.
* For example, if the array is `[1,2,3,4]`, then you can do this operation on the last element, and the array will be `[1,2,3,2].`
* If the element is **odd**, **multiply** it by `2`.
* For example, if the array is `[1,2,3,4]`, then you can do this operation on the first element, and the array will be `[2,2,3,4].`
The **deviation** of the array is the **maximum difference** between any two elements in the array.
Return _the **minimum deviation** the array can have after performing some number of operations._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 1
**Explanation:** You can transform the array to \[1,2,3,2\], then to \[2,2,3,2\], then the deviation will be 3 - 2 = 1.
**Example 2:**
**Input:** nums = \[4,1,5,20,3\]
**Output:** 3
**Explanation:** You can transform the array after two operations to \[4,2,5,5,3\], then the deviation will be 5 - 2 = 3.
**Example 3:**
**Input:** nums = \[2,10,8\]
**Output:** 3
**Constraints:**
* `n == nums.length`
* `2 <= n <= 5 * 104`
* `1 <= nums[i] <= 109` | If you can place balls such that the answer is x then you can do it for y where y < x. Similarly if you cannot place balls such that the answer is x then you can do it for y where y > x. Binary search on the answer and greedily see if it is possible. |
99.8% SC and 68% TC easy python solution | magnetic-force-between-two-balls | 0 | 1 | Feel free to ask... :)\n```\ndef maxDistance(self, position: List[int], m: int) -> int:\n\tposition.sort()\n\tn = len(position)\n\tdef isValid(force):\n\t\tstart = position[0]\n\t\tcount = 1\n\t\twhile(count < m):\n\t\t\tstart += force\n\t\t\ti = bisect_left(position, start)\n\t\t\tif(i == n):\n\t\t\t\treturn False\n\t\t\tstart = position[i]\n\t\t\tcount += 1\n\t\treturn True\n\ti = 1\n\tj = position[n-1] - position[0]\n\twhile(i <= j):\n\t\tmid = i + (j-i)//2\n\t\tx = isValid(mid)\n\t\tif(x):\n\t\t\ti = mid+1\n\t\t\tans = mid\n\t\telse:\n\t\t\tj = mid-1\n\treturn ans\n``` | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
99.8% SC and 68% TC easy python solution | magnetic-force-between-two-balls | 0 | 1 | Feel free to ask... :)\n```\ndef maxDistance(self, position: List[int], m: int) -> int:\n\tposition.sort()\n\tn = len(position)\n\tdef isValid(force):\n\t\tstart = position[0]\n\t\tcount = 1\n\t\twhile(count < m):\n\t\t\tstart += force\n\t\t\ti = bisect_left(position, start)\n\t\t\tif(i == n):\n\t\t\t\treturn False\n\t\t\tstart = position[i]\n\t\t\tcount += 1\n\t\treturn True\n\ti = 1\n\tj = position[n-1] - position[0]\n\twhile(i <= j):\n\t\tmid = i + (j-i)//2\n\t\tx = isValid(mid)\n\t\tif(x):\n\t\t\ti = mid+1\n\t\t\tans = mid\n\t\telse:\n\t\t\tj = mid-1\n\treturn ans\n``` | 1 | You are given an array `nums` of `n` positive integers.
You can perform two types of operations on any element of the array any number of times:
* If the element is **even**, **divide** it by `2`.
* For example, if the array is `[1,2,3,4]`, then you can do this operation on the last element, and the array will be `[1,2,3,2].`
* If the element is **odd**, **multiply** it by `2`.
* For example, if the array is `[1,2,3,4]`, then you can do this operation on the first element, and the array will be `[2,2,3,4].`
The **deviation** of the array is the **maximum difference** between any two elements in the array.
Return _the **minimum deviation** the array can have after performing some number of operations._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 1
**Explanation:** You can transform the array to \[1,2,3,2\], then to \[2,2,3,2\], then the deviation will be 3 - 2 = 1.
**Example 2:**
**Input:** nums = \[4,1,5,20,3\]
**Output:** 3
**Explanation:** You can transform the array after two operations to \[4,2,5,5,3\], then the deviation will be 5 - 2 = 3.
**Example 3:**
**Input:** nums = \[2,10,8\]
**Output:** 3
**Constraints:**
* `n == nums.length`
* `2 <= n <= 5 * 104`
* `1 <= nums[i] <= 109` | If you can place balls such that the answer is x then you can do it for y where y < x. Similarly if you cannot place balls such that the answer is x then you can do it for y where y > x. Binary search on the answer and greedily see if it is possible. |
[Python3] bfs | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | Think of this problem as a tree in which we start from the root `n`. At any node, it connects to up to 3 childrens `n-1`, `n//2` if `n%2 == 0`, `n//3` if `n%3 == 0`. Then we can level order traverse the tree and find the first occurrence of `0` and return its level. \n\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n ans = 0\n queue = [n]\n seen = set()\n while queue: #bfs \n newq = []\n for x in queue: \n if x == 0: return ans \n seen.add(x)\n if x-1 not in seen: newq.append(x-1)\n if x % 2 == 0 and x//2 not in seen: newq.append(x//2)\n if x % 3 == 0 and x//3 not in seen: newq.append(x//3)\n ans += 1\n queue = newq \n```\n\t\nEdit: It turns out that dp also works for this problem per this [post](https://leetcode.com/problems/minimum-number-of-days-to-eat-n-oranges/discuss/794162/C%2B%2BJavaPython-5-lines). \n\t\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n \n @lru_cache(None)\n def fn(n):\n if n <= 1: return n\n return 1 + min(n%2 + fn(n//2), n%3 + fn(n//3))\n \n return fn(n)\n``` | 27 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
[Python3] bfs | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | Think of this problem as a tree in which we start from the root `n`. At any node, it connects to up to 3 childrens `n-1`, `n//2` if `n%2 == 0`, `n//3` if `n%3 == 0`. Then we can level order traverse the tree and find the first occurrence of `0` and return its level. \n\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n ans = 0\n queue = [n]\n seen = set()\n while queue: #bfs \n newq = []\n for x in queue: \n if x == 0: return ans \n seen.add(x)\n if x-1 not in seen: newq.append(x-1)\n if x % 2 == 0 and x//2 not in seen: newq.append(x//2)\n if x % 3 == 0 and x//3 not in seen: newq.append(x//3)\n ans += 1\n queue = newq \n```\n\t\nEdit: It turns out that dp also works for this problem per this [post](https://leetcode.com/problems/minimum-number-of-days-to-eat-n-oranges/discuss/794162/C%2B%2BJavaPython-5-lines). \n\t\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n \n @lru_cache(None)\n def fn(n):\n if n <= 1: return n\n return 1 + min(n%2 + fn(n//2), n%3 + fn(n//3))\n \n return fn(n)\n``` | 27 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
Simple DP - beats 97 % of the submitted solutions. | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n memo = {}\n\n def dp(remaining):\n if remaining <= 1:\n return remaining\n if remaining not in memo:\n memo[remaining] = 1 + min(\n remaining % 2 + dp(remaining // 2),\n remaining % 3 + dp(remaining // 3)\n )\n return memo[remaining]\n \n return dp(n)\n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
Simple DP - beats 97 % of the submitted solutions. | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n memo = {}\n\n def dp(remaining):\n if remaining <= 1:\n return remaining\n if remaining not in memo:\n memo[remaining] = 1 + min(\n remaining % 2 + dp(remaining // 2),\n remaining % 3 + dp(remaining // 3)\n )\n return memo[remaining]\n \n return dp(n)\n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
O(logn) time | O(n) space | solution explained | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe max days can be n if we eat one orange a day. \n\nWe will start with n oranges and eat oranges every day to reduce n to 0 or 1. For each day, we have two options/paths: eat n/2 oranges a day or n/3 oranges\n\nDo DFS to explore all paths and choose the best. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- create a hashmap for memoization i.e to store the min days required to eat x oranges\nkey = oranges left\nvalue = min days required to eat the remaining oranges\n- add base cases to the hashmap i.e days required to eat 0 and 1 oranges\n- define a helper function for DFS\ndfs(oranges left)\n - if x is in the hashmap, we have already found the min days required to eat x oranges, return it\n - recursively find the days required to eat x oranges if we eat x/2 oranges a day or x/3 oranges and update the hashmap with the minimum\n - return the min days from the hashmap\n- call dfs to find min days required to eat n oranges \n\n# Complexity\n- Time complexity: O(dfs recursion) \u2192 O(calls at each level ^ total levels) \u2192 O(2$^{logn}$) \u2192 (memoization using hashmap) \u2192 O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(dfs recursion stack + hashmap) \u2192 O(total levels + n) \u2192 O(logn + n) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n dp = {0: 0, 1: 1}\n\n def dfs(x: int) -> int:\n if x in dp:\n return dp[x]\n dp[x] = 1 + min(x % 2 + dfs(x // 2), x % 3 + dfs(x // 3))\n return dp[x]\n\n return dfs(n)\n \n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
O(logn) time | O(n) space | solution explained | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe max days can be n if we eat one orange a day. \n\nWe will start with n oranges and eat oranges every day to reduce n to 0 or 1. For each day, we have two options/paths: eat n/2 oranges a day or n/3 oranges\n\nDo DFS to explore all paths and choose the best. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- create a hashmap for memoization i.e to store the min days required to eat x oranges\nkey = oranges left\nvalue = min days required to eat the remaining oranges\n- add base cases to the hashmap i.e days required to eat 0 and 1 oranges\n- define a helper function for DFS\ndfs(oranges left)\n - if x is in the hashmap, we have already found the min days required to eat x oranges, return it\n - recursively find the days required to eat x oranges if we eat x/2 oranges a day or x/3 oranges and update the hashmap with the minimum\n - return the min days from the hashmap\n- call dfs to find min days required to eat n oranges \n\n# Complexity\n- Time complexity: O(dfs recursion) \u2192 O(calls at each level ^ total levels) \u2192 O(2$^{logn}$) \u2192 (memoization using hashmap) \u2192 O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(dfs recursion stack + hashmap) \u2192 O(total levels + n) \u2192 O(logn + n) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n dp = {0: 0, 1: 1}\n\n def dfs(x: int) -> int:\n if x in dp:\n return dp[x]\n dp[x] = 1 + min(x % 2 + dfs(x // 2), x % 3 + dfs(x // 3))\n return dp[x]\n\n return dfs(n)\n \n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
Python3 BFS approach with Visited Set for Decision Tree Trimming | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs many people know, using a __BFS__ is often used as a fastest path algorithm because we know that no matter how many paths we take, whatever node\'s path reaches our solution first will have by definition been the fastest.\n\nKnowing this and having read the discussion page, I knew I had to take a look at the TLE issue, which I realized we could just make sure we prune branches we\'ve visited before and let that path go on its own. Not exactly memoization which the problem has tagged, but it works.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStarting from our "node" __N__, we __BFS__ and use a helper function __possibleEating__ to generate any valid values we could possibly travers from that "location".\n\nIf node is valid, add to q and visited, meaning futures visits to same node are ignored\n# Complexity\n- Time complexity: $$O(n^3)$$ maybe(?)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nI\'ll be honest - I\'m a bit iffy on the time and space complexities of tree bfs like this which don\'t contain explicit node counts -> but knowing that we have 3 options to visit each time, at worst case it seems like we visit $$O(n^3)$$ nodes.\n- Space complexity: $$O(n^3)$$ similar to thoughts up-above\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n # bfs -> 3 choices each day -> because bfs min dist\n # return the min days it takes to eat all oranges\n \n # use a set to store previously visited values -> saves time pruning tree\n visited = set()\n\n def possibleEating(num):\n res = [num-1]\n if not num % 2: res.append(num//2)\n if not num % 3: res.append(num - (2 * (num//3)))\n return res\n\n q = deque([n])\n\n time = 1\n while q:\n for _ in range(len(q)):\n curr = q.popleft()\n\n for eat in possibleEating(curr):\n if eat in visited: continue\n\n # found time to eat fruit\n if eat == 0: return time\n\n q.append(eat)\n visited.add(eat)\n time += 1\n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
Python3 BFS approach with Visited Set for Decision Tree Trimming | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs many people know, using a __BFS__ is often used as a fastest path algorithm because we know that no matter how many paths we take, whatever node\'s path reaches our solution first will have by definition been the fastest.\n\nKnowing this and having read the discussion page, I knew I had to take a look at the TLE issue, which I realized we could just make sure we prune branches we\'ve visited before and let that path go on its own. Not exactly memoization which the problem has tagged, but it works.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStarting from our "node" __N__, we __BFS__ and use a helper function __possibleEating__ to generate any valid values we could possibly travers from that "location".\n\nIf node is valid, add to q and visited, meaning futures visits to same node are ignored\n# Complexity\n- Time complexity: $$O(n^3)$$ maybe(?)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nI\'ll be honest - I\'m a bit iffy on the time and space complexities of tree bfs like this which don\'t contain explicit node counts -> but knowing that we have 3 options to visit each time, at worst case it seems like we visit $$O(n^3)$$ nodes.\n- Space complexity: $$O(n^3)$$ similar to thoughts up-above\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n # bfs -> 3 choices each day -> because bfs min dist\n # return the min days it takes to eat all oranges\n \n # use a set to store previously visited values -> saves time pruning tree\n visited = set()\n\n def possibleEating(num):\n res = [num-1]\n if not num % 2: res.append(num//2)\n if not num % 3: res.append(num - (2 * (num//3)))\n return res\n\n q = deque([n])\n\n time = 1\n while q:\n for _ in range(len(q)):\n curr = q.popleft()\n\n for eat in possibleEating(curr):\n if eat in visited: continue\n\n # found time to eat fruit\n if eat == 0: return time\n\n q.append(eat)\n visited.add(eat)\n time += 1\n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
logn time | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n dp = {0:0,1:1} # base case\n\n def dfs(n):\n if n in dp:\n return dp[n]\n\n one = 1 + (n % 2) + dfs(n // 2)\n two = 1 + (n % 3) + dfs(n // 3)\n\n dp[n] = min(one,two)\n return dp[n]\n return dfs(n)\n\n# time complexity -> O(logbase2n->log2(n))\n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
logn time | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n dp = {0:0,1:1} # base case\n\n def dfs(n):\n if n in dp:\n return dp[n]\n\n one = 1 + (n % 2) + dfs(n // 2)\n two = 1 + (n % 3) + dfs(n // 3)\n\n dp[n] = min(one,two)\n return dp[n]\n return dfs(n)\n\n# time complexity -> O(logbase2n->log2(n))\n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
[Python] Simple BFS | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n\n seen = set()\n\n heap = [(0,n)]\n\n while heap:\n count, node = heapq.heappop(heap)\n\n if node == 0: return count\n\n if node % 2 == 0 and node - (node // 2) not in seen:\n heapq.heappush(heap,[count + 1, node - (node // 2)])\n seen.add(node - (node // 2))\n if node % 3 == 0 and node - (2 * (node // 3)) not in seen:\n heapq.heappush(heap,[count + 1, node - (2 * (node // 3))])\n seen.add(node - (2 * (node // 3)))\n if node - 1 not in seen:\n heapq.heappush(heap,[count + 1, node - 1])\n seen.add(node - 1)\n\n\n\n\n \n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
[Python] Simple BFS | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n\n seen = set()\n\n heap = [(0,n)]\n\n while heap:\n count, node = heapq.heappop(heap)\n\n if node == 0: return count\n\n if node % 2 == 0 and node - (node // 2) not in seen:\n heapq.heappush(heap,[count + 1, node - (node // 2)])\n seen.add(node - (node // 2))\n if node % 3 == 0 and node - (2 * (node // 3)) not in seen:\n heapq.heappush(heap,[count + 1, node - (2 * (node // 3))])\n seen.add(node - (2 * (node // 3)))\n if node - 1 not in seen:\n heapq.heappush(heap,[count + 1, node - 1])\n seen.add(node - 1)\n\n\n\n\n \n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
Python - one line | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Code\n```\nclass Solution:\n @cache\n def minDays(self, n: int) -> int: \n return n if n < 2 else 1 + min(n%2 + self.minDays(n//2), n%3 + self.minDays(n//3))\n \n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
Python - one line | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Code\n```\nclass Solution:\n @cache\n def minDays(self, n: int) -> int: \n return n if n < 2 else 1 + min(n%2 + self.minDays(n//2), n%3 + self.minDays(n//3))\n \n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
Concise solution on Python3 | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n \n q = deque([n])\n s = set([n])\n cnt = 0\n\n while q:\n sz = len(q)\n for _ in range(sz):\n cur = q.popleft()\n if cur <= 1:\n return cnt + cur\n \n if cur % 3 == 0 and cur // 3 not in s:\n q.append(cur // 3)\n s.add(cur // 3)\n if cur % 2 == 0 and cur // 2 not in s:\n q.append(cur // 2)\n s.add(cur // 2)\n if cur - 1 not in s:\n q.append(cur - 1)\n s.add(cur - 1)\n cnt += 1\n\n # dummy\n return -1\n\n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
Concise solution on Python3 | minimum-number-of-days-to-eat-n-oranges | 0 | 1 | # Code\n```\nclass Solution:\n def minDays(self, n: int) -> int:\n \n q = deque([n])\n s = set([n])\n cnt = 0\n\n while q:\n sz = len(q)\n for _ in range(sz):\n cur = q.popleft()\n if cur <= 1:\n return cnt + cur\n \n if cur % 3 == 0 and cur // 3 not in s:\n q.append(cur // 3)\n s.add(cur // 3)\n if cur % 2 == 0 and cur // 2 not in s:\n q.append(cur // 2)\n s.add(cur // 2)\n if cur - 1 not in s:\n q.append(cur - 1)\n s.add(cur - 1)\n cnt += 1\n\n # dummy\n return -1\n\n``` | 0 | Given the `root` of a binary tree and an array of `TreeNode` objects `nodes`, return _the lowest common ancestor (LCA) of **all the nodes** in_ `nodes`. All the nodes will exist in the tree, and all values of the tree's nodes are **unique**.
Extending the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of `n` nodes `p1`, `p2`, ..., `pn` in a binary tree `T` is the lowest node that has every `pi` as a **descendant** (where we allow **a node to be a descendant of itself**) for every valid `i` ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[4,7\]
**Output:** 2
**Explanation:** The lowest common ancestor of nodes 4 and 7 is node 2.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[1\]
**Output:** 1
**Explanation:** The lowest common ancestor of a single node is the node itself.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], nodes = \[7,6,2,4\]
**Output:** 5
**Explanation:** The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* All `nodes[i]` will exist in the tree.
* All `nodes[i]` are distinct. | In each step, choose between 2 options:
minOranges = 1 + min( (n%2) + f(n/2), (n%3) + f(n/3) )
where f(n) is the minimum number of days to eat n oranges. |
Simple code using join( ) string method | thousand-separator | 0 | 1 | # Approach\n- convert n to string and reverse the string\n- iterate through the string and select 3 items at a time and also join \'.\' with after 3 items.\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n s=str(n)\n s=s[::-1]\n res = \'.\'.join(s[i:i + 3] for i in range(0, len(s), 3))\n return res[::-1]\n``` | 1 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
Simple code using join( ) string method | thousand-separator | 0 | 1 | # Approach\n- convert n to string and reverse the string\n- iterate through the string and select 3 items at a time and also join \'.\' with after 3 items.\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n s=str(n)\n s=s[::-1]\n res = \'.\'.join(s[i:i + 3] for i in range(0, len(s), 3))\n return res[::-1]\n``` | 1 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
Python 3 by reversing | thousand-separator | 0 | 1 | ```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n s=str(n)\n s=s[::-1]\n res = \'.\'.join(s[i:i + 3] for i in range(0, len(s), 3))\n return res[::-1]\n``` | 39 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
Python 3 by reversing | thousand-separator | 0 | 1 | ```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n s=str(n)\n s=s[::-1]\n res = \'.\'.join(s[i:i + 3] for i in range(0, len(s), 3))\n return res[::-1]\n``` | 39 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
[Python3] 1-line | thousand-separator | 0 | 1 | \n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n return f"{n:,}".replace(",", ".")\n```\n\nAlternatively, \n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n ans = deque()\n while n: \n n, d = divmod(n, 1000)\n ans.appendleft(f"{d:03}" if n else str(d))\n return ".".join(ans) or "0"\n``` | 28 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
[Python3] 1-line | thousand-separator | 0 | 1 | \n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n return f"{n:,}".replace(",", ".")\n```\n\nAlternatively, \n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n ans = deque()\n while n: \n n, d = divmod(n, 1000)\n ans.appendleft(f"{d:03}" if n else str(d))\n return ".".join(ans) or "0"\n``` | 28 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
Python simple join solution | thousand-separator | 0 | 1 | **Python :**\n\n```\ndef thousandSeparator(self, n: int) -> str:\n\tres = str(n)[::-1]\n\tres = \'.\'.join(res[i:i + 3] for i in range(0, len(res), 3))\n\n\treturn res[::-1]\n```\n\n**Like it ? please upvote !** | 4 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
Python simple join solution | thousand-separator | 0 | 1 | **Python :**\n\n```\ndef thousandSeparator(self, n: int) -> str:\n\tres = str(n)[::-1]\n\tres = \'.\'.join(res[i:i + 3] for i in range(0, len(res), 3))\n\n\treturn res[::-1]\n```\n\n**Like it ? please upvote !** | 4 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
Python Solution | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n\n if len(str(n))<=3:\n return str(n)\n else:\n n = list(str(n))\n # print(n)\n for i in range(len(n)-3,-1,-3):\n # print(\'i=\',i)\n n.insert(i,".")\n # print(n)\n if n[0] == \'.\':\n n = n[1:]\n return "".join(n)\n \n\n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
Python Solution | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n\n if len(str(n))<=3:\n return str(n)\n else:\n n = list(str(n))\n # print(n)\n for i in range(len(n)-3,-1,-3):\n # print(\'i=\',i)\n n.insert(i,".")\n # print(n)\n if n[0] == \'.\':\n n = n[1:]\n return "".join(n)\n \n\n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
🔥O(N) SOLVE! 🔥97% BEAT RUNTIME!!!🔥 UPVOTE IF I HELP, PLS:)📈📈📈 | thousand-separator | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n**O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n\n# Code\n```\nclass Solution(object):\n def thousandSeparator(self, n):\n """\n :type n: int\n :rtype: str\n """\n s = \'\'\n str_n = str(n)\n count = 1\n for i in range(len(str_n)-1, -1, -1):\n if count == 3:\n s = \'.\' + str_n[i] + s\n count = 1\n else:\n s = str_n[i] + s\n count += 1\n if s[0] == \'.\':\n s = s[1:]\n return s\n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
🔥O(N) SOLVE! 🔥97% BEAT RUNTIME!!!🔥 UPVOTE IF I HELP, PLS:)📈📈📈 | thousand-separator | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n**O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n\n# Code\n```\nclass Solution(object):\n def thousandSeparator(self, n):\n """\n :type n: int\n :rtype: str\n """\n s = \'\'\n str_n = str(n)\n count = 1\n for i in range(len(str_n)-1, -1, -1):\n if count == 3:\n s = \'.\' + str_n[i] + s\n count = 1\n else:\n s = str_n[i] + s\n count += 1\n if s[0] == \'.\':\n s = s[1:]\n return s\n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
python | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str: \n n = str(n)\n final = []\n count = 0\n for i in range(1,len(n)+1):\n if count ==3:\n final.append(".")\n final.append(n[-i])\n count = 1 \n else:\n final.append(n[-i])\n count+=1\n return "".join(final)[::-1]\n\n\n\n\n\n\n\n\n\n\n \n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
python | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str: \n n = str(n)\n final = []\n count = 0\n for i in range(1,len(n)+1):\n if count ==3:\n final.append(".")\n final.append(n[-i])\n count = 1 \n else:\n final.append(n[-i])\n count+=1\n return "".join(final)[::-1]\n\n\n\n\n\n\n\n\n\n\n \n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
My simple solution! Beats 100.00% of users with Python 3 | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --\nhttps://leetcode.com/problems/thousand-separator/submissions/1108574073>\nhttps://leetcode.com/problems/thousand-separator/submissions/1108574073\n[https://leetcode.com/problems/thousand-separator/submissions/1108574073]()\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n\n res = ""\n\n k = 3\n\n while n:\n\n if k != 0:\n\n dig = n%10\n res = str(dig) + res \n n //= 10\n\n k -=1\n\n else:\n\n res = "." + res\n k = 3\n\n return res if res else "0"\n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
My simple solution! Beats 100.00% of users with Python 3 | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --\nhttps://leetcode.com/problems/thousand-separator/submissions/1108574073>\nhttps://leetcode.com/problems/thousand-separator/submissions/1108574073\n[https://leetcode.com/problems/thousand-separator/submissions/1108574073]()\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n\n res = ""\n\n k = 3\n\n while n:\n\n if k != 0:\n\n dig = n%10\n res = str(dig) + res \n n //= 10\n\n k -=1\n\n else:\n\n res = "." + res\n k = 3\n\n return res if res else "0"\n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
Python O(N) | thousand-separator | 0 | 1 | \n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution(object):\n def thousandSeparator(self, n):\n if n == 0:\n return \'0\'\n top, count = \'\', 0\n while n:\n top = str(n%10) + top\n count += 1\n n //= 10\n if n:\n if count == 3:\n top = \'.\' + top\n count = 0\n return top\n \n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
Python O(N) | thousand-separator | 0 | 1 | \n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution(object):\n def thousandSeparator(self, n):\n if n == 0:\n return \'0\'\n top, count = \'\', 0\n while n:\n top = str(n%10) + top\n count += 1\n n //= 10\n if n:\n if count == 3:\n top = \'.\' + top\n count = 0\n return top\n \n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
another solution from my side......nd its pretty fast | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n n=str(n)\n if len(n)<=3:\n return n\n a=""\n n=list(n)\n n.reverse()\n for i in range(len(n)):\n if (i+1)%3==0 and i!=len(n)-1:\n a+=n[i]+"."\n else:\n a+=n[i]\n \n return a[::-1]\n \n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
another solution from my side......nd its pretty fast | thousand-separator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n n=str(n)\n if len(n)<=3:\n return n\n a=""\n n=list(n)\n n.reverse()\n for i in range(len(n)):\n if (i+1)%3==0 and i!=len(n)-1:\n a+=n[i]+"."\n else:\n a+=n[i]\n \n return a[::-1]\n \n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
Simple solution for beginer | thousand-separator | 0 | 1 | # Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n # using regex style\n # 38ms\n # Beats 54.37% of users with Python3\n """\n import re\n return re.sub("(\\d)(?=(\\d{3})+(?!\\d))", r"\\1.", "%d" % n)\n """\n\n # python built in function\n # 36ms\n # Beats 71.65% of users with Python3\n """\n return "{:,}".format(n).replace(",", ".")\n """\n\n # divmod style\n # 33ms\n # Beats 86.02% of users with Python3\n ret = ""\n while n > 1_000:\n n, r = divmod(n, 1_000)\n ret = ".%03d%s" % (r, ret)\n \n return "{}{}".format(n, ret)\n\n\n``` | 0 | Given an integer `n`, add a dot ( ". ") as the thousands separator and return it in string format.
**Example 1:**
**Input:** n = 987
**Output:** "987 "
**Example 2:**
**Input:** n = 1234
**Output:** "1.234 "
**Constraints:**
* `0 <= n <= 231 - 1` | Each element of target should have a corresponding element in arr, and if it doesn't have a corresponding element, return false. To solve it easiely you can sort the two arrays and check if they are equal. |
Simple solution for beginer | thousand-separator | 0 | 1 | # Code\n```\nclass Solution:\n def thousandSeparator(self, n: int) -> str:\n # using regex style\n # 38ms\n # Beats 54.37% of users with Python3\n """\n import re\n return re.sub("(\\d)(?=(\\d{3})+(?!\\d))", r"\\1.", "%d" % n)\n """\n\n # python built in function\n # 36ms\n # Beats 71.65% of users with Python3\n """\n return "{:,}".format(n).replace(",", ".")\n """\n\n # divmod style\n # 33ms\n # Beats 86.02% of users with Python3\n ret = ""\n while n > 1_000:\n n, r = divmod(n, 1_000)\n ret = ".%03d%s" % (r, ret)\n \n return "{}{}".format(n, ret)\n\n\n``` | 0 | You have a binary tree with a small defect. There is **exactly one** invalid node where its right child incorrectly points to another node at the **same depth** but to the **invalid node's right**.
Given the root of the binary tree with this defect, `root`, return _the root of the binary tree after **removing** this invalid node **and every node underneath it** (minus the node it incorrectly points to)._
**Custom testing:**
The test input is read as 3 lines:
* `TreeNode root`
* `int fromNode` (**not available to** `correctBinaryTree`)
* `int toNode` (**not available to** `correctBinaryTree`)
After the binary tree rooted at `root` is parsed, the `TreeNode` with value of `fromNode` will have its right child pointer pointing to the `TreeNode` with a value of `toNode`. Then, `root` is passed to `correctBinaryTree`.
**Example 1:**
**Input:** root = \[1,2,3\], fromNode = 2, toNode = 3
**Output:** \[1,null,3\]
**Explanation:** The node with value 2 is invalid, so remove it.
**Example 2:**
**Input:** root = \[8,3,1,7,null,9,4,2,null,null,null,5,6\], fromNode = 7, toNode = 4
**Output:** \[8,3,1,null,null,9,4,null,null,5,6\]
**Explanation:** The node with value 7 is invalid, so remove it and the node underneath it, node 2.
**Constraints:**
* The number of nodes in the tree is in the range `[3, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `fromNode != toNode`
* `fromNode` and `toNode` will exist in the tree and will be on the same depth.
* `toNode` is to the **right** of `fromNode`.
* `fromNode.right` is `null` in the initial tree from the test data. | Scan from the back of the integer and use dots to connect blocks with length 3 except the last block. |
Python 2-Line Simple Solution | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | # Intuition\nAll nodes with no indegrees must be in the final list. All other nodes can be reached since they have indegrees, and therefore should not be in the final list.\n\n# Approach\nAdd the "to" node in each edge to a "connected" set. Then iterate through all nodes n and add them to the final list if they are not in the connected set.\n\nThe connected set can be created using a map function to add every "to" value to a set.\n\nThe final list can be created using a filter function to filter out values that exist in the connected set.\n\n# Complexity\n- Time complexity:\nO(N + E) - Iterate through every edge and then every node once.\n\n- Space complexity:\nO(N + E) - Potentially store a number of values equal to the total number of edges in the connected set (E), and then potentially add every node through n to the final list (N).\n\n# Code\n```\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n connected = set(map(lambda e: e[1], edges))\n return list(filter(lambda x: x not in connected, range(n)))\n``` | 3 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
Efficient DFS solution | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def dfs(self, vertex, first=False):\n if vertex in self.reachable:\n return\n if not first:\n self.reachable.add(vertex)\n first = False\n for _vertex in self.adj_matrix[vertex]:\n self.dfs(_vertex)\n\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n self.adj_matrix = defaultdict(list)\n self.reachable = set()\n for edge in edges:\n self.adj_matrix[edge[0]].append(edge[1])\n \n all_nodes = set()\n for i in range(n):\n all_nodes.add(i)\n self.dfs(i, True)\n \n return list(all_nodes - self.reachable)\n \n``` | 2 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
Python3 Solution | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | \n```\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n parent=[False]*n\n for u,v in edges:\n parent[v]=True\n\n ans=[]\n for u in range(n):\n if not parent[u]:\n ans.append(u)\n\n return ans \n``` | 1 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
Indegree Aapproach || Python || O(n) Approach | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n visited=[0]*n\n res=[]\n for i in range(len(edges)):\n visited[edges[i][1]]+=1\n for i in range(n):\n if(visited[i]==0):\n res.append(i)\n return res\n\n\n``` | 1 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
[Python] | O(E)/O(V) | One-liner | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | # Intuition\nIf a node doesn\'t have an inbound edge - we must to include it. All other nodes are reachable, starting from some other node.\n\n# Complexity\n- Time complexity:\n$O(e)$, where $e$ - `len(edges)`\n\n- Space complexity:\n$O(n)$\n\n# Code\n```\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n return set(range(n)) - {b for _, b in edges}\n``` | 1 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
Python/Union Find/Easy | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n l=[i for i in range(n)]\n ans=[]\n for i,j in edges:\n if(l[j]==j):\n l[j]=l[i]\n for i in range(n):\n if(l[i]==i):\n ans.append(i)\n return ans\n``` | 1 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
🐇 Fast and stupid | Java, C++, Python | minimum-number-of-vertices-to-reach-all-nodes | 1 | 1 | # TL;DR\n``` java []\nclass Solution {\n public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {\n var nonRoots = new boolean[n];\n for (var edge: edges) {\n nonRoots[edge.get(1)] = true;\n }\n var result = new LinkedList<Integer>();\n for (int i = 0; i < nonRoots.length; i++) {\n if (!nonRoots[i]) {\n result.add(i);\n }\n }\n return result;\n }\n}\n```\n``` cpp []\nclass Solution {\npublic:\n vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {\n std::vector<bool> nonRoots(n, false);\n for (auto& edge: edges) {\n nonRoots[edge[1]] = true;\n }\n vector<int> result;\n for (int i = 0; i < n; i++) {\n if (!nonRoots[i]) {\n result.push_back(i);\n }\n }\n return result;\n }\n};\n```\n``` python []\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n nonRoots = [False] * n\n for edge in edges:\n nonRoots[edge[1]] = True\n return [i for i, isNonRoot in enumerate(nonRoots) if not isNonRoot]\n```\n\n---\n#### \u26A0\uFE0F Please upvote if you like this solution. \uD83D\uDE43\n---\n\n# Intuition\n\nGiven a directed acyclic graph (DAG), we are asked to find the smallest set of vertices from which all other nodes are reachable. In essence, we need to identify the starting points of all possible paths in the graph, from where every other node can be reached directly or indirectly.\n\nOne key observation is that these "starting points" are essentially vertices that have no incoming edges - that is, no other vertices point to them. The reason is that if a vertex has at least one incoming edge, it means that it can be reached from some other vertex, so including it in the smallest set of vertices would be unnecessary. \n\nSo, if we think about it this way, the problem reduces to **identifying all nodes with no incoming edges**, since all other nodes in the graph are reachable from these nodes. \n\nTo understand why this approach works, consider the converse: if a vertex is not in our answer set, it must have an incoming edge from another vertex. But that means this vertex can be reached from another vertex that must be in our answer set. Hence, we don\'t lose any reachability by excluding vertices with incoming edges from our answer set.\n\n# Approach\n\nThe solution follows directly from the intuition above. First, we initialize a boolean array `nonRoots` of size `n` with all `false` values. This array helps us to keep track of nodes with incoming edges.\n\nNext, we iterate over all given edges. For each edge `fromi -> toi`, we mark `nonRoots[toi]` as `true`. This is because `toi` is reachable from `fromi` and hence not a root.\n\nFinally, we iterate over the `nonRoots` array, and for every `i` that is `false`, we add it to our result. These are the nodes that have no incoming edges and hence are our "root" nodes from which all other nodes are reachable.\n\n# Complexity Analysis\n\n- The time complexity of this solution is $$O(n + m)$$, where $$n$$ is the number of nodes and $$m$$ is the number of edges. We have to iterate over all nodes and edges once.\n\n- The space complexity is $$O(n)$$. We need to maintain an array `nonRoots` of size $$n$$ and a list to hold the result, which in the worst case can hold all $$n$$ nodes. | 1 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
Easily undestandable Python3 solution | minimum-number-of-vertices-to-reach-all-nodes | 0 | 1 | # Intuition\nIn this problem, we only have to find the nodes that cannot be reached by any other node. This is the case as if a node has an incoming edge, it will be found. Therefore, the problem reduces to finding the nodes without any any incoming edges. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialized a simple n sized bool array where the ith node represents if that node has an incoming edge. Then, we can look through the edges array and keep track of all nodes with incoming edges by setting its index to True in the bool array. Finally just return all nodes that do not have any incoming edges. \n\n# Complexity\n- Time complexity:\nO(N) where N is the number of edges \n\n- Space complexity:\nO(N) where N is the number of edges\n\n# Code\n```\nclass Solution:\n def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:\n noIncomingEdgeNode = [False] * n \n result = []\n for (srcNode, dstNode) in edges: \n noIncomingEdgeNode[dstNode] = True\n for i, node in enumerate(noIncomingEdgeNode): \n if not node: \n result.append(i)\n \n return result \n \n``` | 1 | Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i] = [fromi, toi]` represents a directed edge from node `fromi` to node `toi`.
Find _the smallest set of vertices from which all nodes in the graph are reachable_. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,5\],\[3,4\],\[4,2\]\]
**Output:** \[0,3\]
**Explanation:** It's not possible to reach all the nodes from a single vertex. From 0 we can reach \[0,1,2,5\]. From 3 we can reach \[3,4,2,5\]. So we output \[0,3\].
**Example 2:**
**Input:** n = 5, edges = \[\[0,1\],\[2,1\],\[3,1\],\[1,4\],\[2,4\]\]
**Output:** \[0,2,3\]
**Explanation:** Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
**Constraints:**
* `2 <= n <= 10^5`
* `1 <= edges.length <= min(10^5, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi < n`
* All pairs `(fromi, toi)` are distinct. | We need only to check all sub-strings of length k. The number of distinct sub-strings should be exactly 2^k. |
Easy python solution, with 90% SC | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | ```\ndef minOperations(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tans = 0\n\tnums.sort()\n\twhile(nums[-1] > 0):\n\t\tfor i in range(n):\n\t\t\tif(nums[i] % 2):\n\t\t\t\tnums[i] -= 1\n\t\t\t\tans += 1\n\t\tif(nums[-1] > 0):\n\t\t\tfor i in range(n):\n\t\t\t\tnums[i] //= 2\n\t\t\tans += 1\n\treturn ans\n``` | 3 | You are given an integer array `nums`. You have an integer array `arr` of the same length with all values set to `0` initially. You also have the following `modify` function:
You want to use the modify function to covert `arr` to `nums` using the minimum number of calls.
Return _the minimum number of function calls to make_ `nums` _from_ `arr`.
The test cases are generated so that the answer fits in a **32-bit** signed integer.
**Example 1:**
**Input:** nums = \[1,5\]
**Output:** 5
**Explanation:** Increment by 1 (second element): \[0, 0\] to get \[0, 1\] (1 operation).
Double all the elements: \[0, 1\] -> \[0, 2\] -> \[0, 4\] (2 operations).
Increment by 1 (both elements) \[0, 4\] -> \[1, 4\] -> **\[1, 5\]** (2 operations).
Total of operations: 1 + 2 + 2 = 5.
**Example 2:**
**Input:** nums = \[2,2\]
**Output:** 3
**Explanation:** Increment by 1 (both elements) \[0, 0\] -> \[0, 1\] -> \[1, 1\] (2 operations).
Double all the elements: \[1, 1\] -> **\[2, 2\]** (1 operation).
Total of operations: 2 + 1 = 3.
**Example 3:**
**Input:** nums = \[4,2,5\]
**Output:** 6
**Explanation:** (initial)\[0,0,0\] -> \[1,0,0\] -> \[1,0,1\] -> \[2,0,2\] -> \[2,1,2\] -> \[4,2,4\] -> **\[4,2,5\]**(nums).
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j]. Start a bfs from each course i and assign for each course j you visit isReachable[i][j] = True. Answer the queries from the isReachable array. |
Easy python solution, with 90% SC | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | ```\ndef minOperations(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tans = 0\n\tnums.sort()\n\twhile(nums[-1] > 0):\n\t\tfor i in range(n):\n\t\t\tif(nums[i] % 2):\n\t\t\t\tnums[i] -= 1\n\t\t\t\tans += 1\n\t\tif(nums[-1] > 0):\n\t\t\tfor i in range(n):\n\t\t\t\tnums[i] //= 2\n\t\t\tans += 1\n\treturn ans\n``` | 3 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
[Python3] Simple intuition without bitwise operations | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | - For any element in an array, consider it a sequence of addition of 1 and multiplication by 2. eg (`2 = +1, *2`) (`5 = +1, *2, +1`)\n- Each addition operation will be done separately, so we need to simply count all of them\n- But when it comes to the multiplication, we can simply find what is the maximum number of multiply by 2 operations we need to perform from all the elements, since these operations can be performed for multiple element at once and thus can be arranged however we want\n- Then our solution would be simply the sum of the addition operations and the maximum number of multiply operations in any element.\n- Time complexity: `O(32N) = O(N)`\n```python\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n twos = 0\n ones = 0\n for n in nums:\n mul = 0\n while n:\n if n%2: # odd number, just delete 1 so that it\'s now a multiple of 2\n n -= 1\n ones += 1\n else: # multiple of 2, so just divide by 2 \n n //= 2\n mul += 1\n twos = max(twos, mul)\n return ones + twos\n``` | 28 | You are given an integer array `nums`. You have an integer array `arr` of the same length with all values set to `0` initially. You also have the following `modify` function:
You want to use the modify function to covert `arr` to `nums` using the minimum number of calls.
Return _the minimum number of function calls to make_ `nums` _from_ `arr`.
The test cases are generated so that the answer fits in a **32-bit** signed integer.
**Example 1:**
**Input:** nums = \[1,5\]
**Output:** 5
**Explanation:** Increment by 1 (second element): \[0, 0\] to get \[0, 1\] (1 operation).
Double all the elements: \[0, 1\] -> \[0, 2\] -> \[0, 4\] (2 operations).
Increment by 1 (both elements) \[0, 4\] -> \[1, 4\] -> **\[1, 5\]** (2 operations).
Total of operations: 1 + 2 + 2 = 5.
**Example 2:**
**Input:** nums = \[2,2\]
**Output:** 3
**Explanation:** Increment by 1 (both elements) \[0, 0\] -> \[0, 1\] -> \[1, 1\] (2 operations).
Double all the elements: \[1, 1\] -> **\[2, 2\]** (1 operation).
Total of operations: 2 + 1 = 3.
**Example 3:**
**Input:** nums = \[4,2,5\]
**Output:** 6
**Explanation:** (initial)\[0,0,0\] -> \[1,0,0\] -> \[1,0,1\] -> \[2,0,2\] -> \[2,1,2\] -> \[4,2,4\] -> **\[4,2,5\]**(nums).
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j]. Start a bfs from each course i and assign for each course j you visit isReachable[i][j] = True. Answer the queries from the isReachable array. |
[Python3] Simple intuition without bitwise operations | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | - For any element in an array, consider it a sequence of addition of 1 and multiplication by 2. eg (`2 = +1, *2`) (`5 = +1, *2, +1`)\n- Each addition operation will be done separately, so we need to simply count all of them\n- But when it comes to the multiplication, we can simply find what is the maximum number of multiply by 2 operations we need to perform from all the elements, since these operations can be performed for multiple element at once and thus can be arranged however we want\n- Then our solution would be simply the sum of the addition operations and the maximum number of multiply operations in any element.\n- Time complexity: `O(32N) = O(N)`\n```python\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n twos = 0\n ones = 0\n for n in nums:\n mul = 0\n while n:\n if n%2: # odd number, just delete 1 so that it\'s now a multiple of 2\n n -= 1\n ones += 1\n else: # multiple of 2, so just divide by 2 \n n //= 2\n mul += 1\n twos = max(twos, mul)\n return ones + twos\n``` | 28 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Python3・9 lines・T/S: O(n), O(1)・T: 100% | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRephrase the two operations: \n```op == 0```: increment 1; i.e. set rightmost bit to 1 if it is 0\n```op == 1```: multiply all by 2; i.e. left bitshift on all ```nums``` by 1\n\nThen, the minimum number of operations is equal to the minimum number of left bitshifts plus the minimum number of 1-bit in each number represented in binary.\n\nThe minimum number of left bitshifts can be calculated by finding the bit-length of the largest number in ```nums```; i.e. longest length number in binary. This is because we need at least ```max_length - 1``` left bitshifts to move a 1-bit to the most significant bit.\n\n# Example\n\nGiven an array ```[4, 2, 5]```, when represented in binary: ```[100, 10, 101]```\n\n```op == 0```: there are $$4$$ 1-bit in all the numbers (1 in ```100, 10``` each, 2 in ```101```). \nHence we need 4 operations.\n\n```op == 1```: the maximum number is ```101```. \nSince bit-length is $$3$$, at least $$2$$ left shifts needed; i.e. ```_ _ 1``` -> ```_ 1 0``` -> ```1 0 0```\nHence we need 2 operations.\n\nTherefore, answer is $$4+2=6$$ operations.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n\n # count minimum number of left bitshifts\n maximum = max(nums)\n shifts = 0\n while maximum > 1:\n maximum >>= 1\n shifts += 1\n\n # count minimum number of increments (1-bits)\n increments = 0\n for num in nums:\n increments += num.bit_count()\n\n return shifts + increments\n\n```\n\nhttps://leetcode.com/problems/minimum-numbers-of-function-calls-to-make-target-array/submissions/1011775598/ | 0 | You are given an integer array `nums`. You have an integer array `arr` of the same length with all values set to `0` initially. You also have the following `modify` function:
You want to use the modify function to covert `arr` to `nums` using the minimum number of calls.
Return _the minimum number of function calls to make_ `nums` _from_ `arr`.
The test cases are generated so that the answer fits in a **32-bit** signed integer.
**Example 1:**
**Input:** nums = \[1,5\]
**Output:** 5
**Explanation:** Increment by 1 (second element): \[0, 0\] to get \[0, 1\] (1 operation).
Double all the elements: \[0, 1\] -> \[0, 2\] -> \[0, 4\] (2 operations).
Increment by 1 (both elements) \[0, 4\] -> \[1, 4\] -> **\[1, 5\]** (2 operations).
Total of operations: 1 + 2 + 2 = 5.
**Example 2:**
**Input:** nums = \[2,2\]
**Output:** 3
**Explanation:** Increment by 1 (both elements) \[0, 0\] -> \[0, 1\] -> \[1, 1\] (2 operations).
Double all the elements: \[1, 1\] -> **\[2, 2\]** (1 operation).
Total of operations: 2 + 1 = 3.
**Example 3:**
**Input:** nums = \[4,2,5\]
**Output:** 6
**Explanation:** (initial)\[0,0,0\] -> \[1,0,0\] -> \[1,0,1\] -> \[2,0,2\] -> \[2,1,2\] -> \[4,2,4\] -> **\[4,2,5\]**(nums).
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j]. Start a bfs from each course i and assign for each course j you visit isReachable[i][j] = True. Answer the queries from the isReachable array. |
Python3・9 lines・T/S: O(n), O(1)・T: 100% | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRephrase the two operations: \n```op == 0```: increment 1; i.e. set rightmost bit to 1 if it is 0\n```op == 1```: multiply all by 2; i.e. left bitshift on all ```nums``` by 1\n\nThen, the minimum number of operations is equal to the minimum number of left bitshifts plus the minimum number of 1-bit in each number represented in binary.\n\nThe minimum number of left bitshifts can be calculated by finding the bit-length of the largest number in ```nums```; i.e. longest length number in binary. This is because we need at least ```max_length - 1``` left bitshifts to move a 1-bit to the most significant bit.\n\n# Example\n\nGiven an array ```[4, 2, 5]```, when represented in binary: ```[100, 10, 101]```\n\n```op == 0```: there are $$4$$ 1-bit in all the numbers (1 in ```100, 10``` each, 2 in ```101```). \nHence we need 4 operations.\n\n```op == 1```: the maximum number is ```101```. \nSince bit-length is $$3$$, at least $$2$$ left shifts needed; i.e. ```_ _ 1``` -> ```_ 1 0``` -> ```1 0 0```\nHence we need 2 operations.\n\nTherefore, answer is $$4+2=6$$ operations.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n\n # count minimum number of left bitshifts\n maximum = max(nums)\n shifts = 0\n while maximum > 1:\n maximum >>= 1\n shifts += 1\n\n # count minimum number of increments (1-bits)\n increments = 0\n for num in nums:\n increments += num.bit_count()\n\n return shifts + increments\n\n```\n\nhttps://leetcode.com/problems/minimum-numbers-of-function-calls-to-make-target-array/submissions/1011775598/ | 0 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Minimum Numbers of Function Calls to Make Target Array | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n addCount = 0\n doubleCount = 0\n for e in nums:\n if e != 0:\n addCount += 1\n elementDoubleCount = 0\n while e > 1:\n elementDoubleCount += 1\n addCount += e % 2\n e //= 2\n doubleCount = max(elementDoubleCount, doubleCount)\n return doubleCount + addCount\n \n``` | 0 | You are given an integer array `nums`. You have an integer array `arr` of the same length with all values set to `0` initially. You also have the following `modify` function:
You want to use the modify function to covert `arr` to `nums` using the minimum number of calls.
Return _the minimum number of function calls to make_ `nums` _from_ `arr`.
The test cases are generated so that the answer fits in a **32-bit** signed integer.
**Example 1:**
**Input:** nums = \[1,5\]
**Output:** 5
**Explanation:** Increment by 1 (second element): \[0, 0\] to get \[0, 1\] (1 operation).
Double all the elements: \[0, 1\] -> \[0, 2\] -> \[0, 4\] (2 operations).
Increment by 1 (both elements) \[0, 4\] -> \[1, 4\] -> **\[1, 5\]** (2 operations).
Total of operations: 1 + 2 + 2 = 5.
**Example 2:**
**Input:** nums = \[2,2\]
**Output:** 3
**Explanation:** Increment by 1 (both elements) \[0, 0\] -> \[0, 1\] -> \[1, 1\] (2 operations).
Double all the elements: \[1, 1\] -> **\[2, 2\]** (1 operation).
Total of operations: 2 + 1 = 3.
**Example 3:**
**Input:** nums = \[4,2,5\]
**Output:** 6
**Explanation:** (initial)\[0,0,0\] -> \[1,0,0\] -> \[1,0,1\] -> \[2,0,2\] -> \[2,1,2\] -> \[4,2,4\] -> **\[4,2,5\]**(nums).
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j]. Start a bfs from each course i and assign for each course j you visit isReachable[i][j] = True. Answer the queries from the isReachable array. |
Minimum Numbers of Function Calls to Make Target Array | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n addCount = 0\n doubleCount = 0\n for e in nums:\n if e != 0:\n addCount += 1\n elementDoubleCount = 0\n while e > 1:\n elementDoubleCount += 1\n addCount += e % 2\n e //= 2\n doubleCount = max(elementDoubleCount, doubleCount)\n return doubleCount + addCount\n \n``` | 0 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Subtracting or dividing backwards | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | # Intuition\nIt\'s hard to me that how to determine at which step we should add 1 or multiply by two. Since the number of steps remain unchanged, starting from arr to [0 .. 0] is easier.\n\n# Approach\nIf there is an odd in arr, minus one.\nElse divide it by two.\nRepeat the process until [0 .. 0] is obtained.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n ret = 0\n Sum = sum(nums)\n\n while Sum > 0:\n for i in range(len(nums)):\n if nums[i] % 2:\n ret += 1\n nums[i] -= 1\n Sum -= 1\n \n if Sum > 0:\n ret += 1\n nums = [x // 2 for x in nums]\n Sum //= 2\n \n return ret\n\n``` | 0 | You are given an integer array `nums`. You have an integer array `arr` of the same length with all values set to `0` initially. You also have the following `modify` function:
You want to use the modify function to covert `arr` to `nums` using the minimum number of calls.
Return _the minimum number of function calls to make_ `nums` _from_ `arr`.
The test cases are generated so that the answer fits in a **32-bit** signed integer.
**Example 1:**
**Input:** nums = \[1,5\]
**Output:** 5
**Explanation:** Increment by 1 (second element): \[0, 0\] to get \[0, 1\] (1 operation).
Double all the elements: \[0, 1\] -> \[0, 2\] -> \[0, 4\] (2 operations).
Increment by 1 (both elements) \[0, 4\] -> \[1, 4\] -> **\[1, 5\]** (2 operations).
Total of operations: 1 + 2 + 2 = 5.
**Example 2:**
**Input:** nums = \[2,2\]
**Output:** 3
**Explanation:** Increment by 1 (both elements) \[0, 0\] -> \[0, 1\] -> \[1, 1\] (2 operations).
Double all the elements: \[1, 1\] -> **\[2, 2\]** (1 operation).
Total of operations: 2 + 1 = 3.
**Example 3:**
**Input:** nums = \[4,2,5\]
**Output:** 6
**Explanation:** (initial)\[0,0,0\] -> \[1,0,0\] -> \[1,0,1\] -> \[2,0,2\] -> \[2,1,2\] -> \[4,2,4\] -> **\[4,2,5\]**(nums).
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j]. Start a bfs from each course i and assign for each course j you visit isReachable[i][j] = True. Answer the queries from the isReachable array. |
Subtracting or dividing backwards | minimum-numbers-of-function-calls-to-make-target-array | 0 | 1 | # Intuition\nIt\'s hard to me that how to determine at which step we should add 1 or multiply by two. Since the number of steps remain unchanged, starting from arr to [0 .. 0] is easier.\n\n# Approach\nIf there is an odd in arr, minus one.\nElse divide it by two.\nRepeat the process until [0 .. 0] is obtained.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n ret = 0\n Sum = sum(nums)\n\n while Sum > 0:\n for i in range(len(nums)):\n if nums[i] % 2:\n ret += 1\n nums[i] -= 1\n Sum -= 1\n \n if Sum > 0:\n ret += 1\n nums = [x // 2 for x in nums]\n Sum //= 2\n \n return ret\n\n``` | 0 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
67% Tc and 56% SC easy python solution | detect-cycles-in-2d-grid | 0 | 1 | ```\ndef containsCycle(self, grid: List[List[str]]) -> bool:\n\tm, n = len(grid), len(grid[0])\n\tdir = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\t@lru_cache(None)\n\tdef isCycle(i, j, par_i, par_j):\n\t\tif (i, j) in vis:\n\t\t\treturn True\n\t\tvis.add((i, j))\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<m and 0<=j+y<n and grid[i+x][j+y] == grid[i][j] and (i+x, j+y) != (par_i, par_j)):\n\t\t\t\tif(isCycle(i+x, j+y, i, j)):\n\t\t\t\t\treturn True\n\t\treturn False\n\tvis = set()\n\tfor i in range(m):\n\t\tfor j in range(n):\n\t\t\tif((i, j) not in vis and isCycle(i, j, -1, -1)):\n\t\t\t\treturn 1\n\treturn 0\n``` | 2 | Given a 2D array of characters `grid` of size `m x n`, you need to find if there exists any cycle consisting of the **same value** in `grid`.
A cycle is a path of **length 4 or more** in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the **same value** of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle `(1, 1) -> (1, 2) -> (1, 1)` is invalid because from `(1, 2)` we visited `(1, 1)` which was the last visited cell.
Return `true` if any cycle of the same value exists in `grid`, otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "a ", "a ", "a ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "a ", "a ", "a "\]\]
**Output:** true
**Explanation:** There are two valid cycles shown in different colors in the image below:
**Example 2:**
**Input:** grid = \[\[ "c ", "c ", "c ", "a "\],\[ "c ", "d ", "c ", "c "\],\[ "c ", "c ", "e ", "c "\],\[ "f ", "c ", "c ", "c "\]\]
**Output:** true
**Explanation:** There is only one valid cycle highlighted in the image below:
**Example 3:**
**Input:** grid = \[\[ "a ", "b ", "b "\],\[ "b ", "z ", "b "\],\[ "b ", "b ", "a "\]\]
**Output:** false
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 500`
* `grid` consists only of lowercase English letters. | Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. |
67% Tc and 56% SC easy python solution | detect-cycles-in-2d-grid | 0 | 1 | ```\ndef containsCycle(self, grid: List[List[str]]) -> bool:\n\tm, n = len(grid), len(grid[0])\n\tdir = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\t@lru_cache(None)\n\tdef isCycle(i, j, par_i, par_j):\n\t\tif (i, j) in vis:\n\t\t\treturn True\n\t\tvis.add((i, j))\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<m and 0<=j+y<n and grid[i+x][j+y] == grid[i][j] and (i+x, j+y) != (par_i, par_j)):\n\t\t\t\tif(isCycle(i+x, j+y, i, j)):\n\t\t\t\t\treturn True\n\t\treturn False\n\tvis = set()\n\tfor i in range(m):\n\t\tfor j in range(n):\n\t\t\tif((i, j) not in vis and isCycle(i, j, -1, -1)):\n\t\t\t\treturn 1\n\treturn 0\n``` | 2 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
[Python3] DFS concise code | detect-cycles-in-2d-grid | 0 | 1 | - The trick was to keep track of the previous element so that you don\'t go back there wihle doing dfs (took me a long time to figure out)\n- We just check that while doing dfs we reach a node that we have already seen or not\n```python\nclass Solution:\n def containsCycle(self, A: List[List[str]]) -> bool:\n R, C = len(A), len(A[0])\n visited = set()\n \n def neighbors(r, c):\n return [(i, j) for i, j in [(r-1, c), (r+1, c), (r, c-1), (r, c+1)] if 0 <= i < R and 0 <= j < C and A[i][j] == A[r][c]]\n \n def dfs(r, c, x, prev, seen):\n if (r, c) in seen:\n return True\n seen.add((r, c))\n visited.add((r, c))\n\n for i, j in neighbors(r, c):\n if not prev or prev != (i, j):\n if dfs(i, j, x, (r, c), seen):\n return True\n return False\n \n \n for r in range(R):\n for c in range(C):\n if (r, c) not in visited:\n seen = set()\n if dfs(r, c, A[r][c], None, seen):\n return True\n return False\n``` | 10 | Given a 2D array of characters `grid` of size `m x n`, you need to find if there exists any cycle consisting of the **same value** in `grid`.
A cycle is a path of **length 4 or more** in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the **same value** of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle `(1, 1) -> (1, 2) -> (1, 1)` is invalid because from `(1, 2)` we visited `(1, 1)` which was the last visited cell.
Return `true` if any cycle of the same value exists in `grid`, otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "a ", "a ", "a ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "a ", "a ", "a "\]\]
**Output:** true
**Explanation:** There are two valid cycles shown in different colors in the image below:
**Example 2:**
**Input:** grid = \[\[ "c ", "c ", "c ", "a "\],\[ "c ", "d ", "c ", "c "\],\[ "c ", "c ", "e ", "c "\],\[ "f ", "c ", "c ", "c "\]\]
**Output:** true
**Explanation:** There is only one valid cycle highlighted in the image below:
**Example 3:**
**Input:** grid = \[\[ "a ", "b ", "b "\],\[ "b ", "z ", "b "\],\[ "b ", "b ", "a "\]\]
**Output:** false
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 500`
* `grid` consists only of lowercase English letters. | Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. |
[Python3] DFS concise code | detect-cycles-in-2d-grid | 0 | 1 | - The trick was to keep track of the previous element so that you don\'t go back there wihle doing dfs (took me a long time to figure out)\n- We just check that while doing dfs we reach a node that we have already seen or not\n```python\nclass Solution:\n def containsCycle(self, A: List[List[str]]) -> bool:\n R, C = len(A), len(A[0])\n visited = set()\n \n def neighbors(r, c):\n return [(i, j) for i, j in [(r-1, c), (r+1, c), (r, c-1), (r, c+1)] if 0 <= i < R and 0 <= j < C and A[i][j] == A[r][c]]\n \n def dfs(r, c, x, prev, seen):\n if (r, c) in seen:\n return True\n seen.add((r, c))\n visited.add((r, c))\n\n for i, j in neighbors(r, c):\n if not prev or prev != (i, j):\n if dfs(i, j, x, (r, c), seen):\n return True\n return False\n \n \n for r in range(R):\n for c in range(C):\n if (r, c) not in visited:\n seen = set()\n if dfs(r, c, A[r][c], None, seen):\n return True\n return False\n``` | 10 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
Python Solution | detect-cycles-in-2d-grid | 0 | 1 | # Code\n```\nclass Solution:\n def containsCycle(self, grid: List[List[str]]) -> bool:\n rows, cols = len(grid), len(grid[0])\n seen = set()\n\n def dfs(row, col, prev):\n if (row < 0 or row >= rows or\n col < 0 or col >= cols or\n grid[row][col] != grid[prev[0]][prev[1]]): return False\n\n if (row, col) in seen: return True\n\n seen.add((row, col))\n\n curr = (row, col)\n\n directions = [(row + 1, col, curr), (row - 1, col, curr), (row, col + 1, curr), (row, col - 1, curr)]\n for i in range(4):\n if directions[i][0] == prev[0] and directions[i][1] == prev[1]:\n directions.pop(i)\n break\n\n retval = sum(dfs(i[0], i[1], i[2]) for i in directions)\n\n return True if retval > 0 else False\n\n for i in range(rows):\n for j in range(cols):\n if (i, j) not in seen and dfs(i, j, (i, j)):\n print(\'True at\', i, j) \n return True\n\n return False\n``` | 0 | Given a 2D array of characters `grid` of size `m x n`, you need to find if there exists any cycle consisting of the **same value** in `grid`.
A cycle is a path of **length 4 or more** in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the **same value** of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle `(1, 1) -> (1, 2) -> (1, 1)` is invalid because from `(1, 2)` we visited `(1, 1)` which was the last visited cell.
Return `true` if any cycle of the same value exists in `grid`, otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "a ", "a ", "a ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "a ", "a ", "a "\]\]
**Output:** true
**Explanation:** There are two valid cycles shown in different colors in the image below:
**Example 2:**
**Input:** grid = \[\[ "c ", "c ", "c ", "a "\],\[ "c ", "d ", "c ", "c "\],\[ "c ", "c ", "e ", "c "\],\[ "f ", "c ", "c ", "c "\]\]
**Output:** true
**Explanation:** There is only one valid cycle highlighted in the image below:
**Example 3:**
**Input:** grid = \[\[ "a ", "b ", "b "\],\[ "b ", "z ", "b "\],\[ "b ", "b ", "a "\]\]
**Output:** false
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 500`
* `grid` consists only of lowercase English letters. | Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. |
Python Solution | detect-cycles-in-2d-grid | 0 | 1 | # Code\n```\nclass Solution:\n def containsCycle(self, grid: List[List[str]]) -> bool:\n rows, cols = len(grid), len(grid[0])\n seen = set()\n\n def dfs(row, col, prev):\n if (row < 0 or row >= rows or\n col < 0 or col >= cols or\n grid[row][col] != grid[prev[0]][prev[1]]): return False\n\n if (row, col) in seen: return True\n\n seen.add((row, col))\n\n curr = (row, col)\n\n directions = [(row + 1, col, curr), (row - 1, col, curr), (row, col + 1, curr), (row, col - 1, curr)]\n for i in range(4):\n if directions[i][0] == prev[0] and directions[i][1] == prev[1]:\n directions.pop(i)\n break\n\n retval = sum(dfs(i[0], i[1], i[2]) for i in directions)\n\n return True if retval > 0 else False\n\n for i in range(rows):\n for j in range(cols):\n if (i, j) not in seen and dfs(i, j, (i, j)):\n print(\'True at\', i, j) \n return True\n\n return False\n``` | 0 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
BEATS 90%! Python3 BFS | detect-cycles-in-2d-grid | 0 | 1 | # Code\n```\nimport collections\n\n\nclass Solution:\n\n def containsCycle(self, grid: List[List[str]]) -> bool:\n ht = dict()\n q = collections.deque()\n x = y = 0\n for i in range(len(grid)):\n for j in range(len(grid[i])):\n if grid[i][j] not in ht:\n ht[grid[i][j]] = set()\n elif (i, j) not in ht[grid[i][j]]:\n q.append((i, j))\n while len(q) > 0:\n x, y = q.popleft()\n if (x, y) not in ht[grid[i][j]]:\n ht[grid[i][j]].add((x, y))\n elif len(ht[grid[i][j]]) > 2:\n return True\n if 0 < x and grid[x-1][y] == grid[i][j]:\n if (x-1, y) not in ht[grid[i][j]]:\n q.append((x-1, y))\n if 0 < y and grid[x][y-1] == grid[i][j]:\n if (x, y-1) not in ht[grid[i][j]]:\n q.append((x, y-1))\n if x + 1 < len(grid) and grid[x+1][y] == grid[i][j]:\n if (x+1, y) not in ht[grid[i][j]]:\n q.append((x+1, y))\n if y + 1 < len(grid[0]) and grid[x][y+1] == grid[i][j]:\n if (x, y+1) not in ht[grid[i][j]]:\n q.append((x, y+1))\n return False\n``` | 0 | Given a 2D array of characters `grid` of size `m x n`, you need to find if there exists any cycle consisting of the **same value** in `grid`.
A cycle is a path of **length 4 or more** in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the **same value** of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle `(1, 1) -> (1, 2) -> (1, 1)` is invalid because from `(1, 2)` we visited `(1, 1)` which was the last visited cell.
Return `true` if any cycle of the same value exists in `grid`, otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "a ", "a ", "a ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "a ", "a ", "a "\]\]
**Output:** true
**Explanation:** There are two valid cycles shown in different colors in the image below:
**Example 2:**
**Input:** grid = \[\[ "c ", "c ", "c ", "a "\],\[ "c ", "d ", "c ", "c "\],\[ "c ", "c ", "e ", "c "\],\[ "f ", "c ", "c ", "c "\]\]
**Output:** true
**Explanation:** There is only one valid cycle highlighted in the image below:
**Example 3:**
**Input:** grid = \[\[ "a ", "b ", "b "\],\[ "b ", "z ", "b "\],\[ "b ", "b ", "a "\]\]
**Output:** false
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 500`
* `grid` consists only of lowercase English letters. | Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. |
BEATS 90%! Python3 BFS | detect-cycles-in-2d-grid | 0 | 1 | # Code\n```\nimport collections\n\n\nclass Solution:\n\n def containsCycle(self, grid: List[List[str]]) -> bool:\n ht = dict()\n q = collections.deque()\n x = y = 0\n for i in range(len(grid)):\n for j in range(len(grid[i])):\n if grid[i][j] not in ht:\n ht[grid[i][j]] = set()\n elif (i, j) not in ht[grid[i][j]]:\n q.append((i, j))\n while len(q) > 0:\n x, y = q.popleft()\n if (x, y) not in ht[grid[i][j]]:\n ht[grid[i][j]].add((x, y))\n elif len(ht[grid[i][j]]) > 2:\n return True\n if 0 < x and grid[x-1][y] == grid[i][j]:\n if (x-1, y) not in ht[grid[i][j]]:\n q.append((x-1, y))\n if 0 < y and grid[x][y-1] == grid[i][j]:\n if (x, y-1) not in ht[grid[i][j]]:\n q.append((x, y-1))\n if x + 1 < len(grid) and grid[x+1][y] == grid[i][j]:\n if (x+1, y) not in ht[grid[i][j]]:\n q.append((x+1, y))\n if y + 1 < len(grid[0]) and grid[x][y+1] == grid[i][j]:\n if (x, y+1) not in ht[grid[i][j]]:\n q.append((x, y+1))\n return False\n``` | 0 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
98%-Faster Union-Find Approach | detect-cycles-in-2d-grid | 0 | 1 | # Complexity\n- Time complexity: $$O(m*n*log(m*n))$$.\n\n- Space complexity: $$O(m*n)$$.\n\n# Code\n```\nclass UnionFind:\n def __init__(self):\n self.par = {}\n \n def union(self, el1, el2):\n self.par[self.find(el2)] = self.find(el1)\n\n def find(self, el):\n p = self.par.get(el, el)\n if p != el:\n p = self.par[el] = self.find(p)\n \n return p\n\n\nclass Solution:\n def containsCycle(self, grid: List[List[str]]) -> bool:\n uf = UnionFind()\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if i > 0 and j > 0 and grid[i][j-1] == grid[i][j] == grid[i-1][j]:\n if uf.find((i, j-1)) == uf.find((i-1, j)):\n return True\n if j > 0 and grid[i][j-1] == grid[i][j]:\n uf.union((i, j-1), (i, j))\n if i > 0 and grid[i][j] == grid[i-1][j]:\n uf.union((i-1, j), (i, j))\n \n return False\n``` | 0 | Given a 2D array of characters `grid` of size `m x n`, you need to find if there exists any cycle consisting of the **same value** in `grid`.
A cycle is a path of **length 4 or more** in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the **same value** of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle `(1, 1) -> (1, 2) -> (1, 1)` is invalid because from `(1, 2)` we visited `(1, 1)` which was the last visited cell.
Return `true` if any cycle of the same value exists in `grid`, otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "a ", "a ", "a ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "a ", "a ", "a "\]\]
**Output:** true
**Explanation:** There are two valid cycles shown in different colors in the image below:
**Example 2:**
**Input:** grid = \[\[ "c ", "c ", "c ", "a "\],\[ "c ", "d ", "c ", "c "\],\[ "c ", "c ", "e ", "c "\],\[ "f ", "c ", "c ", "c "\]\]
**Output:** true
**Explanation:** There is only one valid cycle highlighted in the image below:
**Example 3:**
**Input:** grid = \[\[ "a ", "b ", "b "\],\[ "b ", "z ", "b "\],\[ "b ", "b ", "a "\]\]
**Output:** false
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 500`
* `grid` consists only of lowercase English letters. | Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. |
98%-Faster Union-Find Approach | detect-cycles-in-2d-grid | 0 | 1 | # Complexity\n- Time complexity: $$O(m*n*log(m*n))$$.\n\n- Space complexity: $$O(m*n)$$.\n\n# Code\n```\nclass UnionFind:\n def __init__(self):\n self.par = {}\n \n def union(self, el1, el2):\n self.par[self.find(el2)] = self.find(el1)\n\n def find(self, el):\n p = self.par.get(el, el)\n if p != el:\n p = self.par[el] = self.find(p)\n \n return p\n\n\nclass Solution:\n def containsCycle(self, grid: List[List[str]]) -> bool:\n uf = UnionFind()\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if i > 0 and j > 0 and grid[i][j-1] == grid[i][j] == grid[i-1][j]:\n if uf.find((i, j-1)) == uf.find((i-1, j)):\n return True\n if j > 0 and grid[i][j-1] == grid[i][j]:\n uf.union((i, j-1), (i, j))\n if i > 0 and grid[i][j] == grid[i-1][j]:\n uf.union((i-1, j), (i, j))\n \n return False\n``` | 0 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
Python 3: UnionFind / Two-Set DFS Solution | detect-cycles-in-2d-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, m, n):\n self.par = {(i, j): (i,j) for i in range(m) for j in range(n)}\n\n def find(self, a):\n p = self.par[a]\n while p != self.par[p]:\n self.par[p] = self.par[self.par[p]]\n p = self.par[p]\n return p\n \n def union(self, a, b):\n par_a, par_b = self.find(a), self.find(b)\n if par_a == par_b:\n return True # cycle detected\n self.par[par_a] = par_b\n return False\n\nclass Solution:\n def containsCycle(self, grid: List[List[str]]) -> bool:\n\n # UNION-FIND\n m, n = len(grid), len(grid[0])\n directions = [(1,0),(0,1)]\n uf = UnionFind(m, n)\n\n for row in range(m):\n for col in range(n):\n for dr, dc in directions:\n r, c = row + dr, col + dc\n if r in range(m) and c in range(n) and grid[row][col] == grid[r][c]:\n if uf.union((row, col), (r, c)):\n return True\n return False\n\n\n # TWO SET CYCLE DETECTION \n m, n = len(grid), len(grid[0])\n directions = [(1,0),(0,1),(-1,0),(0,-1)]\n visited, cycle = set(), set()\n\n def dfs(row, col, from_row, from_col):\n \'\'\'\n Return true if there is a cycle, else false.\n \'\'\'\n\n # check if row col was visited already within the current dfs\n if (row, col) in cycle:\n return True\n\n if (row, col) in visited:\n return False\n\n # pre-order \n visited.add((row, col))\n cycle.add((row, col))\n\n prev_char = grid[row][col]\n for dr, dc in directions:\n r, c = row + dr, col + dc\n \n if r in range(m) and c in range(n) and not (r == from_row and c == from_col):\n cur_char = grid[r][c]\n if cur_char == prev_char and dfs(r, c, row, col):\n return True\n\n # post-order\n cycle.remove((row, col))\n return False\n \n for r in range(m):\n for c in range(n):\n if (r, c) not in visited and dfs(r, c, r, c):\n return True\n return False\n\n\n\n``` | 0 | Given a 2D array of characters `grid` of size `m x n`, you need to find if there exists any cycle consisting of the **same value** in `grid`.
A cycle is a path of **length 4 or more** in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the **same value** of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle `(1, 1) -> (1, 2) -> (1, 1)` is invalid because from `(1, 2)` we visited `(1, 1)` which was the last visited cell.
Return `true` if any cycle of the same value exists in `grid`, otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "a ", "a ", "a ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "b ", "b ", "a "\],\[ "a ", "a ", "a ", "a "\]\]
**Output:** true
**Explanation:** There are two valid cycles shown in different colors in the image below:
**Example 2:**
**Input:** grid = \[\[ "c ", "c ", "c ", "a "\],\[ "c ", "d ", "c ", "c "\],\[ "c ", "c ", "e ", "c "\],\[ "f ", "c ", "c ", "c "\]\]
**Output:** true
**Explanation:** There is only one valid cycle highlighted in the image below:
**Example 3:**
**Input:** grid = \[\[ "a ", "b ", "b "\],\[ "b ", "z ", "b "\],\[ "b ", "b ", "a "\]\]
**Output:** false
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 500`
* `grid` consists only of lowercase English letters. | Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. |
Python 3: UnionFind / Two-Set DFS Solution | detect-cycles-in-2d-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, m, n):\n self.par = {(i, j): (i,j) for i in range(m) for j in range(n)}\n\n def find(self, a):\n p = self.par[a]\n while p != self.par[p]:\n self.par[p] = self.par[self.par[p]]\n p = self.par[p]\n return p\n \n def union(self, a, b):\n par_a, par_b = self.find(a), self.find(b)\n if par_a == par_b:\n return True # cycle detected\n self.par[par_a] = par_b\n return False\n\nclass Solution:\n def containsCycle(self, grid: List[List[str]]) -> bool:\n\n # UNION-FIND\n m, n = len(grid), len(grid[0])\n directions = [(1,0),(0,1)]\n uf = UnionFind(m, n)\n\n for row in range(m):\n for col in range(n):\n for dr, dc in directions:\n r, c = row + dr, col + dc\n if r in range(m) and c in range(n) and grid[row][col] == grid[r][c]:\n if uf.union((row, col), (r, c)):\n return True\n return False\n\n\n # TWO SET CYCLE DETECTION \n m, n = len(grid), len(grid[0])\n directions = [(1,0),(0,1),(-1,0),(0,-1)]\n visited, cycle = set(), set()\n\n def dfs(row, col, from_row, from_col):\n \'\'\'\n Return true if there is a cycle, else false.\n \'\'\'\n\n # check if row col was visited already within the current dfs\n if (row, col) in cycle:\n return True\n\n if (row, col) in visited:\n return False\n\n # pre-order \n visited.add((row, col))\n cycle.add((row, col))\n\n prev_char = grid[row][col]\n for dr, dc in directions:\n r, c = row + dr, col + dc\n \n if r in range(m) and c in range(n) and not (r == from_row and c == from_col):\n cur_char = grid[r][c]\n if cur_char == prev_char and dfs(r, c, row, col):\n return True\n\n # post-order\n cycle.remove((row, col))\n return False\n \n for r in range(m):\n for c in range(n):\n if (r, c) not in visited and dfs(r, c, r, c):\n return True\n return False\n\n\n\n``` | 0 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
[Python3] 2-line | most-visited-sector-in-a-circular-track | 0 | 1 | \n```\nclass Solution:\n def mostVisited(self, n: int, rounds: List[int]) -> List[int]:\n x, xx = rounds[0], rounds[-1]\n return list(range(x, xx+1)) if x <= xx else list(range(1, xx+1)) + list(range(x, n+1))\n``` | 10 | Given an integer `n` and an integer array `rounds`. We have a circular track which consists of `n` sectors labeled from `1` to `n`. A marathon will be held on this track, the marathon consists of `m` rounds. The `ith` round starts at sector `rounds[i - 1]` and ends at sector `rounds[i]`. For example, round 1 starts at sector `rounds[0]` and ends at sector `rounds[1]`
Return _an array of the most visited sectors_ sorted in **ascending** order.
Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).
**Example 1:**
**Input:** n = 4, rounds = \[1,3,1,2\]
**Output:** \[1,2\]
**Explanation:** The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.
**Example 2:**
**Input:** n = 2, rounds = \[2,1,2,1,2,1,2,1,2\]
**Output:** \[2\]
**Example 3:**
**Input:** n = 7, rounds = \[1,3,5,7\]
**Output:** \[1,2,3,4,5,6,7\]
**Constraints:**
* `2 <= n <= 100`
* `1 <= m <= 100`
* `rounds.length == m + 1`
* `1 <= rounds[i] <= n`
* `rounds[i] != rounds[i + 1]` for `0 <= i < m` | Imagine that startTime[i] and endTime[i] form an interval (i.e. [startTime[i], endTime[i]]). The answer is how many times the queryTime laid in those mentioned intervals. |
✅✅✅ 98% faster solution | easy to understand | less code | most-visited-sector-in-a-circular-track | 0 | 1 | \n\n```\nclass Solution:\n def mostVisited(self, n: int, rounds: List[int]) -> List[int]:\n a, b = rounds[0], rounds[-1]\n if a<=b: return [i for i in range(a, b+1)]\n return [i for i in range(1, b+1)] + [i for i in range(a, n+1)]\n``` | 2 | Given an integer `n` and an integer array `rounds`. We have a circular track which consists of `n` sectors labeled from `1` to `n`. A marathon will be held on this track, the marathon consists of `m` rounds. The `ith` round starts at sector `rounds[i - 1]` and ends at sector `rounds[i]`. For example, round 1 starts at sector `rounds[0]` and ends at sector `rounds[1]`
Return _an array of the most visited sectors_ sorted in **ascending** order.
Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).
**Example 1:**
**Input:** n = 4, rounds = \[1,3,1,2\]
**Output:** \[1,2\]
**Explanation:** The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.
**Example 2:**
**Input:** n = 2, rounds = \[2,1,2,1,2,1,2,1,2\]
**Output:** \[2\]
**Example 3:**
**Input:** n = 7, rounds = \[1,3,5,7\]
**Output:** \[1,2,3,4,5,6,7\]
**Constraints:**
* `2 <= n <= 100`
* `1 <= m <= 100`
* `rounds.length == m + 1`
* `1 <= rounds[i] <= n`
* `rounds[i] != rounds[i + 1]` for `0 <= i < m` | Imagine that startTime[i] and endTime[i] form an interval (i.e. [startTime[i], endTime[i]]). The answer is how many times the queryTime laid in those mentioned intervals. |
[PYTHON] simple solution with explanation. | most-visited-sector-in-a-circular-track | 0 | 1 | I spent 45 mins in this question one, so sad...\n\nExplanation:\nif n = 4, rounds = [1,3,1,2]\nthan [1,2,3,4,**1,2**]\noutput is [1,2]\n\nif n = 3 rounds = [3,1,2,3,1]\nthan [3,1,2,**3,1**]\noutput is [1,3]\n\nif n = 4 rounds = [1,4,2,3]\nthan [1,2,3,4,**1,2,3**]\noutput is [1,2,3]\n\nwhich means all steps moved in the middle will happen again and again and again, so they are useless.\nThe only important things are start point and end point.\n\n```\nclass Solution:\n\n def mostVisited(self, n: int, rounds: List[int]) -> List[int]:\n first = rounds[0]\n last = rounds[-1]\n \n if last>=first:\n return [i for i in range(first,last+1)]\n else:\n rec = []\n for i in range(n):\n if i+1<=last or i+1>=first:\n rec.append(i+1)\n return sorted(rec)\n \n``` | 11 | Given an integer `n` and an integer array `rounds`. We have a circular track which consists of `n` sectors labeled from `1` to `n`. A marathon will be held on this track, the marathon consists of `m` rounds. The `ith` round starts at sector `rounds[i - 1]` and ends at sector `rounds[i]`. For example, round 1 starts at sector `rounds[0]` and ends at sector `rounds[1]`
Return _an array of the most visited sectors_ sorted in **ascending** order.
Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).
**Example 1:**
**Input:** n = 4, rounds = \[1,3,1,2\]
**Output:** \[1,2\]
**Explanation:** The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.
**Example 2:**
**Input:** n = 2, rounds = \[2,1,2,1,2,1,2,1,2\]
**Output:** \[2\]
**Example 3:**
**Input:** n = 7, rounds = \[1,3,5,7\]
**Output:** \[1,2,3,4,5,6,7\]
**Constraints:**
* `2 <= n <= 100`
* `1 <= m <= 100`
* `rounds.length == m + 1`
* `1 <= rounds[i] <= n`
* `rounds[i] != rounds[i + 1]` for `0 <= i < m` | Imagine that startTime[i] and endTime[i] form an interval (i.e. [startTime[i], endTime[i]]). The answer is how many times the queryTime laid in those mentioned intervals. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.