title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅ 98.37% O(n) Final Winner | find-the-winner-of-an-array-game | 1 | 1 | # Intuition\nWhen first approaching this problem, we might think about simulating the entire process: comparing numbers, moving the smaller one to the end, and keeping track of the number of consecutive wins. However, a closer inspection reveals a couple of key insights. Firstly, if the game needs only one win (i.e., $ k = 1 $), the winner of the first round is the answer. Secondly, if $ k $ is large enough (i.e., $ k $ is equal to or larger than the length of the array), the maximum element in the array is bound to win eventually. These initial observations allow us to build a strategy that handles these edge cases separately, providing an efficient approach for the main logic.\n\n# Live Coding & More\nhttps://youtu.be/cbFwAvhG_C8?si=ussPA9wySWxCxLp3\n\n# Approach\n1. **Edge Cases**: Check if $ k $ is 1 or if $ k $ is equal to or larger than the length of the array. These cases allow for immediate conclusions.\n2. **Initialization**: Initialize the current winner as the first element and set the consecutive wins count to zero.\n3. **Iteration**: Iterate through the array starting from the second element. For each element:\n - If the current winner is greater, increment the consecutive win count.\n - If the current element is greater, it becomes the new winner and the consecutive win count resets to 1.\n - If at any point the consecutive win count reaches $ k $, the current winner is the answer.\n4. **Final Winner**: If the loop completes without finding an answer, the current winner after the loop is the answer.\n\nThis approach ensures that we only iterate through the list once, making the solution efficient.\n\n# Complexity\n\n- **Time complexity**: $ O(n) $\n The solution iterates through the array once. In the worst-case scenario, we examine all elements in the array. Hence, the time complexity is linear with respect to the size of the array.\n\n- **Space complexity**: $ O(1) $\n The solution uses a constant amount of extra space: a few variables to keep track of the current winner and the consecutive win count. Regardless of the size of the input, the space used remains constant.\n\n# Code\n``` Python []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n if k == 1:\n return max(arr[0], arr[1])\n if k >= len(arr):\n return max(arr)\n \n current_winner = arr[0]\n consecutive_wins = 0\n \n for i in range(1, len(arr)):\n if current_winner > arr[i]:\n consecutive_wins += 1\n else:\n current_winner = arr[i]\n consecutive_wins = 1\n \n if consecutive_wins == k:\n return current_winner\n \n return current_winner\n```\n``` C++ []\nclass Solution {\npublic:\n int getWinner(std::vector<int>& arr, int k) {\n if (k == 1) {\n return std::max(arr[0], arr[1]);\n }\n if (k >= arr.size()) {\n return *std::max_element(arr.begin(), arr.end());\n }\n\n int current_winner = arr[0];\n int consecutive_wins = 0;\n\n for (int i = 1; i < arr.size(); ++i) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins == k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int getWinner(int[] arr, int k) {\n if (k == 1) {\n return Math.max(arr[0], arr[1]);\n }\n if (k >= arr.length) {\n return Arrays.stream(arr).max().getAsInt();\n }\n\n int current_winner = arr[0];\n int consecutive_wins = 0;\n\n for (int i = 1; i < arr.length; i++) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins == k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int GetWinner(int[] arr, int k) {\n if (k == 1) {\n return Math.Max(arr[0], arr[1]);\n }\n if (k >= arr.Length) {\n return arr.Max();\n }\n\n int current_winner = arr[0];\n int consecutive_wins = 0;\n\n for (int i = 1; i < arr.Length; i++) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins == k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n}\n```\n``` Go []\npackage main\n\nfunc getWinner(arr []int, k int) int {\n if k == 1 {\n return max(arr[0], arr[1])\n }\n if k >= len(arr) {\n return maxArr(arr)\n }\n\n current_winner := arr[0]\n consecutive_wins := 0\n\n for i := 1; i < len(arr); i++ {\n if current_winner > arr[i] {\n consecutive_wins++\n } else {\n current_winner = arr[i]\n consecutive_wins = 1\n }\n\n if consecutive_wins == k {\n return current_winner\n }\n }\n\n return current_winner\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n\nfunc maxArr(arr []int) int {\n m := arr[0]\n for _, val := range arr {\n if val > m {\n m = val\n }\n }\n return m\n}\n```\n``` Rust []\nimpl Solution {\n pub fn get_winner(arr: Vec<i32>, k: i32) -> i32 {\n if k == 1 {\n return arr[0].max(arr[1]);\n }\n if k as usize >= arr.len() {\n return *arr.iter().max().unwrap();\n }\n\n let mut current_winner = arr[0];\n let mut consecutive_wins = 0;\n\n for &num in &arr[1..] {\n if current_winner > num {\n consecutive_wins += 1;\n } else {\n current_winner = num;\n consecutive_wins = 1;\n }\n\n if consecutive_wins == k {\n return current_winner;\n }\n }\n\n current_winner\n }\n}\n```\n``` PHP []\nclass Solution {\n function getWinner($arr, $k) {\n if ($k == 1) {\n return max($arr[0], $arr[1]);\n }\n if ($k >= count($arr)) {\n return max($arr);\n }\n\n $current_winner = $arr[0];\n $consecutive_wins = 0;\n\n for ($i = 1; $i < count($arr); $i++) {\n if ($current_winner > $arr[$i]) {\n $consecutive_wins++;\n } else {\n $current_winner = $arr[$i];\n $consecutive_wins = 1;\n }\n\n if ($consecutive_wins == $k) {\n return $current_winner;\n }\n }\n\n return $current_winner;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} arr\n * @param {number} k\n * @return {number}\n */\nvar getWinner = function(arr, k) {\n if (k === 1) {\n return Math.max(arr[0], arr[1]);\n }\n if (k >= arr.length) {\n return Math.max(...arr);\n }\n\n let current_winner = arr[0];\n let consecutive_wins = 0;\n\n for (let i = 1; i < arr.length; i++) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins === k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|------------|---------------------|-------------------|\n| Java | 3 | 55.8 |\n| Rust | 11 | 3.4 |\n| JavaScript | 70 | 51.6 |\n| C++ | 81 | 63.5 |\n| Go | 87 | 8.2 |\n| C# | 156 | 53.8 |\n| PHP | 186 | 31.5 |\n| Python3 | 500 | 29.6 |\n\n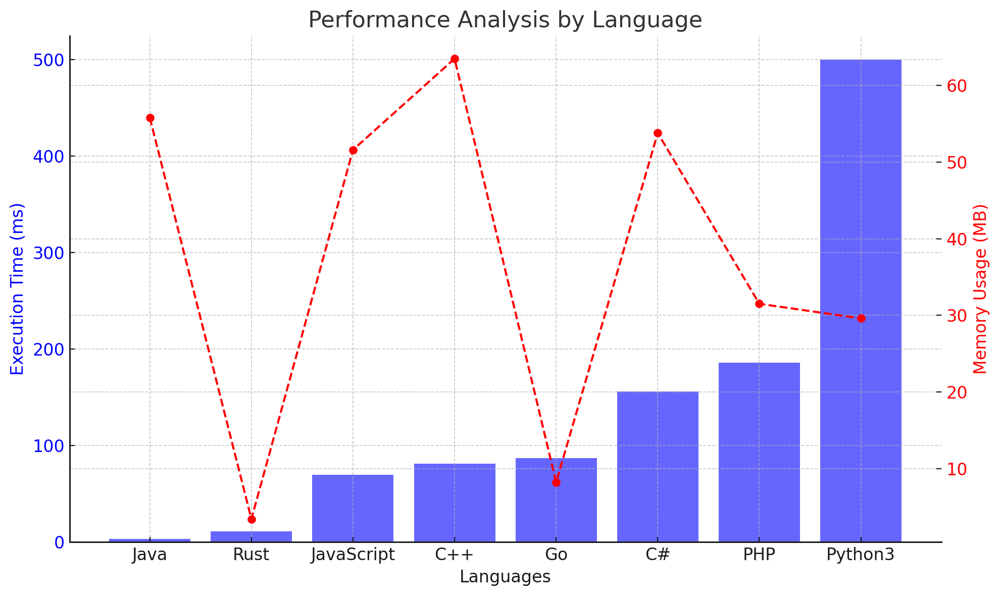\n\n\n# Conclusion\nUnderstanding the rules of the game and the implications of the value of $ k $ were crucial in devising this efficient solution. By handling edge cases separately, we were able to focus on the main logic without unnecessary complications. This problem demonstrates the importance of thoroughly analyzing the problem statement to identify key insights that can simplify the solution. | 103 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | find-the-winner-of-an-array-game | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(With Queue)***\n1. **Initialization:**\n\n - The code initializes a variable `maxElement` to store the maximum element in the `arr`. It starts with the first element of the array.\n - A queue named `queue` is initialized to store the remaining elements in the array.\n1. **Processing the Array:**\n\n - A `for` loop iterates through the elements of the array from the second element (index 1) onwards.\n - In each iteration, the code checks if the current element is greater than the `maxElement`. If it is, the `maxElement` is updated.\n - The current element (the winner of the previous comparison) is stored in the `curr` variable, and the current element is removed from the queue.\n1. **Comparing Elements:**\n\n - The code enters a `while` loop that continues until the queue is not empty.\n - In each iteration of the loop, the code:\n - Retrieves the opponent\'s element from the front of the queue.\n - Compares the `curr` element with the opponent\'s element to determine the winner.\n - If `curr` is greater, it is pushed back to the end of the queue, and a "winstreak" counter is incremented.\n - If the opponent\'s element is greater, it becomes the new `curr`, and the winstreak counter is reset to 1.\n1. **Winning Streak or Maximum Element:**\n\n - After each comparison, the code checks if the winstreak has reached the desired value `k` or if `curr` has become the `maxElement`.\n - If either condition is met, the function returns the current element `curr` as the winner of the game.\n1. **No Unique Winner:**\n\n - If the loop completes without finding a winner (i.e., no winstreak of length `k` occurs), the function returns -1, indicating that there is no unique winner.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int maxElement = arr[0];\n queue<int> queue;\n for (int i = 1; i < arr.size(); i++) {\n maxElement = max(maxElement, arr[i]);\n queue.push(arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n while (!queue.empty()) {\n int opponent = queue.front();\n queue.pop();\n \n if (curr > opponent) {\n queue.push(opponent);\n winstreak++;\n } else {\n queue.push(curr);\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n};\n\n```\n\n```C []\n\n#include <stdlib.h>\n#include <stdio.h>\n#include <limits.h>\n\nint max(int a, int b) {\n return (a > b) ? a : b;\n}\n\nint getWinner(int *arr, int arrSize, int k) {\n int maxElement = arr[0];\n int *queue = (int *)malloc((arrSize - 1) * sizeof(int));\n int front = 0;\n int rear = 0;\n\n for (int i = 1; i < arrSize; i++) {\n maxElement = max(maxElement, arr[i]);\n queue[rear] = arr[i];\n rear++;\n }\n\n int curr = arr[0];\n int winstreak = 0;\n\n while (front != rear) {\n int opponent = queue[front];\n front++;\n\n if (curr > opponent) {\n queue[rear] = opponent;\n rear++;\n winstreak++;\n } else {\n queue[rear] = curr;\n rear++;\n curr = opponent;\n winstreak = 1;\n }\n\n if (winstreak == k || curr == maxElement) {\n free(queue);\n return curr;\n }\n }\n\n free(queue);\n return -1;\n}\n\nint main() {\n int arr[] = {2, 1, 3, 5, 4, 6, 7};\n int k = 2;\n int result = getWinner(arr, 7, k);\n printf("The winner is: %d\\n", result);\n\n return 0;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int maxElement = arr[0];\n Queue<Integer> queue = new LinkedList();\n for (int i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n queue.offer(arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n while (!queue.isEmpty()) {\n int opponent = queue.poll();\n \n if (curr > opponent) {\n queue.offer(opponent);\n winstreak++;\n } else {\n queue.offer(curr);\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n max_element = max(arr)\n queue = deque(arr[1:])\n curr = arr[0]\n winstreak = 0\n\n while queue:\n opponent = queue.popleft()\n if curr > opponent:\n queue.append(opponent)\n winstreak += 1\n else:\n queue.append(curr)\n curr = opponent\n winstreak = 1\n \n if winstreak == k or curr == max_element:\n return curr\n\n```\n\n```javascript []\nvar getWinner = function(arr, k) {\n let maxElement = arr[0];\n let queue = [];\n \n for (let i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n queue.push(arr[i]);\n }\n \n let curr = arr[0];\n let winstreak = 0;\n \n while (queue.length > 0) {\n let opponent = queue.shift();\n \n if (curr > opponent) {\n queue.push(opponent);\n winstreak++;\n } else {\n queue.push(curr);\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak === k || curr === maxElement) {\n return curr;\n }\n }\n \n return -1;\n};\n\n\n```\n\n---\n\n#### ***Approach 2(Without Queue)***\n1. The `getWinner` function takes two parameters: a vector `arr` of integers representing the players\' scores and an integer `k` representing the required win streak.\n\n1. It initializes `maxElement` with the first element of the array `arr`, which is used to keep track of the maximum score in the array.\n\n1. It iterates through the elements of the array to find the maximum score. The `maxElement` variable is updated to store the maximum score in the array.\n\n1. It initializes `curr` with the first element of the array, representing the current player\'s score.\n\n1. It also initializes a variable `winstreak` to 0, which will be used to count the consecutive wins of the current player.\n\n1. The function then iterates through the array from the second element (index 1) to the end.\n\n1. For each player (element) in the array, it compares the current player\'s score (`curr`) with the opponent\'s score. If the current player\'s score is greater than the opponent\'s, the `winstreak` is incremented, indicating a win. Otherwise, the `curr` variable is updated to the opponent\'s score, and the `winstreak` is reset to 1.\n\n1. After each comparison, the code checks if the `winstreak` is equal to `k` or if the current player\'s score is equal to the `maxElement`. If either condition is met, the function returns the current player\'s score, indicating that the player has won the required number of consecutive games or has achieved the maximum score.\n\n1. If the loop finishes without finding a winner, the function returns -1, indicating that there is no unique winner.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int maxElement = arr[0];\n for (int i = 1; i < arr.size(); i++) {\n maxElement = max(maxElement, arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n for (int i = 1; i < arr.size(); i++) {\n int opponent = arr[i];\n \n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n};\n```\n\n```C []\n\n#include <stdio.h>\n#include <limits.h>\n\nint max(int a, int b) {\n return (a > b) ? a : b;\n}\n\nint getWinner(int arr[], int arrSize, int k) {\n int maxElement = arr[0];\n for (int i = 1; i < arrSize; i++) {\n maxElement = max(maxElement, arr[i]);\n }\n\n int curr = arr[0];\n int winstreak = 0;\n\n for (int i = 1; i < arrSize; i++) {\n int opponent = arr[i];\n\n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n\n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n\n return -1;\n}\n\nint main() {\n int arr[] = {2, 1, 3, 5, 4, 6, 7};\n int k = 2;\n int result = getWinner(arr, 7, k);\n printf("The winner is: %d\\n", result);\n\n return 0;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int maxElement = arr[0];\n for (int i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n for (int i = 1; i < arr.length; i++) {\n int opponent = arr[i];\n \n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n max_element = max(arr)\n curr = arr[0]\n winstreak = 0\n\n for i in range(1, len(arr)):\n opponent = arr[i]\n if curr > opponent:\n winstreak += 1\n else:\n curr = opponent\n winstreak = 1\n \n if winstreak == k or curr == max_element:\n return curr\n\n```\n\n```javascript []\nfunction getWinner(arr, k) {\n let maxElement = arr[0];\n for (let i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n }\n\n let curr = arr[0];\n let winstreak = 0;\n\n for (let i = 1; i < arr.length; i++) {\n let opponent = arr[i];\n\n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n\n if (winstreak === k || curr === maxElement) {\n return curr;\n }\n }\n\n return -1;\n}\n\nconst arr = [2, 1, 3, 5, 4, 6, 7];\nconst k = 2;\nconst result = getWinner(arr, k);\nconsole.log(`The winner is: ${result}`);\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | find-the-winner-of-an-array-game | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(With Queue)***\n1. **Initialization:**\n\n - The code initializes a variable `maxElement` to store the maximum element in the `arr`. It starts with the first element of the array.\n - A queue named `queue` is initialized to store the remaining elements in the array.\n1. **Processing the Array:**\n\n - A `for` loop iterates through the elements of the array from the second element (index 1) onwards.\n - In each iteration, the code checks if the current element is greater than the `maxElement`. If it is, the `maxElement` is updated.\n - The current element (the winner of the previous comparison) is stored in the `curr` variable, and the current element is removed from the queue.\n1. **Comparing Elements:**\n\n - The code enters a `while` loop that continues until the queue is not empty.\n - In each iteration of the loop, the code:\n - Retrieves the opponent\'s element from the front of the queue.\n - Compares the `curr` element with the opponent\'s element to determine the winner.\n - If `curr` is greater, it is pushed back to the end of the queue, and a "winstreak" counter is incremented.\n - If the opponent\'s element is greater, it becomes the new `curr`, and the winstreak counter is reset to 1.\n1. **Winning Streak or Maximum Element:**\n\n - After each comparison, the code checks if the winstreak has reached the desired value `k` or if `curr` has become the `maxElement`.\n - If either condition is met, the function returns the current element `curr` as the winner of the game.\n1. **No Unique Winner:**\n\n - If the loop completes without finding a winner (i.e., no winstreak of length `k` occurs), the function returns -1, indicating that there is no unique winner.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int maxElement = arr[0];\n queue<int> queue;\n for (int i = 1; i < arr.size(); i++) {\n maxElement = max(maxElement, arr[i]);\n queue.push(arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n while (!queue.empty()) {\n int opponent = queue.front();\n queue.pop();\n \n if (curr > opponent) {\n queue.push(opponent);\n winstreak++;\n } else {\n queue.push(curr);\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n};\n\n```\n\n```C []\n\n#include <stdlib.h>\n#include <stdio.h>\n#include <limits.h>\n\nint max(int a, int b) {\n return (a > b) ? a : b;\n}\n\nint getWinner(int *arr, int arrSize, int k) {\n int maxElement = arr[0];\n int *queue = (int *)malloc((arrSize - 1) * sizeof(int));\n int front = 0;\n int rear = 0;\n\n for (int i = 1; i < arrSize; i++) {\n maxElement = max(maxElement, arr[i]);\n queue[rear] = arr[i];\n rear++;\n }\n\n int curr = arr[0];\n int winstreak = 0;\n\n while (front != rear) {\n int opponent = queue[front];\n front++;\n\n if (curr > opponent) {\n queue[rear] = opponent;\n rear++;\n winstreak++;\n } else {\n queue[rear] = curr;\n rear++;\n curr = opponent;\n winstreak = 1;\n }\n\n if (winstreak == k || curr == maxElement) {\n free(queue);\n return curr;\n }\n }\n\n free(queue);\n return -1;\n}\n\nint main() {\n int arr[] = {2, 1, 3, 5, 4, 6, 7};\n int k = 2;\n int result = getWinner(arr, 7, k);\n printf("The winner is: %d\\n", result);\n\n return 0;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int maxElement = arr[0];\n Queue<Integer> queue = new LinkedList();\n for (int i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n queue.offer(arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n while (!queue.isEmpty()) {\n int opponent = queue.poll();\n \n if (curr > opponent) {\n queue.offer(opponent);\n winstreak++;\n } else {\n queue.offer(curr);\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n max_element = max(arr)\n queue = deque(arr[1:])\n curr = arr[0]\n winstreak = 0\n\n while queue:\n opponent = queue.popleft()\n if curr > opponent:\n queue.append(opponent)\n winstreak += 1\n else:\n queue.append(curr)\n curr = opponent\n winstreak = 1\n \n if winstreak == k or curr == max_element:\n return curr\n\n```\n\n```javascript []\nvar getWinner = function(arr, k) {\n let maxElement = arr[0];\n let queue = [];\n \n for (let i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n queue.push(arr[i]);\n }\n \n let curr = arr[0];\n let winstreak = 0;\n \n while (queue.length > 0) {\n let opponent = queue.shift();\n \n if (curr > opponent) {\n queue.push(opponent);\n winstreak++;\n } else {\n queue.push(curr);\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak === k || curr === maxElement) {\n return curr;\n }\n }\n \n return -1;\n};\n\n\n```\n\n---\n\n#### ***Approach 2(Without Queue)***\n1. The `getWinner` function takes two parameters: a vector `arr` of integers representing the players\' scores and an integer `k` representing the required win streak.\n\n1. It initializes `maxElement` with the first element of the array `arr`, which is used to keep track of the maximum score in the array.\n\n1. It iterates through the elements of the array to find the maximum score. The `maxElement` variable is updated to store the maximum score in the array.\n\n1. It initializes `curr` with the first element of the array, representing the current player\'s score.\n\n1. It also initializes a variable `winstreak` to 0, which will be used to count the consecutive wins of the current player.\n\n1. The function then iterates through the array from the second element (index 1) to the end.\n\n1. For each player (element) in the array, it compares the current player\'s score (`curr`) with the opponent\'s score. If the current player\'s score is greater than the opponent\'s, the `winstreak` is incremented, indicating a win. Otherwise, the `curr` variable is updated to the opponent\'s score, and the `winstreak` is reset to 1.\n\n1. After each comparison, the code checks if the `winstreak` is equal to `k` or if the current player\'s score is equal to the `maxElement`. If either condition is met, the function returns the current player\'s score, indicating that the player has won the required number of consecutive games or has achieved the maximum score.\n\n1. If the loop finishes without finding a winner, the function returns -1, indicating that there is no unique winner.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int maxElement = arr[0];\n for (int i = 1; i < arr.size(); i++) {\n maxElement = max(maxElement, arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n for (int i = 1; i < arr.size(); i++) {\n int opponent = arr[i];\n \n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n};\n```\n\n```C []\n\n#include <stdio.h>\n#include <limits.h>\n\nint max(int a, int b) {\n return (a > b) ? a : b;\n}\n\nint getWinner(int arr[], int arrSize, int k) {\n int maxElement = arr[0];\n for (int i = 1; i < arrSize; i++) {\n maxElement = max(maxElement, arr[i]);\n }\n\n int curr = arr[0];\n int winstreak = 0;\n\n for (int i = 1; i < arrSize; i++) {\n int opponent = arr[i];\n\n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n\n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n\n return -1;\n}\n\nint main() {\n int arr[] = {2, 1, 3, 5, 4, 6, 7};\n int k = 2;\n int result = getWinner(arr, 7, k);\n printf("The winner is: %d\\n", result);\n\n return 0;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int maxElement = arr[0];\n for (int i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n }\n \n int curr = arr[0];\n int winstreak = 0;\n \n for (int i = 1; i < arr.length; i++) {\n int opponent = arr[i];\n \n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n \n if (winstreak == k || curr == maxElement) {\n return curr;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n max_element = max(arr)\n curr = arr[0]\n winstreak = 0\n\n for i in range(1, len(arr)):\n opponent = arr[i]\n if curr > opponent:\n winstreak += 1\n else:\n curr = opponent\n winstreak = 1\n \n if winstreak == k or curr == max_element:\n return curr\n\n```\n\n```javascript []\nfunction getWinner(arr, k) {\n let maxElement = arr[0];\n for (let i = 1; i < arr.length; i++) {\n maxElement = Math.max(maxElement, arr[i]);\n }\n\n let curr = arr[0];\n let winstreak = 0;\n\n for (let i = 1; i < arr.length; i++) {\n let opponent = arr[i];\n\n if (curr > opponent) {\n winstreak++;\n } else {\n curr = opponent;\n winstreak = 1;\n }\n\n if (winstreak === k || curr === maxElement) {\n return curr;\n }\n }\n\n return -1;\n}\n\nconst arr = [2, 1, 3, 5, 4, 6, 7];\nconst k = 2;\nconst result = getWinner(arr, k);\nconsole.log(`The winner is: ${result}`);\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
Python3 Solution | find-the-winner-of-an-array-game | 0 | 1 | \n```\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n n=len(arr)\n cur=arr[0]\n count=0\n for i in range(1,n):\n if arr[i]>cur:\n cur=arr[i]\n count=0\n count+=1\n if count==k:\n break\n return cur \n``` | 2 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Python3 Solution | find-the-winner-of-an-array-game | 0 | 1 | \n```\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n n=len(arr)\n cur=arr[0]\n count=0\n for i in range(1,n):\n if arr[i]>cur:\n cur=arr[i]\n count=0\n count+=1\n if count==k:\n break\n return cur \n``` | 2 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
✅For Beginners✅ II ✅beats 100%✅ II just for loop & if-condition | find-the-winner-of-an-array-game | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to determine the winner of a game between the first two elements of an integer array A. The game is played by comparing the values of A[0] and A[1] in each round. The larger of the two integers remains in position 0, and the smaller integer is moved to the end of the array. The game continues until one of the integers wins k consecutive rounds, and the code returns the winning integer.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n1. Initialize two variables:\n - `cur`: This variable holds the current winning integer and is initially set to the value of the first element in the array, i.e., `A[0]`.\n - `win`: This variable keeps track of the consecutive wins of the current winning integer and is initially set to 0.\n\n2. Start a loop that iterates through the elements of the array `A` starting from the second element (index 1) because the first element (index 0) is the initial value of `cur`.\n\n3. In each iteration of the loop:\n - Compare the current element `A[i]` with the current winning integer `cur`.\n - If `A[i]` is greater than `cur`, it means that the current element wins the round. Therefore, update the value of `cur` to be `A[i`, as the larger integer is now the current winning integer.\n - Reset the `win` counter to 0 because a new winning integer has emerged.\n\n4. Check if the value of `win` (consecutive wins) has reached the desired number of consecutive wins, which is `k`. If it has reached `k`, it indicates that one of the integers has won `k` consecutive rounds. In this case, break out of the loop because we have found the winner.\n\n5. Continue the loop until either one integer has won `k` consecutive rounds or all elements of the array have been processed.\n\n6. Once the loop ends, return the value of `cur`, which represents the winning integer.\n\nThe code effectively simulates the game between the first two elements of the array and keeps track of the winning integer and the number of consecutive wins. It efficiently determines the winner and returns the result, as it\'s guaranteed that there will be a winner of the game.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int getWinner(vector<int>& A, int k) {\n int cur = A[0], win = 0;\n for (int i = 1; i < A.size(); ++i) {\n if (A[i] > cur) {\n cur = A[i];\n win = 0;\n }\n if (++win == k) break;\n }\n return cur;\n }\n};\n```\n```java []\npublic class Solution {\n public int getWinner(int[] A, int k) {\n int cur = A[0];\n int win = 0;\n \n for (int i = 1; i < A.length; ++i) {\n if (A[i] > cur) {\n cur = A[i];\n win = 0;\n }\n if (++win == k) {\n break;\n }\n }\n \n return cur;\n }\n}\n\n```\n```python []\nclass Solution(object):\n def getWinner(self, arr, k):\n d = dict()\n n = len(arr)\n mx = arr[0]\n for i in range(1, n):\n mx = max(mx, arr[i])\n d[mx] = d[mx] + 1 if mx in d.keys() else 1\n if d[mx] >= k:\n return mx\n return mx\n```\nthanks to : @lee215\n\n\n | 33 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
✅For Beginners✅ II ✅beats 100%✅ II just for loop & if-condition | find-the-winner-of-an-array-game | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to determine the winner of a game between the first two elements of an integer array A. The game is played by comparing the values of A[0] and A[1] in each round. The larger of the two integers remains in position 0, and the smaller integer is moved to the end of the array. The game continues until one of the integers wins k consecutive rounds, and the code returns the winning integer.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n1. Initialize two variables:\n - `cur`: This variable holds the current winning integer and is initially set to the value of the first element in the array, i.e., `A[0]`.\n - `win`: This variable keeps track of the consecutive wins of the current winning integer and is initially set to 0.\n\n2. Start a loop that iterates through the elements of the array `A` starting from the second element (index 1) because the first element (index 0) is the initial value of `cur`.\n\n3. In each iteration of the loop:\n - Compare the current element `A[i]` with the current winning integer `cur`.\n - If `A[i]` is greater than `cur`, it means that the current element wins the round. Therefore, update the value of `cur` to be `A[i`, as the larger integer is now the current winning integer.\n - Reset the `win` counter to 0 because a new winning integer has emerged.\n\n4. Check if the value of `win` (consecutive wins) has reached the desired number of consecutive wins, which is `k`. If it has reached `k`, it indicates that one of the integers has won `k` consecutive rounds. In this case, break out of the loop because we have found the winner.\n\n5. Continue the loop until either one integer has won `k` consecutive rounds or all elements of the array have been processed.\n\n6. Once the loop ends, return the value of `cur`, which represents the winning integer.\n\nThe code effectively simulates the game between the first two elements of the array and keeps track of the winning integer and the number of consecutive wins. It efficiently determines the winner and returns the result, as it\'s guaranteed that there will be a winner of the game.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int getWinner(vector<int>& A, int k) {\n int cur = A[0], win = 0;\n for (int i = 1; i < A.size(); ++i) {\n if (A[i] > cur) {\n cur = A[i];\n win = 0;\n }\n if (++win == k) break;\n }\n return cur;\n }\n};\n```\n```java []\npublic class Solution {\n public int getWinner(int[] A, int k) {\n int cur = A[0];\n int win = 0;\n \n for (int i = 1; i < A.length; ++i) {\n if (A[i] > cur) {\n cur = A[i];\n win = 0;\n }\n if (++win == k) {\n break;\n }\n }\n \n return cur;\n }\n}\n\n```\n```python []\nclass Solution(object):\n def getWinner(self, arr, k):\n d = dict()\n n = len(arr)\n mx = arr[0]\n for i in range(1, n):\n mx = max(mx, arr[i])\n d[mx] = d[mx] + 1 if mx in d.keys() else 1\n if d[mx] >= k:\n return mx\n return mx\n```\nthanks to : @lee215\n\n\n | 33 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
Python 3 solution using array methods | find-the-winner-of-an-array-game | 0 | 1 | \n```\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n if k >= len(arr): return max(arr)\n\n resultIndex = 0\n maxInK = max(arr[resultIndex:resultIndex+k+1])\n while arr[resultIndex] < maxInK:\n resultIndex = arr.index(maxInK)\n maxInK = max(arr[resultIndex:resultIndex+k])\n\n return arr[resultIndex]\n``` | 1 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Python 3 solution using array methods | find-the-winner-of-an-array-game | 0 | 1 | \n```\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n if k >= len(arr): return max(arr)\n\n resultIndex = 0\n maxInK = max(arr[resultIndex:resultIndex+k+1])\n while arr[resultIndex] < maxInK:\n resultIndex = arr.index(maxInK)\n maxInK = max(arr[resultIndex:resultIndex+k])\n\n return arr[resultIndex]\n``` | 1 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
[Python3] bubble-ish sort | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | Algo \nBasic idea is bubble sort. Here, we transform each row into a number which the location of last index of 1. Then, we use a modified bubble sort algo to compute the `ans`. For each row, we find the first value which can be moved to this position via swaps, and update the `ans`. \n\nEdit: added comments to aid understanding. \n\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n #summarizing row into number \n row = [0]*m \n for i in range(m):\n row[i] = next((j for j in reversed(range(n)) if grid[i][j]), 0)\n \n ans = 0\n #sequentially looking for row to fill in \n for k in range(m): \n for i, v in enumerate(row): \n if v <= k: #enough trailing zeros \n ans += i\n row.pop(i) #value used \n break \n else: return -1 #cannot find such row \n return ans \n``` | 13 | Given an `n x n` binary `grid`, in one step you can choose two **adjacent rows** of the grid and swap them.
A grid is said to be **valid** if all the cells above the main diagonal are **zeros**.
Return _the minimum number of steps_ needed to make the grid valid, or **\-1** if the grid cannot be valid.
The main diagonal of a grid is the diagonal that starts at cell `(1, 1)` and ends at cell `(n, n)`.
**Example 1:**
**Input:** grid = \[\[0,0,1\],\[1,1,0\],\[1,0,0\]\]
**Output:** 3
**Example 2:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\]\]
**Output:** -1
**Explanation:** All rows are similar, swaps have no effect on the grid.
**Example 3:**
**Input:** grid = \[\[1,0,0\],\[1,1,0\],\[1,1,1\]\]
**Output:** 0
**Constraints:**
* `n == grid.length` `== grid[i].length`
* `1 <= n <= 200`
* `grid[i][j]` is either `0` or `1` | null |
[Python3] bubble-ish sort | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | Algo \nBasic idea is bubble sort. Here, we transform each row into a number which the location of last index of 1. Then, we use a modified bubble sort algo to compute the `ans`. For each row, we find the first value which can be moved to this position via swaps, and update the `ans`. \n\nEdit: added comments to aid understanding. \n\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n #summarizing row into number \n row = [0]*m \n for i in range(m):\n row[i] = next((j for j in reversed(range(n)) if grid[i][j]), 0)\n \n ans = 0\n #sequentially looking for row to fill in \n for k in range(m): \n for i, v in enumerate(row): \n if v <= k: #enough trailing zeros \n ans += i\n row.pop(i) #value used \n break \n else: return -1 #cannot find such row \n return ans \n``` | 13 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
Easy to understand Python Solution with Comments | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n^2)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n\n # Time : O(n^2)\n # Space : O(n)\n\n n = len(grid)\n zeroesArr = []\n\n # Calculate trailing zeroes for each row \n for i in range(n):\n trailingZeroes = 0\n for j in range(n-1, -1, -1):\n if grid[i][j] == 1:\n break\n trailingZeroes += 1\n zeroesArr.append(trailingZeroes)\n\n # Min number of trailing zeroes expected in 1st row\n minZeroesExpected = n - 1\n res = 0\n\n for i in range(n):\n currMax = -1\n currMaxIndex = -1\n\n # Find closest row with trailing zeroes >= minZeroesExpected\n for j in range(i, n):\n if zeroesArr[j] >= minZeroesExpected:\n currMax = zeroesArr[j]\n currMaxIndex = j\n break\n\n # We couldn\'t find any row with minZeroesExpected\n if currMax < minZeroesExpected:\n return - 1\n \n # Simulate stable swapping of rows \n # Stability in sorting means preserving the relative order between keys with same values\n # we need to maintain relative order of rows since we can only swap two adjacent rows.\n # Bubble Sort is preferred as it\'s a stable sorting algorithm\n while currMaxIndex > i:\n temp = zeroesArr[currMaxIndex]\n zeroesArr[currMaxIndex] = zeroesArr[currMaxIndex - 1]\n zeroesArr[currMaxIndex - 1] = temp\n res += 1\n currMaxIndex -= 1\n\n # Decrease minZeroesExpected for next row by 1\n minZeroesExpected -= 1\n\n return res\n\n\n \n\n\n``` | 0 | Given an `n x n` binary `grid`, in one step you can choose two **adjacent rows** of the grid and swap them.
A grid is said to be **valid** if all the cells above the main diagonal are **zeros**.
Return _the minimum number of steps_ needed to make the grid valid, or **\-1** if the grid cannot be valid.
The main diagonal of a grid is the diagonal that starts at cell `(1, 1)` and ends at cell `(n, n)`.
**Example 1:**
**Input:** grid = \[\[0,0,1\],\[1,1,0\],\[1,0,0\]\]
**Output:** 3
**Example 2:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\]\]
**Output:** -1
**Explanation:** All rows are similar, swaps have no effect on the grid.
**Example 3:**
**Input:** grid = \[\[1,0,0\],\[1,1,0\],\[1,1,1\]\]
**Output:** 0
**Constraints:**
* `n == grid.length` `== grid[i].length`
* `1 <= n <= 200`
* `grid[i][j]` is either `0` or `1` | null |
Easy to understand Python Solution with Comments | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n^2)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n\n # Time : O(n^2)\n # Space : O(n)\n\n n = len(grid)\n zeroesArr = []\n\n # Calculate trailing zeroes for each row \n for i in range(n):\n trailingZeroes = 0\n for j in range(n-1, -1, -1):\n if grid[i][j] == 1:\n break\n trailingZeroes += 1\n zeroesArr.append(trailingZeroes)\n\n # Min number of trailing zeroes expected in 1st row\n minZeroesExpected = n - 1\n res = 0\n\n for i in range(n):\n currMax = -1\n currMaxIndex = -1\n\n # Find closest row with trailing zeroes >= minZeroesExpected\n for j in range(i, n):\n if zeroesArr[j] >= minZeroesExpected:\n currMax = zeroesArr[j]\n currMaxIndex = j\n break\n\n # We couldn\'t find any row with minZeroesExpected\n if currMax < minZeroesExpected:\n return - 1\n \n # Simulate stable swapping of rows \n # Stability in sorting means preserving the relative order between keys with same values\n # we need to maintain relative order of rows since we can only swap two adjacent rows.\n # Bubble Sort is preferred as it\'s a stable sorting algorithm\n while currMaxIndex > i:\n temp = zeroesArr[currMaxIndex]\n zeroesArr[currMaxIndex] = zeroesArr[currMaxIndex - 1]\n zeroesArr[currMaxIndex - 1] = temp\n res += 1\n currMaxIndex -= 1\n\n # Decrease minZeroesExpected for next row by 1\n minZeroesExpected -= 1\n\n return res\n\n\n \n\n\n``` | 0 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
Python Greedy Solution 92% Faster | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | ```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n arr = []\n for row in grid:\n total = 0\n for i in range(len(row)-1,-1,-1):\n if row[i] == 1: break\n total += 1\n \n arr.append(total)\n\n left = []\n res = 0\n\n for i in range(len(grid)-1):\n target = len(grid)-1-i\n index = float("inf")\n temp = []\n \n for j in range(len(arr)):\n if arr[j] >= target:\n index = j\n break\n \n if index == float("inf"):return -1\n\n for j in range(len(arr)):\n if j != index:\n temp.append(arr[j])\n \n left.append(arr[index])\n arr = temp\n res += index\n \n return res\n \n``` | 0 | Given an `n x n` binary `grid`, in one step you can choose two **adjacent rows** of the grid and swap them.
A grid is said to be **valid** if all the cells above the main diagonal are **zeros**.
Return _the minimum number of steps_ needed to make the grid valid, or **\-1** if the grid cannot be valid.
The main diagonal of a grid is the diagonal that starts at cell `(1, 1)` and ends at cell `(n, n)`.
**Example 1:**
**Input:** grid = \[\[0,0,1\],\[1,1,0\],\[1,0,0\]\]
**Output:** 3
**Example 2:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\]\]
**Output:** -1
**Explanation:** All rows are similar, swaps have no effect on the grid.
**Example 3:**
**Input:** grid = \[\[1,0,0\],\[1,1,0\],\[1,1,1\]\]
**Output:** 0
**Constraints:**
* `n == grid.length` `== grid[i].length`
* `1 <= n <= 200`
* `grid[i][j]` is either `0` or `1` | null |
Python Greedy Solution 92% Faster | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | ```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n arr = []\n for row in grid:\n total = 0\n for i in range(len(row)-1,-1,-1):\n if row[i] == 1: break\n total += 1\n \n arr.append(total)\n\n left = []\n res = 0\n\n for i in range(len(grid)-1):\n target = len(grid)-1-i\n index = float("inf")\n temp = []\n \n for j in range(len(arr)):\n if arr[j] >= target:\n index = j\n break\n \n if index == float("inf"):return -1\n\n for j in range(len(arr)):\n if j != index:\n temp.append(arr[j])\n \n left.append(arr[index])\n arr = temp\n res += index\n \n return res\n \n``` | 0 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
Python3 | Easy Approach | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | # Code\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int: \n n = len(grid)\n # count trailing zeros \n count = []\n for i in range(n):\n cnt = 0 \n for j in range(n -1 , -1 , -1 ):\n if grid[i][j] != 0 : \n break \n cnt += 1\n count.append(cnt)\n # Perforn Swapping \n req = n - 1 \n ans = 0 \n for i in range(n):\n check = False \n for j in range(i, n):\n if count[j] >= req:\n while j != i : \n count[j], count[j- 1] = count[j - 1] , count[j]\n j -= 1 \n ans += 1\n req -= 1 \n check = True\n break \n if check == False : \n return - 1 \n return ans \n``` | 0 | Given an `n x n` binary `grid`, in one step you can choose two **adjacent rows** of the grid and swap them.
A grid is said to be **valid** if all the cells above the main diagonal are **zeros**.
Return _the minimum number of steps_ needed to make the grid valid, or **\-1** if the grid cannot be valid.
The main diagonal of a grid is the diagonal that starts at cell `(1, 1)` and ends at cell `(n, n)`.
**Example 1:**
**Input:** grid = \[\[0,0,1\],\[1,1,0\],\[1,0,0\]\]
**Output:** 3
**Example 2:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\]\]
**Output:** -1
**Explanation:** All rows are similar, swaps have no effect on the grid.
**Example 3:**
**Input:** grid = \[\[1,0,0\],\[1,1,0\],\[1,1,1\]\]
**Output:** 0
**Constraints:**
* `n == grid.length` `== grid[i].length`
* `1 <= n <= 200`
* `grid[i][j]` is either `0` or `1` | null |
Python3 | Easy Approach | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | # Code\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int: \n n = len(grid)\n # count trailing zeros \n count = []\n for i in range(n):\n cnt = 0 \n for j in range(n -1 , -1 , -1 ):\n if grid[i][j] != 0 : \n break \n cnt += 1\n count.append(cnt)\n # Perforn Swapping \n req = n - 1 \n ans = 0 \n for i in range(n):\n check = False \n for j in range(i, n):\n if count[j] >= req:\n while j != i : \n count[j], count[j- 1] = count[j - 1] , count[j]\n j -= 1 \n ans += 1\n req -= 1 \n check = True\n break \n if check == False : \n return - 1 \n return ans \n``` | 0 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
[python] leverage syntactic sugar | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | # Approach\nThe same idea as others. Counting the tail zeros and bubble sort.\n\n# Complexity\nO(n^2)\n\n# Code\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n A = [sum(int(x == 0) for x in accumulate(row[::-1])) for row in grid]\n n = len(grid)\n\n res = 0\n for i in range(n):\n for j in range(i, n):\n if A[j] >= n - 1 - i:\n A = A[:i] + A[j:j+1] + A[i:j] + A[j+1:]\n res += j - i\n break\n else:\n return -1\n \n return res\n\n \n``` | 0 | Given an `n x n` binary `grid`, in one step you can choose two **adjacent rows** of the grid and swap them.
A grid is said to be **valid** if all the cells above the main diagonal are **zeros**.
Return _the minimum number of steps_ needed to make the grid valid, or **\-1** if the grid cannot be valid.
The main diagonal of a grid is the diagonal that starts at cell `(1, 1)` and ends at cell `(n, n)`.
**Example 1:**
**Input:** grid = \[\[0,0,1\],\[1,1,0\],\[1,0,0\]\]
**Output:** 3
**Example 2:**
**Input:** grid = \[\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\],\[0,1,1,0\]\]
**Output:** -1
**Explanation:** All rows are similar, swaps have no effect on the grid.
**Example 3:**
**Input:** grid = \[\[1,0,0\],\[1,1,0\],\[1,1,1\]\]
**Output:** 0
**Constraints:**
* `n == grid.length` `== grid[i].length`
* `1 <= n <= 200`
* `grid[i][j]` is either `0` or `1` | null |
[python] leverage syntactic sugar | minimum-swaps-to-arrange-a-binary-grid | 0 | 1 | # Approach\nThe same idea as others. Counting the tail zeros and bubble sort.\n\n# Complexity\nO(n^2)\n\n# Code\n```\nclass Solution:\n def minSwaps(self, grid: List[List[int]]) -> int:\n A = [sum(int(x == 0) for x in accumulate(row[::-1])) for row in grid]\n n = len(grid)\n\n res = 0\n for i in range(n):\n for j in range(i, n):\n if A[j] >= n - 1 - i:\n A = A[:i] + A[j:j+1] + A[i:j] + A[j+1:]\n res += j - i\n break\n else:\n return -1\n \n return res\n\n \n``` | 0 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
[Python] Very simple solution with explanation | get-the-maximum-score | 0 | 1 | ```py\nclass Solution:\n def maxSum(self, nums1: List[int], nums2: List[int]) -> int:\n ## RC ##\n ## APPROACH : GREEDY ##\n ## LOGIC ##\n ## 1. similar to merging 2 sorted arrays\n ## 2. Maintain sum for each array\n ## 3. when you find the same element in both arrays, only take maximum of sum1, sum2 and reset them\n \n p1, p2, sum1, sum2, result = 0, 0, 0, 0, 0\n while(p1 < len(nums1) and p2 < len(nums2)):\n if nums1[p1] == nums2[p2]:\n result += max(sum1, sum2) + nums1[p1]\n sum1, sum2 = 0, 0\n p1, p2 = p1 + 1, p2 + 1\n elif nums1[p1] < nums2[p2]:\n sum1 += nums1[p1]\n p1 += 1\n else:\n sum2 += nums2[p2]\n p2 += 1\n\n while(p1 < len(nums1)):\n sum1 += nums1[p1]\n p1 += 1\n\n while(p2 < len(nums2)):\n sum2 += nums2[p2]\n p2 += 1\n\n return (result + max(sum1 , sum2)) % (10**9 + 7)\n```\nPlease upvote if you like my solution | 6 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
[Python] Very simple solution with explanation | get-the-maximum-score | 0 | 1 | ```py\nclass Solution:\n def maxSum(self, nums1: List[int], nums2: List[int]) -> int:\n ## RC ##\n ## APPROACH : GREEDY ##\n ## LOGIC ##\n ## 1. similar to merging 2 sorted arrays\n ## 2. Maintain sum for each array\n ## 3. when you find the same element in both arrays, only take maximum of sum1, sum2 and reset them\n \n p1, p2, sum1, sum2, result = 0, 0, 0, 0, 0\n while(p1 < len(nums1) and p2 < len(nums2)):\n if nums1[p1] == nums2[p2]:\n result += max(sum1, sum2) + nums1[p1]\n sum1, sum2 = 0, 0\n p1, p2 = p1 + 1, p2 + 1\n elif nums1[p1] < nums2[p2]:\n sum1 += nums1[p1]\n p1 += 1\n else:\n sum2 += nums2[p2]\n p2 += 1\n\n while(p1 < len(nums1)):\n sum1 += nums1[p1]\n p1 += 1\n\n while(p2 < len(nums2)):\n sum2 += nums2[p2]\n p2 += 1\n\n return (result + max(sum1 , sum2)) % (10**9 + 7)\n```\nPlease upvote if you like my solution | 6 | You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts.
You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid.
The **happiness** of each person is calculated as follows:
* Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert).
* Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert).
Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell.
The **grid happiness** is the **sum** of each person's happiness. Return _the **maximum possible grid happiness**._
**Example 1:**
**Input:** m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
**Output:** 240
**Explanation:** Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 \* 30) (0 neighbors) = 120
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
The grid happiness is 120 + 60 + 60 = 240.
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
**Example 2:**
**Input:** m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
**Output:** 260
**Explanation:** Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 \* 20) (2 neighbors) = 80
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
The grid happiness is 90 + 80 + 90 = 260.
**Example 3:**
**Input:** m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
**Output:** 240
**Constraints:**
* `1 <= m, n <= 5`
* `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)` | Partition the array by common integers, and choose the path with larger sum with a DP technique. |
prefix sum | get-the-maximum-score | 0 | 1 | # Code\n```\nclass Solution:\n def maxSum(self, nums1: List[int], nums2: List[int]) -> int:\n MOD = 10 ** 9 + 7\n num2idx1 = {num: i for i, num in enumerate(nums1)}\n num2idx2 = {num: i for i, num in enumerate(nums2)}\n pre1 = []\n cs = 0\n for num in nums1:\n cs += num\n pre1.append(cs)\n pre2 = []\n cs = 0\n for num in nums2:\n cs += num\n pre2.append(cs)\n\n common = [num for num in nums1 if num in num2idx2]\n if not common:\n return max(pre1[-1], pre2[-1])\n \n res = max(pre1[num2idx1[common[0]]], pre2[num2idx2[common[0]]])\n res += max(pre1[-1] - pre1[num2idx1[common[-1]]], pre2[-1] - pre2[num2idx2[common[-1]]])\n for i in range(1, len(common)):\n s1 = pre1[num2idx1[common[i]]] - pre1[num2idx1[common[i - 1]]]\n s2 = pre2[num2idx2[common[i]]] - pre2[num2idx2[common[i - 1]]]\n res += max(s1, s2)\n return res % MOD\n\n\n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
prefix sum | get-the-maximum-score | 0 | 1 | # Code\n```\nclass Solution:\n def maxSum(self, nums1: List[int], nums2: List[int]) -> int:\n MOD = 10 ** 9 + 7\n num2idx1 = {num: i for i, num in enumerate(nums1)}\n num2idx2 = {num: i for i, num in enumerate(nums2)}\n pre1 = []\n cs = 0\n for num in nums1:\n cs += num\n pre1.append(cs)\n pre2 = []\n cs = 0\n for num in nums2:\n cs += num\n pre2.append(cs)\n\n common = [num for num in nums1 if num in num2idx2]\n if not common:\n return max(pre1[-1], pre2[-1])\n \n res = max(pre1[num2idx1[common[0]]], pre2[num2idx2[common[0]]])\n res += max(pre1[-1] - pre1[num2idx1[common[-1]]], pre2[-1] - pre2[num2idx2[common[-1]]])\n for i in range(1, len(common)):\n s1 = pre1[num2idx1[common[i]]] - pre1[num2idx1[common[i - 1]]]\n s2 = pre2[num2idx2[common[i]]] - pre2[num2idx2[common[i - 1]]]\n res += max(s1, s2)\n return res % MOD\n\n\n``` | 0 | You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts.
You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid.
The **happiness** of each person is calculated as follows:
* Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert).
* Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert).
Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell.
The **grid happiness** is the **sum** of each person's happiness. Return _the **maximum possible grid happiness**._
**Example 1:**
**Input:** m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
**Output:** 240
**Explanation:** Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 \* 30) (0 neighbors) = 120
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
The grid happiness is 120 + 60 + 60 = 240.
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
**Example 2:**
**Input:** m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
**Output:** 260
**Explanation:** Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 \* 20) (2 neighbors) = 80
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
The grid happiness is 90 + 80 + 90 = 260.
**Example 3:**
**Input:** m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
**Output:** 240
**Constraints:**
* `1 <= m, n <= 5`
* `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)` | Partition the array by common integers, and choose the path with larger sum with a DP technique. |
Python Solution using Two Pointer in O(n+m) and O(1) | get-the-maximum-score | 0 | 1 | # Code\n```\nclass Solution:\n def maxSum(self, nums1: List[int], nums2: List[int]) -> int:\n i=j=0\n ans=0\n mod=int(1e9+7)\n while(i<len(nums1) or j<len(nums2)):\n c1=c2=0\n while(i<len(nums1) and j<len(nums2) and nums1[i]!=nums2[j]):\n if(nums1[i]>nums2[j]):\n c2+=nums2[j]\n j+=1\n else:\n c1+=nums1[i]\n i+=1\n if(i>=len(nums1) or j>=len(nums2)):\n while(i<len(nums1)):\n c1+=nums1[i]\n i+=1\n while(j<len(nums2)):\n c2+=nums2[j]\n j+=1\n else:\n c1+=nums1[i]\n c2+=nums2[j]\n ans+=max(c1,c2)\n ans%=mod\n i+=1\n j+=1\n return ans\n \n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
Python Solution using Two Pointer in O(n+m) and O(1) | get-the-maximum-score | 0 | 1 | # Code\n```\nclass Solution:\n def maxSum(self, nums1: List[int], nums2: List[int]) -> int:\n i=j=0\n ans=0\n mod=int(1e9+7)\n while(i<len(nums1) or j<len(nums2)):\n c1=c2=0\n while(i<len(nums1) and j<len(nums2) and nums1[i]!=nums2[j]):\n if(nums1[i]>nums2[j]):\n c2+=nums2[j]\n j+=1\n else:\n c1+=nums1[i]\n i+=1\n if(i>=len(nums1) or j>=len(nums2)):\n while(i<len(nums1)):\n c1+=nums1[i]\n i+=1\n while(j<len(nums2)):\n c2+=nums2[j]\n j+=1\n else:\n c1+=nums1[i]\n c2+=nums2[j]\n ans+=max(c1,c2)\n ans%=mod\n i+=1\n j+=1\n return ans\n \n``` | 0 | You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts.
You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid.
The **happiness** of each person is calculated as follows:
* Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert).
* Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert).
Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell.
The **grid happiness** is the **sum** of each person's happiness. Return _the **maximum possible grid happiness**._
**Example 1:**
**Input:** m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
**Output:** 240
**Explanation:** Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 \* 30) (0 neighbors) = 120
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
The grid happiness is 120 + 60 + 60 = 240.
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
**Example 2:**
**Input:** m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
**Output:** 260
**Explanation:** Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 \* 20) (2 neighbors) = 80
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
The grid happiness is 90 + 80 + 90 = 260.
**Example 3:**
**Input:** m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
**Output:** 240
**Constraints:**
* `1 <= m, n <= 5`
* `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)` | Partition the array by common integers, and choose the path with larger sum with a DP technique. |
1539. Kth Missing Positive Number | Simple Solution | kth-missing-positive-number | 0 | 1 | # Intuition\nWe are asked to find the missing smallest positive integer. We can use binary search to find the index of the smallest element which has k missing elements before it. If the element arr[middle] at index middle has p missing elements before it, we can get the number of missing elements before arr[middle+1] as q = arr[middle+1] - arr[middle] - 1 - p. If q >= k, then the required element lies between arr[middle] and arr[middle+1]. Otherwise, the required element lies after arr[middle+1].\n\n# Approach\n1. Set left and right as the first and the last index of the array, respectively.\n2. In each iteration of the loop, find the index middle as the average of left and right.\n3. Find the number of missing elements p before the element arr[middle] using p = arr[middle] - middle - 1.\n4. If p < k, update left = middle+1 and reduce k by p.\n5. Otherwise, update right = middle.\n6. Repeat steps 2-5 until left >= right.\n7. Return left + k as the k-th missing element.\n\n# Complexity\n- Time complexity: **O(log n)**, where n is the length of the given array. This is because we are performing binary search to find the index of the k-th missing element.\n\n- Space complexity: **O(1)**, as we are not using any extra space.\n\n# Code\n``` python []\nclass Solution:\n # O(log(n)) time | O(1) space\n def findKthPositive(self, arr: List[int], k: int) -> int:\n left = 0\n right = len(arr)\n while left < right:\n middle = (left + right) // 2\n if arr[middle] - middle - 1 < k:\n left = middle + 1\n else:\n right = middle\n return left + k\n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
1539. Kth Missing Positive Number | Simple Solution | kth-missing-positive-number | 0 | 1 | # Intuition\nWe are asked to find the missing smallest positive integer. We can use binary search to find the index of the smallest element which has k missing elements before it. If the element arr[middle] at index middle has p missing elements before it, we can get the number of missing elements before arr[middle+1] as q = arr[middle+1] - arr[middle] - 1 - p. If q >= k, then the required element lies between arr[middle] and arr[middle+1]. Otherwise, the required element lies after arr[middle+1].\n\n# Approach\n1. Set left and right as the first and the last index of the array, respectively.\n2. In each iteration of the loop, find the index middle as the average of left and right.\n3. Find the number of missing elements p before the element arr[middle] using p = arr[middle] - middle - 1.\n4. If p < k, update left = middle+1 and reduce k by p.\n5. Otherwise, update right = middle.\n6. Repeat steps 2-5 until left >= right.\n7. Return left + k as the k-th missing element.\n\n# Complexity\n- Time complexity: **O(log n)**, where n is the length of the given array. This is because we are performing binary search to find the index of the k-th missing element.\n\n- Space complexity: **O(1)**, as we are not using any extra space.\n\n# Code\n``` python []\nclass Solution:\n # O(log(n)) time | O(1) space\n def findKthPositive(self, arr: List[int], k: int) -> int:\n left = 0\n right = len(arr)\n while left < right:\n middle = (left + right) // 2\n if arr[middle] - middle - 1 < k:\n left = middle + 1\n else:\n right = middle\n return left + k\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Easy Understanding Python Solution | kth-missing-positive-number | 0 | 1 | Beats 60% of other solutions.\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n a= 0\n b=len(arr)-1\n while a <= b:\n m= a+(b-a)//2\n if arr[m]-m-1 < k:\n a = m+1\n else:\n b = m-1\n return a+k | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
Easy Understanding Python Solution | kth-missing-positive-number | 0 | 1 | Beats 60% of other solutions.\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n a= 0\n b=len(arr)-1\n while a <= b:\n m= a+(b-a)//2\n if arr[m]-m-1 < k:\n a = m+1\n else:\n b = m-1\n return a+k | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
✅Pyhhon3 easiest solution🔥🔥 | kth-missing-positive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Binary search**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- setup counter to 0, and increment at first in while loop.\n- now find position of current counter value.\n- given array is sorted so we can find index of element using binary search.\n- find index of current counter, if not -1 then continue.\n- else if index == -1 then decrement k by 1 and move further.\n- now when k becoms 0 at that time our counter value will be answer.\n- return counter\n\n# Complexity\n- Time complexity: O(Nlog(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n counter = 0\n def binarySearch(k=-1):\n left = 0\n right = len(arr) - 1\n while left <= right:\n mid = (left+right) // 2\n if arr[mid] == k:\n return left+mid\n elif arr[mid] < k:\n left = mid+1\n else:\n right = mid - 1\n return -1\n\n while k:\n counter += 1\n index = binarySearch(counter)\n if not (index+ 1):\n k -= 1\n return counter\n```\n# Please like and comment below :-) | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
✅Pyhhon3 easiest solution🔥🔥 | kth-missing-positive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Binary search**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- setup counter to 0, and increment at first in while loop.\n- now find position of current counter value.\n- given array is sorted so we can find index of element using binary search.\n- find index of current counter, if not -1 then continue.\n- else if index == -1 then decrement k by 1 and move further.\n- now when k becoms 0 at that time our counter value will be answer.\n- return counter\n\n# Complexity\n- Time complexity: O(Nlog(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n counter = 0\n def binarySearch(k=-1):\n left = 0\n right = len(arr) - 1\n while left <= right:\n mid = (left+right) // 2\n if arr[mid] == k:\n return left+mid\n elif arr[mid] < k:\n left = mid+1\n else:\n right = mid - 1\n return -1\n\n while k:\n counter += 1\n index = binarySearch(counter)\n if not (index+ 1):\n k -= 1\n return counter\n```\n# Please like and comment below :-) | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Awesome To Unveil Logic--->Python3 | kth-missing-positive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n list1=[]\n for i in range(1,2001):\n list1.append(i)\n for j in arr:\n if j in list1:\n list1.remove(j)\n return list1[k-1]\n#please upvote me it would encourage me alot\n\n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
Awesome To Unveil Logic--->Python3 | kth-missing-positive-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n list1=[]\n for i in range(1,2001):\n list1.append(i)\n for j in arr:\n if j in list1:\n list1.remove(j)\n return list1[k-1]\n#please upvote me it would encourage me alot\n\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Python3 | kth-missing-positive-number | 0 | 1 | # Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n a = [0] * len(arr)\n a[0] = arr[0] - 1\n\n for i in range(1, len(arr)):\n a[i] = a[i - 1] + (arr[i] - arr[i-1] - 1)\n \n idx = bisect_left(a, k)\n\n return arr[idx - 1] + (k - a[idx - 1]) if idx > 0 else k\n \n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
Python3 | kth-missing-positive-number | 0 | 1 | # Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n a = [0] * len(arr)\n a[0] = arr[0] - 1\n\n for i in range(1, len(arr)):\n a[i] = a[i - 1] + (arr[i] - arr[i-1] - 1)\n \n idx = bisect_left(a, k)\n\n return arr[idx - 1] + (k - a[idx - 1]) if idx > 0 else k\n \n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
🖋Simple Binary Search | 💣Beats 87% | 😎Understand able by NOOBS... | kth-missing-positive-number | 0 | 1 | # Intuition\n Binary search is the best way...\n Use of single WHILE loop!!!\n> Understand able by NOOBS!!!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Best approach by minimum time complaxity...\n Beats 87% as minimum!!!\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 19ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 15mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def findKthPositive(self, arr, k):\n low=0\n high=len(arr)-1\n \n while(low<=high):\n mid=(low+high)//2\n \n if(arr[mid]-(mid+1)<k):\n low=mid+1\n else:\n high=mid-1\n \n return (low+k)\n \n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
🖋Simple Binary Search | 💣Beats 87% | 😎Understand able by NOOBS... | kth-missing-positive-number | 0 | 1 | # Intuition\n Binary search is the best way...\n Use of single WHILE loop!!!\n> Understand able by NOOBS!!!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Best approach by minimum time complaxity...\n Beats 87% as minimum!!!\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 19ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 15mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def findKthPositive(self, arr, k):\n low=0\n high=len(arr)-1\n \n while(low<=high):\n mid=(low+high)//2\n \n if(arr[mid]-(mid+1)<k):\n low=mid+1\n else:\n high=mid-1\n \n return (low+k)\n \n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Simple 🐍python code for beginners😀 | kth-missing-positive-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n i = 1\n while k>0:\n if i not in arr:\n k-=1\n i+=1\n return i-1\n \n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
Simple 🐍python code for beginners😀 | kth-missing-positive-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n i = 1\n while k>0:\n if i not in arr:\n k-=1\n i+=1\n return i-1\n \n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Python3 2 liner solution | kth-missing-positive-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n ans=[i for i in range(1,max(arr)+k+1) if i not in arr]\n return ans[k-1]\n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
Python3 2 liner solution | kth-missing-positive-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findKthPositive(self, arr: List[int], k: int) -> int:\n ans=[i for i in range(1,max(arr)+k+1) if i not in arr]\n return ans[k-1]\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Python| Fastest solution in python 100% | kth-missing-positive-number | 0 | 1 | # Code\n```\nclass Solution:\n def findKthPositive(self, arr: list[int], k: int) -> int:\n if k - (arr[-1] - len(arr)) > 0:\n return arr[-1] + k - (arr[-1] - len(arr))\n l, res = 1, []\n for i in arr:\n if i > l:\n res += [i for i in range(l,i)]\n l = i+1\n elif i == l:\n l = i + 1\n return res[k-1]\n``` | 1 | Given an array `arr` of positive integers sorted in a **strictly increasing order**, and an integer `k`.
Return _the_ `kth` _**positive** integer that is **missing** from this array._
**Example 1:**
**Input:** arr = \[2,3,4,7,11\], k = 5
**Output:** 9
**Explanation:** The missing positive integers are \[1,5,6,8,9,10,12,13,...\]. The 5th missing positive integer is 9.
**Example 2:**
**Input:** arr = \[1,2,3,4\], k = 2
**Output:** 6
**Explanation:** The missing positive integers are \[5,6,7,...\]. The 2nd missing positive integer is 6.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000`
* `1 <= k <= 1000`
* `arr[i] < arr[j]` for `1 <= i < j <= arr.length`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | Notice that numbers with equal sums of row and column indexes belong to the same diagonal. Store them in tuples (sum, row, val), sort them, and then regroup the answer. |
Python| Fastest solution in python 100% | kth-missing-positive-number | 0 | 1 | # Code\n```\nclass Solution:\n def findKthPositive(self, arr: list[int], k: int) -> int:\n if k - (arr[-1] - len(arr)) > 0:\n return arr[-1] + k - (arr[-1] - len(arr))\n l, res = 1, []\n for i in arr:\n if i > l:\n res += [i for i in range(l,i)]\n l = i+1\n elif i == l:\n l = i + 1\n return res[k-1]\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
✔ Python3 Solution | O(N) | can-convert-string-in-k-moves | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def canConvertString(self, s, t, k):\n if len(s) != len(t): return False\n dp = [-1] * 27\n for a, b in zip(s, t):\n n = ord(b) - ord(a)\n dp[n if n >= 0 else 26 + n] += 1\n return all([dp[i] <= (k - i) // 26 for i in range(1, 27)])\n``` | 1 | Given two strings `s` and `t`, your goal is to convert `s` into `t` in `k` moves or less.
During the `ith` (`1 <= i <= k`) move you can:
* Choose any index `j` (1-indexed) from `s`, such that `1 <= j <= s.length` and `j` has not been chosen in any previous move, and shift the character at that index `i` times.
* Do nothing.
Shifting a character means replacing it by the next letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Shifting a character by `i` means applying the shift operations `i` times.
Remember that any index `j` can be picked at most once.
Return `true` if it's possible to convert `s` into `t` in no more than `k` moves, otherwise return `false`.
**Example 1:**
**Input:** s = "input ", t = "ouput ", k = 9
**Output:** true
**Explanation:** In the 6th move, we shift 'i' 6 times to get 'o'. And in the 7th move we shift 'n' to get 'u'.
**Example 2:**
**Input:** s = "abc ", t = "bcd ", k = 10
**Output:** false
**Explanation:** We need to shift each character in s one time to convert it into t. We can shift 'a' to 'b' during the 1st move. However, there is no way to shift the other characters in the remaining moves to obtain t from s.
**Example 3:**
**Input:** s = "aab ", t = "bbb ", k = 27
**Output:** true
**Explanation:** In the 1st move, we shift the first 'a' 1 time to get 'b'. In the 27th move, we shift the second 'a' 27 times to get 'b'.
**Constraints:**
* `1 <= s.length, t.length <= 10^5`
* `0 <= k <= 10^9`
* `s`, `t` contain only lowercase English letters. | null |
✔ Python3 Solution | O(N) | can-convert-string-in-k-moves | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def canConvertString(self, s, t, k):\n if len(s) != len(t): return False\n dp = [-1] * 27\n for a, b in zip(s, t):\n n = ord(b) - ord(a)\n dp[n if n >= 0 else 26 + n] += 1\n return all([dp[i] <= (k - i) // 26 for i in range(1, 27)])\n``` | 1 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
📌📌 Detailed Explanation || Well-Coded || 92% faster 🐍 | can-convert-string-in-k-moves | 0 | 1 | ## IDEA :\n* First we need to calculate the difference of the conversion. for example conversion from `a to b` will have difference of 1.\n* Then we hold a dictiomary (hash map) diff to see how many times we want to convert each difference.\n\n* For example to go from `"aa" to "bb"` we want to go difference 1 for 2 times.\n* This is possible only if we will have k of 27 or above, because to go from a to b we need 1, and each loop starts at 26 (alphabet count).\n\n****\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n\t\tdef canConvertString(self, s: str, t: str, k: int) -> bool:\n\n\t\t\tif len(s)!=len(t):\n\t\t\t\treturn False\n\n\t\t\tdic = defaultdict(int)\n\t\t\tfor a,b in zip(s,t):\n\t\t\t\tif a!=b:\n\t\t\t\t\tif ord(b)>ord(a):\n\t\t\t\t\t\tdiff = ord(b)-ord(a)\n\t\t\t\t\telse:\n\t\t\t\t\t\tdiff = (26-ord(a)+ord(b))\n\n\t\t\t\t\tn = dic[diff]*26 + diff\n\t\t\t\t\tif n>k:\n\t\t\t\t\t\treturn False\n\t\t\t\t\tdic[diff]+=1\n\n\t\t\treturn True\n\n### Explanation :\n\n**Dict Storing Difference as key and value as frequency of that shift require to convert all char with same difference to respective char in \'t\'.**\nExample \n\'\'\'\n\n\ts=abc t=bcd , we require 1 shift three times.So key=1 val=3.\n\n\n**Now for a particular key, we require maximum `26*(val)+diff` number if we want to convert all char with same difference(key) to valid char in \'t\'.**\nExample :\n\'\'\'\n\n\ts = abc t =bcd we require number 1,27,53 to convert s to t.\n\n\n\t\t\t\n**Thanks and Upvote if you got any help or like the Idea !!** \uD83E\uDD1E | 3 | Given two strings `s` and `t`, your goal is to convert `s` into `t` in `k` moves or less.
During the `ith` (`1 <= i <= k`) move you can:
* Choose any index `j` (1-indexed) from `s`, such that `1 <= j <= s.length` and `j` has not been chosen in any previous move, and shift the character at that index `i` times.
* Do nothing.
Shifting a character means replacing it by the next letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Shifting a character by `i` means applying the shift operations `i` times.
Remember that any index `j` can be picked at most once.
Return `true` if it's possible to convert `s` into `t` in no more than `k` moves, otherwise return `false`.
**Example 1:**
**Input:** s = "input ", t = "ouput ", k = 9
**Output:** true
**Explanation:** In the 6th move, we shift 'i' 6 times to get 'o'. And in the 7th move we shift 'n' to get 'u'.
**Example 2:**
**Input:** s = "abc ", t = "bcd ", k = 10
**Output:** false
**Explanation:** We need to shift each character in s one time to convert it into t. We can shift 'a' to 'b' during the 1st move. However, there is no way to shift the other characters in the remaining moves to obtain t from s.
**Example 3:**
**Input:** s = "aab ", t = "bbb ", k = 27
**Output:** true
**Explanation:** In the 1st move, we shift the first 'a' 1 time to get 'b'. In the 27th move, we shift the second 'a' 27 times to get 'b'.
**Constraints:**
* `1 <= s.length, t.length <= 10^5`
* `0 <= k <= 10^9`
* `s`, `t` contain only lowercase English letters. | null |
📌📌 Detailed Explanation || Well-Coded || 92% faster 🐍 | can-convert-string-in-k-moves | 0 | 1 | ## IDEA :\n* First we need to calculate the difference of the conversion. for example conversion from `a to b` will have difference of 1.\n* Then we hold a dictiomary (hash map) diff to see how many times we want to convert each difference.\n\n* For example to go from `"aa" to "bb"` we want to go difference 1 for 2 times.\n* This is possible only if we will have k of 27 or above, because to go from a to b we need 1, and each loop starts at 26 (alphabet count).\n\n****\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n\t\tdef canConvertString(self, s: str, t: str, k: int) -> bool:\n\n\t\t\tif len(s)!=len(t):\n\t\t\t\treturn False\n\n\t\t\tdic = defaultdict(int)\n\t\t\tfor a,b in zip(s,t):\n\t\t\t\tif a!=b:\n\t\t\t\t\tif ord(b)>ord(a):\n\t\t\t\t\t\tdiff = ord(b)-ord(a)\n\t\t\t\t\telse:\n\t\t\t\t\t\tdiff = (26-ord(a)+ord(b))\n\n\t\t\t\t\tn = dic[diff]*26 + diff\n\t\t\t\t\tif n>k:\n\t\t\t\t\t\treturn False\n\t\t\t\t\tdic[diff]+=1\n\n\t\t\treturn True\n\n### Explanation :\n\n**Dict Storing Difference as key and value as frequency of that shift require to convert all char with same difference to respective char in \'t\'.**\nExample \n\'\'\'\n\n\ts=abc t=bcd , we require 1 shift three times.So key=1 val=3.\n\n\n**Now for a particular key, we require maximum `26*(val)+diff` number if we want to convert all char with same difference(key) to valid char in \'t\'.**\nExample :\n\'\'\'\n\n\ts = abc t =bcd we require number 1,27,53 to convert s to t.\n\n\n\t\t\t\n**Thanks and Upvote if you got any help or like the Idea !!** \uD83E\uDD1E | 3 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
Find the residue of modulo | can-convert-string-in-k-moves | 0 | 1 | # Approach\nif two strings have different length, can\'t convert s to t for all k.\nFind the modulo number of shifts by i and its upper bound for i = 1,2,...,25, meaning that do nothing for the residue\'s. \n\n# Complexity\n- Time complexity: O(n), n:length of s\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(26)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canConvertString(self, s: str, t: str, k: int) -> bool:\n if len(s) != len(t):\n return False\n \n k += 1\n L = [0] * 26\n T = [k // 26] * 26\n k %= 26\n\n for i in range(len(s)):\n L[ord(t[i])-ord(s[i])] += 1\n \n for i in range(k):\n T[i] += 1\n\n for i in range(1, 26):\n if L[i] > T[i]:\n return False\n \n return True\n\n``` | 0 | Given two strings `s` and `t`, your goal is to convert `s` into `t` in `k` moves or less.
During the `ith` (`1 <= i <= k`) move you can:
* Choose any index `j` (1-indexed) from `s`, such that `1 <= j <= s.length` and `j` has not been chosen in any previous move, and shift the character at that index `i` times.
* Do nothing.
Shifting a character means replacing it by the next letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Shifting a character by `i` means applying the shift operations `i` times.
Remember that any index `j` can be picked at most once.
Return `true` if it's possible to convert `s` into `t` in no more than `k` moves, otherwise return `false`.
**Example 1:**
**Input:** s = "input ", t = "ouput ", k = 9
**Output:** true
**Explanation:** In the 6th move, we shift 'i' 6 times to get 'o'. And in the 7th move we shift 'n' to get 'u'.
**Example 2:**
**Input:** s = "abc ", t = "bcd ", k = 10
**Output:** false
**Explanation:** We need to shift each character in s one time to convert it into t. We can shift 'a' to 'b' during the 1st move. However, there is no way to shift the other characters in the remaining moves to obtain t from s.
**Example 3:**
**Input:** s = "aab ", t = "bbb ", k = 27
**Output:** true
**Explanation:** In the 1st move, we shift the first 'a' 1 time to get 'b'. In the 27th move, we shift the second 'a' 27 times to get 'b'.
**Constraints:**
* `1 <= s.length, t.length <= 10^5`
* `0 <= k <= 10^9`
* `s`, `t` contain only lowercase English letters. | null |
Find the residue of modulo | can-convert-string-in-k-moves | 0 | 1 | # Approach\nif two strings have different length, can\'t convert s to t for all k.\nFind the modulo number of shifts by i and its upper bound for i = 1,2,...,25, meaning that do nothing for the residue\'s. \n\n# Complexity\n- Time complexity: O(n), n:length of s\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(26)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canConvertString(self, s: str, t: str, k: int) -> bool:\n if len(s) != len(t):\n return False\n \n k += 1\n L = [0] * 26\n T = [k // 26] * 26\n k %= 26\n\n for i in range(len(s)):\n L[ord(t[i])-ord(s[i])] += 1\n \n for i in range(k):\n T[i] += 1\n\n for i in range(1, 26):\n if L[i] > T[i]:\n return False\n \n return True\n\n``` | 0 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
[Python] 💡 Simple and Fast | Time O(n) | Space O(1) | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # \uD83D\uDCA1 Idea\n\n* Record the number of \'(\' in an open bracket count int. \n* If there is a \'))\' or a \') \'then open bracket count -= 1\n* If there is a \'))\' or a \') and open bracket count = 0 an \'(\' must be inserted\n* If there is a single \')\' another \')\' must be inserted\n* At the end of the program and if open bracket count >0 then an \'))\' must be added for each unmatched \'(\'\n\n---\n\n# \uD83D\uDCD1Overview\n* Solution 1: Time O(n), Space O(n) - String Replace <code style="background-color: Green; color: white;">Easy</code>\n* Solution 2: Time O(n), Space O(1) - Case by Case <code style="background-color: OrangeRed; color: white;">Medium</code>\n\n\n---\n\n\n# \uD83C\uDFAFSolution 1: Simple String Replace <code style="background-color: Green; color: white;">Easy</code>\n\n\n## Tricks\n\n* Go through string replacing \'))\' with \'}\'\n* This allows for easy differentiation between \')\' \'))\' when iterating through the input string\n* This makes checking the above conditions a breeze \n\n## Examples\n**Example 1:**\n```\nInput: s = "(()))"\nUsing \'{\' trick\nInput: s = "((})"\n\nVery easy to see the problem running through the string one character at a time\nCase 1: Starting \'(\' has only one \')\' --> add 1\nOutput: 1\n```\n\n**Example 2:**\n```\nInput: s = "))())("\nUsing \'{\' trick\nInput: s = "}(}("\n\nCase 2: Starting \'}\' with no matching \'(\' --> add 1\nCase 3: Ending \'(\' with no maching \'}\' --> add 2\nOutput: 3\n```\n\n**Example 3:**\n```\nInput: s = ")))))))"\nUsing \'{\' trick\nInput: s= "}}} )"\n\nCase 2: \'}\' with no matching \'(\' --> add 1 x (3 times) \nCase 3: \')\' with no matching \'(\' or trailing \')\' --> add 2\n\nOutput: 5\n\n* Case 2 happens 3 times since there are three "}}}"\n* Case 3: we automatically know there is not trailing a \')\' becuase if there were the character would be a \'}\' instead\n```\n\nExamples 1-3 cover all the cases of mismatching brackets there are! You should be ready to try coding a solution :) \n\n## Code\n\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n \n s = s.replace(\'))\', \'}\')\n missing_brackets = 0\n required_closed = 0\n\n for c in s:\n\n # Open Bracket Condition\n if c == \'(\':\n required_closed += 2\n \n # Closed Bracket Condition \n else:\n\t\t\t\n # Case: \')\' \n # Requires additional \')\' \n if c == \')\': \n missing_brackets += 1\n\n # Case: Matching ( for ) or ))\n if required_closed:\n required_closed -= 2\n\n\n # Case: Unmatched ) or ))\n # Need to insert ( to balance string\n else:\n missing_brackets += 1\n\n return missing_brackets + required_closed\n```\n\n---\n\n# \uD83C\uDFAF Solution 2: Case by Case <code style="background-color: OrangeRed; color: white;">Medium</code>\n\n## Implementation\n\n* Implement a boolean that can track \'))\' in O(1) space\n* Update logic from Solution 1 \n\n## Code \n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n \n # Missing \')\' to make valid pair\n missing_closed = 0 \n\n # Required \'(\' to make valid pair\n required_open = 0\n\n # Required \')\' to make valid pair\n required_closed = 0\n\n # Track \'))\' cases \n prev_closed = 0\n\n\n for c in s:\n\n # Open Bracket Condition\n if c == \'(\':\n\n # Failed to make valid pair \n #\')\' Brackets are considered missing and cannot be made valid by subsequent brackets\n # Case: () (\n if required_closed % 2 == 1: \n missing_closed += 1 \n required_closed -= 1\n\n required_closed += 2\n prev_closed = False\n \n # Closed Bracket Condition \n else:\n\n # Match ( with )\n if required_closed:\n required_closed -= 1\n\n # Unmatched ))\n elif prev_closed:\n required_closed -= 1\n\n # Unmatched )\n else:\n required_open += 1\n required_closed += 1\n\n # Bool to track \'))\' \n prev_closed = not prev_closed\n\n return required_open + required_closed + missing_closed\n```\n\nLike if this helped!\nCheers,\nArgent \n | 87 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
[Python] 💡 Simple and Fast | Time O(n) | Space O(1) | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # \uD83D\uDCA1 Idea\n\n* Record the number of \'(\' in an open bracket count int. \n* If there is a \'))\' or a \') \'then open bracket count -= 1\n* If there is a \'))\' or a \') and open bracket count = 0 an \'(\' must be inserted\n* If there is a single \')\' another \')\' must be inserted\n* At the end of the program and if open bracket count >0 then an \'))\' must be added for each unmatched \'(\'\n\n---\n\n# \uD83D\uDCD1Overview\n* Solution 1: Time O(n), Space O(n) - String Replace <code style="background-color: Green; color: white;">Easy</code>\n* Solution 2: Time O(n), Space O(1) - Case by Case <code style="background-color: OrangeRed; color: white;">Medium</code>\n\n\n---\n\n\n# \uD83C\uDFAFSolution 1: Simple String Replace <code style="background-color: Green; color: white;">Easy</code>\n\n\n## Tricks\n\n* Go through string replacing \'))\' with \'}\'\n* This allows for easy differentiation between \')\' \'))\' when iterating through the input string\n* This makes checking the above conditions a breeze \n\n## Examples\n**Example 1:**\n```\nInput: s = "(()))"\nUsing \'{\' trick\nInput: s = "((})"\n\nVery easy to see the problem running through the string one character at a time\nCase 1: Starting \'(\' has only one \')\' --> add 1\nOutput: 1\n```\n\n**Example 2:**\n```\nInput: s = "))())("\nUsing \'{\' trick\nInput: s = "}(}("\n\nCase 2: Starting \'}\' with no matching \'(\' --> add 1\nCase 3: Ending \'(\' with no maching \'}\' --> add 2\nOutput: 3\n```\n\n**Example 3:**\n```\nInput: s = ")))))))"\nUsing \'{\' trick\nInput: s= "}}} )"\n\nCase 2: \'}\' with no matching \'(\' --> add 1 x (3 times) \nCase 3: \')\' with no matching \'(\' or trailing \')\' --> add 2\n\nOutput: 5\n\n* Case 2 happens 3 times since there are three "}}}"\n* Case 3: we automatically know there is not trailing a \')\' becuase if there were the character would be a \'}\' instead\n```\n\nExamples 1-3 cover all the cases of mismatching brackets there are! You should be ready to try coding a solution :) \n\n## Code\n\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n \n s = s.replace(\'))\', \'}\')\n missing_brackets = 0\n required_closed = 0\n\n for c in s:\n\n # Open Bracket Condition\n if c == \'(\':\n required_closed += 2\n \n # Closed Bracket Condition \n else:\n\t\t\t\n # Case: \')\' \n # Requires additional \')\' \n if c == \')\': \n missing_brackets += 1\n\n # Case: Matching ( for ) or ))\n if required_closed:\n required_closed -= 2\n\n\n # Case: Unmatched ) or ))\n # Need to insert ( to balance string\n else:\n missing_brackets += 1\n\n return missing_brackets + required_closed\n```\n\n---\n\n# \uD83C\uDFAF Solution 2: Case by Case <code style="background-color: OrangeRed; color: white;">Medium</code>\n\n## Implementation\n\n* Implement a boolean that can track \'))\' in O(1) space\n* Update logic from Solution 1 \n\n## Code \n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n \n # Missing \')\' to make valid pair\n missing_closed = 0 \n\n # Required \'(\' to make valid pair\n required_open = 0\n\n # Required \')\' to make valid pair\n required_closed = 0\n\n # Track \'))\' cases \n prev_closed = 0\n\n\n for c in s:\n\n # Open Bracket Condition\n if c == \'(\':\n\n # Failed to make valid pair \n #\')\' Brackets are considered missing and cannot be made valid by subsequent brackets\n # Case: () (\n if required_closed % 2 == 1: \n missing_closed += 1 \n required_closed -= 1\n\n required_closed += 2\n prev_closed = False\n \n # Closed Bracket Condition \n else:\n\n # Match ( with )\n if required_closed:\n required_closed -= 1\n\n # Unmatched ))\n elif prev_closed:\n required_closed -= 1\n\n # Unmatched )\n else:\n required_open += 1\n required_closed += 1\n\n # Bool to track \'))\' \n prev_closed = not prev_closed\n\n return required_open + required_closed + missing_closed\n```\n\nLike if this helped!\nCheers,\nArgent \n | 87 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
Python+ detailed explanation | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhile seeing parentheses problem, using stack is my intuition.\nres: record the number of times making insertion\nidx: pointer on s\nstk: store left parenthese\n\nIn this case, if we meet \'(\', just append left parenthese into stack.\nIf we meet one \')\', there is three cases:\n1. nothing in stack. So we need to insert one left parenthese into stack, in order to match right parenthese. So res += 1\n2. \'(\' in stack, also, the next char in s is also a \')\'. Thus, now we have a valid right parenthese. We just need to update the index pointer, and pop the topmost left paren from stack\n3. \'(\' in stack, also, the next char in s is not a \')\'. So we need to add one more \')\' to construct a valid right parenthese. After adding right paren, now we can pop left paren from stack\n\nwhy res += len(stk) * 2?\nAfter traversing s completely, if there are remaining left parentheses, it means there are left parenthese having no matching right parenthese. So we have to add len(stk) * 2 to res.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n stk = list()\n res = 0\n idx = 0\n while (idx < len(s)):\n c = s[idx]\n if (c == \'(\'):\n stk.append(c)\n else: # \u5982\u679C\u662Fright paren\n # Fill in left parenthesis\n if (not stk): # \u5982\u679C\u6CA1\u6709left paren\u5728stack\n res += 1 \n stk.append(\'(\')\n \n # Paired right parenthesis.\n if (idx < len(s) - 1 and s[idx + 1] == \')\'):\n idx += 1\n stk.pop()\n \n # Unpaired right parenthesis.\n else:\n res += 1\n stk.pop()\n \n idx += 1\n \n # Calculate unpaired left parenthesis.\n res += len(stk) * 2\n return res\n \n # # res \u8BB0\u5F55\u63D2\u5165\u6B21\u6570\n # # need \u53D8\u91CF\u8BB0\u5F55\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u91CF\n # need, res = 0, 0\n\n # for i in range(len(s)):\n # if s[i] == \'(\':\n # need += 2\n # # \u5F53\u9047\u5230\u5DE6\u62EC\u53F7\u65F6\uFF0C\u82E5\u5BF9\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u91CF\u4E3A\u5947\u6570\uFF0C\u9700\u8981\u63D2\u5165 1 \u4E2A\u53F3\u62EC\u53F7\u3002\n # # \u56E0\u4E3A\u4E00\u4E2A\u5DE6\u62EC\u53F7\u9700\u8981\u4E24\u4E2A\u53F3\u62EC\u53F7\u561B\uFF0C\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u5FC5\u987B\u662F\u5076\u6570\n # if need %2 == 1:\n # # \u63D2\u5165\u4E00\u4E2A\u53F3\u62EC\u53F7\n # res += 1\n # # \u5BF9\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u51CF\u4E00\n # need -= 1\n\n # elif s[i] == \')\':\n # need -= 1\n # # \u8BF4\u660E\u53F3\u62EC\u53F7\u592A\u591A\u4E86\n # if need == -1:\n # # \u9700\u8981\u63D2\u5165\u4E00\u4E2A\u5DE6\u62EC\u53F7\n # res += 1\n # # \u540C\u65F6\uFF0C\u5BF9\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u53D8\u4E3A 1\n # # -1 -> 1 # \u76F8\u5F53\u4E8E\u662Fadd 2 to need\n # need = 1\n # return need + res\n\n\n \n \n``` | 1 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
Python+ detailed explanation | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhile seeing parentheses problem, using stack is my intuition.\nres: record the number of times making insertion\nidx: pointer on s\nstk: store left parenthese\n\nIn this case, if we meet \'(\', just append left parenthese into stack.\nIf we meet one \')\', there is three cases:\n1. nothing in stack. So we need to insert one left parenthese into stack, in order to match right parenthese. So res += 1\n2. \'(\' in stack, also, the next char in s is also a \')\'. Thus, now we have a valid right parenthese. We just need to update the index pointer, and pop the topmost left paren from stack\n3. \'(\' in stack, also, the next char in s is not a \')\'. So we need to add one more \')\' to construct a valid right parenthese. After adding right paren, now we can pop left paren from stack\n\nwhy res += len(stk) * 2?\nAfter traversing s completely, if there are remaining left parentheses, it means there are left parenthese having no matching right parenthese. So we have to add len(stk) * 2 to res.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n stk = list()\n res = 0\n idx = 0\n while (idx < len(s)):\n c = s[idx]\n if (c == \'(\'):\n stk.append(c)\n else: # \u5982\u679C\u662Fright paren\n # Fill in left parenthesis\n if (not stk): # \u5982\u679C\u6CA1\u6709left paren\u5728stack\n res += 1 \n stk.append(\'(\')\n \n # Paired right parenthesis.\n if (idx < len(s) - 1 and s[idx + 1] == \')\'):\n idx += 1\n stk.pop()\n \n # Unpaired right parenthesis.\n else:\n res += 1\n stk.pop()\n \n idx += 1\n \n # Calculate unpaired left parenthesis.\n res += len(stk) * 2\n return res\n \n # # res \u8BB0\u5F55\u63D2\u5165\u6B21\u6570\n # # need \u53D8\u91CF\u8BB0\u5F55\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u91CF\n # need, res = 0, 0\n\n # for i in range(len(s)):\n # if s[i] == \'(\':\n # need += 2\n # # \u5F53\u9047\u5230\u5DE6\u62EC\u53F7\u65F6\uFF0C\u82E5\u5BF9\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u91CF\u4E3A\u5947\u6570\uFF0C\u9700\u8981\u63D2\u5165 1 \u4E2A\u53F3\u62EC\u53F7\u3002\n # # \u56E0\u4E3A\u4E00\u4E2A\u5DE6\u62EC\u53F7\u9700\u8981\u4E24\u4E2A\u53F3\u62EC\u53F7\u561B\uFF0C\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u5FC5\u987B\u662F\u5076\u6570\n # if need %2 == 1:\n # # \u63D2\u5165\u4E00\u4E2A\u53F3\u62EC\u53F7\n # res += 1\n # # \u5BF9\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u51CF\u4E00\n # need -= 1\n\n # elif s[i] == \')\':\n # need -= 1\n # # \u8BF4\u660E\u53F3\u62EC\u53F7\u592A\u591A\u4E86\n # if need == -1:\n # # \u9700\u8981\u63D2\u5165\u4E00\u4E2A\u5DE6\u62EC\u53F7\n # res += 1\n # # \u540C\u65F6\uFF0C\u5BF9\u53F3\u62EC\u53F7\u7684\u9700\u6C42\u53D8\u4E3A 1\n # # -1 -> 1 # \u76F8\u5F53\u4E8E\u662Fadd 2 to need\n # need = 1\n # return need + res\n\n\n \n \n``` | 1 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
[Python] Simple solution with detailed explanation | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | ```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n ## RC ##\n ## APPROACH : STACK ##\n ## LOGIC ##\n ## 1. Only 3 conditions, open brace -> push to stack\n ## 2. 2 close braces -> pop from stack, if you donot have enough open braces before increment count(indicates one open required)\n ## 3. Only 1 close brace found --> count + 1, to make it 2 close braces, if stack then just pop, if stack is empty then increment count by 2 (one for close brace, one for open brace)\n ## 4. If stack is still left with open braces, we require close braces = twice of that open braces in stack\n \n ## You can even optimize it, without using stack, just counting the left braces.\n \n\t\t## TIME COMPLEXITY : O(N) ##\n\t\t## SPACE COMPLEXITY : O(1) ##\n \n s += "$" # appending dummy character at the end, to make things simpler\n left_braces, count, i = 0, 0, 0\n while( i < len(s)-1 ):\n if s[i] == "(":\n left_braces, i = left_braces + 1, i + 1\n elif s[i] == ")" and s[i+1] == ")":\n if left_braces:\n left_braces -= 1\n else:\n count += 1 # one open brace required\n i += 2\n elif s[i] == ")" and s[i+1] != ")":\n if left_braces:\n count += 1 # one close brace required\n left_braces -= 1\n else:\n count += 2 # one open and one close brace required\n i += 1\n return count + (left_braces * 2) # close braces required at the end for all the remaining left braces\n```\nPlease upvote if you liked my solution. | 23 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
[Python] Simple solution with detailed explanation | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | ```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n ## RC ##\n ## APPROACH : STACK ##\n ## LOGIC ##\n ## 1. Only 3 conditions, open brace -> push to stack\n ## 2. 2 close braces -> pop from stack, if you donot have enough open braces before increment count(indicates one open required)\n ## 3. Only 1 close brace found --> count + 1, to make it 2 close braces, if stack then just pop, if stack is empty then increment count by 2 (one for close brace, one for open brace)\n ## 4. If stack is still left with open braces, we require close braces = twice of that open braces in stack\n \n ## You can even optimize it, without using stack, just counting the left braces.\n \n\t\t## TIME COMPLEXITY : O(N) ##\n\t\t## SPACE COMPLEXITY : O(1) ##\n \n s += "$" # appending dummy character at the end, to make things simpler\n left_braces, count, i = 0, 0, 0\n while( i < len(s)-1 ):\n if s[i] == "(":\n left_braces, i = left_braces + 1, i + 1\n elif s[i] == ")" and s[i+1] == ")":\n if left_braces:\n left_braces -= 1\n else:\n count += 1 # one open brace required\n i += 2\n elif s[i] == ")" and s[i+1] != ")":\n if left_braces:\n count += 1 # one close brace required\n left_braces -= 1\n else:\n count += 2 # one open and one close brace required\n i += 1\n return count + (left_braces * 2) # close braces required at the end for all the remaining left braces\n```\nPlease upvote if you liked my solution. | 23 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
Fast and easy-understanding solution using python, deque | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nChange the string $s$ to a deque and then each time popleft the deque.\n\nIf the character $c$ is \'(\', then update left value to count the number of \'(\'.\n\nIf $c$ is \')\', we then check next character in deque. \nIf nothing in the deque, if left > 0, that means there are \'(\' wait for matching, left -= 1 and we need one more \')\' to match \'(\', thus result adds 1, else left = 0, we need one \'(\' and one \')\' to work with current $c$. \nIf deque still has elements, if next character in deque is \')\', we then check left, if left > 0, left -= 1. Otherwise we need a \'(\' to match the two \')\', result adds 1. If next character in deque is \'(\', if left > 0, left -= 1 and we also need another \')\' to match, so result adds 1, if left = 0, we need one \'(\' and one \')\' to match, result += 2.\n\nAfter all, if we still have left > 0, we add corresponding \'))\' to match.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n result = 0\n s = collections.deque(s)\n left = 0\n while s:\n ele = s.popleft()\n if ele == "(":\n left += 1\n else:\n if not s:\n if left > 0:\n left -= 1\n result += 1\n else:\n result += 2\n else:\n if s[0] == ")":\n s.popleft()\n if left > 0:\n left -= 1\n else:\n result += 1\n else:\n if left > 0:\n left -= 1\n result += 1\n else:\n result += 2\n if left > 0:\n result += left * 2\n return result\n``` | 0 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
Fast and easy-understanding solution using python, deque | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nChange the string $s$ to a deque and then each time popleft the deque.\n\nIf the character $c$ is \'(\', then update left value to count the number of \'(\'.\n\nIf $c$ is \')\', we then check next character in deque. \nIf nothing in the deque, if left > 0, that means there are \'(\' wait for matching, left -= 1 and we need one more \')\' to match \'(\', thus result adds 1, else left = 0, we need one \'(\' and one \')\' to work with current $c$. \nIf deque still has elements, if next character in deque is \')\', we then check left, if left > 0, left -= 1. Otherwise we need a \'(\' to match the two \')\', result adds 1. If next character in deque is \'(\', if left > 0, left -= 1 and we also need another \')\' to match, so result adds 1, if left = 0, we need one \'(\' and one \')\' to match, result += 2.\n\nAfter all, if we still have left > 0, we add corresponding \'))\' to match.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n result = 0\n s = collections.deque(s)\n left = 0\n while s:\n ele = s.popleft()\n if ele == "(":\n left += 1\n else:\n if not s:\n if left > 0:\n left -= 1\n result += 1\n else:\n result += 2\n else:\n if s[0] == ")":\n s.popleft()\n if left > 0:\n left -= 1\n else:\n result += 1\n else:\n if left > 0:\n left -= 1\n result += 1\n else:\n result += 2\n if left > 0:\n result += left * 2\n return result\n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
python3, most intuitive to me, 45% | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe need to process the number of ) seen when 1. a when encountering a (, 2. when we reach the end of the array. \n\nThe logic looks most natural to me compared to other top answers\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n def process():\n nonlocal left, right, res\n if right > 0:\n if right%2==1:\n res += 1 #makes right even\n right += 1\n # handle the rest of even right brackets\n leftneeded = right//2\n if left >= leftneeded:\n left -= leftneeded\n else:\n leftneeded -= left\n res += leftneeded\n left = 0\n right = 0 # all right brackets handled\n left = 0\n right = 0\n res = 0\n for i,c in enumerate(s):\n if c==\'(\':\n process()\n left += 1\n else:\n right += 1\n process()\n res += left*2\n return res\n\n\n \n``` | 0 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
python3, most intuitive to me, 45% | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe need to process the number of ) seen when 1. a when encountering a (, 2. when we reach the end of the array. \n\nThe logic looks most natural to me compared to other top answers\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n def process():\n nonlocal left, right, res\n if right > 0:\n if right%2==1:\n res += 1 #makes right even\n right += 1\n # handle the rest of even right brackets\n leftneeded = right//2\n if left >= leftneeded:\n left -= leftneeded\n else:\n leftneeded -= left\n res += leftneeded\n left = 0\n right = 0 # all right brackets handled\n left = 0\n right = 0\n res = 0\n for i,c in enumerate(s):\n if c==\'(\':\n process()\n left += 1\n else:\n right += 1\n process()\n res += left*2\n return res\n\n\n \n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
Python | 2 methods | stack or balance due | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- stack\n- track balance due for `)`\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ and $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # method 1: stack\n def minInsertions(self, s: str) -> int:\n s = s.replace(\'))\', \'*\')\n ans = 0\n stk = []\n for ch in s:\n if ch == \'(\':\n stk.append(ch)\n else:\n if ch == \')\':\n ans += 1\n if stk and stk[-1] == \'(\':\n stk.pop()\n else:\n stk.append(\'*\')\n for ch in stk:\n ans += 2 if ch == \'(\' else 1\n return ans\n\n # method 2: track balance due\n def minInsertions(self, s: str) -> int:\n ans = rbalance = 0\n for ch in s:\n if ch == \'(\':\n if rbalance & 1:\n ans += 1\n rbalance += 1\n else:\n rbalance += 2\n else:\n rbalance -= 1\n if rbalance < 0:\n ans += 1\n rbalance += 2\n return ans + rbalance\n\n``` | 0 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
Python | 2 methods | stack or balance due | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- stack\n- track balance due for `)`\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ and $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # method 1: stack\n def minInsertions(self, s: str) -> int:\n s = s.replace(\'))\', \'*\')\n ans = 0\n stk = []\n for ch in s:\n if ch == \'(\':\n stk.append(ch)\n else:\n if ch == \')\':\n ans += 1\n if stk and stk[-1] == \'(\':\n stk.pop()\n else:\n stk.append(\'*\')\n for ch in stk:\n ans += 2 if ch == \'(\' else 1\n return ans\n\n # method 2: track balance due\n def minInsertions(self, s: str) -> int:\n ans = rbalance = 0\n for ch in s:\n if ch == \'(\':\n if rbalance & 1:\n ans += 1\n rbalance += 1\n else:\n rbalance += 2\n else:\n rbalance -= 1\n if rbalance < 0:\n ans += 1\n rbalance += 2\n return ans + rbalance\n\n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
Python3 O(1) Constant Storage Solution 🙌 | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nKeep track of open parenthesis and insertions. Key observations:\n\n1. We encounter a (. In this case we increase the open count because we\'ll need to know when all are closed.\n2. We encounter a ). In this case we need to know:\na. Is it a single ) - in this case we pretend that it\'s a )) and decrease the open count, but since it is not a )) in reality, we know we\'ll need to insert a ) so increase the insertion count.\nb. Is it a double, )) - in this case we just make sure to consume both of these characters by increasing the pointer and decrease the open count.\nc. *Note* you decrease the open count in either case because you encountered a closing parenthesis. The only difference is you might have to help a single closing parenthesis out by inserting another one :).\n3. If the open count is negative, well we reset it to zero. This is us because of the fact that we encountered more closing parenthesis than opening parenthesis. We reset to zero because we are inserting an opening brace to compensate.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n # encounter (, )), or )\n insertion_count = 0\n open_count = 0\n\n p = 0\n while p < len(s):\n if s[p] == \'(\':\n open_count += 1\n else:\n open_count -= 1\n\n if open_count < 0:\n open_count = 0\n insertion_count += 1\n\n if p < (len(s) - 1) and s[p+1] == \')\':\n p += 1\n else:\n insertion_count += 1\n \n p += 1\n\n return insertion_count + 2 * open_count\n``` | 0 | Given a parentheses string `s` containing only the characters `'('` and `')'`. A parentheses string is **balanced** if:
* Any left parenthesis `'('` must have a corresponding two consecutive right parenthesis `'))'`.
* Left parenthesis `'('` must go before the corresponding two consecutive right parenthesis `'))'`.
In other words, we treat `'('` as an opening parenthesis and `'))'` as a closing parenthesis.
* For example, `"()) "`, `"())(()))) "` and `"(())()))) "` are balanced, `")() "`, `"())) "` and `"(())) "` are not balanced.
You can insert the characters `'('` and `')'` at any position of the string to balance it if needed.
Return _the minimum number of insertions_ needed to make `s` balanced.
**Example 1:**
**Input:** s = "(())) "
**Output:** 1
**Explanation:** The second '(' has two matching '))', but the first '(' has only ')' matching. We need to add one more ')' at the end of the string to be "(()))) " which is balanced.
**Example 2:**
**Input:** s = "()) "
**Output:** 0
**Explanation:** The string is already balanced.
**Example 3:**
**Input:** s = "))())( "
**Output:** 3
**Explanation:** Add '(' to match the first '))', Add '))' to match the last '('.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of `'('` and `')'` only. | null |
Python3 O(1) Constant Storage Solution 🙌 | minimum-insertions-to-balance-a-parentheses-string | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nKeep track of open parenthesis and insertions. Key observations:\n\n1. We encounter a (. In this case we increase the open count because we\'ll need to know when all are closed.\n2. We encounter a ). In this case we need to know:\na. Is it a single ) - in this case we pretend that it\'s a )) and decrease the open count, but since it is not a )) in reality, we know we\'ll need to insert a ) so increase the insertion count.\nb. Is it a double, )) - in this case we just make sure to consume both of these characters by increasing the pointer and decrease the open count.\nc. *Note* you decrease the open count in either case because you encountered a closing parenthesis. The only difference is you might have to help a single closing parenthesis out by inserting another one :).\n3. If the open count is negative, well we reset it to zero. This is us because of the fact that we encountered more closing parenthesis than opening parenthesis. We reset to zero because we are inserting an opening brace to compensate.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n # encounter (, )), or )\n insertion_count = 0\n open_count = 0\n\n p = 0\n while p < len(s):\n if s[p] == \'(\':\n open_count += 1\n else:\n open_count -= 1\n\n if open_count < 0:\n open_count = 0\n insertion_count += 1\n\n if p < (len(s) - 1) and s[p+1] == \')\':\n p += 1\n else:\n insertion_count += 1\n \n p += 1\n\n return insertion_count + 2 * open_count\n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
Python3 | Prefix xor | O(n) Solution | find-longest-awesome-substring | 0 | 1 | Time Complexity: O(n) -> O(512n) in worst case?\n\n```\nclass Solution:\n def longestAwesome(self, s: str) -> int:\n # li = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]\n li = [2**i for i in range(10)]\n # checker = {0, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512}\n checker = set(li)\n checker.add(0)\n # di: k = prefix xor, v = the first idx I got a new prefix_xor_value.\n di = collections.OrderedDict({0: -1})\n maxLength = prefix_xor = 0\n \n for i in range(len(s)):\n prefix_xor ^= li[int(s[i])]\n # Found a new prefix_xor_value\n if prefix_xor not in di:\n di[prefix_xor] = i\n \n # XOR operation with previous prefix_xor_value\n for key in di.keys():\n if i - di[key] <= maxLength:\n break\n\t\t\t\t# s[di[key] : i] is Awesome Substring\n if key ^ prefix_xor in checker:\n maxLength = i - di[key]\n return maxLength\n \n``` | 1 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Python3 | Prefix xor | O(n) Solution | find-longest-awesome-substring | 0 | 1 | Time Complexity: O(n) -> O(512n) in worst case?\n\n```\nclass Solution:\n def longestAwesome(self, s: str) -> int:\n # li = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]\n li = [2**i for i in range(10)]\n # checker = {0, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512}\n checker = set(li)\n checker.add(0)\n # di: k = prefix xor, v = the first idx I got a new prefix_xor_value.\n di = collections.OrderedDict({0: -1})\n maxLength = prefix_xor = 0\n \n for i in range(len(s)):\n prefix_xor ^= li[int(s[i])]\n # Found a new prefix_xor_value\n if prefix_xor not in di:\n di[prefix_xor] = i\n \n # XOR operation with previous prefix_xor_value\n for key in di.keys():\n if i - di[key] <= maxLength:\n break\n\t\t\t\t# s[di[key] : i] is Awesome Substring\n if key ^ prefix_xor in checker:\n maxLength = i - di[key]\n return maxLength\n \n``` | 1 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
100% | find-longest-awesome-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestAwesome(self, s: str) -> int:\n n = len(s)\n dp = [n + 1] * (1 << 10)\n dp[0] = -1\n res, mask = 0, 0\n for i in range(n):\n mask ^= 1 << int(s[i])\n res = max(res, i - dp[mask])\n for j in range(10):\n res = max(res, i - dp[mask ^ (1 << j)])\n dp[mask] = min(dp[mask], i)\n return res\n``` | 0 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
100% | find-longest-awesome-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestAwesome(self, s: str) -> int:\n n = len(s)\n dp = [n + 1] * (1 << 10)\n dp[0] = -1\n res, mask = 0, 0\n for i in range(n):\n mask ^= 1 << int(s[i])\n res = max(res, i - dp[mask])\n for j in range(10):\n res = max(res, i - dp[mask ^ (1 << j)])\n dp[mask] = min(dp[mask], i)\n return res\n``` | 0 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
Python DP solution. | find-longest-awesome-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem, we are looking for the longest substring that is an awesome string. An awesome string is a string that has an even number of each digit from 0-9. To solve this problem, we can use dynamic programming to keep track of the longest substring that is an awesome string at each index of the input string.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use dynamic programming to solve this problem. We can create an array, `dp`, of length 10 to keep track of the longest substring that is an awesome string at each index of the string. We can also keep track of the current mask of the substring, which is a bitmask that stores the count of each digit in the current substring. To calculate the longest awesome substring at each index, we can iterate through the string and update the mask and the `dp` array accordingly. At each index, we can check if the current substring is an awesome string. If it is, we can update the `dp` array and the longest substring length. \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestAwesome(self, s: str) -> int:\n n = len(s)\n dp = [n + 1] * (1 << 10)\n dp[0] = -1\n res, mask = 0, 0\n for i in range(n):\n mask ^= 1 << int(s[i])\n res = max(res, i - dp[mask])\n for j in range(10):\n res = max(res, i - dp[mask ^ (1 << j)])\n dp[mask] = min(dp[mask], i)\n return res\n``` | 0 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Python DP solution. | find-longest-awesome-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem, we are looking for the longest substring that is an awesome string. An awesome string is a string that has an even number of each digit from 0-9. To solve this problem, we can use dynamic programming to keep track of the longest substring that is an awesome string at each index of the input string.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use dynamic programming to solve this problem. We can create an array, `dp`, of length 10 to keep track of the longest substring that is an awesome string at each index of the string. We can also keep track of the current mask of the substring, which is a bitmask that stores the count of each digit in the current substring. To calculate the longest awesome substring at each index, we can iterate through the string and update the mask and the `dp` array accordingly. At each index, we can check if the current substring is an awesome string. If it is, we can update the `dp` array and the longest substring length. \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestAwesome(self, s: str) -> int:\n n = len(s)\n dp = [n + 1] * (1 << 10)\n dp[0] = -1\n res, mask = 0, 0\n for i in range(n):\n mask ^= 1 << int(s[i])\n res = max(res, i - dp[mask])\n for j in range(10):\n res = max(res, i - dp[mask ^ (1 << j)])\n dp[mask] = min(dp[mask], i)\n return res\n``` | 0 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
✔ Python3 Solution | Clean & Concise | O(n) | find-kth-bit-in-nth-binary-string | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n\n### Recursive Approach\n```\nclass Solution:\n def findKthBit(self, N, K, R = True):\n if K == 1: return \'0\' if R else \'1\'\n mid = (1 << (N - 1))\n if K < mid: return self.findKthBit(N - 1, K, R)\n if K > mid: return self.findKthBit(N - 1, 2 * mid - K, not R)\n return \'1\' if R else \'0\'\n```\n\n### Iterative Approach\n```\nclass Solution:\n def findKthBit(self, N, K):\n ans = 1\n mid = (1 << (N - 1))\n while K > 1:\n if K == mid: return str(ans)\n if K > mid: \n K = 2 * mid - K\n ans ^= 1\n mid >>= 1\n return str(ans^1)\n``` | 1 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
easy O(n) python solution beats 92% | find-kth-bit-in-nth-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findKthBit(self, n: int, k: int) -> str:\n length = 2**n-1\n invert = 0\n while length !=1:\n mid = (length+1)//2\n if k <mid:\n pass\n elif k>mid:\n invert= abs(1-invert)\n k = 2*mid-k\n else:\n return \'1\' if invert==0 else \'0\'\n length = mid-1\n return \'0\' if invert == 0 else \'1\'\n \n``` | 1 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
[Python3] 4-line recursive | find-kth-bit-in-nth-binary-string | 0 | 1 | The first digit is always "0" regardless of `n`. The middle digit at `2**(n-1)` is always `1`. If `k < 2**(n-1)`, one could reduce the problem to `n-1` which is half the size. Otherwise, focus on the other half by reversing the position and "0"/"1". \n\n```\nclass Solution:\n def findKthBit(self, n: int, k: int) -> str:\n if k == 1: return "0"\n if k == 2**(n-1): return "1"\n if k < 2**(n-1): return self.findKthBit(n-1, k)\n return "0" if self.findKthBit(n-1, 2**n-k) == "1" else "1"\n``` | 12 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
Python 4 Lines | Simple Solution | find-kth-bit-in-nth-binary-string | 0 | 1 | ```\nclass Solution:\n def findKthBit(self, n: int, k: int) -> str:\n i, s, hash_map = 1, \'0\', {\'1\': \'0\', \'0\': \'1\'}\n for i in range(1, n):\n s = s + \'1\' + \'\'.join((hash_map[i] for i in s))[::-1]\n return s[k-1] | 1 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
Python 3 || 10 lines, prefix sum, w/example || T/M: 97% / 61% | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | ```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n\n d, ans = defaultdict(list), 0 # Example: nums = [2,2,5,2,5,9,4] target = 9 \n\n pref = enumerate(accumulate(nums, initial = 0)) # pref = [(0, 0),(1, 2),(2, 4),(3, 9),\n # (4,11),(5,16),(6,25),(7,29)]\n \n for i, num in pref: # i num comp d ans\n comp = num - target # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013 \n # 0 0 -9 {0:0} 0\n if comp in d: # 1 2 -7 {0:0,2:1} 0\n ans += 1 # 2 4 -5 {0:0,2:1,4:2} 0 \n d.clear() # 3 9 0 {9:3} 1 <-[2,2,5]\n # 4 11 2 {9:3,11:4} 1\n d[num] = i # 5 16 7 {9:3,11:4,16:5} 1 \n # 6 25 16 {25:6} 2 <-[9]\n return ans # 7 29 20 {25:6, 29:7} 2 <----------return\n\n```\n[https://leetcode.com/problems/maximum-number-of-non-overlapping-subarrays-with-sum-equals-target/submissions/921465408/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 3 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
Python 3 || 10 lines, prefix sum, w/example || T/M: 97% / 61% | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | ```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n\n d, ans = defaultdict(list), 0 # Example: nums = [2,2,5,2,5,9,4] target = 9 \n\n pref = enumerate(accumulate(nums, initial = 0)) # pref = [(0, 0),(1, 2),(2, 4),(3, 9),\n # (4,11),(5,16),(6,25),(7,29)]\n \n for i, num in pref: # i num comp d ans\n comp = num - target # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013 \n # 0 0 -9 {0:0} 0\n if comp in d: # 1 2 -7 {0:0,2:1} 0\n ans += 1 # 2 4 -5 {0:0,2:1,4:2} 0 \n d.clear() # 3 9 0 {9:3} 1 <-[2,2,5]\n # 4 11 2 {9:3,11:4} 1\n d[num] = i # 5 16 7 {9:3,11:4,16:5} 1 \n # 6 25 16 {25:6} 2 <-[9]\n return ans # 7 29 20 {25:6, 29:7} 2 <----------return\n\n```\n[https://leetcode.com/problems/maximum-number-of-non-overlapping-subarrays-with-sum-equals-target/submissions/921465408/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 3 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
[Python] Simple Solution - 2 Sum variant | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | ```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n ## RC ##\n ## APPROACH : HASHMAP - 2 SUM VARIANT ##\n lookup = {0 : -1}\n running_sum = 0\n count = 0\n for i in range(len(nums)):\n running_sum += nums[i]\n if running_sum - target in lookup:\n count += 1\n lookup = {} #reset the map\n lookup[running_sum] = i\n return count\n \n```\nPLEASE UPVOTE IF YOU LIKE MY SOLUTION. | 17 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
[Python] Simple Solution - 2 Sum variant | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | ```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n ## RC ##\n ## APPROACH : HASHMAP - 2 SUM VARIANT ##\n lookup = {0 : -1}\n running_sum = 0\n count = 0\n for i in range(len(nums)):\n running_sum += nums[i]\n if running_sum - target in lookup:\n count += 1\n lookup = {} #reset the map\n lookup[running_sum] = i\n return count\n \n```\nPLEASE UPVOTE IF YOU LIKE MY SOLUTION. | 17 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
python easy || beats 100% | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | ```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n f={}\n f[0]=1;s=0;ans=0\n for j in nums:\n s+=j\n if s-target in f:ans+=1;f={}\n f[s]=1\n return ans\n \n``` | 4 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
python easy || beats 100% | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | ```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n f={}\n f[0]=1;s=0;ans=0\n for j in nums:\n s+=j\n if s-target in f:ans+=1;f={}\n f[s]=1\n return ans\n \n``` | 4 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
Simple Python3 solution with sets and running sums (99%) | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Intuition\nWe want to greedily find the end index of the subarray, but don\'t care about the start index. As long as we end the subarray at the lowest possible index, we "leave room" for as many additional subarrays as possible.\n\nSince we\'re looking at subarrays, we are probably going to want some kind of running sum. However, because the input can contain negative numbers, we can\'t easily use the common approach of a moving window, since we can\'t determine how to change the window borders using only the sum of the current window.\n\n# Approach\nTraverse through *nums* storing the running sum at each index.\n\nNotice that for a list *L*, with *j* > *i*,\n`L[:i] + L[i:j] == L[:j]`, so\n`sum(L[:i]) + sum(L[i:j]) == sum(L[:j])`\nRearranged, this becomes\n`sum(L[:i]) - sum(L[:j]) == sum(L[i:j])`\n\nTherefore, if the difference between the running sum at index *j* and a prior running sum at index *i* is equal to *target*, we know that the sum of the subarray from indices *i* to *j* will be equal to *target*.\nIn other words, *j* is the end of a subarray that sums to target if and only if\n`runningSum[j] - runningSum[i] == target`\nfor some *i*. Instead of looping over each possible *i*, we can rearrange this to\n`runningSum[j] - target == runningSum[i]`. We can now simply compute `runningSum[j] - target` and check if the value is present in our running sums. Since we don\'t need to find the indices of the subarrays, only count them, we can use a set to track running sums instead of a list, reducing the time complexity of checking for a value to `O(1)`.\n\nSo our solution is:\n- Initialize `runningSums = set([0])` and `currentSum = 0`, as well as a tracker `subarraysFound = 0`\n- Iterate over `nums`. For each `num`:\n-- add `num` to `currentSum`\n-- check if `currentSum - target` is in `runningSums`\n-- if it is, we\'ve found the end of a subarray with the target sum. So, increment `subarraysFound`, and reset `runningSums` and `currentSum`\n-- if it\'s not, add `currentSum` to `runningSums`\n- When we\'ve finished iterating over `nums`, return `subarraysFound`\n\n\nTime and space complexity: `O(n)`\n\n# Code\n```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n runningSums = set([0])\n subarraysFound = 0\n currentSum = 0\n for num in nums:\n currentSum += num\n if currentSum - target in runningSums:\n subarraysFound += 1\n runningSums = set([0])\n currentSum = 0\n else:\n runningSums.add(currentSum)\n return subarraysFound\n``` | 0 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
Simple Python3 solution with sets and running sums (99%) | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Intuition\nWe want to greedily find the end index of the subarray, but don\'t care about the start index. As long as we end the subarray at the lowest possible index, we "leave room" for as many additional subarrays as possible.\n\nSince we\'re looking at subarrays, we are probably going to want some kind of running sum. However, because the input can contain negative numbers, we can\'t easily use the common approach of a moving window, since we can\'t determine how to change the window borders using only the sum of the current window.\n\n# Approach\nTraverse through *nums* storing the running sum at each index.\n\nNotice that for a list *L*, with *j* > *i*,\n`L[:i] + L[i:j] == L[:j]`, so\n`sum(L[:i]) + sum(L[i:j]) == sum(L[:j])`\nRearranged, this becomes\n`sum(L[:i]) - sum(L[:j]) == sum(L[i:j])`\n\nTherefore, if the difference between the running sum at index *j* and a prior running sum at index *i* is equal to *target*, we know that the sum of the subarray from indices *i* to *j* will be equal to *target*.\nIn other words, *j* is the end of a subarray that sums to target if and only if\n`runningSum[j] - runningSum[i] == target`\nfor some *i*. Instead of looping over each possible *i*, we can rearrange this to\n`runningSum[j] - target == runningSum[i]`. We can now simply compute `runningSum[j] - target` and check if the value is present in our running sums. Since we don\'t need to find the indices of the subarrays, only count them, we can use a set to track running sums instead of a list, reducing the time complexity of checking for a value to `O(1)`.\n\nSo our solution is:\n- Initialize `runningSums = set([0])` and `currentSum = 0`, as well as a tracker `subarraysFound = 0`\n- Iterate over `nums`. For each `num`:\n-- add `num` to `currentSum`\n-- check if `currentSum - target` is in `runningSums`\n-- if it is, we\'ve found the end of a subarray with the target sum. So, increment `subarraysFound`, and reset `runningSums` and `currentSum`\n-- if it\'s not, add `currentSum` to `runningSums`\n- When we\'ve finished iterating over `nums`, return `subarraysFound`\n\n\nTime and space complexity: `O(n)`\n\n# Code\n```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n runningSums = set([0])\n subarraysFound = 0\n currentSum = 0\n for num in nums:\n currentSum += num\n if currentSum - target in runningSums:\n subarraysFound += 1\n runningSums = set([0])\n currentSum = 0\n else:\n runningSums.add(currentSum)\n return subarraysFound\n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
Prefix sum of latest index with a pointer to the next index | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Intuition\nInital idea was to use sliding window, however, as the array consist of negative number that is not possible.\nHence, this hints to prefix sum.\nNow this is a typical prefix sum, find target. with just ignoring overlaps sub arrays. To do that we keep a start pointer for the next sub array that sums up to the target. The start pointer will always be i + 1 indicating the next possible position of the non overlapping next sub array.\nAlso out prefix hashmap will maintain, sum of latest index, by maintaing sum of latest index we can ensure that the resultant array will aleast be the rightmost portion,\n\n# Approach\nPrefix sum hashmap of latest index\nA next pointer to avoid all the sub arrays whos start point is less than the next pointer\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n\n #prefixsum hashtable\n pre = {\n 0 : -1\n }\n #prefix sum\n p = 0\n #answer count\n c = 0\n #next available starting position for the valid subarray\n #that aint overlapping\n next_ = 0\n\n for i in range(len(nums)):\n #current number\n n = nums[i]\n #updating the prefix sum\n p += n\n #diff\n d = p - target\n #previous index \n idx = pre.get(d,None) \n if idx is not None and idx + 1 >= next_: \n c +=1\n next_ = i + 1\n #updating the prefix sum hashtable\n pre[p] = i\n\n return c\n``` | 0 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
Prefix sum of latest index with a pointer to the next index | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Intuition\nInital idea was to use sliding window, however, as the array consist of negative number that is not possible.\nHence, this hints to prefix sum.\nNow this is a typical prefix sum, find target. with just ignoring overlaps sub arrays. To do that we keep a start pointer for the next sub array that sums up to the target. The start pointer will always be i + 1 indicating the next possible position of the non overlapping next sub array.\nAlso out prefix hashmap will maintain, sum of latest index, by maintaing sum of latest index we can ensure that the resultant array will aleast be the rightmost portion,\n\n# Approach\nPrefix sum hashmap of latest index\nA next pointer to avoid all the sub arrays whos start point is less than the next pointer\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n\n #prefixsum hashtable\n pre = {\n 0 : -1\n }\n #prefix sum\n p = 0\n #answer count\n c = 0\n #next available starting position for the valid subarray\n #that aint overlapping\n next_ = 0\n\n for i in range(len(nums)):\n #current number\n n = nums[i]\n #updating the prefix sum\n p += n\n #diff\n d = p - target\n #previous index \n idx = pre.get(d,None) \n if idx is not None and idx + 1 >= next_: \n c +=1\n next_ = i + 1\n #updating the prefix sum hashtable\n pre[p] = i\n\n return c\n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
Optimal solution O(N) | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Code\n```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n prefix = 0\n count = set([0])\n ans = 0\n\n for n in nums:\n prefix += n\n if prefix - target in count:\n ans += 1\n count = set()\n count.add(prefix)\n return ans\n``` | 0 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
Optimal solution O(N) | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Code\n```\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n prefix = 0\n count = set([0])\n ans = 0\n\n for n in nums:\n prefix += n\n if prefix - target in count:\n ans += 1\n count = set()\n count.add(prefix)\n return ans\n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
Python thought process and debugging steps. Follow along | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Code\n```python []\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n \'\'\'\n Initial thought: Keep two pointers and if the sum is equal to target, increase the count and set p1,p2 to p2+1\n If sum > target: increase p1, reduce s by nums[p1]\n And if sum < target: increase p2, increase s by nums[p2]\n\n Why that won\'t work: Take an example [3,4,-1,4,3,1], target = 6 now p1 = 0 and p2 = 1, sum = 7 Now we incr p1, which isn\'t right\n We would never be able to find [3,4,-1] like that\n\n Another approach: Store the prefix sums and remember which is the last used index\n for each number, we see if a subarray starting from last_used +1 or later can have a sum == target\n If so\n \'\'\'\n ps = {}\n ps[0] = -1\n last_used = -2#We have\'t used anything. -2 so that we get to inclde p[0]\n s = 0\n ans = 0\n for i in range(len(nums)):\n # Prefix sum till ith num\n s += nums[i]\n #We want a subarray with prefix sum rem\n rem = s-target\n # We have a sub array after last_used index\n if rem in ps and ps[rem] >= last_used:\n ans += 1\n last_used = i\n ps[s] = i\n return ans \n``` | 0 | Given an array `nums` and an integer `target`, return _the maximum number of **non-empty** **non-overlapping** subarrays such that the sum of values in each subarray is equal to_ `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 2
**Output:** 2
**Explanation:** There are 2 non-overlapping subarrays \[**1,1**,1,**1,1**\] with sum equals to target(2).
**Example 2:**
**Input:** nums = \[-1,3,5,1,4,2,-9\], target = 6
**Output:** 2
**Explanation:** There are 3 subarrays with sum equal to 6.
(\[5,1\], \[4,2\], \[3,5,1,4,2,-9\]) but only the first 2 are non-overlapping.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
* `0 <= target <= 106` | null |
Python thought process and debugging steps. Follow along | maximum-number-of-non-overlapping-subarrays-with-sum-equals-target | 0 | 1 | # Code\n```python []\nclass Solution:\n def maxNonOverlapping(self, nums: List[int], target: int) -> int:\n \'\'\'\n Initial thought: Keep two pointers and if the sum is equal to target, increase the count and set p1,p2 to p2+1\n If sum > target: increase p1, reduce s by nums[p1]\n And if sum < target: increase p2, increase s by nums[p2]\n\n Why that won\'t work: Take an example [3,4,-1,4,3,1], target = 6 now p1 = 0 and p2 = 1, sum = 7 Now we incr p1, which isn\'t right\n We would never be able to find [3,4,-1] like that\n\n Another approach: Store the prefix sums and remember which is the last used index\n for each number, we see if a subarray starting from last_used +1 or later can have a sum == target\n If so\n \'\'\'\n ps = {}\n ps[0] = -1\n last_used = -2#We have\'t used anything. -2 so that we get to inclde p[0]\n s = 0\n ans = 0\n for i in range(len(nums)):\n # Prefix sum till ith num\n s += nums[i]\n #We want a subarray with prefix sum rem\n rem = s-target\n # We have a sub array after last_used index\n if rem in ps and ps[rem] >= last_used:\n ans += 1\n last_used = i\n ps[s] = i\n return ans \n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
Python 3 || 6 lines, dfs || T/M: 89% / 10% | minimum-cost-to-cut-a-stick | 0 | 1 | ```\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n \n cuts = sorted(chain(cuts,[0,n]))\n \n @lru_cache(None)\n def dfs(l, r):\n length, M = cuts[r] - cuts[l], range(l+1, r)\n return min((dfs(l,i) + dfs(i,r) for i in M),\n default = -length) + length\n \n return dfs(0, len(cuts)-1)\n```\n[https://leetcode.com/problems/minimum-cost-to-cut-a-stick/submissions/958717387/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^3) and space complexity is *O*(*N*^2), in which *N* ~`n`. | 5 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Python 3 || 6 lines, dfs || T/M: 89% / 10% | minimum-cost-to-cut-a-stick | 0 | 1 | ```\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n \n cuts = sorted(chain(cuts,[0,n]))\n \n @lru_cache(None)\n def dfs(l, r):\n length, M = cuts[r] - cuts[l], range(l+1, r)\n return min((dfs(l,i) + dfs(i,r) for i in M),\n default = -length) + length\n \n return dfs(0, len(cuts)-1)\n```\n[https://leetcode.com/problems/minimum-cost-to-cut-a-stick/submissions/958717387/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^3) and space complexity is *O*(*N*^2), in which *N* ~`n`. | 5 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Easy 2 line explanation for 2 liner code | Top down | minimum-cost-to-cut-a-stick | 0 | 1 | ```\n# Intuition\n1) Find cuts between range by binary search in sorted arr\n2) Loop k over cuts \n take min of (0,k) + (k,0) + length \n```\n\n\n\n\n# Code\n```\n\ndef minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n\n @cache\n def help(i=0,j=n):\n x,y = bisect_right(cuts,i), bisect_right(cuts, j-1)\n if x==y: return 0\n return min( help(i,cuts[k]) + help(cuts[k], j) + (j-i) for k in range(x,y) )\n\n return help()\n``` | 2 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Easy 2 line explanation for 2 liner code | Top down | minimum-cost-to-cut-a-stick | 0 | 1 | ```\n# Intuition\n1) Find cuts between range by binary search in sorted arr\n2) Loop k over cuts \n take min of (0,k) + (k,0) + length \n```\n\n\n\n\n# Code\n```\n\ndef minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n\n @cache\n def help(i=0,j=n):\n x,y = bisect_right(cuts,i), bisect_right(cuts, j-1)\n if x==y: return 0\n return min( help(i,cuts[k]) + help(cuts[k], j) + (j-i) for k in range(x,y) )\n\n return help()\n``` | 2 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Pretty beautiful simple and optimal python3 solution | minimum-cost-to-cut-a-stick | 0 | 1 | # Complexity\n- Time complexity: $$O(n ^ 3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n ^ 2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nfrom functools import cache\n\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n\n @cache\n def dp(a, b, i, j):\n if i == j:\n return 0\n\n return min(\n dp(a, cuts[k], i, k) + dp(cuts[k], b, k + 1, j)\n for k in range(i, j)\n ) + b - a\n\n return dp(0, n, 0, len(cuts))\n\n```\n\n## NB\nThe arguments `i` and `j` of DP are uniquely determined by the arguments `a` and `b`, so the true dynamic programming space is `dp[a][b]`.\nHowever, I have explicitly passed them on for ease of understanding. | 1 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Pretty beautiful simple and optimal python3 solution | minimum-cost-to-cut-a-stick | 0 | 1 | # Complexity\n- Time complexity: $$O(n ^ 3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n ^ 2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nfrom functools import cache\n\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n cuts.sort()\n\n @cache\n def dp(a, b, i, j):\n if i == j:\n return 0\n\n return min(\n dp(a, cuts[k], i, k) + dp(cuts[k], b, k + 1, j)\n for k in range(i, j)\n ) + b - a\n\n return dp(0, n, 0, len(cuts))\n\n```\n\n## NB\nThe arguments `i` and `j` of DP are uniquely determined by the arguments `a` and `b`, so the true dynamic programming space is `dp[a][b]`.\nHowever, I have explicitly passed them on for ease of understanding. | 1 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
"Minimum Cost to Cut a Stick"✔ | minimum-cost-to-cut-a-stick | 0 | 1 | # Intuition\nTo find the minimum total cost of the cuts, we can use dynamic programming. We can start by sorting the cuts in ascending order and then consider all possible subproblems.\n\n# Approach\n1. Sort the cuts array in ascending order.\n2. Create a new array called `cuts_arr` by adding 0 at the beginning and `n` at the end, and then appending the sorted cuts array.\n3. Create a 2D array called `dp` with dimensions `(length of cuts_arr) x (length of cuts_arr)`, filled with infinity values.\n4. Initialize the diagonal elements of `dp` with 0, as the cost of cutting a stick of length 0 is 0.\n5. Iterate over the lengths of the stick ranges (starting from 2 up to the length of `cuts_arr`).\n6. Iterate over the start positions of the stick ranges (from 0 to the length of `cuts_arr` minus the current length).\n7. Calculate the end position of the stick range based on the start position and length.\n8. Find the minimum cost by considering each possible cut position within the stick range.\n - Iterate over the cut positions (from the start position plus 1 to the end position minus 1).\n - Calculate the cost of cutting the stick at the current position (equal to the length of the stick range plus the difference between the positions in `cuts_arr`).\n - Update the minimum cost by considering the cost of the left part of the stick range (from the start position to the cut position) and the cost of the right part of the stick range (from the cut position to the end position).\n9. Store the minimum cost in the corresponding position of `dp`.\n10. The minimum total cost of the cuts is stored in `dp[0][-1]`.\n\n# Complexity Analysis\nThe time complexity of this approach is O(n^3), where n is the length of the cuts array. This is because we iterate over all possible stick ranges and for each stick range, we iterate over all possible cut positions within that range.\n\nThe space complexity is O(n^2) to store the `dp` array.\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n # Add the start and end positions to the cuts array\n cuts = [0] + sorted(cuts) + [n]\n m = len(cuts)\n \n # Initialize the dp table with maximum values\n dp = [[float(\'inf\')] * m for _ in range(m)]\n \n # Base case: dp(i, i+1) = 0 since no cuts are made between consecutive positions\n for i in range(m - 1):\n dp[i][i + 1] = 0\n \n # Iterate over the lengths of the cut ranges\n for length in range(2, m):\n # Iterate over the start positions of the cut ranges\n for i in range(m - length):\n # Calculate the end position of the cut range\n j = i + length\n # Find the minimum cost by considering each possible cut position within the range\n for k in range(i + 1, j):\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])\n \n # The minimum cost to cut the entire stick is stored at dp(0, m-1)\n return dp[0][m - 1]\n\n``` | 1 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
"Minimum Cost to Cut a Stick"✔ | minimum-cost-to-cut-a-stick | 0 | 1 | # Intuition\nTo find the minimum total cost of the cuts, we can use dynamic programming. We can start by sorting the cuts in ascending order and then consider all possible subproblems.\n\n# Approach\n1. Sort the cuts array in ascending order.\n2. Create a new array called `cuts_arr` by adding 0 at the beginning and `n` at the end, and then appending the sorted cuts array.\n3. Create a 2D array called `dp` with dimensions `(length of cuts_arr) x (length of cuts_arr)`, filled with infinity values.\n4. Initialize the diagonal elements of `dp` with 0, as the cost of cutting a stick of length 0 is 0.\n5. Iterate over the lengths of the stick ranges (starting from 2 up to the length of `cuts_arr`).\n6. Iterate over the start positions of the stick ranges (from 0 to the length of `cuts_arr` minus the current length).\n7. Calculate the end position of the stick range based on the start position and length.\n8. Find the minimum cost by considering each possible cut position within the stick range.\n - Iterate over the cut positions (from the start position plus 1 to the end position minus 1).\n - Calculate the cost of cutting the stick at the current position (equal to the length of the stick range plus the difference between the positions in `cuts_arr`).\n - Update the minimum cost by considering the cost of the left part of the stick range (from the start position to the cut position) and the cost of the right part of the stick range (from the cut position to the end position).\n9. Store the minimum cost in the corresponding position of `dp`.\n10. The minimum total cost of the cuts is stored in `dp[0][-1]`.\n\n# Complexity Analysis\nThe time complexity of this approach is O(n^3), where n is the length of the cuts array. This is because we iterate over all possible stick ranges and for each stick range, we iterate over all possible cut positions within that range.\n\nThe space complexity is O(n^2) to store the `dp` array.\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n # Add the start and end positions to the cuts array\n cuts = [0] + sorted(cuts) + [n]\n m = len(cuts)\n \n # Initialize the dp table with maximum values\n dp = [[float(\'inf\')] * m for _ in range(m)]\n \n # Base case: dp(i, i+1) = 0 since no cuts are made between consecutive positions\n for i in range(m - 1):\n dp[i][i + 1] = 0\n \n # Iterate over the lengths of the cut ranges\n for length in range(2, m):\n # Iterate over the start positions of the cut ranges\n for i in range(m - length):\n # Calculate the end position of the cut range\n j = i + length\n # Find the minimum cost by considering each possible cut position within the range\n for k in range(i + 1, j):\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])\n \n # The minimum cost to cut the entire stick is stored at dp(0, m-1)\n return dp[0][m - 1]\n\n``` | 1 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Top down dynamic approach (8 lines) | minimum-cost-to-cut-a-stick | 0 | 1 | # Code\n```\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n @cache\n def dp(leftRange, rightRange):\n ans = float(\'inf\')\n for cut in cuts:\n if leftRange < cut < rightRange:\n ans = min(ans, rightRange-leftRange + dp(leftRange, cut) + dp(cut, rightRange))\n return ans if ans != float(\'inf\') else 0\n \n return dp(0, n)\n``` | 1 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Top down dynamic approach (8 lines) | minimum-cost-to-cut-a-stick | 0 | 1 | # Code\n```\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n @cache\n def dp(leftRange, rightRange):\n ans = float(\'inf\')\n for cut in cuts:\n if leftRange < cut < rightRange:\n ans = min(ans, rightRange-leftRange + dp(leftRange, cut) + dp(cut, rightRange))\n return ans if ans != float(\'inf\') else 0\n \n return dp(0, n)\n``` | 1 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Python Easy Solution | minimum-cost-to-cut-a-stick | 0 | 1 | \n\n# Code\n```\nimport sys\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n d={}\n def solve(i,j):\n if (i,j) in d:\n return d[(i,j)]\n ans=sys.maxsize\n cost=j-i\n for cut in cuts:\n if cut<j and cut>i:\n ans=min(ans,solve(i,cut)+solve(cut,j)+cost)\n if ans==sys.maxsize:\n d[(i,j)]=0\n else:\n d[(i,j)]=ans\n return d[(i,j)]\n return solve(0,n)\n``` | 1 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Python Easy Solution | minimum-cost-to-cut-a-stick | 0 | 1 | \n\n# Code\n```\nimport sys\nclass Solution:\n def minCost(self, n: int, cuts: List[int]) -> int:\n d={}\n def solve(i,j):\n if (i,j) in d:\n return d[(i,j)]\n ans=sys.maxsize\n cost=j-i\n for cut in cuts:\n if cut<j and cut>i:\n ans=min(ans,solve(i,cut)+solve(cut,j)+cost)\n if ans==sys.maxsize:\n d[(i,j)]=0\n else:\n d[(i,j)]=ans\n return d[(i,j)]\n return solve(0,n)\n``` | 1 | You are given two linked lists: `list1` and `list2` of sizes `n` and `m` respectively.
Remove `list1`'s nodes from the `ath` node to the `bth` node, and put `list2` in their place.
The blue edges and nodes in the following figure indicate the result:
_Build the result list and return its head._
**Example 1:**
**Input:** list1 = \[0,1,2,3,4,5\], a = 3, b = 4, list2 = \[1000000,1000001,1000002\]
**Output:** \[0,1,2,1000000,1000001,1000002,5\]
**Explanation:** We remove the nodes 3 and 4 and put the entire list2 in their place. The blue edges and nodes in the above figure indicate the result.
**Example 2:**
**Input:** list1 = \[0,1,2,3,4,5,6\], a = 2, b = 5, list2 = \[1000000,1000001,1000002,1000003,1000004\]
**Output:** \[0,1,1000000,1000001,1000002,1000003,1000004,6\]
**Explanation:** The blue edges and nodes in the above figure indicate the result.
**Constraints:**
* `3 <= list1.length <= 104`
* `1 <= a <= b < list1.length - 1`
* `1 <= list2.length <= 104` | Build a dp array where dp[i][j] is the minimum cost to achieve all the cuts between i and j. When you try to get the minimum cost between i and j, try all possible cuts k between them, dp[i][j] = min(dp[i][k] + dp[k][j]) + (j - i) for all possible cuts k between them. |
Image Explanation🏆- [Recursion -> Memo(4 states - 2 states) -> Bottom Up] - C++/Java/Python | minimum-cost-to-cut-a-stick | 1 | 1 | \n\n# Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Minimum Cost to Cut a Stick` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n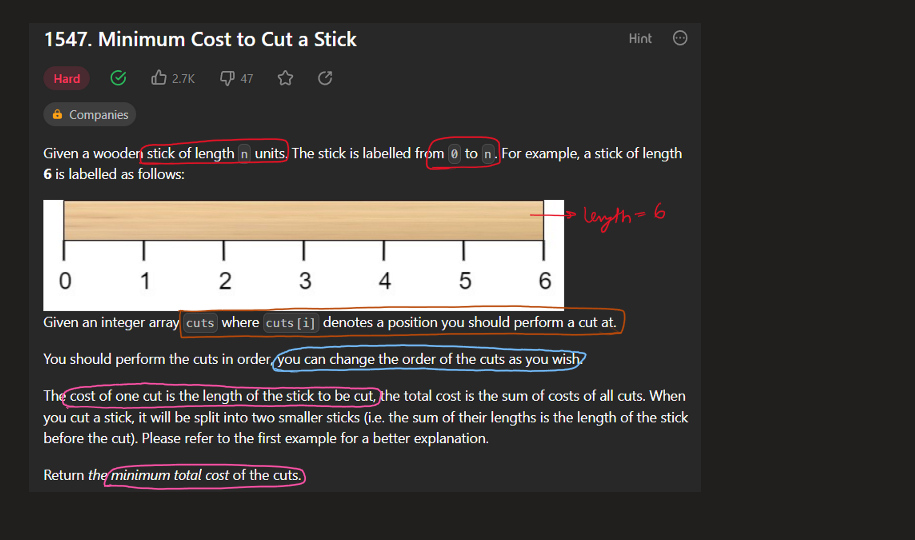\n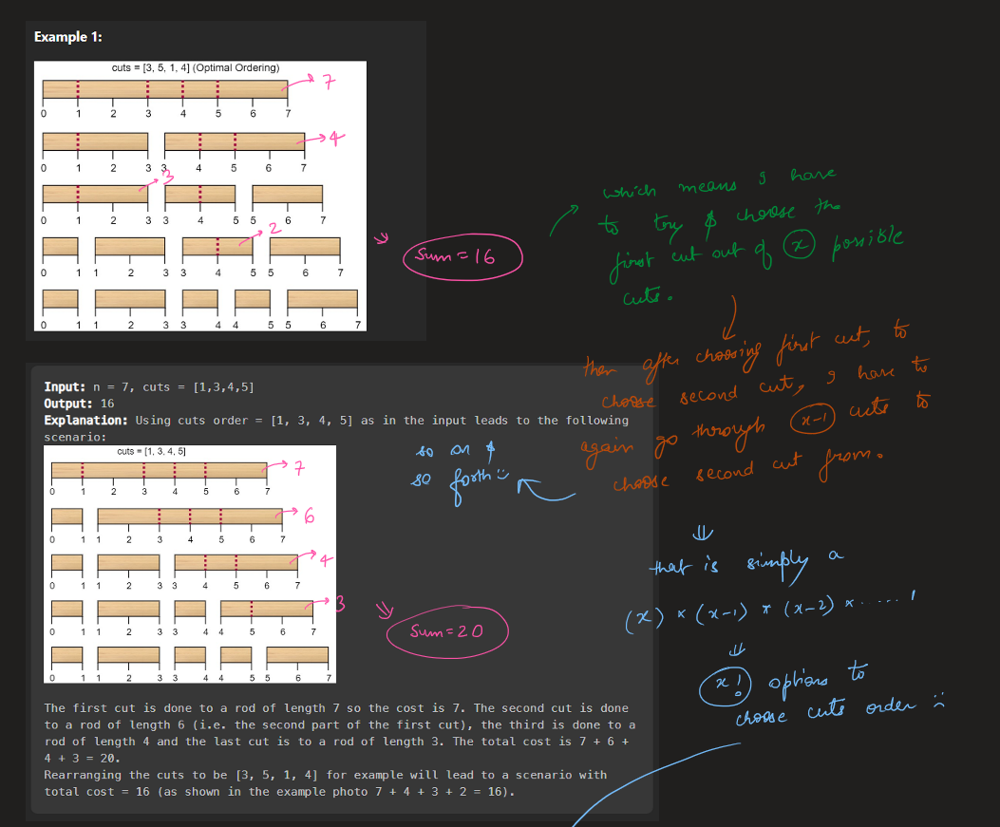\n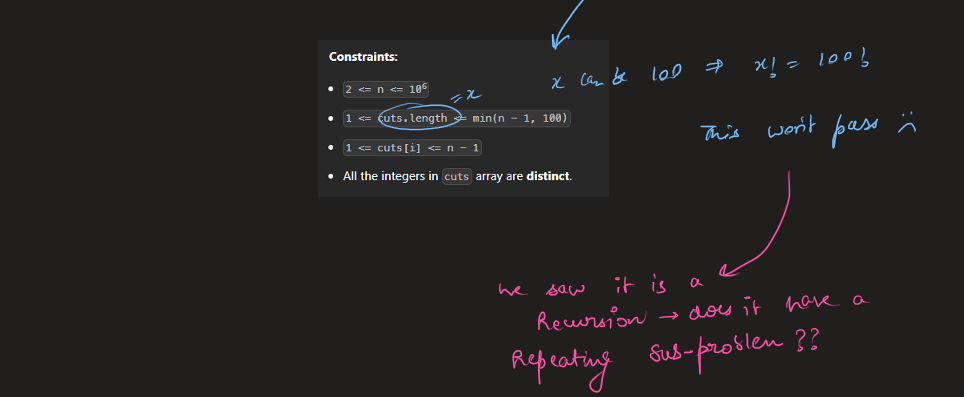\n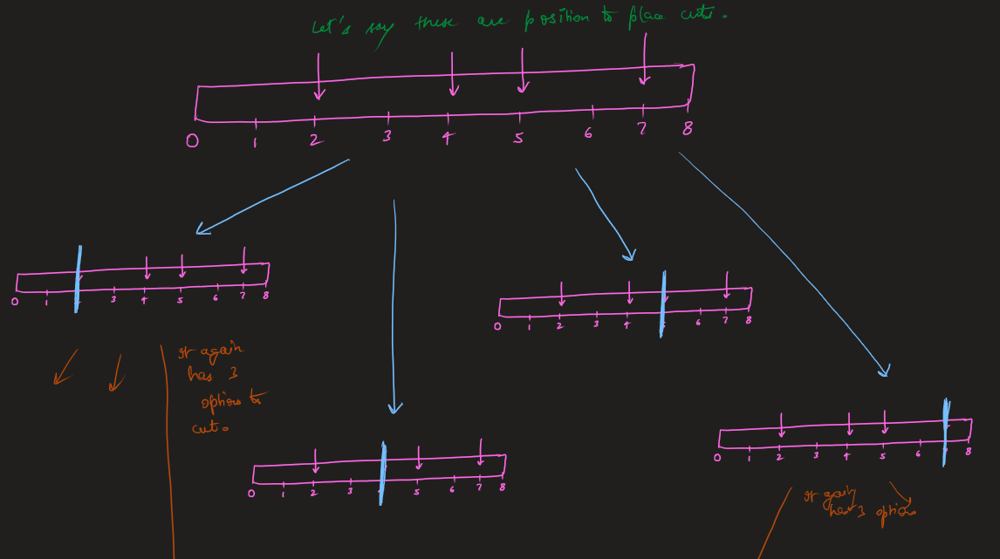\n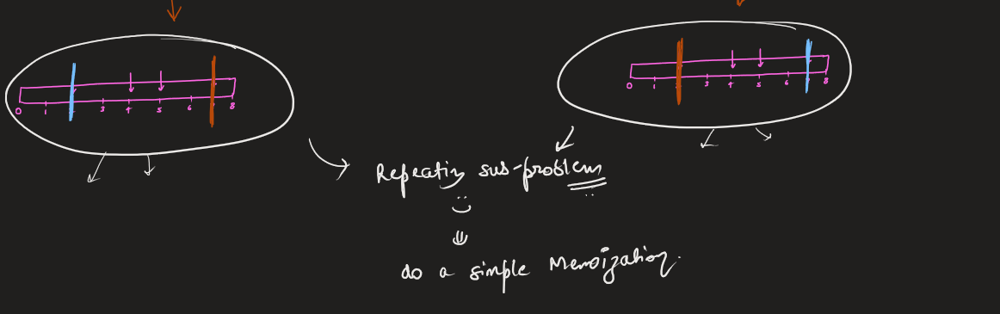\n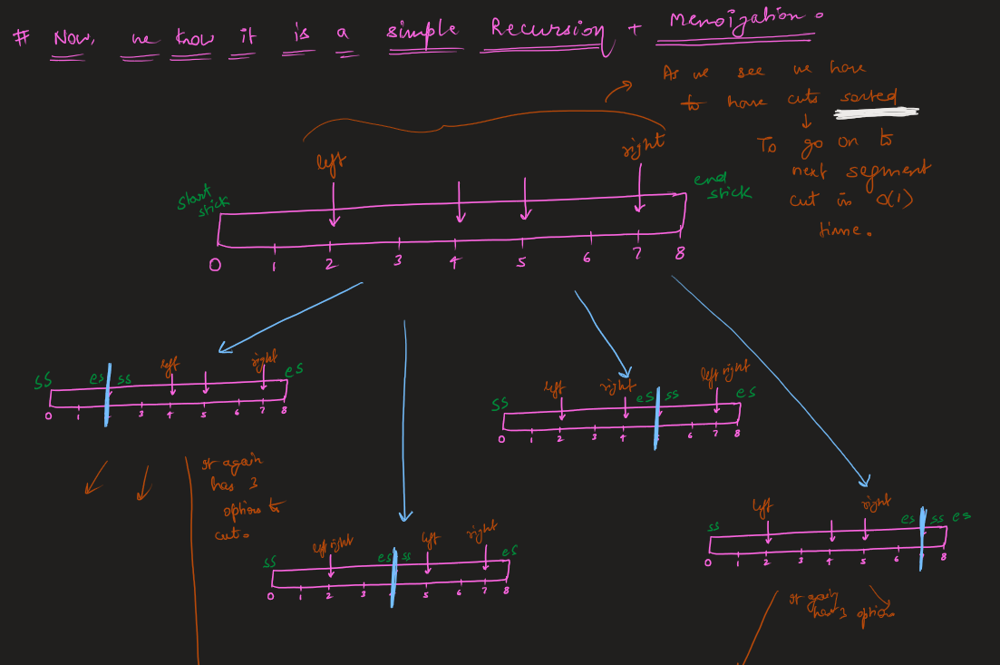\n\n\n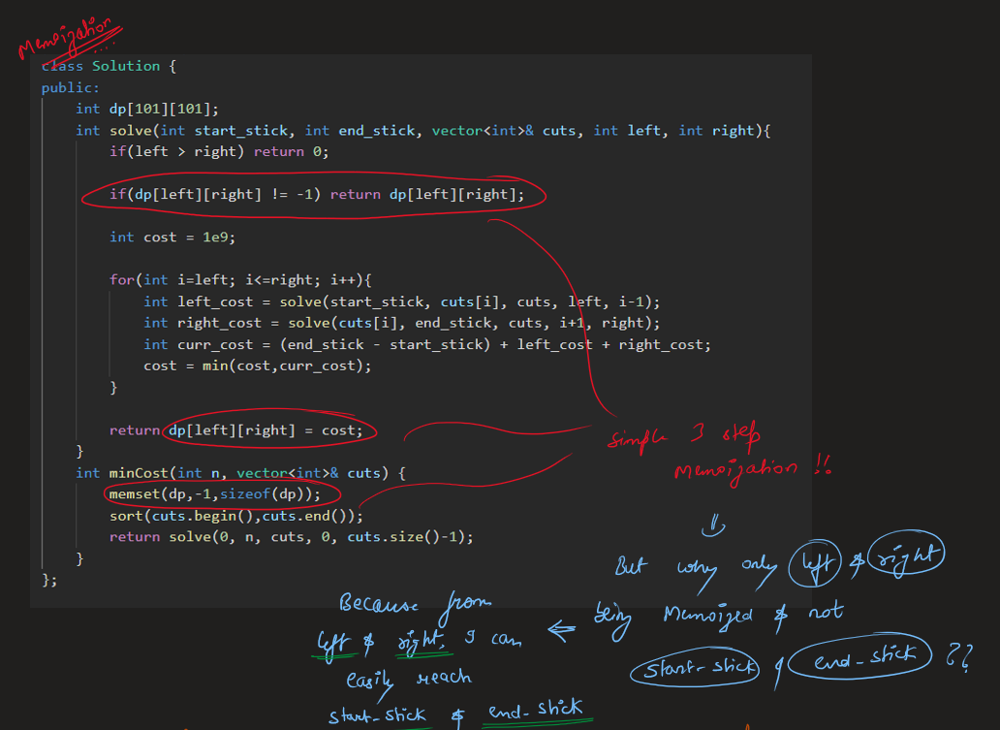\n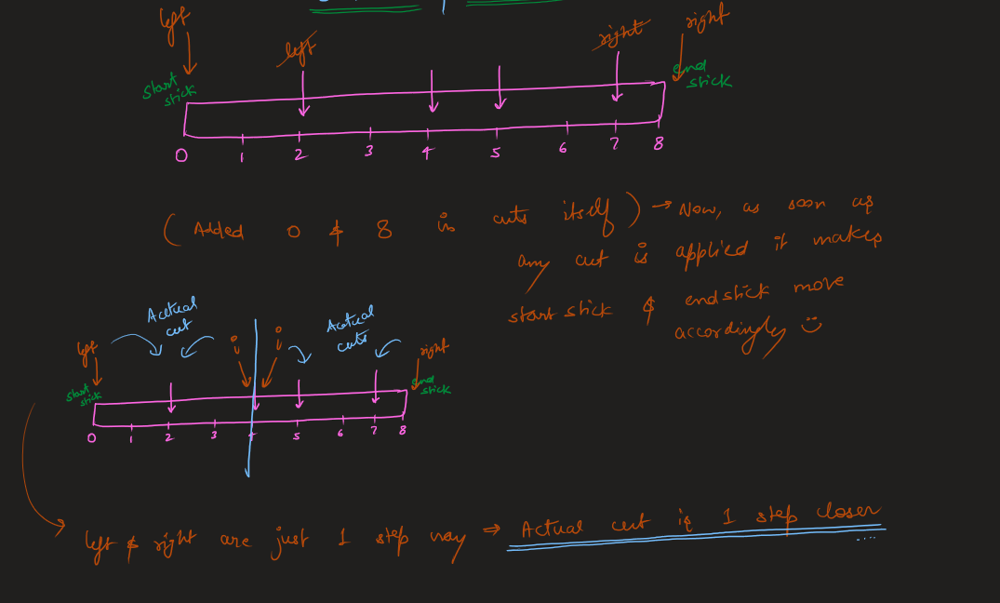\n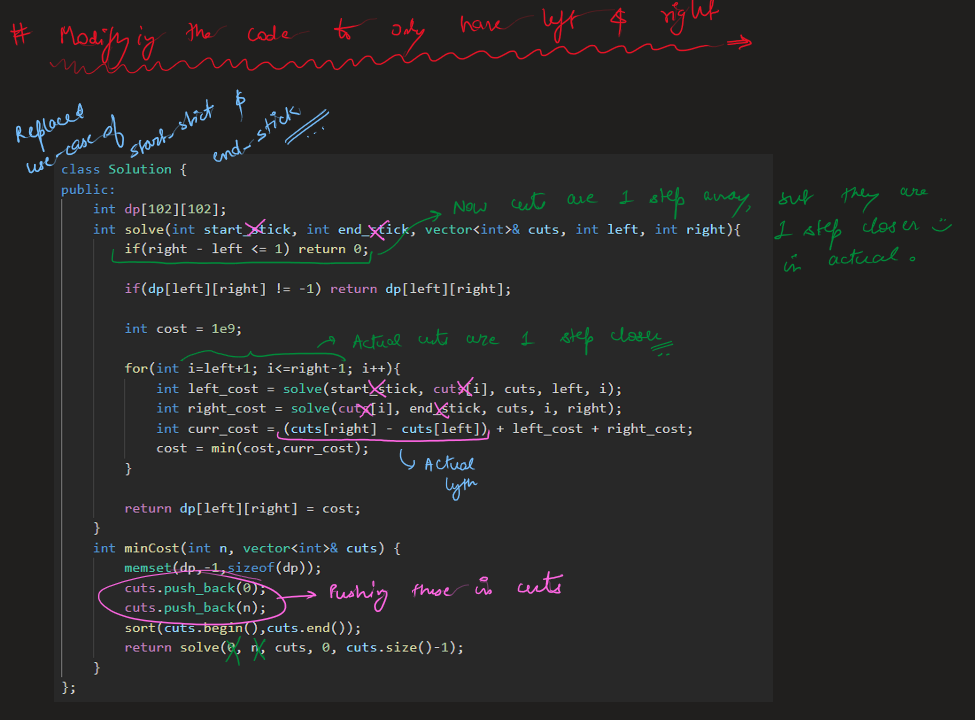\n\n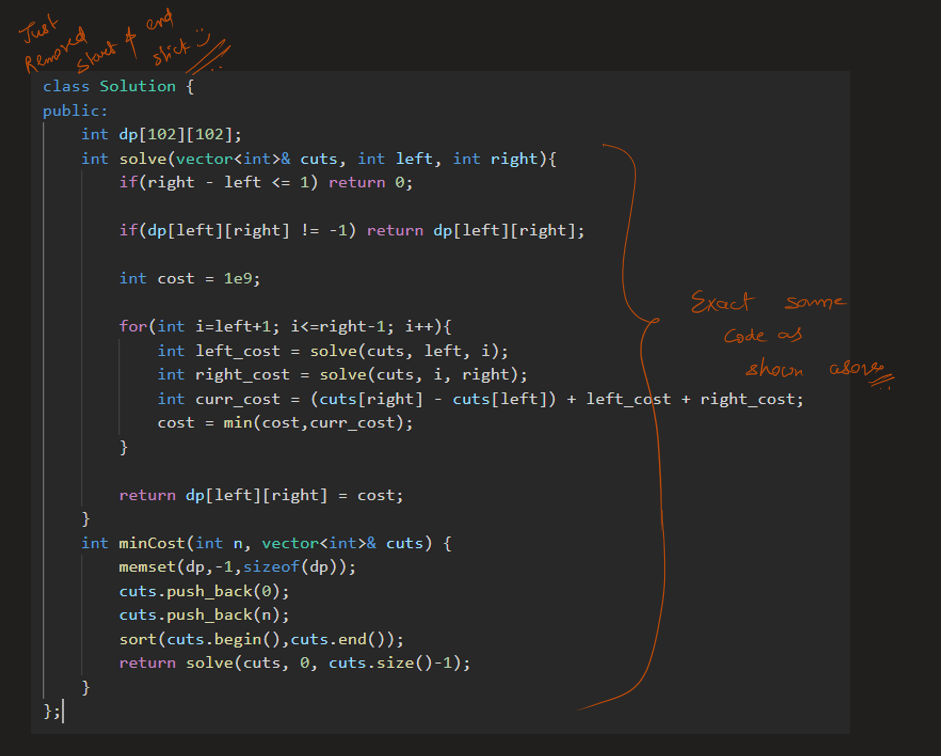\n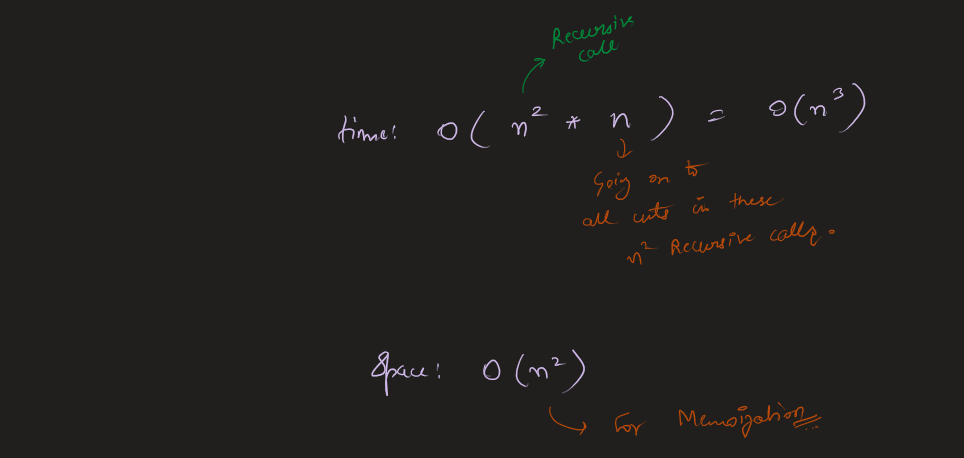\nHere the above n - represents the cuts.size(), you can also take it as m^3 also for time & m^2 for space.\n\n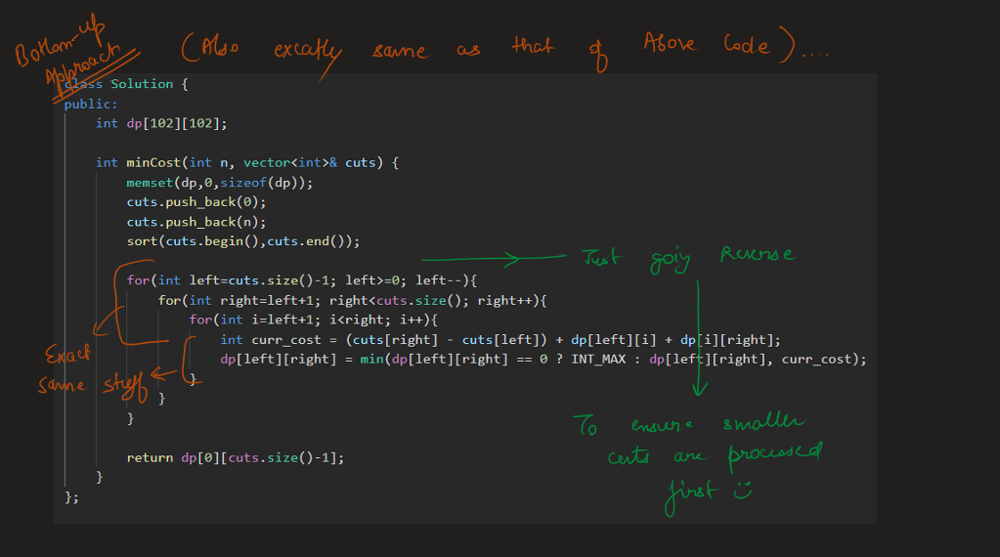\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int dp[101][101];\n int solve(int start_stick, int end_stick, vector<int>& cuts, int left, int right){\n if(left > right) return 0;\n \n if(dp[left][right] != -1) return dp[left][right];\n \n int cost = 1e9;\n \n for(int i=left; i<=right; i++){\n int left_cost = solve(start_stick, cuts[i], cuts, left, i-1);\n int right_cost = solve(cuts[i], end_stick, cuts, i+1, right);\n int curr_cost = (end_stick - start_stick) + left_cost + right_cost;\n cost = min(cost,curr_cost);\n }\n \n return dp[left][right] = cost;\n }\n int minCost(int n, vector<int>& cuts) {\n memset(dp,-1,sizeof(dp));\n sort(cuts.begin(),cuts.end());\n return solve(0, n, cuts, 0, cuts.size()-1);\n }\n};\n```\n```Java []\nclass Solution {\n int[][] dp;\n \n int solve(int start_stick, int end_stick, int[] cuts, int left, int right) {\n if (left > right) return 0;\n\n if (dp[left][right] != -1) return dp[left][right];\n\n int cost = Integer.MAX_VALUE;\n\n for (int i = left; i <= right; i++) {\n int left_cost = solve(start_stick, cuts[i], cuts, left, i - 1);\n int right_cost = solve(cuts[i], end_stick, cuts, i + 1, right);\n int curr_cost = (end_stick - start_stick) + left_cost + right_cost;\n cost = Math.min(cost, curr_cost);\n }\n\n return dp[left][right] = cost;\n }\n \n int minCost(int n, int[] cuts) {\n dp = new int[cuts.length][cuts.length];\n for (int[] row : dp) {\n Arrays.fill(row, -1);\n }\n \n Arrays.sort(cuts);\n return solve(0, n, cuts, 0, cuts.length - 1);\n }\n}\n```\n```Python []\nclass Solution:\n def solve(self, start_stick, end_stick, cuts, left, right, dp):\n if left > right:\n return 0\n\n if dp[left][right] != -1:\n return dp[left][right]\n\n cost = float(\'inf\')\n\n for i in range(left, right + 1):\n left_cost = self.solve(start_stick, cuts[i], cuts, left, i - 1, dp)\n right_cost = self.solve(cuts[i], end_stick, cuts, i + 1, right, dp)\n curr_cost = (end_stick - start_stick) + left_cost + right_cost\n cost = min(cost, curr_cost)\n\n dp[left][right] = cost\n return cost\n\n def minCost(self, n, cuts):\n dp = [[-1] * len(cuts) for _ in range(len(cuts))]\n cuts.sort()\n return self.solve(0, n, cuts, 0, len(cuts) - 1, dp)\n``` | 77 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.