title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
python solution | maximum-number-of-non-overlapping-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nnear about O(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nnear about O(n)\n\n# Code\n```\nclass Solution:\n def maxNumOfSubstrings(self, s: str) -> List[str]:\n\n # storing the intervals of characters\n\n intervals = {}\n for i in range(len(s)):\n if s[i] not in intervals :\n intervals[s[i]] = [i,i]\n else :\n intervals[s[i]].pop()\n intervals[s[i]].append(i)\n \n # merging overlapping intervals\n\n for i in intervals:\n start,end = intervals[i]\n for j in range(start+1,end):\n curStart, curEnd = intervals[s[j]]\n if curStart < start :\n start = curStart\n if curEnd > end :\n end = curEnd\n intervals[i] = [start,end]\n\n # merging overlapping intervals\n\n for i in intervals:\n start,end = intervals[i]\n for j in range(start+1,end):\n curStart, curEnd = intervals[s[j]]\n if curStart < start :\n start = curStart\n if curEnd > end :\n end = curEnd\n intervals[i] = [start,end]\n \n # storing intervals in list\n\n res = []\n for i in intervals:\n res.append(intervals[i])\n res = sorted(res,key = lambda x : x[1])\n\n # finding ans and sotring in ansArr\n\n end = res[0][1]\n start = res[0][0]\n ansArr = [s[res[0][0] : end+1]]\n for i in range(1,len(res)):\n if res[i][0] > end :\n ansArr.append(s[res[i][0] : res[i][1]+1])\n end = res[i][1]\n start = res[i][0]\n\n return ansArr\n\n``` | 0 | Given the `root` of a binary tree, return _the lowest common ancestor (LCA) of two given nodes,_ `p` _and_ `q`. If either node `p` or `q` **does not exist** in the tree, return `null`. All values of the nodes in the tree are **unique**.
According to the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of two nodes `p` and `q` in a binary tree `T` is the lowest node that has both `p` and `q` as **descendants** (where we allow **a node to be a descendant of itself**) ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 10
**Output:** null
**Explanation:** Node 10 does not exist in the tree, so return null.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
**Follow up:** Can you find the LCA traversing the tree, without checking nodes existence? | Notice that it's impossible for any two valid substrings to overlap unless one is inside another. We can start by finding the starting and ending index for each character. From these indices, we can form the substrings by expanding each character's range if necessary (if another character exists in the range with smaller/larger starting/ending index). Sort the valid substrings by length and greedily take those with the smallest length, discarding the ones that overlap those we took. |
Python | Mono Stack of Candidate Substrings | Easy to Understand | Commented | maximum-number-of-non-overlapping-substrings | 0 | 1 | # Approach\nWe scan the string rom left to right while maintaining stack of nested candidate intervals for a valid minimal substring, backtracking as needed. Stack is cleared once a minimal valid substring found, since strings containing it cannot be minimal.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxNumOfSubstrings(self, s: str) -> List[str]:\n # start and end will store start and end indices of individual characters\n start, end = {}, {}\n for idx, char in enumerate(s):\n end[char] = idx\n if char not in start:\n start[char] = idx\n # res will contain all minimal sub-intervals of the string that satisfy condition 2\n # stack will contain nested sub-intervals currently under consideration\n stack, res = [], []\n for idx, char in enumerate(s):\n # Sub-interval does not contain first occurence of character c\n while stack and stack[-1][0] > start[char]:\n stack.pop()\n # Left end of sub-interval must be extended\n if stack and stack[-1][1] < end[char]:\n while len(stack) > 1 and stack[-2][1] < end[char]:\n stack.pop()\n stack[-1][1] = end[char]\n # idx is potential start of minimal sub-interval\n elif idx == start[char] and (not stack or end[char] < stack[-1][1]) :\n stack.append([idx, end[char]])\n # Minimal sub-interval found. All other sub-intervals on the stack containing it cannot be minimal\n if stack and stack[-1][1] == idx:\n res.append(stack[-1])\n stack.clear()\n return [s[start: end + 1] for start, end in res]\n``` | 0 | Given a string `s` of lowercase letters, you need to find the maximum number of **non-empty** substrings of `s` that meet the following conditions:
1. The substrings do not overlap, that is for any two substrings `s[i..j]` and `s[x..y]`, either `j < x` or `i > y` is true.
2. A substring that contains a certain character `c` must also contain all occurrences of `c`.
Find _the maximum number of substrings that meet the above conditions_. If there are multiple solutions with the same number of substrings, _return the one with minimum total length._ It can be shown that there exists a unique solution of minimum total length.
Notice that you can return the substrings in **any** order.
**Example 1:**
**Input:** s = "adefaddaccc "
**Output:** \[ "e ", "f ", "ccc "\]
**Explanation:** The following are all the possible substrings that meet the conditions:
\[
"adefaddaccc "
"adefadda ",
"ef ",
"e ",
"f ",
"ccc ",
\]
If we choose the first string, we cannot choose anything else and we'd get only 1. If we choose "adefadda ", we are left with "ccc " which is the only one that doesn't overlap, thus obtaining 2 substrings. Notice also, that it's not optimal to choose "ef " since it can be split into two. Therefore, the optimal way is to choose \[ "e ", "f ", "ccc "\] which gives us 3 substrings. No other solution of the same number of substrings exist.
**Example 2:**
**Input:** s = "abbaccd "
**Output:** \[ "d ", "bb ", "cc "\]
**Explanation:** Notice that while the set of substrings \[ "d ", "abba ", "cc "\] also has length 3, it's considered incorrect since it has larger total length.
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Read the string from right to left, if the string ends in '0' then the number is even otherwise it is odd. Simulate the steps described in the binary string. |
Python | Mono Stack of Candidate Substrings | Easy to Understand | Commented | maximum-number-of-non-overlapping-substrings | 0 | 1 | # Approach\nWe scan the string rom left to right while maintaining stack of nested candidate intervals for a valid minimal substring, backtracking as needed. Stack is cleared once a minimal valid substring found, since strings containing it cannot be minimal.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxNumOfSubstrings(self, s: str) -> List[str]:\n # start and end will store start and end indices of individual characters\n start, end = {}, {}\n for idx, char in enumerate(s):\n end[char] = idx\n if char not in start:\n start[char] = idx\n # res will contain all minimal sub-intervals of the string that satisfy condition 2\n # stack will contain nested sub-intervals currently under consideration\n stack, res = [], []\n for idx, char in enumerate(s):\n # Sub-interval does not contain first occurence of character c\n while stack and stack[-1][0] > start[char]:\n stack.pop()\n # Left end of sub-interval must be extended\n if stack and stack[-1][1] < end[char]:\n while len(stack) > 1 and stack[-2][1] < end[char]:\n stack.pop()\n stack[-1][1] = end[char]\n # idx is potential start of minimal sub-interval\n elif idx == start[char] and (not stack or end[char] < stack[-1][1]) :\n stack.append([idx, end[char]])\n # Minimal sub-interval found. All other sub-intervals on the stack containing it cannot be minimal\n if stack and stack[-1][1] == idx:\n res.append(stack[-1])\n stack.clear()\n return [s[start: end + 1] for start, end in res]\n``` | 0 | Given the `root` of a binary tree, return _the lowest common ancestor (LCA) of two given nodes,_ `p` _and_ `q`. If either node `p` or `q` **does not exist** in the tree, return `null`. All values of the nodes in the tree are **unique**.
According to the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of two nodes `p` and `q` in a binary tree `T` is the lowest node that has both `p` and `q` as **descendants** (where we allow **a node to be a descendant of itself**) ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 10
**Output:** null
**Explanation:** Node 10 does not exist in the tree, so return null.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
**Follow up:** Can you find the LCA traversing the tree, without checking nodes existence? | Notice that it's impossible for any two valid substrings to overlap unless one is inside another. We can start by finding the starting and ending index for each character. From these indices, we can form the substrings by expanding each character's range if necessary (if another character exists in the range with smaller/larger starting/ending index). Sort the valid substrings by length and greedily take those with the smallest length, discarding the ones that overlap those we took. |
[Python3] greedy | maximum-number-of-non-overlapping-substrings | 0 | 1 | \n```\nclass Solution:\n def maxNumOfSubstrings(self, s: str) -> List[str]:\n locs = {}\n for i, x in enumerate(s): \n locs.setdefault(x, []).append(i)\n \n def fn(lo, hi): \n """Return expanded range covering all chars in s[lo:hi+1]."""\n for xx in locs: \n k0 = bisect_left(locs[xx], lo)\n k1 = bisect_left(locs[xx], hi)\n if k0 < k1 and (locs[xx][0] < lo or hi < locs[xx][-1]): \n lo = min(lo, locs[xx][0])\n hi = max(hi, locs[xx][-1])\n lo, hi = fn(lo, hi)\n return lo, hi\n \n group = set()\n for x in locs: \n group.add(fn(locs[x][0], locs[x][-1]))\n \n ans = [] # ISMP (interval scheduling maximization problem)\n prev = -1 \n for lo, hi in sorted(group, key=lambda x: x[1]): \n if prev < lo: \n ans.append(s[lo:hi+1])\n prev = hi \n return ans \n``` | 1 | Given a string `s` of lowercase letters, you need to find the maximum number of **non-empty** substrings of `s` that meet the following conditions:
1. The substrings do not overlap, that is for any two substrings `s[i..j]` and `s[x..y]`, either `j < x` or `i > y` is true.
2. A substring that contains a certain character `c` must also contain all occurrences of `c`.
Find _the maximum number of substrings that meet the above conditions_. If there are multiple solutions with the same number of substrings, _return the one with minimum total length._ It can be shown that there exists a unique solution of minimum total length.
Notice that you can return the substrings in **any** order.
**Example 1:**
**Input:** s = "adefaddaccc "
**Output:** \[ "e ", "f ", "ccc "\]
**Explanation:** The following are all the possible substrings that meet the conditions:
\[
"adefaddaccc "
"adefadda ",
"ef ",
"e ",
"f ",
"ccc ",
\]
If we choose the first string, we cannot choose anything else and we'd get only 1. If we choose "adefadda ", we are left with "ccc " which is the only one that doesn't overlap, thus obtaining 2 substrings. Notice also, that it's not optimal to choose "ef " since it can be split into two. Therefore, the optimal way is to choose \[ "e ", "f ", "ccc "\] which gives us 3 substrings. No other solution of the same number of substrings exist.
**Example 2:**
**Input:** s = "abbaccd "
**Output:** \[ "d ", "bb ", "cc "\]
**Explanation:** Notice that while the set of substrings \[ "d ", "abba ", "cc "\] also has length 3, it's considered incorrect since it has larger total length.
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Read the string from right to left, if the string ends in '0' then the number is even otherwise it is odd. Simulate the steps described in the binary string. |
[Python3] greedy | maximum-number-of-non-overlapping-substrings | 0 | 1 | \n```\nclass Solution:\n def maxNumOfSubstrings(self, s: str) -> List[str]:\n locs = {}\n for i, x in enumerate(s): \n locs.setdefault(x, []).append(i)\n \n def fn(lo, hi): \n """Return expanded range covering all chars in s[lo:hi+1]."""\n for xx in locs: \n k0 = bisect_left(locs[xx], lo)\n k1 = bisect_left(locs[xx], hi)\n if k0 < k1 and (locs[xx][0] < lo or hi < locs[xx][-1]): \n lo = min(lo, locs[xx][0])\n hi = max(hi, locs[xx][-1])\n lo, hi = fn(lo, hi)\n return lo, hi\n \n group = set()\n for x in locs: \n group.add(fn(locs[x][0], locs[x][-1]))\n \n ans = [] # ISMP (interval scheduling maximization problem)\n prev = -1 \n for lo, hi in sorted(group, key=lambda x: x[1]): \n if prev < lo: \n ans.append(s[lo:hi+1])\n prev = hi \n return ans \n``` | 1 | Given the `root` of a binary tree, return _the lowest common ancestor (LCA) of two given nodes,_ `p` _and_ `q`. If either node `p` or `q` **does not exist** in the tree, return `null`. All values of the nodes in the tree are **unique**.
According to the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of two nodes `p` and `q` in a binary tree `T` is the lowest node that has both `p` and `q` as **descendants** (where we allow **a node to be a descendant of itself**) ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 10
**Output:** null
**Explanation:** Node 10 does not exist in the tree, so return null.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
**Follow up:** Can you find the LCA traversing the tree, without checking nodes existence? | Notice that it's impossible for any two valid substrings to overlap unless one is inside another. We can start by finding the starting and ending index for each character. From these indices, we can form the substrings by expanding each character's range if necessary (if another character exists in the range with smaller/larger starting/ending index). Sort the valid substrings by length and greedily take those with the smallest length, discarding the ones that overlap those we took. |
[Python3] bitwise and | find-a-value-of-a-mysterious-function-closest-to-target | 0 | 1 | Algo\n[Bitwise operations](https://en.wikipedia.org/wiki/Bitwise_operation) can be efficiently carried out in the bit space. Here, the focus is "bitwise and", and an important property of "bitwise and" is that its result cannot be larger than its operands since no unset bits could be set. Furthermore, given a series of number `x1, x2, ..., xn`, their prefix "bitwise and", e..g `x1, x1&x2, x1&x2&x3, ...` can only populate a very small space due to the fact that the bits got unset **sequentially**. For example, if `x1` has `p` set bits, then the above series has at most `p` distinctive numbers. This is a very small set for any numbering system be it 32-bit or 64-bit. \n\nUtilizing this property, this question can be solved in `O(N)` time in contrast to the brute force `O(N^2)` like below which I learned from @qqwqert007 in this [post](https://leetcode.com/problems/find-a-value-of-a-mysterious-function-closest-to-target/discuss/743381/Python-6-lines-O(nlogm)-solution). \n\n```\nclass Solution:\n def closestToTarget(self, arr: List[int], target: int) -> int:\n ans, seen = inf, set()\n for x in arr: \n seen = {ss & x for ss in seen} | {x}\n ans = min(ans, min(abs(ss - target) for ss in seen))\n return ans \n```\n\n```\nclass Solution:\n def closestToTarget(self, arr: List[int], target: int) -> int:\n ans, seen = inf, set()\n for x in arr: \n tmp = set() #new set \n seen.add(0xffffffff)\n for ss in seen:\n ss &= x\n ans = min(ans, abs(ss - target))\n if ss > target: tmp.add(ss) #fine tuning \n seen = tmp\n return ans \n```\n\nA related question is [201. Bitwise AND of Numbers Range](https://leetcode.com/problems/bitwise-and-of-numbers-range/) for which bitwise and is applied to a range. This again can be computed very efficiently if we focus on the much smaller space of possible bits instead of the vast range of numbers. \n```\nclass Solution:\n def rangeBitwiseAnd(self, m: int, n: int) -> int:\n while n > m: \n n &= n-1 #unset last set bit\n return n \n``` | 8 | Winston was given the above mysterious function `func`. He has an integer array `arr` and an integer `target` and he wants to find the values `l` and `r` that make the value `|func(arr, l, r) - target|` minimum possible.
Return _the minimum possible value_ of `|func(arr, l, r) - target|`.
Notice that `func` should be called with the values `l` and `r` where `0 <= l, r < arr.length`.
**Example 1:**
**Input:** arr = \[9,12,3,7,15\], target = 5
**Output:** 2
**Explanation:** Calling func with all the pairs of \[l,r\] = \[\[0,0\],\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[0,1\],\[1,2\],\[2,3\],\[3,4\],\[0,2\],\[1,3\],\[2,4\],\[0,3\],\[1,4\],\[0,4\]\], Winston got the following results \[9,12,3,7,15,8,0,3,7,0,0,3,0,0,0\]. The value closest to 5 is 7 and 3, thus the minimum difference is 2.
**Example 2:**
**Input:** arr = \[1000000,1000000,1000000\], target = 1
**Output:** 999999
**Explanation:** Winston called the func with all possible values of \[l,r\] and he always got 1000000, thus the min difference is 999999.
**Example 3:**
**Input:** arr = \[1,2,4,8,16\], target = 0
**Output:** 0
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `0 <= target <= 107` | null |
python solution | find-a-value-of-a-mysterious-function-closest-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def closestToTarget(self, arr: List[int], target: int) -> int:\n res, s = float(\'inf\'), set()\n for a in arr:\n s = {a & b for b in s} | {a}\n res = min(res, min(abs(a - target) for a in s))\n return res\n``` | 0 | Winston was given the above mysterious function `func`. He has an integer array `arr` and an integer `target` and he wants to find the values `l` and `r` that make the value `|func(arr, l, r) - target|` minimum possible.
Return _the minimum possible value_ of `|func(arr, l, r) - target|`.
Notice that `func` should be called with the values `l` and `r` where `0 <= l, r < arr.length`.
**Example 1:**
**Input:** arr = \[9,12,3,7,15\], target = 5
**Output:** 2
**Explanation:** Calling func with all the pairs of \[l,r\] = \[\[0,0\],\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[0,1\],\[1,2\],\[2,3\],\[3,4\],\[0,2\],\[1,3\],\[2,4\],\[0,3\],\[1,4\],\[0,4\]\], Winston got the following results \[9,12,3,7,15,8,0,3,7,0,0,3,0,0,0\]. The value closest to 5 is 7 and 3, thus the minimum difference is 2.
**Example 2:**
**Input:** arr = \[1000000,1000000,1000000\], target = 1
**Output:** 999999
**Explanation:** Winston called the func with all possible values of \[l,r\] and he always got 1000000, thus the min difference is 999999.
**Example 3:**
**Input:** arr = \[1,2,4,8,16\], target = 0
**Output:** 0
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `0 <= target <= 107` | null |
Python3 solution | find-a-value-of-a-mysterious-function-closest-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to use a set to store the values of the array and the bitwise AND operations between all the elements\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach we are using to solve this problem is to use a set to store the values of the array and the bitwise AND operations between all the elements. We then iterate through the array and calculate the result by taking the difference between the current element and the target, and finding the minimum value in the set. \n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def closestToTarget(self, arr: List[int], target: int) -> int:\n res, s = float(\'inf\'), set()\n for a in arr:\n s = {a & b for b in s} | {a}\n res = min(res, min(abs(a - target) for a in s))\n return res\n``` | 0 | Winston was given the above mysterious function `func`. He has an integer array `arr` and an integer `target` and he wants to find the values `l` and `r` that make the value `|func(arr, l, r) - target|` minimum possible.
Return _the minimum possible value_ of `|func(arr, l, r) - target|`.
Notice that `func` should be called with the values `l` and `r` where `0 <= l, r < arr.length`.
**Example 1:**
**Input:** arr = \[9,12,3,7,15\], target = 5
**Output:** 2
**Explanation:** Calling func with all the pairs of \[l,r\] = \[\[0,0\],\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[0,1\],\[1,2\],\[2,3\],\[3,4\],\[0,2\],\[1,3\],\[2,4\],\[0,3\],\[1,4\],\[0,4\]\], Winston got the following results \[9,12,3,7,15,8,0,3,7,0,0,3,0,0,0\]. The value closest to 5 is 7 and 3, thus the minimum difference is 2.
**Example 2:**
**Input:** arr = \[1000000,1000000,1000000\], target = 1
**Output:** 999999
**Explanation:** Winston called the func with all possible values of \[l,r\] and he always got 1000000, thus the min difference is 999999.
**Example 3:**
**Input:** arr = \[1,2,4,8,16\], target = 0
**Output:** 0
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `0 <= target <= 107` | null |
Python Linear Time Solution | Faster than 70% | find-a-value-of-a-mysterious-function-closest-to-target | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def closestToTarget(self, arr: List[int], target: int) -> int:\n sz, left, right, temp, ans = len(arr), 0, 0, [], inf\n for i in range(len(arr)):\n curr = arr[i]\n temp.append(curr)\n for j in range(left, right + 1):\n ans = min(ans, abs(curr - target))\n curr &= temp[j]\n if curr != temp[-1]: temp.append(curr)\n ans = min(ans, abs(curr - target))\n left, right = right, len(temp)\n return ans\n``` | 0 | Winston was given the above mysterious function `func`. He has an integer array `arr` and an integer `target` and he wants to find the values `l` and `r` that make the value `|func(arr, l, r) - target|` minimum possible.
Return _the minimum possible value_ of `|func(arr, l, r) - target|`.
Notice that `func` should be called with the values `l` and `r` where `0 <= l, r < arr.length`.
**Example 1:**
**Input:** arr = \[9,12,3,7,15\], target = 5
**Output:** 2
**Explanation:** Calling func with all the pairs of \[l,r\] = \[\[0,0\],\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[0,1\],\[1,2\],\[2,3\],\[3,4\],\[0,2\],\[1,3\],\[2,4\],\[0,3\],\[1,4\],\[0,4\]\], Winston got the following results \[9,12,3,7,15,8,0,3,7,0,0,3,0,0,0\]. The value closest to 5 is 7 and 3, thus the minimum difference is 2.
**Example 2:**
**Input:** arr = \[1000000,1000000,1000000\], target = 1
**Output:** 999999
**Explanation:** Winston called the func with all possible values of \[l,r\] and he always got 1000000, thus the min difference is 999999.
**Example 3:**
**Input:** arr = \[1,2,4,8,16\], target = 0
**Output:** 0
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `0 <= target <= 107` | null |
Segment Tree + Sliding Window | O(nlogn) | find-a-value-of-a-mysterious-function-closest-to-target | 0 | 1 | ```\nclass SegmentTree:\n def __init__(self, values):\n self.data = [0 for _ in values] + values\n self.n = len(values)\n\n for idx in reversed(range(1, self.n)):\n self.data[idx] = self.data[2*idx] & self.data[2*idx+1]\n\n\n def query(self, left, right): \n if left>right:\n return -1000000000\n \n right += 1\n left += self.n\n right += self.n\n ans = self.data[left]\n\n while left < right:\n if left % 2:\n ans = ans & self.data[left]\n left += 1\n if right % 2:\n right -= 1 \n ans = ans & self.data[right]\n left //= 2\n right //= 2\n\n return ans\n \n\nclass Solution:\n \n def SlidingWindow(self, arr, target):\n \n st = SegmentTree(arr)\n l = 0\n r = 0\n ans = target + 10**9 # base case when l>r\n \n \n while r<len(arr):\n v = st.query(l, r)\n ans = min(ans, abs(v-target))\n \n if v>=target:\n r+=1\n else:\n if l<r:\n l+=1\n else:\n l+=1\n r+=1\n \n return ans\n \n \n \n \n \n | 5 | Winston was given the above mysterious function `func`. He has an integer array `arr` and an integer `target` and he wants to find the values `l` and `r` that make the value `|func(arr, l, r) - target|` minimum possible.
Return _the minimum possible value_ of `|func(arr, l, r) - target|`.
Notice that `func` should be called with the values `l` and `r` where `0 <= l, r < arr.length`.
**Example 1:**
**Input:** arr = \[9,12,3,7,15\], target = 5
**Output:** 2
**Explanation:** Calling func with all the pairs of \[l,r\] = \[\[0,0\],\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[0,1\],\[1,2\],\[2,3\],\[3,4\],\[0,2\],\[1,3\],\[2,4\],\[0,3\],\[1,4\],\[0,4\]\], Winston got the following results \[9,12,3,7,15,8,0,3,7,0,0,3,0,0,0\]. The value closest to 5 is 7 and 3, thus the minimum difference is 2.
**Example 2:**
**Input:** arr = \[1000000,1000000,1000000\], target = 1
**Output:** 999999
**Explanation:** Winston called the func with all possible values of \[l,r\] and he always got 1000000, thus the min difference is 999999.
**Example 3:**
**Input:** arr = \[1,2,4,8,16\], target = 0
**Output:** 0
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `0 <= target <= 107` | null |
[Python] Num of SubArray & Num of SubSet, Explained | number-of-sub-arrays-with-odd-sum | 0 | 1 | The solution for ***SubArray*** is straight forward with prefix sum:\n* We count not only the prefix sum, but also the number of even & odd prefix sum\n* For a prefix sum is even, we can only get an odd subarray sum by substract an odd prefix sum\n* For a prefix sum is odd, we can only get an odd subarray sum by substract an even prefix sum\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n ans = 0\n running_sum, odd_pf_cnt, even_pf_cnt = 0, 0, 0\n \n for num in arr:\n running_sum += num\n if running_sum % 2:\n odd_pf_cnt += 1\n ans += even_pf_cnt + 1\n else:\n even_pf_cnt += 1\n ans += odd_pf_cnt\n\n return ans % (10 ** 9 + 7)\n```\n\n**One extra solution** for getting the number of ***SubSet*** with odd sum:\n```\n def numOfSubSets(self, arr):\n # count the number of odd numbers and even numbers in the arr\n odd_cnt, even_cnt = 0, 0\n for num in arr:\n if num % 2:\n odd_cnt += 1\n else:\n even_cnt += 1\n # calculate the number of subset from only even numbers\n num_subarray_even = 1\n if even_cnt:\n num_subarray_even = (1 + even_cnt) * even_cnt // 2\n \n # from odd numbers, we can pick 1, 3, 5, ... 2*n + 1 (n = 0, 1, ..)\n k, fk, num_odd_selections = 3, 6, odd_cnt\n while k <= odd_cnt:\n num_odd_selections += num_odd_selections * (odd_cnt - k + 1) * (odd_cnt - k + 2) // fk\n k += 2\n fk = fk * (k - 1) * k\n \n return (num_subarray_even * num_odd_selections) % (10 ** 9 + 7)****\n``` | 1 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
[Python] Num of SubArray & Num of SubSet, Explained | number-of-sub-arrays-with-odd-sum | 0 | 1 | The solution for ***SubArray*** is straight forward with prefix sum:\n* We count not only the prefix sum, but also the number of even & odd prefix sum\n* For a prefix sum is even, we can only get an odd subarray sum by substract an odd prefix sum\n* For a prefix sum is odd, we can only get an odd subarray sum by substract an even prefix sum\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n ans = 0\n running_sum, odd_pf_cnt, even_pf_cnt = 0, 0, 0\n \n for num in arr:\n running_sum += num\n if running_sum % 2:\n odd_pf_cnt += 1\n ans += even_pf_cnt + 1\n else:\n even_pf_cnt += 1\n ans += odd_pf_cnt\n\n return ans % (10 ** 9 + 7)\n```\n\n**One extra solution** for getting the number of ***SubSet*** with odd sum:\n```\n def numOfSubSets(self, arr):\n # count the number of odd numbers and even numbers in the arr\n odd_cnt, even_cnt = 0, 0\n for num in arr:\n if num % 2:\n odd_cnt += 1\n else:\n even_cnt += 1\n # calculate the number of subset from only even numbers\n num_subarray_even = 1\n if even_cnt:\n num_subarray_even = (1 + even_cnt) * even_cnt // 2\n \n # from odd numbers, we can pick 1, 3, 5, ... 2*n + 1 (n = 0, 1, ..)\n k, fk, num_odd_selections = 3, 6, odd_cnt\n while k <= odd_cnt:\n num_odd_selections += num_odd_selections * (odd_cnt - k + 1) * (odd_cnt - k + 2) // fk\n k += 2\n fk = fk * (k - 1) * k\n \n return (num_subarray_even * num_odd_selections) % (10 ** 9 + 7)****\n``` | 1 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Python3 Recursive Solution | number-of-sub-arrays-with-odd-sum | 0 | 1 | ```\n\nclass Solution:\n def odd(self,arr,summ,i,flag):\n #recursion\n if flag==1 and i>0 and summ>0:\n return summ%2\n if i==len(arr):\n return (summ)%2\n if flag==1:\n summ=0\n return self.odd(arr,summ+arr[i],i+1,0)+self.odd(arr,summ,i+1,1)\n \n def numOfSubarrays(self, arr: List[int]) -> int:\n return self.odd(arr,0,0,0)\n\t\t\n\t\t | 4 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Python3 Recursive Solution | number-of-sub-arrays-with-odd-sum | 0 | 1 | ```\n\nclass Solution:\n def odd(self,arr,summ,i,flag):\n #recursion\n if flag==1 and i>0 and summ>0:\n return summ%2\n if i==len(arr):\n return (summ)%2\n if flag==1:\n summ=0\n return self.odd(arr,summ+arr[i],i+1,0)+self.odd(arr,summ,i+1,1)\n \n def numOfSubarrays(self, arr: List[int]) -> int:\n return self.odd(arr,0,0,0)\n\t\t\n\t\t | 4 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Python | O(n) time & O(1) space | prefix sum(detailed explanation) | number-of-sub-arrays-with-odd-sum | 0 | 1 | Keys:\n1) odd number - even numer = odd number(e.g., 9 - 4 = 5)\n2) even number - odd number = odd number(e.g., 8 - 3 = 5)\n3) prefix sum: to obtain the sum of subarray `arr[i + 1, j]`, we can use prefix sum by `sum[0, j] - sum[0, i]`.\n\nIdea:\n1) Keep two counters, `odd_sum` and `even_sum` for the number of odd sums and even sums;\n2) Iterate through the array and during each iteration, keep the the sum of elements we\'ve seen so far in `curr_sum`;\n3) Say the current index is `j`, if `curr_sum` is odd, we can decrease `curr_sum` by any previously seen even sum(say index `i`) to get a subarray `arr[i + 1, j]` with an odd sum; similarly, if `curr_sum` is even, we can decrease `curr_sum` by any previously seen odd sum to get a subarray with an odd sum. \n\n`even_sum` initialize to be 1 since before we start and `curr_sum = 0`, 0 is even.\n\nTime: O(n) - one pass\nSpace: O(1)\n\nHere\'s the code:\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n mod, n = 10 ** 9 + 7, len(arr)\n odd_sum, even_sum, curr_sum, ans = 0, 1, 0, 0\n for i in arr:\n curr_sum += i\n if curr_sum % 2 == 1:\n odd_sum += 1\n ans += even_sum % mod\n else:\n even_sum += 1\n ans += odd_sum % mod\n ans %= mod\n return ans\n```\n\nI know a lot of others also share this idea, but I was having a hard time solving this problem during the contest(got 1 TLE and 1 error before my solution got accepted), and that\'s why I wanna explain it in details.\nIf you find this post helpful, please upvote. Thank you. | 19 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Python | O(n) time & O(1) space | prefix sum(detailed explanation) | number-of-sub-arrays-with-odd-sum | 0 | 1 | Keys:\n1) odd number - even numer = odd number(e.g., 9 - 4 = 5)\n2) even number - odd number = odd number(e.g., 8 - 3 = 5)\n3) prefix sum: to obtain the sum of subarray `arr[i + 1, j]`, we can use prefix sum by `sum[0, j] - sum[0, i]`.\n\nIdea:\n1) Keep two counters, `odd_sum` and `even_sum` for the number of odd sums and even sums;\n2) Iterate through the array and during each iteration, keep the the sum of elements we\'ve seen so far in `curr_sum`;\n3) Say the current index is `j`, if `curr_sum` is odd, we can decrease `curr_sum` by any previously seen even sum(say index `i`) to get a subarray `arr[i + 1, j]` with an odd sum; similarly, if `curr_sum` is even, we can decrease `curr_sum` by any previously seen odd sum to get a subarray with an odd sum. \n\n`even_sum` initialize to be 1 since before we start and `curr_sum = 0`, 0 is even.\n\nTime: O(n) - one pass\nSpace: O(1)\n\nHere\'s the code:\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n mod, n = 10 ** 9 + 7, len(arr)\n odd_sum, even_sum, curr_sum, ans = 0, 1, 0, 0\n for i in arr:\n curr_sum += i\n if curr_sum % 2 == 1:\n odd_sum += 1\n ans += even_sum % mod\n else:\n even_sum += 1\n ans += odd_sum % mod\n ans %= mod\n return ans\n```\n\nI know a lot of others also share this idea, but I was having a hard time solving this problem during the contest(got 1 TLE and 1 error before my solution got accepted), and that\'s why I wanna explain it in details.\nIf you find this post helpful, please upvote. Thank you. | 19 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Python 3 | Easy to understand | Basic | number-of-sub-arrays-with-odd-sum | 0 | 1 | ```\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n ans = 0\n even = 1 #(sum zero before array start)\n odd = 0\n rsum = 0\n for i in range(len(arr)):\n rsum += arr[i]\n if rsum % 2 == 1:\n ans += even\n odd += 1\n else:\n ans += odd\n even += 1\n return ans % (10**9 + 7)\n``` | 4 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Python 3 | Easy to understand | Basic | number-of-sub-arrays-with-odd-sum | 0 | 1 | ```\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n ans = 0\n even = 1 #(sum zero before array start)\n odd = 0\n rsum = 0\n for i in range(len(arr)):\n rsum += arr[i]\n if rsum % 2 == 1:\n ans += even\n odd += 1\n else:\n ans += odd\n even += 1\n return ans % (10**9 + 7)\n``` | 4 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
[Java/Python 3] Count odds and compute, w/ brief explanation and analysis. | number-of-sub-arrays-with-odd-sum | 1 | 1 | 1. Count the number of the odd prefix sum `oddCount`, then the number of the even prefix sum is `arr.length - oddCount`\n2. For each odd prefix sum, its difference between any even prefix sum is also odd subarray sum; \n\n e.g., `arr = [1,2,3,4,5,6,7]`, for a given odd prefix sum `arr[0] + arr[1] = 3`, the difference between even prefix sum `6, 10, 28` are `6 - 3 = 3, 10 - 3 = 7, 28 - 3 = 25`, respectively. They are all odds; Similarly, for the odd prefix sums `arr[0] + ... + arr[4] = 15`, `arr[0] + ... + arr[5] = 21`, their difference between `6, 10, 28` are all odds. Those differneces correspond to `3 * 3 = 9` odd subarrays.\n \nTherefore, in summary, we have `oddCount * evenCount` odd-sum subarrays; \n\nIn addition, the `oddCount` odd prefix sums themselves are also odd-sum subarrays; Hence we have the following formula:\n```\noddCount + oddCount * (arr.length - oddCount) \n```\n```java\n public int numOfSubarrays(int[] arr) {\n long oddCount = 0, prefixSum = 0;\n for (int a : arr) {\n prefixSum += a;\n oddCount += prefixSum % 2;\n }\n oddCount += (arr.length - oddCount) * oddCount;\n return (int)(oddCount % 1_000_000_007); \n }\n```\n```python\n def numOfSubarrays(self, arr: List[int]) -> int:\n odd = sum = 0\n for a in arr:\n sum += a\n odd += sum % 2\n return (odd + odd * (len(arr) - odd)) % (10 ** 9 + 7)\n```\n**Analysis:**\nTime: O(n), space: O(1). | 11 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
[Java/Python 3] Count odds and compute, w/ brief explanation and analysis. | number-of-sub-arrays-with-odd-sum | 1 | 1 | 1. Count the number of the odd prefix sum `oddCount`, then the number of the even prefix sum is `arr.length - oddCount`\n2. For each odd prefix sum, its difference between any even prefix sum is also odd subarray sum; \n\n e.g., `arr = [1,2,3,4,5,6,7]`, for a given odd prefix sum `arr[0] + arr[1] = 3`, the difference between even prefix sum `6, 10, 28` are `6 - 3 = 3, 10 - 3 = 7, 28 - 3 = 25`, respectively. They are all odds; Similarly, for the odd prefix sums `arr[0] + ... + arr[4] = 15`, `arr[0] + ... + arr[5] = 21`, their difference between `6, 10, 28` are all odds. Those differneces correspond to `3 * 3 = 9` odd subarrays.\n \nTherefore, in summary, we have `oddCount * evenCount` odd-sum subarrays; \n\nIn addition, the `oddCount` odd prefix sums themselves are also odd-sum subarrays; Hence we have the following formula:\n```\noddCount + oddCount * (arr.length - oddCount) \n```\n```java\n public int numOfSubarrays(int[] arr) {\n long oddCount = 0, prefixSum = 0;\n for (int a : arr) {\n prefixSum += a;\n oddCount += prefixSum % 2;\n }\n oddCount += (arr.length - oddCount) * oddCount;\n return (int)(oddCount % 1_000_000_007); \n }\n```\n```python\n def numOfSubarrays(self, arr: List[int]) -> int:\n odd = sum = 0\n for a in arr:\n sum += a\n odd += sum % 2\n return (odd + odd * (len(arr) - odd)) % (10 ** 9 + 7)\n```\n**Analysis:**\nTime: O(n), space: O(1). | 11 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Python | DP | Elementary math | [even=i-odd]| Commented | number-of-sub-arrays-with-odd-sum | 0 | 1 | Simple math:\n* even + even = even\n* odd + odd = even\n* odd + even = **odd** (*the only way to get an odd number*)\n\n```dp[i]``` indicates the number of subarrays ending with ```arr[i]``` that summed to an odd number, therefore the number of subarrays ending with ```arr[i]``` that summed to an even number would be ```i-dp[i]```.\n```Python\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n dp = [0] * len(arr)\n dp[0] = arr[0]&1\n for i in range(1,len(arr)):\n if arr[i]&1: # arr[i] is odd\n dp[i] = i - dp[i-1] + 1 # 1 as arr[i] itself\n else: # arr[i] is even\n dp[i] = dp[i-1]\n return sum(dp) % (10**9+7)\n```\n | 5 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Python | DP | Elementary math | [even=i-odd]| Commented | number-of-sub-arrays-with-odd-sum | 0 | 1 | Simple math:\n* even + even = even\n* odd + odd = even\n* odd + even = **odd** (*the only way to get an odd number*)\n\n```dp[i]``` indicates the number of subarrays ending with ```arr[i]``` that summed to an odd number, therefore the number of subarrays ending with ```arr[i]``` that summed to an even number would be ```i-dp[i]```.\n```Python\nclass Solution:\n def numOfSubarrays(self, arr: List[int]) -> int:\n dp = [0] * len(arr)\n dp[0] = arr[0]&1\n for i in range(1,len(arr)):\n if arr[i]&1: # arr[i] is odd\n dp[i] = i - dp[i-1] + 1 # 1 as arr[i] itself\n else: # arr[i] is even\n dp[i] = dp[i-1]\n return sum(dp) % (10**9+7)\n```\n | 5 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
99.7% Python 3 solution with 17 lines, no search, explained | number-of-good-ways-to-split-a-string | 0 | 1 | The following solution yields a 99.64% runtime. For the explanation see below!\n\n```\nclass Solution:\n def numSplits(self, s: str) -> int:\n\t\t# this is not neccessary, but speeds things up\n length = len(s)\n if length == 1: # never splittable\n return 0\n elif length == 2: # always splittable\n return 1\n\t\t\n\t\t# we are recording the first and last occurence of each included letter\n first = {} # max size = 26\n last = {} # max size = 26\n\t\t\n for index, character in enumerate(s): # O(n)\n if character not in first:\n first[character] = index\n last[character] = index\n\t\t\t\n\t\t# we are concatenating the collected indices into a list and sort them\n indices = list(first.values()) + list(last.values()) # max length 26 + 26 = 52\n indices.sort() # sorting is constant O(1) because of the length limit above\n\t\t\n\t\t# all possible splits will be in the middle of this list\n middle = len(indices)//2 # always an integer because indices has an even length\n\t\t\n\t\t# there are this many possible splits between the two \'median\' numbers\n return indices[middle] - indices[middle-1]\n```\n\nLet\'s look at the example **"abacadcac"**. We record the first and last occurence of each letter:\n\n```\nfirst = {\'a\' : 0, \'b\' : 1, \'c\' : 3, \'d\' : 5}\nlast = {\'a\' : 7, \'b\' : 1, \'c\' : 8, \'d\' : 5}\n```\n\nThese two dictionaries can also be visualized like this, with the numbers as small arrows pointing to the indices. Upper row = first, lower row = last.\n\n```\na b c d\n\u25BC \u25BC \u25BC| |\u25BC\n0 1 2 3|4|5 6 7 8\n \u25B2 | |\u25B2 \u25B2 \u25B2\n b d a c\n```\n\nThe two lines represent all possible splits in which there are equally many arrows left of the split as right of the split (not discerning between upper and lower arrows).\n\nIn a sorted list the combined first and last indices look like this:\n\n```\n[0, 1, 1, 3, 5, 5, 7, 8]\n```\n\nThe lines in the arrow example correspond to the middle of this list.\nThe two indices in the middle are `3` and `5`.\nHence, there are `5 - 3` possible ways to split between the 3rd and 5th index.\n\nThanks for upvoting if this was helpful! | 80 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
99.7% Python 3 solution with 17 lines, no search, explained | number-of-good-ways-to-split-a-string | 0 | 1 | The following solution yields a 99.64% runtime. For the explanation see below!\n\n```\nclass Solution:\n def numSplits(self, s: str) -> int:\n\t\t# this is not neccessary, but speeds things up\n length = len(s)\n if length == 1: # never splittable\n return 0\n elif length == 2: # always splittable\n return 1\n\t\t\n\t\t# we are recording the first and last occurence of each included letter\n first = {} # max size = 26\n last = {} # max size = 26\n\t\t\n for index, character in enumerate(s): # O(n)\n if character not in first:\n first[character] = index\n last[character] = index\n\t\t\t\n\t\t# we are concatenating the collected indices into a list and sort them\n indices = list(first.values()) + list(last.values()) # max length 26 + 26 = 52\n indices.sort() # sorting is constant O(1) because of the length limit above\n\t\t\n\t\t# all possible splits will be in the middle of this list\n middle = len(indices)//2 # always an integer because indices has an even length\n\t\t\n\t\t# there are this many possible splits between the two \'median\' numbers\n return indices[middle] - indices[middle-1]\n```\n\nLet\'s look at the example **"abacadcac"**. We record the first and last occurence of each letter:\n\n```\nfirst = {\'a\' : 0, \'b\' : 1, \'c\' : 3, \'d\' : 5}\nlast = {\'a\' : 7, \'b\' : 1, \'c\' : 8, \'d\' : 5}\n```\n\nThese two dictionaries can also be visualized like this, with the numbers as small arrows pointing to the indices. Upper row = first, lower row = last.\n\n```\na b c d\n\u25BC \u25BC \u25BC| |\u25BC\n0 1 2 3|4|5 6 7 8\n \u25B2 | |\u25B2 \u25B2 \u25B2\n b d a c\n```\n\nThe two lines represent all possible splits in which there are equally many arrows left of the split as right of the split (not discerning between upper and lower arrows).\n\nIn a sorted list the combined first and last indices look like this:\n\n```\n[0, 1, 1, 3, 5, 5, 7, 8]\n```\n\nThe lines in the arrow example correspond to the middle of this list.\nThe two indices in the middle are `3` and `5`.\nHence, there are `5 - 3` possible ways to split between the 3rd and 5th index.\n\nThanks for upvoting if this was helpful! | 80 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Python O(n) | number-of-good-ways-to-split-a-string | 0 | 1 | ```\n# TimeComplexity O(n)\n# MemoryComplexity O(n)\n\nclass Solution:\n def numSplits(self, s: str) -> int:\n if not s: return 0\n total = 0\n \n # prefix unique count\n prefix_count = [0]*len(s)\n unique = set()\n for i in range(len(s)):\n unique.add(s[i])\n prefix_count[i] = len(unique)\n \n # checking suffix\n unique.clear()\n for j in range(len(s) - 1, 0, -1):\n unique.add(s[j])\n if prefix_count[j-1] == len(unique):\n total += 1\n \n return total \n``` | 8 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
Python O(n) | number-of-good-ways-to-split-a-string | 0 | 1 | ```\n# TimeComplexity O(n)\n# MemoryComplexity O(n)\n\nclass Solution:\n def numSplits(self, s: str) -> int:\n if not s: return 0\n total = 0\n \n # prefix unique count\n prefix_count = [0]*len(s)\n unique = set()\n for i in range(len(s)):\n unique.add(s[i])\n prefix_count[i] = len(unique)\n \n # checking suffix\n unique.clear()\n for j in range(len(s) - 1, 0, -1):\n unique.add(s[j])\n if prefix_count[j-1] == len(unique):\n total += 1\n \n return total \n``` | 8 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
✔️ [Python] | Simple | Clean approach | beat 95% Easy T: O(N) | number-of-good-ways-to-split-a-string | 0 | 1 | ```\nfrom collections import defaultdict\n\nclass Solution:\n def numSplits(self, s: str) -> int:\n leftD, rightD = defaultdict(int), defaultdict(int)\n ans = 0\n for val in s: rightD[val]+=1\n leftUnique, rightUnique = 0, len(rightD.keys())\n for val in s:\n if leftD.get(val, -1) < 0: \n leftUnique+=1\n leftD[val] = 1\n else: \n leftD[val] += 1 \n rightD[val]-=1\n if rightD[val]<=0: rightUnique-=1\n if leftUnique==rightUnique: ans+=1\n return ans\n```\n\nIf you think this post is helpful for you, **spread your love by hitting a thums up.** Any questions or discussions are welcome!\n\nThank you for reading this solution. | 1 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
✔️ [Python] | Simple | Clean approach | beat 95% Easy T: O(N) | number-of-good-ways-to-split-a-string | 0 | 1 | ```\nfrom collections import defaultdict\n\nclass Solution:\n def numSplits(self, s: str) -> int:\n leftD, rightD = defaultdict(int), defaultdict(int)\n ans = 0\n for val in s: rightD[val]+=1\n leftUnique, rightUnique = 0, len(rightD.keys())\n for val in s:\n if leftD.get(val, -1) < 0: \n leftUnique+=1\n leftD[val] = 1\n else: \n leftD[val] += 1 \n rightD[val]-=1\n if rightD[val]<=0: rightUnique-=1\n if leftUnique==rightUnique: ans+=1\n return ans\n```\n\nIf you think this post is helpful for you, **spread your love by hitting a thums up.** Any questions or discussions are welcome!\n\nThank you for reading this solution. | 1 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Very simple python 🐍 solution using counter Dict with comments | number-of-good-ways-to-split-a-string | 0 | 1 | ```\nimport collections\nclass Solution:\n def numSplits(self, s: str) -> int:\n myS1=collections.Counter() #s1 is now empty\n myS2=collections.Counter(s) #s2 is now has all string \n ways=0 #when len of myS1= len of myS2 --> ways+=1\n\n for letter in s: \n myS1[letter]+=1\n myS2[letter]-=1\n \n if myS2[letter]==0:\n myS2.pop(letter)\n \n if len(myS1)==len(myS2):\n ways+=1 \n return ways \n\n \n``` | 20 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
Very simple python 🐍 solution using counter Dict with comments | number-of-good-ways-to-split-a-string | 0 | 1 | ```\nimport collections\nclass Solution:\n def numSplits(self, s: str) -> int:\n myS1=collections.Counter() #s1 is now empty\n myS2=collections.Counter(s) #s2 is now has all string \n ways=0 #when len of myS1= len of myS2 --> ways+=1\n\n for letter in s: \n myS1[letter]+=1\n myS2[letter]-=1\n \n if myS2[letter]==0:\n myS2.pop(letter)\n \n if len(myS1)==len(myS2):\n ways+=1 \n return ways \n\n \n``` | 20 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Two Hashset Approach | number-of-good-ways-to-split-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thought that appears is the usage of suffix and prefix arrays. We can use hashset to maintain unique characters and store the counts in left and right arrays.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain two arrays, left and right. Iterate from left to right and store the characters in a hashset as we iterate. Then store the length of the set in the array. Similarly iterate the string in reverse order, and then we get right array. \nFinally iterate the string one more time and check if the left and right aray values at a particular index are equal. This is basically splitting of string in two parts, left and right.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSplits(self, s: str) -> int:\n n = len(s)\n\n if n == 1:\n return 1\n \n left = [0]* n\n right = [0]* n\n\n uniqueChars = set()\n\n for i in range(n - 1, -1, -1):\n uniqueChars.add(s[i])\n right[i] = len(uniqueChars)\n\n uniqueChars = set()\n\n for i in range(n):\n uniqueChars.add(s[i])\n left[i] = len(uniqueChars)\n\n total_ways = 0\n\n for i in range(n - 1):\n if left[i] == right[i + 1]:\n total_ways += 1\n\n return total_ways\n``` | 1 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
Two Hashset Approach | number-of-good-ways-to-split-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thought that appears is the usage of suffix and prefix arrays. We can use hashset to maintain unique characters and store the counts in left and right arrays.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain two arrays, left and right. Iterate from left to right and store the characters in a hashset as we iterate. Then store the length of the set in the array. Similarly iterate the string in reverse order, and then we get right array. \nFinally iterate the string one more time and check if the left and right aray values at a particular index are equal. This is basically splitting of string in two parts, left and right.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSplits(self, s: str) -> int:\n n = len(s)\n\n if n == 1:\n return 1\n \n left = [0]* n\n right = [0]* n\n\n uniqueChars = set()\n\n for i in range(n - 1, -1, -1):\n uniqueChars.add(s[i])\n right[i] = len(uniqueChars)\n\n uniqueChars = set()\n\n for i in range(n):\n uniqueChars.add(s[i])\n left[i] = len(uniqueChars)\n\n total_ways = 0\n\n for i in range(n - 1):\n if left[i] == right[i + 1]:\n total_ways += 1\n\n return total_ways\n``` | 1 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Python3 | Solved Using Hashmap and Set | O(N) Time and O(N) Space | number-of-good-ways-to-split-a-string | 0 | 1 | # Intuition\nBasically, I thought of performing linear scan first to obtain frequency map for the entire string. Then, I thought of utilizing a set instance to keep track of number of distinct chars of currently built up left substring and use another hashmap instance to keep track of the current right substring (s.t. left substring + right substring == original string input s). For each new char I process and append to left substring, I check if it\'s a good split. \n\n# Approach\nIf the number of elements in set(tells # distinct chars in left substring) equals number of distinct keys in hashmap(# of distinct chars in right substring), then it\'s a good split! Simply process each char left to right and consider all possible splits and count total good splits! \n\n# Complexity\n- Time complexity:\nO(N), N is number of chars in s! \n\n- Space complexity:\nO(N + N)->O(N), due to hashmap and one set instance! \n\n# Code\n```\nclass Solution:\n def numSplits(self, s: str) -> int:\n #Ex: "aacaba" -> {}(freq map)\n #Built-up set = (a, b, c) \n #Index pos 0 -> built up has 1 key, freq map has 3 keys -> not good!\n #Index pos 1 -> built up has 1 key, freq map has 3 keys -> not good! \n #Index pos 2 -> built up has 2 key, freq map has 2 keys -> good! \n #Index pos 3 -> built up has 2 key , freq map has 2 keys -> good! \n #Index pos 4-> built up has 3 elements, freq map has 1 key -> not good! \n #Index pos 5-> built up has 3 elements, freq map has 0 key -> not good! \n #Ans = 2! \n\n #Ex 2 : s = "abcd" freqmap = {}\n #Built up set = (a, b, c, d) \n #Index pos 0 -> not good \n #index pos 1 -> good! \n #index pos 2 -> not good! \n #index pos 3-> not good! \n #Ans -> 1 good way! \n\n #Approach: First, initialize frequency map via one linear scan of string input!\n #Then, build up left substring and keep track of distinct characters using a set data structure!\n #Also, for each current char we process, update the frequency in freq map and remove key-value\n #pairs if right substring does not contain the particular char no more! \n hm = {} \n left_set = set() \n #initialize frequency map! \n for c in s:\n if c not in hm:\n hm[c] = 1\n else:\n hm[c] += 1\n\n #Add each char to left substring we build over time from left to right! \n #For each new char we append to left substring, consider if it\'s a good split w/\n #respect to right substring!\n\n #initialize num of good splits to 0! \n ans = 0 \n for char in s:\n #record potentially new distinct char part of left substring! \n left_set.add(char)\n #we are removing this char from right substring! \n hm[char] -= 1\n #remove key-val pair for char in hm if there is no more instances of the char in \n #right substring! \n if(hm[char] == 0):\n hm.pop(char)\n #then, check if left and right substring makes a good split! \n if(len(hm.keys()) == len(left_set)):\n ans += 1\n \n return ans \n\n\n \n \n\n\n\n\n\n\n\n``` | 1 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
Python3 | Solved Using Hashmap and Set | O(N) Time and O(N) Space | number-of-good-ways-to-split-a-string | 0 | 1 | # Intuition\nBasically, I thought of performing linear scan first to obtain frequency map for the entire string. Then, I thought of utilizing a set instance to keep track of number of distinct chars of currently built up left substring and use another hashmap instance to keep track of the current right substring (s.t. left substring + right substring == original string input s). For each new char I process and append to left substring, I check if it\'s a good split. \n\n# Approach\nIf the number of elements in set(tells # distinct chars in left substring) equals number of distinct keys in hashmap(# of distinct chars in right substring), then it\'s a good split! Simply process each char left to right and consider all possible splits and count total good splits! \n\n# Complexity\n- Time complexity:\nO(N), N is number of chars in s! \n\n- Space complexity:\nO(N + N)->O(N), due to hashmap and one set instance! \n\n# Code\n```\nclass Solution:\n def numSplits(self, s: str) -> int:\n #Ex: "aacaba" -> {}(freq map)\n #Built-up set = (a, b, c) \n #Index pos 0 -> built up has 1 key, freq map has 3 keys -> not good!\n #Index pos 1 -> built up has 1 key, freq map has 3 keys -> not good! \n #Index pos 2 -> built up has 2 key, freq map has 2 keys -> good! \n #Index pos 3 -> built up has 2 key , freq map has 2 keys -> good! \n #Index pos 4-> built up has 3 elements, freq map has 1 key -> not good! \n #Index pos 5-> built up has 3 elements, freq map has 0 key -> not good! \n #Ans = 2! \n\n #Ex 2 : s = "abcd" freqmap = {}\n #Built up set = (a, b, c, d) \n #Index pos 0 -> not good \n #index pos 1 -> good! \n #index pos 2 -> not good! \n #index pos 3-> not good! \n #Ans -> 1 good way! \n\n #Approach: First, initialize frequency map via one linear scan of string input!\n #Then, build up left substring and keep track of distinct characters using a set data structure!\n #Also, for each current char we process, update the frequency in freq map and remove key-value\n #pairs if right substring does not contain the particular char no more! \n hm = {} \n left_set = set() \n #initialize frequency map! \n for c in s:\n if c not in hm:\n hm[c] = 1\n else:\n hm[c] += 1\n\n #Add each char to left substring we build over time from left to right! \n #For each new char we append to left substring, consider if it\'s a good split w/\n #respect to right substring!\n\n #initialize num of good splits to 0! \n ans = 0 \n for char in s:\n #record potentially new distinct char part of left substring! \n left_set.add(char)\n #we are removing this char from right substring! \n hm[char] -= 1\n #remove key-val pair for char in hm if there is no more instances of the char in \n #right substring! \n if(hm[char] == 0):\n hm.pop(char)\n #then, check if left and right substring makes a good split! \n if(len(hm.keys()) == len(left_set)):\n ans += 1\n \n return ans \n\n\n \n \n\n\n\n\n\n\n\n``` | 1 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Simple solution/intuition in TypeScript / Python | minimum-number-of-increments-on-subarrays-to-form-a-target-array | 0 | 1 | # Intuition\nHere we have:\n- list of integers `target`\n- our goal is to recreate `target` from `initial` list of integers\n\nAn `initial` list consists with `0`-s. It has **the same** structure as in `target`.\n\nThe key to solve this problem is to think about **neighbours** and how they\'re related to each other.\n\nWe should move only in **right** direction and at each step we interested in **decrementing at most** `target[i]`- s as we can.\n\n```\n# Example\ntarget = [3,1,5,4,2]\n\n# Take a look at first two neighbours.\na = 3\nb = 1\n\n# How much \'decrements\' we need to make them 0-s?\n# max(a, b) => 3\n\n# Okay. Let\'s proceed to the next pair:\n\na = 1\nb = 5\n\n# What about this ones?\n# If you repeat the same process before, it WON\'T work\n# since we\'ve already DECREMENTED some points from 3, and 1,\n# respectively. But we have a \'diff\' as b > a and b - a = 4\n# Will it help us somehow?\n\n# At this step try to \'glue\' first integer with this pair \n# and figure out the process of decrementing\n\nseq = [3, 1, 5] => [(2), (0), (4)] => [(1), 0, 4] => [(0), 0, 4] => \n=> [0, 0, (3)] => [0, 0, (2)] => [0, 0, (1)] => [0, 0, (0)]\n\n# For the first step we make 3 decrements, and at the second step 4.\n# diff[0] + diff[1] = 7\n\n# Conclusion: at each step we need to take care about cur. maximum.\n# If it\'s higher than the previous one, increment count of steps as\n# max - min, otherwise continue to move forward.\n``` \n\n# Approach\n1. declare `ans` and `curMax` as `target[0]`\n2. iterate over `target`\n3. if `curMax < target[i]`, increment `ans += target[i] - curMax`\n4. and change `curMax` at each step\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N)** to iterate over `target`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space\n\n# Code in Python3\n```\nclass Solution:\n def minNumberOperations(self, target: List[int]) -> int:\n ans = target[0]\n curMax = target[0]\n\n for i in range(1, len(target)):\n if curMax < target[i]: ans += target[i] - curMax \n\n curMax = target[i]\n \n return ans\n```\n# Code in TypeScript\n```\nfunction minNumberOperations(target: number[]): number {\n let ans = target[0]\n let curMax = target[0]\n\n for (let i = 1; i < target.length; i++) {\n if (curMax < target[i]) ans += target[i] - curMax\n\n curMax = target[i]\n }\n\n return ans\n};\n``` | 1 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Python 3 | Simplest one pass solution. | minimum-number-of-increments-on-subarrays-to-form-a-target-array | 0 | 1 | Check with previous number if it is higher then add the difference otherwise not\n\n```\nclass Solution:\n def minNumberOperations(self, target: List[int]) -> int:\n prev_num = 0\n steps = 0\n for val in target:\n steps += val-prev_num if val > prev_num else 0\n prev_num = val\n return steps\n``` | 7 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | patients-with-a-condition | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef find_patients(patients: pd.DataFrame) -> pd.DataFrame:\n return patients[\n patients[\'conditions\'].str.contains(r\'(^DIAB1)|( DIAB1)\')\n ]\n```\n```SQL []\nSELECT *\n FROM Patients\n WHERE conditions REGEXP \'\\\\bDIAB1\';\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n | 9 | Design a queue that supports `push` and `pop` operations in the front, middle, and back.
Implement the `FrontMiddleBack` class:
* `FrontMiddleBack()` Initializes the queue.
* `void pushFront(int val)` Adds `val` to the **front** of the queue.
* `void pushMiddle(int val)` Adds `val` to the **middle** of the queue.
* `void pushBack(int val)` Adds `val` to the **back** of the queue.
* `int popFront()` Removes the **front** element of the queue and returns it. If the queue is empty, return `-1`.
* `int popMiddle()` Removes the **middle** element of the queue and returns it. If the queue is empty, return `-1`.
* `int popBack()` Removes the **back** element of the queue and returns it. If the queue is empty, return `-1`.
**Notice** that when there are **two** middle position choices, the operation is performed on the **frontmost** middle position choice. For example:
* Pushing `6` into the middle of `[1, 2, 3, 4, 5]` results in `[1, 2, 6, 3, 4, 5]`.
* Popping the middle from `[1, 2, 3, 4, 5, 6]` returns `3` and results in `[1, 2, 4, 5, 6]`.
**Example 1:**
**Input:**
\[ "FrontMiddleBackQueue ", "pushFront ", "pushBack ", "pushMiddle ", "pushMiddle ", "popFront ", "popMiddle ", "popMiddle ", "popBack ", "popFront "\]
\[\[\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[\], \[\]\]
**Output:**
\[null, null, null, null, null, 1, 3, 4, 2, -1\]
**Explanation:**
FrontMiddleBackQueue q = new FrontMiddleBackQueue();
q.pushFront(1); // \[1\]
q.pushBack(2); // \[1, 2\]
q.pushMiddle(3); // \[1, 3, 2\]
q.pushMiddle(4); // \[1, 4, 3, 2\]
q.popFront(); // return 1 -> \[4, 3, 2\]
q.popMiddle(); // return 3 -> \[4, 2\]
q.popMiddle(); // return 4 -> \[2\]
q.popBack(); // return 2 -> \[\]
q.popFront(); // return -1 -> \[\] (The queue is empty)
**Constraints:**
* `1 <= val <= 109`
* At most `1000` calls will be made to `pushFront`, `pushMiddle`, `pushBack`, `popFront`, `popMiddle`, and `popBack`. | null |
😃 Easy Solution || Pandas 🔥🔥 | patients-with-a-condition | 0 | 1 | ```\nimport pandas as pd\n\ndef find_patients(patients: pd.DataFrame) -> pd.DataFrame:\n df = patients[patients[\'conditions\'].str.contains(r\'(^DIAB1)|( DIAB1)\')]\n return df\n \n``` | 1 | Design a queue that supports `push` and `pop` operations in the front, middle, and back.
Implement the `FrontMiddleBack` class:
* `FrontMiddleBack()` Initializes the queue.
* `void pushFront(int val)` Adds `val` to the **front** of the queue.
* `void pushMiddle(int val)` Adds `val` to the **middle** of the queue.
* `void pushBack(int val)` Adds `val` to the **back** of the queue.
* `int popFront()` Removes the **front** element of the queue and returns it. If the queue is empty, return `-1`.
* `int popMiddle()` Removes the **middle** element of the queue and returns it. If the queue is empty, return `-1`.
* `int popBack()` Removes the **back** element of the queue and returns it. If the queue is empty, return `-1`.
**Notice** that when there are **two** middle position choices, the operation is performed on the **frontmost** middle position choice. For example:
* Pushing `6` into the middle of `[1, 2, 3, 4, 5]` results in `[1, 2, 6, 3, 4, 5]`.
* Popping the middle from `[1, 2, 3, 4, 5, 6]` returns `3` and results in `[1, 2, 4, 5, 6]`.
**Example 1:**
**Input:**
\[ "FrontMiddleBackQueue ", "pushFront ", "pushBack ", "pushMiddle ", "pushMiddle ", "popFront ", "popMiddle ", "popMiddle ", "popBack ", "popFront "\]
\[\[\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[\], \[\]\]
**Output:**
\[null, null, null, null, null, 1, 3, 4, 2, -1\]
**Explanation:**
FrontMiddleBackQueue q = new FrontMiddleBackQueue();
q.pushFront(1); // \[1\]
q.pushBack(2); // \[1, 2\]
q.pushMiddle(3); // \[1, 3, 2\]
q.pushMiddle(4); // \[1, 4, 3, 2\]
q.popFront(); // return 1 -> \[4, 3, 2\]
q.popMiddle(); // return 3 -> \[4, 2\]
q.popMiddle(); // return 4 -> \[2\]
q.popBack(); // return 2 -> \[\]
q.popFront(); // return -1 -> \[\] (The queue is empty)
**Constraints:**
* `1 <= val <= 109`
* At most `1000` calls will be made to `pushFront`, `pushMiddle`, `pushBack`, `popFront`, `popMiddle`, and `popBack`. | null |
Pandas - Simple solution | patients-with-a-condition | 0 | 1 | # Approach\n1. Retrieve the content of the `conditions` field.\n2. Create a function to split each `conditions` by a space `\' \'` and check whether it starts with `DIAB1` or not.\n\n# Code\n```\nimport pandas as pd\n\ndef find_patients(patients: pd.DataFrame) -> pd.DataFrame:\n return patients[patients[\'conditions\'].apply(is_valid)]\n\ndef is_valid(content: str) -> bool:\n return any([x.startswith(\'DIAB1\') for x in content.split()])\n``` | 5 | Design a queue that supports `push` and `pop` operations in the front, middle, and back.
Implement the `FrontMiddleBack` class:
* `FrontMiddleBack()` Initializes the queue.
* `void pushFront(int val)` Adds `val` to the **front** of the queue.
* `void pushMiddle(int val)` Adds `val` to the **middle** of the queue.
* `void pushBack(int val)` Adds `val` to the **back** of the queue.
* `int popFront()` Removes the **front** element of the queue and returns it. If the queue is empty, return `-1`.
* `int popMiddle()` Removes the **middle** element of the queue and returns it. If the queue is empty, return `-1`.
* `int popBack()` Removes the **back** element of the queue and returns it. If the queue is empty, return `-1`.
**Notice** that when there are **two** middle position choices, the operation is performed on the **frontmost** middle position choice. For example:
* Pushing `6` into the middle of `[1, 2, 3, 4, 5]` results in `[1, 2, 6, 3, 4, 5]`.
* Popping the middle from `[1, 2, 3, 4, 5, 6]` returns `3` and results in `[1, 2, 4, 5, 6]`.
**Example 1:**
**Input:**
\[ "FrontMiddleBackQueue ", "pushFront ", "pushBack ", "pushMiddle ", "pushMiddle ", "popFront ", "popMiddle ", "popMiddle ", "popBack ", "popFront "\]
\[\[\], \[1\], \[2\], \[3\], \[4\], \[\], \[\], \[\], \[\], \[\]\]
**Output:**
\[null, null, null, null, null, 1, 3, 4, 2, -1\]
**Explanation:**
FrontMiddleBackQueue q = new FrontMiddleBackQueue();
q.pushFront(1); // \[1\]
q.pushBack(2); // \[1, 2\]
q.pushMiddle(3); // \[1, 3, 2\]
q.pushMiddle(4); // \[1, 4, 3, 2\]
q.popFront(); // return 1 -> \[4, 3, 2\]
q.popMiddle(); // return 3 -> \[4, 2\]
q.popMiddle(); // return 4 -> \[2\]
q.popBack(); // return 2 -> \[\]
q.popFront(); // return -1 -> \[\] (The queue is empty)
**Constraints:**
* `1 <= val <= 109`
* At most `1000` calls will be made to `pushFront`, `pushMiddle`, `pushBack`, `popFront`, `popMiddle`, and `popBack`. | null |
Simple Python3 Solution || beats 90% ||🤖💻🧑💻|| upvote please | shuffle-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def restoreString(self, s: str, indices: List[int]) -> str:\n outcome=""\n for i in range(len(s)):\n outcome=outcome+s[indices.index(i)]\n return outcome\n\n \n``` | 7 | You are given a string `s` and an integer array `indices` of the **same length**. The string `s` will be shuffled such that the character at the `ith` position moves to `indices[i]` in the shuffled string.
Return _the shuffled string_.
**Example 1:**
**Input:** s = "codeleet ", `indices` = \[4,5,6,7,0,2,1,3\]
**Output:** "leetcode "
**Explanation:** As shown, "codeleet " becomes "leetcode " after shuffling.
**Example 2:**
**Input:** s = "abc ", `indices` = \[0,1,2\]
**Output:** "abc "
**Explanation:** After shuffling, each character remains in its position.
**Constraints:**
* `s.length == indices.length == n`
* `1 <= n <= 100`
* `s` consists of only lowercase English letters.
* `0 <= indices[i] < n`
* All values of `indices` are **unique**. | Use greedy approach. For each kid check if candies[i] + extraCandies ≥ maximum in Candies[i]. |
Solution of shuffle string problem | shuffle-string | 0 | 1 | # Approach\n- Solved using `zip()` function\n- Python\u2019s `zip()` function creates an iterator that will aggregate elements from two or more iterables\n\n# Complexity\n- Time complexity:\n$$O(n)$$ - as zip() function takes linear time\n\n- Space complexity:\n$$O(n)$$ - as we use extra space for answer\n\n# Code\n```\nclass Solution:\n def restoreString(self, s: str, indices: List[int]) -> str:\n answer = [0] * len(indices)\n for idx, letter in zip(indices, s):\n answer[idx] = letter\n return \'\'.join(answer)\n\n``` | 4 | You are given a string `s` and an integer array `indices` of the **same length**. The string `s` will be shuffled such that the character at the `ith` position moves to `indices[i]` in the shuffled string.
Return _the shuffled string_.
**Example 1:**
**Input:** s = "codeleet ", `indices` = \[4,5,6,7,0,2,1,3\]
**Output:** "leetcode "
**Explanation:** As shown, "codeleet " becomes "leetcode " after shuffling.
**Example 2:**
**Input:** s = "abc ", `indices` = \[0,1,2\]
**Output:** "abc "
**Explanation:** After shuffling, each character remains in its position.
**Constraints:**
* `s.length == indices.length == n`
* `1 <= n <= 100`
* `s` consists of only lowercase English letters.
* `0 <= indices[i] < n`
* All values of `indices` are **unique**. | Use greedy approach. For each kid check if candies[i] + extraCandies ≥ maximum in Candies[i]. |
String Restoration from Indices | shuffle-string | 0 | 1 | This code defines a class Solution with a method restoreString that is used to restore the original string from a given string s and a list of indices indices. The indices list indicates the order in which characters of the original string should be rearranged.\n\nHere\'s a breakdown of the code:\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code is designed to restore the original string by rearranging the characters based on the provided indices. It does so by iterating through the indices list and using it to reconstruct the original string character by character.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1)Initialize an empty string r to store the restored string.\n2)Iterate through the range of the length of the input string s.\n3)For each index i in this range, find the character from the original string s at the index specified by indices.index(i), and append it to the result string r.\n4)Finally, return the restored string r.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the range of the length of the input string, and for each iteration, it performs a search operation in the indices list. This results in a time complexity of O(n^2), where \'n\' is the length of the input string.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe code uses additional space for the result string r, which can be at most the same size as the input string s. Therefore, the space complexity is O(n), where \'n\' is the length of the input string.\n\n# Code\n```\nclass Solution(object):\n def restoreString(self, s, indices):\n """\n :type s: str\n :type indices: List[int]\n :rtype: str\n """\n r=""\n for i in range(len(s)):\n r=r+s[indices.index(i)]\n return r\n``` | 3 | You are given a string `s` and an integer array `indices` of the **same length**. The string `s` will be shuffled such that the character at the `ith` position moves to `indices[i]` in the shuffled string.
Return _the shuffled string_.
**Example 1:**
**Input:** s = "codeleet ", `indices` = \[4,5,6,7,0,2,1,3\]
**Output:** "leetcode "
**Explanation:** As shown, "codeleet " becomes "leetcode " after shuffling.
**Example 2:**
**Input:** s = "abc ", `indices` = \[0,1,2\]
**Output:** "abc "
**Explanation:** After shuffling, each character remains in its position.
**Constraints:**
* `s.length == indices.length == n`
* `1 <= n <= 100`
* `s` consists of only lowercase English letters.
* `0 <= indices[i] < n`
* All values of `indices` are **unique**. | Use greedy approach. For each kid check if candies[i] + extraCandies ≥ maximum in Candies[i]. |
Python 3 lines easy O(n) | shuffle-string | 0 | 1 | Using a list to store all the chars and joining it to return the answer string. \n```\nclass Solution:\n def restoreString(self, s: str, indices: List[int]) -> str:\n res = [\'\'] * len(s)\n for index, char in enumerate(s):\n res[indices[index]] = char\n return "".join(res) | 55 | You are given a string `s` and an integer array `indices` of the **same length**. The string `s` will be shuffled such that the character at the `ith` position moves to `indices[i]` in the shuffled string.
Return _the shuffled string_.
**Example 1:**
**Input:** s = "codeleet ", `indices` = \[4,5,6,7,0,2,1,3\]
**Output:** "leetcode "
**Explanation:** As shown, "codeleet " becomes "leetcode " after shuffling.
**Example 2:**
**Input:** s = "abc ", `indices` = \[0,1,2\]
**Output:** "abc "
**Explanation:** After shuffling, each character remains in its position.
**Constraints:**
* `s.length == indices.length == n`
* `1 <= n <= 100`
* `s` consists of only lowercase English letters.
* `0 <= indices[i] < n`
* All values of `indices` are **unique**. | Use greedy approach. For each kid check if candies[i] + extraCandies ≥ maximum in Candies[i]. |
Simple O(1) Space Python Solution ✅ | minimum-suffix-flips | 0 | 1 | # Intuition\nWe want to find the minimum number of flips required to make all elements of the given binary string \'target\' the same.\n\n# Approach\nWe initialize a counter \'count\' to keep track of the number of flips required. We also initialize a variable \'last\' to store the last encountered character, initially set to \'0\'. We iterate through each character \'b\' in the \'target\' string.\n- If \'last\' is not equal to \'b\', it means a flip is required to make \'b\' the same as \'last\'.\n- In that case, we increment \'count\' by 1 and update \'last\' to be \'b\'.\n- Finally, we return \'count\' as the minimum number of flips required.\n\n# Complexity\n- Time complexity: O(n), where \'n\' is the length of the input string \'target\'. We iterate through the entire string once.\n- Space complexity: O(1), as we are using a constant amount of extra space.\n\n# Code\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n count = 0\n last = \'0\'\n for b in target:\n if last != b:\n count += 1\n last = b\n return count\n``` | 2 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
Simple O(1) Space Python Solution ✅ | minimum-suffix-flips | 0 | 1 | # Intuition\nWe want to find the minimum number of flips required to make all elements of the given binary string \'target\' the same.\n\n# Approach\nWe initialize a counter \'count\' to keep track of the number of flips required. We also initialize a variable \'last\' to store the last encountered character, initially set to \'0\'. We iterate through each character \'b\' in the \'target\' string.\n- If \'last\' is not equal to \'b\', it means a flip is required to make \'b\' the same as \'last\'.\n- In that case, we increment \'count\' by 1 and update \'last\' to be \'b\'.\n- Finally, we return \'count\' as the minimum number of flips required.\n\n# Complexity\n- Time complexity: O(n), where \'n\' is the length of the input string \'target\'. We iterate through the entire string once.\n- Space complexity: O(1), as we are using a constant amount of extra space.\n\n# Code\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n count = 0\n last = \'0\'\n for b in target:\n if last != b:\n count += 1\n last = b\n return count\n``` | 2 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
[Python3] 1-line | minimum-suffix-flips | 0 | 1 | Algo: \n\nTo abstract this problem in math terms, the purpose of it is to simply convert a string composed of `0`\'s and `1`\'s to all `0`\'s using a predefined flip operation that flips everything from a given position to the end. As a result, at any step, one could focus on the left-most `1`. By fliping it, a desirable byproduct is that a continous chunk of `1`\'s connecting to the left-most `1` is set to `0`. An undesirable side effect is that the next `0` will become the left-most `1`. In the next step, you would have to flip this `1`. \n\nIt is not difficult to realize that this problem is to count the number of changes in the string. One caveat is the first character, for which one flip needs to be counted if it is `1`. To unify the operation, we could add a dummy `0` in front so that the string always starts with `0`. \n\nUsing the example given by the problem, the above argument would suggest 3 as the answer as there are in total 3 changes while scanning `010111` (a dummy `0` is added in front) from left to right. \n`10111`\n`01000` after 1st flip\n`00111` after 2nd flip\n`00000` after 3rd flip \n\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n return len(list(groupby("0" + target)))-1\n```\n\nHere, we leverage on `groupby` function of `itertools` module which groups the string for us though the only info we need is the number of groups minus one (`n` groups comes with `n-1` changes from group to group).\n\nFurthermore, the below elegant solution is due to @awice. \n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n ans = flip = 0\n for bulb in target: \n if flip ^ int(bulb): \n flip ^= 1\n ans += 1\n return ans\n```\n\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n ans, prev = 0,"0"\n for c in target: \n if prev != c: ans += 1\n prev = c\n return ans \n``` | 19 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
[Python3] 1-line | minimum-suffix-flips | 0 | 1 | Algo: \n\nTo abstract this problem in math terms, the purpose of it is to simply convert a string composed of `0`\'s and `1`\'s to all `0`\'s using a predefined flip operation that flips everything from a given position to the end. As a result, at any step, one could focus on the left-most `1`. By fliping it, a desirable byproduct is that a continous chunk of `1`\'s connecting to the left-most `1` is set to `0`. An undesirable side effect is that the next `0` will become the left-most `1`. In the next step, you would have to flip this `1`. \n\nIt is not difficult to realize that this problem is to count the number of changes in the string. One caveat is the first character, for which one flip needs to be counted if it is `1`. To unify the operation, we could add a dummy `0` in front so that the string always starts with `0`. \n\nUsing the example given by the problem, the above argument would suggest 3 as the answer as there are in total 3 changes while scanning `010111` (a dummy `0` is added in front) from left to right. \n`10111`\n`01000` after 1st flip\n`00111` after 2nd flip\n`00000` after 3rd flip \n\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n return len(list(groupby("0" + target)))-1\n```\n\nHere, we leverage on `groupby` function of `itertools` module which groups the string for us though the only info we need is the number of groups minus one (`n` groups comes with `n-1` changes from group to group).\n\nFurthermore, the below elegant solution is due to @awice. \n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n ans = flip = 0\n for bulb in target: \n if flip ^ int(bulb): \n flip ^= 1\n ans += 1\n return ans\n```\n\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n ans, prev = 0,"0"\n for c in target: \n if prev != c: ans += 1\n prev = c\n return ans \n``` | 19 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
✅ [Python/C++] O(N) using flips parity | minimum-suffix-flips | 0 | 1 | The strategy here is to keep track of parity of the already made flips. The code is self-explanatory.\n\n```python []\nclass Solution:\n def minFlips(self, target: str) -> int:\n \n flips = 0\n for b in target:\n if flips % 2 == 1 - int(b):\n flips += 1\n\n return flips\n\n```\n```cpp []\nclass Solution\n{\npublic:\n int minFlips(string target)\n {\n int flips = 0;\n \n for (char b : target)\n if ((flips % 2 == 1) == (b == \'0\'))\n flips += 1;\n\n return flips;\n }\n};\n``` | 1 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
✅ [Python/C++] O(N) using flips parity | minimum-suffix-flips | 0 | 1 | The strategy here is to keep track of parity of the already made flips. The code is self-explanatory.\n\n```python []\nclass Solution:\n def minFlips(self, target: str) -> int:\n \n flips = 0\n for b in target:\n if flips % 2 == 1 - int(b):\n flips += 1\n\n return flips\n\n```\n```cpp []\nclass Solution\n{\npublic:\n int minFlips(string target)\n {\n int flips = 0;\n \n for (char b : target)\n if ((flips % 2 == 1) == (b == \'0\'))\n flips += 1;\n\n return flips;\n }\n};\n``` | 1 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python Solution in 3 lines || Easy to understand | minimum-suffix-flips | 0 | 1 | ```\nclass Solution:\n def minFlips(self, target: str) -> int:\n\t\t# to keep counter of number of flip bits\n flips = 0\n\t\t\n\t\t# 0 will become 1 and 1 will become 0 after each move\n\t\t# but the substring before current index in unchanged so traverse from left to right\n for letter in target:\n\t\t\t# we can find the current bit of string using flips%2 because we increment flips once a bit changes.\n\t\t\t# if the current bit not equal to the expected bit we need to flip the string\n\t\t\t\n if int(letter)!=flips%2:\n flips += 1\n return flips\n``` | 3 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
Python Solution in 3 lines || Easy to understand | minimum-suffix-flips | 0 | 1 | ```\nclass Solution:\n def minFlips(self, target: str) -> int:\n\t\t# to keep counter of number of flip bits\n flips = 0\n\t\t\n\t\t# 0 will become 1 and 1 will become 0 after each move\n\t\t# but the substring before current index in unchanged so traverse from left to right\n for letter in target:\n\t\t\t# we can find the current bit of string using flips%2 because we increment flips once a bit changes.\n\t\t\t# if the current bit not equal to the expected bit we need to flip the string\n\t\t\t\n if int(letter)!=flips%2:\n flips += 1\n return flips\n``` | 3 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
73% O(n) TC and 70% O(1) SC easy python solution | minimum-suffix-flips | 0 | 1 | ```\ndef minFlips(self, target: str) -> int:\n\tn = len(target)\n\tans = 0\n\tfor i in range(n):\n\t\tif (target[i] == "0" and ans%2) or (target[i] == "1" and ans%2 == 0):\n\t\t\tans += 1\n\treturn ans\n``` | 1 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
73% O(n) TC and 70% O(1) SC easy python solution | minimum-suffix-flips | 0 | 1 | ```\ndef minFlips(self, target: str) -> int:\n\tn = len(target)\n\tans = 0\n\tfor i in range(n):\n\t\tif (target[i] == "0" and ans%2) or (target[i] == "1" and ans%2 == 0):\n\t\t\tans += 1\n\treturn ans\n``` | 1 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python3 O(N) solution with constant memory (98.27% Runtime) | minimum-suffix-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n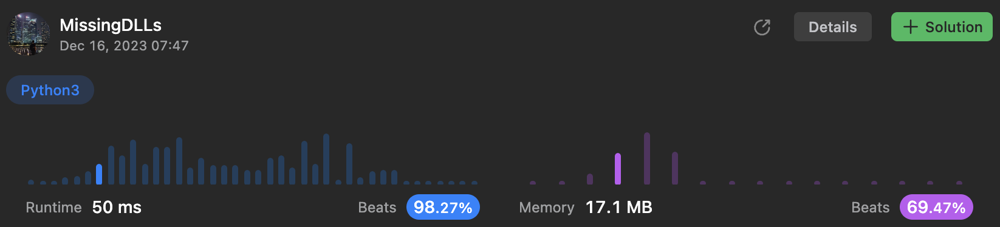\nCount how many times "bit" change occurs from the beginning of the array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- For example, to set specific index\'s bit to 1:\n - XXX...0...XXX becomes XXX...1...111\n - Note 0 ~ i-1th bits are not changed\n- Thus, from beginning of the array, check how many times bit changed from previous value\n- Initially, set previous value to "0" since we start from "000...0" \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n cnt = 0\n p = "0"\n for c in target:\n if c != p:\n cnt += 1\n p = c\n\n return cnt\n``` | 0 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
Python3 O(N) solution with constant memory (98.27% Runtime) | minimum-suffix-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nCount how many times "bit" change occurs from the beginning of the array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- For example, to set specific index\'s bit to 1:\n - XXX...0...XXX becomes XXX...1...111\n - Note 0 ~ i-1th bits are not changed\n- Thus, from beginning of the array, check how many times bit changed from previous value\n- Initially, set previous value to "0" since we start from "000...0" \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n cnt = 0\n p = "0"\n for c in target:\n if c != p:\n cnt += 1\n p = c\n\n return cnt\n``` | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Simple Python Solution Beats 91% | minimum-suffix-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple solution to just increase count when most recent value is different\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n count = 0\n lastVal = "0"\n for char in target:\n if char != lastVal:\n count += 1\n if lastVal == "0":\n lastVal = "1"\n else:\n lastVal = "0"\n return count\n``` | 0 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
Simple Python Solution Beats 91% | minimum-suffix-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple solution to just increase count when most recent value is different\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n count = 0\n lastVal = "0"\n for char in target:\n if char != lastVal:\n count += 1\n if lastVal == "0":\n lastVal = "1"\n else:\n lastVal = "0"\n return count\n``` | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python one-liner | minimum-suffix-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRemove leftmost zeroes, as they don\'t contribute to the final result, then count the number of groups of consecutive zeroes and ones.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n return sum(1 for _ in groupby(target.lstrip(\'0\')))\n``` | 0 | You are given a **0-indexed** binary string `target` of length `n`. You have another binary string `s` of length `n` that is initially set to all zeros. You want to make `s` equal to `target`.
In one operation, you can pick an index `i` where `0 <= i < n` and flip all bits in the **inclusive** range `[i, n - 1]`. Flip means changing `'0'` to `'1'` and `'1'` to `'0'`.
Return _the minimum number of operations needed to make_ `s` _equal to_ `target`.
**Example 1:**
**Input:** target = "10111 "
**Output:** 3
**Explanation:** Initially, s = "00000 ".
Choose index i = 2: "00000 " -> "00111 "
Choose index i = 0: "00111 " -> "11000 "
Choose index i = 1: "11000 " -> "10111 "
We need at least 3 flip operations to form target.
**Example 2:**
**Input:** target = "101 "
**Output:** 3
**Explanation:** Initially, s = "000 ".
Choose index i = 0: "000 " -> "111 "
Choose index i = 1: "111 " -> "100 "
Choose index i = 2: "100 " -> "101 "
We need at least 3 flip operations to form target.
**Example 3:**
**Input:** target = "00000 "
**Output:** 0
**Explanation:** We do not need any operations since the initial s already equals target.
**Constraints:**
* `n == target.length`
* `1 <= n <= 105`
* `target[i]` is either `'0'` or `'1'`. | We need to get the max and min value after changing num and the answer is max - min. Use brute force, try all possible changes and keep the minimum and maximum values. |
Python one-liner | minimum-suffix-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRemove leftmost zeroes, as they don\'t contribute to the final result, then count the number of groups of consecutive zeroes and ones.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFlips(self, target: str) -> int:\n return sum(1 for _ in groupby(target.lstrip(\'0\')))\n``` | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python solution Fast with explanation | number-of-good-leaf-nodes-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought on how to solve this problem is to use a depth-first search (DFS) approach to traverse through the binary tree. For each node, we need to find all its possible distances from its descendants and calculate the number of pairs whose distances are less than the given distance.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can use a depth-first search (DFS) approach to traverse through the binary tree. For each node, we will use a helper function to find all its possible distances from its descendants and calculate the number of pairs whose distances are less than the given distance. \n\nThe helper function will start at the root of the tree and will first check if the root is None. If it is, we will return an empty list. If not, we will check if the root node has no children. If it does not have any children, we will return a list with the distance of 1. If it does have children, we will recursively call the function on the left and right subtrees. We will then loop through the left and right lists and calculate the number of pairs whose distances are less than the given distance. \n\nFinally, we will return a list containing all the distances from the current node to its descendants.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n self.ans = 0\n def dfs(root):\n if not root: return []\n if not root.left and not root.right: return [1]\n left = dfs(root.left)\n right = dfs(root.right)\n for i in left:\n for j in right:\n if i+j <= distance:\n self.ans += 1\n return [i+1 for i in left+right if i+1 < distance]\n dfs(root)\n return self.ans\n``` | 7 | You are given the `root` of a binary tree and an integer `distance`. A pair of two different **leaf** nodes of a binary tree is said to be good if the length of **the shortest path** between them is less than or equal to `distance`.
Return _the number of good leaf node pairs_ in the tree.
**Example 1:**
**Input:** root = \[1,2,3,null,4\], distance = 3
**Output:** 1
**Explanation:** The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
**Example 2:**
**Input:** root = \[1,2,3,4,5,6,7\], distance = 3
**Output:** 2
**Explanation:** The good pairs are \[4,5\] and \[6,7\] with shortest path = 2. The pair \[4,6\] is not good because the length of ther shortest path between them is 4.
**Example 3:**
**Input:** root = \[7,1,4,6,null,5,3,null,null,null,null,null,2\], distance = 3
**Output:** 1
**Explanation:** The only good pair is \[2,5\].
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 210].`
* `1 <= Node.val <= 100`
* `1 <= distance <= 10` | Sort both strings and then check if one of them can break the other. |
Python solution Fast with explanation | number-of-good-leaf-nodes-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought on how to solve this problem is to use a depth-first search (DFS) approach to traverse through the binary tree. For each node, we need to find all its possible distances from its descendants and calculate the number of pairs whose distances are less than the given distance.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can use a depth-first search (DFS) approach to traverse through the binary tree. For each node, we will use a helper function to find all its possible distances from its descendants and calculate the number of pairs whose distances are less than the given distance. \n\nThe helper function will start at the root of the tree and will first check if the root is None. If it is, we will return an empty list. If not, we will check if the root node has no children. If it does not have any children, we will return a list with the distance of 1. If it does have children, we will recursively call the function on the left and right subtrees. We will then loop through the left and right lists and calculate the number of pairs whose distances are less than the given distance. \n\nFinally, we will return a list containing all the distances from the current node to its descendants.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n self.ans = 0\n def dfs(root):\n if not root: return []\n if not root.left and not root.right: return [1]\n left = dfs(root.left)\n right = dfs(root.right)\n for i in left:\n for j in right:\n if i+j <= distance:\n self.ans += 1\n return [i+1 for i in left+right if i+1 < distance]\n dfs(root)\n return self.ans\n``` | 7 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
[Python] Convert to graph + BFS | number-of-good-leaf-nodes-pairs | 0 | 1 | ```\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n graph = collections.defaultdict(list)\n \n def dfs(node, par = None):\n if node:\n graph[node].append(par)\n graph[par].append(node)\n dfs(node.left, node)\n dfs(node.right, node)\n\n dfs(root)\n \n leaves = []\n for node in graph.keys():\n if node and not node.left and not node.right:\n leaves.append(node)\n \n count = 0\n \n for leaf in leaves:\n queue = [(leaf,0)]\n seen = set(queue)\n while queue:\n node,length = queue.pop(0)\n if length>distance:\n break\n if node:\n for nei in graph[node]:\n if nei not in seen:\n seen.add(nei)\n queue.append((nei,length+1))\n if node!=leaf and not node.left and not node.right and length<=distance:\n count+=1\n \n return count//2\n | 28 | You are given the `root` of a binary tree and an integer `distance`. A pair of two different **leaf** nodes of a binary tree is said to be good if the length of **the shortest path** between them is less than or equal to `distance`.
Return _the number of good leaf node pairs_ in the tree.
**Example 1:**
**Input:** root = \[1,2,3,null,4\], distance = 3
**Output:** 1
**Explanation:** The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
**Example 2:**
**Input:** root = \[1,2,3,4,5,6,7\], distance = 3
**Output:** 2
**Explanation:** The good pairs are \[4,5\] and \[6,7\] with shortest path = 2. The pair \[4,6\] is not good because the length of ther shortest path between them is 4.
**Example 3:**
**Input:** root = \[7,1,4,6,null,5,3,null,null,null,null,null,2\], distance = 3
**Output:** 1
**Explanation:** The only good pair is \[2,5\].
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 210].`
* `1 <= Node.val <= 100`
* `1 <= distance <= 10` | Sort both strings and then check if one of them can break the other. |
[Python] Convert to graph + BFS | number-of-good-leaf-nodes-pairs | 0 | 1 | ```\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n graph = collections.defaultdict(list)\n \n def dfs(node, par = None):\n if node:\n graph[node].append(par)\n graph[par].append(node)\n dfs(node.left, node)\n dfs(node.right, node)\n\n dfs(root)\n \n leaves = []\n for node in graph.keys():\n if node and not node.left and not node.right:\n leaves.append(node)\n \n count = 0\n \n for leaf in leaves:\n queue = [(leaf,0)]\n seen = set(queue)\n while queue:\n node,length = queue.pop(0)\n if length>distance:\n break\n if node:\n for nei in graph[node]:\n if nei not in seen:\n seen.add(nei)\n queue.append((nei,length+1))\n if node!=leaf and not node.left and not node.right and length<=distance:\n count+=1\n \n return count//2\n | 28 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
Easy Python Solution with Diagram Explanation | number-of-good-leaf-nodes-pairs | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n\nThe image above gives some idea about the approach. We will traverse the tree using dfs. When we reach the leaf node, we will return `[1]`. For parents of leaf nodes, for e.g. node 2, it has two leaf nodes, 4 and 5, both with distance of 1 from it. For node 1, it has 4 leaf nodes, all with a distance of 2 from it. Basic idea is if a node has a left tree and right tree, compare the distances of nodes in left tree paired with nodes in right, see how many combinations can fulfil the distance requirement.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n total = 0\n def dfs(root):\n if not root.left and not root.right:\n return [1]\n\n descendants = []\n nonlocal total\n left = dfs(root.left) if root.left else []\n right = dfs(root.right) if root.right else []\n\n for i in left:\n if i >= distance: # if left tree leaf node is already > distance on its own, no point checking whether it can be paired with leaf node from right tree\n continue\n for k in right:\n if i + k <= distance:\n total += 1\n \n return [i+1 for i in left+right]\n \n\n dfs(root)\n return total\n \n\n``` | 2 | You are given the `root` of a binary tree and an integer `distance`. A pair of two different **leaf** nodes of a binary tree is said to be good if the length of **the shortest path** between them is less than or equal to `distance`.
Return _the number of good leaf node pairs_ in the tree.
**Example 1:**
**Input:** root = \[1,2,3,null,4\], distance = 3
**Output:** 1
**Explanation:** The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
**Example 2:**
**Input:** root = \[1,2,3,4,5,6,7\], distance = 3
**Output:** 2
**Explanation:** The good pairs are \[4,5\] and \[6,7\] with shortest path = 2. The pair \[4,6\] is not good because the length of ther shortest path between them is 4.
**Example 3:**
**Input:** root = \[7,1,4,6,null,5,3,null,null,null,null,null,2\], distance = 3
**Output:** 1
**Explanation:** The only good pair is \[2,5\].
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 210].`
* `1 <= Node.val <= 100`
* `1 <= distance <= 10` | Sort both strings and then check if one of them can break the other. |
Easy Python Solution with Diagram Explanation | number-of-good-leaf-nodes-pairs | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n\nThe image above gives some idea about the approach. We will traverse the tree using dfs. When we reach the leaf node, we will return `[1]`. For parents of leaf nodes, for e.g. node 2, it has two leaf nodes, 4 and 5, both with distance of 1 from it. For node 1, it has 4 leaf nodes, all with a distance of 2 from it. Basic idea is if a node has a left tree and right tree, compare the distances of nodes in left tree paired with nodes in right, see how many combinations can fulfil the distance requirement.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n total = 0\n def dfs(root):\n if not root.left and not root.right:\n return [1]\n\n descendants = []\n nonlocal total\n left = dfs(root.left) if root.left else []\n right = dfs(root.right) if root.right else []\n\n for i in left:\n if i >= distance: # if left tree leaf node is already > distance on its own, no point checking whether it can be paired with leaf node from right tree\n continue\n for k in right:\n if i + k <= distance:\n total += 1\n \n return [i+1 for i in left+right]\n \n\n dfs(root)\n return total\n \n\n``` | 2 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
Beats 99.35% using recursion in Python | number-of-good-leaf-nodes-pairs | 0 | 1 | The idea is to use recursion for each node.\nIn the `rec(node)` function below, it returns the the number of the leaves from that node for each height. For example, `{1: 1, 2: 3}` means that the node has one leaf with the height 1 and three leaves with the height 2.\nThe point is that if you connect two leaves, there is exactly one root between them, and for that root, the sum of the height of these two nodes is less than or equal to `distance`. After calculating this value (dictionary) for left children and right children, I check all the possible combinations, and if they are less than or equal to `distance`, multiply the numbers and add to `res`.\n\n```\nfrom collections import defaultdict\n\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n def rec(node):\n nonlocal res\n if not node:\n return {}\n elif not node.left and not node.right:\n return {0: 1}\n left_children_dict = rec(node.left)\n right_children_dict = rec(node.right)\n \n for left_height, left_children in left_children_dict.items():\n for right_height, right_children in right_children_dict.items():\n if left_height + right_height + 2 <= distance:\n res += left_children * right_children\n \n combined = defaultdict(int)\n for left_height, left_children in left_children_dict.items():\n combined[left_height + 1] += left_children\n for right_height, right_children in right_children_dict.items():\n combined[right_height + 1] += right_children\n \n return combined\n \n res = 0\n rec(root)\n return res\n``` | 7 | You are given the `root` of a binary tree and an integer `distance`. A pair of two different **leaf** nodes of a binary tree is said to be good if the length of **the shortest path** between them is less than or equal to `distance`.
Return _the number of good leaf node pairs_ in the tree.
**Example 1:**
**Input:** root = \[1,2,3,null,4\], distance = 3
**Output:** 1
**Explanation:** The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
**Example 2:**
**Input:** root = \[1,2,3,4,5,6,7\], distance = 3
**Output:** 2
**Explanation:** The good pairs are \[4,5\] and \[6,7\] with shortest path = 2. The pair \[4,6\] is not good because the length of ther shortest path between them is 4.
**Example 3:**
**Input:** root = \[7,1,4,6,null,5,3,null,null,null,null,null,2\], distance = 3
**Output:** 1
**Explanation:** The only good pair is \[2,5\].
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 210].`
* `1 <= Node.val <= 100`
* `1 <= distance <= 10` | Sort both strings and then check if one of them can break the other. |
Beats 99.35% using recursion in Python | number-of-good-leaf-nodes-pairs | 0 | 1 | The idea is to use recursion for each node.\nIn the `rec(node)` function below, it returns the the number of the leaves from that node for each height. For example, `{1: 1, 2: 3}` means that the node has one leaf with the height 1 and three leaves with the height 2.\nThe point is that if you connect two leaves, there is exactly one root between them, and for that root, the sum of the height of these two nodes is less than or equal to `distance`. After calculating this value (dictionary) for left children and right children, I check all the possible combinations, and if they are less than or equal to `distance`, multiply the numbers and add to `res`.\n\n```\nfrom collections import defaultdict\n\nclass Solution:\n def countPairs(self, root: TreeNode, distance: int) -> int:\n def rec(node):\n nonlocal res\n if not node:\n return {}\n elif not node.left and not node.right:\n return {0: 1}\n left_children_dict = rec(node.left)\n right_children_dict = rec(node.right)\n \n for left_height, left_children in left_children_dict.items():\n for right_height, right_children in right_children_dict.items():\n if left_height + right_height + 2 <= distance:\n res += left_children * right_children\n \n combined = defaultdict(int)\n for left_height, left_children in left_children_dict.items():\n combined[left_height + 1] += left_children\n for right_height, right_children in right_children_dict.items():\n combined[right_height + 1] += right_children\n \n return combined\n \n res = 0\n rec(root)\n return res\n``` | 7 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
50% TC and 80% SC easy python solution | number-of-good-leaf-nodes-pairs | 0 | 1 | ```\ndef countPairs(self, root: TreeNode, distance: int) -> int:\n\tans = [0]\n\tlru_cache(None)\n\tdef dfs(node):\n\t\tif(not node):\n\t\t\treturn []\n\t\tif not(node.left or node.right):\n\t\t\treturn [1]\n\t\tl = dfs(node.left)\n\t\tr = dfs(node.right)\n\t\tfor i in l:\n\t\t\tfor j in r:\n\t\t\t\tif(i+j <= distance):\n\t\t\t\t\tans[0] += 1\n\t\treturn [i+1 for i in l+r]\n\n\tdfs(root)\n\treturn ans[0]\n``` | 4 | You are given the `root` of a binary tree and an integer `distance`. A pair of two different **leaf** nodes of a binary tree is said to be good if the length of **the shortest path** between them is less than or equal to `distance`.
Return _the number of good leaf node pairs_ in the tree.
**Example 1:**
**Input:** root = \[1,2,3,null,4\], distance = 3
**Output:** 1
**Explanation:** The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
**Example 2:**
**Input:** root = \[1,2,3,4,5,6,7\], distance = 3
**Output:** 2
**Explanation:** The good pairs are \[4,5\] and \[6,7\] with shortest path = 2. The pair \[4,6\] is not good because the length of ther shortest path between them is 4.
**Example 3:**
**Input:** root = \[7,1,4,6,null,5,3,null,null,null,null,null,2\], distance = 3
**Output:** 1
**Explanation:** The only good pair is \[2,5\].
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 210].`
* `1 <= Node.val <= 100`
* `1 <= distance <= 10` | Sort both strings and then check if one of them can break the other. |
50% TC and 80% SC easy python solution | number-of-good-leaf-nodes-pairs | 0 | 1 | ```\ndef countPairs(self, root: TreeNode, distance: int) -> int:\n\tans = [0]\n\tlru_cache(None)\n\tdef dfs(node):\n\t\tif(not node):\n\t\t\treturn []\n\t\tif not(node.left or node.right):\n\t\t\treturn [1]\n\t\tl = dfs(node.left)\n\t\tr = dfs(node.right)\n\t\tfor i in l:\n\t\t\tfor j in r:\n\t\t\t\tif(i+j <= distance):\n\t\t\t\t\tans[0] += 1\n\t\treturn [i+1 for i in l+r]\n\n\tdfs(root)\n\treturn ans[0]\n``` | 4 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
SIMPLEST PYTHON SOLUTION | string-compression-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,s,prev,k,ct,n,dct):\n if k<0:\n return float("infinity")\n if i>=n:\n x=0\n if ct>1:\n x=len(str(ct))+1\n elif ct==1:\n x=1\n return x\n if (i,prev,ct,k) in dct:\n return dct[(i,prev,ct,k)]\n if s[i]==prev:\n inc=self.dp(i+1,s,prev,k,ct+1,n,dct)\n else:\n x=0\n if ct>1:\n x=len(str(ct))+1\n elif ct==1:\n x=1\n inc=x+self.dp(i+1,s,s[i],k,1,n,dct)\n exc=self.dp(i+1,s,prev,k-1,ct,n,dct)\n dct[(i,prev,ct,k)]=min(inc,exc)\n return min(inc,exc)\n\n\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n n=len(s)\n return self.dp(0,s,"",k,0,n,{})\n\n \n``` | 1 | [Run-length encoding](http://en.wikipedia.org/wiki/Run-length_encoding) is a string compression method that works by replacing consecutive identical characters (repeated 2 or more times) with the concatenation of the character and the number marking the count of the characters (length of the run). For example, to compress the string `"aabccc "` we replace `"aa "` by `"a2 "` and replace `"ccc "` by `"c3 "`. Thus the compressed string becomes `"a2bc3 "`.
Notice that in this problem, we are not adding `'1'` after single characters.
Given a string `s` and an integer `k`. You need to delete **at most** `k` characters from `s` such that the run-length encoded version of `s` has minimum length.
Find the _minimum length of the run-length encoded version of_ `s` _after deleting at most_ `k` _characters_.
**Example 1:**
**Input:** s = "aaabcccd ", k = 2
**Output:** 4
**Explanation:** Compressing s without deleting anything will give us "a3bc3d " of length 6. Deleting any of the characters 'a' or 'c' would at most decrease the length of the compressed string to 5, for instance delete 2 'a' then we will have s = "abcccd " which compressed is abc3d. Therefore, the optimal way is to delete 'b' and 'd', then the compressed version of s will be "a3c3 " of length 4.
**Example 2:**
**Input:** s = "aabbaa ", k = 2
**Output:** 2
**Explanation:** If we delete both 'b' characters, the resulting compressed string would be "a4 " of length 2.
**Example 3:**
**Input:** s = "aaaaaaaaaaa ", k = 0
**Output:** 3
**Explanation:** Since k is zero, we cannot delete anything. The compressed string is "a11 " of length 3.
**Constraints:**
* `1 <= s.length <= 100`
* `0 <= k <= s.length`
* `s` contains only lowercase English letters. | Dynamic programming + bitmask. dp(peopleMask, idHat) number of ways to wear different hats given a bitmask (people visited) and used hats from 1 to idHat-1. |
SIMPLEST PYTHON SOLUTION | string-compression-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,s,prev,k,ct,n,dct):\n if k<0:\n return float("infinity")\n if i>=n:\n x=0\n if ct>1:\n x=len(str(ct))+1\n elif ct==1:\n x=1\n return x\n if (i,prev,ct,k) in dct:\n return dct[(i,prev,ct,k)]\n if s[i]==prev:\n inc=self.dp(i+1,s,prev,k,ct+1,n,dct)\n else:\n x=0\n if ct>1:\n x=len(str(ct))+1\n elif ct==1:\n x=1\n inc=x+self.dp(i+1,s,s[i],k,1,n,dct)\n exc=self.dp(i+1,s,prev,k-1,ct,n,dct)\n dct[(i,prev,ct,k)]=min(inc,exc)\n return min(inc,exc)\n\n\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n n=len(s)\n return self.dp(0,s,"",k,0,n,{})\n\n \n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
python3 | string-compression-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# We define f(i, curr_run_ch, run_length, nb_dels_remain) to return \n # the minimum, additional, number of characters it will cost to run-length \n # compress the substring s[i..n-1].\n # `curr_run_ch` is the character we have in the current "run", or the same\n # contiguous block of characters. \n # `run_length` is the length of the current "run", or the length of the\n # contiguous block of identical characters.\n\t\t# e.g. if we just encoded "aaaaa", `curr_run_ch` is "a" and `run_length` = 5\n # `nb_dels_remain` is the number of delete operations we have available to us,\n # should we choose to use them\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n # We define f(i, curr_run_ch, run_length, nb_dels_remain) to return \n # the minimum, additional, number of characters it will cost to run-length \n # compress the substring s[i..n-1].\n # `curr_run_ch` is the character we have in the current "run", or the same\n # contiguous block of characters. \n # `run_length` is the length of the current "run", or the length of the\n # contiguous block of identical characters.\n\t\t# e.g. if we just encoded "aaaaa", `curr_run_ch` is "a" and `run_length` = 5\n # `nb_dels_remain` is the number of delete operations we have available to us,\n # should we choose to use them\n memo = {}\n def f(i, curr_run_ch, run_length, nb_dels_remain):\n if i == len(s):\n return 0\n \n key = (i, curr_run_ch, run_length, nb_dels_remain)\n if key in memo:\n return memo[key]\n \n # At character i, we have two possible options, we could choose to either\n # delete this character or keep this character. Each choice we make will\n # incurr some additional run-length encoding length for s[i..n-1]. We return\n # the minimum of the two.\n \n # Delete s[i]\n del_ch_cost = float(\'inf\')\n if nb_dels_remain > 0:\n # Deleting s[i] means the latest character we kept stays the same AND\n # the current run-length of characters stays the same as well\n del_ch_cost = f(i + 1, curr_run_ch, run_length, nb_dels_remain - 1)\n \n # Keep s[i]\n keep_ch_cost = 0\n if s[i] == curr_run_ch:\n\t\t\t # The new character at s[i] we are about to encode is the same as the character in the\n\t\t\t\t# current "run", we could choose to include it into the current run of course.\n # Be careful that if we started with run-length of 1, 9, 99, 999 and etc, encoding another\n # character same as `curr_run_ch` into the same "run" will require an extra digit.\n # e.g. \'a\' => \'2a\' \'9a\' => \'10a\', \'99a\' => \'100a\'\n extra_digit_cost = 0\n if run_length == 1 or len(str(run_length + 1)) > len(str(run_length)):\n extra_digit_cost = 1\n keep_ch_cost = extra_digit_cost + f(i + 1, curr_run_ch, run_length + 1, nb_dels_remain)\n else:\n # s[i] != curr_run_ch, we are going to need to run-length encode at least\n # one instance of s[i] which would cost 1, plus whatever the cost to encode\n # the rest. Of course that also means the current "run" will "reset" and start anew with\n\t\t\t\t# a single character s[i]\n keep_ch_cost = 1 + f(i + 1, s[i], 1, nb_dels_remain)\n \n memo[key] = min(keep_ch_cost, del_ch_cost)\n return memo[key]\n \n return f(0, \'\', 0, k)\n``` | 1 | [Run-length encoding](http://en.wikipedia.org/wiki/Run-length_encoding) is a string compression method that works by replacing consecutive identical characters (repeated 2 or more times) with the concatenation of the character and the number marking the count of the characters (length of the run). For example, to compress the string `"aabccc "` we replace `"aa "` by `"a2 "` and replace `"ccc "` by `"c3 "`. Thus the compressed string becomes `"a2bc3 "`.
Notice that in this problem, we are not adding `'1'` after single characters.
Given a string `s` and an integer `k`. You need to delete **at most** `k` characters from `s` such that the run-length encoded version of `s` has minimum length.
Find the _minimum length of the run-length encoded version of_ `s` _after deleting at most_ `k` _characters_.
**Example 1:**
**Input:** s = "aaabcccd ", k = 2
**Output:** 4
**Explanation:** Compressing s without deleting anything will give us "a3bc3d " of length 6. Deleting any of the characters 'a' or 'c' would at most decrease the length of the compressed string to 5, for instance delete 2 'a' then we will have s = "abcccd " which compressed is abc3d. Therefore, the optimal way is to delete 'b' and 'd', then the compressed version of s will be "a3c3 " of length 4.
**Example 2:**
**Input:** s = "aabbaa ", k = 2
**Output:** 2
**Explanation:** If we delete both 'b' characters, the resulting compressed string would be "a4 " of length 2.
**Example 3:**
**Input:** s = "aaaaaaaaaaa ", k = 0
**Output:** 3
**Explanation:** Since k is zero, we cannot delete anything. The compressed string is "a11 " of length 3.
**Constraints:**
* `1 <= s.length <= 100`
* `0 <= k <= s.length`
* `s` contains only lowercase English letters. | Dynamic programming + bitmask. dp(peopleMask, idHat) number of ways to wear different hats given a bitmask (people visited) and used hats from 1 to idHat-1. |
python3 | string-compression-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# We define f(i, curr_run_ch, run_length, nb_dels_remain) to return \n # the minimum, additional, number of characters it will cost to run-length \n # compress the substring s[i..n-1].\n # `curr_run_ch` is the character we have in the current "run", or the same\n # contiguous block of characters. \n # `run_length` is the length of the current "run", or the length of the\n # contiguous block of identical characters.\n\t\t# e.g. if we just encoded "aaaaa", `curr_run_ch` is "a" and `run_length` = 5\n # `nb_dels_remain` is the number of delete operations we have available to us,\n # should we choose to use them\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n # We define f(i, curr_run_ch, run_length, nb_dels_remain) to return \n # the minimum, additional, number of characters it will cost to run-length \n # compress the substring s[i..n-1].\n # `curr_run_ch` is the character we have in the current "run", or the same\n # contiguous block of characters. \n # `run_length` is the length of the current "run", or the length of the\n # contiguous block of identical characters.\n\t\t# e.g. if we just encoded "aaaaa", `curr_run_ch` is "a" and `run_length` = 5\n # `nb_dels_remain` is the number of delete operations we have available to us,\n # should we choose to use them\n memo = {}\n def f(i, curr_run_ch, run_length, nb_dels_remain):\n if i == len(s):\n return 0\n \n key = (i, curr_run_ch, run_length, nb_dels_remain)\n if key in memo:\n return memo[key]\n \n # At character i, we have two possible options, we could choose to either\n # delete this character or keep this character. Each choice we make will\n # incurr some additional run-length encoding length for s[i..n-1]. We return\n # the minimum of the two.\n \n # Delete s[i]\n del_ch_cost = float(\'inf\')\n if nb_dels_remain > 0:\n # Deleting s[i] means the latest character we kept stays the same AND\n # the current run-length of characters stays the same as well\n del_ch_cost = f(i + 1, curr_run_ch, run_length, nb_dels_remain - 1)\n \n # Keep s[i]\n keep_ch_cost = 0\n if s[i] == curr_run_ch:\n\t\t\t # The new character at s[i] we are about to encode is the same as the character in the\n\t\t\t\t# current "run", we could choose to include it into the current run of course.\n # Be careful that if we started with run-length of 1, 9, 99, 999 and etc, encoding another\n # character same as `curr_run_ch` into the same "run" will require an extra digit.\n # e.g. \'a\' => \'2a\' \'9a\' => \'10a\', \'99a\' => \'100a\'\n extra_digit_cost = 0\n if run_length == 1 or len(str(run_length + 1)) > len(str(run_length)):\n extra_digit_cost = 1\n keep_ch_cost = extra_digit_cost + f(i + 1, curr_run_ch, run_length + 1, nb_dels_remain)\n else:\n # s[i] != curr_run_ch, we are going to need to run-length encode at least\n # one instance of s[i] which would cost 1, plus whatever the cost to encode\n # the rest. Of course that also means the current "run" will "reset" and start anew with\n\t\t\t\t# a single character s[i]\n keep_ch_cost = 1 + f(i + 1, s[i], 1, nb_dels_remain)\n \n memo[key] = min(keep_ch_cost, del_ch_cost)\n return memo[key]\n \n return f(0, \'\', 0, k)\n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Python with Comments 💚 | string-compression-ii | 0 | 1 | ```\nclass Solution:\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n #traverse the string\n #keep track of the status of delete or not delete current character\n #the status includes current index, number of delete, the previous character, and the runing length of previous character\n #return the minium length of compresed between delete or not delete\n\t\t#O(n^2*26*k) = O(n^2*k) time and space\n \n memo = {}\n return self.dfs(s, 0, k, None, 0, memo)\n \n def dfs(self, s, i, k, prev, l, memo):\n if i == len(s):\n return 0\n if (i, k, prev, l) in memo:\n return memo[(i, k, prev, l)]\n \n if k > 0:\n delete = self.dfs(s, i + 1, k - 1, prev, l, memo)\n else:\n\t\t\t#in this case, we cannot delete, set it as INF to choose skip in the end\n delete = float("inf")\n \n if s[i] == prev:\n\t\t #need one more digit for the count\n carry = 1 if l == 1 or len(str(l + 1)) > len(str(l)) else 0\n skip = carry + self.dfs(s, i + 1, k, s[i], l + 1, memo)\n else:\n skip = 1 + self.dfs(s, i + 1, k, s[i], 1, memo)\n \n memo[(i, k, prev, l)] = min(delete, skip)\n \n return memo[(i, k, prev, l)]\n \n``` | 4 | [Run-length encoding](http://en.wikipedia.org/wiki/Run-length_encoding) is a string compression method that works by replacing consecutive identical characters (repeated 2 or more times) with the concatenation of the character and the number marking the count of the characters (length of the run). For example, to compress the string `"aabccc "` we replace `"aa "` by `"a2 "` and replace `"ccc "` by `"c3 "`. Thus the compressed string becomes `"a2bc3 "`.
Notice that in this problem, we are not adding `'1'` after single characters.
Given a string `s` and an integer `k`. You need to delete **at most** `k` characters from `s` such that the run-length encoded version of `s` has minimum length.
Find the _minimum length of the run-length encoded version of_ `s` _after deleting at most_ `k` _characters_.
**Example 1:**
**Input:** s = "aaabcccd ", k = 2
**Output:** 4
**Explanation:** Compressing s without deleting anything will give us "a3bc3d " of length 6. Deleting any of the characters 'a' or 'c' would at most decrease the length of the compressed string to 5, for instance delete 2 'a' then we will have s = "abcccd " which compressed is abc3d. Therefore, the optimal way is to delete 'b' and 'd', then the compressed version of s will be "a3c3 " of length 4.
**Example 2:**
**Input:** s = "aabbaa ", k = 2
**Output:** 2
**Explanation:** If we delete both 'b' characters, the resulting compressed string would be "a4 " of length 2.
**Example 3:**
**Input:** s = "aaaaaaaaaaa ", k = 0
**Output:** 3
**Explanation:** Since k is zero, we cannot delete anything. The compressed string is "a11 " of length 3.
**Constraints:**
* `1 <= s.length <= 100`
* `0 <= k <= s.length`
* `s` contains only lowercase English letters. | Dynamic programming + bitmask. dp(peopleMask, idHat) number of ways to wear different hats given a bitmask (people visited) and used hats from 1 to idHat-1. |
Python with Comments 💚 | string-compression-ii | 0 | 1 | ```\nclass Solution:\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n #traverse the string\n #keep track of the status of delete or not delete current character\n #the status includes current index, number of delete, the previous character, and the runing length of previous character\n #return the minium length of compresed between delete or not delete\n\t\t#O(n^2*26*k) = O(n^2*k) time and space\n \n memo = {}\n return self.dfs(s, 0, k, None, 0, memo)\n \n def dfs(self, s, i, k, prev, l, memo):\n if i == len(s):\n return 0\n if (i, k, prev, l) in memo:\n return memo[(i, k, prev, l)]\n \n if k > 0:\n delete = self.dfs(s, i + 1, k - 1, prev, l, memo)\n else:\n\t\t\t#in this case, we cannot delete, set it as INF to choose skip in the end\n delete = float("inf")\n \n if s[i] == prev:\n\t\t #need one more digit for the count\n carry = 1 if l == 1 or len(str(l + 1)) > len(str(l)) else 0\n skip = carry + self.dfs(s, i + 1, k, s[i], l + 1, memo)\n else:\n skip = 1 + self.dfs(s, i + 1, k, s[i], 1, memo)\n \n memo[(i, k, prev, l)] = min(delete, skip)\n \n return memo[(i, k, prev, l)]\n \n``` | 4 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
[python] Simple clear DP solution | string-compression-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTruly a hard problem.\nThe key point is to think of:\n(1) The definition of dp[i][j] is: for the first i chars, the shortest final length if j chars are deleted.\n(2) The transfer relationship is:\na. if s[i - 1] is deleted, then dp[i][j] = dp[i - 1][j - 1];\nb. if s[i - 1] is not deleted, we should try our best to merge it with the same chars coming before it by removing different chars starting from s[i - 1] to its left. \nFor 2.b, the reason why we remove the different chars from right to left instead of the contrary is that, obviously, we must first remove the near ones than far ones to make it merge with earlier results. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2*k)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n*k)$$\n\n# Code\n```\ndef cost(n):\n if n == 0:\n return 0\n elif n == 1:\n return 1\n elif 1 < n < 10:\n return 2\n elif 10 <= n < 99:\n return 3\n else:\n return 4\n\nclass Solution:\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n dp = [[float(\'inf\')] * (k + 1) for _ in range(len(s) + 1)]\n for i in range(k + 1):\n dp[0][i] = 0\n for i in range(1, len(s) + 1):\n for j in range(k + 1):\n if j > 0:\n dp[i][j] = dp[i - 1][j - 1]\n same, diff = 0, 0\n for p in range(i, 0, -1):\n if j < diff:\n break\n if s[p - 1] == s[i - 1]:\n same += 1\n dp[i][j] = min(dp[i][j], dp[p - 1][j - diff] + cost(same))\n else:\n diff += 1\n return dp[len(s)][k]\n \n``` | 2 | [Run-length encoding](http://en.wikipedia.org/wiki/Run-length_encoding) is a string compression method that works by replacing consecutive identical characters (repeated 2 or more times) with the concatenation of the character and the number marking the count of the characters (length of the run). For example, to compress the string `"aabccc "` we replace `"aa "` by `"a2 "` and replace `"ccc "` by `"c3 "`. Thus the compressed string becomes `"a2bc3 "`.
Notice that in this problem, we are not adding `'1'` after single characters.
Given a string `s` and an integer `k`. You need to delete **at most** `k` characters from `s` such that the run-length encoded version of `s` has minimum length.
Find the _minimum length of the run-length encoded version of_ `s` _after deleting at most_ `k` _characters_.
**Example 1:**
**Input:** s = "aaabcccd ", k = 2
**Output:** 4
**Explanation:** Compressing s without deleting anything will give us "a3bc3d " of length 6. Deleting any of the characters 'a' or 'c' would at most decrease the length of the compressed string to 5, for instance delete 2 'a' then we will have s = "abcccd " which compressed is abc3d. Therefore, the optimal way is to delete 'b' and 'd', then the compressed version of s will be "a3c3 " of length 4.
**Example 2:**
**Input:** s = "aabbaa ", k = 2
**Output:** 2
**Explanation:** If we delete both 'b' characters, the resulting compressed string would be "a4 " of length 2.
**Example 3:**
**Input:** s = "aaaaaaaaaaa ", k = 0
**Output:** 3
**Explanation:** Since k is zero, we cannot delete anything. The compressed string is "a11 " of length 3.
**Constraints:**
* `1 <= s.length <= 100`
* `0 <= k <= s.length`
* `s` contains only lowercase English letters. | Dynamic programming + bitmask. dp(peopleMask, idHat) number of ways to wear different hats given a bitmask (people visited) and used hats from 1 to idHat-1. |
[python] Simple clear DP solution | string-compression-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTruly a hard problem.\nThe key point is to think of:\n(1) The definition of dp[i][j] is: for the first i chars, the shortest final length if j chars are deleted.\n(2) The transfer relationship is:\na. if s[i - 1] is deleted, then dp[i][j] = dp[i - 1][j - 1];\nb. if s[i - 1] is not deleted, we should try our best to merge it with the same chars coming before it by removing different chars starting from s[i - 1] to its left. \nFor 2.b, the reason why we remove the different chars from right to left instead of the contrary is that, obviously, we must first remove the near ones than far ones to make it merge with earlier results. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2*k)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n*k)$$\n\n# Code\n```\ndef cost(n):\n if n == 0:\n return 0\n elif n == 1:\n return 1\n elif 1 < n < 10:\n return 2\n elif 10 <= n < 99:\n return 3\n else:\n return 4\n\nclass Solution:\n def getLengthOfOptimalCompression(self, s: str, k: int) -> int:\n dp = [[float(\'inf\')] * (k + 1) for _ in range(len(s) + 1)]\n for i in range(k + 1):\n dp[0][i] = 0\n for i in range(1, len(s) + 1):\n for j in range(k + 1):\n if j > 0:\n dp[i][j] = dp[i - 1][j - 1]\n same, diff = 0, 0\n for p in range(i, 0, -1):\n if j < diff:\n break\n if s[p - 1] == s[i - 1]:\n same += 1\n dp[i][j] = min(dp[i][j], dp[p - 1][j - diff] + cost(same))\n else:\n diff += 1\n return dp[len(s)][k]\n \n``` | 2 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Time(78%) Memory(99.9%), You can remove triple-for-statement with itertool. | count-good-triplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou can use itertool.\nAnd there are awesome $$O(nlogn)$$ solution using fenwick tree\nLook at the other solution down below\n# Complexity\n- Time complexity: $$O(N^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n cnt = 0\n for i, j, k in itertools.combinations(arr, 3):\n if abs(i-j) <= a and abs(j-k) <= b and abs(k-i) <= c:\n cnt +=1\n return cnt\n``` | 1 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Time(78%) Memory(99.9%), You can remove triple-for-statement with itertool. | count-good-triplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou can use itertool.\nAnd there are awesome $$O(nlogn)$$ solution using fenwick tree\nLook at the other solution down below\n# Complexity\n- Time complexity: $$O(N^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n cnt = 0\n for i, j, k in itertools.combinations(arr, 3):\n if abs(i-j) <= a and abs(j-k) <= b and abs(k-i) <= c:\n cnt +=1\n return cnt\n``` | 1 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Naive Approach || Count Good Triplets | count-good-triplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n count=0\n for i in range(len(arr)):\n for j in range(len(arr)):\n for k in range(len(arr)):\n if i>=0 and i<j and j<k and k<len(arr):\n if abs(arr[i]-arr[j] )<=a and abs(arr[j]-arr[k] )<=b and abs(arr[i]-arr[k] )<=c:\n count+=1\n return count\n``` | 1 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Naive Approach || Count Good Triplets | count-good-triplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n count=0\n for i in range(len(arr)):\n for j in range(len(arr)):\n for k in range(len(arr)):\n if i>=0 and i<j and j<k and k<len(arr):\n if abs(arr[i]-arr[j] )<=a and abs(arr[j]-arr[k] )<=b and abs(arr[i]-arr[k] )<=c:\n count+=1\n return count\n``` | 1 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Pyhton3 solution Triple nested loop | count-good-triplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought on how to solve this problem is to use a triple nested loop. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, I will use a triple nested loop. The outer loop will iterate through each element in the array. For each element, the two inner loops will iterate through the elements after the outer loop\'s current index to make a triplet. After making each triplet, we can then check if each element of the triplet meets the criteria for being a good triplet. If it does, then we can increment our counter. \n# Complexity\n- Time complexity: $$$$O(n^3)$$$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n count = 0\n for i in range(len(arr) - 2):\n for j in range(i + 1, len(arr) - 1):\n if abs(arr[i] - arr[j]) <= a:\n for k in range(j + 1, len(arr)):\n if abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k]) <= c:\n count += 1\n return count\n``` | 1 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Pyhton3 solution Triple nested loop | count-good-triplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought on how to solve this problem is to use a triple nested loop. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, I will use a triple nested loop. The outer loop will iterate through each element in the array. For each element, the two inner loops will iterate through the elements after the outer loop\'s current index to make a triplet. After making each triplet, we can then check if each element of the triplet meets the criteria for being a good triplet. If it does, then we can increment our counter. \n# Complexity\n- Time complexity: $$$$O(n^3)$$$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n count = 0\n for i in range(len(arr) - 2):\n for j in range(i + 1, len(arr) - 1):\n if abs(arr[i] - arr[j]) <= a:\n for k in range(j + 1, len(arr)):\n if abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k]) <= c:\n count += 1\n return count\n``` | 1 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Obvious Brute force that gets accepted | count-good-triplets | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, A: List[int], a: int, b: int, c: int) -> int:\n n = len(A)\n cnt = 0\n for i in range(n):\n for j in range(i+1, n):\n for k in range(j+1, n):\n if abs(A[i]-A[j]) <= a and abs(A[k]-A[j]) <= b and abs(A[i]-A[k]) <= c:\n cnt+=1\n return cnt\n``` | 2 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Obvious Brute force that gets accepted | count-good-triplets | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countGoodTriplets(self, A: List[int], a: int, b: int, c: int) -> int:\n n = len(A)\n cnt = 0\n for i in range(n):\n for j in range(i+1, n):\n for k in range(j+1, n):\n if abs(A[i]-A[j]) <= a and abs(A[k]-A[j]) <= b and abs(A[i]-A[k]) <= c:\n cnt+=1\n return cnt\n``` | 2 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
[PYTHON] Self Explanatory Simple Code | count-good-triplets | 0 | 1 | Runtime: 645 ms, faster than 80.95% of Python3 online submissions for Count Good Triplets.\nMemory Usage: 14 MB, less than 16.30% of Python3 online submissions for Count Good Triplets.\n\n```class Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n co = 0\n for i in range(len(arr)):\n for j in range(i + 1, len(arr)):\n for k in range(j + 1, len(arr)):\n if abs(arr[i] - arr[j]) <= a and abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k]) <= c:\n co += 1\n return co | 3 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
[PYTHON] Self Explanatory Simple Code | count-good-triplets | 0 | 1 | Runtime: 645 ms, faster than 80.95% of Python3 online submissions for Count Good Triplets.\nMemory Usage: 14 MB, less than 16.30% of Python3 online submissions for Count Good Triplets.\n\n```class Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n co = 0\n for i in range(len(arr)):\n for j in range(i + 1, len(arr)):\n for k in range(j + 1, len(arr)):\n if abs(arr[i] - arr[j]) <= a and abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k]) <= c:\n co += 1\n return co | 3 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
simple brute force ||python solution | count-good-triplets | 0 | 1 | Time Complexcity O(N^3)\nSpace complexcity O(1)\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n count=0\n n=len(arr)\n for i in range(n-2):\n for j in range(i+1,n-1):\n for k in range(j+1,n):\n if abs(arr[i]-arr[j])<=a and abs(arr[j]-arr[k])<=b and abs(arr[i]-arr[k])<=c:\n count+=1\n return count\n \n``` | 1 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
simple brute force ||python solution | count-good-triplets | 0 | 1 | Time Complexcity O(N^3)\nSpace complexcity O(1)\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n count=0\n n=len(arr)\n for i in range(n-2):\n for j in range(i+1,n-1):\n for k in range(j+1,n):\n if abs(arr[i]-arr[j])<=a and abs(arr[j]-arr[k])<=b and abs(arr[i]-arr[k])<=c:\n count+=1\n return count\n \n``` | 1 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Python sol with generator and loops | count-good-triplets | 0 | 1 | Python sol with generator and loops\n\n---\n\n**Implementation** by nested loops:\n\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n \n size = len(arr)\n \n good_count = 0\n \n for i in range(size-2):\n for j in range(i+1, size-1):\n for k in range(j+1, size):\n \n ok_a = abs(arr[i] - arr[j]) <= a\n ok_b = abs(arr[j] - arr[k]) <= b\n ok_c = abs(arr[i] - arr[k]) <= c\n \n if all((ok_a, ok_b, ok_c)):\n good_count += 1\n \n \n return good_count\n\n```\n\n---\n\n**Implementation** by generator expression and sum:\n\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n \n \n def is_good(i, j, k):\n \n ok_a = abs(arr[i] - arr[j]) <= a\n ok_b = abs(arr[j] - arr[k]) <= b\n ok_c = abs(arr[i] - arr[k]) <= c\n\n return all((ok_a, ok_b, ok_c))\n \n # -------------------------------------\n \n size = len(arr)\n \n return sum(1 for i in range(size-2) for j in range(i+1, size-1) for k in range(j+1, size) if is_good(i,j,k))\n```\n\n---\n\nReference:\n\n[1] [Python official docs about generator expression](https://www.python.org/dev/peps/pep-0289/) | 28 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Python sol with generator and loops | count-good-triplets | 0 | 1 | Python sol with generator and loops\n\n---\n\n**Implementation** by nested loops:\n\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n \n size = len(arr)\n \n good_count = 0\n \n for i in range(size-2):\n for j in range(i+1, size-1):\n for k in range(j+1, size):\n \n ok_a = abs(arr[i] - arr[j]) <= a\n ok_b = abs(arr[j] - arr[k]) <= b\n ok_c = abs(arr[i] - arr[k]) <= c\n \n if all((ok_a, ok_b, ok_c)):\n good_count += 1\n \n \n return good_count\n\n```\n\n---\n\n**Implementation** by generator expression and sum:\n\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n \n \n def is_good(i, j, k):\n \n ok_a = abs(arr[i] - arr[j]) <= a\n ok_b = abs(arr[j] - arr[k]) <= b\n ok_c = abs(arr[i] - arr[k]) <= c\n\n return all((ok_a, ok_b, ok_c))\n \n # -------------------------------------\n \n size = len(arr)\n \n return sum(1 for i in range(size-2) for j in range(i+1, size-1) for k in range(j+1, size) if is_good(i,j,k))\n```\n\n---\n\nReference:\n\n[1] [Python official docs about generator expression](https://www.python.org/dev/peps/pep-0289/) | 28 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
[Python] Roughly O(n log n) with Fenwick Tree | count-good-triplets | 0 | 1 | This is merely a python spin-off of 2 great solutions.\n1. [Bucket sort ](https://leetcode.com/problems/count-good-triplets/discuss/769821/Java.-O(n).-Well-it-is-really-O(1000-*-n))\n2. [Fenwick tree](https://leetcode.com/problems/count-good-triplets/discuss/951019/Java-Roughly-O(n-log-n)-with-Fenwick-Tree)\n\nI kid you not each of them deserve your full respect. The former is intricate in nature and the latter warrants plenty of understanding to bits manipulation, not to mention these two are merely the prelude to implementations that are solely dependent on programming language and your clear mind. A simple difference in syntax among programming languages could well be the next bug that catches you off-guard. I hope this justifies my contribution.\n\nAttached below is my Fenwick tree implementation. \n\n```\nclass Fenwick:\n def __init__(self, size: int):\n self.partial = [0] * (size + 1)\n self.length = size + 1\n \n def getCum(self, end: int, start: int) -> int:\n return self.getSum(end) - self.getSum(start - 1)\n \n def getSum(self, index0: int) -> int:\n start1 = index0 + 1\n ans = 0\n while start1 > 0:\n ans += self.partial[start1]\n start1 &= (start1 - 1)\n return ans\n \n def addSum(self, i0:int, val: int):\n start1 = i0 + 1\n while True:\n self.partial[start1] += val\n start1 += start1 & (-start1)\n if start1 >= self.length:\n return\n```\n\nUnfortunately, I think it is almost impossible to produce a bug-free implementation under time pressure. So instead of painstakingly memorizing minuscule off-by-one errors that you will surely forget in the next high octane full throttle interview, I would post a log that verrifies my Fenwick tree implementation for your reference.\n\n```\na = [7,3,7,3,12,1,12,2,3]\nfen = Fenwick(len(a))\nfor i, v in enumerate(a):\n fen.addSum(i,v)\n\nb = [v for v in a]\nfor i in range(1, len(a) + 0):\n b[i] += b[i-1]\nprint(b)\n\nfor i in range(1, len(b)):\n right = b[i]\n for j in range(0, i):\n left = b[j]\n print(f"True? {(b[i] - b[j]) == fen.getCum(i , j)} (left,right): ({j},{i}); b[i] - b[j] = {b[i]} - {b[j]} = {b[i] - b[j]}")\n print()\n```\n\nWhat follows will be the solution that makes use of Fenwick tree.\nI specifically commented out the lines that were used to caclulate post array in the old way. In so doing, you should be able to compare and see the difference in runtime by switching through lines.\n\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n pre = [0] * 1001\n post = Fenwick(1001)\n pre[arr[0]] += 1\n vi = 2\n while vi < 0 + len(arr):\n # post[arr[vi]] += 1\n post.addSum(arr[vi], 1)\n vi += 1\n # pi = 1 \n # while pi < 0 + len(post):\n # post[pi] += post[pi-1]\n # pi += 1\n i = 1\n ans = 0\n while i < 0 + len(arr) - 1:\n middle = arr[i]\n aupper = min(1000, middle + a)\n alower = max(0, middle - a)\n bupper = min(1000, middle + b)\n blower = max(0, middle - b)\n traversea = alower\n while traversea <= aupper:\n if pre[traversea]:\n intersectlower = max(blower, traversea - c)\n intersecupper = min(bupper, traversea + c)\n if intersecupper >= intersectlower:\n if not intersectlower:\n # ans += pre[traversea] * post[intersecupper]\n ans += pre[traversea] * post.getSum(intersecupper)\n else:\n # ans += pre[traversea] * (post[intersecupper] - post[intersectlower - 1])\n ans += pre[traversea] * post.getCum(intersecupper, intersectlower)\n traversea += 1\n pre[middle] += 1\n vaftermiddle = arr[i + 1]\n # while vaftermiddle <= 1000:\n # post[vaftermiddle] -= 1\n # vaftermiddle += 1\n post.addSum(vaftermiddle, -1)\n i += 1\n return ans\n``` | 8 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
[Python] Roughly O(n log n) with Fenwick Tree | count-good-triplets | 0 | 1 | This is merely a python spin-off of 2 great solutions.\n1. [Bucket sort ](https://leetcode.com/problems/count-good-triplets/discuss/769821/Java.-O(n).-Well-it-is-really-O(1000-*-n))\n2. [Fenwick tree](https://leetcode.com/problems/count-good-triplets/discuss/951019/Java-Roughly-O(n-log-n)-with-Fenwick-Tree)\n\nI kid you not each of them deserve your full respect. The former is intricate in nature and the latter warrants plenty of understanding to bits manipulation, not to mention these two are merely the prelude to implementations that are solely dependent on programming language and your clear mind. A simple difference in syntax among programming languages could well be the next bug that catches you off-guard. I hope this justifies my contribution.\n\nAttached below is my Fenwick tree implementation. \n\n```\nclass Fenwick:\n def __init__(self, size: int):\n self.partial = [0] * (size + 1)\n self.length = size + 1\n \n def getCum(self, end: int, start: int) -> int:\n return self.getSum(end) - self.getSum(start - 1)\n \n def getSum(self, index0: int) -> int:\n start1 = index0 + 1\n ans = 0\n while start1 > 0:\n ans += self.partial[start1]\n start1 &= (start1 - 1)\n return ans\n \n def addSum(self, i0:int, val: int):\n start1 = i0 + 1\n while True:\n self.partial[start1] += val\n start1 += start1 & (-start1)\n if start1 >= self.length:\n return\n```\n\nUnfortunately, I think it is almost impossible to produce a bug-free implementation under time pressure. So instead of painstakingly memorizing minuscule off-by-one errors that you will surely forget in the next high octane full throttle interview, I would post a log that verrifies my Fenwick tree implementation for your reference.\n\n```\na = [7,3,7,3,12,1,12,2,3]\nfen = Fenwick(len(a))\nfor i, v in enumerate(a):\n fen.addSum(i,v)\n\nb = [v for v in a]\nfor i in range(1, len(a) + 0):\n b[i] += b[i-1]\nprint(b)\n\nfor i in range(1, len(b)):\n right = b[i]\n for j in range(0, i):\n left = b[j]\n print(f"True? {(b[i] - b[j]) == fen.getCum(i , j)} (left,right): ({j},{i}); b[i] - b[j] = {b[i]} - {b[j]} = {b[i] - b[j]}")\n print()\n```\n\nWhat follows will be the solution that makes use of Fenwick tree.\nI specifically commented out the lines that were used to caclulate post array in the old way. In so doing, you should be able to compare and see the difference in runtime by switching through lines.\n\n```\nclass Solution:\n def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:\n pre = [0] * 1001\n post = Fenwick(1001)\n pre[arr[0]] += 1\n vi = 2\n while vi < 0 + len(arr):\n # post[arr[vi]] += 1\n post.addSum(arr[vi], 1)\n vi += 1\n # pi = 1 \n # while pi < 0 + len(post):\n # post[pi] += post[pi-1]\n # pi += 1\n i = 1\n ans = 0\n while i < 0 + len(arr) - 1:\n middle = arr[i]\n aupper = min(1000, middle + a)\n alower = max(0, middle - a)\n bupper = min(1000, middle + b)\n blower = max(0, middle - b)\n traversea = alower\n while traversea <= aupper:\n if pre[traversea]:\n intersectlower = max(blower, traversea - c)\n intersecupper = min(bupper, traversea + c)\n if intersecupper >= intersectlower:\n if not intersectlower:\n # ans += pre[traversea] * post[intersecupper]\n ans += pre[traversea] * post.getSum(intersecupper)\n else:\n # ans += pre[traversea] * (post[intersecupper] - post[intersectlower - 1])\n ans += pre[traversea] * post.getCum(intersecupper, intersectlower)\n traversea += 1\n pre[middle] += 1\n vaftermiddle = arr[i + 1]\n # while vaftermiddle <= 1000:\n # post[vaftermiddle] -= 1\n # vaftermiddle += 1\n post.addSum(vaftermiddle, -1)\n i += 1\n return ans\n``` | 8 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
C++/Python 1 loop vs deque||30ms Beats 100% | find-the-winner-of-an-array-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf k>=len(arr) return max(arr)\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOtherwise use a loop to proceed.\n\n`getWinner` finds the `winner` in an array by iterating through it and keeping track of the maximum value and the `count` of consecutive wins. If the count of consecutive wins reaches `k`, it returns the current `winner`. If the length of the array is less than or equal to k, it returns the maximum value in the array as the winner.\n\n2nd approach is for simulation using deque which is also fast runs in 54ms & beats 98.61%\n# Simulation for testcase\nConsider `arr=[1,8,2,3,7,6,4,5,9] k=8`\n```\nwinner=1 q:[8,2,3,7,6,4,5,9] cout=0\nwinner=8 q:[2,3,7,6,4,5,9,1] cout=1\nwinner=8 q:[3,7,6,4,5,9,1,2] cout=2\nwinner=8 q:[7,6,4,5,9,1,2,3] cout=3\nwinner=8 q:[6,4,5,9,1,2,3,7] cout=4\nwinner=8 q:[4,5,9,1,2,3,7,6] cout=5\nwinner=8 q:[5,9,1,2,3,7,6,4] cout=6\nwinner=8 q:[9,1,2,3,7,6,4,5] cout=7\nwinner=9 q:[1,2,3,7,6,4,5,8] cout=1\nwinner=9 q:[2,3,7,6,4,5,8,1] cout=2\nwinner=9 q:[3,7,6,4,5,8,1,2] cout=3\nwinner=9 q:[7,6,4,5,8,1,2,3] cout=4\nwinner=9 q:[6,4,5,8,1,2,3,7] cout=5\nwinner=9 q:[4,5,8,1,2,3,7,6] cout=6\nwinner=9 q:[5,8,1,2,3,7,6,4] cout=7\nwinner=9 q:[8,1,2,3,7,6,4,5] cout=8\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\ndeque method $$O(n)$$\n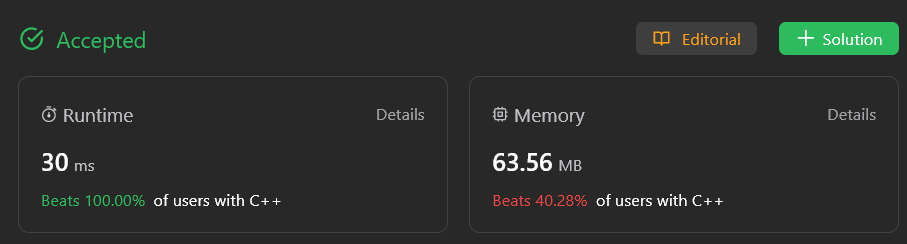\n\n# Code 30ms beats 100%\n```\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int n=arr.size();\n if (n<=k) return *max_element(arr.begin(), arr.end());\n int count=0, winner=arr[0];\n #pragma unroll\n for (int i=1; i<n && count<k; i++) {\n if (arr[i] > winner) {\n winner=arr[i];\n count=1;\n } \n else \n count++;\n }\n return winner;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Python Code with Explanation in comments\n```\n# Define a class called Solution.\nclass Solution:\n # Define a method called getWinner that takes an array \'arr\' and an integer \'k\' as inputs.\n def getWinner(self, arr: List[int], k: int) -> int:\n # Calculate the length of the input array and store it in \'n\'.\n n = len(arr)\n \n # Check if the length of the array is less than or equal to \'k\'.\n if n <= k:\n # If so, return the maximum value in the array as the winner.\n return max(arr)\n \n # Initialize variables to keep track of the count of consecutive wins and the current winner.\n count = 0\n winner = arr[0]\n \n # Iterate through the elements of the array starting from the second element.\n for x in arr[1:]:\n # Check if the current element \'x\' is greater than the current winner.\n if x > winner:\n # If \'x\' is greater, update the winner to \'x\' and reset the count to 1.\n winner = x\n count = 1\n else:\n # If \'x\' is not greater, increment the count.\n count += 1\n \n # Check if the count has reached \'k\'.\n if count == k:\n # If so, break out of the loop.\n break\n \n # Return the winner after the loop completes.\n return winner\n\n```\n# C++ code using deque for simulation runs in 54ms & beats 98.61%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int n=arr.size();\n if (n<=k) return *max_element(arr.begin(), arr.end());\n deque<int> q(arr.begin()+1, arr.end());\n int count=0, winner=arr[0];\n while(count<k){\n int x=q.front();\n if (x>winner){\n q.push_back(winner);\n winner=x;\n count=1;\n q.pop_front();\n }\n else{\n count++;\n q.pop_front();\n q.push_back(x);\n }\n }\n return winner;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 11 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
C++/Python 1 loop vs deque||30ms Beats 100% | find-the-winner-of-an-array-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf k>=len(arr) return max(arr)\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOtherwise use a loop to proceed.\n\n`getWinner` finds the `winner` in an array by iterating through it and keeping track of the maximum value and the `count` of consecutive wins. If the count of consecutive wins reaches `k`, it returns the current `winner`. If the length of the array is less than or equal to k, it returns the maximum value in the array as the winner.\n\n2nd approach is for simulation using deque which is also fast runs in 54ms & beats 98.61%\n# Simulation for testcase\nConsider `arr=[1,8,2,3,7,6,4,5,9] k=8`\n```\nwinner=1 q:[8,2,3,7,6,4,5,9] cout=0\nwinner=8 q:[2,3,7,6,4,5,9,1] cout=1\nwinner=8 q:[3,7,6,4,5,9,1,2] cout=2\nwinner=8 q:[7,6,4,5,9,1,2,3] cout=3\nwinner=8 q:[6,4,5,9,1,2,3,7] cout=4\nwinner=8 q:[4,5,9,1,2,3,7,6] cout=5\nwinner=8 q:[5,9,1,2,3,7,6,4] cout=6\nwinner=8 q:[9,1,2,3,7,6,4,5] cout=7\nwinner=9 q:[1,2,3,7,6,4,5,8] cout=1\nwinner=9 q:[2,3,7,6,4,5,8,1] cout=2\nwinner=9 q:[3,7,6,4,5,8,1,2] cout=3\nwinner=9 q:[7,6,4,5,8,1,2,3] cout=4\nwinner=9 q:[6,4,5,8,1,2,3,7] cout=5\nwinner=9 q:[4,5,8,1,2,3,7,6] cout=6\nwinner=9 q:[5,8,1,2,3,7,6,4] cout=7\nwinner=9 q:[8,1,2,3,7,6,4,5] cout=8\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\ndeque method $$O(n)$$\n\n\n# Code 30ms beats 100%\n```\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int n=arr.size();\n if (n<=k) return *max_element(arr.begin(), arr.end());\n int count=0, winner=arr[0];\n #pragma unroll\n for (int i=1; i<n && count<k; i++) {\n if (arr[i] > winner) {\n winner=arr[i];\n count=1;\n } \n else \n count++;\n }\n return winner;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Python Code with Explanation in comments\n```\n# Define a class called Solution.\nclass Solution:\n # Define a method called getWinner that takes an array \'arr\' and an integer \'k\' as inputs.\n def getWinner(self, arr: List[int], k: int) -> int:\n # Calculate the length of the input array and store it in \'n\'.\n n = len(arr)\n \n # Check if the length of the array is less than or equal to \'k\'.\n if n <= k:\n # If so, return the maximum value in the array as the winner.\n return max(arr)\n \n # Initialize variables to keep track of the count of consecutive wins and the current winner.\n count = 0\n winner = arr[0]\n \n # Iterate through the elements of the array starting from the second element.\n for x in arr[1:]:\n # Check if the current element \'x\' is greater than the current winner.\n if x > winner:\n # If \'x\' is greater, update the winner to \'x\' and reset the count to 1.\n winner = x\n count = 1\n else:\n # If \'x\' is not greater, increment the count.\n count += 1\n \n # Check if the count has reached \'k\'.\n if count == k:\n # If so, break out of the loop.\n break\n \n # Return the winner after the loop completes.\n return winner\n\n```\n# C++ code using deque for simulation runs in 54ms & beats 98.61%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int n=arr.size();\n if (n<=k) return *max_element(arr.begin(), arr.end());\n deque<int> q(arr.begin()+1, arr.end());\n int count=0, winner=arr[0];\n while(count<k){\n int x=q.front();\n if (x>winner){\n q.push_back(winner);\n winner=x;\n count=1;\n q.pop_front();\n }\n else{\n count++;\n q.pop_front();\n q.push_back(x);\n }\n }\n return winner;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 11 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
🚀 96.74% || Simulation Game || Explained Intuition 🚀 | find-the-winner-of-an-array-game | 1 | 1 | # Problem Description\n\nGiven an array of distinct integers, `arr`, and an integer `k`. A game is played between the first **two** elements of the array, `arr[0]` and `arr[1]`. In each round, the **larger** integer remains at position `0`, while the smaller integer is **moved** to the **end** of the array. The game **continues** until one integer wins `k` consecutive rounds. \nThe task is to determine which integer will **win** the game. You can assume that there will **always** be a winner in the game.\n\n- **Constraints:**\n - $2 <= arr.length <= 10^5$\n - $1 <= arr[i] <= 10^6$\n - arr contains **distinct** integers.\n - $1 <= k <= 10^9$\n\n\n---\n\n\n\n# Intuition\n\nHi there, \uD83D\uDE04\n\nLet\'s zoom in\uD83D\uDD0E the details of our problem today.\n\nThe problem is that there is some kind of **games\uD83C\uDFAE** between the numbers of the given array. Each round, the first **two** elements play against eachothers and the **larger** -winner- stays in the position `0` in the array and the **smaller** -loser- goes to the **end** of the array. The winner of the whole game is who wins for `k` **consecutive** round.\nThe task is to find this **winner**.\uD83E\uDD47\n\nSeems cool!\uD83D\uDE0E\n\nDo you have any solutions in mind\uD83E\uDDE0 to solve it?\uD83E\uDD14\nActually, I have one. First thing I thought of was "Why not to **simulate** the game ?". Seems fair enough.\uD83D\uDE4C\n\nBut how can we simulate it ?\uD83E\uDD14\nThere many kind of techniques, One of them is for each element in the array we can let him play `k` rounds or until it **loses**. Unfortunately this solution will give us **TLE** since it will have complexity of $O(N * K)$.\uD83D\uDE22\n\nAnother way to play the simulation ?\nLet\'s see some examples.\n\n```\nEX1 : arr = [2, 1, 7, 3, 4, 5], k = 3\n\nRound1 : winner = 2\narr = [2, 7, 3, 4, 5, 1]\n\nRound2 : winner = 7\narr = [7, 3, 4, 5, 1, 2]\n\nRound3 : winner = 7\narr = [7, 4, 5, 1, 2, 3]\n\nRound4 : winner = 7\narr = [7, 5, 1, 2, 3, 4]\n\nWinner of game = 7\n```\n```\nEX2 : arr = [2, 1, 7, 3], k = 4\n\nRound1 : winner = 2\narr = [2, 7, 3, 1]\n\nRound2 : winner = 7\narr = [7, 3, 1, 2]\n\nRound3 : winner = 7\narr = [7, 1, 2, 3]\n\nRound4 : winner = 7\narr = [7, 2, 3, 1]\n\nRound5 : winner = 7\narr = [7, 3, 1, 2]\n\nWinner of game = 7\n```\n\nDid you **noticed** something in the last two examples ?\uD83E\uDD14\nActually **YES** \uD83E\uDD29! `7` was the winner in the both games. \nIsn\'t `7` is the **largest** element in the these games ?\uD83E\uDD28\nAlso, **YES** !\n\nDo we have an **observation** here ?\uD83E\uDD2F\nAnother **YES**, whenever we encounter the **largest** element as the current winner then we are sure that he will when all the games since no other element is larger than it. \uD83D\uDCAA\n\nAnd we can also be sure of the winner of the game before even start it, HOW ?\uD83E\uDD2F\nSimply if `k` is larger than or equal to array size then the largest element is the winner since in such **games** the winner should defeat all other elements to **win** `k` games and the **only** element can do this is the **largest** element in the array.\n\nGood ! now we have **two** important **observations**. What will we do if the winner of the game **isn\'t** the largest element? How will we get it ?\uD83E\uDD14\nWe can **simulate** the game by tracking the winner and see the current **streak** of his wins and if the current winner has **won** `k` games -from the rules of the game- or it was the **largest** element in our array then it is the winner of the whole game.\uD83E\uDD47 \n\nBut wait, can\'t we **simulate** the game from the beggining **without** considering the **largest** element of the array ?\uD83E\uDD14\nSadly, Since $1 <= k <= 10^9$ and $2 <= arr,length <= 10^5$ then if we simulated the game until one element will when for `k` rounds only we will have **TLE**\uD83D\uDE14 so for that we will have to consider the largest element in our calculations.\n\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n# Approach\n\n1. Find the **maximum** element in the given integer array.\n2. Check if the value of `k` is **greater** than or equal to the size of the array.\n - If **true**, return the **maximum** element, as it\'s the winner and no other element can **defeat** it.\n3. **Initialize** the `current winner` with the **first** element of the array and set the `current streak` to `0`.\n4. Iterate through the array starting from the second element (index 1):\n - Compare the `current winner` with the next element.\n - If the `current winner` is greater, increment the `current streak`.\n - If the next element is greater, reset the streak to 1 and update the `current winner` to the new element.\n - Check if the `current streak` has reached \'k\' or if the `current winner` is the maximum element.\n - If **true**, return the `current winner` as the winner of the game.\n5. The return statement is **dummy** since it can\'t be reached.\n\n## Complexity\n- **Time complexity:**$O(N)$\nSince we are finding the **maximum** element in **linear** time `O(N)` and we are **iterating** over all elements in the array also in **linear** time `O(N)` so the total complexity is `O(N)`.\n- **Space complexity:**$O(1)$\nSince we are using **constant** variables.\n\n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n // Find the maximum element in the array.\n int maxElement = *max_element(arr.begin(), arr.end()); \n\n // If k is greater than or equal to the array size, the maximum element wins.\n if (k >= arr.size())\n return maxElement; \n\n int current_winner = arr[0]; // Initialize the current winner with the first element of the array.\n int current_streak = 0; // Initialize the current streak to 0.\n\n for (int i = 1; i < arr.size(); i++) {\n // If the current winner is greater than the next element, then he will win the next game.\n if (current_winner > arr[i])\n current_streak++; \n\n // the current winner lost the game.\n else {\n current_streak = 1; // Reset the streak since new element becomes the winner.\n current_winner = arr[i]; // Update the current winner.\n }\n\n // If the current streak reaches k or the current winner is the maximum element\n if (current_streak == k || current_winner == maxElement)\n return current_winner; \n }\n\n return current_winner; // Dummy return\n }\n};\n\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n // Find the maximum element in the array.\n int maxElement = Arrays.stream(arr).max().getAsInt();\n\n // If k is greater than or equal to the array size, the maximum element wins.\n if (k >= arr.length) {\n return maxElement;\n }\n\n int currentWinner = arr[0]; // Initialize the current winner with the first element of the array.\n int currentStreak = 0; // Initialize the current streak to 0.\n\n for (int i = 1; i < arr.length; i++) {\n // If the current winner is greater than the next element, then they will win the next game.\n if (currentWinner > arr[i]) {\n currentStreak++;\n\n // the current winner lost the game.\n } else {\n currentStreak = 1; // Reset the streak since a new element becomes the winner.\n currentWinner = arr[i]; // Update the current winner.\n }\n\n // If the current streak reaches k or the current winner is the maximum element\n if (currentStreak == k || currentWinner == maxElement) {\n return currentWinner;\n }\n }\n\n return currentWinner; // Dummy return\n }\n}\n```\n```Python []\nclass Solution:\n def getWinner(self, arr, k):\n # Find the maximum element in the list.\n max_element = max(arr)\n \n # If k is greater than or equal to the list size, the maximum element wins.\n if k >= len(arr):\n return max_element\n \n current_winner = arr[0] # Initialize the current winner with the first element of the list.\n current_streak = 0 # Initialize the current streak to 0.\n \n for i in range(1, len(arr)):\n # If the current winner is greater than the next element, then they will win the next game.\n if current_winner > arr[i]:\n current_streak += 1\n\n # the current winner lost the game.\n else:\n current_streak = 1 # Reset the streak since a new element becomes the winner.\n current_winner = arr[i] # Update the current winner.\n \n # If the current streak reaches k or the current winner is the maximum element\n if current_streak == k or current_winner == max_element:\n return current_winner\n \n return current_winner # Dummy return\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n // Find the maximum element in the array.\n int maxElement = arr[0];\n for (int i = 1; i < arrSize; i++) {\n if (arr[i] > maxElement) {\n maxElement = arr[i];\n }\n }\n\n // If k is greater than or equal to the array size, the maximum element wins.\n if (k >= arrSize) {\n return maxElement;\n }\n\n int current_winner = arr[0]; // Initialize the current winner with the first element of the array.\n int current_streak = 0; // Initialize the current streak to 0.\n\n for (int i = 1; i < arrSize; i++) {\n // If the current winner is greater than the next element, then they will win the next game.\n if (current_winner > arr[i]) {\n current_streak++;\n\n // the current winner lost the game.\n } else {\n current_streak = 1; // Reset the streak since a new element becomes the winner.\n current_winner = arr[i]; // Update the current winner.\n }\n\n // If the current streak reaches k or the current winner is the maximum element\n if (current_streak == k || current_winner == maxElement) {\n return current_winner;\n }\n }\n\n return current_winner; // Dummy return\n}\n```\n\n\n\n\n | 26 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
🚀 96.74% || Simulation Game || Explained Intuition 🚀 | find-the-winner-of-an-array-game | 1 | 1 | # Problem Description\n\nGiven an array of distinct integers, `arr`, and an integer `k`. A game is played between the first **two** elements of the array, `arr[0]` and `arr[1]`. In each round, the **larger** integer remains at position `0`, while the smaller integer is **moved** to the **end** of the array. The game **continues** until one integer wins `k` consecutive rounds. \nThe task is to determine which integer will **win** the game. You can assume that there will **always** be a winner in the game.\n\n- **Constraints:**\n - $2 <= arr.length <= 10^5$\n - $1 <= arr[i] <= 10^6$\n - arr contains **distinct** integers.\n - $1 <= k <= 10^9$\n\n\n---\n\n\n\n# Intuition\n\nHi there, \uD83D\uDE04\n\nLet\'s zoom in\uD83D\uDD0E the details of our problem today.\n\nThe problem is that there is some kind of **games\uD83C\uDFAE** between the numbers of the given array. Each round, the first **two** elements play against eachothers and the **larger** -winner- stays in the position `0` in the array and the **smaller** -loser- goes to the **end** of the array. The winner of the whole game is who wins for `k` **consecutive** round.\nThe task is to find this **winner**.\uD83E\uDD47\n\nSeems cool!\uD83D\uDE0E\n\nDo you have any solutions in mind\uD83E\uDDE0 to solve it?\uD83E\uDD14\nActually, I have one. First thing I thought of was "Why not to **simulate** the game ?". Seems fair enough.\uD83D\uDE4C\n\nBut how can we simulate it ?\uD83E\uDD14\nThere many kind of techniques, One of them is for each element in the array we can let him play `k` rounds or until it **loses**. Unfortunately this solution will give us **TLE** since it will have complexity of $O(N * K)$.\uD83D\uDE22\n\nAnother way to play the simulation ?\nLet\'s see some examples.\n\n```\nEX1 : arr = [2, 1, 7, 3, 4, 5], k = 3\n\nRound1 : winner = 2\narr = [2, 7, 3, 4, 5, 1]\n\nRound2 : winner = 7\narr = [7, 3, 4, 5, 1, 2]\n\nRound3 : winner = 7\narr = [7, 4, 5, 1, 2, 3]\n\nRound4 : winner = 7\narr = [7, 5, 1, 2, 3, 4]\n\nWinner of game = 7\n```\n```\nEX2 : arr = [2, 1, 7, 3], k = 4\n\nRound1 : winner = 2\narr = [2, 7, 3, 1]\n\nRound2 : winner = 7\narr = [7, 3, 1, 2]\n\nRound3 : winner = 7\narr = [7, 1, 2, 3]\n\nRound4 : winner = 7\narr = [7, 2, 3, 1]\n\nRound5 : winner = 7\narr = [7, 3, 1, 2]\n\nWinner of game = 7\n```\n\nDid you **noticed** something in the last two examples ?\uD83E\uDD14\nActually **YES** \uD83E\uDD29! `7` was the winner in the both games. \nIsn\'t `7` is the **largest** element in the these games ?\uD83E\uDD28\nAlso, **YES** !\n\nDo we have an **observation** here ?\uD83E\uDD2F\nAnother **YES**, whenever we encounter the **largest** element as the current winner then we are sure that he will when all the games since no other element is larger than it. \uD83D\uDCAA\n\nAnd we can also be sure of the winner of the game before even start it, HOW ?\uD83E\uDD2F\nSimply if `k` is larger than or equal to array size then the largest element is the winner since in such **games** the winner should defeat all other elements to **win** `k` games and the **only** element can do this is the **largest** element in the array.\n\nGood ! now we have **two** important **observations**. What will we do if the winner of the game **isn\'t** the largest element? How will we get it ?\uD83E\uDD14\nWe can **simulate** the game by tracking the winner and see the current **streak** of his wins and if the current winner has **won** `k` games -from the rules of the game- or it was the **largest** element in our array then it is the winner of the whole game.\uD83E\uDD47 \n\nBut wait, can\'t we **simulate** the game from the beggining **without** considering the **largest** element of the array ?\uD83E\uDD14\nSadly, Since $1 <= k <= 10^9$ and $2 <= arr,length <= 10^5$ then if we simulated the game until one element will when for `k` rounds only we will have **TLE**\uD83D\uDE14 so for that we will have to consider the largest element in our calculations.\n\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n# Approach\n\n1. Find the **maximum** element in the given integer array.\n2. Check if the value of `k` is **greater** than or equal to the size of the array.\n - If **true**, return the **maximum** element, as it\'s the winner and no other element can **defeat** it.\n3. **Initialize** the `current winner` with the **first** element of the array and set the `current streak` to `0`.\n4. Iterate through the array starting from the second element (index 1):\n - Compare the `current winner` with the next element.\n - If the `current winner` is greater, increment the `current streak`.\n - If the next element is greater, reset the streak to 1 and update the `current winner` to the new element.\n - Check if the `current streak` has reached \'k\' or if the `current winner` is the maximum element.\n - If **true**, return the `current winner` as the winner of the game.\n5. The return statement is **dummy** since it can\'t be reached.\n\n## Complexity\n- **Time complexity:**$O(N)$\nSince we are finding the **maximum** element in **linear** time `O(N)` and we are **iterating** over all elements in the array also in **linear** time `O(N)` so the total complexity is `O(N)`.\n- **Space complexity:**$O(1)$\nSince we are using **constant** variables.\n\n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n // Find the maximum element in the array.\n int maxElement = *max_element(arr.begin(), arr.end()); \n\n // If k is greater than or equal to the array size, the maximum element wins.\n if (k >= arr.size())\n return maxElement; \n\n int current_winner = arr[0]; // Initialize the current winner with the first element of the array.\n int current_streak = 0; // Initialize the current streak to 0.\n\n for (int i = 1; i < arr.size(); i++) {\n // If the current winner is greater than the next element, then he will win the next game.\n if (current_winner > arr[i])\n current_streak++; \n\n // the current winner lost the game.\n else {\n current_streak = 1; // Reset the streak since new element becomes the winner.\n current_winner = arr[i]; // Update the current winner.\n }\n\n // If the current streak reaches k or the current winner is the maximum element\n if (current_streak == k || current_winner == maxElement)\n return current_winner; \n }\n\n return current_winner; // Dummy return\n }\n};\n\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n // Find the maximum element in the array.\n int maxElement = Arrays.stream(arr).max().getAsInt();\n\n // If k is greater than or equal to the array size, the maximum element wins.\n if (k >= arr.length) {\n return maxElement;\n }\n\n int currentWinner = arr[0]; // Initialize the current winner with the first element of the array.\n int currentStreak = 0; // Initialize the current streak to 0.\n\n for (int i = 1; i < arr.length; i++) {\n // If the current winner is greater than the next element, then they will win the next game.\n if (currentWinner > arr[i]) {\n currentStreak++;\n\n // the current winner lost the game.\n } else {\n currentStreak = 1; // Reset the streak since a new element becomes the winner.\n currentWinner = arr[i]; // Update the current winner.\n }\n\n // If the current streak reaches k or the current winner is the maximum element\n if (currentStreak == k || currentWinner == maxElement) {\n return currentWinner;\n }\n }\n\n return currentWinner; // Dummy return\n }\n}\n```\n```Python []\nclass Solution:\n def getWinner(self, arr, k):\n # Find the maximum element in the list.\n max_element = max(arr)\n \n # If k is greater than or equal to the list size, the maximum element wins.\n if k >= len(arr):\n return max_element\n \n current_winner = arr[0] # Initialize the current winner with the first element of the list.\n current_streak = 0 # Initialize the current streak to 0.\n \n for i in range(1, len(arr)):\n # If the current winner is greater than the next element, then they will win the next game.\n if current_winner > arr[i]:\n current_streak += 1\n\n # the current winner lost the game.\n else:\n current_streak = 1 # Reset the streak since a new element becomes the winner.\n current_winner = arr[i] # Update the current winner.\n \n # If the current streak reaches k or the current winner is the maximum element\n if current_streak == k or current_winner == max_element:\n return current_winner\n \n return current_winner # Dummy return\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n // Find the maximum element in the array.\n int maxElement = arr[0];\n for (int i = 1; i < arrSize; i++) {\n if (arr[i] > maxElement) {\n maxElement = arr[i];\n }\n }\n\n // If k is greater than or equal to the array size, the maximum element wins.\n if (k >= arrSize) {\n return maxElement;\n }\n\n int current_winner = arr[0]; // Initialize the current winner with the first element of the array.\n int current_streak = 0; // Initialize the current streak to 0.\n\n for (int i = 1; i < arrSize; i++) {\n // If the current winner is greater than the next element, then they will win the next game.\n if (current_winner > arr[i]) {\n current_streak++;\n\n // the current winner lost the game.\n } else {\n current_streak = 1; // Reset the streak since a new element becomes the winner.\n current_winner = arr[i]; // Update the current winner.\n }\n\n // If the current streak reaches k or the current winner is the maximum element\n if (current_streak == k || current_winner == maxElement) {\n return current_winner;\n }\n }\n\n return current_winner; // Dummy return\n}\n```\n\n\n\n\n | 26 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
💯Faster✅💯 Lesser✅3 Methods🔥Simulation Approach🔥Dequeue🔥Two Pointer and Hashtable🔥LinkedList🔥 | find-the-winner-of-an-array-game | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 4 ways to solve this question with detailed explanation of each approach:\n\n# Problem Description: \nWe are given an integer array arr containing distinct integers and an integer k. We need to determine the winner in a game played between the first two elements of the array, arr[0] and arr[1]. In each round of the game, We compare arr[0] with arr[1], and the larger integer wins. The winning integer stays in position 0, while the other integer is moved to the end of the array. The game continues until one integer wins k consecutive rounds, and We need to find the winning integer.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering four different methods to solve this problem:\n1. Simulation Approach\n2. Dequeue\n3. Two Pointer and Hashtable\n\n# 1. Simulation Approach: \n- Initialize $$currentWinner$$ to the first element of the array and $$count$$ to 0.\n- Iterate through the array from the second element to the end.\n- Compare the current element with $$currentWinner$$. If the current element is greater, update $$currentWinner$$ to the current element and reset $$count$$ to 1.\n- If the current element is not greater, increment $$count$$.\n- Check if $$count$$ equals $$k$$. If yes, return $$currentWinner$$.\n- Continue the loop until a winner is found.\n# Complexity\n- \u23F1\uFE0F Time Complexity: $$O(n)$$, where n is the size of the input array. This is because we iterate through the entire array once.\n\n- \uD83D\uDE80 Space Complexity: $$O(1)$$, as we use only a constant amount of extra space for variables.\n\n# Code\n```Python []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n currentWinner = arr[0]\n count = 0\n for i in range(1, len(arr)):\n if arr[i] > currentWinner:\n currentWinner = arr[i]\n count = 1\n else:\n count += 1\n if count == k:\n return currentWinner\n return currentWinner\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int currentWinner = arr[0];\n int count = 0;\n for (int i = 1; i < arr.length; i++) {\n if (arr[i] > currentWinner) {\n currentWinner = arr[i];\n count = 1;\n } else {\n count++;\n }\n if (count == k) {\n return currentWinner;\n }\n }\n return currentWinner;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int currentWinner = arr[0];\n int count = 0;\n for (int i = 1; i < arr.size(); i++) {\n if (arr[i] > currentWinner) {\n currentWinner = arr[i];\n count = 1;\n } else {\n count++;\n }\n if (count == k) {\n return currentWinner;\n }\n }\n return currentWinner;\n }\n};\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n int currentWinner = arr[0];\n int count = 0;\n for (int i = 1; i < arrSize; i++) {\n if (arr[i] > currentWinner) {\n currentWinner = arr[i];\n count = 1;\n } else {\n count++;\n }\n if (count == k) {\n return currentWinner;\n }\n }\n return currentWinner;\n}\n```\n# 2. Dequeue (Queue):\n- Initialize a queue $$q$$ with all elements of the array and $$one$$ to the first element.\n- Initialize $$x$$ to $$k$$, calculate the maximum value $$maxi$$ in the array.\n- If $$k$$ is greater than or equal to the array size, return $$maxi$$.\n- Enter a loop that continues while $$k$$ is greater than 0.\n- In each iteration, dequeue the next element $$two$$ from the queue.\n- Compare $$one$$ and $$two$$. If $$one$$ is greater, decrement $$k$$ and enqueue $$two$$. If $$two$$ is greater, reset $$k$$ to its original value $$x$$, decrement $$k$$, and enqueue $$one$$. Update $$one$$ to be $$two$$.\n- Continue the loop until $$k$$ consecutive wins are reached.\n- Return $$one$$ as the winner.\n# Complexity\n- \u23F1\uFE0F Time Complexity: $$O(n)$$, because we enqueue and dequeue each element once, and in the worst case, we iterate through the array twice.\n\n- \uD83D\uDE80 Space Complexity: $$O(n)$$, as we use a queue to store all the elements of the array.\n\n# Code\n```Python []\nfrom collections import deque\n\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n q = deque(arr)\n one = q.popleft()\n x = k\n maxi = max(arr)\n if k >= len(arr):\n return maxi\n while k:\n two = q.popleft()\n if one > two:\n k -= 1\n q.append(two)\n else:\n k = x\n k -= 1\n q.append(one)\n one = two\n return one\n```\n```Java []\nimport java.util.LinkedList;\nimport java.util.Queue;\n\nclass Solution {\n public int getWinner(int[] arr, int k) {\n Queue<Integer> q = new LinkedList<>();\n for (int i : arr) {\n q.offer(i);\n }\n int one = q.poll();\n int x = k;\n int maxi = Arrays.stream(arr).max().getAsInt();\n if (k >= arr.length) {\n return maxi;\n }\n while (k > 0) {\n int two = q.poll();\n if (one > two) {\n k--;\n q.offer(two);\n } else {\n k = x;\n k--;\n q.offer(one);\n one = two;\n }\n }\n return one;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n queue<int> q;\n for (auto i : arr) {\n q.push(i);\n }\n int one = q.front();\n q.pop();\n int x = k;\n int maxi = *max_element(arr.begin(), arr.end());\n if (k >= arr.size()) {\n return maxi;\n }\n while (k) {\n int two = q.front();\n q.pop();\n if (one > two) {\n k--;\n q.push(two);\n } else {\n k = x;\n k--;\n q.push(one);\n one = two;\n }\n }\n return one;\n }\n};\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n int* queue = (int*)malloc(arrSize * sizeof(int));\n int one = arr[0];\n int x = k;\n int maxi = arr[0];\n for (int i = 1; i < arrSize; i++) {\n queue[i - 1] = arr[i];\n if (arr[i] > maxi) {\n maxi = arr[i];\n }\n }\n if (k >= arrSize) {\n free(queue);\n return maxi;\n }\n int* newQueue = (int*)malloc(arrSize * sizeof(int));\n while (k) {\n int two = queue[0];\n for (int i = 0; i < arrSize - 1; i++) {\n queue[i] = queue[i + 1];\n }\n if (one > two) {\n k--;\n queue[arrSize - 1] = two;\n } else {\n k = x;\n k--;\n queue[arrSize - 1] = one;\n one = two;\n }\n }\n free(queue);\n return one;\n}\n```\n# 3. Two Pointer and Hashtable:\n- Initialize a dictionary $$d$$ to keep track of wins for each integer and two pointers, $$i$$ and $$j$$, to traverse the array.\n- Enter a loop that continues as long as both $$i$$ and $$j$$ are within the array\'s bounds.\n- Compare $$arr[i]$$ and $$arr[j]$$.\n- Update the wins in the dictionary $$d$$ accordingly, and advance the pointers.\n- If $$arr[i]$$ is greater, increment $$i$$. If $$arr[j]$$ is greater, update $$i$$ to be $$j$$ and reset the wins for $$arr[i]$$.\n- Continue the loop until $$k$$ consecutive wins are reached.\n- Return the winner, which is $$arr[i]$$.\n# Complexity\n- \u23F1\uFE0F Time Complexity: $$O(n)$$, because we iterate through the entire array once with the two pointers.\n\n- \uD83D\uDE80 Space Complexity: $$O(n)$$, as we use a dictionary d to store the wins for each integer, which could have n distinct elements.\n\n# Code\n```Python []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n n = len(arr)\n d = {i: 0 for i in arr}\n i, j = 0, 1\n while i < n and j < n:\n if arr[i] > arr[j]:\n d[arr[i]] += 1\n elif arr[i] < arr[j]:\n d[arr[j]] += 1\n i = j\n if d[arr[i]] == k:\n return arr[i]\n j += 1\n return max(arr)\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int n = arr.length;\n HashMap<Integer, Integer> wins = new HashMap<>();\n int i = 0, j = 1;\n while (i < n && j < n) {\n if (arr[i] > arr[j]) {\n wins.put(arr[i], wins.getOrDefault(arr[i], 0) + 1);\n } else if (arr[i] < arr[j]) {\n wins.put(arr[j], wins.getOrDefault(arr[j], 0) + 1);\n i = j;\n }\n if (wins.get(arr[i]) == k) {\n return arr[i];\n }\n j++;\n }\n int maxVal = Arrays.stream(arr).max().getAsInt();\n return maxVal;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int n = arr.size();\n unordered_map<int, int> wins;\n int i = 0, j = 1;\n while (i < n && j < n) {\n if (arr[i] > arr[j]) {\n wins[arr[i]]++;\n } else if (arr[i] < arr[j]) {\n wins[arr[j]]++;\n i = j;\n }\n if (wins[arr[i]] == k) {\n return arr[i];\n }\n j++;\n }\n int maxVal = *max_element(arr.begin(), arr.end());\n return maxVal;\n }\n};\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n int* wins = (int*)malloc(arrSize * sizeof(int));\n for (int i = 0; i < arrSize; i++) {\n wins[i] = 0;\n }\n int i = 0;\n int j = 1;\n while (i < arrSize && j < arrSize) {\n if (arr[i] > arr[j]) {\n wins[i]++;\n } else if (arr[i] < arr[j]) {\n wins[j]++;\n i = j;\n }\n\n if (wins[i] == k) {\n free(wins);\n return arr[i];\n }\n j++;\n }\n int maxVal = arr[0];\n for (int i = 1; i < arrSize; i++) {\n if (arr[i] > maxVal) {\n maxVal = arr[i];\n }\n }\n free(wins);\n return maxVal;\n}\n```\n# \uD83C\uDFC6Conclusion: \nThe optimal approach among the three presented methods would be the "Dequeue (Queue)" approach (Approach 2). This approach efficiently utilizes a queue to simulate the game, making it possible to achieve the result with fewer iterations, which can be particularly useful for large input arrays.\n\n# \uD83D\uDCA1 I invite We to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 43 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
💯Faster✅💯 Lesser✅3 Methods🔥Simulation Approach🔥Dequeue🔥Two Pointer and Hashtable🔥LinkedList🔥 | find-the-winner-of-an-array-game | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 4 ways to solve this question with detailed explanation of each approach:\n\n# Problem Description: \nWe are given an integer array arr containing distinct integers and an integer k. We need to determine the winner in a game played between the first two elements of the array, arr[0] and arr[1]. In each round of the game, We compare arr[0] with arr[1], and the larger integer wins. The winning integer stays in position 0, while the other integer is moved to the end of the array. The game continues until one integer wins k consecutive rounds, and We need to find the winning integer.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering four different methods to solve this problem:\n1. Simulation Approach\n2. Dequeue\n3. Two Pointer and Hashtable\n\n# 1. Simulation Approach: \n- Initialize $$currentWinner$$ to the first element of the array and $$count$$ to 0.\n- Iterate through the array from the second element to the end.\n- Compare the current element with $$currentWinner$$. If the current element is greater, update $$currentWinner$$ to the current element and reset $$count$$ to 1.\n- If the current element is not greater, increment $$count$$.\n- Check if $$count$$ equals $$k$$. If yes, return $$currentWinner$$.\n- Continue the loop until a winner is found.\n# Complexity\n- \u23F1\uFE0F Time Complexity: $$O(n)$$, where n is the size of the input array. This is because we iterate through the entire array once.\n\n- \uD83D\uDE80 Space Complexity: $$O(1)$$, as we use only a constant amount of extra space for variables.\n\n# Code\n```Python []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n currentWinner = arr[0]\n count = 0\n for i in range(1, len(arr)):\n if arr[i] > currentWinner:\n currentWinner = arr[i]\n count = 1\n else:\n count += 1\n if count == k:\n return currentWinner\n return currentWinner\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int currentWinner = arr[0];\n int count = 0;\n for (int i = 1; i < arr.length; i++) {\n if (arr[i] > currentWinner) {\n currentWinner = arr[i];\n count = 1;\n } else {\n count++;\n }\n if (count == k) {\n return currentWinner;\n }\n }\n return currentWinner;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int currentWinner = arr[0];\n int count = 0;\n for (int i = 1; i < arr.size(); i++) {\n if (arr[i] > currentWinner) {\n currentWinner = arr[i];\n count = 1;\n } else {\n count++;\n }\n if (count == k) {\n return currentWinner;\n }\n }\n return currentWinner;\n }\n};\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n int currentWinner = arr[0];\n int count = 0;\n for (int i = 1; i < arrSize; i++) {\n if (arr[i] > currentWinner) {\n currentWinner = arr[i];\n count = 1;\n } else {\n count++;\n }\n if (count == k) {\n return currentWinner;\n }\n }\n return currentWinner;\n}\n```\n# 2. Dequeue (Queue):\n- Initialize a queue $$q$$ with all elements of the array and $$one$$ to the first element.\n- Initialize $$x$$ to $$k$$, calculate the maximum value $$maxi$$ in the array.\n- If $$k$$ is greater than or equal to the array size, return $$maxi$$.\n- Enter a loop that continues while $$k$$ is greater than 0.\n- In each iteration, dequeue the next element $$two$$ from the queue.\n- Compare $$one$$ and $$two$$. If $$one$$ is greater, decrement $$k$$ and enqueue $$two$$. If $$two$$ is greater, reset $$k$$ to its original value $$x$$, decrement $$k$$, and enqueue $$one$$. Update $$one$$ to be $$two$$.\n- Continue the loop until $$k$$ consecutive wins are reached.\n- Return $$one$$ as the winner.\n# Complexity\n- \u23F1\uFE0F Time Complexity: $$O(n)$$, because we enqueue and dequeue each element once, and in the worst case, we iterate through the array twice.\n\n- \uD83D\uDE80 Space Complexity: $$O(n)$$, as we use a queue to store all the elements of the array.\n\n# Code\n```Python []\nfrom collections import deque\n\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n q = deque(arr)\n one = q.popleft()\n x = k\n maxi = max(arr)\n if k >= len(arr):\n return maxi\n while k:\n two = q.popleft()\n if one > two:\n k -= 1\n q.append(two)\n else:\n k = x\n k -= 1\n q.append(one)\n one = two\n return one\n```\n```Java []\nimport java.util.LinkedList;\nimport java.util.Queue;\n\nclass Solution {\n public int getWinner(int[] arr, int k) {\n Queue<Integer> q = new LinkedList<>();\n for (int i : arr) {\n q.offer(i);\n }\n int one = q.poll();\n int x = k;\n int maxi = Arrays.stream(arr).max().getAsInt();\n if (k >= arr.length) {\n return maxi;\n }\n while (k > 0) {\n int two = q.poll();\n if (one > two) {\n k--;\n q.offer(two);\n } else {\n k = x;\n k--;\n q.offer(one);\n one = two;\n }\n }\n return one;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n queue<int> q;\n for (auto i : arr) {\n q.push(i);\n }\n int one = q.front();\n q.pop();\n int x = k;\n int maxi = *max_element(arr.begin(), arr.end());\n if (k >= arr.size()) {\n return maxi;\n }\n while (k) {\n int two = q.front();\n q.pop();\n if (one > two) {\n k--;\n q.push(two);\n } else {\n k = x;\n k--;\n q.push(one);\n one = two;\n }\n }\n return one;\n }\n};\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n int* queue = (int*)malloc(arrSize * sizeof(int));\n int one = arr[0];\n int x = k;\n int maxi = arr[0];\n for (int i = 1; i < arrSize; i++) {\n queue[i - 1] = arr[i];\n if (arr[i] > maxi) {\n maxi = arr[i];\n }\n }\n if (k >= arrSize) {\n free(queue);\n return maxi;\n }\n int* newQueue = (int*)malloc(arrSize * sizeof(int));\n while (k) {\n int two = queue[0];\n for (int i = 0; i < arrSize - 1; i++) {\n queue[i] = queue[i + 1];\n }\n if (one > two) {\n k--;\n queue[arrSize - 1] = two;\n } else {\n k = x;\n k--;\n queue[arrSize - 1] = one;\n one = two;\n }\n }\n free(queue);\n return one;\n}\n```\n# 3. Two Pointer and Hashtable:\n- Initialize a dictionary $$d$$ to keep track of wins for each integer and two pointers, $$i$$ and $$j$$, to traverse the array.\n- Enter a loop that continues as long as both $$i$$ and $$j$$ are within the array\'s bounds.\n- Compare $$arr[i]$$ and $$arr[j]$$.\n- Update the wins in the dictionary $$d$$ accordingly, and advance the pointers.\n- If $$arr[i]$$ is greater, increment $$i$$. If $$arr[j]$$ is greater, update $$i$$ to be $$j$$ and reset the wins for $$arr[i]$$.\n- Continue the loop until $$k$$ consecutive wins are reached.\n- Return the winner, which is $$arr[i]$$.\n# Complexity\n- \u23F1\uFE0F Time Complexity: $$O(n)$$, because we iterate through the entire array once with the two pointers.\n\n- \uD83D\uDE80 Space Complexity: $$O(n)$$, as we use a dictionary d to store the wins for each integer, which could have n distinct elements.\n\n# Code\n```Python []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n n = len(arr)\n d = {i: 0 for i in arr}\n i, j = 0, 1\n while i < n and j < n:\n if arr[i] > arr[j]:\n d[arr[i]] += 1\n elif arr[i] < arr[j]:\n d[arr[j]] += 1\n i = j\n if d[arr[i]] == k:\n return arr[i]\n j += 1\n return max(arr)\n```\n```Java []\nclass Solution {\n public int getWinner(int[] arr, int k) {\n int n = arr.length;\n HashMap<Integer, Integer> wins = new HashMap<>();\n int i = 0, j = 1;\n while (i < n && j < n) {\n if (arr[i] > arr[j]) {\n wins.put(arr[i], wins.getOrDefault(arr[i], 0) + 1);\n } else if (arr[i] < arr[j]) {\n wins.put(arr[j], wins.getOrDefault(arr[j], 0) + 1);\n i = j;\n }\n if (wins.get(arr[i]) == k) {\n return arr[i];\n }\n j++;\n }\n int maxVal = Arrays.stream(arr).max().getAsInt();\n return maxVal;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int getWinner(vector<int>& arr, int k) {\n int n = arr.size();\n unordered_map<int, int> wins;\n int i = 0, j = 1;\n while (i < n && j < n) {\n if (arr[i] > arr[j]) {\n wins[arr[i]]++;\n } else if (arr[i] < arr[j]) {\n wins[arr[j]]++;\n i = j;\n }\n if (wins[arr[i]] == k) {\n return arr[i];\n }\n j++;\n }\n int maxVal = *max_element(arr.begin(), arr.end());\n return maxVal;\n }\n};\n```\n```C []\nint getWinner(int* arr, int arrSize, int k) {\n int* wins = (int*)malloc(arrSize * sizeof(int));\n for (int i = 0; i < arrSize; i++) {\n wins[i] = 0;\n }\n int i = 0;\n int j = 1;\n while (i < arrSize && j < arrSize) {\n if (arr[i] > arr[j]) {\n wins[i]++;\n } else if (arr[i] < arr[j]) {\n wins[j]++;\n i = j;\n }\n\n if (wins[i] == k) {\n free(wins);\n return arr[i];\n }\n j++;\n }\n int maxVal = arr[0];\n for (int i = 1; i < arrSize; i++) {\n if (arr[i] > maxVal) {\n maxVal = arr[i];\n }\n }\n free(wins);\n return maxVal;\n}\n```\n# \uD83C\uDFC6Conclusion: \nThe optimal approach among the three presented methods would be the "Dequeue (Queue)" approach (Approach 2). This approach efficiently utilizes a queue to simulate the game, making it possible to achieve the result with fewer iterations, which can be particularly useful for large input arrays.\n\n# \uD83D\uDCA1 I invite We to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 43 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
✅ 98.37% O(n) Final Winner | find-the-winner-of-an-array-game | 1 | 1 | # Intuition\nWhen first approaching this problem, we might think about simulating the entire process: comparing numbers, moving the smaller one to the end, and keeping track of the number of consecutive wins. However, a closer inspection reveals a couple of key insights. Firstly, if the game needs only one win (i.e., $ k = 1 $), the winner of the first round is the answer. Secondly, if $ k $ is large enough (i.e., $ k $ is equal to or larger than the length of the array), the maximum element in the array is bound to win eventually. These initial observations allow us to build a strategy that handles these edge cases separately, providing an efficient approach for the main logic.\n\n# Live Coding & More\nhttps://youtu.be/cbFwAvhG_C8?si=ussPA9wySWxCxLp3\n\n# Approach\n1. **Edge Cases**: Check if $ k $ is 1 or if $ k $ is equal to or larger than the length of the array. These cases allow for immediate conclusions.\n2. **Initialization**: Initialize the current winner as the first element and set the consecutive wins count to zero.\n3. **Iteration**: Iterate through the array starting from the second element. For each element:\n - If the current winner is greater, increment the consecutive win count.\n - If the current element is greater, it becomes the new winner and the consecutive win count resets to 1.\n - If at any point the consecutive win count reaches $ k $, the current winner is the answer.\n4. **Final Winner**: If the loop completes without finding an answer, the current winner after the loop is the answer.\n\nThis approach ensures that we only iterate through the list once, making the solution efficient.\n\n# Complexity\n\n- **Time complexity**: $ O(n) $\n The solution iterates through the array once. In the worst-case scenario, we examine all elements in the array. Hence, the time complexity is linear with respect to the size of the array.\n\n- **Space complexity**: $ O(1) $\n The solution uses a constant amount of extra space: a few variables to keep track of the current winner and the consecutive win count. Regardless of the size of the input, the space used remains constant.\n\n# Code\n``` Python []\nclass Solution:\n def getWinner(self, arr: List[int], k: int) -> int:\n if k == 1:\n return max(arr[0], arr[1])\n if k >= len(arr):\n return max(arr)\n \n current_winner = arr[0]\n consecutive_wins = 0\n \n for i in range(1, len(arr)):\n if current_winner > arr[i]:\n consecutive_wins += 1\n else:\n current_winner = arr[i]\n consecutive_wins = 1\n \n if consecutive_wins == k:\n return current_winner\n \n return current_winner\n```\n``` C++ []\nclass Solution {\npublic:\n int getWinner(std::vector<int>& arr, int k) {\n if (k == 1) {\n return std::max(arr[0], arr[1]);\n }\n if (k >= arr.size()) {\n return *std::max_element(arr.begin(), arr.end());\n }\n\n int current_winner = arr[0];\n int consecutive_wins = 0;\n\n for (int i = 1; i < arr.size(); ++i) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins == k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int getWinner(int[] arr, int k) {\n if (k == 1) {\n return Math.max(arr[0], arr[1]);\n }\n if (k >= arr.length) {\n return Arrays.stream(arr).max().getAsInt();\n }\n\n int current_winner = arr[0];\n int consecutive_wins = 0;\n\n for (int i = 1; i < arr.length; i++) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins == k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int GetWinner(int[] arr, int k) {\n if (k == 1) {\n return Math.Max(arr[0], arr[1]);\n }\n if (k >= arr.Length) {\n return arr.Max();\n }\n\n int current_winner = arr[0];\n int consecutive_wins = 0;\n\n for (int i = 1; i < arr.Length; i++) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins == k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n}\n```\n``` Go []\npackage main\n\nfunc getWinner(arr []int, k int) int {\n if k == 1 {\n return max(arr[0], arr[1])\n }\n if k >= len(arr) {\n return maxArr(arr)\n }\n\n current_winner := arr[0]\n consecutive_wins := 0\n\n for i := 1; i < len(arr); i++ {\n if current_winner > arr[i] {\n consecutive_wins++\n } else {\n current_winner = arr[i]\n consecutive_wins = 1\n }\n\n if consecutive_wins == k {\n return current_winner\n }\n }\n\n return current_winner\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n\nfunc maxArr(arr []int) int {\n m := arr[0]\n for _, val := range arr {\n if val > m {\n m = val\n }\n }\n return m\n}\n```\n``` Rust []\nimpl Solution {\n pub fn get_winner(arr: Vec<i32>, k: i32) -> i32 {\n if k == 1 {\n return arr[0].max(arr[1]);\n }\n if k as usize >= arr.len() {\n return *arr.iter().max().unwrap();\n }\n\n let mut current_winner = arr[0];\n let mut consecutive_wins = 0;\n\n for &num in &arr[1..] {\n if current_winner > num {\n consecutive_wins += 1;\n } else {\n current_winner = num;\n consecutive_wins = 1;\n }\n\n if consecutive_wins == k {\n return current_winner;\n }\n }\n\n current_winner\n }\n}\n```\n``` PHP []\nclass Solution {\n function getWinner($arr, $k) {\n if ($k == 1) {\n return max($arr[0], $arr[1]);\n }\n if ($k >= count($arr)) {\n return max($arr);\n }\n\n $current_winner = $arr[0];\n $consecutive_wins = 0;\n\n for ($i = 1; $i < count($arr); $i++) {\n if ($current_winner > $arr[$i]) {\n $consecutive_wins++;\n } else {\n $current_winner = $arr[$i];\n $consecutive_wins = 1;\n }\n\n if ($consecutive_wins == $k) {\n return $current_winner;\n }\n }\n\n return $current_winner;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} arr\n * @param {number} k\n * @return {number}\n */\nvar getWinner = function(arr, k) {\n if (k === 1) {\n return Math.max(arr[0], arr[1]);\n }\n if (k >= arr.length) {\n return Math.max(...arr);\n }\n\n let current_winner = arr[0];\n let consecutive_wins = 0;\n\n for (let i = 1; i < arr.length; i++) {\n if (current_winner > arr[i]) {\n consecutive_wins++;\n } else {\n current_winner = arr[i];\n consecutive_wins = 1;\n }\n\n if (consecutive_wins === k) {\n return current_winner;\n }\n }\n\n return current_winner;\n }\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|------------|---------------------|-------------------|\n| Java | 3 | 55.8 |\n| Rust | 11 | 3.4 |\n| JavaScript | 70 | 51.6 |\n| C++ | 81 | 63.5 |\n| Go | 87 | 8.2 |\n| C# | 156 | 53.8 |\n| PHP | 186 | 31.5 |\n| Python3 | 500 | 29.6 |\n\n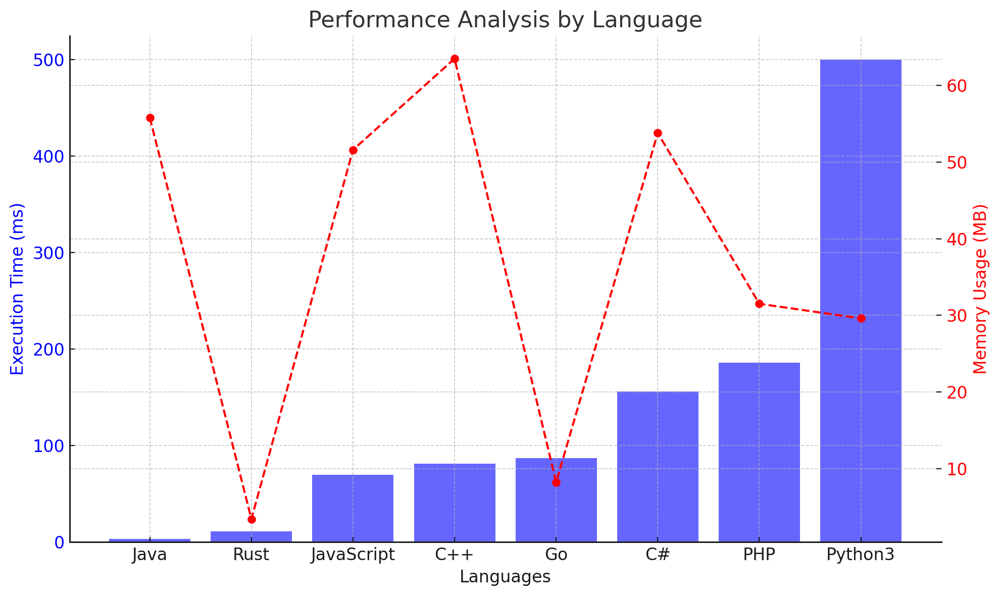\n\n\n# Conclusion\nUnderstanding the rules of the game and the implications of the value of $ k $ were crucial in devising this efficient solution. By handling edge cases separately, we were able to focus on the main logic without unnecessary complications. This problem demonstrates the importance of thoroughly analyzing the problem statement to identify key insights that can simplify the solution. | 103 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.