title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Clear Explanation with Easy Recursive DFS Solution | count-all-possible-routes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry all paths from the start until you run out of fuel. From all the possible paths, keep a count of which paths end on the finishing location from the start. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThere are two insights which make this problem relatively easy to solve. First, note that you aren\'t allowed to travel to the same location which you are one. If this was allowed, then there would be an infinite number of routes since there is no fuel used to travel to the same path. Second, each time you visit a location, there is a different level of fuel left in the tank. If we consider the location and fuel as a tuple, then this acts as a node in a graph. Our task is to find all paths which start from the node (start, fuel) \u2014 where start is the staring location and fuel is the starting fuel \u2014 to (finish, endFuel) where $endFuel \\ge 0$. \n\nThinking of the possible states as a graph allows us to apply a graph traversal algorithm like depth-first search from the starting node (start, fuel).\n\nOn a high level, the algorithm works by exploring all other locations from a given node (index, fuel). If the current index is the finish location, then we can increment our routes count by 1. However, before we do this, we need to check if we have enough fuel left for this path to be considered valid. Next, from this current location, we try to extend the path by exploring all other locations in the locations array and adjusting the amount of fuel we have left. In the end, we return the route count modulo $10^9 + 7$. Since we are going to be making a lot of recursive calls, and the possibility that we are allowed to visit a location multiple times, we cache the route from from (index, fuel) in a dictionary for constant lookup. \n\nFirst, we initialize a cache. The cache is a dictionary where the keys are tuples of (index, fuel) \u2014 the current location and the current fuel \u2014 and the values are the number of valid routes from this state to the finish. Next, for our main ```countRoutes``` method, with first store the modulus for convenience. Next, we call a private recursive method ```_travel```, which takes in all arguments passed to ```countRoutes```. This method will return the number of valid routes from start to finish with the starting fuel. Finally, we return this count after taking the mod value. Now, all we have to do is implement the ```_travel``` method. \n\nThe ```_travel``` method is fairly straightforward. We first initialize a variable ```total``` which stores the number of valid routes. We then check if we have enough fuel left. We can arrive at a location with no fuel left but if we have negative fuel, then this means that the current path being considered is invalid and we can return 0. We then check if the current state is stored in the cache. If it is, then we return the its value from the cache. If not, then we check if the current location is the finish, in which case we have found a valid route and therefore we increment our total count by 1. \n\nNow, to explore all other locations, we iterate over the locations. We need to decrease the fuel by the amount it costs to get to the next location. We then increment total by all the valid routes from the nextLocation. \n\nIn the end, we store the current route count in our cache, and return the total. \n\nNote that I am presenting a solution where we are manually caching the results. In python, we can use the ```@lru_cache(None)``` decorator which will take care of this automatically but this approach provides a deeper understanding. \n\n# Complexity\n- Time complexity: $O(n^2 \\cdot f)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(n \\cdot f)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self) -> None:\n """\n Initialize a cache which will store the number of paths which include a \n particular location with a particular amount of fuel\n """\n\n self.cache = {} # key: (location, fuel), val : routes\n\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n """\n Returns the number of routes possible from start location to the finish location\n with a particular amount of fuel\n\n Args:\n locations: List[int] = fuel costs for travelling between locations which are the indices\n start: int = starting location represented by an index\n finish: int = finishing location represented by an index\n fuel: int = amount of fuel at the start of the journey\n \n Returns:\n routes: int = number of possible routes\n """\n \n # Store the modulus in a variable for convenience\n mod = 10 ** 9 + 7\n\n # Calculate the number of routes from start to finish with starting fuel\n routes = self._travel(locations, start, finish, fuel)\n\n # Return the number of routes module 10**9 + 7\n return routes % mod\n\n def _travel(self, locations: List[int], index: int, finish: int, fuel: int) -> int:\n """\n Returns the number of routes possible from start location to the finish location\n with a particular amount of fuel\n\n Args:\n locations: List[int] = fuel costs for travelling between locations which are the indices\n start: int = starting location represented by an index\n finish: int = finishing location represented by an index\n fuel: int = amount of fuel at the start of the journey\n \n Returns:\n total: int = number of possible routes\n """\n\n # Initialize the total number of routes \n total = 0\n\n # If we are out of fuel, then this current route is invalid and therefore\n # can\'t be considered in our total\n if fuel < 0:\n return 0\n\n # if we have already been to this current location with the current fuel level,\n # then we don\'t need to recalulate the number of valid paths from this state since\n # we have stored that result in our cache and we can return that\n if (index, fuel) in self.cache:\n return self.cache[(index, fuel)]\n \n # If we have a valid amount of fuel and are currently at the finishing point, \n # this route is valid. However, since we can revisit some other locations, we\n # just increment our total route count and continue visiting the other locations\n if index == finish:\n total += 1\n\n # Storing the current locations fuel cost for convenience\n currentCost = locations[index]\n\n # Iterate over the other locations in the array while keeping track of that location\'s\n # fuel cost\n for nextStop, cost in enumerate(locations):\n # We only explore locations different than the current locationn\n if nextStop != index:\n # We subtract the fuel used to get to the next location\n fuelLeft = fuel - abs(cost - currentCost)\n # We increment total to include all paths which lead to the finish \n # from the next location\n total += self._travel(locations, nextStop, finish, fuelLeft)\n \n # We store the number of routes for this state in case it is needed later\n # and return the total number of routes\n self.cache[(index, fuel)] = total \n return total\n\n \n``` | 1 | You are given an array of **distinct** positive integers locations where `locations[i]` represents the position of city `i`. You are also given integers `start`, `finish` and `fuel` representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city `i`, you can pick any city `j` such that `j != i` and `0 <= j < locations.length` and move to city `j`. Moving from city `i` to city `j` reduces the amount of fuel you have by `|locations[i] - locations[j]|`. Please notice that `|x|` denotes the absolute value of `x`.
Notice that `fuel` **cannot** become negative at any point in time, and that you are **allowed** to visit any city more than once (including `start` and `finish`).
Return _the count of all possible routes from_ `start` _to_ `finish`. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** locations = \[2,3,6,8,4\], start = 1, finish = 3, fuel = 5
**Output:** 4
**Explanation:** The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
**Example 2:**
**Input:** locations = \[4,3,1\], start = 1, finish = 0, fuel = 6
**Output:** 5
**Explanation:** The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5
**Example 3:**
**Input:** locations = \[5,2,1\], start = 0, finish = 2, fuel = 3
**Output:** 0
**Explanation:** It is impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.
**Constraints:**
* `2 <= locations.length <= 100`
* `1 <= locations[i] <= 109`
* All integers in `locations` are **distinct**.
* `0 <= start, finish < locations.length`
* `1 <= fuel <= 200` | Sort the arrays, then compute the maximum difference between two consecutive elements for horizontal cuts and vertical cuts. The answer is the product of these maximum values in horizontal cuts and vertical cuts. |
Clear Explanation with Easy Recursive DFS Solution | count-all-possible-routes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry all paths from the start until you run out of fuel. From all the possible paths, keep a count of which paths end on the finishing location from the start. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThere are two insights which make this problem relatively easy to solve. First, note that you aren\'t allowed to travel to the same location which you are one. If this was allowed, then there would be an infinite number of routes since there is no fuel used to travel to the same path. Second, each time you visit a location, there is a different level of fuel left in the tank. If we consider the location and fuel as a tuple, then this acts as a node in a graph. Our task is to find all paths which start from the node (start, fuel) \u2014 where start is the staring location and fuel is the starting fuel \u2014 to (finish, endFuel) where $endFuel \\ge 0$. \n\nThinking of the possible states as a graph allows us to apply a graph traversal algorithm like depth-first search from the starting node (start, fuel).\n\nOn a high level, the algorithm works by exploring all other locations from a given node (index, fuel). If the current index is the finish location, then we can increment our routes count by 1. However, before we do this, we need to check if we have enough fuel left for this path to be considered valid. Next, from this current location, we try to extend the path by exploring all other locations in the locations array and adjusting the amount of fuel we have left. In the end, we return the route count modulo $10^9 + 7$. Since we are going to be making a lot of recursive calls, and the possibility that we are allowed to visit a location multiple times, we cache the route from from (index, fuel) in a dictionary for constant lookup. \n\nFirst, we initialize a cache. The cache is a dictionary where the keys are tuples of (index, fuel) \u2014 the current location and the current fuel \u2014 and the values are the number of valid routes from this state to the finish. Next, for our main ```countRoutes``` method, with first store the modulus for convenience. Next, we call a private recursive method ```_travel```, which takes in all arguments passed to ```countRoutes```. This method will return the number of valid routes from start to finish with the starting fuel. Finally, we return this count after taking the mod value. Now, all we have to do is implement the ```_travel``` method. \n\nThe ```_travel``` method is fairly straightforward. We first initialize a variable ```total``` which stores the number of valid routes. We then check if we have enough fuel left. We can arrive at a location with no fuel left but if we have negative fuel, then this means that the current path being considered is invalid and we can return 0. We then check if the current state is stored in the cache. If it is, then we return the its value from the cache. If not, then we check if the current location is the finish, in which case we have found a valid route and therefore we increment our total count by 1. \n\nNow, to explore all other locations, we iterate over the locations. We need to decrease the fuel by the amount it costs to get to the next location. We then increment total by all the valid routes from the nextLocation. \n\nIn the end, we store the current route count in our cache, and return the total. \n\nNote that I am presenting a solution where we are manually caching the results. In python, we can use the ```@lru_cache(None)``` decorator which will take care of this automatically but this approach provides a deeper understanding. \n\n# Complexity\n- Time complexity: $O(n^2 \\cdot f)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(n \\cdot f)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self) -> None:\n """\n Initialize a cache which will store the number of paths which include a \n particular location with a particular amount of fuel\n """\n\n self.cache = {} # key: (location, fuel), val : routes\n\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n """\n Returns the number of routes possible from start location to the finish location\n with a particular amount of fuel\n\n Args:\n locations: List[int] = fuel costs for travelling between locations which are the indices\n start: int = starting location represented by an index\n finish: int = finishing location represented by an index\n fuel: int = amount of fuel at the start of the journey\n \n Returns:\n routes: int = number of possible routes\n """\n \n # Store the modulus in a variable for convenience\n mod = 10 ** 9 + 7\n\n # Calculate the number of routes from start to finish with starting fuel\n routes = self._travel(locations, start, finish, fuel)\n\n # Return the number of routes module 10**9 + 7\n return routes % mod\n\n def _travel(self, locations: List[int], index: int, finish: int, fuel: int) -> int:\n """\n Returns the number of routes possible from start location to the finish location\n with a particular amount of fuel\n\n Args:\n locations: List[int] = fuel costs for travelling between locations which are the indices\n start: int = starting location represented by an index\n finish: int = finishing location represented by an index\n fuel: int = amount of fuel at the start of the journey\n \n Returns:\n total: int = number of possible routes\n """\n\n # Initialize the total number of routes \n total = 0\n\n # If we are out of fuel, then this current route is invalid and therefore\n # can\'t be considered in our total\n if fuel < 0:\n return 0\n\n # if we have already been to this current location with the current fuel level,\n # then we don\'t need to recalulate the number of valid paths from this state since\n # we have stored that result in our cache and we can return that\n if (index, fuel) in self.cache:\n return self.cache[(index, fuel)]\n \n # If we have a valid amount of fuel and are currently at the finishing point, \n # this route is valid. However, since we can revisit some other locations, we\n # just increment our total route count and continue visiting the other locations\n if index == finish:\n total += 1\n\n # Storing the current locations fuel cost for convenience\n currentCost = locations[index]\n\n # Iterate over the other locations in the array while keeping track of that location\'s\n # fuel cost\n for nextStop, cost in enumerate(locations):\n # We only explore locations different than the current locationn\n if nextStop != index:\n # We subtract the fuel used to get to the next location\n fuelLeft = fuel - abs(cost - currentCost)\n # We increment total to include all paths which lead to the finish \n # from the next location\n total += self._travel(locations, nextStop, finish, fuelLeft)\n \n # We store the number of routes for this state in case it is needed later\n # and return the total number of routes\n self.cache[(index, fuel)] = total \n return total\n\n \n``` | 1 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
python 3 - top down dp | count-all-possible-routes | 0 | 1 | Pay attention on 2 questions: "how to cache" and "time complexity". Evaluate by reading the constraints.\n\n# Intuition\n2 state variables: where you are, and fuel remaining. Sum up all states is ok.\n\nOptimization: if abs(loca[start] - loca[finish]) > fuel -> This means you cannot reach "finish" with the shortest path -> Just return 0 as early exit condition\n\n# Approach\ntop down dp\n\n# Complexity\n- Time complexity:\nO(n * f) -> state variables\n\n- Space complexity:\nO(n * f) -> cache size\n\n# Code\n```\nclass Solution:\n def countRoutes(self, loca: List[int], start: int, finish: int, fuel: int) -> int:\n # state = i, fuel -> do loop on each layer\n\n if abs(loca[start] - loca[finish]) > fuel: return 0 # impossible to reach finish\n\n @lru_cache(None)\n def dp(cur, f_remain): # return number of ways\n if f_remain < 0:\n return 0\n \n res = 1 if cur == finish else 0\n\n for nxt in range(len(loca)):\n if nxt == cur:\n continue\n f_need = abs(loca[nxt] - loca[cur])\n if f_remain >= f_need:\n res += dp(nxt, f_remain - f_need)\n \n return res\n \n return dp(start, fuel) % (10**9 + 7)\n``` | 1 | You are given an array of **distinct** positive integers locations where `locations[i]` represents the position of city `i`. You are also given integers `start`, `finish` and `fuel` representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city `i`, you can pick any city `j` such that `j != i` and `0 <= j < locations.length` and move to city `j`. Moving from city `i` to city `j` reduces the amount of fuel you have by `|locations[i] - locations[j]|`. Please notice that `|x|` denotes the absolute value of `x`.
Notice that `fuel` **cannot** become negative at any point in time, and that you are **allowed** to visit any city more than once (including `start` and `finish`).
Return _the count of all possible routes from_ `start` _to_ `finish`. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** locations = \[2,3,6,8,4\], start = 1, finish = 3, fuel = 5
**Output:** 4
**Explanation:** The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
**Example 2:**
**Input:** locations = \[4,3,1\], start = 1, finish = 0, fuel = 6
**Output:** 5
**Explanation:** The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5
**Example 3:**
**Input:** locations = \[5,2,1\], start = 0, finish = 2, fuel = 3
**Output:** 0
**Explanation:** It is impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.
**Constraints:**
* `2 <= locations.length <= 100`
* `1 <= locations[i] <= 109`
* All integers in `locations` are **distinct**.
* `0 <= start, finish < locations.length`
* `1 <= fuel <= 200` | Sort the arrays, then compute the maximum difference between two consecutive elements for horizontal cuts and vertical cuts. The answer is the product of these maximum values in horizontal cuts and vertical cuts. |
python 3 - top down dp | count-all-possible-routes | 0 | 1 | Pay attention on 2 questions: "how to cache" and "time complexity". Evaluate by reading the constraints.\n\n# Intuition\n2 state variables: where you are, and fuel remaining. Sum up all states is ok.\n\nOptimization: if abs(loca[start] - loca[finish]) > fuel -> This means you cannot reach "finish" with the shortest path -> Just return 0 as early exit condition\n\n# Approach\ntop down dp\n\n# Complexity\n- Time complexity:\nO(n * f) -> state variables\n\n- Space complexity:\nO(n * f) -> cache size\n\n# Code\n```\nclass Solution:\n def countRoutes(self, loca: List[int], start: int, finish: int, fuel: int) -> int:\n # state = i, fuel -> do loop on each layer\n\n if abs(loca[start] - loca[finish]) > fuel: return 0 # impossible to reach finish\n\n @lru_cache(None)\n def dp(cur, f_remain): # return number of ways\n if f_remain < 0:\n return 0\n \n res = 1 if cur == finish else 0\n\n for nxt in range(len(loca)):\n if nxt == cur:\n continue\n f_need = abs(loca[nxt] - loca[cur])\n if f_remain >= f_need:\n res += dp(nxt, f_remain - f_need)\n \n return res\n \n return dp(start, fuel) % (10**9 + 7)\n``` | 1 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
SIMPLE PYTHON SOLUTION USING DP | count-all-possible-routes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,locations,finish,fuel,dct):\n if fuel<0:\n return 0\n if (i,fuel) in dct:\n return dct[(i,fuel)]\n ct=0\n for k in range(len(locations)):\n if i!=k and abs(locations[k]-locations[i])<=fuel:\n ct+=(self.dp(k,locations,finish,fuel-abs(locations[k]-locations[i]),dct))\n if abs(locations[finish]-locations[i])<=fuel:\n dct[(i,fuel)]=ct+1\n return ct+1\n dct[(i,fuel)]=ct\n return ct\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n x=0\n if start==finish:\n x=1\n return ((self.dp(start,locations,finish,fuel,{})//2)+x)%1000000007\n``` | 1 | You are given an array of **distinct** positive integers locations where `locations[i]` represents the position of city `i`. You are also given integers `start`, `finish` and `fuel` representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city `i`, you can pick any city `j` such that `j != i` and `0 <= j < locations.length` and move to city `j`. Moving from city `i` to city `j` reduces the amount of fuel you have by `|locations[i] - locations[j]|`. Please notice that `|x|` denotes the absolute value of `x`.
Notice that `fuel` **cannot** become negative at any point in time, and that you are **allowed** to visit any city more than once (including `start` and `finish`).
Return _the count of all possible routes from_ `start` _to_ `finish`. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** locations = \[2,3,6,8,4\], start = 1, finish = 3, fuel = 5
**Output:** 4
**Explanation:** The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
**Example 2:**
**Input:** locations = \[4,3,1\], start = 1, finish = 0, fuel = 6
**Output:** 5
**Explanation:** The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5
**Example 3:**
**Input:** locations = \[5,2,1\], start = 0, finish = 2, fuel = 3
**Output:** 0
**Explanation:** It is impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.
**Constraints:**
* `2 <= locations.length <= 100`
* `1 <= locations[i] <= 109`
* All integers in `locations` are **distinct**.
* `0 <= start, finish < locations.length`
* `1 <= fuel <= 200` | Sort the arrays, then compute the maximum difference between two consecutive elements for horizontal cuts and vertical cuts. The answer is the product of these maximum values in horizontal cuts and vertical cuts. |
SIMPLE PYTHON SOLUTION USING DP | count-all-possible-routes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,locations,finish,fuel,dct):\n if fuel<0:\n return 0\n if (i,fuel) in dct:\n return dct[(i,fuel)]\n ct=0\n for k in range(len(locations)):\n if i!=k and abs(locations[k]-locations[i])<=fuel:\n ct+=(self.dp(k,locations,finish,fuel-abs(locations[k]-locations[i]),dct))\n if abs(locations[finish]-locations[i])<=fuel:\n dct[(i,fuel)]=ct+1\n return ct+1\n dct[(i,fuel)]=ct\n return ct\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n x=0\n if start==finish:\n x=1\n return ((self.dp(start,locations,finish,fuel,{})//2)+x)%1000000007\n``` | 1 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
Python DP | count-all-possible-routes | 0 | 1 | Try all possible routes with DP\n```python []\nclass Solution:\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n @cache\n def dp(i, fuel):\n cnt = int(i == finish)\n for j in range(len(locations)):\n cost = abs(locations[i] - locations[j])\n if i != j and cost <= fuel:\n cnt += dp(j, fuel - cost)\n return cnt % (10 ** 9 + 7)\n return dp(start, fuel)\n``` | 1 | You are given an array of **distinct** positive integers locations where `locations[i]` represents the position of city `i`. You are also given integers `start`, `finish` and `fuel` representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city `i`, you can pick any city `j` such that `j != i` and `0 <= j < locations.length` and move to city `j`. Moving from city `i` to city `j` reduces the amount of fuel you have by `|locations[i] - locations[j]|`. Please notice that `|x|` denotes the absolute value of `x`.
Notice that `fuel` **cannot** become negative at any point in time, and that you are **allowed** to visit any city more than once (including `start` and `finish`).
Return _the count of all possible routes from_ `start` _to_ `finish`. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** locations = \[2,3,6,8,4\], start = 1, finish = 3, fuel = 5
**Output:** 4
**Explanation:** The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
**Example 2:**
**Input:** locations = \[4,3,1\], start = 1, finish = 0, fuel = 6
**Output:** 5
**Explanation:** The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5
**Example 3:**
**Input:** locations = \[5,2,1\], start = 0, finish = 2, fuel = 3
**Output:** 0
**Explanation:** It is impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.
**Constraints:**
* `2 <= locations.length <= 100`
* `1 <= locations[i] <= 109`
* All integers in `locations` are **distinct**.
* `0 <= start, finish < locations.length`
* `1 <= fuel <= 200` | Sort the arrays, then compute the maximum difference between two consecutive elements for horizontal cuts and vertical cuts. The answer is the product of these maximum values in horizontal cuts and vertical cuts. |
Python DP | count-all-possible-routes | 0 | 1 | Try all possible routes with DP\n```python []\nclass Solution:\n def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int:\n @cache\n def dp(i, fuel):\n cnt = int(i == finish)\n for j in range(len(locations)):\n cost = abs(locations[i] - locations[j])\n if i != j and cost <= fuel:\n cnt += dp(j, fuel - cost)\n return cnt % (10 ** 9 + 7)\n return dp(start, fuel)\n``` | 1 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
Easy Solution for beginners || Beats 95%+✨💫 || 🧛✌️ | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Intuition\nIt seems that you want to replace the question mark (\'?\') in the input string \'s\' with lowercase English alphabets (\'a\' to \'z\') in such a way that adjacent characters are not the same. The code uses a dictionary to keep track of the positions of the question marks and then iterates through the string to perform replacements based on certain conditions.\n\n# Approach\nThe approach followed in the code is to iterate through the positions of the question marks in the string \'s\'. For each position, it tries to replace the question mark with a lowercase English alphabet that is different from its adjacent characters (if any).\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n alp=\'abcdefghijklmnopqrstuvwxyz\'\n #print(dic)\n d=defaultdict(list)\n for i in range(len(s)):\n if s[i]==\'?\':\n d[s[i]].append(i)\n #print(d)\n if len(s)==1:\n return "a"\n for j in d[\'?\']:\n if j > 0 and j < len(s)-1:\n for k in alp:\n if s[j-1] != k and s[j+1] != k:\n #print(s)\n s=s[:j] + k + s[j+1:]\n break\n elif j == 0 and len(s) != 1:\n for k in alp:\n if s[j+1] != k:\n #print(k)\n s=k+s[j+1:]\n break\n elif j == len(s)-1:\n for k in alp:\n if s[j-1] != k:\n #print(k)\n s=s[:j] + k\n break\n return s\n``` | 1 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Easy Solution for beginners || Beats 95%+✨💫 || 🧛✌️ | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Intuition\nIt seems that you want to replace the question mark (\'?\') in the input string \'s\' with lowercase English alphabets (\'a\' to \'z\') in such a way that adjacent characters are not the same. The code uses a dictionary to keep track of the positions of the question marks and then iterates through the string to perform replacements based on certain conditions.\n\n# Approach\nThe approach followed in the code is to iterate through the positions of the question marks in the string \'s\'. For each position, it tries to replace the question mark with a lowercase English alphabet that is different from its adjacent characters (if any).\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n alp=\'abcdefghijklmnopqrstuvwxyz\'\n #print(dic)\n d=defaultdict(list)\n for i in range(len(s)):\n if s[i]==\'?\':\n d[s[i]].append(i)\n #print(d)\n if len(s)==1:\n return "a"\n for j in d[\'?\']:\n if j > 0 and j < len(s)-1:\n for k in alp:\n if s[j-1] != k and s[j+1] != k:\n #print(s)\n s=s[:j] + k + s[j+1:]\n break\n elif j == 0 and len(s) != 1:\n for k in alp:\n if s[j+1] != k:\n #print(k)\n s=k+s[j+1:]\n break\n elif j == len(s)-1:\n for k in alp:\n if s[j-1] != k:\n #print(k)\n s=s[:j] + k\n break\n return s\n``` | 1 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python random choice solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI came up with this random choice solution. \nHowever, I realized that we only need three letters when I checked out the other solutions. LOL\nAnyway, the upper lengh of the string is 100. \nSo I guess there is no big difference in time complexity.\n\n# Code\n```python\nclass Solution:\n def modifyString(self, s: str) -> str:\n s = list("#" + s + "#")\n for i in range(1, len(s) - 1):\n if s[i] == "?":\n while True:\n char = random.choice(string.ascii_lowercase)\n if char not in [s[i-1], s[i+1]]:\n s[i] = char\n break\n\n return "".join(s[1:-1])\n``` | 2 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python random choice solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI came up with this random choice solution. \nHowever, I realized that we only need three letters when I checked out the other solutions. LOL\nAnyway, the upper lengh of the string is 100. \nSo I guess there is no big difference in time complexity.\n\n# Code\n```python\nclass Solution:\n def modifyString(self, s: str) -> str:\n s = list("#" + s + "#")\n for i in range(1, len(s) - 1):\n if s[i] == "?":\n while True:\n char = random.choice(string.ascii_lowercase)\n if char not in [s[i-1], s[i+1]]:\n s[i] = char\n break\n\n return "".join(s[1:-1])\n``` | 2 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
[Python3] one of three letters | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | \n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n s = list(s)\n for i in range(len(s)):\n if s[i] == "?": \n for c in "abc": \n if (i == 0 or s[i-1] != c) and (i+1 == len(s) or s[i+1] != c): \n s[i] = c\n break \n return "".join(s)\n``` | 70 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
[Python3] one of three letters | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | \n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n s = list(s)\n for i in range(len(s)):\n if s[i] == "?": \n for c in "abc": \n if (i == 0 or s[i-1] != c) and (i+1 == len(s) or s[i+1] != c): \n s[i] = c\n break \n return "".join(s)\n``` | 70 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python Easy Solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n new=s\n for i in range(len(s)):\n if new[i]=="?":\n if len(new)==1:\n return "p"\n if i==0:\n lis=[new[i+1]]\n if i==len(s)-1:\n lis=[new[i-1]]\n else:\n lis=[new[i-1],new[i+1]]\n n="a"\n while(n in lis):\n n=chr(ord(n)+1) \n new=new[:i]+n+new[i+1:]\n return new\n``` | 1 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python Easy Solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n new=s\n for i in range(len(s)):\n if new[i]=="?":\n if len(new)==1:\n return "p"\n if i==0:\n lis=[new[i+1]]\n if i==len(s)-1:\n lis=[new[i-1]]\n else:\n lis=[new[i-1],new[i+1]]\n n="a"\n while(n in lis):\n n=chr(ord(n)+1) \n new=new[:i]+n+new[i+1:]\n return new\n``` | 1 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python | Easy Solution✅ | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n if s =="?":\n return "a"\n if len(s) == 1:\n return s\n \n s_list = [x for x in s]\n for index, letter in enumerate(s_list):\n replace_char = {"a","b","c"} \n consecutive_set = set()\n if index == 0 and s_list[index+1] != "?":\n consecutive_set = {s_list[index+1]}\n elif index == len(s_list)-1 and s_list[index-1] != "?":\n consecutive_set = {s_list[index-1]}\n else: \n consecutive_set = {s_list[index-1]} if s_list[index+1] == "?" else {s_list[index-1],s_list[index+1]}\n if letter == "?":\n replace_char = replace_char - consecutive_set\n s_list[index] = replace_char.pop()\n return "".join(s_list)\n``` | 6 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python | Easy Solution✅ | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n if s =="?":\n return "a"\n if len(s) == 1:\n return s\n \n s_list = [x for x in s]\n for index, letter in enumerate(s_list):\n replace_char = {"a","b","c"} \n consecutive_set = set()\n if index == 0 and s_list[index+1] != "?":\n consecutive_set = {s_list[index+1]}\n elif index == len(s_list)-1 and s_list[index-1] != "?":\n consecutive_set = {s_list[index-1]}\n else: \n consecutive_set = {s_list[index-1]} if s_list[index+1] == "?" else {s_list[index-1],s_list[index+1]}\n if letter == "?":\n replace_char = replace_char - consecutive_set\n s_list[index] = replace_char.pop()\n return "".join(s_list)\n``` | 6 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python simple solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | **Python :**\n\n```\ndef modifyString(self, s: str) -> str:\n\ts = list(s)\n\n\tfor i in range(len(s)):\n\t\tif s[i] == \'?\':\n\t\t\tfor c in "abc":\n\t\t\t\tif (i == 0 or s[i - 1] != c) and (i + 1 == len(s) or s[i + 1] != c):\n\t\t\t\t\ts[i] = c\n\t\t\t\t\tbreak\n\n\treturn "".join(s)\n```\n\n**Like it ? please upvote !** | 12 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python simple solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | **Python :**\n\n```\ndef modifyString(self, s: str) -> str:\n\ts = list(s)\n\n\tfor i in range(len(s)):\n\t\tif s[i] == \'?\':\n\t\t\tfor c in "abc":\n\t\t\t\tif (i == 0 or s[i - 1] != c) and (i + 1 == len(s) or s[i + 1] != c):\n\t\t\t\t\ts[i] = c\n\t\t\t\t\tbreak\n\n\treturn "".join(s)\n```\n\n**Like it ? please upvote !** | 12 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Simple Python solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | **Idea:**\nFor every `?` in the string, recplace it with either `a, b, or c`, as there are only two sides for \neach letter therefor there is no need for other letters in the alphabet to recplace it in order to receive a valid string.\n(The spaces added to the beginning and end of the string are in order to skip checking\nevery iteration` if i>0 and i<n.`)\n\n**Time Complexity:** O(n) (where n is the length of the string.)\nWe iterate over every char in the string 4 times:\n- list(s)\n- in the for loop.\n- string[1:n+1] \n- join\n\n**Space Complexity:** O(n) - (for storing `string`)\n\n```\ndef modifyString(self, s: str) -> str:\n string=[" "]+list(s)+[" "]\n n=len(s)\n \n for i in range(1,n+1): \n if string[i]!="?":\n continue\n for letter in "abc":\n if letter!=string[i-1] and letter!=string[i+1]:\n string[i]=letter\n break\n \n return "".join(string[1:n+1])\n```\n\n*Thanx for reading, please **upvote** if it helped you :)* | 3 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Simple Python solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | **Idea:**\nFor every `?` in the string, recplace it with either `a, b, or c`, as there are only two sides for \neach letter therefor there is no need for other letters in the alphabet to recplace it in order to receive a valid string.\n(The spaces added to the beginning and end of the string are in order to skip checking\nevery iteration` if i>0 and i<n.`)\n\n**Time Complexity:** O(n) (where n is the length of the string.)\nWe iterate over every char in the string 4 times:\n- list(s)\n- in the for loop.\n- string[1:n+1] \n- join\n\n**Space Complexity:** O(n) - (for storing `string`)\n\n```\ndef modifyString(self, s: str) -> str:\n string=[" "]+list(s)+[" "]\n n=len(s)\n \n for i in range(1,n+1): \n if string[i]!="?":\n continue\n for letter in "abc":\n if letter!=string[i-1] and letter!=string[i+1]:\n string[i]=letter\n break\n \n return "".join(string[1:n+1])\n```\n\n*Thanx for reading, please **upvote** if it helped you :)* | 3 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python 3 Solution for Beginners ( 3 letter soln) | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | ```\nclass Solution:\n def modifyString(self, s: str) -> str:\n if len(s)==1: #if input contains only a \'?\'\n if s[0]==\'?\':\n return \'a\'\n s=list(s)\n for i in range(len(s)):\n if s[i]==\'?\':\n for c in \'abc\':\n if i==0 and s[i+1]!=c: #if i=0 means it is first letter so there is no s[ i-1]\n s[i]=c\n break\n if i==len(s)-1 and s[i-1]!=c: #if i=len(s) means it is last letter so there is no s[i+1]\n s[i]=c\n break\n if (i>0 and i<len(s)-1) and s[i-1]!=c and s[i+1]!=c: \n s[i]=c\n break\n return \'\'.join(s)\n\t``` | 7 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python 3 Solution for Beginners ( 3 letter soln) | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | ```\nclass Solution:\n def modifyString(self, s: str) -> str:\n if len(s)==1: #if input contains only a \'?\'\n if s[0]==\'?\':\n return \'a\'\n s=list(s)\n for i in range(len(s)):\n if s[i]==\'?\':\n for c in \'abc\':\n if i==0 and s[i+1]!=c: #if i=0 means it is first letter so there is no s[ i-1]\n s[i]=c\n break\n if i==len(s)-1 and s[i-1]!=c: #if i=len(s) means it is last letter so there is no s[i+1]\n s[i]=c\n break\n if (i>0 and i<len(s)-1) and s[i-1]!=c and s[i+1]!=c: \n s[i]=c\n break\n return \'\'.join(s)\n\t``` | 7 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | ```\nclass Solution:\n def modifyString(self, s: str) -> str:\n s: list[str] = list(s)\n alpha: list[str] = list("abcdefghijklmnopqqrstuvwxyz?")\n if len(s) == 1 and s[0] == "?": return "a"\n\n for i in range(len(s)):\n if s[i] == "?":\n if i == 0:\n alpha.remove(s[i + 1])\n elif i == len(s) - 1:\n alpha.remove(s[i - 1])\n else:\n left = s[i - 1]\n right = s[i + 1]\n if left == right: \n alpha.remove(right)\n else:\n alpha.remove(left)\n alpha.remove(right)\n s[i] = alpha[len(alpha) // 2]\n alpha = list("abcdefghijklmnopqqrstuvwxyz?")\n \n return "".join(s)\n``` | 0 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python solution | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | ```\nclass Solution:\n def modifyString(self, s: str) -> str:\n s: list[str] = list(s)\n alpha: list[str] = list("abcdefghijklmnopqqrstuvwxyz?")\n if len(s) == 1 and s[0] == "?": return "a"\n\n for i in range(len(s)):\n if s[i] == "?":\n if i == 0:\n alpha.remove(s[i + 1])\n elif i == len(s) - 1:\n alpha.remove(s[i - 1])\n else:\n left = s[i - 1]\n right = s[i + 1]\n if left == right: \n alpha.remove(right)\n else:\n alpha.remove(left)\n alpha.remove(right)\n s[i] = alpha[len(alpha) // 2]\n alpha = list("abcdefghijklmnopqqrstuvwxyz?")\n \n return "".join(s)\n``` | 0 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Simple solutions | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n # bruteforce solutions\n # 36ms\n # Beats 79.02% of users with Python3\n avail = {\n \'a\': \'a\', \'b\': \'b\', \'c\': \'c\', \'d\': \'d\', \'e\': \'e\', \n \'f\': \'f\', \'g\': \'g\', \'h\': \'h\', \'i\': \'i\', \'j\': \'j\', \'k\': \'k\', \n \'l\': \'l\', \'m\': \'m\', \'n\': \'n\', \'o\': \'o\', \'p\': \'p\', \'q\': \'q\', \n \'r\': \'r\', \'s\': \'s\', \'t\': \'t\', \'u\': \'u\', \'v\': \'v\', \'w\': \'w\', \n \'x\': \'x\', \'y\': \'y\', \'z\': \'z\',\n }\n # prepare for backup copy \n q = avail.copy()\n # remove all reserved words\n _ = [avail.pop(o, None) for o in s]\n \n ret = ""\n for char in s:\n if char == "?":\n if len(avail) == 0:\n avail |= q\n\n _, a = avail.popitem()\n ret += a\n else:\n ret += char\n \n return ret\n``` | 0 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Simple solutions | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n # bruteforce solutions\n # 36ms\n # Beats 79.02% of users with Python3\n avail = {\n \'a\': \'a\', \'b\': \'b\', \'c\': \'c\', \'d\': \'d\', \'e\': \'e\', \n \'f\': \'f\', \'g\': \'g\', \'h\': \'h\', \'i\': \'i\', \'j\': \'j\', \'k\': \'k\', \n \'l\': \'l\', \'m\': \'m\', \'n\': \'n\', \'o\': \'o\', \'p\': \'p\', \'q\': \'q\', \n \'r\': \'r\', \'s\': \'s\', \'t\': \'t\', \'u\': \'u\', \'v\': \'v\', \'w\': \'w\', \n \'x\': \'x\', \'y\': \'y\', \'z\': \'z\',\n }\n # prepare for backup copy \n q = avail.copy()\n # remove all reserved words\n _ = [avail.pop(o, None) for o in s]\n \n ret = ""\n for char in s:\n if char == "?":\n if len(avail) == 0:\n avail |= q\n\n _, a = avail.popitem()\n ret += a\n else:\n ret += char\n \n return ret\n``` | 0 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python3 using range() and filter() | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n l = list(s)\n i = range(ord(\'a\'), ord(\'z\'))\n for c in range(len(l)):\n if l[c] == \'?\':\n prev = l[c-1] if c != 0 else \'a\'\n nxt = l[c+1] if c != len(l)-1 else \'z\'\n l[c] = chr(list(filter(lambda x: x != ord(prev) and x != ord(nxt), i))[0])\n return \'\'.join(l)\n``` | 0 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
Python3 using range() and filter() | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | # Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n l = list(s)\n i = range(ord(\'a\'), ord(\'z\'))\n for c in range(len(l)):\n if l[c] == \'?\':\n prev = l[c-1] if c != 0 else \'a\'\n nxt = l[c+1] if c != len(l)-1 else \'z\'\n l[c] = chr(list(filter(lambda x: x != ord(prev) and x != ord(nxt), i))[0])\n return \'\'.join(l)\n``` | 0 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
EASY SOLUTION FOR BEGINNERS | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | \n# Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n if(len(s)==1):\n return "a"\n if("?" in s):\n i = s.index("?")\n else:\n return s\n al = "abcdefghijklmnopqrstuvwxyz"\n con = s.count("?")\n print(con)\n for j in range(len(s)):\n if(s[j]==\'?\'):\n m,n = j-1,j+1\n if m>=0:\n al = al.replace(str(s[m]),"")\n if n<len(s):\n al = al.replace(str(s[n]),"")\n \n c = ""\n k = 0\n for i in range(0,len(s)):\n if(k>=len(al)):\n k -= len(al)\n if s[i] == \'?\':\n c += al[k]\n k += 1\n else:\n c += s[i]\n print(al)\n return c\n``` | 0 | Given a string `s` containing only lowercase English letters and the `'?'` character, convert **all** the `'?'` characters into lowercase letters such that the final string does not contain any **consecutive repeating** characters. You **cannot** modify the non `'?'` characters.
It is **guaranteed** that there are no consecutive repeating characters in the given string **except** for `'?'`.
Return _the final string after all the conversions (possibly zero) have been made_. If there is more than one solution, return **any of them**. It can be shown that an answer is always possible with the given constraints.
**Example 1:**
**Input:** s = "?zs "
**Output:** "azs "
**Explanation:** There are 25 solutions for this problem. From "azs " to "yzs ", all are valid. Only "z " is an invalid modification as the string will consist of consecutive repeating characters in "zzs ".
**Example 2:**
**Input:** s = "ubv?w "
**Output:** "ubvaw "
**Explanation:** There are 24 solutions for this problem. Only "v " and "w " are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw " and "ubvww ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consist of lowercase English letters and `'?'`. | Treat the graph as undirected. Start a dfs from the root, if you come across an edge in the forward direction, you need to reverse the edge. |
EASY SOLUTION FOR BEGINNERS | replace-all-s-to-avoid-consecutive-repeating-characters | 0 | 1 | \n# Code\n```\nclass Solution:\n def modifyString(self, s: str) -> str:\n if(len(s)==1):\n return "a"\n if("?" in s):\n i = s.index("?")\n else:\n return s\n al = "abcdefghijklmnopqrstuvwxyz"\n con = s.count("?")\n print(con)\n for j in range(len(s)):\n if(s[j]==\'?\'):\n m,n = j-1,j+1\n if m>=0:\n al = al.replace(str(s[m]),"")\n if n<len(s):\n al = al.replace(str(s[n]),"")\n \n c = ""\n k = 0\n for i in range(0,len(s)):\n if(k>=len(al)):\n k -= len(al)\n if s[i] == \'?\':\n c += al[k]\n k += 1\n else:\n c += s[i]\n print(al)\n return c\n``` | 0 | Given a string `s`, return _the number of **distinct** substrings of_ `s`.
A **substring** of a string is obtained by deleting any number of characters (possibly zero) from the front of the string and any number (possibly zero) from the back of the string.
**Example 1:**
**Input:** s = "aabbaba "
**Output:** 21
**Explanation:** The set of distinct strings is \[ "a ", "b ", "aa ", "bb ", "ab ", "ba ", "aab ", "abb ", "bab ", "bba ", "aba ", "aabb ", "abba ", "bbab ", "baba ", "aabba ", "abbab ", "bbaba ", "aabbab ", "abbaba ", "aabbaba "\]
**Example 2:**
**Input:** s = "abcdefg "
**Output:** 28
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters.
**Follow up:** Can you solve this problem in `O(n)` time complexity? | Processing string from left to right, whenever you get a ‘?’, check left character and right character, and select a character not equal to either of them Do take care to compare with replaced occurrence of ‘?’ when checking the left character. |
Python3 Two Pointer Solution | O(1) Space, O(n*m) Time with Indepth Explanation | number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are two types of triples we\'re looking for: \n\n Type 1: Triplet (i, j, k) if nums1[i]^2 == nums2[j] * nums2[k] \n Type 2: Triplet (i, j, k) if nums2[i]^2 == nums1[j] * nums1[k]\n\nNotice the symmetry. It\'s saying we must look for triplets across both arrays. The best way to do this is by running the algorithm twice: once with nums1 as the target (the outer-loop) and again with nums2 as the target.\n\nTo do this without using any space (this can be done using a hashmap to count the instances where the conditions are true for both types), we can use two pointers like a 3Sum problem. In 3Sum, we investigate 1 number and then iterate our pointers over the remainder of a single array, squeezing the Left and Right pointers together. Then, iterate to the next number, shortening the remaining subarray. \n\nThis has a similar approach, except instead of a singular array, we use each number in Array1 `(a1)` and then search for a multiplicative pair in Array2 `(a2)` that would equal to the target of `a1[i]^2`. This works if `a2` is sorted. The time complexity for a sort is `O(nlogn)`, but this pales in comparison to the `O(mn)` runtime of the overall algorithm, so it\'s beneficial to do this. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe ```helper``` function will be used twice, once searching the `nums1` array against `nums2`, and then vice versa. \n\nIn the general case (with `a1 and a2`), sort `a2`, then go through each number in `a1`; our target number will be `a1[i]^2`. To optimally search for the pair in `a2`, we use 2 pointers, starting from the beginning and at the end: `l, r = 0, len(a2) - 1`. Then we iterate over them while `l < r`. \n\nThere are three conditions:\n* `a2[l] * a2[r] > target`: The pair is too large in comparison to our target. To mitigate this, we decrement `r`. This will move our pointer to a smaller number in the leftside (this is why we sorted), lowering our multiplicative result\n* `a2[l] * a2[r] < target`: Our pair isn\'t big enough, so we move our left pointer to the right where larger numbers are sorted, thus growing our multiplicative pair\n* `else: # we found our target`: This has 2 subconditions, when the left and right pointer are equal (i.e, `a2[l] == a2[r]`), and the other when they\'re not. \n * If they\'re equal, that means we shouldn\'t iterate over them to avoid recounting. So, we use the formula for counting pairs:`((n * (n - 1)) // 2)`. This is based on a combination formula, but for only 2 items. Get the size of the window, `n`, and use the formula. We `break` afterward because the numbers are equal, so there are no other pairs to consider between the two numbers.\n * Otherwise, they\'re not equal (but the pair is successful), so we count how many of each number there are and multiply the two together, `res += rightCount * leftCount`. \n\n\nRun this twice on both arrays. This would result in `O(2nm)` runtime, which reduces to `O(nm)`.\n\n# Complexity\n- Time complexity: `O(nm), where n == len(nums1) and m == len(nums2)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(1)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTriplets(self, nums1: List[int], nums2: List[int]) -> int: \n def helper(a1, a2): # a1, a2: array1, array2; symmetry\n # sort the searchable array, a2, to make conditions possible\n a2.sort()\n res = 0\n for n in a1:\n target = n ** 2\n l, r = 0, len(a2) - 1\n while l < r: \n if a2[l] * a2[r] > target:\n r -= 1\n elif a2[l] * a2[r] < target:\n l += 1\n else:\n # if l, r are the same, use combination form and break\n if a2[l] == a2[r]:\n n = (r - l + 1)\n res += ((n * (n - 1))//2)\n break\n # count all the numbers at l and r\n # that are successful pairs\n left, right = a2[l], a2[r]\n leftCount, rightCount = 0, 0\n while l < len(a2) and a2[l] == left:\n leftCount += 1\n l += 1\n while r >= 0 and a2[r] == right:\n rightCount += 1\n r -= 1\n res += rightCount * leftCount\n \n return res\n \n # run it twice for the symmetry between type1/type2\n return helper(nums1, nums2) + helper(nums2, nums1)\n\n``` | 0 | Given two arrays of integers `nums1` and `nums2`, return the number of triplets formed (type 1 and type 2) under the following rules:
* Type 1: Triplet (i, j, k) if `nums1[i]2 == nums2[j] * nums2[k]` where `0 <= i < nums1.length` and `0 <= j < k < nums2.length`.
* Type 2: Triplet (i, j, k) if `nums2[i]2 == nums1[j] * nums1[k]` where `0 <= i < nums2.length` and `0 <= j < k < nums1.length`.
**Example 1:**
**Input:** nums1 = \[7,4\], nums2 = \[5,2,8,9\]
**Output:** 1
**Explanation:** Type 1: (1, 1, 2), nums1\[1\]2 = nums2\[1\] \* nums2\[2\]. (42 = 2 \* 8).
**Example 2:**
**Input:** nums1 = \[1,1\], nums2 = \[1,1,1\]
**Output:** 9
**Explanation:** All Triplets are valid, because 12 = 1 \* 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1\[i\]2 = nums2\[j\] \* nums2\[k\].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2\[i\]2 = nums1\[j\] \* nums1\[k\].
**Example 3:**
**Input:** nums1 = \[7,7,8,3\], nums2 = \[1,2,9,7\]
**Output:** 2
**Explanation:** There are 2 valid triplets.
Type 1: (3,0,2). nums1\[3\]2 = nums2\[0\] \* nums2\[2\].
Type 2: (3,0,1). nums2\[3\]2 = nums1\[0\] \* nums1\[1\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `1 <= nums1[i], nums2[i] <= 105` | Check how many ways you can distribute the balls between the boxes. Consider that one way you will use (x1, x2, x3, ..., xk) where xi is the number of balls from colour i. The probability of achieving this way randomly is ( (ball1 C x1) * (ball2 C x2) * (ball3 C x3) * ... * (ballk C xk)) / (2n C n). The probability of a draw is the sigma of probabilities of different ways to achieve draw. Can you use Dynamic programming to solve this problem in a better complexity ? |
Python3 solution || easy to understand || beginner's friendly | number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def numTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n Map1 = Counter([n * n for n in nums1])\n Map2 = Counter([n * n for n in nums2])\n\n res = 0\n for i in range(len(nums1) - 1):\n for j in range(i + 1, len(nums1)):\n res += Map2[nums1[i] * nums1[j]]\n\n for i in range(len(nums2) - 1):\n for j in range(i + 1, len(nums2)):\n res += Map1[nums2[i] * nums2[j]]\n\n return res\n``` | 0 | Given two arrays of integers `nums1` and `nums2`, return the number of triplets formed (type 1 and type 2) under the following rules:
* Type 1: Triplet (i, j, k) if `nums1[i]2 == nums2[j] * nums2[k]` where `0 <= i < nums1.length` and `0 <= j < k < nums2.length`.
* Type 2: Triplet (i, j, k) if `nums2[i]2 == nums1[j] * nums1[k]` where `0 <= i < nums2.length` and `0 <= j < k < nums1.length`.
**Example 1:**
**Input:** nums1 = \[7,4\], nums2 = \[5,2,8,9\]
**Output:** 1
**Explanation:** Type 1: (1, 1, 2), nums1\[1\]2 = nums2\[1\] \* nums2\[2\]. (42 = 2 \* 8).
**Example 2:**
**Input:** nums1 = \[1,1\], nums2 = \[1,1,1\]
**Output:** 9
**Explanation:** All Triplets are valid, because 12 = 1 \* 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1\[i\]2 = nums2\[j\] \* nums2\[k\].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2\[i\]2 = nums1\[j\] \* nums1\[k\].
**Example 3:**
**Input:** nums1 = \[7,7,8,3\], nums2 = \[1,2,9,7\]
**Output:** 2
**Explanation:** There are 2 valid triplets.
Type 1: (3,0,2). nums1\[3\]2 = nums2\[0\] \* nums2\[2\].
Type 2: (3,0,1). nums2\[3\]2 = nums1\[0\] \* nums1\[1\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `1 <= nums1[i], nums2[i] <= 105` | Check how many ways you can distribute the balls between the boxes. Consider that one way you will use (x1, x2, x3, ..., xk) where xi is the number of balls from colour i. The probability of achieving this way randomly is ( (ball1 C x1) * (ball2 C x2) * (ball3 C x3) * ... * (ballk C xk)) / (2n C n). The probability of a draw is the sigma of probabilities of different ways to achieve draw. Can you use Dynamic programming to solve this problem in a better complexity ? |
Easy understand python solution | number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def numTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n Count1 = Counter(nums1)\n Count2 = Counter(nums2)\n res = 0\n for i in Count1:\n db = Count2.copy()\n while db:\n item = db.popitem()\n Q, r = divmod(i*i, item[0])\n if r == 0 and Q in db:\n res += db[Q]*item[1]*Count1[i]\n db.pop(Q)\n elif r == 0 and Q == item[0]:\n res += comb(item[1],2)*Count1[i]\n \n for i in Count2:\n db = Count1.copy()\n while db:\n item = db.popitem()\n Q, r = divmod(i*i, item[0])\n if r == 0 and Q in db:\n res += db[Q]*item[1]*Count2[i]\n db.pop(Q)\n elif r == 0 and Q == item[0]:\n res += comb(item[1],2)*Count2[i]\n\n return res\n \n\n``` | 0 | Given two arrays of integers `nums1` and `nums2`, return the number of triplets formed (type 1 and type 2) under the following rules:
* Type 1: Triplet (i, j, k) if `nums1[i]2 == nums2[j] * nums2[k]` where `0 <= i < nums1.length` and `0 <= j < k < nums2.length`.
* Type 2: Triplet (i, j, k) if `nums2[i]2 == nums1[j] * nums1[k]` where `0 <= i < nums2.length` and `0 <= j < k < nums1.length`.
**Example 1:**
**Input:** nums1 = \[7,4\], nums2 = \[5,2,8,9\]
**Output:** 1
**Explanation:** Type 1: (1, 1, 2), nums1\[1\]2 = nums2\[1\] \* nums2\[2\]. (42 = 2 \* 8).
**Example 2:**
**Input:** nums1 = \[1,1\], nums2 = \[1,1,1\]
**Output:** 9
**Explanation:** All Triplets are valid, because 12 = 1 \* 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1\[i\]2 = nums2\[j\] \* nums2\[k\].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2\[i\]2 = nums1\[j\] \* nums1\[k\].
**Example 3:**
**Input:** nums1 = \[7,7,8,3\], nums2 = \[1,2,9,7\]
**Output:** 2
**Explanation:** There are 2 valid triplets.
Type 1: (3,0,2). nums1\[3\]2 = nums2\[0\] \* nums2\[2\].
Type 2: (3,0,1). nums2\[3\]2 = nums1\[0\] \* nums1\[1\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `1 <= nums1[i], nums2[i] <= 105` | Check how many ways you can distribute the balls between the boxes. Consider that one way you will use (x1, x2, x3, ..., xk) where xi is the number of balls from colour i. The probability of achieving this way randomly is ( (ball1 C x1) * (ball2 C x2) * (ball3 C x3) * ... * (ballk C xk)) / (2n C n). The probability of a draw is the sigma of probabilities of different ways to achieve draw. Can you use Dynamic programming to solve this problem in a better complexity ? |
Brute Force Slowish | number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def numTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n def count_triplets(nums1: List[int], nums2: List[int]) -> int:\n count = 0\n product_map = defaultdict(int)\n\n for i in range(len(nums1)):\n for j in range(i + 1, len(nums1)):\n product_map[nums1[i] * nums1[j]] += 1\n\n for i in range(len(nums2)):\n square = nums2[i] * nums2[i]\n count += product_map[square]\n\n return count\n\n return count_triplets(nums1, nums2) + count_triplets(nums2, nums1)\n\n``` | 0 | Given two arrays of integers `nums1` and `nums2`, return the number of triplets formed (type 1 and type 2) under the following rules:
* Type 1: Triplet (i, j, k) if `nums1[i]2 == nums2[j] * nums2[k]` where `0 <= i < nums1.length` and `0 <= j < k < nums2.length`.
* Type 2: Triplet (i, j, k) if `nums2[i]2 == nums1[j] * nums1[k]` where `0 <= i < nums2.length` and `0 <= j < k < nums1.length`.
**Example 1:**
**Input:** nums1 = \[7,4\], nums2 = \[5,2,8,9\]
**Output:** 1
**Explanation:** Type 1: (1, 1, 2), nums1\[1\]2 = nums2\[1\] \* nums2\[2\]. (42 = 2 \* 8).
**Example 2:**
**Input:** nums1 = \[1,1\], nums2 = \[1,1,1\]
**Output:** 9
**Explanation:** All Triplets are valid, because 12 = 1 \* 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1\[i\]2 = nums2\[j\] \* nums2\[k\].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2\[i\]2 = nums1\[j\] \* nums1\[k\].
**Example 3:**
**Input:** nums1 = \[7,7,8,3\], nums2 = \[1,2,9,7\]
**Output:** 2
**Explanation:** There are 2 valid triplets.
Type 1: (3,0,2). nums1\[3\]2 = nums2\[0\] \* nums2\[2\].
Type 2: (3,0,1). nums2\[3\]2 = nums1\[0\] \* nums1\[1\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `1 <= nums1[i], nums2[i] <= 105` | Check how many ways you can distribute the balls between the boxes. Consider that one way you will use (x1, x2, x3, ..., xk) where xi is the number of balls from colour i. The probability of achieving this way randomly is ( (ball1 C x1) * (ball2 C x2) * (ball3 C x3) * ... * (ballk C xk)) / (2n C n). The probability of a draw is the sigma of probabilities of different ways to achieve draw. Can you use Dynamic programming to solve this problem in a better complexity ? |
[LC-1577-M | Python3] A Plain Solution | number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers | 0 | 1 | Use `collections.Counter` and iterations to count.\n\n```python3 []\nclass Solution:\n def numTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n sq_cnter1 = Counter([num**2 for num in nums1])\n sq_cnter2 = Counter([num**2 for num in nums2])\n\n def count(nums, sq_cnter):\n n = len(nums)\n cnt = 0\n for i in range(n-1):\n for j in range(i+1, n):\n cnt += sq_cnter[nums[i]*nums[j]]\n return cnt\n \n return count(nums1, sq_cnter2) + count(nums2, sq_cnter1)\n``` | 0 | Given two arrays of integers `nums1` and `nums2`, return the number of triplets formed (type 1 and type 2) under the following rules:
* Type 1: Triplet (i, j, k) if `nums1[i]2 == nums2[j] * nums2[k]` where `0 <= i < nums1.length` and `0 <= j < k < nums2.length`.
* Type 2: Triplet (i, j, k) if `nums2[i]2 == nums1[j] * nums1[k]` where `0 <= i < nums2.length` and `0 <= j < k < nums1.length`.
**Example 1:**
**Input:** nums1 = \[7,4\], nums2 = \[5,2,8,9\]
**Output:** 1
**Explanation:** Type 1: (1, 1, 2), nums1\[1\]2 = nums2\[1\] \* nums2\[2\]. (42 = 2 \* 8).
**Example 2:**
**Input:** nums1 = \[1,1\], nums2 = \[1,1,1\]
**Output:** 9
**Explanation:** All Triplets are valid, because 12 = 1 \* 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1\[i\]2 = nums2\[j\] \* nums2\[k\].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2\[i\]2 = nums1\[j\] \* nums1\[k\].
**Example 3:**
**Input:** nums1 = \[7,7,8,3\], nums2 = \[1,2,9,7\]
**Output:** 2
**Explanation:** There are 2 valid triplets.
Type 1: (3,0,2). nums1\[3\]2 = nums2\[0\] \* nums2\[2\].
Type 2: (3,0,1). nums2\[3\]2 = nums1\[0\] \* nums1\[1\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `1 <= nums1[i], nums2[i] <= 105` | Check how many ways you can distribute the balls between the boxes. Consider that one way you will use (x1, x2, x3, ..., xk) where xi is the number of balls from colour i. The probability of achieving this way randomly is ( (ball1 C x1) * (ball2 C x2) * (ball3 C x3) * ... * (ballk C xk)) / (2n C n). The probability of a draw is the sigma of probabilities of different ways to achieve draw. Can you use Dynamic programming to solve this problem in a better complexity ? |
Python3 solution. | number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition here is to find all the triplets that satisfy the given condition. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a two-pointer technique to solve this problem. We can iterate through each array, and for each element we can use two pointers to calculate the product of the other two elements. If the product is equal to the current element, we can add the triplet to our answer.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Note\nNot the most effient solution\n\n# Code\n```\nclass Solution:\n def numTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n freq1 = self.get_freq(nums1)\n freq2 = self.get_freq(nums2)\n ans = 0\n ans += self.count(freq1, nums2)\n ans += self.count(freq2, nums1)\n return ans\n \n def get_freq(self, nums):\n ans = collections.defaultdict(int)\n n = len(nums)\n for i in range(n):\n ans[nums[i] * nums[i]] += 1\n return ans\n \n def count(self, freq, other):\n ans = 0\n m = len(other)\n for i in range(m):\n for j in range(i+1, m):\n prod = other[i] * other[j]\n if prod in freq:\n ans += freq[prod]\n return ans\n``` | 0 | Given two arrays of integers `nums1` and `nums2`, return the number of triplets formed (type 1 and type 2) under the following rules:
* Type 1: Triplet (i, j, k) if `nums1[i]2 == nums2[j] * nums2[k]` where `0 <= i < nums1.length` and `0 <= j < k < nums2.length`.
* Type 2: Triplet (i, j, k) if `nums2[i]2 == nums1[j] * nums1[k]` where `0 <= i < nums2.length` and `0 <= j < k < nums1.length`.
**Example 1:**
**Input:** nums1 = \[7,4\], nums2 = \[5,2,8,9\]
**Output:** 1
**Explanation:** Type 1: (1, 1, 2), nums1\[1\]2 = nums2\[1\] \* nums2\[2\]. (42 = 2 \* 8).
**Example 2:**
**Input:** nums1 = \[1,1\], nums2 = \[1,1,1\]
**Output:** 9
**Explanation:** All Triplets are valid, because 12 = 1 \* 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1\[i\]2 = nums2\[j\] \* nums2\[k\].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2\[i\]2 = nums1\[j\] \* nums1\[k\].
**Example 3:**
**Input:** nums1 = \[7,7,8,3\], nums2 = \[1,2,9,7\]
**Output:** 2
**Explanation:** There are 2 valid triplets.
Type 1: (3,0,2). nums1\[3\]2 = nums2\[0\] \* nums2\[2\].
Type 2: (3,0,1). nums2\[3\]2 = nums1\[0\] \* nums1\[1\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `1 <= nums1[i], nums2[i] <= 105` | Check how many ways you can distribute the balls between the boxes. Consider that one way you will use (x1, x2, x3, ..., xk) where xi is the number of balls from colour i. The probability of achieving this way randomly is ( (ball1 C x1) * (ball2 C x2) * (ball3 C x3) * ... * (ballk C xk)) / (2n C n). The probability of a draw is the sigma of probabilities of different ways to achieve draw. Can you use Dynamic programming to solve this problem in a better complexity ? |
Python linear solution in O(N) Time complexity and O(1) Space complexity | minimum-time-to-make-rope-colorful | 0 | 1 | ```\nclass Solution:\n def minCost(self, colors: str, neededTime: List[int]) -> int:\n st,ct,total=0,1,0\n sm=neededTime[0]\n mx=neededTime[0]\n for i in range(1,len(colors)):\n if colors[i]==colors[i-1]:\n ct+=1\n sm+=neededTime[i]\n mx=max(mx,neededTime[i])\n else:\n if ct>1:\n total+=(sm-mx)\n ct=1\n st=i\n sm=neededTime[i]\n mx=neededTime[i]\n if ct>1:\n total+=(sm-mx)\n return total\n``` | 5 | Alice has `n` balloons arranged on a rope. You are given a **0-indexed** string `colors` where `colors[i]` is the color of the `ith` balloon.
Alice wants the rope to be **colorful**. She does not want **two consecutive balloons** to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it **colorful**. You are given a **0-indexed** integer array `neededTime` where `neededTime[i]` is the time (in seconds) that Bob needs to remove the `ith` balloon from the rope.
Return _the **minimum time** Bob needs to make the rope **colorful**_.
**Example 1:**
**Input:** colors = "abaac ", neededTime = \[1,2,3,4,5\]
**Output:** 3
**Explanation:** In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.
**Example 2:**
**Input:** colors = "abc ", neededTime = \[1,2,3\]
**Output:** 0
**Explanation:** The rope is already colorful. Bob does not need to remove any balloons from the rope.
**Example 3:**
**Input:** colors = "aabaa ", neededTime = \[1,2,3,4,1\]
**Output:** 2
**Explanation:** Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.
**Constraints:**
* `n == colors.length == neededTime.length`
* `1 <= n <= 105`
* `1 <= neededTime[i] <= 104`
* `colors` contains only lowercase English letters. | null |
Python linear solution in O(N) Time complexity and O(1) Space complexity | minimum-time-to-make-rope-colorful | 0 | 1 | ```\nclass Solution:\n def minCost(self, colors: str, neededTime: List[int]) -> int:\n st,ct,total=0,1,0\n sm=neededTime[0]\n mx=neededTime[0]\n for i in range(1,len(colors)):\n if colors[i]==colors[i-1]:\n ct+=1\n sm+=neededTime[i]\n mx=max(mx,neededTime[i])\n else:\n if ct>1:\n total+=(sm-mx)\n ct=1\n st=i\n sm=neededTime[i]\n mx=neededTime[i]\n if ct>1:\n total+=(sm-mx)\n return total\n``` | 5 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Python 3 || 1578. Minimum Time to Make Rope Colorful | minimum-time-to-make-rope-colorful | 0 | 1 | I\'m not real proud of this one... T/M: 76%/16%\n```\nclass Solution:\n def minCost(self, colors: str, neededTime: List[int]) -> int:\n\t\n arr = list(zip(colors,neededTime))\n\t\t\n groupTime = [list(zip(*g))[1] for k, g in groupby(arr, lambda x: x[0])]\n\t\t\n return sum(neededTime) - sum(max(g) for g in groupTime) | 3 | Alice has `n` balloons arranged on a rope. You are given a **0-indexed** string `colors` where `colors[i]` is the color of the `ith` balloon.
Alice wants the rope to be **colorful**. She does not want **two consecutive balloons** to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it **colorful**. You are given a **0-indexed** integer array `neededTime` where `neededTime[i]` is the time (in seconds) that Bob needs to remove the `ith` balloon from the rope.
Return _the **minimum time** Bob needs to make the rope **colorful**_.
**Example 1:**
**Input:** colors = "abaac ", neededTime = \[1,2,3,4,5\]
**Output:** 3
**Explanation:** In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.
**Example 2:**
**Input:** colors = "abc ", neededTime = \[1,2,3\]
**Output:** 0
**Explanation:** The rope is already colorful. Bob does not need to remove any balloons from the rope.
**Example 3:**
**Input:** colors = "aabaa ", neededTime = \[1,2,3,4,1\]
**Output:** 2
**Explanation:** Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.
**Constraints:**
* `n == colors.length == neededTime.length`
* `1 <= n <= 105`
* `1 <= neededTime[i] <= 104`
* `colors` contains only lowercase English letters. | null |
Python 3 || 1578. Minimum Time to Make Rope Colorful | minimum-time-to-make-rope-colorful | 0 | 1 | I\'m not real proud of this one... T/M: 76%/16%\n```\nclass Solution:\n def minCost(self, colors: str, neededTime: List[int]) -> int:\n\t\n arr = list(zip(colors,neededTime))\n\t\t\n groupTime = [list(zip(*g))[1] for k, g in groupby(arr, lambda x: x[0])]\n\t\t\n return sum(neededTime) - sum(max(g) for g in groupTime) | 3 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Simplest Python UF solution | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | \n# Code\n```\nclass DSU():\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n self.size = 1\n \n def find(self, u):\n if u != self.par[u]:\n self.par[u] = self.find(self.par[u])\n return self.par[u]\n \n def union(self, u, v):\n uu, vv = self.find(u), self.find(v)\n if uu == vv:\n return False\n if self.rank[uu] > self.rank[vv]:\n self.par[vv] = self.par[self.par[vv]]\n self.par[vv] = uu\n elif self.rank[vv] > self.par[uu]:\n self.par[uu] = self.par[self.par[uu]]\n self.par[uu] = vv\n else:\n self.par[uu] = vv\n self.rank[vv] += 1\n self.size += 1\n return True\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf1, uf2, ans = DSU(n), DSU(n), 0\n\n for t, u, v in edges:\n if t == 3 and (not uf1.union(u-1, v-1) or not uf2.union(u-1, v-1)):\n ans += 1\n for t, u, v in edges:\n if t == 1 and not uf1.union(u-1, v-1):\n ans += 1\n elif t == 2 and not uf2.union(u-1, v-1):\n ans += 1\n return ans if uf1.size == n and uf2.size == n else -1\n``` | 2 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
Simplest Python UF solution | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | \n# Code\n```\nclass DSU():\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n self.size = 1\n \n def find(self, u):\n if u != self.par[u]:\n self.par[u] = self.find(self.par[u])\n return self.par[u]\n \n def union(self, u, v):\n uu, vv = self.find(u), self.find(v)\n if uu == vv:\n return False\n if self.rank[uu] > self.rank[vv]:\n self.par[vv] = self.par[self.par[vv]]\n self.par[vv] = uu\n elif self.rank[vv] > self.par[uu]:\n self.par[uu] = self.par[self.par[uu]]\n self.par[uu] = vv\n else:\n self.par[uu] = vv\n self.rank[vv] += 1\n self.size += 1\n return True\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf1, uf2, ans = DSU(n), DSU(n), 0\n\n for t, u, v in edges:\n if t == 3 and (not uf1.union(u-1, v-1) or not uf2.union(u-1, v-1)):\n ans += 1\n for t, u, v in edges:\n if t == 1 and not uf1.union(u-1, v-1):\n ans += 1\n elif t == 2 and not uf2.union(u-1, v-1):\n ans += 1\n return ans if uf1.size == n and uf2.size == n else -1\n``` | 2 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
python 3 - DSU + union by rank + path compression | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Intuition\nAs long as you know DSU, this question is quite straghtforward.\n\nProcess edges in 2 parts:\n- Join all type 3 edges and then type 1 edges. This denotes all Alice edges. And edges with the same parent can be removed.\n- Same process will be done by using type 2 edges instead of type 1.\n\nCheck if all nodes belong to the same parent finally to see if any nodes cannot be reached.\n\n# Approach\nDSU\n\n# Complexity\n- Time complexity:\nO(n * alpha(n)) -> DSU operation on input edges list\n\n- Space complexity:\nO(n) -> DSU structure\'s sc\n\n# Code\n```\nclass DSU:\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n \n def find(self, node):\n if self.par[node] != node:\n self.par[node] = self.find(self.par[node])\n return self.par[node]\n \n def union(self, x, y):\n px, py = self.find(x), self.find(y)\n if self.rank[px] > self.rank[py]: # py to px\n self.par[py] = px\n self.rank[px] += self.rank[py]\n else: # px to py\n self.par[px] = py\n self.rank[py] += self.rank[px]\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n import collections\n type2edge = collections.defaultdict(list)\n for ty, u, v in edges:\n type2edge[ty].append([u, v])\n \n ans = 0\n\n # alice\n dsua = DSU(n+1)\n for u, v in type2edge[3]: # join common\n if dsua.find(u) == dsua.find(v):\n ans += 1\n else:\n dsua.union(u, v)\n for u, v in type2edge[1]:\n if dsua.find(u) == dsua.find(v):\n ans += 1\n else:\n dsua.union(u, v)\n \n for i in range(n):\n dsua.find(i)\n if len(set(dsua.par[1:])) > 1: # diff groups\n return -1\n \n # bob\n dsub = DSU(n+1)\n for u, v in type2edge[3]:\n if dsub.find(u) != dsub.find(v):\n dsub.union(u, v)\n for u, v in type2edge[2]:\n if dsub.find(u) == dsub.find(v):\n ans += 1\n else:\n dsub.union(u, v)\n \n for i in range(n):\n dsub.find(i)\n if len(set(dsub.par[1:])) > 1:\n return -1\n \n return ans\n``` | 2 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
python 3 - DSU + union by rank + path compression | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Intuition\nAs long as you know DSU, this question is quite straghtforward.\n\nProcess edges in 2 parts:\n- Join all type 3 edges and then type 1 edges. This denotes all Alice edges. And edges with the same parent can be removed.\n- Same process will be done by using type 2 edges instead of type 1.\n\nCheck if all nodes belong to the same parent finally to see if any nodes cannot be reached.\n\n# Approach\nDSU\n\n# Complexity\n- Time complexity:\nO(n * alpha(n)) -> DSU operation on input edges list\n\n- Space complexity:\nO(n) -> DSU structure\'s sc\n\n# Code\n```\nclass DSU:\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n \n def find(self, node):\n if self.par[node] != node:\n self.par[node] = self.find(self.par[node])\n return self.par[node]\n \n def union(self, x, y):\n px, py = self.find(x), self.find(y)\n if self.rank[px] > self.rank[py]: # py to px\n self.par[py] = px\n self.rank[px] += self.rank[py]\n else: # px to py\n self.par[px] = py\n self.rank[py] += self.rank[px]\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n import collections\n type2edge = collections.defaultdict(list)\n for ty, u, v in edges:\n type2edge[ty].append([u, v])\n \n ans = 0\n\n # alice\n dsua = DSU(n+1)\n for u, v in type2edge[3]: # join common\n if dsua.find(u) == dsua.find(v):\n ans += 1\n else:\n dsua.union(u, v)\n for u, v in type2edge[1]:\n if dsua.find(u) == dsua.find(v):\n ans += 1\n else:\n dsua.union(u, v)\n \n for i in range(n):\n dsua.find(i)\n if len(set(dsua.par[1:])) > 1: # diff groups\n return -1\n \n # bob\n dsub = DSU(n+1)\n for u, v in type2edge[3]:\n if dsub.find(u) != dsub.find(v):\n dsub.union(u, v)\n for u, v in type2edge[2]:\n if dsub.find(u) == dsub.find(v):\n ans += 1\n else:\n dsub.union(u, v)\n \n for i in range(n):\n dsub.find(i)\n if len(set(dsub.par[1:])) > 1:\n return -1\n \n return ans\n``` | 2 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Python3 Solution | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | \n\n```\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\n ans+=self.dfs(vis,li,com,j)\n return ans\n\n def maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n ans=0\n li=[[] for i in range(n)]\n for l in e:\n if(l[0]==3):\n li[l[1]-1].append(l[2]-1)\n li[l[2]-1].append(l[1]-1)\n vis=[0 for i in range(n)]\n com=0\n for i in range(n):\n if(vis[i]):\n continue\n else:\n com+=1\n temp=self.dfs(vis,li,com,i)\n ans+=(temp-1)\n lia=[[] for i in range(com)]\n lib=[[] for i in range(com)]\n for l in e:\n if(l[0]==1):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lia[a].append(b)\n lia[b].append(a)\n elif(l[0]==2):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lib[a].append(b)\n lib[b].append(a)\n visa=[0 for i in range(com)]\n coma=0\n comb=0\n for i in range(com):\n if(visa[i]):\n continue\n else:\n coma+=1\n if(coma>1):\n return -1\n self.dfs(visa,lia,coma,i)\n \n visb=[0 for i in range(com)]\n for i in range(com):\n if(visb[i]):\n continue\n else:\n comb+=1\n if(comb>1):\n return -1\n self.dfs(visb,lib,comb,i)\n if(coma>1 or comb>1):\n return -1\n ans+=(com-1)*2\n return len(e)-ans\n\n\n``` | 2 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
Python3 Solution | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | \n\n```\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\n ans+=self.dfs(vis,li,com,j)\n return ans\n\n def maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n ans=0\n li=[[] for i in range(n)]\n for l in e:\n if(l[0]==3):\n li[l[1]-1].append(l[2]-1)\n li[l[2]-1].append(l[1]-1)\n vis=[0 for i in range(n)]\n com=0\n for i in range(n):\n if(vis[i]):\n continue\n else:\n com+=1\n temp=self.dfs(vis,li,com,i)\n ans+=(temp-1)\n lia=[[] for i in range(com)]\n lib=[[] for i in range(com)]\n for l in e:\n if(l[0]==1):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lia[a].append(b)\n lia[b].append(a)\n elif(l[0]==2):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lib[a].append(b)\n lib[b].append(a)\n visa=[0 for i in range(com)]\n coma=0\n comb=0\n for i in range(com):\n if(visa[i]):\n continue\n else:\n coma+=1\n if(coma>1):\n return -1\n self.dfs(visa,lia,coma,i)\n \n visb=[0 for i in range(com)]\n for i in range(com):\n if(visb[i]):\n continue\n else:\n comb+=1\n if(comb>1):\n return -1\n self.dfs(visb,lib,comb,i)\n if(coma>1 or comb>1):\n return -1\n ans+=(com-1)*2\n return len(e)-ans\n\n\n``` | 2 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Python short and clean. DSU (Disjoint-Set-Union). Functional programming. | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/editorial/).\n\n# Complexity\n- Time complexity: $$O(e)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is number of nodes`,\n`e is number of edges`.\n\n# Code\n```python\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: list[list[int]]) -> int:\n es = reduce(lambda a, x: a[x[0]].append((x[1], x[2])) or a, edges, ([], [], [], []))\n\n def union_count(dsu: DSU, es: Iterable[tuple[T, T]]) -> int:\n return sum(dsu.union(u, v) or 1 for u, v in es if not dsu.is_connected(u, v))\n\n xs = range(1, n + 1)\n a_dsu, b_dsu = DSU(xs), DSU(xs)\n used = sum((\n union_count(a_dsu, es[3]) and\n union_count(b_dsu, es[3]),\n union_count(a_dsu, es[1]),\n union_count(b_dsu, es[2]),\n ))\n\n return len(edges) - used if a_dsu.ds_count() == b_dsu.ds_count() == 1 else -1\n\n\nT = Hashable\n\n\nclass DSU:\n def __init__(self, xs: Iterable[T] = ()) -> None:\n self.parents: Mapping[T, T] = {x: x for x in xs}\n self.sizes: Mapping[T, int] = {x: 1 for x in xs}\n self.count: int = len(self.parents)\n\n def find(self, u: T) -> T:\n self.parents[u] = u if self.parents[u] == u else self.find(self.parents[u])\n return self.parents[u]\n\n def union(self, u: T, v: T) -> None:\n ur, vr = self.find(u), self.find(v)\n if ur == vr:\n return\n low, high = (ur, vr) if self.sizes[ur] < self.sizes[vr] else (vr, ur)\n self.parents[low] = high\n self.sizes[high] += self.sizes[low]\n self.count -= 1\n\n def is_connected(self, u: T, v: T) -> bool:\n return self.find(u) == self.find(v)\n\n def ds_count(self) -> int:\n return self.count\n``` | 3 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
Python short and clean. DSU (Disjoint-Set-Union). Functional programming. | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/editorial/).\n\n# Complexity\n- Time complexity: $$O(e)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is number of nodes`,\n`e is number of edges`.\n\n# Code\n```python\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: list[list[int]]) -> int:\n es = reduce(lambda a, x: a[x[0]].append((x[1], x[2])) or a, edges, ([], [], [], []))\n\n def union_count(dsu: DSU, es: Iterable[tuple[T, T]]) -> int:\n return sum(dsu.union(u, v) or 1 for u, v in es if not dsu.is_connected(u, v))\n\n xs = range(1, n + 1)\n a_dsu, b_dsu = DSU(xs), DSU(xs)\n used = sum((\n union_count(a_dsu, es[3]) and\n union_count(b_dsu, es[3]),\n union_count(a_dsu, es[1]),\n union_count(b_dsu, es[2]),\n ))\n\n return len(edges) - used if a_dsu.ds_count() == b_dsu.ds_count() == 1 else -1\n\n\nT = Hashable\n\n\nclass DSU:\n def __init__(self, xs: Iterable[T] = ()) -> None:\n self.parents: Mapping[T, T] = {x: x for x in xs}\n self.sizes: Mapping[T, int] = {x: 1 for x in xs}\n self.count: int = len(self.parents)\n\n def find(self, u: T) -> T:\n self.parents[u] = u if self.parents[u] == u else self.find(self.parents[u])\n return self.parents[u]\n\n def union(self, u: T, v: T) -> None:\n ur, vr = self.find(u), self.find(v)\n if ur == vr:\n return\n low, high = (ur, vr) if self.sizes[ur] < self.sizes[vr] else (vr, ur)\n self.parents[low] = high\n self.sizes[high] += self.sizes[low]\n self.count -= 1\n\n def is_connected(self, u: T, v: T) -> bool:\n return self.find(u) == self.find(v)\n\n def ds_count(self) -> int:\n return self.count\n``` | 3 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Beating 98.69% Python Easiest Solution | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | \n\n# Code\n```\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\n ans+=self.dfs(vis,li,com,j)\n return ans\n\n def maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n ans=0\n li=[[] for i in range(n)]\n for l in e:\n if(l[0]==3):\n li[l[1]-1].append(l[2]-1)\n li[l[2]-1].append(l[1]-1)\n vis=[0 for i in range(n)]\n com=0\n for i in range(n):\n if(vis[i]):\n continue\n else:\n com+=1\n temp=self.dfs(vis,li,com,i)\n ans+=(temp-1)\n lia=[[] for i in range(com)]\n lib=[[] for i in range(com)]\n for l in e:\n if(l[0]==1):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lia[a].append(b)\n lia[b].append(a)\n elif(l[0]==2):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lib[a].append(b)\n lib[b].append(a)\n visa=[0 for i in range(com)]\n coma=0\n comb=0\n for i in range(com):\n if(visa[i]):\n continue\n else:\n coma+=1\n if(coma>1):\n return -1\n self.dfs(visa,lia,coma,i)\n \n visb=[0 for i in range(com)]\n for i in range(com):\n if(visb[i]):\n continue\n else:\n comb+=1\n if(comb>1):\n return -1\n self.dfs(visb,lib,comb,i)\n if(coma>1 or comb>1):\n return -1\n ans+=(com-1)*2\n return len(e)-ans\n\n``` | 1 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
Beating 98.69% Python Easiest Solution | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | \n\n# Code\n```\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\n ans+=self.dfs(vis,li,com,j)\n return ans\n\n def maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n ans=0\n li=[[] for i in range(n)]\n for l in e:\n if(l[0]==3):\n li[l[1]-1].append(l[2]-1)\n li[l[2]-1].append(l[1]-1)\n vis=[0 for i in range(n)]\n com=0\n for i in range(n):\n if(vis[i]):\n continue\n else:\n com+=1\n temp=self.dfs(vis,li,com,i)\n ans+=(temp-1)\n lia=[[] for i in range(com)]\n lib=[[] for i in range(com)]\n for l in e:\n if(l[0]==1):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lia[a].append(b)\n lia[b].append(a)\n elif(l[0]==2):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lib[a].append(b)\n lib[b].append(a)\n visa=[0 for i in range(com)]\n coma=0\n comb=0\n for i in range(com):\n if(visa[i]):\n continue\n else:\n coma+=1\n if(coma>1):\n return -1\n self.dfs(visa,lia,coma,i)\n \n visb=[0 for i in range(com)]\n for i in range(com):\n if(visb[i]):\n continue\n else:\n comb+=1\n if(comb>1):\n return -1\n self.dfs(visb,lib,comb,i)\n if(coma>1 or comb>1):\n return -1\n ans+=(com-1)*2\n return len(e)-ans\n\n``` | 1 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Image Explanation🏆- [Easiest & Complete Intuition] - C++/Java/Python | remove-max-number-of-edges-to-keep-graph-fully-traversable | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Remove Max Number of Edges to Keep Graph Fully Traversable` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n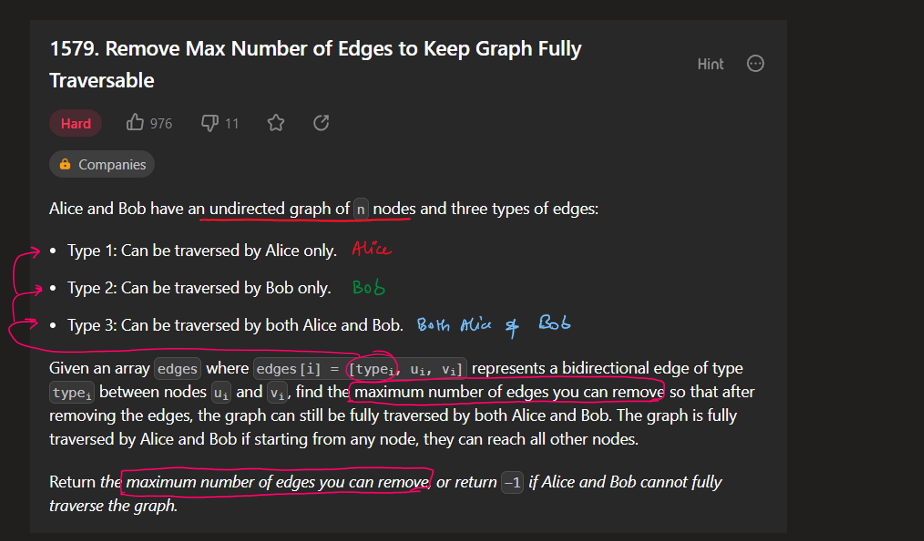\n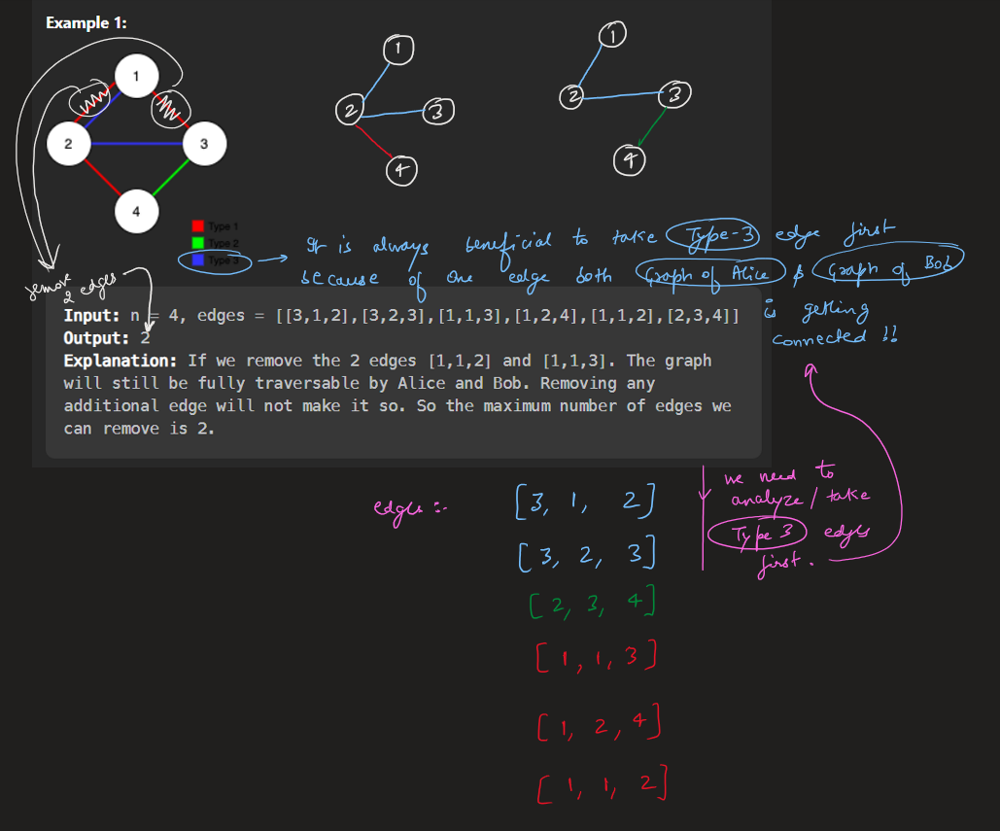\n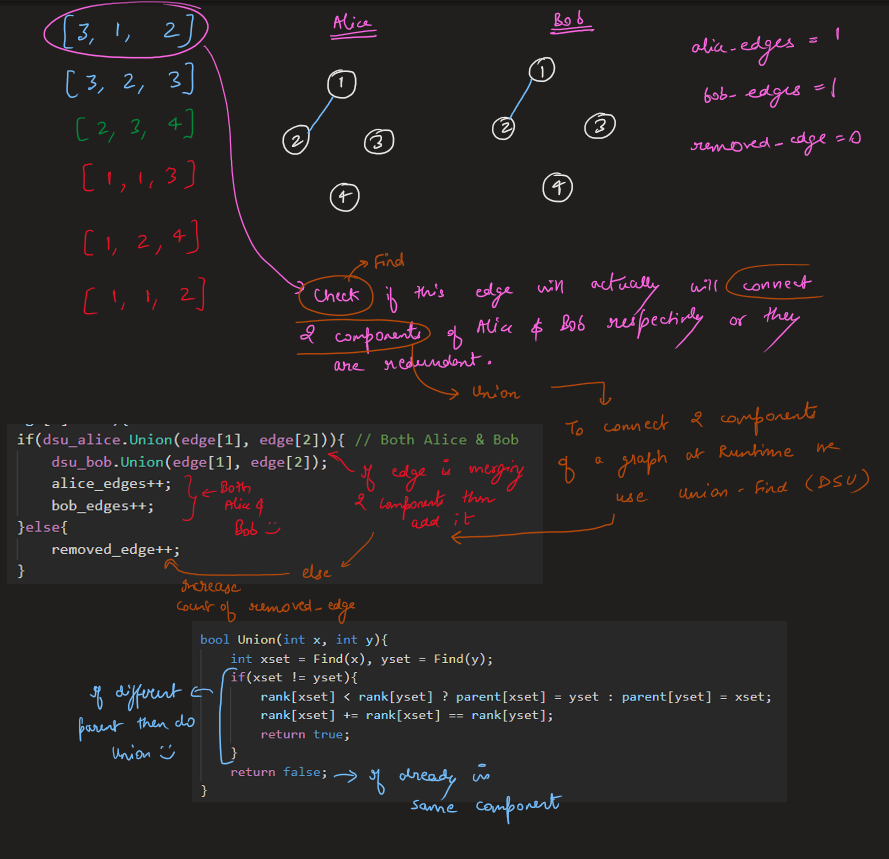\n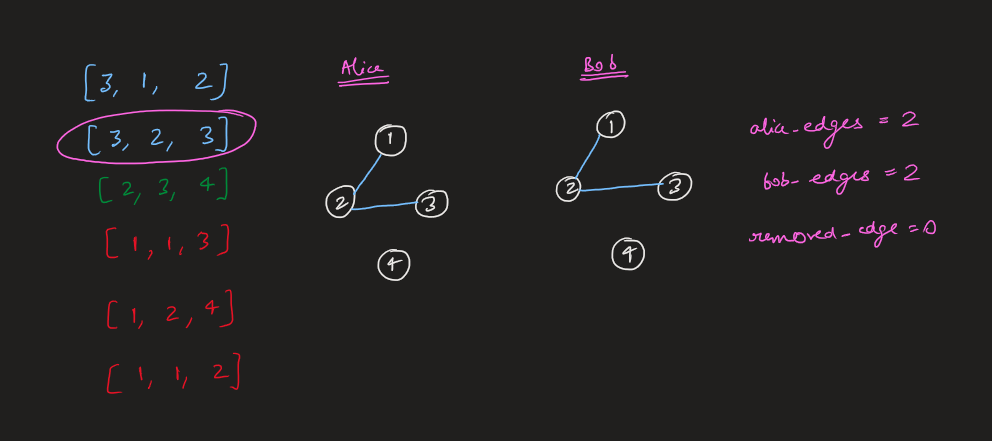\n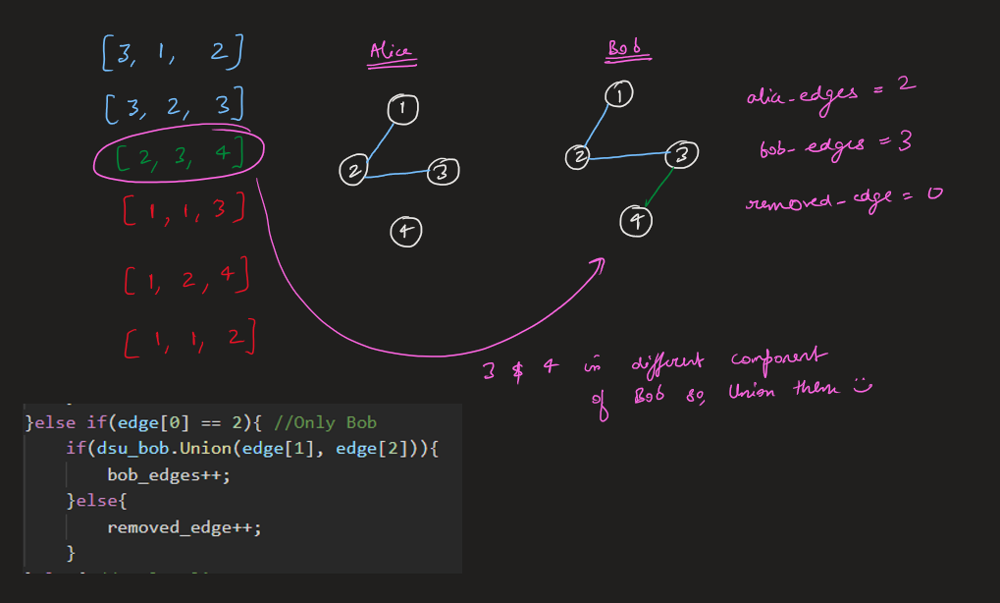\n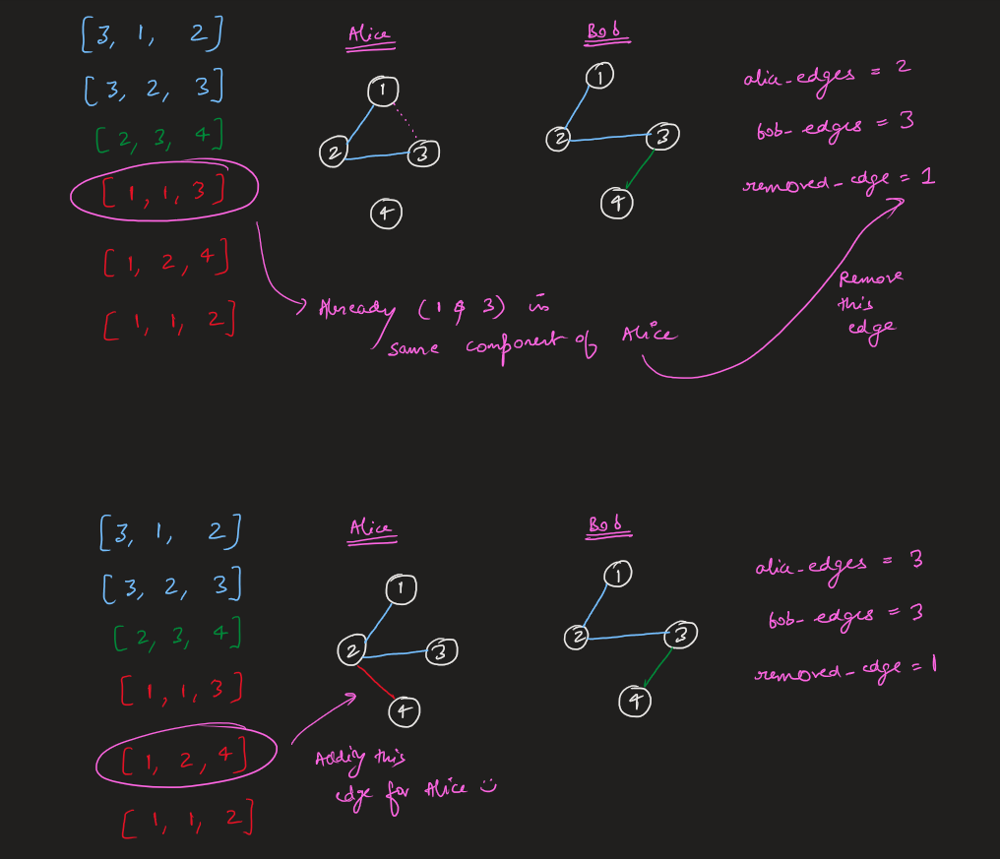\n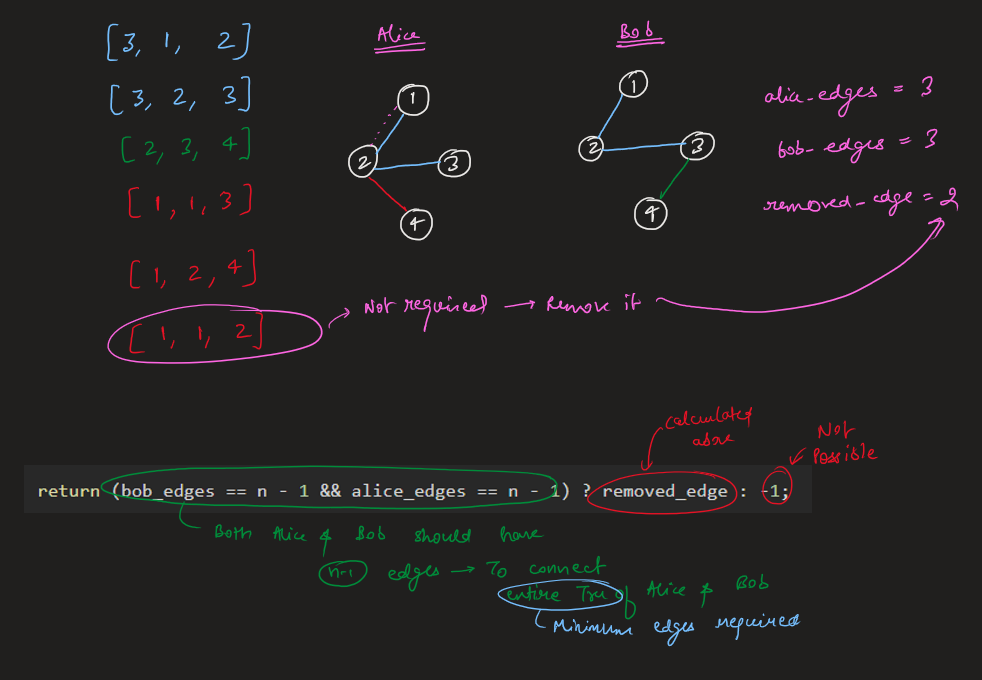\n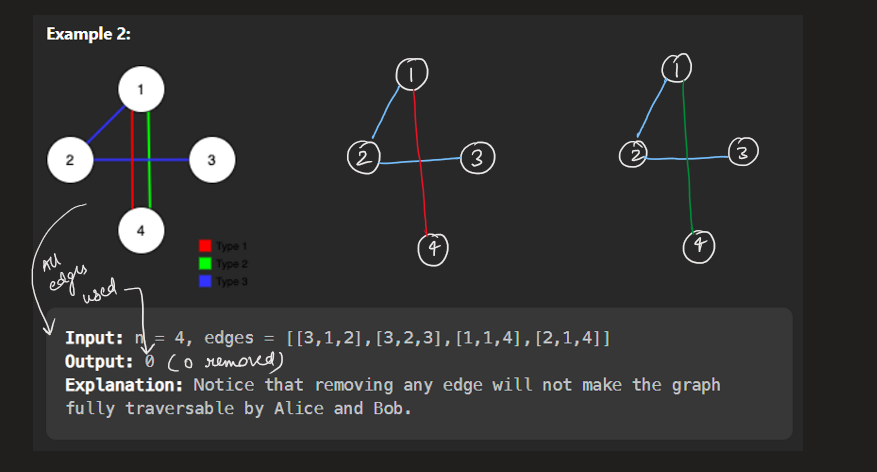\n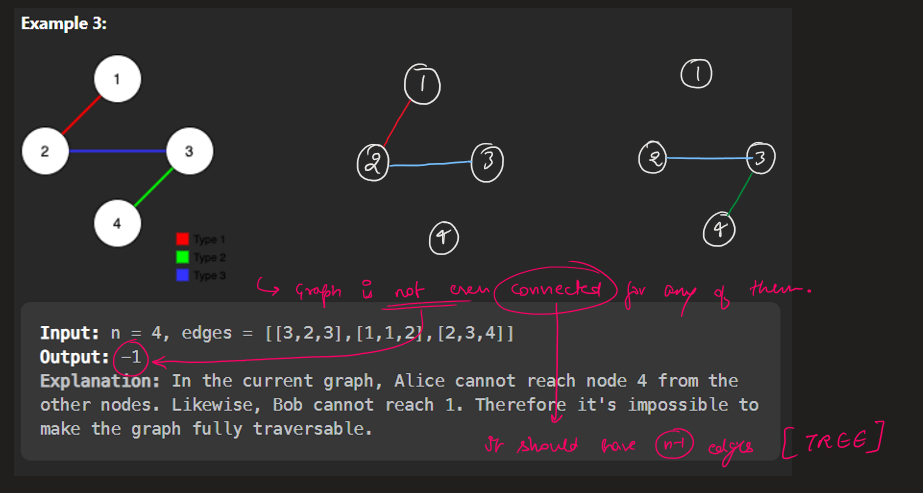\n\n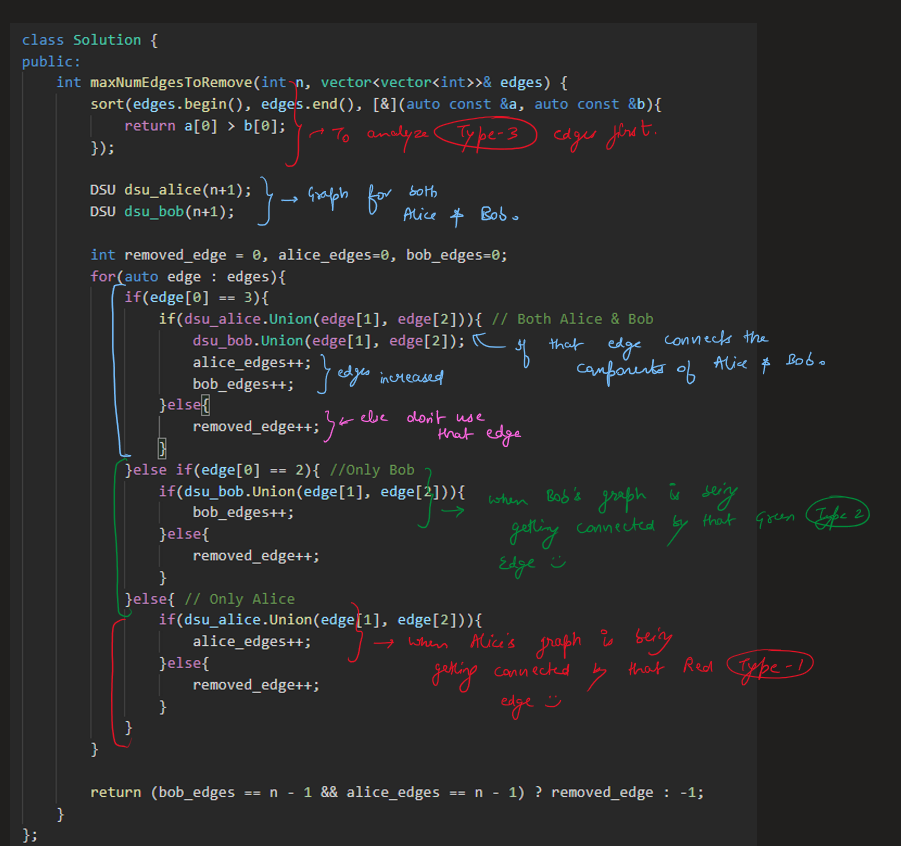\n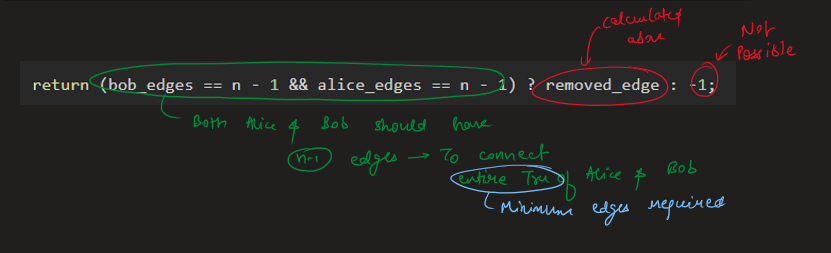\n\n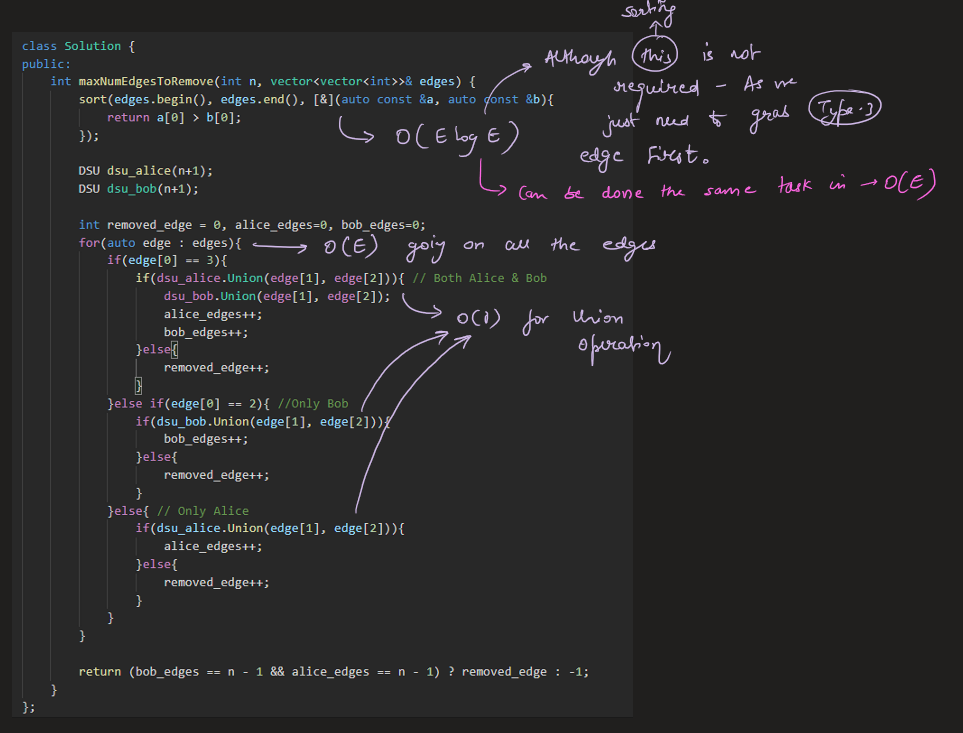\n\n\n# Code\n```C++ []\nclass DSU {\npublic:\n vector<int> parent, rank;\n DSU(int n){\n parent.resize(n, 0);\n rank.resize(n, 0);\n \n for(int i=0;i<n;i++) parent[i] = i;\n }\n \n int Find(int x){\n return parent[x] = parent[x] == x ? x : Find(parent[x]);\n }\n \n bool Union(int x, int y){\n int xset = Find(x), yset = Find(y);\n if(xset != yset){\n rank[xset] < rank[yset] ? parent[xset] = yset : parent[yset] = xset;\n rank[xset] += rank[xset] == rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n sort(edges.begin(), edges.end(), [&](auto const &a, auto const &b){\n return a[0] > b[0];\n });\n\n DSU dsu_alice(n+1);\n DSU dsu_bob(n+1);\n\n int removed_edge = 0, alice_edges=0, bob_edges=0;\n for(auto edge : edges){\n if(edge[0] == 3){\n if(dsu_alice.Union(edge[1], edge[2])){ // Both Alice & Bob\n dsu_bob.Union(edge[1], edge[2]);\n alice_edges++;\n bob_edges++;\n }else{\n removed_edge++;\n }\n }else if(edge[0] == 2){ //Only Bob\n if(dsu_bob.Union(edge[1], edge[2])){\n bob_edges++;\n }else{\n removed_edge++;\n }\n }else{ // Only Alice\n if(dsu_alice.Union(edge[1], edge[2])){\n alice_edges++;\n }else{\n removed_edge++;\n }\n }\n }\n\n return (bob_edges == n - 1 && alice_edges == n - 1) ? removed_edge : -1;\n }\n};\n```\n```Java []\nclass DSU {\n int[] parent;\n int[] rank;\n \n public DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n \n public int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n \n public boolean union(int x, int y) {\n int xset = find(x), yset = find(y);\n if (xset != yset) {\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n } else if (rank[xset] > rank[yset]) {\n parent[yset] = xset;\n } else {\n parent[xset] = yset;\n rank[yset]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> Integer.compare(b[0], a[0]));\n \n DSU dsu_alice = new DSU(n+1);\n DSU dsu_bob = new DSU(n+1);\n \n int removed_edge = 0, alice_edges = 0, bob_edges = 0;\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n if (dsu_alice.union(edge[1], edge[2])) {\n dsu_bob.union(edge[1], edge[2]);\n alice_edges++;\n bob_edges++;\n } else {\n removed_edge++;\n }\n } else if (edge[0] == 2) {\n if (dsu_bob.union(edge[1], edge[2])) {\n bob_edges++;\n } else {\n removed_edge++;\n }\n } else {\n if (dsu_alice.union(edge[1], edge[2])) {\n alice_edges++;\n } else {\n removed_edge++;\n }\n }\n }\n \n return (bob_edges == n - 1 && alice_edges == n - 1) ? removed_edge : -1;\n }\n}\n```\n```Python []\nclass DSU:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n self.rank = [0] * n\n \n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n \n def union(self, x, y):\n xset, yset = self.find(x), self.find(y)\n if xset != yset:\n if self.rank[xset] < self.rank[yset]:\n self.parent[xset] = yset\n elif self.rank[xset] > self.rank[yset]:\n self.parent[yset] = xset\n else:\n self.parent[xset] = yset\n self.rank[yset] += 1\n return True\n return False\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n edges.sort(reverse=True)\n dsu_alice = DSU(n+1)\n dsu_bob = DSU(n+1)\n removed_edge = 0\n alice_edges, bob_edges = 0, 0\n for edge in edges:\n if edge[0] == 3:\n if dsu_alice.union(edge[1], edge[2]):\n dsu_bob.union(edge[1], edge[2])\n alice_edges += 1\n bob_edges += 1\n else:\n removed_edge += 1\n elif edge[0] == 2:\n if dsu_bob.union(edge[1], edge[2]):\n bob_edges += 1\n else:\n removed_edge += 1\n else:\n if dsu_alice.union(edge[1], edge[2]):\n alice_edges += 1\n else:\n removed_edge += 1\n return removed_edge if bob_edges == n - 1 == alice_edges else -1\n``` | 89 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
Image Explanation🏆- [Easiest & Complete Intuition] - C++/Java/Python | remove-max-number-of-edges-to-keep-graph-fully-traversable | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Remove Max Number of Edges to Keep Graph Fully Traversable` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n# Code\n```C++ []\nclass DSU {\npublic:\n vector<int> parent, rank;\n DSU(int n){\n parent.resize(n, 0);\n rank.resize(n, 0);\n \n for(int i=0;i<n;i++) parent[i] = i;\n }\n \n int Find(int x){\n return parent[x] = parent[x] == x ? x : Find(parent[x]);\n }\n \n bool Union(int x, int y){\n int xset = Find(x), yset = Find(y);\n if(xset != yset){\n rank[xset] < rank[yset] ? parent[xset] = yset : parent[yset] = xset;\n rank[xset] += rank[xset] == rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n sort(edges.begin(), edges.end(), [&](auto const &a, auto const &b){\n return a[0] > b[0];\n });\n\n DSU dsu_alice(n+1);\n DSU dsu_bob(n+1);\n\n int removed_edge = 0, alice_edges=0, bob_edges=0;\n for(auto edge : edges){\n if(edge[0] == 3){\n if(dsu_alice.Union(edge[1], edge[2])){ // Both Alice & Bob\n dsu_bob.Union(edge[1], edge[2]);\n alice_edges++;\n bob_edges++;\n }else{\n removed_edge++;\n }\n }else if(edge[0] == 2){ //Only Bob\n if(dsu_bob.Union(edge[1], edge[2])){\n bob_edges++;\n }else{\n removed_edge++;\n }\n }else{ // Only Alice\n if(dsu_alice.Union(edge[1], edge[2])){\n alice_edges++;\n }else{\n removed_edge++;\n }\n }\n }\n\n return (bob_edges == n - 1 && alice_edges == n - 1) ? removed_edge : -1;\n }\n};\n```\n```Java []\nclass DSU {\n int[] parent;\n int[] rank;\n \n public DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n \n public int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n \n public boolean union(int x, int y) {\n int xset = find(x), yset = find(y);\n if (xset != yset) {\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n } else if (rank[xset] > rank[yset]) {\n parent[yset] = xset;\n } else {\n parent[xset] = yset;\n rank[yset]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> Integer.compare(b[0], a[0]));\n \n DSU dsu_alice = new DSU(n+1);\n DSU dsu_bob = new DSU(n+1);\n \n int removed_edge = 0, alice_edges = 0, bob_edges = 0;\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n if (dsu_alice.union(edge[1], edge[2])) {\n dsu_bob.union(edge[1], edge[2]);\n alice_edges++;\n bob_edges++;\n } else {\n removed_edge++;\n }\n } else if (edge[0] == 2) {\n if (dsu_bob.union(edge[1], edge[2])) {\n bob_edges++;\n } else {\n removed_edge++;\n }\n } else {\n if (dsu_alice.union(edge[1], edge[2])) {\n alice_edges++;\n } else {\n removed_edge++;\n }\n }\n }\n \n return (bob_edges == n - 1 && alice_edges == n - 1) ? removed_edge : -1;\n }\n}\n```\n```Python []\nclass DSU:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n self.rank = [0] * n\n \n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n \n def union(self, x, y):\n xset, yset = self.find(x), self.find(y)\n if xset != yset:\n if self.rank[xset] < self.rank[yset]:\n self.parent[xset] = yset\n elif self.rank[xset] > self.rank[yset]:\n self.parent[yset] = xset\n else:\n self.parent[xset] = yset\n self.rank[yset] += 1\n return True\n return False\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n edges.sort(reverse=True)\n dsu_alice = DSU(n+1)\n dsu_bob = DSU(n+1)\n removed_edge = 0\n alice_edges, bob_edges = 0, 0\n for edge in edges:\n if edge[0] == 3:\n if dsu_alice.union(edge[1], edge[2]):\n dsu_bob.union(edge[1], edge[2])\n alice_edges += 1\n bob_edges += 1\n else:\n removed_edge += 1\n elif edge[0] == 2:\n if dsu_bob.union(edge[1], edge[2]):\n bob_edges += 1\n else:\n removed_edge += 1\n else:\n if dsu_alice.union(edge[1], edge[2]):\n alice_edges += 1\n else:\n removed_edge += 1\n return removed_edge if bob_edges == n - 1 == alice_edges else -1\n``` | 89 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Kruskal MST | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Intuition\nMinimum spanning tree with Kruskal algorithm (disjoint set), with some hairs.\n\n# Approach\nFirst attemp to use all type-3 edges (both) (phase 1), then use type-1 (alice-only) and type-2 (bob-only) separatedly (phase 2). Until the tree is built. Register the total edge used.\n\nProof of correctness:\n\n0. ignore the proof of correctness of the MST algorithm\n1. The correctness of "use type-3" first:\n Consider an type-3 edge connects two sets in the phase 1, If we don\'t use it but some other edges at the second phase to connect the two sets, it would costs two edges (one for either alice or bob).\n2. Is there a possible (sub-) spanning tree, whose edges are of mixed type, that has less edge numbers that the pure-type-3 spanning tree?\n -impossible, since the number of edges in the combination of edges from two mixed-spanning tree must be larger or equal to the pure-type-3 tree, with the same reachability.\n\nThus the correctness of the algorithm is proved through the induction.\n\n# Complexity\n- Time complexity:\n$O(|E| * n)$, \nthe $|E|$ is for iterating over all edges, while the $n$ is the worst-case time-complexity of the disjoint set.\n\nNote that there is a ```sorted(edges, ...)``` in my current implementation. This is only for the ease of coding, which means theoretically the sorting (with the time complexity of $O(|E| log(|E|))$) is not needed and the only thing that is needed during the preprocessing is identifying all type-3 edges, which contributes only a O(|E|) time complexity.\n\n- Space complexity:\n$O(n)$ for the disjoint set.\n\n# Code\n```\nclass DS:\n def __init__(self, n: int):\n self.n = n\n self.n_set = n\n self.parent = list(range(n))\n \n def find_root(self, v: int) -> int:\n if self.parent[v] == v:\n return v\n self.parent[v] = self.find_root(self.parent[v])\n return self.parent[v]\n\n def join(self, u: int, v: int) -> bool:\n if self.n_set == 1:\n return False\n u_root = self.find_root(u)\n v_root = self.find_root(v)\n if u_root == v_root:\n return False\n self.parent[u_root] = v_root\n self.n_set -= 1\n return True\n \nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n ds_a = DS(n)\n ds_b = DS(n)\n reordered_edges = sorted(edges, key=lambda x: x[0], reverse=True)\n edges_used = 0\n print(reordered_edges)\n # note: node ids start from 1\n for n_type, u, v in reordered_edges:\n if n_type == 3 and ds_a.n_set != 1:\n if ds_a.join(u - 1, v - 1) and ds_b.join(u - 1, v - 1):\n edges_used += 1\n elif n_type == 1 and ds_a.n_set != 1:\n if ds_a.join(u - 1, v - 1):\n edges_used += 1\n elif n_type == 2 and ds_b.n_set != 1:\n if ds_b.join(u - 1, v - 1):\n edges_used += 1\n\n if ds_b.n_set != 1 or ds_a.n_set != 1:\n return -1\n \n return len(edges) - edges_used\n\n``` | 1 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
Kruskal MST | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Intuition\nMinimum spanning tree with Kruskal algorithm (disjoint set), with some hairs.\n\n# Approach\nFirst attemp to use all type-3 edges (both) (phase 1), then use type-1 (alice-only) and type-2 (bob-only) separatedly (phase 2). Until the tree is built. Register the total edge used.\n\nProof of correctness:\n\n0. ignore the proof of correctness of the MST algorithm\n1. The correctness of "use type-3" first:\n Consider an type-3 edge connects two sets in the phase 1, If we don\'t use it but some other edges at the second phase to connect the two sets, it would costs two edges (one for either alice or bob).\n2. Is there a possible (sub-) spanning tree, whose edges are of mixed type, that has less edge numbers that the pure-type-3 spanning tree?\n -impossible, since the number of edges in the combination of edges from two mixed-spanning tree must be larger or equal to the pure-type-3 tree, with the same reachability.\n\nThus the correctness of the algorithm is proved through the induction.\n\n# Complexity\n- Time complexity:\n$O(|E| * n)$, \nthe $|E|$ is for iterating over all edges, while the $n$ is the worst-case time-complexity of the disjoint set.\n\nNote that there is a ```sorted(edges, ...)``` in my current implementation. This is only for the ease of coding, which means theoretically the sorting (with the time complexity of $O(|E| log(|E|))$) is not needed and the only thing that is needed during the preprocessing is identifying all type-3 edges, which contributes only a O(|E|) time complexity.\n\n- Space complexity:\n$O(n)$ for the disjoint set.\n\n# Code\n```\nclass DS:\n def __init__(self, n: int):\n self.n = n\n self.n_set = n\n self.parent = list(range(n))\n \n def find_root(self, v: int) -> int:\n if self.parent[v] == v:\n return v\n self.parent[v] = self.find_root(self.parent[v])\n return self.parent[v]\n\n def join(self, u: int, v: int) -> bool:\n if self.n_set == 1:\n return False\n u_root = self.find_root(u)\n v_root = self.find_root(v)\n if u_root == v_root:\n return False\n self.parent[u_root] = v_root\n self.n_set -= 1\n return True\n \nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n ds_a = DS(n)\n ds_b = DS(n)\n reordered_edges = sorted(edges, key=lambda x: x[0], reverse=True)\n edges_used = 0\n print(reordered_edges)\n # note: node ids start from 1\n for n_type, u, v in reordered_edges:\n if n_type == 3 and ds_a.n_set != 1:\n if ds_a.join(u - 1, v - 1) and ds_b.join(u - 1, v - 1):\n edges_used += 1\n elif n_type == 1 and ds_a.n_set != 1:\n if ds_a.join(u - 1, v - 1):\n edges_used += 1\n elif n_type == 2 and ds_b.n_set != 1:\n if ds_b.join(u - 1, v - 1):\n edges_used += 1\n\n if ds_b.n_set != 1 or ds_a.n_set != 1:\n return -1\n \n return len(edges) - edges_used\n\n``` | 1 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
✔💯 DAY 395 | DSU | 100% 0ms | [PYTHON/JAVA/C++] | EXPLAINED | Approach 🆙🆙🆙 | remove-max-number-of-edges-to-keep-graph-fully-traversable | 1 | 1 | # Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition \n##### \u2022\tWe have a graph with N nodes and bidirectional edges of three types: Type 1 (Alice only), Type 2 (Bob only), and Type 3 (both Alice and Bob).\n##### \u2022\tWe need to find the maximum number of edges that can be removed while still allowing both Alice and Bob to reach any node starting from any node via the remaining edges.\n##### \u2022\tWe can assume that there are two graphs, one for Alice and one for Bob, where the first graph has edges only of Type 1 and 3, and the second graph has edges only of Type 2 and 3.\n##### \u2022\tAn edge is useful only if it connects two nodes that are not already connected via some other edge or path.\n##### \u2022\tWe can use the Disjoint Set Union (DSU) data structure to detect if two nodes are connected via some path or not in O(\u03B1(N)), where \u03B1(N) is the extremely fast inverse Ackermann function.\n##### \u2022\tWe can use DSU to perform the union of two nodes for an edge, and if the nodes were not connected earlier (i.e., they have a different representative), then we know this edge is needed.\n##### \u2022\tFor every edge, if the two nodes were not connected earlier, we know this edge is required. To get the answer, we can subtract the number of required edges from the total number of edges.\n##### \u2022\tSince Type 3 edges are the most useful (as one Type 3 edge adds two edges, one for Alice and one for Bob), we will first iterate over the edges of Type 3 and add the edge to both graphs.\n##### \u2022\tIn the end, we need to check if the graph for both Alice and Bob is connected or not. If yes, we can say the edges that we didn\'t connect can be removed. To check if the individual graphs are connected, we will check if the number of components in the graph is 1 or not.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tDefine constants for edge types indices: TYPE U, V, ALICE, BOB, BOTH.\n##### \u2022\tDefine the maxNumEdgesToRemove function that takes in the number of nodes (n) and an array of edges (edges).\n##### \u2022\tMove all edges of type BOTH to the start of the array.\n##### \u2022\tCreate two UnionFind data structures, one for Alice and one for Bob.\n##### \u2022\tInitialize a variable added to 0.\n##### \u2022\tIterate over the edges and add them to the appropriate UnionFind data structure.\n##### \u2022\tIf the edge is of type BOTH, add it to both UnionFind data structures.\n##### \u2022\tIf the edge is of type ALICE, add it to the Alice UnionFind data structure.\n##### \u2022\tIf the edge is of type BOB, add it to the Bob UnionFind data structure.\n##### \u2022\tIf the two UnionFind data structures are united, return the number of edges that were not added (edges.length - added).\n##### \u2022\tIf both UnionFind data structures are not united, it is impossible to remove enough edges to make them united, so return -1.\n##### \u2022\tDefine the UnionFind class that takes in the number of elements (n).\n##### \u2022\tInitialize the parent array with n+1 elements and the groups variable to n.\n##### \u2022\tDefine the union function that takes in two elements (u and v) and returns 1 if they were not already in the same group, 0 otherwise.\n##### \u2022\tFind the parent of an element and perform path compression.\n##### \u2022\tDefine the isUnited function that checks if all elements are in the same group and returns true if they are, false otherwise.\n\n\n\n# Code\n```java []\nclass Solution {\n // constants for the edge types indices\n static final int \n TYPE = 0, U = 1, V = 2,\n ALICE = 1, BOB = 2, BOTH = 3;\n\n public int maxNumEdgesToRemove(final int n, final int[][] edges) {\n // Move all edges of type BOTH to the start of the array\n for (int i = 0, j = edges.length - 1; i < j; ) {\n if (edges[i][TYPE] == BOTH) {\n ++i;\n continue;\n }\n final var temp = edges[i];\n edges[i] = edges[j];\n edges[j] = temp;\n --j;\n }\n\n // Create two UnionFind data structures, one for Alice and one for Bob\n final UnionFind \n aliceUf = new UnionFind(n), \n bobUf = new UnionFind(n);\n private int added = 0;\n\n // Iterate over the edges and add them to the appropriate UnionFind data structure\n for (final var edge : edges) {\n final int type = edge[TYPE];\n final int u = edge[U];\n final int v = edge[V];\n\n // Add the edge to both UnionFind data structures if it is of type BOTH\n added += switch (type) {\n case BOTH -> \n aliceUf.union(u, v) | bobUf.union(u, v);\n case ALICE -> aliceUf.union(u, v);\n default -> bobUf.union(u, v);\n };\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (aliceUf.isUnited() && bobUf.isUnited())\n return edges.length - added;\n }\n\n // If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n return -1;\n }\n}\n\nclass UnionFind {\n static final int ZERO = 0;\n final int[] parent;\n int groups;\n\n // Initialize the UnionFind data structure with n groups\n UnionFind(final int n) {\n parent = new int[n + 1];\n groups = n;\n }\n\n // Union two elements and return 1 if they were not already in the same group, 0 otherwise\n int union(final int u, final int v) {\n final int uParent = find(u);\n final int vParent = find(v);\n if (uParent == vParent)\n return 0;\n parent[uParent] = vParent;\n --groups;\n return 1;\n }\n\n // Find the parent of an element and perform path compression\n int find(final int v) {\n if (parent[v] != ZERO)\n return parent[v] = find(parent[v]);\n return v;\n }\n\n // Check if all elements are in the same group\n boolean isUnited() {\n return groups == 1;\n }\n}\n```\n\n```c++ []\nclass Solution {\nprivate:\n // constants for the edge types indices\n static constexpr int \n TYPE = 0, U = 1, V =2,\n ALICE = 1, BOB = 2, BOTH = 3;\n\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Move all edges of type BOTH to the end of the array\n for (int i = 0, j = edges.size() - 1; i < j; ) {\n if (edges[i][TYPE] == BOTH) {\n ++i;\n continue;\n }\n swap(edges[i], edges[j]);\n --j;\n }\n\n // Create two UnionFind data structures, one for Alice and one for Bob\n UnionFind alice_uf(n), bob_uf(n);\n int added = 0;\n\n // Iterate over the edges and add them to the appropriate UnionFind data structure\n for (const auto& edge : edges) {\n const int type = edge[TYPE];\n const int u = edge[U];\n const int v = edge[V];\n\n // Add the edge to both UnionFind data structures if it is of type BOTH\n added += (type == BOTH) ? \n alice_uf.union_(u, v) | bob_uf.union_(u, v) :\n (type == ALICE) ? alice_uf.union_(u, v) : bob_uf.union_(u, v);\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (alice_uf.is_united() && bob_uf.is_united())\n return edges.size() - added;\n }\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (alice_uf.is_united() && bob_uf.is_united())\n return edges.size() - added;\n\n // If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n return -1;\n }\n};\n\nclass UnionFind {\nprivate:\n vector<int> parent;\n int groups;\n\npublic:\n // Initialize the UnionFind data structure with n groups\n UnionFind(int n) : parent(n + 1), groups(n) {\n iota(parent.begin(), parent.end(), 0);\n }\n\n // Union two elements and return 1 if they were not already in the same group, 0 otherwise\n int union_(int u, int v) {\n const int uParent = find_(u);\n const int vParent = find_(v);\n if (uParent == vParent)\n return 0;\n parent[uParent] = vParent;\n --groups;\n return 1;\n }\n\n // Find the parent of an element and perform path compression\n int find_(int v) {\n if (parent[v] != v)\n parent[v] = find_(parent[v]);\n return parent[v];\n }\n\n // Check if all elements are in the same group\n bool is_united() {\n return groups == 1;\n }\n};\n```\n```python []\nclass Solution:\n # constants for the edge types indices\n TYPE, U, V, ALICE, BOB, BOTH = range(6)\n\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n # Move all edges of type BOTH to the end of the array\n i, j = 0, len(edges) - 1\n while i < j:\n if edges[i][self.TYPE] == self.BOTH:\n i += 1\n continue\n edges[i], edges[j] = edges[j], edges[i]\n j -= 1\n\n # Create two UnionFind data structures, one for Alice and one for Bob\n alice_uf, bob_uf = UnionFind(n), UnionFind(n)\n added = 0\n\n # Iterate over the edges and add them to the appropriate UnionFind data structure\n for edge in edges:\n type_, u, v = edge[self.TYPE], edge[self.U], edge[self.V]\n\n # Add the edge to both UnionFind data structures if it is of type BOTH\n if type_ == self.BOTH:\n added += alice_uf.union(u, v) | bob_uf.union(u, v)\n elif type_ == self.ALICE:\n added += alice_uf.union(u, v)\n else:\n added += bob_uf.union(u, v)\n\n # If both UnionFind data structures are united, return the number of edges that were not added\n if alice_uf.is_united() and bob_uf.is_united():\n return len(edges) - added\n\n # If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n if not alice_uf.is_united() or not bob_uf.is_united():\n return -1\n\n # If both UnionFind data structures are united, return the number of edges that were not added\n return len(edges) - added\n\n\nclass UnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n + 1))\n self.groups = n\n\n def union(self, u: int, v: int) -> int:\n u_parent = self.find(u)\n v_parent = self.find(v)\n if u_parent == v_parent:\n return 0\n self.parent[u_parent] = v_parent\n self.groups -= 1\n return 1\n\n def find(self, v: int) -> int:\n if self.parent[v] != v:\n self.parent[v] = self.find(self.parent[v])\n return self.parent[v]\n\n def is_united(self) -> bool:\n return self.groups == 1\n```\n\n\n# Complexity\nTime Complexity:\n1 Moving all edges of type BOTH to the end of the array takes O(n) time.\n\nCreating two UnionFind data structures takes O(n) time.\nIterating over the edges takes O(m) time, where m is the number of edges.\nAdding an edge to a UnionFind data structure takes O(\u03B1(n)) time, where \u03B1(n) is the extremely fast inverse Ackermann function.\nChecking if both UnionFind data structures are united takes O(1) time.\nOverall, the time complexity of the code is O(m \u03B1(n)), where m is the number of edges and n is the number of nodes.\nSpace Complexity:\n\nCreating two UnionFind data structures takes O(n) space.\nCreating the parent array for the UnionFind data structures takes O(n) space.\nCreating the added variable takes O(1) space.\nOverall, the space complexity of the code is O(n).\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nhttps://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/solutions/3468567/day-395-dsu-100-0ms-python-java-c-explained-approach/\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n\n | 26 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
✔💯 DAY 395 | DSU | 100% 0ms | [PYTHON/JAVA/C++] | EXPLAINED | Approach 🆙🆙🆙 | remove-max-number-of-edges-to-keep-graph-fully-traversable | 1 | 1 | # Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition \n##### \u2022\tWe have a graph with N nodes and bidirectional edges of three types: Type 1 (Alice only), Type 2 (Bob only), and Type 3 (both Alice and Bob).\n##### \u2022\tWe need to find the maximum number of edges that can be removed while still allowing both Alice and Bob to reach any node starting from any node via the remaining edges.\n##### \u2022\tWe can assume that there are two graphs, one for Alice and one for Bob, where the first graph has edges only of Type 1 and 3, and the second graph has edges only of Type 2 and 3.\n##### \u2022\tAn edge is useful only if it connects two nodes that are not already connected via some other edge or path.\n##### \u2022\tWe can use the Disjoint Set Union (DSU) data structure to detect if two nodes are connected via some path or not in O(\u03B1(N)), where \u03B1(N) is the extremely fast inverse Ackermann function.\n##### \u2022\tWe can use DSU to perform the union of two nodes for an edge, and if the nodes were not connected earlier (i.e., they have a different representative), then we know this edge is needed.\n##### \u2022\tFor every edge, if the two nodes were not connected earlier, we know this edge is required. To get the answer, we can subtract the number of required edges from the total number of edges.\n##### \u2022\tSince Type 3 edges are the most useful (as one Type 3 edge adds two edges, one for Alice and one for Bob), we will first iterate over the edges of Type 3 and add the edge to both graphs.\n##### \u2022\tIn the end, we need to check if the graph for both Alice and Bob is connected or not. If yes, we can say the edges that we didn\'t connect can be removed. To check if the individual graphs are connected, we will check if the number of components in the graph is 1 or not.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tDefine constants for edge types indices: TYPE U, V, ALICE, BOB, BOTH.\n##### \u2022\tDefine the maxNumEdgesToRemove function that takes in the number of nodes (n) and an array of edges (edges).\n##### \u2022\tMove all edges of type BOTH to the start of the array.\n##### \u2022\tCreate two UnionFind data structures, one for Alice and one for Bob.\n##### \u2022\tInitialize a variable added to 0.\n##### \u2022\tIterate over the edges and add them to the appropriate UnionFind data structure.\n##### \u2022\tIf the edge is of type BOTH, add it to both UnionFind data structures.\n##### \u2022\tIf the edge is of type ALICE, add it to the Alice UnionFind data structure.\n##### \u2022\tIf the edge is of type BOB, add it to the Bob UnionFind data structure.\n##### \u2022\tIf the two UnionFind data structures are united, return the number of edges that were not added (edges.length - added).\n##### \u2022\tIf both UnionFind data structures are not united, it is impossible to remove enough edges to make them united, so return -1.\n##### \u2022\tDefine the UnionFind class that takes in the number of elements (n).\n##### \u2022\tInitialize the parent array with n+1 elements and the groups variable to n.\n##### \u2022\tDefine the union function that takes in two elements (u and v) and returns 1 if they were not already in the same group, 0 otherwise.\n##### \u2022\tFind the parent of an element and perform path compression.\n##### \u2022\tDefine the isUnited function that checks if all elements are in the same group and returns true if they are, false otherwise.\n\n\n\n# Code\n```java []\nclass Solution {\n // constants for the edge types indices\n static final int \n TYPE = 0, U = 1, V = 2,\n ALICE = 1, BOB = 2, BOTH = 3;\n\n public int maxNumEdgesToRemove(final int n, final int[][] edges) {\n // Move all edges of type BOTH to the start of the array\n for (int i = 0, j = edges.length - 1; i < j; ) {\n if (edges[i][TYPE] == BOTH) {\n ++i;\n continue;\n }\n final var temp = edges[i];\n edges[i] = edges[j];\n edges[j] = temp;\n --j;\n }\n\n // Create two UnionFind data structures, one for Alice and one for Bob\n final UnionFind \n aliceUf = new UnionFind(n), \n bobUf = new UnionFind(n);\n private int added = 0;\n\n // Iterate over the edges and add them to the appropriate UnionFind data structure\n for (final var edge : edges) {\n final int type = edge[TYPE];\n final int u = edge[U];\n final int v = edge[V];\n\n // Add the edge to both UnionFind data structures if it is of type BOTH\n added += switch (type) {\n case BOTH -> \n aliceUf.union(u, v) | bobUf.union(u, v);\n case ALICE -> aliceUf.union(u, v);\n default -> bobUf.union(u, v);\n };\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (aliceUf.isUnited() && bobUf.isUnited())\n return edges.length - added;\n }\n\n // If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n return -1;\n }\n}\n\nclass UnionFind {\n static final int ZERO = 0;\n final int[] parent;\n int groups;\n\n // Initialize the UnionFind data structure with n groups\n UnionFind(final int n) {\n parent = new int[n + 1];\n groups = n;\n }\n\n // Union two elements and return 1 if they were not already in the same group, 0 otherwise\n int union(final int u, final int v) {\n final int uParent = find(u);\n final int vParent = find(v);\n if (uParent == vParent)\n return 0;\n parent[uParent] = vParent;\n --groups;\n return 1;\n }\n\n // Find the parent of an element and perform path compression\n int find(final int v) {\n if (parent[v] != ZERO)\n return parent[v] = find(parent[v]);\n return v;\n }\n\n // Check if all elements are in the same group\n boolean isUnited() {\n return groups == 1;\n }\n}\n```\n\n```c++ []\nclass Solution {\nprivate:\n // constants for the edge types indices\n static constexpr int \n TYPE = 0, U = 1, V =2,\n ALICE = 1, BOB = 2, BOTH = 3;\n\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Move all edges of type BOTH to the end of the array\n for (int i = 0, j = edges.size() - 1; i < j; ) {\n if (edges[i][TYPE] == BOTH) {\n ++i;\n continue;\n }\n swap(edges[i], edges[j]);\n --j;\n }\n\n // Create two UnionFind data structures, one for Alice and one for Bob\n UnionFind alice_uf(n), bob_uf(n);\n int added = 0;\n\n // Iterate over the edges and add them to the appropriate UnionFind data structure\n for (const auto& edge : edges) {\n const int type = edge[TYPE];\n const int u = edge[U];\n const int v = edge[V];\n\n // Add the edge to both UnionFind data structures if it is of type BOTH\n added += (type == BOTH) ? \n alice_uf.union_(u, v) | bob_uf.union_(u, v) :\n (type == ALICE) ? alice_uf.union_(u, v) : bob_uf.union_(u, v);\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (alice_uf.is_united() && bob_uf.is_united())\n return edges.size() - added;\n }\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (alice_uf.is_united() && bob_uf.is_united())\n return edges.size() - added;\n\n // If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n return -1;\n }\n};\n\nclass UnionFind {\nprivate:\n vector<int> parent;\n int groups;\n\npublic:\n // Initialize the UnionFind data structure with n groups\n UnionFind(int n) : parent(n + 1), groups(n) {\n iota(parent.begin(), parent.end(), 0);\n }\n\n // Union two elements and return 1 if they were not already in the same group, 0 otherwise\n int union_(int u, int v) {\n const int uParent = find_(u);\n const int vParent = find_(v);\n if (uParent == vParent)\n return 0;\n parent[uParent] = vParent;\n --groups;\n return 1;\n }\n\n // Find the parent of an element and perform path compression\n int find_(int v) {\n if (parent[v] != v)\n parent[v] = find_(parent[v]);\n return parent[v];\n }\n\n // Check if all elements are in the same group\n bool is_united() {\n return groups == 1;\n }\n};\n```\n```python []\nclass Solution:\n # constants for the edge types indices\n TYPE, U, V, ALICE, BOB, BOTH = range(6)\n\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n # Move all edges of type BOTH to the end of the array\n i, j = 0, len(edges) - 1\n while i < j:\n if edges[i][self.TYPE] == self.BOTH:\n i += 1\n continue\n edges[i], edges[j] = edges[j], edges[i]\n j -= 1\n\n # Create two UnionFind data structures, one for Alice and one for Bob\n alice_uf, bob_uf = UnionFind(n), UnionFind(n)\n added = 0\n\n # Iterate over the edges and add them to the appropriate UnionFind data structure\n for edge in edges:\n type_, u, v = edge[self.TYPE], edge[self.U], edge[self.V]\n\n # Add the edge to both UnionFind data structures if it is of type BOTH\n if type_ == self.BOTH:\n added += alice_uf.union(u, v) | bob_uf.union(u, v)\n elif type_ == self.ALICE:\n added += alice_uf.union(u, v)\n else:\n added += bob_uf.union(u, v)\n\n # If both UnionFind data structures are united, return the number of edges that were not added\n if alice_uf.is_united() and bob_uf.is_united():\n return len(edges) - added\n\n # If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n if not alice_uf.is_united() or not bob_uf.is_united():\n return -1\n\n # If both UnionFind data structures are united, return the number of edges that were not added\n return len(edges) - added\n\n\nclass UnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n + 1))\n self.groups = n\n\n def union(self, u: int, v: int) -> int:\n u_parent = self.find(u)\n v_parent = self.find(v)\n if u_parent == v_parent:\n return 0\n self.parent[u_parent] = v_parent\n self.groups -= 1\n return 1\n\n def find(self, v: int) -> int:\n if self.parent[v] != v:\n self.parent[v] = self.find(self.parent[v])\n return self.parent[v]\n\n def is_united(self) -> bool:\n return self.groups == 1\n```\n\n\n# Complexity\nTime Complexity:\n1 Moving all edges of type BOTH to the end of the array takes O(n) time.\n\nCreating two UnionFind data structures takes O(n) time.\nIterating over the edges takes O(m) time, where m is the number of edges.\nAdding an edge to a UnionFind data structure takes O(\u03B1(n)) time, where \u03B1(n) is the extremely fast inverse Ackermann function.\nChecking if both UnionFind data structures are united takes O(1) time.\nOverall, the time complexity of the code is O(m \u03B1(n)), where m is the number of edges and n is the number of nodes.\nSpace Complexity:\n\nCreating two UnionFind data structures takes O(n) space.\nCreating the parent array for the UnionFind data structures takes O(n) space.\nCreating the added variable takes O(1) space.\nOverall, the space complexity of the code is O(n).\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nhttps://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/solutions/3468567/day-395-dsu-100-0ms-python-java-c-explained-approach/\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n\n | 26 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
[Python3] - Union Find - Easy to understand | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n\n def __init__(self, n: int):\n self.root = [i for i in range(n)]\n self.rank = [1 for _ in range(n)]\n self.group = n\n\n def find(self, x: int) -> int:\n if self.root[x] != x: self.root[x] = self.find(self.root[x])\n return self.root[x]\n\n def union(self, x: int, y: int) -> None:\n root_x, root_y = self.find(x), self.find(y)\n if root_x == root_y: return\n if self.rank[root_x] > self.rank[root_y]: self.root[root_y] = root_x\n elif self.rank[root_x] < self.rank[root_y]: self.root[root_x] = root_y\n else:\n self.root[root_y] = root_x\n self.rank[root_x] += 1\n self.group -= 1\n\n def are_connected(self, x: int, y: int) -> bool:\n return self.find(x) == self.find(y)\n\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf_a, uf_b = UnionFind(n), UnionFind(n)\n res = 0\n edges.sort(reverse=True)\n for t, u, v in edges:\n if t == 3:\n if uf_a.are_connected(u - 1, v - 1) or uf_b.are_connected(u - 1, v - 1): res += 1\n else:\n uf_a.union(u - 1, v - 1)\n uf_b.union(u - 1, v - 1)\n if t == 2:\n if uf_b.are_connected(u - 1, v - 1): res += 1\n else: uf_b.union(u - 1, v - 1)\n if t == 1:\n if uf_a.are_connected(u - 1, v - 1): res += 1\n else: uf_a.union(u - 1, v - 1)\n \n return res if uf_a.group == uf_b.group == 1 else -1\n``` | 6 | Alice and Bob have an undirected graph of `n` nodes and three types of edges:
* Type 1: Can be traversed by Alice only.
* Type 2: Can be traversed by Bob only.
* Type 3: Can be traversed by both Alice and Bob.
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return _the maximum number of edges you can remove, or return_ `-1` _if Alice and Bob cannot fully traverse the graph._
**Example 1:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,3\],\[1,2,4\],\[1,1,2\],\[2,3,4\]\]
**Output:** 2
**Explanation:** If we remove the 2 edges \[1,1,2\] and \[1,1,3\]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
**Example 2:**
**Input:** n = 4, edges = \[\[3,1,2\],\[3,2,3\],\[1,1,4\],\[2,1,4\]\]
**Output:** 0
**Explanation:** Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
**Example 3:**
**Input:** n = 4, edges = \[\[3,2,3\],\[1,1,2\],\[2,3,4\]\]
**Output:** -1
**Explanation:** In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
**Constraints:**
* `1 <= n <= 105`
* `1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)`
* `edges[i].length == 3`
* `1 <= typei <= 3`
* `1 <= ui < vi <= n`
* All tuples `(typei, ui, vi)` are distinct. | null |
[Python3] - Union Find - Easy to understand | remove-max-number-of-edges-to-keep-graph-fully-traversable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n\n def __init__(self, n: int):\n self.root = [i for i in range(n)]\n self.rank = [1 for _ in range(n)]\n self.group = n\n\n def find(self, x: int) -> int:\n if self.root[x] != x: self.root[x] = self.find(self.root[x])\n return self.root[x]\n\n def union(self, x: int, y: int) -> None:\n root_x, root_y = self.find(x), self.find(y)\n if root_x == root_y: return\n if self.rank[root_x] > self.rank[root_y]: self.root[root_y] = root_x\n elif self.rank[root_x] < self.rank[root_y]: self.root[root_x] = root_y\n else:\n self.root[root_y] = root_x\n self.rank[root_x] += 1\n self.group -= 1\n\n def are_connected(self, x: int, y: int) -> bool:\n return self.find(x) == self.find(y)\n\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf_a, uf_b = UnionFind(n), UnionFind(n)\n res = 0\n edges.sort(reverse=True)\n for t, u, v in edges:\n if t == 3:\n if uf_a.are_connected(u - 1, v - 1) or uf_b.are_connected(u - 1, v - 1): res += 1\n else:\n uf_a.union(u - 1, v - 1)\n uf_b.union(u - 1, v - 1)\n if t == 2:\n if uf_b.are_connected(u - 1, v - 1): res += 1\n else: uf_b.union(u - 1, v - 1)\n if t == 1:\n if uf_a.are_connected(u - 1, v - 1): res += 1\n else: uf_a.union(u - 1, v - 1)\n \n return res if uf_a.group == uf_b.group == 1 else -1\n``` | 6 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
🚀🚀🚀EASY SOLUTiON EVER !!! || Java || C++ || Python || JS || C# || Ruby || Go 🚀🚀🚀 by PRODONiK | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\nThe problem aims to find the number of special positions in a given matrix. A position is considered special if the element at that position is 1, and there is no other 1 in the same row and the same column.\n\n# Approach\nThe `numSpecial` method iterates over each row in the matrix. For each element with the value 1 in the row, it increments the `ones_in_the_row` variable, indicating the number of 1s in that row. If it\'s the first 1 in the row (`ones_in_the_row == 1`), it marks the corresponding column as potentially special. If it\'s not the first 1 in the row (`ones_in_the_row > 1`), it marks both the current and the previously marked columns as non-special.\n\nThe `columns` array is used to keep track of the status of each column:\n- `0`: Not marked\n- `1`: Potentially special (first 1 in the row)\n- `2`: Not special (more than one 1 in the row)\n\nAfter processing all rows, the method counts the columns marked as potentially special and returns the result.\n\n# Complexity\n- Time complexity: O(m * n)\n The time complexity is linear in the size of the matrix, where `m` is the number of rows and `n` is the number of columns.\n\n- Space complexity: O(n)\n The space complexity is linear in the number of columns, as the `columns` array is used to keep track of the status of each column.\n\n# Code\n```Java []\nclass Solution {\n public int numSpecial (int[][] nums) {\n int result = 0;\n int [] columns = new int [nums[0].length];\n for (int i = 0; i < nums.length; i ++) {\n int ones_in_the_row = 0;\n int column = 0;\n for (int j = 0; j < nums[i].length; j ++) {\n if (nums[i][j] == 1) {\n ones_in_the_row ++;\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n }\n else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n\n }\n for (int column : columns) {\n result += (column == 1 ? 1 : 0);\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& nums) {\n int result = 0;\n std::vector<int> columns(nums[0].size(), 0);\n\n for (int i = 0; i < nums.size(); ++i) {\n int ones_in_the_row = 0;\n int column = 0;\n\n for (int j = 0; j < nums[i].size(); ++j) {\n if (nums[i][j] == 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n for (int column : columns) {\n result += (column == 1 ? 1 : 0);\n }\n\n return result;\n }\n};\n```\n```Python []\nclass Solution:\n def numSpecial(self, nums: List[List[int]]) -> int:\n result = 0\n columns = [0] * len(nums[0])\n\n for i in range(len(nums)):\n ones_in_the_row = 0\n column = 0\n\n for j in range(len(nums[i])):\n if nums[i][j] == 1:\n ones_in_the_row += 1\n\n if ones_in_the_row == 1:\n columns[j] = 1 if columns[j] == 0 else 2\n column = j\n else:\n columns[column] = 2\n columns[j] = 2\n\n result += sum(column == 1 for column in columns)\n return result\n```\n```JavaScript []\nclass Solution {\n numSpecial(nums) {\n let result = 0;\n const columns = new Array(nums[0].length).fill(0);\n\n for (let i = 0; i < nums.length; ++i) {\n let ones_in_the_row = 0;\n let column = 0;\n\n for (let j = 0; j < nums[i].length; ++j) {\n if (nums[i][j] === 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row === 1) {\n columns[j] = columns[j] === 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n result += columns.filter(column => column === 1).length;\n return result;\n }\n}\n```\n```C# []\npublic class Solution {\n public int NumSpecial(int[][] nums) {\n int result = 0;\n int[] columns = new int[nums[0].Length];\n\n for (int i = 0; i < nums.Length; ++i) {\n int ones_in_the_row = 0;\n int column = 0;\n\n for (int j = 0; j < nums[i].Length; ++j) {\n if (nums[i][j] == 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n result += Array.FindAll(columns, column => column == 1).Length;\n return result;\n }\n}\n```\n```Ruby []\nclass Solution\n def num_special(nums)\n result = 0\n columns = Array.new(nums[0].length, 0)\n\n (0...nums.length).each do |i|\n ones_in_the_row = 0\n column = 0\n\n (0...nums[i].length).each do |j|\n if nums[i][j] == 1\n ones_in_the_row += 1\n\n if ones_in_the_row == 1\n columns[j] = columns[j] == 0 ? 1 : 2\n column = j\n else\n columns[column] = 2\n columns[j] = 2\n end\n end\n end\n end\n\n result += columns.count { |column| column == 1 }\n result\n end\nend\n```\n```Go []\ntype Solution struct{}\n\nfunc (s *Solution) NumSpecial(nums [][]int) int {\n\tresult := 0\n\tcolumns := make([]int, len(nums[0]))\n\n\tfor i := 0; i < len(nums); i++ {\n\t\tones_in_the_row := 0\n\t\tcolumn := 0\n\n\t\tfor j := 0; j < len(nums[i]); j++ {\n\t\t\tif nums[i][j] == 1 {\n\t\t\t\tones_in_the_row++\n\n\t\t\t\tif ones_in_the_row == 1 {\n\t\t\t\t\tif columns[j] == 0 {\n\t\t\t\t\t\tcolumns[j] = 1\n\t\t\t\t\t} else {\n\t\t\t\t\t\tcolumns[j] = 2\n\t\t\t\t\t}\n\t\t\t\t\tcolumn = j\n\t\t\t\t} else {\n\t\t\t\t\tcolumns[column] = 2\n\t\t\t\t\tcolumns[j] = 2\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\tfor _, column := range columns {\n\t\tif column == 1 {\n\t\t\tresult++\n\t\t}\n\t}\n\n\treturn result\n}\n```\n\n | 16 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
🚀🚀🚀EASY SOLUTiON EVER !!! || Java || C++ || Python || JS || C# || Ruby || Go 🚀🚀🚀 by PRODONiK | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\nThe problem aims to find the number of special positions in a given matrix. A position is considered special if the element at that position is 1, and there is no other 1 in the same row and the same column.\n\n# Approach\nThe `numSpecial` method iterates over each row in the matrix. For each element with the value 1 in the row, it increments the `ones_in_the_row` variable, indicating the number of 1s in that row. If it\'s the first 1 in the row (`ones_in_the_row == 1`), it marks the corresponding column as potentially special. If it\'s not the first 1 in the row (`ones_in_the_row > 1`), it marks both the current and the previously marked columns as non-special.\n\nThe `columns` array is used to keep track of the status of each column:\n- `0`: Not marked\n- `1`: Potentially special (first 1 in the row)\n- `2`: Not special (more than one 1 in the row)\n\nAfter processing all rows, the method counts the columns marked as potentially special and returns the result.\n\n# Complexity\n- Time complexity: O(m * n)\n The time complexity is linear in the size of the matrix, where `m` is the number of rows and `n` is the number of columns.\n\n- Space complexity: O(n)\n The space complexity is linear in the number of columns, as the `columns` array is used to keep track of the status of each column.\n\n# Code\n```Java []\nclass Solution {\n public int numSpecial (int[][] nums) {\n int result = 0;\n int [] columns = new int [nums[0].length];\n for (int i = 0; i < nums.length; i ++) {\n int ones_in_the_row = 0;\n int column = 0;\n for (int j = 0; j < nums[i].length; j ++) {\n if (nums[i][j] == 1) {\n ones_in_the_row ++;\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n }\n else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n\n }\n for (int column : columns) {\n result += (column == 1 ? 1 : 0);\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& nums) {\n int result = 0;\n std::vector<int> columns(nums[0].size(), 0);\n\n for (int i = 0; i < nums.size(); ++i) {\n int ones_in_the_row = 0;\n int column = 0;\n\n for (int j = 0; j < nums[i].size(); ++j) {\n if (nums[i][j] == 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n for (int column : columns) {\n result += (column == 1 ? 1 : 0);\n }\n\n return result;\n }\n};\n```\n```Python []\nclass Solution:\n def numSpecial(self, nums: List[List[int]]) -> int:\n result = 0\n columns = [0] * len(nums[0])\n\n for i in range(len(nums)):\n ones_in_the_row = 0\n column = 0\n\n for j in range(len(nums[i])):\n if nums[i][j] == 1:\n ones_in_the_row += 1\n\n if ones_in_the_row == 1:\n columns[j] = 1 if columns[j] == 0 else 2\n column = j\n else:\n columns[column] = 2\n columns[j] = 2\n\n result += sum(column == 1 for column in columns)\n return result\n```\n```JavaScript []\nclass Solution {\n numSpecial(nums) {\n let result = 0;\n const columns = new Array(nums[0].length).fill(0);\n\n for (let i = 0; i < nums.length; ++i) {\n let ones_in_the_row = 0;\n let column = 0;\n\n for (let j = 0; j < nums[i].length; ++j) {\n if (nums[i][j] === 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row === 1) {\n columns[j] = columns[j] === 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n result += columns.filter(column => column === 1).length;\n return result;\n }\n}\n```\n```C# []\npublic class Solution {\n public int NumSpecial(int[][] nums) {\n int result = 0;\n int[] columns = new int[nums[0].Length];\n\n for (int i = 0; i < nums.Length; ++i) {\n int ones_in_the_row = 0;\n int column = 0;\n\n for (int j = 0; j < nums[i].Length; ++j) {\n if (nums[i][j] == 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n result += Array.FindAll(columns, column => column == 1).Length;\n return result;\n }\n}\n```\n```Ruby []\nclass Solution\n def num_special(nums)\n result = 0\n columns = Array.new(nums[0].length, 0)\n\n (0...nums.length).each do |i|\n ones_in_the_row = 0\n column = 0\n\n (0...nums[i].length).each do |j|\n if nums[i][j] == 1\n ones_in_the_row += 1\n\n if ones_in_the_row == 1\n columns[j] = columns[j] == 0 ? 1 : 2\n column = j\n else\n columns[column] = 2\n columns[j] = 2\n end\n end\n end\n end\n\n result += columns.count { |column| column == 1 }\n result\n end\nend\n```\n```Go []\ntype Solution struct{}\n\nfunc (s *Solution) NumSpecial(nums [][]int) int {\n\tresult := 0\n\tcolumns := make([]int, len(nums[0]))\n\n\tfor i := 0; i < len(nums); i++ {\n\t\tones_in_the_row := 0\n\t\tcolumn := 0\n\n\t\tfor j := 0; j < len(nums[i]); j++ {\n\t\t\tif nums[i][j] == 1 {\n\t\t\t\tones_in_the_row++\n\n\t\t\t\tif ones_in_the_row == 1 {\n\t\t\t\t\tif columns[j] == 0 {\n\t\t\t\t\t\tcolumns[j] = 1\n\t\t\t\t\t} else {\n\t\t\t\t\t\tcolumns[j] = 2\n\t\t\t\t\t}\n\t\t\t\t\tcolumn = j\n\t\t\t\t} else {\n\t\t\t\t\tcolumns[column] = 2\n\t\t\t\t\tcolumns[j] = 2\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\tfor _, column := range columns {\n\t\tif column == 1 {\n\t\t\tresult++\n\t\t}\n\t}\n\n\treturn result\n}\n```\n\n | 16 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
【Video】Give me 5 minutes - How we think about a solution | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\nCheck row and column direction.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,434\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n\u25A0 MVC(Most Valuable Comment) for me on youtube for the last 7 days\n\n\n\nThank you for your comment @bun_bun17! What you\'re saying is the greatest significance for my presence on YouTube.\n\nThanks everyone who left your comment and thanks everyone who watched videos!\n\n\n---\n\n# Approach\n## How we think about a solution\n\nThe phrase "special positions" implies that only one element in each row and each column has the value 1. Therefore, it seems appropriate to check all rows and columns for this condition.\n\n```\nInput: mat = [[1,0,0],[0,0,1],[1,0,0]]\n\n[1,0,0]\n[0,0,1]\n[1,0,0]\n```\n\nFirst of all, let\'s check row direction.\n```\n\u2192[1,0,0]\n\u2192[0,0,1]\n\u2192[1,0,0]\n```\n\nChecking each row individually, if the sum of elements in a row is 1, there is a potential for that row to have a special position. This is because if the sum is 0, it means there are no positions with a value of 1, and if the sum is 2, it implies there are two positions with a value of 1, which also does not qualify as a special position.\n\n---\n\n\u2B50\uFE0F Points\n\nFind rows with a sum of 1.\n\n---\n\nIn this case, all rows are a sum of 1.\n\n```\n\u2192[1,0,0] = 1\n\u2192[0,0,1] = 1\n\u2192[1,0,0] = 1\n```\nNext, let\'s check column direction. First of all, we need to know index of 1 in each row.\n\n```\n[1,0,0] = index 0 \n[0,0,1] = index 2\n[1,0,0] = index 0\n```\nThen, acutually we do the same thing. Calculate sum of each column.\n```\n \u2193 \u2193\n[1,0,0] = index 0 \n[0,0,1] = index 2\n[1,0,0] = index 0\n```\nIf sum of column is 1, that means we find one of special positions because we iterate the matrix in column direction based on index of possible position. In this case, column index 0 and 2.\n\n---\n\n\u2B50\uFE0F Points\n\nCheck columns based on index of possible position\n\n---\n\nIn the end, we know that only mat[1][2] is special position, because\n```\nsum of column index 0 is 2\nsum of column index 2 is 1\n```\n```\nOutput: 1\n```\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(m * (n + m))$$\n\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n def get_column_sum(col_idx):\n return sum(row[col_idx] for row in mat)\n\n special = 0\n for row in mat:\n if sum(row) == 1:\n col_idx = row.index(1)\n special += get_column_sum(col_idx) == 1\n\n return special\n```\n```javascript []\nvar numSpecial = function(mat) {\n function getColumnSum(colIdx) {\n return mat.reduce((sum, row) => sum + row[colIdx], 0);\n }\n\n let special = 0;\n for (let row of mat) {\n if (row.reduce((acc, val) => acc + val, 0) === 1) {\n const colIdx = row.indexOf(1);\n special += getColumnSum(colIdx) === 1;\n }\n }\n\n return special; \n};\n```\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int special = 0;\n\n for (int[] row : mat) {\n if (getRowSum(row) == 1) {\n int colIdx = getIndexOfOne(row);\n special += (getColumnSum(mat, colIdx) == 1) ? 1 : 0;\n }\n }\n\n return special; \n }\n\n private int getRowSum(int[] row) {\n int sum = 0;\n for (int num : row) {\n sum += num;\n }\n return sum;\n }\n\n private int getColumnSum(int[][] mat, int colIdx) {\n int sum = 0;\n for (int[] row : mat) {\n sum += row[colIdx];\n }\n return sum;\n }\n\n private int getIndexOfOne(int[] row) {\n for (int i = 0; i < row.length; i++) {\n if (row[i] == 1) {\n return i;\n }\n }\n return -1; // If 1 is not found, return -1 or handle accordingly\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int special = 0;\n\n for (const auto& row : mat) {\n if (accumulate(row.begin(), row.end(), 0) == 1) {\n int colIdx = distance(row.begin(), find(row.begin(), row.end(), 1));\n special += getColumnSum(mat, colIdx) == 1;\n }\n }\n\n return special; \n }\n\nprivate:\n int getColumnSum(const vector<vector<int>>& mat, int colIdx) {\n int sum = 0;\n for (const auto& row : mat) {\n sum += row[colIdx];\n }\n return sum;\n }\n};\n```\n\n## Step by step algorithm\n\n1. **Initialize Variables:**\n - `special`: A counter to keep track of the number of special positions.\n\n```python\nspecial = 0\n```\n\n2. **Iterate Over Each Row:**\n - Loop through each row in the matrix `mat`.\n\n```python\nfor row in mat:\n```\n\n3. **Check Sum of Current Row:**\n - Check if the sum of elements in the current row is equal to 1.\n\n```python\nif sum(row) == 1:\n```\n\n4. **Find Column Index with Value 1:**\n - If the sum is 1, find the index of the element with value 1 in the current row. This assumes there is exactly one element with value 1 in the row.\n\n```python\ncol_idx = row.index(1)\n```\n\n5. **Calculate Column Sum:**\n - Use the `get_column_sum` function to calculate the sum of elements in the column with index `col_idx`.\n\n```python\ncol_sum = get_column_sum(col_idx)\n```\n\n - The `get_column_sum` function iterates through each row and accumulates the value in the specified column.\n\n```python\ndef get_column_sum(col_idx):\n return sum(row[col_idx] for row in mat)\n```\n\n6. **Check if Column Sum is 1:**\n - If the column sum is also equal to 1, it indicates that the element at the intersection of the identified row and column is the only \'1\' in its row and column. Increment the `special` counter.\n\n```python\nspecial += col_sum == 1\n```\n\n7. **Return the Result:**\n - The final result is the count of special positions.\n\n```python\nreturn special\n```\n\nIn summary, the algorithm iterates through each row, checks if the sum of elements in the row is 1, finds the corresponding column index with a value of 1, calculates the sum of elements in that column, and increments the `special` counter if both row and column sums are equal to 1. The final result is the count of special positions in the matrix.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/difference-between-ones-and-zeros-in-row-and-column/solutions/4401811/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/swafoNFu99o\n\n\u25A0 Timeline of the video\n\n`0:06` Create number of 1 in each row and column\n`1:16` How to calculate numbers at each position \n`4:03` Coding\n`6:32` Time Complexity and Space Complexity\n`7:02` Explain zip(*grid)\n`8:15` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n | 56 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
【Video】Give me 5 minutes - How we think about a solution | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\nCheck row and column direction.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,434\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n\u25A0 MVC(Most Valuable Comment) for me on youtube for the last 7 days\n\n\n\nThank you for your comment @bun_bun17! What you\'re saying is the greatest significance for my presence on YouTube.\n\nThanks everyone who left your comment and thanks everyone who watched videos!\n\n\n---\n\n# Approach\n## How we think about a solution\n\nThe phrase "special positions" implies that only one element in each row and each column has the value 1. Therefore, it seems appropriate to check all rows and columns for this condition.\n\n```\nInput: mat = [[1,0,0],[0,0,1],[1,0,0]]\n\n[1,0,0]\n[0,0,1]\n[1,0,0]\n```\n\nFirst of all, let\'s check row direction.\n```\n\u2192[1,0,0]\n\u2192[0,0,1]\n\u2192[1,0,0]\n```\n\nChecking each row individually, if the sum of elements in a row is 1, there is a potential for that row to have a special position. This is because if the sum is 0, it means there are no positions with a value of 1, and if the sum is 2, it implies there are two positions with a value of 1, which also does not qualify as a special position.\n\n---\n\n\u2B50\uFE0F Points\n\nFind rows with a sum of 1.\n\n---\n\nIn this case, all rows are a sum of 1.\n\n```\n\u2192[1,0,0] = 1\n\u2192[0,0,1] = 1\n\u2192[1,0,0] = 1\n```\nNext, let\'s check column direction. First of all, we need to know index of 1 in each row.\n\n```\n[1,0,0] = index 0 \n[0,0,1] = index 2\n[1,0,0] = index 0\n```\nThen, acutually we do the same thing. Calculate sum of each column.\n```\n \u2193 \u2193\n[1,0,0] = index 0 \n[0,0,1] = index 2\n[1,0,0] = index 0\n```\nIf sum of column is 1, that means we find one of special positions because we iterate the matrix in column direction based on index of possible position. In this case, column index 0 and 2.\n\n---\n\n\u2B50\uFE0F Points\n\nCheck columns based on index of possible position\n\n---\n\nIn the end, we know that only mat[1][2] is special position, because\n```\nsum of column index 0 is 2\nsum of column index 2 is 1\n```\n```\nOutput: 1\n```\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(m * (n + m))$$\n\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n def get_column_sum(col_idx):\n return sum(row[col_idx] for row in mat)\n\n special = 0\n for row in mat:\n if sum(row) == 1:\n col_idx = row.index(1)\n special += get_column_sum(col_idx) == 1\n\n return special\n```\n```javascript []\nvar numSpecial = function(mat) {\n function getColumnSum(colIdx) {\n return mat.reduce((sum, row) => sum + row[colIdx], 0);\n }\n\n let special = 0;\n for (let row of mat) {\n if (row.reduce((acc, val) => acc + val, 0) === 1) {\n const colIdx = row.indexOf(1);\n special += getColumnSum(colIdx) === 1;\n }\n }\n\n return special; \n};\n```\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int special = 0;\n\n for (int[] row : mat) {\n if (getRowSum(row) == 1) {\n int colIdx = getIndexOfOne(row);\n special += (getColumnSum(mat, colIdx) == 1) ? 1 : 0;\n }\n }\n\n return special; \n }\n\n private int getRowSum(int[] row) {\n int sum = 0;\n for (int num : row) {\n sum += num;\n }\n return sum;\n }\n\n private int getColumnSum(int[][] mat, int colIdx) {\n int sum = 0;\n for (int[] row : mat) {\n sum += row[colIdx];\n }\n return sum;\n }\n\n private int getIndexOfOne(int[] row) {\n for (int i = 0; i < row.length; i++) {\n if (row[i] == 1) {\n return i;\n }\n }\n return -1; // If 1 is not found, return -1 or handle accordingly\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int special = 0;\n\n for (const auto& row : mat) {\n if (accumulate(row.begin(), row.end(), 0) == 1) {\n int colIdx = distance(row.begin(), find(row.begin(), row.end(), 1));\n special += getColumnSum(mat, colIdx) == 1;\n }\n }\n\n return special; \n }\n\nprivate:\n int getColumnSum(const vector<vector<int>>& mat, int colIdx) {\n int sum = 0;\n for (const auto& row : mat) {\n sum += row[colIdx];\n }\n return sum;\n }\n};\n```\n\n## Step by step algorithm\n\n1. **Initialize Variables:**\n - `special`: A counter to keep track of the number of special positions.\n\n```python\nspecial = 0\n```\n\n2. **Iterate Over Each Row:**\n - Loop through each row in the matrix `mat`.\n\n```python\nfor row in mat:\n```\n\n3. **Check Sum of Current Row:**\n - Check if the sum of elements in the current row is equal to 1.\n\n```python\nif sum(row) == 1:\n```\n\n4. **Find Column Index with Value 1:**\n - If the sum is 1, find the index of the element with value 1 in the current row. This assumes there is exactly one element with value 1 in the row.\n\n```python\ncol_idx = row.index(1)\n```\n\n5. **Calculate Column Sum:**\n - Use the `get_column_sum` function to calculate the sum of elements in the column with index `col_idx`.\n\n```python\ncol_sum = get_column_sum(col_idx)\n```\n\n - The `get_column_sum` function iterates through each row and accumulates the value in the specified column.\n\n```python\ndef get_column_sum(col_idx):\n return sum(row[col_idx] for row in mat)\n```\n\n6. **Check if Column Sum is 1:**\n - If the column sum is also equal to 1, it indicates that the element at the intersection of the identified row and column is the only \'1\' in its row and column. Increment the `special` counter.\n\n```python\nspecial += col_sum == 1\n```\n\n7. **Return the Result:**\n - The final result is the count of special positions.\n\n```python\nreturn special\n```\n\nIn summary, the algorithm iterates through each row, checks if the sum of elements in the row is 1, finds the corresponding column index with a value of 1, calculates the sum of elements in that column, and increments the `special` counter if both row and column sums are equal to 1. The final result is the count of special positions in the matrix.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/difference-between-ones-and-zeros-in-row-and-column/solutions/4401811/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/swafoNFu99o\n\n\u25A0 Timeline of the video\n\n`0:06` Create number of 1 in each row and column\n`1:16` How to calculate numbers at each position \n`4:03` Coding\n`6:32` Time Complexity and Space Complexity\n`7:02` Explain zip(*grid)\n`8:15` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n | 56 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | special-positions-in-a-binary-matrix | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Brute Force)***\n1. It iterates through each element of the matrix, checking if it equals 1.\n1. For each element that equals 1, it checks the entire row and column to see if there are any other \'1\'s apart from the current row or column.\n1. If the element has no other \'1\'s in its row and column except for itself, it is considered "special," and the counter \'ans\' is incremented.\n1. Finally, the function returns the count of "special" elements found in the matrix.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n.(m+n)))$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to count the number of "special" elements in the given matrix \'mat\'\n int numSpecial(vector<vector<int>>& mat) {\n int ans = 0; // Variable to store the count of "special" elements\n int m = mat.size(); // Number of rows in the matrix\n int n = mat[0].size(); // Number of columns in the matrix\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n \n bool good = true; // Flag to determine if the element is "special"\n \n // Checking the entire column for other \'1\'s except for the current row\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = false; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n \n // Checking the entire row for other \'1\'s except for the current column\n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = false; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n \n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n \n return ans; // Return the count of "special" elements\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int ans = 0;\n int m = matSize; // Number of rows in the matrix\n int n = *matColSize; // Number of columns in the matrix\n\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n\n int good = 1; // Flag to determine if the element is "special"\n\n // Checking the entire column for other \'1\'s except for the current row\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = 0; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n\n // Checking the entire row for other \'1\'s except for the current column\n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = 0; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n\n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int ans = 0;\n int m = mat.length;\n int n = mat[0].length;\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue;\n }\n \n boolean good = true;\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = false;\n break;\n }\n }\n \n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = false;\n break;\n }\n }\n \n if (good) {\n ans++;\n }\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n ans = 0\n m = len(mat)\n n = len(mat[0])\n \n for row in range(m):\n for col in range(n):\n if mat[row][col] == 0:\n continue\n \n good = True\n for r in range(m):\n if r != row and mat[r][col] == 1:\n good = False\n break\n \n for c in range(n):\n if c != col and mat[row][c] == 1:\n good = False\n break\n \n if good:\n ans += 1\n \n return ans\n\n\n```\n```javascript []\nfunction numSpecial(mat) {\n let ans = 0;\n const m = mat.length; // Number of rows in the matrix\n const n = mat[0].length; // Number of columns in the matrix\n\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n\n let good = true; // Flag to determine if the element is "special"\n\n // Checking the entire column for other \'1\'s except for the current row\n for (let r = 0; r < m; r++) {\n if (r !== row && mat[r][col] === 1) {\n good = false; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n\n // Checking the entire row for other \'1\'s except for the current column\n for (let c = 0; c < n; c++) {\n if (c !== col && mat[row][c] === 1) {\n good = false; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n\n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n```\n\n---\n\n#### ***Approach 2(Pre Count)***\n1. It first calculates the count of \'1\'s in each row and column and stores them in the rowCount and colCount vectors, respectively.\n1. Then, it iterates through each element of the matrix and checks if the element is \'1\' and if its corresponding row and column contain exactly one \'1\'. If so, it counts it as a "special" element.\n1. Finally, it returns the count of "special" elements found in the matrix.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n)$$\n \n\n- *Space complexity:*\n $$O(m+n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to count the number of "special" elements in the given matrix \'mat\'\n int numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(); // Number of rows in the matrix\n int n = mat[0].size(); // Number of columns in the matrix\n\n // Vector to store counts of \'1\'s in each row and column\n vector<int> rowCount(m, 0); // Initialize row count vector with 0s\n vector<int> colCount(n, 0); // Initialize column count vector with 0s\n\n // Counting \'1\'s in each row and column\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n int ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) { // If the element is \'1\'\n if (rowCount[row] == 1 && colCount[col] == 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n }\n};\n\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int m = matSize; // Number of rows in the matrix\n int n = *matColSize; // Number of columns in the matrix\n\n // Array to store counts of \'1\'s in each row and column\n int* rowCount = (int*)calloc(m, sizeof(int)); // Initialize row count array with 0s\n int* colCount = (int*)calloc(n, sizeof(int)); // Initialize column count array with 0s\n\n // Counting \'1\'s in each row and column\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n int ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) { // If the element is \'1\'\n if (rowCount[row] == 1 && colCount[col] == 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n free(rowCount);\n free(colCount);\n return ans; // Return the count of "special" elements\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int m = mat.length;\n int n = mat[0].length;\n int[] rowCount = new int[m];\n int[] colCount = new int[n];\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++;\n colCount[col]++;\n }\n }\n }\n \n int ans = 0;\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n if (rowCount[row] == 1 && colCount[col] == 1) {\n ans++;\n }\n }\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\n\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m = len(mat)\n n = len(mat[0])\n row_count = [0] * m\n col_count = [0] * n\n \n for row in range(m):\n for col in range(n):\n if mat[row][col] == 1:\n row_count[row] += 1\n col_count[col] += 1\n \n ans = 0\n for row in range(m):\n for col in range(n):\n if mat[row][col] == 1:\n if row_count[row] == 1 and col_count[col] == 1:\n ans += 1\n\n return ans\n\n```\n```javascript []\nfunction numSpecial(mat) {\n const m = mat.length; // Number of rows in the matrix\n const n = mat[0].length; // Number of columns in the matrix\n\n // Arrays to store counts of \'1\'s in each row and column\n const rowCount = new Array(m).fill(0); // Initialize row count array with 0s\n const colCount = new Array(n).fill(0); // Initialize column count array with 0s\n\n // Counting \'1\'s in each row and column\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n let ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 1) { // If the element is \'1\'\n if (rowCount[row] === 1 && colCount[col] === 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 38 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | special-positions-in-a-binary-matrix | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Brute Force)***\n1. It iterates through each element of the matrix, checking if it equals 1.\n1. For each element that equals 1, it checks the entire row and column to see if there are any other \'1\'s apart from the current row or column.\n1. If the element has no other \'1\'s in its row and column except for itself, it is considered "special," and the counter \'ans\' is incremented.\n1. Finally, the function returns the count of "special" elements found in the matrix.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n.(m+n)))$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to count the number of "special" elements in the given matrix \'mat\'\n int numSpecial(vector<vector<int>>& mat) {\n int ans = 0; // Variable to store the count of "special" elements\n int m = mat.size(); // Number of rows in the matrix\n int n = mat[0].size(); // Number of columns in the matrix\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n \n bool good = true; // Flag to determine if the element is "special"\n \n // Checking the entire column for other \'1\'s except for the current row\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = false; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n \n // Checking the entire row for other \'1\'s except for the current column\n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = false; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n \n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n \n return ans; // Return the count of "special" elements\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int ans = 0;\n int m = matSize; // Number of rows in the matrix\n int n = *matColSize; // Number of columns in the matrix\n\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n\n int good = 1; // Flag to determine if the element is "special"\n\n // Checking the entire column for other \'1\'s except for the current row\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = 0; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n\n // Checking the entire row for other \'1\'s except for the current column\n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = 0; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n\n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int ans = 0;\n int m = mat.length;\n int n = mat[0].length;\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue;\n }\n \n boolean good = true;\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = false;\n break;\n }\n }\n \n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = false;\n break;\n }\n }\n \n if (good) {\n ans++;\n }\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n ans = 0\n m = len(mat)\n n = len(mat[0])\n \n for row in range(m):\n for col in range(n):\n if mat[row][col] == 0:\n continue\n \n good = True\n for r in range(m):\n if r != row and mat[r][col] == 1:\n good = False\n break\n \n for c in range(n):\n if c != col and mat[row][c] == 1:\n good = False\n break\n \n if good:\n ans += 1\n \n return ans\n\n\n```\n```javascript []\nfunction numSpecial(mat) {\n let ans = 0;\n const m = mat.length; // Number of rows in the matrix\n const n = mat[0].length; // Number of columns in the matrix\n\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n\n let good = true; // Flag to determine if the element is "special"\n\n // Checking the entire column for other \'1\'s except for the current row\n for (let r = 0; r < m; r++) {\n if (r !== row && mat[r][col] === 1) {\n good = false; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n\n // Checking the entire row for other \'1\'s except for the current column\n for (let c = 0; c < n; c++) {\n if (c !== col && mat[row][c] === 1) {\n good = false; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n\n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n```\n\n---\n\n#### ***Approach 2(Pre Count)***\n1. It first calculates the count of \'1\'s in each row and column and stores them in the rowCount and colCount vectors, respectively.\n1. Then, it iterates through each element of the matrix and checks if the element is \'1\' and if its corresponding row and column contain exactly one \'1\'. If so, it counts it as a "special" element.\n1. Finally, it returns the count of "special" elements found in the matrix.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n)$$\n \n\n- *Space complexity:*\n $$O(m+n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to count the number of "special" elements in the given matrix \'mat\'\n int numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(); // Number of rows in the matrix\n int n = mat[0].size(); // Number of columns in the matrix\n\n // Vector to store counts of \'1\'s in each row and column\n vector<int> rowCount(m, 0); // Initialize row count vector with 0s\n vector<int> colCount(n, 0); // Initialize column count vector with 0s\n\n // Counting \'1\'s in each row and column\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n int ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) { // If the element is \'1\'\n if (rowCount[row] == 1 && colCount[col] == 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n }\n};\n\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int m = matSize; // Number of rows in the matrix\n int n = *matColSize; // Number of columns in the matrix\n\n // Array to store counts of \'1\'s in each row and column\n int* rowCount = (int*)calloc(m, sizeof(int)); // Initialize row count array with 0s\n int* colCount = (int*)calloc(n, sizeof(int)); // Initialize column count array with 0s\n\n // Counting \'1\'s in each row and column\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n int ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) { // If the element is \'1\'\n if (rowCount[row] == 1 && colCount[col] == 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n free(rowCount);\n free(colCount);\n return ans; // Return the count of "special" elements\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int m = mat.length;\n int n = mat[0].length;\n int[] rowCount = new int[m];\n int[] colCount = new int[n];\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++;\n colCount[col]++;\n }\n }\n }\n \n int ans = 0;\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n if (rowCount[row] == 1 && colCount[col] == 1) {\n ans++;\n }\n }\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\n\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m = len(mat)\n n = len(mat[0])\n row_count = [0] * m\n col_count = [0] * n\n \n for row in range(m):\n for col in range(n):\n if mat[row][col] == 1:\n row_count[row] += 1\n col_count[col] += 1\n \n ans = 0\n for row in range(m):\n for col in range(n):\n if mat[row][col] == 1:\n if row_count[row] == 1 and col_count[col] == 1:\n ans += 1\n\n return ans\n\n```\n```javascript []\nfunction numSpecial(mat) {\n const m = mat.length; // Number of rows in the matrix\n const n = mat[0].length; // Number of columns in the matrix\n\n // Arrays to store counts of \'1\'s in each row and column\n const rowCount = new Array(m).fill(0); // Initialize row count array with 0s\n const colCount = new Array(n).fill(0); // Initialize column count array with 0s\n\n // Counting \'1\'s in each row and column\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n let ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 1) { // If the element is \'1\'\n if (rowCount[row] === 1 && colCount[col] === 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 38 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
C++/Python one pass||0 ms Beats 100% | special-positions-in-a-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck which rows & columns have exactly one 1!\n\nThe revised C++ code simplifies the loop. The unnecessary copying for column vector is omitted which becomes a fast code, runs in 0 ms and beats 100%!\n\nPython code is in the same manner implemented which runs in 137ms & beats 100%.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a function `check1` to locate the positions of 1\'s in a vector. This`check1` function is useful. The very crucual part is especially when `idx=check1(vect, sz).size()>1`; the columns `j` in `idx` cannot be special indices which can save redundant checking.\n```\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n```\nIt takes a reference to a vector of integers `vect` and an integer `sz` as parameters. The function iterates through the elements of vect and collects the indices where the value is equal to 1 into a new vector `ans`. \n\n```\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n for(int k=i+1; k<m; k++)\n col_j[k]=mat[k][j];\n if (check1(col_j, m).size()==0){\n // cout<<"("<<i<<","<<j<<")";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n\n```\nIt iterates through each row of the matrix (`mat`). For each row, it uses the `check1` function to find the indices of \'1\' in that row (`idx`). If there is exactly one \'1\' in the row and the corresponding column (`j`) has not been marked (`col[j] == 0`), it marks the column, copies the column into `col_j`, and checks if there is exactly one \'1\' in the column using `check1`. If true, it increments the ans counter.\n\nIf there is more than one \'1\' in the row, it marks all the corresponding columns in the `col` vector.\n\nLet\'s consider the testcase\n`[[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,1],[0,0,0,0,1,0,0,0],[1,0,0,0,1,0,0,0],[0,0,1,1,0,0,0,0],[0,0,0,0,0,0,1,0]]`\nThe speical indices are `(0,5), (5,6)`. The process is as follows\n```\nrow0->idx=[5]:(0,5)\nrow1->idx=[4,7] \nrow2->idx=[4] \nrow3->idx=[0,4] \nrow4->idx=[2,3] \nrow5->idx=[6]:(5,6)\n\nans=2\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(m+n)$\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);// check or \n vector<int> col_j(m);\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 for(int k=i+1; k<m; k++)//Check if other 1 in remaining rows\n count_col1+=mat[k][j];\n if (count_col1==0){\n // cout<<"("<<i<<","<<j<<")\\n";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Revised C++ 0 ms Beats 100% \n```\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);//already check or not\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n int count_col1=0;\n for(int k=i+1; k<m; k++)//Check if other 1 in remaining rows\n count_col1+=mat[k][j];\n if (count_col1==0){\n // cout<<"("<<i<<","<<j<<")\\n";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n```\n# Python code runs in 137ms & beats 100%\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n def check1(row):\n ans=[]\n for i, x in enumerate(row):\n if x==1: \n ans.append(i)\n return ans\n m=len(mat)\n n=len(mat[0])\n ans=0\n col=[False]*n\n for row in mat:\n idx=check1(row)\n if len(idx)==1 and not col[j:=idx[0]]:\n col[j]=True\n count_col1=0\n for k in range(m):\n count_col1+=mat[k][j]\n if count_col1==1:\n ans+=1\n else:\n for j in idx:\n col[j]==True\n return ans\n``` | 9 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
C++/Python one pass||0 ms Beats 100% | special-positions-in-a-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck which rows & columns have exactly one 1!\n\nThe revised C++ code simplifies the loop. The unnecessary copying for column vector is omitted which becomes a fast code, runs in 0 ms and beats 100%!\n\nPython code is in the same manner implemented which runs in 137ms & beats 100%.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a function `check1` to locate the positions of 1\'s in a vector. This`check1` function is useful. The very crucual part is especially when `idx=check1(vect, sz).size()>1`; the columns `j` in `idx` cannot be special indices which can save redundant checking.\n```\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n```\nIt takes a reference to a vector of integers `vect` and an integer `sz` as parameters. The function iterates through the elements of vect and collects the indices where the value is equal to 1 into a new vector `ans`. \n\n```\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n for(int k=i+1; k<m; k++)\n col_j[k]=mat[k][j];\n if (check1(col_j, m).size()==0){\n // cout<<"("<<i<<","<<j<<")";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n\n```\nIt iterates through each row of the matrix (`mat`). For each row, it uses the `check1` function to find the indices of \'1\' in that row (`idx`). If there is exactly one \'1\' in the row and the corresponding column (`j`) has not been marked (`col[j] == 0`), it marks the column, copies the column into `col_j`, and checks if there is exactly one \'1\' in the column using `check1`. If true, it increments the ans counter.\n\nIf there is more than one \'1\' in the row, it marks all the corresponding columns in the `col` vector.\n\nLet\'s consider the testcase\n`[[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,1],[0,0,0,0,1,0,0,0],[1,0,0,0,1,0,0,0],[0,0,1,1,0,0,0,0],[0,0,0,0,0,0,1,0]]`\nThe speical indices are `(0,5), (5,6)`. The process is as follows\n```\nrow0->idx=[5]:(0,5)\nrow1->idx=[4,7] \nrow2->idx=[4] \nrow3->idx=[0,4] \nrow4->idx=[2,3] \nrow5->idx=[6]:(5,6)\n\nans=2\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(m+n)$\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);// check or \n vector<int> col_j(m);\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 for(int k=i+1; k<m; k++)//Check if other 1 in remaining rows\n count_col1+=mat[k][j];\n if (count_col1==0){\n // cout<<"("<<i<<","<<j<<")\\n";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Revised C++ 0 ms Beats 100% \n```\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);//already check or not\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n int count_col1=0;\n for(int k=i+1; k<m; k++)//Check if other 1 in remaining rows\n count_col1+=mat[k][j];\n if (count_col1==0){\n // cout<<"("<<i<<","<<j<<")\\n";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n```\n# Python code runs in 137ms & beats 100%\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n def check1(row):\n ans=[]\n for i, x in enumerate(row):\n if x==1: \n ans.append(i)\n return ans\n m=len(mat)\n n=len(mat[0])\n ans=0\n col=[False]*n\n for row in mat:\n idx=check1(row)\n if len(idx)==1 and not col[j:=idx[0]]:\n col[j]=True\n count_col1=0\n for k in range(m):\n count_col1+=mat[k][j]\n if count_col1==1:\n ans+=1\n else:\n for j in idx:\n col[j]==True\n return ans\n``` | 9 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
🚀✅🚀 100% beats Users by TC || Java, C#, Python, Rust, C++, C, Ruby, Go|| 🔥🔥 | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\nThe problem seems to be asking for the number of special positions in a binary matrix. A position is considered special if it contains a 1 and the sum of elements in its row and column is 1.\n\n# Approach\nThe provided code iterates through each element of the matrix and checks if it is 1. If it is, it calculates the sum of elements in its row and column and checks if both sums are equal to 1. If they are, the position is considered special, and the result is incremented.\n\n# Complexity\n- Time complexity: O(m * n^2), where m is the number of rows and n is the number of columns in the matrix.\n- Space complexity: O(1) as no additional space is used.\n\n# Code\n```csharp []\npublic class Solution {\n public int NumSpecial(int[][] mat)\n {\n int result = 0;\n for (int i = 0; i < mat.Length; i++)\n {\n for (int j = 0; j < mat[i].Length; j++)\n {\n if (mat[i][j] == 1)\n {\n int sumx = 0;\n int sumy = 0;\n for (int m = 0; m < mat[i].Length; m++)\n {\n sumx += mat[i][m];\n }\n for (int k = 0; k < mat.Length; k++)\n {\n sumy += mat[k][j];\n }\n if (sumx == 1 && sumy == 1)\n {\n result++;\n }\n }\n }\n }\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int numSpecial(int[][] mat) {\n int result = 0;\n\n // Arrays to store the sums of elements in each row and column\n int[] rowSums = new int[mat.length];\n int[] colSums = new int[mat[0].length];\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[i].length; j++) {\n rowSums[i] += mat[i][j];\n colSums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {\n result++;\n }\n }\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n result = 0\n\n # Lists to store the sums of elements in each row and column\n row_sums = [0] * len(mat)\n col_sums = [0] * len(mat[0])\n\n # Calculate the sums of elements in each row and column\n for i in range(len(mat)):\n for j in range(len(mat[i])):\n row_sums[i] += mat[i][j]\n col_sums[j] += mat[i][j]\n\n # Check if each 1 is special using the precalculated sums\n for i in range(len(mat)):\n for j in range(len(mat[i])):\n if mat[i][j] == 1 and row_sums[i] == 1 and col_sums[j] == 1:\n result += 1\n\n return result\n```\n``` Go []\nfunc numSpecial(mat [][]int) int {\n\tresult := 0\n\n\t// Slices to store the sums of elements in each row and column\n\trowSums := make([]int, len(mat))\n\tcolSums := make([]int, len(mat[0]))\n\n\t// Calculate the sums of elements in each row and column\n\tfor i := 0; i < len(mat); i++ {\n\t\tfor j := 0; j < len(mat[i]); j++ {\n\t\t\trowSums[i] += mat[i][j]\n\t\t\tcolSums[j] += mat[i][j]\n\t\t}\n\t}\n\n\t// Check if each 1 is special using the precalculated sums\n\tfor i := 0; i < len(mat); i++ {\n\t\tfor j := 0; j < len(mat[i]); j++ {\n\t\t\tif mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1 {\n\t\t\t\tresult++\n\t\t\t}\n\t\t}\n\t}\n\n\treturn result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {\n let mut result = 0;\n\n // Vectors to store the sums of elements in each row and column\n let mut row_sums = vec![0; mat.len()];\n let mut col_sums = vec![0; mat[0].len()];\n\n // Calculate the sums of elements in each row and column\n for i in 0..mat.len() {\n for j in 0..mat[i].len() {\n row_sums[i] += mat[i][j];\n col_sums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for i in 0..mat.len() {\n for j in 0..mat[i].len() {\n if mat[i][j] == 1 && row_sums[i] == 1 && col_sums[j] == 1 {\n result += 1;\n }\n }\n }\n\n result\n }\n}\n```\n``` Ruby []\ndef num_special(mat)\n result = 0\n\n # Arrays to store the sums of elements in each row and column\n row_sums = Array.new(mat.length, 0)\n col_sums = Array.new(mat[0].length, 0)\n\n # Calculate the sums of elements in each row and column\n mat.each_with_index do |row, i|\n row.each_with_index do |value, j|\n row_sums[i] += value\n col_sums[j] += value\n end\n end\n\n # Check if each 1 is special using the precalculated sums\n mat.each_with_index do |row, i|\n row.each_with_index do |value, j|\n if value == 1 && row_sums[i] == 1 && col_sums[j] == 1\n result += 1\n end\n end\n end\n\n result\nend\n```\n```Cpp []\n#include <vector>\n\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& mat) {\n int result = 0;\n\n // Vectors to store the sums of elements in each row and column\n std::vector<int> row_sums(mat.size(), 0);\n std::vector<int> col_sums(mat[0].size(), 0);\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[i].size(); j++) {\n row_sums[i] += mat[i][j];\n col_sums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[i].size(); j++) {\n if (mat[i][j] == 1 && row_sums[i] == 1 && col_sums[j] == 1) {\n result++;\n }\n }\n }\n\n return result;\n }\n};\n```\n```c []\n#include <stdlib.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int result = 0;\n\n // Arrays to store the sums of elements in each row and column\n int* rowSums = (int*)malloc(matSize * sizeof(int));\n int* colSums = (int*)malloc(matColSize[0] * sizeof(int));\n\n // Initialize rowSums and colSums to zeros\n for (int i = 0; i < matSize; i++) {\n rowSums[i] = 0;\n }\n for (int j = 0; j < matColSize[0]; j++) {\n colSums[j] = 0;\n }\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < matColSize[0]; j++) {\n rowSums[i] += mat[i][j];\n colSums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < matColSize[0]; j++) {\n if (mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {\n result++;\n }\n }\n }\n\n // Free allocated memory\n free(rowSums);\n free(colSums);\n\n return result;\n}\n```\n\n\n- Please upvote me !!! | 9 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
🚀✅🚀 100% beats Users by TC || Java, C#, Python, Rust, C++, C, Ruby, Go|| 🔥🔥 | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\nThe problem seems to be asking for the number of special positions in a binary matrix. A position is considered special if it contains a 1 and the sum of elements in its row and column is 1.\n\n# Approach\nThe provided code iterates through each element of the matrix and checks if it is 1. If it is, it calculates the sum of elements in its row and column and checks if both sums are equal to 1. If they are, the position is considered special, and the result is incremented.\n\n# Complexity\n- Time complexity: O(m * n^2), where m is the number of rows and n is the number of columns in the matrix.\n- Space complexity: O(1) as no additional space is used.\n\n# Code\n```csharp []\npublic class Solution {\n public int NumSpecial(int[][] mat)\n {\n int result = 0;\n for (int i = 0; i < mat.Length; i++)\n {\n for (int j = 0; j < mat[i].Length; j++)\n {\n if (mat[i][j] == 1)\n {\n int sumx = 0;\n int sumy = 0;\n for (int m = 0; m < mat[i].Length; m++)\n {\n sumx += mat[i][m];\n }\n for (int k = 0; k < mat.Length; k++)\n {\n sumy += mat[k][j];\n }\n if (sumx == 1 && sumy == 1)\n {\n result++;\n }\n }\n }\n }\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int numSpecial(int[][] mat) {\n int result = 0;\n\n // Arrays to store the sums of elements in each row and column\n int[] rowSums = new int[mat.length];\n int[] colSums = new int[mat[0].length];\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[i].length; j++) {\n rowSums[i] += mat[i][j];\n colSums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {\n result++;\n }\n }\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n result = 0\n\n # Lists to store the sums of elements in each row and column\n row_sums = [0] * len(mat)\n col_sums = [0] * len(mat[0])\n\n # Calculate the sums of elements in each row and column\n for i in range(len(mat)):\n for j in range(len(mat[i])):\n row_sums[i] += mat[i][j]\n col_sums[j] += mat[i][j]\n\n # Check if each 1 is special using the precalculated sums\n for i in range(len(mat)):\n for j in range(len(mat[i])):\n if mat[i][j] == 1 and row_sums[i] == 1 and col_sums[j] == 1:\n result += 1\n\n return result\n```\n``` Go []\nfunc numSpecial(mat [][]int) int {\n\tresult := 0\n\n\t// Slices to store the sums of elements in each row and column\n\trowSums := make([]int, len(mat))\n\tcolSums := make([]int, len(mat[0]))\n\n\t// Calculate the sums of elements in each row and column\n\tfor i := 0; i < len(mat); i++ {\n\t\tfor j := 0; j < len(mat[i]); j++ {\n\t\t\trowSums[i] += mat[i][j]\n\t\t\tcolSums[j] += mat[i][j]\n\t\t}\n\t}\n\n\t// Check if each 1 is special using the precalculated sums\n\tfor i := 0; i < len(mat); i++ {\n\t\tfor j := 0; j < len(mat[i]); j++ {\n\t\t\tif mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1 {\n\t\t\t\tresult++\n\t\t\t}\n\t\t}\n\t}\n\n\treturn result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {\n let mut result = 0;\n\n // Vectors to store the sums of elements in each row and column\n let mut row_sums = vec![0; mat.len()];\n let mut col_sums = vec![0; mat[0].len()];\n\n // Calculate the sums of elements in each row and column\n for i in 0..mat.len() {\n for j in 0..mat[i].len() {\n row_sums[i] += mat[i][j];\n col_sums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for i in 0..mat.len() {\n for j in 0..mat[i].len() {\n if mat[i][j] == 1 && row_sums[i] == 1 && col_sums[j] == 1 {\n result += 1;\n }\n }\n }\n\n result\n }\n}\n```\n``` Ruby []\ndef num_special(mat)\n result = 0\n\n # Arrays to store the sums of elements in each row and column\n row_sums = Array.new(mat.length, 0)\n col_sums = Array.new(mat[0].length, 0)\n\n # Calculate the sums of elements in each row and column\n mat.each_with_index do |row, i|\n row.each_with_index do |value, j|\n row_sums[i] += value\n col_sums[j] += value\n end\n end\n\n # Check if each 1 is special using the precalculated sums\n mat.each_with_index do |row, i|\n row.each_with_index do |value, j|\n if value == 1 && row_sums[i] == 1 && col_sums[j] == 1\n result += 1\n end\n end\n end\n\n result\nend\n```\n```Cpp []\n#include <vector>\n\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& mat) {\n int result = 0;\n\n // Vectors to store the sums of elements in each row and column\n std::vector<int> row_sums(mat.size(), 0);\n std::vector<int> col_sums(mat[0].size(), 0);\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[i].size(); j++) {\n row_sums[i] += mat[i][j];\n col_sums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[i].size(); j++) {\n if (mat[i][j] == 1 && row_sums[i] == 1 && col_sums[j] == 1) {\n result++;\n }\n }\n }\n\n return result;\n }\n};\n```\n```c []\n#include <stdlib.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int result = 0;\n\n // Arrays to store the sums of elements in each row and column\n int* rowSums = (int*)malloc(matSize * sizeof(int));\n int* colSums = (int*)malloc(matColSize[0] * sizeof(int));\n\n // Initialize rowSums and colSums to zeros\n for (int i = 0; i < matSize; i++) {\n rowSums[i] = 0;\n }\n for (int j = 0; j < matColSize[0]; j++) {\n colSums[j] = 0;\n }\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < matColSize[0]; j++) {\n rowSums[i] += mat[i][j];\n colSums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < matColSize[0]; j++) {\n if (mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {\n result++;\n }\n }\n }\n\n // Free allocated memory\n free(rowSums);\n free(colSums);\n\n return result;\n}\n```\n\n\n- Please upvote me !!! | 9 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
💯Faster✅💯 Lesser✅2 Methods🔥Brute Force🔥Hashing🔥Python🐍Java☕C++✅C📈 | special-positions-in-a-binary-matrix | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 2 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe problem involves finding the number of special positions in a binary matrix. A special position is defined as a cell with a value of 1 and having all other cells in the same row and column as 0. The task is to determine the count of such special positions in the given binary matrix.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering two different methods to solve this problem:\n1. Brute Force\n2. Hashing\n\n# 1. Brute Force: \n- Iterate through each cell in the matrix.\n- For each cell with a value of 1, check if all other cells in its row and column are 0.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(n^3)`, where n is the size of the matrix.\n\n- \uD83D\uDE80 Space Complexity: `O(1)` - no extra space used.\n\n# Code\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n count = 0\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 1 and sum(mat[i]) == 1 and sum(row[j] for row in mat) == 1:\n count += 1\n return count\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n int sumR = 0;\n int sumC = 0;\n if(mat[i][j]==1){\n for(int k=0;k<mat.length;k++){\n sumR+=mat[k][j];\n }\n for(int k=0;k<mat[0].length;k++){\n sumC+=mat[i][k];\n }\n }\n if(sumR+sumC==2) count++;\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int count = 0;\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1 && accumulate(mat[i].begin(), mat[i].end(), 0) == 1 &&\n accumulate(mat.begin(), mat.end(), 0, [j](int sum, const vector<int>& row) { return sum + row[j]; }) == 1) {\n count++;\n }\n }\n }\n return count;\n }\n};\n```\n# 2. Hashing:\n- Maintain two arrays, rowSum and colSum, to store the sum of each row and column, respectively.\n- Iterate through each cell in the matrix and update the corresponding rowSum and colSum.\n- For each cell with a value of 1, check if its row and column sums are both 1.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(n^2)`, where n is the size of the matrix.\n- \n- \uD83D\uDE80 Space Complexity: `O(n)` - for the rowSum and colSum arrays.\n\n# Code\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n rowSum = [sum(row) for row in mat]\n colSum = [sum(row[j] for row in mat) for j in range(len(mat[0]))]\n count = 0\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 1 and rowSum[i] == 1 and colSum[j] == 1:\n count += 1\n return count\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int[] rowSum = new int[mat.length];\n int[] colSum = new int[mat[0].length];\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n vector<int> rowSum(mat.size(), 0);\n vector<int> colSum(mat[0].size(), 0);\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n int count = 0;\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n};\n```\n```C []\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int* rowSum = (int*)malloc(matSize * sizeof(int));\n int* colSum = (int*)malloc((*matColSize) * sizeof(int));\n memset(rowSum, 0, matSize * sizeof(int));\n memset(colSum, 0, (*matColSize) * sizeof(int));\n\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < *matColSize; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n\n int count = 0;\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < *matColSize; j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n\n free(rowSum);\n free(colSum);\n return count;\n}\n```\n# \uD83C\uDFC6Conclusion: \nIn this problem to find the number of special positions in a binary matrix, we discussed two distinct approaches: the Brute Force method and the Hashing method. and hashing will be a better approach compared to brute force.\n\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 23 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
💯Faster✅💯 Lesser✅2 Methods🔥Brute Force🔥Hashing🔥Python🐍Java☕C++✅C📈 | special-positions-in-a-binary-matrix | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 2 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe problem involves finding the number of special positions in a binary matrix. A special position is defined as a cell with a value of 1 and having all other cells in the same row and column as 0. The task is to determine the count of such special positions in the given binary matrix.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering two different methods to solve this problem:\n1. Brute Force\n2. Hashing\n\n# 1. Brute Force: \n- Iterate through each cell in the matrix.\n- For each cell with a value of 1, check if all other cells in its row and column are 0.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(n^3)`, where n is the size of the matrix.\n\n- \uD83D\uDE80 Space Complexity: `O(1)` - no extra space used.\n\n# Code\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n count = 0\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 1 and sum(mat[i]) == 1 and sum(row[j] for row in mat) == 1:\n count += 1\n return count\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n int sumR = 0;\n int sumC = 0;\n if(mat[i][j]==1){\n for(int k=0;k<mat.length;k++){\n sumR+=mat[k][j];\n }\n for(int k=0;k<mat[0].length;k++){\n sumC+=mat[i][k];\n }\n }\n if(sumR+sumC==2) count++;\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int count = 0;\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1 && accumulate(mat[i].begin(), mat[i].end(), 0) == 1 &&\n accumulate(mat.begin(), mat.end(), 0, [j](int sum, const vector<int>& row) { return sum + row[j]; }) == 1) {\n count++;\n }\n }\n }\n return count;\n }\n};\n```\n# 2. Hashing:\n- Maintain two arrays, rowSum and colSum, to store the sum of each row and column, respectively.\n- Iterate through each cell in the matrix and update the corresponding rowSum and colSum.\n- For each cell with a value of 1, check if its row and column sums are both 1.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(n^2)`, where n is the size of the matrix.\n- \n- \uD83D\uDE80 Space Complexity: `O(n)` - for the rowSum and colSum arrays.\n\n# Code\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n rowSum = [sum(row) for row in mat]\n colSum = [sum(row[j] for row in mat) for j in range(len(mat[0]))]\n count = 0\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 1 and rowSum[i] == 1 and colSum[j] == 1:\n count += 1\n return count\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int[] rowSum = new int[mat.length];\n int[] colSum = new int[mat[0].length];\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n vector<int> rowSum(mat.size(), 0);\n vector<int> colSum(mat[0].size(), 0);\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n int count = 0;\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n};\n```\n```C []\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int* rowSum = (int*)malloc(matSize * sizeof(int));\n int* colSum = (int*)malloc((*matColSize) * sizeof(int));\n memset(rowSum, 0, matSize * sizeof(int));\n memset(colSum, 0, (*matColSize) * sizeof(int));\n\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < *matColSize; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n\n int count = 0;\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < *matColSize; j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n\n free(rowSum);\n free(colSum);\n return count;\n}\n```\n# \uD83C\uDFC6Conclusion: \nIn this problem to find the number of special positions in a binary matrix, we discussed two distinct approaches: the Brute Force method and the Hashing method. and hashing will be a better approach compared to brute force.\n\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 23 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
⭐✅|| STORING EACH ROW AND COL SUM || WELL EXPLAINED (HINDI) || BEATS 100% || ✅⭐ | special-positions-in-a-binary-matrix | 1 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# ALGORITHM\n<!-- Describe your approach to solving the problem. -->\n1)**Matrix ke dimensions nikalo**:\nInput matrix mat ki rows (n) aur columns (m) ka pata lagayein.\n\n2)**Variables ko initialize karein**:\nans naamak ek variable ko 0 se initialize karein. Ye variable special positions ka count store karega.\n\n3)**Row aur column sum vectors ko initialize karein**:\nDo vectors rowsum aur colsum banayein jo har row aur column ke sum ko store karenge.\nrowsum n size ka vector hai jismein shuruwat mein sabhi elements 0 hain.\ncolsum m size ka vector hai jismein shuruwat mein sabhi elements 0 hain.\n\n4)**Row aur column sums nikalein**:\nMatrix ke har element par iterate karein.\nHar element ke liye rowsum aur colsum ko update karein.\n\n5)**Special positions ko check karein**:\nFir se matrix ke har element par iterate karein.\nHar element ke liye check karein ki mat[i][j] 1 hai, rowsum[i] 1 hai, aur colsum[j] 1 hai ya nahi.\nAgar saare conditions satisfy hote hain, to ans ko badhayein.\n\n6)**Result return karein**:\nans mein store kiye gaye special positions ka count return karein.\n\n# Complexity\n- Time complexity:O(n * m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n // Get the number of rows(n) and columns(m) in the matrix\n int n=mat.size();\n int m=mat[0].size();\n int ans=0;\n \n // Vector to store the sum of each row( SIZE OF VECTOR IS n AND ALL ELEMNTS ARE SET 0)\n vector<int>rowsum(n,0);\n // Vector to store the sum of each column of size m and all elements are initially 0\n vector<int>colsum(m,0);\n \n // Calculate the sum of each row and column\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n rowsum[i]+=mat[i][j];\n colsum[j]+=mat[i][j];\n }\n }\n \n // Check for special positions\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n // Check if the current position is 1 and the sum of its row and column is 1\n if(mat[i][j]==1 && rowsum[i]==1 && colsum[j]==1)\n {\n // Increment the ans for special positions\n ans++;\n }\n }\n }\n // Return the total count of special positions\n return ans;\n \n }\n};\n```\n```python []\npython 3 []\ndef column(matrix, i):\n return [row[i] for row in matrix]\nclass Solution:\n \n def numSpecial(self, mat: List[List[int]]) -> int:\n c=0\n for i in range(len(mat)):\n if(mat[i].count(1)==1):\n i=mat[i].index(1)\n col=column(mat,i)\n if(col.count(1)==1):\n c+=1\n \n return c \n```\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n // Get the number of rows (n) and columns (m) in the matrix\n int n = mat.length;\n int m = mat[0].length;\n \n // Initialize a counter for special positions\n int ans = 0;\n \n // Array to store the sum of each row (size of the array is n, and all elements are initially set to 0)\n int[] rowSum = new int[n];\n // Array to store the sum of each column (size of the array is m, and all elements are initially set to 0)\n int[] colSum = new int[m];\n \n // Calculate the sum of each row and column\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n \n // Check for special positions\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n // Check if the current position is 1 and the sum of its row and column is 1\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n // Increment the counter for special positions\n ans++;\n }\n }\n }\n \n // Return the total count of special positions\n return ans;\n }\n}\n```\n | 5 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
⭐✅|| STORING EACH ROW AND COL SUM || WELL EXPLAINED (HINDI) || BEATS 100% || ✅⭐ | special-positions-in-a-binary-matrix | 1 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# ALGORITHM\n<!-- Describe your approach to solving the problem. -->\n1)**Matrix ke dimensions nikalo**:\nInput matrix mat ki rows (n) aur columns (m) ka pata lagayein.\n\n2)**Variables ko initialize karein**:\nans naamak ek variable ko 0 se initialize karein. Ye variable special positions ka count store karega.\n\n3)**Row aur column sum vectors ko initialize karein**:\nDo vectors rowsum aur colsum banayein jo har row aur column ke sum ko store karenge.\nrowsum n size ka vector hai jismein shuruwat mein sabhi elements 0 hain.\ncolsum m size ka vector hai jismein shuruwat mein sabhi elements 0 hain.\n\n4)**Row aur column sums nikalein**:\nMatrix ke har element par iterate karein.\nHar element ke liye rowsum aur colsum ko update karein.\n\n5)**Special positions ko check karein**:\nFir se matrix ke har element par iterate karein.\nHar element ke liye check karein ki mat[i][j] 1 hai, rowsum[i] 1 hai, aur colsum[j] 1 hai ya nahi.\nAgar saare conditions satisfy hote hain, to ans ko badhayein.\n\n6)**Result return karein**:\nans mein store kiye gaye special positions ka count return karein.\n\n# Complexity\n- Time complexity:O(n * m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n // Get the number of rows(n) and columns(m) in the matrix\n int n=mat.size();\n int m=mat[0].size();\n int ans=0;\n \n // Vector to store the sum of each row( SIZE OF VECTOR IS n AND ALL ELEMNTS ARE SET 0)\n vector<int>rowsum(n,0);\n // Vector to store the sum of each column of size m and all elements are initially 0\n vector<int>colsum(m,0);\n \n // Calculate the sum of each row and column\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n rowsum[i]+=mat[i][j];\n colsum[j]+=mat[i][j];\n }\n }\n \n // Check for special positions\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n // Check if the current position is 1 and the sum of its row and column is 1\n if(mat[i][j]==1 && rowsum[i]==1 && colsum[j]==1)\n {\n // Increment the ans for special positions\n ans++;\n }\n }\n }\n // Return the total count of special positions\n return ans;\n \n }\n};\n```\n```python []\npython 3 []\ndef column(matrix, i):\n return [row[i] for row in matrix]\nclass Solution:\n \n def numSpecial(self, mat: List[List[int]]) -> int:\n c=0\n for i in range(len(mat)):\n if(mat[i].count(1)==1):\n i=mat[i].index(1)\n col=column(mat,i)\n if(col.count(1)==1):\n c+=1\n \n return c \n```\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n // Get the number of rows (n) and columns (m) in the matrix\n int n = mat.length;\n int m = mat[0].length;\n \n // Initialize a counter for special positions\n int ans = 0;\n \n // Array to store the sum of each row (size of the array is n, and all elements are initially set to 0)\n int[] rowSum = new int[n];\n // Array to store the sum of each column (size of the array is m, and all elements are initially set to 0)\n int[] colSum = new int[m];\n \n // Calculate the sum of each row and column\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n \n // Check for special positions\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n // Check if the current position is 1 and the sum of its row and column is 1\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n // Increment the counter for special positions\n ans++;\n }\n }\n }\n \n // Return the total count of special positions\n return ans;\n }\n}\n```\n | 5 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
[We💕Simple] One Liner! (Beat 100%) | special-positions-in-a-binary-matrix | 0 | 1 | ## Python3\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n return sum(\n sum(mat[i][col] for i in range(len(mat))) == 1\n for col in [\n row.index(1)\n for row in mat\n if sum(row) == 1\n ]\n )\n\n```\n\n## Kotlin\n``` Kotlin\nclass Solution {\n fun numSpecial(mat: Array<IntArray>): Int =\n mat.mapNotNull { row -> \n row.indexOfFirst { it == 1 }.takeIf { it >= 0 && row.drop(it+1).sum() == 0 }\n }.count { col ->\n mat.sumOf { it[col] } == 1\n }\n}\n```\n\n# Approach\n\n1. **Mapping Rows to Potential Columns**: The function `numSpecial` takes a 2D array `mat` (a matrix) as input. It uses the `mapNotNull` function on this matrix, which processes each row and potentially transforms it to a different value. In this case, the transformation is to identify the column index of the first occurrence of \'1\' in a row.\n\n2. **Identifying Unique \'1\'s in a Row**: Inside `mapNotNull`, `row.indexOfFirst { it == 1 }` finds the index of the first \'1\' in the row. The `takeIf` function is then used to ensure two things:\n - The index is non-negative (i.e., there is at least one \'1\' in the row).\n - All subsequent elements in the row after this \'1\' are zeros (checked by `row.drop(it+1).sum() == 0`).\n3. **Counting Special Elements**: The resulting list from `mapNotNull` contains column indices where there might be a "special" element. The `count` function is then used to count how many of these column indices actually represent a "special" element. This is done by checking for each column index `col` if the sum of all elements in that column (`mat.sumOf { it[col] }`) is equal to 1, which would mean the \'1\' in this column is unique and not shared with other rows.\n\nIn summary, the code strategy is to first identify potential columns for each row where a "special" element could exist. Then, it verifies these potential columns to ensure that they contain only one \'1\' in the entire column. This approach efficiently identifies "special" elements by minimizing the need to repeatedly scan entire rows and columns.\n | 3 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
[We💕Simple] One Liner! (Beat 100%) | special-positions-in-a-binary-matrix | 0 | 1 | ## Python3\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n return sum(\n sum(mat[i][col] for i in range(len(mat))) == 1\n for col in [\n row.index(1)\n for row in mat\n if sum(row) == 1\n ]\n )\n\n```\n\n## Kotlin\n``` Kotlin\nclass Solution {\n fun numSpecial(mat: Array<IntArray>): Int =\n mat.mapNotNull { row -> \n row.indexOfFirst { it == 1 }.takeIf { it >= 0 && row.drop(it+1).sum() == 0 }\n }.count { col ->\n mat.sumOf { it[col] } == 1\n }\n}\n```\n\n# Approach\n\n1. **Mapping Rows to Potential Columns**: The function `numSpecial` takes a 2D array `mat` (a matrix) as input. It uses the `mapNotNull` function on this matrix, which processes each row and potentially transforms it to a different value. In this case, the transformation is to identify the column index of the first occurrence of \'1\' in a row.\n\n2. **Identifying Unique \'1\'s in a Row**: Inside `mapNotNull`, `row.indexOfFirst { it == 1 }` finds the index of the first \'1\' in the row. The `takeIf` function is then used to ensure two things:\n - The index is non-negative (i.e., there is at least one \'1\' in the row).\n - All subsequent elements in the row after this \'1\' are zeros (checked by `row.drop(it+1).sum() == 0`).\n3. **Counting Special Elements**: The resulting list from `mapNotNull` contains column indices where there might be a "special" element. The `count` function is then used to count how many of these column indices actually represent a "special" element. This is done by checking for each column index `col` if the sum of all elements in that column (`mat.sumOf { it[col] }`) is equal to 1, which would mean the \'1\' in this column is unique and not shared with other rows.\n\nIn summary, the code strategy is to first identify potential columns for each row where a "special" element could exist. Then, it verifies these potential columns to ensure that they contain only one \'1\' in the entire column. This approach efficiently identifies "special" elements by minimizing the need to repeatedly scan entire rows and columns.\n | 3 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
🚀🚀 Beats 95% | Easy To Understand | Fully Explained 😎💖 | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\n- We want to find special positions in a binary matrix.\n- A position is special if the element at that position is 1 and all other elements in its row and column are 0.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Iterate through the matrix to find the positions where the element is 1.\n2. Store these positions in a map where the key is the row index and the value is the column index.\n3. For each position in the map, check the entire row and column to ensure that all other elements are 0.\n4. If a position satisfies the condition, increment the count of special positions.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- **Time complexity**:\n- The two nested loops iterate through the matrix, resulting in O(m * n) operations.\n- The final loop iterates through the map, resulting in additional O(m + n) operations.\n- Thus, the overall time complexity is O(m * n + m + n), which simplifies to O(m * n).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity**:\n- We use a map to store positions, which can have at most m entries (number of rows).\n- The space complexity is O(m) for the map.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) \n {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n\n int ans = 0;\n int m = mat.size();\n int n = mat[0].size();\n unordered_map<int, int> mp; // Map to store positions where element is 1\n\n // Find positions where element is 1 and store in the map\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (mat[i][j] == 1)\n mp[i] = j;\n }\n }\n\n // Check each position in the map\n for (auto x : mp) {\n int i = x.first;\n int j = x.second;\n int temp = n - 1;\n int count = 0;\n\n // Check the entire row\n while (temp >= 0) {\n if (mat[i][temp] == 1)\n count++;\n temp--;\n }\n\n temp = m - 1;\n // Check the entire column\n while (temp >= 0) {\n if (mat[temp][j] == 1)\n count++;\n temp--;\n }\n\n if (count == 2)\n ans++; // If count is 2, the position is special\n }\n\n return ans;\n}\n\n};\n```\n\n | 6 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
🚀🚀 Beats 95% | Easy To Understand | Fully Explained 😎💖 | special-positions-in-a-binary-matrix | 1 | 1 | # Intuition\n- We want to find special positions in a binary matrix.\n- A position is special if the element at that position is 1 and all other elements in its row and column are 0.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Iterate through the matrix to find the positions where the element is 1.\n2. Store these positions in a map where the key is the row index and the value is the column index.\n3. For each position in the map, check the entire row and column to ensure that all other elements are 0.\n4. If a position satisfies the condition, increment the count of special positions.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- **Time complexity**:\n- The two nested loops iterate through the matrix, resulting in O(m * n) operations.\n- The final loop iterates through the map, resulting in additional O(m + n) operations.\n- Thus, the overall time complexity is O(m * n + m + n), which simplifies to O(m * n).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity**:\n- We use a map to store positions, which can have at most m entries (number of rows).\n- The space complexity is O(m) for the map.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) \n {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n\n int ans = 0;\n int m = mat.size();\n int n = mat[0].size();\n unordered_map<int, int> mp; // Map to store positions where element is 1\n\n // Find positions where element is 1 and store in the map\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (mat[i][j] == 1)\n mp[i] = j;\n }\n }\n\n // Check each position in the map\n for (auto x : mp) {\n int i = x.first;\n int j = x.second;\n int temp = n - 1;\n int count = 0;\n\n // Check the entire row\n while (temp >= 0) {\n if (mat[i][temp] == 1)\n count++;\n temp--;\n }\n\n temp = m - 1;\n // Check the entire column\n while (temp >= 0) {\n if (mat[temp][j] == 1)\n count++;\n temp--;\n }\n\n if (count == 2)\n ans++; // If count is 2, the position is special\n }\n\n return ans;\n}\n\n};\n```\n\n | 6 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
Python3 Solution | special-positions-in-a-binary-matrix | 0 | 1 | \n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n=len(mat)\n m=len(mat[0])\n ans=0\n transposeMat=list(zip(*mat))\n for i in range(n):\n for j in range(m):\n if mat[i][j]==1 and sum(mat[i])==1 and sum(transposeMat[j])==1:\n ans+=1\n return ans \n``` | 2 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
Python3 Solution | special-positions-in-a-binary-matrix | 0 | 1 | \n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n=len(mat)\n m=len(mat[0])\n ans=0\n transposeMat=list(zip(*mat))\n for i in range(n):\n for j in range(m):\n if mat[i][j]==1 and sum(mat[i])==1 and sum(transposeMat[j])==1:\n ans+=1\n return ans \n``` | 2 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
✅ One Line Solution | special-positions-in-a-binary-matrix | 0 | 1 | (Disclaimer: these are not examples to follow in a real project - they are written for fun and training mostly)\n# Code #1\nTime complexity: $$O(m*n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return sum(sum(rr[j] for rr in M)==1 for r in M if sum(r)==1 and (j:=r.index(1))+1)\n```\n\n# Code #2\nTime complexity: $$O(m*n)$$. Space complexity: $$O(m+n)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return (R:=[sum(r)==1 for r in M]) and (C:=[sum(c)==1 for c in zip(*M)]) and \\\n sum(M[i][j]*R[i]*C[j] for i in range(len(R)) for j in range(len(C)))\n```\n\n# Code #3\nTime complexity: $$O(m*n)$$. Space complexity: $$O(m*n)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return (T:=list(zip(*M))) and sum(sum(T[r.index(1)])==1 for r in M if sum(r)==1)\n``` | 4 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
✅ One Line Solution | special-positions-in-a-binary-matrix | 0 | 1 | (Disclaimer: these are not examples to follow in a real project - they are written for fun and training mostly)\n# Code #1\nTime complexity: $$O(m*n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return sum(sum(rr[j] for rr in M)==1 for r in M if sum(r)==1 and (j:=r.index(1))+1)\n```\n\n# Code #2\nTime complexity: $$O(m*n)$$. Space complexity: $$O(m+n)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return (R:=[sum(r)==1 for r in M]) and (C:=[sum(c)==1 for c in zip(*M)]) and \\\n sum(M[i][j]*R[i]*C[j] for i in range(len(R)) for j in range(len(C)))\n```\n\n# Code #3\nTime complexity: $$O(m*n)$$. Space complexity: $$O(m*n)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return (T:=list(zip(*M))) and sum(sum(T[r.index(1)])==1 for r in M if sum(r)==1)\n``` | 4 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
Easy Solution || Python | special-positions-in-a-binary-matrix | 0 | 1 | # Intuition\nFirst iterating through the matrix gives us the position of ones and we calculate if there are any ones in the respective row or column.\nIn the 2nd iteration we check if the ones are in special position.\n\n\n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(m+n)\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m = len(mat)\n n = len(mat[0])\n row_count = [0] * m\n col_count = [0] * n\n\n special_pos =0 \n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1:\n row_count[i]+=1\n col_count[j]+=1\n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1 and row_count[i] == 1 and col_count[j] == 1:\n special_pos+=1\n return special_pos\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
Easy Solution || Python | special-positions-in-a-binary-matrix | 0 | 1 | # Intuition\nFirst iterating through the matrix gives us the position of ones and we calculate if there are any ones in the respective row or column.\nIn the 2nd iteration we check if the ones are in special position.\n\n\n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(m+n)\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m = len(mat)\n n = len(mat[0])\n row_count = [0] * m\n col_count = [0] * n\n\n special_pos =0 \n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1:\n row_count[i]+=1\n col_count[j]+=1\n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1 and row_count[i] == 1 and col_count[j] == 1:\n special_pos+=1\n return special_pos\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
Simple Solution To count Special Cases | special-positions-in-a-binary-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n answer = 0\n for row in range(len(mat)):\n for column in range(len(mat[row])):\n vertical = sum([i[column] for i in mat])\n horizontal = sum([horizontal for horizontal in mat[row]])\n if vertical == 1 and horizontal == 1 and mat[row][column] == 1:\n answer += 1\n return answer\n \n``` | 1 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
Simple Solution To count Special Cases | special-positions-in-a-binary-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n answer = 0\n for row in range(len(mat)):\n for column in range(len(mat[row])):\n vertical = sum([i[column] for i in mat])\n horizontal = sum([horizontal for horizontal in mat[row]])\n if vertical == 1 and horizontal == 1 and mat[row][column] == 1:\n answer += 1\n return answer\n \n``` | 1 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
Easy solution python || store and access | special-positions-in-a-binary-matrix | 0 | 1 | \n# Complexity\n- Time complexity:O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n row=[0]*len(mat)\n col=[0]*len(mat[0])\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if(mat[i][j]==1):\n row[i]+=1\n col[j]+=1\n ans = 0 \n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if(mat[i][j]==1 and row[i]==1 and col[j]==1 ):\n ans+=1\n return ans\n``` | 1 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
Easy solution python || store and access | special-positions-in-a-binary-matrix | 0 | 1 | \n# Complexity\n- Time complexity:O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n row=[0]*len(mat)\n col=[0]*len(mat[0])\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if(mat[i][j]==1):\n row[i]+=1\n col[j]+=1\n ans = 0 \n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if(mat[i][j]==1 and row[i]==1 and col[j]==1 ):\n ans+=1\n return ans\n``` | 1 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
Solution using sum | special-positions-in-a-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m, n = len(mat), len(mat[0])\n special_count = 0\n\n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1:\n \n if sum(mat[i]) == 1 and sum(mat[k][j] for k in range(m)) == 1:\n special_count += 1\n\n return special_count\n \n``` | 1 | Given an `m x n` binary matrix `mat`, return _the number of special positions in_ `mat`_._
A position `(i, j)` is called **special** if `mat[i][j] == 1` and all other elements in row `i` and column `j` are `0` (rows and columns are **0-indexed**).
**Example 1:**
**Input:** mat = \[\[1,0,0\],\[0,0,1\],\[1,0,0\]\]
**Output:** 1
**Explanation:** (1, 2) is a special position because mat\[1\]\[2\] == 1 and all other elements in row 1 and column 2 are 0.
**Example 2:**
**Input:** mat = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\]
**Output:** 3
**Explanation:** (0, 0), (1, 1) and (2, 2) are special positions.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `mat[i][j]` is either `0` or `1`. | Use two stack one for back history and one for forward history and simulate the functions. Can you do faster by using different data structure ? |
Solution using sum | special-positions-in-a-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m, n = len(mat), len(mat[0])\n special_count = 0\n\n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1:\n \n if sum(mat[i]) == 1 and sum(mat[k][j] for k in range(m)) == 1:\n special_count += 1\n\n return special_count\n \n``` | 1 | You are given a string `s` of even length. Split this string into two halves of equal lengths, and let `a` be the first half and `b` be the second half.
Two strings are **alike** if they have the same number of vowels (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`, `'A'`, `'E'`, `'I'`, `'O'`, `'U'`). Notice that `s` contains uppercase and lowercase letters.
Return `true` _if_ `a` _and_ `b` _are **alike**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "book "
**Output:** true
**Explanation:** a = "bo " and b = "ok ". a has 1 vowel and b has 1 vowel. Therefore, they are alike.
**Example 2:**
**Input:** s = "textbook "
**Output:** false
**Explanation:** a = "text " and b = "book ". a has 1 vowel whereas b has 2. Therefore, they are not alike.
Notice that the vowel o is counted twice.
**Constraints:**
* `2 <= s.length <= 1000`
* `s.length` is even.
* `s` consists of **uppercase and lowercase** letters. | Keep track of 1s in each row and in each column. Then while iterating over matrix, if the current position is 1 and current row as well as current column contains exactly one occurrence of 1. |
Python 3 || 4 lines, w/ explanation || T/M: 95% / 71% | count-unhappy-friends | 0 | 1 | Here\'s how the code works:\n\nWe initialize a defaultdict`sc`, which will store the preferred friends for each pair `u` and friend `v` in the pairs.\n\nWe iterate [u, v] in the pairs list. For each pair in`pairs`, we assign the preferred friends before`u`and `v` to `sc[u]` and `sc[v]` respectively. The preferred friends are determined by taking a slice of the preferences list for the respective friend up to the index where the other friend is found. This allows easy comparison of preferences.\n\nAfter processing all pairs, we iterate over each friend `u`, checking whether there exists a friend `v` in `sc[u]` (i.e., `u` prefers `v`) such that `u` is also present in the preferred friends of `v` (i.e., v`prefers `u` over their current pairing). We check whether any friend in `sc[u]` satisfies this condition.\n\nWe return the count of`True`values, which represents the number of unhappy friends. --*ChatGPT*\n```\nclass Solution:\n\tdef unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n\n\t\tsc = defaultdict()\n\n\t\tfor u,v in pairs:\n\t\t\t\n\t\t\tsc[u],sc[v] = (preferences[u][:preferences[u].index(v)],\n\t\t\t\t\t\t\t\t\t\t preferences[v][:preferences[v].index(u)])\n\t\t\t\n\t\treturn sum(any(u in sc[v] for v in sc[u]) for u in range(n))\n```\n[https://leetcode.com/problems/count-unhappy-friends/submissions/994728034/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*), in which *N* ~`n`. | 3 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Python 3 || 4 lines, w/ explanation || T/M: 95% / 71% | count-unhappy-friends | 0 | 1 | Here\'s how the code works:\n\nWe initialize a defaultdict`sc`, which will store the preferred friends for each pair `u` and friend `v` in the pairs.\n\nWe iterate [u, v] in the pairs list. For each pair in`pairs`, we assign the preferred friends before`u`and `v` to `sc[u]` and `sc[v]` respectively. The preferred friends are determined by taking a slice of the preferences list for the respective friend up to the index where the other friend is found. This allows easy comparison of preferences.\n\nAfter processing all pairs, we iterate over each friend `u`, checking whether there exists a friend `v` in `sc[u]` (i.e., `u` prefers `v`) such that `u` is also present in the preferred friends of `v` (i.e., v`prefers `u` over their current pairing). We check whether any friend in `sc[u]` satisfies this condition.\n\nWe return the count of`True`values, which represents the number of unhappy friends. --*ChatGPT*\n```\nclass Solution:\n\tdef unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n\n\t\tsc = defaultdict()\n\n\t\tfor u,v in pairs:\n\t\t\t\n\t\t\tsc[u],sc[v] = (preferences[u][:preferences[u].index(v)],\n\t\t\t\t\t\t\t\t\t\t preferences[v][:preferences[v].index(u)])\n\t\t\t\n\t\treturn sum(any(u in sc[v] for v in sc[u]) for u in range(n))\n```\n[https://leetcode.com/problems/count-unhappy-friends/submissions/994728034/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*), in which *N* ~`n`. | 3 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
[Python] Make you happy with clean and concise solution | count-unhappy-friends | 0 | 1 | The problem description is not very clear. Please find below clean, concise and self explanatory code. \nTime Complexity: O(n^2). Space Complexity: O(n^2)\nIncluding comments in the code for better understanding. Kindly upvote if you like the solution.\n\n\t\t#Map to get pair mapping\n pairMap = defaultdict(int)\n #To get preference of person i with person j in O(1)\n prefer = {}\n \n #Populating pairMap\n for p1,p2 in pairs:\n pairMap[p1] = p2\n pairMap[p2] = p1\n \n #Populating prefer Map\n for i in range(len(preferences)):\n for j in range(n-1):\n if i not in prefer:\n prefer[i] = {}\n prefer[i][preferences[i][j]] = j\n \n #Looping through preferences again to find if person i is unhappy\n res = 0\n for i in range(len(preferences)):\n for j in range(n-1):\n x = i\n y = pairMap[x]\n u = preferences[x][j]\n v = pairMap[u]\n if prefer[x][u] < prefer[x][y] and prefer[u][x] < prefer[u][v]:\n res+=1\n break\n return res | 18 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
[Python] Make you happy with clean and concise solution | count-unhappy-friends | 0 | 1 | The problem description is not very clear. Please find below clean, concise and self explanatory code. \nTime Complexity: O(n^2). Space Complexity: O(n^2)\nIncluding comments in the code for better understanding. Kindly upvote if you like the solution.\n\n\t\t#Map to get pair mapping\n pairMap = defaultdict(int)\n #To get preference of person i with person j in O(1)\n prefer = {}\n \n #Populating pairMap\n for p1,p2 in pairs:\n pairMap[p1] = p2\n pairMap[p2] = p1\n \n #Populating prefer Map\n for i in range(len(preferences)):\n for j in range(n-1):\n if i not in prefer:\n prefer[i] = {}\n prefer[i][preferences[i][j]] = j\n \n #Looping through preferences again to find if person i is unhappy\n res = 0\n for i in range(len(preferences)):\n for j in range(n-1):\n x = i\n y = pairMap[x]\n u = preferences[x][j]\n v = pairMap[u]\n if prefer[x][u] < prefer[x][y] and prefer[u][x] < prefer[u][v]:\n res+=1\n break\n return res | 18 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
Python | EASY | Explained |99% fast | count-unhappy-friends | 0 | 1 | As per the explanation we got to understand that we first have to make somthing that holds people with their priorities and whats better than a DICT to do so . \nSo we can say as per the first example friend have a preferece:\n0 : 1,2,3\n1 : 3,2,0\n2 : 3,1,0\n3 : 1,2,0\n\nAnd given pairs are = [[0, 1], [2, 3]]\n0 is happy, because 1 is the first preferece\n1 is unhappy, because 3 is its prior preference,\n2 is happy because 3 is its first preference\n3 is also unhappy because 1 is its preferece ans\n\nSo the total count of unhappy friends are 2\n\nStep1: for each, we should check wehther they have a prior preference than the current pair\n use a dictionary:\n {\n 0: [ ],1: [3],2: [ ],3: [1]\n }\n Step2: then we start the iteration, for each key, if the key appear in the dict[value],\n which suggest, the key and the value all have an another prefered choice, then we should\n add the result by 1 at last just return res\n```\n\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n priority = {}\n\t\t#making priority dictonary\n for p1, p2 in pairs:\n priority[p1] = preferences[p1][:preferences[p1].index(p2)]\n priority[p2] = preferences[p2][:preferences[p2].index(p1)]\n #start the iteration\n res = 0 #act as a counter for unhappy friends\n for p1 in priority:\n for p2 in priority[p1]:\n if p1 in priority[p2]:\n res += 1\n break\n return res\n \n``` | 3 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Python | EASY | Explained |99% fast | count-unhappy-friends | 0 | 1 | As per the explanation we got to understand that we first have to make somthing that holds people with their priorities and whats better than a DICT to do so . \nSo we can say as per the first example friend have a preferece:\n0 : 1,2,3\n1 : 3,2,0\n2 : 3,1,0\n3 : 1,2,0\n\nAnd given pairs are = [[0, 1], [2, 3]]\n0 is happy, because 1 is the first preferece\n1 is unhappy, because 3 is its prior preference,\n2 is happy because 3 is its first preference\n3 is also unhappy because 1 is its preferece ans\n\nSo the total count of unhappy friends are 2\n\nStep1: for each, we should check wehther they have a prior preference than the current pair\n use a dictionary:\n {\n 0: [ ],1: [3],2: [ ],3: [1]\n }\n Step2: then we start the iteration, for each key, if the key appear in the dict[value],\n which suggest, the key and the value all have an another prefered choice, then we should\n add the result by 1 at last just return res\n```\n\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n priority = {}\n\t\t#making priority dictonary\n for p1, p2 in pairs:\n priority[p1] = preferences[p1][:preferences[p1].index(p2)]\n priority[p2] = preferences[p2][:preferences[p2].index(p1)]\n #start the iteration\n res = 0 #act as a counter for unhappy friends\n for p1 in priority:\n for p2 in priority[p1]:\n if p1 in priority[p2]:\n res += 1\n break\n return res\n \n``` | 3 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
Beat 99% with clear logic | count-unhappy-friends | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n graph = defaultdict(int)\n for x,y in pairs:\n graph[x] = y\n graph[y] = x\n \n unhappy = set()\n \n def notHappy(u,v,x):\n # return True is u prefer x over v\n return preferences[u].index(x) < preferences[u].index(v)\n \n def checkHappy(x,y):\n # add the unhappy pairs in obtained from x,y\n i = 0\n while preferences[x][i] != y:\n if notHappy(preferences[x][i],graph[preferences[x][i]],x):\n unhappy.add(x)\n unhappy.add(preferences[x][i])\n break\n i += 1\n \n for x,y in pairs:\n if x not in unhappy:\n checkHappy(x,y)\n if y not in unhappy:\n checkHappy(y,x)\n\n return len(unhappy)\n\n``` | 0 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Beat 99% with clear logic | count-unhappy-friends | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n graph = defaultdict(int)\n for x,y in pairs:\n graph[x] = y\n graph[y] = x\n \n unhappy = set()\n \n def notHappy(u,v,x):\n # return True is u prefer x over v\n return preferences[u].index(x) < preferences[u].index(v)\n \n def checkHappy(x,y):\n # add the unhappy pairs in obtained from x,y\n i = 0\n while preferences[x][i] != y:\n if notHappy(preferences[x][i],graph[preferences[x][i]],x):\n unhappy.add(x)\n unhappy.add(preferences[x][i])\n break\n i += 1\n \n for x,y in pairs:\n if x not in unhappy:\n checkHappy(x,y)\n if y not in unhappy:\n checkHappy(y,x)\n\n return len(unhappy)\n\n``` | 0 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
python3 + simulation | count-unhappy-friends | 0 | 1 | # Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n d = {}\n p = {}\n for idx,e in enumerate(preferences):\n d[idx] = e\n c = set()\n for x,y in pairs:\n p[x] = y\n p[y] = x\n for i in range(n):\n team = p[i]\n temp = []\n for m in d[i]:\n if m == team:\n break\n temp.append(m)\n for k in temp:\n if d[k].index(i) < d[k].index(p[k]):\n c.add(i)\n\n return len(c)\n\n\n``` | 0 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
python3 + simulation | count-unhappy-friends | 0 | 1 | # Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n d = {}\n p = {}\n for idx,e in enumerate(preferences):\n d[idx] = e\n c = set()\n for x,y in pairs:\n p[x] = y\n p[y] = x\n for i in range(n):\n team = p[i]\n temp = []\n for m in d[i]:\n if m == team:\n break\n temp.append(m)\n for k in temp:\n if d[k].index(i) < d[k].index(p[k]):\n c.add(i)\n\n return len(c)\n\n\n``` | 0 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.