title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Unhappy Friends: T=O(n^2), S=O(n^2) | count-unhappy-friends | 0 | 1 | # Intuition\n#iterate over pairs (partners)\n#identify the list of friends that each person prefers over their partner\n#check whether the prefered person also prefers me backwards\n#if yes, increment the count as I am unhappy\n#break the inner loop to avoid double counting my unhappiness\n\n# Complexity\n#T=O(n^2),S=O(n^2)\n\n# Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n d, p = {}, preferences\n #T=O(n^2),S=O(n^2) in thw worst case\n for x,y in pairs:\n d[x] = set(p[x][:p[x].index(y)])\n d[y] = set(p[y][:p[y].index(x)])\n \n res = 0\n #T=O(n^2) because dict lookups are O(1)\n for x in d:\n for y in d[x]:\n if x in d[y]:\n res += 1\n break\n return res\n``` | 0 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Unhappy Friends: T=O(n^2), S=O(n^2) | count-unhappy-friends | 0 | 1 | # Intuition\n#iterate over pairs (partners)\n#identify the list of friends that each person prefers over their partner\n#check whether the prefered person also prefers me backwards\n#if yes, increment the count as I am unhappy\n#break the inner loop to avoid double counting my unhappiness\n\n# Complexity\n#T=O(n^2),S=O(n^2)\n\n# Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n d, p = {}, preferences\n #T=O(n^2),S=O(n^2) in thw worst case\n for x,y in pairs:\n d[x] = set(p[x][:p[x].index(y)])\n d[y] = set(p[y][:p[y].index(x)])\n \n res = 0\n #T=O(n^2) because dict lookups are O(1)\n for x in d:\n for y in d[x]:\n if x in d[y]:\n res += 1\n break\n return res\n``` | 0 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
Python Intuitive | count-unhappy-friends | 0 | 1 | # Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n\n partner = {}\n\n for a, b in pairs:\n partner[a] = b\n partner[b] = a\n\n table = collections.defaultdict(dict)\n\n for person, p in enumerate(preferences):\n for rank, friend in enumerate(p):\n table[person][friend] = rank\n\n\n sad = collections.defaultdict(bool)\n\n\n for person in range(n):\n for other in range(person + 1, n):\n if partner[person] == other:\n continue\n \n if table[person][other] < table[person][partner[person]] and table[other][person] < table[other][partner[other]]:\n sad[person] = True\n sad[other] = True\n print(sad)\n\n return sum([1 for b in sad.values() if b == True])\n \n \n\n``` | 0 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Python Intuitive | count-unhappy-friends | 0 | 1 | # Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n\n partner = {}\n\n for a, b in pairs:\n partner[a] = b\n partner[b] = a\n\n table = collections.defaultdict(dict)\n\n for person, p in enumerate(preferences):\n for rank, friend in enumerate(p):\n table[person][friend] = rank\n\n\n sad = collections.defaultdict(bool)\n\n\n for person in range(n):\n for other in range(person + 1, n):\n if partner[person] == other:\n continue\n \n if table[person][other] < table[person][partner[person]] and table[other][person] < table[other][partner[other]]:\n sad[person] = True\n sad[other] = True\n print(sad)\n\n return sum([1 for b in sad.values() if b == True])\n \n \n\n``` | 0 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
Python Slower but Easier to Understand Solution | count-unhappy-friends | 0 | 1 | # Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n lookup = defaultdict(dict)\n for idx, preference in enumerate(preferences):\n for idx2, friend in enumerate(preference):\n lookup[idx][friend] = idx2\n\n unhappy = set()\n\n for (x, y), (u, v) in itertools.combinations(pairs, 2):\n if lookup[x][u] < lookup[x][y] and lookup[u][x] < lookup[u][v]:\n unhappy.add(x)\n unhappy.add(u)\n\n if lookup[x][v] < lookup[x][y] and lookup[v][x] < lookup[v][u]:\n unhappy.add(x)\n unhappy.add(v)\n\n if lookup[y][v] < lookup[y][x] and lookup[v][y] < lookup[v][u]:\n unhappy.add(y)\n unhappy.add(v)\n\n if lookup[y][u] < lookup[y][x] and lookup[u][y] < lookup[u][v]:\n unhappy.add(y)\n unhappy.add(u)\n\n return len(unhappy)\n``` | 0 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Python Slower but Easier to Understand Solution | count-unhappy-friends | 0 | 1 | # Code\n```\nclass Solution:\n def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]) -> int:\n lookup = defaultdict(dict)\n for idx, preference in enumerate(preferences):\n for idx2, friend in enumerate(preference):\n lookup[idx][friend] = idx2\n\n unhappy = set()\n\n for (x, y), (u, v) in itertools.combinations(pairs, 2):\n if lookup[x][u] < lookup[x][y] and lookup[u][x] < lookup[u][v]:\n unhappy.add(x)\n unhappy.add(u)\n\n if lookup[x][v] < lookup[x][y] and lookup[v][x] < lookup[v][u]:\n unhappy.add(x)\n unhappy.add(v)\n\n if lookup[y][v] < lookup[y][x] and lookup[v][y] < lookup[v][u]:\n unhappy.add(y)\n unhappy.add(v)\n\n if lookup[y][u] < lookup[y][x] and lookup[u][y] < lookup[u][v]:\n unhappy.add(y)\n unhappy.add(u)\n\n return len(unhappy)\n``` | 0 | There is a special kind of apple tree that grows apples every day for `n` days. On the `ith` day, the tree grows `apples[i]` apples that will rot after `days[i]` days, that is on day `i + days[i]` the apples will be rotten and cannot be eaten. On some days, the apple tree does not grow any apples, which are denoted by `apples[i] == 0` and `days[i] == 0`.
You decided to eat **at most** one apple a day (to keep the doctors away). Note that you can keep eating after the first `n` days.
Given two integer arrays `days` and `apples` of length `n`, return _the maximum number of apples you can eat._
**Example 1:**
**Input:** apples = \[1,2,3,5,2\], days = \[3,2,1,4,2\]
**Output:** 7
**Explanation:** You can eat 7 apples:
- On the first day, you eat an apple that grew on the first day.
- On the second day, you eat an apple that grew on the second day.
- On the third day, you eat an apple that grew on the second day. After this day, the apples that grew on the third day rot.
- On the fourth to the seventh days, you eat apples that grew on the fourth day.
**Example 2:**
**Input:** apples = \[3,0,0,0,0,2\], days = \[3,0,0,0,0,2\]
**Output:** 5
**Explanation:** You can eat 5 apples:
- On the first to the third day you eat apples that grew on the first day.
- Do nothing on the fouth and fifth days.
- On the sixth and seventh days you eat apples that grew on the sixth day.
**Constraints:**
* `n == apples.length == days.length`
* `1 <= n <= 2 * 104`
* `0 <= apples[i], days[i] <= 2 * 104`
* `days[i] = 0` if and only if `apples[i] = 0`. | Create a matrix “rank” where rank[i][j] holds how highly friend ‘i' views ‘j’. This allows for O(1) comparisons between people |
Prime's Algorithm || Beats 97% | min-cost-to-connect-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n if n <= 1:\n return 0\n \n # Initialize the total cost and a set to track visited nodes\n total_cost = 0\n visited = set()\n \n # Initialize distances with a maximum value for each point\n distances = [float(\'inf\')] * n\n \n # Choose the starting node (here, I choose the first node)\n start_node = 0\n distances[start_node] = 0\n \n min_heap = [(0, start_node)] # Priority queue to select the minimum distance\n \n while min_heap:\n dist, current = heapq.heappop(min_heap)\n \n if current in visited:\n continue\n \n visited.add(current)\n total_cost += dist\n \n for i in range(n):\n if i not in visited:\n # Calculate Manhattan distance between points\n manhattan_dist = abs(points[current][0] - points[i][0]) + abs(points[current][1] - points[i][1])\n \n if manhattan_dist < distances[i]:\n distances[i] = manhattan_dist\n heapq.heappush(min_heap, (manhattan_dist, i))\n \n return total_cost\n\n``` | 2 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Prime's Algorithm || Beats 97% | min-cost-to-connect-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n if n <= 1:\n return 0\n \n # Initialize the total cost and a set to track visited nodes\n total_cost = 0\n visited = set()\n \n # Initialize distances with a maximum value for each point\n distances = [float(\'inf\')] * n\n \n # Choose the starting node (here, I choose the first node)\n start_node = 0\n distances[start_node] = 0\n \n min_heap = [(0, start_node)] # Priority queue to select the minimum distance\n \n while min_heap:\n dist, current = heapq.heappop(min_heap)\n \n if current in visited:\n continue\n \n visited.add(current)\n total_cost += dist\n \n for i in range(n):\n if i not in visited:\n # Calculate Manhattan distance between points\n manhattan_dist = abs(points[current][0] - points[i][0]) + abs(points[current][1] - points[i][1])\n \n if manhattan_dist < distances[i]:\n distances[i] = manhattan_dist\n heapq.heappush(min_heap, (manhattan_dist, i))\n \n return total_cost\n\n``` | 2 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Python3 Solution | min-cost-to-connect-all-points | 0 | 1 | \n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n=len(points)\n def find(parent,x):\n if parent[x]==x:\n return x\n parent[x]=find(parent,parent[x])\n return parent[x]\n\n def union(parent,x,y):\n parent[find(parent,x)]=find(parent,y)\n\n edges=[(abs(points[i][0]-points[j][0])+abs(points[i][1]-points[j][1]),i,j) for i in range(n) for j in range(i+1,n)]\n edges.sort()\n parent=list(range(n))\n minCost,numEdges=0,0\n for cost,u,v in edges:\n if find(parent,u)!=find(parent,v):\n union(parent,u,v)\n minCost+=cost\n numEdges+=1\n\n if numEdges==(n-1):\n break\n\n return minCost \n``` | 2 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Python3 Solution | min-cost-to-connect-all-points | 0 | 1 | \n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n=len(points)\n def find(parent,x):\n if parent[x]==x:\n return x\n parent[x]=find(parent,parent[x])\n return parent[x]\n\n def union(parent,x,y):\n parent[find(parent,x)]=find(parent,y)\n\n edges=[(abs(points[i][0]-points[j][0])+abs(points[i][1]-points[j][1]),i,j) for i in range(n) for j in range(i+1,n)]\n edges.sort()\n parent=list(range(n))\n minCost,numEdges=0,0\n for cost,u,v in edges:\n if find(parent,u)!=find(parent,v):\n union(parent,u,v)\n minCost+=cost\n numEdges+=1\n\n if numEdges==(n-1):\n break\n\n return minCost \n``` | 2 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
✅ 94.85% Prim & Kruskal with Min-Heap | min-cost-to-connect-all-points | 1 | 1 | # Comprehensive Guide to Solving "Min Cost to Connect All Points": Bridging the Gap Efficiently\n\n## Introduction & Problem Statement\n\nHello, algorithmic explorers! Today, we\'re diving into a problem that\'s a fascinating blend of computational geometry and graph theory: "Min Cost to Connect All Points." Imagine you\'re given a set of points on a 2D plane, and your task is to connect them all with lines. Sounds simple? Well, it\'s not just about connecting them; you need to do so with the minimum possible cost, where the cost is defined as the Manhattan distance between points. Intriguing, isn\'t it?\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Graph Theory and MST**: \n This problem can be represented as a graph where each point is a node and the edges are the Manhattan distances between the points. The objective boils down to finding the Minimum Spanning Tree (MST) of this graph.\n \n2. **Manhattan Distance**: \n The edge weight isn\'t just a simple Euclidean distance; it\'s the Manhattan distance, which is the sum of the absolute differences in their Cartesian coordinates.\n\n3. **Constraints**: \n - 1 <= points.length <= 1000\n - $$-10^6 \\leq x_i, y_i \\leq 10^6$$\n - All pairs $$(x_i, y_i)$$ are distinct.\n\n### Strategies to Tackle the Problem\n\n1. **Kruskal\'s Algorithm**: \n This approach utilizes a Union-Find data structure to find the MST efficiently.\n \n2. **Prim\'s Algorithm**: \n This method employs a Priority Queue to select edges with minimum weights iteratively.\n\n---\n\n## Live Coding Prim & Explain\nhttps://youtu.be/7JxI7gt-WEM?si=bCZ7NBlDNRDjUzlw\n\n## Prim\'s Algorithm Explained\n\n### What is Prim\'s Algorithm?\n\nPrim\'s Algorithm is another method for finding the Minimum Spanning Tree. It starts from an arbitrary node and greedily chooses the edge with the smallest weight that connects a visited and an unvisited node.\n\n### The Mechanics of Prim\'s Algorithm in "Min Cost to Connect All Points"\n\n1. **Initialize Priority Queue**: \n - Start from an arbitrary point and initialize a minimum priority queue with its edges.\n\n2. **Visited Nodes Tracking**: \n - Keep track of visited nodes to ensure that each node is visited exactly once.\n\n3. **Iterate and Add to MST**: \n - Pop the edge with the smallest weight from the priority queue. If the edge leads to an unvisited node, add the edge\'s weight to the total MST weight, and insert all edges from that node into the priority queue.\n\n4. **Completion Check**: \n - Continue this process until all nodes have been visited.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n^2 \\log n)$$, due to priority queue operations.\n- **Space Complexity**: $$O(n)$$, for storing the priority queue and visited nodes.\n\n---\n\n# Code Prim\n``` Python []\ndef manhattan_distance(p1: List[int], p2: List[int]) -> int:\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n visited = [False] * n\n heap_dict = {0: 0} \n min_heap = [(0, 0)]\n \n mst_weight = 0\n \n while min_heap:\n w, u = heappop(min_heap)\n \n if visited[u] or heap_dict.get(u, float(\'inf\')) < w:\n continue\n \n visited[u] = True\n mst_weight += w\n \n for v in range(n):\n if not visited[v]:\n new_distance = manhattan_distance(points[u], points[v])\n \n if new_distance < heap_dict.get(v, float(\'inf\')):\n heap_dict[v] = new_distance\n heappush(min_heap, (new_distance, v))\n \n return mst_weight\n```\n``` Go []\ntype Item struct {\n\tdistance, point int\n}\n\ntype PriorityQueue []Item\n\nfunc (pq PriorityQueue) Len() int { return len(pq) }\n\nfunc (pq PriorityQueue) Less(i, j int) bool {\n\treturn pq[i].distance < pq[j].distance\n}\n\nfunc (pq PriorityQueue) Swap(i, j int) {\n\tpq[i], pq[j] = pq[j], pq[i]\n}\n\nfunc (pq *PriorityQueue) Push(x interface{}) {\n\titem := x.(Item)\n\t*pq = append(*pq, item)\n}\n\nfunc (pq *PriorityQueue) Pop() interface{} {\n\told := *pq\n\tn := len(old)\n\titem := old[n-1]\n\t*pq = old[0 : n-1]\n\treturn item\n}\n\nfunc manhattanDistance(p1, p2 []int) int {\n\treturn int(math.Abs(float64(p1[0]-p2[0])) + math.Abs(float64(p1[1]-p2[1])))\n}\n\nfunc minCostConnectPoints(points [][]int) int {\n\tn := len(points)\n\tvisited := make([]bool, n)\n\theapDict := make(map[int]int)\n\tfor i := 0; i < n; i++ {\n\t\theapDict[i] = int(math.MaxInt64) // Initialize all distances to infinity\n\t}\n\theapDict[0] = 0 // Start node\n\n\tpq := make(PriorityQueue, 1)\n\tpq[0] = Item{distance: 0, point: 0}\n\theap.Init(&pq)\n\n\tmstWeight := 0\n\n\tfor pq.Len() > 0 {\n\t\titem := heap.Pop(&pq).(Item)\n\t\tw, u := item.distance, item.point\n\n\t\tif visited[u] || heapDict[u] < w {\n\t\t\tcontinue\n\t\t}\n\n\t\tvisited[u] = true\n\t\tmstWeight += w\n\n\t\tfor v := 0; v < n; v++ {\n\t\t\tif !visited[v] {\n\t\t\t\tnewDistance := manhattanDistance(points[u], points[v])\n\t\t\t\tif newDistance < heapDict[v] {\n\t\t\t\t\theapDict[v] = newDistance\n\t\t\t\t\theap.Push(&pq, Item{distance: newDistance, point: v})\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\treturn mstWeight\n}\n```\n``` Rust []\nuse std::collections::{BinaryHeap, HashMap};\nuse std::cmp::Reverse;\n\nimpl Solution {\n fn manhattan_distance(p1: &[i32], p2: &[i32]) -> i32 {\n (p1[0] - p2[0]).abs() + (p1[1] - p2[1]).abs()\n }\n\n pub fn min_cost_connect_points(points: Vec<Vec<i32>>) -> i32 {\n let n = points.len();\n let mut visited = vec![false; n];\n let mut heap_dict = HashMap::new();\n heap_dict.insert(0, 0);\n let mut min_heap = BinaryHeap::new();\n min_heap.push(Reverse((0, 0)));\n\n let mut mst_weight = 0;\n\n while let Some(Reverse((w, u))) = min_heap.pop() {\n if visited[u] || heap_dict[&u] < w {\n continue;\n }\n\n visited[u] = true;\n mst_weight += w;\n\n for v in 0..n {\n if !visited[v] {\n let new_distance = Self::manhattan_distance(&points[u], &points[v]); // Fix here\n if new_distance < *heap_dict.get(&v).unwrap_or(&i32::MAX) {\n heap_dict.insert(v, new_distance);\n min_heap.push(Reverse((new_distance, v)));\n }\n }\n }\n }\n\n mst_weight\n }\n}\n```\n``` C++ []\nint manhattan_distance(vector<int>& p1, vector<int>& p2) {\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1]);\n}\n\nclass Solution {\npublic:\n int minCostConnectPoints(vector<vector<int>>& points) {\n int n = points.size();\n vector<bool> visited(n, false);\n unordered_map<int, int> heap_dict;\n for(int i = 0; i < n; ++i) {\n heap_dict[i] = INT_MAX; // Initialize all distances to infinity\n }\n heap_dict[0] = 0; // Start node\n \n auto cmp = [](pair<int, int> left, pair<int, int> right) { return left.first > right.first; };\n priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> min_heap(cmp);\n min_heap.push({0, 0});\n \n int mst_weight = 0;\n \n while (!min_heap.empty()) {\n auto [w, u] = min_heap.top();\n min_heap.pop();\n \n if (visited[u] || heap_dict[u] < w) continue;\n \n visited[u] = true;\n mst_weight += w;\n \n for (int v = 0; v < n; ++v) {\n if (!visited[v]) {\n int new_distance = manhattan_distance(points[u], points[v]);\n if (new_distance < heap_dict[v]) {\n heap_dict[v] = new_distance;\n min_heap.push({new_distance, v});\n }\n }\n }\n }\n \n return mst_weight;\n }\n};\n```\n``` Java []\npublic class Solution {\n public static int manhattan_distance(int[] p1, int[] p2) {\n return Math.abs(p1[0] - p2[0]) + Math.abs(p1[1] - p2[1]);\n }\n\n public int minCostConnectPoints(int[][] points) {\n int n = points.length;\n boolean[] visited = new boolean[n];\n HashMap<Integer, Integer> heap_dict = new HashMap<>();\n heap_dict.put(0, 0);\n \n PriorityQueue<int[]> min_heap = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n min_heap.add(new int[]{0, 0});\n \n int mst_weight = 0;\n \n while (!min_heap.isEmpty()) {\n int[] top = min_heap.poll();\n int w = top[0], u = top[1];\n \n if (visited[u] || heap_dict.getOrDefault(u, Integer.MAX_VALUE) < w) continue;\n \n visited[u] = true;\n mst_weight += w;\n \n for (int v = 0; v < n; ++v) {\n if (!visited[v]) {\n int new_distance = manhattan_distance(points[u], points[v]);\n if (new_distance < heap_dict.getOrDefault(v, Integer.MAX_VALUE)) {\n heap_dict.put(v, new_distance);\n min_heap.add(new int[]{new_distance, v});\n }\n }\n }\n }\n \n return mst_weight;\n }\n}\n```\n``` JavaScript []\ndef manhattan_distance(p1: List[int], p2: List[int]) -> int:\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n visited = [False] * n\n heap_dict = {0: 0} \n min_heap = [(0, 0)]\n \n mst_weight = 0\n \n while min_heap:\n w, u = heappop(min_heap)\n \n if visited[u] or heap_dict.get(u, float(\'inf\')) < w:\n continue\n \n visited[u] = True\n mst_weight += w\n \n for v in range(n):\n if not visited[v]:\n new_distance = manhattan_distance(points[u], points[v])\n \n if new_distance < heap_dict.get(v, float(\'inf\')):\n heap_dict[v] = new_distance\n heappush(min_heap, (new_distance, v))\n \n return mst_weight\n```\n``` C# []\npublic class Solution {\n public static int ManhattanDistance(int[] p1, int[] p2) {\n return Math.Abs(p1[0] - p2[0]) + Math.Abs(p1[1] - p2[1]);\n }\n\n public int MinCostConnectPoints(int[][] points) {\n int n = points.Length;\n bool[] visited = new bool[n];\n Dictionary<int, int> heapDict = new Dictionary<int, int>() { {0, 0} };\n var minHeap = new SortedSet<(int w, int u)>() { (0, 0) };\n\n int mstWeight = 0;\n\n while (minHeap.Count > 0) {\n var (w, u) = minHeap.Min;\n minHeap.Remove(minHeap.Min);\n \n if (visited[u] || heapDict[u] < w) continue;\n\n visited[u] = true;\n mstWeight += w;\n\n for (int v = 0; v < n; v++) {\n if (!visited[v]) {\n int newDistance = ManhattanDistance(points[u], points[v]);\n if (newDistance < heapDict.GetValueOrDefault(v, int.MaxValue)) {\n heapDict[v] = newDistance;\n minHeap.Add((newDistance, v));\n }\n }\n }\n }\n\n return mstWeight;\n }\n}\n```\n``` PHP []\nclass Solution {\n function manhattan_distance($p1, $p2) {\n return abs($p1[0] - $p2[0]) + abs($p1[1] - $p2[1]);\n }\n \n function minCostConnectPoints($points) {\n $n = count($points);\n $visited = array_fill(0, $n, false);\n $heap_dict = [0 => 0];\n $min_heap = new SplPriorityQueue();\n $min_heap->insert([0, 0], 0);\n\n $mst_weight = 0;\n\n while (!$min_heap->isEmpty()) {\n list($w, $u) = $min_heap->extract();\n if ($visited[$u] || $heap_dict[$u] < $w) continue;\n\n $visited[$u] = true;\n $mst_weight += $w;\n\n for ($v = 0; $v < $n; $v++) {\n if (!$visited[$v]) {\n $new_distance = $this->manhattan_distance($points[$u], $points[$v]); // Fix here\n if ($new_distance < ($heap_dict[$v] ?? INF)) {\n $heap_dict[$v] = $new_distance;\n $min_heap->insert([$new_distance, $v], -$new_distance);\n }\n }\n }\n }\n\n return $mst_weight;\n }\n}\n```\n\n## Kruskal\'s Algorithm Explained\n\n### What is Kruskal\'s Algorithm?\n\nKruskal\'s Algorithm is an algorithm to find the Minimum Spanning Tree of a graph. It sorts all the edges by weight and adds them one by one, checking that the addition of each edge doesn\'t form a cycle.\n\n### The Essence of Kruskal\'s Algorithm in "Min Cost to Connect All Points"\n\n1. **Initialize Edge List**: \n - Calculate the Manhattan distance between all pairs of points to form an edge list. Each edge is represented by a tuple `(w, u, v)`, where `w` is the weight (Manhattan distance) and `u` and `v` are the nodes (points).\n\n2. **Sort the Edges**: \n - Sort all edges by their weights. This helps us ensure that we\'re considering the smallest weight first, adhering to the "minimum" in Minimum Spanning Tree.\n\n3. **Union-Find for Connectivity**: \n - Use a Union-Find data structure to keep track of connected components. This is crucial for efficiently checking whether adding a new edge would create a cycle.\n\n4. **Iterate and Add to MST**: \n - Iterate through the sorted edge list, adding each edge to the Minimum Spanning Tree if it doesn\'t form a cycle. Keep a counter of the number of edges added, and stop when you\'ve added $$n-1$$ edges, where $$n$$ is the number of nodes.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n^2 \\log n)$$, mainly due to sorting the edge list.\n- **Space Complexity**: $$O(n^2)$$, for storing the edge list and Union-Find data structure.\n\n\n# Code Kruskal \n``` Python []\ndef manhattan_distance(p1: List[int], p2: List[int]) -> int:\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n self.rank = [0 for _ in range(n)]\n \n def find(self, u):\n if self.parent[u] == u:\n return u\n self.parent[u] = self.find(self.parent[u])\n return self.parent[u]\n \n def union(self, u, v):\n u = self.find(u)\n v = self.find(v)\n \n if u == v:\n return False\n \n if self.rank[u] > self.rank[v]:\n u, v = v, u\n \n self.parent[u] = v\n \n if self.rank[u] == self.rank[v]:\n self.rank[v] += 1\n \n return True\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n uf = UnionFind(n)\n \n edges = []\n \n for i in range(n):\n for j in range(i+1, n):\n distance = manhattan_distance(points[i], points[j])\n heappush(edges, (distance, i, j))\n \n mst_weight = 0\n mst_edges = 0\n \n while edges:\n w, u, v = heappop(edges)\n if uf.union(u, v):\n mst_weight += w\n mst_edges += 1\n if mst_edges == n - 1:\n break\n \n return mst_weight\n```\n``` Go []\ntype UnionFind struct {\n\tparent, rank []int\n}\n\nfunc NewUnionFind(n int) *UnionFind {\n\tparent := make([]int, n)\n\trank := make([]int, n)\n\tfor i := range parent {\n\t\tparent[i] = i\n\t}\n\treturn &UnionFind{parent, rank}\n}\n\nfunc (uf *UnionFind) find(u int) int {\n\tif uf.parent[u] == u {\n\t\treturn u\n\t}\n\tuf.parent[u] = uf.find(uf.parent[u])\n\treturn uf.parent[u]\n}\n\nfunc (uf *UnionFind) union(u, v int) bool {\n\tu, v = uf.find(u), uf.find(v)\n\tif u == v {\n\t\treturn false\n\t}\n\tif uf.rank[u] > uf.rank[v] {\n\t\tu, v = v, u\n\t}\n\tuf.parent[u] = v\n\tif uf.rank[u] == uf.rank[v] {\n\t\tuf.rank[v]++\n\t}\n\treturn true\n}\n\nfunc manhattanDistance(p1, p2 []int) int {\n\treturn int(math.Abs(float64(p1[0]-p2[0])) + math.Abs(float64(p1[1]-p2[1])))\n}\n\ntype Edge struct {\n\tdistance, u, v int\n}\n\ntype MinHeap []Edge\n\nfunc (h MinHeap) Len() int { return len(h) }\nfunc (h MinHeap) Less(i, j int) bool { return h[i].distance < h[j].distance }\nfunc (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\nfunc (h *MinHeap) Push(x interface{}) { *h = append(*h, x.(Edge)) }\nfunc (h *MinHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\titem := old[n-1]\n\t*h = old[0 : n-1]\n\treturn item\n}\n\nfunc minCostConnectPoints(points [][]int) int {\n\tn := len(points)\n\tuf := NewUnionFind(n)\n\n\tedges := &MinHeap{}\n\theap.Init(edges)\n\n\tfor i := 0; i < n; i++ {\n\t\tfor j := i + 1; j < n; j++ {\n\t\t\tdistance := manhattanDistance(points[i], points[j])\n\t\t\theap.Push(edges, Edge{distance, i, j})\n\t\t}\n\t}\n\n\tmstWeight := 0\n\tmstEdges := 0\n\n\tfor edges.Len() > 0 {\n\t\tedge := heap.Pop(edges).(Edge)\n\t\tif uf.union(edge.u, edge.v) {\n\t\t\tmstWeight += edge.distance\n\t\t\tmstEdges++\n\t\t\tif mstEdges == n-1 {\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t}\n\n\treturn mstWeight\n}\n```\n``` Rust []\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\n\nstruct UnionFind {\n parent: Vec<usize>,\n rank: Vec<usize>,\n}\n\nimpl UnionFind {\n fn new(n: usize) -> Self {\n Self {\n parent: (0..n).collect(),\n rank: vec![0; n],\n }\n }\n \n fn find(&mut self, u: usize) -> usize {\n if self.parent[u] == u {\n return u;\n }\n self.parent[u] = self.find(self.parent[u]);\n self.parent[u]\n }\n\n fn union(&mut self, mut u: usize, mut v: usize) -> bool {\n u = self.find(u);\n v = self.find(v);\n if u == v {\n return false;\n }\n if self.rank[u] > self.rank[v] {\n std::mem::swap(&mut u, &mut v);\n }\n self.parent[u] = v;\n if self.rank[u] == self.rank[v] {\n self.rank[v] += 1;\n }\n true\n }\n}\n\nfn manhattan_distance(p1: &[i32], p2: &[i32]) -> i32 {\n (p1[0] - p2[0]).abs() + (p1[1] - p2[1]).abs()\n}\n\n\nimpl Solution {\n pub fn min_cost_connect_points(points: Vec<Vec<i32>>) -> i32 {\n let n = points.len();\n let mut uf = UnionFind::new(n);\n let mut edges = BinaryHeap::new();\n\n for i in 0..n {\n for j in (i + 1)..n {\n let distance = manhattan_distance(&points[i], &points[j]);\n edges.push(Reverse((distance, i, j)));\n }\n }\n\n let mut mst_weight = 0;\n let mut mst_edges = 0;\n\n while let Some(Reverse((w, u, v))) = edges.pop() {\n if uf.union(u, v) {\n mst_weight += w;\n mst_edges += 1;\n if mst_edges == n - 1 {\n break;\n }\n }\n }\n\n mst_weight\n }\n}\n```\n``` C++ []\n// todo\n```\n``` Java []\n// todo\n```\n``` JavaScript []\n// todo\n```\n``` C# []\n// todo\n```\n``` PHP []\n// todo\n```\n\n## Performance\n\n| Language | Algorithm | Runtime (ms) | Memory Usage (MB) |\n|------------|-----------|--------------|-------------------|\n| Rust | Prim | 49 | 2.8 |\n| Go | Prim | 71 | 7.5 |\n| Java | Prim | 76 | 45.5 |\n| C++ | Prim | 126 | 14.6 |\n| PHP | Prim | 227 | 30.5 |\n| C# | Prim | 232 | 48.7 |\n| Python3 | Prim | 744 | 20.5 |\n| Python3 | Kruskal | 771 | 84.1 |\n| JavaScript | Prim | 2306 | 93.8 |\n\n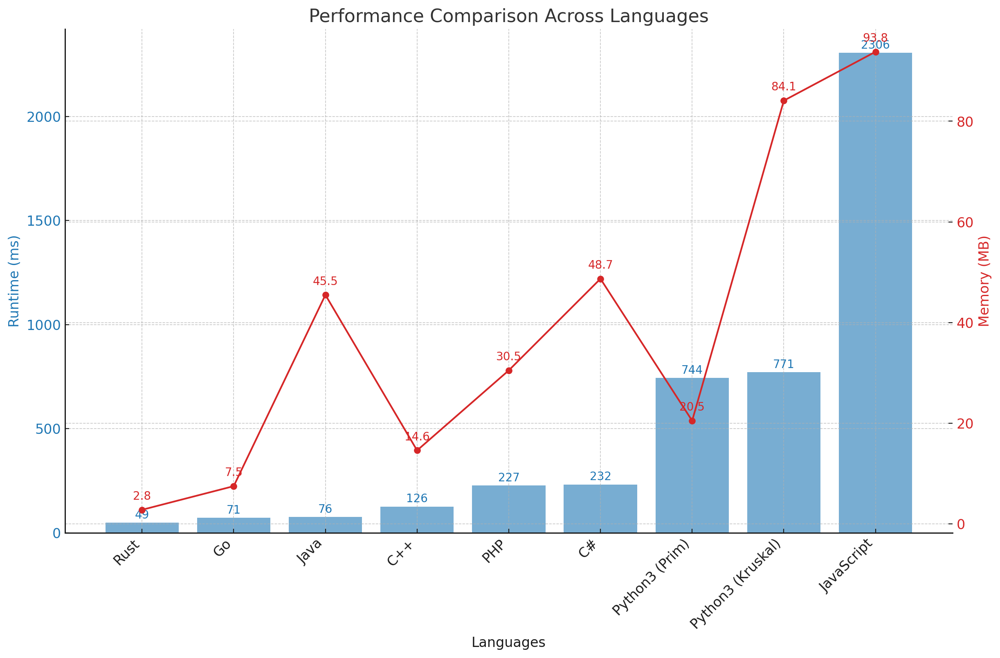\n\n## Live Coding Kruskal & More\nhttps://youtu.be/JgmClRWPMX4?si=2oKw4ZDwb5mmEl3F\n\n## Code Highlights and Best Practices\n\n- Both Kruskal\'s and Prim\'s algorithms are efficient for this problem, but Kruskal\'s algorithm is easier to implement with a Union-Find data structure.\n- Prim\'s algorithm is more intuitive but requires careful handling of the priority queue to ensure optimal performance.\n\nMastering these techniques will not only help you tackle this problem effectively but will also deepen your understanding of graph algorithms, which are incredibly useful in various fields. So, are you ready to connect some points? Let\'s get coding!\n\n | 97 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
✅ 94.85% Prim & Kruskal with Min-Heap | min-cost-to-connect-all-points | 1 | 1 | # Comprehensive Guide to Solving "Min Cost to Connect All Points": Bridging the Gap Efficiently\n\n## Introduction & Problem Statement\n\nHello, algorithmic explorers! Today, we\'re diving into a problem that\'s a fascinating blend of computational geometry and graph theory: "Min Cost to Connect All Points." Imagine you\'re given a set of points on a 2D plane, and your task is to connect them all with lines. Sounds simple? Well, it\'s not just about connecting them; you need to do so with the minimum possible cost, where the cost is defined as the Manhattan distance between points. Intriguing, isn\'t it?\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Graph Theory and MST**: \n This problem can be represented as a graph where each point is a node and the edges are the Manhattan distances between the points. The objective boils down to finding the Minimum Spanning Tree (MST) of this graph.\n \n2. **Manhattan Distance**: \n The edge weight isn\'t just a simple Euclidean distance; it\'s the Manhattan distance, which is the sum of the absolute differences in their Cartesian coordinates.\n\n3. **Constraints**: \n - 1 <= points.length <= 1000\n - $$-10^6 \\leq x_i, y_i \\leq 10^6$$\n - All pairs $$(x_i, y_i)$$ are distinct.\n\n### Strategies to Tackle the Problem\n\n1. **Kruskal\'s Algorithm**: \n This approach utilizes a Union-Find data structure to find the MST efficiently.\n \n2. **Prim\'s Algorithm**: \n This method employs a Priority Queue to select edges with minimum weights iteratively.\n\n---\n\n## Live Coding Prim & Explain\nhttps://youtu.be/7JxI7gt-WEM?si=bCZ7NBlDNRDjUzlw\n\n## Prim\'s Algorithm Explained\n\n### What is Prim\'s Algorithm?\n\nPrim\'s Algorithm is another method for finding the Minimum Spanning Tree. It starts from an arbitrary node and greedily chooses the edge with the smallest weight that connects a visited and an unvisited node.\n\n### The Mechanics of Prim\'s Algorithm in "Min Cost to Connect All Points"\n\n1. **Initialize Priority Queue**: \n - Start from an arbitrary point and initialize a minimum priority queue with its edges.\n\n2. **Visited Nodes Tracking**: \n - Keep track of visited nodes to ensure that each node is visited exactly once.\n\n3. **Iterate and Add to MST**: \n - Pop the edge with the smallest weight from the priority queue. If the edge leads to an unvisited node, add the edge\'s weight to the total MST weight, and insert all edges from that node into the priority queue.\n\n4. **Completion Check**: \n - Continue this process until all nodes have been visited.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n^2 \\log n)$$, due to priority queue operations.\n- **Space Complexity**: $$O(n)$$, for storing the priority queue and visited nodes.\n\n---\n\n# Code Prim\n``` Python []\ndef manhattan_distance(p1: List[int], p2: List[int]) -> int:\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n visited = [False] * n\n heap_dict = {0: 0} \n min_heap = [(0, 0)]\n \n mst_weight = 0\n \n while min_heap:\n w, u = heappop(min_heap)\n \n if visited[u] or heap_dict.get(u, float(\'inf\')) < w:\n continue\n \n visited[u] = True\n mst_weight += w\n \n for v in range(n):\n if not visited[v]:\n new_distance = manhattan_distance(points[u], points[v])\n \n if new_distance < heap_dict.get(v, float(\'inf\')):\n heap_dict[v] = new_distance\n heappush(min_heap, (new_distance, v))\n \n return mst_weight\n```\n``` Go []\ntype Item struct {\n\tdistance, point int\n}\n\ntype PriorityQueue []Item\n\nfunc (pq PriorityQueue) Len() int { return len(pq) }\n\nfunc (pq PriorityQueue) Less(i, j int) bool {\n\treturn pq[i].distance < pq[j].distance\n}\n\nfunc (pq PriorityQueue) Swap(i, j int) {\n\tpq[i], pq[j] = pq[j], pq[i]\n}\n\nfunc (pq *PriorityQueue) Push(x interface{}) {\n\titem := x.(Item)\n\t*pq = append(*pq, item)\n}\n\nfunc (pq *PriorityQueue) Pop() interface{} {\n\told := *pq\n\tn := len(old)\n\titem := old[n-1]\n\t*pq = old[0 : n-1]\n\treturn item\n}\n\nfunc manhattanDistance(p1, p2 []int) int {\n\treturn int(math.Abs(float64(p1[0]-p2[0])) + math.Abs(float64(p1[1]-p2[1])))\n}\n\nfunc minCostConnectPoints(points [][]int) int {\n\tn := len(points)\n\tvisited := make([]bool, n)\n\theapDict := make(map[int]int)\n\tfor i := 0; i < n; i++ {\n\t\theapDict[i] = int(math.MaxInt64) // Initialize all distances to infinity\n\t}\n\theapDict[0] = 0 // Start node\n\n\tpq := make(PriorityQueue, 1)\n\tpq[0] = Item{distance: 0, point: 0}\n\theap.Init(&pq)\n\n\tmstWeight := 0\n\n\tfor pq.Len() > 0 {\n\t\titem := heap.Pop(&pq).(Item)\n\t\tw, u := item.distance, item.point\n\n\t\tif visited[u] || heapDict[u] < w {\n\t\t\tcontinue\n\t\t}\n\n\t\tvisited[u] = true\n\t\tmstWeight += w\n\n\t\tfor v := 0; v < n; v++ {\n\t\t\tif !visited[v] {\n\t\t\t\tnewDistance := manhattanDistance(points[u], points[v])\n\t\t\t\tif newDistance < heapDict[v] {\n\t\t\t\t\theapDict[v] = newDistance\n\t\t\t\t\theap.Push(&pq, Item{distance: newDistance, point: v})\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\treturn mstWeight\n}\n```\n``` Rust []\nuse std::collections::{BinaryHeap, HashMap};\nuse std::cmp::Reverse;\n\nimpl Solution {\n fn manhattan_distance(p1: &[i32], p2: &[i32]) -> i32 {\n (p1[0] - p2[0]).abs() + (p1[1] - p2[1]).abs()\n }\n\n pub fn min_cost_connect_points(points: Vec<Vec<i32>>) -> i32 {\n let n = points.len();\n let mut visited = vec![false; n];\n let mut heap_dict = HashMap::new();\n heap_dict.insert(0, 0);\n let mut min_heap = BinaryHeap::new();\n min_heap.push(Reverse((0, 0)));\n\n let mut mst_weight = 0;\n\n while let Some(Reverse((w, u))) = min_heap.pop() {\n if visited[u] || heap_dict[&u] < w {\n continue;\n }\n\n visited[u] = true;\n mst_weight += w;\n\n for v in 0..n {\n if !visited[v] {\n let new_distance = Self::manhattan_distance(&points[u], &points[v]); // Fix here\n if new_distance < *heap_dict.get(&v).unwrap_or(&i32::MAX) {\n heap_dict.insert(v, new_distance);\n min_heap.push(Reverse((new_distance, v)));\n }\n }\n }\n }\n\n mst_weight\n }\n}\n```\n``` C++ []\nint manhattan_distance(vector<int>& p1, vector<int>& p2) {\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1]);\n}\n\nclass Solution {\npublic:\n int minCostConnectPoints(vector<vector<int>>& points) {\n int n = points.size();\n vector<bool> visited(n, false);\n unordered_map<int, int> heap_dict;\n for(int i = 0; i < n; ++i) {\n heap_dict[i] = INT_MAX; // Initialize all distances to infinity\n }\n heap_dict[0] = 0; // Start node\n \n auto cmp = [](pair<int, int> left, pair<int, int> right) { return left.first > right.first; };\n priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> min_heap(cmp);\n min_heap.push({0, 0});\n \n int mst_weight = 0;\n \n while (!min_heap.empty()) {\n auto [w, u] = min_heap.top();\n min_heap.pop();\n \n if (visited[u] || heap_dict[u] < w) continue;\n \n visited[u] = true;\n mst_weight += w;\n \n for (int v = 0; v < n; ++v) {\n if (!visited[v]) {\n int new_distance = manhattan_distance(points[u], points[v]);\n if (new_distance < heap_dict[v]) {\n heap_dict[v] = new_distance;\n min_heap.push({new_distance, v});\n }\n }\n }\n }\n \n return mst_weight;\n }\n};\n```\n``` Java []\npublic class Solution {\n public static int manhattan_distance(int[] p1, int[] p2) {\n return Math.abs(p1[0] - p2[0]) + Math.abs(p1[1] - p2[1]);\n }\n\n public int minCostConnectPoints(int[][] points) {\n int n = points.length;\n boolean[] visited = new boolean[n];\n HashMap<Integer, Integer> heap_dict = new HashMap<>();\n heap_dict.put(0, 0);\n \n PriorityQueue<int[]> min_heap = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n min_heap.add(new int[]{0, 0});\n \n int mst_weight = 0;\n \n while (!min_heap.isEmpty()) {\n int[] top = min_heap.poll();\n int w = top[0], u = top[1];\n \n if (visited[u] || heap_dict.getOrDefault(u, Integer.MAX_VALUE) < w) continue;\n \n visited[u] = true;\n mst_weight += w;\n \n for (int v = 0; v < n; ++v) {\n if (!visited[v]) {\n int new_distance = manhattan_distance(points[u], points[v]);\n if (new_distance < heap_dict.getOrDefault(v, Integer.MAX_VALUE)) {\n heap_dict.put(v, new_distance);\n min_heap.add(new int[]{new_distance, v});\n }\n }\n }\n }\n \n return mst_weight;\n }\n}\n```\n``` JavaScript []\ndef manhattan_distance(p1: List[int], p2: List[int]) -> int:\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n visited = [False] * n\n heap_dict = {0: 0} \n min_heap = [(0, 0)]\n \n mst_weight = 0\n \n while min_heap:\n w, u = heappop(min_heap)\n \n if visited[u] or heap_dict.get(u, float(\'inf\')) < w:\n continue\n \n visited[u] = True\n mst_weight += w\n \n for v in range(n):\n if not visited[v]:\n new_distance = manhattan_distance(points[u], points[v])\n \n if new_distance < heap_dict.get(v, float(\'inf\')):\n heap_dict[v] = new_distance\n heappush(min_heap, (new_distance, v))\n \n return mst_weight\n```\n``` C# []\npublic class Solution {\n public static int ManhattanDistance(int[] p1, int[] p2) {\n return Math.Abs(p1[0] - p2[0]) + Math.Abs(p1[1] - p2[1]);\n }\n\n public int MinCostConnectPoints(int[][] points) {\n int n = points.Length;\n bool[] visited = new bool[n];\n Dictionary<int, int> heapDict = new Dictionary<int, int>() { {0, 0} };\n var minHeap = new SortedSet<(int w, int u)>() { (0, 0) };\n\n int mstWeight = 0;\n\n while (minHeap.Count > 0) {\n var (w, u) = minHeap.Min;\n minHeap.Remove(minHeap.Min);\n \n if (visited[u] || heapDict[u] < w) continue;\n\n visited[u] = true;\n mstWeight += w;\n\n for (int v = 0; v < n; v++) {\n if (!visited[v]) {\n int newDistance = ManhattanDistance(points[u], points[v]);\n if (newDistance < heapDict.GetValueOrDefault(v, int.MaxValue)) {\n heapDict[v] = newDistance;\n minHeap.Add((newDistance, v));\n }\n }\n }\n }\n\n return mstWeight;\n }\n}\n```\n``` PHP []\nclass Solution {\n function manhattan_distance($p1, $p2) {\n return abs($p1[0] - $p2[0]) + abs($p1[1] - $p2[1]);\n }\n \n function minCostConnectPoints($points) {\n $n = count($points);\n $visited = array_fill(0, $n, false);\n $heap_dict = [0 => 0];\n $min_heap = new SplPriorityQueue();\n $min_heap->insert([0, 0], 0);\n\n $mst_weight = 0;\n\n while (!$min_heap->isEmpty()) {\n list($w, $u) = $min_heap->extract();\n if ($visited[$u] || $heap_dict[$u] < $w) continue;\n\n $visited[$u] = true;\n $mst_weight += $w;\n\n for ($v = 0; $v < $n; $v++) {\n if (!$visited[$v]) {\n $new_distance = $this->manhattan_distance($points[$u], $points[$v]); // Fix here\n if ($new_distance < ($heap_dict[$v] ?? INF)) {\n $heap_dict[$v] = $new_distance;\n $min_heap->insert([$new_distance, $v], -$new_distance);\n }\n }\n }\n }\n\n return $mst_weight;\n }\n}\n```\n\n## Kruskal\'s Algorithm Explained\n\n### What is Kruskal\'s Algorithm?\n\nKruskal\'s Algorithm is an algorithm to find the Minimum Spanning Tree of a graph. It sorts all the edges by weight and adds them one by one, checking that the addition of each edge doesn\'t form a cycle.\n\n### The Essence of Kruskal\'s Algorithm in "Min Cost to Connect All Points"\n\n1. **Initialize Edge List**: \n - Calculate the Manhattan distance between all pairs of points to form an edge list. Each edge is represented by a tuple `(w, u, v)`, where `w` is the weight (Manhattan distance) and `u` and `v` are the nodes (points).\n\n2. **Sort the Edges**: \n - Sort all edges by their weights. This helps us ensure that we\'re considering the smallest weight first, adhering to the "minimum" in Minimum Spanning Tree.\n\n3. **Union-Find for Connectivity**: \n - Use a Union-Find data structure to keep track of connected components. This is crucial for efficiently checking whether adding a new edge would create a cycle.\n\n4. **Iterate and Add to MST**: \n - Iterate through the sorted edge list, adding each edge to the Minimum Spanning Tree if it doesn\'t form a cycle. Keep a counter of the number of edges added, and stop when you\'ve added $$n-1$$ edges, where $$n$$ is the number of nodes.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n^2 \\log n)$$, mainly due to sorting the edge list.\n- **Space Complexity**: $$O(n^2)$$, for storing the edge list and Union-Find data structure.\n\n\n# Code Kruskal \n``` Python []\ndef manhattan_distance(p1: List[int], p2: List[int]) -> int:\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n self.rank = [0 for _ in range(n)]\n \n def find(self, u):\n if self.parent[u] == u:\n return u\n self.parent[u] = self.find(self.parent[u])\n return self.parent[u]\n \n def union(self, u, v):\n u = self.find(u)\n v = self.find(v)\n \n if u == v:\n return False\n \n if self.rank[u] > self.rank[v]:\n u, v = v, u\n \n self.parent[u] = v\n \n if self.rank[u] == self.rank[v]:\n self.rank[v] += 1\n \n return True\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n uf = UnionFind(n)\n \n edges = []\n \n for i in range(n):\n for j in range(i+1, n):\n distance = manhattan_distance(points[i], points[j])\n heappush(edges, (distance, i, j))\n \n mst_weight = 0\n mst_edges = 0\n \n while edges:\n w, u, v = heappop(edges)\n if uf.union(u, v):\n mst_weight += w\n mst_edges += 1\n if mst_edges == n - 1:\n break\n \n return mst_weight\n```\n``` Go []\ntype UnionFind struct {\n\tparent, rank []int\n}\n\nfunc NewUnionFind(n int) *UnionFind {\n\tparent := make([]int, n)\n\trank := make([]int, n)\n\tfor i := range parent {\n\t\tparent[i] = i\n\t}\n\treturn &UnionFind{parent, rank}\n}\n\nfunc (uf *UnionFind) find(u int) int {\n\tif uf.parent[u] == u {\n\t\treturn u\n\t}\n\tuf.parent[u] = uf.find(uf.parent[u])\n\treturn uf.parent[u]\n}\n\nfunc (uf *UnionFind) union(u, v int) bool {\n\tu, v = uf.find(u), uf.find(v)\n\tif u == v {\n\t\treturn false\n\t}\n\tif uf.rank[u] > uf.rank[v] {\n\t\tu, v = v, u\n\t}\n\tuf.parent[u] = v\n\tif uf.rank[u] == uf.rank[v] {\n\t\tuf.rank[v]++\n\t}\n\treturn true\n}\n\nfunc manhattanDistance(p1, p2 []int) int {\n\treturn int(math.Abs(float64(p1[0]-p2[0])) + math.Abs(float64(p1[1]-p2[1])))\n}\n\ntype Edge struct {\n\tdistance, u, v int\n}\n\ntype MinHeap []Edge\n\nfunc (h MinHeap) Len() int { return len(h) }\nfunc (h MinHeap) Less(i, j int) bool { return h[i].distance < h[j].distance }\nfunc (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\nfunc (h *MinHeap) Push(x interface{}) { *h = append(*h, x.(Edge)) }\nfunc (h *MinHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\titem := old[n-1]\n\t*h = old[0 : n-1]\n\treturn item\n}\n\nfunc minCostConnectPoints(points [][]int) int {\n\tn := len(points)\n\tuf := NewUnionFind(n)\n\n\tedges := &MinHeap{}\n\theap.Init(edges)\n\n\tfor i := 0; i < n; i++ {\n\t\tfor j := i + 1; j < n; j++ {\n\t\t\tdistance := manhattanDistance(points[i], points[j])\n\t\t\theap.Push(edges, Edge{distance, i, j})\n\t\t}\n\t}\n\n\tmstWeight := 0\n\tmstEdges := 0\n\n\tfor edges.Len() > 0 {\n\t\tedge := heap.Pop(edges).(Edge)\n\t\tif uf.union(edge.u, edge.v) {\n\t\t\tmstWeight += edge.distance\n\t\t\tmstEdges++\n\t\t\tif mstEdges == n-1 {\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t}\n\n\treturn mstWeight\n}\n```\n``` Rust []\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\n\nstruct UnionFind {\n parent: Vec<usize>,\n rank: Vec<usize>,\n}\n\nimpl UnionFind {\n fn new(n: usize) -> Self {\n Self {\n parent: (0..n).collect(),\n rank: vec![0; n],\n }\n }\n \n fn find(&mut self, u: usize) -> usize {\n if self.parent[u] == u {\n return u;\n }\n self.parent[u] = self.find(self.parent[u]);\n self.parent[u]\n }\n\n fn union(&mut self, mut u: usize, mut v: usize) -> bool {\n u = self.find(u);\n v = self.find(v);\n if u == v {\n return false;\n }\n if self.rank[u] > self.rank[v] {\n std::mem::swap(&mut u, &mut v);\n }\n self.parent[u] = v;\n if self.rank[u] == self.rank[v] {\n self.rank[v] += 1;\n }\n true\n }\n}\n\nfn manhattan_distance(p1: &[i32], p2: &[i32]) -> i32 {\n (p1[0] - p2[0]).abs() + (p1[1] - p2[1]).abs()\n}\n\n\nimpl Solution {\n pub fn min_cost_connect_points(points: Vec<Vec<i32>>) -> i32 {\n let n = points.len();\n let mut uf = UnionFind::new(n);\n let mut edges = BinaryHeap::new();\n\n for i in 0..n {\n for j in (i + 1)..n {\n let distance = manhattan_distance(&points[i], &points[j]);\n edges.push(Reverse((distance, i, j)));\n }\n }\n\n let mut mst_weight = 0;\n let mut mst_edges = 0;\n\n while let Some(Reverse((w, u, v))) = edges.pop() {\n if uf.union(u, v) {\n mst_weight += w;\n mst_edges += 1;\n if mst_edges == n - 1 {\n break;\n }\n }\n }\n\n mst_weight\n }\n}\n```\n``` C++ []\n// todo\n```\n``` Java []\n// todo\n```\n``` JavaScript []\n// todo\n```\n``` C# []\n// todo\n```\n``` PHP []\n// todo\n```\n\n## Performance\n\n| Language | Algorithm | Runtime (ms) | Memory Usage (MB) |\n|------------|-----------|--------------|-------------------|\n| Rust | Prim | 49 | 2.8 |\n| Go | Prim | 71 | 7.5 |\n| Java | Prim | 76 | 45.5 |\n| C++ | Prim | 126 | 14.6 |\n| PHP | Prim | 227 | 30.5 |\n| C# | Prim | 232 | 48.7 |\n| Python3 | Prim | 744 | 20.5 |\n| Python3 | Kruskal | 771 | 84.1 |\n| JavaScript | Prim | 2306 | 93.8 |\n\n\n\n## Live Coding Kruskal & More\nhttps://youtu.be/JgmClRWPMX4?si=2oKw4ZDwb5mmEl3F\n\n## Code Highlights and Best Practices\n\n- Both Kruskal\'s and Prim\'s algorithms are efficient for this problem, but Kruskal\'s algorithm is easier to implement with a Union-Find data structure.\n- Prim\'s algorithm is more intuitive but requires careful handling of the priority queue to ensure optimal performance.\n\nMastering these techniques will not only help you tackle this problem effectively but will also deepen your understanding of graph algorithms, which are incredibly useful in various fields. So, are you ready to connect some points? Let\'s get coding!\n\n | 97 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Easiest py solution using kruskals | min-cost-to-connect-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can think of the given points as nodes of a graph. The weight of an edge between two nodes is the Manhattan distance between the corresponding points. The goal is to find the minimum cost to connect all these points.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo achieve this, we use Kruskal\'s algorithm, a greedy algorithm that finds the Minimum Spanning Tree (MST) of a graph. First, we construct the graph by calculating the Manhattan distances between all pairs of points. Then, we apply Kruskal\'s algorithm on this weighted graph.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(E log E), where E is the number of edges ($$O(n^2)$$)\n\n\n- Space complexity:($$O(n^2)$$)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Graph:\n # Constructor to initialize the graph with \'vertices\' number of vertices\n def __init__(self, vertices):\n self.V = vertices\n self.graph = []\n\n # Function to add an edge to the graph between vertices \'u\' and \'v\' with weight \'w\'\n def add_edge(self, u, v, w):\n self.graph.append([u, v, w])\n\n # Helper function to find the parent of a node \'i\'\n def find_parent(self, parent, i):\n if parent[i] == i:\n return i\n return self.find_parent(parent, parent[i])\n\n # Helper function to perform a union operation between sets of \'u\' and \'v\'\n def union(self, parent, rank, u, v):\n u_set = self.find_parent(parent, u)\n v_set = self.find_parent(parent, v)\n\n if rank[u_set] < rank[v_set]:\n parent[u_set] = v_set\n elif rank[u_set] > rank[v_set]:\n parent[v_set] = u_set\n else:\n parent[v_set] = u_set\n rank[u_set] += 1\n\n # Kruskal\'s algorithm to find the minimum spanning tree\n def kruskal(self):\n result = []\n i, e = 0, 0\n\n # Sort the edges based on their weights\n self.graph = sorted(self.graph, key=lambda item: item[2])\n\n parent = []\n rank = []\n\n # Initialize parent and rank arrays\n for node in range(self.V):\n parent.append(node)\n rank.append(0)\n\n while e < self.V - 1:\n u, v, w = self.graph[i]\n i += 1\n x = self.find_parent(parent, u)\n y = self.find_parent(parent, v)\n\n if x != y:\n e += 1\n result.append([u, v, w])\n self.union(parent, rank, x, y)\n\n return result\n\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n # Initialize a graph with the number of vertices\n g = Graph(len(points))\n\n # Populate the graph with edges and weights\n for i in range(len(points)):\n p1 = points[i]\n for j in range(i + 1, len(points)):\n p2 = points[j]\n d = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n g.add_edge(i, j, d)\n\n # Find the minimum spanning tree using Kruskal\'s algorithm\n mst = g.kruskal()\n\n # Calculate the total cost of the MST\n total_cost = sum(edge[2] for edge in mst)\n\n return total_cost\n\n``` | 1 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Easiest py solution using kruskals | min-cost-to-connect-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can think of the given points as nodes of a graph. The weight of an edge between two nodes is the Manhattan distance between the corresponding points. The goal is to find the minimum cost to connect all these points.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo achieve this, we use Kruskal\'s algorithm, a greedy algorithm that finds the Minimum Spanning Tree (MST) of a graph. First, we construct the graph by calculating the Manhattan distances between all pairs of points. Then, we apply Kruskal\'s algorithm on this weighted graph.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(E log E), where E is the number of edges ($$O(n^2)$$)\n\n\n- Space complexity:($$O(n^2)$$)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Graph:\n # Constructor to initialize the graph with \'vertices\' number of vertices\n def __init__(self, vertices):\n self.V = vertices\n self.graph = []\n\n # Function to add an edge to the graph between vertices \'u\' and \'v\' with weight \'w\'\n def add_edge(self, u, v, w):\n self.graph.append([u, v, w])\n\n # Helper function to find the parent of a node \'i\'\n def find_parent(self, parent, i):\n if parent[i] == i:\n return i\n return self.find_parent(parent, parent[i])\n\n # Helper function to perform a union operation between sets of \'u\' and \'v\'\n def union(self, parent, rank, u, v):\n u_set = self.find_parent(parent, u)\n v_set = self.find_parent(parent, v)\n\n if rank[u_set] < rank[v_set]:\n parent[u_set] = v_set\n elif rank[u_set] > rank[v_set]:\n parent[v_set] = u_set\n else:\n parent[v_set] = u_set\n rank[u_set] += 1\n\n # Kruskal\'s algorithm to find the minimum spanning tree\n def kruskal(self):\n result = []\n i, e = 0, 0\n\n # Sort the edges based on their weights\n self.graph = sorted(self.graph, key=lambda item: item[2])\n\n parent = []\n rank = []\n\n # Initialize parent and rank arrays\n for node in range(self.V):\n parent.append(node)\n rank.append(0)\n\n while e < self.V - 1:\n u, v, w = self.graph[i]\n i += 1\n x = self.find_parent(parent, u)\n y = self.find_parent(parent, v)\n\n if x != y:\n e += 1\n result.append([u, v, w])\n self.union(parent, rank, x, y)\n\n return result\n\n\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n # Initialize a graph with the number of vertices\n g = Graph(len(points))\n\n # Populate the graph with edges and weights\n for i in range(len(points)):\n p1 = points[i]\n for j in range(i + 1, len(points)):\n p2 = points[j]\n d = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n g.add_edge(i, j, d)\n\n # Find the minimum spanning tree using Kruskal\'s algorithm\n mst = g.kruskal()\n\n # Calculate the total cost of the MST\n total_cost = sum(edge[2] for edge in mst)\n\n return total_cost\n\n``` | 1 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
【Video】Improved Prim's algorithm solution - Python, JavaScript, Java and C++ | min-cost-to-connect-all-points | 1 | 1 | # Intuition\nThe main idea of this algorithm is to find the minimum cost to connect all points in a set using a greedy approach based on Prim\'s algorithm. It starts by selecting an arbitrary point as the initial vertex and maintains a priority queue to keep track of the minimum-cost edges to connect the vertices. The algorithm iteratively selects the edge with the smallest cost from the priority queue, adds its cost to the total minimum cost, and marks the corresponding vertex as visited. It then updates the minimum distances to the remaining unvisited vertices and adds new edges to the priority queue if they result in smaller distances. This process continues until all vertices are visited. The algorithm efficiently explores and connects vertices while minimizing the total cost of connections.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/zIHb5fCyjR8\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2335\nThank you for your support!\n\n---\n\n# Approach\n\n**Prim\'s algorithm:**\n\nPrim\'s algorithm is an algorithm for solving the optimization problem of finding the minimum spanning tree in a weighted connected graph within graph theory. A minimum spanning tree is a subset of the edges of the graph that forms a tree containing all vertices while minimizing the total weight of those edges.\n\n**Overview of the Algorithm:**\n\n1. Calculate the distances between each pair of points and use Prim\'s algorithm to form the minimum spanning tree.\n2. Start from an initial point, mark it as visited, and select the point with the smallest distance among the unvisited points.\n3. Calculate the distances from the selected point to the unvisited points and store them in a cache.\n4. Add the minimum cost edge to the priority queue using the distances from the cache.\n5. Repeat the above steps until all points are visited, and calculate the minimum cost.\n\n**Specific Steps:**\n\nInitial State:\n- `n`: Number of points\n- `min_cost`: Minimum cost (initially 0) and return value\n- `visited`: A list to indicate if each point is visited (initially all False)\n- `pq`: Priority queue (initially `(0, 0)` indicating starting from point 0 with cost 0)\n- `cache`: Dictionary for caching distances (initially empty)\n\n**Each Step:**\n\n1. Pop cost and point from `pq` (start from the initial point).\n2. If the point is already visited, skip this point.\n3. Otherwise, mark this point as visited and add the current cost to the minimum cost.\n4. Calculate distances from this point to all unvisited points and store them in the cache. Update the cache if the new distance is smaller.\n5. Add the point with the smallest distance among the unvisited points to the priority queue using distances from the cache.\n6. Repeat steps 3 to 5 until all points are visited.\n7. Return the final minimum cost.\n\n---\n\n# Complexity\n**Time Complexity:**\n- The code uses a priority queue (heap) to efficiently select the minimum-cost edge, and it may iterate over all points.\n- The main loop runs as long as there are elements in the priority queue, which can have up to `n` elements (in the worst case).\n- In each iteration of the main loop, the code performs a constant amount of work for each edge.\n- Therefore, the overall time complexity of the code is O(n^2 * log(n)) due to the priority queue operations.\n\n**Space Complexity:**\n- `visited` is an array of size `n`, which requires O(n) space.\n- `pq` can have up to `n` elements, which also requires O(n) space.\n- `cache` is a dictionary that can store up to `n` key-value pairs, which requires O(n) space.\n- Overall, the space complexity of the code is O(n).\n\n```python []\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n min_cost = 0\n visited = [False] * n\n pq = [(0, 0)] # (cost, vertex)\n cache = {0: 0}\n\n while pq:\n cost, u = heapq.heappop(pq)\n\n if visited[u]:\n continue\n\n visited[u] = True\n min_cost += cost\n\n for v in range(n):\n if not visited[v]:\n dist = abs(points[u][0] - points[v][0]) + abs(points[u][1] - points[v][1])\n if dist < cache.get(v, float(\'inf\')):\n cache[v] = dist\n heapq.heappush(pq, (dist, v))\n\n return min_cost \n```\n```javascript []\n/**\n * @param {number[][]} points\n * @return {number}\n */\nvar minCostConnectPoints = function(points) {\n const n = points.length;\n let minCost = 0;\n const visited = new Array(n).fill(false);\n const distances = new Array(n).fill(Infinity);\n\n distances[0] = 0; // Start from the first point\n\n for (let i = 0; i < n; i++) {\n let u = getMinDistanceVertex(visited, distances);\n visited[u] = true;\n minCost += distances[u];\n\n for (let v = 0; v < n; v++) {\n if (!visited[v]) {\n const dist = Math.abs(points[u][0] - points[v][0]) + Math.abs(points[u][1] - points[v][1]);\n distances[v] = Math.min(distances[v], dist);\n }\n }\n }\n\n return minCost; \n};\n\nvar getMinDistanceVertex = function(visited, distances) {\n let minDist = Infinity;\n let minVertex = -1;\n\n for (let i = 0; i < distances.length; i++) {\n if (!visited[i] && distances[i] < minDist) {\n minDist = distances[i];\n minVertex = i;\n }\n }\n\n return minVertex;\n};\n```\n```java []\nclass Solution {\n public int minCostConnectPoints(int[][] points) {\n int n = points.length;\n int min_cost = 0;\n boolean[] visited = new boolean[n];\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); // [cost, vertex]\n Map<Integer, Integer> cache = new HashMap<>();\n pq.offer(new int[]{0, 0});\n\n while (!pq.isEmpty()) {\n int[] edge = pq.poll();\n int cost = edge[0];\n int u = edge[1];\n\n if (visited[u]) {\n continue;\n }\n\n visited[u] = true;\n min_cost += cost;\n\n for (int v = 0; v < n; v++) {\n if (!visited[v]) {\n int dist = Math.abs(points[u][0] - points[v][0]) + Math.abs(points[u][1] - points[v][1]);\n if (dist < cache.getOrDefault(v, Integer.MAX_VALUE)) {\n cache.put(v, dist);\n pq.offer(new int[]{dist, v});\n }\n }\n }\n }\n\n return min_cost;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minCostConnectPoints(vector<vector<int>>& points) {\n int n = points.size();\n int min_cost = 0;\n std::vector<bool> visited(n, false);\n std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> pq; // {cost, vertex}\n std::unordered_map<int, int> cache;\n pq.push({0, 0});\n\n while (!pq.empty()) {\n auto edge = pq.top();\n pq.pop();\n int cost = edge.first;\n int u = edge.second;\n\n if (visited[u]) {\n continue;\n }\n\n visited[u] = true;\n min_cost += cost;\n\n for (int v = 0; v < n; v++) {\n if (!visited[v]) {\n int dist = std::abs(points[u][0] - points[v][0]) + std::abs(points[u][1] - points[v][1]);\n if (cache.find(v) == cache.end() || dist < cache[v]) {\n cache[v] = dist;\n pq.push({dist, v});\n }\n }\n }\n }\n\n return min_cost;\n }\n};\n```\n\n\n---\n\n\n# Bonus\nThe above code is an improved version of the Prim\'s algorithm. A typical Prim\'s algorithm works as follows:\n\nI believe this code is slower than the above. Because we put all distances into heap regardless of long/short distances, so we execute `while` many times. \n\n## Python\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n min_cost = 0\n visited = [False] * n\n pq = [(0, 0)] # Priority queue to store edges (cost, vertex)\n\n while pq:\n cost, u = heapq.heappop(pq)\n\n if visited[u]:\n continue\n\n visited[u] = True\n min_cost += cost\n\n for v in range(n):\n if not visited[v]:\n dist = abs(points[u][0] - points[v][0]) + abs(points[u][1] - points[v][1])\n heapq.heappush(pq, (dist, v))\n\n return min_cost \n```\n\nThank you for reading. \u2B50\uFE0FPlease upvote this article and don\'t forget to subscribe to my youtube channel!\n\nHave a nice day! | 33 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
【Video】Improved Prim's algorithm solution - Python, JavaScript, Java and C++ | min-cost-to-connect-all-points | 1 | 1 | # Intuition\nThe main idea of this algorithm is to find the minimum cost to connect all points in a set using a greedy approach based on Prim\'s algorithm. It starts by selecting an arbitrary point as the initial vertex and maintains a priority queue to keep track of the minimum-cost edges to connect the vertices. The algorithm iteratively selects the edge with the smallest cost from the priority queue, adds its cost to the total minimum cost, and marks the corresponding vertex as visited. It then updates the minimum distances to the remaining unvisited vertices and adds new edges to the priority queue if they result in smaller distances. This process continues until all vertices are visited. The algorithm efficiently explores and connects vertices while minimizing the total cost of connections.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/zIHb5fCyjR8\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2335\nThank you for your support!\n\n---\n\n# Approach\n\n**Prim\'s algorithm:**\n\nPrim\'s algorithm is an algorithm for solving the optimization problem of finding the minimum spanning tree in a weighted connected graph within graph theory. A minimum spanning tree is a subset of the edges of the graph that forms a tree containing all vertices while minimizing the total weight of those edges.\n\n**Overview of the Algorithm:**\n\n1. Calculate the distances between each pair of points and use Prim\'s algorithm to form the minimum spanning tree.\n2. Start from an initial point, mark it as visited, and select the point with the smallest distance among the unvisited points.\n3. Calculate the distances from the selected point to the unvisited points and store them in a cache.\n4. Add the minimum cost edge to the priority queue using the distances from the cache.\n5. Repeat the above steps until all points are visited, and calculate the minimum cost.\n\n**Specific Steps:**\n\nInitial State:\n- `n`: Number of points\n- `min_cost`: Minimum cost (initially 0) and return value\n- `visited`: A list to indicate if each point is visited (initially all False)\n- `pq`: Priority queue (initially `(0, 0)` indicating starting from point 0 with cost 0)\n- `cache`: Dictionary for caching distances (initially empty)\n\n**Each Step:**\n\n1. Pop cost and point from `pq` (start from the initial point).\n2. If the point is already visited, skip this point.\n3. Otherwise, mark this point as visited and add the current cost to the minimum cost.\n4. Calculate distances from this point to all unvisited points and store them in the cache. Update the cache if the new distance is smaller.\n5. Add the point with the smallest distance among the unvisited points to the priority queue using distances from the cache.\n6. Repeat steps 3 to 5 until all points are visited.\n7. Return the final minimum cost.\n\n---\n\n# Complexity\n**Time Complexity:**\n- The code uses a priority queue (heap) to efficiently select the minimum-cost edge, and it may iterate over all points.\n- The main loop runs as long as there are elements in the priority queue, which can have up to `n` elements (in the worst case).\n- In each iteration of the main loop, the code performs a constant amount of work for each edge.\n- Therefore, the overall time complexity of the code is O(n^2 * log(n)) due to the priority queue operations.\n\n**Space Complexity:**\n- `visited` is an array of size `n`, which requires O(n) space.\n- `pq` can have up to `n` elements, which also requires O(n) space.\n- `cache` is a dictionary that can store up to `n` key-value pairs, which requires O(n) space.\n- Overall, the space complexity of the code is O(n).\n\n```python []\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n min_cost = 0\n visited = [False] * n\n pq = [(0, 0)] # (cost, vertex)\n cache = {0: 0}\n\n while pq:\n cost, u = heapq.heappop(pq)\n\n if visited[u]:\n continue\n\n visited[u] = True\n min_cost += cost\n\n for v in range(n):\n if not visited[v]:\n dist = abs(points[u][0] - points[v][0]) + abs(points[u][1] - points[v][1])\n if dist < cache.get(v, float(\'inf\')):\n cache[v] = dist\n heapq.heappush(pq, (dist, v))\n\n return min_cost \n```\n```javascript []\n/**\n * @param {number[][]} points\n * @return {number}\n */\nvar minCostConnectPoints = function(points) {\n const n = points.length;\n let minCost = 0;\n const visited = new Array(n).fill(false);\n const distances = new Array(n).fill(Infinity);\n\n distances[0] = 0; // Start from the first point\n\n for (let i = 0; i < n; i++) {\n let u = getMinDistanceVertex(visited, distances);\n visited[u] = true;\n minCost += distances[u];\n\n for (let v = 0; v < n; v++) {\n if (!visited[v]) {\n const dist = Math.abs(points[u][0] - points[v][0]) + Math.abs(points[u][1] - points[v][1]);\n distances[v] = Math.min(distances[v], dist);\n }\n }\n }\n\n return minCost; \n};\n\nvar getMinDistanceVertex = function(visited, distances) {\n let minDist = Infinity;\n let minVertex = -1;\n\n for (let i = 0; i < distances.length; i++) {\n if (!visited[i] && distances[i] < minDist) {\n minDist = distances[i];\n minVertex = i;\n }\n }\n\n return minVertex;\n};\n```\n```java []\nclass Solution {\n public int minCostConnectPoints(int[][] points) {\n int n = points.length;\n int min_cost = 0;\n boolean[] visited = new boolean[n];\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); // [cost, vertex]\n Map<Integer, Integer> cache = new HashMap<>();\n pq.offer(new int[]{0, 0});\n\n while (!pq.isEmpty()) {\n int[] edge = pq.poll();\n int cost = edge[0];\n int u = edge[1];\n\n if (visited[u]) {\n continue;\n }\n\n visited[u] = true;\n min_cost += cost;\n\n for (int v = 0; v < n; v++) {\n if (!visited[v]) {\n int dist = Math.abs(points[u][0] - points[v][0]) + Math.abs(points[u][1] - points[v][1]);\n if (dist < cache.getOrDefault(v, Integer.MAX_VALUE)) {\n cache.put(v, dist);\n pq.offer(new int[]{dist, v});\n }\n }\n }\n }\n\n return min_cost;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minCostConnectPoints(vector<vector<int>>& points) {\n int n = points.size();\n int min_cost = 0;\n std::vector<bool> visited(n, false);\n std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> pq; // {cost, vertex}\n std::unordered_map<int, int> cache;\n pq.push({0, 0});\n\n while (!pq.empty()) {\n auto edge = pq.top();\n pq.pop();\n int cost = edge.first;\n int u = edge.second;\n\n if (visited[u]) {\n continue;\n }\n\n visited[u] = true;\n min_cost += cost;\n\n for (int v = 0; v < n; v++) {\n if (!visited[v]) {\n int dist = std::abs(points[u][0] - points[v][0]) + std::abs(points[u][1] - points[v][1]);\n if (cache.find(v) == cache.end() || dist < cache[v]) {\n cache[v] = dist;\n pq.push({dist, v});\n }\n }\n }\n }\n\n return min_cost;\n }\n};\n```\n\n\n---\n\n\n# Bonus\nThe above code is an improved version of the Prim\'s algorithm. A typical Prim\'s algorithm works as follows:\n\nI believe this code is slower than the above. Because we put all distances into heap regardless of long/short distances, so we execute `while` many times. \n\n## Python\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n n = len(points)\n min_cost = 0\n visited = [False] * n\n pq = [(0, 0)] # Priority queue to store edges (cost, vertex)\n\n while pq:\n cost, u = heapq.heappop(pq)\n\n if visited[u]:\n continue\n\n visited[u] = True\n min_cost += cost\n\n for v in range(n):\n if not visited[v]:\n dist = abs(points[u][0] - points[v][0]) + abs(points[u][1] - points[v][1])\n heapq.heappush(pq, (dist, v))\n\n return min_cost \n```\n\nThank you for reading. \u2B50\uFE0FPlease upvote this article and don\'t forget to subscribe to my youtube channel!\n\nHave a nice day! | 33 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Insanely efficient Prim's implementation, beats 99.68% runtime, 99.96% memory | min-cost-to-connect-all-points | 0 | 1 | # Code\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n distances = [[0, 0]] + [[float(\'inf\'), i] for i in range(1, len(points))]\n result = 0\n while distances:\n closest = min(distances)\n result += closest[0]\n x, y = points[closest[1]]\n\n closest[:] = distances[-1][:]\n distances.pop()\n\n for dist in distances:\n x2, y2 = points[dist[1]]\n dist[0] = min(dist[0], abs(x - x2) + abs(y - y2))\n return result\n``` | 0 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Insanely efficient Prim's implementation, beats 99.68% runtime, 99.96% memory | min-cost-to-connect-all-points | 0 | 1 | # Code\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n distances = [[0, 0]] + [[float(\'inf\'), i] for i in range(1, len(points))]\n result = 0\n while distances:\n closest = min(distances)\n result += closest[0]\n x, y = points[closest[1]]\n\n closest[:] = distances[-1][:]\n distances.pop()\n\n for dist in distances:\n x2, y2 = points[dist[1]]\n dist[0] = min(dist[0], abs(x - x2) + abs(y - y2))\n return result\n``` | 0 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
✔Graph || Prims Algorithm✨💎 || Kruskal's Algorithm👀|| Easy to Understand😉😎 | min-cost-to-connect-all-points | 1 | 1 | # Intuition\n- The problem involves finding the minimum cost to connect a set of points using Prim\'s Algorithm, which is a greedy algorithm used for finding the minimum spanning tree (MST) of a graph. \n- In this case, the graph represents the distances between points, and the goal is to connect all points with edges such that the total cost (sum of edge weights) is minimized.\n\n# Approach\n1. **minKey function:** This function is used to find the index of the vertex with the minimum key value that is not yet included in the MST.\n \n - It iterates through all vertices, checks if they are not in the MST (inMST) and have a smaller key value than the current minimum, and updates the minimum index and value accordingly.\n\n1. **MST function:** This function calculates the minimum spanning tree (MST) of the graph using Prim\'s Algorithm. It initializes an array \'key\' to store the key values for each vertex, where key[i] represents the minimum weight of an edge connecting vertex i to the MST. It also initializes an array \'inMST\' to keep track of whether a vertex is included in the MST.\n\n - It starts with the first vertex (0) and sets its key to 0.\n - Then, for V-1 iterations (all vertices except the first one), it selects the vertex \'u\' with the minimum key value that is not in the MST (using minKey function).\n - It includes \'u\' in the MST and updates the key values of its adjacent vertices \'v\' if the edge weight to \'v\' is smaller than the current key value of \'v\'.\n1. **minCostConnectPoints function:** This is the main function that calculates the minimum cost to connect all points.\n\n - It first calculates the Manhattan distances (md) between all pairs of points and populates the \'graph\' matrix with these distances.\n - Then, it calls the MST function to find the minimum cost of connecting all points using Prim\'s Algorithm.\n\n# Complexity\n- Time complexity:\n1. **Calculating Manhattan distances and populating the graph matrix:** This involves two nested loops iterating through all pairs of points, resulting in a time complexity of O(n^2), where \'n\' is the number of points.\n\n1. **MST function (Prim\'s Algorithm):** The time complexity of Prim\'s `Algorithm is O(V^2`) with an adjacency matrix representation of the graph. Since \'V\' is the number of points (vertices), in this case, it is` O(n^2).`\n\n- Space complexity:\n1. **\'graph\' matrix:** `It has a space complexity of O(n^2)` because it stores the distances between all pairs of points.\n\n1. **\'key\' and \'inMST\' arrays:** They both have a space complexity of O(n) because they store information for each point.\n\nOverall, `the space complexity of the algorithm is O(n^2) `due to the \'graph\' matrix and O(n) for the \'key\' and \'inMST\' arrays, making the `space complexity O(n^2)` in total.\n\nPLEASE UPVOTE\u2763\uD83D\uDE0D\n\n# Code\n```\n//Approach-1 (Using 2-D matrix graph) - Prim\'s Algorithm\nclass Solution {\npublic:\n // Function to find the index of the minimum key in \'key\' vector that is not yet included in MST\n int minKey(vector<bool>& inMST, vector<int>& key) {\n int minIndex = 0;\n int minVal = INT_MAX;\n // Loop through all vertices to find the minimum key\n for(int i = 0; i < key.size(); i++) {\n // Check if the vertex is not in MST and its key is smaller than the current minimum value\n if(!inMST[i] && key[i] < minVal) {\n minIndex = i;\n minVal = key[i];\n }\n }\n return minIndex; // Return the index of the minimum key\n }\n\n // Function to calculate the minimum spanning tree (MST) of a given \'graph\' with \'V\' vertices\n int MST(vector<vector<int>>& graph, int V) {\n vector<int> key(V, INT_MAX); // Initialize key values for all vertices to be infinity\n vector<bool> inMST(V, false); // Initialize all vertices as not included in MST\n key[0] = 0; // Start with the first vertex as the source\n \n // Loop through V-1 vertices (all except the first one)\n for(int count = 1; count <= V - 1; count++) {\n int u = minKey(inMST, key); // Find the vertex with the minimum key not in MST\n inMST[u] = true; // Include the selected vertex in MST\n \n // Update the key values of adjacent vertices\n for(int v = 0; v < V; v++) {\n // If there is an edge from \'u\' to \'v\', \'v\' is not in MST, and the edge weight is smaller than \'key[v]\'\n if(graph[u][v] && !inMST[v] && graph[u][v] < key[v]) {\n key[v] = graph[u][v]; // Update the key value of \'v\'\n }\n }\n }\n \n int cost = 0;\n for(int i : key) {\n cost += i; // Calculate the sum of key values, which represents the minimum cost of MST\n }\n return cost; // Return the minimum cost of MST\n }\n\n // Function to calculate the minimum cost to connect all points using Prim\'s Algorithm\n int minCostConnectPoints(vector<vector<int>>& points) {\n int n = points.size();\n vector<vector<int>> graph(n, vector<int>(n)); // Create a 2D matrix \'graph\' to represent the distances between points\n \n // Calculate the Manhattan distance (md) between all pairs of points and populate the \'graph\' matrix\n for(int i = 0; i < n - 1; i++) {\n for(int j = i + 1; j < n; j++) {\n vector<int> p1 = points[i];\n vector<int> p2 = points[j];\n int md = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1]); // Calculate Manhattan distance\n graph[i][j] = md; // Store the distance in both directions since it\'s an undirected graph\n graph[j][i] = md;\n }\n }\n \n return MST(graph, n); // Find and return the minimum cost of connecting all points using MST\n }\n};\n\n```\n# KRUSKAL\'S ALGORITHM\n```\nclass Solution {\npublic:\n vector<int> parent;\n vector<int> rank;\n \n int find (int x) {\n if (x == parent[x]) \n return x;\n \n return parent[x] = find(parent[x]);\n }\n \n void Union (int x, int y) {\n int x_parent = find(x);\n int y_parent = find(y);\n \n if (x_parent == y_parent) \n return;\n \n if(rank[x_parent] > rank[y_parent]) {\n parent[y_parent] = x_parent;\n } else if(rank[x_parent] < rank[y_parent]) {\n parent[x_parent] = y_parent;\n } else {\n parent[x_parent] = y_parent;\n rank[y_parent]++;\n }\n }\n \n int Kruskal(vector<vector<int>> &vec) {\n\n int sum = 0;\n for(auto &temp : vec) {\n \n int u = temp[0];\n int v = temp[1];\n int wt = temp[2];\n \n int parent_u = find(u);\n int parent_v = find(v);\n \n if(parent_u != parent_v) {\n Union(u, v);\n sum += wt;\n }\n \n }\n\n return sum;\n }\n \n int minCostConnectPoints(vector<vector<int>>& points) {\n int V = points.size();\n parent.resize(V);\n\t rank.resize(V, 0);\n \t \n\t for(int i = 0; i<V; i++)\n\t parent[i] = i;\n\n vector<vector<int>> vec;\n \n for(int i = 0; i<V; i++) {\n \n for(int j = i+1; j<V; j++) {\n \n int x1 = points[i][0];\n int y1 = points[i][1];\n \n int x2 = points[j][0];\n int y2 = points[j][1];\n \n int d = abs(x1-x2) + abs(y1-y2);\n \n \n vec.push_back({i, j, d});\n }\n \n }\n \n auto lambda = [&](auto &v1, auto &v2) {\n return v1[2] < v2[2];\n };\n \n sort(begin(vec), end(vec), lambda);\n \n return Kruskal(vec);\n }\n};\n```\n# JAVA\n```\nimport java.util.Arrays;\n\nclass Solution {\n // Function to find the index of the minimum key in \'key\' array that is not yet included in MST\n private int minKey(boolean[] inMST, int[] key) {\n int minIndex = 0;\n int minVal = Integer.MAX_VALUE;\n // Loop through all vertices to find the minimum key\n for (int i = 0; i < key.length; i++) {\n // Check if the vertex is not in MST and its key is smaller than the current minimum value\n if (!inMST[i] && key[i] < minVal) {\n minIndex = i;\n minVal = key[i];\n }\n }\n return minIndex; // Return the index of the minimum key\n }\n\n // Function to calculate the minimum spanning tree (MST) of a given \'graph\' with \'V\' vertices\n private int MST(int[][] graph, int V) {\n int[] key = new int[V];\n boolean[] inMST = new boolean[V];\n Arrays.fill(key, Integer.MAX_VALUE);\n key[0] = 0; // Start with the first vertex as the source\n\n // Loop through V-1 vertices (all except the first one)\n for (int count = 1; count <= V - 1; count++) {\n int u = minKey(inMST, key); // Find the vertex with the minimum key not in MST\n inMST[u] = true; // Include the selected vertex in MST\n\n // Update the key values of adjacent vertices\n for (int v = 0; v < V; v++) {\n // If there is an edge from \'u\' to \'v\', \'v\' is not in MST, and the edge weight is smaller than \'key[v]\'\n if (graph[u][v] > 0 && !inMST[v] && graph[u][v] < key[v]) {\n key[v] = graph[u][v]; // Update the key value of \'v\'\n }\n }\n }\n\n int cost = 0;\n for (int i : key) {\n cost += i; // Calculate the sum of key values, which represents the minimum cost of MST\n }\n return cost; // Return the minimum cost of MST\n }\n\n // Function to calculate the minimum cost to connect all points using Prim\'s Algorithm\n public int minCostConnectPoints(int[][] points) {\n int n = points.length;\n int[][] graph = new int[n][n]; // Create a 2D matrix \'graph\' to represent the distances between points\n\n // Calculate the Manhattan distance (md) between all pairs of points and populate the \'graph\' matrix\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n int[] p1 = points[i];\n int[] p2 = points[j];\n int md = Math.abs(p1[0] - p2[0]) + Math.abs(p1[1] - p2[1]); // Calculate Manhattan distance\n graph[i][j] = md; // Store the distance in both directions since it\'s an undirected graph\n graph[j][i] = md;\n }\n }\n\n return MST(graph, n); // Find and return the minimum cost of connecting all points using MST\n }\n}\n\n```\n# PYTHON\n```\nclass Solution:\n def minKey(self, inMST, key):\n minIndex = 0\n minVal = float(\'inf\')\n for i in range(len(key)):\n if not inMST[i] and key[i] < minVal:\n minIndex = i\n minVal = key[i]\n return minIndex\n\n def MST(self, graph, V):\n key = [float(\'inf\')] * V\n inMST = [False] * V\n key[0] = 0\n \n for count in range(1, V):\n u = self.minKey(inMST, key)\n inMST[u] = True\n \n for v in range(V):\n if graph[u][v] and not inMST[v] and graph[u][v] < key[v]:\n key[v] = graph[u][v]\n \n cost = 0\n for i in key:\n cost += i\n return cost\n\n def minCostConnectPoints(self, points):\n n = len(points)\n graph = [[0] * n for _ in range(n)]\n \n for i in range(n - 1):\n for j in range(i + 1, n):\n p1 = points[i]\n p2 = points[j]\n md = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n graph[i][j] = md\n graph[j][i] = md\n \n return self.MST(graph, n)\n\n```\n# JAVSCRIPT\n\n```\nclass Solution {\n // Function to find the index of the minimum key in \'key\' array that is not yet included in MST\n minKey(inMST, key) {\n let minIndex = 0;\n let minVal = Number.MAX_SAFE_INTEGER;\n // Loop through all vertices to find the minimum key\n for (let i = 0; i < key.length; i++) {\n // Check if the vertex is not in MST and its key is smaller than the current minimum value\n if (!inMST[i] && key[i] < minVal) {\n minIndex = i;\n minVal = key[i];\n }\n }\n return minIndex; // Return the index of the minimum key\n }\n\n // Function to calculate the minimum spanning tree (MST) of a given \'graph\' with \'V\' vertices\n MST(graph, V) {\n const key = new Array(V).fill(Number.MAX_SAFE_INTEGER); // Initialize key values for all vertices to be infinity\n const inMST = new Array(V).fill(false); // Initialize all vertices as not included in MST\n key[0] = 0; // Start with the first vertex as the source\n \n // Loop through V-1 vertices (all except the first one)\n for (let count = 1; count <= V - 1; count++) {\n const u = this.minKey(inMST, key); // Find the vertex with the minimum key not in MST\n inMST[u] = true; // Include the selected vertex in MST\n \n // Update the key values of adjacent vertices\n for (let v = 0; v < V; v++) {\n // If there is an edge from \'u\' to \'v\', \'v\' is not in MST, and the edge weight is smaller than \'key[v]\'\n if (graph[u][v] && !inMST[v] && graph[u][v] < key[v]) {\n key[v] = graph[u][v]; // Update the key value of \'v\'\n }\n }\n }\n \n let cost = 0;\n for (const i of key) {\n cost += i; // Calculate the sum of key values, which represents the minimum cost of MST\n }\n return cost; // Return the minimum cost of MST\n }\n\n // Function to calculate the minimum cost to connect all points using Prim\'s Algorithm\n minCostConnectPoints(points) {\n const n = points.length;\n const graph = new Array(n).fill().map(() => new Array(n).fill(0)); // Create a 2D matrix \'graph\' to represent the distances between points\n \n // Calculate the Manhattan distance (md) between all pairs of points and populate the \'graph\' matrix\n for (let i = 0; i < n - 1; i++) {\n for (let j = i + 1; j < n; j++) {\n const p1 = points[i];\n const p2 = points[j];\n const md = Math.abs(p1[0] - p2[0]) + Math.abs(p1[1] - p2[1]); // Calculate Manhattan distance\n graph[i][j] = md; // Store the distance in both directions since it\'s an undirected graph\n graph[j][i] = md;\n }\n }\n \n return this.MST(graph, n); // Find and return the minimum cost of connecting all points using MST\n }\n}\n\n```\nPLEASE UPVOTE\u2763\uD83D\uDE0D | 6 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
✔Graph || Prims Algorithm✨💎 || Kruskal's Algorithm👀|| Easy to Understand😉😎 | min-cost-to-connect-all-points | 1 | 1 | # Intuition\n- The problem involves finding the minimum cost to connect a set of points using Prim\'s Algorithm, which is a greedy algorithm used for finding the minimum spanning tree (MST) of a graph. \n- In this case, the graph represents the distances between points, and the goal is to connect all points with edges such that the total cost (sum of edge weights) is minimized.\n\n# Approach\n1. **minKey function:** This function is used to find the index of the vertex with the minimum key value that is not yet included in the MST.\n \n - It iterates through all vertices, checks if they are not in the MST (inMST) and have a smaller key value than the current minimum, and updates the minimum index and value accordingly.\n\n1. **MST function:** This function calculates the minimum spanning tree (MST) of the graph using Prim\'s Algorithm. It initializes an array \'key\' to store the key values for each vertex, where key[i] represents the minimum weight of an edge connecting vertex i to the MST. It also initializes an array \'inMST\' to keep track of whether a vertex is included in the MST.\n\n - It starts with the first vertex (0) and sets its key to 0.\n - Then, for V-1 iterations (all vertices except the first one), it selects the vertex \'u\' with the minimum key value that is not in the MST (using minKey function).\n - It includes \'u\' in the MST and updates the key values of its adjacent vertices \'v\' if the edge weight to \'v\' is smaller than the current key value of \'v\'.\n1. **minCostConnectPoints function:** This is the main function that calculates the minimum cost to connect all points.\n\n - It first calculates the Manhattan distances (md) between all pairs of points and populates the \'graph\' matrix with these distances.\n - Then, it calls the MST function to find the minimum cost of connecting all points using Prim\'s Algorithm.\n\n# Complexity\n- Time complexity:\n1. **Calculating Manhattan distances and populating the graph matrix:** This involves two nested loops iterating through all pairs of points, resulting in a time complexity of O(n^2), where \'n\' is the number of points.\n\n1. **MST function (Prim\'s Algorithm):** The time complexity of Prim\'s `Algorithm is O(V^2`) with an adjacency matrix representation of the graph. Since \'V\' is the number of points (vertices), in this case, it is` O(n^2).`\n\n- Space complexity:\n1. **\'graph\' matrix:** `It has a space complexity of O(n^2)` because it stores the distances between all pairs of points.\n\n1. **\'key\' and \'inMST\' arrays:** They both have a space complexity of O(n) because they store information for each point.\n\nOverall, `the space complexity of the algorithm is O(n^2) `due to the \'graph\' matrix and O(n) for the \'key\' and \'inMST\' arrays, making the `space complexity O(n^2)` in total.\n\nPLEASE UPVOTE\u2763\uD83D\uDE0D\n\n# Code\n```\n//Approach-1 (Using 2-D matrix graph) - Prim\'s Algorithm\nclass Solution {\npublic:\n // Function to find the index of the minimum key in \'key\' vector that is not yet included in MST\n int minKey(vector<bool>& inMST, vector<int>& key) {\n int minIndex = 0;\n int minVal = INT_MAX;\n // Loop through all vertices to find the minimum key\n for(int i = 0; i < key.size(); i++) {\n // Check if the vertex is not in MST and its key is smaller than the current minimum value\n if(!inMST[i] && key[i] < minVal) {\n minIndex = i;\n minVal = key[i];\n }\n }\n return minIndex; // Return the index of the minimum key\n }\n\n // Function to calculate the minimum spanning tree (MST) of a given \'graph\' with \'V\' vertices\n int MST(vector<vector<int>>& graph, int V) {\n vector<int> key(V, INT_MAX); // Initialize key values for all vertices to be infinity\n vector<bool> inMST(V, false); // Initialize all vertices as not included in MST\n key[0] = 0; // Start with the first vertex as the source\n \n // Loop through V-1 vertices (all except the first one)\n for(int count = 1; count <= V - 1; count++) {\n int u = minKey(inMST, key); // Find the vertex with the minimum key not in MST\n inMST[u] = true; // Include the selected vertex in MST\n \n // Update the key values of adjacent vertices\n for(int v = 0; v < V; v++) {\n // If there is an edge from \'u\' to \'v\', \'v\' is not in MST, and the edge weight is smaller than \'key[v]\'\n if(graph[u][v] && !inMST[v] && graph[u][v] < key[v]) {\n key[v] = graph[u][v]; // Update the key value of \'v\'\n }\n }\n }\n \n int cost = 0;\n for(int i : key) {\n cost += i; // Calculate the sum of key values, which represents the minimum cost of MST\n }\n return cost; // Return the minimum cost of MST\n }\n\n // Function to calculate the minimum cost to connect all points using Prim\'s Algorithm\n int minCostConnectPoints(vector<vector<int>>& points) {\n int n = points.size();\n vector<vector<int>> graph(n, vector<int>(n)); // Create a 2D matrix \'graph\' to represent the distances between points\n \n // Calculate the Manhattan distance (md) between all pairs of points and populate the \'graph\' matrix\n for(int i = 0; i < n - 1; i++) {\n for(int j = i + 1; j < n; j++) {\n vector<int> p1 = points[i];\n vector<int> p2 = points[j];\n int md = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1]); // Calculate Manhattan distance\n graph[i][j] = md; // Store the distance in both directions since it\'s an undirected graph\n graph[j][i] = md;\n }\n }\n \n return MST(graph, n); // Find and return the minimum cost of connecting all points using MST\n }\n};\n\n```\n# KRUSKAL\'S ALGORITHM\n```\nclass Solution {\npublic:\n vector<int> parent;\n vector<int> rank;\n \n int find (int x) {\n if (x == parent[x]) \n return x;\n \n return parent[x] = find(parent[x]);\n }\n \n void Union (int x, int y) {\n int x_parent = find(x);\n int y_parent = find(y);\n \n if (x_parent == y_parent) \n return;\n \n if(rank[x_parent] > rank[y_parent]) {\n parent[y_parent] = x_parent;\n } else if(rank[x_parent] < rank[y_parent]) {\n parent[x_parent] = y_parent;\n } else {\n parent[x_parent] = y_parent;\n rank[y_parent]++;\n }\n }\n \n int Kruskal(vector<vector<int>> &vec) {\n\n int sum = 0;\n for(auto &temp : vec) {\n \n int u = temp[0];\n int v = temp[1];\n int wt = temp[2];\n \n int parent_u = find(u);\n int parent_v = find(v);\n \n if(parent_u != parent_v) {\n Union(u, v);\n sum += wt;\n }\n \n }\n\n return sum;\n }\n \n int minCostConnectPoints(vector<vector<int>>& points) {\n int V = points.size();\n parent.resize(V);\n\t rank.resize(V, 0);\n \t \n\t for(int i = 0; i<V; i++)\n\t parent[i] = i;\n\n vector<vector<int>> vec;\n \n for(int i = 0; i<V; i++) {\n \n for(int j = i+1; j<V; j++) {\n \n int x1 = points[i][0];\n int y1 = points[i][1];\n \n int x2 = points[j][0];\n int y2 = points[j][1];\n \n int d = abs(x1-x2) + abs(y1-y2);\n \n \n vec.push_back({i, j, d});\n }\n \n }\n \n auto lambda = [&](auto &v1, auto &v2) {\n return v1[2] < v2[2];\n };\n \n sort(begin(vec), end(vec), lambda);\n \n return Kruskal(vec);\n }\n};\n```\n# JAVA\n```\nimport java.util.Arrays;\n\nclass Solution {\n // Function to find the index of the minimum key in \'key\' array that is not yet included in MST\n private int minKey(boolean[] inMST, int[] key) {\n int minIndex = 0;\n int minVal = Integer.MAX_VALUE;\n // Loop through all vertices to find the minimum key\n for (int i = 0; i < key.length; i++) {\n // Check if the vertex is not in MST and its key is smaller than the current minimum value\n if (!inMST[i] && key[i] < minVal) {\n minIndex = i;\n minVal = key[i];\n }\n }\n return minIndex; // Return the index of the minimum key\n }\n\n // Function to calculate the minimum spanning tree (MST) of a given \'graph\' with \'V\' vertices\n private int MST(int[][] graph, int V) {\n int[] key = new int[V];\n boolean[] inMST = new boolean[V];\n Arrays.fill(key, Integer.MAX_VALUE);\n key[0] = 0; // Start with the first vertex as the source\n\n // Loop through V-1 vertices (all except the first one)\n for (int count = 1; count <= V - 1; count++) {\n int u = minKey(inMST, key); // Find the vertex with the minimum key not in MST\n inMST[u] = true; // Include the selected vertex in MST\n\n // Update the key values of adjacent vertices\n for (int v = 0; v < V; v++) {\n // If there is an edge from \'u\' to \'v\', \'v\' is not in MST, and the edge weight is smaller than \'key[v]\'\n if (graph[u][v] > 0 && !inMST[v] && graph[u][v] < key[v]) {\n key[v] = graph[u][v]; // Update the key value of \'v\'\n }\n }\n }\n\n int cost = 0;\n for (int i : key) {\n cost += i; // Calculate the sum of key values, which represents the minimum cost of MST\n }\n return cost; // Return the minimum cost of MST\n }\n\n // Function to calculate the minimum cost to connect all points using Prim\'s Algorithm\n public int minCostConnectPoints(int[][] points) {\n int n = points.length;\n int[][] graph = new int[n][n]; // Create a 2D matrix \'graph\' to represent the distances between points\n\n // Calculate the Manhattan distance (md) between all pairs of points and populate the \'graph\' matrix\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n int[] p1 = points[i];\n int[] p2 = points[j];\n int md = Math.abs(p1[0] - p2[0]) + Math.abs(p1[1] - p2[1]); // Calculate Manhattan distance\n graph[i][j] = md; // Store the distance in both directions since it\'s an undirected graph\n graph[j][i] = md;\n }\n }\n\n return MST(graph, n); // Find and return the minimum cost of connecting all points using MST\n }\n}\n\n```\n# PYTHON\n```\nclass Solution:\n def minKey(self, inMST, key):\n minIndex = 0\n minVal = float(\'inf\')\n for i in range(len(key)):\n if not inMST[i] and key[i] < minVal:\n minIndex = i\n minVal = key[i]\n return minIndex\n\n def MST(self, graph, V):\n key = [float(\'inf\')] * V\n inMST = [False] * V\n key[0] = 0\n \n for count in range(1, V):\n u = self.minKey(inMST, key)\n inMST[u] = True\n \n for v in range(V):\n if graph[u][v] and not inMST[v] and graph[u][v] < key[v]:\n key[v] = graph[u][v]\n \n cost = 0\n for i in key:\n cost += i\n return cost\n\n def minCostConnectPoints(self, points):\n n = len(points)\n graph = [[0] * n for _ in range(n)]\n \n for i in range(n - 1):\n for j in range(i + 1, n):\n p1 = points[i]\n p2 = points[j]\n md = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n graph[i][j] = md\n graph[j][i] = md\n \n return self.MST(graph, n)\n\n```\n# JAVSCRIPT\n\n```\nclass Solution {\n // Function to find the index of the minimum key in \'key\' array that is not yet included in MST\n minKey(inMST, key) {\n let minIndex = 0;\n let minVal = Number.MAX_SAFE_INTEGER;\n // Loop through all vertices to find the minimum key\n for (let i = 0; i < key.length; i++) {\n // Check if the vertex is not in MST and its key is smaller than the current minimum value\n if (!inMST[i] && key[i] < minVal) {\n minIndex = i;\n minVal = key[i];\n }\n }\n return minIndex; // Return the index of the minimum key\n }\n\n // Function to calculate the minimum spanning tree (MST) of a given \'graph\' with \'V\' vertices\n MST(graph, V) {\n const key = new Array(V).fill(Number.MAX_SAFE_INTEGER); // Initialize key values for all vertices to be infinity\n const inMST = new Array(V).fill(false); // Initialize all vertices as not included in MST\n key[0] = 0; // Start with the first vertex as the source\n \n // Loop through V-1 vertices (all except the first one)\n for (let count = 1; count <= V - 1; count++) {\n const u = this.minKey(inMST, key); // Find the vertex with the minimum key not in MST\n inMST[u] = true; // Include the selected vertex in MST\n \n // Update the key values of adjacent vertices\n for (let v = 0; v < V; v++) {\n // If there is an edge from \'u\' to \'v\', \'v\' is not in MST, and the edge weight is smaller than \'key[v]\'\n if (graph[u][v] && !inMST[v] && graph[u][v] < key[v]) {\n key[v] = graph[u][v]; // Update the key value of \'v\'\n }\n }\n }\n \n let cost = 0;\n for (const i of key) {\n cost += i; // Calculate the sum of key values, which represents the minimum cost of MST\n }\n return cost; // Return the minimum cost of MST\n }\n\n // Function to calculate the minimum cost to connect all points using Prim\'s Algorithm\n minCostConnectPoints(points) {\n const n = points.length;\n const graph = new Array(n).fill().map(() => new Array(n).fill(0)); // Create a 2D matrix \'graph\' to represent the distances between points\n \n // Calculate the Manhattan distance (md) between all pairs of points and populate the \'graph\' matrix\n for (let i = 0; i < n - 1; i++) {\n for (let j = i + 1; j < n; j++) {\n const p1 = points[i];\n const p2 = points[j];\n const md = Math.abs(p1[0] - p2[0]) + Math.abs(p1[1] - p2[1]); // Calculate Manhattan distance\n graph[i][j] = md; // Store the distance in both directions since it\'s an undirected graph\n graph[j][i] = md;\n }\n }\n \n return this.MST(graph, n); // Find and return the minimum cost of connecting all points using MST\n }\n}\n\n```\nPLEASE UPVOTE\u2763\uD83D\uDE0D | 6 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
[Python] Simple and Concise MST with Explanation | min-cost-to-connect-all-points | 0 | 1 | ### Introduction\n\nWe need to connect all given `points` in a graph such that the sum of the Manhattan distances between every pair of points connected is the absolute minimum. This is equivalent to finding the total weight of the minimum spanning tree (MST) which connects these `points`.\n\n---\n\n### Implementation\n\n```python\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n d, res = {(x, y): float(\'inf\') if i else 0 for i, (x, y) in enumerate(points)}, 0\n while d:\n x, y = min(d, key=d.get) # obtain the current minimum edge\n res += d.pop((x, y)) # and remove the corresponding point\n for x1, y1 in d: # for the rest of the points, update the minimum manhattan distance\n d[(x1, y1)] = min(d[(x1, y1)], abs(x-x1)+abs(y-y1))\n return res\n```\n\n**TC: O(V<sup>2</sup>)**, V being the number of vertices in the graph. For a detailed explanation of the time complexity, please refer to [this comment](https://leetcode.com/problems/min-cost-to-connect-all-points/discuss/1982821/Python-Simple-and-Concise-MST-with-Explanation/1366981).\n**SC: O(V)**.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 78 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
[Python] Simple and Concise MST with Explanation | min-cost-to-connect-all-points | 0 | 1 | ### Introduction\n\nWe need to connect all given `points` in a graph such that the sum of the Manhattan distances between every pair of points connected is the absolute minimum. This is equivalent to finding the total weight of the minimum spanning tree (MST) which connects these `points`.\n\n---\n\n### Implementation\n\n```python\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n d, res = {(x, y): float(\'inf\') if i else 0 for i, (x, y) in enumerate(points)}, 0\n while d:\n x, y = min(d, key=d.get) # obtain the current minimum edge\n res += d.pop((x, y)) # and remove the corresponding point\n for x1, y1 in d: # for the rest of the points, update the minimum manhattan distance\n d[(x1, y1)] = min(d[(x1, y1)], abs(x-x1)+abs(y-y1))\n return res\n```\n\n**TC: O(V<sup>2</sup>)**, V being the number of vertices in the graph. For a detailed explanation of the time complexity, please refer to [this comment](https://leetcode.com/problems/min-cost-to-connect-all-points/discuss/1982821/Python-Simple-and-Concise-MST-with-Explanation/1366981).\n**SC: O(V)**.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 78 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Purely Kruskal's algorithm. | min-cost-to-connect-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n def calculate_distance(p1, p2):\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n \n n = len(points)\n edges = []\n for i in range(n):\n for j in range(i+1,n):\n distance = calculate_distance(points[i],points[j])\n edges.append((i,j,distance))\n edges.sort(key=lambda x:x[2])\n parents = list(range(n))\n ranks = [0]*n\n min_cost = 0\n def find(i):\n if parents[i]!=i:\n parents[i] = find(parents[i])\n return parents[i]\n def union(i,j):\n rooti = find(i)\n rootj = find(j)\n if rooti!=rootj:\n if ranks[rooti]<=ranks[rootj]:\n parents[rooti] = rootj\n ranks[rootj]+=1\n else:\n parents[rootj] = rooti\n ranks[rooti]+=1\n for v,u,distance in edges:\n if find(u)!=find(v):\n min_cost+=distance\n union(u,v)\n return min_cost\n\n \n``` | 2 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Purely Kruskal's algorithm. | min-cost-to-connect-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n def calculate_distance(p1, p2):\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n \n n = len(points)\n edges = []\n for i in range(n):\n for j in range(i+1,n):\n distance = calculate_distance(points[i],points[j])\n edges.append((i,j,distance))\n edges.sort(key=lambda x:x[2])\n parents = list(range(n))\n ranks = [0]*n\n min_cost = 0\n def find(i):\n if parents[i]!=i:\n parents[i] = find(parents[i])\n return parents[i]\n def union(i,j):\n rooti = find(i)\n rootj = find(j)\n if rooti!=rootj:\n if ranks[rooti]<=ranks[rootj]:\n parents[rooti] = rootj\n ranks[rootj]+=1\n else:\n parents[rootj] = rooti\n ranks[rooti]+=1\n for v,u,distance in edges:\n if find(u)!=find(v):\n min_cost+=distance\n union(u,v)\n return min_cost\n\n \n``` | 2 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Python 95.74% two minimum spanning tree algorithms Clean Code ✅ | min-cost-to-connect-all-points | 0 | 1 | # Prim\'s algorithm\n\n```python []\nclass Solution:\n def minCostConnectPoints(self, points: list[list[int]]) -> int:\n n = len(points)\n visited = [False] * n\n adj_list = [[] for _ in range(n)]\n for i in range(n):\n for j in range(i + 1, n):\n dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])\n adj_list[i].append((dis, j))\n adj_list[j].append((dis, i))\n visited[0] = True\n pq = adj_list[0]\n heapify(pq)\n k = cost = 0\n while k < n - 1:\n dis, v = heappop(pq)\n if not visited[v]:\n visited[v] = True\n cost += dis\n k += 1\n for edge in adj_list[v]:\n heappush(pq, edge)\n return cost\n```\n> 1. Same as Kruskal\'s Algorithms, which requires building $\\frac{n(n-1)}{2}$ edges and using `adj_list` to record edge information`(dis, to)`\n> 2. Starting from the vertex `0`, add its edges to the Priority Queue `pq`, and find the current shortest edge one by one. If the vertices of this edge will not cause a loop, then add this edge to `pq`. Repeat this process until $n-1$ edges are selected.\n\n\n\n# Kruskal\'s algorithm\n```python []\nclass DisjointSet:\n def __init__(self, n: int):\n self.n = n\n self.parent = list(range(self.n))\n self.rank = [0] * self.n\n\n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n root_x, root_y = self.find(x), self.find(y)\n if root_x != root_y:\n if self.rank[root_x] > self.rank[root_y]:\n self.parent[root_y] = root_x\n elif self.rank[root_y] > self.rank[root_x]:\n self.parent[root_x] = root_y\n else:\n self.rank[root_x] += 1\n self.parent[root_y] = root_x\n\n def is_connected(self, x, y):\n return self.find(x) == self.find(y)\n\n\nclass Solution:\n def minCostConnectPoints(self, points: list[list[int]]) -> int:\n n = len(points)\n edges = []\n for i in range(n):\n for j in range(i + 1, n):\n dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])\n edges.append((dis, i, j))\n pq = edges\n heapify(pq)\n dsu = DisjointSet(n)\n k = cost = 0\n while k < n - 1:\n dis, u, v = heappop(pq)\n if not dsu.is_connected(u, v):\n dsu.union(u, v)\n cost += dis\n k += 1\n return cost\n```\n\n> 1. First generate $\\frac{n(n-1)}{2}$ edges for $n$ vertices, and use Priority Queue to take the edge with the smallest weight.\n> 2. Use Disjoint Set to check whether two points on an edge will cause a loop.\n> 3. If the used edges `k` reaches $n-1$, the algorithm ends.\n\n\n\n**THX for reading.\nI would appreciate it very much if you would upvote this.**\n\n\n\n | 4 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Python 95.74% two minimum spanning tree algorithms Clean Code ✅ | min-cost-to-connect-all-points | 0 | 1 | # Prim\'s algorithm\n\n```python []\nclass Solution:\n def minCostConnectPoints(self, points: list[list[int]]) -> int:\n n = len(points)\n visited = [False] * n\n adj_list = [[] for _ in range(n)]\n for i in range(n):\n for j in range(i + 1, n):\n dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])\n adj_list[i].append((dis, j))\n adj_list[j].append((dis, i))\n visited[0] = True\n pq = adj_list[0]\n heapify(pq)\n k = cost = 0\n while k < n - 1:\n dis, v = heappop(pq)\n if not visited[v]:\n visited[v] = True\n cost += dis\n k += 1\n for edge in adj_list[v]:\n heappush(pq, edge)\n return cost\n```\n> 1. Same as Kruskal\'s Algorithms, which requires building $\\frac{n(n-1)}{2}$ edges and using `adj_list` to record edge information`(dis, to)`\n> 2. Starting from the vertex `0`, add its edges to the Priority Queue `pq`, and find the current shortest edge one by one. If the vertices of this edge will not cause a loop, then add this edge to `pq`. Repeat this process until $n-1$ edges are selected.\n\n\n\n# Kruskal\'s algorithm\n```python []\nclass DisjointSet:\n def __init__(self, n: int):\n self.n = n\n self.parent = list(range(self.n))\n self.rank = [0] * self.n\n\n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n root_x, root_y = self.find(x), self.find(y)\n if root_x != root_y:\n if self.rank[root_x] > self.rank[root_y]:\n self.parent[root_y] = root_x\n elif self.rank[root_y] > self.rank[root_x]:\n self.parent[root_x] = root_y\n else:\n self.rank[root_x] += 1\n self.parent[root_y] = root_x\n\n def is_connected(self, x, y):\n return self.find(x) == self.find(y)\n\n\nclass Solution:\n def minCostConnectPoints(self, points: list[list[int]]) -> int:\n n = len(points)\n edges = []\n for i in range(n):\n for j in range(i + 1, n):\n dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])\n edges.append((dis, i, j))\n pq = edges\n heapify(pq)\n dsu = DisjointSet(n)\n k = cost = 0\n while k < n - 1:\n dis, u, v = heappop(pq)\n if not dsu.is_connected(u, v):\n dsu.union(u, v)\n cost += dis\n k += 1\n return cost\n```\n\n> 1. First generate $\\frac{n(n-1)}{2}$ edges for $n$ vertices, and use Priority Queue to take the edge with the smallest weight.\n> 2. Use Disjoint Set to check whether two points on an edge will cause a loop.\n> 3. If the used edges `k` reaches $n-1$, the algorithm ends.\n\n\n\n**THX for reading.\nI would appreciate it very much if you would upvote this.**\n\n\n\n | 4 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Python 3 | Min Spanning Tree | Prim's Algorithm | min-cost-to-connect-all-points | 0 | 1 | ### Explanation\n- This is a typical **minimum spanning tree** question, it can be solved using either *Kruskal* or *Prim*\'s algorithm\n- Below is a **Prim**\'s algorithm implementation\n- Here is a wiki for Pirm\'s algorithm https://en.wikipedia.org/wiki/Prim%27s_algorithm\n- Time Complexity: Prim\'s Algorithm takes `O(NlgN)` but the whole solution is dominated by **`O(N*N)`** due to graph creation (nested loop)\n### Implementation\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n manhattan = lambda p1, p2: abs(p1[0]-p2[0]) + abs(p1[1]-p2[1])\n n, c = len(points), collections.defaultdict(list)\n for i in range(n):\n for j in range(i+1, n):\n d = manhattan(points[i], points[j])\n c[i].append((d, j))\n c[j].append((d, i))\n cnt, ans, visited, heap = 1, 0, [0] * n, c[0]\n visited[0] = 1\n heapq.heapify(heap)\n while heap:\n d, j = heapq.heappop(heap)\n if not visited[j]:\n visited[j], cnt, ans = 1, cnt+1, ans+d\n for record in c[j]: heapq.heappush(heap, record)\n if cnt >= n: break \n return ans\n``` | 111 | You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
**Example 1:**
**Input:** points = \[\[0,0\],\[2,2\],\[3,10\],\[5,2\],\[7,0\]\]
**Output:** 20
**Explanation:**
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
**Example 2:**
**Input:** points = \[\[3,12\],\[-2,5\],\[-4,1\]\]
**Output:** 18
**Constraints:**
* `1 <= points.length <= 1000`
* `-106 <= xi, yi <= 106`
* All pairs `(xi, yi)` are distinct. | Get the total sum and subtract the minimum and maximum value in the array. Finally divide the result by n - 2. |
Python 3 | Min Spanning Tree | Prim's Algorithm | min-cost-to-connect-all-points | 0 | 1 | ### Explanation\n- This is a typical **minimum spanning tree** question, it can be solved using either *Kruskal* or *Prim*\'s algorithm\n- Below is a **Prim**\'s algorithm implementation\n- Here is a wiki for Pirm\'s algorithm https://en.wikipedia.org/wiki/Prim%27s_algorithm\n- Time Complexity: Prim\'s Algorithm takes `O(NlgN)` but the whole solution is dominated by **`O(N*N)`** due to graph creation (nested loop)\n### Implementation\n```\nclass Solution:\n def minCostConnectPoints(self, points: List[List[int]]) -> int:\n manhattan = lambda p1, p2: abs(p1[0]-p2[0]) + abs(p1[1]-p2[1])\n n, c = len(points), collections.defaultdict(list)\n for i in range(n):\n for j in range(i+1, n):\n d = manhattan(points[i], points[j])\n c[i].append((d, j))\n c[j].append((d, i))\n cnt, ans, visited, heap = 1, 0, [0] * n, c[0]\n visited[0] = 1\n heapq.heapify(heap)\n while heap:\n d, j = heapq.heappop(heap)\n if not visited[j]:\n visited[j], cnt, ans = 1, cnt+1, ans+d\n for record in c[j]: heapq.heappush(heap, record)\n if cnt >= n: break \n return ans\n``` | 111 | You have a 2-D `grid` of size `m x n` representing a box, and you have `n` balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
* A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as `1`.
* A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as `-1`.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V " shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return _an array_ `answer` _of size_ `n` _where_ `answer[i]` _is the column that the ball falls out of at the bottom after dropping the ball from the_ `ith` _column at the top, or `-1` _if the ball gets stuck in the box_._
**Example 1:**
**Input:** grid = \[\[1,1,1,-1,-1\],\[1,1,1,-1,-1\],\[-1,-1,-1,1,1\],\[1,1,1,1,-1\],\[-1,-1,-1,-1,-1\]\]
**Output:** \[1,-1,-1,-1,-1\]
**Explanation:** This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
**Example 2:**
**Input:** grid = \[\[-1\]\]
**Output:** \[-1\]
**Explanation:** The ball gets stuck against the left wall.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\],\[1,1,1,1,1,1\],\[-1,-1,-1,-1,-1,-1\]\]
**Output:** \[0,1,2,3,4,-1\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is `1` or `-1`. | Connect each pair of points with a weighted edge, the weight being the manhattan distance between those points. The problem is now the cost of minimum spanning tree in graph with above edges. |
Logical Order Elimination | Modified Kahn's Algorithm | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\nFaced with any substring sorting problems, I\'m drawn to maps and graphs for ease of search space. As such, we can consider this one with not too much of a stretch of the mind. \n\nEach integer value in our selected string has a list of indices at which it appears. IF we make a mapping of these list of indices for each value in order of appearance in s, we can use that against the ordering of appearance of list of values in t (we do not necessarily need to make said list of t, but could if we so chose) \n\nOnce we have this map, our first bet is to actually get the set of unique items in t, which can be done rather nicely with generators that will do the autoskip inclusions as needed. \n\nUsing unique t, our first check is that all of the unique t values are present. If not, then we can skip to returning False. \n\nOtherwise, we need to loop over t, and for each character check if it is in our map. If not, also False. \n\nIf we then loop over values up to this point (such that if we drew say 5 we\'d go from 0 to 4 inclusive) we need to find that the value is in indexes and that the indexes at that point has a starting value at least as advanced or more so than the indexes for the drawn values first appearance. If this does not occur, then they are not in ascending order and may also return False. \n\nIf all of that passes, we need to discard the current item at the front of indexes at the drawn character. If in doing so we now eliminate that list, we need to eliminate the character drawn from indices entirely (this is why we have that second check for inclusion near the top). \n\nIf we manage all of that, there\'s nothing to stop the transformation and can return True. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse collections default dict with collections deque for each character valuation in s \n\nMake a map of the character values -> list of indices of occurrence in order from first to last \n\nMake a set of unique t values \n\n- For each unique t value in unique t values \n - if that value is not in our mapping \n - return False \n\nLoop over t (effectively getting the unique indices for each value of t) \n- as you do, convert your character into its designated key (This is here for other mapping versions of the problem) \n- if we do not have that designated ky in our map \n - return false \n- otherwise, loop over lesser character designations in range to character designation \n - if we have the map at lesser character designation and the map at lesser character designation points to a list whose first index of occurrence is less than the first index of occurrence of our current character designation, it must be that they are not in order, and can return False \n- after completing lesser character loop, remove the most recent occurrence of indexes at character designation by popping left from the map at the character designation \n- if the map now points to an empty list for character designation, remove character designation from the map entirely. \n\n# Complexity\n- Time complexity : O(S + T)\n - O(S) to build s mapping \n - O(T) to build t unique characters \n - O(T) to loop over characters in T \n - within which we do at most O(5) work to loop in range of lesser characters on average \n - Total then is O(S + T + ~5T) -> O(S + C * T) -> O(S + T) \n\n\n- Space complexity : O(S + t) \n - Store O(s) lists of size to account for S, so O(S) \n - Store O(t) \n - Remove storage for potentially all of O(S) \n - Averages out to O(S + t) at worst \n\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool :\n # make a mapping of deque lists called indexes \n indexes = collections.defaultdict(collections.deque)\n # enumerate s \n for index, character in enumerate(s) :\n # indexes at the int cast of character has this index added to it \n indexes[int(character)].append(index)\n\n # get unique values in t \n unique_t_values = set([int(t_i) for t_i in t])\n # for t_v in unique t values \n for t_v in unique_t_values : \n # if not in indexes \n if t_v not in indexes :\n # return False as we are missing pieces \n return False \n \n # loop over t in order given \n for character in t : \n # get the characters integer designation \n character_designation = int(character)\n # update may cause new misses which may prevent future searches \n if character_designation not in indexes : \n return False \n # for index in range up to character designation \n for lesser_character in range(character_designation) : \n # if indexes at lesser character and indexes at lesser character lists 0th item is before indexes at character designations lists 0th item \n if indexes[lesser_character] and indexes[lesser_character][0] < indexes[character_designation][0] : \n # our lists are not transformable, False \n # this is because for any select string mapping of character designations that are greater than their sub indexes \n # it must be such that the index priors sub mapping does not interfere with the index current mapping. \n # this is detailed in the problem statement where they note that values must be in ascending order \n return False \n # after consideration using this most recent index, remove it \n indexes[character_designation].popleft()\n # if length is now zero, remove it \n if len(indexes[character_designation]) == 0 : \n indexes.pop(character_designation)\n \n # if all characters able to sort, return it \n return True \n``` | 0 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
Logical Order Elimination | Modified Kahn's Algorithm | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\nFaced with any substring sorting problems, I\'m drawn to maps and graphs for ease of search space. As such, we can consider this one with not too much of a stretch of the mind. \n\nEach integer value in our selected string has a list of indices at which it appears. IF we make a mapping of these list of indices for each value in order of appearance in s, we can use that against the ordering of appearance of list of values in t (we do not necessarily need to make said list of t, but could if we so chose) \n\nOnce we have this map, our first bet is to actually get the set of unique items in t, which can be done rather nicely with generators that will do the autoskip inclusions as needed. \n\nUsing unique t, our first check is that all of the unique t values are present. If not, then we can skip to returning False. \n\nOtherwise, we need to loop over t, and for each character check if it is in our map. If not, also False. \n\nIf we then loop over values up to this point (such that if we drew say 5 we\'d go from 0 to 4 inclusive) we need to find that the value is in indexes and that the indexes at that point has a starting value at least as advanced or more so than the indexes for the drawn values first appearance. If this does not occur, then they are not in ascending order and may also return False. \n\nIf all of that passes, we need to discard the current item at the front of indexes at the drawn character. If in doing so we now eliminate that list, we need to eliminate the character drawn from indices entirely (this is why we have that second check for inclusion near the top). \n\nIf we manage all of that, there\'s nothing to stop the transformation and can return True. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse collections default dict with collections deque for each character valuation in s \n\nMake a map of the character values -> list of indices of occurrence in order from first to last \n\nMake a set of unique t values \n\n- For each unique t value in unique t values \n - if that value is not in our mapping \n - return False \n\nLoop over t (effectively getting the unique indices for each value of t) \n- as you do, convert your character into its designated key (This is here for other mapping versions of the problem) \n- if we do not have that designated ky in our map \n - return false \n- otherwise, loop over lesser character designations in range to character designation \n - if we have the map at lesser character designation and the map at lesser character designation points to a list whose first index of occurrence is less than the first index of occurrence of our current character designation, it must be that they are not in order, and can return False \n- after completing lesser character loop, remove the most recent occurrence of indexes at character designation by popping left from the map at the character designation \n- if the map now points to an empty list for character designation, remove character designation from the map entirely. \n\n# Complexity\n- Time complexity : O(S + T)\n - O(S) to build s mapping \n - O(T) to build t unique characters \n - O(T) to loop over characters in T \n - within which we do at most O(5) work to loop in range of lesser characters on average \n - Total then is O(S + T + ~5T) -> O(S + C * T) -> O(S + T) \n\n\n- Space complexity : O(S + t) \n - Store O(s) lists of size to account for S, so O(S) \n - Store O(t) \n - Remove storage for potentially all of O(S) \n - Averages out to O(S + t) at worst \n\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool :\n # make a mapping of deque lists called indexes \n indexes = collections.defaultdict(collections.deque)\n # enumerate s \n for index, character in enumerate(s) :\n # indexes at the int cast of character has this index added to it \n indexes[int(character)].append(index)\n\n # get unique values in t \n unique_t_values = set([int(t_i) for t_i in t])\n # for t_v in unique t values \n for t_v in unique_t_values : \n # if not in indexes \n if t_v not in indexes :\n # return False as we are missing pieces \n return False \n \n # loop over t in order given \n for character in t : \n # get the characters integer designation \n character_designation = int(character)\n # update may cause new misses which may prevent future searches \n if character_designation not in indexes : \n return False \n # for index in range up to character designation \n for lesser_character in range(character_designation) : \n # if indexes at lesser character and indexes at lesser character lists 0th item is before indexes at character designations lists 0th item \n if indexes[lesser_character] and indexes[lesser_character][0] < indexes[character_designation][0] : \n # our lists are not transformable, False \n # this is because for any select string mapping of character designations that are greater than their sub indexes \n # it must be such that the index priors sub mapping does not interfere with the index current mapping. \n # this is detailed in the problem statement where they note that values must be in ascending order \n return False \n # after consideration using this most recent index, remove it \n indexes[character_designation].popleft()\n # if length is now zero, remove it \n if len(indexes[character_designation]) == 0 : \n indexes.pop(character_designation)\n \n # if all characters able to sort, return it \n return True \n``` | 0 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
Check If String Is Transformable With Substring Sort Operations. Souvik Hazra | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n idx = defaultdict(deque)\n for i, c in enumerate(s):\n idx[int(c)].append(i)\n for c in t:\n d = int(c)\n if not idx[d]: return False\n for i in range(d):\n if idx[i] and idx[i][0] < idx[d][0]: return False\n idx[d].popleft()\n return True\n``` | 0 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
Check If String Is Transformable With Substring Sort Operations. Souvik Hazra | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n idx = defaultdict(deque)\n for i, c in enumerate(s):\n idx[int(c)].append(i)\n for c in t:\n d = int(c)\n if not idx[d]: return False\n for i in range(d):\n if idx[i] and idx[i][0] < idx[d][0]: return False\n idx[d].popleft()\n return True\n``` | 0 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
Inversions BIT | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BIT():\n def __init__(self, n):\n self.n = n\n self.tree = [0] * (n + 1)\n\n def sum(self, i):\n ans = 0\n i += 1\n while i > 0:\n ans += self.tree[i]\n i -= (i & (-i))\n return ans\n\n def update(self, i, value):\n i += 1\n while i <= self.n:\n self.tree[i] += value\n i += (i & (-i))\n\n\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n if Counter(s)!=Counter(t):\n return False\n ind = defaultdict(deque)\n for id, i in enumerate(t):\n ind[i].append(id)\n a = []\n for i in s:\n a.append(ind[i].popleft())\n n=len(a)\n bt=BIT(n+1)\n ind=defaultdict(lambda :-1)\n for i in range(n):\n inv=bt.sum(n)-bt.sum(a[i])\n bt.update(a[i],1)\n for dig in range(int(s[i])-1,-1,-1):\n if ind[dig]>=i-inv:\n return False\n ind[int(s[i])]=i-inv\n return True\n\n\n``` | 0 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
Inversions BIT | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BIT():\n def __init__(self, n):\n self.n = n\n self.tree = [0] * (n + 1)\n\n def sum(self, i):\n ans = 0\n i += 1\n while i > 0:\n ans += self.tree[i]\n i -= (i & (-i))\n return ans\n\n def update(self, i, value):\n i += 1\n while i <= self.n:\n self.tree[i] += value\n i += (i & (-i))\n\n\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n if Counter(s)!=Counter(t):\n return False\n ind = defaultdict(deque)\n for id, i in enumerate(t):\n ind[i].append(id)\n a = []\n for i in s:\n a.append(ind[i].popleft())\n n=len(a)\n bt=BIT(n+1)\n ind=defaultdict(lambda :-1)\n for i in range(n):\n inv=bt.sum(n)-bt.sum(a[i])\n bt.update(a[i],1)\n for dig in range(int(s[i])-1,-1,-1):\n if ind[dig]>=i-inv:\n return False\n ind[int(s[i])]=i-inv\n return True\n\n\n``` | 0 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
Python (Simple Hashmap) | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s, t):\n dict1 = defaultdict(list)\n\n for i,c in enumerate(s):\n dict1[int(c)].append(i)\n\n for c in t:\n d = int(c)\n\n if not dict1[d]:\n return False\n\n for i in range(d):\n if dict1[i] and dict1[i][0] < dict1[d][0]:\n return False\n \n dict1[d].pop(0)\n\n return True\n\n\n \n\n\n\n \n \n\n\n\n \n``` | 0 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
Python (Simple Hashmap) | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s, t):\n dict1 = defaultdict(list)\n\n for i,c in enumerate(s):\n dict1[int(c)].append(i)\n\n for c in t:\n d = int(c)\n\n if not dict1[d]:\n return False\n\n for i in range(d):\n if dict1[i] and dict1[i][0] < dict1[d][0]:\n return False\n \n dict1[d].pop(0)\n\n return True\n\n\n \n\n\n\n \n \n\n\n\n \n``` | 0 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
Python 3 solution with explanation | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\nIf we have an s[i] in i index we see from what index to what index it can be moved i.e s[i] can be placed at any index in range **lower_index, upper_index** in s\n\n# Approach\nthe intuition is to check where each digit at index i in string s can go upto \nfor example let s = \'3158581\' here 5 at index 2 can\'t go any further before and cant go beyond index 3, so its limits are [2,3] (including 2 and 3) similarly for 5 at index 4 it is [3,5]. we can get this range by calculating count of all numbers before index i that are less than and equal to s[i] and we can get upper limit by len(s)-1-c where c is count of all numbers at index greater than i that are grater than or equal to s[i].\nnow ranges of 5 in above number is [[2,3],[3,5]] we sort this array on first number if equal then second number\nnow get the all indexes of 5 in t (target) in sorted order.\nex: [2,5] \nNote: if len(ranges[5])!=len(indexes[5]) then return False as 5 has diff frequency in s and t\nnow for i in indexes of 5 in t whether check range is satisfying or not.\nfor examples ranges(5) in s:[[2,3],[3,5]] and indexes is [2,5] (both arrays should be sorted) (if diff length return False)\nfor each iteration in length try whether the index is in range or not\nex:\n **for i==0:**\n ind = 2 and range = [2,3]\n here ind is in range go to next iteration\n **for i==1:**\n ind = 5 and range = [3,5]\n here ind is in range go to next iteration\n **as we can attain all indexes 5 is done. similarly do this to all numbers from 0 to 10**\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n #here love is the array that holds ranges of digits from 0 to 9 (len(love)==10)\n #here see is the array that holds indexes of all the digits in t (len(see)==10)\n\n total = [0]*10\n #Total array is the frequency of each digit from 0 to 9 in suffix i.e after index i\n temp = [0]*10\n #Temp array is the frequency of each digit from 0 to 9 is prefix i.e before i\n for i in s:\n total[int(i)]+=1\n love = [[] for i in range(10)]\n ##Love is range \n for i in s:\n ko = int(i)\n lo = sum(temp[:ko+1]) ##Getting lower_value\n temp[ko] += 1 #Updating temp\n total[ko] -= 1 #Updating total\n up = sum(total[ko:])\n up = len(s)-up-1 #getting upper_index\n love[ko].append([lo,up])\n for i in range(len(love)):\n love[i].sort() ##Sorting ranges\n see = [[] for i in range(10)]\n for i in range(len(t)):\n ii = int(t[i])\n see[ii].append(i)\n # for i in range(10):see[i].sort() #No need to sort indexes they are already sorted\n def checkNum(num): #Function that checkes whether indexes are attainable or not for a digit num\n if len(see[num])!=len(love[num]):return False\n for i in range(len(see[num])):\n if see[num][i] not in range(love[num][i][0],love[num][i][1]+1):return False\n return True\n for i in range(10):\n if not checkNum(i):return False\n return True\n``` | 0 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
Python 3 solution with explanation | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\nIf we have an s[i] in i index we see from what index to what index it can be moved i.e s[i] can be placed at any index in range **lower_index, upper_index** in s\n\n# Approach\nthe intuition is to check where each digit at index i in string s can go upto \nfor example let s = \'3158581\' here 5 at index 2 can\'t go any further before and cant go beyond index 3, so its limits are [2,3] (including 2 and 3) similarly for 5 at index 4 it is [3,5]. we can get this range by calculating count of all numbers before index i that are less than and equal to s[i] and we can get upper limit by len(s)-1-c where c is count of all numbers at index greater than i that are grater than or equal to s[i].\nnow ranges of 5 in above number is [[2,3],[3,5]] we sort this array on first number if equal then second number\nnow get the all indexes of 5 in t (target) in sorted order.\nex: [2,5] \nNote: if len(ranges[5])!=len(indexes[5]) then return False as 5 has diff frequency in s and t\nnow for i in indexes of 5 in t whether check range is satisfying or not.\nfor examples ranges(5) in s:[[2,3],[3,5]] and indexes is [2,5] (both arrays should be sorted) (if diff length return False)\nfor each iteration in length try whether the index is in range or not\nex:\n **for i==0:**\n ind = 2 and range = [2,3]\n here ind is in range go to next iteration\n **for i==1:**\n ind = 5 and range = [3,5]\n here ind is in range go to next iteration\n **as we can attain all indexes 5 is done. similarly do this to all numbers from 0 to 10**\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n #here love is the array that holds ranges of digits from 0 to 9 (len(love)==10)\n #here see is the array that holds indexes of all the digits in t (len(see)==10)\n\n total = [0]*10\n #Total array is the frequency of each digit from 0 to 9 in suffix i.e after index i\n temp = [0]*10\n #Temp array is the frequency of each digit from 0 to 9 is prefix i.e before i\n for i in s:\n total[int(i)]+=1\n love = [[] for i in range(10)]\n ##Love is range \n for i in s:\n ko = int(i)\n lo = sum(temp[:ko+1]) ##Getting lower_value\n temp[ko] += 1 #Updating temp\n total[ko] -= 1 #Updating total\n up = sum(total[ko:])\n up = len(s)-up-1 #getting upper_index\n love[ko].append([lo,up])\n for i in range(len(love)):\n love[i].sort() ##Sorting ranges\n see = [[] for i in range(10)]\n for i in range(len(t)):\n ii = int(t[i])\n see[ii].append(i)\n # for i in range(10):see[i].sort() #No need to sort indexes they are already sorted\n def checkNum(num): #Function that checkes whether indexes are attainable or not for a digit num\n if len(see[num])!=len(love[num]):return False\n for i in range(len(see[num])):\n if see[num][i] not in range(love[num][i][0],love[num][i][1]+1):return False\n return True\n for i in range(10):\n if not checkNum(i):return False\n return True\n``` | 0 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
With deques, beats 98% time, 96 space (not sure why though) | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\nPb can be nicely reduced to: \'for each digit of t, check if its first occurence in s is only preceded by bigger numbers\'\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe keep track of the the order of appearance in s via a collection of deque representing the ascending list of indices for each digit [0, ..., 9]. Then we consider each digit of t, pop the smallest corresponding index of s, and check that there are no smaller number before by checking first element of the corresponding deques\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(2n) = O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n O(n) too\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n if s == t:\n return True\n big_table = [deque() for _ in range(10)]\n for i, c in enumerate(s):\n big_table[int(c)].append(i)\n \n for c in t:\n if not big_table[int(c)]: return False\n i = big_table[int(c)].popleft()\n for j in range(int(c)):\n if big_table[j] and big_table[j][0] < i:\n return False\n return True\n\n\n\n``` | 1 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
With deques, beats 98% time, 96 space (not sure why though) | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | # Intuition\nPb can be nicely reduced to: \'for each digit of t, check if its first occurence in s is only preceded by bigger numbers\'\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe keep track of the the order of appearance in s via a collection of deque representing the ascending list of indices for each digit [0, ..., 9]. Then we consider each digit of t, pop the smallest corresponding index of s, and check that there are no smaller number before by checking first element of the corresponding deques\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(2n) = O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n O(n) too\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n if s == t:\n return True\n big_table = [deque() for _ in range(10)]\n for i, c in enumerate(s):\n big_table[int(c)].append(i)\n \n for c in t:\n if not big_table[int(c)]: return False\n i = big_table[int(c)].popleft()\n for j in range(int(c)):\n if big_table[j] and big_table[j][0] < i:\n return False\n return True\n\n\n\n``` | 1 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
[Python3] 8-line deque | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | \n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n if sorted(s) != sorted(t): return False # edge case \n \n pos = [deque() for _ in range(10)]\n for i, ss in enumerate(s): pos[int(ss)].append(i)\n \n for tt in t: \n i = pos[int(tt)].popleft()\n for ii in range(int(tt)): \n if pos[ii] and pos[ii][0] < i: return False # cannot swap \n return True \n``` | 2 | Given two strings `s` and `t`, transform string `s` into string `t` using the following operation any number of times:
* Choose a **non-empty** substring in `s` and sort it in place so the characters are in **ascending order**.
* For example, applying the operation on the underlined substring in `"14234 "` results in `"12344 "`.
Return `true` if _it is possible to transform `s` into `t`_. Otherwise, return `false`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "84532 ", t = "34852 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"84532 " (from index 2 to 3) -> "84352 "
"84352 " (from index 0 to 2) -> "34852 "
**Example 2:**
**Input:** s = "34521 ", t = "23415 "
**Output:** true
**Explanation:** You can transform s into t using the following sort operations:
"34521 " -> "23451 "
"23451 " -> "23415 "
**Example 3:**
**Input:** s = "12345 ", t = "12435 "
**Output:** false
**Constraints:**
* `s.length == t.length`
* `1 <= s.length <= 105`
* `s` and `t` consist of only digits. | The factors of n will be always in the range [1, n]. Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list. |
[Python3] 8-line deque | check-if-string-is-transformable-with-substring-sort-operations | 0 | 1 | \n```\nclass Solution:\n def isTransformable(self, s: str, t: str) -> bool:\n if sorted(s) != sorted(t): return False # edge case \n \n pos = [deque() for _ in range(10)]\n for i, ss in enumerate(s): pos[int(ss)].append(i)\n \n for tt in t: \n i = pos[int(tt)].popleft()\n for ii in range(int(tt)): \n if pos[ii] and pos[ii][0] < i: return False # cannot swap \n return True \n``` | 2 | You are given an array `nums` consisting of non-negative integers. You are also given a `queries` array, where `queries[i] = [xi, mi]`.
The answer to the `ith` query is the maximum bitwise `XOR` value of `xi` and any element of `nums` that does not exceed `mi`. In other words, the answer is `max(nums[j] XOR xi)` for all `j` such that `nums[j] <= mi`. If all elements in `nums` are larger than `mi`, then the answer is `-1`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length` _and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** nums = \[0,1,2,3,4\], queries = \[\[3,1\],\[1,3\],\[5,6\]\]
**Output:** \[3,3,7\]
**Explanation:**
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
**Example 2:**
**Input:** nums = \[5,2,4,6,6,3\], queries = \[\[12,4\],\[8,1\],\[6,3\]\]
**Output:** \[15,-1,5\]
**Constraints:**
* `1 <= nums.length, queries.length <= 105`
* `queries[i].length == 2`
* `0 <= nums[j], xi, mi <= 109` | Suppose the first digit you need is 'd'. How can you determine if it's possible to get that digit there? Consider swapping adjacent characters to maintain relative ordering. |
python 3 99.78% faster and 100% less space | sum-of-all-odd-length-subarrays | 0 | 1 | The idea is to count the frequency of each element in `arr` appearing in the sub array, then sum up `arr[i]*freq[i]`. The key is how to count the `freq[i]` of each element `arr[i]`. Actually, `freq[i] = freq[i-1]-(i+1)//2+(n-i+1)//2`. `n` is the `arr` length.\n\nfor example `arr = [1,4,2,5,3]`, element `arr[0] = 1`. The appearing `freq` of head element `arr[0]` should be how many odd-length sub arrays it can generate. The answer is `(len(arr)+1)//2`. Therefore, the `freq` of element `arr[0] = 1` is `(5+1)//2=3`.\n\nNow let\'s take element `arr[1] = 4` for example, if we take element `arr[0] = 1` out, then `arr[1] = 4` becomes the new head element, thus the `freq` of `arr[1] = 4` in the new subarray could be calculated as the same way of `arr[0] = 1`. It seems that all we need to do is add the `freq` of previous element arr[0] up then we get the `freq` of `arr[1]`.\n\nNo, we also need to minus the subarrays of previous element `arr[0] = 1` when they do not include `arr[1]=4`. In this case, it is `[1]`. This is why `freq[i] = freq[i-1]-(i+1)//2+(n-i+1)//2`.\n\nTo sum up, the core idea is to find the relationship between `freq_current_element` and `freq_previous_element`.\n\n\n\n\n\n```\nclass Solution:\n def sumOddLengthSubarrays(self, arr: List[int]) -> int:\n # corner case\n \n res = 0; freq = 0; n = len(arr)\n for i in range(n):\n freq = freq-(i+1)//2+(n-i+1)//2\n res += freq*arr[i]\n return res\n```\n\n\n | 127 | Given an array of positive integers `arr`, return _the sum of all possible **odd-length subarrays** of_ `arr`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,4,2,5,3\]
**Output:** 58
**Explanation:** The odd-length subarrays of arr and their sums are:
\[1\] = 1
\[4\] = 4
\[2\] = 2
\[5\] = 5
\[3\] = 3
\[1,4,2\] = 7
\[4,2,5\] = 11
\[2,5,3\] = 10
\[1,4,2,5,3\] = 15
If we add all these together we get 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** 3
**Explanation:** There are only 2 subarrays of odd length, \[1\] and \[2\]. Their sum is 3.
**Example 3:**
**Input:** arr = \[10,11,12\]
**Output:** 66
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= 1000`
**Follow up:**
Could you solve this problem in O(n) time complexity? | null |
🚩Easy C++ O(N) Soln. [ FAANG😱 Interview Optimized code ] | sum-of-all-odd-length-subarrays | 1 | 1 | Well, this problem is not as easy as it looks. A bit tricky tbh! \nBut here\'s a simple explaination :\n* No. of even subarrays = Total/2\n* No. of odd subarrays = (Total+1)/2\nTotal subarrays can be found by considering an element and taking all subarrays to its left and right.\nSubarrays to the left = i+1\nSubarrays to the right = n-i\nWe then add 1 i.e (i+1 * n-i )+1 to include the entire array as the subarray.\nAnd that is done for each element from i=0 to i=arr.size()-1\nAnd finally the sum is returned.\n# ***Please upvote if it helps \uD83D\uDE4F.***\n```\nclass Solution {\npublic:\n int sumOddLengthSubarrays(vector<int>& arr) {\n int n = arr.size();\n int sum = 0;\n \n // traverse the array\n for(int i = 0; i < n; i++)\n {\n sum = sum + (((n-i) * (i+1)+1)/2) * arr[i]; //O(n)\n }\n return sum;\n }\n};\n```\nAlso this video helped me. Plz refer this.[https://www.youtube.com/watch?v=LSFcmgq0HYY](http://)\n# ***Please upvote if it helps \uD83D\uDE4F.*** | 40 | Given an array of positive integers `arr`, return _the sum of all possible **odd-length subarrays** of_ `arr`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,4,2,5,3\]
**Output:** 58
**Explanation:** The odd-length subarrays of arr and their sums are:
\[1\] = 1
\[4\] = 4
\[2\] = 2
\[5\] = 5
\[3\] = 3
\[1,4,2\] = 7
\[4,2,5\] = 11
\[2,5,3\] = 10
\[1,4,2,5,3\] = 15
If we add all these together we get 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** 3
**Explanation:** There are only 2 subarrays of odd length, \[1\] and \[2\]. Their sum is 3.
**Example 3:**
**Input:** arr = \[10,11,12\]
**Output:** 66
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= 1000`
**Follow up:**
Could you solve this problem in O(n) time complexity? | null |
4 lines of code beats 99.94% see code with proof very easy | sum-of-all-odd-length-subarrays | 0 | 1 | # Beats 99.94% image for proof:\n\n\n# Code\n```\nclass Solution:\n def sumOddLengthSubarrays(self, arr: List[int]) -> int:\n n=len(arr)\n s=0\n for i in range(n):\n s+=((i+1)*(n-i)+1)//2*arr[i]\n return s\n``` | 1 | Given an array of positive integers `arr`, return _the sum of all possible **odd-length subarrays** of_ `arr`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,4,2,5,3\]
**Output:** 58
**Explanation:** The odd-length subarrays of arr and their sums are:
\[1\] = 1
\[4\] = 4
\[2\] = 2
\[5\] = 5
\[3\] = 3
\[1,4,2\] = 7
\[4,2,5\] = 11
\[2,5,3\] = 10
\[1,4,2,5,3\] = 15
If we add all these together we get 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** 3
**Explanation:** There are only 2 subarrays of odd length, \[1\] and \[2\]. Their sum is 3.
**Example 3:**
**Input:** arr = \[10,11,12\]
**Output:** 66
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= 1000`
**Follow up:**
Could you solve this problem in O(n) time complexity? | null |
very easy approach | sum-of-all-odd-length-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOddLengthSubarrays(self, arr: List[int]) -> int:\n ans=0\n n= len(arr)\n for i in range (n):\n for j in range (i+1,n+1):\n if (j-i)%2:\n ans+=sum (arr[i:j])\n\n \n return ans\n \n``` | 1 | Given an array of positive integers `arr`, return _the sum of all possible **odd-length subarrays** of_ `arr`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,4,2,5,3\]
**Output:** 58
**Explanation:** The odd-length subarrays of arr and their sums are:
\[1\] = 1
\[4\] = 4
\[2\] = 2
\[5\] = 5
\[3\] = 3
\[1,4,2\] = 7
\[4,2,5\] = 11
\[2,5,3\] = 10
\[1,4,2,5,3\] = 15
If we add all these together we get 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** 3
**Explanation:** There are only 2 subarrays of odd length, \[1\] and \[2\]. Their sum is 3.
**Example 3:**
**Input:** arr = \[10,11,12\]
**Output:** 66
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= 1000`
**Follow up:**
Could you solve this problem in O(n) time complexity? | null |
Python Simple Solution | sum-of-all-odd-length-subarrays | 0 | 1 | ```\nclass Solution:\n def sumOddLengthSubarrays(self, arr: List[int]) -> int:\n s=0\n for i in range(len(arr)):\n for j in range(i,len(arr),2):\n s+=sum(arr[i:j+1])\n return s\n``` | 63 | Given an array of positive integers `arr`, return _the sum of all possible **odd-length subarrays** of_ `arr`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,4,2,5,3\]
**Output:** 58
**Explanation:** The odd-length subarrays of arr and their sums are:
\[1\] = 1
\[4\] = 4
\[2\] = 2
\[5\] = 5
\[3\] = 3
\[1,4,2\] = 7
\[4,2,5\] = 11
\[2,5,3\] = 10
\[1,4,2,5,3\] = 15
If we add all these together we get 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** 3
**Explanation:** There are only 2 subarrays of odd length, \[1\] and \[2\]. Their sum is 3.
**Example 3:**
**Input:** arr = \[10,11,12\]
**Output:** 66
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= 1000`
**Follow up:**
Could you solve this problem in O(n) time complexity? | null |
44ms, Python (with comments and detailed walkthrough) | sum-of-all-odd-length-subarrays | 0 | 1 | If you find this post helpful, please **Upvote** :)\n```\nclass Solution(object):\n def sumOddLengthSubarrays(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n\t\t#We declare our output variable with the initial value as the sum of all elements as this is the 1st iteration of the sum of all individual elements.\n result = sum(arr)\n\t\t#Saving length of the input array beforehand for ease of writing\n length = len(arr)\n\t\t#As we already summed up the individual elements, now its time to start groups starting from 3,5,7 and so onnn\n for j in range(3,length+1,2):\n\t\t#Now we need to create pairs for each element with the previous loop sizes\n for i in range(length):\n\t\t\t#This condition is to make we dont search for indexes outside our list\n if (i+j) > length:\n break\n\t\t\t\t\t#We continously add the sum of each sublist to our output variable\n result += sum(arr[i:i+j])\n return result\n ```\n \n\nI will try to explain the logic a bit: \nLets assume the input variable as [1,4,2,5,3]\nWe need to find the sums of the lists:\n[1], [4], [2], [5], [3], [1,4,2], [4,2,5], [2,5,3], [1,4,2,5,3]\n\nThis can also represented in terms of indices \niteration 1: arr[0], arr[1], arr[2] ....arr[4]\niteration 2: arr[0:3], arr[1:4], arr[2:5]\niteration 3: arr[0:5]\n\nSo our main goal should be to generate these indices based on the lenght of the input list.\nIn my code, initiating the result variable as ```sum(arr)``` takes care about the 1st iteration!\n\n```\nfor j in range(3,length+1,2)\n```\ngenerates this for our input list -> [3,5]\n```\nfor i in range(length)\n```\ngenerates this for our input list -> [0,1,2,3,4]\n\nNesting both these loops brings out this logic, along with the condition ``` if (i+j > length: break```\n1st iteration:\n(i,j) = [0:3], [1:4], [2:5]\n2nd iteration:\n(i,j) = [0,5]\n\nWell, this is exactly what we wanted in the first place ryt, we have done, now its just finding the sum of the sublists :)\n\nPlease comment if you have any doubts or suggestions! | 33 | Given an array of positive integers `arr`, return _the sum of all possible **odd-length subarrays** of_ `arr`.
A **subarray** is a contiguous subsequence of the array.
**Example 1:**
**Input:** arr = \[1,4,2,5,3\]
**Output:** 58
**Explanation:** The odd-length subarrays of arr and their sums are:
\[1\] = 1
\[4\] = 4
\[2\] = 2
\[5\] = 5
\[3\] = 3
\[1,4,2\] = 7
\[4,2,5\] = 11
\[2,5,3\] = 10
\[1,4,2,5,3\] = 15
If we add all these together we get 1 + 4 + 2 + 5 + 3 + 7 + 11 + 10 + 15 = 58
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** 3
**Explanation:** There are only 2 subarrays of odd length, \[1\] and \[2\]. Their sum is 3.
**Example 3:**
**Input:** arr = \[10,11,12\]
**Output:** 66
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= 1000`
**Follow up:**
Could you solve this problem in O(n) time complexity? | null |
simple python solution || greedy || prefix sum || nlog(n) | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition and approach\n**since we can use any permutation of list.so we will use greedy approach for purmutation selection of list. we will place the maximum element at the index which is included in most intervals.\n\n**now we have to find the index which occured in most interval. this can be done using "PREFIX SUM". we will initiate freq array of size same as list and all elements are zero.\nthen we will travese the request list and update freq array as following:\n freq[re1[i][0]]+=1 and freq[req[i][1]+1]-=1(take care of n-1 index)\n\nnow we will simply travese freq and update it by freq[i]+=freq[i-1] this will give us frequncy of each element\n\n** now we will sort both nums and freq.\n initiate ans=0 and travese nums while updating ans as following:\n ans=(ans+(freq[i]*nums[i])%1e9+7)%1e9+7\n\n** at the end return your ans.\n\n\n\n# Complexity\n- Time complexity:o(nlog(n))\n\n- Space complexity:o(n)\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, nums: List[int], req: List[List[int]]) -> int:\n n=len(nums)\n r=len(req)\n a=[0 for i in range(n)] //freq list\n for i in range(r):\n a[req[i][0]]+=1\n if(req[i][1]<n-1):\n a[req[i][1]+1]-=1\n \n for i in range(n):\n if(i==0):\n continue\n a[i]+=a[i-1]\n\n a.sort()\n nums.sort()\n ans=0\n N=1e9 + 7\n for i in range(n-1,-1,-1):\n ans+=(a[i]*nums[i])%N\n ans%=N\n return int(ans%N)\n\n``` | 1 | We have an array of integers, `nums`, and an array of `requests` where `requests[i] = [starti, endi]`. The `ith` request asks for the sum of `nums[starti] + nums[starti + 1] + ... + nums[endi - 1] + nums[endi]`. Both `starti` and `endi` are _0-indexed_.
Return _the maximum total sum of all requests **among all permutations** of_ `nums`.
Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], requests = \[\[1,3\],\[0,1\]\]
**Output:** 19
**Explanation:** One permutation of nums is \[2,1,3,4,5\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 1 + 3 + 4 = 8
requests\[1\] -> nums\[0\] + nums\[1\] = 2 + 1 = 3
Total sum: 8 + 3 = 11.
A permutation with a higher total sum is \[3,5,4,2,1\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 5 + 4 + 2 = 11
requests\[1\] -> nums\[0\] + nums\[1\] = 3 + 5 = 8
Total sum: 11 + 8 = 19, which is the best that you can do.
**Example 2:**
**Input:** nums = \[1,2,3,4,5,6\], requests = \[\[0,1\]\]
**Output:** 11
**Explanation:** A permutation with the max total sum is \[6,5,4,3,2,1\] with request sums \[11\].
**Example 3:**
**Input:** nums = \[1,2,3,4,5,10\], requests = \[\[0,2\],\[1,3\],\[1,1\]\]
**Output:** 47
**Explanation:** A permutation with the max total sum is \[4,10,5,3,2,1\] with request sums \[19,18,10\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 105`
* `1 <= requests.length <= 105`
* `requests[i].length == 2`
* `0 <= starti <= endi < n` | null |
simple python solution || greedy || prefix sum || nlog(n) | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition and approach\n**since we can use any permutation of list.so we will use greedy approach for purmutation selection of list. we will place the maximum element at the index which is included in most intervals.\n\n**now we have to find the index which occured in most interval. this can be done using "PREFIX SUM". we will initiate freq array of size same as list and all elements are zero.\nthen we will travese the request list and update freq array as following:\n freq[re1[i][0]]+=1 and freq[req[i][1]+1]-=1(take care of n-1 index)\n\nnow we will simply travese freq and update it by freq[i]+=freq[i-1] this will give us frequncy of each element\n\n** now we will sort both nums and freq.\n initiate ans=0 and travese nums while updating ans as following:\n ans=(ans+(freq[i]*nums[i])%1e9+7)%1e9+7\n\n** at the end return your ans.\n\n\n\n# Complexity\n- Time complexity:o(nlog(n))\n\n- Space complexity:o(n)\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, nums: List[int], req: List[List[int]]) -> int:\n n=len(nums)\n r=len(req)\n a=[0 for i in range(n)] //freq list\n for i in range(r):\n a[req[i][0]]+=1\n if(req[i][1]<n-1):\n a[req[i][1]+1]-=1\n \n for i in range(n):\n if(i==0):\n continue\n a[i]+=a[i-1]\n\n a.sort()\n nums.sort()\n ans=0\n N=1e9 + 7\n for i in range(n-1,-1,-1):\n ans+=(a[i]*nums[i])%N\n ans%=N\n return int(ans%N)\n\n``` | 1 | You are given an array of positive integers `nums` and want to erase a subarray containing **unique elements**. The **score** you get by erasing the subarray is equal to the **sum** of its elements.
Return _the **maximum score** you can get by erasing **exactly one** subarray._
An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
**Example 1:**
**Input:** nums = \[4,2,4,5,6\]
**Output:** 17
**Explanation:** The optimal subarray here is \[2,4,5,6\].
**Example 2:**
**Input:** nums = \[5,2,1,2,5,2,1,2,5\]
**Output:** 8
**Explanation:** The optimal subarray here is \[5,2,1\] or \[1,2,5\].
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | Indexes with higher frequencies should be bound with larger values |
[Python 3] Sweep line Algorithm | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, nums: List[int], requests: List[List[int]]) -> int:\n n = len(nums)\n cnt = [0 for _ in range(n + 1)]\n for i, j in requests:\n cnt[i] += 1\n cnt[j + 1] -= 1\n \n for i in range(1, n + 1):\n cnt[i] += cnt[i - 1]\n \n res = 0\n for v, c in zip(sorted(cnt[:-1]), sorted(nums)):\n res += v * c\n \n return res % (10 ** 9 + 7)\n``` | 1 | We have an array of integers, `nums`, and an array of `requests` where `requests[i] = [starti, endi]`. The `ith` request asks for the sum of `nums[starti] + nums[starti + 1] + ... + nums[endi - 1] + nums[endi]`. Both `starti` and `endi` are _0-indexed_.
Return _the maximum total sum of all requests **among all permutations** of_ `nums`.
Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], requests = \[\[1,3\],\[0,1\]\]
**Output:** 19
**Explanation:** One permutation of nums is \[2,1,3,4,5\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 1 + 3 + 4 = 8
requests\[1\] -> nums\[0\] + nums\[1\] = 2 + 1 = 3
Total sum: 8 + 3 = 11.
A permutation with a higher total sum is \[3,5,4,2,1\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 5 + 4 + 2 = 11
requests\[1\] -> nums\[0\] + nums\[1\] = 3 + 5 = 8
Total sum: 11 + 8 = 19, which is the best that you can do.
**Example 2:**
**Input:** nums = \[1,2,3,4,5,6\], requests = \[\[0,1\]\]
**Output:** 11
**Explanation:** A permutation with the max total sum is \[6,5,4,3,2,1\] with request sums \[11\].
**Example 3:**
**Input:** nums = \[1,2,3,4,5,10\], requests = \[\[0,2\],\[1,3\],\[1,1\]\]
**Output:** 47
**Explanation:** A permutation with the max total sum is \[4,10,5,3,2,1\] with request sums \[19,18,10\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 105`
* `1 <= requests.length <= 105`
* `requests[i].length == 2`
* `0 <= starti <= endi < n` | null |
[Python 3] Sweep line Algorithm | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, nums: List[int], requests: List[List[int]]) -> int:\n n = len(nums)\n cnt = [0 for _ in range(n + 1)]\n for i, j in requests:\n cnt[i] += 1\n cnt[j + 1] -= 1\n \n for i in range(1, n + 1):\n cnt[i] += cnt[i - 1]\n \n res = 0\n for v, c in zip(sorted(cnt[:-1]), sorted(nums)):\n res += v * c\n \n return res % (10 ** 9 + 7)\n``` | 1 | You are given an array of positive integers `nums` and want to erase a subarray containing **unique elements**. The **score** you get by erasing the subarray is equal to the **sum** of its elements.
Return _the **maximum score** you can get by erasing **exactly one** subarray._
An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
**Example 1:**
**Input:** nums = \[4,2,4,5,6\]
**Output:** 17
**Explanation:** The optimal subarray here is \[2,4,5,6\].
**Example 2:**
**Input:** nums = \[5,2,1,2,5,2,1,2,5\]
**Output:** 8
**Explanation:** The optimal subarray here is \[5,2,1\] or \[1,2,5\].
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | Indexes with higher frequencies should be bound with larger values |
Python 3: Simple Sweep Line Solution | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, nums: List[int], requests: List[List[int]]) -> int:\n \n # get the count for each coordiate\n # 0, 1, 2, 3, 4\n # 1 1 1\n # 1 1\n # 1 2 1 1\n # \n\n mod = 10 ** 9 + 7\n N = len(nums)\n sweep_array = [0] * (N + 1)\n\n for s, e in requests:\n sweep_array[s] += 1\n sweep_array[e + 1] -= 1\n \n # get prefix sum\n for i in range(1, N):\n sweep_array[i] += sweep_array[i - 1]\n \n # sort the sweep_array, nums in desc\n nums.sort(reverse=True)\n sweep_array.sort(reverse=True)\n res = 0\n for num, cnt in zip(nums, sweep_array):\n if not cnt:\n break\n res += num * cnt\n return res % mod\n\n``` | 0 | We have an array of integers, `nums`, and an array of `requests` where `requests[i] = [starti, endi]`. The `ith` request asks for the sum of `nums[starti] + nums[starti + 1] + ... + nums[endi - 1] + nums[endi]`. Both `starti` and `endi` are _0-indexed_.
Return _the maximum total sum of all requests **among all permutations** of_ `nums`.
Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], requests = \[\[1,3\],\[0,1\]\]
**Output:** 19
**Explanation:** One permutation of nums is \[2,1,3,4,5\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 1 + 3 + 4 = 8
requests\[1\] -> nums\[0\] + nums\[1\] = 2 + 1 = 3
Total sum: 8 + 3 = 11.
A permutation with a higher total sum is \[3,5,4,2,1\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 5 + 4 + 2 = 11
requests\[1\] -> nums\[0\] + nums\[1\] = 3 + 5 = 8
Total sum: 11 + 8 = 19, which is the best that you can do.
**Example 2:**
**Input:** nums = \[1,2,3,4,5,6\], requests = \[\[0,1\]\]
**Output:** 11
**Explanation:** A permutation with the max total sum is \[6,5,4,3,2,1\] with request sums \[11\].
**Example 3:**
**Input:** nums = \[1,2,3,4,5,10\], requests = \[\[0,2\],\[1,3\],\[1,1\]\]
**Output:** 47
**Explanation:** A permutation with the max total sum is \[4,10,5,3,2,1\] with request sums \[19,18,10\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 105`
* `1 <= requests.length <= 105`
* `requests[i].length == 2`
* `0 <= starti <= endi < n` | null |
Python 3: Simple Sweep Line Solution | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, nums: List[int], requests: List[List[int]]) -> int:\n \n # get the count for each coordiate\n # 0, 1, 2, 3, 4\n # 1 1 1\n # 1 1\n # 1 2 1 1\n # \n\n mod = 10 ** 9 + 7\n N = len(nums)\n sweep_array = [0] * (N + 1)\n\n for s, e in requests:\n sweep_array[s] += 1\n sweep_array[e + 1] -= 1\n \n # get prefix sum\n for i in range(1, N):\n sweep_array[i] += sweep_array[i - 1]\n \n # sort the sweep_array, nums in desc\n nums.sort(reverse=True)\n sweep_array.sort(reverse=True)\n res = 0\n for num, cnt in zip(nums, sweep_array):\n if not cnt:\n break\n res += num * cnt\n return res % mod\n\n``` | 0 | You are given an array of positive integers `nums` and want to erase a subarray containing **unique elements**. The **score** you get by erasing the subarray is equal to the **sum** of its elements.
Return _the **maximum score** you can get by erasing **exactly one** subarray._
An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
**Example 1:**
**Input:** nums = \[4,2,4,5,6\]
**Output:** 17
**Explanation:** The optimal subarray here is \[2,4,5,6\].
**Example 2:**
**Input:** nums = \[5,2,1,2,5,2,1,2,5\]
**Output:** 8
**Explanation:** The optimal subarray here is \[5,2,1\] or \[1,2,5\].
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | Indexes with higher frequencies should be bound with larger values |
Explaining the frequency array | An integral | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nCameras contains the number of cameras at each intersection where cameras[i] = the number of cameras at intersection $i$. Requests contains all the intesection ranges where you used a boost to speed up temporarily.\n\nYour sus score, measuring how likely you are to get pulled over, is given by the sum of, $speed[i] * cameras[i]$ for intersection $i$, across all intersections. Find the maximum sus score you can obtain for any permutation of the number of Cameras at each intersection.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe integral of acceleration is speed (velocity). Before acceleration is integrated, the 1 and -1 offsets represent changes in the rate of change. The rate of change increases by 1, decreases by 1, etc.\n\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, cameras: List[int], requests: List[List[int]]) -> int:\n position = [0] * len(nums)\n acceleration = [0] * len(nums)\n for l,r in requests:\n # speed up\n acceleration[l] += 1\n if r+1 < len(acceleration):\n # slow down\n acceleration[r+1] -= 1\n\n # change acceleration to speed (integral)\n for i in range(1, len(acceleration)):\n acceleration[i] += acceleration[i-1]\n\n # make the max speeds match with the max cameras\n cameras = sorted(cameras)\n speed = sorted(acceleration)\n return sum([n*c for n,c in zip(cameras, speed)]) % ((10**9)+7)\n\n\n``` | 0 | We have an array of integers, `nums`, and an array of `requests` where `requests[i] = [starti, endi]`. The `ith` request asks for the sum of `nums[starti] + nums[starti + 1] + ... + nums[endi - 1] + nums[endi]`. Both `starti` and `endi` are _0-indexed_.
Return _the maximum total sum of all requests **among all permutations** of_ `nums`.
Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], requests = \[\[1,3\],\[0,1\]\]
**Output:** 19
**Explanation:** One permutation of nums is \[2,1,3,4,5\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 1 + 3 + 4 = 8
requests\[1\] -> nums\[0\] + nums\[1\] = 2 + 1 = 3
Total sum: 8 + 3 = 11.
A permutation with a higher total sum is \[3,5,4,2,1\] with the following result:
requests\[0\] -> nums\[1\] + nums\[2\] + nums\[3\] = 5 + 4 + 2 = 11
requests\[1\] -> nums\[0\] + nums\[1\] = 3 + 5 = 8
Total sum: 11 + 8 = 19, which is the best that you can do.
**Example 2:**
**Input:** nums = \[1,2,3,4,5,6\], requests = \[\[0,1\]\]
**Output:** 11
**Explanation:** A permutation with the max total sum is \[6,5,4,3,2,1\] with request sums \[11\].
**Example 3:**
**Input:** nums = \[1,2,3,4,5,10\], requests = \[\[0,2\],\[1,3\],\[1,1\]\]
**Output:** 47
**Explanation:** A permutation with the max total sum is \[4,10,5,3,2,1\] with request sums \[19,18,10\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 105`
* `1 <= requests.length <= 105`
* `requests[i].length == 2`
* `0 <= starti <= endi < n` | null |
Explaining the frequency array | An integral | maximum-sum-obtained-of-any-permutation | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nCameras contains the number of cameras at each intersection where cameras[i] = the number of cameras at intersection $i$. Requests contains all the intesection ranges where you used a boost to speed up temporarily.\n\nYour sus score, measuring how likely you are to get pulled over, is given by the sum of, $speed[i] * cameras[i]$ for intersection $i$, across all intersections. Find the maximum sus score you can obtain for any permutation of the number of Cameras at each intersection.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe integral of acceleration is speed (velocity). Before acceleration is integrated, the 1 and -1 offsets represent changes in the rate of change. The rate of change increases by 1, decreases by 1, etc.\n\n\n# Code\n```\nclass Solution:\n def maxSumRangeQuery(self, cameras: List[int], requests: List[List[int]]) -> int:\n position = [0] * len(nums)\n acceleration = [0] * len(nums)\n for l,r in requests:\n # speed up\n acceleration[l] += 1\n if r+1 < len(acceleration):\n # slow down\n acceleration[r+1] -= 1\n\n # change acceleration to speed (integral)\n for i in range(1, len(acceleration)):\n acceleration[i] += acceleration[i-1]\n\n # make the max speeds match with the max cameras\n cameras = sorted(cameras)\n speed = sorted(acceleration)\n return sum([n*c for n,c in zip(cameras, speed)]) % ((10**9)+7)\n\n\n``` | 0 | You are given an array of positive integers `nums` and want to erase a subarray containing **unique elements**. The **score** you get by erasing the subarray is equal to the **sum** of its elements.
Return _the **maximum score** you can get by erasing **exactly one** subarray._
An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
**Example 1:**
**Input:** nums = \[4,2,4,5,6\]
**Output:** 17
**Explanation:** The optimal subarray here is \[2,4,5,6\].
**Example 2:**
**Input:** nums = \[5,2,1,2,5,2,1,2,5\]
**Output:** 8
**Explanation:** The optimal subarray here is \[5,2,1\] or \[1,2,5\].
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | Indexes with higher frequencies should be bound with larger values |
How to approach this kind of problem - mind map | make-sum-divisible-by-p | 0 | 1 | If you are new to this kind of problems, you would probably get confused. No worries! Here are list of some prior knowledge you may want to go through before touching it.\n\n- [Leetcode 560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/)\nso that you know how to use prefix sum and hashmap to reduce the time complexity from O(n^2) to O(n)\n- [Leetcode 974. Subarray Sums Divisible by K](https://leetcode.com/problems/subarray-sums-divisible-by-k/)\nso that you know how to deal with Modulo operation\n\nLogic\n\n\n\n\nThe question asks for removing a subarray from ```arr``` such that the sum of the remaining array is divisible by ```p```. As shown above, this question could be converted to another question: find one subarray such that the sum of it equals to the ```sum(arr)%p```.\n\nthere are O(n^2) subarrays and to reduce the time complexity to O(n), we have to borrow some space. While we are calculating the running/accumulated sum ```cur==sum(arr[0...j))```, we hope there is some prefix sum ```prev=sum(arr[0...i]))``` such that: ```sum(arr[i...j])==(cur-prev)%p==sum(arr)%p==target```\n\nTherefore, all we need to find is simply ```(cur-target)%p```.\n\nCode\n\n```Python\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n if sum(nums)%p==0:\n return 0\n target = sum(nums) % p\n dic,n = {0:-1},len(nums)\n cur,ret = 0,n\n for i,num in enumerate(nums):\n cur = (cur+num)%p\n if dic.get((cur-target)%p) is not None:\n ret = min(ret,i-dic.get((cur-target)%p))\n dic[cur] = i\n return ret if ret < n else -1\n```\n\n | 138 | Given an array of positive integers `nums`, remove the **smallest** subarray (possibly **empty**) such that the **sum** of the remaining elements is divisible by `p`. It is **not** allowed to remove the whole array.
Return _the length of the smallest subarray that you need to remove, or_ `-1` _if it's impossible_.
A **subarray** is defined as a contiguous block of elements in the array.
**Example 1:**
**Input:** nums = \[3,1,4,2\], p = 6
**Output:** 1
**Explanation:** The sum of the elements in nums is 10, which is not divisible by 6. We can remove the subarray \[4\], and the sum of the remaining elements is 6, which is divisible by 6.
**Example 2:**
**Input:** nums = \[6,3,5,2\], p = 9
**Output:** 2
**Explanation:** We cannot remove a single element to get a sum divisible by 9. The best way is to remove the subarray \[5,2\], leaving us with \[6,3\] with sum 9.
**Example 3:**
**Input:** nums = \[1,2,3\], p = 3
**Output:** 0
**Explanation:** Here the sum is 6. which is already divisible by 3. Thus we do not need to remove anything.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= p <= 109` | null |
How to approach this kind of problem - mind map | make-sum-divisible-by-p | 0 | 1 | If you are new to this kind of problems, you would probably get confused. No worries! Here are list of some prior knowledge you may want to go through before touching it.\n\n- [Leetcode 560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/)\nso that you know how to use prefix sum and hashmap to reduce the time complexity from O(n^2) to O(n)\n- [Leetcode 974. Subarray Sums Divisible by K](https://leetcode.com/problems/subarray-sums-divisible-by-k/)\nso that you know how to deal with Modulo operation\n\nLogic\n\n\n\n\nThe question asks for removing a subarray from ```arr``` such that the sum of the remaining array is divisible by ```p```. As shown above, this question could be converted to another question: find one subarray such that the sum of it equals to the ```sum(arr)%p```.\n\nthere are O(n^2) subarrays and to reduce the time complexity to O(n), we have to borrow some space. While we are calculating the running/accumulated sum ```cur==sum(arr[0...j))```, we hope there is some prefix sum ```prev=sum(arr[0...i]))``` such that: ```sum(arr[i...j])==(cur-prev)%p==sum(arr)%p==target```\n\nTherefore, all we need to find is simply ```(cur-target)%p```.\n\nCode\n\n```Python\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n if sum(nums)%p==0:\n return 0\n target = sum(nums) % p\n dic,n = {0:-1},len(nums)\n cur,ret = 0,n\n for i,num in enumerate(nums):\n cur = (cur+num)%p\n if dic.get((cur-target)%p) is not None:\n ret = min(ret,i-dic.get((cur-target)%p))\n dic[cur] = i\n return ret if ret < n else -1\n```\n\n | 138 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
WEEB DOES PYTHON/C++ | make-sum-divisible-by-p | 0 | 1 | **Python 3**\n\n\tclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n dp = defaultdict(int)\n dp[0] = -1\n target = sum(nums) % p\n curSum = 0\n result = len(nums)\n \n if sum(nums) % p == 0: return 0\n \n for i in range(len(nums)):\n curSum += nums[i]\n \n curMod = curSum % p\n \n temp = (curSum - target) % p\n \n if temp in dp:\n if i - dp[temp] < result:\n result = i - dp[temp]\n \n dp[curMod] = i\n \n return result if result < len(nums) else -1\n\n**C++**\n\t\n\tclass Solution {\n\tpublic:\n\t\tint minSubarray(vector<int>& nums, int p) {\n\t\t\tunordered_map<int, int> dp;\n\t\t\tdp[0] = -1;\n\t\t\tint result = nums.size();\n\t\t\tlong long int curSum = 0;\n\t\t\tint target = 0;\n\t\t\tfor(auto el: nums) target = (target + el) % p;\n\n\t\t\tif(target == 0) return 0;\n\n\t\t\tfor (int i = 0; i < nums.size(); i++){\n\t\t\t\tcurSum += nums[i];\n\n\t\t\t\tint curMod = curSum % p;\n\n\t\t\t\tint temp = (curSum - target) % p;\n\n\t\t\t\tif (dp.find(temp) != dp.end()){\n\t\t\t\t\tif (i - dp[temp] < result){\n\t\t\t\t\t\tresult = i - dp[temp];\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\tdp[curMod] = i;\n\t\t\t}\n\n\t\t\tif (result == nums.size()) return -1;\n\n\t\t\treturn result; \n\t\t}\n\t};\n\nTake a break, watch some anime instead\nCheck out **\u3046\u3061\u306E\u5A18\u306E\u70BA\u306A\u3089\u3070\u3001\u4FFA\u306F\u3082\u3057\u304B\u3057\u305F\u3089\u9B54\u738B\u3082\u5012\u305B\u308B\u304B\u3082\u3057\u308C\u306A\u3044 (If It\'s for My Daughter, I\'d Even Defeat a Demon Lord)**\n\n**Episodes: 12\nGenres: Fantasy, Slice of Life**\n\nIts a really wholesome anime, go watch it \n | 2 | Given an array of positive integers `nums`, remove the **smallest** subarray (possibly **empty**) such that the **sum** of the remaining elements is divisible by `p`. It is **not** allowed to remove the whole array.
Return _the length of the smallest subarray that you need to remove, or_ `-1` _if it's impossible_.
A **subarray** is defined as a contiguous block of elements in the array.
**Example 1:**
**Input:** nums = \[3,1,4,2\], p = 6
**Output:** 1
**Explanation:** The sum of the elements in nums is 10, which is not divisible by 6. We can remove the subarray \[4\], and the sum of the remaining elements is 6, which is divisible by 6.
**Example 2:**
**Input:** nums = \[6,3,5,2\], p = 9
**Output:** 2
**Explanation:** We cannot remove a single element to get a sum divisible by 9. The best way is to remove the subarray \[5,2\], leaving us with \[6,3\] with sum 9.
**Example 3:**
**Input:** nums = \[1,2,3\], p = 3
**Output:** 0
**Explanation:** Here the sum is 6. which is already divisible by 3. Thus we do not need to remove anything.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= p <= 109` | null |
WEEB DOES PYTHON/C++ | make-sum-divisible-by-p | 0 | 1 | **Python 3**\n\n\tclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n dp = defaultdict(int)\n dp[0] = -1\n target = sum(nums) % p\n curSum = 0\n result = len(nums)\n \n if sum(nums) % p == 0: return 0\n \n for i in range(len(nums)):\n curSum += nums[i]\n \n curMod = curSum % p\n \n temp = (curSum - target) % p\n \n if temp in dp:\n if i - dp[temp] < result:\n result = i - dp[temp]\n \n dp[curMod] = i\n \n return result if result < len(nums) else -1\n\n**C++**\n\t\n\tclass Solution {\n\tpublic:\n\t\tint minSubarray(vector<int>& nums, int p) {\n\t\t\tunordered_map<int, int> dp;\n\t\t\tdp[0] = -1;\n\t\t\tint result = nums.size();\n\t\t\tlong long int curSum = 0;\n\t\t\tint target = 0;\n\t\t\tfor(auto el: nums) target = (target + el) % p;\n\n\t\t\tif(target == 0) return 0;\n\n\t\t\tfor (int i = 0; i < nums.size(); i++){\n\t\t\t\tcurSum += nums[i];\n\n\t\t\t\tint curMod = curSum % p;\n\n\t\t\t\tint temp = (curSum - target) % p;\n\n\t\t\t\tif (dp.find(temp) != dp.end()){\n\t\t\t\t\tif (i - dp[temp] < result){\n\t\t\t\t\t\tresult = i - dp[temp];\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\tdp[curMod] = i;\n\t\t\t}\n\n\t\t\tif (result == nums.size()) return -1;\n\n\t\t\treturn result; \n\t\t}\n\t};\n\nTake a break, watch some anime instead\nCheck out **\u3046\u3061\u306E\u5A18\u306E\u70BA\u306A\u3089\u3070\u3001\u4FFA\u306F\u3082\u3057\u304B\u3057\u305F\u3089\u9B54\u738B\u3082\u5012\u305B\u308B\u304B\u3082\u3057\u308C\u306A\u3044 (If It\'s for My Daughter, I\'d Even Defeat a Demon Lord)**\n\n**Episodes: 12\nGenres: Fantasy, Slice of Life**\n\nIts a really wholesome anime, go watch it \n | 2 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
solution | make-sum-divisible-by-p | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n if sum(nums)%p==0:\n return 0\n target = sum(nums) % p\n dic,n = {0:-1},len(nums)\n cur,ret = 0,n\n for i,num in enumerate(nums):\n cur = (cur+num)%p\n if dic.get((cur-target)%p) is not None:\n ret = min(ret,i-dic.get((cur-target)%p))\n dic[cur] = i\n return ret if ret < n else -1\n``` | 0 | Given an array of positive integers `nums`, remove the **smallest** subarray (possibly **empty**) such that the **sum** of the remaining elements is divisible by `p`. It is **not** allowed to remove the whole array.
Return _the length of the smallest subarray that you need to remove, or_ `-1` _if it's impossible_.
A **subarray** is defined as a contiguous block of elements in the array.
**Example 1:**
**Input:** nums = \[3,1,4,2\], p = 6
**Output:** 1
**Explanation:** The sum of the elements in nums is 10, which is not divisible by 6. We can remove the subarray \[4\], and the sum of the remaining elements is 6, which is divisible by 6.
**Example 2:**
**Input:** nums = \[6,3,5,2\], p = 9
**Output:** 2
**Explanation:** We cannot remove a single element to get a sum divisible by 9. The best way is to remove the subarray \[5,2\], leaving us with \[6,3\] with sum 9.
**Example 3:**
**Input:** nums = \[1,2,3\], p = 3
**Output:** 0
**Explanation:** Here the sum is 6. which is already divisible by 3. Thus we do not need to remove anything.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= p <= 109` | null |
solution | make-sum-divisible-by-p | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n if sum(nums)%p==0:\n return 0\n target = sum(nums) % p\n dic,n = {0:-1},len(nums)\n cur,ret = 0,n\n for i,num in enumerate(nums):\n cur = (cur+num)%p\n if dic.get((cur-target)%p) is not None:\n ret = min(ret,i-dic.get((cur-target)%p))\n dic[cur] = i\n return ret if ret < n else -1\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Hashtable with py3 beating 98.80% | make-sum-divisible-by-p | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n n = len(nums)\n totalrem = sum(nums) % p\n if totalrem == 0:\n return 0\n dp = {} // you have to use a dict rather than list to avoid MLE\n presum = 0\n res = float(\'inf\')\n for i,a in enumerate(nums):\n presum += a\n rem = presum % p\n targetrem = (p + rem-totalrem) % p // extra remainder to be removed\n if targetrem in dp:\n res = min(res,i-dp[targetrem]) // closest point to cut\n if rem == totalrem and i!=n-1: // case 2: all nums before shall be removed\n res = min(res,i+1)\n dp[rem] = i\n return res if res != float(\'inf\') else -1\n\n``` | 0 | Given an array of positive integers `nums`, remove the **smallest** subarray (possibly **empty**) such that the **sum** of the remaining elements is divisible by `p`. It is **not** allowed to remove the whole array.
Return _the length of the smallest subarray that you need to remove, or_ `-1` _if it's impossible_.
A **subarray** is defined as a contiguous block of elements in the array.
**Example 1:**
**Input:** nums = \[3,1,4,2\], p = 6
**Output:** 1
**Explanation:** The sum of the elements in nums is 10, which is not divisible by 6. We can remove the subarray \[4\], and the sum of the remaining elements is 6, which is divisible by 6.
**Example 2:**
**Input:** nums = \[6,3,5,2\], p = 9
**Output:** 2
**Explanation:** We cannot remove a single element to get a sum divisible by 9. The best way is to remove the subarray \[5,2\], leaving us with \[6,3\] with sum 9.
**Example 3:**
**Input:** nums = \[1,2,3\], p = 3
**Output:** 0
**Explanation:** Here the sum is 6. which is already divisible by 3. Thus we do not need to remove anything.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= p <= 109` | null |
Hashtable with py3 beating 98.80% | make-sum-divisible-by-p | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n n = len(nums)\n totalrem = sum(nums) % p\n if totalrem == 0:\n return 0\n dp = {} // you have to use a dict rather than list to avoid MLE\n presum = 0\n res = float(\'inf\')\n for i,a in enumerate(nums):\n presum += a\n rem = presum % p\n targetrem = (p + rem-totalrem) % p // extra remainder to be removed\n if targetrem in dp:\n res = min(res,i-dp[targetrem]) // closest point to cut\n if rem == totalrem and i!=n-1: // case 2: all nums before shall be removed\n res = min(res,i+1)\n dp[rem] = i\n return res if res != float(\'inf\') else -1\n\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
google interview | make-sum-divisible-by-p | 0 | 1 | thanks to @lee215\n\n# Intuition\n\n\n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n\n d = {0:-1}\n size = len(nums)\n need = sum(nums)%p\n cur = 0\n res = len(nums)\n\n\n \n for key, val in enumerate(nums):\n cur = (cur+val)%p\n d[cur] = key\n if (cur - need)%p in d:\n res = min(res, key - d[(cur - need) % p]) \n\n return -1 if res == len(nums) else res\n\n \n\n\n\n \n\n \n\n\n\n\n\n\n``` | 0 | Given an array of positive integers `nums`, remove the **smallest** subarray (possibly **empty**) such that the **sum** of the remaining elements is divisible by `p`. It is **not** allowed to remove the whole array.
Return _the length of the smallest subarray that you need to remove, or_ `-1` _if it's impossible_.
A **subarray** is defined as a contiguous block of elements in the array.
**Example 1:**
**Input:** nums = \[3,1,4,2\], p = 6
**Output:** 1
**Explanation:** The sum of the elements in nums is 10, which is not divisible by 6. We can remove the subarray \[4\], and the sum of the remaining elements is 6, which is divisible by 6.
**Example 2:**
**Input:** nums = \[6,3,5,2\], p = 9
**Output:** 2
**Explanation:** We cannot remove a single element to get a sum divisible by 9. The best way is to remove the subarray \[5,2\], leaving us with \[6,3\] with sum 9.
**Example 3:**
**Input:** nums = \[1,2,3\], p = 3
**Output:** 0
**Explanation:** Here the sum is 6. which is already divisible by 3. Thus we do not need to remove anything.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= p <= 109` | null |
google interview | make-sum-divisible-by-p | 0 | 1 | thanks to @lee215\n\n# Intuition\n\n\n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n\n d = {0:-1}\n size = len(nums)\n need = sum(nums)%p\n cur = 0\n res = len(nums)\n\n\n \n for key, val in enumerate(nums):\n cur = (cur+val)%p\n d[cur] = key\n if (cur - need)%p in d:\n res = min(res, key - d[(cur - need) % p]) \n\n return -1 if res == len(nums) else res\n\n \n\n\n\n \n\n \n\n\n\n\n\n\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
[Python] Prefix Sum + Hashmap O(n)/O(n) | make-sum-divisible-by-p | 0 | 1 | # Complexity\n\n* Time: O(n)\n* Space: O(n)\n\nn = size of `nums`\n\n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n \n S = sum(nums)\n R = S % p\n\n if R == 0:\n return 0\n\n pfxrem = 0\n rightmost_rem = {0: -1}\n ans = len(nums)\n for i, v in enumerate(nums):\n\n pfxrem = (pfxrem + v) % p\n\n r = (pfxrem - R) % p\n\n if r in rightmost_rem:\n j = rightmost_rem[r]\n ans = min(ans, i - j)\n rightmost_rem[pfxrem] = i\n\n return ans if ans < len(nums) else -1\n\n``` | 0 | Given an array of positive integers `nums`, remove the **smallest** subarray (possibly **empty**) such that the **sum** of the remaining elements is divisible by `p`. It is **not** allowed to remove the whole array.
Return _the length of the smallest subarray that you need to remove, or_ `-1` _if it's impossible_.
A **subarray** is defined as a contiguous block of elements in the array.
**Example 1:**
**Input:** nums = \[3,1,4,2\], p = 6
**Output:** 1
**Explanation:** The sum of the elements in nums is 10, which is not divisible by 6. We can remove the subarray \[4\], and the sum of the remaining elements is 6, which is divisible by 6.
**Example 2:**
**Input:** nums = \[6,3,5,2\], p = 9
**Output:** 2
**Explanation:** We cannot remove a single element to get a sum divisible by 9. The best way is to remove the subarray \[5,2\], leaving us with \[6,3\] with sum 9.
**Example 3:**
**Input:** nums = \[1,2,3\], p = 3
**Output:** 0
**Explanation:** Here the sum is 6. which is already divisible by 3. Thus we do not need to remove anything.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= p <= 109` | null |
[Python] Prefix Sum + Hashmap O(n)/O(n) | make-sum-divisible-by-p | 0 | 1 | # Complexity\n\n* Time: O(n)\n* Space: O(n)\n\nn = size of `nums`\n\n# Code\n```\nclass Solution:\n def minSubarray(self, nums: List[int], p: int) -> int:\n \n S = sum(nums)\n R = S % p\n\n if R == 0:\n return 0\n\n pfxrem = 0\n rightmost_rem = {0: -1}\n ans = len(nums)\n for i, v in enumerate(nums):\n\n pfxrem = (pfxrem + v) % p\n\n r = (pfxrem - R) % p\n\n if r in rightmost_rem:\n j = rightmost_rem[r]\n ans = min(ans, i - j)\n rightmost_rem[pfxrem] = i\n\n return ans if ans < len(nums) else -1\n\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
SOLID Principles | 100% Memory | Commented and Explained | strange-printer-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is actually similar to whether or not we have edge collisions in polygon coloring for computer graphics. As such, we take the idea of a color bounding box as a polygon of that color, where we are trying to see if we can get to the back of the painting (aka 0) so we have painted all we need to. To get this as a visual application, simply assign each color to an rgb band. The original will show up, and as you go you can find the polygonal size of the rectangles showing and report on it. It\'s really quite interesting in this fashion so I\'ve left as much of it as possible in clear commented code for those interested in setting it up. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe want to track 3 things in our initial set up, so we establish fields for them at init. These are colors yet to reveal, colors not yet revealable, and color boundaries. The colors yet to reveal are those we have yet to process, and initially contains all colors. At each step, we will see if it is a top lying color (meaning we have it on the top of the stack of color boundaries) and if so, we can reveal it to zero and process the boundaries of it. This occurs if we have all values in bounding box of this color, or all values in the bounding box of this color are zero or some mixture of both. If we cannot yet do so, we place it into colors not yet revealable and then will check to see if any change occurred. If no change occurred we have directly conflicting edges and can not process accordingly, and should return False. On change though, we should update colors yet to reveal to the smaller form of those not yet revealable. \n\nTo do all this we need a few functions to help out. The first is our set up function, which gets passed the grid we are going to be working on. \nWe set up our rows and cols of the grid, and get the max dimension as either the max of either of rows or cols or 60 based on problem description. This lets this extend beyond the scope of the problem space. \n\nOur color boundaries all start out with the box going from minimal of row and col for the color and maximal of the row and col for the color, found by looping over the grid. \n\nWhen done with set up we store the grid in its current form. We do this to not modify the original, and to allow us to report out state changes as we go if we so feel that it is appropriate to do so \n\nOur next function is our zero in range function. If a color has been revealed by either all of the cells in the range being that color, or all of the values in that range being that color or zero, we will set all of the cells in that boundary to zero with the zero in range function. It is passed a range of row start, row stop, col start and col stop to work within. \n\nWe also have our test color boundary function. This gets passed a color and pulls from our color boundaries the bounding box for that color. We increment the row stop and col stop by one so that python does go over that range in its for loops. We then loop over all cells in the bounding box, and if there is any cell that is not this color or zero, we return False. Otherwise, after processing all succesfully as either this color or zero, we zero this range and return True. \n\nTo process our colors finally, we do the following \n- while our colors yet to reveal is not an empty set \n - set our colors not yet revealable to an empty set \n - for color in our colors yet to reveal \n - if our test of the color boundary is false, add it to not yet revealable. It will be processed otherwise. \n - if the size of our colors yet to reveal and our colors not yet revealable match, no change occurred in this loop, return False. \n - otherwise, set colors yet to reveal to colors not yet revealable\nIf all colors processed, return True. \n\nTo check if printable, call set up with the target grid, then return the result of processing colors. \n\n# Complexity\n- Time complexity: O(C^2 * Rows * Cols)\n - We loop over colors in process colors \n - we build up a color list, which may have us reprocess colors. This makes it a double loop necessarily of the form I in range N -> J in range I, N, which is known to be N^2 at worst. \n - On each looping of this we loop over rows, nested with cols \n - This is O(C * C * Rows * Cols) where C is colors and rows and cols are the size of the grid \n\n- Space complexity: O(Rows * Cols + Constant) \n - We store the grid \n - The color space boundary is technically a fixed size of color boundary factors, so can be treated as a constant \n\n# Code\n```\nclass Solution:\n # initialize with colors that are about to be revealed and those we cannot reveal yet \n # initialize alongside this the bounding box of a given color area \n def __init__(self) : \n self.colors_yet_to_reveal = set()\n self.colors_not_yet_revealable = set()\n self.color_boundaries = []\n\n def set_up(self, grid) : \n # set up according to grid \n self.rows = len(grid)\n self.cols = len(grid[0])\n # based on problem, should stop at dimension 60, but just in case of hooligans, use this \n self.max_dimension = max(self.rows, self.cols, 60)\n # color boundaries one greater than max dimension for off by one accounding \n self.color_boundaries = [[self.rows, self.cols, 0, 0] for _ in range(self.max_dimension + 1)]\n # loop in range \n for row in range(self.rows) : \n for col in range(self.cols) : \n # get the color \n color = grid[row][col]\n # add it if we don\'t have it yet \n self.colors_yet_to_reveal.add(color)\n # set the boundary box as the min of the value there now and max of value \n # there now compared to the row and col current. This gets the bounding \n # box of the color areas like doing polygon bounding in graphical processing \n self.color_boundaries[color][0] = min(self.color_boundaries[color][0], row)\n self.color_boundaries[color][1] = min(self.color_boundaries[color][1], col)\n self.color_boundaries[color][2] = max(self.color_boundaries[color][2], row)\n self.color_boundaries[color][3] = max(self.color_boundaries[color][3], col)\n # mark the grid as is now for processing \n # this makes it so we don\'t change the original data and can compare on a step by step if needed\n self.grid = grid\n\n # set to zero all values in range for current grid \n def zero_in_range(self, r0, r1, c0, c1) : \n # loop in range \n # could include a print statement or export statement of some kind to see grid as it changes \n for row in range(r0, r1) : \n for col in range(c0, c1) : \n # set to default selected value, in this casce 0 \n self.grid[row][col] = 0\n \n # test color is contiguous in boundary \n def test_color_boundary(self, color) : \n # get stop and start for rows and cols \n r_start, c_start, r_stop, c_stop = self.color_boundaries[color]\n r_stop += 1 \n c_stop += 1 \n # loop in range \n for row in range(r_start, r_stop) : \n for col in range(c_start, c_stop) : \n # if it is not zero and not color, that\'s not good \n # return False \n if self.grid[row][col] > 0 and self.grid[row][col] != color : \n return False \n # otherwise, zero in range and return True \n self.zero_in_range(r_start, r_stop, c_start, c_stop)\n return True \n\n # process colors in grid \n def process_colors(self) :\n # while we still have colors to reveal \n while self.colors_yet_to_reveal : \n # reset your colors not yet revealable at start of each processing loop \n self.colors_not_yet_revealable = set()\n # reveal the current colors you have to reveal \n for color in self.colors_yet_to_reveal : \n # if the color is not yet ready to be revealed \n if self.test_color_boundary(color) == False : \n # mark it as such and continue \n self.colors_not_yet_revealable.add(color)\n # if we have the same amount to reveal as we started with, nothing changed \n # if nothing changed, it\'s not possible, return False \n if len(self.colors_yet_to_reveal) == len(self.colors_not_yet_revealable) : \n return False \n # otherwise, update accordingly. On the loop where self.colors not yet revealable \n # is a set that had nothing added to it, we break \n self.colors_yet_to_reveal = self.colors_not_yet_revealable\n # return True on all colors revealed \n return True \n\n def isPrintable(self, targetGrid: List[List[int]]) -> bool:\n # set up \n self.set_up(targetGrid)\n # return results of processing \n return self.process_colors()\n\n``` | 1 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
SOLID Principles | 100% Memory | Commented and Explained | strange-printer-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is actually similar to whether or not we have edge collisions in polygon coloring for computer graphics. As such, we take the idea of a color bounding box as a polygon of that color, where we are trying to see if we can get to the back of the painting (aka 0) so we have painted all we need to. To get this as a visual application, simply assign each color to an rgb band. The original will show up, and as you go you can find the polygonal size of the rectangles showing and report on it. It\'s really quite interesting in this fashion so I\'ve left as much of it as possible in clear commented code for those interested in setting it up. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe want to track 3 things in our initial set up, so we establish fields for them at init. These are colors yet to reveal, colors not yet revealable, and color boundaries. The colors yet to reveal are those we have yet to process, and initially contains all colors. At each step, we will see if it is a top lying color (meaning we have it on the top of the stack of color boundaries) and if so, we can reveal it to zero and process the boundaries of it. This occurs if we have all values in bounding box of this color, or all values in the bounding box of this color are zero or some mixture of both. If we cannot yet do so, we place it into colors not yet revealable and then will check to see if any change occurred. If no change occurred we have directly conflicting edges and can not process accordingly, and should return False. On change though, we should update colors yet to reveal to the smaller form of those not yet revealable. \n\nTo do all this we need a few functions to help out. The first is our set up function, which gets passed the grid we are going to be working on. \nWe set up our rows and cols of the grid, and get the max dimension as either the max of either of rows or cols or 60 based on problem description. This lets this extend beyond the scope of the problem space. \n\nOur color boundaries all start out with the box going from minimal of row and col for the color and maximal of the row and col for the color, found by looping over the grid. \n\nWhen done with set up we store the grid in its current form. We do this to not modify the original, and to allow us to report out state changes as we go if we so feel that it is appropriate to do so \n\nOur next function is our zero in range function. If a color has been revealed by either all of the cells in the range being that color, or all of the values in that range being that color or zero, we will set all of the cells in that boundary to zero with the zero in range function. It is passed a range of row start, row stop, col start and col stop to work within. \n\nWe also have our test color boundary function. This gets passed a color and pulls from our color boundaries the bounding box for that color. We increment the row stop and col stop by one so that python does go over that range in its for loops. We then loop over all cells in the bounding box, and if there is any cell that is not this color or zero, we return False. Otherwise, after processing all succesfully as either this color or zero, we zero this range and return True. \n\nTo process our colors finally, we do the following \n- while our colors yet to reveal is not an empty set \n - set our colors not yet revealable to an empty set \n - for color in our colors yet to reveal \n - if our test of the color boundary is false, add it to not yet revealable. It will be processed otherwise. \n - if the size of our colors yet to reveal and our colors not yet revealable match, no change occurred in this loop, return False. \n - otherwise, set colors yet to reveal to colors not yet revealable\nIf all colors processed, return True. \n\nTo check if printable, call set up with the target grid, then return the result of processing colors. \n\n# Complexity\n- Time complexity: O(C^2 * Rows * Cols)\n - We loop over colors in process colors \n - we build up a color list, which may have us reprocess colors. This makes it a double loop necessarily of the form I in range N -> J in range I, N, which is known to be N^2 at worst. \n - On each looping of this we loop over rows, nested with cols \n - This is O(C * C * Rows * Cols) where C is colors and rows and cols are the size of the grid \n\n- Space complexity: O(Rows * Cols + Constant) \n - We store the grid \n - The color space boundary is technically a fixed size of color boundary factors, so can be treated as a constant \n\n# Code\n```\nclass Solution:\n # initialize with colors that are about to be revealed and those we cannot reveal yet \n # initialize alongside this the bounding box of a given color area \n def __init__(self) : \n self.colors_yet_to_reveal = set()\n self.colors_not_yet_revealable = set()\n self.color_boundaries = []\n\n def set_up(self, grid) : \n # set up according to grid \n self.rows = len(grid)\n self.cols = len(grid[0])\n # based on problem, should stop at dimension 60, but just in case of hooligans, use this \n self.max_dimension = max(self.rows, self.cols, 60)\n # color boundaries one greater than max dimension for off by one accounding \n self.color_boundaries = [[self.rows, self.cols, 0, 0] for _ in range(self.max_dimension + 1)]\n # loop in range \n for row in range(self.rows) : \n for col in range(self.cols) : \n # get the color \n color = grid[row][col]\n # add it if we don\'t have it yet \n self.colors_yet_to_reveal.add(color)\n # set the boundary box as the min of the value there now and max of value \n # there now compared to the row and col current. This gets the bounding \n # box of the color areas like doing polygon bounding in graphical processing \n self.color_boundaries[color][0] = min(self.color_boundaries[color][0], row)\n self.color_boundaries[color][1] = min(self.color_boundaries[color][1], col)\n self.color_boundaries[color][2] = max(self.color_boundaries[color][2], row)\n self.color_boundaries[color][3] = max(self.color_boundaries[color][3], col)\n # mark the grid as is now for processing \n # this makes it so we don\'t change the original data and can compare on a step by step if needed\n self.grid = grid\n\n # set to zero all values in range for current grid \n def zero_in_range(self, r0, r1, c0, c1) : \n # loop in range \n # could include a print statement or export statement of some kind to see grid as it changes \n for row in range(r0, r1) : \n for col in range(c0, c1) : \n # set to default selected value, in this casce 0 \n self.grid[row][col] = 0\n \n # test color is contiguous in boundary \n def test_color_boundary(self, color) : \n # get stop and start for rows and cols \n r_start, c_start, r_stop, c_stop = self.color_boundaries[color]\n r_stop += 1 \n c_stop += 1 \n # loop in range \n for row in range(r_start, r_stop) : \n for col in range(c_start, c_stop) : \n # if it is not zero and not color, that\'s not good \n # return False \n if self.grid[row][col] > 0 and self.grid[row][col] != color : \n return False \n # otherwise, zero in range and return True \n self.zero_in_range(r_start, r_stop, c_start, c_stop)\n return True \n\n # process colors in grid \n def process_colors(self) :\n # while we still have colors to reveal \n while self.colors_yet_to_reveal : \n # reset your colors not yet revealable at start of each processing loop \n self.colors_not_yet_revealable = set()\n # reveal the current colors you have to reveal \n for color in self.colors_yet_to_reveal : \n # if the color is not yet ready to be revealed \n if self.test_color_boundary(color) == False : \n # mark it as such and continue \n self.colors_not_yet_revealable.add(color)\n # if we have the same amount to reveal as we started with, nothing changed \n # if nothing changed, it\'s not possible, return False \n if len(self.colors_yet_to_reveal) == len(self.colors_not_yet_revealable) : \n return False \n # otherwise, update accordingly. On the loop where self.colors not yet revealable \n # is a set that had nothing added to it, we break \n self.colors_yet_to_reveal = self.colors_not_yet_revealable\n # return True on all colors revealed \n return True \n\n def isPrintable(self, targetGrid: List[List[int]]) -> bool:\n # set up \n self.set_up(targetGrid)\n # return results of processing \n return self.process_colors()\n\n``` | 1 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
python graph + topological sort cycle detection | strange-printer-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPrintable(self, targetGrid: List[List[int]]) -> bool:\n \n n = len(targetGrid)\n m = len(targetGrid[0])\n graph = collections.defaultdict(set)\n indegree = collections.defaultdict(int)\n colors = {}\n for i in range(n):\n for j in range(m):\n if targetGrid[i][j] not in colors:\n colors[targetGrid[i][j]] = [n, m, 0, 0]\n\n for c in colors:\n for i in range(n):\n for j in range(m):\n if targetGrid[i][j] == c:\n colors[c][0] = min(colors[c][0], i)\n colors[c][1] = min(colors[c][1], j)\n colors[c][2] = max(colors[c][2], i)\n colors[c][3] = max(colors[c][3], j)\n \n\n for i in range(colors[c][0], colors[c][2]+1):\n for j in range(colors[c][1], colors[c][3]+1):\n if targetGrid[i][j] != c:\n graph[c].add(targetGrid[i][j])\n \n for node in graph:\n for v in graph[node]:\n indegree[v] +=1\n\n\n\n queue = []\n for c in colors:\n if indegree[c] == 0:\n queue.append(c)\n order = []\n while queue:\n node = queue.pop(0)\n order.append(node)\n for v in graph[node]:\n indegree[v] -=1\n if indegree[v] == 0:\n queue.append(v)\n return len(order) == len(colors.keys())\n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
python graph + topological sort cycle detection | strange-printer-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPrintable(self, targetGrid: List[List[int]]) -> bool:\n \n n = len(targetGrid)\n m = len(targetGrid[0])\n graph = collections.defaultdict(set)\n indegree = collections.defaultdict(int)\n colors = {}\n for i in range(n):\n for j in range(m):\n if targetGrid[i][j] not in colors:\n colors[targetGrid[i][j]] = [n, m, 0, 0]\n\n for c in colors:\n for i in range(n):\n for j in range(m):\n if targetGrid[i][j] == c:\n colors[c][0] = min(colors[c][0], i)\n colors[c][1] = min(colors[c][1], j)\n colors[c][2] = max(colors[c][2], i)\n colors[c][3] = max(colors[c][3], j)\n \n\n for i in range(colors[c][0], colors[c][2]+1):\n for j in range(colors[c][1], colors[c][3]+1):\n if targetGrid[i][j] != c:\n graph[c].add(targetGrid[i][j])\n \n for node in graph:\n for v in graph[node]:\n indegree[v] +=1\n\n\n\n queue = []\n for c in colors:\n if indegree[c] == 0:\n queue.append(c)\n order = []\n while queue:\n node = queue.pop(0)\n order.append(node)\n for v in graph[node]:\n indegree[v] -=1\n if indegree[v] == 0:\n queue.append(v)\n return len(order) == len(colors.keys())\n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python - rectangle overlap graph | strange-printer-ii | 0 | 1 | # Intuition\nKey observation, filling color is on full rectangle only, if one rectangle has other color within its borders, then it has to be painted before that color. This way it can be constructed precedence graph, in another words problem becomes detecting is there cycle or not. More precisely for problem to be solvable it has to be DAG, meaning no cycles, otherwise you got chicken and egg situation. Hard part is to detect overlaps after that cycles can be found with various techniques like indegree counting or dfs with visited flags. \n\n\n# Code\n```\nclass Solution:\n def get_color_borders(self, g, R, C):\n color_border = dict()\n for r in range(R):\n for c in range(C):\n color = g[r][c]\n if color in color_border:\n border = color_border[color]\n border[0], border[1] = min(border[0], r), min(border[1], c)\n border[2], border[3] = max(border[2], r), max(border[3], c)\n else: color_border[color] = [r, c, r, c] \n return color_border\n\n def get_graph_and_indegree(self, color_border, g):\n graph, indeg = defaultdict(set), Counter()\n for color in color_border:\n cb = color_border[color]\n for r, c in product(range(cb[0], cb[2] + 1), range(cb[1], cb[3] + 1)):\n if g[r][c] != color:\n if color not in graph[g[r][c]]:\n graph[g[r][c]].add(color)\n indeg[color] += 1 \n return graph, indeg\n\n def isPrintable(self, g):\n R, C = len(g), len(g[0])\n color_border = self.get_color_borders(g, R, C)\n graph, indeg = self.get_graph_and_indegree(color_border, g)\n\n qu = deque()\n\n for color in color_border:\n if indeg[color] == 0: qu.append(color)\n\n while qu:\n color = qu.popleft()\n for to in graph[color]:\n indeg[to] -= 1\n if indeg[to] == 0: qu.append(to)\n \n return max(indeg.values()) == 0 if indeg else True\n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
Python - rectangle overlap graph | strange-printer-ii | 0 | 1 | # Intuition\nKey observation, filling color is on full rectangle only, if one rectangle has other color within its borders, then it has to be painted before that color. This way it can be constructed precedence graph, in another words problem becomes detecting is there cycle or not. More precisely for problem to be solvable it has to be DAG, meaning no cycles, otherwise you got chicken and egg situation. Hard part is to detect overlaps after that cycles can be found with various techniques like indegree counting or dfs with visited flags. \n\n\n# Code\n```\nclass Solution:\n def get_color_borders(self, g, R, C):\n color_border = dict()\n for r in range(R):\n for c in range(C):\n color = g[r][c]\n if color in color_border:\n border = color_border[color]\n border[0], border[1] = min(border[0], r), min(border[1], c)\n border[2], border[3] = max(border[2], r), max(border[3], c)\n else: color_border[color] = [r, c, r, c] \n return color_border\n\n def get_graph_and_indegree(self, color_border, g):\n graph, indeg = defaultdict(set), Counter()\n for color in color_border:\n cb = color_border[color]\n for r, c in product(range(cb[0], cb[2] + 1), range(cb[1], cb[3] + 1)):\n if g[r][c] != color:\n if color not in graph[g[r][c]]:\n graph[g[r][c]].add(color)\n indeg[color] += 1 \n return graph, indeg\n\n def isPrintable(self, g):\n R, C = len(g), len(g[0])\n color_border = self.get_color_borders(g, R, C)\n graph, indeg = self.get_graph_and_indegree(color_border, g)\n\n qu = deque()\n\n for color in color_border:\n if indeg[color] == 0: qu.append(color)\n\n while qu:\n color = qu.popleft()\n for to in graph[color]:\n indeg[to] -= 1\n if indeg[to] == 0: qu.append(to)\n \n return max(indeg.values()) == 0 if indeg else True\n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python || Clean and Simple Solution using Topological Sorting | strange-printer-ii | 0 | 1 | ```\nfrom collections import defaultdict\nfrom graphlib import CycleError, TopologicalSorter\nfrom itertools import product\n\nMAX_COLOR = 60\n\n\nclass Solution:\n def isPrintable(self, M: list[list[int]]) -> bool:\n g = self.create_graph(M)\n\n try:\n TopologicalSorter(g).prepare()\n return True\n except CycleError:\n return False\n\n @staticmethod\n def create_graph(M: list[list[int]]) -> defaultdict[int, set[int]]:\n m, n = len(M), len(M[0])\n\n g = defaultdict(set)\n\n for c in range(1, MAX_COLOR + 1): # notice that order of traversal, it is from smaller to larger color\n # now, finding the rectangle containing the color "c"\n x1, y1 = m, n # will represent the top left of the square\n x2, y2 = -1, -1 # will represent the bottom right of the square\n\n for i, j in product(range(m), range(n)):\n if M[i][j] == c:\n x1, y1 = min(x1, i), min(y1, j)\n x2, y2 = max(x2, i), max(y2, j)\n\n for i, j in product(range(x1, x2 + 1), range(y1, y2 + 1)):\n if M[i][j] != c:\n g[c].add(M[i][j])\n\n return g\n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
Python || Clean and Simple Solution using Topological Sorting | strange-printer-ii | 0 | 1 | ```\nfrom collections import defaultdict\nfrom graphlib import CycleError, TopologicalSorter\nfrom itertools import product\n\nMAX_COLOR = 60\n\n\nclass Solution:\n def isPrintable(self, M: list[list[int]]) -> bool:\n g = self.create_graph(M)\n\n try:\n TopologicalSorter(g).prepare()\n return True\n except CycleError:\n return False\n\n @staticmethod\n def create_graph(M: list[list[int]]) -> defaultdict[int, set[int]]:\n m, n = len(M), len(M[0])\n\n g = defaultdict(set)\n\n for c in range(1, MAX_COLOR + 1): # notice that order of traversal, it is from smaller to larger color\n # now, finding the rectangle containing the color "c"\n x1, y1 = m, n # will represent the top left of the square\n x2, y2 = -1, -1 # will represent the bottom right of the square\n\n for i, j in product(range(m), range(n)):\n if M[i][j] == c:\n x1, y1 = min(x1, i), min(y1, j)\n x2, y2 = max(x2, i), max(y2, j)\n\n for i, j in product(range(x1, x2 + 1), range(y1, y2 + 1)):\n if M[i][j] != c:\n g[c].add(M[i][j])\n\n return g\n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python (Simple DFS) | strange-printer-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPrintable(self, targetGrid):\n m, n, dict1 = len(targetGrid), len(targetGrid[0]), defaultdict(set)\n\n for c in range(1,61):\n i_mn = j_mn = 60\n i_mx = j_mx = 0\n\n for i in range(m):\n for j in range(n):\n if targetGrid[i][j] == c:\n i_mn = min(i_mn,i)\n i_mx = max(i_mx,i)\n j_mn = min(j_mn,j)\n j_mx = max(j_mx,j)\n\n for i in range(i_mn,i_mx+1):\n for j in range(j_mn,j_mx+1):\n if targetGrid[i][j] != c:\n dict1[c].add(targetGrid[i][j])\n\n def dfs(n):\n if visited[n]: return visited[n] == 1\n visited[n] = 1\n if any(dfs(j) for j in dict1[n]): return True\n visited[n] = 2\n return False \n\n visited = [0]*61\n\n return not any(dfs(i) for i in range(61))\n\n\n\n \n\n\n\n \n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
Python (Simple DFS) | strange-printer-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPrintable(self, targetGrid):\n m, n, dict1 = len(targetGrid), len(targetGrid[0]), defaultdict(set)\n\n for c in range(1,61):\n i_mn = j_mn = 60\n i_mx = j_mx = 0\n\n for i in range(m):\n for j in range(n):\n if targetGrid[i][j] == c:\n i_mn = min(i_mn,i)\n i_mx = max(i_mx,i)\n j_mn = min(j_mn,j)\n j_mx = max(j_mx,j)\n\n for i in range(i_mn,i_mx+1):\n for j in range(j_mn,j_mx+1):\n if targetGrid[i][j] != c:\n dict1[c].add(targetGrid[i][j])\n\n def dfs(n):\n if visited[n]: return visited[n] == 1\n visited[n] = 1\n if any(dfs(j) for j in dict1[n]): return True\n visited[n] = 2\n return False \n\n visited = [0]*61\n\n return not any(dfs(i) for i in range(61))\n\n\n\n \n\n\n\n \n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python 3 | Very fast (beats 100 %) | Implicit directed graph | Search cycle with DFS | strange-printer-ii | 0 | 1 | \n\n# Complexity\n- Time complexity:\n$$O(n*m)$$ to find limits of rectangle of each color.\n$$O(n*m*c)$$ to construct the graph ; $$c$$ is the number of colors.\n$$O(c)$$ to check if there is a cycle in the graph of $$c$$ nodes\n\n-> $$O(n*m*c)$$\n\n- Space complexity:\nrectangle is a dictionnary with $$c$$ keys and its values are lists of 4 integers.\nto_do_after is a dictionnary with $$c$$ keys and values are sets of at most $$c$$ values.\nstatus is a dictionnary (values are integers) of length $$c$$.\n\n-> $$O(c\xB2)$$\n\n# Code\n```\nclass Solution:\n\n def isPrintable(self, grid: List[List[int]]) -> bool: \n # You search limits of each color\'s rectangle \n rectangle = {}\n for i, row in enumerate(grid):\n for j, color in enumerate(row):\n curr = rectangle.get(color, None)\n if not curr:\n rectangle[color] = [i, i + 1, j, j + 1]\n else:\n if i < curr[0]:\n curr[0] = i\n elif i >= curr[1]:\n curr[1] = i + 1\n if j < curr[2]:\n curr[2] = j\n elif j >= curr[3]:\n curr[3] = j + 1\n rectangle[color] = curr\n \n # You construct the dependecies graph\n to_do_after = {}\n for c1 in rectangle.keys():\n x, X, y, Y = rectangle[c1]\n to_do_after[c1] = set()\n for row in grid[x: X]:\n for c2 in row[y: Y]:\n if c2 != c1: \n if c1 in to_do_after.get(c2, []):\n return False\n to_do_after[c1].add(c2)\n \n # You check if there is no cycle in the dependencies graph\n\n def cycle(node):\n status[node] = IN_PROGRESS\n for nn in to_do_after[node]:\n if status[nn] is IN_PROGRESS:\n return True\n elif status[nn] is NOT_VISITED:\n if cycle(nn):\n return True\n status[node] = VISITED\n return False\n \n NOT_VISITED, IN_PROGRESS, VISITED = 1, 2, 3\n status = {c: NOT_VISITED for c in to_do_after.keys()}\n for c in to_do_after.keys():\n if status[c] == NOT_VISITED and cycle(c):\n return False\n return True\n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
Python 3 | Very fast (beats 100 %) | Implicit directed graph | Search cycle with DFS | strange-printer-ii | 0 | 1 | \n\n# Complexity\n- Time complexity:\n$$O(n*m)$$ to find limits of rectangle of each color.\n$$O(n*m*c)$$ to construct the graph ; $$c$$ is the number of colors.\n$$O(c)$$ to check if there is a cycle in the graph of $$c$$ nodes\n\n-> $$O(n*m*c)$$\n\n- Space complexity:\nrectangle is a dictionnary with $$c$$ keys and its values are lists of 4 integers.\nto_do_after is a dictionnary with $$c$$ keys and values are sets of at most $$c$$ values.\nstatus is a dictionnary (values are integers) of length $$c$$.\n\n-> $$O(c\xB2)$$\n\n# Code\n```\nclass Solution:\n\n def isPrintable(self, grid: List[List[int]]) -> bool: \n # You search limits of each color\'s rectangle \n rectangle = {}\n for i, row in enumerate(grid):\n for j, color in enumerate(row):\n curr = rectangle.get(color, None)\n if not curr:\n rectangle[color] = [i, i + 1, j, j + 1]\n else:\n if i < curr[0]:\n curr[0] = i\n elif i >= curr[1]:\n curr[1] = i + 1\n if j < curr[2]:\n curr[2] = j\n elif j >= curr[3]:\n curr[3] = j + 1\n rectangle[color] = curr\n \n # You construct the dependecies graph\n to_do_after = {}\n for c1 in rectangle.keys():\n x, X, y, Y = rectangle[c1]\n to_do_after[c1] = set()\n for row in grid[x: X]:\n for c2 in row[y: Y]:\n if c2 != c1: \n if c1 in to_do_after.get(c2, []):\n return False\n to_do_after[c1].add(c2)\n \n # You check if there is no cycle in the dependencies graph\n\n def cycle(node):\n status[node] = IN_PROGRESS\n for nn in to_do_after[node]:\n if status[nn] is IN_PROGRESS:\n return True\n elif status[nn] is NOT_VISITED:\n if cycle(nn):\n return True\n status[node] = VISITED\n return False\n \n NOT_VISITED, IN_PROGRESS, VISITED = 1, 2, 3\n status = {c: NOT_VISITED for c in to_do_after.keys()}\n for c in to_do_after.keys():\n if status[c] == NOT_VISITED and cycle(c):\n return False\n return True\n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
[Python] Construct Graph and Detect Cycle in the Directed Graph | Easy implementation | strange-printer-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def isPrintable(self, targetGrid: List[List[int]]) -> bool:\n minRow, maxRow = defaultdict(lambda: math.inf), defaultdict(lambda:-math.inf)\n minCol, maxCol = defaultdict(lambda: math.inf), defaultdict(lambda:-math.inf)\n\n # Part 1 - Finding left/right/top/bottom boundaries of a rectangular color block\n M, N = len(targetGrid), len(targetGrid[0])\n for i in range(M):\n for j in range(N):\n color = targetGrid[i][j]\n minRow[color], maxRow[color] = min(minRow[color], i), max(maxRow[color], i)\n minCol[color], maxCol[color] = min(minCol[color], j), max(maxCol[color], j)\n \n # Part 2 - Creation of Graph\n G = defaultdict(list)\n for color in minRow.keys():\n for i in range(minRow[color], maxRow[color] + 1):\n for j in range(minCol[color], maxCol[color] + 1):\n if targetGrid[i][j] != color:\n G[targetGrid[i][j]].append(color)\n \n # Part 3 - Cycle Detection Helper Function\n def dfs_cycle(node):\n visited.add(node)\n dfs_visited.add(node)\n for nei in G[node]:\n if nei in visited and nei in dfs_visited: return True\n if nei not in visited:\n if dfs_cycle(nei): return True\n dfs_visited.remove(node)\n return False\n\n # Part 4 - Cycle Detection in a Directed Graph\n visited, dfs_visited = set(), set()\n for color in minRow.keys():\n if color not in visited:\n if dfs_cycle(color):\n return False \n return True\n\n\n\n\n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
[Python] Construct Graph and Detect Cycle in the Directed Graph | Easy implementation | strange-printer-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def isPrintable(self, targetGrid: List[List[int]]) -> bool:\n minRow, maxRow = defaultdict(lambda: math.inf), defaultdict(lambda:-math.inf)\n minCol, maxCol = defaultdict(lambda: math.inf), defaultdict(lambda:-math.inf)\n\n # Part 1 - Finding left/right/top/bottom boundaries of a rectangular color block\n M, N = len(targetGrid), len(targetGrid[0])\n for i in range(M):\n for j in range(N):\n color = targetGrid[i][j]\n minRow[color], maxRow[color] = min(minRow[color], i), max(maxRow[color], i)\n minCol[color], maxCol[color] = min(minCol[color], j), max(maxCol[color], j)\n \n # Part 2 - Creation of Graph\n G = defaultdict(list)\n for color in minRow.keys():\n for i in range(minRow[color], maxRow[color] + 1):\n for j in range(minCol[color], maxCol[color] + 1):\n if targetGrid[i][j] != color:\n G[targetGrid[i][j]].append(color)\n \n # Part 3 - Cycle Detection Helper Function\n def dfs_cycle(node):\n visited.add(node)\n dfs_visited.add(node)\n for nei in G[node]:\n if nei in visited and nei in dfs_visited: return True\n if nei not in visited:\n if dfs_cycle(nei): return True\n dfs_visited.remove(node)\n return False\n\n # Part 4 - Cycle Detection in a Directed Graph\n visited, dfs_visited = set(), set()\n for color in minRow.keys():\n if color not in visited:\n if dfs_cycle(color):\n return False \n return True\n\n\n\n\n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python | Keep unpaint untill canvas is blank | strange-printer-ii | 0 | 1 | # Code\r\n``` python\r\nclass Solution:\r\n def isPrintable(self, targetGrid):\r\n R, C, limits = len(mat), len(mat[0]), dict()\r\n\r\n for i in range(R): # using corners of color dict as color\'s set as well\r\n for j in range(C):\r\n color = mat[i][j]\r\n if color not in limits: limits[color] = [R, C, 0, 0]\r\n limits[color][0] = min(limits[color][0], i) # min row\r\n limits[color][1] = min(limits[color][1], j) # max col\r\n limits[color][2] = max(limits[color][2], i) # min row\r\n limits[color][3] = max(limits[color][3], j) # max col\r\n\r\n def unpaint(color) -> bool:\r\n # test range of color\r\n r, c, R, C = limits[color]\r\n for i in range(r, R + 1):\r\n for j in range(c, C + 1):\r\n if mat[i][j] not in [0, color]: return False\r\n # unpaint\r\n for i in range(r, R + 1):\r\n for j in range(c, C + 1):\r\n mat[i][j] = 0\r\n\r\n return True\r\n\r\n while limits.keys():\r\n unpainted = list(filter(unpaint, limits.keys()))\r\n if not unpainted: return False\r\n for color in unpainted:\r\n del limits[color]\r\n\r\n return True\r\n``` | 0 | There is a strange printer with the following two special requirements:
* On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
* Once the printer has used a color for the above operation, **the same color cannot be used again**.
You are given a `m x n` matrix `targetGrid`, where `targetGrid[row][col]` is the color in the position `(row, col)` of the grid.
Return `true` _if it is possible to print the matrix_ `targetGrid`_,_ _otherwise, return_ `false`.
**Example 1:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,2,2,1\],\[1,2,2,1\],\[1,1,1,1\]\]
**Output:** true
**Example 2:**
**Input:** targetGrid = \[\[1,1,1,1\],\[1,1,3,3\],\[1,1,3,4\],\[5,5,1,4\]\]
**Output:** true
**Example 3:**
**Input:** targetGrid = \[\[1,2,1\],\[2,1,2\],\[1,2,1\]\]
**Output:** false
**Explanation:** It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
**Constraints:**
* `m == targetGrid.length`
* `n == targetGrid[i].length`
* `1 <= m, n <= 60`
* `1 <= targetGrid[row][col] <= 60` | null |
Python | Keep unpaint untill canvas is blank | strange-printer-ii | 0 | 1 | # Code\r\n``` python\r\nclass Solution:\r\n def isPrintable(self, targetGrid):\r\n R, C, limits = len(mat), len(mat[0]), dict()\r\n\r\n for i in range(R): # using corners of color dict as color\'s set as well\r\n for j in range(C):\r\n color = mat[i][j]\r\n if color not in limits: limits[color] = [R, C, 0, 0]\r\n limits[color][0] = min(limits[color][0], i) # min row\r\n limits[color][1] = min(limits[color][1], j) # max col\r\n limits[color][2] = max(limits[color][2], i) # min row\r\n limits[color][3] = max(limits[color][3], j) # max col\r\n\r\n def unpaint(color) -> bool:\r\n # test range of color\r\n r, c, R, C = limits[color]\r\n for i in range(r, R + 1):\r\n for j in range(c, C + 1):\r\n if mat[i][j] not in [0, color]: return False\r\n # unpaint\r\n for i in range(r, R + 1):\r\n for j in range(c, C + 1):\r\n mat[i][j] = 0\r\n\r\n return True\r\n\r\n while limits.keys():\r\n unpainted = list(filter(unpaint, limits.keys()))\r\n if not unpainted: return False\r\n for color in unpainted:\r\n del limits[color]\r\n\r\n return True\r\n``` | 0 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python solution | rearrange-spaces-between-words | 0 | 1 | ```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n words: list[str] = findall(r"(\\w+)", text)\n len_words, spaces = len(words), text.count(" ")\n reorder_text: str = ""\n\n if len_words == 1: return words[0] + " " * spaces\n\n new_spaces: int = spaces // (len_words - 1)\n\n for index in range(len_words):\n if index == len_words - 1:\n reorder_text += words[index] + " " * ((spaces - (len_words - 1) * new_spaces))\n break\n reorder_text += words[index] + " " * new_spaces\n\n return reorder_text\n``` | 1 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
98.99% Python Straight Forward Solution | rearrange-spaces-between-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n #Count the spaces\n space=text.count(" ")\n #count the words\n words=text.split()\n wrdlen=len(words)\n #Declare the spaces we have to add between the words\n if wrdlen-1>0:\n res=space//(wrdlen-1)\n else:\n res=space\n a=""\n for i in words:\n a=a+i\n #Add the spaces to the front of the word\n if space>=res:\n a=a+" "*res\n space-=res\n #if space are remaining then add it to the end of the a\n if space>0:\n a=a+" "*space\n #Then return the result\n return a\n\n``` | 2 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python - simple and elegant | rearrange-spaces-between-words | 0 | 1 | **Multiple returns**:\n```\nclass Solution(object):\n def reorderSpaces(self, text):\n word_list = text.split()\n words, spaces = len(word_list), text.count(" ")\n \n if words > 1:\n q, r = spaces//(words-1), spaces%(words-1)\n return (" " * q).join(word_list) + " " * r\n else:\n return "".join(word_list) + " " * spaces\n```\n\n**Single return**:\n```\nclass Solution(object):\n def reorderSpaces(self, text):\n word_list = text.split()\n words, spaces = len(word_list), text.count(" ")\n \n if words > 1:\n q, r = spaces//(words-1), spaces%(words-1)\n else:\n q, r = 0, spaces\n \n return (" " * q).join(word_list) + " " * r\n```\n\n**Using *divmod***:\n```\nclass Solution(object):\n def reorderSpaces(self, text):\n word_list = text.split()\n words, spaces = len(word_list), text.count(" ")\n \n if words > 1:\n q, r = divmod(spaces, (words - 1))\n else:\n q, r = 0, spaces\n \n return (" " * q).join(word_list) + " " * r\n```\n\n**Shortened**:\n```\nclass Solution(object):\n def reorderSpaces(self, text):\n w, s = len(text.split()), text.count(" ")\n q, r = (divmod(s, (w - 1))) if w > 1 else (0, s)\n return (" " * q).join(text.split()) + " " * r\n```\n\n**One-liner (not pretty, but did it for fun)**:\n```\nclass Solution(object):\n def reorderSpaces(self, text):\n return "".join(text.split()) + " " * text.count(" ") if len(text.split()) <= 1 else (" " * (text.count(" ")//(len(text.split())-1))).join(text.split()) + " " * (text.count(" ") % (len(text.split())-1))\n``` | 5 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python3 simple solution based on built-in functions | rearrange-spaces-between-words | 0 | 1 | class Solution:\n def reorderSpaces(self, text: str) -> str:\n \n # \n words_list = text.split()\n num_spaces = text.count(\' \')\n num_words = len(words_list)\n # \n if num_words == 1:\n return(words_list[0] + \' \' * num_spaces)\n else:\n q, r = divmod(num_spaces, num_words - 1)\n return( (\' \' * q).join(words_list) + \' \' * r ) | 8 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Clean solution in Python | rearrange-spaces-between-words | 0 | 1 | ```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n spaces = sum(c.isspace() for c in text)\n if not spaces:\n return text\n words = text.split()\n if len(words) > 1:\n q, r = divmod(spaces, (len(words) - 1))\n else:\n q, r = 0, spaces\n return (" " * q).join(words) + " " * r\n``` | 2 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
messy but worked ~ | rearrange-spaces-between-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n\n output = \'\'\n words = text.split()\n\n if len(text) == 1:\n return text\n\n number_of_spaces = text.count(\' \')\n number_of_words = len(words)\n\n if number_of_words == 1:\n output = words[0] + number_of_spaces*\' \'\n return output\n \n add_spaces = number_of_spaces//(number_of_words-1)\n extra_spaces = number_of_spaces%(number_of_words-1)\n \n for word in words[:-1]:\n word += add_spaces * \' \'\n output += word\n if extra_spaces == 0:\n output += words[-1]\n else:\n output += (words[-1] + extra_spaces * \' \')\n return output\n\n \n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python One Line Solution O(n) | rearrange-spaces-between-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str: return (\' \' * (0 if len(words := text.split()) == 1 else text.count(\' \') // (len(words) - 1))).join(words) + \' \' * (text.count(\' \') - (0 if len(words) == 1 else text.count(\' \') // (len(words) - 1)) * (len(words) - 1))\n\n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python3 - Intuitive Approach | rearrange-spaces-between-words | 0 | 1 | # Approach\n1. We iterate through the whole text, in one pass count the number of spaces and part out individual words and add them to words list. \n\n2. We calculate the normalized space amount by dividing number of spaces by number of words (be careful, in case we have only one word we will divide by zero here).\n\n3. We calculate the leftover amount of spaces by subtracting number of spaces from product of normalized amount and number of words except last word.\n\n4. We add words to our output string one by one and after every word we add normalized amount of spaces - except for the last word in list.\n\n5. We check do we have some amount of leftover space, in case we do we multiply an empty space with that amount and add it to our string.\n\n# Complexity\n- Time complexity:\n - O(n)\n\n- Space complexity:\n - O(n)\n\n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n words = []\n numSpaces = 0\n res = ""\n\n i = 0\n while i < len(text):\n if(text[i] == \' \'):\n numSpaces += 1\n i += 1\n continue\n word = ""\n while(i < len(text) and text[i] != \' \'):\n word += text[i]\n i += 1\n words.append(word)\n \n normalized = numSpaces // (1 if len(words) == 1 else len(words) - 1)\n leftover = numSpaces - normalized * (len(words) - 1)\n\n for i in range(len(words)):\n res += words[i]\n for j in range(normalized):\n if i != len(words) - 1:\n res += \' \'\n \n if leftover > 0:\n res += \' \' * leftover\n \n return res\n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Straight forward solutions | rearrange-spaces-between-words | 0 | 1 | # Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n # bruteforce solutions\n # 37ms\n # Beats 62.02% of users with Python3\n space = text.count(" ")\n if space == 0:\n return text\n \n words = text.split()\n n = len(words)\n\n if n == 1:\n return text.strip() + " " * space\n \n diff = space % (n-1)\n ret = (" " * (space // (n-1))).join(words)\n if diff == 0:\n return ret\n\n return ret + " " * diff\n```\n\nPlease upvote if you find this useful :) | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Simple Python code | rearrange-spaces-between-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Count the number of spaces\n- Calculate the number of spaces between words and at the end of the line\n- Join the words with spaces and add trailing spaces\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n $$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n $$O(n)$$ \n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n nSpace = text.count(" ")\n res = text.split()\n\n if len(res) == 1:\n return res[0] + " "*nSpace\n\n nTrail = nSpace % (len(res)-1 or 1)\n nInter = nSpace // (len(res)-1 or 1) \n joinString = \' \'*nInter\n \n\n res = joinString.join(res) + \' \'*nTrail\n return res\n\n \n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Easy Python|Solution|Clear | rearrange-spaces-between-words | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n \n words = text.split()\n num_words = len(words)\n count_space = text.count(" ")\n\n if num_words <= 1 and count_space >0:\n return words[0]+" "*count_space \n elif count_space == 0:\n return text.strip()\n \n\n \n spaces_between = count_space // (num_words - 1)\n extra_spaces = count_space % (num_words - 1) if num_words > 1 else count_space\n\n \n res = ""\n for i, word in enumerate(words):\n res += word\n \n if i < num_words - 1:\n res += " " * spaces_between\n\n \n res += " " * extra_spaces\n\n return res\n\n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python || Easy | rearrange-spaces-between-words | 0 | 1 | # Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n count_space = text.count(\' \')\n words = text.split()\n\n delimeter, rest = 0, count_space\n\n if len(words) > 1:\n delimeter, rest = divmod(count_space, (len(words) - 1))\n\n return (delimeter * \' \').join(words) + (rest * \' \')\n\n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python solution | rearrange-spaces-between-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n spaces=text.count(" ")\n text=text.split()\n if len(text)==1:\n return "".join(text)+" "*spaces\n temp1=" "*(spaces//(len(text)-1))\n temp2=" "*(spaces%(len(text)-1))\n text=temp1.join(text)+temp2\n return text\n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Python Solution - Easy To Read | rearrange-spaces-between-words | 0 | 1 | \n# Code\n```\nclass Solution:\n def reorderSpaces(self, text: str) -> str:\n \n words: list = [word for word in text.split(" ") if word != ""] \n text_spaces_count: int = text.count(" ")\n \n if len(words) == 1: \n return words[0] + " " * text_spaces_count\n \n spaces: int = text_spaces_count // (len(words) - 1)\n string: str = ""\n \n for index in range(len(words)):\n if index == len(words) - 1:\n string += words[index]\n else:\n string += words[index] + (" " * spaces)\n \n string_space_count: int = string.count(" ")\n if string_space_count < text_spaces_count:\n string += " " * (text_spaces_count - string_space_count)\n \n return string\n``` | 0 | You are given a string `text` of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that `text` **contains at least one word**.
Rearrange the spaces so that there is an **equal** number of spaces between every pair of adjacent words and that number is **maximized**. If you cannot redistribute all the spaces equally, place the **extra spaces at the end**, meaning the returned string should be the same length as `text`.
Return _the string after rearranging the spaces_.
**Example 1:**
**Input:** text = " this is a sentence "
**Output:** "this is a sentence "
**Explanation:** There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
**Example 2:**
**Input:** text = " practice makes perfect "
**Output:** "practice makes perfect "
**Explanation:** There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
**Constraints:**
* `1 <= text.length <= 100`
* `text` consists of lowercase English letters and `' '`.
* `text` contains at least one word. | null |
Economical backtracking solution, commented and explained | split-a-string-into-the-max-number-of-unique-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis optimization problem will involve backtracking. The maximum length of s is 16, so there shouldn\'t be too much of a problem with execution time, even though a more general (unlimited length) solution wouldn\'t scale well at all, approaching O($$n!$$) for time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe\'ll work recursively, using depth-first search, and keeping track of the set of substrings that have been used already along the current path. The ***used*** set will grow as we move forward and shrink as we back up.\n\n# Code\n```\nclass Solution:\n def maxUniqueSplit(self, s: str) -> int:\n # DFS-based solution\n used = set() # Working set of substrings\n max_distinct = 0 # Best answer so far\n\n def propose(start, n):\n # DFS helper\n nonlocal max_distinct\n if start == len(s): # Stop recursion\n if n > max_distinct: # Adjust max if appropriate\n max_distinct = n\n else:\n for i in range(start + 1, len(s) + 1): # i is the substring end (+1)\n candidate = s[start:i]\n if candidate not in used: # Unique so far, so legal\n used.add(candidate) # Add to set\n propose(i, n + 1) # Go deeper; next substring\n used.remove(candidate) # Remove (backtracking)\n\n propose(0, 0) # Start here\n return max_distinct\n``` | 2 | Given a string `s`, return _the maximum number of unique substrings that the given string can be split into_.
You can split string `s` into any list of **non-empty substrings**, where the concatenation of the substrings forms the original string. However, you must split the substrings such that all of them are **unique**.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "ababccc "
**Output:** 5
**Explanation**: One way to split maximally is \['a', 'b', 'ab', 'c', 'cc'\]. Splitting like \['a', 'b', 'a', 'b', 'c', 'cc'\] is not valid as you have 'a' and 'b' multiple times.
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation**: One way to split maximally is \['a', 'ba'\].
**Example 3:**
**Input:** s = "aa "
**Output:** 1
**Explanation**: It is impossible to split the string any further.
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lower case English letters. | null |
Python 3 | Backtracking, DFS, clean | Explanations | split-a-string-into-the-max-number-of-unique-substrings | 0 | 1 | ### Explanation\n- The length of `s` is only up to 16, so it won\'t hurt if we exhaustively try out all possibility\n- And intuitively backtracking + DFS is very good at doing job like this\n- Check comment for more detail, pretty standard backtracking problem\n### Implementation\n```\nclass Solution:\n def maxUniqueSplit(self, s: str) -> int:\n ans, n = 0, len(s)\n def dfs(i, cnt, visited):\n nonlocal ans, n\n if i == n: ans = max(ans, cnt); return # stop condition\n for j in range(i+1, n+1): \n if s[i:j] in visited: continue # avoid re-visit/duplicates\n visited.add(s[i:j]) # update visited set\n dfs(j, cnt+1, visited) # backtracking\n visited.remove(s[i:j]) # recover visited set for next possibility\n dfs(0, 0, set()) # function call\n return ans\n``` | 5 | Given a string `s`, return _the maximum number of unique substrings that the given string can be split into_.
You can split string `s` into any list of **non-empty substrings**, where the concatenation of the substrings forms the original string. However, you must split the substrings such that all of them are **unique**.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "ababccc "
**Output:** 5
**Explanation**: One way to split maximally is \['a', 'b', 'ab', 'c', 'cc'\]. Splitting like \['a', 'b', 'a', 'b', 'c', 'cc'\] is not valid as you have 'a' and 'b' multiple times.
**Example 2:**
**Input:** s = "aba "
**Output:** 2
**Explanation**: One way to split maximally is \['a', 'ba'\].
**Example 3:**
**Input:** s = "aa "
**Output:** 1
**Explanation**: It is impossible to split the string any further.
**Constraints:**
* `1 <= s.length <= 16`
* `s` contains only lower case English letters. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.